1 results
An Application of Homogenization Theory to Harmonic Analysis: Harnack Inequalities And Riesz Transforms on Lie Groups of Polynomial Growth
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 4 / 01 August 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-727
- Print publication:
- 01 August 1992
-
- Article
-
- You have access
- Export citation

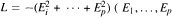 are left invariant Hörmander vector fields) on a connected Lie group
are left invariant Hörmander vector fields) on a connected Lie group 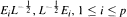 , are bounded on
, are bounded on 