Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:33:58.105Z Has data issue: false hasContentIssue false
  • English
  • Français

An Application of Homogenization Theory to Harmonic Analysis: Harnack Inequalities And Riesz Transforms on Lie Groups of Polynomial Growth

Published online by Cambridge University Press:  20 November 2018

G. Alexopoulos
G. Alexopoulos*
Affiliation:
Université de Paris-Sud Mathématiques, Bât. 425 91405 Orsay Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

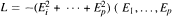We prove a homogenization formula for a sub-Laplacian are left invariant Hörmander vector fields) on a connected Lie group Gof polynomial growth. Then using a rescaling argument inspired from M. Avellanedaand F. H. Lin [2], we prove Harnack inequalities for the positive solutions of the equation (∂/∂t+ L)u= 0. Using these inequalities and further exploiting the algebraic structure of Gwe prove that the Riesz transforms 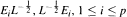, are bounded on Lq,1 < q <+∞ and from L1to weak-L1.

Résumé

Résumé

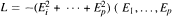On démontre une formule de homogénéisation pour un sous-Laplacien sont des champs de vecteurs de Hörmander invariants à gauche) sur un group de Lie Gconnexe, à croissance polynômiale du volume. Après, en utilisant un argument de rescalarisation inspiré de M. Avellaneda et F. H. Lin [2], on démontre des inégalités de Harnack pour les solutions positives de l'équation (∂/∂t +L)u =0. En utilisant ces inégalités et en exploitant la structure algébrique de G,on démontre que les transformés de Riesz 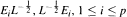sont bornés sur Lq, 1 < q < +∞et de L1dans L1 -faible.

Keywords

22E1522E3043E80HomogenizationLie groupsvolume growthHarnack inequalitiesRiesz transforms
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 4 , 01 August 1992 , pp. 691 - 727
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Aronson, D.C., Bounds for the fundamental solution of a parabolic equation, Bull. Amer. Math. Soc. 73 (1967), 890–896.Google Scholar
2. Avellaneda, M. and Lin, F.H., Compactness methods in the theory of Homogenization, Comm. Pure Appl. Math. 40 (1987), 803–847.Google Scholar
3. Avellaneda, M. and Lin, F.H., Un théorème de Liouville pour des équations elliptiques avec coefficients périodiques, C.R. Acad. Paris (1)609 1989,245–250.Google Scholar
4. Bensoussan, A., Lions, J.L. and Papanicolaou, G., Asymptotic analysis of periodic structures, North Holland Publ., 1978.Google Scholar
5. Besicovitch, A.S., Almost Periodic Functions, Dover Publications, 1954.Google Scholar
6. Bony, J.M., Principe du maximum, inégalité de Harnack et unicité du problème de Cauchy pour les opérateurs elliptiques dégénérés, Ann. Inst. Fourier (1) 19 (1969), 277–304.Google Scholar
7. Christ, M., Lectures on Singular Integral Operators, Regional Conference Series in Mathematics, 77.Google Scholar
8. Christ, M. and Geller, D., Singular integral characterizations of Hardy spaces on homogeneous groups, Duke Math. J. (3. 51 (1984), 547–598.Google Scholar
9. Coifman, R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes, Lecture Notes in Mathematics 242, Springer-Verlag, 1971.Google Scholar
10. David, G., Wavelets, Calderon-Zygmund operators and singular integrals on curves and surfaces, Lecture Notes in Mathematics, to appear.Google Scholar
11. David, G. and Journé, J.L., A boundedness criterion for generalised Calderon-Zygmund operators, Annals of Math. (12) 120 (1984), 371–378.Google Scholar
12. Folland, G.B. and Stein, E., Hardy spaces on Homogeneous groups, Princeton University Press, 1982.Google Scholar
13. Gilbarg, D. and Trudinger, N.S., Elliptic Partial Differential Equations of Second Order, Springer-Verlag, 1983.Google Scholar
14. Guivarc'h, Y., Croissance polynômiale et périodes de fonctions harmoniques, Bull. Se. Math. France 101 (1973), 149–152.Google Scholar
15. Hörmander, L., Hypoelliptic second order operators, Acta Math. 119 (1967), 147–171.Google Scholar
16. Jacobson, N., Lie Algebras, Wiley, 1962.Google Scholar
17. G, P..Lemarié, Continuité sur les espaces de Besov des opérateurs définis par des intégrales singulières, Ann. Inst. Fourier (4) 35 (1985), 175–187.Google Scholar
18. Lohoué, N. and Th, N.. Varopoulos, Remarques sur les transformés de Riesz sur les groupes de Lie nilpotents, C.R. Acad. Paris (I) 11 301 (1985), 559–560.Google Scholar
19. Saloff-Coste, L., Analyse sur les groupes de Lie à croissance polynômiale, Arkiv for Mathematik (2) 28 (1990), 315–331.Google Scholar
20. Stein, E., Singular integrals and differentiability properties of functions, Ann. of Math. Studies, 1970.Google Scholar
21. Stein, E., Topics in Harmonic Analysis, Princeton University Press, 1970.Google Scholar
22. Varadarajan, V.S., Lie groups, Lie algebras and their representations, Prentice-Hall, Englewood Cliffs, N.J.Google Scholar
23. Th, N.. Varopoulos, Fonctions harmoniquespositives sur les groupes de Lie, C.R. Acad. Paris (1)309 (1987), 519–521.Google Scholar
24. Th, N.. Varopoulos, Analysis on Lie groups, J. Funct. Anal. (2) 76 (1988), 346–410.Google Scholar
25. Th, N.. Varopoulos, Saloff-Coste, L. and Coulhon, T., Harmonie Analysis on Lie Groups, to appear.Google Scholar