Let 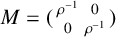$\{b_n\}_{n=1}^{\infty }$ be a sequence of integers larger than 1. We will study the harmonic analysis of the equal-weighted Moran measures $\mu _{\{b_n\},\{{\mathcal D}_n\}}$ with ${\mathcal D}_n=\{0,1,2,\ldots ,q_n-1\}$, where $q_n$ divides $b_n$ for all $n\geq 1.$ In this paper, we first characterize all the maximal orthogonal sets of $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$ via a tree mapping. By this characterization, we give some sufficient conditions for the maximal orthogonal set to be an orthonormal basis.

Let $M=(\begin {smallmatrix}\rho ^{-1} & 0 \\0 & \rho ^{-1} \\\end {smallmatrix})$ be an expanding real matrix with 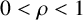$0<\rho <1$, and let 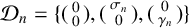${\mathcal D}_n=\{(\begin {smallmatrix} 0\\ 0 \end {smallmatrix}),(\begin {smallmatrix} \sigma _n\\ 0 \end {smallmatrix}),(\begin {smallmatrix} 0\\ \gamma _n \end {smallmatrix})\}$ be digit sets with 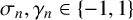$\sigma _n,\gamma _n\in \{-1,1\}$ for each 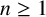$n\ge 1$. Then the infinite convolution

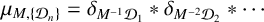$$ \begin{align*}\mu_{M,\{{\mathcal D}_n\}}=\delta_{M^{-1}{\mathcal D}_1}\ast\delta_{M^{-2}{\mathcal D}_2}\ast\cdots\end{align*} $$

is called a Moran–Sierpinski measure. We give a necessary and sufficient condition for 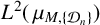$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ to admit an infinite orthogonal set of exponential functions. Furthermore, we give the exact cardinality of orthogonal exponential functions in 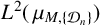$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ when 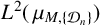$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ does not admit any infinite orthogonal set of exponential functions based on whether 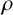$\rho $ is a trinomial number or not.

The completeness of sets of complex exponentials {eiλf(n)⋅:f∈ℤ} in Lp(−π,π), 1<p≤2, is considered under Levinson’s sufficient condition in the non-trivial case λ≥1−(1/p). All such sets are determined explicitly.

A theory of higher rank multiresolution analysis is given in the setting of abelian multiscalings. This theory enables the construction, from a higher rank MRA, of finite wavelet sets whose multidilations have translates forming an orthonormal basis in ${{L}^{2}}({{\mathbb{R}}^{d}})$. While tensor products of uniscaled MRAs provide simple examples we construct many nonseparable higher rank wavelets. In particular we construct Latin square wavelets as rank 2 variants of Haar wavelets. Also we construct nonseparable scaling functions for rank 2 variants of Meyer wavelet scaling functions, and we construct the associated nonseparable wavelets with compactly supported Fourier transforms. On the other hand we show that compactly supported scaling functions for biscaled MRAs are necessarily separable.

the interplay between the behaviour of approximately convex (and approximately affine) functions on the unit ball of a banach space and the geometry of banach $k$-spaces is studied.