Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T10:00:54.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Rank Wavelets

Published online by Cambridge University Press:  20 November 2018

Sean Olphert  and
Stephen C. Power
Sean Olphert
Affiliation:
Department of Mathematics & Statistics, Lancaster University, Lancaster LA1 4YF, UK email: [email protected]@lancaster.ac.uk
Stephen C. Power
Affiliation:
Department of Mathematics & Statistics, Lancaster University, Lancaster LA1 4YF, UK email: [email protected]@lancaster.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A theory of higher rank multiresolution analysis is given in the setting of abelian multiscalings. This theory enables the construction, from a higher rank MRA, of finite wavelet sets whose multidilations have translates forming an orthonormal basis in 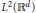${{L}^{2}}({{\mathbb{R}}^{d}})$. While tensor products of uniscaled MRAs provide simple examples we construct many nonseparable higher rank wavelets. In particular we construct Latin square wavelets as rank 2 variants of Haar wavelets. Also we construct nonseparable scaling functions for rank 2 variants of Meyer wavelet scaling functions, and we construct the associated nonseparable wavelets with compactly supported Fourier transforms. On the other hand we show that compactly supported scaling functions for biscaled MRAs are necessarily separable.

Keywords

42C4042A6542A1643A65waveletmulti-scalinghigher rankmultiresolutionLatin squares
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 689 - 720
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Belogay, E. and Y.Wang, Arbitrarily smooth orthogonal nonseparable wavelets in R2. SIAM J. Math. Anal. 30(1999), 678–697. doi:10.1137/S0036141097327732 Google Scholar
[2] Bratteli, O. and Jorgensen, P. E. T., Wavelets through the looking glass: the world of the spectrum. Birkhäuser, Boston, 2002.Google Scholar
[3] Cohen, A. and Daubechies, I., Nonseparable bidimensional wavelet bases. Rev. Mat. Iberoamericana 9(1993), 51–137.Google Scholar
[4] Dai, X., Larson, D. R. and Speegle, D. M., Wavelet sets in Rn, Wavelets, Multiwavelets and Their Applications. Contemp. Math. 216(1998), 15–40.Google Scholar
[5] Dutkay, D. E. and Jorgensen, P. E. T., Methods from multiscale theory and wavelets applied to nonlinear dynamics. In: Wavelets, multiscale systems and hypercomplex analysis, Oper. Theory Adv. Appl. 167, Birkhäuser, Basel, 2006, 87–126.Google Scholar
[6] Eckley, A., Nason, G. P. and Treloar, R. L., Locally stationary wavelet fields with application to the modelling and analysis of image texture. Preprint, 2007.Google Scholar
[7] Grochenig, K. and Madych, W., Multiresolution analysis, Haar bases, and self-similar tilings. IEEE Trans. Inform. Theory 38(1992), 558–568. doi:10.1109/18.119723 Google Scholar
[8] Guo, K., Labate, D., Lim, W. Q., Weiss, G. and E.Wilson, Wavelets with composite dilations and their MRA properties. Appl. Comput. Harmon. Anal. 20(2006), 202–236. doi:10.1016/j.acha.2005.07.002 Google Scholar
[9] He, W. and Lai, M. J., Examples of bivariate nonseparable compactly supported orthonormal continuous wavelets. In: Wavelet Applications in Signal and Image Processing IV, Proceedings, SPIE 3169, 1997, 303–314.Google Scholar
[10] Hernandez, E. and Weiss, G. L., A First Course on Wavelets (Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1996.Google Scholar
[11] Kovacevic, J. and Vetterli, M., Nonseparable multidimensional perfect reconstruction filterbanks. IEEE Trans. Inform. Theory 38(1992), 533–555. doi:10.1109/18.119722 Google Scholar
[12] Li, Y., On a class of bidimensional nonseparable wavelet multipliers. J. Math. Anal. Appl. 270(2002), 543–560. doi:10.1016/S0022-247X(02)00089-6 Google Scholar
[13] Mallat, S., Multiresolution analysis and wavelets. Trans. Amer. Math. Soc. 315(1989), 69–88.Google Scholar
[14] Meyer, Y., Multiresolution Approximations and Wavelet Orthonormal Bases of L2(R). Trans. Amer. Math. Soc. 315(1989), 69–87.Google Scholar
[15] Packer, J. A. and Rieffel, M. A., Wavelet filter functions, the matrix completion problem, and projective modules over C(Tn). J. Fourier Anal. Appl. 9(2003), 101–116. doi:10.1007/s00041-003-0010-4 Google Scholar
[16] Wang, Yang, Wavelets, tiling and spectral sets. Duke Math. J. 114(2002), 43–57. doi:10.1215/S0012-7094-02-11413-6 Google Scholar
[17] Wojtaszczyk, P., A mathematical introduction to wavelets. London Mathematical Society Student Texts 37, Cambridge University Press, Cambridge, 1997.Google Scholar