Writing 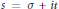 $s\,=\,\sigma \,+\,it$ for a complex variable, it is proved that the modulus of the gamma function,
$s\,=\,\sigma \,+\,it$ for a complex variable, it is proved that the modulus of the gamma function, 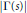 $\left| \Gamma (s) \right|$, is strictly monotone increasing with respect to
$\left| \Gamma (s) \right|$, is strictly monotone increasing with respect to  $\sigma $ whenever
$\sigma $ whenever 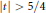 $\left| t \right|\,>\,5/4$. It is also shown that this result is false for
$\left| t \right|\,>\,5/4$. It is also shown that this result is false for 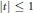 $\left| t \right|\,\le \,1$.
$\left| t \right|\,\le \,1$.
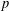 $p$-ADIC GAMMA FUNCTIONS
$p$-ADIC GAMMA FUNCTIONS
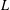 $L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS