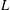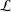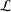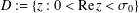Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Wei
and
Wang, Qiong
2020.
Algebraic differential independence concerning the Euler Γ-function and Dirichlet series.
Acta Mathematica Scientia,
Vol. 40,
Issue. 4,
p.
1035.
Chen, Wei
and
Wang, Qiong
2021.
On the Differential and Difference Independence of Γ and ζ.
Acta Mathematica Scientia,
Vol. 41,
Issue. 2,
p.
505.
Lü, Feng
and
Jiang, Shuxin
2023.
On the algebraic differential independence of $$ \Gamma $$ and $$ \zeta $$.
Monatshefte für Mathematik,
Vol. 202,
Issue. 1,
p.
141.
Lü, Feng
2024.
On the algebraic difference independence of Γ and ζ.
Journal of Mathematical Analysis and Applications,
Vol. 538,
Issue. 2,
p.
128446.