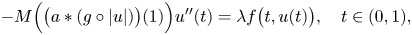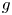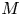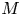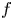A unified characterization of convolution coefficients in nonlocal differential equations

Abstract

In loving memory of my beloved miniature dachshund Maddie (16 March 2002 – 16 March 2020). We consider nonlocal differential equations with convolution coefficients of the form

\[{-}M\Big(\big(a*(g\circ |u|)\big)(1)\Big)u''(t)=\lambda f\big(t,u(t)\big),\quad t\in(0,1), \]

in the case in which $g$ can satisfy very generalized growth conditions; in addition, $M$ is allowed to be both sign-changing and vanishing. Existence of at least one positive solution to this equation equipped with boundary data is considered. We demonstrate that the nonlocal coefficient $M$ allows the forcing term $f$ to be free of almost all assumptions other than continuity.

1. Introduction

For two $L^1((0,\,+\infty ))$ functions, $a$ and $b$, let $(a*b)(t)$ denote the finite convolution of $a$ and $b$ at some $t\ge 0$ – i.e.,

\[ (a*b)(t):=\int_0^ta(t-s)b(s)\ {\rm d}s,\quad t\ge0. \]

In this paper we consider the following convolution-type differential equation, where $\lambda >0$ is a parameter.

(1.1)\begin{equation} {-}M\Big(\big(a*(g\circ |u|)\big)(1)\Big)u''(t)=\lambda f\big(t,u(t)\big),\quad t\in(0,1) \end{equation}

As will be further clarified in § 2, we assume that $M$ is continuous and possibly both sign-changing and vanishing. Moreover, $a\in L^1((0,\,1))$, which is assumed to be a.e. positive, allows for various nonlocal operators to be captured by the convolutional formulation. For example, if we set

\[ a(t):=\frac{1}{\Gamma(\alpha)}t^{\alpha-1},\quad t>0, \]

where $0<\alpha <1$, then $(a*(g\circ u))(1)$ is the $\alpha$-th order Riemann–Liouville fractional integral of $g\circ u$ at $t=1$. Fractional integrals and derivatives are a well studied class of nonlocal operators – see, for example, [1, 7, 19, 32, 33, 45, 46, 53] for some of the research in this area, together with the monographs [35, 47].

Our primary contribution herein is to prove the existence of at least one positive solution to (1.1) when subjected to boundary data and, in particular, to do so whilst making the following contributions.

• • We require only that $g$ satisfy the growth bound

  (1.2)\begin{equation} 0\le\xi_1(u)\le g(u)\le\xi_2(u),\quad u\ge0, \end{equation}
  where both $\xi _1$ and $\xi _2$ are strictly increasing functions. Figure 1 illustrates a possible configuration of $\xi _1$, $\xi _2$, and $g$ satisfying (1.2). Notice that this includes the model case, in which $g(u):=u^p$ for some $p>0$. However, this assumption is more general than other recent assumptions. For example, it has been assumed previously [29, 31] that $g$ satisfies $p$-$q$ growth, i.e., $c_1u^p\le g(u)\le c_2+c_3u^q$, which is clearly a special case of the above with $\xi _1(u):=c_1u^p$ and $\xi _2(u):=c_2+c_3u^q$. Similarly, it has been assumed previously [24] that $g$ is bounded by convex (or concave) functions. Once again, this is obviously a special case in which one further requires the convexity or concavity of the $\xi _i$ functions. So, the generalization investigated here really gets to the heart of the matter inasmuch as what assumptions on $g$ are necessary – i.e., it is sufficient to assume that $g$ is merely bounded above and below by strictly increasing functions. All other assumptions (e.g., convexity, concavity, particular growth regimes such as polynomial growth) are superfluous.

• • We characterize in a numerically precise way the fact that the forcing term $f$ satisfies essentially no restriction other than continuity provided that $M$ assumes both very small and very large positive values. Whilst this observation is not new per se, for it can be recovered in a general sense even from our original work with Kirchhoff equations, cf., [22, Theorem 2.6], in this work we provide a more precise characterization of this phenomenon by utilizing a different growth assumption on $f$. Essentially, we demonstrate that if $M$ is very large at some point and close to zero at another point, then nearly the only assumption needed of $f$ is that it is continuous. This phenomenon is unusual in the theory of boundary value problems (cf., Erbe and Wang [18]), though it has been characterized in the context of boundary value problems with nonlocal boundary conditions [20, 21]. In any case, we demonstrate that this phenomenon exists even under the more general condition imposed on the function $g$.

Figure 1. Illustration of the admissible region for the graph of $g$ satisfying condition (1.2).

Let us mention that an important model case of (1.1) occurs when $a(t)\equiv 1$ and $g(u):=u^p$ for $p\ge 1$. In this case, equation (1.1) reduces to

(1.3)\begin{equation} {-}M\Big(\Vert u\Vert_{L^p}^{p}\Big)u''(t)=\lambda f\big(t,u(t)\big). \end{equation}

In case we instead set $\displaystyle a(t)=\frac {1}{\Gamma (\alpha )}t^{\alpha -1}$, $0<\alpha <1$, as mentioned above, then (1.1) reduces to

\[{-}M\Big(\big(I_{0^+}^{\alpha}(g\circ|u|)\big)(1)\Big)u''(t)=\lambda f\big(t,u(t)\big). \]

where by $(I_{0^+}^{\alpha }u)(t)$ we denote the $\alpha$-th order Riemann–Liouville fractional integral of $u$ at $t$.

More generally, nonlocal equations of the form (1.3), or its relatives, have been well studied in recent years. Two model cases seem to have attracted the most attention. One is (1.3) and its PDE equivalent

(1.4)\begin{equation} {-}M\Big(\Vert u\Vert_{L^p}^{p}\Big)\Delta u(\boldsymbol{x})=\lambda f\big(\boldsymbol{x},u(\boldsymbol{x})\big),\quad x\in\Omega\subset\mathbb{R}^{n}, \end{equation}

whereas the other is

(1.5)\begin{equation} {-}M\Big(\Vert u'\Vert_{L^p}^{p}\Big)u''(t)=\lambda f\big(t,u(t)\big),\quad 0< t<1 \end{equation}

and its PDE equivalent

(1.6)\begin{equation} {-}M\Big(\Vert Du\Vert_{L^p}^{p}\Big)\Delta u(\boldsymbol{x})=\lambda f\big(\boldsymbol{x},u(\boldsymbol{x})\big),\quad x\in\Omega\subset\mathbb{R}^{n}. \end{equation}

Each of (1.3)–(1.6) has its origins in the steady-state version of the Kirchhoff-type wave PDE

\[ u_{tt}-M\Big(\Vert Du\Vert_{L^p}^{p}\Big)\Delta u(\boldsymbol{x})=\lambda f\big(\boldsymbol{x},u(\boldsymbol{x})\big),\quad x\in\Omega\subset\mathbb{R}^{n}. \]

Regarding equations of the type (1.3)–(1.4) some recent contributions include papers by Alves and Covei [3], Corrêa [14], Corrêa, Menezes, and Ferreira [15], do Ó, Lorca, Sánchez, and Ubilla [17], Goodrich [22], Stańczy [51], Wang, Wang, and An [52], Yan and Ma [54], and Yan and Wang [55]. On the other hand, regarding equations of the type (1.5)–(1.6) some recent contributions include papers by Afrouzi, Chung, and Shakeri [2], Ambrosetti and Arcoya [4], Azzouz and Bensedik [5], Boulaaras [8], Boulaaras and Guefaifia [9], Chung [12], Delgado, Morales-Rodrigo, Santos Júnior, and Suárez [16], Graef, Heidarkhani, and Kong [36], Infante [38, 39], and Santos Júnior and Siciliano [48]. In addition to Kirchhoff-like nonlocal differential operators, there is, from a functional analytic viewpoint, a very closely related literature on differential equations equipped with nonlocal boundary operators – see, for example, the papers by Infante, et al. [6, 10, 11, 13, 37, 40–44] and Yang [56, 57], which in addition to the associated mathematical theory, demonstrate applications to the deformation of a beam under a load, the thermodynamics of a heated filament, and nuclear reactor theory. Additionally, Shibata [49, 50], along with Goodrich [28], has provided some nonexistence results for nonlocal ODEs and nonlocal radially symmetric PDEs of the types mentioned above.

Recently, in the setting of both nonlocal ODEs and nonlocal radially symmetric PDEs, we have developed [23, 25–27], together with Lizama [34], a very general methodology for making minimal assumptions of $M$. The methodology utilizes specialized order cones together with topological fixed point theory. An advantage of this methodology is that we are able to make minimal assumptions on the coefficient function $M$. For example, in the study of positive solutions of nonlocal differential equations it is almost always assumed that the nonlocal coefficient $M$ satisfies one of the following three conditions.

1. (1) $M(t)>0$ for all $t\ge 0$ – see, for example, [14, 15, 17, 51, 52]

2. (2) $M(t)$ can only vanish at $0$ or ‘at $+\infty$’ - - see, for example, [4]

3. (3) $M(t)>0$ on a neighbourhood of zero – see, for example, [48]

One can see why such assumptions would be made since if $M(t)=0$, then the differential equation degenerates. Since we are able, by means of our theory, to precisely localize the argument of $M$, i.e., $(a*(g\circ |u|))(1)$, we can avoid making such sweeping assumptions – cf., remark 2.9. Indeed, instead of having to assume that $M(t)>0$ on a pre-specified subset of the real line, our theory simply requires $M(t)$ to be positive somewhere. This is quite different than (1)–(3) above – even than (3), which is the least restrictive of the lot.

So, here we continue the development of this theory by clarifying the generality of the function $g$ and also focussing on the interaction between the behaviour of $M$ and the assumptions required of $f$. And, in particular, we demonstrate that the good aspects of our theory continue to work properly even under the more general assumptions on $g$ utilized herein – not only the minimal assumptions required of $M$, but, furthermore, how $M$ itself can obviate the usual assumptions on $f$.

2. Main result

Throughout this section we denote by $\Vert \cdot \Vert _{\infty }$ the usual maximum norm on $[0,\,1]$, and we will always work within the Banach space $\mathscr {C}([0,\,1])$ equipped with this norm. In addition, we will let $\boldsymbol {1}$ denote the constant function $\boldsymbol {1} : \ \mathbb {R}\rightarrow \{1\}$. Similarly, by $\boldsymbol {0}$ we will denote the constant function $\boldsymbol {0}\ : \mathbb {R}\rightarrow \{0\}$. We will also use the notation

\[ (a*\boldsymbol{1})(c,d):=\int_c^da(1-s)\,{\rm d}s \]

for any $0\le c< d\le 1$.

We next list the assumptions imposed on the various functions appearing in (1.1). In addition, since our approach to studying (1.1) will be via studying the fixed points of an associated Hammerstein integral operator, we will equip (1.1) with boundary data via a Green's function, which we henceforth denote by $G$. The properties of $G$ are listed in condition (H2) below. Observe that condition (H1.2) implies that $(a*\boldsymbol {1})(1)>0$, a fact that will be used in the sequel without explicit mention.

1. H1: The functions $M\ : \ [0,\,+\infty )\rightarrow \mathbb {R}$, $f\ : \ [0,\,1]\times [0,\,+\infty )\rightarrow [0,\,+\infty )$, $g\ : \ [0,\,+\infty )\rightarrow [0,\,+\infty )$, and $a\ : \ (0,\,1]\rightarrow [0,\,+\infty )$ satisfy the following properties.

   1. (1) Each of $M$, $f$, and $g$ is continuous.

   2. (2) $a\in L^1((0,\,1];[0,\,+\infty ))$ is a.e. positive.

   3. (3) There exist numbers $0<\rho _1<\rho _2$ such that $M(t)>0$ for $t\in [\rho _1,\,\rho _2]$.

   4. (4) There exist strictly increasing continuous functions $\xi _1$, $\xi _2\ : \ [0,\,+\infty )\rightarrow [0,\,+\infty )$ such that

      \begin{equation} \xi_1(u)\le g(u)\le\xi_2(u),\quad u\ge0.\nonumber \end{equation}

2. H2: The continuous function $G\ : \ [0,\,1]\times [0,\,1]\rightarrow [0,\,+\infty )$ satisfies each of the following.

   1. (1) There exist numbers $0\le c< d\le 1$ and a constant $\eta _0:=\eta _0(c,\,d)\in (0,\,1]$ such that

      \begin{equation} \min_{t\in[c,d]}G(t,s)\ge\eta_0\mathscr{G}(s),\quad s\in[0,1],\nonumber \end{equation}
      where $\mathscr {G}\ : [0,\,1]\rightarrow [0,\,+\infty )$ denotes the function $\displaystyle \mathscr {G}(s):=\max _{t\in [0,1]}G(t,\,s)$.

   2. (2) With $\eta _0$, $c$, and $d$ as in (H2.1), and both $\rho _1$ and $\rho _2$ as in (H1.3), there exist constants $c_1>0$, $c_2\ge 0$, and $c_3>0$ such that

      \begin{align*} & f(t,u)\ge c_1u,\quad (t,u)\in[c,d]\\& \quad \times\left[\eta_0\xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right),\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(c,d)}\right)\right] \end{align*}
      and that
      \[ f(t,u)\le c_2+c_3u,\quad (t,u)\in[0,1]\times\left[0,\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right)\right]. \]

We will study problem (1.1), equipped with suitable boundary data, by means of the operator $T\ : \mathscr {C}([0,\,1])\rightarrow \mathscr {C}([0,\,1])$ defined by

\[ (Tu)(t):=\lambda\int_0^1\left(M\Big(\big(a*(g\circ |u|)\big)(1)\Big)\right)^{{-}1}G(t,s)f\big(s,u(s)\big)\,{\rm d}s. \]

It will be convenient to restrict the domain of $T$ to specialized sets, which allow us to provide precise control over the argument of $M$. Indeed, this is the strategy that permits us to avoid wide ranging assumptions on $M$ such as the uniform positivity of $M$. In particular, we will work within the order cone

\[ \mathscr{K}:=\left\{u\in\mathscr{C}\big([0,1]\big)\ : \ u\ge0\text{ and }\min_{t\in[c,d]}u(t)\ge\eta_0\Vert u\Vert_{\infty}\right\}. \]

Furthermore, for any $\rho \ge 0$, define the set $\widehat {V}_{\rho }\subseteq \mathscr {K}$ by

\[ \widehat{V}_{\rho}:=\Big\{u\in\mathscr{K}\ : \ \big(a*(g\circ |u|)\big)(1)<\rho\Big\}. \]

Observe that $\widehat {V}_{\rho }$ is (relatively) open in $\mathscr {K}$. Crucially, we note that

\[ \partial\widehat{V}_{\rho}:=\Big\{u\in\mathscr{K}\ : \ \big(a*(g\circ |u|)\big)(1)=\rho\Big\}, \]

which gives us very precise control over the argument of $M$. Since whenever $T$ is restricted to a subset of $\mathscr {K}$ it holds that $u\equiv |u|$, henceforth we will omit the absolute value when performing calculations with $T$.

We begin by providing a result that localizes $u$ in either the case $u\in \widehat {V}_{\rho }$ or $u\in \partial \widehat {V}_{\rho }$ for some $\rho >0$. This lemma will be used repeatedly in the sequel. It also establishes that the $\widehat {V}_{\rho }$ set is bounded, with respect to $\Vert \cdot \Vert _{\infty }$, for each $\rho \ge 0$ – a necessary condition for the application of the topological fixed theorem that we employ later.

Lemma 2.1 Suppose that conditions (H1)–(H2) are satisfied. Then for any $\rho >0$ such that

\begin{align*} \xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)>0, \end{align*}

whenever $u\in \partial \widehat {V}_{\rho }$, it follows that

\begin{align*} \xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)<\Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \end{align*}

In addition, for any $\rho >0$, whenever $u\in \widehat {V}_{\rho }$, it follows that

\begin{align*} \Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \end{align*}

Proof. Let us first suppose that $u\in \partial \widehat {V}_{\rho }$ for some $\rho >0$. Then, on the one hand, we calculate

(2.1)\begin{equation} \begin{aligned} \rho=\big(a*(g\circ u)\big)(1) < \big(a*(\xi_2\circ u)\big)(1) & \le\big(a*(\xi_2\circ\Vert u\Vert_{\infty})\boldsymbol{1}\big)(1)\\ & =\xi_2\big(\Vert u\Vert_{\infty}\big)(a*\boldsymbol{1})(1). \end{aligned} \end{equation}

Then using the fact that $\xi _2$ is strictly increasing, it follows from (2.1) that

(2.2)\begin{equation} \Vert u\Vert_{\infty}>\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right). \end{equation}

On the other hand, we calculate

(2.3)\begin{equation} \begin{aligned} \rho & =\big(a*(g\circ u)\big)(1)>\big(a*(\xi_1\circ u)\big)(1)\\ & \ge\int_c^da(1-s)\xi_1\big(u(s)\big)\ {\rm d}s\\ & \ge\int_c^da(1-s)\xi_1\big(\eta_0\Vert u\Vert_{\infty}\big)\ {\rm d}s\\ & =\xi_1\big(\eta_0\Vert u\Vert_{\infty}\big)(a*\boldsymbol{1})(c,d) \end{aligned} \end{equation}

Then using the fact that $\xi _1$ is strictly increasing, it follows from (2.3) that

(2.4)\begin{equation} \Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \end{equation}

And so from both (2.2) and (2.4) we obtain, for any $\rho >0$, the localization estimate

\[ u\in\partial\widehat{V}_{\rho}\Longrightarrow\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)<\Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \]

Next assume that $u\in \widehat {V}_{\rho }$ for some $\rho >0$. Then, by means of the preceding calculations, we see that the localization

\[ u\in\widehat{V}_{\rho}\Longrightarrow\Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \]

holds. And this completes the proof.

Remark 2.2 We wish to emphasize at this juncture that even though the proof of lemma 2.1 is similar to the related results [24, Lemma 2.3], [26, Lemma 2.4], and [31, Lemma 2.8], it, nonetheless, encompasses far greater generality. Indeed, there is no requirement that either $\xi _1$ or $\xi _2$ satisfy any particular type of growth (e.g., polynomial), and there is no requirement that either function satisfy any convexity or concavity assumption. In addition, even in the model case in which $g(u)=u^p$, here the cases $0< p<1$ and $p\ge 1$ are treated in a unified fashion. And this is not something that has been accomplished before, to the best of our knowledge.

Next we prove a technical lemma regarding how large $M(t)$ needs to be in order for a certain inequality to be satisfied. This result will be used in the existence theorem later. Note that in both the statement of lemma 2.3 as well as the sequel we use the following notation:

\[ \overline{G_{[a,b]}}:=\max_{t\in[0,1]}\int_a^bG(t,s)\ {\rm d}s, \]

for any $0\le a< b\le 1$.

Lemma 2.3 Fix $\rho >0$. Assume that each of conditions (H1) and (H2) is satisfied and that $\displaystyle \xi _2^{-1}(\frac {\rho }{(a*\boldsymbol {1})(1)})>0$. If $u\in \partial \widehat {V}_{\rho }$ and

\[ M(\rho)\ge\lambda\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}, \]

then

\[ \lambda\big(c_2+c_3\Vert u\Vert_{\infty}\big)\big(M(\rho)\big)^{{-}1}\overline{G_{[0,1]}}\le\Vert u\Vert_{\infty}. \]

Proof. First recall that if $u\in \partial \widehat {V}_{\rho }$, then from lemma 2.1 it follows that

(2.5)\begin{equation} 0<\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)<\Vert u\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right). \end{equation}

Note that

(2.6)\begin{equation} \lambda\big(c_2+c_3\Vert u\Vert_{\infty}\big)\big(M(\rho)\big)^{{-}1}\overline{G_{[0,1]}}\le\Vert u\Vert_{\infty} \end{equation}

if and only if

(2.7)\begin{equation} M(\rho)\ge\frac{\lambda\left(c_2+c_3\Vert u\Vert_{\infty}\right)\overline{G_{[0,1]}}}{\Vert u\Vert_{\infty}}. \end{equation}

Now, using (2.5) note that

(2.8)\begin{align} & \frac{\lambda\left(c_2+c_3\Vert u\Vert_{\infty}\right)\overline{G_{[0,1]}}}{\Vert u\Vert_{\infty}}\nonumber\\ & \quad<\left(\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}\lambda\left(c_2+c_3\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right)\right)\overline{G_{[0,1]}}\nonumber\\ & \quad =\lambda\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}. \end{align}

Then, upon combining (2.8) with (2.6)–(2.7) we see that if

\[ M(\rho)\ge\lambda\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}, \]

then

\[ \lambda\big(c_2+c_3\Vert u\Vert_{\infty}\big)\big(M(\rho)\big)^{{-}1}\overline{G_{[0,1]}}\le\Vert u\Vert_{\infty}, \]

which completes the proof.

Lemma 2.4 Assume that conditions (H1)–(H2) hold. Then $T\ : \overline {\widehat {V}_{\rho _2}}\setminus \widehat {V}_{\rho _1}\rightarrow \mathscr {K}$ is completely continuous and, in particular,

\[ T\left(\overline{\widehat{V}_{\rho_2}}\setminus\widehat{V}_{\rho_1}\right)\subseteq\mathscr{K}. \]

Proof. The proof is similar to part of the proof of [20, Theorem 3.1], for example. Therefore, we omit the proof.

We finalize our preliminary lemmata with the following result, known as the Guo-Krasnosel'skiĭ theorem – see, for example, [58]. This will be the topological fixed point theorem that we utilize in our existence theorem.

Lemma 2.5 Let $\mathscr {B}$ be a Banach space and let $\mathscr {K}\subseteq \mathscr {B}$ be a cone. Assume that $\Omega _1$ and $\Omega _2$ are bounded open sets contained in $\mathscr {B}$ such that $\boldsymbol {0}\in \Omega _1$ and $\overline {\Omega }_1\subseteq \Omega _2$. Assume, further, that $T\ : \mathscr {K}\cap (\overline {\Omega }_2\setminus \Omega _1)\rightarrow \mathscr {K}$ is a completely continuous operator. If either

1. (1) $\Vert Ty\Vert \le \Vert y\Vert$ for $y\in \mathscr {K}\cap \partial \Omega _1$ and $\Vert Ty\Vert \ge \Vert y\Vert$ for $y\in \mathscr {K}\cap \partial \Omega _2$; or

2. (2) $\Vert Ty\Vert \ge \Vert y\Vert$ for $y\in \mathscr {K}\cap \partial \Omega _1$ and $\Vert Ty\Vert \le \Vert y\Vert$ for $y\in \mathscr {K}\cap \partial \Omega _2$;

then $T$ has at least one fixed point in $\mathscr {K}\cap (\overline {\Omega }_2\setminus \Omega _1)$.

We now present our existence theorem.

Theorem 2.6 Assume that each of conditions (H1) and (H2) holds. In addition, assume both that

(2.9)\begin{equation} \frac{c_1\lambda\eta_0\overline{G_{[c,d]}}}{M\left(\rho_1\right)}\ge1 \end{equation}

and that

(2.10)\begin{equation} M(\rho_2)\ge\lambda\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}. \end{equation}

If

\[ g(0)<\frac{\rho_1}{(a*\boldsymbol{1})(1)}, \]

then (1.1) equipped with the boundary data inherited from the Green's function $G$ has at least one positive solution, say $u_0$, such that

\[ u_0\in\overline{\widehat{V}_{\rho_2}}\setminus\widehat{V}_{\rho_1}. \]

Moreover, $u_0$ satisfies the localization

\[ \xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right)<\Vert u_0\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right). \]

Proof. First of all, by lemma 2.4 we note that

\[ T\left(\overline{\widehat{V}_{\rho_2}}\setminus\widehat{V}_{\rho_1}\right)\subseteq\mathscr{K}, \]

where $T$ is completely continuous on its domain. Furthermore, we note that

\[ \boldsymbol{0}\in\widehat{V}_{\rho_1} \]

because

\[ \big(a*(g\circ\boldsymbol{0})\boldsymbol{1}\big)(1)=g(0)(a*\boldsymbol{1})(1)<\rho_1 \]

by assumption. And, in addition, we see that

\[ \overline{\widehat{V}_{\rho_1}}\subseteq\widehat{V}_{\rho_2} \]

owing both to the definition of $\widehat {V}_{\rho }$ and to the fact that $\rho _1<\rho _2$. Finally, by lemma 2.1 the sets $\widehat {V}_{\rho _i}$, $i\in \{1,\,2\}$, are bounded. So, each of the technical conditions in lemma 2.5 is satisfied.

We first demonstrate that for each $u\in \partial \widehat {V}_{\rho _1}$ it follows that

(2.11)\begin{equation} \Vert Tu\Vert_{\infty}\ge\Vert u\Vert_{\infty}; \end{equation}

that is, $T$ is a cone expansion on $\partial \widehat {V}_{\rho _1}$. To this end, first note that since $u\in \partial \widehat {V}_{\rho _1}$ it follows that

(2.12)\begin{equation} \big(a*(g\circ u)\big)(1)=\rho_1. \end{equation}

Next recall that $f$ satisfies the growth estimate

(2.13)\begin{align} f(t,u)\ge c_1u,\quad (t,u)\in[c,d]\times\left[\eta_0\xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right),\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(c,d)}\right)\right]. \end{align}

Note that whenever $u\in \partial \widehat {V}_{\rho _1}$, it follows both that

\[ u(t)\ge\eta_0\Vert u\Vert_{\infty}\ge\eta_0\xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right),\quad t\in[a,b] \]

and that

\[ u(t)\le\Vert u\Vert_{\infty}\le\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(c,d)}\right),\quad t\in[0,1]. \]

Consequently, the growth estimate (2.13) is satisfied for any $u\in \partial \widehat {V}_{\rho _1}$. Then it follows from a combination of both (2.12) and (2.13) that, for each $t\in [0,\,1]$,

(2.14)\begin{equation} \begin{aligned} (Tu)(t) & =\lambda\int_0^1\big(M\left(\rho_1\right)\big)^{{-}1}G(t,s)f\big(s,u(s)\big)\ {\rm d}s\\ & \ge\frac{\lambda}{M\left(\rho_1\right)}\int_0^1G(t,s)c_1u(s)\ {\rm d}s\\ & \ge\frac{c_1\lambda}{M\left(\rho_1\right)}\int_{c}^{d}G(t,s)\eta_0\Vert u\Vert_{\infty}\ {\rm d}s\\ & \ge\left(\frac{c_1\lambda\eta_0}{M\left(\rho_1\right)}\int_c^dG(t,s)\ {\rm d}s\right)\Vert u\Vert_{\infty}. \end{aligned} \end{equation}

Now taking the maximum over $t\in [0,\,1]$ on both sides of (2.14) yields

(2.15)\begin{equation} \Vert Tu\Vert_{\infty}\ge\left(\frac{c_1\lambda\eta_0}{M\left(\rho_1\right)}\max_{t\in[0,1]}\int_c^dG(t,s)\ {\rm d}s\right)\Vert u\Vert_{\infty}=\frac{c_1\lambda\eta_0\overline{G_{[c,d]}}}{M\left(\rho_1\right)}\Vert u\Vert_{\infty}. \end{equation}

Finally, using assumption (2.9) in the statement of the theorem, we conclude from inequality (2.15) that

(2.16)\begin{equation} \Vert Tu\Vert_{\infty}\ge\underbrace{\frac{c_1\lambda\eta_0\overline{G_{[a,b]}}}{M\left(\rho_1\right)}}_{\ge1}\Vert u\Vert_{\infty}\ge\Vert u\Vert_{\infty}. \end{equation}

So, inequality (2.16) implies that $T$ is a cone expansion on $\partial \widehat {V}_{\rho _1}$ – that is, inequality (2.11) is satisfied.

We next demonstrate that for each $u\in \partial \widehat {V}_{\rho _2}$ it follows that

(2.17)\begin{equation} \Vert Tu\Vert_{\infty}\le\Vert u\Vert_{\infty}; \end{equation}

that is, $T$ is a cone compression on $\partial \widehat {V}_{\rho _2}$. To this end, first note that since $u\in \partial \widehat {V}_{\rho _2}$ it follows that

(2.18)\begin{equation} \big(a*(g\circ u)\big)(1)=\rho_2. \end{equation}

Next recall that $f$ satisfies the growth estimate

(2.19)\begin{equation} f(t,u)\le c_2+c_3u,\quad (t,u)\in[0,1]\times\left[0,\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right)\right]. \end{equation}

Similar to the first part of the proof, whenever $u\in \partial \widehat {V}_{\rho _2}$ it follows that

(2.20)\begin{equation} u(t)\le\Vert u\Vert_{\infty}\le\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right),\quad t\in[0,1], \end{equation}

where we, once again, have used lemma 2.1; in other words, condition (H2) implies that for each $u\in \partial \widehat {V}_{\rho _2}$ it follows that $f(t,\,u(t))\le c_2+c_3u(t)$, $t\in [0,\,1]$. Then from (2.18)–(2.20), for each $t\in [0,\,1]$, we deduce that

(2.21)\begin{equation} \begin{aligned} (Tu)(t) & =\lambda\int_0^1\big(M\left(\rho_2\right)\big)^{{-}1}G(t,s)f\big(s,u(s)\big)\ {\rm d}s\\ & \le\frac{\lambda}{M\left(\rho_2\right)}\int_0^1G(t,s)\big(c_2+c_3u(s)\big)\ {\rm d}s\\ & \le\frac{\lambda}{M\left(\rho_2\right)}\int_0^1G(t,s)\big(c_2+c_3\Vert u\Vert_{\infty}\big)\ {\rm d}s. \end{aligned} \end{equation}

Taking the maximum over $t\in [0,\,1]$ on both sides of inequality (2.21) yields

(2.22)\begin{equation} \Vert Tu\Vert_{\infty}\le\frac{\lambda}{M\left(\rho_2\right)}\max_{t\in[0,1]}\int_0^1G(t,s)\big(c_2+c_3\Vert u\Vert_{\infty}\big)\ {\rm d}s=\frac{\lambda \overline{G_{[0,1]}}}{M\left(\rho_2\right)}\big(c_2+c_3\Vert u\Vert_{\infty}\big). \end{equation}

Finally, an application of lemma 2.3 to inequality (2.22), keeping in mind assumption (2.10), implies that

(2.23)\begin{equation} \Vert Tu\Vert_{\infty}\le\frac{\lambda \overline{G_{[0,1]}}}{M\left(\rho_2\right)}\big(c_2+c_3\Vert u\Vert_{\infty}\big)\le\Vert u\Vert_{\infty}. \end{equation}

Thus, (2.23) implies the desired inequality (2.17).

All in all, then, by lemma 2.5 we deduce the existence of

\[ u_0\in\overline{\widehat{V}_{\rho_2}}\setminus\widehat{V}_{\rho_1} \]

such that $Tu_0\equiv u_0$. And this function $u_0$ is, therefore, a positive solution of (1.1) equipped with the boundary data inherited from $G$. Finally, the conclusion of lemma 2.1 implies the localization

\[ \xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right)<\Vert u_0\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right). \]

And this completes the proof.

Remark 2.7 Let us consider what conditions (2.9)–(2.10) imply regarding the constants $c_1$, $c_2$, and $c_3$ appearing in the growth condition (H2.2) imposed on the forcing function $f$ in (1.1). Figure 2 provides an idealized drawing of the lower and upper bounding functions for the graph of $f$. In the drawing, the numbers $\alpha _1$, $\alpha _2$, and $\alpha _3$ are defined by

\begin{equation} \alpha_1:=\eta_0\xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right)\nonumber \end{equation}

and

\begin{equation} \alpha_i:=\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_i}{(a*\boldsymbol{1})(c,d)}\right),\quad i\in\{2,3\}.\nonumber \end{equation}

That is, the $\alpha _i$'s are the bounds on the $u$ variable for which $(t,\,u)\mapsto f(t,\,u)$ satisfies the various growth restrictions in condition (H2.2).

Figure 2. The light shaded region shows where the graph of $f$ can live. The dark shaded region is the set $E_0$ referenced in remark 2.7. The numbers $\alpha _i$, $i\in \{1,\,2,\,3\}$, are defined in remark 2.7.

Note first that (2.9) is equivalent to

\[ c_1\ge\frac{M\left(\rho_1\right)}{\lambda\eta_0\overline{G_{[c,d]}}} \]

so that as $M(\rho _1)\to 0^+$, it follows that the lower bound on $c_1$ tends to $0$. More precisely and as in figure 2, define $E_0\subset [0,\,+\infty )$ by

\begin{align*} E_0 & :=\left\{(u,v)\in\mathbb{R}^2\ : \ \eta_0\xi_2^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(1)}\right)\right.\nonumber\\ & \left.\qquad\ \le u\le\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_1}{(a*\boldsymbol{1})(c,d)}\right),\quad 0\le v\le c_1u\right\}. \end{align*}

Then, denoting by $m(E_0)$ the Lebesgue measure of the set $E_0$, we see that

\[ \lim_{M\left(\rho_1\right)\to0^+}m\left(E_0\right)=0. \]

In other words, as $M(\rho _1)$ tends to zero, the restriction $f(t,\,u)\ge c_1u$ is obviated.

On the other hand, (2.10) is equivalent to

\[ M(\rho_2)\ge\lambda\eta_0\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}. \]

So, in a similar way, this implies that if there exists $\rho _2$ such that $M(\rho _2)\gg 1$, then $c_2$ and $c_3$ can be very large, thus implying that the upper bound on $f$ is very mild in this case. Indeed, in terms of the drawing in figure 2, both the slope and the $y$-intercept of the line $u\mapsto c_2+c_3u$ will tend to $+\infty$ as $M(\rho _2)\to +\infty$, which means that the upper bound on $f$ becomes less and less restrictive. Thus, in a simplified sense, we see that if $M$ is alternatively very large somewhere and very close to zero somewhere, then the restrictions on $f$ are obviated, and so, there are then essentially no restrictions on $f$ other than continuity (and nonnegativity).

We conclude with an example in order to clarify the application of theorem 2.6. The example will demonstrate how the nonlocal coefficient $M$ can eliminate nearly all restrictions other than continuity and nonnegativity from $f$.

Example 2.8 Let

\[ g(t):=t+e^t\sin^2{t} \]

and

\[ M(t):=\begin{cases} -3+t,\quad & 0\le t\le 3\\ (t-3)(5-t),\quad & 3\le t\le 5\\ - (t-5)^2,\quad & t\ge5\end{cases}. \]

In addition, set $a\equiv \boldsymbol {1}$ and

\[ G(t,s):=\begin{cases} t(1-s),\quad & 0\le t\le s\le 1\\ s(1-t),\quad & 0\le s\le t\le 1\end{cases}. \]

Then $G$ equips (1.1) with Dirichlet boundary conditions so that we are considering the problem

(2.24)\begin{equation} \begin{aligned} -M\big(\boldsymbol{1}*(g\circ |u|)(1)\big)u''(t) & =\lambda f\big(t,u(t)\big),\quad 0< t<1\\ u(0) & =0\\ u(1) & =0. \end{aligned} \end{equation}

Now, one can show that

\[ \xi_1(t):=t\le g(t)\le e^{2t}=:\xi_2(t). \]

Observe that $\xi _1^{-1}(t)=t$ and $\xi _2^{-1}(t)=\ln {\sqrt {t}}$. In addition, for the Green's function $G$ it is known (see Erbe and Wang [18], for example) that one may choose $\displaystyle c:=\frac {1}{4}$, $\displaystyle d:=\frac {3}{4}$, and $\displaystyle \eta _0=\frac {1}{4}$. Then we calculate

\[ \overline{G_{[c,d]}}=\max_{t\in[0,1]}\int_{\frac{1}{4}}^{\frac{3}{4}}G(t,s)\ {\rm d}s=\frac{15}{32} \]

and

\[ \overline{G_{[0,1]}}=\max_{t\in[0,1]}\int_0^1G(t,s)\ {\rm d}s=\frac{1}{2}. \]

In addition, since $a\equiv \boldsymbol {1}$, it follows that

\[ (a*\boldsymbol{1})(1)=(\boldsymbol{1}*\boldsymbol{1})(1)=1 \]

and that

\[ (a*\boldsymbol{1})(c,d)=(\boldsymbol{1}*\boldsymbol{1})\left(\frac{1}{4},\frac{3}{4}\right):=\int_{\frac{1}{4}}^{\frac{3}{4}}\ {\rm d}s=\frac{1}{2}. \]

Finally, set, for $0<\varepsilon _1<1$,

\[ \rho_1:=3+\varepsilon_1\nonumber \]

and

\[ \rho_2:=4. \]

Note that

\[ g(0)=0<\frac{\rho_1}{(\boldsymbol{1}*\boldsymbol{1})(1)}=\rho_1. \]

Then condition (2.9) is satisfied provided that

(2.25)\begin{equation} \varepsilon_1\left(2-\varepsilon_1\right)=M\left(3+\varepsilon_1\right)\le\frac{15}{128}c_1\lambda, \end{equation}

whereas condition (2.10) is satisfied provided that

\begin{align*} & 1=M(4)=M\left(\rho_2\right)\\ & \quad\ge\lambda\overline{G_{[0,1]}}\left(c_2+\frac{c_3}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(c,d)}\right)\right)\left(\xi_2^{{-}1}\left(\frac{\rho_2}{(a*\boldsymbol{1})(1)}\right)\right)^{{-}1}\\ & \quad=\frac{1}{2}\lambda\big(c_2+32c_3\big)\frac{1}{\ln{2}}\\ & \quad=\frac{1}{\ln{4}}\lambda\big(c_2+32c_3\big), \end{align*}

which is equivalent to

(2.26)\begin{equation} c_2+32c_3\le\frac{\ln{4}}{\lambda}. \end{equation}

Now, since

\[ \lim_{\varepsilon_1\to0^+}\varepsilon_1\left(2-\varepsilon_1\right)=0, \]

it follows that inequality (2.25) can be satisfied for any $\lambda$ and $c_1$ provided that $\varepsilon _1$ is chosen sufficiently close to $0$. So, given any forcing term $f$ satisfying both (H1)–(H2) and inequality (2.26), there exists $\varepsilon _1>0$ sufficiently small such that by theorem 2.6 problem (2.24) admits a positive solution, say

\[ u_0\in\overline{\widehat{V}_{4}}\setminus\widehat{V}_{3+\varepsilon_1}, \]

where $u_0$ satisfies the localization

\[ \ln{\sqrt{3+\varepsilon_1}}=\xi_2^{{-}1}\left(\frac{\rho_1}{(\boldsymbol{1}*\boldsymbol{1})(1)}\right)<\Vert u_0\Vert_{\infty}<\frac{1}{\eta_0}\xi_1^{{-}1}\left(\frac{\rho_2}{(\boldsymbol{1}*\boldsymbol{1})\left(\frac{1}{4},\frac{3}{4}\right)}\right)=32. \]

Finally, observe since

\[ \lim_{\lambda\to0^+}\frac{\ln{4}}{\lambda}={+}\infty, \]

it follows from condition (2.25) that any $f\in \mathscr {C}([0,\,+\infty );[0,\,+\infty ))$ there exists $\lambda _0>0$ sufficiently small such that for each $\lambda \in (0,\,\lambda _0)$ problem (2.24) admits a positive solution. In other words, there is no growth restriction on $f$.

Remark 2.9 Note that the function $g$ in example 2.8

1. (1) alternates between concave and convex;

2. (2) alternates between increasing and decreasing; and

3. (3) does not satisfy

   \[ g(u)\le c_2+c_3u^q, \]
   for any $1\le q<+\infty$, $c_2\ge 0$, and $c_3>0$, seeing as $g$ grows exponentially.

This is seen by the graph of $g$, which is provided in figure 3. Observation (1) implies that the results of [24, 30] cannot be applied. Observation (2) also implies that the results of [24, 30] cannot be applied. And observation (3) implies that the results of [22, 25–27, 29, 31] cannot be applied. Moreover, and as discussed in § 1, other earlier results in the ODEs setting, such as [14, 15, 17, 51, 52], cannot be applied due both to the sign-changing and vanishing nature of the nonlocal coefficient $M$ as defined in (2.24); in particular, both $\displaystyle \lim _{t\to \infty }M(t)=-\infty$ and $M(0)<0$ in contrast to the restrictions imposed (albeit in the PDEs setting) in [4] and [48], respectively. Therefore, the results presented herein are genuinely more broadly applicable than those previously reported in the literature.

Figure 3. Illustration of the graphs of $\xi _1$, $\xi _2$, and $g$ in example 2.8. The shaded region is the area bounded between the graphs of $\xi _1$ and $\xi _2$ – i.e., the admissible region for the graph of $g$.