Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T01:20:14.341Z Has data issue: false hasContentIssue false
  • English
  • Français

On two congruence conjectures of Z.-W. Sun involving Franel numbers

Part of: Combinatorics Elementary classical functions Elementary number theory

Published online by Cambridge University Press:  16 May 2023

Guo-Shuai Mao  and
Yan Liu
Guo-Shuai Mao
Affiliation:
Department of Mathematics, Nanjing University of Information Science and Technology, Nanjing 210044, People's Republic of China ([email protected], [email protected])
Yan Liu
Affiliation:
Department of Mathematics, Nanjing University of Information Science and Technology, Nanjing 210044, People's Republic of China ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we mainly prove the following conjectures of Z.-W. Sun (J. Number Theory 133 (2013), 2914–2928): let $p>2$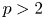 be a prime. If $p=x^2+3y^2$ 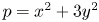with $x,y\in \mathbb {Z}$ and $x\equiv 1\ ({\rm {mod}}\ 3)$, then

\[ x\equiv\frac14\sum_{k=0}^{p-1}(3k+4)\frac{f_k}{2^k}\equiv\frac12\sum_{k=0}^{p-1}(3k+2)\frac{f_k}{({-}4)^k}\ ({\rm{mod}}\ p^2), \]
and if $p\equiv 1\pmod 3$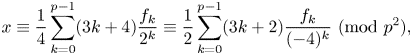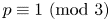, then
\[ \sum_{k=0}^{p-1}\frac{f_k}{2^k}\equiv\sum_{k=0}^{p-1}\frac{f_k}{({-}4)^k}\ ({\rm{mod}}\ p^3), \]
where $f_n=\sum _{k=0}^n\binom {n}k^3$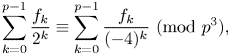 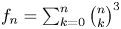stands for the $n$th Franel number.

Keywords

CongruencesFranel numbersp-adic gamma functiongamma function

MSC classification

Primary: 11A07: Congruences; primitive roots; residue systems
Secondary: 05A10: Factorials, binomial coefficients, combinatorial functions 05A19: Combinatorial identities, bijective combinatorics 33B15: Gamma, beta and polygamma functions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 3 , June 2024 , pp. 887 - 905
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Callan, D.. A combinatorial interpretation for an identity of Barrucand. J. Integer Seq. 11 (2008), 08.3.4. 3pp (electronic).Google Scholar
Franel, J.. On a question of Laisant. L'Interméd. Math. 1 (1894), 45–47.Google Scholar
Guo, V. J. W.. Proof of two conjectures of Sun on congruences for Franel numbers. Integr. Transforms Spec. Funct. 24 (2013), 532–539.CrossRefGoogle Scholar
Guo, V. J. W.. Proof of a superconjecture conjectured by Z.-H. Sun. Integr. Transforms Spec. Funct. 25 (2014), 1009–1015.CrossRefGoogle Scholar
Liu, J.-C.. Supercongruences involving $p$-adic gamma functions. Bull. Aust. Math. Soc. 98 (2018), 27–37.CrossRefGoogle Scholar
Liu, J.-C.. On two congruences involving Franel numbers. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Math. 114 (2020), 201.CrossRefGoogle Scholar
Long, L. and Ramakrishna, R.. Some supercongruences occurring in truncated hypergeometric series. Adv. Math. 290 (2016), 773–808.CrossRefGoogle Scholar
Mao, G.-S.. On two congruences involving Apéry and Franel numbers. Res. Math. 75 (2020), 159.CrossRefGoogle Scholar
Mao, G.-S.. Proof of some congruence conjectures of Z.-H. Sun involving Apéry-like numbers. Preprint arXiv:2111.08778.Google Scholar
Mao, G.-S. and Pan, H.. Congruences corresponding to hypergeometric identities I. $_2F_1$ transformations. J. Math. Anal. Appl. 505 (2022), 125527.CrossRefGoogle Scholar
Murty, M. R.. Introduction to $p$-adic analytic number theory. AMS/IP Studies in Advanced Mathematics, vol. 27 (Providence, RI, Somerville, MA: American Mathematical Society, International Press, 2002).Google Scholar
Robert, A. M.. A course in $p$-adic analysis. Graduate Texts in Mathematics, vol. 198 (New York: Springer-Verlag, 2000).CrossRefGoogle Scholar
Schneider, C.. Symbolic summation assists combinatorics. Sém. Lothar. Combin. 56 (2007), B56b.Google Scholar
Sloane, N. J. A.. Sequence A000172 in OEIS (On-Line Encyclopedia of Integer Sequences). http://oeis.org/A000172.Google Scholar
Sun, Z.-H.. Congruences concerning Bernoulli numbers and Bernoulli polynomials. Discrete Appl. Math. 105 (2000), 193–223.CrossRefGoogle Scholar
Sun, Z.-H.. Congruences involving Bernoulli and Euler numbers. J. Number Theory 128 (2008), 280–312.CrossRefGoogle Scholar
Sun, Z.-H.. Super congruences concerning Bernoulli polynomials. Int. J. Number Theory 11 (2015), 2393–2404.CrossRefGoogle Scholar
Sun, Z.-H.. Congruences for sums involving Franel numbers. Int. J. Number Theory 14 (2018), 123–142.CrossRefGoogle Scholar
Sun, Z.-W.. Connections between $p=x^2+3y^2$ and Franel numbers. J. Number Theory 133 (2013), 2914–2928.CrossRefGoogle Scholar
Sun, Z.-W.. Congruences for Franel numbers. Adv. Appl. Math. 51 (2013), 524–535.CrossRefGoogle Scholar
Sury, B., Wang, T.-M. and Zhao, F.-Z.. Identities involving reciprocals of binomial coefficients. J. Integer Seq. 7 (2004), 04.2.8.Google Scholar
Yeung, K. M.. On congruences for Binomial coefficients. J. Number Theory 33 (1989), 1–17.CrossRefGoogle Scholar
Zagier, D.. Integral solutions of Apéry-like recurrence equations. In Groups and symmetries: From Neolithic Scots to John McKay. CRM Proc. Lecture Notes, vol. 47, pp. 349–366 (Providence, RI: Amer. Math. Soc., 2009).Google Scholar