Let E and D be open subsets of $\mathbb {R}^{n+1}$ such that $\overline {D}$ is a compact subset of E, and let v be a supertemperature on E. A temperature u on D is called extendable by v if there is a supertemperature w on E such that $w=u$ on D and $w=v$ on $E\backslash \overline D$ . From earlier work of N. A. Watson, [‘Extendable temperatures’, Bull. Aust. Math. Soc.100 (2019), 297–303], either there is a unique temperature extendable by v, or there are infinitely many; a necessary condition for uniqueness is that the generalised solution of the Dirichlet problem on D corresponding to the restriction of v to $\partial _eD$ is equal to the greatest thermic minorant of v on D. In this paper we first give a condition for nonuniqueness and an example to show that this necessary condition is not sufficient. We then give a uniqueness theorem involving the thermal and cothermal fine topologies and deduce a corollary involving only parabolic and coparabolic tusks.

Let $E$ and $D$ be open subsets of $\mathbb{R}^{n+1}$ such that $\overline{D}$ is a compact subset of $E$, and let $v$ be a supertemperature on $E$. We call a temperature $u$ on $D$extendable by$v$ if there is a supertemperature $w$ on $E$ such that $w=u$ on $D$ and $w=v$ on $E\backslash \overline{D}$. Such a temperature need not be a thermic minorant of $v$ on $D$. We show that either there is a unique temperature extendable by $v$, or there are infinitely many. Examples of temperatures extendable by $v$ include the greatest thermic minorant $GM_{v}^{D}$ of $v$ on $D$, and the Perron–Wiener–Brelot solution of the Dirichlet problem $S\!_{v}^{D}$ on $D$ with boundary values the restriction of $v$ to $\unicode[STIX]{x2202}D$. In the case where these two examples are distinct, we give a formula for producing infinitely many more. Clearly $GM_{v}^{D}$ is the greatest extendable thermic minorant, but we also prove that there is a least one, which is not necessarily equal to $S\!_{v}^{D}$.

It is shown that the Dirichlet problem for the slab 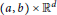$\left( a,\,b \right)\,\times \,{{\mathbb{R}}^{d}}$ with entire boundary data has an entire solution. The proof is based on a generalized Schwarz reflection principle. Moreover, it is shown that for a given entire harmonic function $g$, the inhomogeneous difference equation 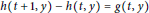$h\left( t\,+\,1,\,y \right)\,-\,h\left( t,\,y \right)\,=\,g\left( t,\,y \right)$ has an entire harmonic solution 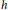$h$.

Let $u$ be a supertemperature on an open set $E$, and let $v$ be a related temperature on an open subset $D$ of $E$. For example, $v$ could be the greatest thermic minorant of $u$ on $D$, if it exists. Putting $w=u$ on $E\setminus D$ and $w=v$ on $D$, we investigate whether $w$, or its lower semicontinuous smoothing, is a supertemperature on $E$. We also give a representation of the greatest thermic minorant on $E$, if it exists, in terms of PWB solutions on an expanding sequence of open subsets of $E$ with union $E$.  In addition, in the case of a nonnegative supertemperature, we prove inequalities that relate reductions to Dirichlet solutions. We also prove that the value of any reduction at a given time depends only on earlier times.

We show that the null limit hypothesis, in the definition of a barrier, can be relaxed for normal boundary points that satisfy a mild additional condition. We also give a simple necessary and sufficient condition for the regularity of semi-singular boundary points.

This paper shows that some characterizations of minimally thin sets connected with a domain having smooth boundary and a half-space in particular also hold for the minimally thin sets at a corner point of a special domain with corners, i.e., the minimally thin set at $\infty$ of a cone.

We give an elementary potential-theoretic proof of a theorem of G. Johnsson: all solutions of Cauchy’s problems for the Laplace equations with an entire data on a sphere extend harmonically to the whole space RN except, perhaps, for the center of the sphere.

Given a domain D in R” and two specified points P0 and P1 in D we consider the problem of minimizing u(p1) over all functions harmonic in D with values between 0 and 1 normalised by the requirement u(P0) = 1/2. We show that when D is suitably regular the problem has a unique solution u* which necessarily takes on boundary values 0 or 1 almost everywhere on the boundary. In the process we prove that it is possible to separate P0 and P1by a harmonic function whose boundary value is supported in an arbitrary set of positive measure. These results depend on the fact that (under suitable regularity conditions) a harmonic function which vanishes on an open subset of the boundary has a normal derivative which is almost everywhere non-vanishing in that set.