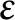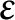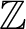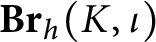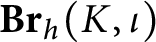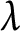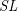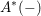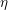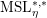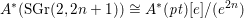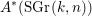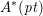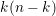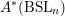Although there is no natural internal product for hermitian forms over an algebra with involution of the first kind, we describe how to multiply two
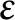 $\varepsilon $
-hermitian forms to obtain a quadratic form over the base field. This allows to define a commutative graded ring structure by taking together bilinear forms and
$\varepsilon $
-hermitian forms to obtain a quadratic form over the base field. This allows to define a commutative graded ring structure by taking together bilinear forms and
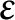 $\varepsilon $
-hermitian forms, which we call the mixed Witt ring of an algebra with involution. We also describe a less powerful version of this construction for unitary involutions, which still defines a ring, but with a grading over
$\varepsilon $
-hermitian forms, which we call the mixed Witt ring of an algebra with involution. We also describe a less powerful version of this construction for unitary involutions, which still defines a ring, but with a grading over
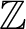 $\mathbb {Z}$
instead of the Klein group.
$\mathbb {Z}$
instead of the Klein group.
We first describe a general framework for defining graded rings out of monoidal functors from monoidal categories with strong symmetry properties to categories of modules. We then give a description of such a strongly symmetric category
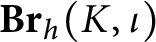 $\mathbf {Br}_h(K,\iota )$
which encodes the usual hermitian Morita theory of algebras with involutions over a field K.
$\mathbf {Br}_h(K,\iota )$
which encodes the usual hermitian Morita theory of algebras with involutions over a field K.
We can therefore apply the general framework to
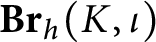 $\mathbf {Br}_h(K,\iota )$
and the Witt group functors to define our mixed Witt rings, and derive their basic properties, including explicit formulas for products of diagonal forms in terms of involution trace forms, explicit computations for the case of quaternion algebras, and reciprocity formulas relative to scalar extensions.
$\mathbf {Br}_h(K,\iota )$
and the Witt group functors to define our mixed Witt rings, and derive their basic properties, including explicit formulas for products of diagonal forms in terms of involution trace forms, explicit computations for the case of quaternion algebras, and reciprocity formulas relative to scalar extensions.
We intend to describe in future articles further properties of those rings, such as a
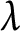 $\lambda $
-ring structure, and relations with the Milnor conjecture and the theory of signatures of hermitian forms.
$\lambda $
-ring structure, and relations with the Milnor conjecture and the theory of signatures of hermitian forms.