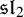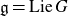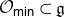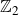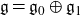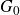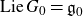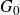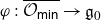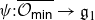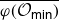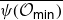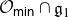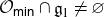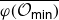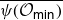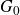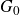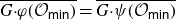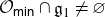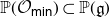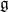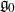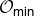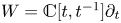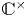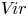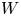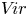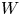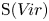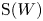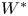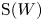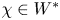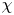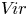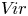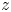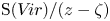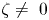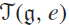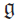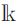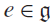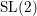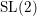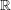We develop techniques to construct isomorphisms between simple affine W-algebras and affine vertex algebras at admissible levels. We then apply these techniques to obtain many new, and conjecturally all, admissible collapsing levels for affine W-algebras. In short, if a simple affine W-algebra at a given level is equal to its affine vertex subalgebra generated by the centraliser of an 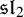${\mathfrak {sl}}_2$-triple associated with the underlying nilpotent orbit, then that level is said to be collapsing. Collapsing levels are important both in representation theory and in theoretical physics. Our approach relies on two fundamental invariants of vertex algebras. The first one is the associated variety, which, in the context of admissible level simple affine W-algebras, leads to the Poisson varieties known as nilpotent Slodowy slices. We exploit the singularities of these varieties to detect possible collapsing levels. The second invariant is the asymptotic datum. We prove a general result asserting that, under appropriate hypotheses, equality of asymptotic data implies isomorphism at the level of vertex algebras. Then we use this to give a sufficient criterion, of combinatorial nature, for an admissible level to be collapsing. Our methods also allow us to study isomorphisms between quotients of W-algebras and extensions of simple affine vertex algebras at admissible levels. Based on such examples, we are led to formulate a general conjecture: for any finite extension of vertex algebras, the induced morphism between associated Poisson varieties is dominant.

Let G be a simple algebraic group with ${\mathfrak g}={\textrm{Lie }} G$ and ${\mathcal O}_{\textsf{min}}\subset{\mathfrak g}$ the minimal nilpotent orbit. For a ${\mathbb Z}_2$-grading ${\mathfrak g}={\mathfrak g}_0\oplus{\mathfrak g}_1$, let $G_0$ be a connected subgroup of G with ${\textrm{Lie }} G_0={\mathfrak g}_0$. We study the $G_0$-equivariant projections $\varphi\,:\,\overline{{\mathcal O}_{\textsf{min}}}\to {\mathfrak g}_0$ and $\psi:\overline{{\mathcal O}_{\textsf{min}}}\to{\mathfrak g}_1$. It is shown that the properties of $\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and $\overline{\psi({\mathcal O}_{\textsf{min}})}$ essentially depend on whether the intersection ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1$ is empty or not. If ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then both $\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and $\overline{\psi({\mathcal O}_{\textsf{min}})}$ contain a 1-parameter family of closed $G_0$-orbits, while if ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1=\varnothing$, then both are $G_0$-prehomogeneous. We prove that $\overline{G{\cdot}\varphi({\mathcal O}_{\textsf{min}})}=\overline{G{\cdot}\psi({\mathcal O}_{\textsf{min}})}$. Moreover, if ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then this common variety is the affine cone over the secant variety of ${\mathbb P}({\mathcal O}_{\textsf{min}})\subset{\mathbb P}({\mathfrak g})$. As a digression, we obtain some invariant-theoretic results on the affine cone over the secant variety of the minimal orbit in an arbitrary simple G-module. In conclusion, we discuss more general projections that are related to either arbitrary reductive subalgebras of ${\mathfrak g}$ in place of ${\mathfrak g}_0$ or spherical nilpotent G-orbits in place of ${\mathcal O}_{\textsf{min}}$.

Let $W = \mathbb {C}[t,t^{-1}]\partial _t$ be the Witt algebra of algebraic vector fields on $\mathbb {C}^\times$ and let $V\!ir$ be the Virasoro algebra, the unique nontrivial central extension of $W$. In this paper, we study the Poisson ideal structure of the symmetric algebras of $V\!ir$ and $W$, as well as several related Lie algebras. We classify prime Poisson ideals and Poisson primitive ideals of $\operatorname {S}(V\!ir)$ and $\operatorname {S}(W)$. In particular, we show that the only functions in $W^*$ which vanish on a nontrivial Poisson ideal (that is, the only maximal ideals of $\operatorname {S}(W)$ with a nontrivial Poisson core) are given by linear combinations of derivatives at a finite set of points; we call such functions local. Given a local function $\chi \in W^*$, we construct the associated Poisson primitive ideal through computing the algebraic symplectic leaf of $\chi$, which gives a notion of coadjoint orbit in our setting. As an application, we prove a structure theorem for subalgebras of $V\!ir$ of finite codimension and show, in particular, that any such subalgebra of $V\!ir$ contains the central element $z$, substantially generalising a result of Ondrus and Wiesner on subalgebras of codimension one. As a consequence, we deduce that $\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple if and only if $\zeta \neq ~0$.

In this paper, we study the center Z of the finite W-algebra $${\mathcal{T}}({\mathfrak{g}},e)$$ associated with a semi-simple Lie algebra $$\mathfrak{g}$$ over an algebraically closed field $$\mathbb{k}$$ of characteristic p≫0, and an arbitrarily given nilpotent element $$e \in{\mathfrak{g}} $$ We obtain an analogue of Veldkamp’s theorem on the center. For the maximal spectrum Specm(Z), we show that its Azumaya locus coincides with its smooth locus of smooth points. The former locus reflects irreducible representations of maximal dimension for $${\mathcal{T}}({\mathfrak{g}},e)$$ .

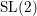We classify the horizontal $\text{SL}(2)$s and $\mathbb{R}$-split polarized mixed Hodge structures on a Mumford–Tate domain.

We continue the study of the closures of GL(V)-orbits in the enhanced nilpotent cone V × N begun by the first two authors. We prove that each closure is an invariant-theoretic quotient of a suitably defined enhanced quiver variety. We conjecture, and prove in special cases, that these enhanced quiver varieties are normal complete intersections, implying that the enhanced nilpotent orbit closures are also normal.