1 Introduction
Vertex algebras have emerged as fundamental objects mediating interactions between representation theory and two-dimensional conformal field theory, three-dimensional topology and, more recently, four-dimensional physics in the guise of the 4D/2D duality. This article concerns two important classes of vertex algebras: the affine Kac-Moody vertex algebras and the affine W-algebras. Examples of W-algebras were first uncovered as vertex algebra extensions of the Virasoro algebra [Reference Fateev and Zamolodchikov41], and these algebras were later perceived to be natural quantisations of Poisson structures of certain completely integrable models (the Gelfand-Dickii brackets in the KP hierarchy, for instance; see the review [Reference Bouwknegt and Schoutens28] and references therein), as well as natural chiralisations of quantised transverse slices. By W-algebra in general we shall mean the quantised Hamiltonian (Drinfeld-Sokolov) reduction of an affine Kac-Moody vertex algebra [Reference Feigin and Frenkel42, Reference Kac, Roan and Wakimoto57], or a quotient thereof.
1.1 Affine vertex algebras, W-algebras and collapsing levels
Let G be a complex connected, simple algebraic group of adjoint type with Lie algebra
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() $k \in \mathbb {C}$
be a complex number, referred to as the level. The universal affine Kac-Moody vertex algebra
$k \in \mathbb {C}$
be a complex number, referred to as the level. The universal affine Kac-Moody vertex algebra
![]() $V^k(\mathfrak {g})$
is constructed from these data, and its simple quotient is denoted
$V^k(\mathfrak {g})$
is constructed from these data, and its simple quotient is denoted
![]() $L_k(\mathfrak {g})$
; see Section 3. The Hamiltonian reduction
$L_k(\mathfrak {g})$
; see Section 3. The Hamiltonian reduction
![]() $H^0_{DS, f}(-)$
takes an additional choice of nilpotent element
$H^0_{DS, f}(-)$
takes an additional choice of nilpotent element
![]() $f \in \mathfrak {g}$
as input, the vertex algebra
$f \in \mathfrak {g}$
as input, the vertex algebra
![]() $\mathscr {W}^k(\mathfrak {g}, f) = H^0_{DS, f}(V^k(\mathfrak {g}))$
depending on f only through its adjoint orbit
$\mathscr {W}^k(\mathfrak {g}, f) = H^0_{DS, f}(V^k(\mathfrak {g}))$
depending on f only through its adjoint orbit
![]() ${\mathbb {O}} = G \cdot f$
. We denote by
${\mathbb {O}} = G \cdot f$
. We denote by
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
the simple quotient of the universal W-algebra
$\mathscr {W}_k(\mathfrak {g}, f)$
the simple quotient of the universal W-algebra
![]() $\mathscr {W}^k(\mathfrak {g}, f)$
. See Section 4 for more details about W-algebras.
$\mathscr {W}^k(\mathfrak {g}, f)$
. See Section 4 for more details about W-algebras.
The theory of vertex algebras is connected to Poisson geometry through the associated variety construction [Reference Arakawa10, Reference Arakawa and Moreau20, Reference Arakawa and Moreau21]. In particular, the associated varieties of the vertex algebras
![]() $L_k(\mathfrak {g})$
and
$L_k(\mathfrak {g})$
and
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
include extensively studied families of Poisson varieties such as nilpotent orbit closures and nilpotent Slodowy slices. The theory of vertex algebras, and in particular the structure of the vertex algebras
$\mathscr {W}_k(\mathfrak {g}, f)$
include extensively studied families of Poisson varieties such as nilpotent orbit closures and nilpotent Slodowy slices. The theory of vertex algebras, and in particular the structure of the vertex algebras
![]() $L_k(\mathfrak {g})$
and
$L_k(\mathfrak {g})$
and
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
at special levels k called admissible levels (see Definition 3.1), is connected as well to the theory of modular functions [Reference Arakawa and van Ekeren13, Reference Arakawa and van Ekeren14, Reference Kac and Wakimoto58, Reference Zhu83]. Both of these themes will be put to use in our investigation of the structure of W-algebras in this work.
$\mathscr {W}_k(\mathfrak {g}, f)$
at special levels k called admissible levels (see Definition 3.1), is connected as well to the theory of modular functions [Reference Arakawa and van Ekeren13, Reference Arakawa and van Ekeren14, Reference Kac and Wakimoto58, Reference Zhu83]. Both of these themes will be put to use in our investigation of the structure of W-algebras in this work.
The universal W-algebras are easy to describe as graded vector spaces. Via spectral sequence arguments, the algebra
![]() $\mathscr {W}^k(\mathfrak {g}, f)$
is seen to have a PBW basis corresponding to a set of strong generators indexed by a basis of the centraliser
$\mathscr {W}^k(\mathfrak {g}, f)$
is seen to have a PBW basis corresponding to a set of strong generators indexed by a basis of the centraliser
![]() $\mathfrak {g}^f$
[Reference de Boer and Tjin27, Reference Frenkel and Ben-Zvi44, Reference Kac and Wakimoto60]. The relations between these generators are, however, extremely complicated and in general are not known explicitly. This hampers direct analysis of the simple quotient
$\mathfrak {g}^f$
[Reference de Boer and Tjin27, Reference Frenkel and Ben-Zvi44, Reference Kac and Wakimoto60]. The relations between these generators are, however, extremely complicated and in general are not known explicitly. This hampers direct analysis of the simple quotient
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
via generators and relations. Though, importantly, it is known that
$\mathscr {W}_k(\mathfrak {g}, f)$
via generators and relations. Though, importantly, it is known that
![]() $\mathscr {W}^k(\mathfrak {g}, f)$
contains an embedded copy of the affine vertex algebra
$\mathscr {W}^k(\mathfrak {g}, f)$
contains an embedded copy of the affine vertex algebra
![]() $V^{k^\natural }(\mathfrak {g}^\natural )$
, where
$V^{k^\natural }(\mathfrak {g}^\natural )$
, where
![]() $\mathfrak {g}^\natural \subset \mathfrak {g}$
denotes the centraliser subalgebra of an
$\mathfrak {g}^\natural \subset \mathfrak {g}$
denotes the centraliser subalgebra of an
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(e, h, f)$
containing f, and
$(e, h, f)$
containing f, and
![]() $k^\natural $
is some level determined by the other data. It follows that the simple quotient
$k^\natural $
is some level determined by the other data. It follows that the simple quotient
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
contains an embedded homomorphic image of the affine vertex algebra, and the level k is then said to be a collapsing level (see Definition 5.3) if the embedded subalgebra coincides with
$\mathscr {W}_k(\mathfrak {g}, f)$
contains an embedded homomorphic image of the affine vertex algebra, and the level k is then said to be a collapsing level (see Definition 5.3) if the embedded subalgebra coincides with
![]() $\mathscr {W}_k(\mathfrak {g}, f)$
itself, that is to say if we have an isomorphism of vertex algebras:
$\mathscr {W}_k(\mathfrak {g}, f)$
itself, that is to say if we have an isomorphism of vertex algebras:
In [Reference Adamović, Kac, Frajria, Papi and Perše4], it was shown that collapsing levels have remarkable applications to the representation theory of affine vertex algebras. They are also useful in elucidating the structure of modular tensor categories of representations of simple W-algebras at admissible, not necessarily collapsing, levels [Reference Arakawa and van Ekeren14]. Furthermore, it has recently been observed [Reference Xie and Yan81] that many collapsing levels for quasi-lisse W-algebras should come from nontrivial isomorphisms of 4D
![]() $N=2$
SUSY field theories, via the 4D/2D duality [Reference Beem, Lemos, Liendo, Peelaers, Rastelli and van Rees25].
$N=2$
SUSY field theories, via the 4D/2D duality [Reference Beem, Lemos, Liendo, Peelaers, Rastelli and van Rees25].
There is a full classification of collapsing levels for the case that f is a minimal nilpotent element
![]() $f_{\text {min}}$
, including the case in which
$f_{\text {min}}$
, including the case in which
![]() $\mathfrak {g}$
is a simple Lie superalgebra ([Reference Adamović, Kac, Frajria, Papi and Perše2, Reference Adamović, Kac, Frajria, Papi and Perše3]). For more general nilpotent elements f, since the commutation relations in
$\mathfrak {g}$
is a simple Lie superalgebra ([Reference Adamović, Kac, Frajria, Papi and Perše2, Reference Adamović, Kac, Frajria, Papi and Perše3]). For more general nilpotent elements f, since the commutation relations in
![]() $\mathscr {W}^k(\mathfrak {g},f)$
are unknown, almost nothing is known about collapsing levels, and to discover them we must appeal to more indirect methods. In this work, we exploit two important invariants of vertex algebras: associated varieties and asymptotic data. The general strategy we use to detect (admissible) collapsing levels is given in Section 6.
$\mathscr {W}^k(\mathfrak {g},f)$
are unknown, almost nothing is known about collapsing levels, and to discover them we must appeal to more indirect methods. In this work, we exploit two important invariants of vertex algebras: associated varieties and asymptotic data. The general strategy we use to detect (admissible) collapsing levels is given in Section 6.
1.2 Associated variety, asymptotic data and main results
To a vertex algebra V one attaches, in a functorial manner, a certain affine Poisson variety
![]() $X_V$
referred to as the associated variety [Reference Arakawa7]. The associated variety of
$X_V$
referred to as the associated variety [Reference Arakawa7]. The associated variety of
![]() $V^k(\mathfrak {g})$
is
$V^k(\mathfrak {g})$
is
![]() $\mathfrak {g}^*$
and the associated varieties of simple affine vertex algebras at admissible levels are nilpotent orbit closures with the induced Kirillov-Kostant-Souriau Poisson structures [Reference Arakawa10]. At the level of associated varieties, the Drinfeld-Sokolov reduction
$\mathfrak {g}^*$
and the associated varieties of simple affine vertex algebras at admissible levels are nilpotent orbit closures with the induced Kirillov-Kostant-Souriau Poisson structures [Reference Arakawa10]. At the level of associated varieties, the Drinfeld-Sokolov reduction
![]() $H^0_{DS, f}(-)$
corresponds to intersection with the Slodowy slice
$H^0_{DS, f}(-)$
corresponds to intersection with the Slodowy slice
![]() $\mathcal {S}_f\cong f+\mathfrak {g}^{e}$
[Reference De Sole and Kac34] [Reference Arakawa10]. In general, the intersection
$\mathcal {S}_f\cong f+\mathfrak {g}^{e}$
[Reference De Sole and Kac34] [Reference Arakawa10]. In general, the intersection
of a nilpotent orbit closure
![]() $\overline {{\mathbb {O}}}$
with a Slodowy slice
$\overline {{\mathbb {O}}}$
with a Slodowy slice
![]() $\mathcal {S}_f$
is referred to as a nilpotent Slodowy slice. Normalisations of nilpotent Slodowy slices are symplectic singularities in the sense of Beauville [Reference Beauville24], and, like nilpotent orbit closures, these varieties are studied for their role in representation theory and in the theory of symplectic singularities.
$\mathcal {S}_f$
is referred to as a nilpotent Slodowy slice. Normalisations of nilpotent Slodowy slices are symplectic singularities in the sense of Beauville [Reference Beauville24], and, like nilpotent orbit closures, these varieties are studied for their role in representation theory and in the theory of symplectic singularities.
The nilpotent Slodowy slices are best understood in the case of minimal degeneration in which
![]() $G \cdot f$
is an open subvariety of the boundaryFootnote
1
of
$G \cdot f$
is an open subvariety of the boundaryFootnote
1
of
![]() ${\mathbb {O}}$
in
${\mathbb {O}}$
in
![]() $\overline {{\mathbb {O}}}$
. In the context of this class of examples, one has the celebrated result of Brieskorn and Slodowy ([Reference Brieskorn29, Reference Slodowy77]) confirming a conjecture of Grothendieck, that the nilpotent Slodowy slice associated with the principal nilpotent orbit
$\overline {{\mathbb {O}}}$
. In the context of this class of examples, one has the celebrated result of Brieskorn and Slodowy ([Reference Brieskorn29, Reference Slodowy77]) confirming a conjecture of Grothendieck, that the nilpotent Slodowy slice associated with the principal nilpotent orbit
![]() ${\mathbb {O}} = {\mathbb {O}}_{\text {prin}}$
and a subregular nilpotent element
${\mathbb {O}} = {\mathbb {O}}_{\text {prin}}$
and a subregular nilpotent element
![]() $f_{\text {subreg}}$
has a simple singularity of the same type as G, for G of type
$f_{\text {subreg}}$
has a simple singularity of the same type as G, for G of type
![]() $A, D, E$
.
$A, D, E$
.
The second invariant of vertex algebras which we make use of, the asymptotic datum (see Definition 2.1), originates in the phenomenon of modular invariance of characters. Consider the character, that is, normalised graded dimension
of an affine vertex algebra or W-algebra V of central charge c. Under favourable circumstances, the character converges to a function of
![]() $\tau $
a variable in the complex upper half plane (having set
$\tau $
a variable in the complex upper half plane (having set
![]() $q = e^{2\pi i \tau }$
). Explicit formulas for these characters, ultimately coming from the Weyl-Kac character formula, yield modular transformation rules, [Reference Kac54, Reference Kac and Wakimoto58], and asymptotic behaviour of
$q = e^{2\pi i \tau }$
). Explicit formulas for these characters, ultimately coming from the Weyl-Kac character formula, yield modular transformation rules, [Reference Kac54, Reference Kac and Wakimoto58], and asymptotic behaviour of
![]() $\chi (\tau )$
of the form
$\chi (\tau )$
of the form
Here
![]() $\tau \downarrow 0$
means
$\tau \downarrow 0$
means
![]() $\tau $
tends to
$\tau $
tends to
![]() $0$
along the positive imaginary axis. The invariants
$0$
along the positive imaginary axis. The invariants
![]() $\mathbf {A}_V$
and
$\mathbf {A}_V$
and
![]() $\mathbf {g}_V$
are called the asymptotic dimension and asymptotic growth of V. Explicit formulas have been given for principal admissible level k by Kac and Wakimoto [Reference Kac and Wakimoto61], and for coprincipal admissible levels in the present work. See Sections 3 and 4 and in particular Propositions 3.8 and 4.10.
$\mathbf {g}_V$
are called the asymptotic dimension and asymptotic growth of V. Explicit formulas have been given for principal admissible level k by Kac and Wakimoto [Reference Kac and Wakimoto61], and for coprincipal admissible levels in the present work. See Sections 3 and 4 and in particular Propositions 3.8 and 4.10.
Plainly the isomorphism (1) entailed by a collapsing level induces an equality of asymptotic data. We now come to our first main theorem, which is a sort of converse (see also Theorem 3.10 and Proposition 6.6).
Theorem 1.1. Assume that k and
![]() $k^\natural $
are admissible levels for
$k^\natural $
are admissible levels for
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {g}^\natural $
, respectively, that
$\mathfrak {g}^\natural $
, respectively, that
![]() $f \in X_{L_k(\mathfrak {g})}$
and that
$f \in X_{L_k(\mathfrak {g})}$
and that
![]() $\chi _{H_{DS,f}^0(L_k(\mathfrak {g}))}(\tau ) \sim \chi _{L_{k^\natural }(\mathfrak {g}^\natural )}(\tau ),$
as
$\chi _{H_{DS,f}^0(L_k(\mathfrak {g}))}(\tau ) \sim \chi _{L_{k^\natural }(\mathfrak {g}^\natural )}(\tau ),$
as
![]() $\tau \downarrow 0$
. Then k is a collapsing level – that is,
$\tau \downarrow 0$
. Then k is a collapsing level – that is,
![]() $\mathscr {W}_k(\mathfrak {g},f) \cong L_{k^\natural }(\mathfrak {g}^\natural )$
.
$\mathscr {W}_k(\mathfrak {g},f) \cong L_{k^\natural }(\mathfrak {g}^\natural )$
.
Using this theorem, we establish many new infinite families of collapsing levels for
![]() $\mathfrak {g}$
of classical type and approximately one hundred collapsing levels for
$\mathfrak {g}$
of classical type and approximately one hundred collapsing levels for
![]() $\mathfrak {g}$
of exceptional type. To give a flavour of our results, we quote the following which is part of Theorem 8.8 and is representative of the results in classical types. See also Theorems 8.7, 9.7, 9.10, 9.14 and 9.16.
$\mathfrak {g}$
of exceptional type. To give a flavour of our results, we quote the following which is part of Theorem 8.8 and is representative of the results in classical types. See also Theorems 8.7, 9.7, 9.10, 9.14 and 9.16.
Theorem 1.2. Let
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
with
$\mathfrak {g}={\mathfrak {sl}}_n$
with
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $k = -n+p/q$
where
$k = -n+p/q$
where
![]() $q \geq 1$
and
$q \geq 1$
and
![]() $p \geq n$
is coprime to q (that is, n is admissible for
$p \geq n$
is coprime to q (that is, n is admissible for
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
). Pick a nilpotent element
$\mathfrak {g}={\mathfrak {sl}}_n$
). Pick a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(q^m,1^s)$
of n, with
$(q^m,1^s)$
of n, with
![]() $m\ge 0$
and
$m\ge 0$
and
![]() $s>0$
. Then k is collapsing if and only if
$s>0$
. Then k is collapsing if and only if
![]() $p=n=h^{\vee }_{{\mathfrak {sl}}_n}$
. Moreover,
$p=n=h^{\vee }_{{\mathfrak {sl}}_n}$
. Moreover,
Similarly, we exhibit here, as an illustration, one of the isomorphisms which we uncover in exceptional types with the help of Theorem 1.1:
The remaining cases in the exceptional types are covered in Theorems 10.1, 10.6, 10.11, 10.18 and 10.16. We conjecture (see Conjectures 9.20 and 10.22) that our list of admissible collapsing levels is exhaustive. We also obtain a number of cases where the simple W-algebra
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is merely a finite extension of its simple affine vertex algebra (see all the above cited theorems).
$\mathscr {W}_k(\mathfrak {g},f)$
is merely a finite extension of its simple affine vertex algebra (see all the above cited theorems).
1.3 Nilpotent Slodowy slices
The nature of the formulas for asymptotic data is such that it is not feasible to find collapsing levels by a naive search for coincidences between respective asymptotic data. For this reason, we turn to the more refined invariant given by the associated variety. Although the problem of determining the associated variety of
![]() $L_k(\mathfrak {g})$
is wide open in general, many of the Poisson varieties arising as associated varieties of simple W-algebras are nilpotent Slodowy slices. More precisely, whenever k is an admissible level for
$L_k(\mathfrak {g})$
is wide open in general, many of the Poisson varieties arising as associated varieties of simple W-algebras are nilpotent Slodowy slices. More precisely, whenever k is an admissible level for
![]() $\mathfrak {g}$
, the associated variety
$\mathfrak {g}$
, the associated variety
![]() $X_{H^0_{DS, f}(L_k(\mathfrak {g}))}$
is the nilpotent Slodowy slice (2) above, with
$X_{H^0_{DS, f}(L_k(\mathfrak {g}))}$
is the nilpotent Slodowy slice (2) above, with
![]() ${\mathbb {O}} = {\mathbb {O}}_k \subset \mathfrak {g}$
a certain nilpotent orbit determined by k [Reference Arakawa10] [Reference Arakawa, van Ekeren and Moreau15]. It is conjectured in general (and confirmed in many cases) that
${\mathbb {O}} = {\mathbb {O}}_k \subset \mathfrak {g}$
a certain nilpotent orbit determined by k [Reference Arakawa10] [Reference Arakawa, van Ekeren and Moreau15]. It is conjectured in general (and confirmed in many cases) that
![]() $H^0_{DS, f}(L_k(\mathfrak {g}))$
is simple, so that
$H^0_{DS, f}(L_k(\mathfrak {g}))$
is simple, so that
![]() $\mathscr {W}_k(\mathfrak {g}, f) = H^0_{DS, f}(L_k(\mathfrak {g}))$
in fact (see Conjecture 4.4). A collapsing level thus induces [Reference Arakawa10], in these cases, an isomorphism
$\mathscr {W}_k(\mathfrak {g}, f) = H^0_{DS, f}(L_k(\mathfrak {g}))$
in fact (see Conjecture 4.4). A collapsing level thus induces [Reference Arakawa10], in these cases, an isomorphism
In particular, the singularity of the nilpotent Slodowy slice in
![]() $\mathfrak {g}$
on the left-hand side should be of the same type as that of the nilpotent orbit closure in
$\mathfrak {g}$
on the left-hand side should be of the same type as that of the nilpotent orbit closure in
![]() $\mathfrak {g}^\natural $
on the right-hand side. We may therefore apply known results on the geometry of nilpotent Slodowy slices to find candidates for collapsing levels.
$\mathfrak {g}^\natural $
on the right-hand side. We may therefore apply known results on the geometry of nilpotent Slodowy slices to find candidates for collapsing levels.
Kraft and Procesi studied nilpotent Slodowy slices for minimal degenerations in the classical types [Reference Kraft and Procesi65, Reference Kraft and Procesi66], motivated by the normality problem for nilpotent orbit closures. They introduced the row/column removal process, reviewed in Section 6 below, and which we now briefly describe. Nilpotent orbits in simple Lie algebras of classical type are parametrised by certain classes of integer partitions and, roughly speaking, the row/column removal rule is a set of combinatorial operations on a pair of partitions ![]() under which the nilpotent Slodowy slice
under which the nilpotent Slodowy slice ![]() remains unchanged up to isomorphism. Using the row/column removal rule, it is possible to identify classes of nilpotent orbits for which an isomorphism of the type (3) holds. Recently, Fu, Juteau, Levy and Sommers [Reference Fu, Juteau, Levy and Sommers47] have complemented the work of Kraft and Procesi by determining the generic singularities of nilpotent orbit closures
remains unchanged up to isomorphism. Using the row/column removal rule, it is possible to identify classes of nilpotent orbits for which an isomorphism of the type (3) holds. Recently, Fu, Juteau, Levy and Sommers [Reference Fu, Juteau, Levy and Sommers47] have complemented the work of Kraft and Procesi by determining the generic singularities of nilpotent orbit closures
![]() $\overline {{\mathbb {O}}}$
in exceptional types, which they did through a study of the nilpotent Slodowy slices
$\overline {{\mathbb {O}}}$
in exceptional types, which they did through a study of the nilpotent Slodowy slices
![]() $\mathcal {S}_{{\mathbb {O}},f}$
at minimal degenerations
$\mathcal {S}_{{\mathbb {O}},f}$
at minimal degenerations
![]() $G \cdot f$
. We make use of these results also in the sequel.
$G \cdot f$
. We make use of these results also in the sequel.
Upgrading the isomorphisms of nilpotent Slodowy slices to collapsing levels is then a matter of computing the level
![]() $k^\natural $
in terms of k and comparing asymptotic data. This is straightforward in principle, but in practice it is extremely complicated, and exact (as opposed to numerical) computations require extensive use of classical cyclotomic product identities such as those presented in Section 7.
$k^\natural $
in terms of k and comparing asymptotic data. This is straightforward in principle, but in practice it is extremely complicated, and exact (as opposed to numerical) computations require extensive use of classical cyclotomic product identities such as those presented in Section 7.
We observe that many of our examples of collapsing levels are of the form
 $$ \begin{align*}-h_{\mathfrak{g}}^\vee+\frac{h_{\mathfrak{g}}^\vee}{q},\end{align*} $$
$$ \begin{align*}-h_{\mathfrak{g}}^\vee+\frac{h_{\mathfrak{g}}^\vee}{q},\end{align*} $$
with
![]() $(h_{\mathfrak {g}}^\vee ,q)=(r^{\vee },q)=1$
, or of the form
$(h_{\mathfrak {g}}^\vee ,q)=(r^{\vee },q)=1$
, or of the form
with
![]() $(h_{\mathfrak {g}}+1 ,q)=1$
,
$(h_{\mathfrak {g}}+1 ,q)=1$
,
![]() $(r^{\vee },q)=r^\vee $
, where
$(r^{\vee },q)=r^\vee $
, where
![]() $h_{\mathfrak {g}}$
is the Coxeter number,
$h_{\mathfrak {g}}$
is the Coxeter number,
![]() $h_{\mathfrak {g}}^\vee $
is the dual Coxeter number, and
$h_{\mathfrak {g}}^\vee $
is the dual Coxeter number, and
![]() $r^{\vee }$
is the lacing number of
$r^{\vee }$
is the lacing number of
![]() $\mathfrak {g}$
, respectively. A level of the first form is called a boundary principal admissible level [Reference Kac, Roan and Wakimoto57] (see also [Reference Kac and Wakimoto62]). The vertex algebras
$\mathfrak {g}$
, respectively. A level of the first form is called a boundary principal admissible level [Reference Kac, Roan and Wakimoto57] (see also [Reference Kac and Wakimoto62]). The vertex algebras
![]() $L_{k}(\mathfrak {g})$
and
$L_{k}(\mathfrak {g})$
and
![]() $\mathscr {W}_{k}(\mathfrak {g},f)$
at boundary principal admissible level k appear as vertex algebras associated with Argyres-Douglas theories via the 4D/2D duality ([Reference Song, Xie and Yan76, Reference Wang and Xie80, Reference Xie, Yan and Yau82]). Collapsing levels which are boundary principal admissible have been studied by Xie and Yan [Reference Xie and Yan81] in this connection, and our results confirm their conjectures [Reference Xie and Yan81, Section 3.4].
$\mathscr {W}_{k}(\mathfrak {g},f)$
at boundary principal admissible level k appear as vertex algebras associated with Argyres-Douglas theories via the 4D/2D duality ([Reference Song, Xie and Yan76, Reference Wang and Xie80, Reference Xie, Yan and Yau82]). Collapsing levels which are boundary principal admissible have been studied by Xie and Yan [Reference Xie and Yan81] in this connection, and our results confirm their conjectures [Reference Xie and Yan81, Section 3.4].
1.4 Related problems
Aside from determination of collapsing levels, the methods we develop in this article can be used to prove other results of a similar flavour, some of which are remarked upon in the body of the text. For instance (see Remark 9.9 for details), if
![]() $\mathfrak {g} = \mathfrak {sp}_n$
and
$\mathfrak {g} = \mathfrak {sp}_n$
and
![]() $k = -h_{\mathfrak {g}}^\vee + p/q$
where q is twice an odd integer and
$k = -h_{\mathfrak {g}}^\vee + p/q$
where q is twice an odd integer and
![]() $p=h+1$
, then for
$p=h+1$
, then for ![]() where
where ![]() ,
,
In addition to such results, we pose a number of conjectures, mostly related to presentation of W-algebras as finite extensions of simple affine vertex algebras. By finite extension we mean here, for definiteness, a vertex algebra W which decomposes as a finite direct sum of irreducible modules over its conformal vertex subalgebra V. In particular, we make the following:
Conjecture 1.3. If W is a finite extension of the vertex algebra V, then the corresponding morphism of Poisson algebraic varieties
![]() $\pi \colon X_W \to X_V$
is a dominant morphism.
$\pi \colon X_W \to X_V$
is a dominant morphism.
The validity of Conjecture 1.3 would imply the widely believed fact that if a finite extension of a vertex algebra is lisse, then so is the vertex algebra. We plan to return to these matters in future work.
Plan of the article
The rest of the article is organised as follows. In Section 2, we collect results on asymptotic data for vertex algebras and their modules. We exhibit a large class of vertex algebras admitting an asymptotic datum (see Proposition 2.6). Section 3 is about affine vertex algebras. The main result of the section describes the asymptotic data of simple affine vertex algebras at admissible levels and of their simple ordinary representations (see Corollary 3.9). Section 4 gathers together several properties of W-algebras. One of the main results of this section is Proposition 4.10, which gives the asymptotic datum of the Drinfeld-Sokolov reduction ![]() for all simple ordinary
for all simple ordinary
![]() $L_k(\mathfrak {g})$
-module
$L_k(\mathfrak {g})$
-module ![]() for admissible k. The notion of collapsing level is introduced in Section 5. In Section 6, we then explain in detail our strategy to find collapsing admissible levels. The identities obtained in Section 7 are useful to compute the asymptotic data in the sections which follow. Our results for the classical types are presented in Sections 8 and 9. See Theorems 8.7 and 8.8 for
for admissible k. The notion of collapsing level is introduced in Section 5. In Section 6, we then explain in detail our strategy to find collapsing admissible levels. The identities obtained in Section 7 are useful to compute the asymptotic data in the sections which follow. Our results for the classical types are presented in Sections 8 and 9. See Theorems 8.7 and 8.8 for
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
, Theorems 9.7 and 9.10 for
$\mathfrak {g}={\mathfrak {sl}}_n$
, Theorems 9.7 and 9.10 for
![]() $\mathfrak {g}=\mathfrak {sp}_n$
, and Theorems 9.14 and 9.16 for
$\mathfrak {g}=\mathfrak {sp}_n$
, and Theorems 9.14 and 9.16 for
![]() $\mathfrak {g}={\mathfrak {so}}_n$
. Our results for the exceptional types are presented in Section 10. See Theorem 10.1 for
$\mathfrak {g}={\mathfrak {so}}_n$
. Our results for the exceptional types are presented in Section 10. See Theorem 10.1 for
![]() $\mathfrak {g}=E_6$
, Theorem 10.6 for
$\mathfrak {g}=E_6$
, Theorem 10.6 for
![]() $\mathfrak {g}=E_7$
, Theorem 10.11 for
$\mathfrak {g}=E_7$
, Theorem 10.11 for
![]() $\mathfrak {g}=E_8$
, Theorem 10.18 for
$\mathfrak {g}=E_8$
, Theorem 10.18 for
![]() $\mathfrak {g}=F_4$
and Theorem 10.16 for
$\mathfrak {g}=F_4$
and Theorem 10.16 for
![]() $\mathfrak {g}=G_2$
. Finally, useful data related to nilpotent orbits in the exceptional types are collected in Appendix 11.
$\mathfrak {g}=G_2$
. Finally, useful data related to nilpotent orbits in the exceptional types are collected in Appendix 11.
2 Asymptotic data of vertex algebras
A vertex algebra is a complex vector space V equipped with a distinguished vector
![]() ${|0\rangle } \in V$
, an endomorphism
${|0\rangle } \in V$
, an endomorphism
![]() $T \in {\mathrm End}\,V$
and a linear map
$T \in {\mathrm End}\,V$
and a linear map
satisfying the following axioms:
-
•
 $a(z)b \in V((z))$
for all
$a(z)b \in V((z))$
for all
 $a,b \in V$
,
$a,b \in V$
, -
• (vacuum axiom)
 ${|0\rangle } (z) = \mathrm {Id}_V$
and
${|0\rangle } (z) = \mathrm {Id}_V$
and
 $a(z) {|0\rangle } \in a+ zV[[z]]$
for all
$a(z) {|0\rangle } \in a+ zV[[z]]$
for all
 $a \in V$
,
$a \in V$
, -
• (translation invariance axiom)
 $[T, a(z)] = \tfrac {\partial }{\partial z} a(z)$
,
$[T, a(z)] = \tfrac {\partial }{\partial z} a(z)$
, -
• (locality axiom)
 $(z-w)^{N_{a,b}} [a(z),b(w)]=0$
for a sufficiently large integer
$(z-w)^{N_{a,b}} [a(z),b(w)]=0$
for a sufficiently large integer
 $N_{a,b}$
, for all
$N_{a,b}$
, for all
 $a,b \in V$
.
$a,b \in V$
.
A vertex algebra V is called conformal if there exists a vector
![]() $\omega $
called the conformal vector such that
$\omega $
called the conformal vector such that
![]() $L(z) = \omega (z) =\sum _{n\in \mathbb {Z}}L_nz^{-n-2}$
satisfies
$L(z) = \omega (z) =\sum _{n\in \mathbb {Z}}L_nz^{-n-2}$
satisfies
-
(a)
 $[L_m,L_n]=(m-n)L_{m+n}+\dfrac {m^3-m}{12}\delta _{m+n,0}c_V$
, where
$[L_m,L_n]=(m-n)L_{m+n}+\dfrac {m^3-m}{12}\delta _{m+n,0}c_V$
, where
 $c_V$
is a constant called the central charge of V,
$c_V$
is a constant called the central charge of V, -
(b)
 $L_0$
acts semisimply on V,
$L_0$
acts semisimply on V, -
(c)
 $L_{-1}=T$
on V.
$L_{-1}=T$
on V.
For a conformal vertex algebra V and a V-module M, we set
![]() $M_d=\{m\in M\colon L_0 m=dm\}$
. The
$M_d=\{m\in M\colon L_0 m=dm\}$
. The
![]() $L_0$
-eigenvalue of a nonzero
$L_0$
-eigenvalue of a nonzero
![]() $L_0$
-eigenvector
$L_0$
-eigenvector
![]() $m \in M$
is called its conformal weight. For an element
$m \in M$
is called its conformal weight. For an element
![]() $a \in V$
of conformal weight
$a \in V$
of conformal weight
![]() $\Delta $
, we write
$\Delta $
, we write
![]() $a(z) = \sum _{n \in \mathbb {Z}} a_n z^{-n-\Delta }$
. Note that in general
$a(z) = \sum _{n \in \mathbb {Z}} a_n z^{-n-\Delta }$
. Note that in general
![]() $a_0 : M_d \rightarrow M_d$
.
$a_0 : M_d \rightarrow M_d$
.
A finitely generated V-module M is called ordinary if
![]() $L_0$
acts semisimply,
$L_0$
acts semisimply,
![]() $\dim M_d<\infty $
for all d, and the conformal weights of M are bounded from below. The minimum conformal weight of a simple ordinary V-module M is called the conformal dimension of M. More generally, a V-module M will be said to be of positive energy (also called admissible) if it possesses a
$\dim M_d<\infty $
for all d, and the conformal weights of M are bounded from below. The minimum conformal weight of a simple ordinary V-module M is called the conformal dimension of M. More generally, a V-module M will be said to be of positive energy (also called admissible) if it possesses a
![]() $\mathbb {Z}_+$
-grading
$\mathbb {Z}_+$
-grading
![]() $M = \bigoplus _{k \in \mathbb {Z}_+} M_k$
such that
$M = \bigoplus _{k \in \mathbb {Z}_+} M_k$
such that
![]() $a_n M_k \subset M_{k-n}$
for all
$a_n M_k \subset M_{k-n}$
for all
![]() $a \in V$
. The normalised character of an ordinary representation M is defined by
$a \in V$
. The normalised character of an ordinary representation M is defined by
A conformal vertex algebra is called conical if
![]() $V=\bigoplus _{\Delta \in \frac {1}{r}\mathbb {Z}_{\ge 0}}V_{\Delta }$
for some
$V=\bigoplus _{\Delta \in \frac {1}{r}\mathbb {Z}_{\ge 0}}V_{\Delta }$
for some
![]() $r\in \mathbb {Z}_{\ge 0}$
and
$r\in \mathbb {Z}_{\ge 0}$
and
![]() $V_0=\mathbb {C}$
. A
$V_0=\mathbb {C}$
. A
![]() $\mathbb {Z}$
-graded conical vertex algebra is said to be of CFT-type. Let V be a vertex algebra of CFT-type. Then V is called self-dual if
$\mathbb {Z}$
-graded conical vertex algebra is said to be of CFT-type. Let V be a vertex algebra of CFT-type. Then V is called self-dual if
![]() $V \cong V'$
as V-modules, where
$V \cong V'$
as V-modules, where
![]() $M'$
denotes the contragredient dual [Reference Frenkel, Huang and Lepowsky46] of the V-module M. Equivalently, V is self-dual if and only if it admits a non-degenerate symmetric invariant bilinear form.
$M'$
denotes the contragredient dual [Reference Frenkel, Huang and Lepowsky46] of the V-module M. Equivalently, V is self-dual if and only if it admits a non-degenerate symmetric invariant bilinear form.
The following definition goes back to [Reference Kac and Wakimoto58, Conjecture 1].Footnote 2
Definition 2.1. A conformal vertex algebra V is said to admit an asymptotic datum if there exist
![]() $\mathbf {A}_V\in \mathbb {R}$
,
$\mathbf {A}_V\in \mathbb {R}$
,
![]() $\mathbf {w}_V \in \mathbb {R}$
,
$\mathbf {w}_V \in \mathbb {R}$
,
![]() $\mathbf {g}_V\in \mathbb {R}$
such that
$\mathbf {g}_V\in \mathbb {R}$
such that
The numbers
![]() $\mathbf {A}_V$
,
$\mathbf {A}_V$
,
![]() $\mathbf {w}_V$
and
$\mathbf {w}_V$
and
![]() $\mathbf {g}_V$
are called the asymptotic dimension of V, the asymptotic weight, and the asymptotic growth, respectively. Similarly, an ordinary V-module M is said to admit an asymptotic datum if there exist
$\mathbf {g}_V$
are called the asymptotic dimension of V, the asymptotic weight, and the asymptotic growth, respectively. Similarly, an ordinary V-module M is said to admit an asymptotic datum if there exist
![]() $\mathbf {A}_M\in \mathbb {C}$
,
$\mathbf {A}_M\in \mathbb {C}$
,
![]() $\mathbf {w}_M,\mathbf {g}_M\in \mathbb {R}$
such that
$\mathbf {w}_M,\mathbf {g}_M\in \mathbb {R}$
such that
For a conformal vertex algebra V and an ordinary V-module M,
is called the quantum dimension of M if it exists ([Reference Dong, Jiao and Xu35]). If both V and M admit asymptotic data,
![]() $\mathbf {g}_V=\mathbf {g}_M$
and
$\mathbf {g}_V=\mathbf {g}_M$
and
![]() $\mathbf {w}_V=\mathbf {w}_M$
, then the quantum dimension of M exists and is equal to the ratio of the asymptotic dimensions:
$\mathbf {w}_V=\mathbf {w}_M$
, then the quantum dimension of M exists and is equal to the ratio of the asymptotic dimensions:
Given a vertex algebra V, one naturally defines a Poisson algebra
![]() $R_V$
, called the Zhu
$R_V$
, called the Zhu
![]() $C_2$
-algebra, as follows ([Reference Zhu83]). Let
$C_2$
-algebra, as follows ([Reference Zhu83]). Let
![]() $C_2(V)$
be the subspace of V spanned by the elements
$C_2(V)$
be the subspace of V spanned by the elements
![]() $a_{(-2)}b$
, where
$a_{(-2)}b$
, where
![]() $a,b \in V$
, and set
$a,b \in V$
, and set
![]() $R_V =V/C_2(V)$
. Then
$R_V =V/C_2(V)$
. Then
![]() $R_V$
acquires a Poisson algebra structure via
$R_V$
acquires a Poisson algebra structure via
where
![]() $\bar {a}$
denotes the image of
$\bar {a}$
denotes the image of
![]() $a\in V$
in the quotient
$a\in V$
in the quotient
![]() $R_V$
.
$R_V$
.
The associated variety [Reference Arakawa7]
![]() $X_V$
of a vertex algebra V is the affine Poisson variety defined by
$X_V$
of a vertex algebra V is the affine Poisson variety defined by
A vertex algebra V is called lisse if
![]() $\dim X_V=0$
. It is called quasi-lisse [Reference Arakawa, Kawasetsu, Kac and Popov17] if
$\dim X_V=0$
. It is called quasi-lisse [Reference Arakawa, Kawasetsu, Kac and Popov17] if
![]() $X_V$
has finitely many symplectic leaves.
$X_V$
has finitely many symplectic leaves.
A vertex algebra V is called rational if any finitely generated positively graded V-module is completely reducible. For a lisse conformal vertex algebra V, any finitely generated V-module is ordinary, and there exist finitely many simple V-modules ([Reference Abe, Buhl and Dong1]).
The following fact is well known.
Proposition 2.2. Let V be a finitely strongly generated, rational, lisse self-dual simple vertex operator algebra of CFT-type. Then any simple V-module M admits an asymptotic datum with
![]() $\mathbf {w}_M=0$
.
$\mathbf {w}_M=0$
.
Proof. We include a proof for completeness. By [Reference Abe, Buhl and Dong1], any simple V-module is ordinary, and there exist finitely many simple V-modules – say, ![]() . Let
. Let
![]() $h_i$
be the conformal dimension of
$h_i$
be the conformal dimension of
![]() $L_i$
. Then
$L_i$
. Then
By Zhu’s theorem [Reference Zhu83], the vector space spanned by
![]() $\chi _{L_i}(\tau )$
,
$\chi _{L_i}(\tau )$
,
![]() $i=0,\dots , r$
is invariant under the natural action of the modular group
$i=0,\dots , r$
is invariant under the natural action of the modular group
![]() $\operatorname {SL}_2(\mathbb {Z})$
. Hence,
$\operatorname {SL}_2(\mathbb {Z})$
. Hence,
 $$ \begin{align*} \chi_{L_i}(\tau)=\sum_{j=1}^r S_{i,j}\chi_{L_j}(-1/\tau) \end{align*} $$
$$ \begin{align*} \chi_{L_i}(\tau)=\sum_{j=1}^r S_{i,j}\chi_{L_j}(-1/\tau) \end{align*} $$
for some
![]() $S_{i,j}\in \mathbb {C}$
,
$S_{i,j}\in \mathbb {C}$
,
![]() $j=0,\dots , r$
. The assertion follows.
$j=0,\dots , r$
. The assertion follows.
The following assertion is widely believed.
Conjecture 2.3. Let V be a rational, lisse, simple, self-dual conformal vertex algebra V,
![]() $\{L_0,\dots , L_r\}$
the complete set of simple V-modules. There exists a unique simple module
$\{L_0,\dots , L_r\}$
the complete set of simple V-modules. There exists a unique simple module
![]() $L_{i_{\circ }}$
with conformal dimension
$L_{i_{\circ }}$
with conformal dimension
![]() $h_{\text {min}}:=h_{i_{\circ }}$
such that
$h_{\text {min}}:=h_{i_{\circ }}$
such that
![]() $h_i> h_{\text {min}}$
for all
$h_i> h_{\text {min}}$
for all
![]() $i\ne i_{\circ }$
, and that
$i\ne i_{\circ }$
, and that
![]() $S_{i i_{\circ }}\ne 0$
for all i.
$S_{i i_{\circ }}\ne 0$
for all i.
In Theorem 4.11, we confirm the uniqueness of the simple module with minimal conformal dimension for exceptional W-algebras ([Reference Arakawa, Futorny and Ramirez12, Reference Kac and Wakimoto60]). See also Conjecture 4.6 and the subsequent remarks.
Proposition 2.4. Let V be as in Conjecture 2.3, with simple modules
![]() $\{L_0,\dots , L_r\}$
ordered so that
$\{L_0,\dots , L_r\}$
ordered so that
![]() $L_0 = V$
, and assume that there exists a unique simple module
$L_0 = V$
, and assume that there exists a unique simple module
![]() $L_{i_{\circ }}$
satisfying the assertion of Conjecture 2.3. Then
$L_{i_{\circ }}$
satisfying the assertion of Conjecture 2.3. Then
for all i. Moreover,
and
where
![]() $\boxtimes $
is the fusion product ([Reference Huang and Lepowsky49, Reference Huang and Lepowsky51, Reference Huang and Lepowsky52, Reference Huang and Lepowsky53]). In particular, the quantum dimension is well defined for all simple V-modules.
$\boxtimes $
is the fusion product ([Reference Huang and Lepowsky49, Reference Huang and Lepowsky51, Reference Huang and Lepowsky52, Reference Huang and Lepowsky53]). In particular, the quantum dimension is well defined for all simple V-modules.
Proof. The assertions except for the last follow from the proof of Proposition 2.2. For the assertion (5), see [Reference Dong, Jiao and Xu35, Remark 4.10].
The number
![]() $c_V-24 h_{\text {min}}$
is called the effective central charge of V in the literature ([Reference Dong and Mason36]).
$c_V-24 h_{\text {min}}$
is called the effective central charge of V in the literature ([Reference Dong and Mason36]).
Remark 2.5. Let V be as in Proposition 2.4. By a result of Huang [Reference Huang50], the category
![]() $V\operatorname {-mod}$
of finitely generated V-modules forms a modular tensor category. In this context, the quantum dimension of a simple V-module is the same as the Frobenius-Perron dimension ([Reference Etingof, Gelaki, Nikshych and Ostrik39]) of V in
$V\operatorname {-mod}$
of finitely generated V-modules forms a modular tensor category. In this context, the quantum dimension of a simple V-module is the same as the Frobenius-Perron dimension ([Reference Etingof, Gelaki, Nikshych and Ostrik39]) of V in
![]() $V\operatorname {-mod}$
.
$V\operatorname {-mod}$
.
Proposition 2.6. Let V be a finitely strongly generated, quasi-lisse vertex operator algebra of CFT-type. Then any simple ordinary V-module L admits an asymptotic datum.
Proof. By [Reference Arakawa, Kawasetsu, Kac and Popov17], the set
![]() $\{L_i\}$
of simple ordinary V-modules is finite, and the characters
$\{L_i\}$
of simple ordinary V-modules is finite, and the characters
![]() $\chi _{L_i}(\tau )$
are solutions of a modular linear differential equation. Since the space spanned by the solutions of a modular linear differential equation is invariant under the natural action of
$\chi _{L_i}(\tau )$
are solutions of a modular linear differential equation. Since the space spanned by the solutions of a modular linear differential equation is invariant under the natural action of
![]() $\operatorname {SL}_2(\mathbb {Z})$
, the assertion follows in a similar manner as Proposition 2.2, except that a solution of a modular linear differential equation may have logarithmic terms – that is, it has the form
$\operatorname {SL}_2(\mathbb {Z})$
, the assertion follows in a similar manner as Proposition 2.2, except that a solution of a modular linear differential equation may have logarithmic terms – that is, it has the form

Let
![]() $\operatorname {Vir}^c$
be the universal Virasoro vertex algebra at central charge
$\operatorname {Vir}^c$
be the universal Virasoro vertex algebra at central charge
![]() $c\in \mathbb {C}$
,
$c\in \mathbb {C}$
,
![]() $\operatorname {Vir}_c$
the unique simple quotient of
$\operatorname {Vir}_c$
the unique simple quotient of
![]() $\operatorname {Vir}^c$
.
$\operatorname {Vir}^c$
.
Lemma 2.7 [Reference Feĭgin and Fuchs43, Reference Kac and Wakimoto58].
A quotient of a universal Virasoro vertex algebra admits an asymptotic datum.
Proof. It is well known that
![]() $\operatorname {Vir}^c$
has length two if
$\operatorname {Vir}^c$
has length two if
![]() $c=1-6(p-q)^2/pq$
for some
$c=1-6(p-q)^2/pq$
for some
![]() $p,q\in \mathbb {Z}_{\geq 2}$
,
$p,q\in \mathbb {Z}_{\geq 2}$
,
![]() $(p,q)=1$
, and otherwise
$(p,q)=1$
, and otherwise
![]() $\operatorname {Vir}^c=\operatorname {Vir}_c$
. Hence, a quotient V of
$\operatorname {Vir}^c=\operatorname {Vir}_c$
. Hence, a quotient V of
![]() $\operatorname {Vir}^c$
is either
$\operatorname {Vir}^c$
is either
![]() $\operatorname {Vir}^c$
or
$\operatorname {Vir}^c$
or
![]() $\operatorname {Vir}_c$
. If
$\operatorname {Vir}_c$
. If
![]() $V=\operatorname {Vir}^c$
, then
$V=\operatorname {Vir}^c$
, then
 $$ \begin{align*} \chi_V(\tau)=\frac{(1-q)q^{(1-c_V)/24}}{\eta(q)}, \end{align*} $$
$$ \begin{align*} \chi_V(\tau)=\frac{(1-q)q^{(1-c_V)/24}}{\eta(q)}, \end{align*} $$
where
![]() $\eta (q)=q^{1/24}\prod _{j\geq 1}(1-q^j)$
. Hence (indicating by
$\eta (q)=q^{1/24}\prod _{j\geq 1}(1-q^j)$
. Hence (indicating by
![]() $+ \cdots $
terms of lower growth),
$+ \cdots $
terms of lower growth),

where we have used l’Hopital’s rule. So V admits an asymptotic datum with
![]() $\mathbf {A}_V=2\pi $
,
$\mathbf {A}_V=2\pi $
,
![]() $\mathbf {w}_V=3$
,
$\mathbf {w}_V=3$
,
![]() $\mathbf {g}_V=1$
.
$\mathbf {g}_V=1$
.
If
![]() $V=\operatorname {Vir}_c$
with
$V=\operatorname {Vir}_c$
with
![]() $c=1-6(p-q)^2/pq$
,
$c=1-6(p-q)^2/pq$
,
![]() $p,q\in \mathbb {Z}_{\geq 2}$
,
$p,q\in \mathbb {Z}_{\geq 2}$
,
![]() $(p,q)=1$
, then as it is well known [Reference Feĭgin and Fuchs43, Reference Kac and Wakimoto58] V admits an asymptotic datum with
$(p,q)=1$
, then as it is well known [Reference Feĭgin and Fuchs43, Reference Kac and Wakimoto58] V admits an asymptotic datum with
![]() $\mathbf {w}_V=0$
,
$\mathbf {w}_V=0$
,

where
![]() $(a, b)$
is the unique solution of
$(a, b)$
is the unique solution of
![]() $pa-qb=1$
in integers
$pa-qb=1$
in integers ![]() and
and ![]() , and
, and
The simple Virasoro vertex algebra
![]() $\operatorname {Vir}_c$
with
$\operatorname {Vir}_c$
with
![]() $c=1-6(p-q)^2/pq$
,
$c=1-6(p-q)^2/pq$
,
![]() $p,q\in \mathbb {Z}_{\geq 2}$
,
$p,q\in \mathbb {Z}_{\geq 2}$
,
![]() $(p,q)=1$
is known to be rational and lisse ([Reference Wang79]). The simple
$(p,q)=1$
is known to be rational and lisse ([Reference Wang79]). The simple
![]() $\operatorname {Vir}_c$
-modules are the
$\operatorname {Vir}_c$
-modules are the
![]() $(p,q)$
-minimal series representations of the Virasoro algebra, and for each simple
$(p,q)$
-minimal series representations of the Virasoro algebra, and for each simple
![]() $\operatorname {Vir}_c$
-module L, we have
$\operatorname {Vir}_c$
-module L, we have
![]() $\mathbf {w}_L=0$
,
$\mathbf {w}_L=0$
,
![]() $\mathbf {g}_L=\mathbf {g}_{\operatorname {Vir}_c}$
and
$\mathbf {g}_L=\mathbf {g}_{\operatorname {Vir}_c}$
and
![]() $\mathbf {A}_L>0$
([Reference Feĭgin and Fuchs43, Reference Kac and Wakimoto58]).
$\mathbf {A}_L>0$
([Reference Feĭgin and Fuchs43, Reference Kac and Wakimoto58]).
Lemma 2.8. Let V be a conformal vertex algebra with central charge
![]() $c=1-6(p-q)^2/pq$
,
$c=1-6(p-q)^2/pq$
,
![]() $p,q\in \mathbb {Z}_{\geq 2}$
,
$p,q\in \mathbb {Z}_{\geq 2}$
,
![]() $(p,q)=1$
, and suppose that V admits an asymptotic datum with
$(p,q)=1$
, and suppose that V admits an asymptotic datum with
![]() $\mathbf {g}_V<1$
. Then V is a direct sum of simple
$\mathbf {g}_V<1$
. Then V is a direct sum of simple
![]() $(p,q)$
-minimal series representations of the Virasoro algebra. If further
$(p,q)$
-minimal series representations of the Virasoro algebra. If further
![]() $\mathbf {A}_V=\mathbf {A}_{\operatorname {Vir}_c}$
, then
$\mathbf {A}_V=\mathbf {A}_{\operatorname {Vir}_c}$
, then
![]() $V\cong \operatorname {Vir}_c$
.
$V\cong \operatorname {Vir}_c$
.
Proof. The vertex algebra homomorphism
![]() $\operatorname {Vir}^c\rightarrow V$
,
$\operatorname {Vir}^c\rightarrow V$
,
![]() $\omega _{\operatorname {Vir}^c}\rightarrow \omega _V$
factors through the embedding
$\omega _{\operatorname {Vir}^c}\rightarrow \omega _V$
factors through the embedding
![]() $\operatorname {Vir}_c\hookrightarrow V$
because otherwise
$\operatorname {Vir}_c\hookrightarrow V$
because otherwise
![]() $\mathbf {g}_V\geq \mathbf {g}_{\operatorname {Vir}^c}=1$
. Thus, the rationality of
$\mathbf {g}_V\geq \mathbf {g}_{\operatorname {Vir}^c}=1$
. Thus, the rationality of
![]() $\operatorname {Vir}_c$
proves the first statement, and so we have
$\operatorname {Vir}_c$
proves the first statement, and so we have
![]() $V=\bigoplus _{i}L_i^{\oplus _{m_i}}$
, where
$V=\bigoplus _{i}L_i^{\oplus _{m_i}}$
, where
![]() $\{L_i\}$
is the set of simple
$\{L_i\}$
is the set of simple
![]() $(p,q)$
-minimal series representations of the Virasoro algebra and
$(p,q)$
-minimal series representations of the Virasoro algebra and
![]() $m_i\in \mathbb {Z}_{\geq 0}\cup \{\infty \}$
. It follows that
$m_i\in \mathbb {Z}_{\geq 0}\cup \{\infty \}$
. It follows that
![]() $\mathbf {A}_V=\sum _i m_i \mathbf {A}_{L_i}$
, and we get the second assertion.
$\mathbf {A}_V=\sum _i m_i \mathbf {A}_{L_i}$
, and we get the second assertion.
Recall that a homomorphism
![]() $f\colon V\rightarrow W$
of conformal vertex algebras is called conformal if
$f\colon V\rightarrow W$
of conformal vertex algebras is called conformal if
![]() $\omega _W=f(\omega _V)$
.
$\omega _W=f(\omega _V)$
.
Proposition 2.9. Let
![]() $f:V\rightarrow W$
be a homomorphism of conformal vertex algebras. Suppose that
$f:V\rightarrow W$
be a homomorphism of conformal vertex algebras. Suppose that
-
•
 $f(\omega _V)\in W_2$
and
$f(\omega _V)\in W_2$
and
 $(\omega _W)_{(2)}f(\omega _V)=0$
,
$(\omega _W)_{(2)}f(\omega _V)=0$
, -
• the simple quotient L of V admits an asymptotic datum,
-
• W is a quotient of a conformal vertex algebra
 $\tilde {W}$
that admits an asymptotic datum.
$\tilde {W}$
that admits an asymptotic datum.
If
![]() $\mathbf {g}_L=\mathbf {g}_{\tilde {W}}$
, then f is conformal.
$\mathbf {g}_L=\mathbf {g}_{\tilde {W}}$
, then f is conformal.
Proof. Our aim is to show that
![]() $\omega =\omega _W-f(\omega _V)$
vanishes. Now, if
$\omega =\omega _W-f(\omega _V)$
vanishes. Now, if
![]() $\omega \ne 0$
, then [Reference Lepowsky and Li67, Theorem 3.11.12] asserts that the commutant subalgebra
$\omega \ne 0$
, then [Reference Lepowsky and Li67, Theorem 3.11.12] asserts that the commutant subalgebra
is conformal with Virasoro vector
![]() $\omega $
of some central charge c. We note that
$\omega $
of some central charge c. We note that
![]() $\omega \notin f(V)$
, for otherwise we would have
$\omega \notin f(V)$
, for otherwise we would have
![]() $\omega _{(0)}\omega = 0$
, which contradicts that
$\omega _{(0)}\omega = 0$
, which contradicts that
![]() $\omega $
is a conformal vector. We thus proceed to show that
$\omega $
is a conformal vector. We thus proceed to show that
![]() $\omega \in f(V)$
and deduce that
$\omega \in f(V)$
and deduce that
![]() $\omega = 0$
by contradiction.
$\omega = 0$
by contradiction.
Consider the homomorphism
![]() $\tilde {f} :\operatorname {Vir}^c \otimes V \rightarrow W$
of conformal vertex algebras that sends the conformal vector
$\tilde {f} :\operatorname {Vir}^c \otimes V \rightarrow W$
of conformal vertex algebras that sends the conformal vector
![]() $\omega ^{(0)}$
of
$\omega ^{(0)}$
of
![]() $\operatorname {Vir}^c $
to
$\operatorname {Vir}^c $
to
![]() $\omega $
, and such that
$\omega $
, and such that
![]() $\tilde {f}({|0\rangle } \otimes v) = f(v)$
for all
$\tilde {f}({|0\rangle } \otimes v) = f(v)$
for all
![]() $v \in V$
. We now have the vertex subalgebra
$v \in V$
. We now have the vertex subalgebra
![]() $U=\tilde {f}(\operatorname {Vir}^c \otimes V)\subset W$
whose simple quotient is isomorphic to
$U=\tilde {f}(\operatorname {Vir}^c \otimes V)\subset W$
whose simple quotient is isomorphic to
![]() $\operatorname {Vir}_c\otimes L$
. We thus have
$\operatorname {Vir}_c\otimes L$
. We thus have
![]() $\mathbf {g}_{\tilde {W}}\ge \mathbf {g}_L+\mathbf {g}_{\operatorname {Vir}_c}$
, and hence,
$\mathbf {g}_{\tilde {W}}\ge \mathbf {g}_L+\mathbf {g}_{\operatorname {Vir}_c}$
, and hence,
![]() $\mathbf {g}_{\operatorname {Vir}_c}=0$
by our hypotheses. From Lemma 2.7, it follows that
$\mathbf {g}_{\operatorname {Vir}_c}=0$
by our hypotheses. From Lemma 2.7, it follows that
![]() $c=0$
.
$c=0$
.
We recall that
![]() $\operatorname {Vir}_0 = \mathbb {C}$
, that the maximal proper ideal of
$\operatorname {Vir}_0 = \mathbb {C}$
, that the maximal proper ideal of
![]() $\operatorname {Vir}^{0}$
is generated by
$\operatorname {Vir}^{0}$
is generated by
![]() $\omega ^{(0)}$
and that this ideal is simple as a
$\omega ^{(0)}$
and that this ideal is simple as a
![]() $\operatorname {Vir}^0$
-module.
$\operatorname {Vir}^0$
-module.
Let N be the maximal ideal of V, so that
![]() $L = V / N$
. We now consider the surjection
$L = V / N$
. We now consider the surjection
and we define
Since
![]() $K \subset L$
is a V-submodule, we have either
$K \subset L$
is a V-submodule, we have either
![]() $K=L$
or
$K=L$
or
![]() $K=0$
.
$K=0$
.
If
![]() $K = 0$
, then
$K = 0$
, then
![]() $\tilde {f}_1$
is an isomorphism because of simplicity of the maximal proper ideal in
$\tilde {f}_1$
is an isomorphism because of simplicity of the maximal proper ideal in
![]() $\operatorname {Vir}^0$
. But then we would have
$\operatorname {Vir}^0$
. But then we would have
![]() $\mathbf {g}_{\tilde {W}} \ge \mathbf {g}_L+\mathbf {g}_{\operatorname {Vir}^0}> \mathbf {g}_L$
since
$\mathbf {g}_{\tilde {W}} \ge \mathbf {g}_L+\mathbf {g}_{\operatorname {Vir}^0}> \mathbf {g}_L$
since
![]() $\mathbf {g}_{\operatorname {Vir}^0}>0$
, and this contradicts our hypotheses.
$\mathbf {g}_{\operatorname {Vir}^0}>0$
, and this contradicts our hypotheses.
Therefore,
![]() $K = L$
. Since
$K = L$
. Since
![]() $(\operatorname {Vir}^0 \otimes V)_2 = \mathbb {C} \omega ^{(0)} \otimes {|0\rangle } \oplus {|0\rangle } \otimes V_2$
, it follows that
$(\operatorname {Vir}^0 \otimes V)_2 = \mathbb {C} \omega ^{(0)} \otimes {|0\rangle } \oplus {|0\rangle } \otimes V_2$
, it follows that
and in particular that
![]() $\omega \in f(V)$
. Thus,
$\omega \in f(V)$
. Thus,
![]() $\omega = 0$
, and we are done.
$\omega = 0$
, and we are done.
3 Admissible affine vertex algebras
Let
![]() $\mathfrak {g}$
be a complex simple Lie algebra of rank
$\mathfrak {g}$
be a complex simple Lie algebra of rank
![]() $\ell $
. Let
$\ell $
. Let
![]() $\mathfrak {g}=\mathfrak {n}_- \mathop {\oplus } \mathfrak {h}\mathop {\oplus } \mathfrak {n}_+$
be a triangular decomposition with a Cartan subalgebra
$\mathfrak {g}=\mathfrak {n}_- \mathop {\oplus } \mathfrak {h}\mathop {\oplus } \mathfrak {n}_+$
be a triangular decomposition with a Cartan subalgebra
![]() $\mathfrak {h}$
,
$\mathfrak {h}$
,
![]() $\Delta $
the root system of
$\Delta $
the root system of
![]() $(\mathfrak {g},\mathfrak {h})$
and
$(\mathfrak {g},\mathfrak {h})$
and
![]() $\Delta _{+}$
a set of positive roots for
$\Delta _{+}$
a set of positive roots for
![]() $\Delta $
,
$\Delta $
,
![]() $\Pi =\{\alpha _1,\dots ,\alpha _{\ell }\}$
the set of simple roots. Let
$\Pi =\{\alpha _1,\dots ,\alpha _{\ell }\}$
the set of simple roots. Let
![]() $\theta $
be the highest root, and
$\theta $
be the highest root, and
![]() $\theta _s$
the highest short root. We also have
$\theta _s$
the highest short root. We also have
![]() $\Delta ^\vee $
the set of coroots. Let P be the weight lattice, Q the root lattice and
$\Delta ^\vee $
the set of coroots. Let P be the weight lattice, Q the root lattice and
![]() $Q^\vee $
the coroot lattice. The lattice P is dual to
$Q^\vee $
the coroot lattice. The lattice P is dual to
![]() $Q^\vee $
, and we write
$Q^\vee $
, and we write
![]() $P^\vee $
for the dual of Q. Recall that the Coxeter number and the dual Coxeter number of
$P^\vee $
for the dual of Q. Recall that the Coxeter number and the dual Coxeter number of
![]() $\mathfrak {g}$
are denoted by
$\mathfrak {g}$
are denoted by
![]() $h_{\mathfrak {g}}$
and
$h_{\mathfrak {g}}$
and
![]() $h_{\mathfrak {g}}^\vee $
, respectively. Identifying
$h_{\mathfrak {g}}^\vee $
, respectively. Identifying
![]() $\mathfrak {h}$
with
$\mathfrak {h}$
with
![]() $\mathfrak {h}^*$
using the inner product
$\mathfrak {h}^*$
using the inner product
 $$ \begin{align*}(~|~)_{\mathfrak{g}}=\displaystyle{\frac{1}{2 h_{\mathfrak{g}}^\vee}}\times\ \text{Killing form of }\ \mathfrak{g},\end{align*} $$
$$ \begin{align*}(~|~)_{\mathfrak{g}}=\displaystyle{\frac{1}{2 h_{\mathfrak{g}}^\vee}}\times\ \text{Killing form of }\ \mathfrak{g},\end{align*} $$
we view
![]() $Q^\vee $
as a sub-lattice of both P and Q. We denote by
$Q^\vee $
as a sub-lattice of both P and Q. We denote by
![]() $\rho $
the Weyl vector (i.e., the half-sum of positive roots).
$\rho $
the Weyl vector (i.e., the half-sum of positive roots).
For ![]() , let
, let ![]() be the irreducible highest weight representation of
be the irreducible highest weight representation of
![]() $\mathfrak {g}$
with highest weight
$\mathfrak {g}$
with highest weight ![]() , and let
, and let
Let
![]() $\widetilde {\mathfrak {g}} = \mathfrak {g}[t,t^{-1}] \oplus \mathbb {C} K \mathop {\oplus } \mathbb {C} D$
be the affine Kac-Moody algebra, with the commutation relations
$\widetilde {\mathfrak {g}} = \mathfrak {g}[t,t^{-1}] \oplus \mathbb {C} K \mathop {\oplus } \mathbb {C} D$
be the affine Kac-Moody algebra, with the commutation relations
for all
![]() $x,y \in \mathfrak {g}$
and all
$x,y \in \mathfrak {g}$
and all
![]() $m,n\in \mathbb {Z}$
. Let
$m,n\in \mathbb {Z}$
. Let
![]() $\widetilde {\mathfrak {g}}=\widehat {\mathfrak {n}}_-\mathop {\oplus } \widetilde {\mathfrak {h}}\mathop {\oplus }\widehat {\mathfrak {n}}_+$
be the standard triangular decomposition – that is,
$\widetilde {\mathfrak {g}}=\widehat {\mathfrak {n}}_-\mathop {\oplus } \widetilde {\mathfrak {h}}\mathop {\oplus }\widehat {\mathfrak {n}}_+$
be the standard triangular decomposition – that is,
![]() $\widetilde {\mathfrak {h}} = \mathfrak {h} \oplus \mathbb {C} K\mathop {\oplus } \mathbb {C} D $
is the Cartan subalgebra of
$\widetilde {\mathfrak {h}} = \mathfrak {h} \oplus \mathbb {C} K\mathop {\oplus } \mathbb {C} D $
is the Cartan subalgebra of
![]() $\widetilde {\mathfrak {g}}$
,
$\widetilde {\mathfrak {g}}$
,
![]() $\widehat {\mathfrak {n}}_+=\mathfrak {n}_+ +t\mathfrak {g}[t]$
,
$\widehat {\mathfrak {n}}_+=\mathfrak {n}_+ +t\mathfrak {g}[t]$
,
![]() $\widehat {\mathfrak {n}}_-=\mathfrak {n}_-+t^{-1}\mathfrak {g}[t^{-1}]$
.
$\widehat {\mathfrak {n}}_-=\mathfrak {n}_-+t^{-1}\mathfrak {g}[t^{-1}]$
.
Let
![]() $\widehat {\mathfrak {g}} =[\widetilde {\mathfrak {g}},\widetilde {\mathfrak {g}}]= \mathfrak {g}[t,t^{-1}] \oplus \mathbb {C} K$
, and let
$\widehat {\mathfrak {g}} =[\widetilde {\mathfrak {g}},\widetilde {\mathfrak {g}}]= \mathfrak {g}[t,t^{-1}] \oplus \mathbb {C} K$
, and let
![]() $\widehat {\mathfrak {h}}=\mathfrak {h}\mathop {\oplus } \mathbb {C} K\subset \widehat {\mathfrak {g}}$
, so that
$\widehat {\mathfrak {h}}=\mathfrak {h}\mathop {\oplus } \mathbb {C} K\subset \widehat {\mathfrak {g}}$
, so that
![]() $\widehat {\mathfrak {g}}=\widehat {\mathfrak {n}}_-\mathop {\oplus } \widehat {\mathfrak {h}}\mathop {\oplus } \widehat {\mathfrak {n}}_+$
. The Cartan subalgebra
$\widehat {\mathfrak {g}}=\widehat {\mathfrak {n}}_-\mathop {\oplus } \widehat {\mathfrak {h}}\mathop {\oplus } \widehat {\mathfrak {n}}_+$
. The Cartan subalgebra
![]() $\widetilde {\mathfrak {h}}$
is equipped with a bilinear form extending that on
$\widetilde {\mathfrak {h}}$
is equipped with a bilinear form extending that on
![]() $\mathfrak {h}$
by
$\mathfrak {h}$
by
We write
![]() $\delta $
and
$\delta $
and ![]() for the elements of
for the elements of
![]() $\widetilde {\mathfrak {h}}^*$
orthogonal to
$\widetilde {\mathfrak {h}}^*$
orthogonal to
![]() $\mathfrak {h}^*$
and dual to K and D, respectively. We have the (real) root system
$\mathfrak {h}^*$
and dual to K and D, respectively. We have the (real) root system
 $$ \begin{align*} \widehat{\Delta}^{\text{re}} &= \{\alpha+n\delta \colon n \in \mathbb{Z}, \alpha \in \Delta\}= \widehat{\Delta}^{\text{re}}_+\sqcup (-\widehat{\Delta}^{\text{re}}_+),\\ \widehat{\Delta}^{\text{re}}_+ &=\{\alpha+n\delta\colon \alpha\in \Delta_+, \ n\ge 0\}\sqcup \{\alpha+n\delta\colon \alpha\in \Delta, \ n> 0\}, \end{align*} $$
$$ \begin{align*} \widehat{\Delta}^{\text{re}} &= \{\alpha+n\delta \colon n \in \mathbb{Z}, \alpha \in \Delta\}= \widehat{\Delta}^{\text{re}}_+\sqcup (-\widehat{\Delta}^{\text{re}}_+),\\ \widehat{\Delta}^{\text{re}}_+ &=\{\alpha+n\delta\colon \alpha\in \Delta_+, \ n\ge 0\}\sqcup \{\alpha+n\delta\colon \alpha\in \Delta, \ n> 0\}, \end{align*} $$
and the affine Weyl group
![]() $\widehat {W}$
generated by reflections
$\widehat {W}$
generated by reflections
![]() $r_\alpha $
for
$r_\alpha $
for
![]() $\alpha \in \widehat {\Delta }^{\text {re}}$
. For
$\alpha \in \widehat {\Delta }^{\text {re}}$
. For
![]() $\alpha \in \mathfrak {h}^*$
, the translation
$\alpha \in \mathfrak {h}^*$
, the translation
![]() $t_\alpha : \widetilde {\mathfrak {h}}^* \rightarrow \widetilde {\mathfrak {h}}^*$
is defined by
$t_\alpha : \widetilde {\mathfrak {h}}^* \rightarrow \widetilde {\mathfrak {h}}^*$
is defined by

For
![]() $\alpha \in Q^\vee $
, we have
$\alpha \in Q^\vee $
, we have
![]() $t_\alpha \in \widehat {W}$
and, in fact,
$t_\alpha \in \widehat {W}$
and, in fact, ![]() . The extended affine Weyl group, which is the group of isometries of
. The extended affine Weyl group, which is the group of isometries of
![]() $\widehat {\Delta }$
, is
$\widehat {\Delta }$
, is ![]() . Here, for R a subset of P,
. Here, for R a subset of P,
![]() $t_R$
stands for the set
$t_R$
stands for the set
![]() $\{t_\alpha \colon \alpha \in R\}$
.
$\{t_\alpha \colon \alpha \in R\}$
.
Let
![]() $\tilde {\mathcal {O}}_k$
be the category
$\tilde {\mathcal {O}}_k$
be the category
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $\widetilde {\mathfrak {g}}$
at level k ([Reference Kac54]), and let
$\widetilde {\mathfrak {g}}$
at level k ([Reference Kac54]), and let
![]() $\tilde {\mathbf {KL}}_k$
be the full subcategory of
$\tilde {\mathbf {KL}}_k$
be the full subcategory of
![]() $\tilde {\mathcal {O}}_k$
consisting of objects on which the action of
$\tilde {\mathcal {O}}_k$
consisting of objects on which the action of
![]() $\mathfrak {g}$
is integrable. The simple objects of
$\mathfrak {g}$
is integrable. The simple objects of
![]() $\tilde {\mathcal {O}}_k$
are the irreducible highest weight representations
$\tilde {\mathcal {O}}_k$
are the irreducible highest weight representations ![]() with
with ![]() such that
such that ![]() , while the simple objects of
, while the simple objects of
![]() $\tilde {\operatorname {KL}}_k$
are those
$\tilde {\operatorname {KL}}_k$
are those ![]() with
with ![]() , where
, where
![]() $P_+$
is the set of dominant integral weights of
$P_+$
is the set of dominant integral weights of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
For a weight ![]() , the corresponding integral root system is
, the corresponding integral root system is
where
![]() $\alpha ^{\vee }=2\alpha /(\alpha |\alpha )$
as usual, and the subgroup
$\alpha ^{\vee }=2\alpha /(\alpha |\alpha )$
as usual, and the subgroup ![]() of
of
![]() $\widehat {W}$
generated by
$\widehat {W}$
generated by
![]() $r_\alpha $
with
$r_\alpha $
with ![]() is called the integral Weyl group of
is called the integral Weyl group of ![]() .
.
Definition 3.1. A weight ![]() is said to be admissible if
is said to be admissible if
-
1.
 is regular dominant – that is,
is regular dominant – that is,  for all
for all  ,
, -
2.
 .
.
Here, ![]() is the affine Weyl vector. An admissible
is the affine Weyl vector. An admissible
![]() $\widetilde {\mathfrak {g}}$
-module is one of the form
$\widetilde {\mathfrak {g}}$
-module is one of the form ![]() for
for ![]() admissible.
admissible.
Given any
![]() $k\in \mathbb {C}$
, let
$k\in \mathbb {C}$
, let
where
![]() $\mathbb {C}_k$
is the one-dimensional representation of
$\mathbb {C}_k$
is the one-dimensional representation of
![]() $\mathfrak {g}[t] \oplus \mathbb {C} K$
on which
$\mathfrak {g}[t] \oplus \mathbb {C} K$
on which
![]() $\mathfrak {g}[t]$
acts by 0 and K acts as a multiplication by the scalar k. There is a unique vertex algebra structure on
$\mathfrak {g}[t]$
acts by 0 and K acts as a multiplication by the scalar k. There is a unique vertex algebra structure on
![]() $V^k(\mathfrak {g})$
such that
$V^k(\mathfrak {g})$
such that
![]() ${|0\rangle }$
is the image of
${|0\rangle }$
is the image of
![]() $1\otimes 1$
in
$1\otimes 1$
in
![]() $V^k(\mathfrak {g})$
and
$V^k(\mathfrak {g})$
and
for all
![]() $x\in \mathfrak {g}$
, where we regard
$x\in \mathfrak {g}$
, where we regard
![]() $\mathfrak {g}$
as a subspace of V through the embedding
$\mathfrak {g}$
as a subspace of V through the embedding
![]() $x \in \mathfrak {g} \hookrightarrow x_{(-1)}{|0\rangle } \in V^k(\mathfrak {g})$
. The vertex algebra
$x \in \mathfrak {g} \hookrightarrow x_{(-1)}{|0\rangle } \in V^k(\mathfrak {g})$
. The vertex algebra
![]() $V^k(\mathfrak {g})$
is called the universal affine vertex algebra associated with
$V^k(\mathfrak {g})$
is called the universal affine vertex algebra associated with
![]() $\mathfrak {g}$
at level k.
$\mathfrak {g}$
at level k.
The vertex algebra
![]() $V^k(\mathfrak {g})$
has a conformal structure given by the Sugawara construction provided that k is noncritical – that is,
$V^k(\mathfrak {g})$
has a conformal structure given by the Sugawara construction provided that k is noncritical – that is,
![]() $k\ne -h^{\vee }_{\mathfrak {g}}$
, with central charge
$k\ne -h^{\vee }_{\mathfrak {g}}$
, with central charge
 $$ \begin{align*}c_{V^{k}(\mathfrak{g})}= \dfrac{k \dim \mathfrak{g} }{k + h_{\mathfrak{g}}^\vee}.\end{align*} $$
$$ \begin{align*}c_{V^{k}(\mathfrak{g})}= \dfrac{k \dim \mathfrak{g} }{k + h_{\mathfrak{g}}^\vee}.\end{align*} $$
A
![]() $V^k(\mathfrak {g})$
-module is the same as a smooth
$V^k(\mathfrak {g})$
-module is the same as a smooth
![]() $\widehat {\mathfrak {g}}$
-module of level k. Recall that a
$\widehat {\mathfrak {g}}$
-module of level k. Recall that a
![]() $\widehat {\mathfrak {g}}$
-module M is smooth if, for all
$\widehat {\mathfrak {g}}$
-module M is smooth if, for all
![]() $a \in \mathfrak {g}$
and
$a \in \mathfrak {g}$
and
![]() $m \in M$
, one has
$m \in M$
, one has
![]() $at^n m = 0$
for all sufficiently large positive
$at^n m = 0$
for all sufficiently large positive
![]() $n \in \mathbb {Z}$
. The highest weight
$n \in \mathbb {Z}$
. The highest weight
![]() $\widetilde {\mathfrak {g}}$
-module
$\widetilde {\mathfrak {g}}$
-module ![]() (regarded as a
(regarded as a
![]() $\widehat {\mathfrak {g}}$
-module and thus
$\widehat {\mathfrak {g}}$
-module and thus
![]() $V^k(\mathfrak {g})$
-module) acquires conformal dimension
$V^k(\mathfrak {g})$
-module) acquires conformal dimension

For a noncritical level k, we consider a
![]() $V^k(\mathfrak {g})$
-module M as a
$V^k(\mathfrak {g})$
-module M as a
![]() $\widetilde {\mathfrak {g}}$
-module by letting D act as the semisimplification of
$\widetilde {\mathfrak {g}}$
-module by letting D act as the semisimplification of
![]() $-L_0$
. In particular, we identify the categories
$-L_0$
. In particular, we identify the categories
![]() $\mathcal {O}_k$
and
$\mathcal {O}_k$
and
![]() $\mathbf {KL}_k$
of
$\mathbf {KL}_k$
of
![]() $\widehat {\mathfrak {g}}$
-modules of level k with the respective full subcategories of
$\widehat {\mathfrak {g}}$
-modules of level k with the respective full subcategories of
![]() $\tilde {\mathcal {O}}_k$
and
$\tilde {\mathcal {O}}_k$
and
![]() $\tilde {\mathbf {KL}}_k$
consisting of modules on which the universal Casimir element C [Reference Kac54, Section 2.5] of
$\tilde {\mathbf {KL}}_k$
consisting of modules on which the universal Casimir element C [Reference Kac54, Section 2.5] of
![]() $\widetilde {\mathfrak {g}}$
acts nilpotently. Accordingly, the affine space
$\widetilde {\mathfrak {g}}$
acts nilpotently. Accordingly, the affine space ![]() is identified with an affine subvariety of
is identified with an affine subvariety of
![]() $\widetilde {\mathfrak {h}}^*$
by the correspondence
$\widetilde {\mathfrak {h}}^*$
by the correspondence
preserving the corresponding linkage relations in
![]() $\mathcal {O}_k$
.
$\mathcal {O}_k$
.
Let
![]() $L_k(\mathfrak {g})$
be the unique simple graded quotient of
$L_k(\mathfrak {g})$
be the unique simple graded quotient of
![]() $V^k(\mathfrak {g})$
. For any graded quotient V of
$V^k(\mathfrak {g})$
. For any graded quotient V of
![]() $V^k(\mathfrak {g})$
, we have
$V^k(\mathfrak {g})$
, we have
![]() $R_V=V/t^{-2}\mathfrak {g}[t^{-1}] V$
. In particular,
$R_V=V/t^{-2}\mathfrak {g}[t^{-1}] V$
. In particular,
![]() $R_{V^k(\mathfrak {g})} \cong \mathbb {C}[\mathfrak {g}^*]$
, and hence,
$R_{V^k(\mathfrak {g})} \cong \mathbb {C}[\mathfrak {g}^*]$
, and hence,
![]() $X_{V^k(\mathfrak {g})}=\mathfrak {g}^*$
. Furthermore,
$X_{V^k(\mathfrak {g})}=\mathfrak {g}^*$
. Furthermore,
![]() $X_{L_k(\mathfrak {g})}$
is a subvariety of
$X_{L_k(\mathfrak {g})}$
is a subvariety of
![]() $\mathfrak {g}^* \cong \mathfrak {g}$
, which is G-invariant and conic.
$\mathfrak {g}^* \cong \mathfrak {g}$
, which is G-invariant and conic.
More generally, let
![]() $\mathfrak {a}$
be a Lie algebra endowed with a symmetric invariant bilinear form
$\mathfrak {a}$
be a Lie algebra endowed with a symmetric invariant bilinear form
![]() $\kappa $
, and
$\kappa $
, and
be the Kac-Moody affinisation of
![]() $\mathfrak {a}$
. It is a Lie algebra with commutation relations
$\mathfrak {a}$
. It is a Lie algebra with commutation relations
for all
![]() $x,y \in \mathfrak {a}$
and all
$x,y \in \mathfrak {a}$
and all
![]() $m,n \in \mathbb {Z}$
. Then the
$m,n \in \mathbb {Z}$
. Then the
![]() $\widehat {\mathfrak {a}}_\kappa $
-module
$\widehat {\mathfrak {a}}_\kappa $
-module
where
![]() $\mathbb {C}$
is the one-dimensional representation of
$\mathbb {C}$
is the one-dimensional representation of
![]() $\mathfrak {a}[t] \oplus \mathbb {C} {\mathbf 1}$
on which
$\mathfrak {a}[t] \oplus \mathbb {C} {\mathbf 1}$
on which
![]() $\mathfrak {a}[t]$
acts by 0 and
$\mathfrak {a}[t]$
acts by 0 and
![]() ${\mathbf 1}$
acts as the identity, has a unique vertex algebra structure such that
${\mathbf 1}$
acts as the identity, has a unique vertex algebra structure such that
![]() ${|0\rangle }$
is the image of
${|0\rangle }$
is the image of
![]() $1\otimes 1$
in
$1\otimes 1$
in
![]() $V^\kappa (\mathfrak {a})$
and
$V^\kappa (\mathfrak {a})$
and
for all
![]() $x\in \mathfrak {a}$
. We have
$x\in \mathfrak {a}$
. We have
![]() $X_{V^\kappa (\mathfrak {a})} \cong \mathfrak {a}^*$
, and, letting
$X_{V^\kappa (\mathfrak {a})} \cong \mathfrak {a}^*$
, and, letting
![]() $L_\kappa (\mathfrak {a})$
be the unique simple graded quotient of
$L_\kappa (\mathfrak {a})$
be the unique simple graded quotient of
![]() $V^\kappa (\mathfrak {a})$
,
$V^\kappa (\mathfrak {a})$
,
![]() $X_{L_\kappa (\mathfrak {a})}$
is a subvariety of
$X_{L_\kappa (\mathfrak {a})}$
is a subvariety of
![]() $\mathfrak {a}^*$
, which is Poisson and conic.
$\mathfrak {a}^*$
, which is Poisson and conic.
For
![]() $M\in \mathcal {O}_k$
on which
$M\in \mathcal {O}_k$
on which
![]() $L_0$
acts semisimply, we consider the multivariable character
$L_0$
acts semisimply, we consider the multivariable character
![]() $\chi _M$
of M defined by
$\chi _M$
of M defined by
We also write, in particular, ![]() .
.
For admissible weight ![]() , a closed form for
, a closed form for ![]() was given in [Reference Kac and Wakimoto59]. It is convenient to write
was given in [Reference Kac and Wakimoto59]. It is convenient to write
![]() $v = 2 \pi \mathrm {i} (-\tau D+z+t K) \in \widetilde {\mathfrak {h}}^*$
as in [Reference Kac54]. Then the character formula is
$v = 2 \pi \mathrm {i} (-\tau D+z+t K) \in \widetilde {\mathfrak {h}}^*$
as in [Reference Kac54]. Then the character formula is

where

The complex number k is said to be admissible for
![]() $\widehat {\mathfrak {g}}$
if
$\widehat {\mathfrak {g}}$
if ![]() is admissible. If this is the case,
is admissible. If this is the case,
![]() $L_k(\mathfrak {g})$
is called a simple admissible affine vertex algebra. By [Reference Kac and Wakimoto61, Proposition 1.2], k is admissible if and only if
$L_k(\mathfrak {g})$
is called a simple admissible affine vertex algebra. By [Reference Kac and Wakimoto61, Proposition 1.2], k is admissible if and only if
 $$ \begin{align} k +h_{\mathfrak{g}}^\vee = \dfrac{p}{q} \text{ with } p,q \in \mathbb{Z}_{\ge 1}, \; (p,q)=1, \; p \ge \begin{cases} h_{\mathfrak{g}}^\vee & \text{if } (r^\vee,q)=1 \\ h_{\mathfrak{g}} & \text{if } (r^\vee,q)=r^\vee, \end{cases} \end{align} $$
$$ \begin{align} k +h_{\mathfrak{g}}^\vee = \dfrac{p}{q} \text{ with } p,q \in \mathbb{Z}_{\ge 1}, \; (p,q)=1, \; p \ge \begin{cases} h_{\mathfrak{g}}^\vee & \text{if } (r^\vee,q)=1 \\ h_{\mathfrak{g}} & \text{if } (r^\vee,q)=r^\vee, \end{cases} \end{align} $$
where
![]() $r^\vee $
is the lacing numberFootnote
3
of
$r^\vee $
is the lacing numberFootnote
3
of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
If k is admissible with
![]() $(r^\vee ,q)=1$
, we say that k is principal. If k is admissible with
$(r^\vee ,q)=1$
, we say that k is principal. If k is admissible with
![]() $(r^\vee ,q)=r^\vee $
, we say that k is coprincipal.
$(r^\vee ,q)=r^\vee $
, we say that k is coprincipal.
Theorem 3.2 [Reference Arakawa10].
Assume that the level
![]() $k= -h_{\mathfrak {g}}^\vee +p/q$
is admissible. Then
$k= -h_{\mathfrak {g}}^\vee +p/q$
is admissible. Then
![]() $X_{L_k(\mathfrak {g})} =\overline {{\mathbb {O}}}_k$
, where
$X_{L_k(\mathfrak {g})} =\overline {{\mathbb {O}}}_k$
, where
![]() ${\mathbb {O}}_k$
is a certain nilpotent orbit of
${\mathbb {O}}_k$
is a certain nilpotent orbit of
![]() $\mathfrak {g}$
which only depends on the denominator q.
$\mathfrak {g}$
which only depends on the denominator q.
In particular, the associated variety of an admissible affine vertex algebra is contained in the nilpotent cone
![]() $\mathcal {N}_{\mathfrak {g}}$
of
$\mathcal {N}_{\mathfrak {g}}$
of
![]() $\mathfrak {g}$
. We note that the converse is not true, and there are affine vertex algebras at non-admissible levels whose associated variety is contained in
$\mathfrak {g}$
. We note that the converse is not true, and there are affine vertex algebras at non-admissible levels whose associated variety is contained in
![]() $\mathcal {N}_{\mathfrak {g}}$
[Reference Arakawa and Moreau19].
$\mathcal {N}_{\mathfrak {g}}$
[Reference Arakawa and Moreau19].
Theorem 3.3 [Reference Arakawa8].
Let k be admissible, ![]() . Then
. Then ![]() is an
is an
![]() $L_k(\mathfrak {g})$
-module if and only if
$L_k(\mathfrak {g})$
-module if and only if ![]() is an admissible weight such that
is an admissible weight such that ![]() for some
for some
![]() $y\in \widetilde {W}$
. Moreover, any
$y\in \widetilde {W}$
. Moreover, any
![]() $L_k(\mathfrak {g})$
-module that lies in
$L_k(\mathfrak {g})$
-module that lies in
![]() $\mathcal {O}_k$
is a direct sum of admissible representations
$\mathcal {O}_k$
is a direct sum of admissible representations ![]() of
of
![]() $\widehat {\mathfrak {g}}$
of level k for
$\widehat {\mathfrak {g}}$
of level k for ![]() satisfying
satisfying ![]() for some
for some
![]() $y\in \widetilde {W}$
.
$y\in \widetilde {W}$
.
For a principal admissible number, let
![]() $\operatorname {Pr}^k$
be the set of admissible weights
$\operatorname {Pr}^k$
be the set of admissible weights ![]() such that
such that ![]() for some
for some
![]() $y\in \widetilde {W}$
. Similarly, for a coprincipal admissible number, let
$y\in \widetilde {W}$
. Similarly, for a coprincipal admissible number, let
![]() $\operatorname {CoPr}^k$
be the set of admissible weights
$\operatorname {CoPr}^k$
be the set of admissible weights ![]() such that
such that ![]() for some
for some
![]() $y\in \widetilde {W}$
. An element of
$y\in \widetilde {W}$
. An element of
![]() $\operatorname {Pr}^k$
(resp.
$\operatorname {Pr}^k$
(resp.
![]() $\operatorname {CoPr}^k$
) is called a principal admissible weight (resp. coprincipal admissible weight) of level k.
$\operatorname {CoPr}^k$
) is called a principal admissible weight (resp. coprincipal admissible weight) of level k.
Occasionally, we shall use
![]() $\operatorname {Adm}^k$
to refer to the set
$\operatorname {Adm}^k$
to refer to the set
![]() $\operatorname {Pr}^k$
or
$\operatorname {Pr}^k$
or
![]() $\operatorname {CoPr}^k$
, according to whether k is a principal or coprincipal admissible number.
$\operatorname {CoPr}^k$
, according to whether k is a principal or coprincipal admissible number.
For ![]() , let us denote by
, let us denote by ![]() the restriction of
the restriction of ![]() to
to
![]() $\mathfrak {h}$
. For
$\mathfrak {h}$
. For ![]() (resp.
(resp. ![]() ), the primitive ideal
), the primitive ideal ![]() is an maximal ideal of
is an maximal ideal of
![]() $U(\mathfrak {g})$
, and
$U(\mathfrak {g})$
, and ![]() if and only if
if and only if ![]() for
for ![]() (resp. for
(resp. for ![]() ) ([Reference Arakawa, Futorny and Ramirez12, Proposition 2.4]). Here and throughout,
) ([Reference Arakawa, Futorny and Ramirez12, Proposition 2.4]). Here and throughout,
![]() $\circ $
denotes the ‘dot’ action
$\circ $
denotes the ‘dot’ action ![]() . Set
. Set
where ![]() .
.
If V is a
![]() $\frac {1}{2}\mathbb {Z}$
-graded vertex algebra, we denote by
$\frac {1}{2}\mathbb {Z}$
-graded vertex algebra, we denote by
![]() $\operatorname {Zhu}(V)$
the Ramond twisted Zhu algebra of V, briefly recalling its construction from ([Reference De Sole and Kac34, Reference Zhu83]). Bilinear products
$\operatorname {Zhu}(V)$
the Ramond twisted Zhu algebra of V, briefly recalling its construction from ([Reference De Sole and Kac34, Reference Zhu83]). Bilinear products
![]() $*_n : V \otimes V \rightarrow V$
are defined by
$*_n : V \otimes V \rightarrow V$
are defined by
 $$\begin{align*}a *_n b = \sum_{j \in \mathbb{Z}_{\ge 0}} \binom{\Delta(a)}{j} a_{(n+j)}b, \end{align*}$$
$$\begin{align*}a *_n b = \sum_{j \in \mathbb{Z}_{\ge 0}} \binom{\Delta(a)}{j} a_{(n+j)}b, \end{align*}$$
for a of conformal weight
![]() $\Delta (a)$
,
$\Delta (a)$
,
![]() $b \in V$
arbitrary. We write in particular
$b \in V$
arbitrary. We write in particular
![]() $a * b = a *_{-1} b$
and
$a * b = a *_{-1} b$
and
![]() $a \circ b = a *_{-2} b$
. Then the Zhu algebra is a quotient of V by the subspace
$a \circ b = a *_{-2} b$
. Then the Zhu algebra is a quotient of V by the subspace
![]() $V \circ V$
spanned by all elements of the form
$V \circ V$
spanned by all elements of the form
![]() $a \circ b$
for
$a \circ b$
for
![]() $a, b \in V$
. The operation
$a, b \in V$
. The operation
![]() $a \otimes b \mapsto a * b$
is well defined in the quotient and turns it into an associative unital algebra with unit
$a \otimes b \mapsto a * b$
is well defined in the quotient and turns it into an associative unital algebra with unit
![]() $[{|0\rangle }]$
.
$[{|0\rangle }]$
.
The fundamental property satisfied by
![]() $\operatorname {Zhu}(V)$
is the existence of a bijection between the set of irreducible
$\operatorname {Zhu}(V)$
is the existence of a bijection between the set of irreducible
![]() $\operatorname {Zhu}(V)$
-modules and the set of irreducible positive energy Ramond twisted V-modules, sending a V-module M to its lowest graded piece
$\operatorname {Zhu}(V)$
-modules and the set of irreducible positive energy Ramond twisted V-modules, sending a V-module M to its lowest graded piece
![]() $M_{\text {low}}$
equipped with the
$M_{\text {low}}$
equipped with the
![]() $\operatorname {Zhu}(V)$
-action
$\operatorname {Zhu}(V)$
-action
![]() $[a] \cdot m = a_0 m$
for
$[a] \cdot m = a_0 m$
for
![]() $a \in V$
and
$a \in V$
and
![]() $m \in M_{\text {low}}$
.
$m \in M_{\text {low}}$
.
For the simple affine vertex algebra
![]() $L_k(\mathfrak {g})$
, we have
$L_k(\mathfrak {g})$
, we have
for some two-sided ideal
![]() $I_k$
of
$I_k$
of
![]() $U(\mathfrak {g})$
.
$U(\mathfrak {g})$
.
The statement of Theorem 3.3 is strengthened by the following assertion.
Theorem 3.4 [Reference Arakawa and van Ekeren14].
Let k be admissible. We have
where the product is taken over ![]() .
.
Theorem 3.5. Let k be admissible, V a conical self-dual conformal vertex algebra, and
![]() $\varphi :V^k(\mathfrak {g})\rightarrow V$
a conformal vertex algebra homomorphism. Then
$\varphi :V^k(\mathfrak {g})\rightarrow V$
a conformal vertex algebra homomorphism. Then
![]() $\varphi $
factors through an embedding
$\varphi $
factors through an embedding
![]() $L_k(\mathfrak {g})\hookrightarrow V$
. In particular, V is a direct sum of admissible
$L_k(\mathfrak {g})\hookrightarrow V$
. In particular, V is a direct sum of admissible
![]() $\widehat {\mathfrak {g}}$
-modules.
$\widehat {\mathfrak {g}}$
-modules.
Proof. It is known [Reference Kac and Wakimoto58] that the maximal proper submodule
![]() $\widetilde {N}$
of
$\widetilde {N}$
of
![]() $V^k(\mathfrak {g})$
is generated by a singular vector
$V^k(\mathfrak {g})$
is generated by a singular vector ![]() of weight – say,
of weight – say, ![]() . Therefore,
. Therefore,
![]() $N = \varphi (\widetilde {N})$
is generated as a
$N = \varphi (\widetilde {N})$
is generated as a
![]() $\widehat {\mathfrak {g}}$
-module by
$\widehat {\mathfrak {g}}$
-module by ![]() , and we shall show that
, and we shall show that ![]() .
.
Let M be an ordinary V-module. Since
![]() $\varphi $
is conformal, the restricted dual
$\varphi $
is conformal, the restricted dual
![]() $M^*=\bigoplus _{d\in \mathbb {C}}\operatorname {\mathrm {Hom}}_{\mathbb {C}}(M_d,\mathbb {C})$
([Reference Frenkel, Huang and Lepowsky46]) as a V-module is the same as the restricted dual of M as a
$M^*=\bigoplus _{d\in \mathbb {C}}\operatorname {\mathrm {Hom}}_{\mathbb {C}}(M_d,\mathbb {C})$
([Reference Frenkel, Huang and Lepowsky46]) as a V-module is the same as the restricted dual of M as a
![]() $V^k(\mathfrak {g})$
-module. In particular, V is self-dual as a
$V^k(\mathfrak {g})$
-module. In particular, V is self-dual as a
![]() $V^k(\mathfrak {g})$
-module.
$V^k(\mathfrak {g})$
-module.
Assume that ![]() . Then we have a non-splitting exact sequence
. Then we have a non-splitting exact sequence
![]() $0\rightarrow N\rightarrow V\rightarrow V/N\rightarrow 0$
of
$0\rightarrow N\rightarrow V\rightarrow V/N\rightarrow 0$
of
![]() $\widehat {\mathfrak {g}}$
-modules. By the self-duality of V, this gives a non-splitting exact sequence
$\widehat {\mathfrak {g}}$
-modules. By the self-duality of V, this gives a non-splitting exact sequence
of
![]() $V^k(\mathfrak {g})$
-modules.
$V^k(\mathfrak {g})$
-modules.
Let ![]() be a weight vector of V of weight
be a weight vector of V of weight ![]() that is mapped to the highest weight vector of
that is mapped to the highest weight vector of
![]() $N^*$
. Since
$N^*$
. Since
![]() $V_0=\mathbb {C}|0{\rangle }$
and (12) is non-split, we have
$V_0=\mathbb {C}|0{\rangle }$
and (12) is non-split, we have ![]() . It follows that
. It follows that ![]() is not a singular vector and also that
is not a singular vector and also that ![]() . Thus,
. Thus, ![]() and
and ![]() are linearly independent vectors of
are linearly independent vectors of ![]() , which are both primitive in the sense of [Reference Moody and Pianzola72, 2.6]. This implies that
, which are both primitive in the sense of [Reference Moody and Pianzola72, 2.6]. This implies that ![]() .
.
Let ![]() be the projective cover of
be the projective cover of ![]() in
in
![]() $\mathcal {O}_k$
and consider the homomorphism
$\mathcal {O}_k$
and consider the homomorphism ![]() that sends the generator of
that sends the generator of ![]() of weight
of weight ![]() to
to ![]() . Since
. Since
![]() $\varphi $
is conformal, the universal Casimir element C of
$\varphi $
is conformal, the universal Casimir element C of
![]() $\widetilde {\mathfrak {g}}$
acts as zero on V. It follows that g factors through a homomorphism
$\widetilde {\mathfrak {g}}$
acts as zero on V. It follows that g factors through a homomorphism ![]() . But then Lemma 3.6 below says that the multiplicity of
. But then Lemma 3.6 below says that the multiplicity of ![]() in
in ![]() is at most one. Since this is a contradiction, we obtain
is at most one. Since this is a contradiction, we obtain ![]() , as desired. The assertion on complete reducibility now follows from Theorem 3.3.
, as desired. The assertion on complete reducibility now follows from Theorem 3.3.
The following assertion is a direct consequence of [Reference Arakawa and Fiebig16, Lemma 6.9].
Lemma 3.6. Let
![]() $\mu \in \widehat {\mathfrak {h}}^*_k$
be dominant, and suppose
$\mu \in \widehat {\mathfrak {h}}^*_k$
be dominant, and suppose ![]() and there is no
and there is no
![]() $\nu $
such that
$\nu $
such that ![]() . Then
. Then ![]() .
.
Proof. We have [Reference Kac and Kazhdan55] ![]() and an exact sequence
and an exact sequence ![]() ; see the discussion just before [Reference Arakawa and Fiebig16, Lemma 6.9] for details. Hence,
; see the discussion just before [Reference Arakawa and Fiebig16, Lemma 6.9] for details. Hence, ![]() . Let
. Let ![]() be a generator of
be a generator of ![]() of weight
of weight ![]() . By [Reference Arakawa and Fiebig16, Lemma 6.9],
. By [Reference Arakawa and Fiebig16, Lemma 6.9], ![]() , and hence,
, and hence, ![]() because
because ![]() is a generator. It follows that
is a generator. It follows that ![]() , and hence,
, and hence, ![]() .
.
If ![]() is an ordinary module over the simple affine vertex algebra
is an ordinary module over the simple affine vertex algebra
![]() $L_k(\mathfrak {g})$
of principal (resp. coprincipal) admissible level k, then
$L_k(\mathfrak {g})$
of principal (resp. coprincipal) admissible level k, then ![]() (resp.
(resp. ![]() ). We have
). We have ![]() for
for ![]() , while
, while ![]() for
for ![]() , where
, where
![]() $\Delta ^{\mathrm {long}}$
is the set of long roots of
$\Delta ^{\mathrm {long}}$
is the set of long roots of
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^{\mathrm {short}}$
is the set of short roots of
$\Delta ^{\mathrm {short}}$
is the set of short roots of
![]() $\Delta $
. The set of simple roots of
$\Delta $
. The set of simple roots of ![]() , both for
, both for ![]() and for
and for ![]() , is given by
, is given by ![]() , where
, where
![]() $\gamma _i = \alpha _i$
for
$\gamma _i = \alpha _i$
for ![]() and
and
 $$ \begin{align*} \gamma_0 = \begin{cases} - \theta +q\delta& \quad \text{if}\ (r^\vee, q) = 1, \\ - \theta_{s}+q\delta /r^{\vee}& \quad \text{if}\ (r^\vee, q) = r^\vee, \end{cases} \end{align*} $$
$$ \begin{align*} \gamma_0 = \begin{cases} - \theta +q\delta& \quad \text{if}\ (r^\vee, q) = 1, \\ - \theta_{s}+q\delta /r^{\vee}& \quad \text{if}\ (r^\vee, q) = r^\vee, \end{cases} \end{align*} $$
where
![]() $\theta _s$
is the highest short root of
$\theta _s$
is the highest short root of
![]() $\Delta $
.
$\Delta $
.
Let
![]() $\phi : \widetilde {\mathfrak {h}}^* \rightarrow \widetilde {\mathfrak {h}}^*$
be the isometry defined to act as the identity on the finite part
$\phi : \widetilde {\mathfrak {h}}^* \rightarrow \widetilde {\mathfrak {h}}^*$
be the isometry defined to act as the identity on the finite part
![]() $\mathfrak {h}^*$
and to act by
$\mathfrak {h}^*$
and to act by
The adjoint
![]() $\phi ^* : \widetilde {\mathfrak {h}} \rightarrow \widetilde {\mathfrak {h}}$
acts by
$\phi ^* : \widetilde {\mathfrak {h}} \rightarrow \widetilde {\mathfrak {h}}$
acts by
We have [Reference Kac and Wakimoto59]
 $$ \begin{align*} \operatorname{Pr}^k &=\bigcup_{\substack{y\in \widetilde{W} \\ y(S_{(q)} )\subset \widehat{\Delta}^{\text{re}}_+}}\operatorname{Pr}^k_y, \quad \operatorname{Pr}^k_y= y\phi(\widehat{P}^{p-h^{\vee}_{\mathfrak{g}}}_{{+}}+\widehat\rho)-\widehat\rho,\\ \operatorname{CoPr}^k &=\bigcup_{\substack{y\in \widetilde{W} \\ y(S_{(q)} )\subset \widehat{\Delta}^{\text{re}}_+}} \operatorname{Pr}^k_y, \quad \operatorname{CoPr}^k_y= y\phi({}^\circ\widehat{P}^{p-h_{\mathfrak{g}}}_{{+}}+\widehat\rho)-\widehat\rho. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}^k &=\bigcup_{\substack{y\in \widetilde{W} \\ y(S_{(q)} )\subset \widehat{\Delta}^{\text{re}}_+}}\operatorname{Pr}^k_y, \quad \operatorname{Pr}^k_y= y\phi(\widehat{P}^{p-h^{\vee}_{\mathfrak{g}}}_{{+}}+\widehat\rho)-\widehat\rho,\\ \operatorname{CoPr}^k &=\bigcup_{\substack{y\in \widetilde{W} \\ y(S_{(q)} )\subset \widehat{\Delta}^{\text{re}}_+}} \operatorname{Pr}^k_y, \quad \operatorname{CoPr}^k_y= y\phi({}^\circ\widehat{P}^{p-h_{\mathfrak{g}}}_{{+}}+\widehat\rho)-\widehat\rho. \end{align*} $$
We have denoted by
![]() $\widehat {P}^{k}_{{+}}$
the set of dominant integral weights of
$\widehat {P}^{k}_{{+}}$
the set of dominant integral weights of
![]() $\widehat {\mathfrak {g}}$
of level k – that is, the set of weights
$\widehat {\mathfrak {g}}$
of level k – that is, the set of weights ![]() such that
such that ![]() for
for
![]() $i=1,\dots , \ell $
, and
$i=1,\dots , \ell $
, and ![]() . Similarly,
. Similarly,
![]() $\widehat {P}^{k}_{{++}}$
will denote the set of regular dominant integral weights, given by
$\widehat {P}^{k}_{{++}}$
will denote the set of regular dominant integral weights, given by ![]() for
for
![]() $i=1,\dots , \ell $
, and
$i=1,\dots , \ell $
, and ![]() . Furthermore,
. Furthermore,
![]() ${}^\circ \widehat {P}^{k}_{{+}}$
is defined similarly to
${}^\circ \widehat {P}^{k}_{{+}}$
is defined similarly to
![]() $\widehat {P}^{k}_{{+}}$
, the condition
$\widehat {P}^{k}_{{+}}$
, the condition ![]() being replaced by
being replaced by ![]() . In particular, we have
. In particular, we have
Proposition 3.7 [Reference Kac and Wakimoto59].
Let k be principal admissible of the form (9), and let
with
![]() $y = t_\beta \overline y$
,
$y = t_\beta \overline y$
,
![]() $\beta \in P^\vee $
,
$\beta \in P^\vee $
,
![]() $\overline y \in W$
, and
$\overline y \in W$
, and
![]() $\nu \in {}^\circ \widehat {P}_+^{p-h^\vee }+\widehat \rho $
. Let
$\nu \in {}^\circ \widehat {P}_+^{p-h^\vee }+\widehat \rho $
. Let
![]() $T \in \mathbb {R}_{>0}$
and
$T \in \mathbb {R}_{>0}$
and
![]() $z \in \mathfrak {h}$
such that
$z \in \mathfrak {h}$
such that
![]() $\alpha (z) \notin \mathbb {Z}$
for all
$\alpha (z) \notin \mathbb {Z}$
for all
![]() $\alpha \in \Delta $
. Then as
$\alpha \in \Delta $
. Then as
![]() $T \rightarrow 0^+$
, one has
$T \rightarrow 0^+$
, one has
where

The proof of the proposition below closely follows the arguments of [Reference Kac and Wakimoto59], with adaptations to the coprincipal case.
Proposition 3.8. Let k be coprincipal admissible of the form (9), and let
with
![]() $y = t_\beta \overline y$
,
$y = t_\beta \overline y$
,
![]() $\beta \in P^\vee $
,
$\beta \in P^\vee $
,
![]() $\overline y \in W$
, and
$\overline y \in W$
, and
![]() $\nu \in {}^\circ \widehat {P}_+^{p-h^\vee }+\widehat {\rho }$
. Let
$\nu \in {}^\circ \widehat {P}_+^{p-h^\vee }+\widehat {\rho }$
. Let
![]() $T \in \mathbb {R}_{>0}$
and
$T \in \mathbb {R}_{>0}$
and
![]() $z \in \mathfrak {h}$
such that
$z \in \mathfrak {h}$
such that
![]() $\alpha (z) \notin \mathbb {Z}$
for all
$\alpha (z) \notin \mathbb {Z}$
for all
![]() $\alpha \in \Delta $
. Then as
$\alpha \in \Delta $
. Then as
![]() $T \rightarrow 0^+$
, we have
$T \rightarrow 0^+$
, we have
where

Proof. The denominator of

is the standard Weyl denominator. Its asymptotic behaviour is well known [Reference Kac54, Proposition 13.13] to be
where
We analyse the numerator by writing it in terms of theta functions. Let m be a positive integer for which the lattice
![]() $\sqrt {m}Q$
is integral, and let
$\sqrt {m}Q$
is integral, and let ![]() , where
, where
![]() $\mu \in P^\vee $
. Then we define
$\mu \in P^\vee $
. Then we define

The modular transformation of these theta functions is given by

where in the sum, ![]() .
.
In the sum defining ![]() , the action of the Weyl group
, the action of the Weyl group ![]() is intertwined with the action of the group
is intertwined with the action of the group ![]() via the automorphism y. The numerator of (13) is thus expressed in terms of theta functions as
via the automorphism y. The numerator of (13) is thus expressed in terms of theta functions as

Now we compute the asymptotic behaviour of
Since ![]() is coprincipal, the lattice
is coprincipal, the lattice
![]() $pq Q$
is integral and we may use the modular transformation formula to write
$pq Q$
is integral and we may use the modular transformation formula to write

(The summands corresponding to nonregular
![]() $\widehat {\mu }$
cancel out in the sum over W.) In the limit
$\widehat {\mu }$
cancel out in the sum over W.) In the limit
![]() $T \rightarrow 0^+$
, the dominant terms in the sum above come from the shortest regular
$T \rightarrow 0^+$
, the dominant terms in the sum above come from the shortest regular
![]() $\mu \in P^\vee $
. Such
$\mu \in P^\vee $
. Such
![]() $\mu $
consist precisely of the W-orbit of
$\mu $
consist precisely of the W-orbit of
![]() $\rho ^\vee $
. We therefore obtain the asymptotic
$\rho ^\vee $
. We therefore obtain the asymptotic

The Weyl denominator formula asserts that

(There is a more standard version of the formula, from which (15) is obtained by applying to the Langlands dual Lie algebra and noting that the duality exchanges
![]() $\rho $
with
$\rho $
with
![]() $\rho ^\vee $
up to a factor of
$\rho ^\vee $
up to a factor of
![]() $\sqrt {r^\vee }$
.) Using (15), we reduce the double sum over W to
$\sqrt {r^\vee }$
.) Using (15), we reduce the double sum over W to
 $$ \begin{align*} \prod_{\alpha \in \Delta_+} 4 \sin\ \frac{\pi (\alpha^\vee | \nu)}{p} \sin\ \pi (\alpha^\vee | z). \end{align*} $$
$$ \begin{align*} \prod_{\alpha \in \Delta_+} 4 \sin\ \frac{\pi (\alpha^\vee | \nu)}{p} \sin\ \pi (\alpha^\vee | z). \end{align*} $$
To deduce the asymptotic behaviour of ![]() , we note that
, we note that
It then follows that

and, combining with (14), finally

The second form for
![]() $\mathbf {g}$
given in the theorem statement follows from the Freudenthal-de Vries strange formula and the fact that Langlands duality exchanges
$\mathbf {g}$
given in the theorem statement follows from the Freudenthal-de Vries strange formula and the fact that Langlands duality exchanges
![]() $\rho $
and
$\rho $
and
![]() $\rho ^\vee $
.
$\rho ^\vee $
.
Corollary 3.9. Let k be an admissible number of the form (9). The admissible affine vertex algebra
![]() $L_k(\mathfrak {g})$
admits an asymptotic datum, and so does any simple ordinary representation
$L_k(\mathfrak {g})$
admits an asymptotic datum, and so does any simple ordinary representation ![]() of
of
![]() $L_k(\mathfrak {g})$
.
$L_k(\mathfrak {g})$
.
-
1. For
 , where
, where
 $n_t=(t^n-t^{-n})/(t-t^{-1})$
,
$n_t=(t^n-t^{-n})/(t-t^{-1})$
,
 $t=e^{\pi \mathrm {i} /p}$
.
$t=e^{\pi \mathrm {i} /p}$
.
-
2. For
 ,
, 
Proof. The assertion follows from Propositions 3.7 and 3.8 by taking the limit
![]() $z \rightarrow 0$
with
$z \rightarrow 0$
with
![]() $\beta =0$
and
$\beta =0$
and
![]() $\bar y=1$
. Let us explain the details for the coprincipal case. The normalised character
$\bar y=1$
. Let us explain the details for the coprincipal case. The normalised character ![]() is just the specialization
is just the specialization ![]() . To prove the first assertion, we therefore apply Proposition 3.8 with
. To prove the first assertion, we therefore apply Proposition 3.8 with
![]() $\beta = 0$
,
$\beta = 0$
,
![]() $\overline y = 1$
,
$\overline y = 1$
, ![]() , and we let z tend to
, and we let z tend to
![]() $0$
along a ray disjoint from the hyperplanes
$0$
along a ray disjoint from the hyperplanes
![]() $(\alpha | z) = 0$
. Comparing the definition of the asymptotic dimension
$(\alpha | z) = 0$
. Comparing the definition of the asymptotic dimension
![]() $\mathbf {A}$
(Definition 2.1 above) with that of
$\mathbf {A}$
(Definition 2.1 above) with that of ![]() yields
yields

Here, we used l’Hopital’s rule.
In the above, we have ![]() since
since ![]() for
for ![]() ,
,
![]() $\alpha \in \Delta _+$
, and
$\alpha \in \Delta _+$
, and ![]() for
for ![]() ,
,
![]() $\alpha \in \Delta _+$
.
$\alpha \in \Delta _+$
.
Note that
![]() $|P /(pq) Q^\vee | = (pq)^\ell |P /Q^\vee |$
and
$|P /(pq) Q^\vee | = (pq)^\ell |P /Q^\vee |$
and ![]() if
if
![]() $r^\vee | q$
. The values of
$r^\vee | q$
. The values of
![]() $|P /Q^\vee |$
and
$|P /Q^\vee |$
and
![]() $|P^\vee / r^\vee Q|$
, as well as other useful data, are collected in Table 1 for each simple Lie algebra.
$|P^\vee / r^\vee Q|$
, as well as other useful data, are collected in Table 1 for each simple Lie algebra.
Table 1 Some data for simple Lie algebras.

Theorem 3.10. Let k be admissible, and let V be a conical self-dual conformal vertex algebra equipped with a vertex algebra homomorphism
![]() $\varphi :V^k(\mathfrak {g})\rightarrow V$
such that
$\varphi :V^k(\mathfrak {g})\rightarrow V$
such that
![]() $\varphi (\omega _{V^k(\mathfrak {g})})\in V_2$
and
$\varphi (\omega _{V^k(\mathfrak {g})})\in V_2$
and
![]() $(\omega _V)_{(2)}\varphi (\omega _{V^k(\mathfrak {g})})=0$
. Assume that V is a quotient of a vertex algebra
$(\omega _V)_{(2)}\varphi (\omega _{V^k(\mathfrak {g})})=0$
. Assume that V is a quotient of a vertex algebra
![]() $\tilde {V}$
that admits an asymptotic datum such that
$\tilde {V}$
that admits an asymptotic datum such that
Then
![]() $\varphi $
factors through a finite extension
$\varphi $
factors through a finite extension
![]() $L_k(\mathfrak {g})\hookrightarrow V$
. If moreover,
$L_k(\mathfrak {g})\hookrightarrow V$
. If moreover,
that is,
Then
![]() $\varphi $
factors through an isomorphism
$\varphi $
factors through an isomorphism
![]() $L_k(\mathfrak {g})\cong V$
.
$L_k(\mathfrak {g})\cong V$
.
Proof. By Proposition 2.9,
![]() $\varphi $
is conformal. Hence, by Theorem 3.5, V is a direct sum of admissible representations
$\varphi $
is conformal. Hence, by Theorem 3.5, V is a direct sum of admissible representations ![]() with
with ![]() if k is principal (resp.
if k is principal (resp. ![]() if k is coprincipal). So we can write
if k is coprincipal). So we can write

with ![]() . In particular, V admits an asymptotic datum with
. In particular, V admits an asymptotic datum with
![]() $\mathbf {g}_V=\mathbf {g}_{L_k(\mathfrak {g})}=\mathbf {g}_{\tilde {V}}$
,
$\mathbf {g}_V=\mathbf {g}_{L_k(\mathfrak {g})}=\mathbf {g}_{\tilde {V}}$
,
![]() $\mathbf {w}_V=0$
,
$\mathbf {w}_V=0$
, ![]() (resp.
(resp. ![]() ). Since
). Since ![]() and
and ![]() for all
for all ![]() (resp.
(resp. ![]() ), we get the first assertion. If, in addition,
), we get the first assertion. If, in addition,
![]() $\mathbf {A}_{\tilde {V}}=\mathbf {A}_{L_k(\mathfrak {g})}$
, then
$\mathbf {A}_{\tilde {V}}=\mathbf {A}_{L_k(\mathfrak {g})}$
, then ![]() , which forces
, which forces ![]() and all others
and all others ![]() are zero, whence the statement.
are zero, whence the statement.
We now briefly discuss some relationships between primitive ideals, associated varieties and conformal dimensions. For a two-sided ideal I of
![]() $U(\mathfrak {g})$
, we denote
$U(\mathfrak {g})$
, we denote
![]() $\operatorname {Var}(I)$
the zero locus of
$\operatorname {Var}(I)$
the zero locus of
![]() $\operatorname {gr}I\subset \operatorname {gr}U(\mathfrak {g})=\mathbb {C}[\mathfrak {g}^*]$
in
$\operatorname {gr}I\subset \operatorname {gr}U(\mathfrak {g})=\mathbb {C}[\mathfrak {g}^*]$
in
![]() $\mathfrak {g}^{*}$
. Now let k be an admissible number with denominator q. We distinguish the following weight:
$\mathfrak {g}^{*}$
. Now let k be an admissible number with denominator q. We distinguish the following weight:

By [Reference Arakawa, van Ekeren and Moreau15, Proposition 2.4],

and
Theorem 3.11 [Reference Arakawa, van Ekeren and Moreau15].
For an admissible number k, we have ![]() .
.
Remark 3.12. Let k be an admissible number, and let ![]() such that
such that ![]() . Since
. Since
![]() $\operatorname {Var}(I_k)=\overline {\mathbb {O}}_k$
by [Reference Arakawa9, Theorem 9.5] (recall (11)) and
$\operatorname {Var}(I_k)=\overline {\mathbb {O}}_k$
by [Reference Arakawa9, Theorem 9.5] (recall (11)) and ![]() is a
is a
![]() $\operatorname {Zhu}(L_k(\mathfrak {g}))$
-module (Theorem 3.3), we have
$\operatorname {Zhu}(L_k(\mathfrak {g}))$
-module (Theorem 3.3), we have
The connection with conformal dimensions is given by the following:
Proposition 3.13. For an admissible number k, the module ![]() has the minimal conformal dimension among the simple
has the minimal conformal dimension among the simple
![]() $L_k(\mathfrak {g})$
-modules that belong to
$L_k(\mathfrak {g})$
-modules that belong to
![]() $\mathcal {O}_k$
.
$\mathcal {O}_k$
.
Proof. By [Reference Arakawa8], a simple
![]() $L_k(\mathfrak {g})$
-module which belongs to
$L_k(\mathfrak {g})$
-module which belongs to
![]() $\mathcal {O}_k$
is an irreducible highest weight module
$\mathcal {O}_k$
is an irreducible highest weight module
![]() $L(\widehat {\mu })$
of highest weight
$L(\widehat {\mu })$
of highest weight ![]() .
.
First, we consider the principal admissible case
![]() $(q,r^{\vee })=1$
. We have, cf. Proposition 3.7 above and preceding remarks,
$(q,r^{\vee })=1$
. We have, cf. Proposition 3.7 above and preceding remarks,
![]() $\widehat {\mu } = y \phi (\widehat {\nu }) - \widehat {\rho }$
where
$\widehat {\mu } = y \phi (\widehat {\nu }) - \widehat {\rho }$
where ![]() and
and
![]() $\nu \in P_{++}^{p}$
, where
$\nu \in P_{++}^{p}$
, where
![]() $y = \overline y t_{-\eta }$
with
$y = \overline y t_{-\eta }$
with
![]() $\eta \in P_+^{\vee , q}$
.
$\eta \in P_+^{\vee , q}$
.
The conformal weight of
![]() $L(\widehat \mu )$
is
$L(\widehat \mu )$
is
 $$\begin{align*}h_{L(\mu)} = \frac{(\mu | \mu + 2\rho)}{2(k+h^\vee_{\mathfrak{g}})} = \frac{|\mu + \rho|^2 - |\rho|^2}{2(k+h^\vee_{\mathfrak{g}})}. \end{align*}$$
$$\begin{align*}h_{L(\mu)} = \frac{(\mu | \mu + 2\rho)}{2(k+h^\vee_{\mathfrak{g}})} = \frac{|\mu + \rho|^2 - |\rho|^2}{2(k+h^\vee_{\mathfrak{g}})}. \end{align*}$$
Now we consider
We show that
![]() $q\nu - p\eta \in P$
is a regular weight. Indeed, suppose
$q\nu - p\eta \in P$
is a regular weight. Indeed, suppose ![]() for some
for some ![]() and put
and put ![]() and
and ![]() . Then
. Then
![]() $qm - pn = 0$
and so p divides m, but this is a contradiction since
$qm - pn = 0$
and so p divides m, but this is a contradiction since
![]() $0 < m < p$
because
$0 < m < p$
because
![]() $\nu $
is regular.
$\nu $
is regular.
The regular elements of P of minimal norm are
![]() $\rho $
and its images under the finite Weyl group, so the claim is proved in the principal admissible case. The coprincipal admissible case is similar. Since
$\rho $
and its images under the finite Weyl group, so the claim is proved in the principal admissible case. The coprincipal admissible case is similar. Since
![]() $(q, r^\vee ) = r^\vee $
, we have
$(q, r^\vee ) = r^\vee $
, we have
![]() $q\nu \in qP \subset P^\vee $
, and hence,
$q\nu \in qP \subset P^\vee $
, and hence,
![]() $q\nu - p\eta \in P^\vee $
. The regular elements of
$q\nu - p\eta \in P^\vee $
. The regular elements of
![]() $P^\vee $
of minimal norm are
$P^\vee $
of minimal norm are
![]() $\rho ^\vee $
and its images under the finite Weyl group, thus proving the claim.
$\rho ^\vee $
and its images under the finite Weyl group, thus proving the claim.
Remark 3.14.
-
1. The weight
 is not the unique element of
is not the unique element of
 $\operatorname {Adm}^k$
that gives the minimal conformal dimension unless
$\operatorname {Adm}^k$
that gives the minimal conformal dimension unless
 $k\in \mathbb {Z}_{\geq 0}$
. Indeed, for
$k\in \mathbb {Z}_{\geq 0}$
. Indeed, for  ,
,
 $L(\hat {\mu })$
has the minimal conformal dimension if and only if
$L(\hat {\mu })$
has the minimal conformal dimension if and only if  with
with
 $w\in W$
such that
$w\in W$
such that
 $w(\alpha )\in \Delta _+$
for
$w(\alpha )\in \Delta _+$
for
 $\alpha \in \Delta _+$
with
$\alpha \in \Delta _+$
with
 $(\rho ,\alpha ^{\vee }) \in q \mathbb {Z}$
(resp.
$(\rho ,\alpha ^{\vee }) \in q \mathbb {Z}$
(resp.  with
with
 $w\in W$
such that
$w\in W$
such that
 $w(\alpha )\in \Delta _+$
for
$w(\alpha )\in \Delta _+$
for
 $\alpha \in \Delta _+$
with
$\alpha \in \Delta _+$
with
 $(\rho ^{\vee },\alpha ^{\vee }) \in q \mathbb {Z}$
).
$(\rho ^{\vee },\alpha ^{\vee }) \in q \mathbb {Z}$
). -
2. The strange formula implies that the asymptotic growth coincides with the effective central charge – that is,
for all
 .
.
4 Asymptotic data of W-algebras
Let f be a nilpotent element of
![]() $\mathfrak {g}$
. Recall [Reference Kac, Roan and Wakimoto57] that a
$\mathfrak {g}$
. Recall [Reference Kac, Roan and Wakimoto57] that a
![]() $\frac {1}{2}\mathbb {Z}$
-grading
$\frac {1}{2}\mathbb {Z}$
-grading
 $$ \begin{align} \mathfrak{g} = \bigoplus_{j \in \frac{1}{2}\mathbb{Z}} \mathfrak{g}_\Gamma^j \end{align} $$
$$ \begin{align} \mathfrak{g} = \bigoplus_{j \in \frac{1}{2}\mathbb{Z}} \mathfrak{g}_\Gamma^j \end{align} $$
is called good for f if
![]() $f \in \mathfrak {g}_\Gamma ^{-1}$
,
$f \in \mathfrak {g}_\Gamma ^{-1}$
,
![]() $\operatorname {\mathrm {ad}} f \colon \mathfrak {g}_\Gamma ^{j} \to \mathfrak {g}_\Gamma ^{j-1}$
is injective for
$\operatorname {\mathrm {ad}} f \colon \mathfrak {g}_\Gamma ^{j} \to \mathfrak {g}_\Gamma ^{j-1}$
is injective for
![]() $j \ge \frac {1}{2}$
and surjective for
$j \ge \frac {1}{2}$
and surjective for ![]() . The grading is called even if
. The grading is called even if
![]() $\mathfrak {g}_\Gamma ^j = 0$
for
$\mathfrak {g}_\Gamma ^j = 0$
for
![]() $j\not \in \mathbb {Z}$
. By the Jacobson-Morosov Theorem, the nilpotent element f embeds into an
$j\not \in \mathbb {Z}$
. By the Jacobson-Morosov Theorem, the nilpotent element f embeds into an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
, and
$(e,h,f)$
, and
![]() $\mathfrak {g}$
thereby inherits a
$\mathfrak {g}$
thereby inherits a
![]() $\frac {1}{2}\mathbb {Z}$
-grading induced by the eigenvalues of
$\frac {1}{2}\mathbb {Z}$
-grading induced by the eigenvalues of
![]() $\operatorname {\mathrm {ad}}(h/2)$
. Such a grading is called a Dynkin grading. All Dynkin gradings are good, but not all good gradings are Dynkin.
$\operatorname {\mathrm {ad}}(h/2)$
. Such a grading is called a Dynkin grading. All Dynkin gradings are good, but not all good gradings are Dynkin.
Let
![]() $x^0_\Gamma $
be the semisimple element of
$x^0_\Gamma $
be the semisimple element of
![]() $\mathfrak {g}$
defining the grading (19) – that is,
$\mathfrak {g}$
defining the grading (19) – that is,
We can assume that
![]() $x^0_\Gamma $
is contained in the Cartan subalgebra
$x^0_\Gamma $
is contained in the Cartan subalgebra
![]() $\mathfrak {h}$
and that
$\mathfrak {h}$
and that
![]() $\alpha (x^0_\Gamma ) \in \frac {1}{2}\mathbb {Z}_{\ge 0}$
for all
$\alpha (x^0_\Gamma ) \in \frac {1}{2}\mathbb {Z}_{\ge 0}$
for all
![]() $\alpha \in \Delta _+$
. For
$\alpha \in \Delta _+$
. For
![]() $j \in \frac {1}{2}\mathbb {Z}$
, we set
$j \in \frac {1}{2}\mathbb {Z}$
, we set
where
![]() $\mathfrak {g}^\alpha $
is the
$\mathfrak {g}^\alpha $
is the
![]() $\alpha $
-root space.
$\alpha $
-root space.
Since the bilinear form
![]() $(x,y) \mapsto (f | [x,y])$
is non-degenerate on
$(x,y) \mapsto (f | [x,y])$
is non-degenerate on
![]() $\mathfrak {g}_\Gamma ^{1/2} \times \mathfrak {g}_\Gamma ^{1/2}$
, the set
$\mathfrak {g}_\Gamma ^{1/2} \times \mathfrak {g}_\Gamma ^{1/2}$
, the set
![]() $\Delta _\Gamma ^{1/2}$
has even cardinality. We set
$\Delta _\Gamma ^{1/2}$
has even cardinality. We set
![]() $\Delta ^0_{\Gamma ,+}= \Delta _\Gamma ^0 \cap \Delta _{+}$
. It is a set of positive roots for
$\Delta ^0_{\Gamma ,+}= \Delta _\Gamma ^0 \cap \Delta _{+}$
. It is a set of positive roots for
![]() $\Delta _\Gamma ^0$
.
$\Delta _\Gamma ^0$
.
Remark 4.1. Unless otherwise specified,
![]() $\Gamma $
will always be the Dynkin grading associated with
$\Gamma $
will always be the Dynkin grading associated with
![]() $(e,h,f)$
. In this case,
$(e,h,f)$
. In this case,
![]() $x^0_\Gamma $
is
$x^0_\Gamma $
is
![]() $h/2$
, and we will briefly write
$h/2$
, and we will briefly write
![]() $x^0$
,
$x^0$
,
![]() $\mathfrak {g}^j$
,
$\mathfrak {g}^j$
,
![]() $\Delta ^j$
,
$\Delta ^j$
,
![]() $\Delta _+^0$
for
$\Delta _+^0$
for
![]() $x_\Gamma ^0$
,
$x_\Gamma ^0$
,
![]() $\mathfrak {g}_\Gamma ^j$
,
$\mathfrak {g}_\Gamma ^j$
,
![]() $\Delta _\Gamma ^j$
,
$\Delta _\Gamma ^j$
,
![]() $\Delta _{\Gamma ,+}^0$
, respectively. However, in type A, even good gradings always exist [Reference Elashvili, Kac and Vinberg38], and it will be convenient to opt for an even good grading that is not necessarily the Dynkin grading.
$\Delta _{\Gamma ,+}^0$
, respectively. However, in type A, even good gradings always exist [Reference Elashvili, Kac and Vinberg38], and it will be convenient to opt for an even good grading that is not necessarily the Dynkin grading.
We denote by
![]() $\mathscr {W}^k(\mathfrak {g},f)$
the universal affine W-algebra associated with
$\mathscr {W}^k(\mathfrak {g},f)$
the universal affine W-algebra associated with
![]() $\mathfrak {g},f$
at level k and a good grading
$\mathfrak {g},f$
at level k and a good grading
![]() $\mathfrak {g}_\Gamma = \bigoplus _{j \in \frac {1}{2}\mathbb {Z}} \mathfrak {g}_\Gamma ^j$
:
$\mathfrak {g}_\Gamma = \bigoplus _{j \in \frac {1}{2}\mathbb {Z}} \mathfrak {g}_\Gamma ^j$
:
where
![]() $H_{DS,f}^\bullet (?)$
is the BRST cohomology functor of the quantized Drinfeld-Sokolov reduction associated with
$H_{DS,f}^\bullet (?)$
is the BRST cohomology functor of the quantized Drinfeld-Sokolov reduction associated with
![]() $\mathfrak {g},f$
([Reference Feigin and Frenkel42, Reference Kac, Roan and Wakimoto57]). The BRST complex of a
$\mathfrak {g},f$
([Reference Feigin and Frenkel42, Reference Kac, Roan and Wakimoto57]). The BRST complex of a
![]() $\widehat {\mathfrak {g}}$
-module M takes the form
$\widehat {\mathfrak {g}}$
-module M takes the form
where
![]() $F^{\text {ch}}$
denotes the Clifford vertex algebra associated with
$F^{\text {ch}}$
denotes the Clifford vertex algebra associated with
![]() $\mathfrak {g}_\Gamma ^{>0} \oplus (\mathfrak {g}_\Gamma ^{>0})^*$
and its canonical symmetric bilinear form, or in the terminology of [Reference Kac, Roan and Wakimoto57] the charged free fermions vertex algebra associated with
$\mathfrak {g}_\Gamma ^{>0} \oplus (\mathfrak {g}_\Gamma ^{>0})^*$
and its canonical symmetric bilinear form, or in the terminology of [Reference Kac, Roan and Wakimoto57] the charged free fermions vertex algebra associated with
![]() $\mathfrak {g}_\Gamma ^{>0} \oplus (\mathfrak {g}_\Gamma ^{>0})^*$
made into a purely odd vector superspace and canonical skew-supersymmetric form, and
$\mathfrak {g}_\Gamma ^{>0} \oplus (\mathfrak {g}_\Gamma ^{>0})^*$
made into a purely odd vector superspace and canonical skew-supersymmetric form, and
![]() $F^{\text {ne}}$
denotes the neutral free fermion vertex algebra associated with
$F^{\text {ne}}$
denotes the neutral free fermion vertex algebra associated with
![]() $\mathfrak {g}_\Gamma ^{1/2}$
and bilinear form
$\mathfrak {g}_\Gamma ^{1/2}$
and bilinear form
![]() $(x,y) \mapsto (f | [x,y])$
. We omit the detailed definition, referring the reader to ([Reference Kac, Roan and Wakimoto57]).
$(x,y) \mapsto (f | [x,y])$
. We omit the detailed definition, referring the reader to ([Reference Kac, Roan and Wakimoto57]).
The W-algebra
![]() $\mathscr {W}^k(\mathfrak {g},f)$
is conformal provided that
$\mathscr {W}^k(\mathfrak {g},f)$
is conformal provided that
![]() $k\ne -h_{\mathfrak {g}}^{\vee }$
and its central charge
$k\ne -h_{\mathfrak {g}}^{\vee }$
and its central charge
![]() $c_{\mathscr {W}^k(\mathfrak {g},f)}$
is given by
$c_{\mathscr {W}^k(\mathfrak {g},f)}$
is given by
 $$ \begin{align}& =\dim \mathfrak{g}_\Gamma^0 -\dfrac{1}{2} \dim \mathfrak{g}_\Gamma^{1/2} -\dfrac{12}{k+h_{\mathfrak{g}}^\vee} | \rho - (k+h_{\mathfrak{g}}^\vee) x^0_\Gamma |^2\qquad \end{align} $$
$$ \begin{align}& =\dim \mathfrak{g}_\Gamma^0 -\dfrac{1}{2} \dim \mathfrak{g}_\Gamma^{1/2} -\dfrac{12}{k+h_{\mathfrak{g}}^\vee} | \rho - (k+h_{\mathfrak{g}}^\vee) x^0_\Gamma |^2\qquad \end{align} $$
([Reference Kac, Roan and Wakimoto57, Theorem 2.2]). Although the vertex algebra structure of
![]() $\mathscr {W}^k(\mathfrak {g},f)$
does not depend on the choice of the good grading of
$\mathscr {W}^k(\mathfrak {g},f)$
does not depend on the choice of the good grading of
![]() $\mathfrak {g}$
([Reference Arakawa, Kuwabara and Malikov18, §3.2.5]), its conformal structure does. In general, we denote by
$\mathfrak {g}$
([Reference Arakawa, Kuwabara and Malikov18, §3.2.5]), its conformal structure does. In general, we denote by
![]() $\mathscr {W}_k(\mathfrak {g},f)$
the unique simple graded quotient of
$\mathscr {W}_k(\mathfrak {g},f)$
the unique simple graded quotient of
![]() $\mathscr {W}^k(\mathfrak {g},f)$
.
$\mathscr {W}^k(\mathfrak {g},f)$
.
Proposition 4.2. The vertex algebra
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is self-dual if the grading (19) is Dynkin.
$\mathscr {W}_k(\mathfrak {g},f)$
is self-dual if the grading (19) is Dynkin.
Proof. By [Reference Arakawa and van Ekeren14, Proposition 6.1 and Remark 6.2], it suffices to show that
![]() $(k+h^{\vee })(h|v)-\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for all
$(k+h^{\vee })(h|v)-\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for all
![]() $v\in \mathfrak {g}^f_0$
. Since
$v\in \mathfrak {g}^f_0$
. Since
![]() $(h|v)={([e,f]|v)}=0$
for
$(h|v)={([e,f]|v)}=0$
for
![]() $v\in \mathfrak {g}^f_0$
, in fact, it is enough to show that
$v\in \mathfrak {g}^f_0$
, in fact, it is enough to show that
![]() $\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
. Note that
$\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
. Note that
![]() $\mathfrak {g}^f_0$
is the centraliser
$\mathfrak {g}^f_0$
is the centraliser
![]() $\mathfrak {g}^\natural $
of the
$\mathfrak {g}^\natural $
of the
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $\{e,h,f\}$
in
$\{e,h,f\}$
in
![]() $\mathfrak {g}$
, which is a reductive Lie subalgebra of
$\mathfrak {g}$
, which is a reductive Lie subalgebra of
![]() $\mathfrak {g}$
. We clearly have
$\mathfrak {g}$
. We clearly have
![]() $\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for
$\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for
![]() $v\in [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
since
$v\in [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
since
![]() $\mathfrak {g}_{>0}$
is a finite-dimensional representation of the semisimple Lie algebra
$\mathfrak {g}_{>0}$
is a finite-dimensional representation of the semisimple Lie algebra
![]() $ [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
. However, Lemma 5.5 below shows that
$ [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
. However, Lemma 5.5 below shows that
![]() $\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for an element v in the centre
$\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} v)=0$
for an element v in the centre
![]() $\mathfrak {z}(\mathfrak {g}^\natural )$
of
$\mathfrak {z}(\mathfrak {g}^\natural )$
of
![]() $\mathfrak {g}^\natural $
as well.
$\mathfrak {g}^\natural $
as well.
We now discuss the associated varieties of affine W-algebras. The associated variety
![]() $X_{\mathscr {W}^k(\mathfrak {g},f) }$
of the universal W-algebra is isomorphic to the Slodowy slice
$X_{\mathscr {W}^k(\mathfrak {g},f) }$
of the universal W-algebra is isomorphic to the Slodowy slice
where
![]() $\mathfrak {g}^{e}$
is the centraliser of e in
$\mathfrak {g}^{e}$
is the centraliser of e in
![]() $\mathfrak {g}$
([Reference De Sole and Kac31]). There is a natural
$\mathfrak {g}$
([Reference De Sole and Kac31]). There is a natural
![]() $\mathbb {C}^*$
-action on
$\mathbb {C}^*$
-action on
![]() $\mathcal {S}_f$
that contracts to f ([Reference Slodowy77]), and the associated variety
$\mathcal {S}_f$
that contracts to f ([Reference Slodowy77]), and the associated variety
![]() $X_{\mathscr {W}_k(\mathfrak {g},f)}$
of the simple quotient is a
$X_{\mathscr {W}_k(\mathfrak {g},f)}$
of the simple quotient is a
![]() $\mathbb {C}^*$
-invariant subvariety of
$\mathbb {C}^*$
-invariant subvariety of
![]() $\mathcal {S}_f$
.
$\mathcal {S}_f$
.
Theorem 4.3 [Reference Arakawa10].
-
1. For any
 $M\in \operatorname {KL}_k$
, we have
$M\in \operatorname {KL}_k$
, we have
 $H_{DS,f}^i(M)=0$
for all
$H_{DS,f}^i(M)=0$
for all
 $i\ne 0$
. In particular, the functor
$i\ne 0$
. In particular, the functor
 $\operatorname {KL}_k\rightarrow \mathscr {W}^k(\mathfrak {g},f)\operatorname {-Mod}$
,
$\operatorname {KL}_k\rightarrow \mathscr {W}^k(\mathfrak {g},f)\operatorname {-Mod}$
,
 $M\mapsto H_{DS,f}^0(M)$
, is exact.
$M\mapsto H_{DS,f}^0(M)$
, is exact. -
2. The
 $\mathscr {W}^k(\mathfrak {g},f)$
-module
$\mathscr {W}^k(\mathfrak {g},f)$
-module
 $H_{DS,f}^0(M)$
is ordinary for any finitely generated object
$H_{DS,f}^0(M)$
is ordinary for any finitely generated object
 $M\in \operatorname {KL}_k$
.
$M\in \operatorname {KL}_k$
. -
3. For any quotient V of
 $V^k(\mathfrak {g})$
, the vertex algebra
$V^k(\mathfrak {g})$
, the vertex algebra
 $H_{DS,f}^{0}(V)$
is a quotient of
$H_{DS,f}^{0}(V)$
is a quotient of
 $\mathscr {W}^k(\mathfrak {g},f)$
provided that it is nonzero, and we have which is a
$\mathscr {W}^k(\mathfrak {g},f)$
provided that it is nonzero, and we have which is a $$ \begin{align*}X_{H_{DS,f}^{0}(V)}= X_V \cap \mathcal{S}_f,\end{align*} $$
$$ \begin{align*}X_{H_{DS,f}^{0}(V)}= X_V \cap \mathcal{S}_f,\end{align*} $$
 $\mathbb {C}^*$
-invariant subvariety of
$\mathbb {C}^*$
-invariant subvariety of
 $\mathcal {S}_f$
([Reference Arakawa10]). In particular,
$\mathcal {S}_f$
([Reference Arakawa10]). In particular,
-
(a)
 $ H_{DS,f}^0(L_k(\mathfrak {g})) \not =0$
if and only if
$ H_{DS,f}^0(L_k(\mathfrak {g})) \not =0$
if and only if
 $f \in X_{L_k(\mathfrak {g})}$
;
$f \in X_{L_k(\mathfrak {g})}$
; -
(b) If
 $G.f\subset X_{L_k(\mathfrak {g})}\subset \mathcal {N}$
, then
$G.f\subset X_{L_k(\mathfrak {g})}\subset \mathcal {N}$
, then
 $H_{DS,f}^{0}(V)$
is quasi-lisse and so is
$H_{DS,f}^{0}(V)$
is quasi-lisse and so is
 $\mathscr {W}_k(\mathfrak {g},f)$
;
$\mathscr {W}_k(\mathfrak {g},f)$
; -
(c) If
 $ X_{L_k(\mathfrak {g})}=\overline {G.f}$
, then
$ X_{L_k(\mathfrak {g})}=\overline {G.f}$
, then
 $H_{DS,f}^{0}(V)$
is lisse and so is
$H_{DS,f}^{0}(V)$
is lisse and so is
 $\mathscr {W}_k(\mathfrak {g},f)$
.
$\mathscr {W}_k(\mathfrak {g},f)$
.
-
Regarding the relationship between the simple W-algebra
![]() $\mathscr {W}_k(\mathfrak {g},f)$
and the reduction
$\mathscr {W}_k(\mathfrak {g},f)$
and the reduction
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
of which it is a quotient, there is the following natural conjecture.
$H_{DS,f}^0(L_k(\mathfrak {g}))$
of which it is a quotient, there is the following natural conjecture.
Conjecture 4.4 [Reference Kac, Roan and Wakimoto57, Reference Kac and Wakimoto61].
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
is either zero or isomorphic to
$H_{DS,f}^0(L_k(\mathfrak {g}))$
is either zero or isomorphic to
![]() $\mathscr {W}_k(\mathfrak {g},f)$
.
$\mathscr {W}_k(\mathfrak {g},f)$
.
This has been proved in many cases. Indeed, we have the following:
Theorem 4.5 [Reference Arakawa and van Ekeren14].
Conjecture 4.4 holds if k is an admissible level,
![]() $f\in X_{L_k(\mathfrak {g})}=\overline {{\mathbb {O}}}_k$
, and f admits an even good grading.
$f\in X_{L_k(\mathfrak {g})}=\overline {{\mathbb {O}}}_k$
, and f admits an even good grading.
Let k be an admissible level. By Theorems 3.2 and 4.3,
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is lisse if
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse if
![]() $f\in {{\mathbb {O}}}_k$
and is quasi-lisse if
$f\in {{\mathbb {O}}}_k$
and is quasi-lisse if
![]() $f\in \overline {{\mathbb {O}}}_k$
. Moreover, under the hypotheses of Theorem 4.5, the associated variety of
$f\in \overline {{\mathbb {O}}}_k$
. Moreover, under the hypotheses of Theorem 4.5, the associated variety of
![]() $ \mathscr {W}_k(\mathfrak {g},f)$
is equal to the nilpotent Slodowy slice
$ \mathscr {W}_k(\mathfrak {g},f)$
is equal to the nilpotent Slodowy slice
Conjecture 4.6 [Reference Arakawa10, Reference Frenkel, Kac and Wakimoto45, Reference Kac and Wakimoto61].
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is rational if k is admissible and
$\mathscr {W}_k(\mathfrak {g},f)$
is rational if k is admissible and
![]() $f\in {{\mathbb {O}}}_k$
.
$f\in {{\mathbb {O}}}_k$
.
Conjecture 4.6 has been settled positively by different methods in a number of cases – namely, for f principal [Reference Arakawa9], for
![]() $\mathfrak {g}$
of type A [Reference Arakawa and van Ekeren14], for
$\mathfrak {g}$
of type A [Reference Arakawa and van Ekeren14], for
![]() $\mathfrak {g}$
of type
$\mathfrak {g}$
of type
![]() $ADE$
and f subregular [Reference Arakawa and van Ekeren14], for
$ADE$
and f subregular [Reference Arakawa and van Ekeren14], for
![]() $\mathfrak {g}$
of type
$\mathfrak {g}$
of type
![]() $B_2$
and f subregular [Reference Fasquel40], for
$B_2$
and f subregular [Reference Fasquel40], for
![]() $\mathfrak {g}$
of type
$\mathfrak {g}$
of type
![]() $B_n$
and f subregular [Reference Creutzig and Linshaw33], for
$B_n$
and f subregular [Reference Creutzig and Linshaw33], for
![]() $\mathfrak {g}$
of type
$\mathfrak {g}$
of type
![]() $C_n$
and f minimal [Reference Creutzig and Linshaw33]. More recently, a general proof has been announced in [Reference McRae71].
$C_n$
and f minimal [Reference Creutzig and Linshaw33]. More recently, a general proof has been announced in [Reference McRae71].
By [Reference De Sole and Kac34], the associative algebra
![]() $\operatorname {Zhu}(\mathscr {W}^k(\mathfrak {g},f))$
is naturally isomorphic to the finite W-algebra [Reference Premet75]
$\operatorname {Zhu}(\mathscr {W}^k(\mathfrak {g},f))$
is naturally isomorphic to the finite W-algebra [Reference Premet75]
![]() $U(\mathfrak {g},f)$
associated with
$U(\mathfrak {g},f)$
associated with
![]() $(\mathfrak {g},f)$
. More generally, we have the following assertion.
$(\mathfrak {g},f)$
. More generally, we have the following assertion.
Theorem 4.7 [Reference Arakawa9].
There exists an isomorphism
where on the right-hand side
![]() $H_{DS,f}^{0}(?)$
is the finite-dimensional analogue of the Drinfeld-Sokolov reduction functor that is denoted by
$H_{DS,f}^{0}(?)$
is the finite-dimensional analogue of the Drinfeld-Sokolov reduction functor that is denoted by
![]() $M\mapsto M_{\dagger }$
in [Reference Losev69].
$M\mapsto M_{\dagger }$
in [Reference Losev69].
By [Reference Ginzburg48, Reference Losev70], see also [Reference Arakawa9, Section 2], we have the following equivalence:
From this, together with Theorems 3.4 and 4.7, we obtain the following:
Corollary 4.8. Let k be an admissible number. We have
where the product is taken over ![]() such that
such that ![]() .
.
The image
![]() $[\omega ]$
of the conformal vector of
$[\omega ]$
of the conformal vector of
![]() $\mathscr {W}^k(\mathfrak {g},f)$
in
$\mathscr {W}^k(\mathfrak {g},f)$
in
![]() $\operatorname {Zhu}(H_{DS,f}^{0}(L_k(\mathfrak {g}))$
acts on
$\operatorname {Zhu}(H_{DS,f}^{0}(L_k(\mathfrak {g}))$
acts on ![]() as the constant multiplication by
as the constant multiplication by

In particular, a simple module of
![]() $H_{DS,f}^{0}(L_k(\mathfrak {g}))$
corresponding to a simple module of
$H_{DS,f}^{0}(L_k(\mathfrak {g}))$
corresponding to a simple module of ![]() via Corollary 4.8 has the conformal dimension
via Corollary 4.8 has the conformal dimension ![]() .
.
For a
![]() $V^k(\mathfrak {g})$
-module M, we consider the character of its reduction – that is, we set
$V^k(\mathfrak {g})$
-module M, we consider the character of its reduction – that is, we set
when it is well defined. Here,
Note that ![]() is well defined for finitely generated objects M of
is well defined for finitely generated objects M of
![]() $\operatorname {KL}_k$
, by Theorem 4.3, and we have
$\operatorname {KL}_k$
, by Theorem 4.3, and we have
Proposition 4.9. Let
![]() $M\in \mathcal {O}_k$
be a
$M\in \mathcal {O}_k$
be a
![]() $V^k(\mathfrak {g})$
-module whose character has asymptotic behaviour
$V^k(\mathfrak {g})$
-module whose character has asymptotic behaviour
and suppose that
![]() $\chi _{H^{\bullet }_{DS, f} (M)}(\tau ,z)$
is well defined. Then
$\chi _{H^{\bullet }_{DS, f} (M)}(\tau ,z)$
is well defined. Then
where

Proof. Let us write
 $$ \begin{align*} \chi_M(\tau,z,t)=\frac{(A_{\widehat{\rho}}\chi_M)(\tau,z,t)}{A_{\widehat{\rho}}(\tau,z,t)}. \end{align*} $$
$$ \begin{align*} \chi_M(\tau,z,t)=\frac{(A_{\widehat{\rho}}\chi_M)(\tau,z,t)}{A_{\widehat{\rho}}(\tau,z,t)}. \end{align*} $$
The asymptotic behaviour of
![]() $A_{\widehat {\rho }}(\tau ,z,t)$
is well known [Reference Kac54, Proposition 13.13] to be
$A_{\widehat {\rho }}(\tau ,z,t)$
is well known [Reference Kac54, Proposition 13.13] to be
where
Hence,
 $$ \begin{align} &\chi_M(\tau,-\tau z,0)\sim \mathbf{A}_M(z) (-{\mathrm{i}} \tau)^{\mathbf{w}_M}e^{\frac{\pi {\mathrm{i}} }{12 \tau}\mathbf{g}_M} \\ &\iff (A_{\widehat{\rho}}\chi_M)(\tau,-\tau z,0)\sim b(\rho,z)A(\rho,z) (-{\mathrm{i}} \tau)^{\mathbf{w}_M-\frac{\ell}{2}} e^{\frac{\pi {\mathrm{i}} }{12 \tau}(\mathbf{g}_M-\dim \mathfrak{g})}. \nonumber \end{align} $$
$$ \begin{align} &\chi_M(\tau,-\tau z,0)\sim \mathbf{A}_M(z) (-{\mathrm{i}} \tau)^{\mathbf{w}_M}e^{\frac{\pi {\mathrm{i}} }{12 \tau}\mathbf{g}_M} \\ &\iff (A_{\widehat{\rho}}\chi_M)(\tau,-\tau z,0)\sim b(\rho,z)A(\rho,z) (-{\mathrm{i}} \tau)^{\mathbf{w}_M-\frac{\ell}{2}} e^{\frac{\pi {\mathrm{i}} }{12 \tau}(\mathbf{g}_M-\dim \mathfrak{g})}. \nonumber \end{align} $$
Now by Theorem 4.3 and the Euler-Poincaré principle (see the discussion in [Reference Kac and Wakimoto61, Section 2]),

Here,
![]() $L_0^{\text {Sug}}$
denotes the zero mode of the Sugawara conformal vector in
$L_0^{\text {Sug}}$
denotes the zero mode of the Sugawara conformal vector in
![]() $V^k(\mathfrak {g})$
while
$V^k(\mathfrak {g})$
while
![]() $L_0^{\text {ch}}$
and
$L_0^{\text {ch}}$
and
![]() $L_0^{\text {ne}}$
denote the conformal vectors in
$L_0^{\text {ne}}$
denote the conformal vectors in
![]() $F^{\text {ch}}$
and
$F^{\text {ch}}$
and
![]() $F^{\text {ne}}$
given in [Reference Kac, Roan and Wakimoto57, Section 2.2], or in [Reference Kac and Wakimoto61, Section 2.1]. We thus have
$F^{\text {ne}}$
given in [Reference Kac, Roan and Wakimoto57, Section 2.2], or in [Reference Kac and Wakimoto61, Section 2.1]. We thus have

in which

We now describe the proof of (27) briefly, referring the reader to [Reference Kac and Wakimoto61, Section 2.2] for details. The numerator of (27) comes directly from the numerator of the expression (13) for ![]() . The modification
. The modification
![]() $z \mapsto z - \tau x_\Gamma ^0$
corresponds to the shift of Virasoro operator
$z \mapsto z - \tau x_\Gamma ^0$
corresponds to the shift of Virasoro operator
![]() $L_0^{\text {Sug}} \mapsto L_0^{\text {Sug}} - (x_\Gamma ^0)_0$
. The Weyl denominator is
$L_0^{\text {Sug}} \mapsto L_0^{\text {Sug}} - (x_\Gamma ^0)_0$
. The Weyl denominator is
![]() $\eta (\tau )^\ell $
times a product of theta functions indexed by
$\eta (\tau )^\ell $
times a product of theta functions indexed by
![]() $\alpha \in \Delta _+$
. At the level of characters, the effect of the tensor product with
$\alpha \in \Delta _+$
. At the level of characters, the effect of the tensor product with
![]() $F^{\text {ch}}$
is to cancel those factors associated with
$F^{\text {ch}}$
is to cancel those factors associated with
![]() $\alpha \in \Delta _{\Gamma }^j$
for
$\alpha \in \Delta _{\Gamma }^j$
for
![]() $j> 0$
. The tensor product with
$j> 0$
. The tensor product with
![]() $F^{\text {ne}}$
reintroduces those factors associated with
$F^{\text {ne}}$
reintroduces those factors associated with
![]() $\alpha \in \Delta _{\Gamma , +}^{1/2}$
(whose cardinality is half that of
$\alpha \in \Delta _{\Gamma , +}^{1/2}$
(whose cardinality is half that of
![]() $\Delta _{\Gamma }^{1/2}$
). Ultimately, this yields the denominator
$\Delta _{\Gamma }^{1/2}$
). Ultimately, this yields the denominator
![]() $\psi (\tau , z - \tau x_\Gamma ^0, t)$
of (27).
$\psi (\tau , z - \tau x_\Gamma ^0, t)$
of (27).
The function
![]() $\psi $
satisfies the asymptotic
$\psi $
satisfies the asymptotic
 $$ \begin{align} \psi(\tau, -\tau z, 0) \sim \prod_{\alpha \in \Delta_{\Gamma, +}^{0} \cup \Delta^{1/2}_{\Gamma, +}} 2 \sin\ \pi(\alpha | z) (-{\mathrm{i}} \tau)^{-\ell/2} e^{\pi {\mathrm{i}} \dim(\mathfrak{g}^f) / 12\tau} \end{align} $$
$$ \begin{align} \psi(\tau, -\tau z, 0) \sim \prod_{\alpha \in \Delta_{\Gamma, +}^{0} \cup \Delta^{1/2}_{\Gamma, +}} 2 \sin\ \pi(\alpha | z) (-{\mathrm{i}} \tau)^{-\ell/2} e^{\pi {\mathrm{i}} \dim(\mathfrak{g}^f) / 12\tau} \end{align} $$
as
![]() $\tau \downarrow 0$
. The asymptotic behaviour of the numerator
$\tau \downarrow 0$
. The asymptotic behaviour of the numerator
![]() $A_{\nu +\widehat {\rho }}(\tau , z - \tau x_\Gamma ^0, t)$
was established in the proof of Proposition 3.8. The required asymptotic follows from (26), (27) and (28), together with the fact that
$A_{\nu +\widehat {\rho }}(\tau , z - \tau x_\Gamma ^0, t)$
was established in the proof of Proposition 3.8. The required asymptotic follows from (26), (27) and (28), together with the fact that
Proposition 4.10. Let
![]() $k =-h_{\mathfrak {g}}^\vee +\dfrac {p}{q}$
be an admissible level, and let
$k =-h_{\mathfrak {g}}^\vee +\dfrac {p}{q}$
be an admissible level, and let
![]() $f \in X_{L_k(\mathfrak {g})}$
. Then
$f \in X_{L_k(\mathfrak {g})}$
. Then ![]() admits an asymptotic datum for all simple ordinary
admits an asymptotic datum for all simple ordinary
![]() $L_k(\mathfrak {g})$
-modules
$L_k(\mathfrak {g})$
-modules ![]() with
with ![]() . Moreover,
. Moreover,
-
1. ([Reference Kac and Wakimoto61]) For
 ,
, 
-
2. For
 ,
, 
In particular,
for any simple ordinary
![]() $L_k(\mathfrak {g})$
-module
$L_k(\mathfrak {g})$
-module ![]() .
.
Proof. Let k be coprincipal and let ![]() . By Proposition 3.8 and Proposition 4.9, we have
. By Proposition 3.8 and Proposition 4.9, we have

where
![]() $\nu $
,
$\nu $
,
![]() $\bar y$
are related with
$\bar y$
are related with ![]() as in Proposition 3.8.
as in Proposition 3.8.
We are interested in the case ![]() which corresponds to
which corresponds to
![]() $\overline y = 1$
,
$\overline y = 1$
,
![]() $\beta = 0$
and
$\beta = 0$
and ![]() . We now simplify the products appearing in the asymptotic above to
. We now simplify the products appearing in the asymptotic above to

The second product here becomes simply
![]() $2^{-|\Delta _{\Gamma }^{1/2}|/2}$
. In the third product, the terms
$2^{-|\Delta _{\Gamma }^{1/2}|/2}$
. In the third product, the terms
![]() $x_\Gamma ^0$
are irrelevant since
$x_\Gamma ^0$
are irrelevant since
![]() $\alpha \in \Delta _{\Gamma , +}^0$
. In the limit
$\alpha \in \Delta _{\Gamma , +}^0$
. In the limit
![]() $z \rightarrow 0$
, this product reduces, by l’Hopital’s rule, to
$z \rightarrow 0$
, this product reduces, by l’Hopital’s rule, to
 $$ \begin{align*} \prod_{\alpha \in \Delta_{\Gamma, +}^{0}} \frac{|\alpha^\vee|/q}{|\alpha|} = \frac{(r^\vee)^{|\Delta_{\Gamma, +}^0 \cap \Delta^{\text{short}}|}}{q^{|\Delta_{\Gamma, +}^0|}}. \end{align*} $$
$$ \begin{align*} \prod_{\alpha \in \Delta_{\Gamma, +}^{0}} \frac{|\alpha^\vee|/q}{|\alpha|} = \frac{(r^\vee)^{|\Delta_{\Gamma, +}^0 \cap \Delta^{\text{short}}|}}{q^{|\Delta_{\Gamma, +}^0|}}. \end{align*} $$
In the fourth product, the limit obtains by simply putting
![]() $z=0$
. Thus, we have obtained the stated formula.
$z=0$
. Thus, we have obtained the stated formula.
Theorem 4.11. Let k be admissible, and let
![]() $f\in \mathfrak {g}$
be a nilpotent element that admits an even good grading.
$f\in \mathfrak {g}$
be a nilpotent element that admits an even good grading.
-
1. Let
 $f\in \overline {\mathbb {O}}_k$
, so that
$f\in \overline {\mathbb {O}}_k$
, so that
 $H_{DS,f}^0(L_k(\mathfrak {g}))\cong \mathscr {W}_k(\mathfrak {g},f)$
(see Theorem 4.5). Then
$H_{DS,f}^0(L_k(\mathfrak {g}))\cong \mathscr {W}_k(\mathfrak {g},f)$
(see Theorem 4.5). Then  is the minimal conformal dimension among simple positive energy representations of
is the minimal conformal dimension among simple positive energy representations of
 $\mathscr {W}_k(\mathfrak {g},f)$
(see (17) and (24)), and we have
$\mathscr {W}_k(\mathfrak {g},f)$
(see (17) and (24)), and we have 
-
2. Suppose further that
 $f\in \mathbb {O}_k$
, so that
$f\in \mathbb {O}_k$
, so that
 $\mathscr {W}_k(\mathfrak {g},f)$
is lisse. Then there exists a unique simple
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse. Then there exists a unique simple
 $\mathscr {W}_k(\mathfrak {g},f)$
-module that has the minimal conformal dimension
$\mathscr {W}_k(\mathfrak {g},f)$
-module that has the minimal conformal dimension  .
.
Proof. First, we treat (1). By Theorem 3.11, ![]() , which contains the orbit
, which contains the orbit
![]() $G.f$
by the assumption. Hence,
$G.f$
by the assumption. Hence, ![]() is nonzero by (23). It follows from Corollary 4.8 that there exists a simple
is nonzero by (23). It follows from Corollary 4.8 that there exists a simple
![]() $\mathscr {W}_k(\mathfrak {g},f)$
-module, corresponding to a simple
$\mathscr {W}_k(\mathfrak {g},f)$
-module, corresponding to a simple ![]() -module, which has the minimal conformal dimension
-module, which has the minimal conformal dimension ![]() among simple positive energy representations of
among simple positive energy representations of
![]() $\mathscr {W}_k(\mathfrak {g},f)$
by Proposition 3.13 and (24). Next, we have
$\mathscr {W}_k(\mathfrak {g},f)$
by Proposition 3.13 and (24). Next, we have

where
![]() $\Gamma $
is a good even grading. Hence, the assertion follows from (21) and the fact that
$\Gamma $
is a good even grading. Hence, the assertion follows from (21) and the fact that
![]() $\dim \mathfrak {g}_{1/2}=0$
, which is true by hypothesis.
$\dim \mathfrak {g}_{1/2}=0$
, which is true by hypothesis.
Now we turn to (2). By [Reference Arakawa and van Ekeren14], each factor ![]() in Corollary 4.8 is a simple algebra, which has a unique simple module. Hence, the assertion follows from Remark 3.14.
in Corollary 4.8 is a simple algebra, which has a unique simple module. Hence, the assertion follows from Remark 3.14.
In view of Proposition 2.4, Theorem 4.11 gives a supporting evidence for Conjecture 4.6.
5 Collapsing levels for W-algebras
In general, if
![]() $\mathfrak {s}$
is a semisimple Lie algebra, we write
$\mathfrak {s}$
is a semisimple Lie algebra, we write
![]() $\kappa _{\mathfrak {s}}$
for the Killing form of
$\kappa _{\mathfrak {s}}$
for the Killing form of
![]() $\mathfrak {s}$
. For now, we assume that
$\mathfrak {s}$
. For now, we assume that
![]() $\mathfrak {s}$
is simple. We denote by
$\mathfrak {s}$
is simple. We denote by
![]() $h_{\mathfrak {s}}^\vee $
its dual Coxeter number and by
$h_{\mathfrak {s}}^\vee $
its dual Coxeter number and by
![]() $(~|~)_{\mathfrak {s}}$
the normalised inner product
$(~|~)_{\mathfrak {s}}$
the normalised inner product
![]() $\dfrac {1}{2h_{\mathfrak {s}}^\vee } \kappa _{\mathfrak {s}}$
so that
$\dfrac {1}{2h_{\mathfrak {s}}^\vee } \kappa _{\mathfrak {s}}$
so that
![]() $(\theta | \theta )=2$
for
$(\theta | \theta )=2$
for
![]() $\theta $
the highest positive root of
$\theta $
the highest positive root of
![]() $\mathfrak {s}$
.
$\mathfrak {s}$
.
As in Section 4, we fix an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
of
$(e,h,f)$
of
![]() $\mathfrak {g}$
, with related notation. In particular, for
$\mathfrak {g}$
, with related notation. In particular, for
![]() $j \in \frac {1}{2}\mathbb {Z}$
, recall that
$j \in \frac {1}{2}\mathbb {Z}$
, recall that
and
![]() $\mathfrak {g}^0$
is the centraliser of h in
$\mathfrak {g}^0$
is the centraliser of h in
![]() $\mathfrak {g}$
. The centraliser
$\mathfrak {g}$
. The centraliser
![]() $\mathfrak {g}^\natural $
of the
$\mathfrak {g}^\natural $
of the
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
in
$(e,h,f)$
in
![]() $\mathfrak {g}$
is given by
$\mathfrak {g}$
is given by
The Lie algebra
![]() $\mathfrak {g}^\natural $
is a reductive subalgebra of
$\mathfrak {g}^\natural $
is a reductive subalgebra of
![]() $\mathfrak {g}$
. The centraliser
$\mathfrak {g}$
. The centraliser
![]() $G^\natural $
of the
$G^\natural $
of the
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
in G is a maximal reductive subgroup of the centraliser of f in G whose Lie algebra is
$(e,h,f)$
in G is a maximal reductive subgroup of the centraliser of f in G whose Lie algebra is
![]() $\mathfrak {g}^\natural $
. We can write
$\mathfrak {g}^\natural $
. We can write
![]() $\mathfrak {g}^\natural = \mathfrak {g}_0^\natural \oplus [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
, with
$\mathfrak {g}^\natural = \mathfrak {g}_0^\natural \oplus [\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
, with
![]() $\mathfrak {g}_0^\natural $
the centre of the reductive Lie algebra
$\mathfrak {g}_0^\natural $
the centre of the reductive Lie algebra
![]() $\mathfrak {g}^\natural $
. Denoting by
$\mathfrak {g}^\natural $
. Denoting by ![]() the simple factors of
the simple factors of
![]() $[\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
, we get
$[\mathfrak {g}^\natural ,\mathfrak {g}^\natural ]$
, we get
 $$ \begin{align*}\mathfrak{g}^\natural=\bigoplus_{i=0}^s \mathfrak{g}^\natural_i.\end{align*} $$
$$ \begin{align*}\mathfrak{g}^\natural=\bigoplus_{i=0}^s \mathfrak{g}^\natural_i.\end{align*} $$
More generally, for
![]() $\mathfrak {g}_\Gamma = \bigoplus _{j \in \frac {1}{2}\mathbb {Z}} \mathfrak {g}_\Gamma ^j$
a good grading for f, we set
$\mathfrak {g}_\Gamma = \bigoplus _{j \in \frac {1}{2}\mathbb {Z}} \mathfrak {g}_\Gamma ^j$
a good grading for f, we set
We note that
![]() $\mathfrak {g}_\Gamma ^\natural $
is not a reductive Lie algebra in general. In fact,
$\mathfrak {g}_\Gamma ^\natural $
is not a reductive Lie algebra in general. In fact,
![]() $\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
$\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
![]() $\mathfrak {g}_\Gamma ^\natural $
. Indeed, by [Reference Elashvili, Kac and Vinberg38, Lemma 1.2],
$\mathfrak {g}_\Gamma ^\natural $
. Indeed, by [Reference Elashvili, Kac and Vinberg38, Lemma 1.2],
![]() $\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
$\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
![]() $\mathfrak {g}^f$
while, on the other hand, since
$\mathfrak {g}^f$
while, on the other hand, since
![]() $\mathfrak {g}^\natural $
is reductive and contained in
$\mathfrak {g}^\natural $
is reductive and contained in
![]() $\bigoplus _{j \ge 0} \mathfrak {g}_\Gamma ^j$
, we have
$\bigoplus _{j \ge 0} \mathfrak {g}_\Gamma ^j$
, we have
![]() $\mathfrak {g}^\natural \subset \mathfrak {g}_\Gamma ^0$
.
$\mathfrak {g}^\natural \subset \mathfrak {g}_\Gamma ^0$
.
Let ![]() . For any element
. For any element
![]() $x \in \mathfrak {g}_i^\natural \subset \mathfrak {g}_\Gamma ^\natural $
, the adjoint action
$x \in \mathfrak {g}_i^\natural \subset \mathfrak {g}_\Gamma ^\natural $
, the adjoint action
![]() $\operatorname {\mathrm {ad}} x$
restricts to an endomorphism of
$\operatorname {\mathrm {ad}} x$
restricts to an endomorphism of
![]() $\mathfrak {g}_\Gamma ^{j}$
, which we denote
$\mathfrak {g}_\Gamma ^{j}$
, which we denote
![]() $\rho _x^{j}$
, for any j. Setting
$\rho _x^{j}$
, for any j. Setting
![]() $\kappa _{\mathfrak {g}_\Gamma ^{j}}(x,x)=\mathrm {tr}(\rho _x^{j} \circ \rho _x^{j} )$
, one defines an invariant bilinear form on
$\kappa _{\mathfrak {g}_\Gamma ^{j}}(x,x)=\mathrm {tr}(\rho _x^{j} \circ \rho _x^{j} )$
, one defines an invariant bilinear form on
![]() $\mathfrak {g}_{i}^\natural $
by (see [Reference Kac and Wakimoto60, Theorem 2.1] for the case where
$\mathfrak {g}_{i}^\natural $
by (see [Reference Kac and Wakimoto60, Theorem 2.1] for the case where
![]() $\Gamma $
is the Dynkin grading)
$\Gamma $
is the Dynkin grading)
Thus, for
![]() $i \not =0$
, there exists a scalar
$i \not =0$
, there exists a scalar
![]() $k_{\Gamma ,i}^\natural $
such that
$k_{\Gamma ,i}^\natural $
such that
Note that
![]() $V^{\phi _{\Gamma ,0}^\natural } (\mathfrak {g}_0^\natural ) \cong M(1)^{\otimes \mathrm {rank}\, \phi _{\Gamma ,0}^\natural }$
, where
$V^{\phi _{\Gamma ,0}^\natural } (\mathfrak {g}_0^\natural ) \cong M(1)^{\otimes \mathrm {rank}\, \phi _{\Gamma ,0}^\natural }$
, where
![]() $M(1)$
is the Heisenberg vertex algebra of central charge 1.
$M(1)$
is the Heisenberg vertex algebra of central charge 1.
Following [Reference Brundan and Goodwin30], we say that two good gradings
![]() $\Gamma ,\Gamma '$
are adjacent if
$\Gamma ,\Gamma '$
are adjacent if

where
![]() $i^-$
denotes the largest half-integer strictly smaller than i and
$i^-$
denotes the largest half-integer strictly smaller than i and
![]() $i^+$
denotes the smallest half-integer strictly greater than i.
$i^+$
denotes the smallest half-integer strictly greater than i.
Lemma 5.1. Let
![]() $\Gamma ,\Gamma '$
be two good gradings for f. If
$\Gamma ,\Gamma '$
be two good gradings for f. If
![]() $\Gamma ,\Gamma '$
are adjacent, then
$\Gamma ,\Gamma '$
are adjacent, then
![]() $\phi _{\Gamma ,i}^\natural =\phi _{\Gamma ',i}^\natural $
for
$\phi _{\Gamma ,i}^\natural =\phi _{\Gamma ',i}^\natural $
for ![]() .
.
Proof. According to [Reference Brundan and Goodwin30, Theorem 2 and Lemma 26], there are Lagrangian subspaces
![]() $\mathfrak {l}_{\Gamma }$
and
$\mathfrak {l}_{\Gamma }$
and
![]() $\mathfrak {l}_{\Gamma '}$
of
$\mathfrak {l}_{\Gamma '}$
of
![]() $\mathfrak {g}_{\Gamma }^{1/2}$
and
$\mathfrak {g}_{\Gamma }^{1/2}$
and
![]() $\mathfrak {g}_{\Gamma '}^{1/2}$
, respectively, with respect to the non-degenerate bilinear form
$\mathfrak {g}_{\Gamma '}^{1/2}$
, respectively, with respect to the non-degenerate bilinear form
![]() $ (f | [ \cdot ,\cdot ])$
such that
$ (f | [ \cdot ,\cdot ])$
such that
where
![]() $\mathfrak {a}^-$
denotes the dual space to the subspace
$\mathfrak {a}^-$
denotes the dual space to the subspace
![]() $\mathfrak {a} \subset \mathfrak {g}$
with respect to the Killing form of
$\mathfrak {a} \subset \mathfrak {g}$
with respect to the Killing form of
![]() $\mathfrak {g}$
. Then for any
$\mathfrak {g}$
. Then for any
![]() $x \in \mathfrak {g}^\natural $
,
$x \in \mathfrak {g}^\natural $
,
 $$ \begin{align*} \kappa_{\mathfrak{g}}(x,x) - \kappa_{\mathfrak{g}_{\Gamma}^0}(x,x)-\kappa_{\mathfrak{g}_{\Gamma}^{1/2}}(x,x) & =2 \kappa_{\mathfrak{l}_\Gamma \oplus \mathfrak{g}_\Gamma^ {>1/2}}(x,x) \\ & = \kappa_{\mathfrak{g}}(x,x) - \kappa_{\mathfrak{g}_{\Gamma'}^0}(x,x)-\kappa_{\mathfrak{g}_{\Gamma'}^{1/2}}(x,x). \end{align*} $$
$$ \begin{align*} \kappa_{\mathfrak{g}}(x,x) - \kappa_{\mathfrak{g}_{\Gamma}^0}(x,x)-\kappa_{\mathfrak{g}_{\Gamma}^{1/2}}(x,x) & =2 \kappa_{\mathfrak{l}_\Gamma \oplus \mathfrak{g}_\Gamma^ {>1/2}}(x,x) \\ & = \kappa_{\mathfrak{g}}(x,x) - \kappa_{\mathfrak{g}_{\Gamma'}^0}(x,x)-\kappa_{\mathfrak{g}_{\Gamma'}^{1/2}}(x,x). \end{align*} $$
Indeed, from the decompositions
 $$ \begin{align*} \mathfrak{g} & = (\mathfrak{l}_\Gamma^- \oplus \mathfrak{g}_\Gamma^ {<-1/2}) \oplus (\mathfrak{k}_{\Gamma}^- \oplus \mathfrak{g}_{\Gamma}^0 \oplus \mathfrak{k}_{\Gamma}) \oplus (\mathfrak{l}_\Gamma \oplus \mathfrak{g}_\Gamma^ {>1/2}), \\ \mathfrak{g} & = (\mathfrak{l}_{\Gamma'}^- \oplus \mathfrak{g}_{\Gamma'}^ {<-1/2}) \oplus (\mathfrak{k}_{\Gamma'}^- \oplus \mathfrak{g}_{\Gamma'}^0 \oplus \mathfrak{k}_{\Gamma'}) \oplus (\mathfrak{l}_{\Gamma'} \oplus \mathfrak{g}_{\Gamma'}^ {>1/2}), \end{align*} $$
$$ \begin{align*} \mathfrak{g} & = (\mathfrak{l}_\Gamma^- \oplus \mathfrak{g}_\Gamma^ {<-1/2}) \oplus (\mathfrak{k}_{\Gamma}^- \oplus \mathfrak{g}_{\Gamma}^0 \oplus \mathfrak{k}_{\Gamma}) \oplus (\mathfrak{l}_\Gamma \oplus \mathfrak{g}_\Gamma^ {>1/2}), \\ \mathfrak{g} & = (\mathfrak{l}_{\Gamma'}^- \oplus \mathfrak{g}_{\Gamma'}^ {<-1/2}) \oplus (\mathfrak{k}_{\Gamma'}^- \oplus \mathfrak{g}_{\Gamma'}^0 \oplus \mathfrak{k}_{\Gamma'}) \oplus (\mathfrak{l}_{\Gamma'} \oplus \mathfrak{g}_{\Gamma'}^ {>1/2}), \end{align*} $$
where
![]() $\mathfrak {k}_\Gamma $
(resp.
$\mathfrak {k}_\Gamma $
(resp.
![]() $\mathfrak {k}_{\Gamma '}$
) is a Lagrangian complement in
$\mathfrak {k}_{\Gamma '}$
) is a Lagrangian complement in
![]() $\mathfrak {g}_\Gamma ^{1/2}$
(resp.
$\mathfrak {g}_\Gamma ^{1/2}$
(resp.
![]() $\mathfrak {g}_{\Gamma '}^{1/2}$
) to
$\mathfrak {g}_{\Gamma '}^{1/2}$
) to
![]() $\unicode{x0142} _\Gamma $
(resp.
$\unicode{x0142} _\Gamma $
(resp.
![]() $\mathfrak {l}_{\Gamma '}$
), we deduce that
$\mathfrak {l}_{\Gamma '}$
), we deduce that
This completes the proof.
Denoting by
![]() $\Gamma _D$
the Dynkin grading, we set
$\Gamma _D$
the Dynkin grading, we set
Remark 5.2. In type A, according to [Reference Brundan and Goodwin30, Lemma 26 and Section 6], there is a chain ![]() of good gradings for f such that
of good gradings for f such that
![]() $\Gamma _0=\Gamma _D$
,
$\Gamma _0=\Gamma _D$
,
![]() $\Gamma _t=\Gamma $
, and for any
$\Gamma _t=\Gamma $
, and for any ![]() ,
,
![]() $\Gamma _{i-1}$
and
$\Gamma _{i-1}$
and
![]() $\Gamma _i$
are adjacent, and one of these good gradings is even. Hence, in type A, we are free to use an even good grading
$\Gamma _i$
are adjacent, and one of these good gradings is even. Hence, in type A, we are free to use an even good grading
![]() $\Gamma $
to compute
$\Gamma $
to compute
![]() $k_i^\natural $
, which is convenient (see the proof of Lemma 8.4).
$k_i^\natural $
, which is convenient (see the proof of Lemma 8.4).
Set
 $$ \begin{align} V^{k^\natural}(\mathfrak{g}^\natural) := V^{\phi_0^\natural} (\mathfrak{g}_0^\natural) \otimes \bigotimes_{i=1}^s V^{k_i^\natural} (\mathfrak{g}_i^\natural). \end{align} $$
$$ \begin{align} V^{k^\natural}(\mathfrak{g}^\natural) := V^{\phi_0^\natural} (\mathfrak{g}_0^\natural) \otimes \bigotimes_{i=1}^s V^{k_i^\natural} (\mathfrak{g}_i^\natural). \end{align} $$
By [Reference Kac and Wakimoto60, Theorem 2.1], there exists an embedding
of vertex algebras. We have
We denote by
![]() $\mathcal {V}^k(\mathfrak {g}^\natural )$
the image in
$\mathcal {V}^k(\mathfrak {g}^\natural )$
the image in
![]() $\mathscr {W}^k(\mathfrak {g},f)$
of the embedding
$\mathscr {W}^k(\mathfrak {g},f)$
of the embedding
![]() $\iota $
, and by
$\iota $
, and by
![]() $\mathcal {V}_k(\mathfrak {g}^\natural )$
the image of
$\mathcal {V}_k(\mathfrak {g}^\natural )$
the image of
![]() $\mathcal {V}^k(\mathfrak {g}^\natural )$
by the canonical projection
$\mathcal {V}^k(\mathfrak {g}^\natural )$
by the canonical projection
![]() $\pi \colon \mathscr {W}^k(\mathfrak {g},f) \twoheadrightarrow \mathscr {W}_k(\mathfrak {g},f)$
.
$\pi \colon \mathscr {W}^k(\mathfrak {g},f) \twoheadrightarrow \mathscr {W}_k(\mathfrak {g},f)$
.
Definition 5.3 [Reference Adamović, Kac, Frajria, Papi and Perše3].
If
![]() $ \mathscr {W}_k(\mathfrak {g},f) \cong \mathcal {V}_k(\mathfrak {g}^\natural )$
, we say that the level k is collapsing.
$ \mathscr {W}_k(\mathfrak {g},f) \cong \mathcal {V}_k(\mathfrak {g}^\natural )$
, we say that the level k is collapsing.
Lemma 5.4. The level k is collapsing if and only if
where
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
stands for
$L_{k^\natural }(\mathfrak {g}^\natural )$
stands for
 $\displaystyle {\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i^\natural )}$
. Equivalently, k is collapsing for
$\displaystyle {\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i^\natural )}$
. Equivalently, k is collapsing for
![]() $\mathscr {W}^k(\mathfrak {g},f)$
if and only if there exists a surjective vertex algebra homomorphism
$\mathscr {W}^k(\mathfrak {g},f)$
if and only if there exists a surjective vertex algebra homomorphism
For example, if
![]() $ \mathscr {W}_k(\mathfrak {g},f) \cong \mathbb {C}$
, then k is collapsing.
$ \mathscr {W}_k(\mathfrak {g},f) \cong \mathbb {C}$
, then k is collapsing.
Proof. If
![]() $\mathscr {W}_k(\mathfrak {g},f) \cong \mathcal {V}_k(\mathfrak {g}^\natural )$
, then
$\mathscr {W}_k(\mathfrak {g},f) \cong \mathcal {V}_k(\mathfrak {g}^\natural )$
, then
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is isomorphic to the quotient of
$\mathscr {W}_k(\mathfrak {g},f)$
is isomorphic to the quotient of
![]() $\bigotimes _{i=0}^s V^{k_i^\natural } (\mathfrak {g}_i)$
by the kernel of the composition
$\bigotimes _{i=0}^s V^{k_i^\natural } (\mathfrak {g}_i)$
by the kernel of the composition
![]() $\pi \circ \iota $
. Since
$\pi \circ \iota $
. Since
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is simple, we deduce that this quotient is isomorphic to
$\mathscr {W}_k(\mathfrak {g},f)$
is simple, we deduce that this quotient is isomorphic to
![]() ${\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)}=L_{k^\natural }(\mathfrak {g}^\natural )$
. Conversely, if
${\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)}=L_{k^\natural }(\mathfrak {g}^\natural )$
. Conversely, if
![]() $ \mathscr {W}_k(\mathfrak {g},f) \cong \bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)$
, then
$ \mathscr {W}_k(\mathfrak {g},f) \cong \bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)$
, then
![]() $\pi \circ \iota $
factorises through
$\pi \circ \iota $
factorises through
![]() $\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)$
, and so
$\bigotimes _{i=0}^s L_{k_i^\natural } (\mathfrak {g}_i)$
, and so
![]() $ \mathscr {W}_k(\mathfrak {g},f)$
is isomorphic to the image of this induced map, so
$ \mathscr {W}_k(\mathfrak {g},f)$
is isomorphic to the image of this induced map, so
![]() $ \mathscr {W}_k(\mathfrak {g},f)\cong \mathcal {V}_k(\mathfrak {g}^\natural )$
.
$ \mathscr {W}_k(\mathfrak {g},f)\cong \mathcal {V}_k(\mathfrak {g}^\natural )$
.
We close this section with a lemma which is used above in the proof of Proposition 4.2.
Lemma 5.5. The centre
![]() $\mathfrak {z}(\mathfrak {g}^\natural )$
of the reductive Lie algebra
$\mathfrak {z}(\mathfrak {g}^\natural )$
of the reductive Lie algebra
![]() $\mathfrak {g}^\natural $
consists of semisimple elements of
$\mathfrak {g}^\natural $
consists of semisimple elements of
![]() $\mathfrak {g}$
. Moreover, for any
$\mathfrak {g}$
. Moreover, for any
![]() $x \in \mathfrak {z}(\mathfrak {g}^\natural )$
, we have
$x \in \mathfrak {z}(\mathfrak {g}^\natural )$
, we have
![]() $\mathrm {tr}_{\mathfrak {g}^{f}}(\operatorname {\mathrm {ad}} x) =0$
and
$\mathrm {tr}_{\mathfrak {g}^{f}}(\operatorname {\mathrm {ad}} x) =0$
and
![]() $\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} x) =0$
, where
$\mathrm {tr}_{\mathfrak {g}_{>0}}(\operatorname {\mathrm {ad}} x) =0$
, where
![]() $\operatorname {\mathrm {ad}}_x$
stands for the endomorphism of
$\operatorname {\mathrm {ad}}_x$
stands for the endomorphism of
![]() $\mathfrak {g}^{f}$
(resp.
$\mathfrak {g}^{f}$
(resp.
![]() $\mathfrak {g}_{>0}$
) induced from the adjoint action of x acting on
$\mathfrak {g}_{>0}$
) induced from the adjoint action of x acting on
![]() $\mathfrak {g}^{f}$
(resp.
$\mathfrak {g}^{f}$
(resp.
![]() $\mathfrak {g}_{>0}$
).
$\mathfrak {g}_{>0}$
).
Proof. As previously mentioned,
![]() $\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
$\mathfrak {g}^\natural $
is a maximal reductive subalgebra of
![]() $\mathfrak {g}^{f}$
([Reference Elashvili, Kac and Vinberg38, Lemma 1.2]). Let
$\mathfrak {g}^{f}$
([Reference Elashvili, Kac and Vinberg38, Lemma 1.2]). Let
![]() $\mathfrak {t}$
be a maximal torus of
$\mathfrak {t}$
be a maximal torus of
![]() $\mathfrak {g}^{0}=\mathfrak {g}^{h}$
containing a maximal torus of
$\mathfrak {g}^{0}=\mathfrak {g}^{h}$
containing a maximal torus of
![]() $\mathfrak {g}^\natural $
, and set
$\mathfrak {g}^\natural $
, and set
We intend to show that
![]() $\mathfrak {z}(\mathfrak {g}^\natural )$
is contained in
$\mathfrak {z}(\mathfrak {g}^\natural )$
is contained in
![]() $\mathfrak {t}^{\natural }$
.
$\mathfrak {t}^{\natural }$
.
We use the decomposition in
![]() $\mathfrak {t}^{\natural }$
-weight spaces of
$\mathfrak {t}^{\natural }$
-weight spaces of
![]() $\mathfrak {g}^{\natural }$
following [Reference Brundan and Goodwin30, Section 2]. For
$\mathfrak {g}^{\natural }$
following [Reference Brundan and Goodwin30, Section 2]. For
![]() $\alpha \in (\mathfrak {t}^{\natural })^*$
and
$\alpha \in (\mathfrak {t}^{\natural })^*$
and
![]() $n \ge 0$
, let
$n \ge 0$
, let
![]() $L(\alpha ,n)$
denote the irreducible
$L(\alpha ,n)$
denote the irreducible
![]() $\mathfrak {t}^{\natural }\oplus \mathfrak {s}$
-modules of dimension
$\mathfrak {t}^{\natural }\oplus \mathfrak {s}$
-modules of dimension
![]() $(n+1)$
on which
$(n+1)$
on which
![]() $\mathfrak {t}^{\natural }$
acts by the weight
$\mathfrak {t}^{\natural }$
acts by the weight
![]() $\alpha $
, where
$\alpha $
, where
![]() $\mathfrak {s}\cong {\mathfrak {sl}}_2$
is the Lie algebra generated by
$\mathfrak {s}\cong {\mathfrak {sl}}_2$
is the Lie algebra generated by
![]() $e,h,f$
. Since each
$e,h,f$
. Since each
![]() $L(\alpha ,n)$
contains a nonzero vector annihilated by f, the set of weights of
$L(\alpha ,n)$
contains a nonzero vector annihilated by f, the set of weights of
![]() $\mathfrak {t}^{\natural }$
on
$\mathfrak {t}^{\natural }$
on
![]() $\mathfrak {g}$
is also the set of weights of
$\mathfrak {g}$
is also the set of weights of
![]() $\mathfrak {t}^\natural $
on
$\mathfrak {t}^\natural $
on
![]() $\mathfrak {g}^{f}$
. Let
$\mathfrak {g}^{f}$
. Let
![]() $\Phi _f \subset (\mathfrak {t}^{\natural })^*$
be the set of all nonzero weights of
$\Phi _f \subset (\mathfrak {t}^{\natural })^*$
be the set of all nonzero weights of
![]() $\mathfrak {t}^{\natural }$
on
$\mathfrak {t}^{\natural }$
on
![]() $\mathfrak {g}^f$
. We have the following decomposition:
$\mathfrak {g}^f$
. We have the following decomposition:

where
![]() $\mathfrak {g}^{\mathfrak {t}^{\natural }}$
is the centraliser of
$\mathfrak {g}^{\mathfrak {t}^{\natural }}$
is the centraliser of
![]() $\mathfrak {t}^{\natural }$
in
$\mathfrak {t}^{\natural }$
in
![]() $\mathfrak {g}$
(it is a Levi subalgebra of
$\mathfrak {g}$
(it is a Levi subalgebra of
![]() $\mathfrak {g}$
) and
$\mathfrak {g}$
) and
This decomposition is compatible with the decomposition
![]() $\mathfrak {g}^f = \mathfrak {g}^\natural \oplus \mathfrak {g}^{f}_{<0}$
, and we have
$\mathfrak {g}^f = \mathfrak {g}^\natural \oplus \mathfrak {g}^{f}_{<0}$
, and we have

where
![]() $\Phi _f^\circ $
denotes the set of all nonzero element of
$\Phi _f^\circ $
denotes the set of all nonzero element of
![]() $\Phi _f$
.
$\Phi _f$
.
Let now
![]() $x \in \mathfrak {z}(\mathfrak {g}^\natural )$
that we write
$x \in \mathfrak {z}(\mathfrak {g}^\natural )$
that we write
![]() $x=x_{0}+\sum _{\alpha \in \Phi _f^\circ } x_\alpha $
relatively to the above decomposition, with
$x=x_{0}+\sum _{\alpha \in \Phi _f^\circ } x_\alpha $
relatively to the above decomposition, with
![]() $x_0 \in \mathfrak {t}^{\natural } $
and
$x_0 \in \mathfrak {t}^{\natural } $
and
![]() $x_\alpha \in \mathfrak {g}^f (\alpha ,0)$
for
$x_\alpha \in \mathfrak {g}^f (\alpha ,0)$
for
![]() $\alpha \in \Phi _f^\circ $
. Let
$\alpha \in \Phi _f^\circ $
. Let
![]() $\alpha ' \in \Phi _f^\circ $
and pick
$\alpha ' \in \Phi _f^\circ $
and pick
![]() $t' \in \mathfrak {t}^{\natural }$
such that
$t' \in \mathfrak {t}^{\natural }$
such that
![]() $\alpha '(t')\not =0$
. From the equalities
$\alpha '(t')\not =0$
. From the equalities
 $$ \begin{align*} 0 &= [y,x] = [y,x_0]+\sum_{\alpha \in \Phi_f^\circ} [y,x_\alpha] = 0 + \sum_{\substack{\alpha \in \Phi_f^\circ \\ \alpha \not=\alpha'}} \alpha(t) x_\alpha + \alpha'(t') x_{\alpha'}, \end{align*} $$
$$ \begin{align*} 0 &= [y,x] = [y,x_0]+\sum_{\alpha \in \Phi_f^\circ} [y,x_\alpha] = 0 + \sum_{\substack{\alpha \in \Phi_f^\circ \\ \alpha \not=\alpha'}} \alpha(t) x_\alpha + \alpha'(t') x_{\alpha'}, \end{align*} $$
we deduce that
![]() $x_{\alpha '}=0$
. Since this is true for each
$x_{\alpha '}=0$
. Since this is true for each
![]() $\alpha \in \Phi _f^\circ $
, we get that
$\alpha \in \Phi _f^\circ $
, we get that
![]() $x=x_0 \in \mathfrak {t}^{\natural }$
. In particular, x is a semisimple elements of
$x=x_0 \in \mathfrak {t}^{\natural }$
. In particular, x is a semisimple elements of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
To show the second assertion, first note that we have the following decomposition:
 $$ \begin{align} \mathfrak{g}= \bigoplus_{\alpha \in \Phi_f} \bigoplus_{n \ge 0} m(\alpha,n) L(\alpha,n), \end{align} $$
$$ \begin{align} \mathfrak{g}= \bigoplus_{\alpha \in \Phi_f} \bigoplus_{n \ge 0} m(\alpha,n) L(\alpha,n), \end{align} $$
where
![]() $m(\alpha ,n) \not =0$
for all
$m(\alpha ,n) \not =0$
for all
![]() $\alpha \in \Phi _f$
. Since
$\alpha \in \Phi _f$
. Since
![]() $\Phi _f$
is a restricted root system in the sense of [Reference Brundan and Goodwin30, Section 2], for
$\Phi _f$
is a restricted root system in the sense of [Reference Brundan and Goodwin30, Section 2], for
![]() $\alpha \in (\mathfrak {t}^\natural )^*$
,
$\alpha \in (\mathfrak {t}^\natural )^*$
,
![]() $\alpha \in \Phi _f$
implies that
$\alpha \in \Phi _f$
implies that
![]() $-\alpha \in \Phi ^f$
and the corresponding root vector spaces have the same dimension. So the second assertion follows from the decompositions (36) and (37).
$-\alpha \in \Phi ^f$
and the corresponding root vector spaces have the same dimension. So the second assertion follows from the decompositions (36) and (37).
6 The main strategy
We describe in this section our general strategy to find new (admissible) collapsing levels using Theorem 3.10. The main difficulty is to find potential candidates for k and f. We explain below our strategy to achieve this.
6.1 Associated variety
If k is collapsing for
![]() $\mathscr {W}^k(\mathfrak {g},f)$
, then certainly
$\mathscr {W}^k(\mathfrak {g},f)$
, then certainly
as Poisson varieties. As we saw in Theorem 4.3, the vertex algebra
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is quasi-lisse whenever
$\mathscr {W}_k(\mathfrak {g},f)$
is quasi-lisse whenever
![]() $f \in \overline {\mathbb {O}}_k$
.
$f \in \overline {\mathbb {O}}_k$
.
Lemma 6.1. Suppose that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is quasi-lisse. If k is collapsing, then
$\mathscr {W}_k(\mathfrak {g},f)$
is quasi-lisse. If k is collapsing, then
![]() $\phi _0^\natural $
is identically zero on
$\phi _0^\natural $
is identically zero on
![]() $\mathfrak {g}_0^\natural $
. In particular, if k is admissible and
$\mathfrak {g}_0^\natural $
. In particular, if k is admissible and
![]() $f\in \overline {\mathbb {O}}_k$
, then k can only be collapsing if
$f\in \overline {\mathbb {O}}_k$
, then k can only be collapsing if
![]() $\phi _0^\natural =0$
.
$\phi _0^\natural =0$
.
Our convention is that
![]() $\phi _0^\natural =0$
when
$\phi _0^\natural =0$
when
![]() $\mathfrak {g}_0^\natural =\{0\}$
.
$\mathfrak {g}_0^\natural =\{0\}$
.
Proof. The associated variety
![]() $X_{L_{k^\natural }(\mathfrak {g}^\natural )} $
is a subvariety of
$X_{L_{k^\natural }(\mathfrak {g}^\natural )} $
is a subvariety of
![]() $(\mathfrak {g}_0^\natural )^*\times (\mathfrak {g}_1^\natural )^*\times \dots \times (\mathfrak {g}_s^\natural )^*$
, and the symplectic leaves of
$(\mathfrak {g}_0^\natural )^*\times (\mathfrak {g}_1^\natural )^*\times \dots \times (\mathfrak {g}_s^\natural )^*$
, and the symplectic leaves of
![]() $(\mathfrak {g}_0^\natural )^*\times (\mathfrak {g}_1^\natural )^*\times \dots \times (\mathfrak {g}_s^\natural )^*$
are the coadjoint orbits of
$(\mathfrak {g}_0^\natural )^*\times (\mathfrak {g}_1^\natural )^*\times \dots \times (\mathfrak {g}_s^\natural )^*$
are the coadjoint orbits of
![]() $G_0^\natural \times \cdots \times G_s^\natural $
, where
$G_0^\natural \times \cdots \times G_s^\natural $
, where
![]() $G_i^\natural $
is the adjoint group of
$G_i^\natural $
is the adjoint group of
![]() $\mathfrak {g}_i^\natural $
. Recall that
$\mathfrak {g}_i^\natural $
. Recall that
![]() $V^{\phi _0^{\natural }}(\mathfrak {g}_0^\natural )$
is a Heisenberg vertex algebra of rank
$V^{\phi _0^{\natural }}(\mathfrak {g}_0^\natural )$
is a Heisenberg vertex algebra of rank
![]() $\dim \mathfrak {g}_0^\natural $
. The associated variety of its simple quotient is
$\dim \mathfrak {g}_0^\natural $
. The associated variety of its simple quotient is
![]() $\mathbb {C}^{ \mathrm {rank}\,\phi _0^\natural }$
, provided that
$\mathbb {C}^{ \mathrm {rank}\,\phi _0^\natural }$
, provided that
![]() $\phi _0^{\natural }\not =0$
. Hence,
$\phi _0^{\natural }\not =0$
. Hence,
![]() $X_{L_{k^\natural }(\mathfrak {g}^\natural )}$
has finitely many symplectic leaves if and only if it is contained in
$X_{L_{k^\natural }(\mathfrak {g}^\natural )}$
has finitely many symplectic leaves if and only if it is contained in
![]() $\mathcal {N}_{\mathfrak {g}_1}\times \dots \times \mathcal {N}_{\mathfrak {g}_s}$
, where
$\mathcal {N}_{\mathfrak {g}_1}\times \dots \times \mathcal {N}_{\mathfrak {g}_s}$
, where
![]() $\mathcal {N}_{\mathfrak {g}_i}$
is the nilpotent cone of
$\mathcal {N}_{\mathfrak {g}_i}$
is the nilpotent cone of
![]() $\mathfrak {g}_i^\natural $
. In particular, we must have
$\mathfrak {g}_i^\natural $
. In particular, we must have
![]() $X_{L_{\phi _0^{\natural }}(\mathfrak {g}_0^\natural )}=\{0\}$
. This happens if and only if
$X_{L_{\phi _0^{\natural }}(\mathfrak {g}_0^\natural )}=\{0\}$
. This happens if and only if
![]() $\phi _0^{\natural }=0$
.
$\phi _0^{\natural }=0$
.
We are thus led to consider levels k for which
![]() $\phi _0^\natural = 0$
(further conditions on k will appear later). Now, for each
$\phi _0^\natural = 0$
(further conditions on k will appear later). Now, for each
![]() $i>0$
, the bilinear form
$i>0$
, the bilinear form
![]() $\phi ^\natural _i$
equals the standard form on the simple component
$\phi ^\natural _i$
equals the standard form on the simple component
![]() $\mathfrak {g}_i^\natural $
, times a well-defined level
$\mathfrak {g}_i^\natural $
, times a well-defined level
![]() $k_i^\natural $
, as per (32). These levels
$k_i^\natural $
, as per (32). These levels
![]() $k_i^\natural $
can then be expressed as functions of the level k, as is done below in Tables 2, 3 and 4 for classical types, and Tables 11–17 for exceptional types. In the tables, we also list
$k_i^\natural $
can then be expressed as functions of the level k, as is done below in Tables 2, 3 and 4 for classical types, and Tables 11–17 for exceptional types. In the tables, we also list
![]() $k_0^\natural $
for those cases in which
$k_0^\natural $
for those cases in which
![]() $\mathfrak {g}_0^\natural \neq 0$
, and since there is no standard normalised form on
$\mathfrak {g}_0^\natural \neq 0$
, and since there is no standard normalised form on
![]() $\mathfrak {g}_0^\natural $
, we now explain what we mean by this. If the centre
$\mathfrak {g}_0^\natural $
, we now explain what we mean by this. If the centre
![]() $\mathfrak {g}_0^\natural $
is one-dimensional, then we choose nonzero
$\mathfrak {g}_0^\natural $
is one-dimensional, then we choose nonzero
![]() $x\in \mathfrak {g}_0^\natural $
and set
$x\in \mathfrak {g}_0^\natural $
and set
![]() $k_{0}^\natural = \phi _{0}^\natural (x,x)$
. Then
$k_{0}^\natural = \phi _{0}^\natural (x,x)$
. Then
![]() $k_0^\natural $
is well defined, as a function of k, up to multiplication by a nonzero scalar. This is sufficient for our purposes since, by Lemma 6.1, we require
$k_0^\natural $
is well defined, as a function of k, up to multiplication by a nonzero scalar. This is sufficient for our purposes since, by Lemma 6.1, we require
![]() $k_0^\natural =0$
. For the vast majority of pairs
$k_0^\natural =0$
. For the vast majority of pairs
![]() $(\mathfrak {g}, f)$
relevant for us, we have
$(\mathfrak {g}, f)$
relevant for us, we have ![]() in fact. Only two exceptions occur (one in type
in fact. Only two exceptions occur (one in type
![]() $E_6$
and one in type
$E_6$
and one in type
![]() $E_7$
), and in both these cases,
$E_7$
), and in both these cases,
![]() $\mathfrak {g}^\natural =\mathfrak {g}_0^\natural \cong \mathbb {C}^2$
. These cases are easily handled separately, and in the tables, we abuse notation by also writing
$\mathfrak {g}^\natural =\mathfrak {g}_0^\natural \cong \mathbb {C}^2$
. These cases are easily handled separately, and in the tables, we abuse notation by also writing
![]() $k_{0}^\natural $
for the value of
$k_{0}^\natural $
for the value of
![]() $\phi _{0}^\natural (x,x)$
for some nonzero
$\phi _{0}^\natural (x,x)$
for some nonzero
![]() $x\in \mathfrak {g}_0^\natural $
.
$x\in \mathfrak {g}_0^\natural $
.
We now call
![]() $k^\natural $
admissible if
$k^\natural $
admissible if
![]() $k_0^\natural =0$
and
$k_0^\natural =0$
and
![]() $k_i^\natural $
is admissible for
$k_i^\natural $
is admissible for
![]() $\mathfrak {g}_i^\natural $
, for each
$\mathfrak {g}_i^\natural $
, for each ![]() .
.
Remark 6.2. It may happen that k is admissible while
![]() $k^\natural $
is not, even if
$k^\natural $
is not, even if
![]() $\mathfrak {g}_0^\natural =0$
. For example, for
$\mathfrak {g}_0^\natural =0$
. For example, for
![]() $\mathfrak {g}=G_2$
, f in the nilpotent orbit labelled
$\mathfrak {g}=G_2$
, f in the nilpotent orbit labelled
![]() $\tilde {A}_1$
(of dimension 8) and
$\tilde {A}_1$
(of dimension 8) and
![]() $k = -4+4/7$
which is a principal admissible level for
$k = -4+4/7$
which is a principal admissible level for
![]() $G_2$
, then
$G_2$
, then
![]() $k^{\natural } = k +3/2=-2+1/14$
is not admissible for
$k^{\natural } = k +3/2=-2+1/14$
is not admissible for
![]() $\mathfrak {g}^\natural \cong {\mathfrak {sl}}_2$
(see Table 11). However, under additional conditions on f and k, we expect that
$\mathfrak {g}^\natural \cong {\mathfrak {sl}}_2$
(see Table 11). However, under additional conditions on f and k, we expect that
![]() $k^\natural $
is admissible if k is admissible. See Conjecture 6.4 below.
$k^\natural $
is admissible if k is admissible. See Conjecture 6.4 below.
Recall
the nilpotent Slodowy slice. Now we assume k and
![]() $k^\natural $
are both admissible, where
$k^\natural $
are both admissible, where
![]() $f\in \overline {\mathbb {O}}_k$
, and we assume that
$f\in \overline {\mathbb {O}}_k$
, and we assume that
![]() $\mathscr {W}_k(\mathfrak {g},f)=H_{DS,f}^0(L_k(\mathfrak {g}))$
(verified if f has a good even grading, and in general if Conjecture 4.4 holds). Then according to Theorem 3.2 and Theorem 4.3,
$\mathscr {W}_k(\mathfrak {g},f)=H_{DS,f}^0(L_k(\mathfrak {g}))$
(verified if f has a good even grading, and in general if Conjecture 4.4 holds). Then according to Theorem 3.2 and Theorem 4.3,
where ![]() are nilpotent orbits in
are nilpotent orbits in ![]() , respectively. This motivates the following definition:
, respectively. This motivates the following definition:
Definition 6.3. We say that a nilpotent Slodowy slice
![]() $\mathcal {S}_{{\mathbb {O}},f}$
is collapsing if
$\mathcal {S}_{{\mathbb {O}},f}$
is collapsing if
![]() $\mathcal {S}_{{\mathbb {O}},f}$
is isomorphic to a product of nilpotent orbit closures in
$\mathcal {S}_{{\mathbb {O}},f}$
is isomorphic to a product of nilpotent orbit closures in
![]() $\mathfrak {g}^\natural $
.
$\mathfrak {g}^\natural $
.
Based on the above analysis, we consider pairs
![]() $({\mathbb {O}},{\mathbb {O}}')$
such that
$({\mathbb {O}},{\mathbb {O}}')$
such that
-
1.
 $\overline {{\mathbb {O}}}=\overline {{\mathbb {O}}}_k$
is the associated variety of some simple admissible affine vertex algebra
$\overline {{\mathbb {O}}}=\overline {{\mathbb {O}}}_k$
is the associated variety of some simple admissible affine vertex algebra
 $L_k(\mathfrak {g})$
,
$L_k(\mathfrak {g})$
, -
2.
 ${\mathbb {O}}' \subset \overline {{\mathbb {O}}}$
,
${\mathbb {O}}' \subset \overline {{\mathbb {O}}}$
, -
3. for
 $f \in {\mathbb {O}}'$
,
$f \in {\mathbb {O}}'$
,
 $\mathcal {S}_{{\mathbb {O}},f}$
is a collapsing nilpotent Slodowy slice which is the associated variety X of the simple admissible affine vertex algebra
$\mathcal {S}_{{\mathbb {O}},f}$
is a collapsing nilpotent Slodowy slice which is the associated variety X of the simple admissible affine vertex algebra
 $L_{k^\natural }(\mathfrak {g}^\natural )$
. (In particular, X is a product of nilpotent orbit closures in
$L_{k^\natural }(\mathfrak {g}^\natural )$
. (In particular, X is a product of nilpotent orbit closures in
 $\mathfrak {g}^{\natural }$
.)
$\mathfrak {g}^{\natural }$
.)
The nilpotent orbit
![]() ${\mathbb {O}}_k$
, for admissible
${\mathbb {O}}_k$
, for admissible
![]() $k= -h_{\mathfrak {g}}^\vee +p/q$
, is given by [Reference Arakawa10, Tables 2–10] and depends only on the denominator q: it is described in terms of the corresponding partition of n for
$k= -h_{\mathfrak {g}}^\vee +p/q$
, is given by [Reference Arakawa10, Tables 2–10] and depends only on the denominator q: it is described in terms of the corresponding partition of n for
![]() $\mathfrak {g}$
simple of classical type – that is,
$\mathfrak {g}$
simple of classical type – that is,
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
,
$\mathfrak {g}={\mathfrak {sl}}_n$
,
![]() $\mathfrak {sp}_n$
or
$\mathfrak {sp}_n$
or
![]() ${\mathfrak {so}}_n$
– and in the Bala-Carter classification for
${\mathfrak {so}}_n$
– and in the Bala-Carter classification for
![]() $\mathfrak {g}$
simple of exceptional type.
$\mathfrak {g}$
simple of exceptional type.
Motivated by the determination of generic singularities of the nilpotent closures
![]() $\overline {{\mathbb {O}}}$
in simple Lie algebras
$\overline {{\mathbb {O}}}$
in simple Lie algebras
![]() $\mathfrak {g}$
of classical types, Kraft and Procesi [Reference Kraft and Procesi64, Reference Kraft and Procesi66] described the smooth equivalences of singularities between Slodowy slices
$\mathfrak {g}$
of classical types, Kraft and Procesi [Reference Kraft and Procesi64, Reference Kraft and Procesi66] described the smooth equivalences of singularities between Slodowy slices
![]() $\mathcal {S}_{{\mathbb {O}}_1,f_1}$
and
$\mathcal {S}_{{\mathbb {O}}_1,f_1}$
and
![]() $\mathcal {S}_{{\mathbb {O}}_2,f_2}$
, where
$\mathcal {S}_{{\mathbb {O}}_2,f_2}$
, where
![]() $\mathcal {S}_{{\mathbb {O}}_2,f_2}$
is obtained from
$\mathcal {S}_{{\mathbb {O}}_2,f_2}$
is obtained from
![]() $\mathcal {S}_{{\mathbb {O}}_1,f_1}$
by the row/column removal rule (see Lemmas 8.2 and 9.2). It turns out that these smooth equivalences actually yield isomorphisms of varieties; see [Reference Li68, Proposition 7.3.2].Footnote
4
Thus, the row/column removal rule, combined with [Reference Arakawa10], yields many pairs
$\mathcal {S}_{{\mathbb {O}}_1,f_1}$
by the row/column removal rule (see Lemmas 8.2 and 9.2). It turns out that these smooth equivalences actually yield isomorphisms of varieties; see [Reference Li68, Proposition 7.3.2].Footnote
4
Thus, the row/column removal rule, combined with [Reference Arakawa10], yields many pairs
![]() $({\mathbb {O}},{\mathbb {O}}')$
satisfying the conditions above in classical types. We consider all such pairs.
$({\mathbb {O}},{\mathbb {O}}')$
satisfying the conditions above in classical types. We consider all such pairs.
For the simple Lie algebras of exceptional types, the authors of [Reference Fu, Juteau, Levy and Sommers47] determine the isomorphism type of most of the Slodowy slices
![]() $\mathcal {S}_{{\mathbb {O}},f}$
for which
$\mathcal {S}_{{\mathbb {O}},f}$
for which
![]() $G.f$
is a minimal degeneration of
$G.f$
is a minimal degeneration of
![]() ${\mathbb {O}}$
(i.e., those for which
${\mathbb {O}}$
(i.e., those for which
![]() $G.f$
is a maximal orbit in
$G.f$
is a maximal orbit in
![]() $\overline {{\mathbb {O}}} \setminus {\mathbb {O}}$
) and also for some of the Slodowy slices for which it is not a minimal degeneration. For the remaining cases, they obtain some weaker information. From their work, together with [Reference Arakawa10], one possibility would be to proceed by finding pairs
$\overline {{\mathbb {O}}} \setminus {\mathbb {O}}$
) and also for some of the Slodowy slices for which it is not a minimal degeneration. For the remaining cases, they obtain some weaker information. From their work, together with [Reference Arakawa10], one possibility would be to proceed by finding pairs
![]() $({\mathbb {O}},{\mathbb {O}}')$
satisfying the above conditions, as in the classical cases.
$({\mathbb {O}},{\mathbb {O}}')$
satisfying the above conditions, as in the classical cases.
In fact, our work is more exhaustive in a sense since in exceptional types, we are able to directly exploit the description of the
![]() $k_i^\natural $
in Tables 11–17 and the central charge (see §6.2 below) to detect all possible collapsing levels. In this way, we find many nontrivial isomorphisms between a Slodowy slice
$k_i^\natural $
in Tables 11–17 and the central charge (see §6.2 below) to detect all possible collapsing levels. In this way, we find many nontrivial isomorphisms between a Slodowy slice
![]() $\mathcal {S}_{{\mathbb {O}},f}$
and a product of nilpotent orbit closures in
$\mathcal {S}_{{\mathbb {O}},f}$
and a product of nilpotent orbit closures in
![]() $\mathfrak {g}^\natural $
. Many of these were observed in [Reference Fu, Juteau, Levy and Sommers47] already, though others seem to be new. However, of course, many of isomorphisms between Slodowy slices obtained in [Reference Fu, Juteau, Levy and Sommers47] do not correspond to collapsing levels and so do not appear in our work.
$\mathfrak {g}^\natural $
. Many of these were observed in [Reference Fu, Juteau, Levy and Sommers47] already, though others seem to be new. However, of course, many of isomorphisms between Slodowy slices obtained in [Reference Fu, Juteau, Levy and Sommers47] do not correspond to collapsing levels and so do not appear in our work.
We remark that all the isomorphisms between nilpotent orbits and nilpotent Slodowy slices that we obtain from collapsing levels are automatically isomorphisms of Poisson varieties.
Roughly speaking, a collapsing Slodowy slice will yield a collapsing level if the asymptotic data of the vertex algebras corresponding to the two sides of (39) can be shown to coincide. In fact, asymptotic data is rather difficult to compute, so the next step in our strategy is to rule out spurious cases by comparing central charges. This is described in §6.2 below.
We close this subsection with a discussion of admissibility of the levels
![]() $k_i^\natural $
.
$k_i^\natural $
.
Conjecture 6.4. If k is admissible and if
![]() $f \in \overline {{\mathbb {O}}}_k$
is such that
$f \in \overline {{\mathbb {O}}}_k$
is such that
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing, then
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing, then
![]() $k^\natural $
is admissible, provided that
$k^\natural $
is admissible, provided that
![]() $k_0^\natural =0$
.
$k_0^\natural =0$
.
We will verify the conjecture in the classical cases in the cases where
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing and the isomorphism between
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing and the isomorphism between
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
and a product of nilpotent orbit closures in
$\mathcal {S}_{{\mathbb {O}}_k,f}$
and a product of nilpotent orbit closures in
![]() $\mathfrak {g}^\natural $
is obtained from the row/column removal rule of Kraft-Procesi (see Lemma 8.4 and Lemma 9.5). We feel that these cases exhaust all possible cases of collapsing nilpotent Slodowy slices so that, together with Lemma 6.5 below, it would complete the proof of the conjecture.
$\mathfrak {g}^\natural $
is obtained from the row/column removal rule of Kraft-Procesi (see Lemma 8.4 and Lemma 9.5). We feel that these cases exhaust all possible cases of collapsing nilpotent Slodowy slices so that, together with Lemma 6.5 below, it would complete the proof of the conjecture.
Lemma 6.5. Conjecture 6.4 is true if
![]() $\mathfrak {g}$
is simple of exceptional type.
$\mathfrak {g}$
is simple of exceptional type.
Proof. Assume that k is admissible. It is known that
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is equidimensional of dimension
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is equidimensional of dimension
![]() $\dim {\mathbb {O}}_k -\dim G.f$
([Reference Ginzburg48, Corollary 1.3.8]). Moreover, by the main result of [Reference Arakawa and Moreau21],
$\dim {\mathbb {O}}_k -\dim G.f$
([Reference Ginzburg48, Corollary 1.3.8]). Moreover, by the main result of [Reference Arakawa and Moreau21],
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is irreducible since k is admissible.
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is irreducible since k is admissible.
If
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing, then, in particular, it is contained in the nilpotent cone
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing, then, in particular, it is contained in the nilpotent cone
![]() $\mathcal {N}_{\mathfrak {g}^\natural }$
of
$\mathcal {N}_{\mathfrak {g}^\natural }$
of
![]() $\mathfrak {g}^\natural $
, and so
$\mathfrak {g}^\natural $
, and so ![]() .
.
The semisimple type of
![]() $\mathfrak {g}^\natural $
and the values of the
$\mathfrak {g}^\natural $
and the values of the
![]() $k_i^\natural $
’s are computed in Tables 11–17. Hence, fixing f, we first consider nilpotent orbits
$k_i^\natural $
’s are computed in Tables 11–17. Hence, fixing f, we first consider nilpotent orbits
![]() ${\mathbb {O}}$
containing
${\mathbb {O}}$
containing
![]() $\overline {G.f}$
such that
$\overline {G.f}$
such that ![]() and such that
and such that
![]() ${\mathbb {O}}={\mathbb {O}}_k$
for some admissible level k for
${\mathbb {O}}={\mathbb {O}}_k$
for some admissible level k for
![]() $\mathfrak {g}$
. This heavily restricts the possibilities for the denominator q of k. Then we can ask whether for such q, the corresponding level
$\mathfrak {g}$
. This heavily restricts the possibilities for the denominator q of k. Then we can ask whether for such q, the corresponding level
![]() $k^\natural $
is admissible for
$k^\natural $
is admissible for
![]() $\mathfrak {g}^\natural $
. Let us illustrate with an example.
$\mathfrak {g}^\natural $
. Let us illustrate with an example.
Assume that
![]() $\mathfrak {g}=F_4$
and that f belongs to the nilpotent orbit labelled
$\mathfrak {g}=F_4$
and that f belongs to the nilpotent orbit labelled
![]() $B_3$
in the Bala-Carter classification (dimension 42). According to Table 12,
$B_3$
in the Bala-Carter classification (dimension 42). According to Table 12,
![]() $\mathfrak {g}^\natural \cong A_1$
. Hence,
$\mathfrak {g}^\natural \cong A_1$
. Hence, ![]() , so
, so ![]() from which we see that
from which we see that
![]() ${\mathbb {O}}_k$
must be
${\mathbb {O}}_k$
must be
![]() $B_3$
,
$B_3$
,
![]() $C_3$
or
$C_3$
or
![]() $F_4(a_2)$
.
$F_4(a_2)$
.
Recall that
![]() $k=-9+p/q$
with
$k=-9+p/q$
with
![]() $(p,q)=1$
and
$(p,q)=1$
and
![]() $p\ge 9$
if q is odd, and
$p\ge 9$
if q is odd, and
![]() $p\ge 12$
if q is even. By [Reference Arakawa10], if
$p\ge 12$
if q is even. By [Reference Arakawa10], if
![]() ${\mathbb {O}}_k = B_3$
, then
${\mathbb {O}}_k = B_3$
, then
![]() $q=8$
, if
$q=8$
, if
![]() ${\mathbb {O}}_k = F_4(a_2)$
, then
${\mathbb {O}}_k = F_4(a_2)$
, then
![]() $q=7$
or
$q=7$
or
![]() $q=10$
, and finally the orbit
$q=10$
, and finally the orbit
![]() $C_3$
cannot occur as
$C_3$
cannot occur as
![]() ${\mathbb {O}}_k$
. Now we examine admissibility of
${\mathbb {O}}_k$
. Now we examine admissibility of
in each case.
-
* If
 $q=7$
, then
$q=7$
, then
 $2 (4 p - 5 q) \ge 2 (4 \times 9 - 5\times 7) =2$
, so
$2 (4 p - 5 q) \ge 2 (4 \times 9 - 5\times 7) =2$
, so
 $k^\natural $
is admissible.
$k^\natural $
is admissible. -
* If
 $q=8$
, then
$q=8$
, then
 $2 (4 p - 5 q)/q = (4 p - 5 \times 8)/4$
and
$2 (4 p - 5 q)/q = (4 p - 5 \times 8)/4$
and
 $4 p - 5 q \ge 4 \times 13 - 5\times 8 =12$
so
$4 p - 5 q \ge 4 \times 13 - 5\times 8 =12$
so
 $k^\natural $
is admissible.
$k^\natural $
is admissible. -
* If
 $q=10$
, then
$q=10$
, then
 $2 (4 p - 5 q)/q = (4 p - 5 \times 10)/5$
and
$2 (4 p - 5 q)/q = (4 p - 5 \times 10)/5$
and
 $4 p - 5 q \ge 4 \times 13 - 5\times 10 =2$
so
$4 p - 5 q \ge 4 \times 13 - 5\times 10 =2$
so
 $k^\natural $
is admissible.
$k^\natural $
is admissible.
In most cases, considerations of orbit dimension, like those above, suffice to reach the desired conclusion. In some cases, however, a more detailed analysis of the Hasse diagrams of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {g}^\natural $
is necessary (we use the diagrams of [Reference Fu, Juteau, Levy and Sommers47]). This is the case, for example, for the minimal nilpotent orbits of
$\mathfrak {g}^\natural $
is necessary (we use the diagrams of [Reference Fu, Juteau, Levy and Sommers47]). This is the case, for example, for the minimal nilpotent orbits of
![]() $F_4$
and
$F_4$
and
![]() $E_7$
. We explain the verification for these two cases.
$E_7$
. We explain the verification for these two cases.
Let us first consider the minimal nilpotent orbit of
![]() $F_4$
(dimension
$F_4$
(dimension
![]() $16$
). In this case,
$16$
). In this case,
![]() $\mathfrak {g}^\natural \cong C_3$
. Since the nilpotent cone of
$\mathfrak {g}^\natural \cong C_3$
. Since the nilpotent cone of
![]() $C_3$
has dimension
$C_3$
has dimension
![]() $18$
, we have
$18$
, we have ![]() . These inequalities are satisfied by
. These inequalities are satisfied by
![]() $6$
nilpotent orbits, but of these, only the orbits
$6$
nilpotent orbits, but of these, only the orbits
![]() $A_1$
(the minimal orbit itself) and
$A_1$
(the minimal orbit itself) and
![]() $A_2 + \widetilde {A}_1$
can occur as
$A_2 + \widetilde {A}_1$
can occur as
![]() ${\mathbb {O}}_k$
.
${\mathbb {O}}_k$
.
If
![]() ${\mathbb {O}}_k = A_2+\tilde {A}_1$
, then
${\mathbb {O}}_k = A_2+\tilde {A}_1$
, then
![]() $q=4$
(here,
$q=4$
(here,
![]() $k = -9 + p/q$
as above), and if
$k = -9 + p/q$
as above), and if
![]() ${\mathbb {O}}_k = A_1$
, then
${\mathbb {O}}_k = A_1$
, then
![]() $q=2$
. Now we examine admissibility of the level
$q=2$
. Now we examine admissibility of the level
in each case.
-
* If
 $q=2$
, then
$q=2$
, then
 $(2p-5q)/(2q) = (p - 5)/2$
and
$(2p-5q)/(2q) = (p - 5)/2$
and
 $p - 5 \ge 13 - 5 = 8 \ge 6=h_{C_3}$
so
$p - 5 \ge 13 - 5 = 8 \ge 6=h_{C_3}$
so
 $k^\natural $
is admissible.
$k^\natural $
is admissible. -
* If
 $q=4$
, then
$q=4$
, then
 $(2p - 5 q)/(2q) = (p - 10)/4$
, but
$(2p - 5 q)/(2q) = (p - 10)/4$
, but
 $p \ge 13$
gives us only
$p \ge 13$
gives us only
 $p - 10 \ge 3$
, not
$p - 10 \ge 3$
, not
 $p - 10 \ge 6$
as required for admissibility.
$p - 10 \ge 6$
as required for admissibility.
To exclude the second case, we observe instead that
![]() $\dim {\mathbb {O}}_{A_2+\tilde {A}_1}-\dim {\mathbb {O}}_{A_1}=18$
. So if
$\dim {\mathbb {O}}_{A_2+\tilde {A}_1}-\dim {\mathbb {O}}_{A_1}=18$
. So if
![]() $\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
were collapsing, then necessarily
$\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
were collapsing, then necessarily
![]() $\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
would be isomorphic to the nilpotent cone
$\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
would be isomorphic to the nilpotent cone
![]() $\mathcal {N}_{C_3}$
of
$\mathcal {N}_{C_3}$
of
![]() $C_3$
since it is irreducible. In particular, it should contain a nilpotent
$C_3$
since it is irreducible. In particular, it should contain a nilpotent
![]() $G^\natural $
-orbit of dimension 16 (corresponding to the subregular nilpotent orbit of
$G^\natural $
-orbit of dimension 16 (corresponding to the subregular nilpotent orbit of
![]() $C_3\cong \mathfrak {sp}_6$
). Here,
$C_3\cong \mathfrak {sp}_6$
). Here,
![]() $G^\natural $
denotes the centraliser in
$G^\natural $
denotes the centraliser in
![]() $F_4$
of the
$F_4$
of the
![]() ${\mathfrak {sl}}_2$
-triple associated with f in the minimal nilpotent orbit
${\mathfrak {sl}}_2$
-triple associated with f in the minimal nilpotent orbit
![]() $A_1$
of
$A_1$
of
![]() $F_4$
whose Lie algebra is
$F_4$
whose Lie algebra is
![]() $\mathfrak {g}^\natural $
. But from the Hasse diagram of the
$\mathfrak {g}^\natural $
. But from the Hasse diagram of the
![]() $F_4$
, we see that this is not possible. Indeed, the Hasse diagram of the
$F_4$
, we see that this is not possible. Indeed, the Hasse diagram of the
![]() $G^\natural $
-action on
$G^\natural $
-action on
![]() $\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
is just the interval between the orbits labelled
$\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
is just the interval between the orbits labelled
![]() ${A_2+\tilde {A}_1}$
and
${A_2+\tilde {A}_1}$
and
![]() $A_1$
in the Hasse diagram of
$A_1$
in the Hasse diagram of
![]() $F_4$
, and the dimension of the corresponding
$F_4$
, and the dimension of the corresponding
![]() $G^\natural $
-orbits would be
$G^\natural $
-orbits would be
![]() $18, 14, 12, 6, 0$
. Since it does not coincide with the Hasse diagram of
$18, 14, 12, 6, 0$
. Since it does not coincide with the Hasse diagram of
![]() $\mathcal {N}_{C_3}$
, this case is ruled out.
$\mathcal {N}_{C_3}$
, this case is ruled out.
Consider now the minimal nilpotent orbit
![]() $A_1$
of
$A_1$
of
![]() $E_7$
(dimension 34). In this case,
$E_7$
(dimension 34). In this case,
![]() $\mathfrak {g}^\natural \cong D_6$
. Since the nilpotent cone of
$\mathfrak {g}^\natural \cong D_6$
. Since the nilpotent cone of
![]() $D_6$
has dimension
$D_6$
has dimension
![]() $60$
, we have
$60$
, we have ![]() . Only the orbits
. Only the orbits
![]() $4 A_1$
and
$4 A_1$
and
![]() $2 A_2 + A_1$
can satisfy this conditions and occur as
$2 A_2 + A_1$
can satisfy this conditions and occur as
![]() ${\mathbb {O}}_k$
.
${\mathbb {O}}_k$
.
If
![]() ${\mathbb {O}}_k = 4 A_1$
, then
${\mathbb {O}}_k = 4 A_1$
, then
![]() $q=2$
(here,
$q=2$
(here,
![]() $k = -18 + p/q$
), and if
$k = -18 + p/q$
), and if
![]() ${\mathbb {O}}_k = 2 A_2+A_1$
, then
${\mathbb {O}}_k = 2 A_2+A_1$
, then
![]() $q=3$
. Now we examine admissibility of the level
$q=3$
. Now we examine admissibility of the level
in each case.
-
* If
 $q=2$
, then
$q=2$
, then
 $(p-4q)/q = (p - 8)/2$
and
$(p-4q)/q = (p - 8)/2$
and
 $p - 8 \ge 19 - 8 = 11 \ge 19=h_{D_6}^\vee $
so
$p - 8 \ge 19 - 8 = 11 \ge 19=h_{D_6}^\vee $
so
 $k^\natural $
is admissible.
$k^\natural $
is admissible. -
* If
 $q=3$
, then
$q=3$
, then
 $(p-4q)/q= (p - 12)/3$
, but
$(p-4q)/q= (p - 12)/3$
, but
 $p \ge 19$
gives us only
$p \ge 19$
gives us only
 $p - 12 \ge 7$
, not
$p - 12 \ge 7$
, not
 $p - 12 \ge 10$
as required for admissibility.
$p - 12 \ge 10$
as required for admissibility.
To exclude the second case, we observe instead that
![]() $\dim {\mathbb {O}}_{2 A_2+A_1}-\dim {\mathbb {O}}_{A_1}=56$
. In
$\dim {\mathbb {O}}_{2 A_2+A_1}-\dim {\mathbb {O}}_{A_1}=56$
. In
![]() $\mathcal {N}_{D_6}$
, there are exactly two nilpotent orbits of dimension 56: there are associated with the partition
$\mathcal {N}_{D_6}$
, there are exactly two nilpotent orbits of dimension 56: there are associated with the partition
![]() $(7,5)$
and
$(7,5)$
and
![]() $(9,1^3)$
. So if
$(9,1^3)$
. So if
![]() $\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
were collapsing, then necessarily
$\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
were collapsing, then necessarily
![]() $\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
would be isomorphic to one of the nilpotent orbit closures of
$\mathcal {S}_{{\mathbb {O}}_{A_2+\tilde {A}_1},A_1}$
would be isomorphic to one of the nilpotent orbit closures of
![]() $D_6$
of dimension 56 since it is irreducible. Both of them contain the nilpotent
$D_6$
of dimension 56 since it is irreducible. Both of them contain the nilpotent
![]() $G^\natural $
-orbit of dimension 54, associated with the partition
$G^\natural $
-orbit of dimension 54, associated with the partition
![]() $(7,3,1^2)$
while, looking at the Hasse diagram of the
$(7,3,1^2)$
while, looking at the Hasse diagram of the
![]() $G^\natural $
-action on
$G^\natural $
-action on
![]() $\mathcal {S}_{{\mathbb {O}}_{2 A_2+A_1},A_1}$
in
$\mathcal {S}_{{\mathbb {O}}_{2 A_2+A_1},A_1}$
in
![]() $E_7$
, we see that this is not possible.
$E_7$
, we see that this is not possible.
The rest of the verifications are left to the reader.
6.2 Central charge
Let k be an admissible level for
![]() $\mathfrak {g}$
. We recall (1) that the nilpotent orbit
$\mathfrak {g}$
. We recall (1) that the nilpotent orbit
![]() $X_{L_k(\mathfrak {g})} \subset \mathcal {N}_{\mathfrak {g}}$
completely determines the denominator q of the level
$X_{L_k(\mathfrak {g})} \subset \mathcal {N}_{\mathfrak {g}}$
completely determines the denominator q of the level
![]() $k=-h_{\mathfrak {g}}^\vee +p/q$
(cf. Theorem 3.2), and (2) that the
$k=-h_{\mathfrak {g}}^\vee +p/q$
(cf. Theorem 3.2), and (2) that the
![]() $k_i^\natural $
, defined by (32) are all polynomials of degree one in k or, equivalently, in p.
$k_i^\natural $
, defined by (32) are all polynomials of degree one in k or, equivalently, in p.
Assume that both k and
![]() $k^\natural $
are admissible. Then both
$k^\natural $
are admissible. Then both
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
and
$L_{k^\natural }(\mathfrak {g}^\natural )$
and
![]() $\mathscr {W}_k(\mathfrak {g},f)$
are conformal vertex algebra since admissible levels are never critical. Denoting by
$\mathscr {W}_k(\mathfrak {g},f)$
are conformal vertex algebra since admissible levels are never critical. Denoting by
![]() $c_V$
the central charge of a conformal vertex algebra V, we recall that
$c_V$
the central charge of a conformal vertex algebra V, we recall that
 $$ \begin{align*}c_{L_{k}(\mathfrak{g})}= \dfrac{k \dim \mathfrak{g} }{k + h_{\mathfrak{g}}^\vee}.\end{align*} $$
$$ \begin{align*}c_{L_{k}(\mathfrak{g})}= \dfrac{k \dim \mathfrak{g} }{k + h_{\mathfrak{g}}^\vee}.\end{align*} $$
If
![]() $\mathfrak {g}_0^\natural = 0$
, then obviously,
$\mathfrak {g}_0^\natural = 0$
, then obviously,

In this case, the possible values of the numerator p of
![]() $k+h_{\mathfrak {g}}^\vee $
for admissible k are determined as solutions of
$k+h_{\mathfrak {g}}^\vee $
for admissible k are determined as solutions of
considered as an equation in an unknown p. Recall that
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))}$
is given in equation (21). If there are no solutions in p to the equation (41), then k is not collapsing. If there are solutions (with
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))}$
is given in equation (21). If there are no solutions in p to the equation (41), then k is not collapsing. If there are solutions (with
![]() $p \ge h_{\mathfrak {g}}$
or
$p \ge h_{\mathfrak {g}}$
or
![]() $p \ge h_{\mathfrak {g}}^\vee $
so as to ensure that
$p \ge h_{\mathfrak {g}}^\vee $
so as to ensure that
![]() $k=-h_{\mathfrak {g}}^{\vee }+p/q$
is admissible), then we proceed to the next step (§6.3).
$k=-h_{\mathfrak {g}}^{\vee }+p/q$
is admissible), then we proceed to the next step (§6.3).
If
![]() $\mathfrak {g}_0^\natural \neq 0$
, then, by Lemma 6.1, the level k can only be collapsing if
$\mathfrak {g}_0^\natural \neq 0$
, then, by Lemma 6.1, the level k can only be collapsing if
![]() $\phi _0^\natural = 0$
. In particular,
$\phi _0^\natural = 0$
. In particular,
![]() $c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
continues to be given by (40). Now the condition
$c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
continues to be given by (40). Now the condition
![]() $\phi _0^\natural = 0$
entirely determines k, and the equation (41), rather than determining p, is simply either true or false. If it is false, then k is not collapsing. If it is true, then we proceed to the next step (§6.3) as before.
$\phi _0^\natural = 0$
entirely determines k, and the equation (41), rather than determining p, is simply either true or false. If it is false, then k is not collapsing. If it is true, then we proceed to the next step (§6.3) as before.
The data needed to compute the levels
![]() $k_i^\natural $
in term of k, for
$k_i^\natural $
in term of k, for ![]() , are collected in Tables 2–4 for the classical types, and in Tables 11–17 for the exceptional types. The data for the exceptional types have been obtained using the software GAP4.
, are collected in Tables 2–4 for the classical types, and in Tables 11–17 for the exceptional types. The data for the exceptional types have been obtained using the software GAP4.
6.3 Asymptotic growth and asymptotic dimension
The first and second steps (§6.1 and §6.2) allow us to detect possible values for admissible k and
![]() $k^\natural $
. As this point, we apply Theorem 3.10, or rather, the following powerful consequence of it.
$k^\natural $
. As this point, we apply Theorem 3.10, or rather, the following powerful consequence of it.
Proposition 6.6. Let k and
![]() $k^{\natural }$
be admissible,
$k^{\natural }$
be admissible,
![]() $f\in \overline {\mathbb {O}}_k$
. Suppose that
$f\in \overline {\mathbb {O}}_k$
. Suppose that
 $$ \begin{align*} &\mathbf{g}_{H^0_{DS,f}(L_k(\mathfrak{g}))}=\mathbf{g}_{L_{k^\natural}(\mathfrak{g}^\natural)}=\sum_{i=1}^s\mathbf{g}_{L_{k_i}(\mathfrak{g}_i)},\\ & \mathbf{A}_{H^0_{DS,f}(L_k(\mathfrak{g}))}=\mathbf{A}_{L_{k^\natural}(\mathfrak{g}^\natural)}=\prod_{i=1}^s\mathbf{A}_{L_{k_i}(\mathfrak{g}_i)}. \end{align*} $$
$$ \begin{align*} &\mathbf{g}_{H^0_{DS,f}(L_k(\mathfrak{g}))}=\mathbf{g}_{L_{k^\natural}(\mathfrak{g}^\natural)}=\sum_{i=1}^s\mathbf{g}_{L_{k_i}(\mathfrak{g}_i)},\\ & \mathbf{A}_{H^0_{DS,f}(L_k(\mathfrak{g}))}=\mathbf{A}_{L_{k^\natural}(\mathfrak{g}^\natural)}=\prod_{i=1}^s\mathbf{A}_{L_{k_i}(\mathfrak{g}_i)}. \end{align*} $$
Then k is collapsing.
Proof. The assertion follows immediately by applying Theorem 3.10, taking for
![]() $\tilde {V} \rightarrow V$
the map
$\tilde {V} \rightarrow V$
the map
![]() $H^0_{DS,f}(L_k(\mathfrak {g})) \rightarrow \mathscr {W}_k(\mathfrak {g},f)$
. Thus,
$H^0_{DS,f}(L_k(\mathfrak {g})) \rightarrow \mathscr {W}_k(\mathfrak {g},f)$
. Thus,
![]() $L_{k^\natural }(\mathfrak {g}^\natural ) \cong \mathscr {W}_k(\mathfrak {g},f)$
, and we conclude that k is collapsing as required.
$L_{k^\natural }(\mathfrak {g}^\natural ) \cong \mathscr {W}_k(\mathfrak {g},f)$
, and we conclude that k is collapsing as required.
This proposition ensures that it is enough to compare the asymptotic growths and the asymptotic dimension of the vertex algebras
![]() $H_{DS,f}^{0}(L_k(\mathfrak {g}))$
and
$H_{DS,f}^{0}(L_k(\mathfrak {g}))$
and
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
that we compute using Corollary 3.9. This is the goal of next sections. In the classical cases, we sometimes directly use the asymptotic growths (when f admits an even good grading) to detect possible values of k instead of the central charge argument because the equation given by the central charge is often difficult to solve.
$L_{k^\natural }(\mathfrak {g}^\natural )$
that we compute using Corollary 3.9. This is the goal of next sections. In the classical cases, we sometimes directly use the asymptotic growths (when f admits an even good grading) to detect possible values of k instead of the central charge argument because the equation given by the central charge is often difficult to solve.
Remark 6.7. In Proposition 6.6, suppose further that
![]() $f\in \mathbb {O}_k$
so that
$f\in \mathbb {O}_k$
so that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is lisse. Then we get that
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse. Then we get that
without the assumption that f admits an even good grading. Indeed,
![]() $f\in \mathbb {O}_k$
implies that
$f\in \mathbb {O}_k$
implies that
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
is lisse by Theorem 4.3. Hence,
$H_{DS,f}^0(L_k(\mathfrak {g}))$
is lisse by Theorem 4.3. Hence,
![]() $L_{k^\natural }(\mathfrak {g}^{\natural })$
must be integrable, and the homomorphism
$L_{k^\natural }(\mathfrak {g}^{\natural })$
must be integrable, and the homomorphism
![]() $\varphi $
of Theorem 3.10 must factor through the embedding
$\varphi $
of Theorem 3.10 must factor through the embedding
![]() $L_{k^\natural }(\mathfrak {g}^{\natural })\hookrightarrow H_{DS,f}^0(L_k(\mathfrak {g}))$
([Reference Dong and Mason37]). In particular,
$L_{k^\natural }(\mathfrak {g}^{\natural })\hookrightarrow H_{DS,f}^0(L_k(\mathfrak {g}))$
([Reference Dong and Mason37]). In particular,
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
is a direct sum of integrable representations of the affine Kac-Moody algebra associated with
$H_{DS,f}^0(L_k(\mathfrak {g}))$
is a direct sum of integrable representations of the affine Kac-Moody algebra associated with
![]() $\mathfrak {g}^{\natural }$
. It follows that the proof of Theorem 3.10 goes through to obtain that
$\mathfrak {g}^{\natural }$
. It follows that the proof of Theorem 3.10 goes through to obtain that
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))\cong L_{k^\natural }(\mathfrak {g}^{\natural })$
.
$H_{DS,f}^0(L_k(\mathfrak {g}))\cong L_{k^\natural }(\mathfrak {g}^{\natural })$
.
If the isomorphism
![]() $\mathscr {W}_k(\mathfrak {g},f)\cong H_{DS,f}^0(L_k(\mathfrak {g}))$
holds, which is the case when f admits an even good grading, Proposition 6.6 gives a necessary and sufficient condition for admissible k to be collapsing. Unfortunately, in general, it gives only a sufficient condition.
$\mathscr {W}_k(\mathfrak {g},f)\cong H_{DS,f}^0(L_k(\mathfrak {g}))$
holds, which is the case when f admits an even good grading, Proposition 6.6 gives a necessary and sufficient condition for admissible k to be collapsing. Unfortunately, in general, it gives only a sufficient condition.
The following proposition will be useful to obtain explicit decompositions of finite extensions of admissible simple affine vertex algebras.
Proposition 6.8. Let k and
![]() $k^{\natural }$
be admissible,
$k^{\natural }$
be admissible,
![]() $f\in \overline {\mathbb {O}}_k$
. Suppose that the associated varieties of
$f\in \overline {\mathbb {O}}_k$
. Suppose that the associated varieties of
![]() $H^0_{DS,f}(L_k(\mathfrak {g}))$
and
$H^0_{DS,f}(L_k(\mathfrak {g}))$
and
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
have the same dimension and are not isomorphic. Then k is not collapsing.
$L_{k^\natural }(\mathfrak {g}^\natural )$
have the same dimension and are not isomorphic. Then k is not collapsing.
Proof. The assumption ensures that
![]() $H^0_{DS,f}(L_k(\mathfrak {g}))$
is nonzero. Hence,
$H^0_{DS,f}(L_k(\mathfrak {g}))$
is nonzero. Hence,
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is a quotient of
$\mathscr {W}_k(\mathfrak {g},f)$
is a quotient of
![]() $H^0_{DS,f}(L_k(\mathfrak {g}))$
, and its associated variety is a Zariski closed subvariety of that of
$H^0_{DS,f}(L_k(\mathfrak {g}))$
, and its associated variety is a Zariski closed subvariety of that of
![]() $H^0_{DS,f}(L_k(\mathfrak {g}))$
. However, since k is admissible, the associated variety of
$H^0_{DS,f}(L_k(\mathfrak {g}))$
. However, since k is admissible, the associated variety of
![]() $H^0_{DS,f}(L_k(\mathfrak {g}))$
is irreducible,
$H^0_{DS,f}(L_k(\mathfrak {g}))$
is irreducible,
![]() $\overline {{\mathbb {O}}_k}$
being unibranch (see [Reference Arakawa and Moreau21]). If k were collapsing, then the associated variety of
$\overline {{\mathbb {O}}_k}$
being unibranch (see [Reference Arakawa and Moreau21]). If k were collapsing, then the associated variety of
![]() $\mathscr {W}_k(\mathfrak {g},f)$
would be isomorphic to the (irreducible) variety
$\mathscr {W}_k(\mathfrak {g},f)$
would be isomorphic to the (irreducible) variety
![]() $X_{L_{k^\natural }(\mathfrak {g}^\natural )}$
and so would have the same dimension as
$X_{L_{k^\natural }(\mathfrak {g}^\natural )}$
and so would have the same dimension as
![]() $X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
by the hypothesis. Then it would be isomorphic to the variety
$X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
by the hypothesis. Then it would be isomorphic to the variety
![]() $X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
since
$X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
since
![]() $X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
is irreducible. This contradicts the non-isomorphism hypothesis.
$X_{H^0_{DS,f}(L_k(\mathfrak {g}))}$
is irreducible. This contradicts the non-isomorphism hypothesis.
7 Some useful product formulas
We recall the well-known identity

and its immediate consequence
 $$ \begin{align} \prod_{j=1}^{n} 2\sin\ {\frac{(j-1/2) \pi}{n}} = 2. \end{align} $$
$$ \begin{align} \prod_{j=1}^{n} 2\sin\ {\frac{(j-1/2) \pi}{n}} = 2. \end{align} $$
In this section, we record some further identities similar to these which will be very helpful when we come to apply Corollary 3.9.
First, from (42), we deduce

Next, we have the following identities.
Lemma 7.1 [Reference Kac54, Reference Kac and Peterson56].
-
1. We have

-
2. For
 $\mathfrak {g}$
simple, not of type
$\mathfrak {g}$
simple, not of type
 $C_\ell $
,
$C_\ell $
,
 $G_2$
,
$G_2$
,
 $F_4$
, we have
$F_4$
, we have 
-
3. We have
 .
. -
4. We have

The lemma is probably known. We provide a proof for the convenience of the reader, and to clear up an ambiguity from [Reference Kac and Peterson56] (see Remark 7.2).
Proof. As a rule, in this proof, we write
![]() $\rho _{\mathfrak {g}}$
(resp.
$\rho _{\mathfrak {g}}$
(resp.
![]() $\rho _{\mathfrak {g}}^\vee $
) for the half-sum of positive roots (resp. coroots) of
$\rho _{\mathfrak {g}}^\vee $
) for the half-sum of positive roots (resp. coroots) of
![]() $\mathfrak {g}$
. For
$\mathfrak {g}$
. For
![]() $p \in \mathbb {Z}_{>0}$
, set
$p \in \mathbb {Z}_{>0}$
, set

Since
![]() $\{ \mathrm {ht}(\alpha ) \colon \alpha \in \Delta _+\}= \{ \mathrm {ht}(\alpha ^\vee ) \colon \alpha \in \Delta _+\}$
, note that for any
$\{ \mathrm {ht}(\alpha ) \colon \alpha \in \Delta _+\}= \{ \mathrm {ht}(\alpha ^\vee ) \colon \alpha \in \Delta _+\}$
, note that for any
![]() $p \ge h_{\mathfrak {g}}$
,
$p \ge h_{\mathfrak {g}}$
,

We use the data of Table 1.
(1) The identity is established in [Reference Kac54, Chapter 13, (13.8.1)] using modular invariance properties. It can also be checked using a case-by-case argument exploiting identities (42) and (44).
(2) We check the identity using a case-by-case argument.
![]() $\ast $
Type
$\ast $
Type
![]() $A_\ell $
. We have
$A_\ell $
. We have
![]() $h_{A_\ell }^\vee +1=\ell +2$
. Since
$h_{A_\ell }^\vee +1=\ell +2$
. Since
![]() $(\rho _{A_\ell } | \alpha ) = \operatorname {ht}(\alpha )$
, we see easily that
$(\rho _{A_\ell } | \alpha ) = \operatorname {ht}(\alpha )$
, we see easily that

So by (1) applied to
![]() $A_{\ell +1}$
, we obtain the expected statement,
$A_{\ell +1}$
, we obtain the expected statement,
![]() $ \varPi _{A_\ell }(\ell +2) =(\ell +2)^{\ell /2} ,$
using the identity (42).
$ \varPi _{A_\ell }(\ell +2) =(\ell +2)^{\ell /2} ,$
using the identity (42).
![]() $\ast $
Type
$\ast $
Type
![]() $B_\ell $
and
$B_\ell $
and
![]() $D_\ell $
. We have
$D_\ell $
. We have
![]() $h_{B_\ell }^\vee =2\ell -1$
and
$h_{B_\ell }^\vee =2\ell -1$
and
![]() $h_{D_\ell }^\vee +1=2\ell -1$
. We first show the statement for
$h_{D_\ell }^\vee +1=2\ell -1$
. We first show the statement for
![]() $D_\ell $
. We have to show that
$D_\ell $
. We have to show that
By (1) applied to
![]() $B_\ell $
, we have
$B_\ell $
, we have
So it suffices to show that the ratio
 $\dfrac {\varPi _{B_\ell }(2\ell -1)}{\varPi _{D_\ell }(2\ell -1)}$
equals
$\dfrac {\varPi _{B_\ell }(2\ell -1)}{\varPi _{D_\ell }(2\ell -1)}$
equals
![]() $2$
. Observing that
$2$
. Observing that
![]() $(\rho _{D_\ell } |\alpha )=\mathrm {ht}(\alpha )$
, we get that
$(\rho _{D_\ell } |\alpha )=\mathrm {ht}(\alpha )$
, we get that

However, observing that
![]() $(\rho _{B_\ell } |\alpha )=\mathrm {ht}(\alpha )$
if
$(\rho _{B_\ell } |\alpha )=\mathrm {ht}(\alpha )$
if
![]() $\alpha $
is long and
$\alpha $
is long and
![]() $(\rho _{B_\ell } |\alpha )=\frac {1}{2}\mathrm {ht}(\alpha )$
if
$(\rho _{B_\ell } |\alpha )=\frac {1}{2}\mathrm {ht}(\alpha )$
if
![]() $\alpha $
is short, we get that
$\alpha $
is short, we get that

Using the identity (42), we show that

From this, we obtain that
 $\dfrac {\varPi _{B_\ell }(2\ell -1)}{\varPi _{D_\ell }(2\ell -1)}=2$
, as desired.
$\dfrac {\varPi _{B_\ell }(2\ell -1)}{\varPi _{D_\ell }(2\ell -1)}=2$
, as desired.
We now turn to the statement for
![]() $B_\ell $
. We have to show that
$B_\ell $
. We have to show that
By (1) applied to
![]() $D_{\ell +1}$
, we have
$D_{\ell +1}$
, we have
So it suffices to show that the ratio
 $\dfrac {\varPi _{D_{\ell +1}}(2\ell )}{\varPi _{B_\ell }(2\ell ) }$
equals
$\dfrac {\varPi _{D_{\ell +1}}(2\ell )}{\varPi _{B_\ell }(2\ell ) }$
equals
![]() $2 (2\ell )^{1/2}$
. As before, computing the heights of roots, we obtain that
$2 (2\ell )^{1/2}$
. As before, computing the heights of roots, we obtain that

Using (42), we show that

whence
 $\dfrac {\varPi _{D_{\ell +1}}(2\ell )}{\varPi _{B_\ell }(2\ell ) }=2 (2\ell )^{1/2},$
as desired.
$\dfrac {\varPi _{D_{\ell +1}}(2\ell )}{\varPi _{B_\ell }(2\ell ) }=2 (2\ell )^{1/2},$
as desired.
![]() $\ast $
Types
$\ast $
Types
![]() $E_6, E_7, E_8$
. By direct calculations, we easily obtain that
$E_6, E_7, E_8$
. By direct calculations, we easily obtain that

Similarly, we get
(3) and (4). We prove both identities together.
By (2), it suffices to check the statement for the non-simply laced cases. We easily check that
It remains to consider the cases where
![]() $\mathfrak {g}$
has type
$\mathfrak {g}$
has type
![]() $B_\ell $
or
$B_\ell $
or
![]() $C_\ell $
.
$C_\ell $
.
![]() $\ast $
Type
$\ast $
Type
![]() $B_\ell $
. Let us first prove the identity (4). By (1) applied to
$B_\ell $
. Let us first prove the identity (4). By (1) applied to
![]() $B_{\ell +1}$
, we have
$B_{\ell +1}$
, we have
Hence, it suffices to show that
 $$ \begin{align*}\dfrac{\varPi_{B_{\ell+1}}(2\ell+1)}{\varPi^\vee_{B_{\ell}}(2\ell+1)}=2(2\ell+1)^{1/2}.\end{align*} $$
$$ \begin{align*}\dfrac{\varPi_{B_{\ell+1}}(2\ell+1)}{\varPi^\vee_{B_{\ell}}(2\ell+1)}=2(2\ell+1)^{1/2}.\end{align*} $$
Using the computations of (2) and the identity (42), we easily obtain the expected equality.
Let us now prove the identity (3) for
![]() $B_\ell $
. By (2) applied to
$B_\ell $
. By (2) applied to
![]() $B_\ell $
, we have
$B_\ell $
, we have
Hence, it suffices to show that
 $$ \begin{align*}\dfrac{\varPi^\vee_{B_{\ell}}(2\ell)}{\varPi_{B_{\ell}}(2\ell)}=2^{1/2}\end{align*} $$
$$ \begin{align*}\dfrac{\varPi^\vee_{B_{\ell}}(2\ell)}{\varPi_{B_{\ell}}(2\ell)}=2^{1/2}\end{align*} $$
since
![]() $|P^\vee /Q^\vee |=2$
for the type
$|P^\vee /Q^\vee |=2$
for the type
![]() $B_\ell $
. Using (42) and the computations of (2), we easily obtain the expected equality.
$B_\ell $
. Using (42) and the computations of (2), we easily obtain the expected equality.
![]() $\ast $
Type
$\ast $
Type
![]() $C_\ell $
. Notice that
$C_\ell $
. Notice that
![]() $h_{C_\ell }= h_{B_\ell }= 2 \ell $
. Hence, it suffices to show that
$h_{C_\ell }= h_{B_\ell }= 2 \ell $
. Hence, it suffices to show that
 $$ \begin{align*}\dfrac{\varPi_{B_{\ell}}^\vee(2\ell)}{\varPi_{C_{\ell}}^\vee(2\ell)}=1\quad \text{and} \quad \dfrac{\varPi_{B_{\ell}}^\vee(2\ell+1)}{\varPi_{C_{\ell}}^\vee(2\ell+1)}=1 \end{align*} $$
$$ \begin{align*}\dfrac{\varPi_{B_{\ell}}^\vee(2\ell)}{\varPi_{C_{\ell}}^\vee(2\ell)}=1\quad \text{and} \quad \dfrac{\varPi_{B_{\ell}}^\vee(2\ell+1)}{\varPi_{C_{\ell}}^\vee(2\ell+1)}=1 \end{align*} $$
since
![]() $|P^\vee /Q^\vee |=2$
for the types
$|P^\vee /Q^\vee |=2$
for the types
![]() $B_\ell $
and
$B_\ell $
and
![]() $C_\ell $
. Again using (42), we easily obtain the expected equalities. This concludes the proof of the lemma.
$C_\ell $
. Again using (42), we easily obtain the expected equalities. This concludes the proof of the lemma.
Remark 7.2. The identities of the lemma are also stated in [Reference Kac and Peterson56, Proposition 4.30]. However, contrary to what should follow from (4.30.2) of [Reference Kac and Peterson56], identity (2) does not hold for the types
![]() $C_\ell $
,
$C_\ell $
,
![]() $\ell \ge 3$
,
$\ell \ge 3$
,
![]() $G_2$
and
$G_2$
and
![]() $F_4$
. For these types, it seems that there is no pleasant formula for
$F_4$
. For these types, it seems that there is no pleasant formula for  .
.
In the next two sections, we study collapsing levels in the classical cases, implementing the strategy described in Section 6.
8 Collapsing levels for type
 ${\mathfrak {sl}}_n$
${\mathfrak {sl}}_n$
Let
![]() $n\in \mathbb {Z}_{>0}$
. In this section, it is assumed that
$n\in \mathbb {Z}_{>0}$
. In this section, it is assumed that
![]() $\mathfrak {g}$
is the simple Lie algebra
$\mathfrak {g}$
is the simple Lie algebra
![]() $\mathfrak {sl}_n$
, the Lie algebra of traceless
$\mathfrak {sl}_n$
, the Lie algebra of traceless
![]() $n \times n$
matrices with coefficients in
$n \times n$
matrices with coefficients in
![]() $\mathbb {C}$
. The Killing form of
$\mathbb {C}$
. The Killing form of
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
is given by
$\mathfrak {g}={\mathfrak {sl}}_n$
is given by
![]() $\kappa _{\mathfrak {g}}(x,y)= 2n \mathrm {tr}(xy)$
and
$\kappa _{\mathfrak {g}}(x,y)= 2n \mathrm {tr}(xy)$
and
![]() $(x|y)_{\mathfrak {g}}=\mathrm {tr}(xy)$
.
$(x|y)_{\mathfrak {g}}=\mathrm {tr}(xy)$
.
Denote by
![]() ${\mathscr {P}}(n)$
the set of partitions of n. As a rule, unless otherwise specified, we write an element
${\mathscr {P}}(n)$
the set of partitions of n. As a rule, unless otherwise specified, we write an element ![]() of
of
![]() ${\mathscr {P}}(n)$
as a decreasing sequence
${\mathscr {P}}(n)$
as a decreasing sequence ![]() omitting zeroes. Thus,
omitting zeroes. Thus,
Let us denote by
![]() $\ge $
the partial order on
$\ge $
the partial order on
![]() ${\mathscr {P}}(n)$
relative to dominance. More precisely, given
${\mathscr {P}}(n)$
relative to dominance. More precisely, given ![]() , we have
, we have ![]() if
if ![]() for
for ![]() .
.
By [Reference Collingwood and McGovern32, Theorem 5.1.1], nilpotent orbits of
![]() ${\mathfrak {sl}}_{n}$
are parametrised by
${\mathfrak {sl}}_{n}$
are parametrised by
![]() ${\mathscr {P}}(n)$
. For
${\mathscr {P}}(n)$
. For ![]() , we shall denote by
, we shall denote by ![]() the corresponding nilpotent orbit of
the corresponding nilpotent orbit of
![]() ${\mathfrak {sl}}_n$
. If
${\mathfrak {sl}}_n$
. If ![]() , then
, then ![]() if and only if
if and only if ![]() .
.
Definition 8.1. Let ![]() . A degeneration of
. A degeneration of ![]() is an element
is an element
![]() $\boldsymbol {\mu } \in {\mathscr {P}}(n)$
such that
$\boldsymbol {\mu } \in {\mathscr {P}}(n)$
such that ![]() – that is,
– that is, ![]() . A degeneration
. A degeneration
![]() $\boldsymbol {\mu }$
of
$\boldsymbol {\mu }$
of ![]() is said to be minimal if
is said to be minimal if
![]() ${\mathbb {O}}_{\boldsymbol {\mu }}$
is open in
${\mathbb {O}}_{\boldsymbol {\mu }}$
is open in ![]() .
.
Fix ![]() . As proved in [Reference Elashvili, Kac and Vinberg38], the set of good gradings for
. As proved in [Reference Elashvili, Kac and Vinberg38], the set of good gradings for ![]() is in bijection with the set of pyramids of shape
is in bijection with the set of pyramids of shape ![]() . We refer to [Reference Brundan and Goodwin30] for the precise construction of pyramids associated with good gradings.
. We refer to [Reference Brundan and Goodwin30] for the precise construction of pyramids associated with good gradings.
For our purpose, let us just recall that a pyramid is a diagram consisting of n boxes each of size 2 units by 2 units drawn in the upper half of the
![]() $xy$
-place, with midpoints having integer coordinates. By the coordinates of the box i, we mean the coordinates of its midpoint. We will also speak of the row number of a box, by which we mean its y-coordinate, and the column number of a box, meaning its x-coordinate. A pyramid of shape
$xy$
-place, with midpoints having integer coordinates. By the coordinates of the box i, we mean the coordinates of its midpoint. We will also speak of the row number of a box, by which we mean its y-coordinate, and the column number of a box, meaning its x-coordinate. A pyramid of shape ![]() consists of r rows, with the
consists of r rows, with the
![]() $i^{\text {th}}$
row consisting of
$i^{\text {th}}$
row consisting of ![]() horizontally consecutive boxes. The rows are positioned so that the boxes of the first row are centred on the y-axis and have y-coordinate
horizontally consecutive boxes. The rows are positioned so that the boxes of the first row are centred on the y-axis and have y-coordinate
![]() $1$
, the boxes of the second row have y-coordinate
$1$
, the boxes of the second row have y-coordinate
![]() $3$
, etc. In addition, no box of row i is permitted to have its x-coordinate smaller than the minimal x-coordinate of the boxes in row
$3$
, etc. In addition, no box of row i is permitted to have its x-coordinate smaller than the minimal x-coordinate of the boxes in row
![]() $i-1$
, nor may its x-coordinate be greater than the maximal x-coordinates of the boxes in row
$i-1$
, nor may its x-coordinate be greater than the maximal x-coordinates of the boxes in row
![]() $i-1$
. We obtain the Dynkin pyramid (corresponding to the Dynkin grading) when the boxes of any row are centred around the y-axis. Note that a good grading is even if and only if the x-coordinates of all boxes have the same parity. This is always the case for the left-adjusted and the right-adjusted pyramids of shape
$i-1$
. We obtain the Dynkin pyramid (corresponding to the Dynkin grading) when the boxes of any row are centred around the y-axis. Note that a good grading is even if and only if the x-coordinates of all boxes have the same parity. This is always the case for the left-adjusted and the right-adjusted pyramids of shape ![]() . For the Dynkin pyramid, this happens if and only if all parts
. For the Dynkin pyramid, this happens if and only if all parts ![]() have the same parity.
have the same parity.
We number the boxes of the pyramid from top right to bottom left and so that col![]() . Then one can choose a representative f in
. Then one can choose a representative f in ![]() as follows. Set
as follows. Set
![]() $f=\sum _{i,j} e_{i,j}$
, where the sum is over all
$f=\sum _{i,j} e_{i,j}$
, where the sum is over all ![]() such that
such that
![]() $\mathrm {row}(i) = \mathrm {row}(j)$
and
$\mathrm {row}(i) = \mathrm {row}(j)$
and
![]() $\mathrm {col}(j)= \mathrm {col}(i)+2$
. Set
$\mathrm {col}(j)= \mathrm {col}(i)+2$
. Set
where
![]() $\tilde {x}_\Gamma ^0=\sum _{i=1}^n \frac {1}{2}\mathrm {col}(i) e_{i,i}$
and
$\tilde {x}_\Gamma ^0=\sum _{i=1}^n \frac {1}{2}\mathrm {col}(i) e_{i,i}$
and
![]() $\varepsilon $
is chosen so that
$\varepsilon $
is chosen so that
![]() $\mathrm {tr}(x_\Gamma ^0)=0$
. Here,
$\mathrm {tr}(x_\Gamma ^0)=0$
. Here,
![]() $e_{i,j}$
stands for the
$e_{i,j}$
stands for the
![]() $(i,j)$
-matrix unit. Then
$(i,j)$
-matrix unit. Then ![]() and
and
yields a good grading  for f (see [Reference Elashvili, Kac and Vinberg38] or [Reference Brundan and Goodwin30, §6]).
for f (see [Reference Elashvili, Kac and Vinberg38] or [Reference Brundan and Goodwin30, §6]).
As an example, we represent in Figure 1 the left-adjusted, the Dynkin and the right-adjusted pyramids for the partition ![]() .
.

Figure 1 Left-adjusted, Dynkin and right-adjusted pyramids of shape ![]()
The following lemma is a refinement of [Reference Kraft and Procesi65, Propositions 4.4 and 5.4]. We refer to [Reference Li68, Propositions 7.3.1 and 7.3.2] for a proof.
Lemma 8.2 (row/column removal rule in
 ${\mathfrak {sl}}_n$
).
${\mathfrak {sl}}_n$
).
Let ![]() and
and
![]() ${\boldsymbol {\mu }}$
a degeneration of
${\boldsymbol {\mu }}$
a degeneration of ![]() . Assume that the first l rows and the first m columns of
. Assume that the first l rows and the first m columns of ![]() and
and
![]() $ {\boldsymbol {\mu }}$
coincide. Denote by
$ {\boldsymbol {\mu }}$
coincide. Denote by ![]() and
and
![]() $\boldsymbol {\mu }'$
the partitions obtained by erasing these l common rows and m common columns. Then
$\boldsymbol {\mu }'$
the partitions obtained by erasing these l common rows and m common columns. Then
as algebraic varieties, with
![]() $f \in {\mathbb {O}}_{{\boldsymbol {\mu }}}$
and
$f \in {\mathbb {O}}_{{\boldsymbol {\mu }}}$
and
![]() $f' \in {\mathbb {O}}_{{\boldsymbol {\mu }'}}$
. In particular, if
$f' \in {\mathbb {O}}_{{\boldsymbol {\mu }'}}$
. In particular, if
![]() $f'=0$
, then
$f'=0$
, then ![]() .
.
By [Reference Arakawa10], if k is an admissible level for
![]() ${\mathfrak {sl}}_n$
, we have
${\mathfrak {sl}}_n$
, we have ![]() , where
, where
Lemma 8.3. Let
![]() $\boldsymbol {\mu }$
be a partition of n such that
$\boldsymbol {\mu }$
be a partition of n such that ![]() . Let
. Let ![]() and
and
![]() $\boldsymbol {\mu }'$
be the partitions obtained from
$\boldsymbol {\mu }'$
be the partitions obtained from ![]() and
and
![]() $\boldsymbol {\mu }$
by erasing all common rows and columns of
$\boldsymbol {\mu }$
by erasing all common rows and columns of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then,
$\boldsymbol {\mu }$
. Then,
![]() $\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
![]() ${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
– that is,
${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
– that is,
![]() $\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
$\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
![]() $\boldsymbol \mu $
is of one of the following types:
$\boldsymbol \mu $
is of one of the following types:
-
(a)
 ,
, -
(b)
 $\boldsymbol {\mu }=(q^m,1^s)$
with
$\boldsymbol {\mu }=(q^m,1^s)$
with  and
and
 $s \ge 0$
,
$s \ge 0$
, -
(c)
 $\boldsymbol {\mu }=(q^{\widetilde m -1},(q-1)^2)$
and
$\boldsymbol {\mu }=(q^{\widetilde m -1},(q-1)^2)$
and
 $\widetilde s = q-2$
.
$\widetilde s = q-2$
.
Here,
![]() $|\boldsymbol {\mu }'|$
stands for the sum of the parts of
$|\boldsymbol {\mu }'|$
stands for the sum of the parts of
![]() $\boldsymbol {\mu }'$
.
$\boldsymbol {\mu }'$
.
Proof. Since ![]() , one can write
, one can write
![]() $\boldsymbol {\mu }=(q^m,\boldsymbol {\nu })$
, with
$\boldsymbol {\mu }=(q^m,\boldsymbol {\nu })$
, with ![]() and
and ![]() with
with
![]() $\nu _1 < q$
. Assume that
$\nu _1 < q$
. Assume that ![]() , the case
, the case ![]() being obvious.
being obvious.
Let ![]() and
and
![]() $\boldsymbol {\mu }"$
be the partitions obtained from
$\boldsymbol {\mu }"$
be the partitions obtained from
![]() $(q^{\widetilde m},\widetilde s)$
and
$(q^{\widetilde m},\widetilde s)$
and
![]() $\boldsymbol {\mu }$
by erasing all common rows of
$\boldsymbol {\mu }$
by erasing all common rows of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then
$\boldsymbol {\mu }$
. Then ![]() and
and
![]() $\boldsymbol {\mu }"=\boldsymbol {\nu }$
. The partition
$\boldsymbol {\mu }"=\boldsymbol {\nu }$
. The partition
![]() $\boldsymbol {\mu }"$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }"$
corresponds to the zero nilpotent orbit of
![]() ${\mathfrak {sl}}_{|\boldsymbol {\mu }"|}$
if and only if
${\mathfrak {sl}}_{|\boldsymbol {\mu }"|}$
if and only if
![]() $\boldsymbol {\nu } = (1^{|\boldsymbol {\nu } |})$
. This leads to the partitions of type (b). We illustrate in Figures 2 the row removal rule in the case where
$\boldsymbol {\nu } = (1^{|\boldsymbol {\nu } |})$
. This leads to the partitions of type (b). We illustrate in Figures 2 the row removal rule in the case where ![]() and
and
![]() $\boldsymbol {\mu }=(3^2,1^4)$
is of type (b).
$\boldsymbol {\mu }=(3^2,1^4)$
is of type (b).

Figure 2 Row removal rule for ![]() and
and
![]() $\boldsymbol {\mu }=(3^2,1^4).$
$\boldsymbol {\mu }=(3^2,1^4).$
Consider now the common columns of ![]() and
and
![]() $\boldsymbol {\mu }$
. Observe that
$\boldsymbol {\mu }$
. Observe that ![]() and
and ![]() have at least one common column if and only if
have at least one common column if and only if
![]() $\widetilde m +1=m+t$
– that is,
$\widetilde m +1=m+t$
– that is,
Assume that this condition holds.
We illustrate in Figures 3 and 4 the row/column removal rule in the case where ![]() ,
,
![]() $\boldsymbol {\mu }=(5^2,4,3)$
, and in the case where
$\boldsymbol {\mu }=(5^2,4,3)$
, and in the case where ![]() ,
,
![]() $\boldsymbol {\mu }=(5^2,4^2)$
.
$\boldsymbol {\mu }=(5^2,4^2)$
.

Figure 3 Row/column removal rule for ![]() and
and
![]() $\boldsymbol {\mu }=(5^2,4,3).$
$\boldsymbol {\mu }=(5^2,4,3).$

Figure 4 Row/column removal rule for ![]() and
and
![]() $\boldsymbol {\mu }=(5^2,4^2).$
$\boldsymbol {\mu }=(5^2,4^2).$
We obtain that ![]() and
and ![]() . Furthermore,
. Furthermore,
![]() $\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
![]() ${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
if and only if
${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
if and only if
![]() ${\nu }_1-\widetilde s=\cdots ={\nu }_t -\widetilde s=1$
. If so, then necessarily,
${\nu }_1-\widetilde s=\cdots ={\nu }_t -\widetilde s=1$
. If so, then necessarily,
![]() $(\widetilde m -m) (q-\widetilde s)=t$
since
$(\widetilde m -m) (q-\widetilde s)=t$
since ![]() and
and
![]() $\boldsymbol {\mu }'$
are partitions of the same integer, whence
$\boldsymbol {\mu }'$
are partitions of the same integer, whence
using
![]() $t = \widetilde m - m +1$
. But condition (46) holds if and only if
$t = \widetilde m - m +1$
. But condition (46) holds if and only if
![]() $q-\widetilde s -1=1$
and
$q-\widetilde s -1=1$
and
![]() $\widetilde m -m=1$
. This leads to the partitions of type (c).
$\widetilde m -m=1$
. This leads to the partitions of type (c).
Conversely, it is easy to verify that if
![]() $\boldsymbol {\mu }$
is of type (a), (b) or (c), then
$\boldsymbol {\mu }$
is of type (a), (b) or (c), then
![]() $\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
![]() ${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
.
${\mathfrak {sl}}_{|\boldsymbol {\mu }'|}$
.
In view of Lemma 8.3, we describe the centraliser
![]() $\mathfrak {g}^\natural $
and the values of the
$\mathfrak {g}^\natural $
and the values of the
![]() $k_i^\natural $
’s for particular
$k_i^\natural $
’s for particular
![]() ${\mathfrak {sl}}_2$
-triples
${\mathfrak {sl}}_2$
-triples
![]() $(e,h,f)$
of
$(e,h,f)$
of
![]() ${\mathfrak {sl}}_n$
.
${\mathfrak {sl}}_n$
.
Lemma 8.4. Let f be a nilpotent element of
![]() ${\mathfrak {sl}}_n$
associated with
${\mathfrak {sl}}_n$
associated with
![]() $\boldsymbol \mu \in {\mathscr {P}}(n)$
, with
$\boldsymbol \mu \in {\mathscr {P}}(n)$
, with
![]() $\boldsymbol \mu $
as in the first column of Table 2. Then the centraliser
$\boldsymbol \mu $
as in the first column of Table 2. Then the centraliser
![]() $\mathfrak {g}^\natural $
of an
$\mathfrak {g}^\natural $
of an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
and the values of the
$(e,h,f)$
and the values of the
![]() $k_i^\natural $
’s are given by Table 2. Moreover, if k is admissible, then so is
$k_i^\natural $
’s are given by Table 2. Moreover, if k is admissible, then so is
![]() $k^\natural $
, provided that
$k^\natural $
, provided that
![]() $k_0^\natural =0$
.
$k_0^\natural =0$
.
Table 2 Centralisers of some
![]() ${\mathfrak {sl}}_2$
-triples
${\mathfrak {sl}}_2$
-triples
![]() $(e,h,f)$
in
$(e,h,f)$
in
![]() ${\mathfrak {sl}}_{n}$
, with
${\mathfrak {sl}}_{n}$
, with
![]() $f \in {\mathbb {O}}_{\boldsymbol \mu }.$
$f \in {\mathbb {O}}_{\boldsymbol \mu }.$

In Table 2, the numbering of the levels
![]() $k_i^\natural $
’s follows the order in which the simple factors of
$k_i^\natural $
’s follows the order in which the simple factors of
![]() $\mathfrak {g}^\natural $
appears.
$\mathfrak {g}^\natural $
appears.
Proof. By Lemma 5.1 and Remark 5.2, in order to describe
![]() $\mathfrak {g}^\natural $
and compute the
$\mathfrak {g}^\natural $
and compute the
![]() $k_i^\natural $
’s, one can use the left-adjusted pyramid of shape
$k_i^\natural $
’s, one can use the left-adjusted pyramid of shape
![]() $\boldsymbol {\mu }$
. This pyramid always corresponds to an even good grading for f.
$\boldsymbol {\mu }$
. This pyramid always corresponds to an even good grading for f.
(1) Consider first the case
![]() $\boldsymbol {\mu }= (q^m,1^s)$
, with s possibly zero. The pyramid consists of a
$\boldsymbol {\mu }= (q^m,1^s)$
, with s possibly zero. The pyramid consists of a
![]() $q \times m$
rectangle surmounted by a vertical strip of dimension
$q \times m$
rectangle surmounted by a vertical strip of dimension
![]() $1 \times s$
on the left as in Figure 5. For example, for
$1 \times s$
on the left as in Figure 5. For example, for
![]() $\boldsymbol {\mu }=(5^3,1^4)$
, we get the pyramid as in Figure 6.
$\boldsymbol {\mu }=(5^3,1^4)$
, we get the pyramid as in Figure 6.

Figure 5 Pyramid for
![]() $(q^m,1^s).$
$(q^m,1^s).$

Figure 6 Pyramid for
![]() $(5^3,1^4).$
$(5^3,1^4).$
From the pyramid, we easily see that

and

First, pick ![]() , with
, with ![]() and
and
![]() $y = \operatorname {diag}(x,x')\in \mathfrak {gl}_{m+s}$
with
$y = \operatorname {diag}(x,x')\in \mathfrak {gl}_{m+s}$
with
![]() $x'=0$
. We have
$x'=0$
. We have
and
![]() $ (t|t)_1^\natural = 2 $
, whence
$ (t|t)_1^\natural = 2 $
, whence
![]() $k^\natural _1 = q k + q n - n.$
This terminates the case
$k^\natural _1 = q k + q n - n.$
This terminates the case
![]() $s=0$
.
$s=0$
.
Assume now
![]() $s\not =0$
. Pick
$s\not =0$
. Pick ![]() , with
, with ![]() and
and
![]() $y =\operatorname {diag}(x,x') \in \mathfrak {gl}_{m+s}$
with
$y =\operatorname {diag}(x,x') \in \mathfrak {gl}_{m+s}$
with ![]() . The projection of t onto the semisimple part of
. The projection of t onto the semisimple part of
![]() $\mathfrak {g}_\Gamma ^0$
is
$\mathfrak {g}_\Gamma ^0$
is ![]() with
with
From this, we get
Choose
![]() $(~|~)_0$
so that
$(~|~)_0$
so that
![]() $(t|t)_0= smn $
, whence
$(t|t)_0= smn $
, whence
![]() $k^\natural _0 = q k + q n - n$
.
$k^\natural _0 = q k + q n - n$
.
Pick finally ![]() , where
, where
![]() $x=0 \in \mathfrak {gl}_m$
and
$x=0 \in \mathfrak {gl}_m$
and
![]() $y = \operatorname {diag}(x,x')\in \mathfrak {gl}_{m+s}$
with
$y = \operatorname {diag}(x,x')\in \mathfrak {gl}_{m+s}$
with ![]() . We have
. We have
and
![]() $(t|t)_2^\natural =2$
, whence
$(t|t)_2^\natural =2$
, whence
![]() $k^\natural _2 = k+ q m - m.$
$k^\natural _2 = k+ q m - m.$
(2) Assume now that
![]() $\boldsymbol \mu =(q^m,(q-1)^2)$
. Here, we easily see that the embedding
$\boldsymbol \mu =(q^m,(q-1)^2)$
. Here, we easily see that the embedding
![]() $\mathfrak {g}^\natural \hookrightarrow \mathfrak {g}^0_\Gamma $
is as follows. We have
$\mathfrak {g}^\natural \hookrightarrow \mathfrak {g}^0_\Gamma $
is as follows. We have


We compute
![]() $k_0^\natural ,k_1^\natural ,k_2^\natural $
similarly as the previous case. So we omit the details.
$k_0^\natural ,k_1^\natural ,k_2^\natural $
similarly as the previous case. So we omit the details.
(3) Finally, assume that
![]() $\boldsymbol \mu =(q^m,s)$
, with
$\boldsymbol \mu =(q^m,s)$
, with
![]() $m \ge 0$
and
$m \ge 0$
and ![]() . Here, we easily see that the embedding
. Here, we easily see that the embedding
![]() $\mathfrak {g}^\natural \hookrightarrow \mathfrak {g}^0_\Gamma $
is as follows. We have
$\mathfrak {g}^\natural \hookrightarrow \mathfrak {g}^0_\Gamma $
is as follows. We have

and

We compute
![]() $k_0^\natural ,k_1^\natural $
as in the first case. So we omit the details.
$k_0^\natural ,k_1^\natural $
as in the first case. So we omit the details.
The last assertion of the lemma is then easy to verify. Indeed, the condition
![]() $k_0^\natural =0$
(when
$k_0^\natural =0$
(when
![]() $k_0^\natural $
appears) implies
$k_0^\natural $
appears) implies
![]() $p=n$
. Then
$p=n$
. Then
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $k_2^\natural = -s+s/q$
(when
$k_2^\natural = -s+s/q$
(when
![]() $k_2^\natural $
appears), which is admissible for
$k_2^\natural $
appears), which is admissible for
![]() ${\mathfrak {sl}}_s$
. If
${\mathfrak {sl}}_s$
. If
![]() $\mathfrak {g}_0^\natural =0$
, then
$\mathfrak {g}_0^\natural =0$
, then
![]() $\boldsymbol \mu =(q^m)$
and
$\boldsymbol \mu =(q^m)$
and
![]() $k_1^\natural = p-n = -m + p-m(q-1)$
, which is admissible for
$k_1^\natural = p-n = -m + p-m(q-1)$
, which is admissible for
![]() ${\mathfrak {sl}}_m$
since
${\mathfrak {sl}}_m$
since
![]() $p-m(q-1) \ge m$
is equivalent to the condition
$p-m(q-1) \ge m$
is equivalent to the condition
![]() $p \ge n$
.
$p \ge n$
.
Remark 8.5. Besides
![]() $\mathfrak {g}$
, f and k, the construction of
$\mathfrak {g}$
, f and k, the construction of
![]() $H^0_{DS, f}(L_k(\mathfrak {g}))$
takes an auxiliary choice of good grading on
$H^0_{DS, f}(L_k(\mathfrak {g}))$
takes an auxiliary choice of good grading on
![]() $\mathfrak {g}$
compatible with f. For all types other than
$\mathfrak {g}$
compatible with f. For all types other than
![]() ${\mathfrak {sl}}_n$
, we use the Dynkin grading, but in this section, we sometimes work with good gradings different than the Dynkin grading. While it is known that
${\mathfrak {sl}}_n$
, we use the Dynkin grading, but in this section, we sometimes work with good gradings different than the Dynkin grading. While it is known that
![]() $H^0_{DS, f}(L_k(\mathfrak {g}))$
, as a vertex algebra, is independent of the choice of good grading, its conformal structure, and therefore in principle its asymptotic datum, can depend on this choice. Since Theorem 3.10 requires self-duality, and by Proposition 4.2 self-duality holds for the Dynkin grading, it is important to verify that the asymptotic datum is independent of the choice of good grading in the cases relevant for us. For
$H^0_{DS, f}(L_k(\mathfrak {g}))$
, as a vertex algebra, is independent of the choice of good grading, its conformal structure, and therefore in principle its asymptotic datum, can depend on this choice. Since Theorem 3.10 requires self-duality, and by Proposition 4.2 self-duality holds for the Dynkin grading, it is important to verify that the asymptotic datum is independent of the choice of good grading in the cases relevant for us. For
![]() $\mathbf {g}$
, this is evident from the formula (see Proposition 4.10). As for
$\mathbf {g}$
, this is evident from the formula (see Proposition 4.10). As for
![]() $\mathbf {A}$
, for the pairs
$\mathbf {A}$
, for the pairs
![]() $(k, f)$
that arise in our search for collapsing levels for
$(k, f)$
that arise in our search for collapsing levels for
![]() ${\mathfrak {sl}}_n$
, the relationship between the orbits
${\mathfrak {sl}}_n$
, the relationship between the orbits
![]() ${\mathbb {O}}_k$
and
${\mathbb {O}}_k$
and
![]() $G. f$
is such that the independence of
$G. f$
is such that the independence of
![]() $\mathbf {A}$
on the choice of good grading can be seen via combinatorial arguments. Namely, we have the following lemma.
$\mathbf {A}$
on the choice of good grading can be seen via combinatorial arguments. Namely, we have the following lemma.
Lemma 8.6. Assume that
![]() $\boldsymbol {\mu }$
is a partition of type (a), (b), (c) as in Lemma 8.3, and pick
$\boldsymbol {\mu }$
is a partition of type (a), (b), (c) as in Lemma 8.3, and pick
![]() $f \in {\mathbb {O}}_{\boldsymbol {\mu }} \subset \overline {{\mathbb {O}}}_k$
. Then the expression given for
$f \in {\mathbb {O}}_{\boldsymbol {\mu }} \subset \overline {{\mathbb {O}}}_k$
. Then the expression given for
![]() $\mathbf {A}_{H^0_{DS, f}(L_k(\mathfrak {g}))}$
in Proposition 4.10 is independent of the choice of good grading
$\mathbf {A}_{H^0_{DS, f}(L_k(\mathfrak {g}))}$
in Proposition 4.10 is independent of the choice of good grading
![]() $\Gamma $
.
$\Gamma $
.
Proof. The expression in question is the product of a term manifestly independent of
![]() $\Gamma $
with
$\Gamma $
with
 $$ \begin{align} \mathbf{A}' = \frac{1}{2^{\frac{|\Delta_\Gamma^{1/2}|}{2}} q^{|\Delta_{\Gamma, +}^0|}} \prod_{\alpha \in \Delta_+ \backslash \Delta_{\Gamma, +}^0} 2 \sin\ {\frac{\pi (x_\Gamma^0 | \alpha)}{q}}. \end{align} $$
$$ \begin{align} \mathbf{A}' = \frac{1}{2^{\frac{|\Delta_\Gamma^{1/2}|}{2}} q^{|\Delta_{\Gamma, +}^0|}} \prod_{\alpha \in \Delta_+ \backslash \Delta_{\Gamma, +}^0} 2 \sin\ {\frac{\pi (x_\Gamma^0 | \alpha)}{q}}. \end{align} $$
Now we consider
![]() $k = -n + p/q$
an admissible level for
$k = -n + p/q$
an admissible level for
![]() $\mathfrak {g} = \mathfrak {sl}_n$
and the Hamiltonian reduction
$\mathfrak {g} = \mathfrak {sl}_n$
and the Hamiltonian reduction
![]() $H^0_{DS, f}(L_k(\mathfrak {g}))$
for some
$H^0_{DS, f}(L_k(\mathfrak {g}))$
for some
![]() $f \in \overline {{\mathbb {O}}}_k$
.
$f \in \overline {{\mathbb {O}}}_k$
.
We first consider the partitions
![]() $(q^m, s)$
of n.
$(q^m, s)$
of n.
The pyramids associated with ![]() all consist of a
all consist of a
![]() $q \times m$
rectangle surmounted by a horizontal strip of dimension
$q \times m$
rectangle surmounted by a horizontal strip of dimension
![]() $s \times 1$
. In Figures 7 and 8, we illustrate two pyramids associated with
$s \times 1$
. In Figures 7 and 8, we illustrate two pyramids associated with
![]() $n=16$
,
$n=16$
,
![]() $q=5$
. In general, there are
$q=5$
. In general, there are
![]() $2(q-s)+1$
distinct pyramids associated with
$2(q-s)+1$
distinct pyramids associated with ![]() .
.

Figure 7 An even good grading.

Figure 8 An odd good grading.
We rewrite (47) as
 $$ \begin{align*} \mathbf{A}' = \prod_{\stackrel{i < j}{x_i=x_j}} \frac{1}{q} \cdot \prod_{\stackrel{i < j}{|x_i-x_j|=1}} \frac{1}{2^{1/2}} \cdot \prod_{\stackrel{i < j}{|x_i-x_j| \ge 1}} 2\sin \frac{\pi |x_i - x_j|}{q}. \end{align*} $$
$$ \begin{align*} \mathbf{A}' = \prod_{\stackrel{i < j}{x_i=x_j}} \frac{1}{q} \cdot \prod_{\stackrel{i < j}{|x_i-x_j|=1}} \frac{1}{2^{1/2}} \cdot \prod_{\stackrel{i < j}{|x_i-x_j| \ge 1}} 2\sin \frac{\pi |x_i - x_j|}{q}. \end{align*} $$
To show that
![]() $\mathbf {A}'$
is independent of
$\mathbf {A}'$
is independent of
![]() $\Gamma $
, we first note that if boxes i and j lie both in the
$\Gamma $
, we first note that if boxes i and j lie both in the
![]() $q \times m$
rectangle or else both in the
$q \times m$
rectangle or else both in the
![]() $s \times 1$
horizontal strip, then the contribution of the pair
$s \times 1$
horizontal strip, then the contribution of the pair
![]() $(i, j)$
to the product above is the same for all choices of
$(i, j)$
to the product above is the same for all choices of
![]() $\Gamma $
. So we may ignore the contributions of such pairs.
$\Gamma $
. So we may ignore the contributions of such pairs.
Now we let i be a box in the
![]() $s \times 1$
strip, and we consider the contribution to the product as j runs along one of the rows of the
$s \times 1$
strip, and we consider the contribution to the product as j runs along one of the rows of the
![]() $q \times m$
rectangle. In the configurations depicted by Figures 7 and 8, this contribution is, respectively,
$q \times m$
rectangle. In the configurations depicted by Figures 7 and 8, this contribution is, respectively,
 $$ \begin{align*} \frac{1}{q} \prod_{j=1}^{n-1} 2\sin\ {\frac{j \pi}{q}} \qquad \text{or} \qquad \frac{1}{2} \prod_{j=1}^{n} 2\sin\ {\frac{(j-1/2) \pi}{n}}. \end{align*} $$
$$ \begin{align*} \frac{1}{q} \prod_{j=1}^{n-1} 2\sin\ {\frac{j \pi}{q}} \qquad \text{or} \qquad \frac{1}{2} \prod_{j=1}^{n} 2\sin\ {\frac{(j-1/2) \pi}{n}}. \end{align*} $$
Indeed, for any of the q possible positions of box i aligned with the
![]() $q \times m$
rectangle, we obtain the first of these products simply because
$q \times m$
rectangle, we obtain the first of these products simply because
![]() $\sin\ {((q-j)\pi /q)} = \sin\ {(j \pi /q)}$
. Similarly, all remaining positions of box i yield the second product. But finally both products are equal to
$\sin\ {((q-j)\pi /q)} = \sin\ {(j \pi /q)}$
. Similarly, all remaining positions of box i yield the second product. But finally both products are equal to
![]() $1$
due to identities (42) and (43), and so all products are equal. Therefore, the value of
$1$
due to identities (42) and (43), and so all products are equal. Therefore, the value of
![]() $\mathbf {A}'$
does not depend on
$\mathbf {A}'$
does not depend on
![]() $\Gamma $
.
$\Gamma $
.
Similar arguments establish independence of
![]() $\mathbf {A}$
on
$\mathbf {A}$
on
![]() $\Gamma $
for nilpotent elements associated with partitions of type
$\Gamma $
for nilpotent elements associated with partitions of type
![]() $(q^m, 1^s)$
or
$(q^m, 1^s)$
or
![]() $(q^m,(q-1)^2)$
.
$(q^m,(q-1)^2)$
.
We are now in a position to state our results on collapsing levels for
![]() ${\mathfrak {sl}}_n$
. We have
${\mathfrak {sl}}_n$
. We have
for an admissible level k and
![]() $f\in \overline {\mathbb {O}}_k$
since any nilpotent element of
$f\in \overline {\mathbb {O}}_k$
since any nilpotent element of
![]() ${\mathfrak {sl}}_n$
admits an even good grading. Moreover,
${\mathfrak {sl}}_n$
admits an even good grading. Moreover,
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is rational if
$\mathscr {W}_k(\mathfrak {g},f)$
is rational if
![]() $f\in {\mathbb {O}}_k$
([Reference Arakawa and van Ekeren14]).
$f\in {\mathbb {O}}_k$
([Reference Arakawa and van Ekeren14]).
First, we consider the case when
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is rational.
$\mathscr {W}_k(\mathfrak {g},f)$
is rational.
Theorem 8.7. Assume that
![]() $k = - h^{\vee }_{\mathfrak {g}} + p/q = -n +p/q$
is admissible for
$k = - h^{\vee }_{\mathfrak {g}} + p/q = -n +p/q$
is admissible for
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
. Pick a nilpotent element
$\mathfrak {g}={\mathfrak {sl}}_n$
. Pick a nilpotent element
![]() $f \in {\mathbb {O}}_k$
so that
$f \in {\mathbb {O}}_k$
so that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is rational. Then k is collapsing if and only if
$\mathscr {W}_k(\mathfrak {g},f)$
is rational. Then k is collapsing if and only if
![]() $n\equiv 0,\pm 1\pmod\ {q}$
and
$n\equiv 0,\pm 1\pmod\ {q}$
and  Furthermore,
Furthermore,
-
1. If
 $n\equiv \pm 1\ \pmod {q}$
, then
$n\equiv \pm 1\ \pmod {q}$
, then  $$ \begin{align*}\mathscr{W}_{-n +n/q}(\mathfrak{sl}_n,f) \cong \mathbb{C}.\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-n +n/q}(\mathfrak{sl}_n,f) \cong \mathbb{C}.\end{align*} $$
-
2. If
 $n\equiv 0\ \pmod {q}$
, where
$n\equiv 0\ \pmod {q}$
, where $$ \begin{align*}\mathscr{W}_{-n + (n+1)/q}(\mathfrak{sl}_n,f) \cong L_{1}(\mathfrak{sl}_{\widetilde m}),\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-n + (n+1)/q}(\mathfrak{sl}_n,f) \cong L_{1}(\mathfrak{sl}_{\widetilde m}),\end{align*} $$
 $\widetilde m$
is defined by (45).
$\widetilde m$
is defined by (45).
Proof. Fix a nilpotent element
![]() $f \in {\mathbb {O}}_k={\mathbb {O}}_{(q^{m},s)}$
, with
$f \in {\mathbb {O}}_k={\mathbb {O}}_{(q^{m},s)}$
, with
![]() $m:=\widetilde m$
and
$m:=\widetilde m$
and
![]() $s:=\widetilde s$
in the notation of (45).
$s:=\widetilde s$
in the notation of (45).
(a) Case
![]() $ s \not =0$
.
$ s \not =0$
.
According to Table 2, we have
![]() $\mathfrak {g}^\natural \cong \mathbb {C} \times {\mathfrak {sl}}_{ m}$
, and
$\mathfrak {g}^\natural \cong \mathbb {C} \times {\mathfrak {sl}}_{ m}$
, and
![]() $k_0^\natural = k_1^\natural = qk + q n-n = p-n$
. If k is collapsing, then necessarily
$k_0^\natural = k_1^\natural = qk + q n-n = p-n$
. If k is collapsing, then necessarily
![]() $k_0^\natural =0$
, whence
$k_0^\natural =0$
, whence
![]() $p=n$
. Assume from now that
$p=n$
. Assume from now that
![]() $p=0$
, whence
$p=0$
, whence
![]() $k_0^\natural = k_1^\natural =0$
. By (48), if k is collapsing, then
$k_0^\natural = k_1^\natural =0$
. By (48), if k is collapsing, then
![]() $\mathscr {W}_k({\mathfrak {sl}}_n,f)\cong \mathbb {C}$
and the asymptotic growth
$\mathscr {W}_k({\mathfrak {sl}}_n,f)\cong \mathbb {C}$
and the asymptotic growth
![]() $\mathbf {g}_{\mathscr {W}_k({\mathfrak {sl}}_n,f)}=\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n)}$
must be
$\mathbf {g}_{\mathscr {W}_k({\mathfrak {sl}}_n,f)}=\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n)}$
must be
![]() $0$
. By Corollary 3.9, we have
$0$
. By Corollary 3.9, we have
![]() $\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural ))} =0$
, while by Proposition 4.10,
$\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural ))} =0$
, while by Proposition 4.10,

since
![]() $\dim \mathfrak {g}^{f} = { m}^2(q-{ s}) +({ m}+1)^2 { s}-1$
. Therefore,
$\dim \mathfrak {g}^{f} = { m}^2(q-{ s}) +({ m}+1)^2 { s}-1$
. Therefore,
![]() $\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n))} =0$
if and only if
$\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n))} =0$
if and only if
![]() ${ s}=1$
or
${ s}=1$
or
![]() ${ s}=q-1$
. The case
${ s}=q-1$
. The case
![]() ${ s}=1$
will be dealt with in Theorem 8.8 with
${ s}=1$
will be dealt with in Theorem 8.8 with
![]() $s=1$
. We consider here only the case
$s=1$
. We consider here only the case
![]() ${ s}=q-1$
.
${ s}=q-1$
.
Our aim is to show that
![]() $\mathscr {W}_{-n + n/q}(\mathfrak {sl}_n,f) \cong \mathbb {C}$
, for f corresponding to the partition
$\mathscr {W}_{-n + n/q}(\mathfrak {sl}_n,f) \cong \mathbb {C}$
, for f corresponding to the partition
![]() $(q^{ m},q-1)$
. By Proposition 6.6 and the above computation, it suffices to show that the asymptotic dimension of
$(q^{ m},q-1)$
. By Proposition 6.6 and the above computation, it suffices to show that the asymptotic dimension of
![]() $H^0_{DS,f}(L_k({\mathfrak {sl}}_n))$
is
$H^0_{DS,f}(L_k({\mathfrak {sl}}_n))$
is
![]() $1$
.
$1$
.
Let
![]() $\mathfrak {g}=\bigoplus _i \mathfrak {g}_\Gamma ^{i}$
be the even good grading for f corresponding to the left-adjusted pyramid of shape
$\mathfrak {g}=\bigoplus _i \mathfrak {g}_\Gamma ^{i}$
be the even good grading for f corresponding to the left-adjusted pyramid of shape
![]() $(q^{{ m}}, s)$
as in the proof of Lemma 8.4. By Proposition 4.10 and Lemma 7.1 (1), we get
$(q^{{ m}}, s)$
as in the proof of Lemma 8.4. By Proposition 4.10 and Lemma 7.1 (1), we get
 $$ \begin{align} \mathbf{A}_{H^0_{DS,f}(L_k({\mathfrak{sl}}_n))} & = \dfrac{1}{q^{|\Delta_{\Gamma,0}^+|} q^{\frac{n-1}{2}} } \prod_{\alpha \in \Delta_+ \setminus \Delta_{\Gamma,+}^{0}} 2 \sin\ \dfrac{\pi (x_\Gamma^0 |\alpha)}{q} , & \end{align} $$
$$ \begin{align} \mathbf{A}_{H^0_{DS,f}(L_k({\mathfrak{sl}}_n))} & = \dfrac{1}{q^{|\Delta_{\Gamma,0}^+|} q^{\frac{n-1}{2}} } \prod_{\alpha \in \Delta_+ \setminus \Delta_{\Gamma,+}^{0}} 2 \sin\ \dfrac{\pi (x_\Gamma^0 |\alpha)}{q} , & \end{align} $$
with
![]() $n=q m + q-1$
and
$n=q m + q-1$
and
![]() $|\Delta _{\Gamma ,0}^+|= \dfrac {{ m}(n-1)}{2}$
. Indeed, by Lemma 8.6, the asymptotic dimension does not depend on the good grading for such an f. For
$|\Delta _{\Gamma ,0}^+|= \dfrac {{ m}(n-1)}{2}$
. Indeed, by Lemma 8.6, the asymptotic dimension does not depend on the good grading for such an f. For ![]() , let
, let
![]() $x_i$
be the x-coordinate of the box labelled i in the pyramid. Note that for
$x_i$
be the x-coordinate of the box labelled i in the pyramid. Note that for
![]() $j \in \mathbb {Z}$
, we have
$j \in \mathbb {Z}$
, we have
In this way, using (50) and the identity (44), we obtain that

Combining this with (49), we verify that
![]() $\mathbf {A}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n)}=1$
, as desired. This concludes this case.
$\mathbf {A}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n)}=1$
, as desired. This concludes this case.
(b) Case
![]() ${ s} =0$
.
${ s} =0$
.
According to Table 2, we have
![]() $\mathfrak {g}^\natural \cong {\mathfrak {sl}}_{ m}$
and
$\mathfrak {g}^\natural \cong {\mathfrak {sl}}_{ m}$
and
![]() $k^\natural =qk +qn -n$
. If k is collapsing, then by (48), we must have
$k^\natural =qk +qn -n$
. If k is collapsing, then by (48), we must have
![]() $\mathbf {g}_{L_{k^\natural }({\mathfrak {sl}}_{{ m}})}=\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n))}$
. We have
$\mathbf {g}_{L_{k^\natural }({\mathfrak {sl}}_{{ m}})}=\mathbf {g}_{H^0_{DS,f}(L_k({\mathfrak {sl}}_n))}$
. We have

since
![]() $\dim \mathfrak {g}^{f} = { m}^2 q -1$
. Solving the equation
$\dim \mathfrak {g}^{f} = { m}^2 q -1$
. Solving the equation

with unknown p, we obtain that p must be either equal to
![]() $n+1$
or
$n+1$
or
![]() $n-1$
. Only the case
$n-1$
. Only the case
![]() $p=n+1$
is greater than
$p=n+1$
is greater than
![]() $h_{\mathfrak {g}}^\vee =n$
.
$h_{\mathfrak {g}}^\vee =n$
.
From now, it is assumed that
![]() $p=n+1$
, whence
$p=n+1$
, whence
![]() $k_1^\natural =1 = -{ m} + ({ m}+1)/1$
. We apply Proposition 6.6 to prove that k is collapsing. It is enough to show that
$k_1^\natural =1 = -{ m} + ({ m}+1)/1$
. We apply Proposition 6.6 to prove that k is collapsing. It is enough to show that
![]() $L_{1}(\mathfrak {sl}_{ m})$
and
$L_{1}(\mathfrak {sl}_{ m})$
and
![]() $H^0_{DS,f}(L_k({\mathfrak {sl}}_n))$
share the same asymptotic dimension. By Corollary 3.9 and Lemma 7.1 (2),
$H^0_{DS,f}(L_k({\mathfrak {sl}}_n))$
share the same asymptotic dimension. By Corollary 3.9 and Lemma 7.1 (2),
However, by Proposition 4.10 and Lemma 7.1 (2),

with
![]() $n=q m$
and
$n=q m$
and
![]() $|\Delta _{\Gamma ,+}^0|= q{ m}({ m}-1)/2$
. Moreover, computing the cardinality of the sets
$|\Delta _{\Gamma ,+}^0|= q{ m}({ m}-1)/2$
. Moreover, computing the cardinality of the sets
![]() $\{\alpha \in \Delta _+ \colon (x_\Gamma ^0|\alpha ) = j \}$
as in the previous case, we obtain by (44) that
$\{\alpha \in \Delta _+ \colon (x_\Gamma ^0|\alpha ) = j \}$
as in the previous case, we obtain by (44) that

Combining this with (52), we get that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{-n + (n+1)/q}(\mathfrak {sl}_n))} =\frac {1}{\sqrt {m}} $
, as expected. This completes the proof.
$\mathbf {A}_{H_{DS,f}^0(L_{-n + (n+1)/q}(\mathfrak {sl}_n))} =\frac {1}{\sqrt {m}} $
, as expected. This completes the proof.
We now consider the partitions
![]() $\boldsymbol \mu \in {\mathscr {P}}(n)$
as in Lemma 9.3 of type (b) and (c). This leads us to the following results.
$\boldsymbol \mu \in {\mathscr {P}}(n)$
as in Lemma 9.3 of type (b) and (c). This leads us to the following results.
Theorem 8.8. Assume that
![]() $k = - n + p/q$
is admissible for
$k = - n + p/q$
is admissible for
![]() $\mathfrak {g}={\mathfrak {sl}}_n$
.
$\mathfrak {g}={\mathfrak {sl}}_n$
.
-
1. Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,1^s)$
, with
$(q^m,1^s)$
, with
 $m\ge 0$
and
$m\ge 0$
and
 $s>0$
. Then k is collapsing if and only if
$s>0$
. Then k is collapsing if and only if
 $p=n=h^{\vee }_{{\mathfrak {sl}}_n}$
. Moreover,
$p=n=h^{\vee }_{{\mathfrak {sl}}_n}$
. Moreover,  $$ \begin{align*}\mathscr{W}_{-n + n/q}(\mathfrak{sl}_n,f) \cong L_{-s+s/q}(\mathfrak{sl}_s).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-n + n/q}(\mathfrak{sl}_n,f) \cong L_{-s+s/q}(\mathfrak{sl}_s).\end{align*} $$
-
2. Assume that
 $\widetilde s =q-2$
, and pick a nilpotent element
$\widetilde s =q-2$
, and pick a nilpotent element
 $f\in \overline {{\mathbb {O}}}_k $
corresponding to the partition
$f\in \overline {{\mathbb {O}}}_k $
corresponding to the partition
 $(q^{m},(q-1)^2)$
, with
$(q^{m},(q-1)^2)$
, with
 $m=\widetilde m-1$
in the notation of (45). Then k is collapsing if and only if
$m=\widetilde m-1$
in the notation of (45). Then k is collapsing if and only if
 $p=n=h^{\vee }_{\mathfrak {g}}$
. Moreover,
$p=n=h^{\vee }_{\mathfrak {g}}$
. Moreover,  $$ \begin{align*}\mathscr{W}_{-n + n/q}(\mathfrak{sl}_n,f) \cong L_{-2+2/q}(\mathfrak{sl}_2).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-n + n/q}(\mathfrak{sl}_n,f) \cong L_{-2+2/q}(\mathfrak{sl}_2).\end{align*} $$
Remark 8.9. For
![]() $s=1$
in (1), the formula has to be understood as
$s=1$
in (1), the formula has to be understood as
Since for
![]() $s=1$
,
$s=1$
,
![]() $\mathbf {g}_{L_{-s+s/q}(\mathfrak {sl}_s)} = \frac {(q-1)(s^2-1)}{q}= 0$
and
$\mathbf {g}_{L_{-s+s/q}(\mathfrak {sl}_s)} = \frac {(q-1)(s^2-1)}{q}= 0$
and
![]() $\mathbf {A}_{L_{-s+s/q}(\mathfrak {sl}_s)}=q^{-(s^2-1)/2}=1$
(see the below proof), the formulas make sense and are compatible with Theorem 8.7
$\mathbf {A}_{L_{-s+s/q}(\mathfrak {sl}_s)}=q^{-(s^2-1)/2}=1$
(see the below proof), the formulas make sense and are compatible with Theorem 8.7
Proof. As in the proof of Theorem 8.7, we let
![]() $\mathfrak {g}=\bigoplus _i \mathfrak {g}_\Gamma ^{i}$
be the even good grading for f corresponding to the left-adjusted pyramid associated with the partition of f.
$\mathfrak {g}=\bigoplus _i \mathfrak {g}_\Gamma ^{i}$
be the even good grading for f corresponding to the left-adjusted pyramid associated with the partition of f.
(1) Fix a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(q^m,1^s)$
. According to Table 2, we have
$(q^m,1^s)$
. According to Table 2, we have
![]() $\mathfrak {g}^\natural \cong \mathbb {C}\times {\mathfrak {sl}}_{m} \times {\mathfrak {sl}}_{s}$
,
$\mathfrak {g}^\natural \cong \mathbb {C}\times {\mathfrak {sl}}_{m} \times {\mathfrak {sl}}_{s}$
,
![]() $k_0^\natural =k_1^\natural = p-n$
and
$k_0^\natural =k_1^\natural = p-n$
and
![]() $k_2^\natural = k+qm - m$
. If k is collapsing, then necessarily
$k_2^\natural = k+qm - m$
. If k is collapsing, then necessarily
![]() $k_0^\natural =0$
– that is,
$k_0^\natural =0$
– that is,
![]() $p=n$
. We assume from now on that
$p=n$
. We assume from now on that
![]() $p=n$
. Hence
$p=n$
. Hence
![]() $k_2^\natural = k + qm - m = - s +s/q$
, which is an admissible level for
$k_2^\natural = k + qm - m = - s +s/q$
, which is an admissible level for
![]() ${\mathfrak {sl}}_s$
. By Proposition 4.10, we get
${\mathfrak {sl}}_s$
. By Proposition 4.10, we get

since
![]() $\dim \mathfrak {g}^f = (m+s)^2 + (q-1)m^2-1$
. By Corollary 3.9 and Lemma 7.1 (1), we have
$\dim \mathfrak {g}^f = (m+s)^2 + (q-1)m^2-1$
. By Corollary 3.9 and Lemma 7.1 (1), we have
 $$ \begin{align*} \mathbf{A}_{L_{-s+s/q}(\mathfrak{sl}_s)} & = \dfrac{1}{q^{s(s-1)/2} q^{(s-1)/2}} = \dfrac{1}{q^{(s^2-1)/2}} .& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{-s+s/q}(\mathfrak{sl}_s)} & = \dfrac{1}{q^{s(s-1)/2} q^{(s-1)/2}} = \dfrac{1}{q^{(s^2-1)/2}} .& \end{align*} $$
However, by Proposition 4.10, we have

with
![]() $|\Delta _{\Gamma ,+}^0 | =\frac {(m+s)(m+s-1)}{2}+ \frac {m(q-1)(m-1)}{2}$
. Indeed, by Lemma 8.6, the asymptotic dimension does not depend on the good grading for such an f. Using the left-adjusted pyramid of shape
$|\Delta _{\Gamma ,+}^0 | =\frac {(m+s)(m+s-1)}{2}+ \frac {m(q-1)(m-1)}{2}$
. Indeed, by Lemma 8.6, the asymptotic dimension does not depend on the good grading for such an f. Using the left-adjusted pyramid of shape
![]() $(q^m,1^s)$
, we easily see that
$(q^m,1^s)$
, we easily see that

using (44). Combining (53) and (54), we conclude that
 $$ \begin{align*}\mathbf{A}_{H_{DS,f}^0(L_{-n+n/q}(\mathfrak{sl}_n))} = \dfrac{1}{q^{(s^2-1)/2}} =\mathbf{A}_{L_{-s+s/q}(\mathfrak{sl}_s)},\end{align*} $$
$$ \begin{align*}\mathbf{A}_{H_{DS,f}^0(L_{-n+n/q}(\mathfrak{sl}_n))} = \dfrac{1}{q^{(s^2-1)/2}} =\mathbf{A}_{L_{-s+s/q}(\mathfrak{sl}_s)},\end{align*} $$
as desired. By Proposition 6.6, it follows that k is collapsing.
(2) Fix a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(q^m,(q-1)^2)$
. According to Table 2, we have
$(q^m,(q-1)^2)$
. According to Table 2, we have
![]() $\mathfrak {g}^\natural \cong \mathbb {C} \times {\mathfrak {sl}}_{m} \times {\mathfrak {sl}}_{2}$
,
$\mathfrak {g}^\natural \cong \mathbb {C} \times {\mathfrak {sl}}_{m} \times {\mathfrak {sl}}_{2}$
,
![]() $k_0^\natural =k_1^\natural = p-n$
and
$k_0^\natural =k_1^\natural = p-n$
and
![]() $k_2^\natural =(q-1)( k+n-m-2)$
. If k is collapsing, then necessarily
$k_2^\natural =(q-1)( k+n-m-2)$
. If k is collapsing, then necessarily
![]() $k_0^\natural =0$
– that is,
$k_0^\natural =0$
– that is,
![]() $p=n$
. We assume from now on that
$p=n$
. We assume from now on that
![]() $p=n$
. Hence,
$p=n$
. Hence,
![]() $k_2^\natural = (q-1)(n/q-m-2)=-2+2/q$
, which is an admissible level for
$k_2^\natural = (q-1)(n/q-m-2)=-2+2/q$
, which is an admissible level for
![]() ${\mathfrak {sl}}_2$
. Note that q is odd since
${\mathfrak {sl}}_2$
. Note that q is odd since
![]() $(q,n)=1$
and
$(q,n)=1$
and
![]() $n=qm +2(q-1)$
. By Proposition 4.10, we get
$n=qm +2(q-1)$
. By Proposition 4.10, we get

since
![]() $\dim \mathfrak {g}^f = m^2+(m+2)^2(q-1)-1$
. Moreover, from (1), we know that
$\dim \mathfrak {g}^f = m^2+(m+2)^2(q-1)-1$
. Moreover, from (1), we know that
However, by Proposition 4.10 and Lemma 8.6, we have

with
![]() $|\Delta _{\Gamma ,+}^0 | =\frac {m(m-1)}{2}+\frac {(m+1)(m+2)(q-1)}{2}$
. Using the left-adjusted pyramid of shape
$|\Delta _{\Gamma ,+}^0 | =\frac {m(m-1)}{2}+\frac {(m+1)(m+2)(q-1)}{2}$
. Using the left-adjusted pyramid of shape
![]() $(q^m,(q-1)^2)$
, we easily see that
$(q^m,(q-1)^2)$
, we easily see that

As in the previous cases, we conclude using (42) and (44) that
as desired. By Proposition 6.6, it follows that k is collapsing.
Remark 8.10. As has been observed in the above proof, if k is collapsing for
![]() $f \in {\mathbb {O}}_{(q^{ m})}$
, with
$f \in {\mathbb {O}}_{(q^{ m})}$
, with
![]() $n = q m$
, then necessarily
$n = q m$
, then necessarily
![]() $k=-n+(n+1)/q$
or
$k=-n+(n+1)/q$
or
![]() $k=-n+(n-1)/q$
. Only the first case leads to an admissible level. However, one may ask whether the following holds:Footnote
5
$k=-n+(n-1)/q$
. Only the first case leads to an admissible level. However, one may ask whether the following holds:Footnote
5
(The two above vertex algebras have the same central charge.)
We propose the following conjectural extension of Theorem 8.8.
Conjecture 8.11. Let
![]() $f \in {\mathfrak {sl}}_n$
be a nilpotent element associated with a partition
$f \in {\mathfrak {sl}}_n$
be a nilpotent element associated with a partition
![]() $(q^m, \boldsymbol \nu )$
, where
$(q^m, \boldsymbol \nu )$
, where ![]() in the notation of (45), and
in the notation of (45), and ![]() is a partition of
is a partition of
![]() $s:= n - q m$
such that
$s:= n - q m$
such that
![]() $\nu _1 < q$
. Then
$\nu _1 < q$
. Then
where
![]() $f'$
is a nilpotent element in
$f'$
is a nilpotent element in
![]() ${\mathfrak {sl}}_s$
associated with the partition
${\mathfrak {sl}}_s$
associated with the partition
![]() $\boldsymbol \nu $
.
$\boldsymbol \nu $
.
Note that Conjecture 8.11 has been proven in the special case where
![]() $n=7$
,
$n=7$
,
![]() $q=3$
and
$q=3$
and
![]() $s=4$
by Francesco Allegra [Reference Allegra6]. This case is, in fact, a particular case of Theorem 8.8 used with f corresponding to the partitions
$s=4$
by Francesco Allegra [Reference Allegra6]. This case is, in fact, a particular case of Theorem 8.8 used with f corresponding to the partitions
![]() $(3^2,1)$
,
$(3^2,1)$
,
![]() $(3,2^2)$
and
$(3,2^2)$
and
![]() $(3,1^4)$
. It seems that this conjecture has been stated in [Reference Xie and Yan81].
$(3,1^4)$
. It seems that this conjecture has been stated in [Reference Xie and Yan81].
The associated variety of
![]() $\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)$
is
$\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)$
is
![]() $\mathcal {S}_{{\mathbb {O}}_{(q^{\widetilde m},\widetilde s)},f}$
, while the associated variety of
$\mathcal {S}_{{\mathbb {O}}_{(q^{\widetilde m},\widetilde s)},f}$
, while the associated variety of
![]() $\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')$
is
$\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')$
is
![]() $\mathcal {S}_{{\mathbb {O}}_{(q^{\widetilde m -m},\widetilde s)},f'}$
. These two nilpotent Slodowy slices are isomorphic by Lemma 8.2. The following proposition gives further evidence for Conjecture 8.11.
$\mathcal {S}_{{\mathbb {O}}_{(q^{\widetilde m -m},\widetilde s)},f'}$
. These two nilpotent Slodowy slices are isomorphic by Lemma 8.2. The following proposition gives further evidence for Conjecture 8.11.
Proposition 8.12. In the above notations, the vertex algebras
![]() $\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)$
and
$\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)$
and
![]() $\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')$
have the same asymptotic growth.
$\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')$
have the same asymptotic growth.
Proof. Write ![]() the partition
the partition
![]() $(q^m,\boldsymbol \nu )$
corresponding to f. Notice that
$(q^m,\boldsymbol \nu )$
corresponding to f. Notice that
![]() $\mathbf {g}_{\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)}=\dim \mathfrak {g}^f -\frac {n}{n q} \dim {\mathfrak {sl}}_n = \sum _{i=1}^{q}( \mu _i^*)^2- 1 -\frac {(n^2-1)}{q}$
and
$\mathbf {g}_{\mathscr {W}_{-n+n/q}({\mathfrak {sl}}_n,f)}=\dim \mathfrak {g}^f -\frac {n}{n q} \dim {\mathfrak {sl}}_n = \sum _{i=1}^{q}( \mu _i^*)^2- 1 -\frac {(n^2-1)}{q}$
and
![]() $\mathbf {g}_{\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')}=\dim \mathfrak {g}^{f} - \frac {s}{s q} \dim {\mathfrak {sl}}_s = \sum _{i=1}^{q}( \mu _i^*-m)^2 - 1 -\frac {(s^2-1)}{q},$
where
$\mathbf {g}_{\mathscr {W}_{-s+s/q}({\mathfrak {sl}}_s,f')}=\dim \mathfrak {g}^{f} - \frac {s}{s q} \dim {\mathfrak {sl}}_s = \sum _{i=1}^{q}( \mu _i^*-m)^2 - 1 -\frac {(s^2-1)}{q},$
where ![]() is the dual partition to
is the dual partition to
![]() $\boldsymbol \mu $
. But we readily verify from the values of the
$\boldsymbol \mu $
. But we readily verify from the values of the
![]() $\mu _i$
’s that the following identity holds:
$\mu _i$
’s that the following identity holds:
![]() $ \sum _{i=1}^{q}( \mu _i^*)^2 - \frac {(n^2-1)}{q} = \sum _{i=1}^{q}( \mu _i^*-m)^2 - \frac {(s^2-1)}{q},$
whence the lemma.
$ \sum _{i=1}^{q}( \mu _i^*)^2 - \frac {(n^2-1)}{q} = \sum _{i=1}^{q}( \mu _i^*-m)^2 - \frac {(s^2-1)}{q},$
whence the lemma.
9 Collapsing levels for types
 $\mathfrak {sp}_n$
and
$\mathfrak {sp}_n$
and
 ${\mathfrak {so}}_n$
${\mathfrak {so}}_n$
Let
![]() $n\in \mathbb {Z}_{> 0}$
. We study in this section collapsing levels for
$n\in \mathbb {Z}_{> 0}$
. We study in this section collapsing levels for
![]() $\mathfrak {sp}_n$
and
$\mathfrak {sp}_n$
and
![]() ${\mathfrak {so}}_n$
.
${\mathfrak {so}}_n$
.
Notations for
 $\mathfrak {sp}_{n}$
$\mathfrak {sp}_{n}$
We realise
![]() $\mathfrak {g}=\mathfrak {sp}_{n}$
as the set of n-size square matrices x such that
$\mathfrak {g}=\mathfrak {sp}_{n}$
as the set of n-size square matrices x such that
![]() $ x^T J_n + J_n x =0$
, where
$ x^T J_n + J_n x =0$
, where
![]() $J_n$
is the anti-diagonal matrix given by
$J_n$
is the anti-diagonal matrix given by
 $$ \begin{align*}J_n := \begin{pmatrix} 0 & U_{n/2} \\ - U_{n/2} & 0 \end{pmatrix},\end{align*} $$
$$ \begin{align*}J_n := \begin{pmatrix} 0 & U_{n/2} \\ - U_{n/2} & 0 \end{pmatrix},\end{align*} $$
where for
![]() $m \in \mathbb {Z}_{\ge 0}$
,
$m \in \mathbb {Z}_{\ge 0}$
,
![]() $U_m$
stands for the m-size square matrix with unit on the anti-diagonal. For an m-size square matrix x, we write
$U_m$
stands for the m-size square matrix with unit on the anti-diagonal. For an m-size square matrix x, we write
![]() $\widehat {x}$
for the matrix
$\widehat {x}$
for the matrix
![]() $U_m x^T U_m$
, where
$U_m x^T U_m$
, where
![]() $x^T$
is the transpose matrix of x. Thus,
$x^T$
is the transpose matrix of x. Thus,

Writing
![]() $e_{i,j}$
for the
$e_{i,j}$
for the
![]() $i,j$
-matrix unit as in the
$i,j$
-matrix unit as in the
![]() ${\mathfrak {sl}}_n$
case, the following matrices give a Chevalley basis for
${\mathfrak {sl}}_n$
case, the following matrices give a Chevalley basis for
![]() $\mathfrak {g}$
:
$\mathfrak {g}$
:

Let
![]() $\sigma _{i,j} \in \{\pm 1\}$
denote the
$\sigma _{i,j} \in \{\pm 1\}$
denote the
![]() $e_{i,j}$
-coefficient of the unique element in the above basis that involves
$e_{i,j}$
-coefficient of the unique element in the above basis that involves
![]() $e_{i,j}$
. The Killing form of
$e_{i,j}$
. The Killing form of
![]() $\mathfrak {g}=\mathfrak {sp}_n$
is given by
$\mathfrak {g}=\mathfrak {sp}_n$
is given by
![]() $\kappa _{\mathfrak {g}}(x,y) = (n+2) \mathrm {tr}(xy)$
and
$\kappa _{\mathfrak {g}}(x,y) = (n+2) \mathrm {tr}(xy)$
and
![]() $(x|y)_{\mathfrak {g}} =\mathrm {tr}(xy)$
.
$(x|y)_{\mathfrak {g}} =\mathrm {tr}(xy)$
.
Set
By [Reference Collingwood and McGovern32, Theorem 5.1.3], nilpotent orbits of
![]() $\mathfrak {sp}_{n}$
are parametrised by
$\mathfrak {sp}_{n}$
are parametrised by
![]() ${\mathscr {P}}_{-1}(n)$
. For
${\mathscr {P}}_{-1}(n)$
. For ![]() , we shall denote by
, we shall denote by ![]() , or simply by
, or simply by ![]() when there is no possible confusion, the corresponding nilpotent orbit of
when there is no possible confusion, the corresponding nilpotent orbit of
![]() $\mathfrak {sp}_{n}$
. As in the case of
$\mathfrak {sp}_{n}$
. As in the case of
![]() ${\mathfrak {sl}}_{n}$
, if
${\mathfrak {sl}}_{n}$
, if ![]() , then
, then ![]() if and only if
if and only if ![]() .
.
Given ![]() , there exists a unique
, there exists a unique ![]() such that
such that ![]() , and if
, and if
![]() $\boldsymbol {\mu }\in {\mathscr {P}}_{-1}(n)$
verifies
$\boldsymbol {\mu }\in {\mathscr {P}}_{-1}(n)$
verifies ![]() , then
, then ![]() .
.
Notations for
 ${\mathfrak {so}}_n$
${\mathfrak {so}}_n$
We realise
![]() ${\mathfrak {so}}_n$
as the set of n-size square matrices x such that
${\mathfrak {so}}_n$
as the set of n-size square matrices x such that
![]() $ x^T K_n + K_n x =0$
, where
$ x^T K_n + K_n x =0$
, where
![]() $K_n$
is the anti-diagonal matrix given by
$K_n$
is the anti-diagonal matrix given by
 $$ \begin{align*}K_n := \begin{pmatrix} 0 & 0 & U_{n/2} \\ 0 & 2 & 0\\ U_{n/2} & 0 & 0 \end{pmatrix} \text{ if }n\text{ is odd}, \qquad K_n := \begin{pmatrix} 0 & U_{n/2} \\ U_{n/2} & 0 \end{pmatrix} \text{ if }n \text{ is even}.\end{align*} $$
$$ \begin{align*}K_n := \begin{pmatrix} 0 & 0 & U_{n/2} \\ 0 & 2 & 0\\ U_{n/2} & 0 & 0 \end{pmatrix} \text{ if }n\text{ is odd}, \qquad K_n := \begin{pmatrix} 0 & U_{n/2} \\ U_{n/2} & 0 \end{pmatrix} \text{ if }n \text{ is even}.\end{align*} $$
Thus, we get that


Writing
![]() $e_{i,j}$
for the
$e_{i,j}$
for the
![]() $i,j$
-matrix unit as in the
$i,j$
-matrix unit as in the
![]() ${\mathfrak {sl}}_n$
case, we see that the following matrices give a Chevalley basis for
${\mathfrak {sl}}_n$
case, we see that the following matrices give a Chevalley basis for
![]() $\mathfrak {g}$
(omitting the last family if n is even):
$\mathfrak {g}$
(omitting the last family if n is even):

As in the
![]() $\mathfrak {sp}_{n}$
case, let
$\mathfrak {sp}_{n}$
case, let
![]() $\sigma _{i,j} \in \{\pm 1\}$
denote the
$\sigma _{i,j} \in \{\pm 1\}$
denote the
![]() $e_{i,j}$
-coefficient of the unique element in the above basis that involves
$e_{i,j}$
-coefficient of the unique element in the above basis that involves
![]() $e_{i,j}$
.
$e_{i,j}$
.
The Killing form of
![]() $\mathfrak {g}={\mathfrak {so}}_n$
is given by
$\mathfrak {g}={\mathfrak {so}}_n$
is given by
![]() $\kappa _{\mathfrak {g}}(x,y)= (n-2) \mathrm {tr}(xy)$
and
$\kappa _{\mathfrak {g}}(x,y)= (n-2) \mathrm {tr}(xy)$
and
![]() $(x|y)_{\mathfrak {g}} =\mathrm {tr}(xy)/2$
. Set
$(x|y)_{\mathfrak {g}} =\mathrm {tr}(xy)/2$
. Set
By [Reference Collingwood and McGovern32, Theorems 5.1.2 and 5.1.4], nilpotent orbits of
![]() ${\mathfrak {so}}_{n}$
are parametrised by
${\mathfrak {so}}_{n}$
are parametrised by
![]() ${\mathscr {P}}_1(n)$
, with the exception that each very even partition
${\mathscr {P}}_1(n)$
, with the exception that each very even partition ![]() (i.e.,
(i.e., ![]() has only even parts) corresponds to two nilpotent orbits. For
has only even parts) corresponds to two nilpotent orbits. For ![]() , not very even, we shall denote by
, not very even, we shall denote by ![]() , or simply by
, or simply by ![]() when there is no possible confusion, the corresponding nilpotent orbit of
when there is no possible confusion, the corresponding nilpotent orbit of
![]() ${\mathfrak {so}}_n$
. For very even
${\mathfrak {so}}_n$
. For very even ![]() , we shall denote by
, we shall denote by ![]() and
and ![]() the two corresponding nilpotent orbits of
the two corresponding nilpotent orbits of
![]() ${\mathfrak {so}}_n$
. In fact, their union forms a single
${\mathfrak {so}}_n$
. In fact, their union forms a single
![]() $O(n)$
-orbit. Thus, nilpotent orbits of
$O(n)$
-orbit. Thus, nilpotent orbits of
![]() $\mathfrak {o}_{n}$
are parametrised by
$\mathfrak {o}_{n}$
are parametrised by
![]() ${\mathscr {P}}_1(n)$
.
${\mathscr {P}}_1(n)$
.
If ![]() , then
, then ![]() if and only if
if and only if ![]() , where
, where ![]() is either
is either ![]() ,
, ![]() or
or ![]() according to whether
according to whether ![]() is very even or not.
is very even or not.
Given ![]() , there exists a unique
, there exists a unique ![]() such that
such that ![]() , and if
, and if
![]() $\boldsymbol {\mu }\in {\mathscr {P}}_{1}(n)$
verifies
$\boldsymbol {\mu }\in {\mathscr {P}}_{1}(n)$
verifies ![]() , then
, then ![]() .
.
Definition 9.1. Assume that ![]() , for
, for
![]() $\varepsilon \in \{\pm 1\}$
. An
$\varepsilon \in \{\pm 1\}$
. An
![]() $\varepsilon $
-degeneration of
$\varepsilon $
-degeneration of ![]() is an element
is an element
![]() $\boldsymbol {\mu } \in {\mathscr {P}}_{\varepsilon }(n)$
such that
$\boldsymbol {\mu } \in {\mathscr {P}}_{\varepsilon }(n)$
such that ![]() – that is,
– that is, ![]() . A
. A
![]() $\varepsilon $
-degeneration
$\varepsilon $
-degeneration
![]() $\boldsymbol {\mu }$
of
$\boldsymbol {\mu }$
of ![]() is said to be minimal if
is said to be minimal if
![]() ${\mathbb {O}}_{\varepsilon ;\boldsymbol {\mu }}$
is open in
${\mathbb {O}}_{\varepsilon ;\boldsymbol {\mu }}$
is open in ![]() .
.
9.1 Symplectic and orthogonal pyramids
As in the
![]() ${\mathfrak {sl}}_n$
case, there is a bijection between the set of good gradings of
${\mathfrak {sl}}_n$
case, there is a bijection between the set of good gradings of
![]() $\mathfrak {sp}_n$
or
$\mathfrak {sp}_n$
or
![]() ${\mathfrak {so}}_n$
compatible with a given nilpotent element and the set of some pyramids of shape the corresponding partition of
${\mathfrak {so}}_n$
compatible with a given nilpotent element and the set of some pyramids of shape the corresponding partition of
![]() ${\mathscr {P}}_\varepsilon (n)$
, with
${\mathscr {P}}_\varepsilon (n)$
, with
![]() $\varepsilon \in \{\pm 1\}$
. Such pyramids are called symplectic pyramids for
$\varepsilon \in \{\pm 1\}$
. Such pyramids are called symplectic pyramids for
![]() $\mathfrak {sp}_n$
(
$\mathfrak {sp}_n$
(
![]() $\varepsilon =-1$
) and orthogonal pyramids for
$\varepsilon =-1$
) and orthogonal pyramids for
![]() ${\mathfrak {so}}_n$
(
${\mathfrak {so}}_n$
(
![]() $\varepsilon =1$
). For
$\varepsilon =1$
). For
![]() $\mathfrak {sp}_n$
and
$\mathfrak {sp}_n$
and
![]() ${\mathfrak {so}}_n$
, we will be only using symplectic or orthogonal Dynkin pyramids. This is a diagram consisting of n boxes each of size
${\mathfrak {so}}_n$
, we will be only using symplectic or orthogonal Dynkin pyramids. This is a diagram consisting of n boxes each of size
![]() $2$
units by
$2$
units by
![]() $2$
units drawn in the
$2$
units drawn in the
![]() $xy$
-plane. As in the
$xy$
-plane. As in the
![]() ${\mathfrak {sl}}_n$
case, the coordinates of a box are the coordinates of its midpoint, and the row and column numbers of a box mean its y- and x-coordinate, respectively, but there are a few differences.
${\mathfrak {sl}}_n$
case, the coordinates of a box are the coordinates of its midpoint, and the row and column numbers of a box mean its y- and x-coordinate, respectively, but there are a few differences.
Let us first explain what are the symplectic Dynkin pyramids of shape ![]() . The parts of
. The parts of ![]() indicate the number of boxes in each row, and the rows are added to the diagram so that we get a symmetric pyramid with respect to the point
indicate the number of boxes in each row, and the rows are added to the diagram so that we get a symmetric pyramid with respect to the point
![]() $(0,0)$
. The only complication is that if some (necessarily even) part
$(0,0)$
. The only complication is that if some (necessarily even) part ![]() of
of ![]() has odd multiplicity, then the first time a row of this length is added to the diagram, it is split into two halves, the right half is added to the next free row in the upper half plane in columns
has odd multiplicity, then the first time a row of this length is added to the diagram, it is split into two halves, the right half is added to the next free row in the upper half plane in columns ![]() and the left half is added to the lower half plane in a centrally symmetric way. We refer the exceptional rows arising in this way to as skew rows. The missing boxes in skew rows are drawn as a box with a cross through it. We number the boxes of the symplectic Dynkin pyramid with labels
and the left half is added to the lower half plane in a centrally symmetric way. We refer the exceptional rows arising in this way to as skew rows. The missing boxes in skew rows are drawn as a box with a cross through it. We number the boxes of the symplectic Dynkin pyramid with labels ![]() in such a way that i and
in such a way that i and
![]() $-i$
appear in centrally symmetric boxes, for
$-i$
appear in centrally symmetric boxes, for ![]() . As a rule, we will number the first
. As a rule, we will number the first
![]() $n/2$
boxes of symplectic Dynkin pyramids from top right to bottom left.
$n/2$
boxes of symplectic Dynkin pyramids from top right to bottom left.
For example, we represent in Figure 9 and Figure 10 the numbered symplectic Dynkin pyramids of shape ![]() and
and ![]() , respectively.
, respectively.

Figure 9 Symplectic Dynkin pyramid of shape
![]() $(5^2,1^2).$
$(5^2,1^2).$

Figure 10 Symplectic Dynkin pyramid of shape
![]() $(5^2,4,2).$
$(5^2,4,2).$
Let us now explain what are the orthogonal Dynkin pyramids of shape ![]() . Assume to start with that n is even. Then the orthogonal Dynkin pyramid is constructed as in the symplectic case, adding rows of lengths determined by the parts of
. Assume to start with that n is even. Then the orthogonal Dynkin pyramid is constructed as in the symplectic case, adding rows of lengths determined by the parts of ![]() working outwards from the x-axis starting with the largest part, in a centrally symmetric way. The only difficulty is if some (necessarily odd) part of
working outwards from the x-axis starting with the largest part, in a centrally symmetric way. The only difficulty is if some (necessarily odd) part of ![]() appears with odd multiplicity. As n is even, the number of distinct parts having odd multiplicity is even. Choose
appears with odd multiplicity. As n is even, the number of distinct parts having odd multiplicity is even. Choose
![]() $i_1 < j_1 < \cdots < i_r < j_r$
such that
$i_1 < j_1 < \cdots < i_r < j_r$
such that ![]() are representatives for all the distinct odd parts of
are representatives for all the distinct odd parts of ![]() having odd multiplicity. Then the first time the part
having odd multiplicity. Then the first time the part ![]() needs to be added to the diagram, the part
needs to be added to the diagram, the part ![]() is also added at the same time, so that the parts
is also added at the same time, so that the parts ![]() and
and ![]() of
of ![]() contribute two centrally symmetric rows to the diagram, one row in the upper half plane with boxes in columns
contribute two centrally symmetric rows to the diagram, one row in the upper half plane with boxes in columns ![]() and the other row in the lower half plane with boxes in columns
and the other row in the lower half plane with boxes in columns ![]() . We will refer to the exceptional rows arising in this way as skew rows. We number the boxes exactly as in the symplectic case.
. We will refer to the exceptional rows arising in this way as skew rows. We number the boxes exactly as in the symplectic case.
For example, we represent in Figure 11 and Figure 12 the numbered orthogonal Dynkin pyramids of shape ![]() and
and ![]() , respectively.
, respectively.

Figure 11 Orthogonal Dynkin pyramid of shape
![]() $(4^2,1^2).$
$(4^2,1^2).$

Figure 12 Orthogonal Dynkin pyramid of shape
![]() $(3,1^3).$
$(3,1^3).$
If n is odd, there is one additional consideration. There must be some odd part appearing with odd multiplicity. Let ![]() be the largest such part, and put
be the largest such part, and put ![]() boxes into the zeroth row in columns
boxes into the zeroth row in columns ![]() ; we also treat this zeroth row as a skew row. Now remove the part
; we also treat this zeroth row as a skew row. Now remove the part ![]() from
from ![]() to obtain a partition of an even number. The remaining parts are then added to the diagram exactly as in the case n even. We number the boxes exactly as in the symplectic Dynkin pyramid with labels
to obtain a partition of an even number. The remaining parts are then added to the diagram exactly as in the case n even. We number the boxes exactly as in the symplectic Dynkin pyramid with labels ![]() in such a way that i and
in such a way that i and
![]() $-i$
appear in centrally symmetric boxes, for
$-i$
appear in centrally symmetric boxes, for ![]() , except that there is here a box numbered
, except that there is here a box numbered
![]() $0$
.
$0$
.
We represent in Figure 13 and Figure 14 two more examples: the numbered orthogonal Dynkin pyramids of shape ![]() and
and ![]() , respectively.
, respectively.

Figure 13 Orthogonal Dynkin pyramid of shape
![]() $(5^3,1^2).$
$(5^3,1^2).$

Figure 14 Orthogonal Dynkin pyramid of shape
![]() $(4^2,3).$
$(4^2,3).$
We can now fix a choice of an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
such that
$(e,h,f)$
such that ![]() by setting
by setting
![]() $f =\sum _{i,j} \sigma _{i,j} e_{i,j}$
for all
$f =\sum _{i,j} \sigma _{i,j} e_{i,j}$
for all ![]() , where the sum of over all pairs
, where the sum of over all pairs
![]() $i,j$
of boxes such in the Dynkin pyramid such that
$i,j$
of boxes such in the Dynkin pyramid such that
 $$ \begin{align*} & \text{either } \mathrm{col}(j)= \mathrm{col}(i)+2 \text{ and } \mathrm{row}(i)=\mathrm{row}(j), \\ & \text{or } \mathrm{col}(j)=1, \; \mathrm{col}(i) = -1 \text{ and } \mathrm{row}(i)= - \mathrm{row}(j) & \\ & \hspace{0.5cm} \text{ is a skew-row in the upper half plane}, \end{align*} $$
$$ \begin{align*} & \text{either } \mathrm{col}(j)= \mathrm{col}(i)+2 \text{ and } \mathrm{row}(i)=\mathrm{row}(j), \\ & \text{or } \mathrm{col}(j)=1, \; \mathrm{col}(i) = -1 \text{ and } \mathrm{row}(i)= - \mathrm{row}(j) & \\ & \hspace{0.5cm} \text{ is a skew-row in the upper half plane}, \end{align*} $$
and
![]() $h = \sum _{i=1}^{n} \mathrm {col}(i) e_{i,i}$
(so
$h = \sum _{i=1}^{n} \mathrm {col}(i) e_{i,i}$
(so
![]() $x^0= \sum _{i=1}^n \frac {1}{2}\mathrm {col}(i) e_{i,i}$
).
$x^0= \sum _{i=1}^n \frac {1}{2}\mathrm {col}(i) e_{i,i}$
).
The following lemma is a refinement of [Reference Kraft and Procesi66, Theorem 12.3]. We refer to [Reference Li68, Propositions 8.5.1 and 8.5.2] for a proof.
Lemma 9.2 (row/column removal rule for
 $\mathfrak {sp}_n$
and
$\mathfrak {sp}_n$
and
 ${\mathfrak {so}}_n$
).
${\mathfrak {so}}_n$
).
Let ![]() , for
, for
![]() $\varepsilon \in \{\pm 1\}$
, and
$\varepsilon \in \{\pm 1\}$
, and
![]() $ {\boldsymbol {\mu }}$
a degeneration of
$ {\boldsymbol {\mu }}$
a degeneration of ![]() . Assume that the first l rows and the first m columns of
. Assume that the first l rows and the first m columns of ![]() and
and
![]() ${\boldsymbol {\mu }}$
coincide, and denote by
${\boldsymbol {\mu }}$
coincide, and denote by ![]() and
and
![]() $\boldsymbol {\mu }'$
the partitions obtained by erasing these l common rows and common m columns. Then
$\boldsymbol {\mu }'$
the partitions obtained by erasing these l common rows and common m columns. Then
as algebraic varieties, with
![]() $f \in {\mathbb {O}}_{\varepsilon; {\boldsymbol {\mu }}}$
and
$f \in {\mathbb {O}}_{\varepsilon; {\boldsymbol {\mu }}}$
and
![]() $f' \in {\mathbb {O}}_{\varepsilon ;{\boldsymbol {\mu }'}}$
. In particular, if
$f' \in {\mathbb {O}}_{\varepsilon ;{\boldsymbol {\mu }'}}$
. In particular, if
![]() $f'=0$
, then
$f'=0$
, then ![]() .
.
By [Reference Arakawa10, Tables 2 and 3], the nilpotent orbit
![]() ${\mathbb {O}}_k$
, for k admissible for
${\mathbb {O}}_k$
, for k admissible for
![]() $\mathfrak {g}=\mathfrak {sp}_n$
or
$\mathfrak {g}=\mathfrak {sp}_n$
or
![]() $\mathfrak {g}={\mathfrak {so}}_n$
, is described as follows:
$\mathfrak {g}={\mathfrak {so}}_n$
, is described as follows:
-
• If k is a principal admissible level for
 $\mathfrak {sp}_n$
(that is, q is odd), then
$\mathfrak {sp}_n$
(that is, q is odd), then  , where
, where  , with
, with  .
. -
• If k is a coprincipal admissible level for
 $\mathfrak {sp}_n$
(that is, q is even), then
$\mathfrak {sp}_n$
(that is, q is even), then  , where
, where  , with
, with  .
. -
• If k is a principal admissible level for
 ${\mathfrak {so}}_n$
(that is, either n is even, or both n and q are odd), then
${\mathfrak {so}}_n$
(that is, either n is even, or both n and q are odd), then  , where
, where  , with
, with  .
. -
• If k is a coprincipal admissible level for
 ${\mathfrak {so}}_n$
(that is, n is odd and q is even), then
${\mathfrak {so}}_n$
(that is, n is odd and q is even), then  , where
, where  , with
, with  .
.
The following lemma is the analog of Lemma 8.3 for
![]() $\mathfrak {sp}_n$
.
$\mathfrak {sp}_n$
.
Lemma 9.3 (Case
 $\mathfrak {sp}_n$
).
$\mathfrak {sp}_n$
).
Let ![]() be such that
be such that ![]() . Fix a partition
. Fix a partition
![]() $\boldsymbol {\mu } \in {\mathscr {P}}_{-1}(n)$
of n such that
$\boldsymbol {\mu } \in {\mathscr {P}}_{-1}(n)$
of n such that ![]() . Let
. Let ![]() and
and
![]() $\boldsymbol {\mu }'$
be the partitions obtained from
$\boldsymbol {\mu }'$
be the partitions obtained from ![]() and
and
![]() $\boldsymbol {\mu }$
by erasing all common rows and columns of
$\boldsymbol {\mu }$
by erasing all common rows and columns of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then,
$\boldsymbol {\mu }$
. Then,
![]() $\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
![]() $\mathfrak {sp}_{|\boldsymbol {\mu }'|}$
– that is,
$\mathfrak {sp}_{|\boldsymbol {\mu }'|}$
– that is,
![]() $\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
$\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
![]() $\boldsymbol \mu $
is of one of the following types:
$\boldsymbol \mu $
is of one of the following types:
-
(a)
 ,
, -
(b)
 $\boldsymbol {\mu }=(q^m,1^s)$
, with q odd, m even,
$\boldsymbol {\mu }=(q^m,1^s)$
, with q odd, m even,
 $s\ge 0$
,
$s\ge 0$
, -
(c)
 $\boldsymbol {\mu }=(q^{\widetilde m-1},q-1,1^{\widetilde s+1})$
, with q odd,
$\boldsymbol {\mu }=(q^{\widetilde m-1},q-1,1^{\widetilde s+1})$
, with q odd, -
(d)
 $\boldsymbol {\mu }=(q^{\widetilde m-1},(q-2)^{2})$
and
$\boldsymbol {\mu }=(q^{\widetilde m-1},(q-2)^{2})$
and
 $\widetilde s = q-4$
, with q odd,
$\widetilde s = q-4$
, with q odd, -
(e)
 $\boldsymbol {\mu }=((\frac {q}{2})^{m},1^s)$
, with q even,
$\boldsymbol {\mu }=((\frac {q}{2})^{m},1^s)$
, with q even,
 $\frac {q}{2},s$
even, m odd or even.
$\frac {q}{2},s$
even, m odd or even. -
(f)
 $\boldsymbol {\mu }=((\frac {q}{2})^{\widetilde m},(\frac {q}{2}-1)^2)$
and
$\boldsymbol {\mu }=((\frac {q}{2})^{\widetilde m},(\frac {q}{2}-1)^2)$
and
 $\widetilde s=\frac {q}{2}-4$
, with q even,
$\widetilde s=\frac {q}{2}-4$
, with q even,
 $\frac {q}{2}$
even,
$\frac {q}{2}$
even, -
(g)
 $\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{m},1^s)$
, with q even,
$\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{m},1^s)$
, with q even,
 $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
 $m,s$
even,
$m,s$
even, -
(h)
 $\boldsymbol {\mu }=((\frac {q}{2})^{\widetilde m +2}, \widetilde s)$
, with q even,
$\boldsymbol {\mu }=((\frac {q}{2})^{\widetilde m +2}, \widetilde s)$
, with q even,
 $\frac {q}{2}$
odd.
$\frac {q}{2}$
odd. -
(i)
 $\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1,1^s)$
, with q even,
$\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1,1^s)$
, with q even,
 $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
 $m,s$
even,
$m,s$
even, -
(j)
 $\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m-1},(\frac {q}{2}-2)^2)$
, and
$\boldsymbol {\mu }=(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m-1},(\frac {q}{2}-2)^2)$
, and
 $\widetilde s=\frac {q}{2}-4$
, with q even,
$\widetilde s=\frac {q}{2}-4$
, with q even,
 $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd, -
(k)
 $\boldsymbol {\mu }=((\frac {q}{2}-1)^2)$
,
$\boldsymbol {\mu }=((\frac {q}{2}-1)^2)$
,
 $\widetilde m=0$
and
$\widetilde m=0$
and
 $\widetilde s=\frac {q}{2}-3$
, with q even,
$\widetilde s=\frac {q}{2}-3$
, with q even,
 $\frac {q}{2}$
odd.
$\frac {q}{2}$
odd.
Here,
![]() $|\boldsymbol {\mu }'|$
stands for the sum of the parts of
$|\boldsymbol {\mu }'|$
stands for the sum of the parts of
![]() $\boldsymbol {\mu }'$
.
$\boldsymbol {\mu }'$
.
Proof. We argue as in the proof of Lemma 8.3. One can assume that ![]() , the case where
, the case where ![]() being obvious. According to the above description of
being obvious. According to the above description of
![]() ${\mathbb {O}}_k$
, five types of partitions for
${\mathbb {O}}_k$
, five types of partitions for ![]() can be distinguished. We consider the different types.
can be distinguished. We consider the different types.
(1) ![]() , with q odd,
, with q odd,
![]() $\widetilde m$
even and
$\widetilde m$
even and ![]() . This case is very similar to that of
. This case is very similar to that of
![]() ${\mathfrak {sl}}_n$
. This leads to the partitions of type (b), the case that
${\mathfrak {sl}}_n$
. This leads to the partitions of type (b), the case that
![]() $\boldsymbol \mu $
is of type
$\boldsymbol \mu $
is of type
![]() $(q^{\widetilde m-1},(q-1)^2)$
being excluded since q and
$(q^{\widetilde m-1},(q-1)^2)$
being excluded since q and
![]() $\widetilde m-2$
are odd.
$\widetilde m-2$
are odd.
(2) ![]() , with q odd,
, with q odd,
![]() $\widetilde m-1$
even,
$\widetilde m-1$
even, ![]() . Assume first that
. Assume first that
![]() $\boldsymbol \mu =(q^{\widetilde m-1},q-1,\boldsymbol \nu )$
, with
$\boldsymbol \mu =(q^{\widetilde m-1},q-1,\boldsymbol \nu )$
, with ![]() and
and ![]() . Then
. Then ![]() and
and
![]() $\boldsymbol \mu '= \boldsymbol \nu $
. So the only possibility for that
$\boldsymbol \mu '= \boldsymbol \nu $
. So the only possibility for that
![]() $\boldsymbol \mu '$
corresponds to the zero orbit is that
$\boldsymbol \mu '$
corresponds to the zero orbit is that
![]() $\nu _i=1$
for any i – that is,
$\nu _i=1$
for any i – that is,
![]() $\boldsymbol \mu $
is of the form (c).
$\boldsymbol \mu $
is of the form (c).
Assume now that
![]() $\boldsymbol \mu =(q^{m},\boldsymbol \nu )$
, with
$\boldsymbol \mu =(q^{m},\boldsymbol \nu )$
, with ![]() even,
even, ![]() and
and ![]() . Let
. Let ![]() and
and
![]() $\boldsymbol {\mu }"$
be the partitions obtained by erasing all common rows of
$\boldsymbol {\mu }"$
be the partitions obtained by erasing all common rows of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then
$\boldsymbol {\mu }$
. Then ![]() and
and
![]() $\boldsymbol \mu "= \boldsymbol \nu $
. If
$\boldsymbol \mu "= \boldsymbol \nu $
. If
![]() $\nu _i=1$
for all i, then we get a partition of type (b). Otherwise, observe that
$\nu _i=1$
for all i, then we get a partition of type (b). Otherwise, observe that ![]() and
and
![]() $\boldsymbol \mu '$
have at least one common column if and only if
$\boldsymbol \mu '$
have at least one common column if and only if
![]() $t=\widetilde m-m+1$
. If so, then
$t=\widetilde m-m+1$
. If so, then
![]() $\nu _t> \widetilde s+1$
and
$\nu _t> \widetilde s+1$
and ![]() ,
, ![]() . The partition
. The partition
![]() $\boldsymbol \mu '$
corresponds to the zero orbit if and only if
$\boldsymbol \mu '$
corresponds to the zero orbit if and only if
![]() $\nu _i-\widetilde s-1=1$
for all i. Then
$\nu _i-\widetilde s-1=1$
for all i. Then
That is,
Since
![]() $\widetilde m-m$
is odd, the only possibility is that
$\widetilde m-m$
is odd, the only possibility is that
![]() $\widetilde m-m=1$
– that is,
$\widetilde m-m=1$
– that is,
![]() $m=\widetilde m-1$
and
$m=\widetilde m-1$
and
![]() $q-\widetilde s-2=2$
; that is,
$q-\widetilde s-2=2$
; that is,
![]() $\widetilde s =q-4$
. Hence,
$\widetilde s =q-4$
. Hence,
![]() $t=2$
and
$t=2$
and
![]() $\nu _1=\nu _2=q-2$
. So
$\nu _1=\nu _2=q-2$
. So
![]() $\boldsymbol \mu $
of the form (d).
$\boldsymbol \mu $
of the form (d).
(3) ![]() , with q even,
, with q even,
![]() $\frac {q}{2}$
even,
$\frac {q}{2}$
even,
![]() $\widetilde m$
odd or even and
$\widetilde m$
odd or even and ![]() . This case is very similar to the
. This case is very similar to the
![]() ${\mathfrak {sl}}_n$
one. So we conclude similarly. This leads to the partitions of type (e) or (f).
${\mathfrak {sl}}_n$
one. So we conclude similarly. This leads to the partitions of type (e) or (f).
(4) ![]() , with q even,
, with q even,
![]() $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
![]() $\widetilde m$
even and
$\widetilde m$
even and ![]() . Assume first that
. Assume first that
![]() $\boldsymbol \mu =(\frac {q}{2}+1,(\frac {q}{2})^{m},\boldsymbol \nu )$
, with
$\boldsymbol \mu =(\frac {q}{2}+1,(\frac {q}{2})^{m},\boldsymbol \nu )$
, with ![]() ,
, ![]() and
and ![]() . Let
. Let ![]() and
and
![]() $\boldsymbol {\mu }"$
be the partitions obtained by erasing all common rows of
$\boldsymbol {\mu }"$
be the partitions obtained by erasing all common rows of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then
$\boldsymbol {\mu }$
. Then ![]() and
and
![]() $\boldsymbol \mu "= \boldsymbol \nu $
. So we are led to the case (3), but the partition
$\boldsymbol \mu "= \boldsymbol \nu $
. So we are led to the case (3), but the partition
![]() $\boldsymbol \mu =(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m-1},(\frac {q}{2}-1)^2)$
is excluded since both
$\boldsymbol \mu =(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m-1},(\frac {q}{2}-1)^2)$
is excluded since both
![]() $\frac {q}{2}$
and
$\frac {q}{2}$
and
![]() $\widetilde m-1$
are odd. So we get only the type (g).
$\widetilde m-1$
are odd. So we get only the type (g).
Assume now that
![]() $\boldsymbol \mu =((\frac {q}{2})^{m},\boldsymbol \nu )$
, with
$\boldsymbol \mu =((\frac {q}{2})^{m},\boldsymbol \nu )$
, with ![]() ,
, ![]() and
and ![]() . Then
. Then ![]() and
and
![]() $\boldsymbol \mu $
have no common rows. Moreover,
$\boldsymbol \mu $
have no common rows. Moreover, ![]() and
and
![]() $\boldsymbol \mu $
have at least one common column if and only if
$\boldsymbol \mu $
have at least one common column if and only if
![]() $m+t=\widetilde m+2$
. If so, then
$m+t=\widetilde m+2$
. If so, then
![]() $\nu _t> \widetilde s$
, and we have
$\nu _t> \widetilde s$
, and we have ![]() ,
, ![]() . The later corresponds to the zero orbit if and only if either
. The later corresponds to the zero orbit if and only if either
![]() $\frac {q}{2}-\widetilde s=1$
and
$\frac {q}{2}-\widetilde s=1$
and
![]() $\nu _i-\widetilde s=1$
for all i, whence
$\nu _i-\widetilde s=1$
for all i, whence
![]() $m+t =\widetilde m+2$
and
$m+t =\widetilde m+2$
and
![]() $\widetilde s=\frac {q}{2}-1$
and, necessarily,
$\widetilde s=\frac {q}{2}-1$
and, necessarily,
![]() $\boldsymbol \mu $
has type (h) with
$\boldsymbol \mu $
has type (h) with
![]() $\widetilde s=0$
. Or
$\widetilde s=0$
. Or
![]() $m=0$
and
$m=0$
and
![]() $\nu _i-\widetilde s=1$
for all i, whence
$\nu _i-\widetilde s=1$
for all i, whence
That is,
Hence, for parity reasons, we get that
![]() $\widetilde m=0$
,
$\widetilde m=0$
, ![]() and
and
![]() $\boldsymbol \mu =((\frac {q}{2}-1)^2)$
. This yields to the partition of type (k).
$\boldsymbol \mu =((\frac {q}{2}-1)^2)$
. This yields to the partition of type (k).
(5) ![]() , with q even,
, with q even,
![]() $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
![]() $\widetilde m-1$
even and
$\widetilde m-1$
even and ![]() .
.
Assume first that the first row of
![]() $\boldsymbol \mu $
if
$\boldsymbol \mu $
if
![]() $\frac {q}{2}+1$
. By erasing the first (common) row of
$\frac {q}{2}+1$
. By erasing the first (common) row of ![]() and
and
![]() $\boldsymbol \mu $
, we go to the situation (3) with
$\boldsymbol \mu $
, we go to the situation (3) with
![]() $\frac {q}{2}$
is place of q. So we get partitions of types (g), (i) or (j).
$\frac {q}{2}$
is place of q. So we get partitions of types (g), (i) or (j).
Assume now that
![]() $\boldsymbol \mu =((\frac {q}{2})^{m},\boldsymbol \nu )$
, with
$\boldsymbol \mu =((\frac {q}{2})^{m},\boldsymbol \nu )$
, with ![]() ,
, ![]() and
and ![]() . Then
. Then ![]() and
and
![]() $\boldsymbol \mu $
have no common rows. Moreover,
$\boldsymbol \mu $
have no common rows. Moreover, ![]() and
and
![]() $\boldsymbol \mu $
have at least one common column only if
$\boldsymbol \mu $
have at least one common column only if
![]() $m+t=\widetilde m+2$
. If so, either
$m+t=\widetilde m+2$
. If so, either
![]() $\nu _t= \widetilde s+1$
and then necessarily
$\nu _t= \widetilde s+1$
and then necessarily
![]() $\boldsymbol \mu $
is of the type (h), or
$\boldsymbol \mu $
is of the type (h), or
![]() $\nu _t> \widetilde s+1$
and we have
$\nu _t> \widetilde s+1$
and we have ![]() and
and ![]() . The later corresponds to the zero nilpotent orbit if and only if either
. The later corresponds to the zero nilpotent orbit if and only if either
![]() $\frac {q}{2}-\widetilde s-1=1$
and
$\frac {q}{2}-\widetilde s-1=1$
and
![]() $\nu _i-\widetilde s-1=1$
for all i, whence
$\nu _i-\widetilde s-1=1$
for all i, whence
![]() $m+t =\widetilde m+1$
and
$m+t =\widetilde m+1$
and
![]() $\widetilde s+1=\frac {q}{2}-1$
, and
$\widetilde s+1=\frac {q}{2}-1$
, and
![]() $\boldsymbol \mu $
has type (h) with
$\boldsymbol \mu $
has type (h) with
![]() $\widetilde s=\frac {q}{2}-2$
, or
$\widetilde s=\frac {q}{2}-2$
, or
![]() $m=0$
and
$m=0$
and
![]() $\nu _i-\widetilde s-1=1$
for all i, whence
$\nu _i-\widetilde s-1=1$
for all i, whence
That is,
whence,
![]() $\frac {q}{2}=1$
and
$\frac {q}{2}=1$
and
![]() $\widetilde s+1=0$
, which is impossible.
$\widetilde s+1=0$
, which is impossible.
Conversely, we easily that all the partitions of type (a)–(k) verify the desired conditions.
We now state the analog of Lemma 8.3 for
![]() ${\mathfrak {so}}_n$
.
${\mathfrak {so}}_n$
.
Lemma 9.4 (Case
 ${\mathfrak {so}}_n$
).
${\mathfrak {so}}_n$
).
Let ![]() be such that
be such that ![]() . Fix a partition
. Fix a partition
![]() $\boldsymbol {\mu }$
of n such that
$\boldsymbol {\mu }$
of n such that ![]() . Let
. Let ![]() and
and
![]() $\boldsymbol {\mu }'$
be the partitions obtained from
$\boldsymbol {\mu }'$
be the partitions obtained from ![]() and
and
![]() $\boldsymbol {\mu }$
by erasing all common rows and columns of
$\boldsymbol {\mu }$
by erasing all common rows and columns of ![]() and
and
![]() $\boldsymbol {\mu }$
. Then,
$\boldsymbol {\mu }$
. Then,
![]() $\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
$\boldsymbol {\mu }'$
corresponds to the zero nilpotent orbit of
![]() $\mathfrak {sp}_{|\boldsymbol {\mu }'|}$
– that is,
$\mathfrak {sp}_{|\boldsymbol {\mu }'|}$
– that is,
![]() $\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
$\boldsymbol {\mu }'=(1^{|\boldsymbol {\mu }'|})$
if and only if
![]() $\boldsymbol \mu \in {\mathscr {P}}_1(n)$
is of one of the following types:
$\boldsymbol \mu \in {\mathscr {P}}_1(n)$
is of one of the following types:
-
(a)
 ,
, -
(b)
 $\boldsymbol {\mu }=(q^m,1^s)$
, with q odd or even, m odd or even,
$\boldsymbol {\mu }=(q^m,1^s)$
, with q odd or even, m odd or even,
 $s\ge 0$
,
$s\ge 0$
, -
(c)
 $\boldsymbol {\mu }=(q^{\widetilde m},(q-1)^{2})$
,
$\boldsymbol {\mu }=(q^{\widetilde m},(q-1)^{2})$
,
 $\widetilde s = q-3$
and
$\widetilde s = q-3$
and
 $\widetilde m$
odd, with q odd,
$\widetilde m$
odd, with q odd, -
(d)
 $\boldsymbol {\mu }=(3^{\widetilde m-1},2^{4})$
,
$\boldsymbol {\mu }=(3^{\widetilde m-1},2^{4})$
,
 $q=3$
,
$q=3$
,
 $\widetilde s=1$
and
$\widetilde s=1$
and
 $\widetilde m$
even,
$\widetilde m$
even, -
(e)
 $\boldsymbol {\mu }=(q^{\widetilde m+1},2^{2})$
,
$\boldsymbol {\mu }=(q^{\widetilde m+1},2^{2})$
,
 $\widetilde s=3$
and
$\widetilde s=3$
and
 $\widetilde m+1$
odd, with q odd,
$\widetilde m+1$
odd, with q odd, -
(f)
 $\boldsymbol {\mu }=(q^{\widetilde m},(q-1)^2,1)$
,
$\boldsymbol {\mu }=(q^{\widetilde m},(q-1)^2,1)$
,
 $\widetilde s = q-2$
and
$\widetilde s = q-2$
and
 $\widetilde m$
even, with q odd,
$\widetilde m$
even, with q odd, -
(g)
 $\boldsymbol {\mu }=(q^{\widetilde m -1},q-1,1^s)$
, with q even,
$\boldsymbol {\mu }=(q^{\widetilde m -1},q-1,1^s)$
, with q even,
 $s\ge 0$
,
$s\ge 0$
, -
(h)
 $\boldsymbol {\mu }=(q^{\widetilde m -1},q-1,2^2)$
and
$\boldsymbol {\mu }=(q^{\widetilde m -1},q-1,2^2)$
and
 $\widetilde s=3$
, with q even,
$\widetilde s=3$
, with q even, -
(i)
 $\boldsymbol {\mu }=(q^{\widetilde m -1},(q-2)^2,1)$
and
$\boldsymbol {\mu }=(q^{\widetilde m -1},(q-2)^2,1)$
and
 $\widetilde s = q-3$
, with q even,
$\widetilde s = q-3$
, with q even, -
(j)
 $\boldsymbol {\mu }=(q+1,q^{m},1^s)$
, with
$\boldsymbol {\mu }=(q+1,q^{m},1^s)$
, with
 $q,m$
even and
$q,m$
even and
 $s\ge 0$
,
$s\ge 0$
, -
(k)
 $\boldsymbol {\mu }=(q+1,q^{m},q-1,1^s)$
, with
$\boldsymbol {\mu }=(q+1,q^{m},q-1,1^s)$
, with
 $q,m$
even and
$q,m$
even and
 $s\ge 0$
,
$s\ge 0$
, -
(l)
 $\boldsymbol {\mu }=(q+1,q^{\widetilde m-1},q-1,2^2)$
and
$\boldsymbol {\mu }=(q+1,q^{\widetilde m-1},q-1,2^2)$
and
 $\widetilde s=3$
, with q even,
$\widetilde s=3$
, with q even, -
(m)
 $\boldsymbol {\mu }=(q+1,q^{\widetilde m-1},(q-2)^2,1)$
and
$\boldsymbol {\mu }=(q+1,q^{\widetilde m-1},(q-2)^2,1)$
and
 $\widetilde s = q-3$
, with q even,
$\widetilde s = q-3$
, with q even, -
(n)
 $\boldsymbol {\mu }=(q^{\widetilde m+1},q-1,1)$
and
$\boldsymbol {\mu }=(q^{\widetilde m+1},q-1,1)$
and
 $\widetilde s=q-1$
, with q even.
$\widetilde s=q-1$
, with q even.
Here,
![]() $|\boldsymbol {\mu }'|$
stands for the sum of the parts of
$|\boldsymbol {\mu }'|$
stands for the sum of the parts of
![]() $\boldsymbol {\mu }'$
.
$\boldsymbol {\mu }'$
.
Proof. The proof is very similar to that of Lemma 9.3. The details are left to the reader.
In particular, by Lemma 9.2, if
![]() $\boldsymbol {\mu }$
is a partition of n as in Lemma 9.3 (resp. Lemma 9.4), the nilpotent Slodowy slice
$\boldsymbol {\mu }$
is a partition of n as in Lemma 9.3 (resp. Lemma 9.4), the nilpotent Slodowy slice
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is isomorphic to a nilpotent orbit closure in
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is isomorphic to a nilpotent orbit closure in
![]() $\mathfrak {sp}_{s}$
(resp.
$\mathfrak {sp}_{s}$
(resp.
![]() ${\mathfrak {so}}_s$
) for
${\mathfrak {so}}_s$
) for
![]() $f \in {\mathbb {O}}_{\varepsilon ;\boldsymbol {\mu }}$
with
$f \in {\mathbb {O}}_{\varepsilon ;\boldsymbol {\mu }}$
with
![]() $\varepsilon =-1$
(resp.
$\varepsilon =-1$
(resp.
![]() $\varepsilon =1$
) and
$\varepsilon =1$
) and
![]() $s:=|\boldsymbol {\mu }'|$
. If
$s:=|\boldsymbol {\mu }'|$
. If
![]() $\boldsymbol {\mu }$
is of type (a), note that
$\boldsymbol {\mu }$
is of type (a), note that
![]() $\mathcal {S}_{{\mathbb {O}}_k,f} \cong \{f\}$
.
$\mathcal {S}_{{\mathbb {O}}_k,f} \cong \{f\}$
.
In view of Lemmas 9.3 and 9.4, we describe the centraliser
![]() $\mathfrak {g}^\natural $
and the values of the
$\mathfrak {g}^\natural $
and the values of the
![]() $k_i^\natural $
’s for particular
$k_i^\natural $
’s for particular
![]() ${\mathfrak {sl}}_2$
-triples
${\mathfrak {sl}}_2$
-triples
![]() $(e,h,f)$
of
$(e,h,f)$
of
![]() $\mathfrak {sp}_n$
and
$\mathfrak {sp}_n$
and
![]() ${\mathfrak {so}}_n$
.
${\mathfrak {so}}_n$
.
Lemma 9.5. Let
![]() $\varepsilon =-1$
(resp.
$\varepsilon =-1$
(resp.
![]() $\varepsilon =1$
), and
$\varepsilon =1$
), and
![]() $f \in {\mathbb {O}}_{\varepsilon ;\boldsymbol \mu }$
a nilpotent element of
$f \in {\mathbb {O}}_{\varepsilon ;\boldsymbol \mu }$
a nilpotent element of
![]() $\mathfrak {sp}_n$
(resp.
$\mathfrak {sp}_n$
(resp.
![]() ${\mathfrak {so}}_n$
) with
${\mathfrak {so}}_n$
) with
![]() $\boldsymbol \mu $
as in the first column of Table 3 (resp. Table 4). Then the centraliser
$\boldsymbol \mu $
as in the first column of Table 3 (resp. Table 4). Then the centraliser
![]() $\mathfrak {g}^\natural $
of an
$\mathfrak {g}^\natural $
of an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
and the
$(e,h,f)$
and the
![]() $k_i^\natural $
’s are given by Table 3 (resp. Table 4). Moreover, if k is admissible, then so is
$k_i^\natural $
’s are given by Table 3 (resp. Table 4). Moreover, if k is admissible, then so is
![]() $k^\natural $
, provided that
$k^\natural $
, provided that
![]() $k_0^\natural =0$
.
$k_0^\natural =0$
.
Table 3 Centralisers of some
![]() ${\mathfrak {sl}}_2$
-triples
${\mathfrak {sl}}_2$
-triples
![]() $(e,h,f)$
in
$(e,h,f)$
in
![]() $\mathfrak {sp}_{n}$
, with
$\mathfrak {sp}_{n}$
, with
![]() $f \in {\mathbb {O}}_{-1;\boldsymbol \mu }.$
$f \in {\mathbb {O}}_{-1;\boldsymbol \mu }.$

Table 4 Centralisers of some
![]() ${\mathfrak {sl}}_2$
-triples
${\mathfrak {sl}}_2$
-triples
![]() $(e,h,f)$
in
$(e,h,f)$
in
![]() ${\mathfrak {so}}_{n}$
, with
${\mathfrak {so}}_{n}$
, with
![]() $f \in {\mathbb {O}}_{1;\boldsymbol \mu }.$
$f \in {\mathbb {O}}_{1;\boldsymbol \mu }.$

In Tables 3 and Table 4, the numbering of the levels
![]() $k_i^\natural $
’s follows the order in which the simple factors of
$k_i^\natural $
’s follows the order in which the simple factors of
![]() $\mathfrak {g}^\natural $
appear.
$\mathfrak {g}^\natural $
appear.
Remark 9.6. In Tables 3 and Table 4, the conclusions for small s or m remain valid, up to possible changes of numbering for the factors
![]() $\mathfrak {g}_i^\natural $
. More specifically, if the factor
$\mathfrak {g}_i^\natural $
. More specifically, if the factor
![]() $\mathfrak {g}_i^\natural $
for some i is isomorphic to
$\mathfrak {g}_i^\natural $
for some i is isomorphic to
![]() $\mathfrak {so}_m$
with
$\mathfrak {so}_m$
with
![]() $m=2$
, then
$m=2$
, then
![]() $\mathfrak {g}_i^\natural \cong \mathbb {C}$
, so i must be replaced by
$\mathfrak {g}_i^\natural \cong \mathbb {C}$
, so i must be replaced by
![]() $0$
and the value of
$0$
and the value of
![]() $k_i^\natural $
remains valid.
$k_i^\natural $
remains valid.
If the factor
![]() $\mathfrak {g}_i^\natural $
for some i – let’s say
$\mathfrak {g}_i^\natural $
for some i – let’s say
![]() $i=1$
– is isomorphic to
$i=1$
– is isomorphic to
![]() $\mathfrak {so}_m$
with
$\mathfrak {so}_m$
with
![]() $m=4$
, then
$m=4$
, then
![]() $\mathfrak {g}_1^\natural $
is not simple and has to replaced by
$\mathfrak {g}_1^\natural $
is not simple and has to replaced by
![]() $\mathfrak {g}_1^\natural \times \mathfrak {g}_2^\natural $
, with
$\mathfrak {g}_1^\natural \times \mathfrak {g}_2^\natural $
, with
![]() $\mathfrak {g}_1^\natural \cong {\mathfrak {sl}}_2$
,
$\mathfrak {g}_1^\natural \cong {\mathfrak {sl}}_2$
,
![]() $\mathfrak {g}_2^\natural \cong {\mathfrak {sl}}_2$
. Moreover, we have to read
$\mathfrak {g}_2^\natural \cong {\mathfrak {sl}}_2$
. Moreover, we have to read
![]() $k_2^\natural = k_1^\natural =\cdots $
instead of
$k_2^\natural = k_1^\natural =\cdots $
instead of
![]() $k_1^\natural =\cdots $
, and the value of
$k_1^\natural =\cdots $
, and the value of
![]() $k_1^\natural $
remains valid.
$k_1^\natural $
remains valid.
If the factor
![]() $\mathfrak {g}_i^\natural $
for some i is isomorphic to
$\mathfrak {g}_i^\natural $
for some i is isomorphic to
![]() $\mathfrak {so}_m$
or
$\mathfrak {so}_m$
or
![]() ${\mathfrak {sl}}_m$
with
${\mathfrak {sl}}_m$
with
![]() $m=1$
, then this factor does not appear (we use the convention that
$m=1$
, then this factor does not appear (we use the convention that
![]() ${\mathfrak {sl}}_1=\mathfrak {so}_1 = 0$
), and we just forget about
${\mathfrak {sl}}_1=\mathfrak {so}_1 = 0$
), and we just forget about
![]() $k_i^\natural $
.
$k_i^\natural $
.
Finally, if the factor
![]() $\mathfrak {g}_i^\natural $
for some i is isomorphic to
$\mathfrak {g}_i^\natural $
for some i is isomorphic to
![]() $\mathfrak {so}_{3} \cong {\mathfrak {sl}}_2$
,
$\mathfrak {so}_{3} \cong {\mathfrak {sl}}_2$
,
![]() $\mathfrak {so}_{6} \cong {\mathfrak {sl}}_3$
or
$\mathfrak {so}_{6} \cong {\mathfrak {sl}}_3$
or
![]() $\mathfrak {sp}_{2} \cong {\mathfrak {sl}}_2$
, then the conclusions remain valid without any change.
$\mathfrak {sp}_{2} \cong {\mathfrak {sl}}_2$
, then the conclusions remain valid without any change.
Proof. We proceed as in Lemma 8.4. In order to describe
![]() $\mathfrak {g}^\natural $
, we use the symplectic (resp. orthogonal) Dynkin pyramid of shape
$\mathfrak {g}^\natural $
, we use the symplectic (resp. orthogonal) Dynkin pyramid of shape
![]() $\boldsymbol {\mu }$
. Indeed, as explained in §9.1, such a pyramid allows to construct an
$\boldsymbol {\mu }$
. Indeed, as explained in §9.1, such a pyramid allows to construct an
![]() ${\mathfrak {sl}}_2$
-triple
${\mathfrak {sl}}_2$
-triple
![]() $(e,h,f)$
with
$(e,h,f)$
with
![]() $f \in {\mathbb {O}}_{\boldsymbol \mu }$
. One easily can compute
$f \in {\mathbb {O}}_{\boldsymbol \mu }$
. One easily can compute
![]() $\mathfrak {g}^0=\mathfrak {g}^{h}$
from the pyramid, and hence,
$\mathfrak {g}^0=\mathfrak {g}^{h}$
from the pyramid, and hence,
![]() $\mathfrak {g}^\natural = \mathfrak {g}^0 \cap \mathfrak {g}^f$
.
$\mathfrak {g}^\natural = \mathfrak {g}^0 \cap \mathfrak {g}^f$
.
Case
![]() $\mathfrak {sp}_n$
. We detail the proof for
$\mathfrak {sp}_n$
. We detail the proof for
![]() $\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{-1}(n)$
. The other cases are dealt with similarly, and the verifications are left to the reader. There are two cases.
$\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{-1}(n)$
. The other cases are dealt with similarly, and the verifications are left to the reader. There are two cases.
(1)
![]() $\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{-1}(n)$
, with q odd, m even, s even. In this case, the orbit
$\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{-1}(n)$
, with q odd, m even, s even. In this case, the orbit
![]() ${\mathbb {O}}_{-1;\boldsymbol \mu }$
is even, and the symplectic Dynkin pyramid associated with the partition
${\mathbb {O}}_{-1;\boldsymbol \mu }$
is even, and the symplectic Dynkin pyramid associated with the partition
![]() $\boldsymbol \mu $
is as in Figure 9 if
$\boldsymbol \mu $
is as in Figure 9 if
![]() $q=5$
,
$q=5$
,
![]() $m=s=2$
. From the pyramid, we obtain that
$m=s=2$
. From the pyramid, we obtain that

To compute
![]() $k_1^{\natural }$
, pick
$k_1^{\natural }$
, pick
![]() $t \in {\mathfrak {g}}^{\natural }$
with
$t \in {\mathfrak {g}}^{\natural }$
with ![]() ,
,
![]() $b=c=0$
and
$b=c=0$
and
![]() $z=0$
in the above description of
$z=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. We obtain that
${\mathfrak {g}}^{\natural }$
. We obtain that
![]() $(t | t)_1^{\natural } = 2$
,
$(t | t)_1^{\natural } = 2$
,
![]() $(t|t)_{\mathfrak {g}} = 2 q$
,
$(t|t)_{\mathfrak {g}} = 2 q$
, ![]() ,
, ![]() . Therefore,
. Therefore, ![]() . To compute
. To compute
![]() $k_2^{\natural }$
, pick
$k_2^{\natural }$
, pick
![]() $t \in {\mathfrak {g}}^{\natural }$
with
$t \in {\mathfrak {g}}^{\natural }$
with ![]() and
and
![]() $x=0$
in the above description of
$x=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. We obtain that
${\mathfrak {g}}^{\natural }$
. We obtain that
![]() $(t | t)_1^{\natural } = 2$
,
$(t | t)_1^{\natural } = 2$
,
![]() $(t|t)_{\mathfrak {g}} = 2$
,
$(t|t)_{\mathfrak {g}} = 2$
, ![]() ,
, ![]() . Therefore,
. Therefore, ![]() .
.
(2)
![]() $\boldsymbol {\mu }=(q^m,1^s)$
, with q even, m odd or even, s even. The orbit
$\boldsymbol {\mu }=(q^m,1^s)$
, with q even, m odd or even, s even. The orbit
![]() ${\mathbb {O}}_{-1;\boldsymbol {\mu }}$
is odd, and we have
${\mathbb {O}}_{-1;\boldsymbol {\mu }}$
is odd, and we have

If
![]() $m=2$
or
$m=2$
or
![]() $m>4$
, we compute
$m>4$
, we compute
![]() $k_1^{\natural }$
by picking
$k_1^{\natural }$
by picking
![]() $t \in {\mathfrak {g}}^{\natural }$
with
$t \in {\mathfrak {g}}^{\natural }$
with ![]() and
and
![]() $y=0$
in the above description of
$y=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. We obtain that
${\mathfrak {g}}^{\natural }$
. We obtain that
![]() $(t | t)_1^{\natural } = 1$
,
$(t | t)_1^{\natural } = 1$
,
![]() $(t|t)_{\mathfrak {g}} = 2 q$
,
$(t|t)_{\mathfrak {g}} = 2 q$
, ![]() ,
,
![]() $\kappa _{\mathfrak {g}^0}(t,t) = 2 m q$
,
$\kappa _{\mathfrak {g}^0}(t,t) = 2 m q$
,
![]() $\kappa _{1/2}(t,t) = 2 s$
. Therefore,
$\kappa _{1/2}(t,t) = 2 s$
. Therefore, ![]() whence the expected result. To compute
whence the expected result. To compute
![]() $k_2^{\natural }$
, pick
$k_2^{\natural }$
, pick
![]() $t \in {\mathfrak {g}}^{\natural }$
with
$t \in {\mathfrak {g}}^{\natural }$
with
![]() $x=0$
and
$x=0$
and ![]() in the above description of
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. We obtain that
${\mathfrak {g}}^{\natural }$
. We obtain that
![]() $(t | t)_2^{\natural } = 2$
,
$(t | t)_2^{\natural } = 2$
,
![]() $(t|t)_{\mathfrak {g}} = 2$
,
$(t|t)_{\mathfrak {g}} = 2$
, ![]() ,
, ![]() ,
,
![]() $\kappa _{1/2}(t,t) = 2 m$
. Therefore,
$\kappa _{1/2}(t,t) = 2 m$
. Therefore, ![]() whence the expected result.
whence the expected result.
Assume
![]() $m=4$
. The isomorphism
$m=4$
. The isomorphism
is obtained through the assignments
with
![]() ${\mathrm {span}}(h_i,e_i,f_i) \cong {\mathfrak {sl}}_2$
. To compute
${\mathrm {span}}(h_i,e_i,f_i) \cong {\mathfrak {sl}}_2$
. To compute
![]() $k_1^{\natural }$
, choose
$k_1^{\natural }$
, choose
![]() $t \in {\mathfrak {g}}^{\natural }$
such that
$t \in {\mathfrak {g}}^{\natural }$
such that
![]() $x= {\mathrm {diag}}(1,1,-1,-1)$
and
$x= {\mathrm {diag}}(1,1,-1,-1)$
and
![]() $y=0$
in the above description of
$y=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. We obtain that
${\mathfrak {g}}^{\natural }$
. We obtain that ![]() . To compute
. To compute
![]() $k_2^{\natural }$
, choose
$k_2^{\natural }$
, choose
![]() $t \in {\mathfrak {g}}^{\natural }$
such that
$t \in {\mathfrak {g}}^{\natural }$
such that
![]() $x= {\mathrm {diag}}(1,-1,1,-1)$
and
$x= {\mathrm {diag}}(1,-1,1,-1)$
and
![]() $y=0$
in the above description of
$y=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. In the same way, we obtain that
${\mathfrak {g}}^{\natural }$
. In the same way, we obtain that ![]() . The computation of
. The computation of
![]() $k_3^{\natural }$
in this case works as in the case
$k_3^{\natural }$
in this case works as in the case
![]() $m>4$
for
$m>4$
for
![]() $k_2^{\natural }$
. This terminates this case following Remark 9.6.
$k_2^{\natural }$
. This terminates this case following Remark 9.6.
Case
![]() ${\mathfrak {so}}_n$
. As for the
${\mathfrak {so}}_n$
. As for the
![]() $\mathfrak {sp}_n$
, we detail the proof only for
$\mathfrak {sp}_n$
, we detail the proof only for
![]() $\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{1}(n)$
. The other cases are dealt with similarly, and the verifications are left to the reader. There are two cases.
$\boldsymbol \mu = (q^m,1^s) \in {\mathscr {P}}_{1}(n)$
. The other cases are dealt with similarly, and the verifications are left to the reader. There are two cases.
(1)
![]() $\boldsymbol {\mu } = (q^m,1^s)$
with q odd.
$\boldsymbol {\mu } = (q^m,1^s)$
with q odd.
(a) Assume first that m is even. Then the orbit
![]() ${\mathbb {O}}_{1;\boldsymbol \mu }$
is even, and from the pyramid, we easily obtain that
${\mathbb {O}}_{1;\boldsymbol \mu }$
is even, and from the pyramid, we easily obtain that


Assume
![]() $m=2$
or
$m=2$
or
![]() $m>4$
. In order to compute
$m>4$
. In order to compute
![]() $k_1^{\natural }$
, pick
$k_1^{\natural }$
, pick
![]() $t \in {\mathfrak {g}}^{\natural }$
with
$t \in {\mathfrak {g}}^{\natural }$
with ![]() and
and
![]() $b=c=0$
,
$b=c=0$
,
![]() $z=0$
in the above description of
$z=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. Then
${\mathfrak {g}}^{\natural }$
. Then
![]() $(t| t)_{1}^\natural = 1$
,
$(t| t)_{1}^\natural = 1$
,
![]() $(t | t )_{\mathfrak {g}} = q$
,
$(t | t )_{\mathfrak {g}} = q$
,
![]() $\kappa _{\mathfrak {g}} (t,t) = 2 q(n-2)$
and
$\kappa _{\mathfrak {g}} (t,t) = 2 q(n-2)$
and
![]() $\kappa _{{\mathfrak {g}}^0} (t,t) = 2m (q-1) + 2(m+s-2)$
. Therefore,
$\kappa _{{\mathfrak {g}}^0} (t,t) = 2m (q-1) + 2(m+s-2)$
. Therefore,
![]() $k_1^{\natural } = qk + q(n-2) -(n-2).$
In order to compute
$k_1^{\natural } = qk + q(n-2) -(n-2).$
In order to compute
![]() $k_2^{\natural }$
, choose
$k_2^{\natural }$
, choose
![]() $t \in {\mathfrak {g}}^{\natural }$
such that
$t \in {\mathfrak {g}}^{\natural }$
such that ![]() and
and
![]() $a=b=c=0$
in the above description of
$a=b=c=0$
in the above description of
![]() ${\mathfrak {g}}^{\natural }$
. Then
${\mathfrak {g}}^{\natural }$
. Then
![]() $(t| t)_{1}^{\natural } = 1$
,
$(t| t)_{1}^{\natural } = 1$
,
![]() $(t | t )_{\mathfrak {g}} = 1$
,
$(t | t )_{\mathfrak {g}} = 1$
,
![]() $\kappa _{\mathfrak {g}} (t,t) = 2(n-2)$
and
$\kappa _{\mathfrak {g}} (t,t) = 2(n-2)$
and
![]() $\kappa _{{\mathfrak {g}}^0} (t,t) = 2(m+s-2)$
. Therefore,
$\kappa _{{\mathfrak {g}}^0} (t,t) = 2(m+s-2)$
. Therefore,
![]() $k_2^{\natural } = k + n-m-s.$
If
$k_2^{\natural } = k + n-m-s.$
If
![]() $m=4$
, using the isomorphism (55) as in the
$m=4$
, using the isomorphism (55) as in the
![]() $\mathfrak {sp}_n$
case, we easily verify that
$\mathfrak {sp}_n$
case, we easily verify that
![]() $k_1^{\natural } = k_2^{\natural } = qk + q(n-2) -(n-2)$
and
$k_1^{\natural } = k_2^{\natural } = qk + q(n-2) -(n-2)$
and
![]() $k_3^{\natural } =k + n-m-s$
. So the same conclusions hold following Remark 9.6.
$k_3^{\natural } =k + n-m-s$
. So the same conclusions hold following Remark 9.6.
(b) Assume now that m is odd. Two cases have to be distinguished.
![]() $\ast $
If s is even, then the orbit
$\ast $
If s is even, then the orbit
![]() ${\mathbb {O}}_{1;\boldsymbol \mu }$
is even and the Dynkin pyramid is as in Figure 15 if
${\mathbb {O}}_{1;\boldsymbol \mu }$
is even and the Dynkin pyramid is as in Figure 15 if
![]() $q=7$
,
$q=7$
,
![]() $m=3$
and
$m=3$
and
![]() $s=2$
.
$s=2$
.

Figure 15 Orthogonal Dynkin Pyramid for
![]() $(7^3,1^4).$
$(7^3,1^4).$
From the pyramid, we obtain that

We compute the
![]() $k_i^{\natural }$
’s as in the case where m is even.
$k_i^{\natural }$
’s as in the case where m is even.
![]() $\ast $
If s is odd, then the orbit
$\ast $
If s is odd, then the orbit
![]() ${\mathbb {O}}_{1;\boldsymbol \mu }$
is even and the Dynkin pyramid is as Figure 16 if
${\mathbb {O}}_{1;\boldsymbol \mu }$
is even and the Dynkin pyramid is as Figure 16 if
![]() $q=7$
,
$q=7$
,
![]() $m=3$
and
$m=3$
and
![]() $s=3$
.
$s=3$
.

Figure 16 Orthogonal Dynkin Pyramid for
![]() $(7^3,1^3).$
$(7^3,1^3).$
From the pyramid, we obtain that

and

The first statement then easily follows. We compute the
![]() $k_i^\natural $
’s as in the case where m is even.
$k_i^\natural $
’s as in the case where m is even.
(2)
![]() $\boldsymbol \mu =(q^m,1^s)$
with q even, m even and
$\boldsymbol \mu =(q^m,1^s)$
with q even, m even and
![]() $s>0$
arbitrary. Here, the orbit
$s>0$
arbitrary. Here, the orbit
![]() ${\mathbb {O}}_{1;\boldsymbol \mu }$
is odd, and we have
${\mathbb {O}}_{1;\boldsymbol \mu }$
is odd, and we have

Let
![]() $\mathfrak {g}_1^\natural $
be the simple component of
$\mathfrak {g}_1^\natural $
be the simple component of
![]() $\mathfrak {g}^\natural $
isomorphic to
$\mathfrak {g}^\natural $
isomorphic to
![]() $\mathfrak {sp}_{m}$
. To compute
$\mathfrak {sp}_{m}$
. To compute
![]() $k_1^\natural $
, pick
$k_1^\natural $
, pick
![]() $t \in \mathfrak {g}^\natural $
with
$t \in \mathfrak {g}^\natural $
with ![]() ,
,
![]() $b=c=0$
,
$b=c=0$
,
![]() $y=0$
in the above description of
$y=0$
in the above description of
![]() $\mathfrak {g}^\natural $
. Then
$\mathfrak {g}^\natural $
. Then
![]() $(t|t)_{\mathfrak {g}^\natural }=2$
,
$(t|t)_{\mathfrak {g}^\natural }=2$
,
![]() $(t|t)_{\mathfrak {g}} = q$
,
$(t|t)_{\mathfrak {g}} = q$
,
![]() $\kappa _{\mathfrak {g}}(t,t)= 2q (n-2)$
,
$\kappa _{\mathfrak {g}}(t,t)= 2q (n-2)$
,
![]() $\kappa _{\mathfrak {g}^{0}}(x,x)= 2 m q$
,
$\kappa _{\mathfrak {g}^{0}}(x,x)= 2 m q$
,
![]() $\kappa _{\mathfrak {g}^{1/2}}(t,t)= 2 s$
. Therefore,
$\kappa _{\mathfrak {g}^{1/2}}(t,t)= 2 s$
. Therefore,
![]() $ 2 k_1^\natural = q k + q (n-2) - n,$
whence the expected result.
$ 2 k_1^\natural = q k + q (n-2) - n,$
whence the expected result.
Assume
![]() $s=3$
or
$s=3$
or
![]() $s>4$
. Let
$s>4$
. Let
![]() $\mathfrak {g}_2^\natural $
be the simple component of
$\mathfrak {g}_2^\natural $
be the simple component of
![]() $\mathfrak {g}^\natural $
isomorphic to
$\mathfrak {g}^\natural $
isomorphic to
![]() ${\mathfrak {so}}_{s}$
. To compute
${\mathfrak {so}}_{s}$
. To compute
![]() $k_2^\natural $
, pick
$k_2^\natural $
, pick ![]() and
and
![]() $x=0$
in the above description of
$x=0$
in the above description of
![]() $\mathfrak {g}^\natural $
. Then
$\mathfrak {g}^\natural $
. Then
![]() $(t|t)_{\mathfrak {g}^\natural }=1$
,
$(t|t)_{\mathfrak {g}^\natural }=1$
,
![]() $(t|t)_{\mathfrak {g}} = 1$
,
$(t|t)_{\mathfrak {g}} = 1$
,
![]() $\kappa _{\mathfrak {g}}(t,t)= 2 (n-2)$
,
$\kappa _{\mathfrak {g}}(t,t)= 2 (n-2)$
,
![]() $\kappa _{\mathfrak {g}^{0}}(x,x)= 2 (s-2)$
,
$\kappa _{\mathfrak {g}^{0}}(x,x)= 2 (s-2)$
,
![]() $\kappa _{\mathfrak {g}^{1/2}}(t,t)= 2 m$
. Therefore,
$\kappa _{\mathfrak {g}^{1/2}}(t,t)= 2 m$
. Therefore,
![]() $ k_2^\natural = k + n-m-s,$
whence the expected result.
$ k_2^\natural = k + n-m-s,$
whence the expected result.
We compute similarly
![]() $k_0^\natural $
for
$k_0^\natural $
for
![]() $s=2$
in which case the
$s=2$
in which case the
![]() $\mathfrak {so}_s$
component is the centre
$\mathfrak {so}_s$
component is the centre
![]() $\mathfrak {g}_0^\natural $
of
$\mathfrak {g}_0^\natural $
of
![]() $\mathfrak {g}^\natural $
. Also, using the isomorphism
$\mathfrak {g}^\natural $
. Also, using the isomorphism
![]() $\mathfrak {so}_4 \cong {\mathfrak {sl}}_2 \times {\mathfrak {sl}}_2$
as in (1),
$\mathfrak {so}_4 \cong {\mathfrak {sl}}_2 \times {\mathfrak {sl}}_2$
as in (1),
![]() $m=4$
case, we easily obtain that
$m=4$
case, we easily obtain that
![]() $ k_2^\natural =k_3^\natural = k + n-m-s.$
$ k_2^\natural =k_3^\natural = k + n-m-s.$
It remains to check the last assertion. We do it for
![]() $\mathfrak {g}=\mathfrak {sp}_m$
and
$\mathfrak {g}=\mathfrak {sp}_m$
and
![]() $\boldsymbol \mu =(q^m,1^s)$
; the other cases can be checked easily as well. In this case,
$\boldsymbol \mu =(q^m,1^s)$
; the other cases can be checked easily as well. In this case,
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_s$
,
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_s$
,
![]() $k_1^\natural =qk + q(\frac {n}{2}+1) - (\frac {n}{2}+1)$
and
$k_1^\natural =qk + q(\frac {n}{2}+1) - (\frac {n}{2}+1)$
and
![]() $k_2^\natural = k + \frac {n}{2}- \frac {m}{2} - \frac {s}{2}$
. Therefore,
$k_2^\natural = k + \frac {n}{2}- \frac {m}{2} - \frac {s}{2}$
. Therefore,
![]() $k_1^\natural = p - (\frac {n}{2}+1)$
, which is a nonnegative integer. In particular, it is admissible for
$k_1^\natural = p - (\frac {n}{2}+1)$
, which is a nonnegative integer. In particular, it is admissible for
![]() $\mathfrak {sp}_m$
. However,
$\mathfrak {sp}_m$
. However,
![]() $k_2^\natural = - (\frac {s}{2}+1) + \frac {p-q \frac {m}{2}}{q}$
, with
$k_2^\natural = - (\frac {s}{2}+1) + \frac {p-q \frac {m}{2}}{q}$
, with
![]() $(p-q \frac {m}{2},q)=1$
and
$(p-q \frac {m}{2},q)=1$
and
![]() $p-q \frac {m}{2} \ge \frac {s}{2}+1$
. So
$p-q \frac {m}{2} \ge \frac {s}{2}+1$
. So
![]() $k_2^\natural $
is admissible for
$k_2^\natural $
is admissible for
![]() $\mathfrak {sp}_s$
.
$\mathfrak {sp}_s$
.
We are now in a position to state our results on collapsing levels for
![]() $\mathfrak {sp}_n$
. First, we consider the case where
$\mathfrak {sp}_n$
. First, we consider the case where
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is lisse – that is,
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse – that is,
![]() $f \in {\mathbb {O}}_k$
.
$f \in {\mathbb {O}}_k$
.
Theorem 9.7. Assume that ![]() is an admissible level for
is an admissible level for
![]() $\mathfrak {g}=\mathfrak {sp}_n$
. Pick a nilpotent element
$\mathfrak {g}=\mathfrak {sp}_n$
. Pick a nilpotent element
![]() $f \in {\mathbb {O}}_k$
so that
$f \in {\mathbb {O}}_k$
so that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is lisse.
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse.
-
1. Assume that k is principal. If
 $p=h_{\mathfrak {sp}_n}^{\vee }=\frac {n}{2}+1$
, then for genericFootnote
6
q, k is collapsing if and only if
$p=h_{\mathfrak {sp}_n}^{\vee }=\frac {n}{2}+1$
, then for genericFootnote
6
q, k is collapsing if and only if
 $n \equiv 0,-1\ \mod q$
. If
$n \equiv 0,-1\ \mod q$
. If
 $n \equiv 0,-1\ \mod q$
, then for generic q, k is collapsing if and only if
$n \equiv 0,-1\ \mod q$
, then for generic q, k is collapsing if and only if
 $p=h_{\mathfrak {sp}_n}^{\vee }$
. Moreover, if
$p=h_{\mathfrak {sp}_n}^{\vee }$
. Moreover, if
 $n \equiv 0,-1\ \mod q$
, then
$n \equiv 0,-1\ \mod q$
, then  $$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n))\cong \mathbb{C}.\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n))\cong \mathbb{C}.\end{align*} $$
-
2. Assume that k is a coprincipal admissible level for
 $\mathfrak {g}=\mathfrak {sp}_n$
. If
$\mathfrak {g}=\mathfrak {sp}_n$
. If
 $p=h_{\mathfrak {sp}_n}+1=n+1$
, then for generic q, k is collapsing if and only if
$p=h_{\mathfrak {sp}_n}+1=n+1$
, then for generic q, k is collapsing if and only if
 $n \equiv 0,1\ \mod \frac {q}{2}$
. If
$n \equiv 0,1\ \mod \frac {q}{2}$
. If
 $n \equiv 0,1\ \mod \frac {q}{2}$
, then for generic q, k is collapsing if and only if
$n \equiv 0,1\ \mod \frac {q}{2}$
, then for generic q, k is collapsing if and only if
 $p=h_{\mathfrak {sp}_n}+1$
Moreover, if
$p=h_{\mathfrak {sp}_n}+1$
Moreover, if
 $n \equiv 0,1\ \mod \frac {q}{2}$
with
$n \equiv 0,1\ \mod \frac {q}{2}$
with
 $\frac {q}{2}$
odd, then and if
$\frac {q}{2}$
odd, then and if $$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n)) \cong \mathbb{C},\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n)) \cong \mathbb{C},\end{align*} $$
 $n \equiv 0,1\ \mod \frac {q}{2}$
with
$n \equiv 0,1\ \mod \frac {q}{2}$
with
 $\frac {q}{2}$
even, then
$\frac {q}{2}$
even, then  $$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n)) \cong L_{1}(\mathfrak{so}_{m}).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong H_{DS,f}^0(L_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n)) \cong L_{1}(\mathfrak{so}_{m}).\end{align*} $$
Note that, in the above statements, the isomorphism
![]() $\mathscr {W}_k(\mathfrak {g},f) \cong H_{DS,f}^0(L_k(\mathfrak {g}))$
holds due to Remark 6.7.
$\mathscr {W}_k(\mathfrak {g},f) \cong H_{DS,f}^0(L_k(\mathfrak {g}))$
holds due to Remark 6.7.
Proof. Let ![]() be the partition corresponding to
be the partition corresponding to
![]() $f \in {\mathbb {O}}_k$
. In the below proof, we always exploit the symplectic Dynkin pyramid of shape
$f \in {\mathbb {O}}_k$
. In the below proof, we always exploit the symplectic Dynkin pyramid of shape ![]() as described in §9.1. Letting
as described in §9.1. Letting ![]() the set of labels, we notice that for
the set of labels, we notice that for
![]() $j \in \frac {1}{2}\mathbb {Z}_{> 0}$
,
$j \in \frac {1}{2}\mathbb {Z}_{> 0}$
,
In this way, the pyramid allows us to compute the central charge and the asymptotic dimension of
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
. Indeed, the central charge of
$H_{DS,f}^0(L_k(\mathfrak {g}))$
. Indeed, the central charge of
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
is given by
$H_{DS,f}^0(L_k(\mathfrak {g}))$
is given by

with
 $$ \begin{align*} |x^0|^2 & = \frac{1}{h_{\mathfrak{g}}^\vee} \sum_{\alpha \in\Delta_+} (x^0 | \alpha)^2, \qquad (\rho|x^0) = \frac{1}{2} \sum_{\alpha \in\Delta_+} (x^0 | \alpha), & \end{align*} $$
$$ \begin{align*} |x^0|^2 & = \frac{1}{h_{\mathfrak{g}}^\vee} \sum_{\alpha \in\Delta_+} (x^0 | \alpha)^2, \qquad (\rho|x^0) = \frac{1}{2} \sum_{\alpha \in\Delta_+} (x^0 | \alpha), & \end{align*} $$
while
![]() $|\rho |^2$
is computed using the strange formula:
$|\rho |^2$
is computed using the strange formula:
However, (56) enables to compute the term  in the asymptotic dimension of
in the asymptotic dimension of
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
in the principal case.
$H_{DS,f}^0(L_k(\mathfrak {g}))$
in the principal case.
For the coprincipal case, note that

and that for
![]() $j \in \frac {1}{2}\mathbb {Z}_{>0}$
,
$j \in \frac {1}{2}\mathbb {Z}_{>0}$
,
 $$ \begin{align} & \# \{\alpha \in \Delta_+^{\mathrm{short}} \colon (x^0|\alpha) = j \}= \# \{ (i,l) \in I \colon 0 < i < |l| , \, |\operatorname{col}(i) - \operatorname{col}(l) |/2 = j \}, \\\nonumber & \# \{\alpha \in \Delta_+^{\mathrm{long}} \colon (x^0|\alpha) = j \}= \# \{ (i,l) \in I \colon i>0, \, l = - i , \, |\operatorname{col}(i) - \operatorname{col}(l) |/2 = j \}. \end{align} $$
$$ \begin{align} & \# \{\alpha \in \Delta_+^{\mathrm{short}} \colon (x^0|\alpha) = j \}= \# \{ (i,l) \in I \colon 0 < i < |l| , \, |\operatorname{col}(i) - \operatorname{col}(l) |/2 = j \}, \\\nonumber & \# \{\alpha \in \Delta_+^{\mathrm{long}} \colon (x^0|\alpha) = j \}= \# \{ (i,l) \in I \colon i>0, \, l = - i , \, |\operatorname{col}(i) - \operatorname{col}(l) |/2 = j \}. \end{align} $$
We now follow the strategy of Section 6.
(1) In this part, q is assumed to be odd. From the description of
![]() ${\mathbb {O}}_k$
, either
${\mathbb {O}}_k$
, either
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m}, \widetilde s)}$
or
${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m}, \widetilde s)}$
or
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m-1},q-1,{\widetilde s}+1)}$
. We consider the two cases separately.
${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m-1},q-1,{\widetilde s}+1)}$
. We consider the two cases separately.
(a) Assume that
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m}, \widetilde s)}$
, with
${\mathbb {O}}_k={\mathbb {O}}_{(q^{\widetilde m}, \widetilde s)}$
, with
![]() $\widetilde m,\widetilde s$
even, and set
$\widetilde m,\widetilde s$
even, and set
![]() $m:=\widetilde m$
,
$m:=\widetilde m$
,
![]() $s:= \widetilde s$
for simplicity. According to Table 3, we have
$s:= \widetilde s$
for simplicity. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
$\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
![]() $k^\natural = p-(\frac {n}{2}+1)$
. Using the symplectic pyramid of shape
$k^\natural = p-(\frac {n}{2}+1)$
. Using the symplectic pyramid of shape
![]() $(q^{m},s)$
, we establish for
$(q^{m},s)$
, we establish for ![]() that
that

The cardinality of roots
![]() $\alpha \in \Delta _+$
such that
$\alpha \in \Delta _+$
such that
![]() $(x^0|\alpha )$
is a half-integer can be computed as follows.
$(x^0|\alpha )$
is a half-integer can be computed as follows.
![]() $\ast $
If
$\ast $
If ![]() , then
, then

![]() $\ast $
If
$\ast $
If
![]() $s-1> \frac {q-1}{2}-\frac {s}{2}+1$
, then
$s-1> \frac {q-1}{2}-\frac {s}{2}+1$
, then

From this, we get an expression of
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))}$
depending on
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))}$
depending on
![]() $q,m,s$
. However,
$q,m,s$
. However,
Fix
![]() $p=h_{\mathfrak {g}}^\vee = \frac {n}{2}+1$
. For generic q, the only solutions of the equation
$p=h_{\mathfrak {g}}^\vee = \frac {n}{2}+1$
. For generic q, the only solutions of the equation
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown s are
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown s are
![]() $s=0$
and
$s=0$
and
![]() $s=q-1$
. Now if we fix
$s=q-1$
. Now if we fix
![]() $s=0$
, for generic q, the only solutions of the equation
$s=0$
, for generic q, the only solutions of the equation
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p are
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p are
Only
![]() $p = \frac {n}{2}+1$
is greater than
$p = \frac {n}{2}+1$
is greater than
![]() $h_{\mathfrak {g}}^\vee $
. If we fix
$h_{\mathfrak {g}}^\vee $
. If we fix
![]() $s=q-1$
, for generic q, the only solution of the equation
$s=q-1$
, for generic q, the only solution of the equation
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
![]() $p = \frac {n}{2}+1$
.
$p = \frac {n}{2}+1$
.
![]() $\ast $
Assume
$\ast $
Assume
![]() $p = \frac {n}{2} + 1$
and
$p = \frac {n}{2} + 1$
and
![]() $s=0$
. In this case,
$s=0$
. In this case,
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
. We aim to apply Proposition 6.6. By Proposition 4.10 and Lemma 7.1 (1), we have
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
. We aim to apply Proposition 6.6. By Proposition 4.10 and Lemma 7.1 (1), we have

with
![]() $n=qm$
and
$n=qm$
and
![]() $|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {m^2}{4}$
since the orbit
$|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {m^2}{4}$
since the orbit ![]() is even. By (56) and the previous computations, we show that
is even. By (56) and the previous computations, we show that

using the identities (42) and (44). Combining (58) and (59), we conclude that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} =1$
, as desired.
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} =1$
, as desired.
![]() $\ast $
Assume
$\ast $
Assume
![]() $p = \frac {n}{2} + 1$
and
$p = \frac {n}{2} + 1$
and
![]() $s=q-1$
. Then
$s=q-1$
. Then
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
. As in the previous case, we aim to apply Proposition 6.6. By Proposition 4.10 and Lemma 7.1 (1), we have
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
. As in the previous case, we aim to apply Proposition 6.6. By Proposition 4.10 and Lemma 7.1 (1), we have

with
![]() $n=qm+q-1$
,
$n=qm+q-1$
,
![]() $|\Delta _+^0| =\frac {(q-1)m(m-1)}{4} +\frac {m^2}{4}$
and
$|\Delta _+^0| =\frac {(q-1)m(m-1)}{4} +\frac {m^2}{4}$
and
![]() $|\Delta ^{1/2}| = (q-1)m$
. Using the identities (42) and (44) and the previous computations, we show that
$|\Delta ^{1/2}| = (q-1)m$
. Using the identities (42) and (44) and the previous computations, we show that

Combining (60) and (61), we conclude that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))}=1$
, as desired.
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))}=1$
, as desired.
(b) Assume now that
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(q^m,q-1,s)}$
, with
${\mathbb {O}}_k={\mathbb {O}}_{(q^m,q-1,s)}$
, with
![]() $m := \widetilde m-1$
,
$m := \widetilde m-1$
,
![]() $s:=\widetilde s+1$
. We argue as in (a). According to Table 3, we have
$s:=\widetilde s+1$
. We argue as in (a). According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m$
, and
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m$
, and
![]() $k_1^\natural = p-(\frac {n}{2}+1)$
. We compute the central charges of
$k_1^\natural = p-(\frac {n}{2}+1)$
. We compute the central charges of
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
and
$H_{DS,f}^0(L_k(\mathfrak {g}))$
and
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
similarly as in (a). Fix
$L_{k^\natural }(\mathfrak {g}^\natural )$
similarly as in (a). Fix
![]() $p=h_{\mathfrak {g}}^\vee = \frac {n}{2}+1$
. Solving the equation
$p=h_{\mathfrak {g}}^\vee = \frac {n}{2}+1$
. Solving the equation
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown s, we get that for generic q, the only solutions are
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown s, we get that for generic q, the only solutions are
![]() $0$
or
$0$
or
![]() $q+1$
, the second one being excluded. Fix
$q+1$
, the second one being excluded. Fix
![]() $s=0$
. Solving the equation
$s=0$
. Solving the equation
![]() $c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p, we get that for generic q, the only solutions are
$c_{H_{DS,f}^0(L_k(\mathfrak {g}))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p, we get that for generic q, the only solutions are
Only
![]() $p = \frac {n}{2}+1$
is greater than
$p = \frac {n}{2}+1$
is greater than
![]() $h_{\mathfrak {g}}^\vee $
. But the case
$h_{\mathfrak {g}}^\vee $
. But the case
![]() $p = \frac {n}{2}+1$
and
$p = \frac {n}{2}+1$
and
![]() $s=0$
has been already dealt with in part (a).
$s=0$
has been already dealt with in part (a).
(2) In this part, q is assumed to be even. It follows from the description of
![]() ${\mathbb {O}}_k$
that either
${\mathbb {O}}_k$
that either
![]() ${\mathbb {O}}_k={\mathbb {O}}_{((\frac {q}{2})^{\widetilde m+1}, \widetilde s+1 )}$
with even
${\mathbb {O}}_k={\mathbb {O}}_{((\frac {q}{2})^{\widetilde m+1}, \widetilde s+1 )}$
with even
![]() $\frac {q}{2}$
, or
$\frac {q}{2}$
, or
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m}, \widetilde s )}$
with odd
${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m}, \widetilde s )}$
with odd
![]() $\frac {q}{2}$
, or
$\frac {q}{2}$
, or
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m -1 },\frac {q}{2}-1, \widetilde s +1)}$
with odd
${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m -1 },\frac {q}{2}-1, \widetilde s +1)}$
with odd
![]() $\frac {q}{2}$
.
$\frac {q}{2}$
.
(a) Assume that
![]() ${\mathbb {O}}_k={\mathbb {O}}_{((\frac {q}{2})^{\widetilde m+1}, \widetilde s+1 )}$
, with
${\mathbb {O}}_k={\mathbb {O}}_{((\frac {q}{2})^{\widetilde m+1}, \widetilde s+1 )}$
, with
![]() $\frac {q}{2}$
even, and set
$\frac {q}{2}$
even, and set
![]() $m:=\widetilde m+1$
,
$m:=\widetilde m+1$
,
![]() $s:=\widetilde s+1$
for simplicity. According to Table 3, we have
$s:=\widetilde s+1$
for simplicity. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {so}_{m}$
, and
$\mathfrak {g}^\natural \cong \mathfrak {so}_{m}$
, and
![]() $k^\natural = p- n$
. The orbit
$k^\natural = p- n$
. The orbit
![]() ${\mathbb {O}}_{k}$
is even. Hence, one can directly use the asymptotic growth. We have
${\mathbb {O}}_{k}$
is even. Hence, one can directly use the asymptotic growth. We have
with
![]() $n=\frac {q m}{2}+ s $
, while
$n=\frac {q m}{2}+ s $
, while

Fixing
![]() $ s =0$
, we find that, for generic q, the only solution of the equation
$ s =0$
, we find that, for generic q, the only solution of the equation
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
![]() $p =n+1$
. Fixing
$p =n+1$
. Fixing
![]() $p = n + 1$
, the only solutions of the equation
$p = n + 1$
, the only solutions of the equation
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
![]() $ s $
are
$ s $
are
![]() $ s =0$
or
$ s =0$
or
![]() $ s =\frac {q}{2}+1$
, the second case being excluded.
$ s =\frac {q}{2}+1$
, the second case being excluded.
From now on, it is assumed that
![]() ${ s }=0$
and
${ s }=0$
and
![]() $p =n+ 1$
. Thus,
$p =n+ 1$
. Thus,
![]() $k^\natural =1$
and
$k^\natural =1$
and
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=\frac m{2}$
. By Corollary 3.9,
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=\frac m{2}$
. By Corollary 3.9,
![]() $\mathbf {A}_{L_1(\mathfrak {sp}_m)} = \dfrac {1}{2}$
, and by Proposition 4.10,
$\mathbf {A}_{L_1(\mathfrak {sp}_m)} = \dfrac {1}{2}$
, and by Proposition 4.10,

with
![]() $|\Delta _+^0| = |\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q \widetilde m(\widetilde m -1)}{8}$
since
$|\Delta _+^0| = |\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q \widetilde m(\widetilde m -1)}{8}$
since
![]() ${\mathbb {O}}_{k}$
is even. Using the symplectic pyramid of shape
${\mathbb {O}}_{k}$
is even. Using the symplectic pyramid of shape
![]() $((\frac {q}{2})^{m})$
, we establish for
$((\frac {q}{2})^{m})$
, we establish for ![]() that
that

From this, we deduce as in previous computations that
whence the statement by Proposition 6.6.
(b) Assume that
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m}, \widetilde s )}$
with
${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{\widetilde m}, \widetilde s )}$
with
![]() $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
![]() $m:=\widetilde m$
even,
$m:=\widetilde m$
even,
![]() $s:= \widetilde s$
even. According to Table 3, we have
$s:= \widetilde s$
even. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
$\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
![]() $k^\natural = \frac {p}{2}- \frac {n+1}{2}$
. Using the symplectic pyramid of shape
$k^\natural = \frac {p}{2}- \frac {n+1}{2}$
. Using the symplectic pyramid of shape
![]() $(\frac {q}{2}+1,(\frac {q}{2})^{m},s)$
, we compute
$(\frac {q}{2}+1,(\frac {q}{2})^{m},s)$
, we compute
![]() $\# \{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha )=j\}$
and
$\# \{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha )=j\}$
and
![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=j\}$
for each j. For
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=j\}$
for each j. For
![]() $s=0$
, we establish that for
$s=0$
, we establish that for ![]()
![]() ,
,
![]() ,
,
![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = 1$
,
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = 1$
,
![]() ,
,
and that for ![]() ,
,
![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j\} =m$
.
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j\} =m$
.
For
![]() $s\not =0$
, we establish that
$s\not =0$
, we establish that

Fixing
![]() $p = n + 1$
, the only solutions of the equation
$p = n + 1$
, the only solutions of the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
![]() $ s $
are
$ s $
are
![]() $ s =0$
and
$ s =0$
and
![]() $ s =\frac {q}{2}-1$
. Fixing
$ s =\frac {q}{2}-1$
. Fixing
![]() $ s =0$
or
$ s =0$
or
![]() $s=\frac {q}{2}-1$
, we find that for generic q the only admissible solution of the equation
$s=\frac {q}{2}-1$
, we find that for generic q the only admissible solution of the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
![]() $p =n+1$
.
$p =n+1$
.
![]() $\ast $
Assume that
$\ast $
Assume that
![]() $p=n+1$
and
$p=n+1$
and
![]() $s =0$
. We have
$s =0$
. We have
![]() $k^\natural =0$
,
$k^\natural =0$
,
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
and
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
and
![]() $\mathbf {A}_{L_1(\mathfrak {sp}_m)} =1$
. Here, we have
$\mathbf {A}_{L_1(\mathfrak {sp}_m)} =1$
. Here, we have ![]() ,
,
![]() $|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q m( m -1)}{8}+\frac {(q-2) }{4}+\frac { m( m -2)}{4}$
,
$|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q m( m -1)}{8}+\frac {(q-2) }{4}+\frac { m( m -2)}{4}$
,
![]() $|\Delta ^{1/2}_+| = m+ m (q-2)$
, and using the above computations, we obtain that
$|\Delta ^{1/2}_+| = m+ m (q-2)$
, and using the above computations, we obtain that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))} =1$
, whence the statement by Proposition 6.6.
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))} =1$
, whence the statement by Proposition 6.6.
![]() $\ast $
Assume that
$\ast $
Assume that
![]() $p=n+1$
and
$p=n+1$
and
![]() $ s =\frac {q}{2}-1$
. We have
$ s =\frac {q}{2}-1$
. We have
![]() $k^\natural =0$
,
$k^\natural =0$
,
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
and
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=0$
and
![]() $\mathbf {A}_{L_1(\mathfrak {sp}_m)} =1$
. Here, we have
$\mathbf {A}_{L_1(\mathfrak {sp}_m)} =1$
. Here, we have ![]() ,
,
![]() $|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q m( m -1)}{8}+\frac { m( m -2)}{4}$
,
$|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| = \frac {q m( m -1)}{8}+\frac { m( m -2)}{4}$
,
![]() $|\Delta ^{1/2}_+| = \frac {q m}{2}$
, and using the above computations, we deduce that
$|\Delta ^{1/2}_+| = \frac {q m}{2}$
, and using the above computations, we deduce that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))} =1$
, whence the statement by Proposition 6.6.
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))} =1$
, whence the statement by Proposition 6.6.
(c) Assume that
![]() ${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1, s )}$
with
${\mathbb {O}}_k={\mathbb {O}}_{(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1, s )}$
with
![]() $\frac {q}{2}$
odd,
$\frac {q}{2}$
odd,
![]() $m:=\widetilde m -1$
even,
$m:=\widetilde m -1$
even,
![]() $s:=\widetilde s +1$
even. According to Table 3, we have
$s:=\widetilde s +1$
even. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
$\mathfrak {g}^\natural \cong \mathfrak {sp}_{m}$
, and
![]() $k^\natural = \frac {p}{2}- \frac {n+1}{2}$
. As in the previous cases, we compute the central charge
$k^\natural = \frac {p}{2}- \frac {n+1}{2}$
. As in the previous cases, we compute the central charge
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}$
using the symplectic pyramid of shape
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}$
using the symplectic pyramid of shape
![]() $(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1, s )$
. We omit here the details. Fixing
$(\frac {q}{2}+1,(\frac {q}{2})^{m},\frac {q}{2}-1, s )$
. We omit here the details. Fixing
![]() $p = n + 1$
, the only solutions of the equation
$p = n + 1$
, the only solutions of the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown
![]() $ s $
are
$ s $
are
![]() $ s =0$
or
$ s =0$
or
![]() $ s =\frac {q}{2}+1$
, the second case being excluded. Fixing
$ s =\frac {q}{2}+1$
, the second case being excluded. Fixing
![]() $ s =0$
, we find that for generic q, the only admissible solution of the equation
$ s =0$
, we find that for generic q, the only admissible solution of the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))}=c_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p is
![]() $p =n+1$
. But the case where
$p =n+1$
. But the case where
![]() $p = n + 1$
and
$p = n + 1$
and
![]() $ s =0$
has been already dealt with in part (2) (b).
$ s =0$
has been already dealt with in part (2) (b).
This terminates the proof of part (2).
Remark 9.8. Since
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $L_1(\mathfrak {so}_m)$
are rational, Theorem 9.7 confirms Conjecture 4.6 for
$L_1(\mathfrak {so}_m)$
are rational, Theorem 9.7 confirms Conjecture 4.6 for
![]() $\mathfrak {g}=\mathfrak {sp}_n$
,
$\mathfrak {g}=\mathfrak {sp}_n$
,
![]() $k+h^{\vee }_{\mathfrak {g}}=h^{\vee }_{\mathfrak {g}}/q$
with
$k+h^{\vee }_{\mathfrak {g}}=h^{\vee }_{\mathfrak {g}}/q$
with
![]() $n\equiv 0,-1\ \pmod {q}$
, q odd, and
$n\equiv 0,-1\ \pmod {q}$
, q odd, and
![]() $k+h^{\vee }_{\mathfrak {g}}=(h^{\vee }_{\mathfrak {g}}+1)/q$
with
$k+h^{\vee }_{\mathfrak {g}}=(h^{\vee }_{\mathfrak {g}}+1)/q$
with
![]() $n\equiv 0,1\ \pmod {q/2}$
, q even.
$n\equiv 0,1\ \pmod {q/2}$
, q even.
Remark 9.9. Although our main goal is to identify collapsing levels (i.e., to prove isomorphisms between certain W-algebras and affine vertex algebras), it is worth remarking that our methods can be used to prove other isomorphisms too, as we now illustrate.
We consider the coprincipal admissible level
![]() $k = -h_{\mathfrak {g}}^\vee + p/q$
, for
$k = -h_{\mathfrak {g}}^\vee + p/q$
, for
![]() $\mathfrak {g} = \mathfrak {sp}_n$
, where q is twice an odd integer and
$\mathfrak {g} = \mathfrak {sp}_n$
, where q is twice an odd integer and
![]() $p=h+1$
. Then
$p=h+1$
. Then ![]() , where
, where ![]() for some
for some
![]() $m, s$
even. Let
$m, s$
even. Let
![]() $f \in {\mathbb {O}}_k$
. In Theorem 9.7 above, we showed that if
$f \in {\mathbb {O}}_k$
. In Theorem 9.7 above, we showed that if
![]() $s=0$
, then
$s=0$
, then
![]() $H_{DS, f}^0(L_{k}(\mathfrak {g}))$
is isomorphic to the trivial vertex algebra
$H_{DS, f}^0(L_{k}(\mathfrak {g}))$
is isomorphic to the trivial vertex algebra
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
If instead
![]() $s=2$
, then the central charge of
$s=2$
, then the central charge of
![]() $H_{DS, f}^0(L_{k}(\mathfrak {g}))$
, which in general is given by the formula
$H_{DS, f}^0(L_{k}(\mathfrak {g}))$
, which in general is given by the formula

and becomes
which is the central charge of the Virasoro minimal model
![]() $\operatorname {Vir}_{2, q/2}$
. The values of
$\operatorname {Vir}_{2, q/2}$
. The values of
![]() $(x_0 | \alpha )$
for
$(x_0 | \alpha )$
for
![]() $\alpha \in \Delta _+$
can be read off from the symplectic pyramid of
$\alpha \in \Delta _+$
can be read off from the symplectic pyramid of ![]() , as was done in the proof of Theorem 9.7, to obtain a formula for the asymptotic dimension
, as was done in the proof of Theorem 9.7, to obtain a formula for the asymptotic dimension
![]() $\mathbf {A}_{H_{DS, f}^0(L_{k}(\mathfrak {g}))}$
. However, the asymptotic dimension of
$\mathbf {A}_{H_{DS, f}^0(L_{k}(\mathfrak {g}))}$
. However, the asymptotic dimension of
![]() $\operatorname {Vir}_{2, q/2}$
is given by formula (6), and the two expressions can be shown to coincide by an elementary, though very tedious, calculation. It follows that
$\operatorname {Vir}_{2, q/2}$
is given by formula (6), and the two expressions can be shown to coincide by an elementary, though very tedious, calculation. It follows that
This gives a yet another evidence for Conjecture 4.4 and Conjecture 4.6.
We now turn to collapsing levels for
![]() $\mathfrak {sp}_n$
in the non lisse cases – that is, we consider the partitions
$\mathfrak {sp}_n$
in the non lisse cases – that is, we consider the partitions
![]() $\boldsymbol \mu \in {\mathscr {P}}_{-1}(n)$
identified in Lemma 9.3 cases (b)–(k). Our study leads us to the following results.
$\boldsymbol \mu \in {\mathscr {P}}_{-1}(n)$
identified in Lemma 9.3 cases (b)–(k). Our study leads us to the following results.
Theorem 9.10. Assume that ![]() is admissible for
is admissible for
![]() $\mathfrak {g}=\mathfrak {sp}_n$
.
$\mathfrak {g}=\mathfrak {sp}_n$
.
-
1. Assume that k is principal – that is, q is odd.
-
(a) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,1^s)$
, with
$(q^m,1^s)$
, with
 $m,s$
even. For generic q, k is collapsing if and only if
$m,s$
even. For generic q, k is collapsing if and only if
 $p=h_{\mathfrak {sp}_n}^{\vee }$
, and
$p=h_{\mathfrak {sp}_n}^{\vee }$
, and  $$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee} + h_{\mathfrak{sp}_s}^{\vee} /q}(\mathfrak{sp}_s).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee} + h_{\mathfrak{sp}_s}^{\vee} /q}(\mathfrak{sp}_s).\end{align*} $$
-
(b) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^{m},q-1,1^{s})$
, with s even. For generic q, k is collapsing only if
$(q^{m},q-1,1^{s})$
, with s even. For generic q, k is collapsing only if
 $p=h_{\mathfrak {sp}_n}^{\vee }$
, and the following inclusion is a finite extension:
$p=h_{\mathfrak {sp}_n}^{\vee }$
, and the following inclusion is a finite extension: 
-
-
2. Assume that k is coprincipal – that is, q is even.
-
(a) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(\frac {q}{2}+1,(\frac {q}{2})^{m},1^s)$
, with
$(\frac {q}{2}+1,(\frac {q}{2})^{m},1^s)$
, with
 $\frac {q}{2}$
odd, m even, s even. If
$\frac {q}{2}$
odd, m even, s even. If
 $p=h_{\mathfrak {sp}_n}+1$
, then k is collapsing if and only if
$p=h_{\mathfrak {sp}_n}+1$
, then k is collapsing if and only if
 $s=0$
or
$s=0$
or
 $s=2$
. If
$s=2$
. If
 $s=2$
, then for generic q, k is collapsing if and only if
$s=2$
, then for generic q, k is collapsing if and only if
 $p=h_{\mathfrak {sp}_n}+1$
. Moreover, if
$p=h_{\mathfrak {sp}_n}+1$
. Moreover, if
 $s=2$
, then
$s=2$
, then  $$ \begin{align*}\qquad \mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee}+h_{\mathfrak{sp}_s}^{\vee}/(q/2)}(\mathfrak{sp}_s).\end{align*} $$
$$ \begin{align*}\qquad \mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee}+h_{\mathfrak{sp}_s}^{\vee}/(q/2)}(\mathfrak{sp}_s).\end{align*} $$
-
(b) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(\frac {q}{2}+1,(\frac {q}{2})^{m}, \frac {q}{2}-1,1^s)$
, with
$(\frac {q}{2}+1,(\frac {q}{2})^{m}, \frac {q}{2}-1,1^s)$
, with
 $\frac {q}{2}$
odd and s even. For generic q, k is collapsing only if
$\frac {q}{2}$
odd and s even. For generic q, k is collapsing only if
 $p=h_{\mathfrak {sp}_n}+1$
, and the following inclusion is a finite extension:
$p=h_{\mathfrak {sp}_n}+1$
, and the following inclusion is a finite extension: 
-
(c) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $((\frac {q}{2})^m,1^s)$
, with
$((\frac {q}{2})^m,1^s)$
, with
 $\frac {q}{2}$
even, m odd or even, and s even. For generic q, k is collapsing only if
$\frac {q}{2}$
even, m odd or even, and s even. For generic q, k is collapsing only if
 $p=h_{\mathfrak {sp}_n}+1$
, and the following inclusion is a finite extension:
$p=h_{\mathfrak {sp}_n}+1$
, and the following inclusion is a finite extension: 
-
Remark 9.11. Similarly to Remark 8.9, notice that (3) and (4) are compatible with (1) for
![]() $s= 0$
, and (5), (6), (7) are compatible with (2) with
$s= 0$
, and (5), (6), (7) are compatible with (2) with
![]() $s= 0$
.
$s= 0$
.
Proof. We argue as in the proof of Theorem 9.7. So we omit some details when the computations are very similar to those considered in Theorem 9.7.
(1) In this part, q is odd.
(a) Fix a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(q^m,1^s)$
. According to Table 3, we have
$(q^m,1^s)$
. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
![]() $k_1^\natural = p-(\frac {n}{2}+1)$
and
$k_1^\natural = p-(\frac {n}{2}+1)$
and
![]() $k_2^\natural = - (\frac {s}{2}+1) + (p-\frac {qm}{2})/q$
. Since f is even,
$k_2^\natural = - (\frac {s}{2}+1) + (p-\frac {qm}{2})/q$
. Since f is even,
![]() $\mathscr {W}_k(\mathfrak {g},f) \cong H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
, and Proposition 6.6 gives a necessary and sufficient condition for that k is collapsing.
$\mathscr {W}_k(\mathfrak {g},f) \cong H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
, and Proposition 6.6 gives a necessary and sufficient condition for that k is collapsing.
By Proposition 4.10, we have
with
![]() $n=qm+s$
, while by Corollary 3.9,
$n=qm+s$
, while by Corollary 3.9,

By solving the equation
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p, we obtain that, for generic q, the only solutions which are nonnegative integers are
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
with unknown p, we obtain that, for generic q, the only solutions which are nonnegative integers are
Only the solution
![]() $p = \frac {n}{2} + 1$
is greater than
$p = \frac {n}{2} + 1$
is greater than
![]() $h_{\mathfrak {g}}^\vee $
. From now on, it is assumed that
$h_{\mathfrak {g}}^\vee $
. From now on, it is assumed that
![]() $p = \frac {n}{2} + 1$
. Then
$p = \frac {n}{2} + 1$
. Then
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $k_2^\natural = -(\frac {s}{2}+1) + (\frac {s}{2}+1)/q$
. We now apply Proposition 6.6 to prove that k is collapsing. By Corollary 3.9 and Lemma 7.1 (1), we have
$k_2^\natural = -(\frac {s}{2}+1) + (\frac {s}{2}+1)/q$
. We now apply Proposition 6.6 to prove that k is collapsing. By Corollary 3.9 and Lemma 7.1 (1), we have
 $$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (\frac{s}{2}+1)/q}(\mathfrak{sp}_s)} & = \dfrac{1}{q^{s^2/4} q^{s/4}} .& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (\frac{s}{2}+1)/q}(\mathfrak{sp}_s)} & = \dfrac{1}{q^{s^2/4} q^{s/4}} .& \end{align*} $$
However, by Proposition 4.10 and Lemma 7.1 (1), we have

with
![]() $n=qm+s$
and
$n=qm+s$
and
![]() $|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {(m+s)^2}{4}$
, since the orbit
$|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {(m+s)^2}{4}$
, since the orbit
![]() $G.f$
is even. Using the pyramid associated with the partition
$G.f$
is even. Using the pyramid associated with the partition
![]() $(q^m,1^s)$
, we establish that for
$(q^m,1^s)$
, we establish that for ![]() ,
,
![]()
![]()
![]() $\# \{\alpha \in \Delta _+ \colon (x^0|\alpha )=q-2j\} = j m^2 ,$
$\# \{\alpha \in \Delta _+ \colon (x^0|\alpha )=q-2j\} = j m^2 ,$
![]() $\# \{\alpha \in \Delta _+ \colon (x^0|\alpha )=q- 2j+1\} = (j-1) m^2+ \frac {m(m+1)}{2} ,$
$\# \{\alpha \in \Delta _+ \colon (x^0|\alpha )=q- 2j+1\} = (j-1) m^2+ \frac {m(m+1)}{2} ,$
We deduce that

by (42) and (44). Combining (62) and (63), we conclude that
as desired.
(b) Fix a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(q^m,q-1,1^s)$
. According to Table 3, we have
$(q^m,q-1,1^s)$
. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
![]() $k_1^\natural = p-(\frac {n}{2}+1)$
and
$k_1^\natural = p-(\frac {n}{2}+1)$
and
![]() $k_2^\natural = - (\frac {s}{2}+1) + \frac {2p-mq-q}{2q}$
, with
$k_2^\natural = - (\frac {s}{2}+1) + \frac {2p-mq-q}{2q}$
, with
![]() $ (2p-mq-q,2q)=1$
. Using the pyramid of shape
$ (2p-mq-q,2q)=1$
. Using the pyramid of shape
![]() $(q^m,q-1,1^s)$
, we establish that for
$(q^m,q-1,1^s)$
, we establish that for ![]() ,
,
![]() ,
,
![]() ,
,
 ,
,

As explained in the proof of Theorem 9.7, the above cardinalities allow us to compute the central charge of
![]() $H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
. By solving the equation
$H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
. By solving the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that for generic q, the only admissible solution is
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that for generic q, the only admissible solution is
![]() $p = \dfrac {n}{2}+1.$
Assume that
$p = \dfrac {n}{2}+1.$
Assume that
![]() $p = \frac {n}{2} + 1$
. Then
$p = \frac {n}{2} + 1$
. Then
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{2q}$
, which is coprincipal admissible for
$k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{2q}$
, which is coprincipal admissible for
![]() $\mathfrak {sp}_s$
. We easily verify that
$\mathfrak {sp}_s$
. We easily verify that
![]() $\mathbf {g}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)}.$
By Corollary 3.9 and Lemma 7.1 (4), we have
$\mathbf {g}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)}.$
By Corollary 3.9 and Lemma 7.1 (4), we have
 $$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (s+1)/(2q)}(\mathfrak{sp}_s)} & = \dfrac{1}{2^{\frac{s}{2}+1} q^{\frac{s}{4}(s+1) }} .& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (s+1)/(2q)}(\mathfrak{sp}_s)} & = \dfrac{1}{2^{\frac{s}{2}+1} q^{\frac{s}{4}(s+1) }} .& \end{align*} $$
However, by Proposition 4.10 and Lemma 7.1 (1),

with
![]() $n=qm+q-1+s$
,
$n=qm+q-1+s$
,
![]() $|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {(m+s)^2}{4}$
and
$|\Delta _+^0| = \frac {(q-1)m(m-1)}{4}+\frac {(m+s)^2}{4}$
and
![]() $|\Delta ^{1/2}|=(q-1)m+s$
. From the above computations, we get that
$|\Delta ^{1/2}|=(q-1)m+s$
. From the above computations, we get that
Since
![]() $\mathbf {g}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)},$
it follows from Theorem 3.10
$\mathbf {g}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n))} = \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)},$
it follows from Theorem 3.10
![]() $\mathscr {W}_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n,f)$
a direct sum of admissible representations of
$\mathscr {W}_{ -(\frac {n}{2}+1) + (\frac {n}{2}+1)/q}(\mathfrak {sp}_n,f)$
a direct sum of admissible representations of
![]() $L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)$
.
$L_{-(\frac {s}{2}+1) + \frac {s+1}{2q}}(\mathfrak {sp}_s)$
.
(2) In this part, q is even.
(a) Pick a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(\frac {q}{2}+1,(\frac {q}{2})^{m}, 1^s)$
, with odd
$(\frac {q}{2}+1,(\frac {q}{2})^{m}, 1^s)$
, with odd
![]() $\frac {q}{2}$
. According to Table 3, we have
$\frac {q}{2}$
. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
![]() $k_1^\natural = \frac {p}{2} - \frac {n+1}{2}$
and
$k_1^\natural = \frac {p}{2} - \frac {n+1}{2}$
and
![]() $k_2^\natural = - (\frac {s}{2}+1) + \frac {2p-mq -q}{2q}$
.
$k_2^\natural = - (\frac {s}{2}+1) + \frac {2p-mq -q}{2q}$
.
Using the pyramid of shape
![]() $(\frac {q}{2}+1,(\frac {q}{2})^{m}, 1^s)$
, we establish that for
$(\frac {q}{2}+1,(\frac {q}{2})^{m}, 1^s)$
, we establish that for ![]() ,
,

that for ![]() ,
,

and that for ![]() ,
,

The above cardinalities allows us to compute the central charge of
![]() $H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
.
$H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))$
.
By solving the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only admissible solution is
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only admissible solution is
![]() $p = n+1$
. Fixing
$p = n+1$
. Fixing
![]() $p=n+1$
, we obtain that the only nonnegative integer solutions the equation
$p=n+1$
, we obtain that the only nonnegative integer solutions the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown s are
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown s are
![]() $s=0$
and
$s=0$
and
![]() $s=2$
. The case where
$s=2$
. The case where
![]() $p=n+1$
and
$p=n+1$
and
![]() $s=0$
has been already dealt with in the proof of Theorem 9.7. We now assume that
$s=0$
has been already dealt with in the proof of Theorem 9.7. We now assume that
![]() $p =n+ 1$
and
$p =n+ 1$
and
![]() $s=2$
. Then
$s=2$
. Then
![]() $k_1^\natural $
,
$k_1^\natural $
,
![]() $k_2^\natural =(\frac {s}{2}+1)/(q/2)$
, and we easily verify that
$k_2^\natural =(\frac {s}{2}+1)/(q/2)$
, and we easily verify that
![]() $\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
. Let us compare the asymptotic dimensions. We obtain here that
$\mathbf {g}_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =\mathbf {g}_{L_{k^\natural }(\mathfrak {g}^\natural )}$
. Let us compare the asymptotic dimensions. We obtain here that
 $$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (s/2+1)/(q/2)}(\mathfrak{sp}_s)} & = \dfrac{1}{(q/2)^{\frac{s^2}{4}+\frac{s}{3}}}& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + (s/2+1)/(q/2)}(\mathfrak{sp}_s)} & = \dfrac{1}{(q/2)^{\frac{s^2}{4}+\frac{s}{3}}}& \end{align*} $$
and that

with
![]() $n=qm/2+q/2+3$
,
$n=qm/2+q/2+3$
,
![]() $|\Delta _+^0| = \frac {(q-2)m(m-1)}{4}+\frac {(m+2)^2}{4}$
,
$|\Delta _+^0| = \frac {(q-2)m(m-1)}{4}+\frac {(m+2)^2}{4}$
,
![]() $|\Delta ^{\mathrm {short}} \cap \Delta _+^0|=|\Delta _+^0|-\frac {m+2}{2}$
and
$|\Delta ^{\mathrm {short}} \cap \Delta _+^0|=|\Delta _+^0|-\frac {m+2}{2}$
and
![]() $|\Delta ^{1/2}|=qm/2+2$
. From the above computations, we can compute the last factor in
$|\Delta ^{1/2}|=qm/2+2$
. From the above computations, we can compute the last factor in
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))}$
, and we get that
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))}$
, and we get that
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))}$
equals
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + (n+1)/q}(\mathfrak {sp}_n))}$
equals
![]() $\mathbf {A}_{L_{ -(\frac {s}{2}+1) + (s/2+1)/(q/2)}(\mathfrak {sp}_s)}$
, whence the expected result.
$\mathbf {A}_{L_{ -(\frac {s}{2}+1) + (s/2+1)/(q/2)}(\mathfrak {sp}_s)}$
, whence the expected result.
(b) Pick a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $(\frac {q}{2}+1,(\frac {q}{2})^m,\frac {q}{2}-1,1^s)$
, with odd
$(\frac {q}{2}+1,(\frac {q}{2})^m,\frac {q}{2}-1,1^s)$
, with odd
![]() $\frac {q}{2}$
. According to Table 3, we have
$\frac {q}{2}$
. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
$\mathfrak {g}^\natural \cong \mathfrak {sp}_m \times \mathfrak {sp}_{s} $
,
![]() $k_1^\natural = \frac {p}{2}- \frac {n+1}{2}$
and
$k_1^\natural = \frac {p}{2}- \frac {n+1}{2}$
and
![]() $k_2^\natural = - (\frac {s}{2}+1) + \frac {p-\frac {qm}{2}-q}{q}$
. Using the pyramid of shape
$k_2^\natural = - (\frac {s}{2}+1) + \frac {p-\frac {qm}{2}-q}{q}$
. Using the pyramid of shape
![]() $(\frac {q}{2}+1,(\frac {q}{2})^m,\frac {q}{2}-1,1^s)$
we establish that for
$(\frac {q}{2}+1,(\frac {q}{2})^m,\frac {q}{2}-1,1^s)$
we establish that for ![]() ,
,
 and that for
and that for ![]() ,
,
![]()

![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = 2,$
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = 2,$
![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=q/2\} = 1,$
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=q/2\} = 1,$
![]()

![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j\} = m,$
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j\} = m,$
By solving the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only solution is
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only solution is
![]() $p = n+1$
. From now on, we assume that
$p = n+1$
. From now on, we assume that
![]() $p=n+1$
. Then
$p=n+1$
. Then
![]() $k_1^\natural =0$
and
$k_1^\natural =0$
and
![]() $k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{q}$
, and we have
$k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{q}$
, and we have
![]() $\mathbf {g}_{\mathscr {W}_{-(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n,f) }= \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{q}}(\mathfrak {sp}_s) }$
.. Moreover,
$\mathbf {g}_{\mathscr {W}_{-(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n,f) }= \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{q}}(\mathfrak {sp}_s) }$
.. Moreover,
 $$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + \frac{s+1}{q}}(\mathfrak{sp}_s)} & = \frac{2^{\frac{s}{2}(\frac{s}{2}-1)}}{q^{\frac{s^2}{4}}(q/2)^{\frac{s}{4}}\sqrt{4}},& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{ -(\frac{s}{2}+1) + \frac{s+1}{q}}(\mathfrak{sp}_s)} & = \frac{2^{\frac{s}{2}(\frac{s}{2}-1)}}{q^{\frac{s^2}{4}}(q/2)^{\frac{s}{4}}\sqrt{4}},& \end{align*} $$
and, as in the previous case, we compute
![]() $\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n))}$
. Here, we get that
$\mathbf {A}_{H_{DS,f}^0(L_{ -(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n))}$
. Here, we get that
and we conclude as in (1) (b).
(c) Fix a nilpotent element
![]() $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
![]() $((\frac {q}{2})^m,1^s)$
, with even
$((\frac {q}{2})^m,1^s)$
, with even
![]() $\frac {q}{2}$
. According to Table 3, we have
$\frac {q}{2}$
. According to Table 3, we have
![]() $\mathfrak {g}^\natural \cong \mathfrak {so}_m \times \mathfrak {sp}_{s} $
,
$\mathfrak {g}^\natural \cong \mathfrak {so}_m \times \mathfrak {sp}_{s} $
,
![]() $k_1^\natural = p-n $
and
$k_1^\natural = p-n $
and
![]() $k_2^\natural = - (\frac {s}{2}+1) + (p-\frac {qm}{2})/q$
. Using the pyramid associated with the partition
$k_2^\natural = - (\frac {s}{2}+1) + (p-\frac {qm}{2})/q$
. Using the pyramid associated with the partition
![]() $((\frac {q}{2})^m,1^s)$
, we establish that for
$((\frac {q}{2})^m,1^s)$
, we establish that for ![]() ,
,
![]() $\# \{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha )=(2j-1)/2\} = ms,$
$\# \{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha )=(2j-1)/2\} = ms,$
![]()
![]() $\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = m,$
and that for
$\# \{\alpha \in \Delta _+^{\mathrm {long}} \colon (x^0|\alpha )=2j-1\} = m,$
and that for ![]() ,
,
![]()
By solving the equation
![]() $c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only solutions are
$c_{H_{DS,f}^0(L_{k}(\mathfrak {sp}_n))} =c_{L_{k^\natural }(\mathfrak {g}^\natural )} $
with unknown p, we obtain that, for generic q, the only solutions are
Only the solution
![]() $p = n + 1$
leads to an admissible level. From now on, it is assumed that
$p = n + 1$
leads to an admissible level. From now on, it is assumed that
![]() $p = n+ 1$
. Then
$p = n+ 1$
. Then
![]() $k_1^\natural =1$
and
$k_1^\natural =1$
and
![]() $k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{q}$
, and we have
$k_2^\natural = -(\frac {s}{2}+1) + \frac {s+1}{q}$
, and we have
![]() $\mathbf {g}_{\mathscr {W}_{-(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n,f) }= \mathbf {g}_{L_{1}(\mathfrak {so}_m) }+ \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{q}}(\mathfrak {sp}_s) } =\frac {m}{2}+\frac {s (2 + q - 2 s + q s)}{2 q}$
.
$\mathbf {g}_{\mathscr {W}_{-(\frac {n}{2}+1) + \frac {n+1}{q}}(\mathfrak {sp}_n,f) }= \mathbf {g}_{L_{1}(\mathfrak {so}_m) }+ \mathbf {g}_{L_{-(\frac {s}{2}+1) + \frac {s+1}{q}}(\mathfrak {sp}_s) } =\frac {m}{2}+\frac {s (2 + q - 2 s + q s)}{2 q}$
.
By Corollary 3.9 and Lemma 7.1 (1),
 $$ \begin{align*} \mathbf{A}_{L_{1}(\mathfrak{so}_m) \otimes L_{ -(\frac{s}{2}+1) + \frac{s+1}{2}}(\mathfrak{sp}_s)} & = \frac{1}{2}\times \frac{2^{\frac{s}{4}(s-1)-1}}{q^{\frac{s}{4}(s+1)}}.& \end{align*} $$
$$ \begin{align*} \mathbf{A}_{L_{1}(\mathfrak{so}_m) \otimes L_{ -(\frac{s}{2}+1) + \frac{s+1}{2}}(\mathfrak{sp}_s)} & = \frac{1}{2}\times \frac{2^{\frac{s}{4}(s-1)-1}}{q^{\frac{s}{4}(s+1)}}.& \end{align*} $$
However, by Proposition 4.10 and Lemma 7.1 (1),

with
![]() $n=qm+s$
,
$n=qm+s$
,
![]() $|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| =\frac {m(m-1)q}{8}+\frac {s(s-2)}{4} $
,
$|\Delta _+^{\mathrm {short}} \cap \Delta _+^0| =\frac {m(m-1)q}{8}+\frac {s(s-2)}{4} $
, ![]() and
and
![]() $|\Delta _+^{1/2}|=ms$
. Using the above computations, we get that
$|\Delta _+^{1/2}|=ms$
. Using the above computations, we get that
and we conclude as in (1) (b).
One can specify the decomposition of the finite extension (1) (b) in Theorem 9.10 assuming that Conjecture 4.4 holds; that is,
(The same arguments work for the the finite extensions in (2) (b) and (c).) Keep the notations of the proof. Denoting by ![]() the highest irreducible representation of
the highest irreducible representation of
![]() $L_{k_2^\natural }(\mathfrak {sp}_s)$
of admissible weight
$L_{k_2^\natural }(\mathfrak {sp}_s)$
of admissible weight ![]() , we get that
, we get that

where ![]() is the lowest
is the lowest
![]() $L_0$
-eigenvalue of
$L_0$
-eigenvalue of ![]() . Moreover, the sum is finite.
. Moreover, the sum is finite.
We have
![]() $p_2- h_{\mathfrak {sp}_s} = (s+1)-s=1$
, where
$p_2- h_{\mathfrak {sp}_s} = (s+1)-s=1$
, where
![]() $k_2^\natural +h_{\mathfrak {sp}_s}^\vee =p_2/q_2$
. Recall that
$k_2^\natural +h_{\mathfrak {sp}_s}^\vee =p_2/q_2$
. Recall that

For generic q, we observe that ![]() is the only fundamental weight for which
is the only fundamental weight for which ![]() . However, we easily verify using Proposition 4.10 that
. However, we easily verify using Proposition 4.10 that
That is,
As a result,
But
![]() $m_0$
must be at most
$m_0$
must be at most
![]() $1$
. So, if
$1$
. So, if
we get
Arguing as above, we conjecture explicit decompositions for the other finite extensions:
Conjecture 9.12. For generic q, we have the following finite extensions:
 $$ \begin{align*} &\hspace{1cm} \mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/(2q)}(\mathfrak{sp}_s) \oplus L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/(2q)}(\mathfrak{sp}_s; \varpi_1).\\ &\hspace{1cm} \mathscr{W}_{-h_{\mathfrak{sp}_n}^\vee + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^\vee+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_s) \oplus L_{-h_{\mathfrak{sp}_s}^\vee+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_s; \varpi_1).\\ & \hspace{1cm} \mathscr{W}_{- h_{\mathfrak{sp}_n}^{\vee}+ (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \\ & \hspace{1cm} \quad \cong L_1({\mathfrak{so}}_m) \otimes (L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_{s})) \oplus (L_1({\mathfrak{so}}_m;\varpi_1) \otimes (L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_{s};\varpi_1)) ). \end{align*} $$
$$ \begin{align*} &\hspace{1cm} \mathscr{W}_{-h_{\mathfrak{sp}_n}^{\vee} + h_{\mathfrak{sp}_n}^{\vee}/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/(2q)}(\mathfrak{sp}_s) \oplus L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/(2q)}(\mathfrak{sp}_s; \varpi_1).\\ &\hspace{1cm} \mathscr{W}_{-h_{\mathfrak{sp}_n}^\vee + (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \cong L_{-h_{\mathfrak{sp}_s}^\vee+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_s) \oplus L_{-h_{\mathfrak{sp}_s}^\vee+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_s; \varpi_1).\\ & \hspace{1cm} \mathscr{W}_{- h_{\mathfrak{sp}_n}^{\vee}+ (h_{\mathfrak{sp}_n}+1)/q}(\mathfrak{sp}_n,f) \\ & \hspace{1cm} \quad \cong L_1({\mathfrak{so}}_m) \otimes (L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_{s})) \oplus (L_1({\mathfrak{so}}_m;\varpi_1) \otimes (L_{-h_{\mathfrak{sp}_s}^{\vee}+(h_{\mathfrak{sp}_s}+1)/q}(\mathfrak{sp}_{s};\varpi_1)) ). \end{align*} $$
Remark 9.13. As it has been observed in the proof of Theorem 9.7 (1), if k is collapsing for
![]() $f \in {\mathbb {O}}_{(q^{m},1^s)}$
, then necessarily
$f \in {\mathbb {O}}_{(q^{m},1^s)}$
, then necessarily
![]() $p=\frac {n}{2}+1$
or
$p=\frac {n}{2}+1$
or
![]() $p=\frac {n+1}{2}$
. Only the first case verifies that
$p=\frac {n+1}{2}$
. Only the first case verifies that
![]() $p \ge h_{\mathfrak {g}}^\vee $
. However, one may wonder whether the following holds:
$p \ge h_{\mathfrak {g}}^\vee $
. However, one may wonder whether the following holds:
(The two above vertex algebras have the same central charge.)
We now state our main results on collapsing levels for
![]() ${\mathfrak {so}}_n$
. Here, also we start with the lisse case – that is,
${\mathfrak {so}}_n$
. Here, also we start with the lisse case – that is,
![]() $f \in {\mathbb {O}}_k$
.
$f \in {\mathbb {O}}_k$
.
Theorem 9.14. Assume that
![]() $k = -h_{\mathfrak {g}}^\vee +p/q=-(n-2)+p/q$
is admissible for
$k = -h_{\mathfrak {g}}^\vee +p/q=-(n-2)+p/q$
is admissible for
![]() $\mathfrak {g}=\mathfrak {so}_n$
. Pick a nilpotent element
$\mathfrak {g}=\mathfrak {so}_n$
. Pick a nilpotent element
![]() $f \in {\mathbb {O}}_k$
so that
$f \in {\mathbb {O}}_k$
so that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is lisse.
$\mathscr {W}_k(\mathfrak {g},f)$
is lisse.
-
1. Assume that q is odd. If
 $p=h_{{\mathfrak {so}}_n}^\vee =n-2$
, then for generic q, k is collapsing if and only if
$p=h_{{\mathfrak {so}}_n}^\vee =n-2$
, then for generic q, k is collapsing if and only if
 $n \equiv 0,1\ \mod q$
. If
$n \equiv 0,1\ \mod q$
. If
 $n \equiv 0,1\ \mod q$
, then for generic q, k is collapsing if and only if
$n \equiv 0,1\ \mod q$
, then for generic q, k is collapsing if and only if
 $p=h_{{\mathfrak {so}}_n}^\vee $
. Moreover, if
$p=h_{{\mathfrak {so}}_n}^\vee $
. Moreover, if
 $n \equiv 0,1\ \mod q$
, then
$n \equiv 0,1\ \mod q$
, then  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+h_{{\mathfrak{so}}_n}^\vee/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g})) \cong \mathbb{C}.\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+h_{{\mathfrak{so}}_n}^\vee/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g})) \cong \mathbb{C}.\end{align*} $$
-
2. Assume that n and q are even. If
 $p=h_{{\mathfrak {so}}_n}+1=n-1$
, then for generic q, k is collapsing if and only if
$p=h_{{\mathfrak {so}}_n}+1=n-1$
, then for generic q, k is collapsing if and only if
 $n \equiv 0,2\ \mod q$
. If
$n \equiv 0,2\ \mod q$
. If
 $n \equiv 0,2\ \mod q$
, then for generic q, k is collapsing if and only if
$n \equiv 0,2\ \mod q$
, then for generic q, k is collapsing if and only if
 $p=h_{{\mathfrak {so}}_n}+1$
. Moreover, if
$p=h_{{\mathfrak {so}}_n}+1$
. Moreover, if
 $n \equiv 0,2\ \mod q$
, then
$n \equiv 0,2\ \mod q$
, then  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g}))\cong \mathbb{C}.\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g}))\cong \mathbb{C}.\end{align*} $$
-
3. Assume that n is odd and that q is even. If
 $p=h_{{\mathfrak {so}}_n}+1=n$
, then for generic q, k is collapsing if and only if
$p=h_{{\mathfrak {so}}_n}+1=n$
, then for generic q, k is collapsing if and only if
 $n \equiv -1,1\ \mod q$
. If
$n \equiv -1,1\ \mod q$
. If
 $n \equiv -1,1\ \mod q$
, then for generic q, k is collapsing if and only if
$n \equiv -1,1\ \mod q$
, then for generic q, k is collapsing if and only if
 $p=h_{{\mathfrak {so}}_n}+1$
. Moreover, if
$p=h_{{\mathfrak {so}}_n}+1$
. Moreover, if
 $n \equiv -1,1\ \mod q$
, then
$n \equiv -1,1\ \mod q$
, then  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g})) \cong \mathbb{C}.\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}({\mathfrak{so}}_n,f) \cong H_{DS,f}^0(L_k(\mathfrak{g})) \cong \mathbb{C}.\end{align*} $$
Proof. We argue as in the proof of Theorem 9.7. We exploit here the orthogonal Dynkin pyramid of shape ![]() corresponding to
corresponding to
![]() $f \in {\mathbb {O}}_k$
. Here, we set
$f \in {\mathbb {O}}_k$
. Here, we set ![]() if n is even, and
if n is even, and ![]() if n is odd. Moreover, for
if n is odd. Moreover, for
![]() $j \in \frac {1}{2}\mathbb {Z}_{> 0}$
,
$j \in \frac {1}{2}\mathbb {Z}_{> 0}$
,

and
with
![]() $\{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha ) = j \}=\varnothing $
if n is even. From this, we compute the central charge and the asymptotic dimension of
$\{\alpha \in \Delta _+^{\mathrm {short}} \colon (x^0|\alpha ) = j \}=\varnothing $
if n is even. From this, we compute the central charge and the asymptotic dimension of
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
using the pyramid exactly as in the case where
$H_{DS,f}^0(L_k(\mathfrak {g}))$
using the pyramid exactly as in the case where
![]() $\mathfrak {g}=\mathfrak {sp}_n$
. Since the proof is very similar to that of Theorem 9.7, we omit the details.
$\mathfrak {g}=\mathfrak {sp}_n$
. Since the proof is very similar to that of Theorem 9.7, we omit the details.
Remark 9.15. As in Remark 9.9, we now comment on a few isomorphisms between W-algebras obtained with similar methods as in the proof of Theorem 9.14 above.
Let
![]() $q>3$
be even and not divisible by
$q>3$
be even and not divisible by
![]() $3$
, let n be odd, and
$3$
, let n be odd, and
![]() $k = -h_{\mathfrak {g}}^\vee + p/q$
a coprincipal admissible level for
$k = -h_{\mathfrak {g}}^\vee + p/q$
a coprincipal admissible level for
![]() $\mathfrak {g} = \mathfrak {so}_n$
, where
$\mathfrak {g} = \mathfrak {so}_n$
, where
![]() $p=h_{\mathfrak {g}}+1$
. Then
$p=h_{\mathfrak {g}}+1$
. Then ![]() , where
, where ![]() . If we choose n so that
. If we choose n so that
![]() $s = 3$
and take
$s = 3$
and take
![]() $f \in {\mathbb {O}}_k$
, then we obtain an isomorphism
$f \in {\mathbb {O}}_k$
, then we obtain an isomorphism
proved by comparison of asymptotic growth and asymptotic dimension.
If q and m are odd so that
![]() $n = mq + 3$
is even, and
$n = mq + 3$
is even, and
![]() $k = -h_{\mathfrak {g}}^\vee + p/q$
is the principal admissible level for
$k = -h_{\mathfrak {g}}^\vee + p/q$
is the principal admissible level for
![]() $\mathfrak {g} = \mathfrak {so}_n$
where
$\mathfrak {g} = \mathfrak {so}_n$
where
![]() $p=h_{\mathfrak {g}}^\vee $
, then
$p=h_{\mathfrak {g}}^\vee $
, then ![]() , where
, where ![]() . If we choose
. If we choose
![]() $f \in {\mathbb {O}}_k$
, then we obtain an isomorphism
$f \in {\mathbb {O}}_k$
, then we obtain an isomorphism
again proved by comparison of asymptotic growth and asymptotic dimension.
Theorem 9.16. Assume that
![]() $k = -h_{\mathfrak {g}}^\vee +p/q=-(n-2)+p/q$
is admissible for
$k = -h_{\mathfrak {g}}^\vee +p/q=-(n-2)+p/q$
is admissible for
![]() $\mathfrak {g}=\mathfrak {so}_n$
.
$\mathfrak {g}=\mathfrak {so}_n$
.
-
1. Assume that q is odd so that k is principal.
-
(a) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,1^s)$
with
$(q^m,1^s)$
with
 $s\ge 3$
. For generic q, k is collapsing only if
$s\ge 3$
. For generic q, k is collapsing only if
 $p=h_{{\mathfrak {so}}_n}^\vee $
or
$p=h_{{\mathfrak {so}}_n}^\vee $
or
 $p=h_{{\mathfrak {so}}_n}^\vee +1$
. Moreover, and (for
$p=h_{{\mathfrak {so}}_n}^\vee +1$
. Moreover, and (for $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +h_{{\mathfrak{so}}_n}^\vee/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +h_{{\mathfrak{so}}_s}^\vee/q}(\mathfrak{so}_s), \end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +h_{{\mathfrak{so}}_n}^\vee/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +h_{{\mathfrak{so}}_s}^\vee/q}(\mathfrak{so}_s), \end{align*} $$
 $m \ge 3$
) we have the following inclusion is a finite extension:
$m \ge 3$
) we have the following inclusion is a finite extension: 
-
(b) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,(q-1)^2)$
. For generic q, k is collapsing if and only if
$(q^m,(q-1)^2)$
. For generic q, k is collapsing if and only if
 $p=h_{{\mathfrak {so}}_n}^\vee $
and
$p=h_{{\mathfrak {so}}_n}^\vee $
and  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +h_{{\mathfrak{so}}_n}^\vee/q}(\mathfrak{so}_{n},f) \cong L_{-2 +2/q}({\mathfrak{sl}}_2), \end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +h_{{\mathfrak{so}}_n}^\vee/q}(\mathfrak{so}_{n},f) \cong L_{-2 +2/q}({\mathfrak{sl}}_2), \end{align*} $$
-
-
2. Assume that q and n are even so that k is principal.
-
(a) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q+1,q^m,1^s)$
, with even m, odd s. Then k is collapsing if and only if
$(q+1,q^m,1^s)$
, with even m, odd s. Then k is collapsing if and only if
 $p=h_{{\mathfrak {so}}_n}+1$
and,
$p=h_{{\mathfrak {so}}_n}+1$
and,  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s).\end{align*} $$
-
(b) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q+1,q^m,q-1,1^s)$
, with even
$(q+1,q^m,q-1,1^s)$
, with even
 $m,s$
,
$m,s$
,
 $s>2$
. Then for generic q, k is collapsing only if
$s>2$
. Then for generic q, k is collapsing only if
 $p=h_{{\mathfrak {so}}_n}+1$
. Moreover, for generic q, we have the following inclusion is a finite extension:
$p=h_{{\mathfrak {so}}_n}+1$
. Moreover, for generic q, we have the following inclusion is a finite extension: 
-
-
3. Assume that n is odd and q is even so that k is coprincipal.
-
(a) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,1^s)$
, with even m and odd s. Then for generic q, k is collapsing only if
$(q^m,1^s)$
, with even m and odd s. Then for generic q, k is collapsing only if
 $p=h_{{\mathfrak {so}}_n}+1$
. Moreover,
$p=h_{{\mathfrak {so}}_n}+1$
. Moreover,  $$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s).\end{align*} $$
$$ \begin{align*}\mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s).\end{align*} $$
-
(b) Pick a nilpotent element
 $f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
$f \in \overline {{\mathbb {O}}}_k$
corresponding to the partition
 $(q^m,q-1,1^s)$
, with even
$(q^m,q-1,1^s)$
, with even
 $m,s$
,
$m,s$
,
 $s>2$
. Then for generic q, k is collapsing only if
$s>2$
. Then for generic q, k is collapsing only if
 $p=n$
. Moreover, for generic q, we have the following inclusion is a finite extension:
$p=n$
. Moreover, for generic q, we have the following inclusion is a finite extension: 
-
Proof. This proof is very similar to that of Theorem 9.10, except that, obviously, we use here orthogonal Dynkin pyramids. We omit the details.
The following conjecture is similar to Conjecture 9.12.
Conjecture 9.17. For generic q, we have the following finite extensions:
 $$ \begin{align*} &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}^\vee+1)/q }(\mathfrak{so}_{n},f) \cong \\ & \hspace{1cm} \qquad L_{1}(\mathfrak{so}_m) \otimes L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}^\vee+1)/q}(\mathfrak{so}_s) \oplus L_{1}(\mathfrak{so}_m;\varpi_1) \otimes L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}^\vee+1)/q}(\mathfrak{so}_s;\varpi_1).\\ &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s) \oplus L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s;\varpi_1).& \\ &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s) \oplus L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s;\varpi_1). \end{align*} $$
$$ \begin{align*} &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee+(h_{{\mathfrak{so}}_n}^\vee+1)/q }(\mathfrak{so}_{n},f) \cong \\ & \hspace{1cm} \qquad L_{1}(\mathfrak{so}_m) \otimes L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}^\vee+1)/q}(\mathfrak{so}_s) \oplus L_{1}(\mathfrak{so}_m;\varpi_1) \otimes L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}^\vee+1)/q}(\mathfrak{so}_s;\varpi_1).\\ &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s) \oplus L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s;\varpi_1).& \\ &\hspace{1cm} \mathscr{W}_{-h_{{\mathfrak{so}}_n}^\vee +(h_{{\mathfrak{so}}_n}+1)/q}(\mathfrak{so}_{n},f) \cong L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s) \oplus L_{-h_{{\mathfrak{so}}_s}^\vee +(h_{{\mathfrak{so}}_s}+1)/q}(\mathfrak{so}_s;\varpi_1). \end{align*} $$
Remark 9.18. Similarly to Remark 8.9, notice that (4) with
![]() $s=0$
or
$s=0$
or
![]() $s=1$
is compatible with (1), (5) with
$s=1$
is compatible with (1), (5) with
![]() $s=1$
is compatible with (2), (7) with
$s=1$
is compatible with (2), (7) with
![]() $s=1$
is compatible with (3), and (8) with
$s=1$
is compatible with (3), and (8) with
![]() $s=0$
is compatible with (3).
$s=0$
is compatible with (3).
Remark 9.19. It might be also interesting to consider the case where
![]() $(n-2,q) \not =1$
. For example, consider the Lie algebra
$(n-2,q) \not =1$
. For example, consider the Lie algebra
![]() $\mathfrak {so}_{27}$
(type
$\mathfrak {so}_{27}$
(type
![]() $B_{13})$
and
$B_{13})$
and
![]() $f \in {\mathbb {O}}_{(5^4,1^7)}$
. We find that
$f \in {\mathbb {O}}_{(5^4,1^7)}$
. We find that
![]() $k= -25+\dfrac {25}{5}=-20$
is not admissible, and
$k= -25+\dfrac {25}{5}=-20$
is not admissible, and
![]() $k_1^\natural = - 5+\dfrac {5}{5}=-4$
is not admissible either. One can wonder whether
$k_1^\natural = - 5+\dfrac {5}{5}=-4$
is not admissible either. One can wonder whether
Other examples are
The last example is interesting because one knows [Reference Arakawa and Moreau21, Theorem 7.1] that, for
![]() $\ell \ge 3$
,
$\ell \ge 3$
,
Conjecture 9.20.
-
1. The cases covered by Theorems 8.7 and 8.8 give the exhaustive list of pairs
 $(f,k)$
where f is a nilpotent element of
$(f,k)$
where f is a nilpotent element of
 ${\mathfrak {sl}}_n$
and k is an admissible collapsing levels for
${\mathfrak {sl}}_n$
and k is an admissible collapsing levels for
 ${\mathfrak {sl}}_n$
.
${\mathfrak {sl}}_n$
. -
2. The cases covered by Theorems 9.7 and 9.10 give the exhaustive list of pairs
 $(f,k)$
where f is a nilpotent element of
$(f,k)$
where f is a nilpotent element of
 $\mathfrak {sp}_n$
and k is an admissible collapsing levels for
$\mathfrak {sp}_n$
and k is an admissible collapsing levels for
 $\mathfrak {sp}_n$
.
$\mathfrak {sp}_n$
. -
3. The cases covered by Theorems 9.14 and 9.16 give the exhaustive list of pairs
 $(f,k)$
where f is a nilpotent element of
$(f,k)$
where f is a nilpotent element of
 ${\mathfrak {so}}_n$
and k is an admissible collapsing levels for
${\mathfrak {so}}_n$
and k is an admissible collapsing levels for
 $\mathfrak {so}_n$
.
$\mathfrak {so}_n$
.
10 Collapsing levels in the exceptional types
In this section, we state our main results and conjectures concerning collapsing levels in the exceptional types. As in the preceding sections, our proofs follow the strategy described in Section 6; considering pairs
![]() $({\mathbb {O}}_k,G.f)$
such that
$({\mathbb {O}}_k,G.f)$
such that
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing. Data on nilpotent orbits,
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is collapsing. Data on nilpotent orbits,
![]() $\mathfrak {sl}_2$
-triples and centralisers, which we will use throughout this section, are recorded in Tables 11, 12, 13, 14–15, 16–17.
$\mathfrak {sl}_2$
-triples and centralisers, which we will use throughout this section, are recorded in Tables 11, 12, 13, 14–15, 16–17.
Table 5 Main asymptotic data in type
![]() $E_6.$
$E_6.$

Table 6 Main asymptotic data in type
![]() $E_7.$
$E_7.$

Table 7 Main asymptotic data in type
![]() $E_8.$
$E_8.$

Table 8 Main asymptotic data in type
![]() $E_8$
.
$E_8$
.

Table 9 Main asymptotic data in type
![]() $G_2.$
$G_2.$

The results of this section are organised by type, the isomorphisms in type
![]() $E_6$
,
$E_6$
,
![]() $E_7$
,
$E_7$
,
![]() $E_8$
,
$E_8$
,
![]() $G_2$
and
$G_2$
and
![]() $F_4$
presented in Theorems 10.1, 10.6, 10.11, 10.16 and 10.18, respectively. In place of f, we write the label of
$F_4$
presented in Theorems 10.1, 10.6, 10.11, 10.16 and 10.18, respectively. In place of f, we write the label of
![]() $G.f$
in the Bala-Carter classification, and
$G.f$
in the Bala-Carter classification, and
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {g}^\natural $
are denoted by their types. The results are summarized in Tables 5, 6, 8, 9 and 10. We present a complete proof only for Theorem 10.1, the others being very similar.
$\mathfrak {g}^\natural $
are denoted by their types. The results are summarized in Tables 5, 6, 8, 9 and 10. We present a complete proof only for Theorem 10.1, the others being very similar.
Table 10 Main asymptotic data in type
![]() $F_4.$
$F_4.$

In the tables, we indicate for each triple
![]() $({\mathbb {O}}_k,G.f,\overline {{\mathbb {O}}^{\natural }}\cong \mathcal {S}_{{\mathbb {O}}_k,f})$
the values of
$({\mathbb {O}}_k,G.f,\overline {{\mathbb {O}}^{\natural }}\cong \mathcal {S}_{{\mathbb {O}}_k,f})$
the values of
![]() $p/q=k+h_{\mathfrak {g}}^\vee $
,
$p/q=k+h_{\mathfrak {g}}^\vee $
,
![]() $k_i^\natural +h_{\mathfrak {g}_i^\natural }^\vee $
, for
$k_i^\natural +h_{\mathfrak {g}_i^\natural }^\vee $
, for ![]() (if
(if
![]() $i>1$
, we write in the first column
$i>1$
, we write in the first column
![]() $k_1^\natural +h_{\mathfrak {g}_1^\natural }^\vee $
, and in second column
$k_1^\natural +h_{\mathfrak {g}_1^\natural }^\vee $
, and in second column
![]() $k_2^\natural +h_{\mathfrak {g}_2^\natural }^\vee $
, etc.), the central charge
$k_2^\natural +h_{\mathfrak {g}_2^\natural }^\vee $
, etc.), the central charge
![]() $c_V$
, the asymptotic growth
$c_V$
, the asymptotic growth
![]() $\mathbf {g}_V$
and the asymptotic dimension
$\mathbf {g}_V$
and the asymptotic dimension
![]() $\mathbf {A}_V$
with V being either
$\mathbf {A}_V$
with V being either
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
or
$H_{DS,f}^0(L_k(\mathfrak {g}))$
or
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
. Then we write in the last column the symbol
$L_{k^\natural }(\mathfrak {g}^\natural )$
. Then we write in the last column the symbol
![]() $\checkmark $
if all invariants match, we write ‘fin. ext.’ if we expect that
$\checkmark $
if all invariants match, we write ‘fin. ext.’ if we expect that
![]() $\mathscr {W}_k(\mathfrak {g},f)$
is a finite extension of
$\mathscr {W}_k(\mathfrak {g},f)$
is a finite extension of
![]() $L_{k^\natural }(\mathfrak {g}^\natural )$
(usually, this happens when all invariants for
$L_{k^\natural }(\mathfrak {g}^\natural )$
(usually, this happens when all invariants for
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
match except the asymptotic dimension, and more details are furnished in the corresponding theorem). As a rule, when one of the invariants does not coincide, we write in first position the invariant corresponding to
$H_{DS,f}^0(L_k(\mathfrak {g}))$
match except the asymptotic dimension, and more details are furnished in the corresponding theorem). As a rule, when one of the invariants does not coincide, we write in first position the invariant corresponding to
![]() $H_{DS,f}^0(L_k(\mathfrak {g}))$
.
$H_{DS,f}^0(L_k(\mathfrak {g}))$
.
Nilpotent orbits are given by their the Bala-Carter classification in the exceptional types. Nilpotent orbits in classical types are given in term of partitions. Note that the associated variety of
![]() $L_k(\mathfrak {g})$
determines the possible denominators q of
$L_k(\mathfrak {g})$
determines the possible denominators q of
![]() $k+h_{\mathfrak {g}}^\vee $
since k is admissible (see Theorem 3.2). So the values of q are always among these possible denominators.
$k+h_{\mathfrak {g}}^\vee $
since k is admissible (see Theorem 3.2). So the values of q are always among these possible denominators.
We also indicate in the table the isomorphism type of
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
(in the third column) when it is known (if so, it is a product of nilpotent orbits in
$\mathcal {S}_{{\mathbb {O}}_k,f}$
(in the third column) when it is known (if so, it is a product of nilpotent orbits in
![]() $\mathfrak {g}^\natural $
). When the isomorphism
$\mathfrak {g}^\natural $
). When the isomorphism
![]() $\overline {{\mathbb {O}}^{\natural }}\cong \mathcal {S}_{{\mathbb {O}}_k,f}$
comes from a minimal degeneration, then we always obtain a minimal nilpotent orbit closure [Reference Fu, Juteau, Levy and Sommers47]. Following Kraft and Procesi [Reference Kraft and Procesi64, Reference Kraft and Procesi66], we refer to the minimal nilpotent orbit
$\overline {{\mathbb {O}}^{\natural }}\cong \mathcal {S}_{{\mathbb {O}}_k,f}$
comes from a minimal degeneration, then we always obtain a minimal nilpotent orbit closure [Reference Fu, Juteau, Levy and Sommers47]. Following Kraft and Procesi [Reference Kraft and Procesi64, Reference Kraft and Procesi66], we refer to the minimal nilpotent orbit
![]() ${\mathbb {O}}_{\text {min}}$
of a simple Lie algebra by the lowercase letters for the ambient simple Lie algebra:
${\mathbb {O}}_{\text {min}}$
of a simple Lie algebra by the lowercase letters for the ambient simple Lie algebra:
![]() $a_k$
,
$a_k$
,
![]() $b_k$
,
$b_k$
,
![]() $c_k$
,
$c_k$
,
![]() $d_k (k\ge 4)$
,
$d_k (k\ge 4)$
,
![]() $g_2$
,
$g_2$
,
![]() $f_4$
,
$f_4$
,
![]() $e_6$
,
$e_6$
,
![]() $e_7$
,
$e_7$
,
![]() $e_8$
. Similarly, we refer to the minimal special nilpotent orbitFootnote
7
for the ambient simple Lie algebra as
$e_8$
. Similarly, we refer to the minimal special nilpotent orbitFootnote
7
for the ambient simple Lie algebra as
![]() $a_k^{sp}$
,
$a_k^{sp}$
,
![]() $b_k^{sp}$
,
$b_k^{sp}$
,
![]() $c_k^{sp}$
,
$c_k^{sp}$
,
![]() $d_k^{sp} (k\ge 4)$
,
$d_k^{sp} (k\ge 4)$
,
![]() $g_2^{sp}$
,
$g_2^{sp}$
,
![]() $f_4^{sp}$
,
$f_4^{sp}$
,
![]() $e_6^{sp}$
,
$e_6^{sp}$
,
![]() $e_7^{sp}$
,
$e_7^{sp}$
,
![]() $e_8^{sp}$
. The nilpotent cone of a Lie algebra of type X will denoted by
$e_8^{sp}$
. The nilpotent cone of a Lie algebra of type X will denoted by
![]() $\mathcal {N}_X$
. In Table 10, the letter m refers to a non-normal type of singularity which is neither a simple surface singularity nor a minimal singularity (see [Reference Fu, Juteau, Levy and Sommers47, §1.8.4]). As for the singularity
$\mathcal {N}_X$
. In Table 10, the letter m refers to a non-normal type of singularity which is neither a simple surface singularity nor a minimal singularity (see [Reference Fu, Juteau, Levy and Sommers47, §1.8.4]). As for the singularity
![]() $a_2^+$
appearing also in Table 10, it refers to the singularity
$a_2^+$
appearing also in Table 10, it refers to the singularity
![]() $a_2$
together with the action of a subgroup
$a_2$
together with the action of a subgroup
![]() $K \subset \mathrm {Aut}({\mathfrak {sl}}_3)$
which lifts a subgroup of the Dynkin diagram of
$K \subset \mathrm {Aut}({\mathfrak {sl}}_3)$
which lifts a subgroup of the Dynkin diagram of
![]() ${\mathfrak {sl}}_3=A_2$
(see [Reference Fu, Juteau, Levy and Sommers47, §1.8.2]).
${\mathfrak {sl}}_3=A_2$
(see [Reference Fu, Juteau, Levy and Sommers47, §1.8.2]).
When the isomorphism type of
![]() $\mathcal {S}_{{\mathbb {O}}_k,f}$
is not known (to the best of our knowledge), we write ‘unknown’.
$\mathcal {S}_{{\mathbb {O}}_k,f}$
is not known (to the best of our knowledge), we write ‘unknown’.
Theorem 10.1. The following isomorphisms hold, providing collapsing levels for
![]() $\mathfrak {g}=E_6$
.
$\mathfrak {g}=E_6$
.
 $$ \begin{align*} & \mathscr{W}_{-12+12/13}(E_6,E_6) \cong \mathbb{C}, && \mathscr{W}_{-12+13/12}(E_6,E_6) \cong \mathbb{C}, \\ & \mathscr{W}_{-12+13/9}(E_6,E_6(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-12+13/6}(E_6,E_6(a_3)) \cong \mathbb{C}, \\ & \mathscr{W}_{-12+13/6}(E_6,A_5) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-12+12/7}(E_6,D_4) \cong L_{-3+3/7}(A_2), \\ & \mathscr{W}_{-12+13/6}(E_6,D_4) \cong L_{-2+4/3}(A_2), && \mathscr{W}_{-12+12/5}(E_6,A_4) \cong L_{-2+2/5}(A_1), \\ & \mathscr{W}_{-12+13/3}(E_6,2A_2+A_1) \cong \mathbb{C}, && \mathscr{W}_{-12+13/3}(E_6,2A_2)\cong L_{-4+7/3}(G_2), \\ & \mathscr{W}_{-12+13/2}(E_6,3 A_1) \cong L_1(A_2). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-12+12/13}(E_6,E_6) \cong \mathbb{C}, && \mathscr{W}_{-12+13/12}(E_6,E_6) \cong \mathbb{C}, \\ & \mathscr{W}_{-12+13/9}(E_6,E_6(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-12+13/6}(E_6,E_6(a_3)) \cong \mathbb{C}, \\ & \mathscr{W}_{-12+13/6}(E_6,A_5) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-12+12/7}(E_6,D_4) \cong L_{-3+3/7}(A_2), \\ & \mathscr{W}_{-12+13/6}(E_6,D_4) \cong L_{-2+4/3}(A_2), && \mathscr{W}_{-12+12/5}(E_6,A_4) \cong L_{-2+2/5}(A_1), \\ & \mathscr{W}_{-12+13/3}(E_6,2A_2+A_1) \cong \mathbb{C}, && \mathscr{W}_{-12+13/3}(E_6,2A_2)\cong L_{-4+7/3}(G_2), \\ & \mathscr{W}_{-12+13/2}(E_6,3 A_1) \cong L_1(A_2). \end{align*} $$
Moreover, the following inclusions are finite extensions:

Proof. We detail below only a few cases. The chief tool to prove the isomorphisms is Theorem 3.10, using data summarised in Table 5.
![]() $\bullet $
Assume
$\bullet $
Assume
![]() $q \ge 12$
. Let
$q \ge 12$
. Let
![]() $p\ge 12$
and
$p\ge 12$
and
![]() $(p,q)=1$
. Computing the central charge, we observe that
$(p,q)=1$
. Computing the central charge, we observe that
![]() $c_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=0$
if and only if
$c_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=0$
if and only if
![]() $(p,q)=(12,13)$
or
$(p,q)=(12,13)$
or
![]() $(p,q)=(13,12)$
. Moreover, in both these cases,
$(p,q)=(13,12)$
. Moreover, in both these cases,
![]() $\mathbf {g}_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=0$
and
$\mathbf {g}_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=0$
and
![]() $\mathbf {A}_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=1$
. By Theorem 3.10, the first two isomorphisms follow.
$\mathbf {A}_{\mathscr {W}_{-12+p/q}(E_6,E_6)}=1$
. By Theorem 3.10, the first two isomorphisms follow.
![]() $\bullet $
Assume that
$\bullet $
Assume that
![]() $q=6$
or
$q=6$
or
![]() $7$
, and pick
$7$
, and pick
![]() $f \in A_5$
. According to Table 13, we have
$f \in A_5$
. According to Table 13, we have
![]() $\mathfrak {g}^\natural \cong {\mathfrak {sl}}_2$
and
$\mathfrak {g}^\natural \cong {\mathfrak {sl}}_2$
and
![]() $k^\natural = k+17/2$
. Computing the central charge, we easily verify that if k is collapsing, then necessarily
$k^\natural = k+17/2$
. Computing the central charge, we easily verify that if k is collapsing, then necessarily
![]() $(p, q) = (13, 6)$
or
$(p, q) = (13, 6)$
or
![]() $(p, q) = (12, 7)$
.
$(p, q) = (12, 7)$
.
![]() $\ast $
Assume first that
$\ast $
Assume first that
![]() $(p, q) = (13, 6)$
. Then
$(p, q) = (13, 6)$
. Then
![]() $k^\natural = -2+2/3$
. Since
$k^\natural = -2+2/3$
. Since
![]() $k = -12+13/6$
and
$k = -12+13/6$
and
![]() $k^\natural = -2+2/3$
are admissible for
$k^\natural = -2+2/3$
are admissible for
![]() $E_6$
and
$E_6$
and
![]() $A_1$
, respectively, it suffices to apply Theorem 3.10 to prove that
$A_1$
, respectively, it suffices to apply Theorem 3.10 to prove that
![]() $\mathscr {W}_{-12+13/6}(E_6,A_5)$
and
$\mathscr {W}_{-12+13/6}(E_6,A_5)$
and
![]() $L_{-2+2/3}(A_1)$
are isomorphic.
$L_{-2+2/3}(A_1)$
are isomorphic.
We easily check using Corollary 3.9 and Proposition 4.10 that
![]() $L_{-2+2/3}(A_1)$
and
$L_{-2+2/3}(A_1)$
and
![]() $H^0_{DS,A_5}(L_{-12+13/6}(E_6))$
share the same asymptotic growth of
$H^0_{DS,A_5}(L_{-12+13/6}(E_6))$
share the same asymptotic growth of
![]() $2$
. Let us compare their asymptotic dimensions. By Corollary 3.9 and Lemma 7.1 (1), we have
$2$
. Let us compare their asymptotic dimensions. By Corollary 3.9 and Lemma 7.1 (1), we have
while by Proposition 4.10 and Lemma 7.1 (2),

with
![]() $|\Delta ^{1/2}|=6$
and
$|\Delta ^{1/2}|=6$
and
![]() $|\Delta _+^0|=1$
. Computing the cardinality of
$|\Delta _+^0|=1$
. Computing the cardinality of
![]() $\{\alpha \in \Delta _+ \colon (x^0 | \alpha )=j \}$
for
$\{\alpha \in \Delta _+ \colon (x^0 | \alpha )=j \}$
for
![]() $j>0$
, we verify that
$j>0$
, we verify that

whence
![]() $\mathbf {A}_{H^0_{DS,A_5}(L_{-12+13/6}(E_6)) }= \frac {1}{3 \sqrt {3}}$
, as required.
$\mathbf {A}_{H^0_{DS,A_5}(L_{-12+13/6}(E_6)) }= \frac {1}{3 \sqrt {3}}$
, as required.
![]() $\ast $
Assume now that
$\ast $
Assume now that
![]() $(p, q) = (12, 7)$
. Here, we obtain that
$(p, q) = (12, 7)$
. Here, we obtain that
and that
Moreover, we can verify that the central charges of
![]() $H^0_{DS,A_5}(L_{-12+12/7}(E_6))$
and
$H^0_{DS,A_5}(L_{-12+12/7}(E_6))$
and
![]() $L_{-2+3/14}(A_1)$
are both equal to
$L_{-2+3/14}(A_1)$
are both equal to
![]() $-25$
. By Theorem 3.10,
$-25$
. By Theorem 3.10,
![]() $\mathscr {W}_{-12+12/7}(E_6,A_5)$
is a finite extension of
$\mathscr {W}_{-12+12/7}(E_6,A_5)$
is a finite extension of
![]() $L_{-2+3/14}(A_1)$
.
$L_{-2+3/14}(A_1)$
.
We argue similarly in all the other cases.
Remark 10.2.
-
1. The associated variety of
 $H_{DS,A_1}^0(L_{-12+13/2}(E_6))$
and that of
$H_{DS,A_1}^0(L_{-12+13/2}(E_6))$
and that of
 $L_{-6+7/2}(A_5)$
have the same dimension, but they are not isomorphic. Indeed, the former is the nilpotent Slodowy slice
$L_{-6+7/2}(A_5)$
have the same dimension, but they are not isomorphic. Indeed, the former is the nilpotent Slodowy slice
 $\mathcal {S}_{3 A_1,A_1}$
in
$\mathcal {S}_{3 A_1,A_1}$
in
 $E_6$
, while the latter is the closure of the nilpotent orbit of
$E_6$
, while the latter is the closure of the nilpotent orbit of
 $A_5={\mathfrak {sl}}_6$
attached to the partition
$A_5={\mathfrak {sl}}_6$
attached to the partition
 $(2^3)$
. These two varieties are not isomorphic since the number of nilpotent
$(2^3)$
. These two varieties are not isomorphic since the number of nilpotent
 $G^\natural $
-orbits in
$G^\natural $
-orbits in
 $\overline {{\mathbb {O}}}_{(2^3)}$
is
$\overline {{\mathbb {O}}}_{(2^3)}$
is
 $4$
, while if
$4$
, while if
 $\mathcal {S}_{3 A_1,A_1}$
had a dense
$\mathcal {S}_{3 A_1,A_1}$
had a dense
 $G^\natural $
-orbit, then the number of
$G^\natural $
-orbit, then the number of
 $G^\natural $
-orbits in
$G^\natural $
-orbits in
 $\mathcal {S}_{3 A_1,A_1}$
would be
$\mathcal {S}_{3 A_1,A_1}$
would be
 $3$
, as we can see from the Hasse diagram of
$3$
, as we can see from the Hasse diagram of
 $E_6$
.
$E_6$
. -
2. Similarly, the nilpotent Slodowy slice
 $\mathcal {S}_{2A_2+A_1,A_2}$
(associated variety of
$\mathcal {S}_{2A_2+A_1,A_2}$
(associated variety of
 $H_{DS,A_2}^0(L_{-12+13/3}(E_6))$
is not isomorphic to the product
$H_{DS,A_2}^0(L_{-12+13/3}(E_6))$
is not isomorphic to the product
 $\mathcal {N}_{A_2}\times \mathcal {N}_{A_2}$
(associated variety of
$\mathcal {N}_{A_2}\times \mathcal {N}_{A_2}$
(associated variety of
 $L_{-3+4/3}(A_2)\otimes L_{-3+4/3}(A_2)$
), and these two varieties have the same dimension.
$L_{-3+4/3}(A_2)\otimes L_{-3+4/3}(A_2)$
), and these two varieties have the same dimension.
Proposition 10.3. The following decompositions hold:

Proof.
![]() $\bullet $
Assume first that
$\bullet $
Assume first that
![]() $(p, q)=(13, 2)$
, and let
$(p, q)=(13, 2)$
, and let
![]() $f \in A_1$
. In this case, we have
$f \in A_1$
. In this case, we have
Moreover, we verify that the central charges of
![]() $H^0_{DS,A_1}(L_{-12+13/2}(E_6))$
and
$H^0_{DS,A_1}(L_{-12+13/2}(E_6))$
and
![]() $L_{-6+7/2}(A_5)$
are both equal to
$L_{-6+7/2}(A_5)$
are both equal to
![]() $-25$
. Arguing as in the proof of Theorem 9.10 (1) (b), we obtain that
$-25$
. Arguing as in the proof of Theorem 9.10 (1) (b), we obtain that

where ![]() is the lowest
is the lowest
![]() $L_0$
-eigenvalue of
$L_0$
-eigenvalue of ![]() . We require
. We require
where ![]() , assuming that all
, assuming that all ![]() , with
, with ![]() . The only possibilities are
. The only possibilities are ![]() or
or ![]() .
.
However, by Proposition 4.10, we easily see that
As a result,
But
![]() $m_0$
must be at most
$m_0$
must be at most
![]() $1$
. We conclude that either
$1$
. We conclude that either
![]() $\mathscr {W}_{-12+13/2}(E_6,A_1) \cong L_{-6+7/2}(A_5) \oplus L_{-6+7/2}(A_5; \varpi _3)$
or that
$\mathscr {W}_{-12+13/2}(E_6,A_1) \cong L_{-6+7/2}(A_5) \oplus L_{-6+7/2}(A_5; \varpi _3)$
or that
![]() $-12+13/2$
is collapsing. But this is impossible by Proposition 6.8 and Remark 10.2.
$-12+13/2$
is collapsing. But this is impossible by Proposition 6.8 and Remark 10.2.
![]() $\bullet $
Assume now
$\bullet $
Assume now
![]() $(p,q)=(13,3)$
and
$(p,q)=(13,3)$
and
![]() $f \in A_2$
. We have
$f \in A_2$
. We have
![]() $\mathscr {W}_{-12+13/3}(E_6,A_2) \cong H_{DS,f}^{0}(L_{-12+13/3}(E_6))$
since f is even. Arguing as in the previous case, we obtain here that the only possible weights are
$\mathscr {W}_{-12+13/3}(E_6,A_2) \cong H_{DS,f}^{0}(L_{-12+13/3}(E_6))$
since f is even. Arguing as in the previous case, we obtain here that the only possible weights are ![]() ,
, ![]() or
or ![]() . Since
. Since
![]() $H_{DS,f}^{0}(L_{-12+13/3}(E_6)) \cong \mathscr {W}_{-12+13/3}(E_6,A_2)$
is a finite direct sum of admissible
$H_{DS,f}^{0}(L_{-12+13/3}(E_6)) \cong \mathscr {W}_{-12+13/3}(E_6,A_2)$
is a finite direct sum of admissible
![]() $L_{-3+4/3}(A_2) \otimes L_{-3+4/3}(A_2)$
-modules, we obtain here from the equalities
$L_{-3+4/3}(A_2) \otimes L_{-3+4/3}(A_2)$
-modules, we obtain here from the equalities
 $$ \begin{align*} &m_0 \mathbf{A}_{L_{-3+4/3}(A_2;0) \otimes L_{-3+4/3}(A_2;0)}+ m_1 \mathbf{A}_{L_{-3+4/3}(A_2;\varpi_1) \otimes L_{-3+4/3}(A_2;\varpi_1)} \\ &\qquad + m_2 \mathbf{A}_{L_{-3+4/3}(A_2;\varpi_2) \otimes L_{-3+4/3}(A_3;\varpi_2)} = 3 \mathbf{A}_{L_{-3+4/3}(A_2) \otimes L_{-3+4/3}(A_2)}, \end{align*} $$
$$ \begin{align*} &m_0 \mathbf{A}_{L_{-3+4/3}(A_2;0) \otimes L_{-3+4/3}(A_2;0)}+ m_1 \mathbf{A}_{L_{-3+4/3}(A_2;\varpi_1) \otimes L_{-3+4/3}(A_2;\varpi_1)} \\ &\qquad + m_2 \mathbf{A}_{L_{-3+4/3}(A_2;\varpi_2) \otimes L_{-3+4/3}(A_3;\varpi_2)} = 3 \mathbf{A}_{L_{-3+4/3}(A_2) \otimes L_{-3+4/3}(A_2)}, \end{align*} $$
and
![]() $m_0=1$
the expected decomposition. Indeed, by Proposition 4.10,
$m_0=1$
the expected decomposition. Indeed, by Proposition 4.10,
For
![]() $(p,q)=(12,7)$
and
$(p,q)=(12,7)$
and
![]() $f \in A_5$
, similar arguments as before Conjecture 9.12 lead to the following conjecture.
$f \in A_5$
, similar arguments as before Conjecture 9.12 lead to the following conjecture.
Conjecture 10.4.
We conjecture the following isomorphisms at non-admissible level.
Conjecture 10.5.
Theorem 10.6. The following isomorphisms hold, providing collapsing levels for
![]() $\mathfrak {g}=E_7$
.
$\mathfrak {g}=E_7$
.
 $$ \begin{align*} & \mathscr{W}_{-18+18/19}(E_7,E_7) \cong \mathbb{C}, && \mathscr{W}_{-18+19/18}(E_7,E_7) \cong \mathbb{C}, \\ & \mathscr{W}_{-18+19/14}(E_7,E_7(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-18+18/13}(E_7,E_6) \cong L_{-2+2/13}(A_1), & \\ & \mathscr{W}_{-18+19/12}(E_7,E_6) \cong L_{-2+3/4}(A_1), && \mathscr{W}_{-18+19/10}(E_7,D_6) \cong L_{-2+2/5}(A_1),\\ & \mathscr{W}_{-18+18/7}(E_7,A_6) \cong \mathbb{C}, && \mathscr{W}_{-18+19/7}(E_7,A_6) \cong L_{1}(A_1), & \\ & \mathscr{W}_{-18+18/7}(E_7,(A_5)") \cong L_{-4+4/7}(G_2), && \mathscr{W}_{-18+18/7}(E_7,D_4) \cong L_{-4+4/7}(C_3), \\ & \mathscr{W}_{-18+19/6}(E_7,E_7(a_5)) \cong \mathbb{C}, && \mathscr{W}_{-18+19/6}(E_7,E_6(a_3)) \cong L_{-2+3/2}(A_1),& \\ & \mathscr{W}_{-18+19/6}(E_7,D_6(a_2)) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-18+19/6}(E_7,(A_5)') \cong L_{-2+2/3}(A_1)\otimes L_{-2+3/2}(A_1), \\ &\mathscr{W}_{-18+19/6}(E_7,(A_5)") \cong L_{-4+7/6}(G_2), && \mathscr{W}_{-18+19/6}(E_7,D_4) \cong L_{-4+7/6}(C_3), & \\ & \mathscr{W}_{-18+19/5}(E_7,A_4+A_2) \cong L_{3}(A_1), && \mathscr{W}_{-18+18/5}(E_7,A_4) \cong L_{-3+3/5}(A_2), & \\ & \mathscr{W}_{-18+19/4}(E_7,A_3+A_2+A_1) \cong L_{2}(A_1), && \mathscr{W}_{-18+19/4}(E_7,D_4(a_1)) \cong L_{-2+3/4}(A_1)^{\otimes 3}, \\ & \mathscr{W}_{-18+19/3}(E_7,2A_2+A_1) \cong L_{1}(A_1), && \mathscr{W}_{-18+19/3}(E_7,A_2+3A_1) \cong L_{- 4+8/3}(G_2), & \\ & \mathscr{W}_{-18+19/3}(E_7,2 A_2) \cong L_{1}(A_1)\otimes L_{- 4+7/3}(G_2), && \mathscr{W}_{-18+19/2}(E_7,4 A_1) \cong \mathbb{C}, \\ & \mathscr{W}_{-18+19/2}(E_7,(3 A_1)') \cong L_{-4+7/2}(C_3), && \mathscr{W}_{-18+19/2}(E_7,(3 A_1)") \cong L_{-9+13/2}(F_4). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-18+18/19}(E_7,E_7) \cong \mathbb{C}, && \mathscr{W}_{-18+19/18}(E_7,E_7) \cong \mathbb{C}, \\ & \mathscr{W}_{-18+19/14}(E_7,E_7(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-18+18/13}(E_7,E_6) \cong L_{-2+2/13}(A_1), & \\ & \mathscr{W}_{-18+19/12}(E_7,E_6) \cong L_{-2+3/4}(A_1), && \mathscr{W}_{-18+19/10}(E_7,D_6) \cong L_{-2+2/5}(A_1),\\ & \mathscr{W}_{-18+18/7}(E_7,A_6) \cong \mathbb{C}, && \mathscr{W}_{-18+19/7}(E_7,A_6) \cong L_{1}(A_1), & \\ & \mathscr{W}_{-18+18/7}(E_7,(A_5)") \cong L_{-4+4/7}(G_2), && \mathscr{W}_{-18+18/7}(E_7,D_4) \cong L_{-4+4/7}(C_3), \\ & \mathscr{W}_{-18+19/6}(E_7,E_7(a_5)) \cong \mathbb{C}, && \mathscr{W}_{-18+19/6}(E_7,E_6(a_3)) \cong L_{-2+3/2}(A_1),& \\ & \mathscr{W}_{-18+19/6}(E_7,D_6(a_2)) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-18+19/6}(E_7,(A_5)') \cong L_{-2+2/3}(A_1)\otimes L_{-2+3/2}(A_1), \\ &\mathscr{W}_{-18+19/6}(E_7,(A_5)") \cong L_{-4+7/6}(G_2), && \mathscr{W}_{-18+19/6}(E_7,D_4) \cong L_{-4+7/6}(C_3), & \\ & \mathscr{W}_{-18+19/5}(E_7,A_4+A_2) \cong L_{3}(A_1), && \mathscr{W}_{-18+18/5}(E_7,A_4) \cong L_{-3+3/5}(A_2), & \\ & \mathscr{W}_{-18+19/4}(E_7,A_3+A_2+A_1) \cong L_{2}(A_1), && \mathscr{W}_{-18+19/4}(E_7,D_4(a_1)) \cong L_{-2+3/4}(A_1)^{\otimes 3}, \\ & \mathscr{W}_{-18+19/3}(E_7,2A_2+A_1) \cong L_{1}(A_1), && \mathscr{W}_{-18+19/3}(E_7,A_2+3A_1) \cong L_{- 4+8/3}(G_2), & \\ & \mathscr{W}_{-18+19/3}(E_7,2 A_2) \cong L_{1}(A_1)\otimes L_{- 4+7/3}(G_2), && \mathscr{W}_{-18+19/2}(E_7,4 A_1) \cong \mathbb{C}, \\ & \mathscr{W}_{-18+19/2}(E_7,(3 A_1)') \cong L_{-4+7/2}(C_3), && \mathscr{W}_{-18+19/2}(E_7,(3 A_1)") \cong L_{-9+13/2}(F_4). \end{align*} $$
Moreover, the following inclusions are finite extensions:

Remark 10.7. In the comments below, we argue as in Remark 10.2 to conclude that the varieties are not isomorphic with the same dimension.
-
1. The associated variety of
 $H_{DS,A_3}^0(L_{-18+19/4}(E_7))$
is not isomorphic to the associated variety of
$H_{DS,A_3}^0(L_{-18+19/4}(E_7))$
is not isomorphic to the associated variety of
 $L_{-2+3/4}(A_1) \otimes L_{-5+7/4}(B_3) $
. The former is the nilpotent Slodowy slice
$L_{-2+3/4}(A_1) \otimes L_{-5+7/4}(B_3) $
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{A_3+A_2+A_1,A_3}$
in
$\mathcal {S}_{A_3+A_2+A_1,A_3}$
in
 $E_7$
, while the later is the closure of the nilpotent orbit of
$E_7$
, while the later is the closure of the nilpotent orbit of
 $a_1 \times {\mathbb {O}}_{1,(3^2,1)} \subset A_1 \times B_3$
.
$a_1 \times {\mathbb {O}}_{1,(3^2,1)} \subset A_1 \times B_3$
. -
2. The associated variety of
 $H_{DS,A_2}^0(L_{-18+19/3}(E_7))$
is not isomorphic to the associated variety of
$H_{DS,A_2}^0(L_{-18+19/3}(E_7))$
is not isomorphic to the associated variety of
 $L_{-6+7/3}(A_5)$
. The former is the nilpotent Slodowy slice
$L_{-6+7/3}(A_5)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{2 A_2+A_1,A_2}$
in
$\mathcal {S}_{2 A_2+A_1,A_2}$
in
 $E_7$
, while the later is the closure of the nilpotent orbit of
$E_7$
, while the later is the closure of the nilpotent orbit of
 $A_5={\mathfrak {sl}}_6$
attached to the partition
$A_5={\mathfrak {sl}}_6$
attached to the partition
 $(3^2)$
.
$(3^2)$
. -
3. The associated variety of
 $H_{DS,2 A_1}^0(L_{-18+19/2}(E_7))$
is not isomorphic to the associated variety of
$H_{DS,2 A_1}^0(L_{-18+19/2}(E_7))$
is not isomorphic to the associated variety of
 $L_{-2+3/2}(A_1) \otimes L_{-7+9/2}(B_4)$
. The former is the nilpotent Slodowy slice
$L_{-2+3/2}(A_1) \otimes L_{-7+9/2}(B_4)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{4 A_1,2 A_1}$
in
$\mathcal {S}_{4 A_1,2 A_1}$
in
 $E_7$
, while the later is the closure of the nilpotent orbit of
$E_7$
, while the later is the closure of the nilpotent orbit of
 $a_1 \times {\mathbb {O}}_{1,(2^4,1)} \subset A_1 \times B_4$
. Here, to conclude that varieties are not isomorphic, one needs to use the singularities of
$a_1 \times {\mathbb {O}}_{1,(2^4,1)} \subset A_1 \times B_4$
. Here, to conclude that varieties are not isomorphic, one needs to use the singularities of
 $\mathcal {S}_{4 A_1,2 A_1}$
as described in [Reference Fu, Juteau, Levy and Sommers47].
$\mathcal {S}_{4 A_1,2 A_1}$
as described in [Reference Fu, Juteau, Levy and Sommers47]. -
4. The associated variety of
 $H_{DS,A_1}^0(L_{-18+19/2}(E_7))$
is not isomorphic to the associated variety of
$H_{DS,A_1}^0(L_{-18+19/2}(E_7))$
is not isomorphic to the associated variety of
 $L_{-10+11/2}(D_6)$
. The former is the nilpotent Slodowy slice
$L_{-10+11/2}(D_6)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{4 A_1,A_1}$
in
$\mathcal {S}_{4 A_1,A_1}$
in
 $E_7$
, while the later is the closure of the nilpotent orbit of
$E_7$
, while the later is the closure of the nilpotent orbit of
 $D_6={\mathfrak {so}}_{12}$
attached to the partition
$D_6={\mathfrak {so}}_{12}$
attached to the partition
 $(3,2^4,1)$
.
$(3,2^4,1)$
.
Proposition 10.8. The following decompositions hold:
 $$ \begin{align*} & \mathscr{W}_{-18+19/8}(E_7,D_5) \cong (L_{-2+3/8}(A_1)\otimes L_{-2+3/4}(A_1)) { \oplus (L_{-2+3/8}(A_1;\varpi_1)\otimes L_{-2+3/4}(A_1;\varpi_1))}, \\ & \mathscr{W}_{-18+19/4}(E_7,A_3) \cong (L_{-2+3/4}(A_1) \otimes L_{-5+7/4}(B_3)) \oplus (L_{-2+3/4}(A_1;\varpi_1) \otimes L_{-5+7/4}(B_3;\varpi_3)) , & \\ & \mathscr{W}_{-18+19/3}(E_7,A_2) \cong L_{-6+7/3}(A_5) {\oplus L_{-6+7/3}(A_5;\varpi_2) \oplus L_{-6+7/3}(A_5;\varpi_4)}, & \\ & \mathscr{W}_{-18+19/2}(E_7,2 A_1) \cong (L_{-2+3/2}(A_1) \otimes L_{-7+9/2}(B_4)) \oplus (L_{-2+3/2}(A_1;\varpi_1) \otimes L_{-7+9/2}(B_4;\varpi_1)) , & \\ & \mathscr{W}_{-18+19/2}(E_7,A_1) \cong L_{-10+11/2}(D_6) {\oplus L_{-10+11/2}(D_6;\varpi_1) }. \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-18+19/8}(E_7,D_5) \cong (L_{-2+3/8}(A_1)\otimes L_{-2+3/4}(A_1)) { \oplus (L_{-2+3/8}(A_1;\varpi_1)\otimes L_{-2+3/4}(A_1;\varpi_1))}, \\ & \mathscr{W}_{-18+19/4}(E_7,A_3) \cong (L_{-2+3/4}(A_1) \otimes L_{-5+7/4}(B_3)) \oplus (L_{-2+3/4}(A_1;\varpi_1) \otimes L_{-5+7/4}(B_3;\varpi_3)) , & \\ & \mathscr{W}_{-18+19/3}(E_7,A_2) \cong L_{-6+7/3}(A_5) {\oplus L_{-6+7/3}(A_5;\varpi_2) \oplus L_{-6+7/3}(A_5;\varpi_4)}, & \\ & \mathscr{W}_{-18+19/2}(E_7,2 A_1) \cong (L_{-2+3/2}(A_1) \otimes L_{-7+9/2}(B_4)) \oplus (L_{-2+3/2}(A_1;\varpi_1) \otimes L_{-7+9/2}(B_4;\varpi_1)) , & \\ & \mathscr{W}_{-18+19/2}(E_7,A_1) \cong L_{-10+11/2}(D_6) {\oplus L_{-10+11/2}(D_6;\varpi_1) }. \end{align*} $$
Proof. We argue as in the proof of Proposition 10.3. More precisely, for f in
![]() $D_5$
or
$D_5$
or
![]() $A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.7.
$A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.7.
For
![]() $(p,q)=(18,11)$
and
$(p,q)=(18,11)$
and
![]() $f \in D_6$
, similar arguments as before Conjecture 9.12 lead to the following conjecture.
$f \in D_6$
, similar arguments as before Conjecture 9.12 lead to the following conjecture.
Conjecture 10.9.
Based on the coincidence of central charges and asymptotic growths and dimensions at the non-admissible levels k and
![]() $k^\natural $
corresponding to
$k^\natural $
corresponding to
![]() $k+18=p/q=18/3$
and
$k+18=p/q=18/3$
and
![]() $k^\natural +4=6/3$
, we conjecture the following:
$k^\natural +4=6/3$
, we conjecture the following:
Conjecture 10.10.
Theorem 10.11. The following isomorphisms hold, providing collapsing levels for
![]() $\mathfrak {g}=E_8$
.
$\mathfrak {g}=E_8$
.
 $$ \begin{align*} & \mathscr{W}_{-30+30/31}(E_8,E_8) \cong \mathbb{C}, && \mathscr{W}_{-30+31/30}(E_8,E_8) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/24}(E_8,E_8(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-30+31/20}(E_8,E_8(a_2)) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+31/18}(E_8,E_7) \cong L_{-2+2/9}(A_1), && \mathscr{W}_{-30+31/15}(E_8,E_8(a_4)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/12}(E_8,D_7) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-30+31/12}(E_8,E_8(a_5)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+30/13}(E_8,E_6) \cong L_{-4+4/13}(G_2), && \mathscr{W}_{-30+31/12}(E_8,E_6) \cong L_{-4+7/12}(G_2), \\ & \mathscr{W}_{-30+31/10}(E_8,E_8(a_6)) \cong \mathbb{C}, && \mathscr{W}_{-30+31/10}(E_8,D_6) \cong L_{-3+3/5}(B_2), \\ & \mathscr{W}_{-30+31/9}(E_8,E_6(a_1)) \cong L_{-3+4/9}(A_2), & & \mathscr{W}_{-30+31/8}(A_7,A_7) \cong \mathbb{C},\\ & \mathscr{W}_{-30+30/7}(E_8,A_6) \cong L_{-2+2/7}(A_1), & & \mathscr{W}_{-30+31/6}(E_8,E_8(a_7)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/6}(E_8,E_8(a_7)) \cong \mathbb{C}, & & \mathscr{W}_{-30+31/6}(E_8,D_6(a_2)) \cong L_{-2+2/3}(A_1)\otimes L_{-2+2/3}(A_1), & \\ & \mathscr{W}_{-30+31/6}(E_8,E_6(a_3)) \cong L_{-4+7/6}(G_2), & & \mathscr{W}_{-30+31/6}(E_8,D_4) \cong L_{-9+13/6}(F_4), \\ & \mathscr{W}_{-30+30/7}(E_8,D_4) \cong L_{-9+9/7}(F_4), & & \mathscr{W}_{-30+31/5}(E_8,A_4+A_3) \cong \mathbb{C}, & \\ & {\mathscr{W}_{-30+32/5}(E_8,A_4+A_3) \cong L_2(A_1)}, & & \mathscr{W}_{-30+31/4}(E_8,2 A_3) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+31/4}(E_8,D_4(a_1)+A_2) \cong L_{-3+3/2}(A_2), & & \mathscr{W}_{-30+31/3}(E_8,2A_2+2A_1) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+32/3}(E_8,2A_2+2A_1) \cong L_1(B_2), & & \mathscr{W}_{-30+31/3}(E_8,2A_2) \cong L_{-4+7/3}(G_2) \otimes L_{-4+7/3}(G_2), & \\ & \mathscr{W}_{-30+31/2}(E_8, 4 A_1) \cong \mathbb{C}, & & \mathscr{W}_{-30+31/2}(E_8,3 A_1) \cong L_{-9+13/2}(F_4). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-30+30/31}(E_8,E_8) \cong \mathbb{C}, && \mathscr{W}_{-30+31/30}(E_8,E_8) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/24}(E_8,E_8(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-30+31/20}(E_8,E_8(a_2)) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+31/18}(E_8,E_7) \cong L_{-2+2/9}(A_1), && \mathscr{W}_{-30+31/15}(E_8,E_8(a_4)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/12}(E_8,D_7) \cong L_{-2+2/3}(A_1), && \mathscr{W}_{-30+31/12}(E_8,E_8(a_5)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+30/13}(E_8,E_6) \cong L_{-4+4/13}(G_2), && \mathscr{W}_{-30+31/12}(E_8,E_6) \cong L_{-4+7/12}(G_2), \\ & \mathscr{W}_{-30+31/10}(E_8,E_8(a_6)) \cong \mathbb{C}, && \mathscr{W}_{-30+31/10}(E_8,D_6) \cong L_{-3+3/5}(B_2), \\ & \mathscr{W}_{-30+31/9}(E_8,E_6(a_1)) \cong L_{-3+4/9}(A_2), & & \mathscr{W}_{-30+31/8}(A_7,A_7) \cong \mathbb{C},\\ & \mathscr{W}_{-30+30/7}(E_8,A_6) \cong L_{-2+2/7}(A_1), & & \mathscr{W}_{-30+31/6}(E_8,E_8(a_7)) \cong \mathbb{C}, \\ & \mathscr{W}_{-30+31/6}(E_8,E_8(a_7)) \cong \mathbb{C}, & & \mathscr{W}_{-30+31/6}(E_8,D_6(a_2)) \cong L_{-2+2/3}(A_1)\otimes L_{-2+2/3}(A_1), & \\ & \mathscr{W}_{-30+31/6}(E_8,E_6(a_3)) \cong L_{-4+7/6}(G_2), & & \mathscr{W}_{-30+31/6}(E_8,D_4) \cong L_{-9+13/6}(F_4), \\ & \mathscr{W}_{-30+30/7}(E_8,D_4) \cong L_{-9+9/7}(F_4), & & \mathscr{W}_{-30+31/5}(E_8,A_4+A_3) \cong \mathbb{C}, & \\ & {\mathscr{W}_{-30+32/5}(E_8,A_4+A_3) \cong L_2(A_1)}, & & \mathscr{W}_{-30+31/4}(E_8,2 A_3) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+31/4}(E_8,D_4(a_1)+A_2) \cong L_{-3+3/2}(A_2), & & \mathscr{W}_{-30+31/3}(E_8,2A_2+2A_1) \cong \mathbb{C}, & \\ & \mathscr{W}_{-30+32/3}(E_8,2A_2+2A_1) \cong L_1(B_2), & & \mathscr{W}_{-30+31/3}(E_8,2A_2) \cong L_{-4+7/3}(G_2) \otimes L_{-4+7/3}(G_2), & \\ & \mathscr{W}_{-30+31/2}(E_8, 4 A_1) \cong \mathbb{C}, & & \mathscr{W}_{-30+31/2}(E_8,3 A_1) \cong L_{-9+13/2}(F_4). \end{align*} $$
Moreover, the following inclusions are finite extensions.

Remark 10.12. In the below comments, we argue as in Remark 10.2 to conclude that the varieties are not isomorphic with the same dimension.
-
1. The associated variety of
 $H_{DS,D_5}^0(L_{-30+31/8}(E_8))$
is not isomorphic to the associated variety of
$H_{DS,D_5}^0(L_{-30+31/8}(E_8))$
is not isomorphic to the associated variety of
 $L_{-5+7/8}(B_3)$
. The former is the nilpotent Slodowy slice
$L_{-5+7/8}(B_3)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{A_7,D_5}$
in
$\mathcal {S}_{A_7,D_5}$
in
 $E_8$
, while the later is the closure of the the nilpotent cone
$E_8$
, while the later is the closure of the the nilpotent cone
 $\mathcal {N}_{B_3}$
of
$\mathcal {N}_{B_3}$
of
 $B_3$
.
$B_3$
. -
2. The associated variety of
 $H_{DS,D_4(a_1)}^0(L_{-30+31/4}(E_8))$
is not isomorphic to the associated variety of
$H_{DS,D_4(a_1)}^0(L_{-30+31/4}(E_8))$
is not isomorphic to the associated variety of
 $L_{-4+7/4}(D_4)$
. The former is the nilpotent Slodowy slice
$L_{-4+7/4}(D_4)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{2 A_3,D_4(a_1)}$
in
$\mathcal {S}_{2 A_3,D_4(a_1)}$
in
 $E_8$
, while the later is the closure of the orbit
$E_8$
, while the later is the closure of the orbit
 ${\mathbb {O}}_{1;(5,3)}$
in
${\mathbb {O}}_{1;(5,3)}$
in
 $D_4$
.
$D_4$
. -
3. The associated variety of
 $H_{DS,A_3}^0(L_{-30+31/4}(E_8))$
is not isomorphic to the associated variety of
$H_{DS,A_3}^0(L_{-30+31/4}(E_8))$
is not isomorphic to the associated variety of
 $L_{-9+11/4}(B_5)$
. The former is the nilpotent Slodowy slice
$L_{-9+11/4}(B_5)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{2 A_3,A_3}$
in
$\mathcal {S}_{2 A_3,A_3}$
in
 $E_8$
, while the later is the closure of the orbit
$E_8$
, while the later is the closure of the orbit
 ${\mathbb {O}}_{1;(4^2,3)}$
in
${\mathbb {O}}_{1;(4^2,3)}$
in
 $B_5$
.
$B_5$
. -
4. The associated variety of
 $H_{DS,A_2}^0(L_{-30+31/3}(E_8))$
is not isomorphic to the associated variety of
$H_{DS,A_2}^0(L_{-30+31/3}(E_8))$
is not isomorphic to the associated variety of
 $L_{-12+13/3}(E_6)$
. The former is the nilpotent Slodowy slice
$L_{-12+13/3}(E_6)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{2 A_2+2 A_1,A_2}$
in
$\mathcal {S}_{2 A_2+2 A_1,A_2}$
in
 $E_8$
, while the later is the closure of the orbit
$E_8$
, while the later is the closure of the orbit
 $2 A_2+A_1$
in
$2 A_2+A_1$
in
 $E_6$
.
$E_6$
. -
5. The associated variety of
 $H_{DS,2A_1}^0(L_{-30+31/2}(E_8))$
is isomorphic to the associated variety of
$H_{DS,2A_1}^0(L_{-30+31/2}(E_8))$
is isomorphic to the associated variety of
 $L_{-11+13/2}(B_6)$
. The former is the nilpotent Slodowy slice
$L_{-11+13/2}(B_6)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{4 A_1, 2A_1}$
in
$\mathcal {S}_{4 A_1, 2A_1}$
in
 $E_8$
, while the later is the closure of the orbit
$E_8$
, while the later is the closure of the orbit
 ${\mathbb {O}}_{1;(2^6,1)}$
in
${\mathbb {O}}_{1;(2^6,1)}$
in
 $B_6$
.
$B_6$
. -
6. The associated variety of
 $H_{DS,A_1}^0(L_{-30+31/2}(E_8))$
is not isomorphic to the associated variety of
$H_{DS,A_1}^0(L_{-30+31/2}(E_8))$
is not isomorphic to the associated variety of
 $L_{-18+19/2}(E_7)$
. Indeed the former is the nilpotent Slodowy slice
$L_{-18+19/2}(E_7)$
. Indeed the former is the nilpotent Slodowy slice
 $\mathcal {S}_{4 A_1,A_1}$
in
$\mathcal {S}_{4 A_1,A_1}$
in
 $E_8$
, while the later is the closure of the orbit
$E_8$
, while the later is the closure of the orbit
 $4 A_1$
in
$4 A_1$
in
 $E_7$
.
$E_7$
.
Proposition 10.13. The following decompositions hold:
 $$ \begin{align*} & \mathscr{W}_{-30+31/8}(E_8,D_5) \cong L_{-3+7/8}(B_3) {\oplus L_{-3+7/8}(B_3;\varpi_3)}, \\ & \mathscr{W}_{-30+31/4}(E_8,D_4(a_1)) \cong L_{-6+7/4}(D_4) \oplus \bigoplus_{i=1,3,4} L_{-6+7/4}(D_4;\varpi_i), \\ & \mathscr{W}_{-30+31/4}(E_8,A_3) \cong L_{-9+11/4}(B_5) \oplus L_{-9+11/4}(B_5;\varpi_1), \\ & \mathscr{W}_{-30+31/3}(E_8,A_2) \cong L_{-12+13/3}(E_6) {\oplus L_{-12+13/3}(E_6;\varpi_1) \oplus L_{-12+13/3}(E_6;\varpi_6)}, \\ & \mathscr{W}_{-30+31/2}(E_8,2 A_1) \cong L_{-11+13/2}(B_6) \oplus L_{-11+13/2}(B_6;\varpi_6) , \\ & \mathscr{W}_{-30+31/2}(E_8,A_1) \cong L_{-18+19/2}(E_7) {\oplus L_{-18+19/2}(E_7;\varpi_7)}. & \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-30+31/8}(E_8,D_5) \cong L_{-3+7/8}(B_3) {\oplus L_{-3+7/8}(B_3;\varpi_3)}, \\ & \mathscr{W}_{-30+31/4}(E_8,D_4(a_1)) \cong L_{-6+7/4}(D_4) \oplus \bigoplus_{i=1,3,4} L_{-6+7/4}(D_4;\varpi_i), \\ & \mathscr{W}_{-30+31/4}(E_8,A_3) \cong L_{-9+11/4}(B_5) \oplus L_{-9+11/4}(B_5;\varpi_1), \\ & \mathscr{W}_{-30+31/3}(E_8,A_2) \cong L_{-12+13/3}(E_6) {\oplus L_{-12+13/3}(E_6;\varpi_1) \oplus L_{-12+13/3}(E_6;\varpi_6)}, \\ & \mathscr{W}_{-30+31/2}(E_8,2 A_1) \cong L_{-11+13/2}(B_6) \oplus L_{-11+13/2}(B_6;\varpi_6) , \\ & \mathscr{W}_{-30+31/2}(E_8,A_1) \cong L_{-18+19/2}(E_7) {\oplus L_{-18+19/2}(E_7;\varpi_7)}. & \end{align*} $$
Proof. We argue as in the proof of Proposition 10.3. More precisely, for f in
![]() $D_5$
,
$D_5$
,
![]() $D_4(a_1)$
or
$D_4(a_1)$
or
![]() $A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.12.
$A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.12.
For other cases, similar arguments as before Conjecture 9.12 lead to the following conjecture.
Conjecture 10.14.

In type
![]() $E_8$
, we make the following conjecture concerning non-admissible levels.
$E_8$
, we make the following conjecture concerning non-admissible levels.
Conjecture 10.15. The following isomorphisms hold.
 $$ \begin{align*} & \mathscr{W}_{-30+32/12}(E_8,E_6) \cong L_{-4+2/3}(G_2) , & & \mathscr{W}_{-24}(E_8,E_6(a_3)) \cong L_{-2}(G_2) , \\ & \mathscr{W}_{-45/2}(E_8,A_4+2A_1) \cong \mathbb{C} , & & \mathscr{W}_{-70/3}(E_8,A_4+A_2+A_1) \cong \mathbb{C}. \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-30+32/12}(E_8,E_6) \cong L_{-4+2/3}(G_2) , & & \mathscr{W}_{-24}(E_8,E_6(a_3)) \cong L_{-2}(G_2) , \\ & \mathscr{W}_{-45/2}(E_8,A_4+2A_1) \cong \mathbb{C} , & & \mathscr{W}_{-70/3}(E_8,A_4+A_2+A_1) \cong \mathbb{C}. \end{align*} $$
For example, in the case of f of Bala-Carter type
![]() $A_4+2A_1$
the conjecture is motivated by the fact that the central charge is
$A_4+2A_1$
the conjecture is motivated by the fact that the central charge is
![]() $0$
and
$0$
and
![]() $k_0^\natural =k_1^\natural =0$
. Similarly, for f of type
$k_0^\natural =k_1^\natural =0$
. Similarly, for f of type
![]() $A_4+A_2+A_1$
, we find
$A_4+A_2+A_1$
, we find
![]() $k_1^\natural =0$
.
$k_1^\natural =0$
.
Theorem 10.16. The following isomorphisms hold, providing collapsing levels for
![]() $G_2$
.
$G_2$
.
 $$ \begin{align*} & \mathscr{W}_{-4+7/12}(G_2,G_2) \cong \mathbb{C}, && \mathscr{W}_{-4+4/7}(G_2,G_2) \cong \mathbb{C} \\ & \mathscr{W}_{-4+7/6}(G_2,G_2(a_1)) \cong \mathbb{C} , && \mathscr{W}_{-4+7/6}(G_2,\tilde A_1) \cong L_{-2+2/3}(A_1), \\ & \mathscr{W}_{-4+7/3}(G_2,A_1) \cong \mathbb{C}, && \mathscr{W}_{-4+8/3}(G_2,A_1) \cong L_{1}(A_1). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-4+7/12}(G_2,G_2) \cong \mathbb{C}, && \mathscr{W}_{-4+4/7}(G_2,G_2) \cong \mathbb{C} \\ & \mathscr{W}_{-4+7/6}(G_2,G_2(a_1)) \cong \mathbb{C} , && \mathscr{W}_{-4+7/6}(G_2,\tilde A_1) \cong L_{-2+2/3}(A_1), \\ & \mathscr{W}_{-4+7/3}(G_2,A_1) \cong \mathbb{C}, && \mathscr{W}_{-4+8/3}(G_2,A_1) \cong L_{1}(A_1). \end{align*} $$
Moreover, the following isomorphism holds.
Proof. To prove the second assertion, we argue as in the proof of Proposition 10.3 using Remark 10.17 below.
Remark 10.17. The associated variety of
![]() $\mathscr {W}_{-4+5/2}(G_2,A_1)$
is not isomorphic to the associated variety of
$\mathscr {W}_{-4+5/2}(G_2,A_1)$
is not isomorphic to the associated variety of
![]() $L_{-2+5/2}(A_1)$
. The former is the nilpotent Slodowy slice
$L_{-2+5/2}(A_1)$
. The former is the nilpotent Slodowy slice
![]() $\mathcal {S}_{\tilde A_1,A_1}$
in
$\mathcal {S}_{\tilde A_1,A_1}$
in
![]() $G_2$
, while the later is the the nilpotent cone in
$G_2$
, while the later is the the nilpotent cone in
![]() $A_1$
, and it is known that
$A_1$
, and it is known that
![]() $\mathcal {S}_{\tilde A_1,A_1}$
is a 2-dimensional non-normal variety.
$\mathcal {S}_{\tilde A_1,A_1}$
is a 2-dimensional non-normal variety.
Table 11 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $G_2.$
$G_2.$

Table 12 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $F_4$
.
$F_4$
.

Table 13 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $E_6.$
$E_6.$

Table 14 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $E_7$
.
$E_7$
.

Table 15 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $E_7$
.
$E_7$
.

Table 16 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $E_8$
.
$E_8$
.

Table 17 Centralisers of
![]() ${\mathfrak {sl}}_2$
-triples in type
${\mathfrak {sl}}_2$
-triples in type
![]() $E_8$
.
$E_8$
.

Theorem 10.18. The following isomorphisms hold, providing collapsing levels for
![]() $\mathfrak {g}=F_4$
.
$\mathfrak {g}=F_4$
.
 $$ \begin{align*} & \mathscr{W}_{-9+13/18}(F_4,F_4) \cong \mathbb{C}, && \mathscr{W}_{-9+9/13}(F_4,F_4) \cong \mathbb{C} \\ & \mathscr{W}_{-9+13/12}(F_4,F_4(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-9+9/7}(F_4,C_3) \cong L_{-2+2/7}(A_1) \\ & \mathscr{W}_{-9+9/7}(F_4,B_3) \cong L_{-2+2/7}(A_1) , && \mathscr{W}_{-9+13/8}(F_4,B_3) \cong L_{1}(A_1) \\ & \mathscr{W}_{-9+13/6}(F_4,F_4(a_3)) \cong \mathbb{C} , && \mathscr{W}_{-9+13/6}(F_4,C_3(a_1)) \cong L_{-2+2/3}(A_1) \\ & \mathscr{W}_{-9+13/6}(F_4,B_3) \cong L_{-2+2/3}(A_1) \otimes L_{-2+2/3}(A_1) , && \mathscr{W}_{-9+13/6}(F_4,\tilde A_2)) \cong L_{-4+7/6}(G_2) \\ & \mathscr{W}_{-9+13/4}(F_4,A_2 +\tilde A_1) \cong \mathbb{C} , && \mathscr{W}_{-9+13/4}(F_4,A_2)) \cong L_{-3+3/2}(A_2), \\ & \mathscr{W}_{-9+13/2}(F_4,A_1)) \cong \mathbb{C}. \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-9+13/18}(F_4,F_4) \cong \mathbb{C}, && \mathscr{W}_{-9+9/13}(F_4,F_4) \cong \mathbb{C} \\ & \mathscr{W}_{-9+13/12}(F_4,F_4(a_1)) \cong \mathbb{C}, && \mathscr{W}_{-9+9/7}(F_4,C_3) \cong L_{-2+2/7}(A_1) \\ & \mathscr{W}_{-9+9/7}(F_4,B_3) \cong L_{-2+2/7}(A_1) , && \mathscr{W}_{-9+13/8}(F_4,B_3) \cong L_{1}(A_1) \\ & \mathscr{W}_{-9+13/6}(F_4,F_4(a_3)) \cong \mathbb{C} , && \mathscr{W}_{-9+13/6}(F_4,C_3(a_1)) \cong L_{-2+2/3}(A_1) \\ & \mathscr{W}_{-9+13/6}(F_4,B_3) \cong L_{-2+2/3}(A_1) \otimes L_{-2+2/3}(A_1) , && \mathscr{W}_{-9+13/6}(F_4,\tilde A_2)) \cong L_{-4+7/6}(G_2) \\ & \mathscr{W}_{-9+13/4}(F_4,A_2 +\tilde A_1) \cong \mathbb{C} , && \mathscr{W}_{-9+13/4}(F_4,A_2)) \cong L_{-3+3/2}(A_2), \\ & \mathscr{W}_{-9+13/2}(F_4,A_1)) \cong \mathbb{C}. \end{align*} $$
Moreover, the following inclusions are finite extensions.

Remark 10.19. In the below comments, we argue as in Remark 10.2 to conclude that the varieties are not isomorphic.
-
1. The associated variety of
 $H_{DS,A_2+\tilde A_1}^0(L_{-9+10/3}(F_4))$
is not isomorphic to the associated variety of
$H_{DS,A_2+\tilde A_1}^0(L_{-9+10/3}(F_4))$
is not isomorphic to the associated variety of
 $L_{-2+5/2}(A_1)$
. The former is the nilpotent Slodowy slice
$L_{-2+5/2}(A_1)$
. The former is the nilpotent Slodowy slice
 $\mathcal {S}_{\tilde A_2+A_1, A_2+\tilde A_1}$
whose singularity at
$\mathcal {S}_{\tilde A_2+A_1, A_2+\tilde A_1}$
whose singularity at
 $f \in A_2+\tilde A_1$
is not normal (see [Reference Fu, Juteau, Levy and Sommers47, §1.8.4]), while the later is the nilpotent cone of
$f \in A_2+\tilde A_1$
is not normal (see [Reference Fu, Juteau, Levy and Sommers47, §1.8.4]), while the later is the nilpotent cone of
 $A_1={\mathfrak {sl}}_2$
.
$A_1={\mathfrak {sl}}_2$
. -
2. The associated variety of
 $H_{DS,A_2}^0(L_{-9+10/3}(F_4,A_2)$
is not isomorphic to the associated variety of
$H_{DS,A_2}^0(L_{-9+10/3}(F_4,A_2)$
is not isomorphic to the associated variety of
 $L_{-2+5/3}(A_2)$
. The former is the nilpotent Slodowy slice
$L_{-2+5/3}(A_2)$
. The former is the nilpotent Slodowy slice
 $\mathcal{S}_{\tilde{\tilde{A}}_2+A_1, A_2}$
, while the later is the nilpotent cone of
$\mathcal{S}_{\tilde{\tilde{A}}_2+A_1, A_2}$
, while the later is the nilpotent cone of
 $A_2$
.
$A_2$
. -
3. The associated variety of
 $H_{DS,\tilde {A}_1}^0(L_{-9+13/4}(F_4))$
is not isomorphic to the associated variety of
$H_{DS,\tilde {A}_1}^0(L_{-9+13/4}(F_4))$
is not isomorphic to the associated variety of
 $L_{-4+5/4}(A_3)$
. Indeed, the former is the nilpotent Slodowy slice
$L_{-4+5/4}(A_3)$
. Indeed, the former is the nilpotent Slodowy slice
 $\mathcal {S}_{A_2+\tilde {A}_1, \tilde {A}_1}$
in
$\mathcal {S}_{A_2+\tilde {A}_1, \tilde {A}_1}$
in
 $F_4$
, while the later is the nilpotent cone of
$F_4$
, while the later is the nilpotent cone of
 $A_3={\mathfrak {sl}}_4$
. But the number of nilpotent
$A_3={\mathfrak {sl}}_4$
. But the number of nilpotent
 $G^\natural $
-orbits in
$G^\natural $
-orbits in
 $\mathcal {N}_{A_3}$
is 5, while the number of
$\mathcal {N}_{A_3}$
is 5, while the number of
 $G^\natural $
-orbits in
$G^\natural $
-orbits in
 $\mathcal {S}_{A_2+\tilde {A}_1, \tilde {A}_1}$
would be 4.
$\mathcal {S}_{A_2+\tilde {A}_1, \tilde {A}_1}$
would be 4.
Proposition 10.20. The following decompositions hold:
 $$ \begin{align*} & \mathscr{W}_{-9+10/3}(F_4,A_2+\tilde A_1) \cong L_{-2+5/2}(A_1) \oplus L_{-2+5/2}(A_1;\varpi_1), \\ & \mathscr{W}_{-9+10/3}(F_4,A_2) \cong L_{-3+5/3}(A_2) \oplus L_{-3+5/3}(A_2;\varpi_1) \oplus L_{-3+5/3}(A_2;\varpi_2), \\ & \mathscr{W}_{-9+13/4}(F_4,\tilde A_1) \cong L_{-4+5/4}(A_3) \oplus \bigoplus_{i=1,2,3}L_{-4+5/4}(A_3;\varpi_i). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-9+10/3}(F_4,A_2+\tilde A_1) \cong L_{-2+5/2}(A_1) \oplus L_{-2+5/2}(A_1;\varpi_1), \\ & \mathscr{W}_{-9+10/3}(F_4,A_2) \cong L_{-3+5/3}(A_2) \oplus L_{-3+5/3}(A_2;\varpi_1) \oplus L_{-3+5/3}(A_2;\varpi_2), \\ & \mathscr{W}_{-9+13/4}(F_4,\tilde A_1) \cong L_{-4+5/4}(A_3) \oplus \bigoplus_{i=1,2,3}L_{-4+5/4}(A_3;\varpi_i). \end{align*} $$
Proof. We argue as in the proof of Proposition 10.3. More precisely, for
![]() $f \in A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.19.
$f \in A_2$
, we can use the fact that f is even. For the other cases, we use Proposition 6.8 and Remark 10.19.
For other cases, similar arguments as before Conjecture 9.12 lead to the following conjecture.
Conjecture 10.21.
 $$ \begin{align*} & \mathscr{W}_{-9+13/10}(F_4,C_3) \cong L_{-2+3/10}(A_1) \oplus L_{-2+3/10}(A_1;\varpi_1), \\ & \mathscr{W}_{-9+9/5}(F_4,B_2) \cong (L_{-2+3/10}(A_1) \otimes L_{-2+3/10}(A_1)) \oplus( L_{-2+3/10}(A_1;\varpi_1) \otimes L_{-2+3/10}(A_1;\varpi_1)). \end{align*} $$
$$ \begin{align*} & \mathscr{W}_{-9+13/10}(F_4,C_3) \cong L_{-2+3/10}(A_1) \oplus L_{-2+3/10}(A_1;\varpi_1), \\ & \mathscr{W}_{-9+9/5}(F_4,B_2) \cong (L_{-2+3/10}(A_1) \otimes L_{-2+3/10}(A_1)) \oplus( L_{-2+3/10}(A_1;\varpi_1) \otimes L_{-2+3/10}(A_1;\varpi_1)). \end{align*} $$
As in the classical cases, we have the following conjecture.
Conjecture 10.22. Assume that
![]() $\mathfrak {g}$
simple of exceptional type. The cases covered by Theorems 10.1, 10.6, 10.11, 10.16 and 10.18 give the exhaustive list of pairs
$\mathfrak {g}$
simple of exceptional type. The cases covered by Theorems 10.1, 10.6, 10.11, 10.16 and 10.18 give the exhaustive list of pairs
![]() $(f,k)$
where f is a nilpotent element of
$(f,k)$
where f is a nilpotent element of
![]() $\mathfrak {g}$
and k is an admissible collapsing levels for
$\mathfrak {g}$
and k is an admissible collapsing levels for
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
Conjecture 10.23. The following isomorphisms hold.
Writing
![]() $k=-9+12/8$
and
$k=-9+12/8$
and
![]() $k^\natural = -4+4/8$
, we find that
$k^\natural = -4+4/8$
, we find that
![]() $\mathscr {W}_{-15/2}(F_4,\tilde A_2)$
and
$\mathscr {W}_{-15/2}(F_4,\tilde A_2)$
and
![]() $L_{-7/2}(G_2)$
have the same central charge and that the (conjectural) formula for asymptotic growth and asymptotic dimension coincide; see Table 10. Similarly, writing
$L_{-7/2}(G_2)$
have the same central charge and that the (conjectural) formula for asymptotic growth and asymptotic dimension coincide; see Table 10. Similarly, writing
![]() $k=-9+9/3$
and
$k=-9+9/3$
and
![]() $k^\natural = -4+6/3$
, we find that
$k^\natural = -4+6/3$
, we find that
![]() $\mathscr {W}_{-6}(F_4,\tilde A_2)$
and
$\mathscr {W}_{-6}(F_4,\tilde A_2)$
and
![]() $L_{-2}(G_2)$
have the same central charge and that the (conjectural) formula for asymptotic growth and asymptotic dimension coincide; see Table 10.
$L_{-2}(G_2)$
have the same central charge and that the (conjectural) formula for asymptotic growth and asymptotic dimension coincide; see Table 10.
11 Centralisers of
 ${\mathfrak {sl}}_2$
-triples in simple exceptional Lie algebras
${\mathfrak {sl}}_2$
-triples in simple exceptional Lie algebras
In this appendix, we collect the data relative to each
![]() ${\mathfrak {sl}}_2$
-triples in simple exceptional Lie algebras. Our results are obtained using the software GAP4 and are summarised in Tables 11, 12, 13, 15 and 17.
${\mathfrak {sl}}_2$
-triples in simple exceptional Lie algebras. Our results are obtained using the software GAP4 and are summarised in Tables 11, 12, 13, 15 and 17.
In the tables, nilpotent orbits are given by the Bala-Carter classification (first column). We indicate in the second column whether the nilpotent orbit is even or not. The third column gives the type of
![]() $\mathfrak {g}^\natural $
, and the last column gives the values of the
$\mathfrak {g}^\natural $
, and the last column gives the values of the
![]() $k_i^\natural $
’s. Obviously, the order follows the order of the simple factors of
$k_i^\natural $
’s. Obviously, the order follows the order of the simple factors of
![]() $\mathfrak {g}^{\natural }$
as appearing in the third column.
$\mathfrak {g}^{\natural }$
as appearing in the third column.
Acknowledgements
The authors wish to express their gratitude to Daniel Juteau for the numerous fruitful discussions on nilpotent Slodowy slices. They are also grateful to Wenbin Yan for several helpful comments concerning collapsing levels in 4D superconformal theory, and they warmly thank Thomas Creutzig and Kazuya Kawasetsu whose question about the isomorphism
![]() $\mathscr {W}_{-14/3}({\mathfrak {sl}}_7) \cong L_{-8/3}({\mathfrak {sl}}_4)$
and corresponding associated varieties was the starting point of this work. TA and JvE wish to thank the University of Lille and the Laboratoire Painlevé for the organisation and the financial support of the conference Geometric and automorphic aspects of W-algebras in 2019 where the collaboration between the three authors started. AM gratefully acknowledges the RIMS of Kyoto, where part of this paper was written, for financial support and its hospitality during her stay in autumn 2018.
$\mathscr {W}_{-14/3}({\mathfrak {sl}}_7) \cong L_{-8/3}({\mathfrak {sl}}_4)$
and corresponding associated varieties was the starting point of this work. TA and JvE wish to thank the University of Lille and the Laboratoire Painlevé for the organisation and the financial support of the conference Geometric and automorphic aspects of W-algebras in 2019 where the collaboration between the three authors started. AM gratefully acknowledges the RIMS of Kyoto, where part of this paper was written, for financial support and its hospitality during her stay in autumn 2018.
Competing interests
The authors have no competing interest to declare.
Funding statement
TA is partially supported by JSPS KAKENHI Grant Numbers J21H04993 and 19KK0065. JvE is supported by the Serrapilheira Institute (grant number Serra – 2023-0001), CNPq grants 310576/2020-2 and 306498/2023-5, and FAPERJ grant 201.445/2021. AM is partially supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research innovation programme (ERC-2020-SyG-854361-HyperK).






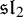







 .
.














































































