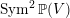 $\operatorname{Sym}^{2}\mathbb{P}(V)$
$\operatorname{Sym}^{2}\mathbb{P}(V)$
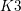 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
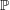 $\mathbb{P}$-objects
$\mathbb{P}$-objects
 $K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION
$K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION