Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T05:26:27.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Formality conjecture for minimal surfaces of Kodaira dimension 0

Part of: Homological algebra Rings and algebras with additional structure Families, fibrations (Co)homology theory

Published online by Cambridge University Press:  18 February 2021

Ruggero Bandiera ,
Marco Manetti  and
Francesco Meazzini
Ruggero Bandiera
Affiliation:
Dipartimento di Matematica Guido Castelnuovo, Università degli studi di Roma La Sapienza, P.le Aldo Moro 5, I-00185Roma, [email protected]
Marco Manetti
Affiliation:
Dipartimento di Matematica Guido Castelnuovo, Università degli studi di Roma La Sapienza, P.le Aldo Moro 5, I-00185Roma, [email protected]
Francesco Meazzini
Affiliation:
Dipartimento di Matematica Guido Castelnuovo, Università degli studi di Roma La Sapienza, P.le Aldo Moro 5, I-00185Roma, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 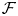$\mathcal {F}$ be a polystable sheaf on a smooth minimal projective surface of Kodaira dimension 0. Then the differential graded (DG) Lie algebra 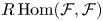$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ of derived endomorphisms of 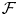$\mathcal {F}$ is formal. The proof is based on the study of equivariant 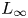$L_{\infty }$ minimal models of DG Lie algebras equipped with a cyclic structure of degree 2 which is non-degenerate in cohomology, and does not rely (even for K3 surfaces) on previous results on the same subject.

Keywords

deformation theorypolystable sheavesformalitydifferential graded Lie algebrasL∞ algebras

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions 14D15: Formal methods; deformations 16W50: Graded rings and modules 18G55: Homotopical algebra
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 2 , February 2021 , pp. 215 - 235
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E. and Saccà, G., Singularities of moduli spaces of sheaves on K3 surfaces and Nakajima quiver varieties, Adv. Math. 329 (2018), 649–703.CrossRefGoogle Scholar
Bandiera, R. and Manetti, M., Algebraic models of local period maps and Yukawa algebras, Lett. Math. Phys. 108 (2018), 2055–2097.10.1007/s11005-018-1064-1CrossRefGoogle Scholar
Bandiera, R., Manetti, M. and Meazzini, F., Deformations of polystable sheaves on surfaces: quadraticity implies formality, Mosc. Math. J. (2020), to appear.Google Scholar
Barth, W., Hulek, K., Peters, C. and van de Ven, A., Compact complex surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 4, second edition (Springer, 2004).10.1007/978-3-642-57739-0CrossRefGoogle Scholar
Beauville, A., Complex algebraic surfaces, London Mathematical Society Lecture Note Series, vol. 68 (Cambridge University Press, 1994).Google Scholar
Budur, N. and Zhang, Z., Formality conjecture for K3 surfaces, Compos. Math. 155 (2018), 902–911.10.1112/S0010437X19007206CrossRefGoogle Scholar
Getzler, E., Lie theory for nilpotent $L_{\infty }$ algebras, Ann. of Math. (2) 170 (2009), 271–301.CrossRefGoogle Scholar
Getzler, E. and Kapranov, M. M., Cyclic operads and cyclic homology, in Geometry, topology, and physics (International Press, Cambridge, MA, 1995), 167–201.Google Scholar
Halperin, S. and Stasheff, J., Obstructions to homotopy equivalences, Adv. Math. 32 (1979), 233–279.10.1016/0001-8708(79)90043-4CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves (Cambridge University Press, 2010).10.1017/CBO9780511711985CrossRefGoogle Scholar
Iacono, D. and Manetti, M., On deformations of pairs (manifold, coherent sheaf), Canad. J. Math. 71 (2019), 1209–1241.CrossRefGoogle Scholar
Kadeishvili, T. V., The algebraic structure in the cohomology of $A(\infty )$-algebras, Soobshch. Akad. Nauk Gruzin. SSR 108 (1982), 249–252 (Russian).Google Scholar
Kaledin, D., Some remarks on formality in families, Mosc. Math. J. 7 (2007), 643–652.10.17323/1609-4514-2007-7-4-643-652CrossRefGoogle Scholar
Kaledin, D. and Lehn, M., Local structure of hyperkähler singularities in O'Grady's examples, Mosc. Math. J. 7 (2007), 653–672.CrossRefGoogle Scholar
Kaledin, D., Lehn, M. and Sorger, Ch., Singular symplectic moduli spaces, Invent. Math. 164 (2006), 591–614.CrossRefGoogle Scholar
Kontsevich, M., Feynman diagram and low dimensional topology, Proc. First Eur. Congr. Math. (1994), 97–122.Google Scholar
Kontsevich, M., Deformation quantization of Poisson manifolds, I, Lett. Math. Phys. 66 (2003), 157–216.10.1023/B:MATH.0000027508.00421.bfCrossRefGoogle Scholar
Lada, T. and Markl, M., Strongly homotopy Lie algebras, Comm. Algebra 23 (1995), 2147–2161.10.1080/00927879508825335CrossRefGoogle Scholar
Lada, T. and Stasheff, J. D., Introduction to sh Lie algebras for physicists, Int. J. Theor. Phys. 32 (1993), 1087–1104.CrossRefGoogle Scholar
Lazarev, A. and Schedler, T., Curved infinity-algebras and their characteristic classes, J. Topol. 5 (2012), 503–528.CrossRefGoogle Scholar
Lunts, V. A., Formality of DG algebras (after Kaledin), J. Algebra 323 (2010), 878–898.CrossRefGoogle Scholar
Manetti, M., Differential graded Lie algebras and formal deformation theory, Algebraic Geometry: Seattle 2005. Proc. Sympos. Pure Math. 80 (2009), 785–810.10.1090/pspum/080.2/2483955CrossRefGoogle Scholar
Manetti, M., On some formality criteria for DG-Lie algebras, J. Algebra 438 (2015), 90–118.10.1016/j.jalgebra.2015.04.029CrossRefGoogle Scholar
Manetti, M., Lie methods in deformation theory. Draft version (2020).Google Scholar
Meazzini, F., A DG-enhancement of $D(\operatorname {QCoh}(X))$ with applications in deformation theory, Preprint (2018), arXiv:1808.05119.Google Scholar
Mukai, S., Symplectic structure of the moduli space of sheaves on an abelian or K3 surface, Invent. Math. 77 (1984), 101–116.CrossRefGoogle Scholar
Neisendorfer, J. and Miller, T., Formal and coformal spaces, Illinois J. Math. 22 (1978), 565–580.10.1215/ijm/1256048467CrossRefGoogle Scholar
O'Grady, K. G., Desingularized moduli spaces of sheaves on a K3, J. Reine Angew. Math. 512 (1999), 49–117.10.1515/crll.1999.056CrossRefGoogle Scholar
O'Grady, K. G., A new six-dimensional irreducible symplectic variety, J. Algebraic Geom. 12 (2003), 435–505.10.1090/S1056-3911-03-00323-0CrossRefGoogle Scholar
Rim, D. S., Equivariant $G$-structure on versal deformations, Trans. Amer. Math. Soc. 257 (1980), 217–226.Google Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, 1994).CrossRefGoogle Scholar
Yoshioka, K., Moduli spaces of stable sheaves on abelian surfaces, Math. Ann. 321 (2001), 817–884.CrossRefGoogle Scholar
Yoshioka, K., Stability and the Fourier-Mukai transform. II, Compos. Math. 145 (2009), 112–142.10.1112/S0010437X08003758CrossRefGoogle Scholar
Yoshioka, K., Fourier-Mukai duality for K3 surfaces via Bridgeland stability condition, J. Geom. Phys. 122 (2017), 103–118.CrossRefGoogle Scholar
Zhang, Z., A note on formality and singularities of moduli spaces, Mosc. Math. J. 12 (2012), 863–879.10.17323/1609-4514-2012-12-4-863-879CrossRefGoogle Scholar