Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T09:07:31.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Autoequivalences of twisted K3 surfaces

Part of: Families, fibrations (Co)homology theory Surfaces and higher-dimensional varieties Forms and linear algebraic groups

Published online by Cambridge University Press:  30 April 2019

Emanuel Reinecke
Emanuel Reinecke*
Affiliation:
Department of Mathematics, University of Michigan, 530 Church Street, Ann Arbor, MI 48109, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Derived equivalences of twisted K3 surfaces induce twisted Hodge isometries between them; that is, isomorphisms of their cohomologies which respect certain natural lattice structures and Hodge structures. We prove a criterion for when a given Hodge isometry arises in this way. In particular, we describe the image of the representation which associates to any autoequivalence of a twisted K3 surface its realization in cohomology: this image is a subgroup of index 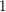$1$ or 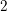$2$ in the group of all Hodge isometries of the twisted K3 surface. We show that both indices can occur.

Keywords

twisted K3 surfacesderived categoriestwisted Hodge structuresdeformations

MSC classification

Primary: 14J28: $K3$ surfaces and Enriques surfaces
Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 14D23: Stacks and moduli problems 11E12: Quadratic forms over global rings and fields
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 5 , May 2019 , pp. 912 - 937
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation under grant no. DMS-1501461 and by the Studienstiftung des deutschen Volkes.

References

Abramovich, D., Corti, A. and Vistoli, A., Twisted bundles and admissible covers , Comm. Algebra 31 (2003), 3547–3618; special issue in honor of Steven L. Kleiman.Google Scholar
Baily, W. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains , Ann. of Math. (2) 84 (1966), 442–528.Google Scholar
Borel, A., Introduction aux groupes arithmétiques , in Publications de l’institut de mathématique de l’université de strasbourg, Actualités Scientifiques et Industrielles, vol. 1341 (Hermann & Cie, Paris, 1969).Google Scholar
Borel, A., Some metric properties of arithmetic quotients of symmetric spaces and an extension theorem , J. Differential Geom. 6 (1972), 543–560; collection of articles dedicated to S. S. Chern and D. C. Spencer on their sixtieth birthdays.10.4310/jdg/1214430642Google Scholar
Borcea, C., Diffeomorphisms of a K3 surface , Math. Ann. 275 (1986), 1–4.Google Scholar
Căldăraru, A., Derived categories of twisted sheaves on Calabi–Yau manifolds, PhD thesis, Cornell University (ProQuest, Ann Arbor, MI, 2000).Google Scholar
Cassels, J., Rational quadratic forms, London Mathematical Society Monographs, vol. 13 (Academic Press, London, 1978).Google Scholar
Canonaco, A. and Stellari, P., Twisted Fourier–Mukai functors , Adv. Math. 212 (2007), 484–503.10.1016/j.aim.2006.10.010Google Scholar
Donaldson, S., Polynomial invariants for smooth four-manifolds , Topology 29 (1990), 257–315.10.1016/0040-9383(90)90001-ZGoogle Scholar
Giraud, J., Cohomologie non abélienne, Grundlehren der mathematischen Wissenschaften, vol. 179 (Springer, Berlin, 1971).Google Scholar
Hosono, S., Lian, B., Oguiso, K. and Yau, S.-T., Autoequivalences of derived category of a K3 surface and monodromy transformations , J. Algebraic Geom. 13 (2004), 513–545.10.1090/S1056-3911-04-00364-9Google Scholar
Huybrechts, D., Macrì, E. and Stellari, P., Stability conditions for generic K3 categories , Compos. Math. 144 (2008), 134–162.10.1112/S0010437X07003065Google Scholar
Huybrechts, D., Macrì, E. and Stellari, P., Derived equivalences of K3 surfaces and orientation , Duke Math. J. 149 (2009), 461–507.10.1215/00127094-2009-043Google Scholar
Hall, J. and Rydh., D., The Hilbert stack , Adv. Math. 253 (2014), 194–233.10.1016/j.aim.2013.12.002Google Scholar
Huybrechts, D. and Stellari, P., Equivalences of twisted K3 surfaces , Math. Ann. 332 (2005), 901–936.10.1007/s00208-005-0662-2Google Scholar
Huybrechts, D. and Stellari, P., Proof of Căldăraru’s conjecture. Appendix to ‘Moduli spaces of twisted sheaves on a projective variety’ by K. Yoshioka , in Moduli spaces and arithmetic geometry, Advanced Studies in Pure Mathematics, vol. 45 (Mathematical Society of Japan, Tokyo, 2006), 31–42.Google Scholar
Huybrechts, D., Lectures on K3 surfaces, Cambridge Studies in Advanced Mathematics, vol. 158 (Cambridge University Press, Cambridge, 2016).Google Scholar
Huybrechts, D., The K3 category of a cubic fourfold , Compos. Math. 153 (2017), 586–620.10.1112/S0010437X16008137Google Scholar
Knudsen, F. and Mumford, D., The projectivity of the moduli space of stable curves. I. Preliminaries on ‘det’ and ‘Div’ , Math. Scand. 39 (1976), 19–55.Google Scholar
Kneser, M., Klassenzahlen indefiniter quadratischer Formen in drei oder mehr Veränderlichen , Arch. Math. (Basel) 7 (1956), 323–332.Google Scholar
Kneser, M., Orthogonale Gruppen über algebraischen Zahlkörpern , J. Reine Angew. Math. 196 (1956), 213–220.Google Scholar
Kovács, S., The cone of curves of a K3 surface , Math. Ann. 300 (1994), 681–691.10.1007/BF01450509Google Scholar
Kodaira, K. and Spencer, D., On deformations of complex analytic structures. III. Stability theorems for complex structures , Ann. of Math. (2) 71 (1960), 43–76.10.2307/1969879Google Scholar
Kudla, S., A note about special cycles on moduli spaces of K3 surfaces , in Arithmetic and geometry of K3 surfaces and Calabi–Yau threefolds, Fields Institute Communications, vol. 67 (Springer, New York, 2013), 411–427.Google Scholar
Lieblich, M., Moduli of twisted sheaves , Duke Math. J. 138 (2007), 23–118.10.1215/S0012-7094-07-13812-2Google Scholar
Lieblich, M., Twisted sheaves and the period-index problem , Compos. Math. 144 (2008), 1–31.Google Scholar
Lieblich, M. and Olsson, M., Fourier–Mukai partners of K3 surfaces in positive characteristic , Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 1001–1033.10.24033/asens.2264Google Scholar
Miranda, R. and Morrison, D., Embeddings of integral quadratic forms (2009), http://web.math.ucsb.edu/∼drm/manuscripts/eiqf.pdf.Google Scholar
Mukai, S., On the moduli space of bundles on K3 surfaces. I , in Vector bundles on algebraic varieties (Bombay, 1984), Studies in Mathematics (Tata Institute of Fundamental Research), vol. 11 (Oxford University Press, Bombay, 1987), 341–413.Google Scholar
Nikulin, V., Integer symmetric bilinear forms and some of their geometric applications , Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), 111–177.Google Scholar
Olsson, M., Deformation theory of representable morphisms of algebraic stacks , Math. Z. 253 (2006), 25–62.10.1007/s00209-005-0875-9Google Scholar
O’Meara, T., Introduction to quadratic forms , in Classics in Mathematics, reprint of the 1973 edition (Springer, Berlin, 2000).Google Scholar
Orlov, D., Equivalences of derived categories and K3 surfaces , J. Math. Sci. (New York) 84 (1997), 1361–1381.Google Scholar
Ploog, D., Groups of autoequivalences of derived categories of smooth projective varieties, PhD thesis, FU Berlin (Logos, Berlin, 2005).Google Scholar
Rizov, J., Moduli stacks of polarized K3 surfaces in mixed characteristic , Serdica Math. J. 32 (2006), 131–178.Google Scholar
Demazure, M. and Grothendieck, A. (eds), Schémas en groupes I: Propriétés générales des schémas en groupes , Séminaire de Géométrie Algébrique du Bois Marie 1962–64 (SGA 3), Lecture Notes in Mathematics, vol. 151 (Springer, Berlin, 1970).Google Scholar
Berthelot, P., Grothendieck, A. and Illusie, L. (eds), Théorie des intersections et théorème de Riemann–Roch , Séminaire de Géométrie Algébrique du Bois Marie 1966–67 (SGA 6), Lecture Notes in Mathematics, vol. 225 (Springer, Berlin, 2006).Google Scholar
The Stacks Project Authors. Stacks Project (2017), http://stacks.math.columbia.edu.Google Scholar
Schürg, T., Toën, B. and Vezzosi, G., Derived algebraic geometry, determinants of perfect complexes, and applications to obstruction theories for maps and complexes , J. Reine Angew. Math. 702 (2015), 1–40.10.1515/crelle-2013-0037Google Scholar
Szendrői, B., Diffeomorphisms and families of Fourier–Mukai transforms in mirror symmetry , in Applications of algebraic geometry to coding theory, physics and computation (Eilat, 2001), NATO Sci. Ser. II Math. Phys. Chem., vol. 36 (Kluwer Academic Publishers, Dordrecht, 2001), 317–337.Google Scholar
Toën, B., K-théorie et cohomologie des champs algébriques, PhD thesis, Université Paul Sabatier-Toulouse III (1999).Google Scholar
Toën, B., Derived Azumaya algebras and generators for twisted derived categories , Invent. Math. 189 (2012), 581–652.10.1007/s00222-011-0372-1Google Scholar
Toën, B. and Vaquié, M., Moduli of objects in dg-categories , Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 387–444.10.1016/j.ansens.2007.05.001Google Scholar