Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T13:16:13.293Z Has data issue: false hasContentIssue false
  • English
  • Français

$K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION

Part of: Cycles and subschemes (Co)homology theory Families, fibrations

Published online by Cambridge University Press:  05 November 2018

Junliang Shen  and
Qizheng Yin
Junliang Shen
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, USA ([email protected])
Qizheng Yin
Affiliation:
Peking University, Beijing International Center for Mathematical Research, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We explore the connection between $K3$ categories and 0-cycles on holomorphic symplectic varieties. In this paper, we focus on Kuznetsov’s noncommutative $K3$ category associated to a nonsingular cubic 4-fold.

By introducing a filtration on the 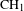$\text{CH}_{1}$-group of a cubic 4-fold $Y$, we conjecture a sheaf/cycle correspondence for the associated $K3$ category 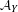${\mathcal{A}}_{Y}$. This is a noncommutative analog of O’Grady’s conjecture concerning derived categories of $K3$ surfaces. We study instances of our conjecture involving rational curves in cubic 4-folds, and verify the conjecture for sheaves supported on low degree rational curves.

Our method provides systematic constructions of (a) the Beauville–Voisin filtration on the 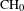$\text{CH}_{0}$-group and (b) algebraically coisotropic subvarieties of a holomorphic symplectic variety which is a moduli space of stable objects in 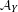${\mathcal{A}}_{Y}$.

Keywords

K3 categoriescubic fourfoldsO’Grady filtrationholomorphic symplectic varietiesBeauville–Voisin conjectures

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions
Secondary: 14C15: (Equivariant) Chow groups and rings; motives 14D20: Algebraic moduli problems, moduli of vector bundles
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1601 - 1627
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addington, N. and Lehn, M., On the symplectic eightfold associated to a Pfaffian cubic fourfold, J. Reine Angew. Math. 731 (2017), 129–137.Google Scholar
Addington, N. and Thomas, R. P., Hodge theory and derived categories of cubic fourfolds, Duke Math. J. 163(10) (2014), 1885–1927.Google Scholar
Atiyah, M. F. and Hirzebruch, F., The Riemann–Roch theorem for analytic embeddings, Topology 1 (1962), 151–166.Google Scholar
Bayer, A., Lahoz, M., Macrì, E., Nuer, H., Perry, A. and Stellari, P., Families of stability conditions, in preparation.Google Scholar
Bayer, A., Lahoz, M., Macrì, E. and Stellari, P., Stability conditions on Kuznetsov components. Appendix joint with X. Zhao, Preprint, 2017, arXiv:1703.10839.Google Scholar
Beauville, A., On the splitting of the Bloch–Beilinson filtration, in Algebraic Cycles and Motives, Vol. 2, London Math. Soc. Lecture Note Ser., Volume 344, pp. 38–53 (Cambridge Univ. Press, Cambridge, 2007).Google Scholar
Beauville, A. and Donagi, R., La variété des droites d’une hypersurface cubique de dimension 4, C. R. Acad. Sci. Paris Sér. I Math. 301(14) (1985), 703–706.Google Scholar
Beauville, A. and Voisin, C., On the Chow ring of a K3 surface, J. Algebraic Geom. 13(3) (2004), 417–426.Google Scholar
Bloch, S. and Srinivas, V., Remarks on correspondences and algebraic cycles, Amer. J. Math. 105(5) (1983), 1235–1253.Google Scholar
Bridgeland, T., Stability conditions on triangulated categories, Ann. of Math. (2) 166(2) (2007), 317–345.Google Scholar
Charles, F. and Pacienza, G., Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles, Preprint, 2014, arXiv:1401.4071v2.Google Scholar
Clemens, C. H. and Griffiths, P. A., The intermediate Jacobian of the cubic threefold, Ann. of Math. (2) 95 (1972), 281–356.Google Scholar
Coskun, I. and Starr, J., Rational curves on smooth cubic hypersurfaces, Int. Math. Res. Not. IMRN 2009(24) (2009), 4626–4641.Google Scholar
Fulton, W., Intersection theory, in Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, second edition, A Series of Modern Surveys in Mathematics, Volume 2 (Springer-Verlag, Berlin, 1998). xiv+470 pp.Google Scholar
Huybrechts, D., Chow groups of K3 surfaces and spherical objects, J. Eur. Math. Soc. 12(6) (2010), 1533–1551.Google Scholar
de Jong, A. J. and Starr, J., Cubic fourfolds and spaces of rational curves, Illinois J. Math. 48(2) (2004), 415–450.Google Scholar
Kuznetsov, A., Derived categories of cubic fourfolds, in Cohomological and Geometric Approaches to Rationality Problems, Progress in Mathematics, Volume 282, pp. 219–243 (Birkhäuser Boston, Inc., Boston, MA, 2010).Google Scholar
Kuznetsov, A., Semiorthogonal decompositions in algebraic geometry, in Proceedings of the International Congress of Mathematicians—Seoul 2014. Vol. II, pp. 635–660 (Kyung Moon Sa, Seoul, 2014).Google Scholar
Kuznetsov, A., Derived categories view on rationality problems, in Rationality Problems in Algebraic Geometry, Lecture Notes in Mathematics, Volume 2172, pp. 67–104 (Fond. CIME/CIME Found. Subser., Springer, Cham, 2016).Google Scholar
Kuznetsov, A. and Markushevich, D., Symplectic structures on moduli spaces of sheaves via the Atiyah class, J. Geom. Phys. 59(7) (2009), 843–860.Google Scholar
Kuznetsov, A. and Perry, A., Derived categories of Gushel–Mukai varieties, Compos. Math. 154(7) (2018), 1362–1406.Google Scholar
Lahoz, M., Lehn, M., Macrì, E. and Stellari, P., Generalized twisted cubics on a cubic fourfold as a moduli space of stable objects, J. Math. Pures Appl. (9) 114 (2018), 85–117.Google Scholar
Laza, R., Sacca, G. and Voisin, C., A hyper-Kähler compactification of the intermediate Jacobian fibration associated with a cubic 4-fold, Acta Math. 218(1) (2017), 55–135.Google Scholar
Lehn, C., Lehn, M., Sorger, C. and van Straten, D., Twisted cubics on cubic fourfolds, J. Reine Angew. Math. 731 (2017), 87–128.Google Scholar
Li, C., Pertusi, L. and Zhao, X., Twisted cubics on cubic fourfolds and stability conditions, Preprint, 2018, arXiv:1802.01134.Google Scholar
Marian, A. and Zhao, X., On the group of zero-cycles of holomorphic symplectic varieties, Preprint, 2017, arXiv:1711.10045v2.Google Scholar
Markushevich, D. and Tikhomirov, A., The Abel–Jacobi map of a moduli component of vector bundles on the cubic threefold, J. Algebraic Geom. 10(1) (2001), 37–62.Google Scholar
Markushevich, D. and Tikhomirov, A., Symplectic structure on a moduli space of sheaves on a cubic fourfold, Izv. Ross. Akad. Nauk Ser. Mat. 67 (2003), 131–158.Google Scholar
Mumford, D., Rational equivalence of 0-cycles on surfaces, J. Math. Kyoto Univ. 9 (1968), 195–204.Google Scholar
O’Grady, K. G., Desingularized moduli spaces of sheaves on a K3, J. Reine Angew. Math. 512 (1999), 49–117.Google Scholar
O’Grady, K. G., Moduli of sheaves and the Chow group of K3 surfaces, J. Math. Pures Appl. (9) 100(5) (2013), 701–718.Google Scholar
Paranjape, K. H., Cohomological and cycle-theoretic connectivity, Ann. of Math. (2) 139(3) (1994), 641–660.Google Scholar
Rojtman, A. A., The torsion of the group of 0-cycles modulo rational equivalence, Ann. of Math. (2) 111(3) (1980), 553–569.Google Scholar
Shen, J., Yin, Q. and Zhao, X., Derived categories of $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties, Preprint, 2017, arXiv:1705.06953v2.Google Scholar
Shen, M., On relations among 1-cycles on cubic hypersurfaces, J. Algebraic Geom. 23(3) (2014), 539–569.Google Scholar
Shen, M. and Vial, C., The Fourier transform for certain hyperkähler fourfolds, Mem. Amer. Math. Soc. 240(1139) (2016), vii+163 pp.Google Scholar
Voisin, C., Théorème de Torelli pour les cubiques de ℙ5, Invent. Math. 86(3) (1986), 577–601.Google Scholar
Voisin, C., Intrinsic pseudo-volume forms and K-correspondences, in The Fano Conference, pp. 761–792 (Univ. Torino, Turin, 2004).Google Scholar
Voisin, C., On the Chow ring of certain algebraic hyper-Kähler manifolds, Pure Appl. Math. Q. 4(3, part 2) (2008), 613–649.Google Scholar
Voisin, C., Rational equivalence of 0-cycles on K3 surfaces and conjectures of Huybrechts and O’Grady, in Recent Advances in Algebraic Geometry, London Mathematical Society Lecture Note Series, Volume 417, pp. 422–436 (Cambridge Univ. Press, Cambridge, 2015).Google Scholar
Voisin, C., Remarks and questions on coisotropic subvarieties and 0-cycles of hyper-Kähler varieties, in K3 Surfaces and their Moduli, Progress in Mathematics, Volume 315, pp. 365–399 (Birkhäuser/Springer, Cham, 2016).Google Scholar
Voisin, C., Hyper-Kähler compactification of the intermediate Jacobian fibration of a cubic fourfold: the twisted case, in Local and Global Methods in Algebraic Geometry, Contemporary Mathematics, Volume 712, pp. 341–355 (American Mathematical Society, Providence, RI, 2018).Google Scholar