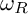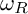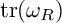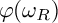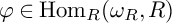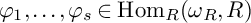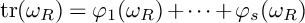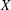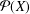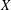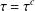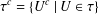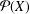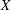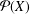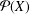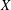3 results
RINGS OF TETER TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 1005-1033
- Print publication:
- December 2022
-
- Article
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
- Export citation
On the Prime Ideals in a Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-319
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation