Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T19:35:08.182Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Prime Ideals in a Commutative Ring

Published online by Cambridge University Press:  20 November 2018

David E. Dobbs
David E. Dobbs*
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996-1300, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

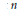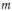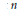If $n$ and $m$ are positive integers, necessary and sufficient conditions are given for the existence of a finite commutative ring $R$ with exactly $n$ elements and exactly 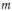$m$ prime ideals. Next, assuming the Axiom of Choice, it is proved that if $R$ is a commutative ring and 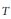$T$ is a commutative $R$-algebra which is generated by a set 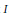$I$, then each chain of prime ideals of 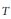$T$ lying over the same prime ideal of $R$ has at most 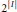${{2}^{\left| I \right|}}$ elements. A polynomial ring example shows that the preceding result is best-possible.

Keywords

13C1513B2504A1014A0513M05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 3 , 01 September 2000 , pp. 312 - 319
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Bourbaki, N., Algèbre Commutative. Masson, Paris, 1983, Chapîtres 8–9.Google Scholar
[2] Dobbs, D. E., On INC-extensions and polynomials with unit content. Canad. Math. Bull. 23 (1980), 37–42.Google Scholar
[3] Dobbs, D. E., Integral extensions with fibers of prescribed cardinality. In: Zero-dimensional commutative rings (eds. D. F. Anderson and D. E. Dobbs), Lecture Notes in Pure and Appl. Math 171(1995), Dekker, New York, 201–207.Google Scholar
[4] Dobbs, D. E., A going-up theorem for arbitrary chains of prime ideals. Comm. Algebra, to appear.Google Scholar
[5] Dobbs, D. E., Fontana, M. and Kabbaj, S., Direct limits of Jaffard domains. Comment. Math. Univ. St. Pauli. 39 (1990), 143–155.Google Scholar
[6] Gilmer, R., Nashier, B. and Nichols, W., On the heights of prime ideals under integral extensions. Arch. Math. 52 (1989), 47–52.Google Scholar
[7] Grothendieck, A. and Dieudonné, J. A., Éléments de Géométrie Algébrique, I. Springer-Verlag, Berlin, 1971.Google Scholar
[8] Halmos, P. R., Naive Set Theory. Van Nostrand, Princeton, 1960.Google Scholar
[9] Kang, B. Y. and Oh, D. Y., Lifting up an infinite chain of prime ideals to a valuation ring. Proc. Amer. Math. Soc. 126 (1998), 645–646.Google Scholar
[10] Kaplansky, I., Commutative Rings. Rev. ed., University of Chicago Press, 1974.Google Scholar
[11] Kelley, J. L., General Topology. Van Nostrand, Princeton, 1955.Google Scholar
[12] Zariski, O. and Samuel, P., Commutative Algebra, I. Van Nostrand, Princeton, 1958.Google Scholar