We prove that the opposite of the category of coalgebras for the Vietoris endofunctor on the category of compact Hausdorff spaces is monadic over $\mathsf {Set}$. We deliver an analogous result for the upper, lower, and convex Vietoris endofunctors acting on the category of stably compact spaces. We provide axiomatizations of the associated (infinitary) varieties. This can be seen as a version of Jónsson–Tarski duality for modal algebras beyond the zero-dimensional setting.

We prove that the category of Nachbin’s compact ordered spaces and order-preserving continuous maps between them is dually equivalent to a variety of algebras, with operations of at most countable arity. Furthermore, we observe that the countable bound on the arity is the best possible: the category of compact ordered spaces is not dually equivalent to any variety of finitary algebras. Indeed, the following stronger results hold: the category of compact ordered spaces is not dually equivalent to (i) any finitely accessible category, (ii) any first-order definable class of structures, and (iii) any class of finitary algebras closed under products and subalgebras. An explicit equational axiomatisation of the dual of the category of compact ordered spaces is obtained; in fact, we provide a finite one, meaning that our description uses only finitely many function symbols and finitely many equational axioms. In preparation for the latter result, we establish a generalisation of a celebrated theorem by Mundici: our result—whose proof is independent of Mundici’s theorem—asserts that the category of unital commutative distributive lattice-ordered monoids is equivalent to the category of what we call MV-monoidal algebras.

Abstract taken directly from the thesis.

E-mail: [email protected]

URL: https://air.unimi.it/retrieve/handle/2434/812809/1698986/phd_unimi_R11882.pdf

Let $L$ be a finite distributive lattice. Let $\text{Su}{{\text{b}}_{0}}(L)$ be the lattice

$$\{S\,|\,S\,\text{is}\,\text{a sublattice of }L\}\cup \{\phi \}$$

and let ${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$ be the length of the shortest maximal chain in $\text{Su}{{\text{b}}_{0}}(L)$. It is proved that if $K$ and $L$ are non-trivial finite distributive lattices, then

$${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K\times L)]={{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K)]+{{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$$

A conjecture from the 1984 Banff Conference on Graphs and Order is thus proved.

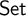
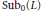
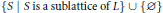
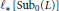
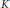
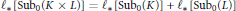
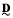Consider the quasi-variety generated by a finite algebra and assume that yields a natural duality on 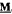based on which is optimal modulo endomorphisms. We shoe that, provided satisfies certain minimality conditions, we can transfer this duality to a natural duality on based on , which is also optimal modulo endormorphisms, for any finite algebra in that has a subalgebra isomorphic to .