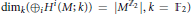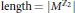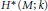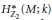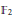A lemma of Tits establishes a connection between the simple connectivity of an incidence geometry and the universal completion of an amalgam induced by a sufficiently transitive group of automorphisms of that geometry. In the present paper, we generalize this lemma to intransitive geometries, thus opening the door for numerous applications. We treat ourselves some amalgams related to intransitive actions of finite orthogonal groups, as a first class of examples.

A ${{\mathbb{Z}}_{2}}$-action with “maximal number of isolated fixed points” (i.e., with only isolated fixed points such that 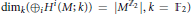${{\dim}_{k}}\left( {{\oplus }_{i}}{{H}^{i}}\left( M;k \right) \right)\,\,=\,\,\left| {{M}^{{{\mathbb{Z}}_{2}}}} \right|,\,k\,=\,\left. {{\mathbb{F}}_{2}} \right)$ on a 3-dimensional, closed manifold determines a binary self-dual code of 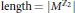$\text{length}\,\text{=}\,\left| {{M}^{{{\mathbb{Z}}_{2}}}} \right|$. In turn this code determines the cohomology algebra 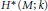${{H}^{*}}\,\left( M;k \right)$ and the equivariant cohomology 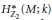$H_{{{\mathbb{Z}}_{2}}}^{*}\,\left( M;k \right)$. Hence, from results on binary self-dual codes one gets information about the cohomology type of 3-manifolds which admit involutions with maximal number of isolated fixed points. In particular, “most” cohomology types of closed 3-manifolds do not admit such involutions. Generalizations of the above result are possible in several directions, e.g., one gets that “most” cohomology types (over 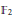${{\mathbb{F}}_{2}}$) of closed 3-manifolds do not admit a non-trivial involution.