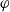1 results
Slope filtrations in families
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 17 May 2012, pp. 249-296
- Print publication:
- April 2013
-
- Article
- Export citation