In this paper, in connection with the program of extending the Curry–Howard isomorphism to classical logic, we study the
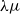 $\lambda \mu$
-calculus of Parigot emphasizing the difference between the original version of Parigot and the version of de Groote in terms of normalization properties. In order to talk about a satisfactory representation of the integers, besides the usual
$\lambda \mu$
-calculus of Parigot emphasizing the difference between the original version of Parigot and the version of de Groote in terms of normalization properties. In order to talk about a satisfactory representation of the integers, besides the usual
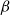 $\beta$
-,
$\beta$
-,
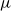 $\mu$
-, and
$\mu$
-, and
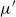 $\mu '$
-reductions, we consider the
$\mu '$
-reductions, we consider the
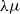 $\lambda \mu$
-calculus augmented with the reduction rules
$\lambda \mu$
-calculus augmented with the reduction rules
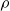 $\rho$
,
$\rho$
,
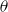 $\theta$
and
$\theta$
and
 $\varepsilon$
. We show that we need all of these rules for this purpose. Then we prove that, with the syntax of Parigot, the calculus enjoys the strong normalization property even when we add the rules
$\varepsilon$
. We show that we need all of these rules for this purpose. Then we prove that, with the syntax of Parigot, the calculus enjoys the strong normalization property even when we add the rules
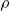 $\rho$
,
$\rho$
,
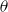 $\theta$
, and
$\theta$
, and
 $\epsilon$
, while the
$\epsilon$
, while the
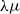 $\lambda \mu$
-calculus presented with the more flexible de Groote-style syntax, in contrast, has only the weak normalization property. In particular, we present a normalization algorithm for the
$\lambda \mu$
-calculus presented with the more flexible de Groote-style syntax, in contrast, has only the weak normalization property. In particular, we present a normalization algorithm for the
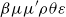 $\beta \mu \mu '\rho \theta \varepsilon$
-reduction in the de Groote-style calculus.
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction in the de Groote-style calculus.
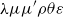 ${\lambda \mu \mu '}\rho \theta \varepsilon$
-calculus
${\lambda \mu \mu '}\rho \theta \varepsilon$
-calculus