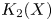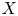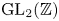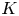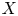1. Introduction
For a positive integer ![]() $N$, let
$N$, let ![]() $Y_1(N)$ and
$Y_1(N)$ and ![]() $X_1(N)$ denote the usual open and closed modular curves over
$X_1(N)$ denote the usual open and closed modular curves over ![]() $\mathbb {Q}$. In this paper, we provide a new perspective on two homomorphisms from the integral homology of the
$\mathbb {Q}$. In this paper, we provide a new perspective on two homomorphisms from the integral homology of the ![]() $\mathbb {C}$-points of
$\mathbb {C}$-points of ![]() $X_1(N)$ to second
$X_1(N)$ to second ![]() $K$-groups of the cyclotomic integer ring
$K$-groups of the cyclotomic integer ring ![]() $\mathbb {Z}[\mu _N]$ and the modular curve
$\mathbb {Z}[\mu _N]$ and the modular curve ![]() $Y_1(N)$:
$Y_1(N)$:
The map ![]() $\Pi _N$ was defined explicitly on slightly larger groups by Busuioc [Reference BusuiocBus08] and the first author [Reference SharifiSha11]. The map
$\Pi _N$ was defined explicitly on slightly larger groups by Busuioc [Reference BusuiocBus08] and the first author [Reference SharifiSha11]. The map ![]() $z_N$ was given an explicit construction in a preprint of Brunault [Reference BrunaultBru22], following earlier constructions by Goncharov [Reference GoncharovGon08] and Brunault [Reference BrunaultBru08] of an analogous map
$z_N$ was given an explicit construction in a preprint of Brunault [Reference BrunaultBru22], following earlier constructions by Goncharov [Reference GoncharovGon08] and Brunault [Reference BrunaultBru08] of an analogous map ![]() $z_N \otimes \mathbb {Q}$ for
$z_N \otimes \mathbb {Q}$ for ![]() $Y(N)$. The
$Y(N)$. The ![]() $p$-adic realization of
$p$-adic realization of ![]() $z_N$ for
$z_N$ for ![]() $p \mid N$ was constructed by Fukaya and Kato in their study [Reference Fukaya and KatoFK24] of a conjecture of the first author [Reference SharifiSha11]. Most of these constructions boil down to the remarkable fact that Steinberg symbols of cyclotomic or Siegel units satisfy relations parallel to the very simple relations satisfied by Manin symbols (although Fukaya and Kato use norm relations among Beilinson–Kato elements and a
$p \mid N$ was constructed by Fukaya and Kato in their study [Reference Fukaya and KatoFK24] of a conjecture of the first author [Reference SharifiSha11]. Most of these constructions boil down to the remarkable fact that Steinberg symbols of cyclotomic or Siegel units satisfy relations parallel to the very simple relations satisfied by Manin symbols (although Fukaya and Kato use norm relations among Beilinson–Kato elements and a ![]() $p$-adic regulator computation); see § 1.1 for more.
$p$-adic regulator computation); see § 1.1 for more.
Our construction is different, and is analogous to the construction of Siegel units on ![]() $Y_1(N)$. Let us specialize to the
$Y_1(N)$. Let us specialize to the ![]() $\Pi _N$-case for a moment to give the idea of our construction, postponing a more careful discussion to § 1.2. Siegel units are pullbacks by an
$\Pi _N$-case for a moment to give the idea of our construction, postponing a more careful discussion to § 1.2. Siegel units are pullbacks by an ![]() $N$-torsion section of theta functions on the universal elliptic curve over
$N$-torsion section of theta functions on the universal elliptic curve over ![]() $Y_1(N)$; these theta functions are uniquely specified by their poles. In our situation, the role of the theta function is played by a ‘big’
$Y_1(N)$; these theta functions are uniquely specified by their poles. In our situation, the role of the theta function is played by a ‘big’ ![]() $1$-cocycle
$1$-cocycle ![]() $\Theta$ on
$\Theta$ on ![]() $\mathrm {GL}_2(\mathbb {Z})$ that is valued in (a quotient of)
$\mathrm {GL}_2(\mathbb {Z})$ that is valued in (a quotient of) ![]() $K_2$ of the function field of
$K_2$ of the function field of ![]() $\mathbb {G}_m^2$. This
$\mathbb {G}_m^2$. This ![]() $\Theta$ is again characterized by its ‘poles’, that is, its image under residue maps to
$\Theta$ is again characterized by its ‘poles’, that is, its image under residue maps to ![]() $K_1$ of function fields of divisors on
$K_1$ of function fields of divisors on ![]() $\mathbb {G}_m^2$. We then pull its restriction to
$\mathbb {G}_m^2$. We then pull its restriction to ![]() $\Gamma _0(N)$ back via a torsion point on
$\Gamma _0(N)$ back via a torsion point on ![]() $\mathbb {G}_m^2$ to obtain a cocycle
$\mathbb {G}_m^2$ to obtain a cocycle
which underlies ![]() $\Pi _N$ described above.
$\Pi _N$ described above.
The construction of the map from ![]() $\Gamma _1(N)$ to
$\Gamma _1(N)$ to ![]() $K_2(Y_1(N))$ is similar,Footnote 1 but the role of
$K_2(Y_1(N))$ is similar,Footnote 1 but the role of ![]() $\mathbb {G}_m^2$ is played by the square
$\mathbb {G}_m^2$ is played by the square ![]() $E^2$ of an elliptic curve, and then
$E^2$ of an elliptic curve, and then ![]() $E$ is varied over the moduli space of elliptic curves. Because the ‘big’ cocycle
$E$ is varied over the moduli space of elliptic curves. Because the ‘big’ cocycle ![]() $\Theta$ is characterized by its poles, it is easy to analyze. In contrast, the specialized cocycle
$\Theta$ is characterized by its poles, it is easy to analyze. In contrast, the specialized cocycle ![]() $\Theta _N$ cannot be so analyzed (it has residues only at primes above
$\Theta _N$ cannot be so analyzed (it has residues only at primes above ![]() $N$, and these carry very little information).
$N$, and these carry very little information).
In particular, we are able to prove the following results (see Theorems 4.3.7 and 7.4.1 for details).
Theorem The map ![]() $\Pi _N$ is Eisenstein with respect to the prime-to-
$\Pi _N$ is Eisenstein with respect to the prime-to-![]() $N$ Hecke operators.
$N$ Hecke operators.
Theorem The map ![]() $z_N$ is equivariant for the prime-to-
$z_N$ is equivariant for the prime-to-![]() $N$ Hecke operators.
$N$ Hecke operators.
These results may be considered in the context of a body of results that suggest close relationships between homology of arithmetic groups and ![]() $K$-groups of algebraic varieties; see, for instance, [Reference StevensSte07, Reference Fukaya, Kato and SharifiFKS14, Reference GoncharovGon19, Reference VenkateshVen19]. Most relevant to our paper is the work of the first author suggesting that the map induced by
$K$-groups of algebraic varieties; see, for instance, [Reference StevensSte07, Reference Fukaya, Kato and SharifiFKS14, Reference GoncharovGon19, Reference VenkateshVen19]. Most relevant to our paper is the work of the first author suggesting that the map induced by ![]() $\Pi _N$ on an Eisenstein quotient of homology is an isomorphism to
$\Pi _N$ on an Eisenstein quotient of homology is an isomorphism to ![]() $K_2(\mathbb {Z}[\mu _N])^+$ away from
$K_2(\mathbb {Z}[\mu _N])^+$ away from ![]() $2$-parts; see Conjecture 4.3.5 for details.
$2$-parts; see Conjecture 4.3.5 for details.
1.1 Background on the maps
We describe in more detail some of the forms of the maps ![]() $\Pi _N$ and
$\Pi _N$ and ![]() $z_N$ that have appeared in the literature. The map
$z_N$ that have appeared in the literature. The map ![]() $\Pi _N$ is most easily defined on a larger homology group relative to the ‘non-infinity cusps’
$\Pi _N$ is most easily defined on a larger homology group relative to the ‘non-infinity cusps’ ![]() $C_1^{\circ }(N)$, which are those that do not lie over the infinity cusp of the modular curve
$C_1^{\circ }(N)$, which are those that do not lie over the infinity cusp of the modular curve ![]() $X_0(N)$. That is, the map
$X_0(N)$. That is, the map ![]() $\Pi _N$ is the restriction of a map
$\Pi _N$ is the restriction of a map
taking image in the slightly larger second ![]() $K$-group of the
$K$-group of the ![]() $N$-integers of
$N$-integers of ![]() $\mathbb {Q}(\mu _N)$.
$\mathbb {Q}(\mu _N)$.
The integral homology relative to the cusps is generated by certain classes ![]() $[u:v]$ of geodesics between cusps known as Manin symbols, where
$[u:v]$ of geodesics between cusps known as Manin symbols, where ![]() $(u,v)$ is a pair of relatively prime integers modulo
$(u,v)$ is a pair of relatively prime integers modulo ![]() $N$.Footnote 2 Those Manin symbols for which both
$N$.Footnote 2 Those Manin symbols for which both ![]() $u$ and
$u$ and ![]() $v$ are nonzero generate the homology relative to the non-infinity cusps.Footnote 3 The map
$v$ are nonzero generate the homology relative to the non-infinity cusps.Footnote 3 The map ![]() $\Pi _N^{\circ }$ was defined in [Reference BusuiocBus08, Reference SharifiSha11] to send each such Manin symbol to a Steinberg symbol of cyclotomic
$\Pi _N^{\circ }$ was defined in [Reference BusuiocBus08, Reference SharifiSha11] to send each such Manin symbol to a Steinberg symbol of cyclotomic ![]() $N$-units in
$N$-units in ![]() $\mathbb {Q}(\mu _N)$:
$\mathbb {Q}(\mu _N)$:
where ![]() $\zeta _N$ is a primitive
$\zeta _N$ is a primitive ![]() $N$th root of unity. The Manin symbols satisfy very simple relations, and to show this map is well defined is to verify that the relations hold at the level of Steinberg symbols, which results from the usual symbol formula
$N$th root of unity. The Manin symbols satisfy very simple relations, and to show this map is well defined is to verify that the relations hold at the level of Steinberg symbols, which results from the usual symbol formula ![]() $\{x,1-x\} = 0$ for
$\{x,1-x\} = 0$ for ![]() $N$-units
$N$-units ![]() $x$ and
$x$ and ![]() $1-x$.
$1-x$.
In [Reference SharifiSha11], the first author conjectured that the ![]() $p$-adic realization of
$p$-adic realization of ![]() $\Pi _N$ (i.e., its tensor product with
$\Pi _N$ (i.e., its tensor product with ![]() $\mathbb {Z}_p$, for which we will use the same notation) for
$\mathbb {Z}_p$, for which we will use the same notation) for ![]() $p$ dividing
$p$ dividing ![]() $N$ is Eisenstein in the sense that for primes
$N$ is Eisenstein in the sense that for primes ![]() $\ell \nmid N$ one has
$\ell \nmid N$ one has
for ![]() $x \in H_1(X_1(N),\mathbb {Z}_p)$, where
$x \in H_1(X_1(N),\mathbb {Z}_p)$, where ![]() $T_{\ell }$ is the
$T_{\ell }$ is the ![]() $\ell$th Hecke operator and
$\ell$th Hecke operator and ![]() $\sigma _{\ell } \in \operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})$ is the arithmetic Frobenius at
$\sigma _{\ell } \in \operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})$ is the arithmetic Frobenius at ![]() $\ell$. For primes
$\ell$. For primes ![]() $\ell \mid N$, he also conjectured that
$\ell \mid N$, he also conjectured that ![]() $\Pi _N(U_{\ell }^*x) = \Pi _N(x)$, where
$\Pi _N(U_{\ell }^*x) = \Pi _N(x)$, where ![]() $U_{\ell }^*$ is the
$U_{\ell }^*$ is the ![]() $\ell$th adjoint Hecke operator.
$\ell$th adjoint Hecke operator.
Fukaya and Kato proved this conjecture in [Reference Fukaya and KatoFK24] by exhibiting ![]() $\Pi _N$ as a specialization at the infinity cusp of the
$\Pi _N$ as a specialization at the infinity cusp of the ![]() $p$-adic realization of
$p$-adic realization of ![]() $z_N$.Footnote 4 Roughly speaking, their map
$z_N$.Footnote 4 Roughly speaking, their map ![]() $z_N$ is also the restriction of a map on relative homology sending
$z_N$ is also the restriction of a map on relative homology sending ![]() $[u:v]$ to a Steinberg symbol
$[u:v]$ to a Steinberg symbol ![]() $\{g_{{u}/{N}},g_{{v}/{N}}\}$ of Siegel units on
$\{g_{{u}/{N}},g_{{v}/{N}}\}$ of Siegel units on ![]() $Y_1(N)$. Via a regulator computation, they show that the
$Y_1(N)$. Via a regulator computation, they show that the ![]() $p$-adic realization of
$p$-adic realization of ![]() $z_N$ is Hecke equivariant for the operators
$z_N$ is Hecke equivariant for the operators ![]() $T_{\ell }$ for
$T_{\ell }$ for ![]() $\ell \nmid N$ and
$\ell \nmid N$ and ![]() $U_{\ell }^*$ for
$U_{\ell }^*$ for ![]() $\ell \mid N$ and they then use the fact that the specialization-at-infinity map is Eisenstein.Footnote 5 The first author has frequently expressed a tentative expectation that the Eisenstein property should hold without passing to the
$\ell \mid N$ and they then use the fact that the specialization-at-infinity map is Eisenstein.Footnote 5 The first author has frequently expressed a tentative expectation that the Eisenstein property should hold without passing to the ![]() $p$-adic realization.
$p$-adic realization.
Here, we give a construction of the maps ![]() $\Pi _N$ and
$\Pi _N$ and ![]() $z_N$ without recourse to explicit symbols or regulator computations.Footnote 6 As mentioned earlier, this also allows us to prove that (1.3) holds for all
$z_N$ without recourse to explicit symbols or regulator computations.Footnote 6 As mentioned earlier, this also allows us to prove that (1.3) holds for all ![]() $\ell \nmid N$ without tensoring with
$\ell \nmid N$ without tensoring with ![]() $\mathbb {Z}_p$. Unlike in the work of Fukaya and Kato, we do not use the Hecke equivariance of
$\mathbb {Z}_p$. Unlike in the work of Fukaya and Kato, we do not use the Hecke equivariance of ![]() $z_N$ to study the Eisenstein property of
$z_N$ to study the Eisenstein property of ![]() $\Pi _N$. Rather, we consider these maps entirely separately.
$\Pi _N$. Rather, we consider these maps entirely separately.
1.2 Our approach
As we have mentioned, our goal in this paper is to provide an alternate construction of the maps ![]() $\Pi _N$ and
$\Pi _N$ and ![]() $z_N$ that is analogous to the construction of Siegel units on
$z_N$ that is analogous to the construction of Siegel units on ![]() $Y_1(N)$ via theta functions on the universal elliptic curve
$Y_1(N)$ via theta functions on the universal elliptic curve ![]() $\mathscr {E}$ over
$\mathscr {E}$ over ![]() $Y_1(N)$. We now describe this approach in more detail.
$Y_1(N)$. We now describe this approach in more detail.
Recall from [Reference KatoKat04, Proposition 1.3] that given a positive integer ![]() $n$ prime to
$n$ prime to ![]() $6N$, there is a theta function
$6N$, there is a theta function ![]() ${}_n \theta$ in
${}_n \theta$ in ![]() $\mathbb {Q}(\mathscr {E})^{\times }$ that is a unit outside of the
$\mathbb {Q}(\mathscr {E})^{\times }$ that is a unit outside of the ![]() $n$-torsion, and which is uniquely specified by the properties that its divisor is
$n$-torsion, and which is uniquely specified by the properties that its divisor is ![]() $n^2(0) - \mathscr {E}[n]$ and that it is invariant under norm maps attached to multiplication by positive integers prime to
$n^2(0) - \mathscr {E}[n]$ and that it is invariant under norm maps attached to multiplication by positive integers prime to ![]() $n$. Siegel units are obtained by pulling back the theta function
$n$. Siegel units are obtained by pulling back the theta function ![]() ${}_n \theta$ to
${}_n \theta$ to ![]() $Y_1(N)$ using
$Y_1(N)$ using ![]() $N$-torsion sections. Though these Siegel units depend upon
$N$-torsion sections. Though these Siegel units depend upon ![]() $n$, they satisfy a distribution relation that permits one to construct an ‘
$n$, they satisfy a distribution relation that permits one to construct an ‘![]() $n=1$’ unit, upon inverting
$n=1$’ unit, upon inverting ![]() $6N$.
$6N$.
The analogues of theta functions in our work are parabolic ![]() $1$-cocycles on
$1$-cocycles on ![]() $\mathrm {GL}_2(\mathbb {Z})$, again valued in second
$\mathrm {GL}_2(\mathbb {Z})$, again valued in second ![]() $K$-groups, but of the function fields of the squares of the multiplicative group
$K$-groups, but of the function fields of the squares of the multiplicative group ![]() $\mathbb {G}_m$ over
$\mathbb {G}_m$ over ![]() $\mathbb {Q}$ and the universal elliptic curve
$\mathbb {Q}$ and the universal elliptic curve ![]() $\mathscr {E}$ over
$\mathscr {E}$ over ![]() $Y_1(N)$. That is, the first is a
$Y_1(N)$. That is, the first is a ![]() $1$-cocycle
$1$-cocycle
where ![]() $\mathrm {GL}_2(\mathbb {Z})$ acts on the
$\mathrm {GL}_2(\mathbb {Z})$ acts on the ![]() $K$-group via pullback of its right-multiplication action on
$K$-group via pullback of its right-multiplication action on ![]() $\mathbb {G}_m^2$, and where
$\mathbb {G}_m^2$, and where ![]() $z_i$ denotes the
$z_i$ denotes the ![]() $i$th coordinate function on
$i$th coordinate function on ![]() $\mathbb {G}_m^2$ (cf. Proposition 3.3.1). The second is a family of
$\mathbb {G}_m^2$ (cf. Proposition 3.3.1). The second is a family of ![]() $1$-cocycles
$1$-cocycles
depending upon a choice of prime ![]() $n \nmid N$. Using
$n \nmid N$. Using ![]() $N$-torsion sections, we pull back the restrictions of these ‘big’ cocycles on
$N$-torsion sections, we pull back the restrictions of these ‘big’ cocycles on ![]() $\Gamma _1(N)$ to obtain
$\Gamma _1(N)$ to obtain ![]() $\Pi _N$ and a map
$\Pi _N$ and a map ![]() ${}_n z_N$ depending on
${}_n z_N$ depending on ![]() $n$ (which we make explicit only at the level of cocycles). As with Siegel units, upon further inverting
$n$ (which we make explicit only at the level of cocycles). As with Siegel units, upon further inverting ![]() $N$, we obtain a map
$N$, we obtain a map ![]() $z_N$ that may be understood as the
$z_N$ that may be understood as the ![]() $n=1$ analogue of the maps
$n=1$ analogue of the maps ![]() ${}_n z_N$.
${}_n z_N$.
Because of the characterization of our big cocycles in terms of their residues, it is easy to provide explicit formulas for and analyze how Hecke operators act on them. In particular, the compatibility of the classes of these ![]() $1$-cocycles with the actions of Hecke operators is verified directly using the equivariance of residue maps for integral matrices of nonzero determinant. The analogous properties of the specialized cocycles follow from the analogous formulas for the big cocycles.
$1$-cocycles with the actions of Hecke operators is verified directly using the equivariance of residue maps for integral matrices of nonzero determinant. The analogous properties of the specialized cocycles follow from the analogous formulas for the big cocycles.
1.2.1 Construction of ‘big’ cocycles
The big cocycles are constructed using three-term motivic complexes. These play the roles of the two-term complex given by the divisor map in the construction of theta functions. Let us describe this in more detail. Taking ![]() $G$ to be
$G$ to be ![]() $\mathbb {G}_m$ or
$\mathbb {G}_m$ or ![]() $\mathscr {E}$ in the respective cases, the ‘motivic complexes’ are homological complexes in degrees
$\mathscr {E}$ in the respective cases, the ‘motivic complexes’ are homological complexes in degrees ![]() $2$,
$2$, ![]() $1$, and
$1$, and ![]() $0$ of the form
$0$ of the form
where the maps are residue maps, and ![]() $D$ and
$D$ and ![]() $x$ vary respectively over irreducible codimension
$x$ vary respectively over irreducible codimension ![]() $1$ and
$1$ and ![]() $2$ cycles of
$2$ cycles of ![]() $G^2$. The first map is given on symbols by the tame symbol, and the second map sends an element of
$G^2$. The first map is given on symbols by the tame symbol, and the second map sends an element of ![]() $K_1(\mathbb {Q}(D)) = \mathbb {Q}(D)^{\times }$ to its divisor. These complexes carry an action of the monoid
$K_1(\mathbb {Q}(D)) = \mathbb {Q}(D)^{\times }$ to its divisor. These complexes carry an action of the monoid ![]() $\Delta$ of integral
$\Delta$ of integral ![]() $2 \times 2$ matrices with nonzero determinant via pullback under the endomorphism of right multiplication. They then also have trace maps with respect to multiplication by positive integers.
$2 \times 2$ matrices with nonzero determinant via pullback under the endomorphism of right multiplication. They then also have trace maps with respect to multiplication by positive integers.
Much as a theta function is uniquely determined by its ‘poles’, or more specifically its norm-invariant divisor, our cocycles are uniquely determined by choices of a trace-fixed ![]() $\mathrm {GL}_2(\mathbb {Z})$-invariant element
$\mathrm {GL}_2(\mathbb {Z})$-invariant element ![]() $Z$ of
$Z$ of ![]() $\bigoplus _x K_0(\mathbb{Q}(x))$, which is to say a formal
$\bigoplus _x K_0(\mathbb{Q}(x))$, which is to say a formal ![]() $\mathbb {Z}$-linear sum of sections of
$\mathbb {Z}$-linear sum of sections of ![]() $G^2$.
$G^2$.
More specifically, given a suitable choice of ![]() $Z$ as above in the image of
$Z$ as above in the image of ![]() $\partial _1$, we choose a lift
$\partial _1$, we choose a lift
of ![]() $Z$. For
$Z$. For ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$, we show that
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$, we show that ![]() $\gamma \eta - \eta \in \operatorname {im} \partial _2$, so there is a unique element
$\gamma \eta - \eta \in \operatorname {im} \partial _2$, so there is a unique element
with residue ![]() $\gamma \eta - \eta$, and the recipe
$\gamma \eta - \eta$, and the recipe ![]() $\gamma \mapsto \Theta ^Z_{\gamma }$ defines a ‘big’ cocycle
$\gamma \mapsto \Theta ^Z_{\gamma }$ defines a ‘big’ cocycle ![]() $\Theta ^Z$ on
$\Theta ^Z$ on ![]() $\mathrm {GL}_2(\mathbb {Z})$. Its cohomology class depends upon the choice of
$\mathrm {GL}_2(\mathbb {Z})$. Its cohomology class depends upon the choice of ![]() $Z$ but not the choice of
$Z$ but not the choice of ![]() $\eta$ (cf. Proposition 6.2.2).
$\eta$ (cf. Proposition 6.2.2).
In the case ![]() $G = \mathbb {G}_m$, the complex (1.6) is left exact, and the kernel of
$G = \mathbb {G}_m$, the complex (1.6) is left exact, and the kernel of ![]() $\partial _2$ is identified with
$\partial _2$ is identified with ![]() $H^2(\mathbb {G}_m^2,2)$. For
$H^2(\mathbb {G}_m^2,2)$. For ![]() $x_0$ the identity in
$x_0$ the identity in ![]() $\mathbb {G}_m^2$, we choose
$\mathbb {G}_m^2$, we choose ![]() $Z$ to be the class
$Z$ to be the class ![]() $e$ of the identity element of the
$e$ of the identity element of the ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed subgroup
$\mathrm {GL}_2(\mathbb {Z})$-fixed subgroup ![]() $K_0(\mathbb{Q}(x_0)) \cong \mathbb {Z}$ of
$K_0(\mathbb{Q}(x_0)) \cong \mathbb {Z}$ of ![]() $\bigoplus _x K_0(\mathbb{Q}(x))$. We choose
$\bigoplus _x K_0(\mathbb{Q}(x))$. We choose ![]() $\eta$ to be the class of
$\eta$ to be the class of ![]() $1-z_1^{-1}$ on the rank
$1-z_1^{-1}$ on the rank ![]() $1$ subtorus defined by
$1$ subtorus defined by ![]() $z_2 = 1$, though as mentioned the class of
$z_2 = 1$, though as mentioned the class of ![]() $\Theta = \Theta ^e$ is independent of this choice. In fact, since we take
$\Theta = \Theta ^e$ is independent of this choice. In fact, since we take ![]() $\eta$ to be trace fixed, the ambiguity inherent in taking the quotient of
$\eta$ to be trace fixed, the ambiguity inherent in taking the quotient of ![]() $K_2(\mathbb {Q}(\mathbb {G}_m^2))$ by
$K_2(\mathbb {Q}(\mathbb {G}_m^2))$ by ![]() $\ker \, \partial _2 = H^2(\mathbb {G}_m^2,2)$ can be further reduced to its trace-invariant part, which is generated by
$\ker \, \partial _2 = H^2(\mathbb {G}_m^2,2)$ can be further reduced to its trace-invariant part, which is generated by ![]() $\{-z_1,-z_2\}$.
$\{-z_1,-z_2\}$.
In the case ![]() $G = \mathscr {E}$, the homology of the motivic complex (1.6) does not vanish anywhere, but if we restrict to its trace-invariant part, then, at least upon inverting
$G = \mathscr {E}$, the homology of the motivic complex (1.6) does not vanish anywhere, but if we restrict to its trace-invariant part, then, at least upon inverting ![]() $6$, it is right exact and the image of the residue map
$6$, it is right exact and the image of the residue map ![]() $\partial _1$ is the kernel of the degree map
$\partial _1$ is the kernel of the degree map ![]() $\bigoplus _x K_0(\mathbb{Q}(x)) \to \mathbb {Z}$. Since there is no meromorphic function on an elliptic curve whose divisor is supported at the origin, the role of
$\bigoplus _x K_0(\mathbb{Q}(x)) \to \mathbb {Z}$. Since there is no meromorphic function on an elliptic curve whose divisor is supported at the origin, the role of ![]() $1 \in K_0(\mathbb{Q}(x_0))$ in the above construction must be replaced by a slightly less canonically chosen trace-invariant and
$1 \in K_0(\mathbb{Q}(x_0))$ in the above construction must be replaced by a slightly less canonically chosen trace-invariant and ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed element
$\mathrm {GL}_2(\mathbb {Z})$-fixed element ![]() $e_n$ that is known to be in the image of
$e_n$ that is known to be in the image of ![]() $\partial _1$, its choice depending on an auxiliary prime
$\partial _1$, its choice depending on an auxiliary prime ![]() $n \nmid N$.
$n \nmid N$.
Remark 1.2.1 (Toric geometry perspective)
We also provide an alternate point of view on the cocycle ![]() $\Theta$ in the
$\Theta$ in the ![]() $\mathbb {G}_m$-case that is tied to toric geometry and which allows us to reduce the ambiguity in
$\mathbb {G}_m$-case that is tied to toric geometry and which allows us to reduce the ambiguity in ![]() $\Theta$ up to torsion of small order. As observed by Brion [Reference BrionBri88], the function that sends a rational cone
$\Theta$ up to torsion of small order. As observed by Brion [Reference BrionBri88], the function that sends a rational cone ![]() $C \subseteq \mathbb {R}^2$ to the generating function
$C \subseteq \mathbb {R}^2$ to the generating function
of the dual cone is additive with respect to subdivisions of cones. (The right-hand series analytically continues from its region of convergence to a rational function.) The differential symbol
gives rise to a map ![]() $K_2(\mathbb {Q}(\mathbb {G}_m^2)) \rightarrow \mathbb {Q}(z_1, z_2)$. We explain in § 5 how the association
$K_2(\mathbb {Q}(\mathbb {G}_m^2)) \rightarrow \mathbb {Q}(z_1, z_2)$. We explain in § 5 how the association ![]() $C \mapsto \phi (C)$ lifts to
$C \mapsto \phi (C)$ lifts to ![]() $K_2(\mathbb {Q}(\mathbb {G}_m^2))$ along this map. For
$K_2(\mathbb {Q}(\mathbb {G}_m^2))$ along this map. For ![]() $\gamma \in \mathrm {SL}_2(\mathbb {Z})$, the image of the cone spanned by
$\gamma \in \mathrm {SL}_2(\mathbb {Z})$, the image of the cone spanned by ![]() $(1,0)$ and
$(1,0)$ and ![]() $\gamma (1,0)$ is a lift of
$\gamma (1,0)$ is a lift of ![]() $\Theta _{\gamma }$. The resulting map is only a cocycle modulo
$\Theta _{\gamma }$. The resulting map is only a cocycle modulo ![]() $\{-z_1, -z_2\}$, and we explain in § 5.4 how it can be modified to avoid even this ambiguity.
$\{-z_1, -z_2\}$, and we explain in § 5.4 how it can be modified to avoid even this ambiguity.
1.2.2 Specialization
To obtain our specialized cocycles, we pull back our big cocycles under ![]() $N$-torsion sections of
$N$-torsion sections of ![]() $G^2$ of the form
$G^2$ of the form ![]() $(1,\iota _N)$, where
$(1,\iota _N)$, where ![]() $\iota _N$ is an
$\iota _N$ is an ![]() $N$-torsion point or section of
$N$-torsion point or section of ![]() $G$. That is, for
$G$. That is, for ![]() $\mathbb {G}_m$, we take
$\mathbb {G}_m$, we take ![]() $\iota _N$ to be a primitive
$\iota _N$ to be a primitive ![]() $N$th root of unity
$N$th root of unity ![]() $\zeta _N$, and for
$\zeta _N$, and for ![]() $\mathscr {E}$, we take
$\mathscr {E}$, we take ![]() $\iota _N \colon Y_1(N) \to \mathscr {E}$ to be the universal
$\iota _N \colon Y_1(N) \to \mathscr {E}$ to be the universal ![]() $N$-torsion section. The values
$N$-torsion section. The values ![]() $\Theta _{\gamma }$ for
$\Theta _{\gamma }$ for ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$ need not be regular at
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$ need not be regular at ![]() $(1,\iota _N)$, but they are for
$(1,\iota _N)$, but they are for ![]() $\gamma$ in the congruence subgroup
$\gamma$ in the congruence subgroup ![]() $\tilde {\Gamma }_0(N)$ of
$\tilde {\Gamma }_0(N)$ of ![]() $\mathrm {GL}_2(\mathbb {Z})$ consisting of matrices with bottom-left entry divisible by
$\mathrm {GL}_2(\mathbb {Z})$ consisting of matrices with bottom-left entry divisible by ![]() $N$. So, we must first restrict to this group prior to taking the pullback.
$N$. So, we must first restrict to this group prior to taking the pullback.
For instance, in the case ![]() $G = \mathbb {G}_m$, upon pulling back via
$G = \mathbb {G}_m$, upon pulling back via ![]() $(1,\zeta _N)$, we obtain a cocycle
$(1,\zeta _N)$, we obtain a cocycle
the right-hand side being the quotient of ![]() $K_2(\mathbb {Q}(\mu _N))$ by a group of order at most
$K_2(\mathbb {Q}(\mu _N))$ by a group of order at most ![]() $2$. The restriction of
$2$. The restriction of ![]() $\Theta _N$ to
$\Theta _N$ to ![]() $\Gamma _1(N)$ is a homomorphism taking image in the corresponding quotient of
$\Gamma _1(N)$ is a homomorphism taking image in the corresponding quotient of ![]() $K_2(\mathbb {Z}[\mu _N])$. In fact, it is easy to see that
$K_2(\mathbb {Z}[\mu _N])$. In fact, it is easy to see that ![]() $\Theta$ is parabolic so that
$\Theta$ is parabolic so that ![]() $\Theta _N$ induces a map from the parabolic homology of the latter group to the quotient of
$\Theta _N$ induces a map from the parabolic homology of the latter group to the quotient of ![]() $K_2$, which in turn yields
$K_2$, which in turn yields ![]() $\Pi _N$.
$\Pi _N$.
The map ![]() ${}_n z_N$ for
${}_n z_N$ for ![]() $Y_1(N)$ is constructed analogously. By pulling back, we obtain a cocycle
$Y_1(N)$ is constructed analogously. By pulling back, we obtain a cocycle
Much as with Siegel units [Reference KatoKat04], upon specialization we can define a universal rational cocycle independent of this choice. That is, the pullbacks of the resulting classes to ![]() $K_2(Y_1(N))$ satisfy natural distribution relations in
$K_2(Y_1(N))$ satisfy natural distribution relations in ![]() $n$ that permit one, upon inverting
$n$ that permit one, upon inverting ![]() $N$, to construct a specialized cocycle
$N$, to construct a specialized cocycle ![]() $\Theta _N$ that should be thought of as the
$\Theta _N$ that should be thought of as the ![]() $n=1$ case of the construction; see Theorem 7.2.2.
$n=1$ case of the construction; see Theorem 7.2.2.
The Eisenstein property of ![]() $\Pi _N$ and Hecke equivariance of
$\Pi _N$ and Hecke equivariance of ![]() $z_N$ follow from analogous properties of the cohomology classes of the big cocycles, as do the explicit formula for
$z_N$ follow from analogous properties of the cohomology classes of the big cocycles, as do the explicit formula for ![]() $\Pi _N$ that arises from (1.3) and its analogue for
$\Pi _N$ that arises from (1.3) and its analogue for ![]() $z_N$ involving Steinberg symbols of Siegel units.
$z_N$ involving Steinberg symbols of Siegel units.
We are, moreover, able to show the expected explicit formula for ![]() $\Theta _N$ as a sum of Steinberg symbols of Siegel units (Beilinson–Kato elements) in Proposition 7.3.1 modulo a subgroup of
$\Theta _N$ as a sum of Steinberg symbols of Siegel units (Beilinson–Kato elements) in Proposition 7.3.1 modulo a subgroup of ![]() $K_2(Y_1(N))$ that vanishes under any standard regulator map. It would be desirable to eliminate this last ambiguity.
$K_2(Y_1(N))$ that vanishes under any standard regulator map. It would be desirable to eliminate this last ambiguity.
1.2.3 Relationship to other topics in the literature
Our construction does not stand in isolation but is related to a rich body of theory that has been developed in different contexts. It is particularly notable that in both cases studied here, one can view the class of the big cocycle ![]() $\Theta$ as arising from a class in equivariant motivic cohomology. We briefly describe this class in the
$\Theta$ as arising from a class in equivariant motivic cohomology. We briefly describe this class in the ![]() $\mathbb {G}_m$-case in § 5.5.
$\mathbb {G}_m$-case in § 5.5.
The equivariant class corresponding to ![]() $\Theta$ provides a kernel to pass between cohomology of
$\Theta$ provides a kernel to pass between cohomology of ![]() $\Gamma _1(N)$ and various
$\Gamma _1(N)$ and various ![]() $K$-groups. Our situation is formally similar to the theory of reductive dual pairs, where the theta function provides a kernel to pass between automorphic forms on different groups, and in fact our proofs of Hecke equivariance are formally similar to the arguments about theta kernels. The idea of using an equivariant class as a kernel has been used in other contexts, for example in Soulé's work [Reference SouléSou79] on the Chern character in algebraic
$K$-groups. Our situation is formally similar to the theory of reductive dual pairs, where the theta function provides a kernel to pass between automorphic forms on different groups, and in fact our proofs of Hecke equivariance are formally similar to the arguments about theta kernels. The idea of using an equivariant class as a kernel has been used in other contexts, for example in Soulé's work [Reference SouléSou79] on the Chern character in algebraic ![]() $K$-theory.
$K$-theory.
Our paper is also related to a number of recent works constructing classes in different flavors of equivariant cohomology [Reference Bergeron, Charollois and GarciaBCG20, Reference Bannai, Hagihara, Yamada and YamamotoBHYY23, Reference Kings and SprangKS24]. The class most relevant to us is the Eisenstein symbol studied in [Reference BeilinsonBei86, Reference FaltingsFal05], but constructed here equivariantly. The possibility of such an equivariant refinement was observed in a different context by Nekovář and Scholl [Reference Nekovář and SchollNS16, § 13]. A closely related story is the theory of polylogarithms [Reference Beilinson and LevinBL91, Reference Huber and KingsHK18], or again, more precisely, the equivariant version of such a theory, as is discussed in [Reference Beilinson, Kings and LevinBKL18, § 3.7].
Our goals are, however, rather different than those of the papers mentioned above: we aim to develop a framework optimized for the analysis of (1.1) and (1.2), with an emphasis on the explicit description of these maps by symbols. This framework can certainly be extended to study other interesting examples as well, such as relating the first homology of Bianchi spaces and Steinberg symbols of elliptic units, or relating the second homology of locally symmetric spaces for ![]() $\mathrm {GL}_3$ and Steinberg symbols of three Siegel units, as proposed in [Reference Fukaya, Kato and SharifiFKS14, § 4.2]. When working in sufficient generality, it will likely be fruitful to systematically proceed in an equivariant fashion.
$\mathrm {GL}_3$ and Steinberg symbols of three Siegel units, as proposed in [Reference Fukaya, Kato and SharifiFKS14, § 4.2]. When working in sufficient generality, it will likely be fruitful to systematically proceed in an equivariant fashion.
1.3 An outline
We briefly summarize the contents of the paper. We start by recalling and establishing certain constructions of motivic cohomology useful to our study in § 2. Most importantly, we employ coniveau spectral sequences to construct Gersten-type complexes in Milnor ![]() $K$-theory, paying special attention to the case of the square of a commutative group scheme.
$K$-theory, paying special attention to the case of the square of a commutative group scheme.
The next three sections treat the case of ![]() $\mathbb {G}_m^2$. In § 3, we construct the big cocycle
$\mathbb {G}_m^2$. In § 3, we construct the big cocycle ![]() $\Theta$ of (1.4). We derive an explicit formula for
$\Theta$ of (1.4). We derive an explicit formula for ![]() $\Theta$ in Proposition 3.3.2 and study its behavior under Hecke operators in Proposition 3.4.4. We then specialize
$\Theta$ in Proposition 3.3.2 and study its behavior under Hecke operators in Proposition 3.4.4. We then specialize ![]() $\Theta$ at a torsion point to construct the cyclotomic cocycle
$\Theta$ at a torsion point to construct the cyclotomic cocycle ![]() $\Theta _N$ of (1.8) in § 4, deriving its explicit formula (Proposition 4.2.4) and its transformation under Hecke operators (Theorem 4.2.11) from the results on
$\Theta _N$ of (1.8) in § 4, deriving its explicit formula (Proposition 4.2.4) and its transformation under Hecke operators (Theorem 4.2.11) from the results on ![]() $\Theta$. We recover the map
$\Theta$. We recover the map ![]() $\Pi _N$ of (1.1) from
$\Pi _N$ of (1.1) from ![]() $\Theta _N$ and verify its Eisenstein property in Theorem 4.3.2. Section 5 has a rather different flavor: in it, we examine the construction of
$\Theta _N$ and verify its Eisenstein property in Theorem 4.3.2. Section 5 has a rather different flavor: in it, we examine the construction of ![]() $\Theta$ through the lens of toric geometry. The main tool is Proposition 5.2.2, which constructs a map from the chain complex of the circle to the motivic complex.
$\Theta$ through the lens of toric geometry. The main tool is Proposition 5.2.2, which constructs a map from the chain complex of the circle to the motivic complex.
In the final two sections of the paper, we turn to the more technically demanding case of ![]() $\mathscr {E}^2$. In § 6, we construct the big cocycles
$\mathscr {E}^2$. In § 6, we construct the big cocycles ![]() ${}_n \Theta$ of (1.5) for primes
${}_n \Theta$ of (1.5) for primes ![]() $n \nmid N$, derive an explicit formula for them in Theorem 6.4.1, and demonstrate their Hecke equivariance in Theorem 6.5.4. In § 7, we specialize these cocycles
$n \nmid N$, derive an explicit formula for them in Theorem 6.4.1, and demonstrate their Hecke equivariance in Theorem 6.5.4. In § 7, we specialize these cocycles ![]() ${}_n \Theta$ using an
${}_n \Theta$ using an ![]() $N$-torsion section to obtain the cocycles
$N$-torsion section to obtain the cocycles ![]() ${}_n \Theta _N$ of (1.9). We construct a ‘universal’ cocycle
${}_n \Theta _N$ of (1.9). We construct a ‘universal’ cocycle ![]() $\Theta _N$ independent of
$\Theta _N$ independent of ![]() $n$ in Theorem 7.2.2, and we derive an explicit formula for it in Proposition 7.3.1. Finally, in Theorem 7.4.1, we construct the map
$n$ in Theorem 7.2.2, and we derive an explicit formula for it in Proposition 7.3.1. Finally, in Theorem 7.4.1, we construct the map ![]() $z_N$ of (1.2) and establish its Hecke equivariance.
$z_N$ of (1.2) and establish its Hecke equivariance.
2. Preliminaries on motivic cohomology
We shall recall basic properties of motivic cohomology groups in § 2.1 and coniveau spectral sequences in § 2.2. We shall use these coniveau spectral sequences to construct Gersten-type complexes in Milnor ![]() $K$-theory that will be central to our later study, paying special attention to the case of the square of a commutative group scheme.
$K$-theory that will be central to our later study, paying special attention to the case of the square of a commutative group scheme.
In § 2.3, we recall the trace maps which will allow us to take fixed parts. In § 2.4, we discuss the particular case of the square of a commutative group scheme of interest to us, introducing our complexes that compute motivic cohomology and various quasi-isomorphic subcomplexes of motivic cohomology groups.
2.1 Motivic cohomology
We shall define motivic cohomology using Bloch's cycle complexes: see, for instance, [Reference BlochBlo86, Reference BlochBlo94, Reference LevineLev99, Reference LevineLev04]. This has a certain psychological advantage for us in that it allows us to think of our classes as coming from cycles. However, which theory of motivic cohomology is used does not matter in our final results, which concern smooth schemes over perfect fields.
Let ![]() $Y$ denote a quasi-projective scheme of finite type over a perfect field
$Y$ denote a quasi-projective scheme of finite type over a perfect field ![]() $F$. For nonnegative integers
$F$. For nonnegative integers ![]() $j$ and
$j$ and ![]() $k$, let
$k$, let ![]() $z^k(Y,j)$ denote the group of codimension
$z^k(Y,j)$ denote the group of codimension ![]() $k$ cycles in
$k$ cycles in ![]() $Y \times \Delta ^j$ (the
$Y \times \Delta ^j$ (the ![]() $F$-fiber product) that meet
$F$-fiber product) that meet ![]() $Y \times \Phi$ for each face
$Y \times \Phi$ for each face ![]() $\Phi$ of the algebraic
$\Phi$ of the algebraic ![]() $j$-simplex
$j$-simplex ![]() $\Delta ^j$ over
$\Delta ^j$ over ![]() $F$ properly. Via alternating sums of face maps, the
$F$ properly. Via alternating sums of face maps, the ![]() $z^k(Y,\cdot )$ form a homological complex with
$z^k(Y,\cdot )$ form a homological complex with ![]() $z^k(Y,j)$ in degree
$z^k(Y,j)$ in degree ![]() $j$. This is Bloch's cycle complex for
$j$. This is Bloch's cycle complex for ![]() $Y$; its homology groups are called higher Chow groups. These complexes admit pullbacks by flat maps and pushforwards by proper maps [Reference BlochBlo86, Proposition 1.3].
$Y$; its homology groups are called higher Chow groups. These complexes admit pullbacks by flat maps and pushforwards by proper maps [Reference BlochBlo86, Proposition 1.3].
For any ![]() $i \in \mathbb {Z}$, we set
$i \in \mathbb {Z}$, we set
We also set ![]() $H^i(Y,k) = 0$ for negative integers
$H^i(Y,k) = 0$ for negative integers ![]() $k$. If
$k$. If ![]() $Y$ is smooth, then
$Y$ is smooth, then ![]() $H^i(Y,k)$ is naturally isomorphic to the
$H^i(Y,k)$ is naturally isomorphic to the ![]() $i$th motivic cohomology group of
$i$th motivic cohomology group of ![]() $Y$ with
$Y$ with ![]() $\mathbb {Z}(k)$-coefficients in the sense of Voevodsky [Reference VoevodskyVoe00] (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 19.1]):Footnote 7
$\mathbb {Z}(k)$-coefficients in the sense of Voevodsky [Reference VoevodskyVoe00] (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 19.1]):Footnote 7
As such, we will refer to the groups ![]() $H^i(Y,k)$ themselves as motivic cohomology groups. (This is slightly nonstandard notation, which hopefully makes some of the typography easier to read.)
$H^i(Y,k)$ themselves as motivic cohomology groups. (This is slightly nonstandard notation, which hopefully makes some of the typography easier to read.)
We briefly summarize a number of standard properties of these groups. To start with, as a consequence of Bloch's strong moving lemma [Reference BlochBlo94, Theorem 0.1], they admit arbitrary pullbacks (see [Reference BlochBlo86, Theorem 4.1]). They also satisfy:
– if
 $Y = \coprod _{h=1}^t Y_h$ is a finite disjoint union of
$Y = \coprod _{h=1}^t Y_h$ is a finite disjoint union of  $F$-schemes, then
$F$-schemes, then  $H^i(Y,k) \cong \bigoplus _{h=1}^t H^i(Y_h,k)$;
$H^i(Y,k) \cong \bigoplus _{h=1}^t H^i(Y_h,k)$;–
 $H^i(Y,k) \cong H^i(Y \times \mathbb {A}^1,k)$ via pullback by the projection morphism
$H^i(Y,k) \cong H^i(Y \times \mathbb {A}^1,k)$ via pullback by the projection morphism  $Y \times _F \mathbb {A}^1 \to Y$ (see [Reference BlochBlo86, Theorem 2.1]);
$Y \times _F \mathbb {A}^1 \to Y$ (see [Reference BlochBlo86, Theorem 2.1]);–
 $H^0(Y, 0) \cong \mathbb {Z}$ if
$H^0(Y, 0) \cong \mathbb {Z}$ if  $Y$ is connected and
$Y$ is connected and  $H^i(Y, 0) = 0$ for
$H^i(Y, 0) = 0$ for  $i \neq 0$;
$i \neq 0$;– if
 $Y$ is smooth, then
$Y$ is smooth, then  $H^1(Y,1)$ is naturally isomorphic to the group of global units on
$H^1(Y,1)$ is naturally isomorphic to the group of global units on  $Y$, and
$Y$, and  $H^2(Y,1)$ is naturally isomorphic to the Picard group of
$H^2(Y,1)$ is naturally isomorphic to the Picard group of  $Y$, while
$Y$, while  $H^i(Y,1) = 0$ for
$H^i(Y,1) = 0$ for  $i \notin \{1,2\}$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Corollary 4.2]);
$i \notin \{1,2\}$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Corollary 4.2]);– if
 $Y$ is smooth, then
$Y$ is smooth, then  $H^i(Y,k) = 0$ for
$H^i(Y,k) = 0$ for  $i > k + \dim Y$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 3.6]);
$i > k + \dim Y$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 3.6]);– if
 $Y$ is a smooth variety over
$Y$ is a smooth variety over  $F$, then
$F$, then  $H^i(Y,k) = 0$ for
$H^i(Y,k) = 0$ for  $i > 2k$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 19.3]);
$i > 2k$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 19.3]);– if
 $f \colon X \rightarrow Y$ is a finite locally free morphism of quasi-projective
$f \colon X \rightarrow Y$ is a finite locally free morphism of quasi-projective  $F$-schemes of finite type (so proper of relative dimension zero), then
$F$-schemes of finite type (so proper of relative dimension zero), then  $f_* f^*$ is multiplication by the degree of
$f_* f^*$ is multiplication by the degree of  $f$ (cf. [Sta24, Lemma 02RH]).
$f$ (cf. [Sta24, Lemma 02RH]).
Suppose that ![]() $Y$ is equidimensional. Then, for any closed
$Y$ is equidimensional. Then, for any closed ![]() $F$-subscheme
$F$-subscheme ![]() $\rho \colon Z \to Y$ of pure codimension
$\rho \colon Z \to Y$ of pure codimension ![]() $c$ and its complement
$c$ and its complement ![]() $\iota \colon U \to Y$, there is an exact Gysin sequence
$\iota \colon U \to Y$, there is an exact Gysin sequence
We refer to the map ![]() $\partial$ as a residue map. It results from the distinguished triangle determined by the left exact sequence of complexes given by pushforward by
$\partial$ as a residue map. It results from the distinguished triangle determined by the left exact sequence of complexes given by pushforward by ![]() $\iota$ and pullback by
$\iota$ and pullback by ![]() $\rho$ given by Bloch's moving lemma.
$\rho$ given by Bloch's moving lemma.
Motivic cohomology also has cup products
which can be constructed by pulling back an external product via the diagonal [Reference BlochBlo86, § 5]. There is then an isomorphism of graded rings
 \[ \bigoplus_{i=0}^{\infty} K_i^M(F) \xrightarrow{\sim} \bigoplus_{i=0}^{\infty} H^i(F,i) \]
\[ \bigoplus_{i=0}^{\infty} K_i^M(F) \xrightarrow{\sim} \bigoplus_{i=0}^{\infty} H^i(F,i) \]
induced by the standard identifications of both sides with ![]() $\mathbb {Z}$ and
$\mathbb {Z}$ and ![]() $F^{\times }$ in degrees
$F^{\times }$ in degrees ![]() $0$ and
$0$ and ![]() $1$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 5.1 and Lemma 5.6]). Recall that the canonical homomorphism
$1$ (see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 5.1 and Lemma 5.6]). Recall that the canonical homomorphism ![]() $K_i^M(F) \to K_i(F)$ to the
$K_i^M(F) \to K_i(F)$ to the ![]() $i$th algebraic
$i$th algebraic ![]() $K$-group of
$K$-group of ![]() $F$ is an isomorphism for
$F$ is an isomorphism for ![]() $i \le 2$, the case of
$i \le 2$, the case of ![]() $i=2$ being Matsumoto's theorem.
$i=2$ being Matsumoto's theorem.
We will need to compare compositions of pushforwards and pullbacks. For instance, we shall often employ the following lemma in the case that the underlying schemes are spectra of fields and ![]() $i=k$, in which case the assertion is one of Milnor
$i=k$, in which case the assertion is one of Milnor ![]() $K$-theory (see also [Reference RostRos96, Rule 1c, p. 329] for a direct formulation of this assertion, noting Theorem 1.4 therein).
$K$-theory (see also [Reference RostRos96, Rule 1c, p. 329] for a direct formulation of this assertion, noting Theorem 1.4 therein).
Lemma 2.1.1 (Base change)
Suppose that

is a cartesian diagram of smooth, equidimensional quasi-projective schemes of finite type over ![]() $F$, with
$F$, with ![]() $\pi _Y$ flat and
$\pi _Y$ flat and ![]() $f$ proper. Then
$f$ proper. Then ![]() $\pi _X$ is flat,
$\pi _X$ is flat, ![]() $f'$ is proper, and
$f'$ is proper, and
as morphisms ![]() $H^{i}(X, k) \rightarrow H^{i+2c}(Y', k)$, where
$H^{i}(X, k) \rightarrow H^{i+2c}(Y', k)$, where ![]() $c = \dim Y - \dim X$ is the relative dimension of f.
$c = \dim Y - \dim X$ is the relative dimension of f.
Proof. The assertions regarding ![]() $\pi _X$ and
$\pi _X$ and ![]() $f'$ are standard. Since
$f'$ are standard. Since ![]() $\pi _X$ and
$\pi _X$ and ![]() $\pi _Y$ are flat, these morphisms are already defined on cycles by taking inverse images and images, so they are defined on the terms of Bloch's cycle complexes, and they are compatible with the boundary maps (cf. [Reference BlochBlo86, Proposition 1.3]). The stated equality of compositions then already holds at the level of complexes (cf. [Reference FultonFul98, Proposition 1.7]).
$\pi _Y$ are flat, these morphisms are already defined on cycles by taking inverse images and images, so they are defined on the terms of Bloch's cycle complexes, and they are compatible with the boundary maps (cf. [Reference BlochBlo86, Proposition 1.3]). The stated equality of compositions then already holds at the level of complexes (cf. [Reference FultonFul98, Proposition 1.7]).
Corollary 2.1.2 (Projection formula)
Let ![]() $f \colon X \to Y$ be a proper, relative dimension c morphism of smooth, equidimensional quasi-projective schemes of finite type over
$f \colon X \to Y$ be a proper, relative dimension c morphism of smooth, equidimensional quasi-projective schemes of finite type over ![]() $F$, and let
$F$, and let ![]() $\alpha \in H^i(X,k)$ and
$\alpha \in H^i(X,k)$ and ![]() $\beta \in H^{i'}(Y,k')$. Then
$\beta \in H^{i'}(Y,k')$. Then
Proof. We need only apply Lemma 2.1.1 to the cartesian square

where ![]() $\Delta _X$ and
$\Delta _X$ and ![]() $\Delta _Y$ are the diagonal embeddings of
$\Delta _Y$ are the diagonal embeddings of ![]() $X$ and
$X$ and ![]() $Y$, respectively.
$Y$, respectively.
We also have the following compatibility of residues with transfers and inclusions of fields.
Lemma 2.1.3 Let ![]() $E/F$ be a finite extension of fields. Then for
$E/F$ be a finite extension of fields. Then for ![]() $v$ a discrete valuation on
$v$ a discrete valuation on ![]() $F$, one has
$F$, one has
as morphisms ![]() $K_n^{M}(E) \rightarrow K_{n-1}^{M}(k(v))$ on Milnor
$K_n^{M}(E) \rightarrow K_{n-1}^{M}(k(v))$ on Milnor ![]() $K$-theory; the sum on the right is over valuations
$K$-theory; the sum on the right is over valuations ![]() $w$ on
$w$ on ![]() $E$ extending
$E$ extending ![]() $v$, the symbols
$v$, the symbols ![]() $\partial _v$ and
$\partial _v$ and ![]() $\partial _w$ are the residue maps on Milnor
$\partial _w$ are the residue maps on Milnor ![]() $K$-theory induced by the valuations
$K$-theory induced by the valuations ![]() $v$ and
$v$ and ![]() $w$, and
$w$, and ![]() $\operatorname {N}$ denotes transfer in Milnor
$\operatorname {N}$ denotes transfer in Milnor ![]() $K$-theory.
$K$-theory.
Similarly, for each ![]() $w \mid v$ as above, we have
$w \mid v$ as above, we have
as morphisms ![]() $K_n^M(F) \rightarrow K_{n-1}^M(k(w))$, where
$K_n^M(F) \rightarrow K_{n-1}^M(k(w))$, where ![]() $\iota$ denotes a map on Milnor
$\iota$ denotes a map on Milnor ![]() $K$-theory induced by inclusions of fields, and
$K$-theory induced by inclusions of fields, and ![]() $e_{k(w)/k(v)}$ is the ramification index.
$e_{k(w)/k(v)}$ is the ramification index.
Proof. This is stated (without proof, but with references) in [Reference RostRos96, Theorem 1.4]; see in particular Rules 3b and 3cs therein.
2.2 Coniveau spectral sequences
Let us recall the coniveau spectral sequence for motivic cohomology. We refer to [Reference DégliseDeg08], which contains many of the details required to set this up. The primary role of this spectral sequence is that it provides complexes that compute motivic cohomology in our situations of interest, and these are also manifestly equivariant for the automorphism group of the ambient variety.
Continuity properties of motivic cohomology [Reference Mazza, Voevodsky and WeibelMVW06, Lemma 3.9] imply that for a finite- type smooth connected variety ![]() $Y$ over a field
$Y$ over a field ![]() $F$ with function field
$F$ with function field ![]() $k(Y)$, we have
$k(Y)$, we have
where the limit is taken over open subvarieties ![]() $U$ of
$U$ of ![]() $Y$.Footnote 8
$Y$.Footnote 8
For ![]() $U$ as above and any irreducible divisor
$U$ as above and any irreducible divisor ![]() $D$ such that
$D$ such that ![]() $D \cap U$ is nonempty, there is a residue homomorphism
$D \cap U$ is nonempty, there is a residue homomorphism
Consider the collection of open sets ![]() $U$ such that
$U$ such that ![]() $D \cap U$ is smooth and nonempty. The collection of sets
$D \cap U$ is smooth and nonempty. The collection of sets ![]() $U - (D \cap U)$ is cofinal in open sets on
$U - (D \cap U)$ is cofinal in open sets on ![]() $Y$, and the collection of
$Y$, and the collection of ![]() $D \cap U$ is cofinal in open sets on
$D \cap U$ is cofinal in open sets on ![]() $D$. Therefore, the residue maps for
$D$. Therefore, the residue maps for ![]() $U$ in the collection induce a residue map
$U$ in the collection induce a residue map
The latter map is determined by the field ![]() $k(Y)$ and the valuation
$k(Y)$ and the valuation ![]() $v$ on it which cuts out
$v$ on it which cuts out ![]() $D$ in
$D$ in ![]() $Y$ (see [Reference DégliseDeg08, Lemma 5.4.5]). When
$Y$ (see [Reference DégliseDeg08, Lemma 5.4.5]). When ![]() $p=q$, it is the residue in Milnor
$p=q$, it is the residue in Milnor ![]() $K$-theory (see [Reference DégliseDeg08, Proposition 6.2.3]).
$K$-theory (see [Reference DégliseDeg08, Proposition 6.2.3]).
With these preliminaries in hand, we recall the coniveau spectral sequence for ![]() $n \ge 0$.
$n \ge 0$.
Theorem 2.2.1 There is a right half-plane spectral sequence with ![]() $E_1$-page
$E_1$-page
where ![]() $Y_p$ denotes the set of points of
$Y_p$ denotes the set of points of ![]() $Y$ of codimension
$Y$ of codimension ![]() $p$ and the differentials are residue maps.
$p$ and the differentials are residue maps.
The coniveau spectral sequence essentially carries the information of ‘all Gysin sequences at once’ and is a limit of spectral sequences attached to these Gysin sequences. We briefly explain its derivation: attached to a decreasing system ![]() $Z = (Z_p)_{p \in \mathbb {Z}}$ of closed
$Z = (Z_p)_{p \in \mathbb {Z}}$ of closed ![]() $F$-subschemes of
$F$-subschemes of ![]() $Y$ with each
$Y$ with each ![]() $Z_p-Z_{p+1}$ smooth,
$Z_p-Z_{p+1}$ smooth, ![]() $Z_p = Y$ for
$Z_p = Y$ for ![]() $p \le 0$, each
$p \le 0$, each ![]() $Z_p$ with
$Z_p$ with ![]() $1 \le p \le n$ of pure codimension
$1 \le p \le n$ of pure codimension ![]() $p$, and
$p$, and ![]() $Z_p = \varnothing$ for
$Z_p = \varnothing$ for ![]() $p > n$, we have Gysin sequences
$p > n$, we have Gysin sequences
for ![]() $0 \le p \le n-1$. For
$0 \le p \le n-1$. For ![]() $D^{p,q} = H^{q-p}(Z_p,n-p)$ and
$D^{p,q} = H^{q-p}(Z_p,n-p)$ and ![]() $E^{p,q} = H^q(Z_p-Z_{p+1},n)$, the exact couple
$E^{p,q} = H^q(Z_p-Z_{p+1},n)$, the exact couple ![]() $(D^{p,q},E^{p,q})$ determined by the exact sequences of (2.2) gives rise to a convergent right half-plane spectral sequence
$(D^{p,q},E^{p,q})$ determined by the exact sequences of (2.2) gives rise to a convergent right half-plane spectral sequence ![]() $E(Z)$ with
$E(Z)$ with ![]() $E_1$-page
$E_1$-page
Note that the ![]() $q$th row of the
$q$th row of the ![]() $E_1$-page of this spectral sequence
$E_1$-page of this spectral sequence ![]() $E(Z)$ is a complex the form
$E(Z)$ is a complex the form
Our convention will be that ![]() $p$th term in this complex has homological degree the twist
$p$th term in this complex has homological degree the twist ![]() $n-p+1$.
$n-p+1$.
If we have two collections ![]() $Z' = (Z'_p)_p$ and
$Z' = (Z'_p)_p$ and ![]() $Z = (Z_p)_p$ of closed subschemes as above with each
$Z = (Z_p)_p$ of closed subschemes as above with each ![]() $Z'_p$ a closed subscheme of
$Z'_p$ a closed subscheme of ![]() $Z_p$, then we obtain morphisms
$Z_p$, then we obtain morphisms ![]() $E^1_{p,q}(Z) \to E^1_{p,q}(Z')$ via composition
$E^1_{p,q}(Z) \to E^1_{p,q}(Z')$ via composition ![]() $j^* \iota _*$ of pushforward and pullback along
$j^* \iota _*$ of pushforward and pullback along
(with ![]() $\iota$ a closed immersion and
$\iota$ a closed immersion and ![]() $j$ an open immersion). In particular, we can take direct limits of the spectral sequences over directed sets of such collections. If we use the collection of all
$j$ an open immersion). In particular, we can take direct limits of the spectral sequences over directed sets of such collections. If we use the collection of all ![]() $Z$, then we obtain the coniveau spectral sequence.
$Z$, then we obtain the coniveau spectral sequence.
The row for ![]() $q = n$ in the
$q = n$ in the ![]() $E_1$-page of the coniveau sequence is a homological complex
$E_1$-page of the coniveau sequence is a homological complex ![]() $\mathsf {K}$ given in degrees
$\mathsf {K}$ given in degrees ![]() $n$ through
$n$ through ![]() $0$ by
$0$ by
It follows from Lemmas 2.1.1 and 2.1.3 that pushforwards by proper maps and pullbacks by flat maps induce morphisms between these sequences via transfer maps and the maps induced by inclusions of fields, respectively, on Milnor ![]() $K$-theory. In this paper, we employ this complex for
$K$-theory. In this paper, we employ this complex for ![]() $n = 2$. So, let us describe this case in more detail.
$n = 2$. So, let us describe this case in more detail.
Example 2.2.2 Suppose that ![]() $n=2$. Then the
$n=2$. Then the ![]() $E_1$-terms of the coniveau sequence in the range
$E_1$-terms of the coniveau sequence in the range ![]() $0 \leq p \leq 2$ and
$0 \leq p \leq 2$ and ![]() $0 \leq q \leq 2$ look like this:
$0 \leq q \leq 2$ look like this:

where the direct sums are over divisors ![]() $D$ and codimension
$D$ and codimension ![]() $2$ points
$2$ points ![]() $x$.
$x$.
Except possibly those with ![]() $p = 0$ and
$p = 0$ and ![]() $q < 0$, all other terms vanish, recalling that the motivic cohomology
$q < 0$, all other terms vanish, recalling that the motivic cohomology ![]() $H^i(F,k)$ of a field
$H^i(F,k)$ of a field ![]() $F$ vanishes when
$F$ vanishes when ![]() $i > k$. In particular, the spectral sequence degenerates, and the row
$i > k$. In particular, the spectral sequence degenerates, and the row
is a complex in homological degrees ![]() $2$,
$2$, ![]() $1$, and
$1$, and ![]() $0$ computing the cohomology groups
$0$ computing the cohomology groups ![]() $H^2(Y, 2)$,
$H^2(Y, 2)$, ![]() $H^3(Y, 2)$, and
$H^3(Y, 2)$, and ![]() $H^4(Y, 2)$, respectively.
$H^4(Y, 2)$, respectively.
As noted after (2.1), the ![]() $D$-component of the map
$D$-component of the map ![]() $\partial _2$ is given by the tame symbol in
$\partial _2$ is given by the tame symbol in ![]() $K$-theory
$K$-theory
for the valuation ![]() $v$ attached to
$v$ attached to ![]() $D$. The map
$D$. The map ![]() $\partial _1$ takes the divisor of
$\partial _1$ takes the divisor of ![]() $f \in k(D)^{\times }$ (i.e., yielding the order of vanishing at
$f \in k(D)^{\times }$ (i.e., yielding the order of vanishing at ![]() $f$ in each
$f$ in each ![]() $K_0k(x) \cong \mathbb {Z}$ for
$K_0k(x) \cong \mathbb {Z}$ for ![]() $x \in D$), which we interpret in the sense of intersection theory if
$x \in D$), which we interpret in the sense of intersection theory if ![]() $D$ is not smooth.
$D$ is not smooth.
Remark 2.2.3 Suppose that ![]() $n \le 2$. For any (connected) open subscheme
$n \le 2$. For any (connected) open subscheme ![]() $U$ of
$U$ of ![]() $Y$, the maps
$Y$, the maps
are injective, as follows for ![]() $n = 2$ from the form of the coniveau spectral sequence for
$n = 2$ from the form of the coniveau spectral sequence for ![]() $U$ in Example 2.2.2, noting that
$U$ in Example 2.2.2, noting that ![]() $k(U) = k(Y)$ (and for
$k(U) = k(Y)$ (and for ![]() $n \le 1$ more easily). Accordingly, we will say that a class in
$n \le 1$ more easily). Accordingly, we will say that a class in ![]() $K_n^M k(Y)$ is defined on
$K_n^M k(Y)$ is defined on ![]() $U$ if it lies in the image of the morphism
$U$ if it lies in the image of the morphism ![]() $H^n(U,n) \rightarrow H^n(k(Y),n)$. Given a class
$H^n(U,n) \rightarrow H^n(k(Y),n)$. Given a class ![]() $\kappa \in K_n^Mk(Y)$ defined on
$\kappa \in K_n^Mk(Y)$ defined on ![]() $U$ and a closed point
$U$ and a closed point ![]() $x \in U$, it is then meaningful to specialize
$x \in U$, it is then meaningful to specialize ![]() $\kappa$ to
$\kappa$ to ![]() $x$ via pullback, producing a class in
$x$ via pullback, producing a class in ![]() $K_n^M k(x)$.
$K_n^M k(x)$.
2.3 Trace maps
Let ![]() $G$ be a smooth, connected commutative group scheme over our base smooth variety
$G$ be a smooth, connected commutative group scheme over our base smooth variety ![]() $Y$ over
$Y$ over ![]() $F$. Let
$F$. Let ![]() $U$ be a nonempty open
$U$ be a nonempty open ![]() $F$-subscheme of a closed
$F$-subscheme of a closed ![]() $F$-subscheme of
$F$-subscheme of ![]() $G$ of pure codimension. Multiplication by any positive integer
$G$ of pure codimension. Multiplication by any positive integer ![]() $m$ defines a morphism
$m$ defines a morphism ![]() $m \colon m^{-1}U \to U$. Pushforward by the finite map given by multiplication by
$m \colon m^{-1}U \to U$. Pushforward by the finite map given by multiplication by ![]() $m$ on
$m$ on ![]() $G$ induces a map
$G$ induces a map
If ![]() $m^{-1}U$ is a subscheme of
$m^{-1}U$ is a subscheme of ![]() $U$, then precomposing the pushforward by
$U$, then precomposing the pushforward by ![]() $m$ with pullback under inclusion gives a morphism
$m$ with pullback under inclusion gives a morphism
denoted by the same symbol, which we refer to as a trace map for ![]() $m$. (The reader might compare with [Reference Kings and RösslerKR17, Definition 2.1.1].)
$m$. (The reader might compare with [Reference Kings and RösslerKR17, Definition 2.1.1].)
In the remainder of this paper, we will frequently be interested in the ‘fixed parts’ of motivic cohomology groups, comprising all elements fixed by all (but finitely many) trace maps ![]() $[p]_*$ for
$[p]_*$ for ![]() $p$ prime not equal to the characteristic of
$p$ prime not equal to the characteristic of ![]() $F$. This frequently isolates a subspace of elements of geometric significance.
$F$. This frequently isolates a subspace of elements of geometric significance.
Example 2.3.1 Let ![]() $z$ denote the coordinate function on
$z$ denote the coordinate function on ![]() $G = \mathbb {G}_m$ over
$G = \mathbb {G}_m$ over ![]() $F$. Choose
$F$. Choose ![]() $m$ not divisible by the characteristic of
$m$ not divisible by the characteristic of ![]() $F$, and suppose that
$F$, and suppose that ![]() $U$ open in
$U$ open in ![]() $G$ satisfies
$G$ satisfies ![]() $m^{-1}U \subset U$. The map
$m^{-1}U \subset U$. The map ![]() $[m]_*$ on
$[m]_*$ on ![]() $H^1(U,1) \subset F(z)^{\times }$ is characterized by the property that for
$H^1(U,1) \subset F(z)^{\times }$ is characterized by the property that for ![]() $f \in H^1(U,1)$ and
$f \in H^1(U,1)$ and ![]() $\alpha \in U(F) \subseteq F^{\times }$,
$\alpha \in U(F) \subseteq F^{\times }$,
with the product taken over ![]() $m$th roots of
$m$th roots of ![]() $\alpha$ inside an algebraic closure of
$\alpha$ inside an algebraic closure of ![]() $F$. The pullback
$F$. The pullback ![]() $[m]^*$ is given more simply by
$[m]^*$ is given more simply by
In particular, for ![]() $U = \mathbb {G}_m-\{1\}$, the norm map
$U = \mathbb {G}_m-\{1\}$, the norm map ![]() $[m]_*$ fixes
$[m]_*$ fixes ![]() $1-z$ in
$1-z$ in ![]() $H^1(\mathbb {G}_m-\{1\},1)$, as follows from the calculation
$H^1(\mathbb {G}_m-\{1\},1)$, as follows from the calculation
 \begin{align} \prod_{i=0}^{m-1} (1-\zeta_m^i z^{1/m}) = 1-z, \end{align}
\begin{align} \prod_{i=0}^{m-1} (1-\zeta_m^i z^{1/m}) = 1-z, \end{align}
where ![]() $\zeta _m$ denotes a primitive
$\zeta _m$ denotes a primitive ![]() $m$th root of unity. (In fact,
$m$th root of unity. (In fact, ![]() $1-z$ is
$1-z$ is ![]() $[m]_*$-fixed even for
$[m]_*$-fixed even for ![]() $m$ divisible by
$m$ divisible by ![]() $\operatorname {char} F$.)
$\operatorname {char} F$.)
Example 2.3.2 Take two smooth connected commutative group schemes ![]() $G_1$ and
$G_1$ and ![]() $G_2$ over
$G_2$ over ![]() $F$, and set
$F$, and set ![]() $G =G_1 \times G_2$. For
$G =G_1 \times G_2$. For ![]() $\nu _j \in H^{i_j}(G_j,k_j)$ with
$\nu _j \in H^{i_j}(G_j,k_j)$ with ![]() $i_j \in \mathbb {Z}$ and
$i_j \in \mathbb {Z}$ and ![]() $k_j \ge 0$, define the exterior product
$k_j \ge 0$, define the exterior product ![]() $\nu _1 \boxtimes \nu _2 \in H^{i_1+i_2}(G, k_1+k_2)$ as the cup product
$\nu _1 \boxtimes \nu _2 \in H^{i_1+i_2}(G, k_1+k_2)$ as the cup product ![]() $\pi _1^* \nu _1 \cup \pi _2^* \nu _2$, with
$\pi _1^* \nu _1 \cup \pi _2^* \nu _2$, with ![]() $\pi _j \colon G \to G_j$ the projection maps. We then have
$\pi _j \colon G \to G_j$ the projection maps. We then have
(To verify this from basic properties, factor the multiplication-by-![]() $m$ map
$m$ map ![]() $[m]$ as a product of corresponding maps
$[m]$ as a product of corresponding maps ![]() $[m]_1$ and
$[m]_1$ and ![]() $[m]_2$ in the first and second coordinates. Then (2.6) follows from the equality
$[m]_2$ in the first and second coordinates. Then (2.6) follows from the equality
where the middle equality is the projection formula of Lemma 2.1.2, together with the analogous assertion with the roles of first and second variables switched.)
The maps ![]() $[m]_*$ commute with each other, with pullback to open subschemes, with pushforward by inclusion of closed subschemes, and with residue maps in Gysin sequences (see [Reference Kings and RösslerKR17, § 2.1]). They also induce a self-map of the
$[m]_*$ commute with each other, with pullback to open subschemes, with pushforward by inclusion of closed subschemes, and with residue maps in Gysin sequences (see [Reference Kings and RösslerKR17, § 2.1]). They also induce a self-map of the ![]() $E_1$-page of the coniveau spectral sequence of Theorem 2.2.1.
$E_1$-page of the coniveau spectral sequence of Theorem 2.2.1.
Remark 2.3.3 For ![]() $x \in G_p$ (i.e., a codimension
$x \in G_p$ (i.e., a codimension ![]() $p$ point) and
$p$ point) and ![]() $y \in G_p$ with
$y \in G_p$ with ![]() $my = x$, the trace map
$my = x$, the trace map
is the sum of norm maps associated to the induced inclusions ![]() $k(x) \hookrightarrow k(y)$ for
$k(x) \hookrightarrow k(y)$ for ![]() $x, y \in G_p$ with
$x, y \in G_p$ with ![]() $my = x$. By [Reference HesselholtHes05, Lemma 14], this is compatible with residues, and so differentials on the
$my = x$. By [Reference HesselholtHes05, Lemma 14], this is compatible with residues, and so differentials on the ![]() $E_1$-page of the coniveau sequence. In particular, we have trace maps on our complexes
$E_1$-page of the coniveau sequence. In particular, we have trace maps on our complexes ![]() $\mathsf {K}^{(n)}(G)$ of (2.3).
$\mathsf {K}^{(n)}(G)$ of (2.3).
2.4 Powers of commutative group schemes
If we start with a smooth, equidimensional quasi-projective scheme ![]() $\mathscr {Y}$ of finite type over
$\mathscr {Y}$ of finite type over ![]() $Y$, then instead of taking a limit of motivic cohomology groups over all open subvarieties of
$Y$, then instead of taking a limit of motivic cohomology groups over all open subvarieties of ![]() $\mathscr {Y}$, it is natural to use only those subvarieties which are themselves defined over
$\mathscr {Y}$, it is natural to use only those subvarieties which are themselves defined over ![]() $Y$. As in § 2.2, we have a coniveau-type spectral sequence for this limit. We are actually interested in only very special cases with finer structure. Correspondingly, we consider here complements of much smaller collections of closed subsets defined over
$Y$. As in § 2.2, we have a coniveau-type spectral sequence for this limit. We are actually interested in only very special cases with finer structure. Correspondingly, we consider here complements of much smaller collections of closed subsets defined over ![]() $Y$ and limits thereof.
$Y$ and limits thereof.
Now let us fix ![]() $n \ge 1$ and let
$n \ge 1$ and let ![]() $\mathscr {Y} = G^n$ be the
$\mathscr {Y} = G^n$ be the ![]() $n$th power of a smooth, connected commutative group scheme
$n$th power of a smooth, connected commutative group scheme ![]() $G$ of relative dimension
$G$ of relative dimension ![]() $1$ over
$1$ over ![]() $Y$, such as
$Y$, such as ![]() $\mathbb {G}_{m/Y}$ or a smooth family of elliptic curves over
$\mathbb {G}_{m/Y}$ or a smooth family of elliptic curves over ![]() $Y$. We use throughout the convention that the monoid
$Y$. We use throughout the convention that the monoid
of integral matrices of nonzero determinant acts by right multiplication on ![]() $G^n$. For example, if
$G^n$. For example, if ![]() $n = 2$ and
$n = 2$ and ![]() $\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta$, then for any
$\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta$, then for any ![]() $g_1, g_2 \in G$, we have
$g_1, g_2 \in G$, we have
This being a right action, the monoid ![]() $\Delta$ then acts on the left on the motivic cohomology groups
$\Delta$ then acts on the left on the motivic cohomology groups ![]() $H^i(G^n,k)$ by pullback.
$H^i(G^n,k)$ by pullback.
Even better, ![]() $\Delta$ acts on the left on the complex
$\Delta$ acts on the left on the complex ![]() $\mathsf {K} = \mathsf {K}^{(n)}(\mathscr {Y})$ of (2.3), also by pullback. That is, if
$\mathsf {K} = \mathsf {K}^{(n)}(\mathscr {Y})$ of (2.3), also by pullback. That is, if ![]() $x \in \mathscr {Y}_q$ is a codimension
$x \in \mathscr {Y}_q$ is a codimension ![]() $q$ point of
$q$ point of ![]() $\mathscr {Y} = G^n$,
$\mathscr {Y} = G^n$, ![]() $\delta \in \Delta$, and
$\delta \in \Delta$, and ![]() $y \in \mathscr {Y}_q$ is such that
$y \in \mathscr {Y}_q$ is such that ![]() $y \cdot \gamma = x$, then pullback yields a map
$y \cdot \gamma = x$, then pullback yields a map ![]() $\gamma ^* \colon k(x) \to k(y)$ of residue fields, and this induces
$\gamma ^* \colon k(x) \to k(y)$ of residue fields, and this induces ![]() $\gamma ^* \colon K_{n-q}^M k(x) \to K_{n-q}^M k(y)$. The pullback map on
$\gamma ^* \colon K_{n-q}^M k(x) \to K_{n-q}^M k(y)$. The pullback map on ![]() $\mathsf {K}_{n-q}$ is the sum of these maps, and the residue maps are clearly equivariant for this action.
$\mathsf {K}_{n-q}$ is the sum of these maps, and the residue maps are clearly equivariant for this action.
Now let us focus on the case ![]() $n = 2$ of interest to us. We consider divisors of the form
$n = 2$ of interest to us. We consider divisors of the form
for nonzero ![]() $\alpha = (i,j) \in \mathbb {Z}^2$. Then
$\alpha = (i,j) \in \mathbb {Z}^2$. Then ![]() $S_{i,j}$ is connected if and only if
$S_{i,j}$ is connected if and only if ![]() $i$ and
$i$ and ![]() $j$ are relatively prime.
$j$ are relatively prime.
Take a finite indexing set ![]() $I \subset \mathbb {Z}^2 - \{(0,0)\}$ with at least two elements and containing at most one representative of each element of
$I \subset \mathbb {Z}^2 - \{(0,0)\}$ with at least two elements and containing at most one representative of each element of ![]() $\mathbb {P}^1(\mathbb {Q})$. We set
$\mathbb {P}^1(\mathbb {Q})$. We set
where we regard ![]() $S_I$ as a closed subscheme of
$S_I$ as a closed subscheme of ![]() $G^2$ with its reduced scheme structure and
$G^2$ with its reduced scheme structure and ![]() $U_I$ as an open subscheme of
$U_I$ as an open subscheme of ![]() $\mathbb {G}_m^2$. We then consider the union of pairwise intersections
$\mathbb {G}_m^2$. We then consider the union of pairwise intersections
 \[ T_I = \bigcup_{\substack{\alpha, \beta \in I \\ \alpha \neq \beta}} (S_{\alpha} \cap S_{\beta}), \]
\[ T_I = \bigcup_{\substack{\alpha, \beta \in I \\ \alpha \neq \beta}} (S_{\alpha} \cap S_{\beta}), \]
which is a finite subgroup scheme of ![]() $G^2$ by our choice of
$G^2$ by our choice of ![]() $I$. Let
$I$. Let
so that ![]() $S_I^{\circ }$ is the disjoint union of the smooth subschemes
$S_I^{\circ }$ is the disjoint union of the smooth subschemes ![]() $S_{\alpha }^{\circ } = S_{\alpha } \cap S_I^{\circ }$ for
$S_{\alpha }^{\circ } = S_{\alpha } \cap S_I^{\circ }$ for ![]() $\alpha \in I$.
$\alpha \in I$.
This fits into the setting above for ![]() $n = 2$ with
$n = 2$ with ![]() $Z_1 = S_I$ and
$Z_1 = S_I$ and ![]() $Z_2 = T_I$, so
$Z_2 = T_I$, so ![]() $Z_0-Z_1 = U_I$ and
$Z_0-Z_1 = U_I$ and ![]() $Z_1-Z_2 = S_I^{\circ }$. We obtain a spectral sequence having the following terms in degrees
$Z_1-Z_2 = S_I^{\circ }$. We obtain a spectral sequence having the following terms in degrees ![]() $(p,q)$ with
$(p,q)$ with ![]() $0 \le p \le 2$ and
$0 \le p \le 2$ and ![]() $0 \le q \le 2$:
$0 \le q \le 2$:

This spectral sequence maps to the coniveau sequence detailed in Example 2.2.2 (with ![]() $Y$ replaced by
$Y$ replaced by ![]() $G^2$). It follows from Remark 2.2.3 that each of the complexes
$G^2$). It follows from Remark 2.2.3 that each of the complexes
injects quasi-isomorphically into the big complex
If we order our indexing sets by ![]() $I \le I'$ if
$I \le I'$ if ![]() $U_{I'} \subseteq U_I$, then the limit complex
$U_{I'} \subseteq U_I$, then the limit complex ![]() $\varinjlim _I \mathsf {K}_I$ is also a quasi-isomorphic subcomplex of
$\varinjlim _I \mathsf {K}_I$ is also a quasi-isomorphic subcomplex of ![]() $\mathsf {K}$. The constructions in this paper can all be carried out using this complex, which is just large enough to allow for the definition of Hecke actions on
$\mathsf {K}$. The constructions in this paper can all be carried out using this complex, which is just large enough to allow for the definition of Hecke actions on ![]() $\mathrm {GL}_2(\mathbb {Z})$-cocycles, in that it is preserved under the pullback action of the monoid
$\mathrm {GL}_2(\mathbb {Z})$-cocycles, in that it is preserved under the pullback action of the monoid ![]() ${\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})}$.
${\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})}$.
3. The square of the multiplicative group
In this section, we shall define a cocycle
where ‘everywhere regular’ means the image of ![]() $H^2(\mathbb {G}_m^2, 2)$. We will primarily work over the base field
$H^2(\mathbb {G}_m^2, 2)$. We will primarily work over the base field ![]() $\mathbb {Q}$, but on occasion we will need to work over a finite base field. We follow the notation for motivic cohomology of § 2.1.
$\mathbb {Q}$, but on occasion we will need to work over a finite base field. We follow the notation for motivic cohomology of § 2.1.
In § 3.1, we begin by computing the motivic cohomology of ![]() $\mathbb {G}_m^r$ for
$\mathbb {G}_m^r$ for ![]() $r \ge 1$. In § 3.2, we introduce explicit symbols in the terms of our motivic complex to be used in the construction. The parabolic cocycle
$r \ge 1$. In § 3.2, we introduce explicit symbols in the terms of our motivic complex to be used in the construction. The parabolic cocycle ![]() $\Theta$ is constructed in § 3.3, and its explicit formula and its parabolicity are verified using its characterizing property. In § 3.4, we then exhibit an Eisenstein property of the class of
$\Theta$ is constructed in § 3.3, and its explicit formula and its parabolicity are verified using its characterizing property. In § 3.4, we then exhibit an Eisenstein property of the class of ![]() $\Theta$ for Hecke operators of all prime levels.
$\Theta$ for Hecke operators of all prime levels.
3.1 Motivic cohomology of  $\mathbb {G}_m^r$
$\mathbb {G}_m^r$
Let ![]() $z$ denote the coordinate function on the multiplicative group
$z$ denote the coordinate function on the multiplicative group ![]() $\mathbb {G}_m$ over a field
$\mathbb {G}_m$ over a field ![]() $F$, normalized so that the value of
$F$, normalized so that the value of ![]() $z$ at the identity element is
$z$ at the identity element is ![]() $1$. The motivic cohomology of
$1$. The motivic cohomology of ![]() $\mathbb {G}_m$ involves classes directly constructed from
$\mathbb {G}_m$ involves classes directly constructed from ![]() $-z$, together with classes pulled back from the motivic cohomology of
$-z$, together with classes pulled back from the motivic cohomology of ![]() $\operatorname {Spec} F$ itself. We extend this description to powers of
$\operatorname {Spec} F$ itself. We extend this description to powers of ![]() $\mathbb {G}_m$.
$\mathbb {G}_m$.
First, we construct suspension isomorphisms in motivic cohomology. Recall the definition of exterior product from Example 2.3.2.
Proposition 3.1.1 Let ![]() $Y$ denote an equidimensional quasi-projective scheme of finite type over
$Y$ denote an equidimensional quasi-projective scheme of finite type over ![]() $F$. There is a natural isomorphism
$F$. There is a natural isomorphism
where the map on the first summand is pullback under projection to the first factor and the map on the second summand is left exterior product with ![]() $-z$, considered as a class in
$-z$, considered as a class in ![]() $H^1(\mathbb {G}_m, 1)$.
$H^1(\mathbb {G}_m, 1)$.
The reason for choosing ![]() $-z$, as opposed to
$-z$, as opposed to ![]() $z$, will be made clear in Lemma 4.1.1. This result is well known and corresponds to the ‘fundamental theorem’ of algebraic
$z$, will be made clear in Lemma 4.1.1. This result is well known and corresponds to the ‘fundamental theorem’ of algebraic ![]() $K$-theory (proved for
$K$-theory (proved for ![]() $K_0$ and
$K_0$ and ![]() $K_1$ by Bass and in general by Quillen).
$K_1$ by Bass and in general by Quillen).
Proof. Consider the canonical embedding ![]() $\iota \colon \mathbb {G}_m \times Y \hookrightarrow \mathbb {A}^1 \times Y$ given by the usual embedding in the first coordinate and the identity in the second. The Gysin sequence has the form
$\iota \colon \mathbb {G}_m \times Y \hookrightarrow \mathbb {A}^1 \times Y$ given by the usual embedding in the first coordinate and the identity in the second. The Gysin sequence has the form
As noted in § 2.1, the pullback ![]() $H^i(Y,k) \to H^i(\mathbb {A}^1 \times Y,k)$ by the projection map is an isomorphism. Thus, it suffices to show that
$H^i(Y,k) \to H^i(\mathbb {A}^1 \times Y,k)$ by the projection map is an isomorphism. Thus, it suffices to show that ![]() $\partial$ is split by a map on the right-hand summand in the theorem, and this follows from
$\partial$ is split by a map on the right-hand summand in the theorem, and this follows from ![]() $\partial (-z \boxtimes x) = \partial (-z) \boxtimes x = x$ for
$\partial (-z \boxtimes x) = \partial (-z) \boxtimes x = x$ for ![]() $x \in H^{i-1}(Y,k-1)$.
$x \in H^{i-1}(Y,k-1)$.
Corollary 3.1.2 Let ![]() $Y$ denote an equidimensional quasi-projective scheme of finite type over a field
$Y$ denote an equidimensional quasi-projective scheme of finite type over a field ![]() $F$, and let
$F$, and let ![]() $r \ge 1$. There is a natural isomorphism
$r \ge 1$. There is a natural isomorphism
 \[ H^i(\mathbb{G}_m^r,k) \cong \bigoplus_{j=0}^{\min(k,r)} H^{i-j}(F,k-j)^{\binom{r}{j}}. \]
\[ H^i(\mathbb{G}_m^r,k) \cong \bigoplus_{j=0}^{\min(k,r)} H^{i-j}(F,k-j)^{\binom{r}{j}}. \]
Proof. This follows by induction on ![]() $r$ by iterating Proposition 3.1.1, that is, taking
$r$ by iterating Proposition 3.1.1, that is, taking ![]() $Y = \mathbb {G}_m^{r-1}$ in the inductive step. Note that
$Y = \mathbb {G}_m^{r-1}$ in the inductive step. Note that ![]() $H^{i-j}(F,k-j) = 0$ if
$H^{i-j}(F,k-j) = 0$ if ![]() $k < j$, so the direct sum stops at the minimum of
$k < j$, so the direct sum stops at the minimum of ![]() $k$ and
$k$ and ![]() $r$.
$r$.
Since ![]() $H^i(F,k) = 0$ for
$H^i(F,k) = 0$ for ![]() $i > k$, we obtain in particular the following corollary.
$i > k$, we obtain in particular the following corollary.
Corollary 3.1.3 The groups ![]() $H^i(\mathbb {G}_m^r,k)$ vanish for all
$H^i(\mathbb {G}_m^r,k)$ vanish for all ![]() $i > k$.
$i > k$.
3.2 Symbols in the complex computing motivic cohomology
Recall from Example 2.2.2 that the coniveau spectral sequence gives rise to a homological complex ![]() $\mathsf {K}$ with nonzero terms in degrees
$\mathsf {K}$ with nonzero terms in degrees ![]() $2$,
$2$, ![]() $1$, and
$1$, and ![]() $0$ given by
$0$ given by
the sums being taken over irreducible divisors and closed points, respectively. This complex computes the cohomology groups ![]() $H^*(\mathbb {G}_m^2, 2)$ in degrees
$H^*(\mathbb {G}_m^2, 2)$ in degrees ![]() $2$ to
$2$ to ![]() $4$ from left to right. Therefore, by Corollary 3.1.3, the sequence is exact in the middle and at the right, and its homology at the left is
$4$ from left to right. Therefore, by Corollary 3.1.3, the sequence is exact in the middle and at the right, and its homology at the left is ![]() $H^2(\mathbb {G}_m^2,2)$. Let
$H^2(\mathbb {G}_m^2,2)$. Let ![]() $\bar {\mathsf {K}}_2$ be the quotient of
$\bar {\mathsf {K}}_2$ be the quotient of ![]() $\mathsf {K}_2$ by the image of
$\mathsf {K}_2$ by the image of ![]() $H^2(\mathbb {G}_m^2, 2)$ so that we get a short exact sequence
$H^2(\mathbb {G}_m^2, 2)$ so that we get a short exact sequence
We shall denote the boundary maps in this complex by the generic symbol ![]() $\partial$.
$\partial$.
The monoid ![]() $\Delta = \mathrm {GL}_2(\mathbb {Q}) \cap M_2(\mathbb {Z})$ acts on the right on
$\Delta = \mathrm {GL}_2(\mathbb {Q}) \cap M_2(\mathbb {Z})$ acts on the right on ![]() $\mathbb {G}_m^2$ by the formula of (2.7). As explained in § 2.4, the complex
$\mathbb {G}_m^2$ by the formula of (2.7). As explained in § 2.4, the complex ![]() $\mathsf {K}$ is correspondingly endowed with a left
$\mathsf {K}$ is correspondingly endowed with a left ![]() $\Delta$-action via pullback. This action descends to an action on
$\Delta$-action via pullback. This action descends to an action on ![]() $\bar {\mathsf {K}}$. For now, we use only the induced action of the group
$\bar {\mathsf {K}}$. For now, we use only the induced action of the group ![]() $\mathrm {GL}_2(\mathbb {Z})$; we will employ the full
$\mathrm {GL}_2(\mathbb {Z})$; we will employ the full ![]() $\Delta$-action in § 3.4.
$\Delta$-action in § 3.4.
Let us define special elements
attached to a primitive vector ![]() $(a,c) \in \mathbb {Z}^2$ or to a matrix
$(a,c) \in \mathbb {Z}^2$ or to a matrix ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$ that satisfy
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$ that satisfy
 \begin{equation} \partial \bigg\langle \!\bigg(\begin{matrix} a & b\\c & d \end{matrix}\bigg) \!\bigg\rangle = \begin{cases} \langle a,c \rangle -\langle -b, -d\rangle & \text{if } \det \gamma=1, \\ \langle -a,-c \rangle -\langle b, d\rangle & \text{if } \det \gamma=-1 \end{cases} \quad \text{and} \quad \partial \langle a,c \rangle = e. \end{equation}
\begin{equation} \partial \bigg\langle \!\bigg(\begin{matrix} a & b\\c & d \end{matrix}\bigg) \!\bigg\rangle = \begin{cases} \langle a,c \rangle -\langle -b, -d\rangle & \text{if } \det \gamma=1, \\ \langle -a,-c \rangle -\langle b, d\rangle & \text{if } \det \gamma=-1 \end{cases} \quad \text{and} \quad \partial \langle a,c \rangle = e. \end{equation}These are:
– the
 $\mathrm {GL}_2(\mathbb {Z})$-fixed class
$\mathrm {GL}_2(\mathbb {Z})$-fixed class  $e \in \mathsf {K}_0$ of the element
$e \in \mathsf {K}_0$ of the element  $1 \in \mathbb {Z}$ supported at the identity of
$1 \in \mathbb {Z}$ supported at the identity of  $\mathbb {G}_m$;
$\mathbb {G}_m$;– for a primitive vector
 $(a,c) \in \mathbb {Z}^2$ and the torus
$(a,c) \in \mathbb {Z}^2$ and the torus  $S_{a,c} = \ker (\mathbb {G}_m^2 \xrightarrow {(x,y) \mapsto x^ay^c} \mathbb {G}_m)$ of (2.8), the image
$S_{a,c} = \ker (\mathbb {G}_m^2 \xrightarrow {(x,y) \mapsto x^ay^c} \mathbb {G}_m)$ of (2.8), the image  $\langle a,c \rangle \in \mathsf {K}_1$ of the invertible function
where
$\langle a,c \rangle \in \mathsf {K}_1$ of the invertible function
where \[ 1-z_1^b z_2^d \in \mathscr{O}(S_{a,c}-\{1\})^{\times} \hookrightarrow K_1( \mathbb{Q}(S_{a,c})), \]
\[ 1-z_1^b z_2^d \in \mathscr{O}(S_{a,c}-\{1\})^{\times} \hookrightarrow K_1( \mathbb{Q}(S_{a,c})), \]
 $\big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ extends
$\big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ extends  $(a,c)$ – this is independent of the choice of
$(a,c)$ – this is independent of the choice of  $(b,d)$, since another choice simply alters the function
$(b,d)$, since another choice simply alters the function  $z_1^b z_2^d$ by a multiple of
$z_1^b z_2^d$ by a multiple of  $z_1^a z_2^c$, which is
$z_1^a z_2^c$, which is  $1$ on
$1$ on  $S_{a,c}$;
$S_{a,c}$;– for
 $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, and its columns
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, and its columns  $v_1= (a,c)$ and
$v_1= (a,c)$ and  $v_2= (b,d)$, the Steinberg symbol
Note that
$v_2= (b,d)$, the Steinberg symbol
Note that \[ \langle \gamma \rangle = \langle v_1, v_2 \rangle = \{1-z_1^az_2^c, 1-z_1^b z_2^d\} \in \mathsf{K}_2. \]
\[ \langle \gamma \rangle = \langle v_1, v_2 \rangle = \{1-z_1^az_2^c, 1-z_1^b z_2^d\} \in \mathsf{K}_2. \]
 $\langle \gamma \rangle = \gamma ^* \langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle$ is the image of
$\langle \gamma \rangle = \gamma ^* \langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle$ is the image of  $(1-z_1^az_2^c) \cup (1-z_1^bz_2^d) \in H^2(\mathbb {G}_m^2 - S_{a,c} \cup S_{b,d},2)$.
$(1-z_1^az_2^c) \cup (1-z_1^bz_2^d) \in H^2(\mathbb {G}_m^2 - S_{a,c} \cup S_{b,d},2)$.
The special elements of the form ![]() $e$,
$e$, ![]() $\langle a,c \rangle$ for
$\langle a,c \rangle$ for ![]() $(a,c) \in \mathbb {Z}^2$ primitive, and
$(a,c) \in \mathbb {Z}^2$ primitive, and ![]() $\langle \gamma \rangle$ for
$\langle \gamma \rangle$ for ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$ together span a subcomplex
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$ together span a subcomplex ![]() $\mathsf {Symb}$ of
$\mathsf {Symb}$ of ![]() $\mathsf {K}$ that we refer to as the symbol complex. We will return to it in §§ 4 and 5. That these symbols satisfy (3.2) follows directly from the description in Example 2.2.2 of the residue maps in
$\mathsf {K}$ that we refer to as the symbol complex. We will return to it in §§ 4 and 5. That these symbols satisfy (3.2) follows directly from the description in Example 2.2.2 of the residue maps in ![]() $\mathsf {K}$ in terms of tame symbols (2.4) and divisors.
$\mathsf {K}$ in terms of tame symbols (2.4) and divisors.
Remark 3.2.1 We note for later use that, for ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, the pullback
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, the pullback ![]() $\gamma ^* \langle 0,1 \rangle$ is supported on the torus
$\gamma ^* \langle 0,1 \rangle$ is supported on the torus ![]() $S_{b,d}$ which is the kernel of
$S_{b,d}$ which is the kernel of ![]() $(z_1, z_2) \mapsto z_1^b z_2^d$. On this divisor, it is given by
$(z_1, z_2) \mapsto z_1^b z_2^d$. On this divisor, it is given by ![]() $\gamma ^* (1-z_1^{-1}) = 1- z_1^{-a} z_2^{-c}$. Thus
$\gamma ^* (1-z_1^{-1}) = 1- z_1^{-a} z_2^{-c}$. Thus
 \begin{equation} \gamma^* \langle 0,1 \rangle = \begin{cases} \langle b,d \rangle & \text{if } \det(\gamma)=1,\\ \langle -b, -d \rangle & \text{if } \det(\gamma)=-1. \end{cases} \end{equation}
\begin{equation} \gamma^* \langle 0,1 \rangle = \begin{cases} \langle b,d \rangle & \text{if } \det(\gamma)=1,\\ \langle -b, -d \rangle & \text{if } \det(\gamma)=-1. \end{cases} \end{equation}3.3 The cocycle
Pulling back the complex ![]() $\bar {\mathsf {K}}_2 \rightarrow \mathsf {K}_1 \rightarrow \mathsf {K}_0$ to the cyclic subgroup generated by
$\bar {\mathsf {K}}_2 \rightarrow \mathsf {K}_1 \rightarrow \mathsf {K}_0$ to the cyclic subgroup generated by ![]() $e \in \mathsf {K}_0$, we get an extension of
$e \in \mathsf {K}_0$, we get an extension of ![]() $\mathbb {Z}$ by
$\mathbb {Z}$ by ![]() $\bar {\mathsf {K}}_2$, and so an extension class in
$\bar {\mathsf {K}}_2$, and so an extension class in
We shall describe a cocycle representing this class more explicitly in Proposition 3.3.1 below. We then give an explicit recipe for ![]() $\Theta _{\gamma }$ as a sum of symbols
$\Theta _{\gamma }$ as a sum of symbols ![]() $\langle \rho \rangle$ with
$\langle \rho \rangle$ with ![]() $\rho \in \mathrm {SL}_2(\mathbb {Z})$ and show that it lies in parabolic cohomology. Because
$\rho \in \mathrm {SL}_2(\mathbb {Z})$ and show that it lies in parabolic cohomology. Because ![]() $H^2(\mathrm {GL}_2(\mathbb {Z}),\mathbb {Z})$ is torsion, a multiple of
$H^2(\mathrm {GL}_2(\mathbb {Z}),\mathbb {Z})$ is torsion, a multiple of ![]() $\Theta$ can actually be lifted to
$\Theta$ can actually be lifted to ![]() $\mathsf {K}_2$; in § 5, we sketch how to do this explicitly.
$\mathsf {K}_2$; in § 5, we sketch how to do this explicitly.
Proposition 3.3.1 There is a ![]() $1$-cocycle
$1$-cocycle
uniquely characterized by the property that
Proof. Since ![]() $(\gamma ^*-1)\langle 0,1 \rangle$ has trivial boundary
$(\gamma ^*-1)\langle 0,1 \rangle$ has trivial boundary ![]() $e-e = 0$, it is the boundary of a unique
$e-e = 0$, it is the boundary of a unique ![]() $\Theta _{\gamma } \in \bar {\mathsf {K}}_2$. Since pullback is a left action, we have
$\Theta _{\gamma } \in \bar {\mathsf {K}}_2$. Since pullback is a left action, we have
for ![]() $\gamma, \gamma ' \in \mathrm {GL}_2(\mathbb {Z})$. That
$\gamma, \gamma ' \in \mathrm {GL}_2(\mathbb {Z})$. That ![]() $\Theta$ is a cocycle therefore follows by the exactness of
$\Theta$ is a cocycle therefore follows by the exactness of ![]() $\bar {\mathsf {K}}$.
$\bar {\mathsf {K}}$.
Next, we give an explicit recipe for values of ![]() $\Theta$ in terms of our special symbols in
$\Theta$ in terms of our special symbols in ![]() $\mathsf {K}_2$ using a standard variant of the Euclidean algorithm, analogous to writing a geodesic between cusps on the modular curve as a sum of Manin symbols. We make the latter analogy precise in § 4.3.
$\mathsf {K}_2$ using a standard variant of the Euclidean algorithm, analogous to writing a geodesic between cusps on the modular curve as a sum of Manin symbols. We make the latter analogy precise in § 4.3.
Given ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, the Euclidean algorithm allows us to find a sequence
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, the Euclidean algorithm allows us to find a sequence ![]() $(v_i)_{i=0}^k$ in
$(v_i)_{i=0}^k$ in ![]() $\mathbb {Z}^2$ for some
$\mathbb {Z}^2$ for some ![]() $k \ge 0$ with
$k \ge 0$ with ![]() $v_0 = (0,1)$ and
$v_0 = (0,1)$ and ![]() $v_k = \det (\gamma ) (b,d)$ and such that the
$v_k = \det (\gamma ) (b,d)$ and such that the ![]() $v_i = (b_i,d_i)$ satisfy
$v_i = (b_i,d_i)$ satisfy ![]() $\det \big (\begin{smallmatrix} b_{i-1} & b_i \\ d_{i-1} & d_i \end{smallmatrix}\big ) = 1$ for all
$\det \big (\begin{smallmatrix} b_{i-1} & b_i \\ d_{i-1} & d_i \end{smallmatrix}\big ) = 1$ for all ![]() $1 \le i \le k$. We call such a sequence
$1 \le i \le k$. We call such a sequence ![]() $(v_i)_{i=0}^k$ a connecting sequence for
$(v_i)_{i=0}^k$ a connecting sequence for ![]() $\gamma$.
$\gamma$.
Proposition 3.3.2 Let ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, and choose a connecting sequence
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, and choose a connecting sequence ![]() $(v_i)_{i=0}^k$ for
$(v_i)_{i=0}^k$ for ![]() $\gamma$. Then we have the following equality in
$\gamma$. Then we have the following equality in ![]() $\bar {\mathsf {K}}_2$:
$\bar {\mathsf {K}}_2$:
 \[ \Theta_{\gamma} = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle. \]
\[ \Theta_{\gamma} = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle. \]
Recall from § 3.2 that ![]() $\langle v_i, -v_{i-1} \rangle$ is the symbol associated to the matrix with first column
$\langle v_i, -v_{i-1} \rangle$ is the symbol associated to the matrix with first column ![]() $v_i$ and second column
$v_i$ and second column ![]() $-v_{i-1}$.
$-v_{i-1}$.
Proof. By (3.3) and (3.2) we have
 \[ \partial \bigg( \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle \bigg) = \sum_{i=1}^k (\langle v_i \rangle - \langle v_{i-1} \rangle) = \langle v_k \rangle - \langle v_0 \rangle = \gamma^* \langle 0,1 \rangle - \langle 0,1 \rangle. \]
\[ \partial \bigg( \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle \bigg) = \sum_{i=1}^k (\langle v_i \rangle - \langle v_{i-1} \rangle) = \langle v_k \rangle - \langle v_0 \rangle = \gamma^* \langle 0,1 \rangle - \langle 0,1 \rangle. \]
Since ![]() $\Theta _{\gamma }$ and
$\Theta _{\gamma }$ and ![]() $\sum _{i=1}^k \langle v_i,-v_{i-1} \rangle$ have the same boundary, they are equal in
$\sum _{i=1}^k \langle v_i,-v_{i-1} \rangle$ have the same boundary, they are equal in ![]() $\bar {\mathsf {K}}_2$.
$\bar {\mathsf {K}}_2$.
Example 3.3.3 Take ![]() $\gamma = \big (\begin{smallmatrix} -1 & 0\\0 & -1 \end{smallmatrix}\big )$. Then
$\gamma = \big (\begin{smallmatrix} -1 & 0\\0 & -1 \end{smallmatrix}\big )$. Then ![]() $v_0 = (0,1)$,
$v_0 = (0,1)$, ![]() $v_1 = (-1,0)$, and
$v_1 = (-1,0)$, and ![]() $v_2 = (0,-1)$ form a connecting sequence for
$v_2 = (0,-1)$ form a connecting sequence for ![]() $\gamma$, so
$\gamma$, so
which equals ![]() $-\{ -z_1, 1-z_2 \}$ in
$-\{ -z_1, 1-z_2 \}$ in ![]() $\bar {\mathsf {K}}_2$.
$\bar {\mathsf {K}}_2$.
We will use a perhaps slightly nonstandard notion of parabolic cohomology for ![]() $\mathrm {GL}_2(\mathbb {Z})$, consistent with our use of right actions of
$\mathrm {GL}_2(\mathbb {Z})$, consistent with our use of right actions of ![]() $\mathrm {GL}_2(\mathbb {Z})$ on group schemes. That is, we define the
$\mathrm {GL}_2(\mathbb {Z})$ on group schemes. That is, we define the ![]() $\mathrm {GL}_2(\mathbb {Z})$-parabolic cohomology group
$\mathrm {GL}_2(\mathbb {Z})$-parabolic cohomology group ![]() $H^1_P(\mathrm {GL}_2(\mathbb {Z}),M)$ for a
$H^1_P(\mathrm {GL}_2(\mathbb {Z}),M)$ for a ![]() $\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-module
$\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-module ![]() $M$ to be the intersection of the kernels of the restriction maps from
$M$ to be the intersection of the kernels of the restriction maps from ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}),M) \to H^1(P,M)$, where
$H^1(\mathrm {GL}_2(\mathbb {Z}),M) \to H^1(P,M)$, where ![]() $P$ runs over all stabilizers of nonzero elements of
$P$ runs over all stabilizers of nonzero elements of ![]() $\mathbb {Z}^2$ under the right action of
$\mathbb {Z}^2$ under the right action of ![]() $\mathrm {GL}_2(\mathbb {Z})$. We say that a
$\mathrm {GL}_2(\mathbb {Z})$. We say that a ![]() $1$-cocycle
$1$-cocycle ![]() $\mathrm {GL}_2(\mathbb {Z}) \to M$ is parabolic if its class lies in the parabolic cohomology group
$\mathrm {GL}_2(\mathbb {Z}) \to M$ is parabolic if its class lies in the parabolic cohomology group ![]() $H^1_P(\mathrm {GL}_2(\mathbb {Z}),M)$.
$H^1_P(\mathrm {GL}_2(\mathbb {Z}),M)$.
Proposition 3.3.4 The cocycle ![]() $\Theta$ is parabolic.
$\Theta$ is parabolic.
Proof. Since the right action of ![]() $\mathrm {GL}_2(\mathbb {Z})$ on the set of relatively prime pairs of integers is transitive, it is enough to verify triviality upon restriction to the stabilizer
$\mathrm {GL}_2(\mathbb {Z})$ on the set of relatively prime pairs of integers is transitive, it is enough to verify triviality upon restriction to the stabilizer ![]() $P_{\infty } = \{ \big (\begin{smallmatrix} 1 & 0 \\ c & \pm 1 \end{smallmatrix}\big ) \mid c \in \mathbb {Z}\}$ of
$P_{\infty } = \{ \big (\begin{smallmatrix} 1 & 0 \\ c & \pm 1 \end{smallmatrix}\big ) \mid c \in \mathbb {Z}\}$ of ![]() $(1,0) \in \mathbb {Z}^2$. If we take
$(1,0) \in \mathbb {Z}^2$. If we take ![]() $\gamma \in P_{\infty }$, then by (3.3),
$\gamma \in P_{\infty }$, then by (3.3),
so ![]() $\Theta _{\gamma } = 0$ in
$\Theta _{\gamma } = 0$ in ![]() $\bar {\mathsf {K}}_2$.
$\bar {\mathsf {K}}_2$.
Remark 3.3.5 The parabolic cocycle ![]() $\Theta$ is also integral in a sense we shall now describe. For this, we employ the theory of motivic cohomology over schemes over Dedekind domains (see the work of Levine [Reference LevineLev99], Geisser [Reference GeisserGei04], and Spitzweck [Reference SpitzweckSpi18]), which we denote as over fields. Take the direct limit of second motivic cohomology groups
$\Theta$ is also integral in a sense we shall now describe. For this, we employ the theory of motivic cohomology over schemes over Dedekind domains (see the work of Levine [Reference LevineLev99], Geisser [Reference GeisserGei04], and Spitzweck [Reference SpitzweckSpi18]), which we denote as over fields. Take the direct limit of second motivic cohomology groups ![]() $\mathsf {K}_{2/\mathbb {Z}} = \varinjlim _U H^2(U,2)$, where
$\mathsf {K}_{2/\mathbb {Z}} = \varinjlim _U H^2(U,2)$, where ![]() $U$ runs over the open
$U$ runs over the open ![]() $\mathbb {Z}$-subschemes of
$\mathbb {Z}$-subschemes of ![]() $\mathbb {G}_m^2{}_{/\mathbb {Z}}$ that are complements of unions of kernels of morphisms
$\mathbb {G}_m^2{}_{/\mathbb {Z}}$ that are complements of unions of kernels of morphisms ![]() $\mathbb {G}_m^2{}_{/\mathbb {Z}} \to \mathbb {G}_m^2{}_{/\mathbb {Z}}$ with
$\mathbb {G}_m^2{}_{/\mathbb {Z}} \to \mathbb {G}_m^2{}_{/\mathbb {Z}}$ with ![]() $(z_1,z_2) \mapsto z_1^az_2^c$ for some primitive
$(z_1,z_2) \mapsto z_1^az_2^c$ for some primitive ![]() $(a,c) \in \mathbb {Z}^2-\{0\}$. There is a canonical injection
$(a,c) \in \mathbb {Z}^2-\{0\}$. There is a canonical injection ![]() $\mathsf {K}_{2/\mathbb {Z}} \hookrightarrow \mathsf {K}_2$, under which the inverse image of
$\mathsf {K}_{2/\mathbb {Z}} \hookrightarrow \mathsf {K}_2$, under which the inverse image of ![]() $H^2(\mathbb {G}_m^2,2)$ is
$H^2(\mathbb {G}_m^2,2)$ is ![]() $H^2(\mathbb {G}_m^2{}_{/\mathbb {Z}},2)$. The statement is then that
$H^2(\mathbb {G}_m^2{}_{/\mathbb {Z}},2)$. The statement is then that
This can be seen directly from the explicit formula of Proposition 3.3.2 or without recourse to this formula using Gysin sequences and Lemma 4.1.2 over finite fields (supposing an expected compatibility of pushforwards and residues as in Lemma 2.1.3 that we did not endeavor to check).
3.4 Hecke actions
We now turn to the action of Hecke operators on the class of our ![]() $1$-cocycle
$1$-cocycle ![]() $\Theta$. To set the stage, suppose that
$\Theta$. To set the stage, suppose that ![]() $\Delta$ is a submonoid of
$\Delta$ is a submonoid of ![]() $M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ and
$M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ and ![]() $\Gamma$ is a finite index subgroup of
$\Gamma$ is a finite index subgroup of ![]() $\mathrm {GL}_2(\mathbb {Z}) \cap \Delta$. We recall the explicit formulas for the action of Hecke operators of double cosets for
$\mathrm {GL}_2(\mathbb {Z}) \cap \Delta$. We recall the explicit formulas for the action of Hecke operators of double cosets for ![]() $\Gamma \backslash \Delta / \Gamma$ on the cohomology
$\Gamma \backslash \Delta / \Gamma$ on the cohomology ![]() $H^1(\Gamma, M)$ for any
$H^1(\Gamma, M)$ for any ![]() $\mathbb {Z}[\Delta ]$-module
$\mathbb {Z}[\Delta ]$-module ![]() $M$.
$M$.
For ![]() $g \in \Delta$, write
$g \in \Delta$, write
 \begin{equation} \Gamma g \Gamma = \coprod_{j=1}^t g_j\Gamma. \end{equation}
\begin{equation} \Gamma g \Gamma = \coprod_{j=1}^t g_j\Gamma. \end{equation}
For ![]() $\gamma \in \Gamma$, there exist a permutation
$\gamma \in \Gamma$, there exist a permutation ![]() $\sigma \in S_t$ (the permutation group on
$\sigma \in S_t$ (the permutation group on ![]() $t$ letters) and elements
$t$ letters) and elements ![]() $\gamma _j \in \Gamma$ such that
$\gamma _j \in \Gamma$ such that ![]() $\gamma g_j = g_{\sigma (j)}\gamma _j$ for
$\gamma g_j = g_{\sigma (j)}\gamma _j$ for ![]() $1 \le j \le t$. For a
$1 \le j \le t$. For a ![]() $1$-cocycle
$1$-cocycle ![]() $\theta \colon \Gamma \to M$ and
$\theta \colon \Gamma \to M$ and ![]() $\gamma \in \Gamma$, we set
$\gamma \in \Gamma$, we set
 \begin{equation} T(g)\theta(\gamma) = \sum_{j=1}^t g_{\sigma(j)}\theta(\gamma_j), \end{equation}
\begin{equation} T(g)\theta(\gamma) = \sum_{j=1}^t g_{\sigma(j)}\theta(\gamma_j), \end{equation}
which in general depends on the chosen coset representatives ![]() $g_j$. The following lemma is well known and verified simply by writing out the definitions.
$g_j$. The following lemma is well known and verified simply by writing out the definitions.
Lemma 3.4.1 For a ![]() $1$-cocycle
$1$-cocycle ![]() $\theta \colon \Gamma \to M$, the cochain
$\theta \colon \Gamma \to M$, the cochain ![]() $T(g)\theta$ is a cocycle with class independent of the choice of double coset decomposition. In particular,
$T(g)\theta$ is a cocycle with class independent of the choice of double coset decomposition. In particular, ![]() $T(g)$ induces a well-defined action on
$T(g)$ induces a well-defined action on ![]() $H^1(\Gamma,M)$. Moreover, this restricts to an action on parabolic cocycles and parabolic cohomology.
$H^1(\Gamma,M)$. Moreover, this restricts to an action on parabolic cocycles and parabolic cohomology.
Remark 3.4.2 The Hecke operators ![]() $T(g)$ of Lemma 3.4.1 arise from left coset decompositions of
$T(g)$ of Lemma 3.4.1 arise from left coset decompositions of ![]() $\Gamma g \Gamma$ for
$\Gamma g \Gamma$ for ![]() $g \in \Delta$. Given a right
$g \in \Delta$. Given a right ![]() $\Delta$-module
$\Delta$-module ![]() $N$, the analogous construction to the above yields right Hecke operators
$N$, the analogous construction to the above yields right Hecke operators ![]() $T^R(g)$ using a decomposition of
$T^R(g)$ using a decomposition of ![]() $\Gamma g \Gamma$ into right cosets, as often found in the literature (see, for example, [Reference ShimuraShi94, Section 8.3]).
$\Gamma g \Gamma$ into right cosets, as often found in the literature (see, for example, [Reference ShimuraShi94, Section 8.3]).
The two operators are related as follows. Write ![]() $*$ for the anti-involution on
$*$ for the anti-involution on ![]() $\mathrm {GL}_2(\mathbb {Q})$ given by
$\mathrm {GL}_2(\mathbb {Q})$ given by ![]() $g^* = (\det g) g^{-1}$. If
$g^* = (\det g) g^{-1}$. If ![]() $\theta \colon \Gamma \to M$ is a left cocycle, then
$\theta \colon \Gamma \to M$ is a left cocycle, then ![]() $\theta ' \colon \gamma \mapsto \theta (\gamma ^{-1})$ is a
$\theta ' \colon \gamma \mapsto \theta (\gamma ^{-1})$ is a ![]() $\Gamma$-cocycle for the right action of
$\Gamma$-cocycle for the right action of ![]() $\Delta$ on
$\Delta$ on ![]() $M$ given by
$M$ given by ![]() $(m, h) \mapsto h^* m$, and the rule
$(m, h) \mapsto h^* m$, and the rule ![]() $\theta \mapsto \theta '$ intertwines the actions of
$\theta \mapsto \theta '$ intertwines the actions of ![]() $T(g)$ and
$T(g)$ and ![]() $T^R(g^*)$. If the action on
$T^R(g^*)$. If the action on ![]() $M$ is trivial, then there is no distinction between left and right cocycles, and the actions of
$M$ is trivial, then there is no distinction between left and right cocycles, and the actions of ![]() $T(g)$ and
$T(g)$ and ![]() $T^R(g^*)$ coincide.
$T^R(g^*)$ coincide.
Returning to our case of interest, we again take
and ![]() $\Gamma = \mathrm {GL}_2(\mathbb {Z})$. The monoid
$\Gamma = \mathrm {GL}_2(\mathbb {Z})$. The monoid ![]() $\Delta$ acts on the right on
$\Delta$ acts on the right on ![]() $\mathbb {G}_m^2(Y)$ for any smooth
$\mathbb {G}_m^2(Y)$ for any smooth ![]() $\mathbb {Q}$-scheme
$\mathbb {Q}$-scheme ![]() $Y$ by formula (2.7), and this right action on
$Y$ by formula (2.7), and this right action on ![]() $\mathbb {G}_m^2$ induces a left pullback action on
$\mathbb {G}_m^2$ induces a left pullback action on ![]() $\mathsf {K}$ as in § 2.4.
$\mathsf {K}$ as in § 2.4.
For example, the pullback by ![]() $\gamma \in \Delta$ of an invertible regular function
$\gamma \in \Delta$ of an invertible regular function ![]() $f$ on
$f$ on ![]() $S_{i,j}-\{1\}$ is the function on
$S_{i,j}-\{1\}$ is the function on ![]() $S_{ai+bj,ci+dj} = S_{i,j}\gamma ^{-1}$ defined by
$S_{ai+bj,ci+dj} = S_{i,j}\gamma ^{-1}$ defined by
and the divisor of ![]() $\gamma ^*f$ is the pullback of the divisor of
$\gamma ^*f$ is the pullback of the divisor of ![]() $f$. This action descends to an action on
$f$. This action descends to an action on ![]() $\bar {\mathsf {K}}$ also, since
$\bar {\mathsf {K}}$ also, since ![]() $M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ acts by pullback on
$M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ acts by pullback on ![]() $H^2(\mathbb {G}_m^2,2)$, compatibly with its morphism to
$H^2(\mathbb {G}_m^2,2)$, compatibly with its morphism to ![]() $\mathsf {K}_2$. In the case of the matrix
$\mathsf {K}_2$. In the case of the matrix ![]() $\big (\begin{smallmatrix} \ell & 0 \\ 0 & \ell \end{smallmatrix}\big )$, we denote this action on
$\big (\begin{smallmatrix} \ell & 0 \\ 0 & \ell \end{smallmatrix}\big )$, we denote this action on ![]() $\mathsf {K}$ more succinctly by
$\mathsf {K}$ more succinctly by ![]() $[\ell ]^*$.
$[\ell ]^*$.
For a prime ![]() $\ell$, let
$\ell$, let ![]() $T_{\ell } = T(g)$ for
$T_{\ell } = T(g)$ for ![]() $g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, where
$g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, where ![]() $T(g)$ is as in (3.5) above for the coset representativesFootnote 9
$T(g)$ is as in (3.5) above for the coset representativesFootnote 9
in ![]() $\Gamma g \Gamma = \coprod _{j=0}^{\ell } g_j \Gamma$. By Lemma 3.4.1, this gives an action of
$\Gamma g \Gamma = \coprod _{j=0}^{\ell } g_j \Gamma$. By Lemma 3.4.1, this gives an action of ![]() $T_{\ell }$ on cohomology independent of the latter decomposition. Let us also define an endomorphism of the complex
$T_{\ell }$ on cohomology independent of the latter decomposition. Let us also define an endomorphism of the complex ![]() $\mathsf {K}$ by the rule
$\mathsf {K}$ by the rule
 \[ T_{\ell}^{\mathsf{K}} = \sum_{j=0}^{\ell} g_j^* \colon \mathsf{K} \to \mathsf{K}. \]
\[ T_{\ell}^{\mathsf{K}} = \sum_{j=0}^{\ell} g_j^* \colon \mathsf{K} \to \mathsf{K}. \]
This depends upon the choice of ![]() $g_j$ and appears primarily as a computational aid.
$g_j$ and appears primarily as a computational aid.
We can now compute the action of ![]() $T_{\ell }$ on the class of
$T_{\ell }$ on the class of ![]() $\Theta$ from the action of
$\Theta$ from the action of ![]() $T_{\ell }^K$ on
$T_{\ell }^K$ on ![]() $e$ of § 3.2.
$e$ of § 3.2.
Lemma 3.4.3 For each prime ![]() $\ell$, we have an equality
$\ell$, we have an equality
of elements of ![]() $\mathsf {K}_0$.
$\mathsf {K}_0$.
Proof. The left-hand side is the sum (with multiplicity) of the classes of the ![]() $\ell +1$ cyclic
$\ell +1$ cyclic ![]() $\ell$-subgroups of
$\ell$-subgroups of ![]() $\mu _{\ell }^2$. This is the sum of the class
$\mu _{\ell }^2$. This is the sum of the class ![]() $[\ell ]^*e$ of
$[\ell ]^*e$ of ![]() $\mu _{\ell }^2$ and
$\mu _{\ell }^2$ and ![]() $\ell$ copies of
$\ell$ copies of ![]() $e$.
$e$.
In the following, note that ![]() $[\ell ]^*$ acts on the cocycle
$[\ell ]^*$ acts on the cocycle ![]() $\Theta$ through its action on
$\Theta$ through its action on ![]() $\bar {\mathsf {K}}_2$.
$\bar {\mathsf {K}}_2$.
Proposition 3.4.4 The ![]() $1$-cocycle
$1$-cocycle ![]() $(T_{\ell } -\ell -[\ell ]^*)\Theta$ has trivial class in
$(T_{\ell } -\ell -[\ell ]^*)\Theta$ has trivial class in ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \bar {\mathsf {K}}_2)$.
$H^1(\mathrm {GL}_2(\mathbb {Z}), \bar {\mathsf {K}}_2)$.
Proof. As the residue of ![]() $\langle 0,1 \rangle$ is
$\langle 0,1 \rangle$ is ![]() $e$, Lemma 3.4.3 and the
$e$, Lemma 3.4.3 and the ![]() $\Delta$-equivariance of the boundary maps in
$\Delta$-equivariance of the boundary maps in ![]() $\mathsf {K}$ imply that
$\mathsf {K}$ imply that ![]() $(T_{\ell }^{\mathsf {K}} - \ell - [\ell ]^*)\langle 0,1 \rangle$ has zero residue. Accordingly there exists
$(T_{\ell }^{\mathsf {K}} - \ell - [\ell ]^*)\langle 0,1 \rangle$ has zero residue. Accordingly there exists ![]() $\psi \in \mathsf {K}_2$ so that
$\psi \in \mathsf {K}_2$ so that
For ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$, let
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$, let ![]() $\sigma$ be a permutation of
$\sigma$ be a permutation of ![]() $\{0,\ldots,\ell \}$, and let
$\{0,\ldots,\ell \}$, and let ![]() $\gamma _j \in \mathrm {GL}_2(\mathbb {Z})$ for
$\gamma _j \in \mathrm {GL}_2(\mathbb {Z})$ for ![]() $0 \le j \le \ell$ be such that
$0 \le j \le \ell$ be such that ![]() $\gamma g_j = g_{\sigma (j)} \gamma _j$. We then have
$\gamma g_j = g_{\sigma (j)} \gamma _j$. We then have
 \begin{align} (\gamma^*-1)T_{\ell}^{\mathsf{K}} \langle 0,1 \rangle &=(\gamma^* -1) \sum_{j=0}^{\ell} g_j^* \langle 0,1 \rangle = \sum_{j=0}^{\ell} g_{\sigma(j)}^*(\gamma_j^*-1) \langle 0,1 \rangle\nonumber\\ &= \partial \bigg( \sum_{j=0}^{\ell} g_{\sigma(j)}^* \Theta_{\gamma_j} \bigg) = \partial (T_{\ell}\Theta)_{\gamma}, \end{align}
\begin{align} (\gamma^*-1)T_{\ell}^{\mathsf{K}} \langle 0,1 \rangle &=(\gamma^* -1) \sum_{j=0}^{\ell} g_j^* \langle 0,1 \rangle = \sum_{j=0}^{\ell} g_{\sigma(j)}^*(\gamma_j^*-1) \langle 0,1 \rangle\nonumber\\ &= \partial \bigg( \sum_{j=0}^{\ell} g_{\sigma(j)}^* \Theta_{\gamma_j} \bigg) = \partial (T_{\ell}\Theta)_{\gamma}, \end{align}
where the last equality follows by definition (3.5) of our Hecke action on ![]() $\mathsf {K}$. Comparing (3.7) and (3.8), we see that
$\mathsf {K}$. Comparing (3.7) and (3.8), we see that
It follows that ![]() $((T_{\ell }-\ell -[\ell ]^*)\Theta )_{\gamma }$ and
$((T_{\ell }-\ell -[\ell ]^*)\Theta )_{\gamma }$ and ![]() $(\gamma ^*-1)\psi$ coincide in
$(\gamma ^*-1)\psi$ coincide in ![]() $\bar {\mathsf {K}}_2$, and therefore the cocycle
$\bar {\mathsf {K}}_2$, and therefore the cocycle ![]() $(T_{\ell }-\ell -[\ell ]^*)\Theta$ is the coboundary of
$(T_{\ell }-\ell -[\ell ]^*)\Theta$ is the coboundary of ![]() $\psi$.
$\psi$.
4. The cyclotomic cocycle
We specialize the cocycle of the previous section at an ![]() $N$-torsion point of
$N$-torsion point of ![]() $\mathbb {G}_m^2$. There are two points to be addressed: classes in
$\mathbb {G}_m^2$. There are two points to be addressed: classes in ![]() $K_2$ of the function field cannot a priori be specialized at a point, and the previous cocycle was valued not in this
$K_2$ of the function field cannot a priori be specialized at a point, and the previous cocycle was valued not in this ![]() $K_2$ but its quotient by everywhere regular classes. To remedy the second issue, we narrow down the regular classes using trace maps.
$K_2$ but its quotient by everywhere regular classes. To remedy the second issue, we narrow down the regular classes using trace maps.
In § 4.1, we calculate the fixed part of the motivic cohomology of ![]() $\mathbb {G}_m^2$ under trace maps. We show that our explicit symbols are contained in the fixed parts of our big complex and use this to reduce the ambiguity in the values of
$\mathbb {G}_m^2$ under trace maps. We show that our explicit symbols are contained in the fixed parts of our big complex and use this to reduce the ambiguity in the values of ![]() $\Theta$. In § 4.2, we construct the explicit cocycle
$\Theta$. In § 4.2, we construct the explicit cocycle ![]() $\Theta _N$ by pulling back
$\Theta _N$ by pulling back ![]() $\Theta$, verify its explicit formula (Proposition 4.2.4), and demonstrate its Eisenstein property (Theorem 4.2.11) for prime-to-level Hecke operators. In § 4.3, we compare with prior work: in particular, we show that
$\Theta$, verify its explicit formula (Proposition 4.2.4), and demonstrate its Eisenstein property (Theorem 4.2.11) for prime-to-level Hecke operators. In § 4.3, we compare with prior work: in particular, we show that ![]() $\Theta _N$ induces the map
$\Theta _N$ induces the map ![]() $\Pi _N$ of (1.1) that is the restriction of the explicit map of [Reference BusuiocBus08, Reference SharifiSha11], and we verify the Eisenstein property of
$\Pi _N$ of (1.1) that is the restriction of the explicit map of [Reference BusuiocBus08, Reference SharifiSha11], and we verify the Eisenstein property of ![]() $\Pi _N$.
$\Pi _N$.
4.1 Fixed parts via suspension
4.1.1 Fixed parts of the cohomology of  $\mathbb {G}_m^2$
$\mathbb {G}_m^2$
The results of § 3.1 imply that the motivic cohomology group ![]() $H^2(\mathbb {G}_m^2,2)$ breaks up as a direct sum of motivic cohomology classes that are
$H^2(\mathbb {G}_m^2,2)$ breaks up as a direct sum of motivic cohomology classes that are ![]() $\mathbb {Z}$-multiples of
$\mathbb {Z}$-multiples of ![]() $(-z_1) \cup (-z_2)$ and sums of classes pulled back via one of the two projection maps. We want to be able to ‘ignore’ the latter classes, and to kill them we will use trace maps.
$(-z_1) \cup (-z_2)$ and sums of classes pulled back via one of the two projection maps. We want to be able to ‘ignore’ the latter classes, and to kill them we will use trace maps.
We work in this subsection over a base field ![]() $F$. For
$F$. For ![]() $r \ge 1$, we define the fixed part of the motivic cohomology group
$r \ge 1$, we define the fixed part of the motivic cohomology group ![]() $H^i(\mathbb {G}_m^r,k)$ as
$H^i(\mathbb {G}_m^r,k)$ as
In general, if ![]() $F$ has zero or sufficiently large characteristic, then this fixed part is the direct summand of
$F$ has zero or sufficiently large characteristic, then this fixed part is the direct summand of ![]() $H^i(\mathbb {G}_m^r,k)$ given by
$H^i(\mathbb {G}_m^r,k)$ given by ![]() $H^i(F,k)$ in the decomposition of Corollary 3.1.2. However, we shall only be interested in these groups in very specific cases: in particular, let us study them for
$H^i(F,k)$ in the decomposition of Corollary 3.1.2. However, we shall only be interested in these groups in very specific cases: in particular, let us study them for ![]() $i = k \le r \in \{1,2\}$.
$i = k \le r \in \{1,2\}$.
Lemma 4.1.1 The element ![]() $-z \in H^1(\mathbb {G}_m,1)$ generates
$-z \in H^1(\mathbb {G}_m,1)$ generates ![]() $H^1(\mathbb {G}_m,1)^{(0)}$.
$H^1(\mathbb {G}_m,1)^{(0)}$.
Proof. The group ![]() $H^1(\mathbb {G}_m, 1)$ consists of the invertible functions on
$H^1(\mathbb {G}_m, 1)$ consists of the invertible functions on ![]() $\mathbb {G}_{m/F}$. As such, each element is uniquely of the form
$\mathbb {G}_{m/F}$. As such, each element is uniquely of the form ![]() $\eta (-z)^k$ for
$\eta (-z)^k$ for ![]() $\eta \in F^{\times }, k \in \mathbb {Z}$.
$\eta \in F^{\times }, k \in \mathbb {Z}$.
Suppose that such a class is ![]() $[m]_*$-fixed for
$[m]_*$-fixed for ![]() $m$ prime to
$m$ prime to ![]() $\operatorname {char} F$. The global unit
$\operatorname {char} F$. The global unit ![]() $-z$ is
$-z$ is ![]() $[m]_*$-fixed for
$[m]_*$-fixed for ![]() $m$ prime to
$m$ prime to ![]() $\operatorname {char} F$ since
$\operatorname {char} F$ since
 \begin{equation} [m]_*(-z) = \prod_{i=0}^{m-1} (-\zeta_m^i z^{1/m}) = - z. \end{equation}
\begin{equation} [m]_*(-z) = \prod_{i=0}^{m-1} (-\zeta_m^i z^{1/m}) = - z. \end{equation}
Thus, we also have ![]() $[m]_* \eta = \eta ^m$ for such
$[m]_* \eta = \eta ^m$ for such ![]() $m$.
$m$.
If ![]() $\operatorname {char} F \neq 2$, then
$\operatorname {char} F \neq 2$, then ![]() $\eta ^2 =\eta$ and so
$\eta ^2 =\eta$ and so ![]() $\eta =1$; in characteristic
$\eta =1$; in characteristic ![]() $2$ the equality
$2$ the equality ![]() $\eta ^3=\eta$ implies the same conclusion. So
$\eta ^3=\eta$ implies the same conclusion. So ![]() $\eta =1$, and the claim follows.
$\eta =1$, and the claim follows.
Let us turn to ![]() $\mathbb {G}_m^2$ over
$\mathbb {G}_m^2$ over ![]() $F$, on which we let
$F$, on which we let ![]() $z_i$ denote the
$z_i$ denote the ![]() $i$th coordinate function.
$i$th coordinate function.
Lemma 4.1.2 The group ![]() $H^1(\mathbb {G}_m^2,1)^{(0)}$ is trivial, and if
$H^1(\mathbb {G}_m^2,1)^{(0)}$ is trivial, and if ![]() $F$ has characteristic not
$F$ has characteristic not ![]() $2$ or
$2$ or ![]() $3$ or is a finite field, then
$3$ or is a finite field, then ![]() $H^2(\mathbb {G}_m^2, 2)^{(0)}$ is
$H^2(\mathbb {G}_m^2, 2)^{(0)}$ is ![]() $\mathbb {Z}$-free of rank
$\mathbb {Z}$-free of rank ![]() $1$, generated by
$1$, generated by ![]() $(-z_1) \cup (-z_2)$.
$(-z_1) \cup (-z_2)$.
Proof. Let us use ![]() $\nu _j$ to denote the class of
$\nu _j$ to denote the class of ![]() $-z_j$ in
$-z_j$ in ![]() $H^1(\mathbb {G}_m^2,1)$. As in Corollary 3.1.2, we have an isomorphism
$H^1(\mathbb {G}_m^2,1)$. As in Corollary 3.1.2, we have an isomorphism
where the maps are given by pullback and (left) cup product with ![]() $1$,
$1$, ![]() $\nu _1$,
$\nu _1$, ![]() $\nu _2$, and
$\nu _2$, and ![]() $\nu _1 \cup \nu _2$, respectively.
$\nu _1 \cup \nu _2$, respectively.
Let ![]() $m \ge 1$ with
$m \ge 1$ with ![]() $\operatorname {char} F \nmid m$. By Example 2.3.2 and (4.2), the class
$\operatorname {char} F \nmid m$. By Example 2.3.2 and (4.2), the class ![]() $\nu _1 \cup \nu _2$ is
$\nu _1 \cup \nu _2$ is ![]() $[m]_*$-fixed. Any class
$[m]_*$-fixed. Any class ![]() $\eta$ that is pulled back from
$\eta$ that is pulled back from ![]() $\operatorname {Spec} F$ satisfies
$\operatorname {Spec} F$ satisfies ![]() $[m]^*\eta = \eta$, so for such
$[m]^*\eta = \eta$, so for such ![]() $\eta$ and any
$\eta$ and any ![]() $\alpha$ among
$\alpha$ among ![]() $1$,
$1$, ![]() $\nu _1$,
$\nu _1$, ![]() $\nu _2$, and
$\nu _2$, and ![]() $\nu _1 \cup \nu _2$, Corollary 2.1.2 yields
$\nu _1 \cup \nu _2$, Corollary 2.1.2 yields
which tells us that the trace maps preserve the summands in (4.3). Thus, we need only consider the summands individually. So, let us suppose that ![]() $\alpha \cup \eta$ is
$\alpha \cup \eta$ is ![]() $[m]_*$-fixed.
$[m]_*$-fixed.
(i) If
 $\alpha = 1$, then
$\alpha = 1$, then  $[m]_*\eta = m^2\eta$. So, if
$[m]_*\eta = m^2\eta$. So, if  $\eta$ is
$\eta$ is  $[m]_*$-fixed, then
$[m]_*$-fixed, then  $(m^2-1)\eta = 0$. If
$(m^2-1)\eta = 0$. If  $\operatorname {char} F \notin \{2,3\}$, then since this is true for
$\operatorname {char} F \notin \{2,3\}$, then since this is true for  $m = 2$ and
$m = 2$ and  $m = 3$, we have
$m = 3$, we have  $\eta = 0$. In the case
$\eta = 0$. In the case  $i = k = 1$, note that if
$i = k = 1$, note that if  $\operatorname {char} F = 2$, then
$\operatorname {char} F = 2$, then  $8\eta = 0$ implies
$8\eta = 0$ implies  $\eta = 0$, and if
$\eta = 0$, and if  $\operatorname {char} F = 3$, then
$\operatorname {char} F = 3$, then  $3\eta = 0$ implies
$3\eta = 0$ implies  $\eta = 0$. If
$\eta = 0$. If  $i = k = 2$ and
$i = k = 2$ and  $F$ is a finite field, then
$F$ is a finite field, then  $H^2(F,2) = 0$, so
$H^2(F,2) = 0$, so  $\eta = 0$.
$\eta = 0$.(ii) If
 $\alpha = \nu _j$, then we have
so if
$\alpha = \nu _j$, then we have
so if \[ [m]_*(\nu_j \cup \eta) = m(\nu_j \cup \eta), \]
\[ [m]_*(\nu_j \cup \eta) = m(\nu_j \cup \eta), \]
 $\nu _j \cup \eta$ is
$\nu _j \cup \eta$ is  $[m]_*$-fixed, then it is
$[m]_*$-fixed, then it is  $(m-1)$-torsion. If
$(m-1)$-torsion. If  $i = k = 1$, then
$i = k = 1$, then  $H^0(F,0) \cong \mathbb {Z}$, so
$H^0(F,0) \cong \mathbb {Z}$, so  $\nu _j \cup \eta = 0$. In general, so long as
$\nu _j \cup \eta = 0$. In general, so long as  $\operatorname {char} F \neq 2$, then
$\operatorname {char} F \neq 2$, then  $\nu _j \cup \eta$ is trivial taking
$\nu _j \cup \eta$ is trivial taking  $m = 2$. If
$m = 2$. If  $i = k = 2$ and
$i = k = 2$ and  $\operatorname {char} F = 2$, then by taking
$\operatorname {char} F = 2$, then by taking  $m=3$, we see that
$m=3$, we see that  $\nu _j \cup \eta$ is
$\nu _j \cup \eta$ is  $2$-torsion in
$2$-torsion in  $F^{\times }$, so trivial.
$F^{\times }$, so trivial.(iii) If
 $\alpha = \nu _1 \cup \nu _2$, then it is indeed
$\alpha = \nu _1 \cup \nu _2$, then it is indeed  $[m]_*$-fixed.
$[m]_*$-fixed.
4.1.2 Fixed parts of complexes
We return to the consideration of ![]() $\mathbb {G}_m^2$ over
$\mathbb {G}_m^2$ over ![]() $\mathbb {Q}$. As explained in Remark 2.3.3, the trace maps
$\mathbb {Q}$. As explained in Remark 2.3.3, the trace maps ![]() $[m]_*$ act on the complex
$[m]_*$ act on the complex ![]() $\mathsf {K}$ as well. We define the fixed complex
$\mathsf {K}$ as well. We define the fixed complex ![]() $\mathsf {K}^{(0)}$ in exactly the same way as (4.1).
$\mathsf {K}^{(0)}$ in exactly the same way as (4.1).
Lemma 4.1.3 The symbols defined in § 3.2 all lie in the fixed part of ![]() $\mathsf {K}$:
$\mathsf {K}$:
Proof. First, note that ![]() $[m]_*e = e$ for all
$[m]_*e = e$ for all ![]() $m$. From (2.5), we see that
$m$. From (2.5), we see that ![]() $\langle a,c \rangle \in \mathsf {K}_1^{(0)}$. Finally, since
$\langle a,c \rangle \in \mathsf {K}_1^{(0)}$. Finally, since ![]() $[m]_*$ on
$[m]_*$ on ![]() $\mathsf {K}_2$ is given by the ‘product of the pushforwards by
$\mathsf {K}_2$ is given by the ‘product of the pushforwards by ![]() $m$ in the first and second variable’ by (2.6), it fixes
$m$ in the first and second variable’ by (2.6), it fixes ![]() $\langle (1,0),(0,1) \rangle$. We then note that
$\langle (1,0),(0,1) \rangle$. We then note that ![]() $\gamma ^*$ and
$\gamma ^*$ and ![]() $[m]_*$ commute.
$[m]_*$ commute.
Proposition 4.1.4 The cocycle ![]() $\Theta$ lifts to a cocycle valued in
$\Theta$ lifts to a cocycle valued in ![]() $\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$.
$\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$.
Proof. Indeed, Proposition 3.3.2 and Lemma 4.1.3 imply that for each ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$, the cocycle
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$, the cocycle ![]() $\Theta _{\gamma }$ is valued in the image of
$\Theta _{\gamma }$ is valued in the image of ![]() $\mathsf {K}_2^{(0)} \rightarrow \bar {\mathsf {K}}_2$. By Lemma 4.1.2, that image is isomorphic to
$\mathsf {K}_2^{(0)} \rightarrow \bar {\mathsf {K}}_2$. By Lemma 4.1.2, that image is isomorphic to ![]() $\mathsf {K}_2^{(0)}/ \langle \{-z_1, -z_2\} \rangle$. Thus
$\mathsf {K}_2^{(0)}/ \langle \{-z_1, -z_2\} \rangle$. Thus ![]() $\Theta$ lifts to that group, and a fortiori to
$\Theta$ lifts to that group, and a fortiori to ![]() $\mathsf {K}_2/ \langle \{-z_1, -z_2\} \rangle$.
$\mathsf {K}_2/ \langle \{-z_1, -z_2\} \rangle$.
In the remainder of this section, we will implicitly regard ![]() $\Theta$ as valued in
$\Theta$ as valued in ![]() $\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$.
$\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$.
Remark 4.1.5 The symbol complex ![]() $\mathsf {Symb}$ defined in § 3.2 is contained in the fixed part under trace maps of the limit complex
$\mathsf {Symb}$ defined in § 3.2 is contained in the fixed part under trace maps of the limit complex ![]() $\varinjlim _I \mathsf {K}_I \subset \mathsf {K}$ of § 2.4. In fact, it is the fixed part of a certain motivic subcomplex
$\varinjlim _I \mathsf {K}_I \subset \mathsf {K}$ of § 2.4. In fact, it is the fixed part of a certain motivic subcomplex ![]() $\mathsf {k}$ of
$\mathsf {k}$ of ![]() $\varinjlim _I \mathsf {K}_I$ that we refer to as the small complex.
$\varinjlim _I \mathsf {K}_I$ that we refer to as the small complex.
To make this precise, for ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$, let us set
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$, let us set ![]() $\mathsf {k}_{\gamma } = \mathsf {K}_I$ for
$\mathsf {k}_{\gamma } = \mathsf {K}_I$ for ![]() $I = \{(a,c),(b,d)\}$. The complex
$I = \{(a,c),(b,d)\}$. The complex ![]() $\mathsf {k}_{\gamma }$ has the form
$\mathsf {k}_{\gamma }$ has the form
where ![]() $S_{a,c}$ and
$S_{a,c}$ and ![]() $S_{b,d}$ are the rank
$S_{b,d}$ are the rank ![]() $1$ tori of (2.8), and the last term is identified with
$1$ tori of (2.8), and the last term is identified with ![]() $\mathbb {Z}$. Using Gysin sequences and the results of § 3.1, it is not hard to see that
$\mathbb {Z}$. Using Gysin sequences and the results of § 3.1, it is not hard to see that ![]() $\mathsf {k}_{\gamma }^{(0)}$ is canonically a direct summand of
$\mathsf {k}_{\gamma }^{(0)}$ is canonically a direct summand of ![]() $\mathsf {k}_{\gamma }$ such that
$\mathsf {k}_{\gamma }$ such that
–
 $\mathsf {k}_{\gamma,2}^{(0)} \cong \mathbb {Z}^4$ is generated by
$\mathsf {k}_{\gamma,2}^{(0)} \cong \mathbb {Z}^4$ is generated by  $\langle \pm (a,c), \pm (b,d) \rangle$,
$\langle \pm (a,c), \pm (b,d) \rangle$,–
 $\mathsf {k}_{\gamma,1}^{(0)} \cong \mathbb {Z}^4$ is generated by
$\mathsf {k}_{\gamma,1}^{(0)} \cong \mathbb {Z}^4$ is generated by  $\langle \pm (a,c) \rangle$ and
$\langle \pm (a,c) \rangle$ and  $\langle \pm (b,d) \rangle$, and
$\langle \pm (b,d) \rangle$, and–
 $\mathsf {k}_{\gamma,0}^{(0)} \cong \mathbb {Z}$ is generated by
$\mathsf {k}_{\gamma,0}^{(0)} \cong \mathbb {Z}$ is generated by  $e$.
$e$.
The homology of ![]() $\mathsf {k}_{\gamma }^{(0)}$ is then concentrated in degree
$\mathsf {k}_{\gamma }^{(0)}$ is then concentrated in degree ![]() $2$, being isomorphic to
$2$, being isomorphic to ![]() $H^2(\mathbb {G}_m^2,2)^{(0)} \cong \mathbb {Z}$.
$H^2(\mathbb {G}_m^2,2)^{(0)} \cong \mathbb {Z}$.
Define the small complex ![]() $\mathsf {k} \subset \mathsf {K}$ to be the span of the
$\mathsf {k} \subset \mathsf {K}$ to be the span of the ![]() $\mathsf {k}_{\gamma }$ for
$\mathsf {k}_{\gamma }$ for ![]() $\gamma \in \mathrm {SL}_2(\mathbb {Z})$. One may verify that the small complex is, like its subcomplexes
$\gamma \in \mathrm {SL}_2(\mathbb {Z})$. One may verify that the small complex is, like its subcomplexes ![]() $\mathsf {k}_{\gamma }$, a quasi-isomorphic subcomplex of
$\mathsf {k}_{\gamma }$, a quasi-isomorphic subcomplex of ![]() $\mathsf {K}$, and from our description of each
$\mathsf {K}$, and from our description of each ![]() $\mathsf {k}_I^{(0)}$, we see that
$\mathsf {k}_I^{(0)}$, we see that ![]() $\mathsf {k}^{(0)}$ is precisely the symbol complex
$\mathsf {k}^{(0)}$ is precisely the symbol complex ![]() $\mathsf {Symb}$. In fact,
$\mathsf {Symb}$. In fact, ![]() $\mathsf {Symb} = \mathsf {k}^{(0)}$ is a
$\mathsf {Symb} = \mathsf {k}^{(0)}$ is a ![]() $\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-direct summand of
$\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-direct summand of ![]() $\mathsf {k}$ with homology
$\mathsf {k}$ with homology ![]() $H^2(\mathbb {G}_m^2,2)^{(0)}$ in degree
$H^2(\mathbb {G}_m^2,2)^{(0)}$ in degree ![]() $2$. In particular, by Proposition 3.3.2, our cocycle
$2$. In particular, by Proposition 3.3.2, our cocycle ![]() $\Theta$ takes values in
$\Theta$ takes values in ![]() $\bar {\mathsf {k}}_2^{(0)} = \,\mathsf {k}_2^{(0)}/\langle (-z_1) \cup (-z_2) \rangle$.
$\bar {\mathsf {k}}_2^{(0)} = \,\mathsf {k}_2^{(0)}/\langle (-z_1) \cup (-z_2) \rangle$.
4.2 Specialization at an  $N$-torsion point
$N$-torsion point
Fix a positive integer ![]() $N \ge 2$. Let us fix the notation for the congruence subgroups of
$N \ge 2$. Let us fix the notation for the congruence subgroups of ![]() $\mathrm {GL}_2(\mathbb {Z})$ that we shall use from this point forward. That is, we set
$\mathrm {GL}_2(\mathbb {Z})$ that we shall use from this point forward. That is, we set
We denote by ![]() $\Gamma _0(N)$ and
$\Gamma _0(N)$ and ![]() $\Gamma _1(N)$ their respective intersections with
$\Gamma _1(N)$ their respective intersections with ![]() $\mathrm {SL}_2(\mathbb {Z})$, as usual. Setting
$\mathrm {SL}_2(\mathbb {Z})$, as usual. Setting ![]() $\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$, we also have associated monoids
$\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$, we also have associated monoids
In this section, we specialize our cocycle ![]() $\Theta$ at the
$\Theta$ at the ![]() $N$-torsion point
$N$-torsion point
with value ![]() $(1,\zeta _N) \in \mathbb {G}_m(\mathbb {Q}(\mu _N))^2$ to obtain a cocycle
$(1,\zeta _N) \in \mathbb {G}_m(\mathbb {Q}(\mu _N))^2$ to obtain a cocycle
4.2.1 The specialized cocycle
We turn to the specialization of ![]() $\Theta$ at the
$\Theta$ at the ![]() $\mathbb {Q}(\mu _N)$-point
$\mathbb {Q}(\mu _N)$-point ![]() $s$ of (4.8), which is given by the map
$s$ of (4.8), which is given by the map ![]() $z_1 \mapsto 1$ and
$z_1 \mapsto 1$ and ![]() $z_2 \mapsto \zeta _N$ on coordinate rings. The stabilizer of
$z_2 \mapsto \zeta _N$ on coordinate rings. The stabilizer of ![]() $s$ in
$s$ in ![]() $\mathrm {GL}_2(\mathbb {Z})$ under its right action on
$\mathrm {GL}_2(\mathbb {Z})$ under its right action on ![]() $\mathbb {G}_m(\mathbb {Q}(\mu _N))^2$ is the congruence subgroup
$\mathbb {G}_m(\mathbb {Q}(\mu _N))^2$ is the congruence subgroup ![]() $\tilde {\Gamma }_1(N)$ of (4.5). For
$\tilde {\Gamma }_1(N)$ of (4.5). For ![]() $j \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, let
$j \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, let ![]() $\sigma _j \in \operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})$ be such that
$\sigma _j \in \operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})$ be such that ![]() $\sigma _j(\zeta _N) = \zeta _N^j$. Via the isomorphism
$\sigma _j(\zeta _N) = \zeta _N^j$. Via the isomorphism
and its composite with ![]() $d \mapsto \sigma _d$, we may consider any
$d \mapsto \sigma _d$, we may consider any ![]() $\mathbb {Z}[\operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})]$-module as a
$\mathbb {Z}[\operatorname {Gal}(\mathbb {Q}(\mu _N)/\mathbb {Q})]$-module as a ![]() $\mathbb {Z}[\tilde {\Gamma }_0(N)]$-module. In particular, we let
$\mathbb {Z}[\tilde {\Gamma }_0(N)]$-module. In particular, we let ![]() $\tilde {\Gamma }_0(N)$ act on
$\tilde {\Gamma }_0(N)$ act on ![]() $K_2(\mathbb {Q}(\mu _N))$ in this fashion.
$K_2(\mathbb {Q}(\mu _N))$ in this fashion.
Note that ![]() $s^*$ is not well defined on the whole of
$s^*$ is not well defined on the whole of ![]() $\mathsf {K}_2$: there is no field map
$\mathsf {K}_2$: there is no field map ![]() $\mathbb {Q}(\mathbb {G}_m^2) \to \mathbb {Q}(\mu _N)$. In order to pull back the values of our cocycle via
$\mathbb {Q}(\mathbb {G}_m^2) \to \mathbb {Q}(\mu _N)$. In order to pull back the values of our cocycle via ![]() $s$, we show that for
$s$, we show that for ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, any lift to
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, any lift to ![]() $\mathsf {K}_2$ of
$\mathsf {K}_2$ of ![]() $\Theta _{\gamma }$ lies in a sufficiently small subgroup of
$\Theta _{\gamma }$ lies in a sufficiently small subgroup of ![]() $\mathsf {K}_2$ upon which
$\mathsf {K}_2$ upon which ![]() $s^*$ can be defined.
$s^*$ can be defined.
For this, let
which is to say the complement in ![]() $\mathbb {G}_m^2$ of the subtori that are the kernels of
$\mathbb {G}_m^2$ of the subtori that are the kernels of ![]() $(z_1, z_2) \mapsto z_1^b z_2^d$ and
$(z_1, z_2) \mapsto z_1^b z_2^d$ and ![]() $(z_1,z_2) \mapsto z_2$. Since
$(z_1,z_2) \mapsto z_2$. Since ![]() $(1,\zeta _N) \in U_{\gamma }$, the specialization map
$(1,\zeta _N) \in U_{\gamma }$, the specialization map
is well defined. The residue of ![]() $\Theta _{\gamma }$ in
$\Theta _{\gamma }$ in ![]() $\mathsf {K}_1$ is
$\mathsf {K}_1$ is ![]() $\langle \det (\gamma )(b,d) \rangle - \langle 0,1 \rangle$. Therefore, any lift of
$\langle \det (\gamma )(b,d) \rangle - \langle 0,1 \rangle$. Therefore, any lift of ![]() $\Theta _{\gamma }$ to
$\Theta _{\gamma }$ to ![]() $\mathsf {K}_2$ is defined on
$\mathsf {K}_2$ is defined on ![]() $U_{\gamma }$ in the sense of Remark 2.2.3.
$U_{\gamma }$ in the sense of Remark 2.2.3.
Proposition 4.1.4 provides a canonical lift of ![]() $\Theta$ to a cocycle valued in
$\Theta$ to a cocycle valued in ![]() $\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$, which we also denote by
$\mathsf {K}_2/\langle \{-z_1, -z_2\} \rangle$, which we also denote by ![]() $\Theta$. The value
$\Theta$. The value ![]() $\Theta _{\gamma }$ lies inside
$\Theta _{\gamma }$ lies inside
where the limit runs over the open ![]() $\mathbb {Q}$-subschemes
$\mathbb {Q}$-subschemes ![]() $U$ of the
$U$ of the ![]() $\mathbb {Q}$-scheme
$\mathbb {Q}$-scheme ![]() $\mathbb {G}_m^2$ containing all multiples of
$\mathbb {G}_m^2$ containing all multiples of ![]() $s$ by an element of
$s$ by an element of ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$. Specialization at
$(\mathbb {Z}/N\mathbb {Z})^{\times }$. Specialization at ![]() $s$ now defines a morphism
$s$ now defines a morphism
where ![]() $Z_N$ is the
$Z_N$ is the ![]() $\tilde {\Gamma }_0(N)$-stable subgroup of
$\tilde {\Gamma }_0(N)$-stable subgroup of ![]() $K_2(\mathbb {Q}(\mu _N))$ generated by the specialization
$K_2(\mathbb {Q}(\mu _N))$ generated by the specialization ![]() $\{-1,-\zeta _N\}$ of the symbol
$\{-1,-\zeta _N\}$ of the symbol ![]() $\{-z_1,-z_2\} \in K_2(\mathbb {Q}(\mathbb {G}_m^2))$ under
$\{-z_1,-z_2\} \in K_2(\mathbb {Q}(\mathbb {G}_m^2))$ under ![]() $s^*$. It therefore makes sense to speak of
$s^*$. It therefore makes sense to speak of
as an element of ![]() $K_2(\mathbb {Q}(\mu _N))/Z_N$, Note that
$K_2(\mathbb {Q}(\mu _N))/Z_N$, Note that
 \[ \{-1,-\zeta_N\} = \begin{cases} \{-1,-1\} & \text{if } N \text{ is odd}, \\ 0 & \text{if } N \text{ is even}, \end{cases} \]
\[ \{-1,-\zeta_N\} = \begin{cases} \{-1,-1\} & \text{if } N \text{ is odd}, \\ 0 & \text{if } N \text{ is even}, \end{cases} \]
so ![]() $Z_N$ is a group of order dividing
$Z_N$ is a group of order dividing ![]() $2$.
$2$.
Proposition 4.2.1 The map
is a parabolic cocycle.
Proof. That ![]() $\Theta _N$ is a cocycle follows from if we can show that
$\Theta _N$ is a cocycle follows from if we can show that ![]() $s^*$ as in (4.10) is a homomorphism of
$s^*$ as in (4.10) is a homomorphism of ![]() $\tilde {\Gamma }_0(N)$-modules. Here, note that
$\tilde {\Gamma }_0(N)$-modules. Here, note that ![]() $\tilde {\Gamma }_0(N)$ acts on
$\tilde {\Gamma }_0(N)$ acts on ![]() $K_2(\mathbb {Q}(\mu _N))$ as in (4.9). Write
$K_2(\mathbb {Q}(\mu _N))$ as in (4.9). Write ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big )$ and note that the two maps
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big )$ and note that the two maps ![]() $\operatorname {Spec} \mathbb {Q}(\mu _N) \rightarrow \mathbb {G}_m^2$ defined by
$\operatorname {Spec} \mathbb {Q}(\mu _N) \rightarrow \mathbb {G}_m^2$ defined by ![]() $\gamma \circ s$ and
$\gamma \circ s$ and ![]() $s \circ \sigma _d$ coincide, since viewed on coordinate rings both send
$s \circ \sigma _d$ coincide, since viewed on coordinate rings both send ![]() $z_1$ to
$z_1$ to ![]() $1 = \zeta _N^c$ and
$1 = \zeta _N^c$ and ![]() $z_2$ to
$z_2$ to ![]() $\zeta _N^d$. In particular,
$\zeta _N^d$. In particular, ![]() $\tilde {\Gamma }_0(N)$ acts on
$\tilde {\Gamma }_0(N)$ acts on ![]() $\mathsf {K}_2(N)$, since for any
$\mathsf {K}_2(N)$, since for any ![]() $\mathbb {Q}$-subscheme
$\mathbb {Q}$-subscheme ![]() $U$ of
$U$ of ![]() $\mathbb {G}_m^2$ with
$\mathbb {G}_m^2$ with ![]() $s \in U(\mathbb {Q}(\mu _N))$, the composition
$s \in U(\mathbb {Q}(\mu _N))$, the composition ![]() $\gamma \circ s = s \circ \sigma _d$ is also a
$\gamma \circ s = s \circ \sigma _d$ is also a ![]() $\mathbb {Q}(\mu _N)$-point of
$\mathbb {Q}(\mu _N)$-point of ![]() $U$. This implies that
$U$. This implies that ![]() $s^* \circ \gamma ^* = \sigma _d \circ s^*$ on
$s^* \circ \gamma ^* = \sigma _d \circ s^*$ on ![]() $\bar {\mathsf {K}}_2(N)$.
$\bar {\mathsf {K}}_2(N)$.
The proof of Proposition 3.3.4 argued that ![]() $\Theta$ is trivial on a lower-triangular parabolic
$\Theta$ is trivial on a lower-triangular parabolic ![]() $P_{\infty }$ in
$P_{\infty }$ in ![]() $\mathrm {GL}_2(\mathbb {Z})$. An arbitrary parabolic
$\mathrm {GL}_2(\mathbb {Z})$. An arbitrary parabolic ![]() $Q$ of
$Q$ of ![]() $\tilde {\Gamma }_0(N)$ has the form
$\tilde {\Gamma }_0(N)$ has the form ![]() $Q = \mu P_{\infty } \mu ^{-1} \cap \tilde {\Gamma }_0(N)$ for some
$Q = \mu P_{\infty } \mu ^{-1} \cap \tilde {\Gamma }_0(N)$ for some ![]() $\mu \in \mathrm {SL}_2(\mathbb {Z})$. For
$\mu \in \mathrm {SL}_2(\mathbb {Z})$. For ![]() $\gamma \in P_{\infty }$, we have
$\gamma \in P_{\infty }$, we have ![]() $\Theta _{\mu \gamma \mu ^{-1}} = (1-(\mu \gamma \mu ^{-1})^*)\Theta _{\mu }$. So long as
$\Theta _{\mu \gamma \mu ^{-1}} = (1-(\mu \gamma \mu ^{-1})^*)\Theta _{\mu }$. So long as ![]() $\Theta _{\mu } \in \mathsf {K}_2(N)$, we then have that
$\Theta _{\mu } \in \mathsf {K}_2(N)$, we then have that ![]() $\Theta |_Q \colon Q \to \mathsf {K}_2(N)$ is a coboundary, and for this it suffices that
$\Theta |_Q \colon Q \to \mathsf {K}_2(N)$ is a coboundary, and for this it suffices that ![]() $\mu = \big (\begin{smallmatrix} a' & b'\\c' & d' \end{smallmatrix}\big )$ satisfies
$\mu = \big (\begin{smallmatrix} a' & b'\\c' & d' \end{smallmatrix}\big )$ satisfies ![]() $N \nmid d'$. On the other hand, the set of
$N \nmid d'$. On the other hand, the set of ![]() $\mu$ with
$\mu$ with ![]() $N \mid d'$ is exactly the coset
$N \mid d'$ is exactly the coset ![]() $\tilde {\Gamma }_0(N)\big (\begin{smallmatrix} 0 & 1\\1 & 0 \end{smallmatrix}\big )$, and in this case
$\tilde {\Gamma }_0(N)\big (\begin{smallmatrix} 0 & 1\\1 & 0 \end{smallmatrix}\big )$, and in this case ![]() $Q = \mu P_{\infty } \mu ^{-1}$. We may then suppose
$Q = \mu P_{\infty } \mu ^{-1}$. We may then suppose ![]() $\mu = \big (\begin{smallmatrix} 0 & 1\\1 & 0 \end{smallmatrix}\big )$, for which
$\mu = \big (\begin{smallmatrix} 0 & 1\\1 & 0 \end{smallmatrix}\big )$, for which ![]() $Q = \{ \big (\begin{smallmatrix} \pm 1 & n \\ 0 & 1 \end{smallmatrix}\big ) \mid n \in \mathbb {Z}\}$. Since
$Q = \{ \big (\begin{smallmatrix} \pm 1 & n \\ 0 & 1 \end{smallmatrix}\big ) \mid n \in \mathbb {Z}\}$. Since ![]() $\Theta _N$ lifts to a map taking the value
$\Theta _N$ lifts to a map taking the value ![]() $\{1-\zeta _N,1-\zeta _N^{-1}\} = 0$ on
$\{1-\zeta _N,1-\zeta _N^{-1}\} = 0$ on ![]() $\big (\begin{smallmatrix} 1 & -1 \\ 0 & 1 \end{smallmatrix}\big )$ and the value
$\big (\begin{smallmatrix} 1 & -1 \\ 0 & 1 \end{smallmatrix}\big )$ and the value ![]() $\{-1,-\zeta _N\} \in Z_N$ on
$\{-1,-\zeta _N\} \in Z_N$ on ![]() $\big (\begin{smallmatrix} -1 & 0 \\ 0 & 1 \end{smallmatrix}\big )$, it is trivial on
$\big (\begin{smallmatrix} -1 & 0 \\ 0 & 1 \end{smallmatrix}\big )$, it is trivial on ![]() $Q$, and we have parabolicity.
$Q$, and we have parabolicity.
We need to modify the notion of connecting sequence of § 3.3 to adapt it to the level ![]() $N$ structure. Specifically, let us refer to a connecting sequence
$N$ structure. Specifically, let us refer to a connecting sequence ![]() $(b_i,d_i)_{i=0}^k$ for
$(b_i,d_i)_{i=0}^k$ for ![]() $\gamma \in \tilde {\Gamma }_0(N)$ with the property that
$\gamma \in \tilde {\Gamma }_0(N)$ with the property that ![]() $N \nmid d_i$ for all
$N \nmid d_i$ for all ![]() $0 \le i \le k$ as an
$0 \le i \le k$ as an ![]() $N$-connecting sequence for
$N$-connecting sequence for ![]() $\gamma$. Note that an
$\gamma$. Note that an ![]() $N$-connecting sequence always exists, as we verify with a little fiddling.
$N$-connecting sequence always exists, as we verify with a little fiddling.
Lemma 4.2.2 Given a primitive vector ![]() $(b,d) \in \mathbb {Z}^2$ with
$(b,d) \in \mathbb {Z}^2$ with ![]() $N \nmid d$, there exists a sequence
$N \nmid d$, there exists a sequence ![]() $(v_i)_{i=0}^k$ in
$(v_i)_{i=0}^k$ in ![]() $\mathbb {Z}^2$ with
$\mathbb {Z}^2$ with ![]() $v_i \wedge v_{i+1} = 1$ for
$v_i \wedge v_{i+1} = 1$ for ![]() $0 \le i < k$ such that
$0 \le i < k$ such that ![]() $v_0 = (0,1)$,
$v_0 = (0,1)$, ![]() $v_k = (b,d)$, and
$v_k = (b,d)$, and ![]() $v_i = (b_i,d_i)$ with
$v_i = (b_i,d_i)$ with ![]() $N \nmid d_i$ for all
$N \nmid d_i$ for all ![]() $0 \le i \le k$.
$0 \le i \le k$.
Proof. Choose any connecting sequence ![]() $(v_i)_{i=0}^k$ with
$(v_i)_{i=0}^k$ with ![]() $v_k = (b,d)$. Suppose that
$v_k = (b,d)$. Suppose that ![]() $v_i$ has second coordinate divisible by
$v_i$ has second coordinate divisible by ![]() $N$. Then neither
$N$. Then neither ![]() $v_{i-1}$ nor
$v_{i-1}$ nor ![]() $v_{i+1}$ does. We will insert another sequence between
$v_{i+1}$ does. We will insert another sequence between ![]() $v_{i-1}$ and
$v_{i-1}$ and ![]() $v_{i+1}$, no element of which has second coordinate divisible by
$v_{i+1}$, no element of which has second coordinate divisible by ![]() $N$. For
$N$. For ![]() $v, w \in \mathbb {Z}^2$, consider
$v, w \in \mathbb {Z}^2$, consider ![]() $v \wedge w$ as an integer via the identification of
$v \wedge w$ as an integer via the identification of ![]() $\bigwedge ^2 \mathbb {Z}^2$ with
$\bigwedge ^2 \mathbb {Z}^2$ with ![]() $\mathbb {Z}$ using the basis vector
$\mathbb {Z}$ using the basis vector ![]() $(1,0) \wedge (0,1)$. Note that
$(1,0) \wedge (0,1)$. Note that ![]() $v_{i-1} \wedge v_i = v_i \wedge v_{i+1} = 1$ for
$v_{i-1} \wedge v_i = v_i \wedge v_{i+1} = 1$ for ![]() $1 \le i \le k-1$. Write
$1 \le i \le k-1$. Write ![]() $t = v_{i-1} \wedge v_{i+1}$. We suppose that
$t = v_{i-1} \wedge v_{i+1}$. We suppose that ![]() $t \geq 1$, the other case being easier. The sequence with
$t \geq 1$, the other case being easier. The sequence with ![]() $v_{i-1},v_i,v_{i+1}$ replaced by
$v_{i-1},v_i,v_{i+1}$ replaced by ![]() $v_{i-1}, v_{i+1}+(1-t) v_i, \ldots, v_{i+1} - v_i, v_{i+1}$ has nearly the desired properties since
$v_{i-1}, v_{i+1}+(1-t) v_i, \ldots, v_{i+1} - v_i, v_{i+1}$ has nearly the desired properties since
for ![]() $1 \le j \leq t-1$. However, the last pair of adjacent vectors
$1 \le j \leq t-1$. However, the last pair of adjacent vectors ![]() $x = v_{i+1}-v_i$ and
$x = v_{i+1}-v_i$ and ![]() $y = v_{i+1}$ satisfies
$y = v_{i+1}$ satisfies ![]() $x \wedge y = -1$, rather than
$x \wedge y = -1$, rather than ![]() $1$. To remedy this, we replace
$1$. To remedy this, we replace ![]() $x,y$ by the sequence
$x,y$ by the sequence ![]() $x, -y, -x, y$.
$x, -y, -x, y$.
Remark 4.2.3 As in Remark 4.1.5, Lemma 4.2.2 tells us that ![]() $\Theta$ restricted to
$\Theta$ restricted to ![]() $\tilde {\Gamma }_0(N)$ takes values in (a quotient of) the degree
$\tilde {\Gamma }_0(N)$ takes values in (a quotient of) the degree ![]() $2$ term of the subcomplex of the small complex
$2$ term of the subcomplex of the small complex ![]() $\mathsf {k}$ spanned by the
$\mathsf {k}$ spanned by the ![]() $\mathsf {k}_{\gamma }$ for those
$\mathsf {k}_{\gamma }$ for those ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ such that
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ such that ![]() $N \nmid c$ and
$N \nmid c$ and ![]() $N \nmid d$.
$N \nmid d$.
We then have the following explicit formula for our cocycle.
Proposition 4.2.4 Let ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, and let
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, and let ![]() $(b_i,d_i)_{i=0}^k$ be an
$(b_i,d_i)_{i=0}^k$ be an ![]() $N$-connecting sequence for
$N$-connecting sequence for ![]() $\gamma$. Then
$\gamma$. Then
 \[ \Theta_{N,\gamma} = \sum_{i=1}^k \{ 1- \zeta_N^{d_i}, 1-\zeta_N^{-d_{i-1}} \}. \]
\[ \Theta_{N,\gamma} = \sum_{i=1}^k \{ 1- \zeta_N^{d_i}, 1-\zeta_N^{-d_{i-1}} \}. \]
Proof. By Proposition 3.3.2, we need only note that
for ![]() $1 \le i \le k$.
$1 \le i \le k$.
Since ![]() $1-\zeta _N^c$ is an
$1-\zeta _N^c$ is an ![]() $N$-unit for all
$N$-unit for all ![]() $c \not \equiv 0 \bmod N$ and the map
$c \not \equiv 0 \bmod N$ and the map ![]() $K_2(\mathbb {Z}[\mu _N,{1}/{N}]) \to K_2(\mathbb {Q}(\mu _N))$ is an injection, we have the following corollary.
$K_2(\mathbb {Z}[\mu _N,{1}/{N}]) \to K_2(\mathbb {Q}(\mu _N))$ is an injection, we have the following corollary.
Corollary 4.2.5 The cocycle ![]() $\Theta _N$ takes values in
$\Theta _N$ takes values in ![]() $K_2(\mathbb {Z}[\mu _N,{1}/{N}])/Z_N$.
$K_2(\mathbb {Z}[\mu _N,{1}/{N}])/Z_N$.
Remark 4.2.6 One could use Remark 3.3.5 to avoid the explicit formula in proving this corollary (assuming the same expected property of integral motivic cohomology), since pullback by ![]() $(1,\zeta _N)$ defines a morphism
$(1,\zeta _N)$ defines a morphism ![]() $\mathsf {K}_{2/\mathbb {Z}}(N) \to K_2(\mathbb {Z}[\mu _N,{1}/{N}])$, where
$\mathsf {K}_{2/\mathbb {Z}}(N) \to K_2(\mathbb {Z}[\mu _N,{1}/{N}])$, where ![]() $\mathsf {K}_{2/\mathbb {Z}}(N) = \mathsf {K}_{2/\mathbb {Z}} \cap \mathsf {K}_2(N)$.
$\mathsf {K}_{2/\mathbb {Z}}(N) = \mathsf {K}_{2/\mathbb {Z}} \cap \mathsf {K}_2(N)$.
In fact, we can do slightly better.
Lemma 4.2.7 If ![]() $N$ is divisible by two distinct primes, then
$N$ is divisible by two distinct primes, then ![]() $\Theta _N$ takes values in
$\Theta _N$ takes values in ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$. Otherwise, its restriction to
$K_2(\mathbb {Z}[\mu _N])/Z_N$. Otherwise, its restriction to ![]() $\Gamma _1(N)$ does.
$\Gamma _1(N)$ does.
Proof. Fix a prime ![]() $\ell$ dividing
$\ell$ dividing ![]() $N$. Let
$N$. Let ![]() $F_{\ell }$ denote the residue field at a prime of
$F_{\ell }$ denote the residue field at a prime of ![]() $\mathbb {Q}(\mu _N)$ over
$\mathbb {Q}(\mu _N)$ over ![]() $\ell$, and consider the tame symbol map
$\ell$, and consider the tame symbol map
of (2.4). The common kernel of the maps ![]() $\delta _{\ell }$ is
$\delta _{\ell }$ is ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$. Thus, it suffices to see that
$K_2(\mathbb {Z}[\mu _N])/Z_N$. Thus, it suffices to see that ![]() $\delta _{\ell } \circ \Theta _N$ is trivial on the congruence subgroups of interest.
$\delta _{\ell } \circ \Theta _N$ is trivial on the congruence subgroups of interest.
Suppose first that ![]() $N$ is divisible by two distinct primes. For any prime
$N$ is divisible by two distinct primes. For any prime ![]() $p \mid N$ with
$p \mid N$ with ![]() $p \neq \ell$, we have that
$p \neq \ell$, we have that ![]() $\tilde {\Gamma }_0(N) \subset \tilde {\Gamma }_0(p)$, so there exists a
$\tilde {\Gamma }_0(N) \subset \tilde {\Gamma }_0(p)$, so there exists a ![]() $p$-connecting sequence
$p$-connecting sequence ![]() $(b_i,d_i)_{i=0}^k$ for any
$(b_i,d_i)_{i=0}^k$ for any ![]() $\gamma \in \tilde {\Gamma }_0(N)$. But then each
$\gamma \in \tilde {\Gamma }_0(N)$. But then each ![]() $1-\zeta _N^{d_i}$ is a unit locally at primes over
$1-\zeta _N^{d_i}$ is a unit locally at primes over ![]() $\ell$, so
$\ell$, so ![]() $\delta _{\ell }(\{1-\zeta _N^{d_i},1-\zeta _N^{-d_{i-1}}\})$ vanishes. By Proposition 4.2.4, we then have
$\delta _{\ell }(\{1-\zeta _N^{d_i},1-\zeta _N^{-d_{i-1}}\})$ vanishes. By Proposition 4.2.4, we then have ![]() $\delta _{\ell }(\Theta _{N,\gamma }) = 1$, independent of
$\delta _{\ell }(\Theta _{N,\gamma }) = 1$, independent of ![]() $\ell$.
$\ell$.
Next, suppose that ![]() $N$ is a power of a prime
$N$ is a power of a prime ![]() $\ell$. Given
$\ell$. Given ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, there exists an
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, there exists an ![]() $\ell$-connecting sequence
$\ell$-connecting sequence ![]() $(b_i,d_i)_{i=0}^k$ for
$(b_i,d_i)_{i=0}^k$ for ![]() $\gamma$. Then each
$\gamma$. Then each ![]() $1-\zeta _N^{d_i}$ has valuation
$1-\zeta _N^{d_i}$ has valuation ![]() $1$ at
$1$ at ![]() $(1-\zeta _N)$, so
$(1-\zeta _N)$, so
 \[ \delta_{\ell}(\{1-\zeta_N^{d_i},1-\zeta_N^{-d_{i-1}}\}) = -\frac{1-\zeta_N^{-d_{i-1}}}{1-\zeta_N^{d_i}} \bmod (1-\zeta_N), \]
\[ \delta_{\ell}(\{1-\zeta_N^{d_i},1-\zeta_N^{-d_{i-1}}\}) = -\frac{1-\zeta_N^{-d_{i-1}}}{1-\zeta_N^{d_i}} \bmod (1-\zeta_N), \]
which reduces to ![]() ${d_{i-1}}/{d_i}$ in
${d_{i-1}}/{d_i}$ in ![]() $\mathbb {F}_{\ell }^{\times }$. Proposition 4.2.4 then yields that
$\mathbb {F}_{\ell }^{\times }$. Proposition 4.2.4 then yields that ![]() $\delta _{\ell }(\Theta _{\gamma }) = \det (\gamma ) d^{-1} \bmod \ell$, which is trivial if
$\delta _{\ell }(\Theta _{\gamma }) = \det (\gamma ) d^{-1} \bmod \ell$, which is trivial if ![]() $\gamma \in \Gamma _1(N)$.
$\gamma \in \Gamma _1(N)$.
4.2.2 Hecke equivariance
We next consider the Hecke equivariance of ![]() $\Theta _N$. Let us set
$\Theta _N$. Let us set
for simplicity, which we also view as a subgroup of ![]() $H^2(\mathbb {G}_m^2,2)$. Over the next few lemmas, we show that the class of
$H^2(\mathbb {G}_m^2,2)$. Over the next few lemmas, we show that the class of ![]() $\Theta$ in
$\Theta$ in ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_2/\Phi )$ is annihilated by all of the operators
$H^1(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_2/\Phi )$ is annihilated by all of the operators ![]() $T_{\ell }-\ell -[\ell ]^*$ for odd primes
$T_{\ell }-\ell -[\ell ]^*$ for odd primes ![]() $\ell$, as well as by
$\ell$, as well as by ![]() $2(T_2-2-[2]^*)$, in order to show the analogous Eisenstein property of
$2(T_2-2-[2]^*)$, in order to show the analogous Eisenstein property of ![]() $\Theta _N$ in Theorem 4.2.11.
$\Theta _N$ in Theorem 4.2.11.
Lemma 4.2.8 For any finite index subgroup ![]() $\Gamma$ of
$\Gamma$ of ![]() $\tilde {\Gamma }_0(N)$, the inclusion
$\tilde {\Gamma }_0(N)$, the inclusion ![]() $\bar {\mathsf {K}}_2(N) \hookrightarrow \mathsf {K}_2/\Phi$ induces an injection on
$\bar {\mathsf {K}}_2(N) \hookrightarrow \mathsf {K}_2/\Phi$ induces an injection on ![]() $H^1(\Gamma, -)$.
$H^1(\Gamma, -)$.
Proof. From Gysin sequences, we see that there is an exact sequence
where the sum ranges over divisors ![]() $D$ containing
$D$ containing ![]() $s$. The lemma follows if we know that the finite index subgroup
$s$. The lemma follows if we know that the finite index subgroup ![]() $\Gamma$ of
$\Gamma$ of ![]() $\tilde {\Gamma }_0(N)$ has trivial invariants on the right-hand group.
$\tilde {\Gamma }_0(N)$ has trivial invariants on the right-hand group.
We claim that the orbit of any divisor ![]() $D$ containing
$D$ containing ![]() $(1,\zeta _N)$ on
$(1,\zeta _N)$ on ![]() $\mathbb {G}_m^2$ under
$\mathbb {G}_m^2$ under ![]() $\mathrm {GL}_2(\mathbb {Z})$ is infinite, so no element of the direct sum can be fixed by the finite index subgroup
$\mathrm {GL}_2(\mathbb {Z})$ is infinite, so no element of the direct sum can be fixed by the finite index subgroup ![]() $\Gamma$. Such a divisor is the vanishing locus of an
$\Gamma$. Such a divisor is the vanishing locus of an ![]() $f \in \mathbb {Q}[z_1^{\pm 1}, z_2^{\pm 1}]$ that is unique up to units, that is, up to some
$f \in \mathbb {Q}[z_1^{\pm 1}, z_2^{\pm 1}]$ that is unique up to units, that is, up to some ![]() $c z_1^i z_2^j$ with
$c z_1^i z_2^j$ with ![]() $c \in \mathbb {Q}^{\times }$ and
$c \in \mathbb {Q}^{\times }$ and ![]() $i, j \in \mathbb {Z}$. Define the support
$i, j \in \mathbb {Z}$. Define the support ![]() $\mathrm {supp}(f)$ of
$\mathrm {supp}(f)$ of ![]() $f$ to be the set of
$f$ to be the set of ![]() $(a,b) \in \mathbb {Z}^2$ for which the coefficient of
$(a,b) \in \mathbb {Z}^2$ for which the coefficient of ![]() $z_1^a z_2^b$ is nonzero. Note that
$z_1^a z_2^b$ is nonzero. Note that ![]() $|\mathrm {supp}(f)| \geq 2$. For any hyperbolic element
$|\mathrm {supp}(f)| \geq 2$. For any hyperbolic element ![]() $\gamma \in \Gamma$, the diameter of
$\gamma \in \Gamma$, the diameter of ![]() $\mathrm {supp}(f)\gamma ^n$ increases without bound as
$\mathrm {supp}(f)\gamma ^n$ increases without bound as ![]() $n \rightarrow \infty$. In particular,
$n \rightarrow \infty$. In particular, ![]() $\mathrm {supp}(f)\gamma ^n$ cannot be a translate of
$\mathrm {supp}(f)\gamma ^n$ cannot be a translate of ![]() $\mathrm {supp}(f)$ for sufficiently large
$\mathrm {supp}(f)$ for sufficiently large ![]() $n$, and therefore
$n$, and therefore ![]() $D \gamma ^n \neq D$ for all
$D \gamma ^n \neq D$ for all ![]() $n \ge 1$.
$n \ge 1$.
Lemma 4.2.9 The kernel of the map on ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}),-)$ induced by the quotient map
$H^1(\mathrm {GL}_2(\mathbb {Z}),-)$ induced by the quotient map ![]() $\mathsf {K}_2/\Phi \twoheadrightarrow \bar {\mathsf {K}}_2$ is
$\mathsf {K}_2/\Phi \twoheadrightarrow \bar {\mathsf {K}}_2$ is ![]() $2$-torsion.
$2$-torsion.
Proof. Recall from Corollary 3.1.2 and Lemma 4.1.2 that ![]() $H^2(\mathbb {G}_m^2,2)$ is the direct sum of subgroups generated by symbols of the form
$H^2(\mathbb {G}_m^2,2)$ is the direct sum of subgroups generated by symbols of the form ![]() $a \cup b$,
$a \cup b$, ![]() $(-z_1) \cup b$,
$(-z_1) \cup b$, ![]() $(-z_2) \cup b$, and
$(-z_2) \cup b$, and ![]() $(-z_1) \cup (-z_2)$ with
$(-z_1) \cup (-z_2)$ with ![]() $a, b \in \mathbb {Q}^{\times }$. It follows that, as a
$a, b \in \mathbb {Q}^{\times }$. It follows that, as a ![]() $\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-module, the group
$\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-module, the group ![]() $H^2(\mathbb {G}_m^2, 2)/\Phi$ is a direct sum of copies of modules
$H^2(\mathbb {G}_m^2, 2)/\Phi$ is a direct sum of copies of modules ![]() $A$ and
$A$ and ![]() $W \otimes _{\mathbb {Z}} A$ with
$W \otimes _{\mathbb {Z}} A$ with ![]() $A$ having trivial
$A$ having trivial ![]() $\mathrm {GL}_2(\mathbb {Z})$-action, where
$\mathrm {GL}_2(\mathbb {Z})$-action, where ![]() $W$ is the group
$W$ is the group ![]() $\mathbb {Z}^2$ endowed with the standard left
$\mathbb {Z}^2$ endowed with the standard left ![]() $\mathrm {GL}_2(\mathbb {Z})$-action.
$\mathrm {GL}_2(\mathbb {Z})$-action.
By the universal coefficient sequence (which is split), it is then enough to verify that the groups ![]() $H_1(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z})$ and
$H_1(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z})$ and ![]() $H_i(\mathrm {GL}_2(\mathbb {Z}), W)$ for
$H_i(\mathrm {GL}_2(\mathbb {Z}), W)$ for ![]() $i \in \{0,1\}$ are
$i \in \{0,1\}$ are ![]() $2$-torsion. In fact,
$2$-torsion. In fact, ![]() $H_1(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z}) \cong \mathrm {GL}_2(\mathbb {Z})^{\mathrm {ab}} \cong (\mathbb {Z}/2\mathbb {Z})^2$. Since
$H_1(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z}) \cong \mathrm {GL}_2(\mathbb {Z})^{\mathrm {ab}} \cong (\mathbb {Z}/2\mathbb {Z})^2$. Since ![]() $\mathrm {SL}_2(\mathbb {Z})$ acts transitively on
$\mathrm {SL}_2(\mathbb {Z})$ acts transitively on ![]() $W-\{0\}$, the coinvariant group
$W-\{0\}$, the coinvariant group ![]() $H_0(\mathrm {GL}_2(\mathbb {Z}),W)$ vanishes, and
$H_0(\mathrm {GL}_2(\mathbb {Z}),W)$ vanishes, and ![]() $H_1(\mathrm {GL}_2(\mathbb {Z}), W)$ is a quotient of
$H_1(\mathrm {GL}_2(\mathbb {Z}), W)$ is a quotient of ![]() $H_1(\mathrm {SL}_2(\mathbb {Z}),W)$. It then suffices to show that the latter group is killed by
$H_1(\mathrm {SL}_2(\mathbb {Z}),W)$. It then suffices to show that the latter group is killed by ![]() $2$.
$2$.
The group ![]() $\mathrm {SL}_2(\mathbb {Z})$ is an amalgamated free product of the cyclic
$\mathrm {SL}_2(\mathbb {Z})$ is an amalgamated free product of the cyclic ![]() $4$-subgroup generated by
$4$-subgroup generated by ![]() $S = \big (\begin{smallmatrix} 0 & 1\\ -1 & 0 \end{smallmatrix}\big )$ and the cyclic
$S = \big (\begin{smallmatrix} 0 & 1\\ -1 & 0 \end{smallmatrix}\big )$ and the cyclic ![]() $6$-subgroup generated by
$6$-subgroup generated by ![]() $T = \big (\begin{smallmatrix} 1 & -1\\ 1 & 0 \end{smallmatrix}\!\big)$ over the
$T = \big (\begin{smallmatrix} 1 & -1\\ 1 & 0 \end{smallmatrix}\!\big)$ over the ![]() $2$-subgroup generated by
$2$-subgroup generated by ![]() $\sigma =S^2=T^3$. Thus we have a Mayer–Vietoris sequence
$\sigma =S^2=T^3$. Thus we have a Mayer–Vietoris sequence
The first two groups vanish because neither ![]() $S$ nor
$S$ nor ![]() $T$ have invariants, and the last is
$T$ have invariants, and the last is ![]() $(\mathbb {Z}/2\mathbb {Z})^2$.
$(\mathbb {Z}/2\mathbb {Z})^2$.
Lemma 4.2.10 The operator ![]() $T_{\ell }-\ell -[\ell ]^*$ kills the class of
$T_{\ell }-\ell -[\ell ]^*$ kills the class of ![]() $\Theta$ (respectively,
$\Theta$ (respectively, ![]() $2 \Theta$) in
$2 \Theta$) in ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_2/\Phi )$ for
$H^1(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_2/\Phi )$ for ![]() $\ell \neq 2$ (respectively, for
$\ell \neq 2$ (respectively, for ![]() $\ell =2$).
$\ell =2$).
Proof. Let ![]() $\tau _{\ell }$ denote the class of
$\tau _{\ell }$ denote the class of ![]() $(T_{\ell }-\ell -[\ell ]^*) \Theta$ in the latter group. Lemma 3.4.4 implies that
$(T_{\ell }-\ell -[\ell ]^*) \Theta$ in the latter group. Lemma 3.4.4 implies that ![]() $\tau _{\ell }$ lies in the kernel of the homomorphism
$\tau _{\ell }$ lies in the kernel of the homomorphism
of Lemma 4.2.9, so is ![]() $2$-torsion. In particular, we have the statement for
$2$-torsion. In particular, we have the statement for ![]() $\ell = 2$.
$\ell = 2$.
This kernel of ![]() $f$ is a quotient of
$f$ is a quotient of ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}),H^2(\mathbb {G}_m^2,2)/\Phi )$. By Lemma 4.1.2 and the decomposition (4.3), the latter group is a direct sum of subgroups on which every
$H^1(\mathrm {GL}_2(\mathbb {Z}),H^2(\mathbb {G}_m^2,2)/\Phi )$. By Lemma 4.1.2 and the decomposition (4.3), the latter group is a direct sum of subgroups on which every ![]() $[m]_*$ acts by one of the scalars
$[m]_*$ acts by one of the scalars ![]() $m$ and
$m$ and ![]() $m^2$. In particular,
$m^2$. In particular, ![]() $\tau _{\ell }$ is killed by any operator
$\tau _{\ell }$ is killed by any operator
 \[ \epsilon = \sum_{m=1}^{\infty} a_m [m]_* \]
\[ \epsilon = \sum_{m=1}^{\infty} a_m [m]_* \]
with ![]() $a_m \in \mathbb {Z}$ and
$a_m \in \mathbb {Z}$ and ![]() $\sum ma_m = \sum m^2 a_m=0$.
$\sum ma_m = \sum m^2 a_m=0$.
Next, let us note that the actions of ![]() $T_{\ell }$ and
$T_{\ell }$ and ![]() $[m]_*$ on
$[m]_*$ on ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2/\Phi )$ commute if
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2/\Phi )$ commute if ![]() $\ell \nmid m$, since by Lemma 2.1.1 the trace map
$\ell \nmid m$, since by Lemma 2.1.1 the trace map ![]() $[m]_*$ commutes with the pullbacks used in the definition of
$[m]_*$ commutes with the pullbacks used in the definition of ![]() $T_{\ell }$ for
$T_{\ell }$ for ![]() $\ell \nmid m$. Consequently,
$\ell \nmid m$. Consequently, ![]() $\tau _{\ell }$ is fixed by each such
$\tau _{\ell }$ is fixed by each such ![]() $[m]_*$. Therefore, so long as the
$[m]_*$. Therefore, so long as the ![]() $a_m$ are zero for
$a_m$ are zero for ![]() $m$ not prime to
$m$ not prime to ![]() $\ell$, the operator
$\ell$, the operator ![]() $\epsilon$ above acts on
$\epsilon$ above acts on ![]() $\tau _{\ell }$ by the scalar
$\tau _{\ell }$ by the scalar ![]() $\sum a_m$, and we conclude that
$\sum a_m$, and we conclude that ![]() $\sum a_m \cdot \tau _{\ell }=0$ for
$\sum a_m \cdot \tau _{\ell }=0$ for ![]() $a_m$ as above such that
$a_m$ as above such that ![]() $a_m = 0$ if
$a_m = 0$ if ![]() $\ell$ divides
$\ell$ divides ![]() $m$. Taking
$m$. Taking ![]() $a_1 = -a_2 = 3a_3 = 3$, we see that
$a_1 = -a_2 = 3a_3 = 3$, we see that ![]() $\tau _{\ell }$ is zero for
$\tau _{\ell }$ is zero for ![]() $\ell \ge 5$ as desired. Taking
$\ell \ge 5$ as desired. Taking ![]() $a_4 = 1$,
$a_4 = 1$, ![]() $a_2= -6$, and
$a_2= -6$, and ![]() $a_1 = 8$, we see that
$a_1 = 8$, we see that ![]() $3\tau _3 = 0$, which is sufficient as
$3\tau _3 = 0$, which is sufficient as ![]() $2\tau _3 = 0$ as well.
$2\tau _3 = 0$ as well.
Let ![]() $\Delta _0(N)$ be the monoid of matrices with lower-left entry divisible by
$\Delta _0(N)$ be the monoid of matrices with lower-left entry divisible by ![]() $N$ and lower-right entry prime to
$N$ and lower-right entry prime to ![]() $N$; see (4.6). For a prime
$N$; see (4.6). For a prime ![]() $\ell$ and
$\ell$ and ![]() $g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$ as before, we let
$g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$ as before, we let ![]() $T_{\ell } = T(g)$ for
$T_{\ell } = T(g)$ for ![]() $\ell \nmid N$, with
$\ell \nmid N$, with ![]() $T(g)$ as in § 3.4.
$T(g)$ as in § 3.4.
Theorem 4.2.11 For primes ![]() $\ell$ not dividing
$\ell$ not dividing ![]() $2N$, we have
$2N$, we have
in ![]() $H^1(\tilde {\Gamma }_0(N),K_2(\mathbb {Q}(\mu _N))/Z_N)$. If
$H^1(\tilde {\Gamma }_0(N),K_2(\mathbb {Q}(\mu _N))/Z_N)$. If ![]() $N$ is odd, we have
$N$ is odd, we have ![]() $2(T_2-2-\sigma _2)\Theta _N = 0$.Footnote 10
$2(T_2-2-\sigma _2)\Theta _N = 0$.Footnote 10
Proof. In Lemma 4.2.10, we proved that for ![]() $\ell \nmid 2N$, the cocycle
$\ell \nmid 2N$, the cocycle ![]() $(T_{\ell } -\ell -[\ell ]^*)\Theta$ is cohomologous to zero when considering
$(T_{\ell } -\ell -[\ell ]^*)\Theta$ is cohomologous to zero when considering ![]() $\Theta$ as a
$\Theta$ as a ![]() $\mathrm {GL}_2(\mathbb {Z})$-cocycle with target
$\mathrm {GL}_2(\mathbb {Z})$-cocycle with target ![]() $\mathsf {K}_2/\langle \{-z_1, -z_2\}\rangle$. For
$\mathsf {K}_2/\langle \{-z_1, -z_2\}\rangle$. For ![]() $\ell \nmid N$, the elements
$\ell \nmid N$, the elements ![]() $g_j$ of (3.6) lie in
$g_j$ of (3.6) lie in ![]() $\Delta _0(N)$ and still provide left coset representatives of
$\Delta _0(N)$ and still provide left coset representatives of ![]() $\tilde {\Gamma }_0(N) \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big ) \tilde {\Gamma }_0(N)$. By Lemma 4.2.8, the class of
$\tilde {\Gamma }_0(N) \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big ) \tilde {\Gamma }_0(N)$. By Lemma 4.2.8, the class of ![]() $(T_{\ell } -\ell -[\ell ]^*)\Theta$ then remains zero when
$(T_{\ell } -\ell -[\ell ]^*)\Theta$ then remains zero when ![]() $\Theta$ is considered as a
$\Theta$ is considered as a ![]() $\tilde {\Gamma }_0(N)$-cocycle with target
$\tilde {\Gamma }_0(N)$-cocycle with target ![]() $\bar {\mathsf {K}}_2(N)$.
$\bar {\mathsf {K}}_2(N)$.
Moreover, the map ![]() $s^* \colon \bar {\mathsf {K}}_2(N) \rightarrow K_2(\mathbb {Q}(\mu _N))/Z_N$ is equivariant for the action of
$s^* \colon \bar {\mathsf {K}}_2(N) \rightarrow K_2(\mathbb {Q}(\mu _N))/Z_N$ is equivariant for the action of ![]() $\Delta _0(N)$ in the sense that
$\Delta _0(N)$ in the sense that ![]() $\sigma _d \circ s^* = s^* \circ \delta$, where
$\sigma _d \circ s^* = s^* \circ \delta$, where ![]() $\delta =\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$; in particular,
$\delta =\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$; in particular, ![]() $\sigma _{\ell } \circ s^* = s^* \circ [\ell ]^*$. Therefore,
$\sigma _{\ell } \circ s^* = s^* \circ [\ell ]^*$. Therefore,
is cohomologous to zero, as a cocycle with target in ![]() $K_2(\mathbb {Q}(\mu _N))/Z_N$.
$K_2(\mathbb {Q}(\mu _N))/Z_N$.
The same argument goes through for ![]() $\ell = 2$ if
$\ell = 2$ if ![]() $N$ is odd by multiplying everything by
$N$ is odd by multiplying everything by ![]() $2$.
$2$.
4.3 Maps on the homology of  $X_1(N)$
$X_1(N)$
In this section, we compare our constructions with others in the literature. We show how the cocycle ![]() $\Theta _N$ induces a map on the homology of the usual closed modular curve
$\Theta _N$ induces a map on the homology of the usual closed modular curve ![]() $X_1(N)$ over
$X_1(N)$ over ![]() $\mathbb {C}$, which is to say the quotient of the extended upper half-plane
$\mathbb {C}$, which is to say the quotient of the extended upper half-plane ![]() $\mathbb {H}^*$ by the congruence subgroup
$\mathbb {H}^*$ by the congruence subgroup ![]() $\Gamma _1(N)$ of
$\Gamma _1(N)$ of ![]() $\mathrm {SL}_2(\mathbb {Z})$. This agrees with the map constructed independently by Busuioc [Reference BusuiocBus08] and the first author [Reference SharifiSha11], which can be defined explicitly on Manin symbols on a slightly larger homology group of
$\mathrm {SL}_2(\mathbb {Z})$. This agrees with the map constructed independently by Busuioc [Reference BusuiocBus08] and the first author [Reference SharifiSha11], which can be defined explicitly on Manin symbols on a slightly larger homology group of ![]() $X_1(N)$, taken relative to some of its cusps. We show that this induced map factors through the quotient of homology by an Eisenstein ideal away from the level, providing a complement to a result of Fukaya and Kato [Reference Fukaya and KatoFK24] on
$X_1(N)$, taken relative to some of its cusps. We show that this induced map factors through the quotient of homology by an Eisenstein ideal away from the level, providing a complement to a result of Fukaya and Kato [Reference Fukaya and KatoFK24] on ![]() $p$-parts for
$p$-parts for ![]() $p \mid N$ that was a conjecture of the first author.
$p \mid N$ that was a conjecture of the first author.
4.3.1 Maps defined on Manin symbols
Let us suppose that ![]() $N \ge 4$. Let
$N \ge 4$. Let ![]() $C_1(N) = \Gamma _1(N) \backslash \mathbb {P}^1(\mathbb {Q})$ denote the cusps in the modular curve
$C_1(N) = \Gamma _1(N) \backslash \mathbb {P}^1(\mathbb {Q})$ denote the cusps in the modular curve ![]() $X_1(N)$, which is taken over
$X_1(N)$, which is taken over ![]() $\mathbb {C}$ in this section. For
$\mathbb {C}$ in this section. For ![]() $\alpha, \beta \in \mathbb {P}^1(\mathbb {Q})$, let
$\alpha, \beta \in \mathbb {P}^1(\mathbb {Q})$, let ![]() $\{\alpha \to \beta \}$ denote the class in the relative homology group
$\{\alpha \to \beta \}$ denote the class in the relative homology group ![]() $H_1(X_1(N),C_1(N),\mathbb {Z})$ of the geodesic in
$H_1(X_1(N),C_1(N),\mathbb {Z})$ of the geodesic in ![]() $\mathbb {H}^*$ from
$\mathbb {H}^*$ from ![]() $\alpha$ to
$\alpha$ to ![]() $\beta$. If
$\beta$. If ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are equivalent cusps, then
$\beta$ are equivalent cusps, then ![]() $\{\alpha \to \beta \}$ lies in the homology of
$\{\alpha \to \beta \}$ lies in the homology of ![]() $X_1(N)$.
$X_1(N)$.
Let us set
for ![]() $\gamma \in \Gamma _1(N)$. This class is independent of the choice of element
$\gamma \in \Gamma _1(N)$. This class is independent of the choice of element ![]() $0 \in \mathbb {H}^*$, and there is a commutative diagram
$0 \in \mathbb {H}^*$, and there is a commutative diagram

where the horizontal and vertical arrows are the standard maps, and all three maps are surjections.
For an abelian group ![]() $M$ with an action of complex conjugation, we let
$M$ with an action of complex conjugation, we let ![]() $M_+$ denote the maximal quotient on which complex conjugation acts trivially.
$M_+$ denote the maximal quotient on which complex conjugation acts trivially.
Proposition 4.3.1 There is a unique ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
$(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
that sends the image of ![]() $\vec {\gamma }$ to
$\vec {\gamma }$ to ![]() $\Theta _{N,\gamma }$ for all
$\Theta _{N,\gamma }$ for all ![]() $\gamma \in \Gamma _1(N)$.
$\gamma \in \Gamma _1(N)$.
Proof. Since the action of ![]() $\tilde {\Gamma }_0(N)$ on
$\tilde {\Gamma }_0(N)$ on ![]() $K_2(\mathbb {Q}(\mu _N))$ is trivial on
$K_2(\mathbb {Q}(\mu _N))$ is trivial on ![]() $\tilde {\Gamma }_1(N)$, the restriction of
$\tilde {\Gamma }_1(N)$, the restriction of ![]() $\Theta _N$ to
$\Theta _N$ to ![]() $\Gamma _1(N)$ induces a
$\Gamma _1(N)$ induces a ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
$(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
where ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ acts by diamond operators on the first term and by the Galois element
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ acts by diamond operators on the first term and by the Galois element ![]() $\sigma _d$ with
$\sigma _d$ with ![]() $\sigma _d(\zeta _N) = \zeta _N^d$ on the last. This homomorphism actually takes values in the subgroup
$\sigma _d(\zeta _N) = \zeta _N^d$ on the last. This homomorphism actually takes values in the subgroup ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$ by Lemma 4.2.7.
$K_2(\mathbb {Z}[\mu _N])/Z_N$ by Lemma 4.2.7.
The composition in (4.12) factors through ![]() $H_1(Y_1(N), \mathbb {Z}) \rightarrow H_1(Y_1(N), \mathbb {Z})_+$, since it is invariant by the natural action
$H_1(Y_1(N), \mathbb {Z}) \rightarrow H_1(Y_1(N), \mathbb {Z})_+$, since it is invariant by the natural action ![]() $Q := \tilde {\Gamma }_1(N)/\Gamma _1(N)$ on the left-hand side. This
$Q := \tilde {\Gamma }_1(N)/\Gamma _1(N)$ on the left-hand side. This ![]() $Q$ is a group of order
$Q$ is a group of order ![]() $2$, and its nontrivial element acts on
$2$, and its nontrivial element acts on ![]() $H_1(Y_1(N),\mathbb {Z})$ by complex conjugation
$H_1(Y_1(N),\mathbb {Z})$ by complex conjugation ![]() $z \mapsto -\bar {z}$.
$z \mapsto -\bar {z}$.
Finally, the composition in (4.12) also factors through ![]() $H_1(Y_1(N), \mathbb {Z}) \rightarrow H_1(X_1(N), \mathbb {Z})$. That is, the cocycle
$H_1(Y_1(N), \mathbb {Z}) \rightarrow H_1(X_1(N), \mathbb {Z})$. That is, the cocycle ![]() $\Theta _N$ is a coboundary, hence trivial, on all parabolic subgroups of
$\Theta _N$ is a coboundary, hence trivial, on all parabolic subgroups of ![]() $\Gamma _1(N)$, which are right stabilizers of nonzero elements of
$\Gamma _1(N)$, which are right stabilizers of nonzero elements of ![]() $\mathbb {P}^1(\mathbb {Q})$. These parabolics are also left stabilizers of elements of
$\mathbb {P}^1(\mathbb {Q})$. These parabolics are also left stabilizers of elements of ![]() $\mathbb {P}^1(\mathbb {Q})$ inside
$\mathbb {P}^1(\mathbb {Q})$ inside ![]() $\mathbb {H}^*$ and thereby generate the kernel of
$\mathbb {H}^*$ and thereby generate the kernel of ![]() $\Gamma _1(N)^{\mathrm {ab}} \rightarrow H_1(X_1(N), \mathbb {Z})$.
$\Gamma _1(N)^{\mathrm {ab}} \rightarrow H_1(X_1(N), \mathbb {Z})$.
Let ![]() $C_1^{\circ }(N) \subset C_1(N)$ denote the set of cusps not lying over
$C_1^{\circ }(N) \subset C_1(N)$ denote the set of cusps not lying over ![]() $\infty \in \Gamma _0(N) \backslash \mathbb {P}^1(\mathbb {Q})$. Given
$\infty \in \Gamma _0(N) \backslash \mathbb {P}^1(\mathbb {Q})$. Given ![]() $u, v \in \mathbb {Z}/N\mathbb {Z}$ with
$u, v \in \mathbb {Z}/N\mathbb {Z}$ with ![]() $(u,v) = (1)$, let
$(u,v) = (1)$, let
where ![]() $\big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with
$\big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with ![]() $(u,v) = (c,d) \bmod N\mathbb {Z}^2$. These Manin symbols for
$(u,v) = (c,d) \bmod N\mathbb {Z}^2$. These Manin symbols for ![]() $u, v \neq 0$ generate the relative homology group
$u, v \neq 0$ generate the relative homology group ![]() $H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z})$. In fact, this group has a presentation on the Manin symbols with relations
$H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z})$. In fact, this group has a presentation on the Manin symbols with relations
the latter for ![]() $u \neq -v$ (cf. [Reference Fukaya and KatoFK24, 3.3.7] and [Reference SharifiSha18, § 5.4]). It also has an action of diamond operators
$u \neq -v$ (cf. [Reference Fukaya and KatoFK24, 3.3.7] and [Reference SharifiSha18, § 5.4]). It also has an action of diamond operators ![]() $\langle j \rangle$ for
$\langle j \rangle$ for ![]() $j \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, given explicitly by
$j \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, given explicitly by
Let us set ![]() $\mathbb {Z}' = \mathbb {Z}[{1}/{2}]$. In general, for an abelian group
$\mathbb {Z}' = \mathbb {Z}[{1}/{2}]$. In general, for an abelian group ![]() $M$ with an action of complex conjugation, let us use
$M$ with an action of complex conjugation, let us use ![]() $m_+$ to denote the image of
$m_+$ to denote the image of ![]() $m \in M$ in
$m \in M$ in ![]() $(M \otimes _{\mathbb {Z}} \mathbb {Z}')_+$. The presentation of
$(M \otimes _{\mathbb {Z}} \mathbb {Z}')_+$. The presentation of ![]() $H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z}')_+$ as a
$H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z}')_+$ as a ![]() $\mathbb {Z}'$-module on the generators
$\mathbb {Z}'$-module on the generators ![]() $[u:v]_+$ has the additional relations
$[u:v]_+$ has the additional relations ![]() $[u:v]_+ = [-u:v]_+$ for all
$[u:v]_+ = [-u:v]_+$ for all ![]() $u, v \neq 0$.
$u, v \neq 0$.
The following construction is due to Busuioc [Reference BusuiocBus08] and the first author [Reference SharifiSha11, Proposition 5.7]. We give a proof that also gives some idea of where it becomes necessary to invert ![]() $2$.
$2$.
Proposition 4.3.2 (Busuioc, Sharifi)
There is a ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
$(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant homomorphism
Proof. For ![]() $\alpha, \beta \in \mathbb {Z}[\mu _N,{1}/{N}]^{\times }$, we denote by
$\alpha, \beta \in \mathbb {Z}[\mu _N,{1}/{N}]^{\times }$, we denote by ![]() $\{\alpha, \beta \}_+$ the projection of the Steinberg symbol to the group
$\{\alpha, \beta \}_+$ the projection of the Steinberg symbol to the group ![]() $(K_2(\mathbb {Z}[\mu _N,{1}/{N}]) \otimes _{\mathbb {Z}} \mathbb {Z}')_+$. Since we kill
$(K_2(\mathbb {Z}[\mu _N,{1}/{N}]) \otimes _{\mathbb {Z}} \mathbb {Z}')_+$. Since we kill ![]() $2$-torsion, we have
$2$-torsion, we have
Now take ![]() $x,y \in \mu _N-\{1\}$. Then
$x,y \in \mu _N-\{1\}$. Then
where the first equality is from invariance under complex conjugation and the second uses bilinearity. Therefore, ![]() $\{1-\zeta _N^a, 1-\zeta _N^b\}_+$ is invariant under changing the sign of either
$\{1-\zeta _N^a, 1-\zeta _N^b\}_+$ is invariant under changing the sign of either ![]() $a$ or
$a$ or ![]() $b$, whence the first relation of (4.13). The second relation of (4.13) follows from this invariance and
$b$, whence the first relation of (4.13). The second relation of (4.13) follows from this invariance and
for ![]() $xy \neq 1$, this equality holding without inverting
$xy \neq 1$, this equality holding without inverting ![]() $2$ and taking quotients trivial under complex conjugation. In turn, this follows from the relation
$2$ and taking quotients trivial under complex conjugation. In turn, this follows from the relation ![]() $\{\eta, 1-\eta \}=0$ with
$\{\eta, 1-\eta \}=0$ with
The restriction of ![]() $\Pi ^{\circ }_N$ to
$\Pi ^{\circ }_N$ to ![]() $H_1(X_1(N),\mathbb {Z})_+$ agrees with the map induced by our cocycle
$H_1(X_1(N),\mathbb {Z})_+$ agrees with the map induced by our cocycle ![]() $\Theta _N$. The first statement in the following is due to Fukaya and Kato [Reference Fukaya and KatoFK24, Theorem 5.3.3] for
$\Theta _N$. The first statement in the following is due to Fukaya and Kato [Reference Fukaya and KatoFK24, Theorem 5.3.3] for ![]() $p \mid N$, after taking
$p \mid N$, after taking ![]() $\mathbb {Z}_p$-coefficients, and in general, a direct proof can be found in [Reference SharifiSha18, Lemma 5.4.1]. For us, the first statement follows from the second, as
$\mathbb {Z}_p$-coefficients, and in general, a direct proof can be found in [Reference SharifiSha18, Lemma 5.4.1]. For us, the first statement follows from the second, as ![]() $\Pi _N$ takes values in
$\Pi _N$ takes values in ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$ by Proposition 4.3.1 (following Lemma 4.2.7, which is related to the aforementioned results).
$K_2(\mathbb {Z}[\mu _N])/Z_N$ by Proposition 4.3.1 (following Lemma 4.2.7, which is related to the aforementioned results).
Proposition 4.3.3 The restriction of ![]() $\Pi ^{\circ }_N$ to
$\Pi ^{\circ }_N$ to ![]() $H_1(X_1(N),\mathbb {Z})_+$ takes values in
$H_1(X_1(N),\mathbb {Z})_+$ takes values in ![]() $(K_2(\mathbb {Z}[\mu _N]) \otimes _{\mathbb {Z}} \mathbb {Z}')_+$ and agrees with the composition of
$(K_2(\mathbb {Z}[\mu _N]) \otimes _{\mathbb {Z}} \mathbb {Z}')_+$ and agrees with the composition of ![]() $\Pi _N$ with the quotient map from
$\Pi _N$ with the quotient map from ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$.
$K_2(\mathbb {Z}[\mu _N])/Z_N$.
Proof. We may write any element of ![]() $H_1(X_1(N),\mathbb {Z})$ as
$H_1(X_1(N),\mathbb {Z})$ as ![]() $\vec {\gamma }$ for some
$\vec {\gamma }$ for some ![]() $\gamma \in \Gamma _1(N)$. Let
$\gamma \in \Gamma _1(N)$. Let ![]() $(b_i,d_i)_{i=0}^k$ be an
$(b_i,d_i)_{i=0}^k$ be an ![]() $N$-connecting sequence for this
$N$-connecting sequence for this ![]() $\gamma$, so in particular
$\gamma$, so in particular ![]() $(b_0,d_0) = (0,1)$ and
$(b_0,d_0) = (0,1)$ and ![]() $(b_k,d_k) = (b,d)$. Then
$(b_k,d_k) = (b,d)$. Then
 \[ \vec{\gamma} = \bigg\{ 0 \to \frac{b}{d} \bigg\} = \sum_{i=1}^k \bigg\{ \frac{b_{i-1}}{d_{i-1}} \to \frac{b_i}{d_i} \bigg \} = \sum_{i=1}^k [d_i:d_{i-1}]_+ = \sum_{i=1}^k [d_i:-d_{i-1}]_+ \]
\[ \vec{\gamma} = \bigg\{ 0 \to \frac{b}{d} \bigg\} = \sum_{i=1}^k \bigg\{ \frac{b_{i-1}}{d_{i-1}} \to \frac{b_i}{d_i} \bigg \} = \sum_{i=1}^k [d_i:d_{i-1}]_+ = \sum_{i=1}^k [d_i:-d_{i-1}]_+ \]
is sent by ![]() $\Pi _N^{\circ }$ to
$\Pi _N^{\circ }$ to ![]() $\sum _{i=1}^k \{1-\zeta _N^{d_i}, 1-\zeta _N^{-d_{i-1}} \}_+$. By Proposition 4.2.4, this sum is the image of
$\sum _{i=1}^k \{1-\zeta _N^{d_i}, 1-\zeta _N^{-d_{i-1}} \}_+$. By Proposition 4.2.4, this sum is the image of ![]() $\Theta _{N,\gamma } = \Pi _N(\vec {\gamma })$.
$\Theta _{N,\gamma } = \Pi _N(\vec {\gamma })$.
4.3.2 Eisenstein property
For a prime ![]() $\ell$, we define the Hecke operator
$\ell$, we define the Hecke operator ![]() $T_{\ell }$ (denoted by
$T_{\ell }$ (denoted by ![]() $U_{\ell }$ if
$U_{\ell }$ if ![]() $\ell \mid N$) on
$\ell \mid N$) on ![]() $H_1(X_1(N),C_1(N),\mathbb {Z})$ to be that arising from a right coset decomposition of
$H_1(X_1(N),C_1(N),\mathbb {Z})$ to be that arising from a right coset decomposition of ![]() $\Gamma _1(N) \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big ) \Gamma _1(N)$. Its adjoint, or dual,
$\Gamma _1(N) \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big ) \Gamma _1(N)$. Its adjoint, or dual, ![]() $T_{\ell }^*$ is similarly the right Hecke operator for
$T_{\ell }^*$ is similarly the right Hecke operator for ![]() $\big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$ (denoted by
$\big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$ (denoted by ![]() $U_{\ell }^*$ if
$U_{\ell }^*$ if ![]() $\ell \mid N$).
$\ell \mid N$).
Remark 4.3.4 The operators ![]() $T_{\ell }$ on relative homology are dual to the corresponding right coset operators on compactly supported cohomology
$T_{\ell }$ on relative homology are dual to the corresponding right coset operators on compactly supported cohomology ![]() $H^1_c(Y_1(N),\mathbb {Z})$, which project to operators that agree with the (left coset) operators
$H^1_c(Y_1(N),\mathbb {Z})$, which project to operators that agree with the (left coset) operators ![]() $T_{\ell }$ on
$T_{\ell }$ on ![]() $H^1(\Gamma _1(N),\mathbb {Z})$ previously defined by Remark 3.4.2.
$H^1(\Gamma _1(N),\mathbb {Z})$ previously defined by Remark 3.4.2.
Note that ![]() $H_1(X_1(N),C_1(N),\mathbb {Z})$ is the left
$H_1(X_1(N),C_1(N),\mathbb {Z})$ is the left ![]() $\Gamma _1(N)$-coinvariant group of the group of degree zero divisors in
$\Gamma _1(N)$-coinvariant group of the group of degree zero divisors in ![]() $\mathbb {Z}[\mathbb {P}^1(\mathbb {Q})]$ under the standard left
$\mathbb {Z}[\mathbb {P}^1(\mathbb {Q})]$ under the standard left ![]() $(M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q}))$-action. Thus, if we choose a set of right coset representatives for the double coset of
$(M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q}))$-action. Thus, if we choose a set of right coset representatives for the double coset of ![]() $\big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ and define
$\big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ and define ![]() $T_{\ell }$ on
$T_{\ell }$ on ![]() $\mathbb {Z}[\mathbb {P}^1(\mathbb {Q})]$ by the sum of their actions, then this induces the
$\mathbb {Z}[\mathbb {P}^1(\mathbb {Q})]$ by the sum of their actions, then this induces the ![]() $T_{\ell }$-action on relative homology.
$T_{\ell }$-action on relative homology.
The adjoint operators preserve the subgroup ![]() $H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z})$, but the operators
$H_1(X_1(N),C_1^{\circ }(N),\mathbb {Z})$, but the operators ![]() $U_{\ell }$ for
$U_{\ell }$ for ![]() $\ell \mid N$ do not. Let us consider the adjoint Hecke algebra
$\ell \mid N$ do not. Let us consider the adjoint Hecke algebra
which also acts on ![]() $H_1(X_1(N),\mathbb {Z})$. Inside this algebra, we have the prime-to-level and full Eisenstein ideals
$H_1(X_1(N),\mathbb {Z})$. Inside this algebra, we have the prime-to-level and full Eisenstein ideals
Since ![]() $\langle \ell \rangle ^* = \langle \ell \rangle ^{-1}$ and
$\langle \ell \rangle ^* = \langle \ell \rangle ^{-1}$ and ![]() $T_{\ell }^* = \langle \ell \rangle ^{-1} T_{\ell }$ for
$T_{\ell }^* = \langle \ell \rangle ^{-1} T_{\ell }$ for ![]() $\ell \nmid N$ in
$\ell \nmid N$ in ![]() $\mathbb {T}^*_N$, note that
$\mathbb {T}^*_N$, note that
The first author has frequently floated the following conjecture that ![]() $\Pi _N$ is Eisenstein, so factors through the quotient of homology by the action of
$\Pi _N$ is Eisenstein, so factors through the quotient of homology by the action of ![]() $I_N$ (or equivalently, that
$I_N$ (or equivalently, that ![]() $\Pi _N(Tx) = 0$ for all
$\Pi _N(Tx) = 0$ for all ![]() $T \in I_N$ and
$T \in I_N$ and ![]() $x \in H_1(X_1(N),\mathbb {Z}')_+$) and, moreover, induces an isomorphism on the quotient by
$x \in H_1(X_1(N),\mathbb {Z}')_+$) and, moreover, induces an isomorphism on the quotient by ![]() $I_N$.
$I_N$.
Conjecture 4.3.5 (Sharifi)
(a) The map
 $\Pi _N$ factors through a map
$\Pi _N$ factors through a map
 \[ \varpi_N \colon H_1(X_1(N),\mathbb{Z}')_+ \otimes_{\mathbb{T}^*_N} \mathbb{T}^*_N/I_N \to (K_2(\mathbb{Z}[\mu_N]) \otimes_{\mathbb{Z}} \mathbb{Z}')_+. \]
\[ \varpi_N \colon H_1(X_1(N),\mathbb{Z}')_+ \otimes_{\mathbb{T}^*_N} \mathbb{T}^*_N/I_N \to (K_2(\mathbb{Z}[\mu_N]) \otimes_{\mathbb{Z}} \mathbb{Z}')_+. \]
(b) The map
 $\varpi _N$ is an isomorphism.
$\varpi _N$ is an isomorphism.
Part (a) of Conjecture 4.3.5 is a stronger form of an earlier conjecture [Reference SharifiSha11, Conjecture 5.8] that the tensor product of ![]() $\Pi _N$ with the identity on
$\Pi _N$ with the identity on ![]() $\mathbb {Z}_p$ for a prime
$\mathbb {Z}_p$ for a prime ![]() $p \mid N$ is Eisenstein. The earlier conjecture was proven by Fukaya and Kato in [Reference Fukaya and KatoFK24, Theorem 5.3.5].Footnote 11 In fact, they showed the following stronger result.
$p \mid N$ is Eisenstein. The earlier conjecture was proven by Fukaya and Kato in [Reference Fukaya and KatoFK24, Theorem 5.3.5].Footnote 11 In fact, they showed the following stronger result.
Theorem 4.3.6 (Fukaya and Kato)
For ![]() $p \mid N$, the map
$p \mid N$, the map ![]() $\Pi _N^{\circ } \otimes _{\mathbb {Z}} \mathrm {id}_{\mathbb {Z}_p}$ factors through a map
$\Pi _N^{\circ } \otimes _{\mathbb {Z}} \mathrm {id}_{\mathbb {Z}_p}$ factors through a map
Though we expect that ![]() $\Pi ^{\circ }_N$ is Eisenstein in general, the induced map
$\Pi ^{\circ }_N$ is Eisenstein in general, the induced map ![]() $\varpi ^{\circ }_N$ is not always an isomorphism. A special case of this conjecture is considered by Lecouturier in [Reference LecouturierLec21, Conjecture 4.32] (see also Conjecture 4.33 therein, which follows from our Conjecture 4.3.5).
$\varpi ^{\circ }_N$ is not always an isomorphism. A special case of this conjecture is considered by Lecouturier in [Reference LecouturierLec21, Conjecture 4.32] (see also Conjecture 4.33 therein, which follows from our Conjecture 4.3.5).
The proof of the result of Fukaya and Kato arises through a description of ![]() $\Pi _N$ as the composition of two maps: first, a Hecke-equivariant map
$\Pi _N$ as the composition of two maps: first, a Hecke-equivariant map ![]() $z_N$ that takes Manin symbols to cup products of Siegel units (i.e., Beilinson–Kato elements); and second, a specialization map induced by pullback at the cusp
$z_N$ that takes Manin symbols to cup products of Siegel units (i.e., Beilinson–Kato elements); and second, a specialization map induced by pullback at the cusp ![]() $0$. The proof of the Hecke equivariance of
$0$. The proof of the Hecke equivariance of ![]() $z_N$ goes through a string of Iwasawa-theoretic and Hida-theoretic constructions and the computation of a
$z_N$ goes through a string of Iwasawa-theoretic and Hida-theoretic constructions and the computation of a ![]() $p$-adic regulator. Their result then follows from the fact that the specialization at zero factors through
$p$-adic regulator. Their result then follows from the fact that the specialization at zero factors through ![]() $I'_N$ and is also trivial on the operators
$I'_N$ and is also trivial on the operators ![]() $U^*_{\ell }-1$ applied to Beilinson–Kato elements.
$U^*_{\ell }-1$ applied to Beilinson–Kato elements.
Though we do not use it to study ![]() $\Pi _N$, we give a construction of a motivic version of the map
$\Pi _N$, we give a construction of a motivic version of the map ![]() $z_N$ and prove its prime-to-level Hecke equivariance in § 7.2. Instead, as a consequence of what we have already done, we obtain a result over
$z_N$ and prove its prime-to-level Hecke equivariance in § 7.2. Instead, as a consequence of what we have already done, we obtain a result over ![]() $\mathbb {Z}'$ for the prime-to-level Eisenstein ideal without any use of Beilinson–Kato elements.Footnote 12 In fact, by Theorem 4.2.11, we have the following result.
$\mathbb {Z}'$ for the prime-to-level Eisenstein ideal without any use of Beilinson–Kato elements.Footnote 12 In fact, by Theorem 4.2.11, we have the following result.
Theorem 4.3.7 The map ![]() $\Pi _N$ factors through a map
$\Pi _N$ factors through a map
Proof. From Theorem 4.2.11, we have that ![]() $T_{\ell }\Theta _N = (\ell +\sigma _{\ell })\Theta _N$ as homomorphisms from
$T_{\ell }\Theta _N = (\ell +\sigma _{\ell })\Theta _N$ as homomorphisms from ![]() $\Gamma _1(N)$ to
$\Gamma _1(N)$ to ![]() $K_2(\mathbb {Z}[\mu _N])/Z_N$. Since
$K_2(\mathbb {Z}[\mu _N])/Z_N$. Since ![]() $\sigma _{\ell } \circ \Pi _N = \Pi _N \circ \langle \ell \rangle$ and noting (4.16), it suffices by Proposition 4.3.2 to check that
$\sigma _{\ell } \circ \Pi _N = \Pi _N \circ \langle \ell \rangle$ and noting (4.16), it suffices by Proposition 4.3.2 to check that
For ![]() $g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, we may choose left coset representatives of
$g = \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, we may choose left coset representatives of ![]() $\Gamma _1(N)g\Gamma _1(N)$ as in (3.4) with bottom-right entry
$\Gamma _1(N)g\Gamma _1(N)$ as in (3.4) with bottom-right entry ![]() $1$ modulo
$1$ modulo ![]() $N$ as follows: for
$N$ as follows: for ![]() $0 \le j < \ell$, set
$0 \le j < \ell$, set ![]() $g_j = \big (\begin{smallmatrix} \ell & j \\ & 1 \end{smallmatrix}\big )$, and set
$g_j = \big (\begin{smallmatrix} \ell & j \\ & 1 \end{smallmatrix}\big )$, and set ![]() $g_{\ell } = \delta _{\ell } \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ with
$g_{\ell } = \delta _{\ell } \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ with ![]() $\delta _{\ell } \in \Gamma _0(N)$ having image
$\delta _{\ell } \in \Gamma _0(N)$ having image ![]() $\ell ^{-1}$ in
$\ell ^{-1}$ in ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$. These agree with the matrices in (3.6) aside from
$(\mathbb {Z}/N\mathbb {Z})^{\times }$. These agree with the matrices in (3.6) aside from ![]() $g_{\ell }$. For the map
$g_{\ell }$. For the map ![]() $\Pi _N$ constructed in Proposition 4.3.1, for
$\Pi _N$ constructed in Proposition 4.3.1, for ![]() $\gamma \in \Gamma _1(N)$, we then have
$\gamma \in \Gamma _1(N)$, we then have
 \[ (T_{\ell}\Theta_N)_{\gamma} = \sum_{j=0}^{\ell} g_{\sigma(j)}^* \Theta_{N,\gamma_j} = \sum_{j=0}^{\ell} \Theta_{N,\gamma_j} = \sum_{j=0}^{\ell} \Pi_N(\vec{\gamma}_j), \]
\[ (T_{\ell}\Theta_N)_{\gamma} = \sum_{j=0}^{\ell} g_{\sigma(j)}^* \Theta_{N,\gamma_j} = \sum_{j=0}^{\ell} \Theta_{N,\gamma_j} = \sum_{j=0}^{\ell} \Pi_N(\vec{\gamma}_j), \]
where ![]() $\gamma g_j = g_{\sigma (j)} \gamma _j$ for
$\gamma g_j = g_{\sigma (j)} \gamma _j$ for ![]() $\sigma$ a permutation of
$\sigma$ a permutation of ![]() $\{0,\ldots,\ell \}$ and
$\{0,\ldots,\ell \}$ and ![]() $\gamma _j \in \Gamma _1(N)$.
$\gamma _j \in \Gamma _1(N)$.
On the other hand, let ![]() $h_j = \big (\begin{smallmatrix} \ell \\ & \ell \end{smallmatrix}\big )g_j^{-1}$ be the adjoint of
$h_j = \big (\begin{smallmatrix} \ell \\ & \ell \end{smallmatrix}\big )g_j^{-1}$ be the adjoint of ![]() $g_j$ so that
$g_j$ so that ![]() $h_j \gamma ^{-1} = \gamma _j^{-1} h_{\sigma (j)}$. Since
$h_j \gamma ^{-1} = \gamma _j^{-1} h_{\sigma (j)}$. Since
for ![]() $\alpha, \beta,\epsilon \in \mathbb {H}^*$ and
$\alpha, \beta,\epsilon \in \mathbb {H}^*$ and ![]() $\{ 0 \to \mu ^{-1} \cdot 0 \} = -\vec {\mu }$ for
$\{ 0 \to \mu ^{-1} \cdot 0 \} = -\vec {\mu }$ for ![]() $\mu \in \Gamma _1(N)$, we have
$\mu \in \Gamma _1(N)$, we have
 \[ T_{\ell}\vec{\gamma} = -T_{\ell} \{0 \to \gamma^{-1} 0\} = -\sum_{j=0}^{\ell} \{ h_j0 \to \gamma_j^{-1} h_{\sigma(j)} 0 \} = -\sum_{j=0}^{\ell} \{ h_{\sigma(j)} 0 \to \gamma_j^{-1} h_{\sigma(j)} 0 \} = \sum_{j=0}^{\ell} \vec{\gamma}_j, \]
\[ T_{\ell}\vec{\gamma} = -T_{\ell} \{0 \to \gamma^{-1} 0\} = -\sum_{j=0}^{\ell} \{ h_j0 \to \gamma_j^{-1} h_{\sigma(j)} 0 \} = -\sum_{j=0}^{\ell} \{ h_{\sigma(j)} 0 \to \gamma_j^{-1} h_{\sigma(j)} 0 \} = \sum_{j=0}^{\ell} \vec{\gamma}_j, \]
hence the result.
5. The  $\mathbb {G}_m^2$-cocycle via toric geometry
$\mathbb {G}_m^2$-cocycle via toric geometry
The aim of this section is to provide a different viewpoint on the above results and minor improvements to some of them. We will describe a map
in the derived category of abelian groups with ![]() $\mathrm {GL}_2(\mathbb {Z})$-action. This map can be used to recover the previous cocycle, and even lift it to
$\mathrm {GL}_2(\mathbb {Z})$-action. This map can be used to recover the previous cocycle, and even lift it to ![]() $\mathsf {K}_2$. Moreover, it allows us to outline the connection of our results with equivariant motivic cohomology, as discussed in § 1.2.3. The key point in the argument is to utilize the behavior of
$\mathsf {K}_2$. Moreover, it allows us to outline the connection of our results with equivariant motivic cohomology, as discussed in § 1.2.3. The key point in the argument is to utilize the behavior of ![]() $K_2$ classes along the boundary of toric compactifications.
$K_2$ classes along the boundary of toric compactifications.
The geometric construction that we give is closely related to joint work in progress of the second named author with Bergeron, Charollois, and Garcia (although that work does not deal with ![]() $K$-theory, rather with differential forms). However, the viewpoint of this section is also close to that taken by numerous other authors on related questions, among which we mention Nori [Reference NoriNor94], Sczech [Reference SczechScz93], Stevens [Reference StevensSte07], Solomon [Reference SolomonSol98], and Garoufalidis and Pommersheim [Reference Garoufalidis and PommersheimGP01]. Particularly relevant is a recent paper of Lim and Park [Reference Lim and ParkLP19], which completes the work of Stevens and lifts a ‘Shintani cocycle’ to the ‘Stevens cocycle’ along a
$K$-theory, rather with differential forms). However, the viewpoint of this section is also close to that taken by numerous other authors on related questions, among which we mention Nori [Reference NoriNor94], Sczech [Reference SczechScz93], Stevens [Reference StevensSte07], Solomon [Reference SolomonSol98], and Garoufalidis and Pommersheim [Reference Garoufalidis and PommersheimGP01]. Particularly relevant is a recent paper of Lim and Park [Reference Lim and ParkLP19], which completes the work of Stevens and lifts a ‘Shintani cocycle’ to the ‘Stevens cocycle’ along a ![]() $\mathrm {dlog}$ map. As with several of the named references, [Reference Lim and ParkLP19] works with cocycles for
$\mathrm {dlog}$ map. As with several of the named references, [Reference Lim and ParkLP19] works with cocycles for ![]() $\mathrm {GL}_n(\mathbb {Q})$ valued in a module of distributions; as such, it does not directly relate to the type of toric geometry that we emphasize here but nonetheless seems very closely related to an infinite level version of our construction.
$\mathrm {GL}_n(\mathbb {Q})$ valued in a module of distributions; as such, it does not directly relate to the type of toric geometry that we emphasize here but nonetheless seems very closely related to an infinite level version of our construction.
At certain points one could proceed by symbols and relations, but we have tried to avoid this. Our point of view would extend without complication to higher dimensions, for instance.
5.1 Residues on  $K_2$ of the function field of a torus
$K_2$ of the function field of a torus
5.1.1 Some toric geometry
It will be helpful to proceed a bit more canonically. Let ![]() $T = \mathbb {G}_m^2$, let
$T = \mathbb {G}_m^2$, let ![]() $X = X_*(T)$ be the cocharacter group of
$X = X_*(T)$ be the cocharacter group of ![]() $T$, and set
$T$, and set ![]() $X_{\mathbb {R}} = X \otimes _{\mathbb {Z}} \mathbb {R} \cong \mathbb {R}^2$. Fix an orientation on
$X_{\mathbb {R}} = X \otimes _{\mathbb {Z}} \mathbb {R} \cong \mathbb {R}^2$. Fix an orientation on ![]() $X_{\mathbb {R}}$, which in particular allows us to make the identification
$X_{\mathbb {R}}$, which in particular allows us to make the identification ![]() $\bigwedge ^2 X \cong \mathbb {Z}$; for
$\bigwedge ^2 X \cong \mathbb {Z}$; for ![]() $x,y \in X$, we accordingly write
$x,y \in X$, we accordingly write ![]() $x \wedge y \in \mathbb {Z}$. Let
$x \wedge y \in \mathbb {Z}$. Let ![]() $X^* = X^*(T)$ be the character group of
$X^* = X^*(T)$ be the character group of ![]() $T$, and denote by
$T$, and denote by
the pairing that describes the composition ![]() $\mathbb {G}_m \to \mathbb {G}_m$.
$\mathbb {G}_m \to \mathbb {G}_m$.
Let us view the torus ![]() $\mathbb {G}_m^2$ as
$\mathbb {G}_m^2$ as ![]() $T = \operatorname {Spec} \mathbb {Q}[X^*]$, and let
$T = \operatorname {Spec} \mathbb {Q}[X^*]$, and let ![]() $\mathbb {Q}(T)$ be the function field of
$\mathbb {Q}(T)$ be the function field of ![]() $T$. For each primitive
$T$. For each primitive ![]() $\lambda \in X$, let
$\lambda \in X$, let ![]() $V_{\lambda } \subset X^*$ be the dual cone of characters which pair non-positively with
$V_{\lambda } \subset X^*$ be the dual cone of characters which pair non-positively with ![]() $\lambda$. Let
$\lambda$. Let ![]() $\mathbb {Q}[V_{\lambda }]$ be the monoid algebra of
$\mathbb {Q}[V_{\lambda }]$ be the monoid algebra of ![]() $V_{\lambda }$. Since each element
$V_{\lambda }$. Since each element ![]() $\nu$ of
$\nu$ of ![]() $V_{\lambda }$ is a regular function on
$V_{\lambda }$ is a regular function on ![]() $T$, we have inclusions
$T$, we have inclusions
In particular, the first inclusion induces an open immersion ![]() $T \rightarrow T_{\lambda }$, where
$T \rightarrow T_{\lambda }$, where
The toric variety ![]() $T_{\lambda }$ has the following properties, all of which are readily proven by choosing coordinates.Footnote 13 The limit
$T_{\lambda }$ has the following properties, all of which are readily proven by choosing coordinates.Footnote 13 The limit ![]() $Q_{\lambda } = \lim _{x \rightarrow \infty } \lambda (x)$ exists in the partial compactification
$Q_{\lambda } = \lim _{x \rightarrow \infty } \lambda (x)$ exists in the partial compactification ![]() $T_{\lambda }$ of
$T_{\lambda }$ of ![]() $T$. In other words, the map
$T$. In other words, the map ![]() $t \mapsto \lambda (t)$, considered as a morphism
$t \mapsto \lambda (t)$, considered as a morphism ![]() $\mathbb {G}_m \rightarrow T_{\lambda }$, extends over
$\mathbb {G}_m \rightarrow T_{\lambda }$, extends over ![]() $\infty \in \mathbb {P}^1$. The complement
$\infty \in \mathbb {P}^1$. The complement ![]() $D_{\lambda } = T_{\lambda } - T$ is a divisor on
$D_{\lambda } = T_{\lambda } - T$ is a divisor on ![]() $T_{\lambda }$, and
$T_{\lambda }$, and ![]() $Q_{\lambda }$ belongs to this divisor. The vanishing order of any
$Q_{\lambda }$ belongs to this divisor. The vanishing order of any ![]() $\chi \in X^*$ along
$\chi \in X^*$ along ![]() $D_{\lambda }$ is given by
$D_{\lambda }$ is given by ![]() $-\langle \lambda, \chi \rangle$. The stabilizer of
$-\langle \lambda, \chi \rangle$. The stabilizer of ![]() $Q_{\lambda }$ under the torus action of
$Q_{\lambda }$ under the torus action of ![]() $T$ on
$T$ on ![]() $T_{\lambda }$ is precisely
$T_{\lambda }$ is precisely ![]() $\lambda (\mathbb {G}_m)$, and this provides a
$\lambda (\mathbb {G}_m)$, and this provides a ![]() $T$-equivariant identification
$T$-equivariant identification
under which ![]() $Q_{\lambda }$ is taken to the identity. Moreover, any choice of
$Q_{\lambda }$ is taken to the identity. Moreover, any choice of ![]() $\mu \in X$ with
$\mu \in X$ with ![]() $\mu \wedge \lambda = 1$ induces an isomorphism
$\mu \wedge \lambda = 1$ induces an isomorphism ![]() $\mathbb {G}_m \xrightarrow {\mu } T \rightarrow T/\lambda (\mathbb {G}_m)$ which permits us to identify
$\mathbb {G}_m \xrightarrow {\mu } T \rightarrow T/\lambda (\mathbb {G}_m)$ which permits us to identify ![]() $D_{\lambda }$ with
$D_{\lambda }$ with ![]() $\mathbb {G}_m$.
$\mathbb {G}_m$.
5.1.2 Residues of classes in  $K_2(\mathbb {Q}(\mathbb {G}_m^2))$
$K_2(\mathbb {Q}(\mathbb {G}_m^2))$
We continue with the notation of § 5.1.1. Our key result, Proposition 5.1.1 below, describes the boundary behavior of classes in ![]() $K_2$ of the function field of
$K_2$ of the function field of ![]() $T$ along toric boundary divisors.
$T$ along toric boundary divisors.
Let ![]() $S^1$ denote the circle, viewed as the quotient of
$S^1$ denote the circle, viewed as the quotient of ![]() $X_{\mathbb {R}}-\{0\}$ by positive scalings:
$X_{\mathbb {R}}-\{0\}$ by positive scalings:
We shall identify points of ![]() $S^1$ with rays
$S^1$ with rays ![]() $\mathbb {R}_+ x \subset X_{\mathbb {R}}$ for
$\mathbb {R}_+ x \subset X_{\mathbb {R}}$ for ![]() $x \in X_{\mathbb {R}}$ nonzero (i.e., half-lines with boundary the origin). A point in
$x \in X_{\mathbb {R}}$ nonzero (i.e., half-lines with boundary the origin). A point in ![]() $S^1$ is rational if it is the image of an element of
$S^1$ is rational if it is the image of an element of ![]() $X$, that is, if the associated ray passes through a point of
$X$, that is, if the associated ray passes through a point of ![]() $X$.
$X$.
Proposition 5.1.1 For ![]() $\kappa \in K_2(\mathbb {Q}(T))$, there is a locally constant function
$\kappa \in K_2(\mathbb {Q}(T))$, there is a locally constant function ![]() $n=n_{\kappa } \colon S^1 - \Sigma \rightarrow \mathbb {Z}$ with
$n=n_{\kappa } \colon S^1 - \Sigma \rightarrow \mathbb {Z}$ with ![]() $\Sigma$ a finite set of rational points, having the following property: if
$\Sigma$ a finite set of rational points, having the following property: if ![]() $n$ is defined on the ray
$n$ is defined on the ray ![]() $\mathbb {R}_+ \lambda$, then the residue of
$\mathbb {R}_+ \lambda$, then the residue of ![]() $\kappa$ along
$\kappa$ along ![]() $D_{\lambda } \cong \mathbb {G}_m$ has the form
$D_{\lambda } \cong \mathbb {G}_m$ has the form ![]() $c z^{n(\lambda )}$ for some scalar
$c z^{n(\lambda )}$ for some scalar ![]() $c \in \mathbb {Q}^{\times }$.
$c \in \mathbb {Q}^{\times }$.
Proof. It is sufficient to analyze the case ![]() $\kappa = \{f, g\}$, in which
$\kappa = \{f, g\}$, in which ![]() $f$ and
$f$ and ![]() $g$ are nonzero elements of
$g$ are nonzero elements of ![]() $\mathbb {Q}[X^*]$, for such symbols generate
$\mathbb {Q}[X^*]$, for such symbols generate ![]() $K_2(\mathbb {Q}(T))$.
$K_2(\mathbb {Q}(T))$.
We may write any ![]() $f \in \mathbb {Q}[X^*]$ as a finite sum
$f \in \mathbb {Q}[X^*]$ as a finite sum
with ![]() $a_{\chi }(f) \in \mathbb {Q}$. Let
$a_{\chi }(f) \in \mathbb {Q}$. Let ![]() $\mathrm {supp}(f)$ denote the finite set
$\mathrm {supp}(f)$ denote the finite set
For a nonzero ![]() $\lambda \in X \otimes _{\mathbb {Z}} \mathbb {R}$, consider the function
$\lambda \in X \otimes _{\mathbb {Z}} \mathbb {R}$, consider the function ![]() $\phi _{f,\lambda } \colon \mathrm {supp}(f) \rightarrow \mathbb {R}$ given by
$\phi _{f,\lambda } \colon \mathrm {supp}(f) \rightarrow \mathbb {R}$ given by
on ![]() $\chi \in \mathrm {supp}(f)$. If
$\chi \in \mathrm {supp}(f)$. If ![]() $\phi _{f,\lambda }$ is injective on the finite set
$\phi _{f,\lambda }$ is injective on the finite set ![]() $\mathrm {supp}(f)$, then we let
$\mathrm {supp}(f)$, then we let ![]() $\chi _{f, \lambda }$ be the unique element
$\chi _{f, \lambda }$ be the unique element ![]() $\chi \in \mathrm {supp}(f)$ maximizing
$\chi \in \mathrm {supp}(f)$ maximizing ![]() $\langle \lambda, \chi \rangle$. It is invariant under rescaling
$\langle \lambda, \chi \rangle$. It is invariant under rescaling ![]() $\lambda$ by a positive real number. Letting
$\lambda$ by a positive real number. Letting ![]() $\Sigma _f$ denote the (finite!) collection of rays
$\Sigma _f$ denote the (finite!) collection of rays ![]() $\mathbb {R}_+ \lambda$ for which
$\mathbb {R}_+ \lambda$ for which ![]() $\phi _{f,\lambda }$ is not injective, we then have a locally constant function
$\phi _{f,\lambda }$ is not injective, we then have a locally constant function
Now fix a rational point of ![]() $S^1 -\Sigma _f$, corresponding to the ray
$S^1 -\Sigma _f$, corresponding to the ray ![]() $\mathbb {R}_+ \lambda$ for some primitive
$\mathbb {R}_+ \lambda$ for some primitive ![]() $\lambda \in X$, and write
$\lambda \in X$, and write
As above, ![]() $v_f$ is the vanishing order of
$v_f$ is the vanishing order of ![]() $f$ along
$f$ along ![]() $T_{\lambda }$; it may be negative. Note that
$T_{\lambda }$; it may be negative. Note that ![]() $f \cdot \chi _f^{-1}$ extends to
$f \cdot \chi _f^{-1}$ extends to ![]() $T_{\lambda }$, because for any
$T_{\lambda }$, because for any ![]() $\chi \in \mathrm {supp}(f)$, the ratio
$\chi \in \mathrm {supp}(f)$, the ratio ![]() $\chi \chi _f^{-1}$ has non-positive pairing with
$\chi \chi _f^{-1}$ has non-positive pairing with ![]() $\lambda$. Since
$\lambda$. Since ![]() $\chi \chi _f^{-1}$ vanishes on
$\chi \chi _f^{-1}$ vanishes on ![]() $D_{\lambda }$ for
$D_{\lambda }$ for ![]() $\chi \in \mathrm {supp}(f)$ with
$\chi \in \mathrm {supp}(f)$ with ![]() $\chi \neq \chi _f$, the value of
$\chi \neq \chi _f$, the value of ![]() $f \cdot \chi _f^{-1}$ along
$f \cdot \chi _f^{-1}$ along ![]() $T_{\lambda }-T$ is the constant
$T_{\lambda }-T$ is the constant ![]() $a_f$.
$a_f$.
Now suppose that ![]() $\mathbb {R}_+ \lambda \notin \Sigma _f$ also does not belong to the set
$\mathbb {R}_+ \lambda \notin \Sigma _f$ also does not belong to the set ![]() $\Sigma _g$ for
$\Sigma _g$ for ![]() $g \in \mathbb {Q}[X^*]$. The image of
$g \in \mathbb {Q}[X^*]$. The image of ![]() $\{f, g \}$ in
$\{f, g \}$ in ![]() $K_1(\mathbb {Q}(D_{\lambda }))$ is therefore the tame symbol given by
$K_1(\mathbb {Q}(D_{\lambda }))$ is therefore the tame symbol given by
 \[ (-1)^{v_fv_g} \frac{g^{v_f}}{f^{v_g}} = c \frac{\chi_g^{v_f}}{\chi_f^{v_g}}, \]
\[ (-1)^{v_fv_g} \frac{g^{v_f}}{f^{v_g}} = c \frac{\chi_g^{v_f}}{\chi_f^{v_g}}, \]
where ![]() $c$ is the constant
$c$ is the constant ![]() $(-1)^{v_fv_g} a_g^{v_f}a_f^{-v_g} \in \mathbb {Q}^{\times }$. The right-hand side defines a function on
$(-1)^{v_fv_g} a_g^{v_f}a_f^{-v_g} \in \mathbb {Q}^{\times }$. The right-hand side defines a function on ![]() $T$, constant on
$T$, constant on ![]() $\lambda (\mathbb {G}_m)$, which extends over
$\lambda (\mathbb {G}_m)$, which extends over ![]() $T_{\lambda }$, and thus can be restricted to
$T_{\lambda }$, and thus can be restricted to ![]() $D_{\lambda }$.
$D_{\lambda }$.
Note that the value of ![]() $\chi _g^{v_f}\chi _f^{-v_g} \in X^*$ on a cocharacter
$\chi _g^{v_f}\chi _f^{-v_g} \in X^*$ on a cocharacter ![]() $\mu$ is given by
$\mu$ is given by
Recall that we are identifying ![]() $D_{\lambda }$ with
$D_{\lambda }$ with ![]() $\mathbb {G}_m$ via any cocharacter
$\mathbb {G}_m$ via any cocharacter ![]() $\mu \colon \mathbb {G}_m \rightarrow T$ with
$\mu \colon \mathbb {G}_m \rightarrow T$ with ![]() $\mu \wedge \lambda =1$; with respect to this identification, the tame symbol above is identified with
$\mu \wedge \lambda =1$; with respect to this identification, the tame symbol above is identified with ![]() $c z^n$, where
$c z^n$, where ![]() $n = \chi _f\wedge \chi _g$. In particular,
$n = \chi _f\wedge \chi _g$. In particular, ![]() $n=n(\lambda )$ is locally constant on the set
$n=n(\lambda )$ is locally constant on the set ![]() $S^1 - \Sigma _f \cup \Sigma _g$ of rays.
$S^1 - \Sigma _f \cup \Sigma _g$ of rays.
Example 5.1.2 Take ![]() $f = 1-z_1$ and
$f = 1-z_1$ and ![]() $g = 1-z_2$. The sets
$g = 1-z_2$. The sets ![]() $\mathrm {supp}(f)$ and
$\mathrm {supp}(f)$ and ![]() $\mathrm {supp}(g)$ in (5.1) are
$\mathrm {supp}(g)$ in (5.1) are ![]() $\{0, (1,0)\}$ and
$\{0, (1,0)\}$ and ![]() $\{0, (0,1)\}$, respectively. Then
$\{0, (0,1)\}$, respectively. Then ![]() $\Sigma _f$ consists of the ray
$\Sigma _f$ consists of the ray ![]() $\mathbb {R}_+ (0,1)$ together with its negative, and
$\mathbb {R}_+ (0,1)$ together with its negative, and ![]() $\Sigma _g$ is the ray
$\Sigma _g$ is the ray ![]() $\mathbb {R}_+ (1,0)$ together with its negative. For
$\mathbb {R}_+ (1,0)$ together with its negative. For ![]() $\lambda = (a,b)$, we have
$\lambda = (a,b)$, we have
 \[ \chi_f = \begin{cases} (1,0) & \text{if } a >0, \\ 0 & \text{if } a < 0, \end{cases} \quad \mathrm{and} \quad \chi_g = \begin{cases} (0,1) & \text{if } b>0, \\ 0 & \text{if } b<0. \end{cases} \]
\[ \chi_f = \begin{cases} (1,0) & \text{if } a >0, \\ 0 & \text{if } a < 0, \end{cases} \quad \mathrm{and} \quad \chi_g = \begin{cases} (0,1) & \text{if } b>0, \\ 0 & \text{if } b<0. \end{cases} \]
Therefore, if we choose the standard orientation where ![]() $(1,0) \wedge (0,1) = 1$, then
$(1,0) \wedge (0,1) = 1$, then ![]() $n=\chi _f \wedge \chi _g$ is given by the function
$n=\chi _f \wedge \chi _g$ is given by the function
 \[ (a,b) \mapsto \begin{cases} 1 & \text{if } a>0 \text{ and } b>0, \\ 0 & \text{if } a <0 \text{ or } b<0, \end{cases} \]
\[ (a,b) \mapsto \begin{cases} 1 & \text{if } a>0 \text{ and } b>0, \\ 0 & \text{if } a <0 \text{ or } b<0, \end{cases} \]
which is to say, the characteristic function of the counterclockwise arc from ![]() $(1,0)$ to
$(1,0)$ to ![]() $(0,1)$ on
$(0,1)$ on ![]() $S^1$, or equivalently of the first quadrant in
$S^1$, or equivalently of the first quadrant in ![]() $\mathbb {R}^2$.
$\mathbb {R}^2$.
5.1.3 Values on symbols
The map ![]() $n$ of Proposition 5.1.1 can be described as a homomorphism from
$n$ of Proposition 5.1.1 can be described as a homomorphism from ![]() $K_2(\mathbb {Q}(T))$ to the set of locally constant functions on
$K_2(\mathbb {Q}(T))$ to the set of locally constant functions on ![]() $S^1$, defined on the complement of a finite set of rational points. If we identify two such functions when they agree off of a finite set, then the target becomes a group under pointwise addition, and the map
$S^1$, defined on the complement of a finite set of rational points. If we identify two such functions when they agree off of a finite set, then the target becomes a group under pointwise addition, and the map ![]() $n$ a group homomorphism. Call this group
$n$ a group homomorphism. Call this group ![]() $\mathsf {Ch}_1$:
$\mathsf {Ch}_1$:
where ![]() $\sim$ is the equivalence relation of agreeing off of a finite set.
$\sim$ is the equivalence relation of agreeing off of a finite set.
Example 5.1.3 For any ![]() $\ell, \ell ' \in S^1_{\mathbb {Q}}$, let
$\ell, \ell ' \in S^1_{\mathbb {Q}}$, let ![]() $[\ell, \ell ']$ be the counterclockwise arc from
$[\ell, \ell ']$ be the counterclockwise arc from ![]() $\ell$ to
$\ell$ to ![]() $\ell '$, which we identify with an element of
$\ell '$, which we identify with an element of ![]() $\mathsf {Ch}_1$ via its characteristic function. (Thus, if
$\mathsf {Ch}_1$ via its characteristic function. (Thus, if ![]() $\ell =\ell '$, then
$\ell =\ell '$, then ![]() $[\ell,\ell ']$ is the zero element.)
$[\ell,\ell ']$ is the zero element.)
Observe that the group ![]() $\mathsf {Ch}_1$ has a presentation with generators the elements
$\mathsf {Ch}_1$ has a presentation with generators the elements ![]() $[\ell, \ell ']$ and relations
$[\ell, \ell ']$ and relations
for ![]() $\ell '$ lying on the counterclockwise arc from
$\ell '$ lying on the counterclockwise arc from ![]() $\ell$ to
$\ell$ to ![]() $\ell ''$ (including both endpoints). Indeed, writing
$\ell ''$ (including both endpoints). Indeed, writing ![]() $\mathsf {G}$ for the abstract group so presented, the homomorphism
$\mathsf {G}$ for the abstract group so presented, the homomorphism ![]() $\mathsf {G} \rightarrow \mathsf {Ch}_1$ is readily seen to be surjective. On the other hand, by recursive use of (5.2), any element of
$\mathsf {G} \rightarrow \mathsf {Ch}_1$ is readily seen to be surjective. On the other hand, by recursive use of (5.2), any element of ![]() $\mathsf {G}$ can be written as a finite sum
$\mathsf {G}$ can be written as a finite sum ![]() $\sum _i m_i [a_i, b_i]$ where
$\sum _i m_i [a_i, b_i]$ where ![]() $m_i \in \mathbb {Z}$ and where the intervals are disjoint except at their endpoints, and the condition of vanishing in
$m_i \in \mathbb {Z}$ and where the intervals are disjoint except at their endpoints, and the condition of vanishing in ![]() $\mathsf {Ch}_1$ then implies that the sum must be empty.
$\mathsf {Ch}_1$ then implies that the sum must be empty.
We can then reformulate Example 5.1.2 as saying that ![]() $\{1-z_1, 1-z_2\} \mapsto [(1,0), (0,1)]$ under
$\{1-z_1, 1-z_2\} \mapsto [(1,0), (0,1)]$ under ![]() $n$. More generally, if
$n$. More generally, if ![]() $\nu _1, \nu _2$ form a positively oriented basis of
$\nu _1, \nu _2$ form a positively oriented basis of ![]() $X$ (i.e.,
$X$ (i.e., ![]() $\nu _1 \wedge \nu _2=1$), then
$\nu _1 \wedge \nu _2=1$), then
where ![]() $\nu _1^*, \nu _2^* \in X^*$ are the dual basis elements.
$\nu _1^*, \nu _2^* \in X^*$ are the dual basis elements.
Remark 5.1.4 For later use, we note that for any ![]() $\ell _1, \ell _2, \ell _3 \in S^1_{\mathbb {Q}}$ we have
$\ell _1, \ell _2, \ell _3 \in S^1_{\mathbb {Q}}$ we have
where ![]() $\delta = 0$ when
$\delta = 0$ when ![]() $\ell _2$ lies on the counterclockwise arc from
$\ell _2$ lies on the counterclockwise arc from ![]() $\ell _1$ to
$\ell _1$ to ![]() $\ell _3$ including endpoints, and
$\ell _3$ including endpoints, and ![]() $\delta =1$ otherwise. (In particular,
$\delta =1$ otherwise. (In particular, ![]() $[\ell _1, \ell _2] + [\ell _2, \ell _1] = 1$ unless
$[\ell _1, \ell _2] + [\ell _2, \ell _1] = 1$ unless ![]() $\ell _1=\ell _2$.) Note that it follows from this that
$\ell _1=\ell _2$.) Note that it follows from this that ![]() $\delta$ satisfies the (homogeneous) cocycle relation
$\delta$ satisfies the (homogeneous) cocycle relation
5.2 Comparison of chain complexes
We continue to suppose that ![]() $T = \mathbb {G}_m^2$, providing an identification
$T = \mathbb {G}_m^2$, providing an identification ![]() $X = \mathbb {Z}^2$. The right automorphism group of
$X = \mathbb {Z}^2$. The right automorphism group of ![]() $T$ is an algebraic group which, consistent with our prior conventions, we consider as acting on the right on
$T$ is an algebraic group which, consistent with our prior conventions, we consider as acting on the right on ![]() $T$. By functoriality, we obtain the usual right action of
$T$. By functoriality, we obtain the usual right action of ![]() $\mathrm {GL}_2(\mathbb {Z})$ on
$\mathrm {GL}_2(\mathbb {Z})$ on ![]() $X$ regarded as row vectors.
$X$ regarded as row vectors.
5.2.1 Alternate description of the chain complex for  $S^1$
$S^1$
The group ![]() $\mathsf {Ch}_1$ introduced above fits into a chain complex that computes the homology of
$\mathsf {Ch}_1$ introduced above fits into a chain complex that computes the homology of ![]() $S^1$.
$S^1$.
Lemma 5.2.1 Let ![]() $\mathsf {Ch}_0$ be the group of finitely supported
$\mathsf {Ch}_0$ be the group of finitely supported ![]() $\mathbb {Z}$-valued functions on the rational points of
$\mathbb {Z}$-valued functions on the rational points of ![]() $S^1$, and define
$S^1$, and define ![]() $\nabla \colon \mathsf {Ch}_1 \rightarrow \mathsf {Ch}_0$ via
$\nabla \colon \mathsf {Ch}_1 \rightarrow \mathsf {Ch}_0$ via
where ![]() $f(x^+)$ (respectively,
$f(x^+)$ (respectively, ![]() $f(x^-)$) is the limit of
$f(x^-)$) is the limit of ![]() $f(y)$ as
$f(y)$ as ![]() $y$ approaches
$y$ approaches ![]() $x$ clockwise (respectively, counterclockwise). Then there is an isomorphism
$x$ clockwise (respectively, counterclockwise). Then there is an isomorphism
in the derived category of ![]() $\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-modules, where
$\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-modules, where ![]() $\mathrm {Chains}_*(S^1)$ denotes the singular chain complex of
$\mathrm {Chains}_*(S^1)$ denotes the singular chain complex of ![]() $S^1$. Here, the left
$S^1$. Here, the left ![]() $\mathrm {GL}_2(\mathbb {Z})$-action on both sides is induced by the right
$\mathrm {GL}_2(\mathbb {Z})$-action on both sides is induced by the right ![]() $\mathrm {GL}_2(\mathbb {Z})$-action on
$\mathrm {GL}_2(\mathbb {Z})$-action on ![]() $X$.
$X$.
Proof. Indeed, the complex
of singular chains is quasi-isomorphic to its truncation ![]() $\operatorname {coker}(d_2) \rightarrow \mathrm {Chains}_0(S^1)$. There is an obvious injection
$\operatorname {coker}(d_2) \rightarrow \mathrm {Chains}_0(S^1)$. There is an obvious injection ![]() $\mathsf {Ch}_0 \rightarrow \mathrm {Chains}_0(S^1)$, as well as a
$\mathsf {Ch}_0 \rightarrow \mathrm {Chains}_0(S^1)$, as well as a ![]() $\mathrm {GL}_2(\mathbb {Z})$-equivariant map
$\mathrm {GL}_2(\mathbb {Z})$-equivariant map ![]() $\mathsf {Ch}_1 \rightarrow \operatorname {coker}(d_2)$ which sends
$\mathsf {Ch}_1 \rightarrow \operatorname {coker}(d_2)$ which sends ![]() $[\ell, \ell ']$ to the singular simplex
$[\ell, \ell ']$ to the singular simplex ![]() $[0,1] \rightarrow S^1$ that proceeds at constant speed from
$[0,1] \rightarrow S^1$ that proceeds at constant speed from ![]() $\ell$ to
$\ell$ to ![]() $\ell '$; to verify this is well defined, one just checks the relation (5.2).
$\ell '$; to verify this is well defined, one just checks the relation (5.2).
Since
these maps provide a morphism of complexes. To see that is a quasi-isomorphism, note that the homology of the complex ![]() $[\mathsf {Ch}_1 \xrightarrow {\nabla } \mathsf {Ch}_0]$ is
$[\mathsf {Ch}_1 \xrightarrow {\nabla } \mathsf {Ch}_0]$ is ![]() $\mathbb {Z}$ in both degrees. That is, the cokernel of
$\mathbb {Z}$ in both degrees. That is, the cokernel of ![]() $\nabla$ is generated by the image of any function that assigns a single rational point on
$\nabla$ is generated by the image of any function that assigns a single rational point on ![]() $S^1$ the value
$S^1$ the value ![]() $1$, and the kernel of
$1$, and the kernel of ![]() $\nabla$ is generated by the constant function with value
$\nabla$ is generated by the constant function with value ![]() $1$ in
$1$ in ![]() $\mathsf {Ch}_1$. These map to generators of
$\mathsf {Ch}_1$. These map to generators of ![]() $H_0(S^1,\mathbb {Z})$ and
$H_0(S^1,\mathbb {Z})$ and ![]() $H_1(S^1,\mathbb {Z})$, respectively.
$H_1(S^1,\mathbb {Z})$, respectively.
5.2.2 The motivic complex via toric geometry
For ![]() $v \in X$ primitive, let
$v \in X$ primitive, let ![]() $[\mathbb {R}_+v]$ denote the characteristic function of the image of
$[\mathbb {R}_+v]$ denote the characteristic function of the image of ![]() $\mathbb {R}_+v$ in
$\mathbb {R}_+v$ in ![]() $S^1$. The indexing of symbols in the following proposition differs from our prior indexing of symbols in
$S^1$. The indexing of symbols in the following proposition differs from our prior indexing of symbols in ![]() $\mathsf {K}$, which was effectively done by characters, rather than cocharacters.
$\mathsf {K}$, which was effectively done by characters, rather than cocharacters.
Proposition 5.2.2 There is a morphism
of complexes of ![]() $\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-modules, where the right-hand complex
$\mathbb {Z}[\mathrm {GL}_2(\mathbb {Z})]$-modules, where the right-hand complex ![]() $\mathsf {K}$ is the coniveau complex computing
$\mathsf {K}$ is the coniveau complex computing ![]() $H^*(\mathbb {G}_m^2, 2)$ of § 3.2. More explicitly, there is a commutative diagram
$H^*(\mathbb {G}_m^2, 2)$ of § 3.2. More explicitly, there is a commutative diagram

where ![]() $f_0(1) = e$ (as in § 3.2),
$f_0(1) = e$ (as in § 3.2),
where ![]() $\nu \in X$ is primitive and
$\nu \in X$ is primitive and ![]() $\nu^{{{\dagger}}}\colon \nu(\mathbb {G}_m) \to \mathbb {G}_m$ denotes the inverse of
$\nu^{{{\dagger}}}\colon \nu(\mathbb {G}_m) \to \mathbb {G}_m$ denotes the inverse of ![]() $\nu$, and
$\nu$, and
for ![]() $\nu _1, \nu _2 \in X$ with
$\nu _1, \nu _2 \in X$ with ![]() $\nu _1 \wedge \nu _2 = 1$ and
$\nu _1 \wedge \nu _2 = 1$ and ![]() $\nu _1^*, \nu _2^* \in X^*$ the dual basis to
$\nu _1^*, \nu _2^* \in X^*$ the dual basis to ![]() $\nu _1, \nu _2$. Moreover,
$\nu _1, \nu _2$. Moreover, ![]() $f_2$ sends the constant function with value
$f_2$ sends the constant function with value ![]() $1$ to the symbol
$1$ to the symbol ![]() $\{-z_1, -z_2\}$.
$\{-z_1, -z_2\}$.
Proof. It is clear that unique ![]() $f_0$ and
$f_0$ and ![]() $f_1$ exist having the specified values and that the right-hand square is commutative. For the
$f_1$ exist having the specified values and that the right-hand square is commutative. For the ![]() $\mathrm {GL}_2(\mathbb {Z})$-equivariance of
$\mathrm {GL}_2(\mathbb {Z})$-equivariance of ![]() $f_1$, we compute
$f_1$, we compute
where, on the right, ![]() $\gamma$ acts as usual by pullback of the right
$\gamma$ acts as usual by pullback of the right ![]() $\Gamma$-action on
$\Gamma$-action on ![]() $T$. Since
$T$. Since ![]() $\nabla$ is injective, it remains only to construct
$\nabla$ is injective, it remains only to construct ![]() $f_2$ satisfying (5.7), and to verify that the left-hand square commutes.
$f_2$ satisfying (5.7), and to verify that the left-hand square commutes.
Observe that if ![]() $\nu _1, \nu _2 \in X \cong \mathbb {Z}^2$ satisfy
$\nu _1, \nu _2 \in X \cong \mathbb {Z}^2$ satisfy ![]() $\nu _1 \wedge \nu _2 = 1$ and have dual basis
$\nu _1 \wedge \nu _2 = 1$ and have dual basis ![]() $\nu _1^*$,
$\nu _1^*$, ![]() $\nu _2^*$, then by (2.4), we have
$\nu _2^*$, then by (2.4), we have
which, together with (5.6), shows that the left-hand square formally commutes on ![]() ${[\mathbb {R}_+ \nu _1, \mathbb {R}_+ \nu _2] \in \mathsf {Ch}_1}$, given the property (5.7).
${[\mathbb {R}_+ \nu _1, \mathbb {R}_+ \nu _2] \in \mathsf {Ch}_1}$, given the property (5.7).
Let ![]() $\mathsf {Symb}_2$ be the subgroup of
$\mathsf {Symb}_2$ be the subgroup of ![]() $K_2(\mathbb {Q}(T))$ generated by all symbols
$K_2(\mathbb {Q}(T))$ generated by all symbols ![]() $\{1-\nu _1^*, 1-\nu _2^*\}$ with
$\{1-\nu _1^*, 1-\nu _2^*\}$ with ![]() $\nu _i^* \in X^*(T)$ and
$\nu _i^* \in X^*(T)$ and ![]() $\nu _1 \wedge \nu _2=1$. Then by (5.3) we have a commutative diagram:
$\nu _1 \wedge \nu _2=1$. Then by (5.3) we have a commutative diagram:

We claim that the map ![]() $n$ of Proposition 5.1.1 restricts to an isomorphism
$n$ of Proposition 5.1.1 restricts to an isomorphism ![]() $\mathsf {Symb}_2 \xrightarrow {\sim } \mathsf {Ch}_1$. Once this is proved, it follows from (5.8) that we can take
$\mathsf {Symb}_2 \xrightarrow {\sim } \mathsf {Ch}_1$. Once this is proved, it follows from (5.8) that we can take ![]() $f_2$ to be the inverse of
$f_2$ to be the inverse of ![]() $n$.
$n$.
By (5.3) again (and the Euclidean algorithm), the image of ![]() $n$ on
$n$ on ![]() $\mathsf {Symb}_2$ contains all
$\mathsf {Symb}_2$ contains all ![]() $[\ell, \ell ']$, so
$[\ell, \ell ']$, so ![]() $n$ is surjective. For injectivity, take
$n$ is surjective. For injectivity, take ![]() $\kappa \in \mathsf {Symb}_2$ with
$\kappa \in \mathsf {Symb}_2$ with ![]() $n(\kappa ) = 0$; then the diagram shows that
$n(\kappa ) = 0$; then the diagram shows that ![]() $\partial \kappa = 0$. It follows, then, that
$\partial \kappa = 0$. It follows, then, that ![]() $\kappa$ lies inside the image of
$\kappa$ lies inside the image of ![]() $H^2(T,2)$. Since
$H^2(T,2)$. Since ![]() $\kappa$ is
$\kappa$ is ![]() $[m]_*$-fixed by Lemma 4.1.3, it follows from Lemma 4.1.2 that
$[m]_*$-fixed by Lemma 4.1.3, it follows from Lemma 4.1.2 that ![]() $\kappa$ is a multiple of
$\kappa$ is a multiple of ![]() $\{-z_1, -z_2\}$. But as in Example 5.1.2, the symbol
$\{-z_1, -z_2\}$. But as in Example 5.1.2, the symbol
maps under ![]() $n$ to the sum of the characteristic functions of the four (strict) quadrants of
$n$ to the sum of the characteristic functions of the four (strict) quadrants of ![]() $\mathbb {R}^2$, which agrees in
$\mathbb {R}^2$, which agrees in ![]() $\mathsf {Ch}_1$ with the constant function
$\mathsf {Ch}_1$ with the constant function ![]() $1$. Therefore,
$1$. Therefore, ![]() $f_2(1) = \{-z_1,-z_2\}$, and
$f_2(1) = \{-z_1,-z_2\}$, and ![]() $\kappa = 0$.
$\kappa = 0$.
Remark 5.2.3 The morphisms ![]() $f_i$ are degreewise injective, and the image of
$f_i$ are degreewise injective, and the image of ![]() $f$ is the symbol complex
$f$ is the symbol complex ![]() $\mathsf {Symb}$ of § 3.2 and Remark 4.1.5. By said remark, the complex
$\mathsf {Symb}$ of § 3.2 and Remark 4.1.5. By said remark, the complex ![]() $[\mathsf {Ch}_2 \rightarrow \mathsf {Ch}_1 \rightarrow \mathbb {Z}]$ is thereby quasi-isomorphic to the fixed part of the small complex
$[\mathsf {Ch}_2 \rightarrow \mathsf {Ch}_1 \rightarrow \mathbb {Z}]$ is thereby quasi-isomorphic to the fixed part of the small complex ![]() $\mathsf {k}$ under the trace maps of § 4.1.
$\mathsf {k}$ under the trace maps of § 4.1.
5.3 The cocycle and Laurent series
We relate our discussion to an invariant of rational cones that has appeared in the literature, and we recover the cocycle ![]() $\Theta$ from the considerations of the prior subsection.
$\Theta$ from the considerations of the prior subsection.
5.3.1 Connection to cocycles valued in Laurent series
We use ‘exponential coordinates’ near the identity. That is, given the coordinate functions ![]() $z_1$,
$z_1$, ![]() $z_2$ on
$z_2$ on ![]() $\mathbb {G}_m^2$, we introduce formal coordinates
$\mathbb {G}_m^2$, we introduce formal coordinates ![]() $u_1$,
$u_1$, ![]() $u_2$ at the identity satisfying
$u_2$ at the identity satisfying ![]() $z_i=e^{u_i}$. For
$z_i=e^{u_i}$. For ![]() $\nu =z_1^m z_2^n \in X^*$, we then formally have
$\nu =z_1^m z_2^n \in X^*$, we then formally have ![]() $\nu =e^{m u_1 + nu_2}$. We will also regard the
$\nu =e^{m u_1 + nu_2}$. We will also regard the ![]() $u_i$ as being linear functions on the Lie algebra
$u_i$ as being linear functions on the Lie algebra ![]() $\mathrm {Lie}(\mathbb {G}_m^2)$ via the isomorphism of formal groups
$\mathrm {Lie}(\mathbb {G}_m^2)$ via the isomorphism of formal groups
Consider the composite map
where the second map sends a Steinberg symbol ![]() $\{f, g\}$ to
$\{f, g\}$ to ![]() ${df}/{f} \wedge {dg}/{g}$, and the third map takes a meromorphic form
${df}/{f} \wedge {dg}/{g}$, and the third map takes a meromorphic form ![]() $\omega$ to
$\omega$ to ![]() $ {\omega }/({du_1 \wedge du_2})$ in the Laurent series field
$ {\omega }/({du_1 \wedge du_2})$ in the Laurent series field ![]() $\mathbb {Q}(\!(u_1, u_2)\!)$, which we take to be the quotient field of
$\mathbb {Q}(\!(u_1, u_2)\!)$, which we take to be the quotient field of ![]() $\mathbb {Q}[\kern-1pt[ u_1,u_2 ]\kern-1pt]$.
$\mathbb {Q}[\kern-1pt[ u_1,u_2 ]\kern-1pt]$.
In particular, given ![]() $\nu _1,\nu _2 \in X$ with
$\nu _1,\nu _2 \in X$ with ![]() $\nu _1 \wedge \nu _2=1$ and dual basis written as
$\nu _1 \wedge \nu _2=1$ and dual basis written as ![]() $\nu _1^* = e^{\lambda _1}, \nu _2^* = e^{\lambda _2}$ (with the
$\nu _1^* = e^{\lambda _1}, \nu _2^* = e^{\lambda _2}$ (with the ![]() $\lambda _i$ linear forms in the
$\lambda _i$ linear forms in the ![]() $u_i$), we calculate
$u_i$), we calculate ![]() $\theta _{\mathrm {L}}$ on
$\theta _{\mathrm {L}}$ on ![]() $[\mathbb {R}_+ \nu _1, \mathbb {R}_+ \nu _2]$ as follows:
$[\mathbb {R}_+ \nu _1, \mathbb {R}_+ \nu _2]$ as follows:
We then regard the last term as the element ![]() $\sum _{\mu \in \mathbb {Z}_{\geq 0} \lambda _1 + \mathbb {Z}_{\geq 0} \lambda _2} e^{-\mu }$ of
$\sum _{\mu \in \mathbb {Z}_{\geq 0} \lambda _1 + \mathbb {Z}_{\geq 0} \lambda _2} e^{-\mu }$ of ![]() $ ({1}/{\lambda _1\lambda _2}) \mathbb {Q}[\kern-1pt[ u_1, u_2 ]\kern-1pt] \subset \mathbb {Q}(\!(u_1,u_2)\!)$.
$ ({1}/{\lambda _1\lambda _2}) \mathbb {Q}[\kern-1pt[ u_1, u_2 ]\kern-1pt] \subset \mathbb {Q}(\!(u_1,u_2)\!)$.
In fact we have the following lemma.
Lemma 5.3.1 Suppose that ![]() $\ell _1, \ell _2 \in S^1$ with
$\ell _1, \ell _2 \in S^1$ with ![]() $\ell _1 \wedge \ell _2> 0$; then
$\ell _1 \wedge \ell _2> 0$; then
 \begin{equation} \theta_{\mathrm{L}}([\ell_1, \ell_2]) = \sum_{\substack{\mu \in X^*\\ \langle \mu, \ell_i \rangle \geq 0}} e^{-\mu}. \end{equation}
\begin{equation} \theta_{\mathrm{L}}([\ell_1, \ell_2]) = \sum_{\substack{\mu \in X^*\\ \langle \mu, \ell_i \rangle \geq 0}} e^{-\mu}. \end{equation}Proof. To verify this, we note that it is possible to choose a sequence ![]() $(x_i)_{i=0}^k$ in
$(x_i)_{i=0}^k$ in ![]() $X$ with
$X$ with ![]() $\ell _1 = \mathbb {R}_+ x_0$ and
$\ell _1 = \mathbb {R}_+ x_0$ and ![]() $\ell _2 = \mathbb {R}_+ x_k$ and
$\ell _2 = \mathbb {R}_+ x_k$ and ![]() $x_i \wedge x_{i+1}=1$ for all
$x_i \wedge x_{i+1}=1$ for all ![]() $0 \le i < k$ and, moreover, with
$0 \le i < k$ and, moreover, with ![]() $x_i$ on the counterclockwise arc from
$x_i$ on the counterclockwise arc from ![]() $\ell _0$ to
$\ell _0$ to ![]() $\ell _1$.
$\ell _1$.
We then apply (5.4) and (5.11) recursively to obtain
 \[ \theta_{\mathrm{L}}([\ell_1, \ell_2]) = \sum_{i=0}^{k-1} \theta_{\mathrm{L}}([x_i, x_{i+1}]) = \sum_{i=0}^{k-1} \sum_{\mu \in C_i^*} e^{-\mu}, \]
\[ \theta_{\mathrm{L}}([\ell_1, \ell_2]) = \sum_{i=0}^{k-1} \theta_{\mathrm{L}}([x_i, x_{i+1}]) = \sum_{i=0}^{k-1} \sum_{\mu \in C_i^*} e^{-\mu}, \]
where ![]() $C_i^*$ is the dual cone to the cone spanned by
$C_i^*$ is the dual cone to the cone spanned by ![]() $x_i, x_{i+1}$. Now it was observed by Brion [Reference BrionBri88, 2.4, Théorème] (see [Reference Barvinok and PommersheimBP99, Prop 8.2(b)] for exposition and exact definitions) that the rule associating a cone
$x_i, x_{i+1}$. Now it was observed by Brion [Reference BrionBri88, 2.4, Théorème] (see [Reference Barvinok and PommersheimBP99, Prop 8.2(b)] for exposition and exact definitions) that the rule associating a cone ![]() $C$ to
$C$ to ![]() $\sum _{\mu \in C^*} e^{-\mu }$ is additive with respect to decompositions of cones into subcones, and therefore the right-hand side is given by (5.12) as claimed.
$\sum _{\mu \in C^*} e^{-\mu }$ is additive with respect to decompositions of cones into subcones, and therefore the right-hand side is given by (5.12) as claimed.
5.3.2 Recovering the cocycle  $\Theta \colon \mathrm {GL}_2(\mathbb {Z}) \rightarrow \bar {\mathsf {K}}_2$
$\Theta \colon \mathrm {GL}_2(\mathbb {Z}) \rightarrow \bar {\mathsf {K}}_2$
Now, and in the remainder of this section, we also work with the left action of ![]() $\Gamma =\mathrm {GL}_2(\mathbb {Z})$ on
$\Gamma =\mathrm {GL}_2(\mathbb {Z})$ on ![]() $S^1$ via the rule
$S^1$ via the rule ![]() $\gamma \cdot \mathbb {R}_+ \nu := \mathbb {R}_+ \nu \gamma ^{-1}$, where we continue to think of
$\gamma \cdot \mathbb {R}_+ \nu := \mathbb {R}_+ \nu \gamma ^{-1}$, where we continue to think of ![]() $X$ as row vectors. (Equivalently, if we regard
$X$ as row vectors. (Equivalently, if we regard ![]() $X$ as column vectors, then
$X$ as column vectors, then ![]() $\gamma \in \Gamma$ acts by left multiplication by its transpose inverse.)
$\gamma \in \Gamma$ acts by left multiplication by its transpose inverse.)
Set ![]() $\ell _0= \mathbb {R}_+ (-1,0)$ so that
$\ell _0= \mathbb {R}_+ (-1,0)$ so that ![]() $f_1(\ell _0)$ is given by the function
$f_1(\ell _0)$ is given by the function ![]() $1-z_1^{-1}$ on the subtorus
$1-z_1^{-1}$ on the subtorus ![]() $\{ (x, 1) \mid x \in \mathbb {G}_m \}$, which is to say the symbol
$\{ (x, 1) \mid x \in \mathbb {G}_m \}$, which is to say the symbol ![]() $\langle 0,1 \rangle$ of § 3.2. Consider the function
$\langle 0,1 \rangle$ of § 3.2. Consider the function
Its composition with the quotient map to ![]() $\bar {\mathsf {K}}_2$ is a cocycle by virtue of (5.4). In fact, this composition coincides with
$\bar {\mathsf {K}}_2$ is a cocycle by virtue of (5.4). In fact, this composition coincides with ![]() $\Theta$, as Proposition 5.2.2 and (5.6) yield that the residue of
$\Theta$, as Proposition 5.2.2 and (5.6) yield that the residue of ![]() $\widetilde {\Theta }(\gamma )$ is
$\widetilde {\Theta }(\gamma )$ is
Example 5.3.2 Let us recover the formula for ![]() $\Theta _{\gamma }$ of Proposition 3.3.2, where
$\Theta _{\gamma }$ of Proposition 3.3.2, where ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Gamma$. Here, for
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Gamma$. Here, for ![]() $\nu \in X$, we abbreviate
$\nu \in X$, we abbreviate ![]() $\mathbb {R}_+\nu$ by
$\mathbb {R}_+\nu$ by ![]() $\nu$. Given a connecting sequence
$\nu$. Given a connecting sequence ![]() $(v_i)_{i=0}^k$ for
$(v_i)_{i=0}^k$ for ![]() $\gamma$ as in § 3.3, we can write
$\gamma$ as in § 3.3, we can write ![]() $[(-1,0), (\det \gamma ) (-d,b)]$ as a sum
$[(-1,0), (\det \gamma ) (-d,b)]$ as a sum ![]() $\sum _{i=1}^k [W v_{i-1}, W v_i]$ with
$\sum _{i=1}^k [W v_{i-1}, W v_i]$ with ![]() $W = \big (\begin{smallmatrix} 0 & -1\\1 & 0 \end{smallmatrix}\big )$. Now if
$W = \big (\begin{smallmatrix} 0 & -1\\1 & 0 \end{smallmatrix}\big )$. Now if ![]() $\nu _1 \wedge \nu _2= 1$, then
$\nu _1 \wedge \nu _2= 1$, then ![]() $f_2$ sends
$f_2$ sends ![]() $[\nu _1, \nu _2]$ to
$[\nu _1, \nu _2]$ to ![]() $\langle -W\nu _2, W \nu _1 \rangle$ in the notation of our previous section. So
$\langle -W\nu _2, W \nu _1 \rangle$ in the notation of our previous section. So
 \[ \tilde{\Theta}(\gamma) = f_2( [ (-1,0), (\det \gamma) (-d,b) ]) = \sum_{i=1}^k f_2([W v_{i-1}, W v_i]) = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle. \]
\[ \tilde{\Theta}(\gamma) = f_2( [ (-1,0), (\det \gamma) (-d,b) ]) = \sum_{i=1}^k f_2([W v_{i-1}, W v_i]) = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle. \]
In effect, the notation of this section absorbed the negative signs by working with the character group of ![]() $\mathbb {G}_m^2$, rather than its cocharacter group.
$\mathbb {G}_m^2$, rather than its cocharacter group.
5.4 Lifting the cocycle
Let ![]() $\Theta$ be the cocycle of Proposition 3.3.1. The obstruction to lifting the class of
$\Theta$ be the cocycle of Proposition 3.3.1. The obstruction to lifting the class of ![]() $\Theta$ to
$\Theta$ to ![]() $\mathsf {K}_2$ lies in the torsion group
$\mathsf {K}_2$ lies in the torsion group ![]() $H^2(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z})$. It follows that a multiple of
$H^2(\mathrm {GL}_2(\mathbb {Z}), \mathbb {Z})$. It follows that a multiple of ![]() $\Theta$ lifts. Here, we will show how to write down an explicit lift of the restriction of
$\Theta$ lifts. Here, we will show how to write down an explicit lift of the restriction of ![]() $12\Theta$ to
$12\Theta$ to ![]() $\mathrm {SL}_2(\mathbb {Z})$ using Proposition 5.2.2.
$\mathrm {SL}_2(\mathbb {Z})$ using Proposition 5.2.2.
To lighten notation, let us write ![]() $f_2(\ell _1, \ell _2)$ for
$f_2(\ell _1, \ell _2)$ for ![]() $f_2([\ell _1, \ell _2])$ and
$f_2([\ell _1, \ell _2])$ and ![]() $\theta _{\mathrm {L}}(\ell _1, \ell _2)$ for
$\theta _{\mathrm {L}}(\ell _1, \ell _2)$ for ![]() $\theta _{\mathrm {L}}([\ell _1,\ell _2])$. By (5.4) and the fact that
$\theta _{\mathrm {L}}([\ell _1,\ell _2])$. By (5.4) and the fact that ![]() $f_2(1) = \{-z_1,-z_2\}$ proven in Proposition 5.2.2, we have
$f_2(1) = \{-z_1,-z_2\}$ proven in Proposition 5.2.2, we have
and therefore, by the definition (5.10) of ![]() $\theta _{\mathrm {L}}$,
$\theta _{\mathrm {L}}$,
We will introduce a ‘correction’ term to ![]() $\theta _{\mathrm {L}}$ to eliminate the right-hand side of (5.15).Footnote 14 Here is the basic idea in a primitive form that does not quite work. Suppose there were a reasonable way to evaluate a value of
$\theta _{\mathrm {L}}$ to eliminate the right-hand side of (5.15).Footnote 14 Here is the basic idea in a primitive form that does not quite work. Suppose there were a reasonable way to evaluate a value of ![]() $\theta _{\mathrm {L}}$ at the origin
$\theta _{\mathrm {L}}$ at the origin ![]() $(u_1, u_2) = (0,0)$. Let
$(u_1, u_2) = (0,0)$. Let ![]() $\theta _{\mathrm {L}}^0$ denote the resulting function from pairs
$\theta _{\mathrm {L}}^0$ denote the resulting function from pairs ![]() $(\ell _1, \ell _2)$ to
$(\ell _1, \ell _2)$ to ![]() $\mathbb {Z}$, which again satisfies (5.15). Then by the latter property and (5.14), the corrected function
$\mathbb {Z}$, which again satisfies (5.15). Then by the latter property and (5.14), the corrected function
would be a homogeneous cocycle, that is, ![]() $f_2'(\ell _1, \ell _2) + f_2'(\ell _2, \ell _3) = f_2'(\ell _1, \ell _3)$. Since
$f_2'(\ell _1, \ell _2) + f_2'(\ell _2, \ell _3) = f_2'(\ell _1, \ell _3)$. Since ![]() $\{-z_1,-z_2\}$ has trivial image in
$\{-z_1,-z_2\}$ has trivial image in ![]() $\bar {\mathsf {K}}_2$, the resulting
$\bar {\mathsf {K}}_2$, the resulting ![]() $1$-cocycle
$1$-cocycle ![]() $\gamma \mapsto f_2'(\ell _0, \gamma \ell _0)$ would lift
$\gamma \mapsto f_2'(\ell _0, \gamma \ell _0)$ would lift ![]() $\Theta$ from
$\Theta$ from ![]() $\bar {\mathsf {K}}_2$ to
$\bar {\mathsf {K}}_2$ to ![]() $\mathsf {K}_2$, as in (5.13).
$\mathsf {K}_2$, as in (5.13).
We will not be able to implement this precisely as stated, but we will be able to do it after replacing the role of the rays ![]() $\ell _1, \ell _2$ by elements of
$\ell _1, \ell _2$ by elements of ![]() $\mathrm {SL}_2(\mathbb {Z})$. To make sense of the evaluation of a value of
$\mathrm {SL}_2(\mathbb {Z})$. To make sense of the evaluation of a value of ![]() $\theta _{\mathrm {L}} \in \mathbb {Q}(\!(u_1, u_2)\!)$ at the origin
$\theta _{\mathrm {L}} \in \mathbb {Q}(\!(u_1, u_2)\!)$ at the origin ![]() $(u_1, u_2) = (0,0)$, we need the auxiliary data of the second column of the matrices in
$(u_1, u_2) = (0,0)$, we need the auxiliary data of the second column of the matrices in ![]() $\mathrm {SL}_2(\mathbb {Z})$; this allows us to take a limit as
$\mathrm {SL}_2(\mathbb {Z})$; this allows us to take a limit as ![]() $(u_1, u_2) \rightarrow 0$ in a specified direction.
$(u_1, u_2) \rightarrow 0$ in a specified direction.
Elements in the image of ![]() $\theta _{\mathrm {L}}$ have the form
$\theta _{\mathrm {L}}$ have the form ![]() $L^{-1} P$, with
$L^{-1} P$, with ![]() $P \in \mathbb {Q}[\kern-1pt[ u_1, u_2 ]\kern-1pt]$ and
$P \in \mathbb {Q}[\kern-1pt[ u_1, u_2 ]\kern-1pt]$ and ![]() $L$ a product of linear forms. Accordingly, we can unambiguously speak of its ‘degree zero’ component
$L$ a product of linear forms. Accordingly, we can unambiguously speak of its ‘degree zero’ component ![]() $\theta _{\mathrm {L}}^0$, namely
$\theta _{\mathrm {L}}^0$, namely ![]() ${P^{(\deg L)}}/{L}$ with
${P^{(\deg L)}}/{L}$ with ![]() $P^{(\deg L)}$ the homogeneous component of
$P^{(\deg L)}$ the homogeneous component of ![]() $P$ of degree the degree of
$P$ of degree the degree of ![]() $L$. This degree zero component is now valued in the rational functions
$L$. This degree zero component is now valued in the rational functions ![]() $\mathbb {Q}(u_1, u_2)$, or more intrinsically via (5.9) as rational functions on the Lie algebra
$\mathbb {Q}(u_1, u_2)$, or more intrinsically via (5.9) as rational functions on the Lie algebra ![]() $\mathrm {Lie} (\mathbb {G}_m^2)$.
$\mathrm {Lie} (\mathbb {G}_m^2)$.
For example, using ![]() $(1-e^{-x})^{-1} = x^{-1} + {1}/{2} + {x}/{12} + O(x^2)$, we deduce that the degree zero component in (5.11) for
$(1-e^{-x})^{-1} = x^{-1} + {1}/{2} + {x}/{12} + O(x^2)$, we deduce that the degree zero component in (5.11) for ![]() $\nu _1, \nu _2 \in X$ with
$\nu _1, \nu _2 \in X$ with ![]() $\nu _1 \wedge \nu _2 = 1$ and dual basis
$\nu _1 \wedge \nu _2 = 1$ and dual basis ![]() $\nu _1^* = e^{\lambda _1}, \nu _2^* = e^{\lambda _2}$ is given by
$\nu _1^* = e^{\lambda _1}, \nu _2^* = e^{\lambda _2}$ is given by
Now given auxiliary vectors ![]() $\nu _1'$ and
$\nu _1'$ and ![]() $\nu _2'$ that are linearly independent from
$\nu _2'$ that are linearly independent from ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ respectively, we define a regularized value of
$\nu _2$ respectively, we define a regularized value of ![]() $\theta _{\mathrm {L}}$ by choosing a decomposition of
$\theta _{\mathrm {L}}$ by choosing a decomposition of ![]() $\theta _{\mathrm {L}}^0(\nu _1,\nu _2)$ as a sum
$\theta _{\mathrm {L}}^0(\nu _1,\nu _2)$ as a sum
where ![]() $A_i$ is a homogeneous rational function in
$A_i$ is a homogeneous rational function in ![]() $(u_1, u_2)$ with poles only along the image of
$(u_1, u_2)$ with poles only along the image of ![]() $\nu _i$; that is to say, if
$\nu _i$; that is to say, if ![]() $\nu _i(t)=(t^{a_1},t^{a_2})$, then
$\nu _i(t)=(t^{a_1},t^{a_2})$, then ![]() $A_i$ has poles along the line spanned by
$A_i$ has poles along the line spanned by ![]() $(a_1, a_2)$. In the example above, for instance, we may take
$(a_1, a_2)$. In the example above, for instance, we may take ![]() $A_1 = \frac {1}{4} + \frac {1}{12} ({\lambda _1}/{\lambda _2})$ and
$A_1 = \frac {1}{4} + \frac {1}{12} ({\lambda _1}/{\lambda _2})$ and ![]() $A_2= \frac {1}{12} ({\lambda _2}/{\lambda _1})$. We now define
$A_2= \frac {1}{12} ({\lambda _2}/{\lambda _1})$. We now define
Here ![]() $A_i(\nu _i')$ means that if
$A_i(\nu _i')$ means that if ![]() $\nu _i'(t) = (t^{a_1}, t^{a_2})$, then we evaluate
$\nu _i'(t) = (t^{a_1}, t^{a_2})$, then we evaluate ![]() $A_i$ at
$A_i$ at ![]() $(a_1, a_2)$. The decomposition
$(a_1, a_2)$. The decomposition ![]() $A_1+A_2$ is not unique, but it is unique up to the constant terms, so the right-hand side of (5.17) does not depend on the choice of decomposition. We should regard this as a ‘regularized value of
$A_1+A_2$ is not unique, but it is unique up to the constant terms, so the right-hand side of (5.17) does not depend on the choice of decomposition. We should regard this as a ‘regularized value of ![]() $\theta _{\mathrm {L}}^0(\nu _1, \nu _2)$ at zero’, where
$\theta _{\mathrm {L}}^0(\nu _1, \nu _2)$ at zero’, where ![]() $\nu _1'$ and
$\nu _1'$ and ![]() $\nu _2'$ are used to perform the regularization.
$\nu _2'$ are used to perform the regularization.
Proposition 5.4.1
(i) There is a unique function
 $\phi \colon \mathrm {SL}_2(\mathbb {Z}) \times \mathrm {SL}_2(\mathbb {Z}) \rightarrow \frac {1}{12} \mathbb {Z}$ which is left
$\phi \colon \mathrm {SL}_2(\mathbb {Z}) \times \mathrm {SL}_2(\mathbb {Z}) \rightarrow \frac {1}{12} \mathbb {Z}$ which is left  $\mathrm {SL}_2(\mathbb {Z})$-invariant and satisfies
(5.18)for all
$\mathrm {SL}_2(\mathbb {Z})$-invariant and satisfies
(5.18)for all \begin{equation} \phi(\gamma_1, \gamma_2) + \phi(\gamma_2, \gamma_3) - \phi(\gamma_1, \gamma_3) = \delta(\gamma_1 \ell_0, \gamma_2 \ell_0, \gamma_3 \ell_0) \end{equation}
\begin{equation} \phi(\gamma_1, \gamma_2) + \phi(\gamma_2, \gamma_3) - \phi(\gamma_1, \gamma_3) = \delta(\gamma_1 \ell_0, \gamma_2 \ell_0, \gamma_3 \ell_0) \end{equation} $\gamma _1, \gamma _2, \gamma _3 \in \mathrm {SL}_2(\mathbb {Z})$.
$\gamma _1, \gamma _2, \gamma _3 \in \mathrm {SL}_2(\mathbb {Z})$.(ii) For
 $\gamma _1, \gamma _2 \in \mathrm {SL}_2(\mathbb {Z})$, set
$\gamma _1, \gamma _2 \in \mathrm {SL}_2(\mathbb {Z})$, set  $\nu _i = \mathbb {R}_+ \gamma _i (-1,0)$ and
$\nu _i = \mathbb {R}_+ \gamma _i (-1,0)$ and  $\nu _i' = \mathbb {R}_+ \gamma _i (0,-1)$ for
$\nu _i' = \mathbb {R}_+ \gamma _i (0,-1)$ for  $i \in \{1,2\}$. If
$i \in \{1,2\}$. If  $\mathbb {R}\nu _1 \neq \mathbb {R}\nu _2$, thenFootnote 15
$\mathbb {R}\nu _1 \neq \mathbb {R}\nu _2$, thenFootnote 15
 \[ \phi(\gamma_1, \gamma_2) = \theta_{\mathrm{L}}^0(\nu_1, \nu_1', \nu_2, \nu_2'). \]
\[ \phi(\gamma_1, \gamma_2) = \theta_{\mathrm{L}}^0(\nu_1, \nu_1', \nu_2, \nu_2'). \]
(iii) The function
 $\mathrm {SL}_2(\mathbb {Z}) \to \mathsf {K}_2$ given by
is a cocycle lifting
$\mathrm {SL}_2(\mathbb {Z}) \to \mathsf {K}_2$ given by
is a cocycle lifting \[ \gamma \mapsto 12 f_2(\ell_0, \gamma \ell_0) - 12\phi(I_2, \gamma) \{-z_1, -z_2\} \]
\[ \gamma \mapsto 12 f_2(\ell_0, \gamma \ell_0) - 12\phi(I_2, \gamma) \{-z_1, -z_2\} \]
 $12 \Theta |_{\mathrm {SL}_2(\mathbb {Z})}$ from
$12 \Theta |_{\mathrm {SL}_2(\mathbb {Z})}$ from  $\bar {\mathsf {K}}_2$ to
$\bar {\mathsf {K}}_2$ to  $\mathsf {K}_2$, where
$\mathsf {K}_2$, where  $I_2$ denotes the
$I_2$ denotes the  $2 \times 2$ identity matrix.
$2 \times 2$ identity matrix.
Proof. For the uniqueness in (i), note that the difference between any two such functions ![]() $\phi$ is a homogeneous cocycle. The group of such cocycles is
$\phi$ is a homogeneous cocycle. The group of such cocycles is ![]() $H^1(\mathrm {SL}_2(\mathbb {Z}),\frac {1}{12}\mathbb {Z}) = 0$, since the abelianization of
$H^1(\mathrm {SL}_2(\mathbb {Z}),\frac {1}{12}\mathbb {Z}) = 0$, since the abelianization of ![]() $\mathrm {SL}_2(\mathbb {Z})$ is torsion. Part (iii) follows from the discussion at the beginning of the section, the cocycle being well defined since
$\mathrm {SL}_2(\mathbb {Z})$ is torsion. Part (iii) follows from the discussion at the beginning of the section, the cocycle being well defined since ![]() $12\phi$ is
$12\phi$ is ![]() $\mathbb {Z}$-valued.
$\mathbb {Z}$-valued.
Take ![]() $\gamma _1, \gamma _2, \gamma _3 \in \mathrm {SL}_2(\mathbb {Z})$, and define
$\gamma _1, \gamma _2, \gamma _3 \in \mathrm {SL}_2(\mathbb {Z})$, and define ![]() $\nu _i, \nu _i'$ for
$\nu _i, \nu _i'$ for ![]() $i \in \{1,2,3\}$ accordingly, as in the discussion preceding the proposition. If the lines
$i \in \{1,2,3\}$ accordingly, as in the discussion preceding the proposition. If the lines ![]() $\mathbb {R} \nu _1, \mathbb {R} \nu _2, \mathbb {R} \nu _3$ are all distinct (i.e., not merely the rays, but the lines themselves), then we claim that
$\mathbb {R} \nu _1, \mathbb {R} \nu _2, \mathbb {R} \nu _3$ are all distinct (i.e., not merely the rays, but the lines themselves), then we claim that
Let us denote the right-hand side of (5.19) more simply by ![]() $\delta$. We are going to deduce the equality of (5.19) from (5.15), replacing the role of
$\delta$. We are going to deduce the equality of (5.19) from (5.15), replacing the role of ![]() $\ell _i$ therein by
$\ell _i$ therein by ![]() $\nu _i$. Splitting
$\nu _i$. Splitting ![]() $\theta _{\mathrm {L}}^0(\nu _i, \nu _j) = A_{ij}+A_{ji}$, where
$\theta _{\mathrm {L}}^0(\nu _i, \nu _j) = A_{ij}+A_{ji}$, where ![]() $A_{ij}$ has poles along
$A_{ij}$ has poles along ![]() $\nu _i=0$ and
$\nu _i=0$ and ![]() $A_{ji}$ has poles along
$A_{ji}$ has poles along ![]() $\nu _j=0$, the left-hand side of (5.15) is
$\nu _j=0$, the left-hand side of (5.15) is
and since each of the three quantities in parentheses has a distinct polar locus, each must be a constant ![]() $c_i$, where these constants values add up to
$c_i$, where these constants values add up to ![]() $c_1+c_2+c_3 = \delta$. A fortiori, the same is true after evaluating each parenthesized quantity thus:
$c_1+c_2+c_3 = \delta$. A fortiori, the same is true after evaluating each parenthesized quantity thus:
which proves (5.19).
Define ![]() $\phi$ on pairs
$\phi$ on pairs ![]() $(\gamma _1, \gamma _2)$ with
$(\gamma _1, \gamma _2)$ with ![]() $\mathbb {R} \nu _1 \neq \mathbb {R} \nu _2$ by the formula in (ii). The identity (5.19) then expresses precisely that the coboundary computation (5.18) is valid when the
$\mathbb {R} \nu _1 \neq \mathbb {R} \nu _2$ by the formula in (ii). The identity (5.19) then expresses precisely that the coboundary computation (5.18) is valid when the ![]() $\nu _i$ are non-proportional. It also uniquely specifies a way to extend this
$\nu _i$ are non-proportional. It also uniquely specifies a way to extend this ![]() $\phi$ to all pairs
$\phi$ to all pairs ![]() $(\gamma _1, \gamma _2)$: we just choose
$(\gamma _1, \gamma _2)$: we just choose ![]() $\gamma _3$ in generic position with respect to both of them and use (5.18) to define
$\gamma _3$ in generic position with respect to both of them and use (5.18) to define ![]() $\phi (\gamma _1, \gamma _2)$. That this is independent of choice of
$\phi (\gamma _1, \gamma _2)$. That this is independent of choice of ![]() $\gamma _3$ follows from the cocycle identity (5.5) for
$\gamma _3$ follows from the cocycle identity (5.5) for ![]() $\delta$. This proves the remainder of (i) and (ii).
$\delta$. This proves the remainder of (i) and (ii).
Remark 5.4.2 The function ![]() $\phi (I_2, \gamma )$ is closely related to the Rademacher
$\phi (I_2, \gamma )$ is closely related to the Rademacher ![]() $\varphi$-function (see [Reference Kirby and MelvinKM94] as a reference on the latter). We evaluate it in the generic case to illustrate this.
$\varphi$-function (see [Reference Kirby and MelvinKM94] as a reference on the latter). We evaluate it in the generic case to illustrate this.
Suppose that the transpose inverse of ![]() $\gamma$ equals
$\gamma$ equals ![]() $\big (\begin{smallmatrix} p & p'\\ q & q' \end{smallmatrix}\big )$ with
$\big (\begin{smallmatrix} p & p'\\ q & q' \end{smallmatrix}\big )$ with ![]() $q > 0$. To compute
$q > 0$. To compute ![]() $\phi (I_2, \gamma )$, we must first of all compute
$\phi (I_2, \gamma )$, we must first of all compute ![]() $\theta _{\mathrm {L}}^0((-1,0),(-p,-q))$, recalling (ii) of Proposition 5.4.1. By (5.12), we must compute the sum
$\theta _{\mathrm {L}}^0((-1,0),(-p,-q))$, recalling (ii) of Proposition 5.4.1. By (5.12), we must compute the sum
where ![]() $C$ is the cone spanned by the dual basis
$C$ is the cone spanned by the dual basis ![]() $(-1,{p}/{q}), (0,-{1}/{q})$ to
$(-1,{p}/{q}), (0,-{1}/{q})$ to ![]() $(-1,0), (-p,-q)$. Now
$(-1,0), (-p,-q)$. Now
Writing ![]() $\lambda _1=u_1- ({p}/{q})u_2$ and
$\lambda _1=u_1- ({p}/{q})u_2$ and ![]() $\lambda _2= ({1}/{q})u_2$, we compute (5.20) as
$\lambda _2= ({1}/{q})u_2$, we compute (5.20) as
 \[ \sum_{\substack{(\alpha, \beta) \in \mathbb{Z}_{\geq 0}^2\\\beta \equiv p \alpha \bmod q}} e^{\alpha \lambda_1 +\beta \lambda_2} = \sum_{(\alpha, \beta) \in \mathbb{Z}_{\geq 0}^2} q^{-1} \bigg(\sum_{\zeta \in \mu_q} \zeta^{ \beta-p\alpha}\bigg) e^{\alpha \lambda_1 + \beta \lambda_2} = q^{-1} \sum_{\zeta \in \mu_q} \frac{1}{(1-\zeta^{-p} e^{\lambda_1})(1-\zeta e^{\lambda_2})}. \]
\[ \sum_{\substack{(\alpha, \beta) \in \mathbb{Z}_{\geq 0}^2\\\beta \equiv p \alpha \bmod q}} e^{\alpha \lambda_1 +\beta \lambda_2} = \sum_{(\alpha, \beta) \in \mathbb{Z}_{\geq 0}^2} q^{-1} \bigg(\sum_{\zeta \in \mu_q} \zeta^{ \beta-p\alpha}\bigg) e^{\alpha \lambda_1 + \beta \lambda_2} = q^{-1} \sum_{\zeta \in \mu_q} \frac{1}{(1-\zeta^{-p} e^{\lambda_1})(1-\zeta e^{\lambda_2})}. \]
All terms above except the term for ![]() $\zeta =1$ are already regular at
$\zeta =1$ are already regular at ![]() $(0,0)$; the
$(0,0)$; the ![]() $\zeta =1$ term contributes
$\zeta =1$ term contributes ![]() $\frac {1}{4} + \frac {1}{12} (\lambda _1 \lambda _2^{-1} + \lambda _2 \lambda _1^{-1})$ by the same computation as (5.16), and thus the degree zero term equals
$\frac {1}{4} + \frac {1}{12} (\lambda _1 \lambda _2^{-1} + \lambda _2 \lambda _1^{-1})$ by the same computation as (5.16), and thus the degree zero term equals
 \[ \frac{1}{q} \bigg( \frac{1}{4} + \frac{1}{12} \bigg(\frac{\lambda_1}{\lambda_2} + \frac{\lambda_2}{\lambda_1}\bigg) \bigg) + \frac{1}{q} \sum_{\zeta \in \mu_q - \{1\}} \frac{1}{(1-\zeta)(1-\zeta^{-p})} \]
\[ \frac{1}{q} \bigg( \frac{1}{4} + \frac{1}{12} \bigg(\frac{\lambda_1}{\lambda_2} + \frac{\lambda_2}{\lambda_1}\bigg) \bigg) + \frac{1}{q} \sum_{\zeta \in \mu_q - \{1\}} \frac{1}{(1-\zeta)(1-\zeta^{-p})} \]
The second term equals ![]() ${1}/{4} - {1}/{4q} + s(p,q)$, where
${1}/{4} - {1}/{4q} + s(p,q)$, where ![]() $s(p,q)$ is the standard Dedekind sum; see [Reference Rademacher and GrosswaldRG72, (18a) and (33a)]. Noting that
$s(p,q)$ is the standard Dedekind sum; see [Reference Rademacher and GrosswaldRG72, (18a) and (33a)]. Noting that
 \[ \frac{\lambda_1}{q \lambda_2}\bigg|_{(0,-1)} =- \frac{p}{q} \quad \mathrm{and} \quad \frac{\lambda_2}{q \lambda_1}\bigg|_{(-p', -q')} = \frac{q'/q}{qp'-pq'} = - \frac{q'}{q}, \]
\[ \frac{\lambda_1}{q \lambda_2}\bigg|_{(0,-1)} =- \frac{p}{q} \quad \mathrm{and} \quad \frac{\lambda_2}{q \lambda_1}\bigg|_{(-p', -q')} = \frac{q'/q}{qp'-pq'} = - \frac{q'}{q}, \]
we get
if ![]() $q > 0$ by [Reference Kirby and MelvinKM94, Theorem 2.2].
$q > 0$ by [Reference Kirby and MelvinKM94, Theorem 2.2].
5.5 Interpretation via equivariant motivic cohomology
Let us explain how the constructions of this section should be regarded as providing a class in equivariant motivic cohomology, and outline how one recovers our cocycle directly from this. Our construction is ad hoc; a suitable theory of equivariant motivic cohomology is not (to our knowledge) developed in the literature.
To simplify our discussion, we take coefficients in ![]() $\mathbb {Z}' := \mathbb {Z}[\frac {1}{6}]$; all cohomology groups should be understood with
$\mathbb {Z}' := \mathbb {Z}[\frac {1}{6}]$; all cohomology groups should be understood with ![]() $\mathbb {Z}'$-coefficients. Let
$\mathbb {Z}'$-coefficients. Let ![]() $\mathsf {D}_{\Gamma }$ be the derived category of
$\mathsf {D}_{\Gamma }$ be the derived category of ![]() $\mathbb {Z}'[\Gamma ]$-modules for
$\mathbb {Z}'[\Gamma ]$-modules for ![]() $\Gamma =\mathrm {GL}_2(\mathbb {Z})$. Let
$\Gamma =\mathrm {GL}_2(\mathbb {Z})$. Let ![]() $\mathsf {K}^{\circ }$ be defined analogously to the complex
$\mathsf {K}^{\circ }$ be defined analogously to the complex ![]() $\mathsf {K}$ of (3.1), but taking
$\mathsf {K}$ of (3.1), but taking ![]() $\mathbb {Z}'$-coefficients and replacing
$\mathbb {Z}'$-coefficients and replacing ![]() $\mathbb {G}_m^2$ by
$\mathbb {G}_m^2$ by ![]() $\mathbb {G}_m^2-\{1\}$; we grade it cohomologically so that it becomes supported in degrees
$\mathbb {G}_m^2-\{1\}$; we grade it cohomologically so that it becomes supported in degrees ![]() $[-2,0]$. This complex computes the motivic cohomology of
$[-2,0]$. This complex computes the motivic cohomology of ![]() $\mathbb {G}_m^2-\{1\}$ with
$\mathbb {G}_m^2-\{1\}$ with ![]() $\mathbb {Z}(2)$-coefficients in degrees
$\mathbb {Z}(2)$-coefficients in degrees ![]() $[2,4]$. With our grading, the motivic cohomology in degree
$[2,4]$. With our grading, the motivic cohomology in degree ![]() $4+i$ is the cohomology of
$4+i$ is the cohomology of ![]() $\mathsf {K}^{\circ }$ in degree
$\mathsf {K}^{\circ }$ in degree ![]() $i$ for
$i$ for ![]() $i \in [-2,0]$.
$i \in [-2,0]$.
As a provisional definition of a particular equivariant motivic cohomology group, we set
Now ![]() $\mathsf {K}^{\circ }$ does not compute the motivic cohomology of
$\mathsf {K}^{\circ }$ does not compute the motivic cohomology of ![]() $\mathbb {G}_m^2-\{1\}$ in full, only its truncation to degrees
$\mathbb {G}_m^2-\{1\}$ in full, only its truncation to degrees ![]() $2$ and greater. In place of
$2$ and greater. In place of ![]() $\mathsf {K}^{\circ }$, a proper definition of motivic cohomology would employ a complex (e.g. of Bloch or Voevodsky) which computes the full motivic cohomology of
$\mathsf {K}^{\circ }$, a proper definition of motivic cohomology would employ a complex (e.g. of Bloch or Voevodsky) which computes the full motivic cohomology of ![]() $\mathbb {G}_m^2-\{1\}$.Footnote 16 However, since
$\mathbb {G}_m^2-\{1\}$.Footnote 16 However, since ![]() $\Gamma$ has no cohomology in degrees greater than
$\Gamma$ has no cohomology in degrees greater than ![]() $2$ upon inverting
$2$ upon inverting ![]() $6$, the above would be isomorphic to a more reasonable definition of equivariant
$6$, the above would be isomorphic to a more reasonable definition of equivariant ![]() $H^3$.
$H^3$.
Let us produce a class in this ![]() $H^3_{\Gamma }$. Lemma 5.2.1 and Proposition 5.2.2 together furnish a map
$H^3_{\Gamma }$. Lemma 5.2.1 and Proposition 5.2.2 together furnish a map
in ![]() $\mathsf {D}_{\Gamma }$. Since
$\mathsf {D}_{\Gamma }$. Since ![]() $\mathrm {Chains}_*(S^1)$ has cohomology in degrees
$\mathrm {Chains}_*(S^1)$ has cohomology in degrees ![]() $-1,0$, the standard action of
$-1,0$, the standard action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $S^1$ induces an exact triangle
$S^1$ induces an exact triangle
in ![]() $\mathsf {D}_{\Gamma }$, where
$\mathsf {D}_{\Gamma }$, where ![]() $(\det )$ refers to twisting the action by
$(\det )$ refers to twisting the action by ![]() $\det \colon \Gamma \rightarrow \langle - 1\rangle$. Had we taken
$\det \colon \Gamma \rightarrow \langle - 1\rangle$. Had we taken ![]() $\mathbb {Z}$-coefficients, the resulting extension class in
$\mathbb {Z}$-coefficients, the resulting extension class in ![]() $H^2(\Gamma,\mathbb {Z}(\det ))$ would have been the equivariant Euler class of
$H^2(\Gamma,\mathbb {Z}(\det ))$ would have been the equivariant Euler class of ![]() $\mathbb {R}^2$ (i.e., the Euler class of the vector bundle on the classifying space
$\mathbb {R}^2$ (i.e., the Euler class of the vector bundle on the classifying space ![]() $\mathrm {EGL}_2(\mathbb {Z})/\mathrm {GL}_2(\mathbb {Z})$ of
$\mathrm {EGL}_2(\mathbb {Z})/\mathrm {GL}_2(\mathbb {Z})$ of ![]() $\mathrm {GL}_2(\mathbb {Z})$ given by
$\mathrm {GL}_2(\mathbb {Z})$ given by ![]() $(\mathrm {EGL}_2(\mathbb {Z}) \times \mathbb {R}^2)/\mathrm {GL}_2(\mathbb {Z})$). On the other hand, since
$(\mathrm {EGL}_2(\mathbb {Z}) \times \mathbb {R}^2)/\mathrm {GL}_2(\mathbb {Z})$). On the other hand, since ![]() $H^i(\Gamma,\mathbb {Z}'(\det )) = 0$ for
$H^i(\Gamma,\mathbb {Z}'(\det )) = 0$ for ![]() $i \in \{1,2\}$, there is a unique splitting in
$i \in \{1,2\}$, there is a unique splitting in ![]() $\mathsf {D}_{\Gamma }$,
$\mathsf {D}_{\Gamma }$,
compatible with the above sequence. In this way, ![]() $h$ splits into components
$h$ splits into components ![]() $h=h_{-1}+h_{-2}[1]$ with
$h=h_{-1}+h_{-2}[1]$ with ![]() $h_{-i} \in \operatorname {Hom}_{\mathsf {D}_{\Gamma }}(\mathbb {Z}'(\det ^{i-1}), \mathsf {K}^{\circ }[-i])$ for
$h_{-i} \in \operatorname {Hom}_{\mathsf {D}_{\Gamma }}(\mathbb {Z}'(\det ^{i-1}), \mathsf {K}^{\circ }[-i])$ for ![]() $i \in \{1,2\}$. This
$i \in \{1,2\}$. This ![]() $h_{-1}$ gives a class in
$h_{-1}$ gives a class in ![]() $H^3_{\Gamma }(\mathbb {G}_m^2-\{1\},2)$, and the class of
$H^3_{\Gamma }(\mathbb {G}_m^2-\{1\},2)$, and the class of ![]() $\Theta$ should be (we did not check details) recovered via
$\Theta$ should be (we did not check details) recovered via
where the last map comes out of a spectral sequence ![]() $H^i(\Gamma,H^j(\mathbb {Q}(\mathbb {G}_m^2),2)) \Rightarrow H^{i+j}_{\Gamma }(\mathbb {Q}(\mathbb {G}_m^2),2)$ computing equivariant cohomology in terms of
$H^i(\Gamma,H^j(\mathbb {Q}(\mathbb {G}_m^2),2)) \Rightarrow H^{i+j}_{\Gamma }(\mathbb {Q}(\mathbb {G}_m^2),2)$ computing equivariant cohomology in terms of ![]() $\Gamma$-cohomology on motivic cohomology.
$\Gamma$-cohomology on motivic cohomology.
6. The square of a universal elliptic curve
In the present section we construct the big cocycles ![]() ${}_n \Theta$ of (1.5) for primes
${}_n \Theta$ of (1.5) for primes ![]() $n \nmid N$. Here, the role of
$n \nmid N$. Here, the role of ![]() $\mathbb {G}_m^2$ is played by the self-product
$\mathbb {G}_m^2$ is played by the self-product ![]() $\mathscr {E}^2$ of the universal elliptic curve over a modular curve. As in the
$\mathscr {E}^2$ of the universal elliptic curve over a modular curve. As in the ![]() $\mathbb {G}_m$-case, our analysis is based on a homological complex
$\mathbb {G}_m$-case, our analysis is based on a homological complex ![]() $\mathsf {K}$ in degrees
$\mathsf {K}$ in degrees ![]() $[2,0]$ that computes the motivic cohomology
$[2,0]$ that computes the motivic cohomology ![]() $H^{4-i}(\mathscr {E}^2, 2)$. Two key differences are as follows.
$H^{4-i}(\mathscr {E}^2, 2)$. Two key differences are as follows.
– The motivic cohomology of
 $\mathscr {E}^2$ is more complicated than that of
$\mathscr {E}^2$ is more complicated than that of  $\mathbb {G}_m^2$. However, through the theory of the Fourier–Mukai transform, one can obtain a reasonable understanding of various isotypical pieces under trace maps. We employ work of Deninger and Murre, taking care with the coefficients.
$\mathbb {G}_m^2$. However, through the theory of the Fourier–Mukai transform, one can obtain a reasonable understanding of various isotypical pieces under trace maps. We employ work of Deninger and Murre, taking care with the coefficients.– The complex
 $\mathsf {K}$ is not exact in degree zero (even after taking fixed parts). This has the following consequence. In the
$\mathsf {K}$ is not exact in degree zero (even after taking fixed parts). This has the following consequence. In the  $\mathbb {G}_m$-case, we made use of an element
$\mathbb {G}_m$-case, we made use of an element  $e \in \mathsf {K}_0$ that is the class of the identity of
$e \in \mathsf {K}_0$ that is the class of the identity of  $\mathbb {G}_m^2$. The analogue here arises from the identity section of
$\mathbb {G}_m^2$. The analogue here arises from the identity section of  $\mathscr {E}^2$, but this is no longer a boundary from
$\mathscr {E}^2$, but this is no longer a boundary from  $\mathsf {K}_1$. The element
$\mathsf {K}_1$. The element  $e_n \in \mathsf {K}_0$ that we use is supported on
$e_n \in \mathsf {K}_0$ that we use is supported on  $n$-torsion for an auxiliary integer
$n$-torsion for an auxiliary integer  $n$; see (6.7). The symbols we work with have correspondingly more involved definitions but do satisfy the same relations as before.
$n$; see (6.7). The symbols we work with have correspondingly more involved definitions but do satisfy the same relations as before.
The contents of the various subsections are as follows. In § 6.1, we give an integral refinement of a result of Deninger and Murre [Reference Denniger and MurreDM91] on the decomposition of the motivic cohomology of an abelian variety into isotypical components for the action of trace maps, with a particular view towards the fixed parts that we employ. In § 6.2, we give an abstract construction of a cocycle ![]() $\Theta ^Z$ as in (1.7) attached to a trace-fixed,
$\Theta ^Z$ as in (1.7) attached to a trace-fixed, ![]() $\mathrm {GL}_2(\mathbb {Z})$-invariant, degree zero formal sum
$\mathrm {GL}_2(\mathbb {Z})$-invariant, degree zero formal sum ![]() $Z$ of points. In § 6.3, we define our explicit symbols in the terms of the big complex and show that they are trace-fixed. Section 6.4 contains the construction of the cocycles
$Z$ of points. In § 6.3, we define our explicit symbols in the terms of the big complex and show that they are trace-fixed. Section 6.4 contains the construction of the cocycles ![]() ${}_n\Theta$. In § 6.5, we consider the compatibility of
${}_n\Theta$. In § 6.5, we consider the compatibility of ![]() ${}_n \Theta$ with two types of prime-to-level Hecke operators, those acting on
${}_n \Theta$ with two types of prime-to-level Hecke operators, those acting on ![]() $\mathrm {GL}_2(\mathbb {Z})$-cocycles and those arising from as correspondences on motivic cohomology. In Theorem 6.5.4, we prove that the two resulting actions agree on the class of
$\mathrm {GL}_2(\mathbb {Z})$-cocycles and those arising from as correspondences on motivic cohomology. In Theorem 6.5.4, we prove that the two resulting actions agree on the class of ![]() ${}_n \Theta$.
${}_n \Theta$.
6.1 Fixed parts via the Fourier–Mukai transform
Let ![]() $Y$ be a smooth, separated, connected scheme of finite type over a field
$Y$ be a smooth, separated, connected scheme of finite type over a field ![]() $F$ of characteristic
$F$ of characteristic ![]() $0$, and let
$0$, and let ![]() $A$ be a family of abelian varieties of relative dimension
$A$ be a family of abelian varieties of relative dimension ![]() $g$ over
$g$ over ![]() $Y$. Set
$Y$. Set ![]() $d = \dim Y$.
$d = \dim Y$.
Let ![]() $\mathbb {Z}' = \mathbb {Z}[{1}/{(2g+1)!}]$. For any integer
$\mathbb {Z}' = \mathbb {Z}[{1}/{(2g+1)!}]$. For any integer ![]() $i$, we set
$i$, we set
As in § 2.3, there are trace maps ![]() $[m]_*$ on
$[m]_*$ on ![]() $H^i(A,\mathbb {Z}'(g))$. There are also pullback maps
$H^i(A,\mathbb {Z}'(g))$. There are also pullback maps ![]() $[m]^*$, and since multiplication by
$[m]^*$, and since multiplication by ![]() $m$ has degree
$m$ has degree ![]() $m^{2g}$ on
$m^{2g}$ on ![]() $A$, we have the relation
$A$, we have the relation
We next prove that ![]() $H^i(A,\mathbb {Z}'(g))$ is the sum of its isotypic components for pullback maps. (We are eventually interested in trace maps
$H^i(A,\mathbb {Z}'(g))$ is the sum of its isotypic components for pullback maps. (We are eventually interested in trace maps ![]() $[m]_*$ as these can also be defined for open subschemes, but we will deduce such results from those on pullbacks.) The argument follows [Reference Denniger and MurreDM91, Theorem 2.19], with an appeal to the integral Grothendieck–Riemann–Roch of Pappas [Reference PappasPap07] to allow us to work over
$[m]_*$ as these can also be defined for open subschemes, but we will deduce such results from those on pullbacks.) The argument follows [Reference Denniger and MurreDM91, Theorem 2.19], with an appeal to the integral Grothendieck–Riemann–Roch of Pappas [Reference PappasPap07] to allow us to work over ![]() $\mathbb {Z}'$.
$\mathbb {Z}'$.
Theorem 6.1.1 For ![]() $i \in \mathbb {Z}$, each class
$i \in \mathbb {Z}$, each class ![]() $\alpha \in H^i(A,\mathbb {Z}'(g))$ is the sum of components
$\alpha \in H^i(A,\mathbb {Z}'(g))$ is the sum of components ![]() $\alpha = \sum _{s=0}^{2g} \alpha _s$ where
$\alpha = \sum _{s=0}^{2g} \alpha _s$ where ![]() $[m]^* \alpha _s = m^{2g-s} \alpha _s$ for all
$[m]^* \alpha _s = m^{2g-s} \alpha _s$ for all ![]() $m \in \mathbb {N}$.
$m \in \mathbb {N}$.
Proof. Let ![]() $A^{\vee }$ be the dual abelian scheme that represents
$A^{\vee }$ be the dual abelian scheme that represents ![]() $\mathrm {Pic}_{A/Y}^0$. Let
$\mathrm {Pic}_{A/Y}^0$. Let ![]() $\mathrm {P}$ be the Poincaré bundle on
$\mathrm {P}$ be the Poincaré bundle on ![]() $A \times _{Y} A^{\vee }$. We may form the Chern character in motivic cohomology:
$A \times _{Y} A^{\vee }$. We may form the Chern character in motivic cohomology:
 \[ e^{c_1(\mathrm{P})} := \sum_{r=0}^{2g+d} \frac{c_1(\mathrm{P})^r}{r!} \in \bigoplus_{r=0}^{2g+d} H^{2r}\bigg(A \times_{Y} A^{\vee}, \mathbb{Z} \bigg[\frac{1}{r!}\bigg](r)\bigg). \]
\[ e^{c_1(\mathrm{P})} := \sum_{r=0}^{2g+d} \frac{c_1(\mathrm{P})^r}{r!} \in \bigoplus_{r=0}^{2g+d} H^{2r}\bigg(A \times_{Y} A^{\vee}, \mathbb{Z} \bigg[\frac{1}{r!}\bigg](r)\bigg). \]
Note that the powers of ![]() $c_1(\mathrm {P})$ beyond
$c_1(\mathrm {P})$ beyond ![]() $2g+d$ vanish because they lie in a Chow group that is evidently zero. Since
$2g+d$ vanish because they lie in a Chow group that is evidently zero. Since ![]() $(1 \times [m]^*) \mathrm {P} \cong \mathrm {P}^{\otimes m}$, we have
$(1 \times [m]^*) \mathrm {P} \cong \mathrm {P}^{\otimes m}$, we have
The diagram
provides a morphism defined on ![]() $\alpha \in H^i(A,\mathbb {Q}(g))$ by
$\alpha \in H^i(A,\mathbb {Q}(g))$ by
known as the Fourier–Mukai transform. By its definition, ![]() $\mathscr {F}$ breaks up as a sum of operators, with the
$\mathscr {F}$ breaks up as a sum of operators, with the ![]() $r$th component
$r$th component ![]() $\mathscr {F}_r$ corresponding to
$\mathscr {F}_r$ corresponding to ![]() ${c_1(\mathrm {P})^r}/{r!}$. That is,
${c_1(\mathrm {P})^r}/{r!}$. That is, ![]() $\mathscr {F} = \sum _{r=0}^{2g+d} \mathscr {F}_r$, where, paying attention to denominators, we have
$\mathscr {F} = \sum _{r=0}^{2g+d} \mathscr {F}_r$, where, paying attention to denominators, we have
Any element of the image of ![]() $\mathscr {F}_r$ transforms under the image of each
$\mathscr {F}_r$ transforms under the image of each ![]() $[m]^*$ by
$[m]^*$ by ![]() $m^r$.
$m^r$.
Now, let ![]() $\mathscr {F}^{\vee }$ be defined dually, with the dual abelian variety
$\mathscr {F}^{\vee }$ be defined dually, with the dual abelian variety ![]() $A^{\vee }$ in place of
$A^{\vee }$ in place of ![]() $A$. For motivic cohomology with
$A$. For motivic cohomology with ![]() $\mathbb {Q}$-coefficients, Deninger and Murre show in [Reference Denniger and MurreDM91, Corollary 2.22] that
$\mathbb {Q}$-coefficients, Deninger and Murre show in [Reference Denniger and MurreDM91, Corollary 2.22] that
(for usual Chow groups, but the argument applies equally to higher Chow groups).Footnote 17
The use of rational coefficients in [Reference Denniger and MurreDM91] is mandated not just by the denominators in the Chern character, but by two applications of the Grothendieck–Riemann–Roch theorem (GRR), both of which arise from [Reference Denniger and MurreDM91, Lemma 2.8] and are used in the subsequent proposition. The first and most consequential application is for the projection morphism ![]() $A^{\vee } \times _S A \to A$, and the second is for the identity section
$A^{\vee } \times _S A \to A$, and the second is for the identity section ![]() $e_A \colon S \to A$.
$e_A \colon S \to A$.
Recall that GRR concerns the behavior of the cup product ![]() $\mathrm {CT}(\mathscr {G}) = e^{c_1(\mathscr {G})} \cup \mathrm {td}(T_X)$ of the Chern character of a coherent sheaf
$\mathrm {CT}(\mathscr {G}) = e^{c_1(\mathscr {G})} \cup \mathrm {td}(T_X)$ of the Chern character of a coherent sheaf ![]() $\mathscr {G}$ on a smooth quasi-projective variety
$\mathscr {G}$ on a smooth quasi-projective variety ![]() $X$ over
$X$ over ![]() $F$ and the Todd class of the tangent bundle
$F$ and the Todd class of the tangent bundle ![]() $T_X$ of
$T_X$ of ![]() $X$ under pushforward by a projective morphism
$X$ under pushforward by a projective morphism ![]() $f \colon X \to Y$, where
$f \colon X \to Y$, where ![]() $Y$ is another such variety. For
$Y$ is another such variety. For ![]() $e$ the relative dimension, it says more precisely regarding the degree
$e$ the relative dimension, it says more precisely regarding the degree ![]() $2r$ component that
$2r$ component that
By [Reference PappasPap07, Theorem 2.2], GRR remains true integrally if ![]() $F$ has characteristic
$F$ has characteristic ![]() $0$ upon inverting the primes dividing
$0$ upon inverting the primes dividing ![]() $(e+r+1)!$ if
$(e+r+1)!$ if ![]() $e \ge 0$ and
$e \ge 0$ and ![]() $(r+1)!$ if
$(r+1)!$ if ![]() $e < 0$. In the two cases of interest to us, we are concerned with
$e < 0$. In the two cases of interest to us, we are concerned with ![]() $\mathrm {CT}_r$ for
$\mathrm {CT}_r$ for ![]() $r \le g$, and
$r \le g$, and ![]() $e = g$ and
$e = g$ and ![]() $e = -g$, respectively. In particular, both applications of GRR go through with coefficients in
$e = -g$, respectively. In particular, both applications of GRR go through with coefficients in ![]() $\mathbb {Z}'=\mathbb {Z}[{1}/{(2g+1)!}]$. Consequently, (6.2) remains valid with coefficients in
$\mathbb {Z}'=\mathbb {Z}[{1}/{(2g+1)!}]$. Consequently, (6.2) remains valid with coefficients in ![]() $\mathbb {Z}'$, and we will use it, as such, in what follows.
$\mathbb {Z}'$, and we will use it, as such, in what follows.
Now let us return to equality (6.2), which we examine when restricted to ![]() $H^i(A, \mathbb {Z}'(g))$. We may write
$H^i(A, \mathbb {Z}'(g))$. We may write ![]() $\mathscr {F}^{\vee } \circ \mathscr {F} = \sum _{s= 0}^{2g+d} \sum _{t=0}^{2g+d} \mathscr {F}^{\vee }_{t} \circ \mathscr {F}_s$, and by definition the composition
$\mathscr {F}^{\vee } \circ \mathscr {F} = \sum _{s= 0}^{2g+d} \sum _{t=0}^{2g+d} \mathscr {F}^{\vee }_{t} \circ \mathscr {F}_s$, and by definition the composition ![]() $\mathscr {F}^{\vee }_{t} \circ \mathscr {F}_s$, restricted to
$\mathscr {F}^{\vee }_{t} \circ \mathscr {F}_s$, restricted to ![]() $H^i(A, \mathbb {Z}'(g))$, has image in
$H^i(A, \mathbb {Z}'(g))$, has image in ![]() $H^{i+ 2(t-g) + 2(s-g)}(A,\mathbb {Z}'[{1}/{s!t!}](s+t-g))$. Therefore (6.2) implies that each such term with
$H^{i+ 2(t-g) + 2(s-g)}(A,\mathbb {Z}'[{1}/{s!t!}](s+t-g))$. Therefore (6.2) implies that each such term with ![]() $t+s \neq 2g$ must vanish. In other words,
$t+s \neq 2g$ must vanish. In other words,
 \[ \mathscr{F}^{\vee} \circ \mathscr{F}|_{H^i(A, \mathbb{Z}'(g))} = \sum_{s=0}^{2g} \mathscr{F}^{\vee}_{2g-s} \circ \mathscr{F}_s = (-1)^g [-1]^* |_{H^i(A, \mathbb{Z}'(g))}, \]
\[ \mathscr{F}^{\vee} \circ \mathscr{F}|_{H^i(A, \mathbb{Z}'(g))} = \sum_{s=0}^{2g} \mathscr{F}^{\vee}_{2g-s} \circ \mathscr{F}_s = (-1)^g [-1]^* |_{H^i(A, \mathbb{Z}'(g))}, \]
where we now understand all the operators to act on motivic cohomology with ![]() $\mathbb {Z}'$-coefficients.
$\mathbb {Z}'$-coefficients.
Take ![]() $\alpha \in H^i(A,\mathbb {Z}'(g))$, and apply
$\alpha \in H^i(A,\mathbb {Z}'(g))$, and apply ![]() $\mathscr {F}^{\vee } \circ \mathscr {F}$ to
$\mathscr {F}^{\vee } \circ \mathscr {F}$ to ![]() $\alpha ' := (-1)^g [-1]^* \alpha$. Now (6.2) implies that the result is
$\alpha ' := (-1)^g [-1]^* \alpha$. Now (6.2) implies that the result is ![]() $\alpha$, so writing
$\alpha$, so writing ![]() $\alpha _s = \mathscr {F}_{2g-s}^{\vee } \mathscr {F}_s \alpha ' \in H^i(A,\mathbb {Z}'(g))$, we have
$\alpha _s = \mathscr {F}_{2g-s}^{\vee } \mathscr {F}_s \alpha ' \in H^i(A,\mathbb {Z}'(g))$, we have
 \begin{equation} \alpha = \sum_{s=0}^{2g} \alpha_s. \end{equation}
\begin{equation} \alpha = \sum_{s=0}^{2g} \alpha_s. \end{equation}
Then ![]() $[m]^*$ acts as
$[m]^*$ acts as ![]() $m^{2g-s}$ on
$m^{2g-s}$ on ![]() $\alpha _s$ for all
$\alpha _s$ for all ![]() $m \ge 1$, as required.
$m \ge 1$, as required.
We can now compute the fixed parts of motivic cohomology groups under trace maps for integers relatively prime to a fixed positive integer ![]() $n$. Let
$n$. Let ![]() $\mathbb {N}_n$ denote the monoid of positive integers prime to
$\mathbb {N}_n$ denote the monoid of positive integers prime to ![]() $n$. We consider the groups
$n$. We consider the groups ![]() $H^i(A,\mathbb {Z}'(g))$ as
$H^i(A,\mathbb {Z}'(g))$ as ![]() $\mathbb {Z}'[\mathbb {N}_n]$-modules for the trace maps. For
$\mathbb {Z}'[\mathbb {N}_n]$-modules for the trace maps. For ![]() $s \ge 0$, set
$s \ge 0$, set
Proposition 6.1.2 We have a direct sum decomposition
 \[ H^i(A,\mathbb{Z}'(g)) = \bigoplus_{s = 0}^{2g} H^i(A,g)^{(s)} \]
\[ H^i(A,\mathbb{Z}'(g)) = \bigoplus_{s = 0}^{2g} H^i(A,g)^{(s)} \]
of ![]() $\mathbb {Z}'[\mathbb {N}_n]$-modules, which is natural in
$\mathbb {Z}'[\mathbb {N}_n]$-modules, which is natural in ![]() $A$ over
$A$ over ![]() $Y$. The group
$Y$. The group ![]() $H^i(A,g)^{(0)}$ is zero unless
$H^i(A,g)^{(0)}$ is zero unless ![]() $i = 2g$, and
$i = 2g$, and ![]() $H^{2g}(A,g)^{(0)}$ is naturally isomorphic to
$H^{2g}(A,g)^{(0)}$ is naturally isomorphic to ![]() $\mathbb {Z}'$ as a
$\mathbb {Z}'$ as a ![]() $\mathbb {Z}'[\mathbb {N}_n]$-module.
$\mathbb {Z}'[\mathbb {N}_n]$-module.
Proof. Write ![]() $\alpha \in H^i(A,\mathbb {Z}'(g))$ as
$\alpha \in H^i(A,\mathbb {Z}'(g))$ as ![]() $\alpha = \sum _{s=0}^{2g} \alpha _s$ as in Theorem 6.1.1. It follows from (6.1) that, for any prime
$\alpha = \sum _{s=0}^{2g} \alpha _s$ as in Theorem 6.1.1. It follows from (6.1) that, for any prime ![]() $\ell \nmid n$, we have
$\ell \nmid n$, we have ![]() $(\ell ^{2g-s}[\ell ]_*- \ell ^{2g})\alpha _s = 0$ for each
$(\ell ^{2g-s}[\ell ]_*- \ell ^{2g})\alpha _s = 0$ for each ![]() $s$. For each
$s$. For each ![]() $0 \le t \le 2g$, let
$0 \le t \le 2g$, let
 \[ \phi_t(\ell) =\prod_{\substack{s=0\\ s\neq t}}^{2g} \ell^{2g} ([\ell]_*-\ell^s) \]
\[ \phi_t(\ell) =\prod_{\substack{s=0\\ s\neq t}}^{2g} \ell^{2g} ([\ell]_*-\ell^s) \]
so that ![]() $\phi _t(\ell )\alpha = \phi _t(\ell )\alpha _t$. Then
$\phi _t(\ell )\alpha = \phi _t(\ell )\alpha _t$. Then ![]() $\phi _t(\ell )$ acts on
$\phi _t(\ell )$ acts on ![]() $\alpha _t$ by the scalar
$\alpha _t$ by the scalar
 \[ r_t(\ell) =\prod_{\substack{s=0\\ s \neq t}}^{2g} \ell^{2g} (\ell^t-\ell^s). \]
\[ r_t(\ell) =\prod_{\substack{s=0\\ s \neq t}}^{2g} \ell^{2g} (\ell^t-\ell^s). \]
There exist primes ![]() $\ell _1, \ldots, \ell _h$ not dividing
$\ell _1, \ldots, \ell _h$ not dividing ![]() $n$ and
$n$ and ![]() $c_1, \ldots, c_h \in \mathbb {Z}'$ such that
$c_1, \ldots, c_h \in \mathbb {Z}'$ such that ![]() $\sum _{j=1}^h c_j r_t(\ell _j) = 1$. (If
$\sum _{j=1}^h c_j r_t(\ell _j) = 1$. (If ![]() $p > 2g+1$, then
$p > 2g+1$, then ![]() $p$ does not divide
$p$ does not divide ![]() $r_t(\ell )$ whenever
$r_t(\ell )$ whenever ![]() $\ell$ is a primitive root modulo
$\ell$ is a primitive root modulo ![]() $p$.) The element
$p$.) The element
 \begin{equation} \phi_t = \sum_{j=1}^h c_j \phi_t(\ell_j) \in \mathbb{Z}'[\mathbb{N}_n] \end{equation}
\begin{equation} \phi_t = \sum_{j=1}^h c_j \phi_t(\ell_j) \in \mathbb{Z}'[\mathbb{N}_n] \end{equation}
then satisfies ![]() $\phi _t(\alpha ) = \alpha _t$. This element
$\phi _t(\alpha ) = \alpha _t$. This element ![]() $\phi _t$ defines a projection of
$\phi _t$ defines a projection of ![]() $H^i(A,\mathbb {Z}'(g))$ onto
$H^i(A,\mathbb {Z}'(g))$ onto ![]() $H^i(A,g)^{(t)}$, and therefore we have that
$H^i(A,g)^{(t)}$, and therefore we have that ![]() $H^i(A,g)^{(t)}$ is a
$H^i(A,g)^{(t)}$ is a ![]() $\mathbb {Z}'[\mathbb {N}_n]$-module direct summand of
$\mathbb {Z}'[\mathbb {N}_n]$-module direct summand of ![]() $H^i(A,\mathbb {Z}'(g))$.
$H^i(A,\mathbb {Z}'(g))$.
Suppose now that ![]() $\alpha \in H^i(A,g)^{(0)}$. Then
$\alpha \in H^i(A,g)^{(0)}$. Then ![]() $\alpha = \phi _0(\alpha ) = \alpha _0$. Referring to (6.3), this
$\alpha = \phi _0(\alpha ) = \alpha _0$. Referring to (6.3), this ![]() $\alpha$ is necessarily of the form
$\alpha$ is necessarily of the form ![]() $\mathscr {F}^{\vee }_{2g} \beta _0$, where
$\mathscr {F}^{\vee }_{2g} \beta _0$, where ![]() $\beta _0 \in H^{i-2g}(A^{\vee },\mathbb {Z}')$. Since
$\beta _0 \in H^{i-2g}(A^{\vee },\mathbb {Z}')$. Since ![]() $H^{i-2g}(A^{\vee },\mathbb {Z}') = 0$ for
$H^{i-2g}(A^{\vee },\mathbb {Z}') = 0$ for ![]() $i \neq 2g$, we actually have
$i \neq 2g$, we actually have ![]() $\alpha = 0$ unless
$\alpha = 0$ unless ![]() $i = 2g$. For
$i = 2g$. For ![]() $i = 2g$, we have the canonical identification
$i = 2g$, we have the canonical identification ![]() $H^0(A^{\vee },\mathbb {Z}') \cong \mathbb {Z}'$, and
$H^0(A^{\vee },\mathbb {Z}') \cong \mathbb {Z}'$, and ![]() $\mathscr {F}^{\vee }_{2g}$ carries
$\mathscr {F}^{\vee }_{2g}$ carries ![]() $1 \in \mathbb {Z}'$ (up to sign) to the fundamental class of the zero section in
$1 \in \mathbb {Z}'$ (up to sign) to the fundamental class of the zero section in ![]() $H^{2g}(A, \mathbb {Z}'(g))$. To verify the final statement, we have by (6.2) that
$H^{2g}(A, \mathbb {Z}'(g))$. To verify the final statement, we have by (6.2) that ![]() $\mathscr {F}_0$ carries the fundamental class of the zero section to a generator for
$\mathscr {F}_0$ carries the fundamental class of the zero section to a generator for ![]() $H^0(A^{\vee }, \mathbb {Z}')$. In summary,
$H^0(A^{\vee }, \mathbb {Z}')$. In summary, ![]() $H^{2g}(A, g)^{(0)}$ is a free
$H^{2g}(A, g)^{(0)}$ is a free ![]() $\mathbb {Z}'$-module of rank
$\mathbb {Z}'$-module of rank ![]() $1$, generated by the fundamental class of the zero section.
$1$, generated by the fundamental class of the zero section.
6.2 The abstract cocycles
Let us now specialize to the case of an elliptic curve ![]() $E$ over a smooth, separated, connected scheme
$E$ over a smooth, separated, connected scheme ![]() $S$ of finite type over a field
$S$ of finite type over a field ![]() $F$. We will apply Theorem 6.1.1 to
$F$. We will apply Theorem 6.1.1 to ![]() $A = E^2$ over
$A = E^2$ over ![]() $S$. For the remainder of this section, we set
$S$. For the remainder of this section, we set
Just as in the case of ![]() $\mathbb {G}_m$, we write down a complex computing the cohomology of
$\mathbb {G}_m$, we write down a complex computing the cohomology of ![]() $E^2$. Recall from Example 2.2.2 that the complex
$E^2$. Recall from Example 2.2.2 that the complex ![]() $\mathsf {K}$ given in homological degrees
$\mathsf {K}$ given in homological degrees ![]() $2$ to
$2$ to ![]() $0$ by
$0$ by
the sums being taken over irreducible divisors and codimension ![]() $2$ points of
$2$ points of ![]() $E^2$ respectively, computes (from left to right) the cohomology
$E^2$ respectively, computes (from left to right) the cohomology ![]() $H^*(E^2, 2)$ in degrees
$H^*(E^2, 2)$ in degrees ![]() $2$ to
$2$ to ![]() $4$.
$4$.
Unlike the case of ![]() $\mathbb {G}_m^2$, none of these cohomology groups of
$\mathbb {G}_m^2$, none of these cohomology groups of ![]() $E^2$ need vanish. However, by Remark 2.3.3, the complex admits trace maps
$E^2$ need vanish. However, by Remark 2.3.3, the complex admits trace maps ![]() $[m]_*$. Set
$[m]_*$. Set
Then ![]() $\mathsf {K}^{(0)}$ can be regarded as the direct limit
$\mathsf {K}^{(0)}$ can be regarded as the direct limit ![]() $\varinjlim _{n} ({}_n \mathsf {K}^{(0)})$, over integers
$\varinjlim _{n} ({}_n \mathsf {K}^{(0)})$, over integers ![]() $n$ ordered by divisibility, of complexes
$n$ ordered by divisibility, of complexes ![]() ${}_n \mathsf {K}^{(0)}$ defined by the fixed part of
${}_n \mathsf {K}^{(0)}$ defined by the fixed part of ![]() $\mathsf {K} \otimes _{\mathbb {Z}} \mathbb {Z}'$ under all
$\mathsf {K} \otimes _{\mathbb {Z}} \mathbb {Z}'$ under all ![]() $m \in \mathbb {N}_n$.
$m \in \mathbb {N}_n$.
Lemma 6.2.1 The sequence ![]() $0 \to \mathsf {K}_2^{(0)} \to \mathsf {K}_1^{(0)} \to \mathsf {K}_0^{(0)}$ is exact.
$0 \to \mathsf {K}_2^{(0)} \to \mathsf {K}_1^{(0)} \to \mathsf {K}_0^{(0)}$ is exact.
Proof. It is enough to prove the same assertion for ![]() ${}_n \mathsf {K}^{(0)}$, since the claim then follows by taking the direct limit. In the following discussion, ‘fixed parts’, or a superscript ‘
${}_n \mathsf {K}^{(0)}$, since the claim then follows by taking the direct limit. In the following discussion, ‘fixed parts’, or a superscript ‘![]() $(0)$’, refers to being fixed under
$(0)$’, refers to being fixed under ![]() $\mathbb {N}_n$.
$\mathbb {N}_n$.
Consider the exact sequence
of ![]() $\mathbb {Z}'[\mathbb {N}_n]$-modules. The map on fixed parts induced by
$\mathbb {Z}'[\mathbb {N}_n]$-modules. The map on fixed parts induced by ![]() $\partial _2$ is injective as
$\partial _2$ is injective as ![]() $H^2(E^2,2)^{(0)}$ is trivial by Proposition 6.1.2.
$H^2(E^2,2)^{(0)}$ is trivial by Proposition 6.1.2.
If ![]() $y \in {}_n\mathsf {K}_1^{(0)}$ has trivial residue (i.e., dies in
$y \in {}_n\mathsf {K}_1^{(0)}$ has trivial residue (i.e., dies in ![]() $\mathsf {K}_0$), then it maps to
$\mathsf {K}_0$), then it maps to ![]() $H^3(E^2,2)^{(0)}$, which equals
$H^3(E^2,2)^{(0)}$, which equals ![]() $0$ by Proposition 6.1.2. Thus, there exists
$0$ by Proposition 6.1.2. Thus, there exists ![]() $x \in \mathsf {K}_2$ with
$x \in \mathsf {K}_2$ with ![]() $\partial _2(x) = y$. For any
$\partial _2(x) = y$. For any ![]() $m \in \mathbb {N}_n$, since
$m \in \mathbb {N}_n$, since ![]() $[m]_*-1$ annihilates
$[m]_*-1$ annihilates ![]() $y$, the element
$y$, the element ![]() $([m]_*-1) x$ lies in the kernel of
$([m]_*-1) x$ lies in the kernel of ![]() $\partial _2$. So, there in turn exists
$\partial _2$. So, there in turn exists ![]() $z_m \in H^2(E^2,\mathbb {Z}'(2))$ that maps to
$z_m \in H^2(E^2,\mathbb {Z}'(2))$ that maps to ![]() $([m]_*-1) x$. Equation (6.4) provides an element
$([m]_*-1) x$. Equation (6.4) provides an element ![]() $\phi _0 \in \mathbb {Z}'[\mathbb {N}_n]$ that projects
$\phi _0 \in \mathbb {Z}'[\mathbb {N}_n]$ that projects ![]() $H^i(E^2,\mathbb {Z}'(2))$ onto its fixed subspace. For
$H^i(E^2,\mathbb {Z}'(2))$ onto its fixed subspace. For ![]() $i = 2$, the fixed part is trivial, so
$i = 2$, the fixed part is trivial, so
In other words, we have ![]() $\phi _0 x \in {}_n \mathsf {K}_2^{(0)}$. Moreover,
$\phi _0 x \in {}_n \mathsf {K}_2^{(0)}$. Moreover, ![]() $\phi _0$ fixes any element of
$\phi _0$ fixes any element of ![]() ${}_n \mathsf {K}_1^{(0)}$, so
${}_n \mathsf {K}_1^{(0)}$, so ![]() $\phi _0 y=y$. Since
$\phi _0 y=y$. Since
the sequence is exact at ![]() ${}_n \mathsf {K}_1^{(0)}$.
${}_n \mathsf {K}_1^{(0)}$.
Now there is a surjective degree map
obtained by composing ![]() $\mathsf {K}_0^{(0)} \rightarrow H^4(E^2, 0)^{(0)}$ with the isomorphism of the latter group with
$\mathsf {K}_0^{(0)} \rightarrow H^4(E^2, 0)^{(0)}$ with the isomorphism of the latter group with ![]() $\mathbb {Z}'$ furnished by Proposition 6.1.
$\mathbb {Z}'$ furnished by Proposition 6.1.
Proposition 6.2.2 Let ![]() $Z \in \mathsf {K}_0^{(0)}$ be a
$Z \in \mathsf {K}_0^{(0)}$ be a ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed class with
$\mathrm {GL}_2(\mathbb {Z})$-fixed class with ![]() $\deg (Z) = 0$ such that there existsFootnote 18
$\deg (Z) = 0$ such that there existsFootnote 18 ![]() $\eta \in \mathsf {K}_1^{(0)}$ with
$\eta \in \mathsf {K}_1^{(0)}$ with ![]() $\partial \eta = Z$. Then there is a
$\partial \eta = Z$. Then there is a ![]() $1$-cocycle
$1$-cocycle
where ![]() $\Theta ^Z_{\gamma }$ is uniquely characterized by the property that
$\Theta ^Z_{\gamma }$ is uniquely characterized by the property that
Moreover, the class of ![]() $\Theta ^Z$ is independent of the choice of
$\Theta ^Z$ is independent of the choice of ![]() $\eta$.
$\eta$.
Proof. By Lemma 6.2.1, a unique ![]() $\Theta ^Z_{\gamma } \in \mathsf {K}_2^{(0)}$ with residue
$\Theta ^Z_{\gamma } \in \mathsf {K}_2^{(0)}$ with residue ![]() $(\gamma ^*-1)\eta$ exists. That the resulting function
$(\gamma ^*-1)\eta$ exists. That the resulting function ![]() $\Theta ^Z$ is a cocycle follows just as in Proposition 3.3.1.
$\Theta ^Z$ is a cocycle follows just as in Proposition 3.3.1.
If ![]() $\eta ' \in \mathsf {K}_1^{(0)}$ also satisfies
$\eta ' \in \mathsf {K}_1^{(0)}$ also satisfies ![]() $\partial \eta ' = Z$, then
$\partial \eta ' = Z$, then ![]() $\eta '$ gives rise to another cocycle
$\eta '$ gives rise to another cocycle ![]() $\Theta '$. By the left exactness in Lemma 6.2.1, there exists
$\Theta '$. By the left exactness in Lemma 6.2.1, there exists ![]() $\psi \in \mathsf {K}_2^{(0)}$ with
$\psi \in \mathsf {K}_2^{(0)}$ with ![]() $\partial \psi = \eta -\eta '$. The cocycles
$\partial \psi = \eta -\eta '$. The cocycles ![]() $\Theta ^Z$ and
$\Theta ^Z$ and ![]() $\Theta '$ are cohomologous since
$\Theta '$ are cohomologous since ![]() $\Theta ^Z_{\gamma } - \Theta '_{\gamma } = (\gamma ^*-1)\psi$.
$\Theta ^Z_{\gamma } - \Theta '_{\gamma } = (\gamma ^*-1)\psi$.
Note that if we can also choose ![]() $\eta$ to be fixed by a parabolic subgroup of
$\eta$ to be fixed by a parabolic subgroup of ![]() $\mathrm {GL}_2(\mathbb {Z})$, then the argument of Proposition 3.3.4 implies that
$\mathrm {GL}_2(\mathbb {Z})$, then the argument of Proposition 3.3.4 implies that ![]() $\Theta ^Z$ is parabolic (with the same meaning as in that proposition).
$\Theta ^Z$ is parabolic (with the same meaning as in that proposition).
In the remaining sections, we specialize to the case that ![]() $E$ is the universal elliptic curve over a modular curve
$E$ is the universal elliptic curve over a modular curve ![]() $Y_1(N)$. In this setting, we will proceed more computationally and produce not only a particularly nice choice of
$Y_1(N)$. In this setting, we will proceed more computationally and produce not only a particularly nice choice of ![]() $Z$ (supported on torsion) but also nice choices of
$Z$ (supported on torsion) but also nice choices of ![]() $\eta$ entirely parallel to the
$\eta$ entirely parallel to the ![]() $\mathbb {G}_m$-case. To do this, we first of all set up a class of natural symbols in
$\mathbb {G}_m$-case. To do this, we first of all set up a class of natural symbols in ![]() $\mathsf {K}$ with which we can compute.
$\mathsf {K}$ with which we can compute.
6.3 Symbols
Fix an integer ![]() $N \geq 4$. We will work over the base scheme
$N \geq 4$. We will work over the base scheme ![]() $Y := Y_1(N)$ over
$Y := Y_1(N)$ over ![]() $\mathbb {Q}$ whose
$\mathbb {Q}$ whose ![]() $S$-points for a
$S$-points for a ![]() $\mathbb {Q}$-scheme
$\mathbb {Q}$-scheme ![]() $S$ parameterize pairs
$S$ parameterize pairs ![]() $(E, P)$ of an elliptic curve
$(E, P)$ of an elliptic curve ![]() $E/S$ and a section
$E/S$ and a section ![]() $P$ of
$P$ of ![]() $E[N]$ that is everywhere of exact order
$E[N]$ that is everywhere of exact order ![]() $N$ (i.e., the associated map from
$N$ (i.e., the associated map from ![]() $\mathbb {Z}/N\mathbb {Z}$ to
$\mathbb {Z}/N\mathbb {Z}$ to ![]() $E[N]$ is a closed immersion of group schemes over
$E[N]$ is a closed immersion of group schemes over ![]() $S$). Though we often omit
$S$). Though we often omit ![]() $N$ from the notation, it should be understood throughout the remainder of this section that we are working at level
$N$ from the notation, it should be understood throughout the remainder of this section that we are working at level ![]() $\Gamma _1(N)$.
$\Gamma _1(N)$.
Our elliptic curve will be taken to be the universal elliptic curve ![]() $\mathscr {E}$ over
$\mathscr {E}$ over ![]() $Y$. Let
$Y$. Let ![]() $\pi \colon \mathscr {E} \to Y$ be the structure morphism. We shall write
$\pi \colon \mathscr {E} \to Y$ be the structure morphism. We shall write
for the square of the universal elliptic curve over ![]() $Y$. We let
$Y$. We let ![]() $\pi _i \colon \mathscr {E}^2 \to \mathscr {E}$ for
$\pi _i \colon \mathscr {E}^2 \to \mathscr {E}$ for ![]() $i \in \{1,2\}$ denote the
$i \in \{1,2\}$ denote the ![]() $i$th projection map.
$i$th projection map.
It will often be useful to add auxiliary ![]() $\Gamma _0(m)$-structure to
$\Gamma _0(m)$-structure to ![]() $Y$. For a positive integer
$Y$. For a positive integer ![]() $m$ prime to
$m$ prime to ![]() $N$, let
$N$, let ![]() $Y_m$ denote the modular curve over
$Y_m$ denote the modular curve over ![]() $\mathbb {Q}$ corresponding to level structure
$\mathbb {Q}$ corresponding to level structure ![]() $\Gamma _1(N) \cap \Gamma _0(m)$. For a
$\Gamma _1(N) \cap \Gamma _0(m)$. For a ![]() $\mathbb {Q}$-scheme
$\mathbb {Q}$-scheme ![]() $S$, the points of
$S$, the points of ![]() $Y_m(S)$ are equivalence classes of triples
$Y_m(S)$ are equivalence classes of triples ![]() $(E,P,K)$, where
$(E,P,K)$, where ![]() $(E, P) \in Y(S)$ and
$(E, P) \in Y(S)$ and ![]() $K$ is an étale-locally cyclic
$K$ is an étale-locally cyclic ![]() $S$-subgroup scheme of order
$S$-subgroup scheme of order ![]() $m$.
$m$.
6.3.1 Symbols on  $\mathscr {E}$
$\mathscr {E}$
Fix a prime number ![]() $n \nmid N$. Denote by
$n \nmid N$. Denote by ![]() $\mathscr {E}'$ the pullback of
$\mathscr {E}'$ the pullback of ![]() $\mathscr {E}$ from
$\mathscr {E}$ from ![]() $Y$ to the modular curve
$Y$ to the modular curve ![]() $Y' = Y_n$. The curve
$Y' = Y_n$. The curve ![]() $\mathscr {E}'$ is equipped with a canonical cyclic subgroup scheme
$\mathscr {E}'$ is equipped with a canonical cyclic subgroup scheme ![]() $\mathscr {K}$ of order
$\mathscr {K}$ of order ![]() $n$.
$n$.
We first define some auxiliary divisors and rational functions on ![]() $\mathscr {E}'$ and
$\mathscr {E}'$ and ![]() $\mathscr {E}$ that we use to construct our symbols in the big complex
$\mathscr {E}$ that we use to construct our symbols in the big complex ![]() $\mathsf {K}$. Note that any
$\mathsf {K}$. Note that any ![]() $S$-subgroup scheme
$S$-subgroup scheme ![]() $\mathsf {G} \subset E[n]$ of the
$\mathsf {G} \subset E[n]$ of the ![]() $n$-torsion of an elliptic curve
$n$-torsion of an elliptic curve ![]() $E$ over a base variety
$E$ over a base variety ![]() $S$ defines a class in
$S$ defines a class in ![]() $H^0(E[n],0)^{(0)}$. Namely,
$H^0(E[n],0)^{(0)}$. Namely, ![]() $\mathsf {G}$ is a union of connected components of
$\mathsf {G}$ is a union of connected components of ![]() $E[n]$, and we associate to
$E[n]$, and we associate to ![]() $\mathsf {G}$ the sum of these components considered in
$\mathsf {G}$ the sum of these components considered in ![]() $H^0(E[n], 0)$; this is automatically
$H^0(E[n], 0)$; this is automatically ![]() $[m]_*$-fixed for
$[m]_*$-fixed for ![]() $m$ relatively prime to
$m$ relatively prime to ![]() $n$.
$n$.
– Set
(6.5) \begin{align} \delta = {}_n \delta = n^2(0) - \mathscr{E}[n] \in H^0(\mathscr{E}[n],0)^{(0)} \quad \mathrm{and} \quad \delta' = {}_n \delta' = n \mathscr{K} - \mathscr{E}'[n] \in H^0(\mathscr{E}'[n],0)^{(0)}. \end{align}
\begin{align} \delta = {}_n \delta = n^2(0) - \mathscr{E}[n] \in H^0(\mathscr{E}[n],0)^{(0)} \quad \mathrm{and} \quad \delta' = {}_n \delta' = n \mathscr{K} - \mathscr{E}'[n] \in H^0(\mathscr{E}'[n],0)^{(0)}. \end{align}
Note that we have an exact sequence
Since ![]() $H^2(\mathscr {E},1)^{(0)} \cong \mathbb {Z}'$ by Theorem 6.1.1, and any element of
$H^2(\mathscr {E},1)^{(0)} \cong \mathbb {Z}'$ by Theorem 6.1.1, and any element of ![]() $H^1(\mathscr {E},1)$ is necessarily an invertible local constant, a variant of an argument of Kato [Reference KatoKat04, 1.10]Footnote 19 yields an exact sequence
$H^1(\mathscr {E},1)$ is necessarily an invertible local constant, a variant of an argument of Kato [Reference KatoKat04, 1.10]Footnote 19 yields an exact sequence
where the degree map is surjective since the class defined by the zero section has degree ![]() $1 \in \mathbb {Z}'$. We also have the analogous sequence for
$1 \in \mathbb {Z}'$. We also have the analogous sequence for ![]() $\mathscr {E}'$. Since
$\mathscr {E}'$. Since ![]() $\delta$ and
$\delta$ and ![]() $\delta '$ have degree zero, we may make the following definition.
$\delta '$ have degree zero, we may make the following definition.
– Let
be the unique ‘theta functions’ with divisors given by \[ \theta = {}_n \theta \in H^1(\mathscr{E} - \mathscr{E}[n],1)^{(0)} \quad \mathrm{and} \quad \theta' = {}_n \theta' \in H^1(\mathscr{E}' - \mathscr{E}'[n],1)^{(0)} \]
\[ \theta = {}_n \theta \in H^1(\mathscr{E} - \mathscr{E}[n],1)^{(0)} \quad \mathrm{and} \quad \theta' = {}_n \theta' \in H^1(\mathscr{E}' - \mathscr{E}'[n],1)^{(0)} \]
 $\delta$ and
$\delta$ and  $\delta '$:
(6.6)
$\delta '$:
(6.6) \begin{equation} \partial \theta = \delta \quad \mathrm{and} \quad \partial \theta'=\delta'. \end{equation}
\begin{equation} \partial \theta = \delta \quad \mathrm{and} \quad \partial \theta'=\delta'. \end{equation}
The morphisms ![]() $Y' \rightarrow Y$ and
$Y' \rightarrow Y$ and ![]() $\mathscr {E}' \rightarrow \mathscr {E}$, as well as
$\mathscr {E}' \rightarrow \mathscr {E}$, as well as ![]() $(\mathscr {E}')^2 \rightarrow \mathscr {E}^2$, where we write
$(\mathscr {E}')^2 \rightarrow \mathscr {E}^2$, where we write
are finite étale of degree ![]() $n+1$.Footnote 20 Let us denote the norm (i.e., pushforward) maps on motivic cohomology induced by these morphisms by
$n+1$.Footnote 20 Let us denote the norm (i.e., pushforward) maps on motivic cohomology induced by these morphisms by ![]() $\operatorname {N}$. Not only do these norms act only on the motivic cohomology of
$\operatorname {N}$. Not only do these norms act only on the motivic cohomology of ![]() $\mathscr {E}'$, but by Lemma 2.1.3 they also give a map of complexes
$\mathscr {E}'$, but by Lemma 2.1.3 they also give a map of complexes ![]() $\mathsf {K}' \rightarrow \mathsf {K}$, with
$\mathsf {K}' \rightarrow \mathsf {K}$, with ![]() $\mathsf {K}'$ being the analogue of
$\mathsf {K}'$ being the analogue of ![]() $\mathsf {K}$ for
$\mathsf {K}$ for ![]() $(\mathscr {E}')^2$. For example, in the direct sum of zero
$(\mathscr {E}')^2$. For example, in the direct sum of zero ![]() $K$-groups of residue fields of codimension
$K$-groups of residue fields of codimension ![]() $1$ points on
$1$ points on ![]() $\mathscr {E}$, we have
$\mathscr {E}$, we have ![]() $\operatorname {N}(\mathscr {K}) = \mathscr {E}[n] + n (0)$ and
$\operatorname {N}(\mathscr {K}) = \mathscr {E}[n] + n (0)$ and ![]() $\operatorname {N}(\mathscr {E}'[n]) = (n+1)\mathscr {E}[n]$. (For the first, for example, the norm of
$\operatorname {N}(\mathscr {E}'[n]) = (n+1)\mathscr {E}[n]$. (For the first, for example, the norm of ![]() $\mathscr {K}$ gives on each elliptic curve fiber of
$\mathscr {K}$ gives on each elliptic curve fiber of ![]() $\mathscr {E} \rightarrow Y$ the sum of all cyclic subgroups of order
$\mathscr {E} \rightarrow Y$ the sum of all cyclic subgroups of order ![]() $n$, which counts the origin with multiplicity
$n$, which counts the origin with multiplicity ![]() $n+1$ and all other points with multiplicity
$n+1$ and all other points with multiplicity ![]() $1$.) Thus, we have
$1$.) Thus, we have
6.3.2 Symbols on  $\mathscr {E}^2$
$\mathscr {E}^2$
We continue to fix an auxiliary prime ![]() $n \nmid N$. We are going to define symbols
$n \nmid N$. We are going to define symbols ![]() $\langle a,c \rangle _n \in \mathsf {K}_1^{(0)}$ for primitive pairs
$\langle a,c \rangle _n \in \mathsf {K}_1^{(0)}$ for primitive pairs ![]() $(a,c) \in \mathbb {Z}^2-\{0\}$ and
$(a,c) \in \mathbb {Z}^2-\{0\}$ and ![]() $\langle \gamma \rangle _n \in \mathsf {K}_2^{(0)}$ for
$\langle \gamma \rangle _n \in \mathsf {K}_2^{(0)}$ for ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$ satisfying relations identical to (3.2), but now with the degree zero element
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$ satisfying relations identical to (3.2), but now with the degree zero element ![]() $e$ in the
$e$ in the ![]() $\mathbb {G}_m^2$ setting replaced by a special
$\mathbb {G}_m^2$ setting replaced by a special ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed and trace-fixed cycle
$\mathrm {GL}_2(\mathbb {Z})$-fixed and trace-fixed cycle ![]() $e_n$ that depends on our choice of
$e_n$ that depends on our choice of ![]() $n$. The symbols, which also depend on
$n$. The symbols, which also depend on ![]() $n$, allow us to give an explicit description of the abstract cocycle
$n$, allow us to give an explicit description of the abstract cocycle ![]() $\Theta ^Z$ of Proposition 6.2.2 in the case
$\Theta ^Z$ of Proposition 6.2.2 in the case ![]() $Z=e_n$.
$Z=e_n$.
As before, an element of ![]() $\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ provides a morphism
$\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ provides a morphism ![]() $\mathscr {E}^2 \rightarrow \mathscr {E}^2$ over
$\mathscr {E}^2 \rightarrow \mathscr {E}^2$ over ![]() $Y$ via right multiplication. We denote by
$Y$ via right multiplication. We denote by ![]() $T_n^{\mathsf {K}}$ the operator on
$T_n^{\mathsf {K}}$ the operator on ![]() $\mathsf {K}$ given by the sum of pullbacks by the representatives
$\mathsf {K}$ given by the sum of pullbacks by the representatives ![]() $g_j$ of (3.6) (replacing
$g_j$ of (3.6) (replacing ![]() $\ell$ by
$\ell$ by ![]() $n$). While the operator
$n$). While the operator ![]() $T_n^{\mathsf {K}}$ depends on the choice of these coset representatives, its action on
$T_n^{\mathsf {K}}$ depends on the choice of these coset representatives, its action on ![]() $\mathrm {GL}_2(\mathbb {Z})$-invariant elements does not.
$\mathrm {GL}_2(\mathbb {Z})$-invariant elements does not.
– In
 $\mathsf {K}_0$, we form the element
(6.7)Here, we view
$\mathsf {K}_0$, we form the element
(6.7)Here, we view \begin{equation} e_n = n ( n^3(0) - nT_n^{\mathsf{K}}(0) + \mathscr{E}[n]^2 ). \end{equation}
\begin{equation} e_n = n ( n^3(0) - nT_n^{\mathsf{K}}(0) + \mathscr{E}[n]^2 ). \end{equation} $H^0(\mathscr {E}[n]^2,0)$ as a subgroup of
$H^0(\mathscr {E}[n]^2,0)$ as a subgroup of  $\mathsf {K}_0$ by the map taking a formal sum of irreducible cycles in
$\mathsf {K}_0$ by the map taking a formal sum of irreducible cycles in  $\mathscr {E}[n]^2$ to the corresponding element of the direct sum of copies of
$\mathscr {E}[n]^2$ to the corresponding element of the direct sum of copies of  $\mathbb {Z}$ given by the zeroth
$\mathbb {Z}$ given by the zeroth  $K$-groups of those cycles. The element
$K$-groups of those cycles. The element  $e_n$ is
$e_n$ is  $\mathrm {GL}_2(\mathbb {Z})$-fixed as a sum of fixed terms.Footnote 21 Note that
$\mathrm {GL}_2(\mathbb {Z})$-fixed as a sum of fixed terms.Footnote 21 Note that  $e_n = V_n^{\mathsf {K}}(0)$, where
(6.8)The element
$e_n = V_n^{\mathsf {K}}(0)$, where
(6.8)The element \begin{equation} V_n^{\mathsf{K}} = n^4 - n^2T_n^{\mathsf{K}} + n[n]^*. \end{equation}
\begin{equation} V_n^{\mathsf{K}} = n^4 - n^2T_n^{\mathsf{K}} + n[n]^*. \end{equation} $e_n$ has degree zero as
$e_n$ has degree zero as  $T_n^{\mathsf {K}}$ has degree
$T_n^{\mathsf {K}}$ has degree  $n(n+1)$ and
$n(n+1)$ and  $[n]^*$ has degree
$[n]^*$ has degree  $n^2$. We will explain the significance of this particular choice of
$n^2$. We will explain the significance of this particular choice of  $e_n$ in Remark 6.3.2.
$e_n$ in Remark 6.3.2.– In
 $\mathsf {K}_1$, we form
(6.9)The external product
$\mathsf {K}_1$, we form
(6.9)The external product \begin{equation} \langle 1, 0 \rangle_n = \delta \boxtimes \theta - \operatorname{N} (\delta' \boxtimes \theta'). \end{equation}
\begin{equation} \langle 1, 0 \rangle_n = \delta \boxtimes \theta - \operatorname{N} (\delta' \boxtimes \theta'). \end{equation} $\delta \boxtimes \theta$ here should be understood to mean the restriction of the function
$\delta \boxtimes \theta$ here should be understood to mean the restriction of the function  $\pi _2^* \theta$ on
$\pi _2^* \theta$ on  $\mathscr {E} \times _Y (\mathscr {E}-\mathscr {E}[n])$ to the divisor defined by
$\mathscr {E} \times _Y (\mathscr {E}-\mathscr {E}[n])$ to the divisor defined by  $\pi _1^{-1}(\delta )$. This defines a class in the direct sum of the multiplicative groups of function fields of the irreducible divisors composing
$\pi _1^{-1}(\delta )$. This defines a class in the direct sum of the multiplicative groups of function fields of the irreducible divisors composing  $\mathscr {E}[n] \times _Y \mathscr {E}$, so also an element of
$\mathscr {E}[n] \times _Y \mathscr {E}$, so also an element of  $\mathsf {K}_1$. Similarly,
$\mathsf {K}_1$. Similarly,  $\delta ' \boxtimes \theta ' \in \mathsf {K}'_1$ is the external product with respect to
$\delta ' \boxtimes \theta ' \in \mathsf {K}'_1$ is the external product with respect to  $(\mathscr {E}')^2 = \mathscr {E}' \times _{Y'} \mathscr {E}'$.
$(\mathscr {E}')^2 = \mathscr {E}' \times _{Y'} \mathscr {E}'$.
More generally, we set
where \[ \langle a,c \rangle_n = \gamma^*\langle 1,0 \rangle_n \in \mathsf{K}_1. \]
\[ \langle a,c \rangle_n = \gamma^*\langle 1,0 \rangle_n \in \mathsf{K}_1. \]
 $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ is arbitrary with first column
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ is arbitrary with first column  $(a,c)$.
$(a,c)$.– In
 $\mathsf {K}_2$, we form
(6.10)Here,
$\mathsf {K}_2$, we form
(6.10)Here, \begin{equation} \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n = \theta \boxtimes \theta - \operatorname{N} (\theta' \boxtimes \theta'). \end{equation}
\begin{equation} \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n = \theta \boxtimes \theta - \operatorname{N} (\theta' \boxtimes \theta'). \end{equation} $\theta \boxtimes \theta$ denotes the Steinberg symbol
$\theta \boxtimes \theta$ denotes the Steinberg symbol  $\{\pi _1^* \theta, \pi _2^* \theta \}$, and
$\{\pi _1^* \theta, \pi _2^* \theta \}$, and  $\theta ' \boxtimes \theta ' \in \mathsf {K}'_2$ is defined analogously.
$\theta ' \boxtimes \theta ' \in \mathsf {K}'_2$ is defined analogously.
In general, for
 $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, we set
(6.11)
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$, we set
(6.11) \begin{equation} \langle \gamma \rangle_n = \gamma^* \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n \in \mathsf{K}_2. \end{equation}
\begin{equation} \langle \gamma \rangle_n = \gamma^* \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n \in \mathsf{K}_2. \end{equation}
In Lemma 6.4.3, we will show that ![]() $\langle a,c \rangle _n$ is independent of the second column of
$\langle a,c \rangle _n$ is independent of the second column of ![]() $\gamma$ used in defining it. For now, let us fix such a choice and show that our symbols are
$\gamma$ used in defining it. For now, let us fix such a choice and show that our symbols are ![]() $[m]_*$-fixed for all
$[m]_*$-fixed for all ![]() $m \in \mathbb {N}_n$.
$m \in \mathbb {N}_n$.
Lemma 6.3.1 The symbols ![]() $e_n$,
$e_n$, ![]() $\langle a,c \rangle _n$, and
$\langle a,c \rangle _n$, and ![]() $\langle \gamma \rangle _n$ defined above satisfy
$\langle \gamma \rangle _n$ defined above satisfy
Proof. Let ![]() $m \in \mathbb {N}_n$. First, note that
$m \in \mathbb {N}_n$. First, note that ![]() $\delta$,
$\delta$, ![]() $\theta$,
$\theta$, ![]() $\delta '$,
$\delta '$, ![]() $\theta '$ are
$\theta '$ are ![]() $[m]_*$-fixed, and therefore their exterior products are as well (see Example 2.3.2). Since
$[m]_*$-fixed, and therefore their exterior products are as well (see Example 2.3.2). Since ![]() $\mathscr {E}' \to \mathscr {E}$ commutes with the multiplication-by-
$\mathscr {E}' \to \mathscr {E}$ commutes with the multiplication-by-![]() $m$ map
$m$ map ![]() $[m]$, the norm maps
$[m]$, the norm maps ![]() $\mathrm {N}$ in (6.9) and (6.10) commute with
$\mathrm {N}$ in (6.9) and (6.10) commute with ![]() $[m]_*$. The Hecke operator
$[m]_*$. The Hecke operator ![]() $T_n^{\mathsf {K}}$ in (6.7) commutes with
$T_n^{\mathsf {K}}$ in (6.7) commutes with ![]() $[m]_*$ in that each
$[m]_*$ in that each

for ![]() $0 \le j \le n$ is a cartesian square. Also,
$0 \le j \le n$ is a cartesian square. Also, ![]() $\mathscr {E}[n]^2$ and each
$\mathscr {E}[n]^2$ and each ![]() $g_j^*(0)$ are
$g_j^*(0)$ are ![]() $[m]_*$-fixed since
$[m]_*$-fixed since ![]() $[m]$ is an automorphism of the corresponding subgroup schemes. It follows that all of the symbols are
$[m]$ is an automorphism of the corresponding subgroup schemes. It follows that all of the symbols are ![]() $[m]_*$-fixed.
$[m]_*$-fixed.
Remark 6.3.2 Let us explain where the strange definition of ![]() $e_n$ in (6.7) comes from. The main issue at hand is that one cannot find a function on
$e_n$ in (6.7) comes from. The main issue at hand is that one cannot find a function on ![]() $\mathscr {E}$ with a single pole at the origin, and therefore (if one is to produce explicit formulas) one needs to choose a
$\mathscr {E}$ with a single pole at the origin, and therefore (if one is to produce explicit formulas) one needs to choose a ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed element of
$\mathrm {GL}_2(\mathbb {Z})$-fixed element of ![]() $\mathsf {K}_0^{(0)}$ somewhat carefully. We will sketch the important feature that this particular formula has.
$\mathsf {K}_0^{(0)}$ somewhat carefully. We will sketch the important feature that this particular formula has.
Take a geometric point ![]() $s$ of
$s$ of ![]() $Y\!$ with associated elliptic curve
$Y\!$ with associated elliptic curve ![]() $E = \mathscr {E}_s$, and fix a basis for
$E = \mathscr {E}_s$, and fix a basis for ![]() $E[n]$, that is, an isomorphism of abelian groups
$E[n]$, that is, an isomorphism of abelian groups ![]() $E[n] \cong (\mathbb {Z}/n\mathbb {Z})^2$. This then identifies
$E[n] \cong (\mathbb {Z}/n\mathbb {Z})^2$. This then identifies ![]() $E[n] \times E[n]$ with
$E[n] \times E[n]$ with ![]() $(\mathbb {Z}/n\mathbb {Z})^2 \times (\mathbb {Z}/n\mathbb {Z})^2$; regarding the two copies of
$(\mathbb {Z}/n\mathbb {Z})^2 \times (\mathbb {Z}/n\mathbb {Z})^2$; regarding the two copies of ![]() $(\mathbb {Z}/n\mathbb {Z})^2$ as the top and bottom rows of a
$(\mathbb {Z}/n\mathbb {Z})^2$ as the top and bottom rows of a ![]() $2 \times 2$ matrix, we may thus regard
$2 \times 2$ matrix, we may thus regard ![]() $E[n] \times E[n] \cong M_2(\mathbb {Z}/n\mathbb {Z})$.
$E[n] \times E[n] \cong M_2(\mathbb {Z}/n\mathbb {Z})$.
Using these coordinates, the fiber of ![]() $e$ above
$e$ above ![]() $s$ is the formal sum
$s$ is the formal sum ![]() $\sum _{M \in M_2(\mathbb {Z}/n\mathbb {Z})} \phi _n(M) M$, where
$\sum _{M \in M_2(\mathbb {Z}/n\mathbb {Z})} \phi _n(M) M$, where
 \[ \phi_n(M) = \begin{cases} n^4-n^3-n^2+n & \text{if } \operatorname{rank}(M) = 0, \\ n-n^2 & \text{if } \operatorname{rank}(M) = 1, \\ n & \text{if } \operatorname{rank}(M) = 2. \end{cases} \]
\[ \phi_n(M) = \begin{cases} n^4-n^3-n^2+n & \text{if } \operatorname{rank}(M) = 0, \\ n-n^2 & \text{if } \operatorname{rank}(M) = 1, \\ n & \text{if } \operatorname{rank}(M) = 2. \end{cases} \]
In detail, this function ![]() $\phi _n$ is the sum of three functions
$\phi _n$ is the sum of three functions ![]() $\phi _n^{0}$,
$\phi _n^{0}$, ![]() $\phi _n^1$, and
$\phi _n^1$, and ![]() $\phi _n^2$ corresponding to the three terms in (6.7):
$\phi _n^2$ corresponding to the three terms in (6.7): ![]() $\phi _n^{0}$, arising from the term
$\phi _n^{0}$, arising from the term ![]() $n^4 (0)$, equals
$n^4 (0)$, equals ![]() $n^4$ in rank
$n^4$ in rank ![]() $0$ and is otherwise zero;
$0$ and is otherwise zero; ![]() $\phi _n^{1}$, arising from the term
$\phi _n^{1}$, arising from the term ![]() $-n^2T_n^{\mathsf {K}}(0)$, equals
$-n^2T_n^{\mathsf {K}}(0)$, equals ![]() $-n^2 \,\mathrm {deg}(T_n) = -n^3-n^2$ in rank
$-n^2 \,\mathrm {deg}(T_n) = -n^3-n^2$ in rank ![]() $0$ and
$0$ and ![]() $-n^2$ in rank
$-n^2$ in rank ![]() $1$; and finally,
$1$; and finally, ![]() $\phi _n^{(2)}$, arising from the term
$\phi _n^{(2)}$, arising from the term ![]() $n E[n]^2$, is simply the constant function with value
$n E[n]^2$, is simply the constant function with value ![]() $n$.
$n$.
The significance of this particular function ![]() $\phi _n$ is that if we push it forward to a
$\phi _n$ is that if we push it forward to a ![]() $\mathbb {Z}$-valued function on
$\mathbb {Z}$-valued function on ![]() $(\mathbb {Z}/n\mathbb {Z})^2$ along any of the maps
$(\mathbb {Z}/n\mathbb {Z})^2$ along any of the maps
which come by taking the product with a fixed element of ![]() $(\mathbb {Z}/n\mathbb {Z})^2$, then the result is zero. This characterizes it up to a scalar among
$(\mathbb {Z}/n\mathbb {Z})^2$, then the result is zero. This characterizes it up to a scalar among ![]() $\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$-invariant functions.
$\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$-invariant functions.
Let us explain why this is a natural property to ask for. In the context of Proposition 6.2.2, if one wants an explicit formula for ![]() $\Theta ^Z$ as an external product of theta functions, it is natural to ask that
$\Theta ^Z$ as an external product of theta functions, it is natural to ask that ![]() $Z$ be an external product of the divisors of those theta functions. In the coordinates just introduced, these correspond to functions on
$Z$ be an external product of the divisors of those theta functions. In the coordinates just introduced, these correspond to functions on ![]() $M_2(\mathbb {Z}/n\mathbb {Z})$ of the form
$M_2(\mathbb {Z}/n\mathbb {Z})$ of the form ![]() $\Phi (M)= f_1(M_1) f_2(M_2)$, where
$\Phi (M)= f_1(M_1) f_2(M_2)$, where ![]() $M_1$ and
$M_1$ and ![]() $M_2$ are the rows of
$M_2$ are the rows of ![]() $M$ and the
$M$ and the ![]() $f_i \colon (\mathbb {Z}/n\mathbb {Z})^2 \rightarrow \mathbb {Z}$ both satisfy
$f_i \colon (\mathbb {Z}/n\mathbb {Z})^2 \rightarrow \mathbb {Z}$ both satisfy ![]() $\sum _{x \in (\mathbb {Z}/n\mathbb {Z})^2} f_i(x) = 0$. If such a function
$\sum _{x \in (\mathbb {Z}/n\mathbb {Z})^2} f_i(x) = 0$. If such a function ![]() $\Phi$ is additionally
$\Phi$ is additionally ![]() $\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$-invariant, then its pushforward to
$\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$-invariant, then its pushforward to ![]() $(\mathbb {Z}/n\mathbb {Z})^2$ along any map
$(\mathbb {Z}/n\mathbb {Z})^2$ along any map ![]() $M \rightarrow vM$ with
$M \rightarrow vM$ with ![]() $v \in (\mathbb {Z}/n\mathbb {Z})^2$ is zero.
$v \in (\mathbb {Z}/n\mathbb {Z})^2$ is zero.
6.4 The explicit cocycle for  $n$
$n$
We turn to the construction of our cocycle for a prime ![]() $n \nmid N$ and the verification of its explicit formula in terms of the symbols of § 6.3. Recall from § 3.3 that a cocycle is parabolic if it has trivial image in the cohomology of all stabilizers of nonzero elements of
$n \nmid N$ and the verification of its explicit formula in terms of the symbols of § 6.3. Recall from § 3.3 that a cocycle is parabolic if it has trivial image in the cohomology of all stabilizers of nonzero elements of ![]() $\mathbb {Z}^2$ under the right action of
$\mathbb {Z}^2$ under the right action of ![]() $\mathrm {GL}_2(\mathbb {Z})$. Much as in Proposition 3.3.2, for
$\mathrm {GL}_2(\mathbb {Z})$. Much as in Proposition 3.3.2, for ![]() $\gamma \in \mathrm {GL}_2(\mathbb {Z})$ with columns
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$ with columns ![]() $v_1$ and
$v_1$ and ![]() $v_2$, we write
$v_2$, we write ![]() $\langle v_1, v_2 \rangle _n$ for
$\langle v_1, v_2 \rangle _n$ for ![]() $\langle \gamma \rangle _n$. Recall also that we defined the notion of a connecting sequence in § 3.3.
$\langle \gamma \rangle _n$. Recall also that we defined the notion of a connecting sequence in § 3.3.
Theorem 6.4.1 Let ![]() $n$ be a prime not dividing
$n$ be a prime not dividing ![]() $N$.
$N$.
(a) There is a parabolic
 $1$-cocycle
$1$-cocycle  ${}_n\Theta \colon \mathrm {GL}_2(\mathbb {Z}) \to \mathsf {K}_2^{(0)}$ uniquely characterized by
for all
${}_n\Theta \colon \mathrm {GL}_2(\mathbb {Z}) \to \mathsf {K}_2^{(0)}$ uniquely characterized by
for all \[ \partial({}_n\Theta_{\gamma}) = (\gamma^*-1)\langle 0,1 \rangle_n \]
\[ \partial({}_n\Theta_{\gamma}) = (\gamma^*-1)\langle 0,1 \rangle_n \]
 $\gamma \in \mathrm {GL}_2(\mathbb {Z})$.
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$.(b) For
 $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$ and a connecting sequence
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$ and a connecting sequence  $(v_i)_{i=0}^k$ for
$(v_i)_{i=0}^k$ for  $\gamma$, we have
(6.12)
$\gamma$, we have
(6.12) \begin{equation} {}_n \Theta_{\gamma} = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle_n. \end{equation}
\begin{equation} {}_n \Theta_{\gamma} = \sum_{i=1}^k \langle v_i, -v_{i-1} \rangle_n. \end{equation}
In order to prove Theorem 6.4.1, we first compute the residues of our symbols.
Lemma 6.4.2 The residue of ![]() $\langle 1,0 \rangle _n$ is
$\langle 1,0 \rangle _n$ is ![]() $e_n$.
$e_n$.
Proof. By (6.6), we have
where, for instance, ![]() $\delta \boxtimes \delta$ denotes the evidently defined external product. By Lemma 2.1.3, taking residues commutes with norms, and therefore
$\delta \boxtimes \delta$ denotes the evidently defined external product. By Lemma 2.1.3, taking residues commutes with norms, and therefore
For the norm ![]() $\operatorname {N}$ corresponding to
$\operatorname {N}$ corresponding to ![]() $(\mathscr {E}')^2 \to \mathscr {E}^2$, we have
$(\mathscr {E}')^2 \to \mathscr {E}^2$, we have
where each of the equalities is inside ![]() $\mathsf {K}^0$. (The final identity is a straightforward computation. See the comparison of (6.17) and (6.18) in the proof of Theorem 6.5.4 below.) For
$\mathsf {K}^0$. (The final identity is a straightforward computation. See the comparison of (6.17) and (6.18) in the proof of Theorem 6.5.4 below.) For ![]() $\delta ' = n \mathscr {K} - \mathscr {E}'[n]$ as in (6.5), we then compute that
$\delta ' = n \mathscr {K} - \mathscr {E}'[n]$ as in (6.5), we then compute that
 \begin{align*} \operatorname{N}(\delta' \boxtimes \delta') &= n^2 \operatorname{N}(\mathscr{K} \boxtimes \mathscr{K}) - n \operatorname{N}(\mathscr{K} \boxtimes \mathscr{E}'[n]) - n \operatorname{N}(\mathscr{E}'[n] \boxtimes \mathscr{K}) + \operatorname{N}(\mathscr{E}'[n]^2)\\ &= n^2 T_n^{\mathsf{K}}(0) - n^2((0) \boxtimes \mathscr{E}[n] + \mathscr{E}[n] \boxtimes (0)) + (-n+1)\mathscr{E}[n]^2. \end{align*}
\begin{align*} \operatorname{N}(\delta' \boxtimes \delta') &= n^2 \operatorname{N}(\mathscr{K} \boxtimes \mathscr{K}) - n \operatorname{N}(\mathscr{K} \boxtimes \mathscr{E}'[n]) - n \operatorname{N}(\mathscr{E}'[n] \boxtimes \mathscr{K}) + \operatorname{N}(\mathscr{E}'[n]^2)\\ &= n^2 T_n^{\mathsf{K}}(0) - n^2((0) \boxtimes \mathscr{E}[n] + \mathscr{E}[n] \boxtimes (0)) + (-n+1)\mathscr{E}[n]^2. \end{align*}
Recalling that ![]() $\delta = n^2(0) - \mathscr {E}[n]$ from (6.5), we have
$\delta = n^2(0) - \mathscr {E}[n]$ from (6.5), we have
and we conclude from the formula (6.7) defining ![]() $e_n$ that
$e_n$ that ![]() $\delta \boxtimes \delta - \operatorname {N}(\delta ' \boxtimes \delta ') = e_n$.
$\delta \boxtimes \delta - \operatorname {N}(\delta ' \boxtimes \delta ') = e_n$.
Lemma 6.4.3 Let ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$. The symbol
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$. The symbol ![]() $\langle a, c \rangle _n = \gamma ^*\langle 1, 0 \rangle _n$ does not depend on the choice of
$\langle a, c \rangle _n = \gamma ^*\langle 1, 0 \rangle _n$ does not depend on the choice of ![]() $(b,d)$ in
$(b,d)$ in ![]() $\gamma$, and its residue is
$\gamma$, and its residue is ![]() $e_n$.
$e_n$.
Proof. Since the residue map ![]() $\mathsf {K}_1 \to \mathsf {K}_0$ is
$\mathsf {K}_1 \to \mathsf {K}_0$ is ![]() $\mathrm {GL}_2(\mathbb {Z})$-equivariant and
$\mathrm {GL}_2(\mathbb {Z})$-equivariant and ![]() $e_n$ is
$e_n$ is ![]() $\mathrm {GL}_2(\mathbb {Z})$-invariant, the symbol
$\mathrm {GL}_2(\mathbb {Z})$-invariant, the symbol ![]() $\gamma ^*\langle 1,0 \rangle$ has residue
$\gamma ^*\langle 1,0 \rangle$ has residue ![]() $e_n$ by Lemma 6.4.2.
$e_n$ by Lemma 6.4.2.
For the first statement, it is enough to see that ![]() $\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )^*$ fixes
$\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )^*$ fixes ![]() $\langle 1, 0 \rangle _n$. For this, recall that
$\langle 1, 0 \rangle _n$. For this, recall that ![]() $\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )$ acts on points of
$\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )$ acts on points of ![]() $\mathscr {E}^2$ via the recipe
$\mathscr {E}^2$ via the recipe ![]() $(E, P, Q) \mapsto (E, P, P+Q)$. Both
$(E, P, Q) \mapsto (E, P, P+Q)$. Both ![]() $\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )^* \langle 1,0 \rangle _n$ and
$\big (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\big )^* \langle 1,0 \rangle _n$ and ![]() $\langle 1,0 \rangle _n$ are meromorphic functions on
$\langle 1,0 \rangle _n$ are meromorphic functions on ![]() $\mathscr {E}[n] \times _{Y} \mathscr {E}$ with the same residue
$\mathscr {E}[n] \times _{Y} \mathscr {E}$ with the same residue ![]() $e_n$. Moreover, they are both invariant under all maps
$e_n$. Moreover, they are both invariant under all maps ![]() $[m]_*$ with
$[m]_*$ with ![]() $m \in \mathbb {N}_n$ by Lemma 6.3.1. They differ, then, by a regular function
$m \in \mathbb {N}_n$ by Lemma 6.3.1. They differ, then, by a regular function ![]() $f$ on
$f$ on ![]() $\mathscr {E}[n] \times _Y \mathscr {E}$ that is fixed under all such
$\mathscr {E}[n] \times _Y \mathscr {E}$ that is fixed under all such ![]() $[m]_*$. Now any regular function on
$[m]_*$. Now any regular function on ![]() $\mathscr {E}[n] \times _{Y} \mathscr {E}$ is necessarily constant along fibers of the map
$\mathscr {E}[n] \times _{Y} \mathscr {E}$ is necessarily constant along fibers of the map ![]() $\mathscr {E} \rightarrow Y$ in the second variable, and thus
$\mathscr {E} \rightarrow Y$ in the second variable, and thus ![]() $f$ is pulled back from a function
$f$ is pulled back from a function ![]() $\bar {f}$ on
$\bar {f}$ on ![]() $\mathscr {E}[n]$. Then the fact that
$\mathscr {E}[n]$. Then the fact that ![]() $f$ is fixed implies that
$f$ is fixed implies that ![]() $([m]_* \bar {f})^{m^2} = \bar {f}$ (where the exponent
$([m]_* \bar {f})^{m^2} = \bar {f}$ (where the exponent ![]() $m^2$ arises from the degree of the map
$m^2$ arises from the degree of the map ![]() $[m]$ in the second variable).
$[m]$ in the second variable).
Now, if one takes ![]() $m \equiv 1 \bmod n$, then
$m \equiv 1 \bmod n$, then ![]() $[m]$ fixes
$[m]$ fixes ![]() $\mathscr {E}[n]$, and one deduces that
$\mathscr {E}[n]$, and one deduces that ![]() $\bar {f}^{m^2} = \bar {f}$ for such
$\bar {f}^{m^2} = \bar {f}$ for such ![]() $m$. In particular, the value of
$m$. In particular, the value of ![]() $\bar {f}$ at any complex point is an
$\bar {f}$ at any complex point is an ![]() $(m^2-1)$th root of unity, so
$(m^2-1)$th root of unity, so ![]() $\bar {f}$ is a constant on both of the geometric components of
$\bar {f}$ is a constant on both of the geometric components of ![]() $\mathscr {E}[n]$ (the identity section and its complement). Since both of these components are preserved by every
$\mathscr {E}[n]$ (the identity section and its complement). Since both of these components are preserved by every ![]() $[m]$, we have
$[m]$, we have ![]() $\bar {f}^{m^2} = \bar {f}$ for all
$\bar {f}^{m^2} = \bar {f}$ for all ![]() $m \in \mathbb {N}_n$. Such a function necessarily satisfies
$m \in \mathbb {N}_n$. Such a function necessarily satisfies ![]() $\bar {f}^{24}=1$, and the class it induces in
$\bar {f}^{24}=1$, and the class it induces in ![]() $H^1(\mathscr {E}[n] \times _{Y} \mathscr {E},\mathbb {Z}'(1))$ is therefore trivial.
$H^1(\mathscr {E}[n] \times _{Y} \mathscr {E},\mathbb {Z}'(1))$ is therefore trivial.
Lemma 6.4.4 Let ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$. Then the residue of
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {GL}_2(\mathbb {Z})$. Then the residue of ![]() $\langle \gamma \rangle _n$ is given by
$\langle \gamma \rangle _n$ is given by
 \[ \partial \langle \gamma \rangle_n = \begin{cases} \langle a,c \rangle_n -\langle -b, -d\rangle_n & \text{if } \det(\gamma) = 1, \\ \langle -a,-c \rangle_n - \langle b,d \rangle_n & \text{if } \det(\gamma) = -1. \end{cases} \]
\[ \partial \langle \gamma \rangle_n = \begin{cases} \langle a,c \rangle_n -\langle -b, -d\rangle_n & \text{if } \det(\gamma) = 1, \\ \langle -a,-c \rangle_n - \langle b,d \rangle_n & \text{if } \det(\gamma) = -1. \end{cases} \]
Proof. We omit the subscripts ![]() $n$ in this proof for brevity of notation, and handle the case
$n$ in this proof for brevity of notation, and handle the case ![]() $\det (\gamma )=1$, the other case being similar. By definition (2.4) of the tame symbol, we have
$\det (\gamma )=1$, the other case being similar. By definition (2.4) of the tame symbol, we have
and similarly for ![]() $\theta ' \boxtimes \theta '$ in
$\theta ' \boxtimes \theta '$ in ![]() $\mathsf {K}'$. Taken together with the compatibility of residues with norms of Lemma 2.1.3, these imply
$\mathsf {K}'$. Taken together with the compatibility of residues with norms of Lemma 2.1.3, these imply
We then compute
 \[ \langle -b,-d \rangle_n = \begin{pmatrix} -b & a \\ -d & c \end{pmatrix}^* \langle 1,0 \rangle_n = \begin{pmatrix} a & b \\ c & d \end{pmatrix}^* \underbrace{ \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}^*(\delta \boxtimes \theta - \operatorname{N}(\delta' \boxtimes \theta'))}_{\theta \boxtimes \delta - \operatorname{N}(\theta' \boxtimes \delta')}. \]
\[ \langle -b,-d \rangle_n = \begin{pmatrix} -b & a \\ -d & c \end{pmatrix}^* \langle 1,0 \rangle_n = \begin{pmatrix} a & b \\ c & d \end{pmatrix}^* \underbrace{ \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}^*(\delta \boxtimes \theta - \operatorname{N}(\delta' \boxtimes \theta'))}_{\theta \boxtimes \delta - \operatorname{N}(\theta' \boxtimes \delta')}. \]
The step under the braces follows readily from the fact that ![]() $\theta, \delta, \theta ', \delta '$ are all invariant under
$\theta, \delta, \theta ', \delta '$ are all invariant under ![]() $[-1]^*$. We also used the fact that
$[-1]^*$. We also used the fact that ![]() $\mathrm {N}$ commutes with
$\mathrm {N}$ commutes with ![]() $\big (\begin{smallmatrix} 0 & 1\\-1 & 0 \end{smallmatrix}\big )^*$, which follows by Lemma 2.1.1.
$\big (\begin{smallmatrix} 0 & 1\\-1 & 0 \end{smallmatrix}\big )^*$, which follows by Lemma 2.1.1.
With the residues of the symbols attached to ![]() $n$ computed, the main theorem follows as in the case of
$n$ computed, the main theorem follows as in the case of ![]() $\mathbb {G}_m^2$.
$\mathbb {G}_m^2$.
Proof of Theorem 6.4.1 The existence and uniqueness of ![]() ${}_n\Theta$ in part (b) follow from Lemma 6.4.3 as in the proof of Proposition 6.2.2. That it is parabolic follows as in Proposition 3.3.4 from the fact that
${}_n\Theta$ in part (b) follow from Lemma 6.4.3 as in the proof of Proposition 6.2.2. That it is parabolic follows as in Proposition 3.3.4 from the fact that ![]() $\gamma ^*\langle 0, 1 \rangle _n = \langle 0, 1 \rangle _n$ for
$\gamma ^*\langle 0, 1 \rangle _n = \langle 0, 1 \rangle _n$ for ![]() $\gamma = \big (\begin{smallmatrix} 1 & 0 \\ c & \pm 1 \end{smallmatrix}\big )$, again by Lemma 6.4.3. Part (c) then follows as
$\gamma = \big (\begin{smallmatrix} 1 & 0 \\ c & \pm 1 \end{smallmatrix}\big )$, again by Lemma 6.4.3. Part (c) then follows as ![]() $\partial \sum _{i=1}^k \langle v_i, - v_{i-1} \rangle _n = (\gamma ^*-1)\langle 0,1 \rangle _n$ by Lemma 6.4.4, as in the proof of Proposition 3.3.2.
$\partial \sum _{i=1}^k \langle v_i, - v_{i-1} \rangle _n = (\gamma ^*-1)\langle 0,1 \rangle _n$ by Lemma 6.4.4, as in the proof of Proposition 3.3.2.
6.5 Hecke actions
We study Hecke operators on the complex ![]() $\mathsf {K}$ arising from correspondences, and we compare their action on the class of the cocycle
$\mathsf {K}$ arising from correspondences, and we compare their action on the class of the cocycle ![]() ${}_n\Theta$ with that of the previously defined Hecke operators on group cohomology (see Lemma 3.4.1).
${}_n\Theta$ with that of the previously defined Hecke operators on group cohomology (see Lemma 3.4.1).
6.5.1 Hecke operators via correspondences
Let us define Hecke operators using correspondences on ![]() $\mathscr {E}$. We restrict ourselves to
$\mathscr {E}$. We restrict ourselves to ![]() $m$th Hecke operators
$m$th Hecke operators ![]() $T'_m$ for
$T'_m$ for ![]() $m \ge 1$ prime to the level
$m \ge 1$ prime to the level ![]() $N$. We have a commutative diagram
$N$. We have a commutative diagram

where the effect of ![]() $\phi$ and
$\phi$ and ![]() $\psi$ on points is given by
$\psi$ on points is given by
The morphisms ![]() $\Phi$ and
$\Phi$ and ![]() $\Psi$ are then defined on fibers by the identity on
$\Psi$ are then defined on fibers by the identity on ![]() $E$ for
$E$ for ![]() $\Phi$ and taking the image under
$\Phi$ and taking the image under ![]() $E \to E/K$ for
$E \to E/K$ for ![]() $\Psi$. We also then have morphisms
$\Psi$. We also then have morphisms ![]() $\Phi ^2$ and
$\Phi ^2$ and ![]() $\Psi ^2$ sending
$\Psi ^2$ sending ![]() $\mathscr {E}^2 \times _Y Y_m$ to
$\mathscr {E}^2 \times _Y Y_m$ to ![]() $\mathscr {E}^2$. All these maps are finite étale.
$\mathscr {E}^2$. All these maps are finite étale.
We define Hecke operators ![]() $T_m'$ on the motivic cohomology of
$T_m'$ on the motivic cohomology of ![]() $Y$ and
$Y$ and ![]() $\mathscr {E}^2$ by the respective rules
$\mathscr {E}^2$ by the respective rules
We also have operators ![]() $[m]'$ acting on motivic cohomology of
$[m]'$ acting on motivic cohomology of ![]() $Y\!$ and
$Y\!$ and ![]() $\mathscr {E}^2$, given by pullback under multiplication by
$\mathscr {E}^2$, given by pullback under multiplication by ![]() $m$, that is, by the morphisms given by
$m$, that is, by the morphisms given by ![]() $m(E,P) = (E,mP)$ on points of
$m(E,P) = (E,mP)$ on points of ![]() $Y$ and given on
$Y$ and given on ![]() $\mathscr {E}^2$ by taking a point
$\mathscr {E}^2$ by taking a point ![]() $x$ in the fiber
$x$ in the fiber ![]() $E^2$ of
$E^2$ of ![]() $(E,P)$ to the point
$(E,P)$ to the point ![]() $mx$ in the fiber
$mx$ in the fiber ![]() $E^2$ of
$E^2$ of ![]() $(E,mP)$.Footnote 22 Note that the operators
$(E,mP)$.Footnote 22 Note that the operators ![]() $[m]'$ arise from diagrams of the same form as (6.13), but replacing
$[m]'$ arise from diagrams of the same form as (6.13), but replacing ![]() $Y_m$ by
$Y_m$ by ![]() $Y$, taking
$Y$, taking ![]() $\phi$ to be the identity map, and defining
$\phi$ to be the identity map, and defining ![]() $\psi$ by
$\psi$ by ![]() $\psi (E, P) = (E, mP)$. In this way, arguments given for
$\psi (E, P) = (E, mP)$. In this way, arguments given for ![]() $T_m'$ will usually adapt to
$T_m'$ will usually adapt to ![]() $[m]'$ without change.
$[m]'$ without change.
The reader might ask why we use the notation ![]() $T'_m$, as opposed to
$T'_m$, as opposed to ![]() $T_m$. The point is this: when we deal with cocycles
$T_m$. The point is this: when we deal with cocycles
there are two reasonable definitions of Hecke operators (both of which preserve coboundaries).
– The fiberwise
 $\mathrm {GL}_2(\mathbb {Z})$-action on
$\mathrm {GL}_2(\mathbb {Z})$-action on  $K_2(k(\mathscr {E}^2))$ extends to an action of
$K_2(k(\mathscr {E}^2))$ extends to an action of  $M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$. Therefore, we can define the
$M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$. Therefore, we can define the  $m$th Hecke operator
$m$th Hecke operator  $T_m$ on
$T_m$ on  $1$-cocycles valued in
$1$-cocycles valued in  $K_2(k(\mathscr {E}^2))$ as in § 3.4.
$K_2(k(\mathscr {E}^2))$ as in § 3.4.– The definition (6.15) also defines operators
 $T'_m$ on the
$T'_m$ on the  $K$-group of the function field of
$K$-group of the function field of  $\mathscr {E}^2$. This induces an operator on cocycles as in (6.16), also denoted by
$\mathscr {E}^2$. This induces an operator on cocycles as in (6.16), also denoted by  $T'_m$.
$T'_m$.
We note that the action of ![]() $T_m$ would exist if we replaced
$T_m$ would exist if we replaced ![]() $\mathscr {E} \rightarrow Y$ by any other family of elliptic curves, whereas
$\mathscr {E} \rightarrow Y$ by any other family of elliptic curves, whereas ![]() $T'_m$ requires that we work with the universal elliptic curve. The primary result of this subsection, Theorem 6.5.4 below, is that the these two operators coincide on the class of the cocycle
$T'_m$ requires that we work with the universal elliptic curve. The primary result of this subsection, Theorem 6.5.4 below, is that the these two operators coincide on the class of the cocycle ![]() ${}_n \Theta$.
${}_n \Theta$.
6.5.2 Hecke equivariance of the cocycle
We can also define Hecke operators ![]() $T'_m \colon \mathsf {K}_i \to \mathsf {K}_i$ on the terms of
$T'_m \colon \mathsf {K}_i \to \mathsf {K}_i$ on the terms of ![]() $\mathsf {K}$ via
$\mathsf {K}$ via ![]() $\Phi ^2_*(\Psi ^2)^*$. These give
$\Phi ^2_*(\Psi ^2)^*$. These give ![]() $\Delta$-equivariant morphisms of complexes, where again
$\Delta$-equivariant morphisms of complexes, where again ![]() $\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$.
$\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$.
Lemma 6.5.1 For each ![]() $m \ge 1$ prime to
$m \ge 1$ prime to ![]() $N$, both
$N$, both ![]() $T_m' \colon \mathsf {K} \rightarrow \mathsf {K}$ and
$T_m' \colon \mathsf {K} \rightarrow \mathsf {K}$ and ![]() $[m]' \colon \mathsf {K} \to \mathsf {K}$ are maps of complexes which are equivariant for the pullback action of
$[m]' \colon \mathsf {K} \to \mathsf {K}$ are maps of complexes which are equivariant for the pullback action of ![]() $\Delta$ for its right action on
$\Delta$ for its right action on ![]() $\mathscr {E}^2$.
$\mathscr {E}^2$.
Proof. The maps ![]() $T_m'$ and
$T_m'$ and ![]() $[m]'$ are compositions of étale pullbacks and finite pushforwards (transfers) in the
$[m]'$ are compositions of étale pullbacks and finite pushforwards (transfers) in the ![]() $K$-theory of fields, and as such commute with residue maps (see Lemma 2.1.3). Thus
$K$-theory of fields, and as such commute with residue maps (see Lemma 2.1.3). Thus ![]() $T_m'$ and
$T_m'$ and ![]() $[m]'$ define maps of complexes.
$[m]'$ define maps of complexes.
The ![]() $\Delta$-action on
$\Delta$-action on ![]() $E^2$ for an elliptic curve
$E^2$ for an elliptic curve ![]() $E$ is equivariant for the reduction
$E$ is equivariant for the reduction ![]() $E^2 \to (E/H)^2$ for any finite subgroup scheme
$E^2 \to (E/H)^2$ for any finite subgroup scheme ![]() $H$, so
$H$, so ![]() $(\Psi ^2)^*$ is equivariant for the pullback action of
$(\Psi ^2)^*$ is equivariant for the pullback action of ![]() $\Delta$. The operators
$\Delta$. The operators ![]() $[m]'$ are
$[m]'$ are ![]() $\Delta$-equivariant, in particular since multiplication by
$\Delta$-equivariant, in particular since multiplication by ![]() $m$ commutes with the
$m$ commutes with the ![]() $\Delta$-action on
$\Delta$-action on ![]() $E^2$. For
$E^2$. For ![]() $\Phi$, we note that
$\Phi$, we note that

is cartesian for any ![]() $\delta \in \Delta$ in that the morphism
$\delta \in \Delta$ in that the morphism ![]() $\Phi ^2$ is flat and the identity on fibers. Therefore,
$\Phi ^2$ is flat and the identity on fibers. Therefore, ![]() $(\Phi ^2)_*$ commutes with pullback by
$(\Phi ^2)_*$ commutes with pullback by ![]() $\delta$, again employing Lemma 2.1.1. Thus, the Hecke actions and pullback
$\delta$, again employing Lemma 2.1.1. Thus, the Hecke actions and pullback ![]() $\Delta$-actions commute.
$\Delta$-actions commute.
For ![]() $m \ge 1$ prime to
$m \ge 1$ prime to ![]() $N$, let us use
$N$, let us use ![]() $T_m^{\mathsf {K}}$ to denote any sum of pullbacks by representatives of the double coset of
$T_m^{\mathsf {K}}$ to denote any sum of pullbacks by representatives of the double coset of ![]() $\big (\begin{smallmatrix} m & \\ & 1 \end{smallmatrix}\big )$, as in § 3.4. (The choice is unimportant, but there is a standard one.)
$\big (\begin{smallmatrix} m & \\ & 1 \end{smallmatrix}\big )$, as in § 3.4. (The choice is unimportant, but there is a standard one.)
Lemma 6.5.2 Let ![]() $m \ge 1$ be prime to
$m \ge 1$ be prime to ![]() $N$.
$N$.
(a) The Hecke operators
 $T'_m$ and
$T'_m$ and  $[m]'$ on
$[m]'$ on  $\mathsf {K}$ commute with
$\mathsf {K}$ commute with  $[\mu ]_*$ for all
$[\mu ]_*$ for all  $\mu$ prime to
$\mu$ prime to  $m$, and in particular they preserve
$m$, and in particular they preserve  $\mathsf {K}^{(0)}$.
$\mathsf {K}^{(0)}$.(b) The Hecke operators
 $T_m^{\mathsf {K}}$ and
$T_m^{\mathsf {K}}$ and  $[m]^*$ on
$[m]^*$ on  $\mathsf {K}$ commute with all
$\mathsf {K}$ commute with all  $[\mu ]_*$ for
$[\mu ]_*$ for  $\mu$ prime to
$\mu$ prime to  $m$, and in particular they preserve
$m$, and in particular they preserve  $\mathsf {K}^{(0)}$.
$\mathsf {K}^{(0)}$.
Proof. The commutativity of ![]() $[\mu ]_*$ with the pushforward map
$[\mu ]_*$ with the pushforward map ![]() $\Phi ^2_*$ is automatic because
$\Phi ^2_*$ is automatic because ![]() $[\mu ]$ and
$[\mu ]$ and ![]() $\Phi ^2$ commute. To see the commutativity with
$\Phi ^2$ commute. To see the commutativity with ![]() $(\Psi ^2)^*$, we note that
$(\Psi ^2)^*$, we note that

is a cartesian diagram, which in turn amounts to the fact that the degree ![]() $m$ isogenies
$m$ isogenies ![]() $E \rightarrow E/K$ underlying
$E \rightarrow E/K$ underlying ![]() $\Psi$ (see (6.14)) induce isomorphisms on
$\Psi$ (see (6.14)) induce isomorphisms on ![]() $\mu$-torsion. Then we apply Lemma 2.1.1. A similar argument applies to both
$\mu$-torsion. Then we apply Lemma 2.1.1. A similar argument applies to both ![]() $[m]'$ and
$[m]'$ and ![]() $[m]^*$, in that they are also isomorphisms on
$[m]^*$, in that they are also isomorphisms on ![]() $\mu$-torsion. Finally, the argument for
$\mu$-torsion. Finally, the argument for ![]() $T_m^{\mathsf {K}}$ has already been given in the course of Lemma 6.3.1.
$T_m^{\mathsf {K}}$ has already been given in the course of Lemma 6.3.1.
The action of ![]() $\Delta$ on the complex
$\Delta$ on the complex ![]() $\mathsf {K}$ provides Hecke operators
$\mathsf {K}$ provides Hecke operators ![]() $T_m$ on
$T_m$ on ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ for
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ for ![]() $m \nmid N$, following the recipe of § 3.4 for the double coset of
$m \nmid N$, following the recipe of § 3.4 for the double coset of ![]() $\big (\begin{smallmatrix} m\\ & 1 \end{smallmatrix}\big )$. The various Hecke operators all commute with one another.
$\big (\begin{smallmatrix} m\\ & 1 \end{smallmatrix}\big )$. The various Hecke operators all commute with one another.
Lemma 6.5.3 Every pair of Hecke operators in the collection of operators ![]() $T_m$,
$T_m$, ![]() $T'_m$,
$T'_m$, ![]() $[m]^*$, and
$[m]^*$, and ![]() $[m]'$ for
$[m]'$ for ![]() $m \ge 1$ prime to
$m \ge 1$ prime to ![]() $N$ commute with each other in their actions on
$N$ commute with each other in their actions on ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$.
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$.
Proof. First, note that these operators all act on ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ since they (or, in the case of
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ since they (or, in the case of ![]() $T_m$, the operators
$T_m$, the operators ![]() $T_m^{\mathsf {K}}$) preserve fixed parts by Lemma 6.5.2. Commutativity between operators of the form
$T_m^{\mathsf {K}}$) preserve fixed parts by Lemma 6.5.2. Commutativity between operators of the form ![]() $T_m$ or
$T_m$ or ![]() $[m]^*$ is standard, as is commutativity between operators of the form
$[m]^*$ is standard, as is commutativity between operators of the form ![]() $T'_m$ or
$T'_m$ or ![]() $[m]'$ for various
$[m]'$ for various ![]() $m$. The operators
$m$. The operators ![]() $[m]^*$ already commute with the operators
$[m]^*$ already commute with the operators ![]() $T'_m$ or
$T'_m$ or ![]() $[m]'$ on
$[m]'$ on ![]() $\mathsf {K}_2$ by Lemma 6.5.1.
$\mathsf {K}_2$ by Lemma 6.5.1.
Given a ![]() $1$-cocycle
$1$-cocycle ![]() $\theta \colon \mathrm {GL}_2(\mathbb {Z}) \to \mathsf {K}_2$, the cocycle
$\theta \colon \mathrm {GL}_2(\mathbb {Z}) \to \mathsf {K}_2$, the cocycle ![]() $T_m \theta$ is defined by the formula of (3.5) for
$T_m \theta$ is defined by the formula of (3.5) for ![]() $g = \big (\begin{smallmatrix} m\\ & 1 \end{smallmatrix}\big )$. It is a sum of terms of the form
$g = \big (\begin{smallmatrix} m\\ & 1 \end{smallmatrix}\big )$. It is a sum of terms of the form ![]() $[\delta ]^* \theta (\gamma ')$ with
$[\delta ]^* \theta (\gamma ')$ with ![]() $\gamma '\in \mathrm {GL}_2(\mathbb {Z})$ and
$\gamma '\in \mathrm {GL}_2(\mathbb {Z})$ and ![]() $\delta \in \Delta$. Any
$\delta \in \Delta$. Any ![]() $T'_{\mu }$ or
$T'_{\mu }$ or ![]() $[\mu ]'$ for
$[\mu ]'$ for ![]() $\mu \in \mathbb {N}_N$ commutes with each
$\mu \in \mathbb {N}_N$ commutes with each ![]() $[\delta ]^*$ by Lemma 6.5.1, so also commutes with
$[\delta ]^*$ by Lemma 6.5.1, so also commutes with ![]() $T_m$ on
$T_m$ on ![]() $\theta$.
$\theta$.
We now proceed to the main result of this section, which unlike the preceding lemmas is not a formality.
Theorem 6.5.4 The actions of ![]() $T_{\ell }$ and
$T_{\ell }$ and ![]() $T_{\ell }'$ coincide on the class of
$T_{\ell }'$ coincide on the class of ![]() ${}_n \Theta$ in
${}_n \Theta$ in ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ for each prime
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2^{(0)})$ for each prime ![]() $\ell \nmid N$. The same is true for the actions of
$\ell \nmid N$. The same is true for the actions of ![]() $[\ell ]^*$ and
$[\ell ]^*$ and ![]() $[\ell ]'$.
$[\ell ]'$.
Proof. Let us say that a cocycle ![]() $\theta \colon \mathrm {GL}_2(\mathbb {Z}) \rightarrow \mathsf {K}_2^{(0)}$ is associated to
$\theta \colon \mathrm {GL}_2(\mathbb {Z}) \rightarrow \mathsf {K}_2^{(0)}$ is associated to ![]() $Z \in \mathsf {K}_0^{(0)}$ if
$Z \in \mathsf {K}_0^{(0)}$ if ![]() $\partial \theta (\gamma ) = (\gamma ^*-1) \eta$ with
$\partial \theta (\gamma ) = (\gamma ^*-1) \eta$ with ![]() $\eta \in \mathsf {K}_1^{(0)}$ such that
$\eta \in \mathsf {K}_1^{(0)}$ such that ![]() $\partial \eta =Z$. Recall that, by Proposition 6.2.2, any two cocycles associated to
$\partial \eta =Z$. Recall that, by Proposition 6.2.2, any two cocycles associated to ![]() $Z$ are cohomologous. To show that the classes of
$Z$ are cohomologous. To show that the classes of ![]() $T_{\ell }'({}_n\Theta )$ and
$T_{\ell }'({}_n\Theta )$ and ![]() $T_{\ell }({}_n\Theta )$ coincide, it therefore suffices to show that
$T_{\ell }({}_n\Theta )$ coincide, it therefore suffices to show that ![]() $T_{\ell }({}_n\Theta )$ and
$T_{\ell }({}_n\Theta )$ and ![]() $T'_{\ell }({}_n\Theta )$ are associated to the same cycle. Let us consider the two cases:
$T'_{\ell }({}_n\Theta )$ are associated to the same cycle. Let us consider the two cases:
– The cocycle
 $T_{\ell } ( {}_n \Theta )$ is associated to
$T_{\ell } ( {}_n \Theta )$ is associated to  $T_{\ell }^{\mathsf {K}} e_n$. Indeed,
$T_{\ell }^{\mathsf {K}} e_n$. Indeed,  $\partial (T_{\ell }^{\mathsf {K}} \langle 0,1 \rangle _n) = T_{\ell }^{\mathsf {K}} e_n$ as
$\partial (T_{\ell }^{\mathsf {K}} \langle 0,1 \rangle _n) = T_{\ell }^{\mathsf {K}} e_n$ as  $T_{\ell }^{\mathsf {K}}$ is a map of complexes, and
$T_{\ell }^{\mathsf {K}}$ is a map of complexes, and  $T_{\ell }^{\mathsf {K}} \langle 0,1 \rangle _n$ belongs to
$T_{\ell }^{\mathsf {K}} \langle 0,1 \rangle _n$ belongs to  $\mathsf {K}_1^{(0)}$ by Lemma 6.5.2. Moreover, for
$\mathsf {K}_1^{(0)}$ by Lemma 6.5.2. Moreover, for  $\gamma \in \mathrm {GL}_2(\mathbb {Z})$, we have
exactly as in equation (3.8) in the proof of Proposition 3.4.4.
$\gamma \in \mathrm {GL}_2(\mathbb {Z})$, we have
exactly as in equation (3.8) in the proof of Proposition 3.4.4. \[ (\gamma^*-1)T_{\ell}^{\mathsf{K}} \langle 0,1 \rangle_n = \partial (T_{\ell}\Theta)_{\gamma} \]
\[ (\gamma^*-1)T_{\ell}^{\mathsf{K}} \langle 0,1 \rangle_n = \partial (T_{\ell}\Theta)_{\gamma} \]
– The cocycle
 $T_{\ell }' ({}_n \Theta )$ is associated to
$T_{\ell }' ({}_n \Theta )$ is associated to  $T_{\ell }' e_n$, since
$T_{\ell }' e_n$, since  $T_{\ell }' \colon \mathsf {K} \to \mathsf {K}$ is a map of complexes that commutes with the
$T_{\ell }' \colon \mathsf {K} \to \mathsf {K}$ is a map of complexes that commutes with the  $\mathrm {GL}_2(\mathbb {Z})$-action by Lemma 6.5.1 and preserves fixed parts by Lemma 6.5.2.
$\mathrm {GL}_2(\mathbb {Z})$-action by Lemma 6.5.1 and preserves fixed parts by Lemma 6.5.2.
We must therefore show that ![]() $T_{\ell }' e_n = T_{\ell }^{\mathsf {K}} e_n$. We claim that it is enough to show the same assertion but replacing
$T_{\ell }' e_n = T_{\ell }^{\mathsf {K}} e_n$. We claim that it is enough to show the same assertion but replacing ![]() $e_n$ by the
$e_n$ by the ![]() $\mathrm {GL}_2(\mathbb {Z})$-fixed class
$\mathrm {GL}_2(\mathbb {Z})$-fixed class ![]() $(0) \in \mathsf {K}_0$. Indeed,
$(0) \in \mathsf {K}_0$. Indeed, ![]() $e_n = V_n^{\mathsf {K}} (0)$, with notation as in (6.8), and
$e_n = V_n^{\mathsf {K}} (0)$, with notation as in (6.8), and ![]() $T_{\ell }^{\mathsf {K}}$ and
$T_{\ell }^{\mathsf {K}}$ and ![]() $V_n^{\mathsf {K}}$ commute in their action on the
$V_n^{\mathsf {K}}$ commute in their action on the ![]() $\mathrm {GL}_2(\mathbb {Z})$-invariant subgroup of
$\mathrm {GL}_2(\mathbb {Z})$-invariant subgroup of ![]() $\mathsf {K}_0$, whereas
$\mathsf {K}_0$, whereas ![]() $T_{\ell }'$ and
$T_{\ell }'$ and ![]() $V_n^{\mathsf {K}}$ commute by Lemma 6.5.1 (noting
$V_n^{\mathsf {K}}$ commute by Lemma 6.5.1 (noting ![]() $V_n^{\mathsf {K}}$ is a sum of various pullback maps).
$V_n^{\mathsf {K}}$ is a sum of various pullback maps).
It therefore only remains to show that ![]() $T_{\ell }'(0) = T_{\ell }^{\mathsf {K}}(0)$. We will describe the fibers of
$T_{\ell }'(0) = T_{\ell }^{\mathsf {K}}(0)$. We will describe the fibers of ![]() $T_{\ell }'(0)$ and
$T_{\ell }'(0)$ and ![]() $T_{\ell }^{\mathsf {K}}(0)$ over a geometric point
$T_{\ell }^{\mathsf {K}}(0)$ over a geometric point ![]() $s$ of
$s$ of ![]() $Y$ and show that they coincide.
$Y$ and show that they coincide.
– The fiber of
 $T_{\ell }'(0)$ is the union of the kernels of all
$T_{\ell }'(0)$ is the union of the kernels of all  $\varphi ^2 \colon E_s^2 \to (E')^2$, where
$\varphi ^2 \colon E_s^2 \to (E')^2$, where  $E_s$ is the fiber of
$E_s$ is the fiber of  $\mathscr {E}$ over
$\mathscr {E}$ over  $s$ and
$s$ and  $\varphi \colon E_s \rightarrow E'$ is an
$\varphi \colon E_s \rightarrow E'$ is an  $\ell$-isogeny. In other words, it is the sum of all
$\ell$-isogeny. In other words, it is the sum of all  $K \times K$ where
$K \times K$ where  $K$ is a cyclic subgroup scheme of
$K$ is a cyclic subgroup scheme of  $E_s$ of order
$E_s$ of order  $\ell$:
(6.17)
$\ell$:
(6.17) \begin{align} T_{\ell}'(0) = \sum_{K} K \times K. \end{align}
\begin{align} T_{\ell}'(0) = \sum_{K} K \times K. \end{align}– The fiber of
 $T_{\ell }^{\mathsf {K}}(0)$ above
$T_{\ell }^{\mathsf {K}}(0)$ above  $s$ is given by those points of
$s$ is given by those points of  $E_s$ in the kernel of some matrix
$E_s$ in the kernel of some matrix  $g_j$ as in (3.6). Regarding
$g_j$ as in (3.6). Regarding  $j$ as valued in
$j$ as valued in  $\mathbb {P}^1(\mathbb {F}_{\ell })$, the kernel of
$\mathbb {P}^1(\mathbb {F}_{\ell })$, the kernel of  $g_j$ is the set of pairs
$g_j$ is the set of pairs  $(P,Q) \in E_s[\ell ]^2$ such that
$(P,Q) \in E_s[\ell ]^2$ such that  $Q/P =-j$ (by which we mean that if we write
$Q/P =-j$ (by which we mean that if we write  $j =a/b$, then
$j =a/b$, then  $aP+bQ=0$), and thus
(6.18)
$aP+bQ=0$), and thus
(6.18) \begin{equation} T_{\ell}^{\mathsf{K}}(0) = \sum_{j \in \mathbb{P}^1(\mathbb{F}_{\ell})} \{ (P, Q) \in E_s[\ell]^2 \mid P/Q = j \}. \end{equation}
\begin{equation} T_{\ell}^{\mathsf{K}}(0) = \sum_{j \in \mathbb{P}^1(\mathbb{F}_{\ell})} \{ (P, Q) \in E_s[\ell]^2 \mid P/Q = j \}. \end{equation}
One easily checks that (6.17) and (6.18) coincide. For example, if we choose a basis to identify ![]() $E_s[\ell ]$ with
$E_s[\ell ]$ with ![]() $\mathbb {F}_{\ell }^2$ and use this to identify
$\mathbb {F}_{\ell }^2$ and use this to identify ![]() $E_s[\ell ]^2$ with
$E_s[\ell ]^2$ with ![]() $M_2(\mathbb {F}_{\ell })$ with the columns giving the coordinates, then (6.17) and (6.18) become identified with the formal sums of matrices with linearly dependent rows and linearly dependent columns, respectively, in both cases counting the zero matrix with multiplicity
$M_2(\mathbb {F}_{\ell })$ with the columns giving the coordinates, then (6.17) and (6.18) become identified with the formal sums of matrices with linearly dependent rows and linearly dependent columns, respectively, in both cases counting the zero matrix with multiplicity ![]() $\ell +1$.
$\ell +1$.
Finally, to see that the classes of ![]() $[\ell ]^*({}_n \Theta )$ and
$[\ell ]^*({}_n \Theta )$ and ![]() $[\ell ]'({}_n \Theta )$ are equal, it is similarly enough to show that
$[\ell ]'({}_n \Theta )$ are equal, it is similarly enough to show that ![]() $[\ell ]^*(0) = [\ell ]'(0)$. This is immediate: both amount to pullback of the zero section by the matrix
$[\ell ]^*(0) = [\ell ]'(0)$. This is immediate: both amount to pullback of the zero section by the matrix ![]() $\big (\begin{smallmatrix} \ell & 0 \\ 0 & \ell \end{smallmatrix}\big )$, so equal
$\big (\begin{smallmatrix} \ell & 0 \\ 0 & \ell \end{smallmatrix}\big )$, so equal ![]() $\mathscr {E}[\ell ]^2$.
$\mathscr {E}[\ell ]^2$.
7. Cocycles for modular curves
In this section, we pull back the cocycles of § 6 to the modular curve via a torsion section.
As before, we fix ![]() $N \ge 4$ and a prime
$N \ge 4$ and a prime ![]() $n \nmid N$, and we write
$n \nmid N$, and we write ![]() $Y = Y_1(N)$ and
$Y = Y_1(N)$ and ![]() $\mathscr {E}$ for the universal elliptic curve above
$\mathscr {E}$ for the universal elliptic curve above ![]() $Y$. The surjection
$Y$. The surjection ![]() $\pi \colon \mathscr {E} \to Y$ has a canonical
$\pi \colon \mathscr {E} \to Y$ has a canonical ![]() $N$-torsion section
$N$-torsion section ![]() $\iota _N \colon Y \to \mathscr {E}[N]$. In § 7.1, we pull back the cocycle
$\iota _N \colon Y \to \mathscr {E}[N]$. In § 7.1, we pull back the cocycle ![]() ${}_n\Theta$ of Theorem 6.4.1 by the section of
${}_n\Theta$ of Theorem 6.4.1 by the section of ![]() $\pi ^2 \colon \mathscr {E}^2 \to Y$ given by
$\pi ^2 \colon \mathscr {E}^2 \to Y$ given by
We denote the result by ![]() ${}_n \Theta _N$. In order to make sense of such a pullback, we must, as in the case of
${}_n \Theta _N$. In order to make sense of such a pullback, we must, as in the case of ![]() $\mathbb {G}_m^2$ described in § 4.2, restrict our cocycle to the congruence subgroup
$\mathbb {G}_m^2$ described in § 4.2, restrict our cocycle to the congruence subgroup ![]() $\tilde {\Gamma }_0(N)$ of
$\tilde {\Gamma }_0(N)$ of ![]() $\mathrm {GL}_2(\mathbb {Z})$ defined in (4.4) to consist of matrices with lower-left entry divisible by
$\mathrm {GL}_2(\mathbb {Z})$ defined in (4.4) to consist of matrices with lower-left entry divisible by ![]() $N$.
$N$.
In § 7.2, we describe modifications that enable us to obtain a universal cocycle ![]() $\Theta _N$ that should be thought of as the ‘
$\Theta _N$ that should be thought of as the ‘![]() $n=1$’ version of the construction; see Theorem 7.2.2. Much as with theta functions, we do not know how to make sense of this on the universal elliptic curve, but we can do so after pullback. The characterizing property of
$n=1$’ version of the construction; see Theorem 7.2.2. Much as with theta functions, we do not know how to make sense of this on the universal elliptic curve, but we can do so after pullback. The characterizing property of ![]() $\Theta _N$ is that it gives rise to each
$\Theta _N$ is that it gives rise to each ![]() ${}_n \Theta _N$ upon application of the Hecke operator
${}_n \Theta _N$ upon application of the Hecke operator ![]() $V_n = n^4 - n^2 T_n + n[n]^*$ or its counterpart
$V_n = n^4 - n^2 T_n + n[n]^*$ or its counterpart ![]() $V'_n = n^4 - n^2 T'_n + n[n]'$. In § 7.3, we prove an explicit formula for this universal cocycle
$V'_n = n^4 - n^2 T'_n + n[n]'$. In § 7.3, we prove an explicit formula for this universal cocycle ![]() $\Theta _N$ modulo a subgroup that vanishes under standard regulator maps.
$\Theta _N$ modulo a subgroup that vanishes under standard regulator maps.
Finally, in § 7.4, we construct the zeta map ![]() $z_N$ of (1.2) and compare with the prior work of Goncharov, Brunault, and Fukaya and Kato. The map
$z_N$ of (1.2) and compare with the prior work of Goncharov, Brunault, and Fukaya and Kato. The map ![]() $z_N$ is constructed in Theorem 7.4.1, where we show that it is Hecke equivariant and takes values in the motivic cohomology of
$z_N$ is constructed in Theorem 7.4.1, where we show that it is Hecke equivariant and takes values in the motivic cohomology of ![]() $X_1(N)$ (over
$X_1(N)$ (over ![]() $\mathbb {Z}[{1}/{N}]$), as opposed to
$\mathbb {Z}[{1}/{N}]$), as opposed to ![]() $Y_1(N)$. We also describe an integral, ordinary
$Y_1(N)$. We also describe an integral, ordinary ![]() $p$-adic analogue in Proposition 7.4.2.
$p$-adic analogue in Proposition 7.4.2.
We suppose that ![]() $\mathbb {Z}' = \mathbb {Z}[\frac {1}{30}]$ throughout this section.
$\mathbb {Z}' = \mathbb {Z}[\frac {1}{30}]$ throughout this section.
7.1 Specialization via an  $N$-torsion section
$N$-torsion section
In this subsection, we pull back our cocycles ![]() ${}_n \Theta$ for primes
${}_n \Theta$ for primes ![]() $n \nmid N$ via the
$n \nmid N$ via the ![]() $N$-torsion section
$N$-torsion section ![]() $s \colon Y \to \mathscr {E}^2$ to obtain cocycles
$s \colon Y \to \mathscr {E}^2$ to obtain cocycles ![]() ${}_n \Theta _N \colon \tilde {\Gamma }_0(N) \to H^2(Y,\mathbb {Z}'(2))$.
${}_n \Theta _N \colon \tilde {\Gamma }_0(N) \to H^2(Y,\mathbb {Z}'(2))$.
7.1.1 Comparison of Hecke operators upon restriction
As in the case of ![]() $\mathbb {G}_m^2$, the section
$\mathbb {G}_m^2$, the section ![]() $s$ is not defined on all of
$s$ is not defined on all of ![]() $\mathsf {K}_2$ but at least on classes ‘regular along
$\mathsf {K}_2$ but at least on classes ‘regular along ![]() $s$’. Writing
$s$’. Writing
where ![]() $U$ runs over the open
$U$ runs over the open ![]() $Y$-subschemes of
$Y$-subschemes of ![]() $\mathscr {E}^2$ containing all prime-to-
$\mathscr {E}^2$ containing all prime-to-![]() $N$ multiples of the image of
$N$ multiples of the image of ![]() $s$, we have a specialization map
$s$, we have a specialization map
and similarly we can pull back by any prime-to-![]() $N$ multiple of
$N$ multiple of ![]() $s$.Footnote 23
$s$.Footnote 23
Now, for ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, we have in fact
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \tilde {\Gamma }_0(N)$, we have in fact ![]() ${}_n \Theta _{\gamma } \in \mathsf {K}_2(N)$. Indeed, write
${}_n \Theta _{\gamma } \in \mathsf {K}_2(N)$. Indeed, write ![]() $U_{\gamma } = \mathscr {E}^2 - S_{0,n} \cup S_{nb,nd}$, that is to say,
$U_{\gamma } = \mathscr {E}^2 - S_{0,n} \cup S_{nb,nd}$, that is to say, ![]() $U_{\gamma }$ is the complement in
$U_{\gamma }$ is the complement in ![]() $\mathscr {E}^2$ of the kernels of the maps
$\mathscr {E}^2$ of the kernels of the maps ![]() $\mathscr {E}^2 \rightarrow \mathscr {E}$ defined by
$\mathscr {E}^2 \rightarrow \mathscr {E}$ defined by ![]() $(P,Q) \mapsto n Q$ and
$(P,Q) \mapsto n Q$ and ![]() $(P,Q) \mapsto n (bP +dQ)$. Then
$(P,Q) \mapsto n (bP +dQ)$. Then ![]() $\partial ({}_n\Theta _{\gamma }) = (\gamma ^*-1)\langle 0,1 \rangle _n$ lies in
$\partial ({}_n\Theta _{\gamma }) = (\gamma ^*-1)\langle 0,1 \rangle _n$ lies in ![]() $H^1(S_{0,n},1)^{(0)} \oplus H^1(S_{nb,nd},1)^{(0)}$ inside
$H^1(S_{0,n},1)^{(0)} \oplus H^1(S_{nb,nd},1)^{(0)}$ inside ![]() $\mathsf {K}_1^{(0)}$. Since
$\mathsf {K}_1^{(0)}$. Since ![]() $s$ and its multiples do not lie on either
$s$ and its multiples do not lie on either ![]() $S_{0,n}$ or
$S_{0,n}$ or ![]() $S_{nb,nd}$, it follows that
$S_{nb,nd}$, it follows that ![]() ${}_n\Theta _{\gamma } \in H^2(U_{\gamma },2)$. Moreover, the image of any prime-to-
${}_n\Theta _{\gamma } \in H^2(U_{\gamma },2)$. Moreover, the image of any prime-to-![]() $N$ multiple of
$N$ multiple of ![]() $s$ is contained in
$s$ is contained in ![]() $U_{\gamma }$ as
$U_{\gamma }$ as ![]() $N \nmid d$. In this way, the cocycle
$N \nmid d$. In this way, the cocycle ![]() ${}_n \Theta$ restricted to
${}_n \Theta$ restricted to ![]() $\tilde {\Gamma }_0(N)$ takes values in
$\tilde {\Gamma }_0(N)$ takes values in ![]() $\mathsf {K}_2(N) \subset \mathsf {K}_2$.Footnote 24
$\mathsf {K}_2(N) \subset \mathsf {K}_2$.Footnote 24
The operators ![]() $T_{\ell }$ and
$T_{\ell }$ and ![]() $T_{\ell }'$ act on
$T_{\ell }'$ act on ![]() $H^1(\tilde {\Gamma }_0(N),\mathsf {K}_2)$ and lift naturally to
$H^1(\tilde {\Gamma }_0(N),\mathsf {K}_2)$ and lift naturally to ![]() $H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2(N))$. For
$H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2(N))$. For ![]() $T_{\ell }$, this is simply because the action of
$T_{\ell }$, this is simply because the action of ![]() $\Delta _0(N)$, as defined in (4.6), sends the section
$\Delta _0(N)$, as defined in (4.6), sends the section ![]() $s$ to a multiple of itself and therefore preserves
$s$ to a multiple of itself and therefore preserves ![]() $\mathsf {K}_2(N)$. For
$\mathsf {K}_2(N)$. For ![]() $T_{\ell }' = \Phi ^2_*(\Psi ^2)^*$ as in § 6.5.1, consider the diagram
$T_{\ell }' = \Phi ^2_*(\Psi ^2)^*$ as in § 6.5.1, consider the diagram

and note that ![]() $\Psi ^2$ preserves
$\Psi ^2$ preserves ![]() $s$, whereas the preimage of the image of
$s$, whereas the preimage of the image of ![]() $s$ under
$s$ under ![]() $\Phi ^2$ is again the image of
$\Phi ^2$ is again the image of ![]() $(s,\mathrm {id})$.
$(s,\mathrm {id})$.
Lemma 7.1.1 For primes ![]() $\ell \nmid N$, the classes of
$\ell \nmid N$, the classes of ![]() $T'_{\ell }({}_n \Theta )$ and
$T'_{\ell }({}_n \Theta )$ and ![]() $T_{\ell }({}_n \Theta )$ coincide in
$T_{\ell }({}_n \Theta )$ coincide in ![]() $H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2(N))$, as do the classes of
$H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2(N))$, as do the classes of ![]() $[\ell ]'({}_n\Theta )$ and
$[\ell ]'({}_n\Theta )$ and ![]() $[\ell ]^*({}_n\Theta )$.
$[\ell ]^*({}_n\Theta )$.
Proof. Theorem 6.5.4 implies that ![]() $T'_{\ell }( {}_n \Theta )$ and
$T'_{\ell }( {}_n \Theta )$ and ![]() $T_{\ell }( {}_n \Theta )$, as well as
$T_{\ell }( {}_n \Theta )$, as well as ![]() $[\ell ]'({}_n\Theta )$ and
$[\ell ]'({}_n\Theta )$ and ![]() $[\ell ]^*({}_n\Theta )$, are cohomologous when considered with target
$[\ell ]^*({}_n\Theta )$, are cohomologous when considered with target ![]() $\mathsf {K}_2$. So it is enough to check the following claim regarding the inclusion
$\mathsf {K}_2$. So it is enough to check the following claim regarding the inclusion ![]() $\mathsf {K}_2(N) \hookrightarrow \mathsf {K}_2$:
$\mathsf {K}_2(N) \hookrightarrow \mathsf {K}_2$:
This injectivity will follow from the Gysin sequence analogous to (4.11) into which the above inclusion fits if one proves the infinitude of all ![]() $\mathrm {GL}_2(\mathbb {Z})$-orbits of irreducible divisors on
$\mathrm {GL}_2(\mathbb {Z})$-orbits of irreducible divisors on ![]() $\mathscr {E}^2$ containing the image of
$\mathscr {E}^2$ containing the image of ![]() $s$. Such a divisor induces a divisor on the fiber
$s$. Such a divisor induces a divisor on the fiber ![]() $E^2$ of
$E^2$ of ![]() $\mathscr {E}^2$ over the generic point of
$\mathscr {E}^2$ over the generic point of ![]() $Y_1(N)$. Restricting to this fiber, it is enough to prove that, for a non-CM elliptic curve over a field
$Y_1(N)$. Restricting to this fiber, it is enough to prove that, for a non-CM elliptic curve over a field ![]() $K$ (in our case, the function field of
$K$ (in our case, the function field of ![]() $Y_1(N)$) and an irreducible
$Y_1(N)$) and an irreducible ![]() $K$-divisor
$K$-divisor ![]() $D$ on
$D$ on ![]() $E^2$, the
$E^2$, the ![]() $\mathrm {SL}_2(\mathbb {Z})$-orbit of
$\mathrm {SL}_2(\mathbb {Z})$-orbit of ![]() $D$ is infinite. In fact, this is even true at the level of the Néron–Severi group: by [Reference Rosen and ShnidmanRS17, Theorem 4.2], the
$D$ is infinite. In fact, this is even true at the level of the Néron–Severi group: by [Reference Rosen and ShnidmanRS17, Theorem 4.2], the ![]() $\mathbb {Q}$-vector space
$\mathbb {Q}$-vector space ![]() $\mathrm {NS}(E^2) \otimes _{\mathbb {Z}} \mathbb {Q}$ realizes the representation of
$\mathrm {NS}(E^2) \otimes _{\mathbb {Z}} \mathbb {Q}$ realizes the representation of ![]() $\mathrm {SL}_2(\mathbb {Z})$ on binary quadratic forms. In this representation, all nonzero orbits are infinite, and the class of
$\mathrm {SL}_2(\mathbb {Z})$ on binary quadratic forms. In this representation, all nonzero orbits are infinite, and the class of ![]() $D$ in the Néron–Severi group is nonzero because its intersection with a suitable hyperplane section is nonzero.
$D$ in the Néron–Severi group is nonzero because its intersection with a suitable hyperplane section is nonzero.
7.1.2 Specialization of the cocycles
Through the right action of ![]() $\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ on
$\Delta = M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ on ![]() $\mathscr {E}^2$, which preserves fibers, any
$\mathscr {E}^2$, which preserves fibers, any ![]() $\delta = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$ acts on the
$\delta = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$ acts on the ![]() $N$-torsion sections of
$N$-torsion sections of ![]() $\mathscr {E}^2 \to Y$. This action of
$\mathscr {E}^2 \to Y$. This action of ![]() $\Delta _0(N)$ does not preserve the section
$\Delta _0(N)$ does not preserve the section ![]() $s$. Indeed, let us agree to write points of
$s$. Indeed, let us agree to write points of ![]() $\mathscr {E}^2$ as triples
$\mathscr {E}^2$ as triples ![]() $((E, P), x, y)$, where
$((E, P), x, y)$, where ![]() $E$ is an elliptic curve and
$E$ is an elliptic curve and ![]() $P$ is an
$P$ is an ![]() $N$-torsion point on
$N$-torsion point on ![]() $E$ (so that
$E$ (so that ![]() $(E,P)$ defines a point of
$(E,P)$ defines a point of ![]() $Y$) and
$Y$) and ![]() $x$,
$x$, ![]() $y$ are points of
$y$ are points of ![]() $E$. With this notation, we compute
$E$. With this notation, we compute ![]() $\delta \circ s$:
$\delta \circ s$:
This does not coincide with ![]() $s \circ [d]'$, where
$s \circ [d]'$, where ![]() $[d]'$ for
$[d]'$ for ![]() $d$ prime to
$d$ prime to ![]() $N$ is the diamond operator on
$N$ is the diamond operator on ![]() $Y_1(N)$ that sends
$Y_1(N)$ that sends ![]() $(E,P)$ to
$(E,P)$ to ![]() $(E, dP)$. Rather,
$(E, dP)$. Rather,
where ![]() $\phi _d \colon \mathscr {E}^2 \rightarrow \mathscr {E}^2$ sends
$\phi _d \colon \mathscr {E}^2 \rightarrow \mathscr {E}^2$ sends ![]() $((E, P), x, y)$ to
$((E, P), x, y)$ to ![]() $((E, d P), x, y)$.
$((E, d P), x, y)$.
Consider the action of ![]() $\Delta _0(N)$ on
$\Delta _0(N)$ on ![]() $H^2(Y_1(N),\mathbb {Z}(2))$ whereby
$H^2(Y_1(N),\mathbb {Z}(2))$ whereby ![]() $\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$ acts as
$\big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \Delta _0(N)$ acts as ![]() $[d]'$, that is,
$[d]'$, that is, ![]() $\Delta _0(N)$ acts through its lower right-hand map to
$\Delta _0(N)$ acts through its lower right-hand map to ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$.
Lemma 7.1.2 The restriction of the pullback map
to the ![]() $\mathbb {Z}[\Delta _0(N)]$-span of the image of
$\mathbb {Z}[\Delta _0(N)]$-span of the image of ![]() ${}_n \Theta$ on
${}_n \Theta$ on ![]() $\tilde {\Gamma }_0(N)$ is
$\tilde {\Gamma }_0(N)$ is ![]() $\Delta _0(N)$-equivariant.
$\Delta _0(N)$-equivariant.
Proof. In fact, if ![]() $x \in \mathsf {K}_2(N)$ is fixed by
$x \in \mathsf {K}_2(N)$ is fixed by ![]() $\phi _d^*$ with
$\phi _d^*$ with ![]() $\phi _d$ as defined above, then by (7.2) we have
$\phi _d$ as defined above, then by (7.2) we have
Thus, we need only show that
for all ![]() $\gamma \in \widetilde {\Gamma }_0(N)$.
$\gamma \in \widetilde {\Gamma }_0(N)$.
By the characterization of ![]() ${}_n \Theta$ in part (a) of Theorem 6.4.1, it is sufficient to verify that
${}_n \Theta$ in part (a) of Theorem 6.4.1, it is sufficient to verify that ![]() $\phi _d^*$ preserves
$\phi _d^*$ preserves ![]() $\mathsf {K}_2^{(0)}$ and fixes
$\mathsf {K}_2^{(0)}$ and fixes ![]() $\langle 0, 1 \rangle _n$. It preserves
$\langle 0, 1 \rangle _n$. It preserves ![]() $\mathsf {K}_2^{(0)}$ as the relevant diagram with
$\mathsf {K}_2^{(0)}$ as the relevant diagram with ![]() $\phi _d$ and
$\phi _d$ and ![]() $[m]$ is evidently cartesian, and it fixes
$[m]$ is evidently cartesian, and it fixes ![]() $\langle 0,1 \rangle _n$ since the latter is ‘pulled back from level
$\langle 0,1 \rangle _n$ since the latter is ‘pulled back from level ![]() $1$’; in particular, it restricts to the same function on the fiber
$1$’; in particular, it restricts to the same function on the fiber ![]() $E^2$ over
$E^2$ over ![]() $(E,P)$ and
$(E,P)$ and ![]() $(E,dP)$.
$(E,dP)$.
Recall that ![]() $T_{\ell }$ acts on the group of cocycles
$T_{\ell }$ acts on the group of cocycles ![]() $\tilde {\Gamma }_0(N) \to H^2(Y, \mathbb {Z}'(2))$ as in (3.5) (where we view
$\tilde {\Gamma }_0(N) \to H^2(Y, \mathbb {Z}'(2))$ as in (3.5) (where we view ![]() $H^2(Y,\mathbb {Z}'(2))$ as a
$H^2(Y,\mathbb {Z}'(2))$ as a ![]() $\mathbb {Z}[\Delta _0(N)]$-module as above), preserving coboundaries, whereas
$\mathbb {Z}[\Delta _0(N)]$-module as above), preserving coboundaries, whereas ![]() $T_{\ell }'$ acts on such cocycles through its action on the motivic cohomology of
$T_{\ell }'$ acts on such cocycles through its action on the motivic cohomology of ![]() $Y$ defined in (6.15). The foregoing lemmas, taken together, have established the following proposition.
$Y$ defined in (6.15). The foregoing lemmas, taken together, have established the following proposition.
Proposition 7.1.3 For ![]() $\gamma \in \tilde {\Gamma }_0(N)$, set
$\gamma \in \tilde {\Gamma }_0(N)$, set
(a) The map
is a parabolic cocycle. \[ {}_n\Theta_N \colon \tilde{\Gamma}_0(N) \to H^2(Y,\mathbb{Z}'(2)), \quad \gamma \mapsto {}_n\Theta_{N,\gamma} \]
\[ {}_n\Theta_N \colon \tilde{\Gamma}_0(N) \to H^2(Y,\mathbb{Z}'(2)), \quad \gamma \mapsto {}_n\Theta_{N,\gamma} \]
(b) For each prime
 $\ell \nmid N$, the cocycles
$\ell \nmid N$, the cocycles  $T_{\ell }({}_n\Theta _N)$ and
$T_{\ell }({}_n\Theta _N)$ and  $T'_{\ell }({}_n\Theta _N)$ are cohomologous.
$T'_{\ell }({}_n\Theta _N)$ are cohomologous.
Proof. For part (a), that ![]() ${}_n \Theta _N$ is a cocycle is clear from Lemmas 7.1.1 and 7.1.2. That it is parabolic at all but the parabolic
${}_n \Theta _N$ is a cocycle is clear from Lemmas 7.1.1 and 7.1.2. That it is parabolic at all but the parabolic ![]() $Q = \{ \big (\begin{smallmatrix} \pm 1 & n \\ 0 & 1 \end{smallmatrix}\!\big) \mid n \in \mathbb {Z}\}$ follows from a nearly identical argument to that of Proposition 4.2.1, using the parabolicity of
$Q = \{ \big (\begin{smallmatrix} \pm 1 & n \\ 0 & 1 \end{smallmatrix}\!\big) \mid n \in \mathbb {Z}\}$ follows from a nearly identical argument to that of Proposition 4.2.1, using the parabolicity of ![]() ${}_n\Theta$ in Theorem 6.4.1(b) and the equivariance of
${}_n\Theta$ in Theorem 6.4.1(b) and the equivariance of ![]() $s^*$ of Lemma 7.1.2. However, to see that
$s^*$ of Lemma 7.1.2. However, to see that ![]() ${}_n \Theta _N$ is a coboundary on the exceptional parabolic
${}_n \Theta _N$ is a coboundary on the exceptional parabolic ![]() $Q$, we argue differently. Since
$Q$, we argue differently. Since ![]() $2$ is invertible in
$2$ is invertible in ![]() $\mathbb {Z}'$ and
$\mathbb {Z}'$ and ![]() $Q \cong \mathbb {Z} \rtimes \mathbb {Z}/2\mathbb {Z}$, it suffices to see that
$Q \cong \mathbb {Z} \rtimes \mathbb {Z}/2\mathbb {Z}$, it suffices to see that ![]() ${}_n \Theta _N$ vanishes on the generator
${}_n \Theta _N$ vanishes on the generator ![]() $\gamma _0 = \big (\begin{smallmatrix} 1 & -1 \\ 0 & 1 \end{smallmatrix}\!\big)$ of the unipotent subgroup of
$\gamma _0 = \big (\begin{smallmatrix} 1 & -1 \\ 0 & 1 \end{smallmatrix}\!\big)$ of the unipotent subgroup of ![]() $Q$. Using (6.12) for the connecting sequence
$Q$. Using (6.12) for the connecting sequence ![]() $v_0=(0,1)$,
$v_0=(0,1)$, ![]() $v_1=(-1,1)$ for
$v_1=(-1,1)$ for ![]() $\gamma _0$ and then applying (6.10) and (6.11), we obtain
$\gamma _0$ and then applying (6.10) and (6.11), we obtain
Since ![]() $\langle \big (\begin{smallmatrix} -1 & 0 \\ 1 & -1 \end{smallmatrix}\big )\rangle$ applied to the section
$\langle \big (\begin{smallmatrix} -1 & 0 \\ 1 & -1 \end{smallmatrix}\big )\rangle$ applied to the section ![]() $s=(0,\iota _N)$ gives
$s=(0,\iota _N)$ gives ![]() $(\iota _N, -\iota _N)$, this becomes
$(\iota _N, -\iota _N)$, this becomes
where ![]() $\iota '_N \colon Y' \to (\mathscr {E}')^2$ is the canonical
$\iota '_N \colon Y' \to (\mathscr {E}')^2$ is the canonical ![]() $N$-torsion section and the norm is from
$N$-torsion section and the norm is from ![]() $Y'$ to
$Y'$ to ![]() $Y$. The two terms in the above expression vanish by the evenness of
$Y$. The two terms in the above expression vanish by the evenness of ![]() $\theta$ and
$\theta$ and ![]() $\theta '$ and the skew-symmetry of the cup product with
$\theta '$ and the skew-symmetry of the cup product with ![]() $\mathbb {Z}'$-coefficients (cf. [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 15.9]).
$\mathbb {Z}'$-coefficients (cf. [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 15.9]).
As for part (b), let ![]() $\ell$ be a prime not dividing
$\ell$ be a prime not dividing ![]() $N$. By Lemma 7.1.2, we have
$N$. By Lemma 7.1.2, we have ![]() $s^* T_{\ell } ({}_n \Theta ) = T_{\ell } ({}_n \Theta _N)$. Moreover,
$s^* T_{\ell } ({}_n \Theta ) = T_{\ell } ({}_n \Theta _N)$. Moreover, ![]() $\iota _N^* \Phi _*\Psi ^* = \phi _*\psi ^*\iota _N^*$ since in the diagram
$\iota _N^* \Phi _*\Psi ^* = \phi _*\psi ^*\iota _N^*$ since in the diagram

the right-hand square commutes and the left-hand square is cartesian. The analogue for ![]() $\mathscr {E}^2$ then holds with
$\mathscr {E}^2$ then holds with ![]() $\iota _N$ replaced by
$\iota _N$ replaced by ![]() $s$, and therefore we have
$s$, and therefore we have ![]() $s^*T'_{\ell }({}_n \Theta ) = T'_{\ell }({}_n \Theta _N)$ as well. Again recalling Lemma 7.1.1, we conclude that the cohomology classes of
$s^*T'_{\ell }({}_n \Theta ) = T'_{\ell }({}_n \Theta _N)$ as well. Again recalling Lemma 7.1.1, we conclude that the cohomology classes of ![]() $T_{\ell }({}_n\Theta _N)$ and
$T_{\ell }({}_n\Theta _N)$ and ![]() $T'_{\ell }({}_n\Theta _N)$ are equal.
$T'_{\ell }({}_n\Theta _N)$ are equal.
There is also a formula for ![]() ${}_n\Theta _{N,\gamma }$ as a sum of cup products of Siegel units that follows in the obvious way by specializing (6.12); we do not write it down here, but we will discuss its ‘
${}_n\Theta _{N,\gamma }$ as a sum of cup products of Siegel units that follows in the obvious way by specializing (6.12); we do not write it down here, but we will discuss its ‘![]() $n=1$’ analogue in the next section.
$n=1$’ analogue in the next section.
7.2 The universal ‘ $n=1$’ cocycle
$n=1$’ cocycle
The cocycle
constructed above depends on the choice of an auxiliary prime ![]() $n$ in addition to the level
$n$ in addition to the level ![]() $N$. As we shall detail, it satisfies a simple distribution relation in
$N$. As we shall detail, it satisfies a simple distribution relation in ![]() $n$ that permits us to construct an ‘
$n$ that permits us to construct an ‘![]() $n=1$’ version rationally.
$n=1$’ version rationally.
7.2.1 Relation between cocycles and statement of the result
Suppose that ![]() $\ell$ is a prime with
$\ell$ is a prime with ![]() $\ell \nmid N$. Set
$\ell \nmid N$. Set
As in § 6.5, the operator ![]() $V_{\ell }'$ acts on
$V_{\ell }'$ acts on ![]() $\mathsf {K}$, and the operator
$\mathsf {K}$, and the operator ![]() $V_{\ell }$ acts on cocycles valued in
$V_{\ell }$ acts on cocycles valued in ![]() $\mathsf {K}_2$. (Strictly speaking, the action of
$\mathsf {K}_2$. (Strictly speaking, the action of ![]() $V_{\ell }$ depends on choice of representatives for the double coset of
$V_{\ell }$ depends on choice of representatives for the double coset of ![]() $\big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, but recall that we made a particular choice in defining
$\big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$, but recall that we made a particular choice in defining ![]() $T_{\ell }$ in § 3.4.) For example, one has by (6.8) the equality
$T_{\ell }$ in § 3.4.) For example, one has by (6.8) the equality ![]() $e_n = V_n(0)$ in
$e_n = V_n(0)$ in ![]() $H^0(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_0)$. Beyond this, these operators act on several closely related groups; for convenience, we summarize some of these actions and their relationships.
$H^0(\mathrm {GL}_2(\mathbb {Z}),\mathsf {K}_0)$. Beyond this, these operators act on several closely related groups; for convenience, we summarize some of these actions and their relationships.
(i) As in the discussion prior to Lemma 7.1.1, the operator
 $V'_{\ell }$ acts directly on
$V'_{\ell }$ acts directly on  $\mathsf {K}_2(N)$, and
$\mathsf {K}_2(N)$, and  $V_{\ell }$ acts on
$V_{\ell }$ acts on  $H^*( \mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2(N))$.
$H^*( \mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2(N))$.(ii) Using double cosets of
 $\tilde {\Gamma }_0(N)$ inside
$\tilde {\Gamma }_0(N)$ inside  $\Delta _0(N)$, the operator
$\Delta _0(N)$, the operator  $V_{\ell }$ acts on
$V_{\ell }$ acts on  $H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$ compatibly with the restriction map
$H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$ compatibly with the restriction map  $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2) \rightarrow H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$.
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2) \rightarrow H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$.(iii) As in Proposition 7.1.3, the operators
 $V_{\ell }$ and
$V_{\ell }$ and  $V'_{\ell }$ both act on
$V'_{\ell }$ both act on  $H^1(\tilde {\Gamma }_0(N), H^2(Y_1(N), \mathbb {Z}'(2)))$. The specialization map
$H^1(\tilde {\Gamma }_0(N), H^2(Y_1(N), \mathbb {Z}'(2)))$. The specialization map  $\mathsf {K}_2(N) \rightarrow H^2(Y_1(N), \mathbb {Z}'(2))$ is equivariant for both operators; this is argued just as in the proof of said proposition.
$\mathsf {K}_2(N) \rightarrow H^2(Y_1(N), \mathbb {Z}'(2))$ is equivariant for both operators; this is argued just as in the proof of said proposition.
The ‘distribution relation’ between our cocycles is then as follows.
Lemma 7.2.1 For any prime ![]() $\ell \nmid N$, the classes of
$\ell \nmid N$, the classes of ![]() $V_{\ell }({}_n\Theta _{N})$ and
$V_{\ell }({}_n\Theta _{N})$ and ![]() $V_n({}_{\ell }\Theta _{N})$ are equal.
$V_n({}_{\ell }\Theta _{N})$ are equal.
Proof. The lemma follows by specialization via ![]() $s^*$, noting point (iii) above, from the claim that
$s^*$, noting point (iii) above, from the claim that
By (7.1), it suffices to prove this instead with target ![]() $\mathsf {K}_2$. Noting point (ii) above, it is, moreover, sufficient to prove the equality inside
$\mathsf {K}_2$. Noting point (ii) above, it is, moreover, sufficient to prove the equality inside ![]() $H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2)$ rather than
$H^1(\mathrm {GL}_2(\mathbb {Z}), \mathsf {K}_2)$ rather than ![]() $H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$, and then, by Theorem 6.5.4, it is sufficient to prove it with the
$H^1(\tilde {\Gamma }_0(N), \mathsf {K}_2)$, and then, by Theorem 6.5.4, it is sufficient to prove it with the ![]() $V$-operators replaced by the
$V$-operators replaced by the ![]() $V'$-operators. But just as in the proof of Theorem 6.5.4, this is a consequence of the fact that
$V'$-operators. But just as in the proof of Theorem 6.5.4, this is a consequence of the fact that ![]() $V'_{\ell } e_n = V'_n e_{\ell } = V'_{\ell } V'_n (0)$.
$V'_{\ell } e_n = V'_n e_{\ell } = V'_{\ell } V'_n (0)$.
Let us state the main theorem of this section.
Theorem 7.2.2 There exists a parabolic cocycle
with class uniquely specified by the property that the classes of ![]() $V_{\ell }(\Theta _N)$ and
$V_{\ell }(\Theta _N)$ and ![]() ${}_{\ell } \Theta _N$ are equal for each
${}_{\ell } \Theta _N$ are equal for each ![]() $\ell$ not dividing
$\ell$ not dividing ![]() $N$. Moreover,
$N$. Moreover, ![]() $T_n$ and
$T_n$ and ![]() $T_n'$ coincide on the class of
$T_n'$ coincide on the class of ![]() $\Theta _N$ for all primes
$\Theta _N$ for all primes ![]() $n \nmid N$.
$n \nmid N$.
The proof requires the following statement about the ring-theoretic structure of the Hecke algebra.
Proposition 7.2.3 Set ![]() $M = H^2(Y, \mathbb {Z}'[{1}/{N}](2))$, and let
$M = H^2(Y, \mathbb {Z}'[{1}/{N}](2))$, and let ![]() $\mathbb {T}_M$ be the subalgebra of the
$\mathbb {T}_M$ be the subalgebra of the ![]() $\mathbb {Z}'[{1}/{N}]$-endomorphism ring of
$\mathbb {Z}'[{1}/{N}]$-endomorphism ring of ![]() $H^1(\tilde {\Gamma }_0(N),M)$ generated by all
$H^1(\tilde {\Gamma }_0(N),M)$ generated by all ![]() $T_{\ell }$ for primes
$T_{\ell }$ for primes ![]() $\ell \nmid N$ and
$\ell \nmid N$ and ![]() $[d]'$ for
$[d]'$ for ![]() $d$ prime to
$d$ prime to ![]() $N$. Then the operators
$N$. Then the operators ![]() $V_n$ for primes
$V_n$ for primes ![]() $n \nmid N$ generate
$n \nmid N$ generate ![]() $\mathbb {T}_M$.
$\mathbb {T}_M$.
We will prove Proposition 7.2.3 in the remainder of this section. Namely, we will show in Lemma 7.2.5 that the algebra ![]() $\mathbb {T}_M$ is a quotient of the
$\mathbb {T}_M$ is a quotient of the ![]() $\mathbb {Z}'[{1}/{N}]$-Hecke algebra
$\mathbb {Z}'[{1}/{N}]$-Hecke algebra ![]() $\mathbb {T}$ of weight
$\mathbb {T}$ of weight ![]() $2$ modular forms for
$2$ modular forms for ![]() $\Gamma _1(N)$, with
$\Gamma _1(N)$, with ![]() $T_{\ell }$ mapping to
$T_{\ell }$ mapping to ![]() $T_{\ell }$ and
$T_{\ell }$ and ![]() $\langle d \rangle$ mapping to
$\langle d \rangle$ mapping to ![]() $[d]'$, and we will show in Proposition 7.2.6 that the
$[d]'$, and we will show in Proposition 7.2.6 that the ![]() $V_n$-operators generate
$V_n$-operators generate ![]() $\mathbb {T}$. This last statement uses the structure of Galois representations attached to level
$\mathbb {T}$. This last statement uses the structure of Galois representations attached to level ![]() $N$ eigenforms.
$N$ eigenforms.
We now prove Theorem 7.2.2 assuming Proposition 7.2.3.
Proof of Theorem 7.2.2 To construct ![]() $\Theta _N$, let us choose operators
$\Theta _N$, let us choose operators ![]() $r_i \in \mathbb {T}_M$ and primes
$r_i \in \mathbb {T}_M$ and primes ![]() $n_i \nmid N$ for
$n_i \nmid N$ for ![]() $1 \le i \le t$ for some
$1 \le i \le t$ for some ![]() $t$ such that
$t$ such that ![]() $\sum _{i=1}^t r_i V_{n_i} = 1$. We then set
$\sum _{i=1}^t r_i V_{n_i} = 1$. We then set ![]() $\Theta _N = \sum _{i=1}^t r_i ({}_{n_i} \Theta _N )$, a parabolic cocycle. By Lemma 7.2.1, we see immediately that, as cohomology classes, we have
$\Theta _N = \sum _{i=1}^t r_i ({}_{n_i} \Theta _N )$, a parabolic cocycle. By Lemma 7.2.1, we see immediately that, as cohomology classes, we have
 \[ V_{\ell}(\Theta_N) = \sum_{i=1}^t r_i V_{n_i} ({}_{\ell} \Theta_N) = {}_{\ell} \Theta_N. \]
\[ V_{\ell}(\Theta_N) = \sum_{i=1}^t r_i V_{n_i} ({}_{\ell} \Theta_N) = {}_{\ell} \Theta_N. \]
Uniqueness follows as, if ![]() $\theta$ is a cocycle with
$\theta$ is a cocycle with ![]() $V_{\ell }\theta = {}_{\ell } \Theta _N$ as cohomology classes for all
$V_{\ell }\theta = {}_{\ell } \Theta _N$ as cohomology classes for all ![]() $\ell \nmid N$, then
$\ell \nmid N$, then ![]() $\theta = \sum _{i=1}^t r_i V_{n_i} \theta = \Theta _N$. To show that
$\theta = \sum _{i=1}^t r_i V_{n_i} \theta = \Theta _N$. To show that ![]() $T_n$ and
$T_n$ and ![]() $T_n'$ coincide, it is enough by Proposition 7.2.3 to show the same for
$T_n'$ coincide, it is enough by Proposition 7.2.3 to show the same for ![]() $V_{\ell } T_n$ and
$V_{\ell } T_n$ and ![]() $V_{\ell } T_n'$. This follows by Lemma 7.1.1 and the commutativity of the two types of Hecke operators on
$V_{\ell } T_n'$. This follows by Lemma 7.1.1 and the commutativity of the two types of Hecke operators on ![]() $H^1(\tilde {\Gamma }_0(N),M)$, which is proved just as in Lemma 6.5.3.
$H^1(\tilde {\Gamma }_0(N),M)$, which is proved just as in Lemma 6.5.3.
7.2.2 Normalizations of Hecke operators
Our conventions regarding Hecke operators on cocycles differ slightly from standard conventions in the literature due to issues of left versus right actions. We briefly describe the precise relationship, which will be useful in using results about Galois representations.
Let ![]() $M_2(\Gamma _1(N))$ denote the complex vector space of weight
$M_2(\Gamma _1(N))$ denote the complex vector space of weight ![]() $2$ modular forms for
$2$ modular forms for ![]() $\Gamma _1(N)$. Elements of
$\Gamma _1(N)$. Elements of ![]() $M_2(\Gamma _1(N))$ are
$M_2(\Gamma _1(N))$ are ![]() $\Gamma _1(N)$-invariant functions on
$\Gamma _1(N)$-invariant functions on ![]() $\mathbb {H}$ for a natural right action on functions, namely,
$\mathbb {H}$ for a natural right action on functions, namely,
for ![]() $\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$. Similarly, elements of
$\gamma = \big (\begin{smallmatrix} a & b\\c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$. Similarly, elements of ![]() $H^1(\Gamma _1(N) \backslash \mathbb {H},\mathbb {C})$ are represented by
$H^1(\Gamma _1(N) \backslash \mathbb {H},\mathbb {C})$ are represented by ![]() $\Gamma _1(N)$-invariant cochains on
$\Gamma _1(N)$-invariant cochains on ![]() $\mathbb {H}$, where we regard
$\mathbb {H}$, where we regard ![]() $\mathrm {SL}_2(\mathbb {Z})$ acting on the right on cochains in a fashion dual to its obvious left action on chains. Correspondingly, it is natural to consider right Hecke operators on these two groups, as is usually done in the literature (cf. Remark 3.4.2); when extending the actions above to
$\mathrm {SL}_2(\mathbb {Z})$ acting on the right on cochains in a fashion dual to its obvious left action on chains. Correspondingly, it is natural to consider right Hecke operators on these two groups, as is usually done in the literature (cf. Remark 3.4.2); when extending the actions above to ![]() $M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ we introduce an extra factor of
$M_2(\mathbb {Z}) \cap \mathrm {GL}_2(\mathbb {Q})$ we introduce an extra factor of ![]() $\det (\gamma )$.
$\det (\gamma )$.
Let us consider the Hecke equivariance of the following two maps:
where the first (due to Eichler and Shimura) sends ![]() $f$ to
$f$ to ![]() $f(z) dz$ and the second sends a cohomology class to the cocycle that, given
$f(z) dz$ and the second sends a cohomology class to the cocycle that, given ![]() $\gamma \in \Gamma _1(N)$, evaluates the cohomology class on the homology class of an arbitrary path from
$\gamma \in \Gamma _1(N)$, evaluates the cohomology class on the homology class of an arbitrary path from ![]() $z$ to
$z$ to ![]() $\gamma z$ (for an arbitrarily chosen
$\gamma z$ (for an arbitrarily chosen ![]() $z \in \mathbb {H}$). These maps intertwine the right Hecke
$z \in \mathbb {H}$). These maps intertwine the right Hecke ![]() $T^R(h)$-actions on all three groups defined by a decomposition
$T^R(h)$-actions on all three groups defined by a decomposition ![]() $\Gamma _1(N) h \Gamma _1(N) = \coprod _{j=1}^t \Gamma _1(N) h_j$. For instance,
$\Gamma _1(N) h \Gamma _1(N) = \coprod _{j=1}^t \Gamma _1(N) h_j$. For instance, ![]() $T^R(h)$ is defined on differential forms as
$T^R(h)$ is defined on differential forms as ![]() $\sum _{j=1}^t h_j^*$, which is clearly compatible with the sum of the actions of the representatives
$\sum _{j=1}^t h_j^*$, which is clearly compatible with the sum of the actions of the representatives ![]() $h_j$ on a modular form.
$h_j$ on a modular form.
Now take ![]() $h = \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ for
$h = \big (\begin{smallmatrix} 1 \\ & \ell \end{smallmatrix}\big )$ for ![]() $\ell \nmid N$. The action of
$\ell \nmid N$. The action of ![]() $T^R(h)$ on
$T^R(h)$ on ![]() $M_2(\Gamma _1(N))$ is readily verified to coincide with the Hecke operator denoted by
$M_2(\Gamma _1(N))$ is readily verified to coincide with the Hecke operator denoted by ![]() $T_{\ell }^*$ by Edixhoven in [Reference EdixhovenEdi92]. By Remark 3.4.2, the corresponding operator on
$T_{\ell }^*$ by Edixhoven in [Reference EdixhovenEdi92]. By Remark 3.4.2, the corresponding operator on ![]() $H^1(\Gamma _1(N),\mathbb {C})$ can also be described as
$H^1(\Gamma _1(N),\mathbb {C})$ can also be described as ![]() $T(h^*)$ (now defined with left cosets), and this operator
$T(h^*)$ (now defined with left cosets), and this operator ![]() $T(h^*) = T( \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$) is exactly our definition of
$T(h^*) = T( \big (\begin{smallmatrix} \ell \\ & 1 \end{smallmatrix}\big )$) is exactly our definition of ![]() $T_{\ell }$.
$T_{\ell }$.
For ![]() $\delta \in \Gamma _0(N)$ with lower right-hand entry
$\delta \in \Gamma _0(N)$ with lower right-hand entry ![]() $d$, the
$d$, the ![]() $T^R(\delta )$-action on cusp forms is the diamond operator
$T^R(\delta )$-action on cusp forms is the diamond operator ![]() $\langle d \rangle$ (denoted by
$\langle d \rangle$ (denoted by ![]() $\langle d \rangle ^*$ in [Reference EdixhovenEdi92]). The
$\langle d \rangle ^*$ in [Reference EdixhovenEdi92]). The ![]() $T(\delta ^{-1}) = T^R(\delta )$-action on a cocycle becomes precomposition with the conjugation
$T(\delta ^{-1}) = T^R(\delta )$-action on a cocycle becomes precomposition with the conjugation ![]() $\gamma \mapsto \delta \gamma \delta ^{-1}$ (since in this case
$\gamma \mapsto \delta \gamma \delta ^{-1}$ (since in this case ![]() $t = 1$ and
$t = 1$ and ![]() $\gamma _1 = \delta \gamma \delta ^{-1}$).
$\gamma _1 = \delta \gamma \delta ^{-1}$).
7.2.3 Comparison of Hecke algebras for  $\Gamma _0$ and
$\Gamma _0$ and  $\Gamma _1$
$\Gamma _1$
Let us view modules for ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$ as having an action of
$(\mathbb {Z}/N\mathbb {Z})^{\times }$ as having an action of ![]() $\Delta _0(N)$ through the quotient map
$\Delta _0(N)$ through the quotient map ![]() $\Delta _0(N) \to (\mathbb {Z}/N\mathbb {Z})^{\times }$ under which a matrix is sent to its lower right-hand corner modulo
$\Delta _0(N) \to (\mathbb {Z}/N\mathbb {Z})^{\times }$ under which a matrix is sent to its lower right-hand corner modulo ![]() $N$. Recall that
$N$. Recall that ![]() $\tilde {\Gamma }_1(N)$ is the analogue of
$\tilde {\Gamma }_1(N)$ is the analogue of ![]() $\Gamma _1(N)$ for
$\Gamma _1(N)$ for ![]() $\mathrm {GL}_2(\mathbb {Z})$ defined in (4.5).
$\mathrm {GL}_2(\mathbb {Z})$ defined in (4.5).
Lemma 7.2.4 Let ![]() $R$ be a commutative ring, and let
$R$ be a commutative ring, and let ![]() $\mathscr {O} = R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$. Then Shapiro's lemma defines an isomorphism
$\mathscr {O} = R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$. Then Shapiro's lemma defines an isomorphism
that is compatible with the action of Hecke operators ![]() $T(g)$ as in (3.5) with
$T(g)$ as in (3.5) with ![]() $g \in \Delta _1(N)$. Moreover, this map is
$g \in \Delta _1(N)$. Moreover, this map is ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant for the action of
$(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant for the action of ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ on the right by precomposition by
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ on the right by precomposition by ![]() $\gamma \mapsto \delta \gamma \delta ^{-1}$ for any
$\gamma \mapsto \delta \gamma \delta ^{-1}$ for any ![]() $\delta \in \tilde {\Gamma }_0(N)$ with image
$\delta \in \tilde {\Gamma }_0(N)$ with image ![]() $d$ in
$d$ in ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$.
Proof. Let us denote the image of a cocycle ![]() $\theta \colon \tilde {\Gamma }_0(N) \rightarrow R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$ under the Shapiro isomorphism by
$\theta \colon \tilde {\Gamma }_0(N) \rightarrow R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$ under the Shapiro isomorphism by ![]() $\overline {\theta }$: it is obtained by restriction of cocycles together with the map
$\overline {\theta }$: it is obtained by restriction of cocycles together with the map ![]() $\phi \colon R[(\mathbb {Z}/N\mathbb {Z})^{\times }] \rightarrow R$ that takes the coefficient of the identity element. For
$\phi \colon R[(\mathbb {Z}/N\mathbb {Z})^{\times }] \rightarrow R$ that takes the coefficient of the identity element. For ![]() $g \in \Delta _0(N)$ and
$g \in \Delta _0(N)$ and ![]() $\gamma \in \tilde {\Gamma }_0(N)$, equation (3.5) states that
$\gamma \in \tilde {\Gamma }_0(N)$, equation (3.5) states that ![]() $T(g)\theta (\gamma ) = \sum _{j=1}^t g_{\sigma (j)}\theta (\gamma _j)$, recalling the notation of § 3.4. If in fact
$T(g)\theta (\gamma ) = \sum _{j=1}^t g_{\sigma (j)}\theta (\gamma _j)$, recalling the notation of § 3.4. If in fact ![]() $g \in \Delta _1(N)$ (as defined in (4.7)) and
$g \in \Delta _1(N)$ (as defined in (4.7)) and ![]() $\gamma \in \tilde {\Gamma }_1(N)$, then we may choose the representatives
$\gamma \in \tilde {\Gamma }_1(N)$, then we may choose the representatives ![]() $g_j$ to also belong to
$g_j$ to also belong to ![]() $\Delta _1(N)$, in which case the
$\Delta _1(N)$, in which case the ![]() $\gamma _j$ belong to
$\gamma _j$ belong to ![]() $\tilde {\Gamma }_1(N)$. We then have
$\tilde {\Gamma }_1(N)$. We then have
 \[ \overline{T(g) \theta}(\gamma) = \sum_{j=1}^t \phi (g_{\sigma(j)} \theta(\gamma_j)) = \sum_{j=1}^t g_{\sigma(j)} \phi(\theta(\gamma_j) ) = \sum_{j=1}^t g_{\sigma(j)} \bar{\theta}(\gamma_j) = (T(g) \overline{\theta})(\gamma). \]
\[ \overline{T(g) \theta}(\gamma) = \sum_{j=1}^t \phi (g_{\sigma(j)} \theta(\gamma_j)) = \sum_{j=1}^t g_{\sigma(j)} \phi(\theta(\gamma_j) ) = \sum_{j=1}^t g_{\sigma(j)} \bar{\theta}(\gamma_j) = (T(g) \overline{\theta})(\gamma). \]
In particular, taking ![]() $g=\big (\begin{smallmatrix} \ell & 0 \\0 & 1 \end{smallmatrix}\big )$ exhibits equivariance for
$g=\big (\begin{smallmatrix} \ell & 0 \\0 & 1 \end{smallmatrix}\big )$ exhibits equivariance for ![]() $T_{\ell }$.
$T_{\ell }$.
Finally, take ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ and a representative
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ and a representative ![]() $\delta \in \tilde {\Gamma }_0(N)$. Then for
$\delta \in \tilde {\Gamma }_0(N)$. Then for ![]() $\gamma \in \tilde {\Gamma }_1(N)$ we get
$\gamma \in \tilde {\Gamma }_1(N)$ we get
so the Shapiro isomorphism is ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$-equivariant.
Now suppose ![]() $6 \in R^{\times }$, and let
$6 \in R^{\times }$, and let ![]() $\mathbb {T}$ denote the
$\mathbb {T}$ denote the ![]() $R$-Hecke algebra of weight
$R$-Hecke algebra of weight ![]() $2$ modular forms for
$2$ modular forms for ![]() $\Gamma _1(N)$ generated by prime-to-level Hecke operators
$\Gamma _1(N)$ generated by prime-to-level Hecke operators ![]() $T_{\ell }$ and diamond operators
$T_{\ell }$ and diamond operators ![]() $\langle \ell \rangle$.
$\langle \ell \rangle$.
Lemma 7.2.5 Let ![]() $M$ be a
$M$ be a ![]() $R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$-module, where
$R[(\mathbb {Z}/N\mathbb {Z})^{\times }]$-module, where ![]() $6 \in R^{\times }$. We equip
$6 \in R^{\times }$. We equip ![]() $M$ with the action of
$M$ with the action of ![]() $\Delta _0(N)$ via the surjection
$\Delta _0(N)$ via the surjection ![]() $\Delta _0(N) \twoheadrightarrow (\mathbb {Z}/N\mathbb {Z})^{\times }$. Let
$\Delta _0(N) \twoheadrightarrow (\mathbb {Z}/N\mathbb {Z})^{\times }$. Let ![]() $\mathbb {T}_M$ be the
$\mathbb {T}_M$ be the ![]() $R$-algebra of endomorphisms of the cohomology group
$R$-algebra of endomorphisms of the cohomology group ![]() $H^1(\tilde {\Gamma }_0(N),M)$ generated by
$H^1(\tilde {\Gamma }_0(N),M)$ generated by ![]() $T_n$ for primes
$T_n$ for primes ![]() $n \nmid N$ and the elements of
$n \nmid N$ and the elements of ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$. Then there is a surjection
$(\mathbb {Z}/N\mathbb {Z})^{\times }$. Then there is a surjection
carrying ![]() $T_n$ to
$T_n$ to ![]() $T_n$ and the diamond operator
$T_n$ and the diamond operator ![]() $\langle d \rangle$ to the action of
$\langle d \rangle$ to the action of ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$.
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$.
Proof. Write ![]() $\mathscr {O}$ for the group algebra of
$\mathscr {O}$ for the group algebra of ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$ over
$(\mathbb {Z}/N\mathbb {Z})^{\times }$ over ![]() $R$, which we view as a quotient of the
$R$, which we view as a quotient of the ![]() $R$-monoid algebra of
$R$-monoid algebra of ![]() $\Delta _0(N)$ through the lower right-hand corner map. Then
$\Delta _0(N)$ through the lower right-hand corner map. Then ![]() $M$ is isomorphic to a quotient of
$M$ is isomorphic to a quotient of ![]() $\mathscr {O}^{\oplus J}$ for some indexing set
$\mathscr {O}^{\oplus J}$ for some indexing set ![]() $J$. Since
$J$. Since ![]() $2$ is invertible in
$2$ is invertible in ![]() $R$, we have
$R$, we have
(see the proof of Proposition 4.3.1), so ![]() $\mathbb {T}$ acts on
$\mathbb {T}$ acts on ![]() $H^1(\tilde {\Gamma }_1(N),M)$. Consider the composition
$H^1(\tilde {\Gamma }_1(N),M)$. Consider the composition
where the first map comes from Shapiro's lemma as in Lemma 7.2.4, and the cokernel of the last map injects into ![]() $H^2(\tilde {\Gamma }_0(N),A)$, for
$H^2(\tilde {\Gamma }_0(N),A)$, for ![]() $A = \ker (\mathscr {O}^{\bigoplus J} \to M)$. We claim that
$A = \ker (\mathscr {O}^{\bigoplus J} \to M)$. We claim that ![]() $H^2(\tilde {\Gamma }_0(N),A)$ is zero, so that the composition in (7.4) is surjective. Since this composition is compatible with the action of Hecke and diamond operators as in Lemma 7.2.4, we will then have the lemma.
$H^2(\tilde {\Gamma }_0(N),A)$ is zero, so that the composition in (7.4) is surjective. Since this composition is compatible with the action of Hecke and diamond operators as in Lemma 7.2.4, we will then have the lemma.
To see the claim, note that the restriction map
is injective since the index ![]() $h = [\tilde {\Gamma }_0(N):\Gamma _0(N) \cap \Gamma (4)]$ is invertible in
$h = [\tilde {\Gamma }_0(N):\Gamma _0(N) \cap \Gamma (4)]$ is invertible in ![]() $R$, and the composition of restriction and corestriction is multiplication by
$R$, and the composition of restriction and corestriction is multiplication by ![]() $h$. The target of restriction is a second cohomology group of an open
$h$. The target of restriction is a second cohomology group of an open ![]() $2$-manifold, hence trivial.
$2$-manifold, hence trivial.
7.2.4 The  $V_n$-operators generate
$V_n$-operators generate
The following result implies Proposition 7.2.3, in view of the results of the previous subsection.
Proposition 7.2.6 Let ![]() $\mathbb {T}$ be the Hecke ring for
$\mathbb {T}$ be the Hecke ring for ![]() $\Gamma _1(N)$ with
$\Gamma _1(N)$ with ![]() $\mathbb {Z}'[{1}/{N}]$-coefficients. The operators
$\mathbb {Z}'[{1}/{N}]$-coefficients. The operators ![]() $V_n$ for primes
$V_n$ for primes ![]() $n \nmid N$ generate the unit ideal of
$n \nmid N$ generate the unit ideal of ![]() $\mathbb {T}$.
$\mathbb {T}$.
Proof. Let ![]() $\mathfrak {v}$ be the ideal of
$\mathfrak {v}$ be the ideal of ![]() $\mathbb {T}$ that the operators
$\mathbb {T}$ that the operators ![]() $V_n$ for
$V_n$ for ![]() $n \nmid N$ generate. Suppose by way of contradiction that
$n \nmid N$ generate. Suppose by way of contradiction that ![]() $\mathfrak {v} \neq \mathbb {T}$. Then
$\mathfrak {v} \neq \mathbb {T}$. Then ![]() $\mathbb {T}/\mathfrak {v}$ is a ring that is finite over
$\mathbb {T}/\mathfrak {v}$ is a ring that is finite over ![]() $\mathbb {Z}'[{1}/{N}]$ and admits a nontrivial homomorphism to a field
$\mathbb {Z}'[{1}/{N}]$ and admits a nontrivial homomorphism to a field ![]() $F$ that is algebraically closed of finite characteristic
$F$ that is algebraically closed of finite characteristic ![]() $p \nmid N$.
$p \nmid N$.
In this situation, there exists an associated continuous, semisimple Galois representation
such that the trace of a Frobenius element ![]() $\varphi _{\ell }$ at any prime
$\varphi _{\ell }$ at any prime ![]() $\ell \nmid Np$ coincides with the image of
$\ell \nmid Np$ coincides with the image of ![]() $T_{\ell }$ in
$T_{\ell }$ in ![]() $F$, and the determinant of
$F$, and the determinant of ![]() $\varphi _{\ell }$ is given by the image of the diamond operator
$\varphi _{\ell }$ is given by the image of the diamond operator ![]() $\langle \ell \rangle$ in
$\langle \ell \rangle$ in ![]() $F^{\times }$, which we will denote by the same symbol. Since
$F^{\times }$, which we will denote by the same symbol. Since ![]() $V_{\ell }$ maps to zero in
$V_{\ell }$ maps to zero in ![]() $F$, this implies that
$F$, this implies that
for ![]() $\ell \nmid Np$.
$\ell \nmid Np$.
By Čebotarev density, ![]() $\rho$ is isomorphic to the direct sum
$\rho$ is isomorphic to the direct sum ![]() $\omega ^2 \oplus \omega ^{-1}\nu$, where
$\omega ^2 \oplus \omega ^{-1}\nu$, where ![]() $\omega$ denotes the mod
$\omega$ denotes the mod ![]() $p$ cyclotomic character and
$p$ cyclotomic character and ![]() $\nu \colon G_{\mathbb {Q}} \rightarrow F^{\times }$ is the composition of the cyclotomic character
$\nu \colon G_{\mathbb {Q}} \rightarrow F^{\times }$ is the composition of the cyclotomic character ![]() $G_{\mathbb {Q}} \rightarrow (\mathbb {Z}/N\mathbb {Z})^{\times }$ and the diamond operator map
$G_{\mathbb {Q}} \rightarrow (\mathbb {Z}/N\mathbb {Z})^{\times }$ and the diamond operator map ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times } \rightarrow F^{\times }$. Restricted to the inertia group above
$(\mathbb {Z}/N\mathbb {Z})^{\times } \rightarrow F^{\times }$. Restricted to the inertia group above ![]() $p$, we get
$p$, we get
which contradicts well-known properties of the Galois representations attached to weight ![]() $2$ eigenforms of level
$2$ eigenforms of level ![]() $N$; that is, the restriction of
$N$; that is, the restriction of ![]() $\rho$ to any inertia group
$\rho$ to any inertia group ![]() $I_p$ at
$I_p$ at ![]() $p$ must be
$p$ must be ![]() $\omega \oplus 1$ or the sum of two tame characters. It is enough to verify this separately for Eisenstein series and cusp forms; in the Eisenstein case only the former case occurs, and in the cuspidal case the two possibilities are distinguished by whether the image of
$\omega \oplus 1$ or the sum of two tame characters. It is enough to verify this separately for Eisenstein series and cusp forms; in the Eisenstein case only the former case occurs, and in the cuspidal case the two possibilities are distinguished by whether the image of ![]() $T_p$ in
$T_p$ in ![]() $F$ is zero or nonzero (see [Reference EdixhovenEdi92, Theorems 2.5–2.6]).
$F$ is zero or nonzero (see [Reference EdixhovenEdi92, Theorems 2.5–2.6]).
Remark 7.2.7 If we are willing to work with ![]() $\mathbb {Q}$-coefficients in place of coefficients in
$\mathbb {Q}$-coefficients in place of coefficients in ![]() $\mathbb {Z}'[{1}/{N}]$, then Proposition 7.2.6 has a much simpler proof. Indeed, each
$\mathbb {Z}'[{1}/{N}]$, then Proposition 7.2.6 has a much simpler proof. Indeed, each ![]() $V_{\ell }$ with
$V_{\ell }$ with ![]() $\ell \nmid N$ is itself a unit in the Hecke algebra acting on group cohomology. The key point is that the
$\ell \nmid N$ is itself a unit in the Hecke algebra acting on group cohomology. The key point is that the ![]() $T_{\ell }$-eigenvalues of any weight
$T_{\ell }$-eigenvalues of any weight ![]() $2$ eigenform for
$2$ eigenform for ![]() $\Gamma _1(N)$ have complex absolute value at most
$\Gamma _1(N)$ have complex absolute value at most ![]() $\ell +1$, and the eigenvalues of diamond operators are roots of unity, so
$\ell +1$, and the eigenvalues of diamond operators are roots of unity, so ![]() $V_{\ell }$ has eigenvalues of complex absolute value at least
$V_{\ell }$ has eigenvalues of complex absolute value at least ![]() $\ell ^3-1-\ell (\ell +1) > 0$.
$\ell ^3-1-\ell (\ell +1) > 0$.
7.3 Explicit formula for the universal cocycle
We cannot quite write down an explicit formula for a cocycle in the universal class of the previous section because of our lack of understanding of the motivic cohomology group ![]() $H^2(Y, \mathbb {Q}(2))$. However, we can at least do it modulo a subgroup
$H^2(Y, \mathbb {Q}(2))$. However, we can at least do it modulo a subgroup ![]() $\mathscr {V}$ which can be seen to vanish under any standard regulator map.
$\mathscr {V}$ which can be seen to vanish under any standard regulator map.
7.3.1 The explicit formula, in brief
For a prime ![]() $n \nmid N$, let
$n \nmid N$, let ![]() $\mathscr {V}_n$ denote the kernel of
$\mathscr {V}_n$ denote the kernel of ![]() $V'_n$ on
$V'_n$ on ![]() $H^2(Y,\mathbb {Q}(2))$, and let
$H^2(Y,\mathbb {Q}(2))$, and let ![]() $\mathscr {V} = \bigcap _{n \nmid N} \mathscr {V}_n$. Remark 7.2.7 implies that the group
$\mathscr {V} = \bigcap _{n \nmid N} \mathscr {V}_n$. Remark 7.2.7 implies that the group ![]() $\mathscr {V}$ maps to zero in any quotient of
$\mathscr {V}$ maps to zero in any quotient of ![]() $H^2(Y, \mathbb {Q}(2))$ that factors through the action of the Hecke algebra on
$H^2(Y, \mathbb {Q}(2))$ that factors through the action of the Hecke algebra on ![]() $H^1(\Gamma _1(N), \mathbb {Q})$.
$H^1(\Gamma _1(N), \mathbb {Q})$.
Proposition 7.3.1 The class of ![]() $\Theta _N$ modulo
$\Theta _N$ modulo ![]() $\mathscr {V}$ equals the class of the cocycle
$\mathscr {V}$ equals the class of the cocycle
 \begin{equation} \tilde{\Gamma}_0(N) \to H^2(Y,\mathbb{Q}(2))/\mathscr{V}, \quad \gamma \mapsto \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \bmod \mathscr{V} \end{equation}
\begin{equation} \tilde{\Gamma}_0(N) \to H^2(Y,\mathbb{Q}(2))/\mathscr{V}, \quad \gamma \mapsto \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \bmod \mathscr{V} \end{equation}
for ![]() $(b_i,d_i)_{i=0}^k$ any
$(b_i,d_i)_{i=0}^k$ any ![]() $N$-connecting sequence for
$N$-connecting sequence for ![]() $\gamma$, where
$\gamma$, where ![]() $g_{{a}/{N}}$ for
$g_{{a}/{N}}$ for ![]() $a$ prime to
$a$ prime to ![]() $N$ is the standard Siegel unit on
$N$ is the standard Siegel unit on ![]() $Y$ (see § 7.3.2).
$Y$ (see § 7.3.2).
Implicit in the statement is the assertion that the right-hand side of (7.5) is independent of the choice of connecting sequence and defines a cocycle.Footnote 25 We explain the proof modulo certain explicit computations with Siegel units that are carried out in the rest of the section.
Proof. We will prove in Lemma 7.3.4 that for ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with both
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with both ![]() $c$ and
$c$ and ![]() $d$ relatively prime to
$d$ relatively prime to ![]() $N$, we have
$N$, we have
for each ![]() $n \nmid N$. For a given
$n \nmid N$. For a given ![]() $N$-connecting sequence
$N$-connecting sequence ![]() $(b_i,d_i)_{i=0}^k$ for
$(b_i,d_i)_{i=0}^k$ for ![]() $\gamma$, let us set
$\gamma$, let us set
 \[ f_{\gamma} = \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \in H^2(Y,\mathbb{Q}(2)) \]
\[ f_{\gamma} = \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \in H^2(Y,\mathbb{Q}(2)) \]
with the understanding that this depends on the connecting sequence. From Proposition 6.4.1(c) and (7.3), we know that
 \[ {}_n \Theta_{N, \gamma} = s^* \sum_{i=1}^k \bigg\langle \!\bigg(\begin{matrix} b_i & -b_{i-1} \\ d_i & -d_{i-1} \end{matrix}\bigg)\!\bigg\rangle_n \stackrel{(7.6)}= \sum_{i=1}^k V_n' (g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}). \]
\[ {}_n \Theta_{N, \gamma} = s^* \sum_{i=1}^k \bigg\langle \!\bigg(\begin{matrix} b_i & -b_{i-1} \\ d_i & -d_{i-1} \end{matrix}\bigg)\!\bigg\rangle_n \stackrel{(7.6)}= \sum_{i=1}^k V_n' (g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}). \]
So, by (7.6), we have that
This equality uniquely determines ![]() $f_{\gamma }$ as an element of
$f_{\gamma }$ as an element of ![]() $H^2(Y,\mathbb {Q}(2))/\mathscr {V}_n$. From this and the fact that
$H^2(Y,\mathbb {Q}(2))/\mathscr {V}_n$. From this and the fact that ![]() ${}_n \Theta _N$ is a cocycle, we see that the quantity
${}_n \Theta _N$ is a cocycle, we see that the quantity ![]() $f_{\gamma } \bmod \mathscr {V}_n$ is independent of choice of connecting sequence, and
$f_{\gamma } \bmod \mathscr {V}_n$ is independent of choice of connecting sequence, and ![]() $\gamma \mapsto f_{\gamma } \bmod \mathscr {V}_n$ is a cocycle. But then the latter two facts are true modulo
$\gamma \mapsto f_{\gamma } \bmod \mathscr {V}_n$ is a cocycle. But then the latter two facts are true modulo ![]() $\mathscr {V} = \bigcap _n \mathscr {V}_n$ as well.
$\mathscr {V} = \bigcap _n \mathscr {V}_n$ as well.
By Theorem 7.2.2, the cocycle ![]() $V'_n(\Theta _N)$ is cohomologous to
$V'_n(\Theta _N)$ is cohomologous to ![]() ${}_n\Theta _N$. In particular, the class of
${}_n\Theta _N$. In particular, the class of ![]() $\gamma \mapsto \Theta _{N,\gamma } - f_{\gamma }$ lies in the kernel of all
$\gamma \mapsto \Theta _{N,\gamma } - f_{\gamma }$ lies in the kernel of all ![]() $V_n'$ acting on
$V_n'$ acting on ![]() $H^1(\tilde {\Gamma }_0(N),M)$ with
$H^1(\tilde {\Gamma }_0(N),M)$ with ![]() $M = H^2(Y,\mathbb {Q}(2))/\mathscr {V}$. To see that this common kernel is zero, consider the injection
$M = H^2(Y,\mathbb {Q}(2))/\mathscr {V}$. To see that this common kernel is zero, consider the injection ![]() $\iota \colon M \hookrightarrow \bigoplus _{n \nmid N} M$ induced by the collection of operators
$\iota \colon M \hookrightarrow \bigoplus _{n \nmid N} M$ induced by the collection of operators ![]() $V'_n$. We must show that the map
$V'_n$. We must show that the map
induced by ![]() $\iota$ is injective. This follows from the surjectivity of the map
$\iota$ is injective. This follows from the surjectivity of the map
which in turn is a consequence of the fact that ![]() $\tilde {\Gamma }_0(N)$-action on the
$\tilde {\Gamma }_0(N)$-action on the ![]() $\mathbb {Q}$-vector space
$\mathbb {Q}$-vector space ![]() $M$ factors through the finite group
$M$ factors through the finite group ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$.
Aside from the change of modular curve, the following is a corollary of Proposition 7.3.1 and its proof. In it, we use ![]() $\mathscr {V}$ to denote the intersection of kernels of the
$\mathscr {V}$ to denote the intersection of kernels of the ![]() $V'_n$ on
$V'_n$ on ![]() $H^2(Y_1(N),\mathbb {Z}'[{1}/{N}](2))$.
$H^2(Y_1(N),\mathbb {Z}'[{1}/{N}](2))$.
Proposition 7.3.2 The cocycle ![]() $\Theta _N$ restricts to a cocycle
$\Theta _N$ restricts to a cocycle
satisfying
 \[ \Theta_{N, \gamma} \equiv \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \bmod \mathscr{V} \]
\[ \Theta_{N, \gamma} \equiv \sum_{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}} \bmod \mathscr{V} \]
for ![]() $\gamma \in \Gamma _1(N)$.
$\gamma \in \Gamma _1(N)$.
Proof. To see that we can work with ![]() $\mathbb {Z}'[{1}/{N}]$-coefficients, note that the only place where we may need to invert further primes (i.e., those dividing
$\mathbb {Z}'[{1}/{N}]$-coefficients, note that the only place where we may need to invert further primes (i.e., those dividing ![]() $\varphi (N)$) in the proof of Proposition 7.3.1 is for the surjectivity of the map in (7.7), but if we replace
$\varphi (N)$) in the proof of Proposition 7.3.1 is for the surjectivity of the map in (7.7), but if we replace ![]() $\tilde {\Gamma }_0(N)$ by
$\tilde {\Gamma }_0(N)$ by ![]() $\tilde {\Gamma }_1(N)$, then this need is alleviated as
$\tilde {\Gamma }_1(N)$, then this need is alleviated as ![]() $\tilde {\Gamma }_1(N)$ acts trivially on
$\tilde {\Gamma }_1(N)$ acts trivially on ![]() $H^2(Y,2)$.
$H^2(Y,2)$.
The second claim is immediate from Proposition 7.3.1, since both cocycles restrict to homomorphisms on ![]() $\Gamma _1(N)$, so are equal (modulo
$\Gamma _1(N)$, so are equal (modulo ![]() $\mathscr {V}$). Set
$\mathscr {V}$). Set ![]() $X = X_1(N)$ (over
$X = X_1(N)$ (over ![]() $\mathbb {Q}$) and
$\mathbb {Q}$) and ![]() $C = X-Y$. We have an exact Gysin sequence
$C = X-Y$. We have an exact Gysin sequence
Each ![]() $V'_n$ for
$V'_n$ for ![]() $n$ not dividing
$n$ not dividing ![]() $N$ acts on
$N$ acts on ![]() $H^1(C,\mathbb {Z}'[{1}/{N}](1)) \cong \mathscr {O}_C^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$. Since this is torsion-free as a
$H^1(C,\mathbb {Z}'[{1}/{N}](1)) \cong \mathscr {O}_C^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$. Since this is torsion-free as a ![]() $\mathbb {Z}'[{1}/{N}]$-module, the argument of Remark 7.2.7 can be applied to show that no nonzero element of
$\mathbb {Z}'[{1}/{N}]$-module, the argument of Remark 7.2.7 can be applied to show that no nonzero element of ![]() $H^1(C,\mathbb {Z}'[{1}/{N}](1))$ is killed by all
$H^1(C,\mathbb {Z}'[{1}/{N}](1))$ is killed by all ![]() $V'_n$ with
$V'_n$ with ![]() $n \nmid N$. From this, we see that
$n \nmid N$. From this, we see that ![]() $\mathscr {V} \subseteq H^2(X,\mathbb {Z}'[{1}/{N}](2))$.
$\mathscr {V} \subseteq H^2(X,\mathbb {Z}'[{1}/{N}](2))$.
It therefore suffices to show that ![]() $\sum _{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}$ has trivial residue in
$\sum _{i=1}^k g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}$ has trivial residue in ![]() $\mathscr {O}_C^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$. It follows from [Reference Fukaya and KatoFK24, Lemma 3.3.12] that the tame symbol of this sum at the cusp
$\mathscr {O}_C^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$. It follows from [Reference Fukaya and KatoFK24, Lemma 3.3.12] that the tame symbol of this sum at the cusp ![]() $\infty \colon \operatorname {Spec} \mathbb {Q}(\mu _N) \to X_1(N)$ has image in
$\infty \colon \operatorname {Spec} \mathbb {Q}(\mu _N) \to X_1(N)$ has image in ![]() $\mathbb {Q}(\mu _N)^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$ equal to
$\mathbb {Q}(\mu _N)^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}'[{1}/{N}]$ equal to
 \[ \prod_{i=1}^k \bigg(\frac{1-\zeta_N^{d_i}}{1-\zeta_N^{d_{i-1}}}\bigg)^{1/12} = 1, \]
\[ \prod_{i=1}^k \bigg(\frac{1-\zeta_N^{d_i}}{1-\zeta_N^{d_{i-1}}}\bigg)^{1/12} = 1, \]
and similarly for the other cusps over the infinity cusp of ![]() $X_0(N)$. At the other, non-infinity cusps, the same lemma tells us that the residues of the individual terms
$X_0(N)$. At the other, non-infinity cusps, the same lemma tells us that the residues of the individual terms ![]() $g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}$ are trivial.
$g_{{d_i}/{N}} \cup g_{{-d_{i-1}}/{N}}$ are trivial.
7.3.2 Review of Siegel units
Let us consider units on the modular curve ![]() $Y(M)$ for
$Y(M)$ for ![]() $M \ge 3$, which is the moduli space of triples
$M \ge 3$, which is the moduli space of triples ![]() $(E,P,Q)$ with
$(E,P,Q)$ with ![]() $E$ an elliptic curve and
$E$ an elliptic curve and ![]() $(P,Q)$ an ordered basis of
$(P,Q)$ an ordered basis of ![]() $E[M]$. The universal elliptic curve
$E[M]$. The universal elliptic curve ![]() $\mathscr {E}(M)$ has two canonical order
$\mathscr {E}(M)$ has two canonical order ![]() $M$ sections
$M$ sections ![]() $\iota _{M,1}, \iota _{M,2} \colon Y(M) \to \mathscr {E}(M)$ corresponding to
$\iota _{M,1}, \iota _{M,2} \colon Y(M) \to \mathscr {E}(M)$ corresponding to ![]() $P$ and
$P$ and ![]() $Q$. For
$Q$. For ![]() $(c,d) \in \mathbb {Z}^2-M\mathbb {Z}^2$ and
$(c,d) \in \mathbb {Z}^2-M\mathbb {Z}^2$ and ![]() $m$ prime to
$m$ prime to ![]() ${M}/{(c,M)} \cdot {M}/{(d,M)}$, let
${M}/{(c,M)} \cdot {M}/{(d,M)}$, let
where ![]() ${}_m \theta \in \mathscr {E}(M)^{\times } \otimes \mathbb {Z}[\frac {1}{6}]$ is the theta function defined analogously to (6.6): it has zeros of multiplicity
${}_m \theta \in \mathscr {E}(M)^{\times } \otimes \mathbb {Z}[\frac {1}{6}]$ is the theta function defined analogously to (6.6): it has zeros of multiplicity ![]() $1$ along nonzero
$1$ along nonzero ![]() $m$-torsion points, and a pole of order
$m$-torsion points, and a pole of order ![]() $m^2-1$ at the identity section.
$m^2-1$ at the identity section.
Next let
for any ![]() $m \equiv 1 \bmod M$ and prime to
$m \equiv 1 \bmod M$ and prime to ![]() $6$, independent of the choice. (In fact, we may define
$6$, independent of the choice. (In fact, we may define ![]() $g_{{c}/{M},{d}/{M}}$ as an element of
$g_{{c}/{M},{d}/{M}}$ as an element of ![]() $\mathscr {O}_{Y(M)}^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}[{1}/{6M}]$.) Then
$\mathscr {O}_{Y(M)}^{\times } \otimes _{\mathbb {Z}} \mathbb {Z}[{1}/{6M}]$.) Then
For any ![]() $m \ge 1$ and
$m \ge 1$ and ![]() $(c,d) \in \mathbb {Z}^2 - M\mathbb {Z}^2$, the Siegel units satisfy the distribution relation
$(c,d) \in \mathbb {Z}^2 - M\mathbb {Z}^2$, the Siegel units satisfy the distribution relation
 \[ \prod_{i = 0}^{m-1} \prod_{j=0}^{m-1} g_{{c}/{Mm} + {i}/{m}, {d}/{Mm} + {j}/{m}} = g_{{c}/{M},{d}/{M}}. \]
\[ \prod_{i = 0}^{m-1} \prod_{j=0}^{m-1} g_{{c}/{Mm} + {i}/{m}, {d}/{Mm} + {j}/{m}} = g_{{c}/{M},{d}/{M}}. \]
The Siegel units ![]() ${}_m g_{0,{d}/{M}}$ and
${}_m g_{0,{d}/{M}}$ and ![]() $g_{0,{d}/{M}}$ are units rationally on
$g_{0,{d}/{M}}$ are units rationally on ![]() $Y_1(M)$. We denote them more simply by
$Y_1(M)$. We denote them more simply by ![]() ${}_m g_{{d}/{M}}$ and
${}_m g_{{d}/{M}}$ and ![]() $g_{{d}/{M}}$, respectively.
$g_{{d}/{M}}$, respectively.
7.3.3 Some computations with Siegel units
Our goal here is to prove (7.6).
Lemma 7.3.3 Let us consider ![]() ${}_n\theta '$ defined analogously to (6.6) as a rational function on the universal elliptic curve
${}_n\theta '$ defined analogously to (6.6) as a rational function on the universal elliptic curve ![]() $\mathscr {E}_n$ over the modular curve
$\mathscr {E}_n$ over the modular curve ![]() $Y_1(Nn)$. For
$Y_1(Nn)$. For ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, we have
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, we have
 \[ (d\iota_N)^*({}_n \theta') = g_{{nd}/{N}}^{-1} \cdot \prod_{j=0}^{n-1} g_{{d}/{N}+{j}/{n}}^n \in \mathscr{O}_{Y'}^{\times} \otimes_{\mathbb{Z}} \mathbb{Q}. \]
\[ (d\iota_N)^*({}_n \theta') = g_{{nd}/{N}}^{-1} \cdot \prod_{j=0}^{n-1} g_{{d}/{N}+{j}/{n}}^n \in \mathscr{O}_{Y'}^{\times} \otimes_{\mathbb{Z}} \mathbb{Q}. \]
Proof. For ![]() $\mathscr {E}_n \rightarrow Y_1(Nn)$, we have canonical order
$\mathscr {E}_n \rightarrow Y_1(Nn)$, we have canonical order ![]() $N$ and order
$N$ and order ![]() $n$ sections
$n$ sections ![]() $\iota _N$ and
$\iota _N$ and ![]() $\iota _n$, respectively. Let
$\iota _n$, respectively. Let ![]() $\phi \colon \mathscr {E}_n\to \mathscr {E}_n$ be translation by
$\phi \colon \mathscr {E}_n\to \mathscr {E}_n$ be translation by ![]() $\iota _n$, that is, given on the fiber over
$\iota _n$, that is, given on the fiber over ![]() $(E,P,Q)$ with
$(E,P,Q)$ with ![]() $P$ of order
$P$ of order ![]() $N$ and
$N$ and ![]() $Q$ of order
$Q$ of order ![]() $n$ by
$n$ by ![]() $\phi (x) = x + Q$. Then
$\phi (x) = x + Q$. Then
 \[ n^2\mathscr{K} - nE[n] = \sum_{j=0}^{n-1} (j\phi)^* (n^2(0)- E[n]), \]
\[ n^2\mathscr{K} - nE[n] = \sum_{j=0}^{n-1} (j\phi)^* (n^2(0)- E[n]), \]
so
 \[ ({}_n\theta')^n = \sum_{j=0}^{n-1} (j\phi)^* {}_n\theta, \]
\[ ({}_n\theta')^n = \sum_{j=0}^{n-1} (j\phi)^* {}_n\theta, \]
where we view ![]() ${}_n \theta$ as the theta function with divisor
${}_n \theta$ as the theta function with divisor ![]() $n^2(0)-E[n]$ on
$n^2(0)-E[n]$ on ![]() $\mathscr {E}_n$. Since, for
$\mathscr {E}_n$. Since, for ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, the section
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$, the section ![]() $d\iota _N+j\iota _n$ has order divisible by
$d\iota _N+j\iota _n$ has order divisible by ![]() $N$, the pullback
$N$, the pullback ![]() $(d\iota _N+j\iota _n)^*{}_n\theta$ is well defined. We then see that
$(d\iota _N+j\iota _n)^*{}_n\theta$ is well defined. We then see that
Taking the product over ![]() $0 \le j \le n-1$ and the
$0 \le j \le n-1$ and the ![]() $n$th root gives the result.
$n$th root gives the result.
Lemma 7.3.4 For ![]() $\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with both
$\gamma = \big (\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big ) \in \mathrm {SL}_2(\mathbb {Z})$ with both ![]() $c$ and
$c$ and ![]() $d$ relatively prime to
$d$ relatively prime to ![]() $N$, we have
$N$, we have
Proof. Note that ![]() $s^* \langle \gamma \rangle _n$ is the pullback of
$s^* \langle \gamma \rangle _n$ is the pullback of ![]() $\langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle _n$ by the section
$\langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle _n$ by the section ![]() $(c\iota _N,d\iota _N)$. We have
$(c\iota _N,d\iota _N)$. We have
 \begin{equation} (c\iota_N,d\iota_N)^*({}_n\theta \boxtimes {}_n \theta) = \frac{g_{{c}/{N}}^{n^2}}{g_{{nc}/{N}}} \cup \frac{g_{{d}/{N}}^{n^2}}{g_{{nd}/{N}}}. \end{equation}
\begin{equation} (c\iota_N,d\iota_N)^*({}_n\theta \boxtimes {}_n \theta) = \frac{g_{{c}/{N}}^{n^2}}{g_{{nc}/{N}}} \cup \frac{g_{{d}/{N}}^{n^2}}{g_{{nd}/{N}}}. \end{equation}
For the ![]() $N$-torsion section of
$N$-torsion section of ![]() $\iota _N \colon Y' \to \mathscr {E}'$ (with
$\iota _N \colon Y' \to \mathscr {E}'$ (with ![]() $Y' = Y_n$ as in § 6.3.1), Lemma 7.3.3 tells us that
$Y' = Y_n$ as in § 6.3.1), Lemma 7.3.3 tells us that
 \begin{equation} (c\iota_N,d\iota_N)^*({}_n \theta' \boxtimes {}_n \theta') = \frac{\prod_{i=0}^{n-1}g_{{c}/{N}+{i}/{n}}^n}{g_{{nc}/{N}}} \cup \frac{\prod_{j=0}^{n-1} g_{{d}/{N}+{j}/{n}}^n}{g_{{nd}/{N}}}. \end{equation}
\begin{equation} (c\iota_N,d\iota_N)^*({}_n \theta' \boxtimes {}_n \theta') = \frac{\prod_{i=0}^{n-1}g_{{c}/{N}+{i}/{n}}^n}{g_{{nc}/{N}}} \cup \frac{\prod_{j=0}^{n-1} g_{{d}/{N}+{j}/{n}}^n}{g_{{nd}/{N}}}. \end{equation}
The individual functions here are defined on ![]() $Y_1(Nn)$, but the product is defined on
$Y_1(Nn)$, but the product is defined on ![]() $Y'$.
$Y'$.
Given that we have a cartesian diagram

Lemma 2.1.1 implies that the norms for ![]() $Y' \to Y$ and
$Y' \to Y$ and ![]() $(\mathscr {E}')^2 \to \mathscr {E}^2$ commute with pullback by the
$(\mathscr {E}')^2 \to \mathscr {E}^2$ commute with pullback by the ![]() $N$-torsion section
$N$-torsion section ![]() $(c\iota _N,d\iota _N)$. Recalling now that
$(c\iota _N,d\iota _N)$. Recalling now that ![]() $\langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle _n = {}_n\theta \boxtimes {}_n\theta - \operatorname {N}({}_n\theta ' \boxtimes {}_n\theta ')$, we then obtain from (7.8) and (7.9) that
$\langle \big (\begin{smallmatrix} 1 & 0\\0 & 1 \end{smallmatrix}\big ) \rangle _n = {}_n\theta \boxtimes {}_n\theta - \operatorname {N}({}_n\theta ' \boxtimes {}_n\theta ')$, we then obtain from (7.8) and (7.9) that
 \begin{align} (c\iota_N,d\iota_N)^* \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n &= \frac{g_{{c}/{N}}^{n^2}}{g_{{nc}/{N}}} \cup \frac{g_{{d}/{N}}^{n^2}}{g_{{nd}/{N}}}\nonumber\\ &\quad - \bigg( \sum_{\langle(\alpha,\beta)\rangle} \frac{\prod_{i=0}^{n-1} g_{{i\alpha}/{n},{c}/{N}+{i\beta}/{n}}^n} {g_{{nc}/{N}}} \cup \frac{\prod_{j=0}^{n-1} g_{{j\alpha}/{n},{d}/{N}+{j\beta}/{n}}^n} {g_{{nd}/{N}}} \bigg), \end{align}
\begin{align} (c\iota_N,d\iota_N)^* \bigg\langle \!\bigg(\begin{matrix} 1 & 0\\0 & 1 \end{matrix}\bigg) \!\bigg\rangle_n &= \frac{g_{{c}/{N}}^{n^2}}{g_{{nc}/{N}}} \cup \frac{g_{{d}/{N}}^{n^2}}{g_{{nd}/{N}}}\nonumber\\ &\quad - \bigg( \sum_{\langle(\alpha,\beta)\rangle} \frac{\prod_{i=0}^{n-1} g_{{i\alpha}/{n},{c}/{N}+{i\beta}/{n}}^n} {g_{{nc}/{N}}} \cup \frac{\prod_{j=0}^{n-1} g_{{j\alpha}/{n},{d}/{N}+{j\beta}/{n}}^n} {g_{{nd}/{N}}} \bigg), \end{align}
where the sum runs over chosen generators of the ![]() $n+1$ cyclic subgroups of order
$n+1$ cyclic subgroups of order ![]() $n$ in
$n$ in ![]() $(\mathbb {Z}/n\mathbb {Z})^2$. Note that in (7.10), we work with the cover
$(\mathbb {Z}/n\mathbb {Z})^2$. Note that in (7.10), we work with the cover ![]() $Y''$ of
$Y''$ of ![]() $Y$ obtained by the additional data of a full level
$Y$ obtained by the additional data of a full level ![]() $n$ structure. The group
$n$ structure. The group ![]() $H^2(Y,\mathbb {Q}(2))$ injects into
$H^2(Y,\mathbb {Q}(2))$ injects into ![]() $H^2(Y'',\mathbb {Q}(2))$ under pullback, since
$H^2(Y'',\mathbb {Q}(2))$ under pullback, since ![]() $Y'' \to Y$ is finite and these groups are
$Y'' \to Y$ is finite and these groups are ![]() $\mathbb {Q}$-vector spaces. We can then compute the norm
$\mathbb {Q}$-vector spaces. We can then compute the norm ![]() $\operatorname {N}({}_n\theta ' \boxtimes {}_n\theta ')$ by taking a sum over the actions of coset representatives for
$\operatorname {N}({}_n\theta ' \boxtimes {}_n\theta ')$ by taking a sum over the actions of coset representatives for ![]() $\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$ modulo the upper triangular subgroup.
$\mathrm {GL}_2(\mathbb {Z}/n\mathbb {Z})$ modulo the upper triangular subgroup.
We now analyze the terms of (7.10). In the second term, we have the following properties.
– The numerators give
 $n^2 T'_n(g_{{c}/{N}} \cup g_{{d}/{N}})$. Indeed, by definition,
$n^2 T'_n(g_{{c}/{N}} \cup g_{{d}/{N}})$. Indeed, by definition,  $T_n' (g_{{c}/{N}} \cup g_{{d}/{N}})$ is obtained by pulling back
$T_n' (g_{{c}/{N}} \cup g_{{d}/{N}})$ is obtained by pulling back  $g_{{c}/{N}} \cup g_{{d}/{N}}$ to
$g_{{c}/{N}} \cup g_{{d}/{N}}$ to  $Y'$ along
$Y'$ along  $\psi \colon (E,P,K) \mapsto (E/K,P+K)$, and then taking the norm
$\psi \colon (E,P,K) \mapsto (E/K,P+K)$, and then taking the norm  $\phi _*$ along
$\phi _*$ along  $Y'/Y$. The pullback
$Y'/Y$. The pullback  $\psi ^*g_{{c}/{N}}$ is given by
$\psi ^*g_{{c}/{N}}$ is given by  $\prod _{i=0}^{n-1} g_{{c}/{N} + {i}/{n}}$, and the norm is as before.
$\prod _{i=0}^{n-1} g_{{c}/{N} + {i}/{n}}$, and the norm is as before.– The cross terms are
by the distribution relation. \[ -n^2g_{{nc}/{N}} \cup g_{{d}/{N}} - ng_{{nc}/{N}} \cup g_{{nd}/{N}} \quad \mathrm{and} \quad -n^2g_{{c}/{N}} \cup g_{{nd}/{N}} - ng_{{nc}/{N}} \cup g_{{nd}/{N}} \]
\[ -n^2g_{{nc}/{N}} \cup g_{{d}/{N}} - ng_{{nc}/{N}} \cup g_{{nd}/{N}} \quad \mathrm{and} \quad -n^2g_{{c}/{N}} \cup g_{{nd}/{N}} - ng_{{nc}/{N}} \cup g_{{nd}/{N}} \]
– The denominators contribute
 $(n+1) g_{{nc}/{N}} \cup g_{{nd}/{N}}$.
$(n+1) g_{{nc}/{N}} \cup g_{{nd}/{N}}$.
Subtracting this from the first term and noting that ![]() $[n]'(g_{{c}/{N}}\cup g_{{d}/{N}}) = g_{{nc}/{N}} \cup g_{{nd}/{N}}$, we obtain
$[n]'(g_{{c}/{N}}\cup g_{{d}/{N}}) = g_{{nc}/{N}} \cup g_{{nd}/{N}}$, we obtain
7.4 Maps on the homology of  $X_1(N)$
$X_1(N)$
We conclude by comparing our cocycle ![]() $\Theta _N$ to related ‘zeta maps’ on the homology of modular curves.
$\Theta _N$ to related ‘zeta maps’ on the homology of modular curves.
7.4.1 Zeta maps with  $\mathbb {Z}'[{1}/{N}]$-coefficients
$\mathbb {Z}'[{1}/{N}]$-coefficients
Since ![]() $\Theta _N$ restricts to a homomorphism on
$\Theta _N$ restricts to a homomorphism on ![]() $\tilde {\Gamma }_1(N)$ which is trivial on parabolic subgroups, we have the following analogue of Proposition 4.3.1. We note that
$\tilde {\Gamma }_1(N)$ which is trivial on parabolic subgroups, we have the following analogue of Proposition 4.3.1. We note that ![]() $H^2(X_1(N),2)$ is preserved by the Hecke and diamond operators on
$H^2(X_1(N),2)$ is preserved by the Hecke and diamond operators on ![]() $H^2(Y_1(N),2)$.
$H^2(Y_1(N),2)$.
Theorem 7.4.1 The map
sending the image of ![]() $\vec \gamma = \{ 0 \to \gamma \cdot 0 \}$ to
$\vec \gamma = \{ 0 \to \gamma \cdot 0 \}$ to ![]() $\Theta _{N,\gamma }$ for all
$\Theta _{N,\gamma }$ for all ![]() $\gamma \in \Gamma _1(N)$ is a Hecke-equivariant homomorphism in the sense that
$\gamma \in \Gamma _1(N)$ is a Hecke-equivariant homomorphism in the sense that ![]() $z_N(T_{\ell } \vec \gamma ) = T'_{\ell } \cdot z_N(\vec \gamma )$ for primes
$z_N(T_{\ell } \vec \gamma ) = T'_{\ell } \cdot z_N(\vec \gamma )$ for primes ![]() $\ell \nmid N$ and
$\ell \nmid N$ and ![]() $z_N(\langle d \rangle \vec \gamma ) = [d]' \cdot z_N(\vec \gamma )$ for
$z_N(\langle d \rangle \vec \gamma ) = [d]' \cdot z_N(\vec \gamma )$ for ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$.
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$.
Proof. The existence of a map to ![]() $H^2(X_1(N),\mathbb {Z}'[{1}/{N}](2))$ follows from Proposition 7.3.2 just as in Proposition 4.3.1, since the induced
$H^2(X_1(N),\mathbb {Z}'[{1}/{N}](2))$ follows from Proposition 7.3.2 just as in Proposition 4.3.1, since the induced ![]() $\tilde {\Gamma }_1(N)$-action on the latter cohomology group is trivial. The Hecke equivariance follows as in the argument of Theorem 4.3.7.
$\tilde {\Gamma }_1(N)$-action on the latter cohomology group is trivial. The Hecke equivariance follows as in the argument of Theorem 4.3.7.
In [Reference GoncharovGon08, Proposition 2.16], Goncharov outlined a construction of an analogue of ![]() $z_N$ for
$z_N$ for ![]() $Y(N)$ via a map from a complex computing the cohomology of the modular curve
$Y(N)$ via a map from a complex computing the cohomology of the modular curve ![]() $Y(N)(\mathbb {C})$ to a certain ‘Euler complex’ involving a Bloch group. In a recent preprint, Brunault [Reference BrunaultBru22, Theorem 4.3] gives what amounts to an explicit construction of a well-defined homomorphism
$Y(N)(\mathbb {C})$ to a certain ‘Euler complex’ involving a Bloch group. In a recent preprint, Brunault [Reference BrunaultBru22, Theorem 4.3] gives what amounts to an explicit construction of a well-defined homomorphism
directly verifying that Steinberg symbols of Siegel units satisfy the Manin relations, improving earlier work in [Reference BrunaultBru08].
The map ![]() $z_N^{\circ }$ agrees on
$z_N^{\circ }$ agrees on ![]() $H_1(X_1(N),\mathbb {Z})$ with the restriction to
$H_1(X_1(N),\mathbb {Z})$ with the restriction to ![]() $\Gamma _1(N)$ of the explicit map
$\Gamma _1(N)$ of the explicit map ![]() $f$ of the proof of Proposition 7.3.1, showing it to be a homomorphism without the need to reduce modulo
$f$ of the proof of Proposition 7.3.1, showing it to be a homomorphism without the need to reduce modulo ![]() $\mathscr {V}$. However, that still leaves an argument needed to show that
$\mathscr {V}$. However, that still leaves an argument needed to show that ![]() $f$ agrees with
$f$ agrees with ![]() $\Theta _N$ on
$\Theta _N$ on ![]() $\Gamma _1(N)$ to deduce the Hecke equivariance of
$\Gamma _1(N)$ to deduce the Hecke equivariance of ![]() $f$.
$f$.
7.4.2 Ordinary zeta maps with  $\mathbb {Z}_p$-coefficients
$\mathbb {Z}_p$-coefficients
Fix a prime ![]() $p \ge 5$ dividing
$p \ge 5$ dividing ![]() $N$. Let
$N$. Let ![]() $\mathbb {T}^*_N$ denote the full adjoint weight
$\mathbb {T}^*_N$ denote the full adjoint weight ![]() $2$ Hecke algebra for
$2$ Hecke algebra for ![]() $\Gamma _1(N)$ over
$\Gamma _1(N)$ over ![]() $\mathbb {Z}_p$ (see (4.15)). We also view it as acting via adjoint operators on
$\mathbb {Z}_p$ (see (4.15)). We also view it as acting via adjoint operators on ![]() $H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Q}_p(2))$; let us use a superscript
$H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Q}_p(2))$; let us use a superscript ![]() $\mathrm {ord}$ to denote the
$\mathrm {ord}$ to denote the ![]() $U_p^*$-ordinary part for this action. This
$U_p^*$-ordinary part for this action. This ![]() $U_p^*$-ordinary part is canonically a direct summand via application of Hida's idempotent in
$U_p^*$-ordinary part is canonically a direct summand via application of Hida's idempotent in ![]() $\mathbb {T}^*_N$.
$\mathbb {T}^*_N$.
In [Reference Fukaya and KatoFK24, Theorem 3.3.9] (see also Lemma 5.2.5 therein), Fukaya and Kato construct the following Hecke-equivariant zeta map to the ![]() $U_p^*$-ordinary part of cohomology (or more precisely, the negative of this map precomposed with an Atkin–Lehner involution).
$U_p^*$-ordinary part of cohomology (or more precisely, the negative of this map precomposed with an Atkin–Lehner involution).
Theorem 7.4.2 (Fukaya and Kato)
There is a ![]() $\mathbb {T}_N^*$-equivariant homomorphism
$\mathbb {T}_N^*$-equivariant homomorphism
where we identify the cup product of Siegel units with its ![]() $U_p^*$-ordinary projection.
$U_p^*$-ordinary projection.
The proof of Theorem 7.4.2 is quite involved but in particular uses a ![]() $p$-adic regulator computation of the values of a related map taken up the cyclotomic tower, which are norm-compatible sequences of Beilinson–Kato elements in Iwasawa cohomology.Footnote 26
$p$-adic regulator computation of the values of a related map taken up the cyclotomic tower, which are norm-compatible sequences of Beilinson–Kato elements in Iwasawa cohomology.Footnote 26
The restriction of the ordinary zeta map ![]() $z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$ to
$z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$ to ![]() $H_1(X_1(N),\mathbb {Z}_p)$ is the étale realization of the zeta map
$H_1(X_1(N),\mathbb {Z}_p)$ is the étale realization of the zeta map ![]() $z_N$ of Theorem 7.4.1. That is, the explicit formula for
$z_N$ of Theorem 7.4.1. That is, the explicit formula for ![]() $z_N(\vec \gamma ) = \Theta _{N,\gamma }$ given in Theorem 6.4.1 agrees in its étale realization with that of
$z_N(\vec \gamma ) = \Theta _{N,\gamma }$ given in Theorem 6.4.1 agrees in its étale realization with that of ![]() $z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$. To see this, note that the group
$z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$. To see this, note that the group ![]() $\mathscr {V}$ providing the ambiguity in the explicit formula for
$\mathscr {V}$ providing the ambiguity in the explicit formula for ![]() $\Theta _N$ of Theorem 6.4.1 vanishes in the étale realization, since the prime-to-level Hecke operators on
$\Theta _N$ of Theorem 6.4.1 vanishes in the étale realization, since the prime-to-level Hecke operators on ![]() $H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Q}_p(2))$ factor through the
$H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Q}_p(2))$ factor through the ![]() $\mathbb {Z}_p$-Hecke algebra of weight
$\mathbb {Z}_p$-Hecke algebra of weight ![]() $2$ modular forms, where each
$2$ modular forms, where each ![]() $V'_{\ell }$ has trivial kernel (see Remark 7.2.7).
$V'_{\ell }$ has trivial kernel (see Remark 7.2.7).
Remark 7.4.3 The operators ![]() $T'_{\ell }$ on
$T'_{\ell }$ on ![]() $H^2(Y,2)$ defined in § 6.5.1 arise from the composition of the operators
$H^2(Y,2)$ defined in § 6.5.1 arise from the composition of the operators ![]() $[\ell ]'$ and the dual (or adjoint) Hecke operators
$[\ell ]'$ and the dual (or adjoint) Hecke operators ![]() $T_{\ell }^*$ (or
$T_{\ell }^*$ (or ![]() $T(\ell )^*$) in [Reference Fukaya and KatoFK24, 1.2.3]. On étale cohomology, where we know that their actions factor through the usual weight
$T(\ell )^*$) in [Reference Fukaya and KatoFK24, 1.2.3]. On étale cohomology, where we know that their actions factor through the usual weight ![]() $2$ Hecke algebra, we have that
$2$ Hecke algebra, we have that ![]() $T'_{\ell }$ acts as
$T'_{\ell }$ acts as ![]() $T_{\ell } = \langle \ell \rangle T_{\ell }^*$. So, the Hecke equivariance at prime-to-level operators in Theorem 7.4.1 matches that of Theorem 7.4.2.
$T_{\ell } = \langle \ell \rangle T_{\ell }^*$. So, the Hecke equivariance at prime-to-level operators in Theorem 7.4.1 matches that of Theorem 7.4.2.
Remark 7.4.4 Jun Wang [Reference WangWan18, § 5.1] (see also [Reference Lecouturier and WangLW22, Theorem 3.7]) proved the analogue of Theorem 7.4.2 for ![]() $p \nmid N$, in which case one need not take ordinary parts. His map is shown to take values in the quotient of
$p \nmid N$, in which case one need not take ordinary parts. His map is shown to take values in the quotient of ![]() $H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))$ by the finite subgroup
$H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))$ by the finite subgroup ![]() $H^2_{\mathrm {\acute {e}t}}(\mathbb {Z}[{1}/{Np}],\mathbb {Z}_p(2))$. The
$H^2_{\mathrm {\acute {e}t}}(\mathbb {Z}[{1}/{Np}],\mathbb {Z}_p(2))$. The ![]() $p$-adic étale realization of our map
$p$-adic étale realization of our map ![]() $z_N$ takes image in
$z_N$ takes image in ![]() $H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))$ and induces Wang's map in the quotient.
$H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))$ and induces Wang's map in the quotient.
In [Reference Fukaya, Kato and SharifiFKS16], it is shown that if ![]() $p \nmid \varphi (N)$, then there exists an integral version of
$p \nmid \varphi (N)$, then there exists an integral version of ![]() $z_N$ to the primitive part of
$z_N$ to the primitive part of ![]() $H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))^{\mathrm {ord}}$ for the action of
$H^2_{\mathrm {\acute {e}t}}(Y_1(N),\mathbb {Z}_p(2))^{\mathrm {ord}}$ for the action of ![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$ by diamond operators, after excluding the
$(\mathbb {Z}/N\mathbb {Z})^{\times }$ by diamond operators, after excluding the ![]() $\omega ^{-2}$-eigenspace for
$\omega ^{-2}$-eigenspace for ![]() $(\mathbb {Z}/p\mathbb {Z})^{\times }$. Let us describe a motivic version of this, without some of these assumptions.
$(\mathbb {Z}/p\mathbb {Z})^{\times }$. Let us describe a motivic version of this, without some of these assumptions.
Let ![]() $\iota \colon (\mathbb {Z}/p\mathbb {Z})^{\times } \to (\mathbb {Z}/N\mathbb {Z})^{\times }$ denote the canonical map that splits reduction modulo
$\iota \colon (\mathbb {Z}/p\mathbb {Z})^{\times } \to (\mathbb {Z}/N\mathbb {Z})^{\times }$ denote the canonical map that splits reduction modulo ![]() $p$. We have an idempotent
$p$. We have an idempotent
 \[ \varepsilon = 1- \frac{1}{p-1} \sum_{a = 1}^{p-1} \omega^2(a)\iota(a) \in \mathbb{Z}_p[(\mathbb{Z}/N\mathbb{Z})^{\times}]. \]
\[ \varepsilon = 1- \frac{1}{p-1} \sum_{a = 1}^{p-1} \omega^2(a)\iota(a) \in \mathbb{Z}_p[(\mathbb{Z}/N\mathbb{Z})^{\times}]. \]
This idempotent applied to ![]() $H^2(X_1(N),\mathbb {Z}_p(2))$ serves to remove the
$H^2(X_1(N),\mathbb {Z}_p(2))$ serves to remove the ![]() $\omega ^{-2}$-eigenspace of
$\omega ^{-2}$-eigenspace of ![]() $(\mathbb {Z}/p\mathbb {Z})^{\times }$, where
$(\mathbb {Z}/p\mathbb {Z})^{\times }$, where ![]() $a \in (\mathbb {Z}/p\mathbb {Z})^{\times }$ acts as
$a \in (\mathbb {Z}/p\mathbb {Z})^{\times }$ acts as ![]() $[\iota (a)]'$.
$[\iota (a)]'$.
Proposition 7.4.5 There exists a unique homomorphism
which
– factors through the
 $U_p$-ordinary projection
$U_p$-ordinary projection  $H_1(X_1(N),\mathbb {Z}_p)_+ \to H_1(X_1(N),\mathbb {Z}_p)_+^{\mathrm {ord}}$ and
$H_1(X_1(N),\mathbb {Z}_p)_+ \to H_1(X_1(N),\mathbb {Z}_p)_+^{\mathrm {ord}}$ and– satisfies
 $z_N^{\mathrm {ord}}(V_n\vec \gamma ) = \varepsilon \cdot {}_n\Theta _{N,\gamma }$ for all primes
$z_N^{\mathrm {ord}}(V_n\vec \gamma ) = \varepsilon \cdot {}_n\Theta _{N,\gamma }$ for all primes  $n \nmid N$ and
$n \nmid N$ and  $\gamma \in \Gamma _1(N)$ with
$\gamma \in \Gamma _1(N)$ with  $\vec \gamma \in H_1(X_1(N),\mathbb {Z}_p)^{\mathrm {ord}}$.
$\vec \gamma \in H_1(X_1(N),\mathbb {Z}_p)^{\mathrm {ord}}$.
It is Hecke equivariant for the prime-to-level Hecke operators in the sense of Theorem 7.4.1.
Proof. The proof mirrors that of Proposition 7.2.6. Consider the ![]() $\mathbb {Z}_p$-algebra of endomorphisms
$\mathbb {Z}_p$-algebra of endomorphisms ![]() $\mathbb {T}_M$ generated by the Hecke operators of
$\mathbb {T}_M$ generated by the Hecke operators of ![]() $T_{\ell }$ for
$T_{\ell }$ for ![]() $\ell \nmid N$,
$\ell \nmid N$, ![]() $U_{\ell }^*$ for
$U_{\ell }^*$ for ![]() $\ell \mid N$, and
$\ell \mid N$, and ![]() $[d]'$ for
$[d]'$ for ![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ acting on
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$ acting on ![]() $H^1(\tilde {\Gamma }_1(N),M) = H^1(\Gamma _1(N),M)_+$. The
$H^1(\tilde {\Gamma }_1(N),M) = H^1(\Gamma _1(N),M)_+$. The ![]() $U_p^*$-ordinary part
$U_p^*$-ordinary part ![]() $\mathbb {T}_M^{\mathrm {ord}}$ of this Hecke algebra acts on
$\mathbb {T}_M^{\mathrm {ord}}$ of this Hecke algebra acts on
First, we note this Hecke algebra ![]() $\mathbb {T}_M^{\mathrm {ord}}$ is a quotient of the Hecke algebra
$\mathbb {T}_M^{\mathrm {ord}}$ is a quotient of the Hecke algebra ![]() $\mathbb {T}^{\mathrm {ord}}$ for
$\mathbb {T}^{\mathrm {ord}}$ for ![]() $U_p$-ordinary modular forms of weight
$U_p$-ordinary modular forms of weight ![]() $2$ for
$2$ for ![]() $\Gamma _1(N)$ that is generated by these operators, by a map taking an operator to its adjoint, that is, via the map that sends
$\Gamma _1(N)$ that is generated by these operators, by a map taking an operator to its adjoint, that is, via the map that sends ![]() $T_{\ell }^*$ to
$T_{\ell }^*$ to ![]() $T_{\ell }$,
$T_{\ell }$, ![]() $U_{\ell }$ to
$U_{\ell }$ to ![]() $U_{\ell }^*$, and
$U_{\ell }^*$, and ![]() $\langle d \rangle ^{-1}$ to
$\langle d \rangle ^{-1}$ to ![]() $[d]'$ (see § 7.2.2). For the direct summand
$[d]'$ (see § 7.2.2). For the direct summand ![]() $\varepsilon \cdot H^1(\tilde {\Gamma }_1(N), M)^{\mathrm {ord}} = H^1(\tilde {\Gamma }_1(N),\varepsilon \cdot M)^{\mathrm {ord}}$, the corresponding Hecke algebra is a quotient of
$\varepsilon \cdot H^1(\tilde {\Gamma }_1(N), M)^{\mathrm {ord}} = H^1(\tilde {\Gamma }_1(N),\varepsilon \cdot M)^{\mathrm {ord}}$, the corresponding Hecke algebra is a quotient of ![]() $\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$.
$\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$.
We claim that the operators ![]() $V_{\ell }^* = \ell ( \ell ^3 - \ell \langle \ell \rangle ^{-1}T_{\ell } + \langle \ell \rangle ^{-1})$ generate
$V_{\ell }^* = \ell ( \ell ^3 - \ell \langle \ell \rangle ^{-1}T_{\ell } + \langle \ell \rangle ^{-1})$ generate ![]() $\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$, which will tell us that the operators
$\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$, which will tell us that the operators ![]() $V_{\ell }$ generate
$V_{\ell }$ generate ![]() $\mathbb {T}_M^{\mathrm {ord}}$. Suppose they do not. We then have a nonzero homomorphism
$\mathbb {T}_M^{\mathrm {ord}}$. Suppose they do not. We then have a nonzero homomorphism ![]() $\phi \colon \varepsilon \cdot \mathbb {T}^{\mathrm {ord}} \to F$ to an algebraically closed field
$\phi \colon \varepsilon \cdot \mathbb {T}^{\mathrm {ord}} \to F$ to an algebraically closed field ![]() $F$ of characteristic
$F$ of characteristic ![]() $p$ such that
$p$ such that ![]() $V_{\ell }^* \in \ker \,\phi$ for all
$V_{\ell }^* \in \ker \,\phi$ for all ![]() $\ell \nmid N$.
$\ell \nmid N$.
Let ![]() $N'$ be the prime-to-
$N'$ be the prime-to-![]() $p$ part of
$p$ part of ![]() $N$. Hida theory (see [Reference HidaHid86, Theorem 1.2]) provides a
$N$. Hida theory (see [Reference HidaHid86, Theorem 1.2]) provides a ![]() $U_p$-ordinary eigenform
$U_p$-ordinary eigenform ![]() $f$ in
$f$ in ![]() $M_2(\Gamma _1(N'p),F)^{\mathrm {ord}}$ such that
$M_2(\Gamma _1(N'p),F)^{\mathrm {ord}}$ such that ![]() $\phi (T_{\ell })$ for
$\phi (T_{\ell })$ for ![]() $\ell \nmid N$ or
$\ell \nmid N$ or ![]() $\phi (U_{\ell })$ for
$\phi (U_{\ell })$ for ![]() $\ell \mid N$ is its
$\ell \mid N$ is its ![]() $\ell$th Fourier coefficient
$\ell$th Fourier coefficient ![]() $a_{\ell }(f) \in F$. Let
$a_{\ell }(f) \in F$. Let ![]() $\omega ^j$ for
$\omega ^j$ for ![]() $1 \le j \le p-1$ be the restriction of the Nebentypus of
$1 \le j \le p-1$ be the restriction of the Nebentypus of ![]() $f$ to
$f$ to ![]() $(\mathbb {Z}/p\mathbb {Z})^{\times }$, where
$(\mathbb {Z}/p\mathbb {Z})^{\times }$, where ![]() $\omega$ denotes the mod
$\omega$ denotes the mod ![]() $p$ cyclotomic character. A result of Ohta [Reference OhtaOht05, Proposition 1.3.5] implies that
$p$ cyclotomic character. A result of Ohta [Reference OhtaOht05, Proposition 1.3.5] implies that ![]() $f$ arises from an eigenform
$f$ arises from an eigenform ![]() $f'$ in the
$f'$ in the ![]() $T_p$-ordinary part of
$T_p$-ordinary part of ![]() $M_{j+2}(\Gamma _1(N'),F)$ with
$M_{j+2}(\Gamma _1(N'),F)$ with ![]() $a_{\ell }(f) = a_{\ell }(f')$ for
$a_{\ell }(f) = a_{\ell }(f')$ for ![]() $\ell \neq p$.
$\ell \neq p$.
As in the proof of Proposition 7.2.6,we may associate to ![]() $f'$ a semisimple Galois representation
$f'$ a semisimple Galois representation ![]() $\rho \colon G_{\mathbb {Q}} \to \mathrm {GL}_2(F)$ satisfying
$\rho \colon G_{\mathbb {Q}} \to \mathrm {GL}_2(F)$ satisfying ![]() $\rho |_{I_p} \simeq \omega ^{j+1} \oplus 1$ (again by [Reference EdixhovenEdi92, Theorem 2.5]). On the other hand, since
$\rho |_{I_p} \simeq \omega ^{j+1} \oplus 1$ (again by [Reference EdixhovenEdi92, Theorem 2.5]). On the other hand, since ![]() $\ell T_{\ell } - 1 - \ell ^3 \langle \ell \rangle \in \ker \,\phi$ for all
$\ell T_{\ell } - 1 - \ell ^3 \langle \ell \rangle \in \ker \,\phi$ for all ![]() $\ell \nmid Np$ by assumption, we must have
$\ell \nmid Np$ by assumption, we must have
for some ![]() $F$-valued Dirichlet character
$F$-valued Dirichlet character ![]() $\chi$ of modulus
$\chi$ of modulus ![]() $N'$, where
$N'$, where ![]() $\varphi _{\ell }$ denotes the Frobenius at
$\varphi _{\ell }$ denotes the Frobenius at ![]() $\ell$. By Čebotarev density, we then have
$\ell$. By Čebotarev density, we then have ![]() $\rho \simeq \omega ^{-1} \oplus \omega ^{j+2}\chi$. This in turn forces
$\rho \simeq \omega ^{-1} \oplus \omega ^{j+2}\chi$. This in turn forces ![]() $j = -2$, but the
$j = -2$, but the ![]() $\omega ^{-2}|_{I_p}$-eigenspace of
$\omega ^{-2}|_{I_p}$-eigenspace of ![]() $\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$ is trivial. Thus, we have the necessary contradiction.
$\varepsilon \cdot \mathbb {T}^{\mathrm {ord}}$ is trivial. Thus, we have the necessary contradiction.
Since the operators ![]() $V_{\ell }$ generate
$V_{\ell }$ generate ![]() $\mathbb {T}_M^{\mathrm {ord}}$, as in the proof of Theorem 7.2.2 we may construct a
$\mathbb {T}_M^{\mathrm {ord}}$, as in the proof of Theorem 7.2.2 we may construct a ![]() $U_p^*$-ordinary parabolic cocycle
$U_p^*$-ordinary parabolic cocycle ![]() $\Theta _N^{\mathrm {ord}} \colon \tilde {\Gamma }_1(N) \to \varepsilon \cdot M$ as a
$\Theta _N^{\mathrm {ord}} \colon \tilde {\Gamma }_1(N) \to \varepsilon \cdot M$ as a ![]() $\mathbb {T}_M$-linear combination of the restrictions of the cocycles
$\mathbb {T}_M$-linear combination of the restrictions of the cocycles ![]() ${}_n \Theta _N$ to
${}_n \Theta _N$ to ![]() $\tilde {\Gamma }_1(N)$, where the coefficients sum to Hida's ordinary idempotent in
$\tilde {\Gamma }_1(N)$, where the coefficients sum to Hida's ordinary idempotent in ![]() $\mathbb {T}_M$. The class of
$\mathbb {T}_M$. The class of ![]() $V_n \Theta _N^{\mathrm {ord}}$ for a prime
$V_n \Theta _N^{\mathrm {ord}}$ for a prime ![]() $n \nmid N$ is the ordinary projection of the class of
$n \nmid N$ is the ordinary projection of the class of ![]() ${}_n \Theta _N$. This in turn gives rise to the homomorphism
${}_n \Theta _N$. This in turn gives rise to the homomorphism ![]() $z_N^{\mathrm {ord}}$ in the statement of the proposition. In particular, note that its image lands in
$z_N^{\mathrm {ord}}$ in the statement of the proposition. In particular, note that its image lands in ![]() $H^2(X_1(N),\mathbb {Z}_p(2))$ via the argument of Proposition 7.3.2.
$H^2(X_1(N),\mathbb {Z}_p(2))$ via the argument of Proposition 7.3.2.
We remark that we do not show that ![]() $z_N^{\mathrm {ord}}$ is equivariant for
$z_N^{\mathrm {ord}}$ is equivariant for ![]() $p$th Hecke operators, as prior to this point we only considered prime-to-level operators on our cocycles. It would be interesting to prove this. Passing to étale cohomology, the explicit formula for
$p$th Hecke operators, as prior to this point we only considered prime-to-level operators on our cocycles. It would be interesting to prove this. Passing to étale cohomology, the explicit formula for ![]() $\Theta _{N,\gamma }$ of Theorem 6.4.1 holds in
$\Theta _{N,\gamma }$ of Theorem 6.4.1 holds in ![]() $H^2_{\mathrm {\acute {e}t}}(Y,\mathbb {Q}_p(2))$ without ambiguity, since
$H^2_{\mathrm {\acute {e}t}}(Y,\mathbb {Q}_p(2))$ without ambiguity, since ![]() $\mathscr {V}$ vanishes there. From this, we see that the
$\mathscr {V}$ vanishes there. From this, we see that the ![]() $\mathbb {Q}_p$-linear extension of the
$\mathbb {Q}_p$-linear extension of the ![]() $p$-adic étale realization of our ordinary zeta map
$p$-adic étale realization of our ordinary zeta map ![]() $z_N^{\mathrm {ord}}$ induces
$z_N^{\mathrm {ord}}$ induces ![]() $\varepsilon$ applied to the restriction of the zeta map
$\varepsilon$ applied to the restriction of the zeta map ![]() $z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$ of Fukaya and Kato to
$z_{N,\mathrm {\acute {e}t}}^{\mathrm {ord}}$ of Fukaya and Kato to ![]() $H_1(X_1(N),\mathbb {Z}_p)$. This is Hecke equivariant for the full Hecke algebra by Theorem 7.4.2.
$H_1(X_1(N),\mathbb {Z}_p)$. This is Hecke equivariant for the full Hecke algebra by Theorem 7.4.2.
Acknowledgements
R.S. thanks T. Fukaya and K. Kato for prior conversations regarding maps on homology, T. Geisser, M. Levine, and M. Spitzweck for answers to questions regarding motivic cohomology, and C. Khare for a conversation on Galois representations. He also thanks T. Smits and F. Vu for a careful reading of a draft of this work, and E. Lecouturier and P. Xu for very helpful comments on the preprint version.
A.V. thanks Aravind Asok for patiently answering questions about motivic cohomology. He also gratefully acknowledges conversations with N. Bergeron, P. Charollois, and L. Garcia.
Finally, we thank the referees for careful readings that resulted in several corrections.
Conflicts of interest
None.
Financial support
The research of R.S. was supported in part by the National Science Foundation under Grant No. DMS-2101889. The research of A.V. was supported in part by the National Science Foundation under Grant No. 1931087.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society, and Cambridge University Press.