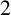1 Introduction
Finite groups with dihedral Sylow
![]() $2$
-subgroups were fully classified by Gorenstein and Walter [Reference Gorenstein and Walter20–Reference Gorenstein and Walter23] (an alternate proof was given by Bender [Reference Bender2, Reference Bender and Glauberman3]). The principal
$2$
-subgroups were fully classified by Gorenstein and Walter [Reference Gorenstein and Walter20–Reference Gorenstein and Walter23] (an alternate proof was given by Bender [Reference Bender2, Reference Bender and Glauberman3]). The principal
![]() $2$
-blocks of such groups were investigated by Brauer [Reference Brauer8], Erdmann [Reference Erdmann15], Landrock [Reference Landrock29], and recently Koshitani and Lassueur [Reference Koshitani and Lassueur28]. As a natural next step, it is desirable to understand arbitrary blocks B of finite groups G with dihedral defect groups D of order
$2$
-blocks of such groups were investigated by Brauer [Reference Brauer8], Erdmann [Reference Erdmann15], Landrock [Reference Landrock29], and recently Koshitani and Lassueur [Reference Koshitani and Lassueur28]. As a natural next step, it is desirable to understand arbitrary blocks B of finite groups G with dihedral defect groups D of order
![]() $2^d\ge 4$
. Brauer [Reference Brauer9] has shown that the number of irreducible characters in B is
$2^d\ge 4$
. Brauer [Reference Brauer9] has shown that the number of irreducible characters in B is
![]() $k(B)=2^{d-2}+3$
, where four of them have height
$k(B)=2^{d-2}+3$
, where four of them have height
![]() $0$
and the remaining characters have height
$0$
and the remaining characters have height
![]() $1$
. However, the number of simple modules in B is
$1$
. However, the number of simple modules in B is
![]() $l(B)=1$
,
$l(B)=1$
,
![]() $2$
or
$2$
or
![]() $3$
depending on three different fusion patterns. (If B is the principal block, the fusion patterns are distinguished by the number of conjugacy classes of involutions: there are three, two or only one such class, respectively.) Based on Brauer’s computations, Cabanes and Picaronny [Reference Cabanes and Picaronny10] have constructed perfect isometries between blocks with dihedral defect groups and the same fusion pattern.
$3$
depending on three different fusion patterns. (If B is the principal block, the fusion patterns are distinguished by the number of conjugacy classes of involutions: there are three, two or only one such class, respectively.) Based on Brauer’s computations, Cabanes and Picaronny [Reference Cabanes and Picaronny10] have constructed perfect isometries between blocks with dihedral defect groups and the same fusion pattern.
The algebra structure of B was first investigated for solvable groups G by Erdmann and Michler [Reference Erdmann and Michler18], and Koshitani [Reference Koshitani27]. The general case of arbitrary groups was subsequently studied by Donovan [Reference Donovan12] and by Erdmann [Reference Erdmann16, Reference Erdmann17] in the framework of tame algebras. Some of the algebras with two simple modules described by Erdmann were not known to occur as block algebras. For
![]() $l(B)=3$
, Linckelmann [Reference Linckelmann30] has lifted the perfect isometries constructed by Cabanes and Picaronny to derived equivalences. This applies in particular to Klein four defect groups (that is,
$l(B)=3$
, Linckelmann [Reference Linckelmann30] has lifted the perfect isometries constructed by Cabanes and Picaronny to derived equivalences. This applies in particular to Klein four defect groups (that is,
![]() $d=2$
) where one has stronger results by Linckelmann [Reference Linckelmann31] and Craven et al. [Reference Craven, Eaton, Kessar and Linckelmann11] on the source algebra of B (the case
$d=2$
) where one has stronger results by Linckelmann [Reference Linckelmann31] and Craven et al. [Reference Craven, Eaton, Kessar and Linckelmann11] on the source algebra of B (the case
![]() $l(B)=2$
does not occur here). The derived equivalence classes for
$l(B)=2$
does not occur here). The derived equivalence classes for
![]() $l(B)=2$
were later found by Holm [Reference Holm25]. The possible Morita equivalence classes in this situation were restricted by Bleher [Reference Bleher4, Reference Bleher5] and Bleher et al. [Reference Bleher, Llosent and Schaefer6] using universal deformation rings. Thereafter, Eisele [Reference Eisele14] proved that certain scalars in Erdmann’s description of the basic algebra cannot arise for
$l(B)=2$
were later found by Holm [Reference Holm25]. The possible Morita equivalence classes in this situation were restricted by Bleher [Reference Bleher4, Reference Bleher5] and Bleher et al. [Reference Bleher, Llosent and Schaefer6] using universal deformation rings. Thereafter, Eisele [Reference Eisele14] proved that certain scalars in Erdmann’s description of the basic algebra cannot arise for
![]() $l(B)=2$
. Finally, using the classification of finite simple groups, a complete list of all Morita equivalence classes of blocks with dihedral defect groups was given recently by Macgregor [Reference Macgregor33].
$l(B)=2$
. Finally, using the classification of finite simple groups, a complete list of all Morita equivalence classes of blocks with dihedral defect groups was given recently by Macgregor [Reference Macgregor33].
Some questions on blocks cannot even be answered when the Morita equivalence class is known. For instance, if B contains real characters
![]() $\chi \in \operatorname {Irr}(B)$
, it is of interest to determine their Frobenius–Schur indicators (F-S indicators for short),
$\chi \in \operatorname {Irr}(B)$
, it is of interest to determine their Frobenius–Schur indicators (F-S indicators for short),
 $$ \begin{align*}\epsilon(\chi):=\frac{1}{|G|}\sum_{g\in G}\chi(g^2),\end{align*} $$
$$ \begin{align*}\epsilon(\chi):=\frac{1}{|G|}\sum_{g\in G}\chi(g^2),\end{align*} $$
in terms of D. Since
![]() $\chi (g^2)$
can only be nonzero when the square of the
$\chi (g^2)$
can only be nonzero when the square of the
![]() $2$
-part of g is conjugate to an element in D, it is plausible that
$2$
-part of g is conjugate to an element in D, it is plausible that
![]() $\epsilon (\chi )$
actually depends on an extension E of D such that
$\epsilon (\chi )$
actually depends on an extension E of D such that
![]() $|E:D|=2$
. In fact, Murray [Reference Murray35] has described the F-S indicators when D is a dihedral group using the decomposition matrix and the so-called extended defect group of B. It is however not clear which combinations of these ingredients can actually occur. The aim of this note is to eliminate two infinite families of Murray’s classification and construct explicit examples for the remaining cases.
$|E:D|=2$
. In fact, Murray [Reference Murray35] has described the F-S indicators when D is a dihedral group using the decomposition matrix and the so-called extended defect group of B. It is however not clear which combinations of these ingredients can actually occur. The aim of this note is to eliminate two infinite families of Murray’s classification and construct explicit examples for the remaining cases.
Theorem 1.1. Let B be real block of a finite group G with dihedral defect group D of order
![]() $2^d\ge 8$
and extended defect group E. Let
$2^d\ge 8$
and extended defect group E. Let
![]() $\epsilon _1,\ldots ,\epsilon _4$
be the F-S indicators of the four irreducible characters of height
$\epsilon _1,\ldots ,\epsilon _4$
be the F-S indicators of the four irreducible characters of height
![]() $0$
in B. There is a unique family of
$0$
in B. There is a unique family of
![]() $2$
-conjugate characters of height
$2$
-conjugate characters of height
![]() $1$
in
$1$
in
![]() $\operatorname {Irr}(B)$
of size
$\operatorname {Irr}(B)$
of size
![]() $2^{d-3}$
. Let
$2^{d-3}$
. Let
![]() $\mu $
be the common F-S indicator of those characters. The possible values for
$\mu $
be the common F-S indicator of those characters. The possible values for
![]() $\epsilon _1,\ldots ,\epsilon _4,\mu $
are given in Table 1, while the remaining
$\epsilon _1,\ldots ,\epsilon _4,\mu $
are given in Table 1, while the remaining
![]() $2^{d-3}-1$
characters (of height
$2^{d-3}-1$
characters (of height
![]() $1$
) all have F-S indicator
$1$
) all have F-S indicator
![]() $1$
. All cases occur for all d as indicated.
$1$
. All cases occur for all d as indicated.
The proof of Theorem 1.1 is given in Section 2. In Section 3, we refine one of the conjectures made in [Reference Sambale41]. In this context, we present two new general results in Section 4. We apply these results in Section 5 to obtain partial information on the F-S indicators of characters in arbitrary tame blocks. Finally, we determine all F-S indicators in real blocks with homocyclic defect group of type
![]() $C_4\times C_4$
.
$C_4\times C_4$
.
Table 1 F-S indicators for Theorem 1.1.

2 Proof of Theorem 1.1
Our notation is fairly standard and follows [Reference Sambale41]. We assume a very basic understanding of fusion systems and refer to [Reference Linckelmann32] occasionally. In the following, let B be a
![]() $2$
-block of a finite group G. We may assume that B is real, that is,
$2$
-block of a finite group G. We may assume that B is real, that is,
![]() $\operatorname {Irr}(B)$
is invariant under complex conjugation (otherwise all characters in
$\operatorname {Irr}(B)$
is invariant under complex conjugation (otherwise all characters in
![]() $\operatorname {Irr}(B)$
have F-S indicator
$\operatorname {Irr}(B)$
have F-S indicator
![]() $0$
). Recall that B determines up to conjugation a unique defect pair
$0$
). Recall that B determines up to conjugation a unique defect pair
![]() $(D,E)$
such that D is a defect group and E is an extended defect group of B (see [Reference Sambale41, Section 3] for details). We remark that
$(D,E)$
such that D is a defect group and E is an extended defect group of B (see [Reference Sambale41, Section 3] for details). We remark that
![]() $D\le E$
and
$D\le E$
and
![]() $|E:D|\le 2$
with equality if and only if B is not the principal block.
$|E:D|\le 2$
with equality if and only if B is not the principal block.
Now let D be a dihedral group of order
![]() $2^d\ge 4$
. Then B is nilpotent if and only if
$2^d\ge 4$
. Then B is nilpotent if and only if
![]() $l(B)=1$
. For
$l(B)=1$
. For
![]() $l(B)>1$
and
$l(B)>1$
and
![]() $d\ge 3$
, we have observed that two type (b) cases in [Reference Murray35, Table 2] have no counterparts in [Reference Murray34, Theorems 1.7, 1.8] for
$d\ge 3$
, we have observed that two type (b) cases in [Reference Murray35, Table 2] have no counterparts in [Reference Murray34, Theorems 1.7, 1.8] for
![]() $d=2$
(that is, D is a Klein four-group). In fact, the following proposition shows that these two cases in [Reference Murray35, Table 2] do not occur.
$d=2$
(that is, D is a Klein four-group). In fact, the following proposition shows that these two cases in [Reference Murray35, Table 2] do not occur.
Proposition 2.1. Let B be a real
![]() $2$
-block of a finite group G with defect pair
$2$
-block of a finite group G with defect pair
![]() $(D,E)$
such that
$(D,E)$
such that
![]() $D\cong D_{2^d}$
with
$D\cong D_{2^d}$
with
![]() $d\ge 3$
. If
$d\ge 3$
. If
![]() $l(B)>1$
, then
$l(B)>1$
, then
![]() $E\cong D\times C_2$
or
$E\cong D\times C_2$
or
![]() $\mathrm {C}_E(D)=\mathrm {Z}(D)$
.
$\mathrm {C}_E(D)=\mathrm {Z}(D)$
.
Proof. Let
![]() $b_D$
be a Brauer correspondent of B in
$b_D$
be a Brauer correspondent of B in
![]() $D\mathrm {C}_G(D)$
. Then by [Reference Murray35, Lemma 2.2], we may choose E in such a way that
$D\mathrm {C}_G(D)$
. Then by [Reference Murray35, Lemma 2.2], we may choose E in such a way that
![]() $b_D^{E\mathrm {C}_G(D)}$
is real with defect pair
$b_D^{E\mathrm {C}_G(D)}$
is real with defect pair
![]() $(D,E)$
. In other words,
$(D,E)$
. In other words,
![]() $(D,b_D,E)$
is a Sylow B-subtriple in the notation of [Reference Murray35]. Since B is not nilpotent, there exists a so-called essential subgroup
$(D,b_D,E)$
is a Sylow B-subtriple in the notation of [Reference Murray35]. Since B is not nilpotent, there exists a so-called essential subgroup
![]() $Q\le D$
in the fusion system
$Q\le D$
in the fusion system
![]() $\mathcal {F}$
of B. Then Q is a Klein four-group and there exists a unique B-subpair
$\mathcal {F}$
of B. Then Q is a Klein four-group and there exists a unique B-subpair
![]() $(Q,b_Q)\le (D,b_D)$
(see [Reference Sambale37, Theorem 1]). Moreover,
$(Q,b_Q)\le (D,b_D)$
(see [Reference Sambale37, Theorem 1]). Moreover,
![]() $b_Q$
is nilpotent with defect group
$b_Q$
is nilpotent with defect group
![]() $\mathrm {C}_D(Q)=Q$
(see [Reference Aschbacher, Kessar and Oliver1, Theorem IV.3.19]). Since Q is essential,
$\mathrm {C}_D(Q)=Q$
(see [Reference Aschbacher, Kessar and Oliver1, Theorem IV.3.19]). Since Q is essential,
The block
![]() $B_Q:=b_Q^{\mathrm {N}_G(Q,b_Q)}$
has defect group
$B_Q:=b_Q^{\mathrm {N}_G(Q,b_Q)}$
has defect group
![]() $\mathrm {N}_D(Q)\cong D_8$
by [Reference Aschbacher, Kessar and Oliver1, Theorem IV.3.19]. By [Reference Navarro36, Corollary 9.21],
$\mathrm {N}_D(Q)\cong D_8$
by [Reference Aschbacher, Kessar and Oliver1, Theorem IV.3.19]. By [Reference Navarro36, Corollary 9.21],
![]() $B_Q$
is the only block of
$B_Q$
is the only block of
![]() $\mathrm {N}_G(Q,b_Q)$
that covers
$\mathrm {N}_G(Q,b_Q)$
that covers
![]() $b_Q$
. Since every subgroup of
$b_Q$
. Since every subgroup of
![]() $S_3$
has trivial Schur multiplier, each
$S_3$
has trivial Schur multiplier, each
![]() $\psi \in \operatorname {Irr}(b_Q)$
extends to its inertial group. The number of extensions is determined by Gallagher’s theorem. If
$\psi \in \operatorname {Irr}(b_Q)$
extends to its inertial group. The number of extensions is determined by Gallagher’s theorem. If
![]() $\psi $
is
$\psi $
is
![]() $\mathrm {N}_G(Q,b_Q)$
-invariant,
$\mathrm {N}_G(Q,b_Q)$
-invariant,
![]() $\operatorname {Irr}(B_Q)$
contains three extensions of
$\operatorname {Irr}(B_Q)$
contains three extensions of
![]() $\psi $
. Since
$\psi $
. Since
![]() $k(B_Q)=5$
, there can be at most one such character
$k(B_Q)=5$
, there can be at most one such character
![]() $\psi $
. If
$\psi $
. If
![]() $\mathrm {N}_G(Q,b_Q)$
has two orbits of length
$\mathrm {N}_G(Q,b_Q)$
has two orbits of length
![]() $2$
in
$2$
in
![]() $\operatorname {Irr}(b_Q)$
, then we would get six characters in
$\operatorname {Irr}(b_Q)$
, then we would get six characters in
![]() $\operatorname {Irr}(B_Q)$
. Therefore, the four characters in
$\operatorname {Irr}(B_Q)$
. Therefore, the four characters in
![]() $\operatorname {Irr}(b_Q)$
distribute into orbits of length
$\operatorname {Irr}(b_Q)$
distribute into orbits of length
![]() $1$
and
$1$
and
![]() $3$
under the action of
$3$
under the action of
![]() $\mathrm {N}_G(Q,b_Q)$
. In particular,
$\mathrm {N}_G(Q,b_Q)$
. In particular,
![]() $\operatorname {Irr}(b_Q)$
contains (at least) three characters with the same F-S indicator.
$\operatorname {Irr}(b_Q)$
contains (at least) three characters with the same F-S indicator.
The possible extended defect groups E were determined in [Reference Murray35, Proposition 4.1]. Suppose that our claim is false. Then we are in case (b), that is,
![]() $E\cong D*C_4$
is a central product. By [Reference Murray35, Lemma 2.6],
$E\cong D*C_4$
is a central product. By [Reference Murray35, Lemma 2.6],
![]() $b_Q$
is real and has extended defect group
$b_Q$
is real and has extended defect group
![]() $\mathrm {C}_E(Q)= Q*E\cong C_4\times C_2$
. However now, [Reference Murray34, Theorem 1.7] implies that exactly two characters in
$\mathrm {C}_E(Q)= Q*E\cong C_4\times C_2$
. However now, [Reference Murray34, Theorem 1.7] implies that exactly two characters in
![]() $\operatorname {Irr}(b_Q)$
have F-S indicator
$\operatorname {Irr}(b_Q)$
have F-S indicator
![]() $1$
. This contradicts the observation above.
$1$
. This contradicts the observation above.
To show that the remaining cases in [Reference Murray35, Table 2] occur, we provide a general construction.
Proposition 2.2. Let
![]() $H<\hat {H}$
be finite groups such that
$H<\hat {H}$
be finite groups such that
![]() $|\hat {H}:H|=2$
. Let E be a Sylow
$|\hat {H}:H|=2$
. Let E be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\hat {H}$
and let
$\hat {H}$
and let
![]() $D:=E\cap H$
. Let
$D:=E\cap H$
. Let
![]() $H\times C_3<G<\hat {H}\times S_3$
such that
$H\times C_3<G<\hat {H}\times S_3$
such that
![]() $H\times S_3\ne G\ne \hat {H}\times C_3$
. Then G has a real
$H\times S_3\ne G\ne \hat {H}\times C_3$
. Then G has a real
![]() $2$
-block B with defect pair isomorphic to
$2$
-block B with defect pair isomorphic to
![]() $(D,E)$
. Moreover, B is Morita equivalent to the principal block
$(D,E)$
. Moreover, B is Morita equivalent to the principal block
![]() $B_0(H)$
of H, and B and
$B_0(H)$
of H, and B and
![]() $B_0(H)$
have the same fusion system.
$B_0(H)$
have the same fusion system.
Proof. Note that
![]() $B_0(H)$
is isomorphic to a (nonreal) block
$B_0(H)$
is isomorphic to a (nonreal) block
![]() $B_0(H)\otimes b$
of
$B_0(H)\otimes b$
of
![]() $H\times C_3$
, where
$H\times C_3$
, where
![]() $b\cong F$
is a nonprincipal block of
$b\cong F$
is a nonprincipal block of
![]() $C_3$
. Clearly,
$C_3$
. Clearly,
![]() $B_0(H)$
and
$B_0(H)$
and
![]() $B_0(H)\otimes b$
have the same fusion system. Let
$B_0(H)\otimes b$
have the same fusion system. Let
be the Fong–Reynolds correspondent of
![]() $B_0(H)\otimes b$
in G. By [Reference Linckelmann32, Theorem 6.8.3], B is Puig equivalent to
$B_0(H)\otimes b$
in G. By [Reference Linckelmann32, Theorem 6.8.3], B is Puig equivalent to
![]() $B_0(H)\otimes b$
(that is, the blocks have the same source algebra). This implies that B is Morita equivalent to
$B_0(H)\otimes b$
(that is, the blocks have the same source algebra). This implies that B is Morita equivalent to
![]() $B_0(H)$
and both blocks have the same fusion system (see [Reference Linckelmann32, Theorem 8.7.1]). In particular, B has defect group D.
$B_0(H)$
and both blocks have the same fusion system (see [Reference Linckelmann32, Theorem 8.7.1]). In particular, B has defect group D.
Let
![]() $\operatorname {Irr}(b)=\{\theta \}$
. Then
$\operatorname {Irr}(b)=\{\theta \}$
. Then
![]() $\chi :=(1_H\times \theta )^G\in \operatorname {Irr}(B)$
is a real character and therefore B is real. Moreover, B is not the principal block of G since otherwise, B cannot cover
$\chi :=(1_H\times \theta )^G\in \operatorname {Irr}(B)$
is a real character and therefore B is real. Moreover, B is not the principal block of G since otherwise, B cannot cover
![]() $B_0(H)\otimes b$
. Therefore, an extended defect group of B must be a Sylow
$B_0(H)\otimes b$
. Therefore, an extended defect group of B must be a Sylow
![]() $2$
-subgroup of G, because
$2$
-subgroup of G, because
![]() $|G:H\times C_3|=2$
. Let
$|G:H\times C_3|=2$
. Let
![]() $e\in E\setminus D$
and
$e\in E\setminus D$
and
![]() $x\in S_3$
an involution. Then,
$x\in S_3$
an involution. Then,
![]() $D\langle ex\rangle $
is a Sylow
$D\langle ex\rangle $
is a Sylow
![]() $2$
-subgroup of G and
$2$
-subgroup of G and
 $$ \begin{align*}E\to D\langle ex\rangle,\quad g\mapsto\begin{cases} g&\text{if }g\in D,\\ gx&\text{if }g\notin D \end{cases} \end{align*} $$
$$ \begin{align*}E\to D\langle ex\rangle,\quad g\mapsto\begin{cases} g&\text{if }g\in D,\\ gx&\text{if }g\notin D \end{cases} \end{align*} $$
is an isomorphism.
Choosing
![]() $(H,\hat {H})=(D,E)$
in Proposition 2.2 shows that there are nilpotent real blocks for every given defect pair
$(H,\hat {H})=(D,E)$
in Proposition 2.2 shows that there are nilpotent real blocks for every given defect pair
![]() $(D,E)$
. Similarly, the choice
$(D,E)$
. Similarly, the choice
![]() $\hat {H}=H\times C_2$
leads to
$\hat {H}=H\times C_2$
leads to
![]() $G=H\times S_3$
and a block with extended defect group
$G=H\times S_3$
and a block with extended defect group
![]() $E\cong D\times C_2$
.
$E\cong D\times C_2$
.
Proof of Theorem 1.1
By Proposition 2.1 and [Reference Murray35, Table 2], it remains to construct examples for each Morita equivalence class and each defect pair. By the remark above, we may assume that B is not nilpotent. Then by [Reference Macgregor33, Theorem 2.1], B is Morita equivalent to
![]() $B_0(H)$
, where H is one of the following groups:
$B_0(H)$
, where H is one of the following groups:
-
(1)
 $\operatorname {PGL}(2,q)$
with
$\operatorname {PGL}(2,q)$
with
 $|q-1|_2=2^{d-1}$
;
$|q-1|_2=2^{d-1}$
; -
(2)
 $\operatorname {PGL}(2,q)$
with
$\operatorname {PGL}(2,q)$
with
 $|q+1|_2=2^{d-1}$
;
$|q+1|_2=2^{d-1}$
; -
(3)
 $\operatorname {PSL}(2,q)$
with
$\operatorname {PSL}(2,q)$
with
 $|q-1|_2=2^d$
;
$|q-1|_2=2^d$
; -
(4)
 $\operatorname {PSL}(2,q)$
with
$\operatorname {PSL}(2,q)$
with
 $|q+1|_2=2^d$
;
$|q+1|_2=2^d$
; -
(5)
 $A_7$
with
$A_7$
with
 $d=3$
.
$d=3$
.
Note that for every
![]() $d\ge 3$
, there exists a prime q congruent to
$d\ge 3$
, there exists a prime q congruent to
![]() $\pm 1+2^d$
modulo
$\pm 1+2^d$
modulo
![]() $2^{d+1}$
by Dirichlet’s theorem. Thus, appropriate groups H exist for every d. Moreover, if
$2^{d+1}$
by Dirichlet’s theorem. Thus, appropriate groups H exist for every d. Moreover, if
![]() $q\equiv 1+2^d\pmod {2^{d+1}}$
, then
$q\equiv 1+2^d\pmod {2^{d+1}}$
, then
![]() $q^2\equiv 1+2^{d+1}\pmod {2^{d+2}}$
. This will be used later on.
$q^2\equiv 1+2^{d+1}\pmod {2^{d+2}}$
. This will be used later on.
For the cases (2) and (5), Murray [Reference Murray35, Table 2] has shown that only
![]() $E\cong D\times C_2$
is possible. Here, we take
$E\cong D\times C_2$
is possible. Here, we take
![]() $G=H\times S_3$
as explained above. In case (4), we find
$G=H\times S_3$
as explained above. In case (4), we find
![]() $E\cong D_{2^{d+1}}$
in [Reference Murray35, Table 2]. Since
$E\cong D_{2^{d+1}}$
in [Reference Murray35, Table 2]. Since
we can take
![]() $\hat {H}:=\operatorname {PGL}(2,q)$
with the required properties.
$\hat {H}:=\operatorname {PGL}(2,q)$
with the required properties.
Suppose now that case (1) occurs. By the remark above, we find a prime p such that
![]() $q=p^2\equiv 1+2^d\pmod {2^{d+1}}$
. Let
$q=p^2\equiv 1+2^d\pmod {2^{d+1}}$
. Let
![]() $\sigma $
be the Frobenius automorphism
$\sigma $
be the Frobenius automorphism
![]() $\mathbb {F}_q\to \mathbb {F}_q$
,
$\mathbb {F}_q\to \mathbb {F}_q$
,
![]() $x\mapsto x^p$
. Then the semilinear group
$x\mapsto x^p$
. Then the semilinear group
![]() $\hat {H}:=H\rtimes \langle \sigma \rangle $
has Sylow
$\hat {H}:=H\rtimes \langle \sigma \rangle $
has Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $E\cong C_{2^{d-1}}\rtimes C_2^2$
, where
$E\cong C_{2^{d-1}}\rtimes C_2^2$
, where
![]() $C_2^2$
acts faithfully on
$C_2^2$
acts faithfully on
![]() $C_{2^{d-1}}$
. (This is type (e) in [Reference Murray35, Proposition 4.1].)
$C_{2^{d-1}}$
. (This is type (e) in [Reference Murray35, Proposition 4.1].)
Next, consider case (3). The choice
![]() $\hat {H}:=\operatorname {PGL}(2,q)$
realises
$\hat {H}:=\operatorname {PGL}(2,q)$
realises
![]() $E\cong D_{2^{d+1}}$
. We may therefore assume that
$E\cong D_{2^{d+1}}$
. We may therefore assume that
![]() $q=p^2$
as above. Then there exists a subgroup
$q=p^2$
as above. Then there exists a subgroup
![]() $\hat {H}$
of
$\hat {H}$
of
![]() ${\operatorname {PGL}(2,q)\rtimes \langle \sigma \rangle }$
of index
${\operatorname {PGL}(2,q)\rtimes \langle \sigma \rangle }$
of index
![]() $2$
with semidihedral Sylow
$2$
with semidihedral Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $E\cong SD_{2^{d+1}}$
. (This group is denoted by
$E\cong SD_{2^{d+1}}$
. (This group is denoted by
![]() $\operatorname {PGL}(2,q)^*$
in [Reference Gorenstein19].) Finally, let
$\operatorname {PGL}(2,q)^*$
in [Reference Gorenstein19].) Finally, let
![]() $d\ge 4$
. Here,
$d\ge 4$
. Here,
![]() $\hat {H}:=H\rtimes \langle \sigma \rangle $
has Sylow
$\hat {H}:=H\rtimes \langle \sigma \rangle $
has Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $E\cong C_{2^{d-1}}\rtimes C_2^2$
as above.
$E\cong C_{2^{d-1}}\rtimes C_2^2$
as above.
3 A refined conjecture
In [Reference Sambale41, Conjecture C], the following conjecture was proposed.
Conjecture 3.1. Let B be a real, nonprincipal
![]() $2$
-block with defect pair
$2$
-block with defect pair
![]() $(D,E)$
and a unique projective indecomposable character
$(D,E)$
and a unique projective indecomposable character
![]() $\Phi $
. Then,
$\Phi $
. Then,
Let
![]() $\Phi _\varphi $
be the projective indecomposable character attached to some
$\Phi _\varphi $
be the projective indecomposable character attached to some
![]() $\varphi \in \operatorname {IBr}(B)$
. Murray [Reference Murray34, Lemma 2.6] has shown that
$\varphi \in \operatorname {IBr}(B)$
. Murray [Reference Murray34, Lemma 2.6] has shown that
![]() $\epsilon (\Phi _\varphi )$
is the multiplicity of
$\epsilon (\Phi _\varphi )$
is the multiplicity of
![]() $\varphi $
as a constituent of the permutation character on
$\varphi $
as a constituent of the permutation character on
![]() $\{x\in G:x^2=1\}$
(see Lemma 4.1 for a refinement). I now believe that the conjecture holds orbit-by-orbit as follows.
$\{x\in G:x^2=1\}$
(see Lemma 4.1 for a refinement). I now believe that the conjecture holds orbit-by-orbit as follows.
Conjecture 3.2. Let B be a real, nonprincipal
![]() $2$
-block with defect pair
$2$
-block with defect pair
![]() $(D,E)$
and a unique projective indecomposable character
$(D,E)$
and a unique projective indecomposable character
![]() $\Phi $
. Then, for every involution
$\Phi $
. Then, for every involution
![]() $x\in G$
,
$x\in G$
,
where
![]() $x^G$
denotes the conjugacy class of x in G.
$x^G$
denotes the conjugacy class of x in G.
Note that
![]() $[\Phi _{\mathrm {C}_G(x)},1_{\mathrm {C}_G(x)}]=|D|[\varphi _{\mathrm {C}_G(x)},1_{\mathrm {C}_G(x)}]^0$
, where
$[\Phi _{\mathrm {C}_G(x)},1_{\mathrm {C}_G(x)}]=|D|[\varphi _{\mathrm {C}_G(x)},1_{\mathrm {C}_G(x)}]^0$
, where
![]() $\operatorname {IBr}(B)=\{\varphi \}$
in the situation of Conjecture 3.2.
$\operatorname {IBr}(B)=\{\varphi \}$
in the situation of Conjecture 3.2.
Proof. Let
![]() $\Omega :=\{x\in G:x^2=1\}$
. Note that the equation in Conjecture 3.2 is also true for
$\Omega :=\{x\in G:x^2=1\}$
. Note that the equation in Conjecture 3.2 is also true for
![]() $x=1$
since B is not principal. Recall that
$x=1$
since B is not principal. Recall that
![]() $\Phi $
vanishes on the elements of even order. By the definition of F-S indicators and Conjecture 3.2,
$\Phi $
vanishes on the elements of even order. By the definition of F-S indicators and Conjecture 3.2,
 $$ \begin{align*} \epsilon(\Phi)&=\frac{1}{|G|}\sum_{g\in G}\Phi(g^2)=\frac{1}{|G|}\sum_{x\in\Omega}\sum_{h\in\mathrm{C}_G(x)^0}\Phi(h^2)=\sum_{x\in\Omega/G}[\Phi_{\mathrm{C}_G(x)},1_{\mathrm{C}_G(x)}]\\ &=\sum_{x\in\Omega/G}|x^G\cap E\setminus D|=|\Omega\cap E\setminus D|=|\{x\in E\setminus D:x^2=1\}|.\\[-50pt] \end{align*} $$
$$ \begin{align*} \epsilon(\Phi)&=\frac{1}{|G|}\sum_{g\in G}\Phi(g^2)=\frac{1}{|G|}\sum_{x\in\Omega}\sum_{h\in\mathrm{C}_G(x)^0}\Phi(h^2)=\sum_{x\in\Omega/G}[\Phi_{\mathrm{C}_G(x)},1_{\mathrm{C}_G(x)}]\\ &=\sum_{x\in\Omega/G}|x^G\cap E\setminus D|=|\Omega\cap E\setminus D|=|\{x\in E\setminus D:x^2=1\}|.\\[-50pt] \end{align*} $$
4 Two general lemmas
In this section, we prove two new results, which are related to Conjecture 3.1. These will be applied in the subsequent sections.
Recall that a B-subsection is a pair
![]() $(x,b_x)$
, where
$(x,b_x)$
, where
![]() $x\in D$
and
$x\in D$
and
![]() $b_x$
is a Brauer correspondent of B in
$b_x$
is a Brauer correspondent of B in
![]() $\mathrm {C}_G(x)$
. In [Reference Sambale41, remark before Theorem 13], we explained that, after conjugation, we may assume that
$\mathrm {C}_G(x)$
. In [Reference Sambale41, remark before Theorem 13], we explained that, after conjugation, we may assume that
![]() $b_x$
has defect pair
$b_x$
has defect pair
![]() $(\mathrm {C}_D(x),\mathrm {C}_E(x))$
(if
$(\mathrm {C}_D(x),\mathrm {C}_E(x))$
(if
![]() $b_x$
is nonreal, then
$b_x$
is nonreal, then
![]() $\mathrm {C}_D(x)=\mathrm {C}_E(x)$
). For
$\mathrm {C}_D(x)=\mathrm {C}_E(x)$
). For
![]() $\chi \in \operatorname {Irr}(B)$
and
$\chi \in \operatorname {Irr}(B)$
and
![]() $\varphi \in \operatorname {IBr}(b_x)$
, we denote the corresponding generalised decomposition number by
$\varphi \in \operatorname {IBr}(b_x)$
, we denote the corresponding generalised decomposition number by
![]() $d_{\chi \varphi }^x$
. In analogy to principal indecomposable modules, we set
$d_{\chi \varphi }^x$
. In analogy to principal indecomposable modules, we set
![]() $\Phi _\varphi ^x:=\sum _{\chi \in \operatorname {Irr}(B)}d_{\chi \varphi }^x\chi $
.
$\Phi _\varphi ^x:=\sum _{\chi \in \operatorname {Irr}(B)}d_{\chi \varphi }^x\chi $
.
The following result generalises [Reference Murray34, Lemma 2.6].
Lemma 4.1. Let B be a real
![]() $2$
-block with defect pair
$2$
-block with defect pair
![]() $(D,E)$
and subsection
$(D,E)$
and subsection
![]() $(x,b)$
. Let
$(x,b)$
. Let
![]() $\pi $
be the Brauer permutation character of the conjugation action of
$\pi $
be the Brauer permutation character of the conjugation action of
![]() $\mathrm {C}_G(x)$
on
$\mathrm {C}_G(x)$
on
![]() ${\Omega _x:=\{y\in G:y^2=x\}}$
. Then the multiplicity of
${\Omega _x:=\{y\in G:y^2=x\}}$
. Then the multiplicity of
![]() $\varphi \in \operatorname {IBr}(b)$
as a constituent of
$\varphi \in \operatorname {IBr}(b)$
as a constituent of
![]() $\pi $
is
$\pi $
is
 $$ \begin{align*}\epsilon(\Phi_\varphi^x)=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)d_{\chi\varphi}^x.\end{align*} $$
$$ \begin{align*}\epsilon(\Phi_\varphi^x)=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)d_{\chi\varphi}^x.\end{align*} $$
In particular,
![]() $\epsilon (\Phi _\varphi ^x)$
is a nonnegative integer. If there is no
$\epsilon (\Phi _\varphi ^x)$
is a nonnegative integer. If there is no
![]() $e\in E\setminus D$
such that
$e\in E\setminus D$
such that
![]() $e^2=x$
, then
$e^2=x$
, then
![]() $\epsilon (\Phi _\varphi ^x)=0$
.
$\epsilon (\Phi _\varphi ^x)=0$
.
Proof. By Brauer’s formula [Reference Brauer8, Theorem 4A] (see also [Reference Sambale41, Lemma 2]),
 $$ \begin{align*} \epsilon(\Phi_\varphi^x)=\sum_{\psi\in\operatorname{Irr}(b)}\epsilon(\psi)d^x_{\psi\varphi}. \end{align*} $$
$$ \begin{align*} \epsilon(\Phi_\varphi^x)=\sum_{\psi\in\operatorname{Irr}(b)}\epsilon(\psi)d^x_{\psi\varphi}. \end{align*} $$
Since
![]() $\Omega _x=\{y\in \mathrm {C}_G(x):y^2=x\}$
, we may assume that
$\Omega _x=\{y\in \mathrm {C}_G(x):y^2=x\}$
, we may assume that
![]() $x\in \mathrm {Z}(G)$
and
$x\in \mathrm {Z}(G)$
and
![]() $B=b$
. By Brauer’s second main theorem, the claim only depends on
$B=b$
. By Brauer’s second main theorem, the claim only depends on
![]() $\varphi $
, and not on B. For
$\varphi $
, and not on B. For
![]() $g\in G^0$
, we compute
$g\in G^0$
, we compute
 $$ \begin{align*} \sum_{\varphi\in\operatorname{IBr}(G)}\epsilon(\Phi_\varphi^x)\varphi(g)&=\sum_{\chi\in\operatorname{Irr}(G)}\epsilon(\chi)\sum_{\varphi\in\operatorname{IBr}(G)}d_{\chi\varphi}^x\varphi(g)=\sum_{\chi\in\operatorname{Irr}(G)}\epsilon(\chi)\chi(xg)\\ &=|\{y\in G:y^2=xg\}|=|\{y\in\mathrm{C}_G(g):y^2=xg\}| \end{align*} $$
$$ \begin{align*} \sum_{\varphi\in\operatorname{IBr}(G)}\epsilon(\Phi_\varphi^x)\varphi(g)&=\sum_{\chi\in\operatorname{Irr}(G)}\epsilon(\chi)\sum_{\varphi\in\operatorname{IBr}(G)}d_{\chi\varphi}^x\varphi(g)=\sum_{\chi\in\operatorname{Irr}(G)}\epsilon(\chi)\chi(xg)\\ &=|\{y\in G:y^2=xg\}|=|\{y\in\mathrm{C}_G(g):y^2=xg\}| \end{align*} $$
[Reference Isaacs26, page 49]. Since g has odd order, there exists a unique power
![]() $\sqrt {g}$
of g such that
$\sqrt {g}$
of g such that
![]() $\sqrt {g}^2=g$
. It is easy to check that the map
$\sqrt {g}^2=g$
. It is easy to check that the map
![]() $\{y\in \mathrm {C}_G(g):y^2=x\}\to \{y\in \mathrm {C}_G(g):y^2=xg\}$
,
$\{y\in \mathrm {C}_G(g):y^2=x\}\to \{y\in \mathrm {C}_G(g):y^2=xg\}$
,
![]() $y\mapsto y\sqrt {g}$
is a bijection. Hence,
$y\mapsto y\sqrt {g}$
is a bijection. Hence,
 $$ \begin{align*}\sum_{\varphi\in\operatorname{IBr}(G)}\epsilon(\Phi_\varphi^x)\varphi(g)=|\{y\in\mathrm{C}_G(g):y^2=x\}|=|\mathrm{C}_G(g)\cap\Omega_x|=\pi(g)\end{align*} $$
$$ \begin{align*}\sum_{\varphi\in\operatorname{IBr}(G)}\epsilon(\Phi_\varphi^x)\varphi(g)=|\{y\in\mathrm{C}_G(g):y^2=x\}|=|\mathrm{C}_G(g)\cap\Omega_x|=\pi(g)\end{align*} $$
for all
![]() $g\in G^0$
. Therefore,
$g\in G^0$
. Therefore,
![]() $\epsilon (\Phi _\varphi ^x)$
is the multiplicity of
$\epsilon (\Phi _\varphi ^x)$
is the multiplicity of
![]() $\varphi $
in
$\varphi $
in
![]() $\pi $
.
$\pi $
.
Now assume that there is no
![]() $e\in E\setminus D$
such that
$e\in E\setminus D$
such that
![]() $e^2=x$
. Then [Reference Murray35, Lemma 1.3] implies
$e^2=x$
. Then [Reference Murray35, Lemma 1.3] implies
 $$ \begin{align*}0=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)\chi(x)=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)\sum_{\varphi\in\operatorname{IBr}(b)}d_{\chi\varphi}^x\varphi(1)=\sum_{\varphi\in\operatorname{IBr}(b)}\epsilon(\Phi_\varphi^x)\varphi(1),\end{align*} $$
$$ \begin{align*}0=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)\chi(x)=\sum_{\chi\in\operatorname{Irr}(B)}\epsilon(\chi)\sum_{\varphi\in\operatorname{IBr}(b)}d_{\chi\varphi}^x\varphi(1)=\sum_{\varphi\in\operatorname{IBr}(b)}\epsilon(\Phi_\varphi^x)\varphi(1),\end{align*} $$
and the second claim follows.
Our second lemma generalises [Reference Sambale41, Theorem 10].
Proposition 4.2. Let B be a real, nonprincipal
![]() $2$
-block with defect pair
$2$
-block with defect pair
![]() $(D,E)$
. Let
$(D,E)$
. Let
![]() $(x,b)$
be a B-subsection such that b is nilpotent with defect pair
$(x,b)$
be a B-subsection such that b is nilpotent with defect pair
![]() $(\mathrm {C}_D(x),\mathrm {C}_E(x))$
, where
$(\mathrm {C}_D(x),\mathrm {C}_E(x))$
, where
![]() $\mathrm {C}_D(x)$
is abelian. Then
$\mathrm {C}_D(x)$
is abelian. Then
![]() $\epsilon (\Phi _\varphi ^x)=|\{e\in E\setminus D:e^2=x\}|,$
where
$\epsilon (\Phi _\varphi ^x)=|\{e\in E\setminus D:e^2=x\}|,$
where
![]() $\operatorname {IBr}(b)=\{\varphi \}$
.
$\operatorname {IBr}(b)=\{\varphi \}$
.
Proof. As in the proof of Lemma 4.1, we may apply Brauer’s formula. Since b has defect pair
![]() $(\mathrm {C}_D(x),\mathrm {C}_E(x))$
and
$(\mathrm {C}_D(x),\mathrm {C}_E(x))$
and
we may assume that
![]() $x\in \mathrm {Z}(G)$
and
$x\in \mathrm {Z}(G)$
and
![]() $B=b$
. Now D is abelian and Conjecture 3.1 holds for B by [Reference Sambale41, Theorem 10]. Since every Brauer correspondent
$B=b$
. Now D is abelian and Conjecture 3.1 holds for B by [Reference Sambale41, Theorem 10]. Since every Brauer correspondent
![]() $\beta $
of B in a section of G is nilpotent with abelian defect groups, Conjecture 3.1 also holds for
$\beta $
of B in a section of G is nilpotent with abelian defect groups, Conjecture 3.1 also holds for
![]() $\beta $
. The claim follows from [Reference Sambale41, Theorem 13].
$\beta $
. The claim follows from [Reference Sambale41, Theorem 13].
In the situation of Proposition 4.2, it is tempting to formalise a local version of Conjecture 3.2: for every
![]() $y\in G$
with
$y\in G$
with
![]() $y^2=x$
,
$y^2=x$
,
(note that
![]() $\mathrm {C}_G(y)\subseteq \mathrm {C}_G(x)$
). We did not find any counterexamples to this equation.
$\mathrm {C}_G(y)\subseteq \mathrm {C}_G(x)$
). We did not find any counterexamples to this equation.
5 Tame blocks
By Murray [Reference Murray34, Theorems 1.7 and 1.8], the F-S indicators of blocks with Klein four defect group are known. As in the proof of Theorem 1.1, one can show that all cases listed there occur. It is tempting to do a similar analysis for other tame blocks, that is,
![]() $2$
-blocks with quaternion or semidihedral defect groups. In this section, we gather some partial results along these lines.
$2$
-blocks with quaternion or semidihedral defect groups. In this section, we gather some partial results along these lines.
Proposition 5.1. Let B be a real tame block of a finite group with defect at least
![]() $3$
. Then B has two or four real irreducible characters of height
$3$
. Then B has two or four real irreducible characters of height
![]() $0$
and they all have F-S indicator
$0$
and they all have F-S indicator
![]() $1$
.
$1$
.
Proof. Let
![]() $(D,E)$
be a defect pair of B. It is well known that B has exactly four irreducible characters of height
$(D,E)$
be a defect pair of B. It is well known that B has exactly four irreducible characters of height
![]() $0$
(see [Reference Sambale38, Theorem 8.1]). By [Reference Gow24, Theorem 5.1], at least one such character has F-S indicator
$0$
(see [Reference Sambale38, Theorem 8.1]). By [Reference Gow24, Theorem 5.1], at least one such character has F-S indicator
![]() $1$
. Since nonreal characters come in pairs of the same degree, B has two or four real irreducible characters of height
$1$
. Since nonreal characters come in pairs of the same degree, B has two or four real irreducible characters of height
![]() $0$
.
$0$
.
To prove the second claim, it suffices to show that
![]() $D/D'$
has a complement in
$D/D'$
has a complement in
![]() $E/D'$
by [Reference Gow24, Theorem 5.6]. Since
$E/D'$
by [Reference Gow24, Theorem 5.6]. Since
![]() $D/D'\cong C_2^2$
, we may assume that
$D/D'\cong C_2^2$
, we may assume that
![]() $E/D'\cong C_4\times C_2$
by way of contradiction. In particular,
$E/D'\cong C_4\times C_2$
by way of contradiction. In particular,
![]() $|E:E'|\ge 8$
. A theorem of Alperin–Feit–Thompson asserts that the number of involutions in E is congruent to
$|E:E'|\ge 8$
. A theorem of Alperin–Feit–Thompson asserts that the number of involutions in E is congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
(see [Reference Isaacs26, Theorem 4.9]). By the remark after [Reference Isaacs26, Theorem 4.9], the number of involutions in D is congruent to
$4$
(see [Reference Isaacs26, Theorem 4.9]). By the remark after [Reference Isaacs26, Theorem 4.9], the number of involutions in D is congruent to
![]() $1$
modulo
$1$
modulo
![]() $4$
. Hence, there exists an involution
$4$
. Hence, there exists an involution
![]() $x\in E\setminus D$
. However, then
$x\in E\setminus D$
. However, then
![]() $\langle x\rangle D'/D'$
is a complement of
$\langle x\rangle D'/D'$
is a complement of
![]() $D/D'$
in
$D/D'$
in
![]() $E/D'$
, which gives a contradiction.
$E/D'$
, which gives a contradiction.
A nonprincipal block of
![]() $G=(C_3\rtimes C_4)\times C_2$
shows that Proposition 5.1 fails for tame blocks of defect
$G=(C_3\rtimes C_4)\times C_2$
shows that Proposition 5.1 fails for tame blocks of defect
![]() $2$
(that is, blocks with Klein four defect group).
$2$
(that is, blocks with Klein four defect group).
We now apply Proposition 4.2 to a concrete example.
Proposition 5.2. Let B be a block with defect pair
![]() $(D,E)$
, where
$(D,E)$
, where
![]() $D\cong Q_8$
. Then B has exactly two real irreducible characters of height
$D\cong Q_8$
. Then B has exactly two real irreducible characters of height
![]() $0$
if and only if one of the following holds:
$0$
if and only if one of the following holds:
-
(1)
 $l(B)=1$
and
$l(B)=1$
and
 $E\in \{Q_{16},SD_{16}\}$
;
$E\in \{Q_{16},SD_{16}\}$
; -
(2) B is Morita equivalent to the principal block of
 $\operatorname {SL}(2,3)$
and
$\operatorname {SL}(2,3)$
and
 $E\notin \{Q_{16},SD_{16}\}$
;
$E\notin \{Q_{16},SD_{16}\}$
; -
(3) B is Morita equivalent to the principal block of
 $\operatorname {SL}(2,5)$
and
$\operatorname {SL}(2,5)$
and
 $E\in \{Q_{16},SD_{16}\}$
.
$E\in \{Q_{16},SD_{16}\}$
.
Proof. Let
![]() $\epsilon _1,\ldots ,\epsilon _4$
be the F-S indicators of the height
$\epsilon _1,\ldots ,\epsilon _4$
be the F-S indicators of the height
![]() $0$
characters
$0$
characters
![]() $\lambda _1,\ldots ,\lambda _4\in \operatorname {Irr}(B)$
. We may choose a B-subsection
$\lambda _1,\ldots ,\lambda _4\in \operatorname {Irr}(B)$
. We may choose a B-subsection
![]() $(x,b)$
such that
$(x,b)$
such that
![]() $|\langle x\rangle |=4$
and b has defect pair
$|\langle x\rangle |=4$
and b has defect pair
![]() $(\langle x\rangle ,\mathrm {C}_E(x))$
. Clearly, b is nilpotent with abelian defect group
$(\langle x\rangle ,\mathrm {C}_E(x))$
. Clearly, b is nilpotent with abelian defect group
![]() $\langle x\rangle $
. Let
$\langle x\rangle $
. Let
![]() $\operatorname {IBr}(b)=\{\varphi _x\}$
. By the orthogonality relations of generalised decomposition numbers (see [Reference Sambale38, Theorem 1.14]), we have
$\operatorname {IBr}(b)=\{\varphi _x\}$
. By the orthogonality relations of generalised decomposition numbers (see [Reference Sambale38, Theorem 1.14]), we have
![]() $d_{\lambda _i,\varphi _x}^x=\pm 1$
for
$d_{\lambda _i,\varphi _x}^x=\pm 1$
for
![]() $1\le i\le 4$
and
$1\le i\le 4$
and
![]() $d_{\chi ,\varphi _x}^x=0$
for
$d_{\chi ,\varphi _x}^x=0$
for
![]() $\chi \in \operatorname {Irr}(B)\setminus \{\lambda _1,\ldots ,\lambda _4\}$
. These numbers depend on the ordinary decomposition matrix of B.
$\chi \in \operatorname {Irr}(B)\setminus \{\lambda _1,\ldots ,\lambda _4\}$
. These numbers depend on the ordinary decomposition matrix of B.
Case 1:
![]() $l(B)=1$
.
$l(B)=1$
.
Here, B is nilpotent with decomposition matrix
![]() $(1,1,1,1,2)^{\mathrm {t}}$
. We may choose our labelling in such a way that
$(1,1,1,1,2)^{\mathrm {t}}$
. We may choose our labelling in such a way that
![]() $(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=(1,1,-1,-1)$
. Similarly, there are elements
$(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=(1,1,-1,-1)$
. Similarly, there are elements
![]() $y,xy\in D$
of order
$y,xy\in D$
of order
![]() $4$
such that
$4$
such that
![]() $(d_{\lambda _1,\varphi _y}^y,\ldots ,d_{\lambda _4,\varphi _y}^y)=(1,-1,1,-1)$
and
$(d_{\lambda _1,\varphi _y}^y,\ldots ,d_{\lambda _4,\varphi _y}^y)=(1,-1,1,-1)$
and
![]() $(d_{\lambda _1,\varphi _{xy}}^{xy},\ldots ,d_{\lambda _4,\varphi _{xy}}^{xy})=(1,-1,-1,1)$
with appropriate labelling. If there exists no
$(d_{\lambda _1,\varphi _{xy}}^{xy},\ldots ,d_{\lambda _4,\varphi _{xy}}^{xy})=(1,-1,-1,1)$
with appropriate labelling. If there exists no
![]() ${e\in E\setminus D}$
such that
${e\in E\setminus D}$
such that
![]() $e^2\in \{x,y,xy\}$
, then
$e^2\in \{x,y,xy\}$
, then
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
by Propositions 4.2 and 5.1. Now suppose that
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
by Propositions 4.2 and 5.1. Now suppose that
![]() $e^2=x$
for some
$e^2=x$
for some
![]() $e\in E\setminus D$
. Then e has order
$e\in E\setminus D$
. Then e has order
![]() $8$
and it follows easily that
$8$
and it follows easily that
![]() $E\cong \{Q_{16},SD_{16}\}$
. In both cases, we have
$E\cong \{Q_{16},SD_{16}\}$
. In both cases, we have
![]() $|\{e\in E\setminus D:e^2=x\}|=2$
and
$|\{e\in E\setminus D:e^2=x\}|=2$
and
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,0,0)$
by Propositions 4.2 and 5.1.
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,0,0)$
by Propositions 4.2 and 5.1.
Now suppose that
![]() $l(B)>1$
. By Macgregor [Reference Macgregor33, Corollary 2.4], there are two cases to consider.
$l(B)>1$
. By Macgregor [Reference Macgregor33, Corollary 2.4], there are two cases to consider.
Case 2: B is Morita equivalent to the principal block of
![]() $\operatorname {SL}(2,3)$
.
$\operatorname {SL}(2,3)$
.
Here,
![]() $l(B)=3$
and B has decomposition matrix
$l(B)=3$
and B has decomposition matrix
 $$ \begin{align*} Q:=\begin{pmatrix} 1&.&.\\ .&1&.\\ .&.&1\\ 1&1&1\\ 1&1&.\\ 1&.&1\\ .&1&1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} Q:=\begin{pmatrix} 1&.&.\\ .&1&.\\ .&.&1\\ 1&1&1\\ 1&1&.\\ 1&.&1\\ .&1&1 \end{pmatrix}. \end{align*} $$
We see that
![]() $\lambda _4$
is real and
$\lambda _4$
is real and
![]() $\epsilon _4=1$
. The orthogonality relations imply that
$\epsilon _4=1$
. The orthogonality relations imply that
![]() $(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=\pm (1,1,1,-1)$
. If there exists
$(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=\pm (1,1,1,-1)$
. If there exists
![]() $e\in E\setminus D$
with
$e\in E\setminus D$
with
![]() $e^2=x$
(that is,
$e^2=x$
(that is,
![]() $E\in \{Q_{16}, SD_{16}\}$
), then
$E\in \{Q_{16}, SD_{16}\}$
), then
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
and otherwise
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
and otherwise
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(0,0,1,1)$
by Propositions 4.2 and 5.1 (after relabelling if necessary).
$(\epsilon _1,\ldots ,\epsilon _4)=(0,0,1,1)$
by Propositions 4.2 and 5.1 (after relabelling if necessary).
Case 3: B is Morita equivalent to the principal block of
![]() $\operatorname {SL}(2,5)$
.
$\operatorname {SL}(2,5)$
.
Here, B has decomposition matrix
 $$ \begin{align*} Q:=\begin{pmatrix} 1&.&.\\ 1&1&.\\ 1&.&1\\ 1&1&1\\ .&1&.\\ .&.&1\\ 2&1&1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} Q:=\begin{pmatrix} 1&.&.\\ 1&1&.\\ 1&.&1\\ 1&1&1\\ .&1&.\\ .&.&1\\ 2&1&1 \end{pmatrix}. \end{align*} $$
It follows that
![]() $\lambda _1$
,
$\lambda _1$
,
![]() $\lambda _4$
are real and
$\lambda _4$
are real and
![]() $(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=\pm (1,-1,-1,1)$
. If
$(d_{\lambda _1,\varphi _x}^x,\ldots ,d_{\lambda _4,\varphi _x}^x)=\pm (1,-1,-1,1)$
. If
![]() ${E\in \{Q_{16},SD_{16}\}}$
, then
${E\in \{Q_{16},SD_{16}\}}$
, then
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,0,0,1)$
, and
$(\epsilon _1,\ldots ,\epsilon _4)=(1,0,0,1)$
, and
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
otherwise.
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
otherwise.
To compute the remaining F-S indicators in the situation of Proposition 5.2, we restrict ourselves further to
![]() $E\in \{Q_{16},SD_{16}\}$
.
$E\in \{Q_{16},SD_{16}\}$
.
Proposition 5.3. Let B be a real block of a finite group G with defect pair
![]() $(D,E)$
such that
$(D,E)$
such that
![]() $D\cong Q_8$
and
$D\cong Q_8$
and
![]() $E\cong \{Q_{16},SD_{16}\}$
. Then the F-S indicators of characters in
$E\cong \{Q_{16},SD_{16}\}$
. Then the F-S indicators of characters in
![]() $\operatorname {Irr}(B)$
are given in Table 2, where the first four characters have height
$\operatorname {Irr}(B)$
are given in Table 2, where the first four characters have height
![]() $0$
. Moreover, all cases occur.
$0$
. Moreover, all cases occur.
Table 2 Some F-S indicators for
![]() $D\cong Q_8$
.
$D\cong Q_8$
.

Proof. We reuse the notation from the proof of Proposition 5.2.
Case 1:
![]() $l(B)=1$
.
$l(B)=1$
.
By Proposition 5.2,
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,0,0)$
. Let
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,0,0)$
. Let
![]() $\operatorname {Irr}(B)=\{\lambda _1,\ldots ,\lambda _4,\psi \}$
and
$\operatorname {Irr}(B)=\{\lambda _1,\ldots ,\lambda _4,\psi \}$
and
![]() $\operatorname {IBr}(B)=\{\varphi \}$
. Then,
$\operatorname {IBr}(B)=\{\varphi \}$
. Then,
with equality if and only if
![]() $E\cong Q_{16}$
by [Reference Murray35, Lemma 1.3]. Hence,
$E\cong Q_{16}$
by [Reference Murray35, Lemma 1.3]. Hence,
![]() $\mu =-1$
if
$\mu =-1$
if
![]() ${E\cong Q_{16}}$
and
${E\cong Q_{16}}$
and
![]() $\mu =1$
if
$\mu =1$
if
![]() $E\cong \textit {SD}_{16}$
. Examples for both cases can be constructed by the remark after Proposition 2.2. The groups are
$E\cong \textit {SD}_{16}$
. Examples for both cases can be constructed by the remark after Proposition 2.2. The groups are
![]() $\mathtt {SmallGroup}(48,18)$
for
$\mathtt {SmallGroup}(48,18)$
for
![]() $E\cong Q_{16}$
and
$E\cong Q_{16}$
and
![]() $\mathtt {SmallGroup}(48,17)$
for
$\mathtt {SmallGroup}(48,17)$
for
![]() $E\cong \textit {SD}_{16}$
in the small groups library [42].
$E\cong \textit {SD}_{16}$
in the small groups library [42].
Now let
![]() $l(B)=3$
and
$l(B)=3$
and
![]() $\operatorname {IBr}(B)=\{\varphi _1,\varphi _2,\varphi _3\}$
. Let
$\operatorname {IBr}(B)=\{\varphi _1,\varphi _2,\varphi _3\}$
. Let
![]() $\psi _1,\psi _2,\psi _3\in \operatorname {Irr}(B)$
be the characters of height
$\psi _1,\psi _2,\psi _3\in \operatorname {Irr}(B)$
be the characters of height
![]() $1$
. Let
$1$
. Let
![]() $\mu _i:=\epsilon (\psi _i)$
for
$\mu _i:=\epsilon (\psi _i)$
for
![]() $i=1,2,3$
.
$i=1,2,3$
.
Case 2: B is Morita equivalent to the principal block of
![]() $\operatorname {SL}(2,3)$
.
$\operatorname {SL}(2,3)$
.
By Proposition 5.2,
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
. Assume first that
$(\epsilon _1,\ldots ,\epsilon _4)=(1,1,1,1)$
. Assume first that
![]() $E\cong Q_{16}$
. Then Lemma 4.1 implies
$E\cong Q_{16}$
. Then Lemma 4.1 implies
for
![]() $i=1,2,3$
. The shape of the decomposition matrix of B yields
$i=1,2,3$
. The shape of the decomposition matrix of B yields
![]() $\mu _1=\mu _2=\mu _3=-1$
as claimed. For the purpose of constructing an infinite family of examples, let q be an odd prime and
$\mu _1=\mu _2=\mu _3=-1$
as claimed. For the purpose of constructing an infinite family of examples, let q be an odd prime and
![]() $H:=\operatorname {SL}(2,q)$
. Let
$H:=\operatorname {SL}(2,q)$
. Let
![]() $\zeta \in \mathbb {F}_{q^2}^\times $
of order
$\zeta \in \mathbb {F}_{q^2}^\times $
of order
![]() $2(q-1)$
. Then,
$2(q-1)$
. Then,
 $$ \begin{align*} \hat{H}:= H\bigg\langle \begin{pmatrix}\zeta&0\\ 0 &\zeta^{-1}\end{pmatrix} \biggr\rangle\le \operatorname{SL}(2,q^{2}) \end{align*} $$
$$ \begin{align*} \hat{H}:= H\bigg\langle \begin{pmatrix}\zeta&0\\ 0 &\zeta^{-1}\end{pmatrix} \biggr\rangle\le \operatorname{SL}(2,q^{2}) \end{align*} $$
is a nonsplit extension with Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $E\cong Q_{2^{d+1}}$
. Thus, we can apply Proposition 2.2 to the pair
$E\cong Q_{2^{d+1}}$
. Thus, we can apply Proposition 2.2 to the pair
![]() $(H,\hat {H})$
. For
$(H,\hat {H})$
. For
![]() $q=3$
, we end up with the (unique) nonprincipal block of
$q=3$
, we end up with the (unique) nonprincipal block of
![]() $G=\mathtt {SmallGroup}(144,124)$
.
$G=\mathtt {SmallGroup}(144,124)$
.
Now assume that
![]() $E\cong \textit {SD}_{16}$
. Here, we need to investigate the generalised decomposition matrix
$E\cong \textit {SD}_{16}$
. Here, we need to investigate the generalised decomposition matrix
![]() $Q^z$
with respect to a B-subsection
$Q^z$
with respect to a B-subsection
![]() $(z,b_z)$
, where
$(z,b_z)$
, where
![]() $\mathrm {Z}(D)=\langle z\rangle $
. The columns of
$\mathrm {Z}(D)=\langle z\rangle $
. The columns of
![]() $Q^z$
lie in the orthogonal complement of the
$Q^z$
lie in the orthogonal complement of the
![]() $\mathbb {Z}$
-module spanned by the columns of the ordinary decomposition matrix and the column
$\mathbb {Z}$
-module spanned by the columns of the ordinary decomposition matrix and the column
![]() $d_{.,\varphi _x}^x$
. It is easy to find a basis of this
$d_{.,\varphi _x}^x$
. It is easy to find a basis of this
![]() $\mathbb {Z}$
-module. Therefore, there exists an integral matrix
$\mathbb {Z}$
-module. Therefore, there exists an integral matrix
![]() $S\in \operatorname {GL}(3,\mathbb {Q})$
such that
$S\in \operatorname {GL}(3,\mathbb {Q})$
such that
 $$ \begin{align*}Q^z=\begin{pmatrix} 1&.&.\\ .&1&.\\ .&.&1\\ 1&1&1\\ -1&-1&.\\ -1&.&-1\\ .&-1&-1 \end{pmatrix}S.\end{align*} $$
$$ \begin{align*}Q^z=\begin{pmatrix} 1&.&.\\ .&1&.\\ .&.&1\\ 1&1&1\\ -1&-1&.\\ -1&.&-1\\ .&-1&-1 \end{pmatrix}S.\end{align*} $$
By Lemma 4.1,
![]() $(\epsilon _1,\ldots ,\epsilon _4,\mu _1,\mu _2,\mu _3)Q^z=(0,0,0)$
. After we multiply both sides with
$(\epsilon _1,\ldots ,\epsilon _4,\mu _1,\mu _2,\mu _3)Q^z=(0,0,0)$
. After we multiply both sides with
![]() $S^{-1}$
, we get
$S^{-1}$
, we get
![]() $\mu _1=\mu _2=\mu _3=1$
as desired. To construct examples, let
$\mu _1=\mu _2=\mu _3=1$
as desired. To construct examples, let
![]() $H:=\operatorname {SL}(2,q)$
for an odd prime q. Let
$H:=\operatorname {SL}(2,q)$
for an odd prime q. Let
![]() $\mathbb {F}_q^\times =\langle \zeta \rangle $
. The conjugation with
$\mathbb {F}_q^\times =\langle \zeta \rangle $
. The conjugation with
![]() $\bigl (\begin {smallmatrix}0&\zeta \\1&\zeta \end {smallmatrix}\bigr )\in \operatorname {GL}(2,q)$
induces an automorphism
$\bigl (\begin {smallmatrix}0&\zeta \\1&\zeta \end {smallmatrix}\bigr )\in \operatorname {GL}(2,q)$
induces an automorphism
![]() $\alpha $
on H of order
$\alpha $
on H of order
![]() $2$
. Then
$2$
. Then
![]() $\hat {H}:=H\rtimes \langle \alpha \rangle $
has Sylow
$\hat {H}:=H\rtimes \langle \alpha \rangle $
has Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $E\cong SD_{2^{d+1}}$
, so we can apply Proposition 2.2. For
$E\cong SD_{2^{d+1}}$
, so we can apply Proposition 2.2. For
![]() $q=3$
, this gives the nonprincipal block of
$q=3$
, this gives the nonprincipal block of
![]() $G=\mathtt {SmallGroup}(144,125)$
.
$G=\mathtt {SmallGroup}(144,125)$
.
Case 3: B is Morita equivalent to the principal block of
![]() $\operatorname {SL}(2,5)$
.
$\operatorname {SL}(2,5)$
.
Here we have
![]() $(\epsilon _1,\ldots ,\epsilon _4)=(1,0,0,1)$
with the labelling of the proof of Proposition 5.2. The decomposition matrix shows further that
$(\epsilon _1,\ldots ,\epsilon _4)=(1,0,0,1)$
with the labelling of the proof of Proposition 5.2. The decomposition matrix shows further that
![]() $\varphi _2=\overline {\varphi _3}$
and therefore
$\varphi _2=\overline {\varphi _3}$
and therefore
![]() $\mu _1=\mu _2=0$
. As before, we have
$\mu _1=\mu _2=0$
. As before, we have
with equality if and only if
![]() $E\cong Q_{16}$
. Hence,
$E\cong Q_{16}$
. Hence,
![]() $\mu _3=-1$
if
$\mu _3=-1$
if
![]() $E\cong Q_{16}$
and
$E\cong Q_{16}$
and
![]() $\mu _3=1$
if
$\mu _3=1$
if
![]() $E\cong \textit {SD}_{16}$
. The former case occurs for a nonprincipal block of
$E\cong \textit {SD}_{16}$
. The former case occurs for a nonprincipal block of
![]() $G=\mathtt {SmallGroup}(720,414)$
and the latter for a nonprincipal block of
$G=\mathtt {SmallGroup}(720,414)$
and the latter for a nonprincipal block of
![]() $G=\mathtt {SmallGroup}(720,415)$
(same construction as in Case 2 with
$G=\mathtt {SmallGroup}(720,415)$
(same construction as in Case 2 with
![]() $q=5$
).
$q=5$
).
If
![]() $E\notin \{Q_{16},SD_{16}\}$
, then one can show that
$E\notin \{Q_{16},SD_{16}\}$
, then one can show that
![]() $E\in \{D,D\times C_2,D*C_4\}$
. It is possible to obtain some further information in these cases, but ultimately, we do not know the F-S indicator
$E\in \{D,D\times C_2,D*C_4\}$
. It is possible to obtain some further information in these cases, but ultimately, we do not know the F-S indicator
![]() $\mu $
of the unique (real) character of height
$\mu $
of the unique (real) character of height
![]() $1$
when
$1$
when
![]() $l(B)=1$
and
$l(B)=1$
and
![]() $E\cong D\times C_2$
. Conjecture 3.1 would imply that
$E\cong D\times C_2$
. Conjecture 3.1 would imply that
![]() $\mu =-1$
.
$\mu =-1$
.
6 Homocyclic defect groups
Since tame blocks have metacyclic defect groups, it is reasonable to look at other classes of
![]() $2$
-blocks with metacyclic defect groups. The corresponding Morita equivalence classes have been determined in [Reference Eaton, Kessar, Külshammer and Sambale13, Theorem 1.1] (combined with [Reference Sambale38, Theorem 8.1]). The only nonnilpotent wild blocks B occur for
$2$
-blocks with metacyclic defect groups. The corresponding Morita equivalence classes have been determined in [Reference Eaton, Kessar, Külshammer and Sambale13, Theorem 1.1] (combined with [Reference Sambale38, Theorem 8.1]). The only nonnilpotent wild blocks B occur for
![]() $D\cong C_{2^n}^2$
, where
$D\cong C_{2^n}^2$
, where
![]() $n\ge 2$
. In this case, B is Morita equivalent to
$n\ge 2$
. In this case, B is Morita equivalent to
![]() $F[D\rtimes C_3]$
. In particular, the Morita equivalence class is uniquely determined by
$F[D\rtimes C_3]$
. In particular, the Morita equivalence class is uniquely determined by
![]() $l(B)$
. We determine the F-S indicators in the special case
$l(B)$
. We determine the F-S indicators in the special case
![]() $n=2$
. Again, these numbers only depend on the extended defect group.
$n=2$
. Again, these numbers only depend on the extended defect group.
Theorem 6.1. Let B be a real
![]() $2$
-block with defect pair
$2$
-block with defect pair
![]() $(D,E)$
such that
$(D,E)$
such that
![]() $D\cong C_4^2$
,
$D\cong C_4^2$
,
![]() $E=D$
or
$E=D$
or
![]() $E\cong \mathtt {SmallGroup}(32,\mathrm {id})$
. Then
$E\cong \mathtt {SmallGroup}(32,\mathrm {id})$
. Then
![]() $(k(B),l(B))\in \{(16,1),(8,3)\}$
and exactly four characters in
$(k(B),l(B))\in \{(16,1),(8,3)\}$
and exactly four characters in
![]() $\operatorname {Irr}(B)$
are
$\operatorname {Irr}(B)$
are
![]() $2$
-rational. The F-S indicators of characters in
$2$
-rational. The F-S indicators of characters in
![]() $\operatorname {Irr}(B)$
are given in Table 3, where the first four characters are
$\operatorname {Irr}(B)$
are given in Table 3, where the first four characters are
![]() $2$
-rational. If
$2$
-rational. If
![]() $l(B)=3$
, then the first three characters are irreducible modulo
$l(B)=3$
, then the first three characters are irreducible modulo
![]() $2$
. All cases occur.
$2$
. All cases occur.
Table 3 F-S indicators for
![]() $D\cong C_4^2$
.
$D\cong C_4^2$
.

Proof. Let
![]() $l(B)=1$
. Then B is nilpotent and the generalised decomposition matrix of B coincides with the character table of D. This shows that
$l(B)=1$
. Then B is nilpotent and the generalised decomposition matrix of B coincides with the character table of D. This shows that
![]() $k(B)=16$
and exactly four characters are
$k(B)=16$
and exactly four characters are
![]() $2$
-rational. The possible groups E can be computed with GAP and examples can be found among the groups of order
$2$
-rational. The possible groups E can be computed with GAP and examples can be found among the groups of order
![]() $96$
as in Proposition 2.2. If B is the principal block (that is,
$96$
as in Proposition 2.2. If B is the principal block (that is,
![]() $E=D$
), then
$E=D$
), then
![]() $\operatorname {Irr}(B)=\operatorname {Irr}(G/\mathrm {O}_{2'}(G))=\operatorname {Irr}(D)$
. In this case, the claim is easy to check. Otherwise, the F-S indicators are determined by [Reference Sambale41, Theorem 10]. We note that the embedding of D in E is not always unique, but the F-S indicators are independent of this embedding (in our situation).
$\operatorname {Irr}(B)=\operatorname {Irr}(G/\mathrm {O}_{2'}(G))=\operatorname {Irr}(D)$
. In this case, the claim is easy to check. Otherwise, the F-S indicators are determined by [Reference Sambale41, Theorem 10]. We note that the embedding of D in E is not always unique, but the F-S indicators are independent of this embedding (in our situation).
Now let
![]() $l(B)=3$
. Suppose first that B is the principal block. By a result of Brauer [Reference Brauer7, Theorem 1], we have
$l(B)=3$
. Suppose first that B is the principal block. By a result of Brauer [Reference Brauer7, Theorem 1], we have
![]() $\operatorname {Irr}(B)=\operatorname {Irr}(G/\mathrm {O}_{2'}(G))=\operatorname {Irr}(D\rtimes C_3)$
. The F-S indicators can be computed easily here. Now let
$\operatorname {Irr}(B)=\operatorname {Irr}(G/\mathrm {O}_{2'}(G))=\operatorname {Irr}(D\rtimes C_3)$
. The F-S indicators can be computed easily here. Now let
![]() $E\ne D$
. We argue as in Proposition 2.1 to exclude most candidates for E. Let
$E\ne D$
. We argue as in Proposition 2.1 to exclude most candidates for E. Let
![]() $(D,b_D)$
be a fixed Brauer pair. By [Reference Sambale41, Proposition 8(i)], the extended stabiliser has the form
$(D,b_D)$
be a fixed Brauer pair. By [Reference Sambale41, Proposition 8(i)], the extended stabiliser has the form
![]() $\mathrm {N}_G(D,b_D)^*=E\mathrm {N}_G(D,b_D)$
. It can be checked that
$\mathrm {N}_G(D,b_D)^*=E\mathrm {N}_G(D,b_D)$
. It can be checked that
![]() $\mathrm {N}_G(D,b_D)/\mathrm {C}_G(D)$
is isomorphic to a Sylow
$\mathrm {N}_G(D,b_D)/\mathrm {C}_G(D)$
is isomorphic to a Sylow
![]() $3$
-subgroup S of
$3$
-subgroup S of
![]() $\operatorname {Aut}(D)$
. Moreover, the normaliser of S in
$\operatorname {Aut}(D)$
. Moreover, the normaliser of S in
![]() $\operatorname {Aut}(S)$
has three conjugacy classes of involutions. Hence, there are at most four possible actions of E on D (including the trivial action). This excludes the cases
$\operatorname {Aut}(S)$
has three conjugacy classes of involutions. Hence, there are at most four possible actions of E on D (including the trivial action). This excludes the cases
![]() $\mathrm {id}\in \{4,12,24,25,26,31,32\}$
. Now let
$\mathrm {id}\in \{4,12,24,25,26,31,32\}$
. Now let
![]() $\mathrm {id}=3$
, that is,
$\mathrm {id}=3$
, that is,
![]() $E\cong C_8\times C_4$
. Then
$E\cong C_8\times C_4$
. Then
![]() $b_D$
is real and nilpotent. By the first part of the proof,
$b_D$
is real and nilpotent. By the first part of the proof,
![]() $b_D$
has exactly
$b_D$
has exactly
![]() $12$
nonreal characters. Under the action of
$12$
nonreal characters. Under the action of
![]() $\mathrm {N}_G(D,b_D)$
, the
$\mathrm {N}_G(D,b_D)$
, the
![]() $16$
characters in
$16$
characters in
![]() $\operatorname {Irr}(b_D)$
distribute into five orbits of length
$\operatorname {Irr}(b_D)$
distribute into five orbits of length
![]() $3$
and one orbit of length
$3$
and one orbit of length
![]() $1$
. In particular, the number of nonreal characters in
$1$
. In particular, the number of nonreal characters in
![]() $\operatorname {Irr}(b_D)$
cannot be
$\operatorname {Irr}(b_D)$
cannot be
![]() $12$
, which gives a contradiction.
$12$
, which gives a contradiction.
Next assume that
![]() $\mathrm {id}=35$
. Here, E acts on D by inverting its elements. In particular, E centralises
$\mathrm {id}=35$
. Here, E acts on D by inverting its elements. In particular, E centralises
![]() $D_1:=\langle x^2:x\in D\rangle \cong C_2^2$
. Fix a B-subpair
$D_1:=\langle x^2:x\in D\rangle \cong C_2^2$
. Fix a B-subpair
![]() $(D_1,b_1)$
. Then
$(D_1,b_1)$
. Then
![]() $b_1$
has defect pair
$b_1$
has defect pair
![]() $(\mathrm {C}_D(D_1),\mathrm {C}_E(D_1))=(D,E)$
. In particular,
$(\mathrm {C}_D(D_1),\mathrm {C}_E(D_1))=(D,E)$
. In particular,
![]() $b_1$
is real. Since S does not centralise
$b_1$
is real. Since S does not centralise
![]() $D_1$
,
$D_1$
,
![]() $b_1$
is nilpotent. By the first part of the proof,
$b_1$
is nilpotent. By the first part of the proof,
![]() $b_1$
has exactly eight characters with F-S indicator
$b_1$
has exactly eight characters with F-S indicator
![]() $-1$
. However, this leads to a contradiction by considering the action of
$-1$
. However, this leads to a contradiction by considering the action of
![]() $\mathrm {N}_G(D,b_D)$
in
$\mathrm {N}_G(D,b_D)$
in
![]() $\operatorname {Irr}(b_1)$
as above. This leaves the cases
$\operatorname {Irr}(b_1)$
as above. This leaves the cases
![]() $\mathrm {id}\in \{11,21,33,34\}$
. In all of those, E splits over D. Hence, all F-S indicators are nonnegative by [Reference Gow24, Theorem 5.6].
$\mathrm {id}\in \{11,21,33,34\}$
. In all of those, E splits over D. Hence, all F-S indicators are nonnegative by [Reference Gow24, Theorem 5.6].
By [Reference Eaton, Kessar, Külshammer and Sambale13], the decomposition matrix of B is
 $$ \begin{align*}Q:=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ 1&1&1\\ 1&1&1\\ 1&1&1\\ 1&1&1\\ 1&1&1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}Q:=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ 1&1&1\\ 1&1&1\\ 1&1&1\\ 1&1&1\\ 1&1&1 \end{pmatrix}.\end{align*} $$
Up to conjugation, there are five nontrivial B-subsections
![]() $(x,b_x)$
,
$(x,b_x)$
,
![]() $(y,b_y)$
,
$(y,b_y)$
,
![]() $(y^{-1},b_y)$
,
$(y^{-1},b_y)$
,
![]() $(z,b_z)$
and
$(z,b_z)$
and
![]() $(z^{-1},b_z)$
, where x is an involution and
$(z^{-1},b_z)$
, where x is an involution and
![]() $y,z$
have order
$y,z$
have order
![]() $4$
. Thus, the complex conjugation fixes exactly four columns of the generalised decomposition matrix
$4$
. Thus, the complex conjugation fixes exactly four columns of the generalised decomposition matrix
![]() $\hat {Q}$
. By Brauer’s permutation lemma, there are exactly four
$\hat {Q}$
. By Brauer’s permutation lemma, there are exactly four
![]() $2$
-rational characters. We stress that the
$2$
-rational characters. We stress that the
![]() $2$
-conjugate characters can still be real since y might be conjugate to
$2$
-conjugate characters can still be real since y might be conjugate to
![]() $y^{-1}$
via an element not fixing
$y^{-1}$
via an element not fixing
![]() $b_y$
. By the shape of Q, we may assume that the first four characters are
$b_y$
. By the shape of Q, we may assume that the first four characters are
![]() $2$
-rational. By [Reference Gow24, Theorem 5.3], two or four of them have F-S indicator
$2$
-rational. By [Reference Gow24, Theorem 5.3], two or four of them have F-S indicator
![]() $1$
.
$1$
.
By [Reference Sambale39, Theorem 15], B is isotypic to the principal block of
![]() $H:=D\rtimes C_3$
. This implies via [Reference Sambale40, Proposition 7.3] that
$H:=D\rtimes C_3$
. This implies via [Reference Sambale40, Proposition 7.3] that
![]() $\hat {Q}$
coincides up to basic sets with the generalised decomposition matrix of H. However, since
$\hat {Q}$
coincides up to basic sets with the generalised decomposition matrix of H. However, since
![]() $l(b_x)=l(b_y)=l(b_z)=1$
, the columns of
$l(b_x)=l(b_y)=l(b_z)=1$
, the columns of
![]() $\hat {Q}$
corresponding to
$\hat {Q}$
corresponding to
![]() $x,y,z$
are uniquely determined up to signs. Using the orthogonality relations, the signs can be chosen such that
$x,y,z$
are uniquely determined up to signs. Using the orthogonality relations, the signs can be chosen such that
 $$ \begin{align*}\hat{Q}=\begin{pmatrix} 1&0&0&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 0&1&0&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 0&0&1&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 1&1&1&3\epsilon_x&-\epsilon_y&-\epsilon_y&-\epsilon_z&-\epsilon_z\\ 1&1&1&-\epsilon_x&(-1+2i)\epsilon_y&(-1-2i)\epsilon_y&\epsilon_z&\epsilon_z\\ 1&1&1&-\epsilon_x&(-1-2i)\epsilon_y&(-1+2i)\epsilon_z&\epsilon_z&\epsilon_z\\ 1&1&1&-\epsilon_x&\epsilon_y&\epsilon_y&(-1+2i)\epsilon_z&(-1-2i)\epsilon_z\\ 1&1&1&-\epsilon_x&\epsilon_y&\epsilon_y&(-1-2i)\epsilon_z&(-1+2i)\epsilon_z \end{pmatrix},\end{align*} $$
$$ \begin{align*}\hat{Q}=\begin{pmatrix} 1&0&0&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 0&1&0&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 0&0&1&\epsilon_x&\epsilon_y&\epsilon_y&\epsilon_z&\epsilon_z\\ 1&1&1&3\epsilon_x&-\epsilon_y&-\epsilon_y&-\epsilon_z&-\epsilon_z\\ 1&1&1&-\epsilon_x&(-1+2i)\epsilon_y&(-1-2i)\epsilon_y&\epsilon_z&\epsilon_z\\ 1&1&1&-\epsilon_x&(-1-2i)\epsilon_y&(-1+2i)\epsilon_z&\epsilon_z&\epsilon_z\\ 1&1&1&-\epsilon_x&\epsilon_y&\epsilon_y&(-1+2i)\epsilon_z&(-1-2i)\epsilon_z\\ 1&1&1&-\epsilon_x&\epsilon_y&\epsilon_y&(-1-2i)\epsilon_z&(-1+2i)\epsilon_z \end{pmatrix},\end{align*} $$
where
![]() $\epsilon _x,\epsilon _y,\epsilon _z\in \{\pm 1\}$
and
$\epsilon _x,\epsilon _y,\epsilon _z\in \{\pm 1\}$
and
![]() $i=\sqrt {-1}$
. Since
$i=\sqrt {-1}$
. Since
![]() $b_x$
,
$b_x$
,
![]() $b_y$
and
$b_y$
and
![]() $b_z$
are nilpotent with abelian defect group, we can apply Proposition 4.2 for each E. This gives a linear system on the vector of F-S indicators. We have checked by computer that there is a unique solution (up to permuting the first three characters). Examples are given by
$b_z$
are nilpotent with abelian defect group, we can apply Proposition 4.2 for each E. This gives a linear system on the vector of F-S indicators. We have checked by computer that there is a unique solution (up to permuting the first three characters). Examples are given by
![]() $G=\mathtt {SmallGroup}(288,a)$
, where
$G=\mathtt {SmallGroup}(288,a)$
, where
![]() $a=67,407,406,405$
for
$a=67,407,406,405$
for
![]() $\mathrm {id}=11,21,33,34$
, respectively.
$\mathrm {id}=11,21,33,34$
, respectively.
It might be possible to conduct a similar analysis for defect groups
![]() $D\cong C_{2^n}^2$
with arbitrary
$D\cong C_{2^n}^2$
with arbitrary
![]() $n\ge 2$
. However, for
$n\ge 2$
. However, for
![]() $n=3$
, there are already
$n=3$
, there are already
![]() $27$
extended defect groups to consider.
$27$
extended defect groups to consider.
Acknowledgments
I thank John Murray for some helpful discussions on the open cases in Section 5. Parts of this paper were written at the University of Valencia, from which I received great hospitality.