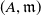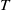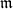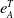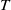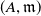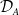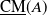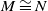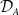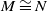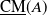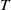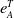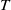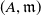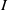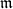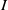A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II

Abstract

Let $(A,\mathfrak{m})$ be a Cohen–Macaulay local ring, and then the notion of a $T$-split sequence was introduced in the part-1 of this paper for the $\mathfrak{m}$-adic filtration with the help of the numerical function $e^T_A$. In this article, we explore the relation between Auslander–Reiten (AR)-sequences and $T$-split sequences. For a Gorenstein ring $(A,\mathfrak{m})$, we define a Hom-finite Krull–Remak–Schmidt category $\mathcal{D}_A$ as a quotient of the stable category $\underline{\mathrm{CM}}(A)$. This category preserves isomorphism, that is, $M\cong N$ in $\mathcal{D}_A$ if and only if $M\cong N$ in $\underline{\mathrm{CM}}(A)$.This article has two objectives: first objective is to extend the notion of $T$-split sequences, and second objective is to explore the function $e^T_A$ and $T$-split sequences. When $(A,\mathfrak{m})$ is an analytically unramified Cohen–Macaulay local ring and $I$ is an $\mathfrak{m}$-primary ideal, then we extend the techniques in part-1 of this paper to the integral closure filtration with respect to $I$ and prove a version of Brauer–Thrall-II for a class of such rings.

1. Introduction

For ease of reference, it is advisable to have a copy of [20] on hand while reading this paper. The notations employed here are consistent with those used in [20].

Let $(A,{\mathfrak{m}})$ be a Cohen–Macaulay local ring of dimension $d \geq 1$ and let ${\mathrm{CM}}(A)$ be the category of maximal Cohen–Macaulay $A$ -modules. In [20], the second author has constructed $T \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$ , a sub-functor of $\mathrm{Ext}^1_A(-, -)$ as follows: Let $M$ be an MCM $A$ -module. Set

\begin{equation*} e^T_A(M) = \lim _{n \rightarrow \infty } \frac {(d-1)!}{n^{d-1}}\ell \left ({\mathrm {Tor}}^A_1(M, \frac {A}{\mathfrak {m}^{n+1}}) \right ). \end{equation*}

This function arose in the second author’s study of certain aspects of the theory of Hilbert functions [15, 16]. Using [15, Theorem 18], we get that $e^T_A(M)$ is a finite number, and it is zero if and only if $M$ is free. Let $s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$ be an exact sequence of MCM $A$ -modules. Then by [17, 2.6], we get that $e^T_A(E) \leq e^T_A(M) + e^T_A(N)$ . Set $e^T(s) = e^T_A(M) + e^T_A(N) - e^T_A(E)$ .

Definition 1.1. We say $s$ is $T$ - split if $e^T_A(s) = 0$ .

Definition 1.2. Let $M, N$ be MCM $A$ -modules. Set

\begin{equation*} T_A(M,N) = \{ s \mid s \ \text {is a $T$-split extension} \}. \end{equation*}

We proved [20, 1.4],

Theorem 1.3. (with notation as above) $T_A \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$ is a sub-functor of $\mathrm{Ext}^1_A(-, -)$ .

Note that the most natural context for the sub-functors of $\mathrm{Ext}$ is exact categories (e.g., see [9, Section 1], [6]).

It is not clear from the definition whether $T_A(M,N)$ is nonzero. Theorem [20, 1.5] shows that there are plenty of $T$ -split extensions if $\dim \mathrm{Ext}^1_A(M,N) \gt 0$ . We proved [20, 1.5]

Theorem 1.4. Let $(A,{\mathfrak{m}})$ be a Cohen–Macaulay local ring and let $M,N$ be MCM $A$ -modules. Then

\begin{equation*} \mathrm {Ext}^1_A(M, N)/T_A(M, N) \quad \text {has finite length.} \end{equation*}

Note Theorem1.4 has no content if $M$ is free on the punctured spectrum of $A$ . One of our motivations of this paper was to investigate $T_A(M, N)$ when $M$ is free on the punctured spectrum of $A$ .

Now assume $(A,{\mathfrak{m}})$ is Henselian and $M$ is an indecomposable MCM $A$ -module with $M_{\mathfrak{p}}$ is free for all $\mathfrak{p}\in$ Spec $^0(A)=$ Spec $(A)\setminus \{\mathfrak{m}\}$ , then a fundamental short exact sequence is known as the Auslander–Reiten (AR)-sequence ending at $M$ exists. For a good introduction to AR-sequences, see [23, Chapter 2].

The following result gives a large number of examples of AR-sequences which are $T$ -split.

Theorem 1.5. Let $(Q,\mathfrak{n})$ be a Henselian regular local ring and $\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$ a regular sequence. Set $I=(f_1,\ldots, f_c)$ and $(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$ . Assume $\dim A = 1$ . Let $M$ be an indecomposable MCM $A$ -module with $\mathrm{cx}_A M\geq 2$ . Assume $M$ is free on Spec $^0(A)$ . Set $M_n= \mathrm{Syz}_n^A(M)$ , then for $n\gg 0$ the AR-sequences ending in $M_n$ are $T$ -split.

For hypersurfaces defined by quadrics, we prove:

Theorem 1.6. Let $(Q,\mathfrak{n})$ be a Henselian regular local ring with algebraically closed residue field $k = Q/\mathfrak{n}$ and let $f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$ . Assume the hypersurface $A = Q/(f)$ is an isolated singularity. Then all but finitely many AR-sequences in $A$ are $T$ -split.

Theorems1.5 and 1.6 show that $T$ -split sequences are abundant in general. However, the following example is important:

Example 1.7. There exists a complete hypersurface isolated singularity $A$ and an indecomposable MCM $A$ -module $M$ such that $T_A(M, N) = 0$ for any MCM $A$ -module $N$ .

Theorem 1.8. Now assume $A$ is Gorenstein. As observed in [17], the function $e^T_A(-)$ is in fact a function on $\underline{\mathrm{CM}}(A)$ the stable category of all MCM $A$ -modules. Let $M$ and $N$ be MCM $A$ -modules. It is well known that we have a natural isomorphism:

\begin{equation*}\eta \colon \underline {\mathrm {Hom}}_A(M,N)\cong \text {Ext}^1_A(\Omega ^{-1}(M),N)\end{equation*}

We denote $\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$ by $\mathcal{R}(M,N)$ . Then $\eta$ induces the following isomorphism:

\begin{equation*}\frac {\underline {\mathrm {Hom}}_A(M,N)}{\mathcal {R}(M,N)}\cong \frac {\text {Ext}^1_A(\Omega ^{-1}(M),N)}{T_A(\Omega ^{-1}(M),N)}.\end{equation*}

Surprisingly,

Proposition 1.9. $\mathcal{R}$ is a relation on $\underline{\mathrm{CM}}(A)$ .

Thus, we may consider the quotient category $\mathcal{D}_A = \underline{\mathrm{CM}}(A)/\mathcal{R}$ . Clearly, $\mathcal{D}_A$ is a Hom-finite additive category. Surprisingly, the following result holds.

Theorem 1.10. Let $(A,\mathfrak{m})$ be a Henselian Gorenstein local ring and let $M$ and $N$ be MCM $A$ -modules. Then the following holds

1. (1) $M\cong N$ in $\mathcal{D}_A$ if and only if $M\cong N$ in $\underline{\mathrm{CM}}(A)$ .

2. (2) $M$ is indecomposable in $\mathcal{D}_A$ if and only if $M$ is indecomposable in $\underline{\mathrm{CM}}(A)$

3. (3) $\mathcal{D}_A$ is a Krull–Remak–Schmidt (KRS) category.

The main application of $T$ -split sequences was to study Weak Brauer–Thrall-II for associated graded modules (Recall Weak Brauer–Thrall-II: Do there exist distinct indecomposable MCM modules $\{M_n\}_{n\geq 1}$ with $G(M_n)$ Cohen–Macaulay and $e(M_n)$ bounded?) for a large class of rings. Note that in [20], the concept was introduced only for the $\mathfrak{m}$ -adic filtration, but for general $I(\ne \mathfrak{m})$ -adic filtrations that method will not work (see [20, Remark 3.2]).

In this article, we extend the results in [20] to a large family of filtrations. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d \geq 1$ and let $I$ be an $\mathfrak{m}$ -primary ideal. Let $\mathcal{F}=\{I_n\}_{n \in \mathbb{Z}}$ where $I_1=\overline{I}$ and $I_n=\overline{I^{n}}$ for $n\gg 0$ be an $I$ -admissible filtration. Note here “–” denotes the integral closure. Let $M$ be an MCM $A$ -module.

Theorem 1.11. Set

\begin{equation*} e_{\mathcal {F}}^T(M) = \lim _{n\to \infty }\frac {(d-1)!}{n^{d-1}}\ell ({\mathrm {Tor}}_1^A(M,A/{I_{n+1}})) \end{equation*}

Then $e_{\mathcal{F}}^T(M) = 0$ if and only if $M$ is free (see [13, Theorem 7.5]). Let $M,N$ be maximal Cohen–Macaulay $A$ -modules and $\alpha \in$ Ext $_A^1(M,N)$ . Let $\alpha$ be given by an extension $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ ; here, $E$ is a maximal Cohen–Macaulay module. Now set

\begin{equation*}e_{\mathcal {F}}^T(\alpha )=e_{\mathcal {F}}^T(M)+e_{\mathcal {F}}^T(N)-e_{\mathcal {F}}^T(E).\end{equation*}

It can be shown that $e_{\mathcal{F}}^T(\alpha ) \geq 0$ , see 3.6.

Definition 1.12. An extension $s\in \mathrm{Ext}_A^1(M,N)$ is $T_{\mathcal{F}}$ -split if $e_{\mathcal{F}}^T(s)=0$ .

As before we can show that ${T_{\mathcal{F}}}(M,N)$ is a submodule of $\mathrm{Ext}^1_A(M,N)$ (see 4.1). Furthermore, ${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-)\times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$ is a sub-functor of $\mathrm{Ext}^1_A(-,-)$ , see 4.2.

Theorem 1.13. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d$ with one of the following conditions:

1. (1) the residue field $k (= A/\mathfrak{m})$ is uncountable.

2. (2) the residue field $k$ is perfect field.

Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$ where $I_1=\overline{I}$ and $I_n= \overline{I^{n}}$ for $n\gg 0$ . Let $M, N$ be MCM $A$ -module then $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$ has finite length.

Next, we prove following theorem.

Theorem 1.14. Let $(A,\mathfrak{m})$ be a complete reduced Cohen–Macaulay local ring of dimension $d\geq 1$ with either uncountable residue field or a perfect residue field. Let $I$ be an $\mathfrak{m}$ -primary ideal. Set $R=A[[X_1,\ldots, X_m]]$ , $J=(I,X_1,\ldots, X_m)$ , $\mathcal{I}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$ , and $\mathcal{J}=\{\overline{J^n}\}_{n \in \mathbb{Z}}$ . If $A$ has an MCM module $M$ with $G_{\mathcal{I}}(M)$ Cohen–Macaulay. Then there exists $\{ E_n \}_{n \geq 1}$ indecomposable MCM $R$ -modules with bounded multiplicity (with respect to $\mathcal{J}$ ) and having $G_{\mathcal{J}}(E_n)$ Cohen–Macaulay for all $n \geq 1$ .

Let $e^T_{\mathcal{F}} \colon \mathrm{Ext}_A^1(M, N) \rightarrow \mathbb{N}$ be the function defined by $\alpha \mapsto e^T_{\mathcal{F}}(\alpha )$ . When $A$ has characteristic $p \gt 0$ , then we can say more about this function. If $V$ is a vector space over a field $k$ , then let $\mathbb{P}(V)$ denote the projective space determined by $V$ .

Theorem 1.15. (with hypotheses as in 1.13 ) Further assume $A$ is of characteristic $p \gt 0$ and that $A$ contains a field $k \cong A/{\mathfrak{m}}$ . If $\mathrm{Ext}_A^1(M, N) \neq T_{\mathcal{F}}(M,N)$ , then the function $e^T_{\mathcal{F}}$ factors as:

\begin{equation*} [\overline {e^T_{\mathcal {F}}}] \colon \mathbb {P}(\mathrm {Ext}^1_A(M, N)/T_{\mathcal {F}}(M, N)) \rightarrow \mathbb {N}\setminus {0}. \end{equation*}

We now describe in brief the contents of this paper. In section 2, we discuss some preliminary results. In section 3, we introduce our function 1.11 and discuss few of its properties. We also discuss in detail the base changes that we need to prove our results. In section 4, we prove Theorem1.13. In the next section, we prove Theorem1.14. In section 6, we prove Theorem1.15. In the next section, we discuss our result on relation between T-split sequences and AR-sequences. In section 8, we prove Theorem1.5. In the next section, we prove Theorem1.6 and construct Example 1.7. In section 10, we prove Proposition 1.9 and Theorem 1.10.

2. Preliminaries

Theorem 2.1. Let $(A,\mathfrak{m})$ be a Noetherian local ring and $I$ be an $\mathfrak{m}$ -primary ideal. Then a filtration $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$ is said to be $I$ -admissible filtration if

1. 1. $I^n\subseteq F_n$ for all $n$ .

2. 2. $F_nF_m \subseteq F_{n + m}$ for all $n,m \in \mathbb{Z}$ .

3. 3. $F_n = IF_{n-1}$ for $n\gg 0$ .

Definition 2.2. A Noetherian local ring $(A,\mathfrak{m})$ is said to be analytically unramified if its $\mathfrak{m}$ -adic completion is reduced.

Theorem 2.3. Let $\overline{\mathfrak{a}}$ denote integral closure of the ideal $\mathfrak{a}$ . If $A$ is analytically unramified then from a result of Rees [21], the integral closure filtration $\mathcal{F}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$ is $I$ -admissible.

Theorem 2.4. Let $(A,\mathfrak{m})$ be a Noetherian local ring, $I$ an $\mathfrak{m}$ -primary ideal, and $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$ a $I$ -admissible filtration. Let $M$ be a finite $A$ -module with dimension $r$ . Then the numerical function $H_{\mathcal{F}}(M,n)= \ell (M/{F_{n+1}}M)$ is known as the Hilbert function of $M$ with respect to $\mathcal{F}$ . For large value of $n$ , $H_{\mathcal{F}}(M,n)$ coincides with a polynomial $P_{\mathcal{F}}(M,n)$ of degree $r$ , and this polynomial is known as the Hilbert polynomial of $M$ with respect to $\mathcal{F}$ . There exist unique integer $e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$ such that Hilbert polynomial of $M$ with respect to $\mathcal{F}$ can be written as:

\begin{equation*}P_{\mathcal {F}}(M,n)= \sum _{i=0}^{r}(-1)^ie_i^{\mathcal {F}}(M)\binom {n+r-i}{r-i}.\end{equation*}

These integers $e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$ are known as the Hilbert coefficients of $M$ with respect to $\mathcal{F}$ . In case of $\mathfrak{m}$ -adic and $I$ -adic filtrations, these coefficients will be denoted as $e_i(M)$ and $e_i^I(M)$ for $i=1,\ldots, r$ , respectively.

Theorem 2.5. Let $(A,\mathfrak{m})$ be a Noetherian local ring and $I$ be an $\mathfrak{m}$ -primary ideal. Let $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$ be an $I$ -admissible filtration and $M$ an $A$ -module with positive dimension. Then an element $x\in F_1\setminus F_2$ is said to be $\mathcal{F}$ -superficial element for $M$ if there exists $c\in \mathbb{N}$ such that for all $n\geq c$ ,

\begin{equation*}(F_{n+1}M:_Mx)\cap F_cM= F_nM.\end{equation*}

The following facts are well known:

1. 1. If $k= A/\mathfrak{m}$ is infinite, then $\mathcal{F}$ -superficial elements for $M$ exist.

2. 2. If $\mathrm{depth}\; M\gt 0$ , then every $\mathcal{F}$ -superficial element for $M$ is also $M$ -regular.

3. 3. If $x$ is $\mathcal{F}$ -superficial element for $M$ and $\mathrm{depth} M \gt 0$ , then $(F_{n+1}M:_Mx)= F_nM$ for $n\gg 0$ .

4. 4. If $x$ is $\mathcal{F}$ -superficial element for $M$ and $\mathrm{depth} M \gt 0$ , then $e_i^{\overline{\mathcal{F}}} (M/xM) = e_i^{\mathcal{F}}(M)$ for $i = 0,1,\ldots, \dim M - 1$ (here $\overline{\mathcal{F}}$ is the obvious quotient filtration of $\mathcal{F}$ ).

Theorem 2.6. A sequence $\underline{x}=x_1,\ldots, x_r$ with $r\leq \dim M$ is said to be $\mathcal{F}$ -superficial sequence for $M$ if $x_1$ is $\mathcal{F}$ -superficial element for $M$ and $x_i$ is $\mathcal{F}/(x_1,\ldots, x_{i-1})$ -superficial element for $M/(x_1,\ldots, x_{i-1})M$ for all $i\leq r$ .

3. The case when $A$ is analytically unramified

Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring with $\dim A = d\geq 1$ and $I$ an $\mathfrak{m}$ -primary ideal. We are primarily interested in the integral closure filtration of $I$ . However, to prove our results, we need the following class of $I$ -admissible filtrations $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$ , where $I_1=\overline{I}$ and $I_n=\overline{I^n}$ for $n\gg 0$ . Let $M$ be an MCM $A$ -module.

Theorem 3.1. The numerical function

\begin{equation*}n\longmapsto \ell ({\mathrm {Tor}}_1^A(M,A/{{I_{n+1}}}))\end{equation*}

is polynomial type; that is, there is a polynomial $t^A_{\mathcal{F}}(M,z)$ which coincides with this numerical function for $n\gg 0$ .

If $M$ is non-free MCM $A$ -module, then $\deg t^A_{\mathcal{F}}(M,z)=d-1$ (see [13, Theorem 7.5]). Note that normalized leading coefficient of $t^A_{\mathcal{F}}(M,z)$ is $e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M))$ .

Theorem 3.2. Set

\begin{align*} e_{\mathcal{F}}^T(M)&=\lim _{n\to \infty }\frac{(d-1)!}{n^{d-1}}\ell ({\mathrm{Tor}}_1^A(M,A/{I_{n+1}}))\\ &=e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M)) \end{align*}

Theorem 3.3. Base change: We need to do several base changes in our arguments.

(I) We first discuss the general setup: Let $\psi \colon (A,{\mathfrak{m}})\rightarrow (B,\mathfrak{n})$ be a flat map such that $B$ is also a Cohen–Macaulay local ring and $({\mathfrak{m}} B =\mathfrak{n}$ . If $M$ is an $A$ -module, then set $M_B= M\otimes _A B$ . If $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$ is an $I$ -admissible filtration, then set $\mathcal{F}_B=\{{I_n B}\}_{n \in \mathbb{Z}}$ . Then,

1. 1. $\ell (N)=\ell (N_B)$ for any finite length $A$ -module $N$ .

2. 2. $\mathcal{F}_B$ is an $IB$ -admissible filtration.

3. 3. $\dim M= \dim M_B$ and $\mathrm{depth} M = \mathrm{depth} M_B$ . In particular, $M$ is an MCM $A$ -module if and only if $M_B$ is MCM $B$ -module.

4. 4. Syz $^A_i(M)\otimes _A B\cong \text{Syz}^B_i(M_B)$ for all $i \geq 0$ .

5. 5. $e_i^{\mathcal{F}}(M)= e_i^{\mathcal{F}_B}(M_B)$ for all $i$ .

6. 6. If $\psi$ is regular and $\mathfrak{a}$ is integrally closed $\mathfrak{m}$ -primary ideal in $A$ , then $\mathfrak{a}B$ is integrally closed in $B$ (for instance, see [11, 2.2(7)]).

(II) Assume $A$ is analytically unramified Cohen–Macaulay local ring and $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$ is an $I$ -admissible filtration with $I$ , $\mathfrak{m}$ -primary and furthermore $I_1=\overline{I}$ and $I_n=\overline{I^n}$ for $n\gg 0$ . We need to base changes as above where $\mathcal{F}_B$ has the property that $I_nB = I^nB = \overline{I^nB}$ whenever $I_n = \overline{I^n}$ . Note this automatically forces $B$ to be analytically unramified. The specific base changes we do are the following:

1. (i) $B = \widehat{A}$ the completion of $A$ . Note that if $J$ is an $\mathfrak{m}$ -primary integrally closed ideal, then $J\widehat{A}$ is also integrally closed, cf., [12, 9.1.1].

2. (ii) If $A$ has a finite residue field, then we can consider the extension $B = A[X]_{({\mathfrak{m}} A[X]}$ . The residue field of $B$ is $k(X)$ which is infinite. Note that if $J$ is an $\mathfrak{m}$ -primary integrally closed ideal, then $J\widehat{A}$ is also integrally closed, cf., [12, 8.4.2].

3. (iii) Assume $\dim A \geq 2$ . Even if $A$ has infinite residue field, there might not exist an $\mathcal{F}$ -superficial element $x$ such that $A/(x)$ is analytically unramified. However, a suitable extension $B$ has this property. To see this, we first observe two facts.

Let $\mathcal{E}$ be a countable set of MCM of $A$ -modules. Assume that the residue field $k$ of $A$ is uncountable if $\mathcal{E}$ is an infinite set. Otherwise, $k$ is infinite.

1. (a) There exist $\underline{x}=x_1,\ldots, x_d\in \overline{I}$ such that $\underline{x}$ is $\mathcal{F}$ -superficial for each $N \in \mathcal{E}$ . This result is well known (for instance, see [18, Lemma 2.2]).

2. (b) There exists a generating set $r_1,\ldots, r_t$ of $I$ such that for each $i$ , $r_i$ is $I$ -superficial and $\mathcal{F}$ -superficial element for each $N \in \mathcal{E}$ (see (a) and [13, Lemma 7.3]).

([7 ], [13, Lemma 7.4, Theorem 7.5]) Choose $r_1,\ldots, r_t$ as in (b). Now consider following flat extension of rings

\begin{equation*}A\rightarrow \hat {A}\rightarrow B=\hat {A}[X_1,\ldots, X_t]_{\mathfrak {m}\hat {A}[X_1,\ldots, X_t]}.\end{equation*}

Let $\zeta = r_1X_1+\ldots +r_tX_t$ . Set $C = B/\zeta B$ and $\mathcal{F}_C=\{I_n C\}$ . For $N \in \mathcal{E}$ , set $N_B = N\otimes _A B$ . Then, we have

1. 1. $B$ is analytically unramified Cohen–Macaulay local ring of dimension $d$ .

2. 2. $N_B$ is MCM $B$ -module for each $N \in \mathcal{E}$ .

3. 3. If $J$ is a integrally closed $\mathfrak{m}$ -primary ideal in $A$ , then $JB$ a integrally closed $\mathfrak{n}$ -primary ideal in $B$ .

4. 4. $I_1C = \overline{I}C = \overline{IC}$ .

5. 5. $I_nC=\overline{I^nC}$ for all $n\gg 0$ .

6. 6. $C$ is analytically unramified Cohen–Macaulay local ring of dimension $d-1$ .

7. 7. $\zeta$ is $\mathcal{F}_B$ -superficial for each $N_B$ (here $N \in \mathcal{E}$ ).

1. (iv) For some of our arguments, we need the residue field of $A$ to be uncountable. If $k$ is finite or countably infinite perfect field do the following: First complete $A$ . By (i), this is possible. So, we may assume $A$ is complete.

Consider extension $\phi \;:\; A\longrightarrow A[[X]]_{\mathfrak{m}A[[X]]}=(B,\mathfrak{n})$ . Set $B_0=B\otimes _Ak=B/\mathfrak{m}B$ . So, $B_0=B/\mathfrak{n}=k((X))$ is uncountable. As $k$ is perfect we get $k((X))$ is $0$ -smooth over $k$ , see [14, 28.7]. Using [14, 28.10], we get $B$ is $\mathfrak{n} (=\mathfrak{m}B)$ -smooth. This implies $\phi$ is regular (see [1, Theorem]).

By I(6) if $\mathfrak{a}$ is an integrally closed $\mathfrak{m}$ -primary ideal in $A$ , then $\mathfrak{a} B$ is integrally closed in $B$ . Thus, ${I_n}B=\overline{I^nB}$ whenever $I_n = \overline{I^n}$ .

Definition 3.4. We say a flat extension $\psi \colon (A,{\mathfrak{m}}) \rightarrow (B,\mathfrak{n})$ with ${\mathfrak{m}} B = \mathfrak{n}$ behaves well with respect to integral closure if for any integrally closed $\mathfrak{m}$ - primary ideal $\mathfrak{a}$ in $A$ , the ideal $\mathfrak{a} B$ is integrally closed in  $B$ .

We need the following result:

Proposition 3.5. Let $(A,\mathfrak{m})$ be analytically unramified Cohen–Macaulay local ring with $\dim A = d\geq 1$ and $I$ an $\mathfrak{m}$ -primary ideal. Let $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$ be a $I$ -admissible filtration where $I_1=\overline{I}$ and $I_n=\overline{I^n}$ for $n\gg 0$ .

1. (1) Let $(B,\mathfrak{n})$ be a flat extension of $A$ which behaves well with respect to integral closure. Set $\mathcal{F}_B = \{{I_nB}\}_{n \in \mathbb{Z}}$ . Then for any MCM $A$ -module $M$ , we have $e^T_{\mathcal{F}}(M) = e^T_{\mathcal{F}_B}(M_B)$ .

2. (2) Let $\dim A \geq 2$ . and the residue field of $A$ is infinite. Let $\mathcal{V}$ be any countable set of MCM $A$ -modules (containing $A$ ). Assume $k = A/{\mathfrak{m}}$ is uncountable if $\mathcal{V}$ is infinite otherwise $k$ is infinite. Then there exists a flat extension $B$ of $A$ which behaves well with respect to integral closure such that there exist $\zeta \in IB$ which is $\mathcal{F}_B$ -superficial with respect to each $N_B$ (for all $N \in \mathcal{V}$ ). Furthermore, if $C = B/\zeta B$ then $C$ is analytically unramified with $IC = \overline{IC}$ and $I_nC = \overline{I^nC}$ for all $n \gg 0$ . Set $N_C = N\otimes _A C$ . Furthermore, $e^T_{\mathcal{F}}(N) = e^T_{\mathcal{F}_C}(N_C)$ for each $N \in \mathcal{V}$ .

Proof. (1) This follows from 3.3(I).

(2) Set $\mathcal{E} = \{ \mathrm{Syz}^A_i(N) \colon i = 0, 1 \ \text{and} \ N \in \mathcal{V}\}$ . Then $\mathcal{E}$ is a countable set and is finite if $\mathcal{V}$ is. Now do the construction in 3.3(I)(iii) and use 2.5(4) and 3.2 to conclude.

The following lemma follows from [17, Theorem 2.6], but here we give a short proof (similar proof also works for ${e_{A}^T}()$ ):

Lemma 3.6. Let $\alpha : 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ be an exact sequence of MCM $A$ -modules. Then ${e_{\mathcal{F}}^T}(E)\leq{e_{\mathcal{F}}^T}(M)+{e_{\mathcal{F}}^T}(N)$ .

Proof. Consider the long exact sequence of $\alpha \otimes _A A/{{I_{n+1}}}$ . We get

\begin{equation*}\ldots \rightarrow {\mathrm {Tor}}_1^A(N,A/{{I_{n+1}}})\rightarrow {\mathrm {Tor}}_1^A(E,A/{{I_{n+1}}})\rightarrow {\mathrm {Tor}}_1^A(M,A/{{I_{n+1}}})\rightarrow \ldots \end{equation*}

So, $\ell ({\mathrm{Tor}}^A_1(E,A/{I_{n+1}}))\leq \ell ({\mathrm{Tor}}^A_1(M,A/{I_{n+1}})) + \ell ({\mathrm{Tor}}^A_1(N,A/{I_{n+1}}))$ . Now from the definition of ${e_{\mathcal{F}}^T}(-)$ , required inequality follows.

Theorem 3.7. Let $M,N$ be maximal Cohen–Macaulay $A$ -modules and $\alpha \in \mathrm{Ext}_A^1(M,N)$ . Let $\alpha$ be given by an extension $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ , here $E$ is a maximal Cohen–Macaulay module. Now set

\begin{equation*}e_{\mathcal {F}}^T(\alpha )=e_{\mathcal {F}}^T(M)+e_{\mathcal {F}}^T(N)-e_{\mathcal {F}}^T(E).\end{equation*}

Theorem 3.8. Let $\alpha _1,\alpha _2\in \mathrm{Ext}^1_A(M,N)$ . Suppose $\alpha _i$ can be given by $0\rightarrow N\rightarrow E_i\rightarrow M\rightarrow 0$ for $i=1,2$ . If $\alpha _1$ and $\alpha _2$ are equivalent, then $E_1\cong E_2$ . So, ${e_{\mathcal{F}}^T}(\alpha _1)={e_{\mathcal{F}}^T}(\alpha _2)$ . This implies ${e_{\mathcal{F}}^T}(\alpha )$ is well defined.

Note that ${e_{\mathcal{F}}^T}(\alpha )\geq 0$ .

Definition 3.9. An extension $s\in$ Ext $_A^1(M,N)$ is $T_{\mathcal{F}}$ -split if $e_{\mathcal{F}}^T(s)=0$ .

Definition 3.10. Let $M,N$ be maximal Cohen–Macaulay $A$ -modules. Set

\begin{equation*}T_{{\mathcal {F}},A}(M,N)=\{s| s \ \text {is a } T_{\mathcal {F}}\text {-split extension}\}.\end{equation*}

Note that if the choice of the ring $A$ is unambiguous from the context, we denote this set as ${T_{\mathcal{F}}}(M,N)$ .

We will need the following two results:

Lemma 3.11. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d\geq 1$ and let $M, N, N_1, E, E_1$ be MCM $A$ -modules. Suppose we have a commutative diagram

If $\alpha$ is $T_{\mathcal{F}}$ -split, then $\beta$ is also $T_{\mathcal{F}}$ -split.

Proof. If $\dim A = 1$ , then we can give an argument similar to [20, Proposition 3.8]. Now assume $d = \dim A \geq 2$ and the result has been proved for all analytically unramified rings of dimension $d -1$ . If the residue field of $A$ is finite, then use 3.3II.(ii). So, we may assume $A/{\mathfrak{m}}$ is infinite. Using 3.5, we may assume that (after going to a flat extension) there exists $\zeta \in I$ such that

1. (i) $\zeta$ is $\mathcal{F}$ -superficial with respect to $A\oplus U \oplus \mathrm{Syz}^A_1(U)$ for each $U$ in the above diagram.

2. (ii) $C = A/\zeta A$ is analytically unramified with $IC = \overline{IC}$ and $I_nC = \overline{I^nC}$ for all $n \gg 0$ .

3. (iii) $e^T_{\mathcal{F}_C}(U/\zeta U) = e^T_{\mathcal{F}}(U)$ for each $U$ in the above diagram.

Notice $\alpha \otimes C$ and $\beta \otimes C$ are exact. For an $A$ -module $V$ , set $\overline{V} = V/\zeta V$ . So, we have a diagram

Note $\alpha \otimes C$ is $T_{\mathcal{F}_C}$ -split. By our induction hypotheses, $\beta \otimes C$ is $T_{\mathcal{F}_C}$ -split. By our construction, it follows that $\beta$ is also $T_{\mathcal{F}}$ -split.

Lemma 3.12. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d\geq 1$ and let $M, M_1, N, E, E_1$ be MCM $A$ -modules. Suppose we have a commutative diagram

If $\beta$ is $T_{\mathcal{F}}$ -split, then $\alpha$ is also $T_{\mathcal{F}}$ -split.

Proof. This is dual to 3.11.

4. $T_{\mathcal{F}}$ -split sequences

In this section, we prove our results regarding $T_{\mathcal{F}}$ .

Theorem 4.1. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d$ . Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F}=\{{I_n}\}$ where $I_1=\overline{I}$ and $I_n= \overline{I^{n}}$ for $n\gg 0$ . Let $M, N$ be MCM $A$ -module, then ${T_{\mathcal{F}}}(M,N)$ is a submodule of $\mathrm{Ext}^1_A(M,N)$ .

Proof. Let $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ be a $T_{\mathcal{F}}$ -split extension and $r\in A$ , then we can define $r\alpha$

Note that first square is pushout diagram. Since $\alpha$ is $T_{\mathcal{F}}$ -split, this implies $r\alpha$ is also $T_{\mathcal{F}}$ -split (see 3.11).

Let $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ and $\alpha' \;:\; 0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$ be two $T_{\mathcal{F}}$ -split extensions. We want to show $\alpha +\alpha '$ is also $T_{\mathcal{F}}$ -split. Note that the addition operation on $\mathrm{Ext}^1_A(M,N)$ is Bear sum, that is, $\alpha +\alpha ':= (\nabla (\alpha \oplus \alpha '))\Delta$ .

Since $\alpha$ and $\alpha '$ are $T_{\mathcal{F}}$ -split, this implies $\alpha \oplus \alpha '\;:\; 0\rightarrow N\oplus N\rightarrow E\oplus E'\rightarrow M\oplus M\rightarrow 0$ also $T_{\mathcal{F}}$ -split. Consider following diagram

Note that first square is pushout diagram. From 3.11, $\nabla (\alpha \oplus \alpha ')$ is $T_{\mathcal{F}}$ -split. Now consider the diagram

Here, second square is pullback diagram. Now from 3.12, $\alpha + \alpha =(\nabla (\alpha \oplus \alpha '))\Delta$ is $T_{\mathcal{F}}$ -split.

We now show

Theorem 4.2. (with hypotheses as in 4.1 ) ${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-) \times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$ is a functor.

Proof. This is similar to [20, 3.13]. We have to use Theorem4.1 and Lemmas 3.11, 3.12.

Remark 4.3. Theorems 4.1 and 4.2 also follows directly from the Lemma 3.6 and [8, Theorem 4.8, Proposition 3.8]. Also see [8, Theorem 4.17]. However, for the sake of completion, we have given a proof of these theorems.

Note that the proof of [8, Theorem 4.8] also works for any totally ordered abelian group in place of  $\mathbb{Z}$ .

The following is one of the main results of our paper.

Theorem 4.4. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d$ with uncountable residue field. Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F}=\{{I_n}\}$ where $I_1=\overline{I}$ and $I_n= \overline{I^{n}}$ for $n\gg 0$ . Let $M, N$ be MCM $A$ -module then $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$ has finite length.

Proof. We prove this theorem by induction. If $\dim A=1$ , then $\mathrm{Ext}^1_A(M,N)$ has finite length. In fact, for any prime ideal $\mathfrak{p}\ne \mathfrak{m}$ , $(\mathrm{Ext}^1_A(M,N))_{\mathfrak{p}}=0$ because $A$ is reduced. Note that for dimension one case, we do not need any assumption on residue field.

We now assume $\dim A \geq 2$ and result is true for dimension $d-1$ .

Let $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0\in \mathrm{Ext}^1_A(M,N)$ and $a\in I$ . Then we have following pushout diagram of $R$ -modules for all $n\geq 1$

Set $\mathcal{V} = \{ M, N, E, E_n \colon n \geq 1 \}$ and set

\begin{equation*}\mathcal {E} = \{ A\} \cup \{ \mathrm {Syz}^A_i(U) \colon i = 0, 1 \ \text {and} \ U \in \mathcal {V} \}.\end{equation*}

We now do the base change as described in 3.3.II.(iii):

\begin{equation*}A\rightarrow \hat {A}\rightarrow B=\hat {A}[X_1,\ldots, X_t]_{\mathfrak {m}\hat {A}[X_1,\ldots, X_t]}\end{equation*}

For any MCM $A$ -module $L$ , set $L_B = L\otimes _{A}B$ .

Let $\mathcal{F}_B = \{ I_nB \}_{n \in \mathbb{Z}}$ . From 3.3.II.(iii), for all $n\geq 1$ , $\zeta$ is $\mathcal{F}_B$ -superficial for

\begin{equation*}B \oplus M_B\oplus N_B \oplus E_{n,B}\oplus \mathrm {Syz}^B_1(M_B)\oplus \mathrm {Syz}^B_1(N_B)\oplus \mathrm {Syz}^B_1(E_{n,B}).\end{equation*}

Set $C = B/\zeta B$ , $\mathcal{F}_C = \{ I_nC \}_{n \in \mathbb{Z}}$ . Then $C$ is analytically unramified with $\dim C = d -1$ . Furthermore, $I_1C = \overline{I_1C}$ and $I_nC = \overline{I^nC}$ for $n \gg 0$ . From 3.5, we have for all $n \geq 0$ ,

\begin{equation*} e^T_{\mathcal {F}}(a^n \alpha ) = e^T_{\mathcal {F}_C,C}(a^n\alpha \otimes C)=e^T_{\mathcal {F}_C,C}(\overline {a^n}(\alpha \otimes C)).\end{equation*}

But from the assumption result is true for $C$ . So

\begin{equation*}e^T_{\mathcal {F}_C, C}(a^n\alpha \otimes C )=e^T_{\mathcal {F}_C, C}(\overline {a^n}(\alpha \otimes C))=0 \quad \text {for $n\gg 0$}. \end{equation*}

This implies $e^T_{\mathcal{F},A}(a^n\alpha )=0$ for $n\gg 0$ . Let $I=(a_1,\ldots, a_u)$ . It follows that

\begin{equation*}(a_1^{n_1},\ldots, a_u^{n_u})\mathrm {Ext}^1_A(M,N)\subseteq {T_{\mathcal {F}}}(M, N).\end{equation*}

So $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$ has finite length.

Theorem 4.5. Let $(A,\mathfrak{m})$ be a Cohen–Macaulay analytically unramified local ring of dimension $d$ with residue field $k$ . Suppose $k$ is perfect field. Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F}=\{{I_n}\}$ where $I_1=\overline{I}$ and $I_n= \overline{I^{n}}$ for $n\gg 0$ . Let $M, N$ be MCM $A$ -module and then $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$ has finite length.

Proof. By 3.3, we may assume $A$ is complete. If $k$ is uncountable, the result follows from Theorem4.4.

Now we consider the case when $k$ is finite or countably infinite. Then by 3.3(iv), there exists a flat local extension $(B,\mathfrak{n})$ of $A$ with $({\mathfrak{m}} B = \mathfrak{n}$ which behaves well with respect to integral closure such that the residue field of $B$ is uncountable. Set $\mathcal{F}_B=\{{I_nB}\}_{n \in \mathbb{Z}}$ , $M_B=M\otimes B$ , and $N_B=N\otimes B$ . Also note that ${I_n}B=\overline{I^nB}$ for $n\gg 0$ .

Let $\alpha \in$ Ext $^1_A(M,N)$ and $a\in \mathfrak{m}$ . Then for all $n\geq 1$ , it is easy to see

\begin{equation*}e^T_{\mathcal {F}}(a^n\alpha )=e^T_{\mathcal {F}_B}((a^n\alpha )\otimes B)=e^T_{\mathcal {F}_B}((a^n\otimes 1)(\alpha \otimes B)).\end{equation*}

From Theorem4.4, $e^T_{\mathcal{F}_B}((a^n\otimes 1)(\alpha \otimes B))=0$ for $n\gg 0$ . So, $e^T_{\mathcal{F}}(a^n\alpha )=0$ for $n\gg 0$ . Therefore, $a^n\alpha \in T_{\mathcal{F}}(M,N)$ for $n\gg 0$ . Now the result follows from the similar argument as in Theorem4.4.

5. Weak Brauer–Thrall-II

We need the following two results.

Lemma 5.1. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d\geq 1$ . Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F}=\{{I_n}\}$ where $I_1=\overline{I}$ and $I_n= \overline{I^{n}}$ for $n\gg 0$ . If $M,N$ and $E$ are MCM modules, thenwe have a $T_{\mathcal{F}}$ -split sequence $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ . Assume $G_{\mathcal{F}}(N)$ is Cohen–Macaulay. Then we have short exact sequence

\begin{equation*}0\rightarrow G_{\mathcal {F}}(N)\rightarrow G_{\mathcal {F}}(E)\rightarrow G_{\mathcal {F}}(M)\rightarrow 0.\end{equation*}

Furthermore, $e_i^{\mathcal{F}}(E)= e_i^{\mathcal{F}}(N)+e_i^{\mathcal{F}}(M)$ for $i=0,\ldots, d$ .

Proof. Follows from an argument similar to [20, Lemma 6.3].

Proposition 5.2. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d\geq 1$ and $I$ an $\mathfrak{m}$ -primary ideal, and $\mathcal{F}=\{\overline{I^n}\}_{n\geq 0}$ . Assume the residue field $k = A/{\mathfrak{m}}$ is either uncountable or a perfect field. Let $M$ and $N$ be MCM $A$ -modules with $G_{\mathcal{F}}(M)$ and $G_{\mathcal{F}}(N)$ Cohen–Macaulay. If there exists only finitely many non-isomorphic MCM $A$ -modules $E$ with $G_{\mathcal{F}}(E)$ Cohen–Macaulay and $e^{\mathcal{F}}(E)= e^{\mathcal{F}}(N)+e^{\mathcal{F}}(M)$ , then $T_{\mathcal{F}}(M,N)$ has finite length (in particular Ext $^1_A(M,N)$ has finite length).

Proof. Follows from an argument similar to [20, Theorem 7.1].

The following result is well known. We indicate a proof for the convenience of the reader.

Lemma 5.3. Let $(A,\mathfrak{m})$ be a Noetherian local ring and $I$ be an ideal of $A$ . Set $B=A[X]$ and $J=(I,X)$ , then $\overline{J^n}=\sum _{i=0}^{n} \overline{I^{n-i}}X^i$ .

Proof. Consider Rees algebra of $I$ , $\mathscr{R}(I)= A[It] = A\oplus It\oplus I^2t^2\oplus \ldots$ . Its integral closure in $A[t]$ is $\overline{\mathscr{R}(I)}= A\oplus \overline{I}t\oplus \overline{I^2}t^2\oplus \ldots$ . By [2, Chapter 5, Exercise 9], we get that $\overline{\mathscr{R}(I)}[X]$ is integral closure of ${\mathscr{R}(I)}[X]$ in $A[t][X]$ . Comparing homogeneous components for all $n$ , we get $\overline{(I,X)^n}=\sum _{i=0}^{n}\overline{I^{n-i}}X^i$ .

Proposition 5.4. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension one and $I$ an $\mathfrak{m}$ -primary ideal. Set $R=A[X]_{(\mathfrak{m},X)}$ , $J=(I,X)$ , $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$ , and $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$ . Then there exists an MCM $R$ -module $E$ with $G_{\mathcal{J}}(E)$ Cohen–Macaulay and dim Ext $^1_R(E,E)\gt 0$ .

Proof. Let $M$ be an MCM $A$ -module. Fix large enough $n$ (say $n_0$ ), then it is easy to see $N=\overline{I^{n_0}}M$ is MCM and $G_{\mathcal{I}}(N)$ is Cohen–Macaulay. From Lemma 5.3, we get $G_{\mathcal{J}}(N\otimes R)= G_{\mathcal{I}}(N)[X]$ . So, $G_{\mathcal{J}}(N\otimes R)$ is Cohen–Macaulay.

From [4, Theorem A.11(b)], dim Ext $^1_R(N\otimes R, N\otimes R) \gt 0$ .

Theorem 5.5. Let $(A,\mathfrak{m})$ be an analytically unramified Cohen–Macaulay local ring of dimension $d\geq 1$ and $I$ an $\mathfrak{m}$ -primary ideal. Set $R=A[X_1,\ldots, X_m]_{(\mathfrak{m},X_1,\ldots, X_m)}$ , $J=(I,X_1,\ldots, X_m)$ , $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$ , and $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$ . Also set $S = \widehat{R}$ and $\mathcal{K}=\{\overline{J^n}S\}_{n\geq 0}$ . If $A$ has an MCM module $M$ with $G_{\mathcal{I}}(M)$ Cohen–Macaulay, then

1. (1) $M\otimes R$ is an MCM $R$ -module with $G_{\mathcal{J}}(M\otimes R)$ Cohen–Macaulay and $\dim \mathrm{Ext}^1_R(M\otimes R,M\otimes R)\gt 0$ .

2. (2) We have $\overline{J^nS} = \overline{J^n}S$ for all $n \geq 1$ . Furthermore, $M\otimes S$ is an MCM $S$ -module with $G_{\mathcal{K}}(M\otimes S)$ Cohen–Macaulay and $\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$ .

Proof. (1) It is sufficient to prove the result for $n=1$ . So, we can assume $R=A[X]$ . It is easy to see $M\otimes R$ is MCM $R$ -module and $G_{\mathcal{J}}(M\otimes R)=G_{\mathcal{I}}(M)[X]$ (follows from Lemma 5.3). So, $G_{\mathcal{J}}(M\otimes R)$ is Cohen–Macaulay.

From [4, Theorem A.11(b)], dim Ext $^1_R(M\otimes R, M\otimes R) \gt 0$ .

(2) The assertion $\overline{J^nS} = \overline{J^n}S$ for all $n \geq 1$ follows from [12, 9.1.1]. For the rest observe that $M\otimes _A S = (M \otimes _A R)\otimes _R S$ . This gives $\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$ . Furthermore, $G_{\mathcal{K}}(S)$ is a flat extension of $G_{\mathcal{J}}(R)$ with zero-dimensional fiber. Notice

\begin{equation*}G_{\mathcal {K}}(M\otimes S) = G_{\mathcal {J}}(M\otimes R)\otimes _{G_{\mathcal {J}}(R)} G_{\mathcal {K}}(S).\end{equation*}

By Theorem [14, 23.3], the result follows.

Theorem 5.6. Let $(A,\mathfrak{m})$ be a complete reduced Cohen–Macaulay local ring of dimension $d\geq 1$ and $I$ an $\mathfrak{m}$ -primary ideal. Assume the residue field $k = A/{\mathfrak{m}}$ is either uncountable or perfect. Set $R=A[[X_1,\ldots, X_m]]$ , $J=(I,X_1,\ldots, X_m)$ , $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$ , and $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$ . If $A$ has an MCM module $M$ with $G_{\mathcal{I}}(M)$ Cohen–Macaulay, then $R$ has infinitely many non-isomorphic MCM modules $D$ with $G_{\mathcal{J}}(D)$ Cohen–Macaulay and bounded multiplicity.

Proof. Follows from 5.1, 5.2, and 5.5.

6. Some results about $e^T_A()$

In this section, we prove Theorem1.15 (see Theorem6.3).

Lemma 6.1. Let $(A,\mathfrak{m}, k)$ be a Cohen–Macaulay local ring and $M,N$ be MCM $A$ -modules. Let $\alpha$ be $T$ -split and $\alpha '$ be any extension and then $e^T_A(\alpha +\alpha ')\leq e^T_A(\alpha ')$ . Also, if char $(A)=p^n\gt 0$ , then $e^T(\alpha +\alpha ')=e^T_A(\alpha ')$ .

Proof. Let $\alpha$ can be represented as $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ and $\alpha '$ as $0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$ . Consider following pullback diagram

From 3.12, $\beta$ is $T$ -split. So, ${e_{A}^T}(E'')={e_{A}^T}(N)+{e_{A}^T}(E')$ .

Now $\alpha +\alpha '$ can be written as $0\rightarrow N\rightarrow Y\rightarrow M\rightarrow 0$ where $Y=E''/S$ and $S=\{(-n,n)\in E''| n\in N\}$ . So, we have following commutative diagram

Here, $\delta$ is natural surjection.

Now from the exact sequence $\gamma \;:\; 0\rightarrow N\rightarrow E''\xrightarrow{\delta } Y\rightarrow 0$ , we get ${e_{A}^T}(\gamma )={e_{A}^T}(N)+{e_{A}^T}(Y)-{e_{A}^T}(E'')$ .

Now we get

\begin{align*} e^T_A(\alpha +\alpha ')&=e^T_A(N)+{e_{A}^T}(M)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E') -{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E'')-{e_{A}^T}(N)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ') -{e_{A}^T}(\gamma ) \end{align*}

So, $e^T_A(\alpha +\alpha ')\leq{e_{A}^T}(\alpha ').$

If char $(A)=p^n \gt 0$ , then we have

\begin{equation*}{e_{A}^T}(\alpha ')\leq {e_{A}^T}((p^n-1)\alpha +\alpha ')\leq \ldots \leq e^T_A(\alpha +\alpha ')\leq {e_{A}^T}(\alpha ') .\end{equation*}

Note that $p^n\alpha =0$ is split exact sequence.

This implies $e^T_A(\alpha +\alpha ')={e_{A}^T}(\alpha ').$

Let $\mathbb{N}$ be the set of non-negative integers.

Remark 6.2. If $char(A) = p^n \gt 0$ , then we have a well defined function

$[e^T_A] \colon \mathrm{Ext}^1_A(M, N)/T_A(M, N) \rightarrow \mathbb{N}$ .

If $V$ is a vector space over a field $k$ , then let $\mathbb{P}(V)$ denote the projective space determined by $V$ .

Theorem 6.3. (with hypotheses as in 6.1) Further assume $A$ is of characteristic $p \gt 0$ and that $A$ contains a field $k \cong A/{\mathfrak{m}}$ . If $\mathrm{Ext}_A^1(M, N) \neq T_A(M,N)$ , then the function $[e^T_A]$ defined in 6.2 factors as:

\begin{equation*} [\overline {e^T_A}] \colon \mathbb {P}(\mathrm {Ext}^1_A(M, N)/T_A(M, N)) \rightarrow \mathbb {N}\setminus {0}. \end{equation*}

Proof. Let $\alpha \in \mathrm{Ext}^1_A(M,N)$ be represented as $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$ . Let $r \in k^*$ and $r\alpha$ be represented as $0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$ . Consider the diagram

Note $\psi \colon E \rightarrow E'$ is an isomorphism. It follows that $e^T(\alpha ) = e^T(r\alpha )$ . The result follows.

Remark 6.4. All the results in this section are also true for ${e_{\mathcal{F}}^T}()$ . The same proofs work in that case also.

Theorem 6.5. For the rest of this section, we consider the following setup:

$(A,{\mathfrak{m}})$ is a complete reduced CM local ring. Also assume $A$ contains a field $k \cong A/{\mathfrak{m}}$ . Furthermore, $k$ is either uncountable or a perfect field. Let $I$ be an $\mathfrak{m}$ -primary ideal and $\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$ be an $I$ -admissible filtration with $I_1 = \overline{I}$ and $I_n = \overline{I^n}$ for $n \gg 0$ . Let $M, N$ be MCM $A$ -modules and consider the function:

\begin{align*} e^T_{\mathcal{F}} &\colon \mathrm{Ext}_A^1(M, N) \rightarrow \mathbb{N} \\ \alpha &\mapsto e^T(\alpha ). \end{align*}

Notice $e^T_{\mathcal{F}}(\alpha ) \leq e^T_{\mathcal{F}}(M) + e^T_{\mathcal{F}}(N)$ . So, $e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))$ is a bounded set.

If $Z$ is a finite set, then set $|Z|$ denote its cardinality.

Set $Z_{\mathcal{F}}(M, N) = | e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))|$ .

Corollary 6.6. (with hypotheses as in 6.5). Further assume $k$ is a finite field and $\mathrm{Ext}^1_A(M, N)$ is nonzero and has finite length as an $A$ -module (and so a finite dimensional $k$ -vector space). Set $c(M, N) = | \mathbb{P}(\mathrm{Ext}_A^1(M, N))|$ . Let $I$ be any $\mathfrak{m}$ -primary ideal and $\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$ be an $I$ -admissible filtration with $I_1 = \overline{I}$ and $I_n = \overline{I^n}$ for $n \gg 0$ . Then $Z_{\mathcal{F}}(M, N) \leq c(M, N)$ .

Proof. We may assume $T_{\mathcal{F}}(M, N) \neq \mathrm{Ext}^1_A(M, N)$ . By 6.3, we get that

\begin{equation*} Z_{\mathcal {F}}(M, N) \leq | \mathbb {P}(\mathrm {Ext}^1_A(M, N)/T_{\mathcal {F}}(M, N)) |. \end{equation*}

Note $| \mathbb{P}(\mathrm{Ext}^1_A(M, N)/T_{\mathcal{F}}(M, N)) |$ is bounded above by $c(M,N)$ . The result follows.

7. T-split sequences and AR-sequences

The goal of this section is to prove the following result:

Theorem 7.1. Let $(A,{\mathfrak{m}})$ be a Henselian Cohen–Macaulay local ring and $M$ be an indecomposable MCM $A$ -module free on the punctured spectrum of $M$ . The following assertions are equivalent:

1. 1. There exists a $T$ -split sequence $\alpha \colon 0 \rightarrow K \rightarrow E \rightarrow M \rightarrow 0$ with $\alpha$ non-split.

2. 2. There exists a $T$ -split sequence $\beta \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$ with $V$ indecomposable and $\beta$ non-split.

3. 3. The AR-sequence ending at $M$ is $T$ -split.

For definition of AR sequences, see [23, Chapter 2]. From [23, Theorem 3.4], we know that for an indecomposable MCM module over $A$ , and then there is an AR-sequence ending in $M$ if and only if $M_{\mathfrak{p}}$ is free for all $\mathfrak{p}\in$ Spec $^0(A)=$ Spec $(A)\setminus \{\mathfrak{m}\}$

Before proving Theorem7.1, we need the following well-known result. We give a proof for the convenience of the reader.

Lemma 7.2. Let $A$ be a Noetherian ring and $N,M$ , and $E$ are finite $A$ -module. Let $N=N_1\oplus N_2$ , and we have following diagram

for $i=1,2$ . Here, $p_i \;:\; N\rightarrow N_i$ is projection map for $i=1,2$ . If $s$ is non-split, then one of the $s_i$ is non-split.

Proof. Let $s_1$ and $s_2$ are split exact sequences. So, we have $g_i\;:\; M_i\rightarrow N_i$ for $i=1,2$ such that $g_if_i=1_{N_i}$ . Consider function $g= (g_1\gamma _1, g_2\gamma _2)\;:\; M\rightarrow N_1\oplus N_2$ . Let $(n_1,n_2)\in N$ and then

\begin{align*} gf(n_1,n_2)&=(g_1\gamma _1f(n_1,n_2), g_2\gamma _2f(n_1,n_2))\\ &=(g_1f_1p_1(n_1,n_2),g_2f_2p_2(n_1,n_2))\\ &=(n_1,n_2) \end{align*}

This implies $g$ is a left inverse of $f$ , so $s$ is split exact sequence.

We now give

Proof of Theorem 7.1. The assertions (iii) $\implies$ (ii) $\implies$ (i) are clear.

(i) $\implies$ (ii). As $A$ is Henselian, the module $K$ splits as a sum of indecomposable modules $K = K_1\oplus K_2 \oplus \cdots \oplus K_r$ . The result follows from Lemma 7.2.

(ii) $\implies$ (iii). Let $\beta \;:\; 0\rightarrow V \rightarrow U\rightarrow M\rightarrow 0$ be $T$ -split and $\beta$ non-split. As $V$ is indecomposable, we have following diagram

Here, $s$ is an AR-sequence ending in $M$ , see [23, 2.3, 2.8]. This implies $s$ is $T$ -split (see [20, Proposition 3.8]).

Remark 7.3. Regarding Proof of Theorem7.1. $(ii) \Rightarrow (iii)$ : The first square is a pushout diagram [6, Proposition 2.12. $(i) \Leftrightarrow (iv)$ ]. Now since we know $T$ is a sub-functor of $\mathrm{Ext}$ coming from an exact substructure of mod $A$ , [8, Theorem 4.8, Proposition 3.8], then the AR-sequence is in $T_A(M,N)$ from definition of Exact structure.

8. Some observation about complete intersection

In this section, we prove Theorem1.5 (see Theorem8.3).

Theorem 8.1. Let $(A,\mathfrak{m})$ be Noetherian local ring and $M$ a finite $A$ -module. We denote the $n$ -th Betti number of $A$ module $M$ as $\beta ^A_n(M)$ . Then complexity of $M$ can be defined as:

\begin{equation*} \text {cx}\, M = \text {inf} \left \{ r\in \mathbb {N}\middle \vert \begin {array}{l} \text {there exists polynomial}\ p(t)\ \text {of degree}\ r-1\\ \text {such that}\ \beta ^A_n(M)\leq p(n)\ \text {for}\ n\gg 0 \end {array}\right \} \end{equation*}

Theorem 8.2. Let $Q$ be a Noetherian ring and $f=f_1,\ldots, f_c$ be a $Q$ -regular sequence. Set $A=Q/(f_1,\ldots, f_c)$ . Let $M$ be a finite $A$ -module. Note projdim $_QM\lt \infty$ .

Let $\mathbb{F}$ is a free resolution of $M$ as an $A$ -module. Let $t_1,\ldots, t_c:\mathbb{F}(+2)\rightarrow \mathbb{F}$ be the Eisenbud operators (see [10, Section 1]). Consider the polynomial ring $B=A[t_1,\ldots, t_c]$ with deg $(t_i)=2$ for $i=1,\ldots, c.$ Let $L$ be an $A$ -module, and then we can think of Tor $_*^A(M,L)=\bigoplus _{i\geq 0}\text{Tor}^A_i(M,L)$ as a $B$ -module (here we give degree $-i$ for an element of Tor $_i^A(M,L)$ ).

Theorem 8.3. Let $(Q,\mathfrak{n},k)$ be a Henselian regular local ring and $\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$ a regular sequence. Assume $k$ is infinite. Set $I=(f_1,\ldots, f_c)$ and $(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$ . Assume $\dim A = 1$ . Let $M$ be an indecomposable MCM $A$ -module with $\mathrm{cx}_AM\ge 2$ and

\begin{equation*}\mathbb {F}: \ldots \rightarrow F_{n+1}\rightarrow F_n\rightarrow F_{n-1}\rightarrow \ldots \end{equation*}

be the minimal free resolution of $M$ . Set $M_r= \mathrm{Syz}_r^A(M)$ . Then there exists $r_0$ such that for all $r\geq r_0$ , there are exact sequences $ \alpha _r \colon 0\rightarrow K_r\rightarrow M_{r+2}\rightarrow M_r\rightarrow 0$ such that

1. (1) $\mathrm{cx} K_r \leq \mathrm{cx} M - 1$ for $r \geq r_0$ .

2. (2) $\alpha _r$ is non-split for $r \geq r_0$ .

3. (3) $\alpha _r$ is $T$ -split for $r \geq r_0$

If furthermore $M$ is free on the punctured spectrum of $A$ , then the AR-sequence ending at $M_r$ is $T$ -split for all $r \geq r_0$ .

Proof. Let $x$ be an $A$ -superficial element. The map $\alpha _n \colon A/{\mathfrak{m}^{n}}\rightarrow A/{\mathfrak{m}^{n+1}}$ defined by $\alpha (a+\mathfrak{m}^n) = ax+\mathfrak{m}^{n+1}$ induces an isomorphism of ${\mathrm{Tor}}^A_i(A/\mathfrak{m}^n,M)$ and ${\mathrm{Tor}}^A_i(A/\mathfrak{m}^{n+1},M)$ for $n \geq \mathrm{red}(A)$ (see [18, Lemma 4.1(3)]).

Fix $n_0\geq \mathrm{red}(A)$ . For $j = 1,\ldots, n_0$ , we have

${\mathrm{Tor}}_*^A(A/\mathfrak{m}^{j},M)= \bigoplus _{i\geq 0}{\mathrm{Tor}}_i^A(A/\mathfrak{m}^{j},M)$ is *-Artinian $B=A[t_1,\ldots, t_c]$ module, where $t_1,\ldots, t_c$ are Eisenbud operators. Then for $i\gg 0$ (say $i \geq i_0$ ) and for $j = 1, \ldots, n_0$ , we have following exact sequence:

\begin{equation*}{\mathrm {Tor}}_{i+2}^A(A/\mathfrak {m}^{j},M)\xrightarrow {\xi } {\mathrm {Tor}}_{i}^A(A/\mathfrak {m}^{j},M) \rightarrow 0.\end{equation*}

Here, $\xi$ is a linear combination of $t_1, \ldots, t_c$ (see [10, Lemma 3.3]).

We have following commutative diagram for $i\geq i_0$

where $\theta _i ={\mathrm{Tor}}^A_i(\alpha _{n_0}, M)$ . As $\theta _i$ and $\theta _{i+2}$ are isomorphisms, we get that the bottom row is also surjective. Iterating we get an exact sequence for all $j \geq 1$ and for all $i \geq i_0$ ,

\begin{equation*}{\mathrm{Tor}}_{i+2}^A(A/\mathfrak{m}^{j},M)\xrightarrow{\xi }{\mathrm{Tor}}_{i}^A(A/\mathfrak{m}^{j},M) \rightarrow 0. \end{equation*}

Note $\xi$ induces a chain map $\xi \colon \mathbb{F}[2] \rightarrow \mathbb{F}$ . As we have a surjection

\begin{equation*}{\mathrm {Tor}}_{i+2}^A(A/\mathfrak {m},M)\xrightarrow {\xi } {\mathrm {Tor}}_{i}^A(A/\mathfrak {m},M) \rightarrow 0, \quad \text {for $i \geq i_0$,} \end{equation*}

by Nakayama Lemma we have surjections $F_{i+2} \xrightarrow{\xi } F_i$ for all $i \geq i_0$ (say with kernel $G_i$ ). Notice we have a short exact sequence of complexes:

\begin{equation*}0 \rightarrow \mathbb {G}_{\geq i_0} \rightarrow \mathbb {F}[2]_{\geq i_0} \xrightarrow {\xi } \mathbb {F}_{\geq i_0}\ \rightarrow 0.\end{equation*}

Thus, we have surjections $M_{i+2} \xrightarrow{\xi } M_i$ for all $i \geq i_0$ , say with kernel $K_i$ . We note that $ \mathbb{G}_{\geq i_0}$ is a free resolution of $K_{i_0}$ and that $K_i$ is (possibly upto a free summand) the $(i-i_0)^{th}$ syzygy of $K_{i_0}$ . It follows that $\mathrm{cx} K_{i} = \mathrm{cx} K_{i_0} \leq \mathrm{cx} M -1$ . We have an exact sequence $\alpha _r \colon 0 \rightarrow K_r \rightarrow M_{r+2} \rightarrow M_r \rightarrow 0$ for all $r \geq r_0$ . Since $M$ is indecomposable, $M_r = \mathrm{Syz}_r^A(M)$ is also indecomposable for all $r \geq 1$ (see [23, Lemma 8.17]). As $\mathrm{cx} M \geq 2$ it follows that $M_{r+2} \ncong M_r$ for all $r \geq 1$ . It follows that $\alpha _r$ is not split for all $r \geq r_0$ .

By 8.2 it follows that for $i \geq i_0$ , we have an exact seqquence

\begin{equation*} 0 \rightarrow {\mathrm {Tor}}^A_1(A/\mathfrak {m}^j, K_i) \rightarrow {\mathrm {Tor}}^A_1(A/\mathfrak {m}^j, M_{i+2}) \rightarrow {\mathrm {Tor}}^A_1(A/\mathfrak {m}^j, M_i) \rightarrow 0,\end{equation*}

for all $j \geq 1$ . Clearly, this implies that $\alpha _i$ is $T$ -split.

Notice $M_r$ is free on Spec $^0(A)$ for all $r \geq 1$ . As $\alpha _r$ is $T$ -split, it follows from 7.1 that the AR-sequence ending at $M_r$ is $T$ -split for all $r \geq r_0$ .

9. $T$ -split sequences on hypersurfaces defined by quadrics

In this section, we prove Theorem1.6 (see Theorem9.4). We also construct Example 1.7 (see 9.5).

Theorem 9.1. In this section, $(Q,\mathfrak{n})$ is a Henselian regular local ring with algebraically closed residue field $k = Q/\mathfrak{n}$ and let $f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$ . Assume the hypersurface $A = Q/(f)$ is an isolated singularity of dimension $d \geq 1$ .

Remark 9.2. Here, we are taking the definition of an Ulrich module as a maximal Cohen–Macaulay module with $e_0(M)=\mu (M)$ (see also [3]).

It is well known that as $f$ is a quadric, the ring $A$ has minimal multiplicity. It follows that $e_0(A) = 2$ and $e_1(A) = 1$ . We also have that if $M$ is MCM, then $N = \mathrm{Syz}^A_1(M)$ is Ulrich, that is, $\mu (N) = e_0(N)$ (furthermore, $e_1(N) =0)$ . As $A$ is also Gorenstein, we get that any MCM $A$ -module $M \cong F \oplus E$ where $F$ is free and $E$ has no-free summands and is a syzygy of an MCM $A$ -module; in particular, $E$ is Ulrich.

The following results compute $e^T(-)$ for MCM $A$ -modules. We also give a sufficient condition for a short exact sequence to be $T$ -split.

Proposition 9.3. (with hypotheses as in 9.1) Let $M, N, U, V$ be MCM $A$ -modules with $M, N$ having no free summands. Then

1. (1) $e^T(M) = \mu (M)$ .

2. (2) Let $U = L \oplus F$ where $F$ is free and $L$ has no free summands. Then $e^T(U) = \mu (L)$ .

3. (3) Let $\alpha \colon 0 \rightarrow N \rightarrow V \rightarrow M \rightarrow 0$ . If $\mu (V) = \mu (N) + \mu (M)$ then

   1. (a) $V$ is Ulrich

   2. (b) $\alpha$ is $T$ -split.

Proof. (1) Note $\mathrm{Syz}^A_1(M)$ is also Ulrich. Using 9.2, we have

\begin{equation*} e^T(M) = e_1(A)\mu (M) - e_1(M) - e_1(\mathrm {Syz}^A_1(M)) = \mu (M). \end{equation*}

(2) Note $e^T(U) = e^T(L) + e^T(F) = \mu (L) + 0 = \mu (L)$ .

(3) We have

\begin{align*} e_0(V) &= e_0(M) + e_0(N), \\ &= \mu (M) + \mu (N) \quad \text{as $M, N$ are Ulrich,} \\ &= \mu (V). \end{align*}

In particular, $V$ is Ulrich. Note that, this also follows from [8, Lemma 5.2.2]. So, $V$ has no free summands. We have

\begin{equation*} e^T(\alpha ) = e^T(M) + e^T(N) - e^T(V) = \mu (M) + \mu (N) - \mu (V) = 0. \end{equation*}

So, $\alpha$ is $T$ -split.

We now state and prove the main result of this section.

Theorem 9.4. (with hypotheses as in 9.1) All but a finitely many AR-sequences of $A$ are $T$ -split.

Proof. We may assume that $A$ is of infinite CM representation type (i.e., there exists infinitely many mutually non-isomorphic indecomposable MCM $A$ -modules); otherwise, there is nothing to prove. The AR-quiver of $A$ is locally finite graph, [23, 5.9]. It follows that for all but finitely many MCM indecomposable $A$ -modules, the middle term of the AR-sequence ending at $M$ and $\mathrm{Syz}^A_1(M)$ will not contain a free summand. Let $M$ be such a indecomposable MCM $A$ -module and let $s \colon 0 \rightarrow \tau (M) \rightarrow V \rightarrow M \rightarrow 0$ be the AR-sequence ending at $M$ . Then by [19, 7.11], we have $\mu (V) = \mu (M) + \mu (\tau (M))$ . Note that the hypotheses of [19, 7.11] are satisfied, especially, there is no irreducible map $A \rightarrow M$ because $V$ has no free summand, [23, 2.12]. The reason for the absence of the irrudicble map $A \rightarrow \mathrm{Syz}^A_1(M)$ due to [19, 2.3, 7.4, 7.6]. By 9.3(3), it follows that $s$ is $T$ -split.

We now give example of an AR-sequence which is not split.

Example 9.5. (with hypotheses as in 9.1) Let $s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$ be an AR-sequence such that $E$ has a free summand. Then

1. (1) $s$ is NOT $T$ -split.

2. (2) If $t \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$ is any non-split exact sequence of MCM $A$ -modules then $t$ is NOT $T$ -split.

Proof. (1) Note $\mu (N) \geq \mu (E) - \mu (M)$ . Furthermore, equality cannot hold for otherwise by Proposition 9.3 we will get $E$ is Ulrich, a contradiction. Let $E = L \oplus F$ with $F \neq 0$ free and $L$ has no free summands. We note that

\begin{align*} e^T(s) &= e^T(N) + e^T(M) - e^T(E), \\ &= \mu (N) + \mu (M) - \mu (L) \\ &\gt \mu (N) + \mu (M) - \mu (E) \gt 0.\\ \end{align*}

Thus, $s$ is NOT $T$ -split.

(2) This follows from Theorem7.1.

10. An application of $T$ -split sequences in Gorenstein case

In this section, we prove Proposition 1.9 (see 10.6). We also prove Theorem1.10 (see 10.10 and 10.11).

Theorem 10.1. Let $(A,\mathfrak{m})$ be a Gorenstein local ring. Let CM $(A)$ denotes the category of MCM $A$ -modules and CM $(A)$ the stable category of CM $(A)$ . Note that objects of CM $(A)$ are same as the objects of CM $(A)$ and if $M$ and $N$ are MCM $A$ -modules, then

\begin{equation*}\underline {\text {Hom}}_{A}(M,N)=\frac {\text {{Hom}}_A(M,N)}{\{f\;:\;M\rightarrow N |\, f\,\, \text {factors through a projective module}\}}.\end{equation*}

Theorem 10.2. (Co-syzygy) Let $(A,\mathfrak{m})$ be a Gorenstein local ring and $M$ be an MCM $A$ -module. Let $M^*=$ Hom $(M,A)$ , and then $M^{**}\cong M$ . Suppose $G\xrightarrow{\epsilon } F\rightarrow M^*\rightarrow 0$ is a minimal presentation of $M^*$ . Dualizing this, we get $0\rightarrow M\rightarrow F^*\xrightarrow{\epsilon ^*} G^*$ . Co-syzygy of $M$ can be defined as coker $(\epsilon ^*)$ and denoted as $\Omega ^{-1}(M)$ . So, we have exact sequence $0\rightarrow M\rightarrow F\rightarrow \Omega ^{-1}(M)\rightarrow 0$ .

Note that co-syzygy does not depend on the minimal presentation, that is, if we take another minimal presentation $G'\xrightarrow{\epsilon '} F'\rightarrow M^*\rightarrow 0$ , then coker $(\epsilon ^*)\cong$ coker $((\epsilon ')^*)$ .

Theorem 10.3. Let $\Omega ^{-1}(M)$ be the co-syzygy of $M$ , and then we have following exact sequence:

\begin{equation*}0\rightarrow M\rightarrow F\rightarrow \Omega ^{-1}(M)\rightarrow 0 \end{equation*}

here $F$ is a free $A$ -module (see 10.2).

For any $f\in \text{{Hom}}_A(M,N)$ , we have following diagram

Here, the first sequare is a pushout diagram.

Remark 10.4. Note that CM $(A)$ is an triangulated category with the projection of the sequence $M\xrightarrow{f}N\xrightarrow{i} C(f)\xrightarrow{-p} \Omega ^{-1}(M)$ in CM $(A)$ as a basic triangles for any morphism $f$ . Exact triangles are triangles isomorphic to a basic triangle (see [5, 4.7]). Also note that for any short exact sequence $0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$ in CM $(A)$ , we have exact triangle $U\rightarrow V\rightarrow W\rightarrow \Omega ^{-1}(U)$ (see [17, Remark 3.3]).

Theorem 10.5. Let $M$ and $N$ be MCM $A$ -modules, and then it is easy to show that

\begin{equation*}\underline {\mathrm {Hom}}_A(M,N)\overset {\eta }\cong \text {Ext}^1_A(\Omega ^{-1}(M),N) \ \text {as}\ A\text {-modules}.\end{equation*}

In fact, the map $\eta \;:\; f\mapsto \alpha _f$ is an isomorphism. It is clear that $\eta$ is natural in $M$ and $N$ .

Let $T_A(\Omega ^{-1}(M),N)$ denotes the set of all $T$ -split sequences in Ext $^1_A(\Omega ^{-1}(M),N)$ . If we denote $\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$ by $\mathcal{R}(M,N)$ , then $\eta$ induces following isomorphism:

\begin{equation*}\frac {\underline {\mathrm {Hom}}_A(M,N)}{\mathcal {R}(M,N)}\cong \frac {\text {Ext}^1_A(\Omega ^{-1}(M),N)}{T_A(\Omega ^{-1}(M),N)}.\end{equation*}

Proposition 10.6. $\mathcal{R}$ is a relation on $\underline{\mathrm{CM}}(A)$ .

Proof. To prove that $\mathcal{R}$ is a relation on CM $(A)$ , we need to show:

if $M_1,M,N,N_1\in$ CM $(A)$ , $u\in \mathcal{R}(M,N)$ , $f\in \underline{{\mathrm{Hom}}}_A(M_1,M)$ , and $g\in \underline{{\mathrm{Hom}}}_A(N,N_1)$ , then $u\circ f\in \mathcal{R}(M_1,N)$ and $g\circ u\in \mathcal{R}(M,N_1)$ .

We first prove $u\circ f\in \mathcal{R}(M_1,N)$ . We have following diagram of exact traingles

Note that the map $h$ exists from the property (TR3) (see [22, Definition 10.2.1]).

So we have following diagram of exact sequences

where $F$ and $G$ are free $A$ -modules. Now since $u\in \mathcal{R}(M,N)$ , this implies $\alpha _u$ is $T$ -split. So from [20, Proposition 3.9], $\alpha _{u\circ f}$ is $T$ -split. In other words, $u\circ f \in \mathcal{R}(M_1,N)$ .

Next, we prove $g\circ u\in \mathcal{R}(M,N_1)$ . We have following diagram of exact traingles

Note that the property (TR3) (see [22, Definition 10.2.1]) guarantees the existence of map $\theta$ .

So we have following diagram of exact sequences

where $F'$ and $G'$ are free $A$ -modules. Now since $u\in \mathcal{R}(M,N)$ , this implies $\alpha _u$ is $T$ -split. So from [20, Proposition 3.8], $\alpha _{g\circ u}$ is $T$ -split. In other words, $g\circ u \in \mathcal{R}(M_1,N)$ .

Remark 10.7. To prove $\alpha _{u\circ f}$ , $\alpha _{g\circ u} \in T_A(M,N)$ , we can use the fact that $T$ is a sub-functor of $\mathrm{Ext}$ coming from exact substructure of mod $A$ (see [8, Theorem 4.8, Proposition 3.8]).

Theorem 10.8. Since $\mathcal{R}$ is a relation on CM $(A)$ , the factor category $\mathcal{D}_A=$ CM $(A)/\mathcal{R}$ is an additive category. Note that objects of $\mathcal{D}_A$ are the same as those of CM $(A)$ , and for any $M,N\in$ Obj $(\mathcal{D}_A)$ , Hom $_{\mathcal{D}_A}(M,N)=\underline{\mathrm{Hom}}_A(M,N)/\mathcal{R}(M,N)$ .

Also note that $\ell (\text{Hom}_{\mathcal{D}_A}(M,N))\lt \infty$ (see [20, Theorem 4.1]).

Next, we want to prove the main result of this section. But, first we prove a lemma.

Lemma 10.9. Let $(A,\mathfrak{m})$ be a Henselian Gorenstein local ring and $M$ be an MCM $A$ -module. Then $\mathcal{R}(M,M)\subseteq$ Jac(End $_A(M))$ in CM $(A)$ .

Proof. We prove this result in three cases:

Case 1: $M$ is indecomposable MCM module.

Let $u\in \mathcal{R}(M,M)$ and if possible assume that $u\notin$ Jac(End $_A(M))$ . This implies $u$ is invertible. Now, we have following diagram of exact sequences

From here, we get $C(u)\cong F$ . Also from the assumption, $\alpha _u$ is $T$ -split. We know that $e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))-e^T(C(u))$ .

So, $e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))$ because $C(u)\cong F$ . This implies

$e^T(\alpha _u)\gt 0$ , but this is a contradiction because $\alpha _u$ is $T$ -split. Therefore, $u\in$ Jac(End $_A(M))$ .

Case 2: $M\cong E^n$ for some indecomposable MCM module $E$ .

It is clear that $\mathcal{R}(M,M)= \mathcal{R}(E^n,E^n)\cong M_n(\mathcal{R}(E,E))$ . Here, $M_n()$ denotes $n\times n$ -matrix.

We also know that End $(E^n)\cong M_n(\underline{\mathrm{End}}(E))$ and

Jac(End $(E^n))\cong M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$ . From the case (1),

$M_n(\mathcal{R}(E,E))\subseteq M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$ .

So, $\mathcal{R}(M,M)\subseteq \text{Jac}(\underline{\mathrm{End}}(M))$ .

Case 3: $M\cong M_1^{r_1}\oplus \ldots \oplus M_q^{r_q}$ with each $M_i$ indecomposable for all $i=1,\ldots, q$ and $M_i\ncong M_j$ if $i\ne j$ (since $A$ is complete, KRS holds for CM $(A)$ ).

We can assume that $q\gt 1$ because $q=1$ case follows from case (2).

Now it is sufficient to prove the following claim.

Claim: Let $E$ and $L$ be MCM $A$ -module. Assume that $E\cong E_1^{a_1}\oplus \ldots \oplus E_n^{a_n}$ and $L\cong L_1^{b_1}\oplus \ldots \oplus L_r^{b_r}$ where $E_i$ and $L_j$ are distinct indecomposable MCM modules and $E_i\ncong L_j$ for $i=1,\ldots, n$ and $j=1,\ldots, r$ . If the lemma is true for $E$ and $L$ , then it is also true for $N=E\oplus L$ .

Proof of the claim: We know that

\begin{equation*} \underline {\mathrm {End}}_A(N)= \begin {pmatrix} \underline {\mathrm {End}}_A(E) & \underline {\mathrm {Hom}}_A(L,E) \\ \underline {\mathrm {Hom}}_A(E,L) & \underline {\mathrm {End}}_A(L) \end {pmatrix}, \end{equation*}

\begin{equation*} \text {Jac}(\underline {\mathrm {End}}_A(N))= \begin {pmatrix} \text {Jac}(\underline {\mathrm {End}}_A(E)) & \underline {\mathrm {Hom}}_A(L,E) \\ \underline {\mathrm {Hom}}_A(E,L) & \text {Jac}(\underline {\mathrm {End}}_A(L)) \end {pmatrix} \end{equation*}

and

\begin{equation*} \mathcal {R}(N,N)= \begin {pmatrix} \mathcal {R}(E,E) & \mathcal {R}(L,E)\\ \mathcal {R}(E,L) & \mathcal {R}(L,L) \end {pmatrix} \end{equation*}

Since the result is true for $E$ and $L$ , this implies $\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$ .

Theorem 10.10. Let $(A,\mathfrak{m})$ be a Henselian Gorenstein local ring, $M$ and $N$ be MCM $A$ -modules. Then $M\cong N$ in $\mathcal{D}_A$ if and only if $M\cong N$ in CM $(A)$ .

Proof. Let $f\;:\;M\rightarrow N$ be an isomorphism in CM $(A)$ . Then, $f$ is an isomorphism of $M$ and $N$ in $\mathcal{D}_A$ .

For the other direction, suppose $ f\;:\;M\rightarrow N$ be an isomorphism in $\mathcal{D}_A$ . Then there exists an isomorphism $g\;:\;N\rightarrow M$ such that $g\circ f=\mu$ and $\mu =1 +\delta$ for some $\delta \in \mathcal{R}(M,M)$ . From Lemma 10.9, $\delta \in$ Jac(End $_A(M))$ . This implies $\mu$ is an isomorphism in CM $(A)$ . Therefore, $g\circ f$ is an isomorphism in CM $(A)$ . Similarly, $f\circ g$ is also an isomorphism in CM $(A)$ . This implies $M\cong N$ in CM $(A)$ .

Proposition 10.11. Let $(A,\mathfrak{m})$ be a Henselian Gorenstein local ring. If $M$ is indecomposable in $\underline{\mathrm{CM}}(A)$ , then it is indecomposable in $\mathcal{D}_A$ . Furthermore, $\mathcal{D}_A$ is a (KRS) category.

Proof. Let $M$ be an MCM $A$ -module, and then $M\cong M_1^{a_1}\oplus \ldots \oplus M_n^{a_n}$ in $\underline{\mathrm{CM}}(A)$ ; here, each $M_i$ is distinct indecomposable non-free MCM $A$ -module.

For any indecomposable non-free MCM module $N$ , we know $\underline{\text{End}}_A(N)$ is a local ring and End $_{\mathcal{D}_A}(N)= \underline{\text{End}}_A(N)/\mathcal{R}(N,N)$ . From Lemma 10.9, $\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$ . So, End $_{\mathcal{D}_A}(N)$ is a local ring. Thus, $N$ is indecomposable in $\mathcal{D}_A$ .

Remark 10.12. The statements of the Lemma 10.9, Theorem 10.10, and Proposition 10.11 are valid for any relation $\mathcal{R}$ coming from a sub-functor of $\mathrm{Ext}$ of the exact substructure of mod $A$ as long as the subadditive function $\phi$ is 0 on free modules ( also see [8, Theorem 4.8]).