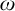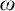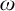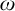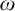1 Introduction
This paper explores the interplay between two model-theoretic finitary conditions on infinite groups:
![]() $\omega $
-categoricity and pseudofiniteness. We recall that a countably infinite first order structure is
$\omega $
-categoricity and pseudofiniteness. We recall that a countably infinite first order structure is
![]() $\omega $
-categorical if any countably infinite N with the same first order theory as M is isomorphic to M, or equivalently, if
$\omega $
-categorical if any countably infinite N with the same first order theory as M is isomorphic to M, or equivalently, if
![]() ${{\mathrm {Aut}}}(M)$
acts oligomorphically on M, that is, has finitely many orbits on
${{\mathrm {Aut}}}(M)$
acts oligomorphically on M, that is, has finitely many orbits on
![]() $M^n$
for all n. We say a structure M is pseudofinite if it is infinite and every first order sentence true of M has a finite model. We make the following conjecture, motivating this paper.
$M^n$
for all n. We say a structure M is pseudofinite if it is infinite and every first order sentence true of M has a finite model. We make the following conjecture, motivating this paper.
Conjecture 1.1. Every
![]() $\omega $
-categorical pseudofinite group G is definably finite-by-abelian-by-finite. More precisely, G has a definable 2-step nilpotent normal subgroup N of finite index which has finite derived subgroup.
$\omega $
-categorical pseudofinite group G is definably finite-by-abelian-by-finite. More precisely, G has a definable 2-step nilpotent normal subgroup N of finite index which has finite derived subgroup.
We shall describe such G as “finite-by-abelian-by-finite”, and note that this is unambiguous: any finite-by-(abelian-by-finite) group is clearly (finite-by-abelian)-by-finite, and conversely, if G has a finite-by-abelian normal subgroup N of finite index, then its derived subgroup
![]() $N'$
is finite and characteristic in N so normal in G, and G is finite-by-(abelian-by-finite). Furthermore, as noted in the introduction to [Reference Evans and Wagner18], we may take N to be characteristic. The upshot is that we may suppose that the normal subgroups of G witnessing “finite-by-abelian-by-finite” are characteristic and hence (by
$N'$
is finite and characteristic in N so normal in G, and G is finite-by-(abelian-by-finite). Furthermore, as noted in the introduction to [Reference Evans and Wagner18], we may take N to be characteristic. The upshot is that we may suppose that the normal subgroups of G witnessing “finite-by-abelian-by-finite” are characteristic and hence (by
![]() $\omega $
-categoricity) definable without parameters, and from now on we just call such a group G an FAF group.
$\omega $
-categoricity) definable without parameters, and from now on we just call such a group G an FAF group.
We show that Conjecture 1.1 reduces to the case of
![]() $\omega $
-categorical pseudofinite p-groups of nilpotency class at most
$\omega $
-categorical pseudofinite p-groups of nilpotency class at most
![]() $2$
.
$2$
.
Proposition 1.2. Conjecture 1.1 holds if every
![]() $\omega $
-categorical pseudofinite p-group of class at most 2 is FAF.
$\omega $
-categorical pseudofinite p-group of class at most 2 is FAF.
It is easy to give examples of
![]() $\omega $
-categorical pseudofinite groups which are abelian (e.g., elementary abelian p-groups), and which are finite-by-abelian but not abelian-by-finite (see also the examples in 2.14). For the latter, the extraspecial p-groups of exponent p (p odd) provide examples: they are
$\omega $
-categorical pseudofinite groups which are abelian (e.g., elementary abelian p-groups), and which are finite-by-abelian but not abelian-by-finite (see also the examples in 2.14). For the latter, the extraspecial p-groups of exponent p (p odd) provide examples: they are
![]() $\omega $
-categorical by [Reference Felgner19], and pseudofinite since they are smoothly approximated (in the sense of [Reference Kantor, Liebeck and Macpherson24]) by finite extraspecial p-groups, as noted in [Reference Kantor, Liebeck and Macpherson24, ‘Added in proof’]. See [Reference Milliet33, Appendix A] for further discussion of the model theory of extraspecial groups. The construction of extraspecial groups is generalized in [Reference Apps2, Theorem A], where it is shown that if G is a finite nilpotent class 2 group and K is a subgroup with
$\omega $
-categorical by [Reference Felgner19], and pseudofinite since they are smoothly approximated (in the sense of [Reference Kantor, Liebeck and Macpherson24]) by finite extraspecial p-groups, as noted in [Reference Kantor, Liebeck and Macpherson24, ‘Added in proof’]. See [Reference Milliet33, Appendix A] for further discussion of the model theory of extraspecial groups. The construction of extraspecial groups is generalized in [Reference Apps2, Theorem A], where it is shown that if G is a finite nilpotent class 2 group and K is a subgroup with
![]() $G'\leq K\leq Z(G)$
, then the central product of
$G'\leq K\leq Z(G)$
, then the central product of
![]() $\aleph _0$
copies of G, amalgamated over K, is
$\aleph _0$
copies of G, amalgamated over K, is
![]() $\omega $
-categorical.
$\omega $
-categorical.
We give a short proof in Section 2 of the following result, an easy consequence of known results on
![]() $\omega $
-categorical groups.
$\omega $
-categorical groups.
Proposition 1.3. Every
![]() $\omega $
-categorical pseudofinite group is nilpotent-by-finite.
$\omega $
-categorical pseudofinite group is nilpotent-by-finite.
We then show that Conjecture 1.1 holds for many of the
![]() $\omega $
-categorical class 2 groups that we know of, in particular (for odd primes p) for the model companion of the theory of exponent p class 2 p-groups described by Saracino and Wood in [Reference Saracino and Wood35], and various generaliations; namely the comprehensive groups of Apps [Reference Apps2] (see Theorems 2.10 and 2.11) and higher nilpotency class generaliations of the Saracino-Wood groups, considered in [Reference Maier31], [Reference Baudisch5], [Reference Baudisch8], and [Reference d’Elbée, Müller, Ramsey and Siniora17]. In particular, we prove the following result (Corollary 2.8 below).
$\omega $
-categorical class 2 groups that we know of, in particular (for odd primes p) for the model companion of the theory of exponent p class 2 p-groups described by Saracino and Wood in [Reference Saracino and Wood35], and various generaliations; namely the comprehensive groups of Apps [Reference Apps2] (see Theorems 2.10 and 2.11) and higher nilpotency class generaliations of the Saracino-Wood groups, considered in [Reference Maier31], [Reference Baudisch5], [Reference Baudisch8], and [Reference d’Elbée, Müller, Ramsey and Siniora17]. In particular, we prove the following result (Corollary 2.8 below).
Theorem 1.4.
-
(i) For p an odd prime, the unique countable existentially closed nilpotent class 2 group of exponent p is not pseudofinite.
-
(ii) The
 $\omega $
-categorical groups
$\omega $
-categorical groups
 $D(n)$
with supersimple rank 1 theory considered by Baudisch in [Reference Baudisch8] are not pseudofinite for
$D(n)$
with supersimple rank 1 theory considered by Baudisch in [Reference Baudisch8] are not pseudofinite for
 $n\geq 2$
.
$n\geq 2$
.
We remark that Baudisch [Reference Baudisch8] showed that the group in (i) has TP
![]() ${}_2$
theory. More recently, d’Elbée, Müller, Ramsey and Siniora [Reference d’Elbée, Müller, Ramsey and Siniora17, Corollary 3.7] have shown it to have an NSOP
${}_2$
theory. More recently, d’Elbée, Müller, Ramsey and Siniora [Reference d’Elbée, Müller, Ramsey and Siniora17, Corollary 3.7] have shown it to have an NSOP
![]() ${}_1$
theory. Part (ii) above shows that not every
${}_1$
theory. Part (ii) above shows that not every
![]() $\omega $
-categorical finite-by-abelian group is pseudofinite, i.e., the converse to our conjecture is false: the groups
$\omega $
-categorical finite-by-abelian group is pseudofinite, i.e., the converse to our conjecture is false: the groups
![]() $D(n)$
for n finite are all finite-by-abelian.
$D(n)$
for n finite are all finite-by-abelian.
A theory has the strict order property if it has a model M such that there is a definable preorder on some power
![]() $M^n$
with an infinite totally ordered subset, and a model has the strict order property if its theory has. We say the model (or theory) is NSOP otherwise. It is easy to see that an
$M^n$
with an infinite totally ordered subset, and a model has the strict order property if its theory has. We say the model (or theory) is NSOP otherwise. It is easy to see that an
![]() $\omega $
-categorical structure with the strict order property is not pseudofinite (see Lemma 2.1). The obvious ways to show that a structure is not pseudofinite are to define a partial ordering which is dense or has no greatest element, or to define a map
$\omega $
-categorical structure with the strict order property is not pseudofinite (see Lemma 2.1). The obvious ways to show that a structure is not pseudofinite are to define a partial ordering which is dense or has no greatest element, or to define a map
![]() $f:X \to X$
which is injective but not surjective, or vice-versa. Such a function cannot be definable in an
$f:X \to X$
which is injective but not surjective, or vice-versa. Such a function cannot be definable in an
![]() $\omega $
-categorical structure, since it would lead to pairs from X at arbitrary “distance” with respect to f. We believe Theorem 1.4 may be the first result proving non-pseudofiniteness of an
$\omega $
-categorical structure, since it would lead to pairs from X at arbitrary “distance” with respect to f. We believe Theorem 1.4 may be the first result proving non-pseudofiniteness of an
![]() $\omega $
-categorical structure without the strict order property, and that (ii) may be the first example of an
$\omega $
-categorical structure without the strict order property, and that (ii) may be the first example of an
![]() $\omega $
-categorical supersimple non-pseudofinite structure. (In the other direction, Kruckman in [Reference Kruckman25, Theorem 4.5] shows that the theory
$\omega $
-categorical supersimple non-pseudofinite structure. (In the other direction, Kruckman in [Reference Kruckman25, Theorem 4.5] shows that the theory
![]() $T_{\mathrm {feq}}^{*}$
of parametrised equivalence relations is
$T_{\mathrm {feq}}^{*}$
of parametrised equivalence relations is
![]() $\omega $
-categorical pseudofinite but not supersimple.) Of course, pseudofiniteness is unknown for many
$\omega $
-categorical pseudofinite but not supersimple.) Of course, pseudofiniteness is unknown for many
![]() $\omega $
-categorical structures – for example it is a well-known open problem posed by Cherlin for the universal homogeneous triangle-free graph (see [Reference Cherlin10, Problem A’], or [Reference Cherlin11]).
$\omega $
-categorical structures – for example it is a well-known open problem posed by Cherlin for the universal homogeneous triangle-free graph (see [Reference Cherlin10, Problem A’], or [Reference Cherlin11]).
Some background on
![]() $\omega $
-categorical groups. The structure of
$\omega $
-categorical groups. The structure of
![]() $\omega $
-categorical groups has been revisited since the early 1970s by many authors, and some substantial literature appears to be little known. We summarize some aspects here, focussing on themes related to Conjecture 1.1.
$\omega $
-categorical groups has been revisited since the early 1970s by many authors, and some substantial literature appears to be little known. We summarize some aspects here, focussing on themes related to Conjecture 1.1.
First, there are several results recovering our intended conclusion, i.e., showing that
![]() $\omega $
-categorical groups satisfying certain model-theoretic hypotheses are FAF. For example, by [Reference Baur, Cherlin and Macintyre9] every
$\omega $
-categorical groups satisfying certain model-theoretic hypotheses are FAF. For example, by [Reference Baur, Cherlin and Macintyre9] every
![]() $\omega $
-categorical superstable group is abelian-by-finite (but under stability only virtual nilpotency is known [Reference Baur, Cherlin and Macintyre9, Reference Felgner20]). This is generalized in [Reference Evans and Wagner18], where it is shown that every
$\omega $
-categorical superstable group is abelian-by-finite (but under stability only virtual nilpotency is known [Reference Baur, Cherlin and Macintyre9, Reference Felgner20]). This is generalized in [Reference Evans and Wagner18], where it is shown that every
![]() $\omega $
-categorical group with supersimple theory is FAF. The latter also generalizes Proposition 6.2.4 from [Reference Cherlin and Hrushovski14] where the same conclusion is obtained for groups interpretable in a smoothly approximable structure; such structures are known to be supersimple. (In [Reference Cherlin and Hrushovski14, Proposition 6.2.4], there are assumptions of finite rank, type amalgamation and modularity—these are shown to hold for smoothly approximable structures in Corollary 2.2.11, Proposition 5.1.15, and Corollary 5.6.4 respectively—note that smooth approximation is equivalent to Lie coordinatisability by [Reference Cherlin and Hrushovski14, Theorem 2].) Finally, by [Reference Dobrowolski and Wagner16], every
$\omega $
-categorical group with supersimple theory is FAF. The latter also generalizes Proposition 6.2.4 from [Reference Cherlin and Hrushovski14] where the same conclusion is obtained for groups interpretable in a smoothly approximable structure; such structures are known to be supersimple. (In [Reference Cherlin and Hrushovski14, Proposition 6.2.4], there are assumptions of finite rank, type amalgamation and modularity—these are shown to hold for smoothly approximable structures in Corollary 2.2.11, Proposition 5.1.15, and Corollary 5.6.4 respectively—note that smooth approximation is equivalent to Lie coordinatisability by [Reference Cherlin and Hrushovski14, Theorem 2].) Finally, by [Reference Dobrowolski and Wagner16], every
![]() $\omega $
-categorical group of finite burden is FAF. In each case, there is some notion of rank, and the arguments often proceed by identifying minimal abelian groups and working with definable isogenies. Some of these results have ring-theoretic analogs, and as noted at the end of this paper, Conjecture 1.1 has a ring-theoretic equivalent, namely Conjecture 3.5.
$\omega $
-categorical group of finite burden is FAF. In each case, there is some notion of rank, and the arguments often proceed by identifying minimal abelian groups and working with definable isogenies. Some of these results have ring-theoretic analogs, and as noted at the end of this paper, Conjecture 1.1 has a ring-theoretic equivalent, namely Conjecture 3.5.
An important construction technique for
![]() $\omega $
-categorical algebraic objects is that of boolean powers. For groups, one takes an
$\omega $
-categorical algebraic objects is that of boolean powers. For groups, one takes an
![]() $\omega $
-categorical or finite group G equipped with the discrete topology, the Stone space S of a countable
$\omega $
-categorical or finite group G equipped with the discrete topology, the Stone space S of a countable
![]() $\omega $
-categorical Boolean algebra B (for example the countable atomless Boolean algebra, in which case S is a Cantor space), and forms the group
$\omega $
-categorical Boolean algebra B (for example the countable atomless Boolean algebra, in which case S is a Cantor space), and forms the group
![]() $B[G]$
consisting of all continuous maps
$B[G]$
consisting of all continuous maps
![]() $S\to G$
, with coordinatewise multiplication as the group operation. There is an analogous construction (see Section 2 of [Reference Apps3], or [Reference Wilson, Campbell and Robertson39, Section 2]) when B is an
$S\to G$
, with coordinatewise multiplication as the group operation. There is an analogous construction (see Section 2 of [Reference Apps3], or [Reference Wilson, Campbell and Robertson39, Section 2]) when B is an
![]() $\omega $
-categorical Boolean ring without a 1: in the case above corresponding to the Cantor set, one obtains the group
$\omega $
-categorical Boolean ring without a 1: in the case above corresponding to the Cantor set, one obtains the group
![]() $B^-(G)$
consisting of all
$B^-(G)$
consisting of all
![]() $f:S \to G$
with
$f:S \to G$
with
![]() $f(x_0)=1_G$
, where
$f(x_0)=1_G$
, where
![]() $x_0\in S$
is specified. It is easily seen that if G is an
$x_0\in S$
is specified. It is easily seen that if G is an
![]() $\omega $
-categorical group which is nilpotent of class 2 but not abelian, and B is infinite, then
$\omega $
-categorical group which is nilpotent of class 2 but not abelian, and B is infinite, then
![]() $B[G]$
and
$B[G]$
and
![]() $B^-[G]$
are
$B^-[G]$
are
![]() $\omega $
-categorical nilpotent class 2 and not FAF (see for example the paragraph before Proposition 4.1 in [Reference Apps2]). By the easy Lemma 3.1 below, such groups are not pseudofinite. For more on Boolean powers of groups, see also [Reference Apps1]. In particular, since any
$\omega $
-categorical nilpotent class 2 and not FAF (see for example the paragraph before Proposition 4.1 in [Reference Apps2]). By the easy Lemma 3.1 below, such groups are not pseudofinite. For more on Boolean powers of groups, see also [Reference Apps1]. In particular, since any
![]() $\omega $
-categorical group has a maximally refined chain of characteristic subgroups with characteristically simple and
$\omega $
-categorical group has a maximally refined chain of characteristic subgroups with characteristically simple and
![]() $\omega $
-categorical or finite successive quotients, [Reference Apps3, Theorem A] gives an approach to structural questions about
$\omega $
-categorical or finite successive quotients, [Reference Apps3, Theorem A] gives an approach to structural questions about
![]() $\omega $
-categorical groups.
$\omega $
-categorical groups.
A number of authors have revisited the subject of
![]() $\omega $
-categorical nilpotent groups, from the viewpoints of Fraïssé limits, existentially closed groups in certain classes, and model companions. We summarize briefly what is known.
$\omega $
-categorical nilpotent groups, from the viewpoints of Fraïssé limits, existentially closed groups in certain classes, and model companions. We summarize briefly what is known.
Saracino and Wood [Reference Saracino and Wood35, Theorem 3.9], among other results, show that for every finite
![]() $m\geq 2$
the collection of nilpotent class 2 groups of exponent m has a model companion, and this model companion is
$m\geq 2$
the collection of nilpotent class 2 groups of exponent m has a model companion, and this model companion is
![]() $\omega $
-categorical. The proof is essentially by identifying appropriate axioms (of the form generalised by Apps, see below). A related thread of work explores groups whose theory has quantifier-elimination. Work of Cherlin and Felgner [Reference Cherlin and Felgner12] reduces the classification to that of QE nilpotent class 2 groups of exponent 4. In [Reference Saracino and Wood36], constructions are given of
$\omega $
-categorical. The proof is essentially by identifying appropriate axioms (of the form generalised by Apps, see below). A related thread of work explores groups whose theory has quantifier-elimination. Work of Cherlin and Felgner [Reference Cherlin and Felgner12] reduces the classification to that of QE nilpotent class 2 groups of exponent 4. In [Reference Saracino and Wood36], constructions are given of
![]() $2^{\aleph _0}$
non-isomorphic countable
$2^{\aleph _0}$
non-isomorphic countable
![]() $\omega $
-categorical such groups. The construction is analogous to that of Henson [Reference Henson21] of homogeneous digraphs: the authors find a family
$\omega $
-categorical such groups. The construction is analogous to that of Henson [Reference Henson21] of homogeneous digraphs: the authors find a family
![]() $\mathcal {F}$
of mutually non-embeddable finite class 2 groups of exponent 4, for each
$\mathcal {F}$
of mutually non-embeddable finite class 2 groups of exponent 4, for each
![]() $S\subset \mathcal {F}$
consider the class of finite class 2 groups of exponent at most 4 not embedding a member of S, and show this class has the amalgamation property; distinct sets S yield non-isomorphic Fraïssé limits. This approach is developed further in [Reference Cherlin, Saracino and Wood15] with a view also to constructions of homogeneous rings.
$S\subset \mathcal {F}$
consider the class of finite class 2 groups of exponent at most 4 not embedding a member of S, and show this class has the amalgamation property; distinct sets S yield non-isomorphic Fraïssé limits. This approach is developed further in [Reference Cherlin, Saracino and Wood15] with a view also to constructions of homogeneous rings.
Apps [Reference Apps2], generalizing the Saracino–Wood construction of model companions for the theory of class 2 p-groups with a given bound on the exponent (not necessarily prime), gives the construction of comprehensive groups described in Section 2 below. The key point is that the centre
![]() $Z(G)$
is specified in advance, together with the exponents of
$Z(G)$
is specified in advance, together with the exponents of
![]() $Z(G)$
,
$Z(G)$
,
![]() $G/Z(G)$
, and G. For given data satisfying certain conditions, the model companion of such a class is described in [Reference Apps2, Theorem D].
$G/Z(G)$
, and G. For given data satisfying certain conditions, the model companion of such a class is described in [Reference Apps2, Theorem D].
Maier in the late 1980s wrote a series of papers on constructions of existentially closed nilpotent groups in various classes. The proofs are based on an intricate adaptation, using Lazard series, of Higman’s amalgamation results for nilpotent groups (see [Reference Higman23]), where the groups are equipped with a common central series. In particular, in [Reference Maier31, Theorem 3.5], Maier shows that for p an odd prime and
![]() $c<p$
the class of groups of nilpotency class c and exponent p has a unique existentially closed member, its model companion, which is
$c<p$
the class of groups of nilpotency class c and exponent p has a unique existentially closed member, its model companion, which is
![]() $\omega $
-categorical. The main focus of Maier’s paper is elsewhere, and he notes that in the case
$\omega $
-categorical. The main focus of Maier’s paper is elsewhere, and he notes that in the case
![]() $c=2$
, Saracino and Wood had already constructed this model companion in [Reference Saracino and Wood35, Theorem 3.9].
$c=2$
, Saracino and Wood had already constructed this model companion in [Reference Saracino and Wood35, Theorem 3.9].
Baudisch [Reference Baudisch5] shows that for an odd prime p the class of finite groups of exponent p and class at most 2, equipped with a predicate for a central subgroup, has the amalgamation property. Its Fraïssé limit will as a group be isomorphic to the model companion of the collection of class 2 exponent p groups. It follows that the latter group has quantifier-elimination once a predicate is added for its centre, and Baudisch also shows that this group does not have simple theory, since there is an infinite descending chain of centralisers of finite sets, each with infinite index in its predecessor. In more recent work Baudisch also shows in [Reference Baudisch8] that its theory is TP
![]() ${}_2$
. He explores in [Reference Baudisch6, Reference Baudisch7] generalizations of the construction in [Reference Baudisch5] to arbitrary nilpotency class
${}_2$
. He explores in [Reference Baudisch6, Reference Baudisch7] generalizations of the construction in [Reference Baudisch5] to arbitrary nilpotency class
![]() $c<p$
. The approach to amalgamation is analogous to that of Maier, and there is a precursor (for
$c<p$
. The approach to amalgamation is analogous to that of Maier, and there is a precursor (for
![]() $c=2$
) in [Reference Saracino37].
$c=2$
) in [Reference Saracino37].
Very recently, d’Elbée, Müller, Ramsey and Siniora [Reference d’Elbée, Müller, Ramsey and Siniora17] have revisited the results of Baudisch and Maier. They give a careful description of the amalgamation in the context of Lie algebras L equipped with a “Lazard series”, that is, a series
![]() $L=L_0\geq L_1 \geq \ldots \geq L_{c+1}=0$
, with
$L=L_0\geq L_1 \geq \ldots \geq L_{c+1}=0$
, with
![]() $[L_i,L_j]\leq L_{i+j}$
for all
$[L_i,L_j]\leq L_{i+j}$
for all
![]() $i,j$
(where
$i,j$
(where
![]() $L_k=0$
for all
$L_k=0$
for all
![]() $k>c$
). They transfer the amalgamation from such “Lazard Lie algebras” to the corresponding class of finite groups (exponent p, class at most c, where
$k>c$
). They transfer the amalgamation from such “Lazard Lie algebras” to the corresponding class of finite groups (exponent p, class at most c, where
![]() $c<p$
, equipped with a Lazard series). This yields a Fraïssé limit
$c<p$
, equipped with a Lazard series). This yields a Fraïssé limit
![]() $\mathbf {G}_{c,p}$
, which is
$\mathbf {G}_{c,p}$
, which is
![]() $\omega $
-categorical, and exactly the model companion of the class of exponent p groups of class at most c constructed by Maier in [Reference Maier31, Theorem 3.5]. They show that the groups
$\omega $
-categorical, and exactly the model companion of the class of exponent p groups of class at most c constructed by Maier in [Reference Maier31, Theorem 3.5]. They show that the groups
![]() $\mathbf {G}_{2,p}$
are NSOP
$\mathbf {G}_{2,p}$
are NSOP
![]() ${}_1$
—it was already known from Baudisch’s work that they do not have supersimple theory. Strikingly, they also show that for
${}_1$
—it was already known from Baudisch’s work that they do not have supersimple theory. Strikingly, they also show that for
![]() $c\geq 3$
the group
$c\geq 3$
the group
![]() $G_{c,p}$
is SOP
$G_{c,p}$
is SOP
![]() ${}_3$
and NSOP
${}_3$
and NSOP
![]() ${}_4$
, and is c-dependent and
${}_4$
, and is c-dependent and
![]() $(c-1)$
-independent (i.e., strictly NSOP
$(c-1)$
-independent (i.e., strictly NSOP
![]() ${}_4$
and strictly NIP
${}_4$
and strictly NIP
![]() ${}_c$
).
${}_c$
).
Structure of the paper. Propositions 1.2 and 1.3, along with Theorem 1.4, are proved in Section 2. We also show in Theorem 2.11 that Apps’s comprehensive groups are not pseudofinite provided they have non-cyclic centre. The section includes a discussion of pseudofiniteness for
![]() $\omega $
-categorical FAF groups. In Section 3 we note that the Boolean power construction does not yield counterexamples to our conjecture, that a counterexample will not arise from an ultraproduct of finite p-groups with large automorphism groups, and present the ring-theoretic analogue of the conjecture.
$\omega $
-categorical FAF groups. In Section 3 we note that the Boolean power construction does not yield counterexamples to our conjecture, that a counterexample will not arise from an ultraproduct of finite p-groups with large automorphism groups, and present the ring-theoretic analogue of the conjecture.
2 Saracino–Wood groups and variants
In this section we reduce our conjecture to the case of nilpotent class 2 groups, and then show that several variants of the Saracino–Wood existentially closed nilpotent class 2 exponent p group (for p an odd prime) are not pseudofinite. We do not consider the case
![]() $p=2$
(where there are analogs of exponent 4). Since it is short and central to the paper, we first include a proof of the following easy result. See also [Reference Kruckman25, Proposition 1.3], where the result is described as folklore.
$p=2$
(where there are analogs of exponent 4). Since it is short and central to the paper, we first include a proof of the following easy result. See also [Reference Kruckman25, Proposition 1.3], where the result is described as folklore.
Lemma 2.1. Let M be an
![]() $\omega $
-categorical pseudofinite structure. Then M does not have the strict order property.
$\omega $
-categorical pseudofinite structure. Then M does not have the strict order property.
Proof. Suppose that M is
![]() $\omega $
-categorical with the strict order property. Then (possibly naming parameters by constants) there is a 0-definable preorder
$\omega $
-categorical with the strict order property. Then (possibly naming parameters by constants) there is a 0-definable preorder
![]() $<$
on some power
$<$
on some power
![]() $M^d$
of M, with an infinite chain. By
$M^d$
of M, with an infinite chain. By
![]() $\omega $
-categoricity there are finitely many 2-types, so by Ramsey’s theorem there is a formula
$\omega $
-categoricity there are finitely many 2-types, so by Ramsey’s theorem there is a formula
![]() $\phi (x,y)$
isolating a complete 2-type and implying the formula
$\phi (x,y)$
isolating a complete 2-type and implying the formula
![]() $x<y$
, and
$x<y$
, and
![]() $\{a_i:i\in \omega \}\in M^d$
such that
$\{a_i:i\in \omega \}\in M^d$
such that
![]() $\phi (a_i,a_j)$
holds whenever
$\phi (a_i,a_j)$
holds whenever
![]() $i<j$
. In particular, some sentence
$i<j$
. In particular, some sentence
![]() $\sigma $
of
$\sigma $
of
![]() ${\mathrm {Th}}(M)$
expresses that
${\mathrm {Th}}(M)$
expresses that
![]() $<$
is a preorder, that
$<$
is a preorder, that
![]() $\phi (x,y)$
implies
$\phi (x,y)$
implies
![]() $x<y$
, that
$x<y$
, that
![]() $\exists x\exists y\phi (x,y)$
, and that
$\exists x\exists y\phi (x,y)$
, and that
![]() $\forall x\forall y\big (\phi (x,y) \to \exists z(\phi (x,z)\wedge \phi (z,y))\big )$
; the last implication holds since
$\forall x\forall y\big (\phi (x,y) \to \exists z(\phi (x,z)\wedge \phi (z,y))\big )$
; the last implication holds since
![]() $M\models \phi (a_1,a_3) \wedge \exists z(\phi (a_1,z)\wedge \phi (z,a_3))$
, and because
$M\models \phi (a_1,a_3) \wedge \exists z(\phi (a_1,z)\wedge \phi (z,a_3))$
, and because
![]() $\phi $
isolates a complete type. Such a sentence clearly has no finite model.
$\phi $
isolates a complete type. Such a sentence clearly has no finite model.
We thus obtain a first step (Proposition 1.3 of the introduction) towards proving Conjecture 1.1.
Corollary 2.2. Let G be an
![]() $\omega $
-categorical pseudofinite group. Then G has a nilpotent 0-definable normal subgroup of finite index.
$\omega $
-categorical pseudofinite group. Then G has a nilpotent 0-definable normal subgroup of finite index.
Proof. By Lemma 2.1, G does not have the strict order property. The result now follows immediately from [Reference Macpherson28, Theorem 1.2].
For any nilpotent group G of class c we write
for the lower central series of G.
Remark 2.3. In arguments below we shall use that if H is a nilpotent group of class 2 and
![]() $x,y\in H$
then for any
$x,y\in H$
then for any
![]() $n\geq 1$
we have
$n\geq 1$
we have
![]() $[x,y]^n=[x^n,y]$
. This is proved easily by induction. In particular, the exponent of
$[x,y]^n=[x^n,y]$
. This is proved easily by induction. In particular, the exponent of
![]() $\gamma _2H$
divides that of
$\gamma _2H$
divides that of
![]() $\gamma _1H/\gamma _2H$
. We also use the identities
$\gamma _1H/\gamma _2H$
. We also use the identities
![]() $[xz,y]=[x,y]^z[z,y]$
and
$[xz,y]=[x,y]^z[z,y]$
and
![]() $[x,y]^{-1}=[y,x]$
, the latter giving
$[x,y]^{-1}=[y,x]$
, the latter giving
![]() $[H,G]=[G,H]$
whenever H is a subgroup of G.
$[H,G]=[G,H]$
whenever H is a subgroup of G.
We aim next for Corollary 2.5, which is just Proposition 1.2 from the Introduction. First, we give a lemma, for which we are very grateful to Laurent Bartholdi for supplying the proof.
Lemma 2.4. Let G be a p-group of class 3, and let
![]() $|\gamma _2G/\gamma _3G|=p^m$
. Then
$|\gamma _2G/\gamma _3G|=p^m$
. Then
![]() $|\gamma _3G|\leq p^{2m^3}$
. In particular G is finite-by-abelian.
$|\gamma _3G|\leq p^{2m^3}$
. In particular G is finite-by-abelian.
Proof. First observe that
![]() $\gamma _2G/\gamma _3G$
has exponent at most
$\gamma _2G/\gamma _3G$
has exponent at most
![]() $p^m$
, and every irredundant generating set has size at most m. Thus
$p^m$
, and every irredundant generating set has size at most m. Thus
![]() $\gamma _2G$
can be generated by
$\gamma _2G$
can be generated by
![]() $\gamma _3 G$
and a set of m commutators
$\gamma _3 G$
and a set of m commutators
![]() $[a,b]$
in G. Let S be the set of these
$[a,b]$
in G. Let S be the set of these
![]() $a,b$
, so S has size at most
$a,b$
, so S has size at most
![]() $2m$
. Let H be the subgroup of G generated by S and
$2m$
. Let H be the subgroup of G generated by S and
![]() $\gamma _3G$
. Then
$\gamma _3G$
. Then
![]() $\gamma _2G\leq H$
, so H is normal in G. Furthermore,
$\gamma _2G\leq H$
, so H is normal in G. Furthermore,
so
For
![]() $x,y\in H$
and
$x,y\in H$
and
![]() $z\in G$
, the Hall–Witt identity
$z\in G$
, the Hall–Witt identity
and the fact that H is normal in G, it now follows that
Since
![]() $\gamma _3G\leq Z(G)$
we now have
$\gamma _3G\leq Z(G)$
we now have
 $$ \begin{align*} \gamma_3G &= [\gamma_2G,G] = [[H,H]\gamma_3G,G]=[[H,H],G]\leq [[G,H],H]\\ & =[[G,H]\gamma_3G,H]=[[H,H],H]. \end{align*} $$
$$ \begin{align*} \gamma_3G &= [\gamma_2G,G] = [[H,H]\gamma_3G,G]=[[H,H],G]\leq [[G,H],H]\\ & =[[G,H]\gamma_3G,H]=[[H,H],H]. \end{align*} $$
Note that since
![]() $\gamma _3G\leq Z(G)$
, for
$\gamma _3G\leq Z(G)$
, for
![]() $x,z\in S$
and
$x,z\in S$
and
![]() $y\in \gamma _2G$
we have
$y\in \gamma _2G$
we have
![]() $[x,y]\in Z(G)$
and so
$[x,y]\in Z(G)$
and so
![]() $[xz,y]=[x,y]^z[z,y]=[x,y][z,y]$
. Hence
$[xz,y]=[x,y]^z[z,y]=[x,y][z,y]$
. Hence
![]() $\gamma _3G$
is generated by a set of commutators
$\gamma _3G$
is generated by a set of commutators
![]() $[x,y]$
where
$[x,y]$
where
![]() $x\in S$
and
$x\in S$
and
![]() $y\in \gamma _2G$
is from a set (of size at most m) which gives a generating set of
$y\in \gamma _2G$
is from a set (of size at most m) which gives a generating set of
![]() $\gamma _2G/\gamma _3G$
. So
$\gamma _2G/\gamma _3G$
. So
![]() $\gamma _3G$
is generated by a set of size at most
$\gamma _3G$
is generated by a set of size at most
![]() $2m^2$
. By Remark 2.3 (applied to the class 2 group
$2m^2$
. By Remark 2.3 (applied to the class 2 group
![]() $\gamma _2G$
),
$\gamma _2G$
),
![]() $\gamma _3G$
has exponent at most
$\gamma _3G$
has exponent at most
![]() $p^m$
. Thus
$p^m$
. Thus
![]() $|\gamma _3G|\leq p^{f(m)}$
where
$|\gamma _3G|\leq p^{f(m)}$
where
![]() $f(m)=2m^3$
.
$f(m)=2m^3$
.
Corollary 2.5. Suppose (A) every
![]() $\omega $
-categorical pseudofinite p-group of class at most 2 is FAF.
$\omega $
-categorical pseudofinite p-group of class at most 2 is FAF.
Then the same conclusion holds for all
![]() $\omega $
-categorical pseudofinite groups.
$\omega $
-categorical pseudofinite groups.
Proof. In the argument below, we may assume that normal subgroups witnessing the FAF condition are characteristic and hence 0-definable; see the discussion of FAF groups after Conjecture 1.1.
Let G be an
![]() $\omega $
-categorical pseudofinite group. By Corollary 2.2 and the last paragraph we may suppose that G is nilpotent. As any periodic nilpotent group is a direct product of its Sylow subgroups, we may further suppose that G is a p-group for some prime p.
$\omega $
-categorical pseudofinite group. By Corollary 2.2 and the last paragraph we may suppose that G is nilpotent. As any periodic nilpotent group is a direct product of its Sylow subgroups, we may further suppose that G is a p-group for some prime p.
Observe that under (A), any pseudofinite
![]() $\omega $
-categorical p-group with a class 2 definable normal subgroup of finite index, or with a finite normal subgoup with class 2 quotient, is FAF. For by (A), the class 2 piece is FAF, and absorbs the finite piece at the top or bottom.
$\omega $
-categorical p-group with a class 2 definable normal subgroup of finite index, or with a finite normal subgoup with class 2 quotient, is FAF. For by (A), the class 2 piece is FAF, and absorbs the finite piece at the top or bottom.
Since there are only finitely many characteristic subgroups, we may suppose by the previous paragraph that G has no proper characteristic subgroup of finite index. Likewise, we may suppose that G has no non-trivial finite characteristic subgroup. Hence we aim to show that G is abelian.
We now use induction on the nilpotency class of G and let
![]() $1\neq \gamma _kG\leq Z(G)$
be the smallest non-trivial term of the lower central series. We need to show
$1\neq \gamma _kG\leq Z(G)$
be the smallest non-trivial term of the lower central series. We need to show
![]() $k=1$
. By assumption (A) and our reduction of G we know that
$k=1$
. By assumption (A) and our reduction of G we know that
![]() $k\neq 2$
. So suppose towards a contradiction that
$k\neq 2$
. So suppose towards a contradiction that
![]() $k\geq 3$
. By induction and since G has no proper characteristic subgroup of finite index,
$k\geq 3$
. By induction and since G has no proper characteristic subgroup of finite index,
![]() $\bar {G}=G/\gamma _kG$
has finite commutator group
$\bar {G}=G/\gamma _kG$
has finite commutator group
![]() $\bar {G}'$
and
$\bar {G}'$
and
![]() $\bar {G}= C_{\bar {G}}(\bar {G}')$
. Thus G has nilpotency class 3. Consider the lower central series
$\bar {G}= C_{\bar {G}}(\bar {G}')$
. Thus G has nilpotency class 3. Consider the lower central series
![]() $G=\gamma _1G>\gamma _2G>\gamma _3G>1$
and note that
$G=\gamma _1G>\gamma _2G>\gamma _3G>1$
and note that
![]() $\gamma _2G/\gamma _3G\cong \bar {G}'$
is finite. By Lemma 2.4, G is finite-by-abelian, with a non-trivial finite characteristic subgroup, contradicting our assumption. Hence
$\gamma _2G/\gamma _3G\cong \bar {G}'$
is finite. By Lemma 2.4, G is finite-by-abelian, with a non-trivial finite characteristic subgroup, contradicting our assumption. Hence
![]() $k=1$
and G is abelian.
$k=1$
and G is abelian.
Our next goal is to show that certain constructions of
![]() $\omega $
-categorical p-groups discussed in the papers [Reference Apps2, Reference Baudisch4–Reference Baudisch6, Reference Cherlin, Saracino and Wood15, Reference Maier31, Reference Saracino and Wood35] are not pseudofinite. In order to make the idea as explicit as possible in the simplest case, we first consider existentially closed class 2 p-groups of exponent p.
$\omega $
-categorical p-groups discussed in the papers [Reference Apps2, Reference Baudisch4–Reference Baudisch6, Reference Cherlin, Saracino and Wood15, Reference Maier31, Reference Saracino and Wood35] are not pseudofinite. In order to make the idea as explicit as possible in the simplest case, we first consider existentially closed class 2 p-groups of exponent p.
Let p be an odd prime. By [Reference Saracino and Wood35, Theorem 3.9], the theory
![]() $T_{{\mathrm {nil2}},p}$
of existentially closed nilpotent class 2 exponent p groups is complete, and is axiomatized by a sentence
$T_{{\mathrm {nil2}},p}$
of existentially closed nilpotent class 2 exponent p groups is complete, and is axiomatized by a sentence
![]() $\rho $
expressing that a model G is a nilpotent, class 2 exponent p group and that the centre is the set of commutators, an axiom scheme expressing that the centre is infinite, and the following axiom scheme
$\rho $
expressing that a model G is a nilpotent, class 2 exponent p group and that the centre is the set of commutators, an axiom scheme expressing that the centre is infinite, and the following axiom scheme
![]() $\Sigma _n:=\{\sigma _n:n>0\}$
. Here
$\Sigma _n:=\{\sigma _n:n>0\}$
. Here
![]() $\sigma _n$
expresses:
$\sigma _n$
expresses:
 $$ \begin{align*}\left(\bigwedge_{i=1}^n [g_i,k]=h_i\right).\end{align*} $$
$$ \begin{align*}\left(\bigwedge_{i=1}^n [g_i,k]=h_i\right).\end{align*} $$
Here linear independence is interpreted in the sense of the
![]() $\mathbb {F}_p$
-vector space
$\mathbb {F}_p$
-vector space
![]() $G/Z(G)$
. As noted in [Reference Saracino and Wood35, Theorem 3.9],
$G/Z(G)$
. As noted in [Reference Saracino and Wood35, Theorem 3.9],
![]() $T_{{\mathrm {nil2}},p}$
is
$T_{{\mathrm {nil2}},p}$
is
![]() $\omega $
-categorical. However, the following lemma yields that
$\omega $
-categorical. However, the following lemma yields that
![]() $\rho \wedge \sigma _1\wedge \sigma _2\wedge \tau $
has no finite model, where
$\rho \wedge \sigma _1\wedge \sigma _2\wedge \tau $
has no finite model, where
![]() $\tau $
expresses that the centre has order at least
$\tau $
expresses that the centre has order at least
![]() $p^2$
.
$p^2$
.
Lemma 2.6. Let p be an odd prime, and let
![]() $(V,W,\beta )$
be a 2-sorted structure where
$(V,W,\beta )$
be a 2-sorted structure where
![]() $V,W$
are vector spaces over
$V,W$
are vector spaces over
![]() $\mathbb {F}_p$
(each sort viewed in the usual language of
$\mathbb {F}_p$
(each sort viewed in the usual language of
![]() $\mathbb {F}_p$
-modules) of dimension at least 2 and
$\mathbb {F}_p$
-modules) of dimension at least 2 and
![]() $\beta :V\times V \to W$
is bilinear. Let
$\beta :V\times V \to W$
is bilinear. Let
![]() $\chi $
be a sentence expressing this information, and
$\chi $
be a sentence expressing this information, and
![]() $\psi $
be the sentence
$\psi $
be the sentence
Then
![]() $\chi \wedge \psi $
has no finite model.
$\chi \wedge \psi $
has no finite model.
Proof. Suppose for a contradiction that
![]() $(V',W',\beta )$
is a finite model of
$(V',W',\beta )$
is a finite model of
![]() $\chi \wedge \psi $
, with
$\chi \wedge \psi $
, with
![]() $\dim (V')=n>1$
and
$\dim (V')=n>1$
and
![]() $\dim (W')=d>1$
. For each
$\dim (W')=d>1$
. For each
![]() $v\in V'$
, the map
$v\in V'$
, the map
![]() $\beta _v:V'\to W'$
given by
$\beta _v:V'\to W'$
given by
![]() $\beta _v(x)=\beta (v,x)$
is linear, and is surjective as
$\beta _v(x)=\beta (v,x)$
is linear, and is surjective as
![]() $(V',W',\beta )\models \psi $
. Thus the kernel
$(V',W',\beta )\models \psi $
. Thus the kernel
![]() $K_v$
of
$K_v$
of
![]() $\beta _v$
has index
$\beta _v$
has index
![]() $p^d$
. Furthermore,
$p^d$
. Furthermore,
![]() $\psi $
ensures that if
$\psi $
ensures that if
![]() $v_1,v_2\in V'$
are linearly independent then any two cosets
$v_1,v_2\in V'$
are linearly independent then any two cosets
![]() $K_{v_1}+a_1$
and
$K_{v_1}+a_1$
and
![]() $K_{v_2}+a_2$
intersect: indeed, if
$K_{v_2}+a_2$
intersect: indeed, if
![]() $w_i=\beta (v_i,a_i)$
for
$w_i=\beta (v_i,a_i)$
for
![]() $i=1,2$
then because
$i=1,2$
then because
![]() $(V',W',\beta )\models \psi $
there is
$(V',W',\beta )\models \psi $
there is
![]() $z\in V'$
with
$z\in V'$
with
![]() $\beta (v_1,z)=w_1\wedge \beta (v_2,z)=w_2$
, and we have
$\beta (v_1,z)=w_1\wedge \beta (v_2,z)=w_2$
, and we have
![]() $z\in (K_{v_1}+a_1) \cap (K_{v_2}+a_2)$
. Thus
$z\in (K_{v_1}+a_1) \cap (K_{v_2}+a_2)$
. Thus
![]() $K_{v_1}+K_{v_2}=V'$
, for if
$K_{v_1}+K_{v_2}=V'$
, for if
![]() $z\in V'$
there is
$z\in V'$
there is
![]() $u_1\in K_{v_1}\cap (K_{v_2}+z)$
, so
$u_1\in K_{v_1}\cap (K_{v_2}+z)$
, so
![]() $u_1=u_2+z$
for some
$u_1=u_2+z$
for some
![]() $u_2\in K_{v_2}$
, and
$u_2\in K_{v_2}$
, and
![]() $z=u_1-u_2\in K_{v_1}+K_{v_2}$
. Thus, we have a collection consisting of
$z=u_1-u_2\in K_{v_1}+K_{v_2}$
. Thus, we have a collection consisting of
![]() $ \frac {p^n-1}{p-1}$
such kernels
$ \frac {p^n-1}{p-1}$
such kernels
![]() $K_v$
, each of codimension d in
$K_v$
, each of codimension d in
![]() $V'$
, such that any two span
$V'$
, such that any two span
![]() $V'$
. By moving to the dual space
$V'$
. By moving to the dual space
![]() $(V')^*$
and taking annihilators, we find a family consisting of
$(V')^*$
and taking annihilators, we find a family consisting of
![]() $\frac {p^n-1}{p-1}$
subspaces of
$\frac {p^n-1}{p-1}$
subspaces of
![]() $(V')^*$
each of dimension d, with pairwise intersection
$(V')^*$
each of dimension d, with pairwise intersection
![]() $\{0\}$
. Since
$\{0\}$
. Since
![]() $d>1$
, this is clearly impossible by counting vectors in
$d>1$
, this is clearly impossible by counting vectors in
![]() $(V')^{*}$
.
$(V')^{*}$
.
Corollary 2.7. Suppose that G is an
![]() $\omega $
-categorical nilpotent group of class 2 and exponent p (where p is an odd prime) with both the centre Z and the group
$\omega $
-categorical nilpotent group of class 2 and exponent p (where p is an odd prime) with both the centre Z and the group
![]() $G/Z$
elementary abelian of rank at least 2, and such that
$G/Z$
elementary abelian of rank at least 2, and such that
![]() $G\models \sigma _1\wedge \sigma _2$
. Then G is not pseudofinite.
$G\models \sigma _1\wedge \sigma _2$
. Then G is not pseudofinite.
Proof. This follows immediately from Lemma 2.6. Indeed, if such G were pseudofinite, then there would be a finite group H satisfying the corresponding conditions. Put
![]() $V=H/Z(H)$
and
$V=H/Z(H)$
and
![]() $W=Z(H)$
– these are elementary abelian p-groups and so vector spaces over
$W=Z(H)$
– these are elementary abelian p-groups and so vector spaces over
![]() $\mathbb {F}_p$
. Let
$\mathbb {F}_p$
. Let
![]() $\beta $
be the commutator map
$\beta $
be the commutator map
![]() $V\times V \to W$
given by
$V\times V \to W$
given by
![]() $[gZ(H),hZ(H)]=[g,h]$
. The axioms
$[gZ(H),hZ(H)]=[g,h]$
. The axioms
![]() $\rho \wedge \sigma _1\wedge \sigma _2$
yield that
$\rho \wedge \sigma _1\wedge \sigma _2$
yield that
![]() $(V,W,\beta )\models \chi \wedge \psi $
, contrary to Lemma 2.6.
$(V,W,\beta )\models \chi \wedge \psi $
, contrary to Lemma 2.6.
This yields almost immediately the following result, and hence gives Theorem 1.4. The groups
![]() $D(n)$
(for n finite) are
$D(n)$
(for n finite) are
![]() $\omega $
-categorical nilpotent class 2 and exponent p, with centre elementary abelian of rank n. By [Reference Baudisch8, Theorem 3], they are supersimple of SU-rank 1. Note that for
$\omega $
-categorical nilpotent class 2 and exponent p, with centre elementary abelian of rank n. By [Reference Baudisch8, Theorem 3], they are supersimple of SU-rank 1. Note that for
![]() $n=1$
the group is extraspecial, so pseudofinite.
$n=1$
the group is extraspecial, so pseudofinite.
Corollary 2.8. Let p be an odd prime.
-
(i) The theory
 $T_{{\mathrm {nil2}},p}$
is not pseudofinite.
$T_{{\mathrm {nil2}},p}$
is not pseudofinite. -
(ii) For
 $n\geq 2$
the group
$n\geq 2$
the group
 $D(n)$
discussed by Baudisch in [Reference Baudisch8] is not pseudofinite.
$D(n)$
discussed by Baudisch in [Reference Baudisch8] is not pseudofinite.
Proof. Case (i) follows immediately from the corollary by the above axiomatisation of
![]() $T_{{\mathrm {nil2}},p}$
. The groups
$T_{{\mathrm {nil2}},p}$
. The groups
![]() $D(n)$
in (ii) are built by an amalgamation argument, working with the class of finite nilpotent class 2 exponent p groups G expanded by linearly independent constants
$D(n)$
in (ii) are built by an amalgamation argument, working with the class of finite nilpotent class 2 exponent p groups G expanded by linearly independent constants
![]() $c_1,\ldots ,c_n$
such that
$c_1,\ldots ,c_n$
such that
![]() $G'\leq \langle c_1,\ldots ,c_n\rangle \leq Z(G)$
. These also satisfy
$G'\leq \langle c_1,\ldots ,c_n\rangle \leq Z(G)$
. These also satisfy
![]() $\sigma _1\wedge \sigma _2$
; this is perhaps most easily verified by working in the category
$\sigma _1\wedge \sigma _2$
; this is perhaps most easily verified by working in the category
![]() $\mathbb {B}^P$
with objects
$\mathbb {B}^P$
with objects
![]() $(V,W,\beta )$
where
$(V,W,\beta )$
where
![]() $V,W$
are vector spaces over
$V,W$
are vector spaces over
![]() $\mathbb {F}_p$
and
$\mathbb {F}_p$
and
![]() $\beta :V\times V \to W$
is an alternating bilinear map, as described in [Reference Baudisch8, Section 3]; we may take
$\beta :V\times V \to W$
is an alternating bilinear map, as described in [Reference Baudisch8, Section 3]; we may take
![]() $W=\langle c_1,\ldots ,c_n\rangle $
.
$W=\langle c_1,\ldots ,c_n\rangle $
.
Remark 2.9. The counting argument in Lemma 2.6 is quite extravagant, and does not seem to require the full strength of
![]() $\psi $
. This suggests a conceivable route to a counterexample to our conjecture, by building a group with sparse satisfaction of
$\psi $
. This suggests a conceivable route to a counterexample to our conjecture, by building a group with sparse satisfaction of
![]() $\sigma _2$
, possibly exploiting the Shelah–Spencer zero-one laws from [Reference Shelah and Spencer38].
$\sigma _2$
, possibly exploiting the Shelah–Spencer zero-one laws from [Reference Shelah and Spencer38].
We now turn to Apps’s more general class of comprehensive groups, which we briefly summarize. First recall that if A is an abelian p-group and
![]() $g\in A$
, then the height
$g\in A$
, then the height
![]() ${\mathrm {ht}}_A(g)$
is defined to be
${\mathrm {ht}}_A(g)$
is defined to be
![]() ${\mathrm {sup}}\{n\geq 0:g=h^{p^n} \mbox {~for some~}h\in A\}$
. A subgroup B of A is pure in A if
${\mathrm {sup}}\{n\geq 0:g=h^{p^n} \mbox {~for some~}h\in A\}$
. A subgroup B of A is pure in A if
![]() ${\mathrm {ht}}_B(g)={\mathrm {ht}}_A(g)$
for all
${\mathrm {ht}}_B(g)={\mathrm {ht}}_A(g)$
for all
![]() $g\in B$
. For a group A of finite exponent, write
$g\in B$
. For a group A of finite exponent, write
![]() ${\mathrm {exp}}(A)$
for the exponent of A. Building on work in [Reference Saracino and Wood35], for p a prime Apps [Reference Apps2] defines a nilpotent class 2 p-group G with centre Z to be comprehensive if it satisfies the following condition, where
${\mathrm {exp}}(A)$
for the exponent of A. Building on work in [Reference Saracino and Wood35], for p a prime Apps [Reference Apps2] defines a nilpotent class 2 p-group G with centre Z to be comprehensive if it satisfies the following condition, where
![]() $|g|$
denotes the order of a group element g,
$|g|$
denotes the order of a group element g,
![]() $G^*=G/Z$
, and for
$G^*=G/Z$
, and for
![]() $g\in G$
,
$g\in G$
,
![]() $g^*$
denotes its image in
$g^*$
denotes its image in
![]() $G^*$
:
$G^*$
:
(
![]() $*$
) Let A be a finite pure subgroup of
$*$
) Let A be a finite pure subgroup of
![]() $G^*$
, let
$G^*$
, let
![]() $\alpha \in {\mathrm {Hom}}(A,Z)$
, let
$\alpha \in {\mathrm {Hom}}(A,Z)$
, let
![]() $w\in Z$
and
$w\in Z$
and
![]() $r\in \mathbb {N}$
, and suppose
$r\in \mathbb {N}$
, and suppose
![]() ${\mathrm {exp}}(\alpha (A))\leq p^r\leq {\mathrm {exp}}(G^*)$
and
${\mathrm {exp}}(\alpha (A))\leq p^r\leq {\mathrm {exp}}(G^*)$
and
![]() $p^r|w|\leq {\mathrm {exp}}(G)$
. Then there is
$p^r|w|\leq {\mathrm {exp}}(G)$
. Then there is
![]() $g\in G$
such that
$g\in G$
such that
![]() $\langle A,g^*\rangle =A\oplus \langle g^*\rangle $
is pure in
$\langle A,g^*\rangle =A\oplus \langle g^*\rangle $
is pure in
![]() $G^*$
,
$G^*$
,
![]() $|g^*|=p^r, g^{p^r}=w$
, and
$|g^*|=p^r, g^{p^r}=w$
, and
![]() $[a, g^*]=\alpha (a)$
for all
$[a, g^*]=\alpha (a)$
for all
![]() $a\in A$
. (Here, the natural map
$a\in A$
. (Here, the natural map
![]() $G^*\times G^*\to Z$
induced by commutation in G is also denoted by
$G^*\times G^*\to Z$
induced by commutation in G is also denoted by
![]() $[-,-]$
.)
$[-,-]$
.)
Given an abelian p-group Z and
![]() $t,u\in \mathbb {N}$
, Apps defines
$t,u\in \mathbb {N}$
, Apps defines
![]() $\mathcal {N}_2(p^u,p^t/Z)$
to be the class of groups G of exponent
$\mathcal {N}_2(p^u,p^t/Z)$
to be the class of groups G of exponent
![]() $p^u$
with centre Z such that
$p^u$
with centre Z such that
![]() ${\mathrm {exp}}(G^*)=p^t$
. He proves the following (restricted below to finite exponent, the area of our interest).
${\mathrm {exp}}(G^*)=p^t$
. He proves the following (restricted below to finite exponent, the area of our interest).
Theorem 2.10 [Reference Apps2, Theorem C].
Let p be prime, Z a countable abelian group of finite exponent
![]() $p^s$
and suppose
$p^s$
and suppose
![]() $t,u\in \mathbb {N}$
with
$t,u\in \mathbb {N}$
with
![]() $s+t\geq u\geq s\geq t$
, with also
$s+t\geq u\geq s\geq t$
, with also
![]() $u> t$
if
$u> t$
if
![]() $p=2$
. Then there is a unique countable comprehensive group G in
$p=2$
. Then there is a unique countable comprehensive group G in
![]() $\mathcal {N}_2(p^u,p^t/Z)$
, and G is
$\mathcal {N}_2(p^u,p^t/Z)$
, and G is
![]() $\omega $
-categorical.
$\omega $
-categorical.
It can be checked that for p an odd prime,
![]() $s=t=u=1$
, and Z an elementary abelian p-group of rank n, the corresponding comprehensive group is exactly Baudisch’s group
$s=t=u=1$
, and Z an elementary abelian p-group of rank n, the corresponding comprehensive group is exactly Baudisch’s group
![]() $D(n)$
.
$D(n)$
.
Theorem 2.11. Let
![]() $Z,p, s,t,u$
and the comprehensive group G be as in Theorem 2.10, with p odd. Assume Z contains an elementary abelian p-group of rank 2 (i.e., Z is not cyclic). Then G is not pseudofinite.
$Z,p, s,t,u$
and the comprehensive group G be as in Theorem 2.10, with p odd. Assume Z contains an elementary abelian p-group of rank 2 (i.e., Z is not cyclic). Then G is not pseudofinite.
Proof. Suppose for a contradiction that G is pseudofinite. Let
![]() $G_0^*$
be the subgroup of
$G_0^*$
be the subgroup of
![]() $G^*$
consisting of elements of height 0 and order p, together with the identity. By [Reference Apps2, Lemma 3.2(a)], the group
$G^*$
consisting of elements of height 0 and order p, together with the identity. By [Reference Apps2, Lemma 3.2(a)], the group
![]() $G_0^*$
is infinite. Let
$G_0^*$
is infinite. Let
![]() $G_0$
be the preimage of
$G_0$
be the preimage of
![]() $G_0^*$
under the map
$G_0^*$
under the map
![]() $G \to G^*$
. Clearly
$G \to G^*$
. Clearly
![]() $G_0$
is characteristic in G, so is
$G_0$
is characteristic in G, so is
![]() $\emptyset $
-definable and so is
$\emptyset $
-definable and so is
![]() $\omega $
-categorical and also pseudofinite. Let
$\omega $
-categorical and also pseudofinite. Let
![]() $Z_0$
be the subgroup of Z consisting of elements of order at most p. Then
$Z_0$
be the subgroup of Z consisting of elements of order at most p. Then
![]() $Z_0$
is an elementary abelian p-group of rank at least 2. Since
$Z_0$
is an elementary abelian p-group of rank at least 2. Since
![]() $[x,y]^p=[x^p,y]$
for any
$[x,y]^p=[x^p,y]$
for any
![]() $x,y\in G_0$
by Remark 2.3, the commutator map
$x,y\in G_0$
by Remark 2.3, the commutator map
![]() $G_0 \times G_0 \to Z$
induces a bilinear map
$G_0 \times G_0 \to Z$
induces a bilinear map
![]() $\beta :G_0^* \times G_0^* \to Z_0$
, and the structure
$\beta :G_0^* \times G_0^* \to Z_0$
, and the structure
![]() $(G_0^*, Z_0, \beta )$
is definable, and so
$(G_0^*, Z_0, \beta )$
is definable, and so
![]() $\omega $
-categorical and pseudofinite. Furthermore, it follows from (
$\omega $
-categorical and pseudofinite. Furthermore, it follows from (
![]() $*$
) that for any linearly independent
$*$
) that for any linearly independent
![]() $g_1,g_2\in G_0^*$
and
$g_1,g_2\in G_0^*$
and
![]() $h_1,h_2\in Z_0$
, there is
$h_1,h_2\in Z_0$
, there is
![]() $k\in G_0^*$
with
$k\in G_0^*$
with
![]() $\beta (g_i,k)=h_i$
for
$\beta (g_i,k)=h_i$
for
![]() $i=1,2$
. This however is impossible by Lemma 2.6.
$i=1,2$
. This however is impossible by Lemma 2.6.
Remark 2.12. Let p be an odd prime and
![]() $m=p^u$
for some
$m=p^u$
for some
![]() $u\geq 1$
. It is shown at the end of Section 3 of [Reference Apps2] that any countable group satisfying the model companion of the theory of class 2 groups of exponent m is a comprehensive group with respect to
$u\geq 1$
. It is shown at the end of Section 3 of [Reference Apps2] that any countable group satisfying the model companion of the theory of class 2 groups of exponent m is a comprehensive group with respect to
![]() $\mathcal {N}_2(p^u,p^u/Z)$
, where
$\mathcal {N}_2(p^u,p^u/Z)$
, where
![]() $Z=(C_{p^u})^\omega $
. Since such Z contains an infinite elementary abelian p-group, the model companion is not pseudofinite.
$Z=(C_{p^u})^\omega $
. Since such Z contains an infinite elementary abelian p-group, the model companion is not pseudofinite.
As mentioned in the introduction, for any odd prime p and
![]() $c<p$
, Maier [Reference Maier31] constructs an
$c<p$
, Maier [Reference Maier31] constructs an
![]() $\omega $
-categorical model companion of the class of exponent p groups of nilpotency class at most c. The construction is described in detail in [Reference d’Elbée, Müller, Ramsey and Siniora17], via an intricate amalgamation of “Lazard” Lie algebras which yields additional information on the model theory of the groups. The countable model of the model companion is denoted
$\omega $
-categorical model companion of the class of exponent p groups of nilpotency class at most c. The construction is described in detail in [Reference d’Elbée, Müller, Ramsey and Siniora17], via an intricate amalgamation of “Lazard” Lie algebras which yields additional information on the model theory of the groups. The countable model of the model companion is denoted
![]() $\mathbf {G}_{c,p}$
. It turns out (personal communication of Christian d’Elbée) that if
$\mathbf {G}_{c,p}$
. It turns out (personal communication of Christian d’Elbée) that if
![]() $c\geq 4$
then
$c\geq 4$
then
![]() $\mathbf {G}_{c,p}$
interprets
$\mathbf {G}_{c,p}$
interprets
![]() $\mathbf {G}_{2,p}$
, which is the countable model of
$\mathbf {G}_{2,p}$
, which is the countable model of
![]() $T_{{\mathop{\mathrm {nil2}}},p}$
; the argument provided by d’Elbée does not handle the case
$T_{{\mathop{\mathrm {nil2}}},p}$
; the argument provided by d’Elbée does not handle the case
![]() $c=3$
. In particular, by Corollary 2.8, we have
$c=3$
. In particular, by Corollary 2.8, we have
Proposition 2.13. Let p be an odd prime and
![]() $3<c<p$
. Then
$3<c<p$
. Then
![]() $\mathbf {G}_{c,p}$
is not pseudofinite.
$\mathbf {G}_{c,p}$
is not pseudofinite.
We have not tried systematically to show that all known groups of this flavour (i.e.,
![]() $\omega $
-categorical model companions, Fraïssé limits in various languages) satisfy Conjecture 1.1. In particular, we only work with odd primes, so for example do not consider the QE nilpotent class 2 groups of exponent 4 mentioned in the introduction.
$\omega $
-categorical model companions, Fraïssé limits in various languages) satisfy Conjecture 1.1. In particular, we only work with odd primes, so for example do not consider the QE nilpotent class 2 groups of exponent 4 mentioned in the introduction.
We finish this section with a brief discussion of which FAF groups are pseudofinite.
Examples 2.14. First, by [Reference Baur, Cherlin and Macintyre9, Theorem 63], every
![]() $\omega $
-categorical abelian-by-finite group has
$\omega $
-categorical abelian-by-finite group has
![]() $\omega $
-stable theory, and hence is smoothly approximable (see e.g., [Reference Cherlin, Harrington and Lachlan13, Corollary 7.4]) and so pseudofinite. As noted in Section 1, extraspecial p-groups of odd exponent p are pseudofinite, whereas by Theorem 2.11 for finite
$\omega $
-stable theory, and hence is smoothly approximable (see e.g., [Reference Cherlin, Harrington and Lachlan13, Corollary 7.4]) and so pseudofinite. As noted in Section 1, extraspecial p-groups of odd exponent p are pseudofinite, whereas by Theorem 2.11 for finite
![]() $n\geq 2$
Baudisch’s groups
$n\geq 2$
Baudisch’s groups
![]() $D(n)$
are not; the groups in both of these classes are finite-by-abelian. At the other extreme to the groups
$D(n)$
are not; the groups in both of these classes are finite-by-abelian. At the other extreme to the groups
![]() $D(n)$
, consider (for an odd prime p and any finite
$D(n)$
, consider (for an odd prime p and any finite
![]() $n\geq 1$
) a vector space V over
$n\geq 1$
) a vector space V over
![]() $\mathbb {F}_{p^n}$
equipped with a non-degenerate symplectic form
$\mathbb {F}_{p^n}$
equipped with a non-degenerate symplectic form
![]() $\beta : V\times V \to \mathbb {F}_{p^n}$
. Define the group
$\beta : V\times V \to \mathbb {F}_{p^n}$
. Define the group
![]() $H(p,n)$
to have universe
$H(p,n)$
to have universe
![]() $V\times \mathbb {F}_{p^n}$
, with group operation
$V\times \mathbb {F}_{p^n}$
, with group operation
![]() $(v_1,x_1)*(v_2,x_2)=(v_1+v_2, x_1+x_2+\beta (v_1,v_2))$
. Then
$(v_1,x_1)*(v_2,x_2)=(v_1+v_2, x_1+x_2+\beta (v_1,v_2))$
. Then
![]() $H(p,n)$
is bi-interpretable with a smoothly approximable structure and so is smoothly approximable and hence pseudofinite (unlike
$H(p,n)$
is bi-interpretable with a smoothly approximable structure and so is smoothly approximable and hence pseudofinite (unlike
![]() $D(n)$
). However, like
$D(n)$
). However, like
![]() $D(n)$
,
$D(n)$
,
![]() $H(p,n)$
is nilpotent class 2 of exponent p with centre elementary abelian of rank n, and is supersimple of SU-rank 1. If
$H(p,n)$
is nilpotent class 2 of exponent p with centre elementary abelian of rank n, and is supersimple of SU-rank 1. If
![]() $n=1$
then
$n=1$
then
![]() $H(p,n)$
is extraspecial (so is isomorphic to
$H(p,n)$
is extraspecial (so is isomorphic to
![]() $D(1)$
).
$D(1)$
).
The groups
![]() $H(p,n)$
are a special case of a more general class of
$H(p,n)$
are a special case of a more general class of
![]() $\omega $
-categorical nilpotent class 2 groups discussed by Apps in [Reference Apps2, Section 2]. Namely, given a finite nilpotent class 2 group G, and subgroup K of G with
$\omega $
-categorical nilpotent class 2 groups discussed by Apps in [Reference Apps2, Section 2]. Namely, given a finite nilpotent class 2 group G, and subgroup K of G with
![]() $G'\leq K\leq Z(G)$
, let
$G'\leq K\leq Z(G)$
, let
![]() $G(\omega ;K)$
denote the (restricted) central product of
$G(\omega ;K)$
denote the (restricted) central product of
![]() $\aleph _0$
copies of G, amalgamated over K, and for
$\aleph _0$
copies of G, amalgamated over K, and for
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n>1$
let
$n>1$
let
![]() $G(n;K)$
be the central product of n copies of G amalgamated over K. Apps shows in [Reference Apps2, Theorem A] that
$G(n;K)$
be the central product of n copies of G amalgamated over K. Apps shows in [Reference Apps2, Theorem A] that
![]() $G(\omega ;K)$
is
$G(\omega ;K)$
is
![]() $\omega $
-categorical.
$\omega $
-categorical.
Question 2.15. Is it true that for any
![]() $G,K$
as above, the group
$G,K$
as above, the group
![]() $G(\omega ,K)$
is pseudofinite and satisfies the limit theory of the groups
$G(\omega ,K)$
is pseudofinite and satisfies the limit theory of the groups
![]() $G(n,K)$
? Are all such groups smoothly approximated by the
$G(n,K)$
? Are all such groups smoothly approximated by the
![]() $G(n,K)$
(and hence supersimple of finite rank)?
$G(n,K)$
(and hence supersimple of finite rank)?
Observe that if G is a finite non-abelian group, then the restricted direct power
![]() $H:=G^\omega $
is not pseudofinite. For define a preorder
$H:=G^\omega $
is not pseudofinite. For define a preorder
![]() $x<y$
on H by putting
$x<y$
on H by putting
![]() $x<y$
if and only if
$x<y$
if and only if
![]() $C_H(x)>C_H(y)$
. Then
$C_H(x)>C_H(y)$
. Then
![]() $H\models (\forall x\in H\setminus Z(H)) (\exists y\in H\setminus Z(H))(x<y)$
; indeed, we could choose y to agree with x on its support, and have a non-central element of G in another entry. Such a sentence could not hold in any finite non-abelian group. In fact, such a group H is also not
$H\models (\forall x\in H\setminus Z(H)) (\exists y\in H\setminus Z(H))(x<y)$
; indeed, we could choose y to agree with x on its support, and have a non-central element of G in another entry. Such a sentence could not hold in any finite non-abelian group. In fact, such a group H is also not
![]() $\omega $
-categorical—see e.g., [Reference Rosenstein34, Theorem 3].
$\omega $
-categorical—see e.g., [Reference Rosenstein34, Theorem 3].
Question 2.16. Does every
![]() $\omega $
-categorical FAF group have supersimple theory?
$\omega $
-categorical FAF group have supersimple theory?
3 Further observations
We begin by noting that the Boolean power construction mentioned in the introduction does not seem to give counterexamples to Conjecture 1.1. Note that in the lemma below, if G is nilpotent of class 2 then so are
![]() $B[G]$
and
$B[G]$
and
![]() $B^-[G]$
.
$B^-[G]$
.
Lemma 3.1. Let G be an
![]() $\omega $
-categorical non-abelian group and let
$\omega $
-categorical non-abelian group and let
![]() $B[G]$
or
$B[G]$
or
![]() $B^-[G]$
be an
$B^-[G]$
be an
![]() $\omega $
-categorical Boolean power of G. Then
$\omega $
-categorical Boolean power of G. Then
![]() $B[G]$
(respectively
$B[G]$
(respectively
![]() $B^-[G]$
) has the strict order property so is not pseudofinite.
$B^-[G]$
) has the strict order property so is not pseudofinite.
Proof. We consider the case when B is the countable atomless Boolean algebra, but the other cases (where B has finitely many atoms, or is an
![]() $\omega $
-categorical Boolean ring without 1) are similar. Let C be the Cantor set. Then
$\omega $
-categorical Boolean ring without 1) are similar. Let C be the Cantor set. Then
![]() $B[G]$
consists of all continuous maps
$B[G]$
consists of all continuous maps
![]() $C\to G$
with finite support. Let
$C\to G$
with finite support. Let
![]() $\{U_i:i\in \omega \}$
be clopen subsets of C, with
$\{U_i:i\in \omega \}$
be clopen subsets of C, with
![]() $U_i\subset U_j$
whenever
$U_i\subset U_j$
whenever
![]() $i<j$
. Also let
$i<j$
. Also let
![]() $g\in G\setminus Z(G)$
and let
$g\in G\setminus Z(G)$
and let
![]() $\phi _i:C\to G$
be the map taking value g on
$\phi _i:C\to G$
be the map taking value g on
![]() $U_i$
and
$U_i$
and
![]() $1$
elsewhere. Then for each i we have
$1$
elsewhere. Then for each i we have
![]() $\phi _i\in B[G]$
, and
$\phi _i\in B[G]$
, and
![]() $C_{B[G]}(\phi _i)$
consists of elements
$C_{B[G]}(\phi _i)$
consists of elements
![]() $\psi $
of
$\psi $
of
![]() $B[G]$
taking any value on
$B[G]$
taking any value on
![]() $C\setminus U_i$
and taking values in
$C\setminus U_i$
and taking values in
![]() $C_G(g)$
on
$C_G(g)$
on
![]() $U_i$
. Hence if
$U_i$
. Hence if
![]() $i>j$
we have
$i>j$
we have
![]() $C_G(\phi _i)<C_G(\phi _j)$
. Thus, the formula
$C_G(\phi _i)<C_G(\phi _j)$
. Thus, the formula
![]() $\phi (x,y)$
expressing
$\phi (x,y)$
expressing
![]() $C_{B[G]}(x)\leq C_{B[G]}(y)$
defines a preorder with an infinite totally ordered subset. Non-pseudofiniteness now follows from Lemma 2.1.
$C_{B[G]}(x)\leq C_{B[G]}(y)$
defines a preorder with an infinite totally ordered subset. Non-pseudofiniteness now follows from Lemma 2.1.
We also pose the following question, aiming to recover a Boolean power structure for a certain class of nilpotent class 2 groups, mimicking the proof of Theorem A of [Reference Apps3] which stems ultimately from an unpublished result of Philip Hall.
Problem 3.2. Find conditions on a locally finite nilpotent class 2 (perhaps
![]() $\omega $
-categorical) group G which guarantee that G is a Boolean power. Suggested conditions are (i) there is no non-trivial characteristic subgroup of G which is properly contained in the derived subgroup
$\omega $
-categorical) group G which guarantee that G is a Boolean power. Suggested conditions are (i) there is no non-trivial characteristic subgroup of G which is properly contained in the derived subgroup
![]() $G'$
, and (ii) G has a subgroup of finite index not containing
$G'$
, and (ii) G has a subgroup of finite index not containing
![]() $G'$
. Find conditions which ensure that G is a filtered Boolean power in the sense of [Reference Macintyre and Rosenstein30].
$G'$
. Find conditions which ensure that G is a filtered Boolean power in the sense of [Reference Macintyre and Rosenstein30].
Let
![]() $f(n)$
be the number of non-isomorphic groups of order n. It is well-known that
$f(n)$
be the number of non-isomorphic groups of order n. It is well-known that
![]() $f(n)$
grows fast for prime power n, in the sense that for prime p we have
$f(n)$
grows fast for prime power n, in the sense that for prime p we have
![]() $f(p^m)\geq p^{\frac {2}{27}m^2(m-6)}$
(see [Reference Higman22]). Given this ubiquity of finite p-groups, we expect there to be many
$f(p^m)\geq p^{\frac {2}{27}m^2(m-6)}$
(see [Reference Higman22]). Given this ubiquity of finite p-groups, we expect there to be many
![]() $\omega $
-categorical class 2 p-groups not of the types described above. Note, though, that the very flexible “Mekler construction” (see [Reference Mekler32]), though it gives examples of nilpotent class 2 exponent p pseudofinite groups (see [Reference Macpherson and Tent29]), does not preserve
$\omega $
-categorical class 2 p-groups not of the types described above. Note, though, that the very flexible “Mekler construction” (see [Reference Mekler32]), though it gives examples of nilpotent class 2 exponent p pseudofinite groups (see [Reference Macpherson and Tent29]), does not preserve
![]() $\omega $
-categoricity so is not likely to give new examples.
$\omega $
-categoricity so is not likely to give new examples.
The deep theory in [Reference Cherlin and Hrushovski14] yields the following consequence.
Proposition 3.3. Suppose that
![]() $d\in \mathbb {N}$
and
$d\in \mathbb {N}$
and
![]() $\mathcal {C}$
is a family of finite groups such that, for all
$\mathcal {C}$
is a family of finite groups such that, for all
![]() $G\in \mathcal {C}$
, the group
$G\in \mathcal {C}$
, the group
![]() ${{\mathrm {Aut}}}(G)$
has at most d orbits on
${{\mathrm {Aut}}}(G)$
has at most d orbits on
![]() $G^4$
. Then the following hold.
$G^4$
. Then the following hold.
-
(i) There is
 $e\in \mathbb {N}$
such that each
$e\in \mathbb {N}$
such that each
 $G\in \mathcal {C}$
has a normal subgroup N of index at most e, with
$G\in \mathcal {C}$
has a normal subgroup N of index at most e, with
 $N'\leq Z(N)$
and
$N'\leq Z(N)$
and
 $|N'|\leq e$
.
$|N'|\leq e$
. -
(ii) Any ultraproduct of members of
 $\mathcal {C}$
is FAF with
$\mathcal {C}$
is FAF with
 $\omega $
-categorical theory.
$\omega $
-categorical theory.
Proof.
-
(i) It follows from the structure theory developed in [Reference Cherlin and Hrushovski14] (see e.g., Theorem 6) that the (sufficiently large) members of
 $\mathcal {C}$
fall into finitely many families
$\mathcal {C}$
fall into finitely many families
 $\mathcal {C}_i$
each associated with an
$\mathcal {C}_i$
each associated with an
 $\omega $
-categorical countably infinite Lie coordinatizable group
$\omega $
-categorical countably infinite Lie coordinatizable group
 $G_i$
whose theory is the collection of sentences which hold in all but finitely many groups in
$G_i$
whose theory is the collection of sentences which hold in all but finitely many groups in
 $\mathcal {C}_i$
. In particular, by [Reference Cherlin and Hrushovski14, Theorem 7] such a group is modular with the type amalgamation property and of finite rank (the rank used in [Reference Cherlin and Hrushovski14] can be taken after the fact to be SU-rank). By [Reference Cherlin and Hrushovski14, Proposition 6.2.4] the group
$\mathcal {C}_i$
. In particular, by [Reference Cherlin and Hrushovski14, Theorem 7] such a group is modular with the type amalgamation property and of finite rank (the rank used in [Reference Cherlin and Hrushovski14] can be taken after the fact to be SU-rank). By [Reference Cherlin and Hrushovski14, Proposition 6.2.4] the group
 $G_i$
is FAF, and the result follows.
$G_i$
is FAF, and the result follows. -
(ii) This is immediate from (i).
Thus, for any construction of an
![]() $\omega $
-categorical pseudofinite not virtually finite-by-abelian group, the
$\omega $
-categorical pseudofinite not virtually finite-by-abelian group, the
![]() $\omega $
-categoricity will not arise directly from richness of the automorphism groups of a class of finite groups. Such a construction will have to involve some model-theoretic argument to obtain
$\omega $
-categoricity will not arise directly from richness of the automorphism groups of a class of finite groups. Such a construction will have to involve some model-theoretic argument to obtain
![]() $\omega $
-categoricity (e.g., back-and-forth, Fraïssé amalgamation, or axiomatizing an appropriate class). We cannot envisage such a construction which eludes the argument against pseudofiniteness given in Section 2.
$\omega $
-categoricity (e.g., back-and-forth, Fraïssé amalgamation, or axiomatizing an appropriate class). We cannot envisage such a construction which eludes the argument against pseudofiniteness given in Section 2.
Remark 3.4. We list the
![]() $\omega $
-categorical nilpotent groups of which we are aware and for which we have not addressed their pseudofiniteness. First, we have not considered the class 2 groups of exponent 4 with quantifier elimination constructed in [Reference Saracino and Wood36], or indeed the Apps comprehensive groups of Theorem 2.10 with
$\omega $
-categorical nilpotent groups of which we are aware and for which we have not addressed their pseudofiniteness. First, we have not considered the class 2 groups of exponent 4 with quantifier elimination constructed in [Reference Saracino and Wood36], or indeed the Apps comprehensive groups of Theorem 2.10 with
![]() $p=2$
, but would expect similar methods to rule out pseudofiniteness. Likewise, as noted before Proposition 2.13, we do not know if Maier’s group
$p=2$
, but would expect similar methods to rule out pseudofiniteness. Likewise, as noted before Proposition 2.13, we do not know if Maier’s group
![]() $\mathbf {G}_{3,p}$
is pseudofinite. In the other direction, we do not know if the finite-by-abelian groups
$\mathbf {G}_{3,p}$
is pseudofinite. In the other direction, we do not know if the finite-by-abelian groups
![]() $G(\omega ,K)$
considered in Question 2.15 are always pseudofinite.
$G(\omega ,K)$
considered in Question 2.15 are always pseudofinite.
Finally, we note that the structure theory for
![]() $\omega $
-categorical rings (not necessarily commutative) has close parallels to that of
$\omega $
-categorical rings (not necessarily commutative) has close parallels to that of
![]() $\omega $
-categorical groups. Thus, we have the following conjecture and proposition. Recall that a ring R is nilpotent (of class r) if
$\omega $
-categorical groups. Thus, we have the following conjecture and proposition. Recall that a ring R is nilpotent (of class r) if
![]() $x_1\ldots x_r=0$
for any
$x_1\ldots x_r=0$
for any
![]() $x_1,\ldots ,x_r\in R$
. We say R is null if
$x_1,\ldots ,x_r\in R$
. We say R is null if
![]() $xy=0$
for any
$xy=0$
for any
![]() $x,y\in R$
.
$x,y\in R$
.
Conjecture 3.5. If R be an
![]() $\omega $
-categorical pseudofinite ring, then R has a definable 2-sided ideal I of finite index which is finite-by-null, i.e., I has a finite 2-sided ideal J such that
$\omega $
-categorical pseudofinite ring, then R has a definable 2-sided ideal I of finite index which is finite-by-null, i.e., I has a finite 2-sided ideal J such that
![]() $I/J$
is null.
$I/J$
is null.
We remark that every supersimple
![]() $\omega $
-categorical ring is in this sense finite-by-null-by-finite (see [Reference Krupinski and Wagner27, Theorem 3.4], and its proof for the definability assertion).
$\omega $
-categorical ring is in this sense finite-by-null-by-finite (see [Reference Krupinski and Wagner27, Theorem 3.4], and its proof for the definability assertion).
Proposition 3.6. Let R be an
![]() $\omega $
-categorical pseudofinite ring. Then R has a definable nilpotent ideal of finite index.
$\omega $
-categorical pseudofinite ring. Then R has a definable nilpotent ideal of finite index.
Proof. By [Reference Krupinski26, Theorem 3.1], any
![]() $\omega $
-categorical ring whose theory does not have the strict order property has a definable nilpotent ideal of finite index (the definability clause comes from the proof in [Reference Krupinski26], using the corresponding definability in Corollary 2.2). The result now follows from Lemma 2.1.
$\omega $
-categorical ring whose theory does not have the strict order property has a definable nilpotent ideal of finite index (the definability clause comes from the proof in [Reference Krupinski26], using the corresponding definability in Corollary 2.2). The result now follows from Lemma 2.1.
Acknowledgments
We warmly thank Bettina Eick for very helpful discussions related to the proof of Corollary 2.5, and Laurent Bartholdi, for allowing us to include the proof of Lemma 2.4 which he provided. We also thank Christian d’Elbée for several very helpful discussions.
Funding
The research of the second author was funded through the Cluster of Excellence by the German Research Foundation (DFG) under Germany’s Excellence Strategy EXC 2044–390685587, Mathematics Münster: Dynamics–Geometry–Structure and by CRC 1442 Geometry: Deformations and Rigidity.