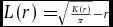Within the second paragraph of page 494 incorrect language was used to characterize the summary characteristics used. Sentences 3–11 of this paragraph should have read:
Second, we calculated three univariate summary characteristics: the nearest neighbour distribution function D(r), the pair-correlation function g(r) and the K-function K(r). The use of multiple summary characteristics holds increased power to characterize variation in spatial patterns (Wiegand et al. 2013). The univariate nearest neighbour distribution function D(r) can be interpreted as the probability that the typical adult tree has its nearest neighbouring adult tree within radius r (or alternatively, the probability that the typical defecation has its nearest neighbouring defecation within radius r). The univariate pair-correlation function g(r) is a non-cumulative normalized neighbourhood density function that gives the expected number of points within rings of radius r and width w centred on a typical point, divided by the mean density of points λ in the study region (Wiegand et al. 2009). We applied g(r) to trees and defecation point patterns separately, using a ring width of 10 m. The K-function K(r) provides a cumulative counterpart to the non-cumulative pair-correlation function g(r) by analysing dispersion and aggregation up to distance r rather than at distance r (Weigand & Moloney 2004). The K-function can be defined as the number of expected points (i.e. either trees or defecations) within circles of radius r extending from a typical point, divided by the mean density of points λ within the study region. Here, we apply the square root transformation L(r) to the K-function to remove scale dependence and stabilize the variance: 
$L( r ) = \scriptstyle\sqrt {\frac{{K( r )}}{\pi }} - r$ (Besag 1977, Wiegand & Moloney 2014).
The authors apologize for this error and any confusion it may have caused.
