Time-series model to predict impact of H1N1 influenza on a children's hospital

Summary

The spring of 2009 witnessed the emergence of a novel influenza A(H1N1) virus resulting in the first influenza pandemic since 1968. In autumn of 2010, the 2009 novel H1N1 influenza strain re-emerged. We performed a retrospective time-series analysis of all patients with laboratory-confirmed H1N1 influenza who presented to our institution during 2009. Cases of influenza were assembled into 3-day aggregates and forecasting models of H1N1 influenza incidence were created. Forecasting estimates of H1N1 incidence for the 2010–2011 season were compared to actual values for our institution to assess model performance. Ninety-five percent confidence intervals calculated around our model's forecasts were accurate to ±3·6 cases per 3-day period for our institution. Our results suggest that time-series models may be useful tools in forecasting the incidence of H1N1 influenza, helping institutions to optimize distribution of resources based on the changing burden of illness.

INTRODUCTION

In the USA, influenza is a common cause of illness and hospitalization in children. Children with chronic medical conditions are at increased risk of morbidity and mortality [1]. A multistate population-based surveillance for influenza-associated hospitalization demonstrated that up to 11% of hospitalized children with laboratory-confirmed influenza required treatment in the intensive care unit with 3% requiring mechanical ventilation [2]. Caring for children with moderate to severe influenza can have a substantial impact on resource utilization in the hospital.

The spring of 2009 witnessed the emergence of a novel influenza A(H1N1) virus of swine origin that resulted in the first influenza pandemic since 1968 with circulation outside the usual influenza season in the Northern Hemisphere [3]. In the USA, the pandemic demonstrated two discrete waves; the first in spring 2009 and a second in late summer and early autumn 2009. Most of the illness of the 2009 pandemic was acute and self-limiting; however, the highest attack rates were reported in children and young adults [3]. As with seasonal influenza, children with chronic medical conditions were at increased risk of complications from H1N1 influenza [4]. In late autumn 2010, the United States Centers for Disease Control and Prevention reported that the 2009 novel H1N1 influenza strain had re-emerged [5].

The application of time-series analysis in the creation of models for infectious disease surveillance [6–8] and resource utilization [9–12] has increased in recent years. The emergence of the H1N1 influenza virus in 2009 and the re-emergence of the same virus in 2010 provided a unique opportunity to investigate the application of time-series analysis techniques in the creation of forecasting models [13]. Accurate surveillance and forecasting of the presentation of H1N1 influenza could have a significant impact on resource utilization and planning for future pandemics and seasonal epidemics.

We hypothesized that a mathematical model could be designed based on analysis of data from our institution, that would effectively capture the periodicity of H1N1 influenza and forecast the incidence of H1N1 influenza presentation to our institution.

METHODS

The Institutional Review Board of the Children's National Medical Center approved this study. We performed a retrospective cohort study identifying all patients with laboratory-confirmed H1N1 influenza infection who presented to the Children's National Medical Center, a 283-bed urban academic tertiary-care children's hospital, between May 2009 and April 2011. Laboratory-confirmed viral infection was defined as identification of H1N1 influenza from a nasopharyngeal or endotracheal specimen by polymerase chain reaction-based techniques. Multiple positive specimens from an individual patient collected within 14 days of one another were considered a unique case [14].

Cases of H1N1 influenza were assembled into 3-day aggregates based on the date of specimen collection. Cases from the 2009 H1N1 influenza pandemic (31 May 2009 to 26 December 2009) were designated as the experimental dataset. Cases from the 2010–2011 H1N1 influenza season (16 December 2010 to 20 April 2011) were designated as the validation dataset.

The experimental dataset was plotted as a time-series and assessed for stationarity using the augmented Dickey–Fuller test for unit roots. Differencing operations were taken in the event that augmented Dickey–Fuller testing suggested the presence of unit roots. Type I error was set at 0·05. The autocorrelation and partial autocorrelation functions were calculated and plotted to aid in the initial identification of a base Box–Jenkins model. Following identification of a base model, non-significant parameters were systematically removed based on the minimization of Akaike's Information Criterion (AIC) to establish our optimal model [15]. To examine the impact that climatological factors have on model performance, we constructed models based on our optimal model that included 3-day averages of maximal and minimal temperature, and precipitation as recorded by the National Climate Data Center for Washington, DC. Maximum-likelihood testing was employed to determine inclusion or exclusion of specific model parameters at a significance level of 0·10. Maximum-likelihood estimation was used to calculate model parameter coefficients.

To assess the performance of our model at forecasting, model estimates were derived and plotted against the validation dataset, forecasting 3, 6 and 15 days into the future. Root mean squared errors (RMSEs) of the forecasts were calculated to derive 95% confidence intervals about the forecasts.

We examined the impact of model updating by recalculating model parameters for our model using data through two time points (29 January 2011 and 28 February 2011). For each update of the model, forecasts were recalculated and compared to the validation datasets. RMSEs of the updated forecasts were calculated to derive 95% confidence intervals about the updated forecasts. All calculations were performed using Stata/IC 10.1 (Stata Corporation, USA).

RESULTS

A total of 462 cases of laboratory-confirmed H1N1 influenza infection in children at the Children's National Medical Center were included in the analysis. Cases of H1N1 influenza infection were assembled into 3-day aggregates and partitioned into experimental (355 cases) and validation (107 cases) datasets. Augmented Dickey–Fuller testing on the experimental datasets demonstrated the presence of unit roots and non-stationarity. First-order differencing of the 3-day aggregates was performed and the resulting differenced series was stationary by augmented Dickey–Fuller testing (P<0·01).

The plot of the autocorrelation function resembled a dampened sine wave while the partial autocorrelation function had significant cut-offs at lags 1 and 6, suggesting an autoregressive process of order 6 with first-order differencing as the base model:

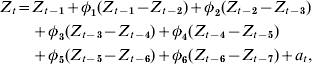
where Z _t=H1N1 cases for time period t, Z _t−i=H1N1 cases for time period t−i, ɸ_t−i=weighted coefficient for H1N1 case difference between time periods t−i and t−(i+1), and a _t=white-noise term for time period t.

Parameters were removed systematically to minimize AIC, including only those parameters significant by maximum-likelihood testing, leading to an autoregressive model with first-order differencing, with significant lags at lag 1 (P=0·001), lag 3 (P=0·039), and lag 6 (P=0·011). We designated this as our optimal model:

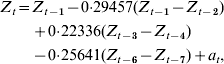
where Z _t=H1N1 cases for time period t, Z _t−i=H1N1 cases for time period t−i, and a _t=white-noise term for time period t.

The addition of 3-day averages of maximal and minimal temperature and precipitation variables to our optimal model did not significantly help to explain the incidence of H1N1 influenza infection by maximum-likelihood testing.

Forecasts were derived for our optimal model and plotted against the validation dataset (Fig. 1). The RMSE was 1·78, 2·02 and 1·92 for the 3-day, 6-day, and 15-day forecasts of the model, respectively. Ninety-five percent confidence intervals calculated around the model's forecasts were accurate to ±3·6, ±4·0 and ±3·8 cases per 3-day time period forecasting 3 days, 6 days and 15 days into the future, respectively. On average for the validation time period, the true H1N1 influenza activity was overestimated by <0·01 cases per 3-day period.

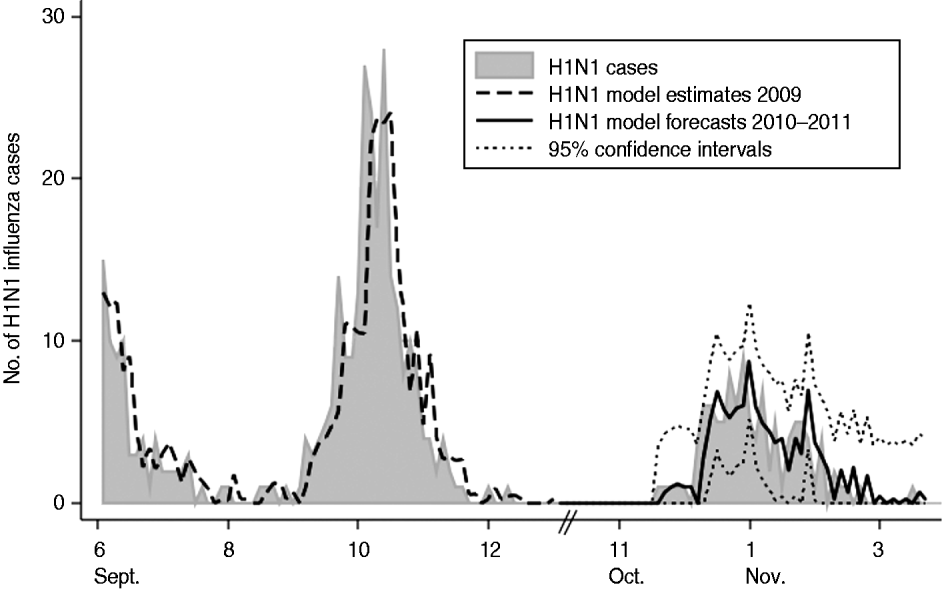
Fig. 1. Plot of actual 3-day incidence of H1N1 influenza cases vs. model estimates and forecasts with 95% confidence intervals for the Children's National Medical Center, forecasting 3 days into the future for 2009–2011. Note: January 2010 to November 2010 not included as H1N1 influenza incidence during this time was zero.

We assessed the value of updating our optimal model at two time periods during the validation time frame (29 January 2011 and 28 February 2011). Updating model parameters with data up to 29 January 2011 reduced the RMSE to 1·62 for the 3-day forecasts for the remaining time points. Updating model parameters with data up to 28 February 2011 reduced the RMSE further to 1·07 for the 3-day forecasts for the remaining time points. Ninety-five percent confidence intervals calculated around the updated models' forecasts were accurate to ±3·3 and ±2·1 cases per 3-day time period for the January and February updates, respectively.

DISCUSSION

The impact of H1N1 on resource utilization during the 2009 pandemic and 2010–2011 seasonal epidemic was substantial in both the outpatient and inpatient settings. Bed utilization, isolation procedures, availability of resources (physicians, nurses, respiratory therapists) and medical equipment (ventilators, nebulization systems) are just a few of the factors inherent to resource utilization affected by the influx of patients with H1N1 influenza. Our identified models, derived from historical data from our institution produced accurate 3-, 6- and 15-day forecasts of H1N1 influenza incidence in our hospital. We believe this model can be used prospectively to anticipate and adjust, in real-time, resource allocation.

During the 2009 pandemic, 20% of patients admitted to our institution required admission to the intensive care unit. One published series of children with H1N1 influenza requiring admission to the intensive care unit reported that 46% of those children required mechanical ventilation [4]. The management of mechanical ventilation in neonates, infants and small children is complex and requires specialized equipment and trained paediatric respiratory therapy personnel.

There has been considerable interest in the possible links between climatological and environmental factors and the incidence of influenza. The inclusion of variables, such as solar radiation, land surface temperature, relative humidity and maximum atmospheric pressure, have contributed to the explanation of seasonal influenza incidence in previously reported models, although often for very specific locations [16, 17].

In our study, we did not demonstrate any association between H1N1 influenza incidence and certain climatological variables. The reasons for this observation are most likely multi-factorial but probably relate to the nature of a virulent novel agent in a largely susceptible population overriding any climatic factors that might affect viral transmission.

Our study focused on the use of time-series analysis, specifically Box–Jenkins modelling, to model and forecast H1N1 incidence for our institution. A number of other modelling approaches have been developed to characterize and quantify the transmission of seasonal and pandemic influenza. Complex mechanistic models exist that incorporate a number of epidemiological variables in an attempt to quantify the transmission potential of pandemic influenza [18, 19].

Our study has a number of limitations. Our model is specific to a single institution and we have no evidence to suggest that it can be generalized to other institutions or communities. Despite the specificity of the model, our objective was to design a model particular to our own institution. While further work is required to assess if similar models can be constructed for institutions in other locations, our experience suggests that these models work well at the local and institutional levels for short-term forecasts of H1N1 influenza incidence.

During the 2009 pandemic it was the policy at our institution, as well as most other institutions, to test for H1N1 influenza in patients who presented with a febrile illness which warranted antiviral treatment and/or hospitalization. This practice, endorsed by the United States Centers for Disease Control and Prevention, most likely led to an increased recognition of cases during the 2009 time period compared to other non-pandemic years like 2010–2011. As such, it is possible that some patients with H1N1 influenza who presented to our institution during the 2010–2011 season with only mild symptoms may have gone unrecognized.

The practical aspects of predicting 3 days into the future are limited and most likely vary among institutions. Our model lost little accuracy when forecasts were derived 6 days and 15 days into the future. Short-term forecasting can help hospital leadership prepare for changes in resource needs brought on by the demands of a surge in viral respiratory admissions.

Using time-series analysis, specifically Box–Jenkins modelling, to create a univariate model of H1N1 influenza incidence allows for the relatively easy creation of an institution-specific forecasting model. As the 2010–2011 resurgence of 2009 novel H1N1 influenza did not follow a similar seasonal incidence as that of 2009, the addition of seasonal components to the model did not help predict incidence as might be expected in seasonal influenza or other respiratory viruses such as respiratory syncytial virus. The lack of a seasonal component limits our model's ability to predict the onset and offset of H1N1 incidence at our institution. A multi-tiered modelling system whereby incidence at the regional or community levels is a component of an institution-specific model like ours may be a solution to this limitation [20].

Our results suggest that time-series models may be useful tools in forecasting the burden of H1N1 influenza infection at the institutional level, helping institutions to optimize distribution of resources based on the changing burden and severity of illness in their respective communities.