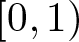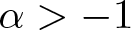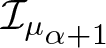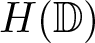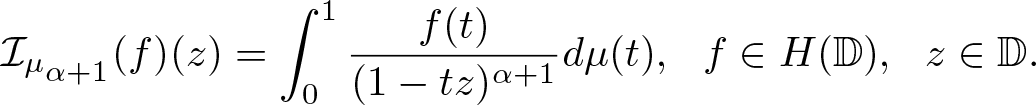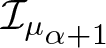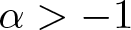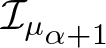1. Introduction
Let ![]() $\mathbb{D}=\{z\in \mathbb{C}:\vert z\vert \lt 1\}$ denote the open unit disk of the complex plane
$\mathbb{D}=\{z\in \mathbb{C}:\vert z\vert \lt 1\}$ denote the open unit disk of the complex plane ![]() $\mathbb{C}$ and
$\mathbb{C}$ and ![]() $H(\mathbb{D})$ denote the space of all analytic functions in
$H(\mathbb{D})$ denote the space of all analytic functions in ![]() $\mathbb{D}$.
$\mathbb{D}$.
The Bloch space ![]() $\mathcal {B}$ consists of those functions
$\mathcal {B}$ consists of those functions ![]() $f\in H(\mathbb{D}) $ for which
$f\in H(\mathbb{D}) $ for which
 \begin{equation*}
\vert \vert f\vert \vert _{\mathcal {B}}=\vert f(0)\vert +\sup_{z\in \mathbb{D}}(1-\vert z\vert ^{2})\vert f'(z)\vert \lt \infty.
\end{equation*}
\begin{equation*}
\vert \vert f\vert \vert _{\mathcal {B}}=\vert f(0)\vert +\sup_{z\in \mathbb{D}}(1-\vert z\vert ^{2})\vert f'(z)\vert \lt \infty.
\end{equation*} The little Bloch space ![]() $\mathcal {B}_{0}$ is the closed subspace of
$\mathcal {B}_{0}$ is the closed subspace of ![]() $\mathcal {B}$ consisting of those functions
$\mathcal {B}$ consisting of those functions ![]() $f\in H(\mathbb{D}) $ such that
$f\in H(\mathbb{D}) $ such that
 \begin{equation*}
\lim_{\vert z\vert \rightarrow 1^{-}}(1-\vert z\vert ^{2})\vert f'(z)\vert =0.
\end{equation*}
\begin{equation*}
\lim_{\vert z\vert \rightarrow 1^{-}}(1-\vert z\vert ^{2})\vert f'(z)\vert =0.
\end{equation*} Let ![]() $0 \lt p\leq\infty$, and the classical Hardy space Hp consists of those functions
$0 \lt p\leq\infty$, and the classical Hardy space Hp consists of those functions ![]() $f\in H(\mathbb{D})$ for which
$f\in H(\mathbb{D})$ for which
 \begin{equation*}
||f||_{p}=\sup_{0\leq r \lt 1} M_p(r, f) \lt \infty,
\end{equation*}
\begin{equation*}
||f||_{p}=\sup_{0\leq r \lt 1} M_p(r, f) \lt \infty,
\end{equation*}where
 \begin{equation*}
M_p(r, f)= \left(\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^p \text{d}\theta \right)^{1/p}, \ 0 \lt p \lt \infty,
\end{equation*}
\begin{equation*}
M_p(r, f)= \left(\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^p \text{d}\theta \right)^{1/p}, \ 0 \lt p \lt \infty,
\end{equation*} \begin{equation*}M_{\infty}(r, f)=\sup_{|z|=r}|f(z)|.\end{equation*}
\begin{equation*}M_{\infty}(r, f)=\sup_{|z|=r}|f(z)|.\end{equation*} For ![]() $0 \lt p \lt \infty$, the Bergman space A p consists of those
$0 \lt p \lt \infty$, the Bergman space A p consists of those ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}||f||^{p}_{A^{p}}=\int_{\mathbb{D}}|f(z)|^{p}\text{d}A(z) \lt \infty,\end{equation*}
\begin{equation*}||f||^{p}_{A^{p}}=\int_{\mathbb{D}}|f(z)|^{p}\text{d}A(z) \lt \infty,\end{equation*} where  $\text{d}A(z)=\frac{\text{d}x\text{d}y}{\pi}$ is the normalized area measure on
$\text{d}A(z)=\frac{\text{d}x\text{d}y}{\pi}$ is the normalized area measure on ![]() $\mathbb{D}$. The reader is referred to [Reference Duren8] for Hardy spaces and [Reference Zhu25] for Bergman spaces and Bloch spaces.
$\mathbb{D}$. The reader is referred to [Reference Duren8] for Hardy spaces and [Reference Zhu25] for Bergman spaces and Bloch spaces.
Let ![]() $f(z)=\sum_{n=0}^{\infty} a_{n}z^{n}\in H(\mathbb{D})$. For any complex parameters t and s with the property that neither
$f(z)=\sum_{n=0}^{\infty} a_{n}z^{n}\in H(\mathbb{D})$. For any complex parameters t and s with the property that neither ![]() $1+t$ nor
$1+t$ nor ![]() $1+t+s$ is a negative integer, the fractional differential operator
$1+t+s$ is a negative integer, the fractional differential operator ![]() $R^{t,s}$ and the fractional integral operator
$R^{t,s}$ and the fractional integral operator ![]() $R_{t,s}$ are defined as follows:
$R_{t,s}$ are defined as follows:
 \begin{equation*}
R^{t,s}f(z)=\sum_{n=0}^{\infty}\frac{\Gamma(2+t)\Gamma(n+2+t+s)}{\Gamma(2+t+s)\Gamma(n+2+t)}a_{n}z^{n},
\end{equation*}
\begin{equation*}
R^{t,s}f(z)=\sum_{n=0}^{\infty}\frac{\Gamma(2+t)\Gamma(n+2+t+s)}{\Gamma(2+t+s)\Gamma(n+2+t)}a_{n}z^{n},
\end{equation*} \begin{equation*}
R_{t,s}f(z)=\sum_{n=0}^{\infty}
\frac{\Gamma(2+t+s)\Gamma(n+2+t)}{\Gamma(2+t)\Gamma(n+2+s+t)}a_{n}z^{n}.
\end{equation*}
\begin{equation*}
R_{t,s}f(z)=\sum_{n=0}^{\infty}
\frac{\Gamma(2+t+s)\Gamma(n+2+t)}{\Gamma(2+t)\Gamma(n+2+s+t)}a_{n}z^{n}.
\end{equation*} Let µ be a finite positive Borel measure on ![]() $[0,1)$ and
$[0,1)$ and ![]() $n\in \mathbb{N}$. We use µn to denote the sequence of order n of µ, that is,
$n\in \mathbb{N}$. We use µn to denote the sequence of order n of µ, that is,  $\mu_{n}=\int_{[0,1)}t^{n}\text{d}\mu(t)$. Let
$\mu_{n}=\int_{[0,1)}t^{n}\text{d}\mu(t)$. Let ![]() $\mathcal {H}_{\mu}$ be the Hankel matrix
$\mathcal {H}_{\mu}$ be the Hankel matrix ![]() $(\mu_{n,k})_{n,k\geq 0}$ with entries
$(\mu_{n,k})_{n,k\geq 0}$ with entries ![]() $\mu_{n,k}=\mu_{n+k}$. The matrix
$\mu_{n,k}=\mu_{n+k}$. The matrix ![]() $\mathcal {H}_{\mu}$ induces an operator on
$\mathcal {H}_{\mu}$ induces an operator on ![]() $ H(\mathbb{D}) $ by its action on the Taylor coefficients:
$ H(\mathbb{D}) $ by its action on the Taylor coefficients:  $a_{n}\rightarrow\displaystyle{\sum_{k=0}^{\infty}}\mu_{n,k}a_{k},\ n\in \mathbb{N}\cup \{0\}.$ The generalized Hilbert operator
$a_{n}\rightarrow\displaystyle{\sum_{k=0}^{\infty}}\mu_{n,k}a_{k},\ n\in \mathbb{N}\cup \{0\}.$ The generalized Hilbert operator ![]() $\mathcal {H}_{\mu}$ defined on the spaces
$\mathcal {H}_{\mu}$ defined on the spaces ![]() $H(\mathbb{D})$ of analytic functions in the unit disc
$H(\mathbb{D})$ of analytic functions in the unit disc ![]() $\mathbb{D}$ is as follows:
$\mathbb{D}$ is as follows:
If ![]() $f\in H(\mathbb{D})$,
$f\in H(\mathbb{D})$,  $f(z)=\displaystyle{\sum_{n=0}^{\infty}}a_{n}z^{n}$, then
$f(z)=\displaystyle{\sum_{n=0}^{\infty}}a_{n}z^{n}$, then
 \begin{equation*}
\mathcal {H}_{\mu}(f)(z)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{\infty}\mu_{n,k}a_{k}\right)z^{n}, \ \ z\in \mathbb{D},
\end{equation*}
\begin{equation*}
\mathcal {H}_{\mu}(f)(z)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{\infty}\mu_{n,k}a_{k}\right)z^{n}, \ \ z\in \mathbb{D},
\end{equation*} whenever the right hand side makes sense and defines an analytic function in ![]() $\mathbb{D}$.
$\mathbb{D}$.
If µ is the Lebesgue measure on ![]() $[0, 1)$, then the matrix
$[0, 1)$, then the matrix ![]() $\mathcal {H}_{\mu}$ reduces to the classical Hilbert matrix
$\mathcal {H}_{\mu}$ reduces to the classical Hilbert matrix  $\mathcal {H}=(\frac{1}{n+k+1})_{n,k\geq 0}$, which induces the classical Hilbert operator
$\mathcal {H}=(\frac{1}{n+k+1})_{n,k\geq 0}$, which induces the classical Hilbert operator ![]() $\mathcal {H}$. The classic Hilbert operator
$\mathcal {H}$. The classic Hilbert operator ![]() $\mathcal {H}$ has been extensively studied on distinct analytic function spaces recently (see [Reference Bao and Wulan2, Reference Diamantopoulos5–Reference Dostanić, Jevtić and Vukotić7, Reference Lanucha, Nowak and Pavlović15]).
$\mathcal {H}$ has been extensively studied on distinct analytic function spaces recently (see [Reference Bao and Wulan2, Reference Diamantopoulos5–Reference Dostanić, Jevtić and Vukotić7, Reference Lanucha, Nowak and Pavlović15]).
It turns out that the integral operator
 \begin{equation*}\mathcal {I}_{\mu}(f)(z)=\int_{0}^{1} \frac{f(t)}{1-tz}\text{d}\mu(t)\end{equation*}
\begin{equation*}\mathcal {I}_{\mu}(f)(z)=\int_{0}^{1} \frac{f(t)}{1-tz}\text{d}\mu(t)\end{equation*} plays a key role when we study the generalized Hilbert operator ![]() $\mathcal {H}_{\mu}$. Galanopoulos and Peláez [Reference Galanopoulos and Peláez10] characterized the measures µ for which the operator
$\mathcal {H}_{\mu}$. Galanopoulos and Peláez [Reference Galanopoulos and Peláez10] characterized the measures µ for which the operator ![]() $\mathcal {I}_{\mu}$ is well defined in H 1 and proved that
$\mathcal {I}_{\mu}$ is well defined in H 1 and proved that ![]() $\mathcal {H}_{\mu}(f)=\mathcal {I}_{\mu}(f)$ for such measures. Chatzifountas, Girela and Peláez [Reference Chatzifountas, Girela and Peláez4] extended this work to H p for all
$\mathcal {H}_{\mu}(f)=\mathcal {I}_{\mu}(f)$ for such measures. Chatzifountas, Girela and Peláez [Reference Chatzifountas, Girela and Peláez4] extended this work to H p for all ![]() $0 \lt p \lt \infty$. Girela and Merchán [Reference Girela and Merchán12] studied these operators acting on certain conformally invariant spaces of analytic functions. The reader is referred to [Reference Girela and Merchán11, Reference Girela and Merchán13, Reference Jevtić and Karapetrović14, Reference Merchán18, Reference Tang and Zhang22] for more on this topic.
$0 \lt p \lt \infty$. Girela and Merchán [Reference Girela and Merchán12] studied these operators acting on certain conformally invariant spaces of analytic functions. The reader is referred to [Reference Girela and Merchán11, Reference Girela and Merchán13, Reference Jevtić and Karapetrović14, Reference Merchán18, Reference Tang and Zhang22] for more on this topic.
In this paper, we consider the generalized integral type Hilbert operator defined as follows:
 \begin{equation*}\mathcal {I}_{\mu_{\alpha+1}}(f)(z)=\int_{0}^{1} \frac{f(t)}{(1-tz)^{\alpha+1}}\text{d}\mu(t),\ \ \ (\alpha \gt -1).\end{equation*}
\begin{equation*}\mathcal {I}_{\mu_{\alpha+1}}(f)(z)=\int_{0}^{1} \frac{f(t)}{(1-tz)^{\alpha+1}}\text{d}\mu(t),\ \ \ (\alpha \gt -1).\end{equation*} If α = 0, then ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is just the integral operator
$\mathcal {I}_{\mu_{\alpha+1}}$ is just the integral operator ![]() $\mathcal {I}_{\mu}$. It is easy to see that
$\mathcal {I}_{\mu}$. It is easy to see that  $R^{-1,\alpha}\mathcal {I}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$ whenever
$R^{-1,\alpha}\mathcal {I}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$ whenever ![]() $\mathcal {I}_{\mu}(f)$ makes sense and defines an analytic function in
$\mathcal {I}_{\mu}(f)$ makes sense and defines an analytic function in ![]() $\mathbb{D}$. Moreover, the operator
$\mathbb{D}$. Moreover, the operator ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is also closely related to the following generalized Hilbert operator:
$\mathcal {I}_{\mu_{\alpha+1}}$ is also closely related to the following generalized Hilbert operator:
 \begin{equation*} \mathcal{H}^{\alpha}_{\mu}(f)(z)=
\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{\infty}\mu_{n,k}a_{k}\right)z^{n}, \ \ (\alpha \gt -1). \end{equation*}
\begin{equation*} \mathcal{H}^{\alpha}_{\mu}(f)(z)=
\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{\infty}\mu_{n,k}a_{k}\right)z^{n}, \ \ (\alpha \gt -1). \end{equation*} When α = 1, the operators ![]() $\mathcal {I}_{\mu_{2}}$ and
$\mathcal {I}_{\mu_{2}}$ and  $\mathcal {H}^{1}_{\mu}$ have been studied in [Reference Li. Zhao and Su16, Reference Ye and Zhou23, Reference Ye and Zhou24] recently.
$\mathcal {H}^{1}_{\mu}$ have been studied in [Reference Li. Zhao and Su16, Reference Ye and Zhou23, Reference Ye and Zhou24] recently.
Let us mention the following results which were obtained by Ye and Zhou [Reference Ye and Zhou23].
Theorem A Let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
(1)
 $\mathcal {I}_{\mu_{2}}$ is bounded from
$\mathcal {I}_{\mu_{2}}$ is bounded from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(2)
 $\mathcal {I}_{\mu_{2}}$ is compact from
$\mathcal {I}_{\mu_{2}}$ is compact from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(3) The measure µ satisfies
 $\int_{0}^{1} \log^{2}\frac{e}{1-t}d\mu(t) \lt \infty.$
$\int_{0}^{1} \log^{2}\frac{e}{1-t}d\mu(t) \lt \infty.$
Theorem B Let ![]() $1 \lt p \lt \infty$ and
$1 \lt p \lt \infty$ and  $\frac{1}{p}+\frac{1}{q}=1$. Suppose µ is a positive Borel measure on
$\frac{1}{p}+\frac{1}{q}=1$. Suppose µ is a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Let ν be the positive Borel measure on
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Let ν be the positive Borel measure on ![]() $[0, 1) $ defined by
$[0, 1) $ defined by ![]() $d\nu(t)=\log\frac{e}{1-t}d\mu(t)$. Then, the following statements are equivalent:
$d\nu(t)=\log\frac{e}{1-t}d\mu(t)$. Then, the following statements are equivalent:
(1)
 $\mathcal {I}_{\mu_{2}}$ is bounded from
$\mathcal {I}_{\mu_{2}}$ is bounded from  $\mathcal {B}$ to A p.
$\mathcal {B}$ to A p.(2)
 $\mathcal {I}_{\mu_{2}}$ is compact from
$\mathcal {I}_{\mu_{2}}$ is compact from  $\mathcal {B}$ to A p.
$\mathcal {B}$ to A p.(3) The measure ν satisfies
 \begin{equation*}\left|\int_{0}^{1} g(t)d\nu(t)\right|\leq C ||g||_{A^{q}}, \ \ \mbox{for every}\ g\in A^{q}. \end{equation*}
\begin{equation*}\left|\int_{0}^{1} g(t)d\nu(t)\right|\leq C ||g||_{A^{q}}, \ \ \mbox{for every}\ g\in A^{q}. \end{equation*}
The condition (3) in Theorem B is rather abstract and difficult to verify in general. In this paper, we shall extend the results for α = 1 to all ![]() $\alpha \gt -1$, and we shall give a new characterization that makes the results more natural and practical. This also allows us to investigate the action of
$\alpha \gt -1$, and we shall give a new characterization that makes the results more natural and practical. This also allows us to investigate the action of ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ from the Bloch space to Hardy spaces and Besov spaces. To state the main results, let us introduce some notions. We let ν be the positive Borel measure on
$\mathcal {I}_{\mu_{\alpha+1}}$ from the Bloch space to Hardy spaces and Besov spaces. To state the main results, let us introduce some notions. We let ν be the positive Borel measure on ![]() $[0, 1) $ defined by
$[0, 1) $ defined by ![]() $\text{d}\nu(t)=\log\frac{e}{1-t}\text{d}\mu(t)$ and
$\text{d}\nu(t)=\log\frac{e}{1-t}\text{d}\mu(t)$ and  $\nu_{n}=\int_{0}^{1} t^{n}\text{d}\nu(t)$. For
$\nu_{n}=\int_{0}^{1} t^{n}\text{d}\nu(t)$. For ![]() $1 \lt p \lt \infty$, we set
$1 \lt p \lt \infty$, we set  $X_{p}=A^{\frac{p}{p-1}}$ and
$X_{p}=A^{\frac{p}{p-1}}$ and ![]() $X_{1}=\mathcal {B}_{0}$ for p = 1. Throughout the paper, we always assume that
$X_{1}=\mathcal {B}_{0}$ for p = 1. Throughout the paper, we always assume that ![]() $\alpha \gt -1$ if there are no additional statements.
$\alpha \gt -1$ if there are no additional statements.
Our main results of this paper are stated as follows.
Theorem 1.1 Let ![]() $1\leq p \lt \infty$, and let µ be a positive Borel measure on
$1\leq p \lt \infty$, and let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
(1) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from
$\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from  $\mathcal {B}$ to A p.
$\mathcal {B}$ to A p.(2) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from  $\mathcal {B}$ to A p.
$\mathcal {B}$ to A p.(3) The measure ν satisfies
 $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lt \infty.$
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lt \infty.$(4) The measure ν satisfies
 $\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{X_{p}}$ for all
$\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{X_{p}}$ for all  $g\in X_{p}$.
$g\in X_{p}$.
Here, we point out that the condition  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$ in Theorems A, B and 1.1 is necessary. The operator
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$ in Theorems A, B and 1.1 is necessary. The operator ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is well defined in the Bloch space
$\mathcal {I}_{\mu_{\alpha+1}}$ is well defined in the Bloch space ![]() $\mathcal {B}$ if and only if
$\mathcal {B}$ if and only if  $\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. In fact, if
$\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. In fact, if ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is well defined in the Bloch space
$\mathcal {I}_{\mu_{\alpha+1}}$ is well defined in the Bloch space ![]() $\mathcal {B}$, take
$\mathcal {B}$, take ![]() $f(z)=\log\frac{e}{1-z}\in \mathcal {B}$ and then
$f(z)=\log\frac{e}{1-z}\in \mathcal {B}$ and then  $|\mathcal {I}_{\mu_{\alpha+1}}(f)(0)| \lt \infty$. Since µ is a positive measure and
$|\mathcal {I}_{\mu_{\alpha+1}}(f)(0)| \lt \infty$. Since µ is a positive measure and ![]() $\log\frac{e}{1-t} \gt 0$ for all
$\log\frac{e}{1-t} \gt 0$ for all ![]() $t\in [0,1)$, we have that
$t\in [0,1)$, we have that
 \begin{equation*}|\mathcal {I}_{\mu_{\alpha+1}}(f)(0)|=\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \infty.\end{equation*}
\begin{equation*}|\mathcal {I}_{\mu_{\alpha+1}}(f)(0)|=\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \infty.\end{equation*} On the other hand, if  $\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then for each
$\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then for each ![]() $f\in \mathcal {B}$,
$f\in \mathcal {B}$, ![]() $0 \lt r \lt 1$ and all
$0 \lt r \lt 1$ and all ![]() $z\in \mathbb{D}$ with
$z\in \mathbb{D}$ with ![]() $|z|\leq r$, we have
$|z|\leq r$, we have
 \begin{equation*} \begin{split}
|\mathcal {I}_{\mu_{\alpha+1}}(f)(z)| &\leq \int_{0}^{1}\frac{|f(t)|}{|1-tz|^{\alpha+1}}\text{d}\mu(t)\leq \frac{1}{(1-|z|)^{\alpha+1}}\int_{0}^{1}|f(t)|\text{d}\mu(t)\\
& \lesssim \frac{||f||_{\mathcal {B}}}{(1-|z|)^{\alpha+1}}\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\lesssim \frac{||f||_{\mathcal {B}}}{(1-|z|)^{\alpha+1}}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
|\mathcal {I}_{\mu_{\alpha+1}}(f)(z)| &\leq \int_{0}^{1}\frac{|f(t)|}{|1-tz|^{\alpha+1}}\text{d}\mu(t)\leq \frac{1}{(1-|z|)^{\alpha+1}}\int_{0}^{1}|f(t)|\text{d}\mu(t)\\
& \lesssim \frac{||f||_{\mathcal {B}}}{(1-|z|)^{\alpha+1}}\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\lesssim \frac{||f||_{\mathcal {B}}}{(1-|z|)^{\alpha+1}}.
\end{split} \end{equation*} This implies that  $\mathcal {I}_{\mu_{\alpha+1}}(f)(z)$ uniformly converges on any compact subset of
$\mathcal {I}_{\mu_{\alpha+1}}(f)(z)$ uniformly converges on any compact subset of ![]() $\mathbb{D}$ and hence is analytic in
$\mathbb{D}$ and hence is analytic in ![]() $\mathbb{D}$.
$\mathbb{D}$.
Throughout the paper, the letter C will denote an absolute constant whose value depends on the parameters indicated in the parentheses and may change from one occurrence to another. We will use the notation ‘![]() $P\lesssim Q$’ if there exists a constant
$P\lesssim Q$’ if there exists a constant ![]() $C=C(\cdot) $ such that ‘
$C=C(\cdot) $ such that ‘![]() $P \leq CQ$’, and ‘
$P \leq CQ$’, and ‘![]() $P \gt rsim Q$’ is understood in an analogous manner. In particular, if ‘
$P \gt rsim Q$’ is understood in an analogous manner. In particular, if ‘![]() $P\lesssim Q$’ and ‘
$P\lesssim Q$’ and ‘![]() $P \gt rsim Q$’ , then we will write ‘
$P \gt rsim Q$’ , then we will write ‘![]() $P\asymp Q$’.
$P\asymp Q$’.
2. Proofs and some related results
We start recalling that for a function ![]() $f(z)=\sum_{n=0}^\infty
a_nz^n$ analytic in
$f(z)=\sum_{n=0}^\infty
a_nz^n$ analytic in ![]() $\mathbb{D}$, the polynomials
$\mathbb{D}$, the polynomials ![]() $\Delta_jf$ are defined as follows:
$\Delta_jf$ are defined as follows:
 \begin{equation*}
\Delta_jf(z)=\sum_{k=2^j}^{2^{j+1}-1} a_kz^k, \quad\text{for}~j\geq 1,
\end{equation*}
\begin{equation*}
\Delta_jf(z)=\sum_{k=2^j}^{2^{j+1}-1} a_kz^k, \quad\text{for}~j\geq 1,
\end{equation*} The polynomials  $\Delta_j=\Delta(\frac{1}{1-z})=\sum^{2^{j+1}-1}_{k=2^{j}}z^{j}$ have the following property (see, e.g. [Reference Pavlović20])
$\Delta_j=\Delta(\frac{1}{1-z})=\sum^{2^{j+1}-1}_{k=2^{j}}z^{j}$ have the following property (see, e.g. [Reference Pavlović20])
 \begin{equation}
||\Delta||_{p}\asymp 2^{j(1-\frac{1}{p})}, \ \ j\in \mathbb{N}, \ 1 \lt p \lt \infty.
\end{equation}
\begin{equation}
||\Delta||_{p}\asymp 2^{j(1-\frac{1}{p})}, \ \ j\in \mathbb{N}, \ 1 \lt p \lt \infty.
\end{equation}Mateljević and Pavlović [Reference Mateljević and Pavlović17] proved the following result.
Lemma 2.1. Let ![]() $1 \lt p \lt \infty$. For a function
$1 \lt p \lt \infty$. For a function ![]() $f\in H(\mathbb{D})$, we define:
$f\in H(\mathbb{D})$, we define:
 \begin{equation*}K_{1}(f):=\int_{\mathbb{D}} |f(z)|^{p}dA(z),\ \ \ K_{2}(f):=\sum_{n=0}^{\infty} 2^{-n}||\Delta_{n}f||^{p}_{p}.\end{equation*}
\begin{equation*}K_{1}(f):=\int_{\mathbb{D}} |f(z)|^{p}dA(z),\ \ \ K_{2}(f):=\sum_{n=0}^{\infty} 2^{-n}||\Delta_{n}f||^{p}_{p}.\end{equation*} Then, ![]() $K_{1}(f)\asymp K_{2}(f)$.
$K_{1}(f)\asymp K_{2}(f)$.
Lemma 2.2. [Reference Pavlović and Mateljević19, Theorem 1]
Let ![]() $0 \lt \beta,p \lt \infty$, and let
$0 \lt \beta,p \lt \infty$, and let ![]() $\{\lambda_{n}\}_{n=0}^{\infty}$ be a sequence of positive numbers. Then,
$\{\lambda_{n}\}_{n=0}^{\infty}$ be a sequence of positive numbers. Then,
 \begin{equation*}\int_{0}^{1}(1-r)^{p\beta-1}\left(\sum_{n=0}^{\infty} \lambda_{n}r^{n}\right)^{p}dr\asymp \sum_{n=0}^{\infty} 2^{-np\beta}\left(\sum_{k\in I_{n}}\lambda_{k}\right)^{p}\end{equation*}
\begin{equation*}\int_{0}^{1}(1-r)^{p\beta-1}\left(\sum_{n=0}^{\infty} \lambda_{n}r^{n}\right)^{p}dr\asymp \sum_{n=0}^{\infty} 2^{-np\beta}\left(\sum_{k\in I_{n}}\lambda_{k}\right)^{p}\end{equation*} where ![]() $I_{0}=\{0\}$,
$I_{0}=\{0\}$, ![]() $I_{n}=[2^{n-1},2^{n})\cap \mathbb{N}$ for
$I_{n}=[2^{n-1},2^{n})\cap \mathbb{N}$ for ![]() $n\in \mathbb{N}$.
$n\in \mathbb{N}$.
The proof of the next result can be found in [Reference Lanucha, Nowak and Pavlović15, Lemma 3.4].
Lemma 2.3. Let ![]() $1 \lt p \lt \infty$, and let
$1 \lt p \lt \infty$, and let ![]() $\gamma=\{\gamma_{k}\}_{k=0}^{\infty}$ be a monotone sequence of positive numbers. Let
$\gamma=\{\gamma_{k}\}_{k=0}^{\infty}$ be a monotone sequence of positive numbers. Let ![]() $g(z)=\sum_{k=0}^{\infty}b_{k}z^{k}$ and
$g(z)=\sum_{k=0}^{\infty}b_{k}z^{k}$ and ![]() $(\gamma g)(z)=\sum_{k=0}^{\infty}b_{k}\gamma_{k}z^{k}$.
$(\gamma g)(z)=\sum_{k=0}^{\infty}b_{k}\gamma_{k}z^{k}$.
(1) If
 $ \{\gamma_{k}\}_{k=0}^{\infty}$ is nondecreasing, then
$ \{\gamma_{k}\}_{k=0}^{\infty}$ is nondecreasing, then
 \begin{equation*}\gamma_{2^{n}}||\Delta_{n} g||_{p}\lesssim||\Delta_{n}(\gamma g)||_{p}\lesssim \gamma_{2^{n+1}}||\Delta_{n} g||_{p}.\end{equation*}
\begin{equation*}\gamma_{2^{n}}||\Delta_{n} g||_{p}\lesssim||\Delta_{n}(\gamma g)||_{p}\lesssim \gamma_{2^{n+1}}||\Delta_{n} g||_{p}.\end{equation*}(2) If
 $ \{\gamma_{k}\}_{k=0}^{\infty}$ is nonincreasing, then
$ \{\gamma_{k}\}_{k=0}^{\infty}$ is nonincreasing, then
 \begin{equation*}\gamma_{2^{n+1}}||\Delta_{n} g||_{p}\lesssim||\Delta_{n}(\gamma g)||_{p}\lesssim \gamma_{2^{n}}||\Delta_{n} g||_{p}.\end{equation*}
\begin{equation*}\gamma_{2^{n+1}}||\Delta_{n} g||_{p}\lesssim||\Delta_{n}(\gamma g)||_{p}\lesssim \gamma_{2^{n}}||\Delta_{n} g||_{p}.\end{equation*}
We also need the following estimates (see, e.g. Proposition 1.4.10 in [Reference Rudin21]).
Lemma 2.4. Let α be any real number and ![]() $z\in \mathbb{D}$. Then
$z\in \mathbb{D}$. Then
 \begin{equation*}
\int^{2\pi}_0\frac{d\theta}{|1-ze^{-i\theta}|^{\alpha}}\asymp
\begin{cases}1 & \quad \text{if} \ \ \alpha \lt 1,\\
\log\frac{2}{1-|z|^2} & \quad \text{if} \ \ \alpha=1,\\
\frac{1}{(1-|z|^2)^{\alpha-1}} & \quad \text{if}\ \ \alpha \gt 1,
\end{cases}
\end{equation*}
\begin{equation*}
\int^{2\pi}_0\frac{d\theta}{|1-ze^{-i\theta}|^{\alpha}}\asymp
\begin{cases}1 & \quad \text{if} \ \ \alpha \lt 1,\\
\log\frac{2}{1-|z|^2} & \quad \text{if} \ \ \alpha=1,\\
\frac{1}{(1-|z|^2)^{\alpha-1}} & \quad \text{if}\ \ \alpha \gt 1,
\end{cases}
\end{equation*}Proof.  $(1)\Rightarrow(3)$
$(1)\Rightarrow(3)$
Suppose that ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded operator from
$\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded operator from ![]() $ \mathcal {B}$ to A p. Take
$ \mathcal {B}$ to A p. Take ![]() $h(z)=\log\frac{e}{1-z}\in \mathcal {B}$, then
$h(z)=\log\frac{e}{1-z}\in \mathcal {B}$, then  $\mathcal {I}_{\mu_{\alpha+1}} (h)\in A^{p}$ and
$\mathcal {I}_{\mu_{\alpha+1}} (h)\in A^{p}$ and  $||\mathcal {I}_{\mu_{\alpha+1}} (h)||_{A^{p}}\lesssim ||h||_{\mathcal {B}}$.
$||\mathcal {I}_{\mu_{\alpha+1}} (h)||_{A^{p}}\lesssim ||h||_{\mathcal {B}}$.
For p = 1, by Hardy’s inequality and Stirling’s formula
 \begin{equation*} \begin{split}
1& \gt rsim||h||_{\mathcal {B}} \gt rsim ||\mathcal {I}_{\mu_{\alpha+1}}(h)||_{A^{1}}=2\int_{0}^{1}M_{1}(r,\mathcal {I}_{\mu_{\alpha+1}}(h))r\text{d}r\\
& =\frac{1}{\pi} \int_{0}^{1} \int_{0}^{2\pi}\left|\int_{0}^{1} \frac{\log\frac{e}{1-t}}{(1-tr\text{e}^{i\theta})^{\alpha+1}}\text{d}\mu(t)\right|\text{d}\theta r\text{d}r\\
& =\frac{1}{\pi}\int_{0}^{1} \int_{0}^{2\pi}\left|\sum_{n=0}^{\infty} \frac{\Gamma(\alpha+1+n)\nu_{n}}{\Gamma(\alpha+1)\Gamma(n+1)}r^{n}\text{e}^{in\theta}\right|\text{d}\theta r \text{d}r\\
& \gt rsim \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(\alpha+1+n)\nu_{n}}{(n+1)\Gamma(\alpha+1)\Gamma(n+1)}r^{n+1} \text{d}r\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha-2}\nu_{n}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
1& \gt rsim||h||_{\mathcal {B}} \gt rsim ||\mathcal {I}_{\mu_{\alpha+1}}(h)||_{A^{1}}=2\int_{0}^{1}M_{1}(r,\mathcal {I}_{\mu_{\alpha+1}}(h))r\text{d}r\\
& =\frac{1}{\pi} \int_{0}^{1} \int_{0}^{2\pi}\left|\int_{0}^{1} \frac{\log\frac{e}{1-t}}{(1-tr\text{e}^{i\theta})^{\alpha+1}}\text{d}\mu(t)\right|\text{d}\theta r\text{d}r\\
& =\frac{1}{\pi}\int_{0}^{1} \int_{0}^{2\pi}\left|\sum_{n=0}^{\infty} \frac{\Gamma(\alpha+1+n)\nu_{n}}{\Gamma(\alpha+1)\Gamma(n+1)}r^{n}\text{e}^{in\theta}\right|\text{d}\theta r \text{d}r\\
& \gt rsim \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(\alpha+1+n)\nu_{n}}{(n+1)\Gamma(\alpha+1)\Gamma(n+1)}r^{n+1} \text{d}r\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha-2}\nu_{n}.
\end{split} \end{equation*} This implies that ![]() $ \sum_{n=0}^{\infty} (n+1)^{\alpha-2}\nu_{n} \lt \infty$.
$ \sum_{n=0}^{\infty} (n+1)^{\alpha-2}\nu_{n} \lt \infty$.
For p > 1, by Lemma 2.1, we have
 \begin{equation*}||h||_{\mathcal {B}} \gt rsim||\mathcal {I}_{\mu_{\alpha+1}} (h)||_{A^{p}}\asymp \sum_{n=0}^{\infty}2^{-n}||\Delta_{n}(\mathcal {I}_{\mu_{\alpha+1}} (h))||^{p}_{p}.\end{equation*}
\begin{equation*}||h||_{\mathcal {B}} \gt rsim||\mathcal {I}_{\mu_{\alpha+1}} (h)||_{A^{p}}\asymp \sum_{n=0}^{\infty}2^{-n}||\Delta_{n}(\mathcal {I}_{\mu_{\alpha+1}} (h))||^{p}_{p}.\end{equation*}It is obvious that
 \begin{equation}
\mathcal {I}_{\mu_{\alpha+1}}(h)(z)=\sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\int_{0}^{1} t^{n}\log\frac{e}{1-t}\text{d}\mu(t)\right)z^{n}.
\end{equation}
\begin{equation}
\mathcal {I}_{\mu_{\alpha+1}}(h)(z)=\sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\int_{0}^{1} t^{n}\log\frac{e}{1-t}\text{d}\mu(t)\right)z^{n}.
\end{equation}Hence, by (2), Lemma 2.3 and (1) we have
 \begin{equation*} \begin{split}
1 & \gt rsim||h||_{\mathcal {B}} \gt rsim \sum_{n=0}^{\infty}2^{-n}||\Delta_{n}(\mathcal {I}_{\mu_{\alpha+1}} (h))||^{p}_{p}\\
&= \sum_{n=0}^{\infty}2^{-n}\left\|\sum^{2^{n+1}-1}_{k=2^{n}}\frac{\Gamma(\alpha+1+k)}{\Gamma(\alpha+1)\Gamma(k+1)}\nu_{k} z^{k}\right\|_{p}^{p}\\
& \gt rsim \sum_{n=0}^{\infty}2^{-n}\nu_{2^{n+1}}^{p}\left\|\Delta_{n}\left(\frac{1}{(1-z)^{\alpha+1}}\right)\right\|^{p}_{p}\\
& \gt rsim \sum_{n=0}^{\infty}2^{n(p\alpha-1)}\nu_{2^{n+1}}^{p} ||\Delta_{n}||_{p}^{p}\\
& \asymp \sum_{n=0}^{\infty}2^{n(p\alpha+p-2)}\nu_{2^{n+1}}^{p}\\
& \asymp \sum_{k=1}^{\infty}k^{(p\alpha+p-3)}\nu_{k}^{p}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
1 & \gt rsim||h||_{\mathcal {B}} \gt rsim \sum_{n=0}^{\infty}2^{-n}||\Delta_{n}(\mathcal {I}_{\mu_{\alpha+1}} (h))||^{p}_{p}\\
&= \sum_{n=0}^{\infty}2^{-n}\left\|\sum^{2^{n+1}-1}_{k=2^{n}}\frac{\Gamma(\alpha+1+k)}{\Gamma(\alpha+1)\Gamma(k+1)}\nu_{k} z^{k}\right\|_{p}^{p}\\
& \gt rsim \sum_{n=0}^{\infty}2^{-n}\nu_{2^{n+1}}^{p}\left\|\Delta_{n}\left(\frac{1}{(1-z)^{\alpha+1}}\right)\right\|^{p}_{p}\\
& \gt rsim \sum_{n=0}^{\infty}2^{n(p\alpha-1)}\nu_{2^{n+1}}^{p} ||\Delta_{n}||_{p}^{p}\\
& \asymp \sum_{n=0}^{\infty}2^{n(p\alpha+p-2)}\nu_{2^{n+1}}^{p}\\
& \asymp \sum_{k=1}^{\infty}k^{(p\alpha+p-3)}\nu_{k}^{p}.
\end{split} \end{equation*} This gives ![]() $ \sum_{n=0}^{\infty} (n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$.
$ \sum_{n=0}^{\infty} (n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$.
Proof.  $(3)\Rightarrow(2)$
$(3)\Rightarrow(2)$
If ![]() $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lt \infty$, then
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lt \infty$, then
 \begin{equation*} \begin{split}
\sum_{n=1}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}&= \sum_{n=1}^{\infty}\left(\sum_{k=2^{n-1}}^{2^{n}-1}(k+1)^{p(\alpha+1)-3}\nu_{k}^{p}\right)\\
& \gt rsim \sum_{n=1}^{\infty}2^{n(p(\alpha+1)-2)}\nu_{2^{n}}^{p}\\
& \gt rsim \sum_{n=1}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
\sum_{n=1}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}&= \sum_{n=1}^{\infty}\left(\sum_{k=2^{n-1}}^{2^{n}-1}(k+1)^{p(\alpha+1)-3}\nu_{k}^{p}\right)\\
& \gt rsim \sum_{n=1}^{\infty}2^{n(p(\alpha+1)-2)}\nu_{2^{n}}^{p}\\
& \gt rsim \sum_{n=1}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p}.
\end{split} \end{equation*}This shows that
 \begin{equation*} \sum_{n=1}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p} \lt \infty.\end{equation*}
\begin{equation*} \sum_{n=1}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p} \lt \infty.\end{equation*}By Lemma 2.2, we have that
 \begin{equation*}\int_{0}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \asymp \sum_{n=0}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p} \lt \infty.\end{equation*}
\begin{equation*}\int_{0}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \asymp \sum_{n=0}^{\infty}2^{-n}\left(\sum_{k=2^{n}}^{2^{n+1}-1}(k+1)^{\alpha-\frac{1}{p}}\nu_{k}\right)^{p} \lt \infty.\end{equation*} Therefore, for any ɛ > 0, there exists ![]() $0 \lt r_{0} \lt 1$ such that
$0 \lt r_{0} \lt 1$ such that
 \begin{equation*}\int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \lt \varepsilon.\end{equation*}
\begin{equation*}\int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \lt \varepsilon.\end{equation*} By the assumption of µ, for the above ɛ > 0, there exists t 0 with ![]() $0 \lt t_{0} \lt 1$ such that
$0 \lt t_{0} \lt 1$ such that
 \begin{equation*}\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \varepsilon.\end{equation*}
\begin{equation*}\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \varepsilon.\end{equation*} Let ![]() $\{f_{k}\}_{k=1}^{\infty}$ be a bounded sequence in
$\{f_{k}\}_{k=1}^{\infty}$ be a bounded sequence in ![]() $\mathcal {B}$ which converges to 0 uniformly on every compact subset of
$\mathcal {B}$ which converges to 0 uniformly on every compact subset of ![]() $\mathbb{D}$. It is clear that
$\mathbb{D}$. It is clear that
 \begin{equation*} \begin{split}
||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||^{p}_{A^{p}}&=\int_{|z|\leq r_{0}}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}\text{d}A(z)+ \int_{r_{0} \lt |z| \lt 1}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}dA(z)\\
& := J_{1,k}+J_{2,k}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||^{p}_{A^{p}}&=\int_{|z|\leq r_{0}}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}\text{d}A(z)+ \int_{r_{0} \lt |z| \lt 1}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}dA(z)\\
& := J_{1,k}+J_{2,k}.
\end{split} \end{equation*} When ![]() $|z|\leq r_{0}$, since
$|z|\leq r_{0}$, since ![]() $\{f_{k}\}_{k=1}^{\infty}$ converges to 0 uniformly on every compact subset of
$\{f_{k}\}_{k=1}^{\infty}$ converges to 0 uniformly on every compact subset of ![]() $\mathbb{D}$, we have
$\mathbb{D}$, we have
 \begin{equation*} \begin{split}
|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|& \leq \int_{0}^{1}\frac{|f_{k}(t)|}{|1-tz|^{1+\alpha}}\text{d}\mu(t)\\
& \lesssim \sup_{|t| \lt t_{0}}|f_{k}(t)|+\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\\
& \lesssim \sup_{|t| \lt t_{0}}|f_{k}(t)|+\varepsilon.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|& \leq \int_{0}^{1}\frac{|f_{k}(t)|}{|1-tz|^{1+\alpha}}\text{d}\mu(t)\\
& \lesssim \sup_{|t| \lt t_{0}}|f_{k}(t)|+\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\\
& \lesssim \sup_{|t| \lt t_{0}}|f_{k}(t)|+\varepsilon.
\end{split} \end{equation*}It follows that
Next, we estimate ![]() $J_{2,k}$.
$J_{2,k}$.
If ![]() $p(\alpha+1)\geq 1$, then by Minkowski inequality and Lemma 2.4, we get
$p(\alpha+1)\geq 1$, then by Minkowski inequality and Lemma 2.4, we get
 \begin{align*} \begin{split}
M_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k})) &\leq \left\{\int_{0}^{2\pi}\left(\int_{0}^{1}\frac{|f_{k}(t)|}{|1-rte^{i\theta}|^{1+\alpha}}{\textrm{d}} \mu(t)\right)^{p} {\textrm{d}} \theta\right\}^{\frac{1}{p}}\\
&\lesssim \int_{0}^{1}\log\frac{e}{1-t}\left(\int_{0}^{2\pi}\frac{{\textrm{d}} \theta}{|1-tre^{i\theta}|^{p(\alpha+1)}}\right)^{\frac{1}{p}} {\textrm{d}} \mu(t)\\
& \lesssim\int_{0}^{1}F(t,r)\log\frac{e}{1-t}{\textrm{d}} \mu(t)\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n},
\end{split} \end{align*}
\begin{align*} \begin{split}
M_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k})) &\leq \left\{\int_{0}^{2\pi}\left(\int_{0}^{1}\frac{|f_{k}(t)|}{|1-rte^{i\theta}|^{1+\alpha}}{\textrm{d}} \mu(t)\right)^{p} {\textrm{d}} \theta\right\}^{\frac{1}{p}}\\
&\lesssim \int_{0}^{1}\log\frac{e}{1-t}\left(\int_{0}^{2\pi}\frac{{\textrm{d}} \theta}{|1-tre^{i\theta}|^{p(\alpha+1)}}\right)^{\frac{1}{p}} {\textrm{d}} \mu(t)\\
& \lesssim\int_{0}^{1}F(t,r)\log\frac{e}{1-t}{\textrm{d}} \mu(t)\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n},
\end{split} \end{align*}where
 \begin{equation*}F(t,r)=\left\{
\begin{array}{cc}
\displaystyle{\frac{1}{(1-tr)^{\alpha+1-\frac{1}{p}}},} & \displaystyle{p(\alpha+1) \gt 1}\\
\displaystyle{\log\frac{e}{1-tr}, } & \displaystyle{p(\alpha+1)=1}
\end{array}\right.\end{equation*}
\begin{equation*}F(t,r)=\left\{
\begin{array}{cc}
\displaystyle{\frac{1}{(1-tr)^{\alpha+1-\frac{1}{p}}},} & \displaystyle{p(\alpha+1) \gt 1}\\
\displaystyle{\log\frac{e}{1-tr}, } & \displaystyle{p(\alpha+1)=1}
\end{array}\right.\end{equation*}By the polar coordinate formula, we have
 \begin{equation*} \begin{split}
J_{2,k}& =\int_{r_{0} \lt |z| \lt 1}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}\text{d}A(z)\\
& \lesssim \int_{r_{0}}^{1}M^{p}_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k}))\text{d}r\\
& \lesssim \int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r\\
& \lesssim \varepsilon.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
J_{2,k}& =\int_{r_{0} \lt |z| \lt 1}|\mathcal {I}_{\mu_{\alpha+1}}(f_{k})(z)|^{p}\text{d}A(z)\\
& \lesssim \int_{r_{0}}^{1}M^{p}_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k}))\text{d}r\\
& \lesssim \int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r\\
& \lesssim \varepsilon.
\end{split} \end{equation*} If ![]() $0 \lt p(\alpha+1) \lt 1$, a similar discussion to the previous one leads to
$0 \lt p(\alpha+1) \lt 1$, a similar discussion to the previous one leads to
 \begin{equation*}M_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k}))\lesssim \int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\lesssim 1.\end{equation*}
\begin{equation*}M_{p}(r,\mathcal {I}_{\mu_{\alpha+1}}(f_{k}))\lesssim \int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t)\lesssim 1.\end{equation*}Note that
 \begin{equation*}\int_{r_{0}}^{1}dr \asymp \int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \lt \varepsilon.\end{equation*}
\begin{equation*}\int_{r_{0}}^{1}dr \asymp \int_{r_{0}}^{1}\left(\sum_{n=0}^{\infty} (n+1)^{\alpha-\frac{1}{p}}\nu_{n}r^{n}\right)^{p}\text{d}r \lt \varepsilon.\end{equation*} This also yields that ![]() $J_{2}\lesssim \varepsilon.$ Therefore,
$J_{2}\lesssim \varepsilon.$ Therefore,
 \begin{equation*}\lim_{k\rightarrow\infty}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||^{p}_{A^{p}}=0.\end{equation*}
\begin{equation*}\lim_{k\rightarrow\infty}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||^{p}_{A^{p}}=0.\end{equation*} This shows that ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is compact.
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is compact.
Let us remark that if ![]() $g(z)=\sum_{n=0}^{\infty} \widehat{g}(n)z^{n}\in H(\mathbb{D})$ and the sequence
$g(z)=\sum_{n=0}^{\infty} \widehat{g}(n)z^{n}\in H(\mathbb{D})$ and the sequence ![]() $\{\widehat{g}(n)\}^{\infty}_{n=0}$ is non-negatively decreasing, then
$\{\widehat{g}(n)\}^{\infty}_{n=0}$ is non-negatively decreasing, then ![]() $g\in H^{p}$
$g\in H^{p}$ ![]() $(p\geq 1)$ if and only if
$(p\geq 1)$ if and only if ![]() $\sum_{n=0}^{\infty} (n+1)^{p-2}\widehat{g}(n)^{p} \lt \infty$ and
$\sum_{n=0}^{\infty} (n+1)^{p-2}\widehat{g}(n)^{p} \lt \infty$ and ![]() $g\in \mathcal {B}_{0}$
$g\in \mathcal {B}_{0}$ ![]() $\Leftrightarrow$
$\Leftrightarrow$ ![]() $g\in VMOA$
$g\in VMOA$ ![]() $\Leftrightarrow$
$\Leftrightarrow$  $\widehat{g}(n)=o(\frac{1}{n})$ (see, e.g. [Reference Pavlović20]). Also,
$\widehat{g}(n)=o(\frac{1}{n})$ (see, e.g. [Reference Pavlović20]). Also, ![]() $g\in A^{p}$ if and only if
$g\in A^{p}$ if and only if ![]() $\sum_{n=0}^{\infty} (n+1)^{p-3}\widehat{g}(n)^{p} \lt \infty$ (see, e.g. [Reference Buckley, Koskela and Vukotić3], Proposition 2.4).
$\sum_{n=0}^{\infty} (n+1)^{p-3}\widehat{g}(n)^{p} \lt \infty$ (see, e.g. [Reference Buckley, Koskela and Vukotić3], Proposition 2.4).
The equivalence ![]() $(3)\Leftrightarrow (4)$ is a consequence of the following proposition.
$(3)\Leftrightarrow (4)$ is a consequence of the following proposition.
Proposition 2.5. Let ![]() $1\leq p \lt \infty$,
$1\leq p \lt \infty$, $\frac{1}{p}+\frac{1}{q}=1$, and let µ be a positive Borel measure on
$\frac{1}{p}+\frac{1}{q}=1$, and let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements hold:
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements hold:
(a) If p > 1, then
 $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$ if and only if
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$ if and only if
 \begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{A^{q}} \ \ \mbox{for all}\ g\in A^{q}.\end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{A^{q}} \ \ \mbox{for all}\ g\in A^{q}.\end{equation*}(b) If p = 1, then
 $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n} \lt \infty$ if and only if
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n} \lt \infty$ if and only if
 \begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{\mathcal {B}} \ \ \mbox{for all}\ g\in \mathcal {B}_{0}.\end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|\lesssim ||g||_{\mathcal {B}} \ \ \mbox{for all}\ g\in \mathcal {B}_{0}.\end{equation*}
Proof. (a). Suppose that ![]() $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$. As we have proved previously,
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu^{p}_{n} \lt \infty$. As we have proved previously, ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded operator from
$\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded operator from ![]() $ \mathcal {B}$ to A p. Since
$ \mathcal {B}$ to A p. Since  $\int_{0}^{1}\log\frac{e}{1-s}d\mu(s) \lt \infty$, it is easy to see that
$\int_{0}^{1}\log\frac{e}{1-s}d\mu(s) \lt \infty$, it is easy to see that
 \begin{equation}
\int_{0}^{1}\vert f(s)\vert \text{d}\mu(s)\lesssim \vert \vert f\vert \vert _{\mathcal {B}} \ \ \ \mbox{for all} \ \ f\in \mathcal {B}.
\end{equation}
\begin{equation}
\int_{0}^{1}\vert f(s)\vert \text{d}\mu(s)\lesssim \vert \vert f\vert \vert _{\mathcal {B}} \ \ \ \mbox{for all} \ \ f\in \mathcal {B}.
\end{equation} For each ![]() $0\leq r \lt 1$,
$0\leq r \lt 1$, ![]() $f\in \mathcal {B}$ and
$f\in \mathcal {B}$ and ![]() $g\in A^{q}$, by (3) and Hölder inequality, we have that
$g\in A^{q}$, by (3) and Hölder inequality, we have that
 \begin{equation*} \begin{split}
& \ \ \ \ \ \int_{\mathbb{D}}\int_{0}^{1}\left| \frac{f(s)g(rz)}{(1-rsz)^{\alpha+1}}
\right| \text{d}\mu(s)dA(z)\\
&\leq \frac{1}{(1-r)^{\alpha+1}}\int_{0}^{1}| f(s)| \text{d}\mu(s)\int_{\mathbb{D}}|g(rz)| dA(z)\\
&\lesssim \frac{|| f||_{\mathcal {B}}}{(1-r)^{\alpha+1}}||g_{r}||_{A^{q}}\lesssim \frac{|| f||_{\mathcal {B}}}{(1-r)^{\alpha+1}}||g||_{A^{q}} \lt \infty,\\
\end{split} \end{equation*}
\begin{equation*} \begin{split}
& \ \ \ \ \ \int_{\mathbb{D}}\int_{0}^{1}\left| \frac{f(s)g(rz)}{(1-rsz)^{\alpha+1}}
\right| \text{d}\mu(s)dA(z)\\
&\leq \frac{1}{(1-r)^{\alpha+1}}\int_{0}^{1}| f(s)| \text{d}\mu(s)\int_{\mathbb{D}}|g(rz)| dA(z)\\
&\lesssim \frac{|| f||_{\mathcal {B}}}{(1-r)^{\alpha+1}}||g_{r}||_{A^{q}}\lesssim \frac{|| f||_{\mathcal {B}}}{(1-r)^{\alpha+1}}||g||_{A^{q}} \lt \infty,\\
\end{split} \end{equation*} where ![]() $g_{r}(z)=g(rz)$. Let
$g_{r}(z)=g(rz)$. Let ![]() $g(z)=\sum_{n=0}^{\infty}b_{n}z^{n}\in A^{q}$. By Fubini’s theorem and a simple calculation through polar coordinate, we have that
$g(z)=\sum_{n=0}^{\infty}b_{n}z^{n}\in A^{q}$. By Fubini’s theorem and a simple calculation through polar coordinate, we have that
 \begin{equation*} \begin{split}
& \ \ \ \ \int_{\mathbb{D}} \overline{\mathcal {I}_{\mu_{\alpha+1}}(f)(rz)}g(rz)\text{d}A(z)\\
& = \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}b_{n}(r^{2}t)^{n}\overline{f(t)}\text{d}\mu(t)\\
& =\int_{0}^{1} R^{0,\alpha-1} g(r^{2}t) \overline{f(t)}d\mu(t).\\
\end{split} \end{equation*}
\begin{equation*} \begin{split}
& \ \ \ \ \int_{\mathbb{D}} \overline{\mathcal {I}_{\mu_{\alpha+1}}(f)(rz)}g(rz)\text{d}A(z)\\
& = \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}b_{n}(r^{2}t)^{n}\overline{f(t)}\text{d}\mu(t)\\
& =\int_{0}^{1} R^{0,\alpha-1} g(r^{2}t) \overline{f(t)}d\mu(t).\\
\end{split} \end{equation*} for all ![]() $0\leq r \lt 1$,
$0\leq r \lt 1$, ![]() $f\in \mathcal {B}$,
$f\in \mathcal {B}$, ![]() $g\in A^{q}$. Recall that the duality
$g\in A^{q}$. Recall that the duality ![]() $(A^{q})^{\ast}\simeq A^{p}$ under the pairing
$(A^{q})^{\ast}\simeq A^{p}$ under the pairing
 \begin{equation*}\langle F, G\rangle=\lim_{r\rightarrow 1^{-}} \int_{\mathbb{D}} F(rz)\overline{G(rz)}\text{d}A(z), \ \ F\in A^{q}, G\in A^{p} .\end{equation*}
\begin{equation*}\langle F, G\rangle=\lim_{r\rightarrow 1^{-}} \int_{\mathbb{D}} F(rz)\overline{G(rz)}\text{d}A(z), \ \ F\in A^{q}, G\in A^{p} .\end{equation*} Therefore, the operator ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded if and only if
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded if and only if
 \begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1} g(t) \overline{f(t)}\text{d}\mu(t)\right|\lesssim ||f||_{\mathcal {B}}||g||_{A^{q}}\ \mbox{for all}\ f \in \mathcal {B},\ g\in A^{q}. \end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1} g(t) \overline{f(t)}\text{d}\mu(t)\right|\lesssim ||f||_{\mathcal {B}}||g||_{A^{q}}\ \mbox{for all}\ f \in \mathcal {B},\ g\in A^{q}. \end{equation*} Now, take ![]() $f(z)=\log\frac{e}{1-z}\in \mathcal {B}$ in above inequality, and we get
$f(z)=\log\frac{e}{1-z}\in \mathcal {B}$ in above inequality, and we get
 \begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)\text{d}\nu(t)\right|\lesssim ||g||_{A^{q}} \ \ \mbox{for all}\ g\in A^{q}.\end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)\text{d}\nu(t)\right|\lesssim ||g||_{A^{q}} \ \ \mbox{for all}\ g\in A^{q}.\end{equation*} Conversely, assume  $h(z)=\sum_{n=0}^{\infty} \widehat{h}(n) z^{n}\in A^{q}$ and the sequence
$h(z)=\sum_{n=0}^{\infty} \widehat{h}(n) z^{n}\in A^{q}$ and the sequence  $\{\widehat{h}(n)\}_{n=0}^{\infty}$ is a decreasing sequence of non-negative real numbers. Since the measure ν satisfies
$\{\widehat{h}(n)\}_{n=0}^{\infty}$ is a decreasing sequence of non-negative real numbers. Since the measure ν satisfies
 \begin{equation*}\int_{0}^{1} R^{0,\alpha-1}h(t)\text{d}\nu(t)\lesssim ||h||_{A^{q}},\end{equation*}
\begin{equation*}\int_{0}^{1} R^{0,\alpha-1}h(t)\text{d}\nu(t)\lesssim ||h||_{A^{q}},\end{equation*}it follows that
 \begin{equation*} \begin{split}
||h||_{A^{q}} & \gt rsim\int_{0}^{1} R^{0,\alpha-1}h(t)\text{d}\nu(t)\\
& = \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}\widehat{h}(n)t^{n}\text{d}\nu(t)\\
& = \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}\widehat{h}(n)\nu_{n}\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\frac{q-3}{q}}\widehat{h}(n)(n+1)^{\alpha-1-\frac{q-3}{q}}\nu_{n}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
||h||_{A^{q}} & \gt rsim\int_{0}^{1} R^{0,\alpha-1}h(t)\text{d}\nu(t)\\
& = \int_{0}^{1} \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}\widehat{h}(n)t^{n}\text{d}\nu(t)\\
& = \sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(n+2)\Gamma(\alpha+1)}\widehat{h}(n)\nu_{n}\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\frac{q-3}{q}}\widehat{h}(n)(n+1)^{\alpha-1-\frac{q-3}{q}}\nu_{n}.
\end{split} \end{equation*} As we remarked before, the sequence  $\{\widehat{h}(n)(n+1)^{\frac{q-3}{q}}\}_{n=0}^{\infty}\in \ell^{q}$. The well-known duality
$\{\widehat{h}(n)(n+1)^{\frac{q-3}{q}}\}_{n=0}^{\infty}\in \ell^{q}$. The well-known duality ![]() $(\ell^{q})^{*}=\ell^{p}$ implies that
$(\ell^{q})^{*}=\ell^{p}$ implies that  $\{(n+1)^{\alpha-1-\frac{q-3}{q}}\nu_{n}\}_{n=0}^{\infty}\in l^{p}$. Therefore,
$\{(n+1)^{\alpha-1-\frac{q-3}{q}}\nu_{n}\}_{n=0}^{\infty}\in l^{p}$. Therefore,
 \begin{equation*}\sum_{n=0}^{\infty} (n+1)^{p\alpha+p-3}\nu^{p}_{n} \lt \infty.\end{equation*}
\begin{equation*}\sum_{n=0}^{\infty} (n+1)^{p\alpha+p-3}\nu^{p}_{n} \lt \infty.\end{equation*} (b). The proof of the necessity is similar to (a). It is enough to notice that ![]() $(\mathcal {B}_{0})^{\ast}\simeq A_{1}$ under the pairing
$(\mathcal {B}_{0})^{\ast}\simeq A_{1}$ under the pairing
 \begin{equation*}\langle F, G\rangle=\lim_{r\rightarrow 1^{-}} \int_{\mathbb{D}} F(rz)\overline{G(rz)}\text{d}A(z), \ \ F\in \mathcal {B}_{0}, G\in A_{1} .\end{equation*}
\begin{equation*}\langle F, G\rangle=\lim_{r\rightarrow 1^{-}} \int_{\mathbb{D}} F(rz)\overline{G(rz)}\text{d}A(z), \ \ F\in \mathcal {B}_{0}, G\in A_{1} .\end{equation*} For the ‘if’ part, let  $h(z)=\sum_{n=0}^{\infty} \widehat{h}(n)z^{n}\in \mathcal {B}_{0}$ and the sequence
$h(z)=\sum_{n=0}^{\infty} \widehat{h}(n)z^{n}\in \mathcal {B}_{0}$ and the sequence  $\{\widehat{h}(n)\}_{n=0}^{\infty}$ is a decreasing sequence of non-negative real numbers, then
$\{\widehat{h}(n)\}_{n=0}^{\infty}$ is a decreasing sequence of non-negative real numbers, then  $\widehat{h}(n)=o(\frac{1}{n}).$ This implies that the sequence
$\widehat{h}(n)=o(\frac{1}{n}).$ This implies that the sequence  $\{(n+1)\widehat{h}(n)\}_{n=0}^{\infty}\in c_{0}$. Arguing as the proof of (a), we have that
$\{(n+1)\widehat{h}(n)\}_{n=0}^{\infty}\in c_{0}$. Arguing as the proof of (a), we have that
 \begin{equation*}||h||_{\mathcal {B}} \gt rsim \sum_{n=0}^{\infty} (n+1)^{\alpha-1}\widehat{h}(n)\nu_{n}.\end{equation*}
\begin{equation*}||h||_{\mathcal {B}} \gt rsim \sum_{n=0}^{\infty} (n+1)^{\alpha-1}\widehat{h}(n)\nu_{n}.\end{equation*} Since ![]() $(c_{0})^{*}=\ell^{1}$, it follows that
$(c_{0})^{*}=\ell^{1}$, it follows that ![]() $\{(n+1)^{\alpha-2}\nu_{n}\}_{n=0}^{\infty}\in \ell^{1}$.
$\{(n+1)^{\alpha-2}\nu_{n}\}_{n=0}^{\infty}\in \ell^{1}$.
Corollary 2.6. Let α > 1, and let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then the following statements are equivalent:
(1) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from
$\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(2) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(3) The measure µ satisfies
 $\sum_{n=0}^{\infty}(n+1)^{\alpha-2}\nu_{n} \lt \infty.$
$\sum_{n=0}^{\infty}(n+1)^{\alpha-2}\nu_{n} \lt \infty.$(4) The measure µ satisfies
 $\int_{0}^{1} \frac{\log\frac{e}{1-t}}{(1-t)^{\alpha-1}}d\mu(t) \lt \infty. $
$\int_{0}^{1} \frac{\log\frac{e}{1-t}}{(1-t)^{\alpha-1}}d\mu(t) \lt \infty. $
Corollary 2.7. Let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then, the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$. Then, the following statements are equivalent:
(1) The operator
 $\mathcal {I}_{\mu_{2}}$ is bounded from
$\mathcal {I}_{\mu_{2}}$ is bounded from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(2) The operator
 $\mathcal {I}_{\mu_{2}}$ is compact from
$\mathcal {I}_{\mu_{2}}$ is compact from  $\mathcal {B}$ to A 1.
$\mathcal {B}$ to A 1.(3) The measure µ satisfies
 $\sum_{n=0}^{\infty}(n+1)^{-1}\nu_{n} \lt \infty.$
$\sum_{n=0}^{\infty}(n+1)^{-1}\nu_{n} \lt \infty.$(4) The measure µ satisfies
 $\int_{0}^{1} \log^{2}\frac{e}{1-t}d\mu(t) \lt \infty.$
$\int_{0}^{1} \log^{2}\frac{e}{1-t}d\mu(t) \lt \infty.$
Corollary 2.8. Let ![]() $\alpha \gt -1$,
$\alpha \gt -1$, ![]() $1\leq p \lt \infty$, and let µ be a positive Borel measure on
$1\leq p \lt \infty$, and let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. If
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. If ![]() $0 \lt p(\alpha+1) \lt 2$, then the operator
$0 \lt p(\alpha+1) \lt 2$, then the operator ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from ![]() $ \mathcal {B}$ to A p.
$ \mathcal {B}$ to A p.
Proof. Since  $\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$, we have that
$\int_{0}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$, we have that ![]() $\nu_{n}\lesssim 1$ for all
$\nu_{n}\lesssim 1$ for all ![]() $n \in \mathbb{N}\cup \{0\}$. If
$n \in \mathbb{N}\cup \{0\}$. If ![]() $0 \lt p(\alpha+1) \lt 2$, then the sum
$0 \lt p(\alpha+1) \lt 2$, then the sum ![]() $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}$ is always finite. This implies that
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}$ is always finite. This implies that ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is compact.
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is compact.
Corollary 2.9. Let ![]() $1\leq p \lt \infty$, and let µ be a finite positive Borel measure on
$1\leq p \lt \infty$, and let µ be a finite positive Borel measure on ![]() $[0, 1)$. If
$[0, 1)$. If ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact) for some
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact) for some ![]() $\alpha \gt -1$, then
$\alpha \gt -1$, then  $\mathcal {I}_{\mu_{\alpha^{'}+1}}$ is bounded (equivalent to compact) from
$\mathcal {I}_{\mu_{\alpha^{'}+1}}$ is bounded (equivalent to compact) from ![]() $ \mathcal {B}$ to A p for any
$ \mathcal {B}$ to A p for any ![]() $-1 \lt \alpha^{'} \lt \alpha$.
$-1 \lt \alpha^{'} \lt \alpha$.
Carleson measures play a key role when we study the generalized Hilbert operators. Recall that if µ is a positive Borel measure on ![]() $[0, 1)$,
$[0, 1)$, ![]() $0\leq\gamma \lt \infty$ and
$0\leq\gamma \lt \infty$ and ![]() $0 \lt s \lt \infty$, then µ is a γ-logarithmic s-Carleson measure if there exists a positive constant C such that
$0 \lt s \lt \infty$, then µ is a γ-logarithmic s-Carleson measure if there exists a positive constant C such that
 \begin{equation*}\mu([t,1))\log^{\gamma}\frac{e}{1-t} \leq C (1-t)^{s}, \ \ \mbox{for all}\ 0\leq t \lt 1 .\end{equation*}
\begin{equation*}\mu([t,1))\log^{\gamma}\frac{e}{1-t} \leq C (1-t)^{s}, \ \ \mbox{for all}\ 0\leq t \lt 1 .\end{equation*}In particular, µ is an s-Carleson measure if γ = 0.
In the following, we provide a sufficient condition and a necessary condition by using the Carleson-type measure.
Corollary 2.10. Suppose ![]() $1 \lt p \lt \infty$,
$1 \lt p \lt \infty$,  $\alpha+1-\frac{2}{p} \gt 0$,
$\alpha+1-\frac{2}{p} \gt 0$,  $\gamma \gt 1+\frac{1}{p}$ and µ is a finite positive Borel measure on
$\gamma \gt 1+\frac{1}{p}$ and µ is a finite positive Borel measure on ![]() $[0, 1)$, then the following statements hold:
$[0, 1)$, then the following statements hold:
(1) If µ is a γ-logarithmic
 $\alpha+1-\frac{2}{p}$-Carleson measure, then
$\alpha+1-\frac{2}{p}$-Carleson measure, then  $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact).
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact).(2) If
 $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded, then µ is a 1-logarithmic
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded, then µ is a 1-logarithmic  $\alpha+1-\frac{2}{p}$-Carleson measure.
$\alpha+1-\frac{2}{p}$-Carleson measure.
Proof. (1) Assuming µ is a γ-logarithmic  $\alpha+1-\frac{2}{p}$-Carleson measure and then integrating by parts, we have that
$\alpha+1-\frac{2}{p}$-Carleson measure and then integrating by parts, we have that
 \begin{equation*} \begin{split}
&\ \ \ \ \ \ \int_{0}^{1} t^{n}\log\frac{2}{1-t}\text{d}\mu(t)\\
&=n \int_{0}^{1} t^{n-1}\mu([t,1))\log\frac{2}{1-t}\text{d}t+\int_{0}^{1} t^{n}\mu([t,1))\frac{\text{d}t}{1-t}\\
& \lesssim n \int_{0}^{1} t^{n-1}(1-t)^{\alpha+1-\frac{2}{p}}\log^{1-\gamma}\frac{e}{1-t}dt+ \int_{0}^{1} t^{n}(1-t)^{\alpha-\frac{2}{p}}\log^{-\gamma}\frac{e}{1-t}\text{d}t.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
&\ \ \ \ \ \ \int_{0}^{1} t^{n}\log\frac{2}{1-t}\text{d}\mu(t)\\
&=n \int_{0}^{1} t^{n-1}\mu([t,1))\log\frac{2}{1-t}\text{d}t+\int_{0}^{1} t^{n}\mu([t,1))\frac{\text{d}t}{1-t}\\
& \lesssim n \int_{0}^{1} t^{n-1}(1-t)^{\alpha+1-\frac{2}{p}}\log^{1-\gamma}\frac{e}{1-t}dt+ \int_{0}^{1} t^{n}(1-t)^{\alpha-\frac{2}{p}}\log^{-\gamma}\frac{e}{1-t}\text{d}t.
\end{split} \end{equation*}It is easy to estimate that
 \begin{equation*} n \int_{0}^{1} t^{n-1}(1-t)^{\alpha+1-\frac{2}{p}}\log^{1-\gamma}\frac{e}{1-t}\text{d}t \asymp \frac{\log^{1-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}} \end{equation*}
\begin{equation*} n \int_{0}^{1} t^{n-1}(1-t)^{\alpha+1-\frac{2}{p}}\log^{1-\gamma}\frac{e}{1-t}\text{d}t \asymp \frac{\log^{1-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}} \end{equation*}and
 \begin{equation*}\int_{0}^{1} t^{n}(1-t)^{\alpha-\frac{2}{p}}\log^{-\gamma}\frac{e}{1-t}\text{d}t\asymp \frac{\log^{-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}}.\end{equation*}
\begin{equation*}\int_{0}^{1} t^{n}(1-t)^{\alpha-\frac{2}{p}}\log^{-\gamma}\frac{e}{1-t}\text{d}t\asymp \frac{\log^{-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}}.\end{equation*}These inequalities imply that
 \begin{equation*}
\nu_{n}= \int_{0}^{1} t^{n}\log\frac{2}{1-t}\text{d}\mu(t)\lesssim \frac{\log^{1-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}}.
\end{equation*}
\begin{equation*}
\nu_{n}= \int_{0}^{1} t^{n}\log\frac{2}{1-t}\text{d}\mu(t)\lesssim \frac{\log^{1-\gamma}(n+1)}{n^{\alpha+1-\frac{2}{p}}}.
\end{equation*}It follows that
 \begin{equation*} \begin{split}
\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lesssim \sum_{n=0}^{\infty}\frac{(\log(n+1))^{p(1-\gamma)}}{n+1}\lesssim 1.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p} \lesssim \sum_{n=0}^{\infty}\frac{(\log(n+1))^{p(1-\gamma)}}{n+1}\lesssim 1.
\end{split} \end{equation*} Theorem 1.1 shows that ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact).
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded (equivalent to compact).
(2) If ![]() $\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded, then for any
$\mathcal {I}_{\mu_{\alpha+1}}: \mathcal {B}\rightarrow A^{p}$ is bounded, then for any ![]() $N\geq 2$, we have
$N\geq 2$, we have
 \begin{equation*} \begin{split}
1 & \gt rsim \sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}\\
& \gt rsim \sum_{n=0}^{N}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}\\
& \gt rsim \nu^{p}_{N} \sum_{n=0}^{N}(n+1)^{p(\alpha+1)-3}\\
& \asymp \nu^{p}_{N}N^{p(\alpha+1)-2}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
1 & \gt rsim \sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}\\
& \gt rsim \sum_{n=0}^{N}(n+1)^{p(\alpha+1)-3}\nu_{n}^{p}\\
& \gt rsim \nu^{p}_{N} \sum_{n=0}^{N}(n+1)^{p(\alpha+1)-3}\\
& \asymp \nu^{p}_{N}N^{p(\alpha+1)-2}.
\end{split} \end{equation*} This implies that ν is an  $\alpha+1-\frac{2}{p}$-Carleson measure which is equivalent to saying that µ is a 1-logarithmic
$\alpha+1-\frac{2}{p}$-Carleson measure which is equivalent to saying that µ is a 1-logarithmic  $\alpha+1-\frac{2}{p}$-Carleson measure.
$\alpha+1-\frac{2}{p}$-Carleson measure.
In fact, the exponent  $1+\frac{1}{p}$ in Corollary 2.10 is sharp.
$1+\frac{1}{p}$ in Corollary 2.10 is sharp.
Proposition 2.11. Let ![]() $1 \lt p \lt \infty$,
$1 \lt p \lt \infty$,  $\frac{1}{p}+\frac{1}{q}=1$ and
$\frac{1}{p}+\frac{1}{q}=1$ and  $\alpha+1-\frac{2}{p} \gt 0$. Then there exist
$\alpha+1-\frac{2}{p} \gt 0$. Then there exist  $1+\frac{1}{p}$-logarithmic
$1+\frac{1}{p}$-logarithmic  $\alpha+1-\frac{2}{p}$-Carleson measure µ and
$\alpha+1-\frac{2}{p}$-Carleson measure µ and ![]() $ g\in A^{q}$ such that
$ g\in A^{q}$ such that
 \begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|=\infty.\end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{0,\alpha-1}g(t)d\nu(t)\right|=\infty.\end{equation*}Proof. Let  $\text{d}\mu(s)=(1-s)^{\alpha-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-s}\text{d}s$. Since
$\text{d}\mu(s)=(1-s)^{\alpha-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-s}\text{d}s$. Since  $\alpha-\frac{2}{p} \gt -1$, we have that
$\alpha-\frac{2}{p} \gt -1$, we have that
 \begin{equation*}\lim_{t\rightarrow 1}\frac{\int_{t}^{1}(1-s)^{\alpha-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-s}\text{d}s}{(1-t)^{\alpha+1-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-t}}=\frac{p}{p(\alpha+1)-2} \gt 0.\end{equation*}
\begin{equation*}\lim_{t\rightarrow 1}\frac{\int_{t}^{1}(1-s)^{\alpha-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-s}\text{d}s}{(1-t)^{\alpha+1-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-t}}=\frac{p}{p(\alpha+1)-2} \gt 0.\end{equation*} This implies that  $\mu([t,1))\lesssim (1-t)^{\alpha+1-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-t}$ for all
$\mu([t,1))\lesssim (1-t)^{\alpha+1-\frac{2}{p}}\log^{-(1+\frac{1}{p})}\frac{e}{1-t}$ for all ![]() $0 \lt t \lt 1$, and hence µ is a
$0 \lt t \lt 1$, and hence µ is a  $1+\frac{1}{p}$-logarithmic
$1+\frac{1}{p}$-logarithmic  $\alpha+1-\frac{2}{p}$-Carleson measure. Choosing a positive real number δ satisfies
$\alpha+1-\frac{2}{p}$-Carleson measure. Choosing a positive real number δ satisfies  $\frac{1}{q} \lt \delta \lt 1$. Let
$\frac{1}{q} \lt \delta \lt 1$. Let
 \begin{equation*}g(z)=\frac{1}{(1-z)^{\frac{2}{q}}}\log^{-\frac{1}{q}}\frac{e}{1-z}(\log\log\frac{e^{2}}{1-z})^{-\delta}, \ \ z\in \mathbb{D}.\end{equation*}
\begin{equation*}g(z)=\frac{1}{(1-z)^{\frac{2}{q}}}\log^{-\frac{1}{q}}\frac{e}{1-z}(\log\log\frac{e^{2}}{1-z})^{-\delta}, \ \ z\in \mathbb{D}.\end{equation*}Arguing as the proof of Lemma 1 in [Reference Avetisyan1], we have that
 \begin{equation*} \begin{split}
M^{q}_{q}(r,g)&=\frac{1}{2\pi}\int_{0}^{2\pi}\frac{1}{|1-re^{i\theta}|^{2}}|\log^{-1}\frac{e}{1-re^{i\theta}}||\log\log\frac{e^{2}}{1-re^{i\theta}}|^{-q\delta}\text{d}\theta\\
& \lesssim \frac{1}{1-r}\log^{-1}\frac{e}{1-r}\left(\log\log\frac{e^{2}}{1-r}\right)^{-q\delta}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
M^{q}_{q}(r,g)&=\frac{1}{2\pi}\int_{0}^{2\pi}\frac{1}{|1-re^{i\theta}|^{2}}|\log^{-1}\frac{e}{1-re^{i\theta}}||\log\log\frac{e^{2}}{1-re^{i\theta}}|^{-q\delta}\text{d}\theta\\
& \lesssim \frac{1}{1-r}\log^{-1}\frac{e}{1-r}\left(\log\log\frac{e^{2}}{1-r}\right)^{-q\delta}.
\end{split} \end{equation*}Therefore,
 \begin{equation*} \begin{split}
||g||_{A^{q}}^{q} &= 2\int_{0}^{1} M^{q}_{q}(r,g)r\text{d}r\\
& \lesssim \int_{0}^{1} \frac{\text{d}r}{(1-r)\log\frac{e}{1-r}\left(\log\log\frac{e^{2}}{1-r}\right)^{q\delta}}\\
& \lesssim 1.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
||g||_{A^{q}}^{q} &= 2\int_{0}^{1} M^{q}_{q}(r,g)r\text{d}r\\
& \lesssim \int_{0}^{1} \frac{\text{d}r}{(1-r)\log\frac{e}{1-r}\left(\log\log\frac{e^{2}}{1-r}\right)^{q\delta}}\\
& \lesssim 1.
\end{split} \end{equation*} This shows that ![]() $g\in A^{q}$.
$g\in A^{q}$.
We now need the fact that the Taylor coefficients  $\widehat{h}(n)$ of the function
$\widehat{h}(n)$ of the function
 \begin{equation*}h(z)=\frac{1}{(1-z)^{a}}\log^{b}\frac{e}{1-z}\left(\log\log\frac{e^{2}}{1-z}\right)^{c}, \ \ a \gt 0, b,c \in \mathbb{R},\end{equation*}
\begin{equation*}h(z)=\frac{1}{(1-z)^{a}}\log^{b}\frac{e}{1-z}\left(\log\log\frac{e^{2}}{1-z}\right)^{c}, \ \ a \gt 0, b,c \in \mathbb{R},\end{equation*} have the property  $\widehat{h}(n)\asymp (n+1)^{a-1}\log^{b}(n+2)\left(\log\log(n+4)\right)^{c}$. The proof of this result is similar to the proof of Theorem 2.31 on pages 192–194 in [Reference Zygmund26], so we omit its proof.
$\widehat{h}(n)\asymp (n+1)^{a-1}\log^{b}(n+2)\left(\log\log(n+4)\right)^{c}$. The proof of this result is similar to the proof of Theorem 2.31 on pages 192–194 in [Reference Zygmund26], so we omit its proof.
It follows that
 \begin{equation*} \begin{split}
R^{0,\alpha-1}g(t)&=\sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(\alpha+1)\Gamma(n+2)}\widehat{g}(n)t^{n}\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha+\frac{2}{q}-2}\log^{-\frac{1}{q}}(n+2)\left(\log\log(n+4)\right)^{-\delta}t^{n}\\
& \asymp \frac{1}{(1-t)^{\alpha+1-\frac{2}{p}}}\log^{-\frac{1}{q}}\frac{e}{1-t}\left(\log\log\frac{e^{2}}{1-t}\right)^{-\delta}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
R^{0,\alpha-1}g(t)&=\sum_{n=0}^{\infty} \frac{\Gamma(n+1+\alpha)}{\Gamma(\alpha+1)\Gamma(n+2)}\widehat{g}(n)t^{n}\\
& \asymp \sum_{n=0}^{\infty} (n+1)^{\alpha+\frac{2}{q}-2}\log^{-\frac{1}{q}}(n+2)\left(\log\log(n+4)\right)^{-\delta}t^{n}\\
& \asymp \frac{1}{(1-t)^{\alpha+1-\frac{2}{p}}}\log^{-\frac{1}{q}}\frac{e}{1-t}\left(\log\log\frac{e^{2}}{1-t}\right)^{-\delta}.
\end{split} \end{equation*} Note that  $\text{d}\nu(t)=\log\frac{e}{1-t}\text{d}\mu(t)=(1-t)^{\alpha-\frac{2}{p}}\log^{-\frac{1}{p}}\frac{e}{1-t}\text{d}t$. Hence,
$\text{d}\nu(t)=\log\frac{e}{1-t}\text{d}\mu(t)=(1-t)^{\alpha-\frac{2}{p}}\log^{-\frac{1}{p}}\frac{e}{1-t}\text{d}t$. Hence,
 \begin{equation*} \left|\int_{0}^{1} R^{0,\alpha-1}g(t)\text{d}d\nu(t)\right|\asymp \int_{0}^{1} \frac{1}{(1-t)\log\frac{e}{1-t}\left(\log\log\frac{e^{2}}{1-t}\right)^{\delta}}\text{d}t
=\infty.
\end{equation*}
\begin{equation*} \left|\int_{0}^{1} R^{0,\alpha-1}g(t)\text{d}d\nu(t)\right|\asymp \int_{0}^{1} \frac{1}{(1-t)\log\frac{e}{1-t}\left(\log\log\frac{e^{2}}{1-t}\right)^{\delta}}\text{d}t
=\infty.
\end{equation*}The proof is complete.
The following Proposition gives a sufficient condition for the operator ![]() $\mathcal {H}^{\alpha}_{\mu}$ to be well defined on
$\mathcal {H}^{\alpha}_{\mu}$ to be well defined on ![]() $\mathcal {B}$ and
$\mathcal {B}$ and  $\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$.
$\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$.
Proposition 2.12. Let µ be a positive Borel measure on ![]() $[0, 1)$. For any s > 0, if µ is an s-Carleson measure, then the operator
$[0, 1)$. For any s > 0, if µ is an s-Carleson measure, then the operator ![]() $\mathcal {H}^{\alpha}_{\mu}$ is well defined on
$\mathcal {H}^{\alpha}_{\mu}$ is well defined on ![]() $\mathcal {B}$ and
$\mathcal {B}$ and  $\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$ for all
$\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)$ for all ![]() $f\in \mathcal {B}$.
$f\in \mathcal {B}$.
Proof. If s > 0 and µ is an s-Carleson measure, then it is easy to check that  $\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$, and hence the operator
$\int_{0}^{1} \log\frac{e}{1-t}\text{d}\mu(t) \lt \infty$, and hence the operator ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is well defined on Bloch space.
$\mathcal {I}_{\mu_{\alpha+1}}$ is well defined on Bloch space.
Now, let ![]() $f(z)=\sum_{n=0}^{\infty} a_{n}z^{n}\in \mathcal {B}$ and
$f(z)=\sum_{n=0}^{\infty} a_{n}z^{n}\in \mathcal {B}$ and  $f_{N}(z)=\sum_{n=0}^{N}a_{n}z^{n}$, then we have that
$f_{N}(z)=\sum_{n=0}^{N}a_{n}z^{n}$, then we have that
 \begin{equation*} \begin{split}
\mathcal{H}^{\alpha}_{\mu}(f_{N})(z)&=
\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\\
& =\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\sum_{k=0}^{N}\int_{0}^{1} t^{n+k}\text{d}\mu(t)a_{k}z^{n}\\
&=\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\int_{0}^{1} f_{N}(t) (tz)^{n}\text{d}\mu(t)\\
&=\mathcal {I}_{\mu_{\alpha+1}}(f_{N})(z),
\end{split} \end{equation*}
\begin{equation*} \begin{split}
\mathcal{H}^{\alpha}_{\mu}(f_{N})(z)&=
\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\\
& =\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\sum_{k=0}^{N}\int_{0}^{1} t^{n+k}\text{d}\mu(t)a_{k}z^{n}\\
&=\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\int_{0}^{1} f_{N}(t) (tz)^{n}\text{d}\mu(t)\\
&=\mathcal {I}_{\mu_{\alpha+1}}(f_{N})(z),
\end{split} \end{equation*} which implies that ![]() $\mathcal{H}^{\alpha}_{\mu}$ is well defined on polynomials. Take
$\mathcal{H}^{\alpha}_{\mu}$ is well defined on polynomials. Take  $p \gt \frac{2}{s}$ and then integrating by parts and using the fact that µ is an s-Carleson measure, we have that
$p \gt \frac{2}{s}$ and then integrating by parts and using the fact that µ is an s-Carleson measure, we have that
 \begin{equation*} \begin{split}
\int_{0}^{1} \frac{1}{(1-t)^{\frac{2}{p}}}d\mu(t)&= \mu([0,1))-\lim_{t\rightarrow 1}\frac{\mu([t,1))}{(1-t)^{\frac{2}{p}}}+\frac{2}{p}\int_{0}^{1} \frac{\mu([t,1))}{(1-t)^{\frac{2}{p}+1}}\text{d}t\\
& \lesssim \mu([0,1))+\int_{0}^{1} (1-t)^{s-\frac{2}{p}-1}\text{d}t\\
& \lesssim \mu([0,1))+ 1 \lesssim1.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
\int_{0}^{1} \frac{1}{(1-t)^{\frac{2}{p}}}d\mu(t)&= \mu([0,1))-\lim_{t\rightarrow 1}\frac{\mu([t,1))}{(1-t)^{\frac{2}{p}}}+\frac{2}{p}\int_{0}^{1} \frac{\mu([t,1))}{(1-t)^{\frac{2}{p}+1}}\text{d}t\\
& \lesssim \mu([0,1))+\int_{0}^{1} (1-t)^{s-\frac{2}{p}-1}\text{d}t\\
& \lesssim \mu([0,1))+ 1 \lesssim1.
\end{split} \end{equation*} Since ![]() $\mathcal {B}\subsetneq A^{p}$, we have that
$\mathcal {B}\subsetneq A^{p}$, we have that
 \begin{equation*} \begin{split}
\int_{0}^{1} |f(t)-f_{N}(t)|\text{d}\mu(t)&\lesssim ||f-f_{N}||_{A^{p}} \int_{0}^{1} \frac{1}{(1-t)^{\frac{2}{p}}}\text{d}\mu(t)\\
& \lesssim ||f-f_{N}||_{A^{p}} \lesssim ||f-f_{N}||_{\mathcal {B}}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
\int_{0}^{1} |f(t)-f_{N}(t)|\text{d}\mu(t)&\lesssim ||f-f_{N}||_{A^{p}} \int_{0}^{1} \frac{1}{(1-t)^{\frac{2}{p}}}\text{d}\mu(t)\\
& \lesssim ||f-f_{N}||_{A^{p}} \lesssim ||f-f_{N}||_{\mathcal {B}}.
\end{split} \end{equation*}This implies that
 \begin{equation*} \begin{split}
&\ \ \ \ \left|\mathcal {I}_{\mu_{\alpha+1}}(f)(z)-\sum_{n=0}^{\infty}
\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\right|\\
& \lesssim \int_{0}^{1} \frac{|f(t)-f_{N}(t)|}{(1-|z|)^{\alpha+1}}\text{d}\mu(t)
\lesssim \frac{1}{(1-|z|)^{\alpha+1}} ||f-f_{N}||_{\mathcal {B}}.
\end{split} \end{equation*}
\begin{equation*} \begin{split}
&\ \ \ \ \left|\mathcal {I}_{\mu_{\alpha+1}}(f)(z)-\sum_{n=0}^{\infty}
\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\right|\\
& \lesssim \int_{0}^{1} \frac{|f(t)-f_{N}(t)|}{(1-|z|)^{\alpha+1}}\text{d}\mu(t)
\lesssim \frac{1}{(1-|z|)^{\alpha+1}} ||f-f_{N}||_{\mathcal {B}}.
\end{split} \end{equation*} Thus, as ![]() $N\rightarrow \infty$, the series
$N\rightarrow \infty$, the series
 \begin{equation*}\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\end{equation*}
\begin{equation*}\sum_{n=0}^{\infty}\frac{\Gamma(n+1+\alpha)}{\Gamma(n+1)\Gamma(\alpha+1)}\left(\sum_{k=0}^{N}\mu_{n,k}a_{k}\right)z^{n}\end{equation*}converges and defines an analytic function
 \begin{equation*}\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)=\int_{0}^{1}\frac{f(t)}{(1-tz)^{1+\alpha}}\text{d}\mu(t).\end{equation*}
\begin{equation*}\mathcal {H}^{\alpha}_{\mu}(f)=\mathcal {I}_{\mu_{\alpha+1}}(f)=\int_{0}^{1}\frac{f(t)}{(1-tz)^{1+\alpha}}\text{d}\mu(t).\end{equation*}The proof is complete.
Corollary 2.13. Suppose ![]() $1 \lt p \lt \infty$,
$1 \lt p \lt \infty$,  $\frac{1}{p}+\frac{1}{q}=1$,
$\frac{1}{p}+\frac{1}{q}=1$,  $\gamma \gt 1+\frac{1}{p}$ and
$\gamma \gt 1+\frac{1}{p}$ and  $\alpha+1-\frac{2}{p} \gt 0$, and let µ be a positive Borel measure on
$\alpha+1-\frac{2}{p} \gt 0$, and let µ be a positive Borel measure on ![]() $[0, 1) $ which is a γ-logarithmic
$[0, 1) $ which is a γ-logarithmic  $\alpha+\frac{2}{q}-1$-Carleson measure. Then
$\alpha+\frac{2}{q}-1$-Carleson measure. Then ![]() $\mathcal {H}_{\mu}^{\alpha}$ is a compact operator from
$\mathcal {H}_{\mu}^{\alpha}$ is a compact operator from ![]() $ \mathcal {B}$ into A p.
$ \mathcal {B}$ into A p.
The Dirichlet type space  $D^{p}_{p-1} $ consists of those functions
$D^{p}_{p-1} $ consists of those functions ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}||f||^{p}_{B^{p}}= |f(0)|^{p}+\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p-1}{\text{d}}A(z) \lt \infty.\end{equation*}
\begin{equation*}||f||^{p}_{B^{p}}= |f(0)|^{p}+\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p-1}{\text{d}}A(z) \lt \infty.\end{equation*} It is known that  $D^{p}_{p-1}\subseteq H^{p}$ for
$D^{p}_{p-1}\subseteq H^{p}$ for ![]() $1\leq p\leq2$. Now, we characterize the measures µ for which
$1\leq p\leq2$. Now, we characterize the measures µ for which ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded (compact) operator from the Bloch space to Hardy spaces.
$\mathcal {I}_{\mu_{\alpha+1}}$ is a bounded (compact) operator from the Bloch space to Hardy spaces.
Theorem 2.14 Let ![]() $1\leq p \lt \infty$, and let µ be a positive Borel measure on
$1\leq p \lt \infty$, and let µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
(1) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from
$\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from  $\mathcal {B}$ to H p.
$\mathcal {B}$ to H p.(2) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from  $\mathcal {B}$ to H p.
$\mathcal {B}$ to H p.(3) The measure ν satisfies
 $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \infty.$
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \infty.$(4) The measure ν satisfies
 \begin{equation*}\left|\int_{0}^{1} R^{-1,\alpha}g(t)d\nu(t)\right|\lesssim ||g||_{Y_{p}}, \ \ \mbox{for all} \ g\in Y_{p},\end{equation*}
\begin{equation*}\left|\int_{0}^{1} R^{-1,\alpha}g(t)d\nu(t)\right|\lesssim ||g||_{Y_{p}}, \ \ \mbox{for all} \ g\in Y_{p},\end{equation*}where
 $ Y_{p}=H^{\frac{p}{p-1}}$ for p > 1 and
$ Y_{p}=H^{\frac{p}{p-1}}$ for p > 1 and  $Y_{1}= VMOA$ for p = 1.
$Y_{1}= VMOA$ for p = 1.
Proof. The proof is similar to the proof of Theorem 1.1, and we omit some specifics. Using the well-known duality  $(H^{\frac{p}{p-1}})^{*}=H^{p}$
$(H^{\frac{p}{p-1}})^{*}=H^{p}$ ![]() $ (1 \lt p \lt \infty)$ and
$ (1 \lt p \lt \infty)$ and ![]() $(\text{VMOA})^{*}=H^{1}$ under the pairing
$(\text{VMOA})^{*}=H^{1}$ under the pairing
 \begin{equation*}\langle F,G\rangle_{H^{2}}=\int_{0}^{2\pi}F(e^{i\theta})\overline{G(e^{i\theta})}\text{d}\theta,\end{equation*}
\begin{equation*}\langle F,G\rangle_{H^{2}}=\int_{0}^{2\pi}F(e^{i\theta})\overline{G(e^{i\theta})}\text{d}\theta,\end{equation*} then arguing as the proof of Proposition 2.5, one can obtain the implications ![]() $(1)\Rightarrow (4)$ and
$(1)\Rightarrow (4)$ and ![]() $(4)\Rightarrow (3)$. The proof of
$(4)\Rightarrow (3)$. The proof of ![]() $(3)\Rightarrow (2)$ is split into
$(3)\Rightarrow (2)$ is split into ![]() $1\leq p \leq 2$ and p > 2. For
$1\leq p \leq 2$ and p > 2. For ![]() $1\leq p\leq 2$, bearing in mind that
$1\leq p\leq 2$, bearing in mind that  $D_{p-1}^{p}\subseteq H^{p}$ and then adapting the proof of the implication
$D_{p-1}^{p}\subseteq H^{p}$ and then adapting the proof of the implication ![]() $(3)\Rightarrow(2)$ in Theorem 1.1, one can deduce that
$(3)\Rightarrow(2)$ in Theorem 1.1, one can deduce that ![]() $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to  $D_{p-1}^{p}$ and hence compact from
$D_{p-1}^{p}$ and hence compact from ![]() $\mathcal {B}$ to H p. For
$\mathcal {B}$ to H p. For ![]() $2 \lt p \lt \infty$, the Hardy–Littlewood Theorem (see [Reference Duren8, Theorem 6.3]) asserts that if
$2 \lt p \lt \infty$, the Hardy–Littlewood Theorem (see [Reference Duren8, Theorem 6.3]) asserts that if  $f(z)=\sum_{n=0}^{\infty}\widehat{f}(n)z^{n}\in H(\mathbb{D})$ and
$f(z)=\sum_{n=0}^{\infty}\widehat{f}(n)z^{n}\in H(\mathbb{D})$ and  $\sum_{n=0}^{\infty} (n+1)^{p-2} |\widehat{f}(n)|^{p} \lt \infty$, then
$\sum_{n=0}^{\infty} (n+1)^{p-2} |\widehat{f}(n)|^{p} \lt \infty$, then
 \begin{equation}
||f||^{p}_{p}\lesssim \sum_{n=0}^{\infty} (n+1)^{p-2} |\widehat{f}(n)|^{p}\end{equation}
\begin{equation}
||f||^{p}_{p}\lesssim \sum_{n=0}^{\infty} (n+1)^{p-2} |\widehat{f}(n)|^{p}\end{equation} Suppose that ![]() $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \infty$, then for any ɛ > 0, there exists a positive integer N such that
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \infty$, then for any ɛ > 0, there exists a positive integer N such that
 \begin{equation}
\sum_{n=N+1}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \varepsilon.\end{equation}
\begin{equation}
\sum_{n=N+1}^{\infty}(n+1)^{p(\alpha+1)-2}\nu_{n}^{p} \lt \varepsilon.\end{equation} Since  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$, there exists t 0 with
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$, there exists t 0 with ![]() $0 \lt t_{0} \lt 1$ such that
$0 \lt t_{0} \lt 1$ such that
 \begin{equation}
\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \varepsilon.\end{equation}
\begin{equation}
\int_{t_{0}}^{1}\log\frac{e}{1-t}\text{d}\mu(t) \lt \varepsilon.\end{equation} Let ![]() $\{f_{k}\}_{k=1}^{\infty}$ be a bounded sequence in
$\{f_{k}\}_{k=1}^{\infty}$ be a bounded sequence in ![]() $\mathcal {B}$, which converges to 0 uniformly on every compact subset of
$\mathcal {B}$, which converges to 0 uniformly on every compact subset of ![]() $\mathbb{D}$. We have to prove that
$\mathbb{D}$. We have to prove that  $\lim_{k\rightarrow0}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p}\rightarrow 0$. By (4) and Stirling’s formula, (5)–(6) we have that
$\lim_{k\rightarrow0}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p}\rightarrow 0$. By (4) and Stirling’s formula, (5)–(6) we have that
 \begin{equation*} \begin{split}
||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p} &\lesssim \sum_{n=0}^{\infty} (n+1)^{p-2}\left|\frac{\Gamma(n+1+\alpha)}{\Gamma(\alpha+1)\Gamma(n+1)}\int_{0}^{1} t^{n}f_{k}(t){\text{d}}\mu(t)\right|^{p}\\
&\lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p}\sum_{n=0}^{N}(n+1)^{p\alpha+p-2}\left (\int_{0}^{t_{0}}t^{n}{\text{d}}\mu(t)\right)^{p} \\
&+ \sum_{n=0}^{N}(n+1)^{p\alpha+p-2}\left(\int_{t_{0}}^{1}\log\frac{e}{1-t}{\text{d}}\mu(t)\right)^{p}\\
&+ \sum_{n=N+1}^{\infty}(n+1)^{p\alpha+p-2}\left(\int_{0}^{1} t^{n}|f_{k}(t)|{\text{d}}\mu(t)\right)^{p}\\
& \lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p}+ \varepsilon^{p} +\sum_{n=N+1}^{\infty}(n+1)^{p\alpha+p-2}\nu_{n}^{p}\\
& \lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p} + \varepsilon^{p}+\varepsilon.\\
\end{split} \end{equation*}
\begin{equation*} \begin{split}
||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p} &\lesssim \sum_{n=0}^{\infty} (n+1)^{p-2}\left|\frac{\Gamma(n+1+\alpha)}{\Gamma(\alpha+1)\Gamma(n+1)}\int_{0}^{1} t^{n}f_{k}(t){\text{d}}\mu(t)\right|^{p}\\
&\lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p}\sum_{n=0}^{N}(n+1)^{p\alpha+p-2}\left (\int_{0}^{t_{0}}t^{n}{\text{d}}\mu(t)\right)^{p} \\
&+ \sum_{n=0}^{N}(n+1)^{p\alpha+p-2}\left(\int_{t_{0}}^{1}\log\frac{e}{1-t}{\text{d}}\mu(t)\right)^{p}\\
&+ \sum_{n=N+1}^{\infty}(n+1)^{p\alpha+p-2}\left(\int_{0}^{1} t^{n}|f_{k}(t)|{\text{d}}\mu(t)\right)^{p}\\
& \lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p}+ \varepsilon^{p} +\sum_{n=N+1}^{\infty}(n+1)^{p\alpha+p-2}\nu_{n}^{p}\\
& \lesssim (\sup_{|w|\leq t_{0}}|f_{k}(w)|)^{p} + \varepsilon^{p}+\varepsilon.\\
\end{split} \end{equation*} This implies that  $\lim_{k\rightarrow0}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p}= 0$.
$\lim_{k\rightarrow0}||\mathcal {I}_{\mu_{\alpha+1}}(f_{k})||_{p}^{p}= 0$.
The analytic Besov space B p ![]() $(1 \lt p \lt \infty)$ consists of those functions
$(1 \lt p \lt \infty)$ consists of those functions ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}||f||^{p}_{B^{p}}= |f(0)|^{p}+\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p-2}{\text{d}}A(z) \lt \infty.\end{equation*}
\begin{equation*}||f||^{p}_{B^{p}}= |f(0)|^{p}+\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p-2}{\text{d}}A(z) \lt \infty.\end{equation*}Lemma 2.1 implies that
 \begin{equation}
f\in B^{p} \Leftrightarrow \sum_{n=0}^{\infty} 2^{-n(p-1)}||\Delta_{n}f'||^{p}_{p} \lt \infty.\end{equation}
\begin{equation}
f\in B^{p} \Leftrightarrow \sum_{n=0}^{\infty} 2^{-n(p-1)}||\Delta_{n}f'||^{p}_{p} \lt \infty.\end{equation} The space B 1 consists of those functions ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}\int_{\mathbb{D}}|f''(z)|{\text{d}}A(z) \lt \infty.\end{equation*}
\begin{equation*}\int_{\mathbb{D}}|f''(z)|{\text{d}}A(z) \lt \infty.\end{equation*} Based on (7), we can obtain the analogue of Theorem 1.1 for Besove spaces B p ![]() $(1\leq p \lt \infty)$.
$(1\leq p \lt \infty)$.
Theorem 2.15 Let ![]() $1\leq p \lt \infty$ and µ be a positive Borel measure on
$1\leq p \lt \infty$ and µ be a positive Borel measure on ![]() $[0, 1)$ with
$[0, 1)$ with  $\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
$\int_{0}^{1} \log\frac{e}{1-t}d\mu(t) \lt \infty$. Then, the following statements are equivalent:
(1) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from
$\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from  $\mathcal {B}$ to B p.
$\mathcal {B}$ to B p.(2) The operator
 $\mathcal {I}_{\mu_{\alpha+1}}$ is compact from
$\mathcal {I}_{\mu_{\alpha+1}}$ is compact from  $\mathcal {B}$ to B p.
$\mathcal {B}$ to B p.(3) The measure µ satisfies
 $\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-1}\nu_{n}^{p} \lt \infty.$
$\sum_{n=0}^{\infty}(n+1)^{p(\alpha+1)-1}\nu_{n}^{p} \lt \infty.$
The proof of this theorem is analogous to Theorem 1.1, and we left it to the interested readers.
Remark 2.16. Let µ be a finite positive Borel measure on ![]() $[0, 1)$ and
$[0, 1)$ and ![]() $f\in H(\mathbb{D})$, and Galanopoulos, Girela and Merchán [Reference Galanopoulos, Girela and Merchán9] introduced a Cesàro-like operator
$f\in H(\mathbb{D})$, and Galanopoulos, Girela and Merchán [Reference Galanopoulos, Girela and Merchán9] introduced a Cesàro-like operator ![]() $\mathcal {C}_{\mu}$ which has been widely studied recently. The operator
$\mathcal {C}_{\mu}$ which has been widely studied recently. The operator ![]() $\mathcal {C}_{\mu}$ is defined by
$\mathcal {C}_{\mu}$ is defined by
 \begin{equation*}\mathcal {C}_{\mu}(f)(z)=\sum^\infty_{n=0}\left(\mu_n\sum^n_{k=0}a_k\right)z^n=\int_{0}^{1}\frac{f(tz)}{1-tz}{\text{d}}\mu(t), \ z\in\mathbb{D}.\end{equation*}
\begin{equation*}\mathcal {C}_{\mu}(f)(z)=\sum^\infty_{n=0}\left(\mu_n\sum^n_{k=0}a_k\right)z^n=\int_{0}^{1}\frac{f(tz)}{1-tz}{\text{d}}\mu(t), \ z\in\mathbb{D}.\end{equation*} We remarked that the proof of Theorem 1.1 can be used to study the action of ![]() $\mathcal{C}_\mu$ from the Bloch space to Bergman spaces, Hardy spaces and Besov spaces. We leave it to the interested readers.
$\mathcal{C}_\mu$ from the Bloch space to Bergman spaces, Hardy spaces and Besov spaces. We leave it to the interested readers.
Funding Statement
The author was supported by the Natural Science Foundation of Hunan Province (No. 2022JJ30369).
Competing Interests
The author declares that there is no conflict of interest.
Availability of Data and Materials
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study: the article describes entirely theoretical research.