Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-17T16:44:23.983Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbolic factors of 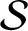${\mathcal S}$-adic subshifts of finite alphabet rank

Part of: Topological dynamics

Published online by Cambridge University Press:  17 March 2022

BASTIÁN ESPINOZA Open the ORCID record for BASTIÁN ESPINOZA [Opens in a new window]
BASTIÁN ESPINOZA*
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, Universidad de Chile, Beauchef 851, Santiago, Chile
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

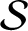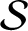This paper studies several aspects of symbolic (i.e. subshift) factors of $\mathcal {S}$ -adic subshifts of finite alphabet rank. First, we address a problem raised by Donoso et al [Interplay between finite topological rank minimal Cantor systems, S-adic subshifts and their complexity. Trans. Amer. Math. Soc. 374(5) (2021), 3453–3489] about the topological rank of symbolic factors of $\mathcal {S}$ -adic subshifts and prove that this rank is at most the one of the extension system, improving on the previous results [B. Espinoza. On symbolic factors of S-adic subshifts of finite alphabet rank. Preprint, 2022, arXiv:2008.13689v2; N. Golestani and M. Hosseini. On topological rank of factors of Cantor minimal systems. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.62. Published online 8 June 2021]. As a consequence of our methods, we prove that finite topological rank systems are coalescent. Second, we investigate the structure of fibers 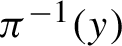$\pi ^{-1}(y)$ of factor maps 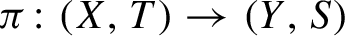$\pi \colon (X,T)\to (Y,S)$ between minimal 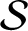${\mathcal S}$ -adic subshifts of finite alphabet rank and show that they have the same finite cardinality for all y in a residual subset of Y. Finally, we prove that the number of symbolic factors (up to conjugacy) of a fixed subshift of finite topological rank is finite, thus extending Durand’s similar theorem on linearly recurrent subshifts [F. Durand. Linearly recurrent subshifts have a finite number of non-periodic subshift factors. Ergod. Th. & Dynam. Sys. 20(4) (2000), 1061–1078].

Keywords

topological rankS-adic representationssubstitutional systems

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 5 , May 2023 , pp. 1511 - 1547
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amini, M., Elliott, G. A. and Golestani, N.. The category of Bratteli diagrams. Canad. J. Math. 67(5) (2015), 990–1023.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions. Elsevier, Amsterdam, 1988.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Finite rank Bratteli diagrams: structure of invariant measures. Trans. Amer. Math. Soc. 365(5) (2013), 2637–2679.CrossRefGoogle Scholar
Berthé, V., Steiner, W., Thuswaldner, J. M. and Yassawi, R.. Recognizability for sequences of morphisms. Ergod. Th. & Dynam. Sys. 39(11) (2019), 2896–2931.CrossRefGoogle Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. Interplay between finite topological rank minimal Cantor systems, $\mathbf{\mathcal{S}}$ -adic subshifts and their complexity. Trans. Amer. Math. Soc. 374(5) (2021), 3453–3489.CrossRefGoogle Scholar
Durand, F., Frank, A. and Maass, A.. Eigenvalues of minimal Cantor systems. J. Eur. Math. Soc. (JEMS) 21(3) (2019), 727–775.CrossRefGoogle Scholar
Durand, F., Host, B. and Skau, C.. Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergod. Th. & Dynam. Sys. 19(4) (1999), 953–993.CrossRefGoogle Scholar
Downarowicz, T. and Maass, A.. Finite-rank Bratteli–Vershik diagrams are expansive. Ergod. Th. & Dynam. Sys. 28(3) (2008), 739–747.CrossRefGoogle Scholar
Downarowicz, T.. The royal couple conceals their mutual relationship: a noncoalescent Toeplitz flow. Israel J. Math. 97 (1997), 239–251.CrossRefGoogle Scholar
Durand, F.. Linearly recurrent subshifts have a finite number of non-periodic subshift factors. Ergod. Th. & Dynam. Sys. 20(4) (2000), 1061–1078.CrossRefGoogle Scholar
Espinoza, B. and Maass, A.. On the automorphism group of minimal $\mathbf{\mathcal{S}}$ -adic subshifts of finite alphabet rank. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.64. Published online 30 June 2021.CrossRefGoogle Scholar
Espinoza, B.. On symbolic factors of $\mathbf{\mathcal{S}}$ -adic subshifts of finite alphabet rank. Preprint, 2022, arXiv:2008.13689v2 [math.DS].Google Scholar
Golestani, N. and Hosseini, M.. On topological rank of factors of Cantor minimal systems. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.62. Published online 8 June 2021.Google Scholar
Giordano, T., Handelman, D. and Hosseini, M.. Orbit equivalence of Cantor minimal systems and their continuous spectra. Math. Z. 289(3–4) (2018), 1199–1218.CrossRefGoogle Scholar
Gjerde, R. and Johansen, Ø.. Bratteli–Vershik models for Cantor minimal systems: applications to Toeplitz flows. Ergod. Th. & Dynam. Sys. 20(6) (2000), 1687–1710.CrossRefGoogle Scholar
Gjerde, R. and Johansen, Ø.. Bratteli–Vershik models for Cantor minimal systems associated to interval exchange transformations. Math. Scand. 90(1) (2002), 87–100.CrossRefGoogle Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(6) (1992), 827–864.CrossRefGoogle Scholar
Rozenberg, G. and Salomaa, A.. Handbook of Formal Languages: Volume 1. Word, Language, Grammar. Springer-Verlag, Berlin, 1997.Google Scholar