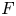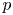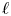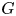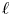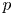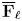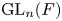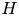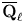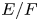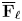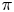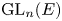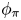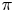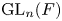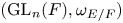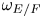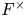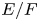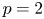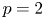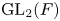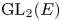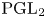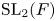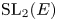1. Introduction
Let ![]() $F$ be a non-archimedean local field of characteristic different from 2 and residual characteristic
$F$ be a non-archimedean local field of characteristic different from 2 and residual characteristic ![]() $p$ and
$p$ and ![]() $G$ the
$G$ the ![]() $F$-points of a reductive group defined over
$F$-points of a reductive group defined over ![]() $F$. Let
$F$. Let ![]() $R$ be an algebraically closed field of characteristic different from
$R$ be an algebraically closed field of characteristic different from ![]() $p$. A representation
$p$. A representation ![]() $\pi$ of a group
$\pi$ of a group ![]() $G$, with coefficients in
$G$, with coefficients in ![]() $R$, is said to be distinguished with respect to a subgroup
$R$, is said to be distinguished with respect to a subgroup ![]() $H$ of
$H$ of ![]() $G$ if it admits a non-trivial
$G$ if it admits a non-trivial ![]() $H$-invariant linear form. More generally, if
$H$-invariant linear form. More generally, if ![]() $\chi$ is a character of
$\chi$ is a character of ![]() $H$, we will say that
$H$, we will say that ![]() $\pi$ is
$\pi$ is ![]() $(H,\chi )$-distinguished if there exists a non-trivial linear functional on the space of
$(H,\chi )$-distinguished if there exists a non-trivial linear functional on the space of ![]() $\pi$ on which
$\pi$ on which ![]() $H$ acts via
$H$ acts via ![]() $\chi$, i.e.
$\chi$, i.e. ![]() $f:\pi \to R$ such that
$f:\pi \to R$ such that
for all ![]() $h \in H$ and
$h \in H$ and ![]() $v \in \pi$.
$v \in \pi$.
Distinguished representations are central objects in the study of the relative Langlands program. The distinction problem is closely related to the Langlands functorial conjectures and it should be possible to characterize the ![]() $(H,\chi )$-distinguished representations as the images with respect to a functorial transfer to
$(H,\chi )$-distinguished representations as the images with respect to a functorial transfer to ![]() $G$ from a third group
$G$ from a third group ![]() $G'$ in many cases. There exists a rich literature, such as [Reference Anandavardhanan and PrasadAP03, Reference Sakellaridis and VenkateshSaVe17, Reference LuLu18, Reference LuLu20], trying to classify all
$G'$ in many cases. There exists a rich literature, such as [Reference Anandavardhanan and PrasadAP03, Reference Sakellaridis and VenkateshSaVe17, Reference LuLu18, Reference LuLu20], trying to classify all ![]() $H$-distinguished complex representations of
$H$-distinguished complex representations of ![]() $G$. Furthermore, when
$G$. Furthermore, when ![]() $\theta$ is the Galois involution of order
$\theta$ is the Galois involution of order ![]() $2$ and
$2$ and ![]() $H=G^{\theta },$ Prasad [Reference PrasadPra15] constructs
$H=G^{\theta },$ Prasad [Reference PrasadPra15] constructs ![]() $\chi _H$ a quadratic character of
$\chi _H$ a quadratic character of ![]() $H$ and gives a precise conjecture for the multiplicity
$H$ and gives a precise conjecture for the multiplicity ![]() $\dim _\mathbb {C}\operatorname {Hom}_H(\pi,\chi _H)$ in terms of the enhanced Langlands parameter of
$\dim _\mathbb {C}\operatorname {Hom}_H(\pi,\chi _H)$ in terms of the enhanced Langlands parameter of ![]() $\pi$.
$\pi$.
More recently, mathematicians have been interested in modular representations of ![]() $p$-adic groups, which are smooth representations with coefficients in
$p$-adic groups, which are smooth representations with coefficients in ![]() $\overline {\mathbf {F}}_{\ell }$, with
$\overline {\mathbf {F}}_{\ell }$, with ![]() $\ell \neq p$. The theory of
$\ell \neq p$. The theory of ![]() $\ell$-modular representations has been initiated by Vignéras in [Reference VignérasVig96]. These works are motivated by a modular local Langlands program and studying congruences between automorphic forms (which have been used to prove many remarkable theorems of arithmetic geometry).
$\ell$-modular representations has been initiated by Vignéras in [Reference VignérasVig96]. These works are motivated by a modular local Langlands program and studying congruences between automorphic forms (which have been used to prove many remarkable theorems of arithmetic geometry).
For modular representations, much remains to be done for the distinction problems. Sécherre and Venketasubramanian have examined the pair ![]() $(G,H) = (\operatorname {GL}_n(F), \operatorname {GL}_{n-1}(F))$ in [Reference Sécherre and VenketasubramanianSéVe17]. Sécherre [Reference SécherreSéc19] also investigated the pair
$(G,H) = (\operatorname {GL}_n(F), \operatorname {GL}_{n-1}(F))$ in [Reference Sécherre and VenketasubramanianSéVe17]. Sécherre [Reference SécherreSéc19] also investigated the pair ![]() $(\operatorname {GL}_{n}(E),\operatorname {GL}_{n}(F))$ for supercuspidal representations with
$(\operatorname {GL}_{n}(E),\operatorname {GL}_{n}(F))$ for supercuspidal representations with ![]() $p$ odd, where
$p$ odd, where ![]() $E$ is a quadratic extension of
$E$ is a quadratic extension of ![]() $F$. Ongoing work by Kurinczuk, Matringe and Sécherre aims at extending the results of the pair
$F$. Ongoing work by Kurinczuk, Matringe and Sécherre aims at extending the results of the pair ![]() $(\operatorname {GL}_{n}(E), \operatorname {GL}_{n}(F))$ to all representations (see [Reference Kurinczuk, Matringe and SécherreKMS23]).
$(\operatorname {GL}_{n}(E), \operatorname {GL}_{n}(F))$ to all representations (see [Reference Kurinczuk, Matringe and SécherreKMS23]).
In this paper, we consider a quadratic field extension ![]() $E/F$ of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic
$E/F$ of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic ![]() $p$. Denote by
$p$. Denote by ![]() $q_F$ (respectively,
$q_F$ (respectively, ![]() $q_E$) the cardinality of the residue field of
$q_E$) the cardinality of the residue field of ![]() $F$ (respectively,
$F$ (respectively, ![]() $E$). Let
$E$). Let ![]() $\ell$ be an odd prime different from
$\ell$ be an odd prime different from ![]() $p$. We are interested in the distinction problems for the pairs
$p$. We are interested in the distinction problems for the pairs ![]() $(\operatorname {GL}_{n}(E),\operatorname {GL}_{n}(F))$ and
$(\operatorname {GL}_{n}(E),\operatorname {GL}_{n}(F))$ and ![]() $(\operatorname {SL}_{2}(E),\operatorname {SL}_{2}(F))$. We also give a modular version of the Prasad conjecture for
$(\operatorname {SL}_{2}(E),\operatorname {SL}_{2}(F))$. We also give a modular version of the Prasad conjecture for ![]() $\operatorname {PGL}_2$.
$\operatorname {PGL}_2$.
We would like to point out that the ongoing work [Reference Kurinczuk, Matringe and SécherreKMS23] of Kurinczuk, Matringe and Sécherre also gives a classification of all irreducible ![]() $\operatorname {GL}_2(F)$-distinguished representations of
$\operatorname {GL}_2(F)$-distinguished representations of ![]() $\operatorname {GL}_{2}(E)$ (at least for
$\operatorname {GL}_{2}(E)$ (at least for ![]() $p\neq 2$). However, our methods and theirs are completely different. They use the gamma factors and the epsilon factors whereas in this article we use Mackey theory.
$p\neq 2$). However, our methods and theirs are completely different. They use the gamma factors and the epsilon factors whereas in this article we use Mackey theory.
1.1 Distinguished supercuspidal representations of  $\operatorname {GL}_n$
$\operatorname {GL}_n$
A ![]() $\overline {\mathbf {Q}}_{\ell }$-representation
$\overline {\mathbf {Q}}_{\ell }$-representation ![]() $(\tilde {\pi },\tilde {V})$ of a
$(\tilde {\pi },\tilde {V})$ of a ![]() $p$-adic group
$p$-adic group ![]() $G$ is said to be
$G$ is said to be ![]() $\ell$-integral if it admits a free
$\ell$-integral if it admits a free ![]() $\overline {\mathbf {Z}}_{\ell }$-submodule
$\overline {\mathbf {Z}}_{\ell }$-submodule ![]() $L$ of
$L$ of ![]() $\tilde {V}$, stable by
$\tilde {V}$, stable by ![]() $G$, such that
$G$, such that ![]() $L \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {Q}}_{\ell } = \tilde {V}$. If
$L \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {Q}}_{\ell } = \tilde {V}$. If ![]() $(\pi,V)$ is an irreducible
$(\pi,V)$ is an irreducible ![]() $\ell$-integral
$\ell$-integral ![]() $\overline {\mathbf {Q}}_{\ell }$-representation and
$\overline {\mathbf {Q}}_{\ell }$-representation and ![]() $L$ is a
$L$ is a ![]() $\overline {\mathbf {Z}}_{\ell }[G]$-lattice of
$\overline {\mathbf {Z}}_{\ell }[G]$-lattice of ![]() $V$ of finite type, then the semi-simplification of
$V$ of finite type, then the semi-simplification of ![]() $L \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {F}}_{\ell }$ does not depend on the choice of
$L \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {F}}_{\ell }$ does not depend on the choice of ![]() $L$ and is called the reduction modulo
$L$ and is called the reduction modulo ![]() $\ell$ of
$\ell$ of ![]() $\pi$ (we refer to [Reference VignérasVig96] for more details). If
$\pi$ (we refer to [Reference VignérasVig96] for more details). If ![]() $\pi$ is an
$\pi$ is an ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $G$, an
$G$, an ![]() $\ell$-integral irreducible
$\ell$-integral irreducible ![]() $\overline {\mathbf {Q}}_{\ell }$-representation
$\overline {\mathbf {Q}}_{\ell }$-representation ![]() $\tilde {\pi }$ is called a
$\tilde {\pi }$ is called a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$ if its reduction modulo
$\pi$ if its reduction modulo ![]() $\ell$ is
$\ell$ is ![]() $\pi$.
$\pi$.
Our first result, discussed in § 3, is the following.
Theorem 1.1 (Theorem 3.4)
Let ![]() $H$ be a closed subgroup of
$H$ be a closed subgroup of ![]() $\operatorname {GL}_n(F)$. Let
$\operatorname {GL}_n(F)$. Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(F)$ which is
$\operatorname {GL}_n(F)$ which is ![]() $H$-distinguished. Then there exists a
$H$-distinguished. Then there exists a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ such that it is supercuspidal and distinguished by
$\pi$ such that it is supercuspidal and distinguished by ![]() $H$.
$H$.
Remark 1.2 Theorem 1.1 is valid even for ![]() $F$ of characteristic 2.
$F$ of characteristic 2.
The proof depends on the type theory and the existence of a projective envelope for supercuspidal types. This is a very general result allowing us to transfer the problem from modular representations to complex representations. As an immediate consequence, we get the following.
Corollary 1.3 (Corollary 3.5)
There is no supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_{2n}(F)$ distinguished by
$\operatorname {GL}_{2n}(F)$ distinguished by ![]() $\operatorname {Sp}_{2n}(F)$.
$\operatorname {Sp}_{2n}(F)$.
We also give two other applications. The first is to study supercuspidal representations of ![]() $\operatorname {GL}_{n}(E)$ distinguished by a Galois involution. For
$\operatorname {GL}_{n}(E)$ distinguished by a Galois involution. For ![]() $\ell \neq 2$, we prove the dichotomy theorem and the disjunction theorem. Let
$\ell \neq 2$, we prove the dichotomy theorem and the disjunction theorem. Let ![]() $\omega _{E/F}$ be the quadratic character of
$\omega _{E/F}$ be the quadratic character of ![]() $F^{\times }$ associated to the field extension
$F^{\times }$ associated to the field extension ![]() $E/F$ by the local class field theory and let
$E/F$ by the local class field theory and let ![]() $\sigma$ be the non-trivial
$\sigma$ be the non-trivial ![]() $F$-automorphism of
$F$-automorphism of ![]() $E$. A representation
$E$. A representation ![]() $\pi$ of
$\pi$ of ![]() $\operatorname {GL}_n(E)$ is said
$\operatorname {GL}_n(E)$ is said ![]() $\sigma$-selfdual if
$\sigma$-selfdual if ![]() $\pi ^{\vee } \simeq \pi ^{\sigma }$, where
$\pi ^{\vee } \simeq \pi ^{\sigma }$, where ![]() $\pi ^{\vee }$ is the contragredient representation of
$\pi ^{\vee }$ is the contragredient representation of ![]() $\pi$.
$\pi$.
Theorem 1.4 (Theorem 3.14)
Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$. Then
$\operatorname {GL}_n(E)$. Then ![]() $\pi$ is
$\pi$ is ![]() $\sigma$-selfdual if and only if it is distinguished or
$\sigma$-selfdual if and only if it is distinguished or ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {GL}_n(F)$. Moreover,
$\operatorname {GL}_n(F)$. Moreover, ![]() $\pi$ cannot be both distinguished and
$\pi$ cannot be both distinguished and ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {GL}_n(F)$.
$\operatorname {GL}_n(F)$.
For the complex representations, it is called the Jacquet conjecture proved by Kable in [Reference KableKab04]. We first show that one can lift ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representations to
$\overline {\mathbf {F}}_{\ell }$-representations to ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-representations. This follows from the fact that since
$\overline {\mathbf {Q}}_{\ell }$-representations. This follows from the fact that since ![]() $\ell$ is odd, the number of inertial classes of such lifts is odd, hence has a fixed point under
$\ell$ is odd, the number of inertial classes of such lifts is odd, hence has a fixed point under ![]() $\sigma$-duality. Then we prove that all these supercuspidal lifts share the same sign due to Schur's lemma. Combining with Theorem 1.1, this allows us to deduce the Jacquet conjecture for modular representations from complex representations.
$\sigma$-duality. Then we prove that all these supercuspidal lifts share the same sign due to Schur's lemma. Combining with Theorem 1.1, this allows us to deduce the Jacquet conjecture for modular representations from complex representations.
Remark 1.5 When ![]() $p\neq 2$, the distinguished supercuspidal representations were studied by Sécherre in [Reference SécherreSéc19] (with no restriction on
$p\neq 2$, the distinguished supercuspidal representations were studied by Sécherre in [Reference SécherreSéc19] (with no restriction on ![]() $\ell$). Our method is different from that used in [Reference SécherreSéc19] and works for
$\ell$). Our method is different from that used in [Reference SécherreSéc19] and works for ![]() $\ell \neq 2$ but for any
$\ell \neq 2$ but for any ![]() $p$. Therefore, combining the results in this paper and in [Reference SécherreSéc19] gives the complete result for distinguished supercuspidal representations for all
$p$. Therefore, combining the results in this paper and in [Reference SécherreSéc19] gives the complete result for distinguished supercuspidal representations for all ![]() $\ell$ and
$\ell$ and ![]() $p$ with
$p$ with ![]() $\ell \neq p$.
$\ell \neq p$.
We also have a characterization using the local Langlands correspondence of Vignéras.
Proposition 1.6 (Proposition 3.15)
Let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$ and
$\operatorname {GL}_n(E)$ and ![]() $\varphi$ its Langlands parameter. Then
$\varphi$ its Langlands parameter. Then ![]() $\pi$ is distinguished (respectively,
$\pi$ is distinguished (respectively, ![]() $\omega _{E/F}$-distinguished) by
$\omega _{E/F}$-distinguished) by ![]() $\operatorname {GL}_n(F)$ if and only if
$\operatorname {GL}_n(F)$ if and only if ![]() $\,\varphi _\pi$ is conjugate-orthogonal (respectively, conjugate-symplectic).
$\,\varphi _\pi$ is conjugate-orthogonal (respectively, conjugate-symplectic).
The last application, is for representations distinguished by a unitary involution. Let ![]() $\ell \neq 2$ and
$\ell \neq 2$ and ![]() $\varsigma$ be a unitary involution of
$\varsigma$ be a unitary involution of ![]() $\operatorname {GL}_n(E)$, that is
$\operatorname {GL}_n(E)$, that is ![]() $\varsigma (g)=\varepsilon \sigma ({}^{t}g^{-1}) \varepsilon ^{-1}$ where
$\varsigma (g)=\varepsilon \sigma ({}^{t}g^{-1}) \varepsilon ^{-1}$ where ![]() $\varepsilon$ is a hermitian matrix in
$\varepsilon$ is a hermitian matrix in ![]() $M_n(E)$.
$M_n(E)$.
Theorem 1.7 (Theorem 3.17)
Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$ and
$\operatorname {GL}_n(E)$ and ![]() $\varsigma$ a unitary involution of
$\varsigma$ a unitary involution of ![]() $G$. Then
$G$. Then ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_n(E)^{\varsigma }$ if and only if
$\operatorname {GL}_n(E)^{\varsigma }$ if and only if ![]() $\pi ^{\sigma }\simeq \pi$.
$\pi ^{\sigma }\simeq \pi$.
This extends the result of [Reference ZouZou22] to the case ![]() $p=2$ when
$p=2$ when ![]() $F$ has characteristic zero.
$F$ has characteristic zero.
1.2 Modular distinguished representations for  $(\operatorname {GL}_{2}(E),\operatorname {GL}_{2}(F))$
$(\operatorname {GL}_{2}(E),\operatorname {GL}_{2}(F))$
In § 4, we complete the classification of all representations of ![]() $\operatorname {GL}_{2}(E)$ distinguished by
$\operatorname {GL}_{2}(E)$ distinguished by ![]() $\operatorname {GL}_{2}(F)$.
$\operatorname {GL}_{2}(F)$.
Let ![]() $\chi _1,\chi _2$ be two characters of
$\chi _1,\chi _2$ be two characters of ![]() $E^{\times }$. We use Mackey theory to show that the principal series representation
$E^{\times }$. We use Mackey theory to show that the principal series representation ![]() $\pi (\chi _1,\chi _2)$ is distinguished by
$\pi (\chi _1,\chi _2)$ is distinguished by ![]() $\operatorname {GL}_2(F)$ if and only if either
$\operatorname {GL}_2(F)$ if and only if either ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with ![]() $\chi _1\neq \chi _2$. (See Lemma 4.3 for more details.)
$\chi _1\neq \chi _2$. (See Lemma 4.3 for more details.)
To get a complete classification, we are just missing irreducible subquotients of non-irreducible principal series. Denote by ![]() $\nu ^{1/2}$ the unramified character of
$\nu ^{1/2}$ the unramified character of ![]() $E^{\times }$ sending a uniformizer to
$E^{\times }$ sending a uniformizer to ![]() $q_E^{1/2}$ where the square root
$q_E^{1/2}$ where the square root ![]() $q_E^{1/2}$ of
$q_E^{1/2}$ of ![]() $q_E$ is fixed. Let
$q_E$ is fixed. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$. When
$E^{\times }$. When ![]() $q_{E} \not \equiv -1 \pmod {\ell }$, we denote by
$q_{E} \not \equiv -1 \pmod {\ell }$, we denote by ![]() $\operatorname {St}_{\chi }$ the twisted Steinberg representation, that is the unique generic irreducible subquotient of
$\operatorname {St}_{\chi }$ the twisted Steinberg representation, that is the unique generic irreducible subquotient of ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$. In the case
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$. In the case ![]() $q_{E} \equiv -1 \pmod {\ell }$, the generic irreducible subquotient of
$q_{E} \equiv -1 \pmod {\ell }$, the generic irreducible subquotient of ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$ is the special representation, denoted by
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$ is the special representation, denoted by ![]() $\operatorname {Sp}_{\chi }$.
$\operatorname {Sp}_{\chi }$.
Theorem 1.8 (Theorem 4.6)
Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$.
$E^{\times }$.
(i) If
 $\ell \nmid q_{E}^2-1$, then
$\ell \nmid q_{E}^2-1$, then  $\operatorname {St}_\chi$ is
$\operatorname {St}_\chi$ is  $\operatorname {GL}_2(F)$-distinguished if and only if
$\operatorname {GL}_2(F)$-distinguished if and only if  $\chi _{|{F^\times }}=\omega _{E/F}$.
$\chi _{|{F^\times }}=\omega _{E/F}$.(ii) If
 $\ell \mid q_{E}+1$, then
$\ell \mid q_{E}+1$, then  $\operatorname {Sp}_\chi$ is
$\operatorname {Sp}_\chi$ is  $\operatorname {GL}_2(F)$-distinguished if and only if
$\operatorname {GL}_2(F)$-distinguished if and only if  $\ell \mid q_{F}+1$ and
$\ell \mid q_{F}+1$ and  $\chi _{|{F^\times }}=\omega _{E/F}$ or
$\chi _{|{F^\times }}=\omega _{E/F}$ or  $\nu ^{1/2}_{|{F^\times }}$.
$\nu ^{1/2}_{|{F^\times }}$.(iii) If
 $\ell \mid q_{E}-1$, then
$\ell \mid q_{E}-1$, then  $\operatorname {St}_\chi$ is
$\operatorname {St}_\chi$ is  $\operatorname {GL}_2(F)$-distinguished if and only if
$\operatorname {GL}_2(F)$-distinguished if and only if  $\chi _{|{F^\times }}=\omega _{E/F}$ or
$\chi _{|{F^\times }}=\omega _{E/F}$ or  $\chi _{|{F^\times }}=\mathbf {1}$ with
$\chi _{|{F^\times }}=\mathbf {1}$ with  $\ell \mid q_{F}-1$.
$\ell \mid q_{F}-1$.
Remark 1.9 From Theorem 1.8, we would like to highlight the fact that we have in the modular case new phenomena that do not appear in the complex setting.
– When
 $q_{F}\equiv 1 \pmod {\ell }$, the Steinberg representation
$q_{F}\equiv 1 \pmod {\ell }$, the Steinberg representation  $\operatorname {St}$ is both
$\operatorname {St}$ is both  $\operatorname {GL}_2(F)$-distinguished and
$\operatorname {GL}_2(F)$-distinguished and  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished.
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished.– When
 $q_{E}\equiv -1 \pmod {\ell }$ and
$q_{E}\equiv -1 \pmod {\ell }$ and  $E/F$ is unramified (that is,
$E/F$ is unramified (that is,  $q_{F}^2\equiv -1 \pmod {\ell }$ and so
$q_{F}^2\equiv -1 \pmod {\ell }$ and so  $q_{F}\not \equiv -1 \pmod {\ell }$) the special representation
$q_{F}\not \equiv -1 \pmod {\ell }$) the special representation  $\operatorname {Sp}$ is neither
$\operatorname {Sp}$ is neither  $\operatorname {GL}_2(F)$-distinguished nor
$\operatorname {GL}_2(F)$-distinguished nor  $(\operatorname {GL}_2(F),\omega _{E/F})$- distinguished. This has been mentioned by Sécherre in [Reference SécherreSéc19, Remark 2.8].
$(\operatorname {GL}_2(F),\omega _{E/F})$- distinguished. This has been mentioned by Sécherre in [Reference SécherreSéc19, Remark 2.8].– When
 $q_{E} \equiv -1 \pmod {\ell }$ and
$q_{E} \equiv -1 \pmod {\ell }$ and  $E/F$ is ramified (that is,
$E/F$ is ramified (that is,  $q_{F} \equiv -1 \pmod {\ell }$) the special representation
$q_{F} \equiv -1 \pmod {\ell }$) the special representation  $\operatorname {Sp}$ is
$\operatorname {Sp}$ is  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished and is also
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished and is also  $(\operatorname {GL}_2(F),\nu ^{1/2}_{|{F^\times }})$-distinguished.
$(\operatorname {GL}_2(F),\nu ^{1/2}_{|{F^\times }})$-distinguished.
1.3 The modulo  $\ell$ Prasad conjecture
$\ell$ Prasad conjecture
In § 5, we discuss the Prasad conjecture for modular representations. In [Reference PrasadPra15], Prasad proposed a conjecture for the multiplicity ![]() $\dim _\mathbb {C} \operatorname {Hom}_{G(F)}(\pi,\chi _G)$ under the local Langlands conjecture, where
$\dim _\mathbb {C} \operatorname {Hom}_{G(F)}(\pi,\chi _G)$ under the local Langlands conjecture, where ![]() $G$ is a quasi-split reductive group defined over
$G$ is a quasi-split reductive group defined over ![]() $F$,
$F$, ![]() $\pi$ is an irreducible smooth representation of
$\pi$ is an irreducible smooth representation of ![]() $G(E)$ lying in a generic
$G(E)$ lying in a generic ![]() $L$-packet and
$L$-packet and ![]() $\chi _G$ is a quadratic character depending on
$\chi _G$ is a quadratic character depending on ![]() $G$ and the quadratic extension
$G$ and the quadratic extension ![]() $E/F$. Since the local Langlands correspondence for the
$E/F$. Since the local Langlands correspondence for the ![]() $\ell$-modular representations of
$\ell$-modular representations of ![]() $G(F)$ has not been set up in general, except for
$G(F)$ has not been set up in general, except for ![]() $G=\operatorname {GL}_n$, we are concerned only with the simplest case where
$G=\operatorname {GL}_n$, we are concerned only with the simplest case where ![]() $G=\operatorname {PGL}_2$.
$G=\operatorname {PGL}_2$.
The modulo ![]() $\ell$ local Langlands correspondence for
$\ell$ local Langlands correspondence for ![]() $\operatorname {GL}_2$ has been defined by Vignéras in [Reference VignérasVig01a], and is a map
$\operatorname {GL}_2$ has been defined by Vignéras in [Reference VignérasVig01a], and is a map ![]() $V : \operatorname {Irr}_R(\operatorname {GL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$, where
$V : \operatorname {Irr}_R(\operatorname {GL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$, where ![]() $\operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$ denotes the set of isomorphism classes of nilpotent semisimple Weil–Deligne representations. Let
$\operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$ denotes the set of isomorphism classes of nilpotent semisimple Weil–Deligne representations. Let ![]() $\pi$ be an irreducible representation of
$\pi$ be an irreducible representation of ![]() $\operatorname {GL}_2(E)$ with central character
$\operatorname {GL}_2(E)$ with central character ![]() $\omega _{\pi }$. Since
$\omega _{\pi }$. Since ![]() $\det V(\pi )=\omega _{\pi }$ as characters of
$\det V(\pi )=\omega _{\pi }$ as characters of ![]() $W_E$, it induces a map
$W_E$, it induces a map
Using this correspondence, the Prasad conjecture is not valid for ![]() $\ell$-modular representations (at least in the non-banal case). Actually, it does not work for any map
$\ell$-modular representations (at least in the non-banal case). Actually, it does not work for any map ![]() $L : \operatorname {Irr}_R(\operatorname {PGL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2)$ having the same semisimple part as
$L : \operatorname {Irr}_R(\operatorname {PGL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2)$ having the same semisimple part as ![]() $PV$ (see § 5.2).
$PV$ (see § 5.2).
In order to propose a solution for ![]() $\ell$-modular representations, we will consider non-nilpotent Weil–Deligne representations as in [Reference Kurinczuk and MatringeKM21]. Let
$\ell$-modular representations, we will consider non-nilpotent Weil–Deligne representations as in [Reference Kurinczuk and MatringeKM21]. Let ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ denote the set of isomorphism classes of semisimple Weil–Deligne representation of
$\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ denote the set of isomorphism classes of semisimple Weil–Deligne representation of ![]() $\operatorname {GL}_2$. Kurinczuk and Matringe define in [Reference Kurinczuk and MatringeKM21] an equivalence relation
$\operatorname {GL}_2$. Kurinczuk and Matringe define in [Reference Kurinczuk and MatringeKM21] an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$, and we denote by
$\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$, and we denote by ![]() $[\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)]$ the quotient set.
$[\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)]$ the quotient set.
Then we define an injection from ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ to
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ to ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ (which is not the trivial one in the non-banal case) in the following way. Let
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ (which is not the trivial one in the non-banal case) in the following way. Let ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $E^\times$. If
$E^\times$. If ![]() $\ell \mid q_E-1$, we denote by
$\ell \mid q_E-1$, we denote by ![]() $\Psi _{\operatorname {St},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation
$\Psi _{\operatorname {St},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation ![]() $\Psi _{\operatorname {St},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ with
$\Psi _{\operatorname {St},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ with ![]() $N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. If
$N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. If ![]() $\ell \mid q_E+1$, let
$\ell \mid q_E+1$, let ![]() $\Psi _{\operatorname {Sp},\chi } := (\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},0)$. We define an injection
$\Psi _{\operatorname {Sp},\chi } := (\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},0)$. We define an injection
by
 \[ P(\Psi) = \left\{\begin{array}{@{}ll}
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{-1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E-1 \mbox{ and } \Psi = \Psi_{
\operatorname{St},\chi}, \\ {\bigg[\chi\nu^{-1/2}
\oplus \chi\nu^{1/2},\begin{pmatrix} 0 & 1 \\ 1 & 0
\end{pmatrix}\bigg]} & \mbox{if } \ell \mid q_E+1 \mbox{
and } \Psi = \Psi_{\operatorname{Sp},\chi}, \\
{}[\Psi] & \mbox{otherwise.} \end{array}\right.
\]
\[ P(\Psi) = \left\{\begin{array}{@{}ll}
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{-1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E-1 \mbox{ and } \Psi = \Psi_{
\operatorname{St},\chi}, \\ {\bigg[\chi\nu^{-1/2}
\oplus \chi\nu^{1/2},\begin{pmatrix} 0 & 1 \\ 1 & 0
\end{pmatrix}\bigg]} & \mbox{if } \ell \mid q_E+1 \mbox{
and } \Psi = \Psi_{\operatorname{Sp},\chi}, \\
{}[\Psi] & \mbox{otherwise.} \end{array}\right.
\]
Then we prove a modulo ![]() $\ell$ version of the Prasad conjecture, using our modified injection
$\ell$ version of the Prasad conjecture, using our modified injection ![]() $P$.
$P$.
Theorem 1.10 (Theorem 5.14)
Let ![]() $\pi$ be an irreducible generic
$\pi$ be an irreducible generic ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {PGL}_2(E)$. Then
$\operatorname {PGL}_2(E)$. Then ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {PGL}_2(F)$ if and only if there exists
$\operatorname {PGL}_2(F)$ if and only if there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F\,|\,W_{E}} \sim P\circ PV(\pi )$.
$\Psi _{F\,|\,W_{E}} \sim P\circ PV(\pi )$.
Remark 1.11 (i) In the banal case, i.e. ![]() $\ell \nmid q_E^2-1$,
$\ell \nmid q_E^2-1$, ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]=\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ and
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]=\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ and ![]() $P$ is the trivial injection, so we found the ‘classical’ Prasad conjecture.
$P$ is the trivial injection, so we found the ‘classical’ Prasad conjecture.
(ii) When ![]() $\ell \mid q_E+1$,
$\ell \mid q_E+1$, ![]() $\ell \mid q_F + 1$ and
$\ell \mid q_F + 1$ and ![]() $\pi = \operatorname {Sp}_\chi$ for a quadratic character
$\pi = \operatorname {Sp}_\chi$ for a quadratic character ![]() $\chi$ of
$\chi$ of ![]() $E^{\times }$ such that
$E^{\times }$ such that ![]() $\chi _{|F^\times }=\omega _{E/F} \nu _{|F^\times }^{1/2}$, then the representation
$\chi _{|F^\times }=\omega _{E/F} \nu _{|F^\times }^{1/2}$, then the representation ![]() $\Psi _F$ is not the Langlands parameter of any representation of
$\Psi _F$ is not the Langlands parameter of any representation of ![]() $\operatorname {PGL}_2(F)$ (nor it is in the image of
$\operatorname {PGL}_2(F)$ (nor it is in the image of ![]() $P$).
$P$).
1.4 Modular distinguished representations for  $(\operatorname {SL}_{2}(E),\operatorname {SL}_{2}(F))$
$(\operatorname {SL}_{2}(E),\operatorname {SL}_{2}(F))$
In the last part, § 6, we use our classification of ![]() $\operatorname {GL}_2(F)$-distinguished representation of
$\operatorname {GL}_2(F)$-distinguished representation of ![]() $\operatorname {GL}_2(E)$ and the restriction method of [Reference Anandavardhanan and PrasadAP03] to classify
$\operatorname {GL}_2(E)$ and the restriction method of [Reference Anandavardhanan and PrasadAP03] to classify ![]() $\operatorname {SL}_2(F)$-distinguished representations for
$\operatorname {SL}_2(F)$-distinguished representations for ![]() $\operatorname {SL}_{2}(E)$ in the modular setting.
$\operatorname {SL}_{2}(E)$ in the modular setting.
Let ![]() $\pi$ be an irreducible
$\pi$ be an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$. Denote by
$\operatorname {GL}_2(E)$. Denote by ![]() $\lg (\pi )$ the length of
$\lg (\pi )$ the length of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ and by
$\pi \vert _{\operatorname {SL}_2(E)}$ and by ![]() $\lg _+(\pi )$ the length of
$\lg _+(\pi )$ the length of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$, where
$\pi \vert _{\operatorname {GL}_2^+(E)}$, where ![]() $\operatorname {GL}_2^+(E)$ is the subgroup of
$\operatorname {GL}_2^+(E)$ is the subgroup of ![]() $\operatorname {GL}_2(E)$, consisting of elements whose determinants belong to
$\operatorname {GL}_2(E)$, consisting of elements whose determinants belong to ![]() $F^{\times }E^{\times 2}$. Let
$F^{\times }E^{\times 2}$. Let ![]() $\mathfrak {p}_{E}$ be a uniformizer of
$\mathfrak {p}_{E}$ be a uniformizer of ![]() $E$, and
$E$, and ![]() $\mathfrak {o}_E$ be the ring of integers of
$\mathfrak {o}_E$ be the ring of integers of ![]() $E$. We fix an
$E$. We fix an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\psi _0$ of
$\psi _0$ of ![]() $E$, which is non-trivial on
$E$, which is non-trivial on ![]() $\mathfrak {o}_E$ and is trivial on both
$\mathfrak {o}_E$ and is trivial on both ![]() $\mathfrak {p}_E$ and
$\mathfrak {p}_E$ and ![]() $F$.
$F$.
For supercuspidal representations, we will adapt the methods of [Reference Anandavardhanan and PrasadAP03] to prove the following theorems.
Theorem 1.12 (Theorem 6.14)
Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$ distinguished by
$\operatorname {GL}_2(E)$ distinguished by ![]() $\operatorname {SL}_2(F)$, and
$\operatorname {SL}_2(F)$, and ![]() $\pi ^+$ the unique irreducible component of
$\pi ^+$ the unique irreducible component of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$ that is
$\pi \vert _{\operatorname {GL}_2^+(E)}$ that is ![]() $\psi _0$-generic. Then
$\psi _0$-generic. Then ![]() $\pi ^+$ is distinguished by
$\pi ^+$ is distinguished by ![]() $\operatorname {SL}_2(F)$. Furthermore, let
$\operatorname {SL}_2(F)$. Furthermore, let ![]() $\tau$ be an irreducible component of
$\tau$ be an irreducible component of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$, distinguished by
$\pi \vert _{\operatorname {SL}_2(E)}$, distinguished by ![]() $\operatorname {SL}_2(F)$. Then
$\operatorname {SL}_2(F)$. Then ![]() $\tau$ is an irreducible component of
$\tau$ is an irreducible component of ![]() $\pi ^+\vert _{\operatorname {SL}_2(E)}$.
$\pi ^+\vert _{\operatorname {SL}_2(E)}$.
Theorem 1.13 (Theorem 6.15)
Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$, and
$\operatorname {GL}_2(E)$, and ![]() $\tau$ an irreducible component of
$\tau$ an irreducible component of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$. Suppose
$\pi \vert _{\operatorname {SL}_2(E)}$. Suppose ![]() $\tau$ is distinguished by
$\tau$ is distinguished by ![]() $\operatorname {SL}_2(F)$. Then,
$\operatorname {SL}_2(F)$. Then,
 \begin{align*}
\mathrm{dim}\mathrm{Hom}{_{\operatorname{SL}_2(F)}}(\tau,\mathbf{1})=
\left\{\begin{array}{@{}ll} 1 & \mbox{if }
\pi\vert_{\operatorname{SL}_2(E)}\cong\tau, \\ 1 & \mbox{if } \lg_+(\pi)=2
\mbox{ and } \lg(\pi)=4, \\ 2 & \mbox{if } \lg_+(\pi)=\lg(\pi)=2,
\\ 4 & \mbox{if } \lg_+(\pi)=\lg(\pi)=4.
\end{array}\right. \end{align*}
\begin{align*}
\mathrm{dim}\mathrm{Hom}{_{\operatorname{SL}_2(F)}}(\tau,\mathbf{1})=
\left\{\begin{array}{@{}ll} 1 & \mbox{if }
\pi\vert_{\operatorname{SL}_2(E)}\cong\tau, \\ 1 & \mbox{if } \lg_+(\pi)=2
\mbox{ and } \lg(\pi)=4, \\ 2 & \mbox{if } \lg_+(\pi)=\lg(\pi)=2,
\\ 4 & \mbox{if } \lg_+(\pi)=\lg(\pi)=4.
\end{array}\right. \end{align*}
The first case and the last case arise only when ![]() $p=2$.
$p=2$.
We also have a criterion for principal series representations. See Theorem 6.16 for more details.
Along the way, we prove the existence of a good lift for supercuspidal representations of ![]() $\operatorname {SL}_2(E)$. Let
$\operatorname {SL}_2(E)$. Let ![]() $\tau$ be an irreducible cuspidal
$\tau$ be an irreducible cuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {SL}_2(E)$, and
$\mathrm {SL}_2(E)$, and ![]() $\tilde {\tau }$ an irreducible cuspidal
$\tilde {\tau }$ an irreducible cuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-representation of
$\overline {\mathbf {Q}}_{\ell }$-representation of ![]() $\mathrm {SL}_2(E)$, which is
$\mathrm {SL}_2(E)$, which is ![]() $\ell$-integral. We say that
$\ell$-integral. We say that ![]() $\tilde {\tau }$ is a good
$\tilde {\tau }$ is a good ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\tau$, if the reduction modulo
$\tau$, if the reduction modulo ![]() $\ell$ of
$\ell$ of ![]() $\tilde {\tau }$ is irreducible and isomorphic to
$\tilde {\tau }$ is irreducible and isomorphic to ![]() $\tau$. We prove in Proposition 6.7 that any supercuspidal representation of
$\tau$. We prove in Proposition 6.7 that any supercuspidal representation of ![]() $\operatorname {SL}_2(E)$ always admits a good
$\operatorname {SL}_2(E)$ always admits a good ![]() $\overline {\mathbf {Q}}_{\ell }$-lift.
$\overline {\mathbf {Q}}_{\ell }$-lift.
2. Notation
Let ![]() $E/F$ be a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic
$E/F$ be a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic ![]() $p$. Denote by
$p$. Denote by ![]() $q_F$ (respectively,
$q_F$ (respectively, ![]() $q_E$) the cardinality of the residue field of
$q_E$) the cardinality of the residue field of ![]() $F$ (respectively,
$F$ (respectively, ![]() $E$). Let
$E$). Let ![]() $W_F$ be the Weil group of
$W_F$ be the Weil group of ![]() $F$. We denote by
$F$. We denote by ![]() $\sigma$ the non-trivial
$\sigma$ the non-trivial ![]() $F$-automorphism of
$F$-automorphism of ![]() $E$.
$E$.
Denote by ![]() $\omega _{E/F}$ the quadratic character of
$\omega _{E/F}$ the quadratic character of ![]() $F^\times$ associated to the quadratic field extension
$F^\times$ associated to the quadratic field extension ![]() $E/F$ by the local class field theory. We may identify the characters of
$E/F$ by the local class field theory. We may identify the characters of ![]() $W_{F}$ and the characters of
$W_{F}$ and the characters of ![]() $F^\times$ by the local class field theory. Let
$F^\times$ by the local class field theory. Let ![]() $\operatorname {Nm}_{E/F}$ be the norm from
$\operatorname {Nm}_{E/F}$ be the norm from ![]() $E$ to
$E$ to ![]() $F$.
$F$.
For ![]() $n \geq 1$, we denote by
$n \geq 1$, we denote by ![]() $\operatorname {GL}_n$ the general linear group, and by
$\operatorname {GL}_n$ the general linear group, and by ![]() $\operatorname {SL}_n$ the special linear group. Denote the standard Borel subgroup of
$\operatorname {SL}_n$ the special linear group. Denote the standard Borel subgroup of ![]() $\operatorname {GL}_n$ by
$\operatorname {GL}_n$ by ![]() $B_n$. Let
$B_n$. Let ![]() $\pi _i$
$\pi _i$ ![]() $(i=1,2)$ be an irreducible representation of
$(i=1,2)$ be an irreducible representation of ![]() $\operatorname {GL}_{n_i}(F)$. Denote by
$\operatorname {GL}_{n_i}(F)$. Denote by ![]() $\pi _1\boxtimes \pi _2$ the tensor product representation of
$\pi _1\boxtimes \pi _2$ the tensor product representation of ![]() $\operatorname {GL}_{n_1}(F)\times \operatorname {GL}_{n_2}(F)$. For a character
$\operatorname {GL}_{n_1}(F)\times \operatorname {GL}_{n_2}(F)$. For a character ![]() $\chi$ of
$\chi$ of ![]() $F^{\times }$, we will also denote by
$F^{\times }$, we will also denote by ![]() $\chi$ the character
$\chi$ the character ![]() $\chi \circ \det$ of
$\chi \circ \det$ of ![]() $\operatorname {GL}_n(F)$. The trivial character will be denoted by
$\operatorname {GL}_n(F)$. The trivial character will be denoted by ![]() $\mathbf {1}$. Let
$\mathbf {1}$. Let ![]() $\nu _n$ be the character
$\nu _n$ be the character ![]() $g\mapsto |\!\det (g)|$ of
$g\mapsto |\!\det (g)|$ of ![]() $\operatorname {GL}_n(F)$.
$\operatorname {GL}_n(F)$.
Let ![]() $H$ be a subgroup of
$H$ be a subgroup of ![]() $G$. Let
$G$. Let ![]() $\pi$ be an irreducible representation of
$\pi$ be an irreducible representation of ![]() $G$. We say that
$G$. We say that ![]() $\pi$ is
$\pi$ is ![]() $H$-distinguished if
$H$-distinguished if ![]() $\operatorname {Hom}_H(\pi,\mathbf {1})\neq 0$. In case that the subgroup
$\operatorname {Hom}_H(\pi,\mathbf {1})\neq 0$. In case that the subgroup ![]() $H$ is clear, we say that
$H$ is clear, we say that ![]() $\pi$ is distinguished sometimes.
$\pi$ is distinguished sometimes.
In this article, ![]() $\ell$ is an odd prime number different from
$\ell$ is an odd prime number different from ![]() $p$ (except for § 3.1, where
$p$ (except for § 3.1, where ![]() $\ell =2$ is also allowed).
$\ell =2$ is also allowed).
Remark 2.1 This paper is written for ![]() $F$ of characteristic different from 2. However, our main theorem, Theorem 3.4, which allows lifting
$F$ of characteristic different from 2. However, our main theorem, Theorem 3.4, which allows lifting ![]() $\ell$-modular supercuspidal distinguished representations to
$\ell$-modular supercuspidal distinguished representations to ![]() $\ell$-adic distinguished representations works without any assumption on the characteristic. Therefore, in § 3.1 only, no assumption on the characteristic of
$\ell$-adic distinguished representations works without any assumption on the characteristic. Therefore, in § 3.1 only, no assumption on the characteristic of ![]() $F$ will be made. After that, we always assume the characteristic to be different from 2 because we use results from the theory of complex representations which are only written with this assumption. For instance, the Jacquet conjecture follows from [Reference KableKab04], written in characteristic zero, but which also works for positive odd characteristic by [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Appendix A] (or [Reference JoJo23]).
$F$ will be made. After that, we always assume the characteristic to be different from 2 because we use results from the theory of complex representations which are only written with this assumption. For instance, the Jacquet conjecture follows from [Reference KableKab04], written in characteristic zero, but which also works for positive odd characteristic by [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Appendix A] (or [Reference JoJo23]).
3. Distinguished supercuspidal representations of  $\operatorname {GL}_n$
$\operatorname {GL}_n$
In this section, we study the distinguished supercuspidal representation of ![]() $\operatorname {GL}_n$. First, we prove a lifting theorem for supercuspidal representations distinguished by an arbitrary closed subgroup
$\operatorname {GL}_n$. First, we prove a lifting theorem for supercuspidal representations distinguished by an arbitrary closed subgroup ![]() $H$. This theorem allows us to study the supercuspidal representations of
$H$. This theorem allows us to study the supercuspidal representations of ![]() $\operatorname {GL}_n(E)$ distinguished by a Galois involution, and extend the result of [Reference SécherreSéc19] to the case
$\operatorname {GL}_n(E)$ distinguished by a Galois involution, and extend the result of [Reference SécherreSéc19] to the case ![]() $p=2$. We also give an application to supercuspidal representations of
$p=2$. We also give an application to supercuspidal representations of ![]() $\operatorname {GL}_n(E)$ distinguished by unitary groups.
$\operatorname {GL}_n(E)$ distinguished by unitary groups.
3.1 Lifting of modular distinguished representation
In this section, ![]() $G=\operatorname {GL}_n(F)$ and
$G=\operatorname {GL}_n(F)$ and ![]() $H$ is an arbitrary closed subgroup of
$H$ is an arbitrary closed subgroup of ![]() $G$. In this part only,
$G$. In this part only, ![]() $F$ could be of any characteristic and we do not require the prime
$F$ could be of any characteristic and we do not require the prime ![]() $\ell$ to be odd, just
$\ell$ to be odd, just ![]() $\ell \neq p$. We want to prove that a supercuspidal
$\ell \neq p$. We want to prove that a supercuspidal ![]() $H$-distinguished
$H$-distinguished ![]() $\overline {\mathbf {F}}_{\ell }$-representation can be lifted to a supercuspidal
$\overline {\mathbf {F}}_{\ell }$-representation can be lifted to a supercuspidal ![]() $H$-distinguished
$H$-distinguished ![]() $\overline {\mathbf {Q}}_{\ell }$-representation. This allows bringing the modular distinction problems to the complex setting. To do that, we use type theory and the existence of a projective envelope.
$\overline {\mathbf {Q}}_{\ell }$-representation. This allows bringing the modular distinction problems to the complex setting. To do that, we use type theory and the existence of a projective envelope.
We start with a few lemmas. Let ![]() $K$ be a finite field extension of
$K$ be a finite field extension of ![]() $F$. We denote by
$F$. We denote by ![]() $\varpi _K$ (respectively,
$\varpi _K$ (respectively, ![]() $\varpi _F$) a uniformizer of
$\varpi _F$) a uniformizer of ![]() $K$ (respectively,
$K$ (respectively, ![]() $F$). Let
$F$). Let ![]() $\mathcal {O}_K$ be the ring of integers of
$\mathcal {O}_K$ be the ring of integers of ![]() $K$, and for an integer
$K$, and for an integer ![]() $i\geq 1$, we denote by
$i\geq 1$, we denote by ![]() $U_K^i$ the subgroup of
$U_K^i$ the subgroup of ![]() $\mathcal {O}_K^{\times }$ defined by
$\mathcal {O}_K^{\times }$ defined by ![]() $U_K^i:=\{1+\varpi _K^{i} u, u \in \mathcal {O}_K\!\}$.
$U_K^i:=\{1+\varpi _K^{i} u, u \in \mathcal {O}_K\!\}$.
Lemma 3.1 Let ![]() $i\geq 1$ and
$i\geq 1$ and ![]() $x\in U_K^i$. Then
$x\in U_K^i$. Then ![]() $x^p \in U_K^{i+1}$.
$x^p \in U_K^{i+1}$.
Proof. Let us write ![]() $x = 1 + \varpi _K^{i} u$, with
$x = 1 + \varpi _K^{i} u$, with ![]() $u \in \mathcal {O}_K$. The binomial expansion gives us
$u \in \mathcal {O}_K$. The binomial expansion gives us ![]() $x^p=1 + p \varpi _K^{i} u + \varpi _K^{2i} u'$, with
$x^p=1 + p \varpi _K^{i} u + \varpi _K^{2i} u'$, with ![]() $u' \in \mathcal {O}_K$. But
$u' \in \mathcal {O}_K$. But ![]() $\varpi _K$ divides
$\varpi _K$ divides ![]() $p$ in
$p$ in ![]() $\mathcal {O}_K$ so
$\mathcal {O}_K$ so ![]() $x^p \in U_K^{i+1}$.
$x^p \in U_K^{i+1}$.
Lemma 3.2 Let ![]() $N \in \mathbb {N}^{*}$. Then there exist two integers
$N \in \mathbb {N}^{*}$. Then there exist two integers ![]() $m\geq 1$ and
$m\geq 1$ and ![]() $s\geq 1$ such that
$s\geq 1$ such that ![]() $\varpi _K^m \in \varpi _F^s U_K^N$.
$\varpi _K^m \in \varpi _F^s U_K^N$.
Proof. Let ![]() $e$ be the ramification index of
$e$ be the ramification index of ![]() $K$ over
$K$ over ![]() $F$. Then
$F$. Then ![]() $\varpi _K^{e} = \varpi _F u$, with
$\varpi _K^{e} = \varpi _F u$, with ![]() $u \in \mathcal {O}_K^{\times }$. Now
$u \in \mathcal {O}_K^{\times }$. Now ![]() $\mathcal {O}_K^{\times } / U_K^1$ is isomorphic to
$\mathcal {O}_K^{\times } / U_K^1$ is isomorphic to ![]() $k_K^{\times }$ the residue field of
$k_K^{\times }$ the residue field of ![]() $K$ of cardinal
$K$ of cardinal ![]() $q_K-1$. Therefore,
$q_K-1$. Therefore, ![]() $x:=u^{q_K-1} \in U_K^1$ and from Lemma 3.1,
$x:=u^{q_K-1} \in U_K^1$ and from Lemma 3.1, ![]() $x^{p^{N}} \in U_K^N$. We get the result with
$x^{p^{N}} \in U_K^N$. We get the result with ![]() $m=e(q_K-1)p^N$ and
$m=e(q_K-1)p^N$ and ![]() $s=(q_K-1)p^N$.
$s=(q_K-1)p^N$.
Let ![]() $G:=\operatorname {GL}_n(F)$. Let
$G:=\operatorname {GL}_n(F)$. Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $G$. Let us write
$G$. Let us write ![]() $\pi = \operatorname {c-Ind}_{J}^{G}(\Lambda )$ (compact induction), for an extended maximal simple type
$\pi = \operatorname {c-Ind}_{J}^{G}(\Lambda )$ (compact induction), for an extended maximal simple type ![]() $(J,\Lambda )$ (for the definition see § 3.1 [Reference Mínguez and SécherreMS14] in which it is called ‘un type simple maximal étendu’). Let
$(J,\Lambda )$ (for the definition see § 3.1 [Reference Mínguez and SécherreMS14] in which it is called ‘un type simple maximal étendu’). Let ![]() $J^{0}$ be the unique maximal compact subgroup of
$J^{0}$ be the unique maximal compact subgroup of ![]() $J$,
$J$, ![]() $J^1$ its maximal normal pro-
$J^1$ its maximal normal pro-![]() $p$-subgroup. There exists a field extension
$p$-subgroup. There exists a field extension ![]() $K$ of
$K$ of ![]() $F$, such that
$F$, such that ![]() $J = K^{\times }J^0=\langle \varpi _K ,J^0 \rangle$. The restricted representation
$J = K^{\times }J^0=\langle \varpi _K ,J^0 \rangle$. The restricted representation ![]() $\lambda :=\Lambda \vert _{J^0}$ is irreducible, and the pair
$\lambda :=\Lambda \vert _{J^0}$ is irreducible, and the pair ![]() $(J^0,\lambda )$ is a maximal simple type. In particular, we have an isomorphism
$(J^0,\lambda )$ is a maximal simple type. In particular, we have an isomorphism ![]() $\lambda \cong \kappa \otimes \rho$, where
$\lambda \cong \kappa \otimes \rho$, where ![]() $\kappa$ is an irreducible representation of
$\kappa$ is an irreducible representation of ![]() $J^0$ with some technical conditions and
$J^0$ with some technical conditions and ![]() $\rho$ is inflated from an irreducible supercuspidal representation of
$\rho$ is inflated from an irreducible supercuspidal representation of ![]() ${J^0/ J^1}$.
${J^0/ J^1}$.
Since ![]() $F^{\times }$ is central in
$F^{\times }$ is central in ![]() $J$,
$J$, ![]() $\varpi _F$ acts on
$\varpi _F$ acts on ![]() $\Lambda$ as a scalar
$\Lambda$ as a scalar ![]() $\bar {\alpha } \in \overline {\mathbf {F}}_{\ell }^\times$. For
$\bar {\alpha } \in \overline {\mathbf {F}}_{\ell }^\times$. For ![]() $R=\overline {\mathbf {F}}_{\ell }$ or
$R=\overline {\mathbf {F}}_{\ell }$ or ![]() $\overline {\mathbf {Z}}_{\ell }$ and
$\overline {\mathbf {Z}}_{\ell }$ and ![]() $\beta \in R^\times$, we denote by
$\beta \in R^\times$, we denote by ![]() $\operatorname {Rep}_{R}^{\beta }(J)$ the categoryFootnote 1 of smooth
$\operatorname {Rep}_{R}^{\beta }(J)$ the categoryFootnote 1 of smooth ![]() $R$-representations of
$R$-representations of ![]() $J$ such that
$J$ such that ![]() $\varpi _F$ acts as the scalar
$\varpi _F$ acts as the scalar ![]() $\beta$.
$\beta$.
Proposition 3.3
(i) The representation
 $\Lambda$ admits a projective envelope
$\Lambda$ admits a projective envelope  $\overline {\mathcal {P}}$ in
$\overline {\mathcal {P}}$ in  $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$.
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$.(ii) Let
 $\alpha \in \overline {\mathbf {Z}}_{\ell }$ be a lift of
$\alpha \in \overline {\mathbf {Z}}_{\ell }$ be a lift of  $\bar {\alpha }$. Then there exists a unique (up to isomorphism) projective object
$\bar {\alpha }$. Then there exists a unique (up to isomorphism) projective object  $\mathcal {P}$ in
$\mathcal {P}$ in  $\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ such that
$\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ such that  $\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$.
$\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$.
Proof. (i) We apply a similar strategy as in [Reference Drevon and SécherreDS23, § 4]. Let ![]() $\eta$ be a character of
$\eta$ be a character of ![]() $J$, trivial on
$J$, trivial on ![]() $J^0$ such that
$J^0$ such that ![]() $\eta (\varpi _F)=\bar {\alpha }$. Let
$\eta (\varpi _F)=\bar {\alpha }$. Let ![]() $\Sigma :=\Lambda \eta ^{-1}$ such that
$\Sigma :=\Lambda \eta ^{-1}$ such that ![]() $\varpi _F$ acts trivially on
$\varpi _F$ acts trivially on ![]() $\Sigma$.
$\Sigma$.
Since ![]() $\Sigma$ is smooth and
$\Sigma$ is smooth and ![]() $J^0$ is compact, there exists an open subgroup
$J^0$ is compact, there exists an open subgroup ![]() $H^2$ of
$H^2$ of ![]() $J^1$ such that
$J^1$ such that ![]() $H^2 \subset \ker (\Sigma _{|J^0})$ and
$H^2 \subset \ker (\Sigma _{|J^0})$ and ![]() $J^0/H^2$ is finite. Since
$J^0/H^2$ is finite. Since ![]() $H^2$ is open in
$H^2$ is open in ![]() $J^0$, there exists an integer
$J^0$, there exists an integer ![]() $N\geq 1$ such that
$N\geq 1$ such that ![]() $U_K^N \subset H^2$. By Lemma 3.2, there exist
$U_K^N \subset H^2$. By Lemma 3.2, there exist ![]() $m,n\geq 1$ such that
$m,n\geq 1$ such that ![]() $\varpi _K^m \in \varpi _F^s U_K^N$. We define a group
$\varpi _K^m \in \varpi _F^s U_K^N$. We define a group ![]() $Q$ by
$Q$ by
The group ![]() $Q$ is finite. Moreover, since
$Q$ is finite. Moreover, since ![]() $\varpi _K^m \in \varpi _F^s H^2$, we have that
$\varpi _K^m \in \varpi _F^s H^2$, we have that ![]() $\langle H^2, \varpi _K^m \rangle =\langle H^2, \varpi _F^s \rangle$. Therefore,
$\langle H^2, \varpi _K^m \rangle =\langle H^2, \varpi _F^s \rangle$. Therefore, ![]() $\Sigma$ is trivial on
$\Sigma$ is trivial on ![]() $\langle H^2, \varpi _F \rangle$ and we can consider
$\langle H^2, \varpi _F \rangle$ and we can consider ![]() $\Sigma$ as a representation of
$\Sigma$ as a representation of ![]() $Q$.
$Q$.
Since ![]() $Q$ is a finite group, by [Reference SerreSer77, Proposition 41] we can consider the projective envelope of
$Q$ is a finite group, by [Reference SerreSer77, Proposition 41] we can consider the projective envelope of ![]() $\Sigma$ in the category of
$\Sigma$ in the category of ![]() $\overline {\mathbf {F}}_{\ell }[Q]$-modules, denoted by
$\overline {\mathbf {F}}_{\ell }[Q]$-modules, denoted by ![]() $\overline {\mathcal {P}}$. We can regard
$\overline {\mathcal {P}}$. We can regard ![]() $\overline {\mathcal {P}}$ as a representation of
$\overline {\mathcal {P}}$ as a representation of ![]() $J$ by inflation. Let
$J$ by inflation. Let
which is compact and ![]() $Q$ is a quotient of
$Q$ is a quotient of ![]() $Q_1$. Since
$Q_1$. Since ![]() $H^2$ is pro-
$H^2$ is pro-![]() $p$, a projective object of
$p$, a projective object of ![]() $Q$ remains projective as a representation of
$Q$ remains projective as a representation of ![]() $Q_1$. Now we show that
$Q_1$. Now we show that ![]() $\overline {\mathcal {P}}$ is projective in
$\overline {\mathcal {P}}$ is projective in ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$. It is due to the fact that
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$. It is due to the fact that ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$ is equivalent to the category of smooth
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$ is equivalent to the category of smooth ![]() $\overline {\mathbf {F}}_{\ell }$-representations of
$\overline {\mathbf {F}}_{\ell }$-representations of ![]() $Q_1$. For arbitrary
$Q_1$. For arbitrary ![]() $\bar {\alpha }$, it follows from the fact that
$\bar {\alpha }$, it follows from the fact that ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$ and
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$ and ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ are equivalent via twisting
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ are equivalent via twisting ![]() $\eta$ with each object in
$\eta$ with each object in ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$.
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{1}(J)$.
(ii) By [Reference SerreSer77, Proposition 42], there is a unique projective ![]() $\overline {\mathbf {Z}}_{\ell }[Q]$-module
$\overline {\mathbf {Z}}_{\ell }[Q]$-module ![]() $\mathcal {P}$ such that
$\mathcal {P}$ such that ![]() $\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$. Like in the first part,
$\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$. Like in the first part, ![]() $\mathcal {P}$ can be lifted to a projective object in
$\mathcal {P}$ can be lifted to a projective object in ![]() $\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$. If
$\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$. If ![]() $\mathcal {P}'$ is another projective in
$\mathcal {P}'$ is another projective in ![]() $\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ with the same properties, then, by projectivity, any isomorphism from
$\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ with the same properties, then, by projectivity, any isomorphism from ![]() $\overline {\mathcal {P}}$ to
$\overline {\mathcal {P}}$ to ![]() $\mathcal {P}' \otimes \overline {\mathbf {F}}_{\ell }$ can be lifted to an isomorphism from
$\mathcal {P}' \otimes \overline {\mathbf {F}}_{\ell }$ can be lifted to an isomorphism from ![]() $\mathcal {P}$ to
$\mathcal {P}$ to ![]() $\mathcal {P}'$.
$\mathcal {P}'$.
Using this projective envelope, we can prove the desired theorem.
Theorem 3.4 Let ![]() $F$ be a non-archimedean local field. Let
$F$ be a non-archimedean local field. Let ![]() $H$ be a closed subgroup of
$H$ be a closed subgroup of ![]() $\operatorname {GL}_n(F)$. Let
$\operatorname {GL}_n(F)$. Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(F)$ which is
$\operatorname {GL}_n(F)$ which is ![]() $H$-distinguished. Then there exists a
$H$-distinguished. Then there exists a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ such that it is supercuspidal and distinguished by
$\pi$ such that it is supercuspidal and distinguished by ![]() $H$.
$H$.
Proof. We write ![]() $\pi = \operatorname {c-Ind}_{J}^{G}(\Lambda )$, for an extended maximal simple type
$\pi = \operatorname {c-Ind}_{J}^{G}(\Lambda )$, for an extended maximal simple type ![]() $(J,\Lambda )$. We have
$(J,\Lambda )$. We have ![]() $\Lambda \in \operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ for
$\Lambda \in \operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ for ![]() $\bar {\alpha }\in \overline {\mathbf {F}}_{\ell }^{\times }$. Let
$\bar {\alpha }\in \overline {\mathbf {F}}_{\ell }^{\times }$. Let ![]() $\bar {\chi }$ be an
$\bar {\chi }$ be an ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\bar {\chi }$ is trivial on
$\bar {\chi }$ is trivial on ![]() $\mathcal {O}_F^{\times }$ and
$\mathcal {O}_F^{\times }$ and ![]() $\bar {\chi }(\varpi _F)=\bar {\alpha }$. Frobenius reciprocity and Mackey formula give us
$\bar {\chi }(\varpi _F)=\bar {\alpha }$. Frobenius reciprocity and Mackey formula give us
Thus, there exists a ![]() $g\in G$ such that
$g\in G$ such that ![]() $\operatorname {Hom}_{J^{g}\cap H}(\Lambda ^{g},\mathbf {1}) \neq 0$. Let
$\operatorname {Hom}_{J^{g}\cap H}(\Lambda ^{g},\mathbf {1}) \neq 0$. Let ![]() $H':=H^{g^{-1}}$ such that
$H':=H^{g^{-1}}$ such that ![]() $J^g \cap H = (J\cap H')^g$. Therefore,
$J^g \cap H = (J\cap H')^g$. Therefore,
Define ![]() $I=\langle J\cap H',\varpi _F\rangle$ and so
$I=\langle J\cap H',\varpi _F\rangle$ and so ![]() $\langle \varpi _F \rangle \subset I\subset J.$ Applying Frobenius reciprocity, we have
$\langle \varpi _F \rangle \subset I\subset J.$ Applying Frobenius reciprocity, we have
Let ![]() $\phi$ be a non-trivial element in
$\phi$ be a non-trivial element in ![]() $\operatorname {Hom}_{I}(\Lambda,\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1})$. Let
$\operatorname {Hom}_{I}(\Lambda,\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1})$. Let ![]() $V$ be the representation space of
$V$ be the representation space of ![]() $\Lambda$. Taking the restriction to
$\Lambda$. Taking the restriction to ![]() $\langle \varpi _F\rangle$, we have
$\langle \varpi _F\rangle$, we have
Since ![]() $\langle \varpi _F\rangle$ acts as the character
$\langle \varpi _F\rangle$ acts as the character ![]() $\bar {\chi }$ on
$\bar {\chi }$ on ![]() $\Lambda$,
$\Lambda$, ![]() $\phi (V)$ is contained in the
$\phi (V)$ is contained in the ![]() $\bar {\chi }$-socle of
$\bar {\chi }$-socle of ![]() $\mathrm {res}_{\langle \varpi _F\rangle }^{I}\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$, which is the maximal subrepresentation where
$\mathrm {res}_{\langle \varpi _F\rangle }^{I}\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$, which is the maximal subrepresentation where ![]() $\langle \varpi _F\rangle$ acts as a multiple of
$\langle \varpi _F\rangle$ acts as a multiple of ![]() $\bar {\chi }$. Meanwhile,
$\bar {\chi }$. Meanwhile,
By Frobenius reciprocity, ![]() $\dim \operatorname {Hom}_{\langle \varpi _F\rangle }(\bar {\chi },\operatorname {Ind}_{\{1\}}^{\langle \varpi _F\rangle }\mathbf {1})=1$. On the other hand,
$\dim \operatorname {Hom}_{\langle \varpi _F\rangle }(\bar {\chi },\operatorname {Ind}_{\{1\}}^{\langle \varpi _F\rangle }\mathbf {1})=1$. On the other hand, ![]() $J\cap H'$ acts trivially on
$J\cap H'$ acts trivially on ![]() $\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$. Since
$\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$. Since ![]() $\Lambda$ is
$\Lambda$ is ![]() $J\cap H'$-distinguished, one can inflate
$J\cap H'$-distinguished, one can inflate ![]() $\bar {\chi }$ to a character of
$\bar {\chi }$ to a character of ![]() $I$, still denoted by
$I$, still denoted by ![]() $\bar {\chi }$. Then the
$\bar {\chi }$. Then the ![]() $\bar {\chi }$-socle of
$\bar {\chi }$-socle of ![]() $\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$ is equivalent to
$\operatorname {Ind}_{J\cap H'}^{I}\mathbf {1}$ is equivalent to ![]() $\bar {\chi }$. Hence,
$\bar {\chi }$. Hence,
By Frobenius reciprocity and the fact that ![]() $J/ I$ is compact, we have
$J/ I$ is compact, we have
where ![]() $\operatorname {c-Ind}_{I}^{J}\bar {\chi }\in \operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ is admissible.
$\operatorname {c-Ind}_{I}^{J}\bar {\chi }\in \operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ is admissible.
Let ![]() $\alpha$ be a root of unity in
$\alpha$ be a root of unity in ![]() $\overline {\mathbf {Z}}_{\ell }$ whose image (after modulo
$\overline {\mathbf {Z}}_{\ell }$ whose image (after modulo ![]() $\ell$) in
$\ell$) in ![]() $\overline {\mathbf {F}}_{\ell }$ is equal to
$\overline {\mathbf {F}}_{\ell }$ is equal to ![]() $\bar {\alpha }$, and denote by
$\bar {\alpha }$, and denote by ![]() $\chi$ a
$\chi$ a ![]() $\overline {\mathbf {Z}}_{\ell }$-lift of
$\overline {\mathbf {Z}}_{\ell }$-lift of ![]() $\bar {\chi }$ such that
$\bar {\chi }$ such that ![]() $\chi$ maps
$\chi$ maps ![]() $\varpi _F$ to
$\varpi _F$ to ![]() $\alpha$. Set
$\alpha$. Set ![]() $\tilde {\chi }=\chi \otimes _{\overline {\mathbf {Z}}_{\ell }}\overline {\mathbf {Q}}_{\ell }$. From Proposition 3.3, let
$\tilde {\chi }=\chi \otimes _{\overline {\mathbf {Z}}_{\ell }}\overline {\mathbf {Q}}_{\ell }$. From Proposition 3.3, let ![]() $\overline {\mathcal {P}}$ be the projective envelope of
$\overline {\mathcal {P}}$ be the projective envelope of ![]() $\Lambda$ in
$\Lambda$ in ![]() $\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ and
$\operatorname {Rep}_{\overline {\mathbf {F}}_{\ell }}^{\bar {\alpha }}(J)$ and ![]() $\mathcal {P}$ a projective object in
$\mathcal {P}$ a projective object in ![]() $\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ such that
$\operatorname {Rep}_{\overline {\mathbf {Z}}_{\ell }}^{\alpha }(J)$ such that ![]() $\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$. Set
$\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell } = \overline {\mathcal {P}}$. Set ![]() $\Lambda |_{J^0}=\kappa \otimes \rho$. Since
$\Lambda |_{J^0}=\kappa \otimes \rho$. Since ![]() $\rho$ corresponds to a supercuspidal representation of
$\rho$ corresponds to a supercuspidal representation of ![]() $J^0/J^1$, a similar argument to [Reference VignérasVig96, Chapitre III, 2.9] gives us the structure of the projective envelope. Let us give some more details. From the structure of the projective envelope for finite groups, we see that if
$J^0/J^1$, a similar argument to [Reference VignérasVig96, Chapitre III, 2.9] gives us the structure of the projective envelope. Let us give some more details. From the structure of the projective envelope for finite groups, we see that if ![]() $\delta$ is an irreducible integral
$\delta$ is an irreducible integral ![]() $\overline {\mathbf {Q}}_{\ell }$-representation of
$\overline {\mathbf {Q}}_{\ell }$-representation of ![]() $J$, then the multiplicity of
$J$, then the multiplicity of ![]() $\delta$ in
$\delta$ in ![]() $\mathcal {P} \otimes \overline {\mathbf {Q}}_{\ell }$ is equal to the multiplicity of
$\mathcal {P} \otimes \overline {\mathbf {Q}}_{\ell }$ is equal to the multiplicity of ![]() $\Lambda$ in
$\Lambda$ in ![]() $r_\ell (\delta )$ (see [Reference Drevon and SécherreDS23, Proposition 4.9]). Moreover, if
$r_\ell (\delta )$ (see [Reference Drevon and SécherreDS23, Proposition 4.9]). Moreover, if ![]() $\Lambda '$ is a subquotient of
$\Lambda '$ is a subquotient of ![]() $\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell }$, then [Reference Drevon and SécherreDS23, Lemma 4.13] says that there exists
$\mathcal {P} \otimes \overline {\mathbf {F}}_{\ell }$, then [Reference Drevon and SécherreDS23, Lemma 4.13] says that there exists ![]() $\delta$ an irreducible integral
$\delta$ an irreducible integral ![]() $\overline {\mathbf {Q}}_{\ell }$-representation of
$\overline {\mathbf {Q}}_{\ell }$-representation of ![]() $J$ such that its modulo
$J$ such that its modulo ![]() $\ell$ reduction contains
$\ell$ reduction contains ![]() $\Lambda$ and
$\Lambda$ and ![]() $\Lambda '$. We show that
$\Lambda '$. We show that ![]() $\Lambda \cong \Lambda '$ by proving that
$\Lambda \cong \Lambda '$ by proving that ![]() $\delta$ is an extended maximal simple type and that
$\delta$ is an extended maximal simple type and that ![]() $\Lambda =r_\ell (\delta )$. In fact, there is an irreducible component
$\Lambda =r_\ell (\delta )$. In fact, there is an irreducible component ![]() $\delta _0$ of
$\delta _0$ of ![]() $\delta \vert _{J^0}$, such that
$\delta \vert _{J^0}$, such that ![]() $\kappa \otimes \rho$ is a subquotient of
$\kappa \otimes \rho$ is a subquotient of ![]() $r_{\ell }(\delta _0)$. Let
$r_{\ell }(\delta _0)$. Let ![]() $\tilde {\kappa }$ be a
$\tilde {\kappa }$ be a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\kappa$ as in [Reference VignérasVig96, Chapitre III, 4.20]. Denote by
$\kappa$ as in [Reference VignérasVig96, Chapitre III, 4.20]. Denote by ![]() $\tilde {\eta }$ the restriction
$\tilde {\eta }$ the restriction ![]() $\tilde {\kappa }\vert _{J^1}$. Since the
$\tilde {\kappa }\vert _{J^1}$. Since the ![]() $\tilde {\eta }$-isotypic part of
$\tilde {\eta }$-isotypic part of ![]() $\delta _0$ is non-trivial, by taking
$\delta _0$ is non-trivial, by taking ![]() $\tilde {\kappa }$-restriction as defined in [Reference VignérasVig01b, Definition 8.1 (c)], there is an irreducible
$\tilde {\kappa }$-restriction as defined in [Reference VignérasVig01b, Definition 8.1 (c)], there is an irreducible ![]() $\overline {\mathbf {Q}}_{\ell }$-representation
$\overline {\mathbf {Q}}_{\ell }$-representation ![]() $\tilde {\rho }$ of
$\tilde {\rho }$ of ![]() $J^0/ J^1$ such that
$J^0/ J^1$ such that ![]() $\delta _0\cong \tilde {\kappa }\otimes \tilde {\rho }$. Then
$\delta _0\cong \tilde {\kappa }\otimes \tilde {\rho }$. Then ![]() $\rho$ is a subquotient of
$\rho$ is a subquotient of ![]() $r_{\ell }(\tilde {\rho })$. Since
$r_{\ell }(\tilde {\rho })$. Since ![]() $\rho$ is supercuspidal, by [Reference HelmHel16, Proposition 5.7] we know
$\rho$ is supercuspidal, by [Reference HelmHel16, Proposition 5.7] we know ![]() $\tilde {\rho }$ is supercuspidal and
$\tilde {\rho }$ is supercuspidal and ![]() $\rho =r_{\ell }(\tilde {\rho })$, which implies that
$\rho =r_{\ell }(\tilde {\rho })$, which implies that ![]() $\delta _0$ is a maximal simple type and
$\delta _0$ is a maximal simple type and ![]() $r_{\ell }(\delta _0)=\kappa \otimes \rho$. Hence,
$r_{\ell }(\delta _0)=\kappa \otimes \rho$. Hence, ![]() $\delta$ is an extended maximal simple type. We conclude that
$\delta$ is an extended maximal simple type. We conclude that ![]() $r_{\ell }(\delta )=\Lambda$. Therefore, we have the following structure of
$r_{\ell }(\delta )=\Lambda$. Therefore, we have the following structure of ![]() $\mathcal {P}$:
$\mathcal {P}$:
(i)
 $\overline {\mathcal {P}}=\mathcal {P} \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {F}}_{\ell }$ is indecomposable of finite length, with each irreducible component isomorphic to
$\overline {\mathcal {P}}=\mathcal {P} \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {F}}_{\ell }$ is indecomposable of finite length, with each irreducible component isomorphic to  $\Lambda$;
$\Lambda$;(ii) let
 $\widetilde {\mathcal {P}} := \mathcal {P} \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {Q}}_{\ell }$ be a
$\widetilde {\mathcal {P}} := \mathcal {P} \otimes _{\overline {\mathbf {Z}}_{\ell }} \overline {\mathbf {Q}}_{\ell }$ be a  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\mathcal {P}$, then
$\mathcal {P}$, then  $\widetilde {\mathcal {P}}$ is isomorphic to the direct sum of extended maximal simple types, which are all the
$\widetilde {\mathcal {P}}$ is isomorphic to the direct sum of extended maximal simple types, which are all the  $\overline {\mathbf {Q}}_{\ell }$-lifts of
$\overline {\mathbf {Q}}_{\ell }$-lifts of  $\Lambda$.
$\Lambda$.
By part (i) and (3.1), we get that
By § I,9.3,(viii) of [Reference VignérasVig96], ![]() $\operatorname {c-Ind}_{I}^{J}\chi$ is a
$\operatorname {c-Ind}_{I}^{J}\chi$ is a ![]() $\overline {\mathbf {Z}}_{\ell }[J]$-lattice of
$\overline {\mathbf {Z}}_{\ell }[J]$-lattice of ![]() $\operatorname {c-Ind}_{I}^{J}\tilde {\chi }$, and the reduction modulo-
$\operatorname {c-Ind}_{I}^{J}\tilde {\chi }$, and the reduction modulo-![]() $\ell$ gives a surjective morphism from
$\ell$ gives a surjective morphism from ![]() $\operatorname {c-Ind}_{I}^{J}\chi$ to
$\operatorname {c-Ind}_{I}^{J}\chi$ to ![]() $\operatorname {c-Ind}_{I}^{J}\bar {\chi }$. By the projectivity of
$\operatorname {c-Ind}_{I}^{J}\bar {\chi }$. By the projectivity of ![]() $\mathcal {P}$, (3.2) implies that
$\mathcal {P}$, (3.2) implies that
Hence, by tensoring with ![]() $\overline {\mathbf {Q}}_{\ell }$ on both sides,
$\overline {\mathbf {Q}}_{\ell }$ on both sides,
From part (ii) and (3.3) there exists a ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts
$\overline {\mathbf {Q}}_{\ell }$-lifts ![]() $\widetilde {\Lambda }$ of
$\widetilde {\Lambda }$ of ![]() $\Lambda$ such that
$\Lambda$ such that ![]() $\operatorname {Hom}_{\overline {\mathbf {Q}}_{\ell }[J]}(\widetilde {\Lambda },\operatorname {Ind}_{J\cap H'}^{J}\mathbf {1}) \neq 0$. Hence,
$\operatorname {Hom}_{\overline {\mathbf {Q}}_{\ell }[J]}(\widetilde {\Lambda },\operatorname {Ind}_{J\cap H'}^{J}\mathbf {1}) \neq 0$. Hence, ![]() $\operatorname {Hom}_{J\cap H'}(\widetilde {\Lambda },\mathbf {1}) \neq 0$.
$\operatorname {Hom}_{J\cap H'}(\widetilde {\Lambda },\mathbf {1}) \neq 0$.
Let ![]() $\widetilde {\pi }:=\operatorname {c-Ind}_{J}^{G}(\widetilde {\Lambda })$, where
$\widetilde {\pi }:=\operatorname {c-Ind}_{J}^{G}(\widetilde {\Lambda })$, where ![]() $\tilde {\Lambda }$ is a
$\tilde {\Lambda }$ is a ![]() $\overline {\mathbf {Q}}_{\ell }$-extended maximal simple type (the discussion before about
$\overline {\mathbf {Q}}_{\ell }$-extended maximal simple type (the discussion before about ![]() $\delta$ shows that
$\delta$ shows that ![]() $\tilde {\Lambda }$ is an extended maximal simple type). Hence,
$\tilde {\Lambda }$ is an extended maximal simple type). Hence, ![]() $\widetilde {\pi }$ is irreducible and supercuspidal. Since the reduction modulo
$\widetilde {\pi }$ is irreducible and supercuspidal. Since the reduction modulo ![]() $\ell$ commutes with
$\ell$ commutes with ![]() $\operatorname {c-Ind}$, we deduce that the representation
$\operatorname {c-Ind}$, we deduce that the representation ![]() $\widetilde {\pi }$ is a
$\widetilde {\pi }$ is a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$. We are left to prove that it is
$\pi$. We are left to prove that it is ![]() $H$-distinguished. As before
$H$-distinguished. As before
and Mackey formula and Frobenius reciprocity give us that ![]() $\widetilde {\pi }$ is
$\widetilde {\pi }$ is ![]() $H$-distinguished.
$H$-distinguished.
The following corollary is an immediate consequence of Theorem 3.4.
Corollary 3.5 When the characteristic of ![]() $F$ is different from 2, there is no supercuspidal
$F$ is different from 2, there is no supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_{2n}(F)$ distinguished by
$\operatorname {GL}_{2n}(F)$ distinguished by ![]() $\operatorname {Sp}_{2n}(F)$.
$\operatorname {Sp}_{2n}(F)$.
Proof. There is no complex supercuspidal representation of ![]() $\operatorname {GL}_{2n}(F)$ distinguished by
$\operatorname {GL}_{2n}(F)$ distinguished by ![]() $\operatorname {Sp}_{2n}(F)$. When the field
$\operatorname {Sp}_{2n}(F)$. When the field ![]() $F$ has characteristic zero, this follows from [Reference Heumos and RallisHR90, Theorem 3.2.2]; and when the field
$F$ has characteristic zero, this follows from [Reference Heumos and RallisHR90, Theorem 3.2.2]; and when the field ![]() $F$ is of characteristic
$F$ is of characteristic ![]() $p$ with
$p$ with ![]() $p\neq 2$, it follows from [Reference PrasadPra19, Theorem 1] (see [Reference PrasadPra19, § 8]). Therefore, the result follows from Theorem 3.4.
$p\neq 2$, it follows from [Reference PrasadPra19, Theorem 1] (see [Reference PrasadPra19, § 8]). Therefore, the result follows from Theorem 3.4.
3.2 The Langlands correspondence modulo  $\ell$ for
$\ell$ for  $\operatorname {GL}_n$
$\operatorname {GL}_n$
In the rest of this paper we will use the modulo ![]() $\ell$ local Langlands correspondence to study distinguished representations. We recall in this section some important results about it.
$\ell$ local Langlands correspondence to study distinguished representations. We recall in this section some important results about it.
The first step to define a modulo ![]() $\ell$ local Langlands correspondence for
$\ell$ local Langlands correspondence for ![]() $\operatorname {GL}_n$ is to define the correspondence for supercuspidal representations. The supercuspidal representations correspond to irreducible representations of the Weil group. This bijection is defined in the modulo
$\operatorname {GL}_n$ is to define the correspondence for supercuspidal representations. The supercuspidal representations correspond to irreducible representations of the Weil group. This bijection is defined in the modulo ![]() $\ell$ case using the modulo
$\ell$ case using the modulo ![]() $\ell$ reduction. This leads to the semisimple Langlands correspondence using the supercuspidal support of a smooth representation.
$\ell$ reduction. This leads to the semisimple Langlands correspondence using the supercuspidal support of a smooth representation.
Let ![]() $R$ be an algebraically closed field of characteristic different from
$R$ be an algebraically closed field of characteristic different from ![]() $p$. We denote by
$p$. We denote by ![]() $\operatorname {Irr}_{R}(\operatorname {GL}_n(F))$ the set of isomorphism classes of smooth irreducible representations of
$\operatorname {Irr}_{R}(\operatorname {GL}_n(F))$ the set of isomorphism classes of smooth irreducible representations of ![]() $\operatorname {GL}_n(F)$ over
$\operatorname {GL}_n(F)$ over ![]() $R$ and by
$R$ and by ![]() $\operatorname {Scusp}_{R}(\operatorname {GL}_n(F))$ the subset of supercuspidal
$\operatorname {Scusp}_{R}(\operatorname {GL}_n(F))$ the subset of supercuspidal ![]() $R$-representations. Let
$R$-representations. Let ![]() $\operatorname {Irr}_{R}(\operatorname {GL}_F):=\cup _{n\geq 1}\operatorname {Irr}_{R}(\operatorname {GL}_n(F))$ and
$\operatorname {Irr}_{R}(\operatorname {GL}_F):=\cup _{n\geq 1}\operatorname {Irr}_{R}(\operatorname {GL}_n(F))$ and ![]() $\operatorname {Scusp}_{R}(\operatorname {GL}_F) := \cup _{n\geq 1}\operatorname {Scusp}_{R}(\operatorname {GL}_n(F))$.
$\operatorname {Scusp}_{R}(\operatorname {GL}_F) := \cup _{n\geq 1}\operatorname {Scusp}_{R}(\operatorname {GL}_n(F))$.
Let ![]() $W_F$ be the Weil group of
$W_F$ be the Weil group of ![]() $F$. It is the subgroup of
$F$. It is the subgroup of ![]() $\operatorname {Gal}(\overline {F}/F)$, where
$\operatorname {Gal}(\overline {F}/F)$, where ![]() $\overline {F}$ is a separable algebraic closure of
$\overline {F}$ is a separable algebraic closure of ![]() $F$, generated by the inertia subgroup
$F$, generated by the inertia subgroup ![]() $I_F$ and a geometric Frobenius element
$I_F$ and a geometric Frobenius element ![]() $\mathrm {Frob}$. Its topology is such that
$\mathrm {Frob}$. Its topology is such that ![]() $I_F$ has the topology induced from
$I_F$ has the topology induced from ![]() $\operatorname {Gal}(\overline {F}/F)$,
$\operatorname {Gal}(\overline {F}/F)$, ![]() $I_F$ is open and the multiplication by
$I_F$ is open and the multiplication by ![]() $\mathrm {Frob}$ is a homeomorphism. Let
$\mathrm {Frob}$ is a homeomorphism. Let ![]() $\operatorname {Irr}_{R}(W_{F})(n)$ be the set of isomorphism classes of smooth irreducible
$\operatorname {Irr}_{R}(W_{F})(n)$ be the set of isomorphism classes of smooth irreducible ![]() $R$-representations of
$R$-representations of ![]() $W_F$ of dimension
$W_F$ of dimension ![]() $n$. Finally, we denote by
$n$. Finally, we denote by ![]() $\operatorname {Mod}_{R}(W_{F})$ the set of isomorphism classes of semisimple smooth
$\operatorname {Mod}_{R}(W_{F})$ the set of isomorphism classes of semisimple smooth ![]() $R$-representations of
$R$-representations of ![]() $W_F$ of finite dimension.
$W_F$ of finite dimension.
In [Reference VignérasVig01a] Vignéras defines a bijection using the modulo ![]() $\ell$ reduction of the local Langlands correspondence over
$\ell$ reduction of the local Langlands correspondence over ![]() $\overline {\mathbf {Q}}_{\ell }$.
$\overline {\mathbf {Q}}_{\ell }$.
Theorem 3.6 [Reference VignérasVig01a, Corollary 2.5]
There exist unique Langlands bijections on ![]() $\overline {\mathbf {F}}_{\ell }$
$\overline {\mathbf {F}}_{\ell }$
which are compatible with modulo ![]() $\ell$ reduction.
$\ell$ reduction.
Let ![]() $\operatorname {MScusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_F)$ be the set of formal finite sums
$\operatorname {MScusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_F)$ be the set of formal finite sums ![]() $\pi _1+\cdots +\pi _r$ of elements of
$\pi _1+\cdots +\pi _r$ of elements of ![]() $\operatorname {Scusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_F)$. The previous bijections induce a bijection
$\operatorname {Scusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_F)$. The previous bijections induce a bijection
Let ![]() $\pi \in \operatorname {Irr}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{n}(F))$. Then
$\pi \in \operatorname {Irr}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{n}(F))$. Then ![]() $\pi$ appears as a subquotient of the parabolic induction of a representation
$\pi$ appears as a subquotient of the parabolic induction of a representation ![]() $\pi _1 \boxtimes \cdots \boxtimes \pi _r$, where
$\pi _1 \boxtimes \cdots \boxtimes \pi _r$, where ![]() $\pi _i \in \operatorname {Scusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{n_i}(F))$ and
$\pi _i \in \operatorname {Scusp}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{n_i}(F))$ and ![]() $\sum n_i =n$. This defines a surjective map with finite fibers, called the supercuspidal support,
$\sum n_i =n$. This defines a surjective map with finite fibers, called the supercuspidal support,
by ![]() $sc(\pi )=\pi _1 + \cdots + \pi _r$.
$sc(\pi )=\pi _1 + \cdots + \pi _r$.
Combining the supercuspidal support and the previous bijections (see [Reference VignérasVig01a, Theorem 1.6]) we get a map, that we call the semisimple Langlands correspondence modulo ![]() $\ell$,
$\ell$,
The previous map ![]() $V_{ss}$ is a surjection but not a bijection. To get a bijection one needs to introduce Weil–Deligne representations.
$V_{ss}$ is a surjection but not a bijection. To get a bijection one needs to introduce Weil–Deligne representations.
Let us start by recalling the definition of Weil–Deligne representations. Let ![]() $\nu : W_{F} \to R^{\times }$ be the unique character trivial on the inertia subgroup of
$\nu : W_{F} \to R^{\times }$ be the unique character trivial on the inertia subgroup of ![]() $W_{F}$, sending a geometric Frobenius element to
$W_{F}$, sending a geometric Frobenius element to ![]() $q_{F}^{-1}$.
$q_{F}^{-1}$.
Definition 3.7 We call a semisimple Weil–Deligne representation of ![]() $\operatorname {GL}_n$ over
$\operatorname {GL}_n$ over ![]() $R$ a couple
$R$ a couple ![]() $(\varphi,N)$ with:
$(\varphi,N)$ with:
(i)
 $\varphi : W_{F} \to \operatorname {GL}_n(R)$ a smooth representation with image composed of semisimple elements;
$\varphi : W_{F} \to \operatorname {GL}_n(R)$ a smooth representation with image composed of semisimple elements;(ii)
 $N \in M_n(R)$ is a matrix such for all
$N \in M_n(R)$ is a matrix such for all  $w\in W_{F}$,
$w\in W_{F}$,  $\varphi (w)N = \nu (w)N\varphi (w)$.
$\varphi (w)N = \nu (w)N\varphi (w)$.
A morphism of Weil–Deligne representations from ![]() $(\varphi,N)$ to
$(\varphi,N)$ to ![]() $(\varphi ',N')$ is a morphism of
$(\varphi ',N')$ is a morphism of ![]() $W_{F}$-representation
$W_{F}$-representation ![]() $f\in \operatorname {Hom}_{W_F}(\varphi,\varphi ')$ such that
$f\in \operatorname {Hom}_{W_F}(\varphi,\varphi ')$ such that ![]() $f\circ N = N' \circ f$. It is an isomorphism if
$f\circ N = N' \circ f$. It is an isomorphism if ![]() $f$ is an isomorphism of
$f$ is an isomorphism of ![]() $W_{F}$-representations. We denote by
$W_{F}$-representations. We denote by ![]() $\operatorname {WDRep}_{R}(W_{F},\operatorname {GL}_n)$ the set of isomorphism classes of semisimple Weil–Deligne representation of
$\operatorname {WDRep}_{R}(W_{F},\operatorname {GL}_n)$ the set of isomorphism classes of semisimple Weil–Deligne representation of ![]() $\operatorname {GL}_n$. When
$\operatorname {GL}_n$. When ![]() $R=\overline {\mathbf {Q}}_{\ell }$, every
$R=\overline {\mathbf {Q}}_{\ell }$, every ![]() $N$ as above is nilpotent. However, this is not the case when
$N$ as above is nilpotent. However, this is not the case when ![]() $R=\overline {\mathbf {F}}_{\ell }$. Therefore, we denote by
$R=\overline {\mathbf {F}}_{\ell }$. Therefore, we denote by ![]() $\operatorname {Nilp}_{R}(W_{F},\operatorname {GL}_n)$ the subset composed of the elements
$\operatorname {Nilp}_{R}(W_{F},\operatorname {GL}_n)$ the subset composed of the elements ![]() $(\phi,N)$ with
$(\phi,N)$ with ![]() $N$ nilpotent.
$N$ nilpotent.
Theorem 3.8 [Reference VignérasVig01a, Theorem 1.8.2]
Let ![]() $\varphi \in \operatorname {Mod}_{\overline {\mathbf {F}}_{\ell }}(W_{F})$. The set consisting of
$\varphi \in \operatorname {Mod}_{\overline {\mathbf {F}}_{\ell }}(W_{F})$. The set consisting of ![]() $\pi \in \operatorname {Irr}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{F})$ such that
$\pi \in \operatorname {Irr}_{\overline {\mathbf {F}}_{\ell }}(\operatorname {GL}_{F})$ such that ![]() $V_{ss}(\pi )=\varphi$ is in bijection with the nilpotent endomorphisms
$V_{ss}(\pi )=\varphi$ is in bijection with the nilpotent endomorphisms ![]() $N$ of
$N$ of ![]() $\pi$, up to conjugation by an isomorphism of
$\pi$, up to conjugation by an isomorphism of ![]() $\varphi$, such that
$\varphi$, such that ![]() $\varphi (w)N = \nu (w)N\varphi (w)$, for all
$\varphi (w)N = \nu (w)N\varphi (w)$, for all ![]() $w\in W_{F}$.
$w\in W_{F}$.
Hence, we get a bijection ![]() $\operatorname {Irr}_R(\operatorname {GL}_{F}) \to \operatorname {Nilp}_{R}(W_{F},\operatorname {GL})$. Vignéras defines the ‘Langlands’ bijection in [Reference VignérasVig01a, § 1.8] using modulo
$\operatorname {Irr}_R(\operatorname {GL}_{F}) \to \operatorname {Nilp}_{R}(W_{F},\operatorname {GL})$. Vignéras defines the ‘Langlands’ bijection in [Reference VignérasVig01a, § 1.8] using modulo ![]() $\ell$ reduction (in a non-naive way), and we call this bijection the
$\ell$ reduction (in a non-naive way), and we call this bijection the ![]() $V$ correspondence:
$V$ correspondence:
3.3 Supercuspidal representations of  $\operatorname {GL}_n(E)$ distinguished by a Galois involution
$\operatorname {GL}_n(E)$ distinguished by a Galois involution
Let ![]() $E/F$ be a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic
$E/F$ be a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2 and residual characteristic ![]() $p$. In this section we are interested in
$p$. In this section we are interested in ![]() $\operatorname {GL}_n(F)$-distinguished supercuspidal
$\operatorname {GL}_n(F)$-distinguished supercuspidal ![]() $\ell$-modular representations of
$\ell$-modular representations of ![]() $\operatorname {GL}_n(E)$. A
$\operatorname {GL}_n(E)$. A ![]() $\operatorname {GL}_n(F)$-distinguished supercuspidal representation is
$\operatorname {GL}_n(F)$-distinguished supercuspidal representation is ![]() $\sigma$-selfdual, that is
$\sigma$-selfdual, that is ![]() $\pi ^{\vee } \simeq \pi ^{\sigma }$ (see [Reference SécherreSéc19, Theorem 4.1]). Let us assume that
$\pi ^{\vee } \simeq \pi ^{\sigma }$ (see [Reference SécherreSéc19, Theorem 4.1]). Let us assume that ![]() $\ell \neq 2$ and let
$\ell \neq 2$ and let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-selfdual supercuspidal representation. The main goal of this section is to prove the dichotomy theorem that
$\sigma$-selfdual supercuspidal representation. The main goal of this section is to prove the dichotomy theorem that ![]() $\pi$ is either distinguished or
$\pi$ is either distinguished or ![]() $\omega _{E/F}$-distinguished, and the disjunction theorem that
$\omega _{E/F}$-distinguished, and the disjunction theorem that ![]() $\pi$ cannot be both distinguished and
$\pi$ cannot be both distinguished and ![]() $\omega _{E/F}$-distinguished. We call it the Jacquet conjecture in the modular setting. For
$\omega _{E/F}$-distinguished. We call it the Jacquet conjecture in the modular setting. For ![]() $p\neq 2$ this is proved in [Reference SécherreSéc19, Theorem 10.8]. Using Theorem 3.4, when
$p\neq 2$ this is proved in [Reference SécherreSéc19, Theorem 10.8]. Using Theorem 3.4, when ![]() $\ell \neq 2$, we will give a different proof of this result that also works for
$\ell \neq 2$, we will give a different proof of this result that also works for ![]() $p=2$ when
$p=2$ when ![]() $F$ has characteristic zero.
$F$ has characteristic zero.
Remark 3.9 In this section we assume ![]() $\ell \neq 2$. When
$\ell \neq 2$. When ![]() $\ell =2$, then
$\ell =2$, then ![]() $p\neq 2$ and the distinguished supercuspidal representations are studied in [Reference SécherreSéc19]. Therefore, combining the results of this section and of [Reference SécherreSéc19] gives a complete result for supercuspidal distinguished representations for all
$p\neq 2$ and the distinguished supercuspidal representations are studied in [Reference SécherreSéc19]. Therefore, combining the results of this section and of [Reference SécherreSéc19] gives a complete result for supercuspidal distinguished representations for all ![]() $\ell$ and
$\ell$ and ![]() $p$ with
$p$ with ![]() $\ell \neq p$ in characteristic zero.
$\ell \neq p$ in characteristic zero.
With Theorem 3.4, we know that we can find a distinguished ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of a distinguished supercuspidal
$\overline {\mathbf {Q}}_{\ell }$-lift of a distinguished supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation whose Langlands parameter is conjugate-orthogonal in the sense of [Reference Gan, Gross and PrasadGGP12, § 7]. With the following lemma, we will show that all the
$\overline {\mathbf {F}}_{\ell }$-representation whose Langlands parameter is conjugate-orthogonal in the sense of [Reference Gan, Gross and PrasadGGP12, § 7]. With the following lemma, we will show that all the ![]() $\sigma$-selfdual
$\sigma$-selfdual ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of a
$\overline {\mathbf {Q}}_{\ell }$-lift of a ![]() $\sigma$-selfdual supercuspidal representations are either all distinguished or all
$\sigma$-selfdual supercuspidal representations are either all distinguished or all ![]() $\omega _{E/F}$-distinguished.
$\omega _{E/F}$-distinguished.
Lemma 3.10 Let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-selfdual irreducible supercuspidal
$\sigma$-selfdual irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$. Suppose that
$\operatorname {GL}_n(E)$. Suppose that ![]() $\tilde {\pi }_1$ and
$\tilde {\pi }_1$ and ![]() $\tilde {\pi }_2$ are two
$\tilde {\pi }_2$ are two ![]() $\sigma$-selfdual irreducible supercuspidal
$\sigma$-selfdual irreducible supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-representations of
$\overline {\mathbf {Q}}_{\ell }$-representations of ![]() $\operatorname {GL}_n(E)$ such that both
$\operatorname {GL}_n(E)$ such that both ![]() $\tilde {\pi }_i$ have modulo
$\tilde {\pi }_i$ have modulo ![]() $\ell$ reduction isomorphic to
$\ell$ reduction isomorphic to ![]() $\pi$. Then
$\pi$. Then ![]() $\tilde {\pi }_1$ and
$\tilde {\pi }_1$ and ![]() $\tilde {\pi }_2$ share the same sign, i.e.
$\tilde {\pi }_2$ share the same sign, i.e. ![]() $\tilde {\pi }_1$ and
$\tilde {\pi }_1$ and ![]() $\tilde {\pi }_2$ are either conjugate-symplectic or conjugate-orthogonal at the same time, but not both.
$\tilde {\pi }_2$ are either conjugate-symplectic or conjugate-orthogonal at the same time, but not both.
Proof. Let us denote by ![]() $\varphi$ (respectively,
$\varphi$ (respectively, ![]() $\tilde {\varphi }_i$) the Langlands parameter of
$\tilde {\varphi }_i$) the Langlands parameter of ![]() $\pi$ (respectively,
$\pi$ (respectively, ![]() $\tilde {\pi }_i$). For
$\tilde {\pi }_i$). For ![]() $i\in \{1,2\}$, since
$i\in \{1,2\}$, since ![]() $\tilde {\pi }_2$ is
$\tilde {\pi }_2$ is ![]() $\sigma$-selfdual,
$\sigma$-selfdual, ![]() $\tilde {\varphi }_i$ is either conjugate-symplectic or conjugate-orthogonal, and let us denote by
$\tilde {\varphi }_i$ is either conjugate-symplectic or conjugate-orthogonal, and let us denote by ![]() $B_i$ the associated bilinear form. We also denote by
$B_i$ the associated bilinear form. We also denote by ![]() $b_i$ the sign of
$b_i$ the sign of ![]() $B_i$. Let us denote by
$B_i$. Let us denote by ![]() $V_i$ the space of
$V_i$ the space of ![]() $\tilde {\varphi }_i$ and by
$\tilde {\varphi }_i$ and by ![]() $V$ the space of
$V$ the space of ![]() $\varphi$. The non-degenerate bilinear form
$\varphi$. The non-degenerate bilinear form ![]() $B_i:V_i \times V_i \to \overline {\mathbf {Q}}_{\ell }$ induces an isomorphism of
$B_i:V_i \times V_i \to \overline {\mathbf {Q}}_{\ell }$ induces an isomorphism of ![]() $W_E$ representation
$W_E$ representation ![]() $f_i : V_i^s \to V_i^{\vee }$, where
$f_i : V_i^s \to V_i^{\vee }$, where ![]() $s \in W_F \setminus W_E$.
$s \in W_F \setminus W_E$.
Since ![]() $\tilde {\varphi }_i$ is a
$\tilde {\varphi }_i$ is a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\varphi$, there exists an
$\varphi$, there exists an ![]() $\overline {\mathbf {Z}}_{\ell }$-lattice
$\overline {\mathbf {Z}}_{\ell }$-lattice ![]() $L_i$ of
$L_i$ of ![]() $V_i$ such that
$V_i$ such that ![]() $L_i \otimes \overline {\mathbf {Q}}_{\ell } \simeq V_i$ and
$L_i \otimes \overline {\mathbf {Q}}_{\ell } \simeq V_i$ and ![]() $L_i \otimes \overline {\mathbf {F}}_{\ell } \simeq V$ (as
$L_i \otimes \overline {\mathbf {F}}_{\ell } \simeq V$ (as ![]() $W_E$ representations). Let
$W_E$ representations). Let ![]() $M_i$ be the
$M_i$ be the ![]() $\overline {\mathbf {Z}}_{\ell }$-lattice of
$\overline {\mathbf {Z}}_{\ell }$-lattice of ![]() $V_i$ such that
$V_i$ such that ![]() $f_i$ induces an isomorphism
$f_i$ induces an isomorphism ![]() $L_i^s \to M_i^{\vee }$. The modulo
$L_i^s \to M_i^{\vee }$. The modulo ![]() $\ell$ reduction does not depend on the lattice, so we also have
$\ell$ reduction does not depend on the lattice, so we also have ![]() $M_i \otimes \overline {\mathbf {Q}}_{\ell } \simeq V_i$ and
$M_i \otimes \overline {\mathbf {Q}}_{\ell } \simeq V_i$ and ![]() $M_i \otimes \overline {\mathbf {F}}_{\ell } \simeq V$. Let
$M_i \otimes \overline {\mathbf {F}}_{\ell } \simeq V$. Let ![]() $B_{i,\overline {\mathbf {Z}}_{\ell }}$ be the restriction of
$B_{i,\overline {\mathbf {Z}}_{\ell }}$ be the restriction of ![]() $B_i$ to
$B_i$ to ![]() $L_i\times M_i$. Its image is a
$L_i\times M_i$. Its image is a ![]() $\overline {\mathbf {Z}}_{\ell }$-lattice of
$\overline {\mathbf {Z}}_{\ell }$-lattice of ![]() $\overline {\mathbf {Q}}_{\ell }$. In addition, by the definition of
$\overline {\mathbf {Q}}_{\ell }$. In addition, by the definition of ![]() $L_i$ and
$L_i$ and ![]() $M_i$ it is non-degenerate as a
$M_i$ it is non-degenerate as a ![]() $\overline {\mathbf {Z}}_{\ell }$-bilinear form. Therefore, its modulo
$\overline {\mathbf {Z}}_{\ell }$-bilinear form. Therefore, its modulo ![]() $\ell$ reduction gives a non-degenerate bilinear form
$\ell$ reduction gives a non-degenerate bilinear form ![]() $\bar {B}_i$ on
$\bar {B}_i$ on ![]() $V$. As
$V$. As ![]() $\ell \neq 2$ the sign
$\ell \neq 2$ the sign ![]() $b_i$ is preserved by reduction modulo
$b_i$ is preserved by reduction modulo ![]() $\ell$, and is the sign of
$\ell$, and is the sign of ![]() $\bar {B}_i$. Moreover,
$\bar {B}_i$. Moreover, ![]() $\pi$ is supercuspidal, so
$\pi$ is supercuspidal, so ![]() $\varphi$ is irreducible. Schur's lemma implies that the sign of a bilinear form on
$\varphi$ is irreducible. Schur's lemma implies that the sign of a bilinear form on ![]() $V$ is unique. Therefore,
$V$ is unique. Therefore, ![]() $b_1=b_2$ and this concludes the proof.
$b_1=b_2$ and this concludes the proof.
Theorem 3.4 and Lemma 3.10 imply the following proposition.
Proposition 3.11 Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$. Then the following assertions are equivalent:
$\operatorname {GL}_n(E)$. Then the following assertions are equivalent:
(i)
 $\pi$ is distinguished;
$\pi$ is distinguished;(ii) there exists a
 $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift  $\tilde {\pi }$ of
$\tilde {\pi }$ of  $\pi$ which is distinguished.
$\pi$ which is distinguished.
Moreover, when these conditions are satisfied, then all the ![]() $\sigma$-selfdual
$\sigma$-selfdual ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts
$\overline {\mathbf {Q}}_{\ell }$-lifts ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ are distinguished.
$\pi$ are distinguished.
Proof. The implication ![]() $\rm (i) \Rightarrow (ii)$ is given by Theorem 3.4 applied with
$\rm (i) \Rightarrow (ii)$ is given by Theorem 3.4 applied with ![]() $\operatorname {GL}_n(E)$ and
$\operatorname {GL}_n(E)$ and ![]() $H=\operatorname {GL}_n(F)$. The other direction
$H=\operatorname {GL}_n(F)$. The other direction ![]() $\rm (ii) \Rightarrow (i)$ follows from an argument of reduction of invariant linear forms as in [Reference Kurinczuk and MatringeKM20, Theorem 3.4].
$\rm (ii) \Rightarrow (i)$ follows from an argument of reduction of invariant linear forms as in [Reference Kurinczuk and MatringeKM20, Theorem 3.4].
To conclude, when ![]() $F$ has characteristic zero, if
$F$ has characteristic zero, if ![]() $\pi$ is distinguished, then all the
$\pi$ is distinguished, then all the ![]() $\sigma$-selfdual
$\sigma$-selfdual ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts of
$\overline {\mathbf {Q}}_{\ell }$-lifts of ![]() $\pi$ are distinguished by Lemma 3.10. For
$\pi$ are distinguished by Lemma 3.10. For ![]() $F$ of positive characteristic, this follows from [Reference SécherreSéc19, Theorem 10.11].
$F$ of positive characteristic, this follows from [Reference SécherreSéc19, Theorem 10.11].
We can now prove the disjunction theorem.
Proposition 3.12 Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$ distinguished by
$\operatorname {GL}_n(E)$ distinguished by ![]() $\operatorname {GL}_n(F)$. Then
$\operatorname {GL}_n(F)$. Then
Proof. We prove the result by contradiction. Let us assume that ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished. Let
$\omega _{E/F}$-distinguished. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$ extending
$E^{\times }$ extending ![]() $\omega _{E/F}$. Let
$\omega _{E/F}$. Let ![]() $\pi ':=\pi (\chi ^{-1} \circ \det )$. Then
$\pi ':=\pi (\chi ^{-1} \circ \det )$. Then ![]() $\pi '$ is a supercuspidal representation and is distinguished since
$\pi '$ is a supercuspidal representation and is distinguished since ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished. Applying Theorem 3.4 to
$\omega _{E/F}$-distinguished. Applying Theorem 3.4 to ![]() $\pi '$ we find a lift
$\pi '$ we find a lift ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ which is
$\pi$ which is ![]() $\widetilde {\omega }_{E/F}$-distinguished, where
$\widetilde {\omega }_{E/F}$-distinguished, where ![]() $\widetilde {\omega }_{E/F}$ is the canonical
$\widetilde {\omega }_{E/F}$ is the canonical ![]() $\ell$-adic lift of
$\ell$-adic lift of ![]() $\omega _{E/F}$, that is the
$\omega _{E/F}$, that is the ![]() $\overline {\mathbf {Q}}_{\ell }$-character of
$\overline {\mathbf {Q}}_{\ell }$-character of ![]() $F^{\times }$ of kernel
$F^{\times }$ of kernel ![]() $\operatorname {Nm}_{E/F}(F^{\times })$.
$\operatorname {Nm}_{E/F}(F^{\times })$.
With Theorem 3.4 we also have a distinguished supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$. Thanks to Proposition 3.11, all
$\pi$. Thanks to Proposition 3.11, all ![]() $\sigma$-selfdual
$\sigma$-selfdual ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts are distinguished by
$\overline {\mathbf {Q}}_{\ell }$-lifts are distinguished by ![]() $\operatorname {GL}_{n}(F)$. In particular,
$\operatorname {GL}_{n}(F)$. In particular, ![]() $\tilde {\pi }$ is
$\tilde {\pi }$ is ![]() $\operatorname {GL}_{n}(F)$-distinguished, which contradicts the fact that a
$\operatorname {GL}_{n}(F)$-distinguished, which contradicts the fact that a ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-representation cannot be both distinguished and
$\overline {\mathbf {Q}}_{\ell }$-representation cannot be both distinguished and ![]() $\omega _{E/F}$-distinguished.
$\omega _{E/F}$-distinguished.
We are left to prove the dichotomy theorem. To do that, we need a theorem analogous to Theorem 3.4 but for ![]() $\sigma$-selfdual representations.
$\sigma$-selfdual representations.
Proposition 3.13 Let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-selfdual supercuspidal representation of
$\sigma$-selfdual supercuspidal representation of ![]() $\operatorname {GL}_n(E)$ over
$\operatorname {GL}_n(E)$ over ![]() $\overline {\mathbf {F}}_{\ell }$. Then there exists a
$\overline {\mathbf {F}}_{\ell }$. Then there exists a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ which is
$\pi$ which is ![]() $\sigma$-selfdual.
$\sigma$-selfdual.
Proof. Let us denote by ![]() $\delta$ the action of
$\delta$ the action of ![]() $\sigma$-duality on
$\sigma$-duality on ![]() $R$-representations, that is
$R$-representations, that is ![]() $V^\delta = (V^\sigma )^{\vee }$. A representation is
$V^\delta = (V^\sigma )^{\vee }$. A representation is ![]() $\sigma$-selfdual if and only if it is
$\sigma$-selfdual if and only if it is ![]() $\delta$ invariant.
$\delta$ invariant.
Let ![]() $[\pi ]$ be the inertial class of
$[\pi ]$ be the inertial class of ![]() $\pi$. Let
$\pi$. Let ![]() $\mathcal {I}$ be the set of inertial classes of supercuspidal
$\mathcal {I}$ be the set of inertial classes of supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts of
$\overline {\mathbf {Q}}_{\ell }$-lifts of ![]() $\pi$. This is a finite set of cardinal a power of
$\pi$. This is a finite set of cardinal a power of ![]() $\ell$ (see [Reference Mínguez and SécherreMS17, Proposition 1.3]). In particular, since
$\ell$ (see [Reference Mínguez and SécherreMS17, Proposition 1.3]). In particular, since ![]() $\ell \neq 2$, this cardinal is odd. The action of
$\ell \neq 2$, this cardinal is odd. The action of ![]() $\delta$ induces an action on inertial classes of representations and since
$\delta$ induces an action on inertial classes of representations and since ![]() $\pi$ is
$\pi$ is ![]() $\delta$-invariant,
$\delta$-invariant, ![]() $\delta$ induces an action on
$\delta$ induces an action on ![]() $\mathcal {I}$. But the cardinal of
$\mathcal {I}$. But the cardinal of ![]() $\mathcal {I}$ is odd and
$\mathcal {I}$ is odd and ![]() $\delta$ is an involution, therefore there exists an inertial class which is
$\delta$ is an involution, therefore there exists an inertial class which is ![]() $\delta$-invariant, that is there exists
$\delta$-invariant, that is there exists ![]() $\tilde {\pi }$ a supercuspidal
$\tilde {\pi }$ a supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$ such that
$\pi$ such that ![]() $[\tilde {\pi }^\delta ]=[\tilde {\pi }]$. Let
$[\tilde {\pi }^\delta ]=[\tilde {\pi }]$. Let ![]() $\tilde {\chi }$ be an unramified character such that
$\tilde {\chi }$ be an unramified character such that ![]() $\tilde {\pi }^\sigma =\tilde {\pi }^{\vee } \otimes \tilde {\chi }$.
$\tilde {\pi }^\sigma =\tilde {\pi }^{\vee } \otimes \tilde {\chi }$.
Since ![]() $\tilde {\chi }$ is unramified, it is trivial on the kernel of the norm map, that is
$\tilde {\chi }$ is unramified, it is trivial on the kernel of the norm map, that is ![]() $\tilde {\chi } = \tilde {\chi }^{\sigma }$. Therefore, there exists an unramified character
$\tilde {\chi } = \tilde {\chi }^{\sigma }$. Therefore, there exists an unramified character ![]() $\tilde {\eta }$ such that
$\tilde {\eta }$ such that ![]() $\tilde {\chi } = \tilde {\eta } \tilde {\eta }^{\sigma } = \tilde {\eta }^2$. Since
$\tilde {\chi } = \tilde {\eta } \tilde {\eta }^{\sigma } = \tilde {\eta }^2$. Since ![]() $\tilde {\pi }$ is
$\tilde {\pi }$ is ![]() $\ell$-integral,
$\ell$-integral, ![]() $\tilde {\chi }$ is also
$\tilde {\chi }$ is also ![]() $\ell$-integral and so is
$\ell$-integral and so is ![]() $\tilde {\eta }$. Let
$\tilde {\eta }$. Let ![]() $\tilde {\pi }':=\tilde {\pi } \otimes \tilde {\eta }^{-1}$ such that
$\tilde {\pi }':=\tilde {\pi } \otimes \tilde {\eta }^{-1}$ such that ![]() $\tilde {\pi }'$ is
$\tilde {\pi }'$ is ![]() $\sigma$-selfdual. Let us denote by
$\sigma$-selfdual. Let us denote by ![]() $\pi '=\pi \otimes \eta ^{-1}$ its reduction modulo
$\pi '=\pi \otimes \eta ^{-1}$ its reduction modulo ![]() $\ell$ where
$\ell$ where ![]() $\eta$ is the reduction modulo
$\eta$ is the reduction modulo ![]() $\ell$ of
$\ell$ of ![]() $\tilde {\eta }$. Since
$\tilde {\eta }$. Since ![]() $\tilde {\pi }'$ is
$\tilde {\pi }'$ is ![]() $\sigma$-selfdual so is
$\sigma$-selfdual so is ![]() $\pi '$. The representations
$\pi '$. The representations ![]() $\pi$ and
$\pi$ and ![]() $\pi '=\pi \otimes \eta ^{-1}$ are both
$\pi '=\pi \otimes \eta ^{-1}$ are both ![]() $\sigma$-selfdual. Thus
$\sigma$-selfdual. Thus ![]() $\pi = \pi \otimes \eta ^{-2}$.
$\pi = \pi \otimes \eta ^{-2}$.
Let ![]() $X_u(\pi )$ be the set of unramified characters
$X_u(\pi )$ be the set of unramified characters ![]() $\xi$ such that
$\xi$ such that ![]() $\pi = \pi \otimes \xi$. It is contained in the cyclic group of order
$\pi = \pi \otimes \xi$. It is contained in the cyclic group of order ![]() $n$ composed of the character
$n$ composed of the character ![]() $\xi$ such that
$\xi$ such that ![]() $\xi ^n=1$ and is characterized by its order
$\xi ^n=1$ and is characterized by its order ![]() $f(\pi )$. Let
$f(\pi )$. Let ![]() $o(\eta )$ be the order of
$o(\eta )$ be the order of ![]() $\eta$. We have
$\eta$. We have ![]() $o(\eta ) \mid 2f(\pi )$. Let
$o(\eta ) \mid 2f(\pi )$. Let ![]() $\tilde {\rho }$ be the canonical
$\tilde {\rho }$ be the canonical ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\eta$. In particular
$\eta$. In particular ![]() $o(\tilde {\rho })=o(\eta ) \mid 2f(\pi )$. Let
$o(\tilde {\rho })=o(\eta ) \mid 2f(\pi )$. Let ![]() $\tilde {\pi }'':=\tilde {\pi }' \otimes \tilde {\rho }$. It is a supercuspidal
$\tilde {\pi }'':=\tilde {\pi }' \otimes \tilde {\rho }$. It is a supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$. To finish the proof, we are left to prove that it is
$\pi$. To finish the proof, we are left to prove that it is ![]() $\sigma$-selfdual. The representation
$\sigma$-selfdual. The representation ![]() $\tilde {\pi }'$ being
$\tilde {\pi }'$ being ![]() $\sigma$-selfdual, we just need to prove that
$\sigma$-selfdual, we just need to prove that ![]() $\tilde {\pi }'' = \tilde {\pi }'' \otimes \tilde {\rho }^2$, that is that
$\tilde {\pi }'' = \tilde {\pi }'' \otimes \tilde {\rho }^2$, that is that ![]() $o(\tilde {\rho }) \mid 2f(\tilde {\pi }')$. The explicit formulas for
$o(\tilde {\rho }) \mid 2f(\tilde {\pi }')$. The explicit formulas for ![]() $f(\tilde {\pi }')$ and
$f(\tilde {\pi }')$ and ![]() $f(\pi )$ show that
$f(\pi )$ show that ![]() $f(\tilde {\pi }')=f(\pi )\ell ^k$ for some integer
$f(\tilde {\pi }')=f(\pi )\ell ^k$ for some integer ![]() $k$ (see, for instance, [Reference Mínguez and SécherreMS14, Remark 3.21]). Thus
$k$ (see, for instance, [Reference Mínguez and SécherreMS14, Remark 3.21]). Thus ![]() $2f(\pi ) \mid 2f(\tilde {\pi }')$ and so
$2f(\pi ) \mid 2f(\tilde {\pi }')$ and so ![]() $o(\tilde {\rho }) \mid 2f(\tilde {\pi }')$. Therefore,
$o(\tilde {\rho }) \mid 2f(\tilde {\pi }')$. Therefore, ![]() $\tilde {\pi }''$ is
$\tilde {\pi }''$ is ![]() $\sigma$-selfdual.
$\sigma$-selfdual.
Theorem 3.14 Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$. Then
$\operatorname {GL}_n(E)$. Then ![]() $\pi$ is
$\pi$ is ![]() $\sigma$-selfdual if and only if it is distinguished or
$\sigma$-selfdual if and only if it is distinguished or ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {GL}_n(F)$. Moreover,
$\operatorname {GL}_n(F)$. Moreover, ![]() $\pi$ cannot be both distinguished and
$\pi$ cannot be both distinguished and ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {GL}_n(F)$.
$\operatorname {GL}_n(F)$.
Proof. Assume that ![]() $\pi$ is
$\pi$ is ![]() $\sigma$-selfdual. Then there exists a
$\sigma$-selfdual. Then there exists a ![]() $\sigma$-selfdual lift
$\sigma$-selfdual lift ![]() $\tilde {\pi }$ by Proposition 3.13. From the dichotomy theorem in the complex case (see [Reference KableKab04] in characteristic zero and [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Theorem A.2] in positive characteristic, or [Reference JoJo23]),
$\tilde {\pi }$ by Proposition 3.13. From the dichotomy theorem in the complex case (see [Reference KableKab04] in characteristic zero and [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Theorem A.2] in positive characteristic, or [Reference JoJo23]), ![]() $\tilde {\pi }$ is either distinguished or
$\tilde {\pi }$ is either distinguished or ![]() $\widetilde {\omega }_{E/F}$-distinguished. Since the reduction modulo
$\widetilde {\omega }_{E/F}$-distinguished. Since the reduction modulo ![]() $\ell$ preserves distinction (see [Reference Kurinczuk and MatringeKM20, Theorem 3.4]), it is also true for
$\ell$ preserves distinction (see [Reference Kurinczuk and MatringeKM20, Theorem 3.4]), it is also true for ![]() $\pi$. The disjunction is Proposition 3.12 and the reciprocity follows from Theorem 4.1.
$\pi$. The disjunction is Proposition 3.12 and the reciprocity follows from Theorem 4.1.
Proposition 3.15 Let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$ and
$\operatorname {GL}_n(E)$ and ![]() $\varphi _\pi$ its Langlands parameter. Then
$\varphi _\pi$ its Langlands parameter. Then ![]() $\pi$ is distinguished if and only if
$\pi$ is distinguished if and only if ![]() $\varphi _\pi$ is conjugate-orthogonal and
$\varphi _\pi$ is conjugate-orthogonal and ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished if and only if
$\omega _{E/F}$-distinguished if and only if ![]() $\varphi _\pi$ is conjugate-symplectic.
$\varphi _\pi$ is conjugate-symplectic.
Proof. A ![]() $\sigma$-selfdual supercuspidal
$\sigma$-selfdual supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation is either distinguished or
$\overline {\mathbf {F}}_{\ell }$-representation is either distinguished or ![]() $\omega _{E/F}$-distinguished by Theorem 3.14. By Proposition 3.11 we can lift a distinguished representation to a distinguished representation. Hence, the result follows from the complex case in [Reference KableKab04] (the results of [Reference KableKab04] are still valid in positive characteristic by [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Appendix A] or [Reference JoJo23]).
$\omega _{E/F}$-distinguished by Theorem 3.14. By Proposition 3.11 we can lift a distinguished representation to a distinguished representation. Hence, the result follows from the complex case in [Reference KableKab04] (the results of [Reference KableKab04] are still valid in positive characteristic by [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and StevensAKMSS21, Appendix A] or [Reference JoJo23]).
3.4 Supercuspidal representations of  $\operatorname {GL}_n(E)$ distinguished by unitary groups
$\operatorname {GL}_n(E)$ distinguished by unitary groups
Another example of application of Theorem 3.4 is for supercuspidal representations distinguished by a unitary involution. Let ![]() $G=\operatorname {GL}_n(E)$ and assume
$G=\operatorname {GL}_n(E)$ and assume ![]() $\ell \neq 2$. Let
$\ell \neq 2$. Let ![]() $\varepsilon$ be an hermitian matrix in
$\varepsilon$ be an hermitian matrix in ![]() $M_n(E)$ (
$M_n(E)$ (![]() $\sigma ({}^{t}\varepsilon )=\varepsilon$). We denote by
$\sigma ({}^{t}\varepsilon )=\varepsilon$). We denote by ![]() $\varsigma$ the unitary involution on
$\varsigma$ the unitary involution on ![]() $G$ defined by
$G$ defined by ![]() $\varsigma (g)=\varepsilon \sigma ({}^{t}g^{-1}) \varepsilon ^{-1}$. In this section, we are interested in supercuspidal
$\varsigma (g)=\varepsilon \sigma ({}^{t}g^{-1}) \varepsilon ^{-1}$. In this section, we are interested in supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representations of
$\overline {\mathbf {F}}_{\ell }$-representations of ![]() $G$ distinguished by
$G$ distinguished by ![]() $G^{\varsigma }$. In particular, we are going to prove that a supercuspidal representation
$G^{\varsigma }$. In particular, we are going to prove that a supercuspidal representation ![]() $\pi$ of
$\pi$ of ![]() $G$ is distinguished by
$G$ is distinguished by ![]() $G^\varsigma$ if and only if it is
$G^\varsigma$ if and only if it is ![]() $\sigma$-invariant. When
$\sigma$-invariant. When ![]() $p\neq 2$, this is proved by Zou in [Reference ZouZou22].
$p\neq 2$, this is proved by Zou in [Reference ZouZou22].
Proposition 3.16 Let ![]() $\pi$ be a
$\pi$ be a ![]() $\sigma$-invariant supercuspidal representation of
$\sigma$-invariant supercuspidal representation of ![]() $\operatorname {GL}_n(E)$ over
$\operatorname {GL}_n(E)$ over ![]() $\overline {\mathbf {F}}_{\ell }$. Then there exists a
$\overline {\mathbf {F}}_{\ell }$. Then there exists a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift ![]() $\tilde {\pi }$ of
$\tilde {\pi }$ of ![]() $\pi$ which is
$\pi$ which is ![]() $\sigma$-invariant.
$\sigma$-invariant.
Proof. We start with the same argument as in the proof of Proposition 3.13. The number of inertial classes of supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-lifts of
$\overline {\mathbf {Q}}_{\ell }$-lifts of ![]() $\pi$ is a power of
$\pi$ is a power of ![]() $\ell$, hence is odd. The involution
$\ell$, hence is odd. The involution ![]() $\sigma$ permutes its elements, so there exists an inertial class
$\sigma$ permutes its elements, so there exists an inertial class ![]() $[\tilde {\pi }]$ which is
$[\tilde {\pi }]$ which is ![]() $\sigma$-invariant. Let
$\sigma$-invariant. Let ![]() $\tilde {\chi }$ be an unramified character such that
$\tilde {\chi }$ be an unramified character such that ![]() $\tilde {\pi }^\sigma =\tilde {\pi } \otimes \tilde {\chi }$.
$\tilde {\pi }^\sigma =\tilde {\pi } \otimes \tilde {\chi }$.
Let us prove that ![]() $\tilde {\pi }$ is, in fact,
$\tilde {\pi }$ is, in fact, ![]() $\sigma$-invariant. As in the proof of Proposition 3.13, let
$\sigma$-invariant. As in the proof of Proposition 3.13, let ![]() $X_u(\tilde {\pi })$ (respectively,
$X_u(\tilde {\pi })$ (respectively, ![]() $X_u(\pi )$) be the set of unramified
$X_u(\pi )$) be the set of unramified ![]() $\overline {\mathbf {Q}}_{\ell }$-characters
$\overline {\mathbf {Q}}_{\ell }$-characters ![]() $\tilde {\xi }$ (respectively, unramified
$\tilde {\xi }$ (respectively, unramified ![]() $\overline {\mathbf {F}}_{\ell }$-characters
$\overline {\mathbf {F}}_{\ell }$-characters ![]() $\xi$) such that
$\xi$) such that ![]() $\tilde {\pi } = \tilde {\pi } \otimes \tilde {\xi }$ (respectively,
$\tilde {\pi } = \tilde {\pi } \otimes \tilde {\xi }$ (respectively, ![]() $\pi = \pi \otimes \xi$). It is characterized by its order
$\pi = \pi \otimes \xi$). It is characterized by its order ![]() $f(\tilde {\pi })$ (respectively,
$f(\tilde {\pi })$ (respectively, ![]() $f(\pi )$). Let
$f(\pi )$). Let ![]() $o(\tilde {\chi })$ be the order of
$o(\tilde {\chi })$ be the order of ![]() $\tilde {\chi }$. To finish the proof, we need to prove that
$\tilde {\chi }$. To finish the proof, we need to prove that ![]() $o(\tilde {\chi })$ divides
$o(\tilde {\chi })$ divides ![]() $f(\tilde {\pi })$. Indeed, this implies that
$f(\tilde {\pi })$. Indeed, this implies that ![]() $\tilde {\chi } \in X_u(\tilde {\pi })$ and
$\tilde {\chi } \in X_u(\tilde {\pi })$ and ![]() $\tilde {\pi }^\sigma \simeq \tilde {\pi } \otimes \tilde {\chi } \simeq \tilde {\pi }$.
$\tilde {\pi }^\sigma \simeq \tilde {\pi } \otimes \tilde {\chi } \simeq \tilde {\pi }$.
Let ![]() $\chi$ be the modulo
$\chi$ be the modulo ![]() $\ell$ reduction of
$\ell$ reduction of ![]() $\tilde {\chi }$ of order
$\tilde {\chi }$ of order ![]() $o(\chi )$. By taking the modulo
$o(\chi )$. By taking the modulo ![]() $\ell$ reduction we have that
$\ell$ reduction we have that ![]() $\pi \simeq \pi \otimes \chi$, thus
$\pi \simeq \pi \otimes \chi$, thus ![]() $\chi \in X_u(\pi )$ and
$\chi \in X_u(\pi )$ and ![]() $o(\chi ) \mid f(\pi )$. In addition, there exists an integer
$o(\chi ) \mid f(\pi )$. In addition, there exists an integer ![]() $a\in \mathbb {N}$ such that
$a\in \mathbb {N}$ such that ![]() $o(\tilde {\chi }) = o(\chi ) \ell ^{a}$. The explicit formulas for
$o(\tilde {\chi }) = o(\chi ) \ell ^{a}$. The explicit formulas for ![]() $f(\tilde {\pi })$ and
$f(\tilde {\pi })$ and ![]() $f(\pi )$ show that there exists an integer
$f(\pi )$ show that there exists an integer ![]() $b \in \mathbb {N}$ such that
$b \in \mathbb {N}$ such that ![]() $f(\tilde {\pi }) = f(\pi ) \ell ^{b}$ and
$f(\tilde {\pi }) = f(\pi ) \ell ^{b}$ and ![]() $f(\pi )$ is prime to
$f(\pi )$ is prime to ![]() $\ell$.
$\ell$.
Since ![]() $\tilde {\chi }$ is unramified, it is trivial on the kernel of the norm map and
$\tilde {\chi }$ is unramified, it is trivial on the kernel of the norm map and ![]() $\tilde {\chi }=\tilde {\chi }^{\sigma }$. In particular,
$\tilde {\chi }=\tilde {\chi }^{\sigma }$. In particular, ![]() $\tilde {\pi }\simeq (\tilde {\pi } \otimes \tilde {\chi })^{\sigma } \simeq \tilde {\pi } \otimes \tilde {\chi }^2$ and
$\tilde {\pi }\simeq (\tilde {\pi } \otimes \tilde {\chi })^{\sigma } \simeq \tilde {\pi } \otimes \tilde {\chi }^2$ and ![]() $o(\tilde {\chi }) \mid 2f(\tilde {\pi })$. Since
$o(\tilde {\chi }) \mid 2f(\tilde {\pi })$. Since ![]() $\ell$ is odd, we get that
$\ell$ is odd, we get that ![]() $a \leq b$. At the end,
$a \leq b$. At the end, ![]() $o(\chi ) \mid f(\pi )$ and
$o(\chi ) \mid f(\pi )$ and ![]() $\ell ^a \mid \ell ^b$ thus
$\ell ^a \mid \ell ^b$ thus ![]() $o(\tilde {\chi }) \mid f(\tilde {\pi })$ and this finishes the proof.
$o(\tilde {\chi }) \mid f(\tilde {\pi })$ and this finishes the proof.
Theorem 3.17 Let ![]() $\pi$ be a supercuspidal
$\pi$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $G=\operatorname {GL}_n(E)$ and
$G=\operatorname {GL}_n(E)$ and ![]() $\varsigma$ a unitary involution of
$\varsigma$ a unitary involution of ![]() $G$. Then
$G$. Then ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $G^{\varsigma }$ if and only if
$G^{\varsigma }$ if and only if ![]() $\pi ^{\sigma }\simeq \pi$.
$\pi ^{\sigma }\simeq \pi$.
Proof. When ![]() $E$ has characteristic zero, since the modulo
$E$ has characteristic zero, since the modulo ![]() $\ell$ reduction preserves
$\ell$ reduction preserves ![]() $\sigma$-invariance and the property of being distinguished for supercuspidal representations [Reference Kurinczuk and MatringeKM20, Theorem 3.4], the result follows from the complex case (see [Reference Hakim and MurnaghanHM02, § 4, Corollary] and [Reference Feigon, Lapid and OffenFLO12, Theorem 0.2]) by Theorem 3.4 and Proposition 3.16. For a field
$\sigma$-invariance and the property of being distinguished for supercuspidal representations [Reference Kurinczuk and MatringeKM20, Theorem 3.4], the result follows from the complex case (see [Reference Hakim and MurnaghanHM02, § 4, Corollary] and [Reference Feigon, Lapid and OffenFLO12, Theorem 0.2]) by Theorem 3.4 and Proposition 3.16. For a field ![]() $E$ of positive characteristic this follows from [Reference ZouZou22, Theorem 1.1].
$E$ of positive characteristic this follows from [Reference ZouZou22, Theorem 1.1].
Remark 3.18 The implication, ![]() $\pi$ distinguished by
$\pi$ distinguished by ![]() $G^{\varsigma }$ implies
$G^{\varsigma }$ implies ![]() $\pi$-invariant, is also proved in [Reference ZouZou22, Theorem 4.1] similarly.
$\pi$-invariant, is also proved in [Reference ZouZou22, Theorem 4.1] similarly.
4. The  $\operatorname {GL}_2(F)$-distinguished representations
$\operatorname {GL}_2(F)$-distinguished representations
This section is devoted to the study of ![]() $\operatorname {GL}_2(F)$-distinguished
$\operatorname {GL}_2(F)$-distinguished ![]() $\ell$-modular representations of
$\ell$-modular representations of ![]() $\operatorname {GL}_2(E)$, with
$\operatorname {GL}_2(E)$, with ![]() $\ell \neq 2$. The case of supercuspidal representations has been dealt with in § 3.3. Using Mackey theory, we will describe non-supercuspidal distinguished representations, hence giving a complete classification of all
$\ell \neq 2$. The case of supercuspidal representations has been dealt with in § 3.3. Using Mackey theory, we will describe non-supercuspidal distinguished representations, hence giving a complete classification of all ![]() $\operatorname {GL}_2(F)$-distinguished representations.
$\operatorname {GL}_2(F)$-distinguished representations.
Before we start, let us recall a result of Sécherre about ![]() $\ell$-modular
$\ell$-modular ![]() $\operatorname {GL}_2(F)$-distinguished representations of
$\operatorname {GL}_2(F)$-distinguished representations of ![]() $\operatorname {GL}_2(E)$. Denote by
$\operatorname {GL}_2(E)$. Denote by ![]() $\mathbf {1}_2$ the trivial character of
$\mathbf {1}_2$ the trivial character of ![]() $\operatorname {GL}_2(F)$.
$\operatorname {GL}_2(F)$.
Theorem 4.1 [Reference SécherreSéc19, Theorem 4.1]
Let ![]() $\pi$ be a distinguished irreducible
$\pi$ be a distinguished irreducible ![]() $\ell$-modular representation of
$\ell$-modular representation of ![]() $\operatorname {GL}_2(E)$. Then:
$\operatorname {GL}_2(E)$. Then:
(i) the central character of
 $\pi$ is trivial on
$\pi$ is trivial on  $F^{\times }$;
$F^{\times }$;(ii) the contragredient representation
 $\pi ^{\vee }$ is distinguished;
$\pi ^{\vee }$ is distinguished;(iii) the space
 $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2)$ has dimension 1;
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2)$ has dimension 1;(iv) the representation
 $\pi$ is
$\pi$ is  $\sigma$-selfdual, that is
$\sigma$-selfdual, that is  $\pi ^{\vee } \simeq \pi ^{\sigma }$.
$\pi ^{\vee } \simeq \pi ^{\sigma }$.
For the complex supercuspidal representations, it was proved by Hakim [Reference HakimHak94] and Prasad [Reference PrasadPra92].
4.1 Non-supercuspidal representations
In § 3.3, we studied when supercuspidal representations are distinguished. In this section, we will deal with non-supercuspidal representations including the principal series representations.
Let us start with an easy lemma that is needed for the rest of this section.
Lemma 4.2 Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$. Then
$E^{\times }$. Then ![]() $\chi \chi ^{\sigma }=\mathbf {1}$ if and only if
$\chi \chi ^{\sigma }=\mathbf {1}$ if and only if ![]() $\chi _{|{F^\times }}=\mathbf {1}$ or
$\chi _{|{F^\times }}=\mathbf {1}$ or ![]() $\chi _{|{F^\times }}=\omega _{E/F}$.
$\chi _{|{F^\times }}=\omega _{E/F}$.
Proof. The condition ![]() $\chi \chi ^{\sigma }=\mathbf {1}$ is equivalent to
$\chi \chi ^{\sigma }=\mathbf {1}$ is equivalent to ![]() $\chi _{|F^\times }$ being trivial on the norm group
$\chi _{|F^\times }$ being trivial on the norm group ![]() $\operatorname {Nm}_{E/F}(E^{\times })$. By the local class field theory the only two characters of
$\operatorname {Nm}_{E/F}(E^{\times })$. By the local class field theory the only two characters of ![]() $F^\times$ trivial on
$F^\times$ trivial on ![]() $\operatorname {Nm}_{E/F}(E^{\times })$ are
$\operatorname {Nm}_{E/F}(E^{\times })$ are ![]() $\mathbf {1}$ and
$\mathbf {1}$ and ![]() $\omega _{E/F}$.
$\omega _{E/F}$.
Let ![]() $\chi _1,\chi _2$ be two characters of
$\chi _1,\chi _2$ be two characters of ![]() $E^{\times }$. Denote by
$E^{\times }$. Denote by ![]() $\pi (\chi _1,\chi _2)$ the principal series representation of
$\pi (\chi _1,\chi _2)$ the principal series representation of ![]() $\operatorname {GL}_2(E)$ induced from
$\operatorname {GL}_2(E)$ induced from ![]() $(\chi _1,\chi _2)$, that is,
$(\chi _1,\chi _2)$, that is, ![]() $\pi (\chi _1,\chi _2)$ is the normalized parabolic induction of
$\pi (\chi _1,\chi _2)$ is the normalized parabolic induction of ![]() $\chi _1\boxtimes \chi _2$ from the standard Borel subgroup to
$\chi _1\boxtimes \chi _2$ from the standard Borel subgroup to ![]() $\operatorname {GL}_2(E)$.
$\operatorname {GL}_2(E)$.
Lemma 4.3 Let ![]() $\pi =\pi (\chi _1,\chi _2)$ be a principal series representation of
$\pi =\pi (\chi _1,\chi _2)$ be a principal series representation of ![]() $\operatorname {GL}_2(E)$. Then
$\operatorname {GL}_2(E)$. Then ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_2(F)$ if and only if either
$\operatorname {GL}_2(F)$ if and only if either ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with ![]() $\chi _1\neq \chi _2$.
$\chi _1\neq \chi _2$.
Moreover, when ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_2(F)$ we have
$\operatorname {GL}_2(F)$ we have
 \[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi,\mathbf{1}_2)=\begin{cases} 2 & \mbox{if } \ell \mid q_F-1, \chi_1=\chi_2 \mbox{ and } \chi_1|_{F^\times}=\mathbf{1}, \\ 1 & \mbox{otherwise}. \end{cases} \]
\[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi,\mathbf{1}_2)=\begin{cases} 2 & \mbox{if } \ell \mid q_F-1, \chi_1=\chi_2 \mbox{ and } \chi_1|_{F^\times}=\mathbf{1}, \\ 1 & \mbox{otherwise}. \end{cases} \]
Proof. Recall that ![]() $B_2(E)$ is the standard Borel subgroup of
$B_2(E)$ is the standard Borel subgroup of ![]() $\operatorname {GL}_2(E)$. Note that
$\operatorname {GL}_2(E)$. Note that ![]() $\operatorname {GL}_2(E)=B_2(E)\operatorname {GL}_2(F)\sqcup B_2(E)\eta \operatorname {GL}_2(F)$ with
$\operatorname {GL}_2(E)=B_2(E)\operatorname {GL}_2(F)\sqcup B_2(E)\eta \operatorname {GL}_2(F)$ with ![]() $\eta =\big (\begin{smallmatrix} 1 & \delta \\ 1 & -\delta \end{smallmatrix}\big )$ and
$\eta =\big (\begin{smallmatrix} 1 & \delta \\ 1 & -\delta \end{smallmatrix}\big )$ and ![]() $E=F[\delta ]$. Denote by
$E=F[\delta ]$. Denote by ![]() $S(X)$ the Schwartz space of
$S(X)$ the Schwartz space of ![]() $X$ consisting of locally constant functions defined on
$X$ consisting of locally constant functions defined on ![]() $X$. There is a short exact sequence
$X$. There is a short exact sequence
of ![]() $\operatorname {GL}_2(F)$-modules and
$\operatorname {GL}_2(F)$-modules and ![]() $\pi$ can be embedded inside
$\pi$ can be embedded inside ![]() $S(\operatorname {GL}_2(E))$. Due to the geometric lemma, one has a short exact sequence
$S(\operatorname {GL}_2(E))$. Due to the geometric lemma, one has a short exact sequence
with ![]() $\delta _{B_2(E)}^{1/2}=\delta _{B_2(F)}$. Applying the functor
$\delta _{B_2(E)}^{1/2}=\delta _{B_2(F)}$. Applying the functor ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$,
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$,
where ![]() $\operatorname {Ext}^1_{F^\times \times F^\times }$ denotes the Ext functor in the category of the finite-dimensional representations of
$\operatorname {Ext}^1_{F^\times \times F^\times }$ denotes the Ext functor in the category of the finite-dimensional representations of ![]() $F^\times \times F^\times$. Thanks to [Reference Drevon and SécherreDS23, Proposition 8.4] that
$F^\times \times F^\times$. Thanks to [Reference Drevon and SécherreDS23, Proposition 8.4] that ![]() $\operatorname {Ext}_{F^\times }^1(\chi,\mathbf {1})\neq 0$ if and only if
$\operatorname {Ext}_{F^\times }^1(\chi,\mathbf {1})\neq 0$ if and only if ![]() $\chi$ is trivial, one has that
$\chi$ is trivial, one has that ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1})\neq 0$ if and only if
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1})\neq 0$ if and only if ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$. If
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$. If ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ and
$\chi _1\chi _2^\sigma =\mathbf {1}$ and ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$, then
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$, then ![]() $\chi _1=\chi _2$. Thus,
$\chi _1=\chi _2$. Thus, ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_2(F)$ if and only if either
$\operatorname {GL}_2(F)$ if and only if either ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ with ![]() $\chi _1\neq \chi _2$.
$\chi _1\neq \chi _2$.
Now, let us assume that ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_2(F)$, that is
$\operatorname {GL}_2(F)$, that is ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }= \chi _2|_{F^\times }=\mathbf {1}$.
$\chi _1|_{F^\times }= \chi _2|_{F^\times }=\mathbf {1}$.
If ![]() $\chi _1\neq \chi _2$, only one of the conditions
$\chi _1\neq \chi _2$, only one of the conditions ![]() $\chi _1\chi _2^\sigma =\mathbf {1}$ or
$\chi _1\chi _2^\sigma =\mathbf {1}$ or ![]() $\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ can be true. We then see from the previous exact sequence that
$\chi _1|_{F^\times }=\chi _2|_{F^\times }=\mathbf {1}$ can be true. We then see from the previous exact sequence that ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2) = \operatorname {Hom}_{F^\times \times F^\times }(\chi _1\boxtimes \chi _2,\mathbf {1})$ or
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2) = \operatorname {Hom}_{F^\times \times F^\times }(\chi _1\boxtimes \chi _2,\mathbf {1})$ or ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2) = \operatorname {Hom}_{E^\times }(\chi _1\chi _2^\sigma,\mathbf {1})$. Therefore,
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi,\mathbf {1}_2) = \operatorname {Hom}_{E^\times }(\chi _1\chi _2^\sigma,\mathbf {1})$. Therefore,
We are left to study the case ![]() $\chi _1=\chi _2$ with
$\chi _1=\chi _2$ with ![]() $\chi _1|_{F^\times }=\mathbf {1}$. Let
$\chi _1|_{F^\times }=\mathbf {1}$. Let ![]() $\chi :=\chi _1=\chi _2$. Note that if
$\chi :=\chi _1=\chi _2$. Note that if ![]() $q_E \not \equiv 1 \pmod {\ell }$ then
$q_E \not \equiv 1 \pmod {\ell }$ then ![]() $\pi (\chi,\chi )$ is irreducible. Thus, by Theorem 4.1,
$\pi (\chi,\chi )$ is irreducible. Thus, by Theorem 4.1, ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi,\chi ),\mathbf {1}_2)=1$. Thus, we assume that
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi,\chi ),\mathbf {1}_2)=1$. Thus, we assume that ![]() $q_E \equiv 1 \pmod {\ell }$. We have two cases.
$q_E \equiv 1 \pmod {\ell }$. We have two cases.
(i) Suppose
 $q_F \equiv -1 \pmod {\ell }$. In this case
$q_F \equiv -1 \pmod {\ell }$. In this case  $(\nu ^{-1/2})_{|F^{\times }}\neq \mathbf {1}$. The representation
$(\nu ^{-1/2})_{|F^{\times }}\neq \mathbf {1}$. The representation  $\pi (\chi,\chi )$ is a direct sum of two irreducible representations: the character
$\pi (\chi,\chi )$ is a direct sum of two irreducible representations: the character  $(\chi \nu ^{-1/2}) \circ \det$ and a twisted Steinberg
$(\chi \nu ^{-1/2}) \circ \det$ and a twisted Steinberg  $\operatorname {St}_{\chi \nu ^{-1/2}}$ (see for instance [Reference VignérasVig89, Theorem 3]). As
$\operatorname {St}_{\chi \nu ^{-1/2}}$ (see for instance [Reference VignérasVig89, Theorem 3]). As  $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \nu ^{-1/2}) \circ \det,\mathbf {1}_2)=0$ and
by Theorem 4.1, we get that
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \nu ^{-1/2}) \circ \det,\mathbf {1}_2)=0$ and
by Theorem 4.1, we get that \[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\operatorname{St}_{\chi \nu^{-1/2}},\mathbf{1}_2) \leq 1 \]
\[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\operatorname{St}_{\chi \nu^{-1/2}},\mathbf{1}_2) \leq 1 \]
 $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi,\chi ),\mathbf {1}_2)=1$.
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi,\chi ),\mathbf {1}_2)=1$.(ii) Suppose
 $q_F \equiv 1 \pmod {\ell }$. This time
$q_F \equiv 1 \pmod {\ell }$. This time  ${(\nu ^{-1/2})}_{|F^{\times }}= \mathbf {1}$. Therefore,
where
${(\nu ^{-1/2})}_{|F^{\times }}= \mathbf {1}$. Therefore,
where \[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\chi,\chi),\mathbf{1}_2)=\dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(V(\mathbf{1},\mathbf{1}),\mathbf{1}_2) \]
\[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\chi,\chi),\mathbf{1}_2)=\dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(V(\mathbf{1},\mathbf{1}),\mathbf{1}_2) \]
 $V(\mathbf {1},\mathbf {1})$ denotes the non-normalized induction.
$V(\mathbf {1},\mathbf {1})$ denotes the non-normalized induction.
Recall that
where ![]() $\eta$ represents the open orbit in double coset
$\eta$ represents the open orbit in double coset ![]() $B_2(E)\backslash \operatorname {GL}_2(E)/\operatorname {GL}_2(F)$. There is a short exact sequence
$B_2(E)\backslash \operatorname {GL}_2(E)/\operatorname {GL}_2(F)$. There is a short exact sequence
Let ![]() $f_1$ be a linear functional defined on a subset consisting of functions in
$f_1$ be a linear functional defined on a subset consisting of functions in ![]() $V(\mathbf {1},\mathbf {1})$ supported on the closed orbit
$V(\mathbf {1},\mathbf {1})$ supported on the closed orbit ![]() $B_2(E)\operatorname {GL}_2(F)$ given by
$B_2(E)\operatorname {GL}_2(F)$ given by
for ![]() $\varphi \in V(\mathbf {1},\mathbf {1})$ supported on
$\varphi \in V(\mathbf {1},\mathbf {1})$ supported on ![]() $B_2(E)\operatorname {GL}_2(F)$. There is a natural extension of
$B_2(E)\operatorname {GL}_2(F)$. There is a natural extension of ![]() $f_1$ to the whole space
$f_1$ to the whole space ![]() $V(\mathbf {1},\mathbf {1})$, still denoted by
$V(\mathbf {1},\mathbf {1})$, still denoted by ![]() $f_1$, due to the embedding
$f_1$, due to the embedding
Then ![]() $f_1$ gives a
$f_1$ gives a ![]() $\operatorname {GL}_2(F)$-invariant linear functional on
$\operatorname {GL}_2(F)$-invariant linear functional on ![]() $\pi$ with support
$\pi$ with support ![]() $B_2(E)\operatorname {GL}_2(F)$. Note that there is a
$B_2(E)\operatorname {GL}_2(F)$. Note that there is a ![]() $\operatorname {GL}_2(E)$-invariant distribution on
$\operatorname {GL}_2(E)$-invariant distribution on ![]() $P^1(E)=B_2(E)\backslash \operatorname {GL}_2(E)$ if and only if
$P^1(E)=B_2(E)\backslash \operatorname {GL}_2(E)$ if and only if ![]() $\delta _{B(E)}=\mathbf {1}$, i.e.
$\delta _{B(E)}=\mathbf {1}$, i.e. ![]() $q_E \equiv 1 \pmod {\ell }$ (see [Reference BourbakiBou04, Chapter VII.6, Theorem 3]). Denote by
$q_E \equiv 1 \pmod {\ell }$ (see [Reference BourbakiBou04, Chapter VII.6, Theorem 3]). Denote by ![]() $d\mu$ the
$d\mu$ the ![]() $\operatorname {GL}_2(E)$-invariant measure on
$\operatorname {GL}_2(E)$-invariant measure on ![]() $P^1(E)$ and so it is
$P^1(E)$ and so it is ![]() $\operatorname {GL}_2(F)$-invariant. Then the restriction of
$\operatorname {GL}_2(F)$-invariant. Then the restriction of ![]() $d\mu$ on
$d\mu$ on ![]() $P^1(F)=B_2(F)\backslash \operatorname {GL}_2(F)$ is zero since
$P^1(F)=B_2(F)\backslash \operatorname {GL}_2(F)$ is zero since ![]() $P^1(F)$ has measure zero with respect to
$P^1(F)$ has measure zero with respect to ![]() $d\mu$. Therefore
$d\mu$. Therefore ![]() $d\mu$ and
$d\mu$ and ![]() $f_1$ generate two different
$f_1$ generate two different ![]() $\operatorname {GL}_2(F)$-invariant linear functionals on
$\operatorname {GL}_2(F)$-invariant linear functionals on ![]() $V(\mathbf {1},\mathbf {1})$. Thus,
$V(\mathbf {1},\mathbf {1})$. Thus, ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(V(\mathbf {1},\mathbf {1}),\mathbf {1}_2)=2$ (the dimension is bounded by 2 by the exact sequence at the beginning of the proof).
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(V(\mathbf {1},\mathbf {1}),\mathbf {1}_2)=2$ (the dimension is bounded by 2 by the exact sequence at the beginning of the proof).
Let us come back to the criterion for being distinguished for irreducible non-supercuspidal representations. By Lemma 4.3, we have the result for all irreducible principal series. We refer to [Reference VignérasVig89] or [Reference VignérasVig96] for the following facts about ![]() $\pi (\chi _1,\chi _2)$. Note that
$\pi (\chi _1,\chi _2)$. Note that ![]() $\pi (\chi _1,\chi _2)$ is reducible if and only if
$\pi (\chi _1,\chi _2)$ is reducible if and only if ![]() $\chi _1=\nu \chi _2$ or
$\chi _1=\nu \chi _2$ or ![]() $\chi _2=\nu \chi _1$. Hence, let
$\chi _2=\nu \chi _1$. Hence, let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$ and we are left to study the irreducible subquotients of
$E^{\times }$ and we are left to study the irreducible subquotients of ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$. If
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$. If ![]() $q_{E} \not \equiv -1 \pmod {\ell }$, then
$q_{E} \not \equiv -1 \pmod {\ell }$, then ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$ has length 2 with irreducible subquotients
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$ has length 2 with irreducible subquotients ![]() $\chi$ and
$\chi$ and ![]() $\operatorname {St}_{\chi }$. If
$\operatorname {St}_{\chi }$. If ![]() $q_{E} \equiv -1 \pmod {\ell }$, the length is 3 and the subquotients are
$q_{E} \equiv -1 \pmod {\ell }$, the length is 3 and the subquotients are ![]() $\chi$,
$\chi$, ![]() $\chi \nu _2$ and
$\chi \nu _2$ and ![]() $\operatorname {Sp}_{\chi }$.
$\operatorname {Sp}_{\chi }$.
Lemma 4.4 Let ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $F^{\times }$. Then
$F^{\times }$. Then ![]() $\operatorname {Ext}^1_{\operatorname {GL}_2(F)}(\mathbf {1}_2,\chi \circ \det )=0$ where
$\operatorname {Ext}^1_{\operatorname {GL}_2(F)}(\mathbf {1}_2,\chi \circ \det )=0$ where ![]() $\operatorname {Ext}^1_{\operatorname {GL}_2(F)}$ is the Ext functor in the category of the smooth representations of
$\operatorname {Ext}^1_{\operatorname {GL}_2(F)}$ is the Ext functor in the category of the smooth representations of ![]() $\operatorname {GL}_2(F)$ with trivial central character.
$\operatorname {GL}_2(F)$ with trivial central character.
Proof. Let ![]() $M$ be an extension of
$M$ be an extension of ![]() $\mathbf {1}_2$ by
$\mathbf {1}_2$ by ![]() $\chi \circ \det$ in the category of the smooth representations of
$\chi \circ \det$ in the category of the smooth representations of ![]() $\operatorname {GL}_2(F)$ with trivial central character. The representation
$\operatorname {GL}_2(F)$ with trivial central character. The representation ![]() $M$ has the form
$M$ has the form
for ![]() $g\in \operatorname {GL}_2(F)$. If
$g\in \operatorname {GL}_2(F)$. If ![]() $g_1,g_2 \in \operatorname {GL}_2(F)$, then
$g_1,g_2 \in \operatorname {GL}_2(F)$, then ![]() $\alpha (g_1g_2)=\alpha (g_1)+\chi (\det (g_1))\alpha (g_2)$. Since
$\alpha (g_1g_2)=\alpha (g_1)+\chi (\det (g_1))\alpha (g_2)$. Since ![]() $M$ has trivial central character,
$M$ has trivial central character, ![]() $\alpha (z)=0$ for every element
$\alpha (z)=0$ for every element ![]() $z$ in the center of
$z$ in the center of ![]() $\operatorname {GL}_2(F)$. It is obvious that
$\operatorname {GL}_2(F)$. It is obvious that ![]() $\alpha (g)=0$ for all
$\alpha (g)=0$ for all ![]() $g$ in
$g$ in ![]() $\operatorname {SL}_2(F)$ since
$\operatorname {SL}_2(F)$ since ![]() $\operatorname {SL}_2(F)$ is a perfect group. Let
$\operatorname {SL}_2(F)$ is a perfect group. Let ![]() $g \in \operatorname {GL}_2(F)$ and
$g \in \operatorname {GL}_2(F)$ and ![]() $t = \det (g) \in F^\times$. By writing
$t = \det (g) \in F^\times$. By writing ![]() $g=g_1g_2$ with
$g=g_1g_2$ with ![]() $g_1=\big (\begin{smallmatrix} t & 0 \\0 & 1 \end{smallmatrix}\big )$ and
$g_1=\big (\begin{smallmatrix} t & 0 \\0 & 1 \end{smallmatrix}\big )$ and ![]() $g_2=g_1^{-1}g \in \operatorname {SL}_2(F)$ we see that
$g_2=g_1^{-1}g \in \operatorname {SL}_2(F)$ we see that ![]() $\alpha (g)=\alpha (g_1)$. Let
$\alpha (g)=\alpha (g_1)$. Let ![]() $\bar {\alpha }:F^\times \to \overline {\mathbf {F}}_{\ell }$ be defined by
$\bar {\alpha }:F^\times \to \overline {\mathbf {F}}_{\ell }$ be defined by ![]() $\bar {\alpha }(t)=\alpha \big (\big (\begin{smallmatrix} t & 0 \\0 & 1 \end{smallmatrix}\big )\big )$. Then for all
$\bar {\alpha }(t)=\alpha \big (\big (\begin{smallmatrix} t & 0 \\0 & 1 \end{smallmatrix}\big )\big )$. Then for all ![]() $g \in \operatorname {GL}_2(F)$,
$g \in \operatorname {GL}_2(F)$, ![]() $\alpha (g)=\bar {\alpha }(\det (g))$. Moreover,
$\alpha (g)=\bar {\alpha }(\det (g))$. Moreover, ![]() $\bar {\alpha }$ is a cocycle satisfying
$\bar {\alpha }$ is a cocycle satisfying ![]() $\bar {\alpha }(t_1t_2)=\bar {\alpha }(t_1)+\chi (t_1)\bar {\alpha }(t_2)$, for
$\bar {\alpha }(t_1t_2)=\bar {\alpha }(t_1)+\chi (t_1)\bar {\alpha }(t_2)$, for ![]() $t_1,t_2 \in F^\times$.
$t_1,t_2 \in F^\times$.
Let ![]() $t_1,t_2 \in F^\times$. The equality
$t_1,t_2 \in F^\times$. The equality ![]() $\bar {\alpha }(t_1t_2)=\bar {\alpha }(t_2t_1)$ gives us that
$\bar {\alpha }(t_1t_2)=\bar {\alpha }(t_2t_1)$ gives us that ![]() $\bar {\alpha }(t_1)+\chi (t_1)\bar {\alpha }(t_2)=\bar {\alpha }(t_2)+\chi (t_2)\bar {\alpha }(t_1)$. If
$\bar {\alpha }(t_1)+\chi (t_1)\bar {\alpha }(t_2)=\bar {\alpha }(t_2)+\chi (t_2)\bar {\alpha }(t_1)$. If ![]() $\chi \neq \mathbf {1}$, then there exists
$\chi \neq \mathbf {1}$, then there exists ![]() $t_1$ such that
$t_1$ such that ![]() $\chi (t_1) \neq 1$. Therefore, for all
$\chi (t_1) \neq 1$. Therefore, for all ![]() $t_2 \in F^\times$, we have
$t_2 \in F^\times$, we have ![]() $\bar {\alpha }(t_2)=c(\chi (t_2)-1)$ where
$\bar {\alpha }(t_2)=c(\chi (t_2)-1)$ where ![]() $c=\bar {\alpha }(t_1)/(\chi (t_1)-1)$ is a constant. Thus, for all
$c=\bar {\alpha }(t_1)/(\chi (t_1)-1)$ is a constant. Thus, for all ![]() $g \in \operatorname {GL}_2(F)$,
$g \in \operatorname {GL}_2(F)$, ![]() $\alpha (g)=c\cdot (\chi (\det (g))-1)$ is a coboundary and the extension
$\alpha (g)=c\cdot (\chi (\det (g))-1)$ is a coboundary and the extension ![]() $M$ splits.
$M$ splits.
We are left with the case ![]() $\chi =\mathbf {1}$. In this case
$\chi =\mathbf {1}$. In this case ![]() $\bar {\alpha }:F^\times \to \overline {\mathbf {F}}_{\ell }$ is a morphism of group. Moreover,
$\bar {\alpha }:F^\times \to \overline {\mathbf {F}}_{\ell }$ is a morphism of group. Moreover, ![]() $\alpha$ is trivial on the center of
$\alpha$ is trivial on the center of ![]() $\operatorname {GL}_2(F)$ so the morphism
$\operatorname {GL}_2(F)$ so the morphism ![]() $\bar {\alpha }$ is trivial on
$\bar {\alpha }$ is trivial on ![]() $F^{\times 2}$ the subgroup of
$F^{\times 2}$ the subgroup of ![]() $F^\times$ of square elements. Since
$F^\times$ of square elements. Since ![]() $F^\times / F^{\times 2}$ is a 2-group and
$F^\times / F^{\times 2}$ is a 2-group and ![]() $\ell \neq 2$, we get that
$\ell \neq 2$, we get that ![]() $\bar {\alpha }$ is trivial, and
$\bar {\alpha }$ is trivial, and ![]() $M$ also splits.
$M$ also splits.
Remark 4.5 (i) If ![]() $\ell =2$, then Lemma 4.4 does not hold any more.
$\ell =2$, then Lemma 4.4 does not hold any more.
(ii) If there is no restriction for the central character, one can easily find the non-trivial extension of ![]() $\mathbf {1}_2$ by
$\mathbf {1}_2$ by ![]() $\mathbf {1}_2$, which is of the form
$\mathbf {1}_2$, which is of the form
where ![]() $\ln$ is the natural logarithm function defined on the multiplicative group consisting of positive real numbers.
$\ln$ is the natural logarithm function defined on the multiplicative group consisting of positive real numbers.
Theorem 4.6 Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$.
$E^{\times }$.
(i) If
 $q_{E}^2\not \equiv 1 \pmod {\ell }$, then
$q_{E}^2\not \equiv 1 \pmod {\ell }$, then  $\operatorname {St}_\chi$ is distinguished if and only if
$\operatorname {St}_\chi$ is distinguished if and only if  $\chi _{|{F^\times }}=\omega _{E/F}$.
$\chi _{|{F^\times }}=\omega _{E/F}$.(ii) If
 $q_{E} \equiv -1 \pmod {\ell }$, then
$q_{E} \equiv -1 \pmod {\ell }$, then  $\operatorname {Sp}_\chi$ is distinguished if and only if
$\operatorname {Sp}_\chi$ is distinguished if and only if  $q_F\equiv -1 \pmod {\ell }$ and
$q_F\equiv -1 \pmod {\ell }$ and  $\chi _{|{F^\times }}=\omega _{E/F}$ or
$\chi _{|{F^\times }}=\omega _{E/F}$ or  $\nu ^{1/2}_{|{F^\times }}$.
$\nu ^{1/2}_{|{F^\times }}$.(iii) If
 $q_{E}\equiv 1 \pmod {\ell }$, then
$q_{E}\equiv 1 \pmod {\ell }$, then  $\operatorname {St}_\chi$ is distinguished if and only if
$\operatorname {St}_\chi$ is distinguished if and only if  $\chi _{|{F^\times }}=\omega _{E/F}$ or
$\chi _{|{F^\times }}=\omega _{E/F}$ or  $\chi _{|{F^\times }}=\mathbf {1}$ with
$\chi _{|{F^\times }}=\mathbf {1}$ with  $q_F\equiv 1 \pmod {\ell }$.
$q_F\equiv 1 \pmod {\ell }$.
Proof. Suppose that ![]() $q_{E}\equiv -1 \pmod {\ell }$. If
$q_{E}\equiv -1 \pmod {\ell }$. If ![]() $\operatorname {Sp}_\chi$ is distinguished, then by Theorem 4.1(ii),
$\operatorname {Sp}_\chi$ is distinguished, then by Theorem 4.1(ii), ![]() $\operatorname {Sp}_\chi$ has trivial central character and so
$\operatorname {Sp}_\chi$ has trivial central character and so ![]() $\chi _{|{F^\times }}^2=1$. Thus, we may assume that
$\chi _{|{F^\times }}^2=1$. Thus, we may assume that ![]() $\chi _{|{F^\times }}^2=\mathbf {1}$. The principal series
$\chi _{|{F^\times }}^2=\mathbf {1}$. The principal series ![]() $\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2})$ has length
$\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2})$ has length ![]() $3$. There are two exact sequences
$3$. There are two exact sequences
and
of ![]() $\operatorname {GL}_2(E)$-modules. Taking the functor
$\operatorname {GL}_2(E)$-modules. Taking the functor ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$, we have the following exact sequence
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$, we have the following exact sequence
where ![]() $\operatorname {Ext}^1_{\operatorname {GL}_2(F)}$ is the Ext functor in the category of the smooth representations of
$\operatorname {Ext}^1_{\operatorname {GL}_2(F)}$ is the Ext functor in the category of the smooth representations of ![]() $\operatorname {GL}_2(F)$ with trivial central character. By Lemma 4.4
$\operatorname {GL}_2(F)$ with trivial central character. By Lemma 4.4
If ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)} (\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2}),\mathbf {1}_2)=0$, then
$\operatorname {Hom}_{\operatorname {GL}_2(F)} (\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2}),\mathbf {1}_2)=0$, then ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=0$ and
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=0$ and ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp}_{\chi }, \mathbf {1}_2)=0$. Hence,
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp}_{\chi }, \mathbf {1}_2)=0$. Hence, ![]() $\operatorname {Sp}_{\chi }$ is not distinguished.
$\operatorname {Sp}_{\chi }$ is not distinguished.
Therefore, we can assume that ![]() $\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2})$ is distinguished. By Lemma 4.3 we get that
$\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2})$ is distinguished. By Lemma 4.3 we get that ![]() $\chi \chi ^{\sigma }=\mathbf {1}$ (that is
$\chi \chi ^{\sigma }=\mathbf {1}$ (that is ![]() $\chi _{|{F^\times }}=\mathbf {1}$ or
$\chi _{|{F^\times }}=\mathbf {1}$ or ![]() $\chi _{|{F^\times }}=\omega _{E/F}$ by Lemma 4.2) or
$\chi _{|{F^\times }}=\omega _{E/F}$ by Lemma 4.2) or ![]() $\chi _{|{F^\times }}\nu ^{1/2}_{|{F^\times }}=\chi _{|{F^\times }}\nu ^{-1/2}_{|{F^\times }}=\mathbf {1}$ (which can only happen if
$\chi _{|{F^\times }}\nu ^{1/2}_{|{F^\times }}=\chi _{|{F^\times }}\nu ^{-1/2}_{|{F^\times }}=\mathbf {1}$ (which can only happen if ![]() $\nu _{|{F^\times }}=\mathbf {1}$, that is if
$\nu _{|{F^\times }}=\mathbf {1}$, that is if ![]() $q_F \equiv -1 \pmod {\ell }$). Moreover, in this case, Lemma 4.3 gives us
$q_F \equiv -1 \pmod {\ell }$). Moreover, in this case, Lemma 4.3 gives us
We have three cases to study.
– Suppose
 $\chi _{|{F^\times }}=\mathbf {1}$. In this case
$\chi _{|{F^\times }}=\mathbf {1}$. In this case  $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=0$ and so
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=0$ and so  $\operatorname {Sp}_{\chi }$ is not distinguished.
$\operatorname {Sp}_{\chi }$ is not distinguished.– Suppose
 $\chi _{|{F^\times }}=\omega _{E/F}$. Now
$\chi _{|{F^\times }}=\omega _{E/F}$. Now  $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=0$ and so
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=0$ and so  $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. If
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. If  $q_F\equiv -1 \pmod {\ell }$, then
$q_F\equiv -1 \pmod {\ell }$, then  $\nu _2|_{\operatorname {GL}_2(F)}=\mathbf {1}_2$. Furthermore, the exact sequence
implies that
$\nu _2|_{\operatorname {GL}_2(F)}=\mathbf {1}_2$. Furthermore, the exact sequence
implies that \[ 0\to \operatorname{Hom}_{\operatorname{GL}_2(F)}(\operatorname{Sp}_\chi,\mathbf{1}_2)\to \operatorname{Hom}_{\operatorname{GL}_2(F)}(J_\chi,\mathbf{1}_2)\to \operatorname{Hom}_{\operatorname{GL}_2(F)}((\chi \circ \det)\nu_2,\mathbf{1}_2)=0 \]
\[ 0\to \operatorname{Hom}_{\operatorname{GL}_2(F)}(\operatorname{Sp}_\chi,\mathbf{1}_2)\to \operatorname{Hom}_{\operatorname{GL}_2(F)}(J_\chi,\mathbf{1}_2)\to \operatorname{Hom}_{\operatorname{GL}_2(F)}((\chi \circ \det)\nu_2,\mathbf{1}_2)=0 \]
 $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp}_\chi,\mathbf {1}_2)=\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. If
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp}_\chi,\mathbf {1}_2)=\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. If  $q_F^2\equiv -1 \pmod {\ell }$, i.e.
$q_F^2\equiv -1 \pmod {\ell }$, i.e.  $E/F$ is unramified, then
$E/F$ is unramified, then  $\nu _2|_{\operatorname {GL}_2(F)}=\omega _{E/F}$. In this case
$\nu _2|_{\operatorname {GL}_2(F)}=\omega _{E/F}$. In this case  $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \circ \det )\nu _2,\mathbf {1}_2)=1$ and so
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \circ \det )\nu _2,\mathbf {1}_2)=1$ and so  $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp},\omega _{E/F})=0$.
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\operatorname {Sp},\omega _{E/F})=0$.– Suppose
 $\chi _{|{F^\times }}=\nu ^{1/2}_{|{F^\times }}$ and
$\chi _{|{F^\times }}=\nu ^{1/2}_{|{F^\times }}$ and  $q_F\equiv -1 \pmod {\ell }$. In the same way,
$q_F\equiv -1 \pmod {\ell }$. In the same way,  $\operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=0$ and so
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=0$ and so  $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. Since
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(J_\chi,\mathbf {1}_2)=1$. Since  $\operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \circ \det )\nu _2,\mathbf {1}_2)=0$ we get that
$\operatorname {Hom}_{\operatorname {GL}_2(F)}((\chi \circ \det )\nu _2,\mathbf {1}_2)=0$ we get that  $\operatorname {Sp}_\chi$ is distinguished.
$\operatorname {Sp}_\chi$ is distinguished.
Suppose ![]() $q_{E}\equiv 1 \pmod {\ell }$. In this case
$q_{E}\equiv 1 \pmod {\ell }$. In this case ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})$ is reducible and semisimple:
$\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})$ is reducible and semisimple: ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})=(\chi \circ \det )\oplus \operatorname {St}_\chi$. If
$\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})=(\chi \circ \det )\oplus \operatorname {St}_\chi$. If ![]() $\operatorname {St}_\chi$ is distinguished, then so is
$\operatorname {St}_\chi$ is distinguished, then so is ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})$. By Lemma 4.3,
$\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2})$. By Lemma 4.3, ![]() $\chi \chi ^{\sigma }=\mathbf {1}$ so
$\chi \chi ^{\sigma }=\mathbf {1}$ so ![]() $\chi _{|{F^\times }}=\mathbf {1}$ or
$\chi _{|{F^\times }}=\mathbf {1}$ or ![]() $\chi _{|{F^\times }}=\omega _{E/F}$ (Lemma 4.2). If
$\chi _{|{F^\times }}=\omega _{E/F}$ (Lemma 4.2). If ![]() $\chi _{|{F^\times }}=\omega _{E/F}$, then
$\chi _{|{F^\times }}=\omega _{E/F}$, then ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)\!=\!0$. Thanks to Lemma 4.3
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)\!=\!0$. Thanks to Lemma 4.3 ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2}),\mathbf {1}_2)\!\geq\! 1$ and so
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\pi (\chi \nu ^{-1/2},\chi \nu ^{-1/2}),\mathbf {1}_2)\!\geq\! 1$ and so ![]() $\operatorname {St}_\chi$ is distinguished. Now if
$\operatorname {St}_\chi$ is distinguished. Now if ![]() $\chi _{|{F^\times }}=\mathbf {1}$,
$\chi _{|{F^\times }}=\mathbf {1}$, ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=1$ and from Lemma 4.3
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)}(\chi \circ \det,\mathbf {1}_2)=1$ and from Lemma 4.3
 \[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\chi\nu^{-1/2},\chi\nu^{-1/2}),\mathbf{1}_2)= \begin{cases} 2, & \mbox{if } q_{F}\equiv 1\ ({\rm mod}\ {\ell}); \\ 1, & \mbox{if } q_{F}\equiv -1\ ({\rm mod}\ {\ell}). \end{cases} \]
\[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\chi\nu^{-1/2},\chi\nu^{-1/2}),\mathbf{1}_2)= \begin{cases} 2, & \mbox{if } q_{F}\equiv 1\ ({\rm mod}\ {\ell}); \\ 1, & \mbox{if } q_{F}\equiv -1\ ({\rm mod}\ {\ell}). \end{cases} \]
Thus, ![]() $\operatorname {St}_\chi$ is distinguished if and only if
$\operatorname {St}_\chi$ is distinguished if and only if ![]() $q_{F}\equiv 1 \pmod {\ell }$.
$q_{F}\equiv 1 \pmod {\ell }$.
The last case is ![]() $q_{E}^2\not \equiv 1 \pmod {\ell }$. We will do a similar argument as
$q_{E}^2\not \equiv 1 \pmod {\ell }$. We will do a similar argument as ![]() $q_{E}\equiv -1 \pmod {\ell }$. We have an exact sequence
$q_{E}\equiv -1 \pmod {\ell }$. We have an exact sequence
of ![]() $\operatorname {GL}_2(E)$-modules. If
$\operatorname {GL}_2(E)$-modules. If ![]() $\operatorname {St}_\chi$ is distinguished then so is
$\operatorname {St}_\chi$ is distinguished then so is ![]() $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$, so
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$, so ![]() $\chi _{|{F^\times }}=\mathbf {1}$ or
$\chi _{|{F^\times }}=\mathbf {1}$ or ![]() $\chi _{|{F^\times }}=\omega _{E/F}$. Taking the functor
$\chi _{|{F^\times }}=\omega _{E/F}$. Taking the functor ![]() $\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$, in the category of the smooth representations of
$\operatorname {Hom}_{\operatorname {GL}_2(F)}(-,\mathbf {1}_2)$, in the category of the smooth representations of ![]() $\operatorname {GL}_2(F)$ with trivial central character, we have
$\operatorname {GL}_2(F)$ with trivial central character, we have
By Lemma 4.4 ![]() $\operatorname {Ext}_{\operatorname {GL}_2(F)}^1(\mathbf {1}_2,\chi \circ \det )=0$. By Lemma 4.3
$\operatorname {Ext}_{\operatorname {GL}_2(F)}^1(\mathbf {1}_2,\chi \circ \det )=0$. By Lemma 4.3 ![]() $\dim \operatorname {Hom}_{\operatorname {GL}_2(F)} (\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2}), \mathbf {1}_2)=1$. Therefore,
$\dim \operatorname {Hom}_{\operatorname {GL}_2(F)} (\pi (\chi \nu ^{1/2},\chi \nu ^{-1/2}), \mathbf {1}_2)=1$. Therefore, ![]() $\operatorname {St}_\chi$ is distinguished if and only if
$\operatorname {St}_\chi$ is distinguished if and only if ![]() $\chi _{|{F^\times }}=\omega _{E/F}$.
$\chi _{|{F^\times }}=\omega _{E/F}$.
Remark 4.7 It can be seen from Theorem 4.6 that there are in the modular case new phenomena that do not appear in the complex setting.
– When
 $q_{F}\equiv 1 \pmod {\ell }$, the Steinberg representation
$q_{F}\equiv 1 \pmod {\ell }$, the Steinberg representation  $\operatorname {St}$ is both
$\operatorname {St}$ is both  $\operatorname {GL}_2(F)$-distinguished and
$\operatorname {GL}_2(F)$-distinguished and  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished.
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished.– When
 $q_{E}\equiv -1 \pmod {\ell }$ and
$q_{E}\equiv -1 \pmod {\ell }$ and  $E/F$ is unramified (that is,
$E/F$ is unramified (that is,  $q_{F}^2\equiv -1 \pmod {\ell }$ and so
$q_{F}^2\equiv -1 \pmod {\ell }$ and so  $q_{F}\not \equiv -1 \pmod {\ell }$) the special representation
$q_{F}\not \equiv -1 \pmod {\ell }$) the special representation  $\operatorname {Sp}$ is neither
$\operatorname {Sp}$ is neither  $\operatorname {GL}_2(F)$-distinguished nor
$\operatorname {GL}_2(F)$-distinguished nor  $(\operatorname {GL}_2(F),\omega _{E/F})$- distinguished. This has been mentioned by Sécherre in [Reference SécherreSéc19, Remark 2.8].
$(\operatorname {GL}_2(F),\omega _{E/F})$- distinguished. This has been mentioned by Sécherre in [Reference SécherreSéc19, Remark 2.8].– When
 $q_{E}\equiv -1 \pmod {\ell }$ and
$q_{E}\equiv -1 \pmod {\ell }$ and  $E/F$ is ramified (and so
$E/F$ is ramified (and so  $q_{F}\equiv -1 \pmod {\ell }$) the special representation
$q_{F}\equiv -1 \pmod {\ell }$) the special representation  $\operatorname {Sp}$ is
$\operatorname {Sp}$ is  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished and is also
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished and is also  $(\operatorname {GL}_2(F),\nu ^{1/2}_{|{F^\times }})$-distinguished.
$(\operatorname {GL}_2(F),\nu ^{1/2}_{|{F^\times }})$-distinguished.
5. The Prasad conjecture for  $\ell$-modular representations of
$\ell$-modular representations of  $\operatorname {PGL}_2$
$\operatorname {PGL}_2$
In [Reference PrasadPra15], Prasad proposed a conjecture for the multiplicity ![]() $\dim \operatorname {Hom}_{G(F)}(\pi,\chi _G)$ under the local Langlands conjecture, where
$\dim \operatorname {Hom}_{G(F)}(\pi,\chi _G)$ under the local Langlands conjecture, where ![]() $G$ is a quasi-split reductive group defined over
$G$ is a quasi-split reductive group defined over ![]() $F$,
$F$, ![]() $\pi$ is an irreducible smooth representation of
$\pi$ is an irreducible smooth representation of ![]() $G(E)$ lying inside a generic
$G(E)$ lying inside a generic ![]() $L$-package and
$L$-package and ![]() $\chi _G$ is a quadratic character depending on
$\chi _G$ is a quadratic character depending on ![]() $G$ and the quadratic extension
$G$ and the quadratic extension ![]() $E/F$. Let us recall briefly the Prasad conjecture for
$E/F$. Let us recall briefly the Prasad conjecture for ![]() $\operatorname {GL}_n$, which has been verified for the complex representations due to the work of Flicker, Prasad, Kable, Matringe and so on.
$\operatorname {GL}_n$, which has been verified for the complex representations due to the work of Flicker, Prasad, Kable, Matringe and so on.
Theorem 5.1 (The Prasad conjecture for  $\operatorname {GL}_{n}$)
$\operatorname {GL}_{n}$)
Let ![]() $\pi$ be a generic irreducible complex representation of
$\pi$ be a generic irreducible complex representation of ![]() $\operatorname {GL}_{n}(E)$ with Langlands parameter
$\operatorname {GL}_{n}(E)$ with Langlands parameter ![]() $\phi _\pi$. Let
$\phi _\pi$. Let ![]() $\chi _G=\omega _{E/F}^{n+1}$. Let
$\chi _G=\omega _{E/F}^{n+1}$. Let ![]() $U_{n,E/F}$ be the quasi-split unitary group. If
$U_{n,E/F}$ be the quasi-split unitary group. If ![]() $\operatorname {Hom}_{\operatorname {GL}_n(F)}(\pi,\chi _G)$ is non-zero, then:
$\operatorname {Hom}_{\operatorname {GL}_n(F)}(\pi,\chi _G)$ is non-zero, then:
(i)
 $\pi ^\vee \cong \pi ^\sigma$;
$\pi ^\vee \cong \pi ^\sigma$;(ii) there exists a parameter
 $\tilde {\phi }$ of
$\tilde {\phi }$ of  $U_{n,E/F}$ such that
$U_{n,E/F}$ such that  $\tilde {\phi }|_{WD_E}=\phi _\pi$;
$\tilde {\phi }|_{WD_E}=\phi _\pi$;(iii)
 $\dim _{\mathbb {C}}\operatorname {Hom}_{\operatorname {GL}_{n}(F)}(\pi,\chi _G)=|F(\phi _\pi )|$ where
and
$\dim _{\mathbb {C}}\operatorname {Hom}_{\operatorname {GL}_{n}(F)}(\pi,\chi _G)=|F(\phi _\pi )|$ where
and \[ F(\phi_\pi):=\big\{\tilde{\phi}:WD_F\rightarrow{}^LU_{n,E/F}\big|\tilde{\phi}|_{WD_E}=\phi_\pi\!\big\} \]
\[ F(\phi_\pi):=\big\{\tilde{\phi}:WD_F\rightarrow{}^LU_{n,E/F}\big|\tilde{\phi}|_{WD_E}=\phi_\pi\!\big\} \]
 $|F(\phi _\pi )|$ denotes its cardinality.
$|F(\phi _\pi )|$ denotes its cardinality.
Conversely, if there exists a parameter ![]() $\tilde {\phi }$ of
$\tilde {\phi }$ of ![]() $U_{n,E/F}$ such that
$U_{n,E/F}$ such that ![]() $\tilde {\phi }|_{WD_E}=\phi _\pi$, then
$\tilde {\phi }|_{WD_E}=\phi _\pi$, then ![]() $\operatorname {Hom}_{\operatorname {GL}_n(F)}(\pi,\chi _G)$ is non-zero.
$\operatorname {Hom}_{\operatorname {GL}_n(F)}(\pi,\chi _G)$ is non-zero.
Since the local Langlands correspondence for the ![]() $\ell$-modular representations of
$\ell$-modular representations of ![]() $G(F)$ has not been set up in general, except for
$G(F)$ has not been set up in general, except for ![]() $G=\operatorname {GL}_n$, we are concerned only with the simplest case where
$G=\operatorname {GL}_n$, we are concerned only with the simplest case where ![]() $G=\operatorname {PGL}_2$.
$G=\operatorname {PGL}_2$.
Theorem 5.2 (The Prasad conjecture for  $\operatorname {PGL}_2$)
$\operatorname {PGL}_2$)
Let ![]() $\pi$ be an irreducible generic complex representation of
$\pi$ be an irreducible generic complex representation of ![]() $\operatorname {PGL}_2(E)$ with Langlands parameter
$\operatorname {PGL}_2(E)$ with Langlands parameter ![]() $\phi _\pi$. Then
$\phi _\pi$. Then ![]() $\operatorname {Hom}_{\operatorname {PGL}_2(F)}(\pi,\omega _{E/F})$ is non-zero if and only if there exists a parameter
$\operatorname {Hom}_{\operatorname {PGL}_2(F)}(\pi,\omega _{E/F})$ is non-zero if and only if there exists a parameter ![]() $\tilde {\phi }$ of
$\tilde {\phi }$ of ![]() $\operatorname {PGL}_2(F)$ such that
$\operatorname {PGL}_2(F)$ such that ![]() $\tilde {\phi }|_{WD_F}=\phi _\pi$.
$\tilde {\phi }|_{WD_F}=\phi _\pi$.
First, we will show that the Prasad conjecture is not valid in the ![]() $\ell$-modular setting (when
$\ell$-modular setting (when ![]() $\ell$ is non-banal), i.e. there exists a parameter
$\ell$ is non-banal), i.e. there exists a parameter ![]() $\tilde {\phi }$ of
$\tilde {\phi }$ of ![]() $\operatorname {PGL}_2(F)$ such that
$\operatorname {PGL}_2(F)$ such that ![]() $\tilde {\phi }|_{WD_F}=\phi _\pi$, however the generic representation
$\tilde {\phi }|_{WD_F}=\phi _\pi$, however the generic representation ![]() $\pi$ is not
$\pi$ is not ![]() $\omega _{E/F}$-distinguished by
$\omega _{E/F}$-distinguished by ![]() $\operatorname {PGL}_2(F)$. Then, we provide a potential solution. To do that we define a non-trivial injection
$\operatorname {PGL}_2(F)$. Then, we provide a potential solution. To do that we define a non-trivial injection ![]() $P$ from nilpotent Weil–Deligne representations
$P$ from nilpotent Weil–Deligne representations ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ to equivalence classes of non-nilpotent one
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ to equivalence classes of non-nilpotent one ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$. Composing the local Langlands correspondence of Vignéras
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$. Composing the local Langlands correspondence of Vignéras ![]() $PV$ with
$PV$ with ![]() $P$ gives us a modular version of the Prasad conjecture. That is, an irreducible generic
$P$ gives us a modular version of the Prasad conjecture. That is, an irreducible generic ![]() $\overline {\mathbf {F}}_{\ell }$-representation
$\overline {\mathbf {F}}_{\ell }$-representation ![]() $\pi$ of
$\pi$ of ![]() $\operatorname {PGL}_2(E)$ is
$\operatorname {PGL}_2(E)$ is ![]() $\omega _{E/F}$-distinguished if and only if there exists
$\omega _{E/F}$-distinguished if and only if there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim P\circ PV(\pi )$.
$\Psi _{F|W_{E}} \sim P\circ PV(\pi )$.
5.1 The Langlands correspondence for  $\operatorname {PGL}_2$
$\operatorname {PGL}_2$
First, we recall how to get a Langlands correspondence for ![]() $\operatorname {PGL}_2$ using the correspondence for
$\operatorname {PGL}_2$ using the correspondence for ![]() $\operatorname {GL}_2$.
$\operatorname {GL}_2$.
Let ![]() $R=\overline {\mathbf {Q}}_{\ell }$ or
$R=\overline {\mathbf {Q}}_{\ell }$ or ![]() $\overline {\mathbf {F}}_{\ell }$. We denote by
$\overline {\mathbf {F}}_{\ell }$. We denote by ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)$ the subset of
$\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)$ the subset of ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ composed of the elements
$\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ composed of the elements ![]() $(\varphi,N)$ such that
$(\varphi,N)$ such that ![]() $\operatorname {Im}(\varphi ) \subset \operatorname {SL}_2(R)$ and
$\operatorname {Im}(\varphi ) \subset \operatorname {SL}_2(R)$ and ![]() $\operatorname {tr}(N)=0$. Let
$\operatorname {tr}(N)=0$. Let ![]() $\operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2) := \operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2) \cap \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$.
$\operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2) := \operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2) \cap \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$.
Remark 5.3 Let ![]() $(\varphi _1,N_1)$ and
$(\varphi _1,N_1)$ and ![]() $(\varphi _2,N_2)$ be two semisimple Weil–Deligne representations with
$(\varphi _2,N_2)$ be two semisimple Weil–Deligne representations with ![]() $\operatorname {Im}(\varphi _1) \subset \operatorname {SL}_2(R)$ and
$\operatorname {Im}(\varphi _1) \subset \operatorname {SL}_2(R)$ and ![]() $\operatorname {Im}(\varphi _2) \subset \operatorname {SL}_2(R)$. If
$\operatorname {Im}(\varphi _2) \subset \operatorname {SL}_2(R)$. If ![]() $(\varphi _1,N_1)$ and
$(\varphi _1,N_1)$ and ![]() $(\varphi _2,N_2)$ are isomorphic in
$(\varphi _2,N_2)$ are isomorphic in ![]() $\operatorname {GL}_2$, then they are also isomorphic in
$\operatorname {GL}_2$, then they are also isomorphic in ![]() $\operatorname {SL}_2$. Indeed, let
$\operatorname {SL}_2$. Indeed, let ![]() $A \in \operatorname {GL}_2(R)$ such that
$A \in \operatorname {GL}_2(R)$ such that ![]() $A^{-1} \varphi _1 A = \varphi _2$ and
$A^{-1} \varphi _1 A = \varphi _2$ and ![]() $A^{-1} N_1 A= N_2$. Since
$A^{-1} N_1 A= N_2$. Since ![]() $R$ is algebraically closed, let
$R$ is algebraically closed, let ![]() $\alpha \in R$ such that
$\alpha \in R$ such that ![]() $\alpha ^2 = \det (A)^{-1}$. Let
$\alpha ^2 = \det (A)^{-1}$. Let ![]() $B:= \alpha A$. Then
$B:= \alpha A$. Then ![]() $B \in \operatorname {SL}_2(R)$ and
$B \in \operatorname {SL}_2(R)$ and ![]() $B^{-1} \varphi _1 B = \varphi _2$,
$B^{-1} \varphi _1 B = \varphi _2$, ![]() $B^{-1} N_1 B= N_2$.
$B^{-1} N_1 B= N_2$.
Let ![]() $L$ be any map
$L$ be any map
such that ![]() $L$ sends the central character to the determinant (that is, if
$L$ sends the central character to the determinant (that is, if ![]() $\pi \in \operatorname {Irr}_R(\operatorname {GL}_2(E))$ and
$\pi \in \operatorname {Irr}_R(\operatorname {GL}_2(E))$ and ![]() $\omega _\pi$ is the central character of
$\omega _\pi$ is the central character of ![]() $\pi$, then
$\pi$, then ![]() $\omega _\pi$ corresponds to
$\omega _\pi$ corresponds to ![]() $\det (L(\pi ))$ via local class field theory). Then
$\det (L(\pi ))$ via local class field theory). Then ![]() $L$ induces a map
$L$ induces a map
making the following diagram commute

where the vertical map on the left-hand side is given by the projection ![]() $\operatorname {GL}_2(E) \to \operatorname {PGL}_2(E)$ and the vertical map on the right-hand side is the inclusion
$\operatorname {GL}_2(E) \to \operatorname {PGL}_2(E)$ and the vertical map on the right-hand side is the inclusion ![]() $\operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2) \subset \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$.
$\operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2) \subset \operatorname {Nilp}_{R}(W_{E},\operatorname {GL}_2)$.
In particular, since the ![]() $V$ correspondence sends the central character to the determinant [Reference Kurinczuk and MatringeKM21, Lemma 6.4], we get a map
$V$ correspondence sends the central character to the determinant [Reference Kurinczuk and MatringeKM21, Lemma 6.4], we get a map ![]() $PV : \operatorname {Irr}_R(\operatorname {PGL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2)$.
$PV : \operatorname {Irr}_R(\operatorname {PGL}_2(E)) \to \operatorname {Nilp}_{R}(W_{E},\operatorname {SL}_2)$.
5.2 Problem with the modular Prasad Conjecture
We shall show that the Prasad conjecture does not hold for ![]() $\ell$-modular representations with the
$\ell$-modular representations with the ![]() $V$ correspondence. One may think that it might work with a different choice of bijection in Theorem 3.8. We will show in this subsection that such kind of bijection does not exist; see Corollary 5.5.
$V$ correspondence. One may think that it might work with a different choice of bijection in Theorem 3.8. We will show in this subsection that such kind of bijection does not exist; see Corollary 5.5.
Let ![]() $L$ be a map
$L$ be a map
such that the semisimple part is given by ![]() $V_{ss}$.
$V_{ss}$.
When ![]() $q_E \equiv -1 \pmod {\ell }$, the image under
$q_E \equiv -1 \pmod {\ell }$, the image under ![]() $L$ of the special representation
$L$ of the special representation ![]() $\operatorname {Sp}$, has
$\operatorname {Sp}$, has ![]() $\nu ^{-1/2} \oplus \nu ^{1/2}$ for the semisimple part.
$\nu ^{-1/2} \oplus \nu ^{1/2}$ for the semisimple part.
Lemma 5.4 Let ![]() $E$ be a quadratic extension of
$E$ be a quadratic extension of ![]() $F$. Let us assume that
$F$. Let us assume that ![]() $q_E \equiv -1 \pmod {\ell }$. Then there exists
$q_E \equiv -1 \pmod {\ell }$. Then there exists ![]() $\Phi _{F} \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Phi _{F} \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Phi _{F|W_{E}}=L(\operatorname {Sp})$.
$\Phi _{F|W_{E}}=L(\operatorname {Sp})$.
Proof. There are three elements in ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ with semisimple part
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$ with semisimple part ![]() $\nu ^{-1/2} \oplus \nu ^{1/2}$ :
$\nu ^{-1/2} \oplus \nu ^{1/2}$ : ![]() $(\nu ^{-1/2} \oplus \nu ^{1/2},0)$,
$(\nu ^{-1/2} \oplus \nu ^{1/2},0)$, ![]() $(\nu ^{-1/2} \oplus \nu ^{1/2},N)$ and
$(\nu ^{-1/2} \oplus \nu ^{1/2},N)$ and ![]() $(\nu ^{1/2} \oplus \nu ^{3/2},N)$, with
$(\nu ^{1/2} \oplus \nu ^{3/2},N)$, with ![]() $N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. Let
$N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. Let ![]() $\nu _{F}$ be a lift of
$\nu _{F}$ be a lift of ![]() $\nu$. The following Weil–Deligne representations in
$\nu$. The following Weil–Deligne representations in ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$,
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$, ![]() $(\nu _{F}^{-1/2} \oplus \nu _{F}^{1/2},0)$,
$(\nu _{F}^{-1/2} \oplus \nu _{F}^{1/2},0)$, ![]() $(\nu _{F}^{-1/2} \oplus \nu _{F}^{1/2},N)$ and
$(\nu _{F}^{-1/2} \oplus \nu _{F}^{1/2},N)$ and ![]() $(\nu _{F}^{1/2} \oplus \nu _{F}^{3/2},N)$ are respective lifts of the previous three elements of
$(\nu _{F}^{1/2} \oplus \nu _{F}^{3/2},N)$ are respective lifts of the previous three elements of ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$. Hence, one of them is a lift of
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$. Hence, one of them is a lift of ![]() $L(\operatorname {Sp})$.
$L(\operatorname {Sp})$.
Corollary 5.5 In the non-banal case, the Prasad conjecture is not true for any map ![]() $L$ as above.
$L$ as above.
Proof. If ![]() $q_E \equiv -1 \pmod {\ell }$ and
$q_E \equiv -1 \pmod {\ell }$ and ![]() $E / F$ is unramified, then by Theorem 4.6, the special representation
$E / F$ is unramified, then by Theorem 4.6, the special representation ![]() $\operatorname {Sp}$ is not
$\operatorname {Sp}$ is not ![]() $\omega _{E/F}$-distinguished. However, the semisimple part of
$\omega _{E/F}$-distinguished. However, the semisimple part of ![]() $L(\operatorname {Sp})$ is
$L(\operatorname {Sp})$ is ![]() $\nu ^{-1/2} \oplus \nu ^{1/2}$. By Lemma 5.4 the Langlands parameter
$\nu ^{-1/2} \oplus \nu ^{1/2}$. By Lemma 5.4 the Langlands parameter ![]() $L(\operatorname {Sp})$ of
$L(\operatorname {Sp})$ of ![]() $\operatorname {Sp}$ can be lifted to
$\operatorname {Sp}$ can be lifted to ![]() $W_F$.
$W_F$.
5.3 Non-nilpotent Weil–Deligne representations
To fix the issue with the Prasad conjecture in the modular setting discussed in the previous paragraph, we want to modify the ![]() $V$ correspondence. In [Reference Kurinczuk and MatringeKM21], Kurinczuk and Matringe modify the local Langlands of Vignéras using non-nilpotent Weil–Deligne representations. We will do something similar to solve our problem.
$V$ correspondence. In [Reference Kurinczuk and MatringeKM21], Kurinczuk and Matringe modify the local Langlands of Vignéras using non-nilpotent Weil–Deligne representations. We will do something similar to solve our problem.
Kurinczuk and Matringe [Reference Kurinczuk and MatringeKM21, Definition 4.8] defined an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$. We recall the definition here. Let
$\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$. We recall the definition here. Let ![]() $(\Phi,U)$ and
$(\Phi,U)$ and ![]() $(\Phi ',U')$ be two Weil–Deligne representations (up to isomorphism) in
$(\Phi ',U')$ be two Weil–Deligne representations (up to isomorphism) in ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$. Then we have the following.
$\operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$. Then we have the following.
(i) If
 $(\Phi,U)$ and
$(\Phi,U)$ and  $(\Phi ',U')$ are indecomposable (as Weil–Deligne representations), we say that
$(\Phi ',U')$ are indecomposable (as Weil–Deligne representations), we say that  $(\Phi,U) \sim (\Phi ',U')$ if there exists
$(\Phi,U) \sim (\Phi ',U')$ if there exists  $\lambda \in R^{\times }$ such that
$\lambda \in R^{\times }$ such that
 \[ (\Phi',U') \simeq (\Phi,\lambda U). \]
\[ (\Phi',U') \simeq (\Phi,\lambda U). \]
(ii) In the general case,
 $(\Phi,U) \sim (\Phi ',U')$ if one can decompose
$(\Phi,U) \sim (\Phi ',U')$ if one can decompose  $(\Phi,U) = \bigoplus _{i=1}^{r} (\Phi _i,U_i)$ and
$(\Phi,U) = \bigoplus _{i=1}^{r} (\Phi _i,U_i)$ and  $(\Phi ',U') = \bigoplus _{i=1}^{r} (\Phi _i',U_i')$ with indecomposable summands such that
$(\Phi ',U') = \bigoplus _{i=1}^{r} (\Phi _i',U_i')$ with indecomposable summands such that  $(\Phi _i,U_i) \sim (\Phi '_i,U'_i)$.
$(\Phi _i,U_i) \sim (\Phi '_i,U'_i)$.
We denote by ![]() $[(\Phi,U)]$ the equivalence class of
$[(\Phi,U)]$ the equivalence class of ![]() $(\Phi,U)$ and by
$(\Phi,U)$ and by
We define also an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)$ through the inclusion
$\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)$ through the inclusion ![]() $\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2) \subset \operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ and we use the notation
$\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2) \subset \operatorname {WDRep}_{R}(W_{E},\operatorname {GL}_2)$ and we use the notation ![]() $[\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)] := \operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)/{\sim }$.
$[\operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)] := \operatorname {WDRep}_{R}(W_{E},\operatorname {SL}_2)/{\sim }$.
Let ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $E^\times$. If
$E^\times$. If ![]() $\ell \mid q_E-1$, we denote by
$\ell \mid q_E-1$, we denote by ![]() $\Psi _{\operatorname {St},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation
$\Psi _{\operatorname {St},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation ![]() $\Psi _{\operatorname {St},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ with
$\Psi _{\operatorname {St},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ with ![]() $N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. In addition, if
$N = \big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. In addition, if ![]() $\ell \mid q_E+1$, we denote by
$\ell \mid q_E+1$, we denote by ![]() $\Psi _{\operatorname {Sp},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation
$\Psi _{\operatorname {Sp},\chi } \in \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$, the Weil–Deligne representation ![]() $\Psi _{\operatorname {Sp},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},0)$. We define an injection
$\Psi _{\operatorname {Sp},\chi } = (\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},0)$. We define an injection
by
 \[ P(\Psi) = \left\{\begin{array}{@{}ll}
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{-1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E-1 \mbox{ and } \Psi =
\Psi_{\operatorname{St},\chi}, \\
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E+1 \mbox{ and } \Psi =
\Psi_{\operatorname{Sp},\chi}, \\ {}[\Psi] &
\mbox{otherwise.} \end{array}\right. \]
\[ P(\Psi) = \left\{\begin{array}{@{}ll}
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{-1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E-1 \mbox{ and } \Psi =
\Psi_{\operatorname{St},\chi}, \\
{\bigg[\chi\nu^{-1/2} \oplus \chi\nu^{1/2},\begin{pmatrix}
0 & 1 \\ 1 & 0 \end{pmatrix}\bigg]} & \mbox{if } \ell \mid
q_E+1 \mbox{ and } \Psi =
\Psi_{\operatorname{Sp},\chi}, \\ {}[\Psi] &
\mbox{otherwise.} \end{array}\right. \]
Since ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)=[\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ due to [Reference Kurinczuk and MatringeKM21, Proposition 4.11],
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)=[\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ due to [Reference Kurinczuk and MatringeKM21, Proposition 4.11], ![]() $P$ is clearly an injection.
$P$ is clearly an injection.
Remark 5.6 (i) When ![]() $\ell$ is banal, that is
$\ell$ is banal, that is ![]() $\ell \nmid q_E^2-1$,
$\ell \nmid q_E^2-1$, ![]() $P$ is just the identity, as we have
$P$ is just the identity, as we have ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)] = \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$.
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)] = \operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)$.
(ii) The map ![]() $P$ is not exactly the
$P$ is not exactly the ![]() $CV$ map of [Reference Kurinczuk and MatringeKM21]. The image is different for non-banal supercuspidal representation and the Steinberg representation when
$CV$ map of [Reference Kurinczuk and MatringeKM21]. The image is different for non-banal supercuspidal representation and the Steinberg representation when ![]() $\ell \mid q_E -1$.
$\ell \mid q_E -1$.
5.4 Lifting for non-irreducible Weil–Deligne representations
In § 4.1 we have described which of the non-supercuspidal irreducible representations are distinguished. To prove the Prasad conjecture, we also need to inquire when Weil–Deligne representations of ![]() $W_E$ can be lifted to
$W_E$ can be lifted to ![]() $W_F$. This is what we do in this section.
$W_F$. This is what we do in this section.
We begin by giving a criterion to lift the semisimple part of a Weil–Deligne representation.
Lemma 5.7 Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$. Let
$E^{\times }$. Let ![]() $\Psi : W_{E} \to \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ defined by
$\Psi : W_{E} \to \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ defined by ![]() $\Psi = \chi \nu ^{-1/2} \oplus \chi ^{-1} \nu ^{1/2}$. Then there exists a semisimple
$\Psi = \chi \nu ^{-1/2} \oplus \chi ^{-1} \nu ^{1/2}$. Then there exists a semisimple ![]() $\Psi _F : W_{F} \to \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ such that
$\Psi _F : W_{F} \to \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ such that ![]() $\Psi _{F|W_{E}} = \Psi$ if and only if
$\Psi _{F|W_{E}} = \Psi$ if and only if ![]() $\chi =\chi ^{\sigma }$ or
$\chi =\chi ^{\sigma }$ or ![]() $\chi \neq \chi ^{\sigma }$ and
$\chi \neq \chi ^{\sigma }$ and ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
Moreover, if ![]() $\chi =\chi ^{\sigma }$ then
$\chi =\chi ^{\sigma }$ then ![]() $\Psi _F = \eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$, with
$\Psi _F = \eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$, with ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\chi =\eta \circ \operatorname {Nm}_{E/F}$. In addition, if
$\chi =\eta \circ \operatorname {Nm}_{E/F}$. In addition, if ![]() $\chi \neq \chi ^{\sigma }$ and
$\chi \neq \chi ^{\sigma }$ and ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$, then
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$, then ![]() $\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$ (which is irreducible).
$\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$ (which is irreducible).
Proof. We have two cases if there is a lift to ![]() $W_{F}$: the two-dimensional representation of
$W_{F}$: the two-dimensional representation of ![]() $W_{F}$ is irreducible or it is the sum of two characters.
$W_{F}$ is irreducible or it is the sum of two characters.
Let us first study when there is a lift which is the sum of two characters. In this case we can lift ![]() $\chi$ to
$\chi$ to ![]() $W_{F}$. This is equivalent to
$W_{F}$. This is equivalent to ![]() $\chi =\eta \circ \operatorname {Nm}_{E/F}$ with
$\chi =\eta \circ \operatorname {Nm}_{E/F}$ with ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ also equivalent to
$F^{\times }$ also equivalent to ![]() $\chi =\chi ^{\sigma }$. If this condition is satisfied, then the lift is
$\chi =\chi ^{\sigma }$. If this condition is satisfied, then the lift is ![]() $\Psi _F = \eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$.
$\Psi _F = \eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$.
Now we deal with the case where there is an irreducible lift. Then this lift must be ![]() $\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$. Let
$\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$. Let ![]() $\mu = \chi \nu ^{-1/2}$. The representation
$\mu = \chi \nu ^{-1/2}$. The representation ![]() $\Psi _F$ is irreducible if and only if
$\Psi _F$ is irreducible if and only if ![]() $\mu \neq \mu ^{\sigma }$ if and only if
$\mu \neq \mu ^{\sigma }$ if and only if ![]() $\chi \neq \chi ^{\sigma }$. Thus, let us assume that
$\chi \neq \chi ^{\sigma }$. Thus, let us assume that ![]() $\chi \neq \chi ^{\sigma }$. In addition, if
$\chi \neq \chi ^{\sigma }$. In addition, if ![]() $\Psi _F$ is a lift of
$\Psi _F$ is a lift of ![]() $\Psi$, then
$\Psi$, then ![]() $\mu ^{\sigma }=\chi ^{-1} \nu ^{1/2}$, that is
$\mu ^{\sigma }=\chi ^{-1} \nu ^{1/2}$, that is ![]() $\mu \mu ^{\sigma }=\mathbf {1}$, or by Lemma 4.2,
$\mu \mu ^{\sigma }=\mathbf {1}$, or by Lemma 4.2, ![]() $\mu _{|F^{\times }}=\mathbf {1}$ or
$\mu _{|F^{\times }}=\mathbf {1}$ or ![]() $\omega _{E/F}$. If these conditions are satisfied, then
$\omega _{E/F}$. If these conditions are satisfied, then ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )$ is an irreducible lift of
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )$ is an irreducible lift of ![]() $\Psi _F$ in
$\Psi _F$ in ![]() $\operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$. We are left to prove at which condition it is in
$\operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$. We are left to prove at which condition it is in ![]() $\operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$. By the previous condition we already have
$\operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$. By the previous condition we already have ![]() $\mu \mu ^{\sigma }=1$. Thus, for
$\mu \mu ^{\sigma }=1$. Thus, for ![]() $w\in W_{E}$,
$w\in W_{E}$, ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(w) \in \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$. Let
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(w) \in \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$. Let ![]() $s\in W_{F} \setminus W_{E}$. Then
$s\in W_{F} \setminus W_{E}$. Then
Therefore, ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(s) \in \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ if and only if
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(s) \in \operatorname {SL}_2(\overline {\mathbf {F}}_{\ell })$ if and only if ![]() $\mu (s^2)=-1$ if and only if
$\mu (s^2)=-1$ if and only if ![]() $\mu _{|F^{\times }}=\omega _{E/F}$. This finishes the proof.
$\mu _{|F^{\times }}=\omega _{E/F}$. This finishes the proof.
Remark 5.8 Note that, when ![]() $\chi$ is quadratic, the case where
$\chi$ is quadratic, the case where ![]() $\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$ is irreducible can only happen when
$\Psi _F = \operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2})$ is irreducible can only happen when ![]() $q_{E}\equiv q_{F}\equiv -1 \pmod {\ell }$. Indeed, we have
$q_{E}\equiv q_{F}\equiv -1 \pmod {\ell }$. Indeed, we have ![]() $\chi ^{\sigma }=\chi \nu$ and
$\chi ^{\sigma }=\chi \nu$ and ![]() $\chi \neq \chi ^{\sigma }$. Therefore,
$\chi \neq \chi ^{\sigma }$. Therefore, ![]() $\nu \neq \mathbf {1}$ and
$\nu \neq \mathbf {1}$ and ![]() $q_{E}\not \equiv 1 \pmod {\ell }$. In addition, since
$q_{E}\not \equiv 1 \pmod {\ell }$. In addition, since ![]() $\chi ^{\sigma }=\chi \nu$, we get that
$\chi ^{\sigma }=\chi \nu$, we get that ![]() $\nu _{|F^{\times }}=\mathbf {1}$ and so that
$\nu _{|F^{\times }}=\mathbf {1}$ and so that ![]() $q_{F}^2\equiv 1 \pmod {\ell }$. Hence,
$q_{F}^2\equiv 1 \pmod {\ell }$. Hence, ![]() $q_{E}\equiv q_{F}\equiv -1 \pmod {\ell }$.
$q_{E}\equiv q_{F}\equiv -1 \pmod {\ell }$.
Now we can examine when a Weil–Deligne representation ![]() $(\Psi,N)$ can be lifted. We will choose
$(\Psi,N)$ can be lifted. We will choose ![]() $N$ such that these representations correspond under
$N$ such that these representations correspond under ![]() $P\circ PV$ to an irreducible generic representation of
$P\circ PV$ to an irreducible generic representation of ![]() $\operatorname {PGL}_2$.
$\operatorname {PGL}_2$.
Lemma 5.9 Let ![]() $q_{E}\equiv -1 \pmod {\ell }$ and
$q_{E}\equiv -1 \pmod {\ell }$ and ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $E^{\times }$. Let
$E^{\times }$. Let ![]() $\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by
$\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by ![]() $\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},N]$, with
$\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},N]$, with ![]() $N=\big (\begin{smallmatrix} 0 & 1 \\ 1 & 0 \end{smallmatrix}\big )$. Then there exists
$N=\big (\begin{smallmatrix} 0 & 1 \\ 1 & 0 \end{smallmatrix}\big )$. Then there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim \Psi$ in
$\Psi _{F|W_{E}} \sim \Psi$ in ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ if and only if
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ if and only if ![]() $q_{F}\equiv -1 \pmod {\ell }$ and
$q_{F}\equiv -1 \pmod {\ell }$ and ![]() $\chi _{|F^{\times }}=\mathbf {1}$ or
$\chi _{|F^{\times }}=\mathbf {1}$ or ![]() $\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
$\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
Proof. If we have a lift ![]() $\Psi _{F}$, then we also have a lift of the semisimple part of
$\Psi _{F}$, then we also have a lift of the semisimple part of ![]() $\Psi$. By Lemma 5.7 this is possible only if
$\Psi$. By Lemma 5.7 this is possible only if ![]() $\chi =\chi ^{\sigma }$ (which is equivalent by Lemma 4.2 to
$\chi =\chi ^{\sigma }$ (which is equivalent by Lemma 4.2 to ![]() $\chi _{|F^{\times }}=\mathbf {1}$ or
$\chi _{|F^{\times }}=\mathbf {1}$ or ![]() $\omega _{E/F}$) or
$\omega _{E/F}$) or ![]() $\chi \neq \chi ^{\sigma }$ and
$\chi \neq \chi ^{\sigma }$ and ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
If ![]() $\chi _{|F^{\times }}=\mathbf {1}$, then by Lemma 5.7, the semisimple part of
$\chi _{|F^{\times }}=\mathbf {1}$, then by Lemma 5.7, the semisimple part of ![]() $\Psi _{F}$ should be
$\Psi _{F}$ should be ![]() $\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$, with
$\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$, with ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\chi =\eta \circ \operatorname {Nm}_{E/F}$. Note that
$\chi =\eta \circ \operatorname {Nm}_{E/F}$. Note that ![]() $\chi _{|F^{\times }}=\mathbf {1}$ implies that
$\chi _{|F^{\times }}=\mathbf {1}$ implies that ![]() $\eta ^2=\mathbf {1}$. If
$\eta ^2=\mathbf {1}$. If ![]() $q_{F} \equiv -1 \pmod {\ell }$, then we can take
$q_{F} \equiv -1 \pmod {\ell }$, then we can take ![]() $\Psi _{F} = [\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N]$. If
$\Psi _{F} = [\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N]$. If ![]() $q_{F} \not \equiv -1 \pmod {\ell }$, then
$q_{F} \not \equiv -1 \pmod {\ell }$, then ![]() $q_{F}^2 \not \equiv 1 \pmod {\ell }$ (
$q_{F}^2 \not \equiv 1 \pmod {\ell }$ (![]() $E$ is a quadratic extension of
$E$ is a quadratic extension of ![]() $F$). In this case,
$F$). In this case, ![]() $[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)]=\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. Since
$[\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)]=\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. Since ![]() $N$ is not nilpotent,
$N$ is not nilpotent, ![]() $\Psi$ cannot be the restriction of an element of
$\Psi$ cannot be the restriction of an element of ![]() $\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$.
$\operatorname {Nilp}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$.
If ![]() $\chi _{|F^{\times }}=\omega _{E/F}$, again by Lemma 5.7, the semisimple part of
$\chi _{|F^{\times }}=\omega _{E/F}$, again by Lemma 5.7, the semisimple part of ![]() $\Psi _{F}$ should be
$\Psi _{F}$ should be ![]() $\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$. This time
$\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2}$. This time ![]() $\eta ^2=\omega _{E/F} \neq \mathbf {1}$. Thus, the only Weil–Deligne representation
$\eta ^2=\omega _{E/F} \neq \mathbf {1}$. Thus, the only Weil–Deligne representation ![]() $[\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2},M]$ is with
$[\eta \nu ^{-1/2} \oplus \eta ^{-1} \nu ^{1/2},M]$ is with ![]() $M=0$ and is not a lift of
$M=0$ and is not a lift of ![]() $\Psi$.
$\Psi$.
Suppose ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$. We get that
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$. We get that ![]() $\nu _{|F^{\times }}=1$ so
$\nu _{|F^{\times }}=1$ so ![]() $q_{F}\equiv -1 \pmod {\ell }$. This time Lemma 5.7 tells us that the semisimple part of
$q_{F}\equiv -1 \pmod {\ell }$. This time Lemma 5.7 tells us that the semisimple part of ![]() $\Psi _{F}$ should be
$\Psi _{F}$ should be ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )$, with
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )$, with ![]() $\mu =\chi \nu ^{-1/2}$. Let
$\mu =\chi \nu ^{-1/2}$. Let ![]() $M=\big (\begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix}\big )$. First, let us show that
$M=\big (\begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix}\big )$. First, let us show that ![]() $\Psi _F:=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu ),M) \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. Let
$\Psi _F:=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu ),M) \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. Let ![]() $s\in W_{F} \setminus W_{E}$. For
$s\in W_{F} \setminus W_{E}$. For ![]() $w \in W_{E}$, we get that
$w \in W_{E}$, we get that ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(w)= \big (\begin{smallmatrix} \mu (w) & 0 \\ 0 & \mu ^{s}(w) \end{smallmatrix}\big )$. Since
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(w)= \big (\begin{smallmatrix} \mu (w) & 0 \\ 0 & \mu ^{s}(w) \end{smallmatrix}\big )$. Since ![]() $\mu ^{\sigma }=\mu \nu$ we get
$\mu ^{\sigma }=\mu \nu$ we get
Since ![]() $\mu (s^2)=-1$, we also have
$\mu (s^2)=-1$, we also have ![]() $\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(s)= \big (\begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix}\big )$. As we are in the case where
$\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu )(s)= \big (\begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix}\big )$. As we are in the case where ![]() $q_{F}\equiv -1 \pmod {\ell }$, the extension
$q_{F}\equiv -1 \pmod {\ell }$, the extension ![]() $E/F$ is ramified. The element
$E/F$ is ramified. The element ![]() $s$ must then be in the inertia subgroup
$s$ must then be in the inertia subgroup ![]() $s\in I_{F}$ and therefore
$s\in I_{F}$ and therefore ![]() $\nu (s)=1$. This gives us
$\nu (s)=1$. This gives us
We have checked that ![]() $\Psi _F=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu ),M) \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. To finish the proof we need to show that
$\Psi _F=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\mu ),M) \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$. To finish the proof we need to show that ![]() $\Psi _{F|W_{E}} \sim \Psi$. We have
$\Psi _{F|W_{E}} \sim \Psi$. We have ![]() $\Psi _{F|W_{E}}=(\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},M)$. In addition,
$\Psi _{F|W_{E}}=(\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},M)$. In addition, ![]() $(\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},M) \sim \Psi$ by [Reference Kurinczuk and MatringeKM21, Lemma 4.23].
$(\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},M) \sim \Psi$ by [Reference Kurinczuk and MatringeKM21, Lemma 4.23].
Lemma 5.10 Let ![]() $q_{E}\equiv 1 \pmod {\ell }$ and
$q_{E}\equiv 1 \pmod {\ell }$ and ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $E^{\times }$. Let
$E^{\times }$. Let ![]() $\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by
$\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by ![]() $\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N]$, with
$\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N]$, with ![]() $N=\big (\begin{smallmatrix} 0 & 1 \\ 1 & 0 \end{smallmatrix}\big )$. Then there exists
$N=\big (\begin{smallmatrix} 0 & 1 \\ 1 & 0 \end{smallmatrix}\big )$. Then there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim \Psi$ if and only if
$\Psi _{F|W_{E}} \sim \Psi$ if and only if ![]() $\chi _{|F^{\times }}=\mathbf {1}$ or
$\chi _{|F^{\times }}=\mathbf {1}$ or ![]() $q_{F}\equiv 1 \pmod {\ell }$ and
$q_{F}\equiv 1 \pmod {\ell }$ and ![]() $\chi _{|F^{\times }}=\omega _{E/F}$.
$\chi _{|F^{\times }}=\omega _{E/F}$.
Proof. By Lemma 5.7 the semisimple part of ![]() $\Psi$ can be lifted to
$\Psi$ can be lifted to ![]() $W_{F}$ if and only if
$W_{F}$ if and only if ![]() $\chi _{|F^{\times }}=\mathbf {1}$ or
$\chi _{|F^{\times }}=\mathbf {1}$ or ![]() $\omega _{E/F}$ (
$\omega _{E/F}$ (![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$ implies that
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$ implies that ![]() $\chi =\chi ^{\sigma }$). Moreover, this lift is
$\chi =\chi ^{\sigma }$). Moreover, this lift is ![]() $\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}$, with
$\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}$, with ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\chi =\eta \circ \operatorname {Nm}_{E/F}$.
$\chi =\eta \circ \operatorname {Nm}_{E/F}$.
If ![]() $\chi _{|F^{\times }}=\mathbf {1}$, then
$\chi _{|F^{\times }}=\mathbf {1}$, then ![]() $\eta ^2=\mathbf {1}$. We can take
$\eta ^2=\mathbf {1}$. We can take ![]() $\Psi _{F} = (\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N)$ (since
$\Psi _{F} = (\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N)$ (since ![]() $\nu _F^2=\mathbf {1}$) and
$\nu _F^2=\mathbf {1}$) and ![]() $\Psi _{F|W_{E}} \sim \Psi$.
$\Psi _{F|W_{E}} \sim \Psi$.
If ![]() $\chi _{|F^{\times }}=\omega _{E/F}$, this time
$\chi _{|F^{\times }}=\omega _{E/F}$, this time ![]() $\eta ^2=\omega _{E/F} \neq \mathbf {1}$. If
$\eta ^2=\omega _{E/F} \neq \mathbf {1}$. If ![]() $q_{F}\equiv -1 \pmod {\ell }$, then
$q_{F}\equiv -1 \pmod {\ell }$, then ![]() $\nu _{F}=\omega _{E/F}$. In this case,
$\nu _{F}=\omega _{E/F}$. In this case, ![]() $\eta ^{-1}=\eta \nu _{F}$. Thus,
$\eta ^{-1}=\eta \nu _{F}$. Thus, ![]() $\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2} = \eta \nu ^{-1/2} \oplus \eta \nu ^{-1/2}$. The only Weil–Deligne representation with this semisimple part is
$\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2} = \eta \nu ^{-1/2} \oplus \eta \nu ^{-1/2}$. The only Weil–Deligne representation with this semisimple part is ![]() $(\eta \nu ^{-1/2} \oplus \eta \nu ^{-1/2},0)$ which is not a lift of
$(\eta \nu ^{-1/2} \oplus \eta \nu ^{-1/2},0)$ which is not a lift of ![]() $\Psi$. If
$\Psi$. If ![]() $q_{F}\equiv 1 \pmod {\ell }$ let
$q_{F}\equiv 1 \pmod {\ell }$ let ![]() $\Psi _{F} := \big (\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}, \big (\begin{smallmatrix} 1 & 0 \\0 & -1 \end{smallmatrix}\big )\big )$. We are left to prove that
$\Psi _{F} := \big (\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}, \big (\begin{smallmatrix} 1 & 0 \\0 & -1 \end{smallmatrix}\big )\big )$. We are left to prove that ![]() $\Psi _{F|W_{E}} \sim \Psi$. Let us remark that
$\Psi _{F|W_{E}} \sim \Psi$. Let us remark that ![]() $N$ is diagonalizable. Therefore,
$N$ is diagonalizable. Therefore, ![]() $(\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ is isomorphic to
$(\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N)$ is isomorphic to ![]() $(\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N')$ with
$(\chi \nu ^{-1/2} \oplus \chi \nu ^{-1/2},N')$ with ![]() $N'=diag(1,-1)$.
$N'=diag(1,-1)$.
Hence, ![]() $\Psi _{F|W_{E}} \sim \Psi$ and we get the result.
$\Psi _{F|W_{E}} \sim \Psi$ and we get the result.
Lemma 5.11 Let ![]() $q_{E}^2\not \equiv 1 \pmod {\ell }$ and
$q_{E}^2\not \equiv 1 \pmod {\ell }$ and ![]() $\chi$ be a quadratic character of
$\chi$ be a quadratic character of ![]() $E^{\times }$. Let
$E^{\times }$. Let ![]() $\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by
$\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by ![]() $\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},N]$, with
$\Psi = [\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2},N]$, with ![]() $N=\big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. Then there exists
$N=\big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$. Then there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim \Psi$ if and only if
$\Psi _{F|W_{E}} \sim \Psi$ if and only if ![]() $\chi _{|F^{\times }}=\mathbf {1}$.
$\chi _{|F^{\times }}=\mathbf {1}$.
Proof. By Lemma 5.7 we can lift the semisimple part if and only if ![]() $\chi _{|F^{\times }}=\mathbf {1}$ or
$\chi _{|F^{\times }}=\mathbf {1}$ or ![]() $\omega _{E/F}$ and this lift is
$\omega _{E/F}$ and this lift is ![]() $\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}$, with
$\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2}$, with ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\chi =\eta \circ \operatorname {Nm}_{E/F}$. If
$\chi =\eta \circ \operatorname {Nm}_{E/F}$. If ![]() $\chi _{|F^{\times }}=\mathbf {1}$, then
$\chi _{|F^{\times }}=\mathbf {1}$, then ![]() $\eta ^2=\mathbf {1}$. We can take
$\eta ^2=\mathbf {1}$. We can take ![]() $\Psi _{F} = (\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N)$ and
$\Psi _{F} = (\eta \nu ^{-1/2} \oplus \eta \nu ^{1/2},N)$ and ![]() $\Psi _{F|W_{E}} \sim \Psi$. If
$\Psi _{F|W_{E}} \sim \Psi$. If ![]() $\chi _{|F^{\times }}=\omega _{E/F}$,
$\chi _{|F^{\times }}=\omega _{E/F}$, ![]() $\eta ^2=\omega _{E/F} \neq \mathbf {1}$. If
$\eta ^2=\omega _{E/F} \neq \mathbf {1}$. If ![]() $(\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2} ,M)$ is a Weil–Deligne representation, then
$(\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2} ,M)$ is a Weil–Deligne representation, then ![]() $M=0$ and this is not a lift of
$M=0$ and this is not a lift of ![]() $\Psi$.
$\Psi$.
Lemma 5.12 Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $E^{\times }$. Let
$E^{\times }$. Let ![]() $\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by
$\Psi \in [\operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{E},\operatorname {SL}_2)]$ defined by ![]() $\Psi = [\chi \nu ^{-1/2} \oplus \chi ^{-1}\nu ^{1/2},N]$, with
$\Psi = [\chi \nu ^{-1/2} \oplus \chi ^{-1}\nu ^{1/2},N]$, with ![]() $N=0$. Then there exists
$N=0$. Then there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim \Psi$ if and only if
$\Psi _{F|W_{E}} \sim \Psi$ if and only if ![]() $\chi =\chi ^{\sigma }$ or
$\chi =\chi ^{\sigma }$ or ![]() $\chi \neq \chi ^{\sigma }$ and
$\chi \neq \chi ^{\sigma }$ and ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$.
Proof. If ![]() $\chi =\chi ^{\sigma }$, take
$\chi =\chi ^{\sigma }$, take ![]() $\eta$ a character of
$\eta$ a character of ![]() $F^{\times }$ such that
$F^{\times }$ such that ![]() $\chi =\eta \circ Nm_{E/F}$. Then
$\chi =\eta \circ Nm_{E/F}$. Then ![]() $\Psi _F = [\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2},N]$ is a lift. In addition, if
$\Psi _F = [\eta \nu ^{-1/2} \oplus \eta ^{-1}\nu ^{1/2},N]$ is a lift. In addition, if ![]() $\chi \neq \chi ^{\sigma }$, Lemma 5.7 tells us that if there is a lift, then
$\chi \neq \chi ^{\sigma }$, Lemma 5.7 tells us that if there is a lift, then ![]() $\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$. In this case, we can take
$\chi _{|F^{\times }}=\omega _{E/F} \nu ^{1/2}_{|F^{\times }}$. In this case, we can take ![]() $\Psi _F = [\operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2}),N]$.
$\Psi _F = [\operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2}),N]$.
5.5 A modulo  $\ell$ Prasad conjecture for
$\ell$ Prasad conjecture for  $\operatorname {PGL}_2$
$\operatorname {PGL}_2$
Now we can gather together all the results of the previous sections to prove a ‘modified’ Prasad conjecture for ![]() $\operatorname {PGL}_2$.
$\operatorname {PGL}_2$.
Let ![]() $PV$ be the correspondence induced by the Vignéras correspondence
$PV$ be the correspondence induced by the Vignéras correspondence
Let us start with the supercuspidal representations.
Proposition 5.13 Let ![]() $\pi$ be an irreducible supercuspidal representation of
$\pi$ be an irreducible supercuspidal representation of ![]() $\operatorname {PGL}_2(E)$ over
$\operatorname {PGL}_2(E)$ over ![]() $\overline {\mathbf {F}}_{\ell }$. Then
$\overline {\mathbf {F}}_{\ell }$. Then ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished if and only if its Langlands parameter
$\omega _{E/F}$-distinguished if and only if its Langlands parameter ![]() $PV(\pi )$ can be lifted to
$PV(\pi )$ can be lifted to ![]() $W_F$.
$W_F$.
Proof. Let ![]() $\pi$ be an irreducible supercuspidal representation of
$\pi$ be an irreducible supercuspidal representation of ![]() $\operatorname {PGL}_2(E)$ over
$\operatorname {PGL}_2(E)$ over ![]() $\overline {\mathbf {F}}_{\ell }$. Let
$\overline {\mathbf {F}}_{\ell }$. Let ![]() $\varphi :=PV(\pi )$ be the Langlands parameter of
$\varphi :=PV(\pi )$ be the Langlands parameter of ![]() $W_E$ associated to
$W_E$ associated to ![]() $\pi$. By Proposition 3.11
$\pi$. By Proposition 3.11 ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished if and only if there exists
$\omega _{E/F}$-distinguished if and only if there exists ![]() $\tilde {\pi }$ a
$\tilde {\pi }$ a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$ which is supercuspidal and
$\pi$ which is supercuspidal and ![]() $\tilde {\omega }_{E/F}$-distinguished. By Theorem 5.2, this happens if and only if the Langlands parameter
$\tilde {\omega }_{E/F}$-distinguished. By Theorem 5.2, this happens if and only if the Langlands parameter ![]() $\tilde {\varphi }$ of
$\tilde {\varphi }$ of ![]() $\tilde {\pi }$, can be extended to
$\tilde {\pi }$, can be extended to ![]() $W_F$. From the definition of the modulo
$W_F$. From the definition of the modulo ![]() $\ell$ Langlands correspondence,
$\ell$ Langlands correspondence, ![]() $\tilde {\varphi }$ is a
$\tilde {\varphi }$ is a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\varphi$. Thus,
$\varphi$. Thus, ![]() $\tilde {\varphi }$ can be extended to
$\tilde {\varphi }$ can be extended to ![]() $W_F$ if and only if
$W_F$ if and only if ![]() $\varphi$ can be extended to
$\varphi$ can be extended to ![]() $W_F$.
$W_F$.
Now let us examine the irreducible generic representations of ![]() $\operatorname {PGL}_2(E)$. Let
$\operatorname {PGL}_2(E)$. Let ![]() $\pi$ be such a representation and denote by
$\pi$ be such a representation and denote by ![]() $PV(\pi )=(\Psi,N)$ its Langlands parameter. We can classify the irreducible generic representations as follows:
$PV(\pi )=(\Psi,N)$ its Langlands parameter. We can classify the irreducible generic representations as follows:
(i) The representation
 $\pi$ is supercuspidal. In this case,
$\pi$ is supercuspidal. In this case,  $\Psi$ is irreducible and
$\Psi$ is irreducible and  $N=0$.
$N=0$.(ii) The representation
 $\pi$ is an irreducible principal series. Here
$\pi$ is an irreducible principal series. Here  $\pi = \pi (\chi \nu ^{-1/2},\chi ^{-1}\nu ^{1/2})$ with
$\pi = \pi (\chi \nu ^{-1/2},\chi ^{-1}\nu ^{1/2})$ with  $\chi ^2\neq \mathbf {1}$. We have
$\chi ^2\neq \mathbf {1}$. We have  $\Psi =\chi \nu ^{-1/2} \oplus \chi ^{-1}\nu ^{1/2}$ and
$\Psi =\chi \nu ^{-1/2} \oplus \chi ^{-1}\nu ^{1/2}$ and  $N=0$
$N=0$(iii) Suppose that
 $\pi$ is the unique generic subquotient of a reducible principal series. Let
$\pi$ is the unique generic subquotient of a reducible principal series. Let  $\chi$ be a quadratic character of
$\chi$ be a quadratic character of  $E^{\times }$ such that
$E^{\times }$ such that  $\pi$ is a subquotient of
$\pi$ is a subquotient of  $\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$.
$\pi (\chi \nu ^{-1/2},\chi \nu ^{1/2})$.
(a) If
 $q_E \not \equiv 1 \pmod {\ell }$, then
$q_E \not \equiv 1 \pmod {\ell }$, then  $\pi = \operatorname {St}_\chi$. In this case,
$\pi = \operatorname {St}_\chi$. In this case,  $\Psi =\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2}$ and
$\Psi =\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2}$ and  $N=\big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$.
$N=\big (\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}\big )$.(b) If
 $q_E \equiv -1 \pmod {\ell }$, this time
$q_E \equiv -1 \pmod {\ell }$, this time  $\pi =\operatorname {Sp}_{\chi }$,
$\pi =\operatorname {Sp}_{\chi }$,  $\Psi =\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2}$ and
$\Psi =\chi \nu ^{-1/2} \oplus \chi \nu ^{1/2}$ and  $N=0$.
$N=0$.
We can summarize the previous results of this article to prove the Prasad conjecture in the modular case.
Theorem 5.14 Let ![]() $\pi$ be an irreducible generic representation of
$\pi$ be an irreducible generic representation of ![]() $\operatorname {PGL}_2(E)$ over
$\operatorname {PGL}_2(E)$ over ![]() $\overline {\mathbf {F}}_{\ell }$. Then
$\overline {\mathbf {F}}_{\ell }$. Then ![]() $\pi$ is
$\pi$ is ![]() $\omega _{E/F}$-distinguished if and only if there exists
$\omega _{E/F}$-distinguished if and only if there exists ![]() $\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that
$\Psi _{F} \in \operatorname {WDRep}_{\overline {\mathbf {F}}_{\ell }}(W_{F},\operatorname {SL}_2)$ such that ![]() $\Psi _{F|W_{E}} \sim P\circ PV(\pi )$.
$\Psi _{F|W_{E}} \sim P\circ PV(\pi )$.
Proof. For supercuspidal representations, the result follows from Proposition 5.13. For irreducible principal series representations it follows from Lemmas 4.3 and 5.12. In addition, for the Steinberg representations or the special representations, it follows from Theorem 4.6 and Lemmas 5.9, 5.10 and 5.11 (depending on the order of ![]() $q_E$ modulo
$q_E$ modulo ![]() $\ell$).
$\ell$).
Remark 5.15 When ![]() $q_E\equiv -1 \pmod {\ell }$,
$q_E\equiv -1 \pmod {\ell }$, ![]() $q_F\equiv -1 \pmod {\ell }$ and
$q_F\equiv -1 \pmod {\ell }$ and ![]() $\chi$ is a quadratic character of
$\chi$ is a quadratic character of ![]() $E^{\times }$ such that
$E^{\times }$ such that ![]() $\chi _{|F^\times }=\omega _{E/F} \nu _{|F^\times }^{1/2}$. We have proved that
$\chi _{|F^\times }=\omega _{E/F} \nu _{|F^\times }^{1/2}$. We have proved that ![]() $P \circ PV(\operatorname {Sp}_{\chi })$ admits a lift to
$P \circ PV(\operatorname {Sp}_{\chi })$ admits a lift to ![]() $W_F$ which is
$W_F$ which is ![]() $\Psi _F=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2}),M)$ with
$\Psi _F=(\operatorname {Ind}_{W_{E}}^{W_{F}}(\chi \nu ^{-1/2}),M)$ with ![]() $M=\big (\begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix}\big )$. The semisimple part of
$M=\big (\begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix}\big )$. The semisimple part of ![]() $\Psi _F$ is irreducible and
$\Psi _F$ is irreducible and ![]() $M$ is non-zero, and so this lift is not the Langlands parameter of any representation of
$M$ is non-zero, and so this lift is not the Langlands parameter of any representation of ![]() $\operatorname {PGL}_2(F)$ (nor it is in the image of
$\operatorname {PGL}_2(F)$ (nor it is in the image of ![]() $P$).
$P$).
6. The  $\operatorname {SL}_2(F)$-distinguished representations
$\operatorname {SL}_2(F)$-distinguished representations
In this section, assuming ![]() $\ell \neq 2$, we classify all the representations of
$\ell \neq 2$, we classify all the representations of ![]() $\operatorname {SL}_2(E)$ distinguished by
$\operatorname {SL}_2(E)$ distinguished by ![]() $\operatorname {SL}_2(F)$. For supercuspidal representations, we will use the restriction method of [Reference Anandavardhanan and PrasadAP03]. Similar to the case
$\operatorname {SL}_2(F)$. For supercuspidal representations, we will use the restriction method of [Reference Anandavardhanan and PrasadAP03]. Similar to the case ![]() $\operatorname {GL}_2(E)$, we will deal with principal series representations using Mackey theory.
$\operatorname {GL}_2(E)$, we will deal with principal series representations using Mackey theory.
6.1 Modulo  $\ell$ representations of
$\ell$ representations of  $\operatorname {SL}_2$
$\operatorname {SL}_2$
We start by recalling some general facts about modulo ![]() $\ell$ representations of
$\ell$ representations of ![]() $\operatorname {SL}_2$.
$\operatorname {SL}_2$.
Recall that ![]() $E/F$ is a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2. Let
$E/F$ is a quadratic extension of locally compact non-archimedean local fields of characteristic different from 2. Let ![]() $\mathfrak {o}_E$ be the ring of integers of
$\mathfrak {o}_E$ be the ring of integers of ![]() $E$, and
$E$, and ![]() $\mathfrak {p}_{E}$ be the maximal ideal of
$\mathfrak {p}_{E}$ be the maximal ideal of ![]() $\mathfrak {o}_E$. Let
$\mathfrak {o}_E$. Let ![]() $\pi$ be an irreducible cuspidal
$\pi$ be an irreducible cuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$. Thanks to [Reference CuiCui20, Proposition 2.35], we have that the restricted representation
$\operatorname {GL}_n(E)$. Thanks to [Reference CuiCui20, Proposition 2.35], we have that the restricted representation ![]() $\pi \vert _{\operatorname {SL}_n(E)}$ is semisimple with finite length and multiplicity-free. Denote by
$\pi \vert _{\operatorname {SL}_n(E)}$ is semisimple with finite length and multiplicity-free. Denote by ![]() $\lg (\pi )$ the length of
$\lg (\pi )$ the length of ![]() $\pi \vert _{\operatorname {SL}_n(E)}$. Let
$\pi \vert _{\operatorname {SL}_n(E)}$. Let
We call ![]() $Y(\pi )$ the twist isomorphism set of
$Y(\pi )$ the twist isomorphism set of ![]() $\pi$. By Corollary 3.8 of [Reference CuiCui20], the cardinality
$\pi$. By Corollary 3.8 of [Reference CuiCui20], the cardinality ![]() $\vert Y(\pi )\vert$ is an integer prime to
$\vert Y(\pi )\vert$ is an integer prime to ![]() $\ell$, and by Proposition 2.37 of [Reference CuiCui20],
$\ell$, and by Proposition 2.37 of [Reference CuiCui20], ![]() $\pi \vert _{\operatorname {SL}_n(F)}$ is multiplicity-free. Hence we deduce from part 3 of Corollary 3.8 of [Reference CuiCui20] that
$\pi \vert _{\operatorname {SL}_n(F)}$ is multiplicity-free. Hence we deduce from part 3 of Corollary 3.8 of [Reference CuiCui20] that
where for any positive integer ![]() $m$, we denote by
$m$, we denote by ![]() $m_{\ell '}$ the largest divisor of
$m_{\ell '}$ the largest divisor of ![]() $m$ which is coprime to
$m$ which is coprime to ![]() $\ell$.
$\ell$.
Lemma 6.1 When ![]() $n=2$, we have
$n=2$, we have
Proof. By (6.1), it is sufficient to prove that the length ![]() $\lg (\pi )$ is coprime to
$\lg (\pi )$ is coprime to ![]() $\ell$. Let
$\ell$. Let ![]() $Z_{E^{\times }}$ be the center of
$Z_{E^{\times }}$ be the center of ![]() $\operatorname {GL}_2(E)$. The length of
$\operatorname {GL}_2(E)$. The length of ![]() $\pi \vert _{Z_{E^{\times }}\operatorname {SL}_2(E)}$ is equal to the length
$\pi \vert _{Z_{E^{\times }}\operatorname {SL}_2(E)}$ is equal to the length ![]() $\lg (\pi )$, which is a divisor of the index
$\lg (\pi )$, which is a divisor of the index ![]() $[\operatorname {GL}_2(E) : Z_{E^{\times }}\operatorname {SL}_2(E)]$, and the latter is equal to
$[\operatorname {GL}_2(E) : Z_{E^{\times }}\operatorname {SL}_2(E)]$, and the latter is equal to ![]() $[ E^{\times }: E^{\times 2}]$, where
$[ E^{\times }: E^{\times 2}]$, where ![]() $E^{\times 2}$ consists of the elements of the form
$E^{\times 2}$ consists of the elements of the form ![]() $x^2$ for
$x^2$ for ![]() $x\in E^{\times }$. By Corollary 5.8 of [Reference NeukirchNeu99], when the characteristic of
$x\in E^{\times }$. By Corollary 5.8 of [Reference NeukirchNeu99], when the characteristic of ![]() $E$ is different from
$E$ is different from ![]() $2$, the index
$2$, the index ![]() $[E^{\times }: E^{\times 2}]$ is equal to
$[E^{\times }: E^{\times 2}]$ is equal to ![]() $2^{2+a}$ where
$2^{2+a}$ where ![]() $a$ is given by
$a$ is given by ![]() $2\mathfrak {o}_E=\mathfrak {p}_E^a$. Hence,
$2\mathfrak {o}_E=\mathfrak {p}_E^a$. Hence, ![]() $\lg (\pi )$ is a power of
$\lg (\pi )$ is a power of ![]() $2$, and we have the desired identity under our assumption
$2$, and we have the desired identity under our assumption ![]() $\ell \neq 2$.
$\ell \neq 2$.
Definition 6.2 Define ![]() $\operatorname {GL}_2^+(E)$ to be a subgroup of
$\operatorname {GL}_2^+(E)$ to be a subgroup of ![]() $\operatorname {GL}_2(E)$, consisting of matrices whose determinant belongs to
$\operatorname {GL}_2(E)$, consisting of matrices whose determinant belongs to ![]() $F^{\times }E^{\times 2}$, where
$F^{\times }E^{\times 2}$, where ![]() $E^{\times 2}$ consists of the elements of the form
$E^{\times 2}$ consists of the elements of the form ![]() $x^2$ for
$x^2$ for ![]() $x\in E^{\times }$. We have
$x\in E^{\times }$. We have ![]() $\operatorname {GL}_2^+(E)=Z_{E^{\times }}\operatorname {SL}_2(E)\operatorname {GL}_2(F)$ where
$\operatorname {GL}_2^+(E)=Z_{E^{\times }}\operatorname {SL}_2(E)\operatorname {GL}_2(F)$ where ![]() $Z_{E^{\times }}$ denotes the center of
$Z_{E^{\times }}$ denotes the center of ![]() $\operatorname {GL}_2(E)$.
$\operatorname {GL}_2(E)$.
Lemma 6.3 Let ![]() $\lg _+(\pi )$ be the length of
$\lg _+(\pi )$ be the length of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$, and
$\pi \vert _{\operatorname {GL}_2^+(E)}$, and
Then we have
Proof. Since the direct components of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$ are
$\pi \vert _{\operatorname {GL}_2^+(E)}$ are ![]() $\operatorname {GL}_2(E)$-conjugate, they share the same length after restricted to
$\operatorname {GL}_2(E)$-conjugate, they share the same length after restricted to ![]() $\operatorname {SL}_2(E)$. We have that
$\operatorname {SL}_2(E)$. We have that ![]() $\lg _+(\pi )$ divides
$\lg _+(\pi )$ divides ![]() $\lg (\pi )$, which is coprime to
$\lg (\pi )$, which is coprime to ![]() $\ell$ by Lemma 6.1. Hence, the Clifford theory in
$\ell$ by Lemma 6.1. Hence, the Clifford theory in ![]() $\ell$-modular setting (see [Reference CuiCui20, Corollary 3.8]) is the same as the complex setting in our case. Meanwhile, since
$\ell$-modular setting (see [Reference CuiCui20, Corollary 3.8]) is the same as the complex setting in our case. Meanwhile, since ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ is multiplicity-free, the restriction
$\pi \vert _{\operatorname {SL}_2(E)}$ is multiplicity-free, the restriction ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$ is multiplicity-free. Then the Clifford theory gives the desired equation
$\pi \vert _{\operatorname {GL}_2^+(E)}$ is multiplicity-free. Then the Clifford theory gives the desired equation ![]() $\lg _+(\pi )=\vert Y_+(\pi )\vert$.
$\lg _+(\pi )=\vert Y_+(\pi )\vert$.
To compute the length ![]() $\lg (\pi )$ we will need to use the local Langlands correspondence.
$\lg (\pi )$ we will need to use the local Langlands correspondence.
6.2 Local Langlands for supercuspidal representations of  $\operatorname {SL}_2$
$\operatorname {SL}_2$
In this section, we use the local Langlands correspondence for ![]() $\operatorname {GL}_2$ to define a correspondence modulo
$\operatorname {GL}_2$ to define a correspondence modulo ![]() $\ell$ for supercuspidal representations of
$\ell$ for supercuspidal representations of ![]() $\operatorname {SL}_2$. As in the complex case, for
$\operatorname {SL}_2$. As in the complex case, for ![]() $\operatorname {SL}_2$, this correspondence is not a bijection, we give a description of the
$\operatorname {SL}_2$, this correspondence is not a bijection, we give a description of the ![]() $L$-packet.
$L$-packet.
Let ![]() $\tau$ be a supercuspidal
$\tau$ be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {SL}_2(E)$. Let
$\operatorname {SL}_2(E)$. Let ![]() $\pi$ be a lift to
$\pi$ be a lift to ![]() $\operatorname {GL}_2(E)$ i.e.
$\operatorname {GL}_2(E)$ i.e. ![]() $\tau \subset \pi |_{\operatorname {SL}_2(E)}$. To
$\tau \subset \pi |_{\operatorname {SL}_2(E)}$. To ![]() $\pi$ we associate by the local Langlands correspondence of Vignéras its Langlands parameter
$\pi$ we associate by the local Langlands correspondence of Vignéras its Langlands parameter ![]() $\varphi _{\pi }: W_{E} \to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$. Let
$\varphi _{\pi }: W_{E} \to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$. Let ![]() $\gamma$ be the projection
$\gamma$ be the projection ![]() $\gamma : \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell }) \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$. Then we define
$\gamma : \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell }) \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$. Then we define ![]() $\varphi _\tau : W_{E} \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ by
$\varphi _\tau : W_{E} \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ by ![]() $\varphi _\tau := \gamma \circ \varphi _{\pi }$. The parameter
$\varphi _\tau := \gamma \circ \varphi _{\pi }$. The parameter ![]() $\varphi _\tau$ does not depend on the choice of the lift
$\varphi _\tau$ does not depend on the choice of the lift ![]() $\pi$ since two lifts differ by a character and so are their Langlands parameters.
$\pi$ since two lifts differ by a character and so are their Langlands parameters.
Let ![]() $\varphi : W_{E} \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ be the parameter of a representation of
$\varphi : W_{E} \to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ be the parameter of a representation of ![]() $\operatorname {SL}_2(E)$. Denote by
$\operatorname {SL}_2(E)$. Denote by ![]() $S_{\varphi }:=C_{\operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })}(\varphi (W_E))$ the centralizer in
$S_{\varphi }:=C_{\operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })}(\varphi (W_E))$ the centralizer in ![]() $\operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ of the image of
$\operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ of the image of ![]() $\varphi$.
$\varphi$.
Proposition 6.4 Let ![]() $\tau$ (respectively,
$\tau$ (respectively, ![]() $\pi$) be a supercuspidal
$\pi$) be a supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {SL}_2(E)$ (respectively,
$\operatorname {SL}_2(E)$ (respectively, ![]() $\operatorname {GL}_2(E)$) and
$\operatorname {GL}_2(E)$) and ![]() $\tau \subset \pi |_{\operatorname {SL}_2(F)}$. Then we have an isomorphism
$\tau \subset \pi |_{\operatorname {SL}_2(F)}$. Then we have an isomorphism
Proof. We follow the strategy of [Reference Gelbart and KnappGK82, Theorem 4.3]. To simplify the notation here, we will simply denote ![]() $\varphi _\tau$ by
$\varphi _\tau$ by ![]() $\varphi$. From the definition of
$\varphi$. From the definition of ![]() $\varphi$, we have that
$\varphi$, we have that ![]() $\varphi =\gamma \circ \varphi _\pi$. Let
$\varphi =\gamma \circ \varphi _\pi$. Let ![]() $s\in S_{\varphi }$ and
$s\in S_{\varphi }$ and ![]() $\tilde {s}\in \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$ such that
$\tilde {s}\in \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$ such that ![]() $\gamma (\tilde {s})=s$. We define a function
$\gamma (\tilde {s})=s$. We define a function ![]() $\chi _s:W_{E} \to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$ by
$\chi _s:W_{E} \to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })$ by
This definition is independent of the choice of ![]() $\tilde {s}$. Moreover, since
$\tilde {s}$. Moreover, since ![]() $\gamma (\chi _s(w))=1$,
$\gamma (\chi _s(w))=1$, ![]() $\chi _s(w)$ is a scalar times the identity. We will denote this scalar again
$\chi _s(w)$ is a scalar times the identity. We will denote this scalar again ![]() $\chi _s(w)$. Hence, we have
$\chi _s(w)$. Hence, we have
Let ![]() $w_1,w_2 \in W_{E}$. Then
$w_1,w_2 \in W_{E}$. Then
 \begin{align*} \chi_s(w_1w_2)\varphi_\pi(w_1w_2) &= \tilde{s}\varphi_\pi(w_1w_2) \tilde{s}^{-1} = \tilde{s}\varphi_\pi(w_1)\varphi_\pi(w_2) \tilde{s}^{-1} \\ &= \tilde{s}\varphi_\pi(w_1)\tilde{s}^{-1}\tilde{s}\varphi_\pi(w_2) \tilde{s}^{-1} \\ &= \chi_s(w_1)\varphi_\pi(w_1) \chi_s(w_2)\varphi_\pi(w_2) \\ &= \chi_s(w_1)\chi_s(w_2)\varphi_\pi(w_1)\varphi_\pi(w_2) = \chi_s(w_1)\chi_s(w_2)\varphi_\pi(w_1w_2). \end{align*}
\begin{align*} \chi_s(w_1w_2)\varphi_\pi(w_1w_2) &= \tilde{s}\varphi_\pi(w_1w_2) \tilde{s}^{-1} = \tilde{s}\varphi_\pi(w_1)\varphi_\pi(w_2) \tilde{s}^{-1} \\ &= \tilde{s}\varphi_\pi(w_1)\tilde{s}^{-1}\tilde{s}\varphi_\pi(w_2) \tilde{s}^{-1} \\ &= \chi_s(w_1)\varphi_\pi(w_1) \chi_s(w_2)\varphi_\pi(w_2) \\ &= \chi_s(w_1)\chi_s(w_2)\varphi_\pi(w_1)\varphi_\pi(w_2) = \chi_s(w_1)\chi_s(w_2)\varphi_\pi(w_1w_2). \end{align*}
Thus, ![]() $\chi _s(w_1w_2)=\chi _s(w_1)\chi _s(w_2)$ and
$\chi _s(w_1w_2)=\chi _s(w_1)\chi _s(w_2)$ and ![]() $\chi _s$ is a character.
$\chi _s$ is a character.
Since ![]() $\varphi _\pi \simeq \chi _s\varphi _\pi$ we have
$\varphi _\pi \simeq \chi _s\varphi _\pi$ we have ![]() $\pi \simeq \pi \otimes (\chi _s \circ \det )$ and
$\pi \simeq \pi \otimes (\chi _s \circ \det )$ and ![]() $\chi _s \in Y(\pi )$. This defines a morphism
$\chi _s \in Y(\pi )$. This defines a morphism ![]() $S_{\varphi } \to Y(\pi )$,
$S_{\varphi } \to Y(\pi )$, ![]() $s \mapsto \chi _s$.
$s \mapsto \chi _s$.
This morphism is surjective. Indeed, if ![]() $\omega \in Y(\pi )$, then
$\omega \in Y(\pi )$, then ![]() $\pi \simeq \pi \otimes (\omega \circ \det )$ and, thus,
$\pi \simeq \pi \otimes (\omega \circ \det )$ and, thus, ![]() $\varphi _\pi \simeq \omega \varphi _\pi$. If
$\varphi _\pi \simeq \omega \varphi _\pi$. If ![]() $\tilde {A}$ implements the equivalence, then
$\tilde {A}$ implements the equivalence, then ![]() $\tilde {A} \varphi _\pi (w) \tilde {A}^{-1} = \omega (w) \varphi _\pi (w)$. Let
$\tilde {A} \varphi _\pi (w) \tilde {A}^{-1} = \omega (w) \varphi _\pi (w)$. Let ![]() $A:=\gamma (\tilde {A})$. Then
$A:=\gamma (\tilde {A})$. Then ![]() $A \in S_{\varphi }$ and
$A \in S_{\varphi }$ and ![]() $\omega = \chi _A$.
$\omega = \chi _A$.
We are left to prove that ![]() $S_{\varphi } \to Y(\pi )$ is injective. Let
$S_{\varphi } \to Y(\pi )$ is injective. Let ![]() $s\in S_{\varphi }$ such that
$s\in S_{\varphi }$ such that ![]() $\chi _s=1$. This implies that
$\chi _s=1$. This implies that ![]() $\tilde {s}$ centralizes the image of
$\tilde {s}$ centralizes the image of ![]() $\varphi _\pi$. Since
$\varphi _\pi$. Since ![]() $\varphi _\pi$ is irreducible, Schur's lemma tells us that
$\varphi _\pi$ is irreducible, Schur's lemma tells us that ![]() $\tilde {s}$ is a scalar. Hence,
$\tilde {s}$ is a scalar. Hence, ![]() $s=1$ and we have the injectivity.
$s=1$ and we have the injectivity.
6.3 Explicit computation of the length
By Proposition 6.4, we compute the length ![]() $\lg (\pi )$ by considering the cardinality of
$\lg (\pi )$ by considering the cardinality of ![]() $S_{\varphi _\tau }$. The method in [Reference ShelstadShe79] can be generalised to the case when
$S_{\varphi _\tau }$. The method in [Reference ShelstadShe79] can be generalised to the case when ![]() $\ell$ is positive, based on which we also obtain the existence of good lift.
$\ell$ is positive, based on which we also obtain the existence of good lift.
Definition 6.5 Let ![]() $\tau$ be an irreducible supercuspidal
$\tau$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {SL}_2(E)$, and
$\mathrm {SL}_2(E)$, and ![]() $\tilde {\tau }$ an irreducible supercuspidal
$\tilde {\tau }$ an irreducible supercuspidal ![]() $\overline {\mathbf {Q}}_{\ell }$-representation of
$\overline {\mathbf {Q}}_{\ell }$-representation of ![]() $\mathrm {SL}_2(E)$, which is
$\mathrm {SL}_2(E)$, which is ![]() $\ell$-integral. We say:
$\ell$-integral. We say:
–
 $\tilde {\tau }$ is a
$\tilde {\tau }$ is a  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$, if
$\tau$, if  $\tau$ is a subquotient of the reduction modulo
$\tau$ is a subquotient of the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\tau }$;
$\tilde {\tau }$;–
 $\tilde {\tau }$ is a good
$\tilde {\tau }$ is a good  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$, if the reduction modulo
$\tau$, if the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\tau }$ is irreducible and isomorphic to
$\tilde {\tau }$ is irreducible and isomorphic to  $\tau$.
$\tau$.
For the case of ![]() $\operatorname {GL}_n(E)$, an irreducible supercuspidal
$\operatorname {GL}_n(E)$, an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_n(E)$ always has a
$\operatorname {GL}_n(E)$ always has a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift, and every
$\overline {\mathbf {Q}}_{\ell }$-lift, and every ![]() $\overline {\mathbf {Q}}_{\ell }$-lift is a good
$\overline {\mathbf {Q}}_{\ell }$-lift is a good ![]() $\overline {\mathbf {Q}}_{\ell }$-lift. The latter property is not true for
$\overline {\mathbf {Q}}_{\ell }$-lift. The latter property is not true for ![]() $\operatorname {SL}_2(E)$. However, we will show the existence of a good
$\operatorname {SL}_2(E)$. However, we will show the existence of a good ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of an irreducible supercuspidal
$\overline {\mathbf {Q}}_{\ell }$-lift of an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {SL}_2(E)$.
$\operatorname {SL}_2(E)$.
Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$ with Langlands parameter
$\operatorname {GL}_2(E)$ with Langlands parameter ![]() $\varphi _\pi$, and
$\varphi _\pi$, and ![]() $\tau \subset \pi \vert _{\operatorname {SL}_2(E)}$. We say
$\tau \subset \pi \vert _{\operatorname {SL}_2(E)}$. We say ![]() $\varphi _{\pi }$ is dihedral if the image of
$\varphi _{\pi }$ is dihedral if the image of ![]() $W_E$ is of the form
$W_E$ is of the form ![]() $\operatorname {Ind}_{W_K}^{W_{E}}\theta$ in
$\operatorname {Ind}_{W_K}^{W_{E}}\theta$ in ![]() $\mathrm {GL}_2(\overline {\mathbf {F}}_{\ell })$ where
$\mathrm {GL}_2(\overline {\mathbf {F}}_{\ell })$ where ![]() $K/E$ is a quadratic field extension,
$K/E$ is a quadratic field extension, ![]() $W_K$ is the Weil group of
$W_K$ is the Weil group of ![]() $K$ and
$K$ and ![]() $\theta$ is a character of
$\theta$ is a character of ![]() $W_K$ which is not invariant under the
$W_K$ which is not invariant under the ![]() $\operatorname {Gal}(K/E)$-action. We say
$\operatorname {Gal}(K/E)$-action. We say ![]() $\varphi _\pi$ is tetrahedral (respectively, octahedral) if the image of
$\varphi _\pi$ is tetrahedral (respectively, octahedral) if the image of ![]() $W_E$ under the map
$W_E$ under the map ![]() $W_E\to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })\to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ is the alternating group
$W_E\to \operatorname {GL}_2(\overline {\mathbf {F}}_{\ell })\to \operatorname {PGL}_2(\overline {\mathbf {F}}_{\ell })$ is the alternating group ![]() $A_4$ (respectively, the symmetric group
$A_4$ (respectively, the symmetric group ![]() $S_4$). (See [Reference Bushnell and HenniartBH06, § 42] for more details.)
$S_4$). (See [Reference Bushnell and HenniartBH06, § 42] for more details.)
Proposition 6.6 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$.
$\operatorname {GL}_2(E)$.
(i) When
 $\varphi _{\pi }$ is dihedral, the length
$\varphi _{\pi }$ is dihedral, the length  $\lg (\pi )$ is 2 or 4.
$\lg (\pi )$ is 2 or 4.(ii) When
 $\varphi _{\pi }$ is not dihedral, then it must be tetrahedral or octahedral, and the length
$\varphi _{\pi }$ is not dihedral, then it must be tetrahedral or octahedral, and the length  $\lg (\pi )$ is 1.
$\lg (\pi )$ is 1.
Proof. Let ![]() $\tilde {\pi }$ be a
$\tilde {\pi }$ be a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$. Then the length
$\pi$. Then the length ![]() $\lg (\tilde {\pi })$ divides the length
$\lg (\tilde {\pi })$ divides the length ![]() $\lg (\pi )$. Suppose
$\lg (\pi )$. Suppose ![]() $\vert Y(\pi )\vert \neq 1$. Then there exists an
$\vert Y(\pi )\vert \neq 1$. Then there exists an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\chi$ of
$\chi$ of ![]() $E^{\times }$ such that
$E^{\times }$ such that ![]() $\pi \otimes \chi \circ \det \cong \pi$. By local class field theory, we identify
$\pi \otimes \chi \circ \det \cong \pi$. By local class field theory, we identify ![]() $\chi$ with an
$\chi$ with an ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $W_E$ such that
$W_E$ such that ![]() $\varphi _{\pi \otimes \chi \circ \det }\cong \chi \varphi _{\pi }\cong \varphi _{\pi }$. Considering the central character, we have that
$\varphi _{\pi \otimes \chi \circ \det }\cong \chi \varphi _{\pi }\cong \varphi _{\pi }$. Considering the central character, we have that ![]() $\chi$ has order
$\chi$ has order ![]() $2$. Then there exists a quadratic field extension
$2$. Then there exists a quadratic field extension ![]() $K/ E$ such that
$K/ E$ such that ![]() $\ker (\chi )=W_K$, which, by Clifford theory implies that
$\ker (\chi )=W_K$, which, by Clifford theory implies that ![]() $\varphi _{\pi }\vert _{W_K}$ is a direct sum of two characters of
$\varphi _{\pi }\vert _{W_K}$ is a direct sum of two characters of ![]() $W_K$. Hence
$W_K$. Hence ![]() $\varphi _\pi =\operatorname {Ind}_{W_K}^{W_{E}}\theta$ where
$\varphi _\pi =\operatorname {Ind}_{W_K}^{W_{E}}\theta$ where ![]() $W_K$ is the Weil group of
$W_K$ is the Weil group of ![]() $K$ and
$K$ and ![]() $\theta$ is an
$\theta$ is an ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $W_K$. Let
$W_K$. Let ![]() $s$ be the non-trivial element in
$s$ be the non-trivial element in ![]() $\mathrm {Gal}(K/ E)$. By a same computation as in [Reference ShelstadShe79, § 11, part (ii)], we deduce that if
$\mathrm {Gal}(K/ E)$. By a same computation as in [Reference ShelstadShe79, § 11, part (ii)], we deduce that if ![]() $\theta / \theta ^{s}$ has order two, then
$\theta / \theta ^{s}$ has order two, then ![]() $\vert S_{\varphi _{\tau }}\vert =4$. When
$\vert S_{\varphi _{\tau }}\vert =4$. When ![]() $(\theta / \theta ^{s})^2\neq \mathbf {1}$, then
$(\theta / \theta ^{s})^2\neq \mathbf {1}$, then ![]() $\vert S_{\varphi _{\tau }}\vert =2$. When
$\vert S_{\varphi _{\tau }}\vert =2$. When ![]() $\theta \cong \theta ^s$ then
$\theta \cong \theta ^s$ then ![]() $\varphi _{\pi }$ is reducible which is not an
$\varphi _{\pi }$ is reducible which is not an ![]() $L$-parameter of an irreducible supercuspidal representation of
$L$-parameter of an irreducible supercuspidal representation of ![]() $\operatorname {GL}_{2}(E)$. Then we obtain the result by applying Lemma 6.1 and Proposition 6.4. On the other hand, let
$\operatorname {GL}_{2}(E)$. Then we obtain the result by applying Lemma 6.1 and Proposition 6.4. On the other hand, let ![]() $\mu _{K/ E}$ be the unique non-trivial character on
$\mu _{K/ E}$ be the unique non-trivial character on ![]() $\mathrm {Gal}(K/ E)$, then we have
$\mathrm {Gal}(K/ E)$, then we have ![]() $\mu _{K/ E}\otimes \varphi _{\pi }\cong \varphi _{\pi }$, hence
$\mu _{K/ E}\otimes \varphi _{\pi }\cong \varphi _{\pi }$, hence ![]() $\vert Y(\pi )\vert \neq 1$. In other words, we show that
$\vert Y(\pi )\vert \neq 1$. In other words, we show that ![]() $\varphi _{\pi }$ is dihedral if and only if
$\varphi _{\pi }$ is dihedral if and only if ![]() $\vert Y(\pi )\vert \neq 1$.
$\vert Y(\pi )\vert \neq 1$.
Suppose that ![]() $\varphi _{\pi }$ is not dihedral, then
$\varphi _{\pi }$ is not dihedral, then ![]() $\vert Y({\pi })\vert =1$, which implies that
$\vert Y({\pi })\vert =1$, which implies that ![]() $p=2$ by [Reference Bushnell and HenniartBH06, § 42]. In this case, the image of a
$p=2$ by [Reference Bushnell and HenniartBH06, § 42]. In this case, the image of a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift ![]() $\tilde {\pi }$ under the projection from
$\tilde {\pi }$ under the projection from ![]() $\operatorname {GL}_2(\overline {\mathbf {Q}}_{\ell })$ to
$\operatorname {GL}_2(\overline {\mathbf {Q}}_{\ell })$ to ![]() $\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ is either isomorphic to
$\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ is either isomorphic to ![]() $S_4$ or
$S_4$ or ![]() $A_4$. For the second case, since any two subgroups of
$A_4$. For the second case, since any two subgroups of ![]() $\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ being isomorphic to
$\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ being isomorphic to ![]() $A_4$ are conjugate to each other, we can choose
$A_4$ are conjugate to each other, we can choose ![]() $\varphi _{\tilde {\pi }}$ such that its image in
$\varphi _{\tilde {\pi }}$ such that its image in ![]() $\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ will be
$\operatorname {PGL}_2(\overline {\mathbf {Q}}_{\ell })$ will be ![]() $N\rtimes C$, where
$N\rtimes C$, where
Since ![]() $\ell \neq 2$, after reduction modulo
$\ell \neq 2$, after reduction modulo ![]() $\ell$ the image of
$\ell$ the image of ![]() $\varphi _{\pi }$ is isomorphic to
$\varphi _{\pi }$ is isomorphic to ![]() $N\rtimes C\cong S_4$ as well. For the case of
$N\rtimes C\cong S_4$ as well. For the case of ![]() $S_4$, it is isomorphic to
$S_4$, it is isomorphic to ![]() $\langle N\rtimes C,\big (\begin{smallmatrix} \sqrt {-1} & 0\\ 0 & 1 \end{smallmatrix}\big )\rangle$. We repeat the similar argument to the case of
$\langle N\rtimes C,\big (\begin{smallmatrix} \sqrt {-1} & 0\\ 0 & 1 \end{smallmatrix}\big )\rangle$. We repeat the similar argument to the case of ![]() $A_4$. This finishes the proof.
$A_4$. This finishes the proof.
Proposition 6.7 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$ and
$\operatorname {GL}_2(E)$ and ![]() $\tilde {\pi }$ a
$\tilde {\pi }$ a ![]() $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of ![]() $\pi$. Let
$\pi$. Let ![]() $\tau$ be an irreducible component of
$\tau$ be an irreducible component of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ and
$\pi \vert _{\operatorname {SL}_2(E)}$ and ![]() $\tilde {\tau }$ an irreducible component of
$\tilde {\tau }$ an irreducible component of ![]() $\tilde {\pi }\vert _{\operatorname {SL}_2(E)}$.
$\tilde {\pi }\vert _{\operatorname {SL}_2(E)}$.
(i) Suppose that
 $\varphi _{\pi }$ is tetrahedral or octahedral. Then
$\varphi _{\pi }$ is tetrahedral or octahedral. Then  $\tilde {\pi }\vert _{\operatorname {SL}_2(E)}\cong \tilde {\tau }$ is a good
$\tilde {\pi }\vert _{\operatorname {SL}_2(E)}\cong \tilde {\tau }$ is a good  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$.
$\tau$.(ii) Suppose that
 $\varphi _{\pi }$ is dihedral.
$\varphi _{\pi }$ is dihedral.(a) If the cardinality of
 $S_{\varphi _{\tilde {\tau }}}$ is
$S_{\varphi _{\tilde {\tau }}}$ is  $4$, then the reduction modulo
$4$, then the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\tau }$ is irreducible. In particular, there exists an irreducible component
$\tilde {\tau }$ is irreducible. In particular, there exists an irreducible component  $\tilde {\tau }'\subset \pi \vert _{\operatorname {SL}_2(E)}$ which is a good
$\tilde {\tau }'\subset \pi \vert _{\operatorname {SL}_2(E)}$ which is a good  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$.
$\tau$.(b) If the cardinality of
 $S_{\varphi _{\tilde {\tau }}}$ is
$S_{\varphi _{\tilde {\tau }}}$ is  $2$, then the reduction modulo
$2$, then the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\tau }$ may be reducible. If it is irreducible, there exists an irreducible component
$\tilde {\tau }$ may be reducible. If it is irreducible, there exists an irreducible component  $\tilde {\tau }'\subset \pi \vert _{\operatorname {SL}_2(E)}$ which is a good
$\tilde {\tau }'\subset \pi \vert _{\operatorname {SL}_2(E)}$ which is a good  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$. If it is reducible, then there exists another
$\tau$. If it is reducible, then there exists another  $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift  $\tilde {\pi }'$ of
$\tilde {\pi }'$ of  $\pi$, such that the cardinality of
$\pi$, such that the cardinality of  $S_{\varphi _{\tilde {\pi }'}}$ is
$S_{\varphi _{\tilde {\pi }'}}$ is  $4$, and there exists an irreducible component
$4$, and there exists an irreducible component  $\tilde {\tau }'\subset \tilde {\pi }'\vert _{\operatorname {SL}_2(F)}$ which is a good
$\tilde {\tau }'\subset \tilde {\pi }'\vert _{\operatorname {SL}_2(F)}$ which is a good  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\tau$.
$\tau$.
Proof.
(i) We have that
 $\varphi _{\tilde {\pi }}$ is tetrahedral or octahedral, hence the reduction modulo
$\varphi _{\tilde {\pi }}$ is tetrahedral or octahedral, hence the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\pi }\vert _{\operatorname {SL}_2(E)}$ is irreducible and isomorphic to
$\tilde {\pi }\vert _{\operatorname {SL}_2(E)}$ is irreducible and isomorphic to  $\tau$ by Proposition 6.6(ii).
$\tau$ by Proposition 6.6(ii).(ii) We have the following.
(a) We first assume that the cardinality of
 $S_{\varphi _{\tilde {\tau }}}$ is
$S_{\varphi _{\tilde {\tau }}}$ is  $4$. We switch the order of restriction to
$4$. We switch the order of restriction to  $\operatorname {SL}_2(E)$ and reduction modulo
$\operatorname {SL}_2(E)$ and reduction modulo  $\ell$. Then by Proposition 6.6(i), we have
$\ell$. Then by Proposition 6.6(i), we have  $\lg (\pi )=\lg (\tilde {\pi })$. Hence, every irreducible component of
$\lg (\pi )=\lg (\tilde {\pi })$. Hence, every irreducible component of  $\tilde {\pi }\vert _{\operatorname {SL}_2}$ is
$\tilde {\pi }\vert _{\operatorname {SL}_2}$ is  $\ell$-integral and its reduction modulo
$\ell$-integral and its reduction modulo  $\ell$ is irreducible. The unicity of Jordan-Hölder components implies the existence of a good
$\ell$ is irreducible. The unicity of Jordan-Hölder components implies the existence of a good  $\overline {\mathbf {Q}}_{\ell }$-lift
$\overline {\mathbf {Q}}_{\ell }$-lift  $\tilde {\tau }$.
$\tilde {\tau }$.(b) Now we assume that the cardinality of
 $S_{\varphi _{\tilde {\tau }}}$ is
$S_{\varphi _{\tilde {\tau }}}$ is  $2$. Then there exists a field extension
$2$. Then there exists a field extension  $K/ E$ and an
$K/ E$ and an  $\ell$-integral
$\ell$-integral  $\overline {\mathbf {Q}}_{\ell }$-quasicharacter
$\overline {\mathbf {Q}}_{\ell }$-quasicharacter  $\tilde {\theta }$ of
$\tilde {\theta }$ of  $K^{\times }$, such that
$K^{\times }$, such that  $\varphi _{\tilde {\pi }}\cong \mathrm {Ind}_{W_K}^{W_{E}}\tilde {\theta }$, and
$\varphi _{\tilde {\pi }}\cong \mathrm {Ind}_{W_K}^{W_{E}}\tilde {\theta }$, and  $(\tilde {\theta }^s/{\tilde {\theta }})^2\neq \mathbf {1}$, where
$(\tilde {\theta }^s/{\tilde {\theta }})^2\neq \mathbf {1}$, where  $\operatorname {Gal}(K/E)=\langle s\rangle$. Let
$\operatorname {Gal}(K/E)=\langle s\rangle$. Let  $\theta$ be the reduction modulo
$\theta$ be the reduction modulo  $\ell$ of
$\ell$ of  $\tilde {\theta }$. Then
$\tilde {\theta }$. Then  $\varphi _{\pi }\cong \mathrm {Ind}_{W_K}^{W_{E}}\theta$. Suppose
$\varphi _{\pi }\cong \mathrm {Ind}_{W_K}^{W_{E}}\theta$. Suppose  $(\theta ^s/{\theta })^2\neq \mathbf {1}$. Then the cardinality of
$(\theta ^s/{\theta })^2\neq \mathbf {1}$. Then the cardinality of  $S_{\varphi _{\tau }}$ is
$S_{\varphi _{\tau }}$ is  $2$ as well. In this case, we apply the same argument as for case (a), and deduce the existence of a good lift. If
$2$ as well. In this case, we apply the same argument as for case (a), and deduce the existence of a good lift. If  $(\theta ^s/{\theta })^2 =\mathbf {1}$, the cardinality of
$(\theta ^s/{\theta })^2 =\mathbf {1}$, the cardinality of  $S_{\varphi _{\tau }}$ is
$S_{\varphi _{\tau }}$ is  $4$, which implies that the length of the reduction modulo
$4$, which implies that the length of the reduction modulo  $\ell$ of each irreducible component in
$\ell$ of each irreducible component in  $\tilde {\pi }\vert _{\operatorname {SL}_2}$ is
$\tilde {\pi }\vert _{\operatorname {SL}_2}$ is  $2$, hence none of them is a good lift of
$2$, hence none of them is a good lift of  $\tau$. Now fix a group embedding from
$\tau$. Now fix a group embedding from  $\overline {\mathbf {F}}_{\ell }^{\times }$ to
$\overline {\mathbf {F}}_{\ell }^{\times }$ to  $\overline {\mathbf {Z}}_{\ell }^{\times }$ by sending an element of
$\overline {\mathbf {Z}}_{\ell }^{\times }$ by sending an element of  $\overline {\mathbf {F}}_{\ell }^{\times }$ to its Teichmuller representative, which gives a natural
$\overline {\mathbf {F}}_{\ell }^{\times }$ to its Teichmuller representative, which gives a natural  $\overline {\mathbf {Q}}_{\ell }$-lift of
$\overline {\mathbf {Q}}_{\ell }$-lift of  $\theta$, denoted by
$\theta$, denoted by  $\tilde {\theta }_{0}$. We deduce that
$\tilde {\theta }_{0}$. We deduce that  $(\tilde {\theta }_{0}^s/{\tilde {\theta }}_{0})^2=\mathbf {1}$. Let
$(\tilde {\theta }_{0}^s/{\tilde {\theta }}_{0})^2=\mathbf {1}$. Let  $\tilde {\pi }'$ be the irreducible supercuspidal
$\tilde {\pi }'$ be the irreducible supercuspidal  $\overline {\mathbf {Q}}_{\ell }$-representation of
$\overline {\mathbf {Q}}_{\ell }$-representation of  $\operatorname {GL}_2(E)$ corresponding to
$\operatorname {GL}_2(E)$ corresponding to  $\varphi _{0}=\mathrm {Ind}_{W_K}^{W_{E}}\tilde {\theta }_{0}$, which is
$\varphi _{0}=\mathrm {Ind}_{W_K}^{W_{E}}\tilde {\theta }_{0}$, which is  $\ell$-integral with reduction modulo
$\ell$-integral with reduction modulo  $\ell$ isomorphic to
$\ell$ isomorphic to  $\pi$, and the cardinality of
$\pi$, and the cardinality of  $Y(\tilde {\pi }')$ is
$Y(\tilde {\pi }')$ is  $4$. We apply the argument for case (a) to finish the proof.
$4$. We apply the argument for case (a) to finish the proof.
6.4 Representations of  $\operatorname {GL}_2(E)$ distinguished by
$\operatorname {GL}_2(E)$ distinguished by  $\operatorname {SL}_2(F)$
$\operatorname {SL}_2(F)$
In the remainder of this paper, we follow the restriction method of [Reference Anandavardhanan and PrasadAP03] since the main strategy of [Reference Anandavardhanan and PrasadAP03] works for ![]() $\overline {\mathbf {F}}_{\ell }$-representations as well. However, in the modular setting, some modifications are still needed in the proofs. For convenience, we state the results which are required for further use.
$\overline {\mathbf {F}}_{\ell }$-representations as well. However, in the modular setting, some modifications are still needed in the proofs. For convenience, we state the results which are required for further use.
For an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation
$\overline {\mathbf {F}}_{\ell }$-representation ![]() $\pi$ of
$\pi$ of ![]() $\operatorname {GL}_2(E)$, we denote by
$\operatorname {GL}_2(E)$, we denote by ![]() $X(\pi )$ the following set
$X(\pi )$ the following set
Proposition 6.8 [Reference Anandavardhanan and PrasadAP03, Proposition 4.1]
Let ![]() $\pi$ be an irreducible
$\pi$ be an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$. Then
$\operatorname {GL}_2(E)$. Then
Proof. Assume that ![]() $\pi$ is
$\pi$ is ![]() $\mathrm {SL}_2(F)$-distinguished. Let
$\mathrm {SL}_2(F)$-distinguished. Let ![]() $Z_{F^\times }$ be the center of
$Z_{F^\times }$ be the center of ![]() $\mathrm {GL}_2(F)$ and
$\mathrm {GL}_2(F)$ and ![]() $Z_{F^\times }'$ be the center of
$Z_{F^\times }'$ be the center of ![]() $\mathrm {SL}_2(F)$. The group
$\mathrm {SL}_2(F)$. The group ![]() $Z_{F^{\times }}'$ is the kernel of determinant that maps
$Z_{F^{\times }}'$ is the kernel of determinant that maps ![]() $Z_{F^{\times }}$ into
$Z_{F^{\times }}$ into ![]() $F^{\times }$. The central character
$F^{\times }$. The central character ![]() $\omega _\pi$ of
$\omega _\pi$ of ![]() $\pi$ is trivial on
$\pi$ is trivial on ![]() $Z_{F^\times }'$ and so there exists a character
$Z_{F^\times }'$ and so there exists a character ![]() $\chi _F$ of
$\chi _F$ of ![]() $F^\times$ such that
$F^\times$ such that ![]() $\chi _F^2=\omega _{\pi }|_{Z_{F^\times\!}}$. Since each smooth
$\chi _F^2=\omega _{\pi }|_{Z_{F^\times\!}}$. Since each smooth ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $F^{\times }$ can be extended to a smooth
$F^{\times }$ can be extended to a smooth ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E^{\times }$, we obtain that after twisting by a smooth
$E^{\times }$, we obtain that after twisting by a smooth ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E^{\times }$, the central character
$E^{\times }$, the central character ![]() $\omega _{\pi }$ of
$\omega _{\pi }$ of ![]() $\pi$ is trivial on
$\pi$ is trivial on ![]() $Z_{F^{\times\!}}$. On the other hand, if
$Z_{F^{\times\!}}$. On the other hand, if ![]() $\pi$ is
$\pi$ is ![]() $(\operatorname {GL}_2(F),\chi )$-distinguished for an
$(\operatorname {GL}_2(F),\chi )$-distinguished for an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\chi$ of
$\chi$ of ![]() $F^{\times }$, then
$F^{\times }$, then ![]() $\pi$ is
$\pi$ is ![]() $\mathrm {SL}_2(F)$-distinguished, and
$\mathrm {SL}_2(F)$-distinguished, and ![]() $\omega _{\pi }$ is trivial on
$\omega _{\pi }$ is trivial on ![]() $Z_{F^{\times }}$ after twisting by a smooth
$Z_{F^{\times }}$ after twisting by a smooth ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E^{\times }$ as explained above. We obtain the fact that if
$E^{\times }$ as explained above. We obtain the fact that if ![]() $\omega _{\pi }$ is never trivial on
$\omega _{\pi }$ is never trivial on ![]() $Z_{F^{\times }}$ after twisting by a smooth
$Z_{F^{\times }}$ after twisting by a smooth ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E^{\times }$, then
$E^{\times }$, then ![]() $\dim \mathrm {Hom}_{\operatorname {SL}_2(F)}(\pi,1)= \vert X(\pi )\vert =0$.
$\dim \mathrm {Hom}_{\operatorname {SL}_2(F)}(\pi,1)= \vert X(\pi )\vert =0$.
Now assume that the central character ![]() $\omega _{\pi }$ is trivial on
$\omega _{\pi }$ is trivial on ![]() $Z_{F^\times\!}$. As in the proof of Proposition 4.1 of [Reference Anandavardhanan and PrasadAP03], we consider the
$Z_{F^\times\!}$. As in the proof of Proposition 4.1 of [Reference Anandavardhanan and PrasadAP03], we consider the ![]() $\overline {\mathbf {F}}_{\ell }$-space
$\overline {\mathbf {F}}_{\ell }$-space ![]() $\mathrm {Hom}_{\mathrm {SL}_2(F)}(\pi,\mathbf {1})$, which has a
$\mathrm {Hom}_{\mathrm {SL}_2(F)}(\pi,\mathbf {1})$, which has a ![]() $\mathrm {GL}_2(F)$-module structure and
$\mathrm {GL}_2(F)$-module structure and ![]() $F^{\times }\cdot \mathrm {SL}_2(F)$ acts trivially. Since
$F^{\times }\cdot \mathrm {SL}_2(F)$ acts trivially. Since ![]() $F^{\times }/ F^{\times 2}$ is a finite abelian group whose order is a power of
$F^{\times }/ F^{\times 2}$ is a finite abelian group whose order is a power of ![]() $2$, our assumption that
$2$, our assumption that ![]() $\ell \neq 2$ implies that
$\ell \neq 2$ implies that ![]() $\mathrm {Hom}_{\mathrm {SL}_2(F)}(\pi,\mathbf {1})$ can decompose into a direct sum of
$\mathrm {Hom}_{\mathrm {SL}_2(F)}(\pi,\mathbf {1})$ can decompose into a direct sum of ![]() $\overline {\mathbf {F}}_{\ell }$-characters of
$\overline {\mathbf {F}}_{\ell }$-characters of ![]() $F^{\times }/ F^{\times 2}$, hence a direct sum of
$F^{\times }/ F^{\times 2}$, hence a direct sum of ![]() $\overline {\mathbf {F}}_{\ell }$-characters of
$\overline {\mathbf {F}}_{\ell }$-characters of ![]() $\mathrm {GL}_2(F)$. In particular, from the definition, for an
$\mathrm {GL}_2(F)$. In particular, from the definition, for an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\chi$ of
$\chi$ of ![]() $\mathrm {GL}_2(F)$ which appears in the direct sum above, we have that
$\mathrm {GL}_2(F)$ which appears in the direct sum above, we have that ![]() $\pi$ is
$\pi$ is ![]() $\chi$-distinguished with respect to
$\chi$-distinguished with respect to ![]() $\mathrm {GL}_2(F)$. Due to Theorem 4.1(iii), the direct sum above is multiplicity-free as
$\mathrm {GL}_2(F)$. Due to Theorem 4.1(iii), the direct sum above is multiplicity-free as ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2(F)$. Hence, we obtain the desired equation.
$\mathrm {GL}_2(F)$. Hence, we obtain the desired equation.
6.5 Supercuspidal case
This subsection focuses on the distinction problems for supercuspidal representations.
Denote by ![]() $\mathrm {U}$ the subgroup of
$\mathrm {U}$ the subgroup of ![]() $\operatorname {GL}_2(E)$ consisting of the upper triangular matrices
$\operatorname {GL}_2(E)$ consisting of the upper triangular matrices ![]() $\big (\begin{smallmatrix} 1 & x \\0 & 1 \end{smallmatrix}\big )$. Then
$\big (\begin{smallmatrix} 1 & x \\0 & 1 \end{smallmatrix}\big )$. Then ![]() $\mathrm {U}\cong E$. Fix an
$\mathrm {U}\cong E$. Fix an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\psi _0$ of
$\psi _0$ of ![]() $E$, which is non-trivial on
$E$, which is non-trivial on ![]() $\mathfrak {o}_E$ and is trivial on both
$\mathfrak {o}_E$ and is trivial on both ![]() $\mathfrak {p}_E$ and
$\mathfrak {p}_E$ and ![]() $F$. Let
$F$. Let ![]() $\pi$ be an irreducible infinite-dimensional
$\pi$ be an irreducible infinite-dimensional ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2(E)$. Then
$\mathrm {GL}_2(E)$. Then ![]() $\pi$ is
$\pi$ is ![]() $\psi _0$-generic, and
$\psi _0$-generic, and ![]() $\pi$ has a unique Whittaker model
$\pi$ has a unique Whittaker model ![]() $\mathcal {W}(\pi,\psi _0)$.
$\mathcal {W}(\pi,\psi _0)$.
Lemma 6.9 Let ![]() $\pi _0$ be an irreducible
$\pi _0$ be an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2^+(E)$ which is of infinite dimension and distinguished by
$\mathrm {GL}_2^+(E)$ which is of infinite dimension and distinguished by ![]() $\operatorname {SL}_2(F)$. Then it has a Whittaker model with respect to
$\operatorname {SL}_2(F)$. Then it has a Whittaker model with respect to ![]() $\psi _0$.
$\psi _0$.
Proof. A similar method as in [Reference Anandavardhanan and PrasadAP03, Lemma 3.1] can be applied here. We repeat the proof for the convenience of the reader. We add some preliminaries at first.
Let ![]() $\pi$ be an irreducible
$\pi$ be an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2(E)$ such that
$\mathrm {GL}_2(E)$ such that ![]() $\pi |_{\operatorname {GL}_2^+(E)}\supset \pi _0$. Up to twisting by an
$\pi |_{\operatorname {GL}_2^+(E)}\supset \pi _0$. Up to twisting by an ![]() ${\overline {\mathbf {F}}_{\ell }}$-character of
${\overline {\mathbf {F}}_{\ell }}$-character of ![]() $F^{\times }$ on
$F^{\times }$ on ![]() $\pi _0$, we can assume that
$\pi _0$, we can assume that ![]() $\pi _0$ is distinguished with respect to
$\pi _0$ is distinguished with respect to ![]() $\mathrm {GL}_2(F)$. Thus, is
$\mathrm {GL}_2(F)$. Thus, is ![]() $\pi$. Recall that
$\pi$. Recall that ![]() $\psi _0$ is a fixed additive
$\psi _0$ is a fixed additive ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E$ which is trivial on
$E$ which is trivial on ![]() $F$, and denote by
$F$, and denote by ![]() $\mathcal {W}(\pi,\psi _0)$ the
$\mathcal {W}(\pi,\psi _0)$ the ![]() $\psi _0$-Whittaker model of
$\psi _0$-Whittaker model of ![]() $\pi$. Let
$\pi$. Let ![]() $W\in \mathcal {W}(\pi,\psi _0)$. By [Reference Kurinczuk and MatringeKM20, § 8.2] we know that the unique
$W\in \mathcal {W}(\pi,\psi _0)$. By [Reference Kurinczuk and MatringeKM20, § 8.2] we know that the unique ![]() $\mathrm {GL}_2(F)$-invariant linear form can be realized as an integration form
$\mathrm {GL}_2(F)$-invariant linear form can be realized as an integration form
where ![]() $d^\times a$ is a Haar measure on
$d^\times a$ is a Haar measure on ![]() $F^\times$, which is non-zero (in [Reference Kurinczuk and MatringeKM20] this integration form is denoted by
$F^\times$, which is non-zero (in [Reference Kurinczuk and MatringeKM20] this integration form is denoted by ![]() $\mathcal {P}_{\pi }$) and
$\mathcal {P}_{\pi }$) and ![]() $\mathrm {GL}_2(F)$-invariant. There is a unique irreducible component of the restricted representation
$\mathrm {GL}_2(F)$-invariant. There is a unique irreducible component of the restricted representation ![]() $\pi \vert _{\mathrm {GL}_2^+(E)}$ that is
$\pi \vert _{\mathrm {GL}_2^+(E)}$ that is ![]() $\psi _0$-generic. Let
$\psi _0$-generic. Let ![]() $\pi _1$ be a non-
$\pi _1$ be a non-![]() $\psi _0$-generic irreducible component of
$\psi _0$-generic irreducible component of ![]() $\mathcal {W}(\pi,\psi _0)\vert _{\mathrm {GL}_2^+(E)}$, and
$\mathcal {W}(\pi,\psi _0)\vert _{\mathrm {GL}_2^+(E)}$, and ![]() $W\in \mathcal {W}(\pi,\psi _0)$ a function belonging to
$W\in \mathcal {W}(\pi,\psi _0)$ a function belonging to ![]() $\pi _1$. Given
$\pi _1$. Given ![]() $g\in \mathrm {GL}_2^+(E)$,
$g\in \mathrm {GL}_2^+(E)$, ![]() $W(g)$ must be zero. Otherwise, it will induce a non-trivial morphism from
$W(g)$ must be zero. Otherwise, it will induce a non-trivial morphism from ![]() $\pi _1$ to the space of
$\pi _1$ to the space of ![]() $\psi _0$-Whittaker functions on
$\psi _0$-Whittaker functions on ![]() $\mathrm {GL}_2^+(E)$, which contradicts the assumption that
$\mathrm {GL}_2^+(E)$, which contradicts the assumption that ![]() $\pi _1$ is not
$\pi _1$ is not ![]() $\psi _0$-generic. Therefore, the
$\psi _0$-generic. Therefore, the ![]() $\mathrm {GL}_2(F)$-invariant linear form can be non-zero only on the
$\mathrm {GL}_2(F)$-invariant linear form can be non-zero only on the ![]() $\psi _0$-generic part of
$\psi _0$-generic part of ![]() $\pi \vert _{\mathrm {GL}^+_2(E)}$, and we conclude that
$\pi \vert _{\mathrm {GL}^+_2(E)}$, and we conclude that ![]() $\pi _0$ is
$\pi _0$ is ![]() $\psi _0$-generic.
$\psi _0$-generic.
Lemma 6.10 Let ![]() $\pi$ be an irreducible
$\pi$ be an irreducible ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2^+(E)$. The restricted representation
$\operatorname {GL}_2^+(E)$. The restricted representation ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ is semisimple with finite length and all irreducible components are conjugate to each other under the action of
$\pi \vert _{\operatorname {SL}_2(E)}$ is semisimple with finite length and all irreducible components are conjugate to each other under the action of ![]() $\operatorname {GL}_2(F)$. Hence, the dimension
$\operatorname {GL}_2(F)$. Hence, the dimension ![]() $\dim \mathrm {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})$ is independent of the choice of irreducible component
$\dim \mathrm {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})$ is independent of the choice of irreducible component ![]() $\tau$ of
$\tau$ of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$.
$\pi \vert _{\operatorname {SL}_2(E)}$.
Proof. The proof of [Reference Anandavardhanan and PrasadAP03, Lemma 3.2] works for ![]() $\overline {\mathbf {F}}_{\ell }$-representations as well.
$\overline {\mathbf {F}}_{\ell }$-representations as well.
Proposition 6.11 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$, which is distinguished with respect to
$\operatorname {GL}_2(E)$, which is distinguished with respect to ![]() $\operatorname {SL}_2(F)$. Then we have
$\operatorname {SL}_2(F)$. Then we have
Assume further that ![]() $\pi$ is distinguished with respect to
$\pi$ is distinguished with respect to ![]() $\operatorname {GL}_2(F)$. Then composition with the norm map
$\operatorname {GL}_2(F)$. Then composition with the norm map ![]() $N_{E/ F}$ induces a bijection from
$N_{E/ F}$ induces a bijection from ![]() $X(\pi )$ to
$X(\pi )$ to ![]() $Y_+(\pi )$.
$Y_+(\pi )$.
Proof. The strategy of [Reference Anandavardhanan and PrasadAP03, Proposition 4.2] can be applied, and we write the proof here for the convenience of the reader. By Proposition 6.8, after twisting ![]() $\pi$ by an
$\pi$ by an ![]() $\overline {\mathbf {F}}_{\ell }$-character of
$\overline {\mathbf {F}}_{\ell }$-character of ![]() $E^{\times }$, we assume that
$E^{\times }$, we assume that ![]() $\pi$ is distinguished with respect to
$\pi$ is distinguished with respect to ![]() $\mathrm {GL}_2(F)$. As in the proof of [Reference Anandavardhanan and PrasadAP03, Proposition 4.2], we give a bijection from
$\mathrm {GL}_2(F)$. As in the proof of [Reference Anandavardhanan and PrasadAP03, Proposition 4.2], we give a bijection from ![]() $X(\pi )$ to
$X(\pi )$ to ![]() $Y_+(\pi )$ given by the composition with the norm map.
$Y_+(\pi )$ given by the composition with the norm map.
Recall that ![]() $\operatorname {Nm}_{E/ F}$ is the norm map from
$\operatorname {Nm}_{E/ F}$ is the norm map from ![]() $E^{\times }$ to
$E^{\times }$ to ![]() $F^{\times }$ and
$F^{\times }$ and ![]() $\chi \in X(\pi )$. Define a map
$\chi \in X(\pi )$. Define a map
via ![]() $\chi \mapsto \chi \circ \operatorname {Nm}_{E/ F}$. Indeed, let
$\chi \mapsto \chi \circ \operatorname {Nm}_{E/ F}$. Indeed, let ![]() $\chi \in X(\pi )$ and
$\chi \in X(\pi )$ and ![]() $\tilde {\chi }$ be a character of
$\tilde {\chi }$ be a character of ![]() $E^{\times }$ such that
$E^{\times }$ such that ![]() $\tilde {\chi }|_{F^\times }=\chi$. By Theorem 4.1,
$\tilde {\chi }|_{F^\times }=\chi$. By Theorem 4.1, ![]() $\pi$ and
$\pi$ and ![]() $\pi \otimes \tilde {\chi }^{-1}$ are
$\pi \otimes \tilde {\chi }^{-1}$ are ![]() $\sigma$-selfdual. Therefore,
$\sigma$-selfdual. Therefore, ![]() $\pi \simeq \pi \otimes \chi \circ \operatorname {Nm}_{E/ F}$ and
$\pi \simeq \pi \otimes \chi \circ \operatorname {Nm}_{E/ F}$ and ![]() $\chi \circ \operatorname {Nm}_{E/ F}\in Y_+(\pi )$.
$\chi \circ \operatorname {Nm}_{E/ F}\in Y_+(\pi )$.
Conversely, let ![]() $\mu \in Y_+(\pi )$. Since
$\mu \in Y_+(\pi )$. Since ![]() $\mu ^{2}=\mathbf {1}$ and
$\mu ^{2}=\mathbf {1}$ and ![]() $\mu \vert _{F^{\times }}=\mathbf {1}$, by Hilbert's theorem
$\mu \vert _{F^{\times }}=\mathbf {1}$, by Hilbert's theorem ![]() $90$, it is trivial on the kernel of
$90$, it is trivial on the kernel of ![]() $\operatorname {Nm}_{E/ F}$. Hence, there exists an
$\operatorname {Nm}_{E/ F}$. Hence, there exists an ![]() $\overline {\mathbf {F}}_{\ell }$-character
$\overline {\mathbf {F}}_{\ell }$-character ![]() $\eta$ of
$\eta$ of ![]() $F^{\times }$, such that
$F^{\times }$, such that ![]() $\mu \cong \eta \circ \operatorname {Nm}_{E/ F}$. Let
$\mu \cong \eta \circ \operatorname {Nm}_{E/ F}$. Let ![]() $\tilde {\eta }$ be an extension of
$\tilde {\eta }$ be an extension of ![]() $\eta$ to
$\eta$ to ![]() $E^{\times }$. Then
$E^{\times }$. Then ![]() $\mu \cong \tilde {\eta }\cdot \tilde {\eta }^{\sigma }$. Since
$\mu \cong \tilde {\eta }\cdot \tilde {\eta }^{\sigma }$. Since ![]() $\pi$ is distinguished with respect to
$\pi$ is distinguished with respect to ![]() $\mathrm {GL}_2(F)$, we have
$\mathrm {GL}_2(F)$, we have
On the other hand, let ![]() $Z_{F^{\times }}$ be the center of
$Z_{F^{\times }}$ be the center of ![]() $\operatorname {GL}_2(F)$. Then
$\operatorname {GL}_2(F)$. Then ![]() $\omega _{\pi \otimes \tilde {\eta }}\vert _{Z_{F^{\times }}}$ is trivial where
$\omega _{\pi \otimes \tilde {\eta }}\vert _{Z_{F^{\times }}}$ is trivial where ![]() $\omega _{\pi \otimes \tilde {\eta }}$ is the central character of
$\omega _{\pi \otimes \tilde {\eta }}$ is the central character of ![]() $\pi \otimes \tilde {\eta }$. By Theorem 3.14,
$\pi \otimes \tilde {\eta }$. By Theorem 3.14, ![]() $\pi \otimes \tilde {\eta }$ is either distinguished or
$\pi \otimes \tilde {\eta }$ is either distinguished or ![]() $\omega _{E/ F}$-distinguished by
$\omega _{E/ F}$-distinguished by ![]() $\operatorname {GL}_2(F)$ but not both. We map
$\operatorname {GL}_2(F)$ but not both. We map ![]() $\mu$ to
$\mu$ to ![]() $\eta$ or
$\eta$ or ![]() $\eta \otimes \omega _{E/ F}$ accordingly. This gives a map from
$\eta \otimes \omega _{E/ F}$ accordingly. This gives a map from ![]() $Y_+(\pi )$ to
$Y_+(\pi )$ to ![]() $X(\pi )$ which is the inverse of
$X(\pi )$ which is the inverse of ![]() $\mathcal {N}$. Hence, we complete the proof.
$\mathcal {N}$. Hence, we complete the proof.
Corollary 6.12 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2(E)$, distinguished by
$\mathrm {GL}_2(E)$, distinguished by ![]() $\mathrm {SL}_2(F)$. The number of
$\mathrm {SL}_2(F)$. The number of ![]() $\mathrm {SL}_2(F)$-invariant linear functionals on
$\mathrm {SL}_2(F)$-invariant linear functionals on ![]() $\pi$ is equal to the length of
$\pi$ is equal to the length of ![]() $\pi \vert _{\mathrm {GL}_2^+(E)}$ and both are
$\pi \vert _{\mathrm {GL}_2^+(E)}$ and both are ![]() $\lg _+(\pi )$.
$\lg _+(\pi )$.
Recall that ![]() $\lg (\pi )$ is the length of
$\lg (\pi )$ is the length of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ and
$\pi \vert _{\operatorname {SL}_2(E)}$ and ![]() $\lg _+(\pi )$ is the length of
$\lg _+(\pi )$ is the length of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$.
$\pi \vert _{\operatorname {GL}_2^+(E)}$.
Proposition 6.13 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\mathrm {GL}_2(E)$ such that
$\mathrm {GL}_2(E)$ such that ![]() $\lg (\pi )$ is different from
$\lg (\pi )$ is different from ![]() $1$. Suppose that
$1$. Suppose that ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {SL}_2(F)$. Then
$\operatorname {SL}_2(F)$. Then ![]() $\lg _+(\pi )$ is different from
$\lg _+(\pi )$ is different from ![]() $1$, and the only irreducible component of
$1$, and the only irreducible component of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$ which is distinguished by
$\pi \vert _{\operatorname {GL}_2^+(E)}$ which is distinguished by ![]() $\operatorname {SL}_2(F)$ is the one that is
$\operatorname {SL}_2(F)$ is the one that is ![]() $\psi _0$-generic (see the beginning of § 6.5 for the definition of
$\psi _0$-generic (see the beginning of § 6.5 for the definition of ![]() $\psi _0$).
$\psi _0$).
Proof. The proof of Proposition 4.4 of [Reference Anandavardhanan and PrasadAP03] can be applied, and we write the proof here for completeness. Suppose that ![]() $\lg _+(\pi )=1$ and denote
$\lg _+(\pi )=1$ and denote ![]() $\pi \vert _{\mathrm {GL}_2^+(E)}$ by
$\pi \vert _{\mathrm {GL}_2^+(E)}$ by ![]() $\pi ^+$. Under this assumption, we have that
$\pi ^+$. Under this assumption, we have that ![]() $\pi ^+\vert _{\mathrm {SL}_2(E)}$ is not irreducible. By Lemma 6.10 we have that the number of
$\pi ^+\vert _{\mathrm {SL}_2(E)}$ is not irreducible. By Lemma 6.10 we have that the number of ![]() $\mathrm {SL}_2(F)$-invariant linear forms is strictly bigger than one. However, by Corollary 6.12, there is only one
$\mathrm {SL}_2(F)$-invariant linear forms is strictly bigger than one. However, by Corollary 6.12, there is only one ![]() $\mathrm {SL}_2(F)$-invariant linear form, which is a contradiction. Hence,
$\mathrm {SL}_2(F)$-invariant linear form, which is a contradiction. Hence, ![]() $\lg _+(\pi )\neq 1$, and the result follows from Lemmas 6.9 and 6.10.
$\lg _+(\pi )\neq 1$, and the result follows from Lemmas 6.9 and 6.10.
Theorem 6.14 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$ distinguished by
$\operatorname {GL}_2(E)$ distinguished by ![]() $\operatorname {SL}_2(F)$, and
$\operatorname {SL}_2(F)$, and ![]() $\pi ^+$ the unique irreducible component of
$\pi ^+$ the unique irreducible component of ![]() $\pi \vert _{\operatorname {GL}_2^+(E)}$ that is
$\pi \vert _{\operatorname {GL}_2^+(E)}$ that is ![]() $\psi _0$-generic. Then
$\psi _0$-generic. Then ![]() $\pi ^+$ is distinguished by
$\pi ^+$ is distinguished by ![]() $\operatorname {SL}_2(F)$. Furthermore, let
$\operatorname {SL}_2(F)$. Furthermore, let ![]() $\tau$ be an irreducible component of
$\tau$ be an irreducible component of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$, distinguished by
$\pi \vert _{\operatorname {SL}_2(E)}$, distinguished by ![]() $\operatorname {SL}_2(F)$. Then
$\operatorname {SL}_2(F)$. Then ![]() $\tau$ is an irreducible component of
$\tau$ is an irreducible component of ![]() $\pi ^+\vert _{\operatorname {SL}_2(E)}$.
$\pi ^+\vert _{\operatorname {SL}_2(E)}$.
Theorem 6.15 Let ![]() $\pi$ be an irreducible supercuspidal
$\pi$ be an irreducible supercuspidal ![]() $\overline {\mathbf {F}}_{\ell }$-representation of
$\overline {\mathbf {F}}_{\ell }$-representation of ![]() $\operatorname {GL}_2(E)$ and
$\operatorname {GL}_2(E)$ and ![]() $\tau$ an irreducible component of
$\tau$ an irreducible component of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$. Suppose
$\pi \vert _{\operatorname {SL}_2(E)}$. Suppose ![]() $\tau$ is distinguished by
$\tau$ is distinguished by ![]() $\operatorname {SL}_2(F)$. Then,
$\operatorname {SL}_2(F)$. Then,
 \[
\mathrm{dim}\mathrm{Hom}{_{\operatorname{SL}_2(F)}}(\tau,\mathbf{1})=
\left\{\begin{array}{@{}ll} 1 & \mbox{if }
\pi\vert_{\operatorname{SL}_2(E)}\cong\tau, \\ 1 & \mbox{if } \lg_+(\pi)=2
\mbox{ and } \lg(\pi)=4, \\ 2 & \mbox{if } \lg_+(\pi)=\lg(\pi)=2,
\\ 4 & \mbox{if } \lg_+(\pi)=\lg(\pi)=4.
\end{array}\right. \]
\[
\mathrm{dim}\mathrm{Hom}{_{\operatorname{SL}_2(F)}}(\tau,\mathbf{1})=
\left\{\begin{array}{@{}ll} 1 & \mbox{if }
\pi\vert_{\operatorname{SL}_2(E)}\cong\tau, \\ 1 & \mbox{if } \lg_+(\pi)=2
\mbox{ and } \lg(\pi)=4, \\ 2 & \mbox{if } \lg_+(\pi)=\lg(\pi)=2,
\\ 4 & \mbox{if } \lg_+(\pi)=\lg(\pi)=4.
\end{array}\right. \]
The first case and the last case arises only when ![]() $p=2$.
$p=2$.
Proof. Let ![]() $\pi ^+\subset \pi |_{\operatorname {GL}_2^+(E)}$ be irreducible and
$\pi ^+\subset \pi |_{\operatorname {GL}_2^+(E)}$ be irreducible and ![]() $\psi _0$-generic. Let
$\psi _0$-generic. Let ![]() $\lg (\pi )'$ be the length of
$\lg (\pi )'$ be the length of ![]() $\pi ^+\vert _{\operatorname {SL}_2(E)}$. Since the components of
$\pi ^+\vert _{\operatorname {SL}_2(E)}$. Since the components of ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ are
$\pi \vert _{\operatorname {SL}_2(E)}$ are ![]() $\operatorname {GL}_2(E)$-conjugate, we deduce that
$\operatorname {GL}_2(E)$-conjugate, we deduce that ![]() $\lg (\pi )'=\lg (\pi )/ \lg _+(\pi )$. By Lemma 6.10, Corollary 6.12 and Theorem 6.14, we summarize that
$\lg (\pi )'=\lg (\pi )/ \lg _+(\pi )$. By Lemma 6.10, Corollary 6.12 and Theorem 6.14, we summarize that ![]() $\mathrm {dim}\mathrm {Hom}{_{\operatorname {SL}_2(F)}}(\pi,\mathbf {1})=\lg _+(\pi )$, and
$\mathrm {dim}\mathrm {Hom}{_{\operatorname {SL}_2(F)}}(\pi,\mathbf {1})=\lg _+(\pi )$, and
We obtain the result by a direct computation.
When ![]() $p$ is odd,
$p$ is odd, ![]() $E^{\times }/ F^{\times }E^{\times 2}$ is of order 2. Since
$E^{\times }/ F^{\times }E^{\times 2}$ is of order 2. Since ![]() $\lg _+(\pi )=\vert Y_+(\pi )\vert$ and the latter is a subset of
$\lg _+(\pi )=\vert Y_+(\pi )\vert$ and the latter is a subset of ![]() $\overline {\mathbf {F}}_{\ell }$-characters of
$\overline {\mathbf {F}}_{\ell }$-characters of ![]() $E^{\times }/ F^{\times }E^{\times 2}$, the case
$E^{\times }/ F^{\times }E^{\times 2}$, the case ![]() $\lg _+(\pi )=4$ can exist only when
$\lg _+(\pi )=4$ can exist only when ![]() $p$ is equal to
$p$ is equal to ![]() $2$.
$2$.
If ![]() $\pi \vert _{\operatorname {SL}_2(E)}$ is irreducible which implies that
$\pi \vert _{\operatorname {SL}_2(E)}$ is irreducible which implies that ![]() $\pi$ is primitive, then
$\pi$ is primitive, then ![]() $p=2$.
$p=2$.
6.6 The principal series representations
In this subsection, we will use Mackey Theory to prove the following theorem, following [Reference LuLu18].
Theorem 6.16 Let ![]() $I(\chi )$ be a principal series representation of
$I(\chi )$ be a principal series representation of ![]() $\operatorname {SL}_2(E)$.
$\operatorname {SL}_2(E)$.
(i) Let
 $\tau$ be an irreducible principal series representation of
$\tau$ be an irreducible principal series representation of  $\operatorname {SL}_2(E)$.
$\operatorname {SL}_2(E)$.(a) If
 $\tau =I(\chi )$ with
$\tau =I(\chi )$ with  $\chi |_{F^\times }=\mathbf {1}$ and
$\chi |_{F^\times }=\mathbf {1}$ and  $\chi \neq \mathbf {1}$, then
$\chi \neq \mathbf {1}$, then  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$.(b) If
 $\tau =I(\chi )$ with
$\tau =I(\chi )$ with  $\chi ^\sigma =\chi$, then
$\chi ^\sigma =\chi$, then  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=2$.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=2$.
(ii) Let
 $\tau$ be an irreducible subrepresentation of
$\tau$ be an irreducible subrepresentation of  $I(\chi )$ distinguished by
$I(\chi )$ distinguished by  $\operatorname {SL}_2(F)$ with
$\operatorname {SL}_2(F)$ with  $q_F\not \equiv 1 \pmod {\ell }$.
$q_F\not \equiv 1 \pmod {\ell }$.
(a) If
 $\chi =\nu ^{\pm 1}$ and
$\chi =\nu ^{\pm 1}$ and  $\ell \nmid q_E^2-1$, then
$\ell \nmid q_E^2-1$, then  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$.(b) If
 $\chi ^2=\mathbf {1},\chi =\chi _F\circ \operatorname {Nm}_{E/F}\neq \mathbf {1}$ and
$\chi ^2=\mathbf {1},\chi =\chi _F\circ \operatorname {Nm}_{E/F}\neq \mathbf {1}$ and  $\ell \nmid q_E^2-1$, then
$\ell \nmid q_E^2-1$, then
 \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=\begin{cases} 3 & \mbox{ if }\chi_F^2=\mathbf{1}, \\ 1 & \mbox{ if }\chi_F^2=\omega_{E/F}. \end{cases} \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=\begin{cases} 3 & \mbox{ if }\chi_F^2=\mathbf{1}, \\ 1 & \mbox{ if }\chi_F^2=\omega_{E/F}. \end{cases} \]
(c) If
 $\ell \mid q_E+1$ and
$\ell \mid q_E+1$ and  $\chi =\nu$, then
$\chi =\nu$, then  $\tau$ is the trivial character and
$\tau$ is the trivial character and  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$. In this case, there are two cuspidal (not supercuspidal) representations inside the Jordan–Holder series of
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$. In this case, there are two cuspidal (not supercuspidal) representations inside the Jordan–Holder series of  $I(\nu )$ which are not distinguished by
$I(\nu )$ which are not distinguished by  $\operatorname {SL}_2(F)$ if
$\operatorname {SL}_2(F)$ if  $E/F$ is unramified. If
$E/F$ is unramified. If  $E/F$ is ramified, then only one of two cuspidal representations is distinguished by
$E/F$ is ramified, then only one of two cuspidal representations is distinguished by  $\operatorname {SL}_2(F)$ with multiplicity two.
$\operatorname {SL}_2(F)$ with multiplicity two.(d) If
 $\ell \mid q_E-1$ and
$\ell \mid q_E-1$ and  $\ell \mid q_F+1$, then
$\ell \mid q_F+1$, then
 \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=\begin{cases} 2 & \mbox{ if }\tau\mbox{ is the Steinberg representation, } \\ 3 & \mbox{ if }\chi=\chi_F\circ \operatorname{Nm}_{E/F}\neq\mathbf{1} \mbox{ with }\chi_F^2=\mathbf{1}, \\ 1 & \mbox{ if }\chi=\chi_F\circ \operatorname{Nm}_{E/F}\mbox{ with }\chi_F^2=\omega_{E/F}. \end{cases} \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=\begin{cases} 2 & \mbox{ if }\tau\mbox{ is the Steinberg representation, } \\ 3 & \mbox{ if }\chi=\chi_F\circ \operatorname{Nm}_{E/F}\neq\mathbf{1} \mbox{ with }\chi_F^2=\mathbf{1}, \\ 1 & \mbox{ if }\chi=\chi_F\circ \operatorname{Nm}_{E/F}\mbox{ with }\chi_F^2=\omega_{E/F}. \end{cases} \]
Let ![]() $B(E)$ be the standard Borel subgroup of
$B(E)$ be the standard Borel subgroup of ![]() $\operatorname {SL}_2(E)$ and
$\operatorname {SL}_2(E)$ and ![]() $B(E)\backslash \operatorname {SL}_2(E)\cong P^1(E)$. Recall that there are two
$B(E)\backslash \operatorname {SL}_2(E)\cong P^1(E)$. Recall that there are two ![]() $F$-rational
$F$-rational ![]() $\operatorname {GL}_2(F)$-orbits in
$\operatorname {GL}_2(F)$-orbits in ![]() $P^1(E)$ which are
$P^1(E)$ which are ![]() $P^1(F)$ and
$P^1(F)$ and ![]() $P^1(E)-P^1(F)$. Moreover, the open orbit
$P^1(E)-P^1(F)$. Moreover, the open orbit ![]() $P^1(E)-P^1(F)$ is isomorphic to
$P^1(E)-P^1(F)$ is isomorphic to ![]() $E^\times \backslash \operatorname {GL}_2(F)$. There is an exact sequence
$E^\times \backslash \operatorname {GL}_2(F)$. There is an exact sequence
where ![]() $E^1=\{e\in E^\times :\operatorname {Nm}_{E/F}(e)=1 \}$. Thus,
$E^1=\{e\in E^\times :\operatorname {Nm}_{E/F}(e)=1 \}$. Thus, ![]() $P^1(E)$ decomposes into three
$P^1(E)$ decomposes into three ![]() $F$-rational
$F$-rational ![]() $\operatorname {SL}_2(F)$-orbits: one closed orbit
$\operatorname {SL}_2(F)$-orbits: one closed orbit ![]() $P^1(F)$ and two open orbits corresponding to
$P^1(F)$ and two open orbits corresponding to ![]() $F^\times /\operatorname {Nm}_{E/F}E^\times =\{\pm 1\}$.
$F^\times /\operatorname {Nm}_{E/F}E^\times =\{\pm 1\}$.
Lemma 6.17 Let ![]() $I(\chi )$ be a principal series representation of
$I(\chi )$ be a principal series representation of ![]() $\operatorname {SL}_2(E)$. Then
$\operatorname {SL}_2(E)$. Then ![]() $\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ), \mathbf {1}) \neq 0$ if and only if either
$\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ), \mathbf {1}) \neq 0$ if and only if either ![]() $\chi |_{F^\times }=\mathbf {1}$ or
$\chi |_{F^\times }=\mathbf {1}$ or ![]() $\chi |_{E^1}=\mathbf {1}$.
$\chi |_{E^1}=\mathbf {1}$.
Proof. Applying Mackey theory, one has an exact sequence
of ![]() $\overline {\mathbf {F}}_{\ell }$-vector spaces. If
$\overline {\mathbf {F}}_{\ell }$-vector spaces. If ![]() $\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ),\mathbf {1})$ is non-zero, then either
$\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ),\mathbf {1})$ is non-zero, then either ![]() $\chi |_{F^\times }$ or
$\chi |_{F^\times }$ or ![]() $\chi |_{E^1}$ is trivial. Conversely, it suffices to show that
$\chi |_{E^1}$ is trivial. Conversely, it suffices to show that ![]() $\chi |_{F^\times }\neq \mathbf {1}$ and
$\chi |_{F^\times }\neq \mathbf {1}$ and ![]() $\chi |_{E^1}=\mathbf {1}$ imply
$\chi |_{E^1}=\mathbf {1}$ imply ![]() $\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ),\mathbf {1})\neq 0$. Note that
$\operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\chi ),\mathbf {1})\neq 0$. Note that ![]() $\operatorname {Ext}^1_{F^\times }(\chi,\mathbf {1})=0$ if and only if
$\operatorname {Ext}^1_{F^\times }(\chi,\mathbf {1})=0$ if and only if ![]() $\chi |_{F^\times }$ is non-trivial; see [Reference Drevon and SécherreDS23, Proposition 8.4]. By the exact sequence, one has
$\chi |_{F^\times }$ is non-trivial; see [Reference Drevon and SécherreDS23, Proposition 8.4]. By the exact sequence, one has
when ![]() $\chi |_{F^\times }\neq \mathbf {1}$. This finishes the proof.
$\chi |_{F^\times }\neq \mathbf {1}$. This finishes the proof.
Lemma 6.18 Suppose that ![]() $\ell \nmid q_F-1$. Assume that
$\ell \nmid q_F-1$. Assume that ![]() $\pi$ (respectively,
$\pi$ (respectively, ![]() $\tau$) is a principal series representation of
$\tau$) is a principal series representation of ![]() $\operatorname {GL}_2(E)$ distinguished by
$\operatorname {GL}_2(E)$ distinguished by ![]() $\operatorname {GL}_2(F)$ (respectively,
$\operatorname {GL}_2(F)$ (respectively, ![]() $\operatorname {SL}_2(F)$) and
$\operatorname {SL}_2(F)$) and ![]() $\tau \subset \pi |_{\operatorname {SL}_2(E)}$. Set
$\tau \subset \pi |_{\operatorname {SL}_2(E)}$. Set ![]() $\pi |_{\operatorname {GL}_2^+(E)}=\oplus _i\pi _i$. Then
$\pi |_{\operatorname {GL}_2^+(E)}=\oplus _i\pi _i$. Then ![]() $\tau \subset \pi _0|_{\operatorname {SL}_2(E)}$ if and only if
$\tau \subset \pi _0|_{\operatorname {SL}_2(E)}$ if and only if ![]() $\pi _0$ is
$\pi _0$ is ![]() $\psi _0$-generic where
$\psi _0$-generic where ![]() $\psi _0$ is a non-degenerate character on
$\psi _0$ is a non-degenerate character on ![]() $E/F$.
$E/F$.
Proof. Suppose that ![]() $\pi =\pi (\chi _1,\chi _2)$ with
$\pi =\pi (\chi _1,\chi _2)$ with ![]() $\chi _1\chi _2$ trivial on
$\chi _1\chi _2$ trivial on ![]() $F^\times$. Then the
$F^\times$. Then the ![]() $\operatorname {GL}_2(F)$-invariant linear functional on
$\operatorname {GL}_2(F)$-invariant linear functional on ![]() $\pi$, up to a constant, is given by
$\pi$, up to a constant, is given by
where ![]() $W$ is the unique right
$W$ is the unique right ![]() $\operatorname {GL}_2(\mathcal {O}_E)$-invariant
$\operatorname {GL}_2(\mathcal {O}_E)$-invariant ![]() $\psi _0$-Whittaker function on
$\psi _0$-Whittaker function on ![]() $\pi$. Since there is a unique
$\pi$. Since there is a unique ![]() $\psi _0$-Whittaker functional on the space of
$\psi _0$-Whittaker functional on the space of ![]() $\pi$, exactly one constituent of the restriction of
$\pi$, exactly one constituent of the restriction of ![]() $\pi$ to
$\pi$ to ![]() $\operatorname {GL}_2^+(E)$ is
$\operatorname {GL}_2^+(E)$ is ![]() $\psi _0$-generic. Thus, the
$\psi _0$-generic. Thus, the ![]() $\operatorname {GL}_2(F)$-invariant functional can be non-zero only on the
$\operatorname {GL}_2(F)$-invariant functional can be non-zero only on the ![]() $\psi _0$-generic part of the restriction of
$\psi _0$-generic part of the restriction of ![]() $\pi$ to
$\pi$ to ![]() $\operatorname {GL}_2^+(E)$. Therefore,
$\operatorname {GL}_2^+(E)$. Therefore, ![]() $\tau \subset \pi _0|_{\operatorname {SL}_2(E)}$, i.e.
$\tau \subset \pi _0|_{\operatorname {SL}_2(E)}$, i.e. ![]() $\pi _0$ is
$\pi _0$ is ![]() $\operatorname {SL}_2(F)$-distinguished if and only if
$\operatorname {SL}_2(F)$-distinguished if and only if ![]() $\pi _0$ is
$\pi _0$ is ![]() $\psi _0$-generic.
$\psi _0$-generic.
Remark 6.19 Let ![]() $\varpi _F$ denote the uniformizer of the ring
$\varpi _F$ denote the uniformizer of the ring ![]() $\mathfrak {o}_F$ of integers of
$\mathfrak {o}_F$ of integers of ![]() $F$. Matringe pointed out that when
$F$. Matringe pointed out that when ![]() $q_F\equiv 1 \pmod {\ell }$,
$q_F\equiv 1 \pmod {\ell }$, ![]() $\pi$ is distinguished by
$\pi$ is distinguished by ![]() $\operatorname {GL}_2(F)$ but
$\operatorname {GL}_2(F)$ but
Thus, this method does not work when we try to determine the multiplicity for the irreducible constituent of ![]() $I(\chi )$ with
$I(\chi )$ with ![]() $\chi ^2=\mathbf {1}$ when
$\chi ^2=\mathbf {1}$ when ![]() $q_F\equiv 1 \pmod {\ell }$.
$q_F\equiv 1 \pmod {\ell }$.
Now we are ready to prove Theorem 6.16.
Proof of Theorem 6.16 (i) Note that if ![]() $\chi \neq \nu ^{\pm 1}$ and
$\chi \neq \nu ^{\pm 1}$ and ![]() $\chi ^2\neq \mathbf {1}$, then
$\chi ^2\neq \mathbf {1}$, then ![]() $I(\chi )$ is irreducible. Then it follows from Lemma 6.17 except that
$I(\chi )$ is irreducible. Then it follows from Lemma 6.17 except that ![]() $\chi =\mathbf {1}$ and
$\chi =\mathbf {1}$ and ![]() $\ell \nmid q_E-1$. It is enough to show that
$\ell \nmid q_E-1$. It is enough to show that ![]() $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\mathbf {1}),\mathbf {1})=2$ when
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\mathbf {1}),\mathbf {1})=2$ when ![]() $\ell \nmid q_E-1$. Note that
$\ell \nmid q_E-1$. Note that ![]() $\pi (\mathbf {1},\mathbf {1})$ is both
$\pi (\mathbf {1},\mathbf {1})$ is both ![]() $\operatorname {GL}_2(F)$-distinguished and
$\operatorname {GL}_2(F)$-distinguished and ![]() $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished with multiplicity one. Thus,
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished with multiplicity one. Thus, ![]() $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\mathbf {1}),\mathbf {1})=2$ by Proposition 6.8.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(I(\mathbf {1}),\mathbf {1})=2$ by Proposition 6.8.
(ii) If ![]() $\tau$ is a trivial character, then
$\tau$ is a trivial character, then ![]() $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$. Let
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=1$. Let ![]() $\tau$ be an infinite-dimensional subrepresentation of
$\tau$ be an infinite-dimensional subrepresentation of ![]() $I(\chi )$.
$I(\chi )$.
(a) If
 $\chi =\nu ^{-1}$, then
$\chi =\nu ^{-1}$, then  $\tau$ is the trivial character. If
$\tau$ is the trivial character. If  $\chi =\nu$ and
$\chi =\nu$ and  $\tau$ is the Steinberg representation
$\tau$ is the Steinberg representation  $\operatorname {St}$, then there exists a short exact sequence
of
$\operatorname {St}$, then there exists a short exact sequence
of \[ 0 \to \operatorname{St} \to I(\nu) \to \mathbf{1} \to 0 \]
\[ 0 \to \operatorname{St} \to I(\nu) \to \mathbf{1} \to 0 \]
 $\operatorname {SL}_2(E)$-representations. Taking the functor
$\operatorname {SL}_2(E)$-representations. Taking the functor  $\operatorname {Hom}_{\operatorname {SL}_2(F)}(-,\mathbf {1})$, one has an exact sequence
Note that
$\operatorname {Hom}_{\operatorname {SL}_2(F)}(-,\mathbf {1})$, one has an exact sequence
Note that \[ 0 \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(\mathbf{1},\mathbf{1}) \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\nu),\mathbf{1}) \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(\operatorname{St},\mathbf{1}) \to \operatorname{Ext}^1_{\operatorname{SL}_2(F)}(\mathbf{1},\mathbf{1}). \]
\[ 0 \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(\mathbf{1},\mathbf{1}) \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\nu),\mathbf{1}) \to \operatorname{Hom}_{\operatorname{SL}_2(F)}(\operatorname{St},\mathbf{1}) \to \operatorname{Ext}^1_{\operatorname{SL}_2(F)}(\mathbf{1},\mathbf{1}). \]
 $\operatorname {Ext}^1_{\operatorname {SL}_2(F)}(\mathbf {1},\mathbf {1})=0$. Thanks to Lemma 6.17, we have
Therefore,
$\operatorname {Ext}^1_{\operatorname {SL}_2(F)}(\mathbf {1},\mathbf {1})=0$. Thanks to Lemma 6.17, we have
Therefore, \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\nu),\mathbf{1})=2. \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\nu),\mathbf{1})=2. \]
 $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {St},\mathbf {1})=2-1=1$.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {St},\mathbf {1})=2-1=1$.(b) If
 $\chi =\chi _F\circ \operatorname {Nm}_{E/F}$ with
$\chi =\chi _F\circ \operatorname {Nm}_{E/F}$ with  $\chi _F^2=\mathbf {1}$, then the irreducible principal series representation
$\chi _F^2=\mathbf {1}$, then the irreducible principal series representation  $\pi (\mathbf {1},\chi )$ is distinguished by
$\pi (\mathbf {1},\chi )$ is distinguished by  $\operatorname {GL}_2(F)$. Furthermore,
There is only one subrepresentation in
$\operatorname {GL}_2(F)$. Furthermore,
There is only one subrepresentation in \[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\mathbf{1},\chi),\chi_F)=1=\dim\operatorname{Hom}_{\operatorname{GL}_2(F)} (\pi(\mathbf{1},\chi),\chi_F\omega_{E/F}). \]
\[ \dim\operatorname{Hom}_{\operatorname{GL}_2(F)}(\pi(\mathbf{1},\chi),\chi_F)=1=\dim\operatorname{Hom}_{\operatorname{GL}_2(F)} (\pi(\mathbf{1},\chi),\chi_F\omega_{E/F}). \]
 $I(\chi )$ which is
$I(\chi )$ which is  $(\mathrm {U},\psi _0)$-generic, which implies that only one constituent in
$(\mathrm {U},\psi _0)$-generic, which implies that only one constituent in  $I(\chi )$ is distinguished by
$I(\chi )$ is distinguished by  $\operatorname {SL}_2(F)$. Thus
$\operatorname {SL}_2(F)$. Thus  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=3$.
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\tau,\mathbf {1})=3$.
If
 $\chi =\chi _F\circ \operatorname {Nm}_{E/F}$ with
$\chi =\chi _F\circ \operatorname {Nm}_{E/F}$ with  $\chi _F^2=\omega _{E/F}$, then
$\chi _F^2=\omega _{E/F}$, then  $\pi (\mathbf {1},\chi )$ is both
$\pi (\mathbf {1},\chi )$ is both  $(\operatorname {GL}_2(F),\chi _F)$-distinguished and
$(\operatorname {GL}_2(F),\chi _F)$-distinguished and  $(\operatorname {GL}_2(F),\chi _F^{-1})$-distinguished. Thus,
Note that two constituents in
$(\operatorname {GL}_2(F),\chi _F^{-1})$-distinguished. Thus,
Note that two constituents in \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\chi),\mathbf{1})=2. \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(I(\chi),\mathbf{1})=2. \]
 $I(\chi )$ are
$I(\chi )$ are  $(\mathrm {U},\psi _0)$-generic. Thus, each one in
$(\mathrm {U},\psi _0)$-generic. Thus, each one in  $I(\chi )$ is distinguished by
$I(\chi )$ is distinguished by  $\operatorname {SL}_2(F)$ with multiplicity one.
$\operatorname {SL}_2(F)$ with multiplicity one.(c) This case is trivial.
If
 $\ell \mid q_E+1$ and
$\ell \mid q_E+1$ and  $\tau$ is a cuspidal non-supercuspidal representation of
$\tau$ is a cuspidal non-supercuspidal representation of  $\operatorname {SL}_2(E)$, then there is a special representation
$\operatorname {SL}_2(E)$, then there is a special representation  $\operatorname {Sp}$ of
$\operatorname {Sp}$ of  $\operatorname {GL}_2(E)$ such that
$\operatorname {GL}_2(E)$ such that  $\tau \subset \operatorname {Sp}|_{\operatorname {SL}_2(E)}$. If
$\tau \subset \operatorname {Sp}|_{\operatorname {SL}_2(E)}$. If  $E/F$ is unramified, then
$E/F$ is unramified, then  $\operatorname {Sp}$ is neither
$\operatorname {Sp}$ is neither  $\operatorname {GL}_2(F)$-distinguished nor
$\operatorname {GL}_2(F)$-distinguished nor  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished. (See [Reference SécherreSéc19, Remark 2.8].) Thus,
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished. (See [Reference SécherreSéc19, Remark 2.8].) Thus,  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {Sp}|_{\operatorname {SL}_2(E)},\mathbf {1})=0$ by Proposition 6.8. If
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {Sp}|_{\operatorname {SL}_2(E)},\mathbf {1})=0$ by Proposition 6.8. If  $E/F$ is ramified, then
$E/F$ is ramified, then  $\operatorname {Sp}$ is not
$\operatorname {Sp}$ is not  $\operatorname {GL}_2(F)$-distinguished but
$\operatorname {GL}_2(F)$-distinguished but  $(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished. It is also
$(\operatorname {GL}_2(F),\omega _{E/F})$-distinguished. It is also  $(\operatorname {GL}_2(F),\nu \vert _{F^{\times }}^{1/2})$-distinguished; see Theorem 4.6(ii). Due to Proposition 6.8,
$(\operatorname {GL}_2(F),\nu \vert _{F^{\times }}^{1/2})$-distinguished; see Theorem 4.6(ii). Due to Proposition 6.8,  $\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {Sp}|_{\operatorname {SL}_2(E)},\mathbf {1})=2$. Note that there is only one constituent in
$\dim \operatorname {Hom}_{\operatorname {SL}_2(F)}(\operatorname {Sp}|_{\operatorname {SL}_2(E)},\mathbf {1})=2$. Note that there is only one constituent in  $\operatorname {Sp}|_{\operatorname {SL}_2(E)}$ which is
$\operatorname {Sp}|_{\operatorname {SL}_2(E)}$ which is  $(\mathrm {U},\psi _0)$-generic, denoted by
$(\mathrm {U},\psi _0)$-generic, denoted by  $\tau$. Thus,
This finishes the proof.
$\tau$. Thus,
This finishes the proof. \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=2. \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\tau,\mathbf{1})=2. \]
(d) If
 $\ell \mid q_E-1$ and
$\ell \mid q_E-1$ and  $\ell \mid q_F+1$, then
$\ell \mid q_F+1$, then  $E/F$ is an unramified field extension. In this case,
$E/F$ is an unramified field extension. In this case,  $I(\mathbf {1})=\mathbf {1}\oplus \operatorname {St}$. Thanks to Theorem 4.6(iii),
If
$I(\mathbf {1})=\mathbf {1}\oplus \operatorname {St}$. Thanks to Theorem 4.6(iii),
If \[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\operatorname{St},\mathbf{1})=2. \]
\[ \dim\operatorname{Hom}_{\operatorname{SL}_2(F)}(\operatorname{St},\mathbf{1})=2. \]
 $\tau \subset I(\chi _F\circ \operatorname {Nm}_{E/F})$ with
$\tau \subset I(\chi _F\circ \operatorname {Nm}_{E/F})$ with  $\chi _F^2=\omega _{E/F}$ or
$\chi _F^2=\omega _{E/F}$ or  $\mathbf {1}$, this case is similar to case (b).
$\mathbf {1}$, this case is similar to case (b).
Remark 6.20 If ![]() $\ell \mid q_F-1$, one can still prove that
$\ell \mid q_F-1$, one can still prove that ![]() $\operatorname {St}$ is distinguished by
$\operatorname {St}$ is distinguished by ![]() $\operatorname {SL}_2(F)$ with multiplicity two due to Theorem 4.6 and that the constituents in
$\operatorname {SL}_2(F)$ with multiplicity two due to Theorem 4.6 and that the constituents in ![]() $I(\chi _F\circ \operatorname {Nm}_{E/F})$ with
$I(\chi _F\circ \operatorname {Nm}_{E/F})$ with ![]() $\chi _F^2=\omega _{E/F}$ are both distinguished by
$\chi _F^2=\omega _{E/F}$ are both distinguished by ![]() $\operatorname {SL}_2(F)$ with multiplicity one. But we cannot determine the situation for
$\operatorname {SL}_2(F)$ with multiplicity one. But we cannot determine the situation for ![]() $\tau \subset I(\chi _F\circ \operatorname {Nm}_{E/F})$ with
$\tau \subset I(\chi _F\circ \operatorname {Nm}_{E/F})$ with ![]() $\chi _F^2=\mathbf {1}$.
$\chi _F^2=\mathbf {1}$.
Acknowledgements
We warmly thank Vincent Sécherre for his remarks and comments which made it possible, in particular, to generalize the results from ![]() $\operatorname {GL}_2$ to
$\operatorname {GL}_2$ to ![]() $\operatorname {GL}_n$. We also thank Nadir Matringe and Alberto Mínguez for useful discussions. We thank an anonymous referee for his useful comments and corrections. The main results were obtained and the paper was written when we were working together at the University of Vienna as postdocs. We would like to thank the University of Vienna for providing such nice working environment.
$\operatorname {GL}_n$. We also thank Nadir Matringe and Alberto Mínguez for useful discussions. We thank an anonymous referee for his useful comments and corrections. The main results were obtained and the paper was written when we were working together at the University of Vienna as postdocs. We would like to thank the University of Vienna for providing such nice working environment.
Conflicts of interest
None.
Financial support
The work of T.L. was partially supported by the ERC, grant agreement 101001159. H.L. was partially supported by NSFC 12301031.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.