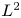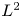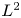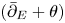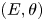Vanishing theorem for tame harmonic bundles via L²-cohomology

Abstract

Using $L^2$-methods, we prove a vanishing theorem for tame harmonic bundles over quasi-compact Kähler manifolds in a very general setting. As a special case, we give a completely new proof of the Kodaira-type vanishing theorems for Higgs bundles due to Arapura. To prove our vanishing theorem, we construct a fine resolution of the Dolbeault complex for tame harmonic bundles via the complex of sheaves of $L^2$-forms, and we establish the Hörmander $L^2$-estimate and solve $(\bar {\partial }_E+\theta )$-equations for Higgs bundles $(E,\theta )$.

1. Introduction

1.1 Main result

Let $(X,\omega )$ be a compact Kähler manifold and let $D$ be a simple normal crossing divisor on $X$. Let $(E,\theta,h)$ be a tame harmonic bundle over $X-D$ such that $\theta$ has nilpotent residues on $D$ (see § 2.1 for the precise definition), and let ${}^\diamond \! E$ be the subsheaf of $\iota _*E$ consisting of sections whose norms with respect to $h$ have sub-polynomial growth (see § 4.2), where $\iota :X-D\hookrightarrow X$ is the inclusion. By Simpson–Mochizuki, ${}^\diamond \! E$ is a locally free coherent sheaf, and $(E,\theta )$ extends to a logarithmic Higgs bundle

\begin{align*} \theta:{}^\diamond\! E\to {}^\diamond\! E\otimes \Omega_X^1(\log D) \end{align*}

such that

\begin{align*} \theta\wedge \theta=0. \end{align*}

We refer to § 4.2 for more details.

In this paper, we prove the following vanishing theorem.

Theorem 1 (Theorem 4.20)

Let $(X,\omega )$ be a compact Kähler manifold of dimension $n$, and let $D$ be a simple normal crossing divisor on $X$. Let $(E,\theta )$ be a tame harmonic bundle on $X-D$ such that $\theta$ has nilpotent residues on $D$, and let $({}^\diamond \! E,\theta )$ be the extension of $(E,\theta )$ on $X$ as introduced above. Let $L$ be a holomorphic line bundle on $X$ equipped with a smooth Hermitian metric $h_L$ such that its curvature $\sqrt {-1}R(h_L)\geq 0$ and has at least $n-k$ positive eigenvalues at every point on $X$ as a real $(1,1)$-form. Let $B$ be a nef line bundle on $X$. Then for the following (Dolbeault) complex of sheaves

(1) \begin{equation} {\rm Dol}({}^\diamond\! E,\theta):={}^\diamond\! E\xrightarrow{\wedge\theta}{}^\diamond\! E\otimes \Omega^1_X(\log D) \xrightarrow{\wedge\theta}\cdots\xrightarrow{\wedge\theta}{}^\diamond\! E\otimes \Omega^n_X(\log D), \end{equation}

the hypercohomology

\[ \mathbb{H}^i\big(X, {\rm Dol}({}^\diamond\! E,\theta)\otimes L\otimes {B} \big)=0 \]

for any $i>n+k$.

Theorem A seems new even if the tame harmonic bundle $(E,\theta,h)$ comes from a complex variation of polarized Hodge structures over $X-D$. It indeed interpolates the Kodaira–Akizuki–Nakano-type vanishing theorems for nilpotent Higgs bundles [Ara19, Theorem 1] by Arapura (in the case that $L$ is ample, see Corollary 4.22), and the log Girbau vanishing theorem by Huang, Liu, Wan and Yang [HLWY23, Corollary 1.2] (in the case that $(E,\theta )=(\mathscr {O}_{X-D},0)$, see Remark 4.21). We stress here that our proof of Theorem A is essentially self-contained (in particular, we do not apply the deep Simpson–Mochizuki correspondence) and is purely in characteristic $0$ (since we are working on Kähler manifolds), comparing with the celebrated vanishing theorem by Arapura [Ara19] whose proof is in characteristic $p$ (see § 1.3 for more details). The main technique in the proof of Theorem A is a new application of $L^2$-methods to tame harmonic bundles, and we hope that it can bring some new input in the study of $L^2$-cohomology for Higgs bundles. Let us also mention a few byproducts of our proof: we construct explicitly complexes of sheaves of $L^2$-forms for tame Higgs bundles which are quasi-isomorphic to the Dolbeault complexes (1) (see Theorem 4.18) in a similar manner (but using different metric) as [Zuc79] in which Zucker did this for variation of polarized Hodge structures over a quasi-projective curve; we also establish the Hörmander $L^2$-estimate and solvability criteria for $(\bar {\partial }_E+\theta )$-equations for Higgs bundles $(E,\theta )$ (see Theorem 3.6 and Corollary 3.7).

If we apply the Simpson–Mochizuki correspondence [Sim90, Moc06] for parabolic Higgs bundles on projective manifolds to Theorem A, we can obtain a vanishing theorem for parabolic Higgs bundles. We refer the readers to Corollary 4.22 for the precise statement.

1.2 Idea of the proof

Let us briefly explain the main idea of our proof of Theorem A. We first construct a complex of $L^2$ fine sheaves for the tame harmonic bundle $(E,\theta,h)$ whose Higgs field $\theta$ has nilpotent residues on $D$, which is quasi-isomorphic to the Dolbeault complex

(2)

For the given Kähler metric $\omega$ on $X$ (we denote the restricted Kähler form $\omega |_{X-D}$ again by $\omega$ over $X-D$) and a smooth Hermitian metric $g$ for $E$ over $X-D$, we let $\mathfrak L^{m}_{(2)}(X,E)_{g,\omega }$ be the sheaf on $X$ of germs of $E$-valued $m$-forms $\sigma$ with measurable coefficients such that $\lvert \sigma \rvert _{g,\omega }^2$ is locally integrable and $(\bar {\partial }+\theta )(\sigma )$ exists weakly as a locally $L^2$, $E$-valued $(m+1)$-form. Here the $L^2$ norms $\lvert \sigma \rvert _{g,\omega }^2$ are induced by $\omega$ on differential forms and by $g$ on elements in $E$. Since $(\bar {\partial }+\theta )^2=0$, it thus gives rise to a complex of fine sheaves

(3)\begin{equation} \mathfrak L^{0}_{(2)}(X,E)_{g,\omega}\stackrel{\bar{\partial}+\theta}{\to} \cdots\stackrel{\bar{\partial}+\theta}{\to} \mathfrak L^{2n}_{(2)}(X,E)_{g,\omega}. \end{equation}

As the harmonic metric $h$ is a canonical metric on $E$, it is quite natural to make the choice that $g$ is the harmonic metric $h$. In addition, we replace the Kähler form $\omega$ by a Poincaré-type metric $\omega _P$ over $X-D$ as [Zuc79, CKS87, KK87]. However, even for the case when $(E,\theta )$ comes from a variation of polarized Hodge structures over $X-D$, it turns out to be a quite difficult problem that $(\mathfrak L_{(2)}^{\bullet }(X,E)_{h,\omega _P},\bar {\partial }+\theta )$ is quasi-isomorphic to ${\rm Dol}({}^\diamond \! E,\theta )$, and one essentially cannot avoid the delicate norm estimate for Hodge metrics near $D$ in [Sch73, Kas85, CKS86] (see, e.g., [Zuc79, JYZ07]). In this paper, we make a slight perturbation $h_{\boldsymbol {a},N}$ of the harmonic metric $h$ (see Lemma 4.11 for more details) as [Moc02, § 4.5.3] such that $h_{\boldsymbol {a},N}$ will degenerate mildly, albeit the norm of harmonic metric $h$ for ${}^\diamond \! E$ is of sub-polynomial growth. In addition, we slightly perturb the Kähler metric $\omega$ on $X-D$ into a complete Kähler metric $\omega _{\boldsymbol {a},N}$ (see Lemma 4.10), which is mutually bounded with the Poincaré metric $\omega _P$ near the divisor $D$. This construction indeed brings us several advantages (among others): we can prove that $(\mathfrak L_{(2)}^{\bullet }(X,E)_{{h_{\boldsymbol {a},N},\omega _{\boldsymbol {a},N}}},\bar {\partial }+\theta )$ is indeed quasi-isomorphic to ${\rm Dol}({}^\diamond \! E,\theta )$, and the negative contribution of the curvature $(E,\theta,{h_{\boldsymbol {a},N}})$ is small enough to be absorbed completely by the curvature $\sqrt {-1} R(h_L)$ of any (partially) positive metrized line bundle $(L,h_L)$.

Thus, we have the following $L^2$ fine resolution of ${\rm Dol}({}^\diamond \! E,\theta )\otimes L$

(4)\begin{equation} (L_{(2)}^{\bullet}(X-D,E\otimes L|_{X-D})_{{h_{\boldsymbol{a},N}}\cdot h_L,{\omega_{\boldsymbol{a},N}}},D''), \end{equation}

where $D'':=\bar {\partial }_{E\otimes L}+\theta \otimes \mathbb {1}_L$ satisfying $D''^2=0$ (we assume $B=\mathscr {O}_X$ here for simplicity). We then reduce the proof of Theorem A to the vanishing of $i$th cohomology of the complex of global sections of (4) for $i>\dim X+k$. To prove this, we first generalize the $L^2$-estimate by Hörmander, Andreotti-Vesentini, Skoda, Demailly and others to Higgs bundles. Roughly speaking, we prove that under certain curvature conditions for Higgs bundles $(E,\theta )$ over $X-D$, we can solve the $D''$-equation as the $\bar {\partial }$-equation in a similar way (see Theorem 3.6 and Corollary 3.7). We then choose the perturbation $h_{\boldsymbol {a},N}$ of $h$ carefully such that such required curvature condition can be fulfilled and it enables us to prove the vanishing result for the $L^2$-cohomology of (4). This idea of solving $D''$-equation for Higgs bundles using $L^2$-method seems a new ingredient as we are aware of.

1.3 Previous results

For $X$ a complex projective manifold with a simple normal crossing divisor $D$, Arapura [Ara19] gives a vanishing theorem for semistable Higgs bundles $(E, \theta )$ over $X-D$ with trivial parabolic structure, trivial Chern classes and nilpotent Higgs field $\theta$. In the spirit of the algebraic proof of the Kodaira vanishing theorem by Deligne and Illusie [DI87], the proof of Arapura's vanishing theorem is reduced to the mod $p$-setting and boils down to a periodic sequence of Higgs bundles $(E_i, \theta _i):=B^i(E, \theta )$ through an operator $B$ raised from the absolute Frobenius morphism, which is due to Lan, Sheng, Yang and Zuo [LSZ19, LSYZ13] and Langer [Lan15]. The dimension of the cohomology $\mathbb {H}^i(X, {\rm Dol}(E_i, \theta _i)\otimes L^{p^i})$ is non-decreasing for $\{(E_i, \theta _i)\}$ and ample line bundle $L$, then Arapura's vanishing theorem follows from Serre's vanishing theorem. With his vanishing theorem, Arapura reproves the Saito's vanishing theorem (see, e.g., Popa [Pop16]) for variation of polarized Hodge structures with unipotent monodromy on the complement of a normal crossing divisor on any complex projective manifold. In the follow-up article [AHL19], Arapura's vanishing theorem for Higgs bundles is generalized to parabolic Higgs bundles. As applications, the vanishing theorem for parabolic Higgs bundle recovers the Saito's vanishing theorem coming from complex variation of Hodge structures over $X-D$. Our main result, Theorem A, is more general compared with the main results in [Ara19] and [AHL19] in the sense that Theorem A applies to general compact Kähler manifolds together with partially ample line bundles. Another new output of this article is that we establish the Hörmander $L^2$-estimate and solve $(\bar {\partial }_E+\theta )$-equations for Higgs bundles $(E,\theta )$, as an important byproduct of the proof of our main theorem.

Notation and conventions

• – A couple $(E,h)$ is a Hermitian vector bundle on a complex manifold $X$ if $E$ is a holomorphic vector bundle on $X$ equipped with a smooth hermitian metric $h$. Here $\bar {\partial }_E$ denotes the complex structure of $E$ and we sometimes simply write $\bar {\partial }$ if no confusion arises.

• – Two hermitian metrics $h$ and $\tilde {h}$ of a holomorphic vector bundle on $X$ are mutually bounded if $C^{-1}h\leq \tilde {h}\leq Ch$ for some constant $C>0$, and we shall denote this by $h\sim h'$.

• – For a hermitian vector bundle $(E,h)$ on a complex manifold, $R(E, h)$ or simply $R(h)$ denotes its Chern curvature.

• – We use $\Delta$ to denote the unit disk in $\mathbb {C}$.

• – The complex manifold $X$ in this paper are always assumed to be connected and of dimension $n$.

• – Throughout the paper we always work over the complex number field $\mathbb {C}$.

2. Technical preliminaries

2.1 Higgs bundle and tame harmonic bundle

In this section we recall the definition of Higgs bundles and tame harmonic bundles. We refer the reader to [Sim88, Sim90, Sim92, Moc02, Moc07] for further details.

Definition 2.1 Let $X$ be a complex manifold. A Higgs bundle on $X$ is a pair $(E,\theta )$ where $E$ is a holomorphic vector bundle with $\bar {\partial }_E$ its complex structure, and $\theta :E\to E\otimes \Omega ^1_X$ is a holomorphic one form with value in $\text {End}(E)$, say Higgs field, satisfying $\theta \wedge \theta =0$.

Let $(E,\theta )$ be a Higgs bundle over a complex manifold $X$. Write $D'':=\bar {\partial }_E+\theta$. Then $D''^2=0$. Suppose $h$ is a smooth hermitian metric of $E$. Denote by $\mathbb {\partial }_h+\bar {\partial }_E$ the Chern connection with respect to $h$, and $\theta ^*_h$ be the adjoint of $\theta$ with respect to $h$. Write $D_h':= {\partial }_h+\theta _h^*$. The metric $h$ is harmonic if the operator $D_h:=D_h'+D''$ is integrable, that is, if $D_h^2=0$.

Definition 2.2 (Harmonic bundle)

A harmonic bundle on a complex manifold $X$ is a Higgs bundle $(E,\theta )$ endowed with a harmonic metric $h$.

Let $X$ be an $n$-dimensional complex manifold, and let $D$ be a simple normal crossing divisor on $X$.

Definition 2.3 (Admissible coordinate)

Let $p$ be a point of $X$, and assume that $\{D_{j}\}_{ j=1,\ldots,\ell }$ are components of $D$ containing $p$. An admissible coordinate around $p$ is the tuple $(U;z_1,\ldots,z_n;\varphi )$ (or simply $(U;z_1,\ldots,z_n)$ if no confusion arises) where

• – $U$ is an open subset of $X$ containing $p$;

• – there is a holomorphic isomorphism $\varphi :U\to \Delta ^n$ such that $\varphi (D_j)=(z_j=0)$ for any $j=1,\ldots,\ell$.

We shall write $U^*:=U-D$, $U(r):=\{z\in U\mid |z_i|< r, \, \forall i=1,\ldots,n\}$ and $U^*(r):=U(r)\cap U^*$.

For any harmonic bundle $(E,\theta,h)$, let $p$ be any point of $X$, and $(U;z_1,\ldots,z_n)$ be an admissible coordinate around $p$. On $U$, we have the description

(5)\begin{equation} \theta=\sum_{j=1}^{\ell}f_j d\log z_j+\sum_{k=\ell+1}^{n}g_k \, dz_k, \end{equation}

where $f_j$ and $g_k$ are holomorphic sections of ${\rm End}(E)$ on $U^*$.

Definition 2.4 (Tameness)

Let $t$ be a formal variable. We have the polynomials $\det (f_j-t)$, and $\det (g_k-t)$, whose coefficients are holomorphic functions defined over $U^*$. When the functions can be extended to the holomorphic functions over $U$, the harmonic bundle is called tame at $p$. A harmonic bundle is tame if it is tame at each point.

Definition 2.5 (Nilpotent residues)

Let $(E, \theta )$ be a Higgs bundle on $X-D$. We say that $\theta$ has nilpotent residues on $D$ if for each component $D_j$ of $D$ and any point $p\in D_j$ one has $\det (f_j-t)|_{U\cap D_j}=(-t)^{{\rm rank} E}$.

Remark 2.6 One should note that the above definition introduced in [Moc02, p. 435] is more general than that in [Ara19, Theorem 1], where the nilpotency of Higgs field $\theta$ is defined to be the local matrix of $\theta$ is nilpotent. We refer the reader to [Ara19] for more details.

Recall that the Poincaré metric $\omega _P$ on $(\Delta ^*)^\ell \times \Delta ^{n-\ell }$ is described as

\[ \omega_P=\sum_{j=1}^{\ell}\frac{\sqrt{-1}dz_j\wedge d\bar{z}_j}{|z_j|^2(\log |z_j|^2)^2}+\sum_{k=\ell+1}^{n}\frac{\sqrt{-1}dz_k\wedge d\bar{z}_k}{(1-|z_k|^2)^2}. \]

Note that

\[ \omega_P=-\sqrt{-1}\partial\overline{\partial} \log \bigg(\prod_{j=1}^{\ell}(-\log |z_j|^2)\cdot \prod_{k=\ell+1}^{n}(1-|z_k|^2)\bigg). \]

For a tame harmonic bundle such that the Higgs field has nilpotent residues, we have the following crucial norm estimate for Higgs field $\theta$. The one-dimensional case is due to Simpson [Sim90, Theorem 1] and Mochizuki [Moc02, Proposition 4.1] in general.

Theorem 2.7 Let $(E,\theta,h)$ be a tame harmonic bundle on $X-D$ such that $\theta$ has nilpotent residues on $D$. Let $f_j,g_k$ be the matrix-valued holomorphic functions as in Definition 2.4. Then there exists a positive constant $C>0$ satisfying that

\begin{align*} &|f_j|_h\leq \frac{C}{-\log |z_j|^2}, \quad \mbox{for}\ j=1,\ldots,\ell;\\ &|g_k|_h \leq C, \quad \mbox{for}\ k=\ell+1,n. \end{align*}

In other words, the norm

\[ | \theta|_{h,\omega_P}\leq C \]

holds over $U^*(r)$ for some constant $C>0$ and $0< r< 1$.

2.2 Curvature property of Higgs bundles

Suppose now $(E, \theta )$ is a Higgs bundle of rank $r$ equipped with a Hermitian metric $h$ over a Kähler manifold $(X,\omega )$ of dimension $n$.

We make the following assumption for $(E,\theta,h)$ throughout this section.

Assumption 2.8 We assume $\bar {\partial }_E\theta _h^*=0$.

We note that Assumption 2.8 is valid for $(E,\theta,h)\otimes (F,h_F)$ where $F$ is a holomorphic line bundle endowed with a hermitian metric $h_F$ and $(E,\theta,h)$ is a harmonic bundle.

Consider the connection $D_h:=D_h'+D''$ (see the paragraph after Definition 2.1). Assumption 2.8 is equivalent to that $\partial _h\theta =0$. Hence, one has the curvature

(6)\begin{equation} F(h)\colon= D_h^2=[D_h',D'']=R(h)+[\theta,\theta^*] \in A^{1,1}(X,\text{End}(E)), \end{equation}

where $R(h)\colon= (\partial _h+\bar {\partial }_E)^2$. Moreover, one can easily see that $(\sqrt {-1}F(h))^{*}=\sqrt {-1}F(h)$. In other words, $\sqrt {-1}F(h)$ is a $(1,1)$-form with $\text {Herm}(E)$-value, where $\text {Herm}(E)$ is the hermitian endomorphism of $(E,h)$.

By Simpson [Sim88], one has the following Kähler identities:

(7)\begin{align} \sqrt{-1}[\Lambda_\omega,D'']=(D_h')^* , \end{align}

(8)\begin{align} \sqrt{-1}[\Lambda_\omega,D_h']=-(D'')^* , \end{align}

where $(D_h')^*$ and $(D'')^*$ are the formally adjoint operators of $D_h'$ and $D''$ with respect to $h$ and $\omega$, and $\Lambda _{\omega }$ is the adjoint operator of $\wedge \omega$ with respect to the Hodge inner product on differential forms. Define the Laplacians

\begin{align*} \Delta'&=D'_hD_h'^*+(D'_h)^*D'_h,\\ \Delta''&=D''(D'')^*+(D'')^*D''. \end{align*}

A standard computation gives the following identity.

Lemma 2.9 (Bochner–Kodaira–Nakano identity for Higgs bundles)

Let $(E,\theta )$ be a Higgs bundle endowed with a smooth Hermitian metric $h$, which satisfies Assumption 2.8. Then

(9) \begin{align} \Delta''=\Delta'+[\sqrt{-1}F(h),\Lambda_\omega]. \end{align}

Proof. By (8), one has

\[ \Delta''=D''(D'')^*+(D'')^*D''=-\sqrt{-1}[D'',[\Lambda_\omega,D_h']]. \]

By the Jacobi identity, one has

\begin{align*} \Delta''&= \sqrt{-1}[D_h',[\Lambda_\omega,D'']]-\sqrt{-1}[\Lambda_{\omega},[D'_h,D'']]\\ &\stackrel{(7)}=[D_h',(D_h')^*]+[\sqrt{-1}[D'_h,D''],\Lambda_{\omega}]\\ &\stackrel{(6)}=\Delta'+[\sqrt{-1}F(h),\Lambda_\omega], \end{align*}

which is the desired equality.

2.3 Notions of positivity

Let us recall the definitions of Nakano positivity and Griffiths negativity for vector bundles in [Dem12, Chapter VII § 6]. Let $E$ be a holomorphic vector bundle endowed with a smooth Hermitian metric $h$. For any $x\in X$, let $e_1,\ldots,e_r$ be a frame of $E$ at $x$, and let $e^1,\ldots,e^r$ be its dual in $E^*$. Let $z_1,\ldots,z_n$ be a local coordinate centered at $x$. Its curvature tensor is written as

\[ R(h) =R_{j\bar{k}\alpha}^\beta dz_j\wedge d\bar{z}_k\otimes e^\alpha\otimes e_\beta \]

Set $R_{j\bar {k}\alpha \bar {\beta }}:=h_{\gamma \bar {\beta }}R_{j\bar {k}\alpha }^\gamma$, where $h_{\gamma \bar {\beta }}=h(e_\gamma,e_\beta )$. We call $(E,h)$ Nakano semi-positive at $x$ if

\[ \sum_{ j,k,\alpha,\beta}R_{j\bar{k}\alpha\bar{\beta}}u^{j\alpha} \overline{u^{k\beta}} \geq 0 \]

for any $u=\sum _{j,\alpha }u^{j\alpha }({\partial }/{\partial z_j})\otimes e_\alpha \in (T_{X}^{1,0}\otimes E)_x$. We call $(E,h)$ Griffiths semi-negative at $x$ if

\[ \sum_{ j,k,\alpha,\beta}R_{j\bar{k}\alpha\bar{\beta}}\xi^j\zeta^\alpha \overline{\xi^k} \overline{\zeta^{\beta}} \leq 0 \]

for any $\xi =\sum _{j}\xi ^j({\partial }/{\partial z_j})\in T_{X,x}^{1,0}$ and any $\zeta =\sum _{\alpha }\zeta ^\alpha e_\alpha \in E_x$.

We write

\[ R(h)\geq_{\text{Nak}} \lambda (\omega\otimes \mathbb{1}_E) \quad \mbox{ for } \lambda\in \mathbb{R} \]

if

\[ \sum_{ j,k,\alpha,\beta}(R_{j\bar{k}\alpha\bar{\beta}}-\lambda\omega_{j\bar{k}}h_{\alpha\bar{\beta}})(x)u^{j\alpha}\overline{u^{k\beta}} \geq 0 \]

for any $x\in X$ and any $u=\sum _{j,\alpha }u^{j\alpha }({\partial }/{\partial z_j})\otimes e_\alpha \in (T_{X}^{1,0}\otimes E)_x$. We use the notation

\[ R(h)\leq_{\text{Gri}} \lambda (\omega\otimes \mathbb{1}_E) \]

if

\[ \sum_{ j,k,\alpha,\beta}(R_{j\bar{k}\alpha\bar{\beta}}-\lambda\omega_{j\bar{k}}h_{\alpha\bar{\beta}})(x)\xi^j\zeta^\alpha \overline{\xi^k} \overline{\zeta^{\beta}} \leq 0 \]

for any $x\in X$, any $\xi =\sum _{j}\xi ^j({\partial }/{\partial z_j})\in T_{X,x}^{1,0}$ and any $\zeta =\sum _{\alpha }\zeta ^\alpha e_\alpha \in E_x$. Note that Nakano semi-positivity (respectively, semi-negativity) implies Griffiths semi-positivity (respectively, semi-negativity).

Lemma 2.10 Let $(E,h)$ be a hermitian vector bundle on a Kähler manifold $(X,\omega )$. If there is a positive constant $C$ such that $|R(h)(x)|_{h,\omega }\leq C$ for any $x\in X$, then

\[ C \omega\otimes \mathbb{1}_{E}\geq_{\text{Nak}} R(h)\geq_{\text{Nak}} -C \omega\otimes \mathbb{1}_{E}. \]

Proof. For any $x\in X$, let $z_1,\ldots,z_n$ be a local coordinate centered at $x$ such that

\[ \omega_x=\sqrt{-1} \sum_{\ell=1}^{n}dz_\ell \wedge d\bar{z}_\ell. \]

Let $e_1,\ldots,e_r$ be a local holomorphic frame of $E$ which is orthonormal at $x$. Write

\[ R(h)=R_{j\bar{k}\alpha}^\beta dz_j\wedge d\bar{z}_k\otimes e^\alpha\otimes e_\beta. \]

Then $R_{j\bar {k}\alpha \bar {\beta }}(x)=R_{j\bar {k}\alpha }^\beta (x)$, and we have

\[ \sum_{ j,k,\alpha,\beta}|R_{j\bar{k}\alpha\bar{\beta}}(x)|^2=|R(h)(x)|^2_{h,\omega}\leq C^2. \]

Hence, for any $u=\sum _{j,\alpha }u^{j\alpha }({\partial }/{\partial z_j})\otimes e_\alpha \in (T_{X}^{1,0}\otimes E)_x$, by using the Cauchy–Schwarz inequality twice, one has

\begin{align*} \bigg|\sum_{ j,k,\alpha,\beta}R_{j\bar{k}\alpha\bar{\beta}}(x) u^{j\alpha}\overline{u^{k\beta}}\bigg|^2&\leq \bigg(\sum_{ k,\beta}\bigg|\sum_{j,\alpha}R_{j\bar{k}\alpha \bar{\beta}}(x)u^{j\alpha}\bigg|^2\bigg) \bigg( \sum_{k,\beta} |\overline{u^{k\beta}}|^2\bigg) \\ &\leq \bigg(\sum_{ k,\beta}\bigg(\sum_{j,\alpha}|R_{j\bar{k} \alpha\bar{\beta}}(x)|^2\bigg) \bigg(\sum_{j,\alpha}|u^{j\alpha}|^2\bigg)\bigg) \bigg( \sum_{k,\beta} |\overline{u^{k\beta}}|^2\bigg) \\ &=|u|_{h,\omega}^4\cdot\sum_{ j,k,\alpha,\beta} |R_{j\bar{k}\alpha\bar{\beta}}(x)|^2 \leq |u|_{h,\omega}^4\cdot C^2. \end{align*}

Hence, one has

\[ -C|u|_{h,\omega}^2\leq \sum_{j,k,\alpha,\beta}R_{j\bar{k} \alpha\bar{\beta}}(x)u^{j\alpha}\overline{u^{k\beta}}\leq C|u|_{h,\omega}^2. \]

The lemma is proved.

The following easy fact will be useful in this paper.

Lemma 2.11 Let $(E_1,h_1)$ and $(E_2,h_2)$ be two hermitian vector bundles over a Kähler manifold $(X,\omega )$ such that $|R(h_1)(x)|_{h_1,\omega }\leq C_1$ and $|R(h_2)(x)|_{h_2,\omega }\leq C_2$ for all $x\in X$. Then for the hermitian vector bundle $(E_1\otimes E_2,h_1h_2)$, one has

\[ |R(h_1h_2)(x)|_{h_1h_2,\omega}\leq \sqrt{2r_2C^2_1+2r_1C^2_2} \]

for all $x\in X$. Here $r_i:={\rm rank} E_i$.

3. $L^2$-method for Higgs bundles

3.1 A quick tour for the simplest case

In this subsection, we assume that $(E,\theta,h)$ is a harmonic bundle over a projective manifold $X$. We will show how to apply Bochner technique to give a simple and quick proof of Theorem A in the case that $D=\varnothing$ and $L$ is ample. The main goal of this subsection is to show the general strategy and we will discuss how to generalize these ideas to prove Theorem A.

For a Higgs bundle $(E,\theta )$ over a projective manifold $X$ of dimension $n$, one has the following holomorphic Dolbeault complex:

(10)\begin{equation} {\rm Dol}(E,\theta):=E\xrightarrow{ \theta}E\otimes \Omega^1_X\xrightarrow{ \theta} \cdots \xrightarrow{ \theta} E\otimes \Omega^n_X. \end{equation}

By Simpson [Sim92], the complex of $\mathscr {C}^{\infty }$ sections of $E$

(11)\begin{equation} \mathscr{A}^0(E)\xrightarrow{D''}\mathscr{A}^1(E)\xrightarrow{D''}\cdots \xrightarrow{D''}\mathscr{A}^{2n}(E) \end{equation}

gives a fine resolution of the above holomorphic Dolbeault complex. Indeed, it can be proven easily from the Dolbeault lemma. Here $\mathscr {A}^m(E)$ is the sheaf of germs of smooth $m$-forms with value in $E$. Hence, the cohomology of the complex of its global sections $(A^\bullet (E),D'' )$ computes the hypercohomology $\mathbb {H}^\bullet (X,{\rm Dol}(E,\theta ))$.

Suppose now $(\tilde {E},\tilde {\theta })$ is a stable Higgs bundle with vanishing Chern classes. By the Simpson correspondence (see [Sim92]), there is a unique (up to a constant rescaling) hermitian metric $\tilde {h}$ over $\tilde {E}$ such that the curvature $F(\tilde {E},\tilde {h})= 0$. For the ample line bundle $L$ on $X$, we choose a smooth Hermitian metric $h_L$ such that its curvature tensor $\sqrt {-1}R(L,h_L)$ is a Kähler form $\omega$.

Let us define a new Higgs bundle $(E,\theta ):=(\tilde {E}\otimes L,\tilde {\theta }\otimes \mathbb {1})$. We introduce a hermitian metric $h$ on $E$ defined by $h:=\tilde {h}\otimes h_L$. One can easily check that $(E,\theta,h)$ satisfies Assumption 2.8 and the curvature

(12)\begin{equation} \sqrt{-1} F(E,h):=\sqrt{-1} R(E,h)+\sqrt{-1} [\theta,\theta^*]= \sqrt{-1} R(L,h_L)\otimes \mathbb{1}_E= \omega\otimes \mathbb{1}_E. \end{equation}

By the Hodge theory, for each $i\in \mathbb {Z}_{\geqslant 0}$, we know that the space of harmonic forms

\[ \mathscr{H}^i:=\{\alpha\in A^i(E)\mid \Delta''\alpha=0 \} \]

is isomorphic to the cohomology $H^i (A^\bullet (E),D'' )\simeq \mathbb {H}^i (X,{\rm Dol}(E,\theta ))$.

Theorem 3.1 (Theorem A in the case that $D=\varnothing$ and $L$ is ample)

With the notation in this subsection, $\mathbb {H}^i (X,{\rm Dol}(\tilde {E},\tilde {\theta })\otimes L)=\mathbb {H}^i (X,{\rm Dol}( {E}, {\theta }) )=0$ for $i>n$.

Proof. Note that ${\rm Dol}(E,\theta )={\rm Dol}(\tilde {E},\tilde {\theta })\otimes L$. It suffices to prove that $\mathscr {H}^i=0$ for $i>n$. We will prove by contradiction. Let us take the Kähler form $\omega :=\sqrt {-1}R(L,h_L)$. Assume that there exists a non-zero $\alpha \in \mathscr {H}^i$. Then by Lemma 2.9, one has

(13)\begin{equation} 0=\Delta''\alpha=\Delta'\alpha+[\sqrt{-1}F(E,h),\Lambda_\omega]\alpha. \end{equation}

An integration by parts yields

\[ \langle \Delta'\alpha,\alpha\rangle_{h,\omega}=\lVert D_h'\alpha\rVert_{h,\omega}^2+\lVert (D_h')^*\alpha\rVert_{h,\omega}^2\geq 0. \]

Hence,

\begin{align*} & 0\geq\int_{X}\langle[\sqrt{-1}F(E,h),\Lambda_\omega]\alpha,\alpha\rangle_{h,\omega}d\text{ Vol}_\omega\\ &\stackrel{(12)}=\int_{X}\langle[\omega\otimes \mathbb{1},\Lambda_\omega]\alpha,\alpha\rangle_{h,\omega}d\text{ Vol}_\omega\\ &\; =\int_{X}(i-n)\lvert\alpha\rvert_{h,\omega}d\text{ Vol}_\omega>0 \end{align*}

for $i>n$. Here $d\text { Vol}_\omega :={\omega ^n}/{n!}$ denotes the volume form of $(X,\omega )$. Hence, the contradiction.

The proof of Theorem 3.1 indicates that, to prove Theorem A in full generality, we shall find a ‘proper’ complex of fine sheaves which is quasi-isomorphic to ${\rm Dol}(E,\theta )$, such that its cohomology of global sections can be computed explicitly. Inspired by the work [Zuc79, DPS01, HLWY23], we will consider the $L^2$-complex as the candidate for this complex of fine sheaves. However, instead of solving $\bar {\partial }$-equation for vector bundles to prove the vanishing theorem, we shall consider $L^2$-estimate and solvability criteria of $(\bar {\partial }_E+\theta )$-equations for Higgs bundles $(E,\theta )$. This is the main content of next subsection.

3.2 Hörmander $L^2$-estimate for Higgs bundles

Solvability criteria for $\bar {\partial }$-equations on complex manifolds are often described as cohomology vanishing theorems. It is essentially based on the abstract theory of functional analysis. Since the Kähler identities (7) and (8) hold for Higgs bundles, it indicates that the following principle should hold.

Principle The package of $L^2$-estimate by Hörmander, Andreotti-Venssetti, Bombieri, Skoda, Demailly et al. should hold without modification for Higgs bundles, provided that $D''=\bar {\partial }+\theta$ is used in place of $\bar {\partial }$ and that $m$-forms are used instead of $(p,q)$-forms.

In this subsection, we work for a very general setup. Let $(E,\bar {\partial }_E,\theta,h)$ be a Higgs bundle together with a Hermitian metric $h$ over a complete Kähler manifold $(M, \omega _M)$ (not necessarily compact). Denote again $D''\colon= \bar {\partial }_E+\theta$. Under a certain curvature condition of $(E,\bar {\partial }_E,\theta,h)$, one can solve the $D''$-equation in the same vein as [Dem12, Chapter VIII, Theorem 4.5]. We follow the standard method of $L^2$ estimate as that in [Dem12, Chapter VIII], and we provide full details for completeness sake. The results in this section will be applied more specifically to modified complete Kähler metrics over complements of simple normal crossing divisors on compact Kähler manifolds in § 4.5.

Let us denote by $A^{m}(M,E)$ (respectively, $A^{p,q}(M,E)$) the set of smooth $E$-valued $m$-forms (respectively, $(p,q)$-forms) on $M$, and denote by $A^{m}_0(M,E)$ (respectively, $A^{p,q}_0(M,E)$) the set of smooth $E$-valued $m$-forms (respectively, $(p,q)$-forms) on $M$ with compact support over the Kähler manifold $(M,\omega _M)$. The pointwise length of $u\in A^m(M,E)$ with respect to the fiber metric induced by $h$ and $\omega _M$, is denoted by $|u|_{h,\omega _M}$. The pointwise inner product of $u$ and $v$ is denoted by $\langle u,v\rangle _{h,\omega _M}$, or simply by $\langle u,v\rangle$. Then the $L^2$-norm of $u$, denoted by $\lVert u\rVert _{h,\omega _M}$, or simply by $\lVert u\rVert$, is defined as the square root of the integral

\[ \lVert u\rVert^2:=\int_{M}|u|^2_{h,\omega_M} \,d\text{ Vol}_{\omega_M}, \]

where $d\text { Vol}_{\omega _M}:={\omega _M^n}/{n!}$, which is finite if $u\in A^m_0(M,E)$. The inner product of $u$ and $v$ associated to this norm is defined by

\[ \langle\langle u,v\rangle\rangle_{h,\omega_M}:= \int_{M}\langle u,v\rangle_{h,\omega_M} \, d\text{ Vol}_{\omega_M}, \]

which is simply denoted by $\langle\langle u,v\rangle\rangle$. Note that the Hodge decomposition $A^m_0(M,E)=\oplus _{p+q=m}A^{p,q}_0(M,E)$ is orthogonal with respect to this inner product $\langle\langle \bullet,\bullet \rangle\rangle$.

We shall denote by $L^{m}_{(2), \, \text {loc}}(M,E)$ (respectively, $L^{p,q}_{(2), \, \text {loc}}(M,E)$) $E$-valued $m$-forms (respectively, $(p,q)$-forms) with locally integrable coefficients. One has a natural decomposition:

\[ L^{m}_{(2), \, \text{loc}}(M,E)=\oplus_{p+q=m} L^{p,q}_{(2), \, \text{loc}}(M,E). \]

Moreover, the operators $D''$ (and $D_h'$, $\bar {\partial }_E$, respectively) act on $L^{m}_{(2), \, \text {loc}}(M,E)$ in the sense of distribution, or precisely speaking, $E$-valued currents. Note that the definition of those objects is independent of the choice of the metrics $\omega _M$ and $h$. A section $s\in L^{m}_{(2), \, \text {loc}}(M,E)$ is said to be in the domain of definition of $D''$, denoted by ${\rm Dom}_{\, \text {loc}}\, D''$, if $D''s\in L^{m+1}_{(2), \, \text {loc}}(M,E)$.

Let $L^{m}_{(2)}(M,E)_{h,\omega _M}$ (respectively, $L^{p,q}_{(2)}(M,E)_{h,\omega _M}$) be the completion of the pre-Hilbert space $A^{m}_0(M,E)$ (respectively, $A^{p,q}_{0}(M,E)$) with respect to the above inner product $\langle\langle \bullet,\bullet \rangle\rangle$. We simply write $L^{m}_{(2)}(M,E)$ (respectively, $L^{p,q}_{(2)}(M,E)$) if no confusion happens. By the Lebesgue's theory of integration, $L^{m}_{(2)}(M,E)$ (respectively, $L^{p,q}_{(2)}(M,E)$) is a subset of $L^{m}_{(2), \, \text {loc}}(M,E)$ (respectively, $L^{p,q}_{(2), \, \text {loc}}(M,E)$). The natural decomposition

\[ L^{m}_{(2)}(M,E)= \bigoplus_{p+q=m} L_{(2)}^{p,q} (M,E) \]

is orthogonal with respect to the inner product $\langle\langle \bullet,\bullet \rangle\rangle$.

Hence, $D''$ (and $D_h'$, $\bar {\partial }_E$, respectively) act on them respectively, and these operators are unbounded, densely defined linear operators

\[ L^m_{(2)}(M,E)\to L^{m+1}_{(2)}(M,E). \]

The domain of definition of $D''$ denoted by $\text { Dom}\, D''$ are defined by

\[ \{u\in L^m_{(2)}(M,E) \mid D'' u\in L^{m+1}_{(2)}(M,E) \}, \]

for which one has $\text { Dom}\, D''\subset {\rm Dom}_{\, \text {loc}}\, D''$. Note that $\text { Dom}\, D''$ depends on the choice of the metric $\omega _M$ and $h$, up to mutual boundedness. Namely, if $\tilde {\omega }_M\sim \omega _M$ and $\tilde {h}\sim h$, $\text { Dom}\, D''$ remains the same in terms of the new metrics $\tilde {\omega }_M$ and $\tilde {h}$.

By the argument in [Dem12, Chapter VIII, Theorem 1.1], this extended operator $D''$ (the so-called weak extension in the literature) is closed, namely its graph is closed. We define $\text { Dom}\, D_h'$ in exactly the same manner.

The following result in [Dem12, Chapter VIII, Theorem 3.2.(a)] is crucial in applying the $L^2$-estimate. Roughly speaking, it gives a condition when the weak extension of $D''$ is the strong one, in terms of the graph norm, and it enables us to apply the integration by parts for $L^2$-sections as in Lemma 3.4.

Theorem 3.2 Let $(M,\omega _M)$ be a complete Kähler manifold and $(E,\bar {\partial }_E,\theta,h)$ is a Higgs bundle on $M$ satisfying Assumption 2.8. Then $A^m_{0}(M,E)$ is dense in $\text { Dom}\, D''$, $\text { Dom}\, D''^*$ and $\text { Dom}\, D''\cap \text { Dom}\, D''^*$, respectively, for the graph norm

\[ u\mapsto \lVert u\rVert +\lVert D''u\rVert, \quad u\mapsto \lVert u\rVert +\lVert (D'')^*u\rVert, \quad u\mapsto \lVert u\rVert +\lVert D''u\rVert+\lVert (D'')^*u\rVert. \]

We recall the following lemma of functional analysis by Von Neumann and Hömander (see, e.g., [Dem12, Chapter VIII, § 1]), which is crucial in obtaining the $L^2$-estimate for Higgs bundles. First we recall the following notation of the adjoint operator $T^*$ and $\text { Dom}\, T^*$: $y\in \text { Dom}\, T^*$ if the linear form

\[ \text{ Dom}\, T\ni x\mapsto \langle\langle Tx,y\rangle\rangle_2 \]

is bounded in $\mathscr {H}_1$-norm. Since $\text { Dom}\, T$ is dense, there exists for every $y$ in $\text { Dom}\, T^*$ a unique element $T^*y$ in $\mathscr {H}_1$ such that $\langle\langle x,T^*y\rangle\rangle _1=\langle\langle Tx,y\rangle\rangle _2$ for all $x\in \text { Dom}\, T$.

Lemma 3.3 If $T:\mathscr {H}_1\to \mathscr {H}_2$ is a closed and densely defined operator, then its adjoint $T^*$ is also closed and densely defined and $(T^*)^*=T$. Furthermore, we have the relation $\ker T^*=(\operatorname {Im} T)^{\perp }$ and its dual $(\ker T)^{\perp } = \overline {\operatorname {Im} T^*}$. In particular, $\ker T\oplus \overline {\operatorname {Im} T^*}=\mathscr {H}_1$.

Note that $A_{m}:=[\sqrt {-1}F(h),\Lambda _{\omega _M}]$ acts on $\wedge ^{m}T_M^*\otimes E$ as a hermitian operator. As $A_m$ is smooth, for any $u\in L^m_{(2),\, \text {loc}}(M,E)$, $A_m(u)\in L^m_{(2),\, \text {loc}}(M,E)$. If $A_m$ is semi-positively definite, $A_m^{{1}/{2}}$ exists as a densely defined hermitian operator from $L^m_{(2) }(M,E)$ to itself. The following result is exactly the same vein as the Kodaira–Nakano inequality (see [Dem82, Lemme 4.4]).

Lemma 3.4 Let $(M,\omega _M)$ be a complete Kähler manifold and $(E,\bar {\partial }_E,\theta,h)$ is a Higgs bundle on $M$ satisfying Assumption 2.8. Assume that $A_m$ is semi-positively definite. Then for every $u\in \text { Dom}\, D''\cap \text { Dom}\, D''^*$, one has

(14)\begin{equation} \lVert D''u\rVert^2+\lVert D''^*u\rVert^2\geq \langle\langle A_mu,u\rangle\rangle :=\int_M \langle A_mu,u\rangle_{h,\omega_M} \, d\text{ Vol}_{\omega_M}. \end{equation}

Proof. Since $(M,\omega _M)$ is complete, by the proof of [Dem12, Chapter VIII, Theorem 3.2.(a)], there exists an exhaustive sequence $\{K_{\nu }\}_{\nu \in \mathbb {N}}$ of compact subsets of $M$ and functions $\rho _\nu$ such that $\rho _\nu =1$ in a neighborhood of $K_\nu$, $\text {Supp}(\rho _\nu )\subset K_{\nu +1}$, $0\leq \rho _\nu \leq 1$, and $|d\rho _\nu |_{\omega _M}\leq 2^{-\nu }$. One can show that $\rho _\nu u\to u$ in the graph norm $u\mapsto \lVert u\rVert +\lVert D''u\rVert +\lVert D''^*u\rVert$. Since $A_m$ is supposed to be semi-positively definite, hence by the monotone convergence theorem

\[ \lim_{\nu\to +\infty}\int_M \langle A_m(\rho_\nu u),\rho_\nu u\rangle_{h,\omega_M} \, d\text{ Vol}_{\omega_M}= \int_M \langle A_m( u), u\rangle_{h,\omega_M} \, d\text{ Vol}_{\omega_M}, \]

which might be $+\infty$ in general. Hence, it suffices to prove (14) under the assumption that $u$ has compact support.

By the convolution arguments in [Dem12, Chapter VIII, Theorem 3.2.(a)], there exists $u_\ell \in A_0^m(M,E)$ such that $u_\ell$ tends to $u$ as $\ell \to \infty$ with respect to the graph norm $\lVert u\rVert +\lVert D''u\rVert +\lVert D''^*u\rVert$, and there is a uniform compact set $K$ such that $\text {Supp}(u_\ell )\subset K$ for all $\ell$. By Lemma 2.9, one has

\[ \langle\langle \Delta''u_\ell,u_\ell\rangle\rangle= \langle\langle \Delta'u_\ell,u_\ell\rangle\rangle+\langle\langle A_mu_\ell,u_\ell\rangle\rangle. \]

As $u_\ell$ has compact support, one applies integration by parts to obtain

\[ \langle\langle \Delta''u_\ell,u_\ell\rangle\rangle=\lVert D''u_\ell\rVert^2+\lVert D''^*u_\ell\rVert^2 \]

and

\[ \langle\langle \Delta'u_\ell,u_\ell\rangle\rangle=\lVert D_h'u_\ell\rVert^2+\lVert D'^*u_\ell\rVert^2\geq 0, \]

which gives rise to

\[ \lVert D''u_\ell\rVert^2+\lVert D''^*u_\ell\rVert^2\geq \langle\langle A_mu_\ell,u_\ell\rangle\rangle. \]

Inequality (14) follows from the above inequality when $\ell$ tends to infinity. The lemma is proved.

Remark 3.5 Suppose that $A_m$ is a semi-positively definite hermitian operator on $\wedge ^{m}T_M^*\otimes E$. For some $v\in L^m_{(2)}(M,E)$, assume that for almost all $x\in M$, there exists a measurable and integrable non-negative function $\alpha (x)$ such that

\[ | \langle v,f\rangle_{h,\omega_M}|^2 \leq \alpha(x) \langle f,A_m(x)f\rangle_{h,\omega_M} \]

for any $f\in A^m_0(M,E)_x$, then the minimum of $\alpha (x)$ is

\[ |A_m^{-{1}/{2}}(x)v|^2_{h,\omega_M}=\langle A_m(x)^{-1}v,v\rangle_{h,\omega_M} \]

if the operator $A_m(x)$ is invertible. Hence, we shall always formally write it in this way even when $A_m(x)$ is no longer invertible, following [Dem12, Chapter VIII, § 4].

Now we are able to state our main result on $L^2$-estimate for Higgs bundles.

Theorem 3.6 (Solving the $D''$-equation for a Higgs bundle)

Let $(M,\omega _M)$ be a complete Kähler manifold and let $(E,\bar {\partial }_E,\theta,h)$ be a Higgs bundle on $M$ satisfying Assumption 2.8. Assume that $A_m$ is semi-positively definite on $\wedge ^mT_M^*\otimes E$ at every $x\in M$. Then for any $v\in L^m_{(2)}(M,E)$ such that $D''v=0$ and

\[ \int_M \langle A_m^{-1}v,v\rangle d\text{ Vol}_{\omega_M}<+\infty, \]

there exists $u\in L^{m-1}_{(2)}(M,E)$ such that $D''u=v$ and

\[ \lVert u\rVert^2\leq\int_M \langle A_m^{-1}v,v\rangle \, d\text{ Vol}_{\omega_M}. \]

Proof. Consider now two closed and densely defined operators

\[ \mathscr{H}_1=L^{m-1}_{(2)}(M,E)\xrightarrow{T=D''}\mathscr{H}_2=L^{m}_{(2)}(M,E)\xrightarrow{S=D''} \mathscr{H}_3=L^{m+1}_{(2)}(M,E). \]

For any $f\in \text { Dom}\, S\cap \text { Dom}\, T^*$, one has

\begin{align*} |\langle\langle f,v\rangle\rangle|^2&=|\int_M \langle f,v\rangle d\text{ Vol}_{\omega_M}|^2\leq |\int_M \langle A_m^{-1}v,v\rangle^{{1}/{2}} \cdot \langle A_mf,f\rangle^{{1}/{2}} d\text{ Vol}_{\omega_M}|^2\\ &\leq \int_M \langle A_m^{-1}v,v\rangle d\text{ Vol}_{\omega_M}\cdot \int_M \langle A_mf,f\rangle d\text{ Vol}_{\omega_M} \end{align*}

by Cauchy–Schwarz inequality. By (14) one has

(15)\begin{equation} |\langle\langle f,v\rangle\rangle|^2\leq C ( \lVert Sf\rVert^2+\lVert T^*f\rVert^2), \end{equation}

where $C:=\int _M \langle A_m^{-1}v,v\rangle \, d\text { Vol}_{\omega _M}>0$.

Note that $T^*\circ S^*=0$ by $S\circ T=0$. For any $f\in \text { Dom}\, T^*$, there is an orthogonal decomposition $f=f_1+f_2$, where $f_1\in \ker S$ and $f_2\in (\ker S)^{\perp }=\overline {\operatorname {Im} S^*}\subset \ker T^*$ by Lemma 3.3. Since $v\in \ker S$, by (15) we then have

\[ |\langle\langle f,v\rangle\rangle|^2=|\langle\langle f_1,v\rangle\rangle|^2\leqslant C ( \lVert Sf_1\rVert^2+\lVert T^*f_1\rVert^2)=C\lVert T^*f_1\rVert^2=C\lVert T^*f\rVert^2. \]

By the Hahn–Banach theorem, we conclude that there is $u\in \text { Dom}\, T$ such that $Tu=v$ with $\lVert u\rVert _2\leq C^{1/2}$. The theorem is proved.

A direct consequence is the following result which can be seen as a Higgs bundle version of Girbau vanishing theorem (see [Dem12, Chapter VII, Theorem 4.2]) in the log setting [HLWY23, Theorem 4.1].

Corollary 3.7 Let $(M,\omega _M)$ be a complete Kähler manifold, and $(\tilde {E},\tilde {\theta },\tilde {h})$ be any harmonic bundle on $M$. Let $L$ be a line bundle on $M$ equipped with a Hermitian metric $h_L$. Assume that

(16)\begin{equation} \langle [\sqrt{-1} R(h_L), \Lambda_{\omega_M}]f, f\rangle_{h_L, \omega_M}\geq \varepsilon \lvert f\rvert_{h_L, \omega_M}^2 \end{equation}

for any $x\in M$ and $f\in (\Lambda ^{p,q}T_M^*\otimes L)_x$ with $p+q=m$. Set $(E,\theta,h):=(\tilde {E}\otimes L,\tilde {\theta }\otimes \mathbb {1}_L,\tilde {h}h_L)$. Then for any $v\in L^m_{(2)}(M,E)$ such that $D''v=0$, there exists $u\in L^{m-1}_{(2)}(M,E)$ such that $D''u=v$ and

\[ \lVert u\rVert^2\leq \frac{\lVert v\rVert^2}{\varepsilon}. \]

Proof. Note that since $(\tilde {E},\tilde {\theta },\tilde {h})$ is a harmonic bundle, both $(\tilde {E},\tilde {\theta },\tilde {h})$ and $(E,\theta,h)$ satisfy Assumption 2.8. Hence,

(17)\begin{align} \sqrt{-1} F(h)&=\sqrt{-1} \Big(R(h)+[\theta,\theta_h^*] \Big)\nonumber\\ &=\sqrt{-1} R(\tilde{h})\otimes \mathbb{1}_L+ \sqrt{-1} R(h_L)\otimes \mathbb{1}_{E}+[\tilde{\theta}\otimes \mathbb{1}_L, \tilde{\theta}_{\tilde{h}}^*\otimes \mathbb{1}_L]\nonumber\\ &=\sqrt{-1} F(\tilde{h})\otimes \mathbb{1}_L+ \sqrt{-1} R(h_L)\otimes \mathbb{1}_{E}\nonumber\\ &= \sqrt{-1} R(h_L)\otimes \mathbb{1}_{E}, \end{align}

where the last equality follows from that $F(\tilde {h})=0$ since $(\tilde {E},\tilde {\theta },\tilde {h})$ is a harmonic bundle. In this case, it is easy to see that for any $f\in (\Lambda ^{m}T_M^*\otimes E)_x$, decomposing $f=\sum _{p+q=m}f^{p,q}$ with $f^{p,q}$ its $(p,q)$-component, one has

\begin{align*} \langle A_mf,f\rangle_{h,\omega_M}&= \sum_{p+q=m}\langle [\sqrt{-1} R(h_L), \Lambda_{\omega_M}]\otimes \mathbb{1}_E(f^{p,q}), f^{p,q}\rangle_{h_L,\omega_M}\\ &\geq \sum_{p+q=m} \varepsilon\lvert f^{p,q}\rvert^2_{h,\omega_M}= \varepsilon\lvert f\rvert^2_{h,\omega_M}. \end{align*}

Hence, $\langle A_m^{-1}f,f\rangle _{h,\omega _M}\leq \varepsilon ^{-1}\lvert f\rvert ^2_{h,\omega _M}$. Applying Theorem 3.6, we conclude that there is $u\in L^{m-1}_{(2)}(M,E)$ such that $D''u=v$ and

\[ \lVert u\rVert^2\leq \int_M \langle A^{-1}_mv,v\rangle_{h,\omega_M}d\text{ Vol}_{\omega_M}\leq \frac{\lVert v\rVert^2}{\varepsilon}. \]

4. Vanishing theorem for tame harmonic bundles

4.1 Parabolic Higgs bundle

In this section, we recall the notions of parabolic Higgs bundles. For more details, refer to [AHL19, §§ 1, 3, 4, 5] and [MY92, § 1]. Let $X$ be a complex manifold, $D=\sum _{i=1}^{\ell }D_i$ be a reduced simple normal crossing divisor, $U=X-D$ be the complement of $D$ and $j:U\to X$ be the inclusion.

Definition 4.1 A parabolic sheaf $(E,{}_{ \boldsymbol {a}}E)$ on $(X, D)$ is a torsion-free $\mathcal {O}_U$-module $E$, together with an $\mathbb {R}^l$-indexed filtration ${}_{ \boldsymbol {a}}E$ (parabolic structure) by coherent subsheaves of $j_*E$ such that

1. (i) $\boldsymbol {a}\in \mathbb {R}^l$ and ${}_{\boldsymbol {a}}E|_U=E$;

2. (ii) for $1\leq i\leq l$, ${}_{\boldsymbol {a}+\boldsymbol {1}_i}E = {}_{\boldsymbol {a}}E\otimes \mathcal {O}_X(D_i)$, where $\boldsymbol {1}_i=(0,\ldots, 0, 1, 0, \ldots, 0)$ with $1$ in the $i$th component;

3. (iii) $_{\boldsymbol {a}+\boldsymbol {\epsilon }}E = {}_{\boldsymbol {a}}E$ for any vector $\boldsymbol {\epsilon }=(\epsilon, \ldots, \epsilon )$ with $0<\epsilon \ll 1$;

4. (iv) the set of weights {$\boldsymbol {a}$ — $_{\boldsymbol {a}}E/_{\boldsymbol {a}-\boldsymbol {\epsilon }}E\not = 0$ for any vector $\boldsymbol {\epsilon }=(\epsilon, \ldots, \epsilon )$ with $0<\epsilon \ll 1$} is discrete in $\mathbb {R}^l$.

A weight is normalized if it lies in $[0,1)^l$. Denote $_{\boldsymbol {0}}E$ by ${}^\diamond \! E$, where $\boldsymbol {0}=(0, \ldots, 0)$. Note that the parabolic structure of $(E,{}_{ \boldsymbol {a}}E)$ is uniquely determined by the filtration for weights lying in $[0,1)^l$. A parabolic bundle on $(X,D)$ consists of a vector bundle $E$ on $X$ with a parabolic structure, such that the filtered subsheaves ${}_{ \boldsymbol {a}}E$ are vector bundles. As pointed out by one of the referees, by the work of Borne and Vistoli the parabolic structure of a parabolic bundle is locally abelian, i.e. it admits a local frame compatible with the filtration (see, e.g., [IS07] and [BV12]).

Definition 4.2 A parabolic Higgs bundle on $(X,D)$ is a parabolic bundle $(E,{}_{ \boldsymbol {a}}E,\theta )$ together with $\mathscr {O}_X$ linear map

\[ \theta:{}^\diamond\! E\to \Omega_X^1(\log D)\otimes {}^\diamond\! E \]

such that

\[ \theta\wedge \theta=0 \]

and

\[ \theta(_{\boldsymbol{a}}E)\subseteq \Omega_X^1(\log D)\otimes {}_{\boldsymbol{a}}E, \]

for $\boldsymbol {a}\in [0, 1)^l$.

A natural class of parabolic Higgs bundles comes from extensions of tame harmonic bundles, as discussed in the following section.

4.2 Extension by an increased order

By a celebrated theorem of Simpson and Mochizuki, there is a natural parabolic Higgs bundle induced by tame harmonic bundle $(E, \theta, h)$.

We recall some notions from [Moc07, § 2.2.1]. Let $(X, D)$ be the pair in § 4.1. Let $E$ be a holomorphic vector bundle with a $\mathscr {C}^\infty$ hermitian metric $h$ over $X-D$.

Let $U$ be an open subset of $X$ with an admissible coordinate $(U; z_1, \ldots, z_n)$ with respect to $D$. For any section $\sigma \in \Gamma (U-D,E|_{U-D})$, let $|\sigma |_h$ denote the norm function of $\sigma$ with respect to the metric $h$. We use the notation $|\sigma |_h\in \mathcal {O}(\prod _{i=1}^{\ell }|z_i|^{-b_i})$ if there exists a positive number $C$ such that $|\sigma |_h\leq C\cdot \prod _{i=1}^{\ell }|z_i|^{-b_i}$. For any $\boldsymbol {b}\in \mathbb {R}^\ell$, say $-\mbox {ord}(\sigma )\leq \boldsymbol {b}$ means the following:

\[ |\sigma|_h=\mathcal{O}\bigg(\prod_{i=1}^{\ell}|z_i|^{-b_i-\varepsilon}\bigg) \]

for any real number $\varepsilon >0$ and $0<|z_i|\ll 1$. For any $\boldsymbol {b}$, the sheaf ${}_{\boldsymbol {b}} E$ is defined as follows:

(18)\begin{equation} \Gamma(U, {}_{\boldsymbol{b}} E):=\{\sigma\in\Gamma(U-D,E|_{U-D})\mid -\mbox{ord}(\sigma)\leq \boldsymbol{b} \}. \end{equation}

The sheaf ${}_{\boldsymbol {b}} E$ is called the extension of $E$ by an increasing order $\boldsymbol {b}$. In particular, we use the notation ${}^\diamond E$ in the case $\boldsymbol {b}=(0,\ldots,0)$.

According to Simpson [Sim90, Theorem 2] and Mochizuki [Moc07, Theorem 8.58], the above extension gives a parabolic Higgs bundle, in particular, $\theta$ preserves the filtration.

Theorem 4.3 (Simpson and Mochizuki)

Let $(X, D)$ be a complex manifold $X$ with a simple normal crossing divisor $D$. If $(E , \theta, h)$ is a tame harmonic bundle on $X-D$, then the corresponding filtration $_{\boldsymbol {b}}E$ according to the increasing order in the extension of $E$ defines a parabolic bundle $(E, {}_{\boldsymbol {b}}E, \theta )$ on $(X,D)$.

Here we also recall the following definition in [Moc07, Definition 2.7].

Definition 4.4 (Acceptable bundle)

Let $(E,\bar {\partial }_E,h)$ be a hermitian vector bundle over $X-D$. We say that $(E,\bar {\partial }_E,h)$ is acceptable at $p\in D$, if the following holds: there is an admissible coordinate $(U;z_1,\ldots,z_n)$ around $p$, such that the norm $\lvert R(E,h) \rvert _{h,\omega _P}\leq C$ for some $C>0$. When $(E_,\bar {\partial }_E,h)$ is acceptable at any point $p$ of $D$, it is called acceptable.

The following deep result by Mochizuki [Moc07, Proposition 8.18] will play an important role throughout this paper.

Theorem 4.5 (Mochizuki)

Let $X$ be a complex manifold and let $D$ be a simple normal crossing divisor on $X$. Assume that $(E,\theta,h)$ is a tame harmonic bundle on $X-D$. Then $(E,h)$ is acceptable.

4.3 Modification of the metric

In this subsection, we work with the following modification of acceptable metric defined in [Moc02, § 4.5.3]. Let us consider the case $X=\Delta ^n$, and $D=\sum _{i=1}^{\ell }D_i$ with $D_i=(z_i=0)$. Let $(E,\bar {\partial }_E,h)$ be an acceptable bundle over $X-D$. For any $\boldsymbol {a}\in \mathbb {R}^\ell _{\geq 0}$ and $N\in \mathbb {Z}$, we define

(19)\begin{equation} \chi(\boldsymbol{a},N):= -\sum_{j=1}^{\ell}a_j\log |z_j|^{2}- N \bigg(\sum_{j=1}^{\ell}\log (-\log |z_j|^2)+ \sum_{k=\ell+1}^{n}\log(1-|z_k|^2)\bigg). \end{equation}

Set $h(\boldsymbol {a},N):=h\cdot e^{-\chi (\boldsymbol {a},N)}$. Then

\[ R(h(\boldsymbol{a},N))=R(h)+\sqrt{-1}\partial\overline{\partial} \chi(\boldsymbol{a},N)=R(h)+N\omega_P. \]

Note that $\Omega _{X^*}=\bigoplus _{i=1}^{n}L_i$ where $L_i$ is the trivial line bundle defined by $L_i:=p_i^*\Omega _{\Delta ^*}$ for $i=1,\ldots,\ell$ and $L_k=p_k^*\Omega _{\Delta }$ for $k=\ell +1,\ldots,n$ where $p_i$ is the projection of $(\Delta ^*)^\ell \times \Delta ^{n-\ell }$ to its $i$th factor. For any $p=1,\ldots,n$, set $h_p$ to be the hermitian metric on $\Omega _{X^*}^p$ induced by $\omega _P$. Then there is a positive constant $C(p,\ell )>0$ depending only on $p$ and $\ell$ such that $|R(h_p)|_{h_p,\omega _P}\leq C(p,\ell )$. Set $C_0:=\sup _{p=0,\ldots,n;\ell =1,\ldots,n}C(p,\ell )$.

Proposition 4.6 Let $(E,\bar {\partial }_E,h)$ be an acceptable bundle over $X-D$, where $X$ is a compact complex manifold and $D$ is a simple normal crossing divisor. Then there is a constant $N_0>0$ such that, for any $x\in D$, one has an admissible coordinate $(U;z_1,\ldots,z_n)$ around $p$ (which can be made arbitrary small) satisfying the following property.

For vector bundles $\mathscr {E}_p:= T_{U^*}^p\otimes E$ and $\mathscr {F}_p:=\Omega _{U^*}^p\otimes E$, which are all equipped with the $\mathscr {C}^\infty$-metric $h_{\mathscr {E}_p}$ and $h_{\mathscr {F}_p}$ induced by $h(\boldsymbol {a},N)$ and $\omega _P$, one has the following estimate:

(20)\begin{equation} \sqrt{-1}R(h_{\mathscr{E}_p})\geqslant_{\text{Nak}} \omega_P\otimes \mathbb{1}_{\mathscr{E}_p}; \quad \sqrt{-1}R(h_{\mathscr{F}_p})\leqslant_{\text{Gri}} 2N \omega_P\otimes \mathbb{1}_{\mathscr{F}_p} \end{equation}

over $U^*$ for any $N\geqslant N_0$. Such $N_0$ does not depend on the choice of $\boldsymbol {a}$.

Proof. As $(E,h)$ is assumed to be acceptable, for any $x\in D$, one can find an admissible coordinate $(U;z_1,\ldots,z_n;\varphi )$ around $x$ such that $|R(h)|_{h,\omega _P}\leq C$. By the above argument, one has $|R(h_p)|_{h_p,\omega _P}\leq C_0$ for the Hermitian metric $h_p$ on $\Omega ^p_{U^*}$. By Lemma 2.11, we conclude that there is a constant $C_1>0$ which depends only on $C_0$ and $C$ such that

\[ |R(h^{-1}_ph)|_{h_p^{-1}h,\omega_P}\leq C_1,\quad |R(h_{p}h)|_{h_ph,\omega_P}\leq C_1 \]

for any $p=0,\ldots,n$, where $h^{-1}_ph$ is the metric for $\mathscr {E}_p$ and $h_ph$ is the metric for $\mathscr {F}_p$. By Lemma 2.10, one has

\[ \sqrt{-1}R(h^{-1}_ph)\geq_{\text{Nak}} -C_1\omega_P\otimes\mathbb{1}_{\mathscr{E}_p},\quad \sqrt{-1}R(h_{p}h)\leq_{\text{Nak}}C_1\omega_P\otimes \mathbb{1}_{\mathscr{F}_p}. \]

As $h_{\mathscr {E}_p}=h^{-1}_ph(\boldsymbol {a},N)$ and $h_{\mathscr {F}_p}=h_ph(\boldsymbol {a},N)$, we then have

\[ \sqrt{-1}R(h_{\mathscr{E}_p})\geq_{\text{Nak}} (N-C_1)\omega_P\otimes\mathbb{1}_{\mathscr{E}_p},\quad \sqrt{-1}R(h_{\mathscr{F}_p})\leq_{\text{Nak}}(N+C_1)\omega_P\otimes \mathbb{1}_{\mathscr{F}_p}. \]

If we take $N_{x}=C_1+1$, then the desired estimate (20) follows for any $N\geq N_x$.

Now we will prove that for points near $x$, the above estimate $N_x$ holds uniformly. As $C_1$ depends only on $C$, one has to prove that there is a constant $C$ such that for any point $z$ near $x$, there is an admissible coordinate with respect to $z$ such that $|R(h)|_{h,\omega _P}\leq C$.

Claim 4.7 Let $\phi :\Delta \to \Delta ^*$ defined by $\phi (t)={t}/{4}+\frac {1}{2}$. Then

\[ \phi^*\frac{\sqrt{-1}dz\wedge d\bar{z}}{|z|^2(\log |z|^2)^2}=\frac{\sqrt{-1}dt\wedge d\bar{t}}{16|\phi(t)|^2(\log |\phi(t)|^2)^2}\leq C_2\sqrt{-1}dt\wedge d\bar{t}\leq C_2\frac{\sqrt{-1}dt\wedge d\bar{t}}{(1-|t|^2)^2}, \]

where $C_2=4 (\log \frac {3}{4})^{-2}$.

For any $z\in U$, we first assume that $z_1=\cdots =z_\ell =0$, namely the components of $D$ passing to $z$ are the same as $x$. Take isomorphisms of unit disk $\{\phi _j\in \text {Aut}(\Delta )\}_{j=\ell +1,\ldots,n}$ such that $\phi _j(z_j)=x_j$. Note that $x_1=\cdots =x_\ell =0$. Hence, $(\mathbb {1}_\Delta,\ldots,\mathbb {1}_\Delta,\phi _{\ell +1},\ldots,\phi _n)\circ \varphi :U\to \Delta ^n$ gives rise to the admissible coordinate for $z$, and the Poincaré metric $\omega _P$ is invariant under this transformation. Hence, one can take $N_z=N_x$.

Now we can assume that $z_1=\cdots =z_m=0$, and that any of $\{z_{m+1},\ldots,z_{\ell }\}$ is not equal to zero, for $m< l$. We first take automorphisms $\{\eta _i\}_{i=m+1,\ldots,\ell }\subset \text {Aut}(\Delta ^*)$ such that $\eta _i(\frac {1}{2})=z_i$. Set $\phi _i=\eta _i\circ \phi :\Delta \to \Delta ^*$ for $i=m+1,\ldots,\ell$. Take isomorphisms of unit disk $\{\phi _j\in \text {Aut}(\Delta )\}_{j=\ell +1,\ldots,n}$ such that $\phi _j(z_j)=x_j$. Then $\varphi ^{-1}\circ (\mathbb {1}_\Delta,\ldots,\mathbb {1}_\Delta,\phi _{m+1},\ldots,\phi _n):\Delta ^n\to X$ will give rise to the desired admissible coordinate for such $z$. By the above claim, one has $|R(h)|_{h,\omega _P}\leq C_2C$. Hence, the above estimate $N_x$ can be made uniformly in $U$. As $X$ and $D$ is compact, one can cover $D$ by finite such open sets, and the desired $N_0$ in the theorem can be achieved.

We now show that these admissible coordinates can be made arbitrarily small. For $0<\varepsilon <1$, set

\begin{align*} \phi_\varepsilon:\Delta_\varepsilon^n&\stackrel{\sim}{\to } \Delta^n\\ (z_1,\ldots,z_n)&\to (\varepsilon^{-1} z_1,\ldots,\varepsilon^{-1} z_n), \end{align*}

where $\Delta _\varepsilon =\{z\in \Delta \mid |z|<\varepsilon \}$. For any admissible coordinate $(U;z_1,\ldots,z_n;\varphi )$ around $x$ such that $|R(h)|_{h,\omega _P}\leq C$, one can introduce a new one $(U(\varepsilon );w_1,\ldots,w_n;\varphi _\varepsilon )$ around $x$ with

\begin{align*} \varphi_\varepsilon:U(\varepsilon)&\stackrel{\sim}{\to} \Delta^n \\ x&\to \phi_\varepsilon\circ \varphi(x). \end{align*}

When $\varepsilon \ll 1$, this admissible coordinate will be arbitrarily small. Note that $\phi _\varepsilon ^*\omega _P\geq \omega _P|_{\Delta _\varepsilon ^n}$. Hence, in the new admissible coordinate $(U(\varepsilon );w_1,\ldots,w_n;\varphi _\varepsilon )$, one still has $\lvert R(h) \rvert _{h,\omega _P}\leq C$. The constant $N_x$ is thus unchanged. The proposition is proved.

This result will be important for us to construct a fine resolution of parabolic Higgs bundles in § 4.5.

4.4 From $L^2$-integrability to $\mathscr {C}^0$-estimate

Note that in order to show the quasi-isomorphism between some complex of sheaves of $L^2$-forms and (1), one has to deduce some norm estimate of sections from the $L^2$-integrability condition. In the case that $(E,\theta )$ is a line bundle with trivial Higgs field, this has been carried out in [DPS01, § 2.4.2] and [HLWY23, Theorem 3.1]. This subsection is devoted to showing this using mean value inequality following [Moc06, Lemma 7.12].

We first recall the following well-known lemma and we provide the proof for the sake of completeness.

Lemma 4.8 Let $(E, h)$ be a Hermitian vector bundle over a complex manifold $X$. Suppose that $R(h)$ is Griffiths semi-negative. Then for any holomorphic section $s\in H^0(X,E)$, one has

\[ \sqrt{-1}\partial\overline{\partial} \log |s|^2_h\geq 0. \]

Proof. Outside the zero locus $(s=0)$, one has

\begin{align*} \sqrt{-1}\partial\overline{\partial} \log |s|^2_h&=\sqrt{-1}\frac{\{\partial_h s,\partial_h s\}_h}{|s|^2_h}-\sqrt{-1}\frac{\{\partial_hs,s\}_h\wedge \{s,\partial_hs\}_h}{|s|^4_h}-\frac{\{\sqrt{-1}R(h)s,s\}_h}{|s|^2_h}\\ &\geq -\frac{\{\sqrt{-1}R(h)s,s\}_h}{|s|^2_h}\geq 0, \end{align*}

where the first inequality is due to Cauchy–Schwarz inequality and the second follows from the assumption that $R(h)$ is Griffiths semi-negative. As $\log |s|_h^2$ is locally bounded from above, it is thus a global plurisubharmonic function on $X$.

Proposition 4.9 With the same setting as Lemma 4.6, for any $x\in D$, we take an admissible coordinate $(U;z_1,\ldots,z_n)$ around $x$ and pick $N\geq N_0$ as in Lemma 4.6. Then for any section $s\in H^0(U^*, \Omega _{U^*}^p\otimes E|_{U^*})$, when $0< r\ll 1$, one has

(21)\begin{equation} |s|_{h,\omega_P}(z)\leq C \lVert s\rVert_{h(\boldsymbol{a},N),\omega_P}\cdot \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i-\delta}\bigg) \end{equation}

for any $\delta >0$ and any $z\in U^*(r)$.

Proof. By Lemma 4.6, for the hermitian vector bundle $(\Omega ^p_{U^*}\otimes E, h_ph(\boldsymbol {a},-N))$ one thus has

\[ R(h_ph(\boldsymbol{a},-N))= R(h_ph(\boldsymbol{a},N))-2N\omega_P\otimes \mathbb{1}_{\Omega^p_{U^*}\otimes E} \leq_{\text{Gri}} 0 \]

over $U^*$ for $N\geq N_0$. For any section $s\in H^0(U^*,\Omega ^p_{U^*}\otimes E)$, by Lemma 4.8 one has

\[ \sqrt{-1}\partial\overline{\partial} \log |s(z)|^2_{h(\boldsymbol{a},-N),\omega_P}\geq 0, \]

where we omit $h_p$ in the subscript for simplicity. For any $z\in U^*(r)$ where $0< r\ll 1$, one has $\log |s(z)|^2_{h(\boldsymbol {a},-N),\omega _P}<0$, and

\begin{align*} \log |s(z)|^2_{h(\boldsymbol{a},-N),\omega_P}&\leq \frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\int_{\Omega_z} \log |s(w)|^2_{h(\boldsymbol{a},-N),\omega_P}d\mbox{vol}_{g}\\ &\leq \log \bigg(\frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\cdot \int_{\Omega_z} |s(w)|^2_{h(\boldsymbol{a},-N),\omega_P}d\mbox{vol}_{g}\bigg)\\ &\leq \log \bigg(C \int_{\Omega_z} \frac{1}{ \prod_{i=1}^{\ell}|w_i|^2}|s(w)|^2_{h(\boldsymbol{a},-N),\omega_P}d\mbox{vol}_{g}\bigg)\\ &\leq \log C_1+ \log \int_{\Omega_z} |s(w)|^2_{h(\boldsymbol{a},-N), \omega_P}\cdot \bigg|\prod_{i=1}^{\ell}(\log |w_i|^2)^2\bigg| \prod_{j=\ell+1}^{n}(1-|w_j|^2)^2 d\mbox{vol}_{\omega_P}\\ & \leq \log C_1+\log \int_{\Omega_z} |s(w)|^2_{h(\boldsymbol{a},N),\omega_P}d\mbox{vol}_{\omega_P}\\ &\leq \log C_1+\log \lVert s\rVert_{h(\boldsymbol{a},N),\omega_P}^2, \end{align*}

where $\Omega _z:=\{w\in U^*\mid |w_i-z_i|\leq {|z_i|}/{2} \text { for } i\leq \ell ; |w_i-z_i|\leq \frac {1}{2} \mbox { for } i>\ell \}$ and $g$ is the Euclidean metric. The first inequality is due to mean value inequality, and the second is Jensen inequality. Hence,

\begin{align*} |s(z)|_{h,\omega_P}&=|s(z)|_{h(\boldsymbol{a},-N),\omega_P}\cdot \bigg(-\prod_{i=1}^{\ell}\log |z_i|^2\bigg)^{{N}/{2}}\cdot \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i}\bigg) \\ &\leq e^{{C_1}/{2}} \lVert s\rVert_{h(\boldsymbol{a},N),\omega_P} \cdot \bigg(-\prod_{i=1}^{\ell}\log |z_i|^2\bigg)^{{N}/{2}}\cdot \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i}\bigg)\\ &\leq C_\delta \lVert s\rVert_{h(\boldsymbol{a},N),\omega_P}\cdot \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i-\delta}\bigg) \end{align*}

for any $\delta >0$ and some positive constant $C_\delta$ depending on $\delta$.

4.5 A fine resolution for Dolbeault complex of Higgs bundles

Let $(E,\theta,h)$ be a tame harmonic bundle on $X-D$, where $(X,\omega )$ is a compact Kähler manifold and $D=\sum _{i=1}^\ell D_i$ is a simple normal crossing divisor on $X$.

Let $L$ be a line bundle on $X$ equipped with a smooth Hermitian metric $h_L$ such that $\sqrt {-1}R(h_L)\geq 0$ and has at least $n-k$ positive eigenvalues. Such a metrized line bundle $(L,h_L)$ is indeed called k-positive in [SS85]. Let $B$ be a nef line bundle on $X$. Let $\sigma _i$ be the section $H^0(X,\mathscr {O}_X(D_i))$ defining $D_i$, and we fix some smooth Hermitian metric $h_i$ for the line bundle $\mathscr {O}_X(D_i)$ such that $|\sigma _i|_{h_i}(z)<1$ for any $z\in X$. Write $\sigma _D:=\prod _{i=1}^{\ell } \sigma _i\in H^0(X,\mathscr {O}_X(D))$ and $h_D:=\prod _{i=1}^{\ell } h_i$ the smooth metric for $\mathscr {O}_X(D)$. Pick a positive constant $N$ greater than $N_0$, where $N_0$ is the constant in Lemma 4.6 such that (20) and Proposition 4.9 hold for $(E, \theta, h)$.

Given a smooth metric $h_B$ on $B$, note that for $\boldsymbol {a}=(a_1,\ldots,a_\ell )\in \mathbb {R}^\ell$ and $\mathscr {L}:=L\otimes {B}|_{X^*}$ equipped with the metric

(22)\begin{equation} h_\mathscr{L}(\boldsymbol{a}):=h_L{h_B}\prod_{i=1}^{\ell}|\sigma_i|^{2a_i}_{h_i}\cdot \bigg(-\prod_{i=1}^{\ell}\log |\sigma_i|_{h_i}^2\bigg)^{N}, \end{equation}

its curvature

(23)\begin{align} \sqrt{-1} R(h_\mathscr{L}(\boldsymbol{a})) &=\sqrt{-1} R(h_L)+ \sqrt{-1} R({h_{B}})+\sum_{i=1}^{\ell} 2\sqrt{-1}a_i R(h_i) \nonumber\\ &\quad +\sqrt{-1} N\sum_{i=1}^{\ell}\frac{\partial \log \lvert \sigma_i\rvert^2_{h_i}\wedge \bar{\partial} \log \lvert \sigma_i\rvert^2_{h_i}}{(\log \lvert \sigma_i\rvert^2_{h_i})^2} -N\sum_{i=1}^{\ell}\frac{\sqrt{-1} R(h_i)}{(\log \lvert \sigma_i\rvert^2_{h_i})^2} \end{align}

Here $R(h_i)$ is the curvature of $(\mathscr {O}_X(D_i),h_i)$.

Let $0\leq \gamma _1(x)\leq \cdots \leq \gamma _n(x)$ be eigenvalues of $\sqrt {-1} R(h_L)$ with respect to $\omega$. Set

\[ \varepsilon_0:=\inf_{X}\gamma_{k+1}(x), \]

which is strictly positive by our assumption on $\sqrt {-1} R(h_L)$.

Lemma 4.10 There exists a smooth hermitian metric $h_{B}$ of $B$, such that upon rescaling $h_i$, for $\boldsymbol {a}\in \mathbb {R}^\ell _{>0}$ sufficiently small, we achieve the following.

1. (i) One has

   (24)\begin{equation} \sqrt{-1} R(h_\mathscr{L}(\boldsymbol{a}))\geq \sqrt{-1} R(h_L)-\varepsilon_1\omega\geq -\varepsilon_1\omega \end{equation}
   for $\varepsilon _1={\varepsilon _0}/{100n^2}$.

2. (ii) The metric

   (25)\begin{equation} \omega_{\boldsymbol{a},N}: = \varepsilon_2\omega+\sqrt{-1} R(h_\mathscr{L}(\boldsymbol{a})) \end{equation}
   is a Kähler metric when restricted on $X^*=X-D$ for $\varepsilon _2={\varepsilon _0}/{10n}$.

3. (iii) One has ${}^\diamond \! E$=${}_{\boldsymbol {a}}E$.

Proof. Let us explain how to achieve part (i). The possible negative contribution for $\sqrt {-1} R(h_\mathscr {L}(\boldsymbol {a}))$ can only come from

\[ \sqrt{-1} R({h_{B}})+\sum_{i=1}^{\ell} 2\sqrt{-1}a_i R(h_i) -N\sum_{i=1}^{\ell}\frac{\sqrt{-1} R(h_i)}{(\log \lvert \sigma_i\rvert^2_{h_i})^2}. \]

As $B$ is nef, one can take $h_{B}$ such that $\sqrt {-1} R({h_{B}})\geq -\frac {1}{2}\varepsilon _1\omega$. As $N$ is fixed, we can replace $h_i$ by $c\cdot h_i$ for $0< c\ll 1$ and let $a_i$ be small enough, such that $\sum _{i=1}^{\ell } 2\sqrt {-1}a_i R(h_i) -N\sum _{i=1}^{\ell }({\sqrt {-1} R(h_i)}/{(\log \lvert \sigma _i\rvert ^2_{h_i})^2})\geq -\frac {1}{2}\varepsilon _1\omega$. This proves part (i). Part (ii) follows directly from part (i).

By Theorem 4.3, ${}^\diamond \! E$ is a parabolic Higgs bundle. By Definition 4.1 (iii), one has ${}^\diamond \! E$=${}_{\boldsymbol {a}}E$ if $\boldsymbol {a}$ is chosen small enough. This proves part (iii).

We know that $\omega _{\boldsymbol {a},N}$ is a complete Kähler metric. Indeed, write $h_i\stackrel {\text {loc}}=e^{-\varphi _i}$ in terms of the trivialization $D_i\cap U=(z_i=0)$ of any admissible coordinate $(U;z_1,\ldots,z_n)$, one has

\begin{align*} \omega_{\boldsymbol{a},N} &=\bigg(\varepsilon_2\omega+\sum_{i=1}^{\ell} 2\sqrt{-1}a_i R(h_i)+ \sqrt{-1} R(h_{M})\bigg)\\ &\quad +N\sum_{i=1}^{\ell}\frac{1}{(\log |z|_i^2+\varphi_i)^2} \bigg(\frac{ d z_i}{z_i}+\partial \varphi_i\bigg)\wedge \bigg(\frac{d\bar{z}_i}{\bar{z}_i}+\bar{\partial} \varphi_i\bigg)\\ &\quad -N\sum_{i=1}^{\ell}\frac{\sqrt{-1}\partial\overline{\partial} \varphi_i}{\log |z|_i^2+\varphi_i}. \end{align*}

From this local expression one can also see that $\omega _{\boldsymbol {a},N}\sim \omega _P$ on any $U^*(r)$ for $0< r<1$. We also can show the following.

Lemma 4.11 For the smooth metric $h_{\boldsymbol {a},N}:=h\cdot \prod _{i=1}^{\ell }|\sigma _i|^{2a_i}_{h_i}\cdot (-\prod _{i=1}^{\ell }\log |\sigma _i|_{h_i}^2)^{N}$ of $E$, it is mutually bounded with $h(\boldsymbol {a},N)$ defined in § 4.3 on any $U^*(r)$ for $0< r<1$.

Let us prove that such construction satisfies the positivity condition in Corollary 3.7.

Proposition 4.12 With the above notation, for any $p+q>n+k$, one has

(26)\begin{equation} \langle [\sqrt{-1} R(h_\mathscr{L}(\boldsymbol{a})), \Lambda_{\omega_{\boldsymbol{a},N}}]f, f\rangle_{\omega_{\boldsymbol{a},N}}\geq \frac{\varepsilon }{2}\lvert f\rvert_{\omega_{\boldsymbol{a},N}}^2 \end{equation}

for any $f\in \Lambda ^{p,q}T_{X^*,x}^*$ and any $x\in X^*$.

Proof. For any point $x\in X^*$, one can choose local coordinate $(z_1,\ldots,z_n)$ around $x$ such that $\omega =\sqrt {-1}\sum _{i=1}^{n} dz_i\wedge d\bar {z}_i$ and $\sqrt {-1} R(h_\mathscr {L}(\boldsymbol {a}))=\sqrt {-1}\sum _{i=1}^{n}\tilde {\gamma }_i dz_i\wedge d\bar {z}_i$ at $x$, where $\tilde {\gamma }_1\leq \cdots \leq \tilde {\gamma }_n$ are eigenvalues of $\sqrt {-1} R(h_\mathscr {L}(\boldsymbol {a}))$ with respect to $\omega$. By (24) one has $\tilde {\gamma }_i\geq \gamma _i-\varepsilon _1$. Let $\lambda _1\leq \cdots \leq \lambda _n$ be eigenvalues of $\sqrt {-1} R(h_\mathscr {L}(\boldsymbol {a}))$ with respect to $\omega _{\boldsymbol {a},N}$. Then $\lambda _i={\tilde {\gamma }_i}/({\varepsilon _2+\tilde {\gamma }_i})$ by Lemma 4.10(ii), and, thus, at each point $x\in X^*$, one has:

• – $-{\varepsilon _1}/({\varepsilon _2-\varepsilon _1})\leq \lambda _i\leq 1$ for $i=1,\ldots,n$;

• – $\lambda _i\geq 1-{\varepsilon _2}/({\varepsilon _0-\varepsilon _1})$ for $i=k+1,\ldots,n$.

We can assume that $p\geq q$. Then

\begin{align*} \langle [\sqrt{-1} R(h_\mathscr{L}(\boldsymbol{a})), \Lambda_{\omega_{\boldsymbol{a},N}}]f, f\rangle_{\omega_{\boldsymbol{a},N}}&\geq \bigg(\sum_{i=1}^{p}\lambda_i+\sum_{j=1}^{q}\lambda_j-\lambda_1-\cdots-\lambda_n\bigg)\lvert f\rvert_{\omega_{\boldsymbol{a},N}}^2 \\ &\geq \bigg((p-k)\bigg(1-\frac{\varepsilon_2}{\varepsilon_0-\varepsilon_1}\bigg)- \frac{k\varepsilon_1}{\varepsilon_2-\varepsilon_1}-(n-q)\bigg)\lvert f\rvert_{\omega_{\boldsymbol{a},N}}^2 \\ &\geq \bigg(1-n\bigg(\frac{\varepsilon_2}{\varepsilon_0-\varepsilon_1}+\frac{\varepsilon_1}{\varepsilon_2-\varepsilon_1}\bigg)\bigg)\lvert f\rvert_{\omega_{\boldsymbol{a},N}}^2 \geq \frac{1}{2}\lvert f\rvert_{\omega_{\boldsymbol{a},N}}^2. \end{align*}

Remark 4.13 Let us mention that Lemma 4.10 and Proposition 4.12 are indeed inspired by the proof of Girbau vanishing theorem in [Dem12, Chapter VII, Theorem 4.2] and its logarithmic generalization in [HLWY23, Theorem 4.1].

We equip ${E}$ with the metric $h_{\boldsymbol {a},N}$ and $X^*$ with the complete Kähler metric $\omega _{\boldsymbol {a},N}$ having the same growth as $\omega _P$ near $D$. Let $\mathfrak L_{(2)}^m(E)_{h_{\boldsymbol {a},N},\omega _{\boldsymbol {a},N}}$ be the sheaf on $X$ (rather than on $X^*$) of germs of $L_2$, $E$-valued $m$-form $u$, for which $D''(u)$ exists weakly as $L^2$-form. Namely, for any open set $U\subset X$, we define

(27)\begin{equation} \mathfrak L_{(2)}^m(E)(U):=\{u\in L^m_{(2)}(U-D,E) \mid D'' u\in L_{(2)}^{m+1}(U-D,E) \}. \end{equation}

Here we write $\mathfrak L_{(2)}^m(E)$ instead of $\mathfrak L_{(2)}^m(E)_{h_{\boldsymbol {a},N},\omega _{\boldsymbol {a},N}}$ for short.

We also define $\mathfrak L_{(2)}^{p,q} (E)$ to be the sheaf on $X$ of germs of $L_2$, $E$-valued $(p,q)$-form, for which $\bar {\partial }_E(u)$ exists weakly as locally $L^2$-form. Namely, for any open set $U\subset X$, one has

(28)\begin{equation} \mathfrak L_{(2)}^{p,q}(E)(U):=\{u\in L^{p,q}_{(2)}(U-D,E)\mid \bar{\partial}_Eu\in L^{p,q+1}_{(2)}(U-D,E)\}. \end{equation}

Note that for any admissible coordinate $(U;z_1,\ldots,z_n)$, as $\omega _{\boldsymbol {a},N}\sim \omega _P$ and $h_{\boldsymbol {a},N}\sim h(\boldsymbol {a},N)$ on any $U^*(r)$ for $0< r<1$, we have that $L^m_{(2)}(U^*(r),E)_{h(\boldsymbol {a},N),\omega _P}$ (in (27)) and $L^{p,q}_{(2)}(U^*(r),E)_{h(\boldsymbol {a},N),\omega _P}$ (in (28)) are the same as those in § 3.2.

The following lemma is a consequence of Theorem 2.7.

Lemma 4.14 Let $(E,\theta,h)$ be a tame harmonic bundle over $X-D$. Suppose $\theta$ has nilpotent residues on $D$. We have that

\[ \mathfrak L_{(2)}^m(E)=\bigoplus_{p+q=m} \mathfrak L_{(2)}^{p,q}(E) \]

and

\[ \theta(\mathfrak L^{p,q}_{(2)}(E))\subset \mathfrak L^{p+1,q}_{(2)}(E). \]

Proof. Since $\theta$ is one-form with value in $\text { End}(E)$, its norm remains unchanged if we replace the metric $h$ by $h(\boldsymbol {a},N):=h\cdot e^{-\chi (\boldsymbol {a},N)}$. One thus has

\[ |\theta|_{h(\boldsymbol{a},N),\omega_P}= |\theta|_{h,\omega_P}\leq C \]

for some $C>0$, where the last inequality follows from Theorem 2.7. (Let us stress here that this is the only place where we use the condition that $\theta$ has nilpotent residues on $D$.) Hence, $\theta$ is a bounded linear operator between Hilbert spaces

\[ L^{p,q}_{(2)}(U-D,E)\to L^{p+1,q}_{(2)}(U-D,E). \]

The theorem follows from that $D''=\bar {\partial }_E+\theta$ and $\bar {\partial }_E\theta =0$.

Proposition 4.15 Let $(E,\theta,h)$ be a tame harmonic bundle over $X-D$. For $x\in D$ and any admissible coordinate $(U;z_1,\ldots,z_n)$ centered at $x$, one has

(29)\begin{equation} \Gamma(U^*(r),\Omega_{U^*(r)}^m\otimes E|_{U^*(r)})\cap \mathfrak L_{(2)}^{m,0}(E)(U(r))=\big( \Omega^m_{X}(\log D)\otimes {}^\diamond\! E\big) (U(r)) \end{equation}

if $0< r\ll 1$. In particular,

(30)\begin{equation} \Omega^m_{X}(\log D)\otimes {}^\diamond\! E\subset \mathfrak L_{(2)}^{m,0}(E). \end{equation}

Proof. Assume that $D\cap U=(z_1\ldots z_\ell =0)$. Write $w_i=\log z_i$ for $i=1,\ldots,\ell$ and $w_j=z_j$ for $j=\ell +1,n$. For the basis $dw_I$ of $\Omega ^{m}_{X}(\log D)$, on $U^*(r)$ with $0< r<1$, one has

\[ |dw_I |_{\omega_P}\leq C_1 \prod_{i=1}^{\ell}(-\log |z_i|^2), \]

for some constant $C_1$.

First, we prove ‘$\supseteq$’ of (29). Pick any section $s\in ( \Omega ^m_{X}(\log D)\otimes {}^\diamond \! E) (U(r))$. One can write

\[ s=\sum_{I}dw_I \otimes e_I \]

with $e_I\in {}^\diamond \! E(U(r))$. Then

\[ |e_I|_h\leq C_2\prod_{i=1}^{\ell}|z_i|^{-\varepsilon} \]

for any $\varepsilon >0$ by the definition of ${}^\diamond \! E$. Therefore, one has

\[ |dw_I\otimes e_I|_{h(\boldsymbol{a},N),\omega_P}\leq |dw_I\otimes e_I|_{h,\omega_P}\cdot e^{-\chi(\boldsymbol{a},N)}=O\bigg(\prod_{i=1}^{\ell}(|z_i|^{a_i-\varepsilon})\bigg) \]

for any $I$, $\varepsilon >0$. This proves that

\[ \int_{U^*(r)}| dw_I\otimes e_\alpha|^2_{h(\boldsymbol{a},N),\omega_P}\omega_P^n=O(1) \]

and, thus,

\[ \Gamma(U^*(r),\Omega_{U^*(r)}^m\otimes E|_{U^*(r)})\cap \mathfrak L_{(2)}^{m,0}(E)(U(r))\supseteq \big( \Omega^m_{X}(\log D)\otimes {}^\diamond\! E\big) (U(r)). \]

Now we prove ‘$\subseteq$’ of (29). For any section $s\in \Gamma (U^*(r),\Omega _{U^*(r)}^m\otimes E|_{U^*(r)})$, we write

\[ s=\sum_{I}dw_I \otimes e_I \]

with $e_I\in E(U^*(r))$. If $s\in \mathfrak L_{(2)}^{m,0}(E)(U(r))$, it follows from Proposition 4.9 that

\[ |s|_{h,\omega_P}(z)\leq C \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i-\delta}\bigg) \]

for any $\delta >0$. Hence,

\[ C \bigg(\prod_{i=1}^{\ell}|z_i|^{-a_i-\delta}\bigg)\geq |s|_{h,\omega_P}=\sum_{I}{|dw_I|_{\omega_P}}|e_I|_{h}\geq \sum_{I} |e_I|_{h} \]

for any $\delta >0$ and $0< r\ll 1$. Therefore, one has

\[ e_I\in {}_{\boldsymbol{a}}E(U(r)). \]

Since ${}_{\boldsymbol {a}}$ is chosen properly such that ${}_{\boldsymbol {a}}E={}^\diamond \! E$, one concludes that

\[ s\in\big( \Omega^m_{X}(\log D)\otimes {}^\diamond\! E\big) (U(r)). \]

This proves that

\[ \Gamma(U^*(r),\Omega_{U^*(r)}^m\otimes E|_{U^*(r)})\cap \mathfrak L_{(2)}^{m,0}(E)(U(r))\subseteq \big( \Omega^m_{X}(\log D)\otimes {}^\diamond\! E\big) (U(r)). \]

Equation (29) follows. Equation (30) is a consequence of (29).

Note that in Theorem 4.15, one does not need to assume that $\theta$ has nilpotent residues on $D$, which is essentially required in Lemma 4.14. For the remainder of § 4.5, we present this nilpotency assumption. Recall that one has $D''^2=0$. Let $(\mathfrak L^\bullet _{(2)}(E),D'')$ be a complex of fine sheaves over $X$ defined by

(31)\begin{equation} \mathfrak L^0_{(2)}(E)\xrightarrow{D''} \mathfrak L^1_{(2)}(E)\xrightarrow{D''} \cdots \xrightarrow{D''} \mathfrak L^m_{(2)}(E). \end{equation}

By (30) and Lemma 4.14, there is a natural inclusion

(32)

and we are going to show that this morphism between two complexes is a quasi-isomorphism.

We now recall a celebrated theorem (in a weaker form) by Demailly [Dem82, Théorème 4.1], which enables us to solve the $\bar {\partial }$-equation on weakly pseudo-convex Kähler manifold (might not be complete). When the metric is complete, it is due to Andreotti and Vesentini [AV65].

Theorem 4.16 (Demailly)

Let $(X,\omega )$ be a Kähler manifold ($\omega$ might not be complete), where $X$ possesses a complete Kähler metric (e.g. $X$ is weakly pseudo-convex). Let $E$ be a vector bundle on $X$ equipped with a smooth hermitian metric $h$ such that

\[ \sqrt{-1}R(E,h)\geq_{\text{Nak}} \varepsilon \omega\otimes \mathbb{1}_E, \]

where $\varepsilon >0$ is a positive constant. Assume that $g\in L^{n,q}_{(2)}(X,E)$ such that $\bar {\partial } g=0$. Then there exists $f\in L^{n,q-1}_{(2)}(X,E)$ such that $\bar {\partial } f=g$ and

\[ \lVert f\rVert_{h,\omega}^2\leqslant \varepsilon^{-1}\lVert g\rVert_{h,\omega}^2. \]

This theorem by Demailly is used to solve the $\bar {\partial }$-equation locally. We first recall the notation used in the following proposition and theorem. Let $(X, \omega )$ be a compact Kähler manifold and let $D=\sum _{i=1}^\ell D_i$ be a simple normal crossing divisor on $X$. Let $(E,\theta,h)$ be a tame harmonic bundle on $X-D$. With the modified Hermitian metric $h_{\boldsymbol {a}, N}$ for $E$ and the complete Kähler metric $\omega _{\boldsymbol {a}, N}$ defined in Lemmas 4.10 and 4.11, we have the sheaves of $L^2$ $E$-valued forms $\mathfrak L_{(2)}^{p,q}(E)_{h_{\boldsymbol {a},N},\omega _{\boldsymbol {a},N}}$ defined in (28). We write $\mathfrak L_{(2)}^{p,q}(E)$ instead of $\mathfrak L_{(2)}^{p,q}(E)_{h_{\boldsymbol {a},N},\omega _{\boldsymbol {a},N}}$ for short.

Proposition 4.17 For any $x\in X$, there is an open set $U\subset X$ (can be made arbitrary small) containing $x$ such that for any $g\in \mathfrak L_{(2)}^{p,q}(E)(U)$ with $q\geq 1$ and $\bar {\partial }_E(g)=0$, there exists a section $f\in \mathfrak L_{(2)}^{p,q-1}(E)(U)$ such that $\bar {\partial }_E f=g$.

Proof. If $x\notin D$, then we can take an open set $U\subset X-D$ containing $x$ which is biholomorphic to a polydisk, and the theorem follows from the usual $L^2$-Dolbeault lemma. Assume $x\in D$. Let $(\tilde {U};z_1,\ldots,z_n)$ be an admissible coordinate around $x$. By Lemma 4.6, $\mathscr {E}_p:= T_{\tilde {U}^*}^p\otimes E$ equipped with the $\mathscr {C}^\infty$-metric ${h}_{\mathscr {E}_p}=h_p^{-1}h(\boldsymbol {a},N)$ induced by $h(\boldsymbol {a},N)$ and $\omega _P$, satisfying

\[ \sqrt{-1}R(h_{\mathscr{E}_p})\geq_{\text{Nak}} \omega_P\otimes \mathbb{1}_{\mathscr{E}_p} \]

for any $p=0,\ldots,n$. Note that $\omega _P|_{\tilde {U}^*(\frac {1}{2})}\sim \omega _{\boldsymbol {a},N}|_{\tilde {U}^*(\frac {1}{2})}$ and $h(\boldsymbol {a},N)|_{\tilde {U}^*(\frac {1}{2})}\sim h_{\boldsymbol {a},N}|_{\tilde {U}^*(\frac {1}{2})}$. Hence, one has

(33)\begin{equation} L_{(2)}^{n,q}(\tilde{U}^*(\tfrac{1}{2}),\mathscr{E}_{n-p})_{h_{\mathscr{E}_{n-p}}, \omega_P}=L_{(2)}^{p,q}(\tilde{U}^*(\tfrac{1}{2}),E)_{h_{\boldsymbol{a},N},\omega_{\boldsymbol{a},N}} \end{equation}

for any $p=0,\ldots,n$. For any $g\in L_{(2)}^{n,q}(\tilde {U}^*(\frac {1}{2}),\mathscr {E}_{n-p})_{h_{\mathscr {E}_{n-p}},\omega _P}$ with $\bar {\partial } (g)=0$, if $q\geq 1$, by Theorem 4.16, there is $f\in L_{(2)}^{n,q-1}(\tilde {U}^*(\frac {1}{2}),\mathscr {E}_{n-p})_{h_{\mathscr {E}_{n-p}},\omega _P}$ such that $\bar {\partial } f=g$. The proposition then follows from (33), and $\tilde {U}^*(\frac {1}{2})$ is the desired open set $U$ in the proposition.

Now we are ready to prove that the $L^2$-complex is the desired fine resolution for our tame harmonic bundle.

Theorem 4.18 The morphism between two complexes in (32) is a quasi-isomorphism.

Proof. Pick any $m\in \{0,\ldots,n\}$. We are going to show that $\iota :\ker \theta /\operatorname {Im} \theta \to \ker D''/\operatorname {Im} D''$ at ${}^\diamond \! E\otimes \Omega ^m_X(\log D)$ is an isomorphism. For any $x\in D$, we pick an open set $U\ni x$ as in Proposition 4.17 and set $U^*=U-D$. Indeed, $U^*=\tilde {U}^*(\frac {1}{2})$ where $(\tilde {U};z_1,\ldots,z_n)$ is an admissible coordinate around $x$ and, thus, $h_{\boldsymbol {a},N}\sim h(\boldsymbol {a},N)$ and $\omega _{\boldsymbol {a},N}\sim \omega _P$ on $U^*$. Pick any $g\in \mathfrak L_{(2)}^{m}(E)(U)$ such that $D''g=0$. By Lemma 4.14, we can write $g=\sum _{p+q=m}g_{p,q}$ where $g_{p,q}\in \mathfrak L_{(2)}^{p,q}(E)(U)$, and let $q_0$ be the largest integer for $q$ such that $g_{p,q}\neq 0$. By Lemma 4.14, we can decompose $D''g$ into bidegrees, such that

\[ \begin{cases} \bar{\partial}_Eg_{m-q_0,q_0}=0\\ \theta g_{m-q_0,q_0}+\bar{\partial}_E g_{m-q_0+1,q_0-1}=0\\ \vdots\\ \theta g_{p_0-1,m-p_0+1}+\bar{\partial}_E g_{p_0,m-p_0}=0\\ \theta g_{p_0,m-p_0}=0 \end{cases} \]

for which the operators act in the sense of distribution. Hence, $g_{m-q_0,q_0}\in \mathfrak L_{(2)}^{m-q_0,q_0}(E)(U)$ with $\bar {\partial }_Eg_{m-q_0,q_0}=0$. Applying Proposition 4.17, there is a section $f_{m-q_0,q_0-1}\in \mathfrak L_{(2)}^{m-q_0,q_0-1}(E)(U)$ such that $\bar {\partial }_E f_{m-q_0,q_0-1}=-g_{m-q_0,q_0}$. By Lemma 4.14, $D''f_{m-q_0,q_0-1}\in \mathfrak L_{(2)}^{m}(E)(U)$, and we define $g':=D''f_{m-q_0,q_0-1}+g\in \mathfrak L_{(2)}^{m}(E)(U)$. One thus has $D''g'=0$. Write $g'=\sum _{p+q=m}g'_{p,q}$ where $g'_{p,q}\in \mathfrak L_{(2)}^{p,q}(E)(U)$. Note that

\[ \begin{cases} g'_{m-q_0,q_0}=\bar{\partial}_E f_{m-q_0,q_0-1}+g_{m-q_0,q_0}=0,\\ g'_{m-q_0+1,q_0-1}=\theta f_{m-q_0,q_0-1} +g_{m-q_0+1,q_0-1} ,\\ g'_{m-q_0+2,q_0-2}= g_{m-q_0+2,q_0-2},\\ \vdots\\ g'_{p_0,m-p_0}= g_{p_0,m-p_0}. \end{cases} \]

We can use the same method to find $f\in \mathfrak L_{(2)}^{m-1}(E)(U)$ such that $g_0=g+D''f\in \mathfrak L_{(2)}^{m,0}(E)(U)$ such that $D''g_0=0$. Decomposing $D''g_0$ into bidegrees we get

\[ \bar{\partial}(g_0)=0, \quad \theta(g_0)=0. \]

By the elliptic regularity of $\bar {\partial }$ one concludes that

\[ g_0\in \Gamma(U^*, \Omega_{U^*}^m\otimes E|_{U^*}). \]

By (29), $g_0\in \Gamma (U,\Omega ^m_{X}(\log D)\otimes {}^\diamond \! E|_U)$, which shows the surjectivity of $\iota$.

Now we prove the injectivity of $\iota$. Let $g \in \Gamma (U,\Omega ^m_{X}(\log D)\otimes {}^\diamond \! E|_U)\subset \mathfrak L_{(2)}^m(E)(U)$ such that $g=D''f$. Write $f=\sum _{p+q=m{-1}}f_{p,q}$ where $f_{p,q}\in \mathfrak L_{(2)}^{p,q}(E)(U)$. Then $g=D''(f_{m-1,0})=\theta (f_{m-1,0})$ thanks to the bidegree condition. Hence,

\[ f_{m-1,0} \in \Gamma(U^*,\Omega_{U^*}^{m-1}\otimes E|_{U^*})\cap \mathfrak L_{(2)}^{m-1,0}(E)(U). \]

By (29) again, $f_{m-1,0}\in \Gamma (U,\Omega ^{m-1}_{X}(\log D)\otimes {}^\diamond \! E|_U)$. The injectivity of $\iota$ follows.

When $m>n$, the exactness of $D''$ can be proven in the same way. Let $g\in \mathfrak L_{(2)}^{m}(E)(U)$ such that $D''g=0$. Applying Proposition 4.17 once again as in the case of $m\leq n$, we can find $f\in \mathfrak L_{(2)}^{m-1}(E)(U)$ such that $D''f+g\in \mathfrak L_{(2)}^{n,m-n}(E)(U)$. As $\theta (D''f+g)=0$, this implies that $\bar {\partial }_E(D''f+g)=0$, and by Proposition 4.17 again one can find $h\in \mathfrak L_{(2)}^{n,m-n-1}(E)(U)$ such that $D''h=\bar {\partial }_Eh=D''f+g$. This shows the exactness of $D''$ when $m>n$. This completes the proof of the theorem.

Remark 4.19 To summarize, let us explain our choice of the perturbation of the metric $h$ by $h_{\boldsymbol {a},N}:=h\cdot \prod _{i=1}^{\ell }|\sigma _i|^{2a_i}_{h_i}\cdot (-\prod _{i=1}^{\ell }\log |\sigma _i|_{h_i}^2)^{N}$.

The input of the factor $\prod _{i=1}^{\ell }|\sigma _i|^{2a_i}_{h_i}$ is to ensure that the sections of ${}^\diamond \! E$ are $L^2$-integrable, which does not seem to be true for the harmonic metric $h$. However, $a_i$ have to be small enough since holomorphic sections of $E$ which are also $L^2$-integrable with respect to $h_{\boldsymbol {a},N}$ only lie on ${}_{\boldsymbol {a}}E$. Due to the semicontinuity of the parabolic structures by Mochizuki (cf. Definition 4.1 (iii) together with Theorem 4.3), ${}_{\boldsymbol {a}}E={}^\diamond \! E$ if $a_i$ are small enough. This is the main context of Theorem 4.15.

The input of $(-\prod _{i=1}^{\ell }\log |\sigma _i|_{h_i}^2)^{N}$ is to add enough local positivity near $D$ such that one can apply the Hörmander–Demailly $L^2$-estimate to obtain the $L^2$-Dolbeault lemma locally around $D$. This is Proposition 4.17. Let us stress here that the fact that $(E,h)$ is acceptable due to Mochizuki is essential to perform such modification of metrics.

4.6 Proof of the main theorem

In this subsection, we will prove the following vanishing theorem for a tame harmonic bundle.

Theorem 4.20 Let $(X,\omega )$ be a compact Kähler manifold of dimension $n$ and let $D$ be a simple normal crossing divisor on $X$. Let $(E,{}_{ \boldsymbol {a}}E,\theta )$ be the parabolic Higgs bundle on $X$ induced by a tame harmonic bundle $(E,\theta,h)$ on $X^*=X-D$ whose Higgs field has nilpotent residues on $D$. Let $L$ be a line bundle on $X$ equipped with a smooth Hermitian metric $h_L$ such that its curvature $\sqrt {-1}R(h_L)\geq 0$ and has at least $n-k$ positive eigenvalues at every point on $X$ as a real (1,1)-form. Let $B$ be a nef line bundle on $X$. Then

\[ \mathbb{H}^m\big(X, ({}^\diamond\! E\otimes \Omega^\bullet_X(\log D),\theta)\otimes L\otimes {B} \big)=0 \]

for any $m>n+k$.

Proof. We will use the notation in § 4.5. Recall that $(X^*,\omega _{\boldsymbol {a},N})$ is a complete Kähler manifold. Write $\mathscr {L}:=L\otimes {B}|_{X^*}$ and we equip it with the metric $g=h_L{h_{B}}$ where $h_{B}$ is properly chosen as Lemma 4.10. Then $g$ is the restriction to $X^*$ of a smooth metric on $X$. We introduce a new Higgs bundle $(\tilde {E},\tilde {\theta },\tilde {h}):=(E\otimes \mathscr {L}, \theta \otimes \mathbb {1}_{\mathscr {L}},h_{\boldsymbol {a},N}\cdot g)$. We still use the notation $D'':=\bar {\partial }_{\tilde {E}}+\tilde {\theta }$ abusively, and $D''^*$ denotes its adjoint with respect to $\tilde {h}$. We will apply Corollary 3.7 to solve the $D''$-equation for this new Higgs bundle.

Note that $h_{\boldsymbol {a},N}g=hh_\mathscr {L}{(\boldsymbol {a})}$ by (22) and Lemma 4.11. By Proposition 4.12, the metrized line bundle $(\mathscr {L},h_\mathscr {L}{(\boldsymbol {a})})$ satisfies the condition in Corollary 3.7 when $m>n+k$. Hence, by Corollary 3.7 for any section $g{\in } L^m_{(2)}(X^*,\tilde {E})_{\tilde {h},\omega _{\boldsymbol {a},N}}$, if $D''g=0$ and $m>n+k$, there exists $f\in L^{m-1}_{(2)}(X^*,\tilde {E})_{\tilde {h},\omega _{\boldsymbol {a},N}}$ such that

\[ D''f=g. \]

Let $\mathfrak L_{(2)}^m(\tilde {E})_{\tilde {h},\omega _{\boldsymbol {a},N}}$ be the sheaf on $X$ (rather than on $X^*$) of germs of locally $L_2$, $\tilde {E}$-valued $m$-forms, for which both $D''(u)$ (as a distribution) exist weakly as locally $L^2$-forms. Namely, for any open set $U\subset X$, one has

(34)\begin{equation} \mathfrak L_{(2)}^m(\tilde{E})(U):=\{u\in L^m_{(2)}(U-D,\tilde{E})_{\tilde{h},\omega_{\boldsymbol{a},N}} \mid D'' u\in L_{(2)}^{m+1}(U-D,E)_{\tilde{h},\omega_{\boldsymbol{a},N}} \}. \end{equation}

Then the above argument proves that the cohomology $H^i$ of the complex of global sections of the sheaves $(\mathfrak L_{(2)}^\bullet (\tilde {E})_{\tilde {h},\omega _{\boldsymbol {a},N}},D'')$ vanishes for $m>n+k$.

As $g$ is smooth over the whole $X$, the metric $\tilde {h}\sim h(\boldsymbol {a},N)$ near $D$ (fix any trivialization of $L\otimes {B}$). Hence, the natural inclusion

(35)

is thus also a quasi-isomorphism by Theorem 4.18.

As the complex $(\mathfrak L_{(2)}^\bullet (\tilde {E})_{\tilde {h},\omega _{\boldsymbol {a},N}},D'')$ is a fine sheaf, its cohomology computes the hypercohomology of the complex $({}^\diamond \! E\otimes L\otimes {B}\otimes \Omega ^\bullet _X(\log D),\tilde {\theta })$. We thus conclude that $\mathbb {H}^m(X,({}^\diamond \! E\otimes L\otimes {B}\otimes \Omega ^\bullet _X(\log D),\tilde {\theta }))=0$ for $m>n+k$. The theorem is proved.

Remark 4.21 Let us show how to derive the log Girbau vanishing theorem in [HLWY23, Corollary 1.2] from Theorem A. In this remark we use the same notation as that in [HLWY23, Corollary 1.2]. With the same setting as Theorem A, let $(E,\theta,h):=(\mathscr {O}_{X-D},0,h)$ where $h$ is the canonical metric on the trivial line bundle $\mathscr {O}_{X-D}$. According to the extension of $(E,\theta,h)$ defined in § 4.2, one has $({}^\diamond \! E,\theta )=(\mathscr {O}_X,0)$. Hence, the Dolbeault complex in (1)

\[ {\rm Dol}({}^\diamond\! E,\theta)=\mathscr{O}_X\xrightarrow{0} \Omega^1_X(\log D) \xrightarrow{0}\cdots\xrightarrow{0} \Omega^n_X(\log D), \]

which is a direct sum of sheaves of logarithmic $p$-forms shifting $p$ places to the right:

\[ {\rm Dol}({}^\diamond\! E,\theta)=\oplus_{p=0}^{n}\Omega^p_X(\log D)[p], \]

where $\Omega ^p_X(\log D)[p]$ is obtained by shifting the single degree complex $\Omega ^p_X(\log D)$ in degree $p$. Hence, if $m>n+k$, by Theorem 4.20 one has

\begin{align*} 0=\mathbb{H}^m\big(X, {\rm Dol}({}^\diamond\! E,\theta)\otimes {N\otimes L} \big) &=\oplus_{p=0}^{n}H^m(X,\Omega^p_X(\log D)\otimes {N\otimes L}[p])\\ &=\oplus_{p=0}^{n}H^{m-p}(X,\Omega^p_X(\log D)\otimes {N\otimes L}). \end{align*}

We thus conclude that

\[ H^{q}(X,\Omega^p_X(\log D)\otimes {N\otimes L}) \]

if $p+q>n+k$. This is the log Girbau vanishing theorem by Huang, Liu, Wan and Yang.

4.7 Vanishing theorem for parabolic Higgs bundles

Let $X$ be a complex projective manifold and let $D$ be a simple normal crossing divisor on $X$. For a parabolic Higgs bundle $(E,{}_{\boldsymbol {a}}E,\theta )$ on $(X,D)$, its parabolic Chern classes, denoted by $\text {para}$-$c_i(E)$, are the usual Chern class of ${}^\diamond \! E$ with a modification along the boundary divisor $D$ (see, e.g., [AHL19, § 3] for more details). With a polarization, i.e. an ample line bundle $H$ on $X$, the parabolic degree $\text {para}$-$\text {deg}(E)$ of $(E,{}_{\boldsymbol {a}}E,\theta )$ is defined to be $\text {para-}c_1(E)\cdot H^{n-1}$. We say $(E,{}_{\boldsymbol {a}}E,\theta )$ slope stable if for any coherent torsion-free subsheaf $V$ of ${}^\diamond \! E$, with $0<\text {rank} V<\text {rank} {}^\diamond \! E=\text {rank} E$ and $\theta (V)\subseteq V\otimes \Omega ^1_X(\log D)$, the condition

\[ \frac{\text{para-deg}(V)}{{\rm rank}(V)}< \frac{\text{para-deg}(E)}{{\rm rank}(E)} \]

is satisfied, where $V$ carries the induced the parabolic structure from $(E,{}_{\boldsymbol {a}}E,\theta )$, i.e. ${}_{\boldsymbol {a}}V:=V\cap {}_{\boldsymbol {a}}E$. A parabolic Higgs bundle $(E,{}_{\boldsymbol {a}}E,\theta )$ is poly-stable if it is a direct sum of slope stable parabolic Higgs bundles. By [IS07], $(E,{}_{\boldsymbol {a}}E,\theta )$ is called locally abelian if in a Zariski neighborhood of any point $x\in X$ there is an isomorphism between the underlying parabolic vector bundle $(E,{}_{\boldsymbol {a}}E)$ and a direct sum of parabolic line bundles.

By the celebrated Simpson–Mochizuki correspondence [Moc06, Theorem 9.4], a parabolic Higgs bundle $(E,{}_{\boldsymbol {a}}E,\theta )$ on $(X,D)$ is poly-stable with trivial parabolic Chern classes and locally abelian if and only if it is induced by a tame harmonic bundle over $X-D$ defined in § 4.2. Based on this deep theorem, our theorem can thus be restated as follows.

Corollary 4.22 Let $(E, {}_{\boldsymbol {a}}E,\theta )$ be a locally abelian poly-stable parabolic Higgs bundle on a projective log pair $(X,D)$ with trivial parabolic Chern classes such that the Higgs field $\theta$ has nilpotent residues on $D$. Let $L$ be a line bundle on $X$ equipped with a smooth metric $h_L$ such that its curvature $\sqrt {-1}R(h_L)\geq 0$ and has at least $n-k$ positive eigenvalues. Let $B$ be a nef line bundle on $X$. Then for the weight-zero filtration ${}^\diamond \! E$ of $(E,{}_{\boldsymbol {a}}E,\theta )$, one has

\begin{align*} \mathbb{H}^m\big(X, ({}^\diamond\! E\otimes \Omega^\bullet_X(\log D),\theta)\otimes L\otimes {B} \big)=0 \end{align*}

for any $m>\dim X+k$.

Remark 4.23 The above corollary essentially generalizes the main theorem [Ara19, Theorem 1] in which he assumed that $\theta$ is nilpotent (see Remark 2.6) and that $L$ is ample.