I. INTRODUCTION
Deep Convolutional Neural Network (DCNN) has been widely used in image classification due to its impressive capability of capturing relevant features of different classes in the data [Reference Krizhevsky, Sutskever and Hinton1–Reference Simonyan and Zisserman3]. However, it is known that the classification accuracy of generic DCNN can be affected by image distortions in the input data: adding small amount of distortion to the test set usually results in a significant reduction in the classification accuracy of the network [Reference Dodge and Karam4].
In computer vision problems, distortion is sometimes unavoidable; it may be a camera artifact, or be caused by the environment. To enhance the robustness of the image classifier against input distortions, since recent years, several studies have proposed promising techniques that can classify severely distorted images (with high noise levels or blurs) by DCNN with high accuracy. For example, Zhou et al. tackle the problem through fine-tuning or re-training of the DCNN network [Reference Zhou, Song and Cheung5], which, however, works well only for several selective types of distortions and requires re-training multiple times using distorted images. Dodge and Karam propose MixQualNet [Reference Dodge and Karam6], which requires identifying the type of image distortion first. Multiple weighted expert networks are trained in the MixQualNet, allowing for handling various types of noises in the input images by weighting the contributions of the expert networks through gating [Reference Dodge and Karam6]. The MixQualNet is more robust to distortion data than a single fine-tuning model, but demands higher computational complexity and hardware cost. Hossain et al. [Reference Hossain, Teng, Zhang, Lim and Lu7] propose to remove high-frequency coefficients of the input data, using the discrete cosine transform (DCT), before sending into the network for training. This model is less affected by the distortion noise, which often contributes to higher frequency components in the DCT domain, and is therefore more robust to distorted data with improved accuracy.
While the deep learning techniques proposed in the aforementioned works have provided significant advancement in improving the accuracy of image classifiers, the robustness is still limited when facing a variety of input image distortions. The existing approaches perform well for some types of distortions, but may not promisingly work as well for others. To address this problem, in this paper, we leverage the advantages of DCT, discrete wavelets transform (DWT), and singular value decomposition (SVD) and propose a new hybrid preprocessing module in the “training” stage to further elevate the robustness and accuracy of the classifier against various types of image distortions.
There have been several studies in the area of image compression that utilizes a hybrid DWT-DCT algorithm to achieve a better coding efficiency [Reference Katharotiya, Patel and Mahesh8, Reference Alsayyh, Mohamad and Abu-ulbeh9]. A combination of 2D-DWT and SVD is used in [Reference Bhagat and Bansal10] to provide efficient compression while keeping the decoding error within an acceptable range. While hybrid DWT-DCT and DWT-SVD preprocessing have been successfully introduced for image compression, its application in robust classifier against image distortions has not been well studied in the literature. In this paper, we propose the hybrid DCT-DWT-SVD algorithm, capitalizing on advantages of the DCT, DWT, and SVD to improve the robustness of the DCNN to image distortions. The input data will first go through the DCT with “zig-zag scanning” in which low-frequency components can be extracted. Next, we determine level-1 or level-2 DWT in a random fashion to capture approximations in the low-frequency band and remove detailed high-frequency sub-band. Random selection allows for maintaining the accuracy for clean data with improved accuracy of the distorted picture by partially removing high-frequency components commonly existed in distorted images. Finally, SVD is applied to retain a fixed number of singular values for feature extraction. During training, all clean data will first go through the DCT-DWT-SVD module before entering the CNN (VGG-16) for training. When testing, the distorted images directly enter the model for classification without having to be processed by the hybrid DCT-DWT-SVD operations.
In this work, five different types of distortions are generated to the images in the datasets SVHN [Reference Yuval, Tao, Adam, Alessandro, Bo and Andrew11] and CIFAR-10/100 [Reference Krizhevsky and Hinton12] for the testing purpose. These five types of distortions include Gaussian noise, speckle noise, salt and pepper noise, motion blur, and Gaussian blur. The experimental results show that the trained DCNN with the proposed DCT-DWT-SVD preprocessing module is robust to all five types of distortions with improved accuracy. The contributions of the paper are summarized as follows:
• We propose a hybrid DCT-DWT-SVD preprocessing module in the DCNN architecture that does not require fine-tuning, re-training, or data augmentation. To our best knowledge, this paper presents the first study in the literature that utilizes the hybrid DCT-DWT-SVD module to combat image distortions in image classifications. Experimental results demonstrate the robustness of the proposed DCT-DWT-SVD module to various types of image distortions.
• When testing, the proposed hybrid module does not require performing noise identification and noise reduction before feeding in the input data. The distorted images directly enter the trained system for classification. The resultant accuracy of the proposed model is better than that of the conventional methods by DCT used in previous papers.
• We introduce the random selection step in determining the size of zig-zag scanning region in DCT and the decomposition level in DWT within the proposed hybrid module. The accuracy of the anti-noise model for both clean data and distorted data can thus be effectively improved.
This paper is organized as follows. Section II reviews the related work in the literature. We elaborate the proposed hybrid DCT-DWT-SVD module in Section III. In Section IV, experiments are conducted to demonstrate the effectiveness and robustness of the hybrid learning module. Finally, a concluding remark is made in Section V.
II. RELATED WORK
Dodge and Karam [Reference Dodge and Karam4] show that the accuracy of image identification of deep network can be significantly influenced by image distortions, and the VGG-16 architecture has been shown to be more robust compared with the other networks [Reference Dodge and Karam13]. Zhou et al. [Reference Zhou, Song and Cheung5] analyze the DNN classifier performance under different distortions, in which re-training and fine-tuning have been proposed to alleviate the effect of image distortions. However, single fine-tuning network may not perform well under various types of distortions. Dodge and Karam [Reference Dodge and Karam6] propose the MixQualNet to deal with various types of noise by mixture of expert-based networks for image classification. Each of the multiple expert networks in MixQualNet is trained with respect to one type of distorted images, leveraging the gating network to weight the contributions of the expert networks. It is shown in [Reference Dodge and Karam6] that the MixQualNet is more robust to distorted data than single fine-tuned models, but is composed of many complex sets of CNN models, rendering very high computational complexity and hardware cost. Ha et al. [Reference Ha, Byun, Kim, Lee, Lee and Lee14] propose an improved version of MixQualNet, termed as Selective DCNN, which employs a tiny CNN to identify the distortion type of the input image and then activates only one expert network based on the result of the tiny CNN. Since only one expert network is activated during inference, the Selective DCNN can effectively reduce the hardware cost. However, this method still needs to train a number of different models, each of which corresponds to a certain type of distortion. To reduce training time and computational complexity, Hossain et al. [Reference Hossain, Teng, Zhang, Lim and Lu7] utilize the DCT before the data entering the network and set a threshold to remove high-frequency coefficients. This approach enhances the robustness of the model to distorted data, since the proposed DCT-based CNN does not heavily rely on high-frequency image details in training the model parameters. However, the classification accuracy of the DCT-based CNN in [Reference Hossain, Teng, Zhang, Lim and Lu7] is still lower than that of the MixQualNet, provided that the type of distorted images has been incorporated in the training stage for the MixQualNet.
III. HYBRID MODULE WITH DCT-DWT-SVD
In this section, we elaborate the proposed hybrid DCT-DWT-SVD module employed in the “training” stage. The rationale behind the DCT-DWT-SVD module is to partially remove high-frequency details from the images used for training such that the proposed model does not heavily rely on these details that are particularly noticeable in distorted images. Embedded within the hybrid module, the “random selection” scheme is introduced in the DCT and DWT stage to determine the number of high-frequency components to be discarded in the hybrid module, allowing for capturing useful features in the clean data and therefore further enhancing the accuracy of classifying the distorted images.
A) The discrete cosine transform
DCT [Reference Ahmed, Natarajan and Rao15] is often used in signal processing and image processing in the frequency domain for lossy data compression (e.g. JPEG [Reference Wallace16]). In particular, DCT has a strong energy concentration characteristic: the information of natural signals transformed by DCT is mostly concentrated in the low-frequency part whereas the high-frequency components generally encode sharp changes that add fine details to the signal. As shown in Fig. 1(a), the DCT coefficients with large magnitudes are in the upper-left corner of the DCT matrix (i.e. the low-frequency part). Typically, zig-zag scanning is adopted to extract the low-frequency components as shown in Fig. 1(b). In contrast with the JPEG [Reference Wallace16] where the block size corresponding to the second type of DCT is usually set to 8 ($8\times 8$![]() block), in this work we use one block with the size identical to that of the original input image.
block), in this work we use one block with the size identical to that of the original input image.

Fig. 1. (a) FDCT and IDCT. (b) The zig-zag scanning.
B) The discrete wavelet transform
DWT utilizes wavelets as the basis functions and decomposes the signal into components associated with multiple frequency bands. The process of the two-dimensional DWT (2D-DWT) is to pass the rows of the 2D signal through a high-pass filter and low-pass filter, then down sample by a factor of two. After that, the 2D-DWT performs the same steps to the columns of the 2D signal again. The region passed by low-pass filter is the low-frequency sub-band which represents the approximation part, and the other regions passing through the high pass filter represent the detailed part. The process of the 2D-DWT is shown in Fig. 2. The 2D-DWT divides the image into four sub-bands, the level-1 DWT and level-2 DWT are shown in Figs 3(a) and 3(b), where LL represents the low-frequency sub-band, HL represents the horizontal high-frequency sub-band, LH represents the vertical high-frequency sub-band, and HH is the diagonal high-frequency sub-band. The LL sub-band generally contains more descriptive features of the image than the other sub-bands. In this paper, we consider “db8” wavelet and “db4” wavelet as the mother wavelet for level-1 and level-2 DWT, respectively. And we utilize “smooth” signal extension to overcome the boundary problem in the 2D-DWT, where the edge components are extended according to the first derivatives on the boundary (Fig. 4).

Fig. 2. Multi-resolution decomposition of the 2D-DWT.
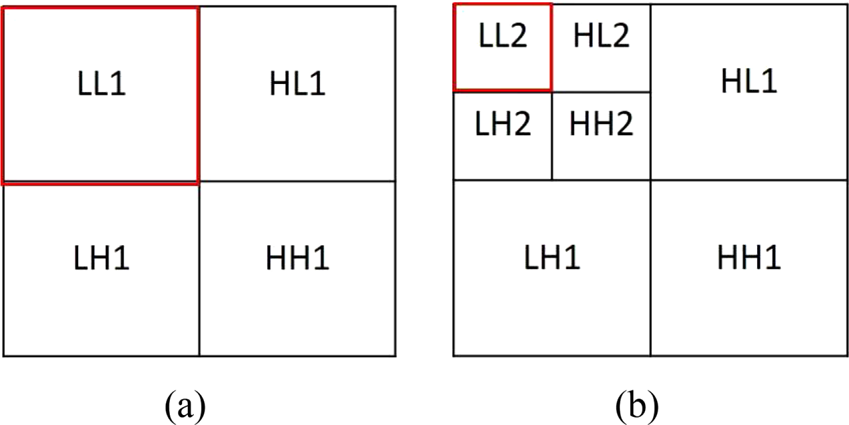
Fig. 3. (a) Single-level decomposition (level-1 DWT). (b) Two-level decomposition (level-2 DWT).

Fig. 4. The “smooth” signal extension mode.
C) Singular value decomposition
SVD is well known for its powerful capability to decompose signals into orthogonal components and is widely used in many signal processing applications, e.g. image compression [Reference Swathi, Shah, Surbhi and Gopichand17] and precoder design for transmitters equipped with multiple antennas in cellular systems. In general, SVD presents a factorization of any matrix $M$![]() into the product of three matrices – an orthogonal matrix $U$
into the product of three matrices – an orthogonal matrix $U$![]() , a diagonal matrix $\Sigma$
, a diagonal matrix $\Sigma$![]() , and the transpose of an orthogonal matrix $V$
, and the transpose of an orthogonal matrix $V$![]() :
:

where the singular values are usually arranged in descending order ($\sigma _1 \geq \sigma _2 \geq \dots \geq \sigma _m$![]() ). The above matrix factorization in (1) can be rewritten as
). The above matrix factorization in (1) can be rewritten as
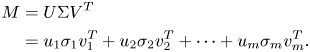
The principle of image compression is to decompose the image into (2), and reserve the components with dominant singular values. A compressed image can thus be generated by appropriately choosing a number of components being retained in (2).
D) DCT-DWT-SVD module integration
In this work, we propose to combine the DCT, DWT, and SVD modules in the preprocessing stage, aiming at integrating the advantages from each technique in order to enhance the robustness and improve classification accuracy for distorted images. It is worthwhile to emphasize that, in contrast with the existing methods in the literature, the proposed hybrid module is used only in the training stage and only the clean (undistorted) images are used for training. The input data first go through the DCT block. Then, the zig-zag scanning is employed to extract low-frequency components. Specifically, as shown in Fig. 1(b), we apply zig-zag scanning in the DCT coefficient matrix starting from the upper-left corner, which corresponds to the low-frequency parts, and remove higher frequency coefficients in order to reduce details more likely to be seen in distorted images. While removing high-frequency components is effective to combat distortions in images, it inevitably discards certain important high-frequency features in the original images as well. To mitigate this effect, in this paper, we proposed to randomly select the zig-zag scanning region in ranges from $5\times 5$![]() to $15\times 15$
to $15\times 15$![]() . Finally, inverse DCT is performed on the remaining DCT coefficients (zig-zag scanning region) to reconstruct the transformed image.
. Finally, inverse DCT is performed on the remaining DCT coefficients (zig-zag scanning region) to reconstruct the transformed image.
Following the DCT operations, the LL-band component of the DCT-approximated images are captured using level-1 or level-2 DWT (Fig. 3), whereas the other high-frequency sub-bands are removed. One promising feature of the DWT is that the basis of wavelet transformation consists of a set of wavelets with infinite length capable of extracting the information of spatial position and frequency in 2D signals. In other words, the high-frequency components decomposed by the DWT are more representative of the spatial and spectral edge details of the original picture than the high-frequency components decomposed by DCT. In this paper, we leverage this important characteristic that distinctive high-frequency components can be extracted from the DCT and DWT. By removing parts of the high-frequency components decomposed by both the DWT and DCT, more distorted parts in the original image can be discarded and distortion-free low-frequency features can thus be retained, which results in a more robust classification performance. In addition, random selection is also introduced here to determine whether level-1 or level-2 DWT is employed in the wavelet transform. At the end of DWT block, the image is reconstructed by inverse DWT. It is worthwhile to note that, while both DCT and DWT play a similar role of contributing to preserving important low-frequency components, placing the DCT operation first before the DWT results in a slightly better classification accuracy. This is because the high-frequency components after the DWT decomposition contain more useful information about clean images, which should not be discarded too early in the whole preprocessing procedure. The final stage of the proposed hybrid module is the SVD block to process the DCT-DWT approximated images and retain prominent components associated with larger singular values. The complete operation of the hybrid DCT-DWT-SVD module is summarized in Algorithm 1.
During training, all clean data will first go through the DCT-DWT-SVD module before entering the CNN (VGG-16) for training. On the other hand, during testing, the distorted images directly enter the VGG-16 model for classification without having to go through the DCT-DWT-SVD module. The whole network is illustrated in Fig. 6. An image transformed by the DCT-DWT-SVD module is shown in Fig. 5. When the number of the selected DCT coefficients is close to $5\times 5$![]() and level-2 is selected in the DWT stage, most of the high-frequency components in the input image are removed after the hybrid preprocessing module. In contrast, if the zig-zag scanning region is close to $15\times 15$
and level-2 is selected in the DWT stage, most of the high-frequency components in the input image are removed after the hybrid preprocessing module. In contrast, if the zig-zag scanning region is close to $15\times 15$![]() in the DCT stage and level-1 is selected in the DWT stage, more high-frequency details will be maintained after the preprocessing module. Since the proportion of the high-frequency components removed in each image is not fixed in both the DCT and DWT stages due to random selection, the subsequent VGG-16 can capture a more diversified low-frequency components reserved in DCT and DWT in the training data. The proposed model does not heavily rely on features with high-frequency details which are often easily affected by various types of distortions. Consequently, the classification accuracy of the distorted images can be effectively improved.
in the DCT stage and level-1 is selected in the DWT stage, more high-frequency details will be maintained after the preprocessing module. Since the proportion of the high-frequency components removed in each image is not fixed in both the DCT and DWT stages due to random selection, the subsequent VGG-16 can capture a more diversified low-frequency components reserved in DCT and DWT in the training data. The proposed model does not heavily rely on features with high-frequency details which are often easily affected by various types of distortions. Consequently, the classification accuracy of the distorted images can be effectively improved.

Fig. 5. Images after being processed by the hybrid DCT-DWT-SVD module with different amounts of low frequency components in the DCT-DWT stage and with six principle components in the SVD stage.

Fig. 6. The proposed DCNN architecture based on the VGG-16 [Reference Simonyan and Zisserman3]. Clean data first go through the DCT-DWT-SVD module before entering the VGG-16 for training. However, the DCT-DWT-SVD module will not be active when testing, with the distorted picture directly entering the model for classification.

E) Deep convolutional neural network
In this paper, we adopt the VGG-16 as the base network, as the VGG-16 architecture [Reference Simonyan and Zisserman3] has been acknowledged to be more robust to image distortions when compared with the AlexNet [Reference Krizhevsky, Sutskever and Hinton1] or GoogleNet [Reference Szegedy2] architectures. The VGG-16 architecture combined with the proposed DCT-DWT-SVD module is shown in Fig. 6, which contains 13 convolutional layers with the kernel size being $3\times 3$![]() . Each convolutional layer is followed by ReLU and the size of max-pooling is $2\times 2$
. Each convolutional layer is followed by ReLU and the size of max-pooling is $2\times 2$![]() . There are 10 channels softmax output layer for SVHN and CIFAR-10, and 100 channels softmax output layer for CIFAR-100, respectively. To prevent from the effects of overfitting and vanishing gradients, we add batch normalization [Reference Sergey and Szegedy18] after each convolutional layer and set dropout probability 0.3 [Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov19] after the first batch normalization, 0.5 before flatten and softmax output layer, and the other dropout probability is set to 0.4. These settings of the dropout probabilities follow from the suggestions in [Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov19] and from trial-and-errors during the simulations. Data augmentation (rotation and shift) [Reference Mikolajczyk and Grochowski20], a well-known and effective step in deep CNN models, is also utilized to combat overfitting. We use stochastic gradient descent [Reference Ruder21] as optimizer and 150 epochs are set with minibatch size 128 for training.
. There are 10 channels softmax output layer for SVHN and CIFAR-10, and 100 channels softmax output layer for CIFAR-100, respectively. To prevent from the effects of overfitting and vanishing gradients, we add batch normalization [Reference Sergey and Szegedy18] after each convolutional layer and set dropout probability 0.3 [Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov19] after the first batch normalization, 0.5 before flatten and softmax output layer, and the other dropout probability is set to 0.4. These settings of the dropout probabilities follow from the suggestions in [Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov19] and from trial-and-errors during the simulations. Data augmentation (rotation and shift) [Reference Mikolajczyk and Grochowski20], a well-known and effective step in deep CNN models, is also utilized to combat overfitting. We use stochastic gradient descent [Reference Ruder21] as optimizer and 150 epochs are set with minibatch size 128 for training.
IV. EXPERIMENTS AND DATASETS
In this section, we discuss different pre-processing methods before training data entering the network to increase the accuracy of CNN for the distortion pictures. The testing data are generated by adding five different types of distortions (Gaussian noise, speckle noise, salt and pepper noise, motion blur, and Gaussian blur) to the images in SVHN [Reference Yuval, Tao, Adam, Alessandro, Bo and Andrew11] and CIFAR-10/100 datasets [Reference Krizhevsky and Hinton12].
A) Generation of distorted images
The SVHN dataset [Reference Yuval, Tao, Adam, Alessandro, Bo and Andrew11] contains more labeled and diversified images with size $32\times 32$![]() taken from street views than the MNIST dataset. The images are divided into 10 classes from digit 0 to digit 9, where 73 257 images are used for training and 26 032 images for testing. There are usually some distracters on the sides of the images that make the classification task more challenging. On the other hand, the CIFAR-10 and CIFAR-100 [Reference Krizhevsky and Hinton12] are labeled images dataset. There are 60 000 $32\times 32$
taken from street views than the MNIST dataset. The images are divided into 10 classes from digit 0 to digit 9, where 73 257 images are used for training and 26 032 images for testing. There are usually some distracters on the sides of the images that make the classification task more challenging. On the other hand, the CIFAR-10 and CIFAR-100 [Reference Krizhevsky and Hinton12] are labeled images dataset. There are 60 000 $32\times 32$![]() color images in CIFAR-10 dataset, all of which are divided into 10 classes. Each class has 6000 images, among which 5000 are used for training and 1000 for testing. Compared with CIFAR-10, CIFAR-100 contains 100 classes and each class has 600 images, 500 for training and 100 for testing.
color images in CIFAR-10 dataset, all of which are divided into 10 classes. Each class has 6000 images, among which 5000 are used for training and 1000 for testing. Compared with CIFAR-10, CIFAR-100 contains 100 classes and each class has 600 images, 500 for training and 100 for testing.
All input data are clean (undistorted) images in the training stage. Five different types of distortions are created in the data set for classification in the testing stage. The range of standard deviations for Gaussian noise and Gaussian blur kernel are from 10 to 50 and from 1 to 5, respectively. We generate the motion blur kernel and move it horizontally by 1 pixel for each step size to simulate motion blur. The size of the motion blur kernel varies from 2 to 10. Salt and pepper noise are added to the input image with SNR from 0.95 to 0.75. We produce a noisy image $S$![]() for speckle noise based on the relation $S = I + G \times I$
for speckle noise based on the relation $S = I + G \times I$![]() , where $I$
, where $I$![]() is the input image and $G$
is the input image and $G$![]() is a uniformly distributed noise with standard deviation varying from 0.1 to 0.5. Examples with increasing levels of distortion for various distortion types are presented in Fig. 7.
is a uniformly distributed noise with standard deviation varying from 0.1 to 0.5. Examples with increasing levels of distortion for various distortion types are presented in Fig. 7.

Fig. 7. Five different distortion levels for five different types of distortions in CIFAR-10.
In the simulations, the curves denoted by VGG-16 is the model trained by clean data without any preprocessing. Retrain-MB refers to the VGG-16 model with re-training for motion blur images [Reference Zhou, Song and Cheung5]. DCT-module [Reference Hossain, Teng, Zhang, Lim and Lu7] and DWT-module respectively use the DCT and DWT in the preprocessing block of the VGG-16 in the training stage. The proposed hybrid DCT-DWT-SVD module (random) performs feature extraction using SVD after the DCT-DWT blocks. Finally, the DCT-DWT-SVD module (none) means the network that does not adopt random selection.
B) Performance comparison
We first justify the effectiveness of introducing random selection in the DCT-DWT stage to the classification accuracy for distorted images. As shown in Fig. 8, we examine the classification accuracy of using only DWT-module before VGG-16 for Gaussian and speckle noise in CIFAR-10 dataset. It can be observed from Fig. 8 that both level-1 and level-2 DWT model lead to better accuracy performance on distortion data than the original VGG-16. As expected, using level-1 DWT in the module can maintain more low-frequency components in the clean data and has a good accuracy when the distortion is not severe. On the other hand, the level-2 DWT model results in a noticeable reduction in the accuracy of clean data but is robust against larger distortions. Figure 8 shows that random selection from level-1 or level-2 DWT in the DWT-module renders a much improved accuracy result, where not only the accuracy in the low-distortion area is comparable to that with level-1 DWT model, but also the accuracy in the high-distortion area is higher than that with level-2 DWT model.

Fig. 8. The classification accuracy of different DWT-module levels with Gaussian Noise and Speckle in CIFAR-10.
When the hybrid DCT-DWT-SVD module is employed, it can be observed from Fig. 9 that randomly selecting the scanning region in the DCT-stage also effectively improves the accuracy of both the clean data and distorted data. As shown in Fig. 9, if the zig-zag scanning region is randomly selected in the region between $5\times 5$![]() and $25\times 25$
and $25\times 25$![]() in the DCT-stage with a fixed level-1 DWT, the DCT-DWT-SVD module maintains a high accuracy of clean data. When the zig-zag scanning region is in the range between $5\times 5 \sim 18\times 18$
in the DCT-stage with a fixed level-1 DWT, the DCT-DWT-SVD module maintains a high accuracy of clean data. When the zig-zag scanning region is in the range between $5\times 5 \sim 18\times 18$![]() and $5\times 5\sim 15\times 15$
and $5\times 5\sim 15\times 15$![]() , we can see that the model results in a slight reduction in the accuracy of clean data but has significantbetter robustness against highly distorted images. In addition, the hybrid DCT-DWT-SVD module with random selection in both the DCT (ranging from $5\times 5$
, we can see that the model results in a slight reduction in the accuracy of clean data but has significantbetter robustness against highly distorted images. In addition, the hybrid DCT-DWT-SVD module with random selection in both the DCT (ranging from $5\times 5$![]() to $15\times 15$
to $15\times 15$![]() ) and DWT (between level-1 and level-2) stages performs better than that when random selection is employed only in the DCT-stage, particularly in the regions of higher distortions.
) and DWT (between level-1 and level-2) stages performs better than that when random selection is employed only in the DCT-stage, particularly in the regions of higher distortions.

Fig. 9. The classification accuracy of various zig-zag selection regions in various types and degrees of noise for images in CIFAR-10.
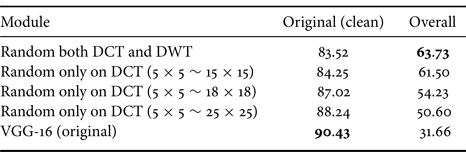
Numerical results of the accuracy performance are presented in Table 1. The proposed hybrid DCT-DWT-SVD module with random selection (denoted by DCT-DWT-SVD module (random)) performs best when testing on distorted images, although it results in slightly lower accuracy than the VGG-16 model when testing only on clean data (i.e.undistorted images). The overall performance in the table refers to the average accuracy over the clean data and distorted images with five levels of distortions.
Table 1. The accuracy ($\%$![]() ) of different random selection regions in the DCT-stage of DCT-DWT-SVD module for image data in CIFAR-10.
) of different random selection regions in the DCT-stage of DCT-DWT-SVD module for image data in CIFAR-10.
In Figs 10, 11, 12, we show the classification accuracy of six different models in various types and degrees of noise for SVHN, CIFAR-10, and CIFAR-100, respectively. In all the images tested, experiments (Figs 10, 11 and 12) show that the retrain-MB network [Reference Zhou, Song and Cheung5] performs well only for the distorted images in the type of motion blur. However, the retrain-MB [Reference Zhou, Song and Cheung5] cannot be well generalized to other types of distortions other than the motion blur. We can see from the figures that the proposed hybrid module with the DCT and DWT as the front stage in the training perform well in all types of image distortions. The DWT-module only is more accurate than the DCT-module [Reference Hossain, Teng, Zhang, Lim and Lu7] under various degrees of noise in both CIFAR-10 (Fig. 11) and CIFAR-100 (Fig. 12). Furthermore, the simulation results show that the DCT-DWT-SVD module (random) has the highest overall accuracy on different types and levels of distortion data. This is because the proposed hybrid module with random selection exploits data with more diversified low-frequency and high-frequency components, allowing to capture more features associated with clean data and with various types of distorted data. Notably, the accuracy of the DCT-DWT-SVD module (random) is higher than that of the DCT-DWT-SVD module (none) when the degree of distortion becomes larger. This shows the benefits of adopting the random selection mechanism, particularly for the highly distorted data. But, the DCT-DWT-SVD module (none) performs slightly better if the data are clean or the distortion is very small.

Fig. 10. The classification accuracy of six different models in various types and degrees of noise in SVHN.
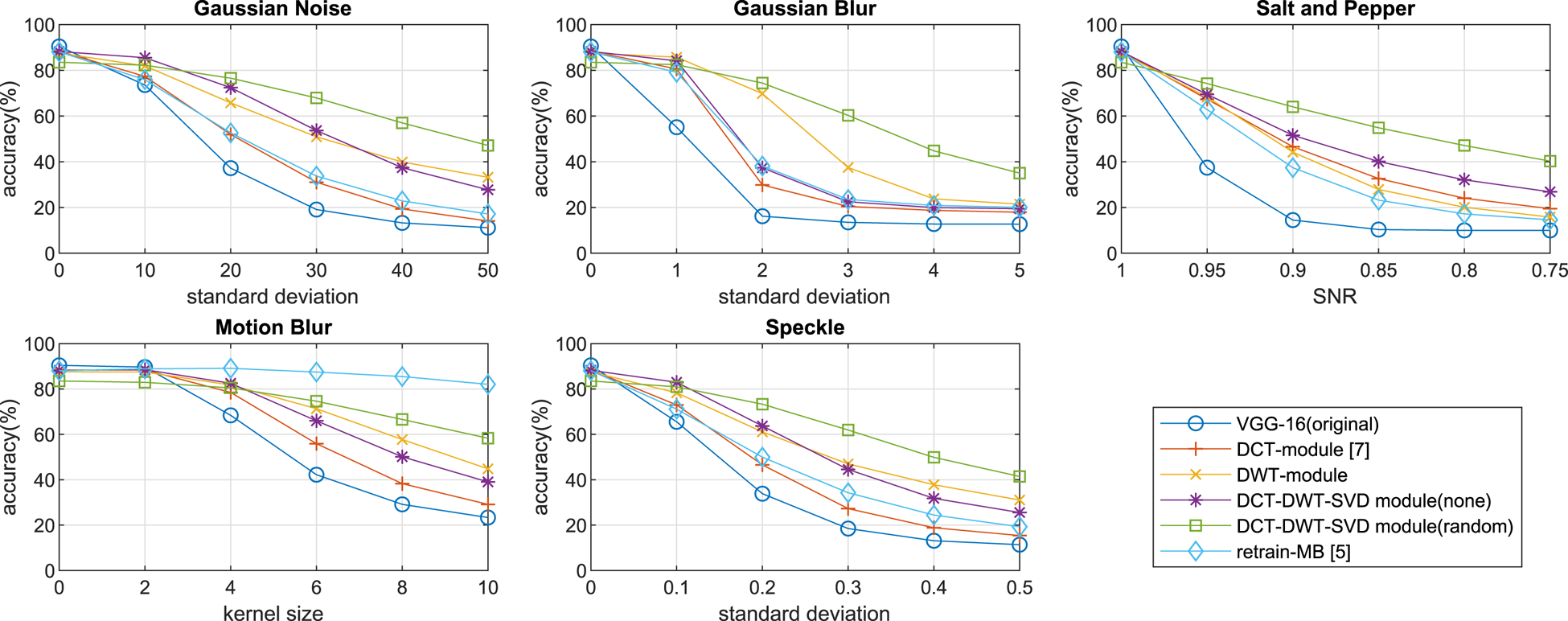
Fig. 11. The classification accuracy of six different models in various types and degrees of noise in CIFAR-10.
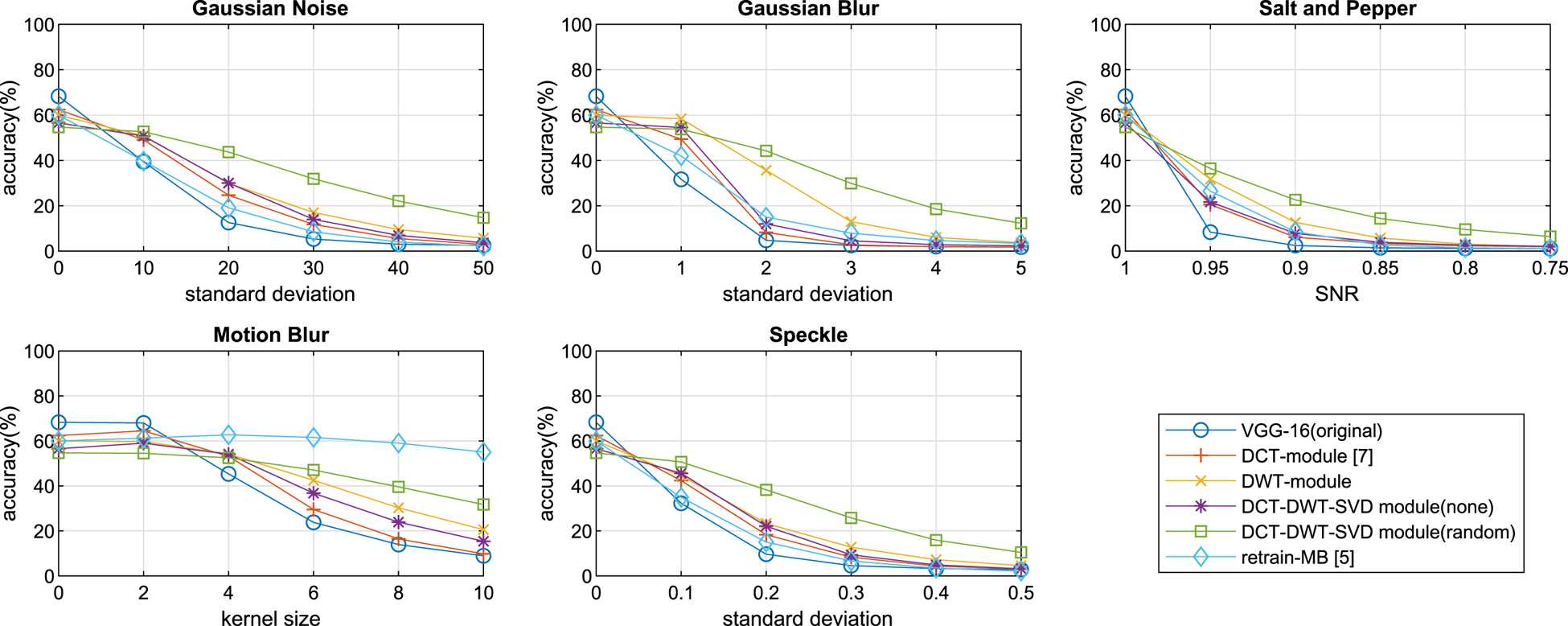
Fig. 12. The classification accuracy of six different models in various types and degrees of noise in CIFAR-100.
We also compare the results of the hybrid module with random-selection DCT but fixed DWT, random-selection DWT but fixed DCT, and DCT-DWT-SVD module (none). Both schemes with random selection outperforms the DCT-DWT-SVD module (none) for identifying highly distorted images. But, both schemes perform worse than the DCT-DWT-SVD module (random). Numerical results are also presented in Tables 2, 3 and 4 for SVHN, CIFAR-10, and CIFAR-100, respectively. The column in overall means the average accuracy and the column in the mixing means the accuracy of the test set that contains all different distortion types and levels. We see that the classification accuracy for the original clean data, the DCT-DWT-SVD module (none) performs slightly better than the DCT-DWT-SVD module (random), but is not suited for classifying highly distorted images, whereas using random selection only in the DCT stage or in the DWT stage, the DCT-DWT-SVD module (random) can perform better with higher overall and mixing accuracy than the DCT-DWT-SVD module (none). This result demonstrates the importance of adopting random selection.
Table 2. The accuracy ($\%$![]() ) of different random selection stages of DCT-DWT-SVD module in SVHN.
) of different random selection stages of DCT-DWT-SVD module in SVHN.

Table 3. The accuracy ($\%$![]() ) of different random selection stages of DCT-DWT-SVD module in CIFAR-10.
) of different random selection stages of DCT-DWT-SVD module in CIFAR-10.

Table 4. The accuracy ($\%$![]() ) of different random selection stages of DCT-DWT-SVD module in CIFAR-100.
) of different random selection stages of DCT-DWT-SVD module in CIFAR-100.

Finally, Table 5 shows the comparison of the number of training parameters needed and corresponding overall accuracy of the five distortion types in CIFAR-10 between the proposed hybrid DCT-DWT-SVD module and the MixQualNet [Reference Dodge and Karam6]. We assume the gating network in the MixQualNet can obtain the perfect target weights. In other words, we assume the MixQualNet has the best performance.
Table 5. Comparison of training parameters and accuracy between DCT-DWT-SVD module and MixQualNet in CIFAR-10 [Reference Dodge and Karam6].

The column MixQualNet (expanded) means that in the training stage, all five distortion types of the inputs are known and are used to train six respective expert networks (1 clean $+$![]() 5 distortions). The column MixQualNet (original) means the original MixQualNet proposed by Dodge and Karam that contains only three expert networks for clean data, Gaussian noise, and Gaussian blur, respectively. From Table 5, we see that the number of training parameters in the model trained with the proposed hybrid DCT-DWT-SVD module is much lower than the MixQualNet (expanded) and MixQualNet (original), while maintaining a comparable overall accuracy. This shows the robustness of the proposed single model trained with the hybrid DCT-DWT-SVD module, which can resist various unknown types of distortions and is thus categorized as a blind method. Note that the overall accuracy of the proposed hybrid DCT-DWT-SVD module is comparable to the MixQualNet (expanded) which must know all distortion types of the inputs. The overall accuracy of the proposed hyrid DCT-DWT-SVD module is higher than the MixQualNet (original) because the unknown distortion types of inputs, like motion blur, salt and pepper noise, and speckle noise, that are not used in the training phase significantly reduce the accuracy of the MixQualNet (original).
5 distortions). The column MixQualNet (original) means the original MixQualNet proposed by Dodge and Karam that contains only three expert networks for clean data, Gaussian noise, and Gaussian blur, respectively. From Table 5, we see that the number of training parameters in the model trained with the proposed hybrid DCT-DWT-SVD module is much lower than the MixQualNet (expanded) and MixQualNet (original), while maintaining a comparable overall accuracy. This shows the robustness of the proposed single model trained with the hybrid DCT-DWT-SVD module, which can resist various unknown types of distortions and is thus categorized as a blind method. Note that the overall accuracy of the proposed hybrid DCT-DWT-SVD module is comparable to the MixQualNet (expanded) which must know all distortion types of the inputs. The overall accuracy of the proposed hyrid DCT-DWT-SVD module is higher than the MixQualNet (original) because the unknown distortion types of inputs, like motion blur, salt and pepper noise, and speckle noise, that are not used in the training phase significantly reduce the accuracy of the MixQualNet (original).
V. CONCLUSION
This paper has studied different preprocessing methods to improve the accuracy of CNN on distorted images. We have proposed a deep neural network based on a hybrid DCT-DWT-SVD pre-processing module with random selection at the training stage. Since DCT and DWT capture low-frequency components and remove high-frequency components in a random manner, and SVD performs feature extraction to enhance features, the proposed deep networks do not heavily rely on high-frequency details in the target objects, therefore achieving better accuracy in classifying distorted (noisy or blurred) images. In addition, we have verified that random selection not only retains the accuracy for clean data, but also enhances the accuracy of identifying high-distortion pictures.
Experimental results have shown that the VGG-16 network trained after the hybrid DCT-DWT-SVD module can effectively improve the accuracy of images degraded by a variety of different degrees of distortions. The proposed hybrid module outperforms the pure DWT method and the pure DCT method [Reference Hossain, Teng, Zhang, Lim and Lu7], as more diversified high-frequency and low-frequency features can be captured with random selection during the training stage. Unlike the traditional fine-tuning process for specific distortions [Reference Zhou, Song and Cheung5], the proposed hybrid module does not need to fine-tune or re-train, and only needs to be trained only once. Finally, we have shown the proposed hybrid module with random selection is robust to many different types of distortions, without having to perform noise identification or noise reduction during testing.
FINANCIAL SUPPORT
This work is partially supported by the “Center for mmWave Smart Radar Systems and Technologies” under the Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE), and partially supported by the Ministry of Science and Technology (MOST) under grants MOST 109-2221-E-009-101, 110-3017-F-009-001, and 110-2221-E-A49-035 in Taiwan.
CONFLICT OF INTEREST
None.
Liang Yao Wang received the B.E. degree in photonics engineering in 2019 and the M.S. degree in electronics engineering in 2021, both from National Yang Ming Chiao Tung University, Taiwan. During his graduate studies, he was a teaching assistant in digital communication. His research interests include deep learning-based image classification, image denoising, and autoencoder.
Sau-Gee Chen received his B.S. degree from National Tsing Hua University, Taiwan, in 1978, M.S. degree and Ph.D. degree in electrical engineering, from the State University of New York at Buffalo, NY, in 1984 and 1988, respectively. He was a professor at the Institute of Electronics, National Chiao Tung University (NCTU), Taiwan, from 1988 to 2021, and was a member of Board of Governor, IEEE Taipei Section, from 2013 to 2020. He was the Chair of the Department of Electronics Engineering, NCTU, during 2012–2015. He was appointed as the Coordinator of IEEE VTS Asia-Pacific Chapters, during 2014–2017. He was the Chair, IEEE Vehicular Technology Society, Taipei Chapter, during 2012–2013. He was Director of Honors Program, College of Electrical & Computer Engineering/College of Computer Science from 2011 to 2012 at NCTU. He also was the director of the Institute of Electronics from 2003 to 2006, all at the same organization. During 2004–2006, he served as an associate editor of IEEE Transactions on Circuits and Systems I. His research interests include digital communication, digital signal processing, and VLSI signal processing. He has published more than 100 conference and journal papers, and holds 20 US and Taiwan patents.
Feng-Tsun Chien received the B.S. degree from National Tsing Hua University (NTHU) in 1995, the M.S. degree from National Taiwan University (NTU) in 1997, and the Ph.D. degree from the University of Southern California (USC), Los Angeles, in 2004, all in electrical engineering. He has been with the Institute of Electronics of National Yang Ming Chiao Tung University (NYCU), Hsinchu, Taiwan, since 2005 and is currently an Associate Professor. He was Fulbright Scholar at the University of California, Los Angeles, during the academic year 2016–2017. He is also affiliated with the Center for mmWave Smart Radar Systems and Technologies of NCTU. Dr. Chien has been serving as a technical program committee member in IEEE ICC (2009–2021) and GLOBECOM (2009–2021). He also served as the Treasurer of the IEEE Vehicular Technology Society, Taipei Chapter, during 2012–2015. His current research interests include wireless communications, statistical signal processing, machine learning, and game theoretic resource allocation.























