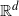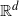1. Introduction
In the spirit of jump-diffusion models, we consider Markov stochastic processes that alternate continuous motions and jumps in some locally compact Polish space E. We call these general processes jump–move processes. In this paper, the state space E is typically not a finite-dimensional Euclidean space, in contrast to standard jump-diffusion models. Many examples of such dynamics have been considered in the literature, including piecewise deterministic processes [Reference Davis6], branching particle systems [Reference Athreya and Ney1, Reference Skorokhod27], spatially structured population models [Reference Bansaye and Méléard2], and some variations of these [Reference Çinlar and Kao4, Reference Löcherbach15], to cite a few. A particular case that will be of special interest to us is when
![]() $E=\cup_{n\geq 0} E_n$
for some disjoint spaces
$E=\cup_{n\geq 0} E_n$
for some disjoint spaces
![]() $E_n$
,
$E_n$
,
![]() $E_0$
consisting of a single element, and the jumps can only occur from
$E_0$
consisting of a single element, and the jumps can only occur from
![]() $E_n$
to
$E_n$
to
![]() $E_{n+1}$
(like a birth) or from
$E_{n+1}$
(like a birth) or from
![]() $E_n$
to
$E_n$
to
![]() $E_{n-1}$
(like a death). We call the latter dynamics a birth–death–move process [Reference Lavancier and Le Guével14, Reference Preston22]. We will provide several illustrations in the particular case of interacting particles in
$E_{n-1}$
(like a death). We call the latter dynamics a birth–death–move process [Reference Lavancier and Le Guével14, Reference Preston22]. We will provide several illustrations in the particular case of interacting particles in
![]() $\mathbb{R}^d$
, with births and deaths. These processes are observed in a wide range of applications, including microbiology [Reference Lavancier and Le Guével14], epidemiology [Reference Masuda and Holme17], and ecology [Reference Pommerening and Grabarnik21, Reference Renshaw and Särkkä24]. The main motivation for this contribution is to provide some foundations for the statistical inference of such processes, especially by studying their ergodic properties.
$\mathbb{R}^d$
, with births and deaths. These processes are observed in a wide range of applications, including microbiology [Reference Lavancier and Le Guével14], epidemiology [Reference Masuda and Holme17], and ecology [Reference Pommerening and Grabarnik21, Reference Renshaw and Särkkä24]. The main motivation for this contribution is to provide some foundations for the statistical inference of such processes, especially by studying their ergodic properties.
In Section 2 we start from a mechanistic general definition of jump–move processes, in the sense that we explicitly construct the process iteratively over time, which equivalently provides a simulation algorithm. This defines a Markov process
![]() $(X_t)_{t\geq 0}$
whose jump intensity function reads
$(X_t)_{t\geq 0}$
whose jump intensity function reads
![]() $\alpha(X_t)$
, for some continuous function
$\alpha(X_t)$
, for some continuous function
![]() $\alpha$
, and that between its jumps follows a continuous Markov motion on E. We then derive, in Section 3, conditions ensuring that the transition kernel of
$\alpha$
, and that between its jumps follows a continuous Markov motion on E. We then derive, in Section 3, conditions ensuring that the transition kernel of
![]() $(X_t)_{t\geq 0}$
forms a Feller semigroup on
$(X_t)_{t\geq 0}$
forms a Feller semigroup on
![]() $C_b(E)$
or on
$C_b(E)$
or on
![]() $C_0(E)$
, where
$C_0(E)$
, where
![]() $C_b(E)$
denotes the set of continuous and bounded functions on E and
$C_b(E)$
denotes the set of continuous and bounded functions on E and
![]() $C_0(E)$
is the set of continuous functions that vanish at infinity. We obtain the natural result that if
$C_0(E)$
is the set of continuous functions that vanish at infinity. We obtain the natural result that if
![]() $\alpha$
is bounded, then a jump–move process is Feller (on
$\alpha$
is bounded, then a jump–move process is Feller (on
![]() $C_b(E)$
or on
$C_b(E)$
or on
![]() $C_0(E)$
) whenever the transition kernel of the jumps and the transition kernel of the inter-jump motion (i.e. the move part) are. Similarly, the infinitesimal generator is just the sum of the generator of the jumps and the generator of the move, the domain corresponding under mild conditions to the domain of the generator of the move.
$C_0(E)$
) whenever the transition kernel of the jumps and the transition kernel of the inter-jump motion (i.e. the move part) are. Similarly, the infinitesimal generator is just the sum of the generator of the jumps and the generator of the move, the domain corresponding under mild conditions to the domain of the generator of the move.
In Section 4, we focus on birth–death–move processes. We obtain simple conditions on the birth and death intensity functions ensuring their ergodicity with a geometric rate of convergence, in line with standard results for simple birth–death processes on
![]() $\mathbb{N}$
[Reference Karlin and McGregor13] and for spatial birth–death processes (the case without move) established by [Reference Møller18] and [Reference Preston22]. This study constitutes our main contribution for statistical applications. It generalizes the results obtained in [Reference Lavancier and Le Guével14], where ergodicity was established under the assumption that the number of individuals n in the population is bounded. Following [Reference Preston22], the main ingredient to establish our more general result is a coupling with a simple birth–death process on
$\mathbb{N}$
[Reference Karlin and McGregor13] and for spatial birth–death processes (the case without move) established by [Reference Møller18] and [Reference Preston22]. This study constitutes our main contribution for statistical applications. It generalizes the results obtained in [Reference Lavancier and Le Guével14], where ergodicity was established under the assumption that the number of individuals n in the population is bounded. Following [Reference Preston22], the main ingredient to establish our more general result is a coupling with a simple birth–death process on
![]() $\mathbb{N}$
, which provides conditions implying that the single element of
$\mathbb{N}$
, which provides conditions implying that the single element of
![]() $E_0$
is an ergodic state for the process. However, the inclusion of inter-jump motions makes this coupling more delicate to justify than for the pure spatial birth–death processes of [Reference Preston22]. We manage to realize the coupling under the assumption that the birth–death–move process is Feller on
$E_0$
is an ergodic state for the process. However, the inclusion of inter-jump motions makes this coupling more delicate to justify than for the pure spatial birth–death processes of [Reference Preston22]. We manage to realize the coupling under the assumption that the birth–death–move process is Feller on
![]() $C_0(E)$
, which necessitates the properties discussed above.
$C_0(E)$
, which necessitates the properties discussed above.
We emphasize that the above results are very general, in the sense that we specify neither E, nor the exact jump transition kernel, nor the form of the inter-jump continuous Markov motion. Our only real working assumption is the boundedness of the intensity function
![]() $\alpha$
. Notably, unlike [Reference Lavancier and Le Guével14], we do not assume that
$\alpha$
. Notably, unlike [Reference Lavancier and Le Guével14], we do not assume that
![]() $\alpha$
is lower-bounded from zero. However, we provide many illustrations in the case where
$\alpha$
is lower-bounded from zero. However, we provide many illustrations in the case where
![]() $(X_t)_{t\geq 0}$
represents the dynamics of a system of particles in
$(X_t)_{t\geq 0}$
represents the dynamics of a system of particles in
![]() $\mathbb{R}^d$
, introduced in Section 2.4. In this situation, we consider continuous inter-jump motions driven by deterministic growth-interacting dynamics, as already exploited in ecology [Reference Häbel, Myllymäki and Pommerening10, Reference Renshaw and Särkkä24], or driven by interacting systems of stochastic differential equations (SDEs), in particular overdamped Langevin dynamics, the Feller properties of which translate straightforwardly to the move part of
$\mathbb{R}^d$
, introduced in Section 2.4. In this situation, we consider continuous inter-jump motions driven by deterministic growth-interacting dynamics, as already exploited in ecology [Reference Häbel, Myllymäki and Pommerening10, Reference Renshaw and Särkkä24], or driven by interacting systems of stochastic differential equations (SDEs), in particular overdamped Langevin dynamics, the Feller properties of which translate straightforwardly to the move part of
![]() $(X_t)_{t\geq 0}$
. As to the jumps, they are continuous Feller in general, but not necessarily Feller on
$(X_t)_{t\geq 0}$
. As to the jumps, they are continuous Feller in general, but not necessarily Feller on
![]() $C_0(E)$
. The picture becomes more intelligible, however, when they consist only of births and deaths. We present in Section 3.3 general birth transition kernels that imply the Feller properties under mild assumptions. On the other hand, a simple uniform death kernel cannot be Feller on
$C_0(E)$
. The picture becomes more intelligible, however, when they consist only of births and deaths. We present in Section 3.3 general birth transition kernels that imply the Feller properties under mild assumptions. On the other hand, a simple uniform death kernel cannot be Feller on
![]() $C_0(E)$
in this setting unless the particles are restricted to a compact subset of
$C_0(E)$
in this setting unless the particles are restricted to a compact subset of
![]() $\mathbb{R}^d$
. We finally show in Section 5 that for a system of interacting particles in
$\mathbb{R}^d$
. We finally show in Section 5 that for a system of interacting particles in
![]() $\mathbb{R}^d$
with births and deaths, we may obtain an explicit Gibbs distribution for the invariant probability measure. This happens when the inter-jump motion is driven by a Langevin dynamics based on some potential function V, and the jump characteristics depend in a suitable way on the same potential V. Our assumptions on V include in particular Riesz potentials, repulsive Lennard-Jones potentials, soft-core potentials, and (regularized) Strauss potentials, which are standard models used in spatial statistics and statistical mechanics.
$\mathbb{R}^d$
with births and deaths, we may obtain an explicit Gibbs distribution for the invariant probability measure. This happens when the inter-jump motion is driven by a Langevin dynamics based on some potential function V, and the jump characteristics depend in a suitable way on the same potential V. Our assumptions on V include in particular Riesz potentials, repulsive Lennard-Jones potentials, soft-core potentials, and (regularized) Strauss potentials, which are standard models used in spatial statistics and statistical mechanics.
We have gathered in the appendix the proofs of the intermediate results used for the coupling described in Section 4. Other proofs, along with additional results, are postponed to supplementary material.
2. Jump–move processes
2.1. Iterative construction
Let E be a Polish space equipped with the Borel
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{E}$
and a distance d. Let
$\mathcal{E}$
and a distance d. Let
![]() $(\Omega,\mathcal{F})$
be a measurable space and
$(\Omega,\mathcal{F})$
be a measurable space and
![]() $(\mathbb{P}_x)_{x \in E}$
a family of probability measures on
$(\mathbb{P}_x)_{x \in E}$
a family of probability measures on
![]() $(\Omega,\mathcal{F}).$
In order to define a jump–move process
$(\Omega,\mathcal{F}).$
In order to define a jump–move process
![]() $(X_t)_{t\geq 0}$
on E, we need three ingredients:
$(X_t)_{t\geq 0}$
on E, we need three ingredients:
-
(i) An intensity function
 $\alpha \;:\; E \rightarrow \mathbb{R}_+$
that governs the inter-jump waiting times.
$\alpha \;:\; E \rightarrow \mathbb{R}_+$
that governs the inter-jump waiting times. -
(ii) A transition kernel K for the jumps, defined on
 $E \times \mathcal{E}.$
$E \times \mathcal{E}.$
-
(iii) A continuous homogeneous Markov process
 $((Y_t)_{t \geq 0}, (\mathbb{P}_x)_{x \in E})$
on E, the distribution of which will drive the inter-jump motion of
$((Y_t)_{t \geq 0}, (\mathbb{P}_x)_{x \in E})$
on E, the distribution of which will drive the inter-jump motion of
 $(X_t)_{t\geq 0}$
.
$(X_t)_{t\geq 0}$
.
Throughout this paper, we will work under the assumption that
![]() $\alpha \;:\; E \rightarrow \mathbb{R}_+ $
is continuous and bounded by
$\alpha \;:\; E \rightarrow \mathbb{R}_+ $
is continuous and bounded by
![]() $\alpha^*>0$
, i.e., for all
$\alpha^*>0$
, i.e., for all
![]() $x\in E$
,
$x\in E$
,
We denote by
![]() $(Q_t^Y)_{t \geq 0}$
the transition kernel of
$(Q_t^Y)_{t \geq 0}$
the transition kernel of
![]() $(Y_t)_{t\geq 0}$
, given by
$(Y_t)_{t\geq 0}$
, given by
The following iterative construction provides clear intuition for the dynamics of the process
![]() $(X_t)_{t\geq 0}$
. It follows closely the presentation in the supplementary material of [Reference Lavancier and Le Guével14], where an algorithm of simulation on a finite time interval is also derived. However, since
$(X_t)_{t\geq 0}$
. It follows closely the presentation in the supplementary material of [Reference Lavancier and Le Guével14], where an algorithm of simulation on a finite time interval is also derived. However, since
![]() $\alpha$
is not lower-bounded from zero, unlike in the previous reference, it is possible that eventually there are no more jumps, a situation taken into account by Equation (2.2) below. The algorithm of simulation adapts straightforwardly to this case.
$\alpha$
is not lower-bounded from zero, unlike in the previous reference, it is possible that eventually there are no more jumps, a situation taken into account by Equation (2.2) below. The algorithm of simulation adapts straightforwardly to this case.
Let
![]() $\big(Y_t^{(j)}\big)_{t \geq 0}$
,
$\big(Y_t^{(j)}\big)_{t \geq 0}$
,
![]() $j\geq 0$
, be a sequence of processes on E identically distributed as
$j\geq 0$
, be a sequence of processes on E identically distributed as
![]() $(Y_t)_{t \geq 0}$
. Set
$(Y_t)_{t \geq 0}$
. Set
![]() $T_0=0$
and let
$T_0=0$
and let
![]() $x_0\in E$
. Then
$x_0\in E$
. Then
![]() $(X_t)_{t\geq 0}$
can be constructed as follows. For
$(X_t)_{t\geq 0}$
can be constructed as follows. For
![]() $j\geq 0$
, iteratively do the following:
$j\geq 0$
, iteratively do the following:
-
(i) Given
 $ X_{T_j}=x_j$
, generate
$ X_{T_j}=x_j$
, generate
 $\big(Y_t^{(j)}\big)_{t \geq 0}$
conditional on
$\big(Y_t^{(j)}\big)_{t \geq 0}$
conditional on
 $ Y_0^{(j)}=x_j$
according to the kernel
$ Y_0^{(j)}=x_j$
according to the kernel
 $(Q_t^{Y}(x_j,.))_{t \geq 0}$
.
$(Q_t^{Y}(x_j,.))_{t \geq 0}$
. -
(ii) Given
 $ X_{T_j}=x_j$
and
$ X_{T_j}=x_j$
and
 $\big(Y_t^{(j)}\big)_{t \geq 0}$
, generate
$\big(Y_t^{(j)}\big)_{t \geq 0}$
, generate
 $ \tau_{j+1}$
according to the following distribution on
$ \tau_{j+1}$
according to the following distribution on
 $\mathbb{R}_+\cup\{+\infty\}$
: (2.2)
$\mathbb{R}_+\cup\{+\infty\}$
: (2.2) \begin{equation} \begin{cases} \mathbb{P}(\tau_{j+1}\leq t)=1-\exp\!\left ( - \int_0^t \alpha \left ( Y_u^{(j)} \right ) \, \text{d} u \right ) \text{ for all } t\in\mathbb{R}_+, \\ \mathbb{P}(\tau_{j+1}=+\infty)=\exp\!\left ( - \int_0^{\infty} \alpha \left ( Y_u^{(j)} \right ) \, \text{d} u \right ).\end{cases} \end{equation}
\begin{equation} \begin{cases} \mathbb{P}(\tau_{j+1}\leq t)=1-\exp\!\left ( - \int_0^t \alpha \left ( Y_u^{(j)} \right ) \, \text{d} u \right ) \text{ for all } t\in\mathbb{R}_+, \\ \mathbb{P}(\tau_{j+1}=+\infty)=\exp\!\left ( - \int_0^{\infty} \alpha \left ( Y_u^{(j)} \right ) \, \text{d} u \right ).\end{cases} \end{equation}
-
(iii) Given
 $ X_{T_j}=x_j$
,
$ X_{T_j}=x_j$
,
 $\big(Y_t^{(j)}\big)_{t \geq 0}$
and
$\big(Y_t^{(j)}\big)_{t \geq 0}$
and
 $ \tau_{j+1}$
,
$ \tau_{j+1}$
,if
 $\tau_{j+1}=\infty$
then set
$\tau_{j+1}=\infty$
then set
 $X_t=Y_{t-T_j}^{(j)}$
for all
$X_t=Y_{t-T_j}^{(j)}$
for all
 $t\geq T_j$
(and stop the iterative construction),
$t\geq T_j$
(and stop the iterative construction),else generate
 $x_{j+1}$
according to the transition kernel
$x_{j+1}$
according to the transition kernel
 $ K (Y_{ \tau_{j+1}}^{(j)}, .)$
.
$ K (Y_{ \tau_{j+1}}^{(j)}, .)$
.
-
(iv) Set
 $ T_{j+1}=T_j+\tau_{j+1}$
,
$ T_{j+1}=T_j+\tau_{j+1}$
,
 $ X_t=Y_{t-T_j}^{(j)}$
for
$ X_t=Y_{t-T_j}^{(j)}$
for
 $t \in [T_j,T_{j+1})$
, and
$t \in [T_j,T_{j+1})$
, and
 $ X_{T_{j+1}}= x_{j+1}$
.
$ X_{T_{j+1}}= x_{j+1}$
.
We denote by
![]() $(\mathcal{F}_t^Y)_{t \geq 0}$
the natural filtration of
$(\mathcal{F}_t^Y)_{t \geq 0}$
the natural filtration of
![]() $(Y_t)_{t\geq 0}$
, i.e.
$(Y_t)_{t\geq 0}$
, i.e.
![]() $\mathcal{F}_t^Y= \sigma ( Y_u, u \leq t)$
, and by
$\mathcal{F}_t^Y= \sigma ( Y_u, u \leq t)$
, and by
![]() $(\mathcal{F}_t)_{t >0}$
the natural filtration of
$(\mathcal{F}_t)_{t >0}$
the natural filtration of
![]() $(X_t)_{t \geq 0}$
. We make these filtrations complete (see [Reference Bass3, Section 20.1]) and abusively use the same notation. The jump–move process
$(X_t)_{t \geq 0}$
. We make these filtrations complete (see [Reference Bass3, Section 20.1]) and abusively use the same notation. The jump–move process
![]() $((X_t)_{t \geq 0}, (\mathbb{P}_x)_{x \in E})$
constructed above is a homogeneous Markov process with respect to
$((X_t)_{t \geq 0}, (\mathbb{P}_x)_{x \in E})$
constructed above is a homogeneous Markov process with respect to
![]() $(\mathcal{F}_t)_{t>0}$
. The trajectories of
$(\mathcal{F}_t)_{t>0}$
. The trajectories of
![]() $(X_t)_{t \geq 0}$
are continuous except at the jump times
$(X_t)_{t \geq 0}$
are continuous except at the jump times
![]() $(T_j)_{j \geq 1}$
, where they are right-continuous. The specific form (2.2) implies that the intensity of jumps is
$(T_j)_{j \geq 1}$
, where they are right-continuous. The specific form (2.2) implies that the intensity of jumps is
![]() $\alpha(X_{t})$
. Denote by
$\alpha(X_{t})$
. Denote by
![]() $N_t=\sum_{j\geq 0} {\mathbf 1}_{T_j\leq t}$
the number of jumps before
$N_t=\sum_{j\geq 0} {\mathbf 1}_{T_j\leq t}$
the number of jumps before
![]() $t\geq 0$
. Under the assumption (2.1), for any
$t\geq 0$
. Under the assumption (2.1), for any
![]() $n \geq 0$
and
$n \geq 0$
and
![]() $t \geq 0$
we have
$t \geq 0$
we have
where
![]() $N^*_t$
follows a Poisson distribution with rate
$N^*_t$
follows a Poisson distribution with rate
![]() $\alpha^*t$
. This in particular implies that
$\alpha^*t$
. This in particular implies that
![]() $(N_t)_{t \geq 0}$
is a non-explosive counting process. All of the aforementioned properties of
$(N_t)_{t \geq 0}$
is a non-explosive counting process. All of the aforementioned properties of
![]() $(X_t)_{t \geq 0}$
are either immediate or verified in [Reference Lavancier and Le Guével14].
$(X_t)_{t \geq 0}$
are either immediate or verified in [Reference Lavancier and Le Guével14].
Note that the above construction only implies the weak Markov property of
![]() $(X_t)_{t\geq 0}$
in general, at least because the process
$(X_t)_{t\geq 0}$
in general, at least because the process
![]() $(Y_t)_{t\geq 0}$
is only assumed to be a (weak) Markov process. A more abstract construction obtained by ‘piecing out’ strong Markov processes is introduced in [Reference Ikeda, Nagasawa and Watanabe11], leading to a strong Markov jump–move process. The strong Markov property can also be obtained in our case by strengthening the assumptions; see Section 3.1.
$(Y_t)_{t\geq 0}$
is only assumed to be a (weak) Markov process. A more abstract construction obtained by ‘piecing out’ strong Markov processes is introduced in [Reference Ikeda, Nagasawa and Watanabe11], leading to a strong Markov jump–move process. The strong Markov property can also be obtained in our case by strengthening the assumptions; see Section 3.1.
The transition kernel of
![]() $(X_t)_{t \geq 0}$
will be denoted, for any
$(X_t)_{t \geq 0}$
will be denoted, for any
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $x \in E$
, and
$x \in E$
, and
![]() $A \in \mathcal{E}$
, by
$A \in \mathcal{E}$
, by
Also, for
![]() $f \in M_b(E)$
, where
$f \in M_b(E)$
, where
![]() $M_b(E)$
is the set of real-valued bounded and measurable functions on E, we will write
$M_b(E)$
is the set of real-valued bounded and measurable functions on E, we will write
![]() $Q_tf(x)=\mathbb{E}_x [ f(X_t)]=\int_E Q_t(x, \text{d} y) f(y)$
. Similarly we will write
$Q_tf(x)=\mathbb{E}_x [ f(X_t)]=\int_E Q_t(x, \text{d} y) f(y)$
. Similarly we will write
![]() $Q_t^Yf(x)=\mathbb{E}_x^Y(f(Y_t))$
.
$Q_t^Yf(x)=\mathbb{E}_x^Y(f(Y_t))$
.
2.2. Special case of the birth–death–move process
A birth–death–move process is the particular case of a jump–move process in which E takes the form
![]() $E= \bigcup_{n=0}^{\infty} E_n$
, with
$E= \bigcup_{n=0}^{\infty} E_n$
, with
![]() $(E_n)_{n \geq 0}$
a sequence of disjoint Polish spaces, and in which the jumps are only births and deaths. We assume that each
$(E_n)_{n \geq 0}$
a sequence of disjoint Polish spaces, and in which the jumps are only births and deaths. We assume that each
![]() $E_n$
is equipped with the Borel
$E_n$
is equipped with the Borel
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{E}_n$
, so that E is associated with the
$\mathcal{E}_n$
, so that E is associated with the
![]() $ \displaystyle \sigma$
-field
$ \displaystyle \sigma$
-field
![]() $\mathcal{E}=\sigma \left ( \bigcup_{n=0}^{\infty} \mathcal{E}_n \right ) $
. We further assume that
$\mathcal{E}=\sigma \left ( \bigcup_{n=0}^{\infty} \mathcal{E}_n \right ) $
. We further assume that
![]() $E_0$
consists of a single element, denoted by
$E_0$
consists of a single element, denoted by
![]() $\text{\O}$
. In this setting, the Markov process
$\text{\O}$
. In this setting, the Markov process
![]() $(Y_t)_{t \geq 0}$
driving the motions of
$(Y_t)_{t \geq 0}$
driving the motions of
![]() $(X_t)_{t \geq 0}$
is supposed to satisfy
$(X_t)_{t \geq 0}$
is supposed to satisfy
We introduce a birth intensity function
![]() $\beta \;:\; E \rightarrow \mathbb{R}_+$
and a death intensity function
$\beta \;:\; E \rightarrow \mathbb{R}_+$
and a death intensity function
![]() $\delta \;:\; E \rightarrow \mathbb{R}_+$
, both assumed to be continuous on E and satisfying
$\delta \;:\; E \rightarrow \mathbb{R}_+$
, both assumed to be continuous on E and satisfying
![]() $\alpha = \beta + \delta.$
We prevent a death in
$\alpha = \beta + \delta.$
We prevent a death in
![]() $E_0$
by assuming that
$E_0$
by assuming that
![]() $\delta(\text{\O})=0.$
The probability transition kernel K for the jumps then reads, for any
$\delta(\text{\O})=0.$
The probability transition kernel K for the jumps then reads, for any
![]() $x \in E$
and
$x \in E$
and
![]() $A \in \mathcal{E}$
,
$A \in \mathcal{E}$
,
where
![]() $K_{\beta} \;:\; E \times \mathcal{E} \rightarrow [0,1]$
is a probability transition kernel for a birth and
$K_{\beta} \;:\; E \times \mathcal{E} \rightarrow [0,1]$
is a probability transition kernel for a birth and
![]() $K_{\delta} \;:\; E \times \mathcal{E} \rightarrow [0,1]$
is a probability transition kernel for a death. They satisfy, for
$K_{\delta} \;:\; E \times \mathcal{E} \rightarrow [0,1]$
is a probability transition kernel for a death. They satisfy, for
![]() $x \in E$
and
$x \in E$
and
![]() $n \geq 0$
,
$n \geq 0$
,
Notice that a simple birth–death process is the particular case in which
![]() $E=\mathbb{N}$
,
$E=\mathbb{N}$
,
![]() $E_n= \{ n \}$
and the intensity functions
$E_n= \{ n \}$
and the intensity functions
![]() $\beta$
and
$\beta$
and
![]() $\delta$
are sequences. More general examples of the inter-jump process Y, of the intensity functions
$\delta$
are sequences. More general examples of the inter-jump process Y, of the intensity functions
![]() $\beta$
and
$\beta$
and
![]() $\delta$
, and of the kernels
$\delta$
, and of the kernels
![]() $K_{\beta}$
and
$K_{\beta}$
and
![]() $K_{\delta}$
are presented in Sections 2.4 and 5; see also [Reference Lavancier and Le Guével14].
$K_{\delta}$
are presented in Sections 2.4 and 5; see also [Reference Lavancier and Le Guével14].
For later purposes, when
![]() $E= \bigcup_{n=0}^{\infty} E_n$
as in the present section, we define the function
$E= \bigcup_{n=0}^{\infty} E_n$
as in the present section, we define the function
![]() $n(.) \;:\; E \rightarrow \mathbb{N}$
by
$n(.) \;:\; E \rightarrow \mathbb{N}$
by
![]() $n(x)=k$
when
$n(x)=k$
when
![]() $x \in E_k$
, so that
$x \in E_k$
, so that
![]() $x \in E_{n(x)}$
is always satisfied.
$x \in E_{n(x)}$
is always satisfied.
2.3. Kolmogorov backward equation
The goal of this section is to present the Kolmogorov backward equation for the transition kernel of the general jump–move process
![]() $(X_t)_{t \geq 0}$
of Section 2.1, providing a more probabilistic viewpoint on its dynamics, and to show that the solution exists and is unique. To obtain these results we use methods similar to those used in [Reference Feller9] for pure jump processes; see also [Reference Preston22]. The key assumption is the boundedness (2.1) of the intensity
$(X_t)_{t \geq 0}$
of Section 2.1, providing a more probabilistic viewpoint on its dynamics, and to show that the solution exists and is unique. To obtain these results we use methods similar to those used in [Reference Feller9] for pure jump processes; see also [Reference Preston22]. The key assumption is the boundedness (2.1) of the intensity
![]() $\alpha$
, which prevents the explosion of the process. The proofs are postponed to Section S-1 of the supplementary material.
$\alpha$
, which prevents the explosion of the process. The proofs are postponed to Section S-1 of the supplementary material.
Theorem 1. For all
![]() $x\in E$
and all
$x\in E$
and all
![]() $A \in \mathcal{E}$
, the function
$A \in \mathcal{E}$
, the function
![]() $t \mapsto Q_t(x,A)$
, for
$t \mapsto Q_t(x,A)$
, for
![]() $t>0$
, satisfies the following Kolmogorov backward equation:
$t>0$
, satisfies the following Kolmogorov backward equation:
 \begin{multline} Q_t(x,A) = \mathbb{E}_x^Y \left [ {\mathbf 1}_{Y_t \in A} \,\text{e}^{ - \int_0^t \alpha(Y_u) \, \text{d} u } \right ] \\+ \int_0^t \int_E Q_{t-s}(y,A) \mathbb{E}_x^Y \left [ K \left (Y_s,dy \right ) \, \alpha(Y_s) \text{e}^{- \int_0^s \alpha(Y_u) \, \text{d} u} \right ] ds.\end{multline}
\begin{multline} Q_t(x,A) = \mathbb{E}_x^Y \left [ {\mathbf 1}_{Y_t \in A} \,\text{e}^{ - \int_0^t \alpha(Y_u) \, \text{d} u } \right ] \\+ \int_0^t \int_E Q_{t-s}(y,A) \mathbb{E}_x^Y \left [ K \left (Y_s,dy \right ) \, \alpha(Y_s) \text{e}^{- \int_0^s \alpha(Y_u) \, \text{d} u} \right ] ds.\end{multline}
In the case of the birth–death–move process of Section 2.2, the above equation reads, for
![]() $x \in E_n$
,
$x \in E_n$
,
 \begin{multline} Q_t(x,A) = \mathbb{E}_x^Y \left [ {\mathbf 1}_{Y_t \in A} \, \text{e}^{ - \int_0^t \alpha(Y_u) \, \text{d} u } \right ] \\ + \int_0^t \int_{E_{n+1}} Q_{t-s}(y,A) \, \mathbb{E}_x^Y \left [ \beta \left (Y_s \right ) K_\beta \left ( Y_s ,dy \right ) \, \text{e}^{ - \int_0^s \alpha(Y_u) \, \text{d} u } \right ] \text{d} s \\ + \int_0^t \int_{E_{n-1}} Q_{t-s}(y,A) \, \mathbb{E}_x^Y \left [ \delta \left (Y_s \right ) K_\delta \left ( Y_s ,dy \right ) \, \text{e}^{ - \int_0^s \alpha(Y_u) \, \text{d} u } \right ] \text{d} s.\end{multline}
\begin{multline} Q_t(x,A) = \mathbb{E}_x^Y \left [ {\mathbf 1}_{Y_t \in A} \, \text{e}^{ - \int_0^t \alpha(Y_u) \, \text{d} u } \right ] \\ + \int_0^t \int_{E_{n+1}} Q_{t-s}(y,A) \, \mathbb{E}_x^Y \left [ \beta \left (Y_s \right ) K_\beta \left ( Y_s ,dy \right ) \, \text{e}^{ - \int_0^s \alpha(Y_u) \, \text{d} u } \right ] \text{d} s \\ + \int_0^t \int_{E_{n-1}} Q_{t-s}(y,A) \, \mathbb{E}_x^Y \left [ \delta \left (Y_s \right ) K_\delta \left ( Y_s ,dy \right ) \, \text{e}^{ - \int_0^s \alpha(Y_u) \, \text{d} u } \right ] \text{d} s.\end{multline}
To show the existence of a unique solution to (2.5), let
![]() $Q_{t,p}(x,A)\;:\!=\;\mathbb{P}_x(X_t \in A , T_p >t)$
be the transition probability from state x to A in time t with less than p jumps. Notice that we can define
$Q_{t,p}(x,A)\;:\!=\;\mathbb{P}_x(X_t \in A , T_p >t)$
be the transition probability from state x to A in time t with less than p jumps. Notice that we can define
![]() $Q_{t,\infty}= \lim \limits_{p \to \infty} Q_{t,p}$
, because
$Q_{t,\infty}= \lim \limits_{p \to \infty} Q_{t,p}$
, because
![]() $Q_{t,p} \leq Q_{t,p+1} \leq 1.$
In the following proposition we use a minimality argument as in [Reference Feller9] to prove that
$Q_{t,p} \leq Q_{t,p+1} \leq 1.$
In the following proposition we use a minimality argument as in [Reference Feller9] to prove that
![]() $Q_{t , \infty}$
is the unique solution to (2.5).
$Q_{t , \infty}$
is the unique solution to (2.5).
Proposition 1. We have that
![]() $Q_{t,\infty}$
is the unique sub-stochastic solution of (2.5), i.e. it is the unique solution satisfying
$Q_{t,\infty}$
is the unique sub-stochastic solution of (2.5), i.e. it is the unique solution satisfying
![]() $Q_{t}(x,E) \leq 1$
for all
$Q_{t}(x,E) \leq 1$
for all
![]() $x\in E$
. Moreover,
$x\in E$
. Moreover,
![]() $Q_{t,\infty}$
is stochastic, i.e.
$Q_{t,\infty}$
is stochastic, i.e.
![]() $Q_{t,\infty}(x,E)=1$
for all
$Q_{t,\infty}(x,E)=1$
for all
![]() $x\in E$
.
$x\in E$
.
To conclude this section, we present an interpretation of
![]() $Q_{t,\infty}$
for the birth–death–move process of Section 2.2, which is much in the spirit of [Reference Preston22]. We write
$Q_{t,\infty}$
for the birth–death–move process of Section 2.2, which is much in the spirit of [Reference Preston22]. We write
![]() $Q_{t,(p)}(x,A)$
for the transition probability from x to A in time t without having entered
$Q_{t,(p)}(x,A)$
for the transition probability from x to A in time t without having entered
![]() $ \bigcup_{k=p+1}^{\infty} E_k$
; that is,
$ \bigcup_{k=p+1}^{\infty} E_k$
; that is,
We can also define
![]() $Q_{t,(\infty)}(x,A) = \lim \limits_{p \rightarrow \infty} \ Q_{t,(p)}(x,A) \leq 1$
by monotonicity.
$Q_{t,(\infty)}(x,A) = \lim \limits_{p \rightarrow \infty} \ Q_{t,(p)}(x,A) \leq 1$
by monotonicity.
Proposition 2. For all
![]() $x\in E$
and all
$x\in E$
and all
![]() $A \in \mathcal{E}$
,
$A \in \mathcal{E}$
,
![]() $Q_{t,(\infty)}(x,A)=Q_{t,\infty}(x,A).$
$Q_{t,(\infty)}(x,A)=Q_{t,\infty}(x,A).$
2.4. Systems of interacting particles in
 $\mathbb{R}^d$
$\mathbb{R}^d$
In this section, we focus on the dynamics of a system of interacting particles in
![]() $\mathbb{R}^d$
. We provide general examples of birth kernels, death kernels, and inter-jump motions in this setting, which in our opinion constitute realistic models for applications and are actually already used in some domains. Some of them, moreover, lead to an explicit Gibbs stationary measure of the dynamics, as we will show in Section 5. These running examples will serve in the rest of the paper to illustrate the theoretical results and make explicit our assumptions.
$\mathbb{R}^d$
. We provide general examples of birth kernels, death kernels, and inter-jump motions in this setting, which in our opinion constitute realistic models for applications and are actually already used in some domains. Some of them, moreover, lead to an explicit Gibbs stationary measure of the dynamics, as we will show in Section 5. These running examples will serve in the rest of the paper to illustrate the theoretical results and make explicit our assumptions.
Let
![]() $W \subset \mathbb{R}^d$
be a closed set where the particles live, equipped with a
$W \subset \mathbb{R}^d$
be a closed set where the particles live, equipped with a
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal{B}$
. A collection of n particles in W is a point configuration for which the ordering does not matter. For this reason, for
$\mathcal{B}$
. A collection of n particles in W is a point configuration for which the ordering does not matter. For this reason, for
![]() $n \geq 1,$
we will identify two elements
$n \geq 1,$
we will identify two elements
![]() $(x_1, \dots,x_n)$
and
$(x_1, \dots,x_n)$
and
![]() $(y_1,\dots,y_n)$
of
$(y_1,\dots,y_n)$
of
![]() $W^n$
if there exists a permutation
$W^n$
if there exists a permutation
![]() $\sigma$
of
$\sigma$
of
![]() $\{1,\dots,n\}$
such that
$\{1,\dots,n\}$
such that
![]() $x_i=y_{\sigma(i)}$
for any
$x_i=y_{\sigma(i)}$
for any
![]() $1 \leq i \leq n$
. Following [Reference Löcherbach15], [Reference Preston22], and others, we thus define
$1 \leq i \leq n$
. Following [Reference Löcherbach15], [Reference Preston22], and others, we thus define
![]() $E_n$
as the space obtained by this identification. Specifically, denoting by
$E_n$
as the space obtained by this identification. Specifically, denoting by
![]() $\pi_n \;:\; (x_1,\dots,x_n) \in W^n \mapsto \{ x_1,\dots,x_n \}$
the associated projection, for
$\pi_n \;:\; (x_1,\dots,x_n) \in W^n \mapsto \{ x_1,\dots,x_n \}$
the associated projection, for
![]() $n\geq 1$
the space
$n\geq 1$
the space
![]() $E_n$
corresponds to
$E_n$
corresponds to
![]() $E_n = \pi_n( W^n) $
equipped with the
$E_n = \pi_n( W^n) $
equipped with the
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal{E}_n=\pi_n (\mathcal{B}^{\otimes n})$
, while
$\mathcal{E}_n=\pi_n (\mathcal{B}^{\otimes n})$
, while
![]() $E_0=\{\text{\O}\}$
consists of just the empty configuration. The general state space of a system of particles is then
$E_0=\{\text{\O}\}$
consists of just the empty configuration. The general state space of a system of particles is then
![]() $E = \cup_{n \geq 0} E_n$
equipped with the
$E = \cup_{n \geq 0} E_n$
equipped with the
![]() $\sigma$
-field
$\sigma$
-field
![]() $ \displaystyle \mathcal{E} = \sigma \left ( \cup_{n \geq 0} \mathcal{E}_n \right ).$
This formalism allows us to go back and forth quite straightforwardly between the space
$ \displaystyle \mathcal{E} = \sigma \left ( \cup_{n \geq 0} \mathcal{E}_n \right ).$
This formalism allows us to go back and forth quite straightforwardly between the space
![]() $E_n$
and the space
$E_n$
and the space
![]() $W^n$
, the latter being in particular more usual for defining the inter-jump motion of n particles, as detailed below. Note that an alternative formalism consists in viewing a configuration of particles as a finite point measure in W, in which case E becomes the set of finite point measures in W; see for instance [Reference Kallenberg12]. We choose in this paper to adopt the former point of view. We denote by
$W^n$
, the latter being in particular more usual for defining the inter-jump motion of n particles, as detailed below. Note that an alternative formalism consists in viewing a configuration of particles as a finite point measure in W, in which case E becomes the set of finite point measures in W; see for instance [Reference Kallenberg12]. We choose in this paper to adopt the former point of view. We denote by
![]() $\|.\|$
the Euclidean norm on
$\|.\|$
the Euclidean norm on
![]() $\mathbb{R}^d$
. If
$\mathbb{R}^d$
. If
![]() $x=\{x_1,\dots,x_n\} \in E_n$
and
$x=\{x_1,\dots,x_n\} \in E_n$
and
![]() $\xi \in W$
, then
$\xi \in W$
, then
![]() $x \cup \xi$
stands for
$x \cup \xi$
stands for
![]() $\{x_1,\dots,x_n,\xi \} \in E_{n+1}$
, and if
$\{x_1,\dots,x_n,\xi \} \in E_{n+1}$
, and if
![]() $1 \leq i \leq n$
, we write
$1 \leq i \leq n$
, we write
![]() $x \, \backslash \, x_i$
for
$x \, \backslash \, x_i$
for
![]() $\{ x_1, \dots, x_{i-1},x_{i+1},\dots, x_n \} \in E_{n-1}.$
$\{ x_1, \dots, x_{i-1},x_{i+1},\dots, x_n \} \in E_{n-1}.$
As long as we are concerned with continuous inter-jump motions, we need to equip E with a distance. Following [Reference Schuhmacher and Xia26], we consider the distance
![]() $d_1$
defined for
$d_1$
defined for
![]() $x=\{x_1,\dots,x_{n(x)} \}$
and
$x=\{x_1,\dots,x_{n(x)} \}$
and
![]() $y=\{y_1,\dots,y_{n(y)} \}$
in E such that
$y=\{y_1,\dots,y_{n(y)} \}$
in E such that
![]() $n(x) \leq n(y)$
by
$n(x) \leq n(y)$
by
 \begin{equation} d_1(x,y) = \frac{1}{n(y)} \left ( \min_{\sigma \in \mathcal{S}_{n(y)}} \sum_{i=1}^{n(x)} (\|x_i-y_{\sigma(i)}\| \wedge 1) + (n(y)-n(x)) \right ), \end{equation}
\begin{equation} d_1(x,y) = \frac{1}{n(y)} \left ( \min_{\sigma \in \mathcal{S}_{n(y)}} \sum_{i=1}^{n(x)} (\|x_i-y_{\sigma(i)}\| \wedge 1) + (n(y)-n(x)) \right ), \end{equation}
with
![]() $d_1(x,\text{\O})=1$
and where
$d_1(x,\text{\O})=1$
and where
![]() $\mathcal{S}_n$
denotes the set of permutations of
$\mathcal{S}_n$
denotes the set of permutations of
![]() $\{1,\dots,n\}$
. The paper [Reference Schuhmacher and Xia26] and Section S-4 in the supplementary material detail some topological properties of
$\{1,\dots,n\}$
. The paper [Reference Schuhmacher and Xia26] and Section S-4 in the supplementary material detail some topological properties of
![]() $(E,d_1)$
. For the purposes of this section, let us quote in particular that
$(E,d_1)$
. For the purposes of this section, let us quote in particular that
![]() $n(.) \;:\; (E,d_1) \rightarrow (\mathbb{N},|.|)$
is continuous and that
$n(.) \;:\; (E,d_1) \rightarrow (\mathbb{N},|.|)$
is continuous and that
![]() $\pi_n$
is continuous. Note that distances other than
$\pi_n$
is continuous. Note that distances other than
![]() $d_1$
could also be chosen, provided these two last properties (at least) are preserved. Incidentally, the Hausdorff distance, which is a common choice of distance between random sets, does not satisfy these properties (see the supplementary material) and is not appropriate in our setting.
$d_1$
could also be chosen, provided these two last properties (at least) are preserved. Incidentally, the Hausdorff distance, which is a common choice of distance between random sets, does not satisfy these properties (see the supplementary material) and is not appropriate in our setting.
We now show how we can easily construct a continuous Markov process
![]() $(Y_t)_{t \geq 0}$
on E from continuous Markov processes on
$(Y_t)_{t \geq 0}$
on E from continuous Markov processes on
![]() $W^n$
for any
$W^n$
for any
![]() $n \geq 1$
. We focus on the case where, for any
$n \geq 1$
. We focus on the case where, for any
![]() $x \in E$
and
$x \in E$
and
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\mathbb{P}_x( (Y_t)_{t \geq 0} \subset E_n)= {\mathbf 1}_{x\in E_n}$
, as we required for birth–death–move processes in Section 2.2. It is then enough to define a process
$\mathbb{P}_x( (Y_t)_{t \geq 0} \subset E_n)= {\mathbf 1}_{x\in E_n}$
, as we required for birth–death–move processes in Section 2.2. It is then enough to define a process
![]() $Y^{|n}$
on each
$Y^{|n}$
on each
![]() $E_n$
. To do so, consider a continuous Markov process
$E_n$
. To do so, consider a continuous Markov process
![]() $(Z_t^{|n})_{t \geq 0}$
on
$(Z_t^{|n})_{t \geq 0}$
on
![]() $W^n$
whose distribution is permutation-equivariant with respect to its initial value
$W^n$
whose distribution is permutation-equivariant with respect to its initial value
![]() $Z^{ \, |n}_0$
. This means that for any permutation
$Z^{ \, |n}_0$
. This means that for any permutation
![]() $\sigma \in \mathcal{S}_n$
, the law of
$\sigma \in \mathcal{S}_n$
, the law of
![]() $Z^{ \, |n}_t = ( Z^{ \, |n}_{t,1}, \dots , Z^{ \, |n}_{t,n} )$
given
$Z^{ \, |n}_t = ( Z^{ \, |n}_{t,1}, \dots , Z^{ \, |n}_{t,n} )$
given
![]() $Z^{ \, |n}_0=(z_{\sigma(1)},\dots,z_{\sigma(n)})$
is the same as the law of
$Z^{ \, |n}_0=(z_{\sigma(1)},\dots,z_{\sigma(n)})$
is the same as the law of
![]() $(Z^{ \, |n}_{t,\sigma(1)}, \dots ,Z^{ \, |n}_{t,\sigma(n)} )$
given
$(Z^{ \, |n}_{t,\sigma(1)}, \dots ,Z^{ \, |n}_{t,\sigma(n)} )$
given
![]() $Z^{ \, |n}_0=(z_1,\dots,z_n)$
. Let
$Z^{ \, |n}_0=(z_1,\dots,z_n)$
. Let
![]() $x= \{x_1,\dots,x_n \} \in E_n$
and take the process
$x= \{x_1,\dots,x_n \} \in E_n$
and take the process
![]() $Z^{ \, |n}_{t}$
with initial state
$Z^{ \, |n}_{t}$
with initial state
![]() $Z^{ \, |n}_0=(x_1,\dots,x_n)$
. Note that, from the previous permutation-equivariance property, the choice of ordering for the coordinates of this initial state does not matter, as will become clear below. We finally define the process
$Z^{ \, |n}_0=(x_1,\dots,x_n)$
. Note that, from the previous permutation-equivariance property, the choice of ordering for the coordinates of this initial state does not matter, as will become clear below. We finally define the process
![]() $Y^{|n}_t$
on
$Y^{|n}_t$
on
![]() $E_n$
starting from x as
$E_n$
starting from x as
Note that the continuity of
![]() $t\to Y^{|n}_t$
(with respect to
$t\to Y^{|n}_t$
(with respect to
![]() $d_1$
) follows from the continuity of
$d_1$
) follows from the continuity of
![]() $t\to Z^{ \, |n}_t$
and the continuity of
$t\to Z^{ \, |n}_t$
and the continuity of
![]() $\pi_n$
. The continuity of
$\pi_n$
. The continuity of
![]() $t\to Y_t$
is then implied by the continuity of
$t\to Y_t$
is then implied by the continuity of
![]() $n(.)$
.
$n(.)$
.
With this construction, the transition kernel of Y reads, for any
![]() $f \in M_b(E)$
,
$f \in M_b(E)$
,
 \begin{align*}Q_t^Yf(x) & = \sum_{n \geq 0}\mathbb{E} \left [ f(Y^{|n}_t) \, |Y^{|n}_0=x\right]{\mathbf 1}_{x \in E_n} \\& = \sum_{n \geq 0}\mathbb{E} \left ( f(\pi_n(Z^{ \, |n}_t)) \left | \right. Z^{ \, |n}_0=(x_{1},\dots,x_{n}) \right ){\mathbf 1}_{x \in E_n},\end{align*}
\begin{align*}Q_t^Yf(x) & = \sum_{n \geq 0}\mathbb{E} \left [ f(Y^{|n}_t) \, |Y^{|n}_0=x\right]{\mathbf 1}_{x \in E_n} \\& = \sum_{n \geq 0}\mathbb{E} \left ( f(\pi_n(Z^{ \, |n}_t)) \left | \right. Z^{ \, |n}_0=(x_{1},\dots,x_{n}) \right ){\mathbf 1}_{x \in E_n},\end{align*}
so that, denoting by
![]() $Q_t^{Z^{ \, |n}}$
the transition kernel of
$Q_t^{Z^{ \, |n}}$
the transition kernel of
![]() $Z^{ \, |n}$
in
$Z^{ \, |n}$
in
![]() $W^n$
, we have
$W^n$
, we have
Note that if we had chosen another ordering for the initial state, i.e.
![]() $Z^{ \, |n}_0=(x_{\sigma(1)},\dots,x_{\sigma(n)})$
for some
$Z^{ \, |n}_0=(x_{\sigma(1)},\dots,x_{\sigma(n)})$
for some
![]() $\sigma \in \mathcal{S}_n$
, then the transition kernel of Y would have remained the same, since by permutation-equivariance
$\sigma \in \mathcal{S}_n$
, then the transition kernel of Y would have remained the same, since by permutation-equivariance
which is
![]() $\mathbb{E} \left ( f(\pi_n(Z^{ \, |n}_t)) \left | \right. Z^{ \, |n}_0=(x_{1},\dots,x_{n}) \right )$
.
$\mathbb{E} \left ( f(\pi_n(Z^{ \, |n}_t)) \left | \right. Z^{ \, |n}_0=(x_{1},\dots,x_{n}) \right )$
.
We are now in a position to present general examples of jump transition kernels and inter-jump motions for a system of particles in W. The first example introduces a death transition kernel where an existing particle dies with a probability that may depend on the distance to the other particles. The next two examples focus on birth transition kernels, driven either by a mixture of densities around each particle or by a Gibbs potential. The last two examples apply the above construction of
![]() $(Y_t)_{t \geq 0}$
on E to introduce inter-jump Langevin diffusions and growth interaction processes.
$(Y_t)_{t \geq 0}$
on E to introduce inter-jump Langevin diffusions and growth interaction processes.
Example 1 (death kernel): Let
![]() $g \;:\; \mathbb{R}_+ \rightarrow \mathbb{R}_+^*$
be a continuous function. For
$g \;:\; \mathbb{R}_+ \rightarrow \mathbb{R}_+^*$
be a continuous function. For
![]() $x=\{x_1,\dots,x_n\}\in E_n$
, set
$x=\{x_1,\dots,x_n\}\in E_n$
, set
![]() $w(x_1,x)=1$
if
$w(x_1,x)=1$
if
![]() $n=1$
, and if
$n=1$
, and if
![]() $n\geq 2$
, for any
$n\geq 2$
, for any
![]() $i\in\{1,\dots,n\}$
set
$i\in\{1,\dots,n\}$
set
with
![]() $z(x)=\sum_{i=1}^n \sum_{k \neq i} g ( \|x_k-x_i\| )$
. A general example of a death transition kernel is
$z(x)=\sum_{i=1}^n \sum_{k \neq i} g ( \|x_k-x_i\| )$
. A general example of a death transition kernel is
 \[\displaystyle K_\delta(x,A)= \sum_{i=1}^{n(x)} w(x_i,x) {\mathbf 1}_{\{x \, \backslash \, x_i\in A\}},\quad x\in E,\ A \in \mathcal{E}.\]
\[\displaystyle K_\delta(x,A)= \sum_{i=1}^{n(x)} w(x_i,x) {\mathbf 1}_{\{x \, \backslash \, x_i\in A\}},\quad x\in E,\ A \in \mathcal{E}.\]
The probability
![]() $w(x_i,x)$
that
$w(x_i,x)$
that
![]() $x_i$
disappears then depends on the distance between
$x_i$
disappears then depends on the distance between
![]() $x_i$
and the other particles in x through g. Uniform deaths correspond to the particular case
$x_i$
and the other particles in x through g. Uniform deaths correspond to the particular case
![]() $w(x_i,x)=1/n(x)$
.
$w(x_i,x)=1/n(x)$
.
Example 2 (birth kernel as a mixture): Let
![]() $\varphi$
be a density function on W, and let
$\varphi$
be a density function on W, and let
![]() $\phi_1 \;:\; W\to \mathbb{R}$
and
$\phi_1 \;:\; W\to \mathbb{R}$
and
![]() $\phi_2\;:\;\mathbb{R}_+\to\mathbb{R}$
be two continuous functions. For
$\phi_2\;:\;\mathbb{R}_+\to\mathbb{R}$
be two continuous functions. For
![]() $x=\{x_1,\dots,x_{n(x)}\}\in E\setminus E_0$
we set
$x=\{x_1,\dots,x_{n(x)}\}\in E\setminus E_0$
we set
![]() $ v(x_i,x) = \exp\left(\phi_1(x_i)+\sum_{k\neq i} \phi_2 \left ( \|x_k-x_i\| \right )\right)$
, and we consider the birth kernel defined for
$ v(x_i,x) = \exp\left(\phi_1(x_i)+\sum_{k\neq i} \phi_2 \left ( \|x_k-x_i\| \right )\right)$
, and we consider the birth kernel defined for
![]() $\Lambda \subset W$
and
$\Lambda \subset W$
and
![]() $x \in E\setminus E_0$
by
$x \in E\setminus E_0$
by
![]() $K_\beta(\text{\O},\Lambda)=\int_\Lambda \varphi(\xi) \text{d} \xi$
and
$K_\beta(\text{\O},\Lambda)=\int_\Lambda \varphi(\xi) \text{d} \xi$
and
 \[ K_\beta (x,\Lambda \cup x) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \dfrac{1}{z(x_i,x)} \int_\Lambda \varphi \left ( \frac{\xi-x_i}{v(x_i,x)} \right ) \, \text{d} \xi,\]
\[ K_\beta (x,\Lambda \cup x) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \dfrac{1}{z(x_i,x)} \int_\Lambda \varphi \left ( \frac{\xi-x_i}{v(x_i,x)} \right ) \, \text{d} \xi,\]
where
![]() $\Lambda \cup x =\{\{u\} \cup x, u\in \Lambda\}$
and
$\Lambda \cup x =\{\{u\} \cup x, u\in \Lambda\}$
and
![]() $z(x_i,x)=\int_W \varphi \left ( (\xi-x_i)/v(x_i,x)\right )\text{d} \xi$
. Note that
$z(x_i,x)=\int_W \varphi \left ( (\xi-x_i)/v(x_i,x)\right )\text{d} \xi$
. Note that
![]() $z(x_i,x)=v(x_i,x)^d$
if
$z(x_i,x)=v(x_i,x)^d$
if
![]() $W=\mathbb{R}^d$
. It is easily checked that
$W=\mathbb{R}^d$
. It is easily checked that
![]() $K_\beta (x,E_{n+1})=K_\beta ( x, W \cup x)= 1$
for
$K_\beta (x,E_{n+1})=K_\beta ( x, W \cup x)= 1$
for
![]() $x \in E_n$
, and in particular this kernel is a genuine birth kernel in the sense that the transition from
$x \in E_n$
, and in particular this kernel is a genuine birth kernel in the sense that the transition from
![]() $E_n$
to
$E_n$
to
![]() $E_{n+1}$
is due only to the addition of a new particle, the existing ones remaining unchanged. Moreover, the new particle is generated as a mixture of distributions driven by
$E_{n+1}$
is due only to the addition of a new particle, the existing ones remaining unchanged. Moreover, the new particle is generated as a mixture of distributions driven by
![]() $\varphi$
, each of them centred at the existing particles. The term
$\varphi$
, each of them centred at the existing particles. The term
![]() $v(x_i,x)$
quantifies the dispersion of births around the particle
$v(x_i,x)$
quantifies the dispersion of births around the particle
![]() $x_i$
, and it depends on the distance between
$x_i$
, and it depends on the distance between
![]() $x_i$
and the other particles through
$x_i$
and the other particles through
![]() $\phi_2$
. A natural example is a mixture of isotropic Gaussian distributions on
$\phi_2$
. A natural example is a mixture of isotropic Gaussian distributions on
![]() $\mathbb{R}^d$
(restricted to W), respectively centred at
$\mathbb{R}^d$
(restricted to W), respectively centred at
![]() $x_i$
with standard deviation
$x_i$
with standard deviation
![]() $v(x_i,x)$
.
$v(x_i,x)$
.
Example 3 (birth kernel based on a Gibbs potential): We introduce a measurable function
![]() $V\;:\; E \rightarrow \mathbb{R}$
, called a potential, satisfying
$V\;:\; E \rightarrow \mathbb{R}$
, called a potential, satisfying
![]() $ z(x)\;:\!=\;\int_W \exp\!(\!-\!(V(x \cup \xi)-V(x))) \, \text{d} \xi < \infty$
for all
$ z(x)\;:\!=\;\int_W \exp\!(\!-\!(V(x \cup \xi)-V(x))) \, \text{d} \xi < \infty$
for all
![]() $x\in E$
, and we consider the birth kernel defined for
$x\in E$
, and we consider the birth kernel defined for
![]() $\Lambda \subset W$
and
$\Lambda \subset W$
and
![]() $x \in E$
by
$x \in E$
by
Note that
![]() $K_\beta ( x, W \cup x)= 1$
for
$K_\beta ( x, W \cup x)= 1$
for
![]() $x \in E$
. With this kernel, given a configuration x, a new particle is more likely to appear in the vicinity of points
$x \in E$
. With this kernel, given a configuration x, a new particle is more likely to appear in the vicinity of points
![]() $\xi\in W$
that make
$\xi\in W$
that make
![]() $V(x \cup \xi)-V(x)$
minimal. This kind of kernel
$V(x \cup \xi)-V(x)$
minimal. This kind of kernel
![]() $K_\beta$
was introduced in [Reference Preston22] for spatial birth–death processes, the case of a birth–death–move process with no move. Their importance is due to the fact that the invariant measure of a spatial birth–death process associated to
$K_\beta$
was introduced in [Reference Preston22] for spatial birth–death processes, the case of a birth–death–move process with no move. Their importance is due to the fact that the invariant measure of a spatial birth–death process associated to
![]() $K_\beta$
, with uniform deaths and specific birth and death intensities, has been explicitly obtained in [Reference Preston22] and corresponds to the Gibbs measure with potential V. This result is the basis of perfect simulation of spatial Gibbs point process models; see [Reference Møller and Waagepetersen19]. We will similarly show in Section 5 that the same Gibbs measure is also invariant for a birth–death–move process associated to the same characteristics for the jumps and a well chosen inter-jump move process
$K_\beta$
, with uniform deaths and specific birth and death intensities, has been explicitly obtained in [Reference Preston22] and corresponds to the Gibbs measure with potential V. This result is the basis of perfect simulation of spatial Gibbs point process models; see [Reference Møller and Waagepetersen19]. We will similarly show in Section 5 that the same Gibbs measure is also invariant for a birth–death–move process associated to the same characteristics for the jumps and a well chosen inter-jump move process
![]() $(Y_t)_{t \geq 0}$
constructed as in the next example.
$(Y_t)_{t \geq 0}$
constructed as in the next example.
Example 4 (Langevin diffusions as inter-jump motions): Let
![]() $g \;:\; \mathbb{R}^d \rightarrow \mathbb{R}^d$
be a globally Lipschitz continuous function,
$g \;:\; \mathbb{R}^d \rightarrow \mathbb{R}^d$
be a globally Lipschitz continuous function,
![]() $\beta >0$
, and
$\beta >0$
, and
![]() $\{ B_{t,i} \} _{1 \leq i \leq n}$
,
$\{ B_{t,i} \} _{1 \leq i \leq n}$
,
![]() $n\geq 1$
, a collection of n independent Brownian motions on
$n\geq 1$
, a collection of n independent Brownian motions on
![]() $\mathbb{R}^d$
. We start from the following system of SDEs, usually called overdamped Langevin equations:
$\mathbb{R}^d$
. We start from the following system of SDEs, usually called overdamped Langevin equations:
For
![]() $z=(z_1,\dots,z_n) \in (\mathbb{R}^d)^n$
, denoting by
$z=(z_1,\dots,z_n) \in (\mathbb{R}^d)^n$
, denoting by
![]() $\Phi_n \;:\; (\mathbb{R}^d)^n \rightarrow (\mathbb{R}^d)^n$
the function defined by
$\Phi_n \;:\; (\mathbb{R}^d)^n \rightarrow (\mathbb{R}^d)^n$
the function defined by
![]() $\Phi_n(z) = (\Phi_{n,1}(z),\dots,\Phi_{n,n}(z))$
with
$\Phi_n(z) = (\Phi_{n,1}(z),\dots,\Phi_{n,n}(z))$
with
![]() $\Phi_{n,i}(z)= \sum_{j \neq i} g ( z_{i}- z_{j})$
, this system of SDEs reads
$\Phi_{n,i}(z)= \sum_{j \neq i} g ( z_{i}- z_{j})$
, this system of SDEs reads
where
![]() $B_t^{\, |n}=(B_{t,1}, \dots, B_{t,n})$
. Since
$B_t^{\, |n}=(B_{t,1}, \dots, B_{t,n})$
. Since
![]() $\Phi_n$
is a permutation-equivariant function, that is, for any
$\Phi_n$
is a permutation-equivariant function, that is, for any
![]() $\sigma \in \mathcal{S}_n$
,
$\sigma \in \mathcal{S}_n$
,
and since
![]() $B_t^{\, |n}$
is exchangeable, we can verify by writing (2.11) in integral form that the law of
$B_t^{\, |n}$
is exchangeable, we can verify by writing (2.11) in integral form that the law of
![]() $Z_t^{|n}$
is permutation-equivariant with respect to its initial state. So when
$Z_t^{|n}$
is permutation-equivariant with respect to its initial state. So when
![]() $W=\mathbb{R}^d$
, we can define each inter-jump process
$W=\mathbb{R}^d$
, we can define each inter-jump process
![]() $Y^{\, |n}$
in
$Y^{\, |n}$
in
![]() $E_n$
from
$E_n$
from
![]() $Z^{\, |n}$
as in (2.8), yielding
$Z^{\, |n}$
as in (2.8), yielding
![]() $(Y_t)_{t \geq 0}$
on E. The same construction can be generalized if
$(Y_t)_{t \geq 0}$
on E. The same construction can be generalized if
![]() $W\subsetneq \mathbb{R}^d$
by considering a Langevin equation with reflecting boundary conditions [Reference Fattler and Grothaus8]. This inter-jump dynamics, associated with the birth kernel of Example 3 and a drift function g related to the potential V, converges to a Gibbs measure on W with potential V (see Section 5).
$W\subsetneq \mathbb{R}^d$
by considering a Langevin equation with reflecting boundary conditions [Reference Fattler and Grothaus8]. This inter-jump dynamics, associated with the birth kernel of Example 3 and a drift function g related to the potential V, converges to a Gibbs measure on W with potential V (see Section 5).
Example 5 (growth interaction processes): This example is motivated by models used in ecology [Reference Comas5, Reference Häbel, Myllymäki and Pommerening10, Reference Renshaw, Comas and Mateu23, Reference Renshaw and Särkkä24]. Each particle consists of a plant located in
![]() $S\subset\mathbb{R}^d$
and associated with a positive mark, which typically represents the size of the plant, so that
$S\subset\mathbb{R}^d$
and associated with a positive mark, which typically represents the size of the plant, so that
![]() $W=S\times \mathbb{R}^+$
here. Births and deaths of plants occur according to a spatial birth-and-death process, while a deterministic growth applies to their mark. Specifically, when a plant appears, its mark is set to zero or generated according to a uniform distribution on
$W=S\times \mathbb{R}^+$
here. Births and deaths of plants occur according to a spatial birth-and-death process, while a deterministic growth applies to their mark. Specifically, when a plant appears, its mark is set to zero or generated according to a uniform distribution on
![]() $[0,\varepsilon]$
for some
$[0,\varepsilon]$
for some
![]() $\varepsilon >0$
[Reference Renshaw and Särkkä24]. Then the mark increases over time, in interaction with the other marks. In order to formally define this inter-jump dynamics, let us denote by
$\varepsilon >0$
[Reference Renshaw and Särkkä24]. Then the mark increases over time, in interaction with the other marks. In order to formally define this inter-jump dynamics, let us denote by
![]() $(U_i(t),m_i(t))_{t \geq 0}$
, for
$(U_i(t),m_i(t))_{t \geq 0}$
, for
![]() $i = 1, \dots , n$
, the components of the process
$i = 1, \dots , n$
, the components of the process
![]() $(Z_t^{|n})_{t \geq 0}$
, where
$(Z_t^{|n})_{t \geq 0}$
, where
![]() $U_i(t) \in S$
and
$U_i(t) \in S$
and
![]() $m_i(t)>0$
, so that
$m_i(t)>0$
, so that
![]() $Z_t^{|n} \in W^n$
. We introduce the system
$Z_t^{|n} \in W^n$
. We introduce the system
where, for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $F_{i,n}$
is a function from
$F_{i,n}$
is a function from
![]() $W^n$
into
$W^n$
into
![]() $\mathbb{R}_+$
. We thus have
$\mathbb{R}_+$
. We thus have
![]() $U_i(t) = U_i(0)$
for all i, and the evolution of the marks
$U_i(t) = U_i(0)$
for all i, and the evolution of the marks
![]() $(m_1(t), \dots ,m_n(t))$
is driven by a deterministic differential equation depending on
$(m_1(t), \dots ,m_n(t))$
is driven by a deterministic differential equation depending on
![]() $(U_1(0),\dots,U_n(0))$
as expected. To define
$(U_1(0),\dots,U_n(0))$
as expected. To define
![]() $Y^{\, |n}$
by (2.8), we finally assume permutation-equivariance, namely that
$Y^{\, |n}$
by (2.8), we finally assume permutation-equivariance, namely that
![]() $F_{\sigma(i),n}(z_1,\dots,z_n)=F_{i,n}(z_{\sigma(1)},\dots,z_{\sigma(n)})$
for all i and all
$F_{\sigma(i),n}(z_1,\dots,z_n)=F_{i,n}(z_{\sigma(1)},\dots,z_{\sigma(n)})$
for all i and all
![]() $\sigma \in \mathcal{S}_n$
, which is satisfied in all of the examples in the aforementioned references.
$\sigma \in \mathcal{S}_n$
, which is satisfied in all of the examples in the aforementioned references.
3. Feller properties and infinitesimal generator
3.1. Feller properties
We assume henceforth that E is a locally compact Polish space. Let
![]() $C_b(E)$
be the set of continuous and bounded functions on E, and let
$C_b(E)$
be the set of continuous and bounded functions on E, and let
![]() $C_0(E)$
be the set of continuous functions that vanish at infinity in the sense that for all
$C_0(E)$
be the set of continuous functions that vanish at infinity in the sense that for all
![]() $ \epsilon>0$
, there exists a compact set
$ \epsilon>0$
, there exists a compact set
![]() $B\in E$
such that
$B\in E$
such that
![]() $x\notin B \Rightarrow |f(x)|<\epsilon$
.
$x\notin B \Rightarrow |f(x)|<\epsilon$
.
Following [Reference Dynkin7] and [Reference Øksendal20], we say that the jump–move process
![]() $(X_t)_{t \geq 0}$
on E with transition kernel
$(X_t)_{t \geq 0}$
on E with transition kernel
![]() $Q_t$
is Feller continuous (or Feller on
$Q_t$
is Feller continuous (or Feller on
![]() $C_b(E)$
) if
$C_b(E)$
) if
![]() $Q_t C_b(E) \subset C_b(E)$
, and we say that it is Feller (or Feller on
$Q_t C_b(E) \subset C_b(E)$
, and we say that it is Feller (or Feller on
![]() $C_0(E)$
) if both
$C_0(E)$
) if both
![]() $ \lim_{t \rightarrow 0} \| Q_tf - f \|_{\infty}= 0$
for any
$ \lim_{t \rightarrow 0} \| Q_tf - f \|_{\infty}= 0$
for any
![]() $f \in C_0(E)$
(strong continuity) and
$f \in C_0(E)$
(strong continuity) and
![]() $Q_t C_0(E) \subset C_0(E)$
.
$Q_t C_0(E) \subset C_0(E)$
.
The following proposition, proved in Section S-2 of the supplementary material, provides information on the continuity property of
![]() $Q_t$
when t goes to 0.
$Q_t$
when t goes to 0.
Proposition 3. We have the following:
-
(i) For any
 $f \in C_b(E)$
and any
$f \in C_b(E)$
and any
 $x \in E$
,
$x \in E$
,
 $\lim_{t \rightarrow 0}\limits Q_tf(x) = f(x)$
.
$\lim_{t \rightarrow 0}\limits Q_tf(x) = f(x)$
. -
(ii) Let
 $ f \in M_b(E)$
. Then
$ f \in M_b(E)$
. Then
 $ \lim_{t \rightarrow 0}\limits \|Q_tf-f\|_{\infty} = 0 $
if and only if
$ \lim_{t \rightarrow 0}\limits \|Q_tf-f\|_{\infty} = 0 $
if and only if
 $ \, \lim_{t \rightarrow 0}\limits \|Q_t^Yf-f\|_{\infty} = 0 . $
$ \, \lim_{t \rightarrow 0}\limits \|Q_t^Yf-f\|_{\infty} = 0 . $
By the second item above, the strong continuity of
![]() $Q_t$
is implied by the strong continuity of
$Q_t$
is implied by the strong continuity of
![]() $Q_t^Y$
, which in turn holds automatically if
$Q_t^Y$
, which in turn holds automatically if
![]() $Q_t^Y \, C_0(E) \subset C_0(E)$
by continuity of
$Q_t^Y \, C_0(E) \subset C_0(E)$
by continuity of
![]() $Y_t$
. We thus obtain the following natural conditions for the jump–move process on E to be Feller continuous or Feller. The proof is given in Section S-2 of the supplementary material.
$Y_t$
. We thus obtain the following natural conditions for the jump–move process on E to be Feller continuous or Feller. The proof is given in Section S-2 of the supplementary material.
Theorem 2. Let
![]() $(X_t)_{t \geq 0}$
be a general jump–move process on E.
$(X_t)_{t \geq 0}$
be a general jump–move process on E.
-
(i) If
 $Q_t^Y \, C_b(E) \subset C_b(E)$
and
$Q_t^Y \, C_b(E) \subset C_b(E)$
and
 $K \, C_b(E) \subset C_b(E)$
, then
$K \, C_b(E) \subset C_b(E)$
, then
 $(X_t)_{t \geq 0}$
is a Feller continuous process.
$(X_t)_{t \geq 0}$
is a Feller continuous process. -
(ii) If
 $Q_t^Y \, C_0(E) \subset C_0(E)$
and
$Q_t^Y \, C_0(E) \subset C_0(E)$
and
 $K \, C_0(E) \subset C_0(E)$
, then
$K \, C_0(E) \subset C_0(E)$
, then
 $(X_t)_{t \geq 0}$
is a Feller process.
$(X_t)_{t \geq 0}$
is a Feller process.
We deduce in particular from this theorem that if
![]() $Q_t^Y \, C_b(E) \subset C_b(E)$
and
$Q_t^Y \, C_b(E) \subset C_b(E)$
and
![]() $K \, C_b(E) \subset C_b(E)$
(or alternatively with
$K \, C_b(E) \subset C_b(E)$
(or alternatively with
![]() $C_0(E)$
instead of
$C_0(E)$
instead of
![]() $C_b(E)$
), then
$C_b(E)$
), then
![]() $(X_t)_{t \geq 0}$
is a strong Markov process for the filtration
$(X_t)_{t \geq 0}$
is a strong Markov process for the filtration
![]() $(\mathcal{F}_t)_{t \geq 0}$
, a property implied by the Feller continuous and Feller properties; see [Reference Bass3]. The Feller property will also be useful to us in Section 4 to construct a coupling between a birth–death–move process and a simple birth–death process on
$(\mathcal{F}_t)_{t \geq 0}$
, a property implied by the Feller continuous and Feller properties; see [Reference Bass3]. The Feller property will also be useful to us in Section 4 to construct a coupling between a birth–death–move process and a simple birth–death process on
![]() $\mathbb{N}$
, with a view to establishing ergodic properties.
$\mathbb{N}$
, with a view to establishing ergodic properties.
In Section 3.3 we investigate the conditions of Theorem 2 for the examples of dynamics of systems of interacting particles in
![]() $\mathbb{R}^d$
introduced in Section 2.4. For these examples, the conditions turn out to be generally satisfied under mild assumptions.
$\mathbb{R}^d$
introduced in Section 2.4. For these examples, the conditions turn out to be generally satisfied under mild assumptions.
3.2. Infinitesimal generator
In this section we compute the infinitesimal generator associated to the jump–move process
![]() $(X_t)_{t \geq 0}$
. We first introduce some notation and recall the definition of the generator; see for instance [Reference Dynkin7]. In connection with this, recall that the family
$(X_t)_{t \geq 0}$
. We first introduce some notation and recall the definition of the generator; see for instance [Reference Dynkin7]. In connection with this, recall that the family
![]() $(Q_t)_{t \geq 0}$
of transition operators is a semigroup on
$(Q_t)_{t \geq 0}$
of transition operators is a semigroup on
![]() $(M_b(E),\|.\|_{\infty}).$
If moreover the process
$(M_b(E),\|.\|_{\infty}).$
If moreover the process
![]() $(X_t)_{t \geq 0}$
is Feller continuous (resp. Feller), then
$(X_t)_{t \geq 0}$
is Feller continuous (resp. Feller), then
![]() $(Q_t)_{t \geq 0}$
is a semigroup on
$(Q_t)_{t \geq 0}$
is a semigroup on
![]() $(C_b(E),\|.\|_{\infty})$
(resp.
$(C_b(E),\|.\|_{\infty})$
(resp.
![]() $(C_0(E),\|.\|_{\infty})$
).
$(C_0(E),\|.\|_{\infty})$
).
Let
![]() $L \subset M_b(E)$
and
$L \subset M_b(E)$
and
![]() $(U_t)_{t \geq 0}$
be a semigroup on
$(U_t)_{t \geq 0}$
be a semigroup on
![]() $(L,\|.\|_{\infty})$
. We set
$(L,\|.\|_{\infty})$
. We set
For
![]() $f \in \mathcal{D}_\mathcal{A}$
, define
$f \in \mathcal{D}_\mathcal{A}$
, define
![]() $\mathcal{A} f = \lim_{t \searrow 0} (U_t f -f)/t.$
The operator
$\mathcal{A} f = \lim_{t \searrow 0} (U_t f -f)/t.$
The operator
![]() $\mathcal{A} \;:\; \mathcal{D}_{\mathcal{A}} \rightarrow L $
is called the infinitesimal generator associated to the semigroup
$\mathcal{A} \;:\; \mathcal{D}_{\mathcal{A}} \rightarrow L $
is called the infinitesimal generator associated to the semigroup
![]() $(U_t)_{t \geq 0}$
and
$(U_t)_{t \geq 0}$
and
![]() $\mathcal{D}_{\mathcal{A}}$
is called the domain of the generator
$\mathcal{D}_{\mathcal{A}}$
is called the domain of the generator
![]() $\mathcal{A}.$
$\mathcal{A}.$
In the following we denote by
![]() $L_0$
(resp.
$L_0$
(resp.
![]() $L_0^Y$
) and
$L_0^Y$
) and
![]() $\mathcal{A}$
(resp.
$\mathcal{A}$
(resp.
![]() $\mathcal{A}^Y$
) the set and the infinitesimal operator associated to
$\mathcal{A}^Y$
) the set and the infinitesimal operator associated to
![]() $(Q_t)_{t \geq 0}$
(resp.
$(Q_t)_{t \geq 0}$
(resp.
![]() $(Q_t^Y)_{t \geq 0}$
). Note that
$(Q_t^Y)_{t \geq 0}$
). Note that
![]() $L_0=L_0^Y$
by Proposition 3.
$L_0=L_0^Y$
by Proposition 3.
Theorem 3. Let
![]() $(X_t)_{t \geq 0}$
be a general jump–move process on a Polish space E. Suppose that if
$(X_t)_{t \geq 0}$
be a general jump–move process on a Polish space E. Suppose that if
![]() $ f \in L_0^Y$
, then
$ f \in L_0^Y$
, then
![]() $\alpha \times f \in L_0^Y$
and
$\alpha \times f \in L_0^Y$
and
![]() $Kf \in L_0^Y$
. Then
$Kf \in L_0^Y$
. Then
![]() $\mathcal{D}_\mathcal{A}=\mathcal{D}_{\mathcal{A}^Y}$
, and for any
$\mathcal{D}_\mathcal{A}=\mathcal{D}_{\mathcal{A}^Y}$
, and for any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
,
$f \in \mathcal{D}_{\mathcal{A}^Y}$
,
This result, proved in Section S-3 of the supplementary material, shows that the generator
![]() $\mathcal{A}$
of the jump–move process
$\mathcal{A}$
of the jump–move process
![]() $(X_t)_{t \geq 0}$
is simply the sum of the generator of the move
$(X_t)_{t \geq 0}$
is simply the sum of the generator of the move
![]() $\mathcal{A}^Y$
and the generator of the jump, specifically of a pure jump Markov process with intensity
$\mathcal{A}^Y$
and the generator of the jump, specifically of a pure jump Markov process with intensity
![]() $\alpha$
and transition kernel K, i.e.
$\alpha$
and transition kernel K, i.e.
![]() $\alpha \times (K- Id)$
(see [Reference Feller9]).
$\alpha \times (K- Id)$
(see [Reference Feller9]).
Note that for a pure jump process,
![]() $Q_t^Y=Id$
for any
$Q_t^Y=Id$
for any
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $L_0^Y=\mathcal{D}_{\mathcal{A}^Y}=M_b(E)$
, and
$L_0^Y=\mathcal{D}_{\mathcal{A}^Y}=M_b(E)$
, and
![]() $\mathcal{A}^Y \equiv 0$
, so that all assumptions of Theorem 3 are trivially true in this setting. More generally, consider a jump–move process with a Feller inter-jump process, i.e.
$\mathcal{A}^Y \equiv 0$
, so that all assumptions of Theorem 3 are trivially true in this setting. More generally, consider a jump–move process with a Feller inter-jump process, i.e.
![]() $Q_t^Y \, C_0(E) \subset C_0(E)$
, and a Feller jump transition, i.e.
$Q_t^Y \, C_0(E) \subset C_0(E)$
, and a Feller jump transition, i.e.
![]() $K \, C_0(E) \subset C_0(E)$
, so that
$K \, C_0(E) \subset C_0(E)$
, so that
![]() $(X_t)_{t \geq 0}$
is Feller by Theorem 2. Then we can take
$(X_t)_{t \geq 0}$
is Feller by Theorem 2. Then we can take
![]() $L_0^Y=C_0(E)$
, and again the assumptions of Theorem 3 are satisfied since
$L_0^Y=C_0(E)$
, and again the assumptions of Theorem 3 are satisfied since
![]() $\alpha$
is bounded.
$\alpha$
is bounded.
3.3. Application to systems of interacting particles in
 $\mathbb{R}^d$
$\mathbb{R}^d$
We go back to the setting of Section 2.4, namely, systems of interacting particles in
![]() $W\subset \mathbb{R}^d$
, in order to investigate whether the examples of dynamics presented therein are (continuous) Feller or not. To do so and be able to check the conditions of Theorem 2, we need to first clarify what the sets
$W\subset \mathbb{R}^d$
, in order to investigate whether the examples of dynamics presented therein are (continuous) Feller or not. To do so and be able to check the conditions of Theorem 2, we need to first clarify what the sets
![]() $ C_b(E)$
and
$ C_b(E)$
and
![]() $ C_0(E) $
are in this framework. Remember that in this setting
$ C_0(E) $
are in this framework. Remember that in this setting
![]() $E = \cup_{n \geq 0} E_n$
, where
$E = \cup_{n \geq 0} E_n$
, where
![]() $E_n = \pi_n( W^n)$
corresponds to the set of unordered n-tuples of W, and we have equipped E with the distance
$E_n = \pi_n( W^n)$
corresponds to the set of unordered n-tuples of W, and we have equipped E with the distance
![]() $d_1$
defined by (2.7). As a first result, it can be verified that
$d_1$
defined by (2.7). As a first result, it can be verified that
![]() $(E,d_1)$
is a locally compact Polish space; see [Reference Schuhmacher and Xia26, Proposition 2.2] and Section S-4 in the supplementary material. To characterize the elements of
$(E,d_1)$
is a locally compact Polish space; see [Reference Schuhmacher and Xia26, Proposition 2.2] and Section S-4 in the supplementary material. To characterize the elements of
![]() $ C_b(E)$
, we shall use the following proposition, proved in the supplementary material.
$ C_b(E)$
, we shall use the following proposition, proved in the supplementary material.
Proposition 4.
Let
![]() $x \in E$
and let
$x \in E$
and let
![]() $(x^{(p)})_{p \geq 1}$
be a sequence converging to x, i.e.
$(x^{(p)})_{p \geq 1}$
be a sequence converging to x, i.e.
![]() $d_1(x^{(p)},x)\to 0$
as
$d_1(x^{(p)},x)\to 0$
as
![]() $p\to\infty$
. Then there exists
$p\to\infty$
. Then there exists
![]() $p_0 \geq 1$
such that for all
$p_0 \geq 1$
such that for all
![]() $p \geq p_0$
,
$p \geq p_0$
,
![]() $n(x^{(p)})=n(x)$
and, when
$n(x^{(p)})=n(x)$
and, when
![]() $n(x)\geq 1$
, there exists a sequence
$n(x)\geq 1$
, there exists a sequence
![]() $(\sigma_{p})_{p \geq p_0}$
of
$(\sigma_{p})_{p \geq p_0}$
of
![]() $\mathcal{S}_{n(x)}$
such that for any
$\mathcal{S}_{n(x)}$
such that for any
![]() $i \in \{ 1 , \dots, n(x) \},$
$i \in \{ 1 , \dots, n(x) \},$
To deal with
![]() $C_0(E)$
, we provide a characterization of the compact sets of each
$C_0(E)$
, we provide a characterization of the compact sets of each
![]() $E_n$
, for
$E_n$
, for
![]() $n \geq 1$
, and an important property of the compact sets of E.
$n \geq 1$
, and an important property of the compact sets of E.
Proposition 5.
Suppose that W is a closed set of
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
-
(i) Let
 $n \geq 1$
and let A be a closed subset of
$n \geq 1$
and let A be a closed subset of
 $(E_n,d_1).$
Then A is compact if and only if the following property holds:
$(E_n,d_1).$
Then A is compact if and only if the following property holds: \[ \forall \, w \in W, \; \exists \, R \geq 0, \; s.t. \; \forall \, x = \{ x_1,...,x_n\} \in A, \; \underset{1 \leq k \leq n}{\max} \{ \|x_k-w\| \} \leq R. \]
\[ \forall \, w \in W, \; \exists \, R \geq 0, \; s.t. \; \forall \, x = \{ x_1,...,x_n\} \in A, \; \underset{1 \leq k \leq n}{\max} \{ \|x_k-w\| \} \leq R. \]
-
(ii) Let A be a compact set of E. Then there exists
 $n_0 \geq 0$
such that
$n_0 \geq 0$
such that
 $A \subset \bigcup_{n=0}^{n_0} E_n. $
$A \subset \bigcup_{n=0}^{n_0} E_n. $
The previous two propositions are the main tools we need to investigate the continuous Feller and Feller properties of the jump kernel K of a jump–move process. Concerning the inter-jump move process
![]() $(Y_t)_{t\geq 0}$
, recall that we can easily define it on each
$(Y_t)_{t\geq 0}$
, recall that we can easily define it on each
![]() $E_n$
from a continuous process
$E_n$
from a continuous process
![]() $(Z^{|n}_t)_{t\geq 0}$
on
$(Z^{|n}_t)_{t\geq 0}$
on
![]() $W^n$
through the projection (2.8). In general, properties on E are not simply derived from properties on
$W^n$
through the projection (2.8). In general, properties on E are not simply derived from properties on
![]() $E_n$
; for instance, we deduce from Proposition 5 that
$E_n$
; for instance, we deduce from Proposition 5 that
![]() $\sum_n f_n {\mathbf 1}_{E_n}$
for
$\sum_n f_n {\mathbf 1}_{E_n}$
for
![]() $f_n\in C_0(E_n)$
is not necessarily in
$f_n\in C_0(E_n)$
is not necessarily in
![]() $C_0(E)$
(take W compact and
$C_0(E)$
(take W compact and
![]() $f_n(x)=n(x)$
). Nonetheless, the formula (2.9) implies that the Feller properties of
$f_n(x)=n(x)$
). Nonetheless, the formula (2.9) implies that the Feller properties of
![]() $(Y_t)_{t\geq 0}$
on
$(Y_t)_{t\geq 0}$
on
![]() $(E,d_1)$
are inherited from those of
$(E,d_1)$
are inherited from those of
![]() $(Z^{|n}_t)_{t\geq 0}$
on
$(Z^{|n}_t)_{t\geq 0}$
on
![]() $W^n$
.
$W^n$
.
Proposition 6.
Let
![]() $(Y_t)_{t \geq 0}$
be defined on E by (2.8). If
$(Y_t)_{t \geq 0}$
be defined on E by (2.8). If
![]() $( Z^{\, |n}_t)_{t \geq 0}$
is a Feller continuous (resp. Feller) process on
$( Z^{\, |n}_t)_{t \geq 0}$
is a Feller continuous (resp. Feller) process on
![]() $W^n$
for every
$W^n$
for every
![]() $n \geq 1$
, then
$n \geq 1$
, then
![]() $(Y_t)_{t \geq 0}$
is a Feller continuous (resp. Feller) process on E.
$(Y_t)_{t \geq 0}$
is a Feller continuous (resp. Feller) process on E.
By this result, standard inter-jump motions are Feller continuous and Feller, as is the case under mild assumptions for our examples 4 and 5, detailed below. Concerning the jump kernels, the global picture is as follows. They are generally Feller continuous, but not necessarily Feller even if the underlying space W is compact, as shown in the following example. However, if we restrict ourselves to birth kernels, then they are generally Feller (see Examples 2 and 3 below). On the other hand, if we restrict ourselves to death kernels, then they are Feller if W is compact, but not otherwise; see Example 1 below. Notice that a birth-and-death jump kernel as in (2.4) is (continuous) Feller when the birth kernel
![]() $K_\beta$
and the death kernel
$K_\beta$
and the death kernel
![]() $K_\delta$
are. So it is generally continuous Feller, and if W is compact, it is generally Feller.
$K_\delta$
are. So it is generally continuous Feller, and if W is compact, it is generally Feller.
Let us make these informal claims more precise through some examples. The first example presents a jump kernel on a set W, possibly compact, that is continuous Feller but not Feller. The other ones correspond to the examples introduced in Section 2.4.
Example Consider the jump kernel K defined by
![]() $Kf(x)= \sum_{i=1}^{n(x)} f(\{x_i\})/n(x)$
for
$Kf(x)= \sum_{i=1}^{n(x)} f(\{x_i\})/n(x)$
for
![]() $f \in M_b(E)$
and
$f \in M_b(E)$
and
![]() $x=\{x_1,\dots,x_{n(x)}\}\in E$
, so that
$x=\{x_1,\dots,x_{n(x)}\}\in E$
, so that
![]() $K(x,E_1)=1$
for any
$K(x,E_1)=1$
for any
![]() $x\in E$
. Let
$x\in E$
. Let
![]() $x^{(p)}$
be a sequence converging to x, from which we define
$x^{(p)}$
be a sequence converging to x, from which we define
![]() $p_0$
and
$p_0$
and
![]() $(\sigma_p)_{p\geq p_0}$
as in Proposition 4. Let
$(\sigma_p)_{p\geq p_0}$
as in Proposition 4. Let
![]() $f \in C_b(E)$
. Then
$f \in C_b(E)$
. Then
![]() $K f(x^{(p)}) = \sum_{i=1}^{n(x)} f( x^{(p)}_{\sigma_p(i)})/n(x)$
tends to
$K f(x^{(p)}) = \sum_{i=1}^{n(x)} f( x^{(p)}_{\sigma_p(i)})/n(x)$
tends to
![]() $\sum_{i=1}^{n(x)} f( x_{i})/n(x) = Kf(x)$
as
$\sum_{i=1}^{n(x)} f( x_{i})/n(x) = Kf(x)$
as
![]() $p\to\infty$
, which shows the continuous Feller property of K, i.e.
$p\to\infty$
, which shows the continuous Feller property of K, i.e.
![]() $K \, C_b(E) \subset C_b(E)$
. Let us now show that K is not Feller. Assume without loss of generality that
$K \, C_b(E) \subset C_b(E)$
. Let us now show that K is not Feller. Assume without loss of generality that
![]() $0\in W$
. Consider the function
$0\in W$
. Consider the function
![]() $f(x)=\max(1-\|x\|,0){\mathbf 1}_{n(x)=1}$
, where we abusively write
$f(x)=\max(1-\|x\|,0){\mathbf 1}_{n(x)=1}$
, where we abusively write
![]() $\|x\|\;:\!=\;\|x_1\|$
when
$\|x\|\;:\!=\;\|x_1\|$
when
![]() $x=\{x_1\}$
,
$x=\{x_1\}$
,
![]() $x_1\in W$
. Note that
$x_1\in W$
. Note that
![]() $f\in C_0(E)$
. Let B be a compact subset of E. From Theorem 5, there exists
$f\in C_0(E)$
. Let B be a compact subset of E. From Theorem 5, there exists
![]() $n_0 \geq 0$
such that
$n_0 \geq 0$
such that
![]() $ B \subset \cup_{n=0}^{n_0} E_n$
. Choose
$ B \subset \cup_{n=0}^{n_0} E_n$
. Choose
![]() $y=\{0,\dots,0\}\in E_{n_0+1}$
. Then
$y=\{0,\dots,0\}\in E_{n_0+1}$
. Then
![]() $y\notin B$
but
$y\notin B$
but
![]() $Kf(y)=1$
, proving that
$Kf(y)=1$
, proving that
![]() $Kf\notin C_0(E)$
.
$Kf\notin C_0(E)$
.
Example 1
(continued) (death kernel): For the death kernel
![]() $K_\delta$
of this example, we have the following:
$K_\delta$
of this example, we have the following:
-
(i)
 $K_\delta C_b (E) \subset C_b(E)$
, and
$K_\delta C_b (E) \subset C_b(E)$
, and -
(ii)
 $K_\delta C_0(E)\subset C_0(E)$
if W is compact, but not necessarily otherwise.
$K_\delta C_0(E)\subset C_0(E)$
if W is compact, but not necessarily otherwise.
To prove the first property, take
![]() $x\in E$
, a sequence
$x\in E$
, a sequence
![]() $(x^{(p)})_{p \geq 0}$
converging to x, and
$(x^{(p)})_{p \geq 0}$
converging to x, and
![]() $p_0$
and
$p_0$
and
![]() $(\sigma_p)_{p\geq p_0}$
from Proposition 4. Then it is not difficult to verify that
$(\sigma_p)_{p\geq p_0}$
from Proposition 4. Then it is not difficult to verify that
![]() $\lim_{p \rightarrow \infty} w(x_{\sigma_p(i)}^{(p)},x^{(p)}) = w(x_i,x)$
by continuity of g. Moreover,
$\lim_{p \rightarrow \infty} w(x_{\sigma_p(i)}^{(p)},x^{(p)}) = w(x_i,x)$
by continuity of g. Moreover,
![]() $ d_1 \left ( x^{(p)} \, \backslash \, x_{ \sigma_p(i)}^{(p)}, x \, \backslash \, x_{i} \right ) \leq \sum_{j \neq i} \|x_{\sigma_p(j)}^{(p)} - x_{j} \|/(n-1)$
, which shows that
$ d_1 \left ( x^{(p)} \, \backslash \, x_{ \sigma_p(i)}^{(p)}, x \, \backslash \, x_{i} \right ) \leq \sum_{j \neq i} \|x_{\sigma_p(j)}^{(p)} - x_{j} \|/(n-1)$
, which shows that
![]() $x^{(p)} \, \backslash \, x_{\sigma_p(i)}^{(p)} \underset{p \rightarrow \infty}{\longrightarrow} x \, \backslash \, x_{i}$
. Therefore, for any
$x^{(p)} \, \backslash \, x_{\sigma_p(i)}^{(p)} \underset{p \rightarrow \infty}{\longrightarrow} x \, \backslash \, x_{i}$
. Therefore, for any
![]() $f\in C_b(E)$
,
$f\in C_b(E)$
,
 \begin{align*} \lim \limits_{p \rightarrow \infty} K_\delta f(x^{(p)}) & = \lim \limits_{p \rightarrow \infty} \sum_{i=1}^{n(x)} w\!\left(x_i^{(p)},x^{(p)}\right) f\!\left(x^{(p)} \, \backslash \, x^{(p)}_i\right) \\ & = \lim \limits_{p \rightarrow \infty} \sum_{i=1}^{n(x)} w\!\left(x_{\sigma_p(i)}^{(p)},x^{(p)}\right) f\!\left(x^{(p)} \, \backslash \, x^{(p)}_{\sigma_p(i)}\right) \\ & = \sum_{i=1}^{n(x)} w(x_{i},x) f(x \backslash \, x_{i}) \\ &= K_\delta f(x).\end{align*}
\begin{align*} \lim \limits_{p \rightarrow \infty} K_\delta f(x^{(p)}) & = \lim \limits_{p \rightarrow \infty} \sum_{i=1}^{n(x)} w\!\left(x_i^{(p)},x^{(p)}\right) f\!\left(x^{(p)} \, \backslash \, x^{(p)}_i\right) \\ & = \lim \limits_{p \rightarrow \infty} \sum_{i=1}^{n(x)} w\!\left(x_{\sigma_p(i)}^{(p)},x^{(p)}\right) f\!\left(x^{(p)} \, \backslash \, x^{(p)}_{\sigma_p(i)}\right) \\ & = \sum_{i=1}^{n(x)} w(x_{i},x) f(x \backslash \, x_{i}) \\ &= K_\delta f(x).\end{align*}
Let us now consider the second claim, (ii). Take
![]() $f \in C_0(E)$
and
$f \in C_0(E)$
and
![]() $\varepsilon >0$
. We fix a compact set A of
$\varepsilon >0$
. We fix a compact set A of
![]() $(E,d_{1})$
such that
$(E,d_{1})$
such that
![]() $|f(x)|< \varepsilon$
for
$|f(x)|< \varepsilon$
for
![]() $x \notin A$
. By Proposition 5,
$x \notin A$
. By Proposition 5,
![]() $ A \subset \bigcup_{n=0}^{n_0} E_n$
for some
$ A \subset \bigcup_{n=0}^{n_0} E_n$
for some
![]() $n_0$
. As a straightforward consequence of Proposition 5 (see the supplementary material), the set
$n_0$
. As a straightforward consequence of Proposition 5 (see the supplementary material), the set
![]() $ B \;:\!=\; \bigcup_{n=0}^{n_0+1} E_n $
is a compact set when W is compact and it satisfies
$ B \;:\!=\; \bigcup_{n=0}^{n_0+1} E_n $
is a compact set when W is compact and it satisfies
![]() $K_\delta(x,A)=0$
for
$K_\delta(x,A)=0$
for
![]() $x \notin B$
. This implies that for
$x \notin B$
. This implies that for
![]() $x\notin B$
,
$x\notin B$
,
 \begin{align} |K_\delta f(x)| & \leq \left | \int_A f(y) K_\delta (x,\text{d} y) \right | + \left | \int_{A^c} f(y) K_\delta (x, \text{d} y) \right | \nonumber \\ & \leq ||f||_{\infty} K_\delta (x,A) + \varepsilon \, K_\delta (x,A^c) \leq \varepsilon,\end{align}
\begin{align} |K_\delta f(x)| & \leq \left | \int_A f(y) K_\delta (x,\text{d} y) \right | + \left | \int_{A^c} f(y) K_\delta (x, \text{d} y) \right | \nonumber \\ & \leq ||f||_{\infty} K_\delta (x,A) + \varepsilon \, K_\delta (x,A^c) \leq \varepsilon,\end{align}
and so
![]() $K_\delta f\in C_0(E)$
. Let us finally show that this result is no longer valid if W is not compact. Assume without loss of generality that
$K_\delta f\in C_0(E)$
. Let us finally show that this result is no longer valid if W is not compact. Assume without loss of generality that
![]() $0\in W$
, and consider as in the previous example the function
$0\in W$
, and consider as in the previous example the function
![]() $f\in C_0(E)$
defined by
$f\in C_0(E)$
defined by
![]() $f(x)=\max(1-\|x\|,0){\mathbf 1}_{n(x)=1}$
. Let B be any compact subset of E. Then
$f(x)=\max(1-\|x\|,0){\mathbf 1}_{n(x)=1}$
. Let B be any compact subset of E. Then
![]() $B_2=B\cap E_2$
is compact because
$B_2=B\cap E_2$
is compact because
![]() $E_2$
is closed and, by Proposition 5, for any
$E_2$
is closed and, by Proposition 5, for any
![]() $x=\{x_1,x_2\} \in B_2$
, there exists
$x=\{x_1,x_2\} \in B_2$
, there exists
![]() $R > 0$
such that
$R > 0$
such that
![]() $\max\{\|x_1\|,\|x_2\|\} \leq R$
. Take
$\max\{\|x_1\|,\|x_2\|\} \leq R$
. Take
![]() $y=\{0,y_2\}$
in
$y=\{0,y_2\}$
in
![]() $E_2$
such that
$E_2$
such that
![]() $\|y_2\|>R+1$
, which is possible since W is not compact. Then
$\|y_2\|>R+1$
, which is possible since W is not compact. Then
![]() $y\notin B$
but
$y\notin B$
but
![]() $K_\delta f(y)=w(y_2,y)$
, proving that
$K_\delta f(y)=w(y_2,y)$
, proving that
![]() $Kf\notin C_0(E)$
.
$Kf\notin C_0(E)$
.
Example 2
(continued) (birth kernel as a mixture): For this example, we shall prove that if
![]() $\mathring W \neq \varnothing$
and if the dispersion function v is continuous, then
$\mathring W \neq \varnothing$
and if the dispersion function v is continuous, then
![]() $K_\beta C_b (E) \subset C_b(E)$
and
$K_\beta C_b (E) \subset C_b(E)$
and
![]() $K_\beta C_0(E)\subset C_0(E)$
. Take
$K_\beta C_0(E)\subset C_0(E)$
. Take
![]() $f\in C_b (E)$
,
$f\in C_b (E)$
,
![]() $x\in E$
, and a sequence
$x\in E$
, and a sequence
![]() $(x^{(p)})_{p \geq 0}$
converging to x, from which we define
$(x^{(p)})_{p \geq 0}$
converging to x, from which we define
![]() $p_0$
and
$p_0$
and
![]() $(\sigma_p)_{p\geq p_0}$
from Proposition 4. We have, for
$(\sigma_p)_{p\geq p_0}$
from Proposition 4. We have, for
![]() $p\geq p_0$
,
$p\geq p_0$
,
 \begin{align*} &K_\beta f(x^{(p)}) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \dfrac{1}{z(x_{\sigma_p(i)}^{(p)},x^{(p)})} \int_{W} f(x^{(p)} \cup \{ \xi \} )\varphi \left ( \frac{\xi-x_{\sigma_p(i)}^{(p)}}{v(x_{\sigma_p(i)}^{(p)},x^{(p)})} \right ) d\xi\\[5pt] &=\dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \frac{\int_{\mathbb{R}^d} {\mathbf 1}_{\{x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \in W\}} f(x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \} ) \varphi(\xi) d\xi}{\int_{\mathbb{R}^d} {\mathbf 1}_{\{x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \in W\}} \varphi(\xi) d\xi}. \end{align*}
\begin{align*} &K_\beta f(x^{(p)}) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \dfrac{1}{z(x_{\sigma_p(i)}^{(p)},x^{(p)})} \int_{W} f(x^{(p)} \cup \{ \xi \} )\varphi \left ( \frac{\xi-x_{\sigma_p(i)}^{(p)}}{v(x_{\sigma_p(i)}^{(p)},x^{(p)})} \right ) d\xi\\[5pt] &=\dfrac{1}{n(x)} \sum_{i=1}^{n(x)} \frac{\int_{\mathbb{R}^d} {\mathbf 1}_{\{x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \in W\}} f(x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \} ) \varphi(\xi) d\xi}{\int_{\mathbb{R}^d} {\mathbf 1}_{\{x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \in W\}} \varphi(\xi) d\xi}. \end{align*}
By continuity of v, the indicator functions involved tend to
![]() ${\mathbf 1}_{\{x_i+ v(x_i ,x)\xi \in W\}}$
for any
${\mathbf 1}_{\{x_i+ v(x_i ,x)\xi \in W\}}$
for any
![]() $x_i+ v(x_i ,x)\xi\in \mathring W$
. On the other hand, for any
$x_i+ v(x_i ,x)\xi\in \mathring W$
. On the other hand, for any
![]() $i\in \{1,...,n(x)\}$
and any
$i\in \{1,...,n(x)\}$
and any
![]() $\xi$
,
$\xi$
,
 \begin{align*} & d_1 \left ( x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \}, x \cup \{ x_{i} + v(x_{i},x) \, \xi \} \right ) \\ & \leq \frac{1}{n(x)+1} \left ( \sum_{j =1}^{n(x)} \|x_{\sigma_p(j)}^{(p)} - x_{j} \| + \|x_{\sigma_p(i)}^{(p)} + v(x_{\sigma_p(i)}^{(p)},x^{(p)}) \, \xi - x_{i} - v(x_{i},x) \, \xi \| \right ) \\ & \leq \frac{1}{n(x)+1} \left ( \sum_{j =1}^{n(x)} \|x_{\sigma_p(j)}^{(p)} - x_{j} \| + \|x_{\sigma_p(i)}^{(p)} - x_{i} \| + \|\xi\| \, |v(x_{\sigma_p(i)}^{(p)},x^{(p)})-v(x_{i},x)| \right ), \end{align*}
\begin{align*} & d_1 \left ( x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \}, x \cup \{ x_{i} + v(x_{i},x) \, \xi \} \right ) \\ & \leq \frac{1}{n(x)+1} \left ( \sum_{j =1}^{n(x)} \|x_{\sigma_p(j)}^{(p)} - x_{j} \| + \|x_{\sigma_p(i)}^{(p)} + v(x_{\sigma_p(i)}^{(p)},x^{(p)}) \, \xi - x_{i} - v(x_{i},x) \, \xi \| \right ) \\ & \leq \frac{1}{n(x)+1} \left ( \sum_{j =1}^{n(x)} \|x_{\sigma_p(j)}^{(p)} - x_{j} \| + \|x_{\sigma_p(i)}^{(p)} - x_{i} \| + \|\xi\| \, |v(x_{\sigma_p(i)}^{(p)},x^{(p)})-v(x_{i},x)| \right ), \end{align*}
which tends to 0 as
![]() $p\to\infty$
. So by continuity of f,
$p\to\infty$
. So by continuity of f,
![]() $ f(x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \} )$
tends to
$ f(x^{(p)} \cup \{ x_{\sigma_p(i)}^{(p)}+ v(x_{\sigma_p(i)}^{(p)} ,x^{(p)})\xi \} )$
tends to
![]() $f(x \cup \{x_i + v(x_i,x)\xi)$
. We conclude by the dominated convergence theorem, since f is bounded and
$f(x \cup \{x_i + v(x_i,x)\xi)$
. We conclude by the dominated convergence theorem, since f is bounded and
![]() $\varphi$
is a density, that
$\varphi$
is a density, that
![]() $K_\beta f(x^{(p)})$
converges to
$K_\beta f(x^{(p)})$
converges to
![]() $ K_\beta f(x)$
as
$ K_\beta f(x)$
as
![]() $p\to\infty$
, which proves that
$p\to\infty$
, which proves that
![]() $K_\beta C_b (E) \subset C_b(E)$
.
$K_\beta C_b (E) \subset C_b(E)$
.
Let us now prove that
![]() $K_\beta C_0(E) \subset C_0(E).$
Let
$K_\beta C_0(E) \subset C_0(E).$
Let
![]() $f \in C_0(E)$
and
$f \in C_0(E)$
and
![]() $\varepsilon >0$
. We fix a compact set
$\varepsilon >0$
. We fix a compact set
![]() $A \subset E$
such that
$A \subset E$
such that
![]() $x \notin A \Rightarrow | f(x) | < \varepsilon$
. By Proposition 5,
$x \notin A \Rightarrow | f(x) | < \varepsilon$
. By Proposition 5,
![]() $A \subset \bigcup_{n=0}^{n_0} E_n$
for some
$A \subset \bigcup_{n=0}^{n_0} E_n$
for some
![]() $n_0$
. Letting
$n_0$
. Letting
![]() $A_n=A \cap E_n$
, for
$A_n=A \cap E_n$
, for
![]() $n=0,\dots,n_0,$
we observe that
$n=0,\dots,n_0,$
we observe that
![]() $A_n$
is a compact set because
$A_n$
is a compact set because
![]() $E_n$
is closed. By Proposition 5, there exists
$E_n$
is closed. By Proposition 5, there exists
![]() $R_n \geq 0$
such that for every
$R_n \geq 0$
such that for every
![]() $a=\{a_1,\dots,a_n\} \in A_n,$
$a=\{a_1,\dots,a_n\} \in A_n,$
![]() $\max_{1 \leq k \leq n} \|a_k\| \leq R_n$
. Now let
$\max_{1 \leq k \leq n} \|a_k\| \leq R_n$
. Now let
![]() $B_{n}= \{ x \in E_{n}, \sum_{k=1}^{n} \|x_k\|/n \leq R_n \}$
and
$B_{n}= \{ x \in E_{n}, \sum_{k=1}^{n} \|x_k\|/n \leq R_n \}$
and
![]() $B = \bigcup_{n=0}^{n_0-1} B_{n}$
. We can verify (see the proof of Proposition 5) that
$B = \bigcup_{n=0}^{n_0-1} B_{n}$
. We can verify (see the proof of Proposition 5) that
![]() $B_n$
is compact and so is B. We claim that if
$B_n$
is compact and so is B. We claim that if
![]() $x\notin B$
, then
$x\notin B$
, then
![]() $K_\beta(x,A)=0$
. Indeed, if
$K_\beta(x,A)=0$
. Indeed, if
![]() $K_\beta (x,A)>0$
, then
$K_\beta (x,A)>0$
, then
![]() $K_\beta (x,A_n) >0$
for some
$K_\beta (x,A_n) >0$
for some
![]() $n\in\{0,\dots,n_0\}$
, but since
$n\in\{0,\dots,n_0\}$
, but since
![]() $ K_\beta(x,A_0) \leq K_\beta(x, \{ \text{\O} \})=0$
, it cannot be
$ K_\beta(x,A_0) \leq K_\beta(x, \{ \text{\O} \})=0$
, it cannot be
![]() $n=0$
. Now, for
$n=0$
. Now, for
![]() $n=1,\dots,n_0$
,
$n=1,\dots,n_0$
,
![]() $K_\beta (x,A_n) >0$
implies that
$K_\beta (x,A_n) >0$
implies that
![]() $x \in E_{n-1}$
and
$x \in E_{n-1}$
and
![]() $A_n \subset \{ z \cup x, \, z \in W \}$
since
$A_n \subset \{ z \cup x, \, z \in W \}$
since
![]() $K_\beta ( x, W \cup x)= 1$
. So
$K_\beta ( x, W \cup x)= 1$
. So
![]() $\max_{1 \leq k \leq n-1} \|x_k\| \leq R_n$
, whereby
$\max_{1 \leq k \leq n-1} \|x_k\| \leq R_n$
, whereby
![]() $x\in B_{n-1}$
. This shows that if
$x\in B_{n-1}$
. This shows that if
![]() $K_\beta (x,A)>0$
then
$K_\beta (x,A)>0$
then
![]() $x\in B$
, as we claimed. We deduce that for any
$x\in B$
, as we claimed. We deduce that for any
![]() $x\notin B$
,
$x\notin B$
,
![]() $|K_\beta f(x)|\leq \epsilon$
as in (3.2).
$|K_\beta f(x)|\leq \epsilon$
as in (3.2).
Example 3
(continued) (birth kernel based on a Gibbs potential): This birth kernel
![]() $K_\beta$
is both Feller continuous and Feller, whenever the potential V is continuous and locally stable. By the latter, we mean that there exists
$K_\beta$
is both Feller continuous and Feller, whenever the potential V is continuous and locally stable. By the latter, we mean that there exists
![]() $\psi\in L^1(W)$
such that for any
$\psi\in L^1(W)$
such that for any
![]() $x\in E$
,
$x\in E$
,
![]() $\exp\!(\!-\!(V(x \cup \xi)-V(x)))\leq \psi(\xi)$
; see for instance [Reference Møller and Waagepetersen19]. Under these conditions, we can prove similarly as in Example 2 that
$\exp\!(\!-\!(V(x \cup \xi)-V(x)))\leq \psi(\xi)$
; see for instance [Reference Møller and Waagepetersen19]. Under these conditions, we can prove similarly as in Example 2 that
![]() $K_\beta C_b(E) \subset C_b(E)$
by use of the dominated convergence theorem and that
$K_\beta C_b(E) \subset C_b(E)$
by use of the dominated convergence theorem and that
![]() $K_\beta C_0(E) \subset C_0(E)$
. Note that the examples of potentials considered in Section 5, leading to an invariant Gibbs measure, are continuous and locally stable.
$K_\beta C_0(E) \subset C_0(E)$
. Note that the examples of potentials considered in Section 5, leading to an invariant Gibbs measure, are continuous and locally stable.
Example 4
(continued) (Langevin diffusions as inter-jump motions): The inter-jump process
![]() $(Y_t)_{t \geq 0}$
, defined through the SDE (2.11), is a Feller continuous and Feller process on E. This is due to the fact that, g being globally Lipschitz, the function
$(Y_t)_{t \geq 0}$
, defined through the SDE (2.11), is a Feller continuous and Feller process on E. This is due to the fact that, g being globally Lipschitz, the function
![]() $\Phi_n$
in (2.11) is also globally Lipschitz for any
$\Phi_n$
in (2.11) is also globally Lipschitz for any
![]() $n\geq 1$
, and so the solution
$n\geq 1$
, and so the solution
![]() $(Z^{\, |n}_t)_{t \geq 0}$
of (2.11) is Feller continuous and Feller (see [Reference Schilling and Partzsch25]). The conclusion then follows from Proposition 6.
$(Z^{\, |n}_t)_{t \geq 0}$
of (2.11) is Feller continuous and Feller (see [Reference Schilling and Partzsch25]). The conclusion then follows from Proposition 6.
Example 5
(continued) (growth interaction processes): In this example, the inter-jump motion is driven by (2.12). If the functions
![]() $F_{1,n}, \dots, F_{n,n}$
are Lipschitz continuous, then
$F_{1,n}, \dots, F_{n,n}$
are Lipschitz continuous, then
![]() $(Y_t)_{t \geq 0}$
is Feller continuous and Feller. Indeed, the solution of (2.12) is continuous in the initial condition
$(Y_t)_{t \geq 0}$
is Feller continuous and Feller. Indeed, the solution of (2.12) is continuous in the initial condition
![]() $Z_0^{|n}$
under this assumption (see [Reference Markley16]), implying the Feller continuity of
$Z_0^{|n}$
under this assumption (see [Reference Markley16]), implying the Feller continuity of
![]() $(Y_t)_{t \geq 0}$
by Proposition 6. Moreover, since the marks
$(Y_t)_{t \geq 0}$
by Proposition 6. Moreover, since the marks
![]() $m_i(t)$
in
$m_i(t)$
in
![]() $(Z_t^{|n})_{t \geq 0}$
are all increasing functions, we have that
$(Z_t^{|n})_{t \geq 0}$
are all increasing functions, we have that
![]() $\|Z_t^{|n}\|\geq \|Z_0^{|n}\|$
. Let
$\|Z_t^{|n}\|\geq \|Z_0^{|n}\|$
. Let
![]() $f\in C_0(W^n)$
,
$f\in C_0(W^n)$
,
![]() $\epsilon>0$
, and
$\epsilon>0$
, and
![]() $R>0$
be such that
$R>0$
be such that
![]() $\|x\|>R\Rightarrow |f(x)|<\epsilon$
. Then, if
$\|x\|>R\Rightarrow |f(x)|<\epsilon$
. Then, if
![]() $\|Z_0^{|n}\|>R$
, we have
$\|Z_0^{|n}\|>R$
, we have
![]() $\|Z_t^{|n}\|\geq R$
and so
$\|Z_t^{|n}\|\geq R$
and so
![]() $f(Z_t^{|n})<\epsilon$
, proving that
$f(Z_t^{|n})<\epsilon$
, proving that
![]() $Z_t^{|n}$
is Feller and so is
$Z_t^{|n}$
is Feller and so is
![]() $(Y_t)_{t \geq 0}$
by Proposition 6.
$(Y_t)_{t \geq 0}$
by Proposition 6.
4. Ergodic properties of birth–death–move processes
In this section we focus on birth–death–move processes as described in Section 2.2. Accordingly, the state space is
![]() $E=\bigcup_{n =0}^{\infty} E_n$
where
$E=\bigcup_{n =0}^{\infty} E_n$
where
![]() $(E_n)_{n \geq 1}$
is a sequence of disjoint locally compact Polish spaces with
$(E_n)_{n \geq 1}$
is a sequence of disjoint locally compact Polish spaces with
![]() $E_0=\{ \text{\O} \}$
, and the jump kernel K reads as in (2.4). Remember that in this setting the jump intensity function is
$E_0=\{ \text{\O} \}$
, and the jump kernel K reads as in (2.4). Remember that in this setting the jump intensity function is
![]() $\alpha=\beta+\delta$
, where
$\alpha=\beta+\delta$
, where
![]() $\beta$
and
$\beta$
and
![]() $\delta$
are the birth and death intensity functions. We introduce the following notation:
$\delta$
are the birth and death intensity functions. We introduce the following notation:
Inspired by [Reference Preston22], we construct in Section 4.1 a coupling between
![]() $(X_t)_{t \geq 0}$
and a simple birth–death process
$(X_t)_{t \geq 0}$
and a simple birth–death process
![]() $(\eta_t)_{t \geq 0}$
on
$(\eta_t)_{t \geq 0}$
on
![]() $\mathbb{N}$
with birth rates
$\mathbb{N}$
with birth rates
![]() $\beta_n $
and death rates
$\beta_n $
and death rates
![]() $\delta_n$
. This coupling allows us to state conditions on the sequences
$\delta_n$
. This coupling allows us to state conditions on the sequences
![]() $(\beta_n)$
and
$(\beta_n)$
and
![]() $(\delta_n)$
ensuring the convergence of the birth–death–move process towards a unique invariant probability measure. This is presented in Section 4.2. A geometric rate of convergence is then derived in Section 4.3, and we characterize some invariant measures in Section 4.4.
$(\delta_n)$
ensuring the convergence of the birth–death–move process towards a unique invariant probability measure. This is presented in Section 4.2. A geometric rate of convergence is then derived in Section 4.3, and we characterize some invariant measures in Section 4.4.
4.1. Coupling of birth–death–move processes
Let
![]() $(X_t)_{t \geq 0}$
be a birth–death–move process, as defined in Section 2.2, and let
$(X_t)_{t \geq 0}$
be a birth–death–move process, as defined in Section 2.2, and let
![]() $(\eta_t)_{t \geq 0}$
be a simple birth–death process on
$(\eta_t)_{t \geq 0}$
be a simple birth–death process on
![]() $\mathbb{N}$
with birth rate
$\mathbb{N}$
with birth rate
![]() $\beta_n$
and death rate
$\beta_n$
and death rate
![]() $\delta_n$
given by (4.1). Note that
$\delta_n$
given by (4.1). Note that
![]() $(\eta_t)_{t \geq 0}$
can be viewed as a birth–death–move process on
$(\eta_t)_{t \geq 0}$
can be viewed as a birth–death–move process on
![]() $\mathbb{N}$
having a constant move process
$\mathbb{N}$
having a constant move process
![]() $y_t =y_0$
, for all
$y_t =y_0$
, for all
![]() $t \geq 0$
. We denote by
$t \geq 0$
. We denote by
![]() $(t_j)_{j \geq 1}$
the jump times of
$(t_j)_{j \geq 1}$
the jump times of
![]() $(\eta_t)_{t \geq 0}$
and by
$(\eta_t)_{t \geq 0}$
and by
![]() $n_t \;:\!=\; \sum_{j \geq 1} {\mathbf 1}_{t_j \leq t}$
the number of jumps before
$n_t \;:\!=\; \sum_{j \geq 1} {\mathbf 1}_{t_j \leq t}$
the number of jumps before
![]() $t \geq 0$
. We also denote by
$t \geq 0$
. We also denote by
![]() $q_t$
the transition kernel of
$q_t$
the transition kernel of
![]() $(\eta_t)_{t \geq 0}$
, i.e.
$(\eta_t)_{t \geq 0}$
, i.e.
![]() $q_t(n,S)=\mathbb{P}(\eta_t\in S|\eta_0=n)$
for any
$q_t(n,S)=\mathbb{P}(\eta_t\in S|\eta_0=n)$
for any
![]() $n\in \mathbb{N}$
and
$n\in \mathbb{N}$
and
![]() $S\in \mathcal{P}(\mathbb{N})$
.
$S\in \mathcal{P}(\mathbb{N})$
.
We define the coupled process
![]() $\check{C}=(X',\eta')$
as a jump–move process on the state space
$\check{C}=(X',\eta')$
as a jump–move process on the state space
![]() $\check{E} = E \times \mathbb{N}$
equipped with the
$\check{E} = E \times \mathbb{N}$
equipped with the
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\check{\mathcal{E}} = \mathcal{E} \otimes \mathcal{P} (\mathbb{N})$
. Denoting by d the distance on E, we also equip
$\check{\mathcal{E}} = \mathcal{E} \otimes \mathcal{P} (\mathbb{N})$
. Denoting by d the distance on E, we also equip
![]() $\check{E}$
with the distance
$\check{E}$
with the distance
![]() $\check{d}((x,k);\;(y,n))\;:\!=\;d(x,y)+ |n-k|/(n\wedge k){\mathbf 1}_{nk \neq 0}$
. To fully characterize
$\check{d}((x,k);\;(y,n))\;:\!=\;d(x,y)+ |n-k|/(n\wedge k){\mathbf 1}_{nk \neq 0}$
. To fully characterize
![]() $\check{C}$
, we now specify its jump intensity function
$\check{C}$
, we now specify its jump intensity function
![]() $ \check{\alpha}$
, its jump kernel
$ \check{\alpha}$
, its jump kernel
![]() $\check{K}$
, and its inter-jump move process
$\check{K}$
, and its inter-jump move process
![]() $\check{Y}$
.
$\check{Y}$
.
The intensity function
![]() $\check{\alpha} \;:\; E \times \mathbb{N} \rightarrow \mathbb{R}_+$
is given by
$\check{\alpha} \;:\; E \times \mathbb{N} \rightarrow \mathbb{R}_+$
is given by
One can easily check that
![]() $\check{\alpha} $
is a continuous function on
$\check{\alpha} $
is a continuous function on
![]() $\check{E}$
, bounded by
$\check{E}$
, bounded by
![]() $2\alpha^*$
.
$2\alpha^*$
.
The transition kernel
![]() $\check{K} \;:\; \check{E} \times \check{\mathcal{E}} \rightarrow [0,1]$
takes the same specific form as in [Reference Preston22]:
$\check{K} \;:\; \check{E} \times \check{\mathcal{E}} \rightarrow [0,1]$
takes the same specific form as in [Reference Preston22]:
-
(i) If
 $x \in E_m, \, m \neq n$
:
$x \in E_m, \, m \neq n$
:  \[ \check{K}((x,n);\; A \times\{n\}) = \dfrac{\alpha (x)}{ \check{\alpha} (x,n)} K(x,A); \]
\[ \check{K}((x,n);\; A \times\{n\}) = \dfrac{\alpha (x)}{ \check{\alpha} (x,n)} K(x,A); \]
 \[ \check{K}((x,n);\; \{x\}\times\{n+1\}) = \dfrac{\beta_n}{ \check{\alpha} (x,n)} ;\]
\[ \check{K}((x,n);\; \{x\}\times\{n+1\}) = \dfrac{\beta_n}{ \check{\alpha} (x,n)} ;\]
 \[ \check{K}((x,n);\; \{x\}\times\{n-1\}) = \dfrac{\delta_n}{ \check{\alpha} (x,n)}. \]
\[ \check{K}((x,n);\; \{x\}\times\{n-1\}) = \dfrac{\delta_n}{ \check{\alpha} (x,n)}. \]
-
(ii) If
 $x \in E_n$
:
$x \in E_n$
:  \[ \check{K}((x,n);\; A\times\{n+1\}) = \dfrac{\beta (x)}{\check{\alpha} (x,n)} K_\beta(x,A) ;\]
\[ \check{K}((x,n);\; A\times\{n+1\}) = \dfrac{\beta (x)}{\check{\alpha} (x,n)} K_\beta(x,A) ;\]
 \[ \check{K}((x,n);\; \{x\}\times\{n+1\}) = \dfrac{\beta_n-\beta(x)}{\check{\alpha} (x,n)}; \]
\[ \check{K}((x,n);\; \{x\}\times\{n+1\}) = \dfrac{\beta_n-\beta(x)}{\check{\alpha} (x,n)}; \]
 \[ \check{K}((x,n);\; A\times\{n-1\}) = \dfrac{\delta_n}{\check{\alpha} (x,n)}K_\delta(x,A); \]
\[ \check{K}((x,n);\; A\times\{n-1\}) = \dfrac{\delta_n}{\check{\alpha} (x,n)}K_\delta(x,A); \]
 \[ \check{K}((x,n);\; A\times\{n\}) = \dfrac{\delta(x)-\delta_n}{\check{\alpha} (x,n)}K_\delta(x,A) . \]
\[ \check{K}((x,n);\; A\times\{n\}) = \dfrac{\delta(x)-\delta_n}{\check{\alpha} (x,n)}K_\delta(x,A) . \]
The inter-jump move process
![]() $\check{Y}$
is finally obtained by an independent coupling of
$\check{Y}$
is finally obtained by an independent coupling of
![]() $(Y_t)_{ t \geq 0}$
and
$(Y_t)_{ t \geq 0}$
and
![]() $(y_t)_{t \geq 0}$
; specifically, its transition kernel
$(y_t)_{t \geq 0}$
; specifically, its transition kernel
![]() $Q_t^{\check{Y}}$
is given, for any
$Q_t^{\check{Y}}$
is given, for any
![]() $(x,p)\in\check{E}$
and
$(x,p)\in\check{E}$
and
![]() $A\times S\in \check{\mathcal{E}}$
, by
$A\times S\in \check{\mathcal{E}}$
, by
 \begin{multline} Q_t^{\check{Y}}((x,p);\; A \times S)= \mathbb{P}( \check{Y}_t \in A \times S | \check{Y}_0=(x,p))\\ =\mathbb{P}(Y_t \in A | Y_0=x) {\mathbf 1}_{p\in S} = Q_t^{Y}(x,A) {\mathbf 1}_{p\in S}.\end{multline}
\begin{multline} Q_t^{\check{Y}}((x,p);\; A \times S)= \mathbb{P}( \check{Y}_t \in A \times S | \check{Y}_0=(x,p))\\ =\mathbb{P}(Y_t \in A | Y_0=x) {\mathbf 1}_{p\in S} = Q_t^{Y}(x,A) {\mathbf 1}_{p\in S}.\end{multline}
This means that
![]() $\check{Y}_t = (Y'_{\!\!t},y'_{\!\!t})=(Y'_{\!\!t},y'_{\!\!0})$
for any
$\check{Y}_t = (Y'_{\!\!t},y'_{\!\!t})=(Y'_{\!\!t},y'_{\!\!0})$
for any
![]() $t\geq 0$
, where
$t\geq 0$
, where
![]() $(Y'_{\!\!t})_{t\geq 0}$
and
$(Y'_{\!\!t})_{t\geq 0}$
and
![]() $(y'_{\!\!t})_{t\geq 0}$
are independent and follow the same distribution as
$(y'_{\!\!t})_{t\geq 0}$
are independent and follow the same distribution as
![]() $(Y_t)_{t\geq 0}$
and
$(Y_t)_{t\geq 0}$
and
![]() $(y_t)_{t\geq 0}$
, respectively. Since Y is a continuous Markov process for the distance d, we can choose a version of Y
′ such that
$(y_t)_{t\geq 0}$
, respectively. Since Y is a continuous Markov process for the distance d, we can choose a version of Y
′ such that
![]() $\check{Y}$
is also continuous for
$\check{Y}$
is also continuous for
![]() $\check{d}$
. Observe moreover that
$\check{d}$
. Observe moreover that
![]() $(\check{Y}_t)_{t \geq 0}$
satisfies
$(\check{Y}_t)_{t \geq 0}$
satisfies
Given
![]() $ \check{\alpha}$
,
$ \check{\alpha}$
,
![]() $\check{K}$
, and
$\check{K}$
, and
![]() $\check{Y}$
as above, the jump–move process
$\check{Y}$
as above, the jump–move process
![]() $\check{C}$
is well defined and can be constructed as in Section 2.1. We denote by
$\check{C}$
is well defined and can be constructed as in Section 2.1. We denote by
![]() $\check{Q}_t$
its transition kernel, by
$\check{Q}_t$
its transition kernel, by
![]() $(\check{T}_j)_{j \geq 1}$
its jump times, and by
$(\check{T}_j)_{j \geq 1}$
its jump times, and by
![]() $\check{N}_t \;:\!=\; \sum_{j \geq 1} {\mathbf 1}_{ \check{T}_j \leq t }$
the number of jumps before
$\check{N}_t \;:\!=\; \sum_{j \geq 1} {\mathbf 1}_{ \check{T}_j \leq t }$
the number of jumps before
![]() $t \geq 0$
. We also set
$t \geq 0$
. We also set
![]() $ \check{\tau}_{j}=\check{T}_j - \check{T}_{j-1}$
. The fact that
$ \check{\tau}_{j}=\check{T}_j - \check{T}_{j-1}$
. The fact that
![]() $\check{C}$
defines a genuine coupling of X with
$\check{C}$
defines a genuine coupling of X with
![]() $\eta$
is the object of the following theorem.
$\eta$
is the object of the following theorem.
Theorem 4. Let
![]() $(X_t)_{t \geq 0}$
be a birth–death–move process on E with transition kernel
$(X_t)_{t \geq 0}$
be a birth–death–move process on E with transition kernel
![]() $Q_t$
, associated to the continuous Markov process Y on E and with jump kernel K, as defined in Section 2.2. Let
$Q_t$
, associated to the continuous Markov process Y on E and with jump kernel K, as defined in Section 2.2. Let
![]() $(\eta_t)_{t \geq 0}$
be a simple birth–death process on
$(\eta_t)_{t \geq 0}$
be a simple birth–death process on
![]() $\mathbb{N}$
with transition kernel
$\mathbb{N}$
with transition kernel
![]() $q_t$
, having a birth rate sequence
$q_t$
, having a birth rate sequence
![]() $(\beta_n)$
and a death rate sequence
$(\beta_n)$
and a death rate sequence
![]() $(\delta_n)$
given by (4.1). Suppose that
$(\delta_n)$
given by (4.1). Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Then the transition kernel
$K C_0(E) \subset C_0(E)$
. Then the transition kernel
![]() $\check{Q}_t$
of the jump–move process
$\check{Q}_t$
of the jump–move process
![]() $\check{C}$
on
$\check{C}$
on
![]() $E\times \mathbb{N}$
constructed above satisfies the following, for any
$E\times \mathbb{N}$
constructed above satisfies the following, for any
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $(x,n) \in E \times \mathbb{N}$
,
$(x,n) \in E \times \mathbb{N}$
,
![]() $A \in \mathcal{E}$
, and
$A \in \mathcal{E}$
, and
![]() $S \in \mathcal{P}(\mathbb{N})$
:
$S \in \mathcal{P}(\mathbb{N})$
:
-
(i)
 $\check{Q}_t((x,n);\; E \times S)=q_t(n,S)$
, and
$\check{Q}_t((x,n);\; E \times S)=q_t(n,S)$
, and -
(ii)
 $\check{Q}_t((x,n);\; A \times \mathbb{N})=Q_t(x,A)$
.
$\check{Q}_t((x,n);\; A \times \mathbb{N})=Q_t(x,A)$
.
If the move
![]() $(Y_t)_{t \geq 0}$
is constant, which is the setting in [Reference Preston22], then the proof is easy under (2.1) by use of the derivative form of the Kolmogorov backward equation. In the general case of a birth–death–move process, this strategy no longer works, and the statement becomes more challenging to prove. We manage to prove it by exploiting the generator of
$(Y_t)_{t \geq 0}$
is constant, which is the setting in [Reference Preston22], then the proof is easy under (2.1) by use of the derivative form of the Kolmogorov backward equation. In the general case of a birth–death–move process, this strategy no longer works, and the statement becomes more challenging to prove. We manage to prove it by exploiting the generator of
![]() $(X_t)_{t \geq 0}$
; see Theorem 3, which explains the Feller conditions in Theorem 4.
$(X_t)_{t \geq 0}$
; see Theorem 3, which explains the Feller conditions in Theorem 4.
Proof of Theorem 4. To prove the first part of the theorem, we use the following lemmas and corollary, proved in the appendix. Fix
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $p \geq 0$
, and let
$p \geq 0$
, and let
Lemma 1.
For any
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $p \geq 0$
,
$p \geq 0$
,
![]() $\psi_p$
is a continuous function.
$\psi_p$
is a continuous function.
Lemma 2. For any
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $p \geq 0$
,
$p \geq 0$
,
![]() $\psi_p$
is right-differentiable and satisfies
$\psi_p$
is right-differentiable and satisfies
Corollary 1.
For any
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $p \geq 0$
,
$p \geq 0$
,
in particular,
![]() $\psi_p$
is differentiable.
$\psi_p$
is differentiable.
Now let
![]() $ w_s(x,n) = \check{Q}_{t-s} ( {\mathbf 1}_E \times q_s({\mathbf 1}_{\{p\}}))(x,n)$
for
$ w_s(x,n) = \check{Q}_{t-s} ( {\mathbf 1}_E \times q_s({\mathbf 1}_{\{p\}}))(x,n)$
for
![]() $s \in [0,t].$
Then, using Corollary 1, we have the following lemma.
$s \in [0,t].$
Then, using Corollary 1, we have the following lemma.
Lemma 3.
For any
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $p \geq 0$
,
$p \geq 0$
,
![]() $s\mapsto w_s$
is differentiable on [0, t] and
$s\mapsto w_s$
is differentiable on [0, t] and
![]() $\partial w_s/\partial s \equiv0$
.
$\partial w_s/\partial s \equiv0$
.
Since
![]() $ w_0(x,n) = \check{Q}_t((x,n);\; E \times \{ p \})$
and
$ w_0(x,n) = \check{Q}_t((x,n);\; E \times \{ p \})$
and
![]() $w_t(x,n) = q_t(n, \{ p \})$
, Lemma 3 implies that these two quantities are equal. The first part of Theorem 4 then follows from the decomposition
$w_t(x,n) = q_t(n, \{ p \})$
, Lemma 3 implies that these two quantities are equal. The first part of Theorem 4 then follows from the decomposition
We turn to the proof of the second part of Theorem 4. Like the first part, it is based on three results that are proved in the appendix. For
![]() $(x,n) \in E \times \mathbb{N}$
and
$(x,n) \in E \times \mathbb{N}$
and
![]() $f \in C_0(E)$
, we set
$f \in C_0(E)$
, we set
Lemma 4.
Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process. Then for any
$(Y_t)_{t \geq 0}$
is a Feller process. Then for any
![]() $(x,n) \in E \times \mathbb{N}$
and any
$(x,n) \in E \times \mathbb{N}$
and any
![]() $f \in C_0(E)$
,
$f \in C_0(E)$
,
![]() $\psi_f$
is a continuous function.
$\psi_f$
is a continuous function.
Lemma 5.
Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Then for any
$K C_0(E) \subset C_0(E)$
. Then for any
![]() $(x,n) \in E \times \mathbb{N}$
and any
$(x,n) \in E \times \mathbb{N}$
and any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
, the function
$f \in \mathcal{D}_{\mathcal{A}^Y}$
, the function
![]() $\psi_f$
is right-differentiable and satisfies
$\psi_f$
is right-differentiable and satisfies
where
![]() $\mathcal{A}$
is the infinitesimal generator of X given by Theorem 3.
$\mathcal{A}$
is the infinitesimal generator of X given by Theorem 3.
Corollary 2.
Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Then for any
$K C_0(E) \subset C_0(E)$
. Then for any
![]() $(x,n) \in E \times \mathbb{N}$
and any
$(x,n) \in E \times \mathbb{N}$
and any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
,
$f \in \mathcal{D}_{\mathcal{A}^Y}$
,
in particular, the function
![]() $\psi_f$
is differentiable with derivative corresponding to (4.3).
$\psi_f$
is differentiable with derivative corresponding to (4.3).
By the Dynkin theorem, the second part of Theorem 4 is implied by the equality
![]() $\check{Q}_t((x,n);\; U \times \mathbb{N}) = Q_t(x,U)$
for any open set
$\check{Q}_t((x,n);\; U \times \mathbb{N}) = Q_t(x,U)$
for any open set
![]() $U\subset E$
, or equivalently
$U\subset E$
, or equivalently
for
![]() $g={\mathbf 1}_U$
. We prove (4.5) first for
$g={\mathbf 1}_U$
. We prove (4.5) first for
![]() $g\in \mathcal{D}_{\mathcal{A}^Y}$
and then for
$g\in \mathcal{D}_{\mathcal{A}^Y}$
and then for
![]() $g \in C_0(E)$
, before getting the result for
$g \in C_0(E)$
, before getting the result for
![]() $g={\mathbf 1}_U$
.
$g={\mathbf 1}_U$
.
Let
![]() $g\in \mathcal{D}_{\mathcal{A}^Y}$
, and for
$g\in \mathcal{D}_{\mathcal{A}^Y}$
, and for
![]() $s\in[0,t]$
define
$s\in[0,t]$
define
![]() $v_s(x,n)=\psi_{Q_s g}(t-s) = \check{Q}_{t-s} \left ( Q_s g \times {\mathbf 1}_\mathbb{N} \right )(x,n)$
. We shall prove that
$v_s(x,n)=\psi_{Q_s g}(t-s) = \check{Q}_{t-s} \left ( Q_s g \times {\mathbf 1}_\mathbb{N} \right )(x,n)$
. We shall prove that
![]() $s\mapsto v_s$
is differentiable with
$s\mapsto v_s$
is differentiable with
![]() $v'_{\!\!s}=0$
. For any
$v'_{\!\!s}=0$
. For any
![]() $h\in \mathbb{R}$
, write
$h\in \mathbb{R}$
, write
![]() $(v_{s+h}(x,n)-v_s(x,n))/h=A_1+A_2+A_3$
with
$(v_{s+h}(x,n)-v_s(x,n))/h=A_1+A_2+A_3$
with
 \begin{align*}A_1 &= \frac1 h\left(\psi_{Q_{s+h} g}(t-s-h) - \psi_{Q_s g}(t-s-h)\right) - \psi_{\mathcal{A} Q_s g}(t-s-h), \\A_2 &= \psi_{\mathcal{A} Q_s g}(t-s-h) - \psi_{\mathcal{A} Q_s g}(t-s), \\A_3 &= \frac 1 h \left(\psi_{Q_s g}(t-s-h) - \psi_{Q_s g}(t-s)\right)+ \psi_{\mathcal{A} Q_s g}(t-s).\end{align*}
\begin{align*}A_1 &= \frac1 h\left(\psi_{Q_{s+h} g}(t-s-h) - \psi_{Q_s g}(t-s-h)\right) - \psi_{\mathcal{A} Q_s g}(t-s-h), \\A_2 &= \psi_{\mathcal{A} Q_s g}(t-s-h) - \psi_{\mathcal{A} Q_s g}(t-s), \\A_3 &= \frac 1 h \left(\psi_{Q_s g}(t-s-h) - \psi_{Q_s g}(t-s)\right)+ \psi_{\mathcal{A} Q_s g}(t-s).\end{align*}
We know by Theorem 3, with
![]() $L_0^Y=C_0(E)$
, that
$L_0^Y=C_0(E)$
, that
![]() $\mathcal{D}_{\mathcal{A}} = \mathcal{D}_{\mathcal{A}^Y}$
, and since
$\mathcal{D}_{\mathcal{A}} = \mathcal{D}_{\mathcal{A}^Y}$
, and since
![]() $Q_s \mathcal{D}_{\mathcal{A}}\subset \mathcal{D}_{\mathcal{A}}$
(see [Reference Dynkin7, Chapter 1, Section 2]), we deduce from Corollary 2 that
$Q_s \mathcal{D}_{\mathcal{A}}\subset \mathcal{D}_{\mathcal{A}}$
(see [Reference Dynkin7, Chapter 1, Section 2]), we deduce from Corollary 2 that
![]() $A_3$
tends to
$A_3$
tends to
![]() $-\partial \psi_{Q_s g}(t-s)/\partial t + \psi_{\mathcal{A} Q_s g}(t-s)=0$
as
$-\partial \psi_{Q_s g}(t-s)/\partial t + \psi_{\mathcal{A} Q_s g}(t-s)=0$
as
![]() $h\to 0$
. Regarding
$h\to 0$
. Regarding
![]() $A_2$
, note that
$A_2$
, note that
![]() $Q_s g\in \mathcal{D}_{\mathcal{A}}$
implies that
$Q_s g\in \mathcal{D}_{\mathcal{A}}$
implies that
![]() $\mathcal{A} Q_s g\in C_0(E)$
(again see [Reference Dynkin7]), so that Lemma 4 applies and
$\mathcal{A} Q_s g\in C_0(E)$
(again see [Reference Dynkin7]), so that Lemma 4 applies and
![]() $A_2\to 0$
as
$A_2\to 0$
as
![]() $h\to 0$
. Regarding
$h\to 0$
. Regarding
![]() $A_1$
, using the linearity of
$A_1$
, using the linearity of
![]() $\psi_f(t)$
in f, we can write
$\psi_f(t)$
in f, we can write
which also tends to 0 as
![]() $h\to 0$
. We therefore obtain that
$h\to 0$
. We therefore obtain that
![]() $v'_{\!\!s}=0$
and so
$v'_{\!\!s}=0$
and so
![]() $v_t(x,n) = (Q_t g \times {\mathbf 1}_\mathbb{N}) (x,n) = \check{Q}_t(g \times {\mathbf 1}_\mathbb{N})(x,n) = v_0(x,n)$
, proving (4.5) when
$v_t(x,n) = (Q_t g \times {\mathbf 1}_\mathbb{N}) (x,n) = \check{Q}_t(g \times {\mathbf 1}_\mathbb{N})(x,n) = v_0(x,n)$
, proving (4.5) when
![]() $g\in \mathcal{D}_{\mathcal{A}^Y}$
.
$g\in \mathcal{D}_{\mathcal{A}^Y}$
.
Now let
![]() $g \in C_0(E).$
By our assumptions and Theorem 2,
$g \in C_0(E).$
By our assumptions and Theorem 2,
![]() $ (X_t)_{t \geq 0}$
is Feller, which implies that
$ (X_t)_{t \geq 0}$
is Feller, which implies that
![]() $C_0(E) = \overline{\mathcal{D}_\mathcal{A}}$
(see [Reference Dynkin7]). So there exists a sequence of functions
$C_0(E) = \overline{\mathcal{D}_\mathcal{A}}$
(see [Reference Dynkin7]). So there exists a sequence of functions
![]() $(g_m)_{m \geq 0}$
in
$(g_m)_{m \geq 0}$
in
![]() $\mathcal{D}_{\mathcal{A}^Y}$
such that
$\mathcal{D}_{\mathcal{A}^Y}$
such that
![]() $\|g_m-g\|_{\infty} \to 0$
as
$\|g_m-g\|_{\infty} \to 0$
as
![]() $m\to\infty$
. The two linear operators
$m\to\infty$
. The two linear operators
![]() $f \in M_b(E) \mapsto \check{Q}_t(f \times {\mathbf 1}_\mathbb{N})$
and
$f \in M_b(E) \mapsto \check{Q}_t(f \times {\mathbf 1}_\mathbb{N})$
and
![]() $f \in M_b(E) \mapsto Q_t(f)$
being bounded, we can take the limit in (4.5) when applied to
$f \in M_b(E) \mapsto Q_t(f)$
being bounded, we can take the limit in (4.5) when applied to
![]() $g_m$
to get the same relation for
$g_m$
to get the same relation for
![]() $g \in C_0(E).$
$g \in C_0(E).$
Finally take
![]() $U \subset E$
an open subset. Then, for any
$U \subset E$
an open subset. Then, for any
![]() $m \geq 0$
, define the function
$m \geq 0$
, define the function
where
![]() $U_m = \{ y \in E, \, d(y,E \backslash U) \geq 1/m \}$
. Then
$U_m = \{ y \in E, \, d(y,E \backslash U) \geq 1/m \}$
. Then
![]() $\phi_m \in C_0(E)$
for any
$\phi_m \in C_0(E)$
for any
![]() $m \geq 0$
, and for any
$m \geq 0$
, and for any
![]() $x \in E$
we have
$x \in E$
we have
![]() $ \phi_m(x) \to {\mathbf 1}_U(x)$
as
$ \phi_m(x) \to {\mathbf 1}_U(x)$
as
![]() $m\to\infty$
. Taking the limit, we obtain by the dominated convergence theorem the relation (4.5) for
$m\to\infty$
. Taking the limit, we obtain by the dominated convergence theorem the relation (4.5) for
![]() $g={\mathbf 1}_U$
, which concludes the proof of the second part of Theorem 4.
$g={\mathbf 1}_U$
, which concludes the proof of the second part of Theorem 4.
4.2. Convergence to an invariant measure
The main interest of the coupling constructed in the previous section is the following specific property.
Proposition 7.
Under the same setting as in Theorem 4, if
![]() $x \in E$
with
$x \in E$
with
![]() $n(x) \leq n$
, then
$n(x) \leq n$
, then
Proof. Let
![]() $x\in E$
and
$x\in E$
and
![]() $n\in\mathbb{N}$
be such that
$n\in\mathbb{N}$
be such that
![]() $n(x)\leq n$
. We show by induction on
$n(x)\leq n$
. We show by induction on
![]() $k \geq 0$
that
$k \geq 0$
that
![]() $\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_k} \in \Gamma , \check{T}_k <+\infty)=0.$
If
$\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_k} \in \Gamma , \check{T}_k <+\infty)=0.$
If
![]() $k=0$
, then
$k=0$
, then
![]() $\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_0} \in \Gamma , \check{T}_0 <+\infty )={\mathbf 1}_{(x,n) \in \Gamma } = 0.$
Suppose next that there exists
$\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_0} \in \Gamma , \check{T}_0 <+\infty )={\mathbf 1}_{(x,n) \in \Gamma } = 0.$
Suppose next that there exists
![]() $k \geq 0$
such that
$k \geq 0$
such that
![]() $\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_k} \in \Gamma , \check{T}_k <+\infty )=0$
. Then
$\mathbb{P}_{(x,n)}(\check{C}_{\check{T}_k} \in \Gamma , \check{T}_k <+\infty )=0$
. Then
 \begin{align*} & \mathbb{P}_{(x,n)}(\check{C}_{\check{T}_{k+1}} \in \Gamma , \check{T}_{k+1} <+\infty) \\ &= \mathbb{E}_{(x,n)} \left [ \mathbb{E}_{(x,n)} \left ( {\mathbf 1}_{ \check{C}_{\check{T}_{k+1}} \in \Gamma} \left | \check{C}_{\check{T}_k}, \left ( \check{Y}_t^{(k)} \right )_{t \geq 0} , \check{\tau}_{k+1} \right. \right ) {\mathbf 1}_{\check{T}_{k+1} <+\infty} \right ] \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{ \check{Y}^{(k)}_{\check{\tau}_{k+1}} \in \Gamma }{\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \; \; \; \text{(by definition of } \check{K} ) \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{ \check{C}_{\check{T}_k} \in \Gamma } {\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \; \; \; \text{(for any } t \geq 0, \; \check{C}_{\check{T}_k} \in \Gamma \Leftrightarrow \check{Y}_t^{(k)} \in \Gamma )\\ & \leq \mathbb{E}_{(x,n)} \left [ {\mathbf 1}_{ \check{C}_{\check{T}_k} \in \Gamma } {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] = \mathbb{P}_{(x,n)} \left [ \check{C}_{\check{T}_k} \in \Gamma, \check{T}_{k} <+\infty \right ] =0,\end{align*}
\begin{align*} & \mathbb{P}_{(x,n)}(\check{C}_{\check{T}_{k+1}} \in \Gamma , \check{T}_{k+1} <+\infty) \\ &= \mathbb{E}_{(x,n)} \left [ \mathbb{E}_{(x,n)} \left ( {\mathbf 1}_{ \check{C}_{\check{T}_{k+1}} \in \Gamma} \left | \check{C}_{\check{T}_k}, \left ( \check{Y}_t^{(k)} \right )_{t \geq 0} , \check{\tau}_{k+1} \right. \right ) {\mathbf 1}_{\check{T}_{k+1} <+\infty} \right ] \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{ \check{Y}^{(k)}_{\check{\tau}_{k+1}} \in \Gamma }{\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \; \; \; \text{(by definition of } \check{K} ) \\ & = \mathbb{E}_{(x,n)} \left [ \check{K} \left ( \check{Y}^{(k)}_{\check{\tau}_{k+1}}, \Gamma \right ) {\mathbf 1}_{ \check{C}_{\check{T}_k} \in \Gamma } {\mathbf 1}_{\check{\tau}_{k+1} <+\infty} {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] \; \; \; \text{(for any } t \geq 0, \; \check{C}_{\check{T}_k} \in \Gamma \Leftrightarrow \check{Y}_t^{(k)} \in \Gamma )\\ & \leq \mathbb{E}_{(x,n)} \left [ {\mathbf 1}_{ \check{C}_{\check{T}_k} \in \Gamma } {\mathbf 1}_{\check{T}_{k} <+\infty} \right ] = \mathbb{P}_{(x,n)} \left [ \check{C}_{\check{T}_k} \in \Gamma, \check{T}_{k} <+\infty \right ] =0,\end{align*}
which proves the induction step. To conclude, recall that
![]() $\mathbb{P}_{(x,n)}( \check{N}_t < \infty )=1$
, and notice that because of the form of
$\mathbb{P}_{(x,n)}( \check{N}_t < \infty )=1$
, and notice that because of the form of
![]() $\Gamma$
one has
$\Gamma$
one has
![]() $ \{ \check{C}_t \in \Gamma \} = \{ \check{C}_{\check{T}_{\check{N}_t} } \in \Gamma \} $
for any
$ \{ \check{C}_t \in \Gamma \} = \{ \check{C}_{\check{T}_{\check{N}_t} } \in \Gamma \} $
for any
![]() $t \geq 0$
. Then
$t \geq 0$
. Then
We deduce from Proposition 7 that for any
![]() $x \in E_m$
with
$x \in E_m$
with
![]() $m \leq n$
,
$m \leq n$
,
In association with Theorem 4, this means that the simple process
![]() $(\eta_t)_{t \geq 0}$
that is coupled with
$(\eta_t)_{t \geq 0}$
that is coupled with
![]() $(X_t)_{t\geq 0}$
converges more slowly to the state 0 than
$(X_t)_{t\geq 0}$
converges more slowly to the state 0 than
![]() $(X_t)_{t \geq 0}$
converges to the state Ø. We can thus build upon renewal theory (see [Reference Feller9]) to prove that Ø is an ergodic state for
$(X_t)_{t \geq 0}$
converges to the state Ø. We can thus build upon renewal theory (see [Reference Feller9]) to prove that Ø is an ergodic state for
![]() $(X_t)_{t \geq 0}$
whenever 0 is an ergodic state for
$(X_t)_{t \geq 0}$
whenever 0 is an ergodic state for
![]() $(\eta_t)_{t \geq 0}$
. Conditions ensuring the latter are either (4.6) or (4.7) below, as established in [Reference Karlin and McGregor13], so that we obtain the following, as verified in the supplementary material.
$(\eta_t)_{t \geq 0}$
. Conditions ensuring the latter are either (4.6) or (4.7) below, as established in [Reference Karlin and McGregor13], so that we obtain the following, as verified in the supplementary material.
Theorem 5. Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Suppose that
$K C_0(E) \subset C_0(E)$
. Suppose that
![]() $\delta_n>0$
for all
$\delta_n>0$
for all
![]() $n \geq 1 $
and one of the following condition holds:
$n \geq 1 $
and one of the following condition holds:
Then
![]() $\mu(A)\;:\!=\;\lim_{t \rightarrow \infty} Q_t(x,A)$
exists for all
$\mu(A)\;:\!=\;\lim_{t \rightarrow \infty} Q_t(x,A)$
exists for all
![]() $x \in E$
and
$x \in E$
and
![]() $A \in \mathcal{E}$
, and is independent of x. Moreover,
$A \in \mathcal{E}$
, and is independent of x. Moreover,
![]() $\mu$
is a probability measure on
$\mu$
is a probability measure on
![]() $(E,\mathcal{E})$
, and it is the unique invariant probability measure for the process, i.e. such that
$(E,\mathcal{E})$
, and it is the unique invariant probability measure for the process, i.e. such that
![]() $\mu(A) = \int_E Q_t(x,A) \, \mu(\text{d} x)$
for any
$\mu(A) = \int_E Q_t(x,A) \, \mu(\text{d} x)$
for any
![]() $A \in \mathcal{E}$
and
$A \in \mathcal{E}$
and
![]() $t \geq 0$
.
$t \geq 0$
.
4.3. Rate of convergence
Based on the coupling constructed in Section 4.1, and under the assumptions of Theorem 5, the rate of convergence of
![]() $Q_t$
towards the invariant measure
$Q_t$
towards the invariant measure
![]() $\mu$
follows from the rate of convergence of the simple birth–death process
$\mu$
follows from the rate of convergence of the simple birth–death process
![]() $\eta$
towards its invariant distribution. This is proven and exploited in [Reference Møller18] in the case of spatial birth–death processes (without move), based upon the coupling of [Reference Preston22]. Since Theorem 4 and Proposition 7 extend this coupling, we deduce in the following theorem the same rates of convergence as in [Reference Møller18]. The proof is the same, and we omit the details.
$\eta$
towards its invariant distribution. This is proven and exploited in [Reference Møller18] in the case of spatial birth–death processes (without move), based upon the coupling of [Reference Preston22]. Since Theorem 4 and Proposition 7 extend this coupling, we deduce in the following theorem the same rates of convergence as in [Reference Møller18]. The proof is the same, and we omit the details.
Theorem 6. Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Let
$K C_0(E) \subset C_0(E)$
. Let
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
be two probability measures on
$\gamma_2$
be two probability measures on
![]() $(E,\mathcal{E})$
, such that one of the two following conditions holds:
$(E,\mathcal{E})$
, such that one of the two following conditions holds:
 \begin{align}(i)& \text{ (4.6) holds true, and for }k=1,2,\ \gamma_k \left ( \bigcup_{n=0}^{n_0} E_n \right ) = 1; \end{align}
\begin{align}(i)& \text{ (4.6) holds true, and for }k=1,2,\ \gamma_k \left ( \bigcup_{n=0}^{n_0} E_n \right ) = 1; \end{align}
 \begin{align}(ii)& \text{ (4.7) holds true, and for }k=1,2,\ \sum_{n=2}^{\infty } \gamma_k ( E_n) \sqrt{\frac{\delta_1 \dots \delta_n}{\beta_1 \dots \beta_{n-1}}}< \infty. \end{align}
\begin{align}(ii)& \text{ (4.7) holds true, and for }k=1,2,\ \sum_{n=2}^{\infty } \gamma_k ( E_n) \sqrt{\frac{\delta_1 \dots \delta_n}{\beta_1 \dots \beta_{n-1}}}< \infty. \end{align}
Then there exist real constants
![]() $c >0$
and
$c >0$
and
![]() $0<r<1$
such that for any
$0<r<1$
such that for any
![]() $t \geq 0$
,
$t \geq 0$
,
Moreover, when the condition (4.8) holds, the constants c and r can be chosen independently of
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2.$
$\gamma_2.$
This result is presented in several particular cases in [Reference Møller18, Corollary 3.1] that are also valid in our setting. In particular, when
![]() $\gamma_1$
corresponds to the invariant measure
$\gamma_1$
corresponds to the invariant measure
![]() $\mu$
obtained in Theorem 5, and
$\mu$
obtained in Theorem 5, and
![]() $\gamma_2$
is a point measure, the assumptions (4.8) and (4.9) simplify and we get the following corollary.
$\gamma_2$
is a point measure, the assumptions (4.8) and (4.9) simplify and we get the following corollary.
Corollary 3.
Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Assume either (4.6) or (4.7), along with the following:
$K C_0(E) \subset C_0(E)$
. Assume either (4.6) or (4.7), along with the following:
 \begin{align} \sum_{n=2}^{\infty} \sqrt{\frac{\beta_1 \dots \beta_{n-1}}{\delta_1 \dots \delta_n}} < \infty \quad\textit{ and } \quad \exists N \geq 0 \; s.t. \; \forall \, n \geq N, \; \beta_n \leq \delta_{n+1}. \end{align}
\begin{align} \sum_{n=2}^{\infty} \sqrt{\frac{\beta_1 \dots \beta_{n-1}}{\delta_1 \dots \delta_n}} < \infty \quad\textit{ and } \quad \exists N \geq 0 \; s.t. \; \forall \, n \geq N, \; \beta_n \leq \delta_{n+1}. \end{align}
Denote by
![]() $\mu$
the invariant measure given by Theorem 5. Then for any
$\mu$
the invariant measure given by Theorem 5. Then for any
![]() $y \in E$
, there exist
$y \in E$
, there exist
![]() $c(y)>0$
and
$c(y)>0$
and
![]() $0<r<1$
(independent of y) such that
$0<r<1$
(independent of y) such that
Moreover, the function
![]() $c(.)$
satisfies
$c(.)$
satisfies
4.4. Characterization of some invariant measures
In general the invariant measure
![]() $\mu$
of a birth–death–move process
$\mu$
of a birth–death–move process
![]() $(X_t)_{t \geq 0}$
, provided it exists, can be a very complicated distribution that mixes the distribution in E due to births and deaths of points, including the probability of being in
$(X_t)_{t \geq 0}$
, provided it exists, can be a very complicated distribution that mixes the distribution in E due to births and deaths of points, including the probability of being in
![]() $E_n$
for each n, with the average distribution on each
$E_n$
for each n, with the average distribution on each
![]() $E_n$
due to the move process Y. In particular, note that according to Theorem 5, Y does not need to be a stationary process for
$E_n$
due to the move process Y. In particular, note that according to Theorem 5, Y does not need to be a stationary process for
![]() $(X_t)_{t \geq 0}$
to converge to an invariant measure. Heuristically, this is because the move process is always eventually ‘killed’ by a return to Ø of
$(X_t)_{t \geq 0}$
to converge to an invariant measure. Heuristically, this is because the move process is always eventually ‘killed’ by a return to Ø of
![]() $(X_t)_{t \geq 0}$
under the hypotheses of Theorem 5.
$(X_t)_{t \geq 0}$
under the hypotheses of Theorem 5.
The situation becomes more intelligible when Y admits an invariant measure that is compatible with the jumps of
![]() $(X_t)_{t \geq 0}$
, as formalized in the next proposition.
$(X_t)_{t \geq 0}$
, as formalized in the next proposition.
Proposition 8.
Suppose that
![]() $(Y_t)_{t \geq 0}$
is a Feller process and that
$(Y_t)_{t \geq 0}$
is a Feller process and that
![]() $K C_0(E) \subset C_0(E)$
. Assume moreover that there exists a finite measure
$K C_0(E) \subset C_0(E)$
. Assume moreover that there exists a finite measure
![]() $\mu$
on E such that for any
$\mu$
on E such that for any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
,
$f \in \mathcal{D}_{\mathcal{A}^Y}$
,
Then for any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
,
$f \in \mathcal{D}_{\mathcal{A}^Y}$
,
![]() $\displaystyle \int_E \mathcal{A} f(x) \, \text{d} \mu(x) = 0$
.
$\displaystyle \int_E \mathcal{A} f(x) \, \text{d} \mu(x) = 0$
.
Proof. By Theorem 3, for any
![]() $f \in \mathcal{D}_{\mathcal{A}^Y}$
,
$f \in \mathcal{D}_{\mathcal{A}^Y}$
,
 \begin{align*} \int_E \mathcal{A} f(x) \, \text{d} \mu(x) & = \int_E \left ( \alpha (x)K f(x)-\alpha(x)f(x) \right ) \, \text{d} \mu(x) + \int_E \mathcal{A}^Y f(x) \, \text{d} \mu(x) \\[5pt] & = \sum_{n \geq 0} \int_{E_n} \mathcal{A}^Y f(x) \, \text{d} \mu_{|E_n}(x) =0. \end{align*}
\begin{align*} \int_E \mathcal{A} f(x) \, \text{d} \mu(x) & = \int_E \left ( \alpha (x)K f(x)-\alpha(x)f(x) \right ) \, \text{d} \mu(x) + \int_E \mathcal{A}^Y f(x) \, \text{d} \mu(x) \\[5pt] & = \sum_{n \geq 0} \int_{E_n} \mathcal{A}^Y f(x) \, \text{d} \mu_{|E_n}(x) =0. \end{align*}
This proposition will be useful for characterizing the invariant measure of the birth–death–move processes considered in Section 5. Indeed, suppose that the hypotheses of Theorem 5 are satisfied. Then
![]() $(X_t)_{t \geq 0}$
converges to a unique invariant measure
$(X_t)_{t \geq 0}$
converges to a unique invariant measure
![]() $\nu$
. Suppose moreover that the pure jump Markov process with intensity
$\nu$
. Suppose moreover that the pure jump Markov process with intensity
![]() $\alpha$
and transition kernel K admits some invariant measure
$\alpha$
and transition kernel K admits some invariant measure
![]() $\mu$
, and that for any
$\mu$
, and that for any
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\mu_{|E_n}$
is also invariant for the move process
$\mu_{|E_n}$
is also invariant for the move process
![]() $Y^{|n}$
on
$Y^{|n}$
on
![]() $E_n$
. Then by Proposition 8 and the uniqueness of
$E_n$
. Then by Proposition 8 and the uniqueness of
![]() $\nu$
, we have that
$\nu$
, we have that
![]() $\nu=\mu$
.
$\nu=\mu$
.
5. Application to pairwise interaction processes on
 $\mathbb{R}^d$
$\mathbb{R}^d$
We present in this section examples of birth–death–move processes, defined through a pairwise potential function V on a compact set
![]() $W\subset \mathbb{R}^d$
, that converge to the Gibbs probability measure associated to V. The specificity is that we make compatible the jump dynamics with the inter-jump diffusion, so that Proposition 8 applies and allows us to characterize this Gibbs measure as the invariant measure.
$W\subset \mathbb{R}^d$
, that converge to the Gibbs probability measure associated to V. The specificity is that we make compatible the jump dynamics with the inter-jump diffusion, so that Proposition 8 applies and allows us to characterize this Gibbs measure as the invariant measure.
When there is no inter-jump motion, this type of convergence is proved in [Reference Preston22] and is a prerequisite for perfect simulation of spatial Gibbs point process models (see [Reference Møller and Waagepetersen19, Chapter 11]). However, the weakness of this approach is that for rigid interactions (as for instance induced by a Lennard-Jones or a Riesz potential; see the examples below), the dynamics based on spatial births and deaths may mix poorly, so that the convergence to the associated Gibbs measure may be very slow. Adding inter-jump motions that do not affect the stationary measure, as done in this section, may alleviate this issue.
Let
![]() $W\;:\!=\; I_1 \times \dots \times I_d$
where, for
$W\;:\!=\; I_1 \times \dots \times I_d$
where, for
![]() $i \in \{1,\dots,d\}$
,
$i \in \{1,\dots,d\}$
,
![]() $I_i$
is a compact interval of
$I_i$
is a compact interval of
![]() $\mathbb{R}$
. Define
$\mathbb{R}$
. Define
![]() $\tilde W_n = \{ (x_1,\dots,x_n) \in (\mathring{W})^n, \; i \neq j \Rightarrow x_i \neq x_j \}$
. As in Section 2.4, we let
$\tilde W_n = \{ (x_1,\dots,x_n) \in (\mathring{W})^n, \; i \neq j \Rightarrow x_i \neq x_j \}$
. As in Section 2.4, we let
![]() $E_0 = \{ \text{\O} \}$
,
$E_0 = \{ \text{\O} \}$
,
![]() $E_n=\pi_n( \tilde W_n)$
for
$E_n=\pi_n( \tilde W_n)$
for
![]() $n\geq 1$
, and
$n\geq 1$
, and
![]() $E=\bigcup_{n=0}^\infty E_n$
.
$E=\bigcup_{n=0}^\infty E_n$
.
We consider a pairwise potential function
![]() $V \;:\; E \to \mathbb{R} \cup \{\infty\}$
, in the sense that there exist
$V \;:\; E \to \mathbb{R} \cup \{\infty\}$
, in the sense that there exist
![]() $a>0$
and
$a>0$
and
![]() $\phi \;:\; \mathbb{R}^d\to\mathbb{R} \cup\{\infty\}$
satisfying
$\phi \;:\; \mathbb{R}^d\to\mathbb{R} \cup\{\infty\}$
satisfying
![]() $\phi(\xi)=\phi(-\xi)$
for all
$\phi(\xi)=\phi(-\xi)$
for all
![]() $\xi\in \mathbb{R}^d$
such that for any
$\xi\in \mathbb{R}^d$
such that for any
![]() $x=\{x_1,\dots,x_n\}\in E_n$
,
$x=\{x_1,\dots,x_n\}\in E_n$
,
when
![]() $n\geq 2$
, while
$n\geq 2$
, while
![]() $V(\{\text{\O} \})=0$
and
$V(\{\text{\O} \})=0$
and
![]() $V(\{\xi\})=a$
for
$V(\{\xi\})=a$
for
![]() $\xi\in W$
. Let
$\xi\in W$
. Let
![]() $\phi_0 \;:\; (0,\infty)\to \mathbb{R}_+$
be a decreasing function with
$\phi_0 \;:\; (0,\infty)\to \mathbb{R}_+$
be a decreasing function with
![]() $\phi_0(r)\to\infty$
as
$\phi_0(r)\to\infty$
as
![]() $r \to 0$
. We will assume the following conditions on
$r \to 0$
. We will assume the following conditions on
![]() $\phi$
:
$\phi$
:
-
(A) The potential is locally stable, i.e. there exists
 $\psi \;:\; W \rightarrow \mathbb{R}_+$
integrable such that
$\psi \;:\; W \rightarrow \mathbb{R}_+$
integrable such that  \begin{equation*} \forall \, n \geq 1, \; \forall \, x \in E_n, \; \forall \, \xi \in W, \; \; \exp\!\left ( - \sum_{i=1}^n \phi(x_i-\xi) \right ) \leq \psi(\xi). \end{equation*}
\begin{equation*} \forall \, n \geq 1, \; \forall \, x \in E_n, \; \forall \, \xi \in W, \; \; \exp\!\left ( - \sum_{i=1}^n \phi(x_i-\xi) \right ) \leq \psi(\xi). \end{equation*}
-
(B) Either
 $\phi$
is bounded, or there exists
$\phi$
is bounded, or there exists
 $r_1>0$
such that
$r_1>0$
such that
 $\phi(\xi)\geq \phi_0(\|\xi\|)$
for all
$\phi(\xi)\geq \phi_0(\|\xi\|)$
for all
 $\|\xi\|<r_1$
.
$\|\xi\|<r_1$
. -
(C) The function
 $\phi$
is weakly differentiable on
$\phi$
is weakly differentiable on
 $\mathbb{R}^d \backslash \{ 0 \}$
,
$\mathbb{R}^d \backslash \{ 0 \}$
,
 $\exp\!(\!-\!\phi)$
is weakly differentiable on
$\exp\!(\!-\!\phi)$
is weakly differentiable on
 $\mathbb{R}^d$
, and for any
$\mathbb{R}^d$
, and for any
 $p > d$
we have
$p > d$
we have
 $\text{e}^{-\phi} \nabla \phi \in L^p_{loc}.$
$\text{e}^{-\phi} \nabla \phi \in L^p_{loc}.$
Let us present some examples of pairwise potentials
![]() $\phi$
that satisfy these assumptions. These are standard instances used in spatial statistics and statistical mechanics.
$\phi$
that satisfy these assumptions. These are standard instances used in spatial statistics and statistical mechanics.
Example (repulsive Lennard-Jones potential): For
![]() $\xi\in\mathbb{R}^d$
,
$\xi\in\mathbb{R}^d$
,
![]() $\phi(\xi)=c\| \xi \|^{-12}$
with
$\phi(\xi)=c\| \xi \|^{-12}$
with
![]() $c>0$
. This potential satisfies the condition (A) with
$c>0$
. This potential satisfies the condition (A) with
![]() $\psi \equiv 1$
and the condition (B). It is moreover differentiable on
$\psi \equiv 1$
and the condition (B). It is moreover differentiable on
![]() $\mathbb{R}^d \backslash \{0 \}$
, and for any
$\mathbb{R}^d \backslash \{0 \}$
, and for any
![]() $\xi \in \mathbb{R}^d \backslash \{0 \}$
,
$\xi \in \mathbb{R}^d \backslash \{0 \}$
,
![]() $\nabla \phi(\xi)= - 12c \xi/\| \xi \|^{14}.$
We deduce that the function
$\nabla \phi(\xi)= - 12c \xi/\| \xi \|^{14}.$
We deduce that the function
![]() $ \text{e}^{-\phi}\nabla \phi$
can be extended to a continuous function on
$ \text{e}^{-\phi}\nabla \phi$
can be extended to a continuous function on
![]() $\mathbb{R}^d$
by setting
$\mathbb{R}^d$
by setting
![]() $( \text{e}^{-\phi}\nabla \phi)(0)=0$
. As a consequence, the condition (C) is satisfied.
$( \text{e}^{-\phi}\nabla \phi)(0)=0$
. As a consequence, the condition (C) is satisfied.
Example (Riesz potential): It is defined on
![]() $\mathbb{R}^d \backslash \{ 0 \}$
by
$\mathbb{R}^d \backslash \{ 0 \}$
by
![]() $\phi(\xi)=c\| \xi \|^{\alpha-d}$
for
$\phi(\xi)=c\| \xi \|^{\alpha-d}$
for
![]() $c>0$
and
$c>0$
and
![]() $0< \alpha < d$
. As in the previous example, we obtain that
$0< \alpha < d$
. As in the previous example, we obtain that
![]() $\phi$
satisfies the conditions (A), (B) and (C).
$\phi$
satisfies the conditions (A), (B) and (C).
Example (soft-core potential):
![]() $\phi(\xi)=- \ln \left ( 1-\exp\!(\!-\!c \|\xi \|^2) \right )$
for
$\phi(\xi)=- \ln \left ( 1-\exp\!(\!-\!c \|\xi \|^2) \right )$
for
![]() $c>0$
. Again this potential satisfies the condition (A) with
$c>0$
. Again this potential satisfies the condition (A) with
![]() $\psi \equiv 1$
and the condition (B). Moreover, for
$\psi \equiv 1$
and the condition (B). Moreover, for
![]() $\xi \in \mathbb{R}^d \backslash \{ 0 \}$
we compute
$\xi \in \mathbb{R}^d \backslash \{ 0 \}$
we compute
![]() $ \nabla \phi(\xi)= - (2 c \text{e}^{-c \|\xi \|^2})(1-\text{e}^{-c \|\xi \|^2}) \, \xi.$
As
$ \nabla \phi(\xi)= - (2 c \text{e}^{-c \|\xi \|^2})(1-\text{e}^{-c \|\xi \|^2}) \, \xi.$
As
![]() $\| \nabla \phi(\xi) \| \sim 1/(c \| \xi \|)$
as
$\| \nabla \phi(\xi) \| \sim 1/(c \| \xi \|)$
as
![]() $\| \xi \|\to 0$
, we also obtain that the function
$\| \xi \|\to 0$
, we also obtain that the function
![]() $ \text{e}^{-\phi}\nabla \phi$
can be extended to a continuous function on
$ \text{e}^{-\phi}\nabla \phi$
can be extended to a continuous function on
![]() $\mathbb{R}^d$
, and the condition (C) follows.
$\mathbb{R}^d$
, and the condition (C) follows.
Example (regularized Strauss potential): For
![]() $R>0$
and
$R>0$
and
![]() $\gamma\geq 0$
, the standard Strauss potential corresponds to
$\gamma\geq 0$
, the standard Strauss potential corresponds to
![]() $\phi(\xi)=\gamma {\mathbf 1}_{\|\xi\|<R}$
. We consider a regularized version by introducing a parameter
$\phi(\xi)=\gamma {\mathbf 1}_{\|\xi\|<R}$
. We consider a regularized version by introducing a parameter
![]() $0<\varepsilon<R$
, so that
$0<\varepsilon<R$
, so that
![]() $\phi(\xi)= \gamma$
if
$\phi(\xi)= \gamma$
if
![]() $ \| \xi \| \leq R - \varepsilon$
,
$ \| \xi \| \leq R - \varepsilon$
,
![]() $\phi(\xi)=0$
if
$\phi(\xi)=0$
if
![]() $ \| \xi \| \geq R + \varepsilon$
, and
$ \| \xi \| \geq R + \varepsilon$
, and
![]() $\phi$
is interpolated between
$\phi$
is interpolated between
![]() $R - \varepsilon$
and
$R - \varepsilon$
and
![]() $R + \varepsilon$
in such a way that it is differentiable. With this regularized version,
$R + \varepsilon$
in such a way that it is differentiable. With this regularized version,
![]() $\phi$
satisfies the condition (A) with
$\phi$
satisfies the condition (A) with
![]() $\psi \equiv 1$
and the conditions (B) and (C).
$\psi \equiv 1$
and the conditions (B) and (C).
Based on a potential V as above, we construct a birth–death–move process
![]() $(X_t)_{t\geq 0}$
with the following characteristics. The birth transition kernel is given as in Example 3 by
$(X_t)_{t\geq 0}$
with the following characteristics. The birth transition kernel is given as in Example 3 by
for any
![]() $x\in E$
and
$x\in E$
and
![]() $\Lambda\subset W$
, where
$\Lambda\subset W$
, where
![]() $ z(x)=\int_W \exp\!(\!-\!(V(x \cup \xi)-V(x))) \, \text{d} \xi$
. Note that by the local stability assumption (A),
$ z(x)=\int_W \exp\!(\!-\!(V(x \cup \xi)-V(x))) \, \text{d} \xi$
. Note that by the local stability assumption (A),
![]() $z(x)<\infty$
for any
$z(x)<\infty$
for any
![]() $x\in E$
. The death transition kernel is just the uniform kernel, a particular case of Example 1, i.e.
$x\in E$
. The death transition kernel is just the uniform kernel, a particular case of Example 1, i.e.
 $$K_\delta f(x) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} f(x \, \backslash \, x_i)$$
$$K_\delta f(x) = \dfrac{1}{n(x)} \sum_{i=1}^{n(x)} f(x \, \backslash \, x_i)$$
for any
![]() $f \in M_b(E)$
and
$f \in M_b(E)$
and
![]() $x=\{x_1,\dots,x_{n(x)}\}\in E$
. For the birth and death intensity functions, we take
$x=\{x_1,\dots,x_{n(x)}\}\in E$
. For the birth and death intensity functions, we take
for any
![]() $x\in E$
. Finally, for the move process, we start with the following Langevin diffusion on
$x\in E$
. Finally, for the move process, we start with the following Langevin diffusion on
![]() $\tilde W_n$
:
$\tilde W_n$
:
with reflecting boundary conditions (see [Reference Fattler and Grothaus8]), and we deduce the move process Y on E as in Example 4.
Proposition 9. The birth–death–move process
![]() $(X_t)_{t\geq 0}$
defined above is a Feller process and converges towards the invariant Gibbs probability measure on W with potential V, i.e. the measure having a density proportional to
$(X_t)_{t\geq 0}$
defined above is a Feller process and converges towards the invariant Gibbs probability measure on W with potential V, i.e. the measure having a density proportional to
![]() $\exp\!(\!-\!V(x))$
with respect to the unit-rate Poisson point process on W.
$\exp\!(\!-\!V(x))$
with respect to the unit-rate Poisson point process on W.
Proof. First note that by the local stability assumption (A),
![]() $\beta(x)\leq e^{-c} \|\psi\|_1/(n(x)\vee 1),$
where
$\beta(x)\leq e^{-c} \|\psi\|_1/(n(x)\vee 1),$
where
![]() $\|\psi\|_1=\int_W \psi(\xi)d\xi$
, so that
$\|\psi\|_1=\int_W \psi(\xi)d\xi$
, so that
![]() $\alpha=\beta +\delta$
is uniformly bounded as required by (2.1).
$\alpha=\beta +\delta$
is uniformly bounded as required by (2.1).
Under the assumptions (B) and (C), [Reference Fattler and Grothaus8] proved that the process
![]() $(Z_{t}^{|n})_{t\geq 0}$
is a well-defined Markov process on
$(Z_{t}^{|n})_{t\geq 0}$
is a well-defined Markov process on
![]() $\tilde W_n$
and is a Feller process. By Proposition 6, Y is then a Feller process on E. On the other hand, the jump transition kernel K given by (2.4) satisfies
$\tilde W_n$
and is a Feller process. By Proposition 6, Y is then a Feller process on E. On the other hand, the jump transition kernel K given by (2.4) satisfies
![]() $KC_0(E)\subset C_0(E)$
, as verified in Examples 1 and 3 in Section 3.3, since W is compact. We thus obtain by Theorem 2 that
$KC_0(E)\subset C_0(E)$
, as verified in Examples 1 and 3 in Section 3.3, since W is compact. We thus obtain by Theorem 2 that
![]() $(X_t)_{t\geq 0}$
is a Feller process. Moreover, by (A) we have that for all
$(X_t)_{t\geq 0}$
is a Feller process. Moreover, by (A) we have that for all
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\beta_n\leq e^{-c} \|\psi\|_1/n$
, so that (4.7) is verified. All assumptions of Theorem 5 are satisfied, which implies that
$\beta_n\leq e^{-c} \|\psi\|_1/n$
, so that (4.7) is verified. All assumptions of Theorem 5 are satisfied, which implies that
![]() $(X_t)_{t\geq 0}$
converges to a unique invariant probability measure as
$(X_t)_{t\geq 0}$
converges to a unique invariant probability measure as
![]() $t\to\infty$
.
$t\to\infty$
.
It remains to characterize this invariant measure. The choices of
![]() $\beta$
,
$\beta$
,
![]() $\delta$
,
$\delta$
,
![]() $K_\beta$
, and
$K_\beta$
, and
![]() $K_\delta$
satisfy the conditions of [Reference Preston22, Theorem 8.1] (see also [Reference Møller and Waagepetersen19, Chapter 11]), which implies that the invariant measure
$K_\delta$
satisfy the conditions of [Reference Preston22, Theorem 8.1] (see also [Reference Møller and Waagepetersen19, Chapter 11]), which implies that the invariant measure
![]() $\mu$
for the birth–death process (without move) having the previous characteristics is the one claimed in the proposition. We deduce that (4.13) holds true. On the other hand, [Reference Fattler and Grothaus8] proved under B and C that
$\mu$
for the birth–death process (without move) having the previous characteristics is the one claimed in the proposition. We deduce that (4.13) holds true. On the other hand, [Reference Fattler and Grothaus8] proved under B and C that
![]() $(Z_{t}^{|n})_{t\geq 0}$
converges towards the invariant measure on
$(Z_{t}^{|n})_{t\geq 0}$
converges towards the invariant measure on
![]() $\tilde W_n$
with a density (with respect to the Lebesgue measure) proportional to
$\tilde W_n$
with a density (with respect to the Lebesgue measure) proportional to
![]() $\exp\!(\!-\!\sum_{1\leq i\neq j\leq n} \phi(x_i-x_j))$
. After projection on
$\exp\!(\!-\!\sum_{1\leq i\neq j\leq n} \phi(x_i-x_j))$
. After projection on
![]() $E_n$
, this means that (4.12) follows, with the same measure
$E_n$
, this means that (4.12) follows, with the same measure
![]() $\mu$
as before. Proposition 8 then applies, and
$\mu$
as before. Proposition 8 then applies, and
![]() $\mu$
is the invariant measure of
$\mu$
is the invariant measure of
![]() $(X_t)_{t\geq 0}$
.
$(X_t)_{t\geq 0}$
.
Appendix. Proofs of lemmas related to Theorem 4
A.1. Proof of Lemma 1
First note that for any
![]() $x \in E$
,
$x \in E$
,
![]() $n \geq 0$
, and
$n \geq 0$
, and
![]() $h > 0$
one has
$h > 0$
one has
 \begin{align*} \mathbb{P}_{(x,n)}(\check{T}_1 \leq h) & = \mathbb{E}_{(x,n)}\left (1-\text{e}^{-\int_0^h \check{\alpha}( \check{Y}_u) \, \text{d} u} \right ) \leq \mathbb{E}_{(x,n)}\left ( \int_0^h \check{\alpha}( \check{Y}_u) \, \text{d} u \right ) \leq 2 \alpha^* h. \end{align*}
\begin{align*} \mathbb{P}_{(x,n)}(\check{T}_1 \leq h) & = \mathbb{E}_{(x,n)}\left (1-\text{e}^{-\int_0^h \check{\alpha}( \check{Y}_u) \, \text{d} u} \right ) \leq \mathbb{E}_{(x,n)}\left ( \int_0^h \check{\alpha}( \check{Y}_u) \, \text{d} u \right ) \leq 2 \alpha^* h. \end{align*}
Next take
![]() $h >0$
. Then
$h >0$
. Then
 \begin{align} \psi_p(t+h) - \psi_p(t) & = \mathbb{E}_{(x,n)} \left [ {\mathbf 1}_{X'_{\!\!\!t+h}\in E} {\mathbf 1}_{\eta'_{\!\!\!t+h}=p} - {\mathbf 1}_{X'_{\!\!t}\in E} {\mathbf 1}_{\eta'_{\!\!t}=p} \right ] \nonumber \\ & = \sum_{k \geq 0} \mathbb{E}_{(x,n)} \left[ \check{Q}_h((X'_{\!\!t},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} |\eta'_{\!\!t} = k \right] \, \mathbb{P}_{(x,n)}(\eta'_{\!\!t} = k). \end{align}
\begin{align} \psi_p(t+h) - \psi_p(t) & = \mathbb{E}_{(x,n)} \left [ {\mathbf 1}_{X'_{\!\!\!t+h}\in E} {\mathbf 1}_{\eta'_{\!\!\!t+h}=p} - {\mathbf 1}_{X'_{\!\!t}\in E} {\mathbf 1}_{\eta'_{\!\!t}=p} \right ] \nonumber \\ & = \sum_{k \geq 0} \mathbb{E}_{(x,n)} \left[ \check{Q}_h((X'_{\!\!t},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} |\eta'_{\!\!t} = k \right] \, \mathbb{P}_{(x,n)}(\eta'_{\!\!t} = k). \end{align}
For any
![]() $k \geq 0$
and
$k \geq 0$
and
![]() $y \in E$
,
$y \in E$
,
 \begin{align*} \left | \check{Q}_h((y,k),E \times \{ p \}) - {\mathbf 1}_{k=p} \right | & = \left | \mathbb{E}_{(y,k)} \left ( {\mathbf 1}_{\eta'_{\!\!h}=p} {\mathbf 1}_{ \check{T}_1 > h} \right ) + \mathbb{E}_{(y,k)} \left ( {\mathbf 1}_{\eta'_{\!\!h}=p} {\mathbf 1}_{ \check{T}_1 \leq h} \right ) - {\mathbf 1}_{k=p} \right | \\ & \leq \mathbb{E}_{(y,k)} \left |( {\mathbf 1}_{\eta'_{\!\!h}=p}- {\mathbf 1}_{k=p} ){\mathbf 1}_{ \check{T}_1 \leq h} \right | + \mathbb{E}_{(y,k)} \left | ( {\mathbf 1}_{\eta'_{\!\!h}=p}- {\mathbf 1}_{k=p} ){\mathbf 1}_{\check{T}_1 >h} \right | \\ & \leq \mathbb{P}_{(x,n)}(\check{T}_1 \leq h) + \mathbb{E}_{(y,k)} \left | ( {\mathbf 1}_{k=p}- {\mathbf 1}_{k=p}) {\mathbf 1}_{\check{T}_1 >h} \right | \\ & \leq 2 \alpha^* h, \end{align*}
\begin{align*} \left | \check{Q}_h((y,k),E \times \{ p \}) - {\mathbf 1}_{k=p} \right | & = \left | \mathbb{E}_{(y,k)} \left ( {\mathbf 1}_{\eta'_{\!\!h}=p} {\mathbf 1}_{ \check{T}_1 > h} \right ) + \mathbb{E}_{(y,k)} \left ( {\mathbf 1}_{\eta'_{\!\!h}=p} {\mathbf 1}_{ \check{T}_1 \leq h} \right ) - {\mathbf 1}_{k=p} \right | \\ & \leq \mathbb{E}_{(y,k)} \left |( {\mathbf 1}_{\eta'_{\!\!h}=p}- {\mathbf 1}_{k=p} ){\mathbf 1}_{ \check{T}_1 \leq h} \right | + \mathbb{E}_{(y,k)} \left | ( {\mathbf 1}_{\eta'_{\!\!h}=p}- {\mathbf 1}_{k=p} ){\mathbf 1}_{\check{T}_1 >h} \right | \\ & \leq \mathbb{P}_{(x,n)}(\check{T}_1 \leq h) + \mathbb{E}_{(y,k)} \left | ( {\mathbf 1}_{k=p}- {\mathbf 1}_{k=p}) {\mathbf 1}_{\check{T}_1 >h} \right | \\ & \leq 2 \alpha^* h, \end{align*}
whereby
On the other hand, with the same calculations for
![]() $h \in [0,t]$
we obtain
$h \in [0,t]$
we obtain
 \begin{align*} \psi_p(t) - \psi_p(t-h) & = \sum_{k \geq 0} \mathbb{E}_{(x,n)}\! \left[ \check{Q}_h((X'_{t-h},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} |\eta'_{t-h} = k \right ] \, \check{Q}_{t-h}((x,n);\; E \times \!\{ k \} ) \\ & \leq 2 \alpha^* h \underset{h \searrow 0}{\longrightarrow} 0. \end{align*}
\begin{align*} \psi_p(t) - \psi_p(t-h) & = \sum_{k \geq 0} \mathbb{E}_{(x,n)}\! \left[ \check{Q}_h((X'_{t-h},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} |\eta'_{t-h} = k \right ] \, \check{Q}_{t-h}((x,n);\; E \times \!\{ k \} ) \\ & \leq 2 \alpha^* h \underset{h \searrow 0}{\longrightarrow} 0. \end{align*}
Therefore the function
![]() $t \in \mathbb{R}_+ \mapsto \psi_q(t)$
is continuous.
$t \in \mathbb{R}_+ \mapsto \psi_q(t)$
is continuous.
A.2. Proof of Lemma 2
Take
![]() $h >0.$
Recall from (A.1) that
$h >0.$
Recall from (A.1) that
For any
![]() $y \in E$
and
$y \in E$
and
![]() $ k \geq 0$
,
$ k \geq 0$
,
where
 \begin{align*}A_1(h)&=\mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{T}_1 > h} \right ),\\A_2(h)&=\mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{N}_h = 1} \right ),\;\text{and}\\A_3(h)&= \mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{T}_2 < h} \right ).\end{align*}
\begin{align*}A_1(h)&=\mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{T}_1 > h} \right ),\\A_2(h)&=\mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{N}_h = 1} \right ),\;\text{and}\\A_3(h)&= \mathbb{E}_{(y,k)} \left ( ( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p} ) {\mathbf 1}_{ \check{T}_2 < h} \right ).\end{align*}
Let us treat each term separately.
First, we clearly have
![]() $A_1(h)=0$
. Second,
$A_1(h)=0$
. Second,
![]() $A_2(h)$
reads
$A_2(h)$
reads
 \begin{align*} &\mathbb{E}_{(y,k)} \left (( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} {\mathbf 1}_{\check{\tau}_2 > h- \check{\tau}_1} \right ) \\ & = \mathbb{E}_{(y,k)} \left [ ( {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{P}_{(y,k)} \left ( \check{\tau}_2 > h- \check{\tau}_1 \left | \check{\mathcal{F}}_{\check{\tau}_1}, \check{Y}^{(1)} \right. \right ) \right ] \\ & = \mathbb{E}_{(y,k)} \left [ ( {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \text{e}^{- \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \right ] \\ & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \mathbb{E}_{(y,k)} \left [ \text{e}^{- \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \left | \check{\mathcal{F}}_{\check{\tau}_1} \right. \right ] \right ] \\ & = \, \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} -{\mathbf 1}_{k=p}) \mathbb{E}_{\check{C}_{\check{\tau}_1}}^{\check{Y}} \left [\text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } \right ] \right ] \\ & = \mathbb{E}_{(y,k)} \!\left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \mathbb{E}_{\check{C}_{\check{\tau}_1}}^{\check{Y}} \left [\text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha}\! \left ( \check{Y}_u \right ) \, \text{d} u } -1 \right ] \right ] + \mathbb{E}_{(y,k)} \!\left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ]\!. \end{align*}
\begin{align*} &\mathbb{E}_{(y,k)} \left (( {\mathbf 1}_{\eta'_{\!\!h}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} {\mathbf 1}_{\check{\tau}_2 > h- \check{\tau}_1} \right ) \\ & = \mathbb{E}_{(y,k)} \left [ ( {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{P}_{(y,k)} \left ( \check{\tau}_2 > h- \check{\tau}_1 \left | \check{\mathcal{F}}_{\check{\tau}_1}, \check{Y}^{(1)} \right. \right ) \right ] \\ & = \mathbb{E}_{(y,k)} \left [ ( {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \text{e}^{- \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \right ] \\ & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \mathbb{E}_{(y,k)} \left [ \text{e}^{- \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \left | \check{\mathcal{F}}_{\check{\tau}_1} \right. \right ] \right ] \\ & = \, \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} -{\mathbf 1}_{k=p}) \mathbb{E}_{\check{C}_{\check{\tau}_1}}^{\check{Y}} \left [\text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } \right ] \right ] \\ & = \mathbb{E}_{(y,k)} \!\left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \mathbb{E}_{\check{C}_{\check{\tau}_1}}^{\check{Y}} \left [\text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha}\! \left ( \check{Y}_u \right ) \, \text{d} u } -1 \right ] \right ] + \mathbb{E}_{(y,k)} \!\left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ]\!. \end{align*}
For the first term above,
For the second term, we have
 \begin{align} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ \, {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}\left | \check{Y}^{(0)}, \check{\tau}_1 \right. \right ] \right ] \nonumber \\ & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \check{K}((Y_{\check{\tau}_1}^{\prime(0)},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} \right ) \right ]. \end{align}
\begin{align} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ \, {\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}\left | \check{Y}^{(0)}, \check{\tau}_1 \right. \right ] \right ] \nonumber \\ & = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \check{K}((Y_{\check{\tau}_1}^{\prime(0)},k);\; E \times \{ p \}) - {\mathbf 1}_{k=p} \right ) \right ]. \end{align}
Following the definition of
![]() $\check{K}$
in Section 4.1, this formula takes one of two forms, depending on whether
$\check{K}$
in Section 4.1, this formula takes one of two forms, depending on whether
![]() $y \notin E_k$
or
$y \notin E_k$
or
![]() $y\in E_k$
. If
$y\in E_k$
. If
![]() $y \notin E_k$
, then
$y \notin E_k$
, then
 \begin{multline*} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } -1 \right ) \right ] {\mathbf 1}_{k=p} \\ + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] {\mathbf 1}_{k=p-1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] {\mathbf 1}_{k=p+1}; \end{multline*}
\begin{multline*} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } -1 \right ) \right ] {\mathbf 1}_{k=p} \\ + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] {\mathbf 1}_{k=p-1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] {\mathbf 1}_{k=p+1}; \end{multline*}
that is,
 \begin{multline} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] \\ = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \right ] \left ( - \alpha_k {\mathbf 1}_{ k=p} + \beta_k {\mathbf 1}_{ k=p-1} + \delta_k {\mathbf 1}_{ k=p+1} \right ). \end{multline}
\begin{multline} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] \\ = \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \right ] \left ( - \alpha_k {\mathbf 1}_{ k=p} + \beta_k {\mathbf 1}_{ k=p-1} + \delta_k {\mathbf 1}_{ k=p+1} \right ). \end{multline}
Since
 \begin{align*} \left | \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] -1 \right | & = \left | \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h \left ( \text{e}^{- \int_0^s \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u}-1 \right ) \text{d} s \right ] \right | \leq 2 \alpha^* h, \end{align*}
\begin{align*} \left | \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \right ] -1 \right | & = \left | \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h \left ( \text{e}^{- \int_0^s \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u}-1 \right ) \text{d} s \right ] \right | \leq 2 \alpha^* h, \end{align*}
we then conclude that
If instead
![]() $y \in E_k$
, we obtain from (A.4)
$y \in E_k$
, we obtain from (A.4)
 \begin{multline*} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] \\= \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p-1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k-\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p-1} \\ + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p+1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \dfrac{\delta(Y_{\check{\tau}_1}^{\prime(0)})-\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} - 1 \right ) \right ] {\mathbf 1}_{k=p} , \end{multline*}
\begin{multline*} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} ({\mathbf 1}_{\eta'_{\!\!\check{\tau}_1}=p} - {\mathbf 1}_{k=p}) \right ] \\= \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p-1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k-\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p-1} \\ + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \right ] {\mathbf 1}_{k=p+1} + \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \left ( \dfrac{\delta(Y_{\check{\tau}_1}^{\prime(0)})-\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} - 1 \right ) \right ] {\mathbf 1}_{k=p} , \end{multline*}
which is the same expression as (A.5). The convergence (A.6) then remains true when the supremum is taken over
![]() $y\in E_k$
, and so over
$y\in E_k$
, and so over
![]() $y\in E$
, i.e.
$y\in E$
, i.e.
Third, for
![]() $A_3(h)$
in (A.3), using (2.3) and defining
$A_3(h)$
in (A.3), using (2.3) and defining
![]() $\check{N}_h^* \sim \mathcal{P}(2\alpha^*h)$
, we have
$\check{N}_h^* \sim \mathcal{P}(2\alpha^*h)$
, we have
Combining the results for
![]() $A_1(h)$
,
$A_1(h)$
,
![]() $A_2(h)$
, and
$A_2(h)$
, and
![]() $A_3(h)$
in (A.3), we get
$A_3(h)$
in (A.3), we get
Finally, coming back to (A.2), we obtain by uniform convergence, for any
![]() $x \in E$
,
$x \in E$
,
where the limit reads
![]() $- \alpha_p \, \psi_p(t) + \beta_{p-1} \, \psi_{p-1}(t) + \delta_{p+1} \, \psi_{p+1}(t)$
, using
$- \alpha_p \, \psi_p(t) + \beta_{p-1} \, \psi_{p-1}(t) + \delta_{p+1} \, \psi_{p+1}(t)$
, using
![]() $\beta_{-1}=0$
.
$\beta_{-1}=0$
.
A.3. Proof of Corollary 1
For
![]() $t\geq 0$
, define
$t\geq 0$
, define
Then G is continuous and right-differentiable on
![]() $\mathbb{R}_+$
by Lemma 2, and
$\mathbb{R}_+$
by Lemma 2, and
![]() $\partial_+G(t)/\partial t =0$
. So G is constant. But
$\partial_+G(t)/\partial t =0$
. So G is constant. But
![]() $G(0)=0$
because
$G(0)=0$
because
![]() $s\mapsto \psi_p(s) $
is bounded on
$s\mapsto \psi_p(s) $
is bounded on
![]() $\mathbb{R}_+$
for any
$\mathbb{R}_+$
for any
![]() $p \geq 0$
. As a consequence we obtain
$p \geq 0$
. As a consequence we obtain
In particular the integrand is continuous by Lemma 1, so
![]() $\psi_p$
is differentiable.
$\psi_p$
is differentiable.
A.4. Proof of Lemma 3
Let us expand
![]() $q_s({\mathbf 1}_{\{p\}})$
as
$q_s({\mathbf 1}_{\{p\}})$
as
Take
![]() $r > p$
. Then for
$r > p$
. Then for
![]() $s\leq t$
, using (2.3) by setting
$s\leq t$
, using (2.3) by setting
![]() $n^*_t \sim \mathcal{P}(\alpha^* t)$
, we have
$n^*_t \sim \mathcal{P}(\alpha^* t)$
, we have
 \begin{align*} \sum_{k=r}^{\infty} \mathbb{P}_k(\eta_s=p) \leq \sum_{k=r}^{\infty} \mathbb{P}_k (n_s \geq k-p) \leq \sum_{k=r}^{\infty} \mathbb{P} (n^*_t \geq k-p) = \sum_{j = r-p}^{\infty} \mathbb{P}(n^*_t \geq j) \underset{r \rightarrow \infty}{\longrightarrow} 0, \end{align*}
\begin{align*} \sum_{k=r}^{\infty} \mathbb{P}_k(\eta_s=p) \leq \sum_{k=r}^{\infty} \mathbb{P}_k (n_s \geq k-p) \leq \sum_{k=r}^{\infty} \mathbb{P} (n^*_t \geq k-p) = \sum_{j = r-p}^{\infty} \mathbb{P}(n^*_t \geq j) \underset{r \rightarrow \infty}{\longrightarrow} 0, \end{align*}
because
![]() $\mathbb{E}(n^*_t) < \infty.$
Coming back to (A.7), we thus have that for any
$\mathbb{E}(n^*_t) < \infty.$
Coming back to (A.7), we thus have that for any
![]() $\varepsilon >0$
, there exists
$\varepsilon >0$
, there exists
![]() $r \geq 0$
such that any
$r \geq 0$
such that any
![]() $d \geq r$
satisfies
$d \geq r$
satisfies
 \begin{equation} \sup\nolimits_{s \in [0,t]} \left \| q_s({\mathbf 1}_{\{p\}}) - \sum_{k =0}^d q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right \|_{\infty} < \varepsilon. \end{equation}
\begin{equation} \sup\nolimits_{s \in [0,t]} \left \| q_s({\mathbf 1}_{\{p\}}) - \sum_{k =0}^d q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right \|_{\infty} < \varepsilon. \end{equation}
Since
![]() $\check{Q}_t$
is a continuous linear operator on
$\check{Q}_t$
is a continuous linear operator on
![]() $M_b(E \times \mathbb{N})$
, we have
$M_b(E \times \mathbb{N})$
, we have
 \begin{align} w_s & = \check{Q}_{t-s} ( {\mathbf 1}_E \times q_s ({\mathbf 1}_{\{p\}})) \nonumber \\ & = \check{Q}_{t-s} \left ( {\mathbf 1}_E \times \lim \limits_{r \rightarrow \infty} \sum_{k =0}^r q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \lim \limits_{r \rightarrow \infty} \check{Q}_{t-s} \left ( {\mathbf 1}_E \times \sum_{k =0}^r q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \lim \limits_{r \rightarrow \infty} \sum_{k =0}^r q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \sum_{k=0}^{\infty} q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ). \end{align}
\begin{align} w_s & = \check{Q}_{t-s} ( {\mathbf 1}_E \times q_s ({\mathbf 1}_{\{p\}})) \nonumber \\ & = \check{Q}_{t-s} \left ( {\mathbf 1}_E \times \lim \limits_{r \rightarrow \infty} \sum_{k =0}^r q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \lim \limits_{r \rightarrow \infty} \check{Q}_{t-s} \left ( {\mathbf 1}_E \times \sum_{k =0}^r q_s(k,\{ p \}) {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \lim \limits_{r \rightarrow \infty} \sum_{k =0}^r q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) \nonumber \\ & = \sum_{k=0}^{\infty} q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ). \end{align}
Let
![]() $\phi_k(s) = q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right )$
. From the Kolmogorov backward equation (2.6), we deduce that
$\phi_k(s) = q_s(k,\{ p \}) \check{Q}_{t-s} \left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right )$
. From the Kolmogorov backward equation (2.6), we deduce that
![]() $\partial q_s(k,\{ p \})/\partial s =- \alpha_k q_s(k,\{ p \}) + \beta_{k} q_s(k+1,\{ p \}) + \delta_k q_s(k-1,\{ p \})$
. Using in addition Corollary 1, we deduce that
$\partial q_s(k,\{ p \})/\partial s =- \alpha_k q_s(k,\{ p \}) + \beta_{k} q_s(k+1,\{ p \}) + \delta_k q_s(k-1,\{ p \})$
. Using in addition Corollary 1, we deduce that
![]() $\phi_k$
is differentiable and
$\phi_k$
is differentiable and
 \begin{multline*} \phi'_k(s) = \left [ - \alpha_k q_s(k,\{ p \}) + \beta_{k} q_s(k+1,\{ p \}) + \delta_k q_s(k-1,\{ p \}) \right ] \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) \\ + q_s(k,\{ p \}) \left [ \alpha_k \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) - \beta_{k-1} \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k-1 \}} \right ) - \delta_{k+1} \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k +1 \}} \right ) \right ]. \end{multline*}
\begin{multline*} \phi'_k(s) = \left [ - \alpha_k q_s(k,\{ p \}) + \beta_{k} q_s(k+1,\{ p \}) + \delta_k q_s(k-1,\{ p \}) \right ] \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) \\ + q_s(k,\{ p \}) \left [ \alpha_k \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) - \beta_{k-1} \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k-1 \}} \right ) - \delta_{k+1} \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k +1 \}} \right ) \right ]. \end{multline*}
Since
and
we can show similarly as for (A.8) that
 $$ \sup\nolimits_{s \in [0,t]} \left \| \sum_{k \geq r} \phi'_k(s) \right \|_{\infty} \underset{r \rightarrow \infty}{\longrightarrow} 0. $$
$$ \sup\nolimits_{s \in [0,t]} \left \| \sum_{k \geq r} \phi'_k(s) \right \|_{\infty} \underset{r \rightarrow \infty}{\longrightarrow} 0. $$
Since by (A.9)
![]() $w_s=\sum_{k\geq 0} \phi_k(s)$
, we deduce that
$w_s=\sum_{k\geq 0} \phi_k(s)$
, we deduce that
![]() $w_s$
is differentiable on [0, t] and
$w_s$
is differentiable on [0, t] and
 \begin{align*} \dfrac{\partial }{\partial s} w_s = &\sum_{k =0}^{\infty} \phi'_k(s) \\ = &\sum_{k=0}^{\infty} \left [ \beta_k q_s(k+1,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times{\mathbf 1}_{\{ k \}} \right ) - \beta_{k-1} q_s(k,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k-1 \}} \right ) \right ] \\ & + \sum_{k=0}^{\infty} \left [ \delta_k q_s(k-1,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) - \delta_{k+1} q_s(k,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times{\mathbf 1}_{\{ k +1 \}} \right ) \right ], \end{align*}
\begin{align*} \dfrac{\partial }{\partial s} w_s = &\sum_{k =0}^{\infty} \phi'_k(s) \\ = &\sum_{k=0}^{\infty} \left [ \beta_k q_s(k+1,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times{\mathbf 1}_{\{ k \}} \right ) - \beta_{k-1} q_s(k,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k-1 \}} \right ) \right ] \\ & + \sum_{k=0}^{\infty} \left [ \delta_k q_s(k-1,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times {\mathbf 1}_{\{ k \}} \right ) - \delta_{k+1} q_s(k,\{ p \}) \check{Q}_{t-s}\left ( {\mathbf 1}_E \times{\mathbf 1}_{\{ k +1 \}} \right ) \right ], \end{align*}
where
![]() $\beta_{-1}=\delta_0=0$
. The first of these two telescoping series vanishes because
$\beta_{-1}=\delta_0=0$
. The first of these two telescoping series vanishes because
![]() $\beta_{-1}=0$
and
$\beta_{-1}=0$
and
The second series vanishes by similar arguments and we have
![]() $\partial w_s/\partial s \equiv0$
.
$\partial w_s/\partial s \equiv0$
.
A.5. Proof of Lemma 4
Let
![]() $h > 0$
; then
$h > 0$
; then
 \begin{align} \psi_f(t+h)-\psi_f(t) & = \mathbb{E}_{(x,n)}\left ( f(X'_{\!\!\!t+h}) {\mathbf 1}_{\eta'_{\!\!\!t+h}\in\mathbb{N}} \right ) - \mathbb{E}_{(x,n)}\left ( f(X'_{\!\!t}) {\mathbf 1}_{\eta'_{\!\!t}\in\mathbb{N}} \right ) \nonumber \\ & = \mathbb{E}_{(x,n)} \left [ \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(X'_{\!\!t},\eta'_{\!\!t}) - f(X'_{\!\!t}){\mathbf 1}_{\eta'_{\!\!t}\in\mathbb{N}} \right ]. \end{align}
\begin{align} \psi_f(t+h)-\psi_f(t) & = \mathbb{E}_{(x,n)}\left ( f(X'_{\!\!\!t+h}) {\mathbf 1}_{\eta'_{\!\!\!t+h}\in\mathbb{N}} \right ) - \mathbb{E}_{(x,n)}\left ( f(X'_{\!\!t}) {\mathbf 1}_{\eta'_{\!\!t}\in\mathbb{N}} \right ) \nonumber \\ & = \mathbb{E}_{(x,n)} \left [ \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(X'_{\!\!t},\eta'_{\!\!t}) - f(X'_{\!\!t}){\mathbf 1}_{\eta'_{\!\!t}\in\mathbb{N}} \right ]. \end{align}
For any
![]() $y \in E$
and
$y \in E$
and
![]() $k \in \mathbb{N}$
one has
$k \in \mathbb{N}$
one has
 \begin{align*} \Big| \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) &- f(y){\mathbf 1}_{k\in \mathbb{N}} \Big | = \left | \mathbb{E}_{(y,k)} \left ( f(X'_{\!\!h}) \right ) - f(y) \right | \\ & \leq 2 \|f\|_{\infty} \mathbb{P}_{(y,k)}(\check{T}_1 \leq h) + \left | \mathbb{E}_{(y,k)} \left ( (f(Y^{\prime(0)}_h)-f(y)) {\mathbf 1}_{\check{T}_1 > h} \right ) \right | \\ & \leq 4 \alpha^* \|f\|_{\infty} h + \left \| Q_h^Yf-f \right \|_{\infty}\!, \end{align*}
\begin{align*} \Big| \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) &- f(y){\mathbf 1}_{k\in \mathbb{N}} \Big | = \left | \mathbb{E}_{(y,k)} \left ( f(X'_{\!\!h}) \right ) - f(y) \right | \\ & \leq 2 \|f\|_{\infty} \mathbb{P}_{(y,k)}(\check{T}_1 \leq h) + \left | \mathbb{E}_{(y,k)} \left ( (f(Y^{\prime(0)}_h)-f(y)) {\mathbf 1}_{\check{T}_1 > h} \right ) \right | \\ & \leq 4 \alpha^* \|f\|_{\infty} h + \left \| Q_h^Yf-f \right \|_{\infty}\!, \end{align*}
where we have used (4.2) in the second-to-last step. Coming back to (A.10), we deduce that
As a Feller process,
![]() $(Y_t)_{t \geq 0}$
is strongly continuous at 0, so that
$(Y_t)_{t \geq 0}$
is strongly continuous at 0, so that
![]() $\psi_f(t+h)\to \psi_f(t)$
as
$\psi_f(t+h)\to \psi_f(t)$
as
![]() $h \searrow 0$
.
$h \searrow 0$
.
On the other hand, for
![]() $h \in [0,t]$
, we can prove similarly that
$h \in [0,t]$
, we can prove similarly that
and
![]() $\psi_f(t-h)\to \psi_f(t)$
as
$\psi_f(t-h)\to \psi_f(t)$
as
![]() $h \searrow 0$
.
$h \searrow 0$
.
A.6. Proof of Lemma 5
Let
![]() $h>0$
. For any
$h>0$
. For any
![]() $t \geq 0$
,
$t \geq 0$
,
 \begin{align*} \left | \dfrac{ \psi_f(t+h)-\psi_f(t) }{h} - \psi_{\mathcal{A} f}(t) \right | & = \left | \check{Q}_t \left ( \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(x,n) - f(x) {\mathbf 1}_{n\in\mathbb{N}}}{h} - \mathcal{A} f(x) \times {\mathbf 1}_{n\in\mathbb{N}} \right ) \right | \\ & \leq \underset{(y,k)\in \check{E}}{\sup} \left | \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}}}{h} - \mathcal{A} f(y) \times{\mathbf 1}_{k\in\mathbb{N}} \right |. \end{align*}
\begin{align*} \left | \dfrac{ \psi_f(t+h)-\psi_f(t) }{h} - \psi_{\mathcal{A} f}(t) \right | & = \left | \check{Q}_t \left ( \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(x,n) - f(x) {\mathbf 1}_{n\in\mathbb{N}}}{h} - \mathcal{A} f(x) \times {\mathbf 1}_{n\in\mathbb{N}} \right ) \right | \\ & \leq \underset{(y,k)\in \check{E}}{\sup} \left | \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}}}{h} - \mathcal{A} f(y) \times{\mathbf 1}_{k\in\mathbb{N}} \right |. \end{align*}
The proof thus consists in showing that
 \[ \underset{(y,k)\in \check{E}}{\sup} \left | \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}}}{h} - \mathcal{A} f(y) \times {\mathbf 1}_{k\in\mathbb{N}} \right | \underset{h \searrow 0}{\longrightarrow} 0. \]
\[ \underset{(y,k)\in \check{E}}{\sup} \left | \dfrac{\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}}}{h} - \mathcal{A} f(y) \times {\mathbf 1}_{k\in\mathbb{N}} \right | \underset{h \searrow 0}{\longrightarrow} 0. \]
For any
![]() $h> 0$
,
$h> 0$
,
![]() $y \in E$
, and
$y \in E$
, and
![]() $k \geq 0$
,
$k \geq 0$
,
 \begin{align*} \dfrac{1}{h} \Big (& \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \Big ) \\ & = \mathbb{E}_{(y,k)} \left [ \dfrac{f(X'_{\!\!h}) -f(y)}{h} \right ] \\ & = \dfrac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_1 >h} \right ] + \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{N}_h=1} \right ] + \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_2 <h} \right ] - f(y) \right ). \end{align*}
\begin{align*} \dfrac{1}{h} \Big (& \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \Big ) \\ & = \mathbb{E}_{(y,k)} \left [ \dfrac{f(X'_{\!\!h}) -f(y)}{h} \right ] \\ & = \dfrac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_1 >h} \right ] + \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{N}_h=1} \right ] + \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_2 <h} \right ] - f(y) \right ). \end{align*}
But
 \begin{align*} \frac{1}{h} & \left ( \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_1 >h} \right ] -f(y) \right ) \\ &= \frac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(Y_h^{\prime(0)}) {\mathbf 1}_{\check{T}_1 >h} \right ] -f(y) \right )\\ & = \dfrac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(0)}_h) \text{e}^{- \int_0^h \check{\alpha}( Y_u^{\prime(0)},k) \, \text{d} u} \right ] - f(y) \right ) \\ & = \mathbb{E}_{y}^Y \left [ \dfrac{f(Y_h) -f(y)}{h} \right ] + \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ f(Y'_{\!\!h}) \left ( \text{e}^{- \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u} -1 + \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ) \right ] \\ &\hspace{0.3cm} - \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ]. \end{align*}
\begin{align*} \frac{1}{h} & \left ( \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_1 >h} \right ] -f(y) \right ) \\ &= \frac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(Y_h^{\prime(0)}) {\mathbf 1}_{\check{T}_1 >h} \right ] -f(y) \right )\\ & = \dfrac{1}{h} \left ( \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(0)}_h) \text{e}^{- \int_0^h \check{\alpha}( Y_u^{\prime(0)},k) \, \text{d} u} \right ] - f(y) \right ) \\ & = \mathbb{E}_{y}^Y \left [ \dfrac{f(Y_h) -f(y)}{h} \right ] + \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ f(Y'_{\!\!h}) \left ( \text{e}^{- \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u} -1 + \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ) \right ] \\ &\hspace{0.3cm} - \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ]. \end{align*}
Using this result and the expression for
![]() $\mathcal{A} f(y)$
from Theorem 3, we can write
$\mathcal{A} f(y)$
from Theorem 3, we can write
 \begin{align*} \dfrac{1}{h} \Big ( &\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \Big) - \mathcal{A} f(y) \\[5pt] &= \dfrac{1}{h} \left ( \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \right ) - \mathcal{A}^Y f(y) + \alpha(y) f(y) - \alpha(y) Kf(y) \\[5pt] &= A_1(h) + A_2(h) + A_3(h) + A_4(h) + A_5(h), \end{align*}
\begin{align*} \dfrac{1}{h} \Big ( &\check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \Big) - \mathcal{A} f(y) \\[5pt] &= \dfrac{1}{h} \left ( \check{Q}_h(f \times {\mathbf 1}_\mathbb{N})(y,k) - f(y) {\mathbf 1}_{k\in\mathbb{N}} \right ) - \mathcal{A}^Y f(y) + \alpha(y) f(y) - \alpha(y) Kf(y) \\[5pt] &= A_1(h) + A_2(h) + A_3(h) + A_4(h) + A_5(h), \end{align*}
where
 \begin{align*} A_1(h) &=\mathbb{E}^Y_y \left [ \dfrac{f(Y_h) -f(y)}{h} \right ] - \mathcal{A}^Y f(y), \\[5pt] A_2(h) &= \check{\alpha}(y,k) f(y) - \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ], \\[5pt] A_3(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ f(Y'_{\!\!h}) \left ( \text{e}^{- \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u} -1 + \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ) \right ], \\[5pt] A_4(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{N}_h=1} \right] - \alpha(y) Kf(y) + (\alpha(y)-\check{\alpha}(y,k))f(y), \\[5pt] A_5(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_2<h} \right]. \end{align*}
\begin{align*} A_1(h) &=\mathbb{E}^Y_y \left [ \dfrac{f(Y_h) -f(y)}{h} \right ] - \mathcal{A}^Y f(y), \\[5pt] A_2(h) &= \check{\alpha}(y,k) f(y) - \dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \int_0^h f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ], \\[5pt] A_3(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ f(Y'_{\!\!h}) \left ( \text{e}^{- \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u} -1 + \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right ) \right ], \\[5pt] A_4(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{N}_h=1} \right] - \alpha(y) Kf(y) + (\alpha(y)-\check{\alpha}(y,k))f(y), \\[5pt] A_5(h) &=\dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{\check{T}_2<h} \right]. \end{align*}
The end of the proof consists in proving that each of these five terms tends uniformly to 0 as
![]() $h \searrow 0$
.
$h \searrow 0$
.
For the first one, note that
and since
![]() $f \in \mathcal{D}_\mathcal{A}^Y$
, by the definition of
$f \in \mathcal{D}_\mathcal{A}^Y$
, by the definition of
![]() $\mathcal{A}^Y$
,
$\mathcal{A}^Y$
,
![]() $\sup_{(y,k) \in \check{E}} \left | A_1(h) \right |$
tends to 0 as
$\sup_{(y,k) \in \check{E}} \left | A_1(h) \right |$
tends to 0 as
![]() $h\to 0$
.
$h\to 0$
.
To show that
![]() ${\sup}_{(y,k) \in \check{E}} | A_2(h)| \underset{h \searrow 0}{\longrightarrow} 0$
, we consider two cases:
${\sup}_{(y,k) \in \check{E}} | A_2(h)| \underset{h \searrow 0}{\longrightarrow} 0$
, we consider two cases:
![]() $y \notin E_k$
and
$y \notin E_k$
and
![]() $y \in E_k$
. First suppose that
$y \in E_k$
. First suppose that
![]() $y \notin E_k$
. Then
$y \notin E_k$
. Then
![]() $\check{\alpha} (y,k) = \alpha (y) + \alpha_k$
and
$\check{\alpha} (y,k) = \alpha (y) + \alpha_k$
and
 \begin{align*} A_2(h) &= \dfrac{1}{h} \int_0^h \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \check{\alpha}(y,k) f(y) - f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \right ] \, \text{d} u \\[5pt] & = \alpha_k \mathbb{E}_{y}^Y \left [ f(y) - f(Y_h) \right ] + \dfrac{1}{h} \int_0^h \mathbb{E}_{y}^Y \left [ \alpha(y) f(y) - f(Y_h) \alpha( Y_u) \right ] \, \text{d} u, \end{align*}
\begin{align*} A_2(h) &= \dfrac{1}{h} \int_0^h \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \check{\alpha}(y,k) f(y) - f(Y'_{\!\!h}) \check{\alpha}( Y'_{\!\!u},k) \right ] \, \text{d} u \\[5pt] & = \alpha_k \mathbb{E}_{y}^Y \left [ f(y) - f(Y_h) \right ] + \dfrac{1}{h} \int_0^h \mathbb{E}_{y}^Y \left [ \alpha(y) f(y) - f(Y_h) \alpha( Y_u) \right ] \, \text{d} u, \end{align*}
where the switch from
![]() $ \mathbb{E}_{(y,k)}^{\check{Y}}$
to
$ \mathbb{E}_{(y,k)}^{\check{Y}}$
to
![]() $\mathbb{E}_{y}^Y$
is a consequence of (4.2), specifically the bivariate generalization of it. Therefore,
$\mathbb{E}_{y}^Y$
is a consequence of (4.2), specifically the bivariate generalization of it. Therefore,
 \begin{align*} & A_2(h) = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \mathbb{E}_y^Y \left [ \alpha(y) f(y) - f(Y_h) \alpha( Y_u) \left | Y_u \right. \right ] \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \alpha(y) f(y) - Q^Y_{h-u} f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \alpha(y) f(y) - f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ &\hspace{5cm}+ \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ f(Y_u) \alpha( Y_u)- Q^Y_{h-u} f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \int_0^1 \left ( f \times \alpha - Q_{hv}^Y (f \times \alpha) \right )(y) \, \text{d} v \\ &\hspace{5cm}+ \int_0^1 \mathbb{E}_y^Y \left [ \alpha( Y_{hv}) \left ( f - Q^Y_{h(1-v)} f \right )(Y_{hv}) \right ] \, \text{d} v. \end{align*}
\begin{align*} & A_2(h) = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \mathbb{E}_y^Y \left [ \alpha(y) f(y) - f(Y_h) \alpha( Y_u) \left | Y_u \right. \right ] \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \alpha(y) f(y) - Q^Y_{h-u} f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ \alpha(y) f(y) - f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ &\hspace{5cm}+ \dfrac{1}{h} \int_0^h \mathbb{E}_y^Y \left [ f(Y_u) \alpha( Y_u)- Q^Y_{h-u} f(Y_u) \alpha( Y_u) \right ] \, \text{d} u \\ & = \alpha_k \left ( f(y) - Q_h^Yf(y) \right ) + \int_0^1 \left ( f \times \alpha - Q_{hv}^Y (f \times \alpha) \right )(y) \, \text{d} v \\ &\hspace{5cm}+ \int_0^1 \mathbb{E}_y^Y \left [ \alpha( Y_{hv}) \left ( f - Q^Y_{h(1-v)} f \right )(Y_{hv}) \right ] \, \text{d} v. \end{align*}
So when
![]() $y \notin E_k$
,
$y \notin E_k$
,
which does not depend on
![]() $(y,k) \in \check{E}$
, and which converges to zero as h goes to 0 by the dominated convergence theorem because
$(y,k) \in \check{E}$
, and which converges to zero as h goes to 0 by the dominated convergence theorem because
![]() $f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. When
$f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. When
![]() $y \in E_k$
, we have
$y \in E_k$
, we have
![]() $\check{\alpha}(y,k) = \beta_k + \delta(y)$
, and using the same computations we obtain the same inequality (A.11), leading to the same convergence. So
$\check{\alpha}(y,k) = \beta_k + \delta(y)$
, and using the same computations we obtain the same inequality (A.11), leading to the same convergence. So
![]() ${\sup}_{(y,k) \in \check{E}} | A_2(h)| \underset{h \searrow 0}{\longrightarrow} 0$
.
${\sup}_{(y,k) \in \check{E}} | A_2(h)| \underset{h \searrow 0}{\longrightarrow} 0$
.
Regarding
![]() $A_3(h)$
, its uniform convergence towards 0 is easily obtained from
$A_3(h)$
, its uniform convergence towards 0 is easily obtained from
 \begin{align*} \left | A_3(h) \right | & \leq \dfrac{\|f\|_{\infty}}{2h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \left ( \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right )^2 \right ] \leq \dfrac{\|f\|_{\infty} \, (2 \alpha^* h)^2}{2h} = 2 h \|f\|_{\infty} ( \alpha^*)^2. \end{align*}
\begin{align*} \left | A_3(h) \right | & \leq \dfrac{\|f\|_{\infty}}{2h} \mathbb{E}_{(y,k)}^{\check{Y}} \left [ \left ( \int_0^h \check{\alpha}( Y'_{\!\!u},k) \, \text{d} u \right )^2 \right ] \leq \dfrac{\|f\|_{\infty} \, (2 \alpha^* h)^2}{2h} = 2 h \|f\|_{\infty} ( \alpha^*)^2. \end{align*}
Let us now prove that
![]() ${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
. We compute
${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
. We compute
 \begin{align*} \dfrac{1}{h} & \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{ \check{N}_t=1} \right ] = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{ \check{\tau}_1 \leq h} {\mathbf 1}_{\check{\tau}_2 > h- \check{\tau}_1} \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(1)}_{h-\check{\tau}_1}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{P}_{(y,k)} \left ( \check{\tau}_2 > h- \check{\tau}_1 \left | \check{\mathcal{F}}_{\check{\tau}_1}, \check{Y}^{(1)} \right. \right ) \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(1)}_{h-\check{\tau}_1}) \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \left | \check{\mathcal{F}}_{\check{\tau}_1} \right. \right ] \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } \right ] \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \\ &+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \left ( \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } -1 \right ) \right ] \right ] . \end{align*}
\begin{align*} \dfrac{1}{h} & \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{ \check{N}_t=1} \right ] = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(X'_{\!\!h}) {\mathbf 1}_{ \check{\tau}_1 \leq h} {\mathbf 1}_{\check{\tau}_2 > h- \check{\tau}_1} \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(1)}_{h-\check{\tau}_1}) {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{P}_{(y,k)} \left ( \check{\tau}_2 > h- \check{\tau}_1 \left | \check{\mathcal{F}}_{\check{\tau}_1}, \check{Y}^{(1)} \right. \right ) \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ f(Y^{\prime(1)}_{h-\check{\tau}_1}) \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u^{(1)} \right ) \, \text{d} u } \left | \check{\mathcal{F}}_{\check{\tau}_1} \right. \right ] \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } \right ] \right ] \\ & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \\ &+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \left ( \text{e}^{ - \int_0^{h-\check{\tau}_1} \check{\alpha} \left ( \check{Y}_u \right ) \, \text{d} u } -1 \right ) \right ] \right ] . \end{align*}
The second term converges uniformly to 0 because its norm is bounded by
 $$ \mathbb{E}_{(y,k)} \left [ \dfrac{{\mathbf 1}_{\check{\tau}_1 \leq h} \, \| f \|_{\infty}}{h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left | \int_0^{h-\check{\tau}_1} \check{\alpha}(\check{Y}_u) \, \text{d} u \right | \right ] \leq \frac{2 h \alpha^* \| f \|_{\infty}}{h} \mathbb{P}_{(y,k)}(\check{\tau}_1 \leq h) \leq 4 h (\alpha^*)^2 \| f \|_{\infty}.$$
$$ \mathbb{E}_{(y,k)} \left [ \dfrac{{\mathbf 1}_{\check{\tau}_1 \leq h} \, \| f \|_{\infty}}{h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left | \int_0^{h-\check{\tau}_1} \check{\alpha}(\check{Y}_u) \, \text{d} u \right | \right ] \leq \frac{2 h \alpha^* \| f \|_{\infty}}{h} \mathbb{P}_{(y,k)}(\check{\tau}_1 \leq h) \leq 4 h (\alpha^*)^2 \| f \|_{\infty}.$$
Let us prove that the first term converges uniformly to
![]() $\alpha(y)Kf(y) - (\alpha(y)-\check{\alpha}(y,k))f(y)$
, proving that
$\alpha(y)Kf(y) - (\alpha(y)-\check{\alpha}(y,k))f(y)$
, proving that
![]() ${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
. We have
${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
. We have
 \begin{multline*} \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \left | \check{Y}^{(0)}, \check{\tau}_1 \right. \right ] \right ] \\ = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \int_{z_1 \in E} \sum_{q \geq 0} \mathbb{E}^{ \check{Y}}_{(z_1,q)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \check{K} \left ( (Y_{\check{\tau}_1}^{\prime(0)},k) ;\; \text{d} z_1 \times \{ q \} \right ) \right ] . \end{multline*}
\begin{multline*} \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \mathbb{E}_{(y,k)} \left [ \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \left | \check{Y}^{(0)}, \check{\tau}_1 \right. \right ] \right ] \\ = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \int_{z_1 \in E} \sum_{q \geq 0} \mathbb{E}^{ \check{Y}}_{(z_1,q)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \check{K} \left ( (Y_{\check{\tau}_1}^{\prime(0)},k) ;\; \text{d} z_1 \times \{ q \} \right ) \right ] . \end{multline*}
We separate as before the cases
![]() $y \notin E_k$
and
$y \notin E_k$
and
![]() $y\in E_k$
. If
$y\in E_k$
. If
![]() $y \notin E_k$
, we obtain
$y \notin E_k$
, we obtain
 \begin{align} \dfrac{1}{h} \mathbb{E}_{(y,k)} \bigg[ {\mathbf 1}_{ \check{\tau}_1 \leq h} & \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \bigg ] \nonumber\\ &= \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E \mathbb{E}^{ \check{Y}}_{(z_1,k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] \nonumber\\ & \hspace{0.5cm}+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \nonumber \\ & \hspace{0.5cm} + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k-1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] . \end{align}
\begin{align} \dfrac{1}{h} \mathbb{E}_{(y,k)} \bigg[ {\mathbf 1}_{ \check{\tau}_1 \leq h} & \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \bigg ] \nonumber\\ &= \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E \mathbb{E}^{ \check{Y}}_{(z_1,k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] \nonumber\\ & \hspace{0.5cm}+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \nonumber \\ & \hspace{0.5cm} + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k-1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] . \end{align}
Let us show that the first term in (A.12) converges to
![]() $\alpha(y) Kf(y)$
:
$\alpha(y) Kf(y)$
:
 \begin{align*} & \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E \mathbb{E}^{\check{Y}}_{(z_1,k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] - \alpha(y) Kf(y) \\[5pt] & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E Q^{\check{Y}}_{h - \check{\tau}_1}(f\times {\mathbf 1}_\mathbb{N})(z_1,k) K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] - \alpha(y) Kf(y)\\ & = \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} \text{d} v \right ] - \alpha(y) Kf(y) \end{align*}
\begin{align*} & \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E \mathbb{E}^{\check{Y}}_{(z_1,k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] - \alpha(y) Kf(y) \\[5pt] & = \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\alpha \left ( Y_{\check{\tau}_1}^{\prime(0)} \right )}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right )} \int_E Q^{\check{Y}}_{h - \check{\tau}_1}(f\times {\mathbf 1}_\mathbb{N})(z_1,k) K(Y_{\check{\tau}_1}^{\prime(0)}, \text{d} z_1) \right ] - \alpha(y) Kf(y)\\ & = \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} \text{d} v \right ] - \alpha(y) Kf(y) \end{align*}
 \begin{align*} & = \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \text{d} v \right ] - \alpha(y) Kf(y) \\[5pt] & \hspace{0.5cm} + \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} -1 \right ) \text{d} v \right ]. \end{align*}
\begin{align*} & = \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \text{d} v \right ] - \alpha(y) Kf(y) \\[5pt] & \hspace{0.5cm} + \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} -1 \right ) \text{d} v \right ]. \end{align*}
But for the last term,
 \begin{multline*} \Big | \mathbb{E}^{\check{Y}}_{(y,k)} \Big [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} -1 \right ) \text{d} v \Big ] \Big | \\[5pt] \leq \alpha^* \| f \|_{\infty} \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u \, \text{d} v \right ] \leq 2 h ( \alpha^*)^2 \| f \|_{\infty}, \end{multline*}
\begin{multline*} \Big | \mathbb{E}^{\check{Y}}_{(y,k)} \Big [ \int_0^1 \alpha \left ( Y'_{\!\!\!hv} \right ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y'_{\!\!\!hv}, \text{d} z_1) \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} -1 \right ) \text{d} v \Big ] \Big | \\[5pt] \leq \alpha^* \| f \|_{\infty} \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \int_0^1 \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u \, \text{d} v \right ] \leq 2 h ( \alpha^*)^2 \| f \|_{\infty}, \end{multline*}
and from (the bivariate version of) (4.2), we can replace
![]() $ \mathbb{E}_{(y,k)}^{\check{Y}}$
by
$ \mathbb{E}_{(y,k)}^{\check{Y}}$
by
![]() $\mathbb{E}_{y}^Y$
in the other term to get
$\mathbb{E}_{y}^Y$
in the other term to get
 \begin{align*} & \left | \mathbb{E}_y^Y \left [ \int_0^1 \alpha( Y_{hv} ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y_{hv}, \text{d} z_1) \text{d} v \right ] - \alpha(y) Kf(y) \right | \\[5pt] & \leq \int_0^1 \left | \mathbb{E}_y^Y \left [ \alpha ( Y_{hv} ) K Q^Y_{h(1 - v)}f(Y_{hv}) - \alpha(Y_{hv}) Kf(Y_{hv}) \right ] \right | \, \text{d} v\\[5pt] & \hspace{5cm} + \int_0^1 \left | \mathbb{E}_y^Y \left [ \alpha(Y_{hv}) Kf(Y_{hv}) - \alpha(y) Kf(y) \right ] \right | \, \text{d} v \\[5pt] & \leq \alpha^* \int_0^1 \| KQ_{h(1-v)}^Yf - Kf \|_{\infty} \, \text{d} v + \int_0^1 \left | Q_{hv}^Y(\alpha \times Kf) (y) - (\alpha \times Kf)(y) \right | \, \text{d} v \\[5pt] & \leq \alpha^* \int_0^1 \| Q_{h(1-v)}^Yf - f \|_{\infty} \, \text{d} v + \int_0^1 \| Q_{hv}^Y(\alpha \times Kf) - (\alpha \times Kf) \|_{\infty} \, \text{d} v, \end{align*}
\begin{align*} & \left | \mathbb{E}_y^Y \left [ \int_0^1 \alpha( Y_{hv} ) \int_E Q^Y_{h(1 - v)}f(z_1) K(Y_{hv}, \text{d} z_1) \text{d} v \right ] - \alpha(y) Kf(y) \right | \\[5pt] & \leq \int_0^1 \left | \mathbb{E}_y^Y \left [ \alpha ( Y_{hv} ) K Q^Y_{h(1 - v)}f(Y_{hv}) - \alpha(Y_{hv}) Kf(Y_{hv}) \right ] \right | \, \text{d} v\\[5pt] & \hspace{5cm} + \int_0^1 \left | \mathbb{E}_y^Y \left [ \alpha(Y_{hv}) Kf(Y_{hv}) - \alpha(y) Kf(y) \right ] \right | \, \text{d} v \\[5pt] & \leq \alpha^* \int_0^1 \| KQ_{h(1-v)}^Yf - Kf \|_{\infty} \, \text{d} v + \int_0^1 \left | Q_{hv}^Y(\alpha \times Kf) (y) - (\alpha \times Kf)(y) \right | \, \text{d} v \\[5pt] & \leq \alpha^* \int_0^1 \| Q_{h(1-v)}^Yf - f \|_{\infty} \, \text{d} v + \int_0^1 \| Q_{hv}^Y(\alpha \times Kf) - (\alpha \times Kf) \|_{\infty} \, \text{d} v, \end{align*}
which converges to 0 as h goes to 0 by the dominated convergence theorem, using the fact that
![]() $f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
and
$f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
and
![]() $KC_0(E) \subset C_0(E)$
. This proves the convergence to
$KC_0(E) \subset C_0(E)$
. This proves the convergence to
![]() $\alpha(y) Kf(y)$
of the first term in (A.12). As for the second and third terms in (A.12), their sum converges to
$\alpha(y) Kf(y)$
of the first term in (A.12). As for the second and third terms in (A.12), their sum converges to
![]() $(\beta_k+\delta_k)f(y)=(\check{\alpha}(y,k) - \alpha(y))f(y)$
. Indeed, for any q,
$(\beta_k+\delta_k)f(y)=(\check{\alpha}(y,k) - \alpha(y))f(y)$
. Indeed, for any q,
 \begin{align*} & \dfrac{1}{h} \left | \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \mathbb{E}^{ \check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},q)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] - f(y) \right | \\ & = \dfrac{1}{h} \left | \int_0^h \mathbb{E}^{\check{Y}}_{(y,k)} \left [\mathbb{E}^{ Y}_{ Y'_{\!\!s}} \left [ f(Y_{h-s}) \right ] \text{e}^{- \int_0^s \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} \right ] \, \text{d} s - f(y) \right | \\ & \leq \left | \int_0^1 \mathbb{E}^{\check{Y}}_{(y,k)}\left [\mathbb{E}^{ Y}_{ Y'_{\!\!hv}} \left [ f(Y_{h(1-v)}) \right ] \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u}-1 \right ) \right ] \, \text{d} v \right | \\ & \hspace{5cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [\mathbb{E}^{ Y}_{ Y_{hv}} \left [ f(Y_{h(1-v)}) \right ] \right ] \, \text{d} v - f(y) \right | \end{align*}
\begin{align*} & \dfrac{1}{h} \left | \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{1}{\check{\alpha} \left ( Y_{\check{\tau}_1}^{\prime(0)},k \right ) } \mathbb{E}^{ \check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},q)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] - f(y) \right | \\ & = \dfrac{1}{h} \left | \int_0^h \mathbb{E}^{\check{Y}}_{(y,k)} \left [\mathbb{E}^{ Y}_{ Y'_{\!\!s}} \left [ f(Y_{h-s}) \right ] \text{e}^{- \int_0^s \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u} \right ] \, \text{d} s - f(y) \right | \\ & \leq \left | \int_0^1 \mathbb{E}^{\check{Y}}_{(y,k)}\left [\mathbb{E}^{ Y}_{ Y'_{\!\!hv}} \left [ f(Y_{h(1-v)}) \right ] \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u}-1 \right ) \right ] \, \text{d} v \right | \\ & \hspace{5cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [\mathbb{E}^{ Y}_{ Y_{hv}} \left [ f(Y_{h(1-v)}) \right ] \right ] \, \text{d} v - f(y) \right | \end{align*}
 \begin{align*} & \leq \int_0^1 \|f\|_{\infty} \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \left | \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u \right | \right] \, \text{d} v + \int_0^1 \left | \mathbb{E}_y^Y \left [ Q_{h(1-v)}^Y f(Y_{hv}) \right ] - f(y) \right | \, \text{d} v\\ & \leq \alpha^* \|f\|_{\infty} h + \int_0^1 \left | Q_h^Yf(y)-f(y) \right | \, \text{d} v \\ & \leq \alpha^* \|f\|_{\infty} h + \|Q_h^Yf-f\|_{\infty}, \end{align*}
\begin{align*} & \leq \int_0^1 \|f\|_{\infty} \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \left | \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k) \, \text{d} u \right | \right] \, \text{d} v + \int_0^1 \left | \mathbb{E}_y^Y \left [ Q_{h(1-v)}^Y f(Y_{hv}) \right ] - f(y) \right | \, \text{d} v\\ & \leq \alpha^* \|f\|_{\infty} h + \int_0^1 \left | Q_h^Yf(y)-f(y) \right | \, \text{d} v \\ & \leq \alpha^* \|f\|_{\infty} h + \|Q_h^Yf-f\|_{\infty}, \end{align*}
which converges to 0 as h goes to 0 by the dominated convergence theorem because
![]() $f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. This completes the proof of the claimed convergence of
$f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. This completes the proof of the claimed convergence of
![]() $A_4(h)$
when
$A_4(h)$
when
![]() $y\notin E_k$
.
$y\notin E_k$
.
Suppose now that
![]() $y \in E_k.$
The expansion carried out in (A.12) becomes in this case
$y \in E_k.$
The expansion carried out in (A.12) becomes in this case
 \begin{align} \dfrac{1}{h} \mathbb{E}_{(y,k)} \Big [ {\mathbf 1}_{ \check{\tau}_1 \leq h} & \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y_{h-\check{\tau}_1}) \right ] \Big ] \nonumber\\ =& \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{ \check{Y}}_{(z_1,k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\beta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ] \nonumber \\ & + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k-\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \nonumber \\ & + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k-1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\delta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ] \nonumber\\ &+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta(Y_{\check{\tau}_1}^{\prime(0)})-\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\delta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ]. \end{align}
\begin{align} \dfrac{1}{h} \mathbb{E}_{(y,k)} \Big [ {\mathbf 1}_{ \check{\tau}_1 \leq h} & \mathbb{E}^{\check{Y}}_{\check{C}_{\check{\tau}_1}} \left [ f(Y_{h-\check{\tau}_1}) \right ] \Big ] \nonumber\\ =& \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{ \check{Y}}_{(z_1,k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\beta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ] \nonumber \\ & + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\beta_k-\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] \right ] \nonumber \\ & + \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k-1)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\delta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ] \nonumber\\ &+ \dfrac{1}{h} \mathbb{E}_{(y,k)} \left [ {\mathbf 1}_{ \check{\tau}_1 \leq h} \dfrac{\delta(Y_{\check{\tau}_1}^{\prime(0)})-\delta_k}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \int_{E } \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k)} \left [ f(Y'_{h-\check{\tau}_1}) \right ] K_\delta \left ( Y_{\check{\tau}_1}^{\prime(0)} , \text{d} z_1 \right ) \right ]. \end{align}
The first, third, and fourth terms above can be treated exactly like the first term in (A.12) to prove that they converge uniformly towards
![]() $\beta(y)K_\beta f(y)$
,
$\beta(y)K_\beta f(y)$
,
![]() $\delta_k K_\delta f(y)$
, and
$\delta_k K_\delta f(y)$
, and
![]() $(\delta(y)-\delta_k)K_\delta f(y)$
, respectively, the sum of which is
$(\delta(y)-\delta_k)K_\delta f(y)$
, respectively, the sum of which is
![]() $\alpha(y)K f(y)$
. For the second term, we compute
$\alpha(y)K f(y)$
. For the second term, we compute
 \begin{align*} \Bigg | \dfrac{1}{h} &\mathbb{E}_{(y,k)} \Bigg [ {\mathbf 1}_{ \check{\tau}_1 \leq h}\dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \Bigg ] \Bigg ] - \beta(y)f(y) \right | \\ & \leq \left | \int_0^1 \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \beta(Y'_{\!\!hv}) \mathbb{E}^{ Y}_{Y'_{\!\!hv}} \left [ f(Y_{h(1-v)}) \right ] \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k+1) \, \text{d} u} -1 \right ) \right ] \, \text{d} v \right | \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) \mathbb{E}^{ Y}_{Y_{hv}} \left [ f(Y_{h(1-v)}) \right ] \right ] \, \text{d} v - \beta(y)f(y) \right | \\ & \leq \alpha^* \| f \|_{\infty} \int_0^1 \int_0^{hv} \mathbb{E}^{Y}_{y} \left[\check{\alpha}(Y_u,k+1)\right] \, \text{d} u \, \text{d} v \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) Q_{h(1-v)}^Y f(Y_{hv}) \right ] \, \text{d} v - \beta(y)f(y) \right | \end{align*}
\begin{align*} \Bigg | \dfrac{1}{h} &\mathbb{E}_{(y,k)} \Bigg [ {\mathbf 1}_{ \check{\tau}_1 \leq h}\dfrac{\beta(Y_{\check{\tau}_1}^{\prime(0)})}{\check{\alpha}(Y_{\check{\tau}_1}^{\prime(0)},k)} \mathbb{E}^{\check{Y}}_{ (Y_{\check{\tau}_1}^{\prime(0)},k+1)} \left [ f(Y'_{h-\check{\tau}_1}) \Bigg ] \Bigg ] - \beta(y)f(y) \right | \\ & \leq \left | \int_0^1 \mathbb{E}^{\check{Y}}_{(y,k)} \left [ \beta(Y'_{\!\!hv}) \mathbb{E}^{ Y}_{Y'_{\!\!hv}} \left [ f(Y_{h(1-v)}) \right ] \left ( \text{e}^{- \int_0^{hv} \check{\alpha}(Y'_{\!\!u},k+1) \, \text{d} u} -1 \right ) \right ] \, \text{d} v \right | \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) \mathbb{E}^{ Y}_{Y_{hv}} \left [ f(Y_{h(1-v)}) \right ] \right ] \, \text{d} v - \beta(y)f(y) \right | \\ & \leq \alpha^* \| f \|_{\infty} \int_0^1 \int_0^{hv} \mathbb{E}^{Y}_{y} \left[\check{\alpha}(Y_u,k+1)\right] \, \text{d} u \, \text{d} v \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) Q_{h(1-v)}^Y f(Y_{hv}) \right ] \, \text{d} v - \beta(y)f(y) \right | \end{align*}
 \begin{align*} & \leq (\alpha^*)^2 \| f \|_{\infty} h + \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) Q_{h(1-v)}^Y f(Y_{hv}) - \beta(Y_{hv})f(Y_{hv}) \right ] \, \text{d} v \right | \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) f(Y_{hv}) \right ] \, \text{d} v - \beta(y)f(y) \right | \\ & \leq (\alpha^*)^2 \| f \|_{\infty} h + \alpha^* \int_0^1 \| Q^Y_{h(1-v)} f - f \|_{\infty} \, \text{d} v + \int_0^1 \| Q^Y_{hv}(\beta \times f) - (\beta \times f) \|_{\infty} \, \text{d} v, \end{align*}
\begin{align*} & \leq (\alpha^*)^2 \| f \|_{\infty} h + \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) Q_{h(1-v)}^Y f(Y_{hv}) - \beta(Y_{hv})f(Y_{hv}) \right ] \, \text{d} v \right | \\ & \hspace{3cm}+ \left | \int_0^1 \mathbb{E}_y^Y \left [ \beta(Y_{hv}) f(Y_{hv}) \right ] \, \text{d} v - \beta(y)f(y) \right | \\ & \leq (\alpha^*)^2 \| f \|_{\infty} h + \alpha^* \int_0^1 \| Q^Y_{h(1-v)} f - f \|_{\infty} \, \text{d} v + \int_0^1 \| Q^Y_{hv}(\beta \times f) - (\beta \times f) \|_{\infty} \, \text{d} v, \end{align*}
which converges to 0 as h goes to 0 by the dominated convergence theorem because
![]() $f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. Given this result and the convergence already proven for the second term in (A.12), we deduce that the second term in (A.13) converges uniformly in (y, k) to
$f \in \mathcal{D}_{\mathcal{A}}^Y \subset C_0(E)$
. Given this result and the convergence already proven for the second term in (A.12), we deduce that the second term in (A.13) converges uniformly in (y, k) to
![]() $(\beta_k - \beta(y)) f(y) = (\check{\alpha}(y,k)-\alpha(y)) f(y).$
$(\beta_k - \beta(y)) f(y) = (\check{\alpha}(y,k)-\alpha(y)) f(y).$
The arguments for
![]() $y \notin E_k$
and
$y \notin E_k$
and
![]() $y \in E_k$
yield the same convergence results, so in conclusion
$y \in E_k$
yield the same convergence results, so in conclusion
that is,
![]() ${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
.
${\sup}_{(y,k) \in \check{E}} | A_4(h)| \underset{h \searrow 0}{\longrightarrow} 0$
.
To finish the proof, it remains to handle
![]() $A_5(h)$
using (2.3) where
$A_5(h)$
using (2.3) where
![]() $\check{N}_h^* \sim \mathcal{P}(2\alpha^*h)$
:
$\check{N}_h^* \sim \mathcal{P}(2\alpha^*h)$
:
which converges uniformly to 0 as h goes to 0.
A.7. Proof of Corollary 2
Let
This function is continuous and right-differentiable on
![]() $\mathbb{R}_+$
from Lemmas 4 and 5, and
$\mathbb{R}_+$
from Lemmas 4 and 5, and
![]() $\partial_+ G(t)/\partial t=0$
. So G is constant. But
$\partial_+ G(t)/\partial t=0$
. So G is constant. But
![]() $G(0)=0$
because
$G(0)=0$
because
![]() $s \geq 0 \mapsto \psi_{\mathcal{A} f}(s)$
is bounded. As a consequence we obtain (4.3). Moreover,
$s \geq 0 \mapsto \psi_{\mathcal{A} f}(s)$
is bounded. As a consequence we obtain (4.3). Moreover,
![]() $\mathcal{A} f \in C_0(E)$
, so by Lemma 4 the function
$\mathcal{A} f \in C_0(E)$
, so by Lemma 4 the function
![]() $s \geq 0 \mapsto \psi_{\mathcal{A} f}(s)$
is continuous. By (4.3) we deduce that
$s \geq 0 \mapsto \psi_{\mathcal{A} f}(s)$
is continuous. By (4.3) we deduce that
![]() $\psi_f$
is differentiable.
$\psi_f$
is differentiable.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/apr.2024.20. It provides the proofs not detailed in the main text. It also describes some topological properties of the space E endowed with the distance
![]() $d_1$
in the case of interacting particles in
$d_1$
in the case of interacting particles in
![]() $\mathbb{R}^d$
, as introduced in Section 2.4.
$\mathbb{R}^d$
, as introduced in Section 2.4.