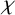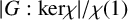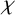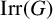1 Introduction
All groups in this paper are finite. We use the notation of [Reference Isaacs3]. Let
![]() $\chi $
be an irreducible character of a group G. Initially, the codegree of
$\chi $
be an irreducible character of a group G. Initially, the codegree of
![]() $\chi $
was defined as
$\chi $
was defined as
![]() $|G|/\chi (1)$
in [Reference Chillag, Mann and Manz1], whereas later, it was defined as
$|G|/\chi (1)$
in [Reference Chillag, Mann and Manz1], whereas later, it was defined as
![]() $|G:\mathrm {ker} \chi |/\chi (1)$
in [Reference Qian, Wang and Wei6]. We will follow the latter definition and take advantage of [Reference Qian, Wang and Wei6, Lemma 2.1]. The codegree of
$|G:\mathrm {ker} \chi |/\chi (1)$
in [Reference Qian, Wang and Wei6]. We will follow the latter definition and take advantage of [Reference Qian, Wang and Wei6, Lemma 2.1]. The codegree of
![]() $\chi $
will be denoted by
$\chi $
will be denoted by
![]() $\mathrm {a}(\chi )$
.
$\mathrm {a}(\chi )$
.
There are several results connecting the structure of the group G and the codegree values of certain subsets of irreducible characters of the group. For example, [Reference Xiaoyou and Lewis7, Theorem 1] shows that if G is solvable and the codegrees of all irreducible nonlinear, monomial, monolithic characters of G are p-power, where p is a fixed prime, then G has a normal Sylow p-subgroup. Let
![]() $N\lhd G$
. In [Reference Qian, Wang and Wei6], the codegree graph
$N\lhd G$
. In [Reference Qian, Wang and Wei6], the codegree graph
![]() $\Gamma (G|N)$
is defined. The vertex set
$\Gamma (G|N)$
is defined. The vertex set
![]() $\mathrm {V}(G|N )$
of
$\mathrm {V}(G|N )$
of
![]() $\Gamma (G|N )$
consists of all primes dividing some integer in
$\Gamma (G|N )$
consists of all primes dividing some integer in
![]() $\mathrm {cod}(G|N)$
, where
$\mathrm {cod}(G|N)$
, where
![]() $\mathrm {cod}(G|N)=\{\mathrm {a}(\chi ): \chi \in \mathrm {Irr}(G), N \not \leq \mathrm {ker}(\chi )\}$
. There is an edge between distinct primes
$\mathrm {cod}(G|N)=\{\mathrm {a}(\chi ): \chi \in \mathrm {Irr}(G), N \not \leq \mathrm {ker}(\chi )\}$
. There is an edge between distinct primes
![]() $p,q \in \mathrm {V}(G|N )$
if
$p,q \in \mathrm {V}(G|N )$
if
![]() $pq$
divides some integer in
$pq$
divides some integer in
![]() $\mathrm {cod}(G|N)$
. Several connections between this graph and the structure of both G and N are proved. For instance, [Reference Qian, Wang and Wei6, Theorem B] shows that if
$\mathrm {cod}(G|N)$
. Several connections between this graph and the structure of both G and N are proved. For instance, [Reference Qian, Wang and Wei6, Theorem B] shows that if
![]() $\Gamma (G|N)$
is disconnected, then it has exactly two connected components and the vertex set of
$\Gamma (G|N)$
is disconnected, then it has exactly two connected components and the vertex set of
![]() $\Gamma (G|N)$
coincides with the set of prime divisors of the order of G when
$\Gamma (G|N)$
coincides with the set of prime divisors of the order of G when
![]() $1<N\lhd G$
.
$1<N\lhd G$
.
The notion of ‘strongly monolithic character’ was introduced in [Reference Erkoç, Güngör and Özkan2, Definition 2.2]. Recall that an irreducible character
![]() $\chi $
is monolithic if
$\chi $
is monolithic if
![]() $G/\!\ker \chi $
has a unique minimal normal subgroup.
$G/\!\ker \chi $
has a unique minimal normal subgroup.
Definition 1.1. Let G be a group. A monolithic character
![]() $\chi $
of G is called strongly monolithic if one of the following conditions is satisfied:
$\chi $
of G is called strongly monolithic if one of the following conditions is satisfied:
-
(i)
 $\mathrm {Z}(\chi )=\ker \chi $
, where Z
$\mathrm {Z}(\chi )=\ker \chi $
, where Z
 $(\chi )=\{g \in G\ : |\chi (g)|=\chi (1)\}$
;
$(\chi )=\{g \in G\ : |\chi (g)|=\chi (1)\}$
; -
(ii)
 $G/\!\ker \chi $
is a p-group whose commutator group is its unique minimal normal subgroup.
$G/\!\ker \chi $
is a p-group whose commutator group is its unique minimal normal subgroup.
Groups all of whose nonlinear irreducible characters are monolithic and having exactly two strongly monolithic characters are classified in [Reference Özkan and Erkoç5, Theorem C].
In this paper, we provide some relations between the structure of a group G and the codegrees of (monomial) strongly monolithic characters of G.
2 Theorems and proofs
Let
![]() $\mathrm {Irr}_{\mathrm {sm}}(G)$
denote the set of strongly monolithic characters of a group G and let
$\mathrm {Irr}_{\mathrm {sm}}(G)$
denote the set of strongly monolithic characters of a group G and let
![]() $\mathrm {Irr}_{\mathrm {msm}}(G)$
denote the set of monomial characters in
$\mathrm {Irr}_{\mathrm {msm}}(G)$
denote the set of monomial characters in
![]() $\mathrm {Irr}_{\mathrm {sm}}(G)$
. We also set
$\mathrm {Irr}_{\mathrm {sm}}(G)$
. We also set
![]() $\mathrm {cod}_{\mathrm {sm}}(G)=\{ \mathrm {a}(\chi ): \chi \in \mathrm {Irr}_{\mathrm {sm}}(G)\}$
and
$\mathrm {cod}_{\mathrm {sm}}(G)=\{ \mathrm {a}(\chi ): \chi \in \mathrm {Irr}_{\mathrm {sm}}(G)\}$
and
![]() $\mathrm {cod}_{\mathrm {msm}}(G)=\{ \mathrm {a}(\chi ): \chi \in \mathrm {Irr}_{\mathrm {msm}}(G)\}$
.
$\mathrm {cod}_{\mathrm {msm}}(G)=\{ \mathrm {a}(\chi ): \chi \in \mathrm {Irr}_{\mathrm {msm}}(G)\}$
.
Let
![]() $N\lhd G$
and
$N\lhd G$
and
![]() $\chi $
be an irreducible character of G with
$\chi $
be an irreducible character of G with
![]() $N \leq \ker \chi $
. Then,
$N \leq \ker \chi $
. Then,
![]() $\chi $
may be viewed as an irreducible character of
$\chi $
may be viewed as an irreducible character of
![]() $G/N$
. It is known that
$G/N$
. It is known that
![]() $\chi $
is a (monomial) strongly monolithic character of G if and only if it is a (monomial) strongly monolithic character of
$\chi $
is a (monomial) strongly monolithic character of G if and only if it is a (monomial) strongly monolithic character of
![]() $G/N$
. Thus,
$G/N$
. Thus,
![]() $\mathrm {Irr}_{\mathrm {sm}}(G/N) \subseteq \mathrm {Irr}_{\mathrm {sm}}(G)$
and
$\mathrm {Irr}_{\mathrm {sm}}(G/N) \subseteq \mathrm {Irr}_{\mathrm {sm}}(G)$
and
![]() $\mathrm {Irr}_{\mathrm {msm}}(G/N) \subseteq \mathrm {Irr}_{\mathrm {msm}}(G)$
. In the proofs, we use these facts without further reference.
$\mathrm {Irr}_{\mathrm {msm}}(G/N) \subseteq \mathrm {Irr}_{\mathrm {msm}}(G)$
. In the proofs, we use these facts without further reference.
Let
![]() $\mathrm {h}(G)$
denote the Fitting length of a solvable group G.
$\mathrm {h}(G)$
denote the Fitting length of a solvable group G.
Lemma 2.1. Let G be a nonabelian group,
![]() $N\lhd G$
and m a fixed positive integer.
$N\lhd G$
and m a fixed positive integer.
-
(a) Then,
 $\mathrm{h}(N)\leq m$
if and only if
$\mathrm{h}(N)\leq m$
if and only if
 $\mathrm{h}(N\ker \chi /\!\ker \chi ) \leq m$
for all strongly monolithic characters
$\mathrm{h}(N\ker \chi /\!\ker \chi ) \leq m$
for all strongly monolithic characters
 $\chi $
of G.
$\chi $
of G. -
(b) Assume further G is solvable. Then,
 $\mathrm{h}(N) \leq m$
if and only if
$\mathrm{h}(N) \leq m$
if and only if
 $\mathrm{h}(N\ker \chi /\!\ker \chi ) \leq m$
for all monomial, strongly monolithic characters
$\mathrm{h}(N\ker \chi /\!\ker \chi ) \leq m$
for all monomial, strongly monolithic characters
 $\chi $
of G.
$\chi $
of G.
Proof. Clearly, the ‘if’ parts of both cases are true. To prove the ‘only if’ parts, assume that the assertions are false and let G be a minimal counterexample for both cases. First, we will show that G has a unique minimal normal subgroup. To see why this is true, assume that G has two distinct minimal normal subgroups
![]() $E_1$
and
$E_1$
and
![]() $E_2$
. Then, for all strongly monolithic characters
$E_2$
. Then, for all strongly monolithic characters
![]() $\chi $
of
$\chi $
of
![]() $G/E_i$
,
$G/E_i$
,
By the minimality of G, we obtain
![]() ${{\mathrm h}}(NE_i/E_i) \leq m\ (i=1,2)$
. Note that the 1–1 homomorphism
${{\mathrm h}}(NE_i/E_i) \leq m\ (i=1,2)$
. Note that the 1–1 homomorphism
![]() $\theta : G \rightarrow G/E_1 \times G/E_1$
given by
$\theta : G \rightarrow G/E_1 \times G/E_1$
given by
![]() $g \mapsto (gE_1, gE_2)$
allows us to see N as a subgroup of
$g \mapsto (gE_1, gE_2)$
allows us to see N as a subgroup of
![]() $NE_1/E_1 \times NE_2/E_2$
, which yields
$NE_1/E_1 \times NE_2/E_2$
, which yields
which is a contradiction. Thus, G has a unique minimal normal subgroup, say M, and so there exists a faithful irreducible character of G.
Now assume that
![]() $1< {\mathrm Z}(G)$
. Then,
$1< {\mathrm Z}(G)$
. Then,
![]() ${\mathrm h}(N)= {{\mathrm h}}(NZ(G)/Z(G)) \leq m$
, which contradicts the choice of G. Thus, G is centreless and so all faithful irreducible characters of G are strongly monolithic by [Reference Isaacs3, Lemma 2.27]. By the hypothesis of the theorem, we obtain the contradiction
${\mathrm h}(N)= {{\mathrm h}}(NZ(G)/Z(G)) \leq m$
, which contradicts the choice of G. Thus, G is centreless and so all faithful irreducible characters of G are strongly monolithic by [Reference Isaacs3, Lemma 2.27]. By the hypothesis of the theorem, we obtain the contradiction
![]() ${\mathrm h}(N) \leq m$
and this completes the proof of item (a).
${\mathrm h}(N) \leq m$
and this completes the proof of item (a).
Now let us assume that G is solvable and prove the ‘only if’ part of item (b). Now, G has a monomial strongly monolithic irreducible character. If
![]() $1<\Phi (G)$
, then
$1<\Phi (G)$
, then
![]() ${\mathrm h}(N)= {\mathrm h}(N \Phi (G)/\Phi (G)) \leq m$
, which contradicts the choice of G. Thus,
${\mathrm h}(N)= {\mathrm h}(N \Phi (G)/\Phi (G)) \leq m$
, which contradicts the choice of G. Thus,
![]() $\Phi (G)=1$
and so
$\Phi (G)=1$
and so
![]() $ \mathrm F(G)=M $
has a complement H in G. Let
$ \mathrm F(G)=M $
has a complement H in G. Let
![]() $ 1\neq \lambda $
be an irreducible character of M. Note that M is abelian and so
$ 1\neq \lambda $
be an irreducible character of M. Note that M is abelian and so
![]() $\lambda (1)=1 $
. Then,
$\lambda (1)=1 $
. Then,
![]() $K:=I_{G}(\lambda )= MI_{H}(\lambda )$
and
$K:=I_{G}(\lambda )= MI_{H}(\lambda )$
and
![]() $M\cap I_H(\lambda )=1$
since M is complemented by H in G. By [Reference Isaacs3, Problem 6.18], there exists an irreducible character
$M\cap I_H(\lambda )=1$
since M is complemented by H in G. By [Reference Isaacs3, Problem 6.18], there exists an irreducible character
![]() $\alpha $
of K such that
$\alpha $
of K such that
![]() $\alpha _M=\lambda $
. Note that
$\alpha _M=\lambda $
. Note that
![]() $\alpha (1)=\lambda (1)=1$
. By [Reference Isaacs3, Theorem 6.11],
$\alpha (1)=\lambda (1)=1$
. By [Reference Isaacs3, Theorem 6.11],
![]() $\alpha ^G $
is irreducible and faithful since
$\alpha ^G $
is irreducible and faithful since
![]() $\lambda \neq 1$
is an irreducible constituent of
$\lambda \neq 1$
is an irreducible constituent of
![]() $(\alpha ^G)_M$
. Thus,
$(\alpha ^G)_M$
. Thus,
![]() $\chi := \alpha ^G$
is faithful and monomial. We have already seen that all faithful irreducible characters of G are strongly monolithic. Thus,
$\chi := \alpha ^G$
is faithful and monomial. We have already seen that all faithful irreducible characters of G are strongly monolithic. Thus,
![]() $\chi $
is a monomial, strongly monolithic character of G and so by hypothesis,
$\chi $
is a monomial, strongly monolithic character of G and so by hypothesis,
![]() ${\mathrm h}(N)= {\mathrm h}(N\ker \chi /\!\ker \chi ) \leq m$
, which is a contradiction. This contradiction completes the proof.
${\mathrm h}(N)= {\mathrm h}(N\ker \chi /\!\ker \chi ) \leq m$
, which is a contradiction. This contradiction completes the proof.
From [Reference Lu and Meng4, Theorem 1.3],
![]() $\mathrm {h}(G) \leq |\mathrm {cod}(G)|-1$
for all solvable groups G. Here, we provide an upper bound for
$\mathrm {h}(G) \leq |\mathrm {cod}(G)|-1$
for all solvable groups G. Here, we provide an upper bound for
![]() $\mathrm {h}(G)$
in terms of the number of the codegrees of just monomial and strongly monolithic characters of a solvable group G.
$\mathrm {h}(G)$
in terms of the number of the codegrees of just monomial and strongly monolithic characters of a solvable group G.
Theorem 2.2. We have
![]() $\mathrm{h}(G) \leq |\mathrm {cod}_{\mathrm {msm}}(G)|+1$
for all finite solvable groups G.
$\mathrm{h}(G) \leq |\mathrm {cod}_{\mathrm {msm}}(G)|+1$
for all finite solvable groups G.
Proof. Let G be a minimal counterexample. Assume that G has no faithful, monomial, strongly monolithic character. By the minimality of G,
for all
![]() $\chi \in \mathrm {Irr}_{\mathrm {msm}}(G)$
. However now, by using Lemma 2.1,
$\chi \in \mathrm {Irr}_{\mathrm {msm}}(G)$
. However now, by using Lemma 2.1,
![]() $\mathrm {h}(G) \leq |\mathrm {cod}_{\mathrm {msm}}(G)|+1$
, which is a contradiction. Thus, G has at least one faithful, monomial, strongly monolithic character and so G has a unique minimal normal subgroup, say M.
$\mathrm {h}(G) \leq |\mathrm {cod}_{\mathrm {msm}}(G)|+1$
, which is a contradiction. Thus, G has at least one faithful, monomial, strongly monolithic character and so G has a unique minimal normal subgroup, say M.
Now assume that
![]() $N\lhd G$
and
$N\lhd G$
and
![]() ${\mathrm h}(G/N)={\mathrm h}(G)$
. We argue that
${\mathrm h}(G/N)={\mathrm h}(G)$
. We argue that
![]() $N=1$
. Otherwise, by the minimality of G,
$N=1$
. Otherwise, by the minimality of G,
which is a contradiction. Thus,
![]() $N=1$
. This implies that
$N=1$
. This implies that
![]() $\Phi (G)=1={\mathrm Z}(G)$
and so
$\Phi (G)=1={\mathrm Z}(G)$
and so
![]() $ \mathrm F(G)=M $
has a complement H in G.
$ \mathrm F(G)=M $
has a complement H in G.
Let
![]() $\psi $
be an irreducible character of
$\psi $
be an irreducible character of
![]() $G/M$
with codegree as large as possible. Since
$G/M$
with codegree as large as possible. Since
![]() $\mathrm {F}(G)=M \leq \ker \psi $
, G has an irreducible character
$\mathrm {F}(G)=M \leq \ker \psi $
, G has an irreducible character
![]() $\theta $
with
$\theta $
with
![]() $a(\psi )< a(\theta )$
by [Reference Lu and Meng4, Lemma 2.11]. Note that
$a(\psi )< a(\theta )$
by [Reference Lu and Meng4, Lemma 2.11]. Note that
![]() $\theta $
is faithful since it does not lie in
$\theta $
is faithful since it does not lie in
![]() $\mathrm {Irr}(G/M)$
. Now let
$\mathrm {Irr}(G/M)$
. Now let
![]() $\chi $
be a faithful irreducible character of G with the largest possible codegree among the faithful irreducible characters of G. We claim that
$\chi $
be a faithful irreducible character of G with the largest possible codegree among the faithful irreducible characters of G. We claim that
![]() $\chi $
is monomial. To see why this is true, let
$\chi $
is monomial. To see why this is true, let
![]() $\lambda $
be an irreducible constituent of
$\lambda $
be an irreducible constituent of
![]() $\chi _M$
. Clearly,
$\chi _M$
. Clearly,
![]() $\lambda \neq 1$
. Now
$\lambda \neq 1$
. Now
![]() $K:=I_{G}(\lambda )= MI_{H}(\lambda )$
and
$K:=I_{G}(\lambda )= MI_{H}(\lambda )$
and
![]() $M\cap I_H(\lambda )=1$
since M is complemented by H in G. Thus, there exists an irreducible character
$M\cap I_H(\lambda )=1$
since M is complemented by H in G. Thus, there exists an irreducible character
![]() $\alpha $
of K such that
$\alpha $
of K such that
![]() $\alpha _M=\lambda $
. Note that
$\alpha _M=\lambda $
. Note that
![]() $\alpha (1)=\lambda (1)=1$
. From [Reference Isaacs3, Theorem 6.11],
$\alpha (1)=\lambda (1)=1$
. From [Reference Isaacs3, Theorem 6.11],
![]() $\alpha ^G $
is irreducible and faithful since
$\alpha ^G $
is irreducible and faithful since
![]() $\lambda \neq 1$
is an irreducible constituent of
$\lambda \neq 1$
is an irreducible constituent of
![]() $(\alpha ^G)_M$
. Moreover,
$(\alpha ^G)_M$
. Moreover,
![]() $\chi =\beta ^G$
for some
$\chi =\beta ^G$
for some
![]() $\beta \in \mathrm {Irr}(K)$
. By the choice of
$\beta \in \mathrm {Irr}(K)$
. By the choice of
![]() $\chi $
,
$\chi $
,
which forces
![]() $\beta (1)=1$
. This means
$\beta (1)=1$
. This means
![]() $\chi $
is monomial as desired. Therefore,
$\chi $
is monomial as desired. Therefore,
![]() $\chi $
is a monomial strongly monolithic character of G and so
$\chi $
is a monomial strongly monolithic character of G and so
![]() $\mathrm {a}(\chi )\in \mathrm {cod}_{\mathrm {msm}}(G)$
. However,
$\mathrm {a}(\chi )\in \mathrm {cod}_{\mathrm {msm}}(G)$
. However,
![]() ${a(\chi )\notin \mathrm {cod}_{\mathrm {msm}}(G/M)}$
since
${a(\chi )\notin \mathrm {cod}_{\mathrm {msm}}(G/M)}$
since
![]() $a(\psi )<a(\theta ) \leq a(\chi )$
which means
$a(\psi )<a(\theta ) \leq a(\chi )$
which means
![]() $|\mathrm {cod}_{\mathrm {msm}}(G/M)| \leq |\mathrm {cod}_{\mathrm {msm}}(G)|-1$
. Thus,
$|\mathrm {cod}_{\mathrm {msm}}(G/M)| \leq |\mathrm {cod}_{\mathrm {msm}}(G)|-1$
. Thus,
This final contradiction completes the proof.
Let
![]() $G=\mathrm {SL}(2,3)$
. Then,
$G=\mathrm {SL}(2,3)$
. Then,
![]() ${\mathrm h}(G)=2=|\mathrm {cod}_{\mathrm {msm}}(G)|+1$
. This example shows that the upper bound in Theorem 2.2 is the best possible.
${\mathrm h}(G)=2=|\mathrm {cod}_{\mathrm {msm}}(G)|+1$
. This example shows that the upper bound in Theorem 2.2 is the best possible.
Theorem 2.3. Let G be a finite nonabelian group. If there exists a fixed prime number p such that
![]() $\chi (1)_p=|G:\ker \chi |_p>1$
for all strongly monolithic characters
$\chi (1)_p=|G:\ker \chi |_p>1$
for all strongly monolithic characters
![]() $\chi $
of G, then
$\chi $
of G, then
![]() ${{\mathrm h}}(G)\leq |\mathrm {cod}_{\mathrm {sm}}(G)|+1$
. In particular, G is solvable.
${{\mathrm h}}(G)\leq |\mathrm {cod}_{\mathrm {sm}}(G)|+1$
. In particular, G is solvable.
Proof. Let G be a minimal counterexample and note that the hypothesis is inherited by factor groups. Assume that G has no faithful strongly monolithic character. By the minimality of G,
for every
![]() $\chi \in \mathrm {Irr}_{\mathrm {sm}}(G)$
. However now, by using Lemma 2.1, we obtain
$\chi \in \mathrm {Irr}_{\mathrm {sm}}(G)$
. However now, by using Lemma 2.1, we obtain
![]() $\mathrm {h}(G) \leq |\mathrm {cod}_{\mathrm {sm}}(G)|+1$
, which is a contradiction. Thus, G has at least one faithful strongly monolithic character and this implies that all faithful irreducible characters of G are strongly monolithic. We also deduce that G has a unique minimal normal subgroup, say M.
$\mathrm {h}(G) \leq |\mathrm {cod}_{\mathrm {sm}}(G)|+1$
, which is a contradiction. Thus, G has at least one faithful strongly monolithic character and this implies that all faithful irreducible characters of G are strongly monolithic. We also deduce that G has a unique minimal normal subgroup, say M.
Let
![]() $\chi $
be an irreducible character of G which does not contain M in its kernel. Then,
$\chi $
be an irreducible character of G which does not contain M in its kernel. Then,
![]() $\chi $
is strongly monolithic since it is faithful and so p does not divide
$\chi $
is strongly monolithic since it is faithful and so p does not divide
![]() $\mathrm {a} (\chi )$
by hypothesis. Therefore, p does not divide the order of M and the action of P on M is Frobenius by [Reference Qian, Wang and Wei6, Theorem A], where P is a Sylow p-subgroup of G. Hence, G is solvable since M is nilpotent and
$\mathrm {a} (\chi )$
by hypothesis. Therefore, p does not divide the order of M and the action of P on M is Frobenius by [Reference Qian, Wang and Wei6, Theorem A], where P is a Sylow p-subgroup of G. Hence, G is solvable since M is nilpotent and
![]() $G/M$
is solvable by the minimality of G.
$G/M$
is solvable by the minimality of G.
Now we argue that
![]() $\Phi (G)=1$
. Otherwise, we would have
$\Phi (G)=1$
. Otherwise, we would have
which is a contradiction. Thus,
![]() $\Phi (G)=1$
which yields
$\Phi (G)=1$
which yields
![]() $\mathrm F(G)=M$
. By using [Reference Lu and Meng4, Lemma 2.11], we deduce that
$\mathrm F(G)=M$
. By using [Reference Lu and Meng4, Lemma 2.11], we deduce that
![]() $|\mathrm {cod}_{\mathrm {sm}}(G/M)| \leq |\mathrm {cod}_{\mathrm {sm}}(G)|-1 $
and so
$|\mathrm {cod}_{\mathrm {sm}}(G/M)| \leq |\mathrm {cod}_{\mathrm {sm}}(G)|-1 $
and so
which is the final contradiction completing the proof.
It is known that if all irreducible character degrees of a finite group G are odd, then G is solvable. We provide an analogue of this fact in terms of codegrees by having an assumption on just the strongly monolithic characters of G.
Theorem 2.4. Let G be a group and assume that
![]() $4\nmid \mathrm{a}(\chi )$
for all strongly monolithic characters
$4\nmid \mathrm{a}(\chi )$
for all strongly monolithic characters
![]() $\chi $
of G. Then, G is solvable. In particular, if
$\chi $
of G. Then, G is solvable. In particular, if
![]() $\mathrm{a}(\chi )$
is odd for all strongly monolithic characters
$\mathrm{a}(\chi )$
is odd for all strongly monolithic characters
![]() $\chi $
of G, then G is solvable.
$\chi $
of G, then G is solvable.
Proof. Assume that the theorem is false and let G be a minimal counterexample. Let
![]() $1< N \lhd G$
. Then, since
$1< N \lhd G$
. Then, since
![]() $G/N$
is solvable by the minimality of G, we conclude that N is not solvable. In particular, N cannot be abelian. Thus,
$G/N$
is solvable by the minimality of G, we conclude that N is not solvable. In particular, N cannot be abelian. Thus,
![]() ${\mathrm Z}(G)=1$
.
${\mathrm Z}(G)=1$
.
It is not difficult to see that G has a unique minimal normal subgroup, say M. Note that M is not abelian. Let
![]() $1\neq \lambda $
be an irreducible character of M and choose an irreducible character
$1\neq \lambda $
be an irreducible character of M and choose an irreducible character
![]() $\chi $
of G with
$\chi $
of G with
![]() $[\chi _M, \lambda ]\neq 0$
. Note that
$[\chi _M, \lambda ]\neq 0$
. Note that
![]() $\chi $
is faithful and so strongly monolithic. Since
$\chi $
is faithful and so strongly monolithic. Since
![]() $4\nmid \mathrm {a}(\chi )$
, we see that
$4\nmid \mathrm {a}(\chi )$
, we see that
![]() $4\nmid \mathrm a(\lambda )$
by [Reference Qian, Wang and Wei6, Lemma 2.1(2)], which means M also satisfies the hypothesis of the theorem. It turns out that
$4\nmid \mathrm a(\lambda )$
by [Reference Qian, Wang and Wei6, Lemma 2.1(2)], which means M also satisfies the hypothesis of the theorem. It turns out that
![]() $M=G$
is a simple group. From the equality
$M=G$
is a simple group. From the equality
 $$ \begin{align*} |G|=\sum_{\chi \in \mathrm{Irr}(G)}\chi(1)^2=1+\sum_{1 \neq \chi \in \mathrm{Irr}(G)}\chi(1)^2, \end{align*} $$
$$ \begin{align*} |G|=\sum_{\chi \in \mathrm{Irr}(G)}\chi(1)^2=1+\sum_{1 \neq \chi \in \mathrm{Irr}(G)}\chi(1)^2, \end{align*} $$
we deduce that G has a nonprincipal irreducible character, say
![]() $\chi $
, with odd degree. Since G is a simple group, we see that
$\chi $
, with odd degree. Since G is a simple group, we see that
![]() $\chi $
is a strongly monolithic character and so
$\chi $
is a strongly monolithic character and so
![]() $4$
does not divide
$4$
does not divide
![]() $\mathrm a(\chi )= |G|/\chi (1)$
by hypothesis. This forces the order of the Sylow 2-subgroup of G to be 2 since
$\mathrm a(\chi )= |G|/\chi (1)$
by hypothesis. This forces the order of the Sylow 2-subgroup of G to be 2 since
![]() $\chi (1)$
is odd. This implies that G has a normal 2-complement. However, this contradicts the simplicity of G.
$\chi (1)$
is odd. This implies that G has a normal 2-complement. However, this contradicts the simplicity of G.
Corollary 2.5. Let G be a group and assume that
![]() $\mathrm{a}(\chi )$
is a prime power for all irreducible characters
$\mathrm{a}(\chi )$
is a prime power for all irreducible characters
![]() $\chi $
of G. Then, G is solvable.
$\chi $
of G. Then, G is solvable.
Proof. Note that all vertices of the graph
![]() $\Gamma (G)$
in [Reference Qian, Wang and Wei6] are isolated and so G has at most two prime divisors by [Reference Qian, Wang and Wei6, Theorem E(2)]. Hence, G is solvable.
$\Gamma (G)$
in [Reference Qian, Wang and Wei6] are isolated and so G has at most two prime divisors by [Reference Qian, Wang and Wei6, Theorem E(2)]. Hence, G is solvable.
Now we generalise Corollary 2.5 by obtaining the solvability of G with the assumption that the codegrees of only the strongly monolithic characters of G are prime powers.
Theorem 2.6. Let G be a group and assume that
![]() $\mathrm a(\chi )$
is a prime power for all strongly monolithic characters
$\mathrm a(\chi )$
is a prime power for all strongly monolithic characters
![]() $\chi $
of G. Then, G is solvable.
$\chi $
of G. Then, G is solvable.
Proof. Assume that the theorem is false and let G be a minimal counterexample. It is not difficult to see that G has a unique minimal normal subgroup, say M.
Let
![]() $1< N \lhd G$
. Then, since
$1< N \lhd G$
. Then, since
![]() $G/N$
is solvable by the minimality of G, we conclude that N is not solvable. Thus,
$G/N$
is solvable by the minimality of G, we conclude that N is not solvable. Thus,
![]() ${\mathrm Z}(G)=1$
and M is nonsolvable. It follows that G has a faithful irreducible character and all such characters are strongly monolithic.
${\mathrm Z}(G)=1$
and M is nonsolvable. It follows that G has a faithful irreducible character and all such characters are strongly monolithic.
Let
![]() $1\neq \lambda $
be an irreducible character of M and choose an irreducible character
$1\neq \lambda $
be an irreducible character of M and choose an irreducible character
![]() $\chi $
of G with
$\chi $
of G with
![]() $[\chi _M, \lambda ]\neq 0$
. Note that
$[\chi _M, \lambda ]\neq 0$
. Note that
![]() $\chi $
is faithful and so strongly monolithic since M is the unique minimal normal subgroup of G. Thus,
$\chi $
is faithful and so strongly monolithic since M is the unique minimal normal subgroup of G. Thus,
![]() $\mathrm a(\chi )$
is a prime power by hypothesis. Now,
$\mathrm a(\chi )$
is a prime power by hypothesis. Now,
![]() $\mathrm a(\lambda )$
is a prime power too, since
$\mathrm a(\lambda )$
is a prime power too, since
![]() $\mathrm a(\lambda ) \mid \mathrm a(\chi )$
by [Reference Qian, Wang and Wei6, Lemma 2.1(2)]. Thus, M also satisfies the hypothesis of the theorem which means
$\mathrm a(\lambda ) \mid \mathrm a(\chi )$
by [Reference Qian, Wang and Wei6, Lemma 2.1(2)]. Thus, M also satisfies the hypothesis of the theorem which means
![]() $G=M$
is a simple group. However, this contradicts [Reference Qian, Wang and Wei6, Lemma 2.3].
$G=M$
is a simple group. However, this contradicts [Reference Qian, Wang and Wei6, Lemma 2.3].
Let p be a prime divisor of the order of a group G and let
![]() $\mathscr {A}$
be either the set of nonlinear, monomial, monolithic characters in
$\mathscr {A}$
be either the set of nonlinear, monomial, monolithic characters in
![]() $\mathrm {Irr(}G\mathrm {)}$
or the set of nonlinear, monomial, monolithic characters in
$\mathrm {Irr(}G\mathrm {)}$
or the set of nonlinear, monomial, monolithic characters in
![]() $\mathrm {IBr(}G\mathrm {)}$
, where IBr(G) denotes the set of irreducible p-Brauer characters of G. If G is solvable and
$\mathrm {IBr(}G\mathrm {)}$
, where IBr(G) denotes the set of irreducible p-Brauer characters of G. If G is solvable and
![]() $\mathrm a(\chi )$
is a power of p for all
$\mathrm a(\chi )$
is a power of p for all
![]() $\chi $
in
$\chi $
in
![]() $\mathscr {A}$
, then G has a normal Sylow p-subgroup by [Reference Xiaoyou and Lewis7, Theorem 1]. We give an analogue of this theorem. Note that we do not assume that G is solvable. In fact, under the hypothesis of the following theorem, we deduce the solvability of G from Theorem 2.6.
$\mathscr {A}$
, then G has a normal Sylow p-subgroup by [Reference Xiaoyou and Lewis7, Theorem 1]. We give an analogue of this theorem. Note that we do not assume that G is solvable. In fact, under the hypothesis of the following theorem, we deduce the solvability of G from Theorem 2.6.
Theorem 2.7. Let G be a group and let p be a fixed prime number. If
![]() $\mathrm{a}(\chi )$
is a power of p for all strongly monolithic characters
$\mathrm{a}(\chi )$
is a power of p for all strongly monolithic characters
![]() $\chi $
of G, then G has a normal Sylow p-subgroup.
$\chi $
of G, then G has a normal Sylow p-subgroup.
Proof. Assume that the theorem is false and let G be a minimal counterexample. First, we argue that G has a unique minimal normal subgroup. To see why this is true, let M and N be two different minimal normal subgroups of G. By the minimality of G, the factor groups
![]() $G/M$
,
$G/M$
,
![]() $G/N$
and so
$G/N$
and so
![]() $G/M \times G/N$
have normal Sylow p-subgroups. Thus, G, which is isomorphic to a subgroup of
$G/M \times G/N$
have normal Sylow p-subgroups. Thus, G, which is isomorphic to a subgroup of
![]() $G/M \times G/N$
, also has a normal Sylow p-subgroup, which is a contradiction with the choice of G. Thus, G has a unique minimal normal subgroup, say M, and so has a faithful irreducible character.
$G/M \times G/N$
, also has a normal Sylow p-subgroup, which is a contradiction with the choice of G. Thus, G has a unique minimal normal subgroup, say M, and so has a faithful irreducible character.
Now we claim that
![]() ${\mathrm Z}(G)=1$
. Otherwise, M is contained in
${\mathrm Z}(G)=1$
. Otherwise, M is contained in
![]() ${\mathrm Z}(G)$
and so normalises P, where P is a Sylow p-subgroup of G. Since G is a minimal counterexample, we obtain
${\mathrm Z}(G)$
and so normalises P, where P is a Sylow p-subgroup of G. Since G is a minimal counterexample, we obtain
![]() $PM \lhd G$
and so, by using a Frattini argument, we see that
$PM \lhd G$
and so, by using a Frattini argument, we see that
![]() $G=N_G(P)M$
, which means P is normal in G which is not the case. Thus,
$G=N_G(P)M$
, which means P is normal in G which is not the case. Thus,
![]() ${\mathrm Z}(G)=1$
as desired. This means all faithful irreducible characters of G are strongly monolithic. It turns out that G has a faithful strongly monolithic character, say
${\mathrm Z}(G)=1$
as desired. This means all faithful irreducible characters of G are strongly monolithic. It turns out that G has a faithful strongly monolithic character, say
![]() $\chi $
. Then,
$\chi $
. Then,
![]() $|G|/\chi (1)=\mathrm a(\chi )$
is a power of p by hypothesis. Thus,
$|G|/\chi (1)=\mathrm a(\chi )$
is a power of p by hypothesis. Thus,
![]() $\mathrm O_p(G) \neq 1$
by [Reference Chillag, Mann and Manz1, Theorem 4] and it follows that
$\mathrm O_p(G) \neq 1$
by [Reference Chillag, Mann and Manz1, Theorem 4] and it follows that
![]() $M\leq \mathrm O_p(G) \leq P $
, which means
$M\leq \mathrm O_p(G) \leq P $
, which means
![]() $P/M$
is a Sylow p-subgroup of
$P/M$
is a Sylow p-subgroup of
![]() $G/M$
. By the minimality of G, we see that
$G/M$
. By the minimality of G, we see that
![]() $P/M \lhd G/M$
, which is equivalent to
$P/M \lhd G/M$
, which is equivalent to
![]() $P \lhd G$
. However, this is a contradiction.
$P \lhd G$
. However, this is a contradiction.