Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-17T13:25:33.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of the Kiefer–Wolfowitz algorithm in the presence of discontinuities

Part of: Mathematical finance Stochastic systems and control

Published online by Cambridge University Press:  23 September 2022

Miklós Rásonyi Open the ORCID record for Miklós Rásonyi [Opens in a new window]  and
Kinga Tikosi
Miklós Rásonyi*
Affiliation:
Rényi Institute, Budapest, and Mathematical Institute, Warsaw
Kinga Tikosi*
Affiliation:
Rényi Institute, Budapest, and Mathematical Institute, Warsaw
*
*Postal address: Reáltanoda utca 13-15, 1053 Budapest, Hungary; ul. Śniadeckich 8, 00-656 Warszawa, Poland.
*Postal address: Reáltanoda utca 13-15, 1053 Budapest, Hungary; ul. Śniadeckich 8, 00-656 Warszawa, Poland.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we estimate the expected error of a stochastic approximation algorithm where the maximum of a function is found using finite differences of a stochastic representation of that function. An error estimate of the order 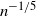$n^{-1/5}$ for the nth iteration is achieved using suitable parameters. The novelty with respect to previous studies is that we allow the stochastic representation to be discontinuous and to consist of possibly dependent random variables (satisfying a mixing condition).

Keywords

Stochastic approximationdependent datathreshold strategies

MSC classification

Primary: 93E35: Stochastic learning and adaptive control
Secondary: 91G60: Numerical methods (including Monte Carlo methods)
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 382 - 406
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkhagen, M. et al. (2021). On stochastic gradient Langevin dynamics with dependent data streams in the logconcave case. Bernoulli 27, 1–33.CrossRefGoogle Scholar
Benveniste, A., Métivier, M. and Priouret, P. (1990). Adaptive Algorithms and Stochastic Approximations. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Cartea, Á., Jaimungal, S. and Penalva, J. (2015). Algorithmic and High-Frequency Trading. Cambridge University Press.Google Scholar
Chau, N. H., Kumar, C., Rásonyi, M. and Sabanis, S. (2019). On fixed gain recursive estimators with discontinuity in the parameters. ESAIM Prob. Statist. 23, 217–244.CrossRefGoogle Scholar
Chau, N. H. et al. (2021). On stochastic gradient Langevin dynamics with dependent data streams: the fully non-convex case. SIAM J. Math. Data Sci. 3, 959–986.CrossRefGoogle Scholar
Durmus, A. and Moulines, É. (2017). Nonasymptotic convergence analysis for the unadjusted Langevin algorithm. Ann. Appl. Prob. 27, 1551–1587.CrossRefGoogle Scholar
Fort, G, Moulines, É., Schreck, A. and Vihola, M. (2016). Convergence of Markovian stochastic approximation with discontinuous dynamics. SIAM J. Control Optimization 54, 866–893.CrossRefGoogle Scholar
Gerencsér, L. (1989). On a class of mixing processes. Stochastics 26, 165–191.Google Scholar
Gerencsér, L. (1992). Rate of convergence of recursive estimators. SIAM J. Control Optimization 30, 1200–1227.CrossRefGoogle Scholar
Gerencsér, L. (1998). SPSA with state-dependent noise—a tool for direct adaptive control. In Proc. 37th IEEE Conference on Decision and Control, Institute of Electrical and Electronics Engineers, Piscataway, NJ, pp. 3451–3456.CrossRefGoogle Scholar
Gerencsér, L. (1999). Convergence rate of moments in stochastic approximation with simultaneous perturbation gradient approximation and resetting. IEEE Trans. Automatic Control 44, 894–905.CrossRefGoogle Scholar
Glasserman, P. and Yao, D. D. (1992). Some guidelines and guarantees for common random numbers. Manag. Sci. 38, 884–908.CrossRefGoogle Scholar
Guasoni, P., Tolomeo, A. and Wang, G. (2019). Should commodity investors follow commodities’ prices? SIAM J. Financial Math. 10, 466–490.CrossRefGoogle Scholar
Kiefer, J. and Wolfowitz, J. (1952). Stochastic estimation of the maximum of a regression function. Ann. Math. Statist. 23, 462–466.CrossRefGoogle Scholar
Kushner, H. J. and Clark, D. S. (1978). Stochastic Approximation for Constrained and Unconstrained Systems. Springer, New York.CrossRefGoogle Scholar
Laruelle, S. and Pagès, G. (2012). Stochastic approximation with averaging innovation applied to finance. Monte Carlo Meth. Appl. 18, 1–51.CrossRefGoogle Scholar
Ljung, L.. (1977). Analysis of recursive stochastic algorithms. IEEE Trans. Automatic Control 22, 551–575.CrossRefGoogle Scholar
Leung, T. and Li, X. (2015). Optimal Mean Reversion Trading. World Scientific, Singapore.Google Scholar
Robbins, H. and Monro, S. (1951). A stochastic approximation method. Ann. Math. Statist. 22, 400–407.CrossRefGoogle Scholar
Sacks, J. (1958). Asymptotic distribution of stochastic approximation procedures. Ann. Math. Statist. 29, 373–405.CrossRefGoogle Scholar
Sichel, H. S., Kleingeld, W. J. and Assibey-Bonsu, W. (1992). A comparative study of three frequency-distribution models for use in ore valuation. J. S. Afr. Inst. Mining Metallurgy 92, 91–99.Google Scholar
TraderGav.com, What is mean reversion trading strategy. Available at https://tradergav.com/what-is-mean-reversion-trading-strategy.Google Scholar
Trading Strategy Guides, (2021). Mean reversion trading strategy with a sneaky secret. Available at https://tradingstrategyguides.com/mean-reversion-trading-strategy.Google Scholar
Trading, Warrior. Mean reversion trading: is it a profitable strategy? Available at https://www.warriortrading.com/mean-reversion.Google Scholar