1. INTRODUCTION
Considerable attention has been given in recent years to the use of thin foil targets irradiated by high-intensity laser pulses for the ion acceleration. Experimental results have shown the advantage of thin targets for collimated ion acceleration, when high-intensity circularly polarized laser beams are normally incident on the target surface (see, for instance, Kar et al., Reference Kar, Borghesi, Bulanov, Key, Liseykina, Macchi, Mackinnon, Patel, Romagnani, Schiavi and Willi2008, Reference Kar, Kakolee, Cherchez, Doria, Macchi, McKenna, Neely, Osterholz, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2013; Henig et al., Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer-terVehn, Tajima, Nickels, Sandner and Habs2009; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009; Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010; Prasad et al., Reference Prasad, Andreev, Ter-Avetisyan, Doria, Quinn, Romagnani, Brenner, Carroll, Dover, Neely, Foster, Gallegos, Green, McKenna, Najmudin, Palmer, Schreiber, Streeter, Tresca, Zepf and Borghesi2011). In addition, laser technology makes it possible now to generate extremely short (femtosecond) and intense (>1022 W/cm2) laser pulses (Mourou et al., Reference Mourou, Tajima and Bulanov2006; Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cechetti, Fuchs, Galimberti, Gizzi, Grismayer, Liseykina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007). Under these conditions, the formation of a double layer in the dense target plasmas by the ponderomotive force of these intense electromagnetic pulses has been considered in several publications (see, for instance, Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaume, Sokolov and Mourou2009; Eliasson et al., Reference Eliasson, Liu, Shao, Sagdeev and Shukla2009; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009; Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Eliezer et al., Reference Eliezer, Nissim, Martinez-Val, Mima and Hora2014). Initially, the radiation pressure (the ponderomotive force per unit area, or the flow of delivered momentum by the wave to the target per unit time and surface) of the incident laser beam pushes the electrons at the target surface producing a sharp density gradient at the surface of the target. There is a build-up of the electron density at this ponderomotively steepened surface, which creates a large space-charge, giving rise to a longitudinal electric field. The electrons on the propagation path of the laser wave are pushed forward by the strong ponderomotive force radiation pressure, while the induced space-charge electric field pulls the ions behind them forming a double layer, consisting of an electron layer located in the downstream (which include a trapped ion population), and an ion charge layer behind it that follows accordingly. The entire structure at the interface of the laser–target interaction is accelerated as a whole. Eliezer et al. (Reference Eliezer, Nissim, Martinez-Val, Mima and Hora2014) have recently studied the stability of such double-layer structure and shown that the laser radiation pressure can accelerate this double-layer structure to very high velocities without breaking it by the Rayleigh–Taylor instability. A recent study and review on radiation pressure acceleration can be found in Schmidt et al. (Reference Schmidt, Boine-Frankenheim and Mulser2015a, Reference Schmidt, Boine-Frankenheim and Mulserb).
In the present work, we apply an Eulerian Vlasov code for the numerical solution of a one-dimensional (1D) relativistic Vlasov–Maxwell equations, to study the ponderomotive force ion acceleration and the formation and evolution of double layers when a high-intensity circularly polarized laser beam is normally incident on the surface of a dense plasma target. The code is noiseless and allows us to follow in details the evolution of the system, especially the phase-space structures of the distribution functions. Three different simulations are presented by varying the thickness of the dense target and/or the intensity of the laser pulse, which are key factors in the formation of the double-layer structure and in the ion acceleration and the formation of neutral plasma jets. We consider an overdense plasma, with the electron density n = 100n cr, where n cr is the critical density. The case of a high density is of interest, because under the condition of an intense laser beam incident on a solid target, the solid target ionizes very rapidly, in a few cycles of the light wave, and the laser beam interacts directly with a plasma with a very high density. In the case of a circular polarization of the laser beam, there is a non-oscillatory radiation pressure applied at the target surface by the incident laser wave. This advantage of circular polarization, especially in reducing electron heating, has been mentioned in several publications (see, for instance, Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaume, Sokolov and Mourou2009; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009; Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010; Kar et al., Reference Kar, Kakolee, Cherchez, Doria, Macchi, McKenna, Neely, Osterholz, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2013). A characteristic parameter of high-power laser beams is the normalized vector potential or quiver momentum ![]() $\left\vert {{\mathop{a}\limits^{\rightharpoonup}}_{\bot}} \right\vert = \left\vert {e {\mathop{A}\limits^{\rightharpoonup}}_ {\bot} /M_{\rm e} c} \right\vert = a_0 $, where
$\left\vert {{\mathop{a}\limits^{\rightharpoonup}}_{\bot}} \right\vert = \left\vert {e {\mathop{A}\limits^{\rightharpoonup}}_ {\bot} /M_{\rm e} c} \right\vert = a_0 $, where ![]() ${\mathop{A}\limits^{\rightharpoonup}}_{\bot} $ is the vector potential of the wave. We choose for a 0 two values, a 0 = 50 and a 0 = 100, for the three simulations we present. For a circularly polarized wave
${\mathop{A}\limits^{\rightharpoonup}}_{\bot} $ is the vector potential of the wave. We choose for a 0 two values, a 0 = 50 and a 0 = 100, for the three simulations we present. For a circularly polarized wave ![]() $2a_0^2 = I{\rm \lambda} _0^2 /1.368 \times {\rm 10}^{{\rm 18}} $, where I is the intensity in W cm−2 and λ0 the laser wavelength in microns. Deuterium plasma is used with M i/M e = 2 × 1836, where M i is the deuterium mass and M e the electron mass. In the first two cases considered, the thickness of the target is kept constant, and the amplitude of the vector potential of the laser is varied from a 0 = 50 to a 0 = 100. In the case a 0 = 50, the laser energy is transferred to the double layer within the target volume itself, and an ion population trapped by the electrons contributes to the formation of a neutral plasma jet. Two events of neutral plasma jet formation takes place during the transition through the target volume in the case with a 0 = 50, which will be followed in details. In the case with a 0 = 100, the whole thin foil is transformed into a double layer and the ponderomotive force acceleration persists beyond the transition through the initial target volume. Electrons pile up in a thin layer at the rear surface (Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010), and only the ions in this electron layer are effectively accelerated, this layer ultimately leading to a neutral plasma jet. In these first two cases, there is no transmission of the laser beam across the moving target. In the third case with a 0 = 100 and a reduced thickness of the target, the entire electron cloud is initially accelerated and completely expelled by the radiation pressure, and the ions are attracted and accelerated by the electron cloud. The main pulse interacts with a modified inhomogeneous plasma. The laser wave travels through the target, does not significantly decay within the target, and there is a transmitted field across the target. Electrons are ejected from the back of the target in the forward direction. D'Humières et al. (Reference d'Humières, Lefebvre, Gremillet and Malka2005, Reference d'Humières, Brantov, Bychenkov, Yu and Tikhonchuk2013) for instance have discussed the features of proton acceleration with high-intensity lasers as a function of the target thickness, and have pointed out that below a given thickness a fraction of the laser energy is transmitted through the target, while above this critical thickness the target is opaque to the laser energy. So the three cases studied show substantial differences in the evolution toward the formation of neutral plasma jets, and in the evolution of the corresponding phase-space structures of the distribution functions.
$2a_0^2 = I{\rm \lambda} _0^2 /1.368 \times {\rm 10}^{{\rm 18}} $, where I is the intensity in W cm−2 and λ0 the laser wavelength in microns. Deuterium plasma is used with M i/M e = 2 × 1836, where M i is the deuterium mass and M e the electron mass. In the first two cases considered, the thickness of the target is kept constant, and the amplitude of the vector potential of the laser is varied from a 0 = 50 to a 0 = 100. In the case a 0 = 50, the laser energy is transferred to the double layer within the target volume itself, and an ion population trapped by the electrons contributes to the formation of a neutral plasma jet. Two events of neutral plasma jet formation takes place during the transition through the target volume in the case with a 0 = 50, which will be followed in details. In the case with a 0 = 100, the whole thin foil is transformed into a double layer and the ponderomotive force acceleration persists beyond the transition through the initial target volume. Electrons pile up in a thin layer at the rear surface (Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010), and only the ions in this electron layer are effectively accelerated, this layer ultimately leading to a neutral plasma jet. In these first two cases, there is no transmission of the laser beam across the moving target. In the third case with a 0 = 100 and a reduced thickness of the target, the entire electron cloud is initially accelerated and completely expelled by the radiation pressure, and the ions are attracted and accelerated by the electron cloud. The main pulse interacts with a modified inhomogeneous plasma. The laser wave travels through the target, does not significantly decay within the target, and there is a transmitted field across the target. Electrons are ejected from the back of the target in the forward direction. D'Humières et al. (Reference d'Humières, Lefebvre, Gremillet and Malka2005, Reference d'Humières, Brantov, Bychenkov, Yu and Tikhonchuk2013) for instance have discussed the features of proton acceleration with high-intensity lasers as a function of the target thickness, and have pointed out that below a given thickness a fraction of the laser energy is transmitted through the target, while above this critical thickness the target is opaque to the laser energy. So the three cases studied show substantial differences in the evolution toward the formation of neutral plasma jets, and in the evolution of the corresponding phase-space structures of the distribution functions.
2. THE RELEVANT EQUATIONS OF THE EULERIAN VLASOV CODE AND THE NUMERICAL METHOD
The relevant equations for the problem we are studying have been presented previously (see, for instance, Shoucri, Reference Shoucri2008a, Reference Shoucrib, Reference Shoucri and Shoucri2010, Reference Shoucri2012; Shoucri & Afeyan, Reference Shoucri and Afeyan2010; Shoucri et al., Reference Shoucri, Lavocat-Dubuis, Matte and Vidal2011). We rewrite these equations in order to fix the notation. Time t is normalized to the inverse laser wave frequency ω−1, length is normalized to l 0 = cω−1, velocity and momentum are normalized respectively to the velocity of light c and to M ec, where M e is the electron mass. The electric field is in units of M eωc/e. The 1D Vlasov equations for the electrons and ions distribution functions f e,i (x, p xe,i, t) verify the relation:
 $$\displaystyle{{\partial f_{{\rm e,i}}} \over {\partial t}} + \displaystyle{{\,p_{x{\rm e,i}}} \over {m_{{\rm e,i}} {\rm \gamma}_{{\rm e,i}}}} \displaystyle{{\partial f_{{\rm e,i}}} \over {\partial x}} + \left( { \mp E_x - \displaystyle{1 \over {2m_{{\rm e,i}} {\rm \gamma} _{{\rm e,i}}}} \displaystyle{{\partial a_ \bot ^2} \over {\partial x}}} \right)\displaystyle{{\partial f_{{\rm e,i}}} \over {\partial p_{x{\rm e,i}}}} = 0,$$
$$\displaystyle{{\partial f_{{\rm e,i}}} \over {\partial t}} + \displaystyle{{\,p_{x{\rm e,i}}} \over {m_{{\rm e,i}} {\rm \gamma}_{{\rm e,i}}}} \displaystyle{{\partial f_{{\rm e,i}}} \over {\partial x}} + \left( { \mp E_x - \displaystyle{1 \over {2m_{{\rm e,i}} {\rm \gamma} _{{\rm e,i}}}} \displaystyle{{\partial a_ \bot ^2} \over {\partial x}}} \right)\displaystyle{{\partial f_{{\rm e,i}}} \over {\partial p_{x{\rm e,i}}}} = 0,$$where γe,i = [1 + (p xe,i/m e,i)2 + (a ⊥/m e,i)2]1/2.
The upper sign in Eq. (1) is for the electron equation and the lower sign for the ion equation, and subscripts e and i denote electrons and ions, respectively. In our normalized units m e = 1, and m i = M i/M e is the ratio of ion-to-electron masses. The longitudinal electric field E x is calculated from Ampère's law:
The transverse electric field ![]() ${\mathop{E}\limits^{\rightharpoonup}}_\bot $ is calculated from the relations:
${\mathop{E}\limits^{\rightharpoonup}}_\bot $ is calculated from the relations:
![]() ${\mathop{a}\limits^{\rightharpoonup}}_\bot = e\vec A/M_{\rm e} c$ is the normalized vector potential.
${\mathop{a}\limits^{\rightharpoonup}}_\bot = e\vec A/M_{\rm e} c$ is the normalized vector potential.
The transverse electromagnetic fields E y, Bz and E z, By for the circularly polarized wave obey Maxwell's equations. With E ± = E y ± B z and F ± = E z ± B y, we write these equations in the following form:
which are integrated along their vacuum characteristics x = ±t. In our normalized units we have the following expressions for the normal current densities:
 $${\mathop {J}\limits^{\rightharpoonup}}_{\bot} = {\mathop {J}\limits^{\rightharpoonup}}_{\bot{\rm e}} + {\mathop {J}\limits^{\rightharpoonup}}_{\bot {\rm i}} ;\quad {\mathop {J}\limits^{\rightharpoonup}}_{\bot {\rm e},{\rm i}} = - \displaystyle{{{\mathop {a}\limits^{\rightharpoonup}}_\bot} \over {m_{{\rm e,i}}}} \int_{ - \infty} ^{ + \infty} {\displaystyle{{\,f_{{\rm e,i}}} \over {{\rm \gamma} _{{\rm e,i}}}}} dp_{x{\rm e,i}}. $$
$${\mathop {J}\limits^{\rightharpoonup}}_{\bot} = {\mathop {J}\limits^{\rightharpoonup}}_{\bot{\rm e}} + {\mathop {J}\limits^{\rightharpoonup}}_{\bot {\rm i}} ;\quad {\mathop {J}\limits^{\rightharpoonup}}_{\bot {\rm e},{\rm i}} = - \displaystyle{{{\mathop {a}\limits^{\rightharpoonup}}_\bot} \over {m_{{\rm e,i}}}} \int_{ - \infty} ^{ + \infty} {\displaystyle{{\,f_{{\rm e,i}}} \over {{\rm \gamma} _{{\rm e,i}}}}} dp_{x{\rm e,i}}. $$The numerical scheme applies a direct solution method of the Vlasov equation as a partial differential equation in phase space. Recent comparisons presented in (Shoucri et al. Reference Shoucri, Lavocat-Dubuis, Matte and Vidal2011) between this code and a particle-in-cell code (Gibbon & Bell, Reference Gibbon and Bell1992), for the problem of ion acceleration and plasma jets formation when a circularly polarized laser beam is normally incident on the surface of an overdense plasma, have shown good agreement between the macroscopic quantities calculated with both codes. We mention also several other applications of Eulerian Vlasov codes to the interaction of a laser beam incident on an overdense plasma (Ruhl & Mulser, Reference Ruhl and Mulser1995; Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005; Eliasson et al., Reference Eliasson, Liu, Shao, Sagdeev and Shukla2009; Grassi et al., Reference Grassi, Fedeli, Macchi, Bulanov and Pegoraro2014).
3. RESULTS
In all the cases considered, we have a forward-propagating circularly polarized laser beam entering the system at the left boundary (x = 0), where the forward-propagating fields at x = 0 are given by E + = 2E 0P r(t)cos (τ) and F − = −2E 0P r(t)sin (τ), E +and F −are defined in Eq. (4). In our normalized units, E 0 = a 0. In the previous expression, τ = t − 1.5t p and t p = 12 (i.e., slightly less than two laser periods) is the pulse duration [full-width at half-maximum (FWHM)] of the laser beam. Time is in units of ω−1. For the time dependence of the laser pulse, the Gaussian shape factor P r(t) is given by:
The forward-propagating laser beam behaves as a Gaussian pulse in time, which reaches its peak at t = 1.5t p = 18. The units of time and space can be easily translated into units of ![]() ${\rm \omega} _{{\rm pe}}^{ - 1} $ and c/ωpe by multiplying them by a factor of 10, since in our calculations ωpe/ω = 10, which corresponds to the value n 0/n cr = 100, which is used in the present work.
${\rm \omega} _{{\rm pe}}^{ - 1} $ and c/ωpe by multiplying them by a factor of 10, since in our calculations ωpe/ω = 10, which corresponds to the value n 0/n cr = 100, which is used in the present work.
3.1. The case of a plasma slab with a width L p = 1.497c/ω and a 0 = 50.
The initial distribution functions for electrons and ions are Maxwellian with temperatures T e = 1 keV for the electrons and T i = 0.1 keV for the ions. We use N = 12,500 grid points in space, and in momentum space we use 1000 grid points for the electrons and 1400 grid points for the ions (the extrema of the electron and ion momentum are ±5 and ±700, respectively). The length of the system is L = 10 in units c/ω. From these parameters we have a grid spacing Δx = 8 × 10−4 and we use a time-step Δt = Δx. We have a vacuum region of length L vac = 2.812 on the left side in front of the plasma slab. The steep ramp in density at the plasma edge on each side of the uniform flat top density of the slab target has a length L edge = 0.24. The length of the plasma slab, with a flat top density of 1 (normalized to 100n cr) is L p = 1.497, and the length of the vacuum region to the right of the slab is 5.211, for a total length of L = 10 The target and its edges thus extend initially from 2.812 to 4.789, with a flat plateau in the density between 3.052 and 4.549. In our units the skin depth c/ωpe = (c/ω)(ω/ωpe) = 0.1c/ω, so the length of the plasma slab with a flat top density of 1 is L p = 1.497 is about 15 skin depths. In free space ω = k for the electromagnetic wave, and as λ = 2π, the condition that λ ≫ L edge is well satisfied.
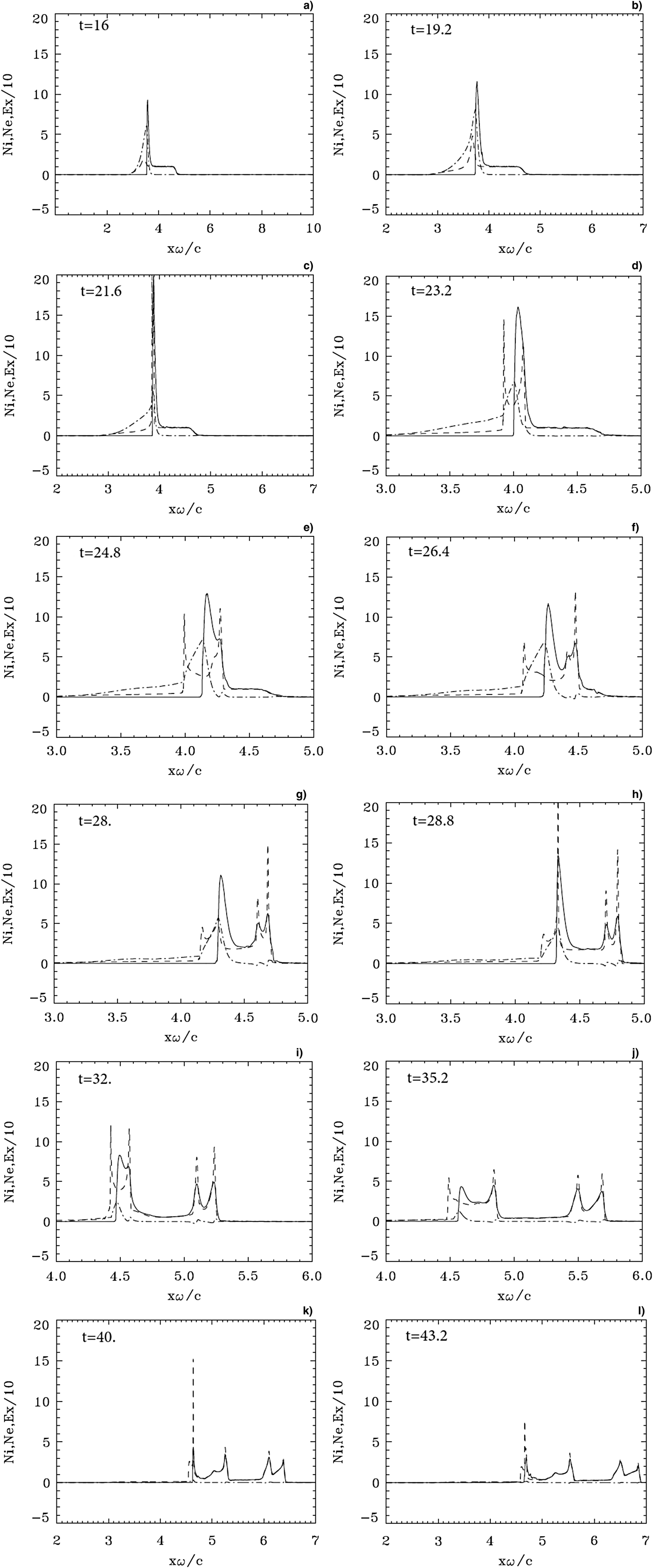
At the beginning the signal in Eq. (6) applied at x = 0 has to travel a distance x ≈ 2.8 to reach the target edge. The ponderomotive force of the radiation pressure will then push the electron edge of the plasma slab. We present in Figure 1 the electron and ion density profiles at times t = 16, 19.2, 21.6, 23.2, 24.8, 26.4, 28.0, 28.8, 32., 35.2, 40.0, and 43.2 (full curves for the electrons and dashed curves for the ions). The electric field (dashed-dotted curves) is also plotted (divided by a factor of 10 to display it on the same scale). In Figure 1a, the profiles at t = 16 show the steep edge of the electron density under the effect of the radiation pressure of the ponderomotive force (full curve), which has moved to the position x ≈ 3.5 (from the initial position x ≈ 2.8) forming a shock profile. There is only little movement in the initial ion density profile (dashed curve), whose edge is still at about x ≈ 2.8. The build-up of the electron density at the target surface creates a space charge, giving rise to a longitudinal electric field. The dash-dotted curve is the electric field resulting from the charge separation, and its penetration in the plasma at the sharp gradient at the surface of the target in Figures 1a and 1b is of the order of 0.1c/ω, which is the value of the skin depth in our normalized units as mentioned previously. As the electromagnetic field has a circular polarization, the ponderomotive force keeps a non-oscillating pressure at the target surface. The temporal variation of the electromagnetic field is very rapid as the FWHM is less than twice the laser period [see Eq. (6)]. The longitudinal electric field builds up very rapidly in time at the plasma–vacuum interface. Figure 1a is presented in the whole domain x = (0, 10) to show the location of the profiles in the simulation box (we will however, modify the horizontal and vertical scales in the course of our discussion to emphasize some important points). In Figure 1b at t = 19.2, we note that the ion density profile (dashed curve) starts to move at the front edge, while the remaining part of the slab specimen to the right of the electron peak still remains unchanged. Figures 3a and 3b for the phase space of the electrons show how the electrons are pushed by the radiation pressure at the left edge, and the electron distribution function shows some strong heating (note that the vertical scales are not the same). From Eq. (6), the laser intensity reaches a peak at a time 1.5t p = 18 at the boundary x = 0. This peak reaches the target surface at the position x ≈ 3.9 at a time t ≈ 21.6 in Figure 1c (we see indeed in Fig. 4 below that the forward-propagating wave E + reaches its peak at the target surface at t = 21.6). Thus, the maximum laser intensity reaches the target edge at about the time we observe the strong acceleration of the ions at the target surface in Figure 1c. This strong acceleration of the ions is also observed in Figure 2a in the phase space of the ions, and the position of the edge in Figure 1c indicates that the accelerated ions are on the vertical edge in Figure 2a, at x ≈ 3.9. The phase space of the electron distribution function in Figure 3c indicates a strong heating of the electron distribution function at the target surface at t ≈ 21.6 (note the variation of the vertical and horizontal scales in Fig. 3). The rapid build-up of the ion density at the target surface has been reported and discussed in several publications (Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005, Reference Macchi, Veghini, Liseykina and Pegoraro2010; Shoucri, Reference Shoucri and Shoucri2010, Reference Shoucri2012; Shoucri & Afeyan, Reference Shoucri and Afeyan2010; Shoucri et al., Reference Shoucri, Lavocat-Dubuis, Matte and Vidal2011). In Figure 1d at t ≈ 23.2, in Figure 1e at t ≈ 24.8 and in Figure 1f at t ≈ 26.4, we see that the ion peak is decreasing slightly leaving a small ion tail behind it, and a double-layer structure is formed, a geometry close to what has been discussed in Figure 1 of Schlegel et al. (Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009), and in Figure 2 of Eliezer et al. (Reference Eliezer, Nissim, Martinez-Val, Mima and Hora2014). This double-layer structure is supported by the radiation pressure of the ponderomotive force of the laser beam. Between the electron and ion peaks in the double layer, there is an electric field providing the restoring force, supported by the space charge provided by the ion population between the ion and electron density peaks (see Fig. 2b). The penetration of this electric field in the steep edge electron layer at the left is of the order of the skin depth 0.1, as we can verify from Figures 1d–1h. Electrons on the propagation path of the laser wave are bunched and pushed forward by the radiation pressure of the ponderomotive force, pulling the ion behind them, and trapping another ion population in their layer. The electron peak is still traveling along the slab (the original slab extends up to x ≈ 4.7 as is clear from Figs 1d and 1e for instance). The left steep edge of the electrons is still subjected to the radiation pressure of the incident laser beam. In Figure 1f at t ≈ 26.4and Figure 1g at t ≈ 28, the right front of the electron density profile propagating in the forward direction crosses the right edge of the original slab around x ≈ 4.7, and forms with the trapped ions a neutral structure which appears in the right half of the electron beam profile in Figure 1h. In Figure 1h at t ≈ 28.8, the electrons at the left surface of the target bunch again under the effect of the ponderomotive force of the laser beam, and we see again the formation of an electron spike and another rapid acceleration event of the ions at the left edge of the electron density profile, which reaches a peak momentum of about 250 in Figure 2c (this second formation of an ion peak takes place while the steep electron edge at the left is still located within the initial slab position). This second acceleration event coincides again with a peak at the target surface of the incident wave E + in Figure 4 at t ≈ 28.8 (note that the reflection of the laser wave in Figure 4 takes place indeed at the position of the electron target surface). The double bump at the right of Figure 1h and the peak on the left are clearly showing their signature in the phase-space structure of the electrons in Figure 3e. The subsequent evolution of the system at and after t ≈ 32 is presented in Figures 1i–1l. A neutral double peak is now free streaming at the right of the system, and the left side of the electron density profile evolves towards the formation of another neutral structure; however the effect of the laser beam pressure is still present, maintaining a small double layer at the target surface. This evolution toward a second neutral structure can be followed in Figures 1j–1l, where the decrease of the incident laser pressure allows the small charge separation at the left edge to decrease and evolve toward neutrality. The two double-bumpy structures are shown in the electron phase space in Figure 3f at t ≈ 35.2. Hence, we finally have two neutral plasma jet bunches with different velocities leaving the original target volume. In Figure 1k at t ≈ 40, we observe another small ion acceleration event, which appears at very low momentum in Figure 2e at t ≈ 40, and as a sharp edge in the phase-space structure at the left in Figure 3g. In Figure 1l at t ≈ 43.2, we essentially see two neutral bunches, corresponding to the two peaks around 300 and 500 in Figure 2f, and the two vorticity-like structures in the electron phase space in Figure 3h. Note the cooling of the electron population in the evolution process leading to the neutral plasma jets.

Fig. 1. Electron (full curves) and ion (dashed curves) density profiles. The electric field (dashed-dotted curves, divided by a factor of 10). Plots at times: (a) t = 16, (b) t = 19.2, (c) t = 21.6, (d) t = 23.2, (e) t = 24.8, (f) t = 26.4, (g) t = 28, (h) t = 28.8, (i) t = 32, (j) t = 35.2, (k) t = 40, (l) t = 43.2.

Fig. 2. Phase-space plots of the ion distribution function. Plots at times: (a) t = 16, (b) t = 25.6, (c) t = 28.8, (d) t = 35.2, (e) t = 40, (f) t = 43.2.

Fig. 3. Phase-space plots of the electron distribution function. Plots at times: (a) t = 11.2, (b) t = 16, (c) t = 21.6, (d) t = 25.6, (e) t = 28.8, (f) t = 35.2 (g) t = 40, (h) t = 43.2.

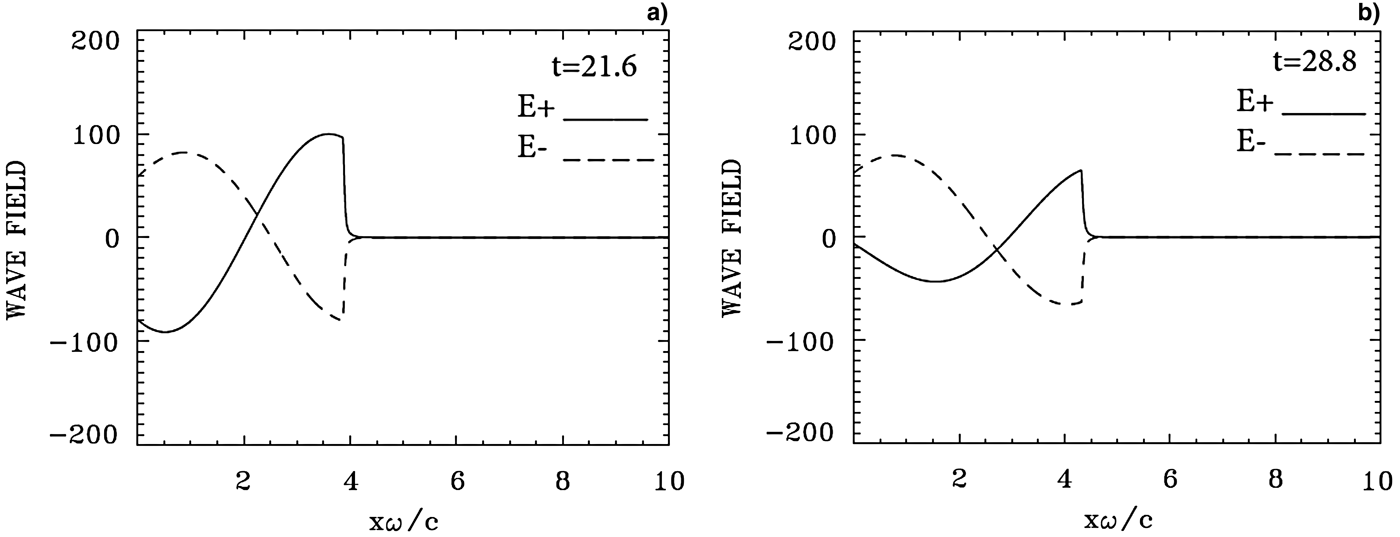
Fig. 4. Incident wave E + (full curve) and reflected wave E − (dashed curve) at t = 21.6 and 28.8. In this case the penetration of the electromagnetic wave in the electron layer at the surface is of the order of the skin depth 0.1c/ω.
As mentioned previously Figure 2 shows the phase-space contour plots of the ion distribution function at t = 16 (during the first rapid acceleration phase of the ions at the target surface presented in Fig. 1c) at t = 25.6, 28.8 (during the second rapid acceleration phase of the ions at the target surface presented in Fig. 1h), and at t = 35.2, 40, and 43.2 when the two neutral plasma jets are formed, and are free-streaming as indicated in Figure 1l. From Figure 2f the ions reach a peak in momentum of about 500. For the maximum momentum M iυ/M ec ≈ 500, we have υ/c ≈ 500/(2 × 1836) = 0.136. A close value of the velocity can also be calculated by a simple inspection following the edge of the shock-like structure of the neutral plasma bump which is free-streaming at the right in Figure 1j at the position x ≈ 5.7at t ≈ 35.2 and in Figure 1l at the position x ≈ 6.8 at t ≈ 43.2, which leads to an average velocity υ/c = 0.1375. This corresponds to an energy of the deuterium ions of ![]() $M_{\rm i} {\rm \upsilon} ^2 /2 = M_{\rm i} c^2 ({\rm \upsilon} /c)^2 /2 =$
$M_{\rm i} {\rm \upsilon} ^2 /2 = M_{\rm i} c^2 ({\rm \upsilon} /c)^2 /2 =$![]() $ 938 \times {\rm 0}{\rm. 0189} = 17.73\,{\rm MeV}$.
$ 938 \times {\rm 0}{\rm. 0189} = 17.73\,{\rm MeV}$.
From Figure 2f the smaller peak of the ions reach a value in momentum of about 340. This corresponds to υ/c = 0.092. A close value for the velocity can also be calculated by simple inspection following the edge of the second shock-like structure of the neutral plasma bump which is free-streaming in Figure 1j at the position x ≈ 4.9 at t ≈ 35.2, and in Figure 1l at the position x ≈ 5.7 at t ≈ 43.2, which leads to an average velocity υ/c = 0.1. This corresponds to an energy of the deuterium ions of the smaller peak of M iυ2/2 = 9.38 MeV.
In Figure 3, we present the phase-space contour plots of the electron distribution function at t = 11.2, 16, 21.6, 25.6, 28.8, 35.2.0, 40, and 40.3. The steep electron edge which is observed at the target surface in Figures 3a–3c is due to the effect of the radiation pressure of the wave, which pushes and rapidly heats the electrons at the target surface. The longitudinal electric field builds up very rapidly in time at the plasma–vacuum interface. Figure 3c at t = 21.6 corresponds to the time where we observe the first rapid acceleration of the ions at the target surface, mentioned in relation to Figure 1c (note the variation of the vertical scale). In Figure 3e at t = 28.8, the vortices-like structures at the right are for the electrons propagating in the neutral plasma jet, ejected from the back of the target in the forward direction, providing the electronic population which neutralizes the ion beam (see Fig. 1h). In Figures 3f–3h, we see the vortices-like structures corresponding to the two bunches of the neutral plasma jets as in Figure 1l. Note the cooling of the electron population when trapped with the ions in the neutral plasma jets. The ions in the neutral plasma jet are free streaming and are not accelerated any more.
Figure 4 presents in the left figure the forward-propagating wave E + [full curve, see Eq. (4) for definitions] and the backward reflected wave E − (dashed curve), at t = 21.6 (at the time of the rapid acceleration of the ions at the target surface observed in Fig. 1c), and at t = 28.8 (at the time of the second rapid acceleration of the ions at the target surface observed in Fig. 1h). We note that the maximum of the incident wave E + is equal to the peak of the laser pulse at t = 21.6 as previously mentioned. Reflection of the wave (dashed curve) takes place at the position of the electron spike at the surface of the target. The electromagnetic wave damps in the plasma over a distance of the order of the skin depth, equal to 0.1 in our normalized units as previously mentioned. There is no penetration in this case of the electromagnetic wave through the target. The strong initial increase of the ion and electron densities at the wave-front plasma-edge interface makes the plasma more opaque. Note that reflection of the laser wave takes place exactly at the position of the surface electron layer. The curves for F + and F − are similar. Note that when E + is at a peak value, F − is zero, and vice versa. Similarly when the reflected wave E − is at its maximum, the backward propagating wave F + is zero.
3.2. The case of a plasma slab with L p = 1.497c/ω and a 0= 100
We use the same target as in Section 3.1 and the same parameters, with the exception that in the present case a 0 = 100. In momentum space, we use 1600 grid points for the electrons and 3400 grid points for the ions (extrema of the electron momentum are ±8 and ±1700 for the ion momentum).
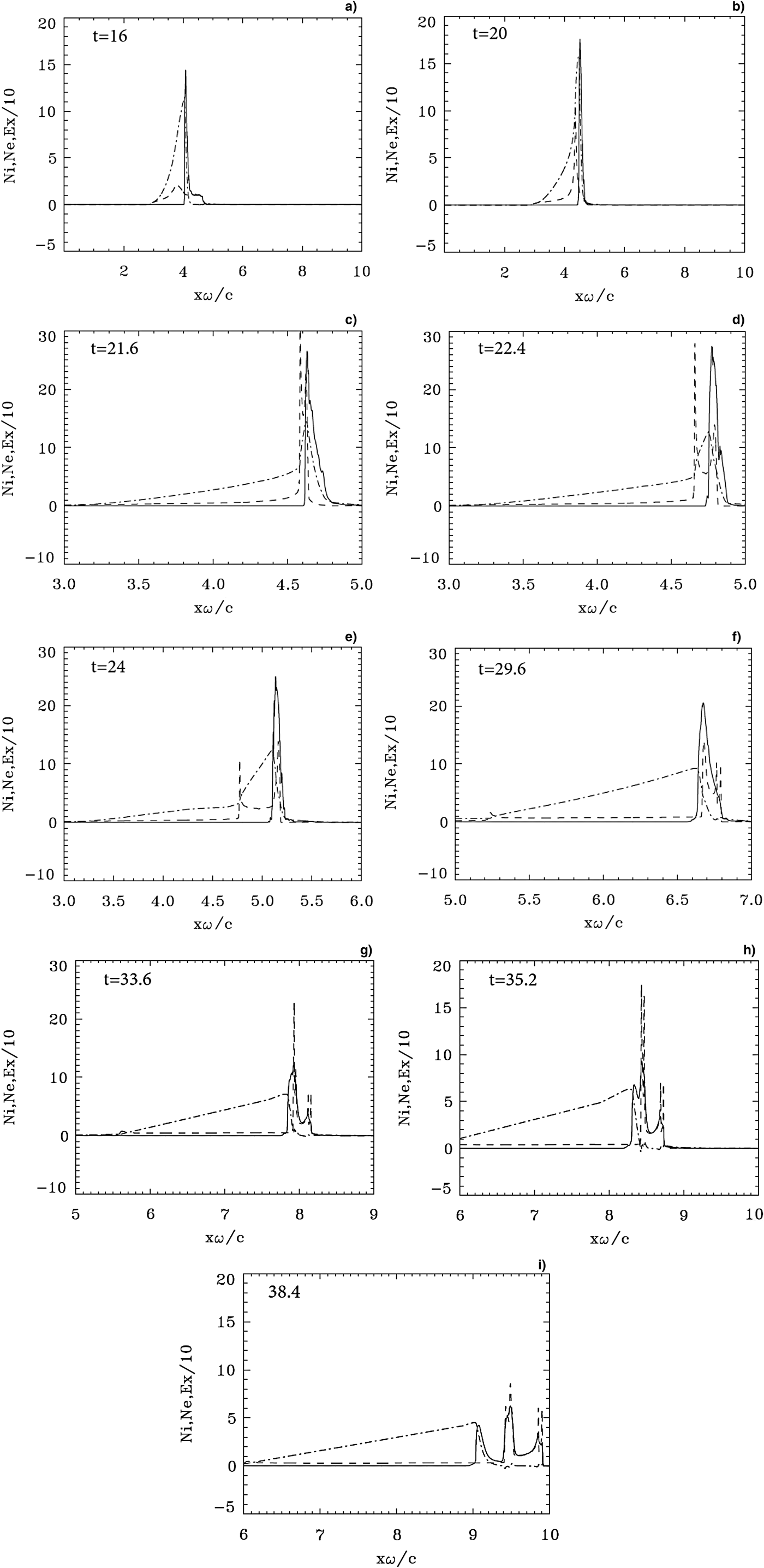
Initially the ponderomotive force or radiation pressure at the target surface is similar to what has been presented in the previous section. Electrons are pushed by the radiation pressure, heated, and accelerated at the target surface and form a steep density spike. An electric field is formed at the target surface due to the charge separation, and its penetration in the plasma beyond the steep edge is of the order of the skin depth 0.1c/ω. The temporal variation of the electromagnetic field is very rapid as the FWHM is less than twice the laser period [see Eq. (6)]. The longitudinal electric field builds up very rapidly in time at the plasma–vacuum interface. We present in Figure 5 some of the results obtained for the density profiles, at times t = 16, 20, 21.6, 22.4, 24, 29.6, 33.6, 35.2 and 38.4. In Figure 5a at t = 16, we observe a more important buildup at the surface of the target compared with Figure 1a. The back of the target does not move yet. In Figure 1b at t = 20, the electron density layer is bunched to a thin layer reaching the back surface of the target. At t = 21.6 (note the change in the scales) we see again a rapid and huge jump in the ion density at the target surface, reaching a peak value above 30, similar to what is presented in Section 3.1 in Figure 1c. In the present case, however, the deformation has penetrated through the entire slab, and a hot electron population diffuses forward from the back of the slab, as can be verified from Figure 7a. The electric field curve is still penetrating a layer of thickness about the skin depth 0.1c/ω inside the steep edge of the electron density. Figure 6a shows the ion distribution function at the time of the rapid acceleration of the ions at t = 21.6, and Figure 7a for the electron distribution function at the same time shows a heating of the electrons at the surface of the target. We observe again the electron peak density separating from the ion peak density in Figure 5d at t = 22.4, in Figure 5e at t = 24, and in the subsequent figures under the effect of the ponderomotive force or the radiation pressure, the structure forms a double layer. Note the slow decrease of the ion peak leaving a small ion population behind it, and the presence of an ion population in the double layer between the ion peak and the electron peak to allow the electric field between the two peaks to exist, and to provide the restoring force. The double-layer structure in Figures 5d and 5e is very close to what is presented in Figure 1 of Schlegel et al. (Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009), and in Figure 2 of Eliezer et al. (Reference Eliezer, Nissim, Martinez-Val, Mima and Hora2014). At this stage the acceleration is continuing under the effect of the radiation pressure of the still growing laser wave, even though the double-layer structure has moved beyond the initial target volume. Electrons are pushed steadily by the radiation pressure, and with the ions in this double-layer structure following behind them, and slowly decaying, while at this stage the solitary-like electron structure appears to be trapping an ion population (see Fig. 5d and the subsequent figures), and the whole thin foil is transformed now into a double layer sustained by the pondromotive force. The restoring force of the space-charge electric field does not reach the intensity where it can balance the ponderomotive force of the laser pressure to keep the two peaks at a constant distance. In Figure 5f, the initial ion peak has almost disappeared, and the figure now is very close to what is discussed in Figure 2 of Tripathi et al. (Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009), and in Macchi et al. (Reference Macchi, Veghini, Liseykina and Pegoraro2010), showing a trapped ion population in the negatively charged electron solitary structure. This transition of the double-layer structure from a shape similar to Figures 5d and 5e, to a shape similar to Figure 5f has been also reported in Figure 7 of Shoucri (Reference Shoucri2012), for more moderate values of ![]() $a_0 = 25/\sqrt 2 $ and density n = 25n cr. In Figure 5g at t = 33.6, we see that the electron solitary structure splits. There are two small electron peaks following and neutralizing two ion peaks, and what appears now as a trapping of the electrons by the ions leads to a cooling of the local electron distribution function. In Figure 5h, there is a small population of excess electrons at the target surface, which detaches from the neutral structure and which is slowing down due to the decrease of the pressure of the decaying laser beam at the target surface. This is further accentuated in Figure 5i at t = 38.4, where we see at the right essentially a structure of two ion peaks neutralized by two electron peaks, giving a neutral plasma structure with double peaks free streaming to the right. The excess electrons forms a third non-neutral electron peak at the left which is further detaching itself from the free-streaming neutral structure, increasing its detachment toward the left as the laser wave pressure decays. So it is the ion population trapped by the electron bunch in Figures 5d and 5e which finally provides the ion population for the neutral plasma jet. Figure 8 at t = 38.4 shows the small incident field E + at x = 9 with a finite value still applying a small pressure on the target surface at x = 9 in Figure 5i. Figure 7d shows the electron distribution function which has further cooled, with two peaks to the right neutralized by the ion peaks as discussed in Figure 5i, and free streaming, and the non-neutral electron peak at the left slowly detaching itself backward toward the left from the free streaming neutral plasma, because of the decay of the pressure exerted by the decaying laser beam.
$a_0 = 25/\sqrt 2 $ and density n = 25n cr. In Figure 5g at t = 33.6, we see that the electron solitary structure splits. There are two small electron peaks following and neutralizing two ion peaks, and what appears now as a trapping of the electrons by the ions leads to a cooling of the local electron distribution function. In Figure 5h, there is a small population of excess electrons at the target surface, which detaches from the neutral structure and which is slowing down due to the decrease of the pressure of the decaying laser beam at the target surface. This is further accentuated in Figure 5i at t = 38.4, where we see at the right essentially a structure of two ion peaks neutralized by two electron peaks, giving a neutral plasma structure with double peaks free streaming to the right. The excess electrons forms a third non-neutral electron peak at the left which is further detaching itself from the free-streaming neutral structure, increasing its detachment toward the left as the laser wave pressure decays. So it is the ion population trapped by the electron bunch in Figures 5d and 5e which finally provides the ion population for the neutral plasma jet. Figure 8 at t = 38.4 shows the small incident field E + at x = 9 with a finite value still applying a small pressure on the target surface at x = 9 in Figure 5i. Figure 7d shows the electron distribution function which has further cooled, with two peaks to the right neutralized by the ion peaks as discussed in Figure 5i, and free streaming, and the non-neutral electron peak at the left slowly detaching itself backward toward the left from the free streaming neutral plasma, because of the decay of the pressure exerted by the decaying laser beam.

Fig. 5. Electron (full curves) and ions (dashed curves) density profiles. The electric field (dashed-dotted curves, divided by a factor of 10). Plots at times: (a) t = 16, (b) t = 20, (c) t = 21.6, (d) t = 22.4, (e) t = 24, (f) t = 29.6, (g) t = 33.6, (h) t = 35.2, (i) t = 38.4.

Fig. 6. Phase-space plots of the ion distribution function. Plots at times: (a) t = 21.6, (b) t = 24, (c) t = 29.6, (d) t = 33.6, (e) t = 38.4, (f) t = 38.4 (zoom).

Fig. 7. Phase-space plots of the electron distribution function. Plots at times: (a) t = 21.6, (b) t = 24, (c) t = 33.6, (d) t = 38.4.

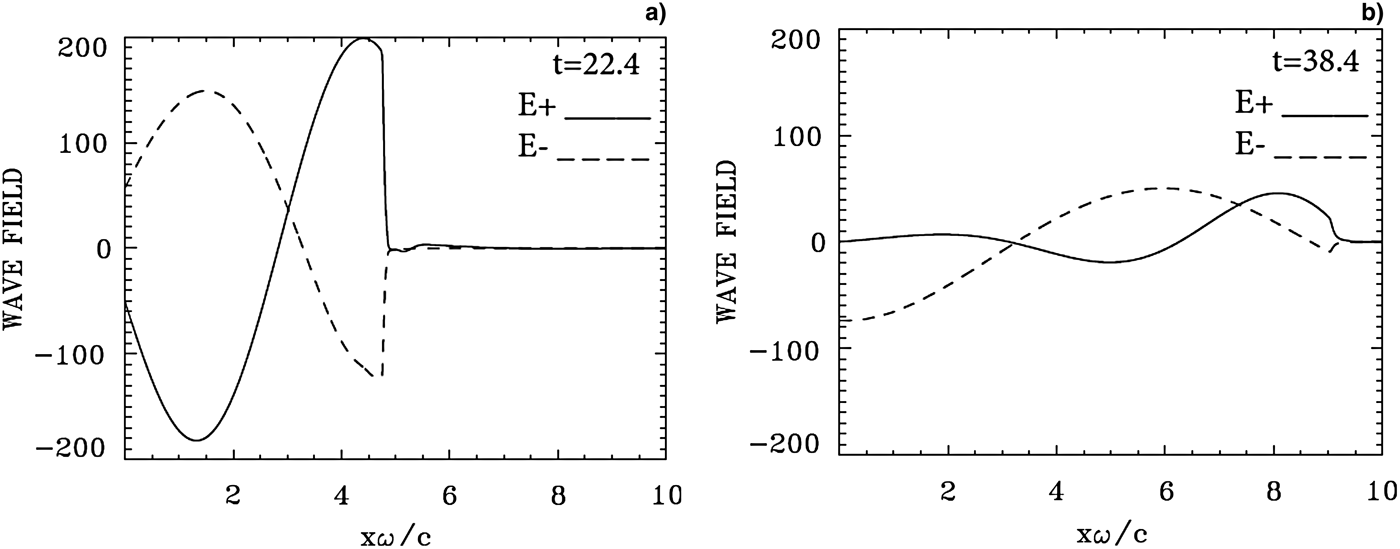
Fig. 8. Incident wave E + (full curve) and reflected wave E − (dashed curve) at: (a) t = 22.4, (b) t = 38.4. Note the very small transmission of the incident wave to the right across the target apparent at t = 22.4.
Figure 6 shows the phase-space contour plots of the ion distribution function at t = 21.6 (when electron are first accelerated), and at t = 24, 29.6, 33.6, and 38.4 (the peak is magnified in Fig. 6f). At the peak value of the normalized ion momentum of 1600 for deuterium, the velocity can be calculated from (allowing for a small relativistic correction) ![]() $1600 = (M_{\rm i} /M_{\rm e} )({\rm \upsilon} /c)/\sqrt {1 - ({\rm \upsilon} /c)^2} $, from which υ/c ≈ 0.4. The corresponding energy is
$1600 = (M_{\rm i} /M_{\rm e} )({\rm \upsilon} /c)/\sqrt {1 - ({\rm \upsilon} /c)^2} $, from which υ/c ≈ 0.4. The corresponding energy is ![]() $M_{\rm i} c^2 (1/\sqrt {1 - ({\rm \upsilon} /c)^2} - 1) \approx 170\,{\rm MeV}$. For the dense peak appearing in Figure 6f around 1200, we can calculate in a similar way υ/c ≈ 0.31, and an energy
$M_{\rm i} c^2 (1/\sqrt {1 - ({\rm \upsilon} /c)^2} - 1) \approx 170\,{\rm MeV}$. For the dense peak appearing in Figure 6f around 1200, we can calculate in a similar way υ/c ≈ 0.31, and an energy ![]() $M_{\rm i} c^2 (1/\sqrt {1 - ({\rm \upsilon} /c)^2} - 1) \approx 97.2\,{\rm MeV}$.
$M_{\rm i} c^2 (1/\sqrt {1 - ({\rm \upsilon} /c)^2} - 1) \approx 97.2\,{\rm MeV}$.
In Figure 7, we present the phase-space contour plots of the electron distribution function at t = 21.6 (at the time of the rapid acceleration of ions shown in Fig. 5c), 24, 33.6, and 38.4. We see in Figures 7a and 7b the initial strong heating of the electrons, together with a slow and small ejection of the electrons from the back of the target, with a steep electron edge observed at the target surface due to the effect of the radiation pressure of the laser beam. We note from Figures 7a–7c how the entire electron population from the initial target volume is pushed forward on the propagation path of the laser beam, far from the initial position of the target. In Figure 7d, we present the phase space on a magnified scale, showing the split in the solitary structure of the electrons into two populations, which we discussed in Figures 5g–5i, the two peaks to the right are for the two electron peaks neutralizing the ions propagating in the neutral plasma jet moving away in the forward direction, and the third peak at the left is for an excess non-neutral electron population which, under the effect of the decaying ponderomotive pressure of the laser beam, is distancing itself from the neutral plasma jet at the right, as discussed in Figure 5i. Note the two vorticity-like structures at the position of the plasma jet in Figure 7d. Note also the cooling in the electron distribution function, after the initial heating apparent in Figures 7a and 7b.
In Figure 8, we present the forward-propagating wave E + (full curves) and the backward reflected wave E − (dashed curves) at t = 22.4 and 38.4 . The curve at t = 22.4, about the time of the maximum of the incident wave E + reaching the target surface, is also about the time of the rapid acceleration of the ions at the target surface in Figures 5c and 7a. The reflection of the wave in Figure 8a takes place at the electron layer surface. We note in Figure 8a that a very small component of the incident wave (full curve) which is transmitted to the right across the target. This small penetration of the laser wave through the target is accompanied by a small ejection of electrons from the back of the target, as we can see from Figures 7a and 7b. This point will be discussed in more details for the results in the next section. We also note the reflection of the decaying laser wave in Figure 8b at t = 38.4 taking place at the surface of the electron peak at the left in Figures 5i and 7d, and providing the small ponderomotive pressure of the surface of the electron peak at the left in Figure 5i, as previously discussed. The curves for F + and F − are similar. Note that when E + is at a peak value, F − is zero, and vice versa. In a similar way when reflected wave E − is at maximum, the backward propagating wave F + is zero.
3.3. The case of a plasma slab with L p = 1.287c/ω and a 0 = 100
We have pointed out in Figure 8a the very small penetration of the laser field beyond the target. In the present case, we reduce slightly the thickness of the slab to allow for a more important penetration of the laser field through the slab. We now have a vacuum region of length L vac = 2.517 on the incident side at the left of the target slab. The steep ramp in density at the plasma edge on each side of the uniform flat top density of the slab target has a length L edge = 0.24. The length of the central plasma slab target, with a flat top density of 1 (or 100n cr) is L p = 1.287, and the remaining vacuum space at the right of the target is 5.716, for a total length of the domain of 10. The initial plasma slab extends from 2.517 to 4.284 and the flat plateau is between 2.757 and 4.044. In our units, the skin depth c/ωpe = (c/ω)(ω/ωpe) = 0.1c/ω; so the thickness of the flat top of the plasma slab is L p ≈ 1.287, about 13 skin depths. We use the same space grid as in Section 3.2. In momentum space, we use 2400 grid points for the electrons and 2000 grid points for the ions (extrema of the electron momentum are ±12 and ±1000 for the ion momentum).
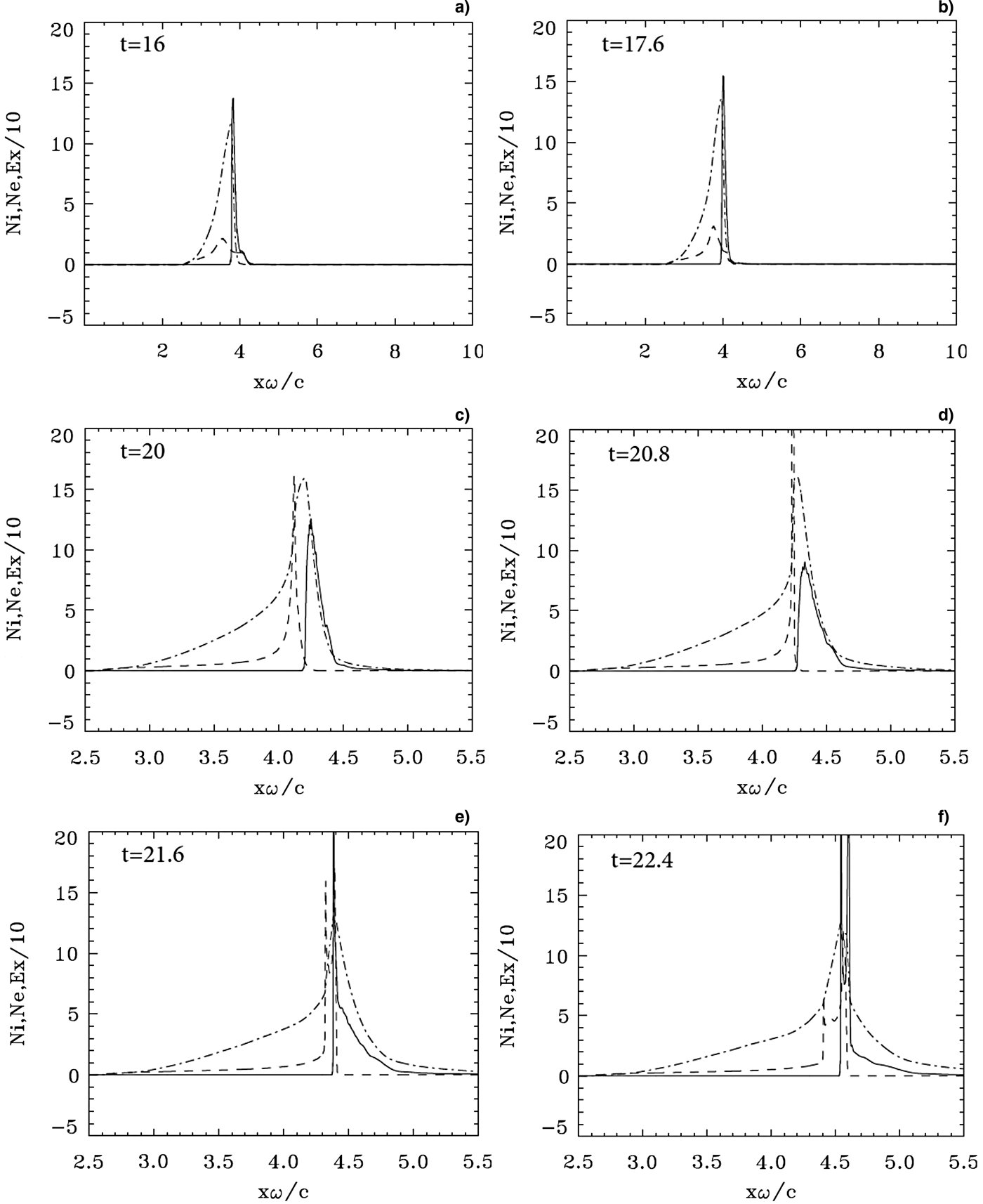
The initial mechanism of the ponderomotive force radiation pressure acceleration at the target surface is similar to what has been presented in the previous sections. We present in Figure 9 some of the results obtained for the density profiles, at times t = 16, 17.6, 20, 20.8, 21.6, and 22.4. We see in Figure 9a that the electron population bunched by the radiation pressure forms a steep layer, but has not yet reached the back of the target, we still see at the right a part of the original slab. The ions (dashed curve) have moved little. In Figure 9b, the bunched electron layer has reached the back limit of the initial target slab at about x ≈ 4.284. The penetration of the electric field (dashed-dotted curve) in the electron layer is of the order of the skin depth 0.1c/ω. We see in Figure 9c at t = 20 and in Figure 9d at t = 20.8, the electron population pushed by the radiation pressure has completely left the location of the initial target, which is now replaced by the structure we see in Figure 9c, where the electron population has been completely expelled by the radiation pressure of the laser beam, did not trap any ion population, and is completely separated from the ion population. Figures 11a and 11b show the electron population forming a cloud and accelerating upward in phase space, and leaking to the right in the forward direction. This is accompanied in Figure 12a–12d by an increased penetration of the incident laser beam through the moving target. In Figure 9c, the ion population forms a spike and is completely separated from the electron population, leaving behind an ion tail. There is a restoring electric field between the ions and the electrons (dashed-dotted curve in Fig. 9c). We observe a rapid increase in the ion spike in Figure 9d and, as indicated also in Figure 10a, in the ion phase space. The ion and electron populations remain separate. Figure 9e at t = 21.6 shows a rapid increase in the electron density at the electron layer surface, and Figure 11c confirms a rapid acceleration of the electrons at the surface of the electron layer, and an ejection of the electrons from the back of the target, coupled with the appearance of a more important longitudinal electric field in the forward direction, and a more important penetration of the laser field through the target in Figure 12b. This ejection of the electrons from the back of the target coupled with the penetration of the laser field through the target has been previously reported (Shoucri et al., Reference Shoucri, Matte and Vidal2013, Reference Shoucri, Matte and Vidal2014). We are still in Figures 9e and 9f at a stage where the radiation pressure at the electron layer surface is very important, the peak value of the laser pulse is still increasing at the target, and its maximum value reaches the actual electron surface at t = 22.4 in Figure 12d, about the time we see the rapid ejection of the electrons from the back of the targets. We note also in Figure 9e a small layer of ions penetrating the electron layer. In Figure 11d, we see the accelerated electrons spiraling in phase space. Similarly, although less violent, spiraling phase-space structures for the electrons were observed in previous simulations at lower laser intensity, when the laser field penetrates through the target (Shoucri et al., Reference Shoucri, Matte and Vidal2013, Reference Shoucri, Matte and Vidal2014). The vertical phase-space spiral structure in Figure 11d translates in the density plot in Figure 9f with two vertical lines for the electron density. A small double layer is formed at the target surface in Figure 9f. We see also in Figure 9f the vertical ion layer corresponding to the vertical line in Figure 10b at t = 22.4, trapped in the electron layer. The target we see in Figure 9f is now submitted to the radiation pressure of the incident laser wave, which is at its maximum at the target surface as seen in Figure 12d. The longitudinal electric field now extends in the forward direction to the right of the target, a situation similar to what was observed in Shoucri et al. (Reference Shoucri, Matte and Vidal2013, Reference Shoucri, Matte and Vidal2014), at a more moderate laser intensity. We note however that in the present situation, this electric field does not seem, at this stage, to play the major role on the double layer, the strong pressure of the incident laser beam on the target surface is still strongly dominant, and we indeed see in Figure 12d that the peak value of the laser beam reaches the steep surface of the electron profile. Figure 11e at t = 23.2 shows the spiraling motion of the electrons interrupted by a rapid acceleration, which makes the follow up difficult with the code. It is possible that these strongly accelerated and escaping electrons, by attempting to leave the target, can lead to the generation of intense space-charge fields which drive the acceleration of ions, similar to the process which is at the basis of the target-normal sheath acceleration mechanism (d'Humières, Reference d'Humiéres and Peshko2012; d'Humières et al., Reference d'Humières, Brantov, Bychenkov, Yu and Tikhonchuk2013; Scisciò et al., Reference Scisciò, d'Humières, Fourmaux, Kieffer, Palumbo and Antici2014).

Fig. 9. Electron (full curves) and ion (dashed curves) density profiles. The electric field (dashed-dotted curves, divided by a factor of 10). Plots at times: (a) t = 16, (b) t = 17.6, (c) t = 20, (d) t = 20.8, (e) t = 21.6, (f) t = 22.4.

Fig. 10. Phase-space plots of the ion distribution function. Plots at times: (a) t = 20.8, (b) t = 22.4.

Fig. 11. Phase-space plots of the electron distribution function. Plots at times: (a) t = 20, (b) t = 20.8, (c) t = 21.6, (d) t = 22.9, (e) t = 23.2. Note the ejection of the electrons to the right in figures (a)–(d), before the spiraling structure develops.

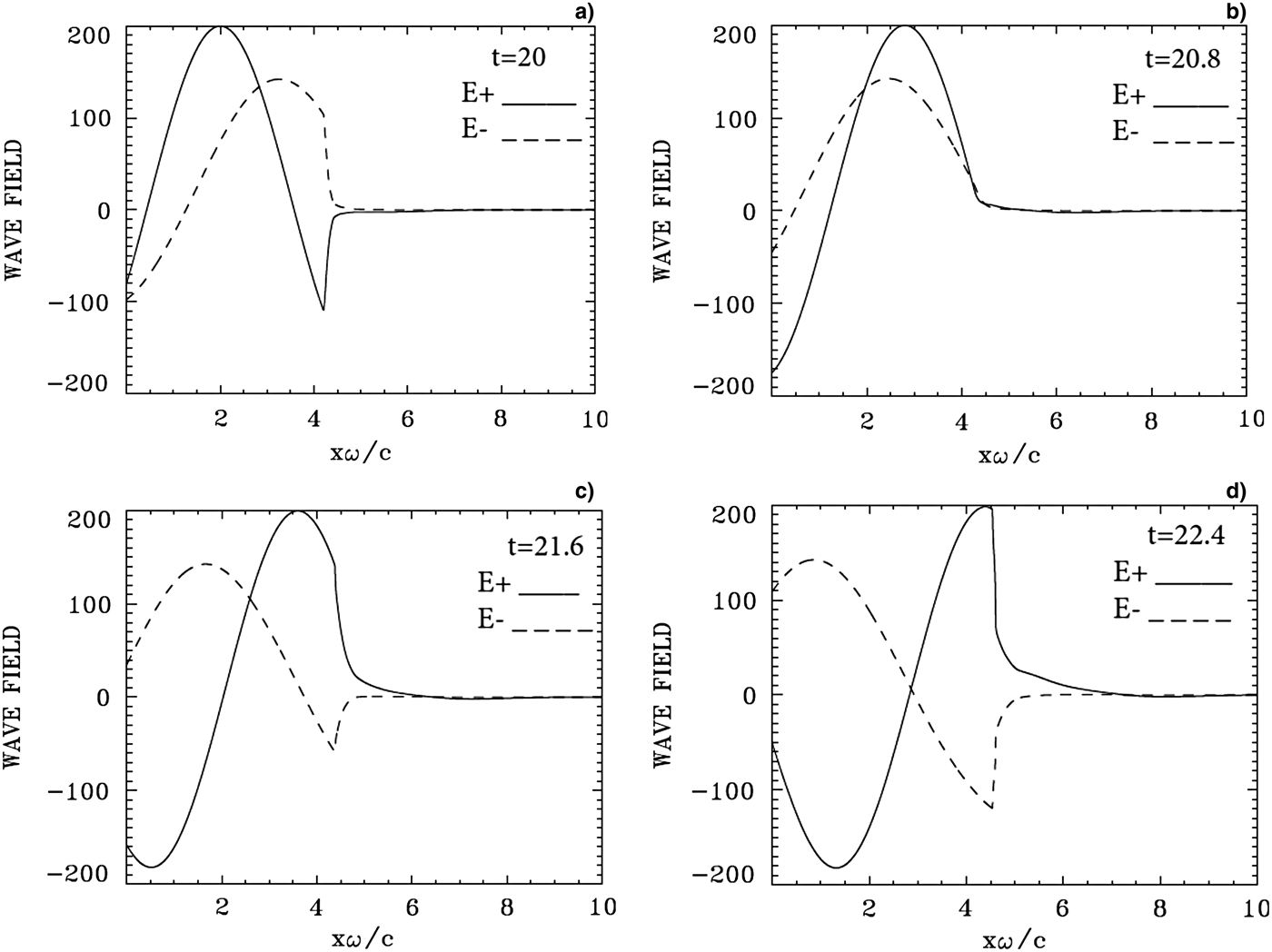
Fig. 12. Incident wave E + (full curve) and reflected wave E − (dashed curve) at: (a) t = 20, (b) t = 20.8, (c) t = 21.6, (d) t = 22.4. Note the penetration of the incident laser beam (full curve) across the target in Figures 12c and 12d.
We present in Figure 10 the phase-space contour plots of the ion distribution function at t = 20.8 (at the time of the rapid rise of the vertical spike of the ion density in Fig. 9d), and at 22.4. The ion peak momentum at this stage is about 900. At this maximum momentum M iυ/M ec ≈ 900 or υ/c ≈ 0.245. This corresponds to an energy of the deuterium ions of M iυ2/2 = 56.35 MeV.
In Figure 11, we present the phase-space contour plots of the electron distribution function at t = 20, 20.8, 21.6, 22.4, and 23.2. We observe the vertical acceleration of the electrons and the ejection of the electron in the forward direction, with a steep electron edge at the target surface due to the effect of the radiation pressure of the wave. Figure 11c at t = 21.6 corresponds to the formation of the spike in electron density we see in Figure 9e. The peak laser field reaches the target surface in Figure 12d at t = 22.4, at the time we see the spiraling of the electrons in phase space as in Figure 11d, and this is followed by a strong acceleration of the electrons as indicated in Figure 11e.
Figure 12 presents the forward-propagating wave E + (full curves) and the backward reflected wave E − (dashed curves), at t = 20, 20.8, 21.6, and 22.4. In Figure 12a, the laser field is reflected at the surface of the electron layer of the target. In Figure 12b, the laser field does not completely decay within the target, there is a transmitted part across the target propagating to the right, which is becoming more important as we move to Figures 12c and 12d. This transmitted part is accompanied by the ejection of the electrons in the forward direction to the right from the back of the target as observed in Figure 11. We note the peak value of E + , arriving at the target surface at t = 22.4 in Figure 12d. We also note that with the present set of parameters, only a fraction of the forward wave E + is transmitted through the target (full curves in Figs 12c and 12d), while another good fraction of the wave is reflected (dashed curves for E −). F + and F − present similar curves. When at the target surface E + and E − are at maximum value, F + and F − are at zero value, and vice versa.
4. CONCLUSION
We have used an Eulerian Vlasov code for the numerical solution of the 1D relativistic Vlasov–Maxwell equations to study the effects of the laser intensity and target thickness on the formation and evolution of a double-layer structure in laser–target interaction, and on the formation of a neutral plasma jet during the interaction of a high-intensity circularly polarized laser beam normally incident on an overdense plasma. The three cases of a high density with n/n cr = 100 considered in the present work are of interest, because under the condition of an intense laser beam incident on a solid target, the solid target ionizes very rapidly, in a few cycles of the light wave, and the laser beam interacts directly with a plasma with a very high density. The results for three different simulations obtained with the same plasma density n/n cr = 100 have been presented, showing different evolution towards the formation of a neutral plasma jet. We have studied two cases where the thickness of the constant density flat-top plateau target is L p = 1.497, with an amplitude of the vector potential of the laser successively equal to a 0 = 50 and a 0 = 100. In these two cases, the target was opaque to the laser beam. With the precision of the Vlasov code, the present study of these two cases provides more insight in the evolution and transformation of the initial homogenous thin foil into a double layer, and ultimately to a neutral plasma jet. By contrast, in the third case, where the flat-top plateau target thickness is reduced to L p = 1.287 with a 0 = 100, we see a penetration of the laser energy across the target and the entire electron population forms a cloud which is accelerated and completely expelled from the back of the target. For the first two cases considered the ponderomotive force or radiation pressure has the dominant role. The electrons are pushed by the radiation pressure, and form a steep gradient at the target surface. This generates a charge separation and an electric field at the plasma edge which accelerates the ions. Under the effect of the radiation pressure acting on the electron surface, the ion peak and the electron peak separate, forming a double-layer structure [very close to what is described in Figure 1 of Schlegel et al. (Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009) and in Figure 2 of Eliezer et al. (Reference Eliezer, Nissim, Martinez-Val, Mima and Hora2014)], with an electric field between the two peaks providing a restoring force, with an additional ion population trapped in the electron thin layer. The laser ponderomotive force pushes the electron density peak and its trapped ion population forward, while the initial ion peak is slowly decaying and following accordingly behind. Note that although the whole thin foil has been transformed into a double-layer structure, and the radiative pressure acceleration is acting on the double layer as a whole, it is the trapped ion population in the electron peak (which is distinct from the initial ion peak of the double layer), which contributes to the formation of the final neutral plasma jet ejected from the back of the target. We note that for the case with a 0 = 50, the radiation pressure had the time to bunch the electrons a second time within the target volume, providing a second trapped ion population and ultimately a second neutral plasma jet of lower velocity. The second case with a 0 = 100 shows the highest velocity reached by the accelerated ions. We also note a behavior of the double-layer evolution close to what is presented here in a recent publication by Shoucri (Reference Shoucri2012), where a case with n/n cr = 25 and ![]() $a_0 = 25/\sqrt 2 $ has been studied, and it was observed that a reduction in the target thickness resulted in a situation where the whole thin foil is transformed into a double-layer structure during the evolution of the system, with an increase in the velocity of the accelerated ion bunch and of the final plasma jet [see Fig. 7 of Shoucri (Reference Shoucri2012)].
$a_0 = 25/\sqrt 2 $ has been studied, and it was observed that a reduction in the target thickness resulted in a situation where the whole thin foil is transformed into a double-layer structure during the evolution of the system, with an increase in the velocity of the accelerated ion bunch and of the final plasma jet [see Fig. 7 of Shoucri (Reference Shoucri2012)].
We mentioned in the previous paragraph that in the first two cases the targets were essentially opaque to the laser beam. By contrast, we noted in the third case with a 0 = 100 when the target thickness has been reduced, that a fraction of the laser energy is transmitted through the target, and the entire electron population forms a cloud accelerated and completely expelled from the back of the target. Scisciò et al. (Reference Scisciò, d'Humières, Fourmaux, Kieffer, Palumbo and Antici2014) and d'Humières et al. (Reference d'Humières, Lefebvre, Gremillet and Malka2005, Reference d'Humières, Brantov, Bychenkov, Yu and Tikhonchuk2013) for instance have discussed the features of proton acceleration with high-intensity lasers as a function of target thickness, where below a given thickness a fraction of the laser energy is transmitted through the target. This thickness delimits two regimes of proton acceleration: The opaque and the transparent regimes. The former corresponds to the first two cases we have studied where the wave does not penetrate through the target, the latter to the transparent regime we studied in the third case. The early evolution of the system in this third case is essentially the same under the effect of the radiation pressure (see Figs 9a and 9b). In the subsequent evolution of the system, however, the target thickness is indeed seen to play a key role in the physical processes involved in the evolution of the density profiles, and the subsequent formation of the plasma emitted from the rear side of the target. We first reach a state where the still growing radiation pressure causes the electron and ion populations to be completely separated in two distinct layers (Figs 9c and 9d) with no ions trapped in the electron layer. The entire electron cloud is then completely expelled by the radiation pressure (Figs 11a and 11b). The electric field between the ion and electron layers provides the restoring force which strongly attracts and accelerates the ions. The laser pulse at the surface of the target, when it peaks at t = 22.4 in Figure 12d, interacts with a modified inhomogeneous plasma. The laser wave travels through the target, does not significantly decay within it and there is a transmitted field across the target. The transmission of the laser field across the target causes the electrons to be ejected from the back of the target in the forward direction, providing an electric field at the back of the target. This usually causes the electrons at the surface of the target to spiral around the target (Shoucri et al., Reference Shoucri, Matte and Vidal2013, Reference Shoucri, Matte and Vidal2014). However, the spiraling event (see Fig. 11d) is higher in the present simulation due to the higher intensity of the laser field. It is difficult at the present stage to say whether the electric field at the right of the target plays an important role in the acceleration process. We are still at a stage where the radiation pressure at the electron layer surface is very important as previously mentioned.
ACKNOWLEDGMENTS
M. Shoucri is grateful to Dr Réjean Girard for his constant interest. The authors are grateful to the Centre de Calcul Scientifique de l'IREQ (CASIR) for the computer time used in the simulations presented in the present work.