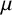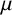THE WEYL TRANSFORM OF A SMOOTH MEASURE ON A REAL-ANALYTIC SUBMANIFOLD

Abstract

If $\mu $ is a smooth measure supported on a real-analytic submanifold of ${\mathbb {R}}^{2n}$ which is not contained in any affine hyperplane, then the Weyl transform of $\mu $ is a compact operator.

1. Introduction

There has been long-standing interest in finding quantum or noncommutative analogues of classical results in harmonic analysis. For example, the noncommutative analogue of the Hausdorff–Young theorem (in greater generality) was proven by Kunze [6] in 1958. Subsequently, there have been more developments in this direction (see [17]). The Weyl transform is a quantum analogue of the Fourier transform. In an earlier work [7], we proved an analogue of a result of Stein about the decay of the Fourier transform of measures supported on a hypersurface of positive Gaussian curvature. Here, we prove a weaker version of that result which applies to submanifolds of arbitrary codimension.

Let $f \in L^1({\mathbb {R}}^n)$ . The Fourier transform of f, denoted by $\hat {f}$ , is given by

$$ \begin{align*} \hat{f}(\xi) = \int_{{\mathbb{R}}^n} f(x) e^{-2\pi i x\cdot \xi}\, dx, \quad \xi \in {\mathbb{R}}^n. \end{align*} $$

The Riemann–Lebesgue lemma [11, Theorem 1.2] states that if $f \in L^1({\mathbb {R}}^n)$ , then

$$ \begin{align*} \lim_{\lvert\xi\rvert \rightarrow \infty}\hat{f}(\xi) = 0. \end{align*} $$

More generally, the Fourier transform of a finite Borel measure $\lambda $ on ${\mathbb {R}}^n$ is given by

$$ \begin{align*} \hat{\lambda}(\xi) = \int_{{\mathbb{R}}^n} e^{-2\pi i x\cdot \xi}\, d\lambda(x), \quad \xi \in {\mathbb{R}}^n. \end{align*} $$

If $\lambda $ is absolutely continuous with respect to the Lebesgue measure m on ${\mathbb {R}}^n$ , that is, $\lambda =fm$ for some $f \in L^1({\mathbb {R}}^n)$ , then the formula above reduces to the usual definition of the Fourier transform of f and

$$ \begin{align*} \lim_{\lvert\xi\rvert \rightarrow \infty}\hat{\lambda}(\xi) = 0. \end{align*} $$

In general, the Fourier transform of a measure need not vanish at infinity. For example, the Fourier transform of $\delta _0$ , the Dirac measure, is identically equal to $1$ . However, the decay of the Fourier transform of a measure can be deduced from certain curvature properties of the support of the measure.

Suppose M is a smooth submanifold of ${\mathbb {R}}^n$ . By a smooth measure on M, we mean a measure of the form $\mu =\psi \sigma $ , where $\sigma $ is the measure on M induced by the Lebesgue measure on ${\mathbb {R}}^n$ and $\psi $ is a smooth function on ${\mathbb {R}}^n$ whose support intersects M in a compact set.

It is well known that if $\mu $ is a smooth measure on a hypersurface in ${\mathbb {R}}^n$ , $n \geq 2$ , whose Gaussian curvature is nonzero everywhere, then

$$ \begin{align*} \lvert\hat{\,\mu}(\xi)\rvert \leq A \lvert\xi\rvert^{(1-n)/2}, \end{align*} $$

where A is a constant independent of $\xi $ (see, for example, [10, Theorem 1, page 348] and [5, Theorem 7.7.14]).

In [7], an analogue of this result for the Weyl transform was proved. Let ${\mathcal {H}} = L^2({\mathbb {R}}^n)$ and ${\mathcal {B}}({\mathcal {H}})$ be the set of bounded operators on ${\mathcal {H}}$ . If $f \in L^1({\mathbb {R}}^{2n})$ , the Weyl transform of f is the operator $W(f) \in {\mathcal {B}}({\mathcal {H}})$ defined by

$$ \begin{align*} (W(f)\varphi)(t) = \int_{{\mathbb{R}}^n}\int_{{\mathbb{R}}^n} f(x,y) e^{\pi i(x \cdot y+2y \cdot t)} \varphi(t+x) \, dx \, dy. \end{align*} $$

More generally, if $\lambda $ is a finite Borel measure on ${\mathbb {R}}^{2n}$ , the Weyl transform of $\lambda $ is the operator $W(\lambda ) \in {\mathcal {B}}({\mathcal {H}})$ defined by

$$ \begin{align*} (W(\lambda)\varphi)(t) = \int_{{\mathbb{R}}^{2n}} e^{\pi i(x \cdot y+2y \cdot t)} \varphi(t+x) \, d\lambda(x,y). \end{align*} $$

The Weyl transform can be expressed in terms of the canonical representation of the Heisenberg group. Recall that the reduced Heisenberg group G is the set of triples

$$ \begin{align*} \{(x,y,z) \mid x,y \in {\mathbb{R}}^n, z \in {\mathbb{C}}, \lvert z\rvert = 1\} \end{align*} $$

with multiplication defined by

$$ \begin{align*} (x,y,z)(x',y',z')=(x+x', y+y', zz'e^{\pi i (x \cdot y'-y \cdot x')}). \end{align*} $$

According to the Stone–von Neumann theorem [3, Theorem 1.50], there is a unique irreducible unitary representation $\rho $ of G such that

$$ \begin{align*} \rho(0,0,z)= zI. \end{align*} $$

The standard realisation of this representation is on the Hilbert space ${\mathcal {H}}$ by the action

(1.1) $$ \begin{align} (\rho(x,y,z)\varphi)(t)= ze^{\pi i (x\cdot y+2y\cdot t)}\varphi(t+x). \end{align} $$

Thus, the Weyl transform of $\lambda $ may be expressed as

(1.2) $$ \begin{align} W(\lambda) = \int_{{\mathbb{R}}^{2n}} \rho(x,y,1) \, d\lambda(x,y), \end{align} $$

where the integral is the weak integral as defined in [9, Definition 3.26].

The analogue of the Riemann–Lebesgue lemma for the Weyl transform is the fact that $W(f)$ is a compact operator if $f \in L^1({\mathbb {R}}^{2n})$ (see, for example, [3, Theorem 1.30] and [14, Theorem 1.3.3]). If $\lambda $ is absolutely continuous with respect to the Lebesgue measure m on ${\mathbb {R}}^{2n}$ , that is, $\lambda =fm$ for some $f \in L^1({\mathbb {R}}^{2n})$ , then $W(\lambda )$ reduces to the usual definition of the Weyl transform of f and hence $W(\lambda )$ is a compact operator.

The main result of [7] is the following theorem.

Theorem 1.1. Suppose S is a compact connected smooth hypersurface in ${\mathbb {R}}^{2n}$ , $n \geq 2$ , whose Gaussian curvature is positive everywhere. Let $\mu $ be a smooth measure on S. Then, $W(\mu )$ is a compact operator. Moreover, when $n\geq 6$ and $p> n$ ,

$$ \begin{align*} W(\mu) \in S^{p}({\mathcal{H}}), \end{align*} $$

where $S^{p}({\mathcal {H}})$ denotes the p-th Schatten class of ${\mathcal {H}}$ .

Naturally, the question of what happens if we consider a submanifold of arbitrary codimension arises.

Let M be a smooth m-dimensional submanifold of ${\mathbb {R}}^n$ , $1 \leq m \leq n-1$ , and let $\mu $ be a smooth measure on M. It is well known that if M is of finite type, that is, at each point, M has at most a finite order of contact with any affine hyperplane, then

$$ \begin{align*} \lvert\hat{\mu}(\xi)\rvert \leq A \lvert\xi\rvert^{-1/k}, \end{align*} $$

where k is the type of M inside the support of $\psi $ (see [10, Theorem 2, page 351]). In particular,

(1.3) $$ \begin{align} \lim_{\lvert\xi\rvert \to \infty} \hat{\mu}(\xi)=0. \end{align} $$

If we consider M to be a real-analytic submanifold of ${\mathbb {R}}^n$ , then the condition of being of finite type is equivalent to M not lying in any affine hyperplane.

The main result of this paper is the following theorem, which is an analogue of (1.3) for the Weyl transform of a smooth measure supported on a real-analytic submanifold of finite type.

Theorem 1.2. Suppose M is a connected real-analytic submanifold of ${\mathbb {R}}^{2n}$ which is not contained in an affine hyperplane. Let $\mu $ be a smooth measure on M. Then, $W(\mu )$ is a compact operator.

In Section 2, we define and study the twisted convolution of finite Borel measures, which is an essential tool required to prove the main result which we prove in Section 3. In Section 4, we prove that if $n=1$ , then the conclusion of Theorem 1.2 holds for a submanifold of finite type without the additional assumption of real analyticity. This also proves Theorem 1.1 partially for $n=1$ .

In [2], Edgar and Rosenblatt proved that the translates of a nonzero function in $L^p({\mathbb {R}}^n)$ , $n \geq 2$ , are linearly independent if and only if $p < 2n/(n-1)$ . In [13, 17], the quantum translation of an operator was defined and it was shown that if X is a nonzero Hilbert–Schmidt operator, then the quantum translates of X are linearly independent. The motivation for quantum translation may be found in [13] (see also [15, 16]).

In [7], as an application of Theorem 1.1, it was shown that for $n \geq 6$ , there exists a nonzero compact operator on $L^2({\mathbb {R}}^n)$ whose quantum translates are linearly dependent. By using an argument similar to that in [7], Theorem 1.2 implies the following result.

Theorem 1.3. There exists a nonzero compact operator T on $L^2({\mathbb {R}}^n)$ and distinct elements $(x_1,y_1), \ldots , (x_{4n+1},y_{4n+1}) \in {\mathbb {R}}^{2n}$ such that $\{(x_1,y_1)\cdot T, \ldots , (x_{4n+1},y_{4n+1})\cdot T\}$ is a linearly dependent set, where $(x_i,y_i)\cdot T = \rho (x_i,y_i,1)T\rho (x_i,y_i,1)^{-1}$ is the quantum translation of T by $(x_i,y_i)$ , $i=1,\ldots , 4n+1$ .

2. Twisted convolution

Recall that if $f,g \in L^1({\mathbb {R}}^{2n})$ , the twisted convolution of f and g, denoted by $f \,\natural \, g$ , is

$$ \begin{align*} f \,\natural \, g (x,y) = \int_{{\mathbb{R}}^n}\int_{{\mathbb{R}}^n} f(x-x',y-y')g(x',y')e^{\pi i (x\cdot y'-y\cdot x')}\, dx' \, dy', \quad (x,y) \in {\mathbb{R}}^{2n}. \end{align*} $$

Twisted convolution turns $L^1({\mathbb {R}}^{2n})$ into a noncommutative Banach algebra. It is well known that the Weyl transform is an algebra homomorphism from $L^1({\mathbb {R}}^{2n})$ to ${\mathcal {B}}({\mathcal {H}})$ , that is, $W(f\,\natural \, g) = W(f)W(g)$ (see, for example, [3, page 26] and [14, page 16]).

Definition 2.1. Let $\mu $ and $\nu $ be finite Borel measures on ${\mathbb {R}}^{2n}$ . The twisted convolution of $\mu $ and $\nu $ is the measure on ${\mathbb {R}}^{2n}$ , denoted by $\mu \,\natural \, \nu $ , given by

$$ \begin{align*} \mu \,\natural \, \nu(E)= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}}\chi_{E}(x+x',y+y')e^{\pi i (x\cdot y'-y\cdot x')}\, d\mu(x,y) \, d\nu(x',y'), \end{align*} $$

where E is a Borel subset of ${\mathbb {R}}^{2n}$ .

It follows from Definition 2.1 that if $f \in C_0({\mathbb {R}}^{2n})$ , then

(2.1) $$ \begin{align} \int_{{\mathbb{R}}^{2n}} f(x,y)\, d(\mu \,\natural \, \nu)(x,y) = \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}}f(x+x',y+y')e^{\pi i (x\cdot y'-y\cdot x')}\, d\mu(x,y) \, d\nu(x',y'). \end{align} $$

Let $f,g \in L^1({\mathbb {R}}^{2n})$ . Let m denote the Lebesgue measure on ${\mathbb {R}}^{2n}$ . Let $\mu _f= fm$ and $\mu _g = gm$ . If E is a Borel subset of ${\mathbb {R}}^{2n}$ , then

$$ \begin{align*} \begin{aligned} \mu_f \,\natural \, \mu_g(E) &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}}\chi_{E}(x+x',y+y')e^{\pi i (x\cdot y'-y\cdot x')}\, d\mu(x,y) \, d\nu(x',y')\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}}\chi_{E}(x+x',y+y')e^{\pi i (x\cdot y'-y\cdot x')}f(x,y)g(x',y')\, dm(x,y) \, dm(x',y')\\ &= \int_{{\mathbb{R}}^{2n}}\chi_{E}(x,y)\int_{{\mathbb{R}}^{2n}} e^{\pi i (x\cdot y'-y\cdot x')}f(x-x',y-y')g(x',y') \, dm(x',y')\, dm(x,y)\\ &= \int_{{\mathbb{R}}^{2n}}\chi_{E}(x,y) (f\,\natural \, g)(x,y)\, dm(x,y) = \mu_{f\,\natural \, g}(E). \end{aligned} \end{align*} $$

Therefore, the two definitions of twisted convolution coincide for $L^1$ functions.

Twisted convolution turns $M({\mathbb {R}}^{2n})$ , the set of finite Borel measures on ${\mathbb {R}}^{2n}$ , into a noncommutative Banach algebra. The following theorem shows that the Weyl transform is an algebra homomorphism from $M({\mathbb {R}}^{2n})$ to ${\mathcal {B}}({\mathcal {H}})$ .

Theorem 2.2. Let $\mu $ and $\nu $ be finite Borel measures on ${\mathbb {R}}^{2n}$ . Then,

$$ \begin{align*} W(\mu \,\natural \, \nu) = W(\mu)W(\nu). \end{align*} $$

Proof. By (1.2) and (2.1),

$$ \begin{align*} \begin{aligned} W(\mu \,\natural \, \nu) &= \int_{{\mathbb{R}}^{2n}} \rho(x,y,1) \,d(\mu \,\natural \, \nu)(x,y)\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}} \rho(x+x',y+y',1) e^{\pi i (x\cdot y' - y\cdot x')} \,d\mu(x,y)\,d\nu(x',y')\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}} \rho(x+x',y+y',e^{\pi i (x\cdot y' - y\cdot x')}) \,d\mu(x,y)\,d\nu(x',y') \ \ \text{(by (1.1))}\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}} \rho((x,y,1)(x',y',1)) \,d\mu(x,y)\,d\nu(x',y')\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}} \rho(x,y,1)\rho(x',y',1) \,d\nu(x',y') \,d\mu(x,y)\\ &= \int_{{\mathbb{R}}^{2n}} \rho(x,y,1)W(\nu) \,d\mu(x,y) = W(\mu)W(\nu). \end{aligned}\\[-43pt] \end{align*} $$

3. The proof

To prove Theorem 1.2, we need a result analogous to a result of Ragozin about the absolute continuity of the convolution of measures supported on analytic submanifolds of ${\mathbb {R}}^n$ (see [8, Theorem 5.1]). In particular, Ragozin proved the absolute continuity of the convolution square of the surface measure on a compact analytic hypersurface of ${\mathbb {R}}^n$ . Later, Thangavelu proved that the twisted convolution of the surface measure on a unit sphere in ${\mathbb {R}}^{2n}$ with itself is absolutely continuous with respect to the Lebesgue measure on ${\mathbb {R}}^{2n}$ (see [12, Proposition 4.3]).

The following theorem is an analogue of [8, Theorem 5.1] for twisted convolutions.

Theorem 3.1. Let $M_1, \ldots , M_k$ be connected real-analytic submanifolds of ${\mathbb {R}}^{2n}$ such that $T_{p_1}M_1 + \cdots + T_{p_k}M_k = {\mathbb {R}}^{2n}$ for some choice of points $p_i \in M_i$ , $i=1, \ldots , k$ , where $T_{p_i}M_i$ denotes the tangent space at $p_i$ of $M_i$ . If $\mu _i$ is a smooth measure on $M_i$ , $i=1, \ldots , k$ , then $\mu _1 \,\natural \, \cdots \,\natural \, \mu _k$ is absolutely continuous with respect to the Lebesgue measure on ${\mathbb {R}}^{2n}$ .

Let $\Sigma _k: M_1 \times \cdots \times M_k \to {\mathbb {R}}^{2n}$ be the map given by $\Sigma _k (p_1,\ldots , p_k)= p_1+ \cdots + p_k$ . We need the following lemma to prove Theorem 3.1.

Lemma 3.2. There exists a smooth function $\varphi _k: M_1 \times \cdots \times M_k \to {\mathbb {C}}$ such that, for a Borel set $E \subseteq {\mathbb {R}}^{2n}$ ,

$$ \begin{align*} \mu_1 \,\natural \, \cdots \,\natural \, \mu_k (E)= (\varphi_k \,\mu_1 \times \cdots \times \mu_k)(\Sigma_k^{-1}(E)), \end{align*} $$

that is, $\mu _1 \,\natural \, \cdots \,\natural \, \mu _k$ is the push-forward of the measure $\varphi _k \,\mu _1 \times \cdots \times \mu _k$ by $\Sigma _k$ .

Proof. We will prove the result by induction on k. First, consider $k=2$ . Observe that by Definition 2.1,

(3.1) $$ \begin{align} \mu_1 \,\natural \, \mu_2 (E)= (\varphi_2 \,\mu_1 \times \mu_2)(\Sigma_2^{-1}(E)), \end{align} $$

where $\varphi _2: {\mathbb {R}}^{2n}\times {\mathbb {R}}^{2n} \to {\mathbb {C}}$ is given by $\varphi _2((x_1,y_1), (x_2,y_2)) = e^{\pi i (x_1\cdot y_2 - y_1 \cdot x_2)}$ .

Assume that there exists a function $\varphi _{k-1}: M_1 \times \cdots \times M_{k-1} \to {\mathbb {C}}$ such that

$$ \begin{align*} \mu_1 \,\natural \, \cdots \,\natural \, \mu_{k-1} (E)= (\varphi_{k-1} \,\mu_1 \times \cdots \times \mu_{k-1})(\Sigma_{k-1}^{-1}(E)). \end{align*} $$

Then,

$$ \begin{align*} \begin{aligned} ((\mu_1 \,\natural \, \cdots & \,\natural \, \mu_{k-1}) \,\natural \, \mu_k) (E)\\ &= \int_{{\mathbb{R}}^{2n}}\int_{{\mathbb{R}}^{2n}}\chi_{E}(x+x_k,y+y_k)e^{\pi i (x\cdot y_k-y\cdot x_k)}\, d(\mu_1 \,\natural \, \cdots \,\natural \, \mu_{k-1})(x,y) \, d\mu_k(x_k,y_k)\\ &= \int_{{\mathbb{R}}^{2n}}\cdots\int_{{\mathbb{R}}^{2n}} [ \chi_{E}(x_1+ \cdots +x_k,y_1 +\cdots +y_k) e^{\pi i ((x_1+\cdots +x_{k-1})\cdot y_k-(y_1+\cdots +y_{k-1})\cdot x_k)} \\ &\hskip 2.2cm \cdot\varphi_{k-1} ((x_1,y_1),\ldots, (x_{k-1},y_{k-1}))] \, d\mu_1(x_1,y_1) \cdots \, d\mu_k(x_k,y_k)\\ &= (\varphi_k \,\mu_1 \times \cdots \times \mu_k)(\Sigma_k^{-1}(E)), \end{aligned} \end{align*} $$

where $\varphi _k: M_1 \times \cdots \times M_k \to {\mathbb {C}}$ is given by

$$ \begin{align*} \varphi_k((x_1,y_1), \ldots, (x_k,y_k))= \varphi_{k-1}((x_1,y_1), \ldots, (x_{k-1},y_{k-1})) e^{\pi i ((x_1+\cdots +x_{k-1})\cdot y_k-(y_1+\cdots +y_{k-1})\cdot x_k)}.\\[-26pt] \end{align*} $$

Theorem 3.1 now follows by the argument in [8, Theorem 5.1]. Here, we give a more streamlined proof using the co-area formula.

Proof of Theorem 3.1.

Let $M_1, \ldots , M_k$ be connected real-analytic submanifolds of ${\mathbb {R}}^{2n}$ . Then, $M_1 \times \cdots \times M_k$ is a connected real-analytic manifold. Let $\tau _{(M_1 \times \cdots \times M_k)}$ denote the Riemannian measure on $M_1 \times \cdots \times M_k$ .

Observe that $\Sigma _k$ is an analytic map. Let $p_i \in M_i$ , $i=1, \ldots , k$ be such that ${T_{p_1}M_1 + \cdots + T_{p_k}M_k = {\mathbb {R}}^{2n}}$ . Then, the rank of $\Sigma _k$ is $2n$ at the point $(p_1, \ldots , p_k)$ . Therefore, the critical set of $\Sigma _k$ is a proper analytic subvariety of $M_1 \times \cdots \times M_k$ and hence has $\tau _{(M_1 \times \cdots \times M_k)}$ measure zero.

If $\mu _i$ is a smooth measure on $M_i$ , $i=1, \ldots , k$ , then $\mu _1 \times \cdots \times \mu _k$ is a smooth measure on $M_1\times \cdots \times M_k$ and so $\varphi _k \, \mu _1 \times \cdots \times \mu _k$ is a smooth measure on $M_1\times \cdots \times M_k$ .

The proof of Theorem 3.1 now follows from the following lemma.

Lemma 3.3. Let M and N be Riemannian manifolds. Let $\tau $ and $\nu $ denote the Riemannian measures on M and N, respectively. Let $\mu = \psi \tau $ be a smooth measure on M. Suppose $f:M \to N$ is a differentiable map. If f is a submersion everywhere except on a set of $\tau $ -measure zero, then the push-forward of $\mu $ by f is absolutely continuous with respect to $\nu $ .

Proof. Let $Z=\{x\in M \mid \ f\ \text {is not a submersion at}\ x\}$ . Then, $\tau (Z)=0$ and so $\mu (Z)=0$ . Let $\mathcal {J}_f$ denote the normal Jacobian of f, that is, the absolute value of the determinant of $df$ restricted to the orthogonal complement of its kernel. Then, $\mathcal {J}_f$ is strictly positive on the set of regular points of f, that is, on $M \setminus Z$ .

Let $f_*\mu $ denote the push-forward of $\mu $ by f. For $x \in N$ , let $\sigma _x$ denote the Riemannian measure on the manifold $f^{-1}(x)$ . Let $U \subseteq N$ be a Borel set. By the co-area formula (see [1, page 159]),

$$ \begin{align*} \begin{aligned} f_*\mu (U) & = \mu(f^{-1}(U)) = \mu(f^{-1}(U)\setminus Z)\\ &= \int_{f^{-1}(U) \setminus Z} d\mu = \int_{f^{-1}(U) \setminus Z} \psi \, d\tau\\ &= \int_{U \setminus f(Z)} \int_{f^{-1}(x)} \frac{\psi(y)}{\mathcal{J}_f(y)} \,d\sigma_x(y) \,d\nu(x), \end{aligned} \end{align*} $$

that is,

$$ \begin{align*}\frac{df_*\mu}{d\nu}(x)=\int_{f^{-1}(x)} \frac{\psi(y)}{\mathcal{J}_f(y)}\,d\sigma_x(y),\end{align*} $$

and so $f_*\mu $ is absolutely continuous with respect to $\nu $ .

We need the following lemma to prove Theorem 1.2.

Lemma 3.4. Let M be a connected real-analytic submanifold of ${\mathbb {R}}^{2n}$ . Assume that M is not contained in any affine hyperplane. Then, there exist points $p_1, \ldots , p_k \in M$ such that $T_{p_1}M + \cdots + T_{p_k}M = {\mathbb {R}}^{2n}$ .

Proof. Suppose $\sum _{p \in M}T_pM \neq {\mathbb {R}}^{2n}$ . Then, there exists a hyperplane Y in ${\mathbb {R}}^{2n}$ such that $\sum _{p \in M}T_pM \subseteq Y$ .

Fix $p \in M$ . Let $q \in M$ . Since M is connected, there exists a differentiable map ${\xi : [0,1] \to M}$ such that $\xi (0)=p$ and $\xi (1)=q$ . By the fundamental theorem of calculus,

$$ \begin{align*} q=p+ \int_0^1 \dot{\xi}(t)\, dt. \end{align*} $$

Since $\dot {\xi }(t) \in Y$ for $t \in [0,1]$ and Y is closed, it follows that $q \in p+ Y$ . This implies that M is contained in the affine hyperplane $p+ Y$ , which is a contradiction.

Hence, $\sum _{p \in M}T_pM ={\mathbb {R}}^{2n}$ . By the Steinitz exchange lemma, there exist finitely many points $p_1, \ldots , p_k \in M$ such that $T_{p_1}M +\cdots +T_{p_k}M = {\mathbb {R}}^{2n}$ .

By possibly adding one more point, we can assume that the integer k obtained in Lemma 3.4 is even.

Proof of Theorem 1.2.

Let $\widetilde {M}= \{-p \:|\: p\in M\}$ . Then, $\widetilde {M}$ is a connected real-analytic submanifold of ${\mathbb {R}}^{2n}$ . Observe that if $p \in M$ , $T_pM = T_{(-p)}\widetilde {M}$ . Therefore, by Lemma 3.4,

(3.2) $$ \begin{align} T_{p_1}M + T_{(-p_2)}\widetilde{M} + \cdots + T_{p_{k-1}}M + T_{(-p_k)}\widetilde{M} = {\mathbb{R}}^{2n}. \end{align} $$

Let $\mu $ be a smooth measure on M. Let $\tilde {\mu }$ denote the push-forward of $\mu $ by the map which sends $p\in M$ to $-p$ . Then, by Theorem 3.1 and (3.2), it follows that $(\mu \,\natural \, \tilde {\mu })^{k/2}$ is absolutely continuous with respect to the Lebesgue measure on ${\mathbb {R}}^{2n}$ . Therefore, $W((\mu \,\natural \, \tilde {\mu })^{k/2})$ is a compact operator.

Observe that $W(\tilde {\mu })= W(\mu )^*$ , where $W(\mu )^*$ is the adjoint of the operator $W(\mu )$ . By Theorem 2.2,

$$ \begin{align*} W((\mu \,\natural \, \tilde{\mu})^{k/2}) = (W(\mu)W(\tilde{\mu}))^{k/2} = (W(\mu)W(\mu)^*)^{k/2}. \end{align*} $$

Since $W(\mu )W(\mu )^*$ is self-adjoint and $(W(\mu )W(\mu )^*)^{k/2}$ is compact, it follows that $W(\mu )W(\mu )^*$ is compact. By the polar decomposition, it follows that $W(\mu )$ is compact.

4. Curve in ${\mathbb {R}}^2$

In this section, we prove the following result, which states that if $n=1$ , the assumption of real analyticity can be removed from Theorem 1.2.

Theorem 4.1. Suppose $M \subseteq {\mathbb {R}}^2$ is a connected smooth hypersurface of finite type. Let $\mu $ be a smooth measure on M. Then, $W(\mu )$ is a compact operator.

We need the following lemma to prove this theorem.

Lemma 4.2. Let $\gamma :[a,b] \to {\mathbb {R}}^2$ be a finite type unit-speed simple smooth curve. Let $\delta :[c,d] \to {\mathbb {R}}^2$ be a unit-speed simple smooth curve. Let $\mu $ and $\nu $ be smooth measures on $\operatorname {Im}(\gamma )$ and $\operatorname {Im}(\delta )$ , respectively. Then, $\mu \,\natural \, \nu $ is absolutely continuous with respect to the Lebesgue measure on ${\mathbb {R}}^2$ .

Proof. Let $E \subseteq {\mathbb {R}}^2$ be a Borel set. Then, by (3.1),

$$ \begin{align*} \mu \,\natural \, \nu (E) = (\varphi_2 \,\mu \times \nu)(\Sigma_2^{-1}(E)), \end{align*} $$

where $\Sigma _2:\operatorname {Im}(\gamma ) \times \operatorname {Im}(\delta ) \to {\mathbb {R}}^2$ is the map given by $\Sigma _2(\gamma (s),\delta (t))= \gamma (s)+\delta (t)$ . Define $S:[a,b]\times [c,d] \to {\mathbb {R}}^2$ by

$$ \begin{align*} S(s,t)= \gamma(s)+\delta(t). \end{align*} $$

Let $T=\{(s,t)\in [a,b]\times [c,d]\:|\: \dot {\gamma }(s)=\pm \dot {\delta }(t)\}$ . Observe that T is the critical set of S. We claim that T has area zero. Suppose T has a positive area. Then, by Fubini’s theorem, there exists $t \in [c,d]$ such that the set $Z=\{s\in [a,b]\:|\: \dot {\gamma }(s)=\pm \dot {\delta }(t)\}$ has positive length. By the Lebesgue differentiation theorem [4, Theorem 3.21], there exists $s' \in [a,b]$ such that $s'$ is a point of density of Z. Then, there exist distinct $s_j \in Z$ such that the sequence $\{s_j\}$ converges to $s'$ , and so the sequence $\{\dot {\gamma }(s_j)\}$ converges to $\dot {\gamma }(s')$ . Let $\vec {v}$ be a unit vector in ${\mathbb {R}}^2$ perpendicular to $\dot {\delta }(t)$ . Then,

$$ \begin{align*} \langle\dot{\gamma}(s_j)\,,\,\vec{v}\rangle = \langle\pm\dot{\delta}(t)\,,\,\vec{v}\rangle = 0, \quad j=1,2,\ldots. \end{align*} $$

Hence, all the coefficients in the Taylor expansion of $\langle \dot {\gamma }(s)\,,\,\vec {v}\rangle $ about $s=s'$ are zero. This contradicts the fact that $\gamma $ is a curve of finite type. Therefore, T has area zero.

Since $\operatorname {Im}(\gamma )$ and $\operatorname {Im}(\delta )$ are smooth submanifolds of ${\mathbb {R}}^2$ , it follows that $\operatorname {Im}(\gamma ) \times \operatorname {Im}(\delta )$ is a smooth submanifold of ${\mathbb {R}}^4$ . Let $\tau $ denote the Riemannian measure on $\operatorname {Im}(\gamma ) \times \operatorname {Im}(\delta )$ . Since $\gamma \times \delta $ is a smooth map and the set T has area zero, it follows that $(\gamma \times \delta )(T)$ has $\tau $ -measure zero.

Observe that $(\gamma \times \delta )(T)$ is the critical set of $\Sigma _2$ . The proof now follows from Lemma 3.3.

Proof of Theorem 4.1.

Suppose $M \subseteq {\mathbb {R}}^2$ is a hypersurface of finite type. Let $\mu $ be a smooth measure on M. Let $\tilde {\mu }$ denote the push-forward of $\mu $ by the map which sends ${p\in M}$ to $-p$ . It follows from Lemma 4.2 that $\mu \,\natural \, \tilde {\mu }$ is absolutely continuous with respect to the Lebesgue measure on ${\mathbb {R}}^2$ . Therefore, $W(\mu \,\natural \, \tilde {\mu })$ is compact. Observe that $W(\tilde {\mu })= W(\mu )^*$ . By Theorem 2.2,

$$ \begin{align*} W(\mu \,\natural \, \tilde{\mu})= W(\mu)W(\tilde{\mu})= W(\mu)W(\mu)^*. \end{align*} $$

Since $W(\mu )W(\mu )^*$ is compact, it follows by the polar decomposition that $W(\mu )$ is compact.