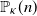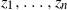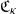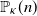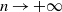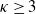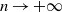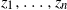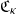1. Introduction
Let
![]() $\mathfrak{C}_\kappa$
be the regular
$\mathfrak{C}_\kappa$
be the regular
![]() $\kappa$
-gon with area 1 positioned on the x-axis, as represented in Figure 1, let
$\kappa$
-gon with area 1 positioned on the x-axis, as represented in Figure 1, let
![]() $r_\kappa=\left(4\tan\left(\frac{\pi}{\kappa}\right)/\kappa\right)^{1/2}$
be its side length, and let
$r_\kappa=\left(4\tan\left(\frac{\pi}{\kappa}\right)/\kappa\right)^{1/2}$
be its side length, and let
![]() $ \theta_\kappa=\frac{(\kappa-2)\pi}{\kappa}$
be the interior angle between two consecutive sides.
$ \theta_\kappa=\frac{(\kappa-2)\pi}{\kappa}$
be the interior angle between two consecutive sides.
For any compact convex domain K of area 1 in
![]() $\mathbb{R}^2$
with non-empty interior and for any
$\mathbb{R}^2$
with non-empty interior and for any
![]() $n\in\mathbb{N}$
, we let
$n\in\mathbb{N}$
, we let
![]() $\mathbb{U}_K^{(n)}$
denote the law of an n-tuple
$\mathbb{U}_K^{(n)}$
denote the law of an n-tuple
![]() $\mathbf{z}[n]\,:\!=\,(\mathbf{z}_1,\cdots,\mathbf{z}_n)$
, where the
$\mathbf{z}[n]\,:\!=\,(\mathbf{z}_1,\cdots,\mathbf{z}_n)$
, where the
![]() $\mathbf{z}_i$
are independent and identically distributed (i.i.d.) and uniform in K.
$\mathbf{z}_i$
are independent and identically distributed (i.i.d.) and uniform in K.
In the special case
![]() $K=\mathfrak{C}_\kappa$
, we write for short
$K=\mathfrak{C}_\kappa$
, we write for short
![]() $\mathbb{U}^{(n)}_{\kappa}\,:\!=\,\mathbb{U}^{(n)}_{\mathfrak{C}_\kappa}$
.
$\mathbb{U}^{(n)}_{\kappa}\,:\!=\,\mathbb{U}^{(n)}_{\mathfrak{C}_\kappa}$
.
An n-tuple of points
![]() $z[n]\in(\mathbb{R}^2)^n$
is said to be in convex position if
$z[n]\in(\mathbb{R}^2)^n$
is said to be in convex position if
![]() $\{z_1,\cdots,z_n\}$
is the vertex set of a convex polygon, which we will refer to as the z[n]-gon; the set of such n-tuples z[n] is denoted by
$\{z_1,\cdots,z_n\}$
is the vertex set of a convex polygon, which we will refer to as the z[n]-gon; the set of such n-tuples z[n] is denoted by
![]() $\mathcal{Z}_n$
. Hence
$\mathcal{Z}_n$
. Hence
is the probability that n i.i.d. random points
![]() $\mathbf{z}[n]$
taken uniformly in K are in convex position, and
$\mathbf{z}[n]$
taken uniformly in K are in convex position, and
is the corresponding probability in the regular
![]() $\kappa$
-gon.
$\kappa$
-gon.

Figure 1.
![]() $\mathfrak{C}_7$
.
$\mathfrak{C}_7$
.
The purpose of this paper is threefold. First we give an equivalent of
![]() $\mathbb{P}_\kappa(n)$
as
$\mathbb{P}_\kappa(n)$
as
![]() $n\to\infty$
(see Theorem 1 below), then we describe the fluctuations of a z[n]-gon with distribution
$n\to\infty$
(see Theorem 1 below), then we describe the fluctuations of a z[n]-gon with distribution
![]() $\mathbb{U}^{(n)}_\kappa$
conditioned to be in convex position (Theorem 8), and we conclude by providing an algorithm to sample such an n-tuple z[n] (Section 6). One of the main contributions of this paper is thus the following theorem.
$\mathbb{U}^{(n)}_\kappa$
conditioned to be in convex position (Theorem 8), and we conclude by providing an algorithm to sample such an n-tuple z[n] (Section 6). One of the main contributions of this paper is thus the following theorem.
Theorem 1.
Let
![]() $\kappa\geq 3$
be an integer. We have
$\kappa\geq 3$
be an integer. We have
where
and
![]() $\mathrm{m}_\kappa$
is the determinant of a deterministic matrix (see Theorem 7), an explicit formula for which is given by
$\mathrm{m}_\kappa$
is the determinant of a deterministic matrix (see Theorem 7), an explicit formula for which is given by
Theorem 1 actually refines a famous result of Bárány [Reference Bárány3] in the case of
![]() $\kappa$
-gons (note, however, that Bárány’s result holds under weaker hypotheses).
$\kappa$
-gons (note, however, that Bárány’s result holds under weaker hypotheses).
Theorem 2. (Bárány [Reference Bárány3].) For any compact convex set K of area 1 with non-empty interior,
where
![]() $\mathrm{AP}^*(K)$
is the supremum of the affine perimeters of all convex sets
$\mathrm{AP}^*(K)$
is the supremum of the affine perimeters of all convex sets
![]() $S\subset K.$
$S\subset K.$
The definition of the affine perimeter will be recalled in Definition 2; we send the interested reader to [Reference Bárány2] for additional details. In the
![]() $\kappa$
-gon case, as will be shown in Lemma 17, we have
$\kappa$
-gon case, as will be shown in Lemma 17, we have
so that one can check that in that particular case, Theorem 1 is compatible with and more precise than Theorem 2.
The quantity
![]() $\mathbb{P}_K(n)$
has been widely studied since the 19th century, and for a large variety of convex sets K, not just regular polygons. Sylvester [Reference Sylvester23] initiated the consideration of this matter, looking at the probability that four points chosen at random in the plane were in convex position. Though Sylvester’s question was ill-posed, it matured in its later formulation into the study of
$\mathbb{P}_K(n)$
has been widely studied since the 19th century, and for a large variety of convex sets K, not just regular polygons. Sylvester [Reference Sylvester23] initiated the consideration of this matter, looking at the probability that four points chosen at random in the plane were in convex position. Though Sylvester’s question was ill-posed, it matured in its later formulation into the study of
![]() $\mathbb{P}_K(4)$
, for any convex shape K of area 1 (see Pfiefer [Reference Pfiefer20] for historical notes). In 1917, Blaschke [Reference Blaschke5] determined the convex domain K that maximizes or minimizes the probability
$\mathbb{P}_K(4)$
, for any convex shape K of area 1 (see Pfiefer [Reference Pfiefer20] for historical notes). In 1917, Blaschke [Reference Blaschke5] determined the convex domain K that maximizes or minimizes the probability
![]() $\mathbb{P}_K(4)$
(on the set of non-flat compact convex domains of
$\mathbb{P}_K(4)$
(on the set of non-flat compact convex domains of
![]() $\mathbb{R}^2$
) by proving that the lower bound is achieved when
$\mathbb{R}^2$
) by proving that the lower bound is achieved when
![]() $K=\triangle$
is a triangle, and the upper bound when
$K=\triangle$
is a triangle, and the upper bound when
![]() $K=\bigcirc$
is a disk; that is,
$K=\bigcirc$
is a disk; that is,
In the same direction, Marckert and Rahmani [Reference Marckert and Rahmani18] proved in 2021 that
This question can be generalized to different values of n, and other dimensions. To this day, the conjecture in dimension 2, that
for all
![]() $n\geq3$
, remains open. Yet the value
$n\geq3$
, remains open. Yet the value
![]() $\mathbb{P}_\bigcirc(n)$
has been known since 2017 to be computable for all
$\mathbb{P}_\bigcirc(n)$
has been known since 2017 to be computable for all
![]() $n\geq3$
, thanks to Marckert’s algebraic formula [Reference Marckert17] in the disk case. Note also that Hilhorst et al. [Reference Hilhorst, Calka and Schehr13] managed in 2008 to derive an asymptotic expansion of
$n\geq3$
, thanks to Marckert’s algebraic formula [Reference Marckert17] in the disk case. Note also that Hilhorst et al. [Reference Hilhorst, Calka and Schehr13] managed in 2008 to derive an asymptotic expansion of
![]() $\log{\mathbb{P}_\bigcirc(n)}$
.
$\log{\mathbb{P}_\bigcirc(n)}$
.
In the case of regular convex polygons, exact formulas are rare, but Valtr proved in 1995 [Reference Valtr24] that for K a parallelogram,
and in 1996 [Reference Valtr25] that when K is a triangle,
The equivalents given at the right-hand side are of course consistent with Theorem 1. Note however that our method will allow us to recover Valtr’s formulas in Section B (our approach avoids discretization arguments, but it largely relies on Valtr’s ideas).
In dimension
![]() $d\geq3$
, if
$d\geq3$
, if
![]() $\triangle^d$
and
$\triangle^d$
and
![]() $\bigcirc^d$
denote respectively a simplex and an ellipsoid of volume 1, the following generalization of Sylvester’s question—that
$\bigcirc^d$
denote respectively a simplex and an ellipsoid of volume 1, the following generalization of Sylvester’s question—that
for any convex domain
![]() $K\subset \mathbb{R}^d$
of volume 1—is a conjecture that remains to be proven (though the right inequality is known as a generalization of Blaschke’s proof in dimension 2). For a comprehensive overview of these matters, we refer to Schneider [Reference Schneider21].
$K\subset \mathbb{R}^d$
of volume 1—is a conjecture that remains to be proven (though the right inequality is known as a generalization of Blaschke’s proof in dimension 2). For a comprehensive overview of these matters, we refer to Schneider [Reference Schneider21].
Canonical ordering of
z
[
n
]-gons. An element of
![]() $z[n]\in\mathcal{Z}_n$
(in convex position) is said to be in convex canonical order if it satisfies the following conditions (see Figure 2):
$z[n]\in\mathcal{Z}_n$
(in convex position) is said to be in convex canonical order if it satisfies the following conditions (see Figure 2):
-
• If
 $(x_i,y_i)$
are the coordinates of
$(x_i,y_i)$
are the coordinates of
 $z_i$
in
$z_i$
in
 $\mathbb{R}^2$
, then
$\mathbb{R}^2$
, then
 $y_1\leq y_i$
for all i (that is,
$y_1\leq y_i$
for all i (that is,
 $z_1$
has the smallest y-component), and among the points having the minimal y-component,
$z_1$
has the smallest y-component), and among the points having the minimal y-component,
 $z_1$
has the smallest x-component.
$z_1$
has the smallest x-component. -
• The sequence
 $(\arg(z_{i+1}-z_i),1\leq i \leq n-1)$
is non-decreasing in
$(\arg(z_{i+1}-z_i),1\leq i \leq n-1)$
is non-decreasing in
 $[0,2\pi]$
.
$[0,2\pi]$
.

Figure 2. Some z[n] in
![]() $\mathcal{C}_7(n)$
.
$\mathcal{C}_7(n)$
.
We denote by
![]() $\overset{\curvearrowleft}{\mathcal{Z}}_n$
the subset of
$\overset{\curvearrowleft}{\mathcal{Z}}_n$
the subset of
![]() $\mathcal{Z}_n$
of n-tuples of points z[n] in convex canonical order. The symmetric group
$\mathcal{Z}_n$
of n-tuples of points z[n] in convex canonical order. The symmetric group
![]() $\mathcal{S}_n$
acts transitively on
$\mathcal{S}_n$
acts transitively on
![]() $\mathcal{Z}_n$
by relabeling the vertex indices; each orbit contains a unique element of
$\mathcal{Z}_n$
by relabeling the vertex indices; each orbit contains a unique element of
![]() $\overset{\curvearrowleft}{\mathcal{Z}}_n$
. We put
$\overset{\curvearrowleft}{\mathcal{Z}}_n$
. We put
![]() $\mathcal{D}_\kappa(n)=\mathcal{Z}_n\cap(\mathfrak{C}_\kappa)^n$
and
$\mathcal{D}_\kappa(n)=\mathcal{Z}_n\cap(\mathfrak{C}_\kappa)^n$
and
![]() $\mathcal{C}_\kappa(n)=\overset{\curvearrowleft}{\mathcal{Z}}_n\cap(\mathfrak{C}_\kappa)^n$
.
$\mathcal{C}_\kappa(n)=\overset{\curvearrowleft}{\mathcal{Z}}_n\cap(\mathfrak{C}_\kappa)^n$
.
Since
![]() $\mathbf{z}[n]$
is picked according to the uniform distribution on
$\mathbf{z}[n]$
is picked according to the uniform distribution on
![]() $(\mathfrak{C}_\kappa)^n$
, and since this measure is the Lebesgue measure
$(\mathfrak{C}_\kappa)^n$
, and since this measure is the Lebesgue measure
![]() $\mathsf{Leb}$
on this set, we have
$\mathsf{Leb}$
on this set, we have
In what follows, we will abandon
![]() $\mathcal{D}_\kappa(n)$
and work mainly in
$\mathcal{D}_\kappa(n)$
and work mainly in
![]() $\mathcal{C}_\kappa(n)$
, as the elements of this set are easier to parametrize. The argument we detail for the computation of
$\mathcal{C}_\kappa(n)$
, as the elements of this set are easier to parametrize. The argument we detail for the computation of
![]() $\mathsf{Leb}(\mathcal{C}_\kappa(n))$
is mainly deterministic, and we will not really be using random variables in the analysis, even though everything could be rewritten in terms of them (but the proof would then be much more cumbersome).
$\mathsf{Leb}(\mathcal{C}_\kappa(n))$
is mainly deterministic, and we will not really be using random variables in the analysis, even though everything could be rewritten in terms of them (but the proof would then be much more cumbersome).
Notation. From now on, we denote by
![]() ${\mathbb{Q}}^{(n)}_{K}$
the law of an n-tuple of points with distribution
${\mathbb{Q}}^{(n)}_{K}$
the law of an n-tuple of points with distribution
![]() $\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in
$\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in
![]() $\mathcal{C}_\kappa(n)$
, and write for short
$\mathcal{C}_\kappa(n)$
, and write for short
![]() $\mathbb{Q}^{(n)}_{\kappa}\,:\!=\,{\mathbb{Q}}^{(n)}_{\mathfrak{C}_\kappa}$
; that is,
$\mathbb{Q}^{(n)}_{\kappa}\,:\!=\,{\mathbb{Q}}^{(n)}_{\mathfrak{C}_\kappa}$
; that is,
This formula represents the measure, but it is not amenable to being used in further computations; we will thus need an alternative geometric understanding of
![]() $\mathcal{C}_\kappa(n)$
, which was inspired by Valtr’s papers.
$\mathcal{C}_\kappa(n)$
, which was inspired by Valtr’s papers.
Limit shape. Bárány [Reference Bárány2] proved in 1999 that the convex hull of an n-tuple
![]() $\mathbf{z}[n]$
with distribution
$\mathbf{z}[n]$
with distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
converges in probability for the Hausdorff topology to an explicit deterministic domain
$\mathbb{Q}^{(n)}_{\kappa}$
converges in probability for the Hausdorff topology to an explicit deterministic domain
![]() $\mathsf{Dom}(K)$
, which has the important property that
$\mathsf{Dom}(K)$
, which has the important property that
In the case of the
![]() $\kappa$
-gon, we represent this domain
$\kappa$
-gon, we represent this domain
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
in Figure 3. We will explain in Lemma 16 how
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
in Figure 3. We will explain in Lemma 16 how
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
is determined using the inner symmetries of
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
is determined using the inner symmetries of
![]() $\mathfrak{C}_\kappa$
.
$\mathfrak{C}_\kappa$
.

Figure 3. For each case
![]() $\kappa=3, 4, 6$
, the inner dashed curve delimits a convex domain
$\kappa=3, 4, 6$
, the inner dashed curve delimits a convex domain
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
inside
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
inside
![]() $\mathfrak{C}_\kappa$
. The dashed curve represents the limit shape of a
$\mathfrak{C}_\kappa$
. The dashed curve represents the limit shape of a
![]() $\mathbf{z}[n]$
-gon taken under
$\mathbf{z}[n]$
-gon taken under
![]() $\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in convex position, as
$\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in convex position, as
![]() $n\to+\infty$
. The curve can be drawn as follows: add the midpoints of the sides of the initial
$n\to+\infty$
. The curve can be drawn as follows: add the midpoints of the sides of the initial
![]() $\kappa$
-gon, and between two consecutive midpoints, add the arc of the parabola which is tangent to the sides and incident to these inner points. The sum of the hatched areas corresponds to the supremum of affine perimeters (for an explanation see Lemma 17 in the appendix).
$\kappa$
-gon, and between two consecutive midpoints, add the arc of the parabola which is tangent to the sides and incident to these inner points. The sum of the hatched areas corresponds to the supremum of affine perimeters (for an explanation see Lemma 17 in the appendix).
Denote by
![]() $d_H$
the Hausdorff distance on the set of compact subsets of
$d_H$
the Hausdorff distance on the set of compact subsets of
![]() $\mathbb{R}^2$
, and for any tuple
$\mathbb{R}^2$
, and for any tuple
![]() ${z}[n]\in(\mathbb{R}^2)^n$
, let
${z}[n]\in(\mathbb{R}^2)^n$
, let
![]() $\mathsf{conv}({z}[n])$
be its convex hull. In the second main contribution of this paper, we detail the fluctuations of the
$\mathsf{conv}({z}[n])$
be its convex hull. In the second main contribution of this paper, we detail the fluctuations of the
![]() $\mathbf{z}[n]$
-gon having distribution
$\mathbf{z}[n]$
-gon having distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
around its limit
$\mathbb{Q}^{(n)}_{\kappa}$
around its limit
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
.
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
.
Theorem 3.
Let
![]() $\kappa \geq 3$
be fixed, and let
$\kappa \geq 3$
be fixed, and let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
. When
$\mathbb{Q}^{(n)}_{\kappa}$
. When
![]() $n\to+\infty$
, we have
$n\to+\infty$
, we have
where
![]() $\Delta$
is a non-trivial random variable.
$\Delta$
is a non-trivial random variable.
This theorem will turn out to be a consequence of the fluctuations of the
![]() $\mathbf{z}[n]$
-gon in distribution (at scale
$\mathbf{z}[n]$
-gon in distribution (at scale
![]() $1/\sqrt{n}$
around its limit) in a functional space, as stated in Theorem 8. We refrain from stating the latter theorem at this point, since we would need to introduce too much material to do so; we postpone this work to Section 5.
$1/\sqrt{n}$
around its limit) in a functional space, as stated in Theorem 8. We refrain from stating the latter theorem at this point, since we would need to introduce too much material to do so; we postpone this work to Section 5.
However, we disclose an element of the proof here: the main idea is to partition each z[n]-gon of
![]() $\mathcal{C}_\kappa(n)$
into
$\mathcal{C}_\kappa(n)$
into
![]() $\kappa$
suitable convex chains, one per corner of the initial polygon
$\kappa$
suitable convex chains, one per corner of the initial polygon
![]() $\mathfrak{C}_\kappa$
. Each of the convex chains will be shown to converge separately towards the arc of the parabola associated with the corresponding ‘corner’ of
$\mathfrak{C}_\kappa$
. Each of the convex chains will be shown to converge separately towards the arc of the parabola associated with the corresponding ‘corner’ of
![]() $\mathfrak{C}_\kappa$
, as introduced in Figure 3.
$\mathfrak{C}_\kappa$
, as introduced in Figure 3.
The convergence results stated in Theorem 8 are reminiscent of the limit theorems concerning lattice convex polygons: in this model, an integer n is given, and a convex (lattice) polygon is a convex polygon contained in the square
![]() $[{-}n,n]^2$
and having vertices with integer coordinates (and any number of sides). Vershik asked whether it was possible to determine the number and typical shape of convex lattice polygons contained in
$[{-}n,n]^2$
and having vertices with integer coordinates (and any number of sides). Vershik asked whether it was possible to determine the number and typical shape of convex lattice polygons contained in
![]() $[{-}n,n]^2$
. Three different solutions were brought to light by Bárány [Reference Bárány1], Vershik [Reference Vershik26], and Sinai [Reference Sinai22] in 1994, which we outline below.
$[{-}n,n]^2$
. Three different solutions were brought to light by Bárány [Reference Bárány1], Vershik [Reference Vershik26], and Sinai [Reference Sinai22] in 1994, which we outline below.
A convex lattice polygon can be decomposed naturally into four parts (delimited by the extreme points in the north/east/south/west directions), which determine four ‘polygonal convex lines’ between them. It is therefore natural to investigate the behavior of these chains, which can be considered, in a first approximation, as convex chains going from (0, 0) to (n, n) in the square
![]() $[0,n]^2$
(up to rotations/translations). For these chains, Bárány [Reference Bárány1], Vershik [Reference Vershik26], and Sinai [Reference Sinai22] proved that when
$[0,n]^2$
(up to rotations/translations). For these chains, Bárány [Reference Bárány1], Vershik [Reference Vershik26], and Sinai [Reference Sinai22] proved that when
![]() $n\to+\infty,$
$n\to+\infty,$
-
(1) the number of these convex polygonal lines is
 $\exp(3(\zeta(3)/\zeta(2))^{1/3} n^{2/3} + o(n^{2/3}))$
, where
$\exp(3(\zeta(3)/\zeta(2))^{1/3} n^{2/3} + o(n^{2/3}))$
, where
 $\zeta$
is the Riemann zeta function,
$\zeta$
is the Riemann zeta function, -
(2) the random number of vertices in such a chain is concentrated around the quantity
 $\left(\zeta(3)^2/\zeta(2)\right)^{-1/3} n^{2/3}$
, and
$\left(\zeta(3)^2/\zeta(2)\right)^{-1/3} n^{2/3}$
, and -
(3) the limit shape of such a chain, normalized in both directions by n, is an arc of a parabola.
These results were refined by Bureaux and Enriquez [Reference Bureaux and Enriquez10] in 2016, and generalized to higher dimensions by Bárány et al. [Reference Bárány, Bureaux and Lund11] in 2018, as well as by Buffière [Reference Buffière9] for zonotopes in 2023.
On a related topic, the paper of Bodini et al. [Reference Bodini, Jacquot, Duchon and Mutafchiev7] gives a characterization of digitally convex polyominoes using combinatorics on words.
Random generation of a
![]() $\mathbf{z}\mathbf{[n]}$
-gon with distribution
$\mathbf{z}\mathbf{[n]}$
-gon with distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
. The naive way of sampling a
$\mathbb{Q}^{(n)}_{\kappa}$
. The naive way of sampling a
![]() $\mathbf{z}[n]$
-gon with distribution
$\mathbf{z}[n]$
-gon with distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
consists in rejection sampling, i.e. sampling points that are
$\mathbb{Q}^{(n)}_{\kappa}$
consists in rejection sampling, i.e. sampling points that are
![]() $\mathbb{U}_n^{(\kappa)}$
-distributed until they are in
$\mathbb{U}_n^{(\kappa)}$
-distributed until they are in
![]() $\mathcal{C}_\kappa(n)$
(or in
$\mathcal{C}_\kappa(n)$
(or in
![]() $\mathcal{D}_\kappa(n)$
). This algorithm works fine for small values of n, but as n grows, computation times become unacceptable (by Theorem 1, the probability of success is less than
$\mathcal{D}_\kappa(n)$
). This algorithm works fine for small values of n, but as n grows, computation times become unacceptable (by Theorem 1, the probability of success is less than
![]() $\frac{k^n}{n^{2n}}$
for some constant k). In particular, the limit shape theorem proven by Bárány cannot be observed empirically using such a method.
$\frac{k^n}{n^{2n}}$
for some constant k). In particular, the limit shape theorem proven by Bárány cannot be observed empirically using such a method.
A comprehensive understanding of the distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
will allow us to determine another distribution
$\mathbb{Q}^{(n)}_{\kappa}$
will allow us to determine another distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, for which we have an exact sampling algorithm (called
${\mathbb{D}}^{(n)}_{\kappa}$
, for which we have an exact sampling algorithm (called
![]() $\kappa$
-sampling and defined in Section 6) that behaves asymptotically like
$\kappa$
-sampling and defined in Section 6) that behaves asymptotically like
![]() $\mathbb{Q}^{(n)}_{\kappa}$
, meaning that
$\mathbb{Q}^{(n)}_{\kappa}$
, meaning that
![]() $d_{V}(\mathbb{Q}^{(n)}_{\kappa},{\mathbb{D}}^{(n)}_{\kappa})\underset{n\to+\infty}{\longrightarrow}0$
, where
$d_{V}(\mathbb{Q}^{(n)}_{\kappa},{\mathbb{D}}^{(n)}_{\kappa})\underset{n\to+\infty}{\longrightarrow}0$
, where
![]() $d_{V}$
is the total variation distance. The distribution
$d_{V}$
is the total variation distance. The distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
is defined in Section 3 and can be viewed as
${\mathbb{D}}^{(n)}_{\kappa}$
is defined in Section 3 and can be viewed as
![]() $\mathbb{Q}^{(n)}_{\kappa}$
conditioned to satisfy a property which occurs with probability going to 1. This algorithm is asymptotically exact (in n, for
$\mathbb{Q}^{(n)}_{\kappa}$
conditioned to satisfy a property which occurs with probability going to 1. This algorithm is asymptotically exact (in n, for
![]() $\kappa$
fixed), for the
$\kappa$
fixed), for the
![]() $\mathbb{Q}^{(n)}_{\kappa}$
-sampling.
$\mathbb{Q}^{(n)}_{\kappa}$
-sampling.
Theorem 4.
The algorithm of
![]() $\kappa$
-sampling samples an n-tuple of points with distribution
$\kappa$
-sampling samples an n-tuple of points with distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
with a complexity of
${\mathbb{D}}^{(n)}_{\kappa}$
with a complexity of
![]() $\mathcal{O}\left(n^{\kappa/2+1}\kappa\log(\kappa)\right).$
$\mathcal{O}\left(n^{\kappa/2+1}\kappa\log(\kappa)\right).$
Contents of the paper. In the second section of this paper, we analyze the properties of an n-tuple
![]() ${z}[n]\in\mathcal{C}_\kappa(n)$
in the light of a new geometric description. In Section 3 we derive the distribution of the important variables of this geometric scheme, using which we provide the proof of Theorem 1 in Section 4. Section 5 is dedicated to the proof of Theorem 3 and the understanding of the fluctuations of z[n] around its limit. In Section 6, we provide the aforementioned algorithm of
${z}[n]\in\mathcal{C}_\kappa(n)$
in the light of a new geometric description. In Section 3 we derive the distribution of the important variables of this geometric scheme, using which we provide the proof of Theorem 1 in Section 4. Section 5 is dedicated to the proof of Theorem 3 and the understanding of the fluctuations of z[n] around its limit. In Section 6, we provide the aforementioned algorithm of
![]() $\kappa$
-sampling and some alternative (more efficient) versions in the cases
$\kappa$
-sampling and some alternative (more efficient) versions in the cases
![]() $\kappa=3$
and
$\kappa=3$
and
![]() $\kappa=4$
. As for the appendices, the first is dedicated to some proofs omitted from the main text, and the second provides a new demonstration of Valtr’s formulas in the triangle and the parallelogram.
$\kappa=4$
. As for the appendices, the first is dedicated to some proofs omitted from the main text, and the second provides a new demonstration of Valtr’s formulas in the triangle and the parallelogram.
2. Geometric aspects
Notation. In the sequel,
![]() $\kappa\geq3$
is considered to be fixed. We will work quite a lot with indices j running through the set of integers
$\kappa\geq3$
is considered to be fixed. We will work quite a lot with indices j running through the set of integers
![]() $\{1,\ldots,\kappa\}$
. By convention, in the case
$\{1,\ldots,\kappa\}$
. By convention, in the case
![]() $j=1$
,
$j=1$
,
![]() $j-1$
stands for
$j-1$
stands for
![]() $\kappa$
, and when
$\kappa$
, and when
![]() $j=\kappa$
,
$j=\kappa$
,
![]() $j+1$
stands for 1 (we do so to avoid tedious notation).
$j+1$
stands for 1 (we do so to avoid tedious notation).
We start by defining the equiangular circumscribed polygon
![]() $\mathsf{ECP}({z}[n])$
associated to
$\mathsf{ECP}({z}[n])$
associated to
![]() ${z}[n]\in \mathcal{C}_\kappa(n)$
, any n-tuple of points in canonical convex order: as represented (in blue) in Figure 4, this is the polygon equal to the intersection of all equiangular polygons whose sides are parallel, one by one, to those of
${z}[n]\in \mathcal{C}_\kappa(n)$
, any n-tuple of points in canonical convex order: as represented (in blue) in Figure 4, this is the polygon equal to the intersection of all equiangular polygons whose sides are parallel, one by one, to those of
![]() $\mathfrak{C}_\kappa$
, and which contain z[n].
$\mathfrak{C}_\kappa$
, and which contain z[n].

Figure 4. On the left, we draw an
![]() $\mathsf{ECP}({z}[n])$
for an n-tuple taken in
$\mathsf{ECP}({z}[n])$
for an n-tuple taken in
![]() $\overset{\curvearrowleft}{\mathcal{C}_7}(n)$
, with distances
$\overset{\curvearrowleft}{\mathcal{C}_7}(n)$
, with distances
![]() $\ell[7]$
from the sides of
$\ell[7]$
from the sides of
![]() $\mathfrak{C}_7$
to those of
$\mathfrak{C}_7$
to those of
![]() $\mathsf{ECP}(z[n])$
. This latter polygon, whose side lengths are given by the tuple of values c[Reference Bodini, Jacquot, Duchon and Mutafchiev7], is drawn with a dashed boundary inside
$\mathsf{ECP}(z[n])$
. This latter polygon, whose side lengths are given by the tuple of values c[Reference Bodini, Jacquot, Duchon and Mutafchiev7], is drawn with a dashed boundary inside
![]() $\mathfrak{C}_7$
. On the right, a six-sided
$\mathfrak{C}_7$
. On the right, a six-sided
![]() $\mathsf{ECP}({z}[n])$
in
$\mathsf{ECP}({z}[n])$
in
![]() $\mathfrak{C}_7$
. One of the sides is reduced to a point: this happens when three consecutive values
$\mathfrak{C}_7$
. One of the sides is reduced to a point: this happens when three consecutive values
![]() $\ell_{{j-1}},\ell_j,\ell_{{j+1}}$
are defined on the same point
$\ell_{{j-1}},\ell_j,\ell_{{j+1}}$
are defined on the same point
![]() $z_i$
in z[n].
$z_i$
in z[n].
We now define some quantities that will allow the description of z[n] in terms of its circumscribed polygon (see also Figure 4).
The distance from the jth side of
![]() $\mathfrak{C}_\kappa$
to z[n] is denoted by
$\mathfrak{C}_\kappa$
to z[n] is denoted by
![]() $\ell_j\,:\!=\,\ell_j({z}[n])$
. The length of the side of
$\ell_j\,:\!=\,\ell_j({z}[n])$
. The length of the side of
![]() $\mathsf{ECP}({z}[n])$
parallel to the x-axis is denoted by
$\mathsf{ECP}({z}[n])$
parallel to the x-axis is denoted by
![]() $c_1\,:\!=\,c_1({z}[n])$
. Then, the consecutive side lengths of
$c_1\,:\!=\,c_1({z}[n])$
. Then, the consecutive side lengths of
![]() $\mathsf{ECP}({z}[n])$
, sorted counterclockwise, are denoted by
$\mathsf{ECP}({z}[n])$
, sorted counterclockwise, are denoted by
![]() $c_1,c_2,\ldots,c_\kappa$
, one or several
$c_1,c_2,\ldots,c_\kappa$
, one or several
![]() $c_i$
possibly being zero.
$c_i$
possibly being zero.
Remark 1. If
![]() $\kappa=3$
, the only possible internal polygons within
$\kappa=3$
, the only possible internal polygons within
![]() $\mathfrak{C}_3$
are equilateral triangles. If
$\mathfrak{C}_3$
are equilateral triangles. If
![]() $\kappa=4$
, only rectangles are admitted. In both these cases, an internal polygon within
$\kappa=4$
, only rectangles are admitted. In both these cases, an internal polygon within
![]() $\mathfrak{C}_\kappa$
has exactly
$\mathfrak{C}_\kappa$
has exactly
![]() $\kappa$
sides. This is no longer true for
$\kappa$
sides. This is no longer true for
![]() $\kappa\geq5$
, as we can see in the right panel of Figure 4. The number of ‘nonzero sides’ of
$\kappa\geq5$
, as we can see in the right panel of Figure 4. The number of ‘nonzero sides’ of
![]() $\mathsf{ECP}({z}[n])$
is bounded above by
$\mathsf{ECP}({z}[n])$
is bounded above by
![]() $\kappa$
, and below by 3 (in fact by 4 for the
$\kappa$
, and below by 3 (in fact by 4 for the
![]() $\kappa=4$
case; it can technically be 2 if all the points in z[n] are aligned, but we may neglect this case).
$\kappa=4$
case; it can technically be 2 if all the points in z[n] are aligned, but we may neglect this case).
Some properties of equiangular circumscribed polygons. A moment’s thought allows one to see that
![]() $\mathsf{ECP}({z}[n])$
is characterized by the
$\mathsf{ECP}({z}[n])$
is characterized by the
![]() $\kappa$
-tuple of distances
$\kappa$
-tuple of distances
![]() $\ell[\kappa]\,:\!=\,(\ell_1({z}[n]),\cdots,\ell_\kappa({z}[n]))$
, and that, in turn,
$\ell[\kappa]\,:\!=\,(\ell_1({z}[n]),\cdots,\ell_\kappa({z}[n]))$
, and that, in turn,
![]() $\ell[\kappa]$
determines the side lengths of the
$\ell[\kappa]$
determines the side lengths of the
![]() $\mathsf{ECP}$
,
$\mathsf{ECP}$
,
![]() $c[\kappa]\,:\!=\,(c_1({z}[n]),\cdots,c_\kappa({z}[n]))$
. In the sequel, since there is no other set of points (except for z[n]) for which
$c[\kappa]\,:\!=\,(c_1({z}[n]),\cdots,c_\kappa({z}[n]))$
. In the sequel, since there is no other set of points (except for z[n]) for which
![]() $\ell[\kappa]$
or
$\ell[\kappa]$
or
![]() $c[\kappa]$
would be defined, we deliberately omit the mention of z[n] when there is no ambiguity.
$c[\kappa]$
would be defined, we deliberately omit the mention of z[n] when there is no ambiguity.
Proposition 1.
Let
![]() $z[n]\in\mathcal{C}_\kappa(n)$
, with the corresponding
$z[n]\in\mathcal{C}_\kappa(n)$
, with the corresponding
![]() $c[\kappa],\ell[\kappa].$
$c[\kappa],\ell[\kappa].$
-
(i) The vectors
 $\ell[\kappa]$
and
$\ell[\kappa]$
and
 $c[\kappa]$
are related by the
$c[\kappa]$
are related by the
 $\kappa$
equations (2.1)where, for all
$\kappa$
equations (2.1)where, for all \begin{equation} c_j=r_\kappa-\mathfrak{cl}_j(\ell[\kappa]),\quad \forall j \in \{1,\ldots,\kappa\},\end{equation}
\begin{equation} c_j=r_\kappa-\mathfrak{cl}_j(\ell[\kappa]),\quad \forall j \in \{1,\ldots,\kappa\},\end{equation}
 $j\in\{1,\ldots,\kappa\}$
,
$j\in\{1,\ldots,\kappa\}$
,
 $\mathfrak{cl}_j(\ell[\kappa])\,:\!=\,\left(\ell_{{j-1}}+\ell_{{j+1}}+2\ell_j\cos(\theta_\kappa)\right)/\sin(\theta_\kappa)$
(here
$\mathfrak{cl}_j(\ell[\kappa])\,:\!=\,\left(\ell_{{j-1}}+\ell_{{j+1}}+2\ell_j\cos(\theta_\kappa)\right)/\sin(\theta_\kappa)$
(here
 $\mathfrak{cl}$
stands for ‘linear combination’).
$\mathfrak{cl}$
stands for ‘linear combination’).
-
(ii) The set
 $\mathcal{L}_\kappa=\ell[\kappa]\left(\mathcal{C}_\kappa(n)\right)$
(of all possible vectors
$\mathcal{L}_\kappa=\ell[\kappa]\left(\mathcal{C}_\kappa(n)\right)$
(of all possible vectors
 $\ell[\kappa]$
) is the set of solutions
$\ell[\kappa]$
) is the set of solutions
 $\ell[\kappa]$
to the system of inequalities
(2.2)together with the conditions
$\ell[\kappa]$
to the system of inequalities
(2.2)together with the conditions \begin{align} \Big\{\quad\mathfrak{cl}_j(\ell[\kappa]) \leq r_\kappa,\quad \forall j \in \{1,\ldots,\kappa\}, \end{align}
\begin{align} \Big\{\quad\mathfrak{cl}_j(\ell[\kappa]) \leq r_\kappa,\quad \forall j \in \{1,\ldots,\kappa\}, \end{align}
 $\ell_j\geq0,j\in\{1,\ldots,\kappa\}.$
$\ell_j\geq0,j\in\{1,\ldots,\kappa\}.$
-
(iii) The perimeter of the z[n]-gon satisfies
 \begin{align*}\sum_{j=1}^\kappa c_j + \frac{2(1+\cos(\theta_\kappa))}{\sin(\theta_\kappa)}\sum_{j=1}^\kappa \ell_j = \kappa r_\kappa. \end{align*}
\begin{align*}\sum_{j=1}^\kappa c_j + \frac{2(1+\cos(\theta_\kappa))}{\sin(\theta_\kappa)}\sum_{j=1}^\kappa \ell_j = \kappa r_\kappa. \end{align*}
Proof.
-
(i) The formulas (2.1) may be deduced from routine computations on the angles and some appropriate applications of Thales’s theorem according to Figure 5 below. Indeed, we have
with (see Figure 5) \begin{align*}\frac{r_\kappa}{\ell_{j-1}/\sin(\theta_\kappa)+c_j+\ell_{j+1}/\sin(\theta_\kappa)}=\frac{a_\kappa}{a_\kappa+\ell_j/\sin(\theta_\kappa)}, \end{align*}
\begin{align*}\frac{r_\kappa}{\ell_{j-1}/\sin(\theta_\kappa)+c_j+\ell_{j+1}/\sin(\theta_\kappa)}=\frac{a_\kappa}{a_\kappa+\ell_j/\sin(\theta_\kappa)}, \end{align*}
 $a_\kappa=\frac{-r_\kappa}{2\cos(\theta_\kappa)}$
.
$a_\kappa=\frac{-r_\kappa}{2\cos(\theta_\kappa)}$
.

Figure 5. Characteristics of an internal polygon.
-
(ii) It is clear that all elements of
 $\mathcal{L}_\kappa$
solve the system (2.2). Let
$\mathcal{L}_\kappa$
solve the system (2.2). Let
 $\ell[\kappa]$
be a solution to (2.2). Draw a
$\ell[\kappa]$
be a solution to (2.2). Draw a
 $\kappa$
-gon and add a straight line
$\kappa$
-gon and add a straight line
 $(l_1)$
at distance
$(l_1)$
at distance
 $\ell_1$
parallel to the first side of
$\ell_1$
parallel to the first side of
 $\mathfrak{C}_\kappa$
, and another one
$\mathfrak{C}_\kappa$
, and another one
 $(l_2)$
at distance
$(l_2)$
at distance
 $\ell_2$
from
$\ell_2$
from
 $\mathfrak{C}_\kappa$
’s second side. The intersection point of these two lines is a vertex
$\mathfrak{C}_\kappa$
’s second side. The intersection point of these two lines is a vertex
 $\mathsf{b}_1$
of the
$\mathsf{b}_1$
of the
 $\mathsf{ECP}$
. Since
$\mathsf{ECP}$
. Since
 $c_2=r_\kappa-\mathfrak{cl}_2(\ell[\kappa])\geq 0$
, a second vertex
$c_2=r_\kappa-\mathfrak{cl}_2(\ell[\kappa])\geq 0$
, a second vertex
 $\mathsf{b}_2$
of the
$\mathsf{b}_2$
of the
 $\mathsf{ECP}$
is at distance
$\mathsf{ECP}$
is at distance
 $c_2$
from
$c_2$
from
 $\mathsf{b}_1$
on
$\mathsf{b}_1$
on
 $(l_2)$
. We can draw
$(l_2)$
. We can draw
 $(l_3)$
parallel to the third side of
$(l_3)$
parallel to the third side of
 $\mathfrak{C}_\kappa$
passing through
$\mathfrak{C}_\kappa$
passing through
 $\mathsf{b}_2$
. With
$\mathsf{b}_2$
. With
 $c_3=r_\kappa-\mathfrak{cl}_3(\ell[\kappa])\geq 0$
, we can set
$c_3=r_\kappa-\mathfrak{cl}_3(\ell[\kappa])\geq 0$
, we can set
 $\mathsf{b}_3$
as the third vertex of the
$\mathsf{b}_3$
as the third vertex of the
 $\mathsf{ECP}$
. Recursively, with all
$\mathsf{ECP}$
. Recursively, with all
 $c_j=r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\geq 0$
, we get all vertices
$c_j=r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\geq 0$
, we get all vertices
 $(\mathsf{b}[\kappa])$
and a full
$(\mathsf{b}[\kappa])$
and a full
 $\mathsf{ECP}$
. Hence, each solution of (2.2) is in
$\mathsf{ECP}$
. Hence, each solution of (2.2) is in
 $\mathcal{L}_\kappa$
.
$\mathcal{L}_\kappa$
.
To get (iii), just sum all of the equations in (2.1) for all values of j.
Contact points. For each z[n] in
![]() $\mathcal{C}_\kappa(n)$
, each side of
$\mathcal{C}_\kappa(n)$
, each side of
![]() $\mathsf{ECP}({z}[n])$
contains at least one element of
$\mathsf{ECP}({z}[n])$
contains at least one element of
![]() $\{z_1,\cdots,z_n\}$
. The jth ‘contact point’
$\{z_1,\cdots,z_n\}$
. The jth ‘contact point’
![]() $\mathsf{cp}_j\,:\!=\,\mathsf{cp}_j({z}[n])$
is the point of
$\mathsf{cp}_j\,:\!=\,\mathsf{cp}_j({z}[n])$
is the point of
![]() $\{z_1,\cdots,z_n\}$
which is on the jth side of
$\{z_1,\cdots,z_n\}$
which is on the jth side of
![]() $\mathsf{ECP}({z}[n])$
, and which is the smallest with respect to the lexicographical order among those with this property. Note that we will work with n-tuples
$\mathsf{ECP}({z}[n])$
, and which is the smallest with respect to the lexicographical order among those with this property. Note that we will work with n-tuples
![]() $\mathbf{z}[n]$
of random variables, so that when
$\mathbf{z}[n]$
of random variables, so that when
![]() $\mathbf{z}[n]$
is
$\mathbf{z}[n]$
is
![]() $\mathbb{Q}^{(n)}_{\kappa}$
-distributed, there is a single point of
$\mathbb{Q}^{(n)}_{\kappa}$
-distributed, there is a single point of
![]() $\{\mathbf{z}_1,\cdots,\mathbf{z}_n\}$
on the jth side of
$\{\mathbf{z}_1,\cdots,\mathbf{z}_n\}$
on the jth side of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
with probability 1; thus the particular choice of the lexicographical order has no importance. However,
$\mathsf{ECP}(\mathbf{z}[n])$
with probability 1; thus the particular choice of the lexicographical order has no importance. However,
![]() $\mathsf{cp}_j=\mathsf{cp}_{{j+1}}$
is possible and occurs with positive probability for all
$\mathsf{cp}_j=\mathsf{cp}_{{j+1}}$
is possible and occurs with positive probability for all
![]() $n\geq1$
.
$n\geq1$
.
Denote by
![]() $\mathsf{b}_j$
the intersection point between the jth and
$\mathsf{b}_j$
the intersection point between the jth and
![]() $(j+1)$
th sides of
$(j+1)$
th sides of
![]() $\mathsf{ECP}({z}[n])$
for all
$\mathsf{ECP}({z}[n])$
for all
![]() $j\in\{1,\ldots,\kappa\}$
(the jth vertex of
$j\in\{1,\ldots,\kappa\}$
(the jth vertex of
![]() $\mathsf{ECP}({z}[n])$
). In the case where the jth side of
$\mathsf{ECP}({z}[n])$
). In the case where the jth side of
![]() $\mathsf{ECP}({z}[n])$
is reduced to a point, i.e.
$\mathsf{ECP}({z}[n])$
is reduced to a point, i.e.
![]() $c_j=0$
, we have
$c_j=0$
, we have
![]() $\mathsf{cp}_{{j-1}}=\mathsf{b}_{{j-1}}=\mathsf{cp}_j=\mathsf{b}_j=\mathsf{cp}_{{j+1}}$
.
$\mathsf{cp}_{{j-1}}=\mathsf{b}_{{j-1}}=\mathsf{cp}_j=\mathsf{b}_j=\mathsf{cp}_{{j+1}}$
.
The triangle with vertices
![]() $\mathsf{cp}_j,\mathsf{cp}_{{j+1}},\mathsf{b}_j$
will be referred to as the jth corner of
$\mathsf{cp}_j,\mathsf{cp}_{{j+1}},\mathsf{b}_j$
will be referred to as the jth corner of
![]() $\mathsf{ECP}({z}[n])$
or
$\mathsf{ECP}({z}[n])$
or
![]() $\mathsf{corner}_j({z}[n])$
(see Figure 6 below for a summary).
$\mathsf{corner}_j({z}[n])$
(see Figure 6 below for a summary).

Figure 6. In
![]() $\mathfrak{C}_7$
, an example of a z[n]-gon, the
$\mathfrak{C}_7$
, an example of a z[n]-gon, the
![]() $\mathsf{ECP}({z}[n])$
, and its vertices
$\mathsf{ECP}({z}[n])$
, and its vertices
![]() $\mathsf{b}[7]$
, as well as the first and second corners (the hashed areas). Here we have
$\mathsf{b}[7]$
, as well as the first and second corners (the hashed areas). Here we have
![]() $s[7]=(2,3,1,2,1,3,0)$
.
$s[7]=(2,3,1,2,1,3,0)$
.
Convex chains between contact points. To get a comprehensive description of z[n] with respect to its circumscribed polygon
![]() $\mathsf{ECP}(z[n])$
, we need to enrich the decomposition between the contact points. For this purpose, let ABC be the triangle with vertices A,B,C (taken in that order) in the plane. For every integer
$\mathsf{ECP}(z[n])$
, we need to enrich the decomposition between the contact points. For this purpose, let ABC be the triangle with vertices A,B,C (taken in that order) in the plane. For every integer
![]() $m\geq 0$
, we denote by
$m\geq 0$
, we denote by
![]() $\mathsf{Chain}_m(ABC)$
the set of
$\mathsf{Chain}_m(ABC)$
the set of
![]() $(m+1)$
-tuples
$(m+1)$
-tuples
![]() $(A,z^{\prime}_1,\ldots,z^{\prime}_{m-1},B)$
such that
$(A,z^{\prime}_1,\ldots,z^{\prime}_{m-1},B)$
such that
![]() $z^{\prime}_1,\ldots,z^{\prime}_{m-1}$
are in the triangle ABC, and
$z^{\prime}_1,\ldots,z^{\prime}_{m-1}$
are in the triangle ABC, and
![]() $(A,z^{\prime}_1,\ldots,z^{\prime}_{m-1},B)\in\overset{\curvearrowleft}{\mathcal{Z}}_{m+1}$
. Hence, m is the number of vectors needed to join the points of any convex chain in
$(A,z^{\prime}_1,\ldots,z^{\prime}_{m-1},B)\in\overset{\curvearrowleft}{\mathcal{Z}}_{m+1}$
. Hence, m is the number of vectors needed to join the points of any convex chain in
![]() $\mathsf{Chain}_{m}(ABC)$
. If
$\mathsf{Chain}_{m}(ABC)$
. If
![]() $A=B$
, we define
$A=B$
, we define
![]() $\mathsf{Chain}_m(ABC)$
only for
$\mathsf{Chain}_m(ABC)$
only for
![]() $m=0$
as the set reduced to the trivial chain
$m=0$
as the set reduced to the trivial chain
![]() $(A,A).$
We can now decompose the z[n]-gon between the contact points as follows.
$(A,A).$
We can now decompose the z[n]-gon between the contact points as follows.
For all
![]() $j\in \{1,\ldots,\kappa\}$
, let
$j\in \{1,\ldots,\kappa\}$
, let
![]() $k\,:\!=\,k(j)\in\{1,\ldots,n\}$
be such that
$k\,:\!=\,k(j)\in\{1,\ldots,n\}$
be such that
![]() $z_k=\mathsf{cp}_j$
, and denote by
$z_k=\mathsf{cp}_j$
, and denote by
![]() $s_j\,:\!=\,s_j(z[n])$
the integer such that
$s_j\,:\!=\,s_j(z[n])$
the integer such that
![]() $z_{k+s_j}=\mathsf{cp}_{{j+1}}$
(eventually
$z_{k+s_j}=\mathsf{cp}_{{j+1}}$
(eventually
![]() $s_j=0$
); the quantity
$s_j=0$
); the quantity
![]() $s_j$
denotes the number of vectors joining the points of the convex chain
$s_j$
denotes the number of vectors joining the points of the convex chain
![]() $(z_k=\mathsf{cp}_j,\ldots,z_{k+s_j}=\mathsf{cp}_{{j+1}})$
. We will refer to the tuple
$(z_k=\mathsf{cp}_j,\ldots,z_{k+s_j}=\mathsf{cp}_{{j+1}})$
. We will refer to the tuple
![]() $s[\kappa]$
as the size vector (see Figure 6 for an example).
$s[\kappa]$
as the size vector (see Figure 6 for an example).
The main technical ingredient of the paper is now tackled in the following structural lemma.
Lemma 1.
For a given
![]() $s[\kappa]$
and
$s[\kappa]$
and
![]() $j\in\{1,\ldots,\kappa\}$
, set
$j\in\{1,\ldots,\kappa\}$
, set
![]() $k=\sum_{t \lt j}s_t$
(so that
$k=\sum_{t \lt j}s_t$
(so that
![]() $\mathsf{cp}_j=z_k$
). Given
$\mathsf{cp}_j=z_k$
). Given
![]() $s[\kappa]$
,
$s[\kappa]$
,
![]() $\mathsf{cp}_j$
, and
$\mathsf{cp}_j$
, and
![]() $\mathsf{cp}_{{j+1}}$
, the set of convex chains
$\mathsf{cp}_{{j+1}}$
, the set of convex chains
![]() $(\mathsf{cp}_j,z_{k+1},\ldots,z_{k+s_j-1},\mathsf{cp}_{{j+1}})$
coincides with the set
$(\mathsf{cp}_j,z_{k+1},\ldots,z_{k+s_j-1},\mathsf{cp}_{{j+1}})$
coincides with the set
![]() $\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
.
$\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
.
Hence, if
![]() $\mathbf{z}[n]$
has distribution
$\mathbf{z}[n]$
has distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
, conditional on
$\mathbb{Q}^{(n)}_{\kappa}$
, conditional on
![]() $({\mathsf{cp}}_j,{\mathsf{cp}}_{{j+1}},\mathbf{s}_j=s_j)$
, the points in the tuple
$({\mathsf{cp}}_j,{\mathsf{cp}}_{{j+1}},\mathbf{s}_j=s_j)$
, the points in the tuple
![]() $(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
have the same distribution as that of
$(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
have the same distribution as that of
![]() $s_j-1$
points
$s_j-1$
points
![]() $(\textbf{z}^{\prime}_{1},\ldots,\textbf{z}^{\prime}_{s_j-1})$
taken uniformly and independently in the triangle
$(\textbf{z}^{\prime}_{1},\ldots,\textbf{z}^{\prime}_{s_j-1})$
taken uniformly and independently in the triangle
![]() $\mathsf{corner}_j$
, conditioned on
$\mathsf{corner}_j$
, conditioned on
![]() $(\mathsf{cp}_j,\textbf{z}^{\prime}_{1},\ldots,\textbf{z}^{\prime}_{s_j-1},\mathsf{cp}_{{j+1}})$
being in
$(\mathsf{cp}_j,\textbf{z}^{\prime}_{1},\ldots,\textbf{z}^{\prime}_{s_j-1},\mathsf{cp}_{{j+1}})$
being in
![]() $\overset{\curvearrowleft}{\mathcal{Z}}_{s_j+1}$
.
$\overset{\curvearrowleft}{\mathcal{Z}}_{s_j+1}$
.

Figure 7. An example in the square case, where the
![]() $\mathsf{ECP}$
is always a rectangle.
$\mathsf{ECP}$
is always a rectangle.
Proof. The first statement is equivalent to saying that there are no restrictions on
![]() $(z_k,\ldots,z_{k+s_j})$
other than those defining
$(z_k,\ldots,z_{k+s_j})$
other than those defining
![]() $\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
: indeed, it is immediate to check that given two consecutive contact points
$\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
: indeed, it is immediate to check that given two consecutive contact points
![]() $z_k=\mathsf{cp}_j$
and
$z_k=\mathsf{cp}_j$
and
![]() $z_{s_j+k}=\mathsf{cp}_{{j+1}}$
, the points of z[n] are in convex position if and only if both subsets
$z_{s_j+k}=\mathsf{cp}_{{j+1}}$
, the points of z[n] are in convex position if and only if both subsets
![]() $S_1$
and
$S_1$
and
![]() $S_2$
of points above and below the straight line joining
$S_2$
of points above and below the straight line joining
![]() $\mathsf{cp}_j$
and
$\mathsf{cp}_j$
and
![]() $\mathsf{cp}_{{j+1}}$
(where both
$\mathsf{cp}_{{j+1}}$
(where both
![]() $S_1$
and
$S_1$
and
![]() $S_2$
contain
$S_2$
contain
![]() $\mathsf{cp}_j$
and
$\mathsf{cp}_j$
and
![]() $\mathsf{cp}_{{j+1}}$
) are in convex position. An example is given in Figure 7.
$\mathsf{cp}_{{j+1}}$
) are in convex position. An example is given in Figure 7.
Because of this property, under
![]() $\mathbb{Q}^{(n)}_{\kappa}$
, the distribution of
$\mathbb{Q}^{(n)}_{\kappa}$
, the distribution of
![]() $(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
, conditional on the position of
$(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
, conditional on the position of
![]() $(\mathsf{cp}_j,\mathsf{cp}_{j+1})$
, is the same as that of
$(\mathsf{cp}_j,\mathsf{cp}_{j+1})$
, is the same as that of
![]() $(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
conditional on the position of all the other points, and it is therefore proportional to the Lebesgue measure on the set of points in convex position in the jth corner (that is, in
$(\textbf{z}_{k+1},\cdots, \textbf{z}_{k+s_j-1})$
conditional on the position of all the other points, and it is therefore proportional to the Lebesgue measure on the set of points in convex position in the jth corner (that is, in
![]() $\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
), which is equivalent to the second statement of the theorem.
$\mathsf{Chain}_{s_j}(\mathsf{corner}_j)$
), which is equivalent to the second statement of the theorem.
The law of chain
![]() $(A,\textbf{u}_1,\cdots,\textbf{u}_k,B)$
conditioned to be in
$(A,\textbf{u}_1,\cdots,\textbf{u}_k,B)$
conditioned to be in
![]() $\mathsf{Chain}_{k+1}(ABC)$
will be called the uniform law in
$\mathsf{Chain}_{k+1}(ABC)$
will be called the uniform law in
![]() $\mathsf{Chain}_{k+1}(ABC)$
.
$\mathsf{Chain}_{k+1}(ABC)$
.
Denote by ◿ the right triangle with vertices (0, 0),(1, 1),(0, 1). For a given non-flat triangle ABC and an integer
![]() $m\geq1$
, let
$m\geq1$
, let
![]() $\mathsf{Aff}_{ABC}$
be the unique affine map that sends ABC onto ◿ (meaning it sends A, B, C to (0, 0),(1, 0),(1, 1), respectively). In the sequel, for
$\mathsf{Aff}_{ABC}$
be the unique affine map that sends ABC onto ◿ (meaning it sends A, B, C to (0, 0),(1, 0),(1, 1), respectively). In the sequel, for
![]() $m\geq0$
, we will denote by ◿
$m\geq0$
, we will denote by ◿
![]() $\mathsf{CC}_m$
a random variable whose law is uniform in
$\mathsf{CC}_m$
a random variable whose law is uniform in
![]() $\mathsf{Chain}_{m}$
(◿), and refer to this random variable as a generic ◿-normalized convex chain of size m.
$\mathsf{Chain}_{m}$
(◿), and refer to this random variable as a generic ◿-normalized convex chain of size m.
From the fundamental property that affine maps preserve convexity, we deduce the following lemma.
Lemma 2.
-
• For a triangle ABC (with non-empty interior), and k points
 $\textbf{u}_1,\cdots,\textbf{u}_k$
with distribution
$\textbf{u}_1,\cdots,\textbf{u}_k$
with distribution
 $\mathbb{U}^{(k)}_{ABC}$
, the probability that the chain
$\mathbb{U}^{(k)}_{ABC}$
, the probability that the chain
 $(A,\textbf{u}_1,\cdots,\textbf{u}_k,B)$
is in the set
$(A,\textbf{u}_1,\cdots,\textbf{u}_k,B)$
is in the set
 $\mathsf{Chain}_{k+1}(ABC)$
does not depend on ABC (so that this value is the same as in the right-triangle case).
$\mathsf{Chain}_{k+1}(ABC)$
does not depend on ABC (so that this value is the same as in the right-triangle case).
-
• The map
 $\mathsf{Aff}_{ABC}$
sends ABC to ◿, sends the uniform distribution on ABC to that of ◿ (as well as
$\mathsf{Aff}_{ABC}$
sends ABC to ◿, sends the uniform distribution on ABC to that of ◿ (as well as
 $\mathbb{U}^{(k)}_{ABC}$
to
$\mathbb{U}^{(k)}_{ABC}$
to
 $\mathbb{U}^{(k)}\!\!$
◿
), and sends the uniform distribution on
$\mathbb{U}^{(k)}\!\!$
◿
), and sends the uniform distribution on
 $\mathsf{Chain}_m(ABC)$
to that on
$\mathsf{Chain}_m(ABC)$
to that on
 $\mathsf{Chain}_{m}$
(◿).
$\mathsf{Chain}_{m}$
(◿).
The affine map
![]() $\varphi$
. In the following, we will work in the spirit of Lemma 1 by mapping every corner of an
$\varphi$
. In the following, we will work in the spirit of Lemma 1 by mapping every corner of an
![]() $\mathsf{ECP}$
to a right triangle. Let
$\mathsf{ECP}$
to a right triangle. Let
![]() ${z}[n]\in\mathcal{C}_\kappa(n)$
, let
${z}[n]\in\mathcal{C}_\kappa(n)$
, let
![]() $c[\kappa]$
be the side lengths of
$c[\kappa]$
be the side lengths of
![]() $\mathsf{ECP}({z}[n])$
, and let
$\mathsf{ECP}({z}[n])$
, and let
![]() $\mathsf{b}[\kappa]$
the vertices of
$\mathsf{b}[\kappa]$
the vertices of
![]() $\mathsf{ECP}({z}[n])$
. For convenience we impose the condition
$\mathsf{ECP}({z}[n])$
. For convenience we impose the condition
![]() $s_j \gt 0$
, so as to have
$s_j \gt 0$
, so as to have
![]() $\mathsf{cp}_j\neq\mathsf{cp}_{{j+1}}$
(the mapping is still definable otherwise). Let
$\mathsf{cp}_j\neq\mathsf{cp}_{{j+1}}$
(the mapping is still definable otherwise). Let
![]() $A^{\prime}_j=(0,c_j),B^{\prime}_j=(0,0),C^{\prime}_j=(c_{{j+1}},0)$
, and define
$A^{\prime}_j=(0,c_j),B^{\prime}_j=(0,0),C^{\prime}_j=(c_{{j+1}},0)$
, and define
![]() $\varphi_j$
as the unique affine map that sends
$\varphi_j$
as the unique affine map that sends
![]() $\mathsf{b}_{{j-1}},\mathsf{b}_j,\mathsf{b}_{{j+1}}$
to
$\mathsf{b}_{{j-1}},\mathsf{b}_j,\mathsf{b}_{{j+1}}$
to
![]() $A^{\prime}_j,B^{\prime}_j,C^{\prime}_j$
, respectively:
$A^{\prime}_j,B^{\prime}_j,C^{\prime}_j$
, respectively:
The map
![]() $\varphi_{j}$
can be seen as the composition of a rotation of the jth corner so as to place the second side (in the clockwise order) parallel to the x-axis; the straightening of the angle of the triangle thus obtained to produce a right triangle; and a translation (which does not play any role). Therefore, the Jacobian determinant of
$\varphi_{j}$
can be seen as the composition of a rotation of the jth corner so as to place the second side (in the clockwise order) parallel to the x-axis; the straightening of the angle of the triangle thus obtained to produce a right triangle; and a translation (which does not play any role). Therefore, the Jacobian determinant of
![]() $\varphi_j$
is the determinant of the matrix
$\varphi_j$
is the determinant of the matrix
![]() $A_j(\theta_\kappa)$
defined as follows:
$A_j(\theta_\kappa)$
defined as follows:
 \begin{align} A_j(\theta_\kappa)\,:\!=\, \underbrace{\begin{pmatrix} 1&\cos(\beta_\kappa) \\[3pt] 0&\sin(\beta_\kappa) \end{pmatrix}^{-1}}_{\text{straightening}} \underbrace{\begin{pmatrix} \cos(-j\beta_\kappa)&\sin(j\beta_\kappa) \\[3pt] -\sin(j\beta_\kappa)&\cos(-j\beta_\kappa) \end{pmatrix}}_{\text{rotation}} ,\end{align}
\begin{align} A_j(\theta_\kappa)\,:\!=\, \underbrace{\begin{pmatrix} 1&\cos(\beta_\kappa) \\[3pt] 0&\sin(\beta_\kappa) \end{pmatrix}^{-1}}_{\text{straightening}} \underbrace{\begin{pmatrix} \cos(-j\beta_\kappa)&\sin(j\beta_\kappa) \\[3pt] -\sin(j\beta_\kappa)&\cos(-j\beta_\kappa) \end{pmatrix}}_{\text{rotation}} ,\end{align}
where
![]() $\beta_\kappa=\pi-\theta_\kappa$
. The Jacobian determinant of
$\beta_\kappa=\pi-\theta_\kappa$
. The Jacobian determinant of
![]() $\varphi_{j}$
is thus
$\varphi_{j}$
is thus
Encoding convex chains in a triangle by simplex products. For all
![]() $\ell\in\mathbb{R}_+$
and
$\ell\in\mathbb{R}_+$
and
![]() $k\in\mathbb{Z}_{ \gt 0}$
, define the simplex
$k\in\mathbb{Z}_{ \gt 0}$
, define the simplex
and the ‘reordered’ simplex
 \begin{align} I [\ell,k]&=\left\{(b_1,\ldots,b_{k}) \text{ where }0 \lt b_1 \lt \ldots \lt b_k \lt \ell,\text{ and } \sum_{i=1}^kb_i=\ell\right\}.\end{align}
\begin{align} I [\ell,k]&=\left\{(b_1,\ldots,b_{k}) \text{ where }0 \lt b_1 \lt \ldots \lt b_k \lt \ell,\text{ and } \sum_{i=1}^kb_i=\ell\right\}.\end{align}
An element
![]() $(a_1,\ldots,a_k)$
of the set
$(a_1,\ldots,a_k)$
of the set
![]() $P[\ell,k]$
encodes k points on the segment
$P[\ell,k]$
encodes k points on the segment
![]() $[0,\ell]$
, whereas an element
$[0,\ell]$
, whereas an element
![]() $(b_1,\ldots,b_{k})$
of
$(b_1,\ldots,b_{k})$
of
![]() $I[\ell,k]$
must be seen as k increasing intervals partitioning the segment
$I[\ell,k]$
must be seen as k increasing intervals partitioning the segment
![]() $[0,\ell]$
.
$[0,\ell]$
.
Nonetheless, the set
![]() $I[\ell,k]$
can actually be identified as a subset of
$I[\ell,k]$
can actually be identified as a subset of
![]() $P[\ell,k-1]$
whose increments are increasing. Indeed, if
$P[\ell,k-1]$
whose increments are increasing. Indeed, if
![]() $(a_1,\ldots,a_{k-1})$
is in
$(a_1,\ldots,a_{k-1})$
is in
![]() $P[\ell,k-1]$
and is such that
$P[\ell,k-1]$
and is such that
![]() $a_1 \lt a_2-a_1 \lt \ldots \lt a_{k-1}-a_{k-2} \lt \ell-a_{k-1}$
, then
$a_1 \lt a_2-a_1 \lt \ldots \lt a_{k-1}-a_{k-2} \lt \ell-a_{k-1}$
, then
![]() $(a_1,a_2-a_1,\ldots,a_{k-1}-a_{k-2},\ell-a_{k-1})$
is in
$(a_1,a_2-a_1,\ldots,a_{k-1}-a_{k-2},\ell-a_{k-1})$
is in
![]() $I[\ell,k]$
. We will sometimes make this identification to present some bijections; nevertheless it is important to remember that topologically,
$I[\ell,k]$
. We will sometimes make this identification to present some bijections; nevertheless it is important to remember that topologically,
![]() $I[\ell,k]$
remains a surface in
$I[\ell,k]$
remains a surface in
![]() $\mathbb{R}^k$
, a
$\mathbb{R}^k$
, a
![]() $(k-1)$
-dimensional simplex, and that useful bijections in measure theory are those whose Jacobian determinant may be computed.
$(k-1)$
-dimensional simplex, and that useful bijections in measure theory are those whose Jacobian determinant may be computed.
Note that the Lebesgue measures of these sets are
 \begin{multline} \mathsf{Leb}_{k}(P[\ell,k])= \int_{P[\ell,k]}\text{d} a[k]=\frac{\ell^{k}}{k!},\\[3pt] \text{ and }\quad\mathsf{Leb}_{k-1}(I[\ell,k])=\int_{I[\ell,k]}\text{d} a[k-1]=\frac{\ell^{k-1}}{k!(k-1)!},\end{multline}
\begin{multline} \mathsf{Leb}_{k}(P[\ell,k])= \int_{P[\ell,k]}\text{d} a[k]=\frac{\ell^{k}}{k!},\\[3pt] \text{ and }\quad\mathsf{Leb}_{k-1}(I[\ell,k])=\int_{I[\ell,k]}\text{d} a[k-1]=\frac{\ell^{k-1}}{k!(k-1)!},\end{multline}
where, for any tuple
![]() $a[k]=(a_1,\ldots,a_k)$
, the notation
$a[k]=(a_1,\ldots,a_k)$
, the notation
![]() $\text{d} a[k]$
stands for
$\text{d} a[k]$
stands for
![]() $\prod_{i=1}^k\text{d} a_i.$
$\prod_{i=1}^k\text{d} a_i.$
An
![]() $m!$
-to-1 map, piecewise linear, from
$m!$
-to-1 map, piecewise linear, from
![]() $\mathsf{Chain}$
to a simplex product. Let abc be a right triangle in c of
$\mathsf{Chain}$
to a simplex product. Let abc be a right triangle in c of
![]() $\mathbb{R}^2$
, and let
$\mathbb{R}^2$
, and let
![]() $d_1=ac$
,
$d_1=ac$
,
![]() $d_2=bc$
denote the distances. For any convex chain
$d_2=bc$
denote the distances. For any convex chain
![]() $\left(a,u_1,\cdots,u_{m-1},b\right)\in\mathsf{Chain}_{m}(abc)$
, we may consider the vectors v[m] joining the points of the convex chain in their order of appearance. Then let the x- and y-coordinates x[m],y[m] of these vectors be given by
$\left(a,u_1,\cdots,u_{m-1},b\right)\in\mathsf{Chain}_{m}(abc)$
, we may consider the vectors v[m] joining the points of the convex chain in their order of appearance. Then let the x- and y-coordinates x[m],y[m] of these vectors be given by
![]() $x_i=\pi_1(v_i),y_i=\pi_2(v_i)$
for all
$x_i=\pi_1(v_i),y_i=\pi_2(v_i)$
for all
![]() $i\in\{1,\ldots,m\}$
, and let
$i\in\{1,\ldots,m\}$
, and let
![]() $(\overset{\circ}{x}_{1} \lt \ldots \lt \overset{\circ}{x}_{m}),(\overset{\circ}{y}_{1} \lt \ldots \lt \overset{\circ}{y}_{m})$
be the tuples of reordered coordinates (see Figure 9 for an example).
$(\overset{\circ}{x}_{1} \lt \ldots \lt \overset{\circ}{x}_{m}),(\overset{\circ}{y}_{1} \lt \ldots \lt \overset{\circ}{y}_{m})$
be the tuples of reordered coordinates (see Figure 9 for an example).

Figure 8. The map
![]() $\varphi_{j}$
.
$\varphi_{j}$
.

Figure 9. A convex chain in a right triangle abc.
Now consider the following surjective mapping (note that we will be working with vectors that are randomly distributed and such that
![]() $\mathbb{P}\left(\exists i\neq j \text{ s.t. } x_i=x_j \text{ or } y_i=y_j\right)=0$
almost surely (a.s.), which ensures that the map
$\mathbb{P}\left(\exists i\neq j \text{ s.t. } x_i=x_j \text{ or } y_i=y_j\right)=0$
almost surely (a.s.), which ensures that the map
![]() $\mathsf{Order}^{(m)}_{abc}$
is well-defined):
$\mathsf{Order}^{(m)}_{abc}$
is well-defined):
 \begin{align} \begin{array}{rccl} \mathsf{Order}^{(m)}_{abc}\,: &\mathsf{Chain}_{m}(a,b,c)&\longrightarrow&I[d_1,m]\times I[d_2,m]\\[3pt] &\left(a,u_1,\cdots,u_{m-1},b\right)&\longmapsto&(\overset{\circ}{x}[m],\overset{\circ}{y}[m])\end{array}.\end{align}
\begin{align} \begin{array}{rccl} \mathsf{Order}^{(m)}_{abc}\,: &\mathsf{Chain}_{m}(a,b,c)&\longrightarrow&I[d_1,m]\times I[d_2,m]\\[3pt] &\left(a,u_1,\cdots,u_{m-1},b\right)&\longmapsto&(\overset{\circ}{x}[m],\overset{\circ}{y}[m])\end{array}.\end{align}
This map is piecewise linear (see Definition 1 below) and has Jacobian determinant 1 since we are in a right triangle.
Definition 1.
(Piecewise linear map.) A map
![]() $g\,:\,E\subset\mathbb{R}^n\to \mathbb{R}^n$
is said to be piecewise linear if the following hold:
$g\,:\,E\subset\mathbb{R}^n\to \mathbb{R}^n$
is said to be piecewise linear if the following hold:
-
• There exists a collection of polytopes
 $(P_i)_{i\in\{1,\ldots,m\}}$
such that
$(P_i)_{i\in\{1,\ldots,m\}}$
such that
 $\bigcup_{i=1}^m P_i = E$
and the interiors
$\bigcup_{i=1}^m P_i = E$
and the interiors
 $P^\circ_i$
of the sets
$P^\circ_i$
of the sets
 $(P_i)_{i\in\{1,\ldots,m\}}$
are pairwise disjoint.
$(P_i)_{i\in\{1,\ldots,m\}}$
are pairwise disjoint.
-
• For all
 $i\in\{1,\ldots,m\}$
,
$i\in\{1,\ldots,m\}$
,
 $g\,:\,P^\circ_i\to \mathbb{R}^n $
is linear.
$g\,:\,P^\circ_i\to \mathbb{R}^n $
is linear.
Piecewise differentiability may be defined in an analogous way (here the term ‘piecewise’ must be understood as g being piecewise differentiable on every
![]() $P^\circ_i$
).
$P^\circ_i$
).
Of course, ‘polytopes’ can be replaced by more general Lebesgue-measurable sets, the union of whose interiors would partition E, up to a Lebesgue-negligible set.
Remark 2. Consider the mapping
where
![]() $(x_{(1)}\leq x_{(2)}\leq x_{(3)})$
is the sorted sequence
$(x_{(1)}\leq x_{(2)}\leq x_{(3)})$
is the sorted sequence
![]() $(x_1,x_2,x_3)$
. The map g is clearly not linear; however, for any
$(x_1,x_2,x_3)$
. The map g is clearly not linear; however, for any
![]() $(x\neq y\neq z)\in\mathbb{R}^3$
, there exists a neighborhood of (x,y,z) on which g is actually linear. At several places in the paper, we use this kind of reordering map, and so we use the term ‘piecewise linearity’ (and ‘piecewise differentiability’) in these cases.
$(x\neq y\neq z)\in\mathbb{R}^3$
, there exists a neighborhood of (x,y,z) on which g is actually linear. At several places in the paper, we use this kind of reordering map, and so we use the term ‘piecewise linearity’ (and ‘piecewise differentiability’) in these cases.
Lemma 3.
Let
![]() $(\overset{\circ}{x}[m],\overset{\circ}{y}[m])\in I[d_1,m]\times I[d_2,m]$
. We have
$(\overset{\circ}{x}[m],\overset{\circ}{y}[m])\in I[d_1,m]\times I[d_2,m]$
. We have
Proof. There are
![]() $m!$
distinct ways of pairing every element of
$m!$
distinct ways of pairing every element of
![]() $\overset{\circ}{x}[m]$
with one of
$\overset{\circ}{x}[m]$
with one of
![]() $\overset{\circ}{y}[m]$
to form m vectors. There exists a unique order that sorts these vectors by increasing slope. This forms the boundary of a convex chain whose vertices in canonical convex order
$\overset{\circ}{y}[m]$
to form m vectors. There exists a unique order that sorts these vectors by increasing slope. This forms the boundary of a convex chain whose vertices in canonical convex order
![]() $(a,u_1,\ldots,u_{m-1},b)$
are in
$(a,u_1,\ldots,u_{m-1},b)$
are in
![]() $\mathsf{Chain}_{m}(abc)$
.
$\mathsf{Chain}_{m}(abc)$
.
This lemma allows us to obtain the Lebesgue measure of the set
![]() $\mathsf{Chain}_{m}(a,b,c)$
, by carrying the Lebesgue measure of
$\mathsf{Chain}_{m}(a,b,c)$
, by carrying the Lebesgue measure of
![]() $I[d_1,m]\times I[d_2,m]$
onto
$I[d_1,m]\times I[d_2,m]$
onto
![]() $\mathsf{Chain}_{m}(abc)$
. In order to compute the Lebesgue measure of
$\mathsf{Chain}_{m}(abc)$
. In order to compute the Lebesgue measure of
![]() $\mathsf{Chain}_{m}(abc)$
, we need to identify the convex chains with m vectors as a subset of
$\mathsf{Chain}_{m}(abc)$
, we need to identify the convex chains with m vectors as a subset of
![]() $\mathbb{R}^{2(m-1)}$
(so that its dimension is
$\mathbb{R}^{2(m-1)}$
(so that its dimension is
![]() $2(m-1)$
, and appears as such). Therefore we introduce
$2(m-1)$
, and appears as such). Therefore we introduce
![]() $\mathsf{Chain}^{\prime}_m(a,b,c)=\{(z_1,\cdots,z_{m-1})\,:\,(a,z_1,\cdots,z_{m-1},b)\in \mathsf{Chain}_{m}(abc)\}$
. By a change of variables we have
$\mathsf{Chain}^{\prime}_m(a,b,c)=\{(z_1,\cdots,z_{m-1})\,:\,(a,z_1,\cdots,z_{m-1},b)\in \mathsf{Chain}_{m}(abc)\}$
. By a change of variables we have
 \begin{align}\nonumber \mathsf{Leb}_{2(m-1)}\left(\mathsf{Chain}^{\prime}_{m}(abc)\right)&=\int_{(\mathbb{R}^2)^{m-1}}\mathbf{1}_{\left\{{\mathsf{Chain}^{\prime}_{m}(abc)}\right\}}\text{d} z[m-1]\\[3pt] \nonumber &=m!(m-1)!\cdot\mathsf{Leb}_{m-1}(I[d_1,m])\cdot\mathsf{Leb}_{m-1}(I[d_2,m])\\[3pt] &=\frac{(d_1d_2)^{m-1}}{m!(m-1)!}.\end{align}
\begin{align}\nonumber \mathsf{Leb}_{2(m-1)}\left(\mathsf{Chain}^{\prime}_{m}(abc)\right)&=\int_{(\mathbb{R}^2)^{m-1}}\mathbf{1}_{\left\{{\mathsf{Chain}^{\prime}_{m}(abc)}\right\}}\text{d} z[m-1]\\[3pt] \nonumber &=m!(m-1)!\cdot\mathsf{Leb}_{m-1}(I[d_1,m])\cdot\mathsf{Leb}_{m-1}(I[d_2,m])\\[3pt] &=\frac{(d_1d_2)^{m-1}}{m!(m-1)!}.\end{align}
Note that the term in
![]() $(m-1)!$
on the second line accounts for the relabeling of the points
$(m-1)!$
on the second line accounts for the relabeling of the points
![]() $(u_1,\cdots,u_{m-1})$
, and
$(u_1,\cdots,u_{m-1})$
, and
![]() $m!$
appears because of Lemma 3.
$m!$
appears because of Lemma 3.
Intuition. For
![]() $\mathbf{z}[n]$
with distribution
$\mathbf{z}[n]$
with distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
, these lemmas reveal that conditional on the position of
$\mathbb{Q}^{(n)}_{\kappa}$
, these lemmas reveal that conditional on the position of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
,
$\mathsf{ECP}(\mathbf{z}[n])$
,
![]() $\mathsf{cp}[\kappa](\mathbf{z}[n])$
, and
$\mathsf{cp}[\kappa](\mathbf{z}[n])$
, and
![]() $s[\kappa](\mathbf{z}[n])$
(all together), the convex chains in each corner are independent. Thus each corner can be considered separately, and by mapping the jth corner of
$s[\kappa](\mathbf{z}[n])$
(all together), the convex chains in each corner are independent. Thus each corner can be considered separately, and by mapping the jth corner of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
to
$\mathsf{ECP}(\mathbf{z}[n])$
to
![]() $A^{\prime}_j,B^{\prime}_j,C^{\prime}_j$
with
$A^{\prime}_j,B^{\prime}_j,C^{\prime}_j$
with
![]() $\varphi_j$
(see (2.3)), we are brought back to the (simpler) study of a convex chain in a right triangle. However, although this big picture is useful for understanding the limit shape theorem, it is unfortunately not sufficient for computing the full asymptotic expansion of
$\varphi_j$
(see (2.3)), we are brought back to the (simpler) study of a convex chain in a right triangle. However, although this big picture is useful for understanding the limit shape theorem, it is unfortunately not sufficient for computing the full asymptotic expansion of
![]() $\mathbb{P}_\kappa(n)$
, mainly because of the fact that the joint distribution of
$\mathbb{P}_\kappa(n)$
, mainly because of the fact that the joint distribution of
![]() $(\ell[\kappa](\mathbf{z}[n]),s[\kappa](\mathbf{z}[n]),\mathsf{cp}[\kappa](\mathbf{z}[n]))$
is intricate and needs to be understood. Hence we need to introduce some more tools to work with the joint distribution.
$(\ell[\kappa](\mathbf{z}[n]),s[\kappa](\mathbf{z}[n]),\mathsf{cp}[\kappa](\mathbf{z}[n]))$
is intricate and needs to be understood. Hence we need to introduce some more tools to work with the joint distribution.
Number of sides of
![]() $\mathsf{ECP}(z[n])$
. For
$\mathsf{ECP}(z[n])$
. For
![]() $z[n]\in\mathcal{C}_\kappa(n)$
and the corresponding
$z[n]\in\mathcal{C}_\kappa(n)$
and the corresponding
![]() $c[\kappa]$
, define the map NZS as follows:
$c[\kappa]$
, define the map NZS as follows:
This map records the indices corresponding to the nonzero sides of
![]() $\mathsf{ECP}({z}[n]).$
Let us also set
$\mathsf{ECP}({z}[n]).$
Let us also set
and define
The following proposition states an equivalent condition on
![]() $\mathbf{s}^{(n)}[\kappa]$
to ensure a ‘full-sided’
$\mathbf{s}^{(n)}[\kappa]$
to ensure a ‘full-sided’
![]() $\mathsf{ECP}$
.
$\mathsf{ECP}$
.
Proposition 2.
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() $\mathbb{Q}^{(n)}_{\kappa}$
. Then
$\mathbb{Q}^{(n)}_{\kappa}$
. Then
![]() $\mathrm{NZS}(\mathbf{z}[n])=\{1,\ldots,\kappa\}$
is equivalent to
$\mathrm{NZS}(\mathbf{z}[n])=\{1,\ldots,\kappa\}$
is equivalent to
![]() $s[\kappa](\mathbf{z}[n])\in\mathbb{N}_\kappa(n).$
$s[\kappa](\mathbf{z}[n])\in\mathbb{N}_\kappa(n).$
Proof. Suppose that the
![]() $\mathsf{ECP}({z}[n])$
has exactly
$\mathsf{ECP}({z}[n])$
has exactly
![]() $\kappa$
nonzero sides, i.e. that if
$\kappa$
nonzero sides, i.e. that if
![]() $\mathbf{c}[\kappa]=c[\kappa](\mathbf{z}[n])$
, then we have
$\mathbf{c}[\kappa]=c[\kappa](\mathbf{z}[n])$
, then we have
![]() $\mathbf{c}_j \gt 0$
for all
$\mathbf{c}_j \gt 0$
for all
![]() $j\in\{1,\ldots,\kappa\}$
. Inside the tuple
$j\in\{1,\ldots,\kappa\}$
. Inside the tuple
![]() $\mathbf{z}[n]$
, consider for all
$\mathbf{z}[n]$
, consider for all
![]() $j\in\{1,\ldots,\kappa\}$
the contact points
$j\in\{1,\ldots,\kappa\}$
the contact points
![]() ${\mathsf{cp}}_{{j-1}}$
,
${\mathsf{cp}}_{{j-1}}$
,
![]() ${\mathsf{cp}}_{j}$
, and
${\mathsf{cp}}_{j}$
, and
![]() ${\mathsf{cp}}_{{j+1}}$
. A small picture suffices to show that we cannot have
${\mathsf{cp}}_{{j+1}}$
. A small picture suffices to show that we cannot have
![]() ${\mathsf{cp}}_{{j-1}}={\mathsf{cp}}_{j}={\mathsf{cp}}_{{j+1}}$
for this is equivalent to
${\mathsf{cp}}_{{j-1}}={\mathsf{cp}}_{j}={\mathsf{cp}}_{{j+1}}$
for this is equivalent to
![]() $\mathbf{c}_j=0$
, and thus is also equivalent to the fact that there exists a nonzero vector leading either
$\mathbf{c}_j=0$
, and thus is also equivalent to the fact that there exists a nonzero vector leading either
![]() ${\mathsf{cp}}_{{j-1}}$
to
${\mathsf{cp}}_{{j-1}}$
to
![]() ${\mathsf{cp}}_{j}$
(i.e.
${\mathsf{cp}}_{j}$
(i.e.
![]() $\mathbf{s}_{{j-1}}\geq1$
), or
$\mathbf{s}_{{j-1}}\geq1$
), or
![]() ${\mathsf{cp}}_{j}$
to
${\mathsf{cp}}_{j}$
to
![]() ${\mathsf{cp}}_{{j+1}}$
(i.e.
${\mathsf{cp}}_{{j+1}}$
(i.e.
![]() $\mathbf{s}_j\geq1$
).
$\mathbf{s}_j\geq1$
).
Therefore the set
![]() ${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
admits another equivalent definition:
${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
admits another equivalent definition:
The following lemma ensures that the overwhelming mass of n-tuples
![]() ${z}[n]\in\mathcal{C}_\kappa(n)$
is actually contained in
${z}[n]\in\mathcal{C}_\kappa(n)$
is actually contained in
![]() ${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n)).$
${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n)).$
Lemma 4.
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() $\mathbb{U}^{(n)}_{\kappa}$
. Denote by
$\mathbb{U}^{(n)}_{\kappa}$
. Denote by
![]() $\widetilde{\mathbb{P}}_\kappa(n)\,:\!=\,n!\ \mathbb{P}\left(\mathbf{z}[n]\in{\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))\right)$
the probability that the
$\widetilde{\mathbb{P}}_\kappa(n)\,:\!=\,n!\ \mathbb{P}\left(\mathbf{z}[n]\in{\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))\right)$
the probability that the
![]() $\mathbf{z}[n]$
are in convex canonical order and additionally that their
$\mathbf{z}[n]$
are in convex canonical order and additionally that their
![]() $\mathsf{ECP}$
has
$\mathsf{ECP}$
has
![]() $\kappa$
nonzero sides. We have
$\kappa$
nonzero sides. We have
The proof of this result requires several arguments related to Bárány’s limit shape theorem, so we send the interested reader to Appendix A for a complete overview of the proof.
Remark 3. Lemma 4 is of paramount importance since it allows us to neglect a subset of
![]() $\mathcal{C}_\kappa(n)$
whose Lebesgue measure becomes insignificant relative to that of
$\mathcal{C}_\kappa(n)$
whose Lebesgue measure becomes insignificant relative to that of
![]() $\mathcal{C}_\kappa(n)$
as
$\mathcal{C}_\kappa(n)$
as
![]() $n\to+\infty$
. To do so, we will assume that all n-tuples of points z[n] we are working with are in
$n\to+\infty$
. To do so, we will assume that all n-tuples of points z[n] we are working with are in
![]() ${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
, so as to force—by Proposition 2—the number of nonzero sides of
${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
, so as to force—by Proposition 2—the number of nonzero sides of
![]() $\mathsf{ECP}({z}[n])$
to be
$\mathsf{ECP}({z}[n])$
to be
![]() $\kappa$
.
$\kappa$
.
Notation. Denote by
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
the distribution of an n-tuple of random points
${\mathbb{D}}^{(n)}_{\kappa}$
the distribution of an n-tuple of random points
![]() $\mathbf{z}[n]$
with distribution
$\mathbf{z}[n]$
with distribution
![]() $\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in
$\mathbb{U}^{(n)}_{\kappa}$
, conditioned to be in
![]() ${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
.
${\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
.
3. Distribution of a convex z[n]-gon
Notation. From now on, we will work with a fixed size vector
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
. We denote by
$s[\kappa]\in\mathbb{N}_\kappa(n)$
. We denote by
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
the subset of all
${\mathcal{C}_\kappa}(s[\kappa])$
the subset of all
![]() ${z}[n]\in{\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
such that
${z}[n]\in{\mathcal{C}_\kappa}(\mathbb{N}_\kappa(n))$
such that
![]() $s[\kappa]({z}[n])=s[\kappa]$
, i.e. the set of n-tuples
$s[\kappa]({z}[n])=s[\kappa]$
, i.e. the set of n-tuples
![]() ${z}[n]\in\mathcal{C}_\kappa(n)$
with a prescribed size vector
${z}[n]\in\mathcal{C}_\kappa(n)$
with a prescribed size vector
![]() $s[\kappa]$
. We will write
$s[\kappa]$
. We will write
![]() $N_j=s_j+s_{{j+1}}-1$
for all
$N_j=s_j+s_{{j+1}}-1$
for all
![]() $j\in\{1,\ldots,\kappa\}$
.
$j\in\{1,\ldots,\kappa\}$
.
The choice to work with a prescribed size vector is not only a technical tool: as a matter of fact, our analysis relies deeply on the computation of the distribution of the size vector, and then on the description of the chains with a prescribed size vector (a foretaste has been given in Lemma 1, for instance). Later in the paper, we will see that the fluctuations of the z[n]-gon in each corner depend also on the fluctuations of the vector
![]() $s[\kappa]$
, so that considerations of this kind cannot be avoided.
$s[\kappa]$
, so that considerations of this kind cannot be avoided.
3.1. Encoding z[n]-gons into side-partitions of
 $\mathsf{ECP}({z}[n])$
$\mathsf{ECP}({z}[n])$
A new geometric description: convex chains between contact points, convex chains in a right triangle, and simplex product. Let us now fix
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
. For all
$s[\kappa]\in\mathbb{N}_\kappa(n)$
. For all
![]() $z[n]\in{\mathcal{C}_\kappa}(s[\kappa])$
, consider the corresponding side lengths
$z[n]\in{\mathcal{C}_\kappa}(s[\kappa])$
, consider the corresponding side lengths
![]() $c[\kappa]$
(which are thus all nonzero), and for all
$c[\kappa]$
(which are thus all nonzero), and for all
![]() $j\in\{1,\ldots,\kappa\}$
, define the side-partition
$j\in\{1,\ldots,\kappa\}$
, define the side-partition
![]() $u^{(j)}[N_j,c_j]=(u_1^{(j)},\ldots,u_{N_j}^{(j)})$
of the jth side length
$u^{(j)}[N_j,c_j]=(u_1^{(j)},\ldots,u_{N_j}^{(j)})$
of the jth side length
![]() $c_j$
of
$c_j$
of
![]() $\mathsf{ECP}({z}[n])$
, which is defined in Figure 10 below and is an element of
$\mathsf{ECP}({z}[n])$
, which is defined in Figure 10 below and is an element of
![]() $P[c_j,N_j]$
. For any side-partition
$P[c_j,N_j]$
. For any side-partition
![]() $u^{(j)}[N_j,c_j]$
thus defined, we set
$u^{(j)}[N_j,c_j]$
thus defined, we set
![]() $u^{(j)}_0\,:\!=\,0$
,
$u^{(j)}_0\,:\!=\,0$
,
![]() $u_{N_j+1}^{(j)}=c_j$
, so that we have
$u_{N_j+1}^{(j)}=c_j$
, so that we have
![]() $u_0^{(j)} \lt u_1^{(j)} \lt \ldots \lt u_{N_j}^{(j)} \lt u_{N_j+1}^{(j)}$
.
$u_0^{(j)} \lt u_1^{(j)} \lt \ldots \lt u_{N_j}^{(j)} \lt u_{N_j+1}^{(j)}$
.

Figure 10. The jth side-partition
![]() $(0=u_0^{(j)} \lt u_1^{(j)} \lt \ldots \lt u_{N_j}^{(j)} \lt u_{N_j+1}^{(j)}=c_j)$
of
$(0=u_0^{(j)} \lt u_1^{(j)} \lt \ldots \lt u_{N_j}^{(j)} \lt u_{N_j+1}^{(j)}=c_j)$
of
![]() $c_j$
, with
$c_j$
, with
![]() $s_j=2$
,
$s_j=2$
,
![]() $s_{{j+1}}=3$
. An alternative way of building the
$s_{{j+1}}=3$
. An alternative way of building the
![]() $u^{(j)}[N_j,c_j]$
will be given in Figure 11. Notice here that we see the contact point on
$u^{(j)}[N_j,c_j]$
will be given in Figure 11. Notice here that we see the contact point on
![]() $c_j$
, but we do not mark it; we treat it the same as the other points.
$c_j$
, but we do not mark it; we treat it the same as the other points.
Main strategy of the proof. Our main strategy is to consider for all
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
the extraction mapping, which encodes a convex z[n]-gon in terms of its
$s[\kappa]\in\mathbb{N}_\kappa(n)$
the extraction mapping, which encodes a convex z[n]-gon in terms of its
![]() $\mathsf{ECP}({z}[n])$
and its side-partitions:
$\mathsf{ECP}({z}[n])$
and its side-partitions:
where
![]() $\mathsf{NiceSet}(s[\kappa])\,:\!=\,\mathsf{Im}(\chi_{s[\kappa]})$
is a strict subset of
$\mathsf{NiceSet}(s[\kappa])\,:\!=\,\mathsf{Im}(\chi_{s[\kappa]})$
is a strict subset of
![]() $(\mathbb{R}^+)^{\kappa}\times\prod_{j=1}^\kappa (\mathbb{R}^+)^{N_j}$
that we now discuss. Recall that for all
$(\mathbb{R}^+)^{\kappa}\times\prod_{j=1}^\kappa (\mathbb{R}^+)^{N_j}$
that we now discuss. Recall that for all
![]() $j\in\{1,\ldots,\kappa\}$
we have set
$j\in\{1,\ldots,\kappa\}$
we have set
![]() $N_j=s_j+s_{{j+1}}-1$
.
$N_j=s_j+s_{{j+1}}-1$
.
In what follows, we need to see the map
![]() $\chi_{s[\kappa]}$
as a ‘nice map’ (a piecewise linear map; see Definition 1) with a ‘nice inverse’ (i.e. with a computable Jacobian determinant), since we will later use this inverse to push forward a measure of
$\chi_{s[\kappa]}$
as a ‘nice map’ (a piecewise linear map; see Definition 1) with a ‘nice inverse’ (i.e. with a computable Jacobian determinant), since we will later use this inverse to push forward a measure of
![]() $\mathsf{NiceSet}(s[\kappa])$
onto the Lebesgue measure on
$\mathsf{NiceSet}(s[\kappa])$
onto the Lebesgue measure on
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
.
${\mathcal{C}_\kappa}(s[\kappa])$
.
Since
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
is a subset of
${\mathcal{C}_\kappa}(s[\kappa])$
is a subset of
![]() $\mathbb{R}^{2n}$
with non-empty interior,
$\mathbb{R}^{2n}$
with non-empty interior,
![]() $\mathsf{NiceSet}(s[\kappa])$
will be seen to be identifiable with a subset of a domain with the same dimension. In order to characterize
$\mathsf{NiceSet}(s[\kappa])$
will be seen to be identifiable with a subset of a domain with the same dimension. In order to characterize
![]() $\mathsf{NiceSet}(s[\kappa])$
, it is relevant to notice that since the
$\mathsf{NiceSet}(s[\kappa])$
, it is relevant to notice that since the
![]() $s[\kappa]$
are fixed, the
$s[\kappa]$
are fixed, the
![]() $u^{(j)}[N_j,c_j]$
allow us to reconstruct the vectors of the convex chains. Since these vectors have increasing slope (as we progress counterclockwise around the z[n]-gon), the
$u^{(j)}[N_j,c_j]$
allow us to reconstruct the vectors of the convex chains. Since these vectors have increasing slope (as we progress counterclockwise around the z[n]-gon), the
![]() $u^{(j)}[N_j,c_j]$
must satisfy a condition that we now detail.
$u^{(j)}[N_j,c_j]$
must satisfy a condition that we now detail.
The image set of
![]() $\chi_{s[\kappa]}$
. Set
$\chi_{s[\kappa]}$
. Set
![]() $\mathcal{L}_\kappa^*\,:\!=\,\{\ell[\kappa]\in\mathcal{L}_\kappa \text{ s.t. for all }j\in\{1,\ldots,\kappa\},c_j \gt 0 \}$
. For any
$\mathcal{L}_\kappa^*\,:\!=\,\{\ell[\kappa]\in\mathcal{L}_\kappa \text{ s.t. for all }j\in\{1,\ldots,\kappa\},c_j \gt 0 \}$
. For any
![]() $\ell[\kappa]\in\mathcal{L}_\kappa^*$
, consider the side lengths
$\ell[\kappa]\in\mathcal{L}_\kappa^*$
, consider the side lengths
![]() $c[\kappa]$
of the
$c[\kappa]$
of the
![]() $\mathsf{ECP}$
induced by
$\mathsf{ECP}$
induced by
![]() $\ell[\kappa].$
For any
$\ell[\kappa].$
For any
![]() $\kappa$
-tuple of side-partitions
$\kappa$
-tuple of side-partitions
![]() $\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
of
$\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
of
![]() $c[\kappa]$
, and all
$c[\kappa]$
, and all
![]() $j\in\{1,\ldots,\kappa\}$
, define the inter-point distances of the side-partition
$j\in\{1,\ldots,\kappa\}$
, define the inter-point distances of the side-partition
![]() $u^{(j)}[N_j,c_j]$
by
$u^{(j)}[N_j,c_j]$
by
![]() $\Delta u^{(j)}_i=u_i^{(j)}-u_{i-1}^{(j)}$
for all
$\Delta u^{(j)}_i=u_i^{(j)}-u_{i-1}^{(j)}$
for all
![]() $i\in\{1,\ldots,N_j+1\}$
. Then define the vectors
$i\in\{1,\ldots,N_j+1\}$
. Then define the vectors
 \begin{align*}v_k^{(j)}=\begin{pmatrix} \Delta u^{{(j)}}_{s_{j}+k}\\[3pt] \Delta u^{{({j+1})}}_k\end{pmatrix},\quad \forall k\in\{1,\ldots,s_{{j+1}}\}. \end{align*}
\begin{align*}v_k^{(j)}=\begin{pmatrix} \Delta u^{{(j)}}_{s_{j}+k}\\[3pt] \Delta u^{{({j+1})}}_k\end{pmatrix},\quad \forall k\in\{1,\ldots,s_{{j+1}}\}. \end{align*}
In words, summing the vectors
![]() $v^{(j)}[s_{{j+1}}]$
allows one to join the point (0, 0) to
$v^{(j)}[s_{{j+1}}]$
allows one to join the point (0, 0) to
![]() $(c_j-u^{(j)}_{s_j},u^{({j+1})}_{s_{{j+1}}})$
. When reordered by increasing slope, these vectors form the boundary of a convex polygon whose vertices form a convex chain. This condition on the vectors must be encoded in the side-partitions when we decompose a z[n]-gon through
$(c_j-u^{(j)}_{s_j},u^{({j+1})}_{s_{{j+1}}})$
. When reordered by increasing slope, these vectors form the boundary of a convex polygon whose vertices form a convex chain. This condition on the vectors must be encoded in the side-partitions when we decompose a z[n]-gon through
![]() $\chi_{s[\kappa]}$
; this condition allows us to identify the image set
$\chi_{s[\kappa]}$
; this condition allows us to identify the image set
![]() $\mathsf{NiceSet}(s[\kappa]).$
$\mathsf{NiceSet}(s[\kappa]).$
We therefore define the following open subset of
![]() $\mathbb{R}^{\kappa}\times\prod_{j=1}^\kappa \mathbb{R}^{N_j}$
:
$\mathbb{R}^{\kappa}\times\prod_{j=1}^\kappa \mathbb{R}^{N_j}$
:
 \begin{multline*} {\mathcal{S}}^{(n)}(s[\kappa])\,:\!=\,\bigg\{\left(\ell[\kappa],w^{(1)},\ldots,w^{(\kappa)}\right)\in\mathcal{L}_\kappa^*\times\prod_{j=1}^\kappa \mathbb{R}^{N_j}\\[3pt] \text{ where }w^{(j)}\,:\!=\,w^{(j)}[N_j,c_j]\in P[c_j,N_j],\\[3pt] \text{ and }\underbrace{\frac{\Delta w^{(j)}_1}{\Delta w^{({j-1})}_{s_{{j-1}}+1}} \lt \ldots \lt \frac{\Delta w^{(j)}_{s_j}}{\Delta w^{({j-1})}_{s_{{j-1}}+s_j}}}_{\text{condition on order of slopes}} \text{ for all }j\in\{1,\ldots,\kappa\}\bigg\}.\end{multline*}
\begin{multline*} {\mathcal{S}}^{(n)}(s[\kappa])\,:\!=\,\bigg\{\left(\ell[\kappa],w^{(1)},\ldots,w^{(\kappa)}\right)\in\mathcal{L}_\kappa^*\times\prod_{j=1}^\kappa \mathbb{R}^{N_j}\\[3pt] \text{ where }w^{(j)}\,:\!=\,w^{(j)}[N_j,c_j]\in P[c_j,N_j],\\[3pt] \text{ and }\underbrace{\frac{\Delta w^{(j)}_1}{\Delta w^{({j-1})}_{s_{{j-1}}+1}} \lt \ldots \lt \frac{\Delta w^{(j)}_{s_j}}{\Delta w^{({j-1})}_{s_{{j-1}}+s_j}}}_{\text{condition on order of slopes}} \text{ for all }j\in\{1,\ldots,\kappa\}\bigg\}.\end{multline*}
Note that we set
![]() $\ell[\kappa]$
in
$\ell[\kappa]$
in
![]() $\mathcal{L}_\kappa^*$
so as to force the construction of any
$\mathcal{L}_\kappa^*$
so as to force the construction of any
![]() $\mathsf{ECP}$
possible (except those having a nonzero side) within
$\mathsf{ECP}$
possible (except those having a nonzero side) within
![]() $\mathfrak{C}_\kappa.$
We consider the increments for the side-partitions because they make up the vectors in each corner as described by Figure 11. Recall the family of mappings
$\mathfrak{C}_\kappa.$
We consider the increments for the side-partitions because they make up the vectors in each corner as described by Figure 11. Recall the family of mappings
![]() $(\varphi_{j})_{j\in\{1,\ldots,\kappa\}}$
introduced in (2.3) together with Figure 8.
$(\varphi_{j})_{j\in\{1,\ldots,\kappa\}}$
introduced in (2.3) together with Figure 8.

Figure 11. The map
![]() $\varphi_j$
(resp.
$\varphi_j$
(resp.
![]() $\varphi_{{j-1}}$
), as introduced in Figure 8, sends the triangle
$\varphi_{{j-1}}$
), as introduced in Figure 8, sends the triangle
![]() $\mathsf{corner}_j$
(resp.
$\mathsf{corner}_j$
(resp.
![]() $\mathsf{corner}_{{j-1}}$
) to the triangle
$\mathsf{corner}_{{j-1}}$
) to the triangle
![]() $A^{\prime}_jB^{\prime}_jC^{\prime}_j$
(resp.
$A^{\prime}_jB^{\prime}_jC^{\prime}_j$
(resp.
![]() $A^{\prime}_{{j-1}}B^{\prime}_{{j-1}}C^{\prime}_{{j-1}}$
). If we perform one more rotation, which is equivalent to setting
$A^{\prime}_{{j-1}}B^{\prime}_{{j-1}}C^{\prime}_{{j-1}}$
). If we perform one more rotation, which is equivalent to setting
![]() $C^{\prime}_{{j-1}}=A^{\prime}_j$
and fixing
$C^{\prime}_{{j-1}}=A^{\prime}_j$
and fixing
![]() $B^{\prime}_{{j-1}},A^{\prime}_j,B^{\prime}_j$
on the same line, we may interpret the side-partitions just as they appear in the right-hand panel.
$B^{\prime}_{{j-1}},A^{\prime}_j,B^{\prime}_j$
on the same line, we may interpret the side-partitions just as they appear in the right-hand panel.
A powerful diffeomorphism. It is quite easy to see that, up to a Lebesgue-null set (we want to avoid treating separately the cases in which several points of z[n] are parallel to the lines of
![]() $\mathfrak{C}_\kappa$
, or more than two
$\mathfrak{C}_\kappa$
, or more than two
![]() $z_i$
are aligned),
$z_i$
are aligned),
![]() $\chi_{s[\kappa]}$
is a bijection between
$\chi_{s[\kappa]}$
is a bijection between
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
and
${\mathcal{C}_\kappa}(s[\kappa])$
and
![]() ${\mathcal{S}}^{(n)}(s[\kappa])$
. The following theorem details some even more important properties of the mapping
${\mathcal{S}}^{(n)}(s[\kappa])$
. The following theorem details some even more important properties of the mapping
![]() $\chi_{s[\kappa]}.$
$\chi_{s[\kappa]}.$
Theorem 5.
For all
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
, the mapping
$s[\kappa]\in\mathbb{N}_\kappa(n)$
, the mapping
is a piecewise diffeomorphism (in the sense of Definition 1) whose Jacobian determinant is constant and equals
![]() $1/\sin(\theta_\kappa)^{n-\kappa}$
(hence the Jacobian determinant does not depend on
$1/\sin(\theta_\kappa)^{n-\kappa}$
(hence the Jacobian determinant does not depend on
![]() $s[\kappa]$
).
$s[\kappa]$
).
In particular, the Lebesgue measure of the set of interest,
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
, satisfies
${\mathcal{C}_\kappa}(s[\kappa])$
, satisfies
Proof of Theorem
5.We need to detail how the inverse mapping of
![]() $\chi_{s[\kappa]}$
is defined to understand its (piecewise) linearity. Pick
$\chi_{s[\kappa]}$
is defined to understand its (piecewise) linearity. Pick
![]() $\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(s[\kappa])$
.
$\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(s[\kappa])$
.
Linearity. Since the tuple
![]() $\ell[\kappa]$
is in
$\ell[\kappa]$
is in
![]() $\mathcal{L}_\kappa^*$
, it defines an equiangular parallel polygon
$\mathcal{L}_\kappa^*$
, it defines an equiangular parallel polygon
![]() $\mathsf{ECP}$
inside
$\mathsf{ECP}$
inside
![]() $\mathfrak{C}_\kappa$
. The map which associates the
$\mathfrak{C}_\kappa$
. The map which associates the
![]() $\mathsf{b}[\kappa]$
to the
$\mathsf{b}[\kappa]$
to the
![]() $\ell[\kappa]$
is piecewise linear: in the classical Cartesian coordinate system, for any
$\ell[\kappa]$
is piecewise linear: in the classical Cartesian coordinate system, for any
![]() $j\in\{1,\ldots,\kappa\}$
, the coordinates of
$j\in\{1,\ldots,\kappa\}$
, the coordinates of
![]() $\mathsf{b}_{j}$
are linear in
$\mathsf{b}_{j}$
are linear in
![]() $\ell_j$
and
$\ell_j$
and
![]() $\ell_{j+1}$
, since
$\ell_{j+1}$
, since
up to a rotation.
Then the contact point
![]() $\mathsf{cp}_j$
is a translation of
$\mathsf{cp}_j$
is a translation of
![]() $\mathsf{b}_{{j-1}}$
by
$\mathsf{b}_{{j-1}}$
by
![]() $u_{s_j}^{(j)}$
along the jth side of the
$u_{s_j}^{(j)}$
along the jth side of the
![]() $\mathsf{ECP}$
. This means that the constructions of the contact points are linear in the
$\mathsf{ECP}$
. This means that the constructions of the contact points are linear in the
![]() $\ell[\kappa]$
and
$\ell[\kappa]$
and
![]() $u_{s_j}^{(j)},j\in\{1,\ldots,\kappa\}$
. To reconstruct the rest of the points, recall the vectors
$u_{s_j}^{(j)},j\in\{1,\ldots,\kappa\}$
. To reconstruct the rest of the points, recall the vectors
 \begin{align*}v_k^{(j)}=\begin{pmatrix} \Delta u^{{(j)}}_{s_{j}+k}\\[3pt] \Delta u^{{({j+1})}}_k \end{pmatrix},\quad \forall k\in\{1,\ldots,s_{{j+1}}-1\}. \end{align*}
\begin{align*}v_k^{(j)}=\begin{pmatrix} \Delta u^{{(j)}}_{s_{j}+k}\\[3pt] \Delta u^{{({j+1})}}_k \end{pmatrix},\quad \forall k\in\{1,\ldots,s_{{j+1}}-1\}. \end{align*}
The convexity condition imposed on the slopes in
![]() ${\mathcal{S}}^{(n)}(s[\kappa])$
forces these vectors to appear in order of increasing slope, so that the map
${\mathcal{S}}^{(n)}(s[\kappa])$
forces these vectors to appear in order of increasing slope, so that the map
![]() $\varphi_j$
sends these vectors in
$\varphi_j$
sends these vectors in
![]() $\mathsf{corner}_j$
to form the boundary of a convex polygon, whose tuple of vertices is thus a convex chain. The construction of the points of this convex chain can hence be rewritten as
$\mathsf{corner}_j$
to form the boundary of a convex polygon, whose tuple of vertices is thus a convex chain. The construction of the points of this convex chain can hence be rewritten as
where
![]() $A_j$
was introduced in (2.3), and inductively for all
$A_j$
was introduced in (2.3), and inductively for all
![]() $k\in\{2,\ldots, s_{{j+1}}-1\},$
$k\in\{2,\ldots, s_{{j+1}}-1\},$
We give an example of this construction in Figure 5. Notice that we have built only
![]() $s_{{j+1}}-1$
vectors, since the
$s_{{j+1}}-1$
vectors, since the
![]() $s_{{j+1}}$
th connects the last point
$s_{{j+1}}$
th connects the last point
![]() $z^{(j)}_{s_j}$
to
$z^{(j)}_{s_j}$
to
![]() $\mathsf{cp}_{{j+1}}$
and is thus determined.
$\mathsf{cp}_{{j+1}}$
and is thus determined.

Figure 12. Vector-building.
We obtain n points
 $(z_1,\ldots,z_n)=(\underbrace{\mathsf{cp}_1,z^{(1)}_2,\ldots,z^{(1)}_{s_1}}_{s_1 \text{ points}},\underbrace{\mathsf{cp}_2,z^{(2)}_2,\ldots,z^{(2)}_{s_2}}_{s_2 \text{ points}},\ldots,{} \underbrace{\mathsf{cp}_\kappa,z^{(\kappa)}_2,\ldots,z^{(\kappa)}_{s_\kappa}}_{s_\kappa \text{ points}}).$
In the end, the whole construction includes only maps that are piecewise linear and piecewise differentiable (Definition 1) in the data
$(z_1,\ldots,z_n)=(\underbrace{\mathsf{cp}_1,z^{(1)}_2,\ldots,z^{(1)}_{s_1}}_{s_1 \text{ points}},\underbrace{\mathsf{cp}_2,z^{(2)}_2,\ldots,z^{(2)}_{s_2}}_{s_2 \text{ points}},\ldots,{} \underbrace{\mathsf{cp}_\kappa,z^{(\kappa)}_2,\ldots,z^{(\kappa)}_{s_\kappa}}_{s_\kappa \text{ points}}).$
In the end, the whole construction includes only maps that are piecewise linear and piecewise differentiable (Definition 1) in the data
![]() $\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
, and thus
$\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
, and thus
![]() $\chi_{s[\kappa]}$
also has these properties.
$\chi_{s[\kappa]}$
also has these properties.
Jacobian. Let us compute the Jacobian determinant of the inverse mapping
![]() $(\chi_{s[\kappa]})^{-1}$
. This requires first the Jacobian determinant of the construction of the contact points
$(\chi_{s[\kappa]})^{-1}$
. This requires first the Jacobian determinant of the construction of the contact points
![]() $\mathsf{cp}[\kappa]$
. To build a contact point, we build the vertices
$\mathsf{cp}[\kappa]$
. To build a contact point, we build the vertices
![]() $\mathsf{b}[\kappa]$
: we fix the y-coordinate of
$\mathsf{b}[\kappa]$
: we fix the y-coordinate of
![]() $\mathsf{b}_\kappa$
and
$\mathsf{b}_\kappa$
and
![]() $\mathsf{b}_1$
as
$\mathsf{b}_1$
as
![]() $\ell_1$
. Now, rotate the figure by
$\ell_1$
. Now, rotate the figure by
![]() $\pi/2-\theta_\kappa$
: in this new system of coordinates, the y-coordinate of
$\pi/2-\theta_\kappa$
: in this new system of coordinates, the y-coordinate of
![]() $\mathsf{b}_1$
and
$\mathsf{b}_1$
and
![]() $\mathsf{b}_2$
is
$\mathsf{b}_2$
is
![]() $\ell_2$
. This determines the coordinates of
$\ell_2$
. This determines the coordinates of
![]() $\mathsf{b}_1$
, and from one rotation to the other, those of
$\mathsf{b}_1$
, and from one rotation to the other, those of
![]() $\mathsf{b}_j$
for all
$\mathsf{b}_j$
for all
![]() $j\in\{1,\ldots,\kappa\}$
. The Jacobian determinant of the whole construction of the
$j\in\{1,\ldots,\kappa\}$
. The Jacobian determinant of the whole construction of the
![]() $\mathsf{b}[\kappa]$
is the determinant of a product of rotation matrices, and is thus 1.
$\mathsf{b}[\kappa]$
is the determinant of a product of rotation matrices, and is thus 1.
Then, as said before, the contact point
![]() $\mathsf{cp}_j$
is built as a translation of
$\mathsf{cp}_j$
is built as a translation of
![]() $u_{s_j}^{(j)}$
from
$u_{s_j}^{(j)}$
from
![]() $\mathsf{b}_{{j-1}}$
on the jth side of
$\mathsf{b}_{{j-1}}$
on the jth side of
![]() $\mathsf{ECP}$
. This operation has Jacobian determinant 1 as well.
$\mathsf{ECP}$
. This operation has Jacobian determinant 1 as well.
For
![]() $j\in\{1,\ldots,\kappa\}$
, the building of
$j\in\{1,\ldots,\kappa\}$
, the building of
![]() $z_k^{(j)}$
,
$z_k^{(j)}$
,
![]() $k\in\{2,\ldots,s_j\}$
, is a translation from
$k\in\{2,\ldots,s_j\}$
, is a translation from
![]() $z^{(j)}_{k-1}$
with the product of the matrix
$z^{(j)}_{k-1}$
with the product of the matrix
![]() $A_j(\theta_\kappa)^{-1}$
with the vector
$A_j(\theta_\kappa)^{-1}$
with the vector
![]() $v^{(j)}_{k-1}$
, for all
$v^{(j)}_{k-1}$
, for all
![]() $j\in\{1,\ldots,\kappa\}$
. So we have
$j\in\{1,\ldots,\kappa\}$
. So we have
 \begin{align}\nonumber \mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)&=\left|\prod_{j=1}^{\kappa}\det\left(A_j(\theta_\kappa)^{-1}\right)^{s_j-1}\right|\\[3pt] &=\sin(\theta_\kappa)^{n-\kappa}. \end{align}
\begin{align}\nonumber \mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)&=\left|\prod_{j=1}^{\kappa}\det\left(A_j(\theta_\kappa)^{-1}\right)^{s_j-1}\right|\\[3pt] &=\sin(\theta_\kappa)^{n-\kappa}. \end{align}
3.2. Working at fixed
 $\ell[\kappa]$
$\ell[\kappa]$
Above, we performed a first ‘conditioning’ based on the size vector
![]() $s[\kappa]$
of the vectors forming the boundary of any z[n]-gon. From this point, the map
$s[\kappa]$
of the vectors forming the boundary of any z[n]-gon. From this point, the map
![]() $\chi_{s[\kappa]}$
encodes z[n] in two parts: the ‘coordinates’
$\chi_{s[\kappa]}$
encodes z[n] in two parts: the ‘coordinates’
![]() $\ell[\kappa]$
of the
$\ell[\kappa]$
of the
![]() $\mathsf{ECP}({z}[n])$
(in the sense that their data is equivalent) and the side-partitions
$\mathsf{ECP}({z}[n])$
(in the sense that their data is equivalent) and the side-partitions
![]() $\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
. We may now perform a second conditioning on the coordinates
$\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
. We may now perform a second conditioning on the coordinates
![]() $\ell[\kappa]$
, by introducing the set
$\ell[\kappa]$
, by introducing the set
This conditioning actually reveals the mass of z[n]-gons contained in an
![]() $\mathsf{ECP}$
of coordinates
$\mathsf{ECP}$
of coordinates
![]() $\ell[\kappa]$
with a repartition
$\ell[\kappa]$
with a repartition
![]() $s[\kappa]$
. Indeed, we have the following lemma.
$s[\kappa]$
. Indeed, we have the following lemma.
Lemma 5.
For all
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
,
$\ell[\kappa]\in\mathcal{L}_\kappa$
,
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
,
$s[\kappa]\in\mathbb{N}_\kappa(n)$
,
Proof. We have
 \begin{multline} \mathsf{Leb}_{2n}(\mathcal{S}^{(n)}(s[\kappa]))=\\[3pt] \int_{\mathbb{R}^\kappa}\mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\underbrace{\int_{\mathbb{R}^{2n-\kappa}} \mathbf{1}_{\left\{{\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])}\right\}} \text{d} u[2n-\kappa]}_{\mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)}\text{d} \ell[\kappa], \end{multline}
\begin{multline} \mathsf{Leb}_{2n}(\mathcal{S}^{(n)}(s[\kappa]))=\\[3pt] \int_{\mathbb{R}^\kappa}\mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\underbrace{\int_{\mathbb{R}^{2n-\kappa}} \mathbf{1}_{\left\{{\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])}\right\}} \text{d} u[2n-\kappa]}_{\mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)}\text{d} \ell[\kappa], \end{multline}
where we let
![]() $\text{d} u[2n-\kappa]=\prod_{j=1}^\kappa \text{d} u^{(j)}[N_j,c_j]$
to lighten the notation. Hence, (3.3) allows us to conclude.
$\text{d} u[2n-\kappa]=\prod_{j=1}^\kappa \text{d} u^{(j)}[N_j,c_j]$
to lighten the notation. Hence, (3.3) allows us to conclude.
This lemma encodes an n-tuple z[n] in convex position in terms of a new geometric description embodied in the coordinates
![]() $\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
. This change of variables comes at the price of the Jacobian computed in Theorem 5. The next step, as suggested by Lemma 5, is to compute, for fixed
$\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
. This change of variables comes at the price of the Jacobian computed in Theorem 5. The next step, as suggested by Lemma 5, is to compute, for fixed
![]() $(\ell[\kappa],s[\kappa])$
, the Lebesgue measure of the set
$(\ell[\kappa],s[\kappa])$
, the Lebesgue measure of the set
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa]).$
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa]).$
The Lebesgue measure of
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. Pick
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. Pick
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
and
$\ell[\kappa]\in\mathcal{L}_\kappa$
and
![]() $\left(u^{(1)},\ldots,u^{(\kappa)}\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. This tuple of side-partitions
$\left(u^{(1)},\ldots,u^{(\kappa)}\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. This tuple of side-partitions
![]() $\left(u^{(1)},\ldots,u^{(\kappa)}\right)$
can be seen as an element of the set
$\left(u^{(1)},\ldots,u^{(\kappa)}\right)$
can be seen as an element of the set
![]() $\prod_{j=1}^\kappa P[c_j,N_j]$
. Indeed, a side-partition
$\prod_{j=1}^\kappa P[c_j,N_j]$
. Indeed, a side-partition
![]() $u^{(j)}\,:\!=\,u^{(j)}[N_j,c_j]$
marks
$u^{(j)}\,:\!=\,u^{(j)}[N_j,c_j]$
marks
![]() $N_j$
points on the segment
$N_j$
points on the segment
![]() $[0,c_j]$
. Nonetheless, just as we did after (2.5) and (2.6), we may instead consider the tuples of distances between points, and reorder each
$[0,c_j]$
. Nonetheless, just as we did after (2.5) and (2.6), we may instead consider the tuples of distances between points, and reorder each
![]() $u^{(j)}$
into increasing increments so as to form
$u^{(j)}$
into increasing increments so as to form
![]() $(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])$
, which is thus an element of
$(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])$
, which is thus an element of
![]() $\prod_{j=1}^\kappa I[c_j,N_j+1]$
. Considering the elements of
$\prod_{j=1}^\kappa I[c_j,N_j+1]$
. Considering the elements of
![]() $\prod_{j=1}^\kappa I[c_j,N_j+1]$
rather than those of
$\prod_{j=1}^\kappa I[c_j,N_j+1]$
rather than those of
![]() $\prod_{j=1}^\kappa P[c_j,N_j]$
prevents us from forming the same convex chain twice. Next we define
$\prod_{j=1}^\kappa P[c_j,N_j]$
prevents us from forming the same convex chain twice. Next we define
a piecewise linear mapping. Given
![]() $(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])\in\prod_{j=1}^\kappa I[c_j,N_j+1]$
, how many distinct n-tuples
$(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])\in\prod_{j=1}^\kappa I[c_j,N_j+1]$
, how many distinct n-tuples
![]() $\left(u^{(1)},\ldots,u^{(\kappa)}\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
can we build out of this object? We answer this question in the following lemma.
$\left(u^{(1)},\ldots,u^{(\kappa)}\right)\in{\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
can we build out of this object? We answer this question in the following lemma.
Lemma 6.
Let
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
,
$s[\kappa]\in\mathbb{N}_\kappa(n)$
,
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
, with the corresponding
$\ell[\kappa]\in\mathcal{L}_\kappa$
, with the corresponding
![]() $c[\kappa]$
. Consider a tuple
$c[\kappa]$
. Consider a tuple
![]() $(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])\in\prod_{j=1}^\kappa I[c_j,N_j+1]$
. Then
$(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1])\in\prod_{j=1}^\kappa I[c_j,N_j+1]$
. Then
 \begin{align} \#\mathsf{Order}_{\ell[\kappa],s[\kappa]}^{-1}\left(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1]\right)=\prod_{j=1}^{\kappa} \left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)s_j!. \end{align}
\begin{align} \#\mathsf{Order}_{\ell[\kappa],s[\kappa]}^{-1}\left(\Delta\widetilde{u}^{(1)}[N_1+1],\ldots,\Delta\widetilde{u}^{(\kappa)}[N_\kappa+1]\right)=\prod_{j=1}^{\kappa} \left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)s_j!. \end{align}
Proof. We need to build
![]() $\kappa$
sets of vectors, the jth being devoted to the construction of the convex chain in the jth corner of the
$\kappa$
sets of vectors, the jth being devoted to the construction of the convex chain in the jth corner of the
![]() $\mathsf{ECP}$
. To form the
$\mathsf{ECP}$
. To form the
![]() $s_j$
vectors in the jth corner, we select
$s_j$
vectors in the jth corner, we select
![]() $s_j$
pieces in
$s_j$
pieces in
![]() $\Delta\widetilde{u}^{(j)}[N_j+1]$
that will account for the x-contributions of the vectors, and we select
$\Delta\widetilde{u}^{(j)}[N_j+1]$
that will account for the x-contributions of the vectors, and we select
![]() $s_j$
pieces (or, complementarily,
$s_j$
pieces (or, complementarily,
![]() $s_{{j+1}}$
pieces) in
$s_{{j+1}}$
pieces) in
![]() $\Delta\widetilde{u}^{({j+1})}[N_{{j+1}}+1]$
that will account for the y-contributions. There are
$\Delta\widetilde{u}^{({j+1})}[N_{{j+1}}+1]$
that will account for the y-contributions. There are
![]() $\prod_{j=1}^{\kappa} \left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)$
ways of choosing these pieces, and
$\prod_{j=1}^{\kappa} \left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)$
ways of choosing these pieces, and
![]() $\prod_{j=1}^{\kappa}s_j!$
ways to pair these elements to form the
$\prod_{j=1}^{\kappa}s_j!$
ways to pair these elements to form the
![]() $s_j$
vectors in each corner (see Figure 13 for an example of the construction).
$s_j$
vectors in each corner (see Figure 13 for an example of the construction).
There exists a unique order that sorts these vectors into convex order in each corner, so that, put together, these pieces form a convex polygon whose set of vertices is a ‘distinct’ n-tuple
![]() ${z}[n]\in{\mathcal{C}_\kappa}(s[\kappa])$
with
${z}[n]\in{\mathcal{C}_\kappa}(s[\kappa])$
with
![]() $\ell[\kappa]({z}[n])=\ell[\kappa]$
. Now, consider
$\ell[\kappa]({z}[n])=\ell[\kappa]$
. Now, consider
![]() $\chi_{s[\kappa]}({z}[n])=\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
: the last entries
$\chi_{s[\kappa]}({z}[n])=\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
: the last entries
![]() $\left(u^{(1)},\ldots,u^{(\kappa)}\right)\,:\!=\,\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
of this tuple form a new distinct element (since z[n] is one as well) of
$\left(u^{(1)},\ldots,u^{(\kappa)}\right)\,:\!=\,\left(u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
of this tuple form a new distinct element (since z[n] is one as well) of
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa]).$
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa]).$

Figure 13. In the first drawing, given a partition in
![]() $I[c_j,s_{{j-1}}+s_j]$
and a partition in
$I[c_j,s_{{j-1}}+s_j]$
and a partition in
![]() $I[c_{{j+1}},s_j+s_{{j+1}}]$
, we randomly pair
$I[c_{{j+1}},s_j+s_{{j+1}}]$
, we randomly pair
![]() $s_j$
pieces of
$s_j$
pieces of
![]() $c_j$
with
$c_j$
with
![]() $s_j$
pieces of
$s_j$
pieces of
![]() $c_{{j+1}}$
to form the vectors in the jth corner. Note that an affine transformation is hiding in the construction of these vectors. In the second drawing, vectors have been reordered by increasing slope. The points
$c_{{j+1}}$
to form the vectors in the jth corner. Note that an affine transformation is hiding in the construction of these vectors. In the second drawing, vectors have been reordered by increasing slope. The points
![]() $\mathsf{cp}_j,\mathsf{cp}_{{j+1}}$
naturally appear as the edges of the convex chain formed by those vectors. In these particular drawings, we took
$\mathsf{cp}_j,\mathsf{cp}_{{j+1}}$
naturally appear as the edges of the convex chain formed by those vectors. In these particular drawings, we took
![]() $s_j=3$
,
$s_j=3$
,
![]() $s_{{j-1}}=2$
,
$s_{{j-1}}=2$
,
![]() $s_{{j+1}}=2$
.
$s_{{j+1}}=2$
.
This allows us to compute the Lebesgue measure of
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. Indeed, the map
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
. Indeed, the map
![]() $\mathsf{Order}_{\ell[\kappa],s[\kappa]}$
carries the Lebesgue measure of
$\mathsf{Order}_{\ell[\kappa],s[\kappa]}$
carries the Lebesgue measure of
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
onto that of
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
onto that of
![]() $\prod_{j=1}^\kappa I[c_j,N_j+1]$
.
$\prod_{j=1}^\kappa I[c_j,N_j+1]$
.
Corollary 1.
For
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
, and
$s[\kappa]\in\mathbb{N}_\kappa(n)$
, and
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
fixed, we have
$\ell[\kappa]\in\mathcal{L}_\kappa$
fixed, we have
 \begin{align} \mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)=\prod_{j=1}^{\kappa}\frac{c_j^{s_j+s_{{j+1}}-1}}{s_j!(s_j+s_{{j+1}}-1)!}. \end{align}
\begin{align} \mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)=\prod_{j=1}^{\kappa}\frac{c_j^{s_j+s_{{j+1}}-1}}{s_j!(s_j+s_{{j+1}}-1)!}. \end{align}
Proof. Indeed, by the previous lemmas, we obtain
 \begin{align} \mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)&=\prod_{j=1}^{\kappa}\left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)s_j! \cdot\mathsf{Leb}_{N_j}\left(I[c_j,N_j+1]\right), \end{align}
\begin{align} \mathsf{Leb}_{2n-\kappa}\left({\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])\right)&=\prod_{j=1}^{\kappa}\left(\begin{smallmatrix}{s_j+s_{{j+1}}} \\[3pt] {s_j}\end{smallmatrix}\right)s_j! \cdot\mathsf{Leb}_{N_j}\left(I[c_j,N_j+1]\right), \end{align}
and we conclude by (2.7).
3.3. The joint distribution of the pair
 $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
Theorem 5 concretizes our understanding of this new equivalent geometric description of the set
![]() ${\mathcal{C}_\kappa}(s[\kappa])$
in terms of the
${\mathcal{C}_\kappa}(s[\kappa])$
in terms of the
![]() $\mathsf{ECP}$
. Let
$\mathsf{ECP}$
. Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, and set
${\mathbb{D}}^{(n)}_{\kappa}$
, and set
![]() $\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
$\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
![]() $\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. By computing the Lebesgue measure of the set
$\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. By computing the Lebesgue measure of the set
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
, we managed to understand the weight of all z[n]-gons contained in any
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
, we managed to understand the weight of all z[n]-gons contained in any
![]() $(\ell[\kappa],s[\kappa])$
-fibration, which is the key to the computation of the joint distribution of the pair
$(\ell[\kappa],s[\kappa])$
-fibration, which is the key to the computation of the joint distribution of the pair
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
.
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
.
Theorem 6.
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, and consider the random variables
${\mathbb{D}}^{(n)}_{\kappa}$
, and consider the random variables
![]() $\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
$\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
![]() $\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. Then for a given
$\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. Then for a given
![]() $s[\kappa]\in\mathbb{N}^\kappa$
, the pair
$s[\kappa]\in\mathbb{N}^\kappa$
, the pair
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
has the joint distribution
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
has the joint distribution
where
 \begin{align} f^{(n)}_{\kappa}\left(\ell[\kappa],s[\kappa]\right)=\frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)} \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}} \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\prod_{j=1}^{\kappa}\frac{c_j^{s_{{j-1}}+s_j-1}}{s_j!(s_{{j-1}}+s_j-1)!}. \end{align}
\begin{align} f^{(n)}_{\kappa}\left(\ell[\kappa],s[\kappa]\right)=\frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)} \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}} \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\prod_{j=1}^{\kappa}\frac{c_j^{s_{{j-1}}+s_j-1}}{s_j!(s_{{j-1}}+s_j-1)!}. \end{align}
Proof. Write
For any continuous bounded test function
![]() $\eta\,:\,\mathbb{R}^{\kappa}\times\mathbb{N}^{\kappa}\to\mathbb{R}$
, we have
$\eta\,:\,\mathbb{R}^{\kappa}\times\mathbb{N}^{\kappa}\to\mathbb{R}$
, we have
which, after the change of variables
![]() $\chi_{s[\kappa]}({z}[n])=\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
, performed at fixed
$\chi_{s[\kappa]}({z}[n])=\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)$
, performed at fixed
![]() $(\ell[\kappa],s[\kappa])$
, gives
$(\ell[\kappa],s[\kappa])$
, gives
 \begin{multline} \mathbb{E}\bigg[\eta\left(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa]\right)\bigg]=\frac{n!}{\widetilde{\mathbb{P}}_\kappa(n)}\sum_{s[\kappa]\in\mathbb{N}_\kappa(n)}\mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)\int_{\mathbb{R}^{\kappa}}\eta(\ell[\kappa],s[\kappa])\\[3pt] \times\left[\int_{\mathbb{R}^{2n-\kappa}}\mathbf{1}_{\left\{{\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(s[\kappa])}\right\}}\text{d} u[2n-\kappa]\right]\text{d} \ell[\kappa]. \end{multline}
\begin{multline} \mathbb{E}\bigg[\eta\left(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa]\right)\bigg]=\frac{n!}{\widetilde{\mathbb{P}}_\kappa(n)}\sum_{s[\kappa]\in\mathbb{N}_\kappa(n)}\mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)\int_{\mathbb{R}^{\kappa}}\eta(\ell[\kappa],s[\kappa])\\[3pt] \times\left[\int_{\mathbb{R}^{2n-\kappa}}\mathbf{1}_{\left\{{\left(\ell[\kappa],u^{(1)}[N_1,c_1],\ldots,u^{(\kappa)}[N_\kappa,c_\kappa]\right)\in{\mathcal{S}}^{(n)}(s[\kappa])}\right\}}\text{d} u[2n-\kappa]\right]\text{d} \ell[\kappa]. \end{multline}
Now,
![]() $\mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)=\sin(\theta_\kappa)^{n-\kappa}$
for all
$\mathrm{Jac}\left((\chi_{s[\kappa]})^{-1}\right)=\sin(\theta_\kappa)^{n-\kappa}$
for all
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
by (3.4), and the last bracket in (3.15) is nothing but the Lebesgue measure of
$s[\kappa]\in\mathbb{N}_\kappa(n)$
by (3.4), and the last bracket in (3.15) is nothing but the Lebesgue measure of
![]() ${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
, which we computed in Corollary 1! Hence substituting (3.9) in (3.15) gives Theorem 6.
${\mathcal{S}}^{(n)}(\ell[\kappa],s[\kappa])$
, which we computed in Corollary 1! Hence substituting (3.9) in (3.15) gives Theorem 6.
In the next section, we are going to exploit the asymptotic stochastic behavior of the pair
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
to deduce an equivalent of
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
to deduce an equivalent of
![]() $\widetilde{\mathbb{P}}_\kappa(n)$
. However, in the particular cases
$\widetilde{\mathbb{P}}_\kappa(n)$
. However, in the particular cases
![]() $\kappa\in\{3,4\}$
, we have
$\kappa\in\{3,4\}$
, we have
![]() ${\mathbb{D}}^{(n)}_{\kappa}=\mathbb{Q}^{(n)}_{\kappa}$
, and the set
${\mathbb{D}}^{(n)}_{\kappa}=\mathbb{Q}^{(n)}_{\kappa}$
, and the set
![]() $\mathcal{L}_\kappa$
is easily computable. Hence we can immediately compute the exact value of
$\mathcal{L}_\kappa$
is easily computable. Hence we can immediately compute the exact value of
![]() $\mathbb{P}_\kappa(n)$
from
$\mathbb{P}_\kappa(n)$
from
![]() $\mathbb{Q}^{(n)}_{\kappa}$
. In Appendix B, we take a look at these computations to recover Valtr’s famous results for the triangle and the parallelogram.
$\mathbb{Q}^{(n)}_{\kappa}$
. In Appendix B, we take a look at these computations to recover Valtr’s famous results for the triangle and the parallelogram.
4. An asymptotic result for convex regular polygons
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, and consider
${\mathbb{D}}^{(n)}_{\kappa}$
, and consider
![]() $\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
$\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
![]() $\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. By symmetry, we have
$\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. By symmetry, we have
![]() $\mathbf{s}^{(n)}_{j}\overset{(d)}{=}\mathbf{s}^{(n)}_{1}$
for all
$\mathbf{s}^{(n)}_{j}\overset{(d)}{=}\mathbf{s}^{(n)}_{1}$
for all
![]() $j\in\{1,\ldots,\kappa\}$
, and since
$j\in\{1,\ldots,\kappa\}$
, and since
![]() $\sum_{j=1}^{\kappa}\mathbf{s}^{(n)}_{j}=n$
, the expectation of
$\sum_{j=1}^{\kappa}\mathbf{s}^{(n)}_{j}=n$
, the expectation of
![]() $\mathbf{s}^{(n)}_{j}$
is given by
$\mathbf{s}^{(n)}_{j}$
is given by
![]() $\mathbb{E}[\mathbf{s}^{(n)}_{j}]=n/\kappa$
. In the sequel we will set
$\mathbb{E}[\mathbf{s}^{(n)}_{j}]=n/\kappa$
. In the sequel we will set
![]() $\mathbf{s}^{(n)}_{\kappa}=n-\sum_{j=1}^{\kappa-1}\mathbf{s}^{(n)}_{j}$
, and we will describe
$\mathbf{s}^{(n)}_{\kappa}=n-\sum_{j=1}^{\kappa-1}\mathbf{s}^{(n)}_{j}$
, and we will describe
![]() $\mathbf{s}^{(n)}[\kappa-1]$
since the last value is determined by the other ones. What we are interested in here are the fluctuations of
$\mathbf{s}^{(n)}[\kappa-1]$
since the last value is determined by the other ones. What we are interested in here are the fluctuations of
![]() $\mathbf{s}^{(n)}[\kappa-1]$
around its expectation, and the asymptotic behavior of the variables
$\mathbf{s}^{(n)}[\kappa-1]$
around its expectation, and the asymptotic behavior of the variables
![]() $\boldsymbol{\ell}^{(n)}[\kappa]$
as n grows. This is all contained in the following theorem.
$\boldsymbol{\ell}^{(n)}[\kappa]$
as n grows. This is all contained in the following theorem.
Theorem 7.
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, and consider
${\mathbb{D}}^{(n)}_{\kappa}$
, and consider
![]() $\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
$\boldsymbol{\ell}^{(n)}[\kappa]=\ell[\kappa](\mathbf{z}[n])$
,
![]() $\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. We introduce the random variables
$\mathbf{s}^{(n)}[\kappa]=s[\kappa](\mathbf{z}[n])$
. We introduce the random variables
![]() $\overline{\boldsymbol{\ell}}^{(n)}[\kappa]=n\boldsymbol{\ell}^{(n)}[\kappa]$
and
$\overline{\boldsymbol{\ell}}^{(n)}[\kappa]=n\boldsymbol{\ell}^{(n)}[\kappa]$
and
![]() $\mathbf{x}_j^{(n)}=\frac{\mathbf{s}^{(n)}_{j}-n/\kappa}{\sqrt{n/\kappa}}$
, for all
$\mathbf{x}_j^{(n)}=\frac{\mathbf{s}^{(n)}_{j}-n/\kappa}{\sqrt{n/\kappa}}$
, for all
![]() $j\in\{1,\ldots,\kappa\}$
. The following convergence in distribution holds in
$j\in\{1,\ldots,\kappa\}$
. The following convergence in distribution holds in
![]() $\mathbb{R}^{2\kappa-1}$
:
$\mathbb{R}^{2\kappa-1}$
:
where the variables
![]() $\overline{\boldsymbol{\ell}}[\kappa]$
are independent from the
$\overline{\boldsymbol{\ell}}[\kappa]$
are independent from the
![]() $\mathbf{x}[\kappa-1]$
; the
$\mathbf{x}[\kappa-1]$
; the
![]() $\overline{\boldsymbol{\ell}}[\kappa]$
are
$\overline{\boldsymbol{\ell}}[\kappa]$
are
![]() $\kappa$
random variables that are exponentially distributed with rate
$\kappa$
random variables that are exponentially distributed with rate
![]() $\displaystyle\frac{2w_\kappa}{\kappa r_\kappa}$
, where
$\displaystyle\frac{2w_\kappa}{\kappa r_\kappa}$
, where
![]() $\displaystyle w_\kappa=\frac{1+\cos(\theta_\kappa)}{\sin(\theta_\kappa)}$
; and
$\displaystyle w_\kappa=\frac{1+\cos(\theta_\kappa)}{\sin(\theta_\kappa)}$
; and
![]() $\mathbf{x}=\mathbf{x}[\kappa-1]$
is a centered Gaussian random vector whose inverse covariance matrix
$\mathbf{x}=\mathbf{x}[\kappa-1]$
is a centered Gaussian random vector whose inverse covariance matrix
![]() $\Sigma_\kappa^{-1}$
of size
$\Sigma_\kappa^{-1}$
of size
![]() $(\kappa-1)\times(\kappa-1)$
is given by
$(\kappa-1)\times(\kappa-1)$
is given by
 \begin{align*}\Sigma_3^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l} 6 & 3\\[3pt] 3 & 6 \end{array}\right),\quad\Sigma_4^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l} 6 & 4 & 2\\[3pt] 4 & 8 & 4\\[3pt] 2 & 4 & 6 \end{array} \right),\quad\Sigma_5^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 6 & 4 & 3 & 2\\[3pt] 4 & 8 & 5 & 3\\[3pt] 3 & 5 & 8 & 4\\[3pt] 2 & 3 & 4 & 6 \end{array} \right), \end{align*}
\begin{align*}\Sigma_3^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l} 6 & 3\\[3pt] 3 & 6 \end{array}\right),\quad\Sigma_4^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l} 6 & 4 & 2\\[3pt] 4 & 8 & 4\\[3pt] 2 & 4 & 6 \end{array} \right),\quad\Sigma_5^{-1}=\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 6 & 4 & 3 & 2\\[3pt] 4 & 8 & 5 & 3\\[3pt] 3 & 5 & 8 & 4\\[3pt] 2 & 3 & 4 & 6 \end{array} \right), \end{align*}
and more generally
 \begin{align*}\Sigma_\kappa^{-1}=\frac{1}{2} \left(\begin{array} {l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 6&4&3&\cdots&\cdots&3&2\\[3pt] 4&8&5&4&\cdots&4&3\\[3pt] 3&5&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&4&\ddots&\ddots&\ddots&4&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&5&3\\[3pt] 3&4&\cdots&4&5&8&4\\[3pt] 2&3&\cdots&\cdots&3&4&6 \end{array} \right).\text{ for }\kappa \geq 6, \end{align*}
\begin{align*}\Sigma_\kappa^{-1}=\frac{1}{2} \left(\begin{array} {l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 6&4&3&\cdots&\cdots&3&2\\[3pt] 4&8&5&4&\cdots&4&3\\[3pt] 3&5&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&4&\ddots&\ddots&\ddots&4&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&5&3\\[3pt] 3&4&\cdots&4&5&8&4\\[3pt] 2&3&\cdots&\cdots&3&4&6 \end{array} \right).\text{ for }\kappa \geq 6, \end{align*}
The determinant
![]() $\mathrm{m}_\kappa=\det\left(\Sigma_\kappa^{-1}\right)$
of the latter matrix has already been mentioned in Theorem 1. The value of this determinant, i.e.
$\mathrm{m}_\kappa=\det\left(\Sigma_\kappa^{-1}\right)$
of the latter matrix has already been mentioned in Theorem 1. The value of this determinant, i.e.
We first state two important intermediate lemmas which will allow us to prove Theorem 7.
Lemma 7.
(Local limit theorem for Poisson variables.) Let
![]() $\kappa$
be a positive integer and
$\kappa$
be a positive integer and
![]() $Y_n$
a Poisson variable of mean
$Y_n$
a Poisson variable of mean
![]() $\frac{n}{\kappa}$
. We have
$\frac{n}{\kappa}$
. We have
 \begin{align*}\sup_{y}\left\vert \sqrt{\frac{n}{\kappa}}\mathbb{P}\left(Y_n=\left\lfloor\frac{n}{\kappa}+y\sqrt{\frac{n}{\kappa}}\right\rfloor\right)-\frac{e^{-y^2/2}}{\sqrt{2\pi}}\right\vert\underset{n\to\infty}{\longrightarrow} 0. \end{align*}
\begin{align*}\sup_{y}\left\vert \sqrt{\frac{n}{\kappa}}\mathbb{P}\left(Y_n=\left\lfloor\frac{n}{\kappa}+y\sqrt{\frac{n}{\kappa}}\right\rfloor\right)-\frac{e^{-y^2/2}}{\sqrt{2\pi}}\right\vert\underset{n\to\infty}{\longrightarrow} 0. \end{align*}
Proof. Pick n i.i.d. random Poisson variables
![]() $X_1,\ldots,X_n$
of mean
$X_1,\ldots,X_n$
of mean
![]() $1/\kappa$
and apply the local limit theorem [Reference Petrov19, Theorem VII.1.1] to
$1/\kappa$
and apply the local limit theorem [Reference Petrov19, Theorem VII.1.1] to
![]() $\widetilde{X}_i=\sqrt{\kappa}(X_i-\frac{1}{\kappa})$
. The support of
$\widetilde{X}_i=\sqrt{\kappa}(X_i-\frac{1}{\kappa})$
. The support of
![]() $\widetilde{X}_1$
is included in
$\widetilde{X}_1$
is included in
![]() $\sqrt{\kappa}\mathbb{Z}-1/\sqrt{\kappa}$
, and
$\sqrt{\kappa}\mathbb{Z}-1/\sqrt{\kappa}$
, and
![]() $X_1+\cdots+X_n$
is a Poisson variable of mean
$X_1+\cdots+X_n$
is a Poisson variable of mean
![]() $n/\kappa.$
$n/\kappa.$
Lemma 8.
Let
![]() $(g_n)_{n\in\mathbb{N}}$
be a sequence of nonnegative measurable functions on
$(g_n)_{n\in\mathbb{N}}$
be a sequence of nonnegative measurable functions on
![]() $\mathbb{R}^d$
. Assume that for every
$\mathbb{R}^d$
. Assume that for every
![]() $\varepsilon \gt 0$
there exists a compact set
$\varepsilon \gt 0$
there exists a compact set
![]() $K_\varepsilon$
such that for all n large enough,
$K_\varepsilon$
such that for all n large enough,
![]() $\int_{K_\varepsilon^c}g_n \lt \varepsilon$
(where
$\int_{K_\varepsilon^c}g_n \lt \varepsilon$
(where
![]() $K_\varepsilon^c$
is the complement of
$K_\varepsilon^c$
is the complement of
![]() $K_\varepsilon$
in
$K_\varepsilon$
in
![]() $\mathbb{R}^d$
), and that
$\mathbb{R}^d$
), and that
![]() $g_n$
uniformly converges on all compact subsets of
$g_n$
uniformly converges on all compact subsets of
![]() $\mathbb{R}^d$
towards a density g (with respect to the Lebesgue measure on
$\mathbb{R}^d$
towards a density g (with respect to the Lebesgue measure on
![]() $\mathbb{R}^d$
). Then there exists a sequence
$\mathbb{R}^d$
). Then there exists a sequence
![]() $(\alpha_n)_{n\in\mathbb{N}}$
such that for n large enough (for small values of n,
$(\alpha_n)_{n\in\mathbb{N}}$
such that for n large enough (for small values of n,
![]() $g_n$
could be zero),
$g_n$
could be zero),
![]() $\frac{1}{\alpha_n}g_n$
is a density and
$\frac{1}{\alpha_n}g_n$
is a density and
![]() $\alpha_n\underset{n\to+\infty}{\longrightarrow}1.$
$\alpha_n\underset{n\to+\infty}{\longrightarrow}1.$
Proof. Take
![]() $\varepsilon \gt 0$
, and choose K such that for n large enough,
$\varepsilon \gt 0$
, and choose K such that for n large enough,
![]() $\int_{K^c}g_n \lt \varepsilon$
. Since g is a density, there exists a compact set H such that
$\int_{K^c}g_n \lt \varepsilon$
. Since g is a density, there exists a compact set H such that
![]() $\int_{H}g\geq 1-\varepsilon$
. Let
$\int_{H}g\geq 1-\varepsilon$
. Let
![]() $S=K\cup H$
. By the uniform convergence, there exists
$S=K\cup H$
. By the uniform convergence, there exists
![]() $m\in\mathbb{N}$
such that for all
$m\in\mathbb{N}$
such that for all
![]() $n\geq m$
, we have
$n\geq m$
, we have
![]() $\int_S \vert g_n-g\vert\leq \varepsilon.$
Then the triangle inequality gives
$\int_S \vert g_n-g\vert\leq \varepsilon.$
Then the triangle inequality gives
 \begin{multline} \int_S g_n \geq \int_S g -\int_S\vert g_n-g\vert\geq 1-2\varepsilon \\[3pt] \text{ and }\quad\int_{\mathbb{R}^d} g_n \leq \int_S g +\int_S\vert g_n-g\vert+\int_{S^c}g_n\leq 1+2\varepsilon. \end{multline}
\begin{multline} \int_S g_n \geq \int_S g -\int_S\vert g_n-g\vert\geq 1-2\varepsilon \\[3pt] \text{ and }\quad\int_{\mathbb{R}^d} g_n \leq \int_S g +\int_S\vert g_n-g\vert+\int_{S^c}g_n\leq 1+2\varepsilon. \end{multline}
This shows
![]() $\alpha_n=\int_{\mathbb{R}^d}g_n$
is finite, well-defined, and nonzero for n large enough, and
$\alpha_n=\int_{\mathbb{R}^d}g_n$
is finite, well-defined, and nonzero for n large enough, and
![]() $\frac{1}{\alpha_n}g_n$
is a density on
$\frac{1}{\alpha_n}g_n$
is a density on
![]() $\mathbb{R}^d$
. From (4.1), we have
$\mathbb{R}^d$
. From (4.1), we have
![]() $\alpha_n\underset{n\to+\infty}{\longrightarrow}1$
, and this concludes the proof.
$\alpha_n\underset{n\to+\infty}{\longrightarrow}1$
, and this concludes the proof.
Notation. Recall that by Proposition 1, if
![]() $z[n]\in\mathcal{C}_\kappa(n)$
, we can express the side lengths
$z[n]\in\mathcal{C}_\kappa(n)$
, we can express the side lengths
![]() $c[\kappa]$
as a function of the boundary distances
$c[\kappa]$
as a function of the boundary distances
![]() $\ell[\kappa]$
of the
$\ell[\kappa]$
of the
![]() $\mathsf{ECP}({z}[n])$
:
$\mathsf{ECP}({z}[n])$
:
with
![]() $\mathfrak{cl}_j(\ell[\kappa])=(\ell_{{j-1}}+\ell_{{j+1}}+2\ell_j\cos(\theta_\kappa))/\sin(\theta_\kappa).$
$\mathfrak{cl}_j(\ell[\kappa])=(\ell_{{j-1}}+\ell_{{j+1}}+2\ell_j\cos(\theta_\kappa))/\sin(\theta_\kappa).$
Proof of Theorem
7. Note that the joint density of
![]() $\left(\left(\overline{\boldsymbol{\ell}}_1,\ldots,\overline{\boldsymbol{\ell}}_\kappa\right),\left(\mathbf{x}_1,\ldots,\mathbf{x}_{\kappa-1}\right)\right)$
on
$\left(\left(\overline{\boldsymbol{\ell}}_1,\ldots,\overline{\boldsymbol{\ell}}_\kappa\right),\left(\mathbf{x}_1,\ldots,\mathbf{x}_{\kappa-1}\right)\right)$
on
![]() $\mathbb{R}_{+}^{\kappa}\times\mathbb{R}^{\kappa-1}$
is given by
$\mathbb{R}_{+}^{\kappa}\times\mathbb{R}^{\kappa-1}$
is given by
 \begin{align*}g_{\kappa}(\overline{\ell}[\kappa],x[\kappa-1])=\left(\sqrt{\frac{\mathrm{m}_\kappa}{(2\pi)^{\kappa-1}}}\exp\left(-\frac{1}{2}x^{t}\Sigma_\kappa^{-1}x\right)\right) \left(\frac{2w_\kappa}{\kappa r_\kappa}\right)^\kappa\exp\left(-\frac{2w_\kappa}{\kappa r_\kappa}\sum_{j=1}^{\kappa}\overline{\ell}_j\right). \end{align*}
\begin{align*}g_{\kappa}(\overline{\ell}[\kappa],x[\kappa-1])=\left(\sqrt{\frac{\mathrm{m}_\kappa}{(2\pi)^{\kappa-1}}}\exp\left(-\frac{1}{2}x^{t}\Sigma_\kappa^{-1}x\right)\right) \left(\frac{2w_\kappa}{\kappa r_\kappa}\right)^\kappa\exp\left(-\frac{2w_\kappa}{\kappa r_\kappa}\sum_{j=1}^{\kappa}\overline{\ell}_j\right). \end{align*}
The proof of Theorem 7 is carried out in two steps:
-
(i) We show the uniform convergence on compact sets of the ‘density’ of the pair
More precisely, we show the uniform convergence on compact sets of a density $$\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1]\right).$$
$$\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1]\right).$$
 $g^{(n)}_{\kappa}$
, introduced in (4.4), that is associated to these random variables.
$g^{(n)}_{\kappa}$
, introduced in (4.4), that is associated to these random variables.
-
(i) (2) We give an argument of uniform integrability for this limit, which allows us to apply Lemma 8 and conclude.
Step 1: Let
![]() $\psi:\mathbb{R}_{+}^\kappa\times\mathbb{R}^{\kappa-1}\to\mathbb{R}$
a bounded continuous function, and let us pass to the limit in the expectation
$\psi:\mathbb{R}_{+}^\kappa\times\mathbb{R}^{\kappa-1}\to\mathbb{R}$
a bounded continuous function, and let us pass to the limit in the expectation
 \begin{multline} \mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1]\right)\right]=\\[3pt] \sum_{s[\kappa]\in\mathbb{N}_\kappa(n)}\int_{\mathbb{R}^\kappa}\psi\left(n\ell[\kappa],\frac{s[\kappa-1]-n/\kappa}{\sqrt{n/\kappa}}\right)f^{(n)}_{\kappa}\left(\ell[\kappa],s[\kappa]\right)\text{d} \ell[\kappa], \end{multline}
\begin{multline} \mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1]\right)\right]=\\[3pt] \sum_{s[\kappa]\in\mathbb{N}_\kappa(n)}\int_{\mathbb{R}^\kappa}\psi\left(n\ell[\kappa],\frac{s[\kappa-1]-n/\kappa}{\sqrt{n/\kappa}}\right)f^{(n)}_{\kappa}\left(\ell[\kappa],s[\kappa]\right)\text{d} \ell[\kappa], \end{multline}
where the joint distribution
![]() $f^{(n)}_{\kappa}$
of the pair
$f^{(n)}_{\kappa}$
of the pair
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
is given in Theorem 6.
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
is given in Theorem 6.
We perform both substitutions
![]() $\overline{\ell}_j=n\ell_j$
and
$\overline{\ell}_j=n\ell_j$
and
![]() $x_j=(s_j-n/\kappa)/\sqrt{n/\kappa}$
in the right-hand side of (4.2). We turn our sum over
$x_j=(s_j-n/\kappa)/\sqrt{n/\kappa}$
in the right-hand side of (4.2). We turn our sum over
![]() $s[\kappa]\in\mathbb{N}_\kappa(n)$
into an integral, in the following way:
$s[\kappa]\in\mathbb{N}_\kappa(n)$
into an integral, in the following way:
 \begin{multline*} \frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\int_{\overline{\mathbb{N}_{\kappa-1}}(n)}\int_{\mathcal{L}_\kappa}\psi\left(n\ell[\kappa],\frac{\lfloor q[\kappa-1]\rfloor-n/\kappa}{\sqrt{n/\kappa}}\right)\\[3pt] \times\prod_{j=1}^{\kappa}\frac{ \left(r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\right)^{\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1}}{\lfloor q_j\rfloor !(\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1)!}\cdot\text{d} \ell[\kappa]\text{d} q[\kappa-1], \end{multline*}
\begin{multline*} \frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\int_{\overline{\mathbb{N}_{\kappa-1}}(n)}\int_{\mathcal{L}_\kappa}\psi\left(n\ell[\kappa],\frac{\lfloor q[\kappa-1]\rfloor-n/\kappa}{\sqrt{n/\kappa}}\right)\\[3pt] \times\prod_{j=1}^{\kappa}\frac{ \left(r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\right)^{\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1}}{\lfloor q_j\rfloor !(\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1)!}\cdot\text{d} \ell[\kappa]\text{d} q[\kappa-1], \end{multline*}
where
![]() $\left\lfloor q_\kappa\right\rfloor$
is set to satisfy
$\left\lfloor q_\kappa\right\rfloor$
is set to satisfy
![]() $\left\lfloor q_\kappa\right\rfloor=n-\sum_{j=1}^{\kappa-1} \left\lfloor q_j\right\rfloor$
(notice that there is no integration with respect to
$\left\lfloor q_\kappa\right\rfloor=n-\sum_{j=1}^{\kappa-1} \left\lfloor q_j\right\rfloor$
(notice that there is no integration with respect to
![]() $q_\kappa$
) and the integration is now done on the region
$q_\kappa$
) and the integration is now done on the region
 $$\overline{\mathbb{N}_{\kappa-1}}(n)\,:\!=\,\left\{q[\kappa-1],\text{ with }q_j \gt 0\text{ and }\sum_{j=1}^{\kappa-1} q_j\leq n\right\}.$$
$$\overline{\mathbb{N}_{\kappa-1}}(n)\,:\!=\,\left\{q[\kappa-1],\text{ with }q_j \gt 0\text{ and }\sum_{j=1}^{\kappa-1} q_j\leq n\right\}.$$
Let us consider the term
 \begin{multline*} \frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\int_{\overline{\mathbb{N}_{\kappa-1}}(n)}\int_{\mathcal{L}_\kappa}\psi\left(n\ell[\kappa],\frac{ q[\kappa-1]-n/\kappa}{\sqrt{n/\kappa}}\right)\\[3pt] \times\prod_{j=1}^{\kappa}\frac{ \left(r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\right)^{\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1}}{\lfloor q_j\rfloor !(\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1)!}\cdot\text{d} \ell[\kappa]\text{d} q[\kappa-1] \end{multline*}
\begin{multline*} \frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\int_{\overline{\mathbb{N}_{\kappa-1}}(n)}\int_{\mathcal{L}_\kappa}\psi\left(n\ell[\kappa],\frac{ q[\kappa-1]-n/\kappa}{\sqrt{n/\kappa}}\right)\\[3pt] \times\prod_{j=1}^{\kappa}\frac{ \left(r_\kappa-\mathfrak{cl}_j(\ell[\kappa])\right)^{\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1}}{\lfloor q_j\rfloor !(\lfloor q_j\rfloor+\lfloor q_{{j+1}}\rfloor-1)!}\cdot\text{d} \ell[\kappa]\text{d} q[\kappa-1] \end{multline*}
(we have removed the floor function in
![]() $\psi$
). This quantity turns out to be the expectation
$\psi$
). This quantity turns out to be the expectation
where for all
![]() $j\in\{1,\ldots,\kappa-1\}$
we set
$j\in\{1,\ldots,\kappa-1\}$
we set
![]() $\overline{\mathbf{x}}^{(n)}_j\,:\!=\,\mathbf{x}^{(n)}_j+\mathbf{U}_j/\sqrt{n/\kappa}$
, with
$\overline{\mathbf{x}}^{(n)}_j\,:\!=\,\mathbf{x}^{(n)}_j+\mathbf{U}_j/\sqrt{n/\kappa}$
, with
![]() $\mathbf{U}_j$
a random variable uniformly distributed in [0, 1].
$\mathbf{U}_j$
a random variable uniformly distributed in [0, 1].
We have replaced a sum by an integral, which amounts to representing a discrete random variable by a continuous one; i.e. if X has a discrete law,
![]() $\mathbb{P}(X=k)=p_k,k\in\mathbb{Z}$
, then
$\mathbb{P}(X=k)=p_k,k\in\mathbb{Z}$
, then
![]() $X\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\lfloor X+U\rfloor$
, where U is uniform in [0, 1]. Then
$X\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\lfloor X+U\rfloor$
, where U is uniform in [0, 1]. Then
We are going to prove first that
![]() $\mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]$
converges to deduce that its counterpart
$\mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]$
converges to deduce that its counterpart
![]() $\mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]$
converges as well, to the same limit.
$\mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]$
converges as well, to the same limit.
After substitution, we obtain
 \begin{multline} \mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]=\\[3pt] \int_{\mathbb{R}^{\kappa-1}}\int_{\mathbb{R}_+^\kappa}\psi(\overline{\ell}[\kappa],x[\kappa-1])g^{(n)}_{\kappa}(\overline{\ell}[\kappa],x[\kappa-1])\text{d} \overline{\ell}[\kappa]\text{d} x[\kappa-1], \end{multline}
\begin{multline} \mathbb{E}\left[\psi\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)\right]=\\[3pt] \int_{\mathbb{R}^{\kappa-1}}\int_{\mathbb{R}_+^\kappa}\psi(\overline{\ell}[\kappa],x[\kappa-1])g^{(n)}_{\kappa}(\overline{\ell}[\kappa],x[\kappa-1])\text{d} \overline{\ell}[\kappa]\text{d} x[\kappa-1], \end{multline}
where, for all
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $g^{(n)}_{\kappa}$
stands for the joint distribution of a pair
$g^{(n)}_{\kappa}$
stands for the joint distribution of a pair
![]() $\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)$
. With the convention
$\left(\overline{\boldsymbol{\ell}}^{(n)}[\kappa],\overline{\mathbf{x}}^{(n)}[\kappa-1]\right)$
. With the convention
![]() $x_\kappa=-\sum_{i=1}^{\kappa-1}x_i$
, the function
$x_\kappa=-\sum_{i=1}^{\kappa-1}x_i$
, the function
![]() $g^{(n)}_{\kappa}$
can be decomposed as follows:
$g^{(n)}_{\kappa}$
can be decomposed as follows:
with
 \begin{align} \omega(n,\kappa)=\frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\left[\frac{1}{\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}}\frac{\kappa^{3n}e^{3n}}{4^n n^{3n}}\right]\left[\bigg(\frac{\kappa r_\kappa}{2w_\kappa}\bigg)^\kappa r_\kappa^{2n-\kappa}\right]\frac{1}{n^\kappa}\sqrt{\frac{n}{\kappa}}^{\kappa-1}, \end{align}
\begin{align} \omega(n,\kappa)=\frac{n!\sin(\theta_\kappa)^{n-\kappa}}{\widetilde{\mathbb{P}}_\kappa(n)}\left[\frac{1}{\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}}\frac{\kappa^{3n}e^{3n}}{4^n n^{3n}}\right]\left[\bigg(\frac{\kappa r_\kappa}{2w_\kappa}\bigg)^\kappa r_\kappa^{2n-\kappa}\right]\frac{1}{n^\kappa}\sqrt{\frac{n}{\kappa}}^{\kappa-1}, \end{align}
and
 \begin{align} h^{(1)}_n\left(\overline{\ell}[\kappa],x[\kappa-1]\right)&=\frac{1}{r_\kappa^{2n-\kappa}}\bigg(\frac{2w_\kappa}{\kappa r_\kappa}\bigg)^\kappa \,\mathbf{1}_{\left\{{\overline{\ell}[\kappa] \in n\mathcal{L}_\kappa}\right\}}\, \prod_{j=1}^{\kappa}\bigg( r_\kappa-\frac{1}{n}\mathfrak{cl}_j(\overline{\ell}[\kappa])\bigg)^{d^{(2)}_j(x[\kappa-1])}, \\[-32pt] \nonumber \end{align}
\begin{align} h^{(1)}_n\left(\overline{\ell}[\kappa],x[\kappa-1]\right)&=\frac{1}{r_\kappa^{2n-\kappa}}\bigg(\frac{2w_\kappa}{\kappa r_\kappa}\bigg)^\kappa \,\mathbf{1}_{\left\{{\overline{\ell}[\kappa] \in n\mathcal{L}_\kappa}\right\}}\, \prod_{j=1}^{\kappa}\bigg( r_\kappa-\frac{1}{n}\mathfrak{cl}_j(\overline{\ell}[\kappa])\bigg)^{d^{(2)}_j(x[\kappa-1])}, \\[-32pt] \nonumber \end{align}
 \begin{align} h^{(2)}_n\left(x[\kappa-1]\right)&= \sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}\frac{4^n n^{3n}}{\kappa^{3n}e^{3n}}\prod_{j=1}^{\kappa}\frac{1}{d^{(1)}_j(x[\kappa-1])!\cdot d^{(2)}_j(x[\kappa-1])!},\end{align}
\begin{align} h^{(2)}_n\left(x[\kappa-1]\right)&= \sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}\frac{4^n n^{3n}}{\kappa^{3n}e^{3n}}\prod_{j=1}^{\kappa}\frac{1}{d^{(1)}_j(x[\kappa-1])!\cdot d^{(2)}_j(x[\kappa-1])!},\end{align}
where
We have arranged the factors so that, as we will see,
![]() $h^{(1)}_n$
and
$h^{(1)}_n$
and
![]() $h^{(2)}_n$
converge to some probability densities.
$h^{(2)}_n$
converge to some probability densities.
Note first that there exists
![]() $\eta \gt 0$
such that
$\eta \gt 0$
such that
![]() $[0,\eta]^\kappa\subset \mathcal{L}_\kappa$
, and thus we have
$[0,\eta]^\kappa\subset \mathcal{L}_\kappa$
, and thus we have
![]() $n\mathcal{L}_\kappa\underset{n\to\infty}{\longrightarrow} \mathbb{R}_{+}^\kappa$
. Then, for every compact
$n\mathcal{L}_\kappa\underset{n\to\infty}{\longrightarrow} \mathbb{R}_{+}^\kappa$
. Then, for every compact
![]() $K\subset \mathbb{R}_{+}^\kappa$
and every
$K\subset \mathbb{R}_{+}^\kappa$
and every
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0\in\mathbb{N}$
such that for all
$n_0\in\mathbb{N}$
such that for all
![]() $n\geq n_0$
,
$n\geq n_0$
,
![]() $K\subset n\mathcal{L}_\kappa$
, i.e.
$K\subset n\mathcal{L}_\kappa$
, i.e.
![]() $\vert\vert\mathbf{1}_{\left\{{\overline{\ell}[\kappa]\in n\mathcal{L}_\kappa}-1\right\}}\vert\vert=0 \lt \varepsilon$
, so that the map
$\vert\vert\mathbf{1}_{\left\{{\overline{\ell}[\kappa]\in n\mathcal{L}_\kappa}-1\right\}}\vert\vert=0 \lt \varepsilon$
, so that the map
![]() $\overline{\ell}[\kappa]\mapsto\mathbf{1}_{\left\{{\overline{\ell}[\kappa]\in n\mathcal{L}_\kappa}\right\}}$
converges uniformly to the constant function 1 on every compact set of
$\overline{\ell}[\kappa]\mapsto\mathbf{1}_{\left\{{\overline{\ell}[\kappa]\in n\mathcal{L}_\kappa}\right\}}$
converges uniformly to the constant function 1 on every compact set of
![]() $\mathbb{R}_+^\kappa$
. Now by the standard approximation
$\mathbb{R}_+^\kappa$
. Now by the standard approximation
![]() $\left(1-\frac{a}{n}\right)^{nb}\underset{n\to+\infty}{\longrightarrow}e^{-ab}$
uniformly for (a,b) on every compact set, we get that
$\left(1-\frac{a}{n}\right)^{nb}\underset{n\to+\infty}{\longrightarrow}e^{-ab}$
uniformly for (a,b) on every compact set, we get that
![]() $h^{(1)}_n$
converges uniformly on every compact set of
$h^{(1)}_n$
converges uniformly on every compact set of
![]() $\mathbb{R}_{+}^\kappa\times\mathbb{R}^{\kappa-1}$
towards
$\mathbb{R}_{+}^\kappa\times\mathbb{R}^{\kappa-1}$
towards
![]() $h^{(1)}$
with
$h^{(1)}$
with
 \begin{align} h^{(1)}\left(\overline{\ell}[\kappa]\right)=\bigg(\frac{2w_\kappa}{\kappa r_\kappa}\bigg)^\kappa\prod_{j=1}^{\kappa}\exp\left(-\frac{2w_\kappa}{\kappa r_\kappa}\overline{\ell}_j\right). \end{align}
\begin{align} h^{(1)}\left(\overline{\ell}[\kappa]\right)=\bigg(\frac{2w_\kappa}{\kappa r_\kappa}\bigg)^\kappa\prod_{j=1}^{\kappa}\exp\left(-\frac{2w_\kappa}{\kappa r_\kappa}\overline{\ell}_j\right). \end{align}
Now, thanks to Corollary 7, for
![]() $x[\kappa-1]$
fixed in
$x[\kappa-1]$
fixed in
![]() $\mathbb{R}^{\kappa-1}$
we have
$\mathbb{R}^{\kappa-1}$
we have
 \begin{multline*} h_n^{(2)}(x[\kappa-1])\underset{n\to +\infty}{\sim}\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}\frac{4^n n^{3n}}{\kappa^{3n}e^{3n}}\bigg(\frac{\kappa}{n}\bigg)^n\bigg(\frac{\kappa}{2n-\kappa}\bigg)^{2n-\kappa}e^{3n-\kappa}\\[3pt] \times\prod_{j=1}^{\kappa}\frac{\sqrt{\kappa}e^{-x_j^2/2}}{\sqrt{2\pi n}}\frac{\sqrt{\kappa}e^{-(x_j+x_{{j+1}})^2/4}}{\sqrt{2\pi (2n-\kappa)}}. \end{multline*}
\begin{multline*} h_n^{(2)}(x[\kappa-1])\underset{n\to +\infty}{\sim}\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}\frac{4^n n^{3n}}{\kappa^{3n}e^{3n}}\bigg(\frac{\kappa}{n}\bigg)^n\bigg(\frac{\kappa}{2n-\kappa}\bigg)^{2n-\kappa}e^{3n-\kappa}\\[3pt] \times\prod_{j=1}^{\kappa}\frac{\sqrt{\kappa}e^{-x_j^2/2}}{\sqrt{2\pi n}}\frac{\sqrt{\kappa}e^{-(x_j+x_{{j+1}})^2/4}}{\sqrt{2\pi (2n-\kappa)}}. \end{multline*}
After simplifications, this actually can be rewritten as the convergence on every compact set of
![]() $\mathbb{R}^{\kappa-1}$
of
$\mathbb{R}^{\kappa-1}$
of
![]() $h_n^{(2)}$
towards
$h_n^{(2)}$
towards
![]() $h^{(2)}$
where
$h^{(2)}$
where
We have established the following uniform convergence on every compact set of
![]() $\mathbb{R}_+^{\kappa}\times\mathbb{R}^{\kappa-1}$
:
$\mathbb{R}_+^{\kappa}\times\mathbb{R}^{\kappa-1}$
:
This concludes Step 1 of our proof.
Step 2: We will apply Lemma 8 to the sequence of functions
![]() $g_n = \frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}, $
and to
$g_n = \frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}, $
and to
![]() $g=g_{\kappa}$
, which is already known to be a density. We therefore need to check that we control the mass of
$g=g_{\kappa}$
, which is already known to be a density. We therefore need to check that we control the mass of
![]() $\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
outside of a certain compact set.
$\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
outside of a certain compact set.
For any compact
![]() $K^{\prime} \subset \mathbb{R}_+^\kappa$
, we have
$K^{\prime} \subset \mathbb{R}_+^\kappa$
, we have
and with
![]() $n\mathcal{L}_\kappa$
being a compact set of
$n\mathcal{L}_\kappa$
being a compact set of
![]() $\mathbb{R}_+^\kappa$
, there exists some
$\mathbb{R}_+^\kappa$
, there exists some
![]() $N\in\mathbb{N}$
such that when
$N\in\mathbb{N}$
such that when
![]() $n\geq N$
, we have the following for all
$n\geq N$
, we have the following for all
![]() $(\overline{\ell}[\kappa],x[\kappa-1])\in (K^{\prime})^c\times \mathbb{R}^{\kappa-1}$
:
$(\overline{\ell}[\kappa],x[\kappa-1])\in (K^{\prime})^c\times \mathbb{R}^{\kappa-1}$
:
Now let
![]() $\varepsilon \gt 0$
be fixed for the rest of this proof, and let us build the compact set
$\varepsilon \gt 0$
be fixed for the rest of this proof, and let us build the compact set
![]() $K_\varepsilon$
outside of which we control the mass of
$K_\varepsilon$
outside of which we control the mass of
![]() $h_n^{(2)}$
. We can reinterpret the map
$h_n^{(2)}$
. We can reinterpret the map
![]() $h_n^{(2)}$
as follows: if
$h_n^{(2)}$
as follows: if
![]() $M_1,M_2$
are two independent multinomial variables, with
$M_1,M_2$
are two independent multinomial variables, with
![]() $M_1\sim\mathcal{M}(n;\frac{1}{\kappa},\ldots,\frac{1}{\kappa})$
and
$M_1\sim\mathcal{M}(n;\frac{1}{\kappa},\ldots,\frac{1}{\kappa})$
and
![]() $M_2\sim\mathcal{M}(2n-\kappa;\frac{1}{\kappa},\ldots,\frac{1}{\kappa})$
, for
$M_2\sim\mathcal{M}(2n-\kappa;\frac{1}{\kappa},\ldots,\frac{1}{\kappa})$
, for
we have
 \begin{align}\nonumber h_n^{(2)}(x[\kappa-1])&=\frac{\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}}{\kappa^\kappa}\frac{4^n n^{3n}}{e^{3n}n!(2n-\kappa)!}\mathbf{P}\left(x[\kappa-1]\right)\\[3pt] &\leq \frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}n^{\kappa-1}\mathbf{P}\left(x[\kappa-1]\right). \end{align}
\begin{align}\nonumber h_n^{(2)}(x[\kappa-1])&=\frac{\sqrt{2\pi^{\kappa+1}\mathrm{m}_\kappa}}{\kappa^\kappa}\frac{4^n n^{3n}}{e^{3n}n!(2n-\kappa)!}\mathbf{P}\left(x[\kappa-1]\right)\\[3pt] &\leq \frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}n^{\kappa-1}\mathbf{P}\left(x[\kappa-1]\right). \end{align}
For n large enough we have both
![]() $n!\geq 2^{-1/2}\sqrt{\pi}n^{n+1/2}e^{-n}$
and the existence of a constant
$n!\geq 2^{-1/2}\sqrt{\pi}n^{n+1/2}e^{-n}$
and the existence of a constant
![]() $\alpha$
such that for all n,
$\alpha$
such that for all n,
![]() $(2n-\kappa)^{2n-\kappa+1/2}\geq \alpha(2n)^{2n-\kappa+1/2}$
, so, setting
$(2n-\kappa)^{2n-\kappa+1/2}\geq \alpha(2n)^{2n-\kappa+1/2}$
, so, setting
![]() $B\,:\!=\,2\pi e^\kappa$
, we have
$B\,:\!=\,2\pi e^\kappa$
, we have
Let
![]() $M_k(i)$
, for
$M_k(i)$
, for
![]() $k\in\{1,2\}$
and
$k\in\{1,2\}$
and
![]() $i\in\{1,\ldots,\kappa\}$
, be the ith entry of the multinomial random variable
$i\in\{1,\ldots,\kappa\}$
, be the ith entry of the multinomial random variable
![]() $M_k$
. Recall that the entry
$M_k$
. Recall that the entry
![]() $M_1(i)$
is a binomial random variable
$M_1(i)$
is a binomial random variable
![]() $\mathcal{B}(n,\frac{1}{\kappa})$
, and that, for
$\mathcal{B}(n,\frac{1}{\kappa})$
, and that, for
![]() $i\neq j$
, the law of
$i\neq j$
, the law of
![]() $M_1(i)$
conditioned on
$M_1(i)$
conditioned on
![]() $M_1(j)=k_j$
is a binomial distribution
$M_1(j)=k_j$
is a binomial distribution
![]() $\mathcal{B}(n-k_j,\frac{1}{\kappa-1})$
. Analogous results hold for
$\mathcal{B}(n-k_j,\frac{1}{\kappa-1})$
. Analogous results hold for
![]() $M_2(i)$
. Now, since these marginals are binomial random variables, they are concentrated around their mean. We will design a compact
$M_2(i)$
. Now, since these marginals are binomial random variables, they are concentrated around their mean. We will design a compact
![]() $K_\varepsilon$
such that
$K_\varepsilon$
such that
![]() $K_\varepsilon^c$
contains the elements
$K_\varepsilon^c$
contains the elements
![]() $x[\kappa-1]$
whose ith entry (for at least one i) is far from its expected value (which will give us exponential small bounds).
$x[\kappa-1]$
whose ith entry (for at least one i) is far from its expected value (which will give us exponential small bounds).
Let us rewrite by presenting the multinomial random variable as Markov chains of a sort. We have
 \begin{multline} \mathbf{P}\left(x[\kappa-1]\right)=\\[3pt] \prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor,M_2(i)=\left\lfloor\frac{2n-\kappa}{\kappa}+(x_i+x_{{i-1}})\sqrt{\frac{n}{\kappa}}\right\rfloor \, \bigg\vert G_1(x,i),G_2(x,i)\bigg) \end{multline}
\begin{multline} \mathbf{P}\left(x[\kappa-1]\right)=\\[3pt] \prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor,M_2(i)=\left\lfloor\frac{2n-\kappa}{\kappa}+(x_i+x_{{i-1}})\sqrt{\frac{n}{\kappa}}\right\rfloor \, \bigg\vert G_1(x,i),G_2(x,i)\bigg) \end{multline}
where
 \begin{multline*} G_1(x,i)\,:\!=\,\bigcap_{j=1}^{i-1}\left\{M_1(j)=\left\lfloor\frac{n}{\kappa}+x_j\sqrt{\frac{n}{\kappa}}\right\rfloor\right\} \text{ and }\\[3pt] G_2(x,i)\,:\!=\,\bigcap_{j=1}^{i-1}\left\{M_2(j)=\left\lfloor\frac{2n-\kappa}{\kappa}+(x_j+x_{{j-1}})\sqrt{\frac{n}{\kappa}}\right\rfloor\right\}. \end{multline*}
\begin{multline*} G_1(x,i)\,:\!=\,\bigcap_{j=1}^{i-1}\left\{M_1(j)=\left\lfloor\frac{n}{\kappa}+x_j\sqrt{\frac{n}{\kappa}}\right\rfloor\right\} \text{ and }\\[3pt] G_2(x,i)\,:\!=\,\bigcap_{j=1}^{i-1}\left\{M_2(j)=\left\lfloor\frac{2n-\kappa}{\kappa}+(x_j+x_{{j-1}})\sqrt{\frac{n}{\kappa}}\right\rfloor\right\}. \end{multline*}
For all
![]() $x[\kappa-1]\in\mathbb{R}^{\kappa-1}$
and
$x[\kappa-1]\in\mathbb{R}^{\kappa-1}$
and
![]() $i\in\{1,\ldots,\kappa-1\}$
, let
$i\in\{1,\ldots,\kappa-1\}$
, let
![]() $Y_i(x)$
be a binomial random variable with the same law as
$Y_i(x)$
be a binomial random variable with the same law as
![]() $M_1(i)\vert G_1(x,i)$
, i.e.
$M_1(i)\vert G_1(x,i)$
, i.e.
A standard inequality for binomial distributions
![]() $\mathbf{x}\sim\mathcal{B}(m,q)$
with
$\mathbf{x}\sim\mathcal{B}(m,q)$
with
![]() $q\in[a,b]$
,
$q\in[a,b]$
,
![]() $0 \lt a \lt b \lt 1$
, [Reference Petrov19, III.5.2], gives the existence of a constant
$0 \lt a \lt b \lt 1$
, [Reference Petrov19, III.5.2], gives the existence of a constant
![]() $C \gt 0$
such that for all x,
$C \gt 0$
such that for all x,
For n large enough, this implies the existence of a constant
![]() $C_\kappa \gt 0$
such that
$C_\kappa \gt 0$
such that
 \begin{align} \mathbf{P}\left(x[\kappa-1]\right)\leq \frac{ \prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor \, \big\vert \, G_1(x,i)\bigg) }{C_\kappa\sqrt{n}^{\kappa-1}}. \end{align}
\begin{align} \mathbf{P}\left(x[\kappa-1]\right)\leq \frac{ \prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor \, \big\vert \, G_1(x,i)\bigg) }{C_\kappa\sqrt{n}^{\kappa-1}}. \end{align}
Controlling the map
![]() $\mathbf{P}$
allows one to control the map
$\mathbf{P}$
allows one to control the map
![]() $h_n^{(2)}$
(recall (4.14)), and thus
$h_n^{(2)}$
(recall (4.14)), and thus
![]() $g_n$
(recall (4.4)). Define the sequence
$g_n$
(recall (4.4)). Define the sequence
![]() $e[\kappa]$
as follows:
$e[\kappa]$
as follows:
![]() $e_1=\sqrt{\kappa}$
, and for all
$e_1=\sqrt{\kappa}$
, and for all
![]() $j\in\{2,\ldots,\kappa-1\}$
,
$j\in\{2,\ldots,\kappa-1\}$
,
We will use
![]() $e[\kappa]$
to define an event of
$e[\kappa]$
to define an event of
![]() $\mathbf{P}$
that has small probability. Let
$\mathbf{P}$
that has small probability. Let
![]() $M \gt 0$
and
$M \gt 0$
and
![]() $t\in\{1,\ldots,\kappa-1\}$
. We define the set
$t\in\{1,\ldots,\kappa-1\}$
. We define the set
Intuitively, forcing the multinomial variable
![]() $M_k$
,
$M_k$
,
![]() $k\in\{1,2\}$
, to be in
$k\in\{1,2\}$
, to be in
![]() $\widehat{B}_M(t)$
is a huge condition for M large, since this requires
$\widehat{B}_M(t)$
is a huge condition for M large, since this requires
![]() $M_k$
to have a coordinate far from its mean. Since for all
$M_k$
to have a coordinate far from its mean. Since for all
![]() $x[\kappa-1]\in \widehat{B}_M(t)$
, by (4.18), we have
$x[\kappa-1]\in \widehat{B}_M(t)$
, by (4.18), we have
we may write (making the small change of variables
![]() $t_i =\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}$
and then taking the supremum on
$t_i =\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}$
and then taking the supremum on
![]() $\widehat{B}_M(t)$
), by (4.17),
$\widehat{B}_M(t)$
), by (4.17),
 \begin{multline} \int_{ \widehat{B}_M(t)}\prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor \, \bigg\vert \, G_1(x,i)\bigg)\text{d} x\\[3pt] \leq\sup_{x\in\widehat{B}_M(t)}\left[\prod_{i=1}^{t-1}\mathbb{P}\left(\left\vert Y_i(x)-\mathbb{E}[Y_i(x)]\right\vert\leq M\sqrt{n}\right)\right]\\[3pt] \times\mathbb{P}\left(\left\vert Y_t(x)-\mathbb{E}[Y_t(x)]\right\vert \gt M\sqrt{n}\right)\left[\prod_{i=t+1}^{\kappa-1}\mathbb{P}\left(\left\vert Y_i(x)-\mathbb{E}[Y_i(x)]\right\vert\in\mathbb{R}\right)\right]\frac{1}{\sqrt{n}^{\kappa-1}}. \end{multline}
\begin{multline} \int_{ \widehat{B}_M(t)}\prod_{i=1}^{\kappa-1}\mathbb{P}\bigg(M_1(i)=\left\lfloor\frac{n}{\kappa}+x_i\sqrt{\frac{n}{\kappa}}\right\rfloor \, \bigg\vert \, G_1(x,i)\bigg)\text{d} x\\[3pt] \leq\sup_{x\in\widehat{B}_M(t)}\left[\prod_{i=1}^{t-1}\mathbb{P}\left(\left\vert Y_i(x)-\mathbb{E}[Y_i(x)]\right\vert\leq M\sqrt{n}\right)\right]\\[3pt] \times\mathbb{P}\left(\left\vert Y_t(x)-\mathbb{E}[Y_t(x)]\right\vert \gt M\sqrt{n}\right)\left[\prod_{i=t+1}^{\kappa-1}\mathbb{P}\left(\left\vert Y_i(x)-\mathbb{E}[Y_i(x)]\right\vert\in\mathbb{R}\right)\right]\frac{1}{\sqrt{n}^{\kappa-1}}. \end{multline}
We bound the terms different from t in the product by 1, and we handle the term in t by Hoeffding’s inequality [Reference Petrov19, III.5.8], i.e.
Let us check that there exists
![]() $M\,:\!=\,M(\varepsilon)$
large enough so that the integral of the map
$M\,:\!=\,M(\varepsilon)$
large enough so that the integral of the map
![]() $\mathbf{P}$
outside of
$\mathbf{P}$
outside of
![]() $K_\varepsilon\,:\!=\,[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}$
is controlled.
$K_\varepsilon\,:\!=\,[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}$
is controlled.
With the decomposition
![]() $A_M\,:\!=\,\mathbb{R}^{\kappa-1}\backslash[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}=\bigsqcup_{t=1}^{\kappa-1}\widehat{B}_M(t)$
, we may write
$A_M\,:\!=\,\mathbb{R}^{\kappa-1}\backslash[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}=\bigsqcup_{t=1}^{\kappa-1}\widehat{B}_M(t)$
, we may write
 \begin{align} \int_{A_M}\mathbf{P}(x[\kappa-1])\text{d} x=\sum_{t=1}^{\kappa-1}\int_{\widehat{B}_M(t)}\mathbf{P}(x[\kappa-1])\text{d} x\leq\frac{2(\kappa-1)}{C_\kappa n^{\kappa-1}}\exp({-}2M^2), \end{align}
\begin{align} \int_{A_M}\mathbf{P}(x[\kappa-1])\text{d} x=\sum_{t=1}^{\kappa-1}\int_{\widehat{B}_M(t)}\mathbf{P}(x[\kappa-1])\text{d} x\leq\frac{2(\kappa-1)}{C_\kappa n^{\kappa-1}}\exp({-}2M^2), \end{align}
where we set
![]() $\text{d} x=\prod_{i=1}^{\kappa-1}\text{d} x_i.$
With
$\text{d} x=\prod_{i=1}^{\kappa-1}\text{d} x_i.$
With
![]() $\varepsilon$
being fixed, we may now choose
$\varepsilon$
being fixed, we may now choose
![]() $M\,:\!=\,M(\varepsilon) \gt 0$
sufficiently large so that
$M\,:\!=\,M(\varepsilon) \gt 0$
sufficiently large so that
For such an M, we put
![]() $K_\varepsilon=[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}$
. In this case, we have indeed
$K_\varepsilon=[{-}M\sqrt{\kappa},M\sqrt{\kappa}]^{\kappa-1}$
. In this case, we have indeed
 \begin{align}\nonumber \int_{K_\varepsilon^c}h_n^{(2)}&\leq\frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}n^{\kappa-1}\int_{A_M}\mathbf{P}(x[\kappa-1])\text{d} x\\[3pt] &\leq\frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}\frac{2(\kappa-1)}{C_\kappa}\exp({-}2M^2) \lt \frac{1}{2}\varepsilon. \end{align}
\begin{align}\nonumber \int_{K_\varepsilon^c}h_n^{(2)}&\leq\frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}n^{\kappa-1}\int_{A_M}\mathbf{P}(x[\kappa-1])\text{d} x\\[3pt] &\leq\frac{2^\kappa\sqrt{\pi}^{\kappa-1}\sqrt{\mathrm{m}_\kappa}}{B\kappa^\kappa}\frac{2(\kappa-1)}{C_\kappa}\exp({-}2M^2) \lt \frac{1}{2}\varepsilon. \end{align}
This completes the proof of Step 2. Indeed, if we sum up, we have uniform convergence of
![]() $\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
to
$\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
to
![]() $g_{\kappa}$
on every compact set, and we have built two compact sets
$g_{\kappa}$
on every compact set, and we have built two compact sets
![]() $K^{\prime}\subset \mathbb{R}_+^{\kappa}$
and
$K^{\prime}\subset \mathbb{R}_+^{\kappa}$
and
![]() $K_\varepsilon\subset \mathbb{R}^{\kappa-1}$
such that for all
$K_\varepsilon\subset \mathbb{R}^{\kappa-1}$
such that for all
![]() $n\geq N$
,
$n\geq N$
,
 \begin{align} \leq 2\underbrace{\int_{(K^{\prime})^c}h^{(1)}}_{\leq 1}\int_{K_\varepsilon^c}h_n^{(2)} \lt \varepsilon, \end{align}
\begin{align} \leq 2\underbrace{\int_{(K^{\prime})^c}h^{(1)}}_{\leq 1}\int_{K_\varepsilon^c}h_n^{(2)} \lt \varepsilon, \end{align}
where the first line comes from (4.4) and the second line comes from the bounds we gave in (4.13) and (4.23).
We may now conclude: we apply Lemma 8, so that there exists a (unique!) sequence normalizing
![]() $\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
into a density. Since
$\frac{1}{\omega(n,\kappa)}g^{(n)}_{\kappa}$
into a density. Since
![]() $g^{(n)}_{\kappa}$
is already a density, this sequence is nothing but
$g^{(n)}_{\kappa}$
is already a density, this sequence is nothing but
![]() $\omega(n,\kappa)$
; hence we have
$\omega(n,\kappa)$
; hence we have
This also proves that
![]() $g^{(n)}_{\kappa}$
converges pointwise to
$g^{(n)}_{\kappa}$
converges pointwise to
![]() $g_{\kappa}$
, or, by definition, that
$g_{\kappa}$
, or, by definition, that
Now, since
by Slutsky’s lemma we have
This ends the proof.
Theorem 1 actually turns out to be a nice corollary of Theorem 7.
Proof of Theorem
1. We saw in (4.26) that the sequence
![]() $\omega(n,\kappa)$
introduced in (4.5) satisfies
$\omega(n,\kappa)$
introduced in (4.5) satisfies
![]() $\omega(n,\kappa)\underset{n\to +\infty}{\longrightarrow}1$
. This allows us to determine
$\omega(n,\kappa)\underset{n\to +\infty}{\longrightarrow}1$
. This allows us to determine
![]() $\widetilde{\mathbb{P}}_\kappa(n)$
. Indeed, Stirling’s formula yields
$\widetilde{\mathbb{P}}_\kappa(n)$
. Indeed, Stirling’s formula yields
Having
![]() $\widetilde{\mathbb{P}}_\kappa(n)\underset{n\to +\infty}{\sim}\mathbb{P}_\kappa(n)$
by Lemma 4, we obtain the expected result.
$\widetilde{\mathbb{P}}_\kappa(n)\underset{n\to +\infty}{\sim}\mathbb{P}_\kappa(n)$
by Lemma 4, we obtain the expected result.
5. Fluctuations around the limit shape
5.1. Basic brick fluctuations
Notation. We say that a point z is the
![]() $\alpha$
-barycenter of (a, b) if
$\alpha$
-barycenter of (a, b) if
![]() $z= \alpha a+(1-\alpha) b$
; in this case,
$z= \alpha a+(1-\alpha) b$
; in this case,
![]() $\alpha$
is called the barycenter parameter.
$\alpha$
is called the barycenter parameter.
Basic building bricks of a
z
[
n
]-gon. For any
![]() $\mathbf{z}[n]$
with distribution
$\mathbf{z}[n]$
with distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
, we have provided an alternative geometric description of the
${\mathbb{D}}^{(n)}_{\kappa}$
, we have provided an alternative geometric description of the
![]() $\mathbf{z}[n]$
-gon in terms of its
$\mathbf{z}[n]$
-gon in terms of its
![]() $\mathsf{ECP}(\mathbf{z}[n])$
, and more specifically in terms of the following:
$\mathsf{ECP}(\mathbf{z}[n])$
, and more specifically in terms of the following:
-
• the boundary distances
 $\boldsymbol{\ell}^{(n)}[\kappa]$
of this
$\boldsymbol{\ell}^{(n)}[\kappa]$
of this
 $\mathsf{ECP},$
$\mathsf{ECP},$
-
• the tuple
 $\mathbf{s}^{(n)}[\kappa]$
counting the vectors in the corners of the
$\mathbf{s}^{(n)}[\kappa]$
counting the vectors in the corners of the
 $\mathsf{ECP}$
, and
$\mathsf{ECP}$
, and -
• the fragmentation of the sides
 $\mathbf{c}^{(n)}[\kappa]$
into side-partitions
$\mathbf{c}^{(n)}[\kappa]$
into side-partitions
 $\mathbf{u}^{(1)}[\mathbf{N}^{(n)}_1],\ldots,\mathbf{u}^{(\kappa)}[\mathbf{N}^{(n)}_\kappa]$
, where
$\mathbf{u}^{(1)}[\mathbf{N}^{(n)}_1],\ldots,\mathbf{u}^{(\kappa)}[\mathbf{N}^{(n)}_\kappa]$
, where
 $\mathbf{N}^{(n)}_j=\mathbf{s}^{(n)}_{j}+\mathbf{s}^{(n)}_{{j+1}}-1$
for all
$\mathbf{N}^{(n)}_j=\mathbf{s}^{(n)}_{j}+\mathbf{s}^{(n)}_{{j+1}}-1$
for all
 $j\in\{1,\ldots,\kappa\}.$
$j\in\{1,\ldots,\kappa\}.$
Notice that the contact points
![]() ${\boldsymbol{\mathsf{cp}}}^{(n)}[\kappa]$
and the vertices
${\boldsymbol{\mathsf{cp}}}^{(n)}[\kappa]$
and the vertices
![]() ${\boldsymbol{\mathsf{b}}}^{(n)}[\kappa]$
of the
${\boldsymbol{\mathsf{b}}}^{(n)}[\kappa]$
of the
![]() $\mathsf{ECP}(\mathbf{z}[n])$
can be recovered using these three data. Indeed,
$\mathsf{ECP}(\mathbf{z}[n])$
can be recovered using these three data. Indeed,
![]() $\boldsymbol{\ell}^{(n)}[\kappa]$
determines the
$\boldsymbol{\ell}^{(n)}[\kappa]$
determines the
![]() $\mathsf{ECP}$
and thus its vertices
$\mathsf{ECP}$
and thus its vertices
![]() ${\boldsymbol{\mathsf{b}}}^{(n)}[\kappa]$
.
${\boldsymbol{\mathsf{b}}}^{(n)}[\kappa]$
.
In (3.15), we see that, conditional on the jth side length
![]() $\mathbf{c}^{(n)}_j=c_j$
and on the size vector
$\mathbf{c}^{(n)}_j=c_j$
and on the size vector
![]() $\mathbf{s}^{(n)}[\kappa]$
, the side-partition
$\mathbf{s}^{(n)}[\kappa]$
, the side-partition
![]() $\left(u_1^{(j)} \lt \ldots \lt u_{\mathbf{N}_j}^{(j)}\right)$
has the law of a reordered
$\left(u_1^{(j)} \lt \ldots \lt u_{\mathbf{N}_j}^{(j)}\right)$
has the law of a reordered
![]() $\mathbf{N}_j$
-tuple of i.i.d. uniform random variables drawn in
$\mathbf{N}_j$
-tuple of i.i.d. uniform random variables drawn in
![]() $[0,c_j].$
The contact point
$[0,c_j].$
The contact point
![]() ${\mathsf{cp}}^{(n)}_j$
is placed on the jth side of the
${\mathsf{cp}}^{(n)}_j$
is placed on the jth side of the
![]() $\mathsf{ECP}$
(on the segment
$\mathsf{ECP}$
(on the segment
![]() $[{\boldsymbol{\mathsf{b}}}^{(n)}_{{j-1}},{\boldsymbol{\mathsf{b}}}^{(n)}_j]$
), at the coordinate
$[{\boldsymbol{\mathsf{b}}}^{(n)}_{{j-1}},{\boldsymbol{\mathsf{b}}}^{(n)}_j]$
), at the coordinate
![]() $\mathbf{u}^{(j)}_{\mathbf{s}^{(n)}_{j}}$
for all
$\mathbf{u}^{(j)}_{\mathbf{s}^{(n)}_{j}}$
for all
![]() $j\in\{1,\ldots,\kappa\}$
. This means that conditional on
$j\in\{1,\ldots,\kappa\}$
. This means that conditional on
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the tuple
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the tuple
![]() ${\mathsf{cp}}^{(n)}[\kappa]$
has independent entries, and
${\mathsf{cp}}^{(n)}[\kappa]$
has independent entries, and
![]() ${\mathsf{cp}}^{(n)}_j$
is a
${\mathsf{cp}}^{(n)}_j$
is a
![]() ${\boldsymbol\beta}_j^{(n)}$
-barycenter of
${\boldsymbol\beta}_j^{(n)}$
-barycenter of
![]() $\left({\boldsymbol{\mathsf{b}}}^{(n)}_{{j-1}},{\boldsymbol{\mathsf{b}}}^{(n)}_j\right)$
, where
$\left({\boldsymbol{\mathsf{b}}}^{(n)}_{{j-1}},{\boldsymbol{\mathsf{b}}}^{(n)}_j\right)$
, where
![]() ${\boldsymbol\beta}_j^{(n)}$
is
${\boldsymbol\beta}_j^{(n)}$
is
![]() $\beta$
-distributed with parameters
$\beta$
-distributed with parameters
![]() $\left(\mathbf{s}^{(n)}_{j},\mathbf{s}^{(n)}_{{j+1}}\right)$
.
$\left(\mathbf{s}^{(n)}_{j},\mathbf{s}^{(n)}_{{j+1}}\right)$
.
For
![]() $j\in\{1,\ldots,\kappa\}$
, the random variable
$j\in\{1,\ldots,\kappa\}$
, the random variable
provides the fluctuations of the barycenter parameter and thus encodes the fluctuations of the contact point
![]() ${\mathsf{cp}}_{j}^{(n)}$
on the jth side
${\mathsf{cp}}_{j}^{(n)}$
on the jth side
![]() $\mathbf{c}^{(n)}_{j}$
of
$\mathbf{c}^{(n)}_{j}$
of
![]() $\mathsf{ECP}(\mathbf{z}[n]).$
$\mathsf{ECP}(\mathbf{z}[n]).$
Fluctuations of basic bricks. We have proved that the boundary distances
![]() $\boldsymbol{\ell}^{(n)}[\kappa]$
behaved as
$\boldsymbol{\ell}^{(n)}[\kappa]$
behaved as
![]() $\frac{1}{n}$
times an exponential distribution, and we will prove in the sequel that the contact points
$\frac{1}{n}$
times an exponential distribution, and we will prove in the sequel that the contact points
![]() ${\mathsf{cp}}^{(n)}[\kappa]$
are typically at distance
${\mathsf{cp}}^{(n)}[\kappa]$
are typically at distance
![]() $\frac{1}{\sqrt{n}}$
around their limit (this is visible in (5.1)). So in order to describe the fluctuations of the
$\frac{1}{\sqrt{n}}$
around their limit (this is visible in (5.1)). So in order to describe the fluctuations of the
![]() $\mathbf{z}[n]$
-gon around its limit, we will state a theorem describing the joint distribution of all basic bricks taken together, rather than providing the fluctuations in
$\mathbf{z}[n]$
-gon around its limit, we will state a theorem describing the joint distribution of all basic bricks taken together, rather than providing the fluctuations in
![]() $\frac{1}{\sqrt{n}}$
of a complicated object for the whole process, which would crush the behavior of some of the bricks. A comprehensive picture of the fluctuations would rely on the concatenation of all the corners’ fluctuations, adjusted to take into account the contact points; we believe that presenting such a picture would not bring any new insight, so we leave it to the interested reader as an exercise.
$\frac{1}{\sqrt{n}}$
of a complicated object for the whole process, which would crush the behavior of some of the bricks. A comprehensive picture of the fluctuations would rely on the concatenation of all the corners’ fluctuations, adjusted to take into account the contact points; we believe that presenting such a picture would not bring any new insight, so we leave it to the interested reader as an exercise.
The ◿-convex chains. Recall Lemma 1 and its notation. Consider for all
![]() $j\in\{1,\ldots,\kappa\}$
the convex chain
$j\in\{1,\ldots,\kappa\}$
the convex chain
![]() $\mathsf{CC}^{(n)}_j=\mathsf{CC}_j^{(n)}(\mathbf{z}[n])$
lying in the jth corner of
$\mathsf{CC}^{(n)}_j=\mathsf{CC}_j^{(n)}(\mathbf{z}[n])$
lying in the jth corner of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
, defined as an element of
$\mathsf{ECP}(\mathbf{z}[n])$
, defined as an element of
![]() $\mathsf{Chain}_{\mathbf{s}^{(n)}_{j}}(\mathsf{corner}_j(\mathbf{z}[n]))$
(this accounts for the decomposition of
$\mathsf{Chain}_{\mathbf{s}^{(n)}_{j}}(\mathsf{corner}_j(\mathbf{z}[n]))$
(this accounts for the decomposition of
![]() $\mathbf{z}[n]$
into convex chains). In order to understand the fluctuations of the jth corner, we will use the normalized version of each of these convex chains:
$\mathbf{z}[n]$
into convex chains). In order to understand the fluctuations of the jth corner, we will use the normalized version of each of these convex chains:
where, for a given non-flat triangle ABC, the mapping
![]() $\mathsf{Aff}_{ABC}$
is the unique map that sends A, B, C to (0, 0),(1, 0),(1, 1), as introduced in Lemma 2. The law of
$\mathsf{Aff}_{ABC}$
is the unique map that sends A, B, C to (0, 0),(1, 0),(1, 1), as introduced in Lemma 2. The law of
![]() $\unicode{x25FF}\mathsf{CC}^{(n)}_j$
depends only on
$\unicode{x25FF}\mathsf{CC}^{(n)}_j$
depends only on
![]() $\mathbf{s}^{(n)}_{j}$
, but the affine mapping
$\mathbf{s}^{(n)}_{j}$
, but the affine mapping
![]() $\mathsf{Aff}_j$
depends on the coordinates of
$\mathsf{Aff}_j$
depends on the coordinates of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
. However, determining the fluctuations of
$\mathsf{ECP}(\mathbf{z}[n])$
. However, determining the fluctuations of
![]() $\mathsf{CC}^{(n)}_j$
amounts to looking at those of
$\mathsf{CC}^{(n)}_j$
amounts to looking at those of
![]() $\unicode{x25FF}\mathsf{CC}^{(n)}_j$
.
$\unicode{x25FF}\mathsf{CC}^{(n)}_j$
.
Recall that a generic ◿-normalized convex chain
![]() $\unicode{x25FF}\mathsf{CC}_m$
of size m is a random variable whose law is that of a convex chain taken uniformly in
$\unicode{x25FF}\mathsf{CC}_m$
of size m is a random variable whose law is that of a convex chain taken uniformly in
![]() $ \mathsf{Chain}_{m}$
(◿). Therefore, a consequence of Lemma 1 and Lemma 2 is the following lemma.
$ \mathsf{Chain}_{m}$
(◿). Therefore, a consequence of Lemma 1 and Lemma 2 is the following lemma.
Lemma 9.
Conditional on
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa],\boldsymbol{\delta}^{(n)}[\kappa])$
, the convex chains
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa],\boldsymbol{\delta}^{(n)}[\kappa])$
, the convex chains
![]() $\unicode{x25FF}\mathsf{CC}^{(n)}[\kappa]$
are independent. Furthermore, for all
$\unicode{x25FF}\mathsf{CC}^{(n)}[\kappa]$
are independent. Furthermore, for all
![]() $j\in\{1,\ldots,\kappa\}$
, the distribution of
$j\in\{1,\ldots,\kappa\}$
, the distribution of
![]() $\unicode{x25FF}\mathsf{CC}_j^{(n)}$
is that of a generic ◿-normalized convex chain of size
$\unicode{x25FF}\mathsf{CC}_j^{(n)}$
is that of a generic ◿-normalized convex chain of size
![]() $\mathbf{s}^{(n)}_{j}$
, i.e.
$\mathbf{s}^{(n)}_{j}$
, i.e.
![]() $\unicode{x25FF}\mathsf{CC}_j^{(n)}\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\unicode{x25FF}\mathsf{CC}_{\mathbf{s}^{(n)}_{j}}$
$\unicode{x25FF}\mathsf{CC}_j^{(n)}\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\unicode{x25FF}\mathsf{CC}_{\mathbf{s}^{(n)}_{j}}$
Thanks to this lemma, it should be clear that we can work on each convex chain separately when
![]() $\mathbf{s}^{(n)}[\kappa]$
is fixed. We introduce some processes in order to describe these fluctuations.
$\mathbf{s}^{(n)}[\kappa]$
is fixed. We introduce some processes in order to describe these fluctuations.
5.2. A parametrization of the normalized convex chains
Let
![]() $m\geq0$
, and let
$m\geq0$
, and let
![]() $\unicode{x25FF}\mathsf{CC}_m=((0,0),\mathbf{z}_1,\ldots,\mathbf{z}_{m-1},(1,1))$
be a generic ◿-normalized convex chain of size m. Rather than considering the tuple of points
$\unicode{x25FF}\mathsf{CC}_m=((0,0),\mathbf{z}_1,\ldots,\mathbf{z}_{m-1},(1,1))$
be a generic ◿-normalized convex chain of size m. Rather than considering the tuple of points
![]() $((0,0),\mathbf{z}_1,\ldots,\mathbf{z}_{m-1},(1,1))$
, we consider the m vectors composing the convex chain. Recall that these vectors are obtained by forming the tuples
$((0,0),\mathbf{z}_1,\ldots,\mathbf{z}_{m-1},(1,1))$
, we consider the m vectors composing the convex chain. Recall that these vectors are obtained by forming the tuples
![]() $\mathbf{u}[m],\mathbf{v}[m]$
of increments of two elements taken uniformly (and independently) in the simplex
$\mathbf{u}[m],\mathbf{v}[m]$
of increments of two elements taken uniformly (and independently) in the simplex
![]() $P[1,m-1]$
. Then the vectors
$P[1,m-1]$
. Then the vectors
![]() $(\mathbf{u}_{i},\mathbf{v}_{i})$
,
$(\mathbf{u}_{i},\mathbf{v}_{i})$
,
![]() $i\in\{1,\ldots,m\}$
, are reordered by increasing slope to form this chain.
$i\in\{1,\ldots,m\}$
, are reordered by increasing slope to form this chain.
In order to use the toolbox of stochastic processes, it is convenient for us to see
![]() $\unicode{x25FF}\mathsf{CC}_m$
as a linear process. For this we will need a suitable parametrization (several choices are possible). For technical reasons, we choose the local slope of
$\unicode{x25FF}\mathsf{CC}_m$
as a linear process. For this we will need a suitable parametrization (several choices are possible). For technical reasons, we choose the local slope of
![]() $\unicode{x25FF}\mathsf{CC}_m$
as the time parameter, and apply the
$\unicode{x25FF}\mathsf{CC}_m$
as the time parameter, and apply the
![]() $\arctan$
function in order to remain in a compact set.
$\arctan$
function in order to remain in a compact set.
Consider the point
![]() $\left(x_{m}(u),y_{m}(u)\right)$
for
$\left(x_{m}(u),y_{m}(u)\right)$
for
![]() $u\in[0, 1]$
, corresponding to the contributions of the previous vectors whose slope are smaller than
$u\in[0, 1]$
, corresponding to the contributions of the previous vectors whose slope are smaller than
![]() $\tan\left(\frac{\pi}{2}u\right)$
, and the process
$\tan\left(\frac{\pi}{2}u\right)$
, and the process
![]() $\mathsf{C}_m$
defined as
$\mathsf{C}_m$
defined as
![]() $\mathsf{C}_m(u)\,:\!=\,\left(x_{m}(u),y_{m}(u)\right)$
for
$\mathsf{C}_m(u)\,:\!=\,\left(x_{m}(u),y_{m}(u)\right)$
for
![]() $u\in[0, 1]$
. Hence, we have
$u\in[0, 1]$
. Hence, we have
where we set
![]() $\tan\left(\frac{\pi}{2}\cdot1\right)=+\infty$
so that
$\tan\left(\frac{\pi}{2}\cdot1\right)=+\infty$
so that
![]() $x_m(1)=y_m(1)=1.$
Note that the tuple
$x_m(1)=y_m(1)=1.$
Note that the tuple
![]() $\unicode{x25FF}\mathsf{CC}_m$
(seen as a set) coincides with the (finite) set
$\unicode{x25FF}\mathsf{CC}_m$
(seen as a set) coincides with the (finite) set
![]() $\{\mathsf{C}_m(u),u\in[0, 1]\}$
.
$\{\mathsf{C}_m(u),u\in[0, 1]\}$
.
Define further the curve
![]() $\mathsf{C}_\infty(u)\,:\!=\,\left(x(u),y(u)\right)$
for all
$\mathsf{C}_\infty(u)\,:\!=\,\left(x(u),y(u)\right)$
for all
![]() $u\in[0, 1]$
, where
$u\in[0, 1]$
, where
 \begin{align}x(u)\,:\!=\,1-\frac{1}{\left(1+\tan\left(\frac{\pi}{2}u\right)\right)^2}\quad\text{ and }\quad y(u)\,:\!=\,\frac{\tan\left(\frac{\pi}{2}u\right)^2}{\left(1+\tan\left(\frac{\pi}{2}u\right)\right)^2}.\end{align}
\begin{align}x(u)\,:\!=\,1-\frac{1}{\left(1+\tan\left(\frac{\pi}{2}u\right)\right)^2}\quad\text{ and }\quad y(u)\,:\!=\,\frac{\tan\left(\frac{\pi}{2}u\right)^2}{\left(1+\tan\left(\frac{\pi}{2}u\right)\right)^2}.\end{align}
We have once more
![]() $x(1)=y(1)=1$
. This curve is actually the parametrization of the parabolic arc lying in ◿, tangent at (0, 0) and (1, 1). It is not surprising to encounter
$x(1)=y(1)=1$
. This curve is actually the parametrization of the parabolic arc lying in ◿, tangent at (0, 0) and (1, 1). It is not surprising to encounter
![]() $\mathsf{C}_\infty$
here, since the convergence in distribution of
$\mathsf{C}_\infty$
here, since the convergence in distribution of
![]() $\mathsf{C}_m$
to
$\mathsf{C}_m$
to
![]() $\mathsf{C}_{\infty}$
that will be stated in Theorem 9 can be seen as a consequence of Bárány’s work on affine perimeters (not a direct consequence, however).
$\mathsf{C}_{\infty}$
that will be stated in Theorem 9 can be seen as a consequence of Bárány’s work on affine perimeters (not a direct consequence, however).
For all
![]() $j\in\{1,\ldots,\kappa\}$
, we let
$j\in\{1,\ldots,\kappa\}$
, we let
![]() $\mathsf{C}^{(n)}_{j}$
be the parametrization in terms of the slope of the jth ◿-normalized convex chain
$\mathsf{C}^{(n)}_{j}$
be the parametrization in terms of the slope of the jth ◿-normalized convex chain
![]() $\unicode{x25FF}\mathsf{CC}_j^{(n)}$
. So now by Lemma 9, we have
$\unicode{x25FF}\mathsf{CC}_j^{(n)}$
. So now by Lemma 9, we have
and conditional on
![]() $\mathbf{s}^{(n)}[\kappa]$
, the
$\mathbf{s}^{(n)}[\kappa]$
, the
![]() $\mathsf{C}^{(n)}_{j}$
,
$\mathsf{C}^{(n)}_{j}$
,
![]() $j\in\{1,\ldots,\kappa\}$
, are independent.
$j\in\{1,\ldots,\kappa\}$
, are independent.
Theorem 9 will also include the convergence in distribution of the fluctuation process
![]() $\mathsf{Y}_m\,:\!=\,\sqrt{m}(\mathsf{C}_m-\mathsf{C}_{\infty})$
to a Gaussian process. This convergence is actually the key that will help us understand the fluctuations of the convex chain
$\mathsf{Y}_m\,:\!=\,\sqrt{m}(\mathsf{C}_m-\mathsf{C}_{\infty})$
to a Gaussian process. This convergence is actually the key that will help us understand the fluctuations of the convex chain
![]() $\unicode{x25FF}\mathsf{CC}_j^{(n)}$
around its limit
$\unicode{x25FF}\mathsf{CC}_j^{(n)}$
around its limit
![]() $\unicode{x25FF}\mathsf{CC}_\infty$
. Indeed, conditional on
$\unicode{x25FF}\mathsf{CC}_\infty$
. Indeed, conditional on
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the processes
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the processes
describe the successive fluctuations of the ◿-convex chain in their corners. We are now able to state the most important result of this section (in which we borrow the notation of Theorem 7).
Theorem 8.
(0) Conditional on
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the processes
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the processes
![]() $\mathsf{C}^{(n)}[\kappa]$
are independent and have the same distribution. For all
$\mathsf{C}^{(n)}[\kappa]$
are independent and have the same distribution. For all
![]() $j\in\{1,\ldots,\kappa\}$
, the process
$j\in\{1,\ldots,\kappa\}$
, the process
![]() $\mathsf{C}^{(n)}_{j}$
converges in
$\mathsf{C}^{(n)}_{j}$
converges in
![]() $D([0, 1],\mathbb{R})$
, which we endow with the Skorokhod topology for the rest of this paper, to the deterministic process
$D([0, 1],\mathbb{R})$
, which we endow with the Skorokhod topology for the rest of this paper, to the deterministic process
![]() $\mathsf{C}_\infty$
introduced in (5.4).
$\mathsf{C}_\infty$
introduced in (5.4).
Furthermore, the ‘fluctuation’ tuple
![]() $\left(\overline{{\boldsymbol\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1],\boldsymbol{\delta}^{(n)}[\kappa],\mathsf{Y}^{(n)}[\kappa]\right)$
converges in distribution in
$\left(\overline{{\boldsymbol\ell}}^{(n)}[\kappa],\mathbf{x}^{(n)}[\kappa-1],\boldsymbol{\delta}^{(n)}[\kappa],\mathsf{Y}^{(n)}[\kappa]\right)$
converges in distribution in
![]() $\mathbb{R}^\kappa\times\mathbb{R}^{\kappa-1}\times\mathbb{R}^{\kappa}\times D([0, 1],\mathbb{R})^\kappa$
(equipped with the corresponding product topology) to a tuple
$\mathbb{R}^\kappa\times\mathbb{R}^{\kappa-1}\times\mathbb{R}^{\kappa}\times D([0, 1],\mathbb{R})^\kappa$
(equipped with the corresponding product topology) to a tuple
![]() $\left(\overline{{\boldsymbol\ell}}[\kappa],\mathbf{x}[\kappa-1],\boldsymbol{\delta}[\kappa],\mathsf{Y}[\kappa]\right)$
with the following properties:
$\left(\overline{{\boldsymbol\ell}}[\kappa],\mathbf{x}[\kappa-1],\boldsymbol{\delta}[\kappa],\mathsf{Y}[\kappa]\right)$
with the following properties:
-
(1) The variables
 $\left(\overline{{\boldsymbol\ell}}[\kappa], \mathbf{x}[\kappa-1]\right)$
and their fluctuations are as already described in Theorem 7.
$\left(\overline{{\boldsymbol\ell}}[\kappa], \mathbf{x}[\kappa-1]\right)$
and their fluctuations are as already described in Theorem 7.
-
(2) Conditional on
 $\left(\overline{{\boldsymbol\ell}}[\kappa], \mathbf{x}[\kappa-1]\right)$
, the variables
$\left(\overline{{\boldsymbol\ell}}[\kappa], \mathbf{x}[\kappa-1]\right)$
, the variables
 $\boldsymbol{\delta}_1,\ldots,\boldsymbol{\delta}_\kappa$
are independent, and for all
$\boldsymbol{\delta}_1,\ldots,\boldsymbol{\delta}_\kappa$
are independent, and for all
 $j\in\{1,\ldots,\kappa\}$
,
$j\in\{1,\ldots,\kappa\}$
,
 $\boldsymbol{\delta}_j$
is a normal random variable with mean
$\boldsymbol{\delta}_j$
is a normal random variable with mean
 $(\mathbf{x}_j-\mathbf{x}_{{j+1}})/4$
and variance
$(\mathbf{x}_j-\mathbf{x}_{{j+1}})/4$
and variance
 $1/8$
.
$1/8$
. -
(3) The tuple
 $\mathsf{Y}^{(n)}[\kappa]$
converges in distribution in D([0, 1]) to the tuple
$\mathsf{Y}^{(n)}[\kappa]$
converges in distribution in D([0, 1]) to the tuple
 $\mathsf{Y}[\kappa]$
, where the processes
$\mathsf{Y}[\kappa]$
, where the processes
 $\mathsf{Y}_1,\ldots,\mathsf{Y}_\kappa$
are i.i.d., and their common distribution is that of
$\mathsf{Y}_1,\ldots,\mathsf{Y}_\kappa$
are i.i.d., and their common distribution is that of
 $\mathsf{Y}_\infty$
, a Gaussian process whose law will be detailed in Theorem 9.
$\mathsf{Y}_\infty$
, a Gaussian process whose law will be detailed in Theorem 9.
This convergence theorem contains the fluctuations of every basic brick of
![]() $\mathsf{ECP}(\mathbf{z}[n])$
.
$\mathsf{ECP}(\mathbf{z}[n])$
.
Proof. We start with the proof of Part 2. Recall (5.1). Conditional on
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
, the
![]() ${\mathsf{cp}}^{(n)}[\kappa]$
are independent, which provides the independence of the
${\mathsf{cp}}^{(n)}[\kappa]$
are independent, which provides the independence of the
![]() $\boldsymbol{\delta}^{(n)}[\kappa]$
(given
$\boldsymbol{\delta}^{(n)}[\kappa]$
(given
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
). It suffices then, to prove the convergence of the marginals; by symmetry, we will prove only the convergence of
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
). It suffices then, to prove the convergence of the marginals; by symmetry, we will prove only the convergence of
![]() $\boldsymbol{\delta}_j^{(n)}= \sqrt{\frac{n}{\kappa}}\left({\boldsymbol\beta}_j(n)-\frac{1}{2}\right)$
.
$\boldsymbol{\delta}_j^{(n)}= \sqrt{\frac{n}{\kappa}}\left({\boldsymbol\beta}_j(n)-\frac{1}{2}\right)$
.
According to the Skorokhod representation theorem, up to a change of probability space, we may assume that
for all
![]() $j\in\{1,\ldots,\kappa\}$
. We may then assume that
$j\in\{1,\ldots,\kappa\}$
. We may then assume that
![]() $\mathbf{s}^{(n)}_{j}=\frac{n}{\kappa}+\mathbf{x}_j\sqrt{\frac{n}{\kappa}}+o(\sqrt{n})$
. In the sequel we drop the
$\mathbf{s}^{(n)}_{j}=\frac{n}{\kappa}+\mathbf{x}_j\sqrt{\frac{n}{\kappa}}+o(\sqrt{n})$
. In the sequel we drop the
![]() $o(\sqrt{n})$
since it provides only negligible contributions.
$o(\sqrt{n})$
since it provides only negligible contributions.
Since
![]() $\beta_j^{(n)}$
is
$\beta_j^{(n)}$
is
![]() $\beta$
-distributed with parameters
$\beta$
-distributed with parameters
![]() $(\mathbf{s}^{(n)}_{j},\mathbf{s}^{(n)}_{{j+1}})$
, we have
$(\mathbf{s}^{(n)}_{j},\mathbf{s}^{(n)}_{{j+1}})$
, we have
![]() $\beta_j^{(n)}\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\frac{\mathbf{T}_j}{\mathbf{T}_j+\mathbf{T}_{{j+1}}}$
where
$\beta_j^{(n)}\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\frac{\mathbf{T}_j}{\mathbf{T}_j+\mathbf{T}_{{j+1}}}$
where
![]() $\mathbf{T}_j$
(resp.
$\mathbf{T}_j$
(resp.
![]() $\mathbf{T}_{{j+1}}$
) is a random variable that is gamma-distributed with parameter
$\mathbf{T}_{{j+1}}$
) is a random variable that is gamma-distributed with parameter
![]() $\mathbf{s}^{(n)}_{j}$
(resp.
$\mathbf{s}^{(n)}_{j}$
(resp.
![]() $\mathbf{s}^{(n)}_{{j+1}}$
), these variables being independent.
$\mathbf{s}^{(n)}_{{j+1}}$
), these variables being independent.
By the central limit theorem, we have
for
![]() $\mathbf{q}_1,\mathbf{q}_2$
two i.i.d. standard Gaussian random variables
$\mathbf{q}_1,\mathbf{q}_2$
two i.i.d. standard Gaussian random variables
![]() $\mathcal{N}(0,1)$
. Hence
$\mathcal{N}(0,1)$
. Hence
This gives the expected result.
Notice now that Part 3 implies Part 0. Indeed, the weak convergence of the processes
![]() $\mathsf{C}^{(n)}_1,\ldots,\mathsf{C}^{(n)}_\kappa$
to
$\mathsf{C}^{(n)}_1,\ldots,\mathsf{C}^{(n)}_\kappa$
to
![]() $\mathsf{C}_\infty$
is a consequence of that of
$\mathsf{C}_\infty$
is a consequence of that of
![]() $\mathsf{Y}^{(n)}_1,\ldots,\mathsf{Y}^{(n)}_\kappa$
to
$\mathsf{Y}^{(n)}_1,\ldots,\mathsf{Y}^{(n)}_\kappa$
to
![]() $\mathsf{Y}_\infty$
. This latter convergence will be the main object of the rest of this section. This is by far the most complicated proof, and we will need to introduce quite a lot of tools to achieve it. We will come back to this proof later.
$\mathsf{Y}_\infty$
. This latter convergence will be the main object of the rest of this section. This is by far the most complicated proof, and we will need to introduce quite a lot of tools to achieve it. We will come back to this proof later.
5.3. Convergence of the normalized convex chain
In order to prove the convergence of
![]() $\mathsf{Y}^{(n)}[\kappa]$
, a new parametrization is required.
$\mathsf{Y}^{(n)}[\kappa]$
, a new parametrization is required.
Notation. Define the maps
![]() $g\,:\,t\in[0, 1]\mapsto\tan\left(\frac{\pi}{2}t\right)$
and
$g\,:\,t\in[0, 1]\mapsto\tan\left(\frac{\pi}{2}t\right)$
and
![]() $\displaystyle h\,:\,t\in[0, 1]\mapsto\frac1{1+g(t)}$
. Let us introduce the following mappings for all
$\displaystyle h\,:\,t\in[0, 1]\mapsto\frac1{1+g(t)}$
. Let us introduce the following mappings for all
![]() $(s,t)\in[0, 1]^2$
:
$(s,t)\in[0, 1]^2$
:
In the following, we will denote by
![]() $\left(\mathsf{Z}^{(1)},\mathsf{Z}^{(2)}\right)$
the coordinates of any process
$\left(\mathsf{Z}^{(1)},\mathsf{Z}^{(2)}\right)$
the coordinates of any process
![]() $\mathsf{Z}$
taking values in
$\mathsf{Z}$
taking values in
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
Recall the definition of the process
![]() $\mathsf{Y}_m$
given in (5.5).
$\mathsf{Y}_m$
given in (5.5).
Theorem 9. The convergence in distribution
holds in
![]() $D([0, 1])^2$
.
$D([0, 1])^2$
.
The sequence of processes
![]() $(\mathsf{Y}_m)$
converges in distribution to a centered Gaussian process
$(\mathsf{Y}_m)$
converges in distribution to a centered Gaussian process
![]() $\mathsf{Y}_\infty$
in
$\mathsf{Y}_\infty$
in
![]() $D([0, 1])^2$
, whose coordinates can be represented as
$D([0, 1])^2$
, whose coordinates can be represented as
 \begin{align} \mathsf{Y}_\infty^{(1)}(t)&=\overline{\mathsf{Y}}^{(1)}(t)+\mathbf{g}_1\cdot x(t)+(\mathbf{g}_1-\mathbf{g}_2)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot x^{\prime}(t), \\[-32pt] \nonumber \end{align}
\begin{align} \mathsf{Y}_\infty^{(1)}(t)&=\overline{\mathsf{Y}}^{(1)}(t)+\mathbf{g}_1\cdot x(t)+(\mathbf{g}_1-\mathbf{g}_2)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot x^{\prime}(t), \\[-32pt] \nonumber \end{align}
 \begin{align} \mathsf{Y}_\infty^{(2)}(t)&=\overline{\mathsf{Y}}^{(2)}(t)+\mathbf{g}_1\cdot y(t)+(\mathbf{g}_1-\mathbf{g}_2)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot y^{\prime}(t),\end{align}
\begin{align} \mathsf{Y}_\infty^{(2)}(t)&=\overline{\mathsf{Y}}^{(2)}(t)+\mathbf{g}_1\cdot y(t)+(\mathbf{g}_1-\mathbf{g}_2)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot y^{\prime}(t),\end{align}
and where the following hold:
-
(i) The mappings x’,y’ are the derivatives of
 $t\mapsto x(t)=\mathsf{C}_\infty^{(1)}(t),t\mapsto y(t)=\mathsf{C}_\infty^{(2)}(t)$
(they are deterministic processes).
$t\mapsto x(t)=\mathsf{C}_\infty^{(1)}(t),t\mapsto y(t)=\mathsf{C}_\infty^{(2)}(t)$
(they are deterministic processes). -
(ii) The random variables
 $\mathbf{g}_1,\mathbf{g}_2$
are independent standard Gaussian variables
$\mathbf{g}_1,\mathbf{g}_2$
are independent standard Gaussian variables
 $\mathcal{N}(0,1)$
.
$\mathcal{N}(0,1)$
. -
(iii) The process
 $\overline{\mathsf{Y}}$
is a centered Gaussian process with variance function(5.17)and with covariance function determined, for
$\overline{\mathsf{Y}}$
is a centered Gaussian process with variance function(5.17)and with covariance function determined, for \begin{align} \mathbb{V}\left[\overline{\mathsf{Y}}^{(p)}(t)\right]=f(0,t)v_p(0,t)+f(0,t)(1-f(0,t))e_p(0,t)^2\quad \forall p\in\{1,2\}\end{align}
\begin{align} \mathbb{V}\left[\overline{\mathsf{Y}}^{(p)}(t)\right]=f(0,t)v_p(0,t)+f(0,t)(1-f(0,t))e_p(0,t)^2\quad \forall p\in\{1,2\}\end{align}
 $(s \lt t)\in[0, 1]^2$
, by (5.18)
$(s \lt t)\in[0, 1]^2$
, by (5.18) \begin{align} \mathrm{cov}\left(\overline{\mathsf{Y}}^{(p)}(s),\overline{\mathsf{Y}}^{(q)}(t)-\overline{\mathsf{Y}}^{(q)}(s)\right)=-f(0,s)f(s,t)e_p(0,s)e_q(s,t)\quad \forall (p,q)\in\{1,2\}^2.\end{align}
\begin{align} \mathrm{cov}\left(\overline{\mathsf{Y}}^{(p)}(s),\overline{\mathsf{Y}}^{(q)}(t)-\overline{\mathsf{Y}}^{(q)}(s)\right)=-f(0,s)f(s,t)e_p(0,s)e_q(s,t)\quad \forall (p,q)\in\{1,2\}^2.\end{align}
-
(iv) The processes
 $\overline{\mathsf{Y}}^{(1)},\overline{\mathsf{Y}}^{(2)}$
are independent from
$\overline{\mathsf{Y}}^{(1)},\overline{\mathsf{Y}}^{(2)}$
are independent from
 $\mathbf{g}_1$
and
$\mathbf{g}_1$
and
 $\mathbf{g}_2$
.
$\mathbf{g}_2$
.
The reason why the functions
![]() $f,e_p,v_p$
appear will be revealed in Proposition 3. Notice that
$f,e_p,v_p$
appear will be revealed in Proposition 3. Notice that
 $$\lim_{t\to1}\frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot x^{\prime}(t) \quad \text{and} \quad \lim_{t\to1}\frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot y^{\prime}(t)$$
$$\lim_{t\to1}\frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot x^{\prime}(t) \quad \text{and} \quad \lim_{t\to1}\frac2{\pi}\frac{\tan\left(\frac{\pi}{2}t\right)}{1+\tan\left(\frac{\pi}{2}t\right)^2}\cdot y^{\prime}(t)$$
are finite, so the process
![]() $\mathsf{Y}_\infty$
is also well-defined at
$\mathsf{Y}_\infty$
is also well-defined at
![]() $t=1$
.
$t=1$
.
Once more, the first assertion (5.14) is a consequence of the second; we will prove only the second one.
Remark 4. (Back to Theorem 8.) The proof of Part 4 of Theorem 8 is an immediate consequence of Theorem 9! Indeed, for all
![]() $j\in\{1,\ldots,\kappa\}$
we have
$j\in\{1,\ldots,\kappa\}$
we have
 \begin{align} \mathsf{Y}_j^{(n)}=\sqrt{\frac{n/\kappa}{\mathbf{s}^{(n)}_{j}}}\sqrt{\mathbf{s}^{(n)}_{j}}\left(\mathsf{C}_{\mathbf{s}^{(n)}_{j}}-\mathsf{C}_\infty\right).\end{align}
\begin{align} \mathsf{Y}_j^{(n)}=\sqrt{\frac{n/\kappa}{\mathbf{s}^{(n)}_{j}}}\sqrt{\mathbf{s}^{(n)}_{j}}\left(\mathsf{C}_{\mathbf{s}^{(n)}_{j}}-\mathsf{C}_\infty\right).\end{align}
By Theorem 9, the term
![]() $\sqrt{\mathbf{s}^{(n)}_{j}}\left(\mathsf{C}_{\mathbf{s}^{(n)}_{j}}-\mathsf{C}_\infty\right)$
converges in distribution to
$\sqrt{\mathbf{s}^{(n)}_{j}}\left(\mathsf{C}_{\mathbf{s}^{(n)}_{j}}-\mathsf{C}_\infty\right)$
converges in distribution to
![]() $\mathsf{Y}_\infty$
, and we know furthermore that
$\mathsf{Y}_\infty$
, and we know furthermore that
![]() $\frac{\mathbf{s}^{(n)}_{j}}{n/\kappa}\xrightarrow[n]{(d)}1$
. Slutsky’s lemma allows us to conclude.
$\frac{\mathbf{s}^{(n)}_{j}}{n/\kappa}\xrightarrow[n]{(d)}1$
. Slutsky’s lemma allows us to conclude.
Remark 5. An immediate consequence of Theorem 9 is that the curve
![]() $\mathcal{C}_m=\{(t,\mathsf{C}_m(t)), t \in [0, 1]\}$
, seen as a compact set, converges in distribution to
$\mathcal{C}_m=\{(t,\mathsf{C}_m(t)), t \in [0, 1]\}$
, seen as a compact set, converges in distribution to
![]() $\mathcal{C}_{\infty}=\{(t,\mathsf{C}_\infty(t)), t \in [0, 1]\}$
, for the Hausdorff distance, as
$\mathcal{C}_{\infty}=\{(t,\mathsf{C}_\infty(t)), t \in [0, 1]\}$
, for the Hausdorff distance, as
![]() $m\to+\infty$
. Furthermore, the term
$m\to+\infty$
. Furthermore, the term
![]() $\sqrt{m}d_H( \mathcal{C}_m,\mathcal{C}_{\infty})$
converges in distribution to a non-trivial random value.
$\sqrt{m}d_H( \mathcal{C}_m,\mathcal{C}_{\infty})$
converges in distribution to a non-trivial random value.
5.4. Proof of Theorem 9
The parametrization of
![]() $\mathsf{C}_m$
in terms of the variables
$\mathsf{C}_m$
in terms of the variables
![]() $(\mathbf{u}[m],\mathbf{v}[m])$
is tricky, since these variables are interconnected (they sum to 1), paired, and then sorted by increasing slope (even if the parametrization in terms of the indicator of the slope allows one to get rid of this difficulty).
$(\mathbf{u}[m],\mathbf{v}[m])$
is tricky, since these variables are interconnected (they sum to 1), paired, and then sorted by increasing slope (even if the parametrization in terms of the indicator of the slope allows one to get rid of this difficulty).
Exponential model. Let
![]() $\boldsymbol{\zeta}[m],\boldsymbol{\xi}[m]$
be two m-tuples of random variables exponentially distributed with mean 1, all these variables being independent. Set
$\boldsymbol{\zeta}[m],\boldsymbol{\xi}[m]$
be two m-tuples of random variables exponentially distributed with mean 1, all these variables being independent. Set
![]() $\boldsymbol{\alpha}_m^{(1)}=\sum_{i=1}^m\boldsymbol{\zeta}_i$
,
$\boldsymbol{\alpha}_m^{(1)}=\sum_{i=1}^m\boldsymbol{\zeta}_i$
,
![]() $\boldsymbol{\alpha}_m^{(2)}=\sum_{i=1}^m\boldsymbol{\xi}_i$
. The following equalities in distribution are classically used to represent order statistics by exponential random variables (a more general result can be found in [Reference Jambunathan14, Theorem 3]):
$\boldsymbol{\alpha}_m^{(2)}=\sum_{i=1}^m\boldsymbol{\xi}_i$
. The following equalities in distribution are classically used to represent order statistics by exponential random variables (a more general result can be found in [Reference Jambunathan14, Theorem 3]):
Lemma 10.
Let
![]() $\mathbf{g}_1,\mathbf{g}_2$
be two independent standard Gaussian variables. The following convergence in distribution holds in
$\mathbf{g}_1,\mathbf{g}_2$
be two independent standard Gaussian variables. The following convergence in distribution holds in
![]() $\mathbb{R}^3$
:
$\mathbb{R}^3$
:
 \begin{align} \sqrt{m}\left[\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right),\left(\frac{m}{\boldsymbol{\alpha}_m^{(2)}}-1\right),\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)\right]\xrightarrow[m]{(d)} \left[\mathbf{g}_1,\mathbf{g}_2,\mathbf{g}_1-\mathbf{g}_2\right].\end{align}
\begin{align} \sqrt{m}\left[\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right),\left(\frac{m}{\boldsymbol{\alpha}_m^{(2)}}-1\right),\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)\right]\xrightarrow[m]{(d)} \left[\mathbf{g}_1,\mathbf{g}_2,\mathbf{g}_1-\mathbf{g}_2\right].\end{align}
Proof. Let us write
 \begin{align*} \sqrt{m}\left(\frac{m}{\boldsymbol{\alpha}_m^{(j)}}-1\right)=\frac{m}{\boldsymbol{\alpha}_m^{(j)}}\times \frac{m-\boldsymbol{\alpha}_m^{(j)}}{\sqrt{m}} \quad \text{ for all }j\in\{1,2\}.\end{align*}
\begin{align*} \sqrt{m}\left(\frac{m}{\boldsymbol{\alpha}_m^{(j)}}-1\right)=\frac{m}{\boldsymbol{\alpha}_m^{(j)}}\times \frac{m-\boldsymbol{\alpha}_m^{(j)}}{\sqrt{m}} \quad \text{ for all }j\in\{1,2\}.\end{align*}
As for the third marginal in the left-hand side of (5.21), write
 \begin{align*} \sqrt{m}\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)=\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\times \left[\frac{m-\boldsymbol{\alpha}_m^{(1)}}{\sqrt{m}}-\frac{m-\boldsymbol{\alpha}_m^{(2)}}{\sqrt{m}}\right].\end{align*}
\begin{align*} \sqrt{m}\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)=\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\times \left[\frac{m-\boldsymbol{\alpha}_m^{(1)}}{\sqrt{m}}-\frac{m-\boldsymbol{\alpha}_m^{(2)}}{\sqrt{m}}\right].\end{align*}
Now, in all these cases, Slutsky’s lemma together with the central limit theorem gives the expected convergence.
We now build an object
![]() $\overline{\mathsf{C}}_m$
close to
$\overline{\mathsf{C}}_m$
close to
![]() $\mathsf{C}_m$
whose convergence is easier to prove. We pair the tuples
$\mathsf{C}_m$
whose convergence is easier to prove. We pair the tuples
![]() $\boldsymbol{\zeta}[m],\boldsymbol{\xi}[m]$
to form m vectors
$\boldsymbol{\zeta}[m],\boldsymbol{\xi}[m]$
to form m vectors
![]() $\mathbf{w}_i=(\boldsymbol{\zeta}_i,\boldsymbol{\xi}_i)$
for all
$\mathbf{w}_i=(\boldsymbol{\zeta}_i,\boldsymbol{\xi}_i)$
for all
![]() $i\in\{1,\ldots,m\}$
. When ordered by increasing slope and summed one by one, these vectors form the boundary of a convex polygon, whose vertices form a convex chain in the triangle
$i\in\{1,\ldots,m\}$
. When ordered by increasing slope and summed one by one, these vectors form the boundary of a convex polygon, whose vertices form a convex chain in the triangle
![]() $\mathsf{Tri}(m)$
of vertices
$\mathsf{Tri}(m)$
of vertices
![]() $(0,0),(\boldsymbol{\alpha}_m^{(1)},0),(\boldsymbol{\alpha}_m^{(1)},\boldsymbol{\alpha}_m^{(2)})$
. If we renormalize the x-coordinates of these vectors by
$(0,0),(\boldsymbol{\alpha}_m^{(1)},0),(\boldsymbol{\alpha}_m^{(1)},\boldsymbol{\alpha}_m^{(2)})$
. If we renormalize the x-coordinates of these vectors by
![]() $\boldsymbol{\alpha}_m^{(1)}$
and the y-coordinates by
$\boldsymbol{\alpha}_m^{(1)}$
and the y-coordinates by
![]() $\boldsymbol{\alpha}_m^{(2)}$
, we obtain a convex chain in ◿ whose law is that of a generic ◿-normalized convex chain. However, we want to study the convex chain before renormalization. Hence, to obtain the analogous process before normalization, we consider the contribution
$\boldsymbol{\alpha}_m^{(2)}$
, we obtain a convex chain in ◿ whose law is that of a generic ◿-normalized convex chain. However, we want to study the convex chain before renormalization. Hence, to obtain the analogous process before normalization, we consider the contribution
![]() $\overline{\mathsf{C}}_m(u)$
of the vectors
$\overline{\mathsf{C}}_m(u)$
of the vectors
![]() $(\boldsymbol{\zeta}_i,\boldsymbol{\xi}_i)$
with slope smaller or equal than
$(\boldsymbol{\zeta}_i,\boldsymbol{\xi}_i)$
with slope smaller or equal than
![]() $u\in[0, 1]$
,
$u\in[0, 1]$
,
We will eventually send
![]() $\overline{\mathsf{C}}_m$
to
$\overline{\mathsf{C}}_m$
to
![]() ${\mathsf{C}}_m$
by sending
${\mathsf{C}}_m$
by sending
![]() $\mathsf{Tri}(m)$
to ◿; in order to control the induced slope modification, we introduce the function
$\mathsf{Tri}(m)$
to ◿; in order to control the induced slope modification, we introduce the function
![]() $\boldsymbol{\alpha}_m$
defined in [0, 1] by
$\boldsymbol{\alpha}_m$
defined in [0, 1] by
 \begin{align}\boldsymbol{\alpha}_m(u)=\frac{2}{\pi}\arctan\left(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\tan\left(\frac{\pi}{2}u\right)\right),\end{align}
\begin{align}\boldsymbol{\alpha}_m(u)=\frac{2}{\pi}\arctan\left(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\tan\left(\frac{\pi}{2}u\right)\right),\end{align}
and such that
![]() $\tan\left(\frac{\pi}{2}\boldsymbol{\alpha}_m(u)\right)=\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\tan\left(\frac{\pi}{2}u\right).$
$\tan\left(\frac{\pi}{2}\boldsymbol{\alpha}_m(u)\right)=\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\tan\left(\frac{\pi}{2}u\right).$
By what we just explained, the link between
![]() $\overline{\mathsf{C}}_m$
and
$\overline{\mathsf{C}}_m$
and
![]() $\mathsf{C}_m$
is the following:
$\mathsf{C}_m$
is the following:
 \begin{align}\mathsf{C}_m&\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\overline{\mathsf{C}}^{(1)}_m\big(\boldsymbol{\alpha}_m(u)\big),\frac{m}{\boldsymbol{\alpha}_m^{(2)}}\overline{\mathsf{C}}^{(2)}_m\big(\boldsymbol{\alpha}_m(u)\big), u\in[0, 1]\right).\end{align}
\begin{align}\mathsf{C}_m&\mathrel{\mathop{\kern 0pt=}\limits^{(d)}}\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\overline{\mathsf{C}}^{(1)}_m\big(\boldsymbol{\alpha}_m(u)\big),\frac{m}{\boldsymbol{\alpha}_m^{(2)}}\overline{\mathsf{C}}^{(2)}_m\big(\boldsymbol{\alpha}_m(u)\big), u\in[0, 1]\right).\end{align}
Indeed, for the example of the first coordinate,
 \begin{align*}\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\overline{\mathsf{C}}^{(1)}_m\big(\boldsymbol{\alpha}_m(u)\big)=\frac{1}{\boldsymbol{\alpha}_m^{(1)}}\sum_{i=1}^m \boldsymbol{\zeta}_i\mathbf{1}_{\left\{{\frac{\boldsymbol{\alpha}_m^{(1)}\boldsymbol{\xi}_i}{\boldsymbol{\alpha}_m^{(2)}\boldsymbol{\zeta}_i}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}, \end{align*}
\begin{align*}\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\overline{\mathsf{C}}^{(1)}_m\big(\boldsymbol{\alpha}_m(u)\big)=\frac{1}{\boldsymbol{\alpha}_m^{(1)}}\sum_{i=1}^m \boldsymbol{\zeta}_i\mathbf{1}_{\left\{{\frac{\boldsymbol{\alpha}_m^{(1)}\boldsymbol{\xi}_i}{\boldsymbol{\alpha}_m^{(2)}\boldsymbol{\zeta}_i}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}, \end{align*}
which takes into account the dilatation of the vectors composing the boundary of the convex chain, as well as the normalization of the slope that is effected by an affine dilatation of ◿.
Decomposition of
![]() $\mathsf{Y}_m$
according to the exponential model. Let us now decompose the process
$\mathsf{Y}_m$
according to the exponential model. Let us now decompose the process
![]() $\mathsf{Y}_m$
into several processes that are easier to manipulate. Let
$\mathsf{Y}_m$
into several processes that are easier to manipulate. Let
![]() $u\in[0, 1]$
; for the pth coordinate,
$u\in[0, 1]$
; for the pth coordinate,
![]() $p\in\{1,2\}$
, we have
$p\in\{1,2\}$
, we have
 \begin{multline}\mathsf{Y}^{(p)}_m(u)=\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\overline{\mathsf{C}}^{(p)}_m\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty^{(p)}\big(\boldsymbol{\alpha}_m(u)\big)\bigg)+\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(p)}\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty^{(p)}\left(u\right)\bigg)\\[3pt] +\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(p)}(u)\Bigg].\end{multline}
\begin{multline}\mathsf{Y}^{(p)}_m(u)=\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\overline{\mathsf{C}}^{(p)}_m\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty^{(p)}\big(\boldsymbol{\alpha}_m(u)\big)\bigg)+\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(p)}\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty^{(p)}\left(u\right)\bigg)\\[3pt] +\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(p)}(u)\Bigg].\end{multline}
Consider
![]() $\mathbf{g}_1,\mathbf{g}_2$
, the two independent standard Gaussian variables of Lemma 10, and let us handle the last two terms of (5.25). Notice first that
$\mathbf{g}_1,\mathbf{g}_2$
, the two independent standard Gaussian variables of Lemma 10, and let us handle the last two terms of (5.25). Notice first that
 \begin{align*}\frac{\mathsf{C}_\infty^{(1)}\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\bigg)-\mathsf{C}_\infty^{(1)}\left(u\right)}{\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)}\xrightarrow[m]{(d)} \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot x^{\prime}(u), \end{align*}
\begin{align*}\frac{\mathsf{C}_\infty^{(1)}\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\bigg)-\mathsf{C}_\infty^{(1)}\left(u\right)}{\bigg(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}-1\bigg)}\xrightarrow[m]{(d)} \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot x^{\prime}(u), \end{align*}
where we have used
![]() $\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\xrightarrow[n]{(d)} 1$
by (5.21). This means that with Lemma 10 we have
$\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}\xrightarrow[n]{(d)} 1$
by (5.21). This means that with Lemma 10 we have
 \begin{multline}\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(1)}\Big(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\Big)-\mathsf{C}_\infty^{(1)}\left(u\right)\bigg)+\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(1)}(u)\Bigg]\\[3pt] \xrightarrow[m]{(d)} \left(\mathbf{g}_1-\mathbf{g}_2\right)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot x^{\prime}(u)+\mathbf{g}_1\cdot x(u).\end{multline}
\begin{multline}\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(1)}\Big(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\Big)-\mathsf{C}_\infty^{(1)}\left(u\right)\bigg)+\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(1)}(u)\Bigg]\\[3pt] \xrightarrow[m]{(d)} \left(\mathbf{g}_1-\mathbf{g}_2\right)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot x^{\prime}(u)+\mathbf{g}_1\cdot x(u).\end{multline}
For the second coordinate, we get a similar convergence of the two last terms:
 \begin{multline}\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(2)}\Big(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\Big)-\mathsf{C}_\infty^{(2)}\left(u\right)\bigg)+\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(2)}(u)\Bigg]\\[3pt] \xrightarrow[m]{(d)}\left(\mathbf{g}_1-\mathbf{g}_2\right)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot y^{\prime}(u)+\mathbf{g}_1\cdot y(u),\end{multline}
\begin{multline}\sqrt{m}\Bigg[\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\bigg(\mathsf{C}_\infty^{(2)}\Big(\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}u\Big)-\mathsf{C}_\infty^{(2)}\left(u\right)\bigg)+\left(\frac{m}{\boldsymbol{\alpha}_m^{(1)}}-1\right)\mathsf{C}_\infty^{(2)}(u)\Bigg]\\[3pt] \xrightarrow[m]{(d)}\left(\mathbf{g}_1-\mathbf{g}_2\right)\cdot \frac2{\pi}\frac{\tan\left(\frac{\pi}{2}u\right)}{1+\tan\left(\frac{\pi}{2}u\right)^2}\cdot y^{\prime}(u)+\mathbf{g}_1\cdot y(u),\end{multline}
where the convergence of (5.26) and (5.27) has to be thought of as a joint convergence including the same Gaussian standard random variables
![]() $\mathbf{g}_1,\mathbf{g}_2$
. This allows us to recover the last two processes mentioned in Theorem 8. For the first one, corresponding to the first term of the decomposition of (5.25), we first need to prove an intermediary lemma.
$\mathbf{g}_1,\mathbf{g}_2$
. This allows us to recover the last two processes mentioned in Theorem 8. For the first one, corresponding to the first term of the decomposition of (5.25), we first need to prove an intermediary lemma.
Lemma 11. Suppose that we have the following convergence in distribution:
in
![]() $D([0, 1])^2$
, for some process
$D([0, 1])^2$
, for some process
![]() $\overline{\mathsf{Y}}$
. Then, for all
$\overline{\mathsf{Y}}$
. Then, for all
![]() $u\in[0, 1]$
, we have
$u\in[0, 1]$
, we have
 \begin{align} \sqrt{m}\left[\overline{\mathsf{C}}_m(u)-\mathsf{C}_\infty(u),\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\left(\overline{\mathsf{C}}_m\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty\big(\boldsymbol{\alpha}_m(u)\big)\right)\right]\xrightarrow[m]{(d)}\left[\overline{\mathsf{Y}}(u),\overline{\mathsf{Y}}(u)\right].\end{align}
\begin{align} \sqrt{m}\left[\overline{\mathsf{C}}_m(u)-\mathsf{C}_\infty(u),\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\left(\overline{\mathsf{C}}_m\big(\boldsymbol{\alpha}_m(u)\big)-\mathsf{C}_\infty\big(\boldsymbol{\alpha}_m(u)\big)\right)\right]\xrightarrow[m]{(d)}\left[\overline{\mathsf{Y}}(u),\overline{\mathsf{Y}}(u)\right].\end{align}
In words, the limiting processes of the two processes on the left-hand side are equal.
Proof. By the strong law of large numbers we have
![]() $\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\xrightarrow[n]{(a.s.)} 1$
, as well as
$\frac{m}{\boldsymbol{\alpha}_m^{(1)}}\xrightarrow[n]{(a.s.)} 1$
, as well as
![]() $\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}$
and thus
$\frac{\boldsymbol{\alpha}_m^{(2)}}{\boldsymbol{\alpha}_m^{(1)}}$
and thus
![]() $\boldsymbol{\alpha}_m(u)\xrightarrow[n]{(a.s.)} u$
for all
$\boldsymbol{\alpha}_m(u)\xrightarrow[n]{(a.s.)} u$
for all
![]() $u\in[0, 1]$
. By (5.28), the sequence of processes
$u\in[0, 1]$
. By (5.28), the sequence of processes
![]() $\left(\sqrt{m}\left(\overline{\mathsf{C}}_m-\mathsf{C}_\infty\right)\right)$
is tight in
$\left(\sqrt{m}\left(\overline{\mathsf{C}}_m-\mathsf{C}_\infty\right)\right)$
is tight in
![]() $D([0, 1]^2)$
. The map
$D([0, 1]^2)$
. The map
![]() $F:u\mapsto \tan\left(\frac{\pi}{2}u\right)$
is a continuous non-decreasing surjective map from [0, 1] to
$F:u\mapsto \tan\left(\frac{\pi}{2}u\right)$
is a continuous non-decreasing surjective map from [0, 1] to
![]() $[0,+\infty]$
(where
$[0,+\infty]$
(where
![]() $[0,+\infty]$
is seen as a compact set). Let
$[0,+\infty]$
is seen as a compact set). Let
![]() $(\mathsf{X}_n)$
be a sequence of processes (with values in
$(\mathsf{X}_n)$
be a sequence of processes (with values in
![]() $\mathbb{R}$
) that converges in distribution to
$\mathbb{R}$
) that converges in distribution to
![]() $\mathsf{X}$
in
$\mathsf{X}$
in
![]() $D([0,+\infty])$
(where, for all
$D([0,+\infty])$
(where, for all
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $\lim_{t\to+\infty}\mathsf{X}_n(t)$
is finite, as is
$\lim_{t\to+\infty}\mathsf{X}_n(t)$
is finite, as is
![]() $\lim_{t\to+\infty}\mathsf{X}(t)$
). This implies that
$\lim_{t\to+\infty}\mathsf{X}(t)$
). This implies that
![]() $\mathsf{X}_n\circ F$
converges in distribution to
$\mathsf{X}_n\circ F$
converges in distribution to
![]() $\mathsf{X}\circ F$
in D([0, 1]). We claim that if
$\mathsf{X}\circ F$
in D([0, 1]). We claim that if
![]() $(a_n,b_n)\xrightarrow[n]{(a.s.)} 1$
, then
$(a_n,b_n)\xrightarrow[n]{(a.s.)} 1$
, then
for the same topology. A proof runs as follows: by the Skorokhod representation theorem, there exists a probability space in which are simultaneously defined some copies
![]() $(\overline{a}_n,\overline{b}_n,\overline{\mathsf{X}}_n)$
of
$(\overline{a}_n,\overline{b}_n,\overline{\mathsf{X}}_n)$
of
![]() $({a_n},{b_n},{\mathsf{X}_n})$
(and
$({a_n},{b_n},{\mathsf{X}_n})$
(and
![]() $\bar{\mathsf{X}}$
a copy of
$\bar{\mathsf{X}}$
a copy of
![]() $\mathsf{X}$
) such that
$\mathsf{X}$
) such that
![]() $(\overline{a}_n,\overline{b}_n,\overline{\mathsf{X}}_n\circ F)\xrightarrow[n]{(a.s.)} (a,b,\overline{\mathsf{X}}\circ F)$
.
$(\overline{a}_n,\overline{b}_n,\overline{\mathsf{X}}_n\circ F)\xrightarrow[n]{(a.s.)} (a,b,\overline{\mathsf{X}}\circ F)$
.
Set
![]() $\lambda_n\,:\,u\mapsto \frac{2}{\pi}\arctan\left(\tan\left(\frac{\pi}{2}u\right)/b_n\right)$
, which is a sequence of strictly increasing continuous functions mapping [0, 1] to itself, with
$\lambda_n\,:\,u\mapsto \frac{2}{\pi}\arctan\left(\tan\left(\frac{\pi}{2}u\right)/b_n\right)$
, which is a sequence of strictly increasing continuous functions mapping [0, 1] to itself, with
![]() $\lambda_n(0)=0$
and
$\lambda_n(0)=0$
and
![]() $\lambda_n(1)=1$
. In particular,
$\lambda_n(1)=1$
. In particular,
![]() $\overline{\mathsf{X}}_n(b_n F(\lambda_n(u)))=\overline{\mathsf{X}}_n(F(u))$
. Hence
$\overline{\mathsf{X}}_n(b_n F(\lambda_n(u)))=\overline{\mathsf{X}}_n(F(u))$
. Hence
since
![]() $(\overline{\mathsf{X}}_n\circ F)$
converges to
$(\overline{\mathsf{X}}_n\circ F)$
converges to
![]() $(\overline{\mathsf{X}}\circ F)$
in D([0, 1]) (and this holds
$(\overline{\mathsf{X}}\circ F)$
in D([0, 1]) (and this holds
![]() $\omega$
by
$\omega$
by
![]() $\omega$
). Furthermore,
$\omega$
). Furthermore,
![]() $\lambda_n(u)\to u $
uniformly in [0, 1], and then, according to Billingsley [Reference Billingsley4, p. 124], we may conclude that the claim holds true.
$\lambda_n(u)\to u $
uniformly in [0, 1], and then, according to Billingsley [Reference Billingsley4, p. 124], we may conclude that the claim holds true.
Notation. In order to prove Theorem 9 (and thus Theorem 8), it remains to prove (5.28). We set
![]() $\overline{\mathsf{Y}}_m\,:\!=\,\sqrt{m}\left(\overline{\mathsf{C}}_m-\mathsf{C}_\infty\right)$
.
$\overline{\mathsf{Y}}_m\,:\!=\,\sqrt{m}\left(\overline{\mathsf{C}}_m-\mathsf{C}_\infty\right)$
.
Lemma 12.
The process
![]() $\overline{\mathsf{Y}}_m$
converges in distribution to
$\overline{\mathsf{Y}}_m$
converges in distribution to
![]() $\overline{\mathsf{Y}}$
in
$\overline{\mathsf{Y}}$
in
![]() $D([0, 1],\mathbb{R}^2)$
, where the process
$D([0, 1],\mathbb{R}^2)$
, where the process
![]() $\overline{\mathsf{Y}}$
is the process introduced in Theorem 9.
$\overline{\mathsf{Y}}$
is the process introduced in Theorem 9.
The proof of this lemma is in two steps, including first the convergence of the finite-dimensional distributions (FDDs) and the tightness of the process. Therefore, we need a suitable parametrization to complete this proof.
Parametrization in the exponential model. Fix some
![]() $k\geq1$
and
$k\geq1$
and
![]() $(0=u_0 \lt u_1 \lt \ldots \lt u_{k-1} \lt u_k=1)$
. We will prove the convergence of
$(0=u_0 \lt u_1 \lt \ldots \lt u_{k-1} \lt u_k=1)$
. We will prove the convergence of
![]() $\mathsf{Y}_m(u_i)$
for all
$\mathsf{Y}_m(u_i)$
for all
![]() $i\in\{1,\ldots,k\}$
(recall that
$i\in\{1,\ldots,k\}$
(recall that
![]() $\mathsf{Y}_m(u_0)=0$
a.s.). Fix, for the moment,
$\mathsf{Y}_m(u_0)=0$
a.s.). Fix, for the moment,
![]() $i\in\{1,\ldots,k\}$
. The random variable
$i\in\{1,\ldots,k\}$
. The random variable
 \begin{align*}\mathbf{n}(u_i)=\mathbf{n}_i\,:\!=\,\left\vert\left\{j;\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{{\boldsymbol{\xi}}_j}{{\boldsymbol{\zeta}}_j}\leq \tan\left(\frac{\pi}{2}u_i\right)\right\}\right\vert \end{align*}
\begin{align*}\mathbf{n}(u_i)=\mathbf{n}_i\,:\!=\,\left\vert\left\{j;\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{{\boldsymbol{\xi}}_j}{{\boldsymbol{\zeta}}_j}\leq \tan\left(\frac{\pi}{2}u_i\right)\right\}\right\vert \end{align*}
counts the number of vectors whose slope is in the interval
![]() $\left(\tan\left(\frac{\pi}{2}u_{i-1}\right),\tan\left(\frac{\pi}{2}u_i\right)\right]$
. We denote by
$\left(\tan\left(\frac{\pi}{2}u_{i-1}\right),\tan\left(\frac{\pi}{2}u_i\right)\right]$
. We denote by
![]() $\left(\mathbf{w}^{(i)}_1,\ldots,\mathbf{w}^{(i)}_{\mathbf{n}_i}\right)$
the sequence of these vectors taken in their initial order. We have
$\left(\mathbf{w}^{(i)}_1,\ldots,\mathbf{w}^{(i)}_{\mathbf{n}_i}\right)$
the sequence of these vectors taken in their initial order. We have
 \begin{align}\overline{\mathsf{C}}_m(u_i)=\frac{1}{m}\sum_{s=1}^i\sum_{j=1}^{\mathbf{n}_s}\mathbf{w}_j^{(s)},\end{align}
\begin{align}\overline{\mathsf{C}}_m(u_i)=\frac{1}{m}\sum_{s=1}^i\sum_{j=1}^{\mathbf{n}_s}\mathbf{w}_j^{(s)},\end{align}
since
![]() $\overline{\mathsf{C}}_m(u_i)$
is obtained by taking the sum of vectors with slopes smaller than or equal to
$\overline{\mathsf{C}}_m(u_i)$
is obtained by taking the sum of vectors with slopes smaller than or equal to
![]() $\tan\left(\frac{\pi}{2}u_i\right)$
. For this i, the variables
$\tan\left(\frac{\pi}{2}u_i\right)$
. For this i, the variables
![]() $\mathbf{w}^{(i)}_j$
are independent and distributed as the law of a pair
$\mathbf{w}^{(i)}_j$
are independent and distributed as the law of a pair
![]() $(\boldsymbol{\zeta},\boldsymbol{\xi})$
conditioned on
$(\boldsymbol{\zeta},\boldsymbol{\xi})$
conditioned on
![]() $\left\{\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{\boldsymbol{\xi}}{\boldsymbol{\zeta}}\leq \tan\left(\frac{\pi}{2}u_i\right) \right\}$
, where
$\left\{\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{\boldsymbol{\xi}}{\boldsymbol{\zeta}}\leq \tan\left(\frac{\pi}{2}u_i\right) \right\}$
, where
![]() $\boldsymbol{\zeta},\boldsymbol{\xi}$
are independent exponential variables with mean 1. Denote by
$\boldsymbol{\zeta},\boldsymbol{\xi}$
are independent exponential variables with mean 1. Denote by
![]() $\mathbf{w}^{(i)}=(\boldsymbol{\zeta}^{(i)},\boldsymbol{\xi}^{(i)})$
a generic random value with this conditional law. Note that the vectors of the sequence
$\mathbf{w}^{(i)}=(\boldsymbol{\zeta}^{(i)},\boldsymbol{\xi}^{(i)})$
a generic random value with this conditional law. Note that the vectors of the sequence
![]() $\left(\mathbf{w}^{(i)}_1,\ldots,\mathbf{w}^{(i)}_{\mathbf{n}_i}\right)$
have the same distribution as
$\left(\mathbf{w}^{(i)}_1,\ldots,\mathbf{w}^{(i)}_{\mathbf{n}_i}\right)$
have the same distribution as
![]() $\mathbf{w}^{(i)}.$
$\mathbf{w}^{(i)}.$
By setting the non-decreasing mapping
we may then set
so that the tuple
![]() $\mathbf{n}[k]$
has a multinomial distribution
$\mathbf{n}[k]$
has a multinomial distribution
![]() $\mathcal{M}(m,p[k]).$
$\mathcal{M}(m,p[k]).$
Proposition 3.
Recall the mappings introduced from (5.9) to (5.13). The following properties of
![]() $\boldsymbol{\zeta}^{(i)}$
and
$\boldsymbol{\zeta}^{(i)}$
and
![]() $\boldsymbol{\xi}^{(i)}$
hold:
$\boldsymbol{\xi}^{(i)}$
hold:
-
1.
 $p_i=f(u_{i-1},u_i)$
;
$p_i=f(u_{i-1},u_i)$
; -
2.
 $\mathbb{E}\left[\boldsymbol{\zeta}^{(i)}\right]=e_1(u_{i-1},u_i)/p_i,\quad\text{ and }\quad\mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]=e_2(u_{i-1},u_i)/p_i$
;
$\mathbb{E}\left[\boldsymbol{\zeta}^{(i)}\right]=e_1(u_{i-1},u_i)/p_i,\quad\text{ and }\quad\mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]=e_2(u_{i-1},u_i)/p_i$
; -
3.
 $\mathbb{V}\left[\boldsymbol{\zeta}^{(i)}\right]=v_1(u_{i-1},u_i)/p_i,\quad\text{ and }\quad\mathbb{V}\left[\boldsymbol{\xi}^{(i)}\right]=v_2(u_{i-1},u_i)/p_i$
;
$\mathbb{V}\left[\boldsymbol{\zeta}^{(i)}\right]=v_1(u_{i-1},u_i)/p_i,\quad\text{ and }\quad\mathbb{V}\left[\boldsymbol{\xi}^{(i)}\right]=v_2(u_{i-1},u_i)/p_i$
; -
4. for all
 $s\in\mathbb{N}$
,
$s\in\mathbb{N}$
,
 $\mathbb{E}\left[\left\vert\boldsymbol{\zeta}^{(i)}\right\vert^s\right]\leq s!\quad\text{ and }\quad\mathbb{E}\left[\left\vert\boldsymbol{\xi}^{(i)}\right\vert^s\right]\leq s!$
.
$\mathbb{E}\left[\left\vert\boldsymbol{\zeta}^{(i)}\right\vert^s\right]\leq s!\quad\text{ and }\quad\mathbb{E}\left[\left\vert\boldsymbol{\xi}^{(i)}\right\vert^s\right]\leq s!$
.
Proof. The first three statements come from standard integral computations. As an illustrative example, let us compute
![]() $\mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]$
:
$\mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]$
:
 \begin{align}\nonumber \mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]&=\frac1{p_i}\int_{(\mathbb{R}_+)^2}ye^{-x-y}\mathbf{1}_{\left\{{\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{y}{x}\leq\tan\left(\frac{\pi}{2}u_i\right)}\right\}}\text{d} x\text{d} y\\[3pt] \nonumber &=\frac1{p_i}\int_{0}^{+\infty}ye^{-y}\int_{\frac{y}{\tan\left(\frac{\pi}{2}u_i\right)}}^{\frac{y}{\tan\left(\frac{\pi}{2}u_{i-1}\right)}}e^{-x}\text{d} x\text{d} y\\[3pt] \nonumber &=\frac1{p_i}\int_{0}^{+\infty}ye^{-(1+\frac{1}{\tan\left(\frac{\pi}{2}u_i\right)})y}\text{d} y-\int_{0}^{+\infty}ye^{-(1+\frac{1}{\tan\left(\frac{\pi}{2}u_{i-1}\right)})y}\text{d} y\\[3pt] &=\frac1{p_i}e_2(u_{i-1},u_i). \end{align}
\begin{align}\nonumber \mathbb{E}\left[\boldsymbol{\xi}^{(i)}\right]&=\frac1{p_i}\int_{(\mathbb{R}_+)^2}ye^{-x-y}\mathbf{1}_{\left\{{\tan\left(\frac{\pi}{2}u_{i-1}\right) \lt \frac{y}{x}\leq\tan\left(\frac{\pi}{2}u_i\right)}\right\}}\text{d} x\text{d} y\\[3pt] \nonumber &=\frac1{p_i}\int_{0}^{+\infty}ye^{-y}\int_{\frac{y}{\tan\left(\frac{\pi}{2}u_i\right)}}^{\frac{y}{\tan\left(\frac{\pi}{2}u_{i-1}\right)}}e^{-x}\text{d} x\text{d} y\\[3pt] \nonumber &=\frac1{p_i}\int_{0}^{+\infty}ye^{-(1+\frac{1}{\tan\left(\frac{\pi}{2}u_i\right)})y}\text{d} y-\int_{0}^{+\infty}ye^{-(1+\frac{1}{\tan\left(\frac{\pi}{2}u_{i-1}\right)})y}\text{d} y\\[3pt] &=\frac1{p_i}e_2(u_{i-1},u_i). \end{align}
The fourth statement comes from the fact the sth moment of an exponential random variable of mean 1 equals
![]() $s!$
.
$s!$
.
The following proposition establishes the link between our parametrization and the limit parabola.
Proposition 4.
For all
![]() $u\in[0, 1]$
, we have, for all
$u\in[0, 1]$
, we have, for all
![]() $m\geq1$
,
$m\geq1$
,
where
![]() $\mathsf{C}_\infty(u)$
is given in (5.4).
$\mathsf{C}_\infty(u)$
is given in (5.4).
Proof. We have
 $$\overline{\mathsf{C}}_m(u)=\frac{1}{m}\sum_{j=1}^m \left(\boldsymbol{\zeta}_j,\boldsymbol{\xi}_j\right)\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}.$$
$$\overline{\mathsf{C}}_m(u)=\frac{1}{m}\sum_{j=1}^m \left(\boldsymbol{\zeta}_j,\boldsymbol{\xi}_j\right)\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}.$$
By linearity of the expectation, it suffices to prove that
Standard integral computations very similar to (5.32) allow us to compute
 $$\mathbb{E}\left[\boldsymbol{\zeta}_j\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}\right]=x(u) \quad \text{and} \quad \mathbb{E}\left[\boldsymbol{\xi}_j\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}\right]=y(u)$$
$$\mathbb{E}\left[\boldsymbol{\zeta}_j\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}\right]=x(u) \quad \text{and} \quad \mathbb{E}\left[\boldsymbol{\xi}_j\mathbf{1}_{\left\{{\frac{\boldsymbol{\xi}_j}{\boldsymbol{\zeta}_j}\leq \tan\left(\frac{\pi}{2}u\right)}\right\}}\right]=y(u)$$
for all
![]() $j\in\{1,\ldots,m\}$
, which is (5.4). It also follows that
$j\in\{1,\ldots,m\}$
, which is (5.4). It also follows that
 \begin{align} \mathsf{C}_\infty(u_i)&=\sum_{s=1}^i \mathbb{E}\left[\left(\boldsymbol{\zeta},\boldsymbol{\xi}\right)\mathbf{1}_{\left\{{\tan\left(\frac{\pi}{2}u_{s-1}\right)\lt \frac{\boldsymbol{\xi}}{\boldsymbol{\zeta}}\leq \tan\left(\frac{\pi}{2}u_s\right)}\right\}}\right] =\sum_{s=1}^i p_s\mathbb{E}\left[\mathbf{w}^{(s)}\right]. \end{align}
\begin{align} \mathsf{C}_\infty(u_i)&=\sum_{s=1}^i \mathbb{E}\left[\left(\boldsymbol{\zeta},\boldsymbol{\xi}\right)\mathbf{1}_{\left\{{\tan\left(\frac{\pi}{2}u_{s-1}\right)\lt \frac{\boldsymbol{\xi}}{\boldsymbol{\zeta}}\leq \tan\left(\frac{\pi}{2}u_s\right)}\right\}}\right] =\sum_{s=1}^i p_s\mathbb{E}\left[\mathbf{w}^{(s)}\right]. \end{align}
We may now come back to the proof of Lemma 12.
Proof of Lemma 12
. We start by proving the convergence of the FDDs of
![]() $\overline{\mathsf{Y}}_m$
to those of
$\overline{\mathsf{Y}}_m$
to those of
![]() $\overline{\mathsf{Y}}.$
$\overline{\mathsf{Y}}.$
FDDs. Let us split
![]() $\overline{\mathsf{Y}}_m(u_i)$
in order to make more visible the convergence result we want to prove. For
$\overline{\mathsf{Y}}_m(u_i)$
in order to make more visible the convergence result we want to prove. For
![]() $i\in\{1,\ldots,k\}$
, we have
$i\in\{1,\ldots,k\}$
, we have
 \begin{align} \overline{\mathsf{Y}}_m(u_i)=\frac{1}{\sqrt{m}}\left(\sum_{s=1}^i\sum_{j=1}^{\mathbf{n}_s}\left(\mathbf{w}_j^{(s)}-\mathbb{E}\left[\mathbf{w}_j^{(s)}\right]\right)\right)+\left(\frac{1}{\sqrt{m}}\sum_{s=1}^i\mathbf{n}_s\mathbb{E}\left[\mathbf{w}^{(s)}\right]-\sqrt{m}\mathsf{C}_\infty(u_i)\right). \end{align}
\begin{align} \overline{\mathsf{Y}}_m(u_i)=\frac{1}{\sqrt{m}}\left(\sum_{s=1}^i\sum_{j=1}^{\mathbf{n}_s}\left(\mathbf{w}_j^{(s)}-\mathbb{E}\left[\mathbf{w}_j^{(s)}\right]\right)\right)+\left(\frac{1}{\sqrt{m}}\sum_{s=1}^i\mathbf{n}_s\mathbb{E}\left[\mathbf{w}^{(s)}\right]-\sqrt{m}\mathsf{C}_\infty(u_i)\right). \end{align}
We decompose the process as suggested by (5.35):
where
![]() $\mathsf{A}_m(u_i)$
is the first contribution of the right-hand side and the second one is rewritten as
$\mathsf{A}_m(u_i)$
is the first contribution of the right-hand side and the second one is rewritten as
 \begin{align} \mathsf{B}_m(u_i) &= \sum_{s=1}^i \left(\frac{\mathbf{n}_s-mp_s}{\sqrt{m}}\right)\mathbb{E}\left[\mathbf{w}^{(s)}\right]. \end{align}
\begin{align} \mathsf{B}_m(u_i) &= \sum_{s=1}^i \left(\frac{\mathbf{n}_s-mp_s}{\sqrt{m}}\right)\mathbb{E}\left[\mathbf{w}^{(s)}\right]. \end{align}
From the fact that
![]() $\mathbf{n}[k]\sim \mathcal{M}(m,p[k])$
and (5.34), a standard consequence of the central limit theorem is that
$\mathbf{n}[k]\sim \mathcal{M}(m,p[k])$
and (5.34), a standard consequence of the central limit theorem is that
where
![]() $\left(\mathbf{b}_s,s\in\{1,\ldots,k\}\right)$
is a centered Gaussian vector with covariance function
$\left(\mathbf{b}_s,s\in\{1,\ldots,k\}\right)$
is a centered Gaussian vector with covariance function
Using a concentration result for
![]() $\mathbf{n}_s$
around
$\mathbf{n}_s$
around
![]() $mp_s$
(for example the Hoeffding inequalities), by the central limit theorem,
$mp_s$
(for example the Hoeffding inequalities), by the central limit theorem,
 \begin{align} \left(\sum_{j=1}^{\mathbf{n}_s}\frac{\mathbf{w}_j^{(s)}-\mathbb{E}\left[\mathbf{w}_j^{(s)}\right]}{\sqrt{m}},s\in\{1,\ldots,k\}\right)\mathrel{\mathop{\kern 0pt\mathrel{\mathop{\kern 0pt\longrightarrow}\limits_{m\to\infty}}}\limits^{(d)}}\left(\sqrt{p_s}\mathbf{G}_s,s\in\{1,\ldots,k\}\right), \end{align}
\begin{align} \left(\sum_{j=1}^{\mathbf{n}_s}\frac{\mathbf{w}_j^{(s)}-\mathbb{E}\left[\mathbf{w}_j^{(s)}\right]}{\sqrt{m}},s\in\{1,\ldots,k\}\right)\mathrel{\mathop{\kern 0pt\mathrel{\mathop{\kern 0pt\longrightarrow}\limits_{m\to\infty}}}\limits^{(d)}}\left(\sqrt{p_s}\mathbf{G}_s,s\in\{1,\ldots,k\}\right), \end{align}
where, for all
![]() $s\in\{1,\ldots,k\}$
, the random variable
$s\in\{1,\ldots,k\}$
, the random variable
![]() $\mathbf{G}_s\,:\!=\,(\mathbf{G}_s^{(1)},\mathbf{G}_s^{(2)})$
is such that the random variables
$\mathbf{G}_s\,:\!=\,(\mathbf{G}_s^{(1)},\mathbf{G}_s^{(2)})$
is such that the random variables
![]() $\mathbf{G}_s^{(1)}$
and
$\mathbf{G}_s^{(1)}$
and
![]() $\mathbf{G}_s^{(2)}$
are independent, and
$\mathbf{G}_s^{(2)}$
are independent, and
![]() $\mathbf{G}_s^{(1)}$
(resp.
$\mathbf{G}_s^{(1)}$
(resp.
![]() $\mathbf{G}_s^{(2)}$
) is a centered Gaussian random variable with variance
$\mathbf{G}_s^{(2)}$
) is a centered Gaussian random variable with variance
![]() $\mathbb{V}\left[\boldsymbol{\zeta}^{(s)}\right]$
(resp.
$\mathbb{V}\left[\boldsymbol{\zeta}^{(s)}\right]$
(resp.
![]() $\mathbb{V}\left[\boldsymbol{\xi}^{(s)}\right]$
), these variables being independent of
$\mathbb{V}\left[\boldsymbol{\xi}^{(s)}\right]$
), these variables being independent of
![]() $\mathbf{b}_s$
. These considerations also allow us to prove that the families of random variables
$\mathbf{b}_s$
. These considerations also allow us to prove that the families of random variables
![]() $(\mathbf{G}_s^{(p)},s\in\{1,\ldots,k\})$
and
$(\mathbf{G}_s^{(p)},s\in\{1,\ldots,k\})$
and
![]() $(\mathbf{b}_s,s\in\{1,\ldots,k\})$
are independent for all
$(\mathbf{b}_s,s\in\{1,\ldots,k\})$
are independent for all
![]() $p\in\{1,2\}$
.
$p\in\{1,2\}$
.
This proves that the FDDs of
![]() $\overline{\mathsf{Y}}_m$
converge to those of
$\overline{\mathsf{Y}}_m$
converge to those of
![]() $\overline{\mathsf{Y}}$
, where
$\overline{\mathsf{Y}}$
, where
 \begin{align} \overline{\mathsf{Y}}(u_i)\,:\!=\,\sum_{s=1}^i\left( \sqrt{p_s}\mathbf{G}_s + \mathbf{b}_s\mathbb{E}\left[\left(\boldsymbol{\xi}^{(s)},\boldsymbol{\zeta}^{(s)}\right)\right]\right), \qquad i\in\{1,\ldots,k\}. \end{align}
\begin{align} \overline{\mathsf{Y}}(u_i)\,:\!=\,\sum_{s=1}^i\left( \sqrt{p_s}\mathbf{G}_s + \mathbf{b}_s\mathbb{E}\left[\left(\boldsymbol{\xi}^{(s)},\boldsymbol{\zeta}^{(s)}\right)\right]\right), \qquad i\in\{1,\ldots,k\}. \end{align}
Tightness. Proving the tightness of the sequence
![]() $(\overline{\mathsf{Y}}_m)_{m\geq0}$
in D([0, 1]) is the tough part of this section. The key point is the following lemma.
$(\overline{\mathsf{Y}}_m)_{m\geq0}$
in D([0, 1]) is the tough part of this section. The key point is the following lemma.
Lemma 13.
Let
![]() $(\mathsf{X}_m)_{m\geq0}$
be a sequence of processes taking their values in D([0, 1]). Assume that for any m,
$(\mathsf{X}_m)_{m\geq0}$
be a sequence of processes taking their values in D([0, 1]). Assume that for any m,
![]() $\mathsf{X}_m=\mathsf{X}^{(1)}_{m}+\mathsf{X}^{(2)}_{m}$
where
$\mathsf{X}_m=\mathsf{X}^{(1)}_{m}+\mathsf{X}^{(2)}_{m}$
where
![]() $\mathsf{X}^{(1)}_{m}$
is a continuous process and
$\mathsf{X}^{(1)}_{m}$
is a continuous process and
![]() $\mathsf{X}^{(2)}_{m}$
is a càdlàg process. If
$\mathsf{X}^{(2)}_{m}$
is a càdlàg process. If
![]() $\mathsf{X}^{(1)}_{m}$
converges in distribution to
$\mathsf{X}^{(1)}_{m}$
converges in distribution to
![]() $\mathsf{X}^{(1)}$
in C([0, 1]), and if
$\mathsf{X}^{(1)}$
in C([0, 1]), and if
![]() $\sup\left\vert\mathsf{X}^{(2)}_{m}\right\vert\xrightarrow[m]{(d)}0$
, then
$\sup\left\vert\mathsf{X}^{(2)}_{m}\right\vert\xrightarrow[m]{(d)}0$
, then
![]() $(\mathsf{X}_m)$
converges in distribution to
$(\mathsf{X}_m)$
converges in distribution to
![]() $\mathsf{X}^{(2)}$
in D([0, 1]).
$\mathsf{X}^{(2)}$
in D([0, 1]).
From this point, the proof is broken into three steps:
-
1. We consider the decomposition
 $\overline{\mathsf{Y}}_m=\overline{\mathcal{Y}}_m+\left(\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m\right)$
, where
$\overline{\mathsf{Y}}_m=\overline{\mathcal{Y}}_m+\left(\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m\right)$
, where
 $\overline{\mathcal{Y}}_m$
is a continuous process and
$\overline{\mathcal{Y}}_m$
is a continuous process and
 $\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m$
is a càdlàg process (on [0, 1]). We want to apply Lemma 13 to
$\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m$
is a càdlàg process (on [0, 1]). We want to apply Lemma 13 to
 $\mathsf{X}^{(1)}_{m}=\overline{\mathcal{Y}}_m$
and
$\mathsf{X}^{(1)}_{m}=\overline{\mathcal{Y}}_m$
and
 $\mathsf{X}^{(2)}_{m}=\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m$
.
$\mathsf{X}^{(2)}_{m}=\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m$
. -
2. We prove the convergence in distribution of the sequence
 $(\overline{\mathcal{Y}}_m)$
to
$(\overline{\mathcal{Y}}_m)$
to
 $\overline{\mathsf{Y}}$
in C([0, 1]).
$\overline{\mathsf{Y}}$
in C([0, 1]). -
3. We prove that
 $\sup_{t\in[0, 1]}\left\vert\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m\right\vert\xrightarrow[m]{(d)}0$
to conclude that
$\sup_{t\in[0, 1]}\left\vert\overline{\mathsf{Y}}_m-\overline{\mathcal{Y}}_m\right\vert\xrightarrow[m]{(d)}0$
to conclude that
 $(\overline{\mathsf{Y}}_m)$
converges in distribution to the same limit
$(\overline{\mathsf{Y}}_m)$
converges in distribution to the same limit
 $\overline{\mathsf{Y}}$
as does
$\overline{\mathsf{Y}}$
as does
 $(\overline{\mathcal{Y}}_m)$
.
$(\overline{\mathcal{Y}}_m)$
.
Step 1: Let us define the process
![]() $\overline{\mathcal{Y}}_m$
properly. Recall the mapping q introduced in (5.31), and for each
$\overline{\mathcal{Y}}_m$
properly. Recall the mapping q introduced in (5.31), and for each
![]() $j\in\{0,\ldots,m\}$
define the ‘jth m-tile’
$j\in\{0,\ldots,m\}$
define the ‘jth m-tile’
as well as the interval
Recall the definition of
![]() $\mathsf{A}_m,{\mathsf{B}}_m$
in (5.37), which satisfies
$\mathsf{A}_m,{\mathsf{B}}_m$
in (5.37), which satisfies
![]() $\overline{\mathsf{Y}}_m(u_i)=\mathsf{A}_m(u_i)+{\mathsf{B}}_m(u_i)$
for any generic point
$\overline{\mathsf{Y}}_m(u_i)=\mathsf{A}_m(u_i)+{\mathsf{B}}_m(u_i)$
for any generic point
![]() $u_i\in[0, 1]$
. We define
$u_i\in[0, 1]$
. We define
![]() $\overline{\mathcal{Y}}_m$
as
$\overline{\mathcal{Y}}_m$
as
where for all
![]() $j\in\{0,\ldots,m\}$
,
$j\in\{0,\ldots,m\}$
,
and
![]() $\mathcal{A}_m,\mathcal{B}_m$
are interpolated between the points
$\mathcal{A}_m,\mathcal{B}_m$
are interpolated between the points
![]() $v_j(m)$
, in order to embed them in the space of continuous processes C([0, 1]), and thus, so is
$v_j(m)$
, in order to embed them in the space of continuous processes C([0, 1]), and thus, so is
![]() $\overline{\mathcal{Y}}_m$
. We have replace the generic points
$\overline{\mathcal{Y}}_m$
. We have replace the generic points
![]() $u_i$
by the m-tiles
$u_i$
by the m-tiles
![]() $v_j(m)$
, which are more suitable for proving the tightness of
$v_j(m)$
, which are more suitable for proving the tightness of
![]() $\mathcal{A}_m,\mathcal{B}_m$
(and thus that of
$\mathcal{A}_m,\mathcal{B}_m$
(and thus that of
![]() $\overline{\mathcal{Y}}_m$
).
$\overline{\mathcal{Y}}_m$
).
Step 2: By construction, the FDDs of
![]() $\overline{\mathcal{Y}}_m$
are the same as those of
$\overline{\mathcal{Y}}_m$
are the same as those of
![]() $\overline{\mathsf{Y}}_m$
on the m-tiles
$\overline{\mathsf{Y}}_m$
on the m-tiles
![]() $v_j(m)$
,
$v_j(m)$
,
![]() $j\in\{1,\ldots,m\}$
, so that it remains to prove only the tightness of
$j\in\{1,\ldots,m\}$
, so that it remains to prove only the tightness of
![]() $(\overline{\mathcal{Y}}_m)$
to prove its convergence in distribution towards
$(\overline{\mathcal{Y}}_m)$
to prove its convergence in distribution towards
![]() $\overline{\mathsf{Y}}$
. By Lemma 14 above (see [Reference Marckert16, Lemma 8]), it suffices to prove the tightness of
$\overline{\mathsf{Y}}$
. By Lemma 14 above (see [Reference Marckert16, Lemma 8]), it suffices to prove the tightness of
![]() $\mathcal{A}_m$
and that of
$\mathcal{A}_m$
and that of
![]() $\mathcal{B}_m$
separately. In fact this establishes the convergence of the FDDs in the sense that
$\mathcal{B}_m$
separately. In fact this establishes the convergence of the FDDs in the sense that
![]() $\left(\overline{\mathcal{Y}}_m\left(\frac{\lfloor mu_i\rfloor}{m}\right),1\leq i\leq k\right)$
converges, that is, at the discretization points. The tightness allows us to see that
$\left(\overline{\mathcal{Y}}_m\left(\frac{\lfloor mu_i\rfloor}{m}\right),1\leq i\leq k\right)$
converges, that is, at the discretization points. The tightness allows us to see that
(the argument is direct from (5.54)).
Lemma 14.
Let
![]() $\left(\mathsf{Z}^{(1)}_m,\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
be a sequence of pairs of processes in
$\left(\mathsf{Z}^{(1)}_m,\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
be a sequence of pairs of processes in
![]() $C([0, 1])^2$
. The tightnesses of both families
$C([0, 1])^2$
. The tightnesses of both families
![]() $\left(\mathsf{Z}^{(1)}_m\right)_{m\geq0}$
and
$\left(\mathsf{Z}^{(1)}_m\right)_{m\geq0}$
and
![]() $\left(\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
in C([0, 1]) imply that of
$\left(\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
in C([0, 1]) imply that of
![]() $\left(\mathsf{Z}^{(1)}_m,\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
in
$\left(\mathsf{Z}^{(1)}_m,\mathsf{Z}^{(2)}_m\right)_{m\geq0}$
in
![]() $C([0, 1])^2$
.
$C([0, 1])^2$
.
A criterion for tightness in C([0, 1]) is the following [Reference Billingsley4, Theorem II.12.3].
Lemma 15.
Let
![]() $(\mathsf{X}_m)_{m\geq0}$
be a sequence of stochastic processes in
$(\mathsf{X}_m)_{m\geq0}$
be a sequence of stochastic processes in
![]() $C\left([0, 1],\mathbb{R}\right)$
. If there exist some positive numbers
$C\left([0, 1],\mathbb{R}\right)$
. If there exist some positive numbers
![]() $\alpha \gt 1,\beta\geq 0$
and a non-decreasing continuous function F on [0, 1] such that, for all
$\alpha \gt 1,\beta\geq 0$
and a non-decreasing continuous function F on [0, 1] such that, for all
![]() $m\in\mathbb{N}$
and
$m\in\mathbb{N}$
and
![]() $(s,t) \in[0, 1]^2$
with
$(s,t) \in[0, 1]^2$
with
![]() $0\leq s\leq t\leq 1$
,
$0\leq s\leq t\leq 1$
,
for all
![]() $\lambda \gt 0$
, then
$\lambda \gt 0$
, then
![]() $(\mathsf{X}_m)_{m\geq0}$
is tight in
$(\mathsf{X}_m)_{m\geq0}$
is tight in
![]() $C\left([0, 1]\right)$
.
$C\left([0, 1]\right)$
.
Note that by Markov’s inequality, it suffices to prove that
![]() $\mathbb{E}\left[\left\vert \mathsf{X}_m(t)-\mathsf{X}_m(s)\right\vert^{\beta}\right]\leq \left\vert F(t)-F(r)\right\vert^{\alpha}$
.
$\mathbb{E}\left[\left\vert \mathsf{X}_m(t)-\mathsf{X}_m(s)\right\vert^{\beta}\right]\leq \left\vert F(t)-F(r)\right\vert^{\alpha}$
.
We are working in
![]() $\mathbb{R}^2$
, so we will apply this criterion twice, one on every coordinate
$\mathbb{R}^2$
, so we will apply this criterion twice, one on every coordinate
![]() $\overline{\mathcal{Y}}_m^{(p)}$
,
$\overline{\mathcal{Y}}_m^{(p)}$
,
![]() $p\in\{1,2\}$
. We shall prove that for both processes,
$p\in\{1,2\}$
. We shall prove that for both processes,
![]() $\beta=4,\alpha=2$
does the job, together with the continuous non-decreasing map
$\beta=4,\alpha=2$
does the job, together with the continuous non-decreasing map
![]() $F=q$
introduced in (5.31), which we extend by setting
$F=q$
introduced in (5.31), which we extend by setting
![]() $F(1)=q(1)=1$
.
$F(1)=q(1)=1$
.
Let
![]() $(s,t) \in[0, 1]^2$
be such that
$(s,t) \in[0, 1]^2$
be such that
![]() $0\leq s \lt t\leq 1$
. There exist
$0\leq s \lt t\leq 1$
. There exist
![]() $j_1 \lt j_2\in\{0,\ldots,m\}$
such that
$j_1 \lt j_2\in\{0,\ldots,m\}$
such that
![]() $s\in I_{j_1}(m)$
and
$s\in I_{j_1}(m)$
and
![]() $t\in I_{j_2}(m)$
, and we assume that
$t\in I_{j_2}(m)$
, and we assume that
![]() $j_1\neq j_2$
(the case
$j_1\neq j_2$
(the case
![]() $j_1=j_2$
will be treated afterwards). We may write, for all
$j_1=j_2$
will be treated afterwards). We may write, for all
![]() $p\in\{1,2\},$
$p\in\{1,2\},$
 \begin{multline} \mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(t)-\mathcal{B}^{(p)}_m(s)\right\vert^{4}\right]\leq \mathrm{Cste}\bigg(\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(t)-\mathcal{B}^{(p)}_m(v_{j_2}(m))\right\vert^{4}\right] \\[3pt] +\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(v_{j_2}(m))-\mathcal{B}^{(p)}_m(v_{j_1+1}(m))\right\vert^{4}\right]+\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(v_{j_1+1}(m))-\mathcal{B}^{(p)}_m(s)\right\vert^{4}\right]\bigg). \end{multline}
\begin{multline} \mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(t)-\mathcal{B}^{(p)}_m(s)\right\vert^{4}\right]\leq \mathrm{Cste}\bigg(\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(t)-\mathcal{B}^{(p)}_m(v_{j_2}(m))\right\vert^{4}\right] \\[3pt] +\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(v_{j_2}(m))-\mathcal{B}^{(p)}_m(v_{j_1+1}(m))\right\vert^{4}\right]+\mathbb{E}\left[\left\vert \mathcal{B}^{(p)}_m(v_{j_1+1}(m))-\mathcal{B}^{(p)}_m(s)\right\vert^{4}\right]\bigg). \end{multline}
Notation. For the sequel, we introduce the random variable
![]() $\mathsf{N}_{[s,t]}$
for
$\mathsf{N}_{[s,t]}$
for
![]() $(s\leq t)\in[0, 1]^2$
, which is binomial-
$(s\leq t)\in[0, 1]^2$
, which is binomial-
![]() $\left(m,q(t)-q(s)\right)$
-distributed. If
$\left(m,q(t)-q(s)\right)$
-distributed. If
![]() $j\in\{0,\ldots,m\}$
and
$j\in\{0,\ldots,m\}$
and
![]() $s=v_{j}(m)$
(or t), we will abuse notation and write
$s=v_{j}(m)$
(or t), we will abuse notation and write
![]() $\mathsf{N}_{[j,t]}=\mathsf{N}_{[v_{j}(m),t]}$
. Notice that
$\mathsf{N}_{[j,t]}=\mathsf{N}_{[v_{j}(m),t]}$
. Notice that
![]() $q(v_j(m))=\frac{j}{m}$
, so that
$q(v_j(m))=\frac{j}{m}$
, so that
![]() $\mathsf{N}_{[j,j+1]}$
is binomial-
$\mathsf{N}_{[j,j+1]}$
is binomial-
![]() $(m,\frac{1}{m})$
-distributed.
$(m,\frac{1}{m})$
-distributed.
Recall (5.37). We have the following equalities in distribution:
where
![]() $\mathbf{w}^{(j_1,j_2)}=(\boldsymbol{\zeta}^{(j_1,j_2)},\boldsymbol{\xi}^{(j_1,j_2)})$
is a random variable distributed as the law of a pair
$\mathbf{w}^{(j_1,j_2)}=(\boldsymbol{\zeta}^{(j_1,j_2)},\boldsymbol{\xi}^{(j_1,j_2)})$
is a random variable distributed as the law of a pair
![]() $(\boldsymbol{\zeta},\boldsymbol{\xi})$
conditioned on
$(\boldsymbol{\zeta},\boldsymbol{\xi})$
conditioned on
where
![]() $\boldsymbol{\zeta},\boldsymbol{\xi}$
are independent exponential variables with mean 1.
$\boldsymbol{\zeta},\boldsymbol{\xi}$
are independent exponential variables with mean 1.
Note that for any random variable
![]() $\mathbf{x}$
that is binomial-(m, p)-distributed,
$\mathbf{x}$
that is binomial-(m, p)-distributed,
Since
![]() $mp\leq m^2p^2$
, for
$mp\leq m^2p^2$
, for
![]() $p\geq1/m$
(and here
$p\geq1/m$
(and here
![]() $q(v_{j_2}(m))-q(v_{j_1+1}(m))\geq 1/m$
), we obtain
$q(v_{j_2}(m))-q(v_{j_1+1}(m))\geq 1/m$
), we obtain
where we have used Proposition 3 to bound
![]() $\mathbb{E}[\big(\boldsymbol{\xi}^{(j_1,j_2)}\big)^4]\leq 4!$
.
$\mathbb{E}[\big(\boldsymbol{\xi}^{(j_1,j_2)}\big)^4]\leq 4!$
.
Now, by the definition of
![]() $\mathcal{B}_m$
,
$\mathcal{B}_m$
,
and since
because
![]() $t\mapsto q(t)$
is convex on [0, 1], using also (5.51), we reach
$t\mapsto q(t)$
is convex on [0, 1], using also (5.51), we reach
In the end, using (5.51) and (5.53) twice in (5.47), we obtain
We may now work on the sequence
![]() $(\mathcal{A}_m)_{m\geq0}$
, so again fix
$(\mathcal{A}_m)_{m\geq0}$
, so again fix
![]() $(s,t) \in[0, 1]^2$
such that
$(s,t) \in[0, 1]^2$
such that
![]() $0\leq s \lt t\leq 1$
. Recall (5.37) and let
$0\leq s \lt t\leq 1$
. Recall (5.37) and let
![]() $\mathbf{w}_1^{(j_1,j_2)},\ldots,\mathbf{w}_{\mathsf{N}_{[j_1+1,j_2]}}^{(j_1,j_2)}$
be a sequence of i.i.d. random variables having the same distribution as
$\mathbf{w}_1^{(j_1,j_2)},\ldots,\mathbf{w}_{\mathsf{N}_{[j_1+1,j_2]}}^{(j_1,j_2)}$
be a sequence of i.i.d. random variables having the same distribution as
![]() $\mathbf{w}^{(j_1,j_2)}$
. We have the equality in distribution
$\mathbf{w}^{(j_1,j_2)}$
. We have the equality in distribution
 \begin{align} \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))&\mathrel{\mathop{\kern 0pt=}\limits^{(d)}} \sum_{i=1}^{\mathsf{N}_{[j_1+1,j_2]}}\frac{\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]}{\sqrt{m}}, \end{align}
\begin{align} \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))&\mathrel{\mathop{\kern 0pt=}\limits^{(d)}} \sum_{i=1}^{\mathsf{N}_{[j_1+1,j_2]}}\frac{\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]}{\sqrt{m}}, \end{align}
so that
 \begin{multline} \mathbb{E}\left[\left\vert \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))\right\vert^{4}\right] =\\[3pt] \sum_{r=0}^{m}\frac{1}{m^2}\mathbb{E}\left[\left\vert\sum_{j=1}^{r}\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]\right\vert^4\right]\mathbb{P}\left(\mathsf{N}_{[j_1+1,j_2]}=r\right). \end{multline}
\begin{multline} \mathbb{E}\left[\left\vert \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))\right\vert^{4}\right] =\\[3pt] \sum_{r=0}^{m}\frac{1}{m^2}\mathbb{E}\left[\left\vert\sum_{j=1}^{r}\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]\right\vert^4\right]\mathbb{P}\left(\mathsf{N}_{[j_1+1,j_2]}=r\right). \end{multline}
If
![]() $\mathbf{H}^{(j_1,j_2)}$
is a random variable having the law of
$\mathbf{H}^{(j_1,j_2)}$
is a random variable having the law of
![]() $\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]$
, then for all
$\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]$
, then for all
![]() $r\in\{1,\ldots,m\}$
,
$r\in\{1,\ldots,m\}$
,
 \begin{align}\nonumber \frac 1{m^2}\mathbb{E}\left[\left\vert\sum_{j=1}^{r}\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]\right\vert^4\right] \leq \frac{r\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^4\right]}{m^2}+\frac{r^2\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^2\right]}{2m^2}. \end{align}
\begin{align}\nonumber \frac 1{m^2}\mathbb{E}\left[\left\vert\sum_{j=1}^{r}\mathbf{w}_1^{(j_1,j_2)}-\mathbb{E}[\mathbf{w}^{(j_1,j_2)}]\right\vert^4\right] \leq \frac{r\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^4\right]}{m^2}+\frac{r^2\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^2\right]}{2m^2}. \end{align}
Therefore,
 \begin{multline} \mathbb{E}\left[\left\vert \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))\right\vert^{4}\right]\leq \frac{\mathbb{E}\left[\mathsf{N}_{[j_1+1,j_2]}\right]\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^4\right]}{m^2}\\[3pt] +\frac{\mathbb{E}\left[\mathsf{N}_{[j_1+1,j_2]}^2\right]\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^2\right]}{2m^2}. \end{multline}
\begin{multline} \mathbb{E}\left[\left\vert \mathcal{A}_m(v_{j_2}(m))-\mathcal{A}_m(v_{j_1+1}(m))\right\vert^{4}\right]\leq \frac{\mathbb{E}\left[\mathsf{N}_{[j_1+1,j_2]}\right]\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^4\right]}{m^2}\\[3pt] +\frac{\mathbb{E}\left[\mathsf{N}_{[j_1+1,j_2]}^2\right]\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^2\right]}{2m^2}. \end{multline}
In the same spirit as in Part 4 of Proposition 3, we may see that for all
![]() $s\in\mathbb{N}$
, we have
$s\in\mathbb{N}$
, we have
![]() $\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^s\right]\leq s!$
. For any random variable
$\mathbb{E}\left[(\mathbf{H}^{(j_1,j_2)})^s\right]\leq s!$
. For any random variable
![]() $\mathbf{x}$
that is binomial-(m,p)-distributed, we have
$\mathbf{x}$
that is binomial-(m,p)-distributed, we have
as soon as
![]() $p\geq 1/m$
(and here
$p\geq 1/m$
(and here
![]() $q(v_{j_2}(m))-q(v_{j_1+1}(m))\geq 1/m$
); hence
$q(v_{j_2}(m))-q(v_{j_1+1}(m))\geq 1/m$
); hence
We can treat the other terms
![]() $\mathcal{A}^{(p)}_m(t)-\mathcal{A}^{(p)}_m(v_{j_2}(m))$
and
$\mathcal{A}^{(p)}_m(t)-\mathcal{A}^{(p)}_m(v_{j_2}(m))$
and
![]() $\mathcal{A}^{(p)}_m(v_{j_1+1}(m))-\mathcal{A}^{(p)}_m(s)$
exactly as we did for the process
$\mathcal{A}^{(p)}_m(v_{j_1+1}(m))-\mathcal{A}^{(p)}_m(s)$
exactly as we did for the process
![]() $\mathcal{B}_m$
in (5.53) and finally find that
$\mathcal{B}_m$
in (5.53) and finally find that
In the case
![]() $j_1=j_2$
, we may immediately write, in both cases
$j_1=j_2$
, we may immediately write, in both cases
![]() $\mathcal{A}_m,\mathcal{B}_m$
(we take
$\mathcal{A}_m,\mathcal{B}_m$
(we take
![]() $\mathcal{B}_m$
here as an example), just as in (5.52),
$\mathcal{B}_m$
here as an example), just as in (5.52),
so that
for every
![]() $p\in\{1,2\}$
, by the same arguments as before. This proves the tightnesses of the sequences of processes
$p\in\{1,2\}$
, by the same arguments as before. This proves the tightnesses of the sequences of processes
![]() $(\mathcal{A}_m),(\mathcal{B}_m)$
.
$(\mathcal{A}_m),(\mathcal{B}_m)$
.
Step 3: In the next step, we prove that
for every
![]() $p\in\{1,2\}$
. Since
$p\in\{1,2\}$
. Since
and for all
![]() $j\in\{0,\ldots,m-1\}$
,
$j\in\{0,\ldots,m-1\}$
,
 \begin{multline} \sup_{t\in I_j(m)}\left\vert\overline{\mathsf{Y}}^{(p)}_m(t)-\overline{\mathcal{Y}}^{(p)}_m(t)\right\vert \leq\sup_{t\in I_j(m)}\left\vert\overline{\mathsf{Y}}^{(p)}_m(t)-\overline{\mathsf{Y}}^{(p)}_m(v_j(m))\right\vert\\[3pt] +\sup_{t\in I_j(m)}\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(t)\right\vert, \end{multline}
\begin{multline} \sup_{t\in I_j(m)}\left\vert\overline{\mathsf{Y}}^{(p)}_m(t)-\overline{\mathcal{Y}}^{(p)}_m(t)\right\vert \leq\sup_{t\in I_j(m)}\left\vert\overline{\mathsf{Y}}^{(p)}_m(t)-\overline{\mathsf{Y}}^{(p)}_m(v_j(m))\right\vert\\[3pt] +\sup_{t\in I_j(m)}\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(t)\right\vert, \end{multline}
the proof of this part consists in showing that both processes
![]() $(\overline{\mathsf{Y}}^{(p)}_m),(\overline{\mathcal{Y}}^{(p)}_m)$
admit fluctuations larger than
$(\overline{\mathsf{Y}}^{(p)}_m),(\overline{\mathcal{Y}}^{(p)}_m)$
admit fluctuations larger than
![]() $\varepsilon \gt 0$
on an interval
$\varepsilon \gt 0$
on an interval
![]() $I_j(m)$
with probability
$I_j(m)$
with probability
![]() $o(1/m)$
. Fix
$o(1/m)$
. Fix
![]() $j\in\{0,\ldots,m-1\}$
for the rest of the proof. Since
$j\in\{0,\ldots,m-1\}$
for the rest of the proof. Since
![]() $(\overline{\mathcal{Y}}^{(p)}_m)$
is linear on every interval
$(\overline{\mathcal{Y}}^{(p)}_m)$
is linear on every interval
![]() $I_j(m)$
, we have, first,
$I_j(m)$
, we have, first,
and second, for all
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
 \begin{align}\nonumber \mathbb{P}\left(\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(v_{j+1}(m))\right\vert\geq \varepsilon\right)&\leq\frac{ \mathbb{E}\left[\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(v_{j+1}(m))\right\vert^4\right]}{\varepsilon^4} \leq \frac{\mathrm{Cste}}{\varepsilon^4m^2}, \end{align}
\begin{align}\nonumber \mathbb{P}\left(\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(v_{j+1}(m))\right\vert\geq \varepsilon\right)&\leq\frac{ \mathbb{E}\left[\left\vert\overline{\mathcal{Y}}^{(p)}_m(v_j(m))-\overline{\mathcal{Y}}^{(p)}_m(v_{j+1}(m))\right\vert^4\right]}{\varepsilon^4} \leq \frac{\mathrm{Cste}}{\varepsilon^4m^2}, \end{align}
where the last inequality comes from the combination of (5.53) and (5.59). By the union bound, we obtain
Let us now handle the process
![]() $(\overline{\mathsf{Y}}^{(p)}_m)$
. Recall its definition (on page 37):
$(\overline{\mathsf{Y}}^{(p)}_m)$
. Recall its definition (on page 37):
![]() $\overline{\mathsf{Y}}^{(p)}_m=\sqrt{m}\left(\mathsf{C}_m^{(p)}-\mathsf{C}_\infty^{(p)}\right)$
. We can write
$\overline{\mathsf{Y}}^{(p)}_m=\sqrt{m}\left(\mathsf{C}_m^{(p)}-\mathsf{C}_\infty^{(p)}\right)$
. We can write
where
is deterministic since
![]() ${\mathsf{C}}_\infty(t)=(x(t),y(t))$
(see (5.4)). This term is easily handled:
${\mathsf{C}}_\infty(t)=(x(t),y(t))$
(see (5.4)). This term is easily handled:
So it suffices to prove that
We return to the definition of
![]() $\overline{\mathsf{C}}_m$
in (5.22). The term
$\overline{\mathsf{C}}_m$
in (5.22). The term
![]() $\left\vert\overline{\mathsf{C}}_m(t)-\overline{\mathsf{C}}_m(v_j(m))\right\vert$
preserves the contribution of the vectors
$\left\vert\overline{\mathsf{C}}_m(t)-\overline{\mathsf{C}}_m(v_j(m))\right\vert$
preserves the contribution of the vectors
![]() $\mathbf{w}[m]$
whose slopes are in the interval
$\mathbf{w}[m]$
whose slopes are in the interval
![]() $\left[\tan\left(\frac{\pi}{2}v_j(m)\right),\tan\left(\frac{\pi}{2}t\right)\right)$
, i.e.
$\left[\tan\left(\frac{\pi}{2}v_j(m)\right),\tan\left(\frac{\pi}{2}t\right)\right)$
, i.e.
In the right-hand side of (5.67), the sum is a sum of non-negative terms; it is thus immediate that
(and a similar property holds for
![]() $\sup_j L_2^{(2)} (j,m)$
). By the union bound,
$\sup_j L_2^{(2)} (j,m)$
). By the union bound,
![]() $\mathbb{P}(\max\{\boldsymbol{\zeta}_i, 1\leq i \leq m\}\geq 3\log m) \leq 1/m^2$
. By Markov, the binomial random variable
$\mathbb{P}(\max\{\boldsymbol{\zeta}_i, 1\leq i \leq m\}\geq 3\log m) \leq 1/m^2$
. By Markov, the binomial random variable
![]() $\mathsf{N}_{[j,j+1]}$
satisfies
$\mathsf{N}_{[j,j+1]}$
satisfies
These two bounds, together with (5.68), yield (5.66).
This completes Step 3 of the proof, as well as the proof as a whole. Indeed, by Lemma 13 and what we proved in Steps 2 and 3, the sequence of processes
![]() $\left(\overline{\mathsf{Y}}_m\right)$
converges in distribution to the same limit as the sequence
$\left(\overline{\mathsf{Y}}_m\right)$
converges in distribution to the same limit as the sequence
![]() $\left(\overline{\mathcal{Y}}_m\right)$
. This limit has been proven to be
$\left(\overline{\mathcal{Y}}_m\right)$
. This limit has been proven to be
![]() $\overline{\mathsf{Y}}$
.
$\overline{\mathsf{Y}}$
.
6. Random generation
In this section, given
![]() $\kappa\geq3$
, we provide an algorithm to sample an n-tuple of points z[n] with distribution
$\kappa\geq3$
, we provide an algorithm to sample an n-tuple of points z[n] with distribution
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
. In Figure 14, we plotted two drawings of
${\mathbb{D}}^{(n)}_{\kappa}$
. In Figure 14, we plotted two drawings of
![]() $\kappa$
-sampling in the cases
$\kappa$
-sampling in the cases
![]() $\kappa=5$
and
$\kappa=5$
and
![]() $\kappa=7$
. In the special cases
$\kappa=7$
. In the special cases
![]() $\kappa=3,4$
where we have
$\kappa=3,4$
where we have
![]() ${\mathbb{D}}^{(n)}_{\kappa}=\mathbb{Q}^{(n)}_{\kappa}$
(recall the discussion on pages 4 and 14), we will provide two alternative sharpened algorithms.
${\mathbb{D}}^{(n)}_{\kappa}=\mathbb{Q}^{(n)}_{\kappa}$
(recall the discussion on pages 4 and 14), we will provide two alternative sharpened algorithms.
6.1. Algorithm of
 $\kappa$
-sampling
$\kappa$
-sampling
The algorithm starts with the computation of the
![]() $\mathsf{ECP}$
. We will use the following notation to express the side lengths with respect to
$\mathsf{ECP}$
. We will use the following notation to express the side lengths with respect to
![]() $\ell[\kappa]$
: put
$\ell[\kappa]$
: put
![]() $\displaystyle P_\kappa=\kappa r_\kappa/w_\kappa$
with
$\displaystyle P_\kappa=\kappa r_\kappa/w_\kappa$
with
![]() $\displaystyle w_\kappa\,:\!=\,\frac{1+\cos(\theta_\kappa)}{\sin(\theta_\kappa)}$
, and recall that by Proposition 1, for
$\displaystyle w_\kappa\,:\!=\,\frac{1+\cos(\theta_\kappa)}{\sin(\theta_\kappa)}$
, and recall that by Proposition 1, for
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
and
$\ell[\kappa]\in\mathcal{L}_\kappa$
and
![]() $\widetilde{c}[\kappa]=\frac{1}{w_\kappa}(r_\kappa-\mathfrak{cl}_j(\ell[\kappa]))_{j\in\{1,\ldots,\kappa\}}$
with
$\widetilde{c}[\kappa]=\frac{1}{w_\kappa}(r_\kappa-\mathfrak{cl}_j(\ell[\kappa]))_{j\in\{1,\ldots,\kappa\}}$
with
![]() $\widetilde{c}=\sum_{j=1}^\kappa\widetilde{c}_j$
, we have
$\widetilde{c}=\sum_{j=1}^\kappa\widetilde{c}_j$
, we have
 \begin{align*}\widetilde{c}+\sum_{j=1}^{\kappa}\ell_j=P_\kappa. \end{align*}
\begin{align*}\widetilde{c}+\sum_{j=1}^{\kappa}\ell_j=P_\kappa. \end{align*}
Algorithm 1
![]() $\kappa$
-sampling
$\kappa$
-sampling

Let us prove that this algorithm returns an n-tuple z[n] that is
![]() ${\mathbb{D}}^{(n)}_{\kappa}$
-distributed, and that this is done within a reasonable amount of time. The notation
${\mathbb{D}}^{(n)}_{\kappa}$
-distributed, and that this is done within a reasonable amount of time. The notation
![]() $\propto$
means that two quantities are proportional.
$\propto$
means that two quantities are proportional.
Proof of Theorem
4. Denote by
![]() $\mathbb{P}_{\mathrm{Alg}}$
the probability of an event in our
$\mathbb{P}_{\mathrm{Alg}}$
the probability of an event in our
![]() $\kappa$
-sampling. The distribution induced in the first step of the algorithm (which is nothing but a rejection algorithm) satisfies
$\kappa$
-sampling. The distribution induced in the first step of the algorithm (which is nothing but a rejection algorithm) satisfies
 \begin{align} \mathbb{P}_{\mathrm{Alg}}\left(\boldsymbol{\ell}^{(n)}[\kappa]\in\prod_{i=1}^{\kappa}\text{d} \ell_i\right) &\propto \, \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\left(P_\kappa-\sum_{j=1}^{\kappa}\ell_j\right)^{2n-\kappa}\prod_{j=1}^{\kappa}\text{d} \ell_j= \, \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\widetilde{c}^{2n-\kappa}\prod_{j=1}^{\kappa}\text{d} \ell_j. \end{align}
\begin{align} \mathbb{P}_{\mathrm{Alg}}\left(\boldsymbol{\ell}^{(n)}[\kappa]\in\prod_{i=1}^{\kappa}\text{d} \ell_i\right) &\propto \, \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\left(P_\kappa-\sum_{j=1}^{\kappa}\ell_j\right)^{2n-\kappa}\prod_{j=1}^{\kappa}\text{d} \ell_j= \, \mathbf{1}_{\left\{{\ell[\kappa]\in\mathcal{L}_\kappa}\right\}}\widetilde{c}^{2n-\kappa}\prod_{j=1}^{\kappa}\text{d} \ell_j. \end{align}
The second step (which is also a rejection algorithm working at
![]() $\ell[\kappa]$
fixed) induces the distribution
$\ell[\kappa]$
fixed) induces the distribution
 \begin{align}\nonumber \mathbb{P}_{\mathrm{Alg}}\left(\mathbf{s}^{(n)}[\kappa]=s[\kappa] \, \big\vert \, \boldsymbol{\ell}^{(n)}[\kappa]\in\prod_{i=1}^{\kappa}\text{d} \ell_i\right)&\propto \, \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}}\prod_{j=1}^{\kappa}\frac{(1/\kappa)^{s_j}}{s_j!}\frac{(\widetilde{c}_j/\widetilde{c})^{N_j}}{N_j!}\\[3pt] &\propto \, \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}}\prod_{j=1}^{\kappa}\frac{(\widetilde{c}_j/\widetilde{c})^{s_j+s_{{j+1}}-1}}{s_j!(s_j+s_{{j+1}}-1)!}. \end{align}
\begin{align}\nonumber \mathbb{P}_{\mathrm{Alg}}\left(\mathbf{s}^{(n)}[\kappa]=s[\kappa] \, \big\vert \, \boldsymbol{\ell}^{(n)}[\kappa]\in\prod_{i=1}^{\kappa}\text{d} \ell_i\right)&\propto \, \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}}\prod_{j=1}^{\kappa}\frac{(1/\kappa)^{s_j}}{s_j!}\frac{(\widetilde{c}_j/\widetilde{c})^{N_j}}{N_j!}\\[3pt] &\propto \, \mathbf{1}_{\left\{{s[\kappa]\in\mathbb{N}_\kappa(n)}\right\}}\prod_{j=1}^{\kappa}\frac{(\widetilde{c}_j/\widetilde{c})^{s_j+s_{{j+1}}-1}}{s_j!(s_j+s_{{j+1}}-1)!}. \end{align}
This gives the appropriate joint distribution for
![]() $(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
as computed in Theorem 6. Now, given
$(\boldsymbol{\ell}^{(n)}[\kappa],\mathbf{s}^{(n)}[\kappa])$
as computed in Theorem 6. Now, given
![]() $\ell[\kappa],c[\kappa],s[\kappa]$
, and since, conditionally on the
$\ell[\kappa],c[\kappa],s[\kappa]$
, and since, conditionally on the
![]() $c[\kappa]$
, the projections of the vectors v[n] are uniform in the
$c[\kappa]$
, the projections of the vectors v[n] are uniform in the
![]() $c[\kappa]$
, the way we are constructing our vectors is valid and so is the building of
$c[\kappa]$
, the way we are constructing our vectors is valid and so is the building of
![]() $z[n].$
$z[n].$
We saw that the
![]() $\ell[\kappa]$
behaves in
$\ell[\kappa]$
behaves in
![]() $c/n$
in Theorem 7, so that
$c/n$
in Theorem 7, so that
![]() $\mathbf{1}_{\left\{{\ell[\kappa]\in n\mathcal{L}_\kappa}\right\}}\to 1$
pointwise and thus the condition
$\mathbf{1}_{\left\{{\ell[\kappa]\in n\mathcal{L}_\kappa}\right\}}\to 1$
pointwise and thus the condition
![]() $\ell[\kappa]\in\mathcal{L}_\kappa$
of Step 1 is satisfied with a probability going to 1 with n. This step costs only the drawing of 2n uniform variates requiring
$\ell[\kappa]\in\mathcal{L}_\kappa$
of Step 1 is satisfied with a probability going to 1 with n. This step costs only the drawing of 2n uniform variates requiring
![]() $\mathcal{O}\left(n\log(n)\right)$
operations. Notice that to perfect the algorithm, one could reuse the unused uniform variates of Step 1 for the next steps.
$\mathcal{O}\left(n\log(n)\right)$
operations. Notice that to perfect the algorithm, one could reuse the unused uniform variates of Step 1 for the next steps.
As for the second step, the probability that the two multinomial samples coincide behaves in
![]() $n^{-\kappa/2}$
. A standard efficient algorithm to simulate a multinomial distribution is the alias method presented by Walker [Reference Walker27], the theoretical basis of which was provided by Kronmal and Peterson [Reference Kronmal and Peterson15]. In our case the complexity of the alias method is
$n^{-\kappa/2}$
. A standard efficient algorithm to simulate a multinomial distribution is the alias method presented by Walker [Reference Walker27], the theoretical basis of which was provided by Kronmal and Peterson [Reference Kronmal and Peterson15]. In our case the complexity of the alias method is
![]() $\mathcal{O}\left(n\kappa\log(\kappa)\right)$
. (There exists other efficient procedures, such as the two-stage method of Brown and Bromberg [Reference Brown and Bromberg8]. For a discussion of the most suitable method of multinomial sampling, we refer to [Reference Davis12].)
$\mathcal{O}\left(n\kappa\log(\kappa)\right)$
. (There exists other efficient procedures, such as the two-stage method of Brown and Bromberg [Reference Brown and Bromberg8]. For a discussion of the most suitable method of multinomial sampling, we refer to [Reference Davis12].)
The last step includes several iterations of sampling and sorting 2n variates, which also has a complexity in
![]() $\mathcal{O}\left(n\log(n)\right)$
.
$\mathcal{O}\left(n\log(n)\right)$
.
The second step is obviously the most costly, and it implies a global complexity of
![]() $\mathcal{O}\left(n^{\kappa/2+1}\kappa\log(\kappa)\right).$
Despite considerable effort, we were not able to make any significant progress in finding an efficient algorithm to reduce the cost of this step.
$\mathcal{O}\left(n^{\kappa/2+1}\kappa\log(\kappa)\right).$
Despite considerable effort, we were not able to make any significant progress in finding an efficient algorithm to reduce the cost of this step.

Figure 14. Two examples of
![]() $\kappa$
-sampling. The set of points is the set of vertices of a convex z[n]-gon, whose boundary is very close to the limit shape drawn inside the
$\kappa$
-sampling. The set of points is the set of vertices of a convex z[n]-gon, whose boundary is very close to the limit shape drawn inside the
![]() $\kappa$
-gon.
$\kappa$
-gon.
6.2. Exact and fast algorithm of
 $\triangle$
-sampling
$\triangle$
-sampling
In the triangular case, the algorithm of
![]() $\triangle$
-sampling avoids the rejection-sampling steps 1 and 2 included in the algorithm of
$\triangle$
-sampling avoids the rejection-sampling steps 1 and 2 included in the algorithm of
![]() $\kappa$
-sampling, which makes the sampling direct and immediately implies a reasonable computation time. Indeed, it happens to be that in the case
$\kappa$
-sampling, which makes the sampling direct and immediately implies a reasonable computation time. Indeed, it happens to be that in the case
![]() $\kappa=3$
, the joint distribution of
$\kappa=3$
, the joint distribution of
![]() ${\boldsymbol\ell}^{(n)}[3],\mathbf{s}^{(n)}[3]$
comes with simplifications (we will show this in Theorem 11) and becomes
${\boldsymbol\ell}^{(n)}[3],\mathbf{s}^{(n)}[3]$
comes with simplifications (we will show this in Theorem 11) and becomes
 \begin{multline} \mathbb{P}\left({\boldsymbol\ell}^{(n)}[3]\in\prod_{j=1}^{3}\mathrm{d}\ell_j,\mathbf{s}^{(n)}[3]=(i,j,k)\right)=\frac{n!\sin(\theta_\kappa)^{n-3}}{\mathbb{P}_{\triangle}(n)((n-1)!)^3}\mathbf{1}_{\left\{{\ell_1+\ell_2+\ell_3\leq\frac{\sqrt{3}}{2}r_3}\right\}} \\[3pt] \times\left(r_3-\frac{2}{\sqrt{3}}(\ell_1+\ell_2+\ell_3)\right)^{2n-3} \left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\mathbf{1}_{\left\{{i+j+k=n}\right\}}\prod_{j=1}^{3}\mathrm{d}\ell_j.\end{multline}
\begin{multline} \mathbb{P}\left({\boldsymbol\ell}^{(n)}[3]\in\prod_{j=1}^{3}\mathrm{d}\ell_j,\mathbf{s}^{(n)}[3]=(i,j,k)\right)=\frac{n!\sin(\theta_\kappa)^{n-3}}{\mathbb{P}_{\triangle}(n)((n-1)!)^3}\mathbf{1}_{\left\{{\ell_1+\ell_2+\ell_3\leq\frac{\sqrt{3}}{2}r_3}\right\}} \\[3pt] \times\left(r_3-\frac{2}{\sqrt{3}}(\ell_1+\ell_2+\ell_3)\right)^{2n-3} \left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\mathbf{1}_{\left\{{i+j+k=n}\right\}}\prod_{j=1}^{3}\mathrm{d}\ell_j.\end{multline}
Algorithm 2
![]() $\triangle$
-sampling
$\triangle$
-sampling

In Figure 15, we plotted an example of
![]() $\triangle$
-sampling. To draw
$\triangle$
-sampling. To draw
![]() $(s_1,s_2,s_3)$
according to three binomial distributions
$(s_1,s_2,s_3)$
according to three binomial distributions
![]() $\displaystyle \mathcal{B}(n-1,\frac{1}{2})$
and conditioned on
$\displaystyle \mathcal{B}(n-1,\frac{1}{2})$
and conditioned on
![]() $s_1+s_2+s_3=n$
, we may do the following:
$s_1+s_2+s_3=n$
, we may do the following:
-
• Draw
 $3n-3$
Bernoulli(
$3n-3$
Bernoulli(
 $\frac{1}{3}$
) random variables
$\frac{1}{3}$
) random variables
 $\mathbf{x}[3n-3]$
.
$\mathbf{x}[3n-3]$
. -
• Set
 $(s_1,s_2,s_3)=\left(\sum_{i=1}^{n-1}\mathbf{x}_i,\sum_{i=n}^{2n-2}\mathbf{x}_i,\sum_{i=2n-1}^{3n-3}\mathbf{x}_i\right)$
.
$(s_1,s_2,s_3)=\left(\sum_{i=1}^{n-1}\mathbf{x}_i,\sum_{i=n}^{2n-2}\mathbf{x}_i,\sum_{i=2n-1}^{3n-3}\mathbf{x}_i\right)$
. -
• Correct
 $\mathbf{x}[3n-3]$
to have
$\mathbf{x}[3n-3]$
to have
 $\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
.
$\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
.
The binomial correction works as follows: if
![]() $\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
, then we have the right distribution. Otherwise, if
$\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
, then we have the right distribution. Otherwise, if
![]() $\sum_{i=1}^{3n-3}\mathbf{x}_i \lt n$
, pick uniformly some
$\sum_{i=1}^{3n-3}\mathbf{x}_i \lt n$
, pick uniformly some
![]() $j\in\{i;\mathbf{x}_i=0\}$
and put
$j\in\{i;\mathbf{x}_i=0\}$
and put
![]() $\mathbf{x}_j=1$
until
$\mathbf{x}_j=1$
until
![]() $\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
. If
$\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
. If
![]() $\sum_{i=1}^{3n-3}\mathbf{x}_i \gt n$
, pick uniformly some
$\sum_{i=1}^{3n-3}\mathbf{x}_i \gt n$
, pick uniformly some
![]() $j\in\{i;\mathbf{x}_i=1\}$
and put
$j\in\{i;\mathbf{x}_i=1\}$
and put
![]() $\mathbf{x}_j=0$
until
$\mathbf{x}_j=0$
until
![]() $\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
.
$\sum_{i=1}^{3n-3}\mathbf{x}_i=n$
.
At the end we get that
 \begin{multline*} \mathbb{P}_{\mathrm{Alg}}\left(\mathbf{s}^{(n)}[3]=(i,j,k)\right) \, \propto \, \left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\frac1{2}\right)^{i}\left(\frac1{2}\right)^{n-1-i}\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\frac1{2}\right)^{n-1}\\[3pt] \times\left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\left(\frac1{2}\right)^{n-1}\mathbf{1}_{\left\{{i+j+k=n}\right\}},\end{multline*}
\begin{multline*} \mathbb{P}_{\mathrm{Alg}}\left(\mathbf{s}^{(n)}[3]=(i,j,k)\right) \, \propto \, \left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\frac1{2}\right)^{i}\left(\frac1{2}\right)^{n-1-i}\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\frac1{2}\right)^{n-1}\\[3pt] \times\left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\left(\frac1{2}\right)^{n-1}\mathbf{1}_{\left\{{i+j+k=n}\right\}},\end{multline*}
so that
The analysis of the sampling of
![]() ${\boldsymbol\ell}_n[3]$
is the same as in the general
${\boldsymbol\ell}_n[3]$
is the same as in the general
![]() $\kappa$
-sampling. In the end, the algorithm of
$\kappa$
-sampling. In the end, the algorithm of
![]() $\triangle$
-generation admits a global complexity of
$\triangle$
-generation admits a global complexity of
![]() $\mathcal{O}\left(n\log(n)\right)$
(in expectation).
$\mathcal{O}\left(n\log(n)\right)$
(in expectation).

Figure 15. A
![]() $\triangle$
-sampling, some z[n]-gon for
$\triangle$
-sampling, some z[n]-gon for
![]() $n=1000$
, close to the limit shape.
$n=1000$
, close to the limit shape.
Algorithm 3.
![]() $\Box$
-sampling
$\Box$
-sampling

6.3. Exact and fast algorithm of
 ${\Box}$
-sampling
${\Box}$
-sampling
In the square case, a fast
![]() ${\Box}$
-sampling can be proposed, which is slightly different from the
${\Box}$
-sampling can be proposed, which is slightly different from the
![]() ${\triangle}$
-sampling and from the
${\triangle}$
-sampling and from the
![]() ${\kappa}$
-sampling. In Figure 16, we plotted an example of this
${\kappa}$
-sampling. In Figure 16, we plotted an example of this
![]() $\Box$
-sampling.
$\Box$
-sampling.
Indeed, in this case, no affine mapping intervenes in the proof since all corners are already right triangles. We may thus consider the law of the positive x-components
![]() $\mathbf{i}_n=\mathbf{s}_4^{(n)}+\mathbf{s}_1^{(n)}$
and y-components
$\mathbf{i}_n=\mathbf{s}_4^{(n)}+\mathbf{s}_1^{(n)}$
and y-components
![]() $\mathbf{j}_n=\mathbf{s}_1^{(n)}+\mathbf{s}_2^{(n)}$
of the vectors forming the boundary of a z[n]-gon. A quick calculus allows us to obtain
$\mathbf{j}_n=\mathbf{s}_1^{(n)}+\mathbf{s}_2^{(n)}$
of the vectors forming the boundary of a z[n]-gon. A quick calculus allows us to obtain
 \begin{multline} \mathbb{P}\left({\boldsymbol\ell}_n[4]\in\prod_{j=1}^{4}\mathrm{d}\ell_j,\mathbf{i}_n=i,\mathbf{j}_n=j\right)=\frac{(n!)^2}{\mathbb{P}_{\Box}(n)((n-1)!)^4}\mathbf{1}_{\left\{{\ell_1+\ell_3\leq1}\right\}}\mathbf{1}_{\left\{{\ell_2+\ell_4\leq1}\right\}} \\[3pt] \times\left(1-(\ell_1+\ell_3)\right)^{n-2}\left(1-(\ell_2+\ell_4)\right)^{n-2}\left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {i-1}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j-1}\end{smallmatrix}\right)\prod_{j=1}^{4}\mathrm{d}\ell_j.\end{multline}
\begin{multline} \mathbb{P}\left({\boldsymbol\ell}_n[4]\in\prod_{j=1}^{4}\mathrm{d}\ell_j,\mathbf{i}_n=i,\mathbf{j}_n=j\right)=\frac{(n!)^2}{\mathbb{P}_{\Box}(n)((n-1)!)^4}\mathbf{1}_{\left\{{\ell_1+\ell_3\leq1}\right\}}\mathbf{1}_{\left\{{\ell_2+\ell_4\leq1}\right\}} \\[3pt] \times\left(1-(\ell_1+\ell_3)\right)^{n-2}\left(1-(\ell_2+\ell_4)\right)^{n-2}\left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {i-1}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j-1}\end{smallmatrix}\right)\prod_{j=1}^{4}\mathrm{d}\ell_j.\end{multline}
In particular, this proves that
![]() $\mathbf{i}_n,\mathbf{j}_n$
are independent, and their law is explicit. It is easier to draw according to this distribution than to consider
$\mathbf{i}_n,\mathbf{j}_n$
are independent, and their law is explicit. It is easier to draw according to this distribution than to consider
![]() $\mathbf{s}^{(n)}[4].$
This approach is, once more, inspired by Valtr’s paper [Reference Valtr24].
$\mathbf{s}^{(n)}[4].$
This approach is, once more, inspired by Valtr’s paper [Reference Valtr24].
The law of a random variable
![]() $\mathbf{k}$
described in the first step satisfies
$\mathbf{k}$
described in the first step satisfies
The probability that two binomial samples are equal is typically
![]() $\frac{1}{\sqrt{n}}$
. A binomial sampling requires
$\frac{1}{\sqrt{n}}$
. A binomial sampling requires
![]() $\mathcal{O}\left(n\right)$
operations, and since this step is the most costly in the
$\mathcal{O}\left(n\right)$
operations, and since this step is the most costly in the
![]() $\Box$
-generation, the whole algorithm has a global complexity of
$\Box$
-generation, the whole algorithm has a global complexity of
![]() $\mathcal{O}(n^{3/2})$
.
$\mathcal{O}(n^{3/2})$
.

Figure 16. A
![]() $\Box$
-sampling, some z[n]-gon for
$\Box$
-sampling, some z[n]-gon for
![]() $n=1000$
, close to the limit shape.
$n=1000$
, close to the limit shape.
Appendix A. Proof of Lemma 4
We decompose
![]() $\mathbb{P}_\kappa(n)$
according to the number of sides of the
$\mathbb{P}_\kappa(n)$
according to the number of sides of the
![]() $\mathsf{ECP}$
we are considering.
$\mathsf{ECP}$
we are considering.
Let
![]() $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
![]() $\mathbb{U}^{(n)}_{\kappa}$
, and write
$\mathbb{U}^{(n)}_{\kappa}$
, and write
 \begin{align*} \mathbb{P}_\kappa(n)&=n!\sum_{\substack{\mathcal{J}\subset\{1,\ldots,\kappa\}\\[3pt] \vert\mathcal{J}\vert\geq 3}}\mathbb{P}\left(\mathbf{z}[n]\in\mathcal{C}_\kappa(n)\cap \mathrm{NZS}(\mathbf{z}[n])=\mathcal{J}\right).\end{align*}
\begin{align*} \mathbb{P}_\kappa(n)&=n!\sum_{\substack{\mathcal{J}\subset\{1,\ldots,\kappa\}\\[3pt] \vert\mathcal{J}\vert\geq 3}}\mathbb{P}\left(\mathbf{z}[n]\in\mathcal{C}_\kappa(n)\cap \mathrm{NZS}(\mathbf{z}[n])=\mathcal{J}\right).\end{align*}
We now borrow some considerations from Bárány ([Reference Bárány2, Reference Bárány3]).
Definition 2.
Given S a convex compact set (non-flat), let
![]() $x_1,\ldots,x_m,x_{m+1}=x_1$
be a subdivision of the boundary
$x_1,\ldots,x_m,x_{m+1}=x_1$
be a subdivision of the boundary
![]() $\partial S$
and let
$\partial S$
and let
![]() $d_i$
be the line supporting S at
$d_i$
be the line supporting S at
![]() $x_i$
for all
$x_i$
for all
![]() $i\in\{1,\ldots,m\}$
. Write
$i\in\{1,\ldots,m\}$
. Write
![]() $y_i$
for the intersection of
$y_i$
for the intersection of
![]() $d_i$
and
$d_i$
and
![]() $d_{i+1}$
(if
$d_{i+1}$
(if
![]() $d_{i}=d_{i+1}$
then
$d_{i}=d_{i+1}$
then
![]() $y_i$
can be any point between
$y_i$
can be any point between
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
). Let
$x_{i+1}$
). Let
![]() $T_i$
denote the triangle with vertices
$T_i$
denote the triangle with vertices
![]() $x_i,y_i,y_{i+1}$
and also its area. We define the affine perimeter of the convex set S as
$x_i,y_i,y_{i+1}$
and also its area. We define the affine perimeter of the convex set S as
where the limit is taken over all sequences of subdivisions x[m] with
![]() $\max_{1,\ldots,m}\vert x_i-x_{i+1}\vert \to 0.$
$\max_{1,\ldots,m}\vert x_i-x_{i+1}\vert \to 0.$
Theorem 10. (Limit shape theorem, Bárány [Reference Bárány2].) Let K be a compact convex domain of
![]() $\mathbb{R}^2$
with nonempty interior.
$\mathbb{R}^2$
with nonempty interior.
-
(1) There exists a convex domain
 $\mathsf{Dom}(K)\subset K$
such that
$\mathsf{Dom}(K)\subset K$
such that
 $\mathrm{AP}(\mathsf{Dom}(K)) \gt \mathrm{AP}(S)$
for all convex sets
$\mathrm{AP}(\mathsf{Dom}(K)) \gt \mathrm{AP}(S)$
for all convex sets
 $S\subset K$
different from
$S\subset K$
different from
 $\mathsf{Dom}(K).$
$\mathsf{Dom}(K).$
-
(2) Let
 $n\geq3$
, and let
$n\geq3$
, and let
 $\mathbf{z}[n]$
have distribution
$\mathbf{z}[n]$
have distribution
 $\mathbb{Q}_K^{(n)}$
. Then for all
$\mathbb{Q}_K^{(n)}$
. Then for all
 $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,  \begin{align*}\lim_{n\to+\infty}\mathbb{P}\left(d_H(\mathsf{conv}(\mathbf{z}[n]),\mathsf{Dom}(K)) \lt \varepsilon\right)=1. \end{align*}
\begin{align*}\lim_{n\to+\infty}\mathbb{P}\left(d_H(\mathsf{conv}(\mathbf{z}[n]),\mathsf{Dom}(K)) \lt \varepsilon\right)=1. \end{align*}
Definition 3.
Define
![]() $\mathrm{AP}^*(K)=\max\{\mathrm{AP}(S), S \text{ convex sets included in }K\}.$
$\mathrm{AP}^*(K)=\max\{\mathrm{AP}(S), S \text{ convex sets included in }K\}.$
In the case of the regular
![]() $\kappa$
-gons, the following result comes as a corollary of the properties of the affine perimeter.
$\kappa$
-gons, the following result comes as a corollary of the properties of the affine perimeter.
Lemma 16.
Let
![]() $p_1,\ldots,p_\kappa$
be the midpoints of the consecutives sides of
$p_1,\ldots,p_\kappa$
be the midpoints of the consecutives sides of
![]() $\mathfrak{C}_\kappa$
, and
$\mathfrak{C}_\kappa$
, and
![]() $y_1,\ldots,y_\kappa$
the vertices of
$y_1,\ldots,y_\kappa$
the vertices of
![]() $\mathfrak{C}_\kappa$
, so that
$\mathfrak{C}_\kappa$
, so that
![]() $p_i$
is the middle of the segment
$p_i$
is the middle of the segment
![]() $[y_i,y_{i+1}]$
(modulo
$[y_i,y_{i+1}]$
(modulo
![]() $\kappa$
). Let
$\kappa$
). Let
![]() $\mathcal{C}_i$
be the unique parabola tangent to
$\mathcal{C}_i$
be the unique parabola tangent to
![]() $p_i y_{i+1}$
at
$p_i y_{i+1}$
at
![]() $p_i$
and tangent to
$p_i$
and tangent to
![]() $y_{i+1} p_{i+1}$
at
$y_{i+1} p_{i+1}$
at
![]() $p_{i+1}.$
The convex domain
$p_{i+1}.$
The convex domain
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
is the subset of
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
is the subset of
![]() $\mathfrak{C}_\kappa$
whose boundary is formed by the parabolas
$\mathfrak{C}_\kappa$
whose boundary is formed by the parabolas
![]() $(\mathcal{C}_i)_{1\leq i\leq \kappa}$
. The set
$(\mathcal{C}_i)_{1\leq i\leq \kappa}$
. The set
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
is thus tangent to
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
is thus tangent to
![]() $\mathfrak{C}_\kappa$
in the
$\mathfrak{C}_\kappa$
in the
![]() $\kappa$
points
$\kappa$
points
![]() $p_1,\ldots,p_\kappa$
.
$p_1,\ldots,p_\kappa$
.
In Figure 17, we represented 3 instances of the convex set
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
in the cases
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
in the cases
![]() $\kappa= 3,4,6$
, which boundary is the dashed curve contained in
$\kappa= 3,4,6$
, which boundary is the dashed curve contained in
![]() $\mathfrak{C}_\kappa$
.
$\mathfrak{C}_\kappa$
.

Figure 17. For each of the cases
![]() $\kappa=3, 4, 6$
, the inner dashed curve is the boundary of the domain
$\kappa=3, 4, 6$
, the inner dashed curve is the boundary of the domain
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
. By the limit shape theorem, it also represents the boundary of a
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
. By the limit shape theorem, it also represents the boundary of a
![]() $\mathbf{z}[n]$
-gon where
$\mathbf{z}[n]$
-gon where
![]() $\mathbf{z}[n]$
is taken under
$\mathbf{z}[n]$
is taken under
![]() $\mathbb{Q}^{(n)}_{\kappa}$
, when
$\mathbb{Q}^{(n)}_{\kappa}$
, when
![]() $n\to+\infty$
.
$n\to+\infty$
.
Proof. Theorem 10 indicates that
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
is the convex domain contained in
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
is the convex domain contained in
![]() $\mathfrak{C}_\kappa$
which maximizes the affine perimeter. By the definition of the affine perimeter, we have
$\mathfrak{C}_\kappa$
which maximizes the affine perimeter. By the definition of the affine perimeter, we have
![]() $\mathrm{AP}(\mathfrak{C}_\kappa)=0$
, so that
$\mathrm{AP}(\mathfrak{C}_\kappa)=0$
, so that
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
lies within the interior of
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
lies within the interior of
![]() $\mathfrak{C}_\kappa$
. In this case (by Bárány [Reference Bárány2]), the boundary of
$\mathfrak{C}_\kappa$
. In this case (by Bárány [Reference Bárány2]), the boundary of
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
is composed of finitely many arcs of parabolas. In order to maximize the affine perimeter,
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
is composed of finitely many arcs of parabolas. In order to maximize the affine perimeter,
![]() $\mathsf{Dom}(\mathfrak{C}_\kappa)$
has to be tangent to at least three sides of
$\mathsf{Dom}(\mathfrak{C}_\kappa)$
has to be tangent to at least three sides of
![]() $\mathfrak{C}_\kappa$
, and the symmetry of
$\mathfrak{C}_\kappa$
, and the symmetry of
![]() $\mathfrak{C}_\kappa$
forces these tangency points to be the
$\mathfrak{C}_\kappa$
forces these tangency points to be the
![]() $\kappa$
midpoints of the sides of
$\kappa$
midpoints of the sides of
![]() $\mathfrak{C}_\kappa$
. Hence between two consecutive midpoints lies an arc of a parabola.
$\mathfrak{C}_\kappa$
. Hence between two consecutive midpoints lies an arc of a parabola.
Lemma 17.
For all
![]() $\kappa\geq 3$
, the supremum of affine perimeters
$\kappa\geq 3$
, the supremum of affine perimeters
![]() $\mathrm{AP}^*(\mathfrak{C}_\kappa)$
is
$\mathrm{AP}^*(\mathfrak{C}_\kappa)$
is
Proof. Using the notation of Lemma 16, we have of course, by symmetry,
Let
![]() $\mathcal{T}_1$
be the area of the triangle with vertices
$\mathcal{T}_1$
be the area of the triangle with vertices
![]() $p_1, y_{2},p_{1}$
. We claim that
$p_1, y_{2},p_{1}$
. We claim that
This property comes from the following fact, due to Blaschke [Reference Blaschke6, p. 38]. Consider a triangle T with vertices a, b, c and with subtriangles (both with dotted areas)
![]() $T^{(1)}$
(with vertices a, d, f) and
$T^{(1)}$
(with vertices a, d, f) and
![]() $T^{(2)}$
(with vertices f, e, c) defined so that
$T^{(2)}$
(with vertices f, e, c) defined so that
![]() $(d,e)\in[a,b]\times[b,c]$
and the segment [d, e] is tangent to the arc of the parabola
$(d,e)\in[a,b]\times[b,c]$
and the segment [d, e] is tangent to the arc of the parabola
![]() $\mathcal{C}$
at f, just as in Figure 18.
$\mathcal{C}$
at f, just as in Figure 18.

Figure 18. Blaschke’s property for arcs of parabolas.
In this case, we have
Therefore, for any integer m, any tuple of points
![]() $x[m]\in\mathcal{C}_1$
, and triangles
$x[m]\in\mathcal{C}_1$
, and triangles
![]() $T_i$
,
$T_i$
,
![]() $i\in\{1,\ldots,m\}$
(both defined as in Definition 2), the quantity
$i\in\{1,\ldots,m\}$
(both defined as in Definition 2), the quantity
![]() $\lim_{x[m]}\sum_{i=1}^{m}\mathsf{Area}\left({T}_i\right)^{1/3}$
is constant; hence
$\lim_{x[m]}\sum_{i=1}^{m}\mathsf{Area}\left({T}_i\right)^{1/3}$
is constant; hence
Now, from easy computations, one gets
which is (A.1).
Proof of Lemma 4. For an n-tuple
![]() $\mathbf{z}[n]$
that is
$\mathbf{z}[n]$
that is
![]() $\mathbb{U}^{(n)}_{\kappa}$
-distributed, Bárány’s Theorem 10 states that for all
$\mathbb{U}^{(n)}_{\kappa}$
-distributed, Bárány’s Theorem 10 states that for all
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
which implies immediately that
Appendix B. Valtr’s results
The surprising simplicity of Valtr’s formulas in the cases of the parallelogram and the triangle can be seen as a consequence of the fact that the sets
![]() $\mathcal{L}_4$
and
$\mathcal{L}_4$
and
![]() $\mathcal{L}_3$
are easily computable. Let us recover these results with Theorem 6.
$\mathcal{L}_3$
are easily computable. Let us recover these results with Theorem 6.
B.1. The triangle
Theorem 11.
(Valtr [Reference Valtr25].) For all
![]() $n\geq3$
, we have
$n\geq3$
, we have
We propose a new proof of Valtr’s result.
Proof. In the case
![]() $\kappa=3$
, the side length of
$\kappa=3$
, the side length of
![]() $\mathfrak{C}_3$
is
$\mathfrak{C}_3$
is
![]() $ r_3=2/3^{1/4}$
. Pick
$ r_3=2/3^{1/4}$
. Pick
![]() $c_1,c_2,c_3,\ell_1,\ell_2,\ell_3$
satisfying the equations
$c_1,c_2,c_3,\ell_1,\ell_2,\ell_3$
satisfying the equations
![]() $(\mathcal{C}_j)_{1\leq j\leq 3}$
. Since the only equiangular polygon with three sides is the equilateral triangle, we have
$(\mathcal{C}_j)_{1\leq j\leq 3}$
. Since the only equiangular polygon with three sides is the equilateral triangle, we have
![]() $c_1=c_2=c_3=c$
. This forces
$c_1=c_2=c_3=c$
. This forces
We thus understand that
 \begin{align*}\mathcal{L}_3=\left\{(\ell_1,\ell_2,\ell_3)\in\left[0, \frac{\sqrt{3}}{2}r_3\right]^3\text{ with }\ell_1+\ell_2+\ell_3\leq \frac{\sqrt{3}}{2}r_3\right\}. \end{align*}
\begin{align*}\mathcal{L}_3=\left\{(\ell_1,\ell_2,\ell_3)\in\left[0, \frac{\sqrt{3}}{2}r_3\right]^3\text{ with }\ell_1+\ell_2+\ell_3\leq \frac{\sqrt{3}}{2}r_3\right\}. \end{align*}
We also have
![]() $\mathbb{N}_3(n)=\left\{(i,j,k)\in \{0,\ldots,n-1\}^3, i+j+k=n\right\}$
, so that we have
$\mathbb{N}_3(n)=\left\{(i,j,k)\in \{0,\ldots,n-1\}^3, i+j+k=n\right\}$
, so that we have
![]() ${\mathbb{D}}_n^{(3)}={\mathbb{Q}}_n^{(3)}$
, and combining this with
${\mathbb{D}}_n^{(3)}={\mathbb{Q}}_n^{(3)}$
, and combining this with
we obtain
 \begin{align*}\mathbb{P}_{\triangle}(n)=n!\sin(\frac{\pi}{3})^{n-3}\sum_{s[3]\in\mathbb{N}_3(n)}\int_{\ell[3]\in\mathcal{L}_3} \prod_{j=1}^{3}\frac{c^{s_{{j-1}}+s_j-1}}{s_j!(s_{{j-1}}+s_j-1)!}\mathrm{d}\ell_1\mathrm{d}\ell_2\mathrm{d}\ell_3. \end{align*}
\begin{align*}\mathbb{P}_{\triangle}(n)=n!\sin(\frac{\pi}{3})^{n-3}\sum_{s[3]\in\mathbb{N}_3(n)}\int_{\ell[3]\in\mathcal{L}_3} \prod_{j=1}^{3}\frac{c^{s_{{j-1}}+s_j-1}}{s_j!(s_{{j-1}}+s_j-1)!}\mathrm{d}\ell_1\mathrm{d}\ell_2\mathrm{d}\ell_3. \end{align*}
Put
![]() $(i,j,k)=s[3]$
and perform the substitution
$(i,j,k)=s[3]$
and perform the substitution
![]() $\ell=\frac{2}{\sqrt{3}}(\ell_1+\ell_2+\ell_3)$
to get
$\ell=\frac{2}{\sqrt{3}}(\ell_1+\ell_2+\ell_3)$
to get
 \begin{align*} \mathbb{P}_{\triangle}(n)&=n!\sin(\frac{\pi}{3})^{n-3}\sum_{(i,j,k)\in\mathbb{N}_3(n)}\int_{0}^{ r_3}\frac{1}{2}\ell^2\frac{( r_3-\ell)^{i+j-1}}{i!(i+j-1)!}\frac{( r_3-\ell)^{j+k-1}}{j!(j+k-1)!}\frac{( r_3-\ell)^{k+i-1}}{k!(k+i-1)!}\left(\frac{\sqrt{3}}{2}\right)^3\mathrm{d}\ell\\[3pt] &=n!\left[\frac{1}{((n-1)!)^3}\sum_{i+j+k=n}\left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\right]\left(\frac{\sqrt{3}}{2}\right)^n\int_0^{ r_3}\frac{1}{2}\ell^2( r_3-\ell)^{2n-3}\mathrm{d}\ell\\[3pt] &=\frac{n!}{((n-1)!)^3} \left(\begin{smallmatrix}{3n-3} \\[3pt] {n}\end{smallmatrix}\right) \frac{(2n-3)!}{(2n)!}\left(\frac{\sqrt{3}}{2}\right)^{n} r_3^{2n}\\[3pt] &=\frac{2^n (3n-3)!}{(2n)!((n-1)!)^3}. \end{align*}
\begin{align*} \mathbb{P}_{\triangle}(n)&=n!\sin(\frac{\pi}{3})^{n-3}\sum_{(i,j,k)\in\mathbb{N}_3(n)}\int_{0}^{ r_3}\frac{1}{2}\ell^2\frac{( r_3-\ell)^{i+j-1}}{i!(i+j-1)!}\frac{( r_3-\ell)^{j+k-1}}{j!(j+k-1)!}\frac{( r_3-\ell)^{k+i-1}}{k!(k+i-1)!}\left(\frac{\sqrt{3}}{2}\right)^3\mathrm{d}\ell\\[3pt] &=n!\left[\frac{1}{((n-1)!)^3}\sum_{i+j+k=n}\left(\begin{smallmatrix}{n-1} \\[3pt] {i}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {j}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {k}\end{smallmatrix}\right)\right]\left(\frac{\sqrt{3}}{2}\right)^n\int_0^{ r_3}\frac{1}{2}\ell^2( r_3-\ell)^{2n-3}\mathrm{d}\ell\\[3pt] &=\frac{n!}{((n-1)!)^3} \left(\begin{smallmatrix}{3n-3} \\[3pt] {n}\end{smallmatrix}\right) \frac{(2n-3)!}{(2n)!}\left(\frac{\sqrt{3}}{2}\right)^{n} r_3^{2n}\\[3pt] &=\frac{2^n (3n-3)!}{(2n)!((n-1)!)^3}. \end{align*}
B.2. The square
Theorem 12.
(Valtr [Reference Valtr24].) For all
![]() $n\geq3$
, we have
$n\geq3$
, we have
Again, we propose a new proof of Valtr’s result.
Proof. Consider a square (i.e. the case
![]() $\kappa=4$
) of side length
$\kappa=4$
) of side length
![]() $ r_4=1$
. Pick
$ r_4=1$
. Pick
![]() $c_1,c_2,c_3,c_4$
and
$c_1,c_2,c_3,c_4$
and
![]() $\ell_1,\ell_2,\ell_3,\ell_4$
satisfying the equations
$\ell_1,\ell_2,\ell_3,\ell_4$
satisfying the equations
![]() $(\mathcal{C}_j)_{1\leq j\leq 4}$
. Since the only equiangular polygons with four sides are rectangles, we have
$(\mathcal{C}_j)_{1\leq j\leq 4}$
. Since the only equiangular polygons with four sides are rectangles, we have
![]() $c_1=c_3$
and
$c_1=c_3$
and
![]() $c_2=c_4$
. This implies
$c_2=c_4$
. This implies
This means in particular that
Just as before, we have
![]() ${\mathbb{D}}_n^{(4)}={\mathbb{Q}}_n^{(4)}$
, so that
${\mathbb{D}}_n^{(4)}={\mathbb{Q}}_n^{(4)}$
, so that
from which we deduce
 \begin{align*}\mathbb{P}_{\Box}(n)=n!\sum_{s[4]\in\mathbb{N}_4(n)}\int_{\ell[4]\in\mathcal{L}_4} \prod_{j=1}^{4}\frac{c_j^{s_{{j-1}}+s_j}}{s_j!(s_{{j-1}}+s_j)!}\mathrm{d}\ell_1\mathrm{d}\ell_2\mathrm{d}\ell_3\mathrm{d}\ell_4, \end{align*}
\begin{align*}\mathbb{P}_{\Box}(n)=n!\sum_{s[4]\in\mathbb{N}_4(n)}\int_{\ell[4]\in\mathcal{L}_4} \prod_{j=1}^{4}\frac{c_j^{s_{{j-1}}+s_j}}{s_j!(s_{{j-1}}+s_j)!}\mathrm{d}\ell_1\mathrm{d}\ell_2\mathrm{d}\ell_3\mathrm{d}\ell_4, \end{align*}
where
![]() $\mathbb{N}_4(n)=\left\{(s_1,s_2,s_3,s_4)\in\mathbb{N}^4\text{ such that }s_1+s_2+s_3+s_4=n\text{ and }s_j+s_{{j+1}}\geq1\right\}$
. Put
$\mathbb{N}_4(n)=\left\{(s_1,s_2,s_3,s_4)\in\mathbb{N}^4\text{ such that }s_1+s_2+s_3+s_4=n\text{ and }s_j+s_{{j+1}}\geq1\right\}$
. Put
![]() $(h,i,j,k)=s[4]$
and perform the substitutions
$(h,i,j,k)=s[4]$
and perform the substitutions
![]() $c_1=1-(\ell_1+\ell_3)$
,
$c_1=1-(\ell_1+\ell_3)$
,
![]() $c_2=1-(\ell_2+\ell_4)$
to get
$c_2=1-(\ell_2+\ell_4)$
to get
 \begin{multline*} \mathbb{P}_{\Box}(n)=n!\sum_{(h,i,j,k)\in\mathbb{N}_4(n)}\int_{0}^1\int_{0}^1 \frac{(1-c_1)c_1^{h+i-1}}{h!(h+i-1)!}\frac{(1-c_2)c_2^{i+j-1}}{i!(i+j-1)!}\\[3pt] \times\frac{c_1^{j+k-1}}{j!(j+k-1)!}\frac{c_2^{h+k-1}}{k!(h+k-1)!}\mathrm{d}c_1\mathrm{d}c_2. \end{multline*}
\begin{multline*} \mathbb{P}_{\Box}(n)=n!\sum_{(h,i,j,k)\in\mathbb{N}_4(n)}\int_{0}^1\int_{0}^1 \frac{(1-c_1)c_1^{h+i-1}}{h!(h+i-1)!}\frac{(1-c_2)c_2^{i+j-1}}{i!(i+j-1)!}\\[3pt] \times\frac{c_1^{j+k-1}}{j!(j+k-1)!}\frac{c_2^{h+k-1}}{k!(h+k-1)!}\mathrm{d}c_1\mathrm{d}c_2. \end{multline*}
This leads to
 \begin{multline} \mathbb{P}_{\Box}(n)=n!\bigg(\int_{0}^1(1-c)c^{n-2}\mathrm{d}c\bigg)^2\\[3pt] \times\sum_{(h,i,j,k)\in\mathbb{N}_4(n)}\frac{1}{h!(h+i-1)!}\frac{1}{i!(i+j-1)!}\frac{1}{j!(j+k-1)!}\frac{1}{k!(h+k-1)!}. \end{multline}
\begin{multline} \mathbb{P}_{\Box}(n)=n!\bigg(\int_{0}^1(1-c)c^{n-2}\mathrm{d}c\bigg)^2\\[3pt] \times\sum_{(h,i,j,k)\in\mathbb{N}_4(n)}\frac{1}{h!(h+i-1)!}\frac{1}{i!(i+j-1)!}\frac{1}{j!(j+k-1)!}\frac{1}{k!(h+k-1)!}. \end{multline}
The integral is a standard beta-integral, so that
It remains to compute the big sum S that appears separately in (B.1):
 \begin{align*} S &=\frac{1}{(n-2)!((n-1)!)^2}\sum_{(h,i,j,k)\in\mathbb{N}_4(n)} \left(\begin{smallmatrix}{n-1} \\[3pt] {h+i}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {j+k}\end{smallmatrix}\right) \left(\begin{smallmatrix}{h+i} \\[3pt] {h}\end{smallmatrix}\right) \left(\begin{smallmatrix}{j+k} \\[3pt] {k}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-2} \\[3pt] {i+j-1}\end{smallmatrix}\right) \\[3pt] &=\frac{1}{(n-2)!((n-1)!)^2}\sum_{r=1}^{n-1}\left(\begin{smallmatrix}{n-1} \\[3pt] {r}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {n-r}\end{smallmatrix}\right) \left(\begin{smallmatrix}{2n-2} \\[3pt] {n-1}\end{smallmatrix}\right)\\[3pt] &=\frac{1}{n!((n-2)!)^2}\left(\begin{smallmatrix}{2n-2} \\[3pt] {n-1}\end{smallmatrix}\right)^2, \end{align*}
\begin{align*} S &=\frac{1}{(n-2)!((n-1)!)^2}\sum_{(h,i,j,k)\in\mathbb{N}_4(n)} \left(\begin{smallmatrix}{n-1} \\[3pt] {h+i}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-1} \\[3pt] {j+k}\end{smallmatrix}\right) \left(\begin{smallmatrix}{h+i} \\[3pt] {h}\end{smallmatrix}\right) \left(\begin{smallmatrix}{j+k} \\[3pt] {k}\end{smallmatrix}\right) \left(\begin{smallmatrix}{n-2} \\[3pt] {i+j-1}\end{smallmatrix}\right) \\[3pt] &=\frac{1}{(n-2)!((n-1)!)^2}\sum_{r=1}^{n-1}\left(\begin{smallmatrix}{n-1} \\[3pt] {r}\end{smallmatrix}\right)\left(\begin{smallmatrix}{n-1} \\[3pt] {n-r}\end{smallmatrix}\right) \left(\begin{smallmatrix}{2n-2} \\[3pt] {n-1}\end{smallmatrix}\right)\\[3pt] &=\frac{1}{n!((n-2)!)^2}\left(\begin{smallmatrix}{2n-2} \\[3pt] {n-1}\end{smallmatrix}\right)^2, \end{align*}
which is Valtr’s formula.
Appendix C. Computation of
 $\mathrm{m}_\kappa$
$\mathrm{m}_\kappa$
In this section, we aim to prove that the determinant
![]() $\mathrm{m}_\kappa$
of the matrix
$\mathrm{m}_\kappa$
of the matrix
![]() $\Sigma_\kappa^{-1}$
of size
$\Sigma_\kappa^{-1}$
of size
![]() $(\kappa-1)\times(\kappa-1)$
, defined in Theorem 7 as
$(\kappa-1)\times(\kappa-1)$
, defined in Theorem 7 as
 \begin{align*}\Sigma_\kappa^{-1}\,:\!=\,\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 6 & 4 & 3 & \cdots & \cdots & 3 & 2\\[3pt] 4 & 8 & 5 & 4 & \cdots & 4 & 3\\[3pt] 3 & 5 & \ddots & \ddots & \ddots & \vdots & \vdots\\[3pt] \vdots & 4 & \ddots & \ddots & \ddots & 4 & \vdots \\[3pt] \vdots & \vdots & \ddots & \ddots & \ddots & 5 & 3\\[3pt] 3 & 4 & \cdots & 4 & 5 & 8 & 4\\[3pt] 2 & 3 & \cdots & \cdots & 3 & 4 & 6 \end{array}\right)\text{ for }\kappa \text{ large enough}, \end{align*}
\begin{align*}\Sigma_\kappa^{-1}\,:\!=\,\frac{1}{2} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 6 & 4 & 3 & \cdots & \cdots & 3 & 2\\[3pt] 4 & 8 & 5 & 4 & \cdots & 4 & 3\\[3pt] 3 & 5 & \ddots & \ddots & \ddots & \vdots & \vdots\\[3pt] \vdots & 4 & \ddots & \ddots & \ddots & 4 & \vdots \\[3pt] \vdots & \vdots & \ddots & \ddots & \ddots & 5 & 3\\[3pt] 3 & 4 & \cdots & 4 & 5 & 8 & 4\\[3pt] 2 & 3 & \cdots & \cdots & 3 & 4 & 6 \end{array}\right)\text{ for }\kappa \text{ large enough}, \end{align*}
is indeed
as given in Theorem 1.
Proof. We define the matrix
![]() $D_\kappa$
as
$D_\kappa$
as
 \begin{align*}D_\kappa\,:\!=\, 2\Sigma_\kappa^{-1} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 4/3&0&\cdots&&0\\[3pt] 0&1&&&\\[3pt] &\ddots&\ddots&\ddots&\vdots\\[3pt] \vdots&&&1&0\\[3pt] 0&\cdots&&0&4/3 \end{array} \right) = \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 8&5&3&\cdots&\cdots&3&8/3\\[3pt] 16/3&8&5&4&\cdots&4&4\\[3pt] 4&5&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&4&\ddots&\ddots&\ddots&4&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&5&4\\[3pt] 4&4&\cdots&4&5&8&16/3\\[3pt] 8/3&3&\cdots&\cdots&3&5&8 \end{array}\right), \end{align*}
\begin{align*}D_\kappa\,:\!=\, 2\Sigma_\kappa^{-1} \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 4/3&0&\cdots&&0\\[3pt] 0&1&&&\\[3pt] &\ddots&\ddots&\ddots&\vdots\\[3pt] \vdots&&&1&0\\[3pt] 0&\cdots&&0&4/3 \end{array} \right) = \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 8&5&3&\cdots&\cdots&3&8/3\\[3pt] 16/3&8&5&4&\cdots&4&4\\[3pt] 4&5&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&4&\ddots&\ddots&\ddots&4&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&5&4\\[3pt] 4&4&\cdots&4&5&8&16/3\\[3pt] 8/3&3&\cdots&\cdots&3&5&8 \end{array}\right), \end{align*}
where, the factor 2 aside, we have just multiplied by
![]() $\frac{4}{3}$
the first and last columns of
$\frac{4}{3}$
the first and last columns of
![]() $\Sigma_\kappa^{-1}$
. This means of course that
$\Sigma_\kappa^{-1}$
. This means of course that
We now decompose
![]() $D_\kappa$
as
$D_\kappa$
as
![]() $D_\kappa\,:\!=\,Q_\kappa+E_\kappa$
with
$D_\kappa\,:\!=\,Q_\kappa+E_\kappa$
with
 \begin{align*}Q_\kappa\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 3&\cdots&\cdots&3\\[3pt] 4&\cdots&\cdots&4\\[3pt] \vdots&&&\vdots\\[3pt] 4&\cdots&\cdots&4\\[3pt] 3&\cdots&\cdots&3 \end{array}\right) \quad\text{ and }\quad E_\kappa\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 5&1&0&\cdots&\cdots&0&-1/3\\[3pt] 4/3&4&\ddots&0&\cdots&0&0\\[3pt] 0&1&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&0&\ddots&\ddots&\ddots&0&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&1&0\\[3pt] 0&0&\cdots&0&\ddots&4&4/3\\[3pt] -1/3&0&\cdots&\cdots&0&1&5 \end{array} \right). \end{align*}
\begin{align*}Q_\kappa\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 3&\cdots&\cdots&3\\[3pt] 4&\cdots&\cdots&4\\[3pt] \vdots&&&\vdots\\[3pt] 4&\cdots&\cdots&4\\[3pt] 3&\cdots&\cdots&3 \end{array}\right) \quad\text{ and }\quad E_\kappa\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 5&1&0&\cdots&\cdots&0&-1/3\\[3pt] 4/3&4&\ddots&0&\cdots&0&0\\[3pt] 0&1&\ddots&\ddots&\ddots&\vdots&\vdots\\[3pt] \vdots&0&\ddots&\ddots&\ddots&0&\vdots\\[3pt] \vdots&\vdots&\ddots&\ddots&\ddots&1&0\\[3pt] 0&0&\cdots&0&\ddots&4&4/3\\[3pt] -1/3&0&\cdots&\cdots&0&1&5 \end{array} \right). \end{align*}
We first claim that
To prove this, notice first that taking two Laplace expansions of the determinant of the
![]() $(m\times m)$
matrix
$(m\times m)$
matrix
 \begin{align*}L_m\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 4&1&0&\cdots&0\\[3pt] 1&\ddots&\ddots&\ddots&\vdots\\[3pt] 0&\ddots&\ddots&\ddots&0\\[3pt] \vdots&\ddots&\ddots&\ddots&1\\[3pt] 0&\cdots&0&1&4 \end{array} \right) \end{align*}
\begin{align*}L_m\,:\!=\, \left(\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 4&1&0&\cdots&0\\[3pt] 1&\ddots&\ddots&\ddots&\vdots\\[3pt] 0&\ddots&\ddots&\ddots&0\\[3pt] \vdots&\ddots&\ddots&\ddots&1\\[3pt] 0&\cdots&0&1&4 \end{array} \right) \end{align*}
gives a constant-recursive sequence of order 2 for its determinant:
which can be solved immediately to get
Taking several Laplace expansions of
![]() $\det(E_\kappa)$
along the first column allows one to either deal with diagonal matrices (leading to the term
$\det(E_\kappa)$
along the first column allows one to either deal with diagonal matrices (leading to the term
![]() $\frac{8}{9}({-}1)^{\kappa-1})$
), or with
$\frac{8}{9}({-}1)^{\kappa-1})$
), or with
![]() $L_{\kappa-2}$
and
$L_{\kappa-2}$
and
![]() $L_{\kappa-3}$
to ultimately get (C.1).
$L_{\kappa-3}$
to ultimately get (C.1).
How do we compute
![]() $\det(D_\kappa)=\det(Q_\kappa+E_\kappa)$
? In general, since the determinant is a multilinear alternating map of the columns of the matrix, for two
$\det(D_\kappa)=\det(Q_\kappa+E_\kappa)$
? In general, since the determinant is a multilinear alternating map of the columns of the matrix, for two
![]() $(m\times m)$
matrices
$(m\times m)$
matrices
![]() $A=(A_i)_{1\leq i\leq m}$
and
$A=(A_i)_{1\leq i\leq m}$
and
![]() $B=(B_i)_{1\leq i\leq m}$
, (where
$B=(B_i)_{1\leq i\leq m}$
, (where
![]() $A_i$
is the ith column of A), we can write
$A_i$
is the ith column of A), we can write
 \begin{align*} \det(A+B)&=\det(A_1+B_1,\ldots,A_m+B_m)\\[3pt] &= \sum_{I\sqcup J=\{1,\ldots,m\}} \det((A_i\mathbf{1}_{\left\{{i\in I}\right\}}+B_i\mathbf{1}_{\left\{{i\in J}\right\}})_{i\in\{1,\ldots,m\}}), \end{align*}
\begin{align*} \det(A+B)&=\det(A_1+B_1,\ldots,A_m+B_m)\\[3pt] &= \sum_{I\sqcup J=\{1,\ldots,m\}} \det((A_i\mathbf{1}_{\left\{{i\in I}\right\}}+B_i\mathbf{1}_{\left\{{i\in J}\right\}})_{i\in\{1,\ldots,m\}}), \end{align*}
where
![]() $I\sqcup J=\{1,\ldots,m\}$
means that I,J forms a partition of
$I\sqcup J=\{1,\ldots,m\}$
means that I,J forms a partition of
![]() $\{1,\ldots,m\}$
.
$\{1,\ldots,m\}$
.
In the case where all columns of B are the same, the sum above only keeps the partitions (I,J) of
![]() $\{1,\ldots,m\}$
where either
$\{1,\ldots,m\}$
where either
![]() $\left\vert J\right\vert=0$
(hence we retrieve
$\left\vert J\right\vert=0$
(hence we retrieve
![]() $\det(A)$
), or
$\det(A)$
), or
![]() $\left\vert J\right\vert=1$
. We therefore introduce the matrix
$\left\vert J\right\vert=1$
. We therefore introduce the matrix
![]() $E_\kappa^{(i)}$
, for all
$E_\kappa^{(i)}$
, for all
![]() $i\in\{1,\ldots,\kappa-1\}$
, which is the matrix
$i\in\{1,\ldots,\kappa-1\}$
, which is the matrix
![]() $E_\kappa$
with its ith column replaced by
$E_\kappa$
with its ith column replaced by
![]() $(3\ 4 \cdots 4\ 3)^t$
. By the previous argument we have
$(3\ 4 \cdots 4\ 3)^t$
. By the previous argument we have
 \begin{align} \det(D_\kappa)=\det(E_\kappa)+\sum_{i=1}^{\kappa-1}\det(E_\kappa^{(i)}). \end{align}
\begin{align} \det(D_\kappa)=\det(E_\kappa)+\sum_{i=1}^{\kappa-1}\det(E_\kappa^{(i)}). \end{align}
We now make the following claim.
Lemma 18
For all
![]() $\kappa$
large enough, we have the following:
$\kappa$
large enough, we have the following:
-
1.
 $\det(E_\kappa^{(i)})=\frac{2}{3}\det(E_\kappa)$
for all
$\det(E_\kappa^{(i)})=\frac{2}{3}\det(E_\kappa)$
for all
 $i\in\{2,\ldots,\kappa-2\},$
$i\in\{2,\ldots,\kappa-2\},$
-
2.
 $\det(E_\kappa^{(1)})=\det(E_\kappa^{(\kappa-1)})=\frac{1}{2}\det(E_\kappa).$
$\det(E_\kappa^{(1)})=\det(E_\kappa^{(\kappa-1)})=\frac{1}{2}\det(E_\kappa).$
This lemma allows us to conclude, since by (C.2), we now have
Proof of Lemma
18. The proof relies on some determinant-preserving column manipulations on
![]() $E_\kappa^{(i)}$
, which provide matrices equal to
$E_\kappa^{(i)}$
, which provide matrices equal to
![]() $E_\kappa$
up to a constant factor.
$E_\kappa$
up to a constant factor.
Pick
![]() $i\in\{2,\ldots,\kappa-2\}$
, and consider the matrix
$i\in\{2,\ldots,\kappa-2\}$
, and consider the matrix
![]() $E_\kappa^{(i)}$
where the ith column is multiplied by
$E_\kappa^{(i)}$
where the ith column is multiplied by
![]() $3/2$
. Then subtract all other columns from the ith. Then add
$3/2$
. Then subtract all other columns from the ith. Then add
![]() $-1/4$
times the first and last columns to the ith column, to obtain
$-1/4$
times the first and last columns to the ith column, to obtain
![]() $E_\kappa$
. This gives the first part.
$E_\kappa$
. This gives the first part.
If
![]() $i=1$
or
$i=1$
or
![]() $\kappa-1$
the same reasoning works: multiply the ith column by 2, and then there exists a linear combination of the columns other than i that can be added to the ith column to retrieve
$\kappa-1$
the same reasoning works: multiply the ith column by 2, and then there exists a linear combination of the columns other than i that can be added to the ith column to retrieve
![]() $E_\kappa$
.
$E_\kappa$
.
Acknowledgements
I would like to express my deepest gratitude to Jean-François Marckert for his valuable guidance and advice throughout the long research and writing process of this paper. I also thank Zoé Varin for her precious help in my struggles with TikZ. Some of the figures in this paper were entirely created by her expert hand. Many thanks to the referees for their wise comments and suggestions, which considerably increased the readability of this paper.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.