Published online by Cambridge University Press: 30 July 2024
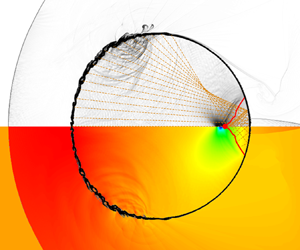
Shock–droplet interaction in the early stage involves intricate wave structures. Investigating this phenomenon is inherently challenging due to the fine spatial and temporal scales involved. Past research has suggested that the occurrence of cavitation, marked by a negative peak pressure, is linked to the focus of the reflected expansion wave. In this study, a high-fidelity compressible numerical approach is utilized to replicate the initial phase of shock–droplet interactions. The location of the negative peak pressure is meticulously documented and compared with experimental measurement and numerical results. Results indicate a strong alignment between the negative peak pressure positions identified through numerical simulations and the focal points identified in theoretical models for low gas–liquid wave velocity ratios. However, this alignment is notably disrupted when dealing with higher gas–liquid wave velocity ratios. Further enhancements are made to the theoretical model, enabling a more precise depiction of internal wave structures and focus points, particularly under conditions of high gas–liquid wave velocity ratios. The study delves into the various factors influencing internal pressure fluctuations within the liquid droplet, categorizing them into four phases: the shock wave effect, relaxation effect, fluctuation effect, and expansion wave effect. Analysing the pressure decrease portion reveals that while the converging of the reflected expansion wave leads to a substantial pressure drop, it accounts for only a fraction of the total pressure variation. Consequently, any model predicting negative peak pressure positions must comprehensively consider all contributing factors.