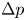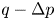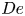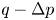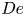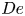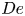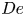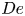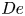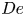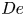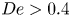doi:10.1017/jfm.2024.455 Ockendon et al. Thin-film flow between a rotating sphere and a nearly vertical moving plate
JFM Perspectives
Onsager's ‘ideal turbulence’ theory
-
- Published online by Cambridge University Press:
- 27 May 2024, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Experimental study on spray in the atmospheric surface layer by raindrops impacting water surface
-
- Published online by Cambridge University Press:
- 27 May 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-monotonic effect of compaction on longitudinal dispersion coefficient of porous media
-
- Published online by Cambridge University Press:
- 04 June 2024, R2
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Secondary motions in turbulent ribbed channel flows
-
- Published online by Cambridge University Press:
- 27 May 2024, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Bacterial barriers
-
- Published online by Cambridge University Press:
- 25 July 2024, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Asymptotic analysis of hydrodynamic forces in a Brinkman penalization method: case of an initial flow around an impulsively started rotating and translating circular cylinder
-
- Published online by Cambridge University Press:
- 27 May 2024, A3
-
- Article
-
- You have access
- HTML
- Export citation
Global stability of the flow past a stepped cylinder
-
- Published online by Cambridge University Press:
- 27 May 2024, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic feature-based deep reinforcement learning for flow control of circular cylinder with sparse surface pressure sensing
-
- Published online by Cambridge University Press:
- 28 May 2024, A4
-
- Article
-
- You have access
- HTML
- Export citation
Thin-film flow between a rotating sphere and a nearly vertical moving plate
-
- Published online by Cambridge University Press:
- 28 May 2024, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational bounds and nonlinear stability of an active nematic suspension
-
- Published online by Cambridge University Press:
- 30 May 2024, A5
-
- Article
-
- You have access
- HTML
- Export citation
Role of streak secondary instabilities on free-stream turbulence-induced transition
-
- Published online by Cambridge University Press:
- 28 May 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
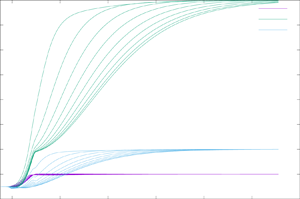
Flow of an Oldroyd-B fluid in a slowly varying contraction: theoretical results for arbitrary values of Deborah number in the ultra-dilute limit
-
- Published online by Cambridge University Press:
- 31 May 2024, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite-size inertial spherical particles in turbulence
-
- Published online by Cambridge University Press:
- 31 May 2024, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Onset of absolute instability on a pitching aerofoil
-
- Published online by Cambridge University Press:
- 29 May 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effect of intermittency in wave forcing on the quasi-biennial oscillation
-
- Published online by Cambridge University Press:
- 31 May 2024, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sedimentation dynamics of passive particles in dilute bacterial suspensions: emergence of bioconvection
-
- Published online by Cambridge University Press:
- 29 May 2024, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fast flow of an Oldroyd-B model fluid through a narrow slowly varying contraction
-
- Published online by Cambridge University Press:
- 31 May 2024, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficient enhancement of turbulent entrainment by small-scale shear instability
-
- Published online by Cambridge University Press:
- 31 May 2024, A20
-
- Article
-
- You have access
- HTML
- Export citation
Flow regimes in emptying–filling boxes with two buoyancy sources of differing strengths and elevations
-
- Published online by Cambridge University Press:
- 24 July 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuation covariance-based study of roll-streak dynamics in Poiseuille flow turbulence
-
- Published online by Cambridge University Press:
- 31 May 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation