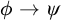1 Introduction
Bi-intuitionistic logic (or Heyting–Brouwer logic) comes rather naturally from adding the algebraic dual of the intuitionistic implication
![]() $\rightarrow $
to the language of intuitionistic logic. This connective is known as ‘co-implication’, and we denote it in what follows by ‘
$\rightarrow $
to the language of intuitionistic logic. This connective is known as ‘co-implication’, and we denote it in what follows by ‘
![]() ’.Footnote
1
In the 1970s, Rauszer started an intense study of various technical aspects of both propositional and predicate bi-intuitionistic logic in a series of interesting articles spanning over a decade [Reference Rauszer18–Reference Rauszer23]. This work has been picked up in recent years by a number of scholars [Reference Badia1–Reference de Groot, Pattinson, Iemhoff, Moortgat and de Queiroz4, Reference Goré and Postniece6, Reference Goré and Shillito7, Reference Kowalski and Ono9, Reference Olkhovikov and Badia13, Reference Pinto and Uustalu17, Reference Skurt26, Reference Tranchini27] and results on all sorts of proof-theoretic and model-theoretic properties of these systems have been produced.
’.Footnote
1
In the 1970s, Rauszer started an intense study of various technical aspects of both propositional and predicate bi-intuitionistic logic in a series of interesting articles spanning over a decade [Reference Rauszer18–Reference Rauszer23]. This work has been picked up in recent years by a number of scholars [Reference Badia1–Reference de Groot, Pattinson, Iemhoff, Moortgat and de Queiroz4, Reference Goré and Postniece6, Reference Goré and Shillito7, Reference Kowalski and Ono9, Reference Olkhovikov and Badia13, Reference Pinto and Uustalu17, Reference Skurt26, Reference Tranchini27] and results on all sorts of proof-theoretic and model-theoretic properties of these systems have been produced.
In this paper we are concerned with refuting the Craig Interpolation Property for predicate bi-intuitionistic logic. In other words, we will show that there are valid implications
![]() $\phi \rightarrow \psi $
with no interpolant in the sense of a formula
$\phi \rightarrow \psi $
with no interpolant in the sense of a formula
![]() $\theta $
in the intersection of the vocabularies of
$\theta $
in the intersection of the vocabularies of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
such that both
$\psi $
such that both
![]() $\phi \rightarrow \theta $
and
$\phi \rightarrow \theta $
and
![]() $\theta \rightarrow \psi $
are valid. Our counterexample is extracted from [Reference Mints, Olkhovikov and Urquhart12] where the Craig interpolation problem for predicate intuitionistic logic with constant domains is solved negatively. More specifically, we consider the implication
$\theta \rightarrow \psi $
are valid. Our counterexample is extracted from [Reference Mints, Olkhovikov and Urquhart12] where the Craig interpolation problem for predicate intuitionistic logic with constant domains is solved negatively. More specifically, we consider the implication
![]() $\phi \rightarrow \psi $
where
$\phi \rightarrow \psi $
where
and
One of the reasons why our construction works is because bi-intuitionistic predicate logic is well-known to be sound with respect to its constant domain semantics [Reference Rauszer21]. Hence, the effect of adding the co-implication connective is that one can restrict attention to Kripke models with constant domains (this has led some authors to question the status of
![]() as an intuitionistic connective [Reference López-Escobar11]).
as an intuitionistic connective [Reference López-Escobar11]).
Rauszer had already studied the interpolation problem for both predicate and propositional versions of bi-intuitionistic logic for global consequence (which we will denote by
![]() $\models ^g$
) in [Reference Rauszer23].Footnote
2
However, she had only established interpolation in a much weaker version properly known as ‘deductive interpolation’ (see [Reference Galatos, Jipsen, Kowalski and Ono5]): if
$\models ^g$
) in [Reference Rauszer23].Footnote
2
However, she had only established interpolation in a much weaker version properly known as ‘deductive interpolation’ (see [Reference Galatos, Jipsen, Kowalski and Ono5]): if
![]() $\phi \vDash ^g \psi $
there is a formula
$\phi \vDash ^g \psi $
there is a formula
![]() $\theta $
in the intersection of the vocabularies of
$\theta $
in the intersection of the vocabularies of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
such that both
$\psi $
such that both
![]() $\phi \vDash ^g \theta $
and
$\phi \vDash ^g \theta $
and
![]() $\theta \vDash ^g \psi $
. Given that in bi-intuitionistic logic the deduction theorem fails for global consequence,Footnote
3
deductive interpolation is not equivalent to the usual Craig interpolation. Craig interpolation for propositional bi-intuitionistic logic was established only recently by a complex proof-theoretic argument [Reference Kowalski and Ono9]. Unfortunately, as we will see, those techniques cannot be extended to the predicate case.
$\theta \vDash ^g \psi $
. Given that in bi-intuitionistic logic the deduction theorem fails for global consequence,Footnote
3
deductive interpolation is not equivalent to the usual Craig interpolation. Craig interpolation for propositional bi-intuitionistic logic was established only recently by a complex proof-theoretic argument [Reference Kowalski and Ono9]. Unfortunately, as we will see, those techniques cannot be extended to the predicate case.
López-Escobar had observed in [Reference López-Escobar11] that bi-intuitionistic predicate logic is not conservative as an extension of intuitionistic predicate logic simply because the axiom of constant domains is derivable in the former. It is known, however, that bi-intuitionistic predicate logic is a conservative extension of constant domain intuitionistic predicate logic [Reference Crolard3]. Then, one could wonder whether this trivialises the result in the present paper given the argument refuting interpolation for the latter in [Reference Mints, Olkhovikov and Urquhart12]. A minute of reflection suffices to show the reader that this is not so, for the argument in [Reference Mints, Olkhovikov and Urquhart12] only establishes that the interpolant does not exist in the language of predicate intuitionistic logic which does not include the new co-implication connective. It does, on the other hand, indicate that the present result is quite natural.
Recently [Reference Shillito25], a number of questions have arisen as to the correctness of Rauszer’s completeness theorem for predicate bi-intuitionistic logic with respect to the Kripke semantics of constant domains. Three fundamental flaws of Rauszer’s proofs are outlined in [Reference Shillito25]: (i) the fact that they mistakenly mix up properties of global and local consequence relations, (ii) the contradictory choice of rooted frames in the completeness proof which would validate non-theorems of bi-intuitionistic logic, and (iii) an incorrect application of some results by Gabbay. Incidentally, there is an alternative completeness argument by Klemke in [Reference Klemke8], where bi-intuitionistic predicate logic is studied possibly for the first time in print (and, as far as we know, independently from Rauszer’s work) and that contains other errors. This paper appears to have been sadly neglected in the history of the subject and it contains valuable techniques such as a version of the unraveling construction used in [Reference Olkhovikov and Badia13] (see [Reference Klemke8, Definition 4.1]).
Let us note, however, that the central result in the present paper does not actually require any appeal to completeness. All we need is (i) that the axiom of constant domains is a theorem of bi-intuitionistic predicate logic and (ii) that bi-intuitionistic predicate logic is sound with respect to the Kripke semantics for intuitionistic logic of constant domains. This is because our implication
![]() $\phi \rightarrow \psi $
described above is a theorem of intuitionistic predicate logic with the addition of the axiom of constant domains, and hence by (i), a theorem of bi-intuitionistic predicate logic. Furthermore, if there would be a proof-theoretic Craig interpolant for this implication, then, by (ii), it would be a semantic interpolant and hence we would get the desired contradiction reasoning as in Theorem 2.
$\phi \rightarrow \psi $
described above is a theorem of intuitionistic predicate logic with the addition of the axiom of constant domains, and hence by (i), a theorem of bi-intuitionistic predicate logic. Furthermore, if there would be a proof-theoretic Craig interpolant for this implication, then, by (ii), it would be a semantic interpolant and hence we would get the desired contradiction reasoning as in Theorem 2.
The article is arranged as follows: in
![]() $\S $
2 we introduce all the required technical preliminaries that we will use in the construction of our counterexample, namely the language of the logic and its models, as well as the notion of a bi-asimulation (among a few other things); in
$\S $
2 we introduce all the required technical preliminaries that we will use in the construction of our counterexample, namely the language of the logic and its models, as well as the notion of a bi-asimulation (among a few other things); in
![]() $\S $
3 we introduce the Craig Interpolation Property, Mints’s counterexample from [Reference Mints, Olkhovikov and Urquhart12] and we show how to adapt the technical argument in that paper to obtain the central result of the present article (Theorem 2); finally, in
$\S $
3 we introduce the Craig Interpolation Property, Mints’s counterexample from [Reference Mints, Olkhovikov and Urquhart12] and we show how to adapt the technical argument in that paper to obtain the central result of the present article (Theorem 2); finally, in
![]() $\S $
4 we provide some concluding remarks on the failure of interpolation described here.
$\S $
4 we provide some concluding remarks on the failure of interpolation described here.
2 Preliminaries and notation
2.1 The first-order language
In this paper we will use ‘first-order’ and ‘predicate’ interchangeably as qualifiers for a logic. We start by fixing some general notational conventions. In this paper, we identify the natural numbers with finite ordinals. We denote by
![]() $\omega $
the smallest infinite ordinal, and by
$\omega $
the smallest infinite ordinal, and by
![]() $\mathbb {N}$
the set
$\mathbb {N}$
the set
![]() $\omega \setminus \{0\}$
. For any
$\omega \setminus \{0\}$
. For any
![]() $n \in \omega $
, we will denote by
$n \in \omega $
, we will denote by
![]() $\bar {o}_n$
the sequence
$\bar {o}_n$
the sequence
![]() $(o_1,\ldots , o_n)$
of objects of any kind; moreover, somewhat abusing the notation, we will denote
$(o_1,\ldots , o_n)$
of objects of any kind; moreover, somewhat abusing the notation, we will denote
![]() $\{o_1,\ldots , o_n\}$
by
$\{o_1,\ldots , o_n\}$
by
![]() $\{\bar {o}_n\}$
. The ordered
$\{\bar {o}_n\}$
. The ordered
![]() $1$
-tuple will be identified with its only member. For any given
$1$
-tuple will be identified with its only member. For any given
![]() $m,n \in \omega $
, the notation
$m,n \in \omega $
, the notation
![]() $(\bar {p}_m)^\frown (\bar {q}_n)$
denotes the concatenation of
$(\bar {p}_m)^\frown (\bar {q}_n)$
denotes the concatenation of
![]() $\bar {p}_m$
and
$\bar {p}_m$
and
![]() $\bar {q}_n$
, and the notation
$\bar {q}_n$
, and the notation
![]() $\bar {p}_n\mapsto \bar {q}_n$
denotes the relation
$\bar {p}_n\mapsto \bar {q}_n$
denotes the relation
![]() $\{(p_i, q_i)\mid 1 \leq i \leq n\}$
; the latter relation is often explicitly assumed to define a function.
$\{(p_i, q_i)\mid 1 \leq i \leq n\}$
; the latter relation is often explicitly assumed to define a function.
More generally, if f is any function, then we will denote by
![]() $dom(f)$
its domain and by
$dom(f)$
its domain and by
![]() $rang(f)$
the image of
$rang(f)$
the image of
![]() $dom(f)$
under f; if
$dom(f)$
under f; if
![]() $rang(f) \subseteq M$
, we will also write
$rang(f) \subseteq M$
, we will also write
![]() $f: dom(f) \to M$
. If
$f: dom(f) \to M$
. If
![]() $f: X \to Y$
is any function, and Z is any set, then we denote by
$f: X \to Y$
is any function, and Z is any set, then we denote by
![]() $[f]Z$
the set
$[f]Z$
the set
![]() $\{q \in Y\mid (\exists p \in Z)(f(p) = q)\}$
; in particular, if
$\{q \in Y\mid (\exists p \in Z)(f(p) = q)\}$
; in particular, if
![]() $\bar {p}_n\mapsto \bar {q}_n$
defines a function, then
$\bar {p}_n\mapsto \bar {q}_n$
defines a function, then
![]() $[\bar {p}_n\mapsto \bar {q}_n]Z$
stands for
$[\bar {p}_n\mapsto \bar {q}_n]Z$
stands for
![]() $\{q_i\mid p_i \in Z,\,1 \leq i \leq n\}$
.
$\{q_i\mid p_i \in Z,\,1 \leq i \leq n\}$
.
For a given set
![]() $\Omega $
and a
$\Omega $
and a
![]() $k\in \omega $
, the notation
$k\in \omega $
, the notation
![]() $\Omega ^k$
(resp.
$\Omega ^k$
(resp.
![]() $\Omega ^{\neq k}$
) will denote the k-th Cartesian power of
$\Omega ^{\neq k}$
) will denote the k-th Cartesian power of
![]() $\Omega $
(resp. the set of all k-tuples from
$\Omega $
(resp. the set of all k-tuples from
![]() $\Omega ^k$
such that their elements are pairwise distinct). We remind the reader that in the special case when
$\Omega ^k$
such that their elements are pairwise distinct). We remind the reader that in the special case when
![]() $k = 0$
it is usual to define
$k = 0$
it is usual to define
![]() $\Omega ^0:= \{\emptyset \} = 1$
, given our earlier convention about the natural numbers. Moreover we will denote the powerset of
$\Omega ^0:= \{\emptyset \} = 1$
, given our earlier convention about the natural numbers. Moreover we will denote the powerset of
![]() $\Omega $
by
$\Omega $
by
![]() $\mathscr {P}(\Omega )$
. We also define that
$\mathscr {P}(\Omega )$
. We also define that
![]() $\Omega ^\ast := \bigcup _{n \geq 0}\Omega ^n$
. Finally, the notation
$\Omega ^\ast := \bigcup _{n \geq 0}\Omega ^n$
. Finally, the notation
![]() $\lvert X\rvert $
will denote the cardinality of the set X, so that, for example,
$\lvert X\rvert $
will denote the cardinality of the set X, so that, for example,
![]() $\lvert X\rvert = \omega $
will mean that X is countably infinite.
$\lvert X\rvert = \omega $
will mean that X is countably infinite.
In this paper, we consider a first-order language without equality based on any set of predicate letters (including
![]() $0$
-ary predicates, that is to say, propositional letters) and individual constants. We do not allow functions, though.
$0$
-ary predicates, that is to say, propositional letters) and individual constants. We do not allow functions, though.
An ordered couple of sets
![]() $\Sigma = (Pred_\Sigma , Const_\Sigma )$
comprising all the predicate letters and constants allowed in a given version of the first-order language will be called the signature of this language. Signatures will be denoted by letters
$\Sigma = (Pred_\Sigma , Const_\Sigma )$
comprising all the predicate letters and constants allowed in a given version of the first-order language will be called the signature of this language. Signatures will be denoted by letters
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Theta $
. For a given signature
$\Theta $
. For a given signature
![]() $\Sigma $
, the elements of
$\Sigma $
, the elements of
![]() $Pred_\Sigma $
will be denoted by
$Pred_\Sigma $
will be denoted by
![]() $P^n$
and
$P^n$
and
![]() $Q^n$
, where
$Q^n$
, where
![]() $n> 0$
indicates the arity, and the elements of
$n> 0$
indicates the arity, and the elements of
![]() $Const_\Sigma $
will be denoted by lowercase Latin letters like a, b, c, d and so on. All these notations and all of the other notations introduced in this section can be decorated by all sorts of sub- and superscripts. We will often use the notation
$Const_\Sigma $
will be denoted by lowercase Latin letters like a, b, c, d and so on. All these notations and all of the other notations introduced in this section can be decorated by all sorts of sub- and superscripts. We will often use the notation
![]() $\Sigma _n$
for the set of n-ary predicates in a given signature
$\Sigma _n$
for the set of n-ary predicates in a given signature
![]() $\Sigma $
. Our signature will not contain function symbols as they are not necessary for the counterexample, and clearly our counterexample in a poorer signature carries over to more complex ones.
$\Sigma $
. Our signature will not contain function symbols as they are not necessary for the counterexample, and clearly our counterexample in a poorer signature carries over to more complex ones.
Even though we have defined signatures as ordered pairs, we will somewhat abuse the notation in the interest of suggestivity and, given a set
![]() $\Pi $
of predicates and a set
$\Pi $
of predicates and a set
![]() $\Delta $
of individual constants outside a given signature
$\Delta $
of individual constants outside a given signature
![]() $\Sigma $
, we will denote by
$\Sigma $
, we will denote by
![]() $\Sigma \cup \Pi \cup \Delta $
the signature where the predicates from
$\Sigma \cup \Pi \cup \Delta $
the signature where the predicates from
![]() $\Pi $
are added to
$\Pi $
are added to
![]() $Pred_\Sigma $
with their respective arities and the constants from
$Pred_\Sigma $
with their respective arities and the constants from
![]() $\Delta $
are added to
$\Delta $
are added to
![]() $Const_\Sigma $
. Moreover, we will write
$Const_\Sigma $
. Moreover, we will write
![]() $\Sigma \subseteq \Theta $
iff there exists a set
$\Sigma \subseteq \Theta $
iff there exists a set
![]() $\Pi $
of predicates and a set
$\Pi $
of predicates and a set
![]() $\Delta $
of individual constants outside
$\Delta $
of individual constants outside
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\Theta = \Sigma \cup \Pi \cup \Delta $
; in other words, iff
$\Theta = \Sigma \cup \Pi \cup \Delta $
; in other words, iff
![]() $\Theta $
extends
$\Theta $
extends
![]() $\Sigma $
as a signature. In case
$\Sigma $
as a signature. In case
![]() $\Pi = Pred_{\Sigma '}$
and
$\Pi = Pred_{\Sigma '}$
and
![]() $\Delta = Const_{\Sigma '}$
, we also express this same fact by writing
$\Delta = Const_{\Sigma '}$
, we also express this same fact by writing
![]() $\Theta = \Sigma \cup \Sigma '$
; furthermore, in case we have
$\Theta = \Sigma \cup \Sigma '$
; furthermore, in case we have
![]() $P \in \Pi $
and
$P \in \Pi $
and
![]() $c \in \Delta $
, we will write
$c \in \Delta $
, we will write
![]() $P \notin \Sigma $
and
$P \notin \Sigma $
and
![]() $c \notin \Sigma $
. Similarly, if
$c \notin \Sigma $
. Similarly, if
![]() $\Theta _1 = \Sigma \cup \Pi _1 \cup \Delta _1$
and
$\Theta _1 = \Sigma \cup \Pi _1 \cup \Delta _1$
and
![]() $\Theta _2 = \Sigma \cup \Pi _2 \cup \Delta _2$
, for pairwise non-overlapping sets of predicates
$\Theta _2 = \Sigma \cup \Pi _2 \cup \Delta _2$
, for pairwise non-overlapping sets of predicates
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
and sets of constants
$\Pi _2$
and sets of constants
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
, we will write that
$\Delta _2$
, we will write that
![]() $\Sigma = \Theta _1 \cap \Theta _2$
.
$\Sigma = \Theta _1 \cap \Theta _2$
.
If
![]() $\Sigma $
is a signature, then the set of first-order formulas is generated from
$\Sigma $
is a signature, then the set of first-order formulas is generated from
![]() $\Sigma $
in the usual way, using the set of logical symbols
$\Sigma $
in the usual way, using the set of logical symbols
![]() (here
(here
![]() stands for the bi-intuitionistic co-implication) and the set of (individual) variables
stands for the bi-intuitionistic co-implication) and the set of (individual) variables
![]() $Var := \{ v_i \mid i < \omega \}$
, and will be denoted by
$Var := \{ v_i \mid i < \omega \}$
, and will be denoted by
![]() $L(\Sigma )$
. The elements of
$L(\Sigma )$
. The elements of
![]() $Var$
will be also denoted by
$Var$
will be also denoted by
![]() $x,y,z, w$
, and the elements of
$x,y,z, w$
, and the elements of
![]() $L(\Sigma )$
by Greek letters like
$L(\Sigma )$
by Greek letters like
![]() $\phi $
,
$\phi $
,
![]() $\psi $
and
$\psi $
and
![]() $\theta $
. As is usual, we will use
$\theta $
. As is usual, we will use
![]() $\neg \phi $
as an abbreviation for
$\neg \phi $
as an abbreviation for
![]() $\phi \to \bot $
.
$\phi \to \bot $
.
For any given signature
![]() $\Sigma $
, and any given
$\Sigma $
, and any given
![]() $\phi \in L(\Sigma )$
, we define
$\phi \in L(\Sigma )$
, we define
![]() $FV(\phi )$
and
$FV(\phi )$
and
![]() $BV(\phi )$
, its sets of free and bound variables, by the usual inductions. These sets are always finite. We will denote the set of
$BV(\phi )$
, its sets of free and bound variables, by the usual inductions. These sets are always finite. We will denote the set of
![]() $L(\Sigma )$
-formulas with free variables among the elements of
$L(\Sigma )$
-formulas with free variables among the elements of
![]() $\bar {x}_n \in Var^{\neq n}$
by
$\bar {x}_n \in Var^{\neq n}$
by
![]() $L_{\bar {x}_n}(\Sigma )$
; in particular,
$L_{\bar {x}_n}(\Sigma )$
; in particular,
![]() $L_\emptyset (\Sigma )$
will stand for the set of
$L_\emptyset (\Sigma )$
will stand for the set of
![]() $\Sigma $
-sentences. If
$\Sigma $
-sentences. If
![]() $\varphi \in L_{\bar {x}_n}(\Sigma )$
(resp.
$\varphi \in L_{\bar {x}_n}(\Sigma )$
(resp.
![]() $\Gamma \subseteq L_{\bar {x}_n}(\Sigma )$
), then we will also express this by writing
$\Gamma \subseteq L_{\bar {x}_n}(\Sigma )$
), then we will also express this by writing
![]() $\varphi (\bar {x}_n)$
(resp.
$\varphi (\bar {x}_n)$
(resp.
![]() $\Gamma (\bar {x}_n)$
).
$\Gamma (\bar {x}_n)$
).
Similarly, given a
![]() $\phi \in L(\Sigma )$
, one can define a signature
$\phi \in L(\Sigma )$
, one can define a signature
![]() $\Theta _\phi $
such that, for any signature
$\Theta _\phi $
such that, for any signature
![]() $\Sigma '$
we have
$\Sigma '$
we have
![]() $\phi \in L(\Sigma ')$
iff
$\phi \in L(\Sigma ')$
iff
![]() $\Theta _\phi \subseteq \Sigma '$
. The definition proceeds by induction on the construction of
$\Theta _\phi \subseteq \Sigma '$
. The definition proceeds by induction on the construction of
![]() $\phi $
and looks as follows:
$\phi $
and looks as follows:
-
•
 $\Theta _{P(\bar {t}_n)} = (\{P^n\}, \{\bar {t}_n\}\cap Const_\Sigma )$
, for any
$\Theta _{P(\bar {t}_n)} = (\{P^n\}, \{\bar {t}_n\}\cap Const_\Sigma )$
, for any
 $P \in \Sigma _n$
and
$P \in \Sigma _n$
and
 $\bar {t}_n \in (Var \cup Const_\Sigma )^n$
.
$\bar {t}_n \in (Var \cup Const_\Sigma )^n$
. -
•
 $\Theta _\bot = \Theta _\top = \emptyset $
.
$\Theta _\bot = \Theta _\top = \emptyset $
. -
•
 $\Theta _{\psi \circ \theta } = \Theta _{\psi }\cup \Theta _{\theta }$
for
$\Theta _{\psi \circ \theta } = \Theta _{\psi }\cup \Theta _{\theta }$
for
 .
. -
•
 $\Theta _{\circ \psi } = \Theta _{\psi }$
for
$\Theta _{\circ \psi } = \Theta _{\psi }$
for
 $\circ \in \{\forall x, \exists x\mid x \in Var\}$
.
$\circ \in \{\forall x, \exists x\mid x \in Var\}$
.
If
![]() $X \subseteq Var$
is finite and
$X \subseteq Var$
is finite and
![]() $f: X \to Const_\Sigma $
, then, for any
$f: X \to Const_\Sigma $
, then, for any
![]() $\phi \in L(\Sigma )$
, we denote by
$\phi \in L(\Sigma )$
, we denote by
![]() $\phi [f] \in L(\Sigma )$
the result of simultaneously replacing every free occurrence of every
$\phi [f] \in L(\Sigma )$
the result of simultaneously replacing every free occurrence of every
![]() $x \in X$
by
$x \in X$
by
![]() $f(x)$
. The precise definition of this operation proceeds by induction on the construction of
$f(x)$
. The precise definition of this operation proceeds by induction on the construction of
![]() $\varphi \in L(\Sigma )$
and runs as follows:
$\varphi \in L(\Sigma )$
and runs as follows:
-
•
 $P(\bar {t}_n) := P(\bar {s}_n)$
, where
$P(\bar {t}_n) := P(\bar {s}_n)$
, where
 $P \in \Sigma _n$
, and
$P \in \Sigma _n$
, and
 $\bar {t}_n, \bar {s}_n \in (Var \cup Const_\Sigma )^n$
are such that, for all
$\bar {t}_n, \bar {s}_n \in (Var \cup Const_\Sigma )^n$
are such that, for all
 $1 \leq i \leq n$
we have:
$1 \leq i \leq n$
we have:  $$ \begin{align*} s_i := \begin{cases} f(t_i),\text{ if }t_i \in X,\\ t_i,\text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} s_i := \begin{cases} f(t_i),\text{ if }t_i \in X,\\ t_i,\text{ otherwise.} \end{cases} \end{align*} $$
-
•
 $(\phi )[f] : = \phi $
for
$(\phi )[f] : = \phi $
for
 $\phi \in \{\bot , \top \}$
.
$\phi \in \{\bot , \top \}$
. -
•
 $(\phi \circ \psi )[f] : = \phi [f]\circ \psi [f]$
, for
$(\phi \circ \psi )[f] : = \phi [f]\circ \psi [f]$
, for
 .
. -
•
 $(Qx\phi )[f] : = Qx(\phi [f\upharpoonright (X \setminus \{x\})])$
, for
$(Qx\phi )[f] : = Qx(\phi [f\upharpoonright (X \setminus \{x\})])$
, for
 $x \in Var$
and
$x \in Var$
and
 $Q \in \{\forall , \exists \}$
.
$Q \in \{\forall , \exists \}$
.
Since
![]() $dom(f)$
is always finite, we will write
$dom(f)$
is always finite, we will write
![]() $\phi [c_1/x_1,\ldots ,c_n/x_n]$
(or, alternatively,
$\phi [c_1/x_1,\ldots ,c_n/x_n]$
(or, alternatively,
![]() $\phi [\bar {c}_n/\bar {x}_n]$
) in place of
$\phi [\bar {c}_n/\bar {x}_n]$
) in place of
![]() $\varphi [f]$
, whenever f is
$\varphi [f]$
, whenever f is
![]() $\bar {x}_n \mapsto \bar {c}_n$
. It is clear that every
$\bar {x}_n \mapsto \bar {c}_n$
. It is clear that every
![]() $\varphi [f]$
can be written in this format. An important particular case is when
$\varphi [f]$
can be written in this format. An important particular case is when
![]() $dom(f) = \{x\}$
, so that we can write
$dom(f) = \{x\}$
, so that we can write
![]() $\phi [f]$
as
$\phi [f]$
as
![]() $\phi [c/x]$
for the corresponding
$\phi [c/x]$
for the corresponding
![]() $c \in Const_\Sigma $
.
$c \in Const_\Sigma $
.
The following lemma states that our substitution operations work as expected. We omit the straightforward but tedious inductive proof.
Lemma 1. Let
![]() $\Sigma $
be a signature, let
$\Sigma $
be a signature, let
![]() $\bar {x}_n \in Var^{\neq n}$
,
$\bar {x}_n \in Var^{\neq n}$
,
![]() $\phi \in L_{\bar {x}_n}(\Sigma )$
,
$\phi \in L_{\bar {x}_n}(\Sigma )$
,
![]() $\bar {y}_m \in Var^{\neq m}$
, and
$\bar {y}_m \in Var^{\neq m}$
, and
![]() $\bar {z}_k \in Var^{\neq k}$
be such that
$\bar {z}_k \in Var^{\neq k}$
be such that
![]() $\{\bar {z}_k\} = \{\bar {x}_n\}\setminus \{\bar {y}_m\}$
. Moreover, let
$\{\bar {z}_k\} = \{\bar {x}_n\}\setminus \{\bar {y}_m\}$
. Moreover, let
![]() $\bar {c}_m \in (Const_\Sigma )^m$
, and let
$\bar {c}_m \in (Const_\Sigma )^m$
, and let
![]() $(i_1,\ldots ,i_m)$
be a permutation of
$(i_1,\ldots ,i_m)$
be a permutation of
![]() $(1,\ldots , m)$
. Then the following statements hold:
$(1,\ldots , m)$
. Then the following statements hold:
-
1.
 $\phi [\bar {c}_m/\bar {y}_m] \in L_{\bar {z}_k}(\Sigma )$
.
$\phi [\bar {c}_m/\bar {y}_m] \in L_{\bar {z}_k}(\Sigma )$
. -
2.
 $\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{i_1}/y_{i_1},\ldots , c_{i_m}/y_{i_m}]$
.
$\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{i_1}/y_{i_1},\ldots , c_{i_m}/y_{i_m}]$
. -
3.
 $\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{1}/y_{1}]\ldots [c_{m}/y_{m}]$
.
$\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{1}/y_{1}]\ldots [c_{m}/y_{m}]$
. -
4. If
 $FV(\phi ) \cap \{\bar {x}_n\} = \{x_{j_1},\ldots ,x_{j_m}\}$
, then
$FV(\phi ) \cap \{\bar {x}_n\} = \{x_{j_1},\ldots ,x_{j_m}\}$
, then
 $\phi [\bar {c}_n/\bar {x}_n] = \phi [c_{j_1}/x_{j_1},\ldots ,c_{j_m}/x_{j_m}]$
.
$\phi [\bar {c}_n/\bar {x}_n] = \phi [c_{j_1}/x_{j_1},\ldots ,c_{j_m}/x_{j_m}]$
. -
5. If
 $\psi \in L_{\bar {x}_n}(\Sigma \cup \{\bar {c}_m\})$
, and
$\psi \in L_{\bar {x}_n}(\Sigma \cup \{\bar {c}_m\})$
, and
 $\{\bar {y}_m\} \cap (\{\bar {x}_n\} \cup BV(\psi )) = \emptyset $
, then there exists a
$\{\bar {y}_m\} \cap (\{\bar {x}_n\} \cup BV(\psi )) = \emptyset $
, then there exists a
 $\chi \in L_{(\bar {x}_n)^\frown (\bar {y}_m)}(\Sigma )$
such that
$\chi \in L_{(\bar {x}_n)^\frown (\bar {y}_m)}(\Sigma )$
such that
 $\chi [\bar {c}_m/\bar {y}_m] = \psi $
.
$\chi [\bar {c}_m/\bar {y}_m] = \psi $
. -
6.
 $\Theta _{\phi [\bar {c}_m/\bar {y}_m]} \subseteq \Theta _\phi \cup \{\bar {c}_m\}$
.
$\Theta _{\phi [\bar {c}_m/\bar {y}_m]} \subseteq \Theta _\phi \cup \{\bar {c}_m\}$
.
Note that Part 2 of the lemma holds just by the notational convention, since permutations of the set of the ordered pairs define one and the same function. Moreover, the joint effect of Parts 2 and 3 is that one can break up
![]() $[\bar {c}_n/\bar {x}_n]$
into a finite set of parts of arbitrary size and then apply those parts to a given
$[\bar {c}_n/\bar {x}_n]$
into a finite set of parts of arbitrary size and then apply those parts to a given
![]() $\phi $
in arbitrary order without affecting the result of a substitution. The latter is something that does not hold for the substitutions of arbitrary terms but is valid in our case due to the restriction to constants.
$\phi $
in arbitrary order without affecting the result of a substitution. The latter is something that does not hold for the substitutions of arbitrary terms but is valid in our case due to the restriction to constants.
The notion of substitution is necessary for a correct inductive definition of a sentence that is independent from the inductive definition of an arbitrary formula. More precisely, let
![]() $\Sigma $
be a signature and let c be any constant, perhaps outside
$\Sigma $
be a signature and let c be any constant, perhaps outside
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() $L_\emptyset (\Sigma )$
is the smallest subset
$L_\emptyset (\Sigma )$
is the smallest subset
![]() $Sent(\Sigma )$
of
$Sent(\Sigma )$
of
![]() $L(\Sigma )$
satisfying the following conditions:
$L(\Sigma )$
satisfying the following conditions:
-
•
 $P(\bar {c}_n), \bot , \top \in Sent(\Sigma )$
for all
$P(\bar {c}_n), \bot , \top \in Sent(\Sigma )$
for all
 $n \geq 1$
,
$n \geq 1$
,
 $P \in \Sigma _n$
, and
$P \in \Sigma _n$
, and
 $\bar {c}_n \in (Const_\Sigma )^n$
.
$\bar {c}_n \in (Const_\Sigma )^n$
. -
• If
 $\phi , \psi \in Sent(\Sigma )$
, then
$\phi , \psi \in Sent(\Sigma )$
, then
 $(\phi \circ \psi ) \in Sent(\Sigma )$
for all
$(\phi \circ \psi ) \in Sent(\Sigma )$
for all
 .
. -
• If
 $x \in Var$
and
$x \in Var$
and
 $\phi [c/x] \in Sent(\Sigma \cup \{c\})$
, then
$\phi [c/x] \in Sent(\Sigma \cup \{c\})$
, then
 $\forall x\phi , \exists x\phi \in Sent(\Sigma )$
.
$\forall x\phi , \exists x\phi \in Sent(\Sigma )$
.
2.2 Semantics
For any given signature
![]() $\Sigma $
, a constant domain intuitionistic Kripke
$\Sigma $
, a constant domain intuitionistic Kripke
![]() $\Sigma $
-model is a structure of the form
$\Sigma $
-model is a structure of the form
![]() $\mathcal {M} = (W, \prec , D, V, I)$
such that:
$\mathcal {M} = (W, \prec , D, V, I)$
such that:
-
• W is a non-empty set of worlds, or nodes.
-
• The accessibility relation
 $\prec \subseteq W \times W$
is reflexive and transitive (i.e., a pre-order).
$\prec \subseteq W \times W$
is reflexive and transitive (i.e., a pre-order). -
• D is a non-empty set (or domain) of objects which is disjoint from W.
-
• The mapping V is a function from
 $Pred_\Sigma \times W$
into the set
$Pred_\Sigma \times W$
into the set
 $\bigcup _{n \geq 0}\mathscr {P}(D^n)$
such that, for every
$\bigcup _{n \geq 0}\mathscr {P}(D^n)$
such that, for every
 $n \geq 0$
, every
$n \geq 0$
, every
 $P \in \Sigma _n$
, and all
$P \in \Sigma _n$
, and all
 $w, v \in W$
, it is true that
$w, v \in W$
, it is true that
 $V(P, w) \subseteq D^n$
and
$V(P, w) \subseteq D^n$
and  $$ \begin{align*} w \prec v \Rightarrow V(P, w) \subseteq V(P, v). \end{align*} $$
$$ \begin{align*} w \prec v \Rightarrow V(P, w) \subseteq V(P, v). \end{align*} $$
Given a
 $P \in \Sigma _n$
, we will sometimes consider the unary projection functions of the form
$P \in \Sigma _n$
, we will sometimes consider the unary projection functions of the form
 $V_P:W \to \mathscr {P}(D^n)$
arising from the binary function V. It is clear that we may view V as the union of the corresponding family of the unary functions, that is to say, that we can assume
$V_P:W \to \mathscr {P}(D^n)$
arising from the binary function V. It is clear that we may view V as the union of the corresponding family of the unary functions, that is to say, that we can assume
 $V = \bigcup _{P \in Pred_\Sigma }V_P$
.
$V = \bigcup _{P \in Pred_\Sigma }V_P$
. -
•
 $I: Const_\Sigma \to D$
is the function interpreting the individual constants.
$I: Const_\Sigma \to D$
is the function interpreting the individual constants.
In what follows, we will always assume the particular case when I is just the identity function on
![]() $Const_\Sigma $
; in other words, we will only consider the constants that are names of themselves.
$Const_\Sigma $
; in other words, we will only consider the constants that are names of themselves.
An interesting particular case arises when
![]() $P \in \Sigma _0$
. In this case, our definition says that
$P \in \Sigma _0$
. In this case, our definition says that
![]() $V_P:W \to \mathscr {P}(D^0)$
, but
$V_P:W \to \mathscr {P}(D^0)$
, but
![]() $\mathscr {P}(D^0) = \mathscr {P}(\{\emptyset \}) = \{\emptyset , \{\emptyset \}\} = \{0,1\} = 2$
, given our identification of natural numbers with the finite ordinals. Therefore,
$\mathscr {P}(D^0) = \mathscr {P}(\{\emptyset \}) = \{\emptyset , \{\emptyset \}\} = \{0,1\} = 2$
, given our identification of natural numbers with the finite ordinals. Therefore,
![]() $V_{P}$
in this case is, in effect, a function from W to
$V_{P}$
in this case is, in effect, a function from W to
![]() $\{0, 1\}$
, and
$\{0, 1\}$
, and
![]() $V_{P}$
returns
$V_{P}$
returns
![]() $1$
for a given w iff
$1$
for a given w iff
![]() $P^0$
holds at w in
$P^0$
holds at w in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Since we will only consider in this paper the models of the type described above, we will simply call them
![]() $\Sigma $
-models.
$\Sigma $
-models.
When we use subscripts and other decorated model notations, we strive for consistency in this respect. Some examples of this notational principle are given below:
As is usual, we denote the reduct of a
![]() $\Sigma $
-model
$\Sigma $
-model
![]() $\mathcal {M}$
to a signature
$\mathcal {M}$
to a signature
![]() $\Theta \subseteq \Sigma $
by
$\Theta \subseteq \Sigma $
by
![]() $\mathcal {M}\upharpoonright \Theta $
.
$\mathcal {M}\upharpoonright \Theta $
.
As for the reverse operation of expanding a model of a smaller signature to a model of a larger signature, if
![]() $\mathcal {M}$
is a
$\mathcal {M}$
is a
![]() $\Sigma $
-model,
$\Sigma $
-model,
![]() $P^{n_1}_1, \ldots , P^{n_k}_k \notin \Sigma $
are pairwise distinct, and
$P^{n_1}_1, \ldots , P^{n_k}_k \notin \Sigma $
are pairwise distinct, and
![]() $\mathbf {A} \subseteq D$
, then, for any given sequence of
$\mathbf {A} \subseteq D$
, then, for any given sequence of
![]() $\pi _1:W\to \mathscr {P}(D^{n_1}), \ldots , \pi _k:W\to \mathscr {P}(D^{n_k})$
of functions monotonic relative to
$\pi _1:W\to \mathscr {P}(D^{n_1}), \ldots , \pi _k:W\to \mathscr {P}(D^{n_k})$
of functions monotonic relative to
![]() $\prec $
, we will denote by
$\prec $
, we will denote by
![]() $(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k; \mathbf {A})$
the unique
$(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k; \mathbf {A})$
the unique
![]() $\Sigma \cup \{ P^{n_1}_1, \ldots ,P^{n_k}_k\}\cup \mathbf {A}$
-model
$\Sigma \cup \{ P^{n_1}_1, \ldots ,P^{n_k}_k\}\cup \mathbf {A}$
-model
![]() $\mathcal {M}'$
such that
$\mathcal {M}'$
such that
![]() $\mathcal {M}'\upharpoonright \Sigma = \mathcal {M}$
,
$\mathcal {M}'\upharpoonright \Sigma = \mathcal {M}$
,
![]() $V'(P^{n_i}_i, w) = \pi _i(w)$
for all
$V'(P^{n_i}_i, w) = \pi _i(w)$
for all
![]() $w \in W$
, and
$w \in W$
, and
![]() $I'(a) = a$
for all
$I'(a) = a$
for all
![]() $1 \leq i \leq k$
and all
$1 \leq i \leq k$
and all
![]() $a \in \mathbf {A}$
. In case
$a \in \mathbf {A}$
. In case
![]() $k = 0$
or
$k = 0$
or
![]() $\mathbf {A} = \emptyset $
, we will write
$\mathbf {A} = \emptyset $
, we will write
![]() $(\mathcal {M};\mathbf {A})$
or
$(\mathcal {M};\mathbf {A})$
or
![]() $(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k)$
, respectively.
$(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k)$
, respectively.
The semantics is given by the following forcing relation defined by induction on the construction of a sentence. If
![]() $\Sigma $
is a signature,
$\Sigma $
is a signature,
![]() $\mathcal {M}$
is a
$\mathcal {M}$
is a
![]() $\Sigma $
-model,
$\Sigma $
-model,
![]() $w \in W$
, and
$w \in W$
, and
![]() $\phi \in L_\emptyset (\Sigma \cup D)$
, then we write that
$\phi \in L_\emptyset (\Sigma \cup D)$
, then we write that
![]() $(\mathcal {M}; D), w \models \phi $
and say that
$(\mathcal {M}; D), w \models \phi $
and say that
![]() $\phi $
is true at w in
$\phi $
is true at w in
![]() $(\mathcal {M}; D)$
iff it follows from the following clauses:
$(\mathcal {M}; D)$
iff it follows from the following clauses:

In the clauses given above, as well as in the similar places below, like Lemma 2 and Definition 4, we also use the symbols
![]() $\forall $
and
$\forall $
and
![]() $\exists $
in the defining part to denote the (classical) quantifiers in the meta-language. We are certain that this creates no ambiguities.
$\exists $
in the defining part to denote the (classical) quantifiers in the meta-language. We are certain that this creates no ambiguities.
Note that the assumption of constant domains allows for a simplification of the clause treating the universal quantifier. The following lemma then spells out the consequences of our definition for the defined connective
![]() $\neg $
.
$\neg $
.
Lemma 2. If
![]() $\Sigma $
is a signature,
$\Sigma $
is a signature,
![]() $\mathcal {M}$
is a
$\mathcal {M}$
is a
![]() $\Sigma $
-model,
$\Sigma $
-model,
![]() $w \in W$
, and
$w \in W$
, and
![]() $\phi \in L_\emptyset (\Sigma \cup D)$
then we have
$\phi \in L_\emptyset (\Sigma \cup D)$
then we have
The proof is immediate by the definition and is omitted.
We then extend this semantics to arbitrary models by setting that for a
![]() $\Sigma $
-model
$\Sigma $
-model
![]() $\mathcal {M}$
, and for a
$\mathcal {M}$
, and for a
![]() $\phi \in L_\emptyset (\Sigma )$
, we have
$\phi \in L_\emptyset (\Sigma )$
, we have
![]() $\mathcal {M}, w\models \phi $
iff
$\mathcal {M}, w\models \phi $
iff
![]() $(\mathcal {M};D), w\models \phi $
. The following theorem is then immediate.
$(\mathcal {M};D), w\models \phi $
. The following theorem is then immediate.
Theorem 1. Let
![]() $\Sigma , \Theta $
be signatures such that
$\Sigma , \Theta $
be signatures such that
![]() $\Sigma \subseteq \Theta $
, let
$\Sigma \subseteq \Theta $
, let
![]() $\mathcal {M}$
be a
$\mathcal {M}$
be a
![]() $\Theta $
-model, let
$\Theta $
-model, let
![]() $w \in W$
, and let
$w \in W$
, and let
![]() $\phi \in L_\emptyset (\Sigma )$
. Then
$\phi \in L_\emptyset (\Sigma )$
. Then
![]() $\mathcal {M}, w \models \phi $
iff
$\mathcal {M}, w \models \phi $
iff
![]() $\mathcal {M}\upharpoonright \Sigma , w \models \phi $
.
$\mathcal {M}\upharpoonright \Sigma , w \models \phi $
.
Theorem 1 is often referred to as Expansion Property in the literature on abstract model theory.
Next, we adopt the standard definitions of validity, satisfiability and of semantic consequence relation. In particular, given a signature
![]() $\Sigma $
, a
$\Sigma $
, a
![]() $\Gamma \cup \{\phi \} \subseteq L_\emptyset (\Sigma )$
, a
$\Gamma \cup \{\phi \} \subseteq L_\emptyset (\Sigma )$
, a
![]() $\Sigma $
-model
$\Sigma $
-model
![]() $\mathcal {M}$
, and a
$\mathcal {M}$
, and a
![]() $w \in W$
, we say that
$w \in W$
, we say that
![]() $(\mathcal {M}, w)$
satisfies
$(\mathcal {M}, w)$
satisfies
![]() $\Gamma $
, and write
$\Gamma $
, and write
![]() $\mathcal {M}, w\models \Gamma $
iff we have
$\mathcal {M}, w\models \Gamma $
iff we have
![]() $\mathcal {M}, w\models \psi $
for all
$\mathcal {M}, w\models \psi $
for all
![]() $\psi \in \Gamma $
. Furthermore, we say that
$\psi \in \Gamma $
. Furthermore, we say that
![]() $\phi $
is a consequence of
$\phi $
is a consequence of
![]() $\Gamma $
and write
$\Gamma $
and write
![]() $\Gamma \models \phi $
iff for every
$\Gamma \models \phi $
iff for every
![]() $\Sigma $
-model
$\Sigma $
-model
![]() $\mathcal {M}$
, and every
$\mathcal {M}$
, and every
![]() $w \in W$
,
$w \in W$
,
![]() $\mathcal {M}, w\models \Gamma $
implies that
$\mathcal {M}, w\models \Gamma $
implies that
![]() $\mathcal {M}, w\models \phi $
. In case
$\mathcal {M}, w\models \phi $
. In case
![]() $\Gamma = \{\psi \}$
for some
$\Gamma = \{\psi \}$
for some
![]() $\psi \in L_\emptyset (\Sigma )$
, we will omit the brackets and simply write
$\psi \in L_\emptyset (\Sigma )$
, we will omit the brackets and simply write
![]() $\psi \models \phi $
, and in case
$\psi \models \phi $
, and in case
![]() $\Gamma = \emptyset $
we will write
$\Gamma = \emptyset $
we will write
![]() $\models \phi $
omitting
$\models \phi $
omitting
![]() $\Gamma $
altogether.
$\Gamma $
altogether.
Having now both the language and its semantic apparatus in place, we can speak of the logical system
![]() $\mathsf {FOBIL}$
of bi-intuitionistic predicate logic. As a model-theoretic language,
$\mathsf {FOBIL}$
of bi-intuitionistic predicate logic. As a model-theoretic language,
![]() $\mathsf {FOBIL}$
can be presented as a fragment of classical first-order logic
$\mathsf {FOBIL}$
can be presented as a fragment of classical first-order logic
![]() $\mathsf {FOCL}$
by means of an appropriate standard translation along the lines of [Reference Olkhovikov15]. On the other hand,
$\mathsf {FOCL}$
by means of an appropriate standard translation along the lines of [Reference Olkhovikov15]. On the other hand,
![]() $\mathsf {FOBIL}$
can be seen as resulting from intuitionistic predicate logic
$\mathsf {FOBIL}$
can be seen as resulting from intuitionistic predicate logic
![]() $\mathsf {FOIL}$
by first restricting its semantics to the constant-domain Kripke models and then adding
$\mathsf {FOIL}$
by first restricting its semantics to the constant-domain Kripke models and then adding
![]() as the new connective to the language. An even closer relation exists between
as the new connective to the language. An even closer relation exists between
![]() $\mathsf {FOBIL}$
and the intuitionistic logic of constant domains
$\mathsf {FOBIL}$
and the intuitionistic logic of constant domains
![]() $\mathsf {CD}$
which can be viewed as the
$\mathsf {CD}$
which can be viewed as the
![]() -free fragment of
-free fragment of
![]() $\mathsf {FOBIL}$
.
$\mathsf {FOBIL}$
.
2.3 Bi-asimulations
An important semantic concept related to bi-intuitionistic predicate logic is the notion of first-order bi-asimulation. This notion can be defined as follows.
Definition 1. Let
![]() $\Sigma $
be a signature, and let
$\Sigma $
be a signature, and let
![]() $\mathcal {M}_0$
,
$\mathcal {M}_0$
,
![]() $\mathcal {M}_1$
be
$\mathcal {M}_1$
be
![]() $\Sigma $
-models. A non-empty relation A is called a first-order bi-asimulation iff the following conditions are satisfied for all
$\Sigma $
-models. A non-empty relation A is called a first-order bi-asimulation iff the following conditions are satisfied for all
![]() $i,j$
such that
$i,j$
such that
![]() $\{i,j\} = \{0,1\}$
, and for all
$\{i,j\} = \{0,1\}$
, and for all
![]() $n \in \omega $
, all
$n \in \omega $
, all
![]() $P \in \Sigma _m$
, all (maybe non-distinct)
$P \in \Sigma _m$
, all (maybe non-distinct)
![]() $j_1, \ldots , j_m \leq n$
, all
$j_1, \ldots , j_m \leq n$
, all
![]() $(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$
and all
$(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$
and all
![]() $(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$
such that
$(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$
such that
![]() $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
:
$(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
:
In the case where we have
![]() $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
in the assumptions of Definition 1, we will say that the first-order bi-asimulation A is from
$(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
in the assumptions of Definition 1, we will say that the first-order bi-asimulation A is from
![]() $(w)^\frown (\bar {a}_n)$
to
$(w)^\frown (\bar {a}_n)$
to
![]() $(v)^\frown (\bar {b}_n)$
. Since we are not going to discuss any other kinds of bi-asimulation relations in this paper, we will omit in what follows the qualification ‘first-order’ and will simply speak of bi-asimulations. The following lemma shows that first-order bi-intuitionistic formulas are preserved under bi-asimulations.
$(v)^\frown (\bar {b}_n)$
. Since we are not going to discuss any other kinds of bi-asimulation relations in this paper, we will omit in what follows the qualification ‘first-order’ and will simply speak of bi-asimulations. The following lemma shows that first-order bi-intuitionistic formulas are preserved under bi-asimulations.
Lemma 3. Let
![]() $\Sigma $
be a signature, let
$\Sigma $
be a signature, let
![]() $\mathcal {M}_0$
,
$\mathcal {M}_0$
,
![]() $\mathcal {M}_1$
be
$\mathcal {M}_1$
be
![]() $\Sigma $
-models, let
$\Sigma $
-models, let
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $i,j$
be such that
$i,j$
be such that
![]() $\{i,j\} = \{0,1\}$
, let
$\{i,j\} = \{0,1\}$
, let
![]() $(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$
and
$(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$
and
![]() $(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$
, and let A be a bi-asimulation between
$(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$
, and let A be a bi-asimulation between
![]() $\mathcal {M}_0$
and
$\mathcal {M}_0$
and
![]() $\mathcal {M}_1$
such that
$\mathcal {M}_1$
such that
![]() $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
. Then for every tuple
$(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$
. Then for every tuple
![]() $\bar {x}_n \in Var^{\neq n}$
and every
$\bar {x}_n \in Var^{\neq n}$
and every
![]() $\phi \in L_{\bar {x}_n}(\Sigma )$
it is true that
$\phi \in L_{\bar {x}_n}(\Sigma )$
it is true that
Proof. By induction on the construction of
![]() $\phi $
.
$\phi $
.
Induction basis. If
![]() $\phi = P(x_{j_1},\ldots ,x_{j_m})$
for some (maybe non-distinct)
$\phi = P(x_{j_1},\ldots ,x_{j_m})$
for some (maybe non-distinct)
![]() $j_1, \ldots , j_m \leq n$
and some
$j_1, \ldots , j_m \leq n$
and some
![]() $P \in \Sigma _m$
, then the statement of the Lemma follows from condition (atom) of Definition 1 and the fact that we have
$P \in \Sigma _m$
, then the statement of the Lemma follows from condition (atom) of Definition 1 and the fact that we have
![]() $\phi [\bar {a}_n/\bar {x}_n] = P(a_{j_1},\ldots ,a_{j_m})$
and
$\phi [\bar {a}_n/\bar {x}_n] = P(a_{j_1},\ldots ,a_{j_m})$
and
![]() $\phi [\bar {b}_n/\bar {x}_n] = P(b_{j_1},\ldots ,b_{j_m})$
.
$\phi [\bar {b}_n/\bar {x}_n] = P(b_{j_1},\ldots ,b_{j_m})$
.
Induction step. The cases when
![]() $\phi = \psi \wedge \theta $
and when
$\phi = \psi \wedge \theta $
and when
![]() $\phi = \psi \vee \theta $
are straightforward. We consider the remaining cases:
$\phi = \psi \vee \theta $
are straightforward. We consider the remaining cases:
Case 1.
![]() $\phi = \psi \to \theta $
. If
$\phi = \psi \to \theta $
. If
![]() $(\mathcal {M}_j; D_j), v\not \models (\psi \to \theta )[\bar {b}_n/\bar {x}_n]$
, then
$(\mathcal {M}_j; D_j), v\not \models (\psi \to \theta )[\bar {b}_n/\bar {x}_n]$
, then
![]() $(\mathcal {M}_j; D_j), v\not \models \psi [\bar {b}_n/\bar {x}_n] \to \theta [\bar {b}_n/\bar {x}_n]$
, and hence there exists a
$(\mathcal {M}_j; D_j), v\not \models \psi [\bar {b}_n/\bar {x}_n] \to \theta [\bar {b}_n/\bar {x}_n]$
, and hence there exists a
![]() $v_0 \mathrel {\succ _j}v$
such that both
$v_0 \mathrel {\succ _j}v$
such that both
![]() $(\mathcal {M}_j; D_j), v_0\models \psi [\bar {b}_n/\bar {x}_n]$
and
$(\mathcal {M}_j; D_j), v_0\models \psi [\bar {b}_n/\bar {x}_n]$
and
![]() $(\mathcal {M}_j; D_j), v_0\not \models \theta [\bar {b}_n/\bar {x}_n]$
. But then, by condition (back), there must be a
$(\mathcal {M}_j; D_j), v_0\not \models \theta [\bar {b}_n/\bar {x}_n]$
. But then, by condition (back), there must be a
![]() $w_0 \mathrel {\succ _i}w$
such that both
$w_0 \mathrel {\succ _i}w$
such that both
![]() $(w_0)^\frown (\bar {a}_n)\mathrel {A}(v_0)^\frown (\bar {b}_n)$
and
$(w_0)^\frown (\bar {a}_n)\mathrel {A}(v_0)^\frown (\bar {b}_n)$
and
![]() $(v_0)^\frown (\bar {b}_n)\mathrel {A}(w_0)^\frown (\bar {a}_n)$
. Now the Induction Hypothesis implies that both
$(v_0)^\frown (\bar {b}_n)\mathrel {A}(w_0)^\frown (\bar {a}_n)$
. Now the Induction Hypothesis implies that both
![]() $(\mathcal {M}_i; D_i), w_0\models \psi [\bar {a}_n/\bar {x}_n]$
and
$(\mathcal {M}_i; D_i), w_0\models \psi [\bar {a}_n/\bar {x}_n]$
and
![]() $(\mathcal {M}_i; D_i), w_0\not \models \theta [\bar {a}_n/\bar {x}_n]$
. Thus we get that
$(\mathcal {M}_i; D_i), w_0\not \models \theta [\bar {a}_n/\bar {x}_n]$
. Thus we get that
Case 2.
![]() . The case is dual to Case 1.
. The case is dual to Case 1.
Case 3.
![]() $\phi = \forall x\psi $
. Then we might have
$\phi = \forall x\psi $
. Then we might have
![]() $x \in \{\bar {x}_n\}$
, but we can always avoid this inconvenience by choosing an
$x \in \{\bar {x}_n\}$
, but we can always avoid this inconvenience by choosing an
![]() $m \geq 0$
, and some pairwise distinct
$m \geq 0$
, and some pairwise distinct
![]() $j_1,\ldots , j_m \leq n$
such that
$j_1,\ldots , j_m \leq n$
such that
![]() $\{x_{j_1},\ldots ,x_{j_m}\} = FV(\forall x\phi )\cap \{\bar {x}_n\}$
. For this m-tuple, we will have,
$\{x_{j_1},\ldots ,x_{j_m}\} = FV(\forall x\phi )\cap \{\bar {x}_n\}$
. For this m-tuple, we will have,
![]() $x \notin \{x_{j_1},\ldots ,x_{j_m}\}$
, and Lemma 1.4 implies that
$x \notin \{x_{j_1},\ldots ,x_{j_m}\}$
, and Lemma 1.4 implies that
But then we reason as follows. If
![]() $(\mathcal {M}_j; D_j), v\not \models (\forall x\psi )[\bar {b}_n/\bar {x}_n] = \forall x(\psi [b_{j_1}/x_{j_1},\ldots , b_{j_m}/x_{j_m}])$
, then we must have
$(\mathcal {M}_j; D_j), v\not \models (\forall x\psi )[\bar {b}_n/\bar {x}_n] = \forall x(\psi [b_{j_1}/x_{j_1},\ldots , b_{j_m}/x_{j_m}])$
, then we must have
![]() $(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}][b/x]$
for some
$(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}][b/x]$
for some
![]() $b \in D_j$
, and hence
$b \in D_j$
, and hence
![]() $(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}, b/x]$
by Lemma 1. Moreover, condition (left) of Definition 1 implies that, for some
$(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}, b/x]$
by Lemma 1. Moreover, condition (left) of Definition 1 implies that, for some
![]() $a \in D_i$
we must have
$a \in D_i$
we must have
![]() $(w)^\frown (\bar {a}_n)^\frown (a)\mathrel {A}(v)^\frown (\bar {b}_n)^\frown (b)$
. Since also
$(w)^\frown (\bar {a}_n)^\frown (a)\mathrel {A}(v)^\frown (\bar {b}_n)^\frown (b)$
. Since also
![]() $FV(\psi )\subseteq \{x_{j_1},\ldots ,x_{j_m}\} \cup \{x\}$
, the Induction Hypothesis is applicable and yields that
$FV(\psi )\subseteq \{x_{j_1},\ldots ,x_{j_m}\} \cup \{x\}$
, the Induction Hypothesis is applicable and yields that
![]() $(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots ,a_{j_m}/x_{j_m}, a/x]$
, whence, further, that
$(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots ,a_{j_m}/x_{j_m}, a/x]$
, whence, further, that
![]() $(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots , a_{j_m}/x_{j_m}][a/x]$
by Lemma 1.
$(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots , a_{j_m}/x_{j_m}][a/x]$
by Lemma 1.
But then it follows (again applying Lemma 1.4) that
Case 4.
![]() $\phi = \exists x\psi $
. The case is dual to Case 3.
$\phi = \exists x\psi $
. The case is dual to Case 3.
Remark 1. Asimulations had been initially introduced by the first author in studying the expressive power of intuitionistic propositional logic in [Reference Olkhovikov14], and they turned out to be equivalent to the intuitionistic bisimulations of [Reference Kurtonina and de Rijke10]. In [Reference Olkhovikov15], they were adapted to
![]() $\mathsf {FOIL}$
, and only a small step was then required to further adapt them to
$\mathsf {FOIL}$
, and only a small step was then required to further adapt them to
![]() $\mathsf {CD}$
; this step was done in [Reference Mints, Olkhovikov and Urquhart12, Definition 6.1] which only differs from Definition 4 in that the condition (forth) is absent. The latter condition first appeared in [Reference Badia1].
$\mathsf {CD}$
; this step was done in [Reference Mints, Olkhovikov and Urquhart12, Definition 6.1] which only differs from Definition 4 in that the condition (forth) is absent. The latter condition first appeared in [Reference Badia1].
Due to the absence of the Boolean, or classical, negation in intuitionistic and bi-intuitionistic logic, the (bi-)asimulations capture an inclusion of theories at the nodes of Kripke models that they connect to one another, rather than the coincidence of such theories. This asymmetry makes it necessary to define (bi-)asimulations as subsets of
![]() $\bigcup _{n \in \omega }((W_0\times (D_0)^n) \times (W_1\times (D_1)^n) )\cup ((W_1\times (D_1)^n) \times (W_0\times (D_0)^n) )$
rather than subsets of
$\bigcup _{n \in \omega }((W_0\times (D_0)^n) \times (W_1\times (D_1)^n) )\cup ((W_1\times (D_1)^n) \times (W_0\times (D_0)^n) )$
rather than subsets of
![]() $\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$
; another option, taken up in [Reference Badia1, Reference Kurtonina and de Rijke10], would be to define (bi-)asimulations as pairs of binary relations, where one relation is a subset of
$\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$
; another option, taken up in [Reference Badia1, Reference Kurtonina and de Rijke10], would be to define (bi-)asimulations as pairs of binary relations, where one relation is a subset of
![]() $\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$
and the other one a subset of
$\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$
and the other one a subset of
![]() $\bigcup _{n \in \omega }(W_1\times (D_1)^n) \times (W_0\times (D_0)^n)$
. The asymmetric nature of (bi)-asimulations also shows itself in the fact that condition (atom) can only be given in the form of an implication and not as a bi-conditional.
$\bigcup _{n \in \omega }(W_1\times (D_1)^n) \times (W_0\times (D_0)^n)$
. The asymmetric nature of (bi)-asimulations also shows itself in the fact that condition (atom) can only be given in the form of an implication and not as a bi-conditional.
A more detailed discussion of the intuitions behind different conditions in the asimulation definition can be found in several published articles; we especially recommend [Reference Olkhovikov14, pp. 350–351] and [Reference Olkhovikov15, p. 812]. Although the explanations there are given relative to the intuitionistic logic, all of them are also applicable to the bi-intuitionistic case. A more general and systematic inquiry into the dependence between the expressive power of a logic and a form of its characteristic simulation relation can be found in [Reference Olkhovikov16], where the first author basically shows, among other things, that, in the presence of classical
![]() $\vee $
and
$\vee $
and
![]() $\wedge $
in the language, the symmetry of a characteristic simulation is equivalent to a presence of a connective expressing non-constant and non-monotone Boolean function.
$\wedge $
in the language, the symmetry of a characteristic simulation is equivalent to a presence of a connective expressing non-constant and non-monotone Boolean function.
Since we are not treating the general theory of bi-asimulations in this paper, but are using them instead, as a technical tool, we omit any further details.
Remark 2. It is rather straightforward to show, by combining the arguments given in [Reference Badia1, Reference Olkhovikov15], that the invariance under bi-asimulations given in Definition 1 defines, for any given signature
![]() $\Sigma $
, the set of natural standard translations of first-order bi-intuitionistic formulas into classical first-order logic. Such a proof, however, is beyond the scope of the present paper.
$\Sigma $
, the set of natural standard translations of first-order bi-intuitionistic formulas into classical first-order logic. Such a proof, however, is beyond the scope of the present paper.
3 Interpolation fails in the bi-intuitionistic setting
3.1 Craig Interpolation Property and Mints’s Counterexample
The Craig Interpolation Property, which was initially defined for
![]() $\mathsf {FOCL}$
, can be considered for
$\mathsf {FOCL}$
, can be considered for
![]() $\mathsf {FOBIL}$
without any changes in the original definition. Therefore, we will say that
$\mathsf {FOBIL}$
without any changes in the original definition. Therefore, we will say that
![]() $\mathsf {FOBIL}$
has Craig Interpolation Property (CIP) iff for any signature
$\mathsf {FOBIL}$
has Craig Interpolation Property (CIP) iff for any signature
![]() $\Sigma $
, and any
$\Sigma $
, and any
![]() $(\phi \to \psi ) \in L_\emptyset (\Sigma )$
such that
$(\phi \to \psi ) \in L_\emptyset (\Sigma )$
such that
![]() $\models \phi \to \psi $
, there exists a
$\models \phi \to \psi $
, there exists a
![]() $\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi )$
such that both
$\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi )$
such that both
![]() $\models \phi \to \theta $
and
$\models \phi \to \theta $
and
![]() $\models \theta \to \psi $
. Any such
$\models \theta \to \psi $
. Any such
![]() $\theta $
is then called an interpolant for
$\theta $
is then called an interpolant for
![]() $\phi \to \psi $
.
$\phi \to \psi $
.
Although CIP holds for both
![]() $\mathsf {FOCL}$
and
$\mathsf {FOCL}$
and
![]() $\mathsf {FOIL}$
, it is known to fail for
$\mathsf {FOIL}$
, it is known to fail for
![]() $\mathsf {CD}$
. The counterexample to CIP for the latter logic was published in [Reference Mints, Olkhovikov and Urquhart12] and is obtained by setting
$\mathsf {CD}$
. The counterexample to CIP for the latter logic was published in [Reference Mints, Olkhovikov and Urquhart12] and is obtained by setting
and
in the definition for CIP given in the previous paragraph. Under these particular settings (fixed throughout the remaining part of this paper), we will call
![]() $\phi \to \psi $
Mints’s Counterexample to CIP. It was shown in [Reference Mints, Olkhovikov and Urquhart12] that
$\phi \to \psi $
Mints’s Counterexample to CIP. It was shown in [Reference Mints, Olkhovikov and Urquhart12] that
![]() $\phi \to \psi $
is valid in
$\phi \to \psi $
is valid in
![]() $\mathsf {CD}$
, but for no
$\mathsf {CD}$
, but for no
![]() -free
-free
![]() $\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi ) = L_\emptyset (\{P^1, Q^1\})$
both
$\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi ) = L_\emptyset (\{P^1, Q^1\})$
both
![]() $\phi \to \theta $
and
$\phi \to \theta $
and
![]() $\theta \to \psi $
are valid in
$\theta \to \psi $
are valid in
![]() $\mathsf {CD}$
.
$\mathsf {CD}$
.
Since
![]() $\mathsf {CD}$
is exactly the
$\mathsf {CD}$
is exactly the
![]() -free fragment of
-free fragment of
![]() $\mathsf {FOBIL}$
, the arguments of [Reference Mints, Olkhovikov and Urquhart12] also show that
$\mathsf {FOBIL}$
, the arguments of [Reference Mints, Olkhovikov and Urquhart12] also show that
![]() $\models \phi \to \psi $
. These arguments, however, are insufficient to show that
$\models \phi \to \psi $
. These arguments, however, are insufficient to show that
![]() $\phi \to \psi $
lacks an interpolant in
$\phi \to \psi $
lacks an interpolant in
![]() $\mathsf {FOBIL}$
due to the richer language of the latter logic. The main purpose of the present paper is to close this gap and to show that Mints’s Counterexample works for
$\mathsf {FOBIL}$
due to the richer language of the latter logic. The main purpose of the present paper is to close this gap and to show that Mints’s Counterexample works for
![]() $\mathsf {FOBIL}$
as well, and that therefore
$\mathsf {FOBIL}$
as well, and that therefore
![]() $\mathsf {FOBIL}$
lacks CIP. The next subsection contains a proof of these claims.
$\mathsf {FOBIL}$
lacks CIP. The next subsection contains a proof of these claims.
3.2 Refuting CIP
Our proof is an improvement on the proof given in [Reference Mints, Olkhovikov and Urquhart12]; it uses many of the same ideas albeit their application to this case requires several adjustments and a slight generalization.
We start by setting
![]() $\Sigma := \{P^1, Q^1\}$
. We will describe two particular
$\Sigma := \{P^1, Q^1\}$
. We will describe two particular
![]() $\Sigma $
-models and a bi-asimulation relation between them, and then we will show how to extend them to models satisfying
$\Sigma $
-models and a bi-asimulation relation between them, and then we will show how to extend them to models satisfying
![]() $\phi $
and failing
$\phi $
and failing
![]() $\psi $
, respectively. The rest of the argument will then be exactly as in [Reference Mints, Olkhovikov and Urquhart12].
$\psi $
, respectively. The rest of the argument will then be exactly as in [Reference Mints, Olkhovikov and Urquhart12].
We start with the definitions of the building blocks for our models (repeating [Reference Mints, Olkhovikov and Urquhart12, Definition 7.1]).
Definition 2.
-
1. A quasi-partition
 $(A,B,C)$
is defined by the following conditions:
$(A,B,C)$
is defined by the following conditions:-
(a)
 $A \cup B \cup C = \mathbb {N}$
;
$A \cup B \cup C = \mathbb {N}$
; -
(b)
 $A,B,C$
are pairwise disjoint;
$A,B,C$
are pairwise disjoint; -
(c)
 $\lvert A\rvert = \lvert C\rvert = \omega $
;
$\lvert A\rvert = \lvert C\rvert = \omega $
; -
(d)
 $\lvert B\rvert \in \{\emptyset , \omega \}$
.
$\lvert B\rvert \in \{\emptyset , \omega \}$
.
-
-
2. A relation
 $\trianglelefteq $
on the set of all quasi-partitions is defined by
$\trianglelefteq $
on the set of all quasi-partitions is defined by  $$\begin{align*}(A,B,C) \trianglelefteq (D,E,F) \Leftrightarrow [ A \subseteq D \wedge F \subseteq C]. \end{align*}$$
$$\begin{align*}(A,B,C) \trianglelefteq (D,E,F) \Leftrightarrow [ A \subseteq D \wedge F \subseteq C]. \end{align*}$$
We immediately fix the following corollary to Definition 2.
Corollary 1. For any quasi-partitions
![]() $(A,B,C)$
and
$(A,B,C)$
and
![]() $(D,E,F)$
, if
$(D,E,F)$
, if
![]() $(A,B,C) \trianglelefteq (D,E,F)$
, then
$(A,B,C) \trianglelefteq (D,E,F)$
, then
![]() $A \cup B \subseteq D \cup E$
.
$A \cup B \subseteq D \cup E$
.
Proof. If
![]() $(A,B,C) \trianglelefteq (D,E,F)$
, then
$(A,B,C) \trianglelefteq (D,E,F)$
, then
![]() $F \subseteq C$
; in other words,
$F \subseteq C$
; in other words,
![]() $\mathbb {N}\setminus (D \cup E) \subseteq \mathbb {N}\setminus (A \cup B)$
. Therefore, by contraposition,
$\mathbb {N}\setminus (D \cup E) \subseteq \mathbb {N}\setminus (A \cup B)$
. Therefore, by contraposition,
![]() $A \cup B \subseteq D \cup E$
.
$A \cup B \subseteq D \cup E$
.
We now fix two special quasi-partitions
![]() $\mathbf {v} = (\mathbf {v}_1, \mathbf {v}_2, \mathbf {v}_3) = ( 3 \mathbb {N}, 3 \mathbb {N} + 1, 3 \mathbb {N} + 2 )$
and
$\mathbf {v} = (\mathbf {v}_1, \mathbf {v}_2, \mathbf {v}_3) = ( 3 \mathbb {N}, 3 \mathbb {N} + 1, 3 \mathbb {N} + 2 )$
and
![]() $\mathbf {w} = (\mathbf {w}_1, \mathbf {w}_2, \mathbf {w}_3) = ( 2 \mathbb {N}, \emptyset , 2 \mathbb {N} + 1)$
. Our (fixed till the end of the present section)
$\mathbf {w} = (\mathbf {w}_1, \mathbf {w}_2, \mathbf {w}_3) = ( 2 \mathbb {N}, \emptyset , 2 \mathbb {N} + 1)$
. Our (fixed till the end of the present section)
![]() $\Sigma $
-models
$\Sigma $
-models
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
are then as follows.
$\mathcal {M}_2$
are then as follows.
Definition 3. The structures
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
are such that:
$\mathcal {M}_2$
are such that:
-
1.
 $W_1 = W_2 = W$
is the set of all quasi-partitions.
$W_1 = W_2 = W$
is the set of all quasi-partitions. -
2.
 $\prec _2 := \trianglelefteq $
, and, for all
$\prec _2 := \trianglelefteq $
, and, for all
 $(A,B,C), (D,E,F)\in W$
, we have
$(A,B,C), (D,E,F)\in W$
, we have
 $(A,B,C)\mathrel {\prec _1}(D,E,F)$
iff
$(A,B,C)\mathrel {\prec _1}(D,E,F)$
iff
 $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and  $$ \begin{align*} (\mathbf{v} \mathrel{\trianglelefteq} (A, B, C) \,\&\, \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert E \cap \mathbf{v}_2\rvert = \omega. \end{align*} $$
$$ \begin{align*} (\mathbf{v} \mathrel{\trianglelefteq} (A, B, C) \,\&\, \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert E \cap \mathbf{v}_2\rvert = \omega. \end{align*} $$
-
3.
 $D_1 = D_2 = \mathbb {N}$
.
$D_1 = D_2 = \mathbb {N}$
. -
4.
 $V_i(P,(A,B,C)) = A \cup B$
,
$V_i(P,(A,B,C)) = A \cup B$
,
 $V_i(Q,(A,B,C)) = A$
for all
$V_i(Q,(A,B,C)) = A$
for all
 $(A,B,C) \in W$
, and
$(A,B,C) \in W$
, and
 $i \in \{1, 2\}$
.
$i \in \{1, 2\}$
. -
5.
 $I_1 = I_2 = \emptyset $
.
$I_1 = I_2 = \emptyset $
.
We now show that
![]() $\mathcal {M}_1$
,
$\mathcal {M}_1$
,
![]() $\mathcal {M}_2$
are
$\mathcal {M}_2$
are
![]() $\Sigma $
-models that can be extended to models verifying
$\Sigma $
-models that can be extended to models verifying
![]() $\phi $
and falsifying
$\phi $
and falsifying
![]() $\psi $
, respectively.
$\psi $
, respectively.
Lemma 4.
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
are
$\mathcal {M}_2$
are
![]() $\Sigma $
-models.
$\Sigma $
-models.
Proof. The extensions of Q are monotonic relative to
![]() $\trianglelefteq $
(hence also relative to
$\trianglelefteq $
(hence also relative to
![]() $\prec _i$
for
$\prec _i$
for
![]() $i \in \{1,2\}$
) by definition of
$i \in \{1,2\}$
) by definition of
![]() $V_i$
. The extensions of P are monotonic relative to
$V_i$
. The extensions of P are monotonic relative to
![]() $\trianglelefteq $
(and thus also relative to
$\trianglelefteq $
(and thus also relative to
![]() $\prec _i$
for
$\prec _i$
for
![]() $i \in \{1,2\}$
) by Corollary 1.
$i \in \{1,2\}$
) by Corollary 1.
The relation
![]() $\prec _2 = \trianglelefteq $
is clearly a pre-order on W. We show that
$\prec _2 = \trianglelefteq $
is clearly a pre-order on W. We show that
![]() $\prec _1$
is a pre-order on the same set.
$\prec _1$
is a pre-order on the same set.
Reflexivity. Let
![]() $(A, B, C) \in W$
. We have
$(A, B, C) \in W$
. We have
![]() $(A,B,C)\mathrel {\prec _1}(A,B,C)$
, since both
$(A,B,C)\mathrel {\prec _1}(A,B,C)$
, since both
![]() $(A,B,C)\mathrel {\trianglelefteq }(A,B,C)$
and
$(A,B,C)\mathrel {\trianglelefteq }(A,B,C)$
and
are trivially satisfied.
Transitivity. Let
![]() $(A, B, C), (D,E,F), (G,H,I) \in W$
be such that
$(A, B, C), (D,E,F), (G,H,I) \in W$
be such that
![]() $(A,B,C)\mathrel {\prec _1}(D,E,F)$
and
$(A,B,C)\mathrel {\prec _1}(D,E,F)$
and
![]() $(D,E,F)\mathrel {\prec _1}(G,H,I)$
. Then we must have both
$(D,E,F)\mathrel {\prec _1}(G,H,I)$
. Then we must have both
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
![]() $(D,E,F)\mathrel {\trianglelefteq }(G,H,I)$
, and thus
$(D,E,F)\mathrel {\trianglelefteq }(G,H,I)$
, and thus
![]() $(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$
.
$(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$
.
On the other hand, we must have both:
and
But then we reason as follows:
Thus we have shown that both
![]() $(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$
and
$(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$
and
whence
![]() $(A,B,C)\mathrel {\prec _1}(G,H,I)$
also follows.
$(A,B,C)\mathrel {\prec _1}(G,H,I)$
also follows.
We pause to state another corollary we need towards our main lemma (Lemma 7).
Lemma 5. For arbitrary
![]() $(A,B,C), (D,E,F) \in W$
, the following statements hold:
$(A,B,C), (D,E,F) \in W$
, the following statements hold:
-
1.
 $\mathbf {v}\mathrel {\prec _1}(A,B,C)$
iff
$\mathbf {v}\mathrel {\prec _1}(A,B,C)$
iff
 $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
$\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
 $\lvert B \cap \mathbf {v}_2\rvert = \omega $
.
$\lvert B \cap \mathbf {v}_2\rvert = \omega $
. -
2. If both
 $\mathbf {v}\mathrel {\prec _1}(A,B,C)$
and
$\mathbf {v}\mathrel {\prec _1}(A,B,C)$
and
 $\mathbf {v}\mathrel {\prec _1}(D,E,F)$
, then
$\mathbf {v}\mathrel {\prec _1}(D,E,F)$
, then  $$ \begin{align*} (A,B,C)\mathrel{\prec_1}(D,E,F) \Leftrightarrow (A,B,C)\mathrel{\trianglelefteq}(D,E,F). \end{align*} $$
$$ \begin{align*} (A,B,C)\mathrel{\prec_1}(D,E,F) \Leftrightarrow (A,B,C)\mathrel{\trianglelefteq}(D,E,F). \end{align*} $$
-
3. If both
 $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
 $(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$
, then
$(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$
, then
 $(A,B,C) = (D,E,F)$
.
$(A,B,C) = (D,E,F)$
.
Proof. (Part 1). We have
![]() $\mathbf {v}\mathrel {\prec _1}(A,B,C)$
iff
$\mathbf {v}\mathrel {\prec _1}(A,B,C)$
iff
![]() $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
$\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
but, since the premise of the latter conditional is trivially true, it holds iff
![]() $\lvert B \cap \mathbf {v}_2\rvert = \omega $
.
$\lvert B \cap \mathbf {v}_2\rvert = \omega $
.
(Part 2). By definition,
![]() $(A,B,C)\mathrel {\prec _1}(D,E,F)$
implies
$(A,B,C)\mathrel {\prec _1}(D,E,F)$
implies
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
. In the other direction, if
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
. In the other direction, if
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and, additionally,
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and, additionally,
![]() $\mathbf {v}\mathrel {\prec _1}(D,E,F)$
, then we must have, by Part 1, that
$\mathbf {v}\mathrel {\prec _1}(D,E,F)$
, then we must have, by Part 1, that
![]() $\lvert E \cap \mathbf {v}_2\rvert = \omega $
. But then also the conditional
$\lvert E \cap \mathbf {v}_2\rvert = \omega $
. But then also the conditional
must be trivially true, whence also
![]() $(A,B,C)\mathrel {\prec _1}(D,E,F)$
follows.
$(A,B,C)\mathrel {\prec _1}(D,E,F)$
follows.
(Part 3). If both
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
![]() $(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$
then we have both
$(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$
then we have both
![]() $A = D$
and
$A = D$
and
![]() $C = F$
. Now
$C = F$
. Now
![]() $B = E$
follows by the fact that
$B = E$
follows by the fact that
![]() $(A,B,C), (D,E,F)$
are quasi-partitions.
$(A,B,C), (D,E,F)$
are quasi-partitions.
In case we have
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
but
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
but
![]() $(A,B,C) \neq (D,E,F)$
, we will write
$(A,B,C) \neq (D,E,F)$
, we will write
![]() $(A,B,C)\mathrel {\triangleleft }(D,E,F)$
.
$(A,B,C)\mathrel {\triangleleft }(D,E,F)$
.
Lemma 6. Fix a surjective
![]() $f: \mathbb {N} \to \mathbf {v}_2$
, and let
$f: \mathbb {N} \to \mathbf {v}_2$
, and let
![]() $\sigma _1: W \to \mathscr {P}(\mathbb {N})$
and
$\sigma _1: W \to \mathscr {P}(\mathbb {N})$
and
![]() $\sigma _2: W \to \{0,1\}$
be defined as follows for all
$\sigma _2: W \to \{0,1\}$
be defined as follows for all
![]() $(A,B,C) \in W$
:
$(A,B,C) \in W$
:
 $$ \begin{align*} \sigma_2(A,B,C):= \begin{cases} 1,\text{ if } \mathbf{w}\mathrel{\triangleleft}(A,B,C),\\ 0,\text{ otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} \sigma_2(A,B,C):= \begin{cases} 1,\text{ if } \mathbf{w}\mathrel{\triangleleft}(A,B,C),\\ 0,\text{ otherwise. } \end{cases} \end{align*} $$
Then
![]() $\sigma _1, \sigma _2$
are monotonic relative to
$\sigma _1, \sigma _2$
are monotonic relative to
![]() $\trianglelefteq $
, and hence also relative to
$\trianglelefteq $
, and hence also relative to
![]() $\prec _i$
for all
$\prec _i$
for all
![]() $i \in \{1,2\}$
.
$i \in \{1,2\}$
.
Furthermore, we define that
![]() $\mathcal {M}^{\prime }_1 := (\mathcal {M}_1; R^1\mapsto \sigma _1)$
and
$\mathcal {M}^{\prime }_1 := (\mathcal {M}_1; R^1\mapsto \sigma _1)$
and
![]() $\mathcal {M}^{\prime }_2 := (\mathcal {M}_2; S^0\mapsto \sigma _2)$
. Then both
$\mathcal {M}^{\prime }_2 := (\mathcal {M}_2; S^0\mapsto \sigma _2)$
. Then both
![]() $\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $
and
$\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $
and
![]() $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $
.
$\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $
.
Proof. We deal with the monotonicity claims first. As for
![]() $\sigma _1$
, if
$\sigma _1$
, if
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
, and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
, and
![]() $n \in \sigma _1(A,B,C)$
, then
$n \in \sigma _1(A,B,C)$
, then
![]() $f(n) \in A \subseteq D$
, hence also
$f(n) \in A \subseteq D$
, hence also
![]() $n \in \sigma _1(D,E,F)$
. As for
$n \in \sigma _1(D,E,F)$
. As for
![]() $\sigma _2$
, if
$\sigma _2$
, if
![]() $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
$(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$
and
![]() $\sigma _2(A,B,C) = 1$
, then
$\sigma _2(A,B,C) = 1$
, then
![]() $\mathbf {w}\mathrel {\triangleleft }(A,B,C)$
, hence also
$\mathbf {w}\mathrel {\triangleleft }(A,B,C)$
, hence also
![]() $\mathbf {w}\mathrel {\triangleleft }(D,E,F)$
and
$\mathbf {w}\mathrel {\triangleleft }(D,E,F)$
and
![]() $\sigma _2(D,E,F) = 1$
.
$\sigma _2(D,E,F) = 1$
.
It remains to show the satisfaction claims for the extended models.
(
![]() $\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $
). Assume that
$\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $
). Assume that
![]() $(A,B,C) \in W$
is such that
$(A,B,C) \in W$
is such that
![]() $\mathbf {v}\mathrel {\prec _1}(A,B,C)$
. Then, by Lemma 5.1, we have
$\mathbf {v}\mathrel {\prec _1}(A,B,C)$
. Then, by Lemma 5.1, we have
![]() $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
$\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$
and
![]() $\lvert B \cap \mathbf {v}_2\rvert = \omega $
. So we choose any
$\lvert B \cap \mathbf {v}_2\rvert = \omega $
. So we choose any
![]() $n \in B \cap \mathbf {v}_2$
and any
$n \in B \cap \mathbf {v}_2$
and any
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $f(m) = n$
. Then
$f(m) = n$
. Then
![]() $f(m) \notin A$
, and hence
$f(m) \notin A$
, and hence
![]() $m \notin \sigma _1(A,B,C)$
; in other words,
$m \notin \sigma _1(A,B,C)$
; in other words,
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models R(m)$
, whence
$(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models R(m)$
, whence
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models \forall xR(x)$
and, by Expansion Property,
$(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models \forall xR(x)$
and, by Expansion Property,
![]() $\mathcal {M}^{\prime }_1,(A, B, C)\not \models \forall xR(x)$
. Since the
$\mathcal {M}^{\prime }_1,(A, B, C)\not \models \forall xR(x)$
. Since the
![]() $\prec _1$
-successor to
$\prec _1$
-successor to
![]() $\mathbf {v}$
was chosen arbitrarily, it follows, by Lemma 2, that
$\mathbf {v}$
was chosen arbitrarily, it follows, by Lemma 2, that
![]() $\mathcal {M}^{\prime }_1,\mathbf {v}\models \neg \forall xR(x)$
.
$\mathcal {M}^{\prime }_1,\mathbf {v}\models \neg \forall xR(x)$
.
Next, if
![]() $n \in \mathbb {N}$
, then consider
$n \in \mathbb {N}$
, then consider
![]() $f(n) \in \mathbf {v}_2$
. Clearly, we have
$f(n) \in \mathbf {v}_2$
. Clearly, we have
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n))$
. If now
$(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n))$
. If now
![]() $(A,B,C) \in W$
is such that
$(A,B,C) \in W$
is such that
![]() $\mathbf {v}\mathrel {\prec _1}(A,B,C)$
and
$\mathbf {v}\mathrel {\prec _1}(A,B,C)$
and
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models Q(f(n))$
, then
$(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models Q(f(n))$
, then
![]() $f(n) \in A$
, thus also
$f(n) \in A$
, thus also
![]() $n \in \sigma _1(A,B,C)$
and, therefore,
$n \in \sigma _1(A,B,C)$
and, therefore,
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models R(n)$
. We have shown that
$(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models R(n)$
. We have shown that
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models Q(f(n)) \to R(n)$
. Summing up, we get that
$(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models Q(f(n)) \to R(n)$
. Summing up, we get that
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n)) \wedge (Q(f(n)) \to R(n))$
for arbitrary
$(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n)) \wedge (Q(f(n)) \to R(n))$
for arbitrary
![]() $n \in \mathbb {N}$
, therefore also
$n \in \mathbb {N}$
, therefore also
![]() $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$
and
$(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$
and
![]() $\mathcal {M}^{\prime }_1,\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$
by Expansion Property.
$\mathcal {M}^{\prime }_1,\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$
by Expansion Property.
(
![]() $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $
). Assume that
$\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $
). Assume that
![]() $n \in \mathbb {N}$
and that
$n \in \mathbb {N}$
and that
![]() $(A,B,C) \in W$
is such that
$(A,B,C) \in W$
is such that
![]() $\mathbf {w}\mathrel {\trianglelefteq }(A,B,C)$
and
$\mathbf {w}\mathrel {\trianglelefteq }(A,B,C)$
and
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models P(n)$
. Then two cases are possible:
$(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models P(n)$
. Then two cases are possible:
Case 1.
![]() $\mathbf {w} = (A,B,C)$
. Then
$\mathbf {w} = (A,B,C)$
. Then
![]() $n \in \mathbf {w}_1 \cup \mathbf {w}_2 = \mathbf {w}_1$
so that
$n \in \mathbf {w}_1 \cup \mathbf {w}_2 = \mathbf {w}_1$
so that
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n)$
, whence also
$(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n)$
, whence also
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n) \vee S$
.
$(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n) \vee S$
.
Case 2.
![]() $\mathbf {w}\mathrel {\triangleleft }(A,B,C)$
. Then
$\mathbf {w}\mathrel {\triangleleft }(A,B,C)$
. Then
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models S$
, therefore also
$(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models S$
, therefore also
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}), (A, B, C)\models Q(n) \vee S$
.
$(\mathcal {M}^{\prime }_2; \mathbb {N}), (A, B, C)\models Q(n) \vee S$
.
Summing up, we have shown that
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models P(n) \to (Q(n) \vee S)$
for arbitrary
$(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models P(n) \to (Q(n) \vee S)$
for arbitrary
![]() $n \in \mathbb {N}$
, whence it follows that
$n \in \mathbb {N}$
, whence it follows that
![]() $(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$
and, after applying Expansion Property, that
$(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$
and, after applying Expansion Property, that
![]() $\mathcal {M}^{\prime }_2,\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$
. However, we also have
$\mathcal {M}^{\prime }_2,\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$
. However, we also have
![]() $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models S$
by definition of
$\mathcal {M}^{\prime }_2,\mathbf {w}\not \models S$
by definition of
![]() $\sigma _2$
, and therefore
$\sigma _2$
, and therefore
![]() $\psi $
fails at
$\psi $
fails at
![]() $(\mathcal {M}^{\prime }_2,\mathbf {w})$
.
$(\mathcal {M}^{\prime }_2,\mathbf {w})$
.
Next, we define a particular bi-asimulation
![]() $\mathbb {A}$
between
$\mathbb {A}$
between
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
such that we have
$\mathcal {M}_2$
such that we have
![]() $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
. The definition looks as follows (cf. [Reference Mints, Olkhovikov and Urquhart12, Definition 7.3]).
$\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
. The definition looks as follows (cf. [Reference Mints, Olkhovikov and Urquhart12, Definition 7.3]).
Definition 4. Relative to the models
![]() ${\cal M}_1$
and
${\cal M}_1$
and
![]() ${\cal M}_2$
given in Definition 3, the relation
${\cal M}_2$
given in Definition 3, the relation
![]() $\mathbb {A}$
is defined as follows:
$\mathbb {A}$
is defined as follows:
-
1.
 $\mathbb {A} \subseteq \bigcup _{k \geq 0} [ (W \times \mathbb {N}^{k}) \times (W \times \mathbb {N}^{k})]$
;
$\mathbb {A} \subseteq \bigcup _{k \geq 0} [ (W \times \mathbb {N}^{k}) \times (W \times \mathbb {N}^{k})]$
; -
2. Given any
 $(A,B,C), (D,E,F)\in W$
, any
$(A,B,C), (D,E,F)\in W$
, any
 $n \geq 0$
and
$n \geq 0$
and
 $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
we have
 $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, iff the following conditions hold:
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, iff the following conditions hold:-
(a) Binary relation
 $[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection.
$[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection. -
(b) If
 $1 \leq k \leq n$
and
$1 \leq k \leq n$
and
 $a_k \in A$
then
$a_k \in A$
then
 $b_k \in D$
.
$b_k \in D$
. -
(c) If
 $1 \leq k \leq n$
and
$1 \leq k \leq n$
and
 $a_k \in B$
, then
$a_k \in B$
, then
 $b_k \in D \cup E$
.
$b_k \in D \cup E$
.
-
Again, we start by pointing out some easy, but important consequences of our definition:
Corollary 2. For any
![]() $(A,B,C), (D,E,F)\in W$
, any
$(A,B,C), (D,E,F)\in W$
, any
![]() $n \geq 0$
, and any
$n \geq 0$
, and any
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
, if we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
, if we have
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, then, for every
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, then, for every
![]() $1 \leq k \leq n$
, we have
$1 \leq k \leq n$
, we have
Proof. Indeed, in the assumptions of the corollary we get the following chain of valid implications:
 $$ \begin{align*} b_k \in F &\Rightarrow b_k \notin D \cup E &&\text{(by}\ F \cap (D \cup E) = \emptyset)\\ &\Rightarrow a_k \notin A \cup B &&\text{(by}\ (A,B,C)^{\frown}(\bar{a}_n)\mathrel{\mathbb{A}}(D,E,F)^{\frown}(\bar{b}_n))\\ &\Rightarrow a_k \in C&&\text{(by}\ \{\bar{a}_n\}\subseteq \mathbb{N}\ \text{and}\ A \cup B \cup C = \mathbb{N}).\\[-34pt] \end{align*} $$
$$ \begin{align*} b_k \in F &\Rightarrow b_k \notin D \cup E &&\text{(by}\ F \cap (D \cup E) = \emptyset)\\ &\Rightarrow a_k \notin A \cup B &&\text{(by}\ (A,B,C)^{\frown}(\bar{a}_n)\mathrel{\mathbb{A}}(D,E,F)^{\frown}(\bar{b}_n))\\ &\Rightarrow a_k \in C&&\text{(by}\ \{\bar{a}_n\}\subseteq \mathbb{N}\ \text{and}\ A \cup B \cup C = \mathbb{N}).\\[-34pt] \end{align*} $$
Corollary 3. For any
![]() $(A,B,C), (D,E,F)\in W$
, any
$(A,B,C), (D,E,F)\in W$
, any
![]() $n \geq 0$
, and any
$n \geq 0$
, and any
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
, we have both
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
, we have both
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and
![]() $(D,E,F)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(A,B,C)^\frown (\bar {a}_n)$
iff the following conditions hold:
$(D,E,F)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(A,B,C)^\frown (\bar {a}_n)$
iff the following conditions hold:
-
1. Binary relation
 $[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection.
$[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection. -
2. For all
 $1 \leq k \leq n$
it is true that
$1 \leq k \leq n$
it is true that
 $a_k \in A$
iff
$a_k \in A$
iff
 $b_k \in D$
.
$b_k \in D$
. -
3. For all
 $1 \leq k \leq n$
it is true that
$1 \leq k \leq n$
it is true that
 $a_k \in C$
iff
$a_k \in C$
iff
 $b_k \in F$
.
$b_k \in F$
.
Proof. The
![]() $(\Rightarrow )$
-part follows from Corollary 2 and condition 2(b) of Definition 4.
$(\Rightarrow )$
-part follows from Corollary 2 and condition 2(b) of Definition 4.
For the
![]() $(\Leftarrow )$
-part, we observe that if
$(\Leftarrow )$
-part, we observe that if
![]() $[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection, then
$[\bar {a}_n \mapsto \bar {b}_n]$
defines a bijection, then
![]() $[\bar {b}_n \mapsto \bar {a}_n]$
also defines a bijection. The satisfaction of condition 2(b) of Definition 4 in both directions is then an immediate consequence of condition 2 of the Corollary, and as for Condition 2(c), we get that, if
$[\bar {b}_n \mapsto \bar {a}_n]$
also defines a bijection. The satisfaction of condition 2(b) of Definition 4 in both directions is then an immediate consequence of condition 2 of the Corollary, and as for Condition 2(c), we get that, if
![]() $1 \leq k \leq n$
and
$1 \leq k \leq n$
and
![]() $a_k \in B$
, then
$a_k \in B$
, then
![]() $a_k \notin C$
, whence
$a_k \notin C$
, whence
![]() $b_k \notin F$
by condition 3 of the Corollary. Therefore,
$b_k \notin F$
by condition 3 of the Corollary. Therefore,
![]() $b_k \in D\cup E$
. Similarly, if
$b_k \in D\cup E$
. Similarly, if
![]() $b_k \in E$
, then
$b_k \in E$
, then
![]() $b_k \notin F$
, whence
$b_k \notin F$
, whence
![]() $a_k \notin C$
by condition 3 of the Corollary. But then
$a_k \notin C$
by condition 3 of the Corollary. But then
![]() $a_k \in A\cup B$
$a_k \in A\cup B$
We can now make the crucial step towards our main result:
Lemma 7. The relation
![]() $\mathbb {A}$
, given in Definition 4, is a bi-asimulation between
$\mathbb {A}$
, given in Definition 4, is a bi-asimulation between
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
, as given in Definition 3, and we have
$\mathcal {M}_2$
, as given in Definition 3, and we have
![]() $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
.
$\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
.
Proof. We check the satisfaction of the conditions given in Definition 1 by
![]() $\mathbb {A}$
. Condition (type) holds by Definition 4.1. Condition (atom) for P and Q follows from Definition 4.2(b) and (c). It is also clear that for any
$\mathbb {A}$
. Condition (type) holds by Definition 4.1. Condition (atom) for P and Q follows from Definition 4.2(b) and (c). It is also clear that for any
![]() $w, v \in W$
we have
$w, v \in W$
we have
![]() $w\mathrel {\mathbb {A}}v$
, so that
$w\mathrel {\mathbb {A}}v$
, so that
![]() $\mathbb {A}$
is non-empty, and, in particular,
$\mathbb {A}$
is non-empty, and, in particular,
![]() $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
holds. We check the remaining conditions in more detail:
$\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
holds. We check the remaining conditions in more detail:
Condition (back)
. Let
![]() $i,j$
be such that
$i,j$
be such that
![]() $\{i, j\} = \{1,2\}$
, let
$\{i, j\} = \{1,2\}$
, let
![]() $(A, B, C),(D,E,F)\in W$
, and let, for some
$(A, B, C),(D,E,F)\in W$
, and let, for some
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that some
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that some
![]() $(G,H,I) \in W$
is such that
$(G,H,I) \in W$
is such that
![]() $(D,E,F)\mathrel {\prec _j}(G,H,I)$
(hence, in particular,
$(D,E,F)\mathrel {\prec _j}(G,H,I)$
(hence, in particular,
![]() $(D,E,F)\trianglelefteq (G,H,I)$
). We have to consider two cases, since B can be either empty or infinite.
$(D,E,F)\trianglelefteq (G,H,I)$
). We have to consider two cases, since B can be either empty or infinite.
Case B1.
![]() $\lvert B\rvert = \omega $
. Then consider the triple
$\lvert B\rvert = \omega $
. Then consider the triple
![]() $(J,K,L)$
such that:
$(J,K,L)$
such that:
 $$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G);\\ K & = (B \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = (C \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$
$$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G);\\ K & = (B \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = (C \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$
We will show that
![]() $(J,K,L)\in W$
and that we have
$(J,K,L)\in W$
and that we have
![]() $(A,B,C)\mathrel {\prec _i}(J,K,L)$
,
$(A,B,C)\mathrel {\prec _i}(J,K,L)$
,
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
. We break down the demonstration of this statement into the following series of claims:
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
. We break down the demonstration of this statement into the following series of claims:
Claim B 1.1.
![]() $J \cup K \cup L = \mathbb {N}$
.
$J \cup K \cup L = \mathbb {N}$
.
Indeed, we know that
 $$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$
$$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$
since
![]() $(G,H,I)\in W$
and, therefore,
$(G,H,I)\in W$
and, therefore,
![]() $G \cup H \cup I = \mathbb {N}$
. On the other hand, we know that
$G \cup H \cup I = \mathbb {N}$
. On the other hand, we know that
 $$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup (B \setminus \{\bar{a}_n\})\cup (C \setminus \{\bar{a}_n\}) &= (A \cup B \cup C)\setminus \{\bar{a}_n\}\\ &= \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$
$$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup (B \setminus \{\bar{a}_n\})\cup (C \setminus \{\bar{a}_n\}) &= (A \cup B \cup C)\setminus \{\bar{a}_n\}\\ &= \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$
since
![]() $(A,B,C)\in W$
and, therefore,
$(A,B,C)\in W$
and, therefore,
![]() $A \cup B \cup C = \mathbb {N}$
. Adding the two equalities together, we get that
$A \cup B \cup C = \mathbb {N}$
. Adding the two equalities together, we get that
as desired.
Claim B1.2. J, K, and L are infinite.
Indeed, A, B, and C are infinite,
![]() $\{\bar {a}_n\}$
is finite, and the following inclusions hold:
$\{\bar {a}_n\}$
is finite, and the following inclusions hold:
Claim B1.3. J, K, and L are pairwise disjoint.
Indeed, take J and K, for example. By definition, we have that
![]() $J \cap K$
is equal to
$J \cap K$
is equal to
By application of distributivity laws, we further get that
 $$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cap (B \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((B \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
$$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cap (B \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((B \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
Next, we know that
![]() $(A,B,C)\in W$
and, therefore,
$(A,B,C)\in W$
and, therefore,
![]() $A \cap B = \emptyset $
, which implies that
$A \cap B = \emptyset $
, which implies that
![]() $(A \setminus \{\bar {a}_n\})\cap (B \setminus \{\bar {a}_n\}) = \emptyset $
.
$(A \setminus \{\bar {a}_n\})\cap (B \setminus \{\bar {a}_n\}) = \emptyset $
.
Moreover, we have
By a parallel argument, we can see that also
![]() $(B \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $
.
$(B \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $
.
Finally, we observe that
![]() $\bar {b}_n \mapsto \bar {a}_n$
is a bijection, and
$\bar {b}_n \mapsto \bar {a}_n$
is a bijection, and
![]() $(G,H,I)\in W$
and, therefore,
$(G,H,I)\in W$
and, therefore,
![]() $G \cap H = \emptyset $
, whence it follows that
$G \cap H = \emptyset $
, whence it follows that
![]() $[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $
.
$[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $
.
Summing up, we see that all the four sets in the union defining
![]() $J \cap K$
are empty and that we have that
$J \cap K$
are empty and that we have that
![]() $J \cap K = \emptyset $
. The other cases are similar.
$J \cap K = \emptyset $
. The other cases are similar.
Claim B1.4.
![]() $(J,K,L)\in W$
.
$(J,K,L)\in W$
.
By Claims B1.1–3.
Claim B1.5.
![]() $(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$
.
$(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$
.
Indeed, if
![]() $a \in A$
, and
$a \in A$
, and
![]() $a \notin \{\bar {a}_n\}$
, then
$a \notin \{\bar {a}_n\}$
, then
![]() $a \in J$
by definition of J. Otherwise we have both
$a \in J$
by definition of J. Otherwise we have both
![]() $a \in A$
and
$a \in A$
and
![]() $a = a_k$
for some
$a = a_k$
for some
![]() $1 \leq k \leq n$
, but then
$1 \leq k \leq n$
, but then
![]() $b_k \in D$
by
$b_k \in D$
by
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
. Next, note that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
. Next, note that
![]() $(D,E,F)\trianglelefteq (G,H,I)$
implies that
$(D,E,F)\trianglelefteq (G,H,I)$
implies that
![]() $D \subseteq G$
, which means that
$D \subseteq G$
, which means that
![]() $b_k \in G$
. But the latter means that
$b_k \in G$
. But the latter means that
![]() $a = a_k \in [\bar {b}_n \mapsto \bar {a}_n](G) \subseteq J$
. Since
$a = a_k \in [\bar {b}_n \mapsto \bar {a}_n](G) \subseteq J$
. Since
![]() $a \in A$
was chosen arbitrarily, we have shown that
$a \in A$
was chosen arbitrarily, we have shown that
![]() $A \subseteq J$
.
$A \subseteq J$
.
Next, if
![]() $a \in L$
, then either
$a \in L$
, then either
![]() $a \in C \setminus \{\bar {a}_n\} \subseteq C$
, or
$a \in C \setminus \{\bar {a}_n\} \subseteq C$
, or
![]() $a \in [\bar {b}_n \mapsto \bar {a}_n](I)$
. In the latter case,
$a \in [\bar {b}_n \mapsto \bar {a}_n](I)$
. In the latter case,
![]() $a = a_k$
for some
$a = a_k$
for some
![]() $1 \leq k \leq n$
, and also
$1 \leq k \leq n$
, and also
![]() $b_k \in I$
. Since
$b_k \in I$
. Since
![]() $(D,E,F)\trianglelefteq (G,H,I)$
implies that
$(D,E,F)\trianglelefteq (G,H,I)$
implies that
![]() $I \subseteq F$
, we get that
$I \subseteq F$
, we get that
![]() $b_k \in F$
, but the latter means, by
$b_k \in F$
, but the latter means, by
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and Corollary 2, that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and Corollary 2, that
![]() $a_k \in C$
. Since
$a_k \in C$
. Since
![]() $a \in L$
was chosen arbitrarily, we have shown that
$a \in L$
was chosen arbitrarily, we have shown that
![]() $L \subseteq C$
.
$L \subseteq C$
.
Claim B1.6.
![]() $(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $
.
$(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $
.
We observe that if
![]() $B \cap \mathbf {v}_2$
is infinite, then so is
$B \cap \mathbf {v}_2$
is infinite, then so is
![]() $(B \setminus \{\bar {a}_n\}) \cap \mathbf {v}_2$
, given that
$(B \setminus \{\bar {a}_n\}) \cap \mathbf {v}_2$
, given that
![]() $\{\bar {a}_n\}$
is finite. But since, according to our definition of K, we have
$\{\bar {a}_n\}$
is finite. But since, according to our definition of K, we have
![]() $(B \setminus \{\bar {a}_n\}) \subseteq K$
,
$(B \setminus \{\bar {a}_n\}) \subseteq K$
,
![]() $K \cap \mathbf {v}_2$
must be infinite, too.
$K \cap \mathbf {v}_2$
must be infinite, too.
Claim B1.7.
![]() $(A,B,C)\mathrel {\prec _i}(J,K,L)$
.
$(A,B,C)\mathrel {\prec _i}(J,K,L)$
.
By Claims B1.5 and B1.6.
Claim B1.8.
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
Indeed, for any given
![]() $1 \leq k \leq n$
, we have
$1 \leq k \leq n$
, we have
![]() $a_k \in J$
iff
$a_k \in J$
iff
![]() $a_k \in [\bar {b}_n \mapsto \bar {a}_n](G)$
iff
$a_k \in [\bar {b}_n \mapsto \bar {a}_n](G)$
iff
![]() $b_k \in G$
, since
$b_k \in G$
, since
![]() $\bar {b}_n \mapsto \bar {a}_n$
defines a bijection. Similarly, we have
$\bar {b}_n \mapsto \bar {a}_n$
defines a bijection. Similarly, we have
![]() $a_k \in L$
iff
$a_k \in L$
iff
![]() $a_k \in [\bar {b}_n \mapsto \bar {a}_n](I)$
iff
$a_k \in [\bar {b}_n \mapsto \bar {a}_n](I)$
iff
![]() $b_k \in I$
. But then our Claim follows from Corollary 3.
$b_k \in I$
. But then our Claim follows from Corollary 3.
The correctness of our construction for Case B1 of condition (back) now follows from Claims B1.4, B1.7, and B1.8.
Case B2.
![]() $B = \emptyset $
. In this case, we partition
$B = \emptyset $
. In this case, we partition
![]() $C \setminus \{\bar {a}_n\}$
into two disjoint infinite sets
$C \setminus \{\bar {a}_n\}$
into two disjoint infinite sets
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, and define
$C_2$
, and define
![]() $(J,K,L)$
as follows:
$(J,K,L)$
as follows:
 $$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G) ;\\ K & = C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = C_2 \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$
$$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G) ;\\ K & = C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = C_2 \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$
We will demonstrate the analogues of all the claims that we have made in the previous case.
Claim B2.1.
![]() $J \cup K \cup L = \mathbb {N}$
.
$J \cup K \cup L = \mathbb {N}$
.
Again, we know that
 $$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$
$$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$
since
![]() $(G,H,I)\in W$
and, therefore,
$(G,H,I)\in W$
and, therefore,
![]() $G \cup H \cup I = \mathbb {N}$
. On the other hand, we know that
$G \cup H \cup I = \mathbb {N}$
. On the other hand, we know that
 $$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup C_1 \cup C_2 &= (A \setminus \{\bar{a}_n\}) \cup (C \setminus \{\bar{a}_n\})\\ &= (A \cup C)\setminus \{\bar{a}_n\} = \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$
$$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup C_1 \cup C_2 &= (A \setminus \{\bar{a}_n\}) \cup (C \setminus \{\bar{a}_n\})\\ &= (A \cup C)\setminus \{\bar{a}_n\} = \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$
since
![]() $(A,B,C)\in W$
and
$(A,B,C)\in W$
and
![]() $B = \emptyset $
and, therefore,
$B = \emptyset $
and, therefore,
![]() $A \cup C = \mathbb {N}$
. Adding the two equalities together, we get that
$A \cup C = \mathbb {N}$
. Adding the two equalities together, we get that
as desired.
Claim B2.2. J, K, and L are infinite.
Indeed, A,
![]() $C_1$
, and
$C_1$
, and
![]() $C_2$
are infinite,
$C_2$
are infinite,
![]() $\{\bar {a}_n\}$
is finite, and the following inclusions hold:
$\{\bar {a}_n\}$
is finite, and the following inclusions hold:
Claim B2.3. J, K, and L are pairwise disjoint.
Indeed, take J and K, for example. By definition, we have that
 $$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap (C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\subseteq ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap ((C \setminus \{\bar{a}_n\})\cup [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
$$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap (C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\subseteq ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap ((C \setminus \{\bar{a}_n\})\cup [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
By application of distributivity laws, we further get that
 $$ \begin{align*} J \cap K &\subseteq ((A \setminus \{\bar{a}_n\}) \cap (C \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((C \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
$$ \begin{align*} J \cap K &\subseteq ((A \setminus \{\bar{a}_n\}) \cap (C \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((C \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$
Next, we know that
![]() $(A,B,C)\in W$
and, therefore,
$(A,B,C)\in W$
and, therefore,
![]() $A \cap C = \emptyset $
, which implies that
$A \cap C = \emptyset $
, which implies that
![]() $(A \setminus \{\bar {a}_n\})\cap (C \setminus \{\bar {a}_n\}) = \emptyset $
.
$(A \setminus \{\bar {a}_n\})\cap (C \setminus \{\bar {a}_n\}) = \emptyset $
.
Moreover, we have
By a parallel argument, we can see that also
![]() $(C \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $
.
$(C \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $
.
Finally, we observe that
![]() $\bar {b}_n \mapsto \bar {a}_n$
is a bijection, and
$\bar {b}_n \mapsto \bar {a}_n$
is a bijection, and
![]() $(G,H,I)\in W$
and, therefore,
$(G,H,I)\in W$
and, therefore,
![]() $G \cap H = \emptyset $
, whence it follows that
$G \cap H = \emptyset $
, whence it follows that
![]() $[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $
.
$[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $
.
Summing up, we see that all the four sets in the union extending
![]() $J \cap K$
are empty and that we have that
$J \cap K$
are empty and that we have that
![]() $J \cap K = \emptyset $
. The other cases are similar.
$J \cap K = \emptyset $
. The other cases are similar.
Claim B2.4.
![]() $(J,K,L)\in W$
.
$(J,K,L)\in W$
.
By Claims B2.1–3.
Claim B2.5.
![]() $(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$
.
$(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$
.
The argument for
![]() $A \subseteq J$
is exactly the same as in Case B1. To see that
$A \subseteq J$
is exactly the same as in Case B1. To see that
![]() $L \subseteq C$
, note that
$L \subseteq C$
, note that
![]() $L = C_2 \cup [\bar {b}_n \mapsto \bar {a}_n](I) \subseteq (C \setminus \{\bar {a}_n\}) \cup [\bar {b}_n \mapsto \bar {a}_n](I)$
, so that the argument used for Case B1 is applicable also here.
$L = C_2 \cup [\bar {b}_n \mapsto \bar {a}_n](I) \subseteq (C \setminus \{\bar {a}_n\}) \cup [\bar {b}_n \mapsto \bar {a}_n](I)$
, so that the argument used for Case B1 is applicable also here.
Claim B2.6.
![]() $(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $
.
$(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $
.
The claim holds trivially since
![]() $\lvert B \cap \mathbf {v}_2\rvert = \omega $
is falsified by the assumption of Case B2.
$\lvert B \cap \mathbf {v}_2\rvert = \omega $
is falsified by the assumption of Case B2.
Claim B2.7.
![]() $(A,B,C)\mathrel {\prec _i}(J,K,L)$
.
$(A,B,C)\mathrel {\prec _i}(J,K,L)$
.
By Claims B2.5 and B2.6.
Claim B2.8.
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
Again the claim follows by the argument used for Claim B1.8 of Case B1.
Condition (forth). Let
![]() $i,j$
be such that
$i,j$
be such that
![]() $\{i, j\} = \{1,2\}$
, let
$\{i, j\} = \{1,2\}$
, let
![]() $(A, B, C), (D,E,F)\in W$
, and let, for some
$(A, B, C), (D,E,F)\in W$
, and let, for some
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that some
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that some
![]() $(J,K,L) \in W$
is such that
$(J,K,L) \in W$
is such that
![]() $(J,K,L)\mathrel {\prec _i}(A,B,C)$
(hence, in particular,
$(J,K,L)\mathrel {\prec _i}(A,B,C)$
(hence, in particular,
![]() $(A,B,C)\mathrel {\trianglerighteq }(J,K,L)$
). Again, we have to consider two cases, since E can be either empty or infinite.
$(A,B,C)\mathrel {\trianglerighteq }(J,K,L)$
). Again, we have to consider two cases, since E can be either empty or infinite.
Case F1.
![]() $\lvert E\rvert = \omega $
. Then consider the triple
$\lvert E\rvert = \omega $
. Then consider the triple
![]() $(G,H,I)$
such that:
$(G,H,I)$
such that:
 $$ \begin{align*} G & = (D \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = (E \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$
$$ \begin{align*} G & = (D \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = (E \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$
We will show that
![]() $(G,H,I)\in W$
and that we have
$(G,H,I)\in W$
and that we have
![]() $(G,H,I)\mathrel {\prec _j}(D,E,F)$
,
$(G,H,I)\mathrel {\prec _j}(D,E,F)$
,
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
. We break down the demonstration of this statement into our usual series of eight claims. The arguments, for the most part, just dualize the arguments given for Case B1 of condition (back), but we spell them out nonetheless.
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
. We break down the demonstration of this statement into our usual series of eight claims. The arguments, for the most part, just dualize the arguments given for Case B1 of condition (back), but we spell them out nonetheless.
Claim F1.1.
![]() $G \cup H \cup I = \mathbb {N}$
.
$G \cup H \cup I = \mathbb {N}$
.
Indeed, we know that
 $$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$
$$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$
since
![]() $(J,K,L)\in W$
and, therefore,
$(J,K,L)\in W$
and, therefore,
![]() $J \cup K \cup L = \mathbb {N}$
. On the other hand, we know that
$J \cup K \cup L = \mathbb {N}$
. On the other hand, we know that
 $$ \begin{align*} (D \setminus \{\bar{b}_n\})\cup (E \setminus \{\bar{b}_n\})\cup (F \setminus \{\bar{b}_n\}) &= (D \cup E \cup F)\setminus \{\bar{b}_n\}\\ &= \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$
$$ \begin{align*} (D \setminus \{\bar{b}_n\})\cup (E \setminus \{\bar{b}_n\})\cup (F \setminus \{\bar{b}_n\}) &= (D \cup E \cup F)\setminus \{\bar{b}_n\}\\ &= \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$
since
![]() $(D,E,F)\in W$
and, therefore,
$(D,E,F)\in W$
and, therefore,
![]() $D \cup E \cup F = \mathbb {N}$
. Adding the two equalities together, we get that
$D \cup E \cup F = \mathbb {N}$
. Adding the two equalities together, we get that
as desired.
Claim F1.2. G, H, and I are infinite.
Indeed, D, E, and F are infinite,
![]() $\{\bar {b}_n\}$
is finite, and the following inclusions hold:
$\{\bar {b}_n\}$
is finite, and the following inclusions hold:
Claim F1.3. G, H, and I are pairwise disjoint.
Indeed, take G and H, for example. By definition, we have that
![]() $G \cap H$
is equal to
$G \cap H$
is equal to
By application of distributivity laws, we further get that
 $$ \begin{align*} G \cap H &= ((D \setminus \{\bar{b}_n\}) \cap (E \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](K))\\ &\qquad\qquad\cup ((E \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](K)). \end{align*} $$
$$ \begin{align*} G \cap H &= ((D \setminus \{\bar{b}_n\}) \cap (E \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](K))\\ &\qquad\qquad\cup ((E \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](K)). \end{align*} $$
Next, we know that
![]() $(D,E,F)\in W$
and, therefore,
$(D,E,F)\in W$
and, therefore,
![]() $D \cap E = \emptyset $
, which implies that
$D \cap E = \emptyset $
, which implies that
![]() $(D \setminus \{\bar {b}_n\})\cap (E \setminus \{\bar {b}_n\}) = \emptyset $
.
$(D \setminus \{\bar {b}_n\})\cap (E \setminus \{\bar {b}_n\}) = \emptyset $
.
Moreover, we have
By a parallel argument, we can see that also
![]() $(E \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](J) = \emptyset $
.
$(E \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](J) = \emptyset $
.
Finally, we observe that
![]() $\bar {a}_n \mapsto \bar {b}_n$
is a bijection, and
$\bar {a}_n \mapsto \bar {b}_n$
is a bijection, and
![]() $(J,K,L)\in W$
and, therefore,
$(J,K,L)\in W$
and, therefore,
![]() $J \cap K = \emptyset $
, whence it follows that
$J \cap K = \emptyset $
, whence it follows that
![]() $[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](K) = \emptyset $
.
$[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](K) = \emptyset $
.
Summing up, we see that all the four sets in the union defining
![]() $G \cap H$
are empty and that we have that
$G \cap H$
are empty and that we have that
![]() $G \cap H = \emptyset $
. The other cases are similar.
$G \cap H = \emptyset $
. The other cases are similar.
Claim F1.4.
![]() $(G,H,I)\in W$
.
$(G,H,I)\in W$
.
By Claims F1.1–3.
Claim F1.5.
![]() $(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$
.
$(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$
.
Indeed, if
![]() $b \in G$
, then either
$b \in G$
, then either
![]() $b \in D \setminus \{\bar {b}_n\} \subseteq D$
, or
$b \in D \setminus \{\bar {b}_n\} \subseteq D$
, or
![]() $b \in [\bar {a}_n \mapsto \bar {b}_n](J)$
. In the latter case,
$b \in [\bar {a}_n \mapsto \bar {b}_n](J)$
. In the latter case,
![]() $b = b_k$
for some
$b = b_k$
for some
![]() $1 \leq k \leq n$
, and also
$1 \leq k \leq n$
, and also
![]() $a_k \in J$
. Since
$a_k \in J$
. Since
![]() $(J,K,L)\trianglelefteq (A,B,C)$
implies that
$(J,K,L)\trianglelefteq (A,B,C)$
implies that
![]() $J \subseteq A$
, we get that
$J \subseteq A$
, we get that
![]() $a_k \in A$
, but the latter means, by
$a_k \in A$
, but the latter means, by
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, that
![]() $b_k \in D$
. Since
$b_k \in D$
. Since
![]() $b \in G$
was chosen arbitrarily, we have shown that
$b \in G$
was chosen arbitrarily, we have shown that
![]() $G \subseteq D$
.
$G \subseteq D$
.
Next, if
![]() $b \in F$
, and
$b \in F$
, and
![]() $b \notin \{\bar {b}_n\}$
, then
$b \notin \{\bar {b}_n\}$
, then
![]() $b \in I$
by definition of F. Otherwise we have both
$b \in I$
by definition of F. Otherwise we have both
![]() $b \in F$
and
$b \in F$
and
![]() $b = b_k$
for some
$b = b_k$
for some
![]() $1 \leq k \leq n$
, but then
$1 \leq k \leq n$
, but then
![]() $a_k \in C$
by
$a_k \in C$
by
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and Corollary 2. Now, note that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
and Corollary 2. Now, note that
![]() $(J,K,L)\mathrel {\trianglelefteq }(A,B,C)$
implies that
$(J,K,L)\mathrel {\trianglelefteq }(A,B,C)$
implies that
![]() $C \subseteq L$
, which means that
$C \subseteq L$
, which means that
![]() $a_k \in L$
. But the latter means that
$a_k \in L$
. But the latter means that
![]() $b = b_k \in [\bar {a}_n \mapsto \bar {b}_n](L) \subseteq I$
. Since
$b = b_k \in [\bar {a}_n \mapsto \bar {b}_n](L) \subseteq I$
. Since
![]() $b \in F$
was chosen arbitrarily, we have shown that
$b \in F$
was chosen arbitrarily, we have shown that
![]() $F \subseteq I$
.
$F \subseteq I$
.
Claim F1.6.
![]() $(\mathbf {v} \trianglelefteq (G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $
.
$(\mathbf {v} \trianglelefteq (G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $
.
We observe that if
![]() $H \cap \mathbf {v}_2$
is infinite, then so is
$H \cap \mathbf {v}_2$
is infinite, then so is
![]() $(E \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$
, given that
$(E \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$
, given that
![]() $H = (E \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](K)$
and
$H = (E \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](K)$
and
![]() $[\bar {a}_n \mapsto \bar {b}_n](K)$
is finite. But then
$[\bar {a}_n \mapsto \bar {b}_n](K)$
is finite. But then
![]() $E \cap \mathbf {v}_2$
must be infinite, too.
$E \cap \mathbf {v}_2$
must be infinite, too.
Claim F1.7.
![]() $(G,H,I)\mathrel {\prec _j}(D,E,F)$
.
$(G,H,I)\mathrel {\prec _j}(D,E,F)$
.
By Claims F1.5 and F1.6.
Claim F1.8.
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
Indeed, for any given
![]() $1 \leq k \leq n$
, we have
$1 \leq k \leq n$
, we have
![]() $b_k \in G$
iff
$b_k \in G$
iff
![]() $b_k \in [\bar {a}_n \mapsto \bar {b}_n](J)$
iff
$b_k \in [\bar {a}_n \mapsto \bar {b}_n](J)$
iff
![]() $a_k \in J$
, since
$a_k \in J$
, since
![]() $\bar {a}_n \mapsto \bar {b}_n$
defines a bijection. Similarly, we have
$\bar {a}_n \mapsto \bar {b}_n$
defines a bijection. Similarly, we have
![]() $b_k \in I$
iff
$b_k \in I$
iff
![]() $b_k \in [\bar {a}_n \mapsto \bar {b}_n](L)$
iff
$b_k \in [\bar {a}_n \mapsto \bar {b}_n](L)$
iff
![]() $a_k \in L$
. But then our Claim follows from Corollary 3.
$a_k \in L$
. But then our Claim follows from Corollary 3.
The correctness of our construction for Case 1 of condition (forth) now follows from Claims F1.4, F1.7, and F1.8.
Case F2.
![]() $E = \emptyset $
. In this case, we partition
$E = \emptyset $
. In this case, we partition
![]() $D \setminus \{\bar {b}_n\}$
into two disjoint infinite sets
$D \setminus \{\bar {b}_n\}$
into two disjoint infinite sets
![]() $D_1$
and
$D_1$
and
![]() $D_2$
. Additionally, in case both
$D_2$
. Additionally, in case both
![]() $D \cap \mathbf {v}_1$
and
$D \cap \mathbf {v}_1$
and
![]() $D \cap \mathbf {v}_2$
are infinite (which means that
$D \cap \mathbf {v}_2$
are infinite (which means that
![]() $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$
and
$(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$
and
![]() $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1$
are infinite, too), we ensure that we have
$(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1$
are infinite, too), we ensure that we have
![]() $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2 \subseteq D_1$
and
$(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2 \subseteq D_1$
and
![]() $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1 \subseteq D_2$
. Then we define
$(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1 \subseteq D_2$
. Then we define
![]() $(G,H,I)$
as follows:
$(G,H,I)$
as follows:
 $$ \begin{align*} G & = D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = D_2 \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$
$$ \begin{align*} G & = D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = D_2 \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$
We will demonstrate our usual eight claims in some detail again, even though the arguments mostly dualize the proofs given for the respective claims in Case B2 of condition (back) (Claim F2.6 being, perhaps, the only exception to this rule).
Claim F2.1.
![]() $G \cup H \cup I = \mathbb {N}$
.
$G \cup H \cup I = \mathbb {N}$
.
Again, we know that
 $$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$
$$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$
since
![]() $(J,K,L)\in W$
and, therefore,
$(J,K,L)\in W$
and, therefore,
![]() $J \cup K \cup L = \mathbb {N}$
. On the other hand, we know that
$J \cup K \cup L = \mathbb {N}$
. On the other hand, we know that
 $$ \begin{align*} (F \setminus \{\bar{b}_n\})\cup D_1 \cup D_2 &= (F \setminus \{\bar{b}_n\}) \cup (D \setminus \{\bar{b}_n\})\\ &= (F \cup D)\setminus \{\bar{b}_n\} = \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$
$$ \begin{align*} (F \setminus \{\bar{b}_n\})\cup D_1 \cup D_2 &= (F \setminus \{\bar{b}_n\}) \cup (D \setminus \{\bar{b}_n\})\\ &= (F \cup D)\setminus \{\bar{b}_n\} = \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$
since
![]() $(D,E,F)\in W$
and
$(D,E,F)\in W$
and
![]() $E = \emptyset $
and, therefore,
$E = \emptyset $
and, therefore,
![]() $D \cup F = \mathbb {N}$
. Adding the two equalities together, we get that
$D \cup F = \mathbb {N}$
. Adding the two equalities together, we get that
as desired.
Claim F2.2. G, H, and I are infinite.
Indeed,
![]() $D_1$
,
$D_1$
,
![]() $D_2$
, and F are infinite,
$D_2$
, and F are infinite,
![]() $\{\bar {b}_n\}$
is finite, and the following inclusions hold:
$\{\bar {b}_n\}$
is finite, and the following inclusions hold:
Claim F2.3. G, H, and I are pairwise disjoint.
Indeed, take G and I, for example. By definition, we have that
 $$ \begin{align*} G \cap I &= ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap (D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\subseteq ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap ((D \setminus \{\bar{b}_n\})\cup [\bar{a}_n \mapsto \bar{b}_n](J)). \end{align*} $$
$$ \begin{align*} G \cap I &= ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap (D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\subseteq ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap ((D \setminus \{\bar{b}_n\})\cup [\bar{a}_n \mapsto \bar{b}_n](J)). \end{align*} $$
By application of distributivity laws, we further get that
 $$ \begin{align*} G \cap I &\subseteq ((F \setminus \{\bar{b}_n\}) \cap (D \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((F \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](L))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](L)). \end{align*} $$
$$ \begin{align*} G \cap I &\subseteq ((F \setminus \{\bar{b}_n\}) \cap (D \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((F \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](L))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](L)). \end{align*} $$
Next, we know that
![]() $(D,E,F)\in W$
and, therefore,
$(D,E,F)\in W$
and, therefore,
![]() $D \cap F = \emptyset $
, which implies that
$D \cap F = \emptyset $
, which implies that
![]() $(D \setminus \{\bar {b}_n\})\cap (F \setminus \{\bar {b}_n\}) = \emptyset $
.
$(D \setminus \{\bar {b}_n\})\cap (F \setminus \{\bar {b}_n\}) = \emptyset $
.
Moreover, we have
By a parallel argument, we can see that also
![]() $(D \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $
.
$(D \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $
.
Finally, we observe that
![]() $\bar {a}_n \mapsto \bar {b}_n$
is a bijection, and
$\bar {a}_n \mapsto \bar {b}_n$
is a bijection, and
![]() $(J,K,L)\in W$
and, therefore,
$(J,K,L)\in W$
and, therefore,
![]() $J \cap L = \emptyset $
, whence it follows that
$J \cap L = \emptyset $
, whence it follows that
![]() $[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $
.
$[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $
.
Summing up, we see that all the four sets in the union extending
![]() $G \cap I$
are empty and that we have
$G \cap I$
are empty and that we have
![]() $G \cap I = \emptyset $
. The other cases are similar.
$G \cap I = \emptyset $
. The other cases are similar.
Claim F2.4.
![]() $(G,H,I)\in W$
.
$(G,H,I)\in W$
.
By Claims F2.1–3.
Claim F2.5.
![]() $(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$
.
$(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$
.
The argument for
![]() $F \subseteq I$
is exactly the same as in Case 1. To see that
$F \subseteq I$
is exactly the same as in Case 1. To see that
![]() $G \subseteq D$
, note that
$G \subseteq D$
, note that
![]() $G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J) \subseteq (D \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](J)$
, so that the argument used for Case F1 is applicable also here.
$G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J) \subseteq (D \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](J)$
, so that the argument used for Case F1 is applicable also here.
Claim F2.6.
![]() $(\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $
.
$(\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $
.
Since we suppose that
![]() $E = \emptyset $
, it will suffice to show that assuming both
$E = \emptyset $
, it will suffice to show that assuming both
![]() $\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$
and
$\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$
and
![]() $\lvert H \cap \mathbf {v}_2\rvert = \omega $
will lead us to a contradiction. Indeed, if
$\lvert H \cap \mathbf {v}_2\rvert = \omega $
will lead us to a contradiction. Indeed, if
![]() $\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$
, then, in particular,
$\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$
, then, in particular,
![]() $\mathbf {v}_1 \subseteq G$
, so that
$\mathbf {v}_1 \subseteq G$
, so that
![]() $\lvert G \cap \mathbf {v}_1\rvert = \omega $
. But we have
$\lvert G \cap \mathbf {v}_1\rvert = \omega $
. But we have
![]() $G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J)$
and
$G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J)$
and
![]() $[\bar {a}_n \mapsto \bar {b}_n](J)$
is finite; therefore, both
$[\bar {a}_n \mapsto \bar {b}_n](J)$
is finite; therefore, both
![]() $\mathbf {v}_1 \cap D_1$
, and its superset,
$\mathbf {v}_1 \cap D_1$
, and its superset,
![]() $\mathbf {v}_1 \cap D$
, must be infinite.
$\mathbf {v}_1 \cap D$
, must be infinite.
If also
![]() $\lvert H \cap \mathbf {v}_2\rvert = \omega $
, then a parallel argument shows that also
$\lvert H \cap \mathbf {v}_2\rvert = \omega $
, then a parallel argument shows that also
![]() $\mathbf {v}_2 \cap D_2$
and
$\mathbf {v}_2 \cap D_2$
and
![]() $\mathbf {v}_2 \cap D$
are infinite.
$\mathbf {v}_2 \cap D$
are infinite.
But, since both
![]() $\mathbf {v}_1 \cap D$
and
$\mathbf {v}_1 \cap D$
and
![]() $\mathbf {v}_2 \cap D$
are infinite, we must have, by the choice of
$\mathbf {v}_2 \cap D$
are infinite, we must have, by the choice of
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, that
$D_2$
, that
![]() $\mathbf {v}_2 \cap (D \setminus \{\bar {b}_n\}) \subseteq D_1$
. On the other hand,
$\mathbf {v}_2 \cap (D \setminus \{\bar {b}_n\}) \subseteq D_1$
. On the other hand,
![]() $D_2 \subseteq (D \setminus \{\bar {b}_n\})$
implies that
$D_2 \subseteq (D \setminus \{\bar {b}_n\})$
implies that
![]() $D_2 = D_2 \cap (D \setminus \{\bar {b}_n\})$
.
$D_2 = D_2 \cap (D \setminus \{\bar {b}_n\})$
.
Therefore,
Since we have
![]() $H = D_2 \cup [\bar {a}_n \mapsto \bar {b}_n](K)$
, and
$H = D_2 \cup [\bar {a}_n \mapsto \bar {b}_n](K)$
, and
![]() $[\bar {a}_n \mapsto \bar {b}_n](K)$
is clearly finite, the set
$[\bar {a}_n \mapsto \bar {b}_n](K)$
is clearly finite, the set
![]() $H \cap \mathbf {v}_2$
can be at most finite, which is a contradiction.
$H \cap \mathbf {v}_2$
can be at most finite, which is a contradiction.
Claim F2.7.
![]() $(G,H,I)\mathrel {\prec _j}(D,E,F)$
.
$(G,H,I)\mathrel {\prec _j}(D,E,F)$
.
By Claims F2.5 and F2.6.
Claim F2.8.
![]() $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
$(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$
, and
![]() $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
$(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$
.
Again the claim follows by the argument used for Claim F1.8 of Case F1.
Condition (left). Let
![]() $i,j$
be such that
$i,j$
be such that
![]() $\{i, j\} = \{1,2\}$
, let
$\{i, j\} = \{1,2\}$
, let
![]() $(A, B, C), (D,E,F)\in W$
, and let, for some
$(A, B, C), (D,E,F)\in W$
, and let, for some
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that
![]() $b \in \mathbb {N}$
. If
$b \in \mathbb {N}$
. If
![]() $b = b_k$
for some
$b = b_k$
for some
![]() $1 \leq k \leq n$
, then we set
$1 \leq k \leq n$
, then we set
![]() $a: = a_k$
. Otherwise, given that
$a: = a_k$
. Otherwise, given that
![]() $b \notin \{\bar {b}_n\}$
, we choose any
$b \notin \{\bar {b}_n\}$
, we choose any
![]() $a \in C \setminus \{\bar {a}_n\}$
. We can do this since C is infinite and
$a \in C \setminus \{\bar {a}_n\}$
. We can do this since C is infinite and
![]() $\{\bar {a}_n\}$
is finite. In both cases we get that
$\{\bar {a}_n\}$
is finite. In both cases we get that
![]() $(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$
by definition of
$(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$
by definition of
![]() $\mathbb {A}$
.
$\mathbb {A}$
.
Condition (right). Let
![]() $i,j$
be such that
$i,j$
be such that
![]() $\{i, j\} = \{1,2\}$
, let
$\{i, j\} = \{1,2\}$
, let
![]() $(A, B, C), (D,E,F)\in W$
, and let, for some
$(A, B, C), (D,E,F)\in W$
, and let, for some
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
$\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$
. Assume, moreover, that we have
![]() $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that
$(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$
, and that
![]() $a \in \mathbb {N}$
. If
$a \in \mathbb {N}$
. If
![]() $a = a_k$
for some
$a = a_k$
for some
![]() $1 \leq k \leq n$
, then we set
$1 \leq k \leq n$
, then we set
![]() $b: = b_k$
. Otherwise, given that
$b: = b_k$
. Otherwise, given that
![]() $a \notin \{\bar {a}_n\}$
, we choose any
$a \notin \{\bar {a}_n\}$
, we choose any
![]() $b \in D \setminus \{\bar {b}_n\}$
. We can do this since D is infinite and
$b \in D \setminus \{\bar {b}_n\}$
. We can do this since D is infinite and
![]() $\{\bar {b}_n\}$
is finite. In both cases we get that
$\{\bar {b}_n\}$
is finite. In both cases we get that
![]() $(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$
by definition of
$(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$
by definition of
![]() $\mathbb {A}$
.
$\mathbb {A}$
.
At this point, it only remains to reap the fruits of the tedious work towards the host of previous lemmas and corollaries:
Theorem 2.
![]() $\mathsf {FOBIL}$
fails CIP.
$\mathsf {FOBIL}$
fails CIP.
Proof. Indeed, we have
![]() $\models \phi \to \psi $
and
$\models \phi \to \psi $
and
![]() $\Theta _\phi \cap \Theta _\psi = \Sigma $
. If now
$\Theta _\phi \cap \Theta _\psi = \Sigma $
. If now
![]() $\theta \in L_\emptyset (\Sigma )$
is such that both
$\theta \in L_\emptyset (\Sigma )$
is such that both
![]() $\models \phi \to \theta $
and
$\models \phi \to \theta $
and
![]() $\models \theta \to \psi $
, then, by Lemma 6, we must have both
$\models \theta \to \psi $
, then, by Lemma 6, we must have both
![]() $\mathcal {M}^{\prime }_1,\mathbf {v}\models \theta $
and
$\mathcal {M}^{\prime }_1,\mathbf {v}\models \theta $
and
![]() $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \theta $
. We also have
$\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \theta $
. We also have
![]() $\mathcal {M}_i = \mathcal {M}^{\prime }_i\upharpoonright \Sigma $
for
$\mathcal {M}_i = \mathcal {M}^{\prime }_i\upharpoonright \Sigma $
for
![]() $i \in \{1,2\}$
and, therefore, by Expansion Property, we get that
$i \in \{1,2\}$
and, therefore, by Expansion Property, we get that
![]() $\mathcal {M}_1,\mathbf {v}\models \theta $
and
$\mathcal {M}_1,\mathbf {v}\models \theta $
and
![]() $\mathcal {M}_2,\mathbf {w}\not \models \theta $
. On the other hand, we know, by Lemma 7, that the relation
$\mathcal {M}_2,\mathbf {w}\not \models \theta $
. On the other hand, we know, by Lemma 7, that the relation
![]() $\mathbb {A}$
, given in Definition 4, is a bi-asimulation between
$\mathbb {A}$
, given in Definition 4, is a bi-asimulation between
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
and that we have
$\mathcal {M}_2$
and that we have
![]() $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
. Therefore,
$\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$
. Therefore,
![]() $\mathcal {M}_1,\mathbf {v}\models \theta $
implies, by Lemma 3, that
$\mathcal {M}_1,\mathbf {v}\models \theta $
implies, by Lemma 3, that
![]() $\mathcal {M}_2,\mathbf {w}\models \theta $
. The obtained contradiction shows that no interpolant exists for
$\mathcal {M}_2,\mathbf {w}\models \theta $
. The obtained contradiction shows that no interpolant exists for
![]() $\phi \to \psi $
.
$\phi \to \psi $
.
Remark 3. Note that Lemma 5.1–2 implies that the submodels generated by
![]() $\mathbf {v}$
and
$\mathbf {v}$
and
![]() $\mathbf {w}$
in
$\mathbf {w}$
in
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
, respectively, are exactly the models
$\mathcal {M}_2$
, respectively, are exactly the models
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
as given in [Reference Mints, Olkhovikov and Urquhart12, Definition 7.2]. Moreover, the proof of Lemma 7 re-uses the constructions given in the proof of [Reference Mints, Olkhovikov and Urquhart12, Lemma 7.2] except for the part treating condition (forth) of Definition 1. However, the arguments showing the correctness of these constructions had to be given anew, since the models
$\mathcal {M}_2$
as given in [Reference Mints, Olkhovikov and Urquhart12, Definition 7.2]. Moreover, the proof of Lemma 7 re-uses the constructions given in the proof of [Reference Mints, Olkhovikov and Urquhart12, Lemma 7.2] except for the part treating condition (forth) of Definition 1. However, the arguments showing the correctness of these constructions had to be given anew, since the models
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
are not bi-intuitionistically equivalent to the models of [Reference Mints, Olkhovikov and Urquhart12, Definition 7.2].
$\mathcal {M}_2$
are not bi-intuitionistically equivalent to the models of [Reference Mints, Olkhovikov and Urquhart12, Definition 7.2].
Thus our main construction in this paper is, in a very precise sense, just an extension of the main construction given in [Reference Mints, Olkhovikov and Urquhart12, Section 7].
4 Conclusion
In this article we have refuted the Craig Interpolation Property for predicate bi-intuitionistic logic, showing how different the situation is from the propositional case that was solved positively in [Reference Kowalski and Ono9]. We proved that Mints’s counterexample [Reference Mints, Olkhovikov and Urquhart12] for predicate intuitionitic logic with constant domains also did the work in the present context. It is clear that, although we allowed constants in our presentation, their role is purely technical, and that due to the nature of Mints’s counterexample, we have also disproved CIP for the purely relational variant of
![]() $\mathsf {FOBIL}$
. The present work still leaves some related open questions, such as the status of the Beth definability property in the bi-intuitionistic setting. For the time being, we have left these and other similar matters as topics for future research.
$\mathsf {FOBIL}$
. The present work still leaves some related open questions, such as the status of the Beth definability property in the bi-intuitionistic setting. For the time being, we have left these and other similar matters as topics for future research.
Acknowledgements
We are grateful to two anonymous referees that provided helpful comments that greatly improved the paper. A special thanks goes to Jim de Groot for providing the command for the typesetting of
![]() .
.
Grigory Olkhovikov is supported by Deutsche Forschungsgemeinschaft (DFG), project OL 589/1-1. Guillermo Badia is partially supported by the Australian Research Council grant DE220100544.
Grigory Olkhovikov would like to dedicate this paper to the memory of his dear co-author, late Professor Grigori Mints, whose strong and incisive mind has been missing in this world since May 29, 2014, and has been deeply missed on every single day since that fateful date. Guillermo Badia most emphatically supports this decision.
An anonymous referee has pointed out that Hiroakira Ono presented an independently obtained version of our central result using a similar idea at a conference in Taiwan in 2018. This result is not published.