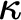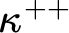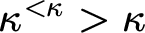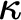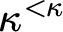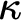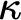1 Introduction
Many of the tree forcings on the Baire space over
![]() $\omega $
have various analogues for higher cardinals. Here we are concerned with club
$\omega $
have various analogues for higher cardinals. Here we are concerned with club
![]() $\kappa $
-Miller forcing [Reference Miller, Baumgartner, Martin and Shelah16] for regular uncountable
$\kappa $
-Miller forcing [Reference Miller, Baumgartner, Martin and Shelah16] for regular uncountable
![]() $\kappa $
, and some of our results apply also to
$\kappa $
, and some of our results apply also to
![]() $\kappa $
-Sacks forcing and some higher amoeba forcings.
$\kappa $
-Sacks forcing and some higher amoeba forcings.
In Section 2 we review some of the common tree higher forcings for uncountable
![]() $\kappa $
. We show that the diamond principle and the inaccessibility of
$\kappa $
. We show that the diamond principle and the inaccessibility of
![]() $\kappa $
can be replaced by the weaker principle
$\kappa $
can be replaced by the weaker principle
![]() $(Dl)_{\kappa }$
in the known theorems about the preservation of
$(Dl)_{\kappa }$
in the known theorems about the preservation of
![]() $\kappa ^+$
in
$\kappa ^+$
in
![]() $\kappa $
-supported iterations of some popular higher tree forcings like Kanamori’s
$\kappa $
-supported iterations of some popular higher tree forcings like Kanamori’s
![]() $\kappa $
-Sacks forcing [Reference Kanamori10], Landver’s versions of filter Sacks forcing [Reference Landver14],
$\kappa $
-Sacks forcing [Reference Kanamori10], Landver’s versions of filter Sacks forcing [Reference Landver14],
![]() $\kappa $
-club Miller forcing [Reference Friedman and Zdomskyy7], and
$\kappa $
-club Miller forcing [Reference Friedman and Zdomskyy7], and
![]() $\kappa $
-club Laver forcing [Reference Brendle, Brooke-Taylor, Friedman and Montoya4].
$\kappa $
-club Laver forcing [Reference Brendle, Brooke-Taylor, Friedman and Montoya4].
In Section 3, we show that under
![]() $\kappa ^{<\kappa } = \kappa $
it is independent whether club
$\kappa ^{<\kappa } = \kappa $
it is independent whether club
![]() $\kappa $
-Miller forcing preserves
$\kappa $
-Miller forcing preserves
![]() $2^\kappa =\kappa ^{++}$
. Petr Simon proved that Sacks forcing collapses the continuum to the bounding number. Under an hypothesis on a
$2^\kappa =\kappa ^{++}$
. Petr Simon proved that Sacks forcing collapses the continuum to the bounding number. Under an hypothesis on a
![]() $\kappa $
-evasion number, we show that club Miller forcing collapses
$\kappa $
-evasion number, we show that club Miller forcing collapses
![]() $2^\kappa $
to the bounding number at
$2^\kappa $
to the bounding number at
![]() $\kappa $
.
$\kappa $
.
In Section 4 we prove that club
![]() $\kappa $
-Miller collapses
$\kappa $
-Miller collapses
![]() $\kappa ^{<\kappa }$
to
$\kappa ^{<\kappa }$
to
![]() $\kappa $
if
$\kappa $
if
![]() $\kappa ^{<\kappa }> \kappa $
. This may serve as a mathematical reason for the assumption
$\kappa ^{<\kappa }> \kappa $
. This may serve as a mathematical reason for the assumption
![]() $\kappa ^{<\kappa } = \kappa $
in work with higher tree forcings.
$\kappa ^{<\kappa } = \kappa $
in work with higher tree forcings.
In Section 5 we answer a question of Brendle, Brooke-Taylor, Friedman and Montoya: We show that the
![]() $(\leq \kappa )$
-support iteration of
$(\leq \kappa )$
-support iteration of
![]() $\kappa $
-Miller forcing with branching into a normal ultrafilter does not have the Laver property.
$\kappa $
-Miller forcing with branching into a normal ultrafilter does not have the Laver property.
Notation: Throughout the paper we let
![]() $\kappa $
be an uncountable regular cardinal. When used, we add additional conditions on
$\kappa $
be an uncountable regular cardinal. When used, we add additional conditions on
![]() $\kappa $
. If
$\kappa $
. If
![]() $\operatorname {\textrm {dom}}(t), i $
are ordinals, we write
$\operatorname {\textrm {dom}}(t), i $
are ordinals, we write
![]() $t \,\hat {} \, \langle i\rangle $
for the concatenation of t with the singleton function
$t \,\hat {} \, \langle i\rangle $
for the concatenation of t with the singleton function
![]() $\{(0,i)\}$
, i.e.,
$\{(0,i)\}$
, i.e.,
![]() $t \,\hat {} \, \langle i\rangle =t \cup \{(\operatorname {\textrm {dom}}(t), i)\}$
. We write
$t \,\hat {} \, \langle i\rangle =t \cup \{(\operatorname {\textrm {dom}}(t), i)\}$
. We write
![]() ${}^{\lambda>} \kappa $
for the set of functions
${}^{\lambda>} \kappa $
for the set of functions
![]() $f \colon \alpha \to \kappa $
for some
$f \colon \alpha \to \kappa $
for some
![]() $\alpha < \lambda $
. The domain
$\alpha < \lambda $
. The domain
![]() $\alpha $
of f is also called the length of f. The set of subsets of
$\alpha $
of f is also called the length of f. The set of subsets of
![]() $\kappa $
of size
$\kappa $
of size
![]() $\kappa $
is denoted by
$\kappa $
is denoted by
![]() $[\kappa ]^\kappa $
.
$[\kappa ]^\kappa $
.
Definition 1.1. Let
![]() $\kappa $
be an infinite cardinal.
$\kappa $
be an infinite cardinal.
-
(1) A tree (on
 $\kappa $
) is a non-empty subset of
$\kappa $
) is a non-empty subset of
 ${}^{\kappa>}\kappa $
that is closed under initial segments. We use the symbol
${}^{\kappa>}\kappa $
that is closed under initial segments. We use the symbol
 $\trianglelefteq $
for the initial segment relation and the symbot
$\trianglelefteq $
for the initial segment relation and the symbot
 $\triangleleft $
for the corresponding strict relation.
$\triangleleft $
for the corresponding strict relation. -
(2) A tree on
 $\kappa $
is called unbounded if
$\kappa $
is called unbounded if  $$ \begin{align*} (\forall t \in p)( \forall \alpha < \kappa )(\exists t' \in p)(\operatorname{\textrm{dom}}(t') \geq \alpha \wedge t' \trianglerighteq t). \end{align*} $$
$$ \begin{align*} (\forall t \in p)( \forall \alpha < \kappa )(\exists t' \in p)(\operatorname{\textrm{dom}}(t') \geq \alpha \wedge t' \trianglerighteq t). \end{align*} $$
-
(3) Let
 $T \subseteq {}^{\kappa>} \kappa $
be a tree and
$T \subseteq {}^{\kappa>} \kappa $
be a tree and
 $s \in T$
. We let
$s \in T$
. We let  $$ \begin{align*}T^{\langle s \rangle} = \{ t \in T \, : \, t \trianglelefteq s \vee s \trianglelefteq t\}. \end{align*} $$
$$ \begin{align*}T^{\langle s \rangle} = \{ t \in T \, : \, t \trianglelefteq s \vee s \trianglelefteq t\}. \end{align*} $$
-
(4) We let
 $[T] = \{x \in {}^\kappa \kappa \, : \, (\forall \alpha < \kappa )( x \restriction \alpha \in T)\}$
. The set
$[T] = \{x \in {}^\kappa \kappa \, : \, (\forall \alpha < \kappa )( x \restriction \alpha \in T)\}$
. The set
 $[T]$
is called the set of branches of T or the body of T.
$[T]$
is called the set of branches of T or the body of T. -
(5) The elements of a tree are called nodes. A node that has at least two immediate
 $\triangleleft $
-successors in p is called a splitting node of p. The set of splitting nodes of p is denoted by
$\triangleleft $
-successors in p is called a splitting node of p. The set of splitting nodes of p is denoted by
 $\operatorname {\textrm {spl}}(p)$
.
$\operatorname {\textrm {spl}}(p)$
. -
(6) Let
 $T \subseteq {}^{\kappa>} \kappa $
be a tree that contains a splitting node. We let the trunk of T,
$T \subseteq {}^{\kappa>} \kappa $
be a tree that contains a splitting node. We let the trunk of T,
 $\operatorname {\textrm {tr}}(T)$
, be the
$\operatorname {\textrm {tr}}(T)$
, be the
 $\trianglelefteq $
-least splitting node of T. If T has no splitting node then we let
$\trianglelefteq $
-least splitting node of T. If T has no splitting node then we let
 $\operatorname {\textrm {tr}}(p) =p$
.
$\operatorname {\textrm {tr}}(p) =p$
. -
(7) Let
 ${\mathbb P}=({\mathbb P},\leq _{{\mathbb P}}) = ({\mathbb P}, \supseteq )$
denote a forcing whose conditions are
${\mathbb P}=({\mathbb P},\leq _{{\mathbb P}}) = ({\mathbb P}, \supseteq )$
denote a forcing whose conditions are
 $(<\kappa )$
-closed unbounded trees. Let G be a P-generic filter. In
$(<\kappa )$
-closed unbounded trees. Let G be a P-generic filter. In
 ${\mathbf {V}}[G]$
we define The function
${\mathbf {V}}[G]$
we define The function $$ \begin{align*} x_G = \bigcup\{ \operatorname{\textrm{tr}}(p) \, : \, p \in G\}. \end{align*} $$
$$ \begin{align*} x_G = \bigcup\{ \operatorname{\textrm{tr}}(p) \, : \, p \in G\}. \end{align*} $$
 $x_G$
is called the generic
$x_G$
is called the generic
 $\kappa $
-real, branch, or function.
$\kappa $
-real, branch, or function.
In the forcings we investigate, the conditions are unbounded trees with additional properties. Subtrees are stronger conditions. In forcing we use the Israeli notation that
![]() $p \leq _{\mathbb P} q$
means that q is stronger than p.Footnote
1
We usually write
$p \leq _{\mathbb P} q$
means that q is stronger than p.Footnote
1
We usually write
![]() $q \subseteq p$
. We write
$q \subseteq p$
. We write
![]() ${\mathbb P} \Vdash \varphi $
if any condition (equivalently, the weakest condition is there is such one) forces
${\mathbb P} \Vdash \varphi $
if any condition (equivalently, the weakest condition is there is such one) forces
![]() $\varphi $
.
$\varphi $
.
We review some general properties. Often the
![]() $\kappa $
-real
$\kappa $
-real
![]() $x_G$
is closely related to the generic filter G:
$x_G$
is closely related to the generic filter G:
Proposition 1.2. Let
![]() ${\mathbb P}= ({\mathbb P}, \supseteq )$
be a forcing whose conditions are
${\mathbb P}= ({\mathbb P}, \supseteq )$
be a forcing whose conditions are
![]() $(<\kappa )$
-closed unbounded trees
$(<\kappa )$
-closed unbounded trees
![]() $p \subseteq {}^{\kappa>}\kappa $
. In addition we assume that
$p \subseteq {}^{\kappa>}\kappa $
. In addition we assume that
![]() ${\mathbb P}$
contains for each
${\mathbb P}$
contains for each
![]() $p\in {\mathbb P}$
and
$p\in {\mathbb P}$
and
![]() $s \in p$
also the condition
$s \in p$
also the condition
![]() $p^{\langle s \rangle }$
(from Definition 1.1(3)). Let G be the generic filter and
$p^{\langle s \rangle }$
(from Definition 1.1(3)). Let G be the generic filter and
![]() $x_G$
be the generic real. Then the following holds.
$x_G$
be the generic real. Then the following holds.
-
(1) For any
 $p,q \in {\mathbb P}$
,
$p,q \in {\mathbb P}$
,
 $p \Vdash x_G \in [q]$
implies
$p \Vdash x_G \in [q]$
implies
 $p \subseteq q$
.
$p \subseteq q$
. -
(2) For any
 $p,q \in {\mathbb P}$
,
$p,q \in {\mathbb P}$
,
 $x_G \in [p] \cap [q]$
implies that p and q are compatible.
$x_G \in [p] \cap [q]$
implies that p and q are compatible. -
(3) The
 $\kappa $
-real
$\kappa $
-real
 $x_G$
determines G via
$x_G$
determines G via
 $G = \{ p \in {\mathbb P} \, : \, x_G \in [p]\}$
.
$G = \{ p \in {\mathbb P} \, : \, x_G \in [p]\}$
.
Proof. (1) If
![]() $p \not \subseteq q$
then there is
$p \not \subseteq q$
then there is
![]() $t \in p \setminus q$
, and
$t \in p \setminus q$
, and
 .
.
(2) Let
![]() . The set
. The set
![]() $D_{p,q}$
is dense in
$D_{p,q}$
is dense in
![]() ${\mathbb P}$
. So there is
${\mathbb P}$
. So there is
![]() $r \in D_{p,q} \cap G$
. We fix such an r. Since
$r \in D_{p,q} \cap G$
. We fix such an r. Since
![]() ${\mathbb P}$
contains only
${\mathbb P}$
contains only
![]() $(<\kappa )$
-closed unbounded trees, we have
$(<\kappa )$
-closed unbounded trees, we have
![]() $x_G \in [p] \cap [q] \cap {}^\kappa \kappa $
. By the definition of
$x_G \in [p] \cap [q] \cap {}^\kappa \kappa $
. By the definition of
![]() $D_{p,q}$
,
$D_{p,q}$
,
![]() $r \Vdash x_G \in [p] \cap [q]$
. Hence by (1),
$r \Vdash x_G \in [p] \cap [q]$
. Hence by (1),
![]() $r \geq p,q$
.
$r \geq p,q$
.
(3) Suppose
![]() $p \in G$
. Then by definition
$p \in G$
. Then by definition
![]() $x_G \in [p]$
. By (2), the set
$x_G \in [p]$
. By (2), the set
![]() $\{p \, : \, x_G \in [p]\}$
is a filter. Since the generic G is a subset of this filter, the latter coincides with G.⊣
$\{p \, : \, x_G \in [p]\}$
is a filter. Since the generic G is a subset of this filter, the latter coincides with G.⊣
2 On the club version
 $\kappa $
-Miller forcing
$\kappa $
-Miller forcing
For an uncountable cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\kappa ^{<\kappa } = \kappa $
and such that
$\kappa ^{<\kappa } = \kappa $
and such that
![]() $\diamondsuit _{\kappa }$
holds, Kanamori [Reference Kanamori10] defined a club version of
$\diamondsuit _{\kappa }$
holds, Kanamori [Reference Kanamori10] defined a club version of
![]() $\kappa $
-Sacks forcing, proved a
$\kappa $
-Sacks forcing, proved a
![]() $\kappa $
-version of Axiom A for it and iterated it with support of size
$\kappa $
-version of Axiom A for it and iterated it with support of size
![]() $\kappa $
, in the style of Baumgartner and Laver [Reference Baumgartner and Laver3]. Later Eisworth [Reference Eisworth6] (again under
$\kappa $
, in the style of Baumgartner and Laver [Reference Baumgartner and Laver3]. Later Eisworth [Reference Eisworth6] (again under
![]() $\kappa ^{<\kappa } = \kappa> \omega $
and
$\kappa ^{<\kappa } = \kappa> \omega $
and
![]() $\diamondsuit _{\kappa }$
) and Rosłanowski and Shelah [Reference Roslanowski and Shelah17–Reference Roslanowski and Shelah20] (mainly for inaccessible
$\diamondsuit _{\kappa }$
) and Rosłanowski and Shelah [Reference Roslanowski and Shelah17–Reference Roslanowski and Shelah20] (mainly for inaccessible
![]() $\kappa $
) investigated versions of
$\kappa $
) investigated versions of
![]() $\kappa $
-properness and
$\kappa $
-properness and
![]() $(<\kappa ^+)$
-support iterations of iterands of length
$(<\kappa ^+)$
-support iterations of iterands of length
![]() $\kappa ^{++}$
for iterands that are in a strong sense proper for the higher cardinal. All of the settings suppose that the iterands are
$\kappa ^{++}$
for iterands that are in a strong sense proper for the higher cardinal. All of the settings suppose that the iterands are
![]() $(<\kappa )$
-closed. An early use of
$(<\kappa )$
-closed. An early use of
![]() $\diamondsuit _{\kappa }$
for showing that the
$\diamondsuit _{\kappa }$
for showing that the
![]() $\kappa $
-supported product of
$\kappa $
-supported product of
![]() $\kappa $
-Silver forcing preserves
$\kappa $
-Silver forcing preserves
![]() $\kappa ^+$
is in Baumgartners proof of [Reference Baumgartner2, Theorem 6.7].Footnote
2
$\kappa ^+$
is in Baumgartners proof of [Reference Baumgartner2, Theorem 6.7].Footnote
2
A careful inspection shows that in the named examples the diamond principle can be replaced by the weaker principle
![]() $(Dl)_{\kappa }$
(see Def. 2.8). We mention here some results that show that
$(Dl)_{\kappa }$
(see Def. 2.8). We mention here some results that show that
![]() $(Dl)_{\kappa }$
is “slightly weaker”: For
$(Dl)_{\kappa }$
is “slightly weaker”: For
![]() $\kappa \geq \aleph _1$
being a successor cardinal,
$\kappa \geq \aleph _1$
being a successor cardinal,
![]() $\diamondsuit _{\kappa }$
and
$\diamondsuit _{\kappa }$
and
![]() $(Dl)_{\kappa }$
are equivalent (see [Reference Kunen12]). For strongly inaccessible
$(Dl)_{\kappa }$
are equivalent (see [Reference Kunen12]). For strongly inaccessible
![]() $\kappa $
, the principle
$\kappa $
, the principle
![]() $(Dl)_{\kappa }$
holds. In Corollary 2.13 we show that under suitable large cardinal hypotheses there is a forcing such that in the extension there is a regular non-strong limit cardinal
$(Dl)_{\kappa }$
holds. In Corollary 2.13 we show that under suitable large cardinal hypotheses there is a forcing such that in the extension there is a regular non-strong limit cardinal
![]() $\kappa $
with
$\kappa $
with
![]() $(Dl)_{\kappa }$
and not
$(Dl)_{\kappa }$
and not
![]() $\diamondsuit _{\kappa }$
.
$\diamondsuit _{\kappa }$
.
The use of the diamond
![]() $\diamondsuit _{\kappa }$
or of the principle
$\diamondsuit _{\kappa }$
or of the principle
![]() $(Dl)_{\kappa }$
poses for many
$(Dl)_{\kappa }$
poses for many
![]() $\kappa $
no additional requirement. In Shelah [Reference Shelah27] it is shown: If
$\kappa $
no additional requirement. In Shelah [Reference Shelah27] it is shown: If
![]() $\kappa $
is a successor and
$\kappa $
is a successor and
![]() $\kappa ^{<\kappa } = \kappa> \aleph _2$
then
$\kappa ^{<\kappa } = \kappa> \aleph _2$
then
![]() $\diamondsuit _{\kappa }$
. On
$\diamondsuit _{\kappa }$
. On
![]() $(Dl)_{\kappa }$
, see Theorem 2.10.
$(Dl)_{\kappa }$
, see Theorem 2.10.
It is not known whether
![]() $\kappa $
-properness in the sense of Eisworth coincides with one of the various versions in the work of Rosłanowski and Shelah. The preservation theorems by Eisworth and by Rosłanowski and Shelah suggest that just replacing
$\kappa $
-properness in the sense of Eisworth coincides with one of the various versions in the work of Rosłanowski and Shelah. The preservation theorems by Eisworth and by Rosłanowski and Shelah suggest that just replacing
![]() $\omega $
by
$\omega $
by
![]() $\kappa $
in the definition of “properness” does in general not suffice to preserve
$\kappa $
in the definition of “properness” does in general not suffice to preserve
![]() $\kappa ^+$
. The preservation of
$\kappa ^+$
. The preservation of
![]() $\kappa ^+$
in iterations is usually guaranteed only under additional requirements on
$\kappa ^+$
in iterations is usually guaranteed only under additional requirements on
![]() $\kappa $
and on the iterands.
$\kappa $
and on the iterands.
There is an instructive example of a
![]() $(<\kappa )$
-closed forcing that is not proper: We write
$(<\kappa )$
-closed forcing that is not proper: We write
![]() $S^\lambda _{\kappa } = \{\alpha < \lambda \, : \, \operatorname {\textrm {cf}}(\alpha ) = \kappa \}$
. In the case of
$S^\lambda _{\kappa } = \{\alpha < \lambda \, : \, \operatorname {\textrm {cf}}(\alpha ) = \kappa \}$
. In the case of
![]() $2^{\mu } = \kappa $
for some
$2^{\mu } = \kappa $
for some
![]() $\mu < \kappa $
,
$\mu < \kappa $
,
![]() $2^{\kappa } = \kappa ^+$
, a non-iterable
$2^{\kappa } = \kappa ^+$
, a non-iterable
![]() $(<\kappa )$
-closed forcing is the
$(<\kappa )$
-closed forcing is the
![]() $\kappa ^{++}$
long iterated forcing
$\kappa ^{++}$
long iterated forcing
![]() ${\mathbb P}_{\textrm {unif}}$
adding a uniformisation to any colouring of a ladder system
${\mathbb P}_{\textrm {unif}}$
adding a uniformisation to any colouring of a ladder system
![]() $\langle C_{\alpha } \, : \, \alpha \in \kappa ^+, \operatorname {\textrm {cf}}(\alpha ) = \kappa \rangle $
, see [Reference Shelah23, Appendix]. However, if
$\langle C_{\alpha } \, : \, \alpha \in \kappa ^+, \operatorname {\textrm {cf}}(\alpha ) = \kappa \rangle $
, see [Reference Shelah23, Appendix]. However, if
![]() $2^{\mu } = \kappa $
, then no continuous ladder system on
$2^{\mu } = \kappa $
, then no continuous ladder system on
 $S^{\kappa ^+}_{\kappa }$
has club uniformisation by [Reference Shelah23, Theorem 3.6]. Thus
$S^{\kappa ^+}_{\kappa }$
has club uniformisation by [Reference Shelah23, Theorem 3.6]. Thus
![]() $(\kappa ^+)^{\mathbf {V}} $
is collapsed by
$(\kappa ^+)^{\mathbf {V}} $
is collapsed by
![]() ${\mathbb P}_{\textrm {unif}}$
.
${\mathbb P}_{\textrm {unif}}$
.
On the other hand Eisworth [Reference Eisworth6] shows for
![]() $\kappa = \aleph _1$
that for a stationary co-stationary
$\kappa = \aleph _1$
that for a stationary co-stationary
 $S\subseteq S^{\aleph _2}_{\aleph _1}$
the forcing adding a uniformisation to any colouring of a ladder system
$S\subseteq S^{\aleph _2}_{\aleph _1}$
the forcing adding a uniformisation to any colouring of a ladder system
![]() $\langle C_{\alpha } \, : \, \alpha \in S\rangle $
is consistent together with CH.
$\langle C_{\alpha } \, : \, \alpha \in S\rangle $
is consistent together with CH.
For inaccessible cardinals
![]() $\kappa $
, Friedman and Zdomskyy [Reference Friedman and Zdomskyy7] and Friedman et al. [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Section 5.2] define a version of club
$\kappa $
, Friedman and Zdomskyy [Reference Friedman and Zdomskyy7] and Friedman et al. [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Section 5.2] define a version of club
![]() $\kappa $
-Miller forcing. We present an equivalent version of the forcing and show that under
$\kappa $
-Miller forcing. We present an equivalent version of the forcing and show that under
![]() $\kappa ^{<\kappa } = \kappa> \omega $
a
$\kappa ^{<\kappa } = \kappa> \omega $
a
![]() $\kappa $
-version of Axiom A holds. For iteration with
$\kappa $
-version of Axiom A holds. For iteration with
![]() $\kappa $
-support we use
$\kappa $
-support we use
![]() $(Dl)_{\kappa }$
.
$(Dl)_{\kappa }$
.
Definition 2.1. Let
![]() $\kappa $
be a regular cardinal such that
$\kappa $
be a regular cardinal such that
![]() $\kappa ^{<\kappa } = \kappa $
. Conditions in the forcing order
$\kappa ^{<\kappa } = \kappa $
. Conditions in the forcing order
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
are trees
${\mathbb Q}^{\textrm {a}}_{\kappa }$
are trees
![]() $p \subseteq {}^{\kappa>}\kappa $
with the following additional properties:
$p \subseteq {}^{\kappa>}\kappa $
with the following additional properties:
-
(1) (Club filter superperfectness) For any
 $s \in p$
there is an extension
$s \in p$
there is an extension
 $t \trianglerighteq s$
in p such that We require that each node has either only one direct successor or splits into a club.
$t \trianglerighteq s$
in p such that We require that each node has either only one direct successor or splits into a club. $$ \begin{align*} \operatorname{\textrm{osucc}}_p(t) := \{\alpha \in \kappa \, : \, t \,\hat{} \, \langle \alpha \rangle \in p \} \mbox{ is club in } \kappa. \end{align*} $$
$$ \begin{align*} \operatorname{\textrm{osucc}}_p(t) := \{\alpha \in \kappa \, : \, t \,\hat{} \, \langle \alpha \rangle \in p \} \mbox{ is club in } \kappa. \end{align*} $$
We write for
 $t \in p$
, for the set of immediate p-successors of t.
$t \in p$
, for the set of immediate p-successors of t. $$ \begin{align*} \operatorname{\textrm{succ}}_p(t) := \{t \,\hat{} \, \langle \alpha \rangle \in \kappa\, :\, t \,\hat{} \, \langle \alpha \rangle \in p \} \end{align*} $$
$$ \begin{align*} \operatorname{\textrm{succ}}_p(t) := \{t \,\hat{} \, \langle \alpha \rangle \in \kappa\, :\, t \,\hat{} \, \langle \alpha \rangle \in p \} \end{align*} $$
-
(2) (Closure of splitting) For each increasing sequence of length
 $< \kappa $
of splitting nodes, the union of the nodes on the sequence is a splitting node of p as well.
$< \kappa $
of splitting nodes, the union of the nodes on the sequence is a splitting node of p as well.
A condition q is stronger than p if
![]() $q \subseteq p$
.
$q \subseteq p$
.
We remark that clauses (1) and (2) imply that any
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is unbounded and has the following closure property:
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is unbounded and has the following closure property:
-
(3) For every increasing sequence
 $\langle t_i \, : \, i < \lambda \rangle $
of length
$\langle t_i \, : \, i < \lambda \rangle $
of length
 $\lambda < \kappa $
of nodes
$\lambda < \kappa $
of nodes
 $t_i \in p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
we have that the limit of the sequence
$t_i \in p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
we have that the limit of the sequence
 $\bigcup \{t_i \, : \, i < \lambda \}$
is also a node in p.
$\bigcup \{t_i \, : \, i < \lambda \}$
is also a node in p.
This clause is sometimes added to the definition, see e.g., [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Definition 74], where the forcing is called
 ${\mathbb {MI}}_{\kappa }^{\textrm {Clubfilter}}$
. Splitting into
${\mathbb {MI}}_{\kappa }^{\textrm {Clubfilter}}$
. Splitting into
![]() $\operatorname {\textrm {osucc}}$
-sets in the club filter is equivalent to splitting into club sets. The forcing
$\operatorname {\textrm {osucc}}$
-sets in the club filter is equivalent to splitting into club sets. The forcing
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
is isomorphic to its version that works only with nodes that are strictly increasing elements of
${\mathbb Q}^{\textrm {a}}_{\kappa }$
is isomorphic to its version that works only with nodes that are strictly increasing elements of
![]() ${}^{\kappa>} \kappa $
. The forcing
${}^{\kappa>} \kappa $
. The forcing
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
is isomorphic to a dense subset of
${\mathbb Q}^{\textrm {a}}_{\kappa }$
is isomorphic to a dense subset of
 ${\mathbb {MI}}_{\kappa }^{\textrm {Clubfilter}}$
and hence their regular open algebras coincide.
${\mathbb {MI}}_{\kappa }^{\textrm {Clubfilter}}$
and hence their regular open algebras coincide.
In [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Proposition 77] it is shown that
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
adds a
${\mathbb Q}^{\textrm {a}}_{\kappa }$
adds a
![]() $\kappa $
-Cohen real, i.e., a generic for
$\kappa $
-Cohen real, i.e., a generic for
![]() $(2^{<\kappa }, \trianglelefteq )$
. This is a sharp contrast to
$(2^{<\kappa }, \trianglelefteq )$
. This is a sharp contrast to
![]() $\omega $
-Miller forcing. The latter preserves P-points and hence does not add Cohen reals.
$\omega $
-Miller forcing. The latter preserves P-points and hence does not add Cohen reals.
Definition 2.2 (See [Reference Kanamori10])
The
![]() $\kappa $
-Sacks forcing
$\kappa $
-Sacks forcing
![]() $\mathbb S_{\kappa }$
. Conditions in
$\mathbb S_{\kappa }$
. Conditions in
![]() $\mathbb S_{\kappa }$
are perfect subtrees of
$\mathbb S_{\kappa }$
are perfect subtrees of
![]() $2^{<\kappa }$
such that each limit of a
$2^{<\kappa }$
such that each limit of a
![]() $(<\kappa )$
-sequence of splitting nodes is a splitting node.
$(<\kappa )$
-sequence of splitting nodes is a splitting node.
Interesting non-equivalent variants of
![]() $\kappa $
-Sacks forcing were introduced by Landver in [Reference Landver14]. He replaces closure of splitting nodes by the requirement that the splitting nodes along each branch must be in a given normal filter over
$\kappa $
-Sacks forcing were introduced by Landver in [Reference Landver14]. He replaces closure of splitting nodes by the requirement that the splitting nodes along each branch must be in a given normal filter over
![]() $\kappa $
.
$\kappa $
.
It is well-known (see e.g., [Reference Friedman and Zdomskyy7, Reference Kanamori10, Reference Roslanowski and Shelah17]) that under
![]() $\kappa ^{<\kappa } = \kappa $
the forcing order
$\kappa ^{<\kappa } = \kappa $
the forcing order
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
fulfils a
${\mathbb Q}^{\textrm {a}}_{\kappa }$
fulfils a
![]() $\kappa $
-version of Axiom A. We define
$\kappa $
-version of Axiom A. We define
![]() $\leq _{\alpha }$
slightly differently from Friedman and Zdomskyy [Reference Friedman and Zdomskyy7, Definition 2.2], so that the premise
$\leq _{\alpha }$
slightly differently from Friedman and Zdomskyy [Reference Friedman and Zdomskyy7, Definition 2.2], so that the premise
![]() $\kappa ^{<\kappa } = \kappa $
suffices for the fusion lemma for one iterand. However, in iterations the inaccessibility of
$\kappa ^{<\kappa } = \kappa $
suffices for the fusion lemma for one iterand. However, in iterations the inaccessibility of
![]() $\kappa $
or the diamond is used in limit steps. See Discussion 2.7. We show that
$\kappa $
or the diamond is used in limit steps. See Discussion 2.7. We show that
![]() $(Dl)_{\kappa }$
suffices.
$(Dl)_{\kappa }$
suffices.
Notation 2.3. We assume
![]() $\kappa ^{<\kappa }= \kappa $
. (This assumption is waived only in Section 4 and taken up again in Section 5.) We fix an enumeration
$\kappa ^{<\kappa }= \kappa $
. (This assumption is waived only in Section 4 and taken up again in Section 5.) We fix an enumeration
![]() $\langle \eta _i \, : \, i <\kappa \rangle $
of
$\langle \eta _i \, : \, i <\kappa \rangle $
of
![]() $\kappa ^{<\kappa }$
such that
$\kappa ^{<\kappa }$
such that
![]() $\eta _i \triangleleft \eta _j$
implies
$\eta _i \triangleleft \eta _j$
implies
![]() $i < j$
.
$i < j$
.
Definition 2.4. For
![]() $\alpha < \kappa $
we let
$\alpha < \kappa $
we let
 $$ \begin{align*}\operatorname{\textrm{spl}}_{\alpha}(p) = \bigl\{ t \in \operatorname{\textrm{spl}}(p) \, : \, \operatorname{\textrm{otp}}(\{s \subsetneq t \, : \, s \in \operatorname{\textrm{spl}}(p)\}) = \alpha\bigr\} \end{align*} $$
$$ \begin{align*}\operatorname{\textrm{spl}}_{\alpha}(p) = \bigl\{ t \in \operatorname{\textrm{spl}}(p) \, : \, \operatorname{\textrm{otp}}(\{s \subsetneq t \, : \, s \in \operatorname{\textrm{spl}}(p)\}) = \alpha\bigr\} \end{align*} $$
and
 $$ \begin{align*}\operatorname{\textrm{cl}}_{\alpha}(p) := \{s \in p \, : \, (\exists \gamma \leq \alpha)(\exists t \in \operatorname{\textrm{spl}}_\gamma(p))( s \subseteq t) \wedge (\exists \beta \leq \alpha)( s = \eta_\beta)\}. \end{align*} $$
$$ \begin{align*}\operatorname{\textrm{cl}}_{\alpha}(p) := \{s \in p \, : \, (\exists \gamma \leq \alpha)(\exists t \in \operatorname{\textrm{spl}}_\gamma(p))( s \subseteq t) \wedge (\exists \beta \leq \alpha)( s = \eta_\beta)\}. \end{align*} $$
We let
![]() $p \leq _ \alpha q$
if
$p \leq _ \alpha q$
if
![]() $p \leq q$
and
$p \leq q$
and
![]() $\operatorname {\textrm {cl}}_{\alpha }(p) = \operatorname {\textrm {cl}}_{\alpha }(q)$
.
$\operatorname {\textrm {cl}}_{\alpha }(p) = \operatorname {\textrm {cl}}_{\alpha }(q)$
.
Note
![]() $|\operatorname {\textrm {cl}}_{\alpha }(p)| \leq |\alpha |+ \aleph _0< \kappa $
.
$|\operatorname {\textrm {cl}}_{\alpha }(p)| \leq |\alpha |+ \aleph _0< \kappa $
.
Lemma 2.5. The forcing
![]() $({\mathbb Q}^{\textrm {a}}_{\kappa },\leq )$
together with the orders
$({\mathbb Q}^{\textrm {a}}_{\kappa },\leq )$
together with the orders
![]() $(\leq _{\alpha })_{\alpha <\kappa }$
fulfils the fusion lemma.
$(\leq _{\alpha })_{\alpha <\kappa }$
fulfils the fusion lemma.
Proof. Let
![]() $\langle p_{\alpha } \, : \, \alpha < \kappa \rangle $
be a fusion sequence, i.e.,
$\langle p_{\alpha } \, : \, \alpha < \kappa \rangle $
be a fusion sequence, i.e.,
![]() $p_{\alpha } \leq _{\alpha } p_\beta $
for
$p_{\alpha } \leq _{\alpha } p_\beta $
for
![]() $\alpha < \beta $
. Then
$\alpha < \beta $
. Then
![]() $\emptyset \in \bigcap p_{\alpha }$
. Now let
$\emptyset \in \bigcap p_{\alpha }$
. Now let
![]() $t \in \bigcap p_{\alpha }$
. For
$t \in \bigcap p_{\alpha }$
. For
![]() $\alpha < \kappa $
, let
$\alpha < \kappa $
, let
![]() $\gamma _{\alpha } $
be maximal
$\gamma _{\alpha } $
be maximal
![]() $\gamma $
such that
$\gamma $
such that
![]() $t \in \operatorname {\textrm {cl}}_\gamma (p_{\alpha })$
. By closure of splitting, the maximum exists. Since the
$t \in \operatorname {\textrm {cl}}_\gamma (p_{\alpha })$
. By closure of splitting, the maximum exists. Since the
![]() $\langle p_{\alpha }\, : \, \alpha < \kappa \rangle $
are increasing in strength we have for
$\langle p_{\alpha }\, : \, \alpha < \kappa \rangle $
are increasing in strength we have for
![]() $\alpha \leq \beta $
,
$\alpha \leq \beta $
,
![]() $\gamma _{\alpha } \geq \gamma _\beta $
. Then let
$\gamma _{\alpha } \geq \gamma _\beta $
. Then let
![]() $\gamma $
be the minimum of the
$\gamma $
be the minimum of the
![]() $\gamma _{\alpha }$
,
$\gamma _{\alpha }$
,
![]() $\alpha < \kappa $
. Let
$\alpha < \kappa $
. Let
![]() $\gamma < \alpha _0 < \kappa $
be such that for any
$\gamma < \alpha _0 < \kappa $
be such that for any
![]() $\alpha \geq \alpha _0$
,
$\alpha \geq \alpha _0$
,
![]() $t \not \in \operatorname {\textrm {cl}}_{\gamma +1}(p_{\alpha })$
. Now we choose an increasing continuous sequence
$t \not \in \operatorname {\textrm {cl}}_{\gamma +1}(p_{\alpha })$
. Now we choose an increasing continuous sequence
![]() $\langle t_{\alpha } \, : \, \alpha _0 \leq \alpha < \kappa \rangle $
such that
$\langle t_{\alpha } \, : \, \alpha _0 \leq \alpha < \kappa \rangle $
such that
![]() $t_{\alpha }$
is a minimal node in
$t_{\alpha }$
is a minimal node in
 $\operatorname {\textrm {spl}}_{\gamma +1}(p_{\alpha })$
above
$\operatorname {\textrm {spl}}_{\gamma +1}(p_{\alpha })$
above
![]() $t_\beta $
,
$t_\beta $
,
![]() $\alpha _0\leq \beta < \alpha $
. There are club many
$\alpha _0\leq \beta < \alpha $
. There are club many
![]() $\alpha $
such that for any
$\alpha $
such that for any
![]() $t_\beta $
,
$t_\beta $
,
![]() $\beta < \alpha $
, there is some
$\beta < \alpha $
, there is some
![]() $i < \alpha $
such that
$i < \alpha $
such that
![]() $t_\beta =\eta _i$
. We take the minimal limit element
$t_\beta =\eta _i$
. We take the minimal limit element
![]() $\beta $
of such a club. Then by definition of
$\beta $
of such a club. Then by definition of
![]() $\leq _{\alpha }$
,
$\leq _{\alpha }$
,
![]() $t_\beta $
stays a
$t_\beta $
stays a
![]() $(\gamma +1)$
-splitting node in all the
$(\gamma +1)$
-splitting node in all the
![]() $p_{\alpha }$
,
$p_{\alpha }$
,
![]() $\alpha <\kappa $
. Its
$\alpha <\kappa $
. Its
![]() $\operatorname {\textrm {osucc}}$
-set in
$\operatorname {\textrm {osucc}}$
-set in
![]() $\bigcap p_{\alpha }$
is a diagonal intersection of
$\bigcap p_{\alpha }$
is a diagonal intersection of
![]() $\operatorname {\textrm {osucc}}_{p_{\alpha }}(t_\beta )$
,
$\operatorname {\textrm {osucc}}_{p_{\alpha }}(t_\beta )$
,
![]() $\alpha < \kappa $
.
$\alpha < \kappa $
.
It is clear that any
![]() $(<\kappa )$
-limit of splitting nodes of
$(<\kappa )$
-limit of splitting nodes of
![]() $\bigcap p_{\alpha }$
is a splitting node in
$\bigcap p_{\alpha }$
is a splitting node in
![]() $\bigcap p_{\alpha }$
.⊣
$\bigcap p_{\alpha }$
.⊣
Lemma 2.6. For every maximal antichain A and every
![]() $\alpha $
and p there is a
$\alpha $
and p there is a
![]() $q \geq _{\alpha } p$
that is compatible with at most
$q \geq _{\alpha } p$
that is compatible with at most
![]() $\kappa $
members of the antichain.
$\kappa $
members of the antichain.
Proof. For any
![]() $t \in \operatorname {\textrm {spl}}_{\alpha }(p)$
we find a club
$t \in \operatorname {\textrm {spl}}_{\alpha }(p)$
we find a club
![]() $C_t \subseteq \operatorname {\textrm {osucc}}_p(t)$
of i such that for any
$C_t \subseteq \operatorname {\textrm {osucc}}_p(t)$
of i such that for any
![]() $i \in C_t$
there is a condition
$i \in C_t$
there is a condition
![]() $q_{t,i}$
with
$q_{t,i}$
with
![]() $p^{\langle t \,\hat {} \, \langle i \rangle \rangle } \leq q_{t,i}$
. Since A is a maximal antichain, there is some
$p^{\langle t \,\hat {} \, \langle i \rangle \rangle } \leq q_{t,i}$
. Since A is a maximal antichain, there is some
![]() $a \in A$
such that there is some
$a \in A$
such that there is some
![]() $r_{t,i} \geq q_{t,i} , a$
. Now we let
$r_{t,i} \geq q_{t,i} , a$
. Now we let
 $$ \begin{align*}q:= \bigcup \{r_{t,i} \, : \, t \in \operatorname{\textrm{spl}}_{\alpha}(p), i \in C_t\}. \end{align*} $$
$$ \begin{align*}q:= \bigcup \{r_{t,i} \, : \, t \in \operatorname{\textrm{spl}}_{\alpha}(p), i \in C_t\}. \end{align*} $$
The union q is a condition and
![]() $q \geq _{\alpha } p$
and q is compatible just with
$q \geq _{\alpha } p$
and q is compatible just with
![]() $|\operatorname {\textrm {spl}}_{\alpha }(p)|\cdot \kappa $
many elements of A.⊣
$|\operatorname {\textrm {spl}}_{\alpha }(p)|\cdot \kappa $
many elements of A.⊣
In Section 4 we will see that the assumption
![]() $\kappa ^{<\kappa } = \kappa $
is essential.
$\kappa ^{<\kappa } = \kappa $
is essential.
In summary
![]() $({\mathbb Q}^{\textrm {a}}_{\kappa }, \leq , (\leq _{\alpha })_{\alpha < \kappa })$
fulfils a
$({\mathbb Q}^{\textrm {a}}_{\kappa }, \leq , (\leq _{\alpha })_{\alpha < \kappa })$
fulfils a
![]() $\kappa $
-version of Axiom A and preserves
$\kappa $
-version of Axiom A and preserves
![]() $\kappa $
.
$\kappa $
.
If
![]() $2^\kappa = \kappa ^+$
then
$2^\kappa = \kappa ^+$
then
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
preserves cardinals strictly above
${\mathbb Q}^{\textrm {a}}_{\kappa }$
preserves cardinals strictly above
![]() $\kappa ^{+}$
.
$\kappa ^{+}$
.
Discussion 2.7. As in the above, we restrict our attention to regular uncountable
![]() $\kappa $
with
$\kappa $
with
![]() $\kappa ^{<\kappa } = \kappa $
. For
$\kappa ^{<\kappa } = \kappa $
. For
![]() $\kappa = \lambda ^+> \aleph _1$
and
$\kappa = \lambda ^+> \aleph _1$
and
![]() $2^\lambda = \kappa $
, by [Reference Shelah27],
$2^\lambda = \kappa $
, by [Reference Shelah27],
![]() $\diamondsuit _{\kappa }$
holds. So only for
$\diamondsuit _{\kappa }$
holds. So only for
![]() $\kappa = \aleph _1$
and for regular non-strong limit cardinals
$\kappa = \aleph _1$
and for regular non-strong limit cardinals
![]() $\kappa $
, it is open whether
$\kappa $
, it is open whether
![]() $\kappa ^{<\kappa } = \kappa $
is sufficient for preserving
$\kappa ^{<\kappa } = \kappa $
is sufficient for preserving
![]() $\kappa ^+$
in iterations with support
$\kappa ^+$
in iterations with support
![]() $\kappa $
of suitable
$\kappa $
of suitable
![]() $(<\kappa )$
-closed tree forcing iterands like
$(<\kappa )$
-closed tree forcing iterands like
![]() $\kappa $
-Sacks forcing (see Definition 2.2) or club
$\kappa $
-Sacks forcing (see Definition 2.2) or club
![]() $\kappa $
-Miller forcing (see Definition 2.1). For Sacks forcing, Kanamori asks this question in [Reference Kanamori10].
$\kappa $
-Miller forcing (see Definition 2.1). For Sacks forcing, Kanamori asks this question in [Reference Kanamori10].
2.1 Fusion sequences for limits of cofinality
 $\kappa $
$\kappa $
In this subsection we show that
![]() $\diamondsuit _{\kappa }$
can be replaced by
$\diamondsuit _{\kappa }$
can be replaced by
![]() $(Dl)_{\kappa }$
as a sufficient condition that the
$(Dl)_{\kappa }$
as a sufficient condition that the
![]() $\kappa $
-support iteration of a tree forcing iterands with Axiom A preserves
$\kappa $
-support iteration of a tree forcing iterands with Axiom A preserves
![]() $\kappa ^+$
. This is a weak partial answer to Kanamori’s question. First we show that
$\kappa ^+$
. This is a weak partial answer to Kanamori’s question. First we show that
![]() $(Dl)_{\kappa }$
can be strictly weaker than
$(Dl)_{\kappa }$
can be strictly weaker than
![]() $\diamondsuit _{\kappa }$
.
$\diamondsuit _{\kappa }$
.
Definition 2.8 (See [Reference Shelah21, Reference Shelah24, Reference Shelah25]).
-
(1) For a regular uncountable
 $\kappa $
and a stationary
$\kappa $
and a stationary
 $S \subseteq \kappa $
we let
$S \subseteq \kappa $
we let
 $(Dl)_S$
mean the following: There is a sequence
$(Dl)_S$
mean the following: There is a sequence
 $\bar {F} = \langle F_\delta \, : \, \delta \in S\rangle $
such that
$\bar {F} = \langle F_\delta \, : \, \delta \in S\rangle $
such that
 $F_\delta \subseteq {}^\delta \delta $
is of cardinality
$F_\delta \subseteq {}^\delta \delta $
is of cardinality
 $< \kappa $
and for every
$< \kappa $
and for every
 $f \in {}^\kappa \kappa $
there are stationarily many
$f \in {}^\kappa \kappa $
there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \restriction \delta \in F_\delta $
.
$f \restriction \delta \in F_\delta $
. -
(2) We write
 $(Dl)^\ast _S$
if in (1) we demand that the set
$(Dl)^\ast _S$
if in (1) we demand that the set
 $\{\delta \in S \, : \, f\restriction \delta \not \in F_\delta \}$
is not stationary.
$\{\delta \in S \, : \, f\restriction \delta \not \in F_\delta \}$
is not stationary.
Fact 2.9. We assume that
![]() $\kappa $
is regular and uncountable and
$\kappa $
is regular and uncountable and
![]() $S \subseteq \kappa $
is stationary.
$S \subseteq \kappa $
is stationary.
-
(1) If
 $\kappa $
is a successor cardinal then
$\kappa $
is a successor cardinal then
 $(Dl)_S$
is equivalent to
$(Dl)_S$
is equivalent to
 $\diamondsuit _S$
and
$\diamondsuit _S$
and
 $(Dl)^\ast _S$
is equivalent to
$(Dl)^\ast _S$
is equivalent to
 $\diamondsuit ^\ast _S$
.
$\diamondsuit ^\ast _S$
. -
(2) If
 $\kappa $
is strongly inaccessible then
$\kappa $
is strongly inaccessible then
 $(Dl)^\ast _S$
holds.
$(Dl)^\ast _S$
holds. -
(3) If
 $S_1 \subseteq S_2$
are stationary in
$S_1 \subseteq S_2$
are stationary in
 $\kappa $
then
$\kappa $
then
 $(Dl)_{S_2}$
implies
$(Dl)_{S_2}$
implies
 $(Dl)_{S_1}$
and the same for the diamond and both
$(Dl)_{S_1}$
and the same for the diamond and both
 $\ast $
-versions.
$\ast $
-versions.
Proof. (1) Is proved by Kunen [Reference Kunen12, Chapter III]. (2) We can let for
![]() $\delta \in S$
,
$\delta \in S$
,
![]() $F_\delta = {}^\delta \delta $
, and we have that
$F_\delta = {}^\delta \delta $
, and we have that
![]() $\langle F_\delta \, : \, \delta \in S\rangle $
is a
$\langle F_\delta \, : \, \delta \in S\rangle $
is a
![]() $(Dl)_S^*$
-sequence.⊣
$(Dl)_S^*$
-sequence.⊣
Theorem 2.10. If
![]() $\mu $
is an uncountable strong limit cardinal and
$\mu $
is an uncountable strong limit cardinal and
![]() $\kappa ^{<\kappa } = \kappa> \mu $
then for all but finitely many regular
$\kappa ^{<\kappa } = \kappa> \mu $
then for all but finitely many regular
![]() $\theta < \mu $
we have
$\theta < \mu $
we have
 $(Dl)^\ast _{\{\delta < \kappa \, : \, \operatorname {\textrm {cf}}(\delta ) = \theta \}}$
.
$(Dl)^\ast _{\{\delta < \kappa \, : \, \operatorname {\textrm {cf}}(\delta ) = \theta \}}$
.
Proof. See [Reference Shelah25].⊣
Lemma 2.11.
-
(1) Assume that
 $\kappa $
is strongly inaccessible and
$\kappa $
is strongly inaccessible and
 $S \subseteq \kappa $
is stationary and
$S \subseteq \kappa $
is stationary and
 ${\mathbb P}$
is a
${\mathbb P}$
is a
 $\kappa $
-c.c. forcing notion of cardinality
$\kappa $
-c.c. forcing notion of cardinality
 $\kappa $
. Then the following holds.
$\kappa $
. Then the following holds.-
(a) In
 $\mathbf {V}^{{\mathbb P}}$
,
$\mathbf {V}^{{\mathbb P}}$
,
 $(Dl)^\ast _S$
holds and hence
$(Dl)^\ast _S$
holds and hence
 $\kappa ^{<\kappa } = \kappa $
.
$\kappa ^{<\kappa } = \kappa $
. -
(b) If
 $\diamondsuit _S$
holds in
$\diamondsuit _S$
holds in
 $\mathbf {V}$
, then it holds also in
$\mathbf {V}$
, then it holds also in
 $\mathbf {V}^{{\mathbb P}}$
.
$\mathbf {V}^{{\mathbb P}}$
.
-
-
(2) If in addition
 ${\mathbb P}$
has the
${\mathbb P}$
has the
 $\theta $
-c.c. for some regular
$\theta $
-c.c. for some regular
 $\theta < \kappa $
then the following holds.
$\theta < \kappa $
then the following holds.-
(a) In
 $\mathbf {V}^{{\mathbb P}}$
the cardinal
$\mathbf {V}^{{\mathbb P}}$
the cardinal
 $\kappa $
is weakly inaccessible.
$\kappa $
is weakly inaccessible. -
(b) We assume yet in addition that
 $\theta \leq \mu < \kappa $
,
$\theta \leq \mu < \kappa $
,
 $\mu $
is regular, and (2.1)Let
$\mu $
is regular, and (2.1)Let $$ \begin{align} \mathbf{V} \models (\forall \alpha < \kappa)(\operatorname{\textrm{cf}}(\alpha) \geq \mu \rightarrow |\alpha|^{<\theta} = |\alpha|). \end{align} $$
$$ \begin{align} \mathbf{V} \models (\forall \alpha < \kappa)(\operatorname{\textrm{cf}}(\alpha) \geq \mu \rightarrow |\alpha|^{<\theta} = |\alpha|). \end{align} $$
 $S= S^\kappa _{\geq \mu } := \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \geq \mu \}$
. If
$S= S^\kappa _{\geq \mu } := \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \geq \mu \}$
. If
 $\mathbf {V} \models \neg \diamondsuit _S$
, so
$\mathbf {V} \models \neg \diamondsuit _S$
, so
 $\mathbf {V}^{{\mathbb P}} \models \neg \diamondsuit _S$
.
$\mathbf {V}^{{\mathbb P}} \models \neg \diamondsuit _S$
.
-
Proof. (1)(a) Since
![]() ${\mathbb P}$
has the
${\mathbb P}$
has the
![]() $\kappa $
-cc., S is also stationary in
$\kappa $
-cc., S is also stationary in
![]() $\mathbf {V}^{{\mathbb P}}$
. We choose an continuously increasing sequence
$\mathbf {V}^{{\mathbb P}}$
. We choose an continuously increasing sequence
![]() $\langle {\mathbb P}_{\alpha } \, : \, \alpha < \kappa \rangle $
of subsets of
$\langle {\mathbb P}_{\alpha } \, : \, \alpha < \kappa \rangle $
of subsets of
![]() ${\mathbb P}$
such that
${\mathbb P}$
such that
![]() $|{\mathbb P}_{\alpha }| < \kappa $
,
$|{\mathbb P}_{\alpha }| < \kappa $
,
![]() ${\mathbb P} = \bigcup \{{\mathbb P}_{\alpha } \, : \, \alpha < \kappa \}$
and
${\mathbb P} = \bigcup \{{\mathbb P}_{\alpha } \, : \, \alpha < \kappa \}$
and
![]() ${\mathbb P}_{\alpha } \leq _{\textrm {ic}} {\mathbb P}$
, i.e.,
${\mathbb P}_{\alpha } \leq _{\textrm {ic}} {\mathbb P}$
, i.e.,
![]() ${\mathbb P}_{\alpha }$
is an incompatibility preserving suborder of
${\mathbb P}_{\alpha }$
is an incompatibility preserving suborder of
![]() ${\mathbb P}$
, incompatibility of two elements of
${\mathbb P}$
, incompatibility of two elements of
![]() ${\mathbb P}_{\alpha }$
within the order
${\mathbb P}_{\alpha }$
within the order
![]() ${\mathbb P}_{\alpha }$
entails their incompatibilty in
${\mathbb P}_{\alpha }$
entails their incompatibilty in
![]() ${\mathbb P}$
. Let
${\mathbb P}$
. Let
![]() $D_\delta $
be the set of canonical
$D_\delta $
be the set of canonical
![]() ${\mathbb P}_\delta $
-names for functions in
${\mathbb P}_\delta $
-names for functions in
![]() ${}^\delta \delta $
. Such a canonical name
${}^\delta \delta $
. Such a canonical name
has, e.g., the form

such that
-
(i) for
 $\gamma < \delta $
,
$\gamma < \delta $
,
 $\beta _\gamma < \kappa $
.
$\beta _\gamma < \kappa $
. -
(ii) for
 $\gamma < \delta $
,
$\gamma < \delta $
,
 $\beta < \beta _\gamma $
,
$\beta < \beta _\gamma $
,
 .
. -
(iii) for
 $\gamma < \delta $
,
$\gamma < \delta $
,
 is a maximal antichain in
is a maximal antichain in
 ${\mathbb P}_\delta $
.
${\mathbb P}_\delta $
.
We let
![]() $P_\delta $
be a name for all evaluations of elements of
$P_\delta $
be a name for all evaluations of elements of
![]() $P_\delta $
, so
$P_\delta $
, so
Since
![]() $\kappa $
is strongly inaccessibly and
$\kappa $
is strongly inaccessibly and
![]() $(|\delta | \cdot |{\mathbb P}_\delta |)^{|{\mathbb P}_\delta |} < \kappa $
, we have that for any
$(|\delta | \cdot |{\mathbb P}_\delta |)^{|{\mathbb P}_\delta |} < \kappa $
, we have that for any
![]() $\delta < \kappa $
,
$\delta < \kappa $
,
![]() $|P_\delta |< \kappa $
and hence
$|P_\delta |< \kappa $
and hence
![]() ${\mathbb P} \Vdash |P_\delta | < \kappa $
.
${\mathbb P} \Vdash |P_\delta | < \kappa $
.
Moreover, since
![]() ${\mathbb P}$
has the
${\mathbb P}$
has the
![]() $\kappa $
-c.c., every
$\kappa $
-c.c., every
![]() ${\mathbb P}$
-name for an elements of
${\mathbb P}$
-name for an elements of
![]() ${}^\delta \delta $
is a
${}^\delta \delta $
is a
![]() ${\mathbb P}_\varepsilon $
-name for some
${\mathbb P}_\varepsilon $
-name for some
![]() $\varepsilon < \kappa $
. We show that
$\varepsilon < \kappa $
. We show that
![]() ${\mathbb P}$
forces that
${\mathbb P}$
forces that
![]() $\langle P_\delta \, : \, \delta \in S \rangle $
has the guessing property of a
$\langle P_\delta \, : \, \delta \in S \rangle $
has the guessing property of a
![]() $(Dl)^\ast _S$
-sequence. Let
$(Dl)^\ast _S$
-sequence. Let
be a canonical
![]() ${\mathbb P}$
-name for a function from
${\mathbb P}$
-name for a function from
![]() $\kappa $
to
$\kappa $
to
![]() $\kappa $
. We have to show that
$\kappa $
. We have to show that
We let

The set
![]() $C_1$
is club in
$C_1$
is club in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() ${\mathbb P}$
force that
${\mathbb P}$
force that
be a
![]() ${\mathbb P}$
-name for a club subset of
${\mathbb P}$
-name for a club subset of
![]() $\kappa $
. Since
$\kappa $
. Since
![]() ${\mathbb P}$
has the
${\mathbb P}$
has the
![]() $\kappa $
-c.c., there is a club
$\kappa $
-c.c., there is a club
![]() $C_2 \in \mathbf {V}$
, such that
$C_2 \in \mathbf {V}$
, such that
. Let
![]() $p \in {\mathbb P}$
. Let
$p \in {\mathbb P}$
. Let
![]() $\delta \in S \cap C_2 \cap C_1$
. For
$\delta \in S \cap C_2 \cap C_1$
. For
![]() $\gamma < \delta $
,
$\gamma < \delta $
,
![]() $\beta < \beta _\gamma $
,
$\beta < \beta _\gamma $
,

. By the definition of
![]() $C_1$
and
$C_1$
and
![]() $P_\delta $
, we have
$P_\delta $
, we have
![]() ${\mathbb P} \Vdash \tau \restriction \delta \in P_\delta $
. Hence (2.2) is proved.
${\mathbb P} \Vdash \tau \restriction \delta \in P_\delta $
. Hence (2.2) is proved.
(1)(b) We let
![]() ${\mathbb P}_{\alpha }$
,
${\mathbb P}_{\alpha }$
,
![]() $\alpha < \kappa $
, be chosen as in the proof of (1)(a). Let
$\alpha < \kappa $
, be chosen as in the proof of (1)(a). Let
![]() $S \subseteq \kappa $
be stationary and let
$S \subseteq \kappa $
be stationary and let
![]() $\langle D_{\alpha } \, : \, \alpha \in S\rangle $
be a
$\langle D_{\alpha } \, : \, \alpha \in S\rangle $
be a
![]() $\diamondsuit _S$
-sequence in
$\diamondsuit _S$
-sequence in
![]() $\mathbf {V}$
. We assume that
$\mathbf {V}$
. We assume that
![]() ${\mathbb P} \subseteq \kappa $
. Then there is a club C such that
${\mathbb P} \subseteq \kappa $
. Then there is a club C such that
![]() ${\mathbb P}_\delta \subseteq \delta $
for
${\mathbb P}_\delta \subseteq \delta $
for
![]() $\delta \in S \cap C$
. Let
$\delta \in S \cap C$
. Let
![]() $\varphi \colon \kappa \to \kappa \times (\kappa \times \kappa )$
be a bijection. By the
$\varphi \colon \kappa \to \kappa \times (\kappa \times \kappa )$
be a bijection. By the
![]() $\kappa $
-c.c, there is a club
$\kappa $
-c.c, there is a club
![]() $C_1 \subseteq C$
such that for
$C_1 \subseteq C$
such that for
![]() $\delta \in C_1$
,
$\delta \in C_1$
,
-
 $(\oplus )_1$
$(\oplus )_1$
 $\varphi \restriction \delta $
is onto
$\varphi \restriction \delta $
is onto
 $\delta \times (\delta \times \delta )$
and
$\delta \times (\delta \times \delta )$
and -
 $(\oplus )_2$
$(\oplus )_2$
 .
.
Let for
![]() $\alpha \in S\cap C_1$
,
$\alpha \in S\cap C_1$
,
We show that
![]() ${\mathbb P}$
forces that
${\mathbb P}$
forces that
![]() $\langle \langle 1_{\mathbb P}, \langle \alpha , D^{\prime }_{\alpha } \rangle \rangle \, : \, \alpha \in S \rangle $
is a name for a diamond sequence on S in
$\langle \langle 1_{\mathbb P}, \langle \alpha , D^{\prime }_{\alpha } \rangle \rangle \, : \, \alpha \in S \rangle $
is a name for a diamond sequence on S in
![]() $\mathbf {V}^{{\mathbb P}}$
.
$\mathbf {V}^{{\mathbb P}}$
.
We let

Then there are stationarily many
![]() $\delta \in S \cap C_1$
such that
$\delta \in S \cap C_1$
such that
![]() $A \cap \delta = D_\delta $
. By the choice of
$A \cap \delta = D_\delta $
. By the choice of
![]() $C_1$
and of
$C_1$
and of
![]() $D^{\prime }_\delta $
, for any such
$D^{\prime }_\delta $
, for any such
![]() $\delta $
we have
$\delta $
we have
(2)(a) Any cardinal
![]() $\delta \in [\theta ,\kappa ]$
in
$\delta \in [\theta ,\kappa ]$
in
![]() $\mathbf {V}$
stays a cardinal in the extension. Since
$\mathbf {V}$
stays a cardinal in the extension. Since
![]() $\kappa $
is regular in the ground model, by the
$\kappa $
is regular in the ground model, by the
![]() $\kappa $
-c.c., it stays regular in the extension.
$\kappa $
-c.c., it stays regular in the extension.
(2)(b) Now let S be the special set as in the premise. A
![]() $\diamondsuit _S^-$
sequence is a
$\diamondsuit _S^-$
sequence is a
![]() $(Dl)_{\kappa }$
-sequence
$(Dl)_{\kappa }$
-sequence
![]() $\langle P_\delta \, : \, \delta < \kappa \rangle $
such that
$\langle P_\delta \, : \, \delta < \kappa \rangle $
such that
![]() $|P_\delta | \leq \delta $
. There is a function
$|P_\delta | \leq \delta $
. There is a function
![]() $f \colon \kappa \to \kappa $
such that for each
$f \colon \kappa \to \kappa $
such that for each
![]() $\delta < \kappa $
, each
$\delta < \kappa $
, each
![]() $P_\delta $
has a
$P_\delta $
has a
![]() ${\mathbb P}_{f(\delta )}$
-name. By the
${\mathbb P}_{f(\delta )}$
-name. By the
![]() $\theta $
-c.c. and the assumption on cardinal expontiation, we have
$\theta $
-c.c. and the assumption on cardinal expontiation, we have
![]() $(\forall \delta \in S)(f(\delta ) \leq \delta )$
. Let
$(\forall \delta \in S)(f(\delta ) \leq \delta )$
. Let
![]() $\langle P_\delta \, : \, \delta \in S\rangle $
be a
$\langle P_\delta \, : \, \delta \in S\rangle $
be a
![]() $\diamondsuit ^-_{S}$
-sequence in
$\diamondsuit ^-_{S}$
-sequence in
![]() $\mathbf {V}^{{\mathbb P}}$
. Then
$\mathbf {V}^{{\mathbb P}}$
. Then
![]() ${\mathbb P} \Vdash |P_\delta | \leq |\delta |$
. We let for
${\mathbb P} \Vdash |P_\delta | \leq |\delta |$
. We let for
![]() $\delta \in S$
,
$\delta \in S$
,
 $$ \begin{align*}D_\delta = \{ x \in {}^\delta \delta \cap \mathbf{V} \, : \, (\exists p \in {\mathbb P}_\delta) (p \Vdash x \in P_\delta)\}. \end{align*} $$
$$ \begin{align*}D_\delta = \{ x \in {}^\delta \delta \cap \mathbf{V} \, : \, (\exists p \in {\mathbb P}_\delta) (p \Vdash x \in P_\delta)\}. \end{align*} $$
Since
![]() ${\mathbb P}$
has the
${\mathbb P}$
has the
![]() $\theta $
-c.c. and since
$\theta $
-c.c. and since
![]() ${\mathbb P} \Vdash |P_\delta | \leq \delta $
, the set
${\mathbb P} \Vdash |P_\delta | \leq \delta $
, the set
![]() $D_\delta $
has size at most
$D_\delta $
has size at most
![]() $|\delta |$
. We show
$|\delta |$
. We show
is a
![]() $\diamondsuit ^-_{S}$
-sequence in
$\diamondsuit ^-_{S}$
-sequence in
![]() $\mathbf {V}$
. Let
$\mathbf {V}$
. Let
![]() $x \subseteq \kappa \in \mathbf {V}$
,
$x \subseteq \kappa \in \mathbf {V}$
,
![]() $C \subseteq \kappa $
be club in
$C \subseteq \kappa $
be club in
![]() $\mathbf {V}$
. By the
$\mathbf {V}$
. By the
![]() $\kappa $
-c.c., C is also a club in
$\kappa $
-c.c., C is also a club in
![]() $\mathbf {V}^{{\mathbb P}}$
. Then for any
$\mathbf {V}^{{\mathbb P}}$
. Then for any
![]() $\delta < \kappa $
,
$\delta < \kappa $
,
![]() $x \cap \delta $
has a
$x \cap \delta $
has a
![]() ${\mathbb P}_\delta $
-name. By assumption,
${\mathbb P}_\delta $
-name. By assumption,
![]() ${\mathbb P} \Vdash \mbox {``}\{ \delta \in C\cap S \, : \, x\restriction \delta \in P_\delta \} \neq \emptyset $
.” We pick
${\mathbb P} \Vdash \mbox {``}\{ \delta \in C\cap S \, : \, x\restriction \delta \in P_\delta \} \neq \emptyset $
.” We pick
![]() $\delta \in C \cap S$
and
$\delta \in C \cap S$
and
![]() $p \in {\mathbb P}$
such that
$p \in {\mathbb P}$
such that
![]() $p \Vdash x\cap \delta \in P_\delta $
. Since
$p \Vdash x\cap \delta \in P_\delta $
. Since
![]() $\delta \in S$
we can choose
$\delta \in S$
we can choose
![]() $p \in {\mathbb P}_\delta $
. Thus
$p \in {\mathbb P}_\delta $
. Thus
![]() $x \cap \delta \in D_\delta $
.⊣
$x \cap \delta \in D_\delta $
.⊣
Remark 2.12. Let
![]() $\kappa $
be strongly inaccessible. For any regular
$\kappa $
be strongly inaccessible. For any regular
![]() $\xi < \kappa $
, the forcing adding
$\xi < \kappa $
, the forcing adding
![]() $\kappa $
many
$\kappa $
many
![]() $\xi $
-Cohen reals, i.e.,
$\xi $
-Cohen reals, i.e.,
 $$ \begin{align*} {\mathbb P}= \{f \, : \, (\exists u \in [\kappa]^{<\xi})( f \colon u \to \{0,1\})\}, \end{align*} $$
$$ \begin{align*} {\mathbb P}= \{f \, : \, (\exists u \in [\kappa]^{<\xi})( f \colon u \to \{0,1\})\}, \end{align*} $$
fulfils the premises of (1) and has the
![]() $\xi ^+$
-cc.
$\xi ^+$
-cc.
Finally we separate
![]() $\diamondsuit _S$
from
$\diamondsuit _S$
from
![]() $(Dl)_S$
for some stationary sets S.
$(Dl)_S$
for some stationary sets S.
Corollary 2.13. If there is a supercompact cardinal
![]() $\kappa $
and a measurable above
$\kappa $
and a measurable above
![]() $\kappa $
,
$\kappa $
,
![]() $\xi < \kappa $
, then is consistent that
$\xi < \kappa $
, then is consistent that
![]() $\kappa $
is strongly inaccessible and for any stationary
$\kappa $
is strongly inaccessible and for any stationary
![]() $S \subseteq \kappa $
,
$S \subseteq \kappa $
,
![]() $(Dl)_{S}$
holds but
$(Dl)_{S}$
holds but
![]() $\diamondsuit _{S}$
fails.
$\diamondsuit _{S}$
fails.
Under the same large cardinal assumptions there is a weakly inaccessible not strongly inaccessible cardinal
![]() $\kappa $
and there is are regular
$\kappa $
and there is are regular
![]() $\xi ^+ < \mu < \kappa $
such that for
$\xi ^+ < \mu < \kappa $
such that for
![]() $S = \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \geq \mu \}$
the principle
$S = \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \geq \mu \}$
the principle
![]() $(Dl)_S$
holds but the diamond
$(Dl)_S$
holds but the diamond
![]() $\diamondsuit _S$
fails.
$\diamondsuit _S$
fails.
Proof. It suffices to force that
![]() $\kappa $
is strongly inaccessible and
$\kappa $
is strongly inaccessible and
![]() $\neg \diamondsuit _{\kappa }$
. Under the named large cardinal assumption there is such a forcing construction in unpublished work by Woodin. Golshani worked Woodin’s construction out in [Reference Golshani8]. Zeman [Reference Zeman29] provides a lower bound on the consistency strength.
$\neg \diamondsuit _{\kappa }$
. Under the named large cardinal assumption there is such a forcing construction in unpublished work by Woodin. Golshani worked Woodin’s construction out in [Reference Golshani8]. Zeman [Reference Zeman29] provides a lower bound on the consistency strength.
For the second part of the corollary, we consider Woodin’s model as the ground model
![]() $\mathbf {V}$
. The iterated modified Radin forcing that is based on a measure sequence forces (2.1).
$\mathbf {V}$
. The iterated modified Radin forcing that is based on a measure sequence forces (2.1).
We apply Lemma 2.11(1) and (2) to a forcing
![]() ${\mathbb P}$
as in Remark 2.12. Such a forcing destroys that
${\mathbb P}$
as in Remark 2.12. Such a forcing destroys that
![]() $\kappa $
is a strong limit but preserves that
$\kappa $
is a strong limit but preserves that
![]() $\kappa $
is weakly inaccessible. According to the second part of the lemma,
$\kappa $
is weakly inaccessible. According to the second part of the lemma,
![]() $\diamondsuit _{S}$
fails in
$\diamondsuit _{S}$
fails in
![]() $\mathbf {V}^{{\mathbb P}}$
. Note that the notion of being a cardinal is not changed by
$\mathbf {V}^{{\mathbb P}}$
. Note that the notion of being a cardinal is not changed by
![]() ${\mathbb P}$
for cardinals of cofinality at least
${\mathbb P}$
for cardinals of cofinality at least
![]() $\xi ^+$
.⊣
$\xi ^+$
.⊣
This concludes our discussion of the principle
![]() $(Dl)_S$
.
$(Dl)_S$
.
Now we return to Miller and Sacks forcing.
Definition 2.14.
-
(1) Let
 ${\mathbb P}_{\alpha }$
be the
${\mathbb P}_{\alpha }$
be the
 $\kappa $
-support iteration of
$\kappa $
-support iteration of
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
. If
${\mathbb Q}^{\textrm {a}}_{\kappa }$
. If
 $p,q \in {\mathbb P}_{\alpha }$
,
$p,q \in {\mathbb P}_{\alpha }$
,
 $\gamma < \kappa $
, and
$\gamma < \kappa $
, and
 $F \subseteq \operatorname {\textrm {supp}}(p)$
we write
$F \subseteq \operatorname {\textrm {supp}}(p)$
we write
 $q \geq _{F,\gamma } p$
if
$q \geq _{F,\gamma } p$
if
 $\forall \beta \in F$
,
$\forall \beta \in F$
,
 $q \restriction \beta \Vdash q(\beta ) \leq _\gamma p(\beta )$
.
$q \restriction \beta \Vdash q(\beta ) \leq _\gamma p(\beta )$
. -
(2) We denote that support of a condition by
 $\operatorname {\textrm {supp}}(p)$
.
$\operatorname {\textrm {supp}}(p)$
.
Lemma 2.15 (Kanamori, proof of [Reference Kanamori10, Theorem 2.2])
Assume
![]() $(Dl)_{\kappa }$
and that
$(Dl)_{\kappa }$
and that
![]() $p \in {\mathbb P}_{\alpha }$
and
$p \in {\mathbb P}_{\alpha }$
and
![]() $p \Vdash _{{\mathbb P}_{\alpha }} \tau \in \textrm {On}$
. Suppose also that
$p \Vdash _{{\mathbb P}_{\alpha }} \tau \in \textrm {On}$
. Suppose also that
![]() $F\subseteq \operatorname {\textrm {supp}}(p)$
and
$F\subseteq \operatorname {\textrm {supp}}(p)$
and
![]() $|F|<\kappa $
, and that
$|F|<\kappa $
, and that
![]() $\gamma < \kappa $
. Then there is a
$\gamma < \kappa $
. Then there is a
![]() $q \geq _{F,\gamma } p$
and an
$q \geq _{F,\gamma } p$
and an
![]() $x \subseteq \textrm {On}$
,
$x \subseteq \textrm {On}$
,
![]() $|x| \leq \kappa $
, such that
$|x| \leq \kappa $
, such that
![]() $q \Vdash \tau \in x$
.
$q \Vdash \tau \in x$
.
Proof. Sketch. We rework Kanamori [Reference Kanamori10, Theorem 2.2] and shows that it works with
![]() $(Dl)_{\kappa }$
instead of
$(Dl)_{\kappa }$
instead of
![]() $\diamondsuit _{\kappa }$
. The modification is: By
$\diamondsuit _{\kappa }$
. The modification is: By
![]() $(<\kappa )$
-closure, in the successor step, we can find a strengthening of all the
$(<\kappa )$
-closure, in the successor step, we can find a strengthening of all the
![]() $<\kappa $
many guesses offered by
$<\kappa $
many guesses offered by
![]() $(Dl)_{\kappa }$
by strengthening successively, in
$(Dl)_{\kappa }$
by strengthening successively, in
![]() $< \kappa $
substeps.⊣
$< \kappa $
substeps.⊣
As a routine conclusion of the technical lemma we get the following:
Theorem 2.16. Assume
![]() $\kappa ^{<\kappa }=\kappa $
and
$\kappa ^{<\kappa }=\kappa $
and
![]() $(Dl)_{\kappa }$
. Let
$(Dl)_{\kappa }$
. Let
![]() $\delta $
be an ordinal and let
$\delta $
be an ordinal and let
![]() be a (
be a (
![]() $\leq \kappa $
)-support iteration of iterands
$\leq \kappa $
)-support iteration of iterands
![]() (in
(in
![]() $\mathbf {V}^{{\mathbb P}_\beta }$
). Then
$\mathbf {V}^{{\mathbb P}_\beta }$
). Then
![]() ${\mathbb P}_{\delta }$
has the following properties.
${\mathbb P}_{\delta }$
has the following properties.
-
(1)
 ${\mathbb P}_{\delta }$
does not collapse
${\mathbb P}_{\delta }$
does not collapse
 $\kappa ^+$
.
$\kappa ^+$
. -
(2) (
 $\kappa $
-properness) For any
$\kappa $
-properness) For any
 $N \prec H(\chi )$
,
$N \prec H(\chi )$
,
 $|N|= \kappa $
with
$|N|= \kappa $
with
 ${}^{<\kappa }N \subseteq N $
and
${}^{<\kappa }N \subseteq N $
and
 $\kappa , p, {\mathbb P}_{\delta } \in N,$
and
$\kappa , p, {\mathbb P}_{\delta } \in N,$
and
 $p \in {\mathbb P}_\delta $
there is a stronger
$p \in {\mathbb P}_\delta $
there is a stronger
 $(N,{\mathbb P}_{\delta })$
generic condition q.
$(N,{\mathbb P}_{\delta })$
generic condition q.
The same holds for any
![]() $\kappa $
-support iteration of
$\kappa $
-support iteration of
![]() $\kappa $
-Sacks forcing. We restate Kanamori’s question:
$\kappa $
-Sacks forcing. We restate Kanamori’s question:
Question 2.17. Can we replace
![]() $(Dl)_{\kappa }$
by
$(Dl)_{\kappa }$
by
![]() $\kappa ^{<\kappa } = \kappa $
in Theorem 2.16?
$\kappa ^{<\kappa } = \kappa $
in Theorem 2.16?
3
 $\kappa ^{++}$
may be preserved or not
$\kappa ^{++}$
may be preserved or not
Here we are concerned with the preservation of
![]() $\kappa ^{++}$
. In this section we show that under the condition
$\kappa ^{++}$
. In this section we show that under the condition
![]() $2^\kappa = \kappa ^{++}$
the preservation of
$2^\kappa = \kappa ^{++}$
the preservation of
![]() $\kappa ^{++}$
by
$\kappa ^{++}$
by
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
is independent from
${\mathbb Q}^{\textrm {a}}_{\kappa }$
is independent from
![]() $\mbox{\sf ZFC}$
.
$\mbox{\sf ZFC}$
.
Definition 3.1. Let
![]() $\mathbb Q$
be a forcing order and let
$\mathbb Q$
be a forcing order and let
![]() $\lambda $
be a cardinal.
$\lambda $
be a cardinal.
![]() $\textrm {Ax}(\mathbb Q, < \lambda )$
is the statement: For any set
$\textrm {Ax}(\mathbb Q, < \lambda )$
is the statement: For any set
![]() $\mathcal D$
of size
$\mathcal D$
of size
![]() $< \lambda $
of dense sets in
$< \lambda $
of dense sets in
![]() $\mathbb Q$
there is a filter
$\mathbb Q$
there is a filter
![]() $G \subseteq \mathbb Q$
such that
$G \subseteq \mathbb Q$
such that
![]() $(\forall D \in \mathcal D)(G \cap D \neq \emptyset )$
. Such a filter is called
$(\forall D \in \mathcal D)(G \cap D \neq \emptyset )$
. Such a filter is called
![]() $\mathcal D$
-generic.
$\mathcal D$
-generic.
Definition 3.2. An amoeba for
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
. See [Reference Laguzzi13]. Let
${\mathbb Q}^{\textrm {a}}_{\kappa }$
. See [Reference Laguzzi13]. Let
![]() $\kappa> \aleph _0$
be an inaccessible cardinal. The amoeba for
$\kappa> \aleph _0$
be an inaccessible cardinal. The amoeba for
![]() $\kappa $
-Miller forcing,
$\kappa $
-Miller forcing,
![]() $\mathbb Q^{\textrm {a,amoeba}}_{\kappa }$
, is the following forcing order: Conditions are of the form
$\mathbb Q^{\textrm {a,amoeba}}_{\kappa }$
, is the following forcing order: Conditions are of the form
![]() $p=(t_p,T_p)$
, where
$p=(t_p,T_p)$
, where
![]() $T_p \in \mathbb Q^a_{\kappa }$
and
$T_p \in \mathbb Q^a_{\kappa }$
and
![]() $t_p$
is a subtree of
$t_p$
is a subtree of
![]() $T_p$
that is
$T_p$
that is
![]() $(<\kappa )$
-closed in the following sense
$(<\kappa )$
-closed in the following sense
-
(a) each increasing sequence of splitting nodes in
 $t_p$
of length
$t_p$
of length
 $(< \kappa )$
is a splitting node of
$(< \kappa )$
is a splitting node of
 $t_p$
(hence
$t_p$
(hence
 $t_p$
has maximal nodes which are of successor length). We write This set is called the set of terminal nodes of
$t_p$
has maximal nodes which are of successor length). We write This set is called the set of terminal nodes of $$ \begin{align*}\operatorname{\textrm{term}}(t_p) = \{ s \in t_p \, : \, (\neg \exists t \triangleright s) t \in t_p\}. \end{align*} $$
$$ \begin{align*}\operatorname{\textrm{term}}(t_p) = \{ s \in t_p \, : \, (\neg \exists t \triangleright s) t \in t_p\}. \end{align*} $$
 $t_p$
. Since
$t_p$
. Since
 $t_p$
is
$t_p$
is
 $(<\kappa )$
-closed, for each
$(<\kappa )$
-closed, for each
 $s \in t_p$
there is a subset
$s \in t_p$
there is a subset
 $F $
of
$F $
of
 $ p^{\langle s \rangle }$
such that for each branch b of
$ p^{\langle s \rangle }$
such that for each branch b of
 $p^{\langle s \rangle }$
terminal
$p^{\langle s \rangle }$
terminal
 $t \trianglerighteq s$
,
$t \trianglerighteq s$
,
 $t \in b$
.
$t \in b$
.
-
(b) For each
 $t \in t_p \cap \operatorname {\textrm {spl}}(p)\setminus \operatorname {\textrm {term}}(t_p)$
we have
$t \in t_p \cap \operatorname {\textrm {spl}}(p)\setminus \operatorname {\textrm {term}}(t_p)$
we have
 $\operatorname {\textrm {osucc}}_{t_p}(t)$
is a closed initial subset of
$\operatorname {\textrm {osucc}}_{t_p}(t)$
is a closed initial subset of
 $\operatorname {\textrm {osucc}}_{T_p}(t)$
.
$\operatorname {\textrm {osucc}}_{T_p}(t)$
.The requirement (b) is used for
 $\bigcup \{t_p \, : \, (t_p,T_p) \in G\} \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. This is used in Theorem 3.4 (4)(b).
$\bigcup \{t_p \, : \, (t_p,T_p) \in G\} \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. This is used in Theorem 3.4 (4)(b).
The forcing order is as follows:
![]() $(t_p,T_p) \leq (t_q,T_q)$
if
$(t_p,T_p) \leq (t_q,T_q)$
if
![]() $T_q \subseteq T_p$
,
$T_q \subseteq T_p$
,
![]() $t_q \supseteq t_p$
and for each
$t_q \supseteq t_p$
and for each
![]() $\eta \in t_p$
,
$\eta \in t_p$
,
 $\operatorname {\textrm {osucc}}_{t_p}(\eta )$
is an initial segment of
$\operatorname {\textrm {osucc}}_{t_p}(\eta )$
is an initial segment of
 $\operatorname {\textrm {osucc}}_{t_q}(\eta )$
.
$\operatorname {\textrm {osucc}}_{t_q}(\eta )$
.
Results about
![]() $\mathbb Q^{\textrm {a,amoeba}}_{\kappa }$
, for inaccessible
$\mathbb Q^{\textrm {a,amoeba}}_{\kappa }$
, for inaccessible
![]() $\kappa $
, can be found in [Reference Laguzzi13].
$\kappa $
, can be found in [Reference Laguzzi13].
Definition 3.3. Now we define
![]() $\leq _{\alpha }$
for
$\leq _{\alpha }$
for
![]() ${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
under the assumption
${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
under the assumption
![]() $\kappa ^{<\kappa } = \kappa $
.
$\kappa ^{<\kappa } = \kappa $
.
-
(1) Let
 $p = (t_p,T_p) \in {\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
.
$p = (t_p,T_p) \in {\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
.We write
This set is called the set of terminal nodes of $$ \begin{align*}\operatorname{\textrm{term}}(t_p) = \{ s \in t_p \, : \, (\neg \exists t \triangleright s) t \in t_p\}. \end{align*} $$
$$ \begin{align*}\operatorname{\textrm{term}}(t_p) = \{ s \in t_p \, : \, (\neg \exists t \triangleright s) t \in t_p\}. \end{align*} $$
 $t_p$
.
$t_p$
.
-
(2) Let
 $\alpha < \kappa $
. We define
$\alpha < \kappa $
. We define  $$ \begin{align*} \begin{aligned} \operatorname{\textrm{spl}}^{\textrm{amoeba}}_{\alpha}(p) = & \big\{ t \in \operatorname{\textrm{spl}}(T_p)\setminus t_p \, : \, \\ & \operatorname{\textrm{otp}}(\{s \in T_p \setminus t_p \, : \, s \subsetneq t \wedge s \in \operatorname{\textrm{spl}}(T_p)\}) = \alpha\big\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{\textrm{spl}}^{\textrm{amoeba}}_{\alpha}(p) = & \big\{ t \in \operatorname{\textrm{spl}}(T_p)\setminus t_p \, : \, \\ & \operatorname{\textrm{otp}}(\{s \in T_p \setminus t_p \, : \, s \subsetneq t \wedge s \in \operatorname{\textrm{spl}}(T_p)\}) = \alpha\big\}. \end{aligned} \end{align*} $$
-
(3) Let
 $\langle \eta _{\alpha } \, : \, \alpha < \kappa \rangle $
enumerate
$\langle \eta _{\alpha } \, : \, \alpha < \kappa \rangle $
enumerate
 $\kappa ^{<\kappa }=\kappa $
and let
$\kappa ^{<\kappa }=\kappa $
and let
 $\alpha < \kappa $
.
$\alpha < \kappa $
.  $$ \begin{align*} \operatorname{\textrm{cl}}^{\textrm{amoeba}}_{\alpha}(p) &:= \{s \in T_p \, : \, (\exists \gamma \leq \alpha)(\exists t \in \operatorname{\textrm{spl}}^{\textrm{amoeba}}_\gamma(p)) (s \subseteq t)\\ &\qquad \wedge (\exists \beta < \alpha)( s = \eta_\beta)\}. \end{align*} $$
$$ \begin{align*} \operatorname{\textrm{cl}}^{\textrm{amoeba}}_{\alpha}(p) &:= \{s \in T_p \, : \, (\exists \gamma \leq \alpha)(\exists t \in \operatorname{\textrm{spl}}^{\textrm{amoeba}}_\gamma(p)) (s \subseteq t)\\ &\qquad \wedge (\exists \beta < \alpha)( s = \eta_\beta)\}. \end{align*} $$
-
(4) For
 $\alpha < \kappa $
we let
$\alpha < \kappa $
we let
 $p = (t_p,T_p) \leq _{\alpha } q = (t_q,T_q)$
if
$p = (t_p,T_p) \leq _{\alpha } q = (t_q,T_q)$
if
 $p \leq q$
,
$p \leq q$
,
 $t_p = t_q$
and
$t_p = t_q$
and
 $\operatorname {\textrm {cl}}^{\textrm {amoeba}}_{\alpha }(p)= \operatorname {\textrm {cl}}^{\textrm {amoeba}}_{\alpha }(q)$
.
$\operatorname {\textrm {cl}}^{\textrm {amoeba}}_{\alpha }(p)= \operatorname {\textrm {cl}}^{\textrm {amoeba}}_{\alpha }(q)$
.
Now we state the positive part of the consistency result.
Theorem 3.4. Suppose that
![]() $\kappa> \omega $
,
$\kappa> \omega $
,
![]() $ \kappa ^{<\kappa } = \kappa $
.
$ \kappa ^{<\kappa } = \kappa $
.
-
(1)
 $\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
and
$\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
and
 $2^\kappa = \kappa ^{++}$
is consistent relative to
$2^\kappa = \kappa ^{++}$
is consistent relative to
 $\mbox{\sf ZFC}$
.
$\mbox{\sf ZFC}$
. -
(2)
 $\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
implies that forcing with
$\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
implies that forcing with
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
does not collapse
${\mathbb Q}^{\textrm {a}}_{\kappa }$
does not collapse
 $\kappa ^{++}$
.
$\kappa ^{++}$
.
Now let
![]() $\kappa $
be inaccessible.
$\kappa $
be inaccessible.
-
(3)
 $\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
and
$\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
and
 $2^\kappa = \kappa ^{++}$
is consistent relative to
$2^\kappa = \kappa ^{++}$
is consistent relative to
 $\mbox{\sf ZFC}$
.
$\mbox{\sf ZFC}$
. -
(4)
 $\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
implies
$\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
implies-
(a) forcing with
 ${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
does not collapse
${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
does not collapse
 $\kappa ^{++}$
and
$\kappa ^{++}$
and -
(b) forcing with
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
does not collapse
${\mathbb Q}^{\textrm {a}}_{\kappa }$
does not collapse
 $\kappa ^{++}$
.
$\kappa ^{++}$
.
-
Proof. (1) and (3). Over a ground model with
![]() $\kappa ^{<\kappa } = \kappa $
,
$\kappa ^{<\kappa } = \kappa $
,
![]() $2^\kappa = \kappa ^+$
and
$2^\kappa = \kappa ^+$
and
![]() $\diamondsuit _{\kappa }$
, one performs the usual iteration with
$\diamondsuit _{\kappa }$
, one performs the usual iteration with
![]() $(\leq \kappa )$
-support as introduced in [Reference Kanamori10]. Any name for
$(\leq \kappa )$
-support as introduced in [Reference Kanamori10]. Any name for
![]() $\kappa ^+$
-many dense subsets of
$\kappa ^+$
-many dense subsets of
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
has an equivalent name that is hereditarily of size
${\mathbb Q}^{\textrm {a}}_{\kappa }$
has an equivalent name that is hereditarily of size
![]() $<\kappa ^{++}$
, and hence there is a book-keeping device.
$<\kappa ^{++}$
, and hence there is a book-keeping device.
(2) Suppose that
![]() $\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
holds in V. Any
$\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
holds in V. Any
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
-name for a function
${\mathbb Q}^{\textrm {a}}_{\kappa }$
-name for a function
![]() $f \colon \mu \to \kappa ^{++}$
for some
$f \colon \mu \to \kappa ^{++}$
for some
![]() $\mu < \kappa ^{++}$
is given by a name that consists of at most
$\mu < \kappa ^{++}$
is given by a name that consists of at most
![]() $\kappa ^+$
dense sets
$\kappa ^+$
dense sets
![]() $\mathcal D$
. By
$\mathcal D$
. By
![]() $\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
there is a
$\textrm {Ax}({\mathbb Q}^{\textrm {a}}_{\kappa }, < \kappa ^{++})$
there is a
![]() $\mathcal D$
-generic filter in V. Thus f cannot be onto.
$\mathcal D$
-generic filter in V. Thus f cannot be onto.
(4)(a) is like (2).
(4)(b) Now for
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
. If
${\mathbb Q}^{\textrm {a}}_{\kappa }$
. If
![]() $D \subseteq {\mathbb Q}^{\textrm {a}}_{\kappa }$
is dense in
$D \subseteq {\mathbb Q}^{\textrm {a}}_{\kappa }$
is dense in
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
, then
${\mathbb Q}^{\textrm {a}}_{\kappa }$
, then
 $$ \begin{align*}\textrm{am}(D) = \{(t_p,T_p) \, : \, (\forall s \in \operatorname{\textrm{term}}(t_p) )(T_p^{\langle s \rangle} \in D)\} \end{align*} $$
$$ \begin{align*}\textrm{am}(D) = \{(t_p,T_p) \, : \, (\forall s \in \operatorname{\textrm{term}}(t_p) )(T_p^{\langle s \rangle} \in D)\} \end{align*} $$
is dense in
![]() ${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
. Any
${\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }$
. Any
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
-name
${\mathbb Q}^{\textrm {a}}_{\kappa }$
-name
![]() for a function
for a function
![]() $f \colon \mu \to \kappa ^{++}$
for some
$f \colon \mu \to \kappa ^{++}$
for some
![]() $\mu < \kappa ^{++}$
is given by a name that consists of at most
$\mu < \kappa ^{++}$
is given by a name that consists of at most
![]() $\kappa ^+$
dense sets
$\kappa ^+$
dense sets
 ,
,
![]() $\alpha < \mu $
, put them into
$\alpha < \mu $
, put them into
![]() $\mathcal D$
. By
$\mathcal D$
. By
![]() $\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
there is a
$\textrm {Ax}({\mathbb Q}^{\textrm {a,amoeba}}_{\kappa }, < \kappa ^{++})$
there is a
![]() $\{\textrm {am}(D) \, : \, D \in \mathcal D\}$
-generic filter G in V. Now
$\{\textrm {am}(D) \, : \, D \in \mathcal D\}$
-generic filter G in V. Now
![]() $T_G=\bigcup \{t_p \, : \, p \in G\}$
is a
$T_G=\bigcup \{t_p \, : \, p \in G\}$
is a
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
-tree. We take any branch b of
${\mathbb Q}^{\textrm {a}}_{\kappa }$
-tree. We take any branch b of
![]() $T_G$
. Then
$T_G$
. Then
 $$ \begin{align*}\{T_p^{\langle s \rangle } \, : \, p=(t_p,T_p) \in G, s \in \operatorname{\textrm{term}}(t_p) \cap b\} \end{align*} $$
$$ \begin{align*}\{T_p^{\langle s \rangle } \, : \, p=(t_p,T_p) \in G, s \in \operatorname{\textrm{term}}(t_p) \cap b\} \end{align*} $$
is a
![]() $\mathcal D$
-generic filter. Thus
$\mathcal D$
-generic filter. Thus
![]() is determined in the ground model and hence cannot be a name for a function from
is determined in the ground model and hence cannot be a name for a function from
![]() $\mu $
onto
$\mu $
onto
![]() $\kappa ^{++}$
.⊣
$\kappa ^{++}$
.⊣
Forcing with
 ${\mathbb Q}^{\text{\rm a}}_{\kappa }$
may collapse
${\mathbb Q}^{\text{\rm a}}_{\kappa }$
may collapse
 $2^\kappa $
to
$2^\kappa $
to
 $\frak b_{\kappa }$
$\frak b_{\kappa }$
Now we come to a complementary scenario:
![]() ${\mathbb Q}^{\textrm{a}}_{\kappa }$
may collapse
${\mathbb Q}^{\textrm{a}}_{\kappa }$
may collapse
![]() $2^\kappa $
to
$2^\kappa $
to
![]() $\frak b_{\kappa }$
. Petr Simon showed that Sacks forcing collapses the continuum to the bounding number [Reference Simon28]. Here we prove, under additional hypotheses, a similar result for the higher case. Our result pertains to
$\frak b_{\kappa }$
. Petr Simon showed that Sacks forcing collapses the continuum to the bounding number [Reference Simon28]. Here we prove, under additional hypotheses, a similar result for the higher case. Our result pertains to
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
.
${\mathbb Q}^{\textrm {a}}_{\kappa }$
.
Definition 3.5. We recall the definition of three cardinal invariants at
![]() $\kappa $
.
$\kappa $
.
-
(1) The ideal of bounded subsets of
 $\kappa $
is
$\kappa $
is
 $J_{\kappa }^{\textrm {bd}} = [\kappa ]^{<\kappa }$
. The order of eventual domination is:
$J_{\kappa }^{\textrm {bd}} = [\kappa ]^{<\kappa }$
. The order of eventual domination is:
 $f \leq _{J^{\textrm {bd}}_{\kappa }} g$
if
$f \leq _{J^{\textrm {bd}}_{\kappa }} g$
if
 $\{\alpha \, : \, f(\alpha ) \not \leq g(\alpha ) \} \in J^{\textrm {bd}}_{\kappa }$
. The bounding number at
$\{\alpha \, : \, f(\alpha ) \not \leq g(\alpha ) \} \in J^{\textrm {bd}}_{\kappa }$
. The bounding number at
 $\kappa $
is the following cardinal
$\kappa $
is the following cardinal  $$ \begin{align*} \frak b_{\kappa} = \min\{|F| \, : \, F \subseteq \kappa^\kappa \wedge (\forall g\in \kappa^\kappa)( \exists f \in F)( f \not\leq_{J_{\kappa}^{\textrm{bd}}} g)\}. \end{align*} $$
$$ \begin{align*} \frak b_{\kappa} = \min\{|F| \, : \, F \subseteq \kappa^\kappa \wedge (\forall g\in \kappa^\kappa)( \exists f \in F)( f \not\leq_{J_{\kappa}^{\textrm{bd}}} g)\}. \end{align*} $$
-
(2) The order of club-domination is defined on functions from
 $\kappa $
to
$\kappa $
to
 $\kappa $
as follows:
$\kappa $
as follows:
 $f \leq _{\textrm {club}} g$
if
$f \leq _{\textrm {club}} g$
if
 $\{\alpha \in \kappa \, : \, f(\alpha ) \leq g(\alpha )\}$
contains a club subset. The bounding number modulo a club at
$\{\alpha \in \kappa \, : \, f(\alpha ) \leq g(\alpha )\}$
contains a club subset. The bounding number modulo a club at
 $\kappa $
is the following cardinal
$\kappa $
is the following cardinal  $$ \begin{align*} \frak b_{\textrm{club},\kappa} = \min\{|F| \, : \, F \subseteq \kappa^\kappa \wedge (\forall g\in \kappa^\kappa)( \exists f \in F)( f \not\leq_{\textrm{club}} g)\}. \end{align*} $$
$$ \begin{align*} \frak b_{\textrm{club},\kappa} = \min\{|F| \, : \, F \subseteq \kappa^\kappa \wedge (\forall g\in \kappa^\kappa)( \exists f \in F)( f \not\leq_{\textrm{club}} g)\}. \end{align*} $$
By [Reference Cummings and Shelah5, Theorem 6],
![]() $\frak b_{\textrm {club},\kappa } = \frak b_{\kappa }$
for any regular uncountable
$\frak b_{\textrm {club},\kappa } = \frak b_{\kappa }$
for any regular uncountable
![]() $\kappa $
.
$\kappa $
.
For any condition p in a tree forcing, in particular for
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
, there is a function mapping each node to the shortest splitting node above it. We work with this function for thinning out trees.
${\mathbb Q}^{\textrm {a}}_{\kappa }$
, there is a function mapping each node to the shortest splitting node above it. We work with this function for thinning out trees.
Definition 3.6.
-
(1) We say
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is nice if the following holds:
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is nice if the following holds:-
(a) For every
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
for every
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
for every
 $\eta \in p$
,
$\eta \in p$
,
 $\eta $
is a strictly increasing function.
$\eta $
is a strictly increasing function. -
(b) If
 $\eta \in \operatorname {\textrm {spl}}(p)$
then
$\eta \in \operatorname {\textrm {spl}}(p)$
then
 $\lg (\eta )$
is a limit ordinal.
$\lg (\eta )$
is a limit ordinal.
-
-
(2) We fix an enumeration
 $\langle \eta _{\alpha } \, : \, \alpha < \kappa \rangle $
of
$\langle \eta _{\alpha } \, : \, \alpha < \kappa \rangle $
of
 ${}^{\kappa> } \kappa $
. Let
${}^{\kappa> } \kappa $
. Let
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. We define as follows: For
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. We define as follows: For $$ \begin{align*} h_p \colon {}^{\kappa>} \kappa \to {}^{\kappa>} \kappa \end{align*} $$
$$ \begin{align*} h_p \colon {}^{\kappa>} \kappa \to {}^{\kappa>} \kappa \end{align*} $$
 $\eta =\eta _{\alpha }\in p\setminus \operatorname {\textrm {spl}}(p)$
we let
$\eta =\eta _{\alpha }\in p\setminus \operatorname {\textrm {spl}}(p)$
we let
 $h_p(\eta )$
be the shortest
$h_p(\eta )$
be the shortest
 $\nu $
such that (
$\nu $
such that (
 $\eta \,\hat {} \, \nu \in \operatorname {\textrm {spl}}(p)$
and
$\eta \,\hat {} \, \nu \in \operatorname {\textrm {spl}}(p)$
and
 $\lg (\eta \,\hat {} \, \nu ) \geq \alpha $
).
$\lg (\eta \,\hat {} \, \nu ) \geq \alpha $
).
For
 $\eta \not \in p$
and for
$\eta \not \in p$
and for
 $\eta \in \operatorname {\textrm {spl}}(p)$
, we let
$\eta \in \operatorname {\textrm {spl}}(p)$
, we let
 $h_p(\eta ) = \emptyset $
.
$h_p(\eta ) = \emptyset $
. -
(3) Let
 $A \subseteq {}^{\kappa>}\kappa $
.
$A \subseteq {}^{\kappa>}\kappa $
.
 $h \colon {}^{\kappa>}\kappa \to {}^{\kappa >} \kappa $
is called increasing on A if for every
$h \colon {}^{\kappa>}\kappa \to {}^{\kappa >} \kappa $
is called increasing on A if for every
 $\eta \in A$
there is
$\eta \in A$
there is
 $(\varrho , \sigma ) \in h(\eta )$
such that
$(\varrho , \sigma ) \in h(\eta )$
such that  $$ \begin{align*}(\forall \alpha \in \operatorname{\textrm{dom}}(\eta))( \eta(\alpha) < \sigma). \end{align*} $$
$$ \begin{align*}(\forall \alpha \in \operatorname{\textrm{dom}}(\eta))( \eta(\alpha) < \sigma). \end{align*} $$
The set of nice conditions in dense in the isomorphic copy of
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
whose conditions contain only strictly increasing nodes. From now on we assume that any
${\mathbb Q}^{\textrm {a}}_{\kappa }$
whose conditions contain only strictly increasing nodes. From now on we assume that any
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
contains only strictly increasing nodes.
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
contains only strictly increasing nodes.
Remark 3.7. If
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is nice and
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
is nice and
![]() $A = \{\eta \,\hat {} \, \langle \alpha \rangle \, : \, \eta \in \operatorname {\textrm {spl}}(p), \eta \,\hat {} \,\langle \alpha \rangle \in p\}$
, then the function
$A = \{\eta \,\hat {} \, \langle \alpha \rangle \, : \, \eta \in \operatorname {\textrm {spl}}(p), \eta \,\hat {} \,\langle \alpha \rangle \in p\}$
, then the function
![]() $h_p$
from Definition 3.6(2) is increasing on A.
$h_p$
from Definition 3.6(2) is increasing on A.
We work with particular evasion numbers, defined as follows.
Definition 3.8.
-
(1) Let
 $\mathfrak {e}^0_{\kappa }$
be the maximal
$\mathfrak {e}^0_{\kappa }$
be the maximal
 $\lambda $
such that for every
$\lambda $
such that for every
 $\mathscr F \subseteq {}^{(^{\kappa>}{\kappa })} \kappa $
of size
$\mathscr F \subseteq {}^{(^{\kappa>}{\kappa })} \kappa $
of size
 $< \lambda $
and every everywhere strictly increasing
$< \lambda $
and every everywhere strictly increasing
 $h \colon {}^{\kappa>}\kappa \to {}^{\kappa >}\kappa $
there is some
$h \colon {}^{\kappa>}\kappa \to {}^{\kappa >}\kappa $
there is some
 $g \colon {}^{\kappa>}\kappa \to \kappa $
with the following property:
$g \colon {}^{\kappa>}\kappa \to \kappa $
with the following property:For every
 $f \in \mathscr F$
and
$f \in \mathscr F$
and
 $\eta \in {}^{\kappa>} \kappa $
there is a stationary set
$\eta \in {}^{\kappa>} \kappa $
there is a stationary set
 $S = S_{h,f,\eta }$
such that for any
$S = S_{h,f,\eta }$
such that for any
 $\delta \in S$
$\delta \in S$
 $$ \begin{align*}g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h(\eta \,\hat{} \,\langle \delta \rangle)) \neq f (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h(\eta \,\hat{} \,\langle \delta \rangle)).\end{align*} $$
$$ \begin{align*}g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h(\eta \,\hat{} \,\langle \delta \rangle)) \neq f (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h(\eta \,\hat{} \,\langle \delta \rangle)).\end{align*} $$
-
(2) Actually we can work with a somewhat more specific variant of
 $\mathfrak {e}_{\kappa }^0$
: Let
$\mathfrak {e}_{\kappa }^0$
: Let
 $\mathfrak {e}^1_{\kappa }$
be the maximal
$\mathfrak {e}^1_{\kappa }$
be the maximal
 $\lambda $
such that for every nice
$\lambda $
such that for every nice
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
and
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
and
 $h = h_p$
and for every
$h = h_p$
and for every
 $\mathscr F \subseteq {}^{({}^{\kappa>} \kappa )} \kappa $
of size
$\mathscr F \subseteq {}^{({}^{\kappa>} \kappa )} \kappa $
of size
 $< \lambda $
there is some
$< \lambda $
there is some
 $g \colon {}^{\kappa>}\kappa \to \kappa $
with the following property:
$g \colon {}^{\kappa>}\kappa \to \kappa $
with the following property:For every
 $f \in \mathscr F$
and
$f \in \mathscr F$
and
 $\eta \in \operatorname {\textrm {spl}}(p)$
there is a stationary set
$\eta \in \operatorname {\textrm {spl}}(p)$
there is a stationary set
 $S = S_{h_p,f,\eta }$
such that for any
$S = S_{h_p,f,\eta }$
such that for any
 $\delta \in S$
$\delta \in S$
 $$ \begin{align*}\eta \,\hat{} \, \langle \delta \rangle \in p \wedge g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \,\langle \delta \rangle)) \neq f (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \,\langle \delta \rangle)).\end{align*} $$
$$ \begin{align*}\eta \,\hat{} \, \langle \delta \rangle \in p \wedge g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \,\langle \delta \rangle)) \neq f (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \,\langle \delta \rangle)).\end{align*} $$
Lemma 3.9. Suppose that
![]() $\kappa = \kappa ^{<\kappa }> \aleph _0$
and that
$\kappa = \kappa ^{<\kappa }> \aleph _0$
and that
![]() ${\mathbb P}$
is the forcing adding
${\mathbb P}$
is the forcing adding
![]() $\lambda = \lambda ^\kappa $
many Cohen reals with support
$\lambda = \lambda ^\kappa $
many Cohen reals with support
![]() $< \kappa $
. Then in the extension we have
$< \kappa $
. Then in the extension we have
 $$ \begin{align*}\frak b_{\kappa} = \frak b_{\textrm{club},\kappa}= \kappa^+ \wedge \mathfrak{e}_{\kappa}^0 = \mathfrak{e}^1_{\kappa} =\lambda.\end{align*} $$
$$ \begin{align*}\frak b_{\kappa} = \frak b_{\textrm{club},\kappa}= \kappa^+ \wedge \mathfrak{e}_{\kappa}^0 = \mathfrak{e}^1_{\kappa} =\lambda.\end{align*} $$
Proof. It is easy to see that the first
![]() $\kappa ^+$
Cohen reals form an unbounded family. Now we work in the forcing extension. Let
$\kappa ^+$
Cohen reals form an unbounded family. Now we work in the forcing extension. Let
![]() ${\mathbb P} = {\mathbb P}_\lambda = \langle {\mathbb P}_{\alpha }, \mathbb Q_\beta \, : \, \beta < \lambda , \alpha \leq \lambda \rangle $
be the iteration,
${\mathbb P} = {\mathbb P}_\lambda = \langle {\mathbb P}_{\alpha }, \mathbb Q_\beta \, : \, \beta < \lambda , \alpha \leq \lambda \rangle $
be the iteration,
![]() $\mathbb Q_{\alpha } = ({}^{\kappa>}\kappa , \triangleleft )$
. Suppose
$\mathbb Q_{\alpha } = ({}^{\kappa>}\kappa , \triangleleft )$
. Suppose
![]() $\mathscr F$
and h are given as in the definition of
$\mathscr F$
and h are given as in the definition of
![]() $\mathfrak {e}_{\kappa }^0$
. Since
$\mathfrak {e}_{\kappa }^0$
. Since
![]() $\mathscr F$
is of size
$\mathscr F$
is of size
![]() $< \lambda $
, there is an initial segment
$< \lambda $
, there is an initial segment
![]() ${\mathbb P}_{\alpha }$
of
${\mathbb P}_{\alpha }$
of
![]() ${\mathbb P}_\lambda $
,
${\mathbb P}_\lambda $
,
![]() $\alpha < \lambda $
and a
$\alpha < \lambda $
and a
![]() $p \in {\mathbb P}_{\alpha }$
, such that p forces that
$p \in {\mathbb P}_{\alpha }$
, such that p forces that
![]() $\mathscr F$
and h are
$\mathscr F$
and h are
![]() ${\mathbb P}_{\alpha }$
-names. We conceive Cohen reals as functions from
${\mathbb P}_{\alpha }$
-names. We conceive Cohen reals as functions from
![]() ${}^{\kappa>} \kappa \to \kappa $
. Since
${}^{\kappa>} \kappa \to \kappa $
. Since
![]() $\kappa ^{<\kappa } = \kappa $
, this is possible. Now let
$\kappa ^{<\kappa } = \kappa $
, this is possible. Now let
![]() $g = c_{\alpha }$
be the
$g = c_{\alpha }$
be the
![]() $\alpha $
-th Cohen real.
$\alpha $
-th Cohen real.
Suppose for a contradiction that there is some
![]() $q \in {\mathbb P}_{\lambda }$
,
$q \in {\mathbb P}_{\lambda }$
,
![]() $q \geq p$
,
$q \geq p$
,
![]() $\eta \in {}^{\kappa>} \kappa $
,
$\eta \in {}^{\kappa>} \kappa $
,
![]() $f \in \mathscr F$
and a name
$f \in \mathscr F$
and a name
![]() such that
such that

Now by induction on
![]() $n < \omega $
we choose
$n < \omega $
we choose
![]() $\delta _{-1} =0$
and increasing
$\delta _{-1} =0$
and increasing
![]() $q_n \geq q$
,
$q_n \geq q$
,
![]() $q_n \in {\mathbb P}_{\lambda }$
, and
$q_n \in {\mathbb P}_{\lambda }$
, and
![]() $\delta _n $
such that
$\delta _n $
such that

and
Then we let
![]() $r = \bigcup q_n$
and we let
$r = \bigcup q_n$
and we let
![]() $\delta = \sup \delta _n$
. Then
$\delta = \sup \delta _n$
. Then
Since h is an increasing function, we have
Hence there is some
![]() $x \in \kappa $
such that
$x \in \kappa $
such that
and
So we reached a contradiction to the Assumption (3.1). For
![]() $\mathfrak {e}^1_{\kappa }$
we work with a name for a subset of
$\mathfrak {e}^1_{\kappa }$
we work with a name for a subset of
![]() $\operatorname {\textrm {osucc}}_p(\eta )$
in Equation (3.1).⊣
$\operatorname {\textrm {osucc}}_p(\eta )$
in Equation (3.1).⊣
In preparation for the next theorem we recall nowhere distributivity and some notions for complete boolean algebras. Two forcings
![]() ${\mathbb P}_1$
,
${\mathbb P}_1$
,
![]() ${\mathbb P}_2$
are said to be equivalent if their regular open algebras
${\mathbb P}_2$
are said to be equivalent if their regular open algebras
![]() $\operatorname {\textrm {RO}}({\mathbb P}_i)$
are isomorphic (for a definition of the regular open algebra of a poset, see, e.g., [Reference Jech9, Corollary 14.12]). Some forcings are characterised up to equivalence just by their density, their closure, and their collapsing behaviour. For a Boolean algebra B, we denote by
$\operatorname {\textrm {RO}}({\mathbb P}_i)$
are isomorphic (for a definition of the regular open algebra of a poset, see, e.g., [Reference Jech9, Corollary 14.12]). Some forcings are characterised up to equivalence just by their density, their closure, and their collapsing behaviour. For a Boolean algebra B, we denote by
![]() $B^+ = B \setminus \{0_B\}$
.
$B^+ = B \setminus \{0_B\}$
.
Definition 3.10 ([Reference Balcar, Simon, Donald Monk and Bonnet1, Definition17])
Let B be a Boolean algebra
![]() $\theta $
,
$\theta $
,
![]() $\lambda $
cardinals. A collection
$\lambda $
cardinals. A collection
![]() $\mathscr P \subseteq \mathscr P(B^+)$
is called a matrix if each member of
$\mathscr P \subseteq \mathscr P(B^+)$
is called a matrix if each member of
![]() $\mathscr P$
is a maximal disjoint subset of
$\mathscr P$
is a maximal disjoint subset of
![]() $B^+$
.
$B^+$
.
A Boolean algebra B is
![]() $( \theta , \lambda )$
-distributive if for every matrix
$( \theta , \lambda )$
-distributive if for every matrix
![]() $\mathscr P = \{P_{\alpha } \, : \, \alpha \in \theta \}$
there is some maximal disjoint set
$\mathscr P = \{P_{\alpha } \, : \, \alpha \in \theta \}$
there is some maximal disjoint set
![]() $Q \subseteq B^+$
such that for each
$Q \subseteq B^+$
such that for each
![]() $q \in Q$
and
$q \in Q$
and
![]() $\alpha \in \theta $
,
$\alpha \in \theta $
,
![]() $|\{p \in P_{\alpha } \, : \, p \cap q \neq 0\}| < \lambda $
.
$|\{p \in P_{\alpha } \, : \, p \cap q \neq 0\}| < \lambda $
.
A Boolean algebra is called
![]() $(\theta ,\lambda )$
-nowhere distributive if for every
$(\theta ,\lambda )$
-nowhere distributive if for every
![]() $x \in B^+$
the algebra
$x \in B^+$
the algebra
![]() $B\restriction x = \{y \in B \, : \, y \leq x\}$
is not
$B\restriction x = \{y \in B \, : \, y \leq x\}$
is not
![]() $(\theta ,\lambda )$
-distributive.
$(\theta ,\lambda )$
-distributive.
Lemma 3.11 ([Reference Balcar, Simon, Donald Monk and Bonnet1, Lemma 1.11])
If a Boolean algebra is
![]() $(\theta ,\lambda )$
-nowhere distributive then there are maximal antichains
$(\theta ,\lambda )$
-nowhere distributive then there are maximal antichains
![]() $\bar {p}^\varepsilon = \langle p^\varepsilon _{\alpha } \, : \, \alpha < \alpha _\varepsilon \rangle $
of
$\bar {p}^\varepsilon = \langle p^\varepsilon _{\alpha } \, : \, \alpha < \alpha _\varepsilon \rangle $
of
![]() ${\mathbb P}$
for
${\mathbb P}$
for
![]() $\varepsilon < \theta $
such that for every
$\varepsilon < \theta $
such that for every
![]() $p \in {\mathbb P}$
for some
$p \in {\mathbb P}$
for some
![]() $\varepsilon < \theta $
$\varepsilon < \theta $
Definition 3.12. Let B be a Boolean algebra. A subset
![]() $D \subseteq B^+$
is called dense if
$D \subseteq B^+$
is called dense if
![]() $(\forall b \in B^+)(\exists d \in D)(d \leq b)$
. The density of a Boolean algebra B is the least size of a dense subset of B. A Boolean algebra B has uniform density if for every
$(\forall b \in B^+)(\exists d \in D)(d \leq b)$
. The density of a Boolean algebra B is the least size of a dense subset of B. A Boolean algebra B has uniform density if for every
![]() $a \in B^ +$
,
$a \in B^ +$
,
![]() $B \restriction a$
has the same density. The density of a forcing order
$B \restriction a$
has the same density. The density of a forcing order
![]() $({\mathbb P},<)$
is the density of the regular open algebra
$({\mathbb P},<)$
is the density of the regular open algebra
![]() $\operatorname {\textrm {RO}}({\mathbb P})$
.
$\operatorname {\textrm {RO}}({\mathbb P})$
.
From the following Lemma, only part (3) will be used later. Part (3) together with Lemma 3.11 gives an alternative proof of part (2).
Lemma 3.13. Let
![]() $\theta < \lambda $
be regular cardinals.
$\theta < \lambda $
be regular cardinals.
-
(1) [Reference Balcar, Simon, Donald Monk and Bonnet1, Theorem 1.15] Suppose that
 ${\mathbb P}$
has the following properties (a) to (c).
${\mathbb P}$
has the following properties (a) to (c).-
(a)
 ${\mathbb P}$
is a
${\mathbb P}$
is a
 $(\theta ,\lambda )$
-nowhere distributive forcing notion,
$(\theta ,\lambda )$
-nowhere distributive forcing notion, -
(b)
 ${\mathbb P}$
has density
${\mathbb P}$
has density
 $\lambda $
,
$\lambda $
, -
(c) in case
 $\theta> \aleph _0$
,
$\theta> \aleph _0$
,
 ${\mathbb P}$
has a
${\mathbb P}$
has a
 $(<\theta )$
-complete dense subset S. The latter means: For any
$(<\theta )$
-complete dense subset S. The latter means: For any
 $\gamma < \theta $
for any
$\gamma < \theta $
for any
 $\leq _{\mathbb P}$
-ascending sequence
$\leq _{\mathbb P}$
-ascending sequence
 $\langle b_i \, : \, i < \gamma \rangle $
of elements
$\langle b_i \, : \, i < \gamma \rangle $
of elements
 $b_i \in S$
, there is an upper bound
$b_i \in S$
, there is an upper bound
 $s \in S$
, i.e., for any i,
$s \in S$
, i.e., for any i,
 $(b_i \leq _{{\mathbb P}} s)$
.
$(b_i \leq _{{\mathbb P}} s)$
.
Then
 ${\mathbb P}$
is equivalent to
${\mathbb P}$
is equivalent to
 $\operatorname {\textrm {Levy}}(\theta ,\lambda )$
.
$\operatorname {\textrm {Levy}}(\theta ,\lambda )$
. -
-
(2) [Reference Shelah26] Under (a) and (b),
 ${\mathbb P}$
collapses
${\mathbb P}$
collapses
 $\lambda $
to
$\lambda $
to
 $\theta $
(and may or may not collapse
$\theta $
(and may or may not collapse
 $\aleph _0$
).
$\aleph _0$
). -
(3) Suppose that
 ${\mathbb P}$
has density
${\mathbb P}$
has density
 $\lambda $
and that there are maximal antichains
$\lambda $
and that there are maximal antichains
 $P_\varepsilon = \langle p_{\varepsilon ,\alpha } \, : \, \alpha < \alpha _\varepsilon \rangle $
for
$P_\varepsilon = \langle p_{\varepsilon ,\alpha } \, : \, \alpha < \alpha _\varepsilon \rangle $
for
 $\varepsilon < \frak b_{\textrm {club}, \kappa }$
as in Lemma 3.11. Then
$\varepsilon < \frak b_{\textrm {club}, \kappa }$
as in Lemma 3.11. Then
 ${\mathbb P}$
collapses
${\mathbb P}$
collapses
 $\lambda $
to
$\lambda $
to
 $\theta $
.
$\theta $
.
Proof. (3) For completeness, we show such a name. We let for
![]() $\varepsilon < \frak b_{\textrm {club}, \kappa }$
,
$\varepsilon < \frak b_{\textrm {club}, \kappa }$
,
![]() $P_\varepsilon $
be a maximal antichain such that for any
$P_\varepsilon $
be a maximal antichain such that for any
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
, there is some
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
, there is some
![]() $\varepsilon < \frak b_{\textrm {club},\kappa }$
such that
$\varepsilon < \frak b_{\textrm {club},\kappa }$
such that
![]() $|\{q \in P_\varepsilon \, : \, q \not \perp p \}| \geq \lambda $
. We enumerate
$|\{q \in P_\varepsilon \, : \, q \not \perp p \}| \geq \lambda $
. We enumerate
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
as
${\mathbb Q}^{\textrm {a}}_{\kappa }$
as
![]() $\langle p_{\alpha } \, : \, \alpha < \lambda \rangle $
such that each condition appears
$\langle p_{\alpha } \, : \, \alpha < \lambda \rangle $
such that each condition appears
![]() $\lambda $
times. For each
$\lambda $
times. For each
![]() $\varepsilon < \frak b_{\textrm {club},\kappa }$
we choose by induction on
$\varepsilon < \frak b_{\textrm {club},\kappa }$
we choose by induction on
![]() $\alpha < \lambda $
a pair
$\alpha < \lambda $
a pair
![]() $(q_{\varepsilon ,\alpha }, r_{\varepsilon , \alpha })$
such that
$(q_{\varepsilon ,\alpha }, r_{\varepsilon , \alpha })$
such that
-
(a)
 $q_{\varepsilon ,\alpha } \in \{s \, : \, (\exists r \in P_\varepsilon )(r \leq s)\}$
and for
$q_{\varepsilon ,\alpha } \in \{s \, : \, (\exists r \in P_\varepsilon )(r \leq s)\}$
and for
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $q_{\varepsilon ,\alpha } \perp q^{\prime }_{\varepsilon ,\beta }$
.
$q_{\varepsilon ,\alpha } \perp q^{\prime }_{\varepsilon ,\beta }$
. -
(b) If
 $|\{q \in P_\varepsilon \, : \, q \not \perp p_{\alpha }\}| = \lambda $
the we choose
$|\{q \in P_\varepsilon \, : \, q \not \perp p_{\alpha }\}| = \lambda $
the we choose
 $r_{\varepsilon ,\alpha } \geq p_{\alpha }, q_{\varepsilon ,\alpha }$
. Otherwise we let
$r_{\varepsilon ,\alpha } \geq p_{\alpha }, q_{\varepsilon ,\alpha }$
. Otherwise we let
 $r_{\varepsilon ,\alpha } = q_{\varepsilon ,\alpha }$
.
$r_{\varepsilon ,\alpha } = q_{\varepsilon ,\alpha }$
.
This is easily done. Then we define a name
of a function from
![]() $\frak b_{\kappa }$
into
$\frak b_{\kappa }$
into
![]() $\lambda $
by letting for
$\lambda $
by letting for
![]() $\varepsilon \in \frak b_{\kappa }$
,
$\varepsilon \in \frak b_{\kappa }$
,

We show that
![]() is a name for a surjection from
is a name for a surjection from
![]() $\frak b_{\kappa }$
to
$\frak b_{\kappa }$
to
![]() $\lambda $
. Given a condition p and
$\lambda $
. Given a condition p and
![]() $\alpha \in \lambda $
, we first choose
$\alpha \in \lambda $
, we first choose
![]() $\varepsilon < \frak b_{\kappa }$
such that
$\varepsilon < \frak b_{\kappa }$
such that
![]() $|\{q \in {\mathbb P}_\varepsilon \, : \, q \not \perp p\}|= \lambda $
and enumerate
$|\{q \in {\mathbb P}_\varepsilon \, : \, q \not \perp p\}|= \lambda $
and enumerate
![]() $\{\beta < \lambda \, : \, p = p_\beta \}$
in increasing order via
$\{\beta < \lambda \, : \, p = p_\beta \}$
in increasing order via
![]() $\langle \beta _\zeta \, : \, \zeta < \lambda \rangle $
.
$\langle \beta _\zeta \, : \, \zeta < \lambda \rangle $
.
Then we choose
![]() $\zeta = \alpha $
and have that
$\zeta = \alpha $
and have that
⊣
Theorem 3.14. Suppose
-
(a)
 $\kappa = \kappa ^{<\kappa }> \omega $
and
$\kappa = \kappa ^{<\kappa }> \omega $
and -
(b)
 $\mathfrak {e}_{\kappa }^1 = \lambda = 2^\kappa $
.
$\mathfrak {e}_{\kappa }^1 = \lambda = 2^\kappa $
.
Then
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
![]() $2^\kappa $
to
$2^\kappa $
to
![]() $\frak b_{\textrm {club},\kappa }$
.
$\frak b_{\textrm {club},\kappa }$
.
Proof. It suffices to show that there are maximal antichains as in the premise of Lemma 3.11. Then Lemma 3.13(3) provides a name for a collapsing function.
-
 $(\otimes )_1$
We fix an enumeration
$(\otimes )_1$
We fix an enumeration
 $\langle \eta _i \, : \, i < \kappa \rangle $
of
$\langle \eta _i \, : \, i < \kappa \rangle $
of
 $\kappa ^{<\kappa }$
such that
$\kappa ^{<\kappa }$
such that-
(a)
 $\eta _i \triangleleft \eta _j $
implies
$\eta _i \triangleleft \eta _j $
implies
 $i < j$
.
$i < j$
. -
(b) For each
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $\lg (\eta _{\alpha }) \leq \alpha $
.
$\lg (\eta _{\alpha }) \leq \alpha $
. -
(c) For each
 $\beta , \varepsilon < \kappa $
if
$\beta , \varepsilon < \kappa $
if
 $\eta \,\hat {} \, \langle \varepsilon \rangle = \eta _\beta $
then
$\eta \,\hat {} \, \langle \varepsilon \rangle = \eta _\beta $
then
 $\beta \geq \varepsilon $
.
$\beta \geq \varepsilon $
.
For
 $\eta \in {}^{\kappa>}\kappa $
, the index of
$\eta \in {}^{\kappa>}\kappa $
, the index of
 $\eta $
is the minimal
$\eta $
is the minimal
 $\alpha $
such that
$\alpha $
such that
 $\eta = \eta _{\alpha }$
.
$\eta = \eta _{\alpha }$
. -
-
 $(\otimes )_2$
We fix a function
$(\otimes )_2$
We fix a function
 $h_\ast \colon \kappa \to \kappa $
such that for any
$h_\ast \colon \kappa \to \kappa $
such that for any
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $h^{-1}[\{\alpha \}] $
is a stationary subset of
$h^{-1}[\{\alpha \}] $
is a stationary subset of
 $\kappa $
.
$\kappa $
. -
 $(\otimes _3)$
Now we define for nice conditions
$(\otimes _3)$
Now we define for nice conditions
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
three sets of nodes If
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
three sets of nodes If $$ \begin{align*} \Lambda^1_{p} = \{\eta \in \operatorname{\textrm{spl}}(p) \, : \, \operatorname{\textrm{otp}}(\{\alpha < \lg(\eta) \, : \, \eta\restriction \alpha \in \operatorname{\textrm{spl}}(p)\}) \mbox{ is a limit ordinal}\}. \end{align*} $$
$$ \begin{align*} \Lambda^1_{p} = \{\eta \in \operatorname{\textrm{spl}}(p) \, : \, \operatorname{\textrm{otp}}(\{\alpha < \lg(\eta) \, : \, \eta\restriction \alpha \in \operatorname{\textrm{spl}}(p)\}) \mbox{ is a limit ordinal}\}. \end{align*} $$
 $\alpha < \lg (\eta )$
and
$\alpha < \lg (\eta )$
and
 $\eta \restriction \alpha \in \operatorname {\textrm {spl}}(p)$
contains a limit order type, say
$\eta \restriction \alpha \in \operatorname {\textrm {spl}}(p)$
contains a limit order type, say
 $\alpha _i$
,
$\alpha _i$
,
 $i \in I$
converge to
$i \in I$
converge to
 $\alpha _{\lim }$
, then it also contains
$\alpha _{\lim }$
, then it also contains
 $\eta \restriction \alpha _{\lim }$
since the latter must be a splitting point, so
$\eta \restriction \alpha _{\lim }$
since the latter must be a splitting point, so
 $\bigcup _{i \in I} \eta \restriction \alpha _{i} = \eta $
. So equivalently we can say that
$\bigcup _{i \in I} \eta \restriction \alpha _{i} = \eta $
. So equivalently we can say that
 $\Lambda ^1_p$
is the set of limits of splitting nodes.
$\Lambda ^1_p$
is the set of limits of splitting nodes.
We choose
 $\Lambda ^1_p$
and not
$\Lambda ^1_p$
and not
 $\operatorname {\textrm {spl}}(p)$
for our thinning out procedures on splitting successors of limit splitting points that are called
$\operatorname {\textrm {spl}}(p)$
for our thinning out procedures on splitting successors of limit splitting points that are called
 $\Lambda ^3_p$
. The point is that after the thinning out according to
$\Lambda ^3_p$
. The point is that after the thinning out according to
 $(\otimes )_4$
we still have a condition, since we thin out at most the successor sets of splitting nodes at successor splitting levels.
$(\otimes )_4$
we still have a condition, since we thin out at most the successor sets of splitting nodes at successor splitting levels.  $$ \begin{align*} \Lambda^2_{p} &= \{\eta\,\hat{} \, \langle \alpha \rangle\, : \, \eta \in \Lambda^1_{p}\}, \\ \Lambda^3_{p} &= \{\eta \,\hat{} \,\langle \alpha \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \alpha \rangle) \, : \, \eta \in \Lambda^1_p, \eta \,\hat{} \, \langle \alpha \rangle \in \Lambda^2_{p}\}. \end{align*} $$
$$ \begin{align*} \Lambda^2_{p} &= \{\eta\,\hat{} \, \langle \alpha \rangle\, : \, \eta \in \Lambda^1_{p}\}, \\ \Lambda^3_{p} &= \{\eta \,\hat{} \,\langle \alpha \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \alpha \rangle) \, : \, \eta \in \Lambda^1_p, \eta \,\hat{} \, \langle \alpha \rangle \in \Lambda^2_{p}\}. \end{align*} $$
For a nice p and
 $\eta \in \Lambda ^1(p)$
we have for any
$\eta \in \Lambda ^1(p)$
we have for any
 $\alpha $
such that
$\alpha $
such that
 $\eta \,\hat {} \, \langle \alpha \rangle \in p$
, that
$\eta \,\hat {} \, \langle \alpha \rangle \in p$
, that
 $\eta \,\hat {} \, \langle \alpha \rangle \not \in \operatorname {\textrm {spl}}(p)$
and
$\eta \,\hat {} \, \langle \alpha \rangle \not \in \operatorname {\textrm {spl}}(p)$
and
 $\eta \,\hat {} \, \langle \alpha \rangle \,\hat {} \, h_p(\eta \,\hat {} \, \langle \alpha \rangle ) \in \Lambda ^3_p$
.
$\eta \,\hat {} \, \langle \alpha \rangle \,\hat {} \, h_p(\eta \,\hat {} \, \langle \alpha \rangle ) \in \Lambda ^3_p$
. -
 $(\otimes )_4$
For
$(\otimes )_4$
For
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
,
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
,
 $g \colon {}^{\kappa>} \kappa \to \kappa $
we define
$g \colon {}^{\kappa>} \kappa \to \kappa $
we define
 $q = q(p,g)$
as the set of
$q = q(p,g)$
as the set of
 $\eta \in p$
such that
$\eta \in p$
such that  $$ \begin{align*} \begin{aligned} &(\forall \alpha < \lg (\eta)) (\eta {\restriction} \alpha \in \Lambda^3_{p} \\ &\rightarrow \eta(\alpha) = \min\{ \xi \, : \, \eta {\restriction} \alpha \, \hat{} \, \langle \xi \rangle \in p \wedge h_{\ast}(\xi) = g (\eta {\restriction} \alpha))\}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &(\forall \alpha < \lg (\eta)) (\eta {\restriction} \alpha \in \Lambda^3_{p} \\ &\rightarrow \eta(\alpha) = \min\{ \xi \, : \, \eta {\restriction} \alpha \, \hat{} \, \langle \xi \rangle \in p \wedge h_{\ast}(\xi) = g (\eta {\restriction} \alpha))\}). \end{aligned} \end{align*} $$
Then
 $q(p,g)$
is a condition and
$q(p,g)$
is a condition and
 $q(p,g) \geq p$
.
$q(p,g) \geq p$
.If
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
, g is as above, and
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
, g is as above, and
 $q = q(p,g)$
, then for any
$q = q(p,g)$
, then for any
 $r \geq q$
,
$r \geq q$
,
 ${\operatorname {\textrm {spl}}(r) \cap \Lambda ^3_{p} = \emptyset }$
.
${\operatorname {\textrm {spl}}(r) \cap \Lambda ^3_{p} = \emptyset }$
. -
 $(\otimes )_5$
Let E be a club and
$(\otimes )_5$
Let E be a club and
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. We say p is suitable for E if for any
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
. We say p is suitable for E if for any
 $\eta \in \operatorname {\textrm {spl}}(p)$
we have is a stationary subset of
$\eta \in \operatorname {\textrm {spl}}(p)$
we have is a stationary subset of $$ \begin{align*} \{\delta < \kappa \, : \, \eta \,\hat{} \, \langle \delta \rangle \in p \wedge \lg(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \delta \rangle)) \not\in E \} \end{align*} $$
$$ \begin{align*} \{\delta < \kappa \, : \, \eta \,\hat{} \, \langle \delta \rangle \in p \wedge \lg(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \delta \rangle)) \not\in E \} \end{align*} $$
 $\kappa $
.
$\kappa $
.
-
 $(\otimes )_6$
For
$(\otimes )_6$
For
 $p, q \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
we define a function as follows. If
$p, q \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
we define a function as follows. If $$ \begin{align*}g_{p,q} \colon {}^{\kappa>} \kappa \to \kappa\end{align*} $$
$$ \begin{align*}g_{p,q} \colon {}^{\kappa>} \kappa \to \kappa\end{align*} $$
 $\nu \in \Lambda ^3_p \cap (q \setminus \operatorname {\textrm {spl}}(q))$
, then we let for the unique
$\nu \in \Lambda ^3_p \cap (q \setminus \operatorname {\textrm {spl}}(q))$
, then we let for the unique $$ \begin{align*}g_{p,q} (\nu) = \min(h_\ast^{-1}[\{\xi\}]) \end{align*} $$
$$ \begin{align*}g_{p,q} (\nu) = \min(h_\ast^{-1}[\{\xi\}]) \end{align*} $$
 $\xi < \kappa $
such that
$\xi < \kappa $
such that
 $\nu \,\hat {} \, \langle \xi \rangle \in q$
. For all other
$\nu \,\hat {} \, \langle \xi \rangle \in q$
. For all other
 $\nu $
, we let
$\nu $
, we let
 $g_{p,q}(\nu ) = 0$
.
$g_{p,q}(\nu ) = 0$
.
-
 $(\otimes )_7$
Let E be club in
$(\otimes )_7$
Let E be club in
 $\kappa $
such that there is a p suitable for E. We show: There is a maximal antichain
$\kappa $
such that there is a p suitable for E. We show: There is a maximal antichain
 $P_E=\langle q_{E,\alpha } \, : \, \alpha < 2^\kappa \rangle $
with the following property: For every
$P_E=\langle q_{E,\alpha } \, : \, \alpha < 2^\kappa \rangle $
with the following property: For every
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
that is suitable for E there are
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
that is suitable for E there are
 $2^\kappa $
mutually incompatible stengthenings
$2^\kappa $
mutually incompatible stengthenings
 $q_{E,\alpha }> p$
,
$q_{E,\alpha }> p$
,
 $\alpha \in A$
for some
$\alpha \in A$
for some
 $A \subseteq 2^\kappa $
,
$A \subseteq 2^\kappa $
,
 $|A| = 2^\kappa $
.
$|A| = 2^\kappa $
.Proof: Let
 $\langle p_{E,\alpha } \, : \, \alpha < 2^\kappa \rangle $
list the
$\langle p_{E,\alpha } \, : \, \alpha < 2^\kappa \rangle $
list the
 $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
that are suitable for E each appearing
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
that are suitable for E each appearing
 $2^\kappa $
times. (In
$2^\kappa $
times. (In
 $(\otimes )_9$
we will see that there are such p, E.) We choose
$(\otimes )_9$
we will see that there are such p, E.) We choose
 $q_{E,\alpha }$
be induction on
$q_{E,\alpha }$
be induction on
 $\alpha $
such that
$\alpha $
such that
 $p_{E,\alpha } \leq q_{E,\alpha }$
and
$p_{E,\alpha } \leq q_{E,\alpha }$
and
 $q_{E,\alpha } \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
and
$q_{E,\alpha } \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
and
 $\beta < \alpha \rightarrow q_\beta \perp q_{E,\alpha }$
. In the end we take any maximal antichain containing
$\beta < \alpha \rightarrow q_\beta \perp q_{E,\alpha }$
. In the end we take any maximal antichain containing
 $\{q_{E,\alpha } \, : \, \alpha < 2^\kappa \}$
as a subset. Since any p that is suitable for E appears at
$\{q_{E,\alpha } \, : \, \alpha < 2^\kappa \}$
as a subset. Since any p that is suitable for E appears at
 $2^\kappa $
many stages as
$2^\kappa $
many stages as
 $p_{E,\alpha }$
, say at stages
$p_{E,\alpha }$
, say at stages
 $\alpha \in A$
, we have
$\alpha \in A$
, we have
 $2^\kappa $
many mutually incompatible
$2^\kappa $
many mutually incompatible
 $q_{E,\alpha }> p=p_{E,\alpha }$
,
$q_{E,\alpha }> p=p_{E,\alpha }$
,
 $\alpha \in A$
.
$\alpha \in A$
.Arriving at
 $\alpha $
, for
$\alpha $
, for
 $\beta < \alpha $
, the function is well defined. By our assumption on
$\beta < \alpha $
, the function is well defined. By our assumption on $$ \begin{align*}f_\beta = g_{p_{E,\alpha}, q_{E,\beta}} \colon {}^{\kappa>}\kappa \to \kappa \end{align*} $$
$$ \begin{align*}f_\beta = g_{p_{E,\alpha}, q_{E,\beta}} \colon {}^{\kappa>}\kappa \to \kappa \end{align*} $$
 $\mathfrak {e}^1_{\kappa } = \lambda $
, there is some g for any
$\mathfrak {e}^1_{\kappa } = \lambda $
, there is some g for any
 $\eta \in \operatorname {\textrm {spl}}(p_{\alpha })$
such that
$\eta \in \operatorname {\textrm {spl}}(p_{\alpha })$
such that
 $\operatorname {\textrm {otp}}(\{\alpha < \lg (\eta ) \, : \, \eta \restriction \alpha \in \operatorname {\textrm {spl}}(p_{\alpha }) \})$
is a limit ordinal +1 there are stationary many
$\operatorname {\textrm {otp}}(\{\alpha < \lg (\eta ) \, : \, \eta \restriction \alpha \in \operatorname {\textrm {spl}}(p_{\alpha }) \})$
is a limit ordinal +1 there are stationary many
 $\delta < \kappa $
such that
$\delta < \kappa $
such that
 $\eta \,\hat {} \, \langle \delta \rangle \in p_{\alpha }$
and We let
$\eta \,\hat {} \, \langle \delta \rangle \in p_{\alpha }$
and We let $$ \begin{align*}f_\beta(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_{p_{E,\alpha}}(\eta \,\hat{} \, \langle \alpha \rangle)) \neq g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_{p_{E,\alpha}}(\eta \,\hat{} \, \langle \alpha \rangle)). \end{align*} $$
$$ \begin{align*}f_\beta(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_{p_{E,\alpha}}(\eta \,\hat{} \, \langle \alpha \rangle)) \neq g (\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_{p_{E,\alpha}}(\eta \,\hat{} \, \langle \alpha \rangle)). \end{align*} $$
 $q_{E,\alpha } = q(p_{E,\alpha },g)$
.
$q_{E,\alpha } = q(p_{E,\alpha },g)$
.
-
 $(\otimes )_8$
We take a club-unbounded family
$(\otimes )_8$
We take a club-unbounded family
 $\langle f^\ast _\varepsilon \, : \, \varepsilon < \frak b_{\kappa } \rangle $
such that the
$\langle f^\ast _\varepsilon \, : \, \varepsilon < \frak b_{\kappa } \rangle $
such that the
 $f^\ast _\varepsilon $
are increasing functions.
$f^\ast _\varepsilon $
are increasing functions.For
 $\alpha < \frak b_{\kappa }$
, we let
$\alpha < \frak b_{\kappa }$
, we let  $$ \begin{align*} E^\ast_{\alpha} = \{ \delta< \kappa \, : \, \delta \mbox{ is a limit } \wedge (\forall \varepsilon < \delta ) (f^\ast_{\alpha}(\varepsilon) < \delta)\}. \end{align*} $$
$$ \begin{align*} E^\ast_{\alpha} = \{ \delta< \kappa \, : \, \delta \mbox{ is a limit } \wedge (\forall \varepsilon < \delta ) (f^\ast_{\alpha}(\varepsilon) < \delta)\}. \end{align*} $$
-
 $(\otimes )_{9}$
Claim: For every p there is an
$(\otimes )_{9}$
Claim: For every p there is an
 $\varepsilon < \frak b_{\kappa }$
such that p is suitable of
$\varepsilon < \frak b_{\kappa }$
such that p is suitable of
 $E^\ast _\varepsilon $
.
$E^\ast _\varepsilon $
.We let
 $$ \begin{align*} \begin{aligned} E_p = & \{\delta < \kappa \, : \, \delta \mbox{ is a limit ordinal and } \\ &(\forall \alpha, \beta < \delta)( \eta_{\alpha} \in p \rightarrow \eta_{\alpha} \,\hat{} \, \langle \beta \rangle, \eta_{\alpha} \,\hat{} \, h_p(\eta_{\alpha}) \in \{\eta_\beta \, : \, \beta < \delta\}))\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} E_p = & \{\delta < \kappa \, : \, \delta \mbox{ is a limit ordinal and } \\ &(\forall \alpha, \beta < \delta)( \eta_{\alpha} \in p \rightarrow \eta_{\alpha} \,\hat{} \, \langle \beta \rangle, \eta_{\alpha} \,\hat{} \, h_p(\eta_{\alpha}) \in \{\eta_\beta \, : \, \beta < \delta\}))\}. \end{aligned} \end{align*} $$
Let
 $g_p (\varepsilon ) $
be the
$g_p (\varepsilon ) $
be the
 $\varepsilon +7$
-th member of
$\varepsilon +7$
-th member of
 $E_p$
. Pick
$E_p$
. Pick
 $\alpha _p=\alpha < \frak b_{\textrm {club}, \kappa }$
such that is a stationary subset of
$\alpha _p=\alpha < \frak b_{\textrm {club}, \kappa }$
such that is a stationary subset of $$ \begin{align*}\{\varepsilon < \kappa \, : \, g_p(\varepsilon) < f^\ast_{\alpha}(\varepsilon)\}\end{align*} $$
$$ \begin{align*}\{\varepsilon < \kappa \, : \, g_p(\varepsilon) < f^\ast_{\alpha}(\varepsilon)\}\end{align*} $$
 $\kappa $
.
$\kappa $
.
Now we show that p is suitable for
 $E^\ast _{\alpha } $
. We have to show: For any
$E^\ast _{\alpha } $
. We have to show: For any
 $\eta \in \operatorname {\textrm {spl}}(p)$
we have is a stationary subset of
$\eta \in \operatorname {\textrm {spl}}(p)$
we have is a stationary subset of $$ \begin{align*} \{\delta < \kappa \, : \, \eta \,\hat{} \, \langle \delta \rangle \in p \wedge \lg(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \delta \rangle)) \not\in E^\ast_{\alpha}\} \end{align*} $$
$$ \begin{align*} \{\delta < \kappa \, : \, \eta \,\hat{} \, \langle \delta \rangle \in p \wedge \lg(\eta \,\hat{} \, \langle \delta \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \delta \rangle)) \not\in E^\ast_{\alpha}\} \end{align*} $$
 $\kappa $
.
$\kappa $
.
Let
 $\eta = \eta _\beta \in \operatorname {\textrm {spl}}(p)$
. By our choice of
$\eta = \eta _\beta \in \operatorname {\textrm {spl}}(p)$
. By our choice of
 $\alpha $
, is a stationary subset of
$\alpha $
, is a stationary subset of $$ \begin{align*}A = \{\varepsilon> \beta \, : \, \varepsilon \in E_p \cap E^*_{\alpha} \wedge g_p(\varepsilon) < f_{\alpha}^\ast(\varepsilon)\} \end{align*} $$
$$ \begin{align*}A = \{\varepsilon> \beta \, : \, \varepsilon \in E_p \cap E^*_{\alpha} \wedge g_p(\varepsilon) < f_{\alpha}^\ast(\varepsilon)\} \end{align*} $$
 $\kappa $
. If
$\kappa $
. If
 $\varepsilon \in A$
, then
$\varepsilon \in A$
, then
 $\zeta = \min \{\gamma \in E_p \, : \, \gamma> \varepsilon \} \in E_p$
and
$\zeta = \min \{\gamma \in E_p \, : \, \gamma> \varepsilon \} \in E_p$
and
 $\zeta < g_p(\varepsilon )$
, since the latter is the
$\zeta < g_p(\varepsilon )$
, since the latter is the
 $\varepsilon +7$
-th member of
$\varepsilon +7$
-th member of
 $E_p$
. By the defition of
$E_p$
. By the defition of
 $E_p$
,
$E_p$
,
 $\varepsilon < \zeta $
and
$\varepsilon < \zeta $
and
 $\zeta \in E_p$
implies that
$\zeta \in E_p$
implies that
 $\eta \,\hat {} \, \langle \varepsilon \rangle \subseteq \{\eta _\gamma \, : \, \gamma < \zeta \}$
, and hence If
$\eta \,\hat {} \, \langle \varepsilon \rangle \subseteq \{\eta _\gamma \, : \, \gamma < \zeta \}$
, and hence If $$ \begin{align*}\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h(\eta \,\hat{} \, \langle \varepsilon \rangle) \in \{\eta_\gamma \, : \, \gamma < \zeta\}. \end{align*} $$
$$ \begin{align*}\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h(\eta \,\hat{} \, \langle \varepsilon \rangle) \in \{\eta_\gamma \, : \, \gamma < \zeta\}. \end{align*} $$
 $\varepsilon \in A$
then
$\varepsilon \in A$
then  $$ \begin{align*} \varepsilon < \zeta < g_p(\varepsilon) < f^\ast_{\alpha}(\varepsilon) < \operatorname{\textrm{succ}}_{E^\ast_{\alpha}}(\varepsilon). \end{align*} $$
$$ \begin{align*} \varepsilon < \zeta < g_p(\varepsilon) < f^\ast_{\alpha}(\varepsilon) < \operatorname{\textrm{succ}}_{E^\ast_{\alpha}}(\varepsilon). \end{align*} $$
Recall, we stipulated properties (a) and (b) of
 $(\otimes )_1$
on the enumeration. Hence
$(\otimes )_1$
on the enumeration. Hence
 $\lg (\eta _\gamma ) \leq \gamma $
and the index of
$\lg (\eta _\gamma ) \leq \gamma $
and the index of
 $\eta \,\hat {} \, \langle \varepsilon \rangle $
is larger than
$\eta \,\hat {} \, \langle \varepsilon \rangle $
is larger than
 $\varepsilon $
. By the definition of
$\varepsilon $
. By the definition of
 $h_p$
we get Hence
$h_p$
we get Hence $$ \begin{align*} \operatorname{\textrm{succ}}_{E^\ast_{\alpha}}(\varepsilon)> \lg(\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \varepsilon \rangle)) \geq \zeta. \end{align*} $$
$$ \begin{align*} \operatorname{\textrm{succ}}_{E^\ast_{\alpha}}(\varepsilon)> \lg(\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h_p(\eta \,\hat{} \, \langle \varepsilon \rangle)) \geq \zeta. \end{align*} $$
 $h_p(\eta \,\hat {} \, \langle \varepsilon \rangle )$
is longer than
$h_p(\eta \,\hat {} \, \langle \varepsilon \rangle )$
is longer than
 $\varepsilon $
. So for any
$\varepsilon $
. So for any
 $\varepsilon \in A$
we have and the claim is proved.
$\varepsilon \in A$
we have and the claim is proved. $$ \begin{align*} \lg(\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h_*(\eta \,\hat{} \, \langle \varepsilon \rangle)) \not\in E^\ast_{\alpha}, \end{align*} $$
$$ \begin{align*} \lg(\eta \,\hat{} \, \langle \varepsilon \rangle \,\hat{} \, h_*(\eta \,\hat{} \, \langle \varepsilon \rangle)) \not\in E^\ast_{\alpha}, \end{align*} $$
Now we show that we now have established the premise of Lemma 3.11. We start with
![]() $\alpha _0< \kappa ^+$
such that there is at all a p that is suitable for
$\alpha _0< \kappa ^+$
such that there is at all a p that is suitable for
![]() $E^\ast _{\alpha _0}$
. Hence p is suitable also for
$E^\ast _{\alpha _0}$
. Hence p is suitable also for
![]() $E^\ast _{\alpha }$
,
$E^\ast _{\alpha }$
,
![]() $\alpha \geq \alpha _0$
. We take for
$\alpha \geq \alpha _0$
. We take for
![]() $\alpha \in [\alpha _0, \kappa ^+)$
an antichain
$\alpha \in [\alpha _0, \kappa ^+)$
an antichain
![]() $P_{E^\ast _{\alpha }}$
as in
$P_{E^\ast _{\alpha }}$
as in
![]() $(\otimes )_7$
. For any
$(\otimes )_7$
. For any
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
there is a
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }$
there is a
![]() $\beta \geq \alpha _0$
such that p is suitable for
$\beta \geq \alpha _0$
such that p is suitable for
![]() $E^\ast _\beta $
. Hence by
$E^\ast _\beta $
. Hence by
![]() $(\otimes )_7$
the set
$(\otimes )_7$
the set
 $\{q \in P_{E^\ast _\beta } \, : \, q \not \perp p\}$
has size
$\{q \in P_{E^\ast _\beta } \, : \, q \not \perp p\}$
has size
![]() $\lambda $
.⊣
$\lambda $
.⊣
Corollary 3.15. It is consistent relative to
![]() $\mbox{\sf ZFC}$
that
$\mbox{\sf ZFC}$
that
![]() $\kappa ^{<\kappa } = \kappa> \omega $
,
$\kappa ^{<\kappa } = \kappa> \omega $
,
![]() $\frak b_{\kappa } = \kappa ^+$
,
$\frak b_{\kappa } = \kappa ^+$
,
![]() $2^\kappa> \kappa ^+$
and
$2^\kappa> \kappa ^+$
and
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
![]() $2^\kappa $
to
$2^\kappa $
to
![]() $\frak b_{\kappa }$
.
$\frak b_{\kappa }$
.
We do not know whether our conditions on the evasion numbers are necessary.
Question 3.16. Does
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapse
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapse
![]() $2^\kappa $
to
$2^\kappa $
to
![]() $\frak b_{\kappa }$
just under the condition
$\frak b_{\kappa }$
just under the condition
![]() $2^\kappa = \kappa ^{++}> \frak b_{\kappa }$
?
$2^\kappa = \kappa ^{++}> \frak b_{\kappa }$
?
4 Waiving
 $\kappa ^{<\kappa } = \kappa $
$\kappa ^{<\kappa } = \kappa $
In this section we collect mathematical reasons for the fact that in higher tree forcings the condition
![]() $\kappa ^{<\kappa } = \kappa $
is very common. We show that under
$\kappa ^{<\kappa } = \kappa $
is very common. We show that under
![]() $\kappa ^{<\kappa }> \kappa $
, the forcing
$\kappa ^{<\kappa }> \kappa $
, the forcing
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
![]() $\kappa ^{<\kappa }$
to
$\kappa ^{<\kappa }$
to
![]() $\kappa $
. We focus on regular
$\kappa $
. We focus on regular
![]() $\kappa $
. This proof of the next theorem is quite complicated and was found before the more general Theorem 4.2. We let it stand because the name is different in particular in the choice of the lengths of trunks that are actually evaluated. If
$\kappa $
. This proof of the next theorem is quite complicated and was found before the more general Theorem 4.2. We let it stand because the name is different in particular in the choice of the lengths of trunks that are actually evaluated. If
![]() $\theta>\omega $
is regular, then then in the next theorem we give a much simpler name of a collapse of
$\theta>\omega $
is regular, then then in the next theorem we give a much simpler name of a collapse of
![]() $\kappa ^\theta $
to
$\kappa ^\theta $
to
![]() $\kappa $
.
$\kappa $
.
Theorem 4.1. If
![]() $\operatorname {\textrm {cf}}(\kappa ) = \kappa =\lambda ^+$
and
$\operatorname {\textrm {cf}}(\kappa ) = \kappa =\lambda ^+$
and
![]() $\kappa \geq \theta ^{++}$
, and
$\kappa \geq \theta ^{++}$
, and
![]() $\kappa ^\theta> \kappa $
, then
$\kappa ^\theta> \kappa $
, then
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
![]() $\kappa ^\theta $
.
$\kappa ^\theta $
.
Proof. By [Reference Shelah22, Lemma 4.4.(3)] for
![]() $\lambda ^+ = \kappa $
there is a sequence
$\lambda ^+ = \kappa $
there is a sequence
![]() $\bar {C}$
and there are T,
$\bar {C}$
and there are T,
![]() $S_i$
,
$S_i$
,
![]() $i < \lambda $
, with the following properties:
$i < \lambda $
, with the following properties:
-
(1)
 $T = \{\alpha \in \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \leq \theta \}$
and
$T = \{\alpha \in \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) \leq \theta \}$
and -
(2) T is the union of stationary sets
 $S_i$
,
$S_i$
,
 $i < \lambda $
, that have the following square property:
$i < \lambda $
, that have the following square property:-
(i) There is
 $\bar {C}^i = \langle C^i_{\alpha } \, : \, \alpha \in S_i\rangle $
,
$\bar {C}^i = \langle C^i_{\alpha } \, : \, \alpha \in S_i\rangle $
, -
(ii)
 $C^i_{\alpha }$
is a closed subset of
$C^i_{\alpha }$
is a closed subset of
 $\alpha $
, not necessarily cofinal in
$\alpha $
, not necessarily cofinal in
 $\alpha $
, however, if
$\alpha $
, however, if
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $C^i_{\alpha }$
is cofinal in
$C^i_{\alpha }$
is cofinal in
 $\alpha $
,
$\alpha $
,
 $C^i_{\alpha } \subseteq T\cap \alpha $
and
$C^i_{\alpha } \subseteq T\cap \alpha $
and
 $\operatorname {\textrm {otp}}(C^i_{\alpha }) \leq \theta $
, and
$\operatorname {\textrm {otp}}(C^i_{\alpha }) \leq \theta $
, and -
(iii) for
 $\alpha \in S_i$
, for any
$\alpha \in S_i$
, for any
 $\beta \in C^i_{\alpha }$
, then
$\beta \in C^i_{\alpha }$
, then
 $\beta \in S_i$
and
$\beta \in S_i$
and
 $C^i_\beta = C^i_{\alpha } \cap \beta $
.
$C^i_\beta = C^i_{\alpha } \cap \beta $
.
-
Again, we choose in the ground model a function
![]() $h_\ast \colon \kappa \to \kappa $
such that for each
$h_\ast \colon \kappa \to \kappa $
such that for each
![]() $\varepsilon \in \kappa $
, there are stationarily many
$\varepsilon \in \kappa $
, there are stationarily many
![]() $\alpha $
with
$\alpha $
with
![]() $h_\ast (\alpha ) = \varepsilon $
.
$h_\ast (\alpha ) = \varepsilon $
.
Now let
![]() $\mathbf G$
be
$\mathbf G$
be
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
generic over
${\mathbb Q}^{\textrm {a}}_{\kappa }$
generic over
![]() $\mathbf {V}$
and let
$\mathbf {V}$
and let
![]() be a name for
be a name for
![]() .
.
First step.
There is a pair
![]() $(i,E)$
such that
$(i,E)$
such that
-
(a) E is club in
 $\kappa ,$
$\kappa ,$
-
(b)
 $ i < \kappa $
, and
$ i < \kappa $
, and -
(c) for every club C of
 $\kappa $
there are stationarily many
$\kappa $
there are stationarily many
 $\alpha \in S_i$
such that
$\alpha \in S_i$
such that
 $C \cap E \cap C^i_{\alpha } = E \cap C^i_{\alpha }$
and
$C \cap E \cap C^i_{\alpha } = E \cap C^i_{\alpha }$
and
 $\operatorname {\textrm {otp}} (E \cap C^i_{\alpha }) = \theta $
.
$\operatorname {\textrm {otp}} (E \cap C^i_{\alpha }) = \theta $
.
A proof is given, e.g., in [Reference Kojman and Shelah11, Fact 3.7].
Let
![]() $S = S_i \cap E$
and
$S = S_i \cap E$
and
![]() $C_{\alpha } = C^i_{\alpha } \cap E$
for
$C_{\alpha } = C^i_{\alpha } \cap E$
for
![]() $\alpha \in S_i$
. Let
$\alpha \in S_i$
. Let
For
![]() $\alpha \in S'$
let
$\alpha \in S'$
let
![]() $\langle \gamma (\alpha ,j) \, : \, j < \theta \rangle $
list
$\langle \gamma (\alpha ,j) \, : \, j < \theta \rangle $
list
![]() $C_{\alpha }$
in increasing order.
$C_{\alpha }$
in increasing order.
Now for each
![]() $\alpha \in S'$
we define a
$\alpha \in S'$
we define a
![]() ${\mathbb P}$
-name
${\mathbb P}$
-name
![]() of a function from
of a function from
![]() $\theta $
into
$\theta $
into
![]() $\kappa $
by letting for
$\kappa $
by letting for
![]() $j \in \theta $
and
$j \in \theta $
and
![]() $\alpha \in S'$
$\alpha \in S'$

Second step.
We show: If
![]() $p \in {\mathbb P}$
and
$p \in {\mathbb P}$
and
![]() $ \nu \in {}^\theta \kappa $
then for some pair
$ \nu \in {}^\theta \kappa $
then for some pair
![]() $(\alpha ,q)$
we have
$(\alpha ,q)$
we have
-
(
 $\alpha $
)
$\alpha $
)
 $\alpha \in S'$
,
$\alpha \in S'$
, -
(
 $\beta $
)
$\beta $
)
 $q \geq p$
, and
$q \geq p$
, and -
(
 $\gamma $
)
$\gamma $
)
 .
.
This is done as follows: For every p and
![]() $\nu $
by induction on
$\nu $
by induction on
![]() $\beta < \kappa $
we choose
$\beta < \kappa $
we choose
![]() $\varrho _\beta $
such that
$\varrho _\beta $
such that
-
(a)
 $\varrho _\beta \in \operatorname {\textrm {spl}}(p)$
,
$\varrho _\beta \in \operatorname {\textrm {spl}}(p)$
, -
(b) for
 $\beta < \gamma < \kappa $
,
$\beta < \gamma < \kappa $
,
 $\varrho _\beta \trianglelefteq \varrho _\gamma $
,
$\varrho _\beta \trianglelefteq \varrho _\gamma $
, -
(c) at limits
 $\delta < \kappa $
,
$\delta < \kappa $
,
 $\varrho _\delta = \bigcup _{\beta <\delta } \varrho _{\beta }$
, and
$\varrho _\delta = \bigcup _{\beta <\delta } \varrho _{\beta }$
, and -
(d) if
 $\gamma = \beta +1$
and
$\gamma = \beta +1$
and
 $\beta \in S$
, and
$\beta \in S$
, and
 $\lg (\varrho _\beta )= \beta $
, then
$\lg (\varrho _\beta )= \beta $
, then
 $g(\varrho _\gamma (\beta )) = \nu (\operatorname {\textrm {otp}}(C_\beta ))$
.
$g(\varrho _\gamma (\beta )) = \nu (\operatorname {\textrm {otp}}(C_\beta ))$
.
Note, for
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $\alpha \in S_i$
,
$\alpha \in S_i$
,
![]() $\gamma (\alpha ,j) = \beta $
:
$\gamma (\alpha ,j) = \beta $
:
So
![]() $\langle \lg (\varrho _\beta ) \, : \, \beta < \kappa \rangle $
is increasing and continuous in
$\langle \lg (\varrho _\beta ) \, : \, \beta < \kappa \rangle $
is increasing and continuous in
![]() $\kappa $
. Hence
$\kappa $
. Hence
![]() $C' = \{\lg (\varrho _\beta ) \, : \, \beta < \kappa \}$
is a club in
$C' = \{\lg (\varrho _\beta ) \, : \, \beta < \kappa \}$
is a club in
![]() $\kappa $
and there is
$\kappa $
and there is
![]() $\alpha $
in
$\alpha $
in
![]() $S'$
such that
$S'$
such that
![]() $C_{\alpha } \subseteq C'$
and
$C_{\alpha } \subseteq C'$
and
![]() $\operatorname {\textrm {cf}}(\alpha ) = \theta $
. By item (d) and Equation (4.2), we have for any
$\operatorname {\textrm {cf}}(\alpha ) = \theta $
. By item (d) and Equation (4.2), we have for any
![]() $j < \theta $
,
$j < \theta $
,
![]() $\gamma (\alpha ,j) \in C_{\alpha }$
, if
$\gamma (\alpha ,j) \in C_{\alpha }$
, if
![]() $\gamma (\alpha ,j) = \beta <\alpha $
then
$\gamma (\alpha ,j) = \beta <\alpha $
then

Since
![]() $p^{[\varrho _{\alpha }]}$
determines
$p^{[\varrho _{\alpha }]}$
determines
, we have

As
![]() $|S'| = \kappa $
, we see that forcing with
$|S'| = \kappa $
, we see that forcing with
![]() ${\mathbb P}$
collapses
${\mathbb P}$
collapses
![]() $\kappa ^\theta $
to
$\kappa ^\theta $
to
![]() $\kappa $
.⊣
$\kappa $
.⊣
Theorem 4.2.
-
(1) If
 $\kappa = \operatorname {\textrm {cf}}(\kappa )> \theta = \operatorname {\textrm {cf}}(\theta ) > \omega $
and
$\kappa = \operatorname {\textrm {cf}}(\kappa )> \theta = \operatorname {\textrm {cf}}(\theta ) > \omega $
and
 $\kappa ^\theta> \kappa $
, then forcing with
$\kappa ^\theta> \kappa $
, then forcing with
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
 $\kappa ^\theta $
to
$\kappa ^\theta $
to
 $\kappa $
.
$\kappa $
. -
(2) If
 $\kappa = \aleph _1$
and
$\kappa = \aleph _1$
and
 $2^\omega> \aleph _1$
, then forcing with
$2^\omega> \aleph _1$
, then forcing with
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
 $2^\omega $
to
$2^\omega $
to
 $\omega _1$
.
$\omega _1$
.
Proof. (1) On
![]() ${}^\theta \kappa $
we define an equivalence relation E as follows:
${}^\theta \kappa $
we define an equivalence relation E as follows:
By Solovay’s theorem, that there are
![]() $\theta $
mutually disjoint stationary subsets of
$\theta $
mutually disjoint stationary subsets of
![]() $\theta $
, the relation E has
$\theta $
, the relation E has
![]() $\kappa ^\theta $
classes. Let
$\kappa ^\theta $
classes. Let
![]() $\langle \varrho _\zeta \, : \, \zeta < \kappa ^\theta \rangle $
list a set of representatives without any repetitions.
$\langle \varrho _\zeta \, : \, \zeta < \kappa ^\theta \rangle $
list a set of representatives without any repetitions.
Again we choose and fix a function
![]() $h_\ast $
from
$h_\ast $
from
![]() $\kappa $
to
$\kappa $
to
![]() $\kappa $
such that for each
$\kappa $
such that for each
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
![]() $h_\ast ^{-1}[\{\alpha \}]$
is a stationary subset of
$h_\ast ^{-1}[\{\alpha \}]$
is a stationary subset of
![]() $\kappa $
. We let
$\kappa $
. We let
be a name for the
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
-generic
${\mathbb Q}^{\textrm {a}}_{\kappa }$
-generic
![]() $\kappa $
-real. Now we define a name for a function
$\kappa $
-real. Now we define a name for a function

by letting
be the minimal
![]() $\zeta \in \kappa ^\theta $
such that there is an increasing continuous sequence
$\zeta \in \kappa ^\theta $
such that there is an increasing continuous sequence
![]() $\langle \alpha _i \, : \, i < \theta \rangle $
converging to
$\langle \alpha _i \, : \, i < \theta \rangle $
converging to
![]() $\delta $
such that
$\delta $
such that

The particular choice of
![]() $\langle \alpha _i \, : \, i < \theta \rangle $
does not matter, since for any two such sequences that are club many
$\langle \alpha _i \, : \, i < \theta \rangle $
does not matter, since for any two such sequences that are club many
![]() $i < \theta $
on which they coincide. We prove that
$i < \theta $
on which they coincide. We prove that
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
forces that
${\mathbb Q}^{\textrm {a}}_{\kappa }$
forces that
![]() is surjective. Given
is surjective. Given
![]() $\zeta \in \kappa ^{\theta }$
we choose by induction on
$\zeta \in \kappa ^{\theta }$
we choose by induction on
![]() $i < \theta $
, a node
$i < \theta $
, a node
![]() $\eta _i \in \operatorname {\textrm {spl}}(p)$
and ordinals
$\eta _i \in \operatorname {\textrm {spl}}(p)$
and ordinals
![]() $\alpha _i \in \kappa $
,
$\alpha _i \in \kappa $
,
![]() $\beta _i \in \kappa $
, with the following properties:
$\beta _i \in \kappa $
, with the following properties:
-
(a)
 $\eta _0 = \operatorname {\textrm {tr}}(p)$
,
$\eta _0 = \operatorname {\textrm {tr}}(p)$
, -
(b)
 $\lg (\eta _i) = \alpha _i$
,
$\lg (\eta _i) = \alpha _i$
, -
(c)
 $\eta _{i+1} \triangleright \eta _i \,\hat {} \, \langle \beta _i\rangle $
(—so
$\eta _{i+1} \triangleright \eta _i \,\hat {} \, \langle \beta _i\rangle $
(—so
 $\eta _{i+1}(\alpha _i) = \beta _i$
—) and
$\eta _{i+1}(\alpha _i) = \beta _i$
—) and
 $\beta _i \in \operatorname {\textrm {osucc}}_{p}(\eta _i)$
is chosen such that
$\beta _i \in \operatorname {\textrm {osucc}}_{p}(\eta _i)$
is chosen such that
 $h_\ast (\beta _i) = \varrho (\alpha _i)$
, and
$h_\ast (\beta _i) = \varrho (\alpha _i)$
, and -
(d)
 $\eta _\delta = \bigcup \{\eta _i \, : \, i < \delta \}$
for limit
$\eta _\delta = \bigcup \{\eta _i \, : \, i < \delta \}$
for limit
 $\delta \leq \theta $
.
$\delta \leq \theta $
.
In the end we let
![]() $q = p^{\langle \eta _\theta \rangle }$
and
$q = p^{\langle \eta _\theta \rangle }$
and
![]() $\delta = \bigcup \{\alpha _i \, : \, i < \theta \}$
have
$\delta = \bigcup \{\alpha _i \, : \, i < \theta \}$
have

(2) Now for the case of
![]() $\kappa = \aleph _1$
. For any limit ordinal
$\kappa = \aleph _1$
. For any limit ordinal
![]() $\delta \in \kappa $
we choose an increasing sequence
$\delta \in \kappa $
we choose an increasing sequence
![]() $\bar {\alpha _\delta } = \langle \alpha _{\delta ,n} \, : \, n<\omega \rangle $
that converges
$\bar {\alpha _\delta } = \langle \alpha _{\delta ,n} \, : \, n<\omega \rangle $
that converges
![]() $\delta $
. Again we let
$\delta $
. Again we let
![]() be a name for the generic branch. We let
be a name for the generic branch. We let
![]() $S = \{\delta < \kappa \, : \, \delta \mbox { limit ordinal}\}$
. We let
$S = \{\delta < \kappa \, : \, \delta \mbox { limit ordinal}\}$
. We let

We define an equivalence relation E on
![]() ${}^\omega \omega $
:
${}^\omega \omega $
:
We let
![]() $\langle \varrho _\zeta \, : \, \zeta \in 2^\omega \rangle $
list a system of representatives without repetitions.
$\langle \varrho _\zeta \, : \, \zeta \in 2^\omega \rangle $
list a system of representatives without repetitions.
Recall:
![]() $\kappa = \omega _1$
and we let
$\kappa = \omega _1$
and we let
![]() $h_\ast \colon \omega _1 \to \omega _1$
be such that for any
$h_\ast \colon \omega _1 \to \omega _1$
be such that for any
![]() $\xi \in \omega _1$
,
$\xi \in \omega _1$
,
![]() $h_\ast ^{-1}[\{\xi \}]$
is stationary in
$h_\ast ^{-1}[\{\xi \}]$
is stationary in
![]() $\omega _1$
.
$\omega _1$
.
Now we define a name
![]() as follows:
as follows:
 if for some
if for some
![]() $m \in \omega $
and
$m \in \omega $
and
![]() $i \in S$
,
$i \in S$
,
 $$ \begin{align} \begin{aligned} p \Vdash & ((m,i) \in w_\delta {}\wedge \\ & n = |\{m' \leq m \, : \, (\exists j < \omega_1) (m',j) \in w_\delta\}| {}\wedge\\ & h_\ast(i) = \gamma). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p \Vdash & ((m,i) \in w_\delta {}\wedge \\ & n = |\{m' \leq m \, : \, (\exists j < \omega_1) (m',j) \in w_\delta\}| {}\wedge\\ & h_\ast(i) = \gamma). \end{aligned} \end{align} $$
We show that
This will finish the proof, since then for any
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
-generic filter G over
${\mathbb Q}^{\textrm {a}}_{\kappa }$
-generic filter G over
![]() $\mathbf {V}$
, in
$\mathbf {V}$
, in
![]() $\mathbf {V}[G]$
the map on S such that
$\mathbf {V}[G]$
the map on S such that
is a collapsing function from S onto
![]() $2^{\omega }$
. Since
$2^{\omega }$
. Since
![]() $\kappa $
is uncountable, also in the extension
$\kappa $
is uncountable, also in the extension
![]() $|S| = \omega _1$
.
$|S| = \omega _1$
.
Heading for (4.5), given p,
![]() $\varrho $
, we show that there are a stronger condition q and some
$\varrho $
, we show that there are a stronger condition q and some
![]() $\delta \in S$
such that
$\delta \in S$
such that
![]() .
.
We choose an increasing continuous sequence
![]() $\langle M_{\alpha } \, : \, \alpha < \omega _1 \rangle $
of countable elementary submodels of
$\langle M_{\alpha } \, : \, \alpha < \omega _1 \rangle $
of countable elementary submodels of
![]() $(H(\chi ), \in ,<)$
such that
$(H(\chi ), \in ,<)$
such that
![]() $\langle \bar {\alpha _\delta } \, : \, \delta \in S \rangle , \omega _1, \varrho , p \in M_0$
.
$\langle \bar {\alpha _\delta } \, : \, \delta \in S \rangle , \omega _1, \varrho , p \in M_0$
.
We take
![]() $\delta \in S$
such that
$\delta \in S$
such that
![]() $M_\delta \cap \omega _1 = \delta $
. Since
$M_\delta \cap \omega _1 = \delta $
. Since
![]() $\langle M_{\alpha } \, : \, \alpha < \omega _1 \rangle $
is increasing and continuous, such a
$\langle M_{\alpha } \, : \, \alpha < \omega _1 \rangle $
is increasing and continuous, such a
![]() $\delta \in S$
exists.
$\delta \in S$
exists.
The aim is to show that there is some node
![]() $\eta \in p$
such that
$\eta \in p$
such that
We let:
 $$ \begin{align*} w^{(\omega)} = \{n < \omega \, : \, (\exists^{\geq \omega} \alpha < \omega_1 )(M_{\alpha} \cap \omega_1 \in [\alpha_{\delta,n}, \alpha_{\delta,n+1}))\}. \end{align*} $$
$$ \begin{align*} w^{(\omega)} = \{n < \omega \, : \, (\exists^{\geq \omega} \alpha < \omega_1 )(M_{\alpha} \cap \omega_1 \in [\alpha_{\delta,n}, \alpha_{\delta,n+1}))\}. \end{align*} $$
We prove that
![]() $w^{(\omega )}$
is infinite. Suppose that
$w^{(\omega )}$
is infinite. Suppose that
![]() $n_0$
is given. Then there is some
$n_0$
is given. Then there is some
![]() $\beta < \delta $
such that
$\beta < \delta $
such that
![]() $M_\beta \cap \omega _1 \geq \alpha _{\delta ,n_0}$
and moreover
$M_\beta \cap \omega _1 \geq \alpha _{\delta ,n_0}$
and moreover
![]() $\beta + \omega < \delta $
, since
$\beta + \omega < \delta $
, since
 $M_\delta \prec (H(\chi ),\in, <)$
and hence
$M_\delta \prec (H(\chi ),\in, <)$
and hence
![]() $M_\delta $
with
$M_\delta $
with
![]() $\omega , \beta \in M_\delta $
fulfils the replacement scheme for the function
$\omega , \beta \in M_\delta $
fulfils the replacement scheme for the function
![]() $\langle (n, \beta +n) \, : \, n < \omega \rangle $
. So
$\langle (n, \beta +n) \, : \, n < \omega \rangle $
. So
![]() $M_{\beta + \omega } \cap \omega _1 < \alpha _{\delta , n_1}$
for some
$M_{\beta + \omega } \cap \omega _1 < \alpha _{\delta , n_1}$
for some
![]() $n_0 < n_1 < \omega $
. Hence all the
$n_0 < n_1 < \omega $
. Hence all the
![]() $M_{\beta +n} \cap \omega _1$
,
$M_{\beta +n} \cap \omega _1$
,
![]() $n \leq \omega $
, are in the interval
$n \leq \omega $
, are in the interval
![]() $[\alpha _{\delta , n_0}, \alpha _{\delta , n_1})$
. The latter interval is the union of
$[\alpha _{\delta , n_0}, \alpha _{\delta , n_1})$
. The latter interval is the union of
![]() $[\alpha _{\delta ,n} \alpha _{\delta , n+1})$
,
$[\alpha _{\delta ,n} \alpha _{\delta , n+1})$
,
![]() $n_0 \leq n <n_1$
. Hence one of these contains
$n_0 \leq n <n_1$
. Hence one of these contains
![]() $M_{\beta +m} \cap \omega _1$
for
$M_{\beta +m} \cap \omega _1$
for
![]() $m $
from an infinite set.
$m $
from an infinite set.
Let
![]() $n_0 < n_1 \dots $
list
$n_0 < n_1 \dots $
list
![]() $w^{(\omega )}$
in increasing order.
$w^{(\omega )}$
in increasing order.
By induction on
![]() $\ell < \omega $
we choose an increasing sequence of splitting nodes
$\ell < \omega $
we choose an increasing sequence of splitting nodes
![]() $\eta _\ell \in \operatorname {\textrm {spl}}(p)$
and
$\eta _\ell \in \operatorname {\textrm {spl}}(p)$
and
![]() $\varepsilon _\ell \in \kappa $
such that such that
$\varepsilon _\ell \in \kappa $
such that such that
-
(
 $\alpha $
)
$\alpha $
)
 $\eta _\ell \triangleleft \eta _{\ell +1,}$
$\eta _\ell \triangleleft \eta _{\ell +1,}$
-
(
 $\beta $
) for
$\beta $
) for
 $\ell \geq 0$
,
$\ell \geq 0$
,
 $i_\ell = \lg (\eta _\ell )= M_{\varepsilon _\ell } \cap \omega _1 \in [\alpha _{\delta ,n_\ell }, \alpha _{\delta ,n_{\ell +1}})$
,
$i_\ell = \lg (\eta _\ell )= M_{\varepsilon _\ell } \cap \omega _1 \in [\alpha _{\delta ,n_\ell }, \alpha _{\delta ,n_{\ell +1}})$
, -
(
 $\gamma $
)
$\gamma $
)
 $\eta _\ell $
is a
$\eta _\ell $
is a
 $\omega $
-limit of splitting nodes and
$\omega $
-limit of splitting nodes and
 $\operatorname {\textrm {range}}(\eta _\ell ) \subseteq M_{\varepsilon _\ell } \cap \omega _1$
, and
$\operatorname {\textrm {range}}(\eta _\ell ) \subseteq M_{\varepsilon _\ell } \cap \omega _1$
, and -
(
 $\delta $
)
$\delta $
)
 $\eta _{\ell +1}(\lg (\eta _\ell ) \in h^{-1}_\ast [\{\varrho (\ell )]$
.
$\eta _{\ell +1}(\lg (\eta _\ell ) \in h^{-1}_\ast [\{\varrho (\ell )]$
.
To find
![]() $\eta _0$
and
$\eta _0$
and
![]() $\varepsilon _0$
we apply the second half of the successor step to
$\varepsilon _0$
we apply the second half of the successor step to
![]() $\operatorname {\textrm {rt}}(p)$
and
$\operatorname {\textrm {rt}}(p)$
and
![]() $M_0$
.
$M_0$
.
We carry out the successor step: Suppose
![]() $\eta _\ell $
and
$\eta _\ell $
and
![]() $\varepsilon _\ell $
are chosen. and
$\varepsilon _\ell $
are chosen. and
![]() $\operatorname {\textrm {dom}}(\eta _\ell ) = i_\ell = M_{\varepsilon _\ell } \cap \omega _1$
has range contained in
$\operatorname {\textrm {dom}}(\eta _\ell ) = i_\ell = M_{\varepsilon _\ell } \cap \omega _1$
has range contained in
![]() $M_{\varepsilon _\ell } \cap \omega _1$
. Hence
$M_{\varepsilon _\ell } \cap \omega _1$
. Hence
We choose
![]() $\alpha $
such that
$\alpha $
such that
![]() $\eta _\ell \,\hat {} \, \langle \alpha \rangle \in p$
and we choose a preliminary
$\eta _\ell \,\hat {} \, \langle \alpha \rangle \in p$
and we choose a preliminary
![]() $\varepsilon ^{\prime }_{\ell +1}$
with the following properties: We let
$\varepsilon ^{\prime }_{\ell +1}$
with the following properties: We let
![]() $\varepsilon ^{\prime }_{\ell +1} \geq \varepsilon _\ell +1$
such that
$\varepsilon ^{\prime }_{\ell +1} \geq \varepsilon _\ell +1$
such that
 $M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1 \in [\alpha _{n_{\ell +1}}, \alpha _{n_{\ell +1} +1})$
. Since
$M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1 \in [\alpha _{n_{\ell +1}}, \alpha _{n_{\ell +1} +1})$
. Since
![]() $\eta _\ell $
is definable from
$\eta _\ell $
is definable from
![]() $M_j$
,
$M_j$
,
![]() $j \leq \varepsilon _\ell $
and p, we have
$j \leq \varepsilon _\ell $
and p, we have
 $ \eta _\ell \in M_{\varepsilon ^{\prime }_{\ell +1}}$
and hence we can do the preliminary step in
$ \eta _\ell \in M_{\varepsilon ^{\prime }_{\ell +1}}$
and hence we can do the preliminary step in
 $M_{\varepsilon ^{\prime }_{\ell +1}}$
.
$M_{\varepsilon ^{\prime }_{\ell +1}}$
.
Since
![]() $S_\ell =h_\ast ^{-1}[\{\varrho (\ell ))\}]$
is in
$S_\ell =h_\ast ^{-1}[\{\varrho (\ell ))\}]$
is in
 $M_{\varepsilon ^{\prime }_{\ell +1}}$
a stationary subset of
$M_{\varepsilon ^{\prime }_{\ell +1}}$
a stationary subset of
![]() $\omega _1$
there are arbitrary large members of
$\omega _1$
there are arbitrary large members of
 $S_\ell \cap (M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1)$
and in particular there are members in
$S_\ell \cap (M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1)$
and in particular there are members in
 $S_\ell \cap (M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1) \cap [\alpha _{\delta , n_{\ell +1}}, \alpha _{\delta , n_{\ell +2}})$
. Thus there is
$S_\ell \cap (M_{\varepsilon ^{\prime }_{\ell +1}} \cap \omega _1) \cap [\alpha _{\delta , n_{\ell +1}}, \alpha _{\delta , n_{\ell +2}})$
. Thus there is
![]() $\alpha \in \omega _1\cap [\alpha _{\delta ,n_{\ell +1}}, \alpha _{\delta ,n_{\ell +2}})$
is such that
$\alpha \in \omega _1\cap [\alpha _{\delta ,n_{\ell +1}}, \alpha _{\delta ,n_{\ell +2}})$
is such that
![]() $h_\ast (\eta _{\ell +1}(i_\ell )) = \varrho (\ell )$
and
$h_\ast (\eta _{\ell +1}(i_\ell )) = \varrho (\ell )$
and
![]() $\eta _\ell \,\hat {} \, \langle \alpha \rangle \in p$
.
$\eta _\ell \,\hat {} \, \langle \alpha \rangle \in p$
.
Then we choose
![]() $\varepsilon _{\ell +1}$
such that
$\varepsilon _{\ell +1}$
such that
![]() $M_{\varepsilon _{\ell +1}} \cap \omega \in [\alpha _{\delta , n_{\ell +1}}, \alpha _{\delta , n_{\ell +1} +1})$
and such that
$M_{\varepsilon _{\ell +1}} \cap \omega \in [\alpha _{\delta , n_{\ell +1}}, \alpha _{\delta , n_{\ell +1} +1})$
and such that
![]() $\eta _{\ell +1} \triangleright \eta _{\ell } \,\hat {} \, \langle \alpha \rangle $
is a splitting node of p that has range
$\eta _{\ell +1} \triangleright \eta _{\ell } \,\hat {} \, \langle \alpha \rangle $
is a splitting node of p that has range
![]() $\subseteq \alpha _{\delta , n_{\ell +1} +1}$
and
$\subseteq \alpha _{\delta , n_{\ell +1} +1}$
and
 $\lg (\eta _{\ell +1}) = M_{\varepsilon _{\ell +1}} \cap \omega _1$
.
$\lg (\eta _{\ell +1}) = M_{\varepsilon _{\ell +1}} \cap \omega _1$
.
Why is there such an
![]() $\eta _{\ell +1}$
? Since limits of splitting nodes are splitting nodes and since the sequence
$\eta _{\ell +1}$
? Since limits of splitting nodes are splitting nodes and since the sequence
![]() $M_{\alpha }$
is continuously increasing, we can find
$M_{\alpha }$
is continuously increasing, we can find
![]() $\eta _{\ell +1}$
by an intermediate
$\eta _{\ell +1}$
by an intermediate
![]() $\omega $
-sequence of nodes
$\omega $
-sequence of nodes
![]() $\eta _{\ell +1,k} \in \operatorname {\textrm {spl}}(p)$
with
$\eta _{\ell +1,k} \in \operatorname {\textrm {spl}}(p)$
with
 $M_{\eta _{\ell +1,k}} \cap \omega _1 = \lg (\eta _{\ell +1,k})> M_{\eta _{\ell ,k}} \cap \kappa $
and the range of
$M_{\eta _{\ell +1,k}} \cap \omega _1 = \lg (\eta _{\ell +1,k})> M_{\eta _{\ell ,k}} \cap \kappa $
and the range of
![]() $\eta _{\ell +1, k} \restriction [i_\ell , \operatorname {\textrm {dom}}(\eta _{\ell +1}))$
is a subset of
$\eta _{\ell +1, k} \restriction [i_\ell , \operatorname {\textrm {dom}}(\eta _{\ell +1}))$
is a subset of
![]() $[\alpha _{\delta ,n_{\ell +1}}, \alpha _{\delta , n_{\ell +1}+1})$
.
$[\alpha _{\delta ,n_{\ell +1}}, \alpha _{\delta , n_{\ell +1}+1})$
.
By Equations (4.3) and (4.4) the argument
![]() $i_\ell $
is determined from
$i_\ell $
is determined from
![]() for some
for some
![]() $m \in {\mathbb Z}$
, for all
$m \in {\mathbb Z}$
, for all
![]() $\ell $
and
$\ell $
and
 . Footnote
3
.
. Footnote
3
.
In the end we let
![]() $\eta = \bigcup \eta _\ell $
. Now the
$\eta = \bigcup \eta _\ell $
. Now the
![]() $n_\ell $
,
$n_\ell $
,
![]() $i_\ell $
,
$i_\ell $
,
![]() $\eta _{\ell +1}$
,
$\eta _{\ell +1}$
,
![]() $\ell \geq 1$
, witness
$\ell \geq 1$
, witness

⊣
Now we sum up all the cases of
![]() $\kappa ^{<\kappa }> \kappa $
for regular
$\kappa ^{<\kappa }> \kappa $
for regular
![]() $\kappa $
.
$\kappa $
.
Theorem 4.3. If
![]() $\kappa $
is a regular uncountable cardinal and
$\kappa $
is a regular uncountable cardinal and
![]() $\kappa ^{<\kappa }> \kappa $
then
$\kappa ^{<\kappa }> \kappa $
then
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
![]() $\kappa ^{<\kappa }$
to
$\kappa ^{<\kappa }$
to
![]() $\kappa $
.
$\kappa $
.
Proof.
-
(1)
 $\kappa $
is a limit cardinal. Then we can write
$\kappa $
is a limit cardinal. Then we can write
 $\kappa ^{<\kappa }$
as
$\kappa ^{<\kappa }$
as
 $\sup \{\kappa ^{\theta ^+} \, : \, \theta < \kappa \}$
. According to Theorem 4.2 part (1) each of the
$\sup \{\kappa ^{\theta ^+} \, : \, \theta < \kappa \}$
. According to Theorem 4.2 part (1) each of the
 $\kappa ^{\theta ^+}$
is collapsed to
$\kappa ^{\theta ^+}$
is collapsed to
 $\kappa $
, and we can combine the names of the collapses and get: Forcing with
$\kappa $
, and we can combine the names of the collapses and get: Forcing with
 ${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
${\mathbb Q}^{\textrm {a}}_{\kappa }$
collapses
 $\kappa ^{<\kappa }$
to
$\kappa ^{<\kappa }$
to
 $\kappa $
.
$\kappa $
. -
(2)
 $\kappa = \theta ^+$
and
$\kappa = \theta ^+$
and
 $\theta> \omega $
is regular. This is Theorem 4.2 part (1).
$\theta> \omega $
is regular. This is Theorem 4.2 part (1). -
(3)
 $\kappa = \omega _1$
. This is Theorem 4.2 part (2).
$\kappa = \omega _1$
. This is Theorem 4.2 part (2). -
(4)
 $\kappa = \theta ^+$
and
$\kappa = \theta ^+$
and
 $\operatorname {\textrm {cf}}(\theta ) < \theta $
.
$\operatorname {\textrm {cf}}(\theta ) < \theta $
.4.1: The first subcase is:
 $\kappa ^\theta = \kappa ^\mu $
for some
$\kappa ^\theta = \kappa ^\mu $
for some
 $\mu \in [\omega _1, \theta )$
. Then we can choose a regular such
$\mu \in [\omega _1, \theta )$
. Then we can choose a regular such
 $\mu $
. Now
$\mu $
. Now
 $\kappa ^\theta = \kappa ^{<\kappa } = \kappa ^\mu $
is collapsed to
$\kappa ^\theta = \kappa ^{<\kappa } = \kappa ^\mu $
is collapsed to
 $\kappa $
by Theorem 4.2 part (1).
$\kappa $
by Theorem 4.2 part (1).4.2: The second subcase is: For all
 $\mu < \theta $
,
$\mu < \theta $
,
 $\kappa ^\mu \leq \kappa $
. Then
$\kappa ^\mu \leq \kappa $
. Then
 $\kappa ^\theta = \kappa ^{\operatorname {\textrm {cf}}(\theta )}$
. This subcase is divided in two subsubcases:
$\kappa ^\theta = \kappa ^{\operatorname {\textrm {cf}}(\theta )}$
. This subcase is divided in two subsubcases:4.2.1: If
 $\operatorname {\textrm {cf}}(\theta )> \omega $
, then by Theorem 4.2 part (1)
$\operatorname {\textrm {cf}}(\theta )> \omega $
, then by Theorem 4.2 part (1)
 $\kappa ^\theta $
is collapsed to
$\kappa ^\theta $
is collapsed to
 $\kappa $
.
$\kappa $
.4.2.2: If
 $\operatorname {\textrm {cf}}(\theta ) = \omega $
, then we need to rework part (2) of Theorem 4.2 to get that also
$\operatorname {\textrm {cf}}(\theta ) = \omega $
, then we need to rework part (2) of Theorem 4.2 to get that also
 $\kappa ^\omega $
is collapsed. We replace
$\kappa ^\omega $
is collapsed. We replace
 $\omega _1$
by
$\omega _1$
by
 $\kappa $
and instead of with countable elementary submodels we work with submodels of cardinality
$\kappa $
and instead of with countable elementary submodels we work with submodels of cardinality
 $< \kappa $
.⊣
$< \kappa $
.⊣
5 On the Laver property
In this section we assume that
![]() $\kappa $
is a measurable cardinal that is measurable after forcing with any
$\kappa $
is a measurable cardinal that is measurable after forcing with any
![]() $(<\kappa )$
-directed forcing. Such a cardinal is gotten by starting with a supercompact cardinal and performing a Laver preparation [Reference Laver15]. Then the supercompactness is indestructible under
$(<\kappa )$
-directed forcing. Such a cardinal is gotten by starting with a supercompact cardinal and performing a Laver preparation [Reference Laver15]. Then the supercompactness is indestructible under
![]() $(<\kappa )$
-directed forcings.
$(<\kappa )$
-directed forcings.
The purpose of this section is to answer a question posed in [Reference Brendle, Brooke-Taylor, Friedman and Montoya4] about the Laver property of an ultrafilter version of Miller forcing. The starting point is the observation in [Reference Brendle, Brooke-Taylor, Friedman and Montoya4] that for normal ultrafilters, each iterand has a version of the Laver property.
Definition 5.1. Given a normal ultrafilter over
![]() $\kappa $
, we define
$\kappa $
, we define
![]() ${\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U)$
, Miller forcing with branching into
${\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U)$
, Miller forcing with branching into
![]() $\mathcal U$
, as follows: A condition
$\mathcal U$
, as follows: A condition
![]() $p \in {\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U)$
is a
$p \in {\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U)$
is a
![]() $(<\kappa )$
-closed superperfect tree
$(<\kappa )$
-closed superperfect tree
![]() $p \subseteq {}^{\kappa>} \kappa $
such that for any splitting node
$p \subseteq {}^{\kappa>} \kappa $
such that for any splitting node
![]() $s \in \operatorname {\textrm {spl}}(p)$
,
$s \in \operatorname {\textrm {spl}}(p)$
,
is an element of
![]() $\mathcal U$
. Subtrees are stronger conditions.
$\mathcal U$
. Subtrees are stronger conditions.
Now we recall the definition of the higher Laver properties.
Definition 5.2 (See [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Definition 79])
Let
![]() $h\colon \kappa \to \kappa \setminus \{0\}$
. A sequence
$h\colon \kappa \to \kappa \setminus \{0\}$
. A sequence
![]() $\langle \varphi _{\alpha } \, : \, \alpha < \kappa \rangle $
is called a h-slalom if for each
$\langle \varphi _{\alpha } \, : \, \alpha < \kappa \rangle $
is called a h-slalom if for each
![]() $\alpha $
,
$\alpha $
,
![]() $\varphi _{\alpha } \in [\kappa ]^{|h(\alpha )|}$
. We say
$\varphi _{\alpha } \in [\kappa ]^{|h(\alpha )|}$
. We say
![]() ${\mathbb P}$
has the h-Laver property if for any
${\mathbb P}$
has the h-Laver property if for any
![]() ${\mathbb P}$
name
${\mathbb P}$
name
and for any
![]() $g \colon \kappa \to \kappa $
such that
$g \colon \kappa \to \kappa $
such that
there is a h-slalom
![]() $\langle \varphi _{\alpha } \, : \, \alpha < \kappa \rangle $
and there is q such that
$\langle \varphi _{\alpha } \, : \, \alpha < \kappa \rangle $
and there is q such that
We answer a question by Brendle, Brooke-Taylor, Friedman, and Montoya:
Proposition 5.3. Assume that
![]() $\kappa $
is supercompact and underwent the Laver preparation. Let
$\kappa $
is supercompact and underwent the Laver preparation. Let
![]() ${\mathbb P} = \langle {\mathbb P}_m, \mathbb Q_n \, : \, n < \omega , m \leq \omega \rangle $
be the countable support iteration of length
${\mathbb P} = \langle {\mathbb P}_m, \mathbb Q_n \, : \, n < \omega , m \leq \omega \rangle $
be the countable support iteration of length
![]() $\omega $
of iterands
$\omega $
of iterands
![]() $\mathbb Q_n= {\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U_n)$
, where
$\mathbb Q_n= {\mathbb Q}^{\textrm {a}}_{\kappa }(\mathcal U_n)$
, where
![]() $\mathcal U_n$
is a normal ultrafilter over
$\mathcal U_n$
is a normal ultrafilter over
![]() $\kappa $
in
$\kappa $
in
![]() $\mathbf {V}^{{\mathbb P}_n}$
. By the Laver preparation
$\mathbf {V}^{{\mathbb P}_n}$
. By the Laver preparation
![]() $\kappa $
is still supercompact in
$\kappa $
is still supercompact in
![]() $\mathbf {V}^{{\mathbb P}_n}$
. For any
$\mathbf {V}^{{\mathbb P}_n}$
. For any
![]() $h \colon \kappa \to \kappa \setminus \{0\}$
there is a
$h \colon \kappa \to \kappa \setminus \{0\}$
there is a
![]() $g \colon \kappa \to \kappa $
and there is a
$g \colon \kappa \to \kappa $
and there is a
![]() ${\mathbb P}$
-name for a function below g that witnesses that
${\mathbb P}$
-name for a function below g that witnesses that
![]() ${\mathbb P}$
does not have the h-Laver property.
${\mathbb P}$
does not have the h-Laver property.
Proof. Let h be given. For each
![]() $\delta < \kappa $
we choose some cardinal
$\delta < \kappa $
we choose some cardinal
![]() $g(\delta ) \in [|h(\delta )|^+, \kappa )$
. For any
$g(\delta ) \in [|h(\delta )|^+, \kappa )$
. For any
![]() $\delta < \kappa $
fix a partition
$\delta < \kappa $
fix a partition
![]() $\langle S_{\delta , \varepsilon } \, : \, \varepsilon < g(\delta ) \rangle $
of
$\langle S_{\delta , \varepsilon } \, : \, \varepsilon < g(\delta ) \rangle $
of
 $S^\kappa _{\aleph _0}= \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) = \aleph _0\}$
into
$S^\kappa _{\aleph _0}= \{\alpha < \kappa \, : \, \operatorname {\textrm {cf}}(\alpha ) = \aleph _0\}$
into
![]() $g(\delta )$
many stationary sets.
$g(\delta )$
many stationary sets.
Let
![]() $\eta _n$
be the
$\eta _n$
be the
![]() $\mathbb Q_n$
-generic
$\mathbb Q_n$
-generic
![]() $\kappa $
-real.
$\kappa $
-real.
Now we define a name for a function that is bounded by g:
 $$ \begin{align} \nu(\delta) = \begin{cases} \varepsilon, & \mbox{ if } \lim_n \langle \eta_n(\delta) \, : \, n<\omega \rangle \in S_{\delta,\varepsilon};\\ 0, & \mbox{ else.} \end{cases} \end{align} $$
$$ \begin{align} \nu(\delta) = \begin{cases} \varepsilon, & \mbox{ if } \lim_n \langle \eta_n(\delta) \, : \, n<\omega \rangle \in S_{\delta,\varepsilon};\\ 0, & \mbox{ else.} \end{cases} \end{align} $$
Now we show:
-
(
 $\ast $
)
$\ast $
)
 $(\forall \varrho \in \prod _{\delta < \kappa } g(\delta ))^{\mathbf {V}}$
, for any condition p for any
$(\forall \varrho \in \prod _{\delta < \kappa } g(\delta ))^{\mathbf {V}}$
, for any condition p for any
 $\varrho $
-slalom
$\varrho $
-slalom
 $\bar {T}= \langle T(\delta ) \, : \, \delta < \kappa \rangle $
in the ground model, for any club C of
$\bar {T}= \langle T(\delta ) \, : \, \delta < \kappa \rangle $
in the ground model, for any club C of
 $\delta < \kappa $
, there is some
$\delta < \kappa $
, there is some
 $\delta \in C$
,
$\delta \in C$
,
 $p \Vdash \nu (\delta ) \not \in T(\delta ))$
.
$p \Vdash \nu (\delta ) \not \in T(\delta ))$
.
Property (
![]() $\ast $
) can be applied in particular to
$\ast $
) can be applied in particular to
![]() $\varrho = h$
,
$\varrho = h$
,
![]() $C= [\alpha , \kappa )$
for some
$C= [\alpha , \kappa )$
for some
![]() $\alpha <\kappa $
, and hence negates the h-Laver property. Let
$\alpha <\kappa $
, and hence negates the h-Laver property. Let
 $\varrho \in \prod _{\delta < \kappa } g(\delta ))^{\mathbf {V}}$
,
$\varrho \in \prod _{\delta < \kappa } g(\delta ))^{\mathbf {V}}$
,
![]() $\langle T(\delta ) \, : \, \delta < \kappa \rangle \in {\mathbf {V}}$
be such that
$\langle T(\delta ) \, : \, \delta < \kappa \rangle \in {\mathbf {V}}$
be such that
![]() $T(\delta ) \in [\kappa ]^{\varrho (\delta )}$
for
$T(\delta ) \in [\kappa ]^{\varrho (\delta )}$
for
![]() $\delta < \kappa $
, p be a condition and let
$\delta < \kappa $
, p be a condition and let
be a
![]() ${\mathbb P}$
-name for a club subset of
${\mathbb P}$
-name for a club subset of
![]() $\kappa $
. We show that
$\kappa $
. We show that
-
(
 $\odot $
) There are
$\odot $
) There are
 $q \geq p$
and
$q \geq p$
and
 $\delta < \kappa $
such that
$\delta < \kappa $
such that
 .
.
By induction on
![]() $n < \omega $
we choose
$n < \omega $
we choose
![]() $p_n$
,
$p_n$
,
![]() $\delta _n$
such that
$\delta _n$
such that
![]() $p_n = \langle p_n(k) \, : \, k \in \omega \rangle $
, where k is the coordinate that runs over the iteration stages, such that
$p_n = \langle p_n(k) \, : \, k \in \omega \rangle $
, where k is the coordinate that runs over the iteration stages, such that
-
(1)
 $p_0 = p$
,
$p_0 = p$
,
 $\delta _0 = 0$
,
$\delta _0 = 0$
, -
(2)
 $p_{n+1} \geq p_n$
,
$p_{n+1} \geq p_n$
,
 $\operatorname {\textrm {dom}}(p_n) = \omega $
,
$\operatorname {\textrm {dom}}(p_n) = \omega $
, -
(3)
 $p_{n} \restriction k \Vdash \operatorname {\textrm {tr}}(p_n(k)) = \eta _{n,k}$
,
$p_{n} \restriction k \Vdash \operatorname {\textrm {tr}}(p_n(k)) = \eta _{n,k}$
, -
(4)
 $\delta _{n+1}> \delta _n$
,
$\delta _{n+1}> \delta _n$
, -
(5)
 $p_n \restriction k \Vdash \delta _{n+1}> \lg (\eta _{n,k})$
,
$p_n \restriction k \Vdash \delta _{n+1}> \lg (\eta _{n,k})$
, -
(6)
 , and
, and -
(7)
 $p_{n+1} \restriction k \Vdash _{{\mathbb P}_k} \lg (\operatorname {\textrm {tr}}(p_{n+1}(k)) \geq \delta _{n+1}$
.
$p_{n+1} \restriction k \Vdash _{{\mathbb P}_k} \lg (\operatorname {\textrm {tr}}(p_{n+1}(k)) \geq \delta _{n+1}$
.
In the end we use that
![]() ${\mathbb P}_\omega $
is
${\mathbb P}_\omega $
is
![]() $(<\kappa )$
-closed and hence we can let
$(<\kappa )$
-closed and hence we can let
![]() $p_\omega $
be a lower bound of
$p_\omega $
be a lower bound of
![]() $p_n$
,
$p_n$
,
![]() $n < \omega $
. We have
$n < \omega $
. We have
Since
![]() $|T(\delta )| < g(\delta )$
, we can choose an
$|T(\delta )| < g(\delta )$
, we can choose an
![]() $\varepsilon \in g(\delta ) \setminus T(\delta )$
. Then we choose
$\varepsilon \in g(\delta ) \setminus T(\delta )$
. Then we choose
![]() $N_n \prec (H(\chi ), \in )$
such that
$N_n \prec (H(\chi ), \in )$
such that
-
(1)
 $\bar {T}$
,
$\bar {T}$
,
 ${\mathbb P}$
,
${\mathbb P}$
,
 $p_\omega \in N_0$
,
$p_\omega \in N_0$
, -
(2)
 $|N_n| < \kappa $
,
$|N_n| < \kappa $
, -
(3)
 $N_n \cap \kappa \in S_{\delta , \varepsilon }$
, and
$N_n \cap \kappa \in S_{\delta , \varepsilon }$
, and -
(4)
 $N_n \in N_{n+1}$
.
$N_n \in N_{n+1}$
.
So there is
![]() $q_1 \geq p_\omega $
such that
$q_1 \geq p_\omega $
such that
![]() $q_1 \in N_1 \cap {\mathbb P}$
,
$q_1 \in N_1 \cap {\mathbb P}$
,
![]() $q_1(0) \geq p_\omega (0)$
,
$q_1(0) \geq p_\omega (0)$
,
![]() $q_1(n) = p_\omega (n)$
for
$q_1(n) = p_\omega (n)$
for
![]() $n>0$
. By induction on n we choose
$n>0$
. By induction on n we choose
![]() $q_n$
such that
$q_n$
such that
and
![]() $q_n(k) = p_\omega (k)$
for
$q_n(k) = p_\omega (k)$
for
![]() $k> n$
. Let
$k> n$
. Let
![]() $q_\omega $
be an upper bound of the
$q_\omega $
be an upper bound of the
![]() $q_n$
. Then
$q_n$
. Then
 $$ \begin{align*} q_\omega \Vdash \lim_n \eta_n(\delta) = \lim_n (N_n \cap \kappa) \in S_{\delta, \varepsilon}. \end{align*} $$
$$ \begin{align*} q_\omega \Vdash \lim_n \eta_n(\delta) = \lim_n (N_n \cap \kappa) \in S_{\delta, \varepsilon}. \end{align*} $$
Hence by Equation (5.1),
and
![]() $\odot $
is proved.⊣
$\odot $
is proved.⊣
Acknowledgments
This research, no. 1191 (Saharon Shelah), was partially supported by European Research Council grant 338821. The authors thank the Technical University of Vienna and the Institute of Discrete Mathematics and Geometry for their hospitality.