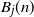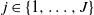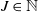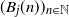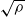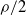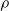1. Introduction
A brief overview of classical Pólya urn models. For
![]() $J\in\mathbb{N}$
, a J-dimensional Pólya urn process
$J\in\mathbb{N}$
, a J-dimensional Pólya urn process
![]() $(B(n))_{n\in\mathbb{N}}$
is an
$(B(n))_{n\in\mathbb{N}}$
is an
![]() $\mathbb{N}^J$
-valued stochastic process which represents the evolution of an urn containing balls of J different colors denoted by
$\mathbb{N}^J$
-valued stochastic process which represents the evolution of an urn containing balls of J different colors denoted by
![]() $1,2,\ldots, J$
. The initial composition of the urn can be specified by a J-dimensional vector B(0) given by
$1,2,\ldots, J$
. The initial composition of the urn can be specified by a J-dimensional vector B(0) given by
![]() $B(0)=\big(B_1(0),\ldots,B_J(0)\big)$
, the jth coordinate
$B(0)=\big(B_1(0),\ldots,B_J(0)\big)$
, the jth coordinate
![]() $B_j(0)$
of B(0) representing the number of balls of color j present in the urn at the beginning of the process, i.e. at time 0. At each subsequent time step
$B_j(0)$
of B(0) representing the number of balls of color j present in the urn at the beginning of the process, i.e. at time 0. At each subsequent time step
![]() $n\geq 1$
, we pick a ball uniformly at random, inspect its color, and put it back into the urn together with a random collection of additional balls, whose colors are given by
$n\geq 1$
, we pick a ball uniformly at random, inspect its color, and put it back into the urn together with a random collection of additional balls, whose colors are given by
![]() $L^{(j)}=(L^{(j,1)},\ldots,L^{(j,J)})$
if the selected ball has color j (which happens with probability proportional to the number of balls of color j already present in the urn). This rule for adding balls can be summed up by the so-called replacement matrix L, which in our case is a random matrix L defined as follows. For
$L^{(j)}=(L^{(j,1)},\ldots,L^{(j,J)})$
if the selected ball has color j (which happens with probability proportional to the number of balls of color j already present in the urn). This rule for adding balls can be summed up by the so-called replacement matrix L, which in our case is a random matrix L defined as follows. For
![]() $J\in\mathbb{N}$
, we write
$J\in\mathbb{N}$
, we write
![]() $[J]\;:\!=\;\{1,\ldots,J\}$
, and we consider a sequence
$[J]\;:\!=\;\{1,\ldots,J\}$
, and we consider a sequence
![]() $(L^{(j)})_{j\in [J]}$
of J independent
$(L^{(j)})_{j\in [J]}$
of J independent
![]() $\mathbb{N}^J$
-valued random (column) vectors. We denote by L the
$\mathbb{N}^J$
-valued random (column) vectors. We denote by L the
![]() $J\times J$
random matrix with column vectors
$J\times J$
random matrix with column vectors
![]() $L^{(j)}$
, so
$L^{(j)}$
, so
![]() $L=\left(L^{(1)},L^{(2)},\ldots,L^{(J)}\right)$
, and by
$L=\left(L^{(1)},L^{(2)},\ldots,L^{(J)}\right)$
, and by
![]() $a_{ij}=\mathbb{E}\left[L^{(j,i)}\right]$
the expectation of
$a_{ij}=\mathbb{E}\left[L^{(j,i)}\right]$
the expectation of
![]() $L^{(j,i)}$
, for all
$L^{(j,i)}$
, for all
![]() $i,j\in [J]$
; finally, we let
$i,j\in [J]$
; finally, we let
![]() $A=(a_{ij})_{i,j\in[J]}$
, so that
$A=(a_{ij})_{i,j\in[J]}$
, so that
![]() $\mathbb{E} L=A$
. We then continue the process, each time taking an independent (of everything else) copy of the replacement matrix L. Note that the model described involves replacement, meaning that the selected ball is placed back into the urn after each draw. However, it is also possible to study a model without replacement by considering the replacement matrix
$\mathbb{E} L=A$
. We then continue the process, each time taking an independent (of everything else) copy of the replacement matrix L. Note that the model described involves replacement, meaning that the selected ball is placed back into the urn after each draw. However, it is also possible to study a model without replacement by considering the replacement matrix
![]() $L-I$
, where I is the
$L-I$
, where I is the
![]() $J\times J$
identity matrix. In this case, it might happen that some diagonal entries of
$J\times J$
identity matrix. In this case, it might happen that some diagonal entries of
![]() $L-I$
are equal to
$L-I$
are equal to
![]() $-1$
, which means a ball is removed from the urn. The urn process is the sequence
$-1$
, which means a ball is removed from the urn. The urn process is the sequence
![]() $(B(n))_{n\geq 1}$
of J-dimensional random vectors with nonnegative integer coordinates, and the jth coordinate
$(B(n))_{n\geq 1}$
of J-dimensional random vectors with nonnegative integer coordinates, and the jth coordinate
![]() $B_j(n)$
of B(n) represents the number of balls of color j in the urn after the nth draw, for
$B_j(n)$
of B(n) represents the number of balls of color j in the urn after the nth draw, for
![]() $j\in [J]$
. We also define
$j\in [J]$
. We also define
![]() $B^{\circ}(n)$
to be the number of balls drawn up to time n; that is,
$B^{\circ}(n)$
to be the number of balls drawn up to time n; that is,
![]() $B^\circ_j(n)$
represents the number of balls of color j drawn up to the nth draw (in particular,
$B^\circ_j(n)$
represents the number of balls of color j drawn up to the nth draw (in particular,
![]() $B^\circ_1(n)+\cdots+B^\circ_J(n)=n$
). As one expects, the limit behavior of
$B^\circ_1(n)+\cdots+B^\circ_J(n)=n$
). As one expects, the limit behavior of
![]() $(B(n))_{n\geq 1}$
and
$(B(n))_{n\geq 1}$
and
![]() $(B^\circ(n))_{n\ge 1}$
depends on the distribution of the replacement matrix L, and in particular on the spectral properties of its mean value matrix A.
$(B^\circ(n))_{n\ge 1}$
depends on the distribution of the replacement matrix L, and in particular on the spectral properties of its mean value matrix A.
The literature on limit theorems for Pólya urn models is enormous and any attempt to give a complete survey here is hopeless, but we mention some relevant references and results in this direction. For additional results, the reader is referred to the cited articles and the references therein. In 1930, in his original article [Reference Pólya10], Pólya investigates a two-color urn process with replacement matrix L being the identity. If L is a non-random, irreducible matrix with exclusively nonnegative entries, then it is well established that the sequence
![]() $B^\circ(n)/n$
converges almost surely to u as n goes to infinity, where u is the left eigenvector associated with
$B^\circ(n)/n$
converges almost surely to u as n goes to infinity, where u is the left eigenvector associated with
![]() $\rho$
, the spectral radius of
$\rho$
, the spectral radius of
![]() $A=\mathbb{E} L$
. The coordinates of u are all nonnegative and normalized in such a way that they sum up to one; see [Reference Athreya and Karlin2, Reference Janson5, Reference Müller and Neininger9, Reference Smythe12] for more details. The second-order behavior of the sequence
$A=\mathbb{E} L$
. The coordinates of u are all nonnegative and normalized in such a way that they sum up to one; see [Reference Athreya and Karlin2, Reference Janson5, Reference Müller and Neininger9, Reference Smythe12] for more details. The second-order behavior of the sequence
![]() $(B^\circ(n))_{n\in\mathbb{N}}$
depends on the second eigenvalue
$(B^\circ(n))_{n\in\mathbb{N}}$
depends on the second eigenvalue
![]() $\lambda_2$
(ordered by real parts) of A. If
$\lambda_2$
(ordered by real parts) of A. If
![]() $\textrm{Re}(\lambda_2)$
, the real part of the second-largest eigenvalue, is less than or equal to
$\textrm{Re}(\lambda_2)$
, the real part of the second-largest eigenvalue, is less than or equal to
![]() $\rho/2$
, then the fluctuations around the limit u are Gaussian (with a random variance). The magnitude of the fluctuations is of order
$\rho/2$
, then the fluctuations around the limit u are Gaussian (with a random variance). The magnitude of the fluctuations is of order
![]() $\sqrt{n}$
when
$\sqrt{n}$
when
![]() $\textrm{Re}(\lambda_2)<\rho/2$
and of order
$\textrm{Re}(\lambda_2)<\rho/2$
and of order
![]() $\log(n)\sqrt{n}$
in the critical case
$\log(n)\sqrt{n}$
in the critical case
![]() $\textrm{Re}(\lambda_2) = \rho/2$
. Conversely, if
$\textrm{Re}(\lambda_2) = \rho/2$
. Conversely, if
![]() $\textrm{Re}(\lambda_2) > \rho/2$
, then the fluctuations are non-Gaussian and of higher order. See Janson [Reference Janson5] for this trichotomy and [Reference Pouyanne11] for an approach based on the spectral decomposition of a suitable finite-difference transition operator on polynomial functions.
$\textrm{Re}(\lambda_2) > \rho/2$
, then the fluctuations are non-Gaussian and of higher order. See Janson [Reference Janson5] for this trichotomy and [Reference Pouyanne11] for an approach based on the spectral decomposition of a suitable finite-difference transition operator on polynomial functions.
Apart from these seminal results, the model of Pólya urns has been extended and more precise asymptotics are known. Several generalizations are considered in [Reference Janson5]. Another possible extension is to consider measure-valued Pólya processes; see the recent work [Reference Janson, Mailler and Villemonais6] for second-order asymptotics of such processes for infinitely many colors and the literature cited there for additional results.
The model and our contribution. In the current paper we consider a modification of the Pólya urn model containing two urns marked
![]() $\mathsf{U}_1$
and
$\mathsf{U}_1$
and
![]() $\mathsf{U}_2$
. For a fixed
$\mathsf{U}_2$
. For a fixed
![]() $J\in\mathbb{N}$
representing the number of colors, we consider the random
$J\in\mathbb{N}$
representing the number of colors, we consider the random
![]() $J\times J$
matrix L as above, with independent column vectors
$J\times J$
matrix L as above, with independent column vectors
![]() $L^{(j)}$
and expectation matrix
$L^{(j)}$
and expectation matrix
![]() $A=\mathbb{E} L$
. With these initial conditions, we define the
$A=\mathbb{E} L$
. With these initial conditions, we define the
![]() $\mathbb{N}^J$
-valued stochastic process
$\mathbb{N}^J$
-valued stochastic process
![]() $(B(n))_{n\in \mathbb{N}}$
as follows, with
$(B(n))_{n\in \mathbb{N}}$
as follows, with
![]() $B(n)=(B_1(n),\ldots,B_J(n))$
. Suppose that at time 0 we have one ball of type (color)
$B(n)=(B_1(n),\ldots,B_J(n))$
. Suppose that at time 0 we have one ball of type (color)
![]() $j_0$
in urn
$j_0$
in urn
![]() $\mathsf{U}_1$
. We draw this ball from urn
$\mathsf{U}_1$
. We draw this ball from urn
![]() $\mathsf{U}_1$
, and we put into urn
$\mathsf{U}_1$
, and we put into urn
![]() $\mathsf{U}_2$
a collection of balls
$\mathsf{U}_2$
a collection of balls
![]() $L^{(j_0)}=(L^{(j_0,1)},\ldots, L^{(j_0,J)})$
(this notation means that for each
$L^{(j_0)}=(L^{(j_0,1)},\ldots, L^{(j_0,J)})$
(this notation means that for each
![]() $i\in [J]$
, we put
$i\in [J]$
, we put
![]() $L^{(j_0,i)}$
balls of type i into urn
$L^{(j_0,i)}$
balls of type i into urn
![]() $\mathsf{U}_2$
). Thus we now have
$\mathsf{U}_2$
). Thus we now have
![]() $\sum_{i=1}^JL^{(j_0,i)}$
balls in urn
$\sum_{i=1}^JL^{(j_0,i)}$
balls in urn
![]() $\mathsf{U}_2$
. At the next step, we draw balls from urn
$\mathsf{U}_2$
. At the next step, we draw balls from urn
![]() $\mathsf{U}_2$
uniformly at random, one after another, and for any ball of type j drawn we add an independent collection of balls with distribution
$\mathsf{U}_2$
uniformly at random, one after another, and for any ball of type j drawn we add an independent collection of balls with distribution
![]() $L^{(j)}$
into urn
$L^{(j)}$
into urn
![]() $\mathsf{U}_1$
. We continue until urn
$\mathsf{U}_1$
. We continue until urn
![]() $\mathsf{U}_2$
is empty, and then we exchange the roles of urns
$\mathsf{U}_2$
is empty, and then we exchange the roles of urns
![]() $\mathsf{U}_1$
and
$\mathsf{U}_1$
and
![]() $\mathsf{U}_2$
. We emphasize that, unlike in the Pólya urn model, in the two-urn model it is more convenient to consider drawing without replacement; that is, the ball drawn in each step is not returned to either urn, but only determines the future addition of balls. In particular, all coefficients of L are nonnegative. For
$\mathsf{U}_2$
. We emphasize that, unlike in the Pólya urn model, in the two-urn model it is more convenient to consider drawing without replacement; that is, the ball drawn in each step is not returned to either urn, but only determines the future addition of balls. In particular, all coefficients of L are nonnegative. For
![]() $j\in [J]$
, by
$j\in [J]$
, by
![]() $B_j(n)$
we denote the total number of balls of type j that have been added to one of these two urns up to (and including) the nth draw.
$B_j(n)$
we denote the total number of balls of type j that have been added to one of these two urns up to (and including) the nth draw.
Graphically, we can draw a random tree in order to visualize the step-by-step evacuation of one urn and the refilling of the other one, as follows: we color the nodes of the tree in colors
![]() $\{1,\ldots,J\}$
; the content of urn
$\{1,\ldots,J\}$
; the content of urn
![]() $\mathsf{U}_1$
represents the root of the tree colored with some fixed
$\mathsf{U}_1$
represents the root of the tree colored with some fixed
![]() $j_0\in \{1,\ldots,J\}$
, i.e. the zero generation; after one draw of the node of type
$j_0\in \{1,\ldots,J\}$
, i.e. the zero generation; after one draw of the node of type
![]() $j_0$
, the content
$j_0$
, the content
![]() $L^{(j_0)}$
of
$L^{(j_0)}$
of
![]() $\mathsf{U}_2$
represents the first generation. Then, after choosing balls (i.e. nodes of the tree at level one) uniformly at random without replacement and putting their offspring in the other urn
$\mathsf{U}_2$
represents the first generation. Then, after choosing balls (i.e. nodes of the tree at level one) uniformly at random without replacement and putting their offspring in the other urn
![]() $\mathsf{U}_1$
, we create step by step the second generation of the tree, and step by step we fill up
$\mathsf{U}_1$
, we create step by step the second generation of the tree, and step by step we fill up
![]() $\mathsf{U}_1$
again. Thus what we propose here is a more refined branching process where the transition from generation k to generation
$\mathsf{U}_1$
again. Thus what we propose here is a more refined branching process where the transition from generation k to generation
![]() $k+1$
is considered after each member of generation k reproduces. If we visualize the process as a random tree that grows after each node is chosen, the quantity
$k+1$
is considered after each member of generation k reproduces. If we visualize the process as a random tree that grows after each node is chosen, the quantity
![]() $B_j(n)$
represents the number of nodes of type j and
$B_j(n)$
represents the number of nodes of type j and
![]() $\sum_{j=1}^JB_j(n)$
represents the total number of nodes in the tree after n steps of the process, that is, after n balls have been drawn from
$\sum_{j=1}^JB_j(n)$
represents the total number of nodes in the tree after n steps of the process, that is, after n balls have been drawn from
![]() $\mathsf{U}_1$
and
$\mathsf{U}_1$
and
![]() $\mathsf{U}_2$
. For better understanding, we illustrate this process in an example in Appendix A and Figure 1.
$\mathsf{U}_2$
. For better understanding, we illustrate this process in an example in Appendix A and Figure 1.

Figure 1. The model with two alternating urns and deterministic replacement matrix after
![]() $n=4$
draws.
$n=4$
draws.
The main focus of the current work is to investigate first- and second-order asymptotics of
![]() $B_j(n)$
as
$B_j(n)$
as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $j\in [J]$
. It may happen that with positive probability
$j\in [J]$
. It may happen that with positive probability
![]() $L^{(j,i)}$
vanishes for all
$L^{(j,i)}$
vanishes for all
![]() $i\in[J]$
. In such a case we do not add any new balls to the urn; we just remove the selected ball of type j. In particular, it can happen that after a finite number
$i\in[J]$
. In such a case we do not add any new balls to the urn; we just remove the selected ball of type j. In particular, it can happen that after a finite number
![]() $n_0$
of steps, both urns are empty; in such a case we define
$n_0$
of steps, both urns are empty; in such a case we define
![]() $B(n)=B(n_0)$
, for
$B(n)=B(n_0)$
, for
![]() $n\ge n_0$
. Since we are interested in the long-term behavior of the urn process, we restrict the analysis to a set where this does not happen, i.e. to the survival event
$n\ge n_0$
. Since we are interested in the long-term behavior of the urn process, we restrict the analysis to a set where this does not happen, i.e. to the survival event
![]() $\mathcal S=\{|B(n)|\to\infty\}$
.
$\mathcal S=\{|B(n)|\to\infty\}$
.
We can also define the corresponding sequence
![]() $(B^\circ(n))_{n\ge 0}$
that represents the types of the balls drawn up to time n. While it is possible to ask about limit theorems for
$(B^\circ(n))_{n\ge 0}$
that represents the types of the balls drawn up to time n. While it is possible to ask about limit theorems for
![]() $B^\circ(n)$
, the method developed in this paper for studying B(n) is directly applicable to
$B^\circ(n)$
, the method developed in this paper for studying B(n) is directly applicable to
![]() $B^\circ(n)$
. Therefore, we focus our attention exclusively on the sequence
$B^\circ(n)$
. Therefore, we focus our attention exclusively on the sequence
![]() $(B(n))_{n\in\mathbb{N}}$
.
$(B(n))_{n\in\mathbb{N}}$
.
The approach we use to investigate
![]() $(B_j(n))_{n\geq 0}$
,
$(B_j(n))_{n\geq 0}$
,
![]() $j\in [J]$
, is to embed it into a multitype discrete-time branching process
$j\in [J]$
, is to embed it into a multitype discrete-time branching process
![]() $(Z_n)_{n\in\mathbb{N}}$
with offspring distribution matrix L. A similar approach using the Athreya–Karlin embedding allowed Janson [Reference Janson5] to study
$(Z_n)_{n\in\mathbb{N}}$
with offspring distribution matrix L. A similar approach using the Athreya–Karlin embedding allowed Janson [Reference Janson5] to study
![]() $(B^\circ_j(n))_{n\geq 0}$
for the Pólya urn model. One difference between our model and the one in [Reference Janson5] is that, in the latter, the process is embedded into a multitype continuous-time Markov branching process, and an individual reproduces after an exponential clock rings. In our model, in the embedded branching process, an individual reproduces after deterministic time 1. The lattice nature of the model manifests itself in the second-order behavior of
$(B^\circ_j(n))_{n\geq 0}$
for the Pólya urn model. One difference between our model and the one in [Reference Janson5] is that, in the latter, the process is embedded into a multitype continuous-time Markov branching process, and an individual reproduces after an exponential clock rings. In our model, in the embedded branching process, an individual reproduces after deterministic time 1. The lattice nature of the model manifests itself in the second-order behavior of
![]() $(B_{j}(n))_{n\geq 0}$
.
$(B_{j}(n))_{n\geq 0}$
.
Assumptions. In this work we use the following assumptions:
-
(GW1) The matrix A has spectral radius
 $\rho>1$
.
$\rho>1$
. -
(GW2) The matrix A is positively regular.
-
(GW3) We have
 $\textbf{0}\neq \sum_{j=1}^J\textrm{Cov}\left[L^{(j)}\right]$
and
$\textbf{0}\neq \sum_{j=1}^J\textrm{Cov}\left[L^{(j)}\right]$
and
 $\textrm{Var}[L^{(i,j)}]<\infty$
for all
$\textrm{Var}[L^{(i,j)}]<\infty$
for all
 $i,j\in[J]$
.
$i,j\in[J]$
. -
(GW4) For every
 $i,j\in[J]$
, the expectation
$i,j\in[J]$
, the expectation
 $\mathbb{E}[ L^{(i,j)}\log L^{(i,j)}]$
is finite.
$\mathbb{E}[ L^{(i,j)}\log L^{(i,j)}]$
is finite.
In the third condition above,
![]() $\textbf{0}$
is the
$\textbf{0}$
is the
![]() $J\times J$
zero matrix, and for
$J\times J$
zero matrix, and for
![]() $j\in[J], \textrm{Cov}\left[L^{(j)}\right]$
represents the
$j\in[J], \textrm{Cov}\left[L^{(j)}\right]$
represents the
![]() $J \times J$
covariance matrix of the vector
$J \times J$
covariance matrix of the vector
![]() $L^{(j)}$
. If the matrix A is irreducible, the Perron–Frobenius theorem ensures that the dominant eigenvalue
$L^{(j)}$
. If the matrix A is irreducible, the Perron–Frobenius theorem ensures that the dominant eigenvalue
![]() $\rho$
of A is real, positive, and simple. If
$\rho$
of A is real, positive, and simple. If
![]() $\rho>1$
, this means that the multitype branching process with offspring distribution matrix L is supercritical, i.e.
$\rho>1$
, this means that the multitype branching process with offspring distribution matrix L is supercritical, i.e.
![]() $\mathbb{P}(\mathcal S)>0$
. If
$\mathbb{P}(\mathcal S)>0$
. If
![]() $\textrm u$
is the corresponding eigenvector for
$\textrm u$
is the corresponding eigenvector for
![]() $\rho$
, then clearly all the entries
$\rho$
, then clearly all the entries
![]() $\textrm u_j$
are strictly greater than zero for any
$\textrm u_j$
are strictly greater than zero for any
![]() $j\in[J]$
, and we assume that
$j\in[J]$
, and we assume that
![]() $\textrm u$
is normalized in such a way that
$\textrm u$
is normalized in such a way that
![]() $\sum_{j\in[J]}\textrm u_j=1$
. First-order asymptotics of
$\sum_{j\in[J]}\textrm u_j=1$
. First-order asymptotics of
![]() $B_j(n)$
,
$B_j(n)$
,
![]() $j\in[J]$
, are determined by
$j\in[J]$
, are determined by
![]() $\rho$
and the vector
$\rho$
and the vector
![]() $\textrm u$
.
$\textrm u$
.
Theorem 1. Assume (GW1), (GW2), and (GW4) hold. Then for any
![]() $j\in [J]$
we have the following strong law of large numbers for the total number of balls of type j after n draws:
$j\in [J]$
we have the following strong law of large numbers for the total number of balls of type j after n draws:
Thus, the first-order behavior of
![]() $B_j(n)$
,
$B_j(n)$
,
![]() $j\in [J]$
resembles the first-order behavior of
$j\in [J]$
resembles the first-order behavior of
![]() $B^\circ_j(n)$
from the model with one urn [Reference Janson5]. In order to understand the second-order asymptotics of
$B^\circ_j(n)$
from the model with one urn [Reference Janson5]. In order to understand the second-order asymptotics of
![]() $B_j(n)$
, we need full information on the spectral decomposition of the mean replacement matrix A. We denote by
$B_j(n)$
, we need full information on the spectral decomposition of the mean replacement matrix A. We denote by
![]() $\sigma_A$
the spectrum of the matrix A and define
$\sigma_A$
the spectrum of the matrix A and define
![]() $\sigma_A^1=\{\lambda\in\sigma_A\;:\;\ |\lambda|>\sqrt{\rho}\}$
,
$\sigma_A^1=\{\lambda\in\sigma_A\;:\;\ |\lambda|>\sqrt{\rho}\}$
,
![]() $\sigma_A^2=\{\lambda\in\sigma_A\;:\;\ |\lambda|=\sqrt{\rho}\}$
, and finally
$\sigma_A^2=\{\lambda\in\sigma_A\;:\;\ |\lambda|=\sqrt{\rho}\}$
, and finally
![]() $\sigma_A^3=\{\lambda\in\sigma_A\;:\;\ |\lambda|<\sqrt{\rho}\}$
. Then we can write
$\sigma_A^3=\{\lambda\in\sigma_A\;:\;\ |\lambda|<\sqrt{\rho}\}$
. Then we can write
For a simple eigenvalue
![]() $\lambda\in\sigma_A$
, we denote by
$\lambda\in\sigma_A$
, we denote by
![]() $\textrm u^\lambda$
and
$\textrm u^\lambda$
and
![]() $\textrm v^\lambda$
the corresponding left and right eigenvectors. We set
$\textrm v^\lambda$
the corresponding left and right eigenvectors. We set
so
![]() $\rho-\gamma$
is the spectral gap of A, and
$\rho-\gamma$
is the spectral gap of A, and
![]() $\Gamma$
is the set of eigenvalues of A where the spectral gap is achieved. For a complex number z we set
$\Gamma$
is the set of eigenvalues of A where the spectral gap is achieved. For a complex number z we set
![]() $\log_\rho z=\frac{\log z}{\log \rho},$
where
$\log_\rho z=\frac{\log z}{\log \rho},$
where
![]() $z\mapsto\log z$
is the principal branch of the natural logarithm. Denote by
$z\mapsto\log z$
is the principal branch of the natural logarithm. Denote by
![]() $\{\textrm e_j\}_{j\in[J]}$
the standard basis vectors in
$\{\textrm e_j\}_{j\in[J]}$
the standard basis vectors in
![]() $\mathbb{R}^J$
. For
$\mathbb{R}^J$
. For
![]() $j\in [J]$
, consider the following row vector in
$j\in [J]$
, consider the following row vector in
![]() $\mathbb{R}^{1\times J}$
:
$\mathbb{R}^{1\times J}$
:
where the ith entry is
![]() $\textrm{w}_{ji}=a_{ji}-\rho\textrm{u}_j=\mathbb{E}[L^{(i,j)}]-\rho\textrm{u}_j$
, for
$\textrm{w}_{ji}=a_{ji}-\rho\textrm{u}_j=\mathbb{E}[L^{(i,j)}]-\rho\textrm{u}_j$
, for
![]() $1\leq i\leq J$
. In the above equation, 1 denotes the vector in
$1\leq i\leq J$
. In the above equation, 1 denotes the vector in
![]() $\mathbb{R}^{1\times J}$
with all entries equal to one. Our main result provides the second-order behavior of
$\mathbb{R}^{1\times J}$
with all entries equal to one. Our main result provides the second-order behavior of
![]() $(B_j(n))_{n\in \mathbb{N}}$
.
$(B_j(n))_{n\in \mathbb{N}}$
.
Theorem 2. Assume that (GW1)–(GW3) hold, all
![]() $\lambda\in\Gamma$
are simple, and there exists
$\lambda\in\Gamma$
are simple, and there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\mathbb{E}\big[\big(L^{(i,j)}\big)^{2+\delta}\big]<\infty$
for all
$\mathbb{E}\big[\big(L^{(i,j)}\big)^{2+\delta}\big]<\infty$
for all
![]() $i,j\in[J]$
. Then for any
$i,j\in[J]$
. Then for any
![]() $j\in[J]$
the following trichotomy holds:
$j\in[J]$
the following trichotomy holds:
-
(i) If
 $\gamma>\sqrt \rho$
, then for any
$\gamma>\sqrt \rho$
, then for any
 $\lambda\in\Gamma$
there exist a 1-periodic, continuous function
$\lambda\in\Gamma$
there exist a 1-periodic, continuous function
 $f_\lambda\;:\;\mathbb{R}\to\mathbb{C}$
and random variables
$f_\lambda\;:\;\mathbb{R}\to\mathbb{C}$
and random variables
 $X,X_\lambda$
such that the following holds:
$X,X_\lambda$
such that the following holds:  \begin{align*}B_j(n)=\rho \textrm u_j \cdot n+\sum_{\lambda\in \Gamma}n^{\log_\rho\lambda}f_\lambda(\log_\rho n-X)X_\lambda+o_{\mathbb{P}}\big(n^{\log_\rho\gamma}\big).\end{align*}
\begin{align*}B_j(n)=\rho \textrm u_j \cdot n+\sum_{\lambda\in \Gamma}n^{\log_\rho\lambda}f_\lambda(\log_\rho n-X)X_\lambda+o_{\mathbb{P}}\big(n^{\log_\rho\gamma}\big).\end{align*}
-
(ii) If
 $\gamma = \sqrt \rho$
and for some
$\gamma = \sqrt \rho$
and for some
 $\lambda\in\sigma^{2}_A$
and
$\lambda\in\sigma^{2}_A$
and
 $i\in[J]$
we have
$i\in[J]$
we have
 $\textrm{w}_j\textrm u^\lambda\neq0$
and
$\textrm{w}_j\textrm u^\lambda\neq0$
and
 $\textrm{Var}[\textrm v^\lambda L\textrm{e}_i]>0$
for
$\textrm{Var}[\textrm v^\lambda L\textrm{e}_i]>0$
for
 $\textrm{w}_j$
defined as in (1), then there exist a 1-periodic, continuous function
$\textrm{w}_j$
defined as in (1), then there exist a 1-periodic, continuous function
 $\psi\;:\;\mathbb{R}\to(0,\infty)$
and a random variable X such that, conditionally on
$\psi\;:\;\mathbb{R}\to(0,\infty)$
and a random variable X such that, conditionally on
 $\mathcal{S}$
, the following convergence in distribution holds:
$\mathcal{S}$
, the following convergence in distribution holds:  \begin{align*}\frac{B_j(n)-\rho \textrm u_j\cdot n}{\sqrt {n\log_{\rho} n}\ \psi(\log_\rho n-X)}\xrightarrow{\scriptscriptstyle{\textrm{d}}} \mathcal{N}(0,1),\qquad \text{as }n\to\infty.\end{align*}
\begin{align*}\frac{B_j(n)-\rho \textrm u_j\cdot n}{\sqrt {n\log_{\rho} n}\ \psi(\log_\rho n-X)}\xrightarrow{\scriptscriptstyle{\textrm{d}}} \mathcal{N}(0,1),\qquad \text{as }n\to\infty.\end{align*}
-
(iii) If
 $\gamma < \sqrt \rho$
and for some
$\gamma < \sqrt \rho$
and for some
 $\lambda\in\sigma^{3}_A$
and some
$\lambda\in\sigma^{3}_A$
and some
 $i\in[J]$
we have
$i\in[J]$
we have
 $\textrm{w}_j\textrm u^\lambda\neq0$
and
$\textrm{w}_j\textrm u^\lambda\neq0$
and
 $\textrm{Var}[\textrm v^\lambda L\textrm{e}_i]>0$
with
$\textrm{Var}[\textrm v^\lambda L\textrm{e}_i]>0$
with
 $\textrm{w}_j$
defined as in (1), then there exist a 1-periodic, continuous function
$\textrm{w}_j$
defined as in (1), then there exist a 1-periodic, continuous function
 $\psi\;:\;\mathbb{R}\to(0,\infty)$
and a random variable X such that, conditionally on
$\psi\;:\;\mathbb{R}\to(0,\infty)$
and a random variable X such that, conditionally on
 $\mathcal{S}$
, the following convergence in distribution holds:
$\mathcal{S}$
, the following convergence in distribution holds:  \begin{align*}\frac{B_j(n)-\rho \textrm u_j\cdot n}{\sqrt n\ \psi(\log_\rho n-X)}\xrightarrow{\scriptscriptstyle{\textrm{d}}} \mathcal{N}(0,1),\qquad \text{as }n\to\infty.\end{align*}
\begin{align*}\frac{B_j(n)-\rho \textrm u_j\cdot n}{\sqrt n\ \psi(\log_\rho n-X)}\xrightarrow{\scriptscriptstyle{\textrm{d}}} \mathcal{N}(0,1),\qquad \text{as }n\to\infty.\end{align*}
A more general and quantified result where the periodic functions are explicitly defined is provided in Theorem 4.
Note that the result above slightly differs from that of the one-urn model, where the functions
![]() $\psi$
and
$\psi$
and
![]() $f_\lambda$
are actually constants. What might be even more surprising is that, in our model, the phase transition occurs at
$f_\lambda$
are actually constants. What might be even more surprising is that, in our model, the phase transition occurs at
![]() $\sqrt{\rho}$
rather than at
$\sqrt{\rho}$
rather than at
![]() $\rho/2$
as observed in the Pólya urn model. The heuristic explanation is as follows: the growth in mean of the corresponding continuous-time branching process is driven by the semigroup
$\rho/2$
as observed in the Pólya urn model. The heuristic explanation is as follows: the growth in mean of the corresponding continuous-time branching process is driven by the semigroup
![]() $e^{tA}$
. In particular, the leading asymptotic is
$e^{tA}$
. In particular, the leading asymptotic is
![]() $e^{t\rho}$
and the next order is
$e^{t\rho}$
and the next order is
![]() $|e^{t \lambda_2}|=e^{t \textrm{Re}\lambda_2}$
. We anticipate observing Gaussian fluctuations in the branching process at the scale
$|e^{t \lambda_2}|=e^{t \textrm{Re}\lambda_2}$
. We anticipate observing Gaussian fluctuations in the branching process at the scale
![]() $\sqrt{e^{t\rho}}$
(with possible polynomial corrections), providing a natural threshold for
$\sqrt{e^{t\rho}}$
(with possible polynomial corrections), providing a natural threshold for
![]() $\textrm{Re}\lambda_2$
in relation to
$\textrm{Re}\lambda_2$
in relation to
![]() $\rho/2$
. On the other hand, the two-urn model is embedded into a discrete-time branching process whose growth in the mean is driven by the semigroup
$\rho/2$
. On the other hand, the two-urn model is embedded into a discrete-time branching process whose growth in the mean is driven by the semigroup
![]() $A^n$
(or
$A^n$
(or
![]() $(I+A)^n$
in the model with no replacement). Thus, the leading term is at scale
$(I+A)^n$
in the model with no replacement). Thus, the leading term is at scale
![]() $\rho^n$
and the subleading term is at scale
$\rho^n$
and the subleading term is at scale
![]() $|\lambda_2|^n$
. As before, we expect to observe Gaussian fluctuations at scale
$|\lambda_2|^n$
. As before, we expect to observe Gaussian fluctuations at scale
![]() $\sqrt{\rho^n}$
, which induce natural distinctions depending on the relative locations of
$\sqrt{\rho^n}$
, which induce natural distinctions depending on the relative locations of
![]() $|\lambda_2|$
and
$|\lambda_2|$
and
![]() $\sqrt{\rho}$
.
$\sqrt{\rho}$
.
Structure of the paper. In Section 2 we introduce multitype branching processes
![]() $(Z_n)_{n\in\mathbb{N}}$
and Crump–Mode–Jagers processes
$(Z_n)_{n\in\mathbb{N}}$
and Crump–Mode–Jagers processes
![]() $(Z_n^{\Phi})_{n\in\mathbb{N}}$
counted with a characteristic
$(Z_n^{\Phi})_{n\in\mathbb{N}}$
counted with a characteristic
![]() $\Phi\;:\;\mathbb{Z}\to \mathbb{R}^{1\times J}$
. Then in Section 3 we show how to relate our model
$\Phi\;:\;\mathbb{Z}\to \mathbb{R}^{1\times J}$
. Then in Section 3 we show how to relate our model
![]() $(B_j(n))$
, with two interacting urns, to a branching process
$(B_j(n))$
, with two interacting urns, to a branching process
![]() $(Z^{\Phi^j}_n)_{n\in \mathbb{N}}$
counted with a characteristic
$(Z^{\Phi^j}_n)_{n\in \mathbb{N}}$
counted with a characteristic
![]() $\Phi^j$
. By applying [Reference Kolesko and Sava-Huss8, Proposition 4.1] to
$\Phi^j$
. By applying [Reference Kolesko and Sava-Huss8, Proposition 4.1] to
![]() $(Z^{\Phi^j}_n)_{n\in\mathbb{N}}$
, we then obtain first-order asymptotics of
$(Z^{\Phi^j}_n)_{n\in\mathbb{N}}$
, we then obtain first-order asymptotics of
![]() $(B_j(n))_{n\in\mathbb{N}}$
for any
$(B_j(n))_{n\in\mathbb{N}}$
for any
![]() $j\in[J]$
(Theorem 1). The main result is proved in Section 4. We conclude with Appendix A, where the model with two interacting urns is illustrated by an example with deterministic replacement matrix, and Appendix B, where higher-moment estimates for
$j\in[J]$
(Theorem 1). The main result is proved in Section 4. We conclude with Appendix A, where the model with two interacting urns is illustrated by an example with deterministic replacement matrix, and Appendix B, where higher-moment estimates for
![]() $(Z_n^{\Phi})$
are given for general characteristics
$(Z_n^{\Phi})$
are given for general characteristics
![]() $\Phi$
.
$\Phi$
.
2. Preliminaries
For the rest of the paper,
![]() $(\Omega,\mathcal{A},\mathbb{P})$
is a probability space on which all the random variables and processes we consider are defined. We write
$(\Omega,\mathcal{A},\mathbb{P})$
is a probability space on which all the random variables and processes we consider are defined. We write
![]() $\xrightarrow{\scriptscriptstyle{a.s.}}$
for almost sure convergence,
$\xrightarrow{\scriptscriptstyle{a.s.}}$
for almost sure convergence,
![]() $\xrightarrow{\scriptscriptstyle{\mathbb{P}}}$
for convergence in probability,
$\xrightarrow{\scriptscriptstyle{\mathbb{P}}}$
for convergence in probability,
![]() $\xrightarrow{\scriptscriptstyle{\textrm{d}}}$
for convergence in distribution, and
$\xrightarrow{\scriptscriptstyle{\textrm{d}}}$
for convergence in distribution, and
![]() $\xrightarrow{\scriptscriptstyle{\textrm{st}}}$
for stable convergence (cf. [Reference Aldous and Eagleson1] for the definition and properties). We also use
$\xrightarrow{\scriptscriptstyle{\textrm{st}}}$
for stable convergence (cf. [Reference Aldous and Eagleson1] for the definition and properties). We also use
![]() $\mathbb{P}^\mathcal{S}$
to denote the conditional probability
$\mathbb{P}^\mathcal{S}$
to denote the conditional probability
![]() $\mathbb{P}[\cdot|\mathcal{S}]$
, and the corresponding convergences are denoted by
$\mathbb{P}[\cdot|\mathcal{S}]$
, and the corresponding convergences are denoted by
![]() $\xrightarrow{\scriptscriptstyle{\mathbb{P}^\mathcal{S}}},\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}},\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}}$
. We use the notation
$\xrightarrow{\scriptscriptstyle{\mathbb{P}^\mathcal{S}}},\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}},\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}}$
. We use the notation
![]() $\mathbb{N} =\{1,2,\ldots,\}$
and
$\mathbb{N} =\{1,2,\ldots,\}$
and
![]() $\mathbb{N}_0 =\{0,1,2,\ldots,\}$
.
$\mathbb{N}_0 =\{0,1,2,\ldots,\}$
.
Stochastic processes. Our convergence results for stochastic processes use the usual space
![]() $\mathcal{D}$
of right-continuous functions with left-hand limits, always equipped with the Skorokhod
$\mathcal{D}$
of right-continuous functions with left-hand limits, always equipped with the Skorokhod
![]() $\textbf{J}_1$
topology. For a finite-dimensional vector space E and any interval
$\textbf{J}_1$
topology. For a finite-dimensional vector space E and any interval
![]() $J\subseteq [-\infty,\infty]$
, we denote by
$J\subseteq [-\infty,\infty]$
, we denote by
![]() $\mathcal{D}(J)=\mathcal{D}(J,E)$
the space of all right-continuous functions from J to E with left-hand limits.
$\mathcal{D}(J)=\mathcal{D}(J,E)$
the space of all right-continuous functions from J to E with left-hand limits.
For an
![]() $n\times m$
matrix
$n\times m$
matrix
![]() $A=(a_{ij})_{i,j}$
with
$A=(a_{ij})_{i,j}$
with
![]() $m,n\in\mathbb{N}$
, the Hilbert–Schmidt norm of A, also called the Frobenius norm, is defined as
$m,n\in\mathbb{N}$
, the Hilbert–Schmidt norm of A, also called the Frobenius norm, is defined as
 \begin{align*}\|A\|_{HS}=\Big(\sum_{i=1}^n\sum_{j=1} ^m|a_{ij}|^2\Big)^{1/2}.\end{align*}
\begin{align*}\|A\|_{HS}=\Big(\sum_{i=1}^n\sum_{j=1} ^m|a_{ij}|^2\Big)^{1/2}.\end{align*}
Since for any vector its Hilbert–Schmidt norm coincides with its Euclidean norm, for the rest of the paper we write only
![]() $\|\cdot\|$
instead of
$\|\cdot\|$
instead of
![]() $\|\cdot\|_{HS}$
.
$\|\cdot\|_{HS}$
.
Ulam–Harris tree
![]() $\mathcal{U}_{\infty}$
. An Ulam–Harris tree
$\mathcal{U}_{\infty}$
. An Ulam–Harris tree
![]() $\mathcal{U}_{\infty}$
is an infinite rooted tree with vertex set
$\mathcal{U}_{\infty}$
is an infinite rooted tree with vertex set
![]() $V_{\infty}= \bigcup_{n \in \mathbb{N}_0} \mathbb{N}^n$
, the set of all finite strings or words
$V_{\infty}= \bigcup_{n \in \mathbb{N}_0} \mathbb{N}^n$
, the set of all finite strings or words
![]() $i_1\cdots i_n$
of positive integers over n letters, including the empty word
$i_1\cdots i_n$
of positive integers over n letters, including the empty word
![]() $\varnothing$
(which we take to be the root), and with an edge joining
$\varnothing$
(which we take to be the root), and with an edge joining
![]() $i_1\cdots i_n$
and
$i_1\cdots i_n$
and
![]() $i_1\cdots i_{n+1}$
for any
$i_1\cdots i_{n+1}$
for any
![]() $n\in \mathbb{N}_0$
and any
$n\in \mathbb{N}_0$
and any
![]() $i_1, \cdots, i_{n+1}\in \mathbb{N}$
. Thus every vertex
$i_1, \cdots, i_{n+1}\in \mathbb{N}$
. Thus every vertex
![]() $v=i_1\cdots i_n$
has outdegree
$v=i_1\cdots i_n$
has outdegree
![]() $\infty$
, and the children of v are the words
$\infty$
, and the children of v are the words
![]() $v1,v2,\ldots$
. We let them have this order so that
$v1,v2,\ldots$
. We let them have this order so that
![]() $\mathcal{U}_{\infty}$
becomes an infinite ordered rooted tree. We will identify
$\mathcal{U}_{\infty}$
becomes an infinite ordered rooted tree. We will identify
![]() $\mathcal{U}_{\infty}$
with its vertex set
$\mathcal{U}_{\infty}$
with its vertex set
![]() $V_{\infty}$
, when there is no risk of confusion in doing so. For vertices
$V_{\infty}$
, when there is no risk of confusion in doing so. For vertices
![]() $v=i_1\cdots i_n$
we also write
$v=i_1\cdots i_n$
we also write
![]() $v=(i_1,\ldots,i_n)$
, and if
$v=(i_1,\ldots,i_n)$
, and if
![]() $u=(j_1,\ldots,j_m)$
we write uv for the concatenation of the words u and v; that is,
$u=(j_1,\ldots,j_m)$
we write uv for the concatenation of the words u and v; that is,
![]() $uv=(j_1,\ldots,j_m,i_1,\ldots,i_n)$
. The parent of
$uv=(j_1,\ldots,j_m,i_1,\ldots,i_n)$
. The parent of
![]() $i_1\cdots i_n$
is
$i_1\cdots i_n$
is
![]() $i_1\cdots i_{n-1}$
. Finally, for
$i_1\cdots i_{n-1}$
. Finally, for
![]() $u \in \mathcal{U}_{\infty}$
, we use the notation
$u \in \mathcal{U}_{\infty}$
, we use the notation
![]() $|u|=n$
to mean
$|u|=n$
to mean
![]() $u \in\mathbb{N}^n$
(i.e. u is a word of length (or height) n; in other words, it is at distance n from the root
$u \in\mathbb{N}^n$
(i.e. u is a word of length (or height) n; in other words, it is at distance n from the root
![]() $\varnothing$
). For any
$\varnothing$
). For any
![]() $u\in V_{\infty}$
, by
$u\in V_{\infty}$
, by
![]() $\mathbb{T}_u$
we mean the subtree of
$\mathbb{T}_u$
we mean the subtree of
![]() $\mathcal{U}_{\infty}$
rooted at u, that is, u together with all infinite paths going away from u, and for
$\mathcal{U}_{\infty}$
rooted at u, that is, u together with all infinite paths going away from u, and for
![]() $u,v\in \mathcal{U}_{\infty}$
we denote by d(u, v) their graph distance. For trees rooted at
$u,v\in \mathcal{U}_{\infty}$
we denote by d(u, v) their graph distance. For trees rooted at
![]() $\varnothing$
, we omit the root and we write only
$\varnothing$
, we omit the root and we write only
![]() $\mathbb{T}$
. For
$\mathbb{T}$
. For
![]() $J\in \mathbb{N}$
, a J-type tree is a pair
$J\in \mathbb{N}$
, a J-type tree is a pair
![]() $(\mathbb{T},\textrm t)$
where
$(\mathbb{T},\textrm t)$
where
![]() $\mathbb{T}$
is a rooted subtree of
$\mathbb{T}$
is a rooted subtree of
![]() $\mathcal{U}_{\infty}$
and
$\mathcal{U}_{\infty}$
and
![]() $\textrm t\;:\;\mathbb{T}\to\{1,\ldots,J\}$
is a function defined on the vertices of
$\textrm t\;:\;\mathbb{T}\to\{1,\ldots,J\}$
is a function defined on the vertices of
![]() $\mathbb{T}$
that returns for each vertex v its type
$\mathbb{T}$
that returns for each vertex v its type
![]() $\textrm t(v)$
.
$\textrm t(v)$
.
Multitype branching processes. Consider the random
![]() $J\times J$
matrix L with independent column vectors
$J\times J$
matrix L with independent column vectors
![]() $L^{(j)}$
, for
$L^{(j)}$
, for
![]() $1\leq j\leq J$
, as in the introduction. Multitype Galton–Watson trees are random variables taking values in the set of J-type trees
$1\leq j\leq J$
, as in the introduction. Multitype Galton–Watson trees are random variables taking values in the set of J-type trees
![]() $(\mathbb{T},\textrm t)$
, where the type function
$(\mathbb{T},\textrm t)$
, where the type function
![]() $\textrm t$
is random and defined in terms of the matrix L. Let
$\textrm t$
is random and defined in terms of the matrix L. Let
![]() $(L(u))_{u\in \mathcal{U}_{\infty}}$
be a family of independent and identically distributed (i.i.d.) copies of L indexed over the vertices of
$(L(u))_{u\in \mathcal{U}_{\infty}}$
be a family of independent and identically distributed (i.i.d.) copies of L indexed over the vertices of
![]() $\mathcal{U}_{\infty}$
. For any
$\mathcal{U}_{\infty}$
. For any
![]() $i\in [J]$
, we define recursively the random labeled tree
$i\in [J]$
, we define recursively the random labeled tree
![]() $\mathbb{T}^{i}$
rooted at
$\mathbb{T}^{i}$
rooted at
![]() $\varnothing$
, with the associated type function
$\varnothing$
, with the associated type function
![]() $\textrm t=\textrm t^{i}\;:\;\mathbb{T}^{i}\to \{1,\ldots,J\}$
, as follows:
$\textrm t=\textrm t^{i}\;:\;\mathbb{T}^{i}\to \{1,\ldots,J\}$
, as follows:
![]() $\varnothing\in\mathbb{T}^{i}$
and
$\varnothing\in\mathbb{T}^{i}$
and
![]() $\textrm t(\varnothing)=i$
. Now suppose that
$\textrm t(\varnothing)=i$
. Now suppose that
![]() $u=j_1\ldots j_m\in\mathbb{T}^{i}$
with
$u=j_1\ldots j_m\in\mathbb{T}^{i}$
with
![]() $\textrm t(u)=j$
, for some
$\textrm t(u)=j$
, for some
![]() $j\in[J]$
. Then
$j\in[J]$
. Then
and we set
![]() $\textrm{t}(u k)=\ell$
whenever
$\textrm{t}(u k)=\ell$
whenever
The multitype branching process
![]() $Z_n=(Z^1_n, \ldots , Z^J_n)$
associated with the pair
$Z_n=(Z^1_n, \ldots , Z^J_n)$
associated with the pair
![]() $(\mathbb{T}^{i_0},\textrm t)$
, and starting from a single particle (or individual) of type
$(\mathbb{T}^{i_0},\textrm t)$
, and starting from a single particle (or individual) of type
![]() $i_0\in [ J]$
at the root
$i_0\in [ J]$
at the root
![]() $\varnothing$
(i.e.,
$\varnothing$
(i.e.,
![]() $\textrm t(\varnothing)=i_0$
) is defined as follows:
$\textrm t(\varnothing)=i_0$
) is defined as follows:
![]() $Z_0=\textrm{e}_{i_0} $
, and for
$Z_0=\textrm{e}_{i_0} $
, and for
![]() $n\geq 1$
,
$n\geq 1$
,
so
![]() $Z_n^i$
represents the number of individuals of type i in the nth generation, or the number of vertices
$Z_n^i$
represents the number of individuals of type i in the nth generation, or the number of vertices
![]() $u\in \mathbb{T}^{i_0}$
with
$u\in \mathbb{T}^{i_0}$
with
![]() $|u|=n$
and
$|u|=n$
and
![]() $\textrm t(u)=i$
. The main results of [Reference Kolesko and Sava-Huss8] that we use in the current paper hold under the assumptions (GW1)–(GW3) on
$\textrm t(u)=i$
. The main results of [Reference Kolesko and Sava-Huss8] that we use in the current paper hold under the assumptions (GW1)–(GW3) on
![]() $(Z_n)_{n\in \mathbb{N}}$
, which we suppose to hold here as well. In particular,
$(Z_n)_{n\in \mathbb{N}}$
, which we suppose to hold here as well. In particular,
![]() $(Z_n)_{n\in\mathbb{N}}$
is a supercritical branching process.
$(Z_n)_{n\in\mathbb{N}}$
is a supercritical branching process.
Spectral decomposition of
A
. Recall the decomposition of the spectrum
![]() $\sigma_A$
of the matrix A as
$\sigma_A$
of the matrix A as
![]() $\sigma_A=\sigma_A^{1}\cup\sigma_A^{2}\cup\sigma_A^{3}$
. From the Jordan–Chevalley decomposition of A (which is unique up to the order of the Jordan blocks) we infer the existence of projections
$\sigma_A=\sigma_A^{1}\cup\sigma_A^{2}\cup\sigma_A^{3}$
. From the Jordan–Chevalley decomposition of A (which is unique up to the order of the Jordan blocks) we infer the existence of projections
![]() $(\pi_\lambda)_{\lambda\in \sigma_A}$
that commute with A and satisfy
$(\pi_\lambda)_{\lambda\in \sigma_A}$
that commute with A and satisfy
![]() $\sum_{\lambda\in\sigma_A}\pi_{\lambda}=I$
and
$\sum_{\lambda\in\sigma_A}\pi_{\lambda}=I$
and
where
![]() $N_{\lambda}=\pi_{\lambda}N_{\lambda}=N_{\lambda}\pi_{\lambda}$
is a nilpotent matrix. Moreover, for any
$N_{\lambda}=\pi_{\lambda}N_{\lambda}=N_{\lambda}\pi_{\lambda}$
is a nilpotent matrix. Moreover, for any
![]() $\lambda_1,\lambda_2\in\sigma_A$
it holds that
$\lambda_1,\lambda_2\in\sigma_A$
it holds that
![]() $\pi_{\lambda_1}\pi_{\lambda_2}=\pi_{\lambda_1}\textbf{1}_{\{\lambda_1=\lambda_2\}}$
. If
$\pi_{\lambda_1}\pi_{\lambda_2}=\pi_{\lambda_1}\textbf{1}_{\{\lambda_1=\lambda_2\}}$
. If
![]() $\lambda\in\sigma_A$
is a simple eigenvalue of A and
$\lambda\in\sigma_A$
is a simple eigenvalue of A and
![]() $\textrm u^\lambda, \textrm v^\lambda$
are the corresponding left and right eigenvectors, normalized in such a way that
$\textrm u^\lambda, \textrm v^\lambda$
are the corresponding left and right eigenvectors, normalized in such a way that
![]() $\textrm v^\lambda\textrm u^\lambda=1$
, then
$\textrm v^\lambda\textrm u^\lambda=1$
, then
![]() $\pi_\lambda=\textrm u^\lambda\textrm v^\lambda$
. If we write
$\pi_\lambda=\textrm u^\lambda\textrm v^\lambda$
. If we write
![]() $N=\sum_{\lambda\in\sigma_A}N_{\lambda}$
, then N is also a nilpotent matrix and we have
$N=\sum_{\lambda\in\sigma_A}N_{\lambda}$
, then N is also a nilpotent matrix and we have
![]() $N\pi_{\lambda}=N_{\lambda}$
. Thus A can be decomposed into its semisimple part
$N\pi_{\lambda}=N_{\lambda}$
. Thus A can be decomposed into its semisimple part
![]() $D=\sum_{\lambda\in\sigma_A}\lambda\pi_{\lambda}$
and a nilpotent part N, as
$D=\sum_{\lambda\in\sigma_A}\lambda\pi_{\lambda}$
and a nilpotent part N, as
![]() $A=D+N$
.
$A=D+N$
.
For any
![]() $\lambda\in\sigma_A$
, we denote by
$\lambda\in\sigma_A$
, we denote by
![]() $d_{\lambda}\geq 0$
the integer such that
$d_{\lambda}\geq 0$
the integer such that
![]() $N_{\lambda}^{d_{\lambda}}\neq 0$
but
$N_{\lambda}^{d_{\lambda}}\neq 0$
but
![]() $N_{\lambda}^{d_{\lambda}+1}=0$
(hence
$N_{\lambda}^{d_{\lambda}+1}=0$
(hence
![]() $d_{\lambda}+1$
is at most the multiplicity of
$d_{\lambda}+1$
is at most the multiplicity of
![]() $\lambda$
). So
$\lambda$
). So
![]() $d_{\lambda}=0$
if and only if
$d_{\lambda}=0$
if and only if
![]() $N_{\lambda}=0$
, and this happens for all
$N_{\lambda}=0$
, and this happens for all
![]() $\lambda$
if and only if A is diagonalizable (that is, A has a complete set of J independent eigenvectors). Since
$\lambda$
if and only if A is diagonalizable (that is, A has a complete set of J independent eigenvectors). Since
![]() $\rho$
is a simple eigenvalue, we have
$\rho$
is a simple eigenvalue, we have
![]() $N_{\rho}=0$
and
$N_{\rho}=0$
and
![]() $d_{\rho}=0$
, and
$d_{\rho}=0$
, and
![]() $\pi_{\rho}=\textrm u\textrm v$
. We set
$\pi_{\rho}=\textrm u\textrm v$
. We set
and for
![]() $i=1,2$
, we define
$i=1,2$
, we define
The process
![]() $\big(W_n^{(i)}\big)_{n\in \mathbb{N}}$
defined by
$\big(W_n^{(i)}\big)_{n\in \mathbb{N}}$
defined by
is a
![]() $\mathcal{A}_n$
-martingale, where
$\mathcal{A}_n$
-martingale, where
![]() $(\mathcal{A}_n)_{n\ge0}$
is the filtration
$(\mathcal{A}_n)_{n\ge0}$
is the filtration
![]() $\mathcal{A}_n=\sigma(\{L(u)\;:\;|u|\le n\})$
. According to [Reference Kolesko and Sava-Huss8, Lemma 2.2],
$\mathcal{A}_n=\sigma(\{L(u)\;:\;|u|\le n\})$
. According to [Reference Kolesko and Sava-Huss8, Lemma 2.2],
![]() $W_n^{(1)}$
converges in
$W_n^{(1)}$
converges in
![]() $\mathcal{L}^2(\Omega,\mathcal{A},\mathbb{P})$
to a random variable
$\mathcal{L}^2(\Omega,\mathcal{A},\mathbb{P})$
to a random variable
![]() $W^{(1)}$
whose expectation is
$W^{(1)}$
whose expectation is
![]() $\mathbb{E} W^{(1)}=\pi^{(1)}\textrm e_{i_0}$
. In particular, we have the convergence
$\mathbb{E} W^{(1)}=\pi^{(1)}\textrm e_{i_0}$
. In particular, we have the convergence
in
![]() $\mathcal{L}^2$
, and the random variable W is given by
$\mathcal{L}^2$
, and the random variable W is given by
![]() $W= \textrm v \cdot W^{(1)}$
with
$W= \textrm v \cdot W^{(1)}$
with
![]() $\mathbb{E} W=\textrm v^{i_0}>0$
. The classical Kesten–Stigum theorem [Reference Kesten and Stigum7] states that under (GW1), (GW2), and (GW4) the convergence above holds almost surely. For the rest of the paper, when we use the random variable W, we always mean the limit random variable from the Kesten–Stigum theorem.
$\mathbb{E} W=\textrm v^{i_0}>0$
. The classical Kesten–Stigum theorem [Reference Kesten and Stigum7] states that under (GW1), (GW2), and (GW4) the convergence above holds almost surely. For the rest of the paper, when we use the random variable W, we always mean the limit random variable from the Kesten–Stigum theorem.
2.1. Branching processes counted with a characteristic
We recall that a characteristic of dimension one is a function
![]() $\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
, so that for each
$\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
, so that for each
![]() $k\in \mathbb{Z}$
,
$k\in \mathbb{Z}$
,
![]() $\Phi(k)$
is an
$\Phi(k)$
is an
![]() $\mathbb{R}^{1\times J}$
-valued random variable defined on the same probability space
$\mathbb{R}^{1\times J}$
-valued random variable defined on the same probability space
![]() $(\Omega,\mathcal{A},\mathbb{P})$
where the Galton–Watson process
$(\Omega,\mathcal{A},\mathbb{P})$
where the Galton–Watson process
![]() $(Z_n)_{n\in\mathbb{N}}$
and its genealogical tree
$(Z_n)_{n\in\mathbb{N}}$
and its genealogical tree
![]() $\mathbb{T}$
are defined. A deterministic characteristic is just a fixed function
$\mathbb{T}$
are defined. A deterministic characteristic is just a fixed function
![]() $\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
. For a random function
$\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
. For a random function
![]() $\Phi\;:\;\mathbb{Z}\to \mathbb{R}^{1\times J}$
and the multitype Galton–Watson tree
$\Phi\;:\;\mathbb{Z}\to \mathbb{R}^{1\times J}$
and the multitype Galton–Watson tree
![]() $\mathbb{T}$
, the process
$\mathbb{T}$
, the process
![]() $(Z^\Phi_n)_{n\in \mathbb{N}}$
which for any
$(Z^\Phi_n)_{n\in \mathbb{N}}$
which for any
![]() $n\in\mathbb{N}$
is defined as
$n\in\mathbb{N}$
is defined as
is called the multitype Crump–Mode–Jagers (CMJ) process counted with characteristic
![]() $\Phi$
, or simply the branching process counted with characteristic
$\Phi$
, or simply the branching process counted with characteristic
![]() $\Phi$
, where
$\Phi$
, where
![]() $\left(\Phi_u\right)_{u\in\mathcal{U}_{\infty}}$
is an i.i.d. copy of
$\left(\Phi_u\right)_{u\in\mathcal{U}_{\infty}}$
is an i.i.d. copy of
![]() $\Phi$
. First- and second-order asymptotics for
$\Phi$
. First- and second-order asymptotics for
![]() $(Z^\Phi_n)_{n\in \mathbb{N}}$
, under mild assumptions on
$(Z^\Phi_n)_{n\in \mathbb{N}}$
, under mild assumptions on
![]() $\Phi$
, are considered in [Reference Kolesko and Sava-Huss8, Proposition 4.1] and in [Reference Kolesko and Sava-Huss8, Theorem 3.5], respectively. We use these two results below for a particular choice of the characteristic
$\Phi$
, are considered in [Reference Kolesko and Sava-Huss8, Proposition 4.1] and in [Reference Kolesko and Sava-Huss8, Theorem 3.5], respectively. We use these two results below for a particular choice of the characteristic
![]() $\Phi$
, and show how the branching process with this particular choice of characteristic can be related to the two-urn model with alternating urns
$\Phi$
, and show how the branching process with this particular choice of characteristic can be related to the two-urn model with alternating urns
![]() $\mathsf{U}_1$
and
$\mathsf{U}_1$
and
![]() $\mathsf{U}_2$
.
$\mathsf{U}_2$
.
The choice of the characteristic. Let
![]() $U\sim\mathsf{Unif}[0,1]$
be a uniform random variable taking values in [0,1] and defined on the probability space
$U\sim\mathsf{Unif}[0,1]$
be a uniform random variable taking values in [0,1] and defined on the probability space
![]() $(\Omega,\mathcal{A},\mathbb{P})$
. For every threshold
$(\Omega,\mathcal{A},\mathbb{P})$
. For every threshold
![]() $x\in[0,1)$
we define the characteristic
$x\in[0,1)$
we define the characteristic
![]() $\Phi^{\mathsf{t}}_{x}\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
by
$\Phi^{\mathsf{t}}_{x}\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
by
or, in a simplified way, for
![]() $1\leq i\leq J$
,
$1\leq i\leq J$
,
 \begin{equation*}\Phi_x^{\mathsf{t}}(k)\textrm{e}_i=\begin{cases}1,&\quad \text{for } k\geq 1,\\[5pt] 1 \text{ with probability } \mathbb{P}(U\leq x)=x,& \quad \text{for } k=0, \\[5pt] 0 \text{ with probability } \mathbb{P}(U> x)=1-x,& \quad \text{for } k=0.\end{cases}\end{equation*}
\begin{equation*}\Phi_x^{\mathsf{t}}(k)\textrm{e}_i=\begin{cases}1,&\quad \text{for } k\geq 1,\\[5pt] 1 \text{ with probability } \mathbb{P}(U\leq x)=x,& \quad \text{for } k=0, \\[5pt] 0 \text{ with probability } \mathbb{P}(U> x)=1-x,& \quad \text{for } k=0.\end{cases}\end{equation*}
Similarly, for
![]() $j\in[J]$
, we define
$j\in[J]$
, we define
![]() $\Phi_{x}^j\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
by
$\Phi_{x}^j\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
by
so
![]() $\Phi_x^j(k)\textrm{e}_i=\Phi^{\mathsf{t}}_x(k)\textrm{e}_i L^{(i,j)}$
. For the uniform random variable U on [0,1], let
$\Phi_x^j(k)\textrm{e}_i=\Phi^{\mathsf{t}}_x(k)\textrm{e}_i L^{(i,j)}$
. For the uniform random variable U on [0,1], let
![]() $(U_u)_{u\in\mathcal{U}_{\infty}}$
be an i.i.d. copy of U. For
$(U_u)_{u\in\mathcal{U}_{\infty}}$
be an i.i.d. copy of U. For
![]() $u\in \mathcal{U}_{\infty}$
, let
$u\in \mathcal{U}_{\infty}$
, let
![]() $ \Phi^{\mathsf{t}}_{x,u}$
(respectively
$ \Phi^{\mathsf{t}}_{x,u}$
(respectively
![]() $ \Phi^j_{x,u}$
) be defined through (2) (respectively (3)) with U, L being replaced by
$ \Phi^j_{x,u}$
) be defined through (2) (respectively (3)) with U, L being replaced by
![]() $U_u,\ L(u)$
. Then the family
$U_u,\ L(u)$
. Then the family
![]() $\big((L(u),\Phi^{\mathsf{t}}_{x,u},\Phi_{x,u}^j)\big)_{u\in \mathcal{U}_{\infty}}$
is an i.i.d. collection of copies of
$\big((L(u),\Phi^{\mathsf{t}}_{x,u},\Phi_{x,u}^j)\big)_{u\in \mathcal{U}_{\infty}}$
is an i.i.d. collection of copies of
![]() $(L,\Phi^{\mathsf{t}}_x,\Phi_x^j)$
, for
$(L,\Phi^{\mathsf{t}}_x,\Phi_x^j)$
, for
![]() $j\in [J]$
.
$j\in [J]$
.
For the characteristic
![]() $\Phi_x^{\mathsf{t}}$
from (2), threshold
$\Phi_x^{\mathsf{t}}$
from (2), threshold
![]() $x\in [0,1)$
, and multitype Galton–Watson tree
$x\in [0,1)$
, and multitype Galton–Watson tree
![]() $\mathbb{T}$
, the process
$\mathbb{T}$
, the process
![]() $\big(Z^{\Phi_x^{\mathsf{t}}}_n\big)_{n\geq 0}$
counts the total number of individuals
$\big(Z^{\Phi_x^{\mathsf{t}}}_n\big)_{n\geq 0}$
counts the total number of individuals
![]() $u\in \mathcal{U}_{\infty}$
born before time n (including the root), and those born at time n with
$u\in \mathcal{U}_{\infty}$
born before time n (including the root), and those born at time n with
![]() $U_u\le x$
, since we have
$U_u\le x$
, since we have
 \begin{align*}Z_n^{\Phi^{\mathsf{t}}_x}&=\sum_{u\in \mathbb{T}}\Phi^{\mathsf{t}}_{x,u}(n-|u|)\textrm{e}_{\textrm t(u)}=\sum_{k=0}^{n-1}\sum_{u\in \mathbb{T}; |u|=k}1+\sum_{u\in \mathbb{T}; \ |u|=n}\textbf{1}_{\{U_u\leq x\}}\\[5pt] &=\sum_{k=0}^{n-1}|Z_k|+\sum_{u\in \mathbb{T}; \ |u|=n}\textbf{1}_{\{U_u\leq x\}},\end{align*}
\begin{align*}Z_n^{\Phi^{\mathsf{t}}_x}&=\sum_{u\in \mathbb{T}}\Phi^{\mathsf{t}}_{x,u}(n-|u|)\textrm{e}_{\textrm t(u)}=\sum_{k=0}^{n-1}\sum_{u\in \mathbb{T}; |u|=k}1+\sum_{u\in \mathbb{T}; \ |u|=n}\textbf{1}_{\{U_u\leq x\}}\\[5pt] &=\sum_{k=0}^{n-1}|Z_k|+\sum_{u\in \mathbb{T}; \ |u|=n}\textbf{1}_{\{U_u\leq x\}},\end{align*}
where
![]() $|Z_n|=\sum_{j=1}^JZ_n^j$
represents the size of the nth generation of the Galton–Watson process. On the other hand,
$|Z_n|=\sum_{j=1}^JZ_n^j$
represents the size of the nth generation of the Galton–Watson process. On the other hand,
![]() $L\textrm e_i=L^{(i)}$
represents the random collection of individuals born from an individual of type i, while
$L\textrm e_i=L^{(i)}$
represents the random collection of individuals born from an individual of type i, while
![]() $L^{(i,j)}=\langle\textrm{e}_j,L\textrm{e}_i\rangle$
represents the random number of offspring of type j of an individual of type i for
$L^{(i,j)}=\langle\textrm{e}_j,L\textrm{e}_i\rangle$
represents the random number of offspring of type j of an individual of type i for
![]() $i,j\in[J]$
. Therefore
$i,j\in[J]$
. Therefore
![]() $Z_n^{\Phi_x^j}$
counts the number of individuals of type j born up to time n, and those of type j born at time
$Z_n^{\Phi_x^j}$
counts the number of individuals of type j born up to time n, and those of type j born at time
![]() $n+1$
but with threshold
$n+1$
but with threshold
![]() $\le x$
, so
$\le x$
, so
![]() $Z_n^{\Phi^j_x}$
can be written as
$Z_n^{\Phi^j_x}$
can be written as
 \begin{align*}Z_n^{\Phi^j_x}&=\sum_{k=0}^{n-1}\sum_{u\in\mathbb{T}; |u|=k}\langle\textrm{e}_j,L(u)\textrm{e}_{\textrm t(u)}\rangle+\sum_{u\in \mathbb{T};|u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
\begin{align*}Z_n^{\Phi^j_x}&=\sum_{k=0}^{n-1}\sum_{u\in\mathbb{T}; |u|=k}\langle\textrm{e}_j,L(u)\textrm{e}_{\textrm t(u)}\rangle+\sum_{u\in \mathbb{T};|u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
since
![]() $Z_{k+1}^j=\sum_{u\in \mathbb{T};|u|=k}\langle\textrm{e}_j,L(u)\textrm{e}_{\textrm t(u)}\rangle$
represents the number of offspring of type j in the
$Z_{k+1}^j=\sum_{u\in \mathbb{T};|u|=k}\langle\textrm{e}_j,L(u)\textrm{e}_{\textrm t(u)}\rangle$
represents the number of offspring of type j in the
![]() $(k+1)$
th generation and
$(k+1)$
th generation and
![]() $|\{u\in \mathbb{T};\;|u|=n+1,\textrm t(u)=j\}|=Z_{n+1}^j$
. Summing up over all
$|\{u\in \mathbb{T};\;|u|=n+1,\textrm t(u)=j\}|=Z_{n+1}^j$
. Summing up over all
![]() $j\in [J]$
gives
$j\in [J]$
gives
 \begin{align*}Z_{n+1}^{\Phi^{\mathsf{t}}_x}-1= \sum_{j=1}^J Z_n^{\Phi^j_x},\end{align*}
\begin{align*}Z_{n+1}^{\Phi^{\mathsf{t}}_x}-1= \sum_{j=1}^J Z_n^{\Phi^j_x},\end{align*}
and an application of [Reference Kolesko and Sava-Huss8, Proposition 4.1] to
![]() $Z_n^{\Phi^{\mathsf{t}}_x}$
and
$Z_n^{\Phi^{\mathsf{t}}_x}$
and
![]() $Z_n^{\Phi^j_x}$
, for
$Z_n^{\Phi^j_x}$
, for
![]() $j\in[J]$
, yields the law of large numbers.
$j\in[J]$
, yields the law of large numbers.
Proposition 1. Under the assumptions (GW1), (GW2), and (GW4), for any threshold
![]() $x\in[0,1)$
and characteristic
$x\in[0,1)$
and characteristic
![]() $\Phi_x^{\mathsf{t}}$
(respectively
$\Phi_x^{\mathsf{t}}$
(respectively
![]() $\Phi_x^j$
,
$\Phi_x^j$
,
![]() $j\in[J]$
) defined in (2) (respectively (3)) we have the following:
$j\in[J]$
) defined in (2) (respectively (3)) we have the following:
 \begin{align*}\lim_{n\to\infty}\dfrac{Z_n^{\Phi^{\mathsf{t}}_x}}{\rho^n}&=\Big(\frac{1}{\rho-1}+x\Big)W,\quad \text{$\mathbb{P}^\mathcal{S}$}\textit{-almost\;surely},\\[5pt] \lim_{n\to\infty}\dfrac{Z_n^{\Phi^j_x}}{\rho^n}&=\Big(\frac{1}{\rho-1}+x\Big)W\rho\textrm u_j,\quad \text{$\mathbb{P}^\mathcal{S}$}\textit{-almost surely}.\end{align*}
\begin{align*}\lim_{n\to\infty}\dfrac{Z_n^{\Phi^{\mathsf{t}}_x}}{\rho^n}&=\Big(\frac{1}{\rho-1}+x\Big)W,\quad \text{$\mathbb{P}^\mathcal{S}$}\textit{-almost\;surely},\\[5pt] \lim_{n\to\infty}\dfrac{Z_n^{\Phi^j_x}}{\rho^n}&=\Big(\frac{1}{\rho-1}+x\Big)W\rho\textrm u_j,\quad \text{$\mathbb{P}^\mathcal{S}$}\textit{-almost surely}.\end{align*}
Proof. Since for any fixed
![]() $x\in[0,1)$
the random variables
$x\in[0,1)$
the random variables
![]() $(\textbf{1}_{\{U_u\leq x\}})_{u\in\mathcal{U}_{\infty}}$
are i.i.d. and Bernoulli-distributed as
$(\textbf{1}_{\{U_u\leq x\}})_{u\in\mathcal{U}_{\infty}}$
are i.i.d. and Bernoulli-distributed as
![]() $\mathsf{Bern}(x)$
, in view of the strong law of large numbers we obtain
$\mathsf{Bern}(x)$
, in view of the strong law of large numbers we obtain
and similarly
For the deterministic characteristic
![]() $\textbf{1}_{\{k\geq 1\}}$
and the corresponding branching process counted with this characteristic, by applying [Reference Kolesko and Sava-Huss8, Proposition 4.1(i)] we get
$\textbf{1}_{\{k\geq 1\}}$
and the corresponding branching process counted with this characteristic, by applying [Reference Kolesko and Sava-Huss8, Proposition 4.1(i)] we get
 \begin{align*}\frac{Z_n^{\Phi_x^{\mathsf{t}}}}{\rho^{n}}&=\frac{1}{\rho}\cdot\overbrace{\frac{1}{\rho^{n-1}}\sum_{k\geq 0}^{n-1}\sum_{|u|=k}1}^{\xrightarrow{\scriptscriptstyle{a.s.}} W\sum_{k\geq 0}\rho^{-k}}+\overbrace{\frac{1}{\rho^{n}}\sum_{|u|=n}\textbf{1}_{\{U_u\leq x\}}}^{\xrightarrow{\scriptscriptstyle{a.s.}} xW}\\[5pt] &\xrightarrow{\scriptscriptstyle{a.s.}} \Big(\frac{1}{\rho}\sum_{k\geq 0}\frac{1}{\rho^{k}}+x\Big)W=\Big(\frac{1}{\rho-1}+x\Big)W,\quad \text{ as }n\to\infty, \end{align*}
\begin{align*}\frac{Z_n^{\Phi_x^{\mathsf{t}}}}{\rho^{n}}&=\frac{1}{\rho}\cdot\overbrace{\frac{1}{\rho^{n-1}}\sum_{k\geq 0}^{n-1}\sum_{|u|=k}1}^{\xrightarrow{\scriptscriptstyle{a.s.}} W\sum_{k\geq 0}\rho^{-k}}+\overbrace{\frac{1}{\rho^{n}}\sum_{|u|=n}\textbf{1}_{\{U_u\leq x\}}}^{\xrightarrow{\scriptscriptstyle{a.s.}} xW}\\[5pt] &\xrightarrow{\scriptscriptstyle{a.s.}} \Big(\frac{1}{\rho}\sum_{k\geq 0}\frac{1}{\rho^{k}}+x\Big)W=\Big(\frac{1}{\rho-1}+x\Big)W,\quad \text{ as }n\to\infty, \end{align*}
and this shows the first part of the claim. For the second one, from the Kesten–Stigum theorem we know that
![]() $\frac{Z_n^j}{\rho^n}\xrightarrow{\scriptscriptstyle{a.s.}} W\textrm{u}_j$
as
$\frac{Z_n^j}{\rho^n}\xrightarrow{\scriptscriptstyle{a.s.}} W\textrm{u}_j$
as
![]() $n\to\infty$
for any
$n\to\infty$
for any
![]() $j\in[J]$
, and for the characteristic
$j\in[J]$
, and for the characteristic
![]() $\Phi_x^j$
, since we have
$\Phi_x^j$
, since we have
 \begin{align*}Z_n^{\Phi_x^j}=\sum_{k=0}^{n}Z_k^j+\sum_{u\in \mathbb{T}; \ |u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
\begin{align*}Z_n^{\Phi_x^j}=\sum_{k=0}^{n}Z_k^j+\sum_{u\in \mathbb{T}; \ |u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
we obtain
 \begin{align*}\frac{Z_n^{\Phi_x^j}}{\rho^{n}}&=\overbrace{\frac{1}{\rho^{n}}\sum_{k=1}^{n}Z_k^j}^{\xrightarrow{\scriptscriptstyle{a.s.}} W\sum_{k\geq 0}\rho^{-k}\textrm{u}_j}+\overbrace{\rho\frac{1}{\rho^{n+1}}\sum_{|u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}}}^{\xrightarrow{\scriptscriptstyle{a.s.}} \rho xW \textrm{u}_j}\\[5pt] &\xrightarrow{\scriptscriptstyle{a.s.}} \Big(\frac{1}{\rho}\sum_{k\geq 0}\frac{1}{\rho^{k}}+x\Big)W\rho \textrm{u}_j=\Big(\frac{1}{\rho-1}+x\Big)W\rho \textrm{u}_j,\quad \textit{ as }n\to\infty, \end{align*}
\begin{align*}\frac{Z_n^{\Phi_x^j}}{\rho^{n}}&=\overbrace{\frac{1}{\rho^{n}}\sum_{k=1}^{n}Z_k^j}^{\xrightarrow{\scriptscriptstyle{a.s.}} W\sum_{k\geq 0}\rho^{-k}\textrm{u}_j}+\overbrace{\rho\frac{1}{\rho^{n+1}}\sum_{|u|=n+1,\textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}}}^{\xrightarrow{\scriptscriptstyle{a.s.}} \rho xW \textrm{u}_j}\\[5pt] &\xrightarrow{\scriptscriptstyle{a.s.}} \Big(\frac{1}{\rho}\sum_{k\geq 0}\frac{1}{\rho^{k}}+x\Big)W\rho \textrm{u}_j=\Big(\frac{1}{\rho-1}+x\Big)W\rho \textrm{u}_j,\quad \textit{ as }n\to\infty, \end{align*}
and the proof is completed.
Following the notation from [Reference Kolesko and Sava-Huss8], for every characteristic
![]() $\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
we define the two vectors
$\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
we define the two vectors
![]() $\textrm{x}_i(\Phi)=\sum_{k\in \mathbb{N}}\mathbb{E}[\Phi(k)]\pi^{(i)}A_i^{-k}$
, for
$\textrm{x}_i(\Phi)=\sum_{k\in \mathbb{N}}\mathbb{E}[\Phi(k)]\pi^{(i)}A_i^{-k}$
, for
![]() $i=1,2$
. In particular, since
$i=1,2$
. In particular, since
![]() $\mathbb{E}[\Phi_x^{\mathsf{t}}(0)]=x\textrm{1}$
, we have
$\mathbb{E}[\Phi_x^{\mathsf{t}}(0)]=x\textrm{1}$
, we have
 \begin{align} \nonumber\textrm{x}_i\left(\Phi_x^{\mathsf{t}}\right)&=x\textrm{1}\pi^{(i)}+\textrm{1}\pi^{(i)}\sum_{k=1}^{\infty}A_i^{-k}=\textrm{1}\pi^{(i)}\left(xI+\sum_{k=1}^{\infty}A_i^{-k}\right)\\[5pt] &=\textrm{1}\pi^{(i)}\left(x + (A_i-I)^{-1}\right),\quad \text{for }i=1,2.\end{align}
\begin{align} \nonumber\textrm{x}_i\left(\Phi_x^{\mathsf{t}}\right)&=x\textrm{1}\pi^{(i)}+\textrm{1}\pi^{(i)}\sum_{k=1}^{\infty}A_i^{-k}=\textrm{1}\pi^{(i)}\left(xI+\sum_{k=1}^{\infty}A_i^{-k}\right)\\[5pt] &=\textrm{1}\pi^{(i)}\left(x + (A_i-I)^{-1}\right),\quad \text{for }i=1,2.\end{align}
For any random characteristic
![]() $\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
that satisfies the assumptions of [Reference Kolesko and Sava-Huss8, Theorem 3.5]—i.e. for which (GW1)–(GW3) hold,
$\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
that satisfies the assumptions of [Reference Kolesko and Sava-Huss8, Theorem 3.5]—i.e. for which (GW1)–(GW3) hold,
![]() $\sum_{k\in \mathbb{Z}}\big\|\mathbb{E}[\Phi(k)]\big\|(\rho^{-k}+\vartheta^{-k})<\infty$
for some
$\sum_{k\in \mathbb{Z}}\big\|\mathbb{E}[\Phi(k)]\big\|(\rho^{-k}+\vartheta^{-k})<\infty$
for some
![]() $\vartheta<\sqrt{\rho}$
, and finally
$\vartheta<\sqrt{\rho}$
, and finally
![]() $\sum_{k\in \mathbb{Z}}\|\textrm{Var}[\Phi(k)]\|\rho^{-k}<\infty$
—we set
$\sum_{k\in \mathbb{Z}}\|\textrm{Var}[\Phi(k)]\|\rho^{-k}<\infty$
—we set
Recall that the constants
![]() $\sigma_{\ell}^2$
, for
$\sigma_{\ell}^2$
, for
![]() $\ell=0,\ldots, J-1$
, are defined as
$\ell=0,\ldots, J-1$
, are defined as
 \begin{equation}\sigma_{\ell}^2=\sigma_{\ell}^2(\Phi)= \frac{\rho^{-\ell}}{(2\ell+1)(\ell !)^2}\sum_{\lambda\in\sigma^2_A}\textrm{Var} \Big[\textrm{x} _2(\Phi) \pi_\lambda (A-\lambda I)^{\ell}L\Big]\textrm{u}.\end{equation}
\begin{equation}\sigma_{\ell}^2=\sigma_{\ell}^2(\Phi)= \frac{\rho^{-\ell}}{(2\ell+1)(\ell !)^2}\sum_{\lambda\in\sigma^2_A}\textrm{Var} \Big[\textrm{x} _2(\Phi) \pi_\lambda (A-\lambda I)^{\ell}L\Big]\textrm{u}.\end{equation}
Let
![]() $\ell$
be the maximal integer such that
$\ell$
be the maximal integer such that
![]() $\sigma_{\ell}(\Phi)>0$
, and set
$\sigma_{\ell}(\Phi)>0$
, and set
![]() $\ell=-\frac12$
if there is no such integer. Then Theorem 3.5 of [Reference Kolesko and Sava-Huss8] states that, for a standard normal variable
$\ell=-\frac12$
if there is no such integer. Then Theorem 3.5 of [Reference Kolesko and Sava-Huss8] states that, for a standard normal variable
![]() $\mathcal{N}(0,1)$
independent of W, the following stable convergence holds:
$\mathcal{N}(0,1)$
independent of W, the following stable convergence holds:
where
![]() $G^\Phi= \sigma_{\ell}(\Phi) \mathcal{N}(0,1)$
if not all
$G^\Phi= \sigma_{\ell}(\Phi) \mathcal{N}(0,1)$
if not all
![]() $\sigma_{\ell}$
are zero, and
$\sigma_{\ell}$
are zero, and
![]() $G^\Phi= \sigma(\Phi)\mathcal{N}(0,1)$
otherwise, while
$G^\Phi= \sigma(\Phi)\mathcal{N}(0,1)$
otherwise, while
![]() $\sigma(\Phi)$
is defined by
$\sigma(\Phi)$
is defined by
and
![]() $\Psi^\Phi$
is the centered characteristic given by
$\Psi^\Phi$
is the centered characteristic given by
Above, the matrices
![]() $\mathsf{P}(k, \ell)$
, for
$\mathsf{P}(k, \ell)$
, for
![]() $k,\ell\in\mathbb{Z}$
are defined as
$k,\ell\in\mathbb{Z}$
are defined as
 \begin{align*} \mathsf{P}(k,\ell)=\begin{cases} -\pi^{(1)}\textbf{1}_{\{\ell<0\}}+\pi^{(2)}\textbf{1}_{\{\ell\geq 0\}}+\pi^{(3)}\textbf{1}_{\{\ell\geq 0\}},\quad \text{if }k\leq 0,\\[5pt] -\pi^{(1)}\textbf{1}_{\{\ell<0\}}-\pi^{(2)}\textbf{1}_{\{\ell<0\}}+\pi^{(3)}\textbf{1}_{\{\ell\geq 0\}},\quad \text{if }k>0. \end{cases}\end{align*}
\begin{align*} \mathsf{P}(k,\ell)=\begin{cases} -\pi^{(1)}\textbf{1}_{\{\ell<0\}}+\pi^{(2)}\textbf{1}_{\{\ell\geq 0\}}+\pi^{(3)}\textbf{1}_{\{\ell\geq 0\}},\quad \text{if }k\leq 0,\\[5pt] -\pi^{(1)}\textbf{1}_{\{\ell<0\}}-\pi^{(2)}\textbf{1}_{\{\ell<0\}}+\pi^{(3)}\textbf{1}_{\{\ell\geq 0\}},\quad \text{if }k>0. \end{cases}\end{align*}
3. The embedding of the urn model into the branching process
Notation. We slightly abuse notation and write
![]() $\Phi^{\mathsf{t}}$
(respectively
$\Phi^{\mathsf{t}}$
(respectively
![]() $\Phi^j$
,
$\Phi^j$
,
![]() $j\in[J]$
) for the whole family
$j\in[J]$
) for the whole family
![]() $\big\{\Phi^{\mathsf{t}}_x\big\}_{x\in[0,1)}$
(respectively
$\big\{\Phi^{\mathsf{t}}_x\big\}_{x\in[0,1)}$
(respectively
![]() $\big\{\Phi^j_x\big\}_{x\in[0,1)}$
) of characteristics indexed over the threshold
$\big\{\Phi^j_x\big\}_{x\in[0,1)}$
) of characteristics indexed over the threshold
![]() $x\in[0,1)$
. We denote by
$x\in[0,1)$
. We denote by
![]() $\mathcal C$
the set of characteristics
$\mathcal C$
the set of characteristics
![]() $\Phi$
which are linear combinations of
$\Phi$
which are linear combinations of
![]() $\Phi^{\mathsf{t}}$
and
$\Phi^{\mathsf{t}}$
and
![]() $\Phi^j$
, for
$\Phi^j$
, for
![]() $j\in[J]$
. Again by abuse of notation, by
$j\in[J]$
. Again by abuse of notation, by
![]() $\Phi\in\mathcal{C}$
we actually refer to the whole family of characteristics
$\Phi\in\mathcal{C}$
we actually refer to the whole family of characteristics
![]() $\{\Phi_x\}_{x\in[0,1)}$
; that is,
$\{\Phi_x\}_{x\in[0,1)}$
; that is,
Extension of
![]() $x\in[0,1)$
to
$x\in[0,1)$
to
![]() $x\in\mathbb{R}$
. Instead of working with thresholds
$x\in\mathbb{R}$
. Instead of working with thresholds
![]() $x\in[0,1)$
and corresponding characteristics
$x\in[0,1)$
and corresponding characteristics
![]() $\Phi_x$
, we can extend the domain of x to the whole of
$\Phi_x$
, we can extend the domain of x to the whole of
![]() $\mathbb{R}$
as follows. For any
$\mathbb{R}$
as follows. For any
![]() $\Phi\in\mathcal C$
and any
$\Phi\in\mathcal C$
and any
![]() $x\in\mathbb{R}$
we define
$x\in\mathbb{R}$
we define
The corresponding CMJ process
![]() $(Z_n^{\Phi_x})_{n\in\mathbb{N}}$
satisfies
$(Z_n^{\Phi_x})_{n\in\mathbb{N}}$
satisfies
![]() $Z_n^{\Phi_x}=Z_0^{\Phi_{x+n}}$
for every
$Z_n^{\Phi_x}=Z_0^{\Phi_{x+n}}$
for every
![]() $n\in\mathbb{N}$
and
$n\in\mathbb{N}$
and
![]() $x\in\mathbb{R}$
, and finally we define
$x\in\mathbb{R}$
, and finally we define
and similarly
![]() $\mathcal{F}^{\Phi}(x)= F_0^{\Phi_{x}}$
. For any
$\mathcal{F}^{\Phi}(x)= F_0^{\Phi_{x}}$
. For any
![]() $x\in\mathbb{R}$
, (7) yields the existence of a Gaussian process
$x\in\mathbb{R}$
, (7) yields the existence of a Gaussian process
![]() $\{\mathcal{G}^{\Phi}(x);\ x\in\mathbb{R}\}$
such that the following convergence holds:
$\{\mathcal{G}^{\Phi}(x);\ x\in\mathbb{R}\}$
such that the following convergence holds:
The Cramér–Wold device implies that, in fact, the convergence holds for finite-dimensional distributions and the limiting process
![]() $\mathcal{G}^{\Phi}$
is jointly Gaussian with
$\mathcal{G}^{\Phi}$
is jointly Gaussian with
![]() $\mathcal{G}^{\Phi}(x)\overset{\textrm{d}}{=} \rho^{\lfloor{x}\rfloor/2}\sigma_\ell(\Phi_{\{x\}}) \mathcal N(0,1)$
or
$\mathcal{G}^{\Phi}(x)\overset{\textrm{d}}{=} \rho^{\lfloor{x}\rfloor/2}\sigma_\ell(\Phi_{\{x\}}) \mathcal N(0,1)$
or
![]() $\mathcal{G}^{\Phi}(x)\overset{\textrm{d}}{=} \rho^{\lfloor{x}\rfloor/2}\sigma(\Phi_{\{x\}}) \mathcal N(0,1)$
depending on the value of the constants
$\mathcal{G}^{\Phi}(x)\overset{\textrm{d}}{=} \rho^{\lfloor{x}\rfloor/2}\sigma(\Phi_{\{x\}}) \mathcal N(0,1)$
depending on the value of the constants
![]() $\sigma_\ell$
or
$\sigma_\ell$
or
![]() $\sigma$
, respectively. Furthermore, we write
$\sigma$
, respectively. Furthermore, we write
![]() $\mathcal{Z}^{\mathsf{t}}, \mathcal{F}^{\mathsf{t}},\mathcal{G}^{\mathsf{t}}$
(respectively
$\mathcal{Z}^{\mathsf{t}}, \mathcal{F}^{\mathsf{t}},\mathcal{G}^{\mathsf{t}}$
(respectively
![]() $\mathcal{Z}^{j},\mathcal{F}^{j},\mathcal{G}^{j}$
) for
$\mathcal{Z}^{j},\mathcal{F}^{j},\mathcal{G}^{j}$
) for
![]() $\mathcal{Z}^{\Phi}, \mathcal{F}^{\Phi},\mathcal{G}^{\Phi}$
if
$\mathcal{Z}^{\Phi}, \mathcal{F}^{\Phi},\mathcal{G}^{\Phi}$
if
![]() $\Phi=\Phi^{\mathsf{t}}$
(respectively
$\Phi=\Phi^{\mathsf{t}}$
(respectively
![]() $\Phi=\Phi^j$
). Since, with probability one, all the random variables
$\Phi=\Phi^j$
). Since, with probability one, all the random variables
![]() $(U_u)_{u\in \mathcal{U}_{\infty}}$
are different, the process
$(U_u)_{u\in \mathcal{U}_{\infty}}$
are different, the process
![]() $(\mathcal{Z}^{\mathsf{t}}(x))_{x\geq 0}$
at its jump point increases by 1. Therefore, the following stopping times are well defined: for
$(\mathcal{Z}^{\mathsf{t}}(x))_{x\geq 0}$
at its jump point increases by 1. Therefore, the following stopping times are well defined: for
![]() $k\in\mathbb{N}$
, define
$k\in\mathbb{N}$
, define
![]() $\tau_k$
as
$\tau_k$
as
Remark 1. With the stopping times
![]() $(\tau_k)_{k\in\mathbb{N}}$
just introduced, we have
$(\tau_k)_{k\in\mathbb{N}}$
just introduced, we have
and this is exactly the number of balls of type j added to the two urns after k draws, for which we seek first- and second-order asymptotics. Our strategy is as follows: first we prove functional limit theorems for the processes
![]() $\{\mathcal{Z}^{\mathsf{t}}(x);\ x\in \mathbb{R}\}$
and
$\{\mathcal{Z}^{\mathsf{t}}(x);\ x\in \mathbb{R}\}$
and
![]() $\{\mathcal{Z}^{j}(x);\ x\in\mathbb{R}\}$
, and then we conclude the corresponding limit theorems for
$\{\mathcal{Z}^{j}(x);\ x\in\mathbb{R}\}$
, and then we conclude the corresponding limit theorems for
![]() $B_j(k)$
, for
$B_j(k)$
, for
![]() $j\in[J]$
. We start with the description of the leading term in the asymptotics of
$j\in[J]$
. We start with the description of the leading term in the asymptotics of
![]() $\mathcal{Z}^{\Phi}(x)$
, for any characteristic
$\mathcal{Z}^{\Phi}(x)$
, for any characteristic
![]() $\Phi\in \mathcal{C}$
.
$\Phi\in \mathcal{C}$
.
Periodic functions. For any
![]() $\lambda\in \mathbb{C}$
, we introduce the function
$\lambda\in \mathbb{C}$
, we introduce the function
where
![]() $\lambda^t=e^{t\log \lambda}$
and
$\lambda^t=e^{t\log \lambda}$
and
![]() $z\mapsto \log z$
is the principal branch of the logarithm. The function
$z\mapsto \log z$
is the principal branch of the logarithm. The function
![]() $l_\lambda$
is continuous and 1-periodic, and it satisfies
$l_\lambda$
is continuous and 1-periodic, and it satisfies
Moreover, the mapping
![]() $x\mapsto \lambda^xl_{\lambda}(x)$
equals
$x\mapsto \lambda^xl_{\lambda}(x)$
equals
![]() $\lambda^x$
for integer x and is linear in between.
$\lambda^x$
for integer x and is linear in between.
Proposition 2. Assume (GW1), (GW2), and (GW4) hold, and for any
![]() $j\in[J]$
let
$j\in[J]$
let
![]() $\Phi=a\Phi^{\mathsf{t}}+b\Phi^j$
, with
$\Phi=a\Phi^{\mathsf{t}}+b\Phi^j$
, with
![]() $a,b\in\mathbb{R}$
. Then it holds that
$a,b\in\mathbb{R}$
. Then it holds that
Proof. Because of the linearity of CMJ processes, for
![]() $x\in \mathbb{R}$
it holds that
$x\in \mathbb{R}$
it holds that
so it suffices to prove the
![]() $\mathbb{P}^\mathcal{S}$
-almost sure convergence for
$\mathbb{P}^\mathcal{S}$
-almost sure convergence for
![]() $\mathcal{Z}^{\mathsf{t}}(x)$
and
$\mathcal{Z}^{\mathsf{t}}(x)$
and
![]() $\mathcal{Z}^{j}(x)$
separately, as
$\mathcal{Z}^{j}(x)$
separately, as
![]() $x\to\infty$
.
$x\to\infty$
.
Case 1:
![]() $x\in[0,1)$
. For
$x\in[0,1)$
. For
![]() $n\in\mathbb{N}$
and
$n\in\mathbb{N}$
and
![]() $x\in[0,1)$
, since
$x\in[0,1)$
, since
![]() $\mathcal{Z}^{\mathsf{t}}(x+n)=Z_n^{\Phi^{\mathsf{t}}_x}$
, in view of Proposition 2.1 we get
$\mathcal{Z}^{\mathsf{t}}(x+n)=Z_n^{\Phi^{\mathsf{t}}_x}$
, in view of Proposition 2.1 we get
Case 2:
![]() $x\in[0,\infty)$
. This case can be reduced to the previous one, where
$x\in[0,\infty)$
. This case can be reduced to the previous one, where
![]() $x\in[0,1)$
, as follows. In view of Equation (13), for any
$x\in[0,1)$
, as follows. In view of Equation (13), for any
![]() $x\in [0,\infty)$
, with
$x\in [0,\infty)$
, with
![]() $m=n+\lfloor x \rfloor$
we obtain
$m=n+\lfloor x \rfloor$
we obtain
In the last equation above, we used the fact that
We still have to prove that the above
![]() $\mathbb{P}^\mathcal{S}$
-almost sure convergence holds for
$\mathbb{P}^\mathcal{S}$
-almost sure convergence holds for
![]() $x\to\infty$
, that is, that
$x\to\infty$
, that is, that
Indeed, from any sequence tending to infinity we may choose a subsequence
![]() $(x_n)$
such that
$(x_n)$
such that
![]() $\{x_n\}$
converges to some
$\{x_n\}$
converges to some
![]() $x_0\in\mathbb{R}$
. Then for any
$x_0\in\mathbb{R}$
. Then for any
![]() $\delta>0$
and large n, in view of
$\delta>0$
and large n, in view of
we have
 \begin{align*}&\frac{\mathcal{Z}^{\mathsf{t}}(\lfloor x_n\rfloor+ x_0-\delta)}{\rho^{\lfloor x_n\rfloor+ x_0-\delta}l_\rho(x_0-\delta)}\cdot\rho^{x_0-\{x_n\}-\delta} \cdot\frac{l_{\rho}(x_0-\delta)}{l_{\rho}(x_n)}\le\frac{\mathcal{Z}^{\mathsf{t}}(x_n)}{\rho^{x_n}l_{\rho}(x_n)}\\[5pt] &\le\frac{\mathcal{Z}^{\mathsf{t}}(\lfloor x_n\rfloor+ x_0+\delta)}{\rho^{\lfloor x_n\rfloor+ x_0+\delta}l_{\rho}(x_0+\delta)}\rho^{x_0-\{x_n\}+\delta}\cdot\frac{l_{\rho}(x_0+\delta)}{l_{\rho}(x_n)}.\end{align*}
\begin{align*}&\frac{\mathcal{Z}^{\mathsf{t}}(\lfloor x_n\rfloor+ x_0-\delta)}{\rho^{\lfloor x_n\rfloor+ x_0-\delta}l_\rho(x_0-\delta)}\cdot\rho^{x_0-\{x_n\}-\delta} \cdot\frac{l_{\rho}(x_0-\delta)}{l_{\rho}(x_n)}\le\frac{\mathcal{Z}^{\mathsf{t}}(x_n)}{\rho^{x_n}l_{\rho}(x_n)}\\[5pt] &\le\frac{\mathcal{Z}^{\mathsf{t}}(\lfloor x_n\rfloor+ x_0+\delta)}{\rho^{\lfloor x_n\rfloor+ x_0+\delta}l_{\rho}(x_0+\delta)}\rho^{x_0-\{x_n\}+\delta}\cdot\frac{l_{\rho}(x_0+\delta)}{l_{\rho}(x_n)}.\end{align*}
Taking the limit first as n goes to infinity and then as
![]() $\delta$
goes to 0, we get the desired convergence, since
$\delta$
goes to 0, we get the desired convergence, since
![]() $x\mapsto l_{\rho}(x)$
is uniformly continuous. The same argument can be used to show that for any
$x\mapsto l_{\rho}(x)$
is uniformly continuous. The same argument can be used to show that for any
![]() $j\in[J]$
we have
$j\in[J]$
we have
and this proves the claim.
An immediate consequence of Proposition 2 is the following corollary.
Corollary 1. Under the assumptions of Proposition 2, for
![]() $\Phi={\rho}\textrm u_j\Phi^{\mathsf{t}}-\Phi^j$
, we have
$\Phi={\rho}\textrm u_j\Phi^{\mathsf{t}}-\Phi^j$
, we have
Also, the strong law of large numbers for
![]() $(B_j(k))_{k\in\mathbb{N}}$
follows immediately from Proposition 2.
$(B_j(k))_{k\in\mathbb{N}}$
follows immediately from Proposition 2.
Proof of Theorem
1. Since
![]() $\tau_k$
goes to infinity as k does, we have
$\tau_k$
goes to infinity as k does, we have
 \begin{align*}\lim_{k\to\infty}\frac{B_j(k)}{k}&=\lim_{k\to\infty}\frac{\mathcal{Z}^{j}(\tau_k)}{\mathcal{Z}^{\mathsf{t}}(\tau_k)}=\lim_{k\to\infty}\frac{\mathcal{Z}^{j}(\tau_k)}{\rho^{\lfloor \tau_k\rfloor}(1+(\rho-1)\{\tau_k\})}\cdot \frac{\rho^{\lfloor \tau_k\rfloor}(1+(\rho-1)\{\tau_k\})}{\mathcal{Z}^{\mathsf{t}}(\tau_k)}\\[5pt] &=\frac{1}{\rho-1}W\rho\textrm{u}_j\cdot \frac{1}{\frac{1}{\rho-1}W}=\rho\textrm{u}_j,\quad \mathbb{P}^\mathcal{S}\text{-almost surely},\end{align*}
\begin{align*}\lim_{k\to\infty}\frac{B_j(k)}{k}&=\lim_{k\to\infty}\frac{\mathcal{Z}^{j}(\tau_k)}{\mathcal{Z}^{\mathsf{t}}(\tau_k)}=\lim_{k\to\infty}\frac{\mathcal{Z}^{j}(\tau_k)}{\rho^{\lfloor \tau_k\rfloor}(1+(\rho-1)\{\tau_k\})}\cdot \frac{\rho^{\lfloor \tau_k\rfloor}(1+(\rho-1)\{\tau_k\})}{\mathcal{Z}^{\mathsf{t}}(\tau_k)}\\[5pt] &=\frac{1}{\rho-1}W\rho\textrm{u}_j\cdot \frac{1}{\frac{1}{\rho-1}W}=\rho\textrm{u}_j,\quad \mathbb{P}^\mathcal{S}\text{-almost surely},\end{align*}
and this finishes the proof.
4. Proof of the main result
The proof is completed in several steps:
-
• In Lemma 1 we investigate compositions of the fluctuations
 $\mathcal{F}^{\mathsf{t}}$
and
$\mathcal{F}^{\mathsf{t}}$
and
 $\mathcal{F}^{j}$
.
$\mathcal{F}^{j}$
. -
• In Theorem 3 we prove weak convergence of the processes
 $\mathcal{X}^{\mathsf{t}}=\mathcal{Z}^{\mathsf{t}}-\mathcal{F}^{\mathsf{t}}$
and
$\mathcal{X}^{\mathsf{t}}=\mathcal{Z}^{\mathsf{t}}-\mathcal{F}^{\mathsf{t}}$
and
 $\mathcal{X}^j=\mathcal{Z}^{j}-\mathcal{F}^{j}$
(rescaled appropriately) to Gaussian processes
$\mathcal{X}^j=\mathcal{Z}^{j}-\mathcal{F}^{j}$
(rescaled appropriately) to Gaussian processes
 $\mathcal{G}^{\mathsf{t}}$
and
$\mathcal{G}^{\mathsf{t}}$
and
 $\mathcal{G}^{j}$
respectively, for any
$\mathcal{G}^{j}$
respectively, for any
 $j\in[J]$
.
$j\in[J]$
. -
• Continuity and strict positivity of the variances of the limiting processes
 $\mathcal{G}^{\mathsf{t}}$
and
$\mathcal{G}^{\mathsf{t}}$
and
 $\mathcal{G}^{j}$
are analyzed in Proposition 4 and in Lemma 2.
$\mathcal{G}^{j}$
are analyzed in Proposition 4 and in Lemma 2. -
• Localization of the stopping times
 $\tau_n$
is done in Proposition 5.
$\tau_n$
is done in Proposition 5. -
• Finally, the limit theorems for
 $B_j(n)$
are given in Proposition 6 and in Theorem 4.
$B_j(n)$
are given in Proposition 6 and in Theorem 4.
4.1. Leading asymptotic terms
We start by describing the leading terms in the asymptotics of
![]() $\mathcal{Z}^{\mathsf{t}}$
and of
$\mathcal{Z}^{\mathsf{t}}$
and of
![]() $\mathcal{Z}^{j}$
for any
$\mathcal{Z}^{j}$
for any
![]() $j\in[J]$
. We recall first that for a characteristic
$j\in[J]$
. We recall first that for a characteristic
![]() $\Phi\in\mathcal{C}$
, the leading term in the asymptotics of
$\Phi\in\mathcal{C}$
, the leading term in the asymptotics of
![]() $\mathcal{Z}^{\Phi}$
is given by
$\mathcal{Z}^{\Phi}$
is given by
![]() $\mathcal{F}^{\Phi}$
; for simplicity of notation, for
$\mathcal{F}^{\Phi}$
; for simplicity of notation, for
![]() $x\in\mathbb{R}$
we write
$x\in\mathbb{R}$
we write
In particular, for
![]() $\Phi=\Phi^{\mathsf{t}}$
and
$\Phi=\Phi^{\mathsf{t}}$
and
![]() $\Phi=\Phi^j$
respectively, we write
$\Phi=\Phi^j$
respectively, we write
Lemma 1. Assume (GW1)–(GW3) hold. Then for sufficiently large arguments the inverse function
![]() $\mathcal{F}^{\mathsf{inv}}=(\mathcal{F}^{\mathsf{t}})^{-1} $
is well defined, and for every
$\mathcal{F}^{\mathsf{inv}}=(\mathcal{F}^{\mathsf{t}})^{-1} $
is well defined, and for every
![]() $j\in[J]$
we have
$j\in[J]$
we have
Proof. For any
![]() $k\in\mathbb{N}_0, x\in[0,1)$
, the equality
$k\in\mathbb{N}_0, x\in[0,1)$
, the equality
together with Equation (5) gives us
that is, for any
![]() $x\ge0$
,
$x\ge0$
,
![]() $\mathcal{F}^{\mathsf{t}}(x)$
is a linear interpolation between
$\mathcal{F}^{\mathsf{t}}(x)$
is a linear interpolation between
![]() $\mathcal{F}^{\mathsf{t}}(\lfloor x\rfloor)$
and
$\mathcal{F}^{\mathsf{t}}(\lfloor x\rfloor)$
and
![]() $\mathcal{F}^{\mathsf{t}}(\lfloor x\rfloor+1)$
. On the other hand, as, in view of (4) and (5), for
$\mathcal{F}^{\mathsf{t}}(\lfloor x\rfloor+1)$
. On the other hand, as, in view of (4) and (5), for
![]() $n\in\mathbb{N}$
we have
$n\in\mathbb{N}$
we have
we conclude that the following holds:
 \begin{align*} &\mathcal{F}^{\mathsf{t}}(x)=\tfrac{\rho^{x}}{\rho-1}l_\rho(x)W+o(\rho^x)\text{ and }\\[5pt] &\big(\mathcal{F}^{\mathsf{t}}\big)'(x)=\rho^{\lfloor x\rfloor}W+o(\rho^x)\text{ for }x\notin\mathbb{Z}. \end{align*}
\begin{align*} &\mathcal{F}^{\mathsf{t}}(x)=\tfrac{\rho^{x}}{\rho-1}l_\rho(x)W+o(\rho^x)\text{ and }\\[5pt] &\big(\mathcal{F}^{\mathsf{t}}\big)'(x)=\rho^{\lfloor x\rfloor}W+o(\rho^x)\text{ for }x\notin\mathbb{Z}. \end{align*}
By the same argument, for
![]() $j\in[J]$
we obtain
$j\in[J]$
we obtain
 \begin{align*} &\mathcal{F}^{j}(x)=\tfrac{\rho^{x}}{\rho-1}l_\rho(x)\rho\textrm{u}_jW+o(\rho^x)\text{ and }\\[5pt] &\big(\mathcal{F}^{j}\big)'(x)=\rho^{\lfloor x\rfloor}\rho\textrm{u}_jW+o(\rho^x)\text{ for }x\notin\mathbb{Z}. \end{align*}
\begin{align*} &\mathcal{F}^{j}(x)=\tfrac{\rho^{x}}{\rho-1}l_\rho(x)\rho\textrm{u}_jW+o(\rho^x)\text{ and }\\[5pt] &\big(\mathcal{F}^{j}\big)'(x)=\rho^{\lfloor x\rfloor}\rho\textrm{u}_jW+o(\rho^x)\text{ for }x\notin\mathbb{Z}. \end{align*}
In particular,
![]() $\mathcal{F}^{\mathsf{t}}$
is eventually increasing
$\mathcal{F}^{\mathsf{t}}$
is eventually increasing
![]() $\mathbb{P}^\mathcal{S}$
-almost surely and thus the inverse function
$\mathbb{P}^\mathcal{S}$
-almost surely and thus the inverse function
![]() $(\mathcal{F}^{\mathsf{t}})^{-1}$
is well defined for large arguments. Furthermore, if
$(\mathcal{F}^{\mathsf{t}})^{-1}$
is well defined for large arguments. Furthermore, if
![]() $\mathcal{F}^{\mathsf{inv}}(t)\notin\mathbb{N}$
and t is large enough then we have
$\mathcal{F}^{\mathsf{inv}}(t)\notin\mathbb{N}$
and t is large enough then we have
since
![]() $\mathcal{F}^{\mathsf{inv}}(t)$
diverges to infinity. Finally, since for large t it holds that
$\mathcal{F}^{\mathsf{inv}}(t)$
diverges to infinity. Finally, since for large t it holds that
we obtain (14).
4.2. Limit theorems for
 $\mathcal{X}^{\mathsf{t}}$
and
$\mathcal{X}^{\mathsf{t}}$
and
 $\mathcal{X}^{j}$
$\mathcal{X}^{j}$
To prove weak convergence of the processes
![]() $\Big\{\frac{1}{n^{\ell+\frac12}\rho^{n/2}\sqrt W}\mathcal{X}^{j}(n+x); \ x\in \mathbb{R}\Big\}$
, we follow the well-known technique: we first prove weak convergence of the finite-dimensional distributions, then prove tightness. According to [Reference Kolesko and Sava-Huss8, Theorem 3.5], the finite-dimensional distributions of the aforementioned processes converge jointly; see also Equation (9) and the discussion thereafter.
$\Big\{\frac{1}{n^{\ell+\frac12}\rho^{n/2}\sqrt W}\mathcal{X}^{j}(n+x); \ x\in \mathbb{R}\Big\}$
, we follow the well-known technique: we first prove weak convergence of the finite-dimensional distributions, then prove tightness. According to [Reference Kolesko and Sava-Huss8, Theorem 3.5], the finite-dimensional distributions of the aforementioned processes converge jointly; see also Equation (9) and the discussion thereafter.
Theorem 3. Suppose that (GW1)–(GW3) hold and L satisfies
![]() $\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
$\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
![]() $\delta\in (0,1)$
. Then for every
$\delta\in (0,1)$
. Then for every
![]() $j\in [J]$
, the family of distributions
$j\in [J]$
, the family of distributions
with respect to
![]() $\mathbb{P}$
is tight in the Skorokhod space
$\mathbb{P}$
is tight in the Skorokhod space
![]() $\mathcal D(\mathbb{R})$
endowed with the standard
$\mathcal D(\mathbb{R})$
endowed with the standard
![]() $\textbf{J}_1$
topology.
$\textbf{J}_1$
topology.
Proof. First let us observe that for any
![]() $k\in\mathbb{Z},\ m\in\mathbb{N}$
, the concatenation is a continuous mapping from
$k\in\mathbb{Z},\ m\in\mathbb{N}$
, the concatenation is a continuous mapping from
![]() $\mathcal{D}([k,k+1))\times\cdots\times\mathcal D([k+m-1,k+m))$
to
$\mathcal{D}([k,k+1))\times\cdots\times\mathcal D([k+m-1,k+m))$
to
![]() $\mathcal D([k,k+m))$
. Consequently, it suffices to prove tightness in the space
$\mathcal D([k,k+m))$
. Consequently, it suffices to prove tightness in the space
![]() $\mathcal D([0,1))$
. For
$\mathcal D([0,1))$
. For
![]() $x\in[0,1)$
,
$x\in[0,1)$
,
![]() $j\in[J]$
, and
$j\in[J]$
, and
![]() $n\in\mathbb{N}$
we set
$n\in\mathbb{N}$
we set
where
![]() $\ell$
may be
$\ell$
may be
![]() $-\frac12$
in Case (i) of [Reference Kolesko and Sava-Huss8, Theorem 3.5], and the characteristic
$-\frac12$
in Case (i) of [Reference Kolesko and Sava-Huss8, Theorem 3.5], and the characteristic
![]() $\Phi^j=(\Phi^j_x)_{x\in[0,1)}$
is defined as in (3). In view of [Reference Billingsley3, Theorem 13.5], it suffices to show that for any
$\Phi^j=(\Phi^j_x)_{x\in[0,1)}$
is defined as in (3). In view of [Reference Billingsley3, Theorem 13.5], it suffices to show that for any
![]() $ 0\leq x\le y\le z<1$
,
$ 0\leq x\le y\le z<1$
,
![]() $\lambda>0$
, and n large enough, it holds that
$\lambda>0$
, and n large enough, it holds that
where
![]() $p:==(2+\delta)/2\in (1,3/2)$
and
$p:==(2+\delta)/2\in (1,3/2)$
and
![]() $C>0$
is some constant. A more restrictive condition is the following inequality:
$C>0$
is some constant. A more restrictive condition is the following inequality:
By Hölder’s inequality, we have
 \begin{align*}\mathbb{E}&\Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{p}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{p}\Big]\\[5pt] &\le\mathbb{E}\left[\mathbb{E}\Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{2}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{2}\Big|\mathcal{A}_n\Big]^{p/2}\right], \end{align*}
\begin{align*}\mathbb{E}&\Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{p}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{p}\Big]\\[5pt] &\le\mathbb{E}\left[\mathbb{E}\Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{2}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{2}\Big|\mathcal{A}_n\Big]^{p/2}\right], \end{align*}
so it remains to show the estimate
for some random variables
![]() $H_n$
with bounded
$H_n$
with bounded
![]() $p/2$
moment. Recalling that for
$p/2$
moment. Recalling that for
![]() $0\leq x<1$
we have
$0\leq x<1$
we have
 \begin{align*}\mathcal{Z}^{j}(n+x)=\sum_{k=0}^{n-1}Z_k^j+\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
\begin{align*}\mathcal{Z}^{j}(n+x)=\sum_{k=0}^{n-1}Z_k^j+\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\textbf{1}_{\{U_u\leq x\}},\end{align*}
we deduce that for
![]() $0\leq x\leq y<1$
,
$0\leq x\leq y<1$
,
We also have
 \begin{align*}\mathcal{F}^{j}(n+y)-\mathcal{F}^{j}(n+x)&=\left(\textrm{x}_1(\Phi^j_y)-\textrm{x}_1(\Phi^j_x)\right)A^n_1 W^{(1)}+\left(\textrm{x}_2(\Phi^j_y)-\textrm{x}_2(\Phi^j_x)\right)A^n_2Z_0\\[5pt] &=(y-x)A\textrm{e}_j^\top\pi^{(1)}A^n_1 W^{(1)}+(y-x)A\textrm{e}_j^\top\pi^{(2)}A^n_2Z_0\\[5pt] &=(y-x)A\textrm{e}_j^\top\big(\pi^{(1)}A^n_1 W^{(1)}+\pi^{(2)}A^n_2Z_0\big)\\[5pt] &=(y-x)F_n^{\Psi}=(y-x)(Z^j_{n+1}-(Z_n^{\Psi}-F_n^{\Psi})),\end{align*}
\begin{align*}\mathcal{F}^{j}(n+y)-\mathcal{F}^{j}(n+x)&=\left(\textrm{x}_1(\Phi^j_y)-\textrm{x}_1(\Phi^j_x)\right)A^n_1 W^{(1)}+\left(\textrm{x}_2(\Phi^j_y)-\textrm{x}_2(\Phi^j_x)\right)A^n_2Z_0\\[5pt] &=(y-x)A\textrm{e}_j^\top\pi^{(1)}A^n_1 W^{(1)}+(y-x)A\textrm{e}_j^\top\pi^{(2)}A^n_2Z_0\\[5pt] &=(y-x)A\textrm{e}_j^\top\big(\pi^{(1)}A^n_1 W^{(1)}+\pi^{(2)}A^n_2Z_0\big)\\[5pt] &=(y-x)F_n^{\Psi}=(y-x)(Z^j_{n+1}-(Z_n^{\Psi}-F_n^{\Psi})),\end{align*}
where
![]() $\Psi\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
is the characteristic given by
$\Psi\;:\;\mathbb{N}_0\to\mathbb{R}^{1\times J}$
is the characteristic given by
![]() $\Psi(k)=\textbf{1}_{\{k=0\}}\textrm{e}_j^{\top}L=\textbf{1}_{\{k=0\}}\langle\textrm{e}_j,L\rangle$
. Hence
$\Psi(k)=\textbf{1}_{\{k=0\}}\textrm{e}_j^{\top}L=\textbf{1}_{\{k=0\}}\langle\textrm{e}_j,L\rangle$
. Hence
![]() $Z_n^{\Psi}$
counts the number of individuals of type j in the
$Z_n^{\Psi}$
counts the number of individuals of type j in the
![]() $(n+1)$
th generation. We then obtain
$(n+1)$
th generation. We then obtain
 \begin{align*}\mathcal{Y}^{j}&(n+y)- \mathcal{Y}^{j}(n+x)=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\left(\mathcal{X}^{j}(n+y)-\mathcal{X}^{j}(n+x)\right)\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\left[(\mathcal{Z}^{j}(n+y)-\mathcal{Z}^{j}(n+x))-(\mathcal{F}^{j}(n+y)-\mathcal{F}^{j}(n+x))\right]\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big[\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\textbf{1}_{\{x< U_u\leq y\}}-(y-x)Z^j_{n+1}+(y-x)(Z_n^{\Psi}-F_n^{\Psi})\Big]\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big[\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\left(\textbf{1}_{\{x< U_u\leq y\}}-(y-x)\right)\cdot 1+(y-x)(Z_n^{\Psi}-F_n^{\Psi})\Big].\end{align*}
\begin{align*}\mathcal{Y}^{j}&(n+y)- \mathcal{Y}^{j}(n+x)=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\left(\mathcal{X}^{j}(n+y)-\mathcal{X}^{j}(n+x)\right)\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\left[(\mathcal{Z}^{j}(n+y)-\mathcal{Z}^{j}(n+x))-(\mathcal{F}^{j}(n+y)-\mathcal{F}^{j}(n+x))\right]\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big[\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\textbf{1}_{\{x< U_u\leq y\}}-(y-x)Z^j_{n+1}+(y-x)(Z_n^{\Psi}-F_n^{\Psi})\Big]\\[5pt] &=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big[\sum_{u\in\mathbb{T}; |u|=n+1; \textrm t(u)=j}\left(\textbf{1}_{\{x< U_u\leq y\}}-(y-x)\right)\cdot 1+(y-x)(Z_n^{\Psi}-F_n^{\Psi})\Big].\end{align*}
Since
![]() $Z_{n+1}^j$
and
$Z_{n+1}^j$
and
![]() $Z_n^{\Psi}-F_n^{\Psi}$
are
$Z_n^{\Psi}-F_n^{\Psi}$
are
![]() $\mathcal{A}_n$
-measurable, by applying Lemma 5 to the intervals
$\mathcal{A}_n$
-measurable, by applying Lemma 5 to the intervals
![]() $I=(x,y)$
,
$I=(x,y)$
,
![]() $J=(y,z)$
, with
$J=(y,z)$
, with
![]() $a_i=1$
,
$a_i=1$
,
![]() $A=(y-x)(Z_n^{\Psi}-F_n^{\Psi})$
, and
$A=(y-x)(Z_n^{\Psi}-F_n^{\Psi})$
, and
![]() $B=(z-y)(Z_n^{\Psi}-F_n^{\Psi})$
, we finally obtain
$B=(z-y)(Z_n^{\Psi}-F_n^{\Psi})$
, we finally obtain
 \begin{align*}\mathbb{E} & \Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{2}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{2}|\mathcal{A}_n\Big]\\[5pt] &\le C \Big(\frac{1}{n^{2\ell+1}\rho^{n}}\Big)^2\big((y-x)(z-y)\big(Z_{n+1}^j\big)^2 +A^4+B^4\big)\\[5pt] & \leq C (z-x)^2 \Big(\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big)^4\left[(Z_n^{\Psi}-F_n^{\Psi})^4+(Z_{n+1}^j)^2\right]=:C|z-x|^2H_n,\end{align*}
\begin{align*}\mathbb{E} & \Big[|\mathcal{Y}^{j}(n+y)-\mathcal{Y}^{j}(n+x)|^{2}\cdot |\mathcal{Y}^{j}(n+z)-\mathcal{Y}^{j}(n+y)|^{2}|\mathcal{A}_n\Big]\\[5pt] &\le C \Big(\frac{1}{n^{2\ell+1}\rho^{n}}\Big)^2\big((y-x)(z-y)\big(Z_{n+1}^j\big)^2 +A^4+B^4\big)\\[5pt] & \leq C (z-x)^2 \Big(\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\Big)^4\left[(Z_n^{\Psi}-F_n^{\Psi})^4+(Z_{n+1}^j)^2\right]=:C|z-x|^2H_n,\end{align*}
for some absolute constant C. We have
![]() $Z_{n+1}^j=Z_n^{\Psi}$
, so Theorem 5(i) implies that
$Z_{n+1}^j=Z_n^{\Psi}$
, so Theorem 5(i) implies that
![]() $\mathbb{E}[(Z_{n+1}^j)^p]=O(\rho^{pn})$
. On the other hand, Corollary 4 yields that
$\mathbb{E}[(Z_{n+1}^j)^p]=O(\rho^{pn})$
. On the other hand, Corollary 4 yields that
![]() $\mathbb{E}\big[(Z_n^{\Psi}-F_n^{\Psi})^{2p}\big] =O(n^{(2\ell+1)p}\rho^{pn})$
. As a consequence, the random variables
$\mathbb{E}\big[(Z_n^{\Psi}-F_n^{\Psi})^{2p}\big] =O(n^{(2\ell+1)p}\rho^{pn})$
. As a consequence, the random variables
![]() $H_n$
have bounded
$H_n$
have bounded
![]() $p/2$
moments, and in turn the process
$p/2$
moments, and in turn the process
![]() $\Big\{\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{j}(n+x); \ x\in \mathbb{R}\Big\}$
is tight in
$\Big\{\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{j}(n+x); \ x\in \mathbb{R}\Big\}$
is tight in
![]() $\mathcal D(\mathbb{R})$
.
$\mathcal D(\mathbb{R})$
.
As a consequence of the previous result we obtain the following.
Corollary 2. Suppose that the assumptions (GW1)–(GW3) hold and that the matrix L satisfies
![]() $\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
$\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
![]() $\delta\in (0,1)$
. Then the family of distributions
$\delta\in (0,1)$
. Then the family of distributions
is tight in the Skorokhod space
![]() $\mathcal D(\mathbb{R})$
endowed with the standard
$\mathcal D(\mathbb{R})$
endowed with the standard
![]() $\textbf{J}_1$
topology.
$\textbf{J}_1$
topology.
Proof. In view of the two equalities
![]() $\mathcal{Z}^{\mathsf{t}}(n+x)-1=\sum_{j=1}^J \mathcal{Z}^{j}(n-1+x)$
and
$\mathcal{Z}^{\mathsf{t}}(n+x)-1=\sum_{j=1}^J \mathcal{Z}^{j}(n-1+x)$
and
![]() $\mathcal{F}^{\mathsf{t}}(n+x)=\sum_{j=1}^J \mathcal{F}^{j}(n-1+x)$
, together with
$\mathcal{F}^{\mathsf{t}}(n+x)=\sum_{j=1}^J \mathcal{F}^{j}(n-1+x)$
, together with
 \begin{align*}\mathcal{Y}^{\mathsf{t}}(n+x)=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{\mathsf{t}}(n+x)=\sum_{j=1}^J\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{j}(n-1+x),\end{align*}
\begin{align*}\mathcal{Y}^{\mathsf{t}}(n+x)=\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{\mathsf{t}}(n+x)=\sum_{j=1}^J\frac{1}{n^{\ell+\frac12}\rho^{n/2}}\mathcal{X}^{j}(n-1+x),\end{align*}
we see that
![]() $\mathcal{Y}^{\mathsf{t}}(n+x)$
can be written as a finite sum of tight processes, so it is tight as well.
$\mathcal{Y}^{\mathsf{t}}(n+x)$
can be written as a finite sum of tight processes, so it is tight as well.
The convergence of the finite-dimensional distributions together with the tightness gives the weak convergence.
Proposition 3. Suppose that the assumptions (GW1)–(GW3) hold and that the matrix L satisfies
![]() $\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
$\mathbb{E}\left[\|L\|^{2+\delta}\right]<\infty$
for some
![]() $\delta\in (0,1)$
. Then we have the following weak convergence of sequences of processes in the Skorokhod space
$\delta\in (0,1)$
. Then we have the following weak convergence of sequences of processes in the Skorokhod space
![]() $\mathcal D(\mathbb{R})$
endowed with the standard
$\mathcal D(\mathbb{R})$
endowed with the standard
![]() $\textbf{J}_1$
topology: for every
$\textbf{J}_1$
topology: for every
![]() $j\in[J]$
it holds that
$j\in[J]$
it holds that
4.3. Properties of the limiting processes
 $\mathcal{G}^{\mathsf{t}}$
and
$\mathcal{G}^{\mathsf{t}}$
and
 $\mathcal{G}^{j}$
$\mathcal{G}^{j}$
Notice that for
![]() $\Phi_0\in\mathcal{C}$
, we have
$\Phi_0\in\mathcal{C}$
, we have
where
![]() $a,b\in \mathbb{R}$
and
$a,b\in \mathbb{R}$
and
![]() $j\in[J]$
. On the other hand, taking
$j\in[J]$
. On the other hand, taking
![]() $a=-\rho\textrm{u}_j$
and
$a=-\rho\textrm{u}_j$
and
![]() $b=1$
, we recover
$b=1$
, we recover
as defined in (1), whose ith entry is given by
![]() $\textrm{w}_{ji}=\mathbb{E}[L^{(i,j)}-\rho\textrm{u}_j]=a_{ji}-\rho\textrm{u}_j$
.
$\textrm{w}_{ji}=\mathbb{E}[L^{(i,j)}-\rho\textrm{u}_j]=a_{ji}-\rho\textrm{u}_j$
.
Proposition 4. For any
![]() $\Phi\in\mathcal C$
and
$\Phi\in\mathcal C$
and
![]() $j\in[J]$
, assume that
$j\in[J]$
, assume that
![]() $\textrm{w}_j\ne \textrm{0}$
and that
$\textrm{w}_j\ne \textrm{0}$
and that
 \begin{align} \sum_{\lambda\in\sigma_A} \sum_{\ell=0}^{J-1}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0. \end{align}
\begin{align} \sum_{\lambda\in\sigma_A} \sum_{\ell=0}^{J-1}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0. \end{align}
-
(i) If
 $\sum_{\lambda\in\sigma_A^{2}}\sum_{\ell=0}^{J-1}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0$
, then for any
$\sum_{\lambda\in\sigma_A^{2}}\sum_{\ell=0}^{J-1}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0$
, then for any
 $x\in[0,1)$
it holds that (16)In particular, the largest
$x\in[0,1)$
it holds that (16)In particular, the largest \begin{align}\max\{0\leq \ell\leq J-1\;:\;\sigma_\ell^2(\Phi_x)>0\}=\max\Big\{\ell\ge 0\;:\;\sum_{\lambda\in\sigma^{2}_A}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0\Big\}.\end{align}
\begin{align}\max\{0\leq \ell\leq J-1\;:\;\sigma_\ell^2(\Phi_x)>0\}=\max\Big\{\ell\ge 0\;:\;\sum_{\lambda\in\sigma^{2}_A}\|\textrm{Var}(\textrm{w}_jN^\ell\pi_{\lambda}L)\|>0\Big\}.\end{align}
 $\ell$
such that
$\ell$
such that
 $\sigma_\ell^2(\Phi_x)>0$
does not depend on x.
$\sigma_\ell^2(\Phi_x)>0$
does not depend on x.
-
(ii) Otherwise, for any
 $x\in[0,1)$
and
$x\in[0,1)$
and
 $0\leq \ell\leq J-1$
, it holds that
$0\leq \ell\leq J-1$
, it holds that  \begin{align*}\sigma_\ell^2(\Phi_x)=0 \quad \text{ and } \quad \sigma^2(\Phi_x)>0.\end{align*}
\begin{align*}\sigma_\ell^2(\Phi_x)=0 \quad \text{ and } \quad \sigma^2(\Phi_x)>0.\end{align*}
Proof. (i) For any
![]() $x\in[0,1)$
, the vector
$x\in[0,1)$
, the vector
![]() $\textrm{x}_2(\Phi_x)$
is given by
$\textrm{x}_2(\Phi_x)$
is given by
If k is at least the right-hand side of Equation (16), then for any
![]() $\lambda\in\sigma^{2}_A$
we have
$\lambda\in\sigma^{2}_A$
we have
![]() $\textrm{w}_jN_\lambda^k(L-A)= 0$
almost surely. Since
$\textrm{w}_jN_\lambda^k(L-A)= 0$
almost surely. Since
![]() $A_2$
is invertible, we have
$A_2$
is invertible, we have
so from the last two matrix equations we get
![]() $\sum_{j\geq 0}A_2^{-j}=A_2\sum_{j\geq 0}A_2^{-j}-A_2$
, which in turn implies
$\sum_{j\geq 0}A_2^{-j}=A_2\sum_{j\geq 0}A_2^{-j}-A_2$
, which in turn implies
![]() $(A_2-I)\sum_{j\geq 0}A_2^{-j}=A_2$
. Multiplying this equation by
$(A_2-I)\sum_{j\geq 0}A_2^{-j}=A_2$
. Multiplying this equation by
![]() $(A_2-I)^{-1}$
from the right and by
$(A_2-I)^{-1}$
from the right and by
![]() $A_2^{-1}$
from the left, we obtain
$A_2^{-1}$
from the left, we obtain
![]() $\sum_{j\geq 1}A_2^{-j}=(A_2-I)^{-1}$
; hence it holds that
$\sum_{j\geq 1}A_2^{-j}=(A_2-I)^{-1}$
; hence it holds that
![]() $(A_2-I)\sum_{j\geq 1}A_2^{-j}\pi_{\lambda}=\pi_{\lambda}$
, and finally it follows that
$(A_2-I)\sum_{j\geq 1}A_2^{-j}\pi_{\lambda}=\pi_{\lambda}$
, and finally it follows that
![]() $\sum_{j\geq 1}A_2^{-j}\pi_{\lambda}=((\lambda-1)I+N_{\lambda})^{-1}$
. In view of the definition (6) of
$\sum_{j\geq 1}A_2^{-j}\pi_{\lambda}=((\lambda-1)I+N_{\lambda})^{-1}$
. In view of the definition (6) of
![]() $\sigma_\ell(\Phi)$
, it is enough to understand the term
$\sigma_\ell(\Phi)$
, it is enough to understand the term
![]() $\textrm{x} _2(\Phi) \pi_\lambda (A-\lambda I)^{\ell}(L-A)$
. It holds that
$\textrm{x} _2(\Phi) \pi_\lambda (A-\lambda I)^{\ell}(L-A)$
. It holds that
 \begin{align*} \textrm{x} _2(\Phi_x) \pi_{\lambda} (A-\lambda I)^{k}&(L-A)=\Big(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j\sum_{j=1}^{\infty}A_2^{-j}\pi_{\lambda}\Big) (A-\lambda I)^{k}\pi_{\lambda}(L-A)\\[5pt] &=\big(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j((\lambda-1)I +N_{\lambda})^{-1}\big) N_{\lambda}^{k}(L-A)\\[5pt] &=\bigg(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j\sum_{j=0}^{d_{\lambda}-1}\left(\begin{array}{c}{-1}\\[2pt] {j}\end{array}\right)(\lambda-1)^{-1-j}N_{\lambda}^j\bigg) N_{\lambda}^{k}\pi_{\lambda}(L-A)= 0, \end{align*}
\begin{align*} \textrm{x} _2(\Phi_x) \pi_{\lambda} (A-\lambda I)^{k}&(L-A)=\Big(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j\sum_{j=1}^{\infty}A_2^{-j}\pi_{\lambda}\Big) (A-\lambda I)^{k}\pi_{\lambda}(L-A)\\[5pt] &=\big(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j((\lambda-1)I +N_{\lambda})^{-1}\big) N_{\lambda}^{k}(L-A)\\[5pt] &=\bigg(x\textrm{w}_j\pi_{\lambda}+\textrm{w}_j\sum_{j=0}^{d_{\lambda}-1}\left(\begin{array}{c}{-1}\\[2pt] {j}\end{array}\right)(\lambda-1)^{-1-j}N_{\lambda}^j\bigg) N_{\lambda}^{k}\pi_{\lambda}(L-A)= 0, \end{align*}
almost surely, and hence
![]() $\sigma_{\ell}^2(\Phi_x)=0$
. On the other hand, if
$\sigma_{\ell}^2(\Phi_x)=0$
. On the other hand, if
![]() $0\leq \ell\leq J-1$
is the maximal number such that
$0\leq \ell\leq J-1$
is the maximal number such that
![]() $\mathbb{P}(\textrm{w}_jN_\lambda^\ell(L-A)\neq 0)>0$
for some
$\mathbb{P}(\textrm{w}_jN_\lambda^\ell(L-A)\neq 0)>0$
for some
![]() $\lambda\in\sigma^{2}_A$
, then for such
$\lambda\in\sigma^{2}_A$
, then for such
![]() $\ell$
and
$\ell$
and
![]() $\lambda$
, similar calculations give
$\lambda$
, similar calculations give
 \begin{align*} \textrm{x} _2(\Phi_x) \pi_\lambda (A-\lambda I)^{\ell}(L-A) &=\bigg(x\textrm{w}_j\pi_\lambda+\textrm{w}_j\sum_{j=0}^{d_\lambda-1}\left(\begin{array}{c}{-1}\\[2pt] {j}\end{array}\right)(\lambda-1)^{-1-j}N_\lambda^j\bigg) N_\lambda^{\ell}\pi_\lambda(L-A)\\[5pt] &=\textrm{w}_j\big(x+(\lambda-1)^{-1}\big) N_\lambda^{\ell}\pi_\lambda(L-A)\neq 0\\[5pt] \end{align*}
\begin{align*} \textrm{x} _2(\Phi_x) \pi_\lambda (A-\lambda I)^{\ell}(L-A) &=\bigg(x\textrm{w}_j\pi_\lambda+\textrm{w}_j\sum_{j=0}^{d_\lambda-1}\left(\begin{array}{c}{-1}\\[2pt] {j}\end{array}\right)(\lambda-1)^{-1-j}N_\lambda^j\bigg) N_\lambda^{\ell}\pi_\lambda(L-A)\\[5pt] &=\textrm{w}_j\big(x+(\lambda-1)^{-1}\big) N_\lambda^{\ell}\pi_\lambda(L-A)\neq 0\\[5pt] \end{align*}
with positive probability, since
![]() $x+(\lambda-1)^{-1}\neq0$
because
$x+(\lambda-1)^{-1}\neq0$
because
![]() $\lambda\notin\mathbb{R}$
. This implies that
$\lambda\notin\mathbb{R}$
. This implies that
![]() $\sigma_\ell^2(\Phi_x)>0$
, and this proves (i).
$\sigma_\ell^2(\Phi_x)>0$
, and this proves (i).
(ii) Assume that
![]() $\textrm{w}_jN^\ell_{\lambda}(L-A)=0$
almost surely for any
$\textrm{w}_jN^\ell_{\lambda}(L-A)=0$
almost surely for any
![]() $\lambda\in\sigma_A^{2}$
and any
$\lambda\in\sigma_A^{2}$
and any
![]() $\ell\ge 0$
. Let
$\ell\ge 0$
. Let
![]() $\textrm{t}_j=\Phi_{0}(1)=a\textrm{1}+b \textrm{e}_j^\top L\in \mathbb{R}^{1\times J}$
be the random row vector whose expectation is
$\textrm{t}_j=\Phi_{0}(1)=a\textrm{1}+b \textrm{e}_j^\top L\in \mathbb{R}^{1\times J}$
be the random row vector whose expectation is
![]() $\mathbb{E}[\mathsf{t}_j]=\textrm{w}_j\neq \textrm{0}$
by assumption, and whose ith entry is denoted by
$\mathbb{E}[\mathsf{t}_j]=\textrm{w}_j\neq \textrm{0}$
by assumption, and whose ith entry is denoted by
![]() $\textrm{t}_{ji}$
. Note that for
$\textrm{t}_{ji}$
. Note that for
![]() $x\in(0,1)$
, in view of (8), we have
$x\in(0,1)$
, in view of (8), we have
 \begin{align*} \sigma^2(\Phi_x)&=\sum_{k=0}^{\infty}\rho^{-k}\textrm{Var}\left[\Phi_x(k)+\Psi^{\Phi_x}(k)\right]\textrm{u} \ge\textrm{Var}\left[\Phi_x(0)+\Psi^{\Phi_x}(0)\right]\textrm{u}\\[5pt] &\ge \mathbb{E}\big[\textrm{Var}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}+\Psi^{\Phi_x}(0)\big|L\big]\textrm{u}\big]+\textrm{Var}\big[\mathbb{E}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}+\Psi^{\Phi_x}(0)\big|L\big]\textrm{u}\big]\\[5pt] &\ge \mathbb{E}\big[\textrm{Var}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}\big|L\big]\textrm{u}\big]=x(1-x)\mathbb{E}\Big[\sum_{i=1}^J \textrm{t}^2_{ji} \textrm u_i\Big] \ge x(1-x)\sum_{i=1}^J \textrm{w}_{ji}^2 \textrm u_i>0, \end{align*}
\begin{align*} \sigma^2(\Phi_x)&=\sum_{k=0}^{\infty}\rho^{-k}\textrm{Var}\left[\Phi_x(k)+\Psi^{\Phi_x}(k)\right]\textrm{u} \ge\textrm{Var}\left[\Phi_x(0)+\Psi^{\Phi_x}(0)\right]\textrm{u}\\[5pt] &\ge \mathbb{E}\big[\textrm{Var}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}+\Psi^{\Phi_x}(0)\big|L\big]\textrm{u}\big]+\textrm{Var}\big[\mathbb{E}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}+\Psi^{\Phi_x}(0)\big|L\big]\textrm{u}\big]\\[5pt] &\ge \mathbb{E}\big[\textrm{Var}\big[\textrm{t}_j\textbf{1}_{\{U\le x\}}\big|L\big]\textrm{u}\big]=x(1-x)\mathbb{E}\Big[\sum_{i=1}^J \textrm{t}^2_{ji} \textrm u_i\Big] \ge x(1-x)\sum_{i=1}^J \textrm{w}_{ji}^2 \textrm u_i>0, \end{align*}
since by assumption
![]() $\textrm{w}_j\neq0$
. Now we prove that
$\textrm{w}_j\neq0$
. Now we prove that
![]() $\sigma^2(\Phi_0)$
does not vanish. We have
$\sigma^2(\Phi_0)$
does not vanish. We have
![]() $\Phi_0(k)=\textrm{w}_j\cdot \textbf{1}_{\{k\geq 1\}}$
, so
$\Phi_0(k)=\textrm{w}_j\cdot \textbf{1}_{\{k\geq 1\}}$
, so
![]() $\Phi_0\;:\;\mathbb{N}_0\mapsto \mathbb{R}^{1\times J}$
is completely deterministic. Assume that
$\Phi_0\;:\;\mathbb{N}_0\mapsto \mathbb{R}^{1\times J}$
is completely deterministic. Assume that
![]() $\sigma^2(\Phi_0)=0$
. Then for any
$\sigma^2(\Phi_0)=0$
. Then for any
![]() $k\in \mathbb{N}_0$
it holds that
$k\in \mathbb{N}_0$
it holds that
![]() $\textrm{Var}\left[\Psi^{\Phi_0}(k)\right]\textrm{u}=0$
, which in turn implies, as
$\textrm{Var}\left[\Psi^{\Phi_0}(k)\right]\textrm{u}=0$
, which in turn implies, as
![]() $\textrm{u}_j>0$
for
$\textrm{u}_j>0$
for
![]() $j\in[J]$
, that for any
$j\in[J]$
, that for any
![]() $k\in \mathbb{N}_0$
and
$k\in \mathbb{N}_0$
and
![]() $j\in[J]$
we have
$j\in[J]$
we have
![]() $\textrm{Var}\left[\Psi^{\Phi_0}(k)\textrm{e}_j\right]=0$
. The latter is equivalent to
$\textrm{Var}\left[\Psi^{\Phi_0}(k)\textrm{e}_j\right]=0$
. The latter is equivalent to
We set
![]() $A_\lambda = \pi_\lambda A+\lambda(I-\pi_\lambda)$
and observe that for any
$A_\lambda = \pi_\lambda A+\lambda(I-\pi_\lambda)$
and observe that for any
![]() $n\in\mathbb{Z}$
and
$n\in\mathbb{Z}$
and
![]() $m\in \mathbb{N}$
we have
$m\in \mathbb{N}$
we have
 \begin{align*} A_{\lambda}^n\pi_{\lambda}=(\lambda I+N_\lambda)^n\pi_{\lambda}=\lambda^{n}\sum_{i=0}^{d_{\lambda}}\lambda^{-i}\left(\begin{array}{c}{n}\\[2pt] {i}\end{array}\right)N_{\lambda}^i\pi_{\lambda}\end{align*}
\begin{align*} A_{\lambda}^n\pi_{\lambda}=(\lambda I+N_\lambda)^n\pi_{\lambda}=\lambda^{n}\sum_{i=0}^{d_{\lambda}}\lambda^{-i}\left(\begin{array}{c}{n}\\[2pt] {i}\end{array}\right)N_{\lambda}^i\pi_{\lambda}\end{align*}
and
 \begin{align*} \sum_{0\le \ell\le m}A_{1}^\ell\pi_{1}&=\sum_{0\le \ell\le m}(I+N_1)^ \ell\pi_{1}=\sum_{0\le \ell\le m}\sum_{i=0}^\ell\left(\begin{array}{c}{\ell}\\[2pt] {i}\end{array}\right)N_1^i\pi_{1} =\sum_{i=0}^{ d_1}N_1^i\sum_{l=i}^{m}\left(\begin{array}{c}{l}\\[2pt] {i}\end{array}\right)\pi_{1}, \end{align*}
\begin{align*} \sum_{0\le \ell\le m}A_{1}^\ell\pi_{1}&=\sum_{0\le \ell\le m}(I+N_1)^ \ell\pi_{1}=\sum_{0\le \ell\le m}\sum_{i=0}^\ell\left(\begin{array}{c}{\ell}\\[2pt] {i}\end{array}\right)N_1^i\pi_{1} =\sum_{i=0}^{ d_1}N_1^i\sum_{l=i}^{m}\left(\begin{array}{c}{l}\\[2pt] {i}\end{array}\right)\pi_{1}, \end{align*}
where in the second equation we have used
![]() $\lambda=1$
(if
$\lambda=1$
(if
![]() $\lambda$
would be in the spectrum of A). Suppose now that for some vector
$\lambda$
would be in the spectrum of A). Suppose now that for some vector
![]() $\textrm{z}\in\mathbb{R}^J$
we have
$\textrm{z}\in\mathbb{R}^J$
we have
and for any
![]() $k\in\mathbb{N}_0$
it holds that
$k\in\mathbb{N}_0$
it holds that
Note that the left-hand side of the previous equation can be rewritten as
 \begin{align*} &\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA^\ell\mathsf{P}(k,\ell)\textrm{z}= \sum_{\lambda\in\sigma_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\mathsf{P}(k,\ell)\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma_A^{1}\cup\sigma_A^{3}}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\mathsf{P}(k,\ell)\textrm{z}\\[5pt] &=-\sum_{\lambda\in\sigma^{1}_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textbf{1}_{\{\ell<0\}}\textrm{z} +\sum_{\lambda\in\sigma^{3}_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textbf{1}_{\{\ell\ge 0\}}\textrm{z}. \end{align*}
\begin{align*} &\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA^\ell\mathsf{P}(k,\ell)\textrm{z}= \sum_{\lambda\in\sigma_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\mathsf{P}(k,\ell)\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma_A^{1}\cup\sigma_A^{3}}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\mathsf{P}(k,\ell)\textrm{z}\\[5pt] &=-\sum_{\lambda\in\sigma^{1}_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textbf{1}_{\{\ell<0\}}\textrm{z} +\sum_{\lambda\in\sigma^{3}_A}\sum_{\ell\in \mathbb{Z}}\textbf{1}_{\{k-\ell-1\ge 1\}}\textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textbf{1}_{\{\ell\ge 0\}}\textrm{z}. \end{align*}
Setting
![]() $-n=k-2\ge -2$
, we get
$-n=k-2\ge -2$
, we get
 \begin{align*} 0&=\sum_{\lambda\in\sigma^{1}_A}\sum_{\ell\le -n}\textrm{w}_jA_{\lambda}^\ell\textbf{1}_{\{\ell<0\}}\pi_{\lambda}\textrm{z} =\sum_{\lambda\in\sigma^{1}_A}\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}A_{\lambda}^{-n}\pi_{\lambda}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^{1}_A}\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}(\lambda\pi_{\lambda}+N_\lambda)^{-n}\pi_{\lambda}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^{1}_A}\lambda^{-n}\sum_{i=0}^{d_{\lambda}}\left(\begin{array}{c}{-n}\\[2pt] {i}\end{array}\right)\lambda^{-i}\Big(\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}N_{\lambda}^i\pi_{\lambda}\textrm{z}\Big),\end{align*}
\begin{align*} 0&=\sum_{\lambda\in\sigma^{1}_A}\sum_{\ell\le -n}\textrm{w}_jA_{\lambda}^\ell\textbf{1}_{\{\ell<0\}}\pi_{\lambda}\textrm{z} =\sum_{\lambda\in\sigma^{1}_A}\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}A_{\lambda}^{-n}\pi_{\lambda}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^{1}_A}\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}(\lambda\pi_{\lambda}+N_\lambda)^{-n}\pi_{\lambda}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^{1}_A}\lambda^{-n}\sum_{i=0}^{d_{\lambda}}\left(\begin{array}{c}{-n}\\[2pt] {i}\end{array}\right)\lambda^{-i}\Big(\textrm{w}_j(I-A_{\lambda}^{-1})^{-1}N_{\lambda}^i\pi_{\lambda}\textrm{z}\Big),\end{align*}
which in view of Lemma 6 implies that
Now we can use the decomposition
 \begin{align*}(I-A_{\lambda}^{-1})^{-1}\pi_\lambda=\sum_{i=0}^{d_\lambda-1}c_iN^i_\lambda\pi_\lambda,\end{align*}
\begin{align*}(I-A_{\lambda}^{-1})^{-1}\pi_\lambda=\sum_{i=0}^{d_\lambda-1}c_iN^i_\lambda\pi_\lambda,\end{align*}
for some
![]() $c_0,\ldots,c_{d_\lambda-1}$
, and since
$c_0,\ldots,c_{d_\lambda-1}$
, and since
![]() $(I-A_{\lambda}^{-1})^{-1}$
is invertible, we conclude that the matrix
$(I-A_{\lambda}^{-1})^{-1}$
is invertible, we conclude that the matrix
![]() $(I-A_{\lambda}^{-1})^{-1}\pi_\lambda$
is not nilpotent and hence
$(I-A_{\lambda}^{-1})^{-1}\pi_\lambda$
is not nilpotent and hence
![]() $c_0\neq0$
. Now, taking
$c_0\neq0$
. Now, taking
![]() $i=d_{\lambda-1}$
in (19), we infer that
$i=d_{\lambda-1}$
in (19), we infer that
![]() $c_0\textrm{w}_jN_\lambda^{d_{\lambda}-1}\textrm{z}=0$
; that is, we have
$c_0\textrm{w}_jN_\lambda^{d_{\lambda}-1}\textrm{z}=0$
; that is, we have
![]() $\textrm{w}_jN_{\lambda}^{d_{\lambda}-1}\textrm{z}=0$
. Recursively, we see that for
$\textrm{w}_jN_{\lambda}^{d_{\lambda}-1}\textrm{z}=0$
. Recursively, we see that for
![]() $i=d_{\lambda}-1,d_{\lambda}-2,\ldots,0$
Equation (19) implies
$i=d_{\lambda}-1,d_{\lambda}-2,\ldots,0$
Equation (19) implies
![]() $\textrm{w}_jN_\lambda^i\textrm{z}=0$
, for any
$\textrm{w}_jN_\lambda^i\textrm{z}=0$
, for any
![]() $\lambda\in\sigma_A^{1}$
. Taking this into account and setting
$\lambda\in\sigma_A^{1}$
. Taking this into account and setting
![]() $n=k-2>0 $
, from the condition (18) we get
$n=k-2>0 $
, from the condition (18) we get
 \begin{align*} 0&=\sum_{\lambda\in\sigma^3_A}\sum_{0\le \ell\le n} \textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textrm{z} =\sum_{\lambda\in\sigma^3_A\setminus\{1\}}\sum_{0\le \ell\le n} \textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textrm{z} +\textbf{1}_{\{1\in\sigma^{3}_A\}}\sum_{0\le \ell\le n} \textrm{w}_jA_{1}^\ell\pi_{1}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^3_A\setminus\{1\}} \textrm{w}_j(A_{\lambda}-I)^{-1}(A_{\lambda}^{n+1}-I)\pi_{\lambda}\textrm{z} +\textbf{1}_{\{1\in\sigma^{3}_A\}}\sum_{0\le \ell\le n} \textrm{w}_j(I+N_1)^\ell\pi_{1}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^3_A\setminus\{1\}}\sum_{i=0}^{d_\lambda-1}\textrm{w}_j(A_{\lambda}-I)^{-1}N^i_\lambda\pi_\lambda \textrm{z}\lambda^np_{\lambda,i}(n)+\textbf{1}_{\{1\in\sigma^{3}_A\}} \sum_{i=0}^{d_1-1}\textrm{w}_jN^i_1\pi_1 \textrm{z} p_{1,i+1}(n)+c, \end{align*}
\begin{align*} 0&=\sum_{\lambda\in\sigma^3_A}\sum_{0\le \ell\le n} \textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textrm{z} =\sum_{\lambda\in\sigma^3_A\setminus\{1\}}\sum_{0\le \ell\le n} \textrm{w}_jA_{\lambda}^\ell\pi_{\lambda}\textrm{z} +\textbf{1}_{\{1\in\sigma^{3}_A\}}\sum_{0\le \ell\le n} \textrm{w}_jA_{1}^\ell\pi_{1}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^3_A\setminus\{1\}} \textrm{w}_j(A_{\lambda}-I)^{-1}(A_{\lambda}^{n+1}-I)\pi_{\lambda}\textrm{z} +\textbf{1}_{\{1\in\sigma^{3}_A\}}\sum_{0\le \ell\le n} \textrm{w}_j(I+N_1)^\ell\pi_{1}\textrm{z}\\[5pt] &=\sum_{\lambda\in\sigma^3_A\setminus\{1\}}\sum_{i=0}^{d_\lambda-1}\textrm{w}_j(A_{\lambda}-I)^{-1}N^i_\lambda\pi_\lambda \textrm{z}\lambda^np_{\lambda,i}(n)+\textbf{1}_{\{1\in\sigma^{3}_A\}} \sum_{i=0}^{d_1-1}\textrm{w}_jN^i_1\pi_1 \textrm{z} p_{1,i+1}(n)+c, \end{align*}
where
![]() $p_{\gamma,i}$
is some polynomial of degree i and c does not depend on n. Lemma 6 implies that
$p_{\gamma,i}$
is some polynomial of degree i and c does not depend on n. Lemma 6 implies that
and also
The same argument as before gives that
![]() $\textrm{w}_jN_\lambda^i\textrm{z}=0,$
for any
$\textrm{w}_jN_\lambda^i\textrm{z}=0,$
for any
![]() $\lambda\in\sigma_A^{3}$
and
$\lambda\in\sigma_A^{3}$
and
![]() $i<d_\lambda$
. Suppose now that
$i<d_\lambda$
. Suppose now that
![]() $\sigma^2(\Phi_0)=0$
and also
$\sigma^2(\Phi_0)=0$
and also
![]() $\sigma_\ell^2(\Phi_0)=0$
for all
$\sigma_\ell^2(\Phi_0)=0$
for all
![]() $0\leq \ell\leq J$
. Then by setting
$0\leq \ell\leq J$
. Then by setting
![]() $\textrm{z}=(L-A)\textrm e_j$
with
$\textrm{z}=(L-A)\textrm e_j$
with
![]() $j\in [J]$
we conclude that for any
$j\in [J]$
we conclude that for any
![]() $\lambda\in \sigma_A$
and
$\lambda\in \sigma_A$
and
![]() $\ell\ge 0$
,
$\ell\ge 0$
,
This contradicts the assumption.
Continuity of the limit processes
![]() $\boldsymbol{\mathcal{G}}^{\mathsf{t}}$
and
$\boldsymbol{\mathcal{G}}^{\mathsf{t}}$
and
![]() $\boldsymbol{\mathcal{G}}^{\textbf{\textit{j}}}$
$\boldsymbol{\mathcal{G}}^{\textbf{\textit{j}}}$
We recall once again the notation
![]() $\mathcal{G}^{\Phi}(x)=\rho^{\lfloor x\rfloor/2}G^{\Phi_{\{x\}}}$
, where
$\mathcal{G}^{\Phi}(x)=\rho^{\lfloor x\rfloor/2}G^{\Phi_{\{x\}}}$
, where
![]() $G^{\Phi_{\{x\}}}\overset{\textrm{d}}{=}\sigma_\ell(\Phi_{\{x\}})\mathcal{N}$
or
$G^{\Phi_{\{x\}}}\overset{\textrm{d}}{=}\sigma_\ell(\Phi_{\{x\}})\mathcal{N}$
or
![]() $G^{\Phi_{\{x\}}}\overset{\textrm{d}}{=}\sigma(\Phi_{\{x\}})\mathcal{N}$
, with
$G^{\Phi_{\{x\}}}\overset{\textrm{d}}{=}\sigma(\Phi_{\{x\}})\mathcal{N}$
, with
![]() $\mathcal{N}\;:\!=\;\mathcal{N}(0,1)$
denoting a standard normal variable independent of W, and
$\mathcal{N}\;:\!=\;\mathcal{N}(0,1)$
denoting a standard normal variable independent of W, and
![]() $\mathcal{G}^{\mathsf{t}}$
(respectively
$\mathcal{G}^{\mathsf{t}}$
(respectively
![]() $\mathcal{G}^{\Phi}$
) denoting
$\mathcal{G}^{\Phi}$
) denoting
![]() $\mathcal{G}^{\Phi}$
if
$\mathcal{G}^{\Phi}$
if
![]() $\Phi=\Phi^{\mathsf{t}}$
(respectively
$\Phi=\Phi^{\mathsf{t}}$
(respectively
![]() $\Phi=\Phi^i$
).
$\Phi=\Phi^i$
).
Lemma 2. For
![]() $j\in[J]$
, let
$j\in[J]$
, let
![]() $\mathcal{H}(x)=\rho \textrm{u}_j \mathcal{G}^{\mathsf{t}}(x)-\mathcal{G}^{j}(x)$
. Under the assumptions of Theorem 3,
$\mathcal{H}(x)=\rho \textrm{u}_j \mathcal{G}^{\mathsf{t}}(x)-\mathcal{G}^{j}(x)$
. Under the assumptions of Theorem 3,
![]() $\mathcal{H}(x)$
is continuous for any
$\mathcal{H}(x)$
is continuous for any
![]() $x\in [0,\infty)$
.
$x\in [0,\infty)$
.
Proof. Since
![]() $\mathcal{H}$
is a linear combination of the Gaussian processes
$\mathcal{H}$
is a linear combination of the Gaussian processes
![]() $\mathcal{G}^{\mathsf{t}}$
and
$\mathcal{G}^{\mathsf{t}}$
and
![]() $\mathcal{G}^{j}$
, it is enough to show continuity for the two terms separately. We start with the continuity of
$\mathcal{G}^{j}$
, it is enough to show continuity for the two terms separately. We start with the continuity of
![]() $\mathcal{G}^{j}$
. For any
$\mathcal{G}^{j}$
. For any
![]() $0\le x\le y\le 1$
, since either
$0\le x\le y\le 1$
, since either
or
depending on whether we are in Case (i) or Case (ii) of Theorem 3.5 in [Reference Kolesko and Sava-Huss8], we have to upper-bound
![]() $\sigma^2(\Phi^j_{y}-\Phi^j_{x})$
and
$\sigma^2(\Phi^j_{y}-\Phi^j_{x})$
and
![]() $\sigma_\ell^2(\Phi^j_{y}-\Phi^j_{x})$
by some power of
$\sigma_\ell^2(\Phi^j_{y}-\Phi^j_{x})$
by some power of
![]() $|y-x|$
. The definition of
$|y-x|$
. The definition of
![]() $\sigma^2(\Phi)$
applied to the characteristic
$\sigma^2(\Phi)$
applied to the characteristic
![]() $\Phi^j_{y}-\Phi^j_{x}$
yields
$\Phi^j_{y}-\Phi^j_{x}$
yields
 \begin{align*} &\sigma^2(\Phi^j_{y}-\Phi^j_{x})=\sum_{k<0}\rho^{-k}\textrm{Var}[\textrm{e}_j\pi^{(1)}(y-x)A^{k-1})(L-A)]\textrm{u} \\[5pt] + &\textrm{Var}[\textrm{e}_j\textbf{1}_{\{x< U\le y\}}-\textrm{e}_j\pi^{(1)}(y-x)A^{-1}(L-A)]\textrm{u} +\rho\textrm{Var}[(y-x)e_j\pi^{(3)}(L-A)]\textrm{u} \le C(y-x). \end{align*}
\begin{align*} &\sigma^2(\Phi^j_{y}-\Phi^j_{x})=\sum_{k<0}\rho^{-k}\textrm{Var}[\textrm{e}_j\pi^{(1)}(y-x)A^{k-1})(L-A)]\textrm{u} \\[5pt] + &\textrm{Var}[\textrm{e}_j\textbf{1}_{\{x< U\le y\}}-\textrm{e}_j\pi^{(1)}(y-x)A^{-1}(L-A)]\textrm{u} +\rho\textrm{Var}[(y-x)e_j\pi^{(3)}(L-A)]\textrm{u} \le C(y-x). \end{align*}
On the other hand, as for
![]() $\Phi^j_{y}-\Phi^j_{x}$
it holds that
$\Phi^j_{y}-\Phi^j_{x}$
it holds that
![]() $\textrm{x}_2=\textrm{x}_2(\Phi^j_{y}-\Phi^j_{x})=(y-x)\textrm{e}_j\pi^{(2)}$
, we conclude that
$\textrm{x}_2=\textrm{x}_2(\Phi^j_{y}-\Phi^j_{x})=(y-x)\textrm{e}_j\pi^{(2)}$
, we conclude that
 \begin{align*} \sigma_\ell^2(\Phi^j_{y}-\Phi^j_{x})= \frac{\rho^{-\ell}}{(2\ell+1)(\ell!)^2}\sum_{\lambda\in\sigma^2_A}\textrm{Var} \left[\textrm{x} _2 \pi_\lambda (A-\lambda I)^{\ell}L\right]\textrm{u}\le C(y-x)^2. \end{align*}
\begin{align*} \sigma_\ell^2(\Phi^j_{y}-\Phi^j_{x})= \frac{\rho^{-\ell}}{(2\ell+1)(\ell!)^2}\sum_{\lambda\in\sigma^2_A}\textrm{Var} \left[\textrm{x} _2 \pi_\lambda (A-\lambda I)^{\ell}L\right]\textrm{u}\le C(y-x)^2. \end{align*}
In particular, in both of the cases (i) and (ii) of [Reference Kolesko and Sava-Huss8, Theorem 3.5] we have
and therefore, since
![]() $\mathcal{G}^{j}$
is Gaussian, we obtain
$\mathcal{G}^{j}$
is Gaussian, we obtain
which by the Kolmogorov continuity theorem implies that
![]() $\mathcal{G}^{j}$
is continuous. The same calculations as for
$\mathcal{G}^{j}$
is continuous. The same calculations as for
![]() $\mathcal{G}^{j}$
can be carried out to prove that
$\mathcal{G}^{j}$
can be carried out to prove that
![]() $\mathcal{G}^{\mathsf{t}}$
is continuous, so also
$\mathcal{G}^{\mathsf{t}}$
is continuous, so also
![]() $\mathcal{H}(x)=\rho\textrm{u}_j\mathcal{G}^{\mathsf{t}}(x)-\mathcal{G}^{j}(x)$
is continuous.
$\mathcal{H}(x)=\rho\textrm{u}_j\mathcal{G}^{\mathsf{t}}(x)-\mathcal{G}^{j}(x)$
is continuous.
Localization of the stopping times
This section addresses the localization of the stopping times
![]() $(\tau_k)_{k\in\mathbb{N}}$
. On the non-extinction event
$(\tau_k)_{k\in\mathbb{N}}$
. On the non-extinction event
![]() $\mathcal{S}$
, for any
$\mathcal{S}$
, for any
![]() $n\in\mathbb{N}$
, we define the random variable
$n\in\mathbb{N}$
, we define the random variable
and we define the function
![]() $h\;:\;\mathbb{R}\to\mathbb{R}$
by
$h\;:\;\mathbb{R}\to\mathbb{R}$
by
Note that
![]() $h^{-1}$
is uniformly continuous and given by
$h^{-1}$
is uniformly continuous and given by
![]() $h^{-1}(x)=\lfloor x\rfloor+\log_\rho\big(1+(\rho-1)\{x\}\big)$
.
$h^{-1}(x)=\lfloor x\rfloor+\log_\rho\big(1+(\rho-1)\{x\}\big)$
.
Proposition 5. Under the assumptions (GW1)–(GW3), and if for
![]() $k\in\mathbb{N}$
we set
$k\in\mathbb{N}$
we set
![]() $t_k=h(T_k)$
, then for
$t_k=h(T_k)$
, then for
![]() $(\tau_k)$
defined as in (10), we have
$(\tau_k)$
defined as in (10), we have
Proof. By Proposition 2, the following
![]() $\mathbb{P}^\mathcal{S}$
-almost sure convergence holds:
$\mathbb{P}^\mathcal{S}$
-almost sure convergence holds:
We recall that
![]() $l_{\rho}\;:\;[0,\infty)\to\mathbb{R}$
is defined as
$l_{\rho}\;:\;[0,\infty)\to\mathbb{R}$
is defined as
![]() $l_{\rho}(x)=(1+(\rho-1)\{x\})\rho^{-\{x\}}$
. Since
$l_{\rho}(x)=(1+(\rho-1)\{x\})\rho^{-\{x\}}$
. Since
![]() $\mathcal{Z}^{\mathsf{t}}(\tau_k)=k$
, we infer that for any
$\mathcal{Z}^{\mathsf{t}}(\tau_k)=k$
, we infer that for any
![]() $\delta>0$
and large enough k we have
$\delta>0$
and large enough k we have
This can be rewritten as
Notice that we have
and the inverse of the increasing function
![]() $h^{-1}(x)$
is given by
$h^{-1}(x)$
is given by
![]() $ \lfloor x\rfloor +\frac{\rho^{\{x\}}-1}{\rho-1}=h(x)$
, which then yields the following inequalities:
$ \lfloor x\rfloor +\frac{\rho^{\{x\}}-1}{\rho-1}=h(x)$
, which then yields the following inequalities:
From the uniform continuity of h(x), by letting
![]() $\delta\to 0$
, we obtain the claim.
$\delta\to 0$
, we obtain the claim.
The above proposition implies that
4.4. Limit theorems for
 $B_j$
$B_j$
Proposition 6. Under the assumptions of Theorem 3, let
![]() $\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
be any characteristic such that the following stable convergence holds:
$\Phi\;:\;\mathbb{Z}\to\mathbb{R}^{1\times J}$
be any characteristic such that the following stable convergence holds:
for some continuous Gaussian process
![]() $\mathcal{G}^{\Phi}$
with
$\mathcal{G}^{\Phi}$
with
![]() $\textrm{Var} \left[\mathcal{G}^{\Phi}(x)\right]>0$
, for any
$\textrm{Var} \left[\mathcal{G}^{\Phi}(x)\right]>0$
, for any
![]() $x\in\mathbb{R}$
. Then there exists a continuous, positive, 1-periodic function
$x\in\mathbb{R}$
. Then there exists a continuous, positive, 1-periodic function
![]() $\psi^{\Phi}$
such that for
$\psi^{\Phi}$
such that for
![]() $\tau_n$
as in (10) and
$\tau_n$
as in (10) and
![]() $T_n=\log_\rho\frac{n(\rho-1)}{W}$
, it holds that
$T_n=\log_\rho\frac{n(\rho-1)}{W}$
, it holds that
 \begin{align} \frac{\mathcal{X}^{\Phi}(\tau_n)}{ \sqrt n (\log_\rho n)^{l+\frac12}\psi^{\Phi}(T_n) }\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal N(0,1),\quad \text{ as } n\to\infty. \end{align}
\begin{align} \frac{\mathcal{X}^{\Phi}(\tau_n)}{ \sqrt n (\log_\rho n)^{l+\frac12}\psi^{\Phi}(T_n) }\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal N(0,1),\quad \text{ as } n\to\infty. \end{align}
Proof. The key idea in the proof is to use the functional limit theorem for
![]() $\mathcal{X}^{\Phi}$
to replace
$\mathcal{X}^{\Phi}$
to replace
![]() $\mathcal{X}^{\Phi}(\tau_n)$
by
$\mathcal{X}^{\Phi}(\tau_n)$
by
![]() $\mathcal{X}^{\Phi}(t_n)$
. Recall that for h as defined in (20), which is continuous and strictly increasing, we have used the notation
$\mathcal{X}^{\Phi}(t_n)$
. Recall that for h as defined in (20), which is continuous and strictly increasing, we have used the notation
![]() $t_n=h(\log_\rho n-\log_\rho\frac{W}{\rho-1})=h(T_n)$
. Furthermore, for any
$t_n=h(\log_\rho n-\log_\rho\frac{W}{\rho-1})=h(T_n)$
. Furthermore, for any
![]() $x\in\mathbb{R}$
and
$x\in\mathbb{R}$
and
![]() $n\in\mathbb{N}$
it holds that
$n\in\mathbb{N}$
it holds that
![]() $h(n+x)=n+h(x)$
. Consequently, by (21), we have
$h(n+x)=n+h(x)$
. Consequently, by (21), we have
and the latter convergence can be rewritten as
 \begin{align*} \frac{\mathcal{X}^{\Phi} \big(h(n+x)\big)}{\Big(n^{2\ell+1}\rho^{n} W\textrm{Var} \left[\mathcal{G}^{\Phi}\big(h(x)\big)\right]\Big)^{1/2}}\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)\quad\text{in }\mathcal D(\mathbb{R}), \end{align*}
\begin{align*} \frac{\mathcal{X}^{\Phi} \big(h(n+x)\big)}{\Big(n^{2\ell+1}\rho^{n} W\textrm{Var} \left[\mathcal{G}^{\Phi}\big(h(x)\big)\right]\Big)^{1/2}}\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)\quad\text{in }\mathcal D(\mathbb{R}), \end{align*}
for some stationary and continuous process G with
![]() $G(0)\overset{\textrm{D}}{=}\mathcal N(0,1)$
. Note that one consequence of the convergence in (21) is the following property of the limiting process:
$G(0)\overset{\textrm{D}}{=}\mathcal N(0,1)$
. Note that one consequence of the convergence in (21) is the following property of the limiting process:
![]() $\mathcal{G}^{\Phi}(x+1)\overset{\textrm{d}}{=}\sqrt\rho \mathcal{G}^{\Phi}(x)$
. Hence, the previous convergence is equivalent to
$\mathcal{G}^{\Phi}(x+1)\overset{\textrm{d}}{=}\sqrt\rho \mathcal{G}^{\Phi}(x)$
. Hence, the previous convergence is equivalent to
 \begin{align*} \frac{\mathcal{X}^{\Phi} \big(h(n+x)\big)}{\Big(\big((n+x)\vee 1\big)^{2\ell+1}\rho^{n+x}\rho^{-\{x\}}W\textrm{Var} \left[\mathcal{G}^{\Phi}\big(h(\{x\})\big)\right]\Big)^{1/2}}\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)\quad\text{in }\mathcal D(\mathbb{R}).\end{align*}
\begin{align*} \frac{\mathcal{X}^{\Phi} \big(h(n+x)\big)}{\Big(\big((n+x)\vee 1\big)^{2\ell+1}\rho^{n+x}\rho^{-\{x\}}W\textrm{Var} \left[\mathcal{G}^{\Phi}\big(h(\{x\})\big)\right]\Big)^{1/2}}\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)\quad\text{in }\mathcal D(\mathbb{R}).\end{align*}
In other words, for the function
![]() $\psi^\Phi$
defined by
$\psi^\Phi$
defined by
which is continuous and positive, and for
 \begin{align*} X(x)=\frac{\mathcal{X}^{\Phi} \big(h(x)\big)}{\Big(\big(x\vee 1\big)^{2\ell+1}\rho^{x}\frac{W}{\rho-1}\Big)^{1/2} \psi^\Phi(x)}, \end{align*}
\begin{align*} X(x)=\frac{\mathcal{X}^{\Phi} \big(h(x)\big)}{\Big(\big(x\vee 1\big)^{2\ell+1}\rho^{x}\frac{W}{\rho-1}\Big)^{1/2} \psi^\Phi(x)}, \end{align*}
it holds that
![]() $X(n+x)\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)$
, and therefore an application of Lemma 3(ii) with
$X(n+x)\xrightarrow{\scriptscriptstyle{\textrm{st},\mathcal{S}}} G(x)$
, and therefore an application of Lemma 3(ii) with
![]() $a_n= \log_\rho n$
yields
$a_n= \log_\rho n$
yields
Since
![]() $h^{-1}(x)$
is uniformly continuous, by Proposition 5 we get
$h^{-1}(x)$
is uniformly continuous, by Proposition 5 we get
We claim that from Lemma 3(i) with
![]() $N_n= \lfloor{\log_{\rho} n}\rfloor$
and
$N_n= \lfloor{\log_{\rho} n}\rfloor$
and
![]() $\delta_n=2^{-n}$
it follows that
$\delta_n=2^{-n}$
it follows that
Indeed, for fixed
![]() $m\in\mathbb{N}$
, on the event
$m\in\mathbb{N}$
, on the event
![]() $|\log_{\rho} W|\le k_m-2\delta_m-1-\log_\rho(\rho-1)$
and
$|\log_{\rho} W|\le k_m-2\delta_m-1-\log_\rho(\rho-1)$
and
![]() $|h^{-1}(\tau_n)-h^{-1}(t_n)|\le \delta_m$
we have
$|h^{-1}(\tau_n)-h^{-1}(t_n)|\le \delta_m$
we have
In turn, for any
![]() $\varepsilon>0$
we get
$\varepsilon>0$
we get
 \begin{align*} &\mathbb{P}^\mathcal{S}\Big(\big|X\big(h^{-1}(\tau_n)\big)-X\big(h^{-1}(t_n)\big)\big|>\varepsilon\Big)\le \mathbb{P}^\mathcal{S}\big( \omega(X_{N_{m}},k_m,\delta_{m})>\varepsilon\big)\\[5pt] &+\mathbb{P}^\mathcal{S}\big(|\log_\rho W|> k_m-2\delta_m-1-\log_\rho(\rho-1)\big) +\mathbb{P}^\mathcal{S}\big(|h^{-1}(\tau_n)-h^{-1}(t_n)|> \delta_m\big).\end{align*}
\begin{align*} &\mathbb{P}^\mathcal{S}\Big(\big|X\big(h^{-1}(\tau_n)\big)-X\big(h^{-1}(t_n)\big)\big|>\varepsilon\Big)\le \mathbb{P}^\mathcal{S}\big( \omega(X_{N_{m}},k_m,\delta_{m})>\varepsilon\big)\\[5pt] &+\mathbb{P}^\mathcal{S}\big(|\log_\rho W|> k_m-2\delta_m-1-\log_\rho(\rho-1)\big) +\mathbb{P}^\mathcal{S}\big(|h^{-1}(\tau_n)-h^{-1}(t_n)|> \delta_m\big).\end{align*}
Taking the limit first as
![]() $n\to\infty$
and then as
$n\to\infty$
and then as
![]() $m\to\infty$
and using (24), we get (25). Finally, (25) and (23) imply that
$m\to\infty$
and using (24), we get (25). Finally, (25) and (23) imply that
 \begin{align*}\frac{\mathcal{X}^{\Phi}(\tau_n)}{\big(h^{-1}(\tau_n)\vee 1\big)^{\ell+\frac12}\sqrt n\rho^{(h^{-1}(\tau_n)-h^{-1}(t_n))/2} \psi^\Phi(h^{-1}(\tau_n))}=X\big(h^{-1}(\tau_n)\big)\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} G(0),\end{align*}
\begin{align*}\frac{\mathcal{X}^{\Phi}(\tau_n)}{\big(h^{-1}(\tau_n)\vee 1\big)^{\ell+\frac12}\sqrt n\rho^{(h^{-1}(\tau_n)-h^{-1}(t_n))/2} \psi^\Phi(h^{-1}(\tau_n))}=X\big(h^{-1}(\tau_n)\big)\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} G(0),\end{align*}
which together with (24) and the
![]() $\mathbb{P}^\mathcal{S}$
-almost sure convergence of
$\mathbb{P}^\mathcal{S}$
-almost sure convergence of
![]() $\frac{\psi^\Phi(h^{-1}(\tau_n))}{\psi^\Phi(h^{-1}(t_n))}$
and
$\frac{\psi^\Phi(h^{-1}(\tau_n))}{\psi^\Phi(h^{-1}(t_n))}$
and
![]() $\frac{h^{-1}(\tau_n)}{\log_\rho n}$
to 1 yields that
$\frac{h^{-1}(\tau_n)}{\log_\rho n}$
to 1 yields that
 \begin{align*} \frac{\mathcal{X}^{\Phi}(\tau_n)}{\sqrt n(\log_\rho n)^{\ell+\frac12} \psi^\Phi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal N(0,1);\end{align*}
\begin{align*} \frac{\mathcal{X}^{\Phi}(\tau_n)}{\sqrt n(\log_\rho n)^{\ell+\frac12} \psi^\Phi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal N(0,1);\end{align*}
that is, (22) holds. This completes the proof.
Using the auxiliary result that we have just proved, we can now state and prove our main result.
Theorem 4. Suppose that (15) holds and all assumptions from Theorem 3 are satisfied. Then there exists a continuous, positive, and 1-periodic function
![]() $\psi$
such that, for
$\psi$
such that, for
![]() $T_n=\log_{\rho}\frac{n(\rho-1)}{W}$
and any
$T_n=\log_{\rho}\frac{n(\rho-1)}{W}$
and any
![]() $j\in[J]$
, we have
$j\in[J]$
, we have
 \begin{align*} \frac{B_j(n)-\mathcal{F}^{j}\big(\mathcal{F}^{\mathsf{inv}}(n)\big)}{\sqrt n(\log_{\rho} n)^{\ell+\frac12}\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1), \quad \text{as }n\to\infty. \end{align*}
\begin{align*} \frac{B_j(n)-\mathcal{F}^{j}\big(\mathcal{F}^{\mathsf{inv}}(n)\big)}{\sqrt n(\log_{\rho} n)^{\ell+\frac12}\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1), \quad \text{as }n\to\infty. \end{align*}
Proof. Since for any
![]() $j\in[J]$
we have
$j\in[J]$
we have
![]() $\mathcal{Z}^{j}(\tau_n)=B_j(n)$
and
$\mathcal{Z}^{j}(\tau_n)=B_j(n)$
and
![]() $\mathcal{X}^{j}(n)=\mathcal{Z}^{j}(n)-\mathcal{F}^{j}(n)$
, we can write
$\mathcal{X}^{j}(n)=\mathcal{Z}^{j}(n)-\mathcal{F}^{j}(n)$
, we can write
 \begin{align*}B_j(n)&=\mathcal{F}^{j}(\tau_n)+\mathcal{X}^{j}(\tau_n)\\[5pt] &=\mathcal{F}^{j}\big(\mathcal{F}^{\mathsf{inv}}(n)\big)+\mathcal{X}^{j}(\tau_n)+(\mathcal{F}^{j}\circ \mathcal{F}^{\mathsf{inv}}\circ \mathcal{F}^{\mathsf{t}}(\tau_n)-\mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))).\end{align*}
\begin{align*}B_j(n)&=\mathcal{F}^{j}(\tau_n)+\mathcal{X}^{j}(\tau_n)\\[5pt] &=\mathcal{F}^{j}\big(\mathcal{F}^{\mathsf{inv}}(n)\big)+\mathcal{X}^{j}(\tau_n)+(\mathcal{F}^{j}\circ \mathcal{F}^{\mathsf{inv}}\circ \mathcal{F}^{\mathsf{t}}(\tau_n)-\mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))).\end{align*}
From the fact that
![]() $\mathcal{F}^{\mathsf{t}}(\tau_n)=n-\mathcal{X}^{\mathsf{t}}(\tau_n)$
together with Lemma 1, we obtain
$\mathcal{F}^{\mathsf{t}}(\tau_n)=n-\mathcal{X}^{\mathsf{t}}(\tau_n)$
together with Lemma 1, we obtain
and therefore
By Proposition 4 (positivity of the variances of the limiting process) and Lemma 2 (continuity of the limit processes), the characteristics
![]() $\Phi=\Phi^j-\rho\textrm{u}_j\Phi^{\mathsf{t}}$
and
$\Phi=\Phi^j-\rho\textrm{u}_j\Phi^{\mathsf{t}}$
and
![]() $\Phi=\Phi^{\mathsf{t}}$
and the corresponding processes
$\Phi=\Phi^{\mathsf{t}}$
and the corresponding processes
![]() $\mathcal{X}^{\Phi}$
with these characteristics satisfy the assumptions of Proposition 6. Thus we can apply Proposition 6 to the processes
$\mathcal{X}^{\Phi}$
with these characteristics satisfy the assumptions of Proposition 6. Thus we can apply Proposition 6 to the processes
![]() $\mathcal{X}^{\Phi}=\mathcal{X}^{j}-\rho\textrm{u}_j\mathcal{X}^{\mathsf{t}}$
and to
$\mathcal{X}^{\Phi}=\mathcal{X}^{j}-\rho\textrm{u}_j\mathcal{X}^{\mathsf{t}}$
and to
![]() $\mathcal{X}^{\mathsf{t}}$
to obtain
$\mathcal{X}^{\mathsf{t}}$
to obtain
 \begin{align*}\frac{\mathcal{X}^{j}(\tau_n)-{\rho}\textrm{u}_j\mathcal{X}^{\mathsf{t}}(\tau_n)}{ \sqrt n (\log_\rho n)^{\ell+\frac12}\psi(T_n)} \xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}}\mathcal N(0,1),\end{align*}
\begin{align*}\frac{\mathcal{X}^{j}(\tau_n)-{\rho}\textrm{u}_j\mathcal{X}^{\mathsf{t}}(\tau_n)}{ \sqrt n (\log_\rho n)^{\ell+\frac12}\psi(T_n)} \xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}}\mathcal N(0,1),\end{align*}
for some function
![]() $\psi$
which is continuous, positive, and 1-periodic; moreover,
$\psi$
which is continuous, positive, and 1-periodic; moreover,
![]() $\frac{\mathcal{X}^{\mathsf{t}}(\tau_n)}{ \sqrt n (\log_\rho n)^{\ell+\frac12} }\cdot o(1) \xrightarrow{\scriptscriptstyle{\mathbb{P}}} 0$
as
$\frac{\mathcal{X}^{\mathsf{t}}(\tau_n)}{ \sqrt n (\log_\rho n)^{\ell+\frac12} }\cdot o(1) \xrightarrow{\scriptscriptstyle{\mathbb{P}}} 0$
as
![]() $n\to\infty$
, which completes the proof.
$n\to\infty$
, which completes the proof.
Finally, in view of Theorem 4, it suffices to find an expansion of
![]() $\mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))$
up to an error of order
$\mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))$
up to an error of order
![]() $o(n^{\log_\rho\gamma})$
to prove Theorem 2 ; the latter will then follow immediately from the next corollary.
$o(n^{\log_\rho\gamma})$
to prove Theorem 2 ; the latter will then follow immediately from the next corollary.
Corollary 3. Under the assumptions of Theorem 4, suppose that all eigenvalues in
![]() $\Gamma$
are simple. Then the following hold:
$\Gamma$
are simple. Then the following hold:
-
(i) If
 $\gamma \gt \sqrt \rho$
, then for any
$\gamma \gt \sqrt \rho$
, then for any
 $\lambda\in\Gamma$
there exist a 1-periodic, continuous function
$\lambda\in\Gamma$
there exist a 1-periodic, continuous function
 $f_{\lambda}\;:\;\mathbb{R}\to\mathbb{C}$
and a random variable
$f_{\lambda}\;:\;\mathbb{R}\to\mathbb{C}$
and a random variable
 $X_{\lambda}$
such that
$X_{\lambda}$
such that  \begin{align*}B_j(n)=\rho\textrm{u}_j\cdot n+\sum_{\lambda\in \Gamma}n^{\log_{\rho}\lambda}f_{\lambda}(T_n)X_{\lambda}+o_{\mathbb{P}}\Big(n^{\log_{\rho}\gamma}\Big).\end{align*}
\begin{align*}B_j(n)=\rho\textrm{u}_j\cdot n+\sum_{\lambda\in \Gamma}n^{\log_{\rho}\lambda}f_{\lambda}(T_n)X_{\lambda}+o_{\mathbb{P}}\Big(n^{\log_{\rho}\gamma}\Big).\end{align*}
-
(ii) If
 $\gamma=\sqrt \rho$
, then there is a 1-periodic, continuous function
$\gamma=\sqrt \rho$
, then there is a 1-periodic, continuous function
 $\psi\;:\;\mathbb{R}\to(0,\infty)$
such that the following convergence holds:
$\psi\;:\;\mathbb{R}\to(0,\infty)$
such that the following convergence holds:  \begin{align*}\frac{B_j(n)-\rho\textrm{u}_j\cdot n}{\sqrt n(\log_{\rho} n)^{\frac12}\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1),\quad \text{as }n\to\infty.\end{align*}
\begin{align*}\frac{B_j(n)-\rho\textrm{u}_j\cdot n}{\sqrt n(\log_{\rho} n)^{\frac12}\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1),\quad \text{as }n\to\infty.\end{align*}
-
(iii) If
 $\gamma<\sqrt \rho$
, then there is a 1-periodic, continuous function
$\gamma<\sqrt \rho$
, then there is a 1-periodic, continuous function
 $\psi\;:\;\mathbb{R}\to(0,\infty)$
such that the following convergence holds:
$\psi\;:\;\mathbb{R}\to(0,\infty)$
such that the following convergence holds:  \begin{align*}\frac{B_j(n)-\rho\textrm{u}_j\cdot n}{\sqrt n\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1),\quad \text{as }n\to\infty.\end{align*}
\begin{align*}\frac{B_j(n)-\rho\textrm{u}_j\cdot n}{\sqrt n\psi(T_n)}\xrightarrow{\scriptscriptstyle{\textrm{d},\mathcal{S}}} \mathcal{N}(0,1),\quad \text{as }n\to\infty.\end{align*}
Proof. We handle the case (i) in detail; the other two cases are identical, so we leave the details to the interested reader. If
![]() $\gamma>\sqrt \rho$
, then by (5) we have
$\gamma>\sqrt \rho$
, then by (5) we have
 \begin{align*} \mathcal{F}^{\Phi}(n)&= \textrm{x}_1(\Phi)A^n_1 W^{(1)}+\textrm{x}_2(\Phi)A^n_2Z_0 = \sum_{\lambda\in\Gamma\cup\{\rho\}}\lambda^n\textrm{x}_1(\Phi)\pi_{\lambda}W^{(1)}+o(\gamma^n)\\[5pt] &=\rho^n\textrm{x}_1(\Phi) W\textrm u+\sum_{\lambda\in\Gamma}\lambda^n\textrm{x}_1(\Phi) W_{\lambda} \textrm u^{\lambda}+o(\gamma^n),\end{align*}
\begin{align*} \mathcal{F}^{\Phi}(n)&= \textrm{x}_1(\Phi)A^n_1 W^{(1)}+\textrm{x}_2(\Phi)A^n_2Z_0 = \sum_{\lambda\in\Gamma\cup\{\rho\}}\lambda^n\textrm{x}_1(\Phi)\pi_{\lambda}W^{(1)}+o(\gamma^n)\\[5pt] &=\rho^n\textrm{x}_1(\Phi) W\textrm u+\sum_{\lambda\in\Gamma}\lambda^n\textrm{x}_1(\Phi) W_{\lambda} \textrm u^{\lambda}+o(\gamma^n),\end{align*}
where we define
![]() $W_{\lambda} \textrm u^{\lambda}=\pi_{\lambda} W^{(\lambda)}$
for some scalar random variable
$W_{\lambda} \textrm u^{\lambda}=\pi_{\lambda} W^{(\lambda)}$
for some scalar random variable
![]() $W_{\lambda}$
(this can be done since
$W_{\lambda}$
(this can be done since
![]() $\pi_{\lambda}$
is a projection on the space spanned by the eigenvector
$\pi_{\lambda}$
is a projection on the space spanned by the eigenvector
![]() $\textrm u^\lambda$
). In particular, as
$\textrm u^\lambda$
). In particular, as
![]() $\mathcal{F}^{j}$
and
$\mathcal{F}^{j}$
and
![]() $\mathcal{F}^{\mathsf{t}}$
are piecewise linear between consecutive integer arguments, we conclude that
$\mathcal{F}^{\mathsf{t}}$
are piecewise linear between consecutive integer arguments, we conclude that
and taking into account that
![]() $\textrm{x}_1(\Phi_{0}^j)= \frac{\lambda}{\lambda-1}\textrm{e}_j^\top\pi_\lambda$
, we finally get
$\textrm{x}_1(\Phi_{0}^j)= \frac{\lambda}{\lambda-1}\textrm{e}_j^\top\pi_\lambda$
, we finally get
By the same argument, we also obtain
 \begin{align*} \mathcal{F}^{\mathsf{t}}(x)=\sum_{j=1}^{J} \mathcal{F}^{j}(x-1)=\frac{\rho^x}{\rho-1}l_\rho(x) W+\sum_{\lambda\in\Gamma}\frac{\lambda^x}{\lambda-1}l_\lambda(x) W_\lambda \Big(\sum_{i=1}^{J}\textrm{u}_{i}^\lambda\Big) +o(\gamma^x).\end{align*}
\begin{align*} \mathcal{F}^{\mathsf{t}}(x)=\sum_{j=1}^{J} \mathcal{F}^{j}(x-1)=\frac{\rho^x}{\rho-1}l_\rho(x) W+\sum_{\lambda\in\Gamma}\frac{\lambda^x}{\lambda-1}l_\lambda(x) W_\lambda \Big(\sum_{i=1}^{J}\textrm{u}_{i}^\lambda\Big) +o(\gamma^x).\end{align*}
In particular, it holds that
 \begin{align*} \mathcal{F}^j(x)=\rho \textrm{u}_j\cdot \mathcal{F}^{\mathsf{t}}(x)+\sum_{\lambda\in\Gamma}\frac{\lambda^{x}}{\lambda-1}l_\lambda(x)\Big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\Big(\sum_{i=1}^J\textrm{u}_i^\lambda\Big)\Big) W_\lambda+o(\gamma^x).\end{align*}
\begin{align*} \mathcal{F}^j(x)=\rho \textrm{u}_j\cdot \mathcal{F}^{\mathsf{t}}(x)+\sum_{\lambda\in\Gamma}\frac{\lambda^{x}}{\lambda-1}l_\lambda(x)\Big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\Big(\sum_{i=1}^J\textrm{u}_i^\lambda\Big)\Big) W_\lambda+o(\gamma^x).\end{align*}
Since for
![]() $\lambda\in \Gamma$
we have
$\lambda\in \Gamma$
we have
and
![]() $\mathcal{F}^{\mathsf{inv}}(n)=t_n+o(1)=h(T_n)+o(1)$
, we deduce that
$\mathcal{F}^{\mathsf{inv}}(n)=t_n+o(1)=h(T_n)+o(1)$
, we deduce that
 \begin{align*} \mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))& =\rho \textrm{u}_j\cdot n+\sum_{\lambda\in\Gamma}n^{\log_\rho \lambda} \frac{l_\lambda(h(T_n))}{l_\rho(h(T_n))^{\log_\rho \lambda}} \cdot\Big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\Big(\sum_{i=1}^J \textrm{u}_i^\lambda\Big)\Big)\Big(\frac{\rho-1}{ W}\Big)^{\log_\rho \lambda} \frac{W_\lambda}{\lambda-1}\\[5pt] &+o_{\mathbb{P}}(n^{\log_\rho\gamma}),\end{align*}
\begin{align*} \mathcal{F}^{j}(\mathcal{F}^{\mathsf{inv}}(n))& =\rho \textrm{u}_j\cdot n+\sum_{\lambda\in\Gamma}n^{\log_\rho \lambda} \frac{l_\lambda(h(T_n))}{l_\rho(h(T_n))^{\log_\rho \lambda}} \cdot\Big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\Big(\sum_{i=1}^J \textrm{u}_i^\lambda\Big)\Big)\Big(\frac{\rho-1}{ W}\Big)^{\log_\rho \lambda} \frac{W_\lambda}{\lambda-1}\\[5pt] &+o_{\mathbb{P}}(n^{\log_\rho\gamma}),\end{align*}
and thus (i) holds with
 \begin{align*}f_\lambda(x)=\frac{l_\lambda(h(x))}{l_\rho(h(x))^{\log_\rho \lambda}}\quad \text{ and} \quad X_\lambda= \big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\big(\sum_{i=1}^J\textrm{u}_i^\lambda\big)\big)\Big(\frac{\rho-1}{ W}\Big)^{\log_\rho \lambda} \frac{W_\lambda}{\lambda-1},\end{align*}
\begin{align*}f_\lambda(x)=\frac{l_\lambda(h(x))}{l_\rho(h(x))^{\log_\rho \lambda}}\quad \text{ and} \quad X_\lambda= \big(\lambda\textrm{u}_j^\lambda-\rho \textrm u_j\big(\sum_{i=1}^J\textrm{u}_i^\lambda\big)\big)\Big(\frac{\rho-1}{ W}\Big)^{\log_\rho \lambda} \frac{W_\lambda}{\lambda-1},\end{align*}
for every
![]() $\lambda\in \Gamma$
.
$\lambda\in \Gamma$
.
In the case
![]() $\gamma=\sqrt \rho$
we have
$\gamma=\sqrt \rho$
we have
and for
![]() $\gamma<\sqrt \rho$
we have
$\gamma<\sqrt \rho$
we have
In both cases we can use the same approach as in the proof of (i), after an application of Theorem 4; this proves (ii) and (iii).
Appendix A. Example
We illustrate here the model with two alternating urns using an example with
![]() $J=3$
colors (
$J=3$
colors (
![]() $1= \text{black}$
,
$1= \text{black}$
,
![]() $2= \text{red}$
, and
$2= \text{red}$
, and
![]() $3=\text{green}$
in the tree from Figure 1) and deterministic replacement matrix L given by
$3=\text{green}$
in the tree from Figure 1) and deterministic replacement matrix L given by
 \begin{equation*}L=\begin{pmatrix}1\;\;\;\; & 0\;\;\;\; & 2\\[5pt] 0\;\;\;\; & 2\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 1\;\;\;\; & 1\end{pmatrix}\end{equation*}
\begin{equation*}L=\begin{pmatrix}1\;\;\;\; & 0\;\;\;\; & 2\\[5pt] 0\;\;\;\; & 2\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 1\;\;\;\; & 1\end{pmatrix}\end{equation*}
and
![]() $j_0=1$
; that is, we start with one black ball in
$j_0=1$
; that is, we start with one black ball in
![]() $\mathsf{U}_1$
at time 0, so
$\mathsf{U}_1$
at time 0, so
![]() $B(0)=(1,0,0)$
. The first column
$B(0)=(1,0,0)$
. The first column
![]() $L^{(1)}$
of L tells us that when we draw a black ball from some urn, we add one black and one green ball to the other urn, so
$L^{(1)}$
of L tells us that when we draw a black ball from some urn, we add one black and one green ball to the other urn, so
![]() $\mathsf{U}_2$
is given by the nodes at level one of the tree and
$\mathsf{U}_2$
is given by the nodes at level one of the tree and
![]() $B(1)=(2,0,1)$
. Since after one step
$B(1)=(2,0,1)$
. Since after one step
![]() $\mathsf{U}_1$
has been emptied, we proceed to draw balls step by step from
$\mathsf{U}_1$
has been emptied, we proceed to draw balls step by step from
![]() $\mathsf{U_2}$
(from the first level of the tree). After drawing a green ball from
$\mathsf{U_2}$
(from the first level of the tree). After drawing a green ball from
![]() $\mathsf{U}_2$
, since the third column of the matrix L gives the number of balls of each color added to the other urn, with probability
$\mathsf{U}_2$
, since the third column of the matrix L gives the number of balls of each color added to the other urn, with probability
![]() $1/2$
the number of balls added after two steps is
$1/2$
the number of balls added after two steps is
![]() $B(2)=(4,1,2)$
and with probability
$B(2)=(4,1,2)$
and with probability
![]() $1/2$
it is
$1/2$
it is
![]() $B(2)=(3,0,2)$
. Then
$B(2)=(3,0,2)$
. Then
![]() $B(3)=(5,1,3)$
and
$B(3)=(5,1,3)$
and
![]() $\mathsf{U}_2$
has been emptied, so we proceed again to
$\mathsf{U}_2$
has been emptied, so we proceed again to
![]() $\mathsf{U}_1$
, which now contains 6 balls, and with probability
$\mathsf{U}_1$
, which now contains 6 balls, and with probability
![]() $1/6$
we have
$1/6$
we have
![]() $B(4)=(5,3,4)$
; now we have started to build the third level of the random tree and to fill
$B(4)=(5,3,4)$
; now we have started to build the third level of the random tree and to fill
![]() $\mathsf{U}_2$
again.
$\mathsf{U}_2$
again.
Appendix B. Higher-order estimates and additional results
Higher-moment estimates for
![]() $Z_n^{\Phi}$
. We provide here, for a general random characteristic
$Z_n^{\Phi}$
. We provide here, for a general random characteristic
![]() $\Phi$
, higher-moment estimates for the random variable
$\Phi$
, higher-moment estimates for the random variable
![]() ${Z_n^{\Phi}-\textrm{x}_1A^n_1 W^{(1)}-\textrm{x}_2A^n_2Z_0}$
. These estimates are needed in the proof of Theorem 3 for the characteristics
${Z_n^{\Phi}-\textrm{x}_1A^n_1 W^{(1)}-\textrm{x}_2A^n_2Z_0}$
. These estimates are needed in the proof of Theorem 3 for the characteristics
![]() $\Phi^{\mathsf{t}}$
and
$\Phi^{\mathsf{t}}$
and
![]() $\Phi^j$
which fulfill the assumptions of the next result. Recall that
$\Phi^j$
which fulfill the assumptions of the next result. Recall that
![]() $\Phi$
is called centered if
$\Phi$
is called centered if
![]() $\mathbb{E}[\Phi(k)]=\textrm{0}\in \mathbb{R}^{1\times J}$
for any
$\mathbb{E}[\Phi(k)]=\textrm{0}\in \mathbb{R}^{1\times J}$
for any
![]() $k\in\mathbb{Z}$
.
$k\in\mathbb{Z}$
.
Theorem 5. Let
![]() $p\in[1,2]$
, and let
$p\in[1,2]$
, and let
![]() $\Phi\;:\;\mathbb{Z}\to \mathbb{C}^{1\times J}$
be a random characteristic. Moreover, assume that (GW1)–(GW3) hold and the second moment of L is finite. Then the following hold:
$\Phi\;:\;\mathbb{Z}\to \mathbb{C}^{1\times J}$
be a random characteristic. Moreover, assume that (GW1)–(GW3) hold and the second moment of L is finite. Then the following hold:
-
(i) If
 $\sum_{k\in \mathbb{Z}}\big(\mathbb{E}\big[ \|\Phi(k)\|^p\big]\big)^{1/p} \rho^{-k} <\infty$
, then
$\sum_{k\in \mathbb{Z}}\big(\mathbb{E}\big[ \|\Phi(k)\|^p\big]\big)^{1/p} \rho^{-k} <\infty$
, then
 $\mathbb{E}\big[|Z^\Phi_n|^{p}\big]=O(\rho ^{pn})$
.
$\mathbb{E}\big[|Z^\Phi_n|^{p}\big]=O(\rho ^{pn})$
. -
(ii) If
 $\sum_{k\leq n}\big(\mathbb{E}\big[ \|\Phi(k)\|^p\big]\big)^{1/p} \rho^{-k} =O(n^r) $
for some
$\sum_{k\leq n}\big(\mathbb{E}\big[ \|\Phi(k)\|^p\big]\big)^{1/p} \rho^{-k} =O(n^r) $
for some
 $r\ge0$
, then
$r\ge0$
, then
 $\mathbb{E}\big[|Z^\Phi_n|^p\big]=O(\rho ^{pn}n^{pr})$
.
$\mathbb{E}\big[|Z^\Phi_n|^p\big]=O(\rho ^{pn}n^{pr})$
.
If in addition
![]() $\Phi$
is centered, then the following hold:
$\Phi$
is centered, then the following hold:
-
(i) If
 $\sum_{k\in \mathbb{Z}}\big(\mathbb{E}\big[ \|\Phi(k)\|^{2p}\big]\big)^{1/p}\rho^{-k}<\infty$
, then
$\sum_{k\in \mathbb{Z}}\big(\mathbb{E}\big[ \|\Phi(k)\|^{2p}\big]\big)^{1/p}\rho^{-k}<\infty$
, then
 $\mathbb{E}\left[|Z^\Phi_n|^{2p}\right]=O(\rho^{np})$
.
$\mathbb{E}\left[|Z^\Phi_n|^{2p}\right]=O(\rho^{np})$
. -
(ii) If
 $\sum_{k\le n}\big(\mathbb{E}\big[ \|\Phi(k)\|^{2p}\big]\big)^{1/p}\rho^{-k}=O(\rho^nn^r)$
, then
$\sum_{k\le n}\big(\mathbb{E}\big[ \|\Phi(k)\|^{2p}\big]\big)^{1/p}\rho^{-k}=O(\rho^nn^r)$
, then
 $\mathbb{E}\left[|Z^\Phi_n|^{2p}\right]=O(\rho^{np}n^{pr})$
.
$\mathbb{E}\left[|Z^\Phi_n|^{2p}\right]=O(\rho^{np}n^{pr})$
.
Proof. From the decomposition
it is enough to get the desired bound on each term separately. If v is the right eigenvector of A for the eigenvalue
![]() $\rho>1$
, then it holds that
$\rho>1$
, then it holds that
and further we have
 \begin{align*} \big|Z_n^{\mathbb{E}\Phi}\big|& \le \sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\| \|Z_k\| \le \sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\| \big\lt\textbf{1}, Z_k\big\gt\\[5pt] &\le \min_i\textrm{v}_i^{-1}\sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\|\big\lt\textrm{v}, Z_k\big\gt \le \min_i\textrm{v}_i^{-1}\sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\|\big\lt\textrm{v}, \rho^k W_k^{(1)}\big\gt\\[5pt] &=\rho^n \times \min_i\textrm{v}_i^{-1}\sum_{k\le n} \|\mathbb{E}\Phi(k)\| \rho^{-k}\big\lt\textrm{v}, W_{n-k}^{(1)}\big\gt. \end{align*}
\begin{align*} \big|Z_n^{\mathbb{E}\Phi}\big|& \le \sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\| \|Z_k\| \le \sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\| \big\lt\textbf{1}, Z_k\big\gt\\[5pt] &\le \min_i\textrm{v}_i^{-1}\sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\|\big\lt\textrm{v}, Z_k\big\gt \le \min_i\textrm{v}_i^{-1}\sum_{k\ge 0} \|\mathbb{E}\Phi(n-k)\|\big\lt\textrm{v}, \rho^k W_k^{(1)}\big\gt\\[5pt] &=\rho^n \times \min_i\textrm{v}_i^{-1}\sum_{k\le n} \|\mathbb{E}\Phi(k)\| \rho^{-k}\big\lt\textrm{v}, W_{n-k}^{(1)}\big\gt. \end{align*}
In view of Lemma 2.2 from [Reference Kolesko and Sava-Huss8], the random variables
![]() $\big\lt \textrm{v}, W_k^{(1)}\big\gt$
are bounded in
$\big\lt \textrm{v}, W_k^{(1)}\big\gt$
are bounded in
![]() $\mathcal{L}^2$
, and therefore by Minkowski’s inequality the
$\mathcal{L}^2$
, and therefore by Minkowski’s inequality the
![]() $\mathcal{L}^2$
norm of
$\mathcal{L}^2$
norm of
![]() $Z_n^{\mathbb{E}\Phi}$
is bounded by a multiple of
$Z_n^{\mathbb{E}\Phi}$
is bounded by a multiple of
![]() $\rho^n\sum_{k\le n} \|\mathbb{E}\Phi(k)\| \rho^{-k}$
. As a result we get
$\rho^n\sum_{k\le n} \|\mathbb{E}\Phi(k)\| \rho^{-k}$
. As a result we get
in the case (i) and
in the case (ii). By Jensen’s inequality, the pth moment of
![]() $Z_n^{\mathbb{E}\Phi}$
, for
$Z_n^{\mathbb{E}\Phi}$
, for
![]() $p\in[1,2]$
, is of order
$p\in[1,2]$
, is of order
![]() $O(\rho^{pn})$
in the case (i) and of order
$O(\rho^{pn})$
in the case (i) and of order
![]() $O(n^{pr}\rho^{pn})$
in the case (ii).
$O(n^{pr}\rho^{pn})$
in the case (ii).
Now we focus on the case with a centered characteristic
![]() $\Psi\;:\!=\;\Phi-\mathbb{E}\Phi$
. We consider an increasing sequence
$\Psi\;:\!=\;\Phi-\mathbb{E}\Phi$
. We consider an increasing sequence
![]() $(G_n)_{n\in\mathbb{N}}$
of subsets of
$(G_n)_{n\in\mathbb{N}}$
of subsets of
![]() $\mathcal{U}_{\infty}$
that satisfies the following:
$\mathcal{U}_{\infty}$
that satisfies the following:
![]() $\cup_{n\geq 1}G_n=\mathcal{U}_{\infty}$
; for any
$\cup_{n\geq 1}G_n=\mathcal{U}_{\infty}$
; for any
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $G_n=n$
; if
$G_n=n$
; if
![]() $u\in G_n$
, then for any
$u\in G_n$
, then for any
![]() $v\leq u$
,
$v\leq u$
,
![]() $v\in G_n$
. Such a sequence can be constructed using the diagonal method. If
$v\in G_n$
. Such a sequence can be constructed using the diagonal method. If
![]() $\mathcal{G}_n=\sigma\left(\{L(u)\;:\; u\in G_n\}\right)$
, then one can see that
$\mathcal{G}_n=\sigma\left(\{L(u)\;:\; u\in G_n\}\right)$
, then one can see that
![]() $\sum_{u\in G_k}\Psi_u(n-|u|)\textrm{e}_{\textrm t{(u)}}$
is a
$\sum_{u\in G_k}\Psi_u(n-|u|)\textrm{e}_{\textrm t{(u)}}$
is a
![]() $\mathcal{G}_k$
-martingale. Indeed, for any
$\mathcal{G}_k$
-martingale. Indeed, for any
![]() $u\in G_k$
both
$u\in G_k$
both
![]() $\textrm t(u)$
and
$\textrm t(u)$
and
![]() $\Psi_u$
are
$\Psi_u$
are
![]() $\mathcal{G}_k$
-measurable, and the fact that
$\mathcal{G}_k$
-measurable, and the fact that
![]() $\Psi$
is centered gives the martingale property. By the Topchii–Vatutin inequality [Reference Topchǐ and Vatutin13, Theorem 2] applied to
$\Psi$
is centered gives the martingale property. By the Topchii–Vatutin inequality [Reference Topchǐ and Vatutin13, Theorem 2] applied to
![]() $\sum_{u\in G_n}\Psi_u(n-|u|)\textrm{e}_{\textrm t{(u)}}$
we get
$\sum_{u\in G_n}\Psi_u(n-|u|)\textrm{e}_{\textrm t{(u)}}$
we get
 \begin{align*} \mathbb{E}\Big[\Big|\sum_{u\in\mathbb{T}}&\Psi_u(n-|u|)\textrm{e}_{\textrm t(u)}\Big|^p\Big]\le C_p\mathbb{E}\Big[\sum_{u\in\mathbb{T}}\big|\Psi_u(n-|u|)\textrm{e}_{\textrm t(u)}\big|^p\Big]\\[5pt] &\le C_p \sum_{k\ge 0}\mathbb{E}\big[\|\Psi(n-k)\|^p\big] \rho^{k} \le 2^p C_p \sum_{k\ge 0} \mathbb{E}\big[\|\Phi(n-k)\|^p \big]\rho^k\\[5pt] &\le 2^p C_p \Big(\sum_{k\ge 0} \big(\mathbb{E}\big[\|\Phi(n-k)\|^p \big]\big)^{1/p}\rho^{k/p}\Big)^p \le 2^p C_p \Big(\sum_{k\ge 0} \big(\mathbb{E}\big[\|\Phi(n-k)\|^p \big]\big)^{1/p}\rho^k\Big)^p\\[5pt] &\le 2^p C_p\rho^{pn} \Big(\sum_{k\le n} \big(\mathbb{E}\big[\|\Phi(k)\|^p \big]\big)^{1/p}\rho^{-k}\Big)^p, \end{align*}
\begin{align*} \mathbb{E}\Big[\Big|\sum_{u\in\mathbb{T}}&\Psi_u(n-|u|)\textrm{e}_{\textrm t(u)}\Big|^p\Big]\le C_p\mathbb{E}\Big[\sum_{u\in\mathbb{T}}\big|\Psi_u(n-|u|)\textrm{e}_{\textrm t(u)}\big|^p\Big]\\[5pt] &\le C_p \sum_{k\ge 0}\mathbb{E}\big[\|\Psi(n-k)\|^p\big] \rho^{k} \le 2^p C_p \sum_{k\ge 0} \mathbb{E}\big[\|\Phi(n-k)\|^p \big]\rho^k\\[5pt] &\le 2^p C_p \Big(\sum_{k\ge 0} \big(\mathbb{E}\big[\|\Phi(n-k)\|^p \big]\big)^{1/p}\rho^{k/p}\Big)^p \le 2^p C_p \Big(\sum_{k\ge 0} \big(\mathbb{E}\big[\|\Phi(n-k)\|^p \big]\big)^{1/p}\rho^k\Big)^p\\[5pt] &\le 2^p C_p\rho^{pn} \Big(\sum_{k\le n} \big(\mathbb{E}\big[\|\Phi(k)\|^p \big]\big)^{1/p}\rho^{-k}\Big)^p, \end{align*}
and the latter expression is of the order
![]() $O(\rho^{pn})$
in the case (i) and
$O(\rho^{pn})$
in the case (i) and
![]() $O(n^{pr}\rho^{pn})$
in the case (ii). This finishes the proof of the first two statements (i) and (ii).
$O(n^{pr}\rho^{pn})$
in the case (ii). This finishes the proof of the first two statements (i) and (ii).
Now we turn to the proof of (iii) and (iv). Observe that the Burkholder–Davis–Gundy inequality [Reference Burkholder, Davis and Gundy4, Theorem 1.1] yields
 \begin{align*} \mathbb{E}\Big[\big|Z_n^{\Phi}\big|^{2p}\Big]&= \mathbb{E}\Big[\Big|\sum_u \Phi_u(n-|u|)\textrm{e}_{\textrm t(u)}\Big|^{2p}\Big]\\[5pt] &\le C_p\mathbb{E}\Big[\Big|\sum_u \big|\Phi_u(n-|u|)\textrm{e}_{\textrm t(u)}\big|^2\Big|^{p}\Big] =C_p\mathbb{E}\Big[\big|Z_n^{\Psi}\big|^{p}\Big], \end{align*}
\begin{align*} \mathbb{E}\Big[\big|Z_n^{\Phi}\big|^{2p}\Big]&= \mathbb{E}\Big[\Big|\sum_u \Phi_u(n-|u|)\textrm{e}_{\textrm t(u)}\Big|^{2p}\Big]\\[5pt] &\le C_p\mathbb{E}\Big[\Big|\sum_u \big|\Phi_u(n-|u|)\textrm{e}_{\textrm t(u)}\big|^2\Big|^{p}\Big] =C_p\mathbb{E}\Big[\big|Z_n^{\Psi}\big|^{p}\Big], \end{align*}
where
![]() $\Psi$
is a new characteristic defined by
$\Psi$
is a new characteristic defined by
![]() $\Psi_u(k)\textrm{e}_i:==\big|\Phi_u(k)\textrm{e}_{i}\big|^2$
, i.e. the components of
$\Psi_u(k)\textrm{e}_i:==\big|\Phi_u(k)\textrm{e}_{i}\big|^2$
, i.e. the components of
![]() $\Psi(k)$
are squares of the components of
$\Psi(k)$
are squares of the components of
![]() $\Phi$
. Clearly
$\Phi$
. Clearly
![]() $\|\Psi(k)\|\le \|\Phi(k)\|^2$
, and as a consequence (iii) and (iv) follow from (i) and (ii) respectively applied to the characteristic
$\|\Psi(k)\|\le \|\Phi(k)\|^2$
, and as a consequence (iii) and (iv) follow from (i) and (ii) respectively applied to the characteristic
![]() $\Psi$
.
$\Psi$
.
Corollary 4. Let
![]() $\Phi\;:\;\mathbb{Z}\to \mathbb{C}^{1\times J}$
be a random characteristic such that
$\Phi\;:\;\mathbb{Z}\to \mathbb{C}^{1\times J}$
be a random characteristic such that
for some
![]() $\vartheta<\sqrt{\rho}$
, and
$\vartheta<\sqrt{\rho}$
, and
Suppose that
![]() $\mathbb{E}\left[\|L\|^{2p}\right]<\infty$
for some
$\mathbb{E}\left[\|L\|^{2p}\right]<\infty$
for some
![]() $p\in(1,2)$
. Then, for
$p\in(1,2)$
. Then, for
![]() $F_n^\Phi$
defined by (5), it holds that
$F_n^\Phi$
defined by (5), it holds that
 \begin{align*}\mathbb{E}\Big[\big|Z_n^{\Phi}-F^\Phi_n\big|^{2p}\Big]=\begin{cases}O\big(\rho^{np}\big)&\textit{if for all}\;\, \text{$0\leq \ell \leq J-1$, }\sigma_\ell=0,\\[5pt] O\big(n^{(2\ell+1)p}\rho^{np}\big)\quad&\textit{if}\; \text{$0\leq \ell\leq J-1$}\; \textit{is maximal with }\sigma_\ell>0. \end{cases}\end{align*}
\begin{align*}\mathbb{E}\Big[\big|Z_n^{\Phi}-F^\Phi_n\big|^{2p}\Big]=\begin{cases}O\big(\rho^{np}\big)&\textit{if for all}\;\, \text{$0\leq \ell \leq J-1$, }\sigma_\ell=0,\\[5pt] O\big(n^{(2\ell+1)p}\rho^{np}\big)\quad&\textit{if}\; \text{$0\leq \ell\leq J-1$}\; \textit{is maximal with }\sigma_\ell>0. \end{cases}\end{align*}
Proof. The decomposition from Equation (18) in [Reference Kolesko and Sava-Huss8] yields
where
![]() $\Psi_1$
and
$\Psi_1$
and
![]() $\Psi_2$
are two random centered characteristics such that
$\Psi_2$
are two random centered characteristics such that
-
• for any
 $k\in \mathbb{Z}$
we can decompose
$k\in \mathbb{Z}$
we can decompose
 $\Psi_1$
as
$\Psi_1$
as
 $\Psi_1(k)=\Psi_1'(k)(L-A)$
for some deterministic characteristic
$\Psi_1(k)=\Psi_1'(k)(L-A)$
for some deterministic characteristic
 $\Psi_1'(k)$
(see the paragraph after Equation (19) in [Reference Kolesko and Sava-Huss8]) and
$\Psi_1'(k)$
(see the paragraph after Equation (19) in [Reference Kolesko and Sava-Huss8]) and
 $\sum_{k\in \mathbb{Z}}\mathbb{E}\left[\|\Psi_1(k)\|^2\right]\rho^{-k}<\infty$
, and
$\sum_{k\in \mathbb{Z}}\mathbb{E}\left[\|\Psi_1(k)\|^2\right]\rho^{-k}<\infty$
, and -
•
 $Z_n^{\Psi_2}=\textrm{x}_2\pi^{(2)} (Z_n-A^n_2Z_0)$
, i.e.
$Z_n^{\Psi_2}=\textrm{x}_2\pi^{(2)} (Z_n-A^n_2Z_0)$
, i.e.
 $\Psi_2(k)=\textrm{x}_2\pi^{(2)}A^{k-1}(L-A)\textbf{1}_{\{k>0\}}$
, for some row vector
$\Psi_2(k)=\textrm{x}_2\pi^{(2)}A^{k-1}(L-A)\textbf{1}_{\{k>0\}}$
, for some row vector
 $\textrm{x}_2$
.
$\textrm{x}_2$
.
Moreover, the last term
![]() $o(\rho^{n/2})$
in (28) is deterministic. By Minkowski’s inequality, we have
$o(\rho^{n/2})$
in (28) is deterministic. By Minkowski’s inequality, we have
We estimate each of the two terms on the right-hand side separately. In view of Lemma 4, there is a constant
![]() $C>0$
such that
$C>0$
such that
and, in particular,
Theorem 5(iii) applied to
![]() $\Psi_1$
yields
$\Psi_1$
yields
![]() $\mathbb{E}\big[\big(Z^{\Psi_1}_{n}\big)^{2p}\big]=O(\rho^{np})$
. In order to deal with the second term
$\mathbb{E}\big[\big(Z^{\Psi_1}_{n}\big)^{2p}\big]=O(\rho^{np})$
. In order to deal with the second term
![]() $\mathbb{E}\left[\big(Z^{\Psi_2}_{n}\big)^{2p}\right]$
on the left-hand side of (29), note that by the definition of
$\mathbb{E}\left[\big(Z^{\Psi_2}_{n}\big)^{2p}\right]$
on the left-hand side of (29), note that by the definition of
![]() $\ell$
we may write
$\ell$
we may write
 \begin{align*} \Psi_2(k)&=\textbf{1}_{\{k>0\}}\textrm{x}_2\pi^{(2)} \sum_{j=0}^{J-1}\left(\begin{array}{c}{k-1}\\[2pt] {j}\end{array}\right)D^{k-1-j}N^{j}(L-A)\\[5pt] &=\textbf{1}_{\{k>0\}}\textrm{x}_2\pi^{(2)} \sum_{j=0}^{(J-1)\wedge \ell}\left(\begin{array}{c}{k-1}\\[2pt] {j}\end{array}\right)D^{k-1-j}N^{j}(L-A). \end{align*}
\begin{align*} \Psi_2(k)&=\textbf{1}_{\{k>0\}}\textrm{x}_2\pi^{(2)} \sum_{j=0}^{J-1}\left(\begin{array}{c}{k-1}\\[2pt] {j}\end{array}\right)D^{k-1-j}N^{j}(L-A)\\[5pt] &=\textbf{1}_{\{k>0\}}\textrm{x}_2\pi^{(2)} \sum_{j=0}^{(J-1)\wedge \ell}\left(\begin{array}{c}{k-1}\\[2pt] {j}\end{array}\right)D^{k-1-j}N^{j}(L-A). \end{align*}
In particular, as k goes to infinity we have
and by Theorem 5(iv) applied to
![]() $\Psi_2$
, we obtain
$\Psi_2$
, we obtain
![]() $\mathbb{E}\big[\big(Z^{\Psi_2}_{n}\big)^{2p}\big]=O(n^{(2\ell+1)p}\rho^{np})$
, which together with (29) proves the desired.
$\mathbb{E}\big[\big(Z^{\Psi_2}_{n}\big)^{2p}\big]=O(n^{(2\ell+1)p}\rho^{np})$
, which together with (29) proves the desired.
For any function
![]() $f\;:\;\mathbb{R}\to\mathbb{R}$
, let
$f\;:\;\mathbb{R}\to\mathbb{R}$
, let
be the modulus of continuity of f on the interval
![]() $[-k,k]$
.
$[-k,k]$
.
Lemma 3. For a stochastic process X taking values in the Skorokhod space
![]() $\mathcal D(\mathbb{R})$
, and for
$\mathcal D(\mathbb{R})$
, and for
![]() $n\in \mathbb{N}$
, let
$n\in \mathbb{N}$
, let
![]() $X_n(t)= X(t+n)$
. Furthermore, suppose that
$X_n(t)= X(t+n)$
. Furthermore, suppose that
![]() $Y=(Y(t))_{t\in\mathbb{R}}$
is a stationary process with almost surely continuous trajectories. Then we have the following:
$Y=(Y(t))_{t\in\mathbb{R}}$
is a stationary process with almost surely continuous trajectories. Then we have the following:
-
(i) If
 $X_n\xrightarrow{\scriptscriptstyle{\textrm{d}}} Y$
,
$X_n\xrightarrow{\scriptscriptstyle{\textrm{d}}} Y$
,
 $N_n$
is a sequence of natural numbers diverging to infinity, and
$N_n$
is a sequence of natural numbers diverging to infinity, and
 $\delta_n\searrow0$
, then there is a sequence
$\delta_n\searrow0$
, then there is a sequence
 $k_n\nearrow\infty$
such that (30)
$k_n\nearrow\infty$
such that (30) \begin{align}\omega(X_{N_{n}},k_n,\delta_{n})\xrightarrow{\scriptscriptstyle{\mathbb{P}}}0,\quad\text{as }n\to\infty.\end{align}
\begin{align}\omega(X_{N_{n}},k_n,\delta_{n})\xrightarrow{\scriptscriptstyle{\mathbb{P}}}0,\quad\text{as }n\to\infty.\end{align}
-
(ii) If, for some real-valued random variable S independent of Y, it holds that
 $(S,X_n)\xrightarrow{\scriptscriptstyle{\textrm{d}}}(S,Y)$
as
$(S,X_n)\xrightarrow{\scriptscriptstyle{\textrm{d}}}(S,Y)$
as
 $n\to\infty$
, then for any sequence
$n\to\infty$
, then for any sequence
 $a_n$
that diverges to infinity we have (31)
$a_n$
that diverges to infinity we have (31) \begin{align}X(a_n+S)\xrightarrow{\scriptscriptstyle{\textrm{d}}} Y(0),\quad \text{as } n\to\infty .\end{align}
\begin{align}X(a_n+S)\xrightarrow{\scriptscriptstyle{\textrm{d}}} Y(0),\quad \text{as } n\to\infty .\end{align}
Proof. (i): Fix
![]() $\delta>0$
and
$\delta>0$
and
![]() $k\in \mathbb{N}$
. Then the mapping
$k\in \mathbb{N}$
. Then the mapping
![]() $\mathcal D(\mathbb{R})\ni f\mapsto \omega(f,k,\delta)\in\mathbb{R}$
is continuous at any
$\mathcal D(\mathbb{R})\ni f\mapsto \omega(f,k,\delta)\in\mathbb{R}$
is continuous at any
![]() $f\in\mathcal C(\mathbb{R})$
. The continuous mapping theorem yields
$f\in\mathcal C(\mathbb{R})$
. The continuous mapping theorem yields
Hence, for any
![]() $\varepsilon >0$
we have
$\varepsilon >0$
we have
Since
![]() $\varepsilon$
is arbitrary, we can take the limit as
$\varepsilon$
is arbitrary, we can take the limit as
![]() $\varepsilon$
goes to 0, and from the continuity of Y we conclude that
$\varepsilon$
goes to 0, and from the continuity of Y we conclude that
In particular, there is
![]() $n(k)>n(k-1)$
such that for all
$n(k)>n(k-1)$
such that for all
![]() $n\ge n(k)$
it holds that
$n\ge n(k)$
it holds that
Now for
![]() $n\ge n(1)$
we set
$n\ge n(1)$
we set
![]() $k_n=k$
whenever
$k_n=k$
whenever
![]() $n(k)\le n<n(k+1)$
. Clearly
$n(k)\le n<n(k+1)$
. Clearly
![]() $k_n\nearrow\infty$
and it holds that
$k_n\nearrow\infty$
and it holds that
which implies (30); this proves the first part of the claim.
(ii): The convergence in (31) holds if for any subsequence
![]() $n_k$
we can choose a further subsequence
$n_k$
we can choose a further subsequence
![]() $n_{k_l}$
along which the convergence holds. Since we may replace the sequence
$n_{k_l}$
along which the convergence holds. Since we may replace the sequence
![]() $a_n$
by a subsequence
$a_n$
by a subsequence
![]() $a_{n_k}$
, it suffices to show the convergence (31) along some subsequence. Thus, without loss of generality, we may assume that
$a_{n_k}$
, it suffices to show the convergence (31) along some subsequence. Thus, without loss of generality, we may assume that
![]() $\{a_n\}\to a$
for some
$\{a_n\}\to a$
for some
![]() $a\in[0,1]$
. For
$a\in[0,1]$
. For
![]() $N_n=\lfloor a_n\rfloor$
and
$N_n=\lfloor a_n\rfloor$
and
![]() $\delta_n=2|\{a_n\}-a|$
, we infer from Part (i) the existence of a sequence
$\delta_n=2|\{a_n\}-a|$
, we infer from Part (i) the existence of a sequence
![]() $k_n\nearrow\infty$
such that (30) holds.
$k_n\nearrow\infty$
such that (30) holds.
For
![]() $Z_n= X(N_n+\{a_n\}+S)-X(N_n+a+S)$
, once again by Part (i) of the proof, we have
$Z_n= X(N_n+\{a_n\}+S)-X(N_n+a+S)$
, once again by Part (i) of the proof, we have
and thus, by Slutsky’s theorem, it suffices to prove
Next, observe that the mapping
![]() $\mathbb{R}\times\mathcal D(\mathbb{R})\ni(s,x)\mapsto x(a+s)\in \mathbb{R}$
is continuous at any point
$\mathbb{R}\times\mathcal D(\mathbb{R})\ni(s,x)\mapsto x(a+s)\in \mathbb{R}$
is continuous at any point
![]() $(s,x)\in \mathbb{R}\times \mathcal C(\mathbb{R})$
. Therefore, by the continuous mapping theorem we have
$(s,x)\in \mathbb{R}\times \mathcal C(\mathbb{R})$
. Therefore, by the continuous mapping theorem we have
and this completes the proof.
Lemma 4. Suppose that X is a random
![]() $k\times m$
matrix with
$k\times m$
matrix with
![]() $\mathbb{E}[\|X\|^r]<\infty$
for some
$\mathbb{E}[\|X\|^r]<\infty$
for some
![]() $r>1$
. Then, for any
$r>1$
. Then, for any
![]() $q<r$
, there is a constant
$q<r$
, there is a constant
![]() $C=C(m,k,q,r,X)>0$
such that for any
$C=C(m,k,q,r,X)>0$
such that for any
![]() $m\times k$
deterministic matrix A it holds that
$m\times k$
deterministic matrix A it holds that
Proof. Without loss of generality, by the homogeneity of both sides, we may also assume that
![]() $\|A\|= 1$
. Now let
$\|A\|= 1$
. Now let
![]() $N=\{a\in\mathbb{R}^{m\times k}\;:\;aX=0\ \text{ almost surely}\}$
be a linear subspace of
$N=\{a\in\mathbb{R}^{m\times k}\;:\;aX=0\ \text{ almost surely}\}$
be a linear subspace of
![]() $\mathbb{R}^{m\times k}$
and V its orthogonal complement. As both functions
$\mathbb{R}^{m\times k}$
and V its orthogonal complement. As both functions
defined on the compact space
![]() $V\cap\{\|x\|=1\}$
are continuous and do not vanish, they achieve their minimum and maximum. We define
$V\cap\{\|x\|=1\}$
are continuous and do not vanish, they achieve their minimum and maximum. We define
Finally, by writing
![]() $A=A_1+A_2$
with
$A=A_1+A_2$
with
![]() $A_1\in N$
and
$A_1\in N$
and
![]() $A_2\in V$
, we obtain
$A_2\in V$
, we obtain
and this completes the proof.
Lemma 5. Let I, J be two disjoint subintervals of [0,1], let
![]() $N\in\mathbb{N}$
, and let
$N\in\mathbb{N}$
, and let
![]() $U_1,\ldots U_N$
be an independent collection of random variables uniformly distributed on [0,1]. Then for any sequence
$U_1,\ldots U_N$
be an independent collection of random variables uniformly distributed on [0,1]. Then for any sequence
![]() $a\in\ell^2$
and any numbers
$a\in\ell^2$
and any numbers
![]() $A,B\in \mathbb{R}$
, we have
$A,B\in \mathbb{R}$
, we have
 \begin{align*}\mathbb{E}\Big[\Big|\sum_{i=1}^N(\textbf{1}_{\{U_i\in I\}}-|I|)a_i& +A\Big|^2\cdot\Big|\sum_{i=1}^N(\textbf{1}_{\{U_i\in J\}}-|J|)a_i+B\Big|^2\Big] \\[5pt] & \leq C|I| |J|\|a\|^2(A^2+B^2+\|a\|^2)+A^2B^2\\[5pt] & \lesssim |I||J|\|a\|^4 +A^4+B^4,\end{align*}
\begin{align*}\mathbb{E}\Big[\Big|\sum_{i=1}^N(\textbf{1}_{\{U_i\in I\}}-|I|)a_i& +A\Big|^2\cdot\Big|\sum_{i=1}^N(\textbf{1}_{\{U_i\in J\}}-|J|)a_i+B\Big|^2\Big] \\[5pt] & \leq C|I| |J|\|a\|^2(A^2+B^2+\|a\|^2)+A^2B^2\\[5pt] & \lesssim |I||J|\|a\|^4 +A^4+B^4,\end{align*}
for some absolute constant
![]() $C>0$
.
$C>0$
.
Proof. For ease of notation, for
![]() $i=1,\ldots,N$
we set
$i=1,\ldots,N$
we set
so
![]() $\mathbb{E}[q_i]=\mathbb{E}[r_i]=\mathbb{E}[q_i q_j]=\mathbb{E}[r_i r_j]=0$
, for
$\mathbb{E}[q_i]=\mathbb{E}[r_i]=\mathbb{E}[q_i q_j]=\mathbb{E}[r_i r_j]=0$
, for
![]() $i\ne j$
. Simple calculations give
$i\ne j$
. Simple calculations give
 \begin{align*} \mathbb{E}[q_i^2]&=\big(|I|-|I|^2\big)a_i^2\quad \text{and}\quad \mathbb{E}[q_ir_i]=-|I||J|a_i^2, \\[5pt] \mathbb{E}[q_i^2r_i]&=\big(-|I||J|+2|I|^2|J|\big)a_i^3\quad \text{and} \quad \mathbb{E}[q_i^2r_i^2]=\big(|I||J|(|I|-3|I||J|+|J|)\big)a_i^4. \end{align*}
\begin{align*} \mathbb{E}[q_i^2]&=\big(|I|-|I|^2\big)a_i^2\quad \text{and}\quad \mathbb{E}[q_ir_i]=-|I||J|a_i^2, \\[5pt] \mathbb{E}[q_i^2r_i]&=\big(-|I||J|+2|I|^2|J|\big)a_i^3\quad \text{and} \quad \mathbb{E}[q_i^2r_i^2]=\big(|I||J|(|I|-3|I||J|+|J|)\big)a_i^4. \end{align*}
We first have
Expanding the expectation, we get
 \begin{align*} \mathbb{E}\Big[\Big|\sum_{i\le N}q_i+A\Big|^2\cdot\Big|\sum_{i\le N}r_i+B\Big|^2\Big]= \sum_{i_1,i_2,j_1,j_2}\mathbb{E}[q_{i_1}q_{i_2}r_{j_1}r_{j_2}]+2A\sum_{i,j_1,j_2}\mathbb{E}[q_ir_{j_1}r_{j_2}]\\[5pt] +2B\sum_{i_1,i_2,j}\mathbb{E}[q_{i_1}q_{i_2}r_{j}]+4AB\sum_{i,j}\mathbb{E}[q_ir_j]+A^2B^2=:= I+II+III+IV+A^2B^2. \end{align*}
\begin{align*} \mathbb{E}\Big[\Big|\sum_{i\le N}q_i+A\Big|^2\cdot\Big|\sum_{i\le N}r_i+B\Big|^2\Big]= \sum_{i_1,i_2,j_1,j_2}\mathbb{E}[q_{i_1}q_{i_2}r_{j_1}r_{j_2}]+2A\sum_{i,j_1,j_2}\mathbb{E}[q_ir_{j_1}r_{j_2}]\\[5pt] +2B\sum_{i_1,i_2,j}\mathbb{E}[q_{i_1}q_{i_2}r_{j}]+4AB\sum_{i,j}\mathbb{E}[q_ir_j]+A^2B^2=:= I+II+III+IV+A^2B^2. \end{align*}
We show that each of the terms I, II, III, IV is bounded by a multiple of the term
![]() $|I| |J|N(A^2+B^2+N)$
. Note that a nontrivial term of the form
$|I| |J|N(A^2+B^2+N)$
. Note that a nontrivial term of the form
![]() $\mathbb{E}[q_{i_1}q_{i_2}r_{j_1}r_{j_2}]$
is either of the form
$\mathbb{E}[q_{i_1}q_{i_2}r_{j_1}r_{j_2}]$
is either of the form
![]() $E[q_i^2r_j^2]$
or of the form
$E[q_i^2r_j^2]$
or of the form
![]() $\mathbb{E}[q_{i_1}q_{i_2}r_{i_1}r_{i_2}]$
, which in turn implies
$\mathbb{E}[q_{i_1}q_{i_2}r_{i_1}r_{i_2}]$
, which in turn implies
 \begin{align*} I&=\sum_{i,j}\mathbb{E}[q_i^2r_j^2]+4\sum_{i\neq j}\mathbb{E}[q_ir_i]\mathbb{E}[q_jr_j]=|I||J|(|I|-3|I||J|+|J|)\sum a_i^4\\[5pt] & +2(|I|-|I|^2)(|J|-|J|^2)\sum_{i\neq j}a_i^2a_j^2+4|I|^2|J|^2\sum_{i\neq j}a_i^2a_j^2 \le 8|I||J|\|a\|^4. \end{align*}
\begin{align*} I&=\sum_{i,j}\mathbb{E}[q_i^2r_j^2]+4\sum_{i\neq j}\mathbb{E}[q_ir_i]\mathbb{E}[q_jr_j]=|I||J|(|I|-3|I||J|+|J|)\sum a_i^4\\[5pt] & +2(|I|-|I|^2)(|J|-|J|^2)\sum_{i\neq j}a_i^2a_j^2+4|I|^2|J|^2\sum_{i\neq j}a_i^2a_j^2 \le 8|I||J|\|a\|^4. \end{align*}
Next,
![]() $\mathbb{E}[q_{i_1}q_{i_2}r_{j}]$
is nonzero if it is of the form
$\mathbb{E}[q_{i_1}q_{i_2}r_{j}]$
is nonzero if it is of the form
![]() $\mathbb{E}[q_i^2r_i]$
. Hence, we have
$\mathbb{E}[q_i^2r_i]$
. Hence, we have
 \begin{align*}III &= 2B\sum_i\mathbb{E}[q^2_ir_i]=2B(-|I||J|+2|I|^2|J|)\sum_{i}a_i^3 =2B|I||J|(2|I|-1)\sum_{i}a_i^3\\[5pt] & \le 4|I||J||B|\|a\|^3.\end{align*}
\begin{align*}III &= 2B\sum_i\mathbb{E}[q^2_ir_i]=2B(-|I||J|+2|I|^2|J|)\sum_{i}a_i^3 =2B|I||J|(2|I|-1)\sum_{i}a_i^3\\[5pt] & \le 4|I||J||B|\|a\|^3.\end{align*}
By symmetry, we have
Finally, by the same reasoning as above, we get
and the claim follows from putting together the four quantities.
Lemma 6. Let
![]() $l,N\in\mathbb{N}$
and let
$l,N\in\mathbb{N}$
and let
![]() $\lambda_1,\ldots,\lambda_\ell$
be different, nonzero complex numbers. For
$\lambda_1,\ldots,\lambda_\ell$
be different, nonzero complex numbers. For
![]() $(i,j)\in\mathbb{N}_0\times [\ell]$
we define
$(i,j)\in\mathbb{N}_0\times [\ell]$
we define
![]() $f_{i,j}\;:\;\mathbb{Z}\to\mathbb{C}$
by
$f_{i,j}\;:\;\mathbb{Z}\to\mathbb{C}$
by
![]() $f_{i,j}(k)= k^i\lambda_j^k$
. Then the collection of functions
$f_{i,j}(k)= k^i\lambda_j^k$
. Then the collection of functions
![]() $\{f_{i,j}\;:\;(i,j)\in\mathbb{N}_0\times [\ell]\}$
is linearly independent. In particular, if, for any
$\{f_{i,j}\;:\;(i,j)\in\mathbb{N}_0\times [\ell]\}$
is linearly independent. In particular, if, for any
![]() $i\in\mathbb{N}_0$
and
$i\in\mathbb{N}_0$
and
![]() $j\le \ell$
,
$j\le \ell$
,
![]() $p_{j,i}$
is a polynomial of degree i, then the collection of functions
$p_{j,i}$
is a polynomial of degree i, then the collection of functions
![]() $\{k\mapsto \lambda_j^{k} p_{j,i}(k)\;:\;(i,j)\in\mathbb{N}_0\times [\ell]\}$
is also linearly independent.
$\{k\mapsto \lambda_j^{k} p_{j,i}(k)\;:\;(i,j)\in\mathbb{N}_0\times [\ell]\}$
is also linearly independent.
Proof. Let
![]() $h=\sum_{i,j}c_{i,j}f_{i,j}$
be a finite linear combination of the functions
$h=\sum_{i,j}c_{i,j}f_{i,j}$
be a finite linear combination of the functions
![]() $f_{i,j}$
. Our aim is to show that
$f_{i,j}$
. Our aim is to show that
By
![]() $d_j(h)$
we denote the maximal power i such that the element
$d_j(h)$
we denote the maximal power i such that the element
![]() $f_{i-1,j}$
appears in the combination of h. Furthermore, we set
$f_{i-1,j}$
appears in the combination of h. Furthermore, we set
![]() $d(h)= d_1(h)+\ldots d_\ell(h)$
. We prove the claim by induction on d(h). If
$d(h)= d_1(h)+\ldots d_\ell(h)$
. We prove the claim by induction on d(h). If
![]() $d(h)=1$
then
$d(h)=1$
then
![]() $h(k)=\lambda_j^k$
for some j and the conclusion follows. Now suppose that (33) holds for any h with
$h(k)=\lambda_j^k$
for some j and the conclusion follows. Now suppose that (33) holds for any h with
![]() $d(h)=n$
and take h with
$d(h)=n$
and take h with
![]() $d(h)=n+1$
. If
$d(h)=n+1$
. If
![]() $d_j(h)\le1$
for all
$d_j(h)\le1$
for all
![]() $j\le \ell$
, then
$j\le \ell$
, then
![]() $h(k)=\sum_{m=1}^{n+1}c_{j_m}\lambda_{j_m}^k$
for some
$h(k)=\sum_{m=1}^{n+1}c_{j_m}\lambda_{j_m}^k$
for some
![]() $j_1,\ldots,j_{n+1}\le n+1$
. Since
$j_1,\ldots,j_{n+1}\le n+1$
. Since
![]() $\big(\lambda_{j_m}^{-N+1}f_{0,j_m}(k)\big)_{1\le k,m\le n+1}$
forms a Vandermonde matrix, this implies (33).
$\big(\lambda_{j_m}^{-N+1}f_{0,j_m}(k)\big)_{1\le k,m\le n+1}$
forms a Vandermonde matrix, this implies (33).
Therefore, we may now assume that for some
![]() $j_0\le \ell$
we have
$j_0\le \ell$
we have
![]() $d_{j_0}(h)\ge2$
. We denote by
$d_{j_0}(h)\ge2$
. We denote by
![]() $\nabla$
the difference operator defined by
$\nabla$
the difference operator defined by
![]() $\nabla f(k)= f(k+1)-f(k)$
, and
$\nabla f(k)= f(k+1)-f(k)$
, and
![]() $m_{j_0}$
is defined by
$m_{j_0}$
is defined by
![]() $m_{j_0}f(k)=\lambda_{j_0}^kf(k)$
. We now define a linear operator
$m_{j_0}f(k)=\lambda_{j_0}^kf(k)$
. We now define a linear operator
![]() $\nabla_{{j_0}}= m_{j_0}\nabla m_{j_0}^{-1}$
. Clearly
$\nabla_{{j_0}}= m_{j_0}\nabla m_{j_0}^{-1}$
. Clearly
![]() $\nabla_{j_0}$
acts on the linear combinations g of
$\nabla_{j_0}$
acts on the linear combinations g of
![]() $f_{i,j}$
with
$f_{i,j}$
with
![]() $d_{j}(\nabla_{j_0}g)\le d_{j}(g)$
and also
$d_{j}(\nabla_{j_0}g)\le d_{j}(g)$
and also
![]() $d_{j_0}(\nabla_{j_0}f_{i,j_0})=d_{j_0}(f_{i,j_0})-1 $
. In particular,
$d_{j_0}(\nabla_{j_0}f_{i,j_0})=d_{j_0}(f_{i,j_0})-1 $
. In particular,
![]() $1\le \nabla_{j_0}h\le n$
, and hence by the induction hypothesis
$1\le \nabla_{j_0}h\le n$
, and hence by the induction hypothesis
![]() $\nabla_{j_0}h(k)\neq0$
for some
$\nabla_{j_0}h(k)\neq0$
for some
![]() $k\ge N$
, which finally implies that
$k\ge N$
, which finally implies that
![]() $h(k)\neq0$
or
$h(k)\neq0$
or
![]() $h(k+1)\neq0$
, thus proving (33).
$h(k+1)\neq0$
, thus proving (33).
Acknowledgements
We are very grateful to the two anonymous referees for their suggestions and positive criticism, which substantially improved the quality and the presentation of the paper.
Funding information
This research was funded in part by the Austrian Science Fund (FWF) 10.55776/P34129. For open access purposes, the authors have applied a CC BY public copyright license to any author-accepted manuscript version arising from this submission.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.