1. Introduction
Significant advances have been achieved in recent years in understanding the structure and motion of freely propagating premixed flames, including the role of intrinsic flame instabilities and flame-turbulence interactions, using a hydrodynamic theory. Following the multi-scale approach proposed by Clavin & Williams (Reference Clavin and Williams1982), a general theory of multi-dimensional flames in arbitrary flow fields has been derived systematically from the general governing equations by Matalon & Matkowsky (Reference Matalon and Matkowsky1982, Reference Matalon and Matkowsky1983), and generalized by Matalon, Cui & Bechtold (Reference Matalon, Cui and Bechtold2003) to account for salient physical properties, including temperature-dependent transport, differential and preferential diffusion (i.e. anon-unity and distinct Lewis numbers for the fuel and oxidizer), and effects due to stoichiometry and reaction orders. The main assumption behind this theory is that the flame is thin relative to all other fluid dynamic length scales and can be treated as a surface of density discontinuity when determining the flow field. The instantaneous shape and location of the flame surface, and expressions relating the pressure and velocities across this surface were obtained by asymptotic matching. Of paramount importance is the flame speed-flame stretch relation that has captivated the interest of experimentalists whose raw data from measurements in laboratory configurations was found to correlate well with this prediction. The hydrodynamic theory has been used in analytical and numerical studies to successfully unravel mechanisms of flame instability, their onset and their nonlinear growth. Moreover, since the complexity of the chemistry is captured elegantly by fewer physicochemical parameters, the restriction on numerical time step and mesh size in turbulent flame calculations is alleviated making it an ideal model for fundamental understanding, which is free of turbulence modelling assumptions, empiricism and/or ad hoc adjustable parameters. The approach was successfully implemented in two and three dimensions for planar and spherically expanding turbulent flames (Creta & Matalon Reference Creta and Matalon2011; Fogla, Creta & Matalon Reference Fogla, Creta and Matalon2015; Patyal & Matalon Reference Patyal and Matalon2018; Mohan & Matalon Reference Mohan and Matalon2021, Reference Mohan and Matalon2022; Patyal & Matalon Reference Patyal and Matalon2022), capturing many important morphological features, such as multiply folded and disjoint surfaces, pinching of surface elements and the creation of pockets of unburned gas, all of which are commonly observed in laboratory flames. Additionally, predictions of flame characteristics, including the turbulent flame speed that is arguably one of the most important properties, were found to compare well with empirical correlations suggested in the literature (Fogla, Creta & Matalon Reference Fogla, Creta and Matalon2017).
The objective of this study is the derivation of a hydrodynamic theory of premixed flames propagating in closed vessels. There are significant differences when the flame propagates in an open or closed space. Consider, for example, a flame initiated from a small ignition source at the centre of a spherical vessel containing a combustible mixture. The outwardly propagating flame appears at first smooth and spherical but, after reaching a critical size, it spontaneously turns into a highly cellular structure. For mixtures deficient in their more mobile component (sub-unity Lewis numbers), such as lean hydrogen–air, the critical flame size at the onset of instability is of the order of the flame thickness and the observed instability is thermo-diffusive in nature. In mixtures for which the Lewis number is greater than one, such as rich hydrogen–air, the critical flame size at the onset of instability is of the order of several flame thicknesses. The average cell size of the developing flame is significantly larger, with the flame surface bearing resemblance to that of a soccer ball. Such mixtures are thermo-diffusively stable, and the observed instability is hydrodynamic in nature. It is the well-known Darrieus–Landau instability (Darrieus Reference Darrieus1938; Landau Reference Landau1944) induced by gas expansion that results from the heat released by the chemical reactions (Istratov & Librovich Reference Istratov and Librovich1969; Bechtold & Matalon Reference Bechtold and Matalon1987; Addabbo, Bechtold & Matalon Reference Addabbo, Bechtold and Matalon2002). The increase in surface area of the corrugated flame, further augmented by the continuous creation of cells as the flame grows bigger, results in enhanced fuel consumption and an increased propagation speed. In open space, this development occurs under nearly isobaric conditions; the mean pressure remains virtually constant and equal to the ambient pressure. In a closed vessel, the mean pressure increases in time, the gas is compressed and its temperature rises, leading to higher flame temperatures and a subsequent increase in propagation speed. The self-acceleration of the flame would be significantly affected by combustion instabilities and, in a turbulent environment, by the highly vortical field within which the flame is propagating. The role of intrinsic combustion instabilities and flame-turbulence interactions when the flame is propagating in a confined environment have not been thoroughly investigated. Fundamental understanding of the flame morphology, the dependence of the burning rate on the state of the gas, the onset of instabilities, self-wrinkling and self-acceleration of the flame surface, and the effects of turbulence all have practical implications on the design of engineering devices. It is also important from a safety perspective, to prevent undesirable phenomena such as knocking or the onset of detonations.
Expanding flames in spherical chambers are frequently used in the laboratory to ascertain the laminar flame speeds and Markstein lengths of various fuel mixtures experimentally, owing to a well-defined stretch rate that diminishes as the flame grows bigger. The continuously changing temperature and pressure of the unburned mixture, the unknown effect of pressure buildup and the onset of flame instabilities poses significant challenges in the accuracy of data reduction and limit the range of mixtures that can be studied. Moreover, the measurements are prone to yielding widely different values of burning velocities (Andrews & Bradley Reference Andrews and Bradley1972). Some investigators addressed these issues by modifying their experimental device to alleviate the rapid changes in pressure and allowing nearly constant-pressure measurements (Tse, Zhu & Law Reference Tse, Zhu and Law2000, Reference Tse, Zhu and Law2004). Others have limited measurements to the initial stages of flame propagation by assuming a negligible pressure rise and unconfined conditions (Bradley et al. Reference Bradley, Hicks, Lawes, Sheppard and Woolley1998). The accuracy of the burning velocity values determined by the confined flame method compared with those obtained from unconfined conditions were recently examined, noting that a slight pressure rise contributes to an increase in burned gas density and an inward flow of the expanded burned gas (Chen, Burke & Ju Reference Chen, Burke and Ju2009; Omari & Tartakovsky Reference Omari and Tartakovsky2016), both of which significantly affect the measured data. Fundamental understanding of the fluid dynamical consequences when the flame propagates in a closed vessel, the dependence of the burning rate on pressure buildup and the onset or delay of instabilities and cellularity will contribute greatly to the experimental effort.
Earlier hydrodynamic studies of confined flames, including the original work of Sivashinsky (Reference Sivashinsky1979) and the stability analyses of McGreevy & Matalon (Reference McGreevy and Matalon1994a,Reference McGreevy and Matalonb), treated the flame as a structureless surface of discontinuity. The present work is the first asymptotic theory that resolves the structure of the thin but finite flame zone, and captures the effect of pressure rise, flow conditions and mixture properties on the flame speed; it follows a previous exploration by Bechtold & Matalon (Reference Bechtold and Matalon2000) that sowed the seeds of this paper. The analysis shows that the flame speed of confined flames is modified not only by flame stretch, representing the distortion of an element of the flame surface, but also by variations of the flame thickness that combine to describe the deformation of a volume element of the flame zone, or the voluminal stretch. This concept, first introduced by Buckmaster (Reference Buckmaster1979) in the context of slowly varying flames, has not been apparent in the hydrodynamic theory of freely propagating flames owing to the assumption of a constant flame thickness. Elements of this idea, referred to as mass-based flame stretch, were exploited by de-Goey and co-workers (van Oijen et al. Reference van Oijen, Donini, Bastiaans, ten Thije Boonkkamp and de Goey2016) in their numerical simulations. In addition to the voluminal stretch, the flame speed is shown to be also modified by the rate of pressure increase. The two ingredients, voluminal stretch and pressure rise, arising from physicochemical influences associated with the internal flame structure, are modulated when cast in dimensional form by two pressure-dependent Markstein lengths of the order of the flame thickness. Since the increase in burning rate as the pressure rises causes the flame to become thinner, their effects diminish during combustion and become negligible in the latter stages of propagation. While this assertion has been phenomenologically recognized, it is the first time that it has been quantified in a detailed analysis.
Flame stretch is an asymptotic concept that is unambiguously defined when the flame is confined to a surface. It measures the distortion of the flame that results from its motion and from the fluid velocity gradient it experiences, and can be expressed in terms of properties of the flame surface, such as curvature and propagation speed, and of the underlying velocity field (Matalon Reference Matalon1983). For freely propagating flames, it may be also expressed as a combination of the curvature of the flame front and the hydrodynamic strain it experiences. This representation is particularly convenient in general computational studies because the strain rate is implemented in most fluid dynamical codes. However, it requires specifying an isosurface within the flame zone that represents the flame front, and accommodating for the velocity divergence that, although it vanishes on either side of the flame, is not zero within the numerically resolved flame zone due to gas expansion (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). It is shown that under confinement, flame stretch is not a simple combination of the surface curvature and hydrodynamic strain, because the velocity divergence is not zero even outside the flame zone owing to adiabatic compression. Even in the hydrodynamic limit, when the flame is confined to a surface, the contribution of the velocity divergence at the flame front is essential to balance the local strain rate and properly evaluate the stretch rate.
In the freely propagating flame theory, the chemical activity is confined to a thin layer embedded within the flame zone and centred near the location where the temperature reaches its maximum value – the adiabatic flame temperature. For a given mixture, the adiabatic flame temperature is a constant that depends on the total heat release. In a closed vessel the flame temperature exceeds the adiabatic value and varies in time as a consequence of pressure rise. Moreover, the temperature in the burned gas continues to increase due to adiabatic compression. These conditions preclude the use of the standard activation energy asymptotic approximation, which has greatly facilitated analyses of combustion problems by confining the chemical activity to a reaction sheet. The temporal change of flame temperature requires readjusting the reaction zone thickness from one time to the next, while the continual increase in temperature in the burned gas prevents expressing the jump in temperature gradient across the reaction sheet in closed form. Consequently, we employ a delta-function model that has been used in the literature when encountering similar technical difficulties (Matkowsky & Sivashinsky Reference Matkowsky and Sivashinsky1978; Buckmaster & Ludford Reference Buckmaster and Ludford1983; Margolis & Matkowsky Reference Margolis and Matkowsky1983). In this approach, the reaction rate takes the form of a Dirac delta function with a strength expressed as an Arrhenius form of the instantaneous flame temperature. The jump conditions across the reaction sheet are then determined by direct integration of the governing equations. We demonstrate that a formal asymptotic approach can be carried out by adopting the Newtonian approximation (Van Dyke Reference Van Dyke1954; Cole Reference Cole1957), whereby the ratio of specific heats is assumed near unity. In this limit the flame temperature is near its adiabatic value, delaying the aforementioned difficulties to higher orders. The restriction placed on the ratio of specific heats leads to a description of flame propagation that is not as rich as the more general case, but provides justification for the delta-function model employed without this limitation.
2. Governing equations
A homogeneous combustible mixture consisting of two reactants, both appearing in small quantities relative to an abundant inert gas, resides in a closed vessel. The mass fraction of the deficient and excess reactants in the mixture are ![]() $Y_{D_0}$ and
$Y_{D_0}$ and ![]() $Y_{E_0}$, respectively, with the index
$Y_{E_0}$, respectively, with the index ![]() $i=D,E$ representing the deficient/excess reactant and the subscript 0 identifying conditions of the given initial mixture. In a lean mixture, the fuel is the deficient component, while in a rich mixture the deficient component is the oxidizer. Upon ignition, a flame separating the fresh mixture from the burned products propagates throughout the vessel. The chemical activity is modelled by a single overall step:
$i=D,E$ representing the deficient/excess reactant and the subscript 0 identifying conditions of the given initial mixture. In a lean mixture, the fuel is the deficient component, while in a rich mixture the deficient component is the oxidizer. Upon ignition, a flame separating the fresh mixture from the burned products propagates throughout the vessel. The chemical activity is modelled by a single overall step:
Here ![]() $\mathcal {C}_{i}$ represents the chemical symbol and
$\mathcal {C}_{i}$ represents the chemical symbol and ![]() $\nu _{i}$ the stoichiometric coefficient of species
$\nu _{i}$ the stoichiometric coefficient of species ![]() $i$. The reaction rate is given by
$i$. The reaction rate is given by
where ![]() $\tilde \rho$ is the density and
$\tilde \rho$ is the density and ![]() $\tilde T$ the temperature of the mixture,
$\tilde T$ the temperature of the mixture, ![]() $Y_i$ and
$Y_i$ and ![]() $W_{i}$ are the mass fraction and molecular weight of species
$W_{i}$ are the mass fraction and molecular weight of species ![]() $i$,
$i$, ![]() $E$ is the overall activation energy,
$E$ is the overall activation energy, ![]() $\mathcal {R}$ is the gas constant and
$\mathcal {R}$ is the gas constant and ![]() $\mathcal {B}$ a pre-exponential factor. To allow for mixture compositions ranging from lean to rich conditions, we introduce the excess-to-deficient reactant mass ratio
$\mathcal {B}$ a pre-exponential factor. To allow for mixture compositions ranging from lean to rich conditions, we introduce the excess-to-deficient reactant mass ratio
where ![]() $\nu =\nu _{E}W_{E}/\nu _{D}W_{D}$ is the mass-weighted stoichiometric coefficient ratio. As defined,
$\nu =\nu _{E}W_{E}/\nu _{D}W_{D}$ is the mass-weighted stoichiometric coefficient ratio. As defined, ![]() $\varPhi$ is always larger than one, with
$\varPhi$ is always larger than one, with ![]() $\varPhi = 1$ corresponding to a stoichiometric mixture. Hence,
$\varPhi = 1$ corresponding to a stoichiometric mixture. Hence, ![]() $\varPhi$ is equal to the equivalence ratio for fuel-rich mixtures and to the reciprocal of the equivalence ratio for fuel-lean mixtures.
$\varPhi$ is equal to the equivalence ratio for fuel-rich mixtures and to the reciprocal of the equivalence ratio for fuel-lean mixtures.
Deflagrative combustion phenomena are highly subsonic and a low-Mach-number approximation may be employed for their description; the characteristic Mach number ![]() ${Ma}$ is defined as the ratio of the laminar flame speed to the speed of sound in the initial fresh mixture. For
${Ma}$ is defined as the ratio of the laminar flame speed to the speed of sound in the initial fresh mixture. For ![]() ${Ma} \ll 1$, the pressure in the vessel is rapidly equalized such that spatial variations remain relatively small. The pressure may then be decomposed into the mean pressure
${Ma} \ll 1$, the pressure in the vessel is rapidly equalized such that spatial variations remain relatively small. The pressure may then be decomposed into the mean pressure ![]() $\tilde P = \tilde P(t)$ and small fluctuations of
$\tilde P = \tilde P(t)$ and small fluctuations of ![]() $O({Ma}^2)$ that balance the small changes in momentum. The temporal variations of the mean pressure
$O({Ma}^2)$ that balance the small changes in momentum. The temporal variations of the mean pressure ![]() $\tilde P(t)$ are determined by integrating the energy equation throughout the entire domain, after neglecting the small viscous dissipation term. For impermeable walls, and in the absence of heat losses, one finds that
$\tilde P(t)$ are determined by integrating the energy equation throughout the entire domain, after neglecting the small viscous dissipation term. For impermeable walls, and in the absence of heat losses, one finds that
where ![]() $t$ is the time variable,
$t$ is the time variable, ![]() $P_0, \rho _0,T_0$ the pressure, density and temperature of the fresh unburned mixture,
$P_0, \rho _0,T_0$ the pressure, density and temperature of the fresh unburned mixture, ![]() $Q$ the total heat release,
$Q$ the total heat release, ![]() $c_v$ the specific heat at constant volume (assumed constant) and
$c_v$ the specific heat at constant volume (assumed constant) and ![]() $\tilde {\mathbb {V}}$ the volume of the vessel. A consequence of this quasi-isobaric approximation is the simplification of the equation of state to
$\tilde {\mathbb {V}}$ the volume of the vessel. A consequence of this quasi-isobaric approximation is the simplification of the equation of state to
where ![]() $\bar W$ is the mean molecular weight of the mixture (assumed constant).
$\bar W$ is the mean molecular weight of the mixture (assumed constant).
The equations governing the combustion process consist of the Navier–Stokes equations supplemented by mass balance equations for the two reactants and an energy equation for the mixture. To express these equations in dimensionless form, the hydrodynamic length scale ![]() $l$ is used as a unit length, the laminar flame speed
$l$ is used as a unit length, the laminar flame speed ![]() $S_{L}$ as a unit speed and the ratio
$S_{L}$ as a unit speed and the ratio ![]() $l/S_{L}$ as a unit of time. The hydrodynamic length characterizes the lateral size of the flame or the average wavelength of corrugations evolving on its surface. Diffusion processes introduce an additional length scale
$l/S_{L}$ as a unit of time. The hydrodynamic length characterizes the lateral size of the flame or the average wavelength of corrugations evolving on its surface. Diffusion processes introduce an additional length scale ![]() $l_d = \mathcal {D}_{th} /S_{L}$, where
$l_d = \mathcal {D}_{th} /S_{L}$, where ![]() $\mathcal {D}_{th} = \lambda _{{0}}/\rho _{0} c_p$ is the thermal diffusivity of the initial fresh mixture with
$\mathcal {D}_{th} = \lambda _{{0}}/\rho _{0} c_p$ is the thermal diffusivity of the initial fresh mixture with ![]() $\lambda _0$ the thermal conductivity and
$\lambda _0$ the thermal conductivity and ![]() $c_p$ the specific heat at constant pressure (assumed constant). The ratio of the diffusion-to-hydrodynamic length scales,
$c_p$ the specific heat at constant pressure (assumed constant). The ratio of the diffusion-to-hydrodynamic length scales, ![]() $\delta \equiv l_d/l$, is a representative measure of the flame thickness. Pressure, density and temperature are scaled with respect to their values in the initial fresh mixture
$\delta \equiv l_d/l$, is a representative measure of the flame thickness. Pressure, density and temperature are scaled with respect to their values in the initial fresh mixture ![]() $P_0, \rho _0,T_0$. The transport coefficients, including the viscosity
$P_0, \rho _0,T_0$. The transport coefficients, including the viscosity ![]() $\tilde \mu$ and thermal conductivity
$\tilde \mu$ and thermal conductivity ![]() $\tilde \lambda$ of the mixture, and the diffusion coefficients
$\tilde \lambda$ of the mixture, and the diffusion coefficients ![]() $\tilde \rho \mathcal {D}_i$ where
$\tilde \rho \mathcal {D}_i$ where ![]() $\mathcal {D}_i$ is the molecular diffusivity of species
$\mathcal {D}_i$ is the molecular diffusivity of species ![]() $i$ (into the inert gas), depend on temperature. Scaled by their values in the initial fresh mixture, the dimensionless coefficients
$i$ (into the inert gas), depend on temperature. Scaled by their values in the initial fresh mixture, the dimensionless coefficients
are assumed to have the same temperature dependence such that their ratios, consisting of the Prandtl ![]() $\Pr \equiv \tilde \mu c_p/\tilde \lambda$ and Lewis
$\Pr \equiv \tilde \mu c_p/\tilde \lambda$ and Lewis ![]() ${{Le}_i \equiv \tilde \lambda / \tilde \rho \mathcal {D}_i c_p}$ numbers, remain constant. The common transport coefficient (in dimensionless form) takes the form
${{Le}_i \equiv \tilde \lambda / \tilde \rho \mathcal {D}_i c_p}$ numbers, remain constant. The common transport coefficient (in dimensionless form) takes the form ![]() $\lambda (T) = T^a$, with
$\lambda (T) = T^a$, with ![]() $1/2 \le a \le 1$. The laminar flame speed for a two-reactant model obeying (2.2) in the large activation energy limit (Bechtold & Matalon Reference Bechtold and Matalon1999), is given by
$1/2 \le a \le 1$. The laminar flame speed for a two-reactant model obeying (2.2) in the large activation energy limit (Bechtold & Matalon Reference Bechtold and Matalon1999), is given by
 \begin{equation} S_{L} = \sqrt{4 \left(\frac{\tilde \rho_a}{\rho_{{0}}}\right)^{2} \frac{\tilde \lambda_a}{\lambda_{{0}}} \frac{\mathcal{D}_{th} {(1 + \beta ( \varPhi - 1)/2{Le}_E)}} {\beta^{3} {\nu_{E}^{{-}1} {\nu_{D}^{{-}1} }} {Le}_E^{{-}1}{Le}_D^{{-}1} } \frac{\rho_0 Y_{D_0} \mathcal{B}}{ \nu_D W_{D}}} \exp({-E/2\mathcal{R} \tilde T_{a}}), \end{equation}
\begin{equation} S_{L} = \sqrt{4 \left(\frac{\tilde \rho_a}{\rho_{{0}}}\right)^{2} \frac{\tilde \lambda_a}{\lambda_{{0}}} \frac{\mathcal{D}_{th} {(1 + \beta ( \varPhi - 1)/2{Le}_E)}} {\beta^{3} {\nu_{E}^{{-}1} {\nu_{D}^{{-}1} }} {Le}_E^{{-}1}{Le}_D^{{-}1} } \frac{\rho_0 Y_{D_0} \mathcal{B}}{ \nu_D W_{D}}} \exp({-E/2\mathcal{R} \tilde T_{a}}), \end{equation}where
 \begin{equation} \beta = \frac{E(\tilde T_a - T_0) }{ \mathcal{R} \tilde T_{a}^{2} },\quad \tilde T_a =T_0 + \frac {(Q/c_p) Y_{D_0} }{ \nu_{D}W_{D} } \end{equation}
\begin{equation} \beta = \frac{E(\tilde T_a - T_0) }{ \mathcal{R} \tilde T_{a}^{2} },\quad \tilde T_a =T_0 + \frac {(Q/c_p) Y_{D_0} }{ \nu_{D}W_{D} } \end{equation}
are, respectively, the Zel'dovich number and adiabatic flame temperature. The subscript ![]() $a$ stands for values evaluated at the adiabatic temperature, namely
$a$ stands for values evaluated at the adiabatic temperature, namely ![]() $\tilde \lambda _a = \tilde \lambda (\tilde T_a)$ and
$\tilde \lambda _a = \tilde \lambda (\tilde T_a)$ and ![]() $\tilde \rho _a/\rho _{{0}} = T_0 / \tilde T_a$. Below, only when the same symbols are used for both dimensional and dimensionless variables, the dimensional quantities are distinguished by a ‘tilde’ accent.
$\tilde \rho _a/\rho _{{0}} = T_0 / \tilde T_a$. Below, only when the same symbols are used for both dimensional and dimensionless variables, the dimensional quantities are distinguished by a ‘tilde’ accent.
In dimensionless form, the governing equations are
where ![]() $\mathrm {D}/\mathrm {D} t \equiv \partial /\partial t + \boldsymbol v \boldsymbol {\cdot } \boldsymbol \nabla$ is the convective derivative,
$\mathrm {D}/\mathrm {D} t \equiv \partial /\partial t + \boldsymbol v \boldsymbol {\cdot } \boldsymbol \nabla$ is the convective derivative, ![]() $\boldsymbol v$ is the gas velocity,
$\boldsymbol v$ is the gas velocity, ![]() $\boldsymbol {\varSigma }$ is the viscous stress tensor given by
$\boldsymbol {\varSigma }$ is the viscous stress tensor given by
with ![]() $\boldsymbol E$ and
$\boldsymbol E$ and ![]() $\boldsymbol I$ the strain rate and unit tensors (the superscript
$\boldsymbol I$ the strain rate and unit tensors (the superscript ![]() $\mathrm {T}$ denoting the transpose) and
$\mathrm {T}$ denoting the transpose) and
the reaction rate. Consistent with the low-Mach-number approximation, the pressure has been expressed as ![]() $P(t) + \gamma {Ma}^2 p(\boldsymbol x,t)$, where
$P(t) + \gamma {Ma}^2 p(\boldsymbol x,t)$, where ![]() $P$ is the spatially uniform (or mean) pressure in the vessel and
$P$ is the spatially uniform (or mean) pressure in the vessel and ![]() $p$ is the dynamic pressure. In view of (2.4), the overall or mean pressure is obtained from
$p$ is the dynamic pressure. In view of (2.4), the overall or mean pressure is obtained from
where the integration is performed over the entire volume ![]() ${\mathbb {V}}$ expressed in units of the hydrodynamic length
${\mathbb {V}}$ expressed in units of the hydrodynamic length ![]() $l$. In addition to the Prandtl number
$l$. In addition to the Prandtl number ![]() $\Pr$ and Lewis number
$\Pr$ and Lewis number ![]() ${Le}_D, {Le}_E$, the parameters appearing in these equations are: the ratio of specific heats
${Le}_D, {Le}_E$, the parameters appearing in these equations are: the ratio of specific heats ![]() $\gamma = {c_p/ c_v}$, the heat release parameter
$\gamma = {c_p/ c_v}$, the heat release parameter ![]() $q = (Q Y_{D_{{0}}} / \nu _{D}W_{D})/ c_p T_0$ that represents the ratio of the total heat released per unit mass of the deficient reactant to the enthalpy of the initial mixture, the adiabatic flame temperature
$q = (Q Y_{D_{{0}}} / \nu _{D}W_{D})/ c_p T_0$ that represents the ratio of the total heat released per unit mass of the deficient reactant to the enthalpy of the initial mixture, the adiabatic flame temperature ![]() $T_a = 1+ q$ and the activation energy parameter
$T_a = 1+ q$ and the activation energy parameter ![]() $\beta _0 = E/\mathcal {R}T_0$ related to the Zel'dovich number
$\beta _0 = E/\mathcal {R}T_0$ related to the Zel'dovich number ![]() $\beta$ via
$\beta$ via ![]() $\beta _0 = (T_a^2/q) \beta$. The Damköhler number
$\beta _0 = (T_a^2/q) \beta$. The Damköhler number ![]() $\mathbb {D}$, representing the ratio of the flow to the chemical reaction times, is given by
$\mathbb {D}$, representing the ratio of the flow to the chemical reaction times, is given by
where ![]() $\tilde {\mathcal {B}}$ is the scaled pre-exponential factor (in units of s
$\tilde {\mathcal {B}}$ is the scaled pre-exponential factor (in units of s![]() $^{-1}$). When substituting for the laminar flame speed (2.7), the Damköhler number simplifies to
$^{-1}$). When substituting for the laminar flame speed (2.7), the Damköhler number simplifies to
For a stoichiometric mixture, ![]() $\varPhi = 1$, the Damköhler number depends on the Lewis numbers of both reactants, while for a mixture remote from stoichiometry, it depends primarily on the Lewis number of the deficient reactant.
$\varPhi = 1$, the Damköhler number depends on the Lewis numbers of both reactants, while for a mixture remote from stoichiometry, it depends primarily on the Lewis number of the deficient reactant.
An expression for the end pressure ![]() $P = P_{e}$, defined as the mean pressure in the vessel at time
$P = P_{e}$, defined as the mean pressure in the vessel at time ![]() $t= t_e$, namely the time when the flame has consumed all the available reactant, can be obtained by integrating the combined energy and appropriate species equations
$t= t_e$, namely the time when the flame has consumed all the available reactant, can be obtained by integrating the combined energy and appropriate species equations
 \begin{align} & \frac{\partial}{\partial t} \left(\rho \left(\frac{qY_{D}}{{Y_{D_{0}}}}+T \right) \right) + \boldsymbol\nabla \boldsymbol{\cdot} \left({\rho {\boldsymbol v} \left(\frac{qY_{D}}{{Y_{D_{0}}} }+T \right) } \right) - \delta \boldsymbol\nabla \boldsymbol{\cdot}\left(\lambda \boldsymbol\nabla \left(\frac{qY_{D} }{{Y_{D_{0}}} } {Le}_D^{{-}1}+T \right) \right) \nonumber\\ &\quad =\frac{\gamma -1}{\gamma} \frac{\mathrm{d}P}{\mathrm{d}t} \end{align}
\begin{align} & \frac{\partial}{\partial t} \left(\rho \left(\frac{qY_{D}}{{Y_{D_{0}}}}+T \right) \right) + \boldsymbol\nabla \boldsymbol{\cdot} \left({\rho {\boldsymbol v} \left(\frac{qY_{D}}{{Y_{D_{0}}} }+T \right) } \right) - \delta \boldsymbol\nabla \boldsymbol{\cdot}\left(\lambda \boldsymbol\nabla \left(\frac{qY_{D} }{{Y_{D_{0}}} } {Le}_D^{{-}1}+T \right) \right) \nonumber\\ &\quad =\frac{\gamma -1}{\gamma} \frac{\mathrm{d}P}{\mathrm{d}t} \end{align}over the entire volume. For impermeable and rigid walls, and in the absence of heat losses, it simplifies to
which can be integrated in time from ![]() $t = 0$ to
$t = 0$ to ![]() $t= t_e$, to give
$t= t_e$, to give ![]() $P_{e} = 1 + \gamma q$. If combustion was to occur uniformly throughout the vessel as in a stirred reactor, such that
$P_{e} = 1 + \gamma q$. If combustion was to occur uniformly throughout the vessel as in a stirred reactor, such that ![]() $\rho = 1$, the final temperature would be the constant-volume adiabatic temperature
$\rho = 1$, the final temperature would be the constant-volume adiabatic temperature ![]() $1 + \gamma q$. However, owing to the fluid dynamics associated with the flame propagation, neither the density nor the temperature remain spatially uniform. It should be noted that in determining
$1 + \gamma q$. However, owing to the fluid dynamics associated with the flame propagation, neither the density nor the temperature remain spatially uniform. It should be noted that in determining ![]() $P_{e}$ we have assumed that a flame already exists at
$P_{e}$ we have assumed that a flame already exists at ![]() $t=0$. In other words, the theory does not describe the short ignition event that is expected to have a minor effect on the end pressure level.
$t=0$. In other words, the theory does not describe the short ignition event that is expected to have a minor effect on the end pressure level.
The governing equations (2.9)–(2.17) will be analysed using a multi-scale approach that exploits the disparity in length scales associated with the fluid dynamics, diffusion and chemical reactions. The flame zone consisting of the region where diffusion and chemical reactions occur may be treated as an internal layer of ![]() $O(\delta )$, with
$O(\delta )$, with ![]() $\delta \ll 1$, that separates the unburned gas from the burned products. Consequently, the governing equations in the hydrodynamic regions on either side of the flame zone are greatly simplified, but they remain dependent on the instantaneous shape and location of the flame surface, or equivalently, on the flame propagation speed. The latter, which is the focus of the subsequent analysis, depends on the diffusion and chemical processes occurring inside the flame zone, on the pressure buildup and on the interaction of the flame with the local flow conditions.
$\delta \ll 1$, that separates the unburned gas from the burned products. Consequently, the governing equations in the hydrodynamic regions on either side of the flame zone are greatly simplified, but they remain dependent on the instantaneous shape and location of the flame surface, or equivalently, on the flame propagation speed. The latter, which is the focus of the subsequent analysis, depends on the diffusion and chemical processes occurring inside the flame zone, on the pressure buildup and on the interaction of the flame with the local flow conditions.
In the following sections we start by examining the simplifications that result in the hydrodynamic zones. We then analyse the physicochemical processes occurring in the thin but finite flame zone and derive explicit expressions for the flame speed and overall pressure rise. Following a general discussion of the results, applicable to general time-dependent multi-dimensional flames in vessels of arbitrary geometry, we provide a complete description of planar and spherical flames. We conclude with general comments about and future applications of the derived hydrodynamic theory.
3. The hydrodynamic zones
In the limit ![]() $\delta \to 0$, the flame zone shrinks to a surface described by
$\delta \to 0$, the flame zone shrinks to a surface described by ![]() $\psi (\boldsymbol x,t) = 0$ and referred to as the flame front. It separates the unburned gas in the region
$\psi (\boldsymbol x,t) = 0$ and referred to as the flame front. It separates the unburned gas in the region ![]() $\psi (\boldsymbol x, t) < 0$ from the burned products in the region
$\psi (\boldsymbol x, t) < 0$ from the burned products in the region ![]() $\psi (\boldsymbol x,t) > 0$, and is characterized by the geometric factors
$\psi (\boldsymbol x,t) > 0$, and is characterized by the geometric factors
defined to represent the unit normal pointing towards the burned gas region and the propagation speed (in the laboratory frame) of the flame surface back along its normal. The determination of the instantaneous shape and location of the flame front and/or the propagation speed depend on the diffusion and reaction processes occurring inside the flame zone, as discussed in the next section.
To leading order in ![]() $\delta$, diffusion and chemical reactions are negligible on either side of the flame front, i.e.
$\delta$, diffusion and chemical reactions are negligible on either side of the flame front, i.e. ![]() $\psi (\boldsymbol x,t) \lessgtr 0$, and the governing equations reduce to
$\psi (\boldsymbol x,t) \lessgtr 0$, and the governing equations reduce to
The combination of the continuity (3.2) and energy (3.5) equations implies that the volume dilatation rate is
namely, fluid elements on either side of the flame are progressively compressed. Integrating (2.9)–(2.13) across the flame zone and taking the limit ![]() $\delta \to 0$ yield the Rankine–Hugoniot (RH) jump conditions
$\delta \to 0$ yield the Rankine–Hugoniot (RH) jump conditions
where the bracket ![]() $[\![ \,\,]\!]$ denotes the jump across the flame front, i.e.
$[\![ \,\,]\!]$ denotes the jump across the flame front, i.e. ![]() $[\![ \varTheta ]\!]=\varTheta |_{{\psi =0^+}} - \varTheta |_{{\psi =0^-}}$. Comments regarding the
$[\![ \varTheta ]\!]=\varTheta |_{{\psi =0^+}} - \varTheta |_{{\psi =0^-}}$. Comments regarding the ![]() $O(\delta )$ corrections will be discussed below, following the flame zone analysis.
$O(\delta )$ corrections will be discussed below, following the flame zone analysis.
Given that the fresh mixture in the vessel is initially homogeneous, and assuming that the deficient reactant is completely consumed in the flame zone, (3.4a,b) yield
The energy equation (3.5), when combined with the equation of state (3.6), shows that the function
referred to as the entropy function (the entropy of the gas is proportional to ![]() $\ln \mathcal {E}$), satisfies
$\ln \mathcal {E}$), satisfies
Since the state of the fresh gas is initially uniform and the entropy ahead of the flame is conserved along particle paths, ![]() $\mathcal {E} = 1$ in the unburned gas region. In the burned gas region
$\mathcal {E} = 1$ in the unburned gas region. In the burned gas region ![]() $\mathcal {E}=\mathcal {E}(\boldsymbol x, t)$ is determined by solving (3.13). As a consequence,
$\mathcal {E}=\mathcal {E}(\boldsymbol x, t)$ is determined by solving (3.13). As a consequence,
The temperature and density of the unburned gas remain spatially uniform, but their values increase in time because of gas compression, a conclusion that remains true to all orders in ![]() $\delta$. By contrast, the temporally varying temperature and density at the moving front,
$\delta$. By contrast, the temporally varying temperature and density at the moving front,
are advected with the flow downstream such that the burned gas is no longer spatially uniform. Here and below, subscripts ![]() $b$ and
$b$ and ![]() $u$ will be used to denote conditions on the burned/unburned side of the flame front; i.e. at
$u$ will be used to denote conditions on the burned/unburned side of the flame front; i.e. at ![]() $\psi = 0^{\pm }$, respectively. The flame temperature
$\psi = 0^{\pm }$, respectively. The flame temperature ![]() $T_{f}$, defined as the temperature at
$T_{f}$, defined as the temperature at ![]() $\psi = 0^+$, is given to leading order by
$\psi = 0^+$, is given to leading order by ![]() $T_b$ and is seen to exceed the adiabatic flame temperature
$T_b$ and is seen to exceed the adiabatic flame temperature ![]() $T_a$ as a result of adiabatic compression. On the other hand, the extent of gas expansion across the flame,
$T_a$ as a result of adiabatic compression. On the other hand, the extent of gas expansion across the flame,
diminishes as the pressure rises.
To complete the formulation, an equation describing the evolution of the flame surface ![]() $\psi (\boldsymbol x,t)=0$ or, equivalently, the propagation speed
$\psi (\boldsymbol x,t)=0$ or, equivalently, the propagation speed ![]() $V_{f}$, must be derived. It is customary to use instead of the propagation speed, the flame speed, which is defined as the propagation speed relative to the flow of fresh mixture, namely
$V_{f}$, must be derived. It is customary to use instead of the propagation speed, the flame speed, which is defined as the propagation speed relative to the flow of fresh mixture, namely
where the ![]() $^*$ denotes conditions at
$^*$ denotes conditions at ![]() $\psi =0^-$. The local mass burning rate
$\psi =0^-$. The local mass burning rate
refers to the normal mass flux at the cold edge of the flame zone as viewed from an observer moving with the flame front. The flame speed, burning rate and mean pressure rise depend on the physicochemical processes occurring inside the flame zone, as discussed next.
4. The flame zone
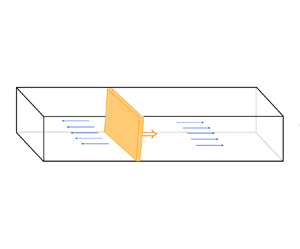
It is convenient in the following analysis to introduce a curvilinear coordinate system attached to the flame front, as shown in figure 1. The flame front is parametrized by the surface coordinates ![]() $(\xi _1,\xi _2)$ aligned with the principal directions of curvature at each point of the surface, and
$(\xi _1,\xi _2)$ aligned with the principal directions of curvature at each point of the surface, and ![]() ${\boldsymbol e_1}, {\boldsymbol e_2}$ denote unit vectors tangential to the parametric curves
${\boldsymbol e_1}, {\boldsymbol e_2}$ denote unit vectors tangential to the parametric curves ![]() $\xi _2 = {\rm const.}$ and
$\xi _2 = {\rm const.}$ and ![]() $\xi _1 = {\rm const.}$, respectively. The three vectors
$\xi _1 = {\rm const.}$, respectively. The three vectors ![]() $\boldsymbol e_{1},\boldsymbol e_{2},\boldsymbol n$, with
$\boldsymbol e_{1},\boldsymbol e_{2},\boldsymbol n$, with ![]() $\boldsymbol n = \boldsymbol e_1 \times \boldsymbol e_2$, form an orthogonal triad of unit vectors and (
$\boldsymbol n = \boldsymbol e_1 \times \boldsymbol e_2$, form an orthogonal triad of unit vectors and (![]() $\xi _1, \xi _2, n$) may be taken as the coordinates of an arbitrary point P in space at time
$\xi _1, \xi _2, n$) may be taken as the coordinates of an arbitrary point P in space at time ![]() $t$. The vector position
$t$. The vector position ![]() $\boldsymbol r$ of the point P with respect to the fixed rectangular coordinate system may be expressed in terms of the distance
$\boldsymbol r$ of the point P with respect to the fixed rectangular coordinate system may be expressed in terms of the distance ![]() $n$ from the flame front and the position vector
$n$ from the flame front and the position vector ![]() $\boldsymbol r_f$ of the projection of P on the surface, namely
$\boldsymbol r_f$ of the projection of P on the surface, namely
which serves as the transformation from the rectangular to the moving intrinsic surface coordinate system. The unit vectors ![]() $\boldsymbol e_1$ and
$\boldsymbol e_1$ and ![]() $\boldsymbol e_2$ are given by
$\boldsymbol e_2$ are given by
where ![]() $a_i = |\partial \boldsymbol r_f /\partial \xi _i|$. The gas velocity may be decomposed as
$a_i = |\partial \boldsymbol r_f /\partial \xi _i|$. The gas velocity may be decomposed as ![]() $\boldsymbol v = \boldsymbol v_{\perp } + v_n \boldsymbol n$, where
$\boldsymbol v = \boldsymbol v_{\perp } + v_n \boldsymbol n$, where ![]() $v_n$ is the velocity component oriented normal to the flame surface and
$v_n$ is the velocity component oriented normal to the flame surface and ![]() $\boldsymbol v_{\perp } = v_1 \boldsymbol e_1 + v_2 \boldsymbol e_2$. Consequently,
$\boldsymbol v_{\perp } = v_1 \boldsymbol e_1 + v_2 \boldsymbol e_2$. Consequently, ![]() $m \equiv \rho (v_n - V_{f} )$ is the normal mass flux. Computation of the vector differential operators involve the scale factors
$m \equiv \rho (v_n - V_{f} )$ is the normal mass flux. Computation of the vector differential operators involve the scale factors
where ![]() $\kappa _1$ and
$\kappa _1$ and ![]() $\kappa _2$ are the principal curvatures in the
$\kappa _2$ are the principal curvatures in the ![]() $\xi _1$ and
$\xi _1$ and ![]() $\xi _2$ directions, respectively. The sum
$\xi _2$ directions, respectively. The sum ![]() $\kappa = \kappa _1 + \kappa _2$ is referred below as the curvature of the flame surface. The gradient operator then takes the form
$\kappa = \kappa _1 + \kappa _2$ is referred below as the curvature of the flame surface. The gradient operator then takes the form
where ![]() $\boldsymbol \nabla _{s}$ is its surface component. The divergence of a vector
$\boldsymbol \nabla _{s}$ is its surface component. The divergence of a vector ![]() $\boldsymbol b$, with components
$\boldsymbol b$, with components ![]() $(b_1,b_2,b_3)$ in the directions
$(b_1,b_2,b_3)$ in the directions ![]() $\boldsymbol e_1$,
$\boldsymbol e_1$, ![]() $\boldsymbol e_2$ and
$\boldsymbol e_2$ and ![]() $\boldsymbol n$ respectively, is given by
$\boldsymbol n$ respectively, is given by
and the Laplacian of a scalar ![]() $\varphi$ is
$\varphi$ is
Transforming the governing equations also requires expressing time derivatives in the moving frame, using
with ![]() $\dot {\boldsymbol {\xi }} = l_1 \dot \xi _1 \boldsymbol e_1 + l_2 \dot \xi _2 \boldsymbol e_2$, where the ‘dot’ corresponds to differentiation with respect to time, and
$\dot {\boldsymbol {\xi }} = l_1 \dot \xi _1 \boldsymbol e_1 + l_2 \dot \xi _2 \boldsymbol e_2$, where the ‘dot’ corresponds to differentiation with respect to time, and ![]() $V_{f} = - \partial n/\partial t$. We will avoid writing the general equations in the moving curvilinear system and express only the relevant terms at each stage of the analysis. Further details can be found in Matalon et al. (Reference Matalon, Cui and Bechtold2003, appendix B).
$V_{f} = - \partial n/\partial t$. We will avoid writing the general equations in the moving curvilinear system and express only the relevant terms at each stage of the analysis. Further details can be found in Matalon et al. (Reference Matalon, Cui and Bechtold2003, appendix B).

Figure 1. The intrinsic curvilinear coordinates (![]() $\xi _1, \xi _2, n$) to the flame surface. The blue and magenta vectors correspond to the normal component of the gas velocity
$\xi _1, \xi _2, n$) to the flame surface. The blue and magenta vectors correspond to the normal component of the gas velocity ![]() $v_n \boldsymbol n$ and normal propagation velocity
$v_n \boldsymbol n$ and normal propagation velocity ![]() $- V_{f} \boldsymbol n$, respectively.
$- V_{f} \boldsymbol n$, respectively.
To examine the internal structure of the flame zone, centred near the surface along which ![]() $n=0$, we introduce the stretched conductivity-weighted coordinate
$n=0$, we introduce the stretched conductivity-weighted coordinate
with ![]() $\delta \ll 1$, and seek solutions that match those in the hydrodynamic zones as
$\delta \ll 1$, and seek solutions that match those in the hydrodynamic zones as ![]() $\eta \to \mp \infty$. Although it is straightforward to simplify the governing equations in the flame zone using this transformation, they remain intractable analytically due to the highly nonlinear reaction rate term. A common simplification that has paved the way to most of the theoretical advances in combustion is the activation energy asymptotic approximation. The activation energy of chemical reactions occurring in combustion systems is typically large compared with the thermal energy of the fresh mixture, such that
$\eta \to \mp \infty$. Although it is straightforward to simplify the governing equations in the flame zone using this transformation, they remain intractable analytically due to the highly nonlinear reaction rate term. A common simplification that has paved the way to most of the theoretical advances in combustion is the activation energy asymptotic approximation. The activation energy of chemical reactions occurring in combustion systems is typically large compared with the thermal energy of the fresh mixture, such that ![]() $\beta _0 \gg 1$ or, equivalently, the Zel'dovich number
$\beta _0 \gg 1$ or, equivalently, the Zel'dovich number ![]() $\beta = q \beta _0/T_a^2 \gg 1$ (in the following analysis it is more convenient to use
$\beta = q \beta _0/T_a^2 \gg 1$ (in the following analysis it is more convenient to use ![]() $\beta _0$). As a result, the chemical activity is confined to a thin layer embedded within the flame zone and centred about the location where the temperature is near its maximum value – the flame temperature
$\beta _0$). As a result, the chemical activity is confined to a thin layer embedded within the flame zone and centred about the location where the temperature is near its maximum value – the flame temperature ![]() $T_{f}$. In the limit
$T_{f}$. In the limit ![]() $\beta _0 \to \infty$, the reaction rate
$\beta _0 \to \infty$, the reaction rate ![]() $\omega$ takes the form of a Dirac delta function of strength
$\omega$ takes the form of a Dirac delta function of strength ![]() ${\sim }\exp {(-\beta _0/T_{f}})$; i.e. an Arrhenius form of temperature
${\sim }\exp {(-\beta _0/T_{f}})$; i.e. an Arrhenius form of temperature ![]() $T_{f}$. This approximation has been implemented in one of two ways: as a formal asymptotic approach, in which the solution is expressed in terms of gauge functions that depend on
$T_{f}$. This approximation has been implemented in one of two ways: as a formal asymptotic approach, in which the solution is expressed in terms of gauge functions that depend on ![]() $\beta _0$, or as a model – the delta-function model with
$\beta _0$, or as a model – the delta-function model with ![]() $\beta _0$ treated as a finite parameter (Matkowsky & Sivashinsky Reference Matkowsky and Sivashinsky1978; Buckmaster & Ludford Reference Buckmaster and Ludford1983; Margolis & Matkowsky Reference Margolis and Matkowsky1983). The latter, which captures the essence of activation energy asymptotics, was used primarily when encountering technical difficulties that prevented the use of a formal approach.
$\beta _0$ treated as a finite parameter (Matkowsky & Sivashinsky Reference Matkowsky and Sivashinsky1978; Buckmaster & Ludford Reference Buckmaster and Ludford1983; Margolis & Matkowsky Reference Margolis and Matkowsky1983). The latter, which captures the essence of activation energy asymptotics, was used primarily when encountering technical difficulties that prevented the use of a formal approach.
A systematic asymptotic approach was used to describe the dynamics of freely propagating flames (Matalon & Matkowsky Reference Matalon and Matkowsky1982; Matalon et al. Reference Matalon, Cui and Bechtold2003). In this case, the flame temperature is constant and equal to ![]() $T_a$ and the reaction zone spans the region where
$T_a$ and the reaction zone spans the region where ![]() $T - T_a = O(1/\beta _0)$ such that
$T - T_a = O(1/\beta _0)$ such that ![]() $\omega = O(1)$. The reaction rate (2.16) is exponentially small, and hence, negligible in the preheat zone where
$\omega = O(1)$. The reaction rate (2.16) is exponentially small, and hence, negligible in the preheat zone where ![]() $T < T_a$, and vanishes identically in the post-reaction zone where the deficient reactant or both reactants for a stoichiometric mixture are completely consumed. The solution in the reaction zone that constitutes a balance between the diffusion and chemical reaction rates provides, through asymptotic matching, jump conditions across the reaction sheet that can be used to facilitate the determination of the solution in the flame zone. The analysis also requires adopting a near-equidiffusion formulation (Buckmaster & Ludford Reference Buckmaster and Ludford1982), whereby
$T < T_a$, and vanishes identically in the post-reaction zone where the deficient reactant or both reactants for a stoichiometric mixture are completely consumed. The solution in the reaction zone that constitutes a balance between the diffusion and chemical reaction rates provides, through asymptotic matching, jump conditions across the reaction sheet that can be used to facilitate the determination of the solution in the flame zone. The analysis also requires adopting a near-equidiffusion formulation (Buckmaster & Ludford Reference Buckmaster and Ludford1982), whereby ![]() ${Le}_i^{-1} = 1 - {le}_i/\beta _0$, and a near-stoichiometric mixture limit (Bechtold & Matalon Reference Bechtold and Matalon1999) where
${Le}_i^{-1} = 1 - {le}_i/\beta _0$, and a near-stoichiometric mixture limit (Bechtold & Matalon Reference Bechtold and Matalon1999) where ![]() $Y_{E_0} - \nu Y_{D_0} = O(1/\beta _0)$, such that
$Y_{E_0} - \nu Y_{D_0} = O(1/\beta _0)$, such that ![]() $\varPhi = 1 + \varphi /\beta _0$ with
$\varPhi = 1 + \varphi /\beta _0$ with ![]() $\varphi = O(1)$ representing the deviation from stoichiometry.
$\varphi = O(1)$ representing the deviation from stoichiometry.
When propagating in a closed vessel, the flame temperature ![]() $T_{f}$ varies in time and exceeds the adiabatic flame temperature
$T_{f}$ varies in time and exceeds the adiabatic flame temperature ![]() $T_a$. The reaction rate may then be expressed in the form
$T_a$. The reaction rate may then be expressed in the form
ensuring that the chemical reaction remains confined to a thin layer where ![]() $T - T_{f} = O(1/\beta _0)$. Retaining a reaction–diffusion balance inside the thin reaction layer, however, requires rescaling the equations from one time to the next by readjusting the reaction zone thickness with an exponentially small scale that balances the factor
$T - T_{f} = O(1/\beta _0)$. Retaining a reaction–diffusion balance inside the thin reaction layer, however, requires rescaling the equations from one time to the next by readjusting the reaction zone thickness with an exponentially small scale that balances the factor ![]() $\exp {(\beta _0/T_a - \beta _0/T_{f})}$. This constitutes a technical difficulty that prevents the use of a formal asymptotic approach. A resolution can be obtained if one adopts a Newtonian approximation (Van Dyke Reference Van Dyke1954; Cole Reference Cole1957), whereby
$\exp {(\beta _0/T_a - \beta _0/T_{f})}$. This constitutes a technical difficulty that prevents the use of a formal asymptotic approach. A resolution can be obtained if one adopts a Newtonian approximation (Van Dyke Reference Van Dyke1954; Cole Reference Cole1957), whereby ![]() $(\gamma - 1)/\gamma$ is treated as a small parameter. In this limit,
$(\gamma - 1)/\gamma$ is treated as a small parameter. In this limit, ![]() $T_{f} \sim T_a$ and the factor
$T_{f} \sim T_a$ and the factor ![]() $\exp {(\beta _0/T_a - \beta _0/T_{f})}$ remains, to leading order, an
$\exp {(\beta _0/T_a - \beta _0/T_{f})}$ remains, to leading order, an ![]() $O(1)$ quantity. This approach is implemented in § 7. Although the Newtonian approximation accounts for gas compression, the increase in density translates entirely into a pressure rise, with the temperature minimally affected. To allow for gas compression to modify both the temperature and pressure, as anticipated physically, and circumvent the aforementioned difficulty, we use instead the delta-function approach.
$O(1)$ quantity. This approach is implemented in § 7. Although the Newtonian approximation accounts for gas compression, the increase in density translates entirely into a pressure rise, with the temperature minimally affected. To allow for gas compression to modify both the temperature and pressure, as anticipated physically, and circumvent the aforementioned difficulty, we use instead the delta-function approach.
The reaction rate in the governing equations is now replaced by the Dirac delta function of strength ![]() ${\sim }\exp {(-\beta _0/T_{f})}$, and
${\sim }\exp {(-\beta _0/T_{f})}$, and ![]() $\beta _0$ is subsequently treated as a finite parameter. The chemical reaction is now confined to a surface located, without loss of generality, at
$\beta _0$ is subsequently treated as a finite parameter. The chemical reaction is now confined to a surface located, without loss of generality, at ![]() $\eta = 0$. For consistency with earlier studies, we retain the near-equidiffusion and near-stoichiometric assumptions and use the same scaling for the temperature–mass fraction coupling functions, namely
$\eta = 0$. For consistency with earlier studies, we retain the near-equidiffusion and near-stoichiometric assumptions and use the same scaling for the temperature–mass fraction coupling functions, namely
 \begin{equation} \left.\begin{gathered} T + qY_{D}/Y_{D_0} = H + \beta_0^{{-}1} h_{D} + \cdots, \\ T +qY_{E}/\nu Y_{D_0} = H + \beta_0^{{-}1} (h_{E} + q \varphi) + \cdots, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} T + qY_{D}/Y_{D_0} = H + \beta_0^{{-}1} h_{D} + \cdots, \\ T +qY_{E}/\nu Y_{D_0} = H + \beta_0^{{-}1} (h_{E} + q \varphi) + \cdots, \end{gathered}\right\} \end{equation}where the enthalpy functions satisfy
 \begin{equation} \left.\begin{gathered} \rho \frac{\mathrm{D}H}{\mathrm{D}t} - \delta \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla H ) = \frac{\gamma - 1}{\gamma} \frac{\mathrm{d}P}{\mathrm{d}t}, \\ \rho \frac{\mathrm{D}h_i}{\mathrm{D}t} - \delta \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla h_i ) ={-} \delta {le}_i \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla (H - T)). \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \rho \frac{\mathrm{D}H}{\mathrm{D}t} - \delta \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla H ) = \frac{\gamma - 1}{\gamma} \frac{\mathrm{d}P}{\mathrm{d}t}, \\ \rho \frac{\mathrm{D}h_i}{\mathrm{D}t} - \delta \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla h_i ) ={-} \delta {le}_i \boldsymbol\nabla \boldsymbol{\cdot} (\lambda \boldsymbol\nabla (H - T)). \end{gathered}\right\} \end{equation}
The enthalpy perturbations ![]() $h_{D}$ and
$h_{D}$ and ![]() $h_{E}$ may then be used as the dependent variables replacing the mass fractions. Since the deficient reactant is depleted by the chemical reaction,
$h_{E}$ may then be used as the dependent variables replacing the mass fractions. Since the deficient reactant is depleted by the chemical reaction,
in the burned gas region ![]() $(\eta \ge 0)$. At the reaction sheet (
$(\eta \ge 0)$. At the reaction sheet (![]() $\eta =0$),
$\eta =0$),
representing, respectively, the flame temperature and the mass of unconsumed reactant leaking through the reaction sheet. A direct integration of the governing equations across ![]() $\eta = 0$ yields the following jump relations:
$\eta = 0$ yields the following jump relations:
 \begin{gather} \left.\begin{gathered} {}[\rho] = [T] = [H] = [h_i] = [\boldsymbol v] = 0, \\ [p] = \frac{4}{3} \Pr \left[\lambda \frac{\partial v_n}{\partial\eta}\right],\quad \left[\frac{\partial\boldsymbol v_{{\perp}}}{\partial\eta}\right] = 0, \\ \left[\frac{\partial H}{\partial\eta}\right] = 0,\quad \left[\frac{\partial h_i}{\partial\eta}\right] ={-}{le}_i \left[\frac{\partial T}{\partial\eta}\right], \end{gathered}\right\} \end{gather}
\begin{gather} \left.\begin{gathered} {}[\rho] = [T] = [H] = [h_i] = [\boldsymbol v] = 0, \\ [p] = \frac{4}{3} \Pr \left[\lambda \frac{\partial v_n}{\partial\eta}\right],\quad \left[\frac{\partial\boldsymbol v_{{\perp}}}{\partial\eta}\right] = 0, \\ \left[\frac{\partial H}{\partial\eta}\right] = 0,\quad \left[\frac{\partial h_i}{\partial\eta}\right] ={-}{le}_i \left[\frac{\partial T}{\partial\eta}\right], \end{gathered}\right\} \end{gather} \begin{gather} \left[\frac{\partial T}{\partial\eta}\right] ={-} qP \left(\frac{T_{f}}{T_a}\right)^{2} \sqrt\frac{\lambda_b}{\lambda_a}\sqrt {\frac{1 + (h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi)/2T_{f}^{2} } { 1 + q\varphi /2T_a^2}} \exp\left({\frac{\beta_0}{2T_a} - \frac{\beta_0}{2T_{f}}}\right). \end{gather}
\begin{gather} \left[\frac{\partial T}{\partial\eta}\right] ={-} qP \left(\frac{T_{f}}{T_a}\right)^{2} \sqrt\frac{\lambda_b}{\lambda_a}\sqrt {\frac{1 + (h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi)/2T_{f}^{2} } { 1 + q\varphi /2T_a^2}} \exp\left({\frac{\beta_0}{2T_a} - \frac{\beta_0}{2T_{f}}}\right). \end{gather}
Here ![]() $\lambda _b = \lambda (T_b)$ and the bracket
$\lambda _b = \lambda (T_b)$ and the bracket ![]() $[\,\,]$ denotes the jump, i.e.
$[\,\,]$ denotes the jump, i.e. ![]() $[\varTheta ] =\varTheta |_{{\eta =0^+}} - \varTheta |_{{\eta =0^-}}$. To avoid confusion, we note the distinction between the single brackets
$[\varTheta ] =\varTheta |_{{\eta =0^+}} - \varTheta |_{{\eta =0^-}}$. To avoid confusion, we note the distinction between the single brackets ![]() $[\,\,]$ used here to represent the jump across the reaction zone from the double brackets
$[\,\,]$ used here to represent the jump across the reaction zone from the double brackets ![]() $[\![ \,\,]\!]$ used earlier that represent the jump across the entire flame zone. The relations (4.14)–(4.15) constitute an obvious generalization of those derived systematically in the Newtonian limit (§ 7), and reduce to the corresponding relations for freely propagation flames (Matalon et al. Reference Matalon, Cui and Bechtold2003) when
$[\![ \,\,]\!]$ used earlier that represent the jump across the entire flame zone. The relations (4.14)–(4.15) constitute an obvious generalization of those derived systematically in the Newtonian limit (§ 7), and reduce to the corresponding relations for freely propagation flames (Matalon et al. Reference Matalon, Cui and Bechtold2003) when ![]() $P=1$. Although the jump in temperature gradient includes the factor
$P=1$. Although the jump in temperature gradient includes the factor ![]() $\exp {(\beta _0/2 T_a - \beta _0/2T_{f})}$, which is exponentially large when
$\exp {(\beta _0/2 T_a - \beta _0/2T_{f})}$, which is exponentially large when ![]() $\beta _0$ is formally treated as a large parameter, this factor is quite moderate, approximately 1–2 for practical values of the physical parameters.
$\beta _0$ is formally treated as a large parameter, this factor is quite moderate, approximately 1–2 for practical values of the physical parameters.
To describe the combustion field in the flame zone (![]() $-\infty < \eta < \infty$), all variables are expanded in power series of
$-\infty < \eta < \infty$), all variables are expanded in power series of ![]() $\delta$, namely
$\delta$, namely
 \begin{equation} \left.\begin{gathered} m = m^{(0)}(\eta, \xi_1,\xi_2,t) + \delta m^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ T = T^{(0)}(\eta, \xi_1,\xi_2,t) + \delta T^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ H = H^{(0)}(\eta, \xi_1,\xi_2,t) + \delta H^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ h_i = h_i^{(0)}(\eta, \xi_1,\xi_2,t) + \delta h_i^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ v_n = v_n^{(0)}(\eta, \xi_1,\xi_2,t) + \delta v_n^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ \boldsymbol v_{{\perp}} = \boldsymbol v_{{\perp}}^{(0)}(\eta, \xi_1,\xi_2,t) + \delta \boldsymbol v_{{\perp}}^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ p = p^{(0)}(\eta, \xi_1,\xi_2,t) + \delta p^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} m = m^{(0)}(\eta, \xi_1,\xi_2,t) + \delta m^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ T = T^{(0)}(\eta, \xi_1,\xi_2,t) + \delta T^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ H = H^{(0)}(\eta, \xi_1,\xi_2,t) + \delta H^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ h_i = h_i^{(0)}(\eta, \xi_1,\xi_2,t) + \delta h_i^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ v_n = v_n^{(0)}(\eta, \xi_1,\xi_2,t) + \delta v_n^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ \boldsymbol v_{{\perp}} = \boldsymbol v_{{\perp}}^{(0)}(\eta, \xi_1,\xi_2,t) + \delta \boldsymbol v_{{\perp}}^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots, \\ p = p^{(0)}(\eta, \xi_1,\xi_2,t) + \delta p^{(1)}(\eta, \xi_1,\xi_2,t) + \cdots. \end{gathered}\right\} \end{equation}
The mean pressure ![]() $P(t)$ has not been explicitly expanded, but it too will be determined to
$P(t)$ has not been explicitly expanded, but it too will be determined to ![]() $O(\delta )$ when evaluating the integral in (2.17). The equations that need to be solved at each order are obtained by applying the transformation
$O(\delta )$ when evaluating the integral in (2.17). The equations that need to be solved at each order are obtained by applying the transformation ![]() $(n,\xi _1,\xi _2,t) \mapsto (\eta,\xi _1,\xi _2,t)$ to the governing equations, noting that
$(n,\xi _1,\xi _2,t) \mapsto (\eta,\xi _1,\xi _2,t)$ to the governing equations, noting that
They must be solved for ![]() $\eta \lessgtr 0$ subject to the jump conditions (4.14) across
$\eta \lessgtr 0$ subject to the jump conditions (4.14) across ![]() $\eta = 0$. The matching conditions for the state variables are readily available from (3.11) and (3.14), namely
$\eta = 0$. The matching conditions for the state variables are readily available from (3.11) and (3.14), namely
 \begin{equation} \left.\begin{gathered} Y_D \sim \left\{\begin{array}{@{}ll@{}} {Y_{D_{0}}}, \\ 0, \end{array}\right.\quad Y_E \sim \left\{\begin{array}{@{}ll@{}} {Y_{E_{0}}} & \text{as}\ \eta \to -\infty, \\ \nu {Y_{D_{0}}} \varphi/\beta_0 & \text{as}\ \eta \to +\infty, \end{array}\right.\\ \rho \sim \left\{\begin{array}{@{}ll@{}} P^{1/\gamma}, \\ P / T_b, \end{array}\right.\quad T \sim \left\{\begin{array}{@{}ll@{}} P^{(\gamma -1)/\gamma} & \text{as}\ \eta \to -\infty, \\ T_b & \text{as}\ \eta \to +\infty, \end{array}\right. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} Y_D \sim \left\{\begin{array}{@{}ll@{}} {Y_{D_{0}}}, \\ 0, \end{array}\right.\quad Y_E \sim \left\{\begin{array}{@{}ll@{}} {Y_{E_{0}}} & \text{as}\ \eta \to -\infty, \\ \nu {Y_{D_{0}}} \varphi/\beta_0 & \text{as}\ \eta \to +\infty, \end{array}\right.\\ \rho \sim \left\{\begin{array}{@{}ll@{}} P^{1/\gamma}, \\ P / T_b, \end{array}\right.\quad T \sim \left\{\begin{array}{@{}ll@{}} P^{(\gamma -1)/\gamma} & \text{as}\ \eta \to -\infty, \\ T_b & \text{as}\ \eta \to +\infty, \end{array}\right. \end{gathered}\right\} \end{equation}
where ![]() $T_b = T_b^{(0)}(t) + \delta T_b^{(1)}(t) + \cdots$, with
$T_b = T_b^{(0)}(t) + \delta T_b^{(1)}(t) + \cdots$, with ![]() $T_b^{(0)} = P^{(\gamma -1)/ \gamma } + q$. Consequently,
$T_b^{(0)} = P^{(\gamma -1)/ \gamma } + q$. Consequently, ![]() $H \sim T_b$ as
$H \sim T_b$ as ![]() $\eta \to \pm \infty$, but the enthalpy perturbations that satisfy
$\eta \to \pm \infty$, but the enthalpy perturbations that satisfy ![]() $h_D = h_E \sim 0$ as
$h_D = h_E \sim 0$ as ![]() $\eta \to - \infty$ remain to be determined on the burned side as
$\eta \to - \infty$ remain to be determined on the burned side as ![]() $\eta \to + \infty$.
$\eta \to + \infty$.
To leading order,
 \begin{equation} \left.\begin{gathered} \frac{\partial m^{(0)}}{\partial \eta }=0, \\ m^{(0)}\frac{\partial T^{(0)}}{\partial \eta} - \frac{\partial^{2}T^{(0)}}{\partial \eta ^{2}} = 0, \\ m^{(0)}\frac{\partial H^{(0)}}{\partial \eta } - \frac{\partial^{2}H^{(0)}}{\partial \eta ^{2}} =0, \\ m^{(0)}\frac{\partial h_i^{(0)}}{\partial \eta } - \frac{\partial^{2}h_i^{(0)}}{\partial \eta ^{2}} ={-} {le}_i \left( \frac{\partial ^{2} H^{(0)}}{\partial \eta ^{2}} - \frac{\partial ^{2} T^{(0)}}{\partial \eta ^{2}} \right), \\ m^{(0)}\frac{\partial v_n^{(0)}}{\partial \eta } - \frac{4}{3}\Pr \frac{\partial ^{2}v_n^{(0)}}{\partial \eta ^{2}} ={-}\frac{\partial p^{(0)} }{\partial \eta }, \\ m^{(0)}\frac{\partial \boldsymbol v_{{\perp}}^{(0)}}{\partial \eta } -\Pr \frac{\partial^{2}\boldsymbol v_{{\perp}}^{(0)}}{\partial \eta ^{2}} = 0. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial m^{(0)}}{\partial \eta }=0, \\ m^{(0)}\frac{\partial T^{(0)}}{\partial \eta} - \frac{\partial^{2}T^{(0)}}{\partial \eta ^{2}} = 0, \\ m^{(0)}\frac{\partial H^{(0)}}{\partial \eta } - \frac{\partial^{2}H^{(0)}}{\partial \eta ^{2}} =0, \\ m^{(0)}\frac{\partial h_i^{(0)}}{\partial \eta } - \frac{\partial^{2}h_i^{(0)}}{\partial \eta ^{2}} ={-} {le}_i \left( \frac{\partial ^{2} H^{(0)}}{\partial \eta ^{2}} - \frac{\partial ^{2} T^{(0)}}{\partial \eta ^{2}} \right), \\ m^{(0)}\frac{\partial v_n^{(0)}}{\partial \eta } - \frac{4}{3}\Pr \frac{\partial ^{2}v_n^{(0)}}{\partial \eta ^{2}} ={-}\frac{\partial p^{(0)} }{\partial \eta }, \\ m^{(0)}\frac{\partial \boldsymbol v_{{\perp}}^{(0)}}{\partial \eta } -\Pr \frac{\partial^{2}\boldsymbol v_{{\perp}}^{(0)}}{\partial \eta ^{2}} = 0. \end{gathered}\right\} \end{equation}
Conservation of mass implies that ![]() $m^{(0)} = M$ independent of
$m^{(0)} = M$ independent of ![]() $\eta$. The solution of the state variables that satisfies the jump relations at
$\eta$. The solution of the state variables that satisfies the jump relations at ![]() $\eta =0$ and the matching conditions as
$\eta =0$ and the matching conditions as ![]() $\eta \rightarrow \pm \infty$ is
$\eta \rightarrow \pm \infty$ is
with ![]() $H^{(0)} = T_b^{(0)}$ independent of
$H^{(0)} = T_b^{(0)}$ independent of ![]() $\eta$. The top and bottom expressions correspond to
$\eta$. The top and bottom expressions correspond to ![]() $\eta < 0$ and
$\eta < 0$ and ![]() $\eta > 0$, respectively, a notation that is also kept below. The solution of the velocity and pressure that satisfies the jump relations at
$\eta > 0$, respectively, a notation that is also kept below. The solution of the velocity and pressure that satisfies the jump relations at ![]() $\eta = 0$ is given by
$\eta = 0$ is given by
 \begin{equation} \left.\begin{gathered} v_n^{(0)} = v_n^{(0)}|_{{\eta ={-}\infty}} + \frac{1}{P} \left\{\begin{array}{@{}l@{}} q M \,\text{e}^{M \eta} \\ q M \end{array}\right.,\quad \boldsymbol v_{{\perp}}^{(0)} =\boldsymbol v_{{\perp}}^{(0)}|_{{\eta ={-}\infty}},\\ p^{(0)}= p^{(0)}|_{{\eta ={-}\infty}} + \frac{1}{P} \left\{\begin{array}{@{}l@{}} \left(\dfrac{4}{3} \Pr -1\right) qM^2 \,\text{e}^{M \eta}, \\ - q M^2, \end{array}\right. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} v_n^{(0)} = v_n^{(0)}|_{{\eta ={-}\infty}} + \frac{1}{P} \left\{\begin{array}{@{}l@{}} q M \,\text{e}^{M \eta} \\ q M \end{array}\right.,\quad \boldsymbol v_{{\perp}}^{(0)} =\boldsymbol v_{{\perp}}^{(0)}|_{{\eta ={-}\infty}},\\ p^{(0)}= p^{(0)}|_{{\eta ={-}\infty}} + \frac{1}{P} \left\{\begin{array}{@{}l@{}} \left(\dfrac{4}{3} \Pr -1\right) qM^2 \,\text{e}^{M \eta}, \\ - q M^2, \end{array}\right. \end{gathered}\right\} \end{equation}
where it can be verified that the behaviour as ![]() $\eta \to \pm \infty$ confirms the RH relations across the flame. Finally, the jump relation for the temperature gradient yields an expression for the burning rate, given by
$\eta \to \pm \infty$ confirms the RH relations across the flame. Finally, the jump relation for the temperature gradient yields an expression for the burning rate, given by
 \begin{equation} M = P \left(\frac{T_{f}}{T_a}\right)^{2} \sqrt\frac{\lambda_b}{\lambda_a} \sqrt {\frac{1 + q \varphi / 2T_{f}^{2}} {1 + q\varphi /2 T_a^2}} \exp\left({\frac{\beta_0}{2T_a} - \frac{\beta_0}{2T_{f}}}\right), \end{equation}
\begin{equation} M = P \left(\frac{T_{f}}{T_a}\right)^{2} \sqrt\frac{\lambda_b}{\lambda_a} \sqrt {\frac{1 + q \varphi / 2T_{f}^{2}} {1 + q\varphi /2 T_a^2}} \exp\left({\frac{\beta_0}{2T_a} - \frac{\beta_0}{2T_{f}}}\right), \end{equation}
where here, ![]() $T_{f} = T_b^{(0)}$. Below, we will use
$T_{f} = T_b^{(0)}$. Below, we will use ![]() $T_{f}$ and
$T_{f}$ and ![]() $T_b^{(0)}$ interchangeably when only the leading order of flame temperature is needed in a given expression. Equation (4.22) shows that, to leading order, the burning rate depends only on time and simplifies to
$T_b^{(0)}$ interchangeably when only the leading order of flame temperature is needed in a given expression. Equation (4.22) shows that, to leading order, the burning rate depends only on time and simplifies to ![]() $M=1$ for a freely propagating flame, as it should.
$M=1$ for a freely propagating flame, as it should.
We now proceed to the next order in the perturbation scheme. Before writing the simplified equations to ![]() $O(\delta )$ we note that since
$O(\delta )$ we note that since ![]() $\lambda = \lambda (T)$ and
$\lambda = \lambda (T)$ and ![]() $T \sim T^{(0)}(\eta, t)$, the transformation (4.17a–c) implies that
$T \sim T^{(0)}(\eta, t)$, the transformation (4.17a–c) implies that
 \begin{equation} \left.\begin{gathered} \frac{\partial}{\partial t} = \frac{\partial}{\partial t} + \frac{\partial \eta}{\partial t} \frac{\partial}{\partial \eta} + O(\delta), \qquad \boldsymbol\nabla_{s} = \boldsymbol\nabla_{s} + O(\delta), \\ \lambda \frac{\partial \eta}{\partial t} = \int^0_{\eta} \lambda_T \frac{\partial T}{\partial t} \mathrm{d} \eta' = \left\{\begin{array}{@{}l@{}} \dot T_{f} \displaystyle\int^0_{\eta} \lambda_T \,\mathrm{d} \eta' - \dfrac{\dot M}{M} \left(\lambda \eta + \displaystyle\int^0_{\eta} \lambda \, \mathrm{d} \eta' \right), \\ - \lambda_T \dot T_{f} \eta, \end{array}\right. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial}{\partial t} = \frac{\partial}{\partial t} + \frac{\partial \eta}{\partial t} \frac{\partial}{\partial \eta} + O(\delta), \qquad \boldsymbol\nabla_{s} = \boldsymbol\nabla_{s} + O(\delta), \\ \lambda \frac{\partial \eta}{\partial t} = \int^0_{\eta} \lambda_T \frac{\partial T}{\partial t} \mathrm{d} \eta' = \left\{\begin{array}{@{}l@{}} \dot T_{f} \displaystyle\int^0_{\eta} \lambda_T \,\mathrm{d} \eta' - \dfrac{\dot M}{M} \left(\lambda \eta + \displaystyle\int^0_{\eta} \lambda \, \mathrm{d} \eta' \right), \\ - \lambda_T \dot T_{f} \eta, \end{array}\right. \end{gathered}\right\} \end{equation}
where ![]() $\lambda _T = \mathrm {d} \lambda /\mathrm {d} T$ and the ‘dot’, here and thereafter, signifies differentiation with respect to
$\lambda _T = \mathrm {d} \lambda /\mathrm {d} T$ and the ‘dot’, here and thereafter, signifies differentiation with respect to ![]() $t$.
$t$.
The continuity equation takes the form
where ![]() $\kappa$ is the local curvature of the flame surface taken to be positive when the surface is concave towards the burned gas, as per the convention adopted earlier, and
$\kappa$ is the local curvature of the flame surface taken to be positive when the surface is concave towards the burned gas, as per the convention adopted earlier, and
 \begin{equation} {\mathbb{K}} ={-} V_{f} \kappa +\underbrace{\frac{1}{a_1 a_2} \left(\frac{\partial(a_2v_1)}{\partial\xi_1} + \frac{\partial(a_1v_2)}{\partial\xi_2}\right)}_{\boldsymbol\nabla_{s}\ \boldsymbol{\cdot}\ \boldsymbol v_{{\perp}}} \end{equation}
\begin{equation} {\mathbb{K}} ={-} V_{f} \kappa +\underbrace{\frac{1}{a_1 a_2} \left(\frac{\partial(a_2v_1)}{\partial\xi_1} + \frac{\partial(a_1v_2)}{\partial\xi_2}\right)}_{\boldsymbol\nabla_{s}\ \boldsymbol{\cdot}\ \boldsymbol v_{{\perp}}} \end{equation}
is the (dimensionless) stretch rate experienced by the flame (Matalon et al. Reference Matalon, Cui and Bechtold2003, appendix A), both being independent of ![]() $\eta$. Its influence on the flame propagation will be discussed in § 5. The solution of (4.24), which satisfies continuity at
$\eta$. Its influence on the flame propagation will be discussed in § 5. The solution of (4.24), which satisfies continuity at ![]() $\eta =0$, takes the form
$\eta =0$, takes the form
 \begin{equation} m^{(1)} = A + \left\{\begin{array}{@{}l@{}} g(\eta), \\ \lambda_b \left(M \kappa - \dfrac{P}{T_{f}} \mathbb{K} - \dfrac{ \dot P}{T_{f}} + \dfrac{\gamma - 1}{\gamma} \dfrac{T_{u} \dot P}{T_{f}^2} \right) \eta, \end{array}\right. \end{equation}
\begin{equation} m^{(1)} = A + \left\{\begin{array}{@{}l@{}} g(\eta), \\ \lambda_b \left(M \kappa - \dfrac{P}{T_{f}} \mathbb{K} - \dfrac{ \dot P}{T_{f}} + \dfrac{\gamma - 1}{\gamma} \dfrac{T_{u} \dot P}{T_{f}^2} \right) \eta, \end{array}\right. \end{equation}
where ![]() $A = A(\xi _1,\xi _2,t)$ remains to be determined, and
$A = A(\xi _1,\xi _2,t)$ remains to be determined, and
 \begin{align} g(\eta) &= \left(M \kappa - \frac{\dot M P}{ M \vartheta(\eta)}\right) \mathcal{J}_1(\eta) + \left(\frac{\dot M P}{M} - P \mathbb{K} - \dot P \right) \mathcal{J}_2(\eta) \nonumber\\ &\quad + \frac{\gamma -1}{\gamma}\dot P T_{u} \left(\frac{\mathcal{J}_3(\eta)}{\vartheta} - \mathcal{J}_4(\eta)\right). \end{align}
\begin{align} g(\eta) &= \left(M \kappa - \frac{\dot M P}{ M \vartheta(\eta)}\right) \mathcal{J}_1(\eta) + \left(\frac{\dot M P}{M} - P \mathbb{K} - \dot P \right) \mathcal{J}_2(\eta) \nonumber\\ &\quad + \frac{\gamma -1}{\gamma}\dot P T_{u} \left(\frac{\mathcal{J}_3(\eta)}{\vartheta} - \mathcal{J}_4(\eta)\right). \end{align}Here
 \begin{equation} \left.\begin{gathered} \mathcal{J}_1 (\eta) = \int_{0}^{\eta} \lambda(\eta') \, \mathrm{d} \eta',\quad \mathcal{J}_2 (\eta) = \int_{0}^{\eta} \frac{\lambda(\eta')}{\vartheta(\eta')} \mathrm{d}\eta', \\ \mathcal{J}_3 (\eta) = \int_{0}^{\eta} \frac{\mathrm{d}}{\mathrm{d}\vartheta} (\lambda(\eta')) \, \mathrm{d} \eta',\quad \mathcal{J}_4 (\eta) = \int_{0}^{\eta} \frac{\mathrm{d}}{\mathrm{d}\vartheta} \left(\frac{\lambda(\eta')}{\vartheta(\eta')}\right)\mathrm{d} \eta', \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \mathcal{J}_1 (\eta) = \int_{0}^{\eta} \lambda(\eta') \, \mathrm{d} \eta',\quad \mathcal{J}_2 (\eta) = \int_{0}^{\eta} \frac{\lambda(\eta')}{\vartheta(\eta')} \mathrm{d}\eta', \\ \mathcal{J}_3 (\eta) = \int_{0}^{\eta} \frac{\mathrm{d}}{\mathrm{d}\vartheta} (\lambda(\eta')) \, \mathrm{d} \eta',\quad \mathcal{J}_4 (\eta) = \int_{0}^{\eta} \frac{\mathrm{d}}{\mathrm{d}\vartheta} \left(\frac{\lambda(\eta')}{\vartheta(\eta')}\right)\mathrm{d} \eta', \end{gathered}\right\} \end{equation}
where ![]() $\vartheta$ is the leading-order temperature in the preheat zone, namely
$\vartheta$ is the leading-order temperature in the preheat zone, namely ![]() $\vartheta (\eta ) = T_{u} + q \,\text{e}^{M \eta }$, and
$\vartheta (\eta ) = T_{u} + q \,\text{e}^{M \eta }$, and ![]() $T_{u} = P^{(\gamma -1)/ \gamma }$ is the temperature on the unburned side of the flame zone. For simplicity of notation, we have displayed explicitly only the dependence on
$T_{u} = P^{(\gamma -1)/ \gamma }$ is the temperature on the unburned side of the flame zone. For simplicity of notation, we have displayed explicitly only the dependence on ![]() $\eta$, which is needed for integration, although
$\eta$, which is needed for integration, although ![]() $g$ is a function of
$g$ is a function of ![]() $\xi _1, \xi _2, \eta$ and
$\xi _1, \xi _2, \eta$ and ![]() $t$ and the integrals
$t$ and the integrals ![]() $\mathcal {J}_i$ depend on both
$\mathcal {J}_i$ depend on both ![]() $\eta$ and
$\eta$ and ![]() $t$. The same notation is adopted below.
$t$. The same notation is adopted below.
The remaining equations describing the combustion field are
and
 \begin{align} M
\frac{\partial{h_i^{(1)}} }{\partial\eta} -
\frac{\partial^2{h_i^{(1)}}}{\partial\eta^2} &={-} (m^{(1)}
+\lambda \kappa ) \frac{\partial {h_i^{(0)}}}{\partial
\eta} - \lambda \rho^{(0)}
\left(\frac{\partial{h_i^{(0)}}}{\partial t} +
\frac{\partial \eta}{\partial t} \frac{\partial
h_i^{(0)}}{\partial \eta}\right) \nonumber\\ &\quad +{le}_i
\left(\frac{\partial^2~T^{(1)}}{\partial\eta^2} -
\frac{\partial^2H^{(1)}}{\partial\eta^2} - \lambda \kappa
\frac{\partial T^{(0)}}{\partial\eta}\right),
\end{align}
\begin{align} M
\frac{\partial{h_i^{(1)}} }{\partial\eta} -
\frac{\partial^2{h_i^{(1)}}}{\partial\eta^2} &={-} (m^{(1)}
+\lambda \kappa ) \frac{\partial {h_i^{(0)}}}{\partial
\eta} - \lambda \rho^{(0)}
\left(\frac{\partial{h_i^{(0)}}}{\partial t} +
\frac{\partial \eta}{\partial t} \frac{\partial
h_i^{(0)}}{\partial \eta}\right) \nonumber\\ &\quad +{le}_i
\left(\frac{\partial^2~T^{(1)}}{\partial\eta^2} -
\frac{\partial^2H^{(1)}}{\partial\eta^2} - \lambda \kappa
\frac{\partial T^{(0)}}{\partial\eta}\right),
\end{align}
for ![]() ${h_D^{(1)}}$ and
${h_D^{(1)}}$ and ![]() ${h_E^{(1)}}$. They must satisfy the
${h_E^{(1)}}$. They must satisfy the ![]() $O(\delta )$ contributions of the jump relations (4.14) across
$O(\delta )$ contributions of the jump relations (4.14) across ![]() $\eta =0$, namely
$\eta =0$, namely
 \begin{equation} \left.\begin{gathered}
{}[T^{(1)}] = [H^{(1)}] = [{h_i^{(1)}}] = 0, \\
\left[\frac{\partial H^{(1)}}{\partial\eta}\right] =
0,\quad \left[ \frac{\partial{h_i^{(1)}}}{\partial\eta}
\right] ={-}{le}_i \left[\frac{\partial
T^{(1)}}{\partial\eta}\right],\\ \left[\frac{\partial
T^{(1)}}{\partial\eta}\right] ={-} \frac{q M}{2 T_{f}^2}
\left({h_{D}^{{\ast}}}^{(1)} + \frac{{h_{E}^{{\ast}}}^{(1)}
- {h_{D}^{{\ast}}}^{(1)} }{2 + q \varphi/T_{f}^2} \right) -
q \frac{\partial M}{\partial T_{f}} T_b^{(1)},
\end{gathered}\right\}
\end{equation}
\begin{equation} \left.\begin{gathered}
{}[T^{(1)}] = [H^{(1)}] = [{h_i^{(1)}}] = 0, \\
\left[\frac{\partial H^{(1)}}{\partial\eta}\right] =
0,\quad \left[ \frac{\partial{h_i^{(1)}}}{\partial\eta}
\right] ={-}{le}_i \left[\frac{\partial
T^{(1)}}{\partial\eta}\right],\\ \left[\frac{\partial
T^{(1)}}{\partial\eta}\right] ={-} \frac{q M}{2 T_{f}^2}
\left({h_{D}^{{\ast}}}^{(1)} + \frac{{h_{E}^{{\ast}}}^{(1)}
- {h_{D}^{{\ast}}}^{(1)} }{2 + q \varphi/T_{f}^2} \right) -
q \frac{\partial M}{\partial T_{f}} T_b^{(1)},
\end{gathered}\right\}
\end{equation}
and the matching conditions ![]() $H^{(1)} = T^{(1)} = {h_i^{(1)}} \sim 0$ as
$H^{(1)} = T^{(1)} = {h_i^{(1)}} \sim 0$ as ![]() $\eta \rightarrow -\infty$, where
$\eta \rightarrow -\infty$, where
 \begin{equation} \frac{\partial M}{\partial T_{f}} = M \left\{\frac{2}{T_{f}} + \left.\frac{1}{2\lambda_b} \lambda_T \right|_{{T_{f}}} - \frac{q \varphi/ 2T_{f}^3}{1 + q \varphi / 2T_{f}^{2}}+ \frac{\beta_0}{2 T_{f}^2}\right\}. \end{equation}
\begin{equation} \frac{\partial M}{\partial T_{f}} = M \left\{\frac{2}{T_{f}} + \left.\frac{1}{2\lambda_b} \lambda_T \right|_{{T_{f}}} - \frac{q \varphi/ 2T_{f}^3}{1 + q \varphi / 2T_{f}^{2}}+ \frac{\beta_0}{2 T_{f}^2}\right\}. \end{equation}
We note that the equations for ![]() $h_{D}^{(1)}$ and
$h_{D}^{(1)}$ and ![]() $h_{E}^{(1)}$ combine naturally into a single equation when introducing
$h_{E}^{(1)}$ combine naturally into a single equation when introducing
as the effective enthalpy and (reduced) Lewis number of the mixture. Then
 \begin{gather} \begin{aligned}[b] M \frac{\partial{\mathcal H}^{(1)} }{\partial\eta} - \frac{\partial^2{\mathcal H}^{(1)}}{\partial\eta^2} &={-} (m^{(1)} +\lambda \kappa) \frac{\partial {\mathcal H}^{(0)} }{\partial \eta } - \lambda \rho^{(0)} \left(\frac{\partial{\mathcal H}^{(0)} }{\partial t} + \frac{\partial \eta}{\partial t} \frac{\partial {\mathcal H}^{(0)}}{\partial \eta}\right)\\ &\quad + {le_{eff}} \left( \frac{\partial^2~T^{(1)}}{\partial\eta^2} - \frac{\partial^2H^{(1)}}{\partial\eta^2} - \lambda \kappa \frac{\partial T^{(0)}}{\partial\eta } \right),\end{aligned} \end{gather}
\begin{gather} \begin{aligned}[b] M \frac{\partial{\mathcal H}^{(1)} }{\partial\eta} - \frac{\partial^2{\mathcal H}^{(1)}}{\partial\eta^2} &={-} (m^{(1)} +\lambda \kappa) \frac{\partial {\mathcal H}^{(0)} }{\partial \eta } - \lambda \rho^{(0)} \left(\frac{\partial{\mathcal H}^{(0)} }{\partial t} + \frac{\partial \eta}{\partial t} \frac{\partial {\mathcal H}^{(0)}}{\partial \eta}\right)\\ &\quad + {le_{eff}} \left( \frac{\partial^2~T^{(1)}}{\partial\eta^2} - \frac{\partial^2H^{(1)}}{\partial\eta^2} - \lambda \kappa \frac{\partial T^{(0)}}{\partial\eta } \right),\end{aligned} \end{gather}
and the jump relations across ![]() $\eta =0$ simplify to
$\eta =0$ simplify to
 \begin{equation} \left.\begin{gathered} {}[T^{(1)}] = [{\mathcal H}^{(1)}] = 0,\quad \left[\frac{\partial T^{(1)}}{\partial\eta}\right] ={-} \frac{q M}{2 T_{f}^2} {{\mathcal H}^{*}}^{(1)} - q \frac{\partial M}{\partial T_{f}} T_b^{(1)}, \\ \left[\frac{\partial {\mathcal H}^{(1)} }{\partial\eta}\right] ={-}{le_{eff}} \left[\frac{\partial T^{(1)}}{\partial\eta}\right]. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} {}[T^{(1)}] = [{\mathcal H}^{(1)}] = 0,\quad \left[\frac{\partial T^{(1)}}{\partial\eta}\right] ={-} \frac{q M}{2 T_{f}^2} {{\mathcal H}^{*}}^{(1)} - q \frac{\partial M}{\partial T_{f}} T_b^{(1)}, \\ \left[\frac{\partial {\mathcal H}^{(1)} }{\partial\eta}\right] ={-}{le_{eff}} \left[\frac{\partial T^{(1)}}{\partial\eta}\right]. \end{gathered}\right\} \end{equation}
We are left to address (4.29)–(4.36) for ![]() $T^{(1)}, H^{(1)}$ and
$T^{(1)}, H^{(1)}$ and ![]() ${\mathcal H}^{(1)}$, respectively, subject to the jump relations (4.37).
${\mathcal H}^{(1)}$, respectively, subject to the jump relations (4.37).
The solution in the burned gas region (![]() $\eta > 0$) is
$\eta > 0$) is
 \begin{equation} \left.\begin{gathered} T^{(1)} = T_b^{(1)}+ q \lambda_b \frac{\gamma-1}{\gamma} \frac{\dot P}{M T_{f}} \eta, \\ H^{(1)} = T^{(1)},\quad {\mathcal H}^{(1)} = B, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} T^{(1)} = T_b^{(1)}+ q \lambda_b \frac{\gamma-1}{\gamma} \frac{\dot P}{M T_{f}} \eta, \\ H^{(1)} = T^{(1)},\quad {\mathcal H}^{(1)} = B, \end{gathered}\right\} \end{equation}
where ![]() $T_b^{(1)}$ and
$T_b^{(1)}$ and ![]() $B$ remain to be determined. In the preheat zone (
$B$ remain to be determined. In the preheat zone (![]() $\eta < 0$) the temperature equation (4.29) takes the form
$\eta < 0$) the temperature equation (4.29) takes the form
 \begin{align} \left.\begin{gathered} M \frac{\partial T^{(1)}}{\partial\eta} - \frac{\partial^2~T^{(1)}}{\partial\eta^2} ={-} Aq M \,{\rm e}^{M\eta} - q s(\eta) M \,{\rm e}^{M\eta}, \\ s(\eta) = g(\eta) + \kappa \lambda(\eta)- \frac{\gamma-1}{\gamma} \frac{\dot P}{M} \frac{\lambda(\eta)}{\vartheta (\eta)} + \frac{\dot M}{M} \frac{P}{\vartheta(\eta)} \mathcal{J}_1(\eta) - \frac{\gamma -1}{\gamma} \frac{T_{u} \dot P}{\vartheta(\eta)} \mathcal{J}_3(\eta), \end{gathered}\right\} \end{align}
\begin{align} \left.\begin{gathered} M \frac{\partial T^{(1)}}{\partial\eta} - \frac{\partial^2~T^{(1)}}{\partial\eta^2} ={-} Aq M \,{\rm e}^{M\eta} - q s(\eta) M \,{\rm e}^{M\eta}, \\ s(\eta) = g(\eta) + \kappa \lambda(\eta)- \frac{\gamma-1}{\gamma} \frac{\dot P}{M} \frac{\lambda(\eta)}{\vartheta (\eta)} + \frac{\dot M}{M} \frac{P}{\vartheta(\eta)} \mathcal{J}_1(\eta) - \frac{\gamma -1}{\gamma} \frac{T_{u} \dot P}{\vartheta(\eta)} \mathcal{J}_3(\eta), \end{gathered}\right\} \end{align}
and the general solution that satisfies continuity at ![]() $\eta =0$ is
$\eta =0$ is
 \begin{equation} T^{(1)} = T_b^{(1)} + D ({\rm e}^{M\eta} -1)+ A q \eta \,\text{e}^{M\eta} + q \int_{\eta}^{0} s(\eta')(\text{e}^{M\eta'} - \text{e}^{M\eta}) \,\mathrm{d}\eta'. \end{equation}
\begin{equation} T^{(1)} = T_b^{(1)} + D ({\rm e}^{M\eta} -1)+ A q \eta \,\text{e}^{M\eta} + q \int_{\eta}^{0} s(\eta')(\text{e}^{M\eta'} - \text{e}^{M\eta}) \,\mathrm{d}\eta'. \end{equation}
Similarly, the solution of (4.30) that is continuous and smooth at ![]() $\eta =0$ is
$\eta =0$ is
 \begin{equation} H^{(1)} = T_b^{(1)}+ \frac{\gamma-1}{\gamma} \frac{q \lambda_b \dot P}{M^2 T_{f}} \left\{( \text{e}^{M \eta }-1) + \frac{M T_{f}}{\lambda_b} {\int_{\eta}^{0}} \frac{\lambda(\eta') }{ \vartheta(\eta')}(\text{e}^{M \eta} - \text{e}^{M \eta'})\,\mathrm{d}\eta'\right\}. \end{equation}
\begin{equation} H^{(1)} = T_b^{(1)}+ \frac{\gamma-1}{\gamma} \frac{q \lambda_b \dot P}{M^2 T_{f}} \left\{( \text{e}^{M \eta }-1) + \frac{M T_{f}}{\lambda_b} {\int_{\eta}^{0}} \frac{\lambda(\eta') }{ \vartheta(\eta')}(\text{e}^{M \eta} - \text{e}^{M \eta'})\,\mathrm{d}\eta'\right\}. \end{equation}
Matching as ![]() $\eta \rightarrow -\infty$ yields
$\eta \rightarrow -\infty$ yields
 \begin{equation} \left.\begin{gathered} T_b^{(1)} = \frac{\gamma-1}{\gamma} \frac{q \lambda_b \dot P}{M^2 T_{f}} \left(1+ \frac{M T_{f}}{\lambda_b} \int_{-\infty}^{0} \frac{\lambda(\eta') }{ \vartheta(\eta')} \text{e}^{M\eta'} \mathrm{d} \eta'\right), \\ D = T_b^{(1)} + q \int_{-\infty}^{0} s(\eta') \,\text{e}^{M\eta'} \mathrm{d}\eta'. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} T_b^{(1)} = \frac{\gamma-1}{\gamma} \frac{q \lambda_b \dot P}{M^2 T_{f}} \left(1+ \frac{M T_{f}}{\lambda_b} \int_{-\infty}^{0} \frac{\lambda(\eta') }{ \vartheta(\eta')} \text{e}^{M\eta'} \mathrm{d} \eta'\right), \\ D = T_b^{(1)} + q \int_{-\infty}^{0} s(\eta') \,\text{e}^{M\eta'} \mathrm{d}\eta'. \end{gathered}\right\} \end{equation} Although an explicit solution can also be written for ![]() ${\mathcal H}^{(1)}$, it suffices for our purpose to integrate (4.36) from
${\mathcal H}^{(1)}$, it suffices for our purpose to integrate (4.36) from ![]() $\eta = -\infty$ to
$\eta = -\infty$ to ![]() $\eta = 0^-$ and use the matching condition
$\eta = 0^-$ and use the matching condition ![]() ${\mathcal H}^{(1)} \sim 0$ as
${\mathcal H}^{(1)} \sim 0$ as ![]() $\eta \rightarrow -\infty$ and the jump conditions (4.37). One finds that
$\eta \rightarrow -\infty$ and the jump conditions (4.37). One finds that
 \begin{equation} \left.\begin{gathered} M B = q {le_{eff}} \left\{\int_{-\infty}^0 \left( s(\eta') + \frac{\gamma-1}{\gamma} \frac{\dot P}{M} \dfrac{\lambda(\eta')}{\vartheta (\eta')} \right) (1 + M \eta')M \,{\rm e}^{M \eta'} \,\mathrm{d} \eta' \right. \\ \quad \left.- M \kappa \int_{-\infty}^0 \lambda(\eta') \,{\rm e}^{M \eta'} \,\mathrm{d} \eta' \right\}, \\ \frac{q M}{2 T_{f}^2} B ={-} \frac{\gamma-1}{\gamma} \frac{q \lambda_b}{M T_{f}} \dot P + MD + q A - q\frac{\partial M}{\partial T_{f}} T_b^{(1)}. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} M B = q {le_{eff}} \left\{\int_{-\infty}^0 \left( s(\eta') + \frac{\gamma-1}{\gamma} \frac{\dot P}{M} \dfrac{\lambda(\eta')}{\vartheta (\eta')} \right) (1 + M \eta')M \,{\rm e}^{M \eta'} \,\mathrm{d} \eta' \right. \\ \quad \left.- M \kappa \int_{-\infty}^0 \lambda(\eta') \,{\rm e}^{M \eta'} \,\mathrm{d} \eta' \right\}, \\ \frac{q M}{2 T_{f}^2} B ={-} \frac{\gamma-1}{\gamma} \frac{q \lambda_b}{M T_{f}} \dot P + MD + q A - q\frac{\partial M}{\partial T_{f}} T_b^{(1)}. \end{gathered}\right\} \end{equation}This results in the determination of all the unknown functions
 \begin{align} \left.\begin{gathered} T_b^{(1)} = \frac{\gamma-1}{\gamma} \frac{\dot P}{M^2} \left\{ J_1 + \frac{q\lambda_b }{ T_{f}} \right\}, \\ B ={-} {le_{eff}} \frac{P}{M^2} \left\{ J_2 \left(\mathbb{K} + \frac{\dot P}{P} - \frac{\dot M}{M} \right)- \dot T_{u} J_3 \right\}, \\ D = T_b^{(1)} + \frac{P}{M^2} \left\{ J_1\left(\mathbb{K} + \frac{\dot P}{P} - \frac{\dot M}{M} \right) - \left(\frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right)\dot T_{u} \right\}, \\ A = \frac{\partial M}{\partial T_{f}} T_b^{(1)} - \left( \frac{P}{M} \mathbb{K} + \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P}{M} \right) \right) \left( \frac{J_1}{q} - \frac{{le_{eff}}}{2 \, {T_{f}^2}} J_3 \right) - \frac{\dot T_{u} P}{qM} \left( \frac{\lambda_b}{T_f} - \frac{\lambda_u}{T_{u}} - \frac{q{le_{eff}} }{2 T_{f}^2} J_3 \right) \end{gathered}\right\} \end{align}
\begin{align} \left.\begin{gathered} T_b^{(1)} = \frac{\gamma-1}{\gamma} \frac{\dot P}{M^2} \left\{ J_1 + \frac{q\lambda_b }{ T_{f}} \right\}, \\ B ={-} {le_{eff}} \frac{P}{M^2} \left\{ J_2 \left(\mathbb{K} + \frac{\dot P}{P} - \frac{\dot M}{M} \right)- \dot T_{u} J_3 \right\}, \\ D = T_b^{(1)} + \frac{P}{M^2} \left\{ J_1\left(\mathbb{K} + \frac{\dot P}{P} - \frac{\dot M}{M} \right) - \left(\frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right)\dot T_{u} \right\}, \\ A = \frac{\partial M}{\partial T_{f}} T_b^{(1)} - \left( \frac{P}{M} \mathbb{K} + \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P}{M} \right) \right) \left( \frac{J_1}{q} - \frac{{le_{eff}}}{2 \, {T_{f}^2}} J_3 \right) - \frac{\dot T_{u} P}{qM} \left( \frac{\lambda_b}{T_f} - \frac{\lambda_u}{T_{u}} - \frac{q{le_{eff}} }{2 T_{f}^2} J_3 \right) \end{gathered}\right\} \end{align}expressed in terms of the (convergent) definite integrals
 \begin{equation} \left.\begin{gathered}
J_1 = \int_{T_{u}}^{T_{f}} \frac{\lambda(x) }{x} \mathrm{d}\kern 0.06em x,\quad J_2 = \int_{T_{u}}^{T_{f}} \frac{\lambda(x) }{x}
\ln {\left( \frac{q}{x - T_{u} } \right)} \mathrm{d}\kern 0.06em x, \\
J_3 ={-} \int_{T_{u}}^{T_{f}}
\frac{\mathrm{d}}{\mathrm{d}\kern 0.06em x} \left(\frac{\lambda(x)
}{x}\right) \ln{\left(\frac{q}{x - T_{u} } \right)} ={-}
\frac{\dot J_2}{\dot T_u}. \end{gathered}\right\}
\end{equation}
\begin{equation} \left.\begin{gathered}
J_1 = \int_{T_{u}}^{T_{f}} \frac{\lambda(x) }{x} \mathrm{d}\kern 0.06em x,\quad J_2 = \int_{T_{u}}^{T_{f}} \frac{\lambda(x) }{x}
\ln {\left( \frac{q}{x - T_{u} } \right)} \mathrm{d}\kern 0.06em x, \\
J_3 ={-} \int_{T_{u}}^{T_{f}}
\frac{\mathrm{d}}{\mathrm{d}\kern 0.06em x} \left(\frac{\lambda(x)
}{x}\right) \ln{\left(\frac{q}{x - T_{u} } \right)} ={-}
\frac{\dot J_2}{\dot T_u}. \end{gathered}\right\}
\end{equation}
Note that ![]() $J_1, J_2 >0$ and
$J_1, J_2 >0$ and ![]() $J_3 >0$ for
$J_3 >0$ for ![]() $\lambda (T) = T^a$ for
$\lambda (T) = T^a$ for ![]() $a<1$. For
$a<1$. For ![]() $\lambda (T) = T$, they can be evaluated such that
$\lambda (T) = T$, they can be evaluated such that ![]() $J_1 = J_2 = q$ and
$J_1 = J_2 = q$ and ![]() $J_3 = 0$. At the initial time, the limits of integration are from
$J_3 = 0$. At the initial time, the limits of integration are from ![]() $1$ to
$1$ to ![]() $T_a$ and the corresponding integrals will be denoted with the accent ‘hat’, i.e.
$T_a$ and the corresponding integrals will be denoted with the accent ‘hat’, i.e. ![]() $\hat {J}_1$ and
$\hat {J}_1$ and ![]() $\hat {J}_2$. They are identical to the integrals appearing in a similar context in the freely propagating flame theory.
$\hat {J}_2$. They are identical to the integrals appearing in a similar context in the freely propagating flame theory.
We have now obtained solutions correct to ![]() $O(\delta )$ for the state variables
$O(\delta )$ for the state variables ![]() $\rho, T$, the enthalpy functions
$\rho, T$, the enthalpy functions ![]() $H, {\mathcal H}$, or equivalently the mass fractions
$H, {\mathcal H}$, or equivalently the mass fractions ![]() $Y_{D}, Y_{E}$, and mass flux
$Y_{D}, Y_{E}$, and mass flux ![]() $m$ inside the flame zone. The latter, which determines the burning rate, is the primary focus of this study. Although one can also solve the fluid mechanics equations to the same order, the algebra is rather lengthy and beyond the scope of this paper.
$m$ inside the flame zone. The latter, which determines the burning rate, is the primary focus of this study. Although one can also solve the fluid mechanics equations to the same order, the algebra is rather lengthy and beyond the scope of this paper.
5. Flame speed and pressure rise
We proceed in deriving explicit expressions for the burning rate and/or flame speed, the flame temperature and the overall pressure rise in the vessel.
5.1. The flame speed
The burning rate ![]() $m^*$, as defined in (3.18), is obtained by matching the hydrodynamic solution
$m^*$, as defined in (3.18), is obtained by matching the hydrodynamic solution ![]() $m_{hyd} = m^{(0)}_{hyd} + \delta m^{(1)}_{hyd}$ at
$m_{hyd} = m^{(0)}_{hyd} + \delta m^{(1)}_{hyd}$ at ![]() $n=0^-$ with the corresponding solution in the flame zone, namely
$n=0^-$ with the corresponding solution in the flame zone, namely ![]() $m \sim m^{(0)} + \delta m^{(1)}$ as
$m \sim m^{(0)} + \delta m^{(1)}$ as ![]() $\eta \to -\infty$. Evidently, to leading order,
$\eta \to -\infty$. Evidently, to leading order,
To proceed to the next order, we note that as ![]() $\eta \to -\infty$,
$\eta \to -\infty$,
 \begin{equation} \left.\begin{gathered} \mathcal{J}_2 \sim \frac{J_1}{MT_{u}} + \frac{\mathcal{J}_1 (\eta)}{T_{u}}, \\ T_{u} \left( \frac{\mathcal{J}_3} {\vartheta(\eta)} - \mathcal{J}_4 \right) \sim{-} \frac{\dot J_1}{M \dot T_{u}} + \frac{J_1}{M T_{u}} + \dfrac{\mathcal{J}_1 (\eta)}{T_{u}}, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \mathcal{J}_2 \sim \frac{J_1}{MT_{u}} + \frac{\mathcal{J}_1 (\eta)}{T_{u}}, \\ T_{u} \left( \frac{\mathcal{J}_3} {\vartheta(\eta)} - \mathcal{J}_4 \right) \sim{-} \frac{\dot J_1}{M \dot T_{u}} + \frac{J_1}{M T_{u}} + \dfrac{\mathcal{J}_1 (\eta)}{T_{u}}, \end{gathered}\right\} \end{equation}such that
 \begin{align} m \sim M + \delta \left\{ A - \frac{P}{MT_{u}} \left(\left({\mathbb{K}} + \frac{1}{\gamma} \frac{\dot P}{P} - \frac{\dot M}{M} \right) J_1 + \dot J_1 \right) + \left( M \kappa - \frac{P\mathbb{K}}{T_{u}} - \frac{\dot P}{\gamma T_{u}} \right) \mathcal{J}_1(\eta)\right\}. \end{align}
\begin{align} m \sim M + \delta \left\{ A - \frac{P}{MT_{u}} \left(\left({\mathbb{K}} + \frac{1}{\gamma} \frac{\dot P}{P} - \frac{\dot M}{M} \right) J_1 + \dot J_1 \right) + \left( M \kappa - \frac{P\mathbb{K}}{T_{u}} - \frac{\dot P}{\gamma T_{u}} \right) \mathcal{J}_1(\eta)\right\}. \end{align}
The hydrodynamic solution to ![]() $O(\delta )$ at
$O(\delta )$ at ![]() $n = 0^-$ takes the form
$n = 0^-$ takes the form
 \begin{equation} m_{hyd} \sim M + \delta \left\{ m^{(1)}_{hyd}|_{n=0^-} + \left.\frac{\partial m^{(0)}_{hyd}}{\partial n}\right|_{n=0^-} \mathcal{J}_1(\eta) \right\}, \end{equation}
\begin{equation} m_{hyd} \sim M + \delta \left\{ m^{(1)}_{hyd}|_{n=0^-} + \left.\frac{\partial m^{(0)}_{hyd}}{\partial n}\right|_{n=0^-} \mathcal{J}_1(\eta) \right\}, \end{equation}
where, here and below, it is understood that ![]() $M$ must be expanded to
$M$ must be expanded to ![]() $O(\delta )$, namely replaced by
$O(\delta )$, namely replaced by ![]() $M + \delta (\partial {M}/\partial {T_{f}})T_b^{(1)}$ with the
$M + \delta (\partial {M}/\partial {T_{f}})T_b^{(1)}$ with the ![]() $O(\delta )$ retained when necessary. Matching then yields an expression for
$O(\delta )$ retained when necessary. Matching then yields an expression for ![]() $m^*$ which, after dividing by
$m^*$ which, after dividing by ![]() $\rho _u$, gives the expression
$\rho _u$, gives the expression
 \begin{equation} S_{f} =
\frac{M}{\rho_u} - \frac{\delta}{M} \left\{ \mathcal{M}_1
\left( \mathbb{K} - \frac{\dot M}{M}\right) + \mathcal{M}_2
\frac{\dot P}{P} \right\} + \unicode{x2134}(\delta).
\end{equation}
\begin{equation} S_{f} =
\frac{M}{\rho_u} - \frac{\delta}{M} \left\{ \mathcal{M}_1
\left( \mathbb{K} - \frac{\dot M}{M}\right) + \mathcal{M}_2
\frac{\dot P}{P} \right\} + \unicode{x2134}(\delta).
\end{equation}
The flame speed ![]() $S_{f}$ is modulated by two time-dependent coefficients
$S_{f}$ is modulated by two time-dependent coefficients
 \begin{equation} \left.\begin{gathered} \mathcal{M}_1 = \frac{ T_{f}}{q} J_1+ \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q} T_{u} J_2, \\ \mathcal{M}_2 = \mathcal{M}_1- \frac{\gamma -1}{\gamma} \left\{J_1+ \left( \frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right) \frac{T_{u}T_{f}}{q}+ \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q}T_{u}^2 J_3 \right\}, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \mathcal{M}_1 = \frac{ T_{f}}{q} J_1+ \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q} T_{u} J_2, \\ \mathcal{M}_2 = \mathcal{M}_1- \frac{\gamma -1}{\gamma} \left\{J_1+ \left( \frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right) \frac{T_{u}T_{f}}{q}+ \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q}T_{u}^2 J_3 \right\}, \end{gathered}\right\} \end{equation}
which results from (5.3) after expressing the scaled parameters ![]() ${le_{eff}}$ and
${le_{eff}}$ and ![]() $\varphi$ in terms of the effective Lewis number
$\varphi$ in terms of the effective Lewis number ![]() $Le_{eff}$ and the excess-to-deficient reactant mass ratio
$Le_{eff}$ and the excess-to-deficient reactant mass ratio ![]() $\varPhi$ while using the Zel'dovich number
$\varPhi$ while using the Zel'dovich number ![]() $\beta$ in lieu of
$\beta$ in lieu of ![]() $\beta _0$. Matching the gradients does not reveal new information because the gradient of the mass flux to leading order can also be deduced from the continuity equation (3.2) when evaluated at
$\beta _0$. Matching the gradients does not reveal new information because the gradient of the mass flux to leading order can also be deduced from the continuity equation (3.2) when evaluated at ![]() $n=0^-$. The
$n=0^-$. The ![]() $O(\delta )$ correction to the flame speed consists of two terms; the first will be recognized below as the voluminal stretch and the second is the proportionate time rate of change of the pressure; the coefficients
$O(\delta )$ correction to the flame speed consists of two terms; the first will be recognized below as the voluminal stretch and the second is the proportionate time rate of change of the pressure; the coefficients ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$, which can arguably be referred to as Markstein numbers, will be further discussed below.
$\mathcal {M}_2$, which can arguably be referred to as Markstein numbers, will be further discussed below.
The flame speed, as defined in (3.17), is based on the prevalent convention that it is measured relative to the velocity of the fresh unburned gas. It is often convenient to relate the propagation speed to the gas velocity of the burned gas and define the flame speed as ![]() $S_{f}^{b} \equiv m^{b}/\rho _b$, where the superscript
$S_{f}^{b} \equiv m^{b}/\rho _b$, where the superscript ![]() $^{b}$ here and below signifies that the quantity is measured relative to the burned gas. This requires evaluating the mass flux
$^{b}$ here and below signifies that the quantity is measured relative to the burned gas. This requires evaluating the mass flux ![]() $m^{b}$ at the burned edge of the flame, i.e. at
$m^{b}$ at the burned edge of the flame, i.e. at ![]() $n=0^+$, which is directly obtained by matching with the solution (4.26) as
$n=0^+$, which is directly obtained by matching with the solution (4.26) as ![]() $\eta \to +\infty$. The flame speed is then given by
$\eta \to +\infty$. The flame speed is then given by
 \begin{equation} \frac{\rho_b}{\rho_u} S_{f}^{b} = \frac{M}{\rho_u} - \frac{\delta}{M}\left\{\mathcal{M}_1^{b} \left( \mathbb{K} - \frac{\dot M}{M} \right) + \mathcal{M}_2^{b} \frac{\dot P}{P} \right\} + \unicode{x2134}(\delta), \end{equation}
\begin{equation} \frac{\rho_b}{\rho_u} S_{f}^{b} = \frac{M}{\rho_u} - \frac{\delta}{M}\left\{\mathcal{M}_1^{b} \left( \mathbb{K} - \frac{\dot M}{M} \right) + \mathcal{M}_2^{b} \frac{\dot P}{P} \right\} + \unicode{x2134}(\delta), \end{equation}with time-dependent coefficients
 \begin{equation} \left.\begin{gathered} \mathcal{M}_1^{b} = \frac{T_{u}}{q} J_1 + \left( \frac{T_a}{T_{f}}\right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q} T_{u} J_2,\\ \mathcal{M}_2^{b} = \mathcal{M}_1^{b}- \frac{\gamma -1}{\gamma} T_{u}^2 \left\{\frac{1}{q} \left( \frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right) + \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q}J_3 \right\}, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \mathcal{M}_1^{b} = \frac{T_{u}}{q} J_1 + \left( \frac{T_a}{T_{f}}\right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q} T_{u} J_2,\\ \mathcal{M}_2^{b} = \mathcal{M}_1^{b}- \frac{\gamma -1}{\gamma} T_{u}^2 \left\{\frac{1}{q} \left( \frac{\lambda_u}{T_{u}} - \frac{\lambda_b}{T_{f}}\right) + \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2 q}J_3 \right\}, \end{gathered}\right\} \end{equation}
which may be referred to as the burned Markstein numbers. Here too, matching the gradients does not reveal new information; the gradient of the mass flux to leading order can be also deduced from the continuity equation (3.2) when evaluated at ![]() $n=0^+$.
$n=0^+$.
From the above relations, it can be verified that there is an ![]() $O(\delta )$ jump in the normal mass flux across the entire flame given by
$O(\delta )$ jump in the normal mass flux across the entire flame given by
 \begin{equation} [\![ m ]\!] = \frac{\delta}{M} \left\{\rho_u J_1 \left(\mathbb{K} - \frac{\dot M}{M}\right) + \frac{\mathrm{d}}{\mathrm{d}t}(\rho_u J_1)\right\}. \end{equation}
\begin{equation} [\![ m ]\!] = \frac{\delta}{M} \left\{\rho_u J_1 \left(\mathbb{K} - \frac{\dot M}{M}\right) + \frac{\mathrm{d}}{\mathrm{d}t}(\rho_u J_1)\right\}. \end{equation}Although the mass flux is conserved across an infinitesimally thin flame, when accounting for the finite (albeit small) thickness of the flame zone, the normal mass flux leaving the flame differs from that into the flame due to transverse transport and/or mass accumulation. One also notes that the jump in the gas velocity across the flame given by
always increases in time, a direct result of the rise in flame temperature.
Although the density and temperature of the unburned gas ![]() $\rho _u$ and
$\rho _u$ and ![]() $T_u$ remain spatially uniform to all orders in
$T_u$ remain spatially uniform to all orders in ![]() $\delta$, the state of the burned gas is modified to
$\delta$, the state of the burned gas is modified to ![]() $O(\delta )$ by corrections arising from variations in the flame temperature. In particular, the temperature is determined by solving
$O(\delta )$ by corrections arising from variations in the flame temperature. In particular, the temperature is determined by solving
subject to
 \begin{align} T_{f} &= T_{u} + q - \frac{\delta P}{M^2} \left\{ \frac{\gamma-1}{\gamma} \left( J_1 + \frac{q\lambda_b }{ T_{u} + q} \right) \frac{\dot P}{P} \right\} \nonumber\\ &\quad - ({Le}_D -1) \frac{\delta }{M} \left\{\left( \frac{P J_2}{M} \right) \mathbb{K} + \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{P J_2}{M} \right)\right\} \end{align}
\begin{align} T_{f} &= T_{u} + q - \frac{\delta P}{M^2} \left\{ \frac{\gamma-1}{\gamma} \left( J_1 + \frac{q\lambda_b }{ T_{u} + q} \right) \frac{\dot P}{P} \right\} \nonumber\\ &\quad - ({Le}_D -1) \frac{\delta }{M} \left\{\left( \frac{P J_2}{M} \right) \mathbb{K} + \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{P J_2}{M} \right)\right\} \end{align}
at ![]() $n=0^+$, with appropriate boundary conditions to
$n=0^+$, with appropriate boundary conditions to ![]() $O(\delta )$ at the vessel's walls. The expression for
$O(\delta )$ at the vessel's walls. The expression for ![]() $T_{f}$ results from matching with the solution in the flame zone as
$T_{f}$ results from matching with the solution in the flame zone as ![]() $\eta \to + \infty$. Although the flame temperature
$\eta \to + \infty$. Although the flame temperature ![]() $T_{f}$ varies primarily in time as a result of the pressure rise, there are small changes in temperature associated with flame stretch that depend on the Lewis number of the deficient reactant, i.e. the fuel in a lean mixture and the oxidizer in a rich mixture. The dependence on flame stretch was corroborated with direct numerical simulations for freely expanding spherical flames (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015) where it was shown that, depending on the equivalence ratio that determines whether
$T_{f}$ varies primarily in time as a result of the pressure rise, there are small changes in temperature associated with flame stretch that depend on the Lewis number of the deficient reactant, i.e. the fuel in a lean mixture and the oxidizer in a rich mixture. The dependence on flame stretch was corroborated with direct numerical simulations for freely expanding spherical flames (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015) where it was shown that, depending on the equivalence ratio that determines whether ![]() ${Le}_D$ is above/below one, the flame temperature is lower/higher than its adiabatic value and increases/decreases towards
${Le}_D$ is above/below one, the flame temperature is lower/higher than its adiabatic value and increases/decreases towards ![]() $T_a$ when
$T_a$ when ![]() ${\mathbb {K}} \to 0$.
${\mathbb {K}} \to 0$.
The equations describing the flow field and state variables in the hydrodynamic zones were presented in § 3 to leading order. To extend the results to ![]() $O(\delta )$, (2.9)–(2.13) must be considered with the reaction term set to zero and diffusion added as correction terms. For the determination of the flow field, the
$O(\delta )$, (2.9)–(2.13) must be considered with the reaction term set to zero and diffusion added as correction terms. For the determination of the flow field, the ![]() $O(\delta )$ corrections to the RH conditions (3.9) must be derived, as carried out in Matalon & Matkowsky (Reference Matalon and Matkowsky1982) for freely propagating flames. Not being the focus of this work, the derivation will not be pursued here. For configurations that depend on a single spatial coordinate, such as planar or spherical flames, the velocity field is directly determined from the continuity equation (3.7) which, when extended to
$O(\delta )$ corrections to the RH conditions (3.9) must be derived, as carried out in Matalon & Matkowsky (Reference Matalon and Matkowsky1982) for freely propagating flames. Not being the focus of this work, the derivation will not be pursued here. For configurations that depend on a single spatial coordinate, such as planar or spherical flames, the velocity field is directly determined from the continuity equation (3.7) which, when extended to ![]() $O(\delta )$ takes the form
$O(\delta )$ takes the form
and needs to be solved subject to the jump condition (5.9) across the flame surface. The momentum equation is used a posteriori to evaluate the dynamic pressure.
As a final remark, we note that the expressions for the flame speed and Markstein lengths (relative to burned or unburned gas), and the flame temperature simplify to the corresponding expressions for freely propagating flames. With ![]() $P= T_{u} =1$, the flame temperature, to leading order, is the adiabatic flame temperature
$P= T_{u} =1$, the flame temperature, to leading order, is the adiabatic flame temperature ![]() $T_a = 1+q$ and the density is a piecewise constant function with
$T_a = 1+q$ and the density is a piecewise constant function with ![]() $\rho _u = 1$ and
$\rho _u = 1$ and ![]() $\rho _b = 1/T_a$. Then, the flame speed depends on a single Markstein number
$\rho _b = 1/T_a$. Then, the flame speed depends on a single Markstein number ![]() $\mathcal {M}_1$ that takes the form
$\mathcal {M}_1$ that takes the form
where ![]() $\sigma = \rho _u / \rho _b$ is the unburned-to-burned density ratio. The stretch-corrected flame speed and temperature reduce to
$\sigma = \rho _u / \rho _b$ is the unburned-to-burned density ratio. The stretch-corrected flame speed and temperature reduce to
 \begin{equation} \left.\begin{gathered} S_f = 1 - \delta \mathcal{M}_1 {\mathbb{K}}, \\ T_{f} = T_{a} - \delta \left\{({Le}_D -1) \int_{1}^{\sigma} \frac{\lambda(x) }{x} \ln {\left(\frac{\sigma - 1}{x - 1}\right)} \mathrm{d}\kern 0.06em x\right\} \mathbb{K}, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} S_f = 1 - \delta \mathcal{M}_1 {\mathbb{K}}, \\ T_{f} = T_{a} - \delta \left\{({Le}_D -1) \int_{1}^{\sigma} \frac{\lambda(x) }{x} \ln {\left(\frac{\sigma - 1}{x - 1}\right)} \mathrm{d}\kern 0.06em x\right\} \mathbb{K}, \end{gathered}\right\} \end{equation}as in Matalon et al. (Reference Matalon, Cui and Bechtold2003).
5.2. Pressure rise
The pressure rise in the vessel is determined from (2.17) where the integral on the right-hand side is to be carried out over the entire volume. In the hydrodynamic limit it simplifies to
where the integration is carried out across the flame zone and over the entire flame surface ![]() $\mathcal {A}_{f}$. Since the chemical reaction rate
$\mathcal {A}_{f}$. Since the chemical reaction rate ![]() $\omega$ is replaced by a Dirac delta function, the latter simplifies to
$\omega$ is replaced by a Dirac delta function, the latter simplifies to
The integrand consists of the jump in temperature gradient across the reaction sheet, namely the fraction of the total heat generated by the chemical reaction and conducted in different proportions to the burned and unburned gas. Under adiabatic conditions, more heat is transported to the fresh mixture justifying the assertion that the pressure always rises. The jump in temperature gradient across ![]() $\eta =0$ is obtained directly from the solution constructed in the previous section, such that
$\eta =0$ is obtained directly from the solution constructed in the previous section, such that
 \begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{\gamma q {\mathbb{A}}_{f}}{{\mathbb{V}}} \left\{ M - \delta \left(\frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q} \left(\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{P J_2}{M} \right)+ \frac{PJ_2}{M} \frac{1}{{\mathbb{A}}_{f}} \int_{\mathcal{A}_{f}} \mathbb{K} \, \mathrm{d} \mathcal{A}\right)\right\}, \end{equation}
\begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{\gamma q {\mathbb{A}}_{f}}{{\mathbb{V}}} \left\{ M - \delta \left(\frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q} \left(\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{P J_2}{M} \right)+ \frac{PJ_2}{M} \frac{1}{{\mathbb{A}}_{f}} \int_{\mathcal{A}_{f}} \mathbb{K} \, \mathrm{d} \mathcal{A}\right)\right\}, \end{equation}
where ![]() ${\mathbb {A}}_{f}$ is the flame surface area. For consistency,
${\mathbb {A}}_{f}$ is the flame surface area. For consistency, ![]() $O(\delta ^2)$ terms in the curly bracketed expression must be discarded. It may be verified when using (4.22) that the factor multiplying the last term in this equation decreases in time implying that the influence of flame stretch diminishes as the pressure rises. Equation (5.18) can be also expressed as
$O(\delta ^2)$ terms in the curly bracketed expression must be discarded. It may be verified when using (4.22) that the factor multiplying the last term in this equation decreases in time implying that the influence of flame stretch diminishes as the pressure rises. Equation (5.18) can be also expressed as
 \begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{\gamma}{{\mathbb{V}}}\int_{\mathcal{A}_{f}} (q m^* + T_{f} [\![ m]\!]) \,\mathrm{d} \mathcal{A} + \delta \left(\frac{{\mathbb{A}}_{f}}{\mathbb{V}} \right)^{2} \gamma(\gamma-1) q J_1, \end{equation}
\begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{\gamma}{{\mathbb{V}}}\int_{\mathcal{A}_{f}} (q m^* + T_{f} [\![ m]\!]) \,\mathrm{d} \mathcal{A} + \delta \left(\frac{{\mathbb{A}}_{f}}{\mathbb{V}} \right)^{2} \gamma(\gamma-1) q J_1, \end{equation}a form found useful in the next section.
5.3. Flame stretch
Flame stretch, first introduced by Karlovitz et al. (Reference Karlovitz, Denniston, Knapschaefer and Wells1953), is a measure of the deformation of the flame surface resulting from its motion and from the underlying flow field. It is defined as the proportionate rate of change of the area of an infinitesimal surface element ![]() $A$ of the flame front, namely
$A$ of the flame front, namely ![]() ${\mathbb {K}} \equiv A^{-1} \,\mathrm {d}{A}/\mathrm {d}{t}$. The stretch rate appeared naturally in the mass conservation equation (4.24) when expressed in terms of intrinsic surface coordinates, and may be expressed in the coordinate-free form as
${\mathbb {K}} \equiv A^{-1} \,\mathrm {d}{A}/\mathrm {d}{t}$. The stretch rate appeared naturally in the mass conservation equation (4.24) when expressed in terms of intrinsic surface coordinates, and may be expressed in the coordinate-free form as
obtained from the basic definition (Matalon Reference Matalon1983). The first term corresponds to the surface dilatation resulting from the motion of the flame front, and the second term is the surface extension/compression resulting from the underlying velocity gradient on the surface of the flame front. The curvature can be evaluated from ![]() $\kappa = - \boldsymbol \nabla \boldsymbol {\cdot } {\boldsymbol n}$, evaluated at the flame front. Since
$\kappa = - \boldsymbol \nabla \boldsymbol {\cdot } {\boldsymbol n}$, evaluated at the flame front. Since ![]() $\boldsymbol v_{\perp }$ is continuous across the flame (to leading order), the stretch rate is uniquely defined on the flame surface and can be evaluated from (5.20) on either side of the interface.
$\boldsymbol v_{\perp }$ is continuous across the flame (to leading order), the stretch rate is uniquely defined on the flame surface and can be evaluated from (5.20) on either side of the interface.
It is often stated that flame stretch is a combination of curvature and strain, a statement that requires careful consideration. When expanding the right-hand side of (5.20), one finds that
where ![]() $K_S = - \boldsymbol n \boldsymbol {\cdot } \boldsymbol E \boldsymbol {\cdot } \boldsymbol n$ is the local strain rate. It must be noted that the first two terms on the right-hand side admit different values when evaluated on the unburned and burned sides of the flame front. Thus, using (5.21) to determine the stretch rate requires specifying on which side of the flame front this expression is to be evaluated. For a freely propagating flame in the hydrodynamic limit,
$K_S = - \boldsymbol n \boldsymbol {\cdot } \boldsymbol E \boldsymbol {\cdot } \boldsymbol n$ is the local strain rate. It must be noted that the first two terms on the right-hand side admit different values when evaluated on the unburned and burned sides of the flame front. Thus, using (5.21) to determine the stretch rate requires specifying on which side of the flame front this expression is to be evaluated. For a freely propagating flame in the hydrodynamic limit, ![]() $\boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v = 0$ on either side of the flame and the stretch rate is indeed a combination of curvature and strain, but each of these components have different expressions when evaluated on the unburned and burned sides. On the unburned side of the flame,
$\boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v = 0$ on either side of the flame and the stretch rate is indeed a combination of curvature and strain, but each of these components have different expressions when evaluated on the unburned and burned sides. On the unburned side of the flame, ![]() $\boldsymbol v \boldsymbol {\cdot } \boldsymbol n - V_{f} \sim 1$ and
$\boldsymbol v \boldsymbol {\cdot } \boldsymbol n - V_{f} \sim 1$ and ![]() ${\mathbb {K}} = \kappa + K_S^{u}$; on the burned side of the flame
${\mathbb {K}} = \kappa + K_S^{u}$; on the burned side of the flame ![]() ${\boldsymbol v \boldsymbol {\cdot } \boldsymbol n - V_{f} \sim \sigma}$, where
${\boldsymbol v \boldsymbol {\cdot } \boldsymbol n - V_{f} \sim \sigma}$, where ![]() $\sigma$ is the unburned-to-burned density ratio and
$\sigma$ is the unburned-to-burned density ratio and ![]() ${\mathbb {K}} = \sigma \kappa + K_S^{b}$. Both yield the same value for the stretch rate because
${\mathbb {K}} = \sigma \kappa + K_S^{b}$. Both yield the same value for the stretch rate because ![]() $[\![ K_S ]\!] = - (\sigma - 1) \kappa$, a relation derived in Matalon et al. (Reference Matalon, Cui and Bechtold2003). For a flame propagating in a closed vessel, the stretch rate is not just a combination of curvature and strain because the volume dilatation rate
$[\![ K_S ]\!] = - (\sigma - 1) \kappa$, a relation derived in Matalon et al. (Reference Matalon, Cui and Bechtold2003). For a flame propagating in a closed vessel, the stretch rate is not just a combination of curvature and strain because the volume dilatation rate ![]() $\boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v \ne 0$ due to gas compression, but may be expressed in the form
$\boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v \ne 0$ due to gas compression, but may be expressed in the form
A planar flame, for example, is not stretched, but in a closed vessel it experiences normal strain that balances the volume dilatation rate, thus ensuring that ![]() ${\mathbb {K}} = 0$. Similarly, a spherical flame experiences normal straining and a non-zero dilatation rate such that (5.22) simplifies to
${\mathbb {K}} = 0$. Similarly, a spherical flame experiences normal straining and a non-zero dilatation rate such that (5.22) simplifies to ![]() ${\mathbb {K}} = - V_{f} \kappa$ as it should. These examples will be further discussed in § 6.
${\mathbb {K}} = - V_{f} \kappa$ as it should. These examples will be further discussed in § 6.
Although the flame zone expressed in units of the diffusion length ![]() $l_d$ is of infinite extent, the distance required for the temperature to rise from the cold value
$l_d$ is of infinite extent, the distance required for the temperature to rise from the cold value ![]() $T_{u}$ to the flame temperature
$T_{u}$ to the flame temperature ![]() $T_f$ occurs over a relatively small multiple of this length. The flame thickness may therefore be defined as the distance from the reaction zone to the point where the temperature falls within
$T_f$ occurs over a relatively small multiple of this length. The flame thickness may therefore be defined as the distance from the reaction zone to the point where the temperature falls within ![]() $1\,\%$ of
$1\,\%$ of ![]() $T_{u}$. For a freely propagating flame (
$T_{u}$. For a freely propagating flame (![]() $M=1$), this distance is constant; typically
$M=1$), this distance is constant; typically ![]() $l_{f} \approx 7 l_d$ with an accuracy of
$l_{f} \approx 7 l_d$ with an accuracy of ![]() $10^{-4}$. Under confinement, however,
$10^{-4}$. Under confinement, however, ![]() $l_{f} \sim 1/M$ and, since
$l_{f} \sim 1/M$ and, since ![]() $M$ increases in time due to the pressure rise, the flame becomes consistently thinner when propagating towards the end of the vessel, as shown in figure 2(a). The graph exhibits the dependence of
$M$ increases in time due to the pressure rise, the flame becomes consistently thinner when propagating towards the end of the vessel, as shown in figure 2(a). The graph exhibits the dependence of ![]() $l_{f}$ on time, represented by
$l_{f}$ on time, represented by ![]() $P(t)$, for various values of
$P(t)$, for various values of ![]() $q$, with
$q$, with ![]() $\varphi =0, \lambda = T^{0.7}$ and
$\varphi =0, \lambda = T^{0.7}$ and ![]() $\beta = 10$. Changes in equivalence ratio and/or the dependence
$\beta = 10$. Changes in equivalence ratio and/or the dependence ![]() $\lambda (T)$ show no significant quantitative difference in the behaviour of
$\lambda (T)$ show no significant quantitative difference in the behaviour of ![]() $l_{f}$.
$l_{f}$.

Figure 2. The dependence of (a) the flame thickness ![]() $l_f$ and (b) the flame temperature
$l_f$ and (b) the flame temperature ![]() $T_{f}$ scaled by the adiabatic flame temperature
$T_{f}$ scaled by the adiabatic flame temperature ![]() $T_a$ on pressure
$T_a$ on pressure ![]() $P(t)$ representing time, for various values of the heat release parameter
$P(t)$ representing time, for various values of the heat release parameter ![]() $q$; the curves end at
$q$; the curves end at ![]() $P = P_{e}$ marked on the axis.
$P = P_{e}$ marked on the axis.
Due to the significant decrease in the flame thickness with time, the correction to the flame speed resulting from the physicochemical processes occurring inside the flame zone has been expressed in (5.5) as a multiple of ![]() $\delta /M$, which being proportional to
$\delta /M$, which being proportional to ![]() $l_{f}/l$, is a more accurate measure of its thickness. The proportionate time rate of change of the flame thickness
$l_{f}/l$, is a more accurate measure of its thickness. The proportionate time rate of change of the flame thickness ![]() ${l_{f}}^{-1} \,\mathrm {d}{l_{f}}/\mathrm {d}{t} = - \dot M/M$ combines with the proportionate time rate of change of the area of a flame surface element to define a voluminal stretch rate
${l_{f}}^{-1} \,\mathrm {d}{l_{f}}/\mathrm {d}{t} = - \dot M/M$ combines with the proportionate time rate of change of the area of a flame surface element to define a voluminal stretch rate
where ![]() $V = l_{f} A$ is an infinitesimal volume element of the flame zone. Accordingly, the flame speed (5.5) was found to depend on the voluminal stretch rate that measures the local deformation of a volume element of the flame zone. The voluminal stretch concept was first introduced by Buckmaster (Reference Buckmaster1979) in the context of slowly varying flames, as noted in the introduction.
$V = l_{f} A$ is an infinitesimal volume element of the flame zone. Accordingly, the flame speed (5.5) was found to depend on the voluminal stretch rate that measures the local deformation of a volume element of the flame zone. The voluminal stretch concept was first introduced by Buckmaster (Reference Buckmaster1979) in the context of slowly varying flames, as noted in the introduction.
5.4. The effective Lewis number
Although distinct Lewis numbers were assumed for the two reactants, the burning rate was found to depend on a stoichiometry-weighted combination of the two, or an effective Lewis number of the form
 \begin{equation} \left.\begin{gathered} Le_{eff} = \frac{{Le}_E + {Le}_D (1 + \varDelta)}{2+ \varDelta},\\ \varDelta = \left(\frac{T_a}{{T_{f}}} \right)^{2} \beta(\varPhi - 1),\quad \varPhi \sim \left\{\begin{array}{@{}ll@{}} 1/\phi & \text{lean mixtures}, \\ \phi & \text{rich mixtures}, \end{array}\right. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} Le_{eff} = \frac{{Le}_E + {Le}_D (1 + \varDelta)}{2+ \varDelta},\\ \varDelta = \left(\frac{T_a}{{T_{f}}} \right)^{2} \beta(\varPhi - 1),\quad \varPhi \sim \left\{\begin{array}{@{}ll@{}} 1/\phi & \text{lean mixtures}, \\ \phi & \text{rich mixtures}, \end{array}\right. \end{gathered}\right\} \end{equation}
where ![]() $\phi$ is the equivalence ratio and
$\phi$ is the equivalence ratio and ![]() $\varDelta$ measures the deviation from stoichiometry. It is an average of the Lewis numbers of fuel and oxidizer, with a heavier weight on the deficient component in the mixture. The effective Lewis number is the mean value of
$\varDelta$ measures the deviation from stoichiometry. It is an average of the Lewis numbers of fuel and oxidizer, with a heavier weight on the deficient component in the mixture. The effective Lewis number is the mean value of ![]() ${Le}_D$ and
${Le}_D$ and ![]() ${Le}_E$ for a stoichiometric mixture (
${Le}_E$ for a stoichiometric mixture (![]() $\varDelta = 0$) and tends towards
$\varDelta = 0$) and tends towards ![]() ${Le}_D$ for conditions sufficiently far from stoichiometry (
${Le}_D$ for conditions sufficiently far from stoichiometry (![]() $\varDelta \gg 1$). It also varies in time due to the dependence of
$\varDelta \gg 1$). It also varies in time due to the dependence of ![]() $T_{f}/T_a$ on pressure shown in figure 2(b). The figure displays the dependence of the (leading-order) flame temperature scaled by the adiabatic temperature
$T_{f}/T_a$ on pressure shown in figure 2(b). The figure displays the dependence of the (leading-order) flame temperature scaled by the adiabatic temperature ![]() $T_a$ on pressure, which varies in time from
$T_a$ on pressure, which varies in time from ![]() $P=1$ initially to the end pressure
$P=1$ initially to the end pressure ![]() $P_{e}=1 + \gamma q$; the latter is shown on the axis for each value of
$P_{e}=1 + \gamma q$; the latter is shown on the axis for each value of ![]() $q$. Given that
$q$. Given that ![]() $T_{f}/T_a$ does not increase considerably, and the uncertainty in accurately specifying the individual Lewis numbers, a time-averaged value can serve as the representative
$T_{f}/T_a$ does not increase considerably, and the uncertainty in accurately specifying the individual Lewis numbers, a time-averaged value can serve as the representative ![]() $Le_{eff}$.
$Le_{eff}$.
Figure 3 shows the dependence of ![]() $Le_{eff}$, averaged over the total propagation time, on the equivalence ratio
$Le_{eff}$, averaged over the total propagation time, on the equivalence ratio ![]() $\phi$ of the mixture, for several fuels burning in air. They are plotted for the representative value
$\phi$ of the mixture, for several fuels burning in air. They are plotted for the representative value ![]() $q=6$, which characterizes mixtures of various heat releases
$q=6$, which characterizes mixtures of various heat releases ![]() $Q$ and mass fractions
$Q$ and mass fractions ![]() $Y_{D_{{0}}}$. The determination of the effective
$Y_{D_{{0}}}$. The determination of the effective ![]() $Le_{eff}$ requires specifying the limiting Lewis numbers; the fuel Lewis number
$Le_{eff}$ requires specifying the limiting Lewis numbers; the fuel Lewis number ![]() ${Le}_F$ for lean mixtures and the oxygen Lewis number
${Le}_F$ for lean mixtures and the oxygen Lewis number ![]() ${Le}_O$ for rich mixtures. These values are defined as the ratio of the thermal diffusivity of the mixture to the binary diffusivity of the fuel/oxygen into N
${Le}_O$ for rich mixtures. These values are defined as the ratio of the thermal diffusivity of the mixture to the binary diffusivity of the fuel/oxygen into N![]() $_2$, as per the dilute-mixture assumption used when adopting Fick's law in the governing equations; they were estimated near the lean/rich flammability limits and are marked by a dashed line in the figure. The formula (5.24) then provides the distribution of
$_2$, as per the dilute-mixture assumption used when adopting Fick's law in the governing equations; they were estimated near the lean/rich flammability limits and are marked by a dashed line in the figure. The formula (5.24) then provides the distribution of ![]() $Le_{eff}$ as a function of the equivalence ratio
$Le_{eff}$ as a function of the equivalence ratio ![]() $\phi$, approaching the respective limiting Lewis numbers for lean and rich mixtures. A monotonically decreasing curve results for heavy hydrocarbon fuels with
$\phi$, approaching the respective limiting Lewis numbers for lean and rich mixtures. A monotonically decreasing curve results for heavy hydrocarbon fuels with ![]() ${Le}_F > 1$, and a monotonically increasing curve results for light fuels with
${Le}_F > 1$, and a monotonically increasing curve results for light fuels with ![]() ${Le}_F < 1$, such as hydrogen and methane. The transitional curves display a weak dependence on the Zel'dovich number, which has been specified in this figure as
${Le}_F < 1$, such as hydrogen and methane. The transitional curves display a weak dependence on the Zel'dovich number, which has been specified in this figure as ![]() $\beta = 10$.
$\beta = 10$.

Figure 3. The dependence of the effective Lewis number ![]() $Le_{eff}$, averaged over the total propagation time, on the mixture equivalence ratio for several fuels burning in air. The dashed lines mark the limiting Lewis numbers; the fuel Lewis number
$Le_{eff}$, averaged over the total propagation time, on the mixture equivalence ratio for several fuels burning in air. The dashed lines mark the limiting Lewis numbers; the fuel Lewis number ![]() ${Le}_F$ for lean mixtures and the oxygen Lewis number
${Le}_F$ for lean mixtures and the oxygen Lewis number ![]() ${Le}_O$ for rich mixtures.
${Le}_O$ for rich mixtures.
5.5. The Markstein numbers
When viewed on the hydrodynamic scale, the flame is effectively an interface embedded in the flow field; the preheat zone of the flame collapses to ![]() $\psi = 0^-$ and the post-reaction zone of the flame to
$\psi = 0^-$ and the post-reaction zone of the flame to ![]() $\psi = 0^+$. The propagation speed can be expressed relative to either the unburned or burned gas. When expressed relative to the unburned gas, the flame speed
$\psi = 0^+$. The propagation speed can be expressed relative to either the unburned or burned gas. When expressed relative to the unburned gas, the flame speed ![]() $S_{f}$ exhibits a linear dependence on the voluminal stretch rate, modulated by a parameter
$S_{f}$ exhibits a linear dependence on the voluminal stretch rate, modulated by a parameter ![]() $\mathcal {M}_1$, and on the rate of pressure rise, modulated by a parameter
$\mathcal {M}_1$, and on the rate of pressure rise, modulated by a parameter ![]() $\mathcal {M}_2$. Similarly, when expressed relative to the burned gas, the flame speed
$\mathcal {M}_2$. Similarly, when expressed relative to the burned gas, the flame speed ![]() $S_{f}^{b}$ exhibits a linear dependence on the voluminal stretch rate, modulated by a parameter
$S_{f}^{b}$ exhibits a linear dependence on the voluminal stretch rate, modulated by a parameter ![]() $\mathcal {M}^{b}_1$, and on the rate of pressure rise, modulated by a parameter
$\mathcal {M}^{b}_1$, and on the rate of pressure rise, modulated by a parameter ![]() $\mathcal {M}^{b}_2$. We note that unlike
$\mathcal {M}^{b}_2$. We note that unlike ![]() $S_{f}$, which mimics the diffusion and reaction processes occurring in the entire flame zone and is not evaluated at any specific isotherm,
$S_{f}$, which mimics the diffusion and reaction processes occurring in the entire flame zone and is not evaluated at any specific isotherm, ![]() $S_{f}^{b}$ is effectively evaluated at the flame temperature
$S_{f}^{b}$ is effectively evaluated at the flame temperature ![]() $T = T_{f}$. This has practical implications when seeking comparison with experimental and/or numerical simulations aimed at quantifying the dependence of the flame speed on stretch and pressure rise. Measurements and simulations that resolve the flame structure require selecting an isotherm to represent the flame surface, and the burned Markstein numbers in that regard are the most relevant ones. Indeed, it has been established that the most appropriate isotherm for the evaluation of the flame speed, which is well conditioned and displays the best agreement with the theory, must be sufficiently close to the burned side of the flame (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). The flame speed
$T = T_{f}$. This has practical implications when seeking comparison with experimental and/or numerical simulations aimed at quantifying the dependence of the flame speed on stretch and pressure rise. Measurements and simulations that resolve the flame structure require selecting an isotherm to represent the flame surface, and the burned Markstein numbers in that regard are the most relevant ones. Indeed, it has been established that the most appropriate isotherm for the evaluation of the flame speed, which is well conditioned and displays the best agreement with the theory, must be sufficiently close to the burned side of the flame (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). The flame speed ![]() $S_{f}$ and Markstein numbers
$S_{f}$ and Markstein numbers ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$, on the other hand, are the appropriate expressions to use for the evolving flame front when determining the flow field in the hydrodynamic regions.
$\mathcal {M}_2$, on the other hand, are the appropriate expressions to use for the evolving flame front when determining the flow field in the hydrodynamic regions.
Although the Markstein numbers (5.6) and (5.8) are pressure dependent, for a given mixture they are mostly affected by the effective Lewis number ![]() $Le_{eff}$. Given that their dependence on time for a wide range of
$Le_{eff}$. Given that their dependence on time for a wide range of ![]() $Le_{eff}$ is quite moderate, they can be represented by an average value. In figure 4 we show the variation of the Markstein numbers (unburned and burned, averaged over the total propagation time) of selected fuels burning in air across the entire range of the stoichiometric spectrum, which evidently mirror the variation of
$Le_{eff}$ is quite moderate, they can be represented by an average value. In figure 4 we show the variation of the Markstein numbers (unburned and burned, averaged over the total propagation time) of selected fuels burning in air across the entire range of the stoichiometric spectrum, which evidently mirror the variation of ![]() $Le_{eff}$ on the equivalence ratio. We note that the second member on the right-hand side of (5.8) is identically zero for
$Le_{eff}$ on the equivalence ratio. We note that the second member on the right-hand side of (5.8) is identically zero for ![]() $\lambda (T)=T$ and negligibly small otherwise, implying that
$\lambda (T)=T$ and negligibly small otherwise, implying that ![]() $\mathcal {M}_2^{b} \approx \mathcal {M}_1^{b} = \mathcal {M}^{b}$. For the unburned coefficients,
$\mathcal {M}_2^{b} \approx \mathcal {M}_1^{b} = \mathcal {M}^{b}$. For the unburned coefficients, ![]() $\mathcal {M}_2 < \mathcal {M}_1$, but the difference is typically small and does not exceed
$\mathcal {M}_2 < \mathcal {M}_1$, but the difference is typically small and does not exceed ![]() $20\,\%$.
$20\,\%$.

Figure 4. The dependence of the Markstein numbers (averaged over the total propagation time) on the mixture equivalence ratio ![]() $\phi$ for several fuels burning in air.
$\phi$ for several fuels burning in air.
There are circumstances where despite the moderate variation of the Markstein numbers with time they may change sign during the propagation. This becomes particularly relevant when attempting to extract the burned Markstein number from experimental measurements. Since the integrals ![]() $J_1$ and
$J_1$ and ![]() $J_2$ are both positive,
$J_2$ are both positive, ![]() $\mathcal {M}^{b}$ is strictly positive for
$\mathcal {M}^{b}$ is strictly positive for ![]() $Le_{eff} > {Le}^{cr}_{eff}$ and negative otherwise, where
$Le_{eff} > {Le}^{cr}_{eff}$ and negative otherwise, where
In most cases, ![]() $\mathcal {M}^{b}$ is either positive or negative, but in a limited range of sub-unity Lewis number, estimated as
$\mathcal {M}^{b}$ is either positive or negative, but in a limited range of sub-unity Lewis number, estimated as ![]() $0.75 \lessapprox Le_{eff} \lessapprox 0.82$, it may change sign during the propagation. The implication being that in such cases, the location where flame speed measurements are taken to estimate the Markstein numbers becomes important. Two examples illustrating this effect are shown in figure 5, where the dependence of
$0.75 \lessapprox Le_{eff} \lessapprox 0.82$, it may change sign during the propagation. The implication being that in such cases, the location where flame speed measurements are taken to estimate the Markstein numbers becomes important. Two examples illustrating this effect are shown in figure 5, where the dependence of ![]() $\mathcal {M}^{b}$ on time is shown for several values of the equivalence ratio. For a sufficiently lean hydrogen–air mixture, such as
$\mathcal {M}^{b}$ on time is shown for several values of the equivalence ratio. For a sufficiently lean hydrogen–air mixture, such as ![]() $\phi \le 0.775$, the Markstein number is strictly negative and becomes strictly positive for
$\phi \le 0.775$, the Markstein number is strictly negative and becomes strictly positive for ![]() $\phi \ge 0.845$; it changes sign during the propagation when
$\phi \ge 0.845$; it changes sign during the propagation when ![]() $\phi \approx 0.8$. The opposite trend is observed for a rich octane–air mixture when diluted with CO
$\phi \approx 0.8$. The opposite trend is observed for a rich octane–air mixture when diluted with CO![]() $_2$ to increase the effective Lewis number; the Markstein number is strictly positive for
$_2$ to increase the effective Lewis number; the Markstein number is strictly positive for ![]() $\phi \le 1.98$, negative for
$\phi \le 1.98$, negative for ![]() $\phi \ge 2.92$ and changes sign during the propagation when
$\phi \ge 2.92$ and changes sign during the propagation when ![]() $\phi \approx 2.4$.
$\phi \approx 2.4$.

Figure 5. Two cases illustrating circumstances where the ‘burned’ Markstein number ![]() $\mathcal {M}^{b}$ may change sign during the propagation. Results are shown for the (a) H
$\mathcal {M}^{b}$ may change sign during the propagation. Results are shown for the (a) H![]() $_2$–air mixture and (b) C
$_2$–air mixture and (b) C![]() $_8$H
$_8$H![]() $_{18}$–air–CO
$_{18}$–air–CO![]() $_2$ mixture.
$_2$ mixture.
6. Planar and spherical flames
The asymptotic theory derived in the previous sections is used next to examine flame propagation in two canonical configurations: a planar flame propagating in a rectangular channel of length ![]() $L$ and a centrally ignited outwardly propagating flame in a spherical vessel of radius
$L$ and a centrally ignited outwardly propagating flame in a spherical vessel of radius ![]() $L$ (see figure 6). The results are illustrated below for vessels of length/radius
$L$ (see figure 6). The results are illustrated below for vessels of length/radius ![]() $L =100$, measured in units of the hydrodynamic length scale
$L =100$, measured in units of the hydrodynamic length scale ![]() $l$. For typical
$l$. For typical ![]() $\delta = l_d/l \sim 0.02 - 0.002$, it corresponds to approximately 1000–10 000 flame thicknesses. Different mixtures will be represented by varying the heat release parameter
$\delta = l_d/l \sim 0.02 - 0.002$, it corresponds to approximately 1000–10 000 flame thicknesses. Different mixtures will be represented by varying the heat release parameter ![]() $q$ and effective Lewis number
$q$ and effective Lewis number ![]() $Le_{eff}$, assuming stoichiometric conditions
$Le_{eff}$, assuming stoichiometric conditions ![]() $\varphi =0$, a power law
$\varphi =0$, a power law ![]() $\lambda = T^a$ with
$\lambda = T^a$ with ![]() $a= 0.7$ and ratio of specific heats
$a= 0.7$ and ratio of specific heats ![]() $\gamma = 1.4$.
$\gamma = 1.4$.

Figure 6. Flame configurations: (a) planar flame propagating from left to right and (b) outwardly propagating spherical flame; the blue arrows show the flow direction.
6.1. Planar flame
We consider first the propagation of a planar flame travelling from left to right in a rectangular channel, as shown in figure 6(a). If the channel's width (in the ![]() $y$ and
$y$ and ![]() $z$ directions) is chosen as the hydrodynamic length scale
$z$ directions) is chosen as the hydrodynamic length scale ![]() $l$, the flame surface area
$l$, the flame surface area ![]() ${\mathbb {A}}_f =1$ and the ratio
${\mathbb {A}}_f =1$ and the ratio ![]() ${\mathbb {A}}_f /{\mathbb {V}} = 1/L$. The flame front is described by
${\mathbb {A}}_f /{\mathbb {V}} = 1/L$. The flame front is described by ![]() $\psi (x,t) \equiv x_f (t) - x = 0$, such that
$\psi (x,t) \equiv x_f (t) - x = 0$, such that ![]() $0 < x < x_f$ corresponds to the burned gas and
$0 < x < x_f$ corresponds to the burned gas and ![]() $x_f < x < L$ to the unburned gas region. The propagation speed is then given by
$x_f < x < L$ to the unburned gas region. The propagation speed is then given by ![]() $V_{f} = - \dot x_f$.
$V_{f} = - \dot x_f$.
To leading order, the gas velocity determined from (5.13) and satisfying ![]() $u(0,t) = u(L,t)=0$ is given by
$u(0,t) = u(L,t)=0$ is given by
 \begin{equation} u(x,t) = \left\{\begin{array}{@{}ll@{}} \dfrac{\dot{P}}{\gamma P}(L - x), & x_f < x < L, \\ -\dfrac{\dot{P}}{\gamma P} x, & 0 < x < x_f, \end{array}\right. \end{equation}
\begin{equation} u(x,t) = \left\{\begin{array}{@{}ll@{}} \dfrac{\dot{P}}{\gamma P}(L - x), & x_f < x < L, \\ -\dfrac{\dot{P}}{\gamma P} x, & 0 < x < x_f, \end{array}\right. \end{equation}
with the pressure obtained by solving ![]() $\dot P = \gamma q M/L$ subject to
$\dot P = \gamma q M/L$ subject to ![]() $P(0)=1$, and
$P(0)=1$, and ![]() $M$ given by (4.22). The RH relation
$M$ given by (4.22). The RH relation ![]() $[\![ \rho (\dot {x}_f - u)]\!] =0$ then yields an expression for the flame position,
$[\![ \rho (\dot {x}_f - u)]\!] =0$ then yields an expression for the flame position,
where ![]() $P_{e} = 1+ \gamma q$ is the end pressure. In a sufficiently long channel (
$P_{e} = 1+ \gamma q$ is the end pressure. In a sufficiently long channel (![]() $L \gg 1$), the pressure increases linearly in time, namely
$L \gg 1$), the pressure increases linearly in time, namely ![]() $P \sim 1 + \gamma qt/L$, and the velocity simplifies to
$P \sim 1 + \gamma qt/L$, and the velocity simplifies to
where the additional ![]() $O(1/L)$ contribution in the unburned gas comes from the expansion of
$O(1/L)$ contribution in the unburned gas comes from the expansion of ![]() $M$. When
$M$. When ![]() $L \to \infty$, the solution tends to that of a planar flame propagating from the closed end of a semi-infinite channel towards an open end at a speed
$L \to \infty$, the solution tends to that of a planar flame propagating from the closed end of a semi-infinite channel towards an open end at a speed ![]() $\dot x_f \sim 1+q$. Determining the state of the burned gas requires first solving the advection equation
$\dot x_f \sim 1+q$. Determining the state of the burned gas requires first solving the advection equation
for the entropy function, subject to ![]() $\mathcal {E} = \mathcal {E}_b$ at
$\mathcal {E} = \mathcal {E}_b$ at ![]() $x = x_f$. The general solution is
$x = x_f$. The general solution is ![]() $\mathcal {E} = f(xP^{1/\gamma })$, where the function
$\mathcal {E} = f(xP^{1/\gamma })$, where the function ![]() $f(\zeta )$ is determined from the relation
$f(\zeta )$ is determined from the relation
Evidently, ![]() $f(0) = 1+q$ and
$f(0) = 1+q$ and ![]() $f(\zeta ) \sim 1$ as
$f(\zeta ) \sim 1$ as ![]() $\zeta \to \infty$, but the values of interest are limited to
$\zeta \to \infty$, but the values of interest are limited to ![]() $\zeta$ corresponding to
$\zeta$ corresponding to ![]() $1 \le P < P_{e}$, with the end point determined by the parameters
$1 \le P < P_{e}$, with the end point determined by the parameters ![]() $\gamma$ and
$\gamma$ and ![]() $q$.
$q$.
Next we examine the influences arising from the finite thickness of the flame. Evidently, the planar flame surface is not stretched; although it experiences normal strain, the strain rate ![]() $K_S = - \partial u / \partial x$ balances the dilatation rate resulting from gas compression such that
$K_S = - \partial u / \partial x$ balances the dilatation rate resulting from gas compression such that ![]() ${\mathbb {K}} = K_S + \boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v = 0$. The flame thickness however decreases as the pressure rises and the influence of the internal structure on the flame speed, given by (5.5), diminishes in time. Equation (5.18) for the pressure simplifies to
${\mathbb {K}} = K_S + \boldsymbol \nabla \boldsymbol {\cdot } \boldsymbol v = 0$. The flame thickness however decreases as the pressure rises and the influence of the internal structure on the flame speed, given by (5.5), diminishes in time. Equation (5.18) for the pressure simplifies to
 \begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac {\gamma q}{L} \left\{ M - \delta\left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P J_2}{M} \right) \right\}, \end{equation}
\begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac {\gamma q}{L} \left\{ M - \delta\left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P J_2}{M} \right) \right\}, \end{equation}
with the only changes at ![]() $O(\delta )$ resulting from non-unity Lewis number effects. Their contributions however are generally small and amount to less than
$O(\delta )$ resulting from non-unity Lewis number effects. Their contributions however are generally small and amount to less than ![]() $5\,\%$ for typical values of
$5\,\%$ for typical values of ![]() $\delta$ and a wide range of
$\delta$ and a wide range of ![]() $Le_{eff}$. The RH condition (5.9) combined with (5.19) yields
$Le_{eff}$. The RH condition (5.9) combined with (5.19) yields
 \begin{equation} x_{f} = \left(1 - \frac{P_{e} - P}{P_{e}-1} P^{{-}1/\gamma} \right) L + \frac{\delta}{q } \left(\frac{T_f J_1}{M} - \frac{T_a \widehat{J_1}}{ P^{1/\gamma}} \right), \end{equation}
\begin{equation} x_{f} = \left(1 - \frac{P_{e} - P}{P_{e}-1} P^{{-}1/\gamma} \right) L + \frac{\delta}{q } \left(\frac{T_f J_1}{M} - \frac{T_a \widehat{J_1}}{ P^{1/\gamma}} \right), \end{equation}
relating flame location to pressure. Although the gas velocity is affected to ![]() $O(\delta )$ by the corresponding variations in pressure, the velocity in the burned gas includes an additional correction resulting from the right-hand side of (5.13), such that
$O(\delta )$ by the corresponding variations in pressure, the velocity in the burned gas includes an additional correction resulting from the right-hand side of (5.13), such that
 \begin{equation} u ={-} \left.\frac{\dot{P}}{\gamma P} x + \delta \lambda f'(x P^{1/\gamma})\right|^x_{x=0}, \quad 0 < x < x_f, \end{equation}
\begin{equation} u ={-} \left.\frac{\dot{P}}{\gamma P} x + \delta \lambda f'(x P^{1/\gamma})\right|^x_{x=0}, \quad 0 < x < x_f, \end{equation}
where the prime in ![]() $f^{\prime }$ denotes differentiation with respect to the function's argument and
$f^{\prime }$ denotes differentiation with respect to the function's argument and ![]() $\lambda$ at the wall is evaluated at
$\lambda$ at the wall is evaluated at ![]() $T(0) = P^{(\gamma - 1)/\gamma } T_a$. Overall, the contributions arising from the internal flame structure on the propagation of a planar flame are small.
$T(0) = P^{(\gamma - 1)/\gamma } T_a$. Overall, the contributions arising from the internal flame structure on the propagation of a planar flame are small.
The results are illustrated in figures 7 and 8 for a representative value ![]() $\delta = 0.05$, starting with the solution of an unconfined planar flame at
$\delta = 0.05$, starting with the solution of an unconfined planar flame at ![]() $x = 0$. Although the computations account for the
$x = 0$. Although the computations account for the ![]() $O(\delta )$ corrections, the solutions appear indistinguishable from their leading-order counterparts.
$O(\delta )$ corrections, the solutions appear indistinguishable from their leading-order counterparts.

Figure 7. (a) The pressure ![]() $P$ and (b) the mass burning rate
$P$ and (b) the mass burning rate ![]() $m^*$ as a function of time, for a planar flame propagating in a closed channel, for various values of the heat release parameter
$m^*$ as a function of time, for a planar flame propagating in a closed channel, for various values of the heat release parameter ![]() $q$.
$q$.

Figure 8. (a) Density and (b) temperature profiles of a planar flame in a closed channel at equal time intervals, for a representative value ![]() $q=6$.
$q=6$.
Figure 7 shows the dependence of the pressure ![]() $P$ and burning rate
$P$ and burning rate ![]() $m^*$ on time, for several values of the heat release parameter
$m^*$ on time, for several values of the heat release parameter ![]() $q$. The pressure and burning rate, which at first grow linearly, increase rapidly after the flame has travelled beyond the middle of the vessel. Although the transition appears to occur earlier for larger values of
$q$. The pressure and burning rate, which at first grow linearly, increase rapidly after the flame has travelled beyond the middle of the vessel. Although the transition appears to occur earlier for larger values of ![]() $q$, the duration of flame propagation is also shortened. Note that the overall pressure increases by nearly ten fold, approaching
$q$, the duration of flame propagation is also shortened. Note that the overall pressure increases by nearly ten fold, approaching ![]() $P_{e} = 1 + \gamma q$ when the flame reaches the end of the channel.
$P_{e} = 1 + \gamma q$ when the flame reaches the end of the channel.
Density and temperature profiles at equal time intervals are shown in figure 8. The gas on both sides of the flame is compressed continuously as the pressure rises. In the unburned gas region the density and temperature remain spatially uniform but vary in time. The larger pressure translates primarily in increasing the density of the fresh mixture, which reaches a value of approximately five times its initial value, near the end of propagation. The temporally increasing temperature and density of the moving flame front are advected with the flow upstream such that their values in the burned gas region are no longer spatially uniform. A temperature gradient is established in the burned gas region and is responsible for the re-illumination observed in photographic records of flames propagating in closed spherical bombs at the centre of the vessel, a phenomenon known as the Flamm-Mache effect (Flamm & Mache Reference Flamm and Mache1917; Lewis & von Elbe Reference Lewis and von Elbe1987). The finite temperature gradient observed at ![]() $x=0$ can be smoothed out in a thin thermal boundary layer to ensure the adiabaticity condition at the wall.
$x=0$ can be smoothed out in a thin thermal boundary layer to ensure the adiabaticity condition at the wall.
Velocity profiles are plotted in figure 9(a) for the representative value ![]() $q = 6$. Initially the burned gas trapped between the flame and the left wall is at rest, the flame advances at a speed
$q = 6$. Initially the burned gas trapped between the flame and the left wall is at rest, the flame advances at a speed ![]() $\dot x_{f} \sim 1+q$ and the fresh mixture is forced to the right at a constant velocity
$\dot x_{f} \sim 1+q$ and the fresh mixture is forced to the right at a constant velocity ![]() $u^* \sim q$. As the flame propagates forward, the fresh mixture is being forced against a denser gas causing it to slow down, gradually coming to rest at the end of the channel. The jump in velocity across the flame increases due to the higher flame temperature and the burned gas is swiftly advected away from the flame at an increasing speed. The flame propagation speed
$u^* \sim q$. As the flame propagates forward, the fresh mixture is being forced against a denser gas causing it to slow down, gradually coming to rest at the end of the channel. The jump in velocity across the flame increases due to the higher flame temperature and the burned gas is swiftly advected away from the flame at an increasing speed. The flame propagation speed ![]() $\dot x_{f} = S_{f} + u^*$ results from a balance between the increasing flame speed and the gradual reduction in gas velocity ahead of the flame front. The flame speed
$\dot x_{f} = S_{f} + u^*$ results from a balance between the increasing flame speed and the gradual reduction in gas velocity ahead of the flame front. The flame speed ![]() $S_{f}$ and propagation speed
$S_{f}$ and propagation speed ![]() $\dot x_{f}$ are shown in figure 9(b) for increasing values of
$\dot x_{f}$ are shown in figure 9(b) for increasing values of ![]() $q$, starting respectively from
$q$, starting respectively from ![]() $1$ and
$1$ and ![]() $1+q$ at time
$1+q$ at time ![]() $t=0$ to a common value when the flame reaches the end of the vessel and
$t=0$ to a common value when the flame reaches the end of the vessel and ![]() $u^*=0$. Being an intrinsic property of the combustion process, the flame speed (dashed curves) increases continuously in time and is higher for larger values of heat release. The propagation speed (solid curves) on the other hand depends on the flow conditions, such that the flame accelerates throughout the vessel for low values of
$u^*=0$. Being an intrinsic property of the combustion process, the flame speed (dashed curves) increases continuously in time and is higher for larger values of heat release. The propagation speed (solid curves) on the other hand depends on the flow conditions, such that the flame accelerates throughout the vessel for low values of ![]() $q$ and decelerates for large values of
$q$ and decelerates for large values of ![]() $q$. Indeed, the velocity profiles shown in figure 9(a) at equal time intervals demonstrate that the flame for
$q$. Indeed, the velocity profiles shown in figure 9(a) at equal time intervals demonstrate that the flame for ![]() $q=6$ decelerates throughout the channel.
$q=6$ decelerates throughout the channel.

Figure 9. Planar flames propagating in a closed channel: (a) velocity profiles at equal time intervals, for a representative value ![]() $q=6$, and (b) flame speed
$q=6$, and (b) flame speed ![]() $S_{f}$ (dashed curves) and propagation speed
$S_{f}$ (dashed curves) and propagation speed ![]() $\dot x_f$ (solid curves) as a function of time for various values of
$\dot x_f$ (solid curves) as a function of time for various values of ![]() $q$.
$q$.
6.2. Spherical flame
We consider now the propagation of a centrally ignited flame in a closed spherical vessel of radius ![]() $L$, as shown in figure 6(b). The flame front is described by
$L$, as shown in figure 6(b). The flame front is described by ![]() $\psi (r,t) = R(t) - r = 0$, such that
$\psi (r,t) = R(t) - r = 0$, such that ![]() $0 < r < R$ corresponds to the burned gas and
$0 < r < R$ corresponds to the burned gas and ![]() $R < r < L$ to the unburned gas region. The propagation speed is then given by
$R < r < L$ to the unburned gas region. The propagation speed is then given by ![]() $V_{f} = - \dot R$. The ratio of the flame surface area to the volume of the vessel,
$V_{f} = - \dot R$. The ratio of the flame surface area to the volume of the vessel, ![]() ${\mathbb {A}}_{f}/{\mathbb {V}} = 3 R^2/L^3$, increases in time as the flame propagates outward.
${\mathbb {A}}_{f}/{\mathbb {V}} = 3 R^2/L^3$, increases in time as the flame propagates outward.
To leading order, the gas velocity determined from (5.13) and satisfying ![]() $u(0,t) = u(L,t)=0$ is given by
$u(0,t) = u(L,t)=0$ is given by
 \begin{equation} v(r,t) = \left\{\begin{array}{@{}ll@{}} \dfrac{\dot P}{3 \gamma P} \left(\dfrac{L^3}{r^2} - r \right), & R < r < L, \\ -\dfrac{\dot P}{3 \gamma P} r, & 0 < r < R, \end{array}\right. \end{equation}
\begin{equation} v(r,t) = \left\{\begin{array}{@{}ll@{}} \dfrac{\dot P}{3 \gamma P} \left(\dfrac{L^3}{r^2} - r \right), & R < r < L, \\ -\dfrac{\dot P}{3 \gamma P} r, & 0 < r < R, \end{array}\right. \end{equation}
with the pressure obtained by solving ![]() $\dot P = 3 \gamma q M R^2/L^3$ subject to
$\dot P = 3 \gamma q M R^2/L^3$ subject to ![]() $P(0) =1$, and
$P(0) =1$, and ![]() $M$ given by (4.22). The RH relation
$M$ given by (4.22). The RH relation ![]() $[[ \rho (\dot R - v) ]] = 0$ then yields the following expression for the flame position:
$[[ \rho (\dot R - v) ]] = 0$ then yields the following expression for the flame position:
 \begin{equation} R(t) = \left(1 - \frac{P_{e} - P}{P_{e} -1} P^{{-}1/\gamma} \right)^{1/3}L. \end{equation}
\begin{equation} R(t) = \left(1 - \frac{P_{e} - P}{P_{e} -1} P^{{-}1/\gamma} \right)^{1/3}L. \end{equation}Determining the state of the burned gas requires solving the advection equation
for the entropy function, subject to ![]() $\mathcal {E} = \mathcal {E}_b$ at
$\mathcal {E} = \mathcal {E}_b$ at ![]() $r = R$. The general solution is
$r = R$. The general solution is ![]() $\mathcal {E} = f(r P^{1/3\gamma })$ where the function
$\mathcal {E} = f(r P^{1/3\gamma })$ where the function ![]() $f(\zeta )$ is obtained from the relation
$f(\zeta )$ is obtained from the relation
 \begin{equation} f(\zeta) = 1+ \frac{q}{P^{(\gamma-1)/\gamma}}\quad \text{for}\ \zeta = \left(P^{1/\gamma}-\frac{P_e-P}{P_e-1}\right)^{1/3} L. \end{equation}
\begin{equation} f(\zeta) = 1+ \frac{q}{P^{(\gamma-1)/\gamma}}\quad \text{for}\ \zeta = \left(P^{1/\gamma}-\frac{P_e-P}{P_e-1}\right)^{1/3} L. \end{equation}
Similar to the equivalent function for the planar solution, ![]() $f(0) = 1+q$ and
$f(0) = 1+q$ and ![]() $f(\zeta ) \sim 1$ as
$f(\zeta ) \sim 1$ as ![]() $\zeta \to \infty$; its relevance is limited to values of
$\zeta \to \infty$; its relevance is limited to values of ![]() $\zeta$ corresponding to
$\zeta$ corresponding to ![]() $1 \le P \le P_{e}$.
$1 \le P \le P_{e}$.
Next, we examine the influences that result from the finite thickness of the flame. Unlike the planar flame, the surface of the spherical flame is stretched at a rate ![]() $\mathbb {K} = 2\dot R/R$ apparent from the fundamental expression (5.20). We recall that for a flame under confinement, the stretch rate is not a simple combination of curvature and strain, and is obtained only when combined with the volume dilatation rate. Moreover, the flame experiences normal strain at different rates on the unburned and burned sides of the flame surface, given by
$\mathbb {K} = 2\dot R/R$ apparent from the fundamental expression (5.20). We recall that for a flame under confinement, the stretch rate is not a simple combination of curvature and strain, and is obtained only when combined with the volume dilatation rate. Moreover, the flame experiences normal strain at different rates on the unburned and burned sides of the flame surface, given by
respectively. When substituted in (5.22) with the curvature term ![]() $(M/\rho )\kappa$ evaluated appropriately, one finds that
$(M/\rho )\kappa$ evaluated appropriately, one finds that
as expected. The flame speed is given by (5.5), with the corrections resulting from flame stretch most significant when the flame is relatively small. Equation (5.18) for the pressure simplifies to
 \begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{3\gamma q R^2}{L^3} \left\{ M - \delta \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q R^2} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P J_2}{M} R^2 \right) \right\} \end{equation}
\begin{equation} \frac{\mathrm{d}P}{\mathrm{d}t} = \frac{3\gamma q R^2}{L^3} \left\{ M - \delta \left( \frac{T_a}{T_{f} } \right)^{2} \frac{\beta(Le_{eff} - 1)}{2q R^2} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{P J_2}{M} R^2 \right) \right\} \end{equation}
with the only changes at ![]() $O(\delta )$ resulting from non-unity Lewis number effects. As for the planar flame, their contribution is generally small for a wide range of
$O(\delta )$ resulting from non-unity Lewis number effects. As for the planar flame, their contribution is generally small for a wide range of ![]() $Le_{eff}$. The RH condition (5.9) combined with (5.19) yields the equation
$Le_{eff}$. The RH condition (5.9) combined with (5.19) yields the equation
relating the flame location to the pressure. The gas velocity is affected to ![]() $O(\delta )$ by the pressure variations, with an additional correction in the burned gas region resulting from the right-hand side of (5.13). One finds that
$O(\delta )$ by the pressure variations, with an additional correction in the burned gas region resulting from the right-hand side of (5.13). One finds that
where ![]() $\lambda = \lambda (T)$ is evaluated at the origin where
$\lambda = \lambda (T)$ is evaluated at the origin where ![]() $T(0) = P^{(\gamma - 1)/\gamma } T_a$.
$T(0) = P^{(\gamma - 1)/\gamma } T_a$.
The results presented below correspond to a spherical flame evolving from a small unconfined flame kernel and, unless otherwise specified, ![]() $\delta =0.05$. Although the computations account for the
$\delta =0.05$. Although the computations account for the ![]() $O(\delta )$ corrections, their contributions are generally small except for the flame speed and propagation speed; the solutions of the state variables remain indistinguishable from their leading-order counterparts.
$O(\delta )$ corrections, their contributions are generally small except for the flame speed and propagation speed; the solutions of the state variables remain indistinguishable from their leading-order counterparts.
The dependence of the pressure level ![]() $P$ on time is shown in figure 10(a) for several values of the heat release parameter
$P$ on time is shown in figure 10(a) for several values of the heat release parameter ![]() $q$. The initial linear rise in
$q$. The initial linear rise in ![]() $P$ appears much slower than for a planar flame, but the sharp increase occurring after the flame has travelled beyond the middle of the vessel is more rapid, being proportional to the flame surface area
$P$ appears much slower than for a planar flame, but the sharp increase occurring after the flame has travelled beyond the middle of the vessel is more rapid, being proportional to the flame surface area ![]() $R^2$. When increasing
$R^2$. When increasing ![]() $q$, the transition appears to occur at an earlier time, but the duration of flame propagation is also shorter. Unlike the planar flame, the effect of flame stretch on the flame speed and, consequently, on the mass burning rate
$q$, the transition appears to occur at an earlier time, but the duration of flame propagation is also shorter. Unlike the planar flame, the effect of flame stretch on the flame speed and, consequently, on the mass burning rate ![]() $m^*$ is evident in figure 10(b). In the absence of stretch, with
$m^*$ is evident in figure 10(b). In the absence of stretch, with ![]() $P \sim 1$ during the early stages of propagation the flame speed would remain close to the laminar flame speed with
$P \sim 1$ during the early stages of propagation the flame speed would remain close to the laminar flame speed with ![]() $m^* \sim 1$. The incipient spherical flame, however, is highly stretched such that
$m^* \sim 1$. The incipient spherical flame, however, is highly stretched such that ![]() $S_{f}$, and consequently
$S_{f}$, and consequently ![]() $m^*$, are significantly lower for practically all values of the unburned Markstein number
$m^*$, are significantly lower for practically all values of the unburned Markstein number ![]() $\mathcal {M}_1$. This behaviour changes at later times due to the diminished effect of stretch on one hand and the pressure rise on the other.
$\mathcal {M}_1$. This behaviour changes at later times due to the diminished effect of stretch on one hand and the pressure rise on the other.

Figure 10. The pressure ![]() $P$ and burning rate
$P$ and burning rate ![]() $m^*$ as a function of time, for a spherically expanding flame in a closed vessel at various values of the heat release parameter
$m^*$ as a function of time, for a spherically expanding flame in a closed vessel at various values of the heat release parameter ![]() $q$ and
$q$ and ![]() $Le_{eff} = 1$.
$Le_{eff} = 1$.
Profiles of density and temperature are shown in figure 11 at equal time intervals for the representative value of ![]() $q = 6$. The results are similar to those observed for planar flames. The gas on both sides of the flame is compressed continuously as the pressure rises. In the unburned gas the density and temperature remain spatially uniform, but vary in time. The pressure rise translates primarily in increasing the gas density with the temperature increasing only slightly. In the burned gas the density and temperature are no longer spatially uniform; the temporally varying temperature and density of the moving flame front are advected with the flow in the burned gas region. The temperature increases significantly reaching its maximum value at the centre of the vessel, as observed by Flamm & Mache (Reference Flamm and Mache1917).
$q = 6$. The results are similar to those observed for planar flames. The gas on both sides of the flame is compressed continuously as the pressure rises. In the unburned gas the density and temperature remain spatially uniform, but vary in time. The pressure rise translates primarily in increasing the gas density with the temperature increasing only slightly. In the burned gas the density and temperature are no longer spatially uniform; the temporally varying temperature and density of the moving flame front are advected with the flow in the burned gas region. The temperature increases significantly reaching its maximum value at the centre of the vessel, as observed by Flamm & Mache (Reference Flamm and Mache1917).

Figure 11. Density and temperature profiles of a spherical flame in a closed vessel at equal time intervals, for a representative value ![]() $q=6$.
$q=6$.
Velocity profiles at equal time intervals are shown in figure 12 for ![]() $q=6$,
$q=6$, ![]() $Le_{eff} = 1$ and two values of
$Le_{eff} = 1$ and two values of ![]() $\delta$. The sharp discontinuity represents the flame location. Initially the burned gas is at rest and the propagating flame drives the fresh mixture ahead into motion. As the flame grows outwards, the velocity across the flame increases because of the higher flame temperature and the burned gas is swiftly advected away from the flame at an increasing speed. The fresh mixture that moves against a denser gas slows down, coming to rest at the end of the vessel. Two profiles are shown at each time; the dashed curves correspond to the leading-order solution, absent of flame stretch effects, and the solid curves to the complete solution. For
$\delta$. The sharp discontinuity represents the flame location. Initially the burned gas is at rest and the propagating flame drives the fresh mixture ahead into motion. As the flame grows outwards, the velocity across the flame increases because of the higher flame temperature and the burned gas is swiftly advected away from the flame at an increasing speed. The fresh mixture that moves against a denser gas slows down, coming to rest at the end of the vessel. Two profiles are shown at each time; the dashed curves correspond to the leading-order solution, absent of flame stretch effects, and the solid curves to the complete solution. For ![]() $\delta = 0.05$, the expanding stretched flame is seen to propagate slower, lagging behind the solution predicted in the absence of stretch. When stretch effects are underplayed, as for
$\delta = 0.05$, the expanding stretched flame is seen to propagate slower, lagging behind the solution predicted in the absence of stretch. When stretch effects are underplayed, as for ![]() $\delta = 0.001$, the solutions with and without the
$\delta = 0.001$, the solutions with and without the ![]() $O(\delta )$ corrections appear closer.
$O(\delta )$ corrections appear closer.

Figure 12. Velocity profiles of a spherical flame propagating in a closed vessel at equal time intervals. The dashed lines correspond to the leading-order solution, absent of stretch effects, and the solid lines to the solution with ![]() $O(\delta )$ contributions included; for
$O(\delta )$ contributions included; for ![]() $q=6$ and
$q=6$ and ![]() $Le_{eff} = 1$. Results are shown for (a)
$Le_{eff} = 1$. Results are shown for (a) ![]() $\delta = 0.05$ and (b)
$\delta = 0.05$ and (b) ![]() $\delta = 0.001$.
$\delta = 0.001$.
We now consider the effects of flame stretch on the propagation speed and its dependence on the properties of the combustible mixture. It is instructive to examine first the simplifications that result when the flame propagates in a sufficiently large vessel (![]() $L \gg 1$). In this limit, the equation for the pressure takes the form
$L \gg 1$). In this limit, the equation for the pressure takes the form
with the velocity field given by
 \begin{equation} v(r,t) \sim q \left(1 - \delta \frac{\beta(Le_{eff} - 1)}{2} \hat J_2 {\mathbb{K}}\right) \left\{\begin{array}{@{}ll@{}} \dfrac{R^2}{r^2} - \dfrac{R^2}{L^3} r, & R < r < L, \\ -\dfrac{ R^2}{L^3} r, & 0 < r < R. \end{array}\right. \end{equation}
\begin{equation} v(r,t) \sim q \left(1 - \delta \frac{\beta(Le_{eff} - 1)}{2} \hat J_2 {\mathbb{K}}\right) \left\{\begin{array}{@{}ll@{}} \dfrac{R^2}{r^2} - \dfrac{R^2}{L^3} r, & R < r < L, \\ -\dfrac{ R^2}{L^3} r, & 0 < r < R. \end{array}\right. \end{equation}
When ![]() $L \to \infty$, we recover the solution of a centrally ignited freely propagating spherical flame; the pocket of burned gas encompassed by the flame remains at rest, the unburned gas forced forward decays according to the inverse of the square of radial distance, and the flame propagation speed is given by
$L \to \infty$, we recover the solution of a centrally ignited freely propagating spherical flame; the pocket of burned gas encompassed by the flame remains at rest, the unburned gas forced forward decays according to the inverse of the square of radial distance, and the flame propagation speed is given by
The propagation speed highlights the combined effects of stretch and differential diffusion, as shown in figure 13(a). In mixtures with ![]() $Le_{eff} > {Le}^{cr}_{eff}$, for which
$Le_{eff} > {Le}^{cr}_{eff}$, for which ![]() $\mathcal {M}_1^{b} > 0$, the spherical flame expands slower as compared with the unstretched flame (dashed line) and accelerates toward the asymptotic value
$\mathcal {M}_1^{b} > 0$, the spherical flame expands slower as compared with the unstretched flame (dashed line) and accelerates toward the asymptotic value ![]() $\dot R = 1+q$, associated with the (burned) laminar flame speed. In mixtures with
$\dot R = 1+q$, associated with the (burned) laminar flame speed. In mixtures with ![]() $Le_{eff} < {Le}^{cr}_{eff}$ the flame expands at a relatively faster rate that is gradually reduced due to stretching and decelerates towards the asymptotic value
$Le_{eff} < {Le}^{cr}_{eff}$ the flame expands at a relatively faster rate that is gradually reduced due to stretching and decelerates towards the asymptotic value ![]() $\dot R = 1+q$. This stretch-dominated behaviour was observed experimentally in various mixtures (Strehlow Reference Strehlow1984; Kwon, Tseng & Faeth Reference Kwon, Tseng and Faeth1992; Beeckmann et al. Reference Beeckmann, Hesse, Kruse, Berens, Peters, Pitsch and Matalon2017) by varying the equivalence ratio, and confirmed theoretically by Frankel & Sivashinsky (Reference Frankel and Sivashinsky1983), Bechtold & Matalon (Reference Bechtold and Matalon1987) and Addabbo et al. (Reference Addabbo, Bechtold and Matalon2002). It persists when the propagation occurs in a closed vessel as illustrated in figure 13(b) for
$\dot R = 1+q$. This stretch-dominated behaviour was observed experimentally in various mixtures (Strehlow Reference Strehlow1984; Kwon, Tseng & Faeth Reference Kwon, Tseng and Faeth1992; Beeckmann et al. Reference Beeckmann, Hesse, Kruse, Berens, Peters, Pitsch and Matalon2017) by varying the equivalence ratio, and confirmed theoretically by Frankel & Sivashinsky (Reference Frankel and Sivashinsky1983), Bechtold & Matalon (Reference Bechtold and Matalon1987) and Addabbo et al. (Reference Addabbo, Bechtold and Matalon2002). It persists when the propagation occurs in a closed vessel as illustrated in figure 13(b) for ![]() $\delta = 0.001$, but is limited to the early time before the flame encounters a significantly denser gas and slows down until reaching the end of the vessel. The intersection of the curves for various
$\delta = 0.001$, but is limited to the early time before the flame encounters a significantly denser gas and slows down until reaching the end of the vessel. The intersection of the curves for various ![]() $Le_{eff}$ with the dashed line corresponding to the leading-order solution occurs when the flame zone contributions vanish, namely at radii within
$Le_{eff}$ with the dashed line corresponding to the leading-order solution occurs when the flame zone contributions vanish, namely at radii within ![]() $O(\delta )$ of each other. For
$O(\delta )$ of each other. For ![]() $\delta = 0.05$, stretch effects extend to larger radii as shown in figure 14. For
$\delta = 0.05$, stretch effects extend to larger radii as shown in figure 14. For ![]() $Le_{eff} > {Le}^{cr}_{eff}$, the flame accelerates, reaches a peak at nearly the midway point to the vessel wall before slowing down, while for smaller values of
$Le_{eff} > {Le}^{cr}_{eff}$, the flame accelerates, reaches a peak at nearly the midway point to the vessel wall before slowing down, while for smaller values of ![]() $Le_{eff}$, the flame undergoes monotonic deceleration throughout the bulk of the propagation. Finally, we note that the small increase in speed observed when
$Le_{eff}$, the flame undergoes monotonic deceleration throughout the bulk of the propagation. Finally, we note that the small increase in speed observed when ![]() $R \approx 100$ is due to the limitation of the model that does not account for the interaction of the flame zone with the vessel's walls.
$R \approx 100$ is due to the limitation of the model that does not account for the interaction of the flame zone with the vessel's walls.

Figure 13. Propagation speed of spherical flames for various ![]() $Le_{eff}$; plots correspond to
$Le_{eff}$; plots correspond to ![]() $q=6$ and
$q=6$ and ![]() $\delta =0.001$; the dashed line indicates the solution (leading-order) in the absence of stretch effects. (a) Freely propagating flame. (b) Propagation in a closed vessel.
$\delta =0.001$; the dashed line indicates the solution (leading-order) in the absence of stretch effects. (a) Freely propagating flame. (b) Propagation in a closed vessel.

Figure 14. Propagation speed of spherical flames for various ![]() $Le_{eff}$; plots correspond to
$Le_{eff}$; plots correspond to ![]() $q=6$ and
$q=6$ and ![]() $\delta =0.05$; the dashed line indicates the solution (leading-order) in the absence of stretch effects.
$\delta =0.05$; the dashed line indicates the solution (leading-order) in the absence of stretch effects.
Since the problem under consideration is inherently unsteady, it is appropriate to comment on the initial state of the mixture and its effect on the flame propagation. As noted earlier, the present theory does not describe the ignition event and assumes that a flame already exists at ![]() $t=0$. However, when igniting the mixture, a small pocket of burned gas of radius
$t=0$. However, when igniting the mixture, a small pocket of burned gas of radius ![]() $R_0$ and temperature
$R_0$ and temperature ![]() $T_a$ is first formed and then propagates outward. Accounting for this condition when integrating (2.21) leads to
$T_a$ is first formed and then propagates outward. Accounting for this condition when integrating (2.21) leads to
which modifies the dependence of the flame size on pressure (6.16) to read
Since the initial kernel of radius ![]() $R_0$ is of the order of the flame thickness
$R_0$ is of the order of the flame thickness ![]() $\delta$, the correction term is extremely small and can be neglected.
$\delta$, the correction term is extremely small and can be neglected.
Constant volume combustion chambers are commonly used in the laboratory to determine the laminar flame speed of different mixtures. In one approach, measurements of centrally ignited expanding flames are taken up to a limited distance and the laminar flame speed is determined by extrapolating the data to the zero-stretch limit; namely from the asymptotic value ![]() $\dot R = 1 + q$ shown in figure 13(a). Data are collected during the early stages of propagation when pressure rise is minimal so that the burned gas enclosed by the flame remains essentially at rest and, thus,
$\dot R = 1 + q$ shown in figure 13(a). Data are collected during the early stages of propagation when pressure rise is minimal so that the burned gas enclosed by the flame remains essentially at rest and, thus, ![]() $\dot {R} = S_{f}^{b}$. The laminar flame speed is then given by
$\dot {R} = S_{f}^{b}$. The laminar flame speed is then given by ![]() $S_{f} = (\rho _b/\rho _u) S_{f}^{b}$ with
$S_{f} = (\rho _b/\rho _u) S_{f}^{b}$ with ![]() $\rho _b$ and
$\rho _b$ and ![]() $\rho _u$ taken as constants. However, unless the experimental set-up ensures that the ambient pressure remains constant, the results may be tainted by small pressure changes, effects due to compression and by the inward flow of burned gas that becomes substantial when the flame grows bigger as shown in figure 12. The present theory provides a means for estimating these effects in sufficiently large chambers. The dependence of the flame radius on the pressure level given by (6.10), and the gas velocity in the burned gas given by (6.9), may be used to more accurately determine the distance where measurements can be taken without being significantly affected by fluid motion and compressibility effects. Figure 13(b) illustrates a scenario where the laminar flame speed can be reasonably estimated from measurements taken up to
$\rho _u$ taken as constants. However, unless the experimental set-up ensures that the ambient pressure remains constant, the results may be tainted by small pressure changes, effects due to compression and by the inward flow of burned gas that becomes substantial when the flame grows bigger as shown in figure 12. The present theory provides a means for estimating these effects in sufficiently large chambers. The dependence of the flame radius on the pressure level given by (6.10), and the gas velocity in the burned gas given by (6.9), may be used to more accurately determine the distance where measurements can be taken without being significantly affected by fluid motion and compressibility effects. Figure 13(b) illustrates a scenario where the laminar flame speed can be reasonably estimated from measurements taken up to ![]() $R \approx 30$, in contrast to the conditions presented in figure 14.
$R \approx 30$, in contrast to the conditions presented in figure 14.
Another approach to determine the laminar flame speed involves the use of smaller spherical vessels with thick walls that can accommodate higher pressures. Transducers measure the pressure history as the flame propagates outward, and flame location, propagation speed and flow velocities are then determined from theoretically derived relationships, which are essentially the leading-order expressions presented here. Our theory provides corrections to these quantities that account for effects resulting from the internal flame structure, as given by (6.16) and (6.17). When included in data extrapolation these contributions may lead to better accuracy.
The same reasoning to the aforementioned comments applies to the determination of the Markstein length that, as the present theory demonstrates, is affected by the rise in pressure and flame temperature. Additionally, the experimental pursuit may be hampered by onset of the hydrodynamic instability that may be enhanced by the attenuated influence of diffusion on the thinner flames that result under confinement.
7. The Newtonian limit
A formal asymptotic approach of the flame zone analysis can be carried out when adopting the Newtonian limit ![]() $(\gamma -1)/ \gamma \ll 1$, in lieu of the delta-function model used above. It requires adopting the distinguished limit
$(\gamma -1)/ \gamma \ll 1$, in lieu of the delta-function model used above. It requires adopting the distinguished limit
with ![]() $\epsilon = \beta _0^{-1} \ll 1$. Here we use
$\epsilon = \beta _0^{-1} \ll 1$. Here we use ![]() $\epsilon$ as the perturbation parameter to avoid confusion with
$\epsilon$ as the perturbation parameter to avoid confusion with ![]() $\beta _0$ treated earlier in the delta-function model as a finite parameter.
$\beta _0$ treated earlier in the delta-function model as a finite parameter.
We start by examining the implication of the Newtonian limit on the solution in the hydrodynamic zones. The entropy in the homogeneous fresh mixture remains constant, ![]() $\mathcal {E} =1$, while in the burned gas it is given by
$\mathcal {E} =1$, while in the burned gas it is given by ![]() $\mathcal {E} = T_a + \epsilon \hat \gamma \mathcal {E}_1 + \cdots$, with
$\mathcal {E} = T_a + \epsilon \hat \gamma \mathcal {E}_1 + \cdots$, with ![]() $\mathcal {E}_1$ determined by solving
$\mathcal {E}_1$ determined by solving
The density and temperature are then given by
 \begin{equation} \left.\begin{gathered} \rho \sim \left\{\begin{array}{@{}ll@{}} P - \epsilon \hat{\gamma} P \ln P, & \psi(\boldsymbol x,t) < 0, \\ \dfrac{P}{T_a} - \epsilon \hat{\gamma} \left( \dfrac{P}{ T_a}\ln P + \dfrac{P}{ T_a^2} \mathcal{E}_1(\boldsymbol x,t) \right), & \psi(\boldsymbol x,t) > 0, \end{array}\right. \\ T \sim \left\{\begin{array}{@{}ll@{}} 1 + \epsilon \hat{\gamma} \ln P, & \psi(\boldsymbol x,t) < 0, \\ T_a + \epsilon \hat{\gamma} (T_a \ln P + \mathcal{E}_1(\boldsymbol x,t)), & \psi(\boldsymbol x,t) > 0, \end{array}\right. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \rho \sim \left\{\begin{array}{@{}ll@{}} P - \epsilon \hat{\gamma} P \ln P, & \psi(\boldsymbol x,t) < 0, \\ \dfrac{P}{T_a} - \epsilon \hat{\gamma} \left( \dfrac{P}{ T_a}\ln P + \dfrac{P}{ T_a^2} \mathcal{E}_1(\boldsymbol x,t) \right), & \psi(\boldsymbol x,t) > 0, \end{array}\right. \\ T \sim \left\{\begin{array}{@{}ll@{}} 1 + \epsilon \hat{\gamma} \ln P, & \psi(\boldsymbol x,t) < 0, \\ T_a + \epsilon \hat{\gamma} (T_a \ln P + \mathcal{E}_1(\boldsymbol x,t)), & \psi(\boldsymbol x,t) > 0, \end{array}\right. \end{gathered}\right\} \end{equation}
with the flame temperature given by ![]() $T_{f} \sim T_a + \epsilon \hat {\gamma } \ln P$. Gas compression leads to a pressure rise that minimally affects the temperature but, as shown below, alters the burning rate in a more meaningful way.
$T_{f} \sim T_a + \epsilon \hat {\gamma } \ln P$. Gas compression leads to a pressure rise that minimally affects the temperature but, as shown below, alters the burning rate in a more meaningful way.
The solution in the flame zone requires, as before, introducing the stretching transformation (4.8), expanding all variables in powers of ![]() $\delta$ and seeking solutions that match those in the hydrodynamic zones as
$\delta$ and seeking solutions that match those in the hydrodynamic zones as ![]() $\eta \to \mp \infty$. Instead of replacing the reaction rate by a Dirac delta function, the thin reaction zone centred near
$\eta \to \mp \infty$. Instead of replacing the reaction rate by a Dirac delta function, the thin reaction zone centred near ![]() $\eta =0$ is now resolved on the
$\eta =0$ is now resolved on the ![]() $\hat \eta = \eta /\epsilon$ scale, with
$\hat \eta = \eta /\epsilon$ scale, with ![]() $\epsilon \ll \delta$. The equations in the flame zone that do not contain explicitly the reaction rate term, can be directly integrated with respect to
$\epsilon \ll \delta$. The equations in the flame zone that do not contain explicitly the reaction rate term, can be directly integrated with respect to ![]() $\hat \eta$ to provide, through matching, the jump conditions (4.14) across
$\hat \eta$ to provide, through matching, the jump conditions (4.14) across ![]() $\eta =0$. The exception is the energy equation that determines the jump in the temperature gradient. To this end, we retain the near-equidiffusion and near-stoichiometric assumptions and expand the temperature and mass fractions about their values at
$\eta =0$. The exception is the energy equation that determines the jump in the temperature gradient. To this end, we retain the near-equidiffusion and near-stoichiometric assumptions and expand the temperature and mass fractions about their values at ![]() $\eta =0$, such that
$\eta =0$, such that
 \begin{equation} \left.\begin{gathered} T = T_ a + \epsilon (\hat{\gamma} \ln P + {\theta}(\hat \eta, \xi_1,\xi_2, t))+\cdots, \\ T + qY_{D}/Y_{D_0} = T_a + \epsilon (\hat{\gamma} \ln P + \hat h_{D}(\hat \eta, \xi_1,\xi_2, t))+ \cdots, \\ T +qY_{E}/\nu Y_{D_0} = T_a + \epsilon (\hat{\gamma} \ln P + q \varphi + \hat h_{E}(\hat \eta, \xi_1,\xi_2,t)) + \cdots . \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} T = T_ a + \epsilon (\hat{\gamma} \ln P + {\theta}(\hat \eta, \xi_1,\xi_2, t))+\cdots, \\ T + qY_{D}/Y_{D_0} = T_a + \epsilon (\hat{\gamma} \ln P + \hat h_{D}(\hat \eta, \xi_1,\xi_2, t))+ \cdots, \\ T +qY_{E}/\nu Y_{D_0} = T_a + \epsilon (\hat{\gamma} \ln P + q \varphi + \hat h_{E}(\hat \eta, \xi_1,\xi_2,t)) + \cdots . \end{gathered}\right\} \end{equation}
where use has been made of ![]() $Y_{E_0} = \nu Y_{D_0} (1 + \epsilon \varphi )$. Being conserved scalars, the enthalpies satisfy
$Y_{E_0} = \nu Y_{D_0} (1 + \epsilon \varphi )$. Being conserved scalars, the enthalpies satisfy ![]() $\partial ^2 \hat h_i / \partial \hat \eta ^2 = 0$, and the bounded solutions remain independent of
$\partial ^2 \hat h_i / \partial \hat \eta ^2 = 0$, and the bounded solutions remain independent of ![]() $\hat \eta$ such that
$\hat \eta$ such that
As a consequence, the energy equation simplifies to
 \begin{equation} \left.\begin{gathered} - \frac{\partial^{2} \theta}{\partial \hat{\eta}^{2}} = \varLambda (h_{D}^{{\ast}} - {\theta}) (h_{E}^{{\ast}} + q \varphi - {\theta}) \exp({\theta /T_a^{2}}), \\ \varLambda = \frac {q^2 P^{2 + \hat \gamma/T_a^{2}}}{4T_a^6 ( 1 + q\varphi / 2 T_a^2)}= O(1), \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} - \frac{\partial^{2} \theta}{\partial \hat{\eta}^{2}} = \varLambda (h_{D}^{{\ast}} - {\theta}) (h_{E}^{{\ast}} + q \varphi - {\theta}) \exp({\theta /T_a^{2}}), \\ \varLambda = \frac {q^2 P^{2 + \hat \gamma/T_a^{2}}}{4T_a^6 ( 1 + q\varphi / 2 T_a^2)}= O(1), \end{gathered}\right\} \end{equation}consisting of a balance between the diffusion and chemical reaction rates. The associated matching conditions are
where the latter results from the fact that ![]() $T(\eta, \xi _1,\xi _2, t)$ for
$T(\eta, \xi _1,\xi _2, t)$ for ![]() $\eta > 0$ is, to leading order, independent of
$\eta > 0$ is, to leading order, independent of ![]() $\eta$, and
$\eta$, and ![]() $h_{D}^*$ is effectively the perturbation of the flame temperature in the post-reaction region. A first integral of (7.6) can be obtained after multiplying both sides of the equation by
$h_{D}^*$ is effectively the perturbation of the flame temperature in the post-reaction region. A first integral of (7.6) can be obtained after multiplying both sides of the equation by ![]() $\partial \theta / \partial \hat {\eta }$. Using the matching conditions (7.7) one finds that
$\partial \theta / \partial \hat {\eta }$. Using the matching conditions (7.7) one finds that
 \begin{align} \left.\left(\frac{\partial T}{\partial\eta} \right)^{2}\right|_{\eta = 0^-} &= 2 \varLambda \int_{-\infty}^{h_{D}^{{\ast}}} (h_{D}^{{\ast}} - {\theta}) (h_{E}^{{\ast}} + q \varphi - {\theta}) \exp({\theta/T_a^{2}}) \,\mathrm{d}{\theta} \nonumber\\ &= 2 \varLambda T_a^{4}(h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi + 2T_a^2) \exp({h_{D}^{{\ast}}/ T_a^{2}}), \end{align}
\begin{align} \left.\left(\frac{\partial T}{\partial\eta} \right)^{2}\right|_{\eta = 0^-} &= 2 \varLambda \int_{-\infty}^{h_{D}^{{\ast}}} (h_{D}^{{\ast}} - {\theta}) (h_{E}^{{\ast}} + q \varphi - {\theta}) \exp({\theta/T_a^{2}}) \,\mathrm{d}{\theta} \nonumber\\ &= 2 \varLambda T_a^{4}(h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi + 2T_a^2) \exp({h_{D}^{{\ast}}/ T_a^{2}}), \end{align}
which can be expressed as a jump relation for the temperature gradient across the action zone (![]() $\eta = 0$), namely
$\eta = 0$), namely
 \begin{equation} \left[\frac{\partial T}{\partial\eta} \right] ={-} q P^{1+ {\hat{\gamma}}/{2 T_a^{2}}} \sqrt{\frac{1 + (h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi )/2 T_a^{2} } { 1 + q\varphi /2 T_a^2}} \exp({{h_{D}^{{\ast}} / 2 T_a^{2}}}). \end{equation}
\begin{equation} \left[\frac{\partial T}{\partial\eta} \right] ={-} q P^{1+ {\hat{\gamma}}/{2 T_a^{2}}} \sqrt{\frac{1 + (h_{E}^{{\ast}} - h_{D}^{{\ast}} + q \varphi )/2 T_a^{2} } { 1 + q\varphi /2 T_a^2}} \exp({{h_{D}^{{\ast}} / 2 T_a^{2}}}). \end{equation}The jump in the temperature gradient (4.15) adopted in the delta-function model is a straightforward generalization of this relation.
The solution in the flame zone can be easily deduced from the results derived in § 4 by taking the limit ![]() $(\gamma -1)/ \gamma \ll 1$ and will not be repeated here. The resulting leading-order expressions for pressure and burning rate are
$(\gamma -1)/ \gamma \ll 1$ and will not be repeated here. The resulting leading-order expressions for pressure and burning rate are
with ![]() $\alpha = 1 + \hat \gamma /2 T_a^2$. A closed form solution can then be obtained for the planar flame, for which
$\alpha = 1 + \hat \gamma /2 T_a^2$. A closed form solution can then be obtained for the planar flame, for which ![]() ${\mathbb {A}}_{f}/{\mathbb {V}} = 1/L$. One finds that
${\mathbb {A}}_{f}/{\mathbb {V}} = 1/L$. One finds that
 \begin{equation} P = \left(\frac{L}{L - q(\alpha-1)t }\right)^{{1}/{(\alpha -1)}},\quad M = \left(\frac{L}{L - q(\alpha-1)t }\right)^{{\alpha}/{(\alpha -1)}}, \end{equation}
\begin{equation} P = \left(\frac{L}{L - q(\alpha-1)t }\right)^{{1}/{(\alpha -1)}},\quad M = \left(\frac{L}{L - q(\alpha-1)t }\right)^{{\alpha}/{(\alpha -1)}}, \end{equation}consistent with the results shown in figure 7. The flame location and propagation speed are given by
Similar to the observations in figure 9(b), when propagating forward, the flame accelerates for ![]() $\alpha >2$ (small values of
$\alpha >2$ (small values of ![]() $q$) and decelerates for
$q$) and decelerates for ![]() $\alpha < 2$ (large values of
$\alpha < 2$ (large values of ![]() $q$); steady propagation results when
$q$); steady propagation results when ![]() $\alpha = 2$. For the spherical flame,
$\alpha = 2$. For the spherical flame, ![]() ${\mathbb {A}}_{f}/{\mathbb {V}} = 3R^2/L^3$ and when integrated numerically, (7.10a,b) yield results that are consistent with those in the previous section. Here too, steady propagation results when
${\mathbb {A}}_{f}/{\mathbb {V}} = 3R^2/L^3$ and when integrated numerically, (7.10a,b) yield results that are consistent with those in the previous section. Here too, steady propagation results when ![]() $\alpha = 2$, with
$\alpha = 2$, with ![]() $\dot R = 1+q$ and
$\dot R = 1+q$ and ![]() $P = (1 - q T_a^2 t^3/L^3)^{-1}$.
$P = (1 - q T_a^2 t^3/L^3)^{-1}$.
8. Conclusions
A general theory of premixed flames propagating in closed vessels is developed using a multi-scale approach that exploits the disparity in length scales associated with the fluid dynamics, diffusion and chemical reactions. The formulation reduces the problem to the analysis of a free boundary fluid dynamical problem, where the free boundary is the flame surface that separates burned gases from the unburned combustible mixture. By resolving the internal structure of the flame zone, explicit expressions for the flame speed and temperature, and their dependence on the flow and mixture conditions are derived. The flame speed is shown to be modified by the voluminal stretch rate, which quantifies the deformation of a volume element of the flame zone that results from the motion of the flame and the underlying flow field, and by the rate of pressure rise. Both effects are modulated by Markstein numbers of the order of the flame thickness that depend on the heat release, mixture composition and diffusion properties of the reactants, while capturing the effects of temperature-dependent transport and stoichiometry. The flame temperature rises above the adiabatic flame temperature as a result of the pressure buildup, with a weak dependence on the Lewis number of the deficient reactant. Integration across the entire volume of the vessel yields an equation for the pressure buildup and its dependence on the burning rate and mixture properties. The determination of the flow field and the evolution of the flame surface are strongly coupled. The fluid velocity is affected by the progressive increase in density and temperature resulting from the combined effects of heat release, adiabatic compression and pressure buildup, while the instantaneous shape and location of the flame surface relies on the local flow conditions through the stretch rate, and on the pressure and mixture compositions through the Markstein numbers.
The present hydrodynamic theory differs significantly from that of freely propagating flames. Unlike the latter where the flame propagates under nearly isobaric conditions and its structure remains quasi-steady, combustion in a closed vessel is accompanied by an increase in pressure that leads to a decrease in flame thickness and a diminishing effect of its influence on the propagation. The temperature along the flame surface exceeds the adiabatic flame temperature, and keeps increasing in the burned gas region due to adiabatic compression. The flame speed depends not only on the conventional stretch rate, which measures the distortion of the flame surface, but also on the rate of decrease of the flame thickness, as well as on the rate of pressure buildup. The flow field ahead and behind the confined flame is strongly affected by gas compression. Although thermo-diffusive effects are captured by Markstein numbers, similar to the freely propagating flame theory, these are now pressure dependent and in some circumstances may change sign during the course of propagation.
To illustrate the richness of the current theory, we employ it to study the propagation of a planar flame in a rectangular channel and a centrally ignited expanding flame in a spherical vessel, demonstrating the role of compression and heat release on the burning rate and flame speed, and the effect of confinement on the flow field induced by the flame motion. During the early stages of propagation, the pressure rise is moderate and the flame propagates in a quasi-steady manner. When the flame reaches a distance of roughly one third of the vessel's size, the sharp increase in pressure results in an appreciable increase in burning rate. Influences resulting from the internal flame structure are primarily manifested through flame stretch and have therefore a minimal effect on the unstretched planar flame. Spherical flames on the other hand are found to accelerate or decelerate for different Lewis numbers during the initial stage of propagation when stretch effects are substantial, before they inevitably decelerate due to gas compression. The fundamental insights will serve to guide the experimental effort, since measurements of flame speed and Markstein length are often carried out in constant volume chambers.
The hydrodynamic model is amenable to further the study of flames of arbitrary shape within closed vessels of general configuration. The detailed analysis presented in this study identifies the causes and effects of various mechanisms involved in the combustion process and permits the construction of instructive models to numerically simulate the evolution of multi-dimensional and corrugated flames in closed vessels. The main limitation is the assumption that variations inside the flame zone due to enhanced chemistry or turbulence, which could potentially alter its internal structure, are not physically resolved. Though the model represents general chemical reactions via a single overall step, it is valid where chemical kinetic parameters such as the activation energy remain fairly constant with pressure rise. It is also limited to cases where the overall kinetics are not substantially affected by drastic increases in pressure and temperature (Westbrook et al. Reference Westbrook, Pitz, Herbinet, Curran and Silke2009), mixing with burned products (Dagan et al. Reference Dagan, Chakroun, Shanbhogue and Ghoniem2019) or a high degree of turbulence (Aspden, Day & Bell Reference Aspden, Day and Bell2015). Future studies will leverage the model to analyse the stability properties of confined flames and their propagation in turbulent media of moderate intensity, neither of which are currently well understood.
Declaration of interests
The authors report no conflict of interest.
Author contributions
All authors contributed equally to theoretical derivations, reaching conclusions and in writing the paper.