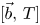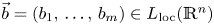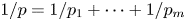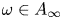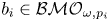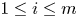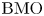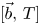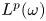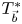The commutators of multilinear Calderón–Zygmund operators on weighted Hardy spaces

Abstract

In this paper, we study the behaviours of the commutators $[\vec b,\,T]$ generated by multilinear Calderón–Zygmund operators $T$ with $\vec b=(b_1,\,\ldots,\,b_m)\in L_{\rm loc}(\mathbb {R}^n)$ on weighted Hardy spaces. We show that for some $p_i\in (0,\,1]$ with $1/p=1/p_1+\cdots +1/p_m$, $\omega \in A_\infty$ and $b_i\in \mathcal {BMO}_{\omega,p_i}$ ($1\le i\le m$), which are a class of non-trivial subspaces of ${\rm BMO}$, the commutators $[\vec b,\,T]$ are bounded from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$ to $L^p(\omega )$. Meanwhile, we also establish the corresponding results for a class of maximal truncated multilinear commutators $T_{\vec b}^*$.

1. Introduction and main results

This paper is devoted to exploring the behaviours of the commutators of multilinear operators in weighted Hardy spaces. As well known, multilinear Calderón–Zygmund theory was introduced and first investigated by Coifman and Meyer [1, 2]. Later on, the topic was retaken by several authors: including Grafakos and Torres [10], Lerner et al. [15] and Cruz-Uribe et al. [4], etc. We first recall the definition of multilinear Calderón–Zygmund operators.

Definition 1.1 Assume that $K(y_0,\,y_1,\,\ldots,\,y_m)$ is a function defined away from the diagonal $y_0=y_1=\cdots =y_m$ in $(\mathbb {R}^n)^{m+1}$, which satisfies the following estimates

(1.1)\begin{equation} |\partial_{y_0}^{\alpha_0}\cdots\partial_{y_m}^{\alpha_m}K(y_0,y_1,\ldots,y_m)|\leq \frac{A_\alpha}{(\sum_{k,l=0}^m|y_k-y_l|)^{mn+|\alpha|}} , \end{equation}

for all $\alpha =(\alpha _0,\,\cdots,\,\alpha _m)$ such that $|\alpha |=|\alpha _0|+\cdots +|\alpha _m|\leq N$, where $|\alpha _j|$ is the order of each multi-index $\alpha _j$, and $N$ is a large integer to be determined later. An m-linear Calderón–Zygmund operator is a multilinear operator $T$ that satisfies

\[ T:L^{q_1}\times\cdots\times L^{q_m}\to L^q \]

for some $1< q_1,\,\ldots,\,q_m<\infty$ and $1/q=1/q_1+\cdots +1/q_m,$ $T$ has the integral representation

\[ T(f_1,\ldots,f_m)(x)=\int_{(\mathbb{R}^n)^m}K(x,y_1,\ldots,y_m)\prod_{j=1}^m f_j(y_j){\rm d}y_j \]

whenever $f_i\in L_c^\infty$ and $x\notin \cap _i {\rm supp} f_i.$

It was shown in [9] that if $T$ is an $m$-linear Calderón–Zygmund operator, $1/p_1+\cdots +1/p_m=1/p$ and $p_0=\min \{p_j,\,j=1,\,\ldots,\,m\}>1$, then $T$ is bounded from $L^{p_1}(\omega )\times \cdots \times L^{p_m}(\omega )$ into $L^p(\omega )$, provided that the weight $\omega$ is in the class $A_{p_0}$(see subsection 2.1 for the definition of $A_{p_0}$). In 2001, Grafakos and Kalton [8] discussed the boundedness of multilinear Calderón–Zygmund operators on the product of Hardy spaces. Later on, Cruz-Uribe et al. [4] generalized the results in [8] to the weighted Hardy spaces. Precisely,

Theorem A. (cf. [4]) Let $0< p_1,\,\ldots,\,p_m<\infty$, $\omega _i\in A_\infty$, $1\leq i\leq m$ and

\[ \frac{1}{p}=\frac{1}{p_1}+\cdots+\frac{1}{p_m}. \]

Suppose that $T$ is an $m$-linear Calderón–Zygmund operator associated to a kernel $K$ that satisfies (1.1) with

\[ N\geq \max\Bigg\{\left\lfloor mn\left(\frac{q_{\omega_i}}{p_i}-1\right)\right\rfloor_+,1\leq i\leq m\Bigg\}+(m-1)n. \]

Then

\[ \big\|T(\vec f)\big\|_{L^p(\nu_{\vec \omega})} \lesssim\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega_i)}, \]

where $\nu _{\vec \omega }=\Pi _{i=1}^m\omega _i^{p/p_i}$, $q_\omega :=\inf \{ q>1:\omega \in A_q \}$.

In this paper, we will focus on the commutators of multilinear operators. For an $m$-linear Calderón–Zygmund operator $T$ and a collection of locally integral functions $\vec b=(b_1,\,\ldots,\,b_m)$, the multilinear commutators generated by $T$ and $\vec b$ are defined as follows:

\[ [\vec b, T](f_1,\ldots,f_m)=\sum_{j=1}^m [b_j,T](f_1,\ldots,f_m), \]

where

\[ [b_j,T](f_1,\ldots,f_m):=b_j T(f_1,\ldots,f_m)-T(f_1,\ldots,f_{j-1},b_jf_j,f_{j+1},\ldots,f_m). \]

The $m$-linear commutators were considered by Pérez and Torres in [20]. Lerner et al. [15] introduced the multiple weight $A_{\vec P}$ (see definition 3.5 in [15]), and they proved that when $\vec b\in ({\rm BMO})^m$, $[\vec b,\,T]$ is bounded from $L^{p_1}(\omega _1)\times \cdots \times L^{p_m}(\omega _m)$ to $L^p(\nu _{\vec \omega })$ for $\vec \omega =(\omega _1,\,\ldots,\,\omega _m)\in A_{\vec P}$, the multiple Muckenhoupt class, where $1/p_1+\cdots +1/p_m=1/p$ and $\nu _{\vec \omega }=\prod _{i=1}^m\omega _i^{p/p_i}$. Moreover, inspired by the remarkable work of Lerner et al. [16], Kunwar and Ou [14] obtained the Bloom type two-weight inequalities of $[\vec b,\,T]$. Precisely, $1< p_i<\infty$ and $1/p_1+\cdots +1/p_m=1/p$, $\lambda _i,\,\mu _i\in A_{p_i}$, $\nu _i=(\mu _i/\lambda _i)^{1/p_i}$, $\nu _{\vec \lambda }=\prod _{i=1}^m\lambda _i^{p/p_i}$, for $b\in \rm {BMO}_{\nu _i}$(see definition in [14]), $i=1,\,\ldots,\,m$, it holds that

\[ \|[\vec b, T](f_1,\ldots,f_m)\|_{L^p(\nu_{\vec\lambda})} \lesssim\Bigg(\sum_{i=1}^m\|b_i\|_{BMO_{\nu_i}}\Bigg)\prod_{i=1}^m\|f_i\|_{L^{p_i}(\mu_i)}. \]

On the other hand, for $m=1$, in the endpoint case, Harboure et al. [11] showed that for general $b\in \rm {BMO}(\mathbb {R}^n)$, the linear commutator $[b,\,T]$ cannot be bounded from $H^1(\mathbb {R}^n)$ to $L^1(\mathbb {R}^n)$. However, Liang et al. [19] and Huy et al. [13] found out $\mathcal {BMO}_{\omega,p}$ (see subsection 2.2 for the definition and properties), a non-trivial subspace of ${\rm BMO}(\mathbb {R}^n)$ for some Muckenhoupt weights $\omega$ and $0< p\le 1$, such that $[b,\,{T}]$ is bounded from the weighted Hardy spaces $H^p(\omega )$ to the weighted Lebesgue spaces $L^p(\omega )$, when $b\in \mathcal {BMO}_{\omega,p}$. For the multilinear setting, He and Liang [12] recently proved that $[\vec b,\, T]$ is bounded from $H^1(\omega )\times \cdots \times H^1(\omega )$ to $L^{1/m}(\omega )$, when $\vec b\in (\mathcal {BMO}_{\omega,1})^m$.

Based on the results above, it is natural to ask the following question.

Question. Is $[\vec b,\,T]$ bounded from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$ to $L^{p}(\omega )$ for some $0< p_i<1,\,~1\leq i\leq m$, when $b_i\in \mathcal {BMO}_{\omega,p_i}$, the non-trivial subspaces of ${\rm BMO}(\mathbb {R}^n)$?

One of the main purpose in this paper is to address the question above. Our result can be formulated as follows.

Theorem 1.2 Let $0< p_i\leq 1,$ $1\leq i\leq m,$ and

\[ \frac{1}{p}=\frac{1}{p_1}+\cdots+\frac{1}{p_m}. \]

Suppose that $\omega \in A_{\infty }$ with $\int _{\mathbb {R}^n}\frac {\omega (x)}{(1+|x|)^{np_0}}<\infty$ with $p_0=\min _{1\le i\le m}p_i,$ $T$ is an $m$-linear Calderón–Zygmund operator with $K$ that satisfies (1.1) with

(1.2)\begin{equation} N\geq \max\Bigg\{\left\lfloor mn\left(\frac{q_{\omega}}{p_i}-1\right)\right\rfloor_+,1\leq i\leq m\Bigg\}+(m-1)n. \end{equation}

Then for $\vec b=(b_1,\,b_2,\,\ldots,\,b_m)$, $b_i\in \mathcal {BMO}_{\omega,p_i},\,1\le i\le m,$

\[ \big\|[\vec b,T](\vec f)\big\|_{L^p(\omega)}\lesssim\Bigg(\sum_{j=1}^m\| b_j\|_{\mathcal{BMO}_{\omega, p_j}}\Bigg)\prod_{i=1}^m\|f_i\|_{H^{p_i}({\omega})}. \]

Moreover, we consider the maximal truncated multilinear commutators. Let $K$ satisfy (1.1), the maximal truncated multilinear operator is defined by

(1.3)\begin{equation} T^*(\vec f)(x):=\sup_{\delta>0} |T_\delta(\vec f)(x)| =\sup_{\delta>0}\Bigg|\int_{\mathbb{R}^n}K_\delta(x,y_1,\ldots,y_m)\prod_{j=1}^mf_j(y_j){\rm d}y_j\Bigg|, \end{equation}

where $K_\delta (x,\,y_1,\,\ldots,\,y_m)=\phi (\sqrt {|x-y_1|^2+\cdots +|x-y_m|^2}/2\delta )K(x,\,y_1,\,\ldots,\,y_m)$ and $\phi (x)$ is a smooth function on $\mathbb {R}^n$, which vanishes if $|x|\leq 1/4$ and is equal to 1 if $|x|>1/2$. Given a collection of locally integral functions $\vec b=(b_1,\,\ldots,\,b_m)$, the maximal truncated multilinear commutators are defined by

\[ T^*_{\vec b}(\vec f)(x):=\sum_{i=1}^mT^{*}_{b_i}(\vec f)(x), \]

where

(1.4)\begin{equation} T^{*}_{b_i}(\vec f)(x) =\sup_{\delta>0}\Bigg|\int_{\mathbb{R}^n}(b_i(x_i)-b_i(y_i)) K_\delta(x,y_1,\ldots,y_m)\prod_{j=1}^m f_j(y_j){\rm d}y_j\Bigg|. \end{equation}

The boundedness of $T^*$ on the weighted Lebesgue spaces was first given by Grafakos and Torres [9]. Subsequently, Grafakos and Kalton [8] and Li et al. [18] successively discussed the boundedness of $T^*$ on Hardy spaces and weighted Hardy spaces. Recently, Wen et al. [21] extended and improved the results of [8] and [18] as follows.

Theorem B. (cf. [21]) Let $0< p_1,\,\ldots,\,p_m<\infty$, $\omega _i\in A_\infty$, $1\leq i\leq m$, and

\[ \frac{1}{p}=\frac{1}{p_1}+\cdots+\frac{1}{p_m}. \]

Suppose that $T^*$ is defined as in (1.3) and $K$ satisfies (1.1) with $N$ as in theorem A. Then

\[ \big\|T^*(\vec f)\big\|_{L^p(\nu_{\vec \omega})}\lesssim \prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega_i)}, \]

where $\nu _{\vec \omega }=\prod _{i=1}^m\omega _i^{p/p_i}$.

Inspired by the results above, for the maximal truncated multilinear commutator $T^*_{\vec b}$, we can obtain the following theorem.

Theorem 1.3 Let $0< p_i\leq 1,$ $1\leq i\leq m,$ and

\[ \frac{1}{p}=\frac{1}{p_1}+\cdots+\frac{1}{p_m}. \]

Suppose that $\omega \in A_{\infty }$ and satisfies $\int _{\mathbb {R}^n}{\omega (x)}/{(1+|x|)^{np_0}}<\infty$ with $p_0=\min _{1\le i\le m}p_i,$ $T^*_{\vec {b}}$ is defined as in (1.4) and $K$ satisfies (1.1) with $N$ as in theorem 1.2. Then for $\vec b=(b_1,\,b_2,\,\ldots,\,b_m),$ $b_i\in \mathcal {BMO}_{\omega,p_i},\, 1\le i\le m,$

\[ \big\|T^*_{\vec b}(\vec f)\big\|_{L^p(\omega)}\lesssim \Bigg(\sum_{j=1}^m\| b_j\|_{\mathcal{BMO}_{\omega, p_j}}\Bigg)\prod_{i=1}^m\|f_i\|_{H^{p_i}({\omega})}. \]

Remark 1.4 (i) It is worth noting that for some $p_i>1$, $i=1,\,2,\,\ldots,\,m$, the results of theorems 1.2 and 1.3 still hold. (ii) Moreover, theorem 1.2 extends the result in [12] for $p_i=1$ to the cases for certain $0< p_i<1(i=1,\,\ldots,\,m)$. (iii) For the general different $\omega _i\in A_\infty$ with $\int _{\mathbb {R}^n}{\omega (x)}/{(1+|x|)^{np_i}}{\rm d}x<\infty$, $1\le i\le m$, our method doesn't work. It would be interesting to know whether $[\vec b,\,T]$ or $T_{\vec b}^*$ with $b_i\in \mathcal {BMO}_{\omega _i,p_i}$ ($1\le i\le m$) are bounded from $H^{p_1}(\omega _1)\times \cdots \times H^{p_m}(\omega _m)$ to $L^{p}(\nu _{\vec \omega })$ for the different Muckenhoupt weights $\omega _i$, $1\le i\le m$, with $\nu _{\vec \omega }=\prod _{i=1}^m \omega _i^{p/p_i}$.

The rest of this paper is organized as follows. We will recall some definitions and known results about Muckenhoupt weights, $\mathcal {BMO}_{\omega,p}$ spaces and weighted Hardy spaces in $\S$ 2. The proof of theorem 1.2 will be given in $\S$ 3. Finally, we will prove theorem 1.3 in $\S$ 4. We remark that some ideas in our arguments are taken from [4, 13, 19, 21], in which the multilinear Calderón–Zygmund operators and the linear commutators of Calderón–Zygmund operators were dealt with.

Finally, we make some conventions on notation. Throughout the whole paper, we denote by $C$ a positive constant which is independent of the main parameters, but it may vary from line to line. We denote $f\lesssim g$, $f\approx g$ if $f\leq Cg$ and $f\lesssim g \lesssim f$ respectively. For $1\leq p\leq \infty,$ $p'$ is the conjugate index of $p$, and $1/p+1/p'=1$. $E^c=\mathbb {R}^n\backslash E$ is the complementary set of any measurable subset $E$ of $\mathbb {R}^n$. Any cube $\tilde{Q}$ is denoted as $\tilde Q:=8\sqrt {n}Q,$ where the cube is with the same centre and $8$ times the side length of $Q$.

2. Preliminaries

In this section, we recall some auxiliary facts and lemmas, which will be used in our arguments.

2.1 Muckenhoupt weights

A non-negative measurable function $\omega$ is said to be in the Muckenhoupt class $A_p$ with $1< p<\infty$, if there exists a constant $C>0$ such that

\[ [\omega]_{A_p,Q}=\Bigg(\frac{1}{|Q|}\int_Q\omega(x){\rm d}x\Bigg) \Bigg(\frac{1}{|Q|}\int_Q\omega(x)^{1-p'}{\rm d}x\Bigg)^{p-1}\leq C \]

for all cubes $Q\subset \mathbb {R}^n$, where $1/p+1/{p'}=1.$ And we denote $[w]_{A_p}:=\sup _{Q}[\omega ]_{A_p,Q}$. When $p=1$, a non-negative measurable function $\omega$ is said to belong $A_1$ if

\[ \frac{1}{|Q|}\int_Q\omega(y){\rm d}y\lesssim{\rm{ess}}\inf_{x\in Q}\omega(x) \]

for all cubes $Q\subset \mathbb {R}^n$. We denote $A_\infty :=\cup _{p\ge 1}A_p$ and by $q_\omega :=\inf \{q>1:\omega \in A_q\}$ for $\omega \in A_\infty$. It is well known that if $\omega \in A_p$ for $1< p<\infty,$ then $\omega \in A_r$ for all $r>p$ and $\omega \in A_q$ for some $1\leq q< p.$ Then we give some important results about $A_p$ weight that will be used later on.

Lemma 2.1 [7]

Let $\omega \in A_p,\,~p\geq 1$. Then, for any cube $Q$ and $\lambda >1,$

\[ \omega(\lambda Q)\lesssim \lambda^{np}\omega(Q). \]

Lemma 2.2 [4]

Let $\omega \in A_\infty,$ $0< p<\infty$ and $\max \{1,\,p\}< q<\infty$. Then for any collection of cubes $\{Q_k\}_{k=1}^\infty$ in $\mathbb {R}^n$ and non-negative integrable functions $\{f_k\}_{k=1}^\infty$ with $\operatorname {supp}{f_k}\subset Q_k,$ we have

\[ \Bigg\|\sum_{k=1}^\infty f_k\Bigg\|_{L^p(\omega)}\lesssim\Bigg\|\sum_{k=1}^\infty\Bigg(\frac{1}{\omega(Q_k)}\int_{Q_k}f_k(x)^q\omega(x){\rm d}x\Bigg)^{1/q}\chi_{ Q_k}\Bigg\|_{L^p(\omega)}. \]

2.2 ${\mathcal {BMO}_{\omega,p}}$ spaces and basic facts

This subsection is concerning with the definition of ${\mathcal {BMO}_{\omega,p}}$ and its basic properties.

Definition of ${\mathcal {BMO}_{\omega,p}}$. Let $p\in (0,\,\infty )$, $\omega \in A_\infty$ and satisfy $\int _{\mathbb {R}^n}{\omega (x)}/{(1+|x|)^{np}}{\rm d}x<\infty$. A locally integrable function $b$ is said to be in $\mathcal {BMO}_{\omega,p}$ if

\[ \| b\|_{\mathcal{BMO}_{\omega,p}}:=\sup_{Q}\Bigg\{\Bigg(\frac{1}{\omega(Q)}\int_{Q^c}\frac{\omega(x)}{|x-x_0|^{np}}{\rm d}x\Bigg)^{1/p} \int_{Q}|b(y)-b_Q|{\rm d}y\Bigg\}<\infty, \]

where the supremum is taken over all cubes $Q:=Q(x_0,\,l)\subset \mathbb {R}^n$ with $x_0\in \mathbb {R}^n$ and $l\in (0,\,\infty )$. Here and hereafter,

\[ \omega(Q):=\int_Q \omega(z){\rm d}z\quad \mathrm{and}\quad b_Q:=\frac{1}{|Q|}\int_Q b(z){\rm d}z. \]

A locally integrable function $b$ is said to be in $\mathrm {BMO}$ if

\[ \| b\|_{\mathrm{BMO}}:=\sup_{Q\subset\mathbb{R}^n}\frac{1}{|Q|}\int_Q|b(x)-b_Q|{\rm d}x<\infty, \]

where the supremum is taken over all cubes $Q\subset \mathbb {R}^n.$

Basic facts ([13, 19]).  (i)  $\mathcal {BMO}_{\omega,p}\subset {\rm BMO}$, which is a proper inclusion.

(ii)  Let $0< p\leq 1$, $\omega \in A_\infty$ such that $\int _{\mathbb {R}^n}{\omega (x)}/{(1+|x|)^{np}}{\rm d}x<\infty$. Any Lipschitz function $b$ with compact support belongs to $\mathcal {BMO}_{\omega,p}$.

Lemma 2.3 [19]

Let $\omega \in A_{\infty }$ and $q\in [1,\,\infty ).$ Then for $b\in {\rm BMO}$ and any cube $Q:=Q(x_0,\,l)\subset \mathbb {R}^n$ with some $x_0\in \mathbb {R}^n$ and $l\in (0,\,\infty ),$

\[ \Bigg(\frac{1}{\omega(Q)}\int_Q|b(x)-b_Q|^q\omega(x){\rm d}x\Bigg)^{1/q}\lesssim\| b\|_{\rm BMO}. \]

2.3 Weighted Hardy spaces

Let $\mathscr {S}$ be the Schwartz class of smooth functions. For a large integer $N_0$, denote

\[ \mathfrak{S}_{N_0}=\Bigg\{\phi\in\mathscr{S}(\mathbb{R}^n):\int_{\mathbb{R}^n}(1+|x|)^{N_0} \Bigg(\sum_{|\beta|\leq N_0}\Bigg|\frac{\partial^\beta}{\partial x^\beta}\phi(x)\Bigg|^2\Bigg){\rm d}x\leq1\Bigg\}. \]

Given $\omega \in A_\infty$ and $0< p<\infty$, the weighted Hardy spaces $H^p(\omega )$ is defined by

\[ H^p(\omega)=\{f\in\mathscr{S}'(\mathbb{R}^n):\mathcal{M}_{N_0}(f)\in L^p(\omega)\} \]

with the quasi-norm

\[ \|f\|_{H^p(\omega)}=\|\mathcal{M}_{N_0}(f)\|_{L^p(\omega)}, \]

where $\mathcal {M}_{N_0}(f)$ is given by

\[ \mathcal{M}_{N_0}(f)(x)=\sup_{\phi\in\mathfrak{S}_{N_0}}\sup_{t>0}|\phi_t\ast f(x)|. \]

Given an integer $N\geq 0$, we say that a function $a$ is an $(H^p(\omega ),\,\infty,\,N)$-atom if

\[ \operatorname{supp} a_k\subset Q_k,\quad \|a_k\|_{L^\infty}\leq\big(\omega(Q_k)\big)^{{-}1/p} ,\quad \int_{\mathbb{R}^n}x^\alpha a_k(x){\rm d}x=0,\quad |\alpha|\leq N. \]

For $\omega \in A_\infty$ and $0< p<\infty$, denote $S_\omega :=\lfloor n(q_\omega /p-1)\rfloor _+$. Let $N\geq S_\omega$, we define

\[ \mathcal{O}_N=\Bigg\{f\in C_{0}^{\infty}:\int_{\mathbb{R}^n}x^\alpha f(x){\rm d}x=0,\quad 0\leq|\alpha|\leq N\Bigg\}. \]

Then $\mathcal {O}_N$ is dense in $H^p(\omega )$ (see [4, 5]).

In addition, we have the following finite atomic decomposition which was given in [5].

Lemma 2.4 [5]

Given $0< p<\infty$ and $\omega \in A_\infty,$ $S_\omega :=\lfloor n(q_\omega /p-1)\rfloor _+,$ fix $N\geq S_\omega$. Then if $f\in \mathcal {O}_N,$ there exists a finite sequence $\{a_k\}_{k=1}^{M}$ of $(H^p(\omega ),\,\infty,\,N)$-atoms with supports $Q_k,$ and a non-negative sequence $\{\lambda _i\}_{i=1}^{M}$ such that $f=\sum _{k =1}^M\lambda _k a_k$ and

\[ \sum_{k=1}^M\lambda_k^p\lesssim\|f\|_{H^p(\omega)}^p. \]

3. The proof of theorem 1.2

This section is devoted to proving theorem 1.2. First, we need to prove a weighted norm inequality for $[\vec b,\,T].$ To do so, we will make use of some recent developments in the theory of Harmonic analysis on the domination of multilinear operators by sparse operators. Next, we sketch the basic definitions.

A collection of cubes $\mathcal {S}$ is called a sparse family if each cube $Q\in \mathcal {S}$ contains measurable subset $E_Q\subset Q$ such that $|E_Q|\geq 1/2|Q|$ and the family $\{E_Q\}_{Q\in \mathcal {S}}$ is pairwise disjoint. Given a sparse family $\mathcal {S}$, the sparse operator $\mathcal {T}_{\mathcal {S},b}$ defined with a locally integrable function $b$ by Lerner et al. in [16],

\[ \mathcal{T}_{\mathcal{S},b}(f)(x)=\sum_{Q\in\mathcal{S}}|b(x)-b_Q|f_Q\chi_Q(x). \]

Let $\mathcal {T}_{\mathcal {S},b}^\star$ denote the adjoint operator to $\mathcal {T}_{\mathcal {S},b}:$

\[ \mathcal{T}_{\mathcal{S},b}^\star(f)(x) =\sum_{Q\in\mathcal{S}}\Bigg(\frac{1}{|Q|}\int_Q|b(y)-b_Q|f(y){\rm d}y\Bigg)\chi_Q(x). \]

Proposition 3.1 [16]

Let $1< p<\infty$ and $\omega \in A_p$, then for $b\in {\rm BMO}$, given any sparse linear operators $\mathcal {T}_{\mathcal {S},b}(f)$ and $\mathcal {T}_{\mathcal {S},b}^\star (f)$ have

\[ \|\mathcal{T}_{\mathcal{S},b}(f)\|_{L^p(\omega)} \lesssim[\omega]_{A_p}^{\max\{1,p'/p\}}\|b\|_{\rm BMO}\|f\|_{L^p(\omega)} \]

and

\[ \|\mathcal{T}_{\mathcal{S},b}^\star(f)\|_{L^p(\omega)} \lesssim[\omega]_{A_p}^{\max\{1,p'/p\}}\|b\|_{\rm BMO}\|f\|_{L^p(\omega)}. \]

In a similar way, for $b_l\in L_{loc}^1$, $l=1,\,\ldots,\,m$, given a sparse family $\mathcal {S}$ we define the multilinear sparse operator:

\[ \mathcal{T}_{\mathcal{S},b_l}(f_1,\ldots,f_m)(x)=\sum_{Q\in \mathcal{S}} |b_l(x)-b_{l,Q}| \prod_{i=1}^m f_{i,Q}\chi_Q(x). \]

Let $\mathcal {T}_{\mathcal {S},b_l}^\star$ denote the adjoint operator to $\mathcal {T}_{\mathcal {S}, b_l}$:

\[ \mathcal{T}_{\mathcal{S},b_l}^\star(f_1,\ldots,f_m)(x)=\sum_{Q\in \mathcal{S}} \Bigg(\frac{1}{|Q|}\int_Q|b_l(y)-b_{l,Q}|f_l(y){\rm d}y\Bigg) \prod_{i=1,i\neq l}^mf_{i,Q}\chi_Q(x). \]

The following pointwise sparse domination for the multilinear commutators of Calderón–Zygmund operators was proved by Kunwar and Ou [14]:

Proposition 3.2 [14]

Let $T$ be an $m$-linear Calderón–Zygmund operator with $K$ satisfying (1.1) with $N$ as in theorem 1.2. Given locally integral functions $\vec b=(b_1,\,\ldots,\,b_m)$ on $\mathbb {R}^n$. Then for any bounded functions $\vec f=(f_1,\,\ldots,\,f_m)$ with compact support, there exists $3^n$ sparse families $\mathcal {S}_j$ such that

\begin{align*} \big|[\vec b,T](f_1,\ldots,f_m)(x)\big|& \lesssim\sum_{i=1}^m\Bigg(\sum_{j=1}^{3^n}\big(\mathcal{T}_{\mathcal{S}_j,b_i}(|f_1|,\ldots,|f_m|)(x)\\ & \quad +\mathcal{T}_{\mathcal{S}_j,b_i}^\star(|f_1|,\ldots,|f_m|)(x)\big)\Bigg). \end{align*}

Next, we prove the following weighted estimate for $[\vec b,\,T]$.

Lemma 3.3 Let $T$ be an $m$-linear Calderón–Zygmund operator with $K$ that satisfies (1.1) with $N$ as in theorem 1.2. Fix $\omega \in A_p$, $1< p<\infty$. Given functions $\vec b=(b_1,\,\ldots,\,b_m)$ which $b_i\in {\rm BMO}$, $i=1,\,\ldots,\,m$. Then for any bounded functions $\vec f=(f_1,\,\ldots,\,f_m)$ with compact support, we have

\[ \big\|[\vec b, T](f_1,\ldots,f_m)\big\|_{L^p(\omega)}\lesssim\Bigg(\sum_{i=1}^m\|b_i\|_{\rm BMO}\Bigg)\|f_l\|_{L^p(\omega)}\prod_{j=1,j\neq l}^m\|f_j\|_{L^\infty},~~l=1,2,\ldots,m. \]

Proof. By linearity it is enough to consider the operator with only one symbol. For $1\leq k\leq m$, fix $b_k\in {\rm BMO}$ and consider the operator $[b_k,\,T](f_1,\,\ldots,\,f_m)(x)$. By proposition 3.2, it suffices to prove this estimate for any multilinear sparse operators $\mathcal {T}_{\mathcal {S},b_k}$, $\mathcal {T}_{\mathcal {S},b_k}^\star$ and non-negative functions $f_1,\,\ldots,\,f_m$. By the definition of the sparse operator, we have

\begin{align*} \mathcal{T}_{\mathcal{S},b_k}(f_1,\ldots,f_m)(x) & \leq \prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}\sum_{Q\in \mathcal{S}} |b_k(x)-b_{k,Q}|f_{l,Q}\chi_Q(x)\\ & =\mathcal{T}_{\mathcal{S},b_k}( f_l)(x)\prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}. \end{align*}

Then, by proposition 3.1, we obtain

\[ \|\mathcal{T}_{\mathcal{S},b_k}(f_1,\ldots,f_m)\|_{L^p(\omega)} \lesssim\|b_k\|_{\rm BMO}\|f_l\|_{L^p(\omega)}\prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}, \]

Next, we estimate $\mathcal {T}_{\mathcal {S},b_k}^\star$ in two different cases:

Case 1: $k= l$,

\begin{align*} \mathcal{T}_{\mathcal{S},b_k}^\star(f_1,\ldots,f_m)(x) & \leq \prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}\sum_{Q\in \mathcal{S}} \Bigg(\frac{1}{|Q|}\int_Q|b_k(y)-b_{k,Q}||f_k(y)|{\rm d}y\Bigg)\chi_Q(x)\\ & =\mathcal{T}_{\mathcal{S},b_k}^\star( f_k)(x)\prod_{i=1,l\neq l}^m\|f_i\|_{L^\infty}. \end{align*}

Then, by proposition 3.1, we have that

\[ \|\mathcal{T}_{\mathcal{S},b_k}^\star(f_1,\ldots,f_m)\|_{L^p(\omega)} \lesssim\|b_k\|_{\rm BMO}\|f_l\|_{L^p(\omega)}\prod_{i=1,i\neq k}^m\|f_i\|_{L^\infty}. \]

Case 2: $k\neq l$,

\begin{align*} \mathcal{T}_{\mathcal{S},b_k}^\star(f_1,\ldots,f_m)(x) & \leq \prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}\sum_{Q\in \mathcal{S}} \Bigg(\frac{1}{|Q|}\int_Q|b_k(y)-b_{k,Q}|{\rm d}y\Bigg)f_{l,Q}\chi_Q(x)\\ & \lesssim \|b_k\|_{\rm BMO}\prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty} \sum_{Q\in \mathcal{S}}f_{l,Q}\chi_Q(x)\\ & = :\|b_k\|_{\rm BMO}\prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty} \mathcal{T}_{\mathcal{S}}(f_l)(x), \end{align*}

Recall the well-known bound for the sparse operator $\mathcal {T}_S$ (see [3]):

\[ \|\mathcal{T}_{\mathcal{S}} (f_l)\|_{L^p(\omega)} \lesssim[\omega]_{A_p}^{\max\{1,p'/p\}}\|f_l\|_{L^p(\omega)},~~ p\in(1,\infty). \]

Thus, we have

\[ \|\mathcal{T}_{\mathcal{S},b_k}^\star(f_1,\ldots,f_m)\|_{L^p(\omega)} \lesssim\|b_k\|_{\rm BMO}\|f_l\|_{L^p(\omega)}\prod_{i=1,i\neq l}^m\|f_i\|_{L^\infty}, \]

which completes the proof of lemma 3.3.

We also need the following lemma:

Lemma 3.4 [17]

Let $T$ be an $m$-linear Calderón–Zygmund operator with $K$ that satisfies (1.1) with $N$ as in theorem 1.2. Let $0< p_i\leq 1,$ $a_i$ be an $(H^{p_i}(\omega ),\,\infty,\,N)$-atom supported in $Q_k$, and $c_i$ be the centre of $Q_{i},$ $l_i$ be the side length of $Q_i,$ $i=1,\,\ldots,\,m$. Assume $\tilde Q_1\cap \cdots \cap \tilde Q_m\neq \emptyset$. Then for any $x\in (\tilde Q_1\cap \cdots \cap \tilde Q_m)^c,$ we have

\[ |T(a_1,\ldots,a_m)(x)| \lesssim\prod_{i=1}^m\frac{\big(\omega(Q_{i})\big)^{{-}1/p_i}|Q_{i}|^{1+(N+1)/nm}} {(|x-c_{i}|+l_{i})^{n+(N+1)/m}}. \]

Now, we are in the position to prove theorem 1.2.

Proof of theorem 1.2. Proof of theorem 1.2

By linearity, it is enough to consider the operator with only one symbol. For $1\leq l\leq m$, fix then $b_l\in \mathcal {BMO}_{\omega,p_l}$ and consider the operator $[b_l,\,T](f_1,\,\ldots,\,f_m)(x)$. By lemma 2.4, we will work with finite sums of weighted Hardy atoms and obtain estimates independent of the number of terms in each sum. We write $f_i$ as a finite sum of atoms,

\[ f_i=\sum_{k_i=1}^M\lambda_{i,k_i}a_{i,k_i},\quad i=1,2,\ldots,m, \]

where $\lambda _{i,k_i}\geq 0$ and $a_{i,k_i}$ are $(H^{p_i}(\omega ),\,\infty,\,N)$-atoms. They are supported in cubes $Q_{i,k_i}$, $\|a_{i,k_i}\|_{L^\infty }\leq (\omega (Q_{i,k_i}))^{-1/p_i}$, $\int _{Q_{i,k_i}} x^\beta a_{i,k_i}(x){\rm d}x=0$ for all $|\beta |\leq N,$ and

\[ \sum_{k_i}\lambda_{i,k_i}^{p_i}\lesssim\|f_i\|_{H^{p_i}(\omega)}^{p_i}. \]

Denote the centre of $Q_{i,k_i}$ by $c_{i,k_i}$ and the side length of $Q_{i,k_i}$ by $l_{i,k_i}$. Using multilinearity we write

\[ [b_l,T](f_1,\ldots,f_m)(x) =\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}[b_l,T](a_{1,k_1},\ldots,a_{m,k_m})(x). \]

Then, we decompose $[b_l,\,T](f_1,\,\ldots,\,f_m)(x)$ into two parts, for $x\in \mathbb {R}^n$

\[ \big|[b_l,T](f_1,\ldots,f_m)(x)\big|\leq I_1(x)+I_2(x), \]

where

\begin{align*} I_1(x)& =\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m} \big|[b_l,T](a_{1,k_1},\ldots,a_{m,k_m})(x)\big| \chi_{\tilde Q_{1,k_1}\cap\cdots\cap \tilde Q_{m,k_m}},\\ I_2(x)& =\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m} \big|[b_l,T](a_{1,k_1},\ldots,a_{m,k_m})(x)\big| \chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}. \end{align*}

Now, let us begin to discuss $\|I_1\|_{L^p(\omega )}$. For fixed $k_1,\,\ldots,\,k_m$, assume that

\[ \tilde Q_{1,k_1}\cap\cdots\cap\tilde Q_{m,k_m}\neq\emptyset, \]

since otherwise there is nothing needed to be proved. Suppose that $\omega (\tilde Q_{1,k_1})$ has the smallest value among $\omega (\tilde Q_{i,k_i}),\,~i=1,\,2,\,\ldots,\,m$. For $q\in (q_\omega,\,\infty )$, by lemma 3.3, we have

\begin{align*} & \Bigg(\frac{1}{\omega(\tilde Q_{1,k_1})}\int_{\tilde Q_{1,k_1}}\big|[b_l,T](a_{1,k_1},\ldots,a_{m,k_m})(x)\big|^q\omega(x){\rm d}x\Bigg)^{1/q}\\ & \qquad\leq\big(\omega(\tilde Q_{1,k_1})\big)^{{-}1/q} \big\|[b_l,T](a_{1,k_1},\ldots,a_{m,k_m})\big\|_{L^q(\omega)}\\ & \qquad\lesssim\|b_l\|_{\rm BMO}\big(\omega(\tilde Q_{1,k_1})\big)^{{-}1/q}\|a_{1,k_1}\|_{L^q(\omega)}\prod_{i=2}^m\|a_{i,k_i}\|_{L^\infty}\\ & \qquad\lesssim\|b_l\|_{\rm BMO}\big(\omega(\tilde Q_{1,k_1})\big)^{{-}1/q}\big(\omega(Q_{1,k_1})\big)^{1/q-1/p_1} \prod_{i=2}^m\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}\\ & \qquad\lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}. \end{align*}

By lemma 2.2 and Hölder's inequality, we obtain

\begin{align*} \|I_1\|_{L^p(\omega)} & \lesssim \|b_l\|_{\rm BMO}\Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m} \prod_{i=1}^m\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i} \chi_{\tilde Q_{1,k_1}}\Bigg\|_{L^p(\omega)}\\ & \lesssim \|b_l\|_{\rm BMO}\Bigg\|\prod_{i=1}^m\Bigg(\sum_{k_i}\lambda_{i,k_i} \big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}\chi_{\tilde Q_{1,k_1}}\Bigg)\Bigg\|_{L^p(\omega)}\\ & \lesssim \|b_l\|_{\rm BMO}\prod_{i=1}^m \Bigg\|\sum_{k_i}\lambda_{i,k_i} \big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}\omega({\cdot})^{1/p_i}\chi_{\tilde Q_{1,k_1}}\Bigg\|_{L^{p_i}}\\ & \lesssim \|b_l\|_{\rm BMO}\prod_{i=1}^m \Bigg(\sum_{k_i}\lambda_{i,k_i}^{p_i}\Bigg)^{1/p_i} \lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \end{align*}

Thus,

\[ \|I_1\|_{L^p(\omega)}\lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

Next, we estimate $\|I_2\|_{L^p(\omega )}$, we split it again

\begin{align*} \|I_2\|_{L^p(\omega)}& \lesssim\Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}\big|b_l-b_{l,{Q_{l,k_l}}}\big|\\ & \quad\times|T(a_{1,k_1},\ldots,a_{l,k_l},\ldots,a_{m,k_m})|\chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}\Bigg\|_{L^p(\omega)}\\ & \quad+\Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}\\ & \quad\times \big|T\big(a_{1,k_1},\ldots,(b_l-b_{l,{Q_{l,k_l}}}) a_{l,k_l},\ldots,a_{m,k_m}\big)\big| \chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}\Bigg\|_{L^p(\omega)}\\ & =:\|I_{21}\|_{L^p(\omega)}+\|I_{22}\|_{L^p(\omega)}. \end{align*}

For $\|I_{21}\|_{L^p(\omega )}$, using the Hölder inequality and lemma 3.4, we get

\begin{align*} \|I_{21}\|_{L^p(\omega)} & \lesssim\Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}|b_l-b_{l,{Q_{l,k_l}}}| \prod_{i=1}^m\\ & \quad \times \frac{\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}|Q_{i,k_i}|^{1+(N+1)/nm}} {(l_{i,k_i}+|\cdot{-}c_{i,k_i}|)^{n+(N+1)/m}}\Bigg\|_{L^p(\omega)}\\ & \lesssim\Bigg\|\Bigg(\sum_{k_l}\frac{\lambda_{l,k_l} \big(\omega(Q_{l,k_l})\big)^{{-}1/p_l}|b_l-b_{l,{Q_{l,k_l}}}| l_{l,k_l}^{n+(N+1)/m}}{(l_{l,k_l}+|\cdot{-}c_{l,k_l}|)^{n+(N+1)/m}}\Bigg)\\ & \quad\times\prod_{i=1,i\neq l}^m\Bigg(\sum_{k_i} \frac{\lambda_{i,k_i}\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}l_{i,k_i}^{n+(N+1)/m}} {(l_{i,k_i}+|\cdot{-}c_{i,k_i}|)^{n+(N+1)/m}}\Bigg)\Bigg\|_{L^p(\omega)}\\ & \lesssim \Bigg\|\sum_{k_l}\frac{\lambda_{l,k_l} \big(\omega(Q_{l,k_l})\big)^{{-}1/p_l} |b_l-b_{l,{Q_{l,k_l}}}|l_{l,k_l}^{n+(N+1)/m}} {(l_{l,k_l}+|\cdot{-}c_{l,k_l}|)^{n+(N+1)/m}}\Bigg\|_{L^{p_l}(\omega)}\\ & \quad\times\prod_{i=1,i\neq l}^m\Bigg\|\sum_{k_i}\frac{\lambda_{i,k_i} \big(\omega(Q_{i,k_i})\big)^{{-}1/p_i}l_{i,k_i}^{n+(N+1)/m}} {(l_{i,k_i}+|\cdot{-}c_{i,k_i}|)^{n+(N+1)/m}} \Bigg\|_{L^{p_i}(\omega)}\ = :& J_1\cdot J_2. \end{align*}

For $J_2$, by (1.2) and lemma 2.1, we have

\begin{align*} & \Bigg\|\sum_{k_i}\frac{\lambda_{i,k_i}\big(\omega(Q_{i,k_i})\big)^{{-}1/p_i} l_{i,k_i}^{n+(N+1)/m}}{(l_{i,k_i}+|\cdot{-}c_{i,k_i}|)^{n+(N+1)/m}} \Bigg\|_{L^{p_i}(\omega)}^{p_i}\\ & \quad\leq\sum_{k_i}\lambda_{i,k_i}^{p_i}\Bigg(\int_{Q_{i,k_i}} \frac{\big(\omega(Q_{i,k_i})\big)^{{-}1}l_{i,k_i}^{p_in+p_i(N+1)/m}\omega(x)}{(l_{i,k_i}+|x-c_{i,k_i}|)^{p_in+p_i(N+1)/m}}{\rm d}x\\ & \qquad+\sum_{j=1}^\infty\int_{2^jQ_{i,k_i}\backslash2^{j-1}Q_{i,k_i}} \frac{\big(\omega(Q_{i,k_i})\big)^{{-}1}l_{i,k_i}^{p_in+p_i(N+1)/m}\omega(x)}{(l_{i,k_i}+|x-c_{i,k_i}|)^{p_in+p_i(N+1)/m}}{\rm d}x\Bigg)\\ & \quad\lesssim\sum_{k_i}\lambda_{i,k_i}^{p_i}\big(\omega(Q_{i,k_i})\big)^{{-}1} \Bigg(\sum_{j=0}^\infty\frac{\omega(2^jQ_{i,k_i})}{2^{j(p_in+p_i(N+1)/m)}}\Bigg)\\ & \quad\lesssim\sum_{k_i}\lambda_{i,k_i}^{p_i}\big(\omega(Q_{i,k_i})\big)^{{-}1} \Bigg(\sum_{j=1}^\infty\frac{\omega(Q_{i,k_i})}{2^{j(p_in+p_i(N+1)/m-nq_\omega)}}\Bigg)\\ & \quad\lesssim\sum_{k_i}\lambda_{i,k_i}^{p_i}\lesssim\|f_i\|_{H^{p_i}(\omega)}^{p_i}. \end{align*}

For $J_1$, by (1.2) and lemmas 2.1 and 2.3, we obtain

\begin{align*} & \Bigg\|\sum_{k_l}\frac{\lambda_{l,k_l} \big(\omega(Q_{l,k_l})\big)^{{-}1/p_l} |b_l-b_{l,{Q_{l,k_l}}}|l_{l,k_l}^{n+(N+1)/m}} {(l_{l,k_l}+|\cdot{-}c_{l,k_l}|)^{n+(N+1)/m}}\Bigg\|_{L^{p_l}(\omega)}^{p_l}\\ & \quad\lesssim\sum_{k_l}\lambda_{l,k_l}^{p_l}\big(\omega(Q_{l,k_l})\big)^{{-}1}\Bigg(\int_{Q_{l,k_l}} \frac{|b_l(x)-b_{l,{Q_{l,k_l}}}|^{p_l}l_{l,k_l}^{p_ln+p_l(N+1)/m}\omega(x)} {(l_{l,k_l}+|x-c_{l,k_l}|)^{p_ln+p_l(N+1)/m}}{\rm d}x\\ & \qquad+\sum_{j=1}^\infty\int_{2^{j+1}Q_{l,k_l}\backslash2^jQ_{l,k_l}} \frac{|b_l(x)-b_{l,{Q_{l,k_l}}}|^{p_l}l_{l,k_l}^{p_ln+p_l(N+1)/m}\omega(x)} {(l_{l,k_l}+|x-c_{l,k_l}|)^{p_ln+p_l(N+1)/m}}{\rm d}x\Bigg)\\ & \quad\lesssim\|b_l\|_{\rm BMO}^{p_l}\|f_l\|_{H^{p_l}(\omega)}^{p_l}. \end{align*}

Thus,

\[ \|I_{21}\|_{L^p(\omega)}\lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

To estimate $\|I_{22}\|_{L^p(\omega )}$, we write

\[ \|I_{22}\|_{L^p(\omega)}=\Bigg\|T\Bigg(f_1,\ldots,\sum_{k_l}\lambda_{l,k_l} (b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l},\ldots,f_m\Bigg)\Bigg\|_{L^p(\omega)}. \]

By the boundedness of $T$ from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$ to $L^p(\omega )$, we only need to show

\[ \Bigg\|\sum_{k_l}\lambda_{l,k_l}(b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\Bigg\|_{H^{p_l}({\omega})} \lesssim\|f_l\|_{H^{p_l}(\omega)}\|b_l\|_{\mathcal{BMO}_{\omega,p_l}}, \]

that is,

(3.1)\begin{equation} \Bigg\|\sum_{k_l}\lambda_{l,k_l}\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big) \Bigg\|_{L^{p_l}(\omega)}\lesssim\|f_l\|_{H^{p_l}(\omega)}\|b_l\|_{\mathcal{BMO}_{\omega,p_l}}. \end{equation}

We write

\begin{align*} & \Bigg\|\sum_{k_l}\lambda_{l,k_l}\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big) \Bigg\|_{L^{p_l}(\omega)}^{p_l}\\ & \quad\leq\sum_{k_l}\lambda_{l,k_l}^{p_l}\int_{2Q_{l,k_l}} \big|\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big)(x)\big|^{p_l}\omega(x){\rm d}x\\ & \qquad+\sum_{k_l}\lambda_{l,k_l}^{p_l}\int_{(2Q_{l,k_l})^c} \big|\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big)(x)\big|^{p_l}\omega(x){\rm d}x=:{L_1}+{L_2}. \end{align*}

For $L_1$, by Hölder's inequality for $t/p_l$ $(q_{\omega }< t<\infty )$, lemma 2.3 and the boundedness of $\mathcal {M}_N$ on $L^t(\omega )$, we obtain

\begin{align*} {L_1}& =\sum_{k_l}\lambda_{l,k_l}^{p_1}\int_{2Q_{l,k_l}}\big|\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big)(x)\big|^{p_l}\omega(x){\rm d}x\\ & \leq\sum_{k_l}\lambda_{l,k_l}^{p_l}\big\|\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big)\big\|_{L^t(\omega)}^{p_l} \Bigg(\int_{2Q_{l,k_l}}\omega(x){\rm d}x\Bigg)^{1-p_l/t}\\ & \lesssim\sum_{k_l}\lambda_{l,k_l}^{p_l}\big\|( b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big\|_{L^t(\omega)}^{p_l}\big(\omega(Q_{l,k_l})\big)^{1-p_l/t}\\ & \lesssim\sum_{k_l}\lambda_{l,k_l}^{p_l} \| b_l\|_{\mathrm{BMO}}^{p_l}\lesssim\|f_l\|_{H^{p_l}(\omega)}^{p_l} \| b_l\|_{\mathcal{BMO}_{\omega,p_l}}^{p_l}. \end{align*}

For ${L_2}$, note that for $x\in (2Q_{l,k_l})^c$ and $y\in Q_{l,k_l}$, $|x-y|\approx |x-c_{l,k_l}|$. Then, for $\phi \in \mathfrak {S}_N$, $t>0$, we have

\begin{align*} & \frac{1}{t^n}\Bigg|\int_{Q_{l,k_l}} (b_l(y)-b_{l,Q_{l,k_l}})a_{l,k_l}(y)\phi\big(\frac{x-y}{t}\big){\rm d}y\Bigg|\\ & \lesssim\frac{1}{|x-c_{l,k_l}|^n}\int_{Q_{l,k_l}}|b_l(y)-b_{l,Q_{l,k_l}}||a_{l,k_l}(y)|{\rm d}y\\ & \lesssim\frac{1}{|x-c_{l,k_l}|^n\big(\omega(Q_{l,k_l})\big)^{1/p_l}}\int_{Q_{l,k_l}}|b_l(y)-b_{l,Q_{l,k_l}}|{\rm d}y. \end{align*}

This, together with the definition of $\mathcal {BMO}_{\omega,p_l},$ deduces that

\[ {L_2}\lesssim\sum_{k_l}\lambda_{l,k_l}^{p_l} \| b_l\|_{\mathcal{BMO}_{\omega,p_l}}^{p_l} \lesssim\|f_l\|_{H^{p_l}(\omega)}^{p_l}\| b_l\|_{\mathcal{BMO}_{\omega,p_l}}^{p_l}. \]

Summing up the estimates of ${L_1}$ and $L_2$, we obtain

\[ \|I_{22}\|_{L^p(\omega)}\lesssim \| b_l\|_{\mathcal{BMO}_{\omega,p_l}}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

Combining the estimates in both cases, there is

\[ \big\|[\vec b,T](\vec f)\big\|_{L^p(\omega)}\lesssim\Bigg(\sum_{j=1}^m\| b_j\|_{\mathcal{BMO}_{\omega, p_j}}\Bigg)\prod_{i=1}^m\|f_i\|_{H^{p_i}({\omega})}, \]

which completes the proof of theorem 1.2.

4. The proof of theorem 1.3

Before proving theorem 1.3, we need to prove a weighted norm inequality for $T_{\vec b}^*$. We first recall some definitions and results. Given $\vec f=(f_1,\,\ldots,\,f_m),$ we define the multilinear maximal operator $\mathcal {M}$ by

\[ \mathcal{M}(\vec f)(x)=\sup_{Q\ni x}\prod_{i=1}^m\frac{1}{|Q|}\int_Q|f_i(y_i)|{\rm d}y_i, \]

where the supremum is taken over all cubes $Q$ containing $x$.

For $\rho >0$, let $M_\rho$ be the maximal function

\[ M_\rho (f)(x)=M(|f|^\rho)^{1/\rho}(x)=\Bigg(\sup_{Q\ni x}\frac{1}{|Q|}\int_{Q}|f(y)|^\rho {\rm d}y\Bigg)^{1/\rho}. \]

Also, let $M^\sharp$ be the sharp maximal function of Fefferman-Stein [6],

\[ M^\sharp(f)(x)=\sup_{Q\ni x} \inf_c\frac{1}{|Q|}\int_Q|f(y)-c|{\rm d}y\approx \sup_{Q\ni x}\frac{1}{|Q|}\int_Q|f(y)-f_Q|{\rm d}y, \]

and

\[ M_\rho^\sharp(f)(x)=\big(M^\sharp(|f|^\rho)(x)\big)^{1/\rho}=\Bigg(\sup_{Q\ni x} \inf_c\frac{1}{|Q|}\int_Q\big||f(y)|^\rho-c\big|{\rm d}y\Bigg)^{1/\rho}. \]

The maximal function $\mathcal {M}_{L(\log L)}(\vec f)(x)$ is defined by

\[ \mathcal{M}_{L(\log L)}(\vec f)(x)=\sup_{Q\ni x}\prod_{i=1}^m\|f_i\|_{L(\log L),Q}, \]

and $\mathcal {M}_{L(\log L)}(\vec f)$ is pointwise controlled by a multiple of $\prod _{j=1}^m M^2(f_j)(x)$.

We will use the following form of classical result of Fefferman and Stein [6]. Let $0< p,\,\rho <\infty$ and $\omega \in A_\infty.$ Then

\[ \int_{\mathbb{R}^n}\big(M_\rho (f)(x)\big)^p\omega(x){\rm d}x \lesssim\int_{\mathbb{R}^n}\big(M_\rho^\sharp (f)(x)\big)^p\omega(x){\rm d}x, \]

for all functions $f$ for which the left-hand side is finite.

Lemma 4.1 Let $T^*_{\vec {b}}$ be defined as in (1.4) and $K$ satisfies (1.1) with $N$ as in theorem 1.2. Fix $\omega \in A_p,$ $1< p<\infty$. Given functions $\vec b=(b_1,\,\ldots,\,b_m)$ which $b_i\in {\rm BMO},$ $i=1,\,\ldots,\,m$. Then for any bounded functions $\vec f=(f_1,\,\ldots,\,f_m)$ with compact support, we have

\[ \big\|T^*_{\vec b}(f_1,\ldots,f_m)\big\|_{L^p(\omega)} \lesssim\Bigg(\sum_{i=1}^m\|b_i\|_{\rm BMO}\Bigg)\|f_l\|_{L^p(\omega)}\prod_{j=1,j\neq l}^m\|f_j\|_{L^\infty},\quad l=1,2,\ldots,m. \]

Proof. By sublinearity, it is enough to consider the operator with only one symbol. For $1\leq i\leq m$, fix $b_i\in {\rm BMO}$ and consider the operator $T_{b_i}^*(\vec f)(x)$. Let $0<\delta <\varepsilon$ with $0<\delta <1/m$, Xue [22] proved:

(4.1)\begin{equation} M_\delta^\sharp(T_{b_i}^*(\vec f))(x) \lesssim\|b_i\|_{\rm BMO}\Bigg(\mathcal{M}_{L(\log L)}(\vec f)(x) +M_\varepsilon( T^*(\vec f))(x)\Bigg), \end{equation}

and

(4.2)\begin{equation} M_\delta^\sharp(T^*(\vec f))(x)\lesssim\mathcal{M}(\vec f)(x). \end{equation}

Taking $0<\delta <\varepsilon <1/m$, using (4.1) and (4.2) and the Fefferman–Stein inequality, we have

\begin{align*} \|T_{b_i}^*(\vec f)\|_{L^p(\omega)} & \leq \|M_\delta(T_{b_i}^*(\vec f))\|_{L^p(\omega)}\lesssim\|M_\delta^\sharp(T_{b_i}^*(\vec f))\|_{L^p(\omega)}\\ & \lesssim\|b_i\|_{\rm BMO}\big(\|\mathcal{M}_{L(\log L)}(\vec f)\|_{L^p(\omega)} +\|M_\varepsilon( T^*(\vec f))\|_{L^p(\omega)}\big)\\ & \lesssim\|b_i\|_{\rm BMO}\big(\|\mathcal{M}_{L(\log L)}(\vec f)\|_{L^p(\omega)} +\|M_\varepsilon^\sharp( T^*(\vec f))\|_{L^p(\omega)}\big)\\ & \lesssim\|b_i\|_{\rm BMO}\big(\|\mathcal{M}_{L(\log L)}(\vec f)\|_{L^p(\omega)} +\|\mathcal{M}(\vec f)\|_{L^p(\omega)}\big)\\ & \lesssim\|b_i\|_{\rm BMO}\|\mathcal{M}_{L(\log L)}(\vec f)\|_{L^p(\omega)}\lesssim\|b_i\|_{\rm BMO}\Bigg\|\prod_{j=1}^m M^2(f_j)\Bigg\|_{L^p(\omega)}\\ & \lesssim\|b_i\|_{\rm BMO}\prod_{j=1,j\neq l}^m\|M^2(f_j)\|_{L^\infty}\|M^2(f_l)\|_{L^p(\omega)}\\ & \lesssim\|b_i\|_{\rm BMO}\|f_l\|_{L^p(\omega)}\prod_{j=1,j\neq l}^m\|f_j\|_{L^\infty}. \end{align*}

To apply the Fefferman–Stein inequality in the above computations, we need to check that $\|M_\delta (T_{b_i}^*)(\vec f)\|_{L^p(\omega )}$ and $\|M_\varepsilon ( T^*(\vec f))\|_{L^p(\omega )}$ are finite. Note that $\omega \in A_p$, $\omega$ is also in $A_{p_0}$ with $pm< p_0<\infty$. So with $\varepsilon < p/p_0<1/m$ and the boundedness of Hardy–Littlewood maximal function, we have

\begin{align*} \|M_\varepsilon(T^*(\vec f))\|_{L^p(\omega)} & \leq \|M_{p/p_0}(T^*(\vec f))\|_{L^p(\omega)} =\|M(T^*(\vec f)^{p/p_0})\|_{L^{p_0}(\omega)}^{p_0/p}\\ & \lesssim\|T^*(\vec f)^{p/p_0}\|_{L^{p_0}(\omega)}^{p_0/p} = \|T^*(\vec f)\|_{L^{p}(\omega)}. \end{align*}

Then it is enough to prove $\|T^*(\vec f)\|_{L^{p}(\omega )}$ is finite for each family $\vec f$ of bounded functions with compact support for which $\|\mathcal {M}_{L(\log L)}(\vec f)\|_{L^p(\omega )}$ is finite. The arguments are as follows.

Without loss of generality, we assume $\operatorname {supp} f_i\subset Q(0,\,l)$ for $i=1,\,\ldots,\,m$. The weight $\omega$ is also in $L_{loc}^r$ for $r$ sufficiently close to 1 such that its dual exponent $r'$ satisfies $1/m < pr'<\infty.$ Thus, it follows from Hölder's inequality and the boundedness of $T^*$

(4.3)\begin{align} \|T^*(\vec f)\chi_{2Q}\|_{L^{p}(\omega)} & \leq \Bigg(\int_{2Q}|T^*(\vec f)(x)|^{pr'}{\rm d}x\Bigg)^{1/pr'} \Bigg(\int_{2Q}\omega(x)^rdx\Bigg)^{1/pr}\nonumber\\ & \lesssim\|T^*(\vec f)\|_{L^{pr'}}\lesssim \prod_{i=1}^m \|f_i\|_{L^{s_i}}<\infty, \end{align}

where $1/pr'=\sum _{i=1}^m 1/s_i$. For $x\in (2Q)^c$, $y_i\in Q$, we have $|x-y_i|\approx |x|$, $i=1,\,\ldots,\,m$,

(4.4)\begin{align} |T^*(\vec f)(x)| & \lesssim\int_{(Q(0,l))^m}\frac{\prod_{i=1}^m|f_i(y_i)|} {(\sum_{i=1}^m|x-y_i|)^{mn}}{\rm d}y_i\nonumber\\ & \lesssim\prod_{i=1}^m\frac{1}{|x|^n}\int_{Q(0,|x|)}|f_i(y_i)|{\rm d}y_i\lesssim\mathcal{M}(\vec f)(x)\lesssim\mathcal{M}_{L(\log L)}(\vec f)(x). \end{align}

Fom the assumption $\|\mathcal {M}_{L(\log L)}(\vec f)\|_{L^p(\omega )}$ is finite, we have

\[ \|T^*(\vec f)\chi_{(2Q)^c}\|_{L^{p}(\omega)}\lesssim \|\mathcal{M}_{L(\log L)}(\vec f)\chi_{(2Q)^c}\|_{L^{p}(\omega)}<\infty. \]

Thus, we obtain $\|M_\varepsilon ( T^*(\vec f))\|_{L^p(\omega )}$ is finite.

Next, we show $\|M_\delta (T_{b_i}^*)(\vec f)\|_{L^p(\omega )}$ is finite. It suffices to prove $\|T_{b_i}^*(\vec f)\|_{L^p(\omega )}$ is finite. First, we assume $b_i$ is bounded,

\begin{align*} T_{b_i}^*(\vec f)(x) & =\sup_{\delta>0}\Bigg|\int_{(\mathbb{R}^n)^m}(b_i(x)-b_i(y_j)) K_{\delta}(x,y_1,\ldots,y_m)\prod_{i=1}^mf_i(y_i){\rm d}y_i\Bigg|\\ & \leq |b_i(x)|T^*(\vec f)(x)+T^*(f_1,\ldots,b_if_i,\ldots,f_m)(x)\\ & \lesssim T^*(\vec f)(x)+T^*(f_1,\ldots,b_if_i,\ldots,f_m)(x). \end{align*}

Thus, following the similar arguments as (4.3), we have

\begin{align*} \|T_{b_i}^*(\vec f)\chi_{2Q}\|_{L^p(\omega)} & \lesssim\|T^*(\vec f)\chi_{2Q}\|_{L^p(\omega)} +\|T^*(f_1,\ldots,b_if_i,\ldots,f_m)\chi_{2Q}\|_{L^p(\omega)}\\ & \lesssim \prod_{i=1}^m \|f_i\|_{L^{s_i}(\omega)}<\infty. \end{align*}

On the other hand, for $x\in (2Q)^c$, note that $b$ is bounded, then similar to the arguments of (4.4), we have

\[ T_{b_i}^*(\vec f)(x)\lesssim\mathcal{M}_{L(\log L)}(\vec f)(x). \]

From the assumption, we obtain

\[ \|T_{b_i}^*(\vec f)\chi_{(2Q)^c}\|_{L^p(\omega)} \lesssim\|M_{L(\log L)}(\vec f)\chi_{(2Q)^c}\|_{L^p(\omega)}<\infty. \]

Thus, we proved $\|T_{b_i}^*(\vec f)\|_{L^p(\omega )}$ is finite when $b_i$ is bounded.

For general $b,$ we use the limiting argument as in [16]. Let $\{b_{i,j}\}$ be a sequence of functions such that

\[ b_{i,j}(x)= \begin{cases} j, & b_i(x)>j \\ b_i(x), & |b_i(x)|\leq j,\\ - j, & b_i(x)<{-}j. \end{cases} \]

Note that the sequence converges pointwise to $b_i$ almost everywhere, and $\|b_{i,j}\|_{\rm BMO}\lesssim \|b_i\|_{\rm BMO}$.

Since the family $\vec f$ is bounded with compact support and $T^*$ is bounded, we have that $T_{b_{i,j}}^*(\vec f)$ convergence to $T_{b_{i}}^*(\vec f)$ in $L^p$ is for every $1< p<\infty$. It follows that for a subsequence $\{b_{i,j'}\}\subset \{b_{i,j}\}$, $T^*_{b_{i,j'}}(\vec f)$ convergence to $T^*_{b_i}(\vec f)$ is almost everywhere. Then by Fatou's lemma, we get the required estimate. Thus, we complete the proof of lemma 4.1.

Lemma 4.2 [18, 21]

Let $T^*$ be defined as in (1.3) and $K$ satisfies (1.1) with $N$ as in theorem 1.2. For $0< p_i\leq 1,$ let $a_i$ be an $(H^{p_i}(\omega ),\,\infty,\,N)$-atom supported in $Q_k$, and $c_i$ be the centre of $Q_{i}$, $l_i$ be the side length of $Q_i$, $i=1,\,\ldots,\,m$. Assume $\tilde Q_1\cap \cdots \cap \tilde Q_m\neq \emptyset,$ then for any $x\in (\tilde Q_1\cap \cdots \cap \tilde Q_m)^c,$ we have

\[ |T^*(a_1,\ldots,a_m)(x)| \lesssim\prod_{i=1}^m\frac{\big(\omega(Q_{i})\big)^{{-}1/p_i}|Q_{i}|^{1+(N+1)/nm}} {(|x-c_{i}|+l_{i})^{n+(N+1)/m}}. \]

Now, we are in the position to prove theorem 1.3.

Proof of theorem 1.3. Proof of theorem 1.3

We use the same arguments as in proving theorem 1.2. By sublinearity, it is enough to consider the operator with only one symbol. For $1\leq l\leq m$, fix then $b_l\in \mathcal {BMO}_{\omega,p_l}$ and consider the operator $T^*_{b_l}(f_1,\,\ldots,\,f_m)(x)$. By lemma 2.4, we will work with finite sums of weighted Hardy atoms and obtain estimates independent of the number of terms in each sum. We write $f_i$ as a finite sum of atoms,

\[ f_i=\sum_{k_i=1}^M\lambda_{i,k_i}a_{i,k_i},\quad i=1,2,\ldots,m, \]

where $\lambda _{i,k_i}\geq 0$ and $a_{i,k_i}$ are $(H^{p_i}(\omega ),\,\infty,\,N)$-atoms. They are supported in cubes $Q_{i,k_i}$, $\|a_{i,k_i}\|_{L^\infty }\leq (\omega (Q_{i,k_i}))^{-1/p_i}$, $\int _{Q_{i,k_i}} x^\beta a_{i,k_i}(x){\rm d}x=0$ for all $|\beta |\leq N,$ and

\[ \sum_{k_i}\lambda_{i,k_i}^{p_i}\lesssim\|f_i\|_{H^{p_i}(\omega)}^{p_i}. \]

Denote the centre of $Q_{i,k_i}$ by $c_{i,k_i}$ and the side length of $Q_{i,k_i}$ by $l_{i,k_i}$. Using multi-sublinearity, we write

\[ T^*_{b_l}(f_1,\ldots,f_m)(x) \leq\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}T^*_{b_l}(a_{1,k_1},\ldots,a_{m,k_m})(x). \]

Then, we decompose $T^*_{b_l}(f_1,\,\ldots,\,f_m)(x)$ into two parts, for $x\in \mathbb {R}^n$

\[ T^*_{b_l}(f_1,\ldots,f_m)(x)\leq I(x)+II(x), \]

where

\begin{align*} & I(x):=\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m} T^*_{b_l}(a_{1,k_1},\ldots,a_{m,k_m})(x) \chi_{\tilde Q_{1,k_1}\cap\cdots\cap \tilde Q_{m,k_m}},\\ & II(x):=\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m} T^*_{b_l}(a_{1,k_1},\ldots,a_{m,k_m})(x) \chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}. \end{align*}

By lemmas 2.2 and 4.1 and the same arguments as estimating $I_1$ in the proof of theorem 1.2, we have

\[ \|I\|_{L^p(\omega)}\lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

Next, we estimate $\|II\|_{L^p(\omega )}$, we split it again

\begin{align*} \|II\|_{L^p(\omega)}& \lesssim \Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}\big|b_l-b_{l,{Q_{l,k_l}}}\big|\\ & \quad\times T^*(a_{1,k_1},\ldots,a_{l,k_l},\ldots,a_{m,k_m}) \chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}\Bigg\|_{L^p(\omega)}\\ & \quad+\Bigg\|\sum_{k_1,\ldots,k_m}\lambda_{1,k_1}\cdots\lambda_{m,k_m}\\ & \quad\times T^*\big(a_{1,k_1},\ldots,(b_l-b_{l,{Q_{l,k_l}}}) a_{l,k_l},\ldots,a_{m,k_m}\big) \chi_{\tilde Q_{1,k_1}^c\cup\cdots\cup \tilde Q_{m,k_m}^c}\Bigg\|_{L^p(\omega)}\\ & \quad=:\|II_{1}\|_{L^p(\omega)}+\|II_{2}\|_{L^p(\omega)}. \end{align*}

Using lemmas 2.3 and 4.2 and the same arguments as estimating $I_{21}$ in the proof of theorem 1.2, we can obtain

\[ \|II_{1}\|_{L^p(\omega)}\lesssim\|b_l\|_{\rm BMO}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

To estimate $\|II_{2}\|_{L^p(\omega )}$, for any $k_i\in \{1,\,2,\,\ldots,\,M\}$, $i=1,\,\ldots,\,m$, we only need to show

\begin{align*} & \Bigg\|T^*\big(\lambda_{1,k_1} a_{1,k_1},\ldots,\lambda_{l,k_l}(b_l-b_{l,{Q_{l,k_l}}}) a_{l,k_l},\ldots,\lambda_{m,k_m}a_{m,k_m}\big)\Bigg\|_{L^p(\omega)}\\ & \quad\lesssim \|b_l\|_{\mathcal{BMO}_{\omega,p_l}}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \end{align*}

By the boundedness of $T^*$ from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$ to $L^p(\omega )$, we need to show

\[ \big\|\lambda_{i,k_i}a_{i,k_i}\big\|_{H^{p_i}({\omega})} \lesssim\|f_i\|_{H^{p_i}(\omega)},\quad k_i\in\{1,\ldots,M\}, \quad i\in\{1,\ldots,m\}\backslash l, \]

and

\[ \big\|\lambda_{l,k_l}(b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big\|_{H^{p_l}({\omega})} \lesssim\|f_l\|_{H^{p_l}(\omega)}\|b_l\|_{\mathcal{BMO}_{\omega,p_l}}, \quad k_l\in\{1,\ldots,M\}. \]

Using the same argument as (3.1), we can obtain

\[ \big\|\lambda_{i,k_i}\mathcal{M}_N(a_{i,k_i}) \big\|_{L^{p_i}(\omega)} \lesssim\|f_i\|_{H^{p_i}(\omega)},\quad k_i\in\{1,\ldots,M\},\quad i\in\{1,\ldots,m\}\backslash l, \]

and

\[ \big\|\lambda_{l,k_l}\mathcal{M}_N\big((b_l-b_{l,{Q_{l,k_l}}})a_{l,k_l}\big) \big\|_{L^{p_l}(\omega)}\lesssim\|f_l\|_{H^{p_l}(\omega)}\|b_l\|_{\mathcal{BMO}_{\omega,p_l}}, \quad k_l\in\{1,\ldots,M\}. \]

Thus,

\[ \|II_{2}\|_{L^p(\omega)}\lesssim \| b_l\|_{\mathcal{BMO}_{\omega,p_l}}\prod_{i=1}^m\|f_i\|_{H^{p_i}(\omega)}. \]

Combining the estimates in both cases, there is

\[ \big\|T^*_{\vec b}(\vec f)\big\|_{L^p(\omega)}\lesssim\Bigg(\sum_{j=1}^m\| b_j\|_{\mathcal{BMO}_{\omega, p_j}}\Bigg)\prod_{i=1}^m\|f_i\|_{H^{p_i}({\omega})}, \]

which completes the proof of theorem 1.3.