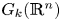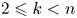1. Introduction
For a path-connected space $X$![]() we denote its topological complexity by $\mathrm {TC}(X)$
we denote its topological complexity by $\mathrm {TC}(X)$![]() . In [Reference Pavešić9] the author considered the problem of finding $\mathrm {TC}(G_k(\mathbb {R}^{n}))$
. In [Reference Pavešić9] the author considered the problem of finding $\mathrm {TC}(G_k(\mathbb {R}^{n}))$![]() for various $2\leqslant k< n$
for various $2\leqslant k< n$![]() (in this paper, $G_k(\mathbb {R}^{n})$
(in this paper, $G_k(\mathbb {R}^{n})$![]() denotes the real Grassmann manifold of $k$
denotes the real Grassmann manifold of $k$![]() -dimensional subspaces in $\mathbb {R}^{n}$
-dimensional subspaces in $\mathbb {R}^{n}$![]() ). Unfortunately, there is a problem with the proof of the main lemma of that paper (lemma 4.4) and the consequential results on the topological complexity (theorems 4.5, 4.8 and 4.12); see [Reference Pavešić10]. In this paper we reconsider this problem, and as an outcome correct and improve several results from [Reference Pavešić9]. As in [Reference Pavešić9], we use the cohomology method to obtain our results.
). Unfortunately, there is a problem with the proof of the main lemma of that paper (lemma 4.4) and the consequential results on the topological complexity (theorems 4.5, 4.8 and 4.12); see [Reference Pavešić10]. In this paper we reconsider this problem, and as an outcome correct and improve several results from [Reference Pavešić9]. As in [Reference Pavešić9], we use the cohomology method to obtain our results.
This paper closely follows and builds on the ideas presented in [Reference Pavešić9] (so, for background, motivation and all undefined notions, the reader is advised to consult [Reference Pavešić9]). Throughout the paper we will use, as much as possible, the notation from [Reference Pavešić9]. In particular, we will be working with the unreduced topological complexity, as defined by Farber in [Reference Farber5] (e.g. by this definition the topological complexity of a contractible space is equal to 1).
The paper is organized as follows. In § 2 we describe the cohomology method mentioned above and give an overview of the cohomology of real Grassmannians. In § 3 we consider the case $k=2$![]() . We obtain the exact value of the zero-divisor cup-length of $G_2(\mathbb {R}^{2^{s}+1})$
. We obtain the exact value of the zero-divisor cup-length of $G_2(\mathbb {R}^{2^{s}+1})$![]() (denoted by $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))$
(denoted by $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))$![]() , and defined in § 2) for $s\geqslant 2$
, and defined in § 2) for $s\geqslant 2$![]() ; additionally, for $s\geqslant 3$
; additionally, for $s\geqslant 3$![]() , $2^{s}+4\leqslant n\leqslant 2^{s+1}$
, $2^{s}+4\leqslant n\leqslant 2^{s+1}$![]() we prove a lower bound for $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$
we prove a lower bound for $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$![]() . These results show that the value of the zero-divisor cup-length given in [Reference Pavešić9, theorem 4.5] is not correct; what is more interesting, our results improve lower bounds for topological complexity stated in the same theorem. Section 4 is devoted to the case $k=3$
. These results show that the value of the zero-divisor cup-length given in [Reference Pavešić9, theorem 4.5] is not correct; what is more interesting, our results improve lower bounds for topological complexity stated in the same theorem. Section 4 is devoted to the case $k=3$![]() . Separately, we prove lower bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$
. Separately, we prove lower bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$![]() in the cases $n=2^{s}+1$
in the cases $n=2^{s}+1$![]() (for $s\geqslant 3$
(for $s\geqslant 3$![]() ), and $2^{s}+3\leqslant n\leqslant 2^{s+1}$
), and $2^{s}+3\leqslant n\leqslant 2^{s+1}$![]() (for $s\geqslant 2$
(for $s\geqslant 2$![]() ). The first result shows that the corresponding result from [Reference Pavešić9, theorem 4.8] is not correct, and improves the stated lower bound for topological complexity of $G_3(\mathbb {R}^{2^{s}+1})$
). The first result shows that the corresponding result from [Reference Pavešić9, theorem 4.8] is not correct, and improves the stated lower bound for topological complexity of $G_3(\mathbb {R}^{2^{s}+1})$![]() (for $s\geqslant 5$
(for $s\geqslant 5$![]() ). In § 5 we give a general lower bound for $\mathrm {zcl}(G_k(\mathbb {R}^{n}))$
). In § 5 we give a general lower bound for $\mathrm {zcl}(G_k(\mathbb {R}^{n}))$![]() (for $k\geqslant 4$
(for $k\geqslant 4$![]() ). For $k\geqslant 9$
). For $k\geqslant 9$![]() this result improves the bounds stated in [Reference Pavešić9, theorem 4.10].
this result improves the bounds stated in [Reference Pavešić9, theorem 4.10].
2. Background and notation
As mentioned in the Introduction, to obtain our results we use the so-called cohomology method, which we now (briefly) explain.
Let $\Delta :X\rightarrow X\times X$![]() denote the diagonal map. Then the elements of
denote the diagonal map. Then the elements of
are called zero-divisors. Furthermore, the zero-divisor cup-length of $X$![]() , denoted by $\mathrm {zcl}(X)$
, denoted by $\mathrm {zcl}(X)$![]() , is defined to be the maximum number of elements from $\mathrm {Ker}\,\Delta ^{*}$
, is defined to be the maximum number of elements from $\mathrm {Ker}\,\Delta ^{*}$![]() whose product is non-zero. In [Reference Farber5], Farber proved that $\mathrm {zcl}(X)$
whose product is non-zero. In [Reference Farber5], Farber proved that $\mathrm {zcl}(X)$![]() gives a lower bound for $\mathrm {TC}(X)$
gives a lower bound for $\mathrm {TC}(X)$![]() , that is $\mathrm {TC}(X)\geqslant \mathrm {zcl}(X)+1$
, that is $\mathrm {TC}(X)\geqslant \mathrm {zcl}(X)+1$![]() . Hence, a lower bound for $\mathrm {zcl}(X)$
. Hence, a lower bound for $\mathrm {zcl}(X)$![]() immediately gives a lower bound for $\mathrm {TC}(X)$
immediately gives a lower bound for $\mathrm {TC}(X)$![]() . Note that for every $w\in H^{*}(X;\mathbb {Z}_2)$
. Note that for every $w\in H^{*}(X;\mathbb {Z}_2)$![]() the element
the element
is in $\mathrm {Ker}\,\Delta ^{*}$![]() (since $\Delta ^{*}(z(w))=w\cdot 1+1\cdot w=0$
(since $\Delta ^{*}(z(w))=w\cdot 1+1\cdot w=0$![]() ). Then, by [Reference Cohen and Suciu2, lemma 5.2], $\mathrm {Ker}\,\Delta ^{*}$
). Then, by [Reference Cohen and Suciu2, lemma 5.2], $\mathrm {Ker}\,\Delta ^{*}$![]() is generated as an ideal by these elements, that is by the set $\{z(w)\,:\,w\in H^{*}(X;\mathbb {Z}_2)\}$
is generated as an ideal by these elements, that is by the set $\{z(w)\,:\,w\in H^{*}(X;\mathbb {Z}_2)\}$![]() . So, if $\mathrm {zcl}(X)=t$
. So, if $\mathrm {zcl}(X)=t$![]() , then there are classes $x_1,\,x_2,\,\ldots,\,x_t\in {H}^{*}(X;\mathbb {Z}_2)$
, then there are classes $x_1,\,x_2,\,\ldots,\,x_t\in {H}^{*}(X;\mathbb {Z}_2)$![]() such that $z(x_1)z(x_2)\cdots z(x_t)\neq 0$
such that $z(x_1)z(x_2)\cdots z(x_t)\neq 0$![]() .
.
To get the best possible results on $\mathrm {TC}(G_k(\mathbb {R}^{n}))$![]() using the cohomology method, one requires fine understanding of the cohomology algebra $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
using the cohomology method, one requires fine understanding of the cohomology algebra $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . There are several ways to describe this algebra; in this paper we will use the one due to Borel (see [Reference Borel1]):
. There are several ways to describe this algebra; in this paper we will use the one due to Borel (see [Reference Borel1]):
where $w_1,\,w_2,\,\ldots,\,w_k$![]() are the Stiefel–Whitney classes of the canonical $k$
are the Stiefel–Whitney classes of the canonical $k$![]() -dimensional vector bundle over $G_k(\mathbb {R}^{n})$
-dimensional vector bundle over $G_k(\mathbb {R}^{n})$![]() , and $I_{k,n}=(\overline {w}_{n-k+1},\,\overline {w}_{n-k+2},\,\ldots,\,\overline {w}_{n})$
, and $I_{k,n}=(\overline {w}_{n-k+1},\,\overline {w}_{n-k+2},\,\ldots,\,\overline {w}_{n})$![]() is the ideal generated by dual classes.
is the ideal generated by dual classes.
Although Borel's description of $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() appears simple enough, it turns out that performing concrete calculations in this algebra can be rather difficult. Hence, one usually needs to apply some additional methods and properties of $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
appears simple enough, it turns out that performing concrete calculations in this algebra can be rather difficult. Hence, one usually needs to apply some additional methods and properties of $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . The following result gives an additive basis for this algebra (see, e.g. [Reference Jaworowski7, Reference Petrović, Prvulović and Radovanović11]).
. The following result gives an additive basis for this algebra (see, e.g. [Reference Jaworowski7, Reference Petrović, Prvulović and Radovanović11]).
Proposition 2.1 The set $B_{k,n-k}=\{w_1^{a_1}\cdots w_k^{a_k}\,:\,0\leqslant a_1+\cdots +a_k\leqslant n-k\}$![]() is an additive basis for $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
is an additive basis for $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() .
.
The height of a class $c\in \widetilde {H}^{*}(X;\mathbb {Z}_2)$![]() , denoted by $\mathrm {ht}(c)$
, denoted by $\mathrm {ht}(c)$![]() , is the largest $m\in \mathbb {N}$
, is the largest $m\in \mathbb {N}$![]() such that $c^{m}\neq 0$
such that $c^{m}\neq 0$![]() . For $k\geqslant 2$
. For $k\geqslant 2$![]() , the height of $w_1\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
, the height of $w_1\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() is obtained by Stong in [Reference Stong12]: if $2\leqslant k\leqslant n-k$
is obtained by Stong in [Reference Stong12]: if $2\leqslant k\leqslant n-k$![]() and $s$
and $s$![]() is the unique positive integer such that $2^{s}< n\leqslant 2^{s+1}$
is the unique positive integer such that $2^{s}< n\leqslant 2^{s+1}$![]() , then
, then
In this paper we will often use Stong's method from [Reference Stong12] for calculations in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() (later this method was generalized by Korbaš and Lörinc to all flag manifolds, see [Reference Korbaš and Lörinc8]). In what follows we briefly explain this method.
(later this method was generalized by Korbaš and Lörinc to all flag manifolds, see [Reference Korbaš and Lörinc8]). In what follows we briefly explain this method.
Let $\mathrm {Flag}(\mathbb {R}^{n})$![]() denote the (real) complete flag manifold ($n\geqslant 2$
denote the (real) complete flag manifold ($n\geqslant 2$![]() ). Denote by $e_i:=w_1(\gamma _i)$
). Denote by $e_i:=w_1(\gamma _i)$![]() the first Stiefel–Whitney class of the canonical line bundle $\gamma _i$
the first Stiefel–Whitney class of the canonical line bundle $\gamma _i$![]() over $\mathrm {Flag}(\mathbb {R}^{n})$
over $\mathrm {Flag}(\mathbb {R}^{n})$![]() , for $1\leqslant i\leqslant n$
, for $1\leqslant i\leqslant n$![]() . Then we have the map $\pi :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow G_k(\mathbb {R}^{n})$
. Then we have the map $\pi :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow G_k(\mathbb {R}^{n})$![]() , given by
, given by
The following result will be very useful for our calculations in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() (and $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
(and $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() ).
).
Proposition 2.2
(1) The set $B_n=\{e_1^{a_1}e_2^{a_2}\cdots e_{n-1}^{a_{n-1}}\,:\,0\leqslant a_i\leqslant n-i\}$
 is an additive basis for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
is an additive basis for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ .
.(2) $\mathrm {ht}(e_i)=n-1$
 for $1\leqslant i\leqslant n$
for $1\leqslant i\leqslant n$ . In particular $e_i^{n}=0$
. In particular $e_i^{n}=0$ for $1\leqslant i\leqslant n$
for $1\leqslant i\leqslant n$ .
.(3) A monomial $e_1^{a_1}e_2^{a_2}\cdots e_n^{a_n}\in H^{\binom {n}{2}}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
 is non-zero if and only if $(a_1,\,a_2,\,\ldots,\,a_n)$
is non-zero if and only if $(a_1,\,a_2,\,\ldots,\,a_n)$ is a permutation of the $n$
is a permutation of the $n$ -tuple $(n-1,\,n-2,\,\ldots,\,1,\,0)$
-tuple $(n-1,\,n-2,\,\ldots,\,1,\,0)$ .
.(4) If $u\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
 and
\[ v=e_1^{k-1}e_2^{k-2}\cdots e_{k-1}\cdot e_{k+1}^{n-k-1}e_{k+2}^{n-k-2}\cdots e_{n-1}\in H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2), \]then $\pi ^{*}(u)\cdot v\in H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
and
\[ v=e_1^{k-1}e_2^{k-2}\cdots e_{k-1}\cdot e_{k+1}^{n-k-1}e_{k+2}^{n-k-2}\cdots e_{n-1}\in H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2), \]then $\pi ^{*}(u)\cdot v\in H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
 , and $u\neq 0$
, and $u\neq 0$ if and only if $\pi ^{*}(u)\cdot v\neq 0$
if and only if $\pi ^{*}(u)\cdot v\neq 0$ .
.(5) For $1\leqslant i\leqslant k,$
 $\pi ^{*}(w_{i})$
$\pi ^{*}(w_{i})$ is the $i$
is the $i$ -th elementary symmetric polynomial in the variables $e_{1},\,e_{2},\,\ldots,\,e_{k}$
-th elementary symmetric polynomial in the variables $e_{1},\,e_{2},\,\ldots,\,e_{k}$ .
.
Heights of the classes $z(w_1)$![]() and $z(w_k)$
and $z(w_k)$![]() will be very useful in our calculations. In what follows we determine these values.
will be very useful in our calculations. In what follows we determine these values.
It turns out that if $\mathrm {ht}(w)$![]() is known, then $\mathrm {ht}(z(w))$
is known, then $\mathrm {ht}(z(w))$![]() can easily be calculated. This is proven in lemma 4.3 from [Reference Pavešić9]. Namely, one has: if $w\in H^{*}(X;\mathbb {Z}_2)$
can easily be calculated. This is proven in lemma 4.3 from [Reference Pavešić9]. Namely, one has: if $w\in H^{*}(X;\mathbb {Z}_2)$![]() and $t$
and $t$![]() is the unique non-negative integer such that $2^{t}\leqslant \mathrm {ht}(w)<2^{t+1}$
is the unique non-negative integer such that $2^{t}\leqslant \mathrm {ht}(w)<2^{t+1}$![]() , then
, then
We will apply this identity for $X=G_k(\mathbb {R}^{n})$![]() , when $2\leqslant k\leqslant n-k$
, when $2\leqslant k\leqslant n-k$![]() . If $2^{s}< n\leqslant 2^{s+1}$
. If $2^{s}< n\leqslant 2^{s+1}$![]() , then (2.1) implies
, then (2.1) implies
On the other hand, proposition 2.1 implies $w_k^{n-k}\neq 0$![]() , so $\mathrm {ht}(w_k)=n-k$
, so $\mathrm {ht}(w_k)=n-k$![]() (by observing dimension we conclude that $w_k^{n-k+1}=0$
(by observing dimension we conclude that $w_k^{n-k+1}=0$![]() ). Hence, if $t$
). Hence, if $t$![]() is the unique non-negative integer such that $2^{t}\leqslant n-k<2^{t+1}$
is the unique non-negative integer such that $2^{t}\leqslant n-k<2^{t+1}$![]() , then (2.2) implies
, then (2.2) implies
The following lemma will be particularly useful in § 3.
Lemma 2.3 Let $m,\,k,\,n\in \mathbb {N},$![]() $k< n,$
$k< n,$![]() and $d_1,\,\ldots,\,d_m\in \mathbb {N}$
and $d_1,\,\ldots,\,d_m\in \mathbb {N}$![]() be such that $d_1+\cdots +d_m\geqslant 2k(n-k)$
be such that $d_1+\cdots +d_m\geqslant 2k(n-k)$![]() . If $x_i\in H^{d_i}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
. If $x_i\in H^{d_i}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() for $1\leqslant i\leqslant m,$
for $1\leqslant i\leqslant m,$![]() then
then
Proof. Note that the product $p=z(x_1)\cdots z(x_m)$![]() is the sum of certain classes of the form $x\otimes y+y\otimes x$
is the sum of certain classes of the form $x\otimes y+y\otimes x$![]() , for some $x,\,y\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
, for some $x,\,y\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . Since $p$
. Since $p$![]() is in dimension at least $2k(n-k)=2\dim G_k(\mathbb {R}^{n})$
is in dimension at least $2k(n-k)=2\dim G_k(\mathbb {R}^{n})$![]() , so is $x\otimes y$
, so is $x\otimes y$![]() , and hence $x,\,y\in H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
, and hence $x,\,y\in H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() or $x\otimes y=y\otimes x=0$
or $x\otimes y=y\otimes x=0$![]() . There is only one non-zero class in $H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
. There is only one non-zero class in $H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , namely $w_k^{n-k}$
, namely $w_k^{n-k}$![]() (by proposition 2.1), and hence $x\otimes y=y\otimes x=0$
(by proposition 2.1), and hence $x\otimes y=y\otimes x=0$![]() or $x\otimes y=w_k^{n-k}\otimes w_k^{n-k}=y\otimes x$
or $x\otimes y=w_k^{n-k}\otimes w_k^{n-k}=y\otimes x$![]() . In both cases $x\otimes y+y\otimes x=0$
. In both cases $x\otimes y+y\otimes x=0$![]() , which implies $p=0$
, which implies $p=0$![]() .
.
Also, we recall some results from [Reference Pavešić9] that will be used in our calculations.
Lemma 2.4
(a) If $2^{s}< n\leqslant 2^{s+1},$
 then $w_1^{2^{s}} w_2^{n-2^{s}-1}\,{\neq}\,0$
then $w_1^{2^{s}} w_2^{n-2^{s}-1}\,{\neq}\,0$ and $w_1^{2^{s}}w_2^{n-2^{s}}\,{=}\,0$
and $w_1^{2^{s}}w_2^{n-2^{s}}\,{=}\,0$ in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ .
.(b) If $2^{s}+3\leqslant n\leqslant 2^{s+1}$
 and $t\,{=}\,n-2^{s},$
and $t\,{=}\,n-2^{s},$ then $w_1^{2^{s}} w_2^{2^{s}}w_3^{t-3}\,{\neq}\, 0$
then $w_1^{2^{s}} w_2^{2^{s}}w_3^{t-3}\,{\neq}\, 0$ in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$ .
.
Throughout the paper we use the same notation as in this section.
Finally, let us say a few words on lemma 4.4 from [Reference Pavešić9] and our strategy that bypasses the application of this lemma. In lemma 4.4 from [Reference Pavešić9] the author assumes that $u_1,\,\ldots,\,u_n\in H^{*}(X;\mathbb {Z}_2)$![]() and $k_1,\,\ldots,\,k_n\in \mathbb {N}$
and $k_1,\,\ldots,\,k_n\in \mathbb {N}$![]() are such that $u_1^{k_1}\cdots u_n^{k_n}\neq 0$
are such that $u_1^{k_1}\cdots u_n^{k_n}\neq 0$![]() , and wants to prove that $A=z(u_1)^{2^{r_1}-1}\cdots z(u_n)^{2^{r_n}-1}\neq 0$
, and wants to prove that $A=z(u_1)^{2^{r_1}-1}\cdots z(u_n)^{2^{r_n}-1}\neq 0$![]() , where $r_i$
, where $r_i$![]() is the unique integer such that $2^{r_i-1}\leqslant k_i<2^{r_i}$
is the unique integer such that $2^{r_i-1}\leqslant k_i<2^{r_i}$![]() for $1\leqslant i\leqslant n$
for $1\leqslant i\leqslant n$![]() . For this he notices that after expanding $A$
. For this he notices that after expanding $A$![]() one summand is $u_1^{k_1}\cdots u_n^{k_n}\otimes u_1^{2^{r_1}-k_1-1}\cdots u_n^{2^{r_n}-k_n-1}$
one summand is $u_1^{k_1}\cdots u_n^{k_n}\otimes u_1^{2^{r_1}-k_1-1}\cdots u_n^{2^{r_n}-k_n-1}$![]() , which is nonzero, and from this immediately concludes that $A\neq 0$
, which is nonzero, and from this immediately concludes that $A\neq 0$![]() . As we will see in the proofs of our results, the problem is that the set
. As we will see in the proofs of our results, the problem is that the set
can contain more than one element, and hence that the corresponding summands of $A$![]() with the first coordinate equal to $u_1^{k_1}\cdots u_n^{k_n}$
with the first coordinate equal to $u_1^{k_1}\cdots u_n^{k_n}$![]() may cancel out. So, in our proofs we choose the $n$
may cancel out. So, in our proofs we choose the $n$![]() -tuple $(k_1,\,\ldots,\,k_n)$
-tuple $(k_1,\,\ldots,\,k_n)$![]() a bit more carefully to ensure that
a bit more carefully to ensure that
and that this further leads to $A\neq 0$![]() (note: in our applications the degree of $z(u_i)$
(note: in our applications the degree of $z(u_i)$![]() in $A$
in $A$![]() will not always be $2^{r_i}-1$
will not always be $2^{r_i}-1$![]() , so we will have slightly different formulas than the one given above).
, so we will have slightly different formulas than the one given above).
3. Zero-divisor cup-length of $G_2(\mathbb {R}^{n})$
Let $s$![]() be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$
be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$![]() . In this section we consider $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$
. In this section we consider $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$![]() . We note that propositions 3.7 and 3.10, that we prove in this section, show that the corresponding results of [Reference Pavešić9, theorem 4.5] are not correct (see also remark 3.9). Fortunately, correct versions give better lower bounds for the topological complexity of $G_2(\mathbb {R}^{n})$
. We note that propositions 3.7 and 3.10, that we prove in this section, show that the corresponding results of [Reference Pavešić9, theorem 4.5] are not correct (see also remark 3.9). Fortunately, correct versions give better lower bounds for the topological complexity of $G_2(\mathbb {R}^{n})$![]() .
.
We will compare our results with the following upper bound from [Reference Pavešić9] (this result is a consequence of a general result from [Reference Costa and Farber3, theorem 1]).
Proposition 3.1 If $1\leqslant k< n,$![]() then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)$
then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)$![]() . In fact, if $k\neq 1$
. In fact, if $k\neq 1$![]() and $(k,\,n)\neq (2,\,2^{d}+1)$
and $(k,\,n)\neq (2,\,2^{d}+1)$![]() for all $d\in \mathbb {N},$
for all $d\in \mathbb {N},$![]() then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)-1$
then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)-1$![]() .
.
3.1 Preliminary lemmas
Let $n$![]() be a positive integer and $n=\sum _{i=0}^{t}\alpha _i\cdot 2^{i}$
be a positive integer and $n=\sum _{i=0}^{t}\alpha _i\cdot 2^{i}$![]() , where $\alpha _i\in \{0,\,1\}$
, where $\alpha _i\in \{0,\,1\}$![]() for $0\leqslant i\leqslant t$
for $0\leqslant i\leqslant t$![]() and $\alpha _t=1$
and $\alpha _t=1$![]() , its representation in base 2. Then we write $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$
, its representation in base 2. Then we write $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$![]() .
.
As we use $\mathbb {Z}_2$![]() coefficient the following special case of Lucas’ theorem will be particularly useful to us: if $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$
coefficient the following special case of Lucas’ theorem will be particularly useful to us: if $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$![]() and $m:=(\beta _r,\,\ldots,\,\beta _1,\,\beta _0)_2$
and $m:=(\beta _r,\,\ldots,\,\beta _1,\,\beta _0)_2$![]() , then
, then
We will use the following two consequences of Lucas’ theorem throughout the paper. Let $w\in H^{*}(X;\mathbb {Z}_2)$![]() . By Lucas’ theorem, $\binom {2^{m}}{i}$
. By Lucas’ theorem, $\binom {2^{m}}{i}$![]() is even for $1\leqslant i\leqslant 2^{m}-1$
is even for $1\leqslant i\leqslant 2^{m}-1$![]() , and so
, and so
On the other hand, by Lucas’ theorem $\binom {2^{m}-1}{i}$![]() is odd for all $0\leqslant i\leqslant 2^{m}-1$
is odd for all $0\leqslant i\leqslant 2^{m}-1$![]() , and hence
, and hence

We will also need the following result.
Lemma 3.2 Let $n$![]() be a non-negative integer. Then:
be a non-negative integer. Then:
(a) $\binom {2n}{n}$
 is odd if and only if $n=0;$
is odd if and only if $n=0;$
(b) $\binom {2n}{n+1}$
 is odd if and only if $n=2^{t+1}-1$
is odd if and only if $n=2^{t+1}-1$ for some $t\in \mathbb {N}_0$
for some $t\in \mathbb {N}_0$ .
.
Proof. Part (a) immediately follows from Lucas’ theorem.
For part (b) we note that $C_n=\binom {2n}{n}-\binom {2n}{n+1}$![]() is the $n$
is the $n$![]() -th Catalan number. Then the result follows from part (a) and the fact that $C_n$
-th Catalan number. Then the result follows from part (a) and the fact that $C_n$![]() (for $n\geqslant 1$
(for $n\geqslant 1$![]() ) is odd if and only if $n=2^{t+1}-1$
) is odd if and only if $n=2^{t+1}-1$![]() for some $t\in \mathbb {N}_0$
for some $t\in \mathbb {N}_0$![]() (see [Reference Eğecioğlu4]).
(see [Reference Eğecioğlu4]).
Lemma 3.3 Let $0\leqslant m\leqslant n-2$![]() and $\alpha _0,\,\alpha _1,\,\ldots,\,\alpha _{n-1-m}\in \mathbb {Z}_2$
and $\alpha _0,\,\alpha _1,\,\ldots,\,\alpha _{n-1-m}\in \mathbb {Z}_2$![]() . Then:
. Then:
(a) $\sum _{i=0}^{n-1-m} \alpha _ie_1^{m+i}e_2^{n-1-i}=0$
 in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ iff $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$
iff $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$ ;
;(b) for a polynomial $p\in H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
 in classes $e_1$
in classes $e_1$ and $e_2$
and $e_2$ one has
\[ p\cdot e_3^{n-3}e_4^{n-4}\cdots e_{n-1}=0\quad{in}\quad H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2) \]if and only if $p=0$
one has
\[ p\cdot e_3^{n-3}e_4^{n-4}\cdots e_{n-1}=0\quad{in}\quad H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2) \]if and only if $p=0$
 in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ .
.
Proof.
(a) By proposition 2.1 from [Reference González, Gutiérrez, Gutiérrez and Lara6] we have $e_2^{n-1}=e_1^{n-1}+e_1^{n-2}e_2+\dots +e_1e_2^{n-2}$
 (we use this proposition for $m=1$
(we use this proposition for $m=1$ , $k=n-1$
, $k=n-1$ and $i=n-2$
and $i=n-2$ ). Since $e_1^{n}=0$
). Since $e_1^{n}=0$ (by proposition 2.2(2)), we have
\[ \sum_{i=0}^{n-1-m} \alpha_ie_1^{m+i}e_2^{n-1-i}=\sum_{i=1}^{n-1-m}(\alpha_i+\alpha_0)e_1^{m+i}e_2^{n-1-i}. \]Since $e_1^{m+1}e_2^{n-2},\,e_1^{m+2}e_2^{n-3},\,\ldots,\,e_1^{n-1}e_2^{m}$
(by proposition 2.2(2)), we have
\[ \sum_{i=0}^{n-1-m} \alpha_ie_1^{m+i}e_2^{n-1-i}=\sum_{i=1}^{n-1-m}(\alpha_i+\alpha_0)e_1^{m+i}e_2^{n-1-i}. \]Since $e_1^{m+1}e_2^{n-2},\,e_1^{m+2}e_2^{n-3},\,\ldots,\,e_1^{n-1}e_2^{m}$
 are in the additive basis $B_n$
are in the additive basis $B_n$ (from proposition 2.2(1)), the last sum is zero if and only if $\alpha _1+\alpha _0=\alpha _2+\alpha _0=\dots =\alpha _{n-1-m}+\alpha _0=0$
(from proposition 2.2(1)), the last sum is zero if and only if $\alpha _1+\alpha _0=\alpha _2+\alpha _0=\dots =\alpha _{n-1-m}+\alpha _0=0$ , i.e. if and only if $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$
, i.e. if and only if $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$ .
.(b) As in part (a) we use the identities $e_2^{n-1}=e_1^{n-1}+e_1^{n-2}e_2+\dots +e_1e_2^{n-2}$
 and $e_1^{n}=e_2^{n}=0$
and $e_1^{n}=e_2^{n}=0$ to express $p$
to express $p$ in the form $\sum \alpha _{i,j}e_1^{i}e_2^{j}$
in the form $\sum \alpha _{i,j}e_1^{i}e_2^{j}$ , where $\alpha _{i,j}\in \{0,\,1\}$
, where $\alpha _{i,j}\in \{0,\,1\}$ , $0\leqslant i\leqslant n-1$
, $0\leqslant i\leqslant n-1$ and $0\leqslant j\leqslant n-2$
and $0\leqslant j\leqslant n-2$ . Then $\sum \alpha _{i,j}e_1^{i}e_2^{j}e_3^{n-3}e_4^{n-4}\cdots e_{n-1}$
. Then $\sum \alpha _{i,j}e_1^{i}e_2^{j}e_3^{n-3}e_4^{n-4}\cdots e_{n-1}$ ($=pe_3^{n-3}e_4^{n-4}\cdots e_{n-1}$
($=pe_3^{n-3}e_4^{n-4}\cdots e_{n-1}$ ) is a sum of the elements from the basis $B_n$
) is a sum of the elements from the basis $B_n$ from proposition 2.2(1); so this sum is zero if and only if $\alpha _{ij}=0$
from proposition 2.2(1); so this sum is zero if and only if $\alpha _{ij}=0$ for all $i,\,j$
for all $i,\,j$ , i.e. if and only if $p=0$
, i.e. if and only if $p=0$ (since $p$
(since $p$ is also represented in the basis $B_{n}$
is also represented in the basis $B_{n}$ ).
).
Remark 3.4 We will use the following consequence of part a) of this lemma. Let $p=\sum _{i=0}^{b-a} \alpha _ie_1^{a+i}e_2^{b-i}\in H^{a+b}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() for some $0\leqslant a\leqslant n-2$
for some $0\leqslant a\leqslant n-2$![]() , $a\leqslant b\leqslant n-1$
, $a\leqslant b\leqslant n-1$![]() . If there exist $0\leqslant i'\neq i''\leqslant b-a$
. If there exist $0\leqslant i'\neq i''\leqslant b-a$![]() such that $\alpha _{i'}=0$
such that $\alpha _{i'}=0$![]() and $\alpha _{i''}=1$
and $\alpha _{i''}=1$![]() , then $p\neq 0$
, then $p\neq 0$![]() .
.
Furthermore, if $q\in H^{c}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , where $c\leqslant 2n-3$
, where $c\leqslant 2n-3$![]() , is written as a sum of some monomials of the form $e_1^{i}e_2^{j}$
, is written as a sum of some monomials of the form $e_1^{i}e_2^{j}$![]() , then after removing all summands with $i\geqslant n$
, then after removing all summands with $i\geqslant n$![]() or $j\geqslant n$
or $j\geqslant n$![]() (since they are 0 by proposition 2.2(2)), we get that $q$
(since they are 0 by proposition 2.2(2)), we get that $q$![]() is written in the same way as $p$
is written in the same way as $p$![]() above.
above.
Lemma 3.5 If $2^{s}< n\leqslant 2^{s+1}$![]() and $a,\,b\in \mathbb {N}_0$
and $a,\,b\in \mathbb {N}_0$![]() are such that $a+2b=2(n-2),$
are such that $a+2b=2(n-2),$![]() then $w_1^{a}w_2^{b}\neq 0$
then $w_1^{a}w_2^{b}\neq 0$![]() in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() if and only if
if and only if
Proof. By proposition 2.2(4), $w_1^{a}w_2^{b}\neq 0$![]() in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() if and only if
if and only if
in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . After expanding we have
. After expanding we have

Note that by proposition 2.2(3) the only non-zero monomials in this sum are the ones for $i$![]() that satisfies $(i+1+b,\,a-i+b)\in \{(n-1,\,n-2),\,(n-2,\,n-1)\}$
that satisfies $(i+1+b,\,a-i+b)\in \{(n-1,\,n-2),\,(n-2,\,n-1)\}$![]() and $\binom {a}{i}$
and $\binom {a}{i}$![]() is odd, i.e. $i\in \{n-2-b,\,n-3-b\}$
is odd, i.e. $i\in \{n-2-b,\,n-3-b\}$![]() and $\binom {a}{i}$
and $\binom {a}{i}$![]() is odd.
is odd.
If $i=n-2-b$![]() , then $\binom {a}{i}=\binom {2(n-2-b)}{n-2-b}=\binom {2m}{m}$
, then $\binom {a}{i}=\binom {2(n-2-b)}{n-2-b}=\binom {2m}{m}$![]() (here $2m=2(n-2-b)=a$
(here $2m=2(n-2-b)=a$![]() ). By lemma 3.2 this number is odd only if $m=0$
). By lemma 3.2 this number is odd only if $m=0$![]() , i.e. $(a,\,b)=(0,\,n-2)$
, i.e. $(a,\,b)=(0,\,n-2)$![]() .
.
Let us now consider the case $i=n-3-b$![]() . Then $\binom {a}{i}=\binom {2(n-2-b)}{n-3-b}=\binom {2m}{m-1}=\binom {2m}{m+1}$
. Then $\binom {a}{i}=\binom {2(n-2-b)}{n-3-b}=\binom {2m}{m-1}=\binom {2m}{m+1}$![]() (again $2m=2(n-2-b)=a$
(again $2m=2(n-2-b)=a$![]() ). By lemma 3.2 this number is odd if and only if $m=2^{l}-1$
). By lemma 3.2 this number is odd if and only if $m=2^{l}-1$![]() for some $l\geqslant 1$
for some $l\geqslant 1$![]() . Then $a=2^{l+1}-2$
. Then $a=2^{l+1}-2$![]() and $b=n-2^{l}-1\geqslant 0$
and $b=n-2^{l}-1\geqslant 0$![]() , which completes our proof.
, which completes our proof.
Remark 3.6 If $w_1^{a}w_2^{b}\neq 0$![]() and $a+2b=2(n-2),$
and $a+2b=2(n-2),$![]() then, by proposition 2.1, $w_1^{a}w_2^{b}=w_2^{n-2}$
then, by proposition 2.1, $w_1^{a}w_2^{b}=w_2^{n-2}$![]() (since $w_2^{n-2}$
(since $w_2^{n-2}$![]() is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() ).
).
3.2 Some exact values
In this section we calculate $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$![]() for $n=2^{s}+1$
for $n=2^{s}+1$![]() .
.
In the proof of the main result we will use the following observation. Let $n\geqslant 4$![]() . Then, by proposition 2.1, every class in $H^{1}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
. Then, by proposition 2.1, every class in $H^{1}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() is of the form $\alpha w_1$
is of the form $\alpha w_1$![]() , $\alpha \in \mathbb {Z}_2$
, $\alpha \in \mathbb {Z}_2$![]() , while every class in $H^{2}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
, while every class in $H^{2}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() is of the form $\beta w_1^{2}+\gamma w_2$
is of the form $\beta w_1^{2}+\gamma w_2$![]() , $\beta,\,\gamma \in \mathbb {Z}_2$
, $\beta,\,\gamma \in \mathbb {Z}_2$![]() . Since $z(w_1^{2})=z(w_1)^{2}$
. Since $z(w_1^{2})=z(w_1)^{2}$![]() , we conclude: if $\mathrm {zcl}(G_2(\mathbb {R}^{n}))=t$
, we conclude: if $\mathrm {zcl}(G_2(\mathbb {R}^{n}))=t$![]() , then there are $a,\,b,\,c\in \mathbb {N}_0$
, then there are $a,\,b,\,c\in \mathbb {N}_0$![]() such that $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$
such that $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$![]() , where $a+b+c=t$
, where $a+b+c=t$![]() and $x_1,\,\ldots,\,x_c$
and $x_1,\,\ldots,\,x_c$![]() are some classes of $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
are some classes of $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() each in dimension at least 3.
each in dimension at least 3.
Proposition 3.7 For $s\geqslant 2$![]() and $n=2^{s}+1$
and $n=2^{s}+1$![]() one has
one has
Proof. First, we prove that $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-3}\neq 0$![]() . After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$
. After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$![]() , for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
, for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$
. By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$![]() (for $l\geqslant 2$
(for $l\geqslant 2$![]() ) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-3}{2^{s}-2^{l}}$
) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-3}{2^{s}-2^{l}}$![]() . By Lucas’ theorem each of these binomial coefficients is odd, so $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-3}$
. By Lucas’ theorem each of these binomial coefficients is odd, so $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-3}$![]() contains $w_2^{n-2}\otimes \sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$
contains $w_2^{n-2}\otimes \sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$![]() . Since $w_2^{n-2}$
. Since $w_2^{n-2}$![]() is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() (by proposition 2.1), it is enough to prove $\sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}\neq 0$
(by proposition 2.1), it is enough to prove $\sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}\neq 0$![]() (in $H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$
(in $H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$![]() ).
).
Note that by lemma 2.4, $w_1^{2^{s}}w_2=0$![]() , and so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}=0$
, and so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}=0$![]() for $2\leqslant l\leqslant s-1$
for $2\leqslant l\leqslant s-1$![]() . Hence, it is enough to prove that $w_1w_2^{2^{s}-3}=w_1w_2^{n-4}\neq 0$
. Hence, it is enough to prove that $w_1w_2^{2^{s}-3}=w_1w_2^{n-4}\neq 0$![]() , which follows from the fact that $w_1w_2^{n-4}$
, which follows from the fact that $w_1w_2^{n-4}$![]() is in the additive basis $B_{2,n-2}$
is in the additive basis $B_{2,n-2}$![]() (proposition 2.1). So, $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))\geqslant 2^{s+1}+2^{s}-4$
(proposition 2.1). So, $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))\geqslant 2^{s+1}+2^{s}-4$![]() .
.
Let us now prove that $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))\leqslant 2^{s+1}+2^{s}-4$![]() . Suppose that this is not the case and let $a,\,b,\,c\in \mathbb {N}_0$
. Suppose that this is not the case and let $a,\,b,\,c\in \mathbb {N}_0$![]() and $x_1,\,\ldots,\,x_c\in H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$
and $x_1,\,\ldots,\,x_c\in H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$![]() be some classes each in dimension at least 3, such that $a+b+c\geqslant 2^{s+1}+2^{s}-3$
be some classes each in dimension at least 3, such that $a+b+c\geqslant 2^{s+1}+2^{s}-3$![]() and $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$
and $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$![]() . By lemma 2.3, we have $a+2b+3c\leqslant 4(2^{s}-1)-1=2^{s+2}-5$
. By lemma 2.3, we have $a+2b+3c\leqslant 4(2^{s}-1)-1=2^{s+2}-5$![]() , and hence $b+2c\leqslant 2^{s}-2$
, and hence $b+2c\leqslant 2^{s}-2$![]() . Furthermore, since $z(w_1)^{2^{s+1}}=0$
. Furthermore, since $z(w_1)^{2^{s+1}}=0$![]() (by (2.3)), we have $a\leqslant 2^{s+1}-1$
(by (2.3)), we have $a\leqslant 2^{s+1}-1$![]() and hence $b+c=(a+b+c)-a\geqslant 2^{s}-2$
and hence $b+c=(a+b+c)-a\geqslant 2^{s}-2$![]() . This implies $b=2^{s}-2$
. This implies $b=2^{s}-2$![]() and $c=0$
and $c=0$![]() . Finally, $a+b+c\geqslant 2^{s+1}+2^{s}-3$
. Finally, $a+b+c\geqslant 2^{s+1}+2^{s}-3$![]() and $a\leqslant 2^{s+1}-1$
and $a\leqslant 2^{s+1}-1$![]() imply $a=2^{s+1}-1$
imply $a=2^{s+1}-1$![]() .
.
So, it is enough to prove $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-2}=0$![]() . Suppose that this is not the case. Note that the dimension of $A$
. Suppose that this is not the case. Note that the dimension of $A$![]() is $2^{s+1}-1+2(2^{s}-2)=4(n-2)-1$
is $2^{s+1}-1+2(2^{s}-2)=4(n-2)-1$![]() , so every summand of $A$
, so every summand of $A$![]() is of the form $x'\otimes x''$
is of the form $x'\otimes x''$![]() where one of the classes $x'$
where one of the classes $x'$![]() and $x''$
and $x''$![]() has dimension $2(n-2)$
has dimension $2(n-2)$![]() and the other $2(n-2)-1$
and the other $2(n-2)-1$![]() . Note that, by proposition 2.1, the only class in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
. Note that, by proposition 2.1, the only class in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() of dimension $2(n-2)$
of dimension $2(n-2)$![]() (resp. $2(n-2)-1$
(resp. $2(n-2)-1$![]() ) is $w_2^{n-2}$
) is $w_2^{n-2}$![]() (resp. $w_1w_2^{n-3}$
(resp. $w_1w_2^{n-3}$![]() ). By symmetry, this and $A\neq 0$
). By symmetry, this and $A\neq 0$![]() imply $A=w_2^{n-2}\otimes w_1w_2^{n-3}+w_1w_2^{n-3}\otimes w_2^{n-2}$
imply $A=w_2^{n-2}\otimes w_1w_2^{n-3}+w_1w_2^{n-3}\otimes w_2^{n-2}$![]() . Now, we proceed as in the first part of the proof to prove that the coefficient of $w_2^{n-2}\otimes w_1w_2^{n-3}$
. Now, we proceed as in the first part of the proof to prove that the coefficient of $w_2^{n-2}\otimes w_1w_2^{n-3}$![]() in $A$
in $A$![]() is zero. By lemma 3.5 each such summand in $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-2}$
is zero. By lemma 3.5 each such summand in $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-2}$![]() is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}$
is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}$![]() (for some $1\leqslant l\leqslant s$
(for some $1\leqslant l\leqslant s$![]() ) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-2}{2^{s}-2^{l}}$
) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-2}{2^{s}-2^{l}}$![]() . By Lucas’ theorem this coefficient is 1, so it is enough to prove $\sum _{l=1}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$
. By Lucas’ theorem this coefficient is 1, so it is enough to prove $\sum _{l=1}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$![]() .
.
Again, by lemma 2.4, $w_1^{2^{s}}w_2=0$![]() , so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$
, so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$![]() for $2\leqslant l\leqslant s-1$
for $2\leqslant l\leqslant s-1$![]() . Hence, the previous sum is equal to $w_1^{2^{s+1}-3}+w_1w_2^{2^{s}-2}$
. Hence, the previous sum is equal to $w_1^{2^{s+1}-3}+w_1w_2^{2^{s}-2}$![]() . By (2.1), $w_1^{2^{s+1}-3}\neq 0$
. By (2.1), $w_1^{2^{s+1}-3}\neq 0$![]() , so $w_1^{2^{s+1}-3}=w_1w_2^{n-3}=w_1w_2^{2^{s}-2}$
, so $w_1^{2^{s+1}-3}=w_1w_2^{n-3}=w_1w_2^{2^{s}-2}$![]() , and hence $A=0$
, and hence $A=0$![]() .
.
Remark 3.8 By proposition 3.1, $\mathrm {TC}(G_2(\mathbb {R}^{2^{s}+1}))\leqslant 2^{s+2}-4$![]() , so there is a gap of $2^{s}-1$
, so there is a gap of $2^{s}-1$![]() between our lower bound and this bound. For example, $9\leqslant \mathrm {TC}(G_2(\mathbb {R}^{5})) \leqslant 12$
between our lower bound and this bound. For example, $9\leqslant \mathrm {TC}(G_2(\mathbb {R}^{5})) \leqslant 12$![]() .
.
Remark 3.9 Ideas from this paper can be used to prove the following:
(1) If $s\geqslant 1$
 , then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+2}))=3\cdot 2^{s}-2$
, then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+2}))=3\cdot 2^{s}-2$ (one has $z(w_1)^{2^{s+1}-2}z(w_2)^{2^{s}}\neq 0$
(one has $z(w_1)^{2^{s+1}-2}z(w_2)^{2^{s}}\neq 0$ ). So, by proposition 3.1, $3\cdot 2^{s}-1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+2}))\leqslant 2^{s+2}-1$
). So, by proposition 3.1, $3\cdot 2^{s}-1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+2}))\leqslant 2^{s+2}-1$ .
.(2) If $s\geqslant 2$
 , then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+3}))=3\cdot 2^{s}$
, then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+3}))=3\cdot 2^{s}$ (one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+1}\neq 0$
(one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+1}\neq 0$ ). So, by proposition 3.1, $3\cdot 2^{s}+1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+3}))\leqslant 2^{s+2}+3$
). So, by proposition 3.1, $3\cdot 2^{s}+1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+3}))\leqslant 2^{s+2}+3$ .
.
Complete proofs of these results can be found in the extended version of this paper which is available on the author's website.
3.3 General bounds for $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$
Let $2^{s}+4\leqslant n\leqslant 2^{s+1}$![]() and $t=n-2^{s}$
and $t=n-2^{s}$![]() . Also, we assume $s\geqslant 3$
. Also, we assume $s\geqslant 3$![]() (i.e. $n\neq 8$
(i.e. $n\neq 8$![]() ). Furthermore, let $r$
). Furthermore, let $r$![]() be the unique integer such that $2^{r-1}< t\leqslant 2^{r}$
be the unique integer such that $2^{r-1}< t\leqslant 2^{r}$![]() . Since $t\geqslant 4$
. Since $t\geqslant 4$![]() , we have $r\geqslant 2$
, we have $r\geqslant 2$![]() . Let $j$
. Let $j$![]() be the smallest positive integer such that the digit on position $j$
be the smallest positive integer such that the digit on position $j$![]() in the binary representation of $t-2$
in the binary representation of $t-2$![]() is equal to 1 ($j$
is equal to 1 ($j$![]() is well-defined since $t-2\geqslant 2$
is well-defined since $t-2\geqslant 2$![]() ); in other words, $t-2$
); in other words, $t-2$![]() has the binary representation of the following form
has the binary representation of the following form
for some $\alpha _0,\,\alpha _{j+1},\,\alpha _{j+2},\,\ldots,\,\alpha _{m-1}\in \{0,\,1\}$![]() and $1\leqslant j\leqslant m$
and $1\leqslant j\leqslant m$![]() . Since $2^{m}\leqslant t-2\leqslant 2^{r}-2\leqslant 2^{s}-2$
. Since $2^{m}\leqslant t-2\leqslant 2^{r}-2\leqslant 2^{s}-2$![]() , we additionally have $1\leqslant j\leqslant m< r\leqslant s$
, we additionally have $1\leqslant j\leqslant m< r\leqslant s$![]() .
.
Proposition 3.10 If $n,$![]() $s,$
$s,$![]() $t,$
$t,$![]() $r$
$r$![]() and $j$
and $j$![]() are as above, then
are as above, then
and $\mathrm {TC}(G_2(\mathbb {R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{r}-\varepsilon -1$![]() , where $\varepsilon =\left \{\begin {smallmatrix} 2^{j},\, & \mbox {if }t\mbox { is even} \\ 2^{j}+1,\, & \mbox {otherwise.} \end {smallmatrix}\right.$
, where $\varepsilon =\left \{\begin {smallmatrix} 2^{j},\, & \mbox {if }t\mbox { is even} \\ 2^{j}+1,\, & \mbox {otherwise.} \end {smallmatrix}\right.$![]()
Proof. It is enough to prove that $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+2^{r}-\varepsilon -1}\neq 0$![]() . After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$
. After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$![]() , for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
, for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$
. By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$![]() , $0\leqslant l\leqslant s$
, $0\leqslant l\leqslant s$![]() , with coefficient $\alpha _l=\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}=\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}$
, with coefficient $\alpha _l=\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}=\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}$![]() . (Note: if $2^{r}+2^{l}-\varepsilon -t<0$
. (Note: if $2^{r}+2^{l}-\varepsilon -t<0$![]() , then $2^{s}+2^{r}-\varepsilon -1<2^{s}+t-2^{l}-1$
, then $2^{s}+2^{r}-\varepsilon -1<2^{s}+t-2^{l}-1$![]() and hence $\alpha _l=0$
and hence $\alpha _l=0$![]() , so there is no need to discard summands $\alpha _lw_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$
, so there is no need to discard summands $\alpha _lw_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$![]() when $2^{r}+2^{l}-\varepsilon -t<0$
when $2^{r}+2^{l}-\varepsilon -t<0$![]() .) Since $w_2^{n-2}$
.) Since $w_2^{n-2}$![]() is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$
is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$![]() (by proposition 2.1), it is enough to prove
(by proposition 2.1), it is enough to prove

Let us first consider the case when $t$![]() is even. Then $\varepsilon =2^{j}$
is even. Then $\varepsilon =2^{j}$![]() . Note that $2^{s}+2^{r}-2^{j}-1=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +1$
. Note that $2^{s}+2^{r}-2^{j}-1=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +1$![]() ($j< r$
($j< r$![]() ). So, by Lucas’ theorem, $\alpha _0$
). So, by Lucas’ theorem, $\alpha _0$![]() and $\alpha _s$
and $\alpha _s$![]() are even (since both $2^{s}+t-2$
are even (since both $2^{s}+t-2$![]() and $t-1$
and $t-1$![]() have digit 1 on the $j$
have digit 1 on the $j$![]() -th position in the binary representation), while $\alpha _j$
-th position in the binary representation), while $\alpha _j$![]() is odd (since $2^{s}+t-1-2^{j}$
is odd (since $2^{s}+t-1-2^{j}$![]() has digit 0 on the $j$
has digit 0 on the $j$![]() -th position in the binary representation).
-th position in the binary representation).
Let us denote $\tau =2^{r}-2^{j}-t$![]() . Note that $t-2+2^{j}\leqslant 2^{r}$
. Note that $t-2+2^{j}\leqslant 2^{r}$![]() , i.e. $\tau \geqslant -2$
, i.e. $\tau \geqslant -2$![]() . By proposition 2.2.(4), $A\neq 0$
. By proposition 2.2.(4), $A\neq 0$![]() if and only if
if and only if

and, by part (b) of lemma 3.3, if and only if

To prove that $p_1\neq 0$![]() we will use remark 3.4, i.e. we write $p_1$
we will use remark 3.4, i.e. we write $p_1$![]() as in remark 3.4 and find suitable indices $i'$
as in remark 3.4 and find suitable indices $i'$![]() and $i''$
and $i''$![]() (as in that remark). We denote
(as in that remark). We denote

Let us observe a monomial $e_1^{a}e_2^{b}$![]() that appears in the inner sum for $l$
that appears in the inner sum for $l$![]() . Then $a+b=2^{s+1}+2\tau$
. Then $a+b=2^{s+1}+2\tau$![]() and $a-b=(2i+1-2^{s-l})2^{l+1}$
and $a-b=(2i+1-2^{s-l})2^{l+1}$![]() , i.e. $2^{l+1}\parallel a-b$
, i.e. $2^{l+1}\parallel a-b$![]() for $s\neq l$
for $s\neq l$![]() (i.e. $2^{l+1}\mid a-b$
(i.e. $2^{l+1}\mid a-b$![]() and $2^{l+2}\nmid a-b$
and $2^{l+2}\nmid a-b$![]() ) and $a=b$
) and $a=b$![]() for $s=l$
for $s=l$![]() ; so, $e_1^{a}e_2^{b}$
; so, $e_1^{a}e_2^{b}$![]() appears only once in $q_1$
appears only once in $q_1$![]() and its coefficient is $\alpha _l$
and its coefficient is $\alpha _l$![]() . Now, since $\alpha _s$
. Now, since $\alpha _s$![]() is even this implies that the coefficient of $(e_1e_2)^{2^{s}+\tau }$
is even this implies that the coefficient of $(e_1e_2)^{2^{s}+\tau }$![]() in $q_1$
in $q_1$![]() is 0, and since $\alpha _0$
is 0, and since $\alpha _0$![]() is even that the coefficients of $e_1^{2^{s}+\tau -1}e_2^{2^{s}+\tau +1}$
is even that the coefficients of $e_1^{2^{s}+\tau -1}e_2^{2^{s}+\tau +1}$![]() and $e_1^{2^{s}+\tau +2^{j}-1}e_2^{2^{s}+\tau -2^{j}+1}$
and $e_1^{2^{s}+\tau +2^{j}-1}e_2^{2^{s}+\tau -2^{j}+1}$![]() in $q_1$
in $q_1$![]() are 0. On the other hand, since $\alpha _j$
are 0. On the other hand, since $\alpha _j$![]() is odd the coefficient of $e_1^{2^{s}+\tau +2^{j}}e_2^{2^{s}+\tau -2^{j}}$
is odd the coefficient of $e_1^{2^{s}+\tau +2^{j}}e_2^{2^{s}+\tau -2^{j}}$![]() in $q_1$
in $q_1$![]() is 1.
is 1.
Now, we expand $p_1=(e_1^{2}+e_1e_2)q_1$![]() . Note that the degree of each monomial in $p_1$
. Note that the degree of each monomial in $p_1$![]() is $2^{s+1}+2\tau +2=2^{s+1}+2^{r+1}-2t-2^{j+1}+2\leqslant 2^{s+1}+4(t-1)-2t-2=2n-6$
is $2^{s+1}+2\tau +2=2^{s+1}+2^{r+1}-2t-2^{j+1}+2\leqslant 2^{s+1}+4(t-1)-2t-2=2n-6$![]() , and hence, after removing all monomials of the form $e_1^{a}e_2^{b}$
, and hence, after removing all monomials of the form $e_1^{a}e_2^{b}$![]() when $a\geqslant n$
when $a\geqslant n$![]() or $b\geqslant n$
or $b\geqslant n$![]() , we get $p_1$
, we get $p_1$![]() written as in remark 3.4. Let us observe a monomial $e_1^{a}e_2^{b}$
written as in remark 3.4. Let us observe a monomial $e_1^{a}e_2^{b}$![]() in $p_1$
in $p_1$![]() . By the previous identity, its coefficient is the sum of coefficients of $e_1^{a-2}e_2^{b}$
. By the previous identity, its coefficient is the sum of coefficients of $e_1^{a-2}e_2^{b}$![]() and $e_1^{a-1}e_2^{b-1}$
and $e_1^{a-1}e_2^{b-1}$![]() in $q_1$
in $q_1$![]() . So, the coefficient of $(e_1e_2)^{2^{s}+\tau +1}$
. So, the coefficient of $(e_1e_2)^{2^{s}+\tau +1}$![]() is 0, while the coefficient of $e_1^{2^{s}+\tau +2^{j}+1}e_2^{2^{s}+\tau -2^{j}+1}$
is 0, while the coefficient of $e_1^{2^{s}+\tau +2^{j}+1}e_2^{2^{s}+\tau -2^{j}+1}$![]() is 1. Since $2^{s}+\tau +2^{j}+1=2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$
is 1. Since $2^{s}+\tau +2^{j}+1=2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$![]() , the degrees of $e_1$
, the degrees of $e_1$![]() and $e_2$
and $e_2$![]() in these monomials are less than $n$
in these monomials are less than $n$![]() , so we can apply lemma 3.3 and remark 3.4 to conclude $p_1\neq 0$
, so we can apply lemma 3.3 and remark 3.4 to conclude $p_1\neq 0$![]() .
.
Finally, we consider the case when $t$![]() is odd. Then $\varepsilon =2^{j}+1$
is odd. Then $\varepsilon =2^{j}+1$![]() . Note that $2^{s}+2^{r}-2^{j}-2=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +2$
. Note that $2^{s}+2^{r}-2^{j}-2=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +2$![]() , while $t-2=2^{j+1}t'+2^{j}+1<2^{r}\leqslant 2^{s}$
, while $t-2=2^{j+1}t'+2^{j}+1<2^{r}\leqslant 2^{s}$![]() for some $t'\geqslant 0$
for some $t'\geqslant 0$![]() . So, by Lucas’ theorem, we have that $\alpha _0=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}+1}$
. So, by Lucas’ theorem, we have that $\alpha _0=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}+1}$![]() and $\alpha _1=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}}$
and $\alpha _1=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}}$![]() are even, while
are even, while
is odd.
Let us denote $\theta =2^{r}-2^{j}-t-1$![]() . Note that $2^{j}+t-2\leqslant 2^{r}+1$
. Note that $2^{j}+t-2\leqslant 2^{r}+1$![]() , i.e. $\theta \geqslant -4$
, i.e. $\theta \geqslant -4$![]() . By proposition 2.2.(4), $A\neq 0$
. By proposition 2.2.(4), $A\neq 0$![]() if and only if
if and only if

and, by lemma 3.3(b), if and only if $p_2=\sum _{l=0}^{s}\alpha _l (e_1+e_2)^{2^{s+1}-2^{l+1}+1}(e_1e_2)^{2^{l}+\theta } e_1$![]() is non-zero. Let us denote
is non-zero. Let us denote

Now, as in the previous part of the proof we conclude: the coefficients of $e_1^{2^{s}+\theta -1}e_2^{2^{s}+\theta +1}$![]() , $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +2}$
, $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +2}$![]() and $e_1^{2^{s}+\theta -3}e_2^{2^{s}+\theta +3}$
and $e_1^{2^{s}+\theta -3}e_2^{2^{s}+\theta +3}$![]() in $q_2$
in $q_2$![]() are 0 (since $\alpha _0$
are 0 (since $\alpha _0$![]() and $\alpha _1$
and $\alpha _1$![]() are even); the coefficient of $e_1^{2^{s}+\theta -4}e_2^{2^{s}+\theta +4}$
are even); the coefficient of $e_1^{2^{s}+\theta -4}e_2^{2^{s}+\theta +4}$![]() in $q_2$
in $q_2$![]() is 1 (since $\alpha _2$
is 1 (since $\alpha _2$![]() is odd). So, in the polynomial $p_2=(e_1^{2}+e_1e_2)q_2$
is odd). So, in the polynomial $p_2=(e_1^{2}+e_1e_2)q_2$![]() the coefficient of $e_1^{2^{s}+\theta }e_2^{2^{s}+\theta +2}$
the coefficient of $e_1^{2^{s}+\theta }e_2^{2^{s}+\theta +2}$![]() is 0, while the coefficient of $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +4}$
is 0, while the coefficient of $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +4}$![]() is 1. Since the total degree of each monomial of $p_2$
is 1. Since the total degree of each monomial of $p_2$![]() is $2^{s+1}+2\theta +2=2^{s+1}+2^{r+1}-2^{j+1}-2t\leqslant 2^{s+1}+4t-8-2t=2n-8$
is $2^{s+1}+2\theta +2=2^{s+1}+2^{r+1}-2^{j+1}-2t\leqslant 2^{s+1}+4t-8-2t=2n-8$![]() and $2^{s}+\theta +4=2^{s}+2^{r}-2^{j}-t+3\leqslant 2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$
and $2^{s}+\theta +4=2^{s}+2^{r}-2^{j}-t+3\leqslant 2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$![]() , we can apply lemma 3.3 and remark 3.4 to conclude $p_2\neq 0$
, we can apply lemma 3.3 and remark 3.4 to conclude $p_2\neq 0$![]() .
.
4. Zero-divisor cup-length of $G_3(\mathbb {R}^{n})$
Let $s$![]() be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$
be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$![]() . In this section we give some bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$
. In this section we give some bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$![]() .
.
In the following proposition we consider the case $n=2^{s}+1$![]() . This result will show that the corresponding result of [Reference Pavešić9, theorem 4.8] is not correct (see also remark 4.2). Fortunately, this proposition gives a better lower bound for topological complexity.
. This result will show that the corresponding result of [Reference Pavešić9, theorem 4.8] is not correct (see also remark 4.2). Fortunately, this proposition gives a better lower bound for topological complexity.
Proposition 4.1 Let $n=2^{s}+1,$![]() where $s\geqslant 3$
where $s\geqslant 3$![]() . Then
. Then
Proof. It is enough to show $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s-1}+2^{s-2}-2}z(w_3)^{2^{s-1}-4}\neq 0$![]() .
.
First, we prove that $w_1^{2^{s}}w_3=0$![]() . By proposition 2.2, this follows from
. By proposition 2.2, this follows from

Since $w_1^{2^{s}}w_3=0$![]() , we have
, we have

Let us observe all classes of the form $w_3^{n-3}\otimes x$![]() for some $x\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$
for some $x\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$![]() after expanding the expression for $A$
after expanding the expression for $A$![]() ; since $w_3^{n-3}$
; since $w_3^{n-3}$![]() is the only non-zero class in $H^{3(n-3)}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$
is the only non-zero class in $H^{3(n-3)}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$![]() (by proposition 2.1), to prove that $A$
(by proposition 2.1), to prove that $A$![]() is non-zero it is enough to show that the sum of all such $x$
is non-zero it is enough to show that the sum of all such $x$![]() is non-zero. To do so, we determine all monomials $x'$
is non-zero. To do so, we determine all monomials $x'$![]() and $x''$
and $x''$![]() in classes $w_1$
in classes $w_1$![]() and $w_2$
and $w_2$![]() , such that $w_1^{2^{s}}x'=w_3^{n-3}=w_3^{2^{s}-2}$
, such that $w_1^{2^{s}}x'=w_3^{n-3}=w_3^{2^{s}-2}$![]() and $w_3^{2^{s-1}-4}x''=w_3^{2^{s}-2}$
and $w_3^{2^{s-1}-4}x''=w_3^{2^{s}-2}$![]() .
.
Let $x'=w_1^{a}w_2^{b}$![]() be such that $w_1^{2^{s}+a}w_2^{b}=w_3^{2^{s}-2}$
be such that $w_1^{2^{s}+a}w_2^{b}=w_3^{2^{s}-2}$![]() . Then $a+2b=2(2^{s}-3)$
. Then $a+2b=2(2^{s}-3)$![]() . We use proposition 2.2:
. We use proposition 2.2:

Note that by proposition 2.2(3) the only non-zero monomials in this sum are the ones for $i$![]() that satisfies $(i+b+2,\,a-i+b+1)\in \{(2^{s}-1,\,2^{s}-2),\,(2^{s}-2,\,2^{s}-1)\}$
that satisfies $(i+b+2,\,a-i+b+1)\in \{(2^{s}-1,\,2^{s}-2),\,(2^{s}-2,\,2^{s}-1)\}$![]() and $\binom {a}{i}$
and $\binom {a}{i}$![]() is odd, i.e. $i\in \{2^{s}-3-b,\,2^{s}-4-b\}$
is odd, i.e. $i\in \{2^{s}-3-b,\,2^{s}-4-b\}$![]() and $\binom {a}{i}$
and $\binom {a}{i}$![]() is odd.
is odd.
If $i=2^{s}-3-b$![]() , then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-3-b}=\binom {2\delta }{\delta }$
, then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-3-b}=\binom {2\delta }{\delta }$![]() (here $2\delta =2(2^{s}-3-b)=a$
(here $2\delta =2(2^{s}-3-b)=a$![]() ). By lemma 3.2, this number is odd only if $\delta =0$
). By lemma 3.2, this number is odd only if $\delta =0$![]() , i.e. $(a,\,b)=(0,\,2^{s}-3)$
, i.e. $(a,\,b)=(0,\,2^{s}-3)$![]() . Let us now consider the case $i=2^{s}-4-b$
. Let us now consider the case $i=2^{s}-4-b$![]() . Then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-4-b}=\binom {2\delta }{\delta -1}=\binom {2\delta }{\delta +1}$
. Then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-4-b}=\binom {2\delta }{\delta -1}=\binom {2\delta }{\delta +1}$![]() . Again, by lemma 3.2, this number is odd only if $\delta =2^{l}-1$
. Again, by lemma 3.2, this number is odd only if $\delta =2^{l}-1$![]() , and hence $a=2^{l+1}-2$
, and hence $a=2^{l+1}-2$![]() and $b=2^{s}-2^{l}-2$
and $b=2^{s}-2^{l}-2$![]() for some $1\leqslant l\leqslant s-1$
for some $1\leqslant l\leqslant s-1$![]() .
.
Let us now go back to our expression for $A$![]() . Here we only consider pairs $(a,\,b)$
. Here we only consider pairs $(a,\,b)$![]() that satisfy $a\leqslant 2^{s}-1$
that satisfy $a\leqslant 2^{s}-1$![]() and $b\leqslant 2^{s-1}+2^{s-2}-2$
and $b\leqslant 2^{s-1}+2^{s-2}-2$![]() ; hence $b=2^{s}-2^{l}-2$
; hence $b=2^{s}-2^{l}-2$![]() only if $l\in \{s-2,\,s-1\}$
only if $l\in \{s-2,\,s-1\}$![]() , so we have two pairs to consider: $(a,\,b)\in \{(2^{s-1}-2,\,2^{s-1}+2^{s-2}-2),\,(2^{s}-2,\,2^{s-1}-2)\}=P$
, so we have two pairs to consider: $(a,\,b)\in \{(2^{s-1}-2,\,2^{s-1}+2^{s-2}-2),\,(2^{s}-2,\,2^{s-1}-2)\}=P$![]() .
.
Next, let $x''=w_1^{a'}w_2^{b'}$![]() be such that $w_1^{a'}w_2^{b'}w_3^{2^{s-1}-4}=w_3^{2^{s}-2}$
be such that $w_1^{a'}w_2^{b'}w_3^{2^{s-1}-4}=w_3^{2^{s}-2}$![]() . We denote the set of all such pairs $(a',\,b')$
. We denote the set of all such pairs $(a',\,b')$![]() with $P'$
with $P'$![]() . Clearly, if $(a',\,b')\in P'$
. Clearly, if $(a',\,b')\in P'$![]() , then $a'+2b'=3(2^{s-1}+2)$
, then $a'+2b'=3(2^{s-1}+2)$![]() , and hence $a'+b'\geqslant 3(2^{s-2}+1)$
, and hence $a'+b'\geqslant 3(2^{s-2}+1)$![]() ; also, by observing $A$
; also, by observing $A$![]() , it is clear that $a'\leqslant 2^{s}-1$
, it is clear that $a'\leqslant 2^{s}-1$![]() .
.
Now, to prove that $A$![]() is non-zero, it is enough to prove that $B$
is non-zero, it is enough to prove that $B$![]() is non-zero, where $B$
is non-zero, where $B$![]() is equal to
is equal to
By proposition 2.2.(4), this is equivalent to $p=\pi ^{*}(B)e_1^{2}e_2e_{4}^{n-4}\cdots e_{n-1}\neq 0$![]() . In what follows we will be working with the additive basis
. In what follows we will be working with the additive basis
for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , given by proposition 2.2(1) and the canonical homeomorphism $\sigma :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow \mathrm {Flag}(\mathbb {R}^{n})$
, given by proposition 2.2(1) and the canonical homeomorphism $\sigma :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow \mathrm {Flag}(\mathbb {R}^{n})$![]() defined by
defined by
Let $d_{3,n-3}=e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}$![]() . Then
. Then

Note that the monomials of $p_2$![]() belong to $\widetilde {B}_{2^{s}+1}$
belong to $\widetilde {B}_{2^{s}+1}$![]() ; indeed, the degree of $e_1$
; indeed, the degree of $e_1$![]() in each monomial is at most $2^{s-1}+1+2^{s-1}-4+2=2^{s}-1$
in each monomial is at most $2^{s-1}+1+2^{s-1}-4+2=2^{s}-1$![]() , the degree of $e_2$
, the degree of $e_2$![]() is at most $2^{s-1}+1+2^{s-1}-4+1=2^{s}-2$
is at most $2^{s-1}+1+2^{s-1}-4+1=2^{s}-2$![]() , and the degree of $e_3$
, and the degree of $e_3$![]() is at most $2^{s-1}+1+2^{s-1}-4=2^{s}-3$
is at most $2^{s-1}+1+2^{s-1}-4=2^{s}-3$![]() . In particular, each monomial of $p_2$
. In particular, each monomial of $p_2$![]() is not divisible by $e_3^{2^{s}}$
is not divisible by $e_3^{2^{s}}$![]() . Finally, $p_2\neq 0$
. Finally, $p_2\neq 0$![]() since $e_1^{2^{s}-1}e_2^{2^{s-1}-3}e_3^{2^{s-1}-4}e_4^{n-4}\cdots e_{n-1}$
since $e_1^{2^{s}-1}e_2^{2^{s-1}-3}e_3^{2^{s-1}-4}e_4^{n-4}\cdots e_{n-1}$![]() has coefficient 1 in $p_2$
has coefficient 1 in $p_2$![]() .
.
On the other hand,

Since $a'+b'\geqslant 3(2^{s-2}+1)$![]() , the degree of $e_1$
, the degree of $e_1$![]() (resp. $e_2$
(resp. $e_2$![]() ) in each monomial of this sum is at most $2^{s}+2^{s-1}+2^{s-2}-1-a'-b'\leqslant 2^{s}-4$
) in each monomial of this sum is at most $2^{s}+2^{s-1}+2^{s-2}-1-a'-b'\leqslant 2^{s}-4$![]() (resp. $2^{s}+2^{s-1}+2^{s-2}-2-a'-b'\leqslant 2^{s}-5$
(resp. $2^{s}+2^{s-1}+2^{s-2}-2-a'-b'\leqslant 2^{s}-5$![]() ), and hence, after expansion, each monomial (if any) of $p_3$
), and hence, after expansion, each monomial (if any) of $p_3$![]() is in $\widetilde {B}_{2^{s}+1}$
is in $\widetilde {B}_{2^{s}+1}$![]() and divisible by $e_3^{2^{s}}$
and divisible by $e_3^{2^{s}}$![]() (note: it is possible that $p_3=0$
(note: it is possible that $p_3=0$![]() ).
).
Hence, $p_2$![]() and $p_3$
and $p_3$![]() do not have any common monomials from $\widetilde {B}_{2^{s}+1}$
do not have any common monomials from $\widetilde {B}_{2^{s}+1}$![]() , and so there are no cancellations between monomials of $p_2$
, and so there are no cancellations between monomials of $p_2$![]() and $p_3$
and $p_3$![]() . Now, $p_2\neq 0$
. Now, $p_2\neq 0$![]() implies $p=p_2+p_3\neq 0$
implies $p=p_2+p_3\neq 0$![]() .
.
Remark 4.2 Ideas from this paper can be used to prove the following: if $s\geqslant 4$![]() , then $\mathrm {zcl}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}$
, then $\mathrm {zcl}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}$![]() (one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+2^{s-1}}z(w_3)\neq 0$
(one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+2^{s-1}}z(w_3)\neq 0$![]() ). Hence, $\mathrm {TC}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}+1$
). Hence, $\mathrm {TC}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}+1$![]() . Complete proof of this result can be found in the extended version of this paper which is available on the author's website.
. Complete proof of this result can be found in the extended version of this paper which is available on the author's website.
Proposition 4.3 Let $s\geqslant 2,$![]() $n=2^{s}+t\leqslant 2^{s+1},$
$n=2^{s}+t\leqslant 2^{s+1},$![]() $t\geqslant 3$
$t\geqslant 3$![]() and $2^{r-1}< t\leqslant 2^{r}$
and $2^{r-1}< t\leqslant 2^{r}$![]() . Then
. Then
Also, if $t-3\geqslant 2^{s-1},$![]() then $\mathrm {zcl}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}-1$
then $\mathrm {zcl}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}-1$![]() and $\mathrm {TC}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}$
and $\mathrm {TC}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}$![]() .
.
Proof. For the first inequality it is enough to show
Note that $w_1^{2^{s}}w_3^{2^{r}}=0$![]() . Indeed, this follows from proposition 2.2(4), $e_i^{2^{s}+2^{r}}=0$
. Indeed, this follows from proposition 2.2(4), $e_i^{2^{s}+2^{r}}=0$![]() for $i\in \{1,\,2,\,3\}$
for $i\in \{1,\,2,\,3\}$![]() and the following calculations:
and the following calculations:

Similarly, one proves that $w_2^{2^{s}}w_3^{2^{r}}=0$![]() , $w_1^{2^{s}}w_2^{2^{s}+2^{r}}=0$
, $w_1^{2^{s}}w_2^{2^{s}+2^{r}}=0$![]() and $w_1^{2^{s}+2^{r}}w_2^{2^{s}}=0$
and $w_1^{2^{s}+2^{r}}w_2^{2^{s}}=0$![]() .
.
Note that $2^{r}\geqslant t\geqslant 3$![]() implies $r\geqslant 2$
implies $r\geqslant 2$![]() . Now, we consider the cases $2\leqslant r\leqslant s-1$
. Now, we consider the cases $2\leqslant r\leqslant s-1$![]() and $r=s$
and $r=s$![]() separately.
separately.
Case 1: $2\leqslant r\leqslant s-1$![]() . We have
. We have

Since $2^{s}-1=2^{s-1}+\dots +2^{r+1}+2^{r}+2^{r}-1$![]() and $2^{s}-2^{r+1}=2^{s-1}+\dots +2^{r+1}$
and $2^{s}-2^{r+1}=2^{s-1}+\dots +2^{r+1}$![]() , in a similar way we get
, in a similar way we get
Since the dimension of $w_1^{2^{s}}w_2^{2^{s}}$![]() is greater than the dimension of the class $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$
is greater than the dimension of the class $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$![]() , after expanding the expression for $A$
, after expanding the expression for $A$![]() , there is only one summand with the first coordinate in dimension $3\cdot 2^{s}+2^{r}-1$
, there is only one summand with the first coordinate in dimension $3\cdot 2^{s}+2^{r}-1$![]() , and this summand is $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\otimes w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$
, and this summand is $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\otimes w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$![]() . Hence, it is enough to prove that $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\neq 0$
. Hence, it is enough to prove that $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\neq 0$![]() and $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\neq 0$
and $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\neq 0$![]() .
.
First, we prove that $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\neq 0$![]() . Since $e_i^{2^{s+1}}=0$
. Since $e_i^{2^{s+1}}=0$![]() for $i\in \{1,\,2,\,3\}$
for $i\in \{1,\,2,\,3\}$![]() (by proposition 2.2(2)), by proposition 2.2(4) it is enough to prove that
(by proposition 2.2(2)), by proposition 2.2(4) it is enough to prove that

is non-zero in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , i.e. that $w_1^{2^{r}-1}w_3^{2^{s}}$
, i.e. that $w_1^{2^{r}-1}w_3^{2^{s}}$![]() is non-zero in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$
is non-zero in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . Observe the inclusion $i:G_3(\mathbb {R}^{n-2^{s}})\subset G_3(\mathbb {R}^{n})$
. Observe the inclusion $i:G_3(\mathbb {R}^{n-2^{s}})\subset G_3(\mathbb {R}^{n})$![]() . Note that the height of $i^{*}(w_1)$
. Note that the height of $i^{*}(w_1)$![]() in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$
in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$![]() is $2^{r}-1$
is $2^{r}-1$![]() (by (2.1)). So, let $x$
(by (2.1)). So, let $x$![]() be a class in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$
be a class in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$![]() such that $i^{*}(w_1)^{2^{r}-1} x\in H^{3(n-2^{s}-3)}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$
such that $i^{*}(w_1)^{2^{r}-1} x\in H^{3(n-2^{s}-3)}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$![]() is non-zero (this class exists by Poincare's duality); further, let $\widetilde {x}\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$
is non-zero (this class exists by Poincare's duality); further, let $\widetilde {x}\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$![]() be such that $i^{*}(\widetilde {x})=x$
be such that $i^{*}(\widetilde {x})=x$![]() . Then, by [Reference Stong12, lemma 1], the value of $w_1^{2^{r}-1}\widetilde {x}\cdot w_3^{2^{s}}$
. Then, by [Reference Stong12, lemma 1], the value of $w_1^{2^{r}-1}\widetilde {x}\cdot w_3^{2^{s}}$![]() is the same as the value of $i^{*}(w_1^{2^{r}-1} \widetilde {x})=i^{*}(w_1)^{2^{r}-1} x$
is the same as the value of $i^{*}(w_1^{2^{r}-1} \widetilde {x})=i^{*}(w_1)^{2^{r}-1} x$![]() , which is non-zero. Hence, $w_1^{2^{r}-1}w_3^{2^{s}}\neq 0$
, which is non-zero. Hence, $w_1^{2^{r}-1}w_3^{2^{s}}\neq 0$![]() .
.
Finally, we prove that $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\neq 0$![]() . This will immediately follow from the identity $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r}}w_3^{2^{r}}=w_1^{2^{s}}w_2^{2^{s}}=w_3^{2^{s}}\neq 0$
. This will immediately follow from the identity $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r}}w_3^{2^{r}}=w_1^{2^{s}}w_2^{2^{s}}=w_3^{2^{s}}\neq 0$![]() , which we now prove. Since $e_i^{2^{s}+2^{r}}=0$
, which we now prove. Since $e_i^{2^{s}+2^{r}}=0$![]() for $i\in \{1,\,2,\,3\}$
for $i\in \{1,\,2,\,3\}$![]() , by proposition 2.2(4) this follows from (here $d_{3,n-3}=e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}$
, by proposition 2.2(4) this follows from (here $d_{3,n-3}=e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}$![]() )
)

Since $w_3^{2^{s}}\in B_{3,n-3}$![]() , we have $w_3^{2^{s}}\neq 0$
, we have $w_3^{2^{s}}\neq 0$![]() , which completes our proof.
, which completes our proof.
Case 2: $r=s$![]() . Then $A=z(w_1)^{2^{s}-1}(w_1^{2^{s}}\otimes w_3^{2^{s}}+w_3^{2^{s}}\otimes w_1^{2^{s}})$
. Then $A=z(w_1)^{2^{s}-1}(w_1^{2^{s}}\otimes w_3^{2^{s}}+w_3^{2^{s}}\otimes w_1^{2^{s}})$![]() . Since after expanding $A$
. Since after expanding $A$![]() there is only one summand with the first coordinate in dimension $2^{s+2}-1$
there is only one summand with the first coordinate in dimension $2^{s+2}-1$![]() , and this summand is $w_1^{2^{s}-1}w_3^{2^{s}}\otimes w_1^{2^{s}}$
, and this summand is $w_1^{2^{s}-1}w_3^{2^{s}}\otimes w_1^{2^{s}}$![]() , it is enough to prove $w_1^{2^{s}-1}w_3^{2^{s}}\neq 0$
, it is enough to prove $w_1^{2^{s}-1}w_3^{2^{s}}\neq 0$![]() and $w_1^{2^{s}}\neq 0$
and $w_1^{2^{s}}\neq 0$![]() . The second follows from $w_1^{2^{s}}\in B_{3,n-3}$
. The second follows from $w_1^{2^{s}}\in B_{3,n-3}$![]() , and the first one is proven after the calculations for $p_2$
, and the first one is proven after the calculations for $p_2$![]() .
.
Suppose now that $t-3\geqslant 2^{s-1}$![]() . We will prove that
. We will prove that
which implies $\mathrm {zcl}(G_3(\mathbb {R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{s-1}-1$![]() .
.
Let us observe all summands of $B$![]() with the first coordinate in dimension $9\cdot 2^{s-1}$
with the first coordinate in dimension $9\cdot 2^{s-1}$![]() . Note that
. Note that
so the only monomial of this form is $w_1^{2^{s}}w_2^{2^{s}}w_3^{2^{s-1}}\otimes w_1^{2^{s}-1}$![]() , and hence it is enough to prove that $w_1^{2^{s}}w_2^{2^{s}}w_3^{2^{s-1}}\neq 0$
, and hence it is enough to prove that $w_1^{2^{s}}w_2^{2^{s}}w_3^{2^{s-1}}\neq 0$![]() and $w_1^{2^{s}-1}\neq 0$
and $w_1^{2^{s}-1}\neq 0$![]() . This follows from lemma 2.4 (indeed, since $t-3\geqslant 2^{s-1}$
. This follows from lemma 2.4 (indeed, since $t-3\geqslant 2^{s-1}$![]() , both monomials divide $w_1^{2^{s}}w_2^{2^{s}}w_3^{t-3}\neq 0$
, both monomials divide $w_1^{2^{s}}w_2^{2^{s}}w_3^{t-3}\neq 0$![]() ).
).
5. Zero-divisor cup-length of $G_k(\mathbb {R}^{n})$
In this section we give a lower bound for $G_k(\mathbb {R}^{n})$![]() for $k\geqslant 4$
for $k\geqslant 4$![]() .
.
Proposition 5.1 Let $4\leqslant k< n$![]() and $2^{s}+k\leqslant n\leqslant 2^{s+1}$
and $2^{s}+k\leqslant n\leqslant 2^{s+1}$![]() . Then
. Then
Proof. Let $2^{r-1}< k\leqslant 2^{r}$![]() . Then $\lceil \log _2 k\rceil =r$
. Then $\lceil \log _2 k\rceil =r$![]() , so it is enough to prove
, so it is enough to prove

First, let us prove that $p=\prod _{i=0}^{r-2}w_{2^{i}}^{2^{s}}$![]() is non-zero in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$
is non-zero in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$![]() . Let $d_{k,n-k}=e_1^{k-1}\cdots e_{k-1} e_{k+1}^{n-k-1}\cdots e_{n-1}$
. Let $d_{k,n-k}=e_1^{k-1}\cdots e_{k-1} e_{k+1}^{n-k-1}\cdots e_{n-1}$![]() . Since $e_i^{2^{s+1}}=0$
. Since $e_i^{2^{s+1}}=0$![]() for $1\leqslant i\leqslant k$
for $1\leqslant i\leqslant k$![]() (by proposition 2.2(2)) and $k':=\sum _{i=0}^{r-2}2^{i}=2^{r-1}-1< k$
(by proposition 2.2(2)) and $k':=\sum _{i=0}^{r-2}2^{i}=2^{r-1}-1< k$![]() we have
we have

where $[2^{0},\,2^{1},\,\ldots,\,2^{r-2}]=\binom {2^{0}+2^{1}+\dots +2^{r-2}}{2^{0}}\binom {2^{1}+\dots +2^{r-2}}{2^{1}}\cdots \binom {2^{r-2}}{2^{r-2}}$![]() denotes the multinomial coefficient. By Lucas’ theorem, this coefficient is odd. Also, for $1\leqslant i\leqslant k$
denotes the multinomial coefficient. By Lucas’ theorem, this coefficient is odd. Also, for $1\leqslant i\leqslant k$![]() the degree of $e_i$
the degree of $e_i$![]() in each monomial in the last expression for $p_1$
in each monomial in the last expression for $p_1$![]() is at most $2^{s}+k-i\leqslant n-i$
is at most $2^{s}+k-i\leqslant n-i$![]() , so all monomials in this expression are distinct members of the basis $B_n$
, so all monomials in this expression are distinct members of the basis $B_n$![]() for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , and hence $p_1\neq 0$
, and hence $p_1\neq 0$![]() . So, by proposition 2.2(4), $p\neq 0$
. So, by proposition 2.2(4), $p\neq 0$![]() .
.
Now, let us observe all summands after expanding $A$![]() with first coordinate in dimension $(2^{r-1}-1)\cdot 2^{s}$
with first coordinate in dimension $(2^{r-1}-1)\cdot 2^{s}$![]() . The dimension of $p$
. The dimension of $p$![]() is $(2^{r-1}-1)\cdot 2^{s}$
is $(2^{r-1}-1)\cdot 2^{s}$![]() , and it is easy to see that the only term of this form is $p\otimes w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}$
, and it is easy to see that the only term of this form is $p\otimes w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}$![]() . So, to finish the proof it is enough to prove $w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}\neq 0$
. So, to finish the proof it is enough to prove $w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}\neq 0$![]() . In fact, we prove that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$
. In fact, we prove that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$![]() . Since $e_i^{2^{s+1}}=0$
. Since $e_i^{2^{s+1}}=0$![]() for $1\leqslant i\leqslant k$
for $1\leqslant i\leqslant k$![]() , we have
, we have

Now, as above, $2^{s}+k\leqslant n$![]() implies that all monomials in the last expression for $p_2$
implies that all monomials in the last expression for $p_2$![]() are distinct members of the basis $B_n$
are distinct members of the basis $B_n$![]() for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$
for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$![]() , and hence $p_2\neq 0$
, and hence $p_2\neq 0$![]() . By proposition 2.2(4), it follows that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$
. By proposition 2.2(4), it follows that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$![]() .
.
Acknowledgements
The author would like to thank Prof. Petar Pavešić for valuable comments and helpful discussions on the subject. Also, the author would like to thank the anonymous referee for carefully reading the paper and for providing many useful comments and suggestions that improved the paper, and Prof. Mark Grant for pointing to us the paper [Reference Cohen and Suciu2]. The author is partially supported by Ministry of Education, Science and Technological Development of Republic of Serbia (Grant No. 45103-9/2021-14/200104).