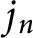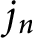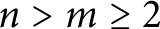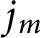1 Introduction
Let
![]() $j(z)$
be the classical elliptic modular invariant that can be defined as
$j(z)$
be the classical elliptic modular invariant that can be defined as
 $$ \begin{align*} j(z)=1728\frac{E_4^3(z)}{E_4^3(z)-E_6^2(z)}, \end{align*} $$
$$ \begin{align*} j(z)=1728\frac{E_4^3(z)}{E_4^3(z)-E_6^2(z)}, \end{align*} $$
where z is in the upper half plane, and
![]() $E_k(z)$
denotes the normalized Eisenstein series of weight k for the modular group
$E_k(z)$
denotes the normalized Eisenstein series of weight k for the modular group
![]() $\operatorname {SL}_2(\mathbb {Z})$
. It is well known that
$\operatorname {SL}_2(\mathbb {Z})$
. It is well known that
![]() $j(z)$
is holomorphic on the upper half plane with a simple pole at infinity and is invariant under the action of
$j(z)$
is holomorphic on the upper half plane with a simple pole at infinity and is invariant under the action of
![]() $\operatorname {SL}_2(\mathbb {Z})$
. For each
$\operatorname {SL}_2(\mathbb {Z})$
. For each
![]() $n\ge 1$
recall that the nth Hecke operator
$n\ge 1$
recall that the nth Hecke operator
![]() $T_n$
of weight
$T_n$
of weight
![]() $0$
acts on a modular function
$0$
acts on a modular function
![]() $f(z)$
through the formula
$f(z)$
through the formula
 $$ \begin{align*} T_n(f)(z):=n^{-1}\sum_{\substack{ad=n, \\ 0 \le b\le d-1}}f\left(\frac{az+b}{d}\right). \end{align*} $$
$$ \begin{align*} T_n(f)(z):=n^{-1}\sum_{\substack{ad=n, \\ 0 \le b\le d-1}}f\left(\frac{az+b}{d}\right). \end{align*} $$
We define
See [Reference Asai, Kaneko and Ninomiya1, Reference Bruinier, Kohnen and Ono3] for more details and applications of the modular functions
![]() $j_n(z)$
. One interesting aspect of
$j_n(z)$
. One interesting aspect of
![]() $j_n(z)$
is that each function can be written as a monic polynomial in
$j_n(z)$
is that each function can be written as a monic polynomial in
![]() $j(z)$
of degree n, denoted
$j(z)$
of degree n, denoted
![]() $\varphi _n$
. That is,
$\varphi _n$
. That is,
The first three
![]() $\varphi _n$
are
$\varphi _n$
are
The zeros of modular functions in the fundamental domain of
![]() $\operatorname {SL}_2(\mathbb {Z})$
have been studied by various authors. Rankin and Swinnerton-Dyer proved in [Reference Rankin and Swinnerton-Dyer13] that all the zeros of Eisenstein series
$\operatorname {SL}_2(\mathbb {Z})$
have been studied by various authors. Rankin and Swinnerton-Dyer proved in [Reference Rankin and Swinnerton-Dyer13] that all the zeros of Eisenstein series
![]() $E_k$
in the fundamental domain of
$E_k$
in the fundamental domain of
![]() $\operatorname {SL}_2(\mathbb {Z})$
lie on the unit circle. By extending the work of [Reference Rankin and Swinnerton-Dyer13] Nozaki [Reference Nozaki11] showed that the zeros of
$\operatorname {SL}_2(\mathbb {Z})$
lie on the unit circle. By extending the work of [Reference Rankin and Swinnerton-Dyer13] Nozaki [Reference Nozaki11] showed that the zeros of
![]() $E_k$
and
$E_k$
and
![]() $E_{k+12}$
interlace on the unit circle, which was first observed by Gekeler [Reference Gekeler6]. Griffin et al. [Reference Griffin, Kenshur, Price, Vandenberg-Daves, Xue and Zhu8] further refined the method of [Reference Nozaki11] to present a necessary and sufficient condition for the zeros of
$E_{k+12}$
interlace on the unit circle, which was first observed by Gekeler [Reference Gekeler6]. Griffin et al. [Reference Griffin, Kenshur, Price, Vandenberg-Daves, Xue and Zhu8] further refined the method of [Reference Nozaki11] to present a necessary and sufficient condition for the zeros of
![]() $E_k$
and
$E_k$
and
![]() $E_{k+a}$
to interlace.
$E_{k+a}$
to interlace.
In a different scenario, Asai et al. [Reference Asai, Kaneko and Ninomiya1] showed that all the zeros of the modular function
![]() $j_n(z)$
in the fundamental domain are simple and lie on the unit circle. By improving their work, Jermann [Reference Jermann10] proved that for
$j_n(z)$
in the fundamental domain are simple and lie on the unit circle. By improving their work, Jermann [Reference Jermann10] proved that for
![]() $n\ge 1$
the zeros of
$n\ge 1$
the zeros of
![]() $j_n(z)$
and
$j_n(z)$
and
![]() $j_{n+1}(z)$
interlace on the unit circle of the fundamental domain.
$j_{n+1}(z)$
interlace on the unit circle of the fundamental domain.
On the other hand, inspired by the analogy between the zeros of Eisenstein series and orthogonal polynomials, the authors [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5] proved the following Stieltjes interlacing property between the zeros of Eisenstein series.
Theorem 1.1 ([Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Theorem 1.2])
Let
![]() $n>m\ge 24 $
and
$n>m\ge 24 $
and
![]() $m\ne 26$
, then between every two zeros of
$m\ne 26$
, then between every two zeros of
![]() $E_m(z)$
on the unit circle of the fundamental domain there is a zero of
$E_m(z)$
on the unit circle of the fundamental domain there is a zero of
![]() $E_n(z)$
.
$E_n(z)$
.
This interlacing property was first observed by Stieltjes [Reference Szegő14, Theorem 3.3.3] for the zeros of orthogonal polynomials and has received continuous attention in the area of numerical analysis and approximation theory, see for example [Reference Beardon and Driver2, Reference Driver, Jooste and Jordaan4, Reference Gibson7]. Our goal is to investigate the Stieltjes interlacing property in the context of modular functions. With this goal and Theorem 1.1 in mind, it is natural to ask whether the Stieltjes interlacing property holds for the zeros of
![]() $j_n$
. In this paper, we will adopt the method and results from [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5] to show that the Stieltjes interlacing property also holds in this situation. More precisely, we will prove the following result.
$j_n$
. In this paper, we will adopt the method and results from [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5] to show that the Stieltjes interlacing property also holds in this situation. More precisely, we will prove the following result.
Theorem 1.2 Let
![]() $n>m\ge 2$
be positive integers. Then on the unit circle in the fundamental domain, between every two zeros of
$n>m\ge 2$
be positive integers. Then on the unit circle in the fundamental domain, between every two zeros of
![]() $j_m(z)$
, there exists a zero of
$j_m(z)$
, there exists a zero of
![]() $j_n(z)$
.
$j_n(z)$
.
Let us briefly describe the basic idea used in the works of [Reference Asai, Kaneko and Ninomiya1, Reference Jermann10]. Suppose that
![]() $0\le x\le 1/2$
, and let
$0\le x\le 1/2$
, and let
![]() $z=x+iy$
be over the unit circle between i and
$z=x+iy$
be over the unit circle between i and
![]() $e^{\pi i/3}$
. Both works were based on studying the function
$e^{\pi i/3}$
. Both works were based on studying the function
 $$ \begin{align*} F_n(x) := j_n\left(x+i\sqrt{1-x^2}\right) e^{-2\pi n\sqrt{1-x^2}} = j_n(z) e^{-2\pi ny}, \end{align*} $$
$$ \begin{align*} F_n(x) := j_n\left(x+i\sqrt{1-x^2}\right) e^{-2\pi n\sqrt{1-x^2}} = j_n(z) e^{-2\pi ny}, \end{align*} $$
which is a real function over this interval. Clearly,
![]() $F_n(x)=0$
if and only if
$F_n(x)=0$
if and only if
![]() $j_n(z)=0$
. Furthermore, the function
$j_n(z)=0$
. Furthermore, the function
![]() $F_n(x)$
is closely approximated by
$F_n(x)$
is closely approximated by
![]() $2\cos (2\pi nx)$
. A nice bound on the remainder ([Reference Asai, Kaneko and Ninomiya1, Key Lemma] and [Reference Jermann10, Lemma 2.1])
$2\cos (2\pi nx)$
. A nice bound on the remainder ([Reference Asai, Kaneko and Ninomiya1, Key Lemma] and [Reference Jermann10, Lemma 2.1])
then enabled the authors of both papers to prove the desired results on the location of zeros of
![]() $F_n$
or
$F_n$
or
![]() $j_n$
. This idea in a certain sense implies that if a separation property holds for the zeros of
$j_n$
. This idea in a certain sense implies that if a separation property holds for the zeros of
![]() $2\cos (2\pi nx)$
, then the same property will likely hold for the zeros of
$2\cos (2\pi nx)$
, then the same property will likely hold for the zeros of
![]() $F_n$
. In this aspect, the following result serves as the starting point as well as a motivation for Theorem 1.2.
$F_n$
. In this aspect, the following result serves as the starting point as well as a motivation for Theorem 1.2.
Proposition 1.3 Let
![]() $ n>m\ge 2$
be positive integers. Then on the interval
$ n>m\ge 2$
be positive integers. Then on the interval
 $[0, \frac {1}{2}]$
, between any two zeros of
$[0, \frac {1}{2}]$
, between any two zeros of
![]() $2\cos (2\pi m x)$
, there exists a zero of
$2\cos (2\pi m x)$
, there exists a zero of
![]() $2\cos (2\pi n x)$
.
$2\cos (2\pi n x)$
.
We will prove this proposition after some preparation in Section 2.
We give an outline of the paper. This paper follows a similar structure to our previous paper [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5], and many lemmas and propositions have similar proofs. In Section 2, we give some preliminary definitions and lemmas. In particular, we will prove Proposition 1.3, which serves as a prototype of the proof for Theorem 1.2 and the Stieltjes interlacing property in general. We then split the proof of Theorem 1.2 into multiple cases. In Section 3, we consider the easier case when
![]() $\frac {n}{m}$
is relatively large. When
$\frac {n}{m}$
is relatively large. When
![]() $\frac {n}{m}$
is relatively small, we follow the method in [Reference Jermann10] and divide the interval
$\frac {n}{m}$
is relatively small, we follow the method in [Reference Jermann10] and divide the interval
 $\left [0, \frac {1}{2} \right ]$
into two subintervals; we consider the zeros on the subinterval
$\left [0, \frac {1}{2} \right ]$
into two subintervals; we consider the zeros on the subinterval
 $\left [0, \frac {1}{2} - \frac {\log m}{5m}\right ]$
in Section 4 and zeros on
$\left [0, \frac {1}{2} - \frac {\log m}{5m}\right ]$
in Section 4 and zeros on
 $\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
in Section 5. In Section 6, we combine all of the cases to complete the proof of Theorem 1.2 and discuss an application on the polynomials
$\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
in Section 5. In Section 6, we combine all of the cases to complete the proof of Theorem 1.2 and discuss an application on the polynomials
![]() $\varphi _n$
.
$\varphi _n$
.
2 Notation and preliminary lemmas
In this section, we will set up some necessary notation and prove some lemmas for later applications.
Recall from Section 1 that for
![]() $z=x+iy$
on the unit circle between i and
$z=x+iy$
on the unit circle between i and
![]() $e^{\pi i /3}$
and
$e^{\pi i /3}$
and
 $x \in [0, \frac {1}{2}]$
,
$x \in [0, \frac {1}{2}]$
,
and
Definition 2.1 ([Reference Jermann10, (12)])
For
![]() $0 \leq k \leq m - 1$
, let
$0 \leq k \leq m - 1$
, let
![]() $x_{m,k}$
be the kth zero of
$x_{m,k}$
be the kth zero of
![]() $\cos (2\pi mx)$
on
$\cos (2\pi mx)$
on
 $[0,\frac {1}{2}]$
, counting from
$[0,\frac {1}{2}]$
, counting from
![]() $\frac {1}{2}$
. More precisely,
$\frac {1}{2}$
. More precisely,
 $$ \begin{align*}x_{m, k} = \frac{1}{2} - \frac{k}{2m} - \frac{1}{4m} = \frac{1}{2} - \frac{2k + 1}{4m}.\end{align*} $$
$$ \begin{align*}x_{m, k} = \frac{1}{2} - \frac{k}{2m} - \frac{1}{4m} = \frac{1}{2} - \frac{2k + 1}{4m}.\end{align*} $$
Definition 2.2 [Reference Jermann10]
For
![]() $0\le k\le m-1$
, let
$0\le k\le m-1$
, let
![]() $u_{m,k}$
be the real part of the kth zero of
$u_{m,k}$
be the real part of the kth zero of
![]() $j_m(z)$
on the unit circle between i and
$j_m(z)$
on the unit circle between i and
![]() $e^{\pi i/3}$
, counting from
$e^{\pi i/3}$
, counting from
![]() $e^{\pi i/3}$
. Equivalently,
$e^{\pi i/3}$
. Equivalently,
![]() $u_{m,k}$
is the kth zero of
$u_{m,k}$
is the kth zero of
![]() $F_m(x)$
on
$F_m(x)$
on
 $[0,\frac {1}{2}]$
, counting from
$[0,\frac {1}{2}]$
, counting from
![]() $\frac {1}{2}$
. Thus,
$\frac {1}{2}$
. Thus,
![]() $u_{m, k} < u_{m, k-1}$
for all
$u_{m, k} < u_{m, k-1}$
for all
![]() $1 \leq k \leq m- 1$
. Throughout the paper, we simply refer to
$1 \leq k \leq m- 1$
. Throughout the paper, we simply refer to
![]() $u_{m,k}$
as the zeros of
$u_{m,k}$
as the zeros of
![]() $j_m(z)$
.
$j_m(z)$
.
Remark We typically use k for an index for the zeros of
![]() $j_m(z)$
and
$j_m(z)$
and
![]() $\ell $
as an index for the zeros of
$\ell $
as an index for the zeros of
![]() $j_n(z)$
.
$j_n(z)$
.
A good upper bound for the distance between
![]() $x_{m,k}$
and
$x_{m,k}$
and
![]() $u_{m,k}$
plays a fundamental role in studying the location of zeros of
$u_{m,k}$
plays a fundamental role in studying the location of zeros of
![]() $j_m$
. Jermann developed the following upper bound in [Reference Jermann10].
$j_m$
. Jermann developed the following upper bound in [Reference Jermann10].
Lemma 2.3 ([Reference Jermann10, Lemma 2.3])
Let
![]() $m\ge 4$
. Then
$m\ge 4$
. Then
 $$ \begin{align*} |u_{m,k}-x_{m,k}|<\frac{1}{11m}. \end{align*} $$
$$ \begin{align*} |u_{m,k}-x_{m,k}|<\frac{1}{11m}. \end{align*} $$
Borrowing an idea from [Reference Griffin, Kenshur, Price, Vandenberg-Daves, Xue and Zhu8, Lemma 3.5], we will present a stronger upper bound for the distance
![]() $|u_{m,k}-x_{m,k}|$
.
$|u_{m,k}-x_{m,k}|$
.
Note that [Reference Jermann10, Corollary 2.2] gives the bound
 $$ \begin{align*} |T_m(x)|\le e^{-2\pi m(\frac{1}{2}-x)}+e^{-\frac{\sqrt{3}}2\pi m}m <1.1. \end{align*} $$
$$ \begin{align*} |T_m(x)|\le e^{-2\pi m(\frac{1}{2}-x)}+e^{-\frac{\sqrt{3}}2\pi m}m <1.1. \end{align*} $$
The improved upper bound for
![]() $|u_{m,k}-x_{m,k}|$
is stated as follows.
$|u_{m,k}-x_{m,k}|$
is stated as follows.
Lemma 2.4 Let
 $\delta _{m,k}=\frac {1}{2}-\frac {k}{2m}=x_{m,k}+\frac {1}{4m}$
and
$\delta _{m,k}=\frac {1}{2}-\frac {k}{2m}=x_{m,k}+\frac {1}{4m}$
and
 $$ \begin{align*}\gamma_{m,k}=\frac{1}{11.919m}\left(e^{-2\pi m(\frac{1}{2}-\delta_{m,k})}+e^{-\frac{\sqrt{3}}2\pi m}m\right) = \frac{1}{11.919m}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right).\end{align*} $$
$$ \begin{align*}\gamma_{m,k}=\frac{1}{11.919m}\left(e^{-2\pi m(\frac{1}{2}-\delta_{m,k})}+e^{-\frac{\sqrt{3}}2\pi m}m\right) = \frac{1}{11.919m}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right).\end{align*} $$
Then for
![]() $m \geq 1$
and
$m \geq 1$
and
![]() $k \geq 0$
,
$k \geq 0$
,
 $$ \begin{align*}|u_{m,k}-x_{m,k}|< \gamma_{m,k} = \frac{1}{11.919m}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right).\end{align*} $$
$$ \begin{align*}|u_{m,k}-x_{m,k}|< \gamma_{m,k} = \frac{1}{11.919m}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right).\end{align*} $$
As a corollary, we have the following slight improvement of Lemma 2.3:
 $$ \begin{align*}|u_{m,k}-x_{m,k}|\le \gamma_{m,0} < \frac{1}{11.139m}.\end{align*} $$
$$ \begin{align*}|u_{m,k}-x_{m,k}|\le \gamma_{m,0} < \frac{1}{11.139m}.\end{align*} $$
Proof We have computationally verified both upper bounds are valid for
![]() $m < 4$
. For
$m < 4$
. For
![]() $m \geq 4$
, we follow the methods of [Reference Jermann10, Lemma 2.3] and [Reference Griffin, Kenshur, Price, Vandenberg-Daves, Xue and Zhu8, Lemma 3.5]. First note that
$m \geq 4$
, we follow the methods of [Reference Jermann10, Lemma 2.3] and [Reference Griffin, Kenshur, Price, Vandenberg-Daves, Xue and Zhu8, Lemma 3.5]. First note that
 $$ \begin{align*} F_m(x_{m,k}\pm \gamma_{m,k})&= 2\cos(2\pi m(x_{m,k}\pm \gamma_{m,k}))+T_m(x_{m,k}\pm \gamma_{m,k})\\ &= \pm(-1)^{m+k} 2\sin(2\pi m\gamma_{m,k})+T_n(x_{m,k}\pm \gamma_{m,k}). \end{align*} $$
$$ \begin{align*} F_m(x_{m,k}\pm \gamma_{m,k})&= 2\cos(2\pi m(x_{m,k}\pm \gamma_{m,k}))+T_m(x_{m,k}\pm \gamma_{m,k})\\ &= \pm(-1)^{m+k} 2\sin(2\pi m\gamma_{m,k})+T_n(x_{m,k}\pm \gamma_{m,k}). \end{align*} $$
On the interval
 $|x-x_{m,k}|\leq \frac {1}{4m}$
, one has
$|x-x_{m,k}|\leq \frac {1}{4m}$
, one has
 $|T_m(x)|\leq e^{-2\pi m(\frac {1}{2}-\delta _{m,k})}+e^{-\frac {\sqrt {3}}2\pi m}m$
, according to [Reference Jermann10, Corollary 2.2]. Also,
$|T_m(x)|\leq e^{-2\pi m(\frac {1}{2}-\delta _{m,k})}+e^{-\frac {\sqrt {3}}2\pi m}m$
, according to [Reference Jermann10, Corollary 2.2]. Also,
 $$ \begin{align*}0<2\pi m \left\lvert \gamma_{m,k} \right\lvert<\frac{\pi}{6}(1.07),\end{align*} $$
$$ \begin{align*}0<2\pi m \left\lvert \gamma_{m,k} \right\lvert<\frac{\pi}{6}(1.07),\end{align*} $$
because for
![]() $m \geq 1$
, one has
$m \geq 1$
, one has
![]() $e^{0}+e^{-\frac {\sqrt {3}}2\pi m}m<1.07$
.
$e^{0}+e^{-\frac {\sqrt {3}}2\pi m}m<1.07$
.
Using the fact that
 $\sin (\theta )> \frac {\sin (\frac {\pi }{6}(1.07))\theta }{(\frac {\pi }{6}(1.07))}$
when
$\sin (\theta )> \frac {\sin (\frac {\pi }{6}(1.07))\theta }{(\frac {\pi }{6}(1.07))}$
when
![]() $0<\theta <\pi (1.07)/6$
, we get that
$0<\theta <\pi (1.07)/6$
, we get that
 $$ \begin{align*}|2\sin(2\pi m\gamma_{m,k})| & > \frac{24\sin\left(\frac{\pi(1.07)}{6}\right)}{1.07}m\gamma_{m,k} > 11.919m\gamma_{m, k} \\ &= e^{-2\pi m(\frac{1}{2}-\delta_{m,k})}+e^{-\frac{\sqrt{3}}2\pi m}m\geq |T_m(x_{m,k}\pm\gamma_{m,k})|.\end{align*} $$
$$ \begin{align*}|2\sin(2\pi m\gamma_{m,k})| & > \frac{24\sin\left(\frac{\pi(1.07)}{6}\right)}{1.07}m\gamma_{m,k} > 11.919m\gamma_{m, k} \\ &= e^{-2\pi m(\frac{1}{2}-\delta_{m,k})}+e^{-\frac{\sqrt{3}}2\pi m}m\geq |T_m(x_{m,k}\pm\gamma_{m,k})|.\end{align*} $$
This implies that
![]() $F_m(x_{m,k}+ \gamma _{m,k})F_m(x_{m,k}- \gamma _{m,k})<0$
, and thus we have the desired bound.▪
$F_m(x_{m,k}+ \gamma _{m,k})F_m(x_{m,k}- \gamma _{m,k})<0$
, and thus we have the desired bound.▪
In the next result, we derive a condition on the values of
![]() $m,n, k$
, and
$m,n, k$
, and
![]() $\ell $
in order for the Stieltjes interlacing to happen.
$\ell $
in order for the Stieltjes interlacing to happen.
Lemma 2.5 Let
![]() $n>m\ge 2$
,
$n>m\ge 2$
,
![]() $0\le k\le m-1$
, and
$0\le k\le m-1$
, and
![]() $0\le \ell \le n-1$
. Then
$0\le \ell \le n-1$
. Then
![]() $x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
if and only if
$x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
if and only if
 $$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{n}{m} < \frac{2\ell + 1}{2k + 1}.\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{n}{m} < \frac{2\ell + 1}{2k + 1}.\end{align*} $$
Proof By Definition 2.1,
 $$ \begin{align*}\frac{1}{2} - \frac{2k + 1}{4m}> \frac{1}{2} - \frac{2\ell + 1}{4n} > \frac{1}{2} - \frac{2k + 3}{4m}\end{align*} $$
$$ \begin{align*}\frac{1}{2} - \frac{2k + 1}{4m}> \frac{1}{2} - \frac{2\ell + 1}{4n} > \frac{1}{2} - \frac{2k + 3}{4m}\end{align*} $$
happens if and only if
 $$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{n}{m} < \frac{2\ell + 1}{2k + 1},\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{n}{m} < \frac{2\ell + 1}{2k + 1},\end{align*} $$
as desired.▪
Corollary 2.6 If
![]() $n> m$
and
$n> m$
and
![]() $x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
, then
$x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
, then
![]() $\ell> k$
.
$\ell> k$
.
Proof Suppose on the contrary that
![]() $\ell \leq k$
. Then by Lemma 2.5,
$\ell \leq k$
. Then by Lemma 2.5,
 $$ \begin{align*}\frac{n}{m} < \frac{2\ell + 1}{2k + 1} \leq 1,\end{align*} $$
$$ \begin{align*}\frac{n}{m} < \frac{2\ell + 1}{2k + 1} \leq 1,\end{align*} $$
contradicting the assumption that
![]() $n> m$
. Thus,
$n> m$
. Thus,
![]() $\ell> k$
, as desired.▪
$\ell> k$
, as desired.▪
To show the Stieltjes interlacing property, special attention is needed for the behavior of the zeros of
![]() $F_n$
(or
$F_n$
(or
![]() $2\cos (2\pi nx)$
) closest to the endpoints 0 or
$2\cos (2\pi nx)$
) closest to the endpoints 0 or
![]() $\frac {1}{2}$
.
$\frac {1}{2}$
.
Lemma 2.7 compares the zeros of
![]() $2\cos (2\pi nx)$
and
$2\cos (2\pi nx)$
and
![]() $2\cos (2\pi m x)$
closest to
$2\cos (2\pi m x)$
closest to
![]() $\frac {1}{2}$
.
$\frac {1}{2}$
.
Lemma 2.7 If
![]() $n> m \geq 2$
, then
$n> m \geq 2$
, then
![]() $x_{n, 0}> x_{m, 0}$
.
$x_{n, 0}> x_{m, 0}$
.
Proof By Definition 2.1,
 $$ \begin{align*}x_{n, 0} - x_{m, 0} = \left(\frac{1}{2} - \frac{1}{4n}\right) - \left(\frac{1}{2} - \frac{1}{4m}\right) = \frac{1}{4m} - \frac{1}{4n}> 0,\end{align*} $$
$$ \begin{align*}x_{n, 0} - x_{m, 0} = \left(\frac{1}{2} - \frac{1}{4n}\right) - \left(\frac{1}{2} - \frac{1}{4m}\right) = \frac{1}{4m} - \frac{1}{4n}> 0,\end{align*} $$
which completes the proof.▪
The next lemma compares the zeros of
![]() $F_n$
and
$F_n$
and
![]() $F_m$
closest to
$F_m$
closest to
![]() $\frac {1}{2}$
. It is a direct corollary of the interlacing property in [Reference Jermann10, Theorem 3.1].
$\frac {1}{2}$
. It is a direct corollary of the interlacing property in [Reference Jermann10, Theorem 3.1].
Lemma 2.8 ([Reference Jermann10, Theorem 3.1])
If
![]() $n> m \geq 2$
, then
$n> m \geq 2$
, then
![]() $u_{n, 0}> u_{m, 0}$
.
$u_{n, 0}> u_{m, 0}$
.
Lemma 2.9 compares the zeros of
![]() $2\cos (2\pi nx)$
and
$2\cos (2\pi nx)$
and
![]() $2\cos (2\pi m x)$
closest to
$2\cos (2\pi m x)$
closest to
![]() $0$
.
$0$
.
Lemma 2.9 If
![]() $n> m \geq 2$
, then
$n> m \geq 2$
, then
![]() $x_{m, m - 1}> x_{n, n - 1}$
.
$x_{m, m - 1}> x_{n, n - 1}$
.
Proof By Definition 2.1, since
![]() $n> m$
,
$n> m$
,
 $$ \begin{align*} x_{m, m - 1} - x_{n, n - 1} &= \frac{2(n - 1) + 1}{4n} - \frac{2(m - 1) + 1}{4m} = \frac{1}{4m} - \frac{1}{4n}> 0, \end{align*} $$
$$ \begin{align*} x_{m, m - 1} - x_{n, n - 1} &= \frac{2(n - 1) + 1}{4n} - \frac{2(m - 1) + 1}{4m} = \frac{1}{4m} - \frac{1}{4n}> 0, \end{align*} $$
hence the claim.▪
The next lemma compares the zeros of
![]() $F_n$
and
$F_n$
and
![]() $F_m$
closest to
$F_m$
closest to
![]() $0$
. It is again a corollary of the interlacing property in [Reference Jermann10, Theorem 3.1].
$0$
. It is again a corollary of the interlacing property in [Reference Jermann10, Theorem 3.1].
Lemma 2.10 ([Reference Jermann10, Theorem 3.1])
If
![]() $n> m \geq 2$
, then
$n> m \geq 2$
, then
![]() $u_{m, m - 1}> u_{n, n - 1}$
.
$u_{m, m - 1}> u_{n, n - 1}$
.
We now prove Proposition 1.3. This will illustrate how Lemmas 2.7–2.10 are applied to show Stieltjes interlacing. Similar to the proof of [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Proposition 1.5], the main part of the proof is simple, but extra care must be taken to ensure there are no problems with the zeros closest to
![]() $0$
and
$0$
and
![]() $\frac {1}{2}$
. Similar work will be carried out in later sections as well.
$\frac {1}{2}$
. Similar work will be carried out in later sections as well.
Proof of Proposition 1.3
It suffices to prove the proposition for consecutive zeros of
![]() $2\cos (2\pi mx)$
. By Definition 2.1, the distance between two consecutive zeros of
$2\cos (2\pi mx)$
. By Definition 2.1, the distance between two consecutive zeros of
![]() $2\cos (2\pi mx)$
is
$2\cos (2\pi mx)$
is
![]() $\frac {1}{2m}$
, and similarly, the distance between two consecutive zeros of
$\frac {1}{2m}$
, and similarly, the distance between two consecutive zeros of
![]() $2\cos (2\pi nx)$
is
$2\cos (2\pi nx)$
is
![]() $\frac {1}{2n}$
. Since
$\frac {1}{2n}$
. Since
![]() $m < n$
,
$m < n$
,
 $\frac {1}{2n} < \frac {1}{2m}$
, which means that the distance between any two consecutive zeros of
$\frac {1}{2n} < \frac {1}{2m}$
, which means that the distance between any two consecutive zeros of
![]() $2\cos (2\pi nx)$
is smaller than the distance between any two consecutive zeros of
$2\cos (2\pi nx)$
is smaller than the distance between any two consecutive zeros of
![]() $2\cos (2\pi mx)$
. This, combined with Lemmas 2.7 and 2.9, concludes the proof.▪
$2\cos (2\pi mx)$
. This, combined with Lemmas 2.7 and 2.9, concludes the proof.▪
For ease of notation, define
 $$ \begin{align*} I_{m, k, n, \ell} = \left[\frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}\right]. \end{align*} $$
$$ \begin{align*} I_{m, k, n, \ell} = \left[\frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}\right]. \end{align*} $$
Lemma 2.11 ([Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Lemma 2.4])
If
![]() $(x_{m, k} - x_{n, \ell })(u_{m, k} - u_{n, \ell }) \leq 0$
, then
$(x_{m, k} - x_{n, \ell })(u_{m, k} - u_{n, \ell }) \leq 0$
, then
 $$ \begin{align*}\frac{n}{m} \in I_{m, k, n, \ell}.\end{align*} $$
$$ \begin{align*}\frac{n}{m} \in I_{m, k, n, \ell}.\end{align*} $$
Proof Following the proof of [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Lemma 2.4], we note that if
![]() $(x_{m, k} - x_{n, \ell })(u_{m, k} - u_{n, \ell }) \leq 0$
, then
$(x_{m, k} - x_{n, \ell })(u_{m, k} - u_{n, \ell }) \leq 0$
, then
By Lemma 2.4, we conclude that
 $$ \begin{align*}\left\lvert \frac{2\ell + 1}{4n} - \frac{2k + 1}{4m} \right\lvert < \frac{1}{11.919m}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{1}{11.919n}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
$$ \begin{align*}\left\lvert \frac{2\ell + 1}{4n} - \frac{2k + 1}{4m} \right\lvert < \frac{1}{11.919m}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{1}{11.919n}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
or equivalently,
 $$ \begin{align*}\left\lvert (2\ell + 1) - (2k + 1)\frac{n}{m} \right\lvert < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right).\end{align*} $$
$$ \begin{align*}\left\lvert (2\ell + 1) - (2k + 1)\frac{n}{m} \right\lvert < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right).\end{align*} $$
If
 $\frac {n}{m} \leq \frac {2\ell + 1}{2k + 1}$
, then
$\frac {n}{m} \leq \frac {2\ell + 1}{2k + 1}$
, then
 $$ \begin{align*}(2\ell + 1) - (2k + 1)\frac{n}{m} < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
$$ \begin{align*}(2\ell + 1) - (2k + 1)\frac{n}{m} < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
so
 $$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{n}{m} \leq \frac{2\ell + 1}{2k + 1} < \frac{2\ell + 1 + \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{n}{m} \leq \frac{2\ell + 1}{2k + 1} < \frac{2\ell + 1 + \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
as desired.
Otherwise, if
 $\frac {n}{m}> \frac {2\ell + 1}{2k + 1}$
, then
$\frac {n}{m}> \frac {2\ell + 1}{2k + 1}$
, then
 $$ \begin{align*}(2k + 1)\frac{n}{m} - (2\ell + 1) < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
$$ \begin{align*}(2k + 1)\frac{n}{m} - (2\ell + 1) < \frac{n}{m}\cdot\frac{4}{11.919}\left(e^{-k\pi} + e^{-\frac{\sqrt{3}}{2}\pi m}m\right) + \frac{4}{11.919}\left(e^{-\ell \pi} + e^{-\frac{\sqrt{3}}{2}\pi n}n\right),\end{align*} $$
so
 $$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1}{2k + 1} < \frac{n}{m} < \frac{2\ell + 1 + \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1}{2k + 1} < \frac{n}{m} < \frac{2\ell + 1 + \frac{4}{11.919}\!\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\!\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
as desired.▪
The next lemma will give a sufficient condition for the zeros of
![]() $F_n$
to interlace.
$F_n$
to interlace.
Lemma 2.12 ([Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Lemma 2.11])
Suppose
![]() $n> m \geq 2$
. If
$n> m \geq 2$
. If
![]() $\frac {n}{m}$
lies in the gap between
$\frac {n}{m}$
lies in the gap between
![]() $I_{m, k + 1, n, \ell }$
and
$I_{m, k + 1, n, \ell }$
and
![]() $I_{m, k, n, \ell }$
, or equivalently,
$I_{m, k, n, \ell }$
, or equivalently,
 $$ \begin{align*}\frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{n}{m} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{n}{m} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)},\end{align*} $$
then
![]() $u_{m, k}> u_{n, \ell } > u_{m, k + 1}$
.
$u_{m, k}> u_{n, \ell } > u_{m, k + 1}$
.
Proof The proof follows similarly to [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Lemma 2.11]. Since
 $$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1}{2k + 3} < \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}\end{align*} $$
and
 $$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1}{2k + 1},\end{align*} $$
$$ \begin{align*}\frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1}{2k + 1},\end{align*} $$
we know that
![]() $x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
by Lemma 2.5. Moreover, since
$x_{m, k}> x_{n, \ell } > x_{m, k + 1}$
by Lemma 2.5. Moreover, since
![]() $\frac {n}{m} \not \in I_{m, k, n, \ell }$
and
$\frac {n}{m} \not \in I_{m, k, n, \ell }$
and
![]() $\frac {n}{m} \not \in I_{m, k + 1, n, \ell }$
, by Lemma 2.11, we conclude that
$\frac {n}{m} \not \in I_{m, k + 1, n, \ell }$
, by Lemma 2.11, we conclude that
![]() $u_{m, k}> u_{n, \ell } > u_{m, k + 1}$
, as desired.
$u_{m, k}> u_{n, \ell } > u_{m, k + 1}$
, as desired.
We now check to make sure that the interval is nonempty to ensure that the lemma is nontrivial. Using the bound
![]() $e^{0}+e^{-\frac {\sqrt {3}}2\pi m}m<1.07$
for
$e^{0}+e^{-\frac {\sqrt {3}}2\pi m}m<1.07$
for
![]() $m \geq 1$
, note that
$m \geq 1$
, note that
 $$ \begin{align*} &\left(2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &> \left(2\ell + 1 - \frac{4}{11.919}1.07\right)\left(2k + 3 - \frac{4}{11.919}1.07\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}1.07\right)\left(2k + 1 + \frac{4}{11.919}1.07\right)\\ &> \left(2\ell + 0.64\right)\left(2k + 2.64\right) - \left(2\ell + 1.36\right)\left(2k + 1.36\right)\\ &= 2.56\ell - 1.44k - 0.16\\ &> 0, \end{align*} $$
$$ \begin{align*} &\left(2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &> \left(2\ell + 1 - \frac{4}{11.919}1.07\right)\left(2k + 3 - \frac{4}{11.919}1.07\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}1.07\right)\left(2k + 1 + \frac{4}{11.919}1.07\right)\\ &> \left(2\ell + 0.64\right)\left(2k + 2.64\right) - \left(2\ell + 1.36\right)\left(2k + 1.36\right)\\ &= 2.56\ell - 1.44k - 0.16\\ &> 0, \end{align*} $$
since
![]() $\ell> k$
by Corollary 2.6.▪
$\ell> k$
by Corollary 2.6.▪
3
 $\frac {n}{m}$
is large
$\frac {n}{m}$
is large
Throughout the rest of this paper, improving on the estimate in [Reference Jermann10, Corollary 2.2], we use the bounds
 $$ \begin{align*}e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m < 1.01 \qquad \text{and} \qquad e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m < 0.052\end{align*} $$
$$ \begin{align*}e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m < 1.01 \qquad \text{and} \qquad e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m < 0.052\end{align*} $$
for
![]() $k \geq 0$
and
$k \geq 0$
and
![]() $m \geq 2$
.
$m \geq 2$
.
This section treats the case when n is large relative to m.
Proposition 3.1 Let
![]() $2 \leq m < n$
be positive integers such that
$2 \leq m < n$
be positive integers such that
![]() $\frac {n}{m}> 1.434$
. Then between every two zeros of
$\frac {n}{m}> 1.434$
. Then between every two zeros of
![]() $F_m(x)$
, there exists a zero of
$F_m(x)$
, there exists a zero of
![]() $F_n(x)$
.
$F_n(x)$
.
Proof By Definition 2.1 and Lemma 2.4, for each
![]() $0\le k\le m-1$
and
$0\le k\le m-1$
and
![]() $0\le \ell \le n-1$
,
$0\le \ell \le n-1$
,
 $$ \begin{align*} u_{m, k} - u_{m, k + 1} &\geq x_{m, k} - x_{m, k + 1} - \left\lvert x_{m, k} - u_{m, k} \right\lvert - \left\lvert x_{m, k + 1} - u_{m, k + 1} \right\lvert\\ &> \frac{1}{2m} - \frac{1}{11.919m}\!\left(\! e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m \!\right) - \frac{1}{11.919m} \!\left(\! e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m \!\right)\\ &> \frac{1}{2m} - \frac{1}{11.919m}(1.062)\\ &> \frac{1}{2n} + \frac{1}{11.919n}(1.062)\\ &> \frac{1}{2n} + \frac{1}{11.919n}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) + \frac{1}{11.919n}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> x_{n, \ell} - x_{n, \ell + 1} + \left\lvert x_{n, \ell} - u_{n, \ell} \right\lvert + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert\\ &\geq u_{n, \ell} - u_{n, \ell + 1}, \end{align*} $$
$$ \begin{align*} u_{m, k} - u_{m, k + 1} &\geq x_{m, k} - x_{m, k + 1} - \left\lvert x_{m, k} - u_{m, k} \right\lvert - \left\lvert x_{m, k + 1} - u_{m, k + 1} \right\lvert\\ &> \frac{1}{2m} - \frac{1}{11.919m}\!\left(\! e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m \!\right) - \frac{1}{11.919m} \!\left(\! e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m \!\right)\\ &> \frac{1}{2m} - \frac{1}{11.919m}(1.062)\\ &> \frac{1}{2n} + \frac{1}{11.919n}(1.062)\\ &> \frac{1}{2n} + \frac{1}{11.919n}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) + \frac{1}{11.919n}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> x_{n, \ell} - x_{n, \ell + 1} + \left\lvert x_{n, \ell} - u_{n, \ell} \right\lvert + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert\\ &\geq u_{n, \ell} - u_{n, \ell + 1}, \end{align*} $$
where the fourth inequality follows since
![]() $\frac {n}{m}> 1.434$
.
$\frac {n}{m}> 1.434$
.
4 Zeros close to
 $0$
$0$
In this section, we investigate the behavior of zeros of
![]() $j_n$
and
$j_n$
and
![]() $j_m$
close to the endpoint
$j_m$
close to the endpoint
![]() $0$
when
$0$
when
![]() $\frac {n}{m}$
is relatively small.
$\frac {n}{m}$
is relatively small.
First, we correct a minor mistake in [Reference Jermann10]. Jermann claims in [Reference Jermann10, (26)] that if
 $x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then
$x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then
 $k \geq \frac {\log m}{3}$
. However, this is not true for
$k \geq \frac {\log m}{3}$
. However, this is not true for
![]() $10 < m < 1809$
. In fact, if
$10 < m < 1809$
. In fact, if
 $x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
and
$x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
and
![]() $10<m<1809$
, then one can only get
$10<m<1809$
, then one can only get
 $k \geq \frac {2\log m}{5} - \frac {1}{2}$
. Thus, we need to modify [Reference Jermann10, Lemma 3.3] and its proof slightly; we also give a weaker version of [Reference Jermann10, Lemma 3.3] that is more applicable to us.
$k \geq \frac {2\log m}{5} - \frac {1}{2}$
. Thus, we need to modify [Reference Jermann10, Lemma 3.3] and its proof slightly; we also give a weaker version of [Reference Jermann10, Lemma 3.3] that is more applicable to us.
Lemma 4.1 ([Reference Jermann10, Lemma 3.3])
For
![]() $m \geq 191$
and
$m \geq 191$
and
 $k \geq \frac {2\log m}{5} - \frac {1}{2}$
,
$k \geq \frac {2\log m}{5} - \frac {1}{2}$
,
 $$ \begin{align*}|x_{m, k} - u_{m, k}| < \frac{1}{10m(m+1)}.\end{align*} $$
$$ \begin{align*}|x_{m, k} - u_{m, k}| < \frac{1}{10m(m+1)}.\end{align*} $$
Moreover, for
![]() $m \geq 30$
and
$m \geq 30$
and
 $k \geq \frac {2\log m}{5} - \frac {1}{2}$
,
$k \geq \frac {2\log m}{5} - \frac {1}{2}$
,
 $$ \begin{align*}|x_{m, k} - u_{m, k}| < \frac{1}{6m(m+1)}.\end{align*} $$
$$ \begin{align*}|x_{m, k} - u_{m, k}| < \frac{1}{6m(m+1)}.\end{align*} $$
Proof We will follow the proof of [Reference Jermann10, Lemma 3.3] closely here with necessary modifications to take care of the aforementioned mistake.
Assume on the contrary that
 $$ \begin{align*} \frac{1}{4m}>|x_{m, k} - u_{m, k}|\ge \frac{1}{cm(m+1)}. \end{align*} $$
$$ \begin{align*} \frac{1}{4m}>|x_{m, k} - u_{m, k}|\ge \frac{1}{cm(m+1)}. \end{align*} $$
Here, we write c in place of 6 or 10. Then by the Taylor approximation for
![]() $\sin (x)$
,
$\sin (x)$
,
 $$ \begin{align*} |2\cos(2\pi m u_{m,k})|&= |2\sin(2\pi m(x_{m, k} - u_{m, k}))|\ge 2\sin\left(\frac{2\pi m}{cm(m+1)}\right) \\ &\ge \frac{4\pi}{c(m+1)}-\frac{8\pi^3}{3c^3(m+1)^3}. \end{align*} $$
$$ \begin{align*} |2\cos(2\pi m u_{m,k})|&= |2\sin(2\pi m(x_{m, k} - u_{m, k}))|\ge 2\sin\left(\frac{2\pi m}{cm(m+1)}\right) \\ &\ge \frac{4\pi}{c(m+1)}-\frac{8\pi^3}{3c^3(m+1)^3}. \end{align*} $$
On the other hand, for
 $k\ge \frac {2\log m}{5}-\frac {1}{2}$
, estimates by taking the derivative and [Reference Jermann10, Corollary 2.2] gives that
$k\ge \frac {2\log m}{5}-\frac {1}{2}$
, estimates by taking the derivative and [Reference Jermann10, Corollary 2.2] gives that
 $$ \begin{align*} |2\cos(2\pi m u_{m,k})| &\le e^{-\pi k} + e^{-\pi m \frac{\sqrt{3}}{2}} m \\ &\le {e}^{\frac{\pi}{2}}m^{-\frac{2\pi}{5}}+e^{-\pi m \frac{\sqrt{3}}{2}} m < \frac{4\pi}{c(m+1)}-\frac{8\pi^3}{3c^3(m+1)^3} \end{align*} $$
$$ \begin{align*} |2\cos(2\pi m u_{m,k})| &\le e^{-\pi k} + e^{-\pi m \frac{\sqrt{3}}{2}} m \\ &\le {e}^{\frac{\pi}{2}}m^{-\frac{2\pi}{5}}+e^{-\pi m \frac{\sqrt{3}}{2}} m < \frac{4\pi}{c(m+1)}-\frac{8\pi^3}{3c^3(m+1)^3} \end{align*} $$
for
![]() $m \geq 30$
when
$m \geq 30$
when
![]() $c = 6$
and
$c = 6$
and
![]() $m \geq 191$
when
$m \geq 191$
when
![]() $c = 10$
, which gives a contradiction.▪
$c = 10$
, which gives a contradiction.▪
The correctness of [Reference Jermann10, Theorem 3.1] thus relies on making sure that
![]() $j_n$
and
$j_n$
and
![]() $j_{n+1}$
interlace for
$j_{n+1}$
interlace for
![]() $11 \leq n \leq 190$
. We have computationally verified that they do.
$11 \leq n \leq 190$
. We have computationally verified that they do.
We may now prove the main result of this section.
Proposition 4.2 Let
![]() $30 \leq m < n$
be positive integers such that
$30 \leq m < n$
be positive integers such that
![]() $\frac {n}{m} \leq 1.434$
. Let r be the smallest value for k such that
$\frac {n}{m} \leq 1.434$
. Let r be the smallest value for k such that
![]() $x_{m, k}$
lies in the interval
$x_{m, k}$
lies in the interval
 $[0, \frac {1}{2} - \frac {\log m}{5m}]$
. Then for
$[0, \frac {1}{2} - \frac {\log m}{5m}]$
. Then for
![]() $r \leq k \leq m - 2$
, between
$r \leq k \leq m - 2$
, between
![]() $u_{m, k}$
and
$u_{m, k}$
and
![]() $u_{m, k+1}$
, there exists a zero of
$u_{m, k+1}$
, there exists a zero of
![]() $F_n(x)$
.
$F_n(x)$
.
Proof This proof follows similarly to [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5, Proposition 4.2]. By [Reference Jermann10, Theorem 3.1], we are done if
![]() $n = m + 1$
. Thus, we assume that
$n = m + 1$
. Thus, we assume that
![]() $n \geq m + 2$
.
$n \geq m + 2$
.
We know that if
 $x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then by Definition 2.1,
$x_{m, k} \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then by Definition 2.1,
 $k \geq \frac {2\log m}{5} - \frac {1}{2}$
. Similarly, if
$k \geq \frac {2\log m}{5} - \frac {1}{2}$
. Similarly, if
 $x_{n, \ell } \in [0, \frac {1}{2} - \frac {\log n}{5n}]$
, then
$x_{n, \ell } \in [0, \frac {1}{2} - \frac {\log n}{5n}]$
, then
 $\ell \geq \frac {2\log n}{5} - \frac {1}{2}$
. Since
$\ell \geq \frac {2\log n}{5} - \frac {1}{2}$
. Since
![]() $m < n$
,
$m < n$
,
 $\frac {1}{2} - \frac {\log m}{5m}<\frac {1}{2} - \frac {\log n}{5n}$
, so if
$\frac {1}{2} - \frac {\log m}{5m}<\frac {1}{2} - \frac {\log n}{5n}$
, so if
 $x_{n, \ell } \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then
$x_{n, \ell } \in [0, \frac {1}{2} - \frac {\log m}{5m}]$
, then
 $\ell \geq \frac {2\log n}{5} - \frac {1}{2}$
.
$\ell \geq \frac {2\log n}{5} - \frac {1}{2}$
.
Also,
 $$ \begin{align} \frac{1}{3n(n+1)} + \frac{1}{3m(m+1)} < \frac{2}{3m(m+1)} < \frac{1}{1.434m^2} \leq \frac{1}{mn} \leq \frac{(n - m)}{2mn} = \frac{1}{2m} - \frac{1}{2n}. \end{align} $$
$$ \begin{align} \frac{1}{3n(n+1)} + \frac{1}{3m(m+1)} < \frac{2}{3m(m+1)} < \frac{1}{1.434m^2} \leq \frac{1}{mn} \leq \frac{(n - m)}{2mn} = \frac{1}{2m} - \frac{1}{2n}. \end{align} $$
Thus, by Lemma 4.1, for k and
![]() $\ell $
such that
$\ell $
such that
![]() $x_{m, k}, x_{m, k + 1}, x_{n, \ell },$
and
$x_{m, k}, x_{m, k + 1}, x_{n, \ell },$
and
![]() $x_{n, \ell + 1}$
lie in the interval
$x_{n, \ell + 1}$
lie in the interval
 $[0, \frac {1}{2} - \frac {\log m}{5m}]$
,
$[0, \frac {1}{2} - \frac {\log m}{5m}]$
,
 $$ \begin{align} u_{m, k} - u_{m, k + 1} &\geq x_{m, k} - x_{m, k + 1} - \left\lvert x_{m, k} - u_{m, k} \right\lvert - \left\lvert x_{m, k + 1} - u_{m, k + 1} \right\lvert\nonumber\\ &> \frac{1}{2m} - \frac{1}{3m(m+1)}\nonumber\\ &> \frac{1}{2n} + \frac{1}{3n(n+1)}\nonumber\\ &\geq x_{n, \ell} - x_{n, \ell + 1} + \left\lvert x_{n, \ell} - u_{n, \ell} \right\lvert + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert\nonumber\\ &\geq u_{n, \ell} - u_{n, \ell + 1}, \end{align} $$
$$ \begin{align} u_{m, k} - u_{m, k + 1} &\geq x_{m, k} - x_{m, k + 1} - \left\lvert x_{m, k} - u_{m, k} \right\lvert - \left\lvert x_{m, k + 1} - u_{m, k + 1} \right\lvert\nonumber\\ &> \frac{1}{2m} - \frac{1}{3m(m+1)}\nonumber\\ &> \frac{1}{2n} + \frac{1}{3n(n+1)}\nonumber\\ &\geq x_{n, \ell} - x_{n, \ell + 1} + \left\lvert x_{n, \ell} - u_{n, \ell} \right\lvert + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert\nonumber\\ &\geq u_{n, \ell} - u_{n, \ell + 1}, \end{align} $$
where the the third inequality is due to (4.1).
We note that k and
![]() $\ell $
such that
$\ell $
such that
![]() $x_{m, k}, x_{m, k + 1}, x_{n, \ell },$
and
$x_{m, k}, x_{m, k + 1}, x_{n, \ell },$
and
![]() $x_{n, \ell + 1}$
lie in the interval
$x_{n, \ell + 1}$
lie in the interval
 $[0, \frac {1}{2} - \frac {\log m}{5m}]$
exists because
$[0, \frac {1}{2} - \frac {\log m}{5m}]$
exists because
![]() $10 < m < n$
and Proposition 1.3.
$10 < m < n$
and Proposition 1.3.
By the distance inequality (4.2), to show the Stieltjes interlacing on the interval
 $[0, \frac {1}{2} - \frac {\log m}{5m}]$
, we only need to check the zeros closest to the endpoints. The two zeros closest to
$[0, \frac {1}{2} - \frac {\log m}{5m}]$
, we only need to check the zeros closest to the endpoints. The two zeros closest to
![]() $0$
are covered by Lemma 2.10, so it remains to verify that there is a zero of
$0$
are covered by Lemma 2.10, so it remains to verify that there is a zero of
![]() $F_n$
between
$F_n$
between
![]() $u_{m, r}$
and
$u_{m, r}$
and
![]() $u_{m, r+1}$
. Let
$u_{m, r+1}$
. Let
![]() $u_{n, \ell + 1}$
be the closest zero of
$u_{n, \ell + 1}$
be the closest zero of
![]() $F_n$
smaller than
$F_n$
smaller than
![]() $u_{m, r+1}$
. By Lemma 4.1 and (4.1),
$u_{m, r+1}$
. By Lemma 4.1 and (4.1),
 $$ \begin{align*} x_{n, \ell} &= x_{n, \ell + 1} + \frac{1}{2n}\\ &\leq u_{n, \ell + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \frac{1}{2n}\\ &< u_{m, r + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \frac{1}{2n}\\ &\leq x_{m, r + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \left\lvert x_{m, r + 1} - u_{m, r + 1} \right\lvert + \frac{1}{2n}\\ &= x_{m, r} + \frac{1}{2n} - \frac{1}{2m} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \left\lvert x_{m, r + 1} - u_{m, r + 1} \right\lvert\\ &< x_{m, r} + \frac{1}{2n} - \frac{1}{2m} + \frac{1}{6n(n+1)} + \frac{1}{6m(m+1)}\\ &< x_{m, r}. \end{align*} $$
$$ \begin{align*} x_{n, \ell} &= x_{n, \ell + 1} + \frac{1}{2n}\\ &\leq u_{n, \ell + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \frac{1}{2n}\\ &< u_{m, r + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \frac{1}{2n}\\ &\leq x_{m, r + 1} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \left\lvert x_{m, r + 1} - u_{m, r + 1} \right\lvert + \frac{1}{2n}\\ &= x_{m, r} + \frac{1}{2n} - \frac{1}{2m} + \left\lvert x_{n, \ell + 1} - u_{n, \ell + 1} \right\lvert + \left\lvert x_{m, r + 1} - u_{m, r + 1} \right\lvert\\ &< x_{m, r} + \frac{1}{2n} - \frac{1}{2m} + \frac{1}{6n(n+1)} + \frac{1}{6m(m+1)}\\ &< x_{m, r}. \end{align*} $$
Then (4.2) applies, so
By the choice of
![]() $u_{n, \ell + 1}$
, we conclude that
$u_{n, \ell + 1}$
, we conclude that
![]() $u_{n, \ell }$
lies between
$u_{n, \ell }$
lies between
![]() $u_{m, r}$
and
$u_{m, r}$
and
![]() $u_{m, r+1}$
, as desired.▪
$u_{m, r+1}$
, as desired.▪
5 Zeros close to
 $\frac {1}{2}$
$\frac {1}{2}$
In this section, we study the case when
![]() $\frac {n}{m}$
is relatively small and the zeros involved are close to the endpoint
$\frac {n}{m}$
is relatively small and the zeros involved are close to the endpoint
![]() $\frac {1}{2}$
. This case is difficult because the distance inequality
$\frac {1}{2}$
. This case is difficult because the distance inequality
![]() $u_{n,\ell }-u_{n,\ell +1} < u_{m,k}-u_{m,k+1}$
that was used in the previous cases is hard to establish. To overcome this difficulty we will follow the treatment in Section 5 of [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5] closely. Our goal is to prove the following result.
$u_{n,\ell }-u_{n,\ell +1} < u_{m,k}-u_{m,k+1}$
that was used in the previous cases is hard to establish. To overcome this difficulty we will follow the treatment in Section 5 of [Reference Frendreiss, Gao, Lei, Woodall, Xue and Zhu5] closely. Our goal is to prove the following result.
Proposition 5.1 Let
![]() $10 < m < n$
be positive integers such that
$10 < m < n$
be positive integers such that
![]() $\frac {n}{m} \leq 1.434$
. Then on the interval
$\frac {n}{m} \leq 1.434$
. Then on the interval
 $\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, between any two zeros of
$\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, between any two zeros of
![]() $F_m$
, there exists a zero of
$F_m$
, there exists a zero of
![]() $F_n$
.
$F_n$
.
Proposition 5.1 is implied by Proposition 1.3 and the following two lemmas whose proofs will occupy the remaining section.
Lemma 5.2 Let
![]() $10 < m < n$
be positive integers such that
$10 < m < n$
be positive integers such that
![]() $\frac {n}{m} \leq 1.434$
. Suppose that
$\frac {n}{m} \leq 1.434$
. Suppose that
 $\frac {1}{2} \geq x_{m, k}> x_{n, \ell } > x_{m, k + 1} \geq \frac {1}{2} - \frac {\log m}{2m}$
and
$\frac {1}{2} \geq x_{m, k}> x_{n, \ell } > x_{m, k + 1} \geq \frac {1}{2} - \frac {\log m}{2m}$
and
![]() $u_{n, \ell } \geq u_{m, k}$
. Then
$u_{n, \ell } \geq u_{m, k}$
. Then
![]() $u_{m, k}> u_{n, \ell + 1} > u_{m, k + 1}$
.
$u_{m, k}> u_{n, \ell + 1} > u_{m, k + 1}$
.
Lemma 5.3 Let
![]() $10 < m < n$
be positive integers such that
$10 < m < n$
be positive integers such that
![]() $\frac {n}{m} \leq 1.434$
. Suppose that
$\frac {n}{m} \leq 1.434$
. Suppose that
 $\frac {1}{2} \geq x_{m, k}> x_{n, \ell } > x_{m, k + 1} \geq \frac {1}{2} - \frac {\log m}{2m}$
and
$\frac {1}{2} \geq x_{m, k}> x_{n, \ell } > x_{m, k + 1} \geq \frac {1}{2} - \frac {\log m}{2m}$
and
![]() $u_{n, \ell } \leq u_{m, k + 1}$
. Then
$u_{n, \ell } \leq u_{m, k + 1}$
. Then
![]() $u_{m, k}> u_{n, \ell - 1} > u_{m, k + 1}$
.
$u_{m, k}> u_{n, \ell - 1} > u_{m, k + 1}$
.
5.1 Proof of Lemma 5.2
Proof of Lemma 5.2
By the assumptions, we know that
![]() $\frac {n}{m} \in I_{m, k, n, \ell }$
by Lemma 2.11. We wish to show that
$\frac {n}{m} \in I_{m, k, n, \ell }$
by Lemma 2.11. We wish to show that
 $$ \begin{align} \frac{2\ell + 3 + \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} \end{align} $$
$$ \begin{align} \frac{2\ell + 3 + \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} \end{align} $$
and
 $$ \begin{align} \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 3 - \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \end{align} $$
$$ \begin{align} \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell + 3 - \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \end{align} $$
so
![]() $\frac {n}{m} \in I_{m, k, n, \ell }$
implies that
$\frac {n}{m} \in I_{m, k, n, \ell }$
implies that
![]() $u_{m, k}> u_{n, \ell + 1} > u_{m, k + 1}$
by Proposition 2.12.
$u_{m, k}> u_{n, \ell + 1} > u_{m, k + 1}$
by Proposition 2.12.
Again by our assumptions, we know that
![]() $\ell> k$
by Corollary 2.6,
$\ell> k$
by Corollary 2.6,
![]() $10 < m < n$
, and by Lemma 2.5,
$10 < m < n$
, and by Lemma 2.5,
 $\frac {2\ell + 1}{2k + 3} < \frac {n}{m} \leq 1.434$
. Moreover, since we are on the interval
$\frac {2\ell + 1}{2k + 3} < \frac {n}{m} \leq 1.434$
. Moreover, since we are on the interval
 $\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, as mentioned in [Reference Jermann10, (27)],
$\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, as mentioned in [Reference Jermann10, (27)],
![]() $k \leq \log m$
. Thus, (5.1) holds by Lemma 5.4, and (5.2) holds by Lemma 5.5.▪
$k \leq \log m$
. Thus, (5.1) holds by Lemma 5.4, and (5.2) holds by Lemma 5.5.▪
The proofs of Lemmas 5.4 and 5.5, which were needed above, are now shown.
Lemma 5.4 If
![]() $\ell> k$
are non-negative integers and
$\ell> k$
are non-negative integers and
![]() $10 < m < n$
are positive integers such that
$10 < m < n$
are positive integers such that
![]() $k \leq \log m$
, then (5.1) holds.
$k \leq \log m$
, then (5.1) holds.
Proof Note that the function
 $f(m) := e^{-\frac {\sqrt {3}}2\pi m}m$
is decreasing in m for
$f(m) := e^{-\frac {\sqrt {3}}2\pi m}m$
is decreasing in m for
![]() $m \geq 1$
. Thus, since
$m \geq 1$
. Thus, since
![]() $\ell> k$
,
$\ell> k$
,
![]() $m < n$
, and
$m < n$
, and
![]() $k \leq \log m$
(or equivalently,
$k \leq \log m$
(or equivalently,
![]() $e^k \leq m$
),
$e^k \leq m$
),
 $$ \begin{align*} &\left(2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 3 + \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right) \\ &\quad = 4(\ell - k) - \frac{4}{11.919}(2k + 3)\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) \\ &\qquad - \frac{4}{11.919}(2\ell + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) - \frac{4}{11.919}(2\ell + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad + \left(\frac{4}{11.919}\right)^2\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) \\ &\qquad - \left(\frac{4}{11.919}\right)^2\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\quad > 4(\ell - k) - \frac{16}{11.919}(\ell - k) - \frac{4}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) \\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) - \left(\frac{4}{11.919}\right)^2(1.01)^2 \\ &\quad > 2.54 - \frac{8}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right) \\ &\qquad - \frac{8}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right). \end{align*} $$
$$ \begin{align*} &\left(2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 3 + \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right) \\ &\quad = 4(\ell - k) - \frac{4}{11.919}(2k + 3)\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) \\ &\qquad - \frac{4}{11.919}(2\ell + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right) - \frac{4}{11.919}(2\ell + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad + \left(\frac{4}{11.919}\right)^2\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) \\ &\qquad - \left(\frac{4}{11.919}\right)^2\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\quad > 4(\ell - k) - \frac{16}{11.919}(\ell - k) - \frac{4}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) \\ &\qquad - \frac{4}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \frac{4}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) - \left(\frac{4}{11.919}\right)^2(1.01)^2 \\ &\quad > 2.54 - \frac{8}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right) \\ &\qquad - \frac{8}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right). \end{align*} $$
Moreover,
 $$ \begin{align*}g(k) := \frac{8}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right) + \frac{8}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right)\end{align*} $$
$$ \begin{align*}g(k) := \frac{8}{11.919}(2k + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right) + \frac{8}{11.919}(2k + 1)\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi e^k}e^k\right)\end{align*} $$
is decreasing for
![]() $k \geq 0$
, and
$k \geq 0$
, and
![]() $g(0) < 2.54$
. Thus, for
$g(0) < 2.54$
. Thus, for
![]() $k \geq 0$
, (5.1) holds.▪
$k \geq 0$
, (5.1) holds.▪
Lemma 5.5 Let
![]() $k, \ell $
be non-negative integers such that
$k, \ell $
be non-negative integers such that
 $\frac {2\ell + 1}{2k + 3} < 1.434$
. Moreover, if
$\frac {2\ell + 1}{2k + 3} < 1.434$
. Moreover, if
![]() $k \leq 1$
, suppose that
$k \leq 1$
, suppose that
![]() $\ell> k$
and
$\ell> k$
and
![]() $u_{n, \ell } \geq u_{m, k}$
. If m and n are positive integers greater than
$u_{n, \ell } \geq u_{m, k}$
. If m and n are positive integers greater than
![]() $10$
such that
$10$
such that
![]() $\frac {n}{m} \leq 1.434$
, then (5.2) holds.
$\frac {n}{m} \leq 1.434$
, then (5.2) holds.
Proof First, suppose
![]() $k \geq 2$
. Then
$k \geq 2$
. Then
 $$ \begin{align*} &\left(2\ell + 3 - \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\quad = 2(2k + 1) - \frac{4}{11.919}(2k + 1)\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n + e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &\qquad - \frac{4}{11.919}(2\ell + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) - \frac{4}{11.919}(2\ell + 1)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad + \left(\frac{4}{11.919}\right)^2\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \left(\frac{4}{11.919}\right)^2\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\quad > 2(2k + 1) - \frac{4(1.062)}{11.919}(2k + 1) - \frac{16}{11.919}(\ell + 1)(1.01) - \left(\frac{4}{11.919}\right)^2(1.01)^2\\ &\quad = (2k + 3) \\ &\quad \left(\left(2 - \frac{4(1.062)}{11.919}\right) - \frac{8(1.01)}{11.919}\frac{2\ell + 1}{2k + 3} - \frac{\left(\frac{4}{11.919}\right)^2(1.01)^2 + 2\left(2 - \frac{4(1.062)}{11.919}\right) + \frac{8(1.01)}{11.919}}{2k + 3}\right)\\ & \quad > (2k + 3) \\ &\quad \left(\left(2 - \frac{4(1.062)}{11.919}\right) - \frac{8(1.01)}{11.919}1.434 - \frac{\left(\frac{4}{11.919}\right)^2(1.01)^2 + 2\left(2 - \frac{4(1.062)}{11.919}\right) + \frac{8(1.01)}{11.919}}{7}\right)\\ &\quad > 0, \end{align*} $$
$$ \begin{align*} &\left(2\ell + 3 - \frac{4}{11.919}\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 - \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\qquad - \left(2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\right)\left(2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\right)\\ &\quad = 2(2k + 1) - \frac{4}{11.919}(2k + 1)\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n + e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &\qquad - \frac{4}{11.919}(2\ell + 3)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) - \frac{4}{11.919}(2\ell + 1)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad + \left(\frac{4}{11.919}\right)^2\left(e^{-(\ell + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\qquad - \left(\frac{4}{11.919}\right)^2\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)\\ &\quad > 2(2k + 1) - \frac{4(1.062)}{11.919}(2k + 1) - \frac{16}{11.919}(\ell + 1)(1.01) - \left(\frac{4}{11.919}\right)^2(1.01)^2\\ &\quad = (2k + 3) \\ &\quad \left(\left(2 - \frac{4(1.062)}{11.919}\right) - \frac{8(1.01)}{11.919}\frac{2\ell + 1}{2k + 3} - \frac{\left(\frac{4}{11.919}\right)^2(1.01)^2 + 2\left(2 - \frac{4(1.062)}{11.919}\right) + \frac{8(1.01)}{11.919}}{2k + 3}\right)\\ & \quad > (2k + 3) \\ &\quad \left(\left(2 - \frac{4(1.062)}{11.919}\right) - \frac{8(1.01)}{11.919}1.434 - \frac{\left(\frac{4}{11.919}\right)^2(1.01)^2 + 2\left(2 - \frac{4(1.062)}{11.919}\right) + \frac{8(1.01)}{11.919}}{7}\right)\\ &\quad > 0, \end{align*} $$
as desired. We are now left with the cases for
![]() $k= 0,1$
. Since
$k= 0,1$
. Since
![]() $\ell>k$
and
$\ell>k$
and
 $\frac {2\ell + 1}{2k + 3} < 1.434$
, we are able to explicitly write the three cases that are possible.
$\frac {2\ell + 1}{2k + 3} < 1.434$
, we are able to explicitly write the three cases that are possible.
Case 1:
![]() $k = 0$
.
$k = 0$
.
We must have
![]() $\ell = 1$
. Then since
$\ell = 1$
. Then since
![]() $\frac {n}{m} \leq 1.434$
, by Definition 2.1,
$\frac {n}{m} \leq 1.434$
, by Definition 2.1,
 $$ \begin{align*} x_{m, 0} - x_{n, 1} &= \frac{3}{4n} - \frac{1}{4m}\\ &> \frac{1.01}{11.919m} + \frac{0.052}{11.919n}\\ &> \frac{1}{11.919m}\left(1+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 0} - u_{m, 0}| + |x_{n, 1} - u_{n, 1}|, \end{align*} $$
$$ \begin{align*} x_{m, 0} - x_{n, 1} &= \frac{3}{4n} - \frac{1}{4m}\\ &> \frac{1.01}{11.919m} + \frac{0.052}{11.919n}\\ &> \frac{1}{11.919m}\left(1+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 0} - u_{m, 0}| + |x_{n, 1} - u_{n, 1}|, \end{align*} $$
so
![]() $u_{m, 0}> u_{n, 1}$
, contradicting the assumption that
$u_{m, 0}> u_{n, 1}$
, contradicting the assumption that
![]() $u_{n, 1} \geq u_{m, 0}$
. Thus, this case is not possible.
$u_{n, 1} \geq u_{m, 0}$
. Thus, this case is not possible.
Case 2:
![]() $k = 1, \ell = 2$
.
$k = 1, \ell = 2$
.
Since
![]() $\frac {n}{m} \leq 1.434$
, by Definition 2.1,
$\frac {n}{m} \leq 1.434$
, by Definition 2.1,
 $$ \begin{align*} x_{m, 1} - x_{n, 2} &= \frac{5}{4n} - \frac{3}{4m}\\ &> \frac{0.052}{11.919m} + \frac{0.002}{11.919n}\\ &> \frac{1}{11.919m}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-2\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 1} - u_{m, 1}| + |x_{n, 2} - u_{n, 2}|, \end{align*} $$
$$ \begin{align*} x_{m, 1} - x_{n, 2} &= \frac{5}{4n} - \frac{3}{4m}\\ &> \frac{0.052}{11.919m} + \frac{0.002}{11.919n}\\ &> \frac{1}{11.919m}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-2\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 1} - u_{m, 1}| + |x_{n, 2} - u_{n, 2}|, \end{align*} $$
so
![]() $u_{m, 1}> u_{n, 2}$
, contradicting the assumption that
$u_{m, 1}> u_{n, 2}$
, contradicting the assumption that
![]() $u_{n, 2} \geq u_{m, 1}$
. Thus, this case is not possible.
$u_{n, 2} \geq u_{m, 1}$
. Thus, this case is not possible.
Case 3:
![]() $k = 1, \ell = 3$
.
$k = 1, \ell = 3$
.
Since
![]() $\frac {n}{m} \leq 1.434$
, by Definition 2.1,
$\frac {n}{m} \leq 1.434$
, by Definition 2.1,
 $$ \begin{align*} x_{m, 1} - x_{n, 3} &= \frac{7}{4n} - \frac{3}{4m}\\ &> \frac{0.052}{11.919m} + \frac{0.001}{11.919n}\\ &> \frac{1}{11.919m}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-3\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 1} - u_{m, 1}| + |x_{n, 3} - u_{n, 3}|, \end{align*} $$
$$ \begin{align*} x_{m, 1} - x_{n, 3} &= \frac{7}{4n} - \frac{3}{4m}\\ &> \frac{0.052}{11.919m} + \frac{0.001}{11.919n}\\ &> \frac{1}{11.919m}\left(e^{-\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right) + \frac{1}{11.919n}\left(e^{-3\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)\\ &> |x_{m, 1} - u_{m, 1}| + |x_{n, 3} - u_{n, 3}|, \end{align*} $$
so
![]() $u_{m, 1}> u_{n, 3}$
, contradicting the assumption that
$u_{m, 1}> u_{n, 3}$
, contradicting the assumption that
![]() $u_{n, 3} \geq u_{m, 1}$
. Thus, this case is not possible.
$u_{n, 3} \geq u_{m, 1}$
. Thus, this case is not possible.
We have covered all possible cases, and thus conclude the proof of Lemma 5.5.
We now prove the second lemma necessary for Proposition 5.1.
5.2 Proof of Lemma 5.3
Proof of Lemma 5.3
By the assumptions, we have that
![]() $\frac {n}{m} \in I_{m, k + 1, n, \ell }$
by Lemma 2.11. Moreover, recall that
$\frac {n}{m} \in I_{m, k + 1, n, \ell }$
by Lemma 2.11. Moreover, recall that
![]() $\ell> k \geq 0$
by Corollary 2.6. We wish to show that
$\ell> k \geq 0$
by Corollary 2.6. We wish to show that
 $$ \begin{align} \frac{2\ell - 1 + \frac{4}{11.919}\left(e^{-(\ell - 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}\right)} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}\right)}{2k + 3 + \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} \end{align} $$
$$ \begin{align} \frac{2\ell - 1 + \frac{4}{11.919}\left(e^{-(\ell - 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}\right)} < \frac{2\ell + 1 - \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}\right)}{2k + 3 + \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} \end{align} $$
and
 $$ \begin{align} \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell - 1 - \frac{4}{11.919}\left(e^{-(\ell - 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \end{align} $$
$$ \begin{align} \frac{2\ell + 1 + \frac{4}{11.919}\left(e^{-\ell\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 3 - \frac{4}{11.919}\left(e^{-(k + 1)\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)} < \frac{2\ell - 1 - \frac{4}{11.919}\left(e^{-(\ell - 1)\pi}+e^{-\frac{\sqrt{3}}2\pi n}n\right)}{2k + 1 + \frac{4}{11.919}\left(e^{-k\pi}+e^{-\frac{\sqrt{3}}2\pi m}m\right)}, \end{align} $$
so
![]() $\frac {n}{m} \in I_{m, k + 1, n, \ell }$
implies that
$\frac {n}{m} \in I_{m, k + 1, n, \ell }$
implies that
![]() $u_{m, k}> u_{n, \ell - 1} > u_{m, k + 1}$
by Lemma 2.12.
$u_{m, k}> u_{n, \ell - 1} > u_{m, k + 1}$
by Lemma 2.12.
Note that by letting
![]() $k = k' - 1$
and
$k = k' - 1$
and
![]() $\ell = \ell ' + 1$
, (5.3) is the same as (5.2), which was proven in Lemma 5.5, but with
$\ell = \ell ' + 1$
, (5.3) is the same as (5.2), which was proven in Lemma 5.5, but with
![]() $k'$
and
$k'$
and
![]() $\ell '$
instead of k and
$\ell '$
instead of k and
![]() $\ell $
. We see that
$\ell $
. We see that
 $\frac {2\ell ' + 1}{2k' + 3} \leq \frac {2\ell + 1}{2k + 3} < \frac {n}{m} \leq 1.434$
by Lemma 2.5. Moreover, if
$\frac {2\ell ' + 1}{2k' + 3} \leq \frac {2\ell + 1}{2k + 3} < \frac {n}{m} \leq 1.434$
by Lemma 2.5. Moreover, if
![]() $k \geq 1$
, then
$k \geq 1$
, then
![]() $k' \geq 2$
, so (5.3) holds by Lemma 5.5. Thus, it remains to consider the case when
$k' \geq 2$
, so (5.3) holds by Lemma 5.5. Thus, it remains to consider the case when
![]() $k = 0$
.
$k = 0$
.
Similarly, by letting
![]() $\ell = \ell ' + 1$
and leaving k unchanged, (5.4) is the same as (5.1), which was proven in Lemma 5.4, but with
$\ell = \ell ' + 1$
and leaving k unchanged, (5.4) is the same as (5.1), which was proven in Lemma 5.4, but with
![]() $\ell '$
instead of
$\ell '$
instead of
![]() $\ell $
. Since we are on the interval
$\ell $
. Since we are on the interval
 $\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, as mentioned in [Reference Jermann10, (27)],
$\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, as mentioned in [Reference Jermann10, (27)],
![]() $k \leq \log m$
. Then if
$k \leq \log m$
. Then if
![]() $\ell> k + 1$
, (5.4) holds by Lemma 5.4. Thus, it remains to consider the case where
$\ell> k + 1$
, (5.4) holds by Lemma 5.4. Thus, it remains to consider the case where
![]() $\ell = k + 1$
.
$\ell = k + 1$
.
Thus, Lemma 5.3 holds in all cases except when
![]() $k = 0$
and
$k = 0$
and
![]() $\ell \geq 2$
, or when
$\ell \geq 2$
, or when
![]() $\ell = k + 1$
. We now show that each of these cases cannot happen.
$\ell = k + 1$
. We now show that each of these cases cannot happen.
Case 1:
![]() $k = 0$
and
$k = 0$
and
![]() $\ell \geq 2$
.
$\ell \geq 2$
.
Recall that
![]() $x_{m, 0}> x_{n, \ell } > x_{m, 1}$
by our assumptions. By Lemma 2.5, we have that
$x_{m, 0}> x_{n, \ell } > x_{m, 1}$
by our assumptions. By Lemma 2.5, we have that
 $$ \begin{align*}\frac{n}{m}> \frac{2\ell + 1}{2k + 3} \geq \frac{5}{3} > 1.434,\end{align*} $$
$$ \begin{align*}\frac{n}{m}> \frac{2\ell + 1}{2k + 3} \geq \frac{5}{3} > 1.434,\end{align*} $$
contradicting the assumption that
![]() $\frac {n}{m} \leq 1.434$
. Thus, this case is not possible.
$\frac {n}{m} \leq 1.434$
. Thus, this case is not possible.
Case 2:
![]() $\ell = k + 1$
. Recall that
$\ell = k + 1$
. Recall that
![]() $x_{m, k}> x_{n, k + 1} > x_{m, k + 1}$
by our assumptions. Since we are on the interval
$x_{m, k}> x_{n, k + 1} > x_{m, k + 1}$
by our assumptions. Since we are on the interval
 $\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, we know that
$\left [\frac {1}{2} - \frac {\log m}{2m}, \frac {1}{2}\right ]$
, we know that
![]() $k + 1 \leq \log m < \log n$
by [Reference Jermann10, (27)]. Let
$k + 1 \leq \log m < \log n$
by [Reference Jermann10, (27)]. Let
![]() $\hat {x}_{n, k}$
be as defined in [Reference Jermann10, Section 3]. Then by [Reference Jermann10, Lemma 3.4],
$\hat {x}_{n, k}$
be as defined in [Reference Jermann10, Section 3]. Then by [Reference Jermann10, Lemma 3.4],
 $$ \begin{align*}\hat{x}_{n, k + 1} - x_{n, k + 1} = \frac{w_{k + 1}}{n} \qquad \text{and} \qquad \hat{x}_{m, k + 1} - x_{m, k + 1} = \frac{w_{k + 1}}{m},\end{align*} $$
$$ \begin{align*}\hat{x}_{n, k + 1} - x_{n, k + 1} = \frac{w_{k + 1}}{n} \qquad \text{and} \qquad \hat{x}_{m, k + 1} - x_{m, k + 1} = \frac{w_{k + 1}}{m},\end{align*} $$
where
![]() $w_k$
is independent of n (or m) and
$w_k$
is independent of n (or m) and
 $\left \lvert w_k \right \lvert \le \frac {1}{12}$
for all
$\left \lvert w_k \right \lvert \le \frac {1}{12}$
for all
![]() $k\le \log m$
. Following the method of [Reference Jermann10, Lemma 3.5] and applying Definition 2.1,
$k\le \log m$
. Following the method of [Reference Jermann10, Lemma 3.5] and applying Definition 2.1,
 $$ \begin{align*} \hat{x}_{n, k + 1} - \hat{x}_{m, k + 1} &= x_{n, k + 1} - x_{m, k + 1} - w_{k + 1}\left(\frac{1}{m} - \frac{1}{n}\right)\\ &\geq \frac{2k + 3}{4}\left(\frac{1}{m} - \frac{1}{n}\right) - \frac{1}{12}\left(\frac{1}{m} - \frac{1}{n}\right)\\ &= \frac{3k + 4}{6}\left(\frac{n - m}{mn}\right)> 0. \end{align*} $$
$$ \begin{align*} \hat{x}_{n, k + 1} - \hat{x}_{m, k + 1} &= x_{n, k + 1} - x_{m, k + 1} - w_{k + 1}\left(\frac{1}{m} - \frac{1}{n}\right)\\ &\geq \frac{2k + 3}{4}\left(\frac{1}{m} - \frac{1}{n}\right) - \frac{1}{12}\left(\frac{1}{m} - \frac{1}{n}\right)\\ &= \frac{3k + 4}{6}\left(\frac{n - m}{mn}\right)> 0. \end{align*} $$
Moreover, by [Reference Jermann10, Lemma 3.6],
 $$ \begin{align*}\left\lvert \hat{x}_{n, k + 1} - u_{n, k + 1} \right\lvert < \frac{1}{20n(n+1)}\qquad \text{and} \qquad \left\lvert \hat{x}_{m, k + 1} - u_{m, k + 1} \right\lvert < \frac{1}{20m(m+1)}.\end{align*} $$
$$ \begin{align*}\left\lvert \hat{x}_{n, k + 1} - u_{n, k + 1} \right\lvert < \frac{1}{20n(n+1)}\qquad \text{and} \qquad \left\lvert \hat{x}_{m, k + 1} - u_{m, k + 1} \right\lvert < \frac{1}{20m(m+1)}.\end{align*} $$
Since
![]() $\frac {n}{m} \leq 1.434$
, we get
$\frac {n}{m} \leq 1.434$
, we get
 $$ \begin{align*} \left\lvert \hat{x}_{n, k + 1} - u_{n, k + 1} \right\lvert + \left\lvert \hat{x}_{m, k + 1} - u_{m, k + 1} \right\lvert &< \frac{1}{20n(n+1)} + \frac{1}{20m(m+1)}\\ &< \frac{1}{10m(m+1)}\\ &< \frac{4}{6 \cdot 1.434m^2}\\ &\leq \frac{3k + 4}{6}\left(\frac{n - m}{nm}\right)\\ &< \hat{x}_{n, k + 1} - \hat{x}_{m, k + 1},\end{align*} $$
$$ \begin{align*} \left\lvert \hat{x}_{n, k + 1} - u_{n, k + 1} \right\lvert + \left\lvert \hat{x}_{m, k + 1} - u_{m, k + 1} \right\lvert &< \frac{1}{20n(n+1)} + \frac{1}{20m(m+1)}\\ &< \frac{1}{10m(m+1)}\\ &< \frac{4}{6 \cdot 1.434m^2}\\ &\leq \frac{3k + 4}{6}\left(\frac{n - m}{nm}\right)\\ &< \hat{x}_{n, k + 1} - \hat{x}_{m, k + 1},\end{align*} $$
so
![]() $u_{n, k + 1}> u_{m, k + 1}$
. This contradicts our initial assumption that
$u_{n, k + 1}> u_{m, k + 1}$
. This contradicts our initial assumption that
![]() $u_{n, k + 1} \leq u_{m, k + 1}$
, so we conclude that this case is not possible.
$u_{n, k + 1} \leq u_{m, k + 1}$
, so we conclude that this case is not possible.
We have exhausted all cases, so the proof of Lemma 5.3 is complete.▪
6 Proof of Theorem 1.2 and discussion
Proof of Theorem 1.2
It suffices to show the theorem for consecutive zeros of
![]() $F_m$
. By Proposition 3.1, the theorem is proved for
$F_m$
. By Proposition 3.1, the theorem is proved for
![]() $2 \leq m < n$
such that
$2 \leq m < n$
such that
![]() $\frac {n}{m}> 1.434$
. For
$\frac {n}{m}> 1.434$
. For
![]() $m \geq 30$
, as the length of the intersection interval
$m \geq 30$
, as the length of the intersection interval
 $$ \begin{align*}\left[\frac{1}{2} - \frac{\log m }{2m}, \frac{1}{2} - \frac{\log m}{5m}\right]=\left[0,\frac{1}{2} - \frac{\log m}{5m}\right]\cap \left[\frac{1}{2} - \frac{\log m }{2m},\frac{1}{2}\right]\end{align*} $$
$$ \begin{align*}\left[\frac{1}{2} - \frac{\log m }{2m}, \frac{1}{2} - \frac{\log m}{5m}\right]=\left[0,\frac{1}{2} - \frac{\log m}{5m}\right]\cap \left[\frac{1}{2} - \frac{\log m }{2m},\frac{1}{2}\right]\end{align*} $$
is
 $$ \begin{align*} \frac{1}{2}-\frac{\log m}{5m}-\frac{1}{2}+\frac{\log m}{2m}=\frac{3\log m}{10}\frac{1}{m}\ge \frac{3\log 30}{10}\frac{1}{m}>\frac{1}{2m}+\frac{2}{11m}, \end{align*} $$
$$ \begin{align*} \frac{1}{2}-\frac{\log m}{5m}-\frac{1}{2}+\frac{\log m}{2m}=\frac{3\log m}{10}\frac{1}{m}\ge \frac{3\log 30}{10}\frac{1}{m}>\frac{1}{2m}+\frac{2}{11m}, \end{align*} $$
by Lemma 2.3 there is at least one zero (not two zeros as incorrectly and unnecessarily claimed in the proof of [Reference Jermann10, Theorem 3.1]) of
![]() $F_m$
in this interval. Thus, by Propositions 4.2 and 5.1, we conclude that for
$F_m$
in this interval. Thus, by Propositions 4.2 and 5.1, we conclude that for
![]() $30 \leq m < n$
such that
$30 \leq m < n$
such that
![]() $\frac {n}{m} \leq 1.434$
, the theorem is proven. It remains to check the case when
$\frac {n}{m} \leq 1.434$
, the theorem is proven. It remains to check the case when
![]() $2 \leq m \leq 29$
and
$2 \leq m \leq 29$
and
![]() $\frac {n}{m} \leq 1.434$
, which has been verified computationally and by using [Reference Jermann10, Theorem 3.1].
$\frac {n}{m} \leq 1.434$
, which has been verified computationally and by using [Reference Jermann10, Theorem 3.1].
As a corollary we obtain the following indivisibility among the polynomials
![]() $\varphi _n$
in Section 1.
$\varphi _n$
in Section 1.
Corollary 6.1 If
![]() $2\le m <n\le 2m$
, then
$2\le m <n\le 2m$
, then
![]() $\varphi _m\nmid \varphi _n.$
$\varphi _m\nmid \varphi _n.$
Proof Suppose on the contrary that
![]() $\varphi _m\mid \varphi _n$
.
$\varphi _m\mid \varphi _n$
.
By Theorem 1.2, there are at least
![]() $m-1$
zeros of
$m-1$
zeros of
![]() $\varphi _n$
that are not shared by
$\varphi _n$
that are not shared by
![]() $\varphi _m$
. There are m more zeros of
$\varphi _m$
. There are m more zeros of
![]() $\varphi _n$
from
$\varphi _n$
from
![]() $\varphi _m$
, and two extra zeros of
$\varphi _m$
, and two extra zeros of
![]() $\varphi _n$
closest to the two endpoints by Lemmas 2.8 and 2.10. Thus, the total number of zeros of
$\varphi _n$
closest to the two endpoints by Lemmas 2.8 and 2.10. Thus, the total number of zeros of
![]() $\varphi _n$
is at least
$\varphi _n$
is at least
![]() $m+(m-1)+2=2m+1$
, which is a contradiction.▪
$m+(m-1)+2=2m+1$
, which is a contradiction.▪
We end the paper with the following well-known conjecture due to Ono [Reference Ono12, Problem 4.30]. It has been verified by us using SAGE for
![]() $n\le 500$
, see also [Reference Guerzhoy9] for a partial result towards the conjecture. Clearly this conjecture implies Corollary 6.1.
$n\le 500$
, see also [Reference Guerzhoy9] for a partial result towards the conjecture. Clearly this conjecture implies Corollary 6.1.
Conjecture 6.2 Each polynomial
![]() $\varphi _n$
for
$\varphi _n$
for
![]() $n\ge 1$
is irreducible over
$n\ge 1$
is irreducible over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
APPENDIX A Data
In this appendix, we supply the relevant data for
![]() $n\le 10$
. In Table A.1, the real parts of zeros of
$n\le 10$
. In Table A.1, the real parts of zeros of
![]() $j_n(z)$
in the fundamental domain are calculated using Mathematica. For comparison, the zeros of
$j_n(z)$
in the fundamental domain are calculated using Mathematica. For comparison, the zeros of
![]() $\cos (2\pi n x)$
in the interval
$\cos (2\pi n x)$
in the interval
![]() $(0,0.5)$
are given in Table A.2. Note that these data are ordered decreasingly according to the convention in this paper. In Figure A.1, we plot the real parts of zeros of
$(0,0.5)$
are given in Table A.2. Note that these data are ordered decreasingly according to the convention in this paper. In Figure A.1, we plot the real parts of zeros of
![]() $j_n(z)$
to help visualize the statement of Theorem 1.2.
$j_n(z)$
to help visualize the statement of Theorem 1.2.
Table A.1 Real parts of zeros of
![]() $j_n(z)$
.
$j_n(z)$
.

Table A.2 Zeros of
![]() $\cos (2\pi nx)$
in
$\cos (2\pi nx)$
in
 $(0,\frac {1}{2})$
.
$(0,\frac {1}{2})$
.


Figure A.1 Real parts of zeros of
![]() $j_n(z)$
.
$j_n(z)$
.
Acknowledgment
This research was conducted during the
![]() $2021$
REU program at Clemson University, supported by NSF-DMS Grant 1547399. We want to thank the referee for advice and for pointing out the references related to Conjecture 6.2.
$2021$
REU program at Clemson University, supported by NSF-DMS Grant 1547399. We want to thank the referee for advice and for pointing out the references related to Conjecture 6.2.