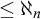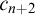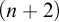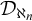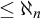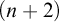1 Introduction
Motivated by problems in general topology, Birkhoff [Reference Birkhoff1], Tukey [Reference Tukey15], and Day [Reference Day2] studied some natural classes of directed sets. Later, Schmidt [Reference Schmidt9] and Isbell [Reference Isbell4, Reference Isbell5] investigated uncountable directed sets under the Tukey order
![]() $<_T$
. In [Reference Todorčević12], Todorčević showed that under
$<_T$
. In [Reference Todorčević12], Todorčević showed that under
![]() ${\mathsf {PFA}}$
there are only five cofinal types in the class
${\mathsf {PFA}}$
there are only five cofinal types in the class
![]() $\mathcal D_{\aleph _1}$
of all cofinal types of size
$\mathcal D_{\aleph _1}$
of all cofinal types of size
![]() $\leq \aleph _1$
under the Tukey order, namely,
$\leq \aleph _1$
under the Tukey order, namely,
![]() $\{1,\omega ,\omega _1,\omega \times \omega _1,[\omega _1]^{<\omega }\}$
. In the other direction, Todorčević showed that under
$\{1,\omega ,\omega _1,\omega \times \omega _1,[\omega _1]^{<\omega }\}$
. In the other direction, Todorčević showed that under
![]() $\operatorname {\mathrm {CH}}$
there are
$\operatorname {\mathrm {CH}}$
there are
![]() $2^{\mathfrak c}$
many non-equivalent cofinal types in this class. Later in [Reference Todorčević14] this was extended to all transitive relations on
$2^{\mathfrak c}$
many non-equivalent cofinal types in this class. Later in [Reference Todorčević14] this was extended to all transitive relations on
![]() $\omega _1$
. Recently, Kuzeljević and Todorčević [Reference Kuzeljević and Todorčević6] initiated the study of the class
$\omega _1$
. Recently, Kuzeljević and Todorčević [Reference Kuzeljević and Todorčević6] initiated the study of the class
![]() $\mathcal D_{\aleph _2}$
. They showed in
$\mathcal D_{\aleph _2}$
. They showed in
![]() $\operatorname {\mathrm {ZFC}}$
that this class contains at least fourteen different cofinal types which can be constructed from two basic types of directed sets and their products:
$\operatorname {\mathrm {ZFC}}$
that this class contains at least fourteen different cofinal types which can be constructed from two basic types of directed sets and their products:
![]() $(\kappa ,\in )$
and
$(\kappa ,\in )$
and
![]() $([\kappa ]^{<\theta },\subseteq )$
, where
$([\kappa ]^{<\theta },\subseteq )$
, where
![]() $\kappa \in \{1,\omega ,\omega _1,\omega _2\}$
and
$\kappa \in \{1,\omega ,\omega _1,\omega _2\}$
and
![]() $\theta \in \{\omega ,\omega _1\}$
.
$\theta \in \{\omega ,\omega _1\}$
.
In this paper, we extend the work of Todorčević and his collaborators and uncover a connection between the classes of the
![]() $\mathcal D_{\aleph _n}$
’s and the Catalan numbers. Denote
$\mathcal D_{\aleph _n}$
’s and the Catalan numbers. Denote
![]() $V_k:=\{1, \omega _k, [\omega _k]^{<\omega _m} \mid 0\leq m<k\}$
,
$V_k:=\{1, \omega _k, [\omega _k]^{<\omega _m} \mid 0\leq m<k\}$
,
![]() $\mathcal F_n:=\bigcup _{k\leq n} V_k$
and finally let
$\mathcal F_n:=\bigcup _{k\leq n} V_k$
and finally let
![]() $\mathcal S_n$
be the set of all finite products of elements of
$\mathcal S_n$
be the set of all finite products of elements of
![]() $\mathcal F_n$
. Recall (see Section 3) that the n-Catalan number is equal to the cardinality of the set of all Dyck n-paths. The set
$\mathcal F_n$
. Recall (see Section 3) that the n-Catalan number is equal to the cardinality of the set of all Dyck n-paths. The set
![]() $\mathcal K_n$
of all Dyck n-paths admits a natural ordering
$\mathcal K_n$
of all Dyck n-paths admits a natural ordering
![]() $\vartriangleleft $
, and the connection we uncover is as follows.
$\vartriangleleft $
, and the connection we uncover is as follows.
Theorem A. The posets
![]() and
and
![]() $(\mathcal K_{n+2},\vartriangleleft )$
are isomorphic. In particular, the class
$(\mathcal K_{n+2},\vartriangleleft )$
are isomorphic. In particular, the class
![]() $\mathcal D_{\aleph _n}$
has size at least the
$\mathcal D_{\aleph _n}$
has size at least the
![]() $(n+2)$
-Catalan number.
$(n+2)$
-Catalan number.
A natural question which arises is whether an interval determined by two successive elements of
![]() forms an empty interval in
forms an empty interval in
![]() $(\mathcal D_{ \aleph _n},<_T)$
. In [Reference Kuzeljević and Todorčević6], the authors showed that there are two intervals of
$(\mathcal D_{ \aleph _n},<_T)$
. In [Reference Kuzeljević and Todorčević6], the authors showed that there are two intervals of
![]() $\mathcal S_2$
that are indeed empty in
$\mathcal S_2$
that are indeed empty in
![]() $\mathcal D_{\aleph _2}$
, and they also showed that consistently, under
$\mathcal D_{\aleph _2}$
, and they also showed that consistently, under
![]() $\operatorname {\mathrm {GCH}}$
and the existence of a non-reflecting stationary subset of
$\operatorname {\mathrm {GCH}}$
and the existence of a non-reflecting stationary subset of
![]() $E^{\omega _2}_\omega $
, two intervals of
$E^{\omega _2}_\omega $
, two intervals of
![]() $\mathcal S_2$
that are nonempty in
$\mathcal S_2$
that are nonempty in
![]() $\mathcal D_{\aleph _2}$
.
$\mathcal D_{\aleph _2}$
.
In this paper, we prove:
Theorem B. Assuming
![]() $\operatorname {\mathrm {GCH}}$
, for every positive integer n, all intervals of
$\operatorname {\mathrm {GCH}}$
, for every positive integer n, all intervals of
![]() $\mathcal S_n$
that form an empty interval in
$\mathcal S_n$
that form an empty interval in
![]() $\mathcal D_{\aleph _n}$
are identified, and counterexamples are constructed to the other cases.
$\mathcal D_{\aleph _n}$
are identified, and counterexamples are constructed to the other cases.
1.1 Organization of this paper
In Section 2 we analyze the Tukey order of directed sets using characteristics of the ideal of bounded subsets.
In Section 3 we consider the poset
![]() and show it is isomorphic to the poset of good
and show it is isomorphic to the poset of good
![]() $(n+2)$
-paths (Dyck paths) with the natural order. As a corollary we get that the cardinality of
$(n+2)$
-paths (Dyck paths) with the natural order. As a corollary we get that the cardinality of
![]() $\mathcal D_{ \aleph _n}$
is greater than or equal to the Catalan number
$\mathcal D_{ \aleph _n}$
is greater than or equal to the Catalan number
![]() $c_{n+2}$
. Furthermore, we address the basic question of whether a specific interval in the poset
$c_{n+2}$
. Furthermore, we address the basic question of whether a specific interval in the poset
![]() is empty, i.e., considering an element C and a successor of it E, is there a directed set
is empty, i.e., considering an element C and a successor of it E, is there a directed set
![]() $D\in \mathcal D_{\aleph _n}$
such that
$D\in \mathcal D_{\aleph _n}$
such that
![]() $C<_T D <_T E$
? We answer this question in Theorem 3.5 using results from the next two sections.
$C<_T D <_T E$
? We answer this question in Theorem 3.5 using results from the next two sections.
In Section 4 we present sufficient conditions on an interval of the poset
![]() which enable us to prove there is no directed set inside.
which enable us to prove there is no directed set inside.
In Section 5 we present cardinal arithmetic assumptions, enough to construct on specific intervals of the poset
![]() a directed set inside.
a directed set inside.
In Section 6 we finish with a remark about future research.
In the Appendix diagrams of the posets
![]() and
and
![]() are presented.
are presented.
1.2 Notation
For a set of ordinals C, we write
![]() $\operatorname {\mathrm {acc}}(C):=\{\alpha <\sup (C) \mid \sup (C\cap \alpha )=\alpha>0\}$
. For
$\operatorname {\mathrm {acc}}(C):=\{\alpha <\sup (C) \mid \sup (C\cap \alpha )=\alpha>0\}$
. For
![]() $\alpha <\gamma $
where
$\alpha <\gamma $
where
![]() $\alpha $
is a regular cardinal, denote
$\alpha $
is a regular cardinal, denote
![]() $E^\gamma _\alpha :=\{ \beta <\gamma \mid \operatorname {\mathrm {cf}}(\beta )=\alpha \}$
. The set of all infinite (resp. infinite and regular) cardinals below
$E^\gamma _\alpha :=\{ \beta <\gamma \mid \operatorname {\mathrm {cf}}(\beta )=\alpha \}$
. The set of all infinite (resp. infinite and regular) cardinals below
![]() $\kappa $
is denoted by
$\kappa $
is denoted by
![]() $\operatorname {\mathrm {Card}}(\kappa )$
(resp.
$\operatorname {\mathrm {Card}}(\kappa )$
(resp.
![]() $\operatorname {\mathrm {Reg}}(\kappa )$
). For a cardinal
$\operatorname {\mathrm {Reg}}(\kappa )$
). For a cardinal
![]() $\kappa $
we denote by
$\kappa $
we denote by
![]() $\kappa ^+$
the successor cardinal of
$\kappa ^+$
the successor cardinal of
![]() $\kappa $
, and by
$\kappa $
, and by
![]() $\kappa ^{+n}$
the nth-successor cardinal. For a function
$\kappa ^{+n}$
the nth-successor cardinal. For a function
![]() $f:X\rightarrow Y$
and a set
$f:X\rightarrow Y$
and a set
![]() $A\subseteq X$
, we denote
$A\subseteq X$
, we denote
![]() $f"A:=\{f(x)\mid x\in A\}$
. For a set A and a cardinal
$f"A:=\{f(x)\mid x\in A\}$
. For a set A and a cardinal
![]() $\theta $
, we write
$\theta $
, we write
![]() $[A]^{\theta }:=\{X\subseteq A \mid |X|=\theta \}$
and define
$[A]^{\theta }:=\{X\subseteq A \mid |X|=\theta \}$
and define
![]() $[A]^{\leq \theta }$
and
$[A]^{\leq \theta }$
and
![]() $[A]^{<\theta }$
similarly. For a sequence of sets
$[A]^{<\theta }$
similarly. For a sequence of sets
![]() $\langle A_i\mid i\in A \rangle $
, let
$\langle A_i\mid i\in A \rangle $
, let
![]() $\prod _{i\in I} D_i:=\{f:I\rightarrow \bigcup _{i\in I} D_i \mid \forall i\in I[f(i)\in D_i] \}$
.
$\prod _{i\in I} D_i:=\{f:I\rightarrow \bigcup _{i\in I} D_i \mid \forall i\in I[f(i)\in D_i] \}$
.
1.3 Preliminaries
A partial ordered set
![]() $(D,\leq _D)$
is directed iff for every
$(D,\leq _D)$
is directed iff for every
![]() $x,y\in D$
there is
$x,y\in D$
there is
![]() $z\in D$
such that
$z\in D$
such that
![]() $x\leq _D z$
and
$x\leq _D z$
and
![]() $y\leq _D z$
. We say that a subset X of a directed set D is bounded if there is some
$y\leq _D z$
. We say that a subset X of a directed set D is bounded if there is some
![]() $d\in D$
such that
$d\in D$
such that
![]() $x\leq _D d$
for each
$x\leq _D d$
for each
![]() $x\in X$
. Otherwise, X is unbounded in D. We say that a subset X of a directed D is cofinal if for every
$x\in X$
. Otherwise, X is unbounded in D. We say that a subset X of a directed D is cofinal if for every
![]() $d\in D$
there exists some
$d\in D$
there exists some
![]() $x\in X$
such that
$x\in X$
such that
![]() $d\leq _D x$
. Let
$d\leq _D x$
. Let
![]() $\operatorname {\mathrm {cf}}(D)$
denote the minimal cardinality of a cofinal subset of D. If D and E are two directed sets, we say that
$\operatorname {\mathrm {cf}}(D)$
denote the minimal cardinality of a cofinal subset of D. If D and E are two directed sets, we say that
![]() $f:D\rightarrow E$
is a Tukey function if
$f:D\rightarrow E$
is a Tukey function if
![]() $f"X:=\{f(x)\mid x\in X\}$
is unbounded in E whenever X is unbounded in D. If such a Tukey function exists we say that D is Tukey reducible to E, and write
$f"X:=\{f(x)\mid x\in X\}$
is unbounded in E whenever X is unbounded in D. If such a Tukey function exists we say that D is Tukey reducible to E, and write
![]() $D\leq _T E$
. If
$D\leq _T E$
. If
![]() $D\leq _T E$
and
$D\leq _T E$
and
![]() $E\not \leq _T D$
, we write
$E\not \leq _T D$
, we write
![]() $D<_T E$
. A function
$D<_T E$
. A function
![]() $g:E\rightarrow D$
is called a convergent/cofinal map from E to D if for every
$g:E\rightarrow D$
is called a convergent/cofinal map from E to D if for every
![]() $d\in D$
there is an
$d\in D$
there is an
![]() $e_d\in E$
such that for every
$e_d\in E$
such that for every
![]() $c\geq e_d$
we have
$c\geq e_d$
we have
![]() $g(c)\geq d$
. There is a convergent map
$g(c)\geq d$
. There is a convergent map
![]() $g:E\rightarrow D$
iff
$g:E\rightarrow D$
iff
![]() $D\leq _T E$
. Note that for a convergent map
$D\leq _T E$
. Note that for a convergent map
![]() $g:E\rightarrow D$
and a cofinal subset
$g:E\rightarrow D$
and a cofinal subset
![]() $Y\subseteq E$
, the set
$Y\subseteq E$
, the set
![]() $g"Y$
is cofinal in D. We say that two directed sets D and E are cofinally/Tukey equivalent and write
$g"Y$
is cofinal in D. We say that two directed sets D and E are cofinally/Tukey equivalent and write
![]() $D\equiv _T E$
iff
$D\equiv _T E$
iff
![]() $D\leq _T E$
and
$D\leq _T E$
and
![]() $D\geq _T E$
. Formally, a cofinal type is an equivalence class under the Tukey order, we abuse the notation and call every representative of the class a cofinal type. Notice that a directed set D is cofinally equivalent to any cofinal subset of D. In [Reference Tukey15], Tukey proved that
$D\geq _T E$
. Formally, a cofinal type is an equivalence class under the Tukey order, we abuse the notation and call every representative of the class a cofinal type. Notice that a directed set D is cofinally equivalent to any cofinal subset of D. In [Reference Tukey15], Tukey proved that
![]() $D\equiv _T E$
iff there is a directed set
$D\equiv _T E$
iff there is a directed set
![]() $(X, \leq _X)$
such that both D and E are isomorphic to a cofinal subset of X. We denote by
$(X, \leq _X)$
such that both D and E are isomorphic to a cofinal subset of X. We denote by
![]() $\mathcal D_\kappa $
the set of all cofinal types of directed sets of cofinality
$\mathcal D_\kappa $
the set of all cofinal types of directed sets of cofinality
![]() $\leq \kappa $
.
$\leq \kappa $
.
Consider a sequence of directed sets
![]() $\langle D_i \mid i\in I \rangle $
, we define the directed set which is the product of them
$\langle D_i \mid i\in I \rangle $
, we define the directed set which is the product of them
![]() $(\prod _{i\in I} D_i,\leq )$
ordered by everywhere-dominance, i.e., for two elements
$(\prod _{i\in I} D_i,\leq )$
ordered by everywhere-dominance, i.e., for two elements
![]() $d, e \in \prod _{i\in I} D_i$
we let
$d, e \in \prod _{i\in I} D_i$
we let
![]() $ d \leq e$
if and only if
$ d \leq e$
if and only if
![]() $ d(i)\leq _{D_i} e(i)$
for each
$ d(i)\leq _{D_i} e(i)$
for each
![]() $i\in I$
. For
$i\in I$
. For
![]() $X\subseteq \prod _{i\in I} D_i$
, let
$X\subseteq \prod _{i\in I} D_i$
, let
![]() $\pi _{D_i}$
be the projection to the i-coordinate. A simple observation [Reference Todorčević12, Proposition 2] is that if n is finite, then
$\pi _{D_i}$
be the projection to the i-coordinate. A simple observation [Reference Todorčević12, Proposition 2] is that if n is finite, then
![]() $D_1\times \dots \times D_n$
is the least upper bound of
$D_1\times \dots \times D_n$
is the least upper bound of
![]() $D_1,\dots ,D_n$
in the Tukey order. Similarly, we define a
$D_1,\dots ,D_n$
in the Tukey order. Similarly, we define a
![]() $\theta $
-support product
$\theta $
-support product
![]() $\prod ^{\leq \theta }_{i\in I}D_i$
; for each
$\prod ^{\leq \theta }_{i\in I}D_i$
; for each
![]() $i\in I$
, we fix some element
$i\in I$
, we fix some element
![]() $0_{D_i}\in D_i$
(usually minimal). Every element
$0_{D_i}\in D_i$
(usually minimal). Every element
![]() $v\in \prod ^{\leq \theta }_{i\in I}D_i$
is such that
$v\in \prod ^{\leq \theta }_{i\in I}D_i$
is such that
![]() $|\operatorname {\mathrm {supp}}(v)|\leq \theta $
, where
$|\operatorname {\mathrm {supp}}(v)|\leq \theta $
, where
![]() $\operatorname {\mathrm {supp}}(v):=\{ i\in I \mid v(i)\not = 0_{D_i}\}$
. The order is coordinate wise.
$\operatorname {\mathrm {supp}}(v):=\{ i\in I \mid v(i)\not = 0_{D_i}\}$
. The order is coordinate wise.
2 Characteristics of directed sets
We commence this section with the following two lemmas which will be used throughout the paper.
Lemma 2.1 (Pouzet [Reference Pouzet7]).
Suppose D is a directed set such that
![]() $\operatorname {\mathrm {cf}}(D)=\kappa $
is infinite, then there exists a cofinal directed set
$\operatorname {\mathrm {cf}}(D)=\kappa $
is infinite, then there exists a cofinal directed set
![]() $P\subseteq D$
of size
$P\subseteq D$
of size
![]() $\kappa $
such that every subset of size
$\kappa $
such that every subset of size
![]() $\kappa $
of P is unbounded
$\kappa $
of P is unbounded
Proof Let
![]() $X\subseteq D$
be a cofinal subset of cardinality
$X\subseteq D$
be a cofinal subset of cardinality
![]() $\kappa $
and let
$\kappa $
and let
![]() $\{x_\alpha \mid \alpha <\kappa \}$
be an enumeration of X. Let
$\{x_\alpha \mid \alpha <\kappa \}$
be an enumeration of X. Let
![]() $P:=\{ x_\alpha \mid \alpha <\kappa \text { and for all } \beta <\alpha [x_\alpha \not <_D x_\beta ] \}$
. We claim that P is cofinal. In order to prove this, fix
$P:=\{ x_\alpha \mid \alpha <\kappa \text { and for all } \beta <\alpha [x_\alpha \not <_D x_\beta ] \}$
. We claim that P is cofinal. In order to prove this, fix
![]() $d\in D$
. As X is cofinal in D, fix a minimal
$d\in D$
. As X is cofinal in D, fix a minimal
![]() $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
![]() $d<_D x_\alpha $
. If
$d<_D x_\alpha $
. If
![]() $x_\alpha \in P$
, then we are done. If not, then fix some
$x_\alpha \in P$
, then we are done. If not, then fix some
![]() $\beta <\alpha $
minimal such that
$\beta <\alpha $
minimal such that
![]() $x_\alpha <_D x_\beta $
. We claim that
$x_\alpha <_D x_\beta $
. We claim that
![]() $x_\beta \in P$
, i.e., there is no
$x_\beta \in P$
, i.e., there is no
![]() $\gamma <\beta $
such that
$\gamma <\beta $
such that
![]() $x_\beta <_D x_\gamma $
. Suppose there is some
$x_\beta <_D x_\gamma $
. Suppose there is some
![]() $\gamma <\beta $
such that
$\gamma <\beta $
such that
![]() $x_\beta <_D x_\gamma $
, then
$x_\beta <_D x_\gamma $
, then
![]() $x_\alpha <_D x_\gamma $
, which is a contradiction to the minimality of
$x_\alpha <_D x_\gamma $
, which is a contradiction to the minimality of
![]() $\beta $
. Note that
$\beta $
. Note that
![]() $d<_D x_\beta \in P$
as sought. As P is cofinal in D,
$d<_D x_\beta \in P$
as sought. As P is cofinal in D,
![]() $\operatorname {\mathrm {cf}}(D)=\kappa $
,
$\operatorname {\mathrm {cf}}(D)=\kappa $
,
![]() $P\subseteq X$
and
$P\subseteq X$
and
![]() $|X|=\kappa $
, we get that
$|X|=\kappa $
, we get that
![]() $|P|=\kappa $
.
$|P|=\kappa $
.
Finally, let us show that every subset of size
![]() $\kappa $
of P is unbounded. Suppose on the contrary that
$\kappa $
of P is unbounded. Suppose on the contrary that
![]() $X\subseteq P$
is a bounded subset of P of size
$X\subseteq P$
is a bounded subset of P of size
![]() $\kappa $
. Fix some
$\kappa $
. Fix some
![]() $x_\beta \in P$
above X and
$x_\beta \in P$
above X and
![]() $\beta <\alpha <\kappa $
such that
$\beta <\alpha <\kappa $
such that
![]() $x_\alpha \in X$
, but this is an absurd as
$x_\alpha \in X$
, but this is an absurd as
![]() $x_\alpha <_D x_\beta $
and
$x_\alpha <_D x_\beta $
and
![]() $x_\alpha \in P$
.
$x_\alpha \in P$
.
Fact 2.2 (Kuzeljević–Todorčević [Reference Kuzeljević and Todorčević6, Lemma 2.3]).
Let
![]() $\lambda \geq \omega $
be a regular cardinal and
$\lambda \geq \omega $
be a regular cardinal and
![]() $n<\omega $
be positive. The directed set
$n<\omega $
be positive. The directed set
![]() $[\lambda ^{+n}]^{\leq \lambda }$
contains a cofinal subset
$[\lambda ^{+n}]^{\leq \lambda }$
contains a cofinal subset
![]() $\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }}$
of size
$\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }}$
of size
![]() $\lambda ^{+n}$
with the property that every subset of
$\lambda ^{+n}$
with the property that every subset of
![]() $\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }}$
of size
$\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }}$
of size
![]() $>\lambda $
is unbounded in
$>\lambda $
is unbounded in
![]() $[\lambda ^{+n}]^{\leq \lambda }$
. In particular,
$[\lambda ^{+n}]^{\leq \lambda }$
. In particular,
![]() $[\lambda ^{+n}]^{\leq \lambda }$
belongs to
$[\lambda ^{+n}]^{\leq \lambda }$
belongs to
![]() $\mathcal D_{\lambda ^{+n}}$
, i.e.
$\mathcal D_{\lambda ^{+n}}$
, i.e.
![]() $\operatorname {\mathrm {cf}}([\lambda ^{+n}]^{\leq \lambda }) \leq \lambda ^{+n}$
.
$\operatorname {\mathrm {cf}}([\lambda ^{+n}]^{\leq \lambda }) \leq \lambda ^{+n}$
.
Recall that any directed set is Tukey equivalent to any of its cofinal subsets, hence
![]() $\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }} \equiv _T [\lambda ^{+n}]^{\leq \lambda }$
.
$\mathfrak D_{[\lambda ^{+n}]^{\leq \lambda }} \equiv _T [\lambda ^{+n}]^{\leq \lambda }$
.
As part of our analysis of the class
![]() $\mathcal D_{\aleph _n}$
, we would like to find certain traits of directed sets which distinguish them from one another in the Tukey order. This was done previously, in [Reference Isbell4, Reference Schmidt9, Reference Todorčević14]. We use that the language of cardinal functions of ideals.
$\mathcal D_{\aleph _n}$
, we would like to find certain traits of directed sets which distinguish them from one another in the Tukey order. This was done previously, in [Reference Isbell4, Reference Schmidt9, Reference Todorčević14]. We use that the language of cardinal functions of ideals.
Definition 2.3. For a set D and an ideal
![]() $\mathcal I$
over D, consider the following cardinal characteristics of
$\mathcal I$
over D, consider the following cardinal characteristics of
![]() $\mathcal I$
:
$\mathcal I$
:
-
•
 $\operatorname {\mathrm {add}}(\mathcal I):=\min \{\kappa \mid \mathcal A \subseteq I,~ |\mathcal A|=\kappa , ~\bigcup \mathcal A\notin \mathcal I\}$
;
$\operatorname {\mathrm {add}}(\mathcal I):=\min \{\kappa \mid \mathcal A \subseteq I,~ |\mathcal A|=\kappa , ~\bigcup \mathcal A\notin \mathcal I\}$
; -
•
 $ \operatorname {\mathrm {non}}(\mathcal I):=\min \{|X|\mid X\subseteq D,~ X\notin \mathcal I \}$
;
$ \operatorname {\mathrm {non}}(\mathcal I):=\min \{|X|\mid X\subseteq D,~ X\notin \mathcal I \}$
; -
•
 $ \operatorname {\mathrm {out}}(\mathcal I):=\min \{ \theta \leq |D|^+\mid \mathcal I\cap [D]^{\theta }=\emptyset \}$
;
$ \operatorname {\mathrm {out}}(\mathcal I):=\min \{ \theta \leq |D|^+\mid \mathcal I\cap [D]^{\theta }=\emptyset \}$
; -
•
 $\operatorname {\mathrm {in}}(\mathcal I, \kappa ) = \{ \theta \leq \kappa \mid \forall X\in [D]^\kappa ~\exists Y\in [X]^\theta \cap \mathcal I \}$
.
$\operatorname {\mathrm {in}}(\mathcal I, \kappa ) = \{ \theta \leq \kappa \mid \forall X\in [D]^\kappa ~\exists Y\in [X]^\theta \cap \mathcal I \}$
.
Notice that
![]() $\operatorname {\mathrm {add}}(\mathcal I)\leq \operatorname {\mathrm {non}}(\mathcal I) \leq \operatorname {\mathrm {out}}(\mathcal I)$
.
$\operatorname {\mathrm {add}}(\mathcal I)\leq \operatorname {\mathrm {non}}(\mathcal I) \leq \operatorname {\mathrm {out}}(\mathcal I)$
.
Definition 2.4. For a directed set D, denote by
![]() $\mathcal I_{\operatorname {\mathrm {bd}}}(D) $
the ideal of bounded subsets of D.
$\mathcal I_{\operatorname {\mathrm {bd}}}(D) $
the ideal of bounded subsets of D.
Proposition 2.5. Let D be a directed set. Then
![]() $:$
$:$
-
(1)
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
is the minimal size of an unbounded subset of D, so every subset of size less than
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
is the minimal size of an unbounded subset of D, so every subset of size less than
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
is bounded.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
is bounded. -
(2) If
 $\theta <\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then there exists in D some bounded subset of size
$\theta <\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then there exists in D some bounded subset of size
 $\theta $
.
$\theta $
. -
(3) If
 $\theta \geq \operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then every subset X of size
$\theta \geq \operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then every subset X of size
 $\theta $
is unbounded in D.
$\theta $
is unbounded in D. -
(4) If
 $\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, then for every
$\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, then for every
 $X\in [D]^\kappa $
there exists some
$X\in [D]^\kappa $
there exists some
 $B\in [X]^{\theta }$
bounded.
$B\in [X]^{\theta }$
bounded. -
(5) For every
 $\theta <\operatorname {\mathrm {add}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
and a family
$\theta <\operatorname {\mathrm {add}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
and a family
 $\mathcal A$
of size
$\mathcal A$
of size
 $\theta $
of bounded subsets of D, the subset
$\theta $
of bounded subsets of D, the subset
 $\bigcup \mathcal A$
is also bounded in D.
$\bigcup \mathcal A$
is also bounded in D.
Let us consider another intuitive feature of a directed set, containing information about the cardinality of hereditary unbounded subsets, this was considered previously by Isbell [Reference Isbell4].
Definition 2.6 (Hereditary unbounded sets).
For a directed set D, set
Proposition 2.7. Let D be a directed set. Then
![]() $:$
$:$
-
• If
 $\operatorname {\mathrm {cf}}(D)$
is an infinite cardinal, then
$\operatorname {\mathrm {cf}}(D)$
is an infinite cardinal, then
 $\operatorname {\mathrm {cf}}(D)\in \operatorname {\mathrm {hu}}(D)$
.
$\operatorname {\mathrm {cf}}(D)\in \operatorname {\mathrm {hu}}(D)$
. -
• If
 $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\leq \kappa \leq |D|$
, then
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\leq \kappa \leq |D|$
, then
 $ \kappa \in \operatorname {\mathrm {hu}}(D)$
.
$ \kappa \in \operatorname {\mathrm {hu}}(D)$
. -
• For an infinite cardinal
 $\kappa $
we have that
$\kappa $
we have that
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\kappa ))=\operatorname {\mathrm {cf}}(\kappa )$
,
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\kappa ))=\operatorname {\mathrm {cf}}(\kappa )$
,
 $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\kappa $
and
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\kappa $
and
 $\operatorname {\mathrm {hu}}(\kappa )=\{\lambda \in \operatorname {\mathrm {Card}}(\kappa ^+) \mid \lambda =\operatorname {\mathrm {cf}}(\kappa )\}$
.
$\operatorname {\mathrm {hu}}(\kappa )=\{\lambda \in \operatorname {\mathrm {Card}}(\kappa ^+) \mid \lambda =\operatorname {\mathrm {cf}}(\kappa )\}$
. -
• If
 $\kappa =\operatorname {\mathrm {cf}}(D)=\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then
$\kappa =\operatorname {\mathrm {cf}}(D)=\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
, then
 $D\equiv _T\kappa $
.
$D\equiv _T\kappa $
. -
• For two infinite cardinals
 $\kappa>\theta $
we have that
$\kappa>\theta $
we have that
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}([\kappa ]^{<\theta }))=\operatorname {\mathrm {cf}}(\theta )$
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}([\kappa ]^{<\theta }))=\operatorname {\mathrm {cf}}(\theta )$
. -
• For a regular cardinal
 $\kappa $
and a positive
$\kappa $
and a positive
 $n<\omega $
,
$n<\omega $
,
 $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\mathfrak D_{[\kappa ^{+n}]^{\leq \kappa }}))>\kappa $
and
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\mathfrak D_{[\kappa ^{+n}]^{\leq \kappa }}))>\kappa $
and
 $\operatorname {\mathrm {hu}}(\mathfrak D_{[\kappa ^{+n}]^{\leq \kappa }}) = \{ \kappa ^{+(m+1)}\mid m< n\}$
.
$\operatorname {\mathrm {hu}}(\mathfrak D_{[\kappa ^{+n}]^{\leq \kappa }}) = \{ \kappa ^{+(m+1)}\mid m< n\}$
. -
• If
 $\kappa =\operatorname {\mathrm {cf}}(D)$
is regular,
$\kappa =\operatorname {\mathrm {cf}}(D)$
is regular,
 $\theta =\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
and
$\theta =\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
and
 $\theta ^{+n}=\kappa $
for some
$\theta ^{+n}=\kappa $
for some
 $n<\omega $
, then
$n<\omega $
, then
 $D\equiv _T [\kappa ]^{<\theta }$
.
$D\equiv _T [\kappa ]^{<\theta }$
.
In the rest of this section we consider various scenarios in which the traits of a certain directed set give us information about its position in the poset
![]() $(\mathcal D_{\kappa }, <_T )$
.
$(\mathcal D_{\kappa }, <_T )$
.
Lemma 2.8. Suppose D is a directed set,
![]() $\kappa $
is an infinite regular cardinal and
$\kappa $
is an infinite regular cardinal and
![]() $X\subseteq D$
is an unbounded subset of size
$X\subseteq D$
is an unbounded subset of size
![]() $\kappa $
such that every subset of X of size
$\kappa $
such that every subset of X of size
![]() $<\kappa $
is bounded. Then
$<\kappa $
is bounded. Then
![]() $\kappa \in \operatorname {\mathrm {hu}}(D)$
.
$\kappa \in \operatorname {\mathrm {hu}}(D)$
.
Proof Enumerate
![]() $X:=\{x_\alpha \mid \alpha <\kappa \}$
, by the assumption, for every
$X:=\{x_\alpha \mid \alpha <\kappa \}$
, by the assumption, for every
![]() $\alpha <\kappa $
we may fix some
$\alpha <\kappa $
we may fix some
![]() $z_\alpha \in D$
above the bounded initial segment
$z_\alpha \in D$
above the bounded initial segment
![]() $\{x_\beta \mid \beta <\alpha \}$
. We show that
$\{x_\beta \mid \beta <\alpha \}$
. We show that
![]() $Z:=\{z_\alpha \mid \alpha <\kappa \}$
, witnesses
$Z:=\{z_\alpha \mid \alpha <\kappa \}$
, witnesses
![]() $\kappa \in \operatorname {\mathrm {hu}}(D)$
. First, let us show that
$\kappa \in \operatorname {\mathrm {hu}}(D)$
. First, let us show that
![]() $|Z|=\kappa $
. Suppose on the contrary that
$|Z|=\kappa $
. Suppose on the contrary that
![]() $Z:=\{z_\alpha \mid \alpha <\kappa \}$
is of cardinality
$Z:=\{z_\alpha \mid \alpha <\kappa \}$
is of cardinality
![]() $< \kappa $
. Then for some
$< \kappa $
. Then for some
![]() $\alpha <\kappa $
, the element
$\alpha <\kappa $
, the element
![]() $z_\alpha $
is above the subset X, hence X is bounded which is absurd. Now, let us prove that Z is hereditarily unbounded. We claim that every subset of Z of cardinality
$z_\alpha $
is above the subset X, hence X is bounded which is absurd. Now, let us prove that Z is hereditarily unbounded. We claim that every subset of Z of cardinality
![]() $\kappa $
is also unbounded. Suppose not, let us fix some
$\kappa $
is also unbounded. Suppose not, let us fix some
![]() $W\in [Z]^\kappa $
bounded by some
$W\in [Z]^\kappa $
bounded by some
![]() $d\in D$
, but then d is above X contradicting the fact that X is unbounded.
$d\in D$
, but then d is above X contradicting the fact that X is unbounded.
Lemma 2.9. Suppose D is a directed set and
![]() $\kappa $
is an infinite cardinal in
$\kappa $
is an infinite cardinal in
![]() $\operatorname {\mathrm {hu}}(D)$
, then
$\operatorname {\mathrm {hu}}(D)$
, then
![]() $\kappa \leq _TD$
.
$\kappa \leq _TD$
.
Proof Fix
![]() $X\subseteq D$
of cardinality
$X\subseteq D$
of cardinality
![]() $\kappa $
such that every subset of X of size
$\kappa $
such that every subset of X of size
![]() $\kappa $
is unbounded and a one-to-one function
$\kappa $
is unbounded and a one-to-one function
![]() $f:\kappa \rightarrow X$
, notice that f is a Tukey function from
$f:\kappa \rightarrow X$
, notice that f is a Tukey function from
![]() $\kappa $
to D as sought.
$\kappa $
to D as sought.
Corollary 2.10. Suppose D is directed set,
![]() $\kappa $
is regular and
$\kappa $
is regular and
![]() $X\subseteq D$
is an unbounded subset of size
$X\subseteq D$
is an unbounded subset of size
![]() $\kappa $
such that every subset of X of size
$\kappa $
such that every subset of X of size
![]() $< \kappa $
is bounded, then
$< \kappa $
is bounded, then
![]() $\kappa \leq _T D$
.
$\kappa \leq _T D$
.
The reader may check the following:
-
• For any two infinite cardinals
 $\lambda $
and
$\lambda $
and
 $\kappa $
of the same cofinality, we have
$\kappa $
of the same cofinality, we have
 $\lambda \equiv _T \kappa $
.
$\lambda \equiv _T \kappa $
. -
• For an infinite regular cardinal
 $\kappa $
, we have
$\kappa $
, we have
 $\kappa \equiv _T [\kappa ]^{<\kappa }$
.
$\kappa \equiv _T [\kappa ]^{<\kappa }$
. -
•
 $\operatorname {\mathrm {hu}}(\prod ^{<\omega }_{n<\omega }\omega _{n+1}) = \{\omega _n \mid n<\omega \}$
.
$\operatorname {\mathrm {hu}}(\prod ^{<\omega }_{n<\omega }\omega _{n+1}) = \{\omega _n \mid n<\omega \}$
.
Lemma 2.11. Suppose D and E are two directed sets such that for some
![]() $\theta \in \operatorname {\mathrm {hu}}(D)$
regular we have
$\theta \in \operatorname {\mathrm {hu}}(D)$
regular we have
![]() $\theta>\operatorname {\mathrm {cf}}(E)$
, then
$\theta>\operatorname {\mathrm {cf}}(E)$
, then
![]() $D\not \leq _T E$
.
$D\not \leq _T E$
.
Proof By passing to a cofinal subset, we may assume that
![]() $|E|=\operatorname {\mathrm {cf}}(E)$
. Fix
$|E|=\operatorname {\mathrm {cf}}(E)$
. Fix
![]() $\theta \in \operatorname {\mathrm {hu}}(D)$
regular such that
$\theta \in \operatorname {\mathrm {hu}}(D)$
regular such that
![]() $\operatorname {\mathrm {cf}}(E)<\theta $
and
$\operatorname {\mathrm {cf}}(E)<\theta $
and
![]() $X\in [D]^\theta $
witnessing
$X\in [D]^\theta $
witnessing
![]() $\theta \in \operatorname {\mathrm {hu}}(D)$
, i.e., every subset of X of size
$\theta \in \operatorname {\mathrm {hu}}(D)$
, i.e., every subset of X of size
![]() $\theta $
is unbounded. Suppose on the contrary that there exists a Tukey function
$\theta $
is unbounded. Suppose on the contrary that there exists a Tukey function
![]() $f:D\rightarrow E$
. By the pigeonhole principle, there exists some
$f:D\rightarrow E$
. By the pigeonhole principle, there exists some
![]() $Z\in [X]^{\theta }$
and
$Z\in [X]^{\theta }$
and
![]() $e\in E$
such that
$e\in E$
such that
![]() $f"Z=\{e\}$
. As f is Tukey and the subset
$f"Z=\{e\}$
. As f is Tukey and the subset
![]() $Z\subseteq X$
is unbounded,
$Z\subseteq X$
is unbounded,
![]() $f"Z$
is unbounded in E which is absurd.
$f"Z$
is unbounded in E which is absurd.
Notice that for every directed set D, if
![]() $\operatorname {\mathrm {cf}}(D)>1$
, then
$\operatorname {\mathrm {cf}}(D)>1$
, then
![]() $\operatorname {\mathrm {cf}}(D)$
is an infinite cardinal.
$\operatorname {\mathrm {cf}}(D)$
is an infinite cardinal.
As a corollary from the previous lemma,
![]() $\lambda \not \leq _T \kappa $
for any two regular cardinals
$\lambda \not \leq _T \kappa $
for any two regular cardinals
![]() $\lambda>\kappa $
where
$\lambda>\kappa $
where
![]() $\lambda $
is infinite. Furthermore, the reader can check that
$\lambda $
is infinite. Furthermore, the reader can check that
![]() $\lambda \not \leq _T\kappa $
, whenever
$\lambda \not \leq _T\kappa $
, whenever
![]() $\lambda <\kappa $
are infinite regular cardinals.
$\lambda <\kappa $
are infinite regular cardinals.
Lemma 2.12. Suppose C and D are directed sets such that
![]() $C\leq _T D$
, then
$C\leq _T D$
, then
![]() $\operatorname {\mathrm {cf}}(C)\leq \operatorname {\mathrm {cf}}(D)$
.
$\operatorname {\mathrm {cf}}(C)\leq \operatorname {\mathrm {cf}}(D)$
.
Proof Suppose
![]() $|D|=\operatorname {\mathrm {cf}}(D)$
and let
$|D|=\operatorname {\mathrm {cf}}(D)$
and let
![]() $f:C\rightarrow D$
be a Tukey function. As f is Tukey, for every
$f:C\rightarrow D$
be a Tukey function. As f is Tukey, for every
![]() $d\in D$
the set
$d\in D$
the set
![]() $\{x\in C\mid f(x)=d\}$
is bounded in C by some
$\{x\in C\mid f(x)=d\}$
is bounded in C by some
![]() $c_d\in C$
. Note that for every
$c_d\in C$
. Note that for every
![]() $x\in C$
, we have
$x\in C$
, we have
![]() $x\leq _C c_{f(x)}$
, hence the set
$x\leq _C c_{f(x)}$
, hence the set
![]() $\{c_d \mid d\in D\}$
is cofinal in C. So
$\{c_d \mid d\in D\}$
is cofinal in C. So
![]() $\operatorname {\mathrm {cf}}(C)\leq |D|=\operatorname {\mathrm {cf}}(D)$
as sought.
$\operatorname {\mathrm {cf}}(C)\leq |D|=\operatorname {\mathrm {cf}}(D)$
as sought.
Lemma 2.13. Let
![]() $\kappa $
and
$\kappa $
and
![]() $\theta $
be two cardinals such that
$\theta $
be two cardinals such that
![]() $\theta <\kappa =\operatorname {\mathrm {cf}}(\kappa )$
.
$\theta <\kappa =\operatorname {\mathrm {cf}}(\kappa )$
.
Suppose D is a directed set such that
![]() $\operatorname {\mathrm {cf}}(D)\leq \kappa $
and
$\operatorname {\mathrm {cf}}(D)\leq \kappa $
and
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\geq \theta $
, then
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\geq \theta $
, then
![]() $D\leq _T [\kappa ]^{<\theta }$
. Furthermore, if
$D\leq _T [\kappa ]^{<\theta }$
. Furthermore, if
![]() $\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, then
$\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, then
![]() $D<_T [\kappa ]^{<\theta }$
.
$D<_T [\kappa ]^{<\theta }$
.
Proof First, we show that there exists a Tukey function
![]() $f:D \rightarrow [\kappa ]^{<\theta }$
. Let us fix a cofinal subset
$f:D \rightarrow [\kappa ]^{<\theta }$
. Let us fix a cofinal subset
![]() $X\subseteq D$
of cardinality
$X\subseteq D$
of cardinality
![]() $\leq \kappa $
such that every subset of X of cardinality
$\leq \kappa $
such that every subset of X of cardinality
![]() $< \theta $
is bounded. As
$< \theta $
is bounded. As
![]() $|X|\leq \kappa $
we may fix an injection
$|X|\leq \kappa $
we may fix an injection
![]() $f:X\rightarrow [\kappa ]^{1}$
, we will show f is a Tukey function. Let
$f:X\rightarrow [\kappa ]^{1}$
, we will show f is a Tukey function. Let
![]() $Y\subseteq X$
be a subset unbounded in D, this implies
$Y\subseteq X$
be a subset unbounded in D, this implies
![]() $|Y|\geq \theta $
. As f is an injection, the set
$|Y|\geq \theta $
. As f is an injection, the set
![]() $\bigcup f"Y$
is of cardinality
$\bigcup f"Y$
is of cardinality
![]() $\geq \theta $
. Note that every subset of
$\geq \theta $
. Note that every subset of
![]() $[\kappa ]^{<\theta }$
whose union is of cardinality
$[\kappa ]^{<\theta }$
whose union is of cardinality
![]() $\geq \theta $
is unbounded in
$\geq \theta $
is unbounded in
![]() $[\kappa ]^{<\theta }$
, hence
$[\kappa ]^{<\theta }$
, hence
![]() $f"Y$
is an unbounded subset in
$f"Y$
is an unbounded subset in
![]() $[\kappa ]^{<\theta }$
as sought.
$[\kappa ]^{<\theta }$
as sought.
Assume
![]() $\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, we are left to show that
$\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\kappa )$
, we are left to show that
![]() $[\kappa ]^{<\theta }\not \leq _T D$
. Suppose on the contrary that
$[\kappa ]^{<\theta }\not \leq _T D$
. Suppose on the contrary that
![]() $g:[\kappa ]^{<\theta }\rightarrow D$
is a Tukey function. We split to two cases:
$g:[\kappa ]^{<\theta }\rightarrow D$
is a Tukey function. We split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $| g" [\kappa ]^1| < \kappa $
. As
$| g" [\kappa ]^1| < \kappa $
. As
![]() $\kappa $
is regular, by the pigeonhole principle there exists a set
$\kappa $
is regular, by the pigeonhole principle there exists a set
![]() $X\subseteq [\kappa ]^1$
of cardinality
$X\subseteq [\kappa ]^1$
of cardinality
![]() $\kappa $
, and
$\kappa $
, and
![]() $d\in D$
such that
$d\in D$
such that
![]() $g(x)=d$
for each
$g(x)=d$
for each
![]() $x\in X$
. Notice
$x\in X$
. Notice
![]() $g"X$
is a bounded subset of D. As
$g"X$
is a bounded subset of D. As
![]() $X\subseteq [\kappa ]^1$
is of cardinality
$X\subseteq [\kappa ]^1$
is of cardinality
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa>\theta $
, it is unbounded in
$\kappa>\theta $
, it is unbounded in
![]() $[\kappa ]^{<\theta }$
. Since g is a Tukey function, we get that
$[\kappa ]^{<\theta }$
. Since g is a Tukey function, we get that
![]() $g"X$
is unbounded which is absurd.
$g"X$
is unbounded which is absurd.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|g"[\kappa ]^1| = \kappa $
. Let
$|g"[\kappa ]^1| = \kappa $
. Let
![]() $X:=g"[\kappa ]^1$
, by our assumption on D, there exists a bounded subset
$X:=g"[\kappa ]^1$
, by our assumption on D, there exists a bounded subset
![]() $B\in [X]^{\theta }$
. Since B is of size
$B\in [X]^{\theta }$
. Since B is of size
![]() $\theta $
, we get that
$\theta $
, we get that
![]() $(g^{-1} [B])\cap [\kappa ]^1$
is of cardinality
$(g^{-1} [B])\cap [\kappa ]^1$
is of cardinality
![]() $\geq \theta $
, hence unbounded in
$\geq \theta $
, hence unbounded in
![]() $[\kappa ]^{<\theta }$
, which is absurd to the assumption g is Tukey.
$[\kappa ]^{<\theta }$
, which is absurd to the assumption g is Tukey.
Remark 2.14. For every two directed sets, D and E, if
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D) )<\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E) )$
, then
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D) )<\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E) )$
, then
![]() $D\not \leq _T E$
. For example,
$D\not \leq _T E$
. For example,
![]() $\theta \not \leq _T [\kappa ]^{\leq \theta }$
.
$\theta \not \leq _T [\kappa ]^{\leq \theta }$
.
Lemma 2.15. Let
![]() $\kappa $
be a regular infinite cardinal. Suppose D and E are two directed sets such that
$\kappa $
be a regular infinite cardinal. Suppose D and E are two directed sets such that
![]() $|D|\geq \kappa $
and
$|D|\geq \kappa $
and
![]() $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, then
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))\in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, then
![]() $D\not \leq _T E$
.
$D\not \leq _T E$
.
Proof Let
![]() $\theta :=\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
. By the definition of
$\theta :=\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))$
. By the definition of
![]() $\operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, as
$\operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, as
![]() $\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, we know that
$\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
, we know that
![]() $\theta \leq \kappa $
. Notice that every subset of D of size
$\theta \leq \kappa $
. Notice that every subset of D of size
![]() $\geq \theta $
is unbounded in D and every subset of size
$\geq \theta $
is unbounded in D and every subset of size
![]() $\kappa $
of E contains a bounded subset in E of size
$\kappa $
of E contains a bounded subset in E of size
![]() $\theta $
.
$\theta $
.
Suppose on the contrary that there exists a Tukey function
![]() $f:D\rightarrow E$
. We split to two cases:
$f:D\rightarrow E$
. We split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|f"D|<\kappa $
, then by the pigeonhole principle there exists some
$|f"D|<\kappa $
, then by the pigeonhole principle there exists some
![]() $X\in [D]^\kappa $
and
$X\in [D]^\kappa $
and
![]() $e\in E$
such that
$e\in E$
such that
![]() $f"X=\{e\}$
. As
$f"X=\{e\}$
. As
![]() $|X|=\kappa \geq \theta $
, we know that X is unbounded in D, but
$|X|=\kappa \geq \theta $
, we know that X is unbounded in D, but
![]() $f"X$
is bounded in E which is absurd as f is a Tukey function.
$f"X$
is bounded in E which is absurd as f is a Tukey function.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|f"D|\geq \kappa $
, by the assumption there exists a subset
$|f"D|\geq \kappa $
, by the assumption there exists a subset
![]() $Y\in [f"D]^\theta $
which is bounded in E. Notice that
$Y\in [f"D]^\theta $
which is bounded in E. Notice that
![]() $X:=f^{-1}Y$
is a subset of D of size
$X:=f^{-1}Y$
is a subset of D of size
![]() $\geq \theta $
, hence unbounded in D. So X is an unbounded subset of D such that
$\geq \theta $
, hence unbounded in D. So X is an unbounded subset of D such that
![]() $f"X=Y$
is bounded in E, contradicting the fact that f is a Tukey function.
$f"X=Y$
is bounded in E, contradicting the fact that f is a Tukey function.
Lemma 2.16. Suppose
![]() $\kappa $
is a regular uncountable cardinal, C and
$\kappa $
is a regular uncountable cardinal, C and
![]() $\langle D_m \mid m<n\rangle $
are directed sets such that
$\langle D_m \mid m<n\rangle $
are directed sets such that
![]() $|C|<\kappa \leq \operatorname {\mathrm {cf}}(D_m)$
and
$|C|<\kappa \leq \operatorname {\mathrm {cf}}(D_m)$
and
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_m))>\theta $
for every
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_m))>\theta $
for every
![]() $m<n$
. Then
$m<n$
. Then
![]() $\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}} (C\times \prod _{m<n}{D_m}),\kappa ) $
.
$\theta \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}} (C\times \prod _{m<n}{D_m}),\kappa ) $
.
Proof Suppose
![]() $X\subseteq C\times \prod _{m<n}{D_m}$
is of size
$X\subseteq C\times \prod _{m<n}{D_m}$
is of size
![]() $\kappa $
, we show that X contains a bounded subset of size
$\kappa $
, we show that X contains a bounded subset of size
![]() $\theta $
. As
$\theta $
. As
![]() $|C|<\kappa $
, by the pigeonhole principle we can fix some
$|C|<\kappa $
, by the pigeonhole principle we can fix some
![]() $Y\in [X]^\kappa $
and
$Y\in [X]^\kappa $
and
![]() $c\in C$
such that
$c\in C$
such that
![]() $\pi _C " Y=\{c\}$
. Suppose on the contrary that some subset
$\pi _C " Y=\{c\}$
. Suppose on the contrary that some subset
![]() $Z\subseteq Y$
of size
$Z\subseteq Y$
of size
![]() $\theta $
is unbounded, it must be that for some
$\theta $
is unbounded, it must be that for some
![]() $m<n$
the set
$m<n$
the set
![]() $\pi _{D_m}"Z$
is unbounded in
$\pi _{D_m}"Z$
is unbounded in
![]() $D_m$
, but this is absurd as
$D_m$
, but this is absurd as
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_m))>\theta $
and
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_m))>\theta $
and
![]() $|\pi _{D_m}"Z|\leq \theta $
.
$|\pi _{D_m}"Z|\leq \theta $
.
Lemma 2.17. Suppose
![]() $C,D$
and E are directed sets such that
$C,D$
and E are directed sets such that
![]() $:$
$:$
-
• for every partition
 $D=\bigcup _{\gamma <\kappa } D_\gamma $
, there exists an ordinal
$D=\bigcup _{\gamma <\kappa } D_\gamma $
, there exists an ordinal
 $\gamma <\kappa $
, and an unbounded
$\gamma <\kappa $
, and an unbounded
 $X\subseteq D_\gamma $
of size
$X\subseteq D_\gamma $
of size
 $\kappa $
;
$\kappa $
; -
•
 $|C|\leq \kappa $
;
$|C|\leq \kappa $
; -
•
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
.
Then
![]() $D\not \leq _T C\times E$
.
$D\not \leq _T C\times E$
.
Proof Suppose on the contrary, that there exists a Tukey function
![]() $h:D \rightarrow C \times E$
. For
$h:D \rightarrow C \times E$
. For
![]() $c\in C$
, let
$c\in C$
, let
![]() $D_c:=\{x\in D \mid \exists e\in E [h(x)=(c,e)]\}$
. Since h is a function,
$D_c:=\{x\in D \mid \exists e\in E [h(x)=(c,e)]\}$
. Since h is a function,
![]() $D:=\bigcup _{c\in C} D_c$
is a partition to
$D:=\bigcup _{c\in C} D_c$
is a partition to
![]() $\leq \kappa $
many sets. By the assumption, there exists
$\leq \kappa $
many sets. By the assumption, there exists
![]() $c\in C$
and an unbounded subset
$c\in C$
and an unbounded subset
![]() $X\subseteq D_c$
of cardinality
$X\subseteq D_c$
of cardinality
![]() $\kappa $
. Enumerate
$\kappa $
. Enumerate
![]() $X=\{x_\xi \mid \xi <\kappa \}$
and let
$X=\{x_\xi \mid \xi <\kappa \}$
and let
![]() $e_\xi \in E$
be such that
$e_\xi \in E$
be such that
![]() $h(x_\xi ) =(c,e_\xi )$
, for each
$h(x_\xi ) =(c,e_\xi )$
, for each
![]() $\xi <\kappa $
. As
$\xi <\kappa $
. As
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
, there exists some upper bound
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
, there exists some upper bound
![]() $e\in E$
to the set
$e\in E$
to the set
![]() $\{e_\xi \mid \xi <\kappa \}$
. Since X is unbounded and h is Tukey,
$\{e_\xi \mid \xi <\kappa \}$
. Since X is unbounded and h is Tukey,
![]() $h"X=\{(c,e_\xi )\mid \xi <\kappa \}$
must be unbounded, which is absurd as
$h"X=\{(c,e_\xi )\mid \xi <\kappa \}$
must be unbounded, which is absurd as
![]() $(c,e)$
is bounding it.
$(c,e)$
is bounding it.
Note that the lemma is also true when the partition of D is of size less than
![]() $\kappa $
.
$\kappa $
.
3 The Catalan structure
The sequence of Catalan numbers
![]() $\langle c_n \mid n<\omega \rangle =\langle 1,1,2,5,14,42,\dots \rangle $
is an ubiquitous sequence of integers with many characterizations, for a comprehensive review of the subject, we refer the reader to Stanley’s book [Reference Stanley11]. One of the many representations of
$\langle c_n \mid n<\omega \rangle =\langle 1,1,2,5,14,42,\dots \rangle $
is an ubiquitous sequence of integers with many characterizations, for a comprehensive review of the subject, we refer the reader to Stanley’s book [Reference Stanley11]. One of the many representations of
![]() $c_n$
, is the number of good n-paths (Dyck paths), where a good n-path is a monotonic lattice path along the edges of a grid with
$c_n$
, is the number of good n-paths (Dyck paths), where a good n-path is a monotonic lattice path along the edges of a grid with
![]() $n\times n$
square cells, which do not pass above the diagonal. A monotonic path is one which starts in the lower left corner, finishes in the upper right corner, and consists entirely of edges pointing rightwards or upwards. An equivalent representation of a good n-path, which we will consider from now on, is a vector
$n\times n$
square cells, which do not pass above the diagonal. A monotonic path is one which starts in the lower left corner, finishes in the upper right corner, and consists entirely of edges pointing rightwards or upwards. An equivalent representation of a good n-path, which we will consider from now on, is a vector
![]() $\vec p$
of the columns’ heights of the path (ignoring the first trivial column), i.e., a vector
$\vec p$
of the columns’ heights of the path (ignoring the first trivial column), i.e., a vector
![]() $\vec p=\langle p_0,\dots ,p_{n-2}\rangle $
of length
$\vec p=\langle p_0,\dots ,p_{n-2}\rangle $
of length
![]() $n-1$
of
$n-1$
of
![]() $\leq $
-increasing numbers satisfying
$\leq $
-increasing numbers satisfying
![]() $0\leq p_k\leq k+1$
, for every
$0\leq p_k\leq k+1$
, for every
![]() $0\leq k\leq n-2$
. We consider the poset
$0\leq k\leq n-2$
. We consider the poset
![]() $(\mathcal K_n,\vartriangleleft )$
where
$(\mathcal K_n,\vartriangleleft )$
where
![]() $\mathcal K_n$
is the set of all good n-paths and the relation
$\mathcal K_n$
is the set of all good n-paths and the relation
![]() $\vartriangleleft $
is defined such that
$\vartriangleleft $
is defined such that
![]() $\vec a \vartriangleleft \vec b$
if and only if the two paths are distinct and for every k with
$\vec a \vartriangleleft \vec b$
if and only if the two paths are distinct and for every k with
![]() $0\leq k\leq n-2$
we have
$0\leq k\leq n-2$
we have
![]() $b_k\leq a_k$
, in other words, the path
$b_k\leq a_k$
, in other words, the path
![]() $\vec b$
is below the path
$\vec b$
is below the path
![]() $\vec a$
(allowing overlaps). Notice that for two distinct good n-paths
$\vec a$
(allowing overlaps). Notice that for two distinct good n-paths
![]() $\vec a$
and
$\vec a$
and
![]() $\vec b$
, either
$\vec b$
, either
![]() $\vec a \not \vartriangleleft \vec b$
or
$\vec a \not \vartriangleleft \vec b$
or
![]() $\vec b \not \vartriangleleft \vec a$
. A good n-path
$\vec b \not \vartriangleleft \vec a$
. A good n-path
![]() $\vec b$
is an immediate successor of a good n-path
$\vec b$
is an immediate successor of a good n-path
![]() $\vec a$
if
$\vec a$
if
![]() $\vec a\vartriangleleft \vec b$
and
$\vec a\vartriangleleft \vec b$
and
![]() $\vec a-\vec b$
is a vector with value
$\vec a-\vec b$
is a vector with value
![]() $0$
at all coordinates except one of them which gets the value
$0$
at all coordinates except one of them which gets the value
![]() $1$
.
$1$
.

Figure 1 The good
![]() $4$
-path
$4$
-path
![]() $\langle 1,1,3\rangle $
.
$\langle 1,1,3\rangle $
.
Suppose
![]() $\vec a$
and
$\vec a$
and
![]() $\vec b$
are two good n-paths where
$\vec b$
are two good n-paths where
![]() $\vec b$
is an immediate successor of
$\vec b$
is an immediate successor of
![]() $\vec a$
. Let
$\vec a$
. Let
![]() $i\leq n-2$
be the unique coordinate on which
$i\leq n-2$
be the unique coordinate on which
![]() $\vec a$
and
$\vec a$
and
![]() $\vec b$
are different and
$\vec b$
are different and
![]() $a_i$
be the value of
$a_i$
be the value of
![]() $\vec a$
on this coordinate, i.e.,
$\vec a$
on this coordinate, i.e.,
![]() $a_i=b_i+1 $
. We say that the pair
$a_i=b_i+1 $
. We say that the pair
![]() $(\vec a, \vec b)$
is on the k-diagonal if and only if
$(\vec a, \vec b)$
is on the k-diagonal if and only if
![]() $i+1-a_i=k$
and
$i+1-a_i=k$
and
![]() $\vec b$
is an immediate successor of
$\vec b$
is an immediate successor of
![]() $\vec a$
(Figure 1).
$\vec a$
(Figure 1).
In this section we show the connection between the Catalan numbers and cofinal types. Let us fix
![]() $n<\omega $
. Recall that for every
$n<\omega $
. Recall that for every
![]() $k<\omega $
, we set
$k<\omega $
, we set
![]() $V_k:=\{1, \omega _k, [\omega _k]^{<\omega _m} \mid 0\leq m<k\}$
,
$V_k:=\{1, \omega _k, [\omega _k]^{<\omega _m} \mid 0\leq m<k\}$
,
![]() $\mathcal F_n:=\bigcup _{k\leq n} V_k$
and let
$\mathcal F_n:=\bigcup _{k\leq n} V_k$
and let
![]() $\mathcal S_n$
be the set of all finite products of elements in
$\mathcal S_n$
be the set of all finite products of elements in
![]() $\mathcal F_n$
. Our goal is to construct a coding which gives rise to an order-isomorphism between
$\mathcal F_n$
. Our goal is to construct a coding which gives rise to an order-isomorphism between
![]() and
and
![]() $(\mathcal K_{n+2},\vartriangleleft )$
.
$(\mathcal K_{n+2},\vartriangleleft )$
.
To do that, we first consider a “canonical form” of directed sets in
![]() $\mathcal S_n$
. By Lemma 2.13 the following hold:
$\mathcal S_n$
. By Lemma 2.13 the following hold:
-
(a) For all
 $0\leq l<m<k<\omega $
we have
$0\leq l<m<k<\omega $
we have
 $1<_T \omega _k<_T [\omega _k]^{<\omega _m} <_T [\omega _k]^{<\omega _l} $
.
$1<_T \omega _k<_T [\omega _k]^{<\omega _m} <_T [\omega _k]^{<\omega _l} $
. -
(b) For all
 $0\leq l\leq t<m\leq k<\omega $
with
$0\leq l\leq t<m\leq k<\omega $
with
 $(l,k)\neq (t,m)$
we have
$(l,k)\neq (t,m)$
we have
 $[\omega _m]^{<\omega _t} <_T [\omega _k]^{<\omega _l}$
and
$[\omega _m]^{<\omega _t} <_T [\omega _k]^{<\omega _l}$
and
 $\omega _m <_T [\omega _k]^{<\omega _l}$
.
$\omega _m <_T [\omega _k]^{<\omega _l}$
.
Notice that (a) implies
![]() $(V_k,<_T)$
is linearly ordered. A basic fact is that for two directed sets C and D such that
$(V_k,<_T)$
is linearly ordered. A basic fact is that for two directed sets C and D such that
![]() $C\leq _T D$
, we have
$C\leq _T D$
, we have
![]() $C\times D \equiv _T D$
. Hence, for every
$C\times D \equiv _T D$
. Hence, for every
![]() $D\in \mathcal S_n$
we can find a sequence of elements
$D\in \mathcal S_n$
we can find a sequence of elements
![]() $\langle D^k \mid k\leq n \rangle $
, where
$\langle D^k \mid k\leq n \rangle $
, where
![]() $D^k\in V_k$
for every
$D^k\in V_k$
for every
![]() $k\leq n$
, such that
$k\leq n$
, such that
![]() $D\equiv _T \prod _{k\leq n}D^k$
. As we are analyzing the class
$D\equiv _T \prod _{k\leq n}D^k$
. As we are analyzing the class
![]() $\mathcal D_{\aleph _n}$
under the Tukey relation
$\mathcal D_{\aleph _n}$
under the Tukey relation
![]() $<_T$
, two directed sets which are of the same
$<_T$
, two directed sets which are of the same
![]() $\equiv _T$
-equivalence class are indistinguishable, so from now on we consider only elements of this form in
$\equiv _T$
-equivalence class are indistinguishable, so from now on we consider only elements of this form in
![]() $\mathcal S_n$
.
$\mathcal S_n$
.
We define a function
![]() $\mathfrak F:\mathcal S_n \rightarrow \mathcal S_n$
as follows: Fix
$\mathfrak F:\mathcal S_n \rightarrow \mathcal S_n$
as follows: Fix
![]() $D\in \mathcal S_n$
where
$D\in \mathcal S_n$
where
![]() $D=\prod _{k\leq n} D^k$
. Next, we construct a sequence
$D=\prod _{k\leq n} D^k$
. Next, we construct a sequence
![]() $\langle D_k \mid k\leq n \rangle $
by reverse recursion on
$\langle D_k \mid k\leq n \rangle $
by reverse recursion on
![]() $k\leq n$
. At the top case, set
$k\leq n$
. At the top case, set
![]() $D_n:=D^n$
. Next, for
$D_n:=D^n$
. Next, for
![]() $0\leq k< n$
. If by (b), we get that
$0\leq k< n$
. If by (b), we get that
![]() $D^{k} <_T D^{m}$
for some
$D^{k} <_T D^{m}$
for some
![]() $k<m\leq n$
, then set
$k<m\leq n$
, then set
![]() $D_{k}:=1$
. Else, let
$D_{k}:=1$
. Else, let
![]() $D_{k}:=D^{k}$
. Finally, let
$D_{k}:=D^{k}$
. Finally, let
![]() $\mathfrak F(D) := \prod _{k\leq n} D_{k}$
. Notice that we constructed
$\mathfrak F(D) := \prod _{k\leq n} D_{k}$
. Notice that we constructed
![]() $\mathfrak F(D)$
such that
$\mathfrak F(D)$
such that
![]() $\mathfrak F(D) \equiv _T D$
. We define
$\mathfrak F(D) \equiv _T D$
. We define
![]() $\mathcal T_n:=\operatorname {\mathrm {Im}}(\mathfrak F)$
.
$\mathcal T_n:=\operatorname {\mathrm {Im}}(\mathfrak F)$
.
The coding. We encode each product
![]() $D\in \mathcal T_n$
by an
$D\in \mathcal T_n$
by an
![]() $(n+2)$
-good path
$(n+2)$
-good path
![]() $\vec v_D:=\langle v_0,\dots , v_{n}\rangle $
. Recall that
$\vec v_D:=\langle v_0,\dots , v_{n}\rangle $
. Recall that
![]() $D:=\prod _{k\leq n} D_k$
, where
$D:=\prod _{k\leq n} D_k$
, where
![]() $D_k\in V_k$
for every
$D_k\in V_k$
for every
![]() $k\leq n$
. We define by reverse recursion on
$k\leq n$
. We define by reverse recursion on
![]() $0\leq k \leq n$
, the elements of the vector
$0\leq k \leq n$
, the elements of the vector
![]() $\vec v_D$
such that
$\vec v_D$
such that
![]() $v_k\leq k+1$
as follows: Suppose one of the elements of
$v_k\leq k+1$
as follows: Suppose one of the elements of
![]() $\langle [\omega _k]^{<\omega },\dots , [\omega _k]^{<\omega _{k-1}} ,\omega _k \rangle $
is equal to
$\langle [\omega _k]^{<\omega },\dots , [\omega _k]^{<\omega _{k-1}} ,\omega _k \rangle $
is equal to
![]() $D_k$
, then let
$D_k$
, then let
![]() $v_{k}$
be its coordinate (starting from
$v_{k}$
be its coordinate (starting from
![]() $0$
). Suppose this is not the case, then if
$0$
). Suppose this is not the case, then if
![]() $k=n$
, we let
$k=n$
, we let
![]() $v_{k}:=n+1$
else
$v_{k}:=n+1$
else
![]() $v_{k}:=\min \{ v_{k+1}, k+1\}$
.
$v_{k}:=\min \{ v_{k+1}, k+1\}$
.
Notice that by (b), if
![]() $0\leq i<j\leq n$
, then
$0\leq i<j\leq n$
, then
![]() $v_i \leq v_j$
. Hence, every element
$v_i \leq v_j$
. Hence, every element
![]() $D\in \mathcal T_n$
is encoded as a good
$D\in \mathcal T_n$
is encoded as a good
![]() $(n+2)$
-path.
$(n+2)$
-path.
To see that the coding is one-to-one, suppose
![]() $C,D\in \mathcal T_n$
are distinct. Let
$C,D\in \mathcal T_n$
are distinct. Let
![]() $k:=\max \{ i\leq n \mid C_i\neq D_i\}$
. We split to two cases:
$k:=\max \{ i\leq n \mid C_i\neq D_i\}$
. We split to two cases:
![]() $\blacktriangleright $
Suppose both
$\blacktriangleright $
Suppose both
![]() $C_k$
and
$C_k$
and
![]() $D_k$
are not equal to
$D_k$
are not equal to
![]() $1$
, then clearly the column height of
$1$
, then clearly the column height of
![]() $\vec v_C$
and
$\vec v_C$
and
![]() $\vec v_D$
are different at coordinate
$\vec v_D$
are different at coordinate
![]() $k+1$
.
$k+1$
.
![]() $\blacktriangleright $
Suppose one of them is equal to
$\blacktriangleright $
Suppose one of them is equal to
![]() $1$
, say
$1$
, say
![]() $C_k$
, then
$C_k$
, then
![]() $D_k\neq 1$
. Let
$D_k\neq 1$
. Let
![]() $\vec v_C:=\langle v^C_0,\dots v^C_n\rangle $
and
$\vec v_C:=\langle v^C_0,\dots v^C_n\rangle $
and
![]() $\vec v_D:=\langle v^D_0,\dots v^D_n\rangle $
. Suppose
$\vec v_D:=\langle v^D_0,\dots v^D_n\rangle $
. Suppose
![]() $k=n$
, then clearly
$k=n$
, then clearly
![]() $v^D_n < v^C_n$
. Suppose
$v^D_n < v^C_n$
. Suppose
![]() $k<n$
, then
$k<n$
, then
![]() $v^D_i = v^C_i$
for
$v^D_i = v^C_i$
for
![]() $k<i\leq n$
. By the coding,
$k<i\leq n$
. By the coding,
![]() $v^D_k<k+1$
and by (b)
$v^D_k<k+1$
and by (b)
![]() $v^D_k<v^D_{k+1}=v^C_{k+1}$
, but
$v^D_k<v^D_{k+1}=v^C_{k+1}$
, but
![]() $v^C_k:=\min \{ k+1, v^C_{k+1}\}$
. Hence
$v^C_k:=\min \{ k+1, v^C_{k+1}\}$
. Hence
![]() $v^D_k < v^C_k$
as sought.
$v^D_k < v^C_k$
as sought.
To see that the coding is onto, let us fix a good
![]() $(n+2)$
-path
$(n+2)$
-path
![]() $\vec v:=\langle v_0, \dots , v_n \rangle $
. We construct
$\vec v:=\langle v_0, \dots , v_n \rangle $
. We construct
![]() $\langle D_k \mid k\leq n \rangle $
by reverse recursion on
$\langle D_k \mid k\leq n \rangle $
by reverse recursion on
![]() $k\leq n$
. At the top case, set
$k\leq n$
. At the top case, set
![]() $D_n$
to be the
$D_n$
to be the
![]() $v_n$
element of the vector
$v_n$
element of the vector
![]() $\langle [\omega _n]^{<\omega },\dots , [\omega _n]^{<\omega _{n-1}} ,\omega _n, 1\rangle $
. For
$\langle [\omega _n]^{<\omega },\dots , [\omega _n]^{<\omega _{n-1}} ,\omega _n, 1\rangle $
. For
![]() $k<n$
, if
$k<n$
, if
![]() $v_k=v_{k+1}$
, let
$v_k=v_{k+1}$
, let
![]() $D_{k}:=1$
. Else, let
$D_{k}:=1$
. Else, let
![]() $D_k$
be the kth element of the vector
$D_k$
be the kth element of the vector
![]() $\langle [\omega _k]^{<\omega },\dots , [\omega _k]^{<\omega _{k-1}} ,\omega _k, 1\rangle $
. Let
$\langle [\omega _k]^{<\omega },\dots , [\omega _k]^{<\omega _{k-1}} ,\omega _k, 1\rangle $
. Let
![]() $D=\prod _{k\leq n} D_k$
, notice that as
$D=\prod _{k\leq n} D_k$
, notice that as
![]() $\vec v$
represents a good
$\vec v$
represents a good
![]() $(n+2)$
-path we have
$(n+2)$
-path we have
![]() $D=\mathfrak F(D)$
, hence
$D=\mathfrak F(D)$
, hence
![]() $D \in \mathcal T_n$
. Furthermore,
$D \in \mathcal T_n$
. Furthermore,
![]() $\vec v_D =\vec v$
, hence the coding is onto as sought. As a Corollary we get that
$\vec v_D =\vec v$
, hence the coding is onto as sought. As a Corollary we get that
![]() $|\mathcal T_n|=c_{n+2}$
.
$|\mathcal T_n|=c_{n+2}$
.
In Figure 2 we present all good
![]() $4$
-paths and the corresponding types in
$4$
-paths and the corresponding types in
![]() $\mathcal T_2$
they encode.
$\mathcal T_2$
they encode.

Figure 2 All good
![]() $4$
-paths and the corresponding types in
$4$
-paths and the corresponding types in
![]() $\mathcal T_2$
they encode.
$\mathcal T_2$
they encode.
Lemma 3.1. Suppose
![]() $C,D\in \mathcal T_n$
and
$C,D\in \mathcal T_n$
and
![]() $\vec v_D \vartriangleleft \vec v_C$
, then
$\vec v_D \vartriangleleft \vec v_C$
, then
![]() $D\leq _T C$
.
$D\leq _T C$
.
Proof Let
![]() $D = \prod _{k\leq n} D_k$
and
$D = \prod _{k\leq n} D_k$
and
![]() $C=\prod _{k\leq n} C_k$
. Note that if
$C=\prod _{k\leq n} C_k$
. Note that if
![]() $D_k\leq _T C$
for every
$D_k\leq _T C$
for every
![]() $k\leq n$
, then
$k\leq n$
, then
![]() $D\leq _T C$
as sought. Fix
$D\leq _T C$
as sought. Fix
![]() $k\leq n$
, if
$k\leq n$
, if
![]() $D_k=1$
, then clearly
$D_k=1$
, then clearly
![]() $D_k\leq C$
. Suppose
$D_k\leq C$
. Suppose
![]() $D_k\neq 1$
, we split to two cases:
$D_k\neq 1$
, we split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $C_k\neq 1$
. As
$C_k\neq 1$
. As
![]() $v^C_k <v^D_k$
and by (a) we have
$v^C_k <v^D_k$
and by (a) we have
![]() $D_k \leq _T C_k\leq _T C$
as sought.
$D_k \leq _T C_k\leq _T C$
as sought.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $C_k=1$
, let
$C_k=1$
, let
![]() $m:=\max \{i\leq n \mid k< i,~v^C_i= v^C_k\}$
. As
$m:=\max \{i\leq n \mid k< i,~v^C_i= v^C_k\}$
. As
![]() $v^C_i \leq i+1$
, by the coding m is well-defined and
$v^C_i \leq i+1$
, by the coding m is well-defined and
![]() $v^C_m= v^C_k\leq k<m$
. Notice that
$v^C_m= v^C_k\leq k<m$
. Notice that
![]() $C_m=[\omega _m]^{<\omega _p}$
where
$C_m=[\omega _m]^{<\omega _p}$
where
![]() $p=v^C_m$
and
$p=v^C_m$
and
![]() $D_k\equiv _T [\omega _k]^{<\omega _p}$
. So by (b),
$D_k\equiv _T [\omega _k]^{<\omega _p}$
. So by (b),
![]() $D_k\leq _T C_m\leq _T C$
as sought.
$D_k\leq _T C_m\leq _T C$
as sought.
Lemma 3.2. Suppose
![]() $C,D\in \mathcal T_n$
and
$C,D\in \mathcal T_n$
and
![]() $\vec v_D \not \vartriangleleft \vec v_C$
, then
$\vec v_D \not \vartriangleleft \vec v_C$
, then
![]() $D\not \leq _T C$
.
$D\not \leq _T C$
.
Proof Let
![]() $D=\prod _{k\leq n} D_k$
,
$D=\prod _{k\leq n} D_k$
,
![]() $C=\prod _{k\leq n} C_k$
,
$C=\prod _{k\leq n} C_k$
,
![]() $\vec v_C:=\langle v_0^C,\dots , v_n^C\rangle $
and
$\vec v_C:=\langle v_0^C,\dots , v_n^C\rangle $
and
![]() $\vec v_D:=\langle v_0^D,\dots , v_n^D\rangle $
As
$\vec v_D:=\langle v_0^D,\dots , v_n^D\rangle $
As
![]() $\vec v_D \not \vartriangleleft \vec v_C$
, we can define
$\vec v_D \not \vartriangleleft \vec v_C$
, we can define
![]() $i=\min \{k\leq n \mid v^C_k>v^D_k\}$
.
$i=\min \{k\leq n \mid v^C_k>v^D_k\}$
.
Let
![]() $p:=v^D_i$
and
$p:=v^D_i$
and
![]() $r=\max \{k\leq n \mid v_i^D = v_k^D\}$
, notice that
$r=\max \{k\leq n \mid v_i^D = v_k^D\}$
, notice that
![]() $p\leq i$
. We define a directed set F such that
$p\leq i$
. We define a directed set F such that
![]() $F\leq _T D$
.
$F\leq _T D$
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $p=i$
and let
$p=i$
and let
![]() $F=\omega _i$
. If
$F=\omega _i$
. If
![]() $r=i$
, then clearly
$r=i$
, then clearly
![]() $F=D_i$
and
$F=D_i$
and
![]() $F\leq _T D$
as sought. Else, by the coding
$F\leq _T D$
as sought. Else, by the coding
![]() $D_r=[\omega _r]^{<\omega _p}$
. By Lemma 2.13, we have
$D_r=[\omega _r]^{<\omega _p}$
. By Lemma 2.13, we have
![]() $F\leq _T D$
as sought.
$F\leq _T D$
as sought.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $p<i$
and let
$p<i$
and let
![]() $F=\mathfrak D_{[\omega _i]^{<\omega _{p}}}$
. By the coding
$F=\mathfrak D_{[\omega _i]^{<\omega _{p}}}$
. By the coding
![]() $D_r=[\omega _r]^{<\omega _p}$
and by Clause (b), we have
$D_r=[\omega _r]^{<\omega _p}$
and by Clause (b), we have
![]() $F\leq _T D$
as sought.
$F\leq _T D$
as sought.
Notice that
![]() $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(F)) = \omega _p$
and
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(F)) = \omega _p$
and
![]() $\operatorname {\mathrm {cf}}(F)=\omega _i$
. As
$\operatorname {\mathrm {cf}}(F)=\omega _i$
. As
![]() $F\leq _T D$
, it is enough to verify that
$F\leq _T D$
, it is enough to verify that
![]() $F\not \leq _T C$
.
$F\not \leq _T C$
.
As
![]() $\vec v_C$
is a good
$\vec v_C$
is a good
![]() $(n+2)$
-path, we know that
$(n+2)$
-path, we know that
![]() $v_k^C>p$
for every
$v_k^C>p$
for every
![]() $k\geq i$
. Consider
$k\geq i$
. Consider
![]() $A:=\{i\leq k\leq n \mid C_k \neq 1 \}$
. We split to two cases:
$A:=\{i\leq k\leq n \mid C_k \neq 1 \}$
. We split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $A=\emptyset $
. Then
$A=\emptyset $
. Then
![]() $\operatorname {\mathrm {cf}}(\prod _{k\leq n} C_k) <\omega _i$
. As
$\operatorname {\mathrm {cf}}(\prod _{k\leq n} C_k) <\omega _i$
. As
![]() $\operatorname {\mathrm {cf}}(F)=\omega _i$
, by Lemma 2.12 we have that
$\operatorname {\mathrm {cf}}(F)=\omega _i$
, by Lemma 2.12 we have that
![]() $F\not \leq _T \prod _{k\leq n} C_k$
as sought.
$F\not \leq _T \prod _{k\leq n} C_k$
as sought.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $A\neq \emptyset $
. Let
$A\neq \emptyset $
. Let
![]() $E:=\prod _{k<i} C_k \times \prod _{k\in A} C_k$
Notice that
$E:=\prod _{k<i} C_k \times \prod _{k\in A} C_k$
Notice that
![]() $\operatorname {\mathrm {cf}}(\prod _{k<i} C_k)<\omega _i$
,
$\operatorname {\mathrm {cf}}(\prod _{k<i} C_k)<\omega _i$
,
![]() $\prod _{i\leq k \leq n} C_k \equiv _T \prod _{k\in A} C_k$
and
$\prod _{i\leq k \leq n} C_k \equiv _T \prod _{k\in A} C_k$
and
![]() $C\equiv _T E$
. Furthermore, for each
$C\equiv _T E$
. Furthermore, for each
![]() $k\in A$
, we have
$k\in A$
, we have
![]() $\operatorname {\mathrm {non}}(\mathcal I_{bd}(C_k))>\omega _p$
. By Lemma 2.16, we have
$\operatorname {\mathrm {non}}(\mathcal I_{bd}(C_k))>\omega _p$
. By Lemma 2.16, we have
![]() $\omega _p\in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\omega _i)$
. Recall
$\omega _p\in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\omega _i)$
. Recall
![]() $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(F)) = \omega _p$
. By Lemma 2.15, we get that
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(F)) = \omega _p$
. By Lemma 2.15, we get that
![]() $F\not \leq _T E$
, hence
$F\not \leq _T E$
, hence
![]() $F\not \leq _T C$
as sought.
$F\not \leq _T C$
as sought.
Theorem 3.3. The posets
![]() $(\mathcal T_n, <_T)$
and
$(\mathcal T_n, <_T)$
and
![]() $(\mathcal K_{n+2},\vartriangleleft )$
are isomorphic.
$(\mathcal K_{n+2},\vartriangleleft )$
are isomorphic.
Proof Define f from
![]() $(\mathcal T_n,<_T)$
to
$(\mathcal T_n,<_T)$
to
![]() $(\mathcal K_{n+2},\vartriangleleft )$
, where for
$(\mathcal K_{n+2},\vartriangleleft )$
, where for
![]() $C\in \mathcal T_n$
, we let
$C\in \mathcal T_n$
, we let
![]() $f(C):=\vec v_C$
. By Lemmas 3.1 and 3.2, this is indeed an isomorphism of posets.
$f(C):=\vec v_C$
. By Lemmas 3.1 and 3.2, this is indeed an isomorphism of posets.
Furthermore, we claim that
![]() $\mathcal T_n$
contains one unique representative from each equivalence class of
$\mathcal T_n$
contains one unique representative from each equivalence class of
![]() $(\mathcal S_n,\equiv _T)$
. Recall that the function
$(\mathcal S_n,\equiv _T)$
. Recall that the function
![]() $\mathfrak F$
is preserving Tukey equivalence classes. Consider two distinct
$\mathfrak F$
is preserving Tukey equivalence classes. Consider two distinct
![]() $C,D\in \mathcal T_n$
. As the coding is a bijection,
$C,D\in \mathcal T_n$
. As the coding is a bijection,
![]() $\vec v_C$
and
$\vec v_C$
and
![]() $\vec v_D$
are different. Notice that either
$\vec v_D$
are different. Notice that either
![]() $\vec v_C \not \vartriangleleft \vec v_D$
or
$\vec v_C \not \vartriangleleft \vec v_D$
or
![]() $\vec v_D \not \vartriangleleft \vec v_C$
, hence by Lemma 3.2,
$\vec v_D \not \vartriangleleft \vec v_C$
, hence by Lemma 3.2,
![]() $C\not \equiv _T D$
as sought.
$C\not \equiv _T D$
as sought.
Consider the poset
![]() $(\mathcal T_n, <_T)$
, clearly
$(\mathcal T_n, <_T)$
, clearly
![]() $1$
is a minimal element and by Lemma 2.13,
$1$
is a minimal element and by Lemma 2.13,
![]() $[\omega _n]^{<\omega }$
is a maximal element. By the previous theorem, the set of immediate successors of an element D in the poset
$[\omega _n]^{<\omega }$
is a maximal element. By the previous theorem, the set of immediate successors of an element D in the poset
![]() $(\mathcal T_n, <_T)$
, is the set of all directed sets
$(\mathcal T_n, <_T)$
, is the set of all directed sets
![]() $C\in \mathcal T_n$
such that
$C\in \mathcal T_n$
such that
![]() $\vec v_C$
is an
$\vec v_C$
is an
![]() $\vartriangleleft $
-immediate successor of
$\vartriangleleft $
-immediate successor of
![]() $\vec v_D$
.
$\vec v_D$
.
Lemma 3.4. Suppose
![]() $G,H\in \mathcal T_n$
, H is an immediate successor of G in the poset
$G,H\in \mathcal T_n$
, H is an immediate successor of G in the poset
![]() $(\mathcal T_n, <_T)$
and
$(\mathcal T_n, <_T)$
and
![]() $(\vec v_G, \vec v_H)$
are on the l-diagonal. Then there are
$(\vec v_G, \vec v_H)$
are on the l-diagonal. Then there are
![]() $C, E, M, N$
directed sets such that
$C, E, M, N$
directed sets such that
![]() $:$
$:$
-
•
 $G\equiv _T C\times M\times E$
and
$G\equiv _T C\times M\times E$
and
 $H\equiv _T C\times N \times E$
;
$H\equiv _T C\times N \times E$
; -
• for some
 $k\leq n$
,
$k\leq n$
,
 $\operatorname {\mathrm {cf}}(N)=\omega _k$
,
$\operatorname {\mathrm {cf}}(N)=\omega _k$
,
 $|C|<\omega _k$
and either
$|C|<\omega _k$
and either
 $E\equiv _T 1$
or
$E\equiv _T 1$
or
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
.
Furthermore,
-
• If
 $l=0$
, then
$l=0$
, then
 $M=1$
and
$M=1$
and
 $N=\omega _k$
.
$N=\omega _k$
. -
• If
 $l=1$
, then
$l=1$
, then
 $k>1$
and
$k>1$
and
 $M=\omega _k$
and
$M=\omega _k$
and
 $N=[\omega _k]^{<\omega _{k-1}}$
.
$N=[\omega _k]^{<\omega _{k-1}}$
. -
• If
 $l>1$
, then
$l>1$
, then
 $k>l$
and
$k>l$
and
 $M=[\omega _k]^{<\omega _{k-l+1}}$
and
$M=[\omega _k]^{<\omega _{k-l+1}}$
and
 $N=[\omega _k]^{<\omega _{k-l}}$
.
$N=[\omega _k]^{<\omega _{k-l}}$
.
Proof As H is an immediate successor of G in the poset
![]() $(\mathcal T_n, <_T)$
, we know that
$(\mathcal T_n, <_T)$
, we know that
![]() $\vec v_H$
is an immediate successor of
$\vec v_H$
is an immediate successor of
![]() $\vec v_H$
in
$\vec v_H$
in
![]() $(\mathcal K_{n+2},\vartriangleleft )$
. Let k be the unique
$(\mathcal K_{n+2},\vartriangleleft )$
. Let k be the unique
![]() $k\leq n$
such that
$k\leq n$
such that
![]() $v^k_G = v^k_H +1$
.
$v^k_G = v^k_H +1$
.
Let
![]() $\vec v_G:=\langle v^0_G, \dots , v^n_G \rangle $
be a good
$\vec v_G:=\langle v^0_G, \dots , v^n_G \rangle $
be a good
![]() $(n+2)$
-path coded by G. We construct
$(n+2)$
-path coded by G. We construct
![]() $\langle M_i \mid i\leq n \rangle $
by letting
$\langle M_i \mid i\leq n \rangle $
by letting
![]() $M_i$
be the ith element of the vector
$M_i$
be the ith element of the vector
![]() $\langle [\omega _i]^{<\omega },\dots , [\omega _i]^{<\omega _{i-1}} ,\omega _i, 1\rangle $
for every
$\langle [\omega _i]^{<\omega },\dots , [\omega _i]^{<\omega _{i-1}} ,\omega _i, 1\rangle $
for every
![]() $i\leq n$
. Notice that
$i\leq n$
. Notice that
![]() $G\equiv _T \prod _{i\leq n} M_i$
. Similarly, we may construct
$G\equiv _T \prod _{i\leq n} M_i$
. Similarly, we may construct
![]() $\langle N_i \mid i\leq n \rangle $
such that
$\langle N_i \mid i\leq n \rangle $
such that
![]() $H\equiv _T \prod _{i\leq n} N_i$
. Clearly,
$H\equiv _T \prod _{i\leq n} N_i$
. Clearly,
![]() $M_i=N_i$
for every
$M_i=N_i$
for every
![]() $i\neq k$
.
$i\neq k$
.
Let
![]() $C:=\prod _{i<k} M_i$
and
$C:=\prod _{i<k} M_i$
and
![]() $E:=\prod _{i>k} M_i$
. Notice that
$E:=\prod _{i>k} M_i$
. Notice that
![]() $|C|=\operatorname {\mathrm {cf}}(C)<\omega _k$
and either
$|C|=\operatorname {\mathrm {cf}}(C)<\omega _k$
and either
![]() $E\equiv _T 1$
or
$E\equiv _T 1$
or
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
. Moreover,
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
. Moreover,
![]() $G\equiv _T C\times M_k \times E$
and
$G\equiv _T C\times M_k \times E$
and
![]() $H\equiv _TC\times N_k \times E$
. We split to cases:
$H\equiv _TC\times N_k \times E$
. We split to cases:
-
• If
 $l=0$
, then
$l=0$
, then
 $v^k_H=k+1$
, hence
$v^k_H=k+1$
, hence
 $M_k=1$
and
$M_k=1$
and
 $N_k=\omega _k$
.
$N_k=\omega _k$
. -
• If
 $l=1$
, then
$l=1$
, then
 $v^k_H=k$
, hence
$v^k_H=k$
, hence
 $M_k=\omega _k$
and
$M_k=\omega _k$
and
 $N_k=[\omega _k]^{<\omega _{k-1}}$
.
$N_k=[\omega _k]^{<\omega _{k-1}}$
. -
• If
 $l>1$
, then
$l>1$
, then
 $v^k_H=k-l+1$
, hence
$v^k_H=k-l+1$
, hence
 $M_k=[\omega _k]^{<\omega _{k-l+1}}$
and
$M_k=[\omega _k]^{<\omega _{k-l+1}}$
and
 $N_k=[\omega _k]^{<\omega _{k-l}}$
.
$N_k=[\omega _k]^{<\omega _{k-l}}$
.
Theorem 3.5. Suppose
![]() $G,H\in \mathcal T_n$
, H is an immediate successor of G in the poset
$G,H\in \mathcal T_n$
, H is an immediate successor of G in the poset
![]() $(\mathcal T_n, <_T)$
and
$(\mathcal T_n, <_T)$
and
![]() $(\vec v_G, \vec v_H)$
are on the l-diagonal.
$(\vec v_G, \vec v_H)$
are on the l-diagonal.
-
• If
 $l=0$
, then there is no directed set
$l=0$
, then there is no directed set
 $D\in \mathcal D_{\aleph _n}$
such that
$D\in \mathcal D_{\aleph _n}$
such that
 $G<_T D<_T H$
.
$G<_T D<_T H$
. -
• If
 $l>0$
, then consistently there exist a directed set
$l>0$
, then consistently there exist a directed set
 $D\in \mathcal D_{\aleph _n}$
such that
$D\in \mathcal D_{\aleph _n}$
such that
 $G<_T D<_T H$
.
$G<_T D<_T H$
.
Proof Let
![]() $C,E, M, N$
be as in the previous lemma, so
$C,E, M, N$
be as in the previous lemma, so
![]() $G\equiv _T C\times M\times E$
,
$G\equiv _T C\times M\times E$
,
![]() $H\equiv _T C\times N \times E$
and for some
$H\equiv _T C\times N \times E$
and for some
![]() $k\leq n$
,
$k\leq n$
,
![]() $|C|<\omega _k$
and either
$|C|<\omega _k$
and either
![]() $E\equiv _T 1$
or
$E\equiv _T 1$
or
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
. We split to three cases:
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\omega _{k-l}$
. We split to three cases:
-
• Suppose
 $l=0$
, then
$l=0$
, then
 $G\equiv _T C\times E $
and
$G\equiv _T C\times E $
and
 $H\equiv _T C\times \omega _k \times E$
, by Theorem 4.1 there is no directed set D such that
$H\equiv _T C\times \omega _k \times E$
, by Theorem 4.1 there is no directed set D such that
 $G<_T D <_T H$
.
$G<_T D <_T H$
. -
• Suppose
 $l=1$
, then
$l=1$
, then
 $k\geq 1$
and
$k\geq 1$
and
 $N=[\omega _k]^{<\omega _{k-1}}$
and
$N=[\omega _k]^{<\omega _{k-1}}$
and
 $M=\omega _k$
.
$M=\omega _k$
.-
– Suppose
 $k=1$
, then under the assumption
$k=1$
, then under the assumption
 $\mathfrak b =\omega _1$
, by Theorem 5.9 there exists a directed set D such that
$\mathfrak b =\omega _1$
, by Theorem 5.9 there exists a directed set D such that
 $G<_T D <_T H$
.
$G<_T D <_T H$
. -
– Suppose
 $k>1$
, then under the assumption
$k>1$
, then under the assumption
 $2^{\aleph _{k-2}} = \aleph _{k-1}$
and
$2^{\aleph _{k-2}} = \aleph _{k-1}$
and
 $2^{\aleph _{k-1}}= \aleph _k$
, by Corollary 5.1 there exists a directed set D such that
$2^{\aleph _{k-1}}= \aleph _k$
, by Corollary 5.1 there exists a directed set D such that
 $G<_T D <_T H$
.
$G<_T D <_T H$
.
-
-
• Suppose
 $l>1$
, then
$l>1$
, then
 $k\geq 2$
. Let
$k\geq 2$
. Let
 $\theta =\omega _{k-l}$
and
$\theta =\omega _{k-l}$
and
 $\lambda = \omega _{k-1}$
. Notice
$\lambda = \omega _{k-1}$
. Notice
 $N=[\omega _k]^{\leq \theta }$
and
$N=[\omega _k]^{\leq \theta }$
and
 $M=[\omega _k]^{<\theta }$
. In Corollary 5.11, we shall show that under the assumption
$M=[\omega _k]^{<\theta }$
. In Corollary 5.11, we shall show that under the assumption
 $\lambda ^{\theta }<\lambda ^+$
and
$\lambda ^{\theta }<\lambda ^+$
and
 $ \clubsuit ^{\omega _{k-1}}_{J}(S,1) $
for some stationary set
$ \clubsuit ^{\omega _{k-1}}_{J}(S,1) $
for some stationary set
 $S\subseteq E^{\omega _k}_{\theta }$
, there exists a directed set D such that
$S\subseteq E^{\omega _k}_{\theta }$
, there exists a directed set D such that
 $G<_T D <_T H$
.
$G<_T D <_T H$
.
4 Empty intervals in
 $D_{\aleph _n}$
$D_{\aleph _n}$
Consider two successive directed sets in the poset
![]() $(\mathcal T_n , <_T)$
, we can ask whether there exists some other directed set in between in the Tukey order. The following theorem give us a scenario in which there is a no such directed set.
$(\mathcal T_n , <_T)$
, we can ask whether there exists some other directed set in between in the Tukey order. The following theorem give us a scenario in which there is a no such directed set.
Theorem 4.1. Let
![]() $\kappa $
be a regular cardinal. Suppose C and E are two directed sets such that
$\kappa $
be a regular cardinal. Suppose C and E are two directed sets such that
![]() $\operatorname {\mathrm {cf}}(C)<\kappa $
and either
$\operatorname {\mathrm {cf}}(C)<\kappa $
and either
![]() $E\equiv _T 1$
or
$E\equiv _T 1$
or
![]() $\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
and
$\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
and
![]() $\kappa \leq \operatorname {\mathrm {cf}}(E)$
. Then there is no directed set D such that
$\kappa \leq \operatorname {\mathrm {cf}}(E)$
. Then there is no directed set D such that
![]() $C\times E <_T D <_T C\times \kappa \times E$
.
$C\times E <_T D <_T C\times \kappa \times E$
.
Lemma 4.2. Let
![]() $\kappa $
be a regular cardinal. Suppose C is a directed set such that
$\kappa $
be a regular cardinal. Suppose C is a directed set such that
![]() $\operatorname {\mathrm {cf}}(C)<\kappa $
, then there is no directed set D such that
$\operatorname {\mathrm {cf}}(C)<\kappa $
, then there is no directed set D such that
![]() $C <_T D <_T C \times \kappa $
.
$C <_T D <_T C \times \kappa $
.
Proof Suppose D is a directed set such that
![]() $C <_T D <_T C \times \kappa $
. Let us assume D is a directed set of size
$C <_T D <_T C \times \kappa $
. Let us assume D is a directed set of size
![]() $\operatorname {\mathrm {cf}}(D)$
such that every subset of D of size
$\operatorname {\mathrm {cf}}(D)$
such that every subset of D of size
![]() $\operatorname {\mathrm {cf}}(D)$
is unbounded in D. By Lemma 2.12 we get that
$\operatorname {\mathrm {cf}}(D)$
is unbounded in D. By Lemma 2.12 we get that
![]() $\operatorname {\mathrm {cf}}(C) \leq \operatorname {\mathrm {cf}}(D)\leq \kappa $
. We split to two cases:
$\operatorname {\mathrm {cf}}(C) \leq \operatorname {\mathrm {cf}}(D)\leq \kappa $
. We split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\operatorname {\mathrm {cf}}(C)\leq \operatorname {\mathrm {cf}}(D) <\kappa $
. Let
$\operatorname {\mathrm {cf}}(C)\leq \operatorname {\mathrm {cf}}(D) <\kappa $
. Let
![]() $g:D\rightarrow C\times \kappa $
be a Tukey function. As
$g:D\rightarrow C\times \kappa $
be a Tukey function. As
![]() $|D|=\operatorname {\mathrm {cf}}(D)<\kappa $
and
$|D|=\operatorname {\mathrm {cf}}(D)<\kappa $
and
![]() $\kappa $
is regular there exists some
$\kappa $
is regular there exists some
![]() $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
![]() $g"D \subseteq C\times \alpha $
. We claim that
$g"D \subseteq C\times \alpha $
. We claim that
![]() $\pi _C \circ g$
is a Tukey function from D to C, hence
$\pi _C \circ g$
is a Tukey function from D to C, hence
![]() $D\leq _T C$
which is absurd. Suppose
$D\leq _T C$
which is absurd. Suppose
![]() $X\subseteq D$
is unbounded in D, as g is a Tukey function, we know that
$X\subseteq D$
is unbounded in D, as g is a Tukey function, we know that
![]() $g"X$
is unbounded in
$g"X$
is unbounded in
![]() $C\times \kappa $
. But as
$C\times \kappa $
. But as
![]() $(\pi _{\kappa }\circ g)"X$
is bounded by
$(\pi _{\kappa }\circ g)"X$
is bounded by
![]() $\alpha $
, we get that
$\alpha $
, we get that
![]() $(\pi _{C}\circ g)" X$
is unbounded in C as sought.
$(\pi _{C}\circ g)" X$
is unbounded in C as sought.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\operatorname {\mathrm {cf}}(D)=\kappa $
, notice that
$\operatorname {\mathrm {cf}}(D)=\kappa $
, notice that
![]() $\kappa \in \operatorname {\mathrm {hu}}(D)$
is regular so by Lemma 2.9 we get that
$\kappa \in \operatorname {\mathrm {hu}}(D)$
is regular so by Lemma 2.9 we get that
![]() $\kappa \leq _T D$
. We also know that
$\kappa \leq _T D$
. We also know that
![]() $C\leq _T D$
, thus
$C\leq _T D$
, thus
![]() $\kappa \times C \leq _T D$
which is absurd.
$\kappa \times C \leq _T D$
which is absurd.
Note that
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
implies that
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))> \kappa $
implies that
![]() $\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
.
$\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
.
Lemma 4.3. Let
![]() $\kappa $
be a regular cardinal. Suppose C and E are two directed sets such that
$\kappa $
be a regular cardinal. Suppose C and E are two directed sets such that
![]() $\operatorname {\mathrm {cf}}(C)<\kappa \leq \operatorname {\mathrm {cf}}(E)$
and
$\operatorname {\mathrm {cf}}(C)<\kappa \leq \operatorname {\mathrm {cf}}(E)$
and
![]() $\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
. Then there is no directed set D such that
$\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
. Then there is no directed set D such that
![]() $C\times E <_T D <_T C\times \kappa \times E$
.
$C\times E <_T D <_T C\times \kappa \times E$
.
Proof Suppose D is a directed set such that
![]() $C\times E \leq _T D \leq _T C\times \kappa \times E$
, we will show that either
$C\times E \leq _T D \leq _T C\times \kappa \times E$
, we will show that either
![]() $D\equiv _T C\times E$
or
$D\equiv _T C\times E$
or
![]() $D\equiv _T C\times \kappa \times E$
. We may assume that every subset of D of size
$D\equiv _T C\times \kappa \times E$
. We may assume that every subset of D of size
![]() $\operatorname {\mathrm {cf}}(D)$
is unbounded and
$\operatorname {\mathrm {cf}}(D)$
is unbounded and
![]() $|C|=\operatorname {\mathrm {cf}}(C)$
. By Lemma 2.12, we have that
$|C|=\operatorname {\mathrm {cf}}(C)$
. By Lemma 2.12, we have that
![]() $\operatorname {\mathrm {cf}}(E)=\operatorname {\mathrm {cf}}(D)$
.
$\operatorname {\mathrm {cf}}(E)=\operatorname {\mathrm {cf}}(D)$
.
Suppose first there exists some unbounded subset
![]() $X\in [D]^{\kappa }$
such that every subset
$X\in [D]^{\kappa }$
such that every subset
![]() $Y\in [X]^{<\kappa }$
is bounded. By Corollary 2.10, this implies that
$Y\in [X]^{<\kappa }$
is bounded. By Corollary 2.10, this implies that
![]() $\kappa \leq _T D$
. But as
$\kappa \leq _T D$
. But as
![]() $C\times E\leq _T D$
and
$C\times E\leq _T D$
and
![]() $D \leq _T C\times \kappa \times E$
, this implies that
$D \leq _T C\times \kappa \times E$
, this implies that
![]() $C\times \kappa \times E \equiv _T D$
as sought.
$C\times \kappa \times E \equiv _T D$
as sought.
Hereafter, suppose for every unbounded subset
![]() $X\in [D]^{\kappa }$
there exists some subset
$X\in [D]^{\kappa }$
there exists some subset
![]() $Y\in [X]^{<\kappa }$
unbounded. Let
$Y\in [X]^{<\kappa }$
unbounded. Let
![]() $g:D\rightarrow C\times \kappa \times E$
be a Tukey function. Define
$g:D\rightarrow C\times \kappa \times E$
be a Tukey function. Define
![]() $h:=\pi _{C\times E} \circ g$
. Now, there are two main cases to consider:
$h:=\pi _{C\times E} \circ g$
. Now, there are two main cases to consider:
-
▸ Suppose every unbounded subset
 $X\subseteq D$
of size
$X\subseteq D$
of size
 $\lambda>\kappa $
which contain no unbounded subset of smaller cardinality is such that
$\lambda>\kappa $
which contain no unbounded subset of smaller cardinality is such that
 $h"X$
is unbounded in
$h"X$
is unbounded in
 $C\times E$
.
$C\times E$
.We show that h is Tukey, it is enough to verify that for every cardinal
 $\omega \leq \mu \leq \kappa $
and every unbounded subset
$\omega \leq \mu \leq \kappa $
and every unbounded subset
 $X\subseteq D$
of size
$X\subseteq D$
of size
 $\mu $
which contain no unbounded subset of smaller cardinality is such that
$\mu $
which contain no unbounded subset of smaller cardinality is such that
 $h"X$
is unbounded in
$h"X$
is unbounded in
 $C\times E$
.
$C\times E$
.As g is Tukey, the set
 $g"X$
is unbounded in
$g"X$
is unbounded in
 $C\times \kappa \times E$
. Notice that if the set
$C\times \kappa \times E$
. Notice that if the set
 $\pi _{C\times E}\circ g" X$
is unbounded, then we are done. Assume that
$\pi _{C\times E}\circ g" X$
is unbounded, then we are done. Assume that
 $\pi _{C\times E}\circ g" X$
is bounded, then
$\pi _{C\times E}\circ g" X$
is bounded, then
 $\pi _{\kappa } \circ g"X$
is unbounded.
$\pi _{\kappa } \circ g"X$
is unbounded. $\blacktriangleright \blacktriangleright $
Suppose
$\blacktriangleright \blacktriangleright $
Suppose
 $|X|<\kappa $
. As
$|X|<\kappa $
. As
 $|g"X|<\kappa $
, we have that
$|g"X|<\kappa $
, we have that
 $\pi _{\kappa } \circ g"X$
is bounded, which is absurd.
$\pi _{\kappa } \circ g"X$
is bounded, which is absurd. $\blacktriangleright \blacktriangleright $
Suppose
$\blacktriangleright \blacktriangleright $
Suppose
 $ |X|=\kappa $
, by the case assumption there exists some
$ |X|=\kappa $
, by the case assumption there exists some
 $Y \in [X]^{<\kappa }$
unbounded in D. But this is absurd as the assumption on X was that X contains no subset of size smaller than
$Y \in [X]^{<\kappa }$
unbounded in D. But this is absurd as the assumption on X was that X contains no subset of size smaller than
 $|X|$
which is unbounded.
$|X|$
which is unbounded. $\blacktriangleright \blacktriangleright $
Suppose
$\blacktriangleright \blacktriangleright $
Suppose
 $|X|>\kappa $
, by the case assumption,
$|X|>\kappa $
, by the case assumption,
 $h"X$
is unbounded in
$h"X$
is unbounded in
 $C\times E$
as sought.
$C\times E$
as sought. -
▸ Suppose for some unbounded subset
 $X\subseteq D$
of size
$X\subseteq D$
of size
 $\lambda>\kappa $
which contains no unbounded subset of smaller cardinality is such that
$\lambda>\kappa $
which contains no unbounded subset of smaller cardinality is such that
 $h"X$
is bounded in
$h"X$
is bounded in
 $C\times E$
. As g is Tukey,
$C\times E$
. As g is Tukey,
 $\pi _{\kappa }\circ g"X$
is unbounded.
$\pi _{\kappa }\circ g"X$
is unbounded.Let
 $X_\alpha := X\cap g^{-1} (C\times \{\alpha \}\times E )$
and
$X_\alpha := X\cap g^{-1} (C\times \{\alpha \}\times E )$
and
 $U_\alpha :=\bigcup _{\beta \leq \alpha } X_\beta $
for every
$U_\alpha :=\bigcup _{\beta \leq \alpha } X_\beta $
for every
 $\alpha <\kappa $
. As g is Tukey and
$\alpha <\kappa $
. As g is Tukey and
 $g"U_\alpha $
is bounded, we get that
$g"U_\alpha $
is bounded, we get that
 $U_\alpha $
is also bounded by some
$U_\alpha $
is also bounded by some
 $y_\alpha \in D$
. Let
$y_\alpha \in D$
. Let
 $Y:=\{y_\alpha \mid \alpha <\kappa \}$
. We claim that Y is of cardinality
$Y:=\{y_\alpha \mid \alpha <\kappa \}$
. We claim that Y is of cardinality
 $\kappa $
. If it wasn’t, then by the pigeonhole principle as
$\kappa $
. If it wasn’t, then by the pigeonhole principle as
 $\kappa $
is regular there would be some
$\kappa $
is regular there would be some
 $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
 $y_\alpha $
bounds the set X in D and that is absurd. Similarly, as X is unbounded, the set Y and also every subset of it of size
$y_\alpha $
bounds the set X in D and that is absurd. Similarly, as X is unbounded, the set Y and also every subset of it of size
 $\kappa $
must be unbounded.
$\kappa $
must be unbounded.Next, we aim to get
 $Z\in [Y]^\kappa $
such that
$Z\in [Y]^\kappa $
such that
 $\pi _{C\times E}\circ g"Z$
is bounded by some
$\pi _{C\times E}\circ g"Z$
is bounded by some
 $(c,e)\in C\times E$
. This can be done as follows: As
$(c,e)\in C\times E$
. This can be done as follows: As
 $|C|<\kappa $
and
$|C|<\kappa $
and
 $\kappa $
is regular, by the pigeonhole principle, there exists some
$\kappa $
is regular, by the pigeonhole principle, there exists some
 $Z_0\in [Y]^\kappa $
and
$Z_0\in [Y]^\kappa $
and
 $c\in C$
such that
$c\in C$
such that
 $g"Z_0 \subseteq \{c\}\times \kappa \times E$
. Similarly, if
$g"Z_0 \subseteq \{c\}\times \kappa \times E$
. Similarly, if
 $|\pi _{E}\circ g" Z_0|<\kappa $
, by the pigeonhole principle, there exists some
$|\pi _{E}\circ g" Z_0|<\kappa $
, by the pigeonhole principle, there exists some
 $Z\in [Z_0]^\kappa $
and
$Z\in [Z_0]^\kappa $
and
 $e\in E$
such that
$e\in E$
such that
 $g"Z \subseteq \{c\}\times \kappa \times \{e\}$
. Else, if
$g"Z \subseteq \{c\}\times \kappa \times \{e\}$
. Else, if
 $|\pi _{E}" Z_0|=\kappa $
, then as
$|\pi _{E}" Z_0|=\kappa $
, then as
 $\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
for some
$\kappa \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E),\kappa )$
for some
 $B\in [\pi _{E}\circ g" Z_0]^{\kappa }$
and
$B\in [\pi _{E}\circ g" Z_0]^{\kappa }$
and
 $e\in E$
, B is bounded in E by e. Fix some
$e\in E$
, B is bounded in E by e. Fix some
 $Z\in [Z_0]^\kappa $
such that
$Z\in [Z_0]^\kappa $
such that
 $g"Z\subseteq \{c\}\times \kappa \times B$
.
$g"Z\subseteq \{c\}\times \kappa \times B$
.Note that Z is a subset of Y of size
 $\kappa $
, hence, unbounded in D. By the assumption, there exists some subset
$\kappa $
, hence, unbounded in D. By the assumption, there exists some subset
 $W\in [Z]^{<\kappa }$
unbounded in D. Note that as
$W\in [Z]^{<\kappa }$
unbounded in D. Note that as
 $\kappa $
is regular, for some
$\kappa $
is regular, for some
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $\pi _{\kappa } \circ g"W\subseteq \alpha $
. As g is Tukey, the subset
$\pi _{\kappa } \circ g"W\subseteq \alpha $
. As g is Tukey, the subset
 $g"W\subseteq \{c\}\times \kappa \times E$
is unbounded in
$g"W\subseteq \{c\}\times \kappa \times E$
is unbounded in
 $C\times \kappa \times E$
, but this is absurd as
$C\times \kappa \times E$
, but this is absurd as
 $g"W$
is bounded by
$g"W$
is bounded by
 $(c,\alpha ,e)$
.
$(c,\alpha ,e)$
.
5 Non-empty intervals
In this section we consider three types of intervals in the poset
![]() $(\mathcal T_n, <_T)$
and show each one can consistently have a directed set inside.
$(\mathcal T_n, <_T)$
and show each one can consistently have a directed set inside.
5.1 Directed set between
 $ \theta ^+ \times \theta ^{++}$
and
$ \theta ^+ \times \theta ^{++}$
and
 $[\theta ^{++}]^{\leq \theta }$
$[\theta ^{++}]^{\leq \theta }$
In [Reference Kuzeljević and Todorčević6, Theorem 1.1], the authors constructed a directed set between
![]() $\omega _1\times \omega _2$
and
$\omega _1\times \omega _2$
and
![]() $[\omega _2]^{\leq \omega }$
under the assumption
$[\omega _2]^{\leq \omega }$
under the assumption
![]() $2^{\aleph _0}=\aleph _1$
,
$2^{\aleph _0}=\aleph _1$
,
![]() $2^{\aleph _1}=\aleph _2$
and the existence of an
$2^{\aleph _1}=\aleph _2$
and the existence of an
![]() $\aleph _2$
-Souslin tree. In this subsection we generalize this result while waiving the assumption concerning the Souslin tree. The main corollary of this subsection is:
$\aleph _2$
-Souslin tree. In this subsection we generalize this result while waiving the assumption concerning the Souslin tree. The main corollary of this subsection is:
Corollary 5.1. Assume
![]() $\theta $
is an infinite cardinal such that
$\theta $
is an infinite cardinal such that
![]() $2^\theta = \theta ^+$
,
$2^\theta = \theta ^+$
,
![]() $2^{\theta ^+}= \theta ^{++}$
. Suppose C and E are directed sets such that
$2^{\theta ^+}= \theta ^{++}$
. Suppose C and E are directed sets such that
![]() $\operatorname {\mathrm {cf}}(C)\leq \theta ^+$
and either
$\operatorname {\mathrm {cf}}(C)\leq \theta ^+$
and either
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta ^+$
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta ^+$
or
![]() $E\equiv _T 1$
. Then there exists a directed set D such that
$E\equiv _T 1$
. Then there exists a directed set D such that
![]() $ C\times \theta ^+ \times \theta ^{++}\times E <_T C\times D\times E <_T C\times [\theta ^{++}]^{\leq \theta }\times E.$
$ C\times \theta ^+ \times \theta ^{++}\times E <_T C\times D\times E <_T C\times [\theta ^{++}]^{\leq \theta }\times E.$
The result follows immediately from Theorems 5.3 and 5.4. First, we prove the following required lemma.
Lemma 5.2. Suppose
![]() $\theta $
is a infinite cardinal and
$\theta $
is a infinite cardinal and
![]() $D,J, E$
are three directed sets such that
$D,J, E$
are three directed sets such that
![]() $:$
$:$
-
•
 $\operatorname {\mathrm {cf}}(D)=\operatorname {\mathrm {cf}}(J)=\theta ^{++};$
$\operatorname {\mathrm {cf}}(D)=\operatorname {\mathrm {cf}}(J)=\theta ^{++};$
-
•
 $\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
$\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
 $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(J))\leq \theta ^+;$
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(J))\leq \theta ^+;$
-
•
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
 $E\equiv _T 1;$
$E\equiv _T 1;$
-
•
 $D\times E\leq _T J\times E$
.
$D\times E\leq _T J\times E$
.
Then
![]() $J\times E\not \leq _T D\times E$
. In particular,
$J\times E\not \leq _T D\times E$
. In particular,
![]() $D\times E <_T J\times E$
.
$D\times E <_T J\times E$
.
Proof Notice that D is a directed set such that every subset of size
![]() $\theta ^{++}$
contains a bounded subset of size
$\theta ^{++}$
contains a bounded subset of size
![]() $\theta ^+$
. Let us fix a cofinal subset
$\theta ^+$
. Let us fix a cofinal subset
![]() $A\subseteq J$
of size
$A\subseteq J$
of size
![]() $\theta ^{++}$
such that every subset of A of size
$\theta ^{++}$
such that every subset of A of size
![]() $>\theta $
is unbounded in J.
$>\theta $
is unbounded in J.
Suppose on the contrary that
![]() $J\times E\leq _T D\times E$
. As
$J\times E\leq _T D\times E$
. As
![]() $D\times E\leq _T J\times E$
we get that
$D\times E\leq _T J\times E$
we get that
![]() $D\times E\equiv _T J\times E$
, hence there exists some directed set X such that both
$D\times E\equiv _T J\times E$
, hence there exists some directed set X such that both
![]() $D\times E$
and
$D\times E$
and
![]() $J\times E$
are cofinal subsets of X.
$J\times E$
are cofinal subsets of X.
We may assume that D has an enumeration
![]() $D:=\{d_\alpha \mid \alpha <\theta ^{++}\}$
such that for every
$D:=\{d_\alpha \mid \alpha <\theta ^{++}\}$
such that for every
![]() $\beta <\alpha <\theta ^{++}$
we have
$\beta <\alpha <\theta ^{++}$
we have
![]() $d_\alpha \not <d_\beta $
. Fix some
$d_\alpha \not <d_\beta $
. Fix some
![]() $e\in E$
. Now, for each
$e\in E$
. Now, for each
![]() $a\in A$
take a unique
$a\in A$
take a unique
![]() $x_a\in D$
and some
$x_a\in D$
and some
![]() $e_a\in E$
such that
$e_a\in E$
such that
![]() $(a,e)\leq _X (x_a,e_a)$
. To do that, enumerate
$(a,e)\leq _X (x_a,e_a)$
. To do that, enumerate
![]() $A=\{a_\alpha \mid \alpha <\theta ^{++}\}$
. Suppose we have constructed already the increasing sequence
$A=\{a_\alpha \mid \alpha <\theta ^{++}\}$
. Suppose we have constructed already the increasing sequence
![]() $\langle \nu _\beta \mid \beta <\alpha \rangle $
of elements in
$\langle \nu _\beta \mid \beta <\alpha \rangle $
of elements in
![]() $\theta ^{++}$
. Pick some
$\theta ^{++}$
. Pick some
![]() $\xi <\theta ^{++}$
above
$\xi <\theta ^{++}$
above
![]() $\{ \nu _\beta \mid \beta <\alpha \}$
. As
$\{ \nu _\beta \mid \beta <\alpha \}$
. As
![]() $D\times E$
is a directed set we may fix some
$D\times E$
is a directed set we may fix some
![]() $(x_{a_\alpha },e_a):=(d_{\nu _\alpha },e_a)\in D\times E$
above
$(x_{a_\alpha },e_a):=(d_{\nu _\alpha },e_a)\in D\times E$
above
![]() $(a_\alpha ,e)$
and
$(a_\alpha ,e)$
and
![]() $(d_\xi ,e)$
.
$(d_\xi ,e)$
.
Set
![]() $T=\{x_a\mid a\in A\}$
, since
$T=\{x_a\mid a\in A\}$
, since
![]() $A\times E$
is cofinal in X, the set
$A\times E$
is cofinal in X, the set
![]() $T\times E$
is also cofinal in X and
$T\times E$
is also cofinal in X and
![]() $D\times E$
. As
$D\times E$
. As
![]() $|T|=\theta ^{++}$
we get that there exists some subset
$|T|=\theta ^{++}$
we get that there exists some subset
![]() $B\in [T]^{\theta ^+}$
bounded in D. Let
$B\in [T]^{\theta ^+}$
bounded in D. Let
![]() $c\in D$
be such that
$c\in D$
be such that
![]() $b\leq c$
for each
$b\leq c$
for each
![]() $b\in B$
. Consider the set
$b\in B$
. Consider the set
![]() $K=\{a\in A \mid x_a \in B \}$
. Since either
$K=\{a\in A \mid x_a \in B \}$
. Since either
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
![]() $E\equiv _T 1$
, as
$E\equiv _T 1$
, as
![]() $\{e_a\mid a\in K\}$
is of size
$\{e_a\mid a\in K\}$
is of size
![]() $\leq \theta ^+$
, it is bounded in E by some
$\leq \theta ^+$
, it is bounded in E by some
![]() $\tilde e\in E$
. So
$\tilde e\in E$
. So
![]() $P:=\{(x_a, e_a)\mid a\in K\}$
is bounded in X. Since B is of size
$P:=\{(x_a, e_a)\mid a\in K\}$
is bounded in X. Since B is of size
![]() $>\theta $
, the set K is also of size
$>\theta $
, the set K is also of size
![]() $>\theta $
. Thus, by the assumption on A, the set
$>\theta $
. Thus, by the assumption on A, the set
![]() $K\times \{e\}$
is unbounded in
$K\times \{e\}$
is unbounded in
![]() $J\times E$
, but also in X because
$J\times E$
, but also in X because
![]() $J\times E$
is a cofinal subset of X. Then, for each
$J\times E$
is a cofinal subset of X. Then, for each
![]() $a\in K$
we have
$a\in K$
we have
![]() $(a,e)\leq _X (x_a,e_a) \leq _X (c,\tilde e)$
, contradicting the unboundedness of
$(a,e)\leq _X (x_a,e_a) \leq _X (c,\tilde e)$
, contradicting the unboundedness of
![]() $K\times \{e\}$
in
$K\times \{e\}$
in
![]() $J\times E$
.
$J\times E$
.
Theorem 5.3. Suppose
![]() $\theta $
is an infinite cardinal and
$\theta $
is an infinite cardinal and
![]() $C,D,E$
are directed sets such that
$C,D,E$
are directed sets such that
![]() $:$
$:$
-
(1)
 $\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
.
$\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
. -
(2) For every partition
 $D=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
$D=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
 $\gamma <\theta ^+$
, and an unbounded
$\gamma <\theta ^+$
, and an unbounded
 $K\subseteq D_\gamma $
of size
$K\subseteq D_\gamma $
of size
 $\theta ^+$
.
$\theta ^+$
. -
(3)
 $\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
$\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
. -
(4)
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
 $E\equiv _T 1$
.
$E\equiv _T 1$
. -
(5) C is a directed set such that
 $\operatorname {\mathrm {cf}}(C)\leq \theta ^+$
.
$\operatorname {\mathrm {cf}}(C)\leq \theta ^+$
.
Then
![]() $ C\times \theta ^+ \times \theta ^{++}\times E <_T C\times D\times E <_T C\times [\theta ^{++}]^{\leq \theta }\times E.$
$ C\times \theta ^+ \times \theta ^{++}\times E <_T C\times D\times E <_T C\times [\theta ^{++}]^{\leq \theta }\times E.$
Proof As
![]() $\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
, we may assume that every subset of D of size
$\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
, we may assume that every subset of D of size
![]() $\theta ^{++}$
is unbounded.
$\theta ^{++}$
is unbounded.
Claim 5.3.1.
![]() $\theta ^+\times \theta ^{++}\leq _T D$
.
$\theta ^+\times \theta ^{++}\leq _T D$
.
Proof As
![]() $\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
, we get by Lemma 2.9 that
$\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
, we get by Lemma 2.9 that
![]() $\theta ^{++}\leq _T D$
. Let K be an unbounded subset of D of size
$\theta ^{++}\leq _T D$
. Let K be an unbounded subset of D of size
![]() $\theta ^+$
, as every subset of size
$\theta ^+$
, as every subset of size
![]() $\theta $
is bounded, by Corollary 2.10 we get that
$\theta $
is bounded, by Corollary 2.10 we get that
![]() $\theta ^+\leq _T D$
. Hence,
$\theta ^+\leq _T D$
. Hence,
![]() $\theta ^+\times \theta ^{++} \leq _T D$
as sought.
$\theta ^+\times \theta ^{++} \leq _T D$
as sought.
Claim 5.3.2.
![]() $D \leq _T [\theta ^{++}]^{\leq \theta }$
.
$D \leq _T [\theta ^{++}]^{\leq \theta }$
.
Proof As
![]() $\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
and
$\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
and
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
, by Lemma 2.13,
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
, by Lemma 2.13,
![]() $D \leq _T [\theta ^{++}]^{\leq \theta }$
as sought.
$D \leq _T [\theta ^{++}]^{\leq \theta }$
as sought.
Notice this implies that
![]() $ C\times \theta ^+ \times \theta ^{++}\times E \leq _T C\times D\times E \leq _T C\times [\theta ^{++}]^{\leq \theta }\times E.$
$ C\times \theta ^+ \times \theta ^{++}\times E \leq _T C\times D\times E \leq _T C\times [\theta ^{++}]^{\leq \theta }\times E.$
By Lemma 2.17, as
![]() $|C\times \theta ^+|\leq \theta ^+$
,
$|C\times \theta ^+|\leq \theta ^+$
,
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\theta ^{++}\times E))>\theta ^+$
and Clause (2) we get that
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(\theta ^{++}\times E))>\theta ^+$
and Clause (2) we get that
![]() $D\not \leq _T C\times \theta ^+\times \theta ^{++}\times E$
.
$D\not \leq _T C\times \theta ^+\times \theta ^{++}\times E$
.
Claim 5.3.3.
![]() $C\times [\theta ^{++}]^{\leq \theta }\times E \not \leq _T C\times D\times E$
.
$C\times [\theta ^{++}]^{\leq \theta }\times E \not \leq _T C\times D\times E$
.
Proof Recall that
![]() $\mathfrak D_{ [\theta ^{++}]^{\leq \theta }}\equiv _T [\theta ^{++}]^{\leq \theta }$
. Notice that following:
$\mathfrak D_{ [\theta ^{++}]^{\leq \theta }}\equiv _T [\theta ^{++}]^{\leq \theta }$
. Notice that following:
-
•
 $\operatorname {\mathrm {cf}}(C\times D)=\operatorname {\mathrm {cf}}(C\times \mathfrak D_{[\theta ^{++}]^{\leq \theta }})=\theta ^{++}$
.
$\operatorname {\mathrm {cf}}(C\times D)=\operatorname {\mathrm {cf}}(C\times \mathfrak D_{[\theta ^{++}]^{\leq \theta }})=\theta ^{++}$
. -
• By Clause (3) we have that
 $\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(C\times D), \theta ^{++})$
and
$\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(C\times D), \theta ^{++})$
and
 $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(C\times \mathfrak D_{ [\theta ^{++}]^{\leq \theta }}))\leq \theta ^{+}$
.
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}(C\times \mathfrak D_{ [\theta ^{++}]^{\leq \theta }}))\leq \theta ^{+}$
. -
•
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta ^+$
or
 $E=1$
.
$E=1$
. -
•
 $C\times D\times E\leq _T C\times \mathfrak D_{[\theta ^{++}]^{\leq \theta }}\times E$
.
$C\times D\times E\leq _T C\times \mathfrak D_{[\theta ^{++}]^{\leq \theta }}\times E$
.
So by Lemma 5.2 we are done.
We are left with proving the following theorem, in which we define a directed set
![]() $D_c$
using a coloring c.
$D_c$
using a coloring c.
Theorem 5.4. Suppose
![]() $\theta $
is an infinite cardinal such that
$\theta $
is an infinite cardinal such that
![]() $2^\theta = \theta ^+$
and
$2^\theta = \theta ^+$
and
![]() $2^{\theta ^+}=\theta ^{++}$
. Then there exists a directed set D such that
$2^{\theta ^+}=\theta ^{++}$
. Then there exists a directed set D such that
![]() $:$
$:$
-
(1)
 $\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
.
$\operatorname {\mathrm {cf}}(D)=\theta ^{++}$
. -
(2) For every partition
 $D=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
$D=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
 $\gamma <\theta ^+$
, and an unbounded
$\gamma <\theta ^+$
, and an unbounded
 $K\subseteq D_\gamma $
of size
$K\subseteq D_\gamma $
of size
 $\theta ^+$
.
$\theta ^+$
. -
(3)
 $\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
$\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D), \theta ^{++})$
and
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D))=\theta ^+$
.
The rest of this subsection is dedicated to proving Theorem 5.4. The arithmetic hypothesis will only play a role later on. Let
![]() $\theta $
be an infinite cardinal. For two sets of ordinals A and B, we denote
$\theta $
be an infinite cardinal. For two sets of ordinals A and B, we denote
![]() $A\circledast B:= \{(\alpha ,\beta )\in A\times B\mid \alpha <\beta \}$
. Recall that by [Reference Inamdar and Rinot3, Corollary 7.3],
$A\circledast B:= \{(\alpha ,\beta )\in A\times B\mid \alpha <\beta \}$
. Recall that by [Reference Inamdar and Rinot3, Corollary 7.3],
![]() ${\mathsf {onto}}(\mathcal S,J^{\operatorname {\mathrm {bd}}}[\theta ^{++}],\theta ^+)$
holds for
${\mathsf {onto}}(\mathcal S,J^{\operatorname {\mathrm {bd}}}[\theta ^{++}],\theta ^+)$
holds for
![]() $\mathcal S:=[\theta ^{++}]^{\theta ^{++}}$
. This means that we may fix a coloring
$\mathcal S:=[\theta ^{++}]^{\theta ^{++}}$
. This means that we may fix a coloring
![]() $c:[\theta ^{++}]^2\rightarrow \theta ^+$
such that for every
$c:[\theta ^{++}]^2\rightarrow \theta ^+$
such that for every
![]() $S\in \mathcal S$
and unbounded
$S\in \mathcal S$
and unbounded
![]() $B\subseteq \theta ^{++}$
, there exists
$B\subseteq \theta ^{++}$
, there exists
![]() $\delta \in S$
such that
$\delta \in S$
such that
![]() $c"(\{\delta \}\circledast B)=\theta ^+$
.
$c"(\{\delta \}\circledast B)=\theta ^+$
.
We fix some
![]() $S\in \mathcal S$
. For our purpose, it will suffice to assume that S is nothing but the whole of
$S\in \mathcal S$
. For our purpose, it will suffice to assume that S is nothing but the whole of
![]() $\theta ^{++}$
. Let
$\theta ^{++}$
. Let
Consider
![]() $D_{c}$
ordered by inclusion, and notice that
$D_{c}$
ordered by inclusion, and notice that
![]() $D_{c}$
is a directed set since
$D_{c}$
is a directed set since
![]() $\operatorname {\mathrm {NS}}_{\theta ^+}$
is an ideal.
$\operatorname {\mathrm {NS}}_{\theta ^+}$
is an ideal.
Proposition 5.5. The following hold
![]() $:$
$:$
-
•
 $[\theta ^{++}]^{\leq \theta } \subseteq D_{c} \subseteq [\theta ^{++}]^{\leq \theta ^+}$
.
$[\theta ^{++}]^{\leq \theta } \subseteq D_{c} \subseteq [\theta ^{++}]^{\leq \theta ^+}$
. -
•
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_c))\geq \operatorname {\mathrm {add}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_c))\geq \theta ^+$
, i.e., every family of bounded subsets of
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_c))\geq \operatorname {\mathrm {add}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_c))\geq \theta ^+$
, i.e., every family of bounded subsets of
 $D_{c}$
of size
$D_{c}$
of size
 $< \theta ^+$
is bounded.
$< \theta ^+$
is bounded. -
• If
 $2^{\theta ^+}=\theta ^{++}$
, then
$2^{\theta ^+}=\theta ^{++}$
, then
 $|D_c|=\theta ^{++}$
, and hence
$|D_c|=\theta ^{++}$
, and hence
 $D_c\in \mathcal D_{\theta ^{++}}$
.
$D_c\in \mathcal D_{\theta ^{++}}$
.
Lemma 5.6. For every partition
![]() $D_{c}=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
$D_{c}=\bigcup _{\gamma <\theta ^+} D_\gamma $
, there is an ordinal
![]() $\gamma <\theta ^+$
, and an unbounded
$\gamma <\theta ^+$
, and an unbounded
![]() $E\subseteq D_\gamma $
of size
$E\subseteq D_\gamma $
of size
![]() $\theta ^+$
.
$\theta ^+$
.
Proof As
![]() $[\theta ^{++}]^1$
is a subset of
$[\theta ^{++}]^1$
is a subset of
![]() $D_{c}$
, the family
$D_{c}$
, the family
![]() $\{D_{\gamma }\mid \gamma <\theta ^+\}$
is a partition of the set
$\{D_{\gamma }\mid \gamma <\theta ^+\}$
is a partition of the set
![]() $[\theta ^{++}]^1$
to at most
$[\theta ^{++}]^1$
to at most
![]() $\theta ^+$
many sets. As
$\theta ^+$
many sets. As
![]() $\theta ^+<\theta ^{++}=\operatorname {\mathrm {cf}}(\theta ^{++})$
, by the pigeonhole principle we get that for some
$\theta ^+<\theta ^{++}=\operatorname {\mathrm {cf}}(\theta ^{++})$
, by the pigeonhole principle we get that for some
![]() $\gamma <\theta ^+$
and
$\gamma <\theta ^+$
and
![]() $b\in [\theta ^{++}]^{\theta ^{++}}$
, we have
$b\in [\theta ^{++}]^{\theta ^{++}}$
, we have
![]() $[b]^1 \subseteq D_{\gamma }$
. Notice that by the assumption on the coloring c, there exists some
$[b]^1 \subseteq D_{\gamma }$
. Notice that by the assumption on the coloring c, there exists some
![]() $\delta \in S$
and
$\delta \in S$
and
![]() $\delta <b'\in [b]^{\theta ^+}$
such that
$\delta <b'\in [b]^{\theta ^+}$
such that
![]() $c"(\delta \circledast b')=\theta ^+$
. Clearly the set
$c"(\delta \circledast b')=\theta ^+$
. Clearly the set
![]() $E:=[b']^1$
is a subset of
$E:=[b']^1$
is a subset of
![]() $ D_{\gamma }$
of size
$ D_{\gamma }$
of size
![]() $\theta ^+$
which is unbounded in
$\theta ^+$
which is unbounded in
![]() $D_{c}$
.
$D_{c}$
.
Lemma 5.7. Suppose
![]() $2^{\theta }=\theta ^+$
, then
$2^{\theta }=\theta ^+$
, then
![]() $\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_{c}),\theta ^{++})$
.
$\theta ^+ \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_{c}),\theta ^{++})$
.
Proof We follow the proof of [Reference Kuzeljević and Todorčević6, Lemma 5.4].
Let
![]() $D'$
be a subset of
$D'$
be a subset of
![]() $D_{c}$
of size
$D_{c}$
of size
![]() $\theta ^{++}$
we will show it contains a bounded subset of size
$\theta ^{++}$
we will show it contains a bounded subset of size
![]() $\theta ^+$
, let us enumerate it as
$\theta ^+$
, let us enumerate it as
![]() $\{T_\gamma \mid \gamma <\theta ^{++}\}$
. Let, for each
$\{T_\gamma \mid \gamma <\theta ^{++}\}$
. Let, for each
![]() $X\in D_{c}$
and
$X\in D_{c}$
and
![]() $\gamma \in S$
,
$\gamma \in S$
,
![]() $N^X_\gamma $
denote the non-stationary set
$N^X_\gamma $
denote the non-stationary set
![]() $\{c(\gamma ,\beta )\mid \beta \in X\setminus (\gamma +1)\}$
, and let
$\{c(\gamma ,\beta )\mid \beta \in X\setminus (\gamma +1)\}$
, and let
![]() $G^X_\gamma $
denote a club in
$G^X_\gamma $
denote a club in
![]() $\theta ^+$
disjoint from
$\theta ^+$
disjoint from
![]() $N^X_\gamma $
.
$N^X_\gamma $
.
As
![]() $2^{\theta }=\theta ^+$
we may fix a sufficiently large regular cardinal
$2^{\theta }=\theta ^+$
we may fix a sufficiently large regular cardinal
![]() $\chi $
, and an elementary submodel
$\chi $
, and an elementary submodel
![]() $M\prec H_{\chi }$
of cardinality
$M\prec H_{\chi }$
of cardinality
![]() $\theta ^+$
containing all the relevant objects and such that
$\theta ^+$
containing all the relevant objects and such that
![]() $M^{\theta } \subseteq M$
. Denote
$M^{\theta } \subseteq M$
. Denote
![]() $\delta =M\cap \theta ^{++}$
, notice
$\delta =M\cap \theta ^{++}$
, notice
![]() $\delta \in E^{\theta ^{++}}_{\theta ^+}$
. Fix an increasing sequence
$\delta \in E^{\theta ^{++}}_{\theta ^+}$
. Fix an increasing sequence
![]() $\langle \gamma _\xi \mid \xi <\theta ^+\rangle $
in
$\langle \gamma _\xi \mid \xi <\theta ^+\rangle $
in
![]() $\delta $
such that
$\delta $
such that
![]() $\sup \{\gamma _\xi \mid \xi <\theta ^+\}=\delta $
. Enumerate
$\sup \{\gamma _\xi \mid \xi <\theta ^+\}=\delta $
. Enumerate
![]() $\delta \cap S=\{s_\xi \mid \xi <\theta ^+\}$
. In order to simplify notation, let
$\delta \cap S=\{s_\xi \mid \xi <\theta ^+\}$
. In order to simplify notation, let
![]() $G^\gamma _\xi $
denote the set
$G^\gamma _\xi $
denote the set
![]() $G^{T_\gamma }_{s_\xi }$
for each
$G^{T_\gamma }_{s_\xi }$
for each
![]() $\gamma <\theta ^{++}$
and
$\gamma <\theta ^{++}$
and
![]() $\xi <\theta ^+$
.
$\xi <\theta ^+$
.
We construct by recursion on
![]() $\xi <\theta ^+$
three sequences
$\xi <\theta ^+$
three sequences
![]() $\langle \delta _\xi \mid \xi <\theta ^+\rangle $
,
$\langle \delta _\xi \mid \xi <\theta ^+\rangle $
,
![]() $\langle \Gamma _\xi \mid \xi <\theta ^+\rangle $
and
$\langle \Gamma _\xi \mid \xi <\theta ^+\rangle $
and
![]() $\langle \eta _\xi \mid \xi <\theta ^+\rangle $
with the following properties:
$\langle \eta _\xi \mid \xi <\theta ^+\rangle $
with the following properties:
-
(1)
 $\langle \delta _\xi \mid \xi <\theta ^+\rangle $
is an increasing sequence converging to
$\langle \delta _\xi \mid \xi <\theta ^+\rangle $
is an increasing sequence converging to
 $\delta $
.
$\delta $
. -
(2)
 $\langle \Gamma _\xi \mid \xi <\theta ^+ \rangle $
is a decreasing
$\langle \Gamma _\xi \mid \xi <\theta ^+ \rangle $
is a decreasing
 $\subseteq $
-chain of stationary subsets of
$\subseteq $
-chain of stationary subsets of
 $\theta ^{++}$
each one containing
$\theta ^{++}$
each one containing
 $\delta $
and definable in M.
$\delta $
and definable in M. -
(3)
 $\langle \eta _\xi \mid \xi <\theta ^+ \rangle $
is an increasing sequence of ordinals below
$\langle \eta _\xi \mid \xi <\theta ^+ \rangle $
is an increasing sequence of ordinals below
 $\theta ^+$
.
$\theta ^+$
. -
(4)
 $G^\delta _{\zeta } \cap \eta _{\mu } = G^{\delta _{\mu }}_{\zeta }\cap \eta _{\mu } $
for
$G^\delta _{\zeta } \cap \eta _{\mu } = G^{\delta _{\mu }}_{\zeta }\cap \eta _{\mu } $
for
 $\zeta \leq \mu <\theta ^+$
.
$\zeta \leq \mu <\theta ^+$
.
![]() $\blacktriangleright $
Base case: Let
$\blacktriangleright $
Base case: Let
![]() $\eta _0$
be the first limit point of
$\eta _0$
be the first limit point of
![]() $G^\delta _0$
. Notice that
$G^\delta _0$
. Notice that
![]() $G^\delta _0\cap \eta _0$
is an infinite set of size
$G^\delta _0\cap \eta _0$
is an infinite set of size
![]() $\leq \theta $
below
$\leq \theta $
below
![]() $\delta $
, hence it is inside of M. Let
$\delta $
, hence it is inside of M. Let
Since
![]() $\delta \in \Gamma _0$
, the set
$\delta \in \Gamma _0$
, the set
![]() $\Gamma _0$
is stationary in
$\Gamma _0$
is stationary in
![]() $\theta ^{++}$
. Let
$\theta ^{++}$
. Let
![]() $\delta _0:=\min (\Gamma _0)$
.
$\delta _0:=\min (\Gamma _0)$
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\xi _0<\theta ^+$
, and that
$\xi _0<\theta ^+$
, and that
![]() $\delta _\xi $
,
$\delta _\xi $
,
![]() $\Gamma _\xi $
and
$\Gamma _\xi $
and
![]() $\eta _\xi $
have been constructed for each
$\eta _\xi $
have been constructed for each
![]() $\xi <\xi _0$
. Let
$\xi <\xi _0$
. Let
![]() $\eta _{\xi _0}$
be the first limit point of
$\eta _{\xi _0}$
be the first limit point of
![]() $G^\delta _{\xi _0}\setminus \sup \{\eta _\xi \mid \xi <\xi _0\}$
. Consider the set
$G^\delta _{\xi _0}\setminus \sup \{\eta _\xi \mid \xi <\xi _0\}$
. Consider the set
Since
![]() $\Gamma _{\xi _0}$
belongs to M, and since
$\Gamma _{\xi _0}$
belongs to M, and since
![]() $\delta \in \Gamma _{\xi _0}$
, it must be that
$\delta \in \Gamma _{\xi _0}$
, it must be that
![]() $\Gamma _{\xi _0}$
is stationary in
$\Gamma _{\xi _0}$
is stationary in
![]() $\theta ^{++}$
. Since
$\theta ^{++}$
. Since
![]() $\Gamma _{\xi _0}$
is cofinal in
$\Gamma _{\xi _0}$
is cofinal in
![]() $\theta ^{++}$
and belongs to M, the set
$\theta ^{++}$
and belongs to M, the set
![]() $\delta \cap \Gamma _{\xi _0}$
is cofinal in
$\delta \cap \Gamma _{\xi _0}$
is cofinal in
![]() $\delta $
. Define
$\delta $
. Define
![]() $\delta _{\xi _0}$
be the minimal ordinal in
$\delta _{\xi _0}$
be the minimal ordinal in
![]() $\delta \cap \Gamma _{\xi _0}$
greater than both
$\delta \cap \Gamma _{\xi _0}$
greater than both
![]() $\sup \{\delta _\xi \mid \xi <\xi _0\}$
and
$\sup \{\delta _\xi \mid \xi <\xi _0\}$
and
![]() $\gamma _{\xi _0}$
. It is clear from the construction that conditions
$\gamma _{\xi _0}$
. It is clear from the construction that conditions
![]() $(1-4)$
are satisfied.
$(1-4)$
are satisfied.
The following claim gives us the wanted result.
Claim 5.7.1. The set
![]() $\{T_{\delta _\xi }\mid \xi <\theta ^+\}$
is a subset of
$\{T_{\delta _\xi }\mid \xi <\theta ^+\}$
is a subset of
![]() $D'$
of size
$D'$
of size
![]() $\theta ^+$
which is bounded in
$\theta ^+$
which is bounded in
![]() $D_{c}$
.
$D_{c}$
.
Proof As the order on
![]() $D_{c}$
is
$D_{c}$
is
![]() $\subseteq $
, it suffices to prove that the union
$\subseteq $
, it suffices to prove that the union
![]() $T=\bigcup _{\xi <\theta ^+} T_{\delta _\xi }\in D_{c}$
. Since, for each
$T=\bigcup _{\xi <\theta ^+} T_{\delta _\xi }\in D_{c}$
. Since, for each
![]() $\xi <\theta ^+$
, both
$\xi <\theta ^+$
, both
![]() $\delta _\xi $
and
$\delta _\xi $
and
![]() $\langle T_\gamma \mid \gamma <\theta ^{++} \rangle $
belong to M, it must be that
$\langle T_\gamma \mid \gamma <\theta ^{++} \rangle $
belong to M, it must be that
![]() $T_{\delta _\xi }\in M$
. Since
$T_{\delta _\xi }\in M$
. Since
![]() $\theta ^+\in M$
and
$\theta ^+\in M$
and
![]() $M\models |T_{\delta _\xi }|\leq \theta ^+$
, we have
$M\models |T_{\delta _\xi }|\leq \theta ^+$
, we have
![]() $T_{\delta _\xi }\subseteq M$
. Thus
$T_{\delta _\xi }\subseteq M$
. Thus
![]() $T\subseteq M$
and furthermore
$T\subseteq M$
and furthermore
![]() $T\subseteq \delta $
. This means that, in order to prove that
$T\subseteq \delta $
. This means that, in order to prove that
![]() $T\in D_{c}$
, it is enough to prove that for each
$T\in D_{c}$
, it is enough to prove that for each
![]() $t \in S\cap \delta $
, the set
$t \in S\cap \delta $
, the set
![]() $\{c(t,\beta )\mid \beta \in T\setminus (t+1)\}$
is non-stationary in
$\{c(t,\beta )\mid \beta \in T\setminus (t+1)\}$
is non-stationary in
![]() $\theta ^+$
. Fix some
$\theta ^+$
. Fix some
![]() $t\in S\cap \delta $
. Let
$t\in S\cap \delta $
. Let
![]() $\zeta <\theta ^+$
be such that
$\zeta <\theta ^+$
be such that
![]() $s_\zeta = t$
. Define
$s_\zeta = t$
. Define
 $$ \begin{align*}G:=G^\delta_\zeta \cap (\bigcap_{\xi\leq \zeta} G^{\delta_\xi}_\zeta)\cap (\triangle_{\xi<\theta^+} G^{\delta_\xi}_\zeta).\end{align*} $$
$$ \begin{align*}G:=G^\delta_\zeta \cap (\bigcap_{\xi\leq \zeta} G^{\delta_\xi}_\zeta)\cap (\triangle_{\xi<\theta^+} G^{\delta_\xi}_\zeta).\end{align*} $$
Since the intersection of
![]() $< \theta ^+$
-many clubs in
$< \theta ^+$
-many clubs in
![]() $\theta ^+$
is a club, and since diagonal intersection of
$\theta ^+$
is a club, and since diagonal intersection of
![]() $\theta ^+$
many clubs is a club, we know that G is a club in
$\theta ^+$
many clubs is a club, we know that G is a club in
![]() $\theta ^+$
.
$\theta ^+$
.
We will prove that
![]() $G\cap \{c(t,\beta )\mid \beta \in T\setminus (t+1)\}=\emptyset $
. Suppose
$G\cap \{c(t,\beta )\mid \beta \in T\setminus (t+1)\}=\emptyset $
. Suppose
![]() $\alpha <\theta ^+$
is such that
$\alpha <\theta ^+$
is such that
![]() $\alpha \in G \cap \{c(t,\beta )\mid \beta \in T\setminus (t+1)\}$
. This means that
$\alpha \in G \cap \{c(t,\beta )\mid \beta \in T\setminus (t+1)\}$
. This means that
![]() $\alpha \in G$
and that for some
$\alpha \in G$
and that for some
![]() $\mu <\theta ^+$
and
$\mu <\theta ^+$
and
![]() $\beta \in T_{\delta _\mu }\setminus (t+1)$
we have
$\beta \in T_{\delta _\mu }\setminus (t+1)$
we have
![]() $\alpha = c(t,\beta )$
. So
$\alpha = c(t,\beta )$
. So
![]() $\alpha \in N^{T_{\delta _\mu }}_{t}$
. Note that this implies that
$\alpha \in N^{T_{\delta _\mu }}_{t}$
. Note that this implies that
![]() $\alpha \notin G^{\delta _\mu }_\zeta $
. Let us split to three cases:
$\alpha \notin G^{\delta _\mu }_\zeta $
. Let us split to three cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\mu \leq \zeta $
, then since
$\mu \leq \zeta $
, then since
![]() $\alpha \in \bigcap _{\xi \leq \zeta } G^{\delta _\xi }_\zeta $
, we have that
$\alpha \in \bigcap _{\xi \leq \zeta } G^{\delta _\xi }_\zeta $
, we have that
![]() $\alpha \in G^{\delta _\mu }_\zeta $
which is clearly contradicting
$\alpha \in G^{\delta _\mu }_\zeta $
which is clearly contradicting
![]() $\alpha \notin G^{\delta _\mu }_\zeta $
.
$\alpha \notin G^{\delta _\mu }_\zeta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\mu>\zeta $
and
$\mu>\zeta $
and
![]() $\alpha <\eta _\mu $
. Then by
$\alpha <\eta _\mu $
. Then by
![]() $(4)$
, we have that
$(4)$
, we have that
![]() $G^\delta _\zeta \cap \eta _\mu =G^{\delta _\mu }_\zeta \cap \eta _\mu $
. As
$G^\delta _\zeta \cap \eta _\mu =G^{\delta _\mu }_\zeta \cap \eta _\mu $
. As
![]() $\alpha \not \in G^{\delta _\mu }_\zeta $
and
$\alpha \not \in G^{\delta _\mu }_\zeta $
and
![]() $\alpha <\eta _\mu $
, it must be that
$\alpha <\eta _\mu $
, it must be that
![]() $\alpha \notin G^\delta _\zeta $
. Recall that
$\alpha \notin G^\delta _\zeta $
. Recall that
![]() $\alpha \in G$
, but this is absurd as
$\alpha \in G$
, but this is absurd as
![]() $G\subseteq G^\delta _\zeta $
and
$G\subseteq G^\delta _\zeta $
and
![]() $\alpha \notin G^\delta _\zeta $
.
$\alpha \notin G^\delta _\zeta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\mu>\zeta $
and
$\mu>\zeta $
and
![]() $\alpha \geq \eta _\mu \geq \mu $
. As
$\alpha \geq \eta _\mu \geq \mu $
. As
![]() $\alpha \in G$
, we have that
$\alpha \in G$
, we have that
![]() $\alpha \in \triangle _{\xi <\theta ^+} G^{\delta _\xi }_\zeta $
. As
$\alpha \in \triangle _{\xi <\theta ^+} G^{\delta _\xi }_\zeta $
. As
![]() $\alpha>\mu $
, we get that
$\alpha>\mu $
, we get that
![]() $\alpha \in G^{\delta _\mu }_\zeta $
which is clearly contradicting
$\alpha \in G^{\delta _\mu }_\zeta $
which is clearly contradicting
![]() $\alpha \notin G^{\delta _\mu }_\zeta $
.
$\alpha \notin G^{\delta _\mu }_\zeta $
.
5.2 Directed set between
 $\omega \times \omega _1$
and
$\omega \times \omega _1$
and
 $[\omega _1]^{<\omega }$
$[\omega _1]^{<\omega }$
As mentioned in [Reference Raghavan and Todorčević8], by the results of Todorčević [Reference Todorčević13], it follows that under the assumption
![]() $\mathfrak b=\omega _1$
there exists a directed set of size
$\mathfrak b=\omega _1$
there exists a directed set of size
![]() $\omega _1$
between the directed sets
$\omega _1$
between the directed sets
![]() $\omega \times \omega _1$
and
$\omega \times \omega _1$
and
![]() $[\omega _1]^{<\omega }$
. In this subsection we spell out the details of this construction.
$[\omega _1]^{<\omega }$
. In this subsection we spell out the details of this construction.
For two functions
![]() $f,g\in {}^{\omega }\omega $
, we define the order
$f,g\in {}^{\omega }\omega $
, we define the order
![]() $<^*$
by
$<^*$
by
![]() $f<^*g$
iff the set
$f<^*g$
iff the set
![]() $\{n<\omega \mid g(n)\geq f(n)\}$
is finite. Furthermore, by
$\{n<\omega \mid g(n)\geq f(n)\}$
is finite. Furthermore, by
![]() $f\lhd g$
we means that there exists
$f\lhd g$
we means that there exists
![]() $m<\omega $
such that for all
$m<\omega $
such that for all
![]() $n<m$
we have
$n<m$
we have
![]() $f(n)\leq g(n)$
and
$f(n)\leq g(n)$
and
![]() $f(k)<g(k)$
whenever
$f(k)<g(k)$
whenever
![]() $m\leq k<\omega $
. Assuming
$m\leq k<\omega $
. Assuming
![]() $f\leq ^* g$
, we let
$f\leq ^* g$
, we let
![]() $\Delta (f,g):=\min \{m<\omega \mid \forall n\geq m [f(n)\leq g(n)]\}$
.
$\Delta (f,g):=\min \{m<\omega \mid \forall n\geq m [f(n)\leq g(n)]\}$
.
The following fact is a special case of [Reference Todorčević13, Theorem 1.1] in the case
![]() $n=0$
, for complete details we give the proof as suggested by the referee.
$n=0$
, for complete details we give the proof as suggested by the referee.
Fact 5.8 (Todorčević [Reference Todorčević13, Theorem 1.1]).
Suppose A is an uncountable sequence of
![]() ${}^{\omega }\omega $
of increasing functions which are
${}^{\omega }\omega $
of increasing functions which are
![]() $<^*$
-increasing and
$<^*$
-increasing and
![]() $\leq ^*$
-unbounded, then there are
$\leq ^*$
-unbounded, then there are
![]() $f,g\in A$
such that
$f,g\in A$
such that
![]() $f\lhd g$
.
$f\lhd g$
.
Proof Let
![]() $A:=\{g_\alpha \mid \alpha <\omega _1\}$
be an uncountable sequence of increasing functions of
$A:=\{g_\alpha \mid \alpha <\omega _1\}$
be an uncountable sequence of increasing functions of
![]() ${}^{\omega }\omega $
which are
${}^{\omega }\omega $
which are
![]() $<^*$
-increasing and
$<^*$
-increasing and
![]() $\leq ^*$
-unbounded.
$\leq ^*$
-unbounded.
Let us fix a countable elementary sub-model
![]() $M\prec (H_{\omega _2},\in )$
with
$M\prec (H_{\omega _2},\in )$
with
![]() $A\in M$
. Let
$A\in M$
. Let
![]() $\delta :=\omega _1\cap M$
,
$\delta :=\omega _1\cap M$
,
![]() $B:=\omega _1\setminus (\delta +1)$
and write
$B:=\omega _1\setminus (\delta +1)$
and write
![]() $B_n:=\{\beta \in B\mid \Delta (g_\delta ,g_\beta )=n \}$
. As
$B_n:=\{\beta \in B\mid \Delta (g_\delta ,g_\beta )=n \}$
. As
![]() $B=\bigcup _{n<\omega }B_n$
, let us fix some
$B=\bigcup _{n<\omega }B_n$
, let us fix some
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $B_n$
is uncountable. As
$B_n$
is uncountable. As
![]() $\{g_\alpha \mid \alpha \in B_n\}$
is unbounded, we get that the set
$\{g_\alpha \mid \alpha \in B_n\}$
is unbounded, we get that the set
![]() $K:=\{m<\omega \mid \sup \{g_\beta (m)\mid \beta \in B_n\} = \omega \}$
is non-empty, so consider the minimal element,
$K:=\{m<\omega \mid \sup \{g_\beta (m)\mid \beta \in B_n\} = \omega \}$
is non-empty, so consider the minimal element,
![]() $m:=\min (K)$
. For
$m:=\min (K)$
. For
![]() $t\in {}^{m}\omega $
, denote
$t\in {}^{m}\omega $
, denote
![]() $B^t_n:=\{\beta \in B_n \mid t\subseteq g_\beta \}$
. By minimality of m, the set
$B^t_n:=\{\beta \in B_n \mid t\subseteq g_\beta \}$
. By minimality of m, the set
![]() $\{ t\in {}^{m}\omega \mid B^t_n \neq \emptyset \}$
is finite, so we can easily find some
$\{ t\in {}^{m}\omega \mid B^t_n \neq \emptyset \}$
is finite, so we can easily find some
![]() $t\in {}^{m}\omega $
such that
$t\in {}^{m}\omega $
such that
![]() $\sup \{ g_\beta (m)\mid \beta \in B^t_n\}=\omega $
.
$\sup \{ g_\beta (m)\mid \beta \in B^t_n\}=\omega $
.
Note that the set
![]() $\{\beta < \omega _1 \mid t\subseteq g_\beta \}$
is a non-empty set that is definable from A and t, hence it is in M. Let us fix some
$\{\beta < \omega _1 \mid t\subseteq g_\beta \}$
is a non-empty set that is definable from A and t, hence it is in M. Let us fix some
![]() $\alpha \in M\cap \omega _1$
such that
$\alpha \in M\cap \omega _1$
such that
![]() $t\subseteq g_\alpha $
. Put
$t\subseteq g_\alpha $
. Put
![]() $k:=\Delta (g_\alpha ,g_\delta )$
, and then pick
$k:=\Delta (g_\alpha ,g_\delta )$
, and then pick
![]() $\beta \in B^t_n$
such that
$\beta \in B^t_n$
such that
![]() $g_\beta (m)>g_\alpha (k+n)$
. Of course,
$g_\beta (m)>g_\alpha (k+n)$
. Of course,
![]() $\alpha <\delta <\beta $
. We claim that
$\alpha <\delta <\beta $
. We claim that
![]() $g_\alpha \vartriangleleft g_\beta $
as sought.
$g_\alpha \vartriangleleft g_\beta $
as sought.
Let us divide to three cases:
-
• If
 $i<m$
, then
$i<m$
, then
 $g_\alpha (i)=t(i)=g_\beta (i)$
.
$g_\alpha (i)=t(i)=g_\beta (i)$
. -
• If
 $m\leq i\leq k+n$
, then
$m\leq i\leq k+n$
, then
 $g_\alpha (i)\leq g_\alpha (k+n)<g_\beta (m)\leq g_\beta (i)$
recall that every function in A is increasing.
$g_\alpha (i)\leq g_\alpha (k+n)<g_\beta (m)\leq g_\beta (i)$
recall that every function in A is increasing. -
• If
 $k+n<i<\omega $
, then
$k+n<i<\omega $
, then
 $\Delta (g_\alpha ,g_\delta )=k<i$
and
$\Delta (g_\alpha ,g_\delta )=k<i$
and
 $g_\alpha (i)\leq g_\delta (i)$
, as well as
$g_\alpha (i)\leq g_\delta (i)$
, as well as
 $\Delta (g_\delta ,g_\beta )=n<i$
and
$\Delta (g_\delta ,g_\beta )=n<i$
and
 $g_\delta (i)\leq g_\beta (i)$
. Altogether,
$g_\delta (i)\leq g_\beta (i)$
. Altogether,
 $g_\alpha (i)\leq g_\beta (i)$
.
$g_\alpha (i)\leq g_\beta (i)$
.
Theorem 5.9. Assume
![]() $\mathfrak b =\omega _1$
. Suppose E is a directed set such that
$\mathfrak b =\omega _1$
. Suppose E is a directed set such that
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
or
![]() $E\equiv _T 1$
. Then there exists a directed set D such that
$E\equiv _T 1$
. Then there exists a directed set D such that
Proof Let
![]() $\mathcal F:=\langle f_\alpha \mid \alpha <\omega _1 \rangle \subseteq {}^{\omega }\omega $
witness
$\mathcal F:=\langle f_\alpha \mid \alpha <\omega _1 \rangle \subseteq {}^{\omega }\omega $
witness
![]() $\mathfrak b=\omega _1$
. Recall
$\mathfrak b=\omega _1$
. Recall
![]() $\mathcal F$
is a
$\mathcal F$
is a
![]() $<^*$
-increasing and unbounded sequence, i.e., for every
$<^*$
-increasing and unbounded sequence, i.e., for every
![]() $g\in {}^{\omega }\omega $
, there exists some
$g\in {}^{\omega }\omega $
, there exists some
![]() $\alpha <\omega _1$
such that
$\alpha <\omega _1$
such that
![]() $f_\beta \not \leq ^* g$
, whenever
$f_\beta \not \leq ^* g$
, whenever
![]() $\alpha <\beta <\omega _1$
.
$\alpha <\beta <\omega _1$
.
For a finite set of functions
![]() $F\subseteq {}^{\omega }\omega $
, we define a function
$F\subseteq {}^{\omega }\omega $
, we define a function
![]() $h:=\max (F)$
which is
$h:=\max (F)$
which is
![]() $\lhd $
-above every function in F by letting
$\lhd $
-above every function in F by letting
![]() $h(n):=\max \{f(n)\mid f\in F\}$
. We consider the directed set
$h(n):=\max \{f(n)\mid f\in F\}$
. We consider the directed set
![]() $D:=\{ \max (F)\mid F\subseteq \mathcal F,~ |F|<\aleph _0 \}$
, ordered by the relation
$D:=\{ \max (F)\mid F\subseteq \mathcal F,~ |F|<\aleph _0 \}$
, ordered by the relation
![]() $\lhd $
, clearly D is a directed set.
$\lhd $
, clearly D is a directed set.
Claim 5.9.1. Every uncountable subset
![]() $X\subseteq D$
contains a countable
$X\subseteq D$
contains a countable
![]() $B\subset X$
which is unbounded in D.
$B\subset X$
which is unbounded in D.
Proof Let X be an uncountable subset of D. As
![]() $\mathcal F$
is a
$\mathcal F$
is a
![]() $<^*$
-increasing and unbounded, also X contains an uncountable
$<^*$
-increasing and unbounded, also X contains an uncountable
![]() $<^*$
-unbounded subset
$<^*$
-unbounded subset
![]() $Y\subseteq X$
. As no function
$Y\subseteq X$
. As no function
![]() $g:\omega \rightarrow \omega $
is
$g:\omega \rightarrow \omega $
is
![]() $<^*$
-bounding the set Y, we can find an infinite countable subset
$<^*$
-bounding the set Y, we can find an infinite countable subset
![]() $B\subseteq Y$
and
$B\subseteq Y$
and
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $\{f(n)\mid f\in B \}$
is infinite. Clearly B is
$\{f(n)\mid f\in B \}$
is infinite. Clearly B is
![]() $\lhd $
-unbounded in D as sought.
$\lhd $
-unbounded in D as sought.
Claim 5.9.2.
![]() $\omega \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\omega _1) $
.
$\omega \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D),\omega _1) $
.
Proof We show that every uncountable subset of D contains a countable infinite bounded subset. Let
![]() $A\subseteq D$
be an uncountable set, we may refine A and assume that it is
$A\subseteq D$
be an uncountable set, we may refine A and assume that it is
![]() $<^*$
-increasing and unbounded. We enumerate
$<^*$
-increasing and unbounded. We enumerate
![]() $A:=\{g_\alpha \mid \alpha <\omega _1\}$
and define a coloring
$A:=\{g_\alpha \mid \alpha <\omega _1\}$
and define a coloring
![]() $c:[\omega _1]^2\rightarrow 2$
, letting for
$c:[\omega _1]^2\rightarrow 2$
, letting for
![]() $\alpha <\beta <\omega _1$
the color
$\alpha <\beta <\omega _1$
the color
![]() $c(\alpha ,\beta )=1$
iff
$c(\alpha ,\beta )=1$
iff
![]() $g_\alpha \lhd g_\beta $
. Recall that Erdös and Rado showed that
$g_\alpha \lhd g_\beta $
. Recall that Erdös and Rado showed that
![]() $\omega _1\rightarrow (\omega _1,\omega +1)^2$
, so either there is an uncountable homogeneous set of color
$\omega _1\rightarrow (\omega _1,\omega +1)^2$
, so either there is an uncountable homogeneous set of color
![]() $0$
or there exists an homogeneous set of color
$0$
or there exists an homogeneous set of color
![]() $1$
of order-type
$1$
of order-type
![]() $\omega +1$
. Notice that Fact 5.8 contradicts the first alternative, so the second one must hold. Let
$\omega +1$
. Notice that Fact 5.8 contradicts the first alternative, so the second one must hold. Let
![]() $X\subseteq \omega _1$
be a set such that
$X\subseteq \omega _1$
be a set such that
![]() $\operatorname {\mathrm {otp}}(X)=\omega +1$
and
$\operatorname {\mathrm {otp}}(X)=\omega +1$
and
![]() $c"[X]^2=\{1\}$
, notice that
$c"[X]^2=\{1\}$
, notice that
![]() $\{g_\alpha \mid \alpha \in X\}$
is an infinite countable subset of A which is
$\{g_\alpha \mid \alpha \in X\}$
is an infinite countable subset of A which is
![]() $\lhd $
-bounded by the function
$\lhd $
-bounded by the function
![]() $g_{\max (X)}\in A$
as sought.here
$g_{\max (X)}\in A$
as sought.here
Note that
![]() $\operatorname {\mathrm {cf}}(D)=\omega _1$
, hence
$\operatorname {\mathrm {cf}}(D)=\omega _1$
, hence
![]() $D\times E \leq _T [\omega _1]^{<\omega }\times E$
.
$D\times E \leq _T [\omega _1]^{<\omega }\times E$
.
Claim 5.9.3.
![]() $\omega \times \omega _1\times E\leq _T D\times E$
.
$\omega \times \omega _1\times E\leq _T D\times E$
.
Proof As every subset of D of size
![]() $\omega _1$
is unbounded, we get by Lemma 2.9 that
$\omega _1$
is unbounded, we get by Lemma 2.9 that
![]() $\omega _1\leq _T D$
. As D is a directed set, every finite subset of D is bounded. By Claim 5.9.1, D contains an infinite countable unbounded subset, so by Corollary 2.10 we have
$\omega _1\leq _T D$
. As D is a directed set, every finite subset of D is bounded. By Claim 5.9.1, D contains an infinite countable unbounded subset, so by Corollary 2.10 we have
![]() $\omega \leq _T D$
. Finally,
$\omega \leq _T D$
. Finally,
![]() $\omega \times \omega _1 \leq _T D$
as sought.
$\omega \times \omega _1 \leq _T D$
as sought.
Claim 5.9.4.
![]() $D\not \leq _T\omega \times E$
.
$D\not \leq _T\omega \times E$
.
Proof Recall that either
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
or
![]() $E\equiv _T 1$
. Note that if
$E\equiv _T 1$
. Note that if
![]() $E\equiv _T 1$
, then as
$E\equiv _T 1$
, then as
![]() $\operatorname {\mathrm {cf}}(D)=\omega _1>\operatorname {\mathrm {cf}}(\omega )$
, we have by Lemma 2.12 that
$\operatorname {\mathrm {cf}}(D)=\omega _1>\operatorname {\mathrm {cf}}(\omega )$
, we have by Lemma 2.12 that
![]() $D\not \leq _T\omega \times E$
as sought. Note that for every partition
$D\not \leq _T\omega \times E$
as sought. Note that for every partition
![]() $D=\bigcup \{D_n\mid n<\omega \}$
of D, there exists some
$D=\bigcup \{D_n\mid n<\omega \}$
of D, there exists some
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $D_n$
is uncountable, and by Claim 5.9.1, there exists some
$D_n$
is uncountable, and by Claim 5.9.1, there exists some
![]() $X\subseteq D_n$
infinite and unbounded in D. As
$X\subseteq D_n$
infinite and unbounded in D. As
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
, by Lemma 2.17 we have
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\omega $
, by Lemma 2.17 we have
![]() $D\not \leq _T\omega \times E$
as sought.
$D\not \leq _T\omega \times E$
as sought.
Claim 5.9.5.
![]() $[\omega _1]^{<\omega } \not \leq _T D\times E$
.
$[\omega _1]^{<\omega } \not \leq _T D\times E$
.
Proof By Claim 5.9.2, every uncountable subset of D contains an infinite countable bounded subset and every countable subset of
![]() $E $
is bounded, we get that
$E $
is bounded, we get that
![]() $\omega \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D\times E),\omega _1)$
. As
$\omega \in \operatorname {\mathrm {in}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D\times E),\omega _1)$
. As
![]() $\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}([\omega _1]^{<\omega }))=\omega $
by Lemma 2.15 we get that
$\operatorname {\mathrm {out}}(\mathcal I_{\operatorname {\mathrm {bd}}}([\omega _1]^{<\omega }))=\omega $
by Lemma 2.15 we get that
![]() $[\omega _1]^{<\omega } \not \leq _T D\times E$
as sought.
$[\omega _1]^{<\omega } \not \leq _T D\times E$
as sought.
5.3 Directed set between
 $[\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }$
and
$[\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }$
and
 $[\lambda ^+]^{< \theta }$
$[\lambda ^+]^{< \theta }$
In [Reference Kuzeljević and Todorčević6, Theorem 1.2], the authors constructed a directed set between
![]() $[\omega _1]^{<\omega }\times [\omega _2]^{\leq \omega }$
and
$[\omega _1]^{<\omega }\times [\omega _2]^{\leq \omega }$
and
![]() $[\omega _2]^{< \omega }$
under the assumption
$[\omega _2]^{< \omega }$
under the assumption
![]() $2^{\aleph _0}=\aleph _1$
,
$2^{\aleph _0}=\aleph _1$
,
![]() $2^{\aleph _1}=\aleph _2$
and the existence of a non-reflecting stationary subset of
$2^{\aleph _1}=\aleph _2$
and the existence of a non-reflecting stationary subset of
![]() $E^{\omega _2}_\omega $
. In this subsection we generalize this result while waiving the assumption concerning the non-reflecting stationary set.
$E^{\omega _2}_\omega $
. In this subsection we generalize this result while waiving the assumption concerning the non-reflecting stationary set.
We commence by recalling some classic guessing principles and introducing a weak one, named
![]() $ \clubsuit ^\mu _{J}(S,1) $
, which will be useful for our construction.
$ \clubsuit ^\mu _{J}(S,1) $
, which will be useful for our construction.
Definition 5.10. For a stationary subset
![]() $ S\subseteq \kappa $
:
$ S\subseteq \kappa $
:
-
(1)
 $ \diamondsuit (S) $
asserts the existence of a sequence
$ \diamondsuit (S) $
asserts the existence of a sequence
 $ \langle C_\alpha \mid \alpha \in S \rangle $
such that:
$ \langle C_\alpha \mid \alpha \in S \rangle $
such that:-
• for all
 $ \alpha \in S $
,
$ \alpha \in S $
,
 $ C_\alpha \subseteq \alpha $
;
$ C_\alpha \subseteq \alpha $
; -
• for every
 $B\subseteq \kappa $
, the set
$B\subseteq \kappa $
, the set
 $\{\alpha \in S\mid B\cap \alpha =C_\alpha \}$
is stationary.
$\{\alpha \in S\mid B\cap \alpha =C_\alpha \}$
is stationary.
-
-
(2)
 $ \clubsuit (S) $
asserts the existence of a sequence
$ \clubsuit (S) $
asserts the existence of a sequence
 $ \langle C_\alpha \mid \alpha \in S \rangle $
such that:
$ \langle C_\alpha \mid \alpha \in S \rangle $
such that:-
• for all
 $ \alpha \in S\cap \operatorname {\mathrm {acc}}(\kappa ) $
,
$ \alpha \in S\cap \operatorname {\mathrm {acc}}(\kappa ) $
,
 $ C_\alpha $
is a cofinal subset of
$ C_\alpha $
is a cofinal subset of
 $\alpha $
of order type
$\alpha $
of order type
 $\operatorname {\mathrm {cf}}(\alpha )$
;
$\operatorname {\mathrm {cf}}(\alpha )$
; -
• for every cofinal subset
 $ B\subseteq \kappa $
, the set
$ B\subseteq \kappa $
, the set
 $\{\alpha \in S \mid C_\alpha \subseteq B \}$
is stationary.
$\{\alpha \in S \mid C_\alpha \subseteq B \}$
is stationary.
-
-
(3)
 $ \clubsuit ^\mu _{J}(S,1) $
asserts the existence of a sequence
$ \clubsuit ^\mu _{J}(S,1) $
asserts the existence of a sequence
 $ \langle C_\alpha \mid \alpha \in S \rangle $
such that:
$ \langle C_\alpha \mid \alpha \in S \rangle $
such that:-
• for all
 $ \alpha \in S\cap \operatorname {\mathrm {acc}}(\kappa ) $
,
$ \alpha \in S\cap \operatorname {\mathrm {acc}}(\kappa ) $
,
 $ C_\alpha $
is a cofinal subset of
$ C_\alpha $
is a cofinal subset of
 $\alpha $
of order type
$\alpha $
of order type
 $\operatorname {\mathrm {cf}}(\alpha )$
;
$\operatorname {\mathrm {cf}}(\alpha )$
; -
• for every partition
 $\langle A_\beta \mid \beta <\mu \rangle $
of
$\langle A_\beta \mid \beta <\mu \rangle $
of
 $\kappa $
there exists some
$\kappa $
there exists some
 $\beta <\mu $
such that the set
$\beta <\mu $
such that the set
 $\{\alpha \in S \mid \sup (C_\alpha \cap A_\beta )=\alpha \}$
is stationary.
$\{\alpha \in S \mid \sup (C_\alpha \cap A_\beta )=\alpha \}$
is stationary.
-
Recall that by a Theorem of Shelah [Reference Shelah10], for every uncountable cardinal
![]() $\lambda $
which satisfy
$\lambda $
which satisfy
![]() $2^\lambda = \lambda ^+$
and every stationary
$2^\lambda = \lambda ^+$
and every stationary
![]() $S\subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
,
$S\subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
,
![]() $\Diamond (S)$
holds. It is clear that
$\Diamond (S)$
holds. It is clear that
![]() $\Diamond (S) \Rightarrow \clubsuit (S) \Rightarrow \clubsuit ^\lambda _{J}(S,1) $
. The main corollary of this subsection is:
$\Diamond (S) \Rightarrow \clubsuit (S) \Rightarrow \clubsuit ^\lambda _{J}(S,1) $
. The main corollary of this subsection is:
Corollary 5.11. Let
![]() $\theta <\lambda $
be two regular cardinals. Assume
$\theta <\lambda $
be two regular cardinals. Assume
![]() $\lambda ^{\theta }<\lambda ^+$
and
$\lambda ^{\theta }<\lambda ^+$
and
![]() $\clubsuit ^\lambda _{J}(S,1) $
holds for some stationary
$\clubsuit ^\lambda _{J}(S,1) $
holds for some stationary
![]() $S\subseteq E^{\lambda ^+}_\theta $
. Suppose C and E are two directed sets such that
$S\subseteq E^{\lambda ^+}_\theta $
. Suppose C and E are two directed sets such that
![]() $\operatorname {\mathrm {cf}}(C)<\lambda ^+$
and
$\operatorname {\mathrm {cf}}(C)<\lambda ^+$
and
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
![]() $E\equiv _T 1$
. Then there exists a directed set
$E\equiv _T 1$
. Then there exists a directed set
![]() $D_{\mathcal C}$
such that
$D_{\mathcal C}$
such that
![]() $:$
$:$
In the rest of this subsection we prove this result.
Suppose
![]() $\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
is a C-sequence for some stationary set
$\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
is a C-sequence for some stationary set
![]() $S\subseteq E^{\lambda ^+}_\theta $
, i.e.,
$S\subseteq E^{\lambda ^+}_\theta $
, i.e.,
![]() $C_\alpha $
is a cofinal subset of
$C_\alpha $
is a cofinal subset of
![]() $\alpha $
of order-type
$\alpha $
of order-type
![]() $\theta $
, whenever
$\theta $
, whenever
![]() $\alpha \in S$
. We define the directed set
$\alpha \in S$
. We define the directed set
![]() $D_{\mathcal C} :=\{ Y\in [\lambda ^+]^{\leq \theta }\mid \forall \alpha \in S [|Y\cap C_\alpha |<\theta ] \}$
ordered by
$D_{\mathcal C} :=\{ Y\in [\lambda ^+]^{\leq \theta }\mid \forall \alpha \in S [|Y\cap C_\alpha |<\theta ] \}$
ordered by
![]() $\subseteq $
. Notice that
$\subseteq $
. Notice that
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_{\mathcal C}))= \theta $
and
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(D_{\mathcal C}))= \theta $
and
![]() $[\lambda ^+]^{< \theta }\subseteq D_{\mathcal C}$
.
$[\lambda ^+]^{< \theta }\subseteq D_{\mathcal C}$
.
Recall that by Hausdorff’s formula
![]() $(\lambda ^+)^\theta = \max \{\lambda ^+,\lambda ^\theta \}$
, so if
$(\lambda ^+)^\theta = \max \{\lambda ^+,\lambda ^\theta \}$
, so if
![]() $\lambda ^{\theta }<\lambda ^+$
, then
$\lambda ^{\theta }<\lambda ^+$
, then
![]() $(\lambda ^+)^\theta =\lambda ^+$
. So we may assume
$(\lambda ^+)^\theta =\lambda ^+$
. So we may assume
![]() $|D_{\mathcal C}|=\lambda ^+$
.
$|D_{\mathcal C}|=\lambda ^+$
.
Claim 5.11.1. Suppose
![]() $|D_{\mathcal C}|=\lambda ^+$
, then
$|D_{\mathcal C}|=\lambda ^+$
, then
![]() $[\lambda ^+]^{\leq \theta } \leq _T D_{\mathcal C}$
.
$[\lambda ^+]^{\leq \theta } \leq _T D_{\mathcal C}$
.
Proof Fix a bijection
![]() $\phi :D_{\mathcal C}\rightarrow \lambda ^+$
. Denote
$\phi :D_{\mathcal C}\rightarrow \lambda ^+$
. Denote
![]() $X:=\{x\cup \{\phi (x)\}\mid x\in D_{\mathcal C}\}$
, clearly X is cofinal subset of
$X:=\{x\cup \{\phi (x)\}\mid x\in D_{\mathcal C}\}$
, clearly X is cofinal subset of
![]() $D_{\mathcal C}$
. Let us fix some injective function
$D_{\mathcal C}$
. Let us fix some injective function
![]() $g:[\lambda ^+]^{\leq \theta } \rightarrow X$
. We claim that g is a Tukey function, which witness that
$g:[\lambda ^+]^{\leq \theta } \rightarrow X$
. We claim that g is a Tukey function, which witness that
![]() $[\lambda ^+]^{\leq \theta } \leq _T D_{\mathcal C}$
. Fix some
$[\lambda ^+]^{\leq \theta } \leq _T D_{\mathcal C}$
. Fix some
![]() $B\subseteq [\lambda ^+]^{\leq \theta }$
unbounded in
$B\subseteq [\lambda ^+]^{\leq \theta }$
unbounded in
![]() $ [\lambda ^+]^{\leq \theta }$
, note that
$ [\lambda ^+]^{\leq \theta }$
, note that
![]() $|B|>\theta $
. As g is injective, we get that
$|B|>\theta $
. As g is injective, we get that
![]() $g"B$
is a set of size
$g"B$
is a set of size
![]() $>\theta $
. Notice that there exists
$>\theta $
. Notice that there exists
![]() $Z\in [\lambda ^+]^{\theta ^+}$
such that
$Z\in [\lambda ^+]^{\theta ^+}$
such that
![]() $Z\subseteq \bigcup g"B$
. Assume that
$Z\subseteq \bigcup g"B$
. Assume that
![]() $g"B$
is bounded by
$g"B$
is bounded by
![]() $d\in D_{\mathcal C}$
in
$d\in D_{\mathcal C}$
in
![]() $D_{\mathcal C}$
. As
$D_{\mathcal C}$
. As
![]() $D_{\mathcal C}$
is ordered by
$D_{\mathcal C}$
is ordered by
![]() $\subseteq $
, we get that
$\subseteq $
, we get that
![]() $Z\subseteq d$
, so
$Z\subseteq d$
, so
![]() $|d|\geq \theta ^+$
. But this is a absurd as every set in
$|d|\geq \theta ^+$
. But this is a absurd as every set in
![]() $D_{\mathcal C}$
is of size
$D_{\mathcal C}$
is of size
![]() $\leq \theta $
.
$\leq \theta $
.
Notice that by Lemma 2.13 and Claim 5.11.1, as
![]() $(\lambda ^+)^\theta =\lambda ^+$
we have
$(\lambda ^+)^\theta =\lambda ^+$
we have
![]() $ [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta } \leq _T [\lambda ]^{<\theta } \times D_{\mathcal C} \leq _T [\lambda ^+]^{< \theta }.$
Hence,
$ [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta } \leq _T [\lambda ]^{<\theta } \times D_{\mathcal C} \leq _T [\lambda ^+]^{< \theta }.$
Hence,
![]() $C\times [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }\times E\leq _T C\times [\lambda ]^{<\theta } \times D_{\mathcal C}\times E \leq _T C\times [\lambda ^+]^{< \theta } \times E.$
$C\times [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }\times E\leq _T C\times [\lambda ]^{<\theta } \times D_{\mathcal C}\times E \leq _T C\times [\lambda ^+]^{< \theta } \times E.$
Claim 5.11.2. Suppose
![]() $\mathcal C$
is a
$\mathcal C$
is a
![]() $ \clubsuit ^\lambda _{J}(S,1) $
-sequence and
$ \clubsuit ^\lambda _{J}(S,1) $
-sequence and
![]() $:$
$:$
-
(i) C is a directed set such that
 $|C|<\lambda ^+$
;
$|C|<\lambda ^+$
; -
(ii) E is a directed set such that
 $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta $
and
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}}(E))>\theta $
and
 $\operatorname {\mathrm {cf}}(E)\geq \lambda ^+$
.
$\operatorname {\mathrm {cf}}(E)\geq \lambda ^+$
.
Then
![]() $ C\times D_{\mathcal C} \not \leq _T C\times E$
.
$ C\times D_{\mathcal C} \not \leq _T C\times E$
.
Proof Suppose that
![]() $f: C\times D_{\mathcal C} \rightarrow C\times E$
is a Tukey function. Fix some
$f: C\times D_{\mathcal C} \rightarrow C\times E$
is a Tukey function. Fix some
![]() $o\in C$
and for each
$o\in C$
and for each
![]() $\xi <\lambda ^+$
, denote
$\xi <\lambda ^+$
, denote
![]() $(c_\xi , x_\xi ) := f(o,\{\xi \})$
. Consider the set
$(c_\xi , x_\xi ) := f(o,\{\xi \})$
. Consider the set
![]() $\{(c_\xi ,x_\xi ) \mid \xi <\lambda ^+\}$
. For every
$\{(c_\xi ,x_\xi ) \mid \xi <\lambda ^+\}$
. For every
![]() $c\in C$
, we define
$c\in C$
, we define
![]() $A_c:=\{\xi <\lambda ^+ \mid c_\xi =c\}$
, clearly
$A_c:=\{\xi <\lambda ^+ \mid c_\xi =c\}$
, clearly
![]() $\langle A_c \mid c\in C \rangle $
is a partition of
$\langle A_c \mid c\in C \rangle $
is a partition of
![]() $\lambda ^+$
to less than
$\lambda ^+$
to less than
![]() $\lambda ^+$
many sets.
$\lambda ^+$
many sets.
As
![]() $\mathcal C$
is a
$\mathcal C$
is a
![]() $ \clubsuit ^\lambda _{J}(S,1) $
-sequence, there exists some
$ \clubsuit ^\lambda _{J}(S,1) $
-sequence, there exists some
![]() $c\in C$
and
$c\in C$
and
![]() $\alpha \in S$
such that
$\alpha \in S$
such that
![]() $|C_\alpha \cap A_c|=\theta $
. Let us fix some
$|C_\alpha \cap A_c|=\theta $
. Let us fix some
![]() $B\in [C_\alpha \cap A_c]^{\theta }$
. Notice that the set
$B\in [C_\alpha \cap A_c]^{\theta }$
. Notice that the set
![]() $G:=\{(o,\{\xi \})\mid \xi \in B\}$
is unbounded in
$G:=\{(o,\{\xi \})\mid \xi \in B\}$
is unbounded in
![]() $ C\times D_{\mathcal C}$
, hence as f is Tukey,
$ C\times D_{\mathcal C}$
, hence as f is Tukey,
![]() $f"G$
is unbounded in
$f"G$
is unbounded in
![]() $C\times E$
. The subset
$C\times E$
. The subset
![]() $\{x_\xi \mid \xi \in B\}$
of E is of size
$\{x_\xi \mid \xi \in B\}$
of E is of size
![]() $\theta $
, hence bounded by some e. Note that
$\theta $
, hence bounded by some e. Note that
![]() $f"G=\{( c,x_\xi )\mid \xi \in B\}$
is bounded by
$f"G=\{( c,x_\xi )\mid \xi \in B\}$
is bounded by
![]() $(c,e)$
in
$(c,e)$
in
![]() $ C\times E$
which is absurd.
$ C\times E$
which is absurd.
By the previous claim, as
![]() $\lambda ^\theta <\lambda ^+$
, we get that
$\lambda ^\theta <\lambda ^+$
, we get that
![]() $ C\times D_{\mathcal C}\times [\lambda ]^{<\theta } \times E \not \leq _T C\times [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }\times E $
. The following claim gives a negative answer to the question of whether there is a C-sequence
$ C\times D_{\mathcal C}\times [\lambda ]^{<\theta } \times E \not \leq _T C\times [\lambda ]^{<\theta }\times [\lambda ^+]^{\leq \theta }\times E $
. The following claim gives a negative answer to the question of whether there is a C-sequence
![]() $\mathcal C$
such that
$\mathcal C$
such that
![]() $D_{\mathcal C} \equiv _T [\lambda ^+]^{<\theta }$
.
$D_{\mathcal C} \equiv _T [\lambda ^+]^{<\theta }$
.
In the following claim we use the fact that the sets in the sequence
![]() $\mathcal C$
are of a bounded cofinality.
$\mathcal C$
are of a bounded cofinality.
Claim 5.11.3. Assume
![]() $\lambda ^\theta <\lambda ^+$
. Suppose
$\lambda ^\theta <\lambda ^+$
. Suppose
![]() $S\subseteq E^{\lambda ^+}_\theta $
is a stationary set and
$S\subseteq E^{\lambda ^+}_\theta $
is a stationary set and
![]() $\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
is a C-sequence, then
$\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
is a C-sequence, then
![]() $D_{\mathcal C}\not \geq _T [\lambda ^+]^{<\theta }$
.
$D_{\mathcal C}\not \geq _T [\lambda ^+]^{<\theta }$
.
Proof Let
![]() $S\subseteq E^{\lambda ^+}_\theta $
and
$S\subseteq E^{\lambda ^+}_\theta $
and
![]() $\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
be a C-sequence. Suppose we have
$\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
be a C-sequence. Suppose we have
![]() $ [\lambda ^+]^{< \theta } \leq _T D_{\mathcal C} $
, let
$ [\lambda ^+]^{< \theta } \leq _T D_{\mathcal C} $
, let
![]() $f:[\lambda ^+]^{< \theta } \rightarrow D_{\mathcal C}$
be a Tukey function and
$f:[\lambda ^+]^{< \theta } \rightarrow D_{\mathcal C}$
be a Tukey function and
![]() $Y:=f"[\lambda ^+]^{1}$
. Let us split to two cases:
$Y:=f"[\lambda ^+]^{1}$
. Let us split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Y|<\lambda ^+$
. By the pigeonhole principle, we can find a subset
$|Y|<\lambda ^+$
. By the pigeonhole principle, we can find a subset
![]() $Q\subseteq [\lambda ]^1$
of size
$Q\subseteq [\lambda ]^1$
of size
![]() $\theta $
such that
$\theta $
such that
![]() $f"Q=\{x\}$
for some
$f"Q=\{x\}$
for some
![]() $x\in D_{\mathcal C}$
. As f is Tukey and Q is unbounded in
$x\in D_{\mathcal C}$
. As f is Tukey and Q is unbounded in
![]() $[\lambda ^+]^{< \theta }$
, the set
$[\lambda ^+]^{< \theta }$
, the set
![]() $f"Q$
is unbounded which is absurd.
$f"Q$
is unbounded which is absurd.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Y|=\lambda ^+$
. As f is Tukey, every subset of Y of size
$|Y|=\lambda ^+$
. As f is Tukey, every subset of Y of size
![]() $\theta $
is unbounded which is absurd to the following claim.
$\theta $
is unbounded which is absurd to the following claim.
Subclaim 5.11.3.1. There is no subset
![]() $Y\subseteq D_{\mathcal C}$
of size
$Y\subseteq D_{\mathcal C}$
of size
![]() $\lambda ^+$
such that every subset of Y of size
$\lambda ^+$
such that every subset of Y of size
![]() $\theta $
is unbounded.
$\theta $
is unbounded.
Proof Assume towards a contradiction that Y is such a set. As
![]() $\lambda ^{\theta }<\lambda ^+$
, we may refine Y and assume that
$\lambda ^{\theta }<\lambda ^+$
, we may refine Y and assume that
![]() $Y=\{y_\alpha \mid \alpha <\lambda ^+\}$
is a
$Y=\{y_\alpha \mid \alpha <\lambda ^+\}$
is a
![]() $\Delta $
-system with a root R separated by a club
$\Delta $
-system with a root R separated by a club
![]() $C\subseteq \lambda ^+$
, i.e., such that for every
$C\subseteq \lambda ^+$
, i.e., such that for every
![]() $\alpha <\beta <\lambda ^+$
,
$\alpha <\beta <\lambda ^+$
,
![]() $y_\alpha \setminus R <\eta < y_\beta \setminus R$
for some
$y_\alpha \setminus R <\eta < y_\beta \setminus R$
for some
![]() $\eta \in C$
.
$\eta \in C$
.
We define an increasing sequence of ordinals
![]() $\langle \beta _\nu \mid \nu \leq \theta ^2\rangle $
where for each
$\langle \beta _\nu \mid \nu \leq \theta ^2\rangle $
where for each
![]() $\nu \leq \theta ^2$
we let
$\nu \leq \theta ^2$
we let
![]() $\beta _\nu :=\sup \{y_\xi \mid \xi <\nu \}$
. As C is a club, we get that
$\beta _\nu :=\sup \{y_\xi \mid \xi <\nu \}$
. As C is a club, we get that
![]() $\beta _{\theta \cdot \nu }\in C$
for each
$\beta _{\theta \cdot \nu }\in C$
for each
![]() $\nu <\theta $
.
$\nu <\theta $
.
We aim to construct a subset
![]() $X=\{x_j \mid j <\theta \}$
of Y, we split to two cases: Suppose
$X=\{x_j \mid j <\theta \}$
of Y, we split to two cases: Suppose
![]() $\beta _{\theta ^2}\in S$
. Recall that
$\beta _{\theta ^2}\in S$
. Recall that
![]() $\operatorname {\mathrm {otp}} (C_{\beta _{\theta ^2}})=\theta $
and
$\operatorname {\mathrm {otp}} (C_{\beta _{\theta ^2}})=\theta $
and
![]() $\sup (C_{\beta _{\theta ^2}})=\beta _{\theta ^2}$
, so for every
$\sup (C_{\beta _{\theta ^2}})=\beta _{\theta ^2}$
, so for every
![]() $j <\theta $
we have that the interval
$j <\theta $
we have that the interval
![]() $[\beta _{\theta \cdot j},\beta _{\theta \cdot (j+1)})$
contains
$[\beta _{\theta \cdot j},\beta _{\theta \cdot (j+1)})$
contains
![]() $<\theta $
many elements of the ladder
$<\theta $
many elements of the ladder
![]() $C_{\beta _{\theta ^2}}$
, let us fix some
$C_{\beta _{\theta ^2}}$
, let us fix some
![]() $x_j\in Y$
such that
$x_j\in Y$
such that
![]() $x_j\setminus R\subset [\beta _{\theta \cdot j},\beta _{\theta \cdot (j+1)})$
and
$x_j\setminus R\subset [\beta _{\theta \cdot j},\beta _{\theta \cdot (j+1)})$
and
![]() $x_j\setminus R$
is disjoint from
$x_j\setminus R$
is disjoint from
![]() $C_{\beta _{\theta ^2}}$
. If
$C_{\beta _{\theta ^2}}$
. If
![]() $\beta _{\theta ^2}\notin S$
, define
$\beta _{\theta ^2}\notin S$
, define
![]() $X:=\{x_j \mid j<\theta \}$
where
$X:=\{x_j \mid j<\theta \}$
where
![]() $x_j:= y_{\theta \cdot j}$
.
$x_j:= y_{\theta \cdot j}$
.
Let us show that
![]() $X=\{x_j \mid j <\theta \}$
is a bounded subset of Y, which is a contradiction to the assumption. It is enough to show that for every
$X=\{x_j \mid j <\theta \}$
is a bounded subset of Y, which is a contradiction to the assumption. It is enough to show that for every
![]() $\alpha \in S$
, we have that
$\alpha \in S$
, we have that
![]() $|(\bigcup X)\cap C_\alpha |<\theta $
. Let
$|(\bigcup X)\cap C_\alpha |<\theta $
. Let
![]() $\alpha \in S$
.
$\alpha \in S$
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha>\beta _{\theta ^2}$
, as
$\alpha>\beta _{\theta ^2}$
, as
![]() $C_\alpha $
is a cofinal subset of
$C_\alpha $
is a cofinal subset of
![]() $\alpha $
of order-type
$\alpha $
of order-type
![]() $\theta $
and
$\theta $
and
![]() $\bigcup X$
is bounded by
$\bigcup X$
is bounded by
![]() $\beta _{\theta ^2}$
it is clear that
$\beta _{\theta ^2}$
it is clear that
![]() $|(\bigcup X)\cap C_\alpha |<\theta $
.
$|(\bigcup X)\cap C_\alpha |<\theta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha <\beta _{\theta ^2}$
. As
$\alpha <\beta _{\theta ^2}$
. As
![]() $C_\alpha $
if cofinal in
$C_\alpha $
if cofinal in
![]() $\alpha $
and of order-type
$\alpha $
and of order-type
![]() $\theta $
, there exists some
$\theta $
, there exists some
![]() $j <\theta $
such that for all
$j <\theta $
such that for all
![]() $j <\rho <\theta $
, we have
$j <\rho <\theta $
, we have
![]() $(x_\rho \setminus R)\cap C_\alpha =\emptyset $
. As
$(x_\rho \setminus R)\cap C_\alpha =\emptyset $
. As
![]() $x_\rho \in D_{\mathcal C_R}$
for every
$x_\rho \in D_{\mathcal C_R}$
for every
![]() $\rho <\theta $
and
$\rho <\theta $
and
![]() $\theta $
is regular, we get that
$\theta $
is regular, we get that
![]() $|(\bigcup X)\cap C_\alpha |<\theta $
as sought.
$|(\bigcup X)\cap C_\alpha |<\theta $
as sought.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha = \beta _{\theta ^2}$
. Notice this implies that we are in the first case of the construction of the set X. Recall that the
$\alpha = \beta _{\theta ^2}$
. Notice this implies that we are in the first case of the construction of the set X. Recall that the
![]() $\Delta $
-system
$\Delta $
-system
![]() $\{x_j \mid j <\theta \}$
is such that
$\{x_j \mid j <\theta \}$
is such that
![]() $(x_j\setminus R )\cap C_\alpha =\emptyset $
, hence
$(x_j\setminus R )\cap C_\alpha =\emptyset $
, hence
![]() $(\bigcup X)\cap C_{\alpha } = R \cap C_\alpha $
. Recall that as
$(\bigcup X)\cap C_{\alpha } = R \cap C_\alpha $
. Recall that as
![]() $x_0\in D_{\mathcal C}$
, we get that
$x_0\in D_{\mathcal C}$
, we get that
![]() $R \cap C_\alpha $
is of size
$R \cap C_\alpha $
is of size
![]() $<\theta $
, hence also
$<\theta $
, hence also
![]() $(\bigcup X)\cap C_{\alpha }$
is as sought.
$(\bigcup X)\cap C_{\alpha }$
is as sought.
Claim 5.11.4. Assume
![]() $\lambda ^\theta <\lambda ^+$
. Suppose C and E are two directed sets such that
$\lambda ^\theta <\lambda ^+$
. Suppose C and E are two directed sets such that
![]() $|C|<\lambda ^+$
and either
$|C|<\lambda ^+$
and either
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
![]() $E\equiv _T 1$
. Then for every C-sequence
$E\equiv _T 1$
. Then for every C-sequence
![]() $\mathcal C$
on a stationary
$\mathcal C$
on a stationary
![]() $S\subseteq E^{\lambda ^+}_\theta $
,
$S\subseteq E^{\lambda ^+}_\theta $
,
![]() $C\times [\lambda ^+]^{<\theta } \times E\not \leq _T C\times D_{\mathcal C} \times E$
.
$C\times [\lambda ^+]^{<\theta } \times E\not \leq _T C\times D_{\mathcal C} \times E$
.
Proof Let
![]() $\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
be a C-sequence where
$\mathcal C:=\langle C_\alpha \mid \alpha \in S \rangle $
be a C-sequence where
![]() $S\subseteq E^{\lambda ^+}_\theta $
. Suppose on the contrary that
$S\subseteq E^{\lambda ^+}_\theta $
. Suppose on the contrary that
![]() $C\times [\lambda ^+]^{<\theta } \times E \leq _T C\times D_{\mathcal C} \times E$
. Hence,
$C\times [\lambda ^+]^{<\theta } \times E \leq _T C\times D_{\mathcal C} \times E$
. Hence,
![]() $[\lambda ^+]^{<\theta }\leq _T C\times D_{\mathcal C} \times E$
, let us fix a Tukey function
$[\lambda ^+]^{<\theta }\leq _T C\times D_{\mathcal C} \times E$
, let us fix a Tukey function
![]() $f:[\lambda ^+]^{<\theta }\rightarrow C\times D_{\mathcal C}\times E$
witnessing that. Consider
$f:[\lambda ^+]^{<\theta }\rightarrow C\times D_{\mathcal C}\times E$
witnessing that. Consider
![]() $X=[\lambda ^+]^1$
.
$X=[\lambda ^+]^1$
.
By the pigeonhole principle, there exists some
![]() $c\in C$
and some set
$c\in C$
and some set
![]() $Z\subseteq X$
of size
$Z\subseteq X$
of size
![]() $\lambda ^+$
such that
$\lambda ^+$
such that
![]() $f"Z \subseteq \{ c\}\times D_{\mathcal C}\times E$
. Let
$f"Z \subseteq \{ c\}\times D_{\mathcal C}\times E$
. Let
![]() $Y:=\pi _{D_{\mathcal C}} (f"Z)$
. Let us split to two cases:
$Y:=\pi _{D_{\mathcal C}} (f"Z)$
. Let us split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Y|< \lambda ^+$
. By the pigeonhole principle, we can find a subset
$|Y|< \lambda ^+$
. By the pigeonhole principle, we can find a subset
![]() $Q\subseteq Z$
of size
$Q\subseteq Z$
of size
![]() $\theta $
such that
$\theta $
such that
![]() $f"Q=\{c\}\times \{x\}\times E$
for some
$f"Q=\{c\}\times \{x\}\times E$
for some
![]() $x\in D_{\mathcal C}$
. As f is Tukey and Q is unbounded, we must have that
$x\in D_{\mathcal C}$
. As f is Tukey and Q is unbounded, we must have that
![]() $f"Q$
is unbounded, but this is absurd as
$f"Q$
is unbounded, but this is absurd as
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
.
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Y|=\lambda ^+$
. As f is Tukey and either
$|Y|=\lambda ^+$
. As f is Tukey and either
![]() $\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
$\operatorname {\mathrm {non}}(\mathcal I_{\operatorname {\mathrm {bd}}} (E))>\theta $
or
![]() $E=1$
, every subset of Y of size
$E=1$
, every subset of Y of size
![]() $\theta $
is unbounded which is impossible by Claim 5.11.3.1.
$\theta $
is unbounded which is impossible by Claim 5.11.3.1.
5.4 Structure of
 $D_{\mathcal C}$
$D_{\mathcal C}$
In [Reference Todorčević12, Lemmas 1, 2], Todorčević defined for every
![]() $\kappa $
regular and
$\kappa $
regular and
![]() $S\subseteq \kappa $
the directed set
$S\subseteq \kappa $
the directed set
![]() $D(S):=\{C\subseteq [S]^{\leq \omega } \mid \forall \alpha <\omega _1[\sup (C\cap \alpha )\in C]\}$
ordered by inclusion; and studied the structure of such directed sets. In this section we follow this line of study but for directed sets of the form
$D(S):=\{C\subseteq [S]^{\leq \omega } \mid \forall \alpha <\omega _1[\sup (C\cap \alpha )\in C]\}$
ordered by inclusion; and studied the structure of such directed sets. In this section we follow this line of study but for directed sets of the form
![]() $D_{\mathcal C}$
, constructing a large
$D_{\mathcal C}$
, constructing a large
![]() $<_T$
-antichain and chain of directed sets using
$<_T$
-antichain and chain of directed sets using
![]() $\theta $
-support product.
$\theta $
-support product.
5.4.1 Antichain
Theorem 5.12. Suppose
![]() $2^\lambda =\lambda ^+$
,
$2^\lambda =\lambda ^+$
,
![]() $\lambda ^\theta <\lambda ^+$
, then there exists a family
$\lambda ^\theta <\lambda ^+$
, then there exists a family
![]() $\mathcal F$
of size
$\mathcal F$
of size
![]() $2^{\lambda ^+}$
of directed sets of the form
$2^{\lambda ^+}$
of directed sets of the form
![]() $D_{\mathcal C}$
such that every two of them are Tukey incomparable.
$D_{\mathcal C}$
such that every two of them are Tukey incomparable.
Proof As
![]() $2^\lambda =\lambda ^+$
holds, by Shelah’s Theorem we get that
$2^\lambda =\lambda ^+$
holds, by Shelah’s Theorem we get that
![]() $\diamondsuit (S)$
holds for every
$\diamondsuit (S)$
holds for every
![]() $S\subseteq E^{\lambda ^+}_\theta $
stationary subset. Let us fix some stationary subset
$S\subseteq E^{\lambda ^+}_\theta $
stationary subset. Let us fix some stationary subset
![]() $S\subseteq E^{\lambda ^+}_\theta $
and a partition of S into
$S\subseteq E^{\lambda ^+}_\theta $
and a partition of S into
![]() $\lambda ^+$
-many stationary subsets
$\lambda ^+$
-many stationary subsets
![]() $\langle S_\alpha \mid \alpha <\lambda ^+ \rangle $
. For each
$\langle S_\alpha \mid \alpha <\lambda ^+ \rangle $
. For each
![]() $S_\alpha $
we fix a
$S_\alpha $
we fix a
![]() $\clubsuit (S_\alpha )$
sequence
$\clubsuit (S_\alpha )$
sequence
![]() $\langle C_\beta \mid \beta \in S_\alpha \rangle $
.
$\langle C_\beta \mid \beta \in S_\alpha \rangle $
.
Let us fix a family
![]() $\mathcal F$
of size
$\mathcal F$
of size
![]() $2^{\lambda ^+}$
of subsets of
$2^{\lambda ^+}$
of subsets of
![]() $S $
such that for every two
$S $
such that for every two
![]() $R,T\in \mathcal F$
there exists some
$R,T\in \mathcal F$
there exists some
![]() $S_\alpha $
such that
$S_\alpha $
such that
![]() $R\setminus T \supseteq S_\alpha $
. For each
$R\setminus T \supseteq S_\alpha $
. For each
![]() $T\in \mathcal F$
let us define a C-sequence
$T\in \mathcal F$
let us define a C-sequence
![]() $\mathcal C_T:= \langle C_\alpha \mid \alpha \in T \rangle $
. Clearly the following lemma shows the family
$\mathcal C_T:= \langle C_\alpha \mid \alpha \in T \rangle $
. Clearly the following lemma shows the family
![]() $\{ D_{\mathcal C_T} \mid T\in \mathcal F \}$
is as sought.
$\{ D_{\mathcal C_T} \mid T\in \mathcal F \}$
is as sought.
Claim 5.12.1. Suppose
![]() $\mathcal C_T:=\langle C_\beta \mid \beta \in T \rangle $
and
$\mathcal C_T:=\langle C_\beta \mid \beta \in T \rangle $
and
![]() $\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
are two C-sequences such that
$\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
are two C-sequences such that
![]() $T,R\subseteq E^{\lambda ^+}_\theta $
are stationary subsets. Then if
$T,R\subseteq E^{\lambda ^+}_\theta $
are stationary subsets. Then if
![]() $\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
$\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
![]() $\clubsuit $
-sequence, then
$\clubsuit $
-sequence, then
![]() $D_{\mathcal C_T}\not \leq _T D_{\mathcal C_R}$
.
$D_{\mathcal C_T}\not \leq _T D_{\mathcal C_R}$
.
Proof Suppose
![]() $f:D_{\mathcal C_T} \rightarrow D_{\mathcal C_R}$
is a Tukey function. Fix a subset
$f:D_{\mathcal C_T} \rightarrow D_{\mathcal C_R}$
is a Tukey function. Fix a subset
![]() $W\subseteq [\lambda ^+]^1\subseteq D_{\mathcal C_T}$
of size
$W\subseteq [\lambda ^+]^1\subseteq D_{\mathcal C_T}$
of size
![]() $\lambda ^+$
, we split to two cases:
$\lambda ^+$
, we split to two cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $f"W \subseteq [\alpha ]^{\theta }$
for some
$f"W \subseteq [\alpha ]^{\theta }$
for some
![]() $\alpha <\lambda ^+$
. As
$\alpha <\lambda ^+$
. As
![]() $\lambda ^\theta <\lambda ^+$
, by the pigeonhole principle we can find a subset
$\lambda ^\theta <\lambda ^+$
, by the pigeonhole principle we can find a subset
![]() $X\subseteq W $
of size
$X\subseteq W $
of size
![]() $\lambda ^+$
such that
$\lambda ^+$
such that
![]() $f"X = \{z\}$
for some
$f"X = \{z\}$
for some
![]() $z\in D_{\mathcal C_R}$
. As
$z\in D_{\mathcal C_R}$
. As
![]() $\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
$\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
![]() $\clubsuit $
-sequence and
$\clubsuit $
-sequence and
![]() $\bigcup X \in [\lambda ^+]^{\lambda ^+}$
, there exists some
$\bigcup X \in [\lambda ^+]^{\lambda ^+}$
, there exists some
![]() $\beta \in T\setminus R$
such that
$\beta \in T\setminus R$
such that
![]() $C_\beta \subseteq \bigcup X$
. So X is an unbounded subset of
$C_\beta \subseteq \bigcup X$
. So X is an unbounded subset of
![]() $\mathcal C_T$
such that
$\mathcal C_T$
such that
![]() $f"X$
is bounded in
$f"X$
is bounded in
![]() $\mathcal C_R$
which is absurd.
$\mathcal C_R$
which is absurd.
![]() $\blacktriangleright $
As
$\blacktriangleright $
As
![]() $|f"W|=\lambda ^+$
, using
$|f"W|=\lambda ^+$
, using
![]() $\lambda ^\theta <\lambda ^+$
we may fix a subset
$\lambda ^\theta <\lambda ^+$
we may fix a subset
![]() $Y=\{y_\beta \mid \beta <\lambda ^+\}\subseteq f"W$
which forms a
$Y=\{y_\beta \mid \beta <\lambda ^+\}\subseteq f"W$
which forms a
![]() $\Delta $
-system with a root
$\Delta $
-system with a root
![]() $R_1$
. In other words, for
$R_1$
. In other words, for
![]() $\alpha <\beta <\lambda ^+$
we have
$\alpha <\beta <\lambda ^+$
we have
![]() $y_\alpha \setminus R_1 < y_\beta \setminus R_1 $
and
$y_\alpha \setminus R_1 < y_\beta \setminus R_1 $
and
![]() $y_\alpha \cap y_\beta =R_1$
. For each
$y_\alpha \cap y_\beta =R_1$
. For each
![]() $\alpha <\lambda ^+$
, we fix
$\alpha <\lambda ^+$
, we fix
![]() $x_\alpha \in W$
such that
$x_\alpha \in W$
such that
![]() $f(x_\alpha )=y_\alpha $
. Finally, without loss of generality we may use the
$f(x_\alpha )=y_\alpha $
. Finally, without loss of generality we may use the
![]() $\Delta $
-system lemma again and refine our set Y to get that there exists a club
$\Delta $
-system lemma again and refine our set Y to get that there exists a club
![]() $E\subseteq \lambda ^+$
such that, for all
$E\subseteq \lambda ^+$
such that, for all
![]() $\alpha <\beta <\lambda ^+$
we have:
$\alpha <\beta <\lambda ^+$
we have:
-
•
 $x_\alpha \cap x_\beta = \emptyset $
;
$x_\alpha \cap x_\beta = \emptyset $
; -
•
 $y_\alpha \cap y_\beta = R_1 $
;
$y_\alpha \cap y_\beta = R_1 $
; -
• there exists some
 $\gamma \in E$
such that
$\gamma \in E$
such that
 $x_\alpha < \gamma < x_\beta $
and
$x_\alpha < \gamma < x_\beta $
and
 $y_\alpha \setminus R_1 < \gamma < y_\beta \setminus R_1 $
;
$y_\alpha \setminus R_1 < \gamma < y_\beta \setminus R_1 $
; -
•
 $f(x_\alpha ) = y_\alpha $
.
$f(x_\alpha ) = y_\alpha $
.
Furthermore, we may assume that between any two elements of
![]() $\xi <\eta $
in E there exists a unique
$\xi <\eta $
in E there exists a unique
![]() $\alpha <\lambda ^+$
such that
$\alpha <\lambda ^+$
such that
![]() $\xi < x_\alpha \cup (y_\alpha \setminus R_1)<\eta $
.
$\xi < x_\alpha \cup (y_\alpha \setminus R_1)<\eta $
.
As
![]() $\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
$\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
![]() $\clubsuit $
-sequence, there exists some
$\clubsuit $
-sequence, there exists some
![]() $\beta \in (T\setminus R)\cap \operatorname {\mathrm {acc}}(E)$
such that
$\beta \in (T\setminus R)\cap \operatorname {\mathrm {acc}}(E)$
such that
![]() $C_\beta \subseteq \bigcup \{x_\alpha \mid \alpha <\lambda ^+\}$
. Construct by recursion an increasing sequence
$C_\beta \subseteq \bigcup \{x_\alpha \mid \alpha <\lambda ^+\}$
. Construct by recursion an increasing sequence
![]() $\langle \beta _\nu \mid \nu <\theta \rangle \subseteq C_\beta $
and a sequence
$\langle \beta _\nu \mid \nu <\theta \rangle \subseteq C_\beta $
and a sequence
![]() $\langle z_\nu \mid \nu <\theta \rangle \subseteq \{x_\alpha \mid \alpha <\lambda ^+\}$
such that
$\langle z_\nu \mid \nu <\theta \rangle \subseteq \{x_\alpha \mid \alpha <\lambda ^+\}$
such that
![]() $\beta _\nu \in z_\nu <\beta $
.
$\beta _\nu \in z_\nu <\beta $
.
Clearly,
![]() $\{z_\nu \mid \nu <\theta \}$
is unbounded in
$\{z_\nu \mid \nu <\theta \}$
is unbounded in
![]() $ D_{\mathcal C_T}$
, so the following claim proves f is not a Tukey function.
$ D_{\mathcal C_T}$
, so the following claim proves f is not a Tukey function.
Subclaim 5.12.1.1. The subset
![]() $\{ f(z_\nu )\mid \nu <\theta \}$
is bounded in
$\{ f(z_\nu )\mid \nu <\theta \}$
is bounded in
![]() $D_{\mathcal C_R}$
.
$D_{\mathcal C_R}$
.
Proof Let
![]() $Y:=\bigcup f(z_\nu )$
and
$Y:=\bigcup f(z_\nu )$
and
![]() $\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
, we will show that for every
$\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
, we will show that for every
![]() $\alpha \in R$
, we have
$\alpha \in R$
, we have
![]() $|Y\cap C_\alpha |<\theta $
. By the refinement we did previously it is clear that
$|Y\cap C_\alpha |<\theta $
. By the refinement we did previously it is clear that
![]() $\{f(z_\nu )\setminus R_1\mid \nu <\theta \}$
is a pairwise disjoint sequence, where for each
$\{f(z_\nu )\setminus R_1\mid \nu <\theta \}$
is a pairwise disjoint sequence, where for each
![]() $\nu <\theta $
we have some element
$\nu <\theta $
we have some element
![]() $\gamma _\nu \in E$
such that
$\gamma _\nu \in E$
such that
![]() $f(z_\nu )\setminus R_1 < \gamma _\nu < f(z_{\nu +1}) \setminus R_1<\beta $
. Let
$f(z_\nu )\setminus R_1 < \gamma _\nu < f(z_{\nu +1}) \setminus R_1<\beta $
. Let
![]() $\alpha \in R$
.
$\alpha \in R$
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha>\beta $
. As
$\alpha>\beta $
. As
![]() $C_\alpha $
is cofinal in
$C_\alpha $
is cofinal in
![]() $\alpha $
and of order-type
$\alpha $
and of order-type
![]() $\theta $
, then
$\theta $
, then
![]() $|Y\cap C_\alpha |<\theta $
.
$|Y\cap C_\alpha |<\theta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha <\beta $
. As
$\alpha <\beta $
. As
![]() $C_\alpha $
is cofinal in
$C_\alpha $
is cofinal in
![]() $\alpha $
and of order-type
$\alpha $
and of order-type
![]() $\theta $
, there exists some
$\theta $
, there exists some
![]() $\nu <\theta $
such that for all
$\nu <\theta $
such that for all
![]() $\nu <\rho <\theta $
, we have
$\nu <\rho <\theta $
, we have
![]() $(f(z_\rho )\setminus R_1)\cap C_\alpha =\emptyset $
. As
$(f(z_\rho )\setminus R_1)\cap C_\alpha =\emptyset $
. As
![]() $f(z_\rho )\in D_{\mathcal C_R}$
for every
$f(z_\rho )\in D_{\mathcal C_R}$
for every
![]() $\rho <\theta $
and
$\rho <\theta $
and
![]() $\theta $
is regular, we get that
$\theta $
is regular, we get that
![]() $|Y\cap C_\alpha |<\theta $
as sought.
$|Y\cap C_\alpha |<\theta $
as sought.
As
![]() $\beta \notin R$
there are no more cases to consider.
$\beta \notin R$
there are no more cases to consider.
Corollary 5.13. Suppose
![]() $2^\lambda =\lambda ^+$
,
$2^\lambda =\lambda ^+$
,
![]() $\lambda ^\theta <\lambda ^+$
and
$\lambda ^\theta <\lambda ^+$
and
![]() $S\subseteq E^{\lambda ^+}_\theta $
is a stationary subset. Then there exists a family
$S\subseteq E^{\lambda ^+}_\theta $
is a stationary subset. Then there exists a family
![]() $\mathcal F$
of directed sets of the form
$\mathcal F$
of directed sets of the form
![]() $D_{\mathcal C}\times [\lambda ]^{<\theta }$
of size
$D_{\mathcal C}\times [\lambda ]^{<\theta }$
of size
![]() $2^{\lambda ^+}$
such that every two of them are Tukey incomparable.
$2^{\lambda ^+}$
such that every two of them are Tukey incomparable.
Proof Clearly by the same arguments of Theorem 5.12 the following lemma is suffices to get the wanted result.
Claim 5.13.1. Suppose
![]() $\mathcal C_T:=\langle C_\beta \mid \beta \in T \rangle $
and
$\mathcal C_T:=\langle C_\beta \mid \beta \in T \rangle $
and
![]() $\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
are two C-sequences such that
$\mathcal C_R:=\langle C_\beta \mid \beta \in R \rangle $
are two C-sequences such that
![]() $T,R\subseteq E^{\lambda ^+}_\theta $
are stationary subsets such that
$T,R\subseteq E^{\lambda ^+}_\theta $
are stationary subsets such that
![]() $T\setminus R$
is stationary. Then if
$T\setminus R$
is stationary. Then if
![]() $\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
$\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
![]() $\clubsuit $
-sequence, then
$\clubsuit $
-sequence, then
![]() $ D_{\mathcal C_T}\times [\lambda ]^{<\theta }\not \leq _T D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
.
$ D_{\mathcal C_T}\times [\lambda ]^{<\theta }\not \leq _T D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
.
Proof Suppose
![]() $f: D_{\mathcal C_T} \times [\lambda ]^{<\theta }\rightarrow D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
is a Tukey function. Consider
$f: D_{\mathcal C_T} \times [\lambda ]^{<\theta }\rightarrow D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
is a Tukey function. Consider
![]() $Q=f"([\lambda ^+]^1\times \{\emptyset \} )$
, let us split to two cases:
$Q=f"([\lambda ^+]^1\times \{\emptyset \} )$
, let us split to two cases:
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $|Q|<\lambda ^+$
, then by the pigeonhole principle, there exists
$|Q|<\lambda ^+$
, then by the pigeonhole principle, there exists
![]() $x\in D_{\mathcal C_R}$
,
$x\in D_{\mathcal C_R}$
,
![]() $F\in [\lambda ]^{<\theta }$
and a set
$F\in [\lambda ]^{<\theta }$
and a set
![]() $W\subseteq [\lambda ^+]^1$
of size
$W\subseteq [\lambda ^+]^1$
of size
![]() $\lambda ^+$
such that
$\lambda ^+$
such that
![]() $f"( W\times \{\emptyset \}) =\{(x,F)\}$
. As
$f"( W\times \{\emptyset \}) =\{(x,F)\}$
. As
![]() $\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
$\langle C_\beta \mid \beta \in T\setminus R \rangle $
is a
![]() $\clubsuit $
-sequence and
$\clubsuit $
-sequence and
![]() $\bigcup W \in [\lambda ^+]^{\lambda ^+}$
, we may fix some
$\bigcup W \in [\lambda ^+]^{\lambda ^+}$
, we may fix some
![]() $\beta \in T\setminus R$
such that
$\beta \in T\setminus R$
such that
![]() $C_\beta \subseteq \bigcup W$
. Hence
$C_\beta \subseteq \bigcup W$
. Hence
![]() $W\times \{\emptyset \}$
is unbounded in
$W\times \{\emptyset \}$
is unbounded in
![]() $D_{\mathcal C_T}\times [\lambda ]^{<\theta }$
but
$D_{\mathcal C_T}\times [\lambda ]^{<\theta }$
but
![]() $f"(W\times \{\emptyset \})$
is bounded in
$f"(W\times \{\emptyset \})$
is bounded in
![]() $D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
which is absurd as f is Tukey.
$D_{\mathcal C_R}\times [\lambda ]^{<\theta }$
which is absurd as f is Tukey.
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $|Q|=\lambda ^+$
, then by the pigeonhole principle there exists some
$|Q|=\lambda ^+$
, then by the pigeonhole principle there exists some
![]() $F\in [\lambda ]^{<\theta }$
and a set
$F\in [\lambda ]^{<\theta }$
and a set
![]() $W\subseteq [\lambda ^+]^1$
of size
$W\subseteq [\lambda ^+]^1$
of size
![]() $\lambda ^+$
such that,
$\lambda ^+$
such that,
![]() $f"(W\times \{\emptyset \}) \subseteq D_{\mathcal C_R}\times \{F\} $
. Let
$f"(W\times \{\emptyset \}) \subseteq D_{\mathcal C_R}\times \{F\} $
. Let
![]() $Y:=\pi _0(f"(W\times \{\emptyset \}))$
. Next, we may continue with the same proof as in Lemma 5.12.1.
$Y:=\pi _0(f"(W\times \{\emptyset \}))$
. Next, we may continue with the same proof as in Lemma 5.12.1.
5.4.2 Chain
Theorem 5.14. Suppose
![]() $2^\lambda =\lambda ^+$
,
$2^\lambda =\lambda ^+$
,
![]() $\lambda ^\theta <\lambda ^+$
. Then there exists a family
$\lambda ^\theta <\lambda ^+$
. Then there exists a family
![]() $\mathcal F=\{D_{\mathcal C_\xi } \mid \xi <\lambda ^+\}$
of Tukey incomparable directed sets of the form
$\mathcal F=\{D_{\mathcal C_\xi } \mid \xi <\lambda ^+\}$
of Tukey incomparable directed sets of the form
![]() $D_{\mathcal C}$
such that
$D_{\mathcal C}$
such that
![]() $\langle \prod ^{\leq \theta }_{\zeta <\xi } D_{\mathcal C_\zeta } \mid \xi <\lambda ^+\rangle $
is a
$\langle \prod ^{\leq \theta }_{\zeta <\xi } D_{\mathcal C_\zeta } \mid \xi <\lambda ^+\rangle $
is a
![]() $<_T$
-increasing chain.
$<_T$
-increasing chain.
Proof As in Theorem 5.12, we fix a partition
![]() $\langle S_\zeta \mid \zeta <\lambda ^+\rangle $
of
$\langle S_\zeta \mid \zeta <\lambda ^+\rangle $
of
![]() $E^{\lambda ^+}_\theta $
to stationary subsets such that there exists a
$E^{\lambda ^+}_\theta $
to stationary subsets such that there exists a
![]() $\clubsuit (S_\zeta ) $
-sequence
$\clubsuit (S_\zeta ) $
-sequence
![]() $\mathcal C_\zeta $
for
$\mathcal C_\zeta $
for
![]() $\zeta <\lambda ^+$
. Note that for every
$\zeta <\lambda ^+$
. Note that for every
![]() $A\in [\lambda ^+]^{<\lambda ^+}$
, we have
$A\in [\lambda ^+]^{<\lambda ^+}$
, we have
![]() $|\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }|=\lambda ^+$
. Note that for every
$|\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }|=\lambda ^+$
. Note that for every
![]() $A,B \in [\lambda ^+]^{<\lambda ^+}$
such that
$A,B \in [\lambda ^+]^{<\lambda ^+}$
such that
![]() $A\subset B$
, we have
$A\subset B$
, we have
![]() $\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } \leq _T \prod ^{\leq \theta }_{\zeta \in B} D_{\mathcal C_\zeta }$
. The following claim gives us the wanted result.
$\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } \leq _T \prod ^{\leq \theta }_{\zeta \in B} D_{\mathcal C_\zeta }$
. The following claim gives us the wanted result.
Claim 5.14.1. Suppose
![]() $A\in [\lambda ^+]^{<\lambda ^+}$
and
$A\in [\lambda ^+]^{<\lambda ^+}$
and
![]() $\xi \in \lambda ^+\setminus A$
, then
$\xi \in \lambda ^+\setminus A$
, then
![]() $ D_{\mathcal C_\xi } \not \leq _T \prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } $
. In particular,
$ D_{\mathcal C_\xi } \not \leq _T \prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } $
. In particular,
![]() $\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } <_T \prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }\times D_{\mathcal C_\xi }$
.
$\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta } <_T \prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }\times D_{\mathcal C_\xi }$
.
Proof Let
![]() $D:=D_{\mathcal C_\xi }$
and
$D:=D_{\mathcal C_\xi }$
and
![]() $E:=\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }$
. Note that as
$E:=\prod ^{\leq \theta }_{\zeta \in A} D_{\mathcal C_\zeta }$
. Note that as
![]() $2^\lambda =\lambda ^+$
, then
$2^\lambda =\lambda ^+$
, then
![]() $(\lambda ^+)^\lambda = \lambda ^+$
, so
$(\lambda ^+)^\lambda = \lambda ^+$
, so
![]() $|E|=\lambda ^+$
. Suppose
$|E|=\lambda ^+$
. Suppose
![]() $f:D \rightarrow E$
is a Tukey function. Consider
$f:D \rightarrow E$
is a Tukey function. Consider
![]() $Q=f"[\lambda ^+]^1$
, let us split to cases:
$Q=f"[\lambda ^+]^1$
, let us split to cases:
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Q|< \lambda ^+$
, then by pigeonhole principle, there exists
$|Q|< \lambda ^+$
, then by pigeonhole principle, there exists
![]() $e\in E$
and a subset
$e\in E$
and a subset
![]() $X\subseteq D$
of size
$X\subseteq D$
of size
![]() $\lambda ^+$
such that
$\lambda ^+$
such that
![]() $f"X =\{e\}$
. As
$f"X =\{e\}$
. As
![]() $\langle C_\beta \mid \beta \in S_\xi \rangle $
is a
$\langle C_\beta \mid \beta \in S_\xi \rangle $
is a
![]() $\clubsuit $
-sequence, there exists some
$\clubsuit $
-sequence, there exists some
![]() $\beta \in S_\xi $
such that
$\beta \in S_\xi $
such that
![]() $C_\beta \subseteq \bigcup X$
. So X is an unbounded subset of D such that
$C_\beta \subseteq \bigcup X$
. So X is an unbounded subset of D such that
![]() $f"X$
is bounded in E which is absurd.
$f"X$
is bounded in E which is absurd.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $|Q|=\lambda ^+$
. Let us enumerate
$|Q|=\lambda ^+$
. Let us enumerate
![]() $Q:=\{q_\alpha \mid \alpha <\lambda ^+\}$
. Recall that for every
$Q:=\{q_\alpha \mid \alpha <\lambda ^+\}$
. Recall that for every
![]() $\zeta \in A$
,
$\zeta \in A$
,
![]() $D_{\mathcal C_{\zeta }}\subseteq [\lambda ^+]^{\leq \theta }$
. Let
$D_{\mathcal C_{\zeta }}\subseteq [\lambda ^+]^{\leq \theta }$
. Let
![]() $z_\alpha := \bigcup \{ q_\alpha (\zeta ) \times \{\zeta \} \mid \zeta \in A, ~q_\alpha (\zeta )\neq 0_{D_{\mathcal C_\zeta }}\}$
, notice that
$z_\alpha := \bigcup \{ q_\alpha (\zeta ) \times \{\zeta \} \mid \zeta \in A, ~q_\alpha (\zeta )\neq 0_{D_{\mathcal C_\zeta }}\}$
, notice that
![]() $z_\alpha \in [\lambda ^+ \times A]^{\leq \theta }$
. We fix a bijection
$z_\alpha \in [\lambda ^+ \times A]^{\leq \theta }$
. We fix a bijection
![]() $\phi :\lambda ^+\times A \rightarrow \lambda ^+$
.
$\phi :\lambda ^+\times A \rightarrow \lambda ^+$
.
As
![]() $\{\phi "z_\alpha \mid \alpha <\lambda ^+\}$
is a subset of
$\{\phi "z_\alpha \mid \alpha <\lambda ^+\}$
is a subset of
![]() $[\lambda ^+]^{\leq \theta }$
of size
$[\lambda ^+]^{\leq \theta }$
of size
![]() $\lambda ^+$
and
$\lambda ^+$
and
![]() $\lambda ^\theta <\lambda ^+$
, by the
$\lambda ^\theta <\lambda ^+$
, by the
![]() $\Delta $
-system lemma, we may refine our sequence Q and re-index such that
$\Delta $
-system lemma, we may refine our sequence Q and re-index such that
![]() $\{\phi "z_\alpha \mid \alpha <\lambda ^+\}$
will be a
$\{\phi "z_\alpha \mid \alpha <\lambda ^+\}$
will be a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $R'$
.
$R'$
.
For each
![]() $\alpha <\lambda ^+$
and
$\alpha <\lambda ^+$
and
![]() $\zeta \in A$
, let
$\zeta \in A$
, let
![]() $y_{\alpha ,\zeta }:=\{ \beta <\lambda ^+ \mid \beta \in q_\alpha (\zeta )\}$
. We claim that for each
$y_{\alpha ,\zeta }:=\{ \beta <\lambda ^+ \mid \beta \in q_\alpha (\zeta )\}$
. We claim that for each
![]() $\zeta \in A$
, the set
$\zeta \in A$
, the set
![]() $\{y_{\alpha ,\zeta }\mid \zeta \in A\}$
is a
$\{y_{\alpha ,\zeta }\mid \zeta \in A\}$
is a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $R_{\zeta }:=\{\beta <\lambda ^+\mid (\beta ,\zeta )\in \phi ^{-1}[R'] \}$
. Let us show that whenever
$R_{\zeta }:=\{\beta <\lambda ^+\mid (\beta ,\zeta )\in \phi ^{-1}[R'] \}$
. Let us show that whenever
![]() $\alpha <\beta <\lambda ^+$
, we have
$\alpha <\beta <\lambda ^+$
, we have
![]() $y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } = R_{\zeta } $
. Notice that
$y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } = R_{\zeta } $
. Notice that
![]() $\delta \in y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } \iff \delta \in q_\alpha (\zeta )\cap q_\beta (\zeta ) \iff (\delta ,\zeta )\in z_\alpha \cap z_\beta \iff \phi (\delta ,\zeta ) \in \phi "(z_\alpha \cap z_\beta )=\phi "z_\alpha \cap \phi "z_\beta = R' \iff (\delta ,\zeta )\in \phi ^{-1}R' \iff \delta \in R_{\zeta }$
. For each
$\delta \in y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } \iff \delta \in q_\alpha (\zeta )\cap q_\beta (\zeta ) \iff (\delta ,\zeta )\in z_\alpha \cap z_\beta \iff \phi (\delta ,\zeta ) \in \phi "(z_\alpha \cap z_\beta )=\phi "z_\alpha \cap \phi "z_\beta = R' \iff (\delta ,\zeta )\in \phi ^{-1}R' \iff \delta \in R_{\zeta }$
. For each
![]() $\alpha <\lambda ^+$
, we fix
$\alpha <\lambda ^+$
, we fix
![]() $x_\alpha \in [\lambda ^+]^1$
such that
$x_\alpha \in [\lambda ^+]^1$
such that
![]() $f(x_\alpha )=q_\alpha $
.
$f(x_\alpha )=q_\alpha $
.
We use the
![]() $\Delta $
-system lemma again and refine our sequence such that there exists a club
$\Delta $
-system lemma again and refine our sequence such that there exists a club
![]() $C\subseteq \lambda ^+$
and for all
$C\subseteq \lambda ^+$
and for all
![]() $\alpha <\beta <\lambda ^+$
we have:
$\alpha <\beta <\lambda ^+$
we have:
-
(1) for every
 $\zeta \in A$
, we have
$\zeta \in A$
, we have
 $y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } = R_{\zeta } $
;
$y_{\alpha ,\zeta }\cap y_{\beta ,\zeta } = R_{\zeta } $
; -
(2)
 $x_\alpha \cap x_\beta = \emptyset $
;
$x_\alpha \cap x_\beta = \emptyset $
; -
(3) there exists some
 $\gamma \in C$
such that
$\gamma \in C$
such that
 $x_\alpha \cup (\bigcup _{\zeta \in A} (y_{\alpha ,\zeta }\setminus R_\zeta ))< \gamma < x_\beta \cup (\bigcup _{\zeta \in A } (y_{\beta ,\zeta }\setminus R_\zeta ) )$
.
$x_\alpha \cup (\bigcup _{\zeta \in A} (y_{\alpha ,\zeta }\setminus R_\zeta ))< \gamma < x_\beta \cup (\bigcup _{\zeta \in A } (y_{\beta ,\zeta }\setminus R_\zeta ) )$
.
Furthermore, we may assume that between any two elements of
![]() $\gamma <\delta $
in C there exists some
$\gamma <\delta $
in C there exists some
![]() $\alpha <\lambda ^+$
such that
$\alpha <\lambda ^+$
such that
![]() $\gamma <x_\alpha \cup (\bigcup _{\zeta \in A } (y_{\alpha ,\zeta }\setminus R_\zeta ))<\delta $
. We continue in the spirit of Claim 5.11.3.1.
$\gamma <x_\alpha \cup (\bigcup _{\zeta \in A } (y_{\alpha ,\zeta }\setminus R_\zeta ))<\delta $
. We continue in the spirit of Claim 5.11.3.1.
As
![]() $\langle C_\beta \mid \beta \in S_\xi \rangle $
is a
$\langle C_\beta \mid \beta \in S_\xi \rangle $
is a
![]() $\clubsuit $
-sequence, there exists some
$\clubsuit $
-sequence, there exists some
![]() $\beta \in S_\xi \cap \operatorname {\mathrm {acc}}(C)$
such that
$\beta \in S_\xi \cap \operatorname {\mathrm {acc}}(C)$
such that
![]() $C_\beta \subseteq \bigcup \{x_\alpha \mid \alpha <\lambda ^+\}$
. Construct by recursion an increasing sequence
$C_\beta \subseteq \bigcup \{x_\alpha \mid \alpha <\lambda ^+\}$
. Construct by recursion an increasing sequence
![]() $\langle \beta _\nu \mid \nu <\theta \rangle \subseteq C_\beta $
and a sequence
$\langle \beta _\nu \mid \nu <\theta \rangle \subseteq C_\beta $
and a sequence
![]() $\langle w_\nu \mid \nu <\theta \rangle \subseteq \{x_\alpha \mid \alpha <\lambda ^+\}$
such that
$\langle w_\nu \mid \nu <\theta \rangle \subseteq \{x_\alpha \mid \alpha <\lambda ^+\}$
such that
![]() ${\beta _\nu \in w_\nu <\beta }$
.
${\beta _\nu \in w_\nu <\beta }$
.
Clearly,
![]() $\{w_\nu \mid \nu <\theta \}$
is unbounded in
$\{w_\nu \mid \nu <\theta \}$
is unbounded in
![]() $ D_{\mathcal C_\xi }$
, so the following Claim proves f is not a Tukey function.
$ D_{\mathcal C_\xi }$
, so the following Claim proves f is not a Tukey function.
Subclaim 5.14.1.1. The subset
![]() $\{ f(w_\nu )\mid \nu <\theta \}$
is bounded in E.
$\{ f(w_\nu )\mid \nu <\theta \}$
is bounded in E.
Proof For each
![]() $\zeta \in A$
, let
$\zeta \in A$
, let
![]() $W_\zeta := \bigcup _{\nu <\theta } f(w_\nu )(\zeta )$
. We will show that
$W_\zeta := \bigcup _{\nu <\theta } f(w_\nu )(\zeta )$
. We will show that
![]() $W_\zeta \in D_{\mathcal C_\zeta }$
, as
$W_\zeta \in D_{\mathcal C_\zeta }$
, as
![]() $|\{\zeta \in A\mid W_\zeta \neq \emptyset \}|\leq \theta $
this will imply that
$|\{\zeta \in A\mid W_\zeta \neq \emptyset \}|\leq \theta $
this will imply that
![]() $\prod ^{\leq \theta }_{\zeta \in A} W_\zeta $
is well defined and an element of E. Clearly
$\prod ^{\leq \theta }_{\zeta \in A} W_\zeta $
is well defined and an element of E. Clearly
![]() $f(w_\nu )\leq _E \prod ^{\leq \theta }_{\zeta \in A} W_\zeta $
for every
$f(w_\nu )\leq _E \prod ^{\leq \theta }_{\zeta \in A} W_\zeta $
for every
![]() $\nu <\theta $
, so the set
$\nu <\theta $
, so the set
![]() $\{ f(w_\nu )\mid \nu <\theta \}$
is bounded in E as sought.
$\{ f(w_\nu )\mid \nu <\theta \}$
is bounded in E as sought.
Let
![]() $\mathcal C_{\zeta }:=\langle C_\alpha \mid \alpha \in S_\zeta \rangle $
, we will show that for every
$\mathcal C_{\zeta }:=\langle C_\alpha \mid \alpha \in S_\zeta \rangle $
, we will show that for every
![]() $\alpha \in S_\zeta $
, we have
$\alpha \in S_\zeta $
, we have
![]() $|W_\zeta \cap C_\alpha |<\theta $
. By the refinement we did previously it is clear that
$|W_\zeta \cap C_\alpha |<\theta $
. By the refinement we did previously it is clear that
![]() $\{f(w_\nu )(\zeta )\setminus R_\zeta \mid \nu <\theta \}$
is a pairwise disjoint sequence, where for each
$\{f(w_\nu )(\zeta )\setminus R_\zeta \mid \nu <\theta \}$
is a pairwise disjoint sequence, where for each
![]() $\nu <\theta $
we have some element
$\nu <\theta $
we have some element
![]() $\gamma _\nu \in C$
such that
$\gamma _\nu \in C$
such that
![]() $f(w_\nu )(\zeta )\setminus R_\zeta < \gamma _\nu < f(w_{\nu +1})(\zeta )\setminus R_\zeta $
. Furthermore,
$f(w_\nu )(\zeta )\setminus R_\zeta < \gamma _\nu < f(w_{\nu +1})(\zeta )\setminus R_\zeta $
. Furthermore,
![]() $f(w_\nu )(\zeta )\subseteq \beta $
for every
$f(w_\nu )(\zeta )\subseteq \beta $
for every
![]() $\nu <\theta $
. Let
$\nu <\theta $
. Let
![]() $\alpha \in S_\zeta $
.
$\alpha \in S_\zeta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha>\beta $
. As
$\alpha>\beta $
. As
![]() $C_\alpha $
if cofinal in
$C_\alpha $
if cofinal in
![]() $\alpha $
and of order-type
$\alpha $
and of order-type
![]() $\theta $
, then
$\theta $
, then
![]() $|W_\zeta \cap C_\alpha |<\theta $
.
$|W_\zeta \cap C_\alpha |<\theta $
.
![]() $\blacktriangleright $
Suppose
$\blacktriangleright $
Suppose
![]() $\alpha <\beta $
. As
$\alpha <\beta $
. As
![]() $C_\alpha $
if cofinal in
$C_\alpha $
if cofinal in
![]() $\alpha $
and of order-type
$\alpha $
and of order-type
![]() $\theta $
, there exists some
$\theta $
, there exists some
![]() $\nu <\theta $
such that for all
$\nu <\theta $
such that for all
![]() $\nu <\rho <\theta $
, we have
$\nu <\rho <\theta $
, we have
![]() $(f(w_\rho )(\zeta )\setminus R_\zeta )\cap C_\alpha =\emptyset $
. As
$(f(w_\rho )(\zeta )\setminus R_\zeta )\cap C_\alpha =\emptyset $
. As
![]() $f(w_\rho )(\zeta )\in D_{\mathcal C_\zeta }$
for every
$f(w_\rho )(\zeta )\in D_{\mathcal C_\zeta }$
for every
![]() $\rho <\theta $
, we get that
$\rho <\theta $
, we get that
![]() $|W_\zeta \cap C_\alpha |<\theta $
as sought.
$|W_\zeta \cap C_\alpha |<\theta $
as sought.
As
![]() $\beta \notin S_\zeta $
there are no more cases to consider.
$\beta \notin S_\zeta $
there are no more cases to consider.
6 Concluding remarks
A natural continuation of this line of research is analysing the class
![]() $\mathcal D_{\kappa }$
for cardinals
$\mathcal D_{\kappa }$
for cardinals
![]() $\kappa \geq \aleph _\omega $
. As a preliminary finding we notice that the poset
$\kappa \geq \aleph _\omega $
. As a preliminary finding we notice that the poset
![]() $(\mathcal P(\omega ),\subset )$
can be embedded by a function
$(\mathcal P(\omega ),\subset )$
can be embedded by a function
![]() $\mathfrak F$
into the class
$\mathfrak F$
into the class
![]() $\mathcal D_{\aleph _\omega }$
under the Tukey order. Furthermore, for every two successive elements
$\mathcal D_{\aleph _\omega }$
under the Tukey order. Furthermore, for every two successive elements
![]() $A,B$
in the poset
$A,B$
in the poset
![]() $(\mathcal P(\omega ),\subset )$
, i.e.,
$(\mathcal P(\omega ),\subset )$
, i.e.,
![]() $A\subset B $
and
$A\subset B $
and
![]() $|B\setminus A|=1$
, there is no directed set D such that
$|B\setminus A|=1$
, there is no directed set D such that
![]() $\mathfrak F(A)<_T D <_T \mathfrak F(B)$
. The embedding is defined via
$\mathfrak F(A)<_T D <_T \mathfrak F(B)$
. The embedding is defined via
![]() $\mathfrak F(A):= \prod ^{<\omega }_{n\in A} \omega _{n+1}$
, and the furthermore part can be proved by Lemma 4.3. As a corollary, we get that in
$\mathfrak F(A):= \prod ^{<\omega }_{n\in A} \omega _{n+1}$
, and the furthermore part can be proved by Lemma 4.3. As a corollary, we get that in
![]() $\operatorname {\mathrm {ZFC}}$
the cardinality of
$\operatorname {\mathrm {ZFC}}$
the cardinality of
![]() $\mathcal D_{\aleph _\omega }$
is at least
$\mathcal D_{\aleph _\omega }$
is at least
![]() $2^{\aleph _0}$
.
$2^{\aleph _0}$
.
A Appendix: Tukey ordering of simple elements of the class
 $\mathcal D_{\aleph _2}$
and
$\mathcal D_{\aleph _2}$
and
 $\mathcal D_{\aleph _3}$
$\mathcal D_{\aleph _3}$
We present each of the posets
![]() $(\mathcal T_{2},<_T)$
and
$(\mathcal T_{2},<_T)$
and
![]() $(\mathcal T_{3},<_T)$
in a diagram. In both diagrams below, for any two directed sets A and B, an arrow
$(\mathcal T_{3},<_T)$
in a diagram. In both diagrams below, for any two directed sets A and B, an arrow
![]() $A\rightarrow B$
, represents the fact that
$A\rightarrow B$
, represents the fact that
![]() $A<_T B$
. If the arrow is dashed, then under
$A<_T B$
. If the arrow is dashed, then under
![]() $\operatorname {\mathrm {GCH}}$
there exists a directed set in between. If the arrow is not dashed, then there is no directed set in between A and B. Every two directed sets A and B such that there is no directed path (in the obvious sense) from A to B, are such that
$\operatorname {\mathrm {GCH}}$
there exists a directed set in between. If the arrow is not dashed, then there is no directed set in between A and B. Every two directed sets A and B such that there is no directed path (in the obvious sense) from A to B, are such that
![]() $A\not \leq _T B$
. Note that this implies that any two directed sets on the same horizontal level are incompatible in the Tukey order (Figures 3 and 4).
$A\not \leq _T B$
. Note that this implies that any two directed sets on the same horizontal level are incompatible in the Tukey order (Figures 3 and 4).

Figure 3 Tukey ordering of
![]() $(\mathcal T_{2},<_T)$
.
$(\mathcal T_{2},<_T)$
.

Figure 4 Tukey ordering of
![]() $(\mathcal T_{3},<_T).$
$(\mathcal T_{3},<_T).$
Acknowledgments
This paper presents several results from the author’s Ph.D. research at Bar-Ilan University under the supervision of Assaf Rinot to whom he wishes to express his deep appreciation. Our thanks go to Tanmay Inamdar for many illuminating discussions. We thank the referee for their effort and for writing a detailed thoughtful report that improved this paper.
Funding
The author is supported by the European Research Council (grant agreement ERC-2018-StG 802756).