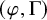1 Introduction
The Fontaine–Mazur conjecture predicts that representations of Galois groups of number fields which are sufficiently nice should come from geometry. In practice, the way one proves this is by proving so-called automorphy lifting theorems, relating the Galois representations of interest to Galois representations already known to have the desired properties.
In this context, if
![]() $\rho :\operatorname {\mathrm {Gal}}_{F}\rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbf {Q}}}_p)$
is the representation, ‘sufficiently nice’ includes a condition on the local Galois group at p called being geometric. In the present paper, motivated by a question of Andreatta–Iovita–Pilloni [Reference Andreatta, Iovita and PilloniAIP18], we consider a characteristic p analogue of this conjecture. There is no definition of ‘geometric’ for a Galois representation with positive characteristic coefficients, but we replace it with the condition trianguline:
$\rho :\operatorname {\mathrm {Gal}}_{F}\rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbf {Q}}}_p)$
is the representation, ‘sufficiently nice’ includes a condition on the local Galois group at p called being geometric. In the present paper, motivated by a question of Andreatta–Iovita–Pilloni [Reference Andreatta, Iovita and PilloniAIP18], we consider a characteristic p analogue of this conjecture. There is no definition of ‘geometric’ for a Galois representation with positive characteristic coefficients, but we replace it with the condition trianguline:
Theorem. Assume
![]() $p\geq 5$
, and let L be a finite extension of
$p\geq 5$
, and let L be a finite extension of
![]() ${\mathbf {F}}_p(\!(u)\!)$
. Let
${\mathbf {F}}_p(\!(u)\!)$
. Let
![]() $\rho :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathscr {O}}_L)$
be an odd continuous Galois representation unramified away from p such that the
$\rho :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathscr {O}}_L)$
be an odd continuous Galois representation unramified away from p such that the
![]() $(\varphi ,\Gamma )$
-module
$(\varphi ,\Gamma )$
-module
![]() $D_{\mathrm {rig}}(\rho |_{\operatorname {\mathrm {Gal}}_{Q_p}})$
is trianguline with regular parameters. Assume, moreover, that the reduction
$D_{\mathrm {rig}}(\rho |_{\operatorname {\mathrm {Gal}}_{Q_p}})$
is trianguline with regular parameters. Assume, moreover, that the reduction
![]() $\overline {\rho }$
is modular and satisfies certain additional technical hypotheses. Then
$\overline {\rho }$
is modular and satisfies certain additional technical hypotheses. Then
![]() $\rho $
is the twist of the Galois representation corresponding to a point on the extended eigencurve
$\rho $
is the twist of the Galois representation corresponding to a point on the extended eigencurve
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2}$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2}$
.
The eigencurve
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}$
was originally constructed by Coleman–Mazur, and it is a rigid analytic space whose points correspond to overconvergent modular forms. Points corresponding to classical eigenforms (of varying weight and level) are dense, so we can think of it as a moduli space of p-adic modular forms. Each point of the eigencurve has a Galois representation attached, but Kisin [Reference KisinKis03] showed that the Galois representations at nonclassical points are not geometric at p. Instead, they are trianguline (though he did not use this terminology; it was introduced subsequently by Colmez). A converse was proved by Emerton [Reference EmertonEme11, Theorem 1.2.4] when the coefficients are p-adic.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}$
was originally constructed by Coleman–Mazur, and it is a rigid analytic space whose points correspond to overconvergent modular forms. Points corresponding to classical eigenforms (of varying weight and level) are dense, so we can think of it as a moduli space of p-adic modular forms. Each point of the eigencurve has a Galois representation attached, but Kisin [Reference KisinKis03] showed that the Galois representations at nonclassical points are not geometric at p. Instead, they are trianguline (though he did not use this terminology; it was introduced subsequently by Colmez). A converse was proved by Emerton [Reference EmertonEme11, Theorem 1.2.4] when the coefficients are p-adic.
Given a p-adic Galois representation
![]() $\rho $
, there is an associated object
$\rho $
, there is an associated object
![]() $D_{\mathrm {rig}}(\rho )$
called a
$D_{\mathrm {rig}}(\rho )$
called a
![]() $(\varphi ,\Gamma )$
-module; at the expense of making the coefficients more complicated, the Galois representation can be captured as the action of a semilinear operator
$(\varphi ,\Gamma )$
-module; at the expense of making the coefficients more complicated, the Galois representation can be captured as the action of a semilinear operator
![]() $\varphi $
together with the action of a one-dimensional p-adic Lie group
$\varphi $
together with the action of a one-dimensional p-adic Lie group
![]() $\Gamma $
. Then even if
$\Gamma $
. Then even if
![]() $\rho $
is irreducible, it is possible for
$\rho $
is irreducible, it is possible for
![]() $D_{\mathrm {rig}}(\rho )$
to be reducible. Kisin showed that this happens in small neighborhoods of classical points on the eigencurve; if
$D_{\mathrm {rig}}(\rho )$
to be reducible. Kisin showed that this happens in small neighborhoods of classical points on the eigencurve; if
![]() $\rho _x$
is the Galois representation attached to a point x, there is an exact sequence
$\rho _x$
is the Galois representation attached to a point x, there is an exact sequence
where
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are rank-
$D_2$
are rank-
![]() $1\ (\varphi ,\Gamma )$
-modules. There is a basis element
$1\ (\varphi ,\Gamma )$
-modules. There is a basis element
![]() $\mathbf {e}_1$
of
$\mathbf {e}_1$
of
![]() $D_1$
such that
$D_1$
such that
![]() $\varphi $
acts on
$\varphi $
acts on
![]() $\mathbf {e}_1$
by the
$\mathbf {e}_1$
by the
![]() $U_p$
-eigenvalue at x and
$U_p$
-eigenvalue at x and
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\mathbf {e}_1$
trivially. This construction was extended over (a normalization of) the eigencurve in separate work of [Reference Kedlaya, Pottharst and XiaoKPX14] and [Reference LiuLiu15].
$\mathbf {e}_1$
trivially. This construction was extended over (a normalization of) the eigencurve in separate work of [Reference Kedlaya, Pottharst and XiaoKPX14] and [Reference LiuLiu15].
The eigencurve is equipped with a map
![]() $\mathrm {wt}:\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}\rightarrow \mathscr {W}^{\mathrm {rig}}$
to weight space, which we may view as the disjoint union of
$\mathrm {wt}:\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}\rightarrow \mathscr {W}^{\mathrm {rig}}$
to weight space, which we may view as the disjoint union of
![]() $p-1$
rigid analytic open unit disks. The existence of Galois representations attached to eigenforms means it is also equipped with a morphism
$p-1$
rigid analytic open unit disks. The existence of Galois representations attached to eigenforms means it is also equipped with a morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}\rightarrow {\mathbf {G}}_m^{\mathrm {rig}}\times \coprod _{\overline {\rho }}R_{\overline {\rho }}$
, where the
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2}^{\mathrm {rig}}\rightarrow {\mathbf {G}}_m^{\mathrm {rig}}\times \coprod _{\overline {\rho }}R_{\overline {\rho }}$
, where the
![]() $R_{\overline {\rho }}$
are Galois deformation rings (more precisely, deformation rings of pseudocharacters), and
$R_{\overline {\rho }}$
are Galois deformation rings (more precisely, deformation rings of pseudocharacters), and
![]() ${\mathbf {G}}_m^{\mathrm {rig}}$
corresponds to the eigenvalue of the Hecke operator
${\mathbf {G}}_m^{\mathrm {rig}}$
corresponds to the eigenvalue of the Hecke operator
![]() $U_p$
. The triangulation results of [Reference KisinKis03], [Reference Kedlaya, Pottharst and XiaoKPX14] and [Reference LiuLiu15] mean that we can combine these two maps to get a morphism
$U_p$
. The triangulation results of [Reference KisinKis03], [Reference Kedlaya, Pottharst and XiaoKPX14] and [Reference LiuLiu15] mean that we can combine these two maps to get a morphism
 $$\begin{align*}\mathscr{X}_{\operatorname{\mathrm{GL}}_2}\rightarrow \coprod_{\overline{\rho}}X_{\mathrm{{tri}},\overline{\rho}}^{\psi,\kappa,\mathrm{rig}} \end{align*}$$
$$\begin{align*}\mathscr{X}_{\operatorname{\mathrm{GL}}_2}\rightarrow \coprod_{\overline{\rho}}X_{\mathrm{{tri}},\overline{\rho}}^{\psi,\kappa,\mathrm{rig}} \end{align*}$$
to a moduli space of trianguline Galois representations (here, the decorations
![]() $\psi $
and
$\psi $
and
![]() $\kappa $
simply mean we are fixing the determinant and the parameters of the triangulation). The result of [Reference EmertonEme11] then shows that this morphism surjects onto certain components.
$\kappa $
simply mean we are fixing the determinant and the parameters of the triangulation). The result of [Reference EmertonEme11] then shows that this morphism surjects onto certain components.
More recently, the construction of the eigencurve has been extended to mixed characteristic by Andreatta–Pilloni–Iovita [Reference Andreatta, Iovita and PilloniAIP18], [Reference Andreatta, Iovita and PilloniAIP16] and Johansson–Newton [Reference Johansson and NewtonJN16], using Huber’s theory of adic spaces instead of Tate’s theory of rigid analytic spaces. These authors construct pseudorigid spaces containing characteristic
![]() $0$
eigenvarieties as open subspaces, with nonempty characteristic p loci.
$0$
eigenvarieties as open subspaces, with nonempty characteristic p loci.
In previous work, we generalized the construction of
![]() $(\varphi ,\Gamma )$
-module to families of Galois representations with pseudorigid coefficients [Reference BellovinBel23b] and showed that the triangulation of the eigencurve extends to the boundary characteristic p points [Reference BellovinBel23a]. This yields an analogous morphism
$(\varphi ,\Gamma )$
-module to families of Galois representations with pseudorigid coefficients [Reference BellovinBel23b] and showed that the triangulation of the eigencurve extends to the boundary characteristic p points [Reference BellovinBel23a]. This yields an analogous morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2}\rightarrow \coprod X_{\mathrm {{tri}},\overline {\rho }}^{\psi ,\kappa }$
of pseudorigid spaces. In the present paper, we use that machinery to prove a modularity result for Galois representations trianguline at p, characterizing the image in many components.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2}\rightarrow \coprod X_{\mathrm {{tri}},\overline {\rho }}^{\psi ,\kappa }$
of pseudorigid spaces. In the present paper, we use that machinery to prove a modularity result for Galois representations trianguline at p, characterizing the image in many components.
The proof rests on the Taylor–Wiles patching method, as reformulated in [Reference ScholzeSch18]. This is the source of the aforementioned technical hypotheses on
![]() $\overline {\rho }$
(which amount to assumptions about the image of
$\overline {\rho }$
(which amount to assumptions about the image of
![]() $\overline {\rho }$
being sufficiently big). However, there are a number of technical complications. For example, to carry out some preliminary reductions, we first prove a version of the Jacquet–Langlands correspondence on eigenvarieties extending the construction of [Reference BirkbeckBir19], and we characterize the image of the cyclic base change morphism
$\overline {\rho }$
being sufficiently big). However, there are a number of technical complications. For example, to carry out some preliminary reductions, we first prove a version of the Jacquet–Langlands correspondence on eigenvarieties extending the construction of [Reference BirkbeckBir19], and we characterize the image of the cyclic base change morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of [Reference Johansson and NewtonJN19a]. The latter uses the construction of an auxiliary ‘
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of [Reference Johansson and NewtonJN19a]. The latter uses the construction of an auxiliary ‘
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed’ eigenvariety, which may be of independent interest. This permits us to transfer the problem to overconvergent quaternionic modular forms over a cyclic totally real extension of
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed’ eigenvariety, which may be of independent interest. This permits us to transfer the problem to overconvergent quaternionic modular forms over a cyclic totally real extension of
![]() ${\mathbf {Q}}$
.
${\mathbf {Q}}$
.
The modules of quaternionic automorphic forms we patch are those constructed in [Reference Johansson and NewtonJN16]. We construct trianguline deformation rings which act on them, and we patch by introducing ramification at additional primes. But the construction of trianguline deformation rings is delicate because in general triangulations of
![]() $(\varphi ,\Gamma )$
-modules do not interact well with integral structures on the corresponding Galois representation. Thus, we crucially use the pseudorigid theory of triangulations (and not just the rigid analytic theory) to ensure that we can construct an integral quotient of a Galois deformation ring whose analytic points are trianguline, with Frobenius eigenvalues bounded by a fixed slope.
$(\varphi ,\Gamma )$
-modules do not interact well with integral structures on the corresponding Galois representation. Thus, we crucially use the pseudorigid theory of triangulations (and not just the rigid analytic theory) to ensure that we can construct an integral quotient of a Galois deformation ring whose analytic points are trianguline, with Frobenius eigenvalues bounded by a fixed slope.
This leads to a further difficulty, which is that it is difficult to study the components of the trianguline deformation ring directly. Instead, we patch families of overconvergent automorphic forms, which lets us compare the Galois representation we are interested in with ‘nearby’ potentially Barsotti–Tate representations which are known to be automorphic. Along the way, we construct local pieces of a patched quaternionic eigenvariety
![]() $\mathscr {X}_{\underline D^{\times }}^{\infty }$
, together with a morphism to a trianguline variety and a patched module of overconvergent modular forms. We note that it is only possible to patch families of overconvergent automorphic forms because we constructed an integral model of the trianguline variety; we know almost nothing about its structure away from nice points in the analytic locus, but understanding it better would be very interesting. We also hope to glue these local patched modules in future work.
$\mathscr {X}_{\underline D^{\times }}^{\infty }$
, together with a morphism to a trianguline variety and a patched module of overconvergent modular forms. We note that it is only possible to patch families of overconvergent automorphic forms because we constructed an integral model of the trianguline variety; we know almost nothing about its structure away from nice points in the analytic locus, but understanding it better would be very interesting. We also hope to glue these local patched modules in future work.
We have not attempted to work in maximum generality. In particular, it should be possible to relax the ramification condition and prove an overconvergent modularity lifting theorem for certain totally real fields. However, this would require constructing and studying a cyclic base change morphism for more general extensions of number fields. We expect that it is possible to construct these morphisms for the middle-degree eigenvariety over a totally real field, which would lead to stronger trianguline modularity theorems in characteristic
![]() $0$
. But we were forced to assume the degree of the cyclic extension was prime to p to characterize the image of a base change morphism in positive characteristic, so additional work would be required to strengthen our results in positive characteristic.
$0$
. But we were forced to assume the degree of the cyclic extension was prime to p to characterize the image of a base change morphism in positive characteristic, so additional work would be required to strengthen our results in positive characteristic.
We further remark that our ‘big image’ condition on the residual Galois representation is stronger than the standard one. This is to ensure that we have access to the necessary cohomological vanishing theorems to permit us to work with middle-degree eigenvarieties.
The work of Breuil–Hellmann–Schraen [Reference Breuil, Hellmann and SchraenBHS17] constructs a similar patched eigenvariety for unitary groups, using completed cohomology rather than overconvergent cohomology. It would be extremely interesting to relate these two constructions.
We now describe the structure of this paper. We begin by recalling the theory of trianguline
![]() $(\varphi ,\Gamma )$
-modules and their deformations; this permits us to construct and study pseudorigid trianguline varieties (generalizing those of [Reference ChenevierChe13] and [Reference Breuil, Hellmann and SchraenBHS17]). We compute the dimension of these pseudorigid trianguline varieties with fixed determinant and weight, and we show that they have an integral model after bounding the slopes of the rank-
$(\varphi ,\Gamma )$
-modules and their deformations; this permits us to construct and study pseudorigid trianguline varieties (generalizing those of [Reference ChenevierChe13] and [Reference Breuil, Hellmann and SchraenBHS17]). We compute the dimension of these pseudorigid trianguline varieties with fixed determinant and weight, and we show that they have an integral model after bounding the slopes of the rank-
![]() $1$
constituents.
$1$
constituents.
We then turn to the automorphic theory we will need. We prove that so-called twist classical points are very Zariski dense in the eigenvariety
![]() $\mathscr {X}_{\underline D^{\times }}$
, which permits us to interpolate the Jacquet–Langlands correspondence to extended eigenvarieties and permits us to conclude that
$\mathscr {X}_{\underline D^{\times }}$
, which permits us to interpolate the Jacquet–Langlands correspondence to extended eigenvarieties and permits us to conclude that
![]() $\mathscr {X}_{\underline D^{\times }}$
is reduced (extending the results of [Reference BirkbeckBir19] and [Reference ChenevierChe05]). We also study the cyclic base change morphism
$\mathscr {X}_{\underline D^{\times }}$
is reduced (extending the results of [Reference BirkbeckBir19] and [Reference ChenevierChe05]). We also study the cyclic base change morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of [Reference Johansson and NewtonJN19a]; when F is totally real and
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of [Reference Johansson and NewtonJN19a]; when F is totally real and
![]() $[F:{\mathbf {Q}}]$
is prime to p, we show that
$[F:{\mathbf {Q}}]$
is prime to p, we show that
![]() $x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
is in the image if and only if it is fixed by
$x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
is in the image if and only if it is fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. To do this, we study the
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. To do this, we study the
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus in the Hilbert eigenvariety, and show that classical points are dense in it.
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus in the Hilbert eigenvariety, and show that classical points are dense in it.
Finally, we turn to the patching argument. We show that our modules of integral overconvergent automorphic forms are projective at maximal points of weight space, and we show that we can add certain kinds of level structure. Then using the standard Taylor–Wiles patching construction, we construct a patched module with the support we expect. This permits us to deduce the desired modularity statement by deformation from potentially Barsotti–Tate points in characteristic
![]() $0$
. This last step requires the results of [Reference KisinKis09b].
$0$
. This last step requires the results of [Reference KisinKis09b].
Notation
We fix some running notation and hypotheses. In Section 2, we assume that
![]() $p\geq 3$
because we only developed the theory of
$p\geq 3$
because we only developed the theory of
![]() $(\varphi ,\Gamma )$
-modules over pseudorigid spaces in that situation. In Sections 3 and 5, we assume
$(\varphi ,\Gamma )$
-modules over pseudorigid spaces in that situation. In Sections 3 and 5, we assume
![]() $p\geq 5$
; we need this hypothesis to construct eigenvarieties (and the Jacquet–Langlands and cyclic base change morphisms between them) at tame level
$p\geq 5$
; we need this hypothesis to construct eigenvarieties (and the Jacquet–Langlands and cyclic base change morphisms between them) at tame level
![]() $1$
and later to apply Taylor–Wiles patching.
$1$
and later to apply Taylor–Wiles patching.
We normalize class field theory so that it sends uniformizers to geometric Frobenius, and we normalize Hodge–Tate weights so that the cyclotomic character has Hodge–Tate weight
![]() $-1$
.
$-1$
.
If X is a group isomorphic to
![]() $X_0\times {\mathbf {Z}}_p^{\oplus r}\times {\mathbf {Z}}^{\oplus s}$
, where
$X_0\times {\mathbf {Z}}_p^{\oplus r}\times {\mathbf {Z}}^{\oplus s}$
, where
![]() $X_0$
is a finite group, we let
$X_0$
is a finite group, we let
![]() $\widehat X:=\underline{\mathrm{Hom}}(X,{\mathbf {G}}_m^{\operatorname {\mathrm {ad}}})$
denote the functor
$\widehat X:=\underline{\mathrm{Hom}}(X,{\mathbf {G}}_m^{\operatorname {\mathrm {ad}}})$
denote the functor
![]() $R\mapsto \operatorname {\mathrm {Hom}}_{\mathrm {cts}}(X,R^{\times })$
.
$R\mapsto \operatorname {\mathrm {Hom}}_{\mathrm {cts}}(X,R^{\times })$
.
2 Trianguline varieties and Galois deformation rings
2.1 Galois deformation rings
Let
![]() ${\mathbf {E}}/{\mathbf {Q}}_p$
be a finite extension, with ring of integers
${\mathbf {E}}/{\mathbf {Q}}_p$
be a finite extension, with ring of integers
![]() ${\mathscr {O}}_E$
, uniformizer
${\mathscr {O}}_E$
, uniformizer
![]() $\varpi _E$
, and residue field
$\varpi _E$
, and residue field
![]() ${\mathbf {F}}$
, and let G be a profinite group satisfying Mazur’s condition
${\mathbf {F}}$
, and let G be a profinite group satisfying Mazur’s condition
![]() $\Phi _p$
. The two cases we will be most interested in are
$\Phi _p$
. The two cases we will be most interested in are
![]() $G=\operatorname {\mathrm {Gal}}_K$
and
$G=\operatorname {\mathrm {Gal}}_K$
and
![]() $G=\operatorname {\mathrm {Gal}}_{F,S}$
, where K is a finite extension of
$G=\operatorname {\mathrm {Gal}}_{F,S}$
, where K is a finite extension of
![]() ${\mathbf {Q}}_p$
, and F is a number field, and S is a set of places of F.
${\mathbf {Q}}_p$
, and F is a number field, and S is a set of places of F.
Suppose we have a continuous homomorphism
![]() $\overline {\rho }:G\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
. Then we may construct the universal framed deformation ring
$\overline {\rho }:G\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
. Then we may construct the universal framed deformation ring
![]() $R_{\overline {\rho }}^\square $
, which prorepresents the functor
$R_{\overline {\rho }}^\square $
, which prorepresents the functor
on the category of complete local Noetherian
![]() ${\mathscr {O}}_E$
-algebras with residue field
${\mathscr {O}}_E$
-algebras with residue field
![]() ${\mathbf {F}}$
, of lifts of
${\mathbf {F}}$
, of lifts of
![]() $\overline {\rho }$
, that is, deformations of
$\overline {\rho }$
, that is, deformations of
![]() $\overline {\rho }$
together with a basis. If
$\overline {\rho }$
together with a basis. If
![]() $\operatorname {\mathrm {End}}_G(\overline {\rho })={\mathbf {F}}$
(for example, if
$\operatorname {\mathrm {End}}_G(\overline {\rho })={\mathbf {F}}$
(for example, if
![]() $\overline {\rho }$
is absolutely irreducible), we additionally have the universal (unframed) deformation ring
$\overline {\rho }$
is absolutely irreducible), we additionally have the universal (unframed) deformation ring
![]() $R_{\overline {\rho }}$
parametrizing deformations of
$R_{\overline {\rho }}$
parametrizing deformations of
![]() $\rho $
.
$\rho $
.
If R is a complete local Noetherian
![]() ${\mathscr {O}}_E$
-algebra with maximal ideal
${\mathscr {O}}_E$
-algebra with maximal ideal
![]() $\mathfrak {m}_R$
and finite residue field, and
$\mathfrak {m}_R$
and finite residue field, and
![]() $\psi :\operatorname {\mathrm {Gal}}_K\rightarrow R^{\times }$
is a continuous character such that
$\psi :\operatorname {\mathrm {Gal}}_K\rightarrow R^{\times }$
is a continuous character such that
![]() $\det \overline {\rho }=\psi \mod \mathfrak {m}_R$
, there is a quotient
$\det \overline {\rho }=\psi \mod \mathfrak {m}_R$
, there is a quotient
![]() $R\mathop {\widehat \otimes } R_{\overline {\rho }}^\square \twoheadrightarrow R_{\overline {\rho }}^{\square ,\psi }$
parametrizing lifts of
$R\mathop {\widehat \otimes } R_{\overline {\rho }}^\square \twoheadrightarrow R_{\overline {\rho }}^{\square ,\psi }$
parametrizing lifts of
![]() $\overline {\rho }$
with determinant
$\overline {\rho }$
with determinant
![]() $\psi $
. Indeed, there is a homomorphism
$\psi $
. Indeed, there is a homomorphism
![]() $R_{\det \overline {\rho }}\rightarrow R_{\overline {\rho }}^\square $
given by the determinant map, and the choice of
$R_{\det \overline {\rho }}\rightarrow R_{\overline {\rho }}^\square $
given by the determinant map, and the choice of
![]() $\psi $
defines a homomorphism
$\psi $
defines a homomorphism
![]() $R_{\det \overline {\rho }}\rightarrow R$
; then
$R_{\det \overline {\rho }}\rightarrow R$
; then
![]() $R_{\overline {\rho }}^{\square ,\psi }=R\mathop {\widehat \otimes }_{R_{\det \overline {\rho }}}R_{\overline {\rho }}^\square $
. If
$R_{\overline {\rho }}^{\square ,\psi }=R\mathop {\widehat \otimes }_{R_{\det \overline {\rho }}}R_{\overline {\rho }}^\square $
. If
![]() $\operatorname {\mathrm {End}}_G(\overline {\rho })={\mathbf {F}}$
, there is similarly a quotient
$\operatorname {\mathrm {End}}_G(\overline {\rho })={\mathbf {F}}$
, there is similarly a quotient
![]() $R\mathop {\widehat \otimes } R_{\overline {\rho }}\twoheadrightarrow R_{\overline {\rho }}^\psi $
parametrizing deformations of
$R\mathop {\widehat \otimes } R_{\overline {\rho }}\twoheadrightarrow R_{\overline {\rho }}^\psi $
parametrizing deformations of
![]() $\overline {\rho }$
with determinant
$\overline {\rho }$
with determinant
![]() $\psi $
.
$\psi $
.
Now, we specialize to the arithmetic situations of interest. Let
![]() $K/{\mathbf {Q}}_p$
be a finite extension, and assume that
$K/{\mathbf {Q}}_p$
be a finite extension, and assume that
![]() $\operatorname {\mathrm {Hom}}(K,E)$
has cardinality
$\operatorname {\mathrm {Hom}}(K,E)$
has cardinality
![]() $[K:{\mathbf {Q}}_p]$
. Then by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 3.37],
$[K:{\mathbf {Q}}_p]$
. Then by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 3.37],
![]() $R_{\overline {\rho }}^\square $
is a complete intersection, and by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 4.21] the irreducible components of
$R_{\overline {\rho }}^\square $
is a complete intersection, and by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 4.21] the irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_{\overline {\rho }}^\square $
are in bijection with the irreducible components of
$\operatorname {\mathrm {Spec}} R_{\overline {\rho }}^\square $
are in bijection with the irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_{\det \overline {\rho }}$
. More precisely, if
$\operatorname {\mathrm {Spec}} R_{\det \overline {\rho }}$
. More precisely, if
![]() $\mu :=\mu _{p^\infty }(K)$
denotes the p-power roots of unity in
$\mu :=\mu _{p^\infty }(K)$
denotes the p-power roots of unity in
![]() $K^{\times }$
, local class field theory identifies it with a subgroup of
$K^{\times }$
, local class field theory identifies it with a subgroup of
![]() $\operatorname {\mathrm {Gal}}_K^{\mathrm {ab}}$
; by [Reference Böckle, Iyengar and PaškūnasBIP23a, Lemma 4.1]
$\operatorname {\mathrm {Gal}}_K^{\mathrm {ab}}$
; by [Reference Böckle, Iyengar and PaškūnasBIP23a, Lemma 4.1]
![]() $R_{\det \overline {\rho }}$
is a power series ring over
$R_{\det \overline {\rho }}$
is a power series ring over
![]() ${\mathscr {O}}_E[\mu ]$
, so its irreducible components are in bijection with characters
${\mathscr {O}}_E[\mu ]$
, so its irreducible components are in bijection with characters
![]() $\chi :\mu \rightarrow {\mathscr {O}}_E^{\times }$
. There are quotients
$\chi :\mu \rightarrow {\mathscr {O}}_E^{\times }$
. There are quotients
![]() $R_{\overline {\rho }}^\square \twoheadrightarrow R_{\overline {\rho }}^{\square ,\chi }$
parametrizing lifts of
$R_{\overline {\rho }}^\square \twoheadrightarrow R_{\overline {\rho }}^{\square ,\chi }$
parametrizing lifts of
![]() $\overline {\rho }$
whose determinant restricted to
$\overline {\rho }$
whose determinant restricted to
![]() $\mu $
(via the Artin map) agrees with
$\mu $
(via the Artin map) agrees with
![]() $\chi $
, and by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 4.5, Corollary 4.19] the rings
$\chi $
, and by [Reference Böckle, Iyengar and PaškūnasBIP23a, Corollary 4.5, Corollary 4.19] the rings
![]() $R_{\overline {\rho }}^{\square ,\chi }$
are normal domains and complete intersections. In particular,
$R_{\overline {\rho }}^{\square ,\chi }$
are normal domains and complete intersections. In particular,
![]() $R_{\overline {\rho }}^{\square }$
is reduced.
$R_{\overline {\rho }}^{\square }$
is reduced.
Let F be a number field, and let
![]() $\Sigma _p:=\{v\mid p\}$
. If
$\Sigma _p:=\{v\mid p\}$
. If
![]() $\rho :\operatorname {\mathrm {Gal}}_F\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
is a continuous representation and v is a place of F, we let
$\rho :\operatorname {\mathrm {Gal}}_F\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
is a continuous representation and v is a place of F, we let
![]() $\rho _v$
denote
$\rho _v$
denote
![]() $\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
. Suppose that
$\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
. Suppose that
![]() $\overline {\rho }$
is absolutely irreducible, and let S be a finite set of places of F containing
$\overline {\rho }$
is absolutely irreducible, and let S be a finite set of places of F containing
![]() $\Sigma _p$
and the infinite places such that
$\Sigma _p$
and the infinite places such that
![]() $\overline {\rho }$
is unramified outside S. Then we let
$\overline {\rho }$
is unramified outside S. Then we let
![]() $R_{\overline {\rho },S}$
denote the universal deformation ring parametrizing deformations unramified outside of S, and we let
$R_{\overline {\rho },S}$
denote the universal deformation ring parametrizing deformations unramified outside of S, and we let
![]() $R_{\overline {\rho },S}^{\square }$
denote the universal deformation ring whose A-points are deformations
$R_{\overline {\rho },S}^{\square }$
denote the universal deformation ring whose A-points are deformations
![]() $\rho _A$
of
$\rho _A$
of
![]() $\overline {\rho }$
unramified outside of S, together with bases for
$\overline {\rho }$
unramified outside of S, together with bases for
![]() $\rho _A|_{\operatorname {\mathrm {Gal}}_{F_v}}$
for each
$\rho _A|_{\operatorname {\mathrm {Gal}}_{F_v}}$
for each
![]() $v\in \Sigma _p$
. We also let
$v\in \Sigma _p$
. We also let
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square }:=\otimes _{v\in \Sigma _p}R_{\overline {\rho }_v}^{\square }$
.
$R_{\overline {\rho },\mathrm {loc}}^{\square }:=\otimes _{v\in \Sigma _p}R_{\overline {\rho }_v}^{\square }$
.
If
![]() $\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
is a continuous character as above, we let
$\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
is a continuous character as above, we let
 $$ \begin{align*} R_{\overline{\rho},S}^\psi&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},S}}R_{\overline{\rho},S} \\ R_{\overline{\rho},S}^{\square,\psi}&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},S}}R_{\overline{\rho},S}^{\square} \\ R_{\overline{\rho},\mathrm{loc}}^{\square,\psi}&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},\mathrm{loc}}}R_{\overline{\rho},\mathrm{loc}}^{\square}. \end{align*} $$
$$ \begin{align*} R_{\overline{\rho},S}^\psi&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},S}}R_{\overline{\rho},S} \\ R_{\overline{\rho},S}^{\square,\psi}&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},S}}R_{\overline{\rho},S}^{\square} \\ R_{\overline{\rho},\mathrm{loc}}^{\square,\psi}&:=R\mathop{\widehat\otimes}_{R_{\det\overline{\rho},\mathrm{loc}}}R_{\overline{\rho},\mathrm{loc}}^{\square}. \end{align*} $$
For any place
![]() $v\in \Sigma _p$
, restriction from
$v\in \Sigma _p$
, restriction from
![]() $\operatorname {\mathrm {Gal}}_{F,S}$
to
$\operatorname {\mathrm {Gal}}_{F,S}$
to
![]() $\operatorname {\mathrm {Gal}}_{F_v}$
defines a homomorphism
$\operatorname {\mathrm {Gal}}_{F_v}$
defines a homomorphism
![]() $R_{\overline {\rho }_v}^\square \rightarrow R_{\overline {\rho },S}^\square $
, and so we obtain homomorphisms
$R_{\overline {\rho }_v}^\square \rightarrow R_{\overline {\rho },S}^\square $
, and so we obtain homomorphisms
and
We can relate our local and global deformation rings more precisely:
Lemma 2.1.1. Suppose that
![]() $p\nmid d$
. Let
$p\nmid d$
. Let
![]() $h^1$
denote the dimension (as an
$h^1$
denote the dimension (as an
![]() ${\mathbf {F}}$
-vector space) of
${\mathbf {F}}$
-vector space) of
 $$\begin{align*}\ker\,\left(H^1(\operatorname{\mathrm{Gal}}_{F,S},\operatorname{\mathrm{ad}}^0(\overline{\rho}))\rightarrow \prod_{v\in \Sigma_p}H^1(\operatorname{\mathrm{Gal}}_{F_v},\operatorname{\mathrm{ad}}^0(\overline{\rho}_v))\right), \end{align*}$$
$$\begin{align*}\ker\,\left(H^1(\operatorname{\mathrm{Gal}}_{F,S},\operatorname{\mathrm{ad}}^0(\overline{\rho}))\rightarrow \prod_{v\in \Sigma_p}H^1(\operatorname{\mathrm{Gal}}_{F_v},\operatorname{\mathrm{ad}}^0(\overline{\rho}_v))\right), \end{align*}$$
let
![]() $\delta _F:=\dim _{{\mathbf {F}}}H^0(\operatorname {\mathrm {Gal}}_{F,S},\operatorname {\mathrm {ad}}\overline {\rho })$
, and for
$\delta _F:=\dim _{{\mathbf {F}}}H^0(\operatorname {\mathrm {Gal}}_{F,S},\operatorname {\mathrm {ad}}\overline {\rho })$
, and for
![]() $v\in \Sigma _p$
let
$v\in \Sigma _p$
let
![]() $\delta _v:=\dim _{{\mathbf {F}}}H^0(\operatorname {\mathrm {Gal}}_{F_v},\operatorname {\mathrm {ad}}\overline {\rho }_v)$
. Then
$\delta _v:=\dim _{{\mathbf {F}}}H^0(\operatorname {\mathrm {Gal}}_{F_v},\operatorname {\mathrm {ad}}\overline {\rho }_v)$
. Then
![]() $R_{\overline {\rho },S}^{\square ,\psi }$
can be topologically generated over
$R_{\overline {\rho },S}^{\square ,\psi }$
can be topologically generated over
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
by
$R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
by
![]() $g:=h^1+\sum _{v\in \Sigma _p}\delta _v-\delta _F$
elements.
$g:=h^1+\sum _{v\in \Sigma _p}\delta _v-\delta _F$
elements.
Proof. Let
![]() $\mathfrak {m}_{\mathrm {{loc}}}$
denote the maximal ideal of
$\mathfrak {m}_{\mathrm {{loc}}}$
denote the maximal ideal of
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
, and let
$R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
, and let
![]() $\mathfrak {m}_S$
denote the maximal ideal of
$\mathfrak {m}_S$
denote the maximal ideal of
![]() $R_{\overline {\rho },S}^{\square ,\psi }$
. We need to compute the relative tangent space
$R_{\overline {\rho },S}^{\square ,\psi }$
. We need to compute the relative tangent space
![]() $\left (\mathfrak {m}_S/(\mathfrak {m}_S^2,\mathfrak {m}_{\mathrm {{loc}}})\right )^\ast $
of
$\left (\mathfrak {m}_S/(\mathfrak {m}_S^2,\mathfrak {m}_{\mathrm {{loc}}})\right )^\ast $
of
![]() $R_{\overline {\rho },S}^{\square ,\psi }/\mathfrak {m}_{\mathrm {{loc}}}$
. But the maximal ideal of R is contained in
$R_{\overline {\rho },S}^{\square ,\psi }/\mathfrak {m}_{\mathrm {{loc}}}$
. But the maximal ideal of R is contained in
![]() $\mathfrak {m}_{\mathrm {{loc}}}$
, so we may assume that
$\mathfrak {m}_{\mathrm {{loc}}}$
, so we may assume that
![]() $\psi $
is constant, and the result follows from [Reference KisinKis09b, Lemma 3.2.2].
$\psi $
is constant, and the result follows from [Reference KisinKis09b, Lemma 3.2.2].
2.2 Deformations of trianguline
 $(\varphi ,\Gamma )$
-modules
$(\varphi ,\Gamma )$
-modules
Trianguline
![]() $(\varphi ,\Gamma )$
-modules are those which are extensions of
$(\varphi ,\Gamma )$
-modules are those which are extensions of
![]() $(\varphi ,\Gamma )$
-modules of character type. More precisely,
$(\varphi ,\Gamma )$
-modules of character type. More precisely,
Definition 2.2.1. Let X be a pseudorigid space over
![]() $\mathscr {O}_E$
for some finite extension
$\mathscr {O}_E$
for some finite extension
![]() $E/{\mathbf {Q}}_p$
, let
$E/{\mathbf {Q}}_p$
, let
![]() $K/{\mathbf {Q}}_p$
be a finite extension and let
$K/{\mathbf {Q}}_p$
be a finite extension and let
![]() $\underline \delta =(\delta _1,\ldots ,\delta _d):(K^{\times })^d\rightarrow \Gamma (X,\mathscr {O}_X^{\times })$
be a d-tuple of continuous characters. A
$\underline \delta =(\delta _1,\ldots ,\delta _d):(K^{\times })^d\rightarrow \Gamma (X,\mathscr {O}_X^{\times })$
be a d-tuple of continuous characters. A
![]() $(\varphi ,\Gamma _{K})$
-module D is trianguline with parameter
$(\varphi ,\Gamma _{K})$
-module D is trianguline with parameter
![]() $\underline \delta $
if (possibly after enlarging E) there is an increasing filtration
$\underline \delta $
if (possibly after enlarging E) there is an increasing filtration
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D$
by
$\operatorname {\mathrm {Fil}}^{\bullet } D$
by
![]() $(\varphi ,\Gamma _{K})$
-modules and a set of line bundles
$(\varphi ,\Gamma _{K})$
-modules and a set of line bundles
![]() $\mathscr {L}_1,\ldots ,\mathscr {L}_d$
such that
$\mathscr {L}_1,\ldots ,\mathscr {L}_d$
such that
![]() $\operatorname {\mathrm {gr}}^iD\cong \Lambda _{X,\mathrm {rig},K}(\delta _i)\otimes \mathscr {L}_i$
for all i.
$\operatorname {\mathrm {gr}}^iD\cong \Lambda _{X,\mathrm {rig},K}(\delta _i)\otimes \mathscr {L}_i$
for all i.
If
![]() $X=\operatorname {\mathrm {Spa}} R$
where R is a field, we say that D is strictly trianguline with parameter
$X=\operatorname {\mathrm {Spa}} R$
where R is a field, we say that D is strictly trianguline with parameter
![]() $\underline \delta $
if for each i,
$\underline \delta $
if for each i,
![]() $\operatorname {\mathrm {Fil}}^{i+1}D$
is the unique sub-
$\operatorname {\mathrm {Fil}}^{i+1}D$
is the unique sub-
![]() $(\varphi ,\Gamma _{K})$
-module of D containing
$(\varphi ,\Gamma _{K})$
-module of D containing
![]() $\operatorname {\mathrm {Fil}}^iD$
such that
$\operatorname {\mathrm {Fil}}^iD$
such that
![]() $\operatorname {\mathrm {gr}}^{i+1}D\cong \Lambda _{R,\mathrm {rig},K}(\delta _{i+1})$
.
$\operatorname {\mathrm {gr}}^{i+1}D\cong \Lambda _{R,\mathrm {rig},K}(\delta _{i+1})$
.
As in the characteristic
![]() $0$
situation treated in [Reference Bellache and ChenevierBC09, §2.3], we may define and study deformations of trianguline
$0$
situation treated in [Reference Bellache and ChenevierBC09, §2.3], we may define and study deformations of trianguline
![]() $(\varphi ,\Gamma )$
-modules:
$(\varphi ,\Gamma )$
-modules:
Definition 2.2.2. Let R be a finite extension of
![]() ${\mathbf {F}}_p(\!(u)\!)$
, and let D be a fixed
${\mathbf {F}}_p(\!(u)\!)$
, and let D be a fixed
![]() $(\varphi ,\Gamma _{K})$
-module of rank d over
$(\varphi ,\Gamma _{K})$
-module of rank d over
![]() $\Lambda _{R,\mathrm {rig},K}$
equipped with a triangulation
$\Lambda _{R,\mathrm {rig},K}$
equipped with a triangulation
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D$
with parameter
$\operatorname {\mathrm {Fil}}^{\bullet } D$
with parameter
![]() $\underline \delta $
. Let
$\underline \delta $
. Let
![]() $\mathcal {C}_R$
denote the category of Artin local
$\mathcal {C}_R$
denote the category of Artin local
![]() ${\mathbf {Z}}_p$
-algebras
${\mathbf {Z}}_p$
-algebras
![]() $R'$
equipped with an isomorphism
$R'$
equipped with an isomorphism
![]() $R'/\mathfrak {m}_{R^{\prime }}\xrightarrow {\sim }R$
. The trianguline deformation functor
$R'/\mathfrak {m}_{R^{\prime }}\xrightarrow {\sim }R$
. The trianguline deformation functor
![]() $\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}:\mathcal {C}_R\rightarrow \underline {\mathrm {Set}}$
is defined to be the set of isomorphism classes
$\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}:\mathcal {C}_R\rightarrow \underline {\mathrm {Set}}$
is defined to be the set of isomorphism classes
where
![]() $D_{R^{\prime }}$
is a
$D_{R^{\prime }}$
is a
![]() $(\varphi ,\Gamma _{K})$
-module over
$(\varphi ,\Gamma _{K})$
-module over
![]() $\Lambda _{R^{\prime },\mathrm {rig},K}$
,
$\Lambda _{R^{\prime },\mathrm {rig},K}$
,
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D_{R^{\prime }}$
is a triangulation, and
$\operatorname {\mathrm {Fil}}^{\bullet } D_{R^{\prime }}$
is a triangulation, and
![]() $\iota :R\otimes _{R^{\prime }}D_{R^{\prime }}\xrightarrow {\sim }D$
is an isomorphism which also defines isomorphisms
$\iota :R\otimes _{R^{\prime }}D_{R^{\prime }}\xrightarrow {\sim }D$
is an isomorphism which also defines isomorphisms
![]() $R\otimes _{R^{\prime }}\operatorname {\mathrm {Fil}}^iD_{R^{\prime }}\xrightarrow {\sim }\operatorname {\mathrm {Fil}}^iD$
.
$R\otimes _{R^{\prime }}\operatorname {\mathrm {Fil}}^iD_{R^{\prime }}\xrightarrow {\sim }\operatorname {\mathrm {Fil}}^iD$
.
One of the consequences of the proof of [Reference BellovinBel23b, Proposition 5.1] is that when
![]() $d=1$
,
$d=1$
,
![]() $\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}$
is formally smooth. As in the characteristic
$\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}$
is formally smooth. As in the characteristic
![]() $0$
situation, the same is true for general d, so long as the parameter satisfies a certain regularity condition. Note that the regularity condition in here is slightly different than in characteristic
$0$
situation, the same is true for general d, so long as the parameter satisfies a certain regularity condition. Note that the regularity condition in here is slightly different than in characteristic
![]() $0$
; the additional characters avoided in the statement of [Reference Bellache and ChenevierBC09, Proposition 2.3.10] do not make sense in characteristic p.
$0$
; the additional characters avoided in the statement of [Reference Bellache and ChenevierBC09, Proposition 2.3.10] do not make sense in characteristic p.
Proposition 2.2.3. Suppose the parameter
![]() $\underline \delta $
of
$\underline \delta $
of
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D$
satisfies the property that
$\operatorname {\mathrm {Fil}}^{\bullet } D$
satisfies the property that
![]() $\delta _i\delta _j^{-1}\neq \chi _{\mathrm {cyc}}\circ \operatorname {\mathrm {Nm}}_{K/{\mathbf {Q}}_p}$
for any
$\delta _i\delta _j^{-1}\neq \chi _{\mathrm {cyc}}\circ \operatorname {\mathrm {Nm}}_{K/{\mathbf {Q}}_p}$
for any
![]() $i<j$
. Then
$i<j$
. Then
![]() $\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}$
is formally smooth.
$\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}$
is formally smooth.
Proof. The proof is essentially identical to that of [Reference Bellache and ChenevierBC09, Proposition 2.3.10], but we sketch it here for the convenience of the reader. We proceed by induction on d; the case
![]() $d=1$
follows from the proof of [Reference BellovinBel23b, Proposition 5.1], so we assume the result for trianguline deformations of
$d=1$
follows from the proof of [Reference BellovinBel23b, Proposition 5.1], so we assume the result for trianguline deformations of
![]() $(\varphi ,\Gamma )$
-modules of rank
$(\varphi ,\Gamma )$
-modules of rank
![]() $d-1$
. Let
$d-1$
. Let
![]() $I\subset R'$
be a square-zero ideal. We need to prove that
$I\subset R'$
be a square-zero ideal. We need to prove that
![]() $\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}(R')\rightarrow \mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}(R'/I)$
is surjective, so we may factor
$\mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}(R')\rightarrow \mathrm {Def}_{D,\operatorname {\mathrm {Fil}}^{\bullet }}(R'/I)$
is surjective, so we may factor
![]() $R'\twoheadrightarrow R'/I$
into a series of small extensions and assume that I is principal and
$R'\twoheadrightarrow R'/I$
into a series of small extensions and assume that I is principal and
![]() $I\mathfrak {m}_{R^{\prime }}=0$
. By the inductive hypothesis, we may find a trianguline deformation
$I\mathfrak {m}_{R^{\prime }}=0$
. By the inductive hypothesis, we may find a trianguline deformation
![]() $D'$
of
$D'$
of
![]() $\operatorname {\mathrm {Fil}}^{d-1}D$
over
$\operatorname {\mathrm {Fil}}^{d-1}D$
over
![]() $\Lambda _{R^{\prime },\mathrm {rig},L}$
. By twisting, we may assume that
$\Lambda _{R^{\prime },\mathrm {rig},L}$
. By twisting, we may assume that
![]() $\delta _d$
is trivial. Then we need to show that the natural map
$\delta _d$
is trivial. Then we need to show that the natural map
![]() $H_{\varphi ,\Gamma }^1(D')\rightarrow H_{\varphi ,\Gamma }^1(\operatorname {\mathrm {Fil}}^{d-1})$
is surjective. But the cokernel of this map is
$H_{\varphi ,\Gamma }^1(D')\rightarrow H_{\varphi ,\Gamma }^1(\operatorname {\mathrm {Fil}}^{d-1})$
is surjective. But the cokernel of this map is
![]() $H_{\varphi ,\Gamma }^2(I\otimes _{R^{\prime }/\mathfrak {m}_{R^{\prime }}}\operatorname {\mathrm {Fil}}^{d-1}D(\delta _d^{-1}))=I\otimes _{R^{\prime }/\mathfrak {m}_{R^{\prime }}}H_{\varphi ,\Gamma }^2(\operatorname {\mathrm {Fil}}^{d-1}D(\delta _d^{-1}))$
, which is
$H_{\varphi ,\Gamma }^2(I\otimes _{R^{\prime }/\mathfrak {m}_{R^{\prime }}}\operatorname {\mathrm {Fil}}^{d-1}D(\delta _d^{-1}))=I\otimes _{R^{\prime }/\mathfrak {m}_{R^{\prime }}}H_{\varphi ,\Gamma }^2(\operatorname {\mathrm {Fil}}^{d-1}D(\delta _d^{-1}))$
, which is
![]() $0$
by assumption and [Reference BellovinBel23b, Corollary 4.11].
$0$
by assumption and [Reference BellovinBel23b, Corollary 4.11].
In order to build moduli spaces of trianguline
![]() $(\varphi ,\Gamma )$
-modules, we will use moduli spaces of characters, as in [Reference BellovinBel23a, §2.3]. If G is a commutative p-adic Lie group and
$(\varphi ,\Gamma )$
-modules, we will use moduli spaces of characters, as in [Reference BellovinBel23a, §2.3]. If G is a commutative p-adic Lie group and
![]() $G'\subset G$
is a compact subgroup such that
$G'\subset G$
is a compact subgroup such that
![]() $G/G'$
is free and finitely generated, then we have
$G/G'$
is free and finitely generated, then we have
![]() $\widehat {G'}:=\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![G']\!]$
and the pseudorigid spaces
$\widehat {G'}:=\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![G']\!]$
and the pseudorigid spaces
![]() $\widehat {G'}^{\mathrm {{an}}}$
and
$\widehat {G'}^{\mathrm {{an}}}$
and
![]() $\widehat {G}^{\mathrm {{an}}}:=\operatorname {\mathrm {Spa}}({\mathbf {Z}}[G/G'],{\mathbf {Z}}){\times }_{{\mathbf {Z}}}\widehat {G'}^{\mathrm {{an}}}$
. If X is a pseudorigid space, we also have the pseudorigid space
$\widehat {G}^{\mathrm {{an}}}:=\operatorname {\mathrm {Spa}}({\mathbf {Z}}[G/G'],{\mathbf {Z}}){\times }_{{\mathbf {Z}}}\widehat {G'}^{\mathrm {{an}}}$
. If X is a pseudorigid space, we also have the pseudorigid space
![]() $\widehat G_X$
, which represents the functor
$\widehat G_X$
, which represents the functor
on the category of adic spaces over X.
In particular, if K is a finite extension of
![]() ${\mathbf {Q}}_p$
, we will be interested in
${\mathbf {Q}}_p$
, we will be interested in
![]() $\widehat {K^{\times }}^{\mathrm {{an}}}$
and
$\widehat {K^{\times }}^{\mathrm {{an}}}$
and
![]() $\widehat {(K^{\times })^d}^{\mathrm {{an}}}$
for
$\widehat {(K^{\times })^d}^{\mathrm {{an}}}$
for
![]() $d\geq 1$
:
$d\geq 1$
:
Definition 2.2.4. We let
![]() $\mathcal {T}:=\widehat {K^{\times }}^{\mathrm {{an}}}$
, and for any
$\mathcal {T}:=\widehat {K^{\times }}^{\mathrm {{an}}}$
, and for any
![]() $d\geq 1$
, we write
$d\geq 1$
, we write
![]() $\mathcal {T}^d:=\widehat {(K^{\times })^d}^{\mathrm {{an}}}$
.
$\mathcal {T}^d:=\widehat {(K^{\times })^d}^{\mathrm {{an}}}$
.
We see that
![]() $\widehat {K^{\times }}^{\mathrm {{an}}}\cong {\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}{\times }_{{\mathbf {Z}}}\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
, and
$\widehat {K^{\times }}^{\mathrm {{an}}}\cong {\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}{\times }_{{\mathbf {Z}}}\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
, and
![]() $\mathcal {T}^d\cong {\mathbf {G}}_m^{\operatorname {\mathrm {ad}},d}{\times }_{{\mathbf {Z}}}\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]^{\mathrm {{an}}}$
. Since
$\mathcal {T}^d\cong {\mathbf {G}}_m^{\operatorname {\mathrm {ad}},d}{\times }_{{\mathbf {Z}}}\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]^{\mathrm {{an}}}$
. Since
![]() ${\mathscr {O}}_K^{\times }$
is compact,
${\mathscr {O}}_K^{\times }$
is compact,
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
is a quasicompact pseudorigid space; it has a finite cover
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
is a quasicompact pseudorigid space; it has a finite cover
![]() $\{U_i:=\operatorname {\mathrm {Spa}} R_i\}$
by affinoid subspaces, and
$\{U_i:=\operatorname {\mathrm {Spa}} R_i\}$
by affinoid subspaces, and
![]() ${\mathbf {G}}_{m,U_i}$
is a rising union of relative annuli
${\mathbf {G}}_{m,U_i}$
is a rising union of relative annuli
![]() $C_{U_i,h}:=\operatorname {\mathrm {Spa}} R_i\left \langle u^hT, u^hT^{-1}\right \rangle $
.
$C_{U_i,h}:=\operatorname {\mathrm {Spa}} R_i\left \langle u^hT, u^hT^{-1}\right \rangle $
.
If
![]() $K={\mathbf {Q}}_p$
, then
$K={\mathbf {Q}}_p$
, then
![]() $\widehat {{\mathbf {Q}}_p^{\times }}^{\mathrm {{an}}}$
has connected components indexed by the elements of
$\widehat {{\mathbf {Q}}_p^{\times }}^{\mathrm {{an}}}$
has connected components indexed by the elements of
![]() $\mu _{p-1}$
, each of which is isomorphic to
$\mu _{p-1}$
, each of which is isomorphic to
![]() $\left (\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathbf {Z}}_p]\!]\right )^{\mathrm {{an}}}\times {\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
.
$\left (\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathbf {Z}}_p]\!]\right )^{\mathrm {{an}}}\times {\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
.
Remark 2.2.5. In the pseudorigid setting (unlike the classical rigid analytic setting), it is not true that
![]() $\widehat {G_1\times G_2}^{\mathrm {{an}}}\cong \widehat {G_1}^{\mathrm {{an}}}\times \widehat {G_2}^{\mathrm {{an}}}$
. Indeed,
$\widehat {G_1\times G_2}^{\mathrm {{an}}}\cong \widehat {G_1}^{\mathrm {{an}}}\times \widehat {G_2}^{\mathrm {{an}}}$
. Indeed,
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_1,T_2]\!]^{\mathrm {{an}}}$
consists of all valuations which do not vanish on all three of
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_1,T_2]\!]^{\mathrm {{an}}}$
consists of all valuations which do not vanish on all three of
![]() $p, T_1, T_2$
. But
$p, T_1, T_2$
. But
also excludes valuations vanishing at both p and
![]() $T_1$
(or both p and
$T_1$
(or both p and
![]() $T_2$
). In particular,
$T_2$
). In particular,
![]() $\mathcal {T}^d$
is not a product of copies of
$\mathcal {T}^d$
is not a product of copies of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Definition 2.2.6. We say that a continuous character
![]() $\kappa :K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is regular if for all maximal points
$\kappa :K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is regular if for all maximal points
![]() $x\in X$
, the residual character
$x\in X$
, the residual character
![]() $\kappa _x:K^{\times }\rightarrow k(x)^{\times }$
is not of the form
$\kappa _x:K^{\times }\rightarrow k(x)^{\times }$
is not of the form
-
•
 $\alpha \mapsto \alpha ^{-\mathbf {i}}$
or
$\alpha \mapsto \alpha ^{-\mathbf {i}}$
or
 $\alpha \mapsto \alpha ^{\mathbf {i}+\mathbf {1}}\lvert \alpha \rvert $
for
$\alpha \mapsto \alpha ^{\mathbf {i}+\mathbf {1}}\lvert \alpha \rvert $
for
 $\mathbf {i}\in {\mathbf {Z}}_{\geq 0}^{\operatorname {\mathrm {Hom}}(K,k(x))}$
(if x is a characteristic
$\mathbf {i}\in {\mathbf {Z}}_{\geq 0}^{\operatorname {\mathrm {Hom}}(K,k(x))}$
(if x is a characteristic
 $0$
point), or
$0$
point), or -
• trivial or
 $\chi _{\mathrm {cyc}}\circ \operatorname {\mathrm {Nm}}_{K/{\mathbf {Q}}_p}$
(if x is a characteristic p point).
$\chi _{\mathrm {cyc}}\circ \operatorname {\mathrm {Nm}}_{K/{\mathbf {Q}}_p}$
(if x is a characteristic p point).
The space of regular parameters
![]() $\mathcal {T}_{\mathrm {reg}}^d\subset \mathcal {T}^d$
is the Zariski-open subspace whose X-points are given by parameters
$\mathcal {T}_{\mathrm {reg}}^d\subset \mathcal {T}^d$
is the Zariski-open subspace whose X-points are given by parameters
![]() $\underline \delta :(K^{\times })^d\rightarrow {\mathscr {O}}(X)^{\times }$
such that
$\underline \delta :(K^{\times })^d\rightarrow {\mathscr {O}}(X)^{\times }$
such that
![]() $\delta _i\delta _j^{-1}:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is regular for all
$\delta _i\delta _j^{-1}:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is regular for all
![]() $j>i$
.
$j>i$
.
Consider the functor
![]() $\mathcal {S}_d^\square $
on pseudorigid spaces defined via
$\mathcal {S}_d^\square $
on pseudorigid spaces defined via
where D is a trianguline
![]() $(\varphi ,\Gamma _K)$
-module with filtration
$(\varphi ,\Gamma _K)$
-module with filtration
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D$
and regular parameter
$\operatorname {\mathrm {Fil}}^{\bullet } D$
and regular parameter
![]() $\underline \delta \in \mathcal {T}_{\mathrm {reg}}^d$
, and
$\underline \delta \in \mathcal {T}_{\mathrm {reg}}^d$
, and
![]() $\underline \nu $
is a sequence of trivializations
$\underline \nu $
is a sequence of trivializations
![]() $\nu _i:\operatorname {\mathrm {gr}}^iD\xrightarrow {\sim }\Lambda _{X,\mathrm {rig},K}$
. There is a natural transformation
$\nu _i:\operatorname {\mathrm {gr}}^iD\xrightarrow {\sim }\Lambda _{X,\mathrm {rig},K}$
. There is a natural transformation
![]() $\mathcal {S}_d^\square \rightarrow \mathcal {T}_{\mathrm {reg}}^d$
given on X-points by
$\mathcal {S}_d^\square \rightarrow \mathcal {T}_{\mathrm {reg}}^d$
given on X-points by
Exactly as in [Reference ChenevierChe13, Théorème 3.3] and [Reference Hellmann and SchraenHS16, Theorem 2.4], we have the following:
Proposition 2.2.7. The functor
![]() $\mathcal {S}_d^\square $
is representable by a pseudorigid space, which we also denote
$\mathcal {S}_d^\square $
is representable by a pseudorigid space, which we also denote
![]() $\mathcal {S}_d^\square $
, and the morphism
$\mathcal {S}_d^\square $
, and the morphism
![]() $\mathcal {S}_d^\square \rightarrow \mathcal {T}_{\mathrm {reg}}^d$
is smooth of relative dimension
$\mathcal {S}_d^\square \rightarrow \mathcal {T}_{\mathrm {reg}}^d$
is smooth of relative dimension
![]() $\frac {d(d-1)}{2}[K:{\mathbf {Q}}_p]$
.
$\frac {d(d-1)}{2}[K:{\mathbf {Q}}_p]$
.
One proves by induction on d that if D is a trianguline
![]() $(\varphi ,\Gamma _K)$
-module over X with parameter
$(\varphi ,\Gamma _K)$
-module over X with parameter
![]() $\underline \delta \in (\mathcal {T}_{\mathrm {reg}})^d$
, then
$\underline \delta \in (\mathcal {T}_{\mathrm {reg}})^d$
, then
![]() $H_{\varphi ,\Gamma _K}^1(D)$
is a vector bundle over X of rank
$H_{\varphi ,\Gamma _K}^1(D)$
is a vector bundle over X of rank
![]() $d[K:{\mathbf {Q}}_p]$
(the regularity assumption ensures that
$d[K:{\mathbf {Q}}_p]$
(the regularity assumption ensures that
![]() $H_{\varphi ,\Gamma _K}^0(D)=H_{\varphi ,\Gamma _K}^2(D)=0$
). Now,
$H_{\varphi ,\Gamma _K}^0(D)=H_{\varphi ,\Gamma _K}^2(D)=0$
). Now,
![]() $\mathcal {S}_1^\square =\mathcal {T}=\mathcal {T}_{\mathrm {reg}}^1$
, so
$\mathcal {S}_1^\square =\mathcal {T}=\mathcal {T}_{\mathrm {reg}}^1$
, so
![]() $\mathcal {S}_1^\square $
is representable and is smooth of the correct dimension over
$\mathcal {S}_1^\square $
is representable and is smooth of the correct dimension over
![]() $\mathcal {T}_{\mathrm {reg}}^1$
. Then one may proceed by induction on d again and construct
$\mathcal {T}_{\mathrm {reg}}^1$
. Then one may proceed by induction on d again and construct
![]() $\mathcal {S}_d^\square $
as the moduli space of extensions of the universal
$\mathcal {S}_d^\square $
as the moduli space of extensions of the universal
![]() $(\varphi ,\Gamma _K)$
-module of character type
$(\varphi ,\Gamma _K)$
-module of character type
![]() $\Lambda _{\mathcal {T},\mathrm {rig},K}(\delta _{\mathrm {univ}})$
by the universal object
$\Lambda _{\mathcal {T},\mathrm {rig},K}(\delta _{\mathrm {univ}})$
by the universal object
![]() $D_{d-1,\mathrm {univ}}$
over
$D_{d-1,\mathrm {univ}}$
over
![]() $\mathcal {S}_{d-1}^\square $
. For a specified regular parameter
$\mathcal {S}_{d-1}^\square $
. For a specified regular parameter
![]() $\underline \delta =(\delta _1,\ldots ,\delta _d)\in \mathcal {T}_{\mathrm {reg}}^d(X)$
, the fiber
$\underline \delta =(\delta _1,\ldots ,\delta _d)\in \mathcal {T}_{\mathrm {reg}}^d(X)$
, the fiber
![]() $\mathcal {S}_d^\square |_{\underline \delta }$
is equal to
$\mathcal {S}_d^\square |_{\underline \delta }$
is equal to
![]() $\operatorname {\mathrm {Ext}}^1(\Lambda _{X,\mathrm {rig},K}(\delta _d),D_{d-1,\mathrm {univ}}|_{(\delta _1,\ldots ,\delta _{d-1})})=H_{\varphi ,\Gamma _K}^1(D_{d-1,\mathrm {univ}}|_{(\delta _1,\ldots ,\delta _{d-1})}(\delta _d^{-1}))$
. This is a rank-
$\operatorname {\mathrm {Ext}}^1(\Lambda _{X,\mathrm {rig},K}(\delta _d),D_{d-1,\mathrm {univ}}|_{(\delta _1,\ldots ,\delta _{d-1})})=H_{\varphi ,\Gamma _K}^1(D_{d-1,\mathrm {univ}}|_{(\delta _1,\ldots ,\delta _{d-1})}(\delta _d^{-1}))$
. This is a rank-
![]() $(d-1)$
vector bundle over X, and the claim follows.
$(d-1)$
vector bundle over X, and the claim follows.
We also introduce variants of
![]() $\mathcal {S}_d^\square $
with families of fixed determinant and weights. More precisely, suppose X is a pseudorigid space and we have a continuous character
$\mathcal {S}_d^\square $
with families of fixed determinant and weights. More precisely, suppose X is a pseudorigid space and we have a continuous character
![]() $\delta _{\det }:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
and a d-tuple of continuous characters
$\delta _{\det }:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
and a d-tuple of continuous characters
![]() $\underline \kappa :=(\kappa _1,\ldots ,\kappa _d):{\mathscr {O}}_K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
. We say that
$\underline \kappa :=(\kappa _1,\ldots ,\kappa _d):{\mathscr {O}}_K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
. We say that
![]() $\delta _{\det }$
and
$\delta _{\det }$
and
![]() $\underline \kappa $
are compatible if
$\underline \kappa $
are compatible if
![]() $\delta _{\det }|_{{\mathscr {O}}_K^{\times }}=\kappa _1\cdots \kappa _d$
. If
$\delta _{\det }|_{{\mathscr {O}}_K^{\times }}=\kappa _1\cdots \kappa _d$
. If
![]() $\delta _{\det }$
and
$\delta _{\det }$
and
![]() $\underline \kappa $
are compatible, we consider the functors
$\underline \kappa $
are compatible, we consider the functors
![]() $\mathcal {S}_d^{\square ,\delta _{\det }}$
and
$\mathcal {S}_d^{\square ,\delta _{\det }}$
and
![]() $\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
on pseudorigid spaces over X defined via
$\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
on pseudorigid spaces over X defined via
and
Proposition 2.2.8. The functor
![]() $\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
is representable by a pseudorigid space over X, which we also denote
$\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
is representable by a pseudorigid space over X, which we also denote
![]() $\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
, and the morphism
$\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }$
, and the morphism
![]() $\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }\rightarrow X$
is smooth and surjective of relative dimension
$\mathcal {S}_d^{\square ,\delta _{\det },\underline \kappa }\rightarrow X$
is smooth and surjective of relative dimension
![]() $\frac {d(d-1)}{2}[K:{\mathbf {Q}}_p]+d-1$
.
$\frac {d(d-1)}{2}[K:{\mathbf {Q}}_p]+d-1$
.
Proof. Set
![]() $Y:=\widehat {({\mathscr {O}}_K^{\times })^d}^{\mathrm {{an}}}$
. Then there is a morphism
$Y:=\widehat {({\mathscr {O}}_K^{\times })^d}^{\mathrm {{an}}}$
. Then there is a morphism
![]() $\mathcal {T}^d\rightarrow {\mathbf {G}}_{m,Y}$
, given by
$\mathcal {T}^d\rightarrow {\mathbf {G}}_{m,Y}$
, given by
![]() $\underline \delta \mapsto \left (\delta _1|_{{\mathscr {O}}_K^{\times }},\ldots ,\delta _d|_{{\mathscr {O}}_K^{\times }},\delta _1(\varpi _K)\cdots \delta _d(\varpi _K)\right )$
, and it is smooth of relative dimension
$\underline \delta \mapsto \left (\delta _1|_{{\mathscr {O}}_K^{\times }},\ldots ,\delta _d|_{{\mathscr {O}}_K^{\times }},\delta _1(\varpi _K)\cdots \delta _d(\varpi _K)\right )$
, and it is smooth of relative dimension
![]() $d-1$
. The choice of
$d-1$
. The choice of
![]() $\delta _{\det }$
and
$\delta _{\det }$
and
![]() $\underline \kappa $
define a morphism
$\underline \kappa $
define a morphism
![]() $X\rightarrow {\mathbf {G}}_{m,Y}$
, and we have a pullback square
$X\rightarrow {\mathbf {G}}_{m,Y}$
, and we have a pullback square

Then the result follows from Proposition 2.2.7.
Example 2.2.9. In the example of most interest to us, we will take
![]() $K={\mathbf {Q}}_p$
,
$K={\mathbf {Q}}_p$
,
![]() $d=2$
, and
$d=2$
, and
![]() $R={\mathbf {Z}}_p[\![T_0]\!]$
, where
$R={\mathbf {Z}}_p[\![T_0]\!]$
, where
![]() $T_0:=\operatorname {\mathrm {T}}({\mathbf {Z}}_p)$
for a split maximal torus
$T_0:=\operatorname {\mathrm {T}}({\mathbf {Z}}_p)$
for a split maximal torus
![]() $\operatorname {\mathrm {T}}\subset \operatorname {\mathrm {GL}}_2/{\mathbf {Z}}_p$
. Fix an unramified character
$\operatorname {\mathrm {T}}\subset \operatorname {\mathrm {GL}}_2/{\mathbf {Z}}_p$
. Fix an unramified character
![]() $\psi _0:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}\rightarrow R^{\times }$
. There is a universal pair of characters
$\psi _0:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}\rightarrow R^{\times }$
. There is a universal pair of characters
![]() $\lambda _1,\lambda _2:{\mathbf {Z}}_p^{\times }\rightrightarrows R^{\times }$
, and we set
$\lambda _1,\lambda _2:{\mathbf {Z}}_p^{\times }\rightrightarrows R^{\times }$
, and we set
![]() $\psi :=\left ( \lambda _1\lambda _2 \chi _{\mathrm {{cyc}}}\right )^{-1}\psi _0$
and
$\psi :=\left ( \lambda _1\lambda _2 \chi _{\mathrm {{cyc}}}\right )^{-1}\psi _0$
and
![]() $\underline \kappa :(\lambda _2^{-1},\left (\lambda _1\chi _{\mathrm {{cyc}}}\right )^{-1})$
. Then the morphism
$\underline \kappa :(\lambda _2^{-1},\left (\lambda _1\chi _{\mathrm {{cyc}}}\right )^{-1})$
. Then the morphism
![]() $\mathcal {S}_2^{\square }\rightarrow \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is the natural projection
$\mathcal {S}_2^{\square }\rightarrow \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is the natural projection
![]() $\mathcal {S}_d^{\square }\rightarrow \widehat {({\mathbf {Z}}_p^{\times })^2}$
, composed with taking inverses and swapping factors. Furthermore,
$\mathcal {S}_d^{\square }\rightarrow \widehat {({\mathbf {Z}}_p^{\times })^2}$
, composed with taking inverses and swapping factors. Furthermore,
![]() $\mathcal {T}$
is two-dimensional and irreducible (corresponding to a choice of
$\mathcal {T}$
is two-dimensional and irreducible (corresponding to a choice of
![]() $\delta _1$
); fixing the determinant means the remaining degrees of freedom are the one-dimensional irreducible space
$\delta _1$
); fixing the determinant means the remaining degrees of freedom are the one-dimensional irreducible space
![]() $\widehat {{\mathbf {Z}}_p^{\times }}$
(corresponding to the choice of
$\widehat {{\mathbf {Z}}_p^{\times }}$
(corresponding to the choice of
![]() $\delta _2|_{{\mathbf {Z}}_p^{\times }}$
), and the generically one-dimensional space of extensions between them. We see that, in this case,
$\delta _2|_{{\mathbf {Z}}_p^{\times }}$
), and the generically one-dimensional space of extensions between them. We see that, in this case,
![]() $\mathcal {S}_2^{\square ,\delta _{\psi },\underline \kappa }$
is four-dimensional and an
$\mathcal {S}_2^{\square ,\delta _{\psi },\underline \kappa }$
is four-dimensional and an
![]() ${\mathbf {A}}^1$
-torsor over a dense open subspace of
${\mathbf {A}}^1$
-torsor over a dense open subspace of
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \widehat {({\mathbf {Z}}_p^{\times })^2}$
. Hence, it is irreducible.
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \widehat {({\mathbf {Z}}_p^{\times })^2}$
. Hence, it is irreducible.
2.3 Structure of trianguline varieties
Let
![]() $K/{\mathbf {Q}}_p$
be a finite extension, and let
$K/{\mathbf {Q}}_p$
be a finite extension, and let
![]() $\overline {\rho }:\operatorname {\mathrm {Gal}}_K\rightarrow \operatorname {\mathrm {GL}}_d(k)$
be a continuous representation, where k is a finite field containing the residue field of K. The fiber product
$\overline {\rho }:\operatorname {\mathrm {Gal}}_K\rightarrow \operatorname {\mathrm {GL}}_d(k)$
be a continuous representation, where k is a finite field containing the residue field of K. The fiber product
![]() $(\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square })^{\mathrm {{an}}}{\times }_{\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p}\mathcal {T}^d$
exists as a pseudorigid space, and it is contained in the fiber product
$(\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square })^{\mathrm {{an}}}{\times }_{\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p}\mathcal {T}^d$
exists as a pseudorigid space, and it is contained in the fiber product
(with complement of codimension
![]() $\geq 2$
if
$\geq 2$
if
![]() $d\geq 2$
). Let
$d\geq 2$
). Let
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
be the Zariski closure in the latter of the set of maximal points
$X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
be the Zariski closure in the latter of the set of maximal points
![]() $x=\{(\rho _x,\underline \delta _x)\}$
, where
$x=\{(\rho _x,\underline \delta _x)\}$
, where
![]() $\rho _x$
is a (framed) lift of
$\rho _x$
is a (framed) lift of
![]() $\overline {\rho }$
and
$\overline {\rho }$
and
![]() $\underline \delta _x\in \mathcal {T}_{\mathrm {reg}}^d(L)$
is a regular parameter of
$\underline \delta _x\in \mathcal {T}_{\mathrm {reg}}^d(L)$
is a regular parameter of
![]() $D_{\mathrm {rig}}(\rho _x)$
.
$D_{\mathrm {rig}}(\rho _x)$
.
Let R be a complete local Noetherian
![]() ${\mathbf {Z}}_p$
-algebra with finite residue field. Fix an d-tuple of characters
${\mathbf {Z}}_p$
-algebra with finite residue field. Fix an d-tuple of characters
![]() $\underline \kappa :=(\kappa _1,\ldots ,\kappa _d)$
, where
$\underline \kappa :=(\kappa _1,\ldots ,\kappa _d)$
, where
![]() $\kappa _i:{\mathscr {O}}_K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
and
$\kappa _i:{\mathscr {O}}_K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
and
![]() $X:=\left (\operatorname {\mathrm {Spa}} R\right )^{\mathrm {{an}}}$
, and fix a character
$X:=\left (\operatorname {\mathrm {Spa}} R\right )^{\mathrm {{an}}}$
, and fix a character
![]() $\psi :\operatorname {\mathrm {Gal}}_K\rightarrow R^{\times }$
. Over the pseudorigid space X, a character
$\psi :\operatorname {\mathrm {Gal}}_K\rightarrow R^{\times }$
. Over the pseudorigid space X, a character
![]() $\psi :\operatorname {\mathrm {Gal}}_K\rightarrow {\mathscr {O}}(X)^{\times }$
corresponds to a rank-
$\psi :\operatorname {\mathrm {Gal}}_K\rightarrow {\mathscr {O}}(X)^{\times }$
corresponds to a rank-
![]() $1\ (\varphi ,\Gamma )$
-module of the form
$1\ (\varphi ,\Gamma )$
-module of the form
![]() $D_{\mathrm {rig}}(\delta _{\psi })$
, for some character
$D_{\mathrm {rig}}(\delta _{\psi })$
, for some character
![]() $\delta _{\psi }:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
. If
$\delta _{\psi }:K^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
. If
![]() $\delta _{\psi }$
and
$\delta _{\psi }$
and
![]() $\underline \kappa $
are compatible, we may define
$\underline \kappa $
are compatible, we may define
to be the Zariski closure of the set of maximal points
![]() $x=\{(\rho _x,\underline \delta _x)\}$
, where
$x=\{(\rho _x,\underline \delta _x)\}$
, where
![]() $\rho _x$
is a framed lift of
$\rho _x$
is a framed lift of
![]() $\overline {\rho }$
with determinant
$\overline {\rho }$
with determinant
![]() $\psi $
and
$\psi $
and
![]() $\underline \delta _x\in \mathcal {T}_{\mathrm {reg}}^d(L)$
is a regular parameter of
$\underline \delta _x\in \mathcal {T}_{\mathrm {reg}}^d(L)$
is a regular parameter of
![]() $D_{\mathrm {rig}}(\rho _x)$
such that
$D_{\mathrm {rig}}(\rho _x)$
such that
![]() $\delta _i|_{{\mathscr {O}}_K^{\times }}=\kappa _i$
.
$\delta _i|_{{\mathscr {O}}_K^{\times }}=\kappa _i$
.
In order to study the structure of
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
and
$X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
and
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
, we will need to know something about the essential image of the functor from Galois representations to
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
, we will need to know something about the essential image of the functor from Galois representations to
![]() $(\varphi ,\Gamma )$
-modules. We refer the reader to [Reference BellovinBel23b] for details on definitions of pseudorigid overconvergent period rings and the construction of
$(\varphi ,\Gamma )$
-modules. We refer the reader to [Reference BellovinBel23b] for details on definitions of pseudorigid overconvergent period rings and the construction of
![]() $(\varphi ,\Gamma )$
-modules in the pseudorigid setting. However, we note here that
$(\varphi ,\Gamma )$
-modules in the pseudorigid setting. However, we note here that
![]() $\Lambda _{R,[0,b],K}$
is the coordinate ring of a closed annulus over
$\Lambda _{R,[0,b],K}$
is the coordinate ring of a closed annulus over
![]() $\operatorname {\mathrm {Spa}} R$
,
$\operatorname {\mathrm {Spa}} R$
,
![]() $\Lambda _{R,(0,b],K}$
is the ring of global functions on a half-open annulus over
$\Lambda _{R,(0,b],K}$
is the ring of global functions on a half-open annulus over
![]() $\operatorname {\mathrm {Spa}} R$
, and
$\operatorname {\mathrm {Spa}} R$
, and
![]() $\Lambda _{R,{\mathrm {rig}},K}:=\varprojlim _{b\rightarrow 0}\Lambda _{R,(0,b],K}$
. As in the work of [Reference Cherbonnier and ColmezCC98] and [Reference Berger and ColmezBC08],
$\Lambda _{R,{\mathrm {rig}},K}:=\varprojlim _{b\rightarrow 0}\Lambda _{R,(0,b],K}$
. As in the work of [Reference Cherbonnier and ColmezCC98] and [Reference Berger and ColmezBC08],
![]() $(\varphi ,\Gamma )$
-modules attached to Galois representations are constructed over
$(\varphi ,\Gamma )$
-modules attached to Galois representations are constructed over
![]() $\Lambda _{R,[0,b],K}$
for some
$\Lambda _{R,[0,b],K}$
for some
![]() $b>0$
(which depends in subtle ways on the representation).
$b>0$
(which depends in subtle ways on the representation).
Lemma 2.3.1. The functor
![]() $M\rightsquigarrow D_{\mathrm {rig},K}(M)$
from
$M\rightsquigarrow D_{\mathrm {rig},K}(M)$
from
![]() $\operatorname {\mathrm {Gal}}_K$
-representations to their associated
$\operatorname {\mathrm {Gal}}_K$
-representations to their associated
![]() $(\varphi ,\Gamma )$
-modules is formally smooth.
$(\varphi ,\Gamma )$
-modules is formally smooth.
Proof. We need to show that if D is a projective
![]() $(\varphi ,\Gamma _K)$
-module over a pseudoaffinoid algebra
$(\varphi ,\Gamma _K)$
-module over a pseudoaffinoid algebra
![]() $R'$
, and
$R'$
, and
![]() $I\subset R'$
is a square-zero ideal such that
$I\subset R'$
is a square-zero ideal such that
![]() $(R'/I)\otimes _{R^{\prime }}D$
arises from a family of Galois representations, then D also arises from a family of Galois representations. Indeed, we have a short exact sequence
$(R'/I)\otimes _{R^{\prime }}D$
arises from a family of Galois representations, then D also arises from a family of Galois representations. Indeed, we have a short exact sequence
By assumption,
![]() $D':=(R'/I)\otimes _{R^{\prime }}D$
arises from a family of
$D':=(R'/I)\otimes _{R^{\prime }}D$
arises from a family of
![]() $\operatorname {\mathrm {Gal}}_K$
representations
$\operatorname {\mathrm {Gal}}_K$
representations
![]() $M'$
over
$M'$
over
![]() $R'/I$
, and since
$R'/I$
, and since
it arises from a family of
![]() $\operatorname {\mathrm {Gal}}_K$
representations
$\operatorname {\mathrm {Gal}}_K$
representations
![]() $M"$
over
$M"$
over
![]() $R'/\operatorname {\mathrm {ann}}_{R^{\prime }}I$
. Since D has a model
$R'/\operatorname {\mathrm {ann}}_{R^{\prime }}I$
. Since D has a model
![]() $D_b$
over
$D_b$
over
![]() $\Lambda _{R^{\prime },(0,b],K}$
, we have a commutative diagram
$\Lambda _{R^{\prime },(0,b],K}$
, we have a commutative diagram

By construction,
![]() $\widetilde \Lambda _{R^{\prime },(0,b]}\otimes _{R^{\prime }}D"\cong \widetilde \Lambda _{R^{\prime },(0,b]}\otimes \left (\widetilde \Lambda _{R_0',[0,b]}\otimes _{R_0'}M_0"\right )$
and
$\widetilde \Lambda _{R^{\prime },(0,b]}\otimes _{R^{\prime }}D"\cong \widetilde \Lambda _{R^{\prime },(0,b]}\otimes \left (\widetilde \Lambda _{R_0',[0,b]}\otimes _{R_0'}M_0"\right )$
and
![]() $\widetilde \Lambda _{R^{\prime },(0,b]}\otimes _{R^{\prime }}D'\cong \widetilde \Lambda _{R^{\prime },(0,b]}\otimes \left (\widetilde \Lambda _{R_0',[0,b]}\otimes _{R_0'}M_0'\right )$
, for some integral models
$\widetilde \Lambda _{R^{\prime },(0,b]}\otimes _{R^{\prime }}D'\cong \widetilde \Lambda _{R^{\prime },(0,b]}\otimes \left (\widetilde \Lambda _{R_0',[0,b]}\otimes _{R_0'}M_0'\right )$
, for some integral models
![]() $M_0"$
and
$M_0"$
and
![]() $M_0'$
(perhaps after localizing on
$M_0'$
(perhaps after localizing on
![]() $\operatorname {\mathrm {Spa}} R'$
and shrinking b). Therefore, we have quasi-isomorphisms
$\operatorname {\mathrm {Spa}} R'$
and shrinking b). Therefore, we have quasi-isomorphisms
 $$ \begin{align*} [M"]&\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},[0,b]}\otimes_{R_0'}M_0"\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},[0,b/p]}\otimes_{R_0'}M_0"] \\ &\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},(0,b]}\otimes_{R^{\prime}}D" \xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},(0,b/p]}\otimes_{R^{\prime}}D"] \end{align*} $$
$$ \begin{align*} [M"]&\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},[0,b]}\otimes_{R_0'}M_0"\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},[0,b/p]}\otimes_{R_0'}M_0"] \\ &\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},(0,b]}\otimes_{R^{\prime}}D" \xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},(0,b/p]}\otimes_{R^{\prime}}D"] \end{align*} $$
and
 $$ \begin{align*} [M']&\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},[0,b]}\otimes_{R_0'}M_0'\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},[0,b/p]}\otimes_{R_0'}M_0'] \\ &\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},(0,b]}\otimes_{R^{\prime}}D'\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},(0,b/p]}\otimes_{R^{\prime}}D']. \end{align*} $$
$$ \begin{align*} [M']&\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},[0,b]}\otimes_{R_0'}M_0'\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},[0,b/p]}\otimes_{R_0'}M_0'] \\ &\xrightarrow\sim [\widetilde\Lambda_{R^{\prime},(0,b]}\otimes_{R^{\prime}}D'\xrightarrow{\varphi-1}\widetilde\Lambda_{R^{\prime},(0,b/p]}\otimes_{R^{\prime}}D']. \end{align*} $$
Then the snake lemma implies that we have an exact sequence
of
![]() $R'$
-modules equipped with continuous
$R'$
-modules equipped with continuous
![]() $R'$
-linear actions of
$R'$
-linear actions of
![]() $\operatorname {\mathrm {Gal}}_K$
, with
$\operatorname {\mathrm {Gal}}_K$
, with
![]() $M'$
finite projective over
$M'$
finite projective over
![]() $R'/I$
and
$R'/I$
and
![]() $M"\cong (R'/\operatorname {\mathrm {ann}}_{R^{\prime }}I)\otimes _{R^{\prime }/I}M'$
. It follows that
$M"\cong (R'/\operatorname {\mathrm {ann}}_{R^{\prime }}I)\otimes _{R^{\prime }/I}M'$
. It follows that
![]() $M:=\left (\widetilde \Lambda _{R^{\prime },\mathrm {rig},K}\otimes D\right )^{\varphi =1}$
is a projective
$M:=\left (\widetilde \Lambda _{R^{\prime },\mathrm {rig},K}\otimes D\right )^{\varphi =1}$
is a projective
![]() $R'$
-module of the same rank and
$R'$
-module of the same rank and
![]() $D_{\mathrm {rig},K}(M)=D$
.
$D_{\mathrm {rig},K}(M)=D$
.
In [Reference Breuil, Hellmann and SchraenBHS17, §2.2], the authors show that the characteristic
![]() $0$
locus
$0$
locus
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\mathrm {rig}}$
of the trianguline variety is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\mathrm {rig}}$
of the trianguline variety is equidimensional of dimension
![]() $d^2+[K:{\mathbf {Q}}_p]\frac {d(d+1)}{2}$
, and generically smooth. We note that if
$d^2+[K:{\mathbf {Q}}_p]\frac {d(d+1)}{2}$
, and generically smooth. We note that if
![]() $\psi :\operatorname {\mathrm {Gal}}_K\rightarrow {\mathscr {O}}_E^{\times }$
is a crystalline character, where
$\psi :\operatorname {\mathrm {Gal}}_K\rightarrow {\mathscr {O}}_E^{\times }$
is a crystalline character, where
![]() $E/{\mathbf {Q}}_p$
is a finite extension and
$E/{\mathbf {Q}}_p$
is a finite extension and
![]() ${\mathscr {O}}_E$
is its ring of integers, then an identical argument shows that the rigid analytic locus
${\mathscr {O}}_E$
is its ring of integers, then an identical argument shows that the rigid analytic locus
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\mathrm {rig}}\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi }$
is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\mathrm {rig}}\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi }$
is equidimensional of dimension
![]() $d^2-1+[K:{\mathbf {Q}}_p]\frac {(d+2)(d-1)}{2}$
(indeed, [Reference Böckle, Iyengar and PaškūnasBIP23b, Theorem 1.2] provides the necessary crystalline lifts with fixed determinant).
$d^2-1+[K:{\mathbf {Q}}_p]\frac {(d+2)(d-1)}{2}$
(indeed, [Reference Böckle, Iyengar and PaškūnasBIP23b, Theorem 1.2] provides the necessary crystalline lifts with fixed determinant).
Unfortunately, we cannot rule out components of
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
or
$X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
or
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi }$
supported entirely in characteristic p, and so to deduce the same result in the pseudorigid setting, we need to repeat a large part of the argument in a neighborhood of the characteristic p fiber.
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi }$
supported entirely in characteristic p, and so to deduce the same result in the pseudorigid setting, we need to repeat a large part of the argument in a neighborhood of the characteristic p fiber.
Proposition 2.3.2.
-
1. The space
 $X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(equipped with its underlying reduced structure) is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(equipped with its underlying reduced structure) is equidimensional of dimension
 $d^2+[K:{\mathbf {Q}}_p]\frac {d(d+1)}{2}$
.
$d^2+[K:{\mathbf {Q}}_p]\frac {d(d+1)}{2}$
. -
2. If
 $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
is nonempty, it is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
is nonempty, it is equidimensional of dimension
 $d^2-1+[K:{\mathbf {Q}}_p]\frac {d(d-1)}{2}+\dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
.
$d^2-1+[K:{\mathbf {Q}}_p]\frac {d(d-1)}{2}+\dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
. -
3. There is an open subspace
 $Z\subset \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
such that morphism
$Z\subset \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
such that morphism
 $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }|_Z\rightarrow Z$
is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }|_Z\rightarrow Z$
is equidimensional of dimension
 $d^2-1+[K:{\mathbf {Q}}_p]\frac {d(d-1)}{2}$
.
$d^2-1+[K:{\mathbf {Q}}_p]\frac {d(d-1)}{2}$
.
Proof. The proofs of the first two parts are very similar to that of [Reference Breuil, Hellmann and SchraenBHS17, Théorème 2.6], and we will prove them simultaneously. By construction, there is a universal framed deformation
![]() $\rho _{\mathrm {univ}}:\operatorname {\mathrm {Gal}}_K\rightarrow \operatorname {\mathrm {GL}}_d(R_{\overline {\rho }}^\square )$
of
$\rho _{\mathrm {univ}}:\operatorname {\mathrm {Gal}}_K\rightarrow \operatorname {\mathrm {GL}}_d(R_{\overline {\rho }}^\square )$
of
![]() $\overline {\rho }$
, and we may pull it back to
$\overline {\rho }$
, and we may pull it back to
![]() $X_{\mathrm {{tri}},\overline {\rho }}^\square $
(resp.
$X_{\mathrm {{tri}},\overline {\rho }}^\square $
(resp.
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
). Then for any irreducible open affinoid
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
). Then for any irreducible open affinoid
![]() $X\subset X\rightarrow X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(resp.
$X\subset X\rightarrow X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(resp.
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
), by [Reference BellovinBel23a, Corollary 5.10] there is a sequence of blow-ups and normalizations
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
), by [Reference BellovinBel23a, Corollary 5.10] there is a sequence of blow-ups and normalizations
![]() $f:\widetilde X\rightarrow X$
and an open subspace
$f:\widetilde X\rightarrow X$
and an open subspace
![]() $U\subset \widetilde X$
containing the characteristic p locus such that
$U\subset \widetilde X$
containing the characteristic p locus such that
![]() $f^\ast \rho _{\mathrm {univ}}|_U$
is trianguline with parameters
$f^\ast \rho _{\mathrm {univ}}|_U$
is trianguline with parameters
![]() $f^\ast \underline \delta $
. Shrinking U if necessary, we may assume that
$f^\ast \underline \delta $
. Shrinking U if necessary, we may assume that
![]() $f^\ast \underline \delta $
is regular (indeed, the preimage of
$f^\ast \underline \delta $
is regular (indeed, the preimage of
![]() $\mathcal {T}_{\mathrm {reg}}^d$
in U is open, and by construction U contains a Zariski dense set of points corresponding to trianguline representations with regular parameters). Furthermore, there is a Zariski-dense and open subspace
$\mathcal {T}_{\mathrm {reg}}^d$
in U is open, and by construction U contains a Zariski dense set of points corresponding to trianguline representations with regular parameters). Furthermore, there is a Zariski-dense and open subspace
![]() $V\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(resp.
$V\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
(resp.
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
) such that
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
) such that
![]() $f^{-1}(V)\subset U$
and f defines an isomorphism
$f^{-1}(V)\subset U$
and f defines an isomorphism
![]() $f^{-1}(V)\xrightarrow \sim V$
.
$f^{-1}(V)\xrightarrow \sim V$
.
Over U, the
![]() $(\varphi ,\Gamma _K)$
-module
$(\varphi ,\Gamma _K)$
-module
![]() $D:=D_{\mathrm {rig},K}(f^\ast \rho _{\mathrm {univ}})$
is equipped with an increasing filtration
$D:=D_{\mathrm {rig},K}(f^\ast \rho _{\mathrm {univ}})$
is equipped with an increasing filtration
![]() $\operatorname {\mathrm {Fil}}^{\bullet } D$
such that
$\operatorname {\mathrm {Fil}}^{\bullet } D$
such that
![]() $\operatorname {\mathrm {gr}}^iD\cong \Lambda _{U,\mathrm {rig},K}(f^\ast \delta _i)\otimes \mathscr {L}_i$
for some line bundle
$\operatorname {\mathrm {gr}}^iD\cong \Lambda _{U,\mathrm {rig},K}(f^\ast \delta _i)\otimes \mathscr {L}_i$
for some line bundle
![]() $\mathscr {L}_i$
on U. We may therefore construct a
$\mathscr {L}_i$
on U. We may therefore construct a
![]() ${\mathbf {G}}_{m,U}^d$
-torsor
${\mathbf {G}}_{m,U}^d$
-torsor
![]() $U^\square \rightarrow U$
trivializing each of the
$U^\square \rightarrow U$
trivializing each of the
![]() $\mathscr {L}_i$
; since
$\mathscr {L}_i$
; since
![]() $U^\square $
carries the data
$U^\square $
carries the data
![]() $(D,\operatorname {\mathrm {Fil}}^{\bullet } D, f^\ast \underline \delta , \underline \nu )$
, where
$(D,\operatorname {\mathrm {Fil}}^{\bullet } D, f^\ast \underline \delta , \underline \nu )$
, where
![]() $\underline \nu $
is the set of trivializations
$\underline \nu $
is the set of trivializations
![]() $\nu _i:\operatorname {\mathrm {gr}}^iD\xrightarrow \sim \Lambda _{U,\mathrm {rig},K}(f^\ast \delta _i)$
, there is a morphism
$\nu _i:\operatorname {\mathrm {gr}}^iD\xrightarrow \sim \Lambda _{U,\mathrm {rig},K}(f^\ast \delta _i)$
, there is a morphism
![]() $U^\square \rightarrow \mathcal {S}_d^\square $
.
$U^\square \rightarrow \mathcal {S}_d^\square $
.
Let
![]() $V^\square \subset U^\square $
denote the pullback of
$V^\square \subset U^\square $
denote the pullback of
![]() $U^\square \rightarrow U$
to V. We claim that
$U^\square \rightarrow U$
to V. We claim that
![]() $V^\square \rightarrow \mathcal {S}_d^\square $
is smooth of relative dimension
$V^\square \rightarrow \mathcal {S}_d^\square $
is smooth of relative dimension
![]() $d^2$
. To see this, suppose we have a pseudoaffinoid algebra
$d^2$
. To see this, suppose we have a pseudoaffinoid algebra
![]() $R'$
, a morphism
$R'$
, a morphism
![]() $\operatorname {\mathrm {Spa}} R'\rightarrow \mathcal {S}_d^\square $
and a square-zero ideal
$\operatorname {\mathrm {Spa}} R'\rightarrow \mathcal {S}_d^\square $
and a square-zero ideal
![]() $I\subset R'$
such that the composition
$I\subset R'$
such that the composition
![]() $\operatorname {\mathrm {Spa}} R'/I\hookrightarrow \operatorname {\mathrm {Spa}} R'\rightarrow \mathcal {S}_d^\square $
is in the image of
$\operatorname {\mathrm {Spa}} R'/I\hookrightarrow \operatorname {\mathrm {Spa}} R'\rightarrow \mathcal {S}_d^\square $
is in the image of
![]() $V^\square $
. Then there is a ring of definition
$V^\square $
. Then there is a ring of definition
![]() $R_0'\subset R'/I$
such that the homomorphism
$R_0'\subset R'/I$
such that the homomorphism
![]() $R_{\overline {\rho }}^\square \rightarrow R'/I$
factors through
$R_{\overline {\rho }}^\square \rightarrow R'/I$
factors through
![]() $R_0'$
; we let
$R_0'$
; we let
![]() $M_0'\cong R_0^{\prime \oplus d}$
be the pullback of the universal framed deformation to
$M_0'\cong R_0^{\prime \oplus d}$
be the pullback of the universal framed deformation to
![]() $R_0'$
and we let
$R_0'$
and we let
![]() $M':=R'/I\otimes _{R_0'}M_0'$
.
$M':=R'/I\otimes _{R_0'}M_0'$
.
By Lemma 2.3.1, there is a
![]() $\operatorname {\mathrm {Gal}}_K$
-representation M over
$\operatorname {\mathrm {Gal}}_K$
-representation M over
![]() $R'$
such that
$R'$
such that
![]() $(R'/I)\otimes _{R^{\prime }}M\xrightarrow {\sim }M'$
. It follows that
$(R'/I)\otimes _{R^{\prime }}M\xrightarrow {\sim }M'$
. It follows that
![]() $M_0'$
and its basis lift to a free module
$M_0'$
and its basis lift to a free module
![]() $M_0$
over some ring of definition
$M_0$
over some ring of definition
![]() $R_0'\subset R'$
such that
$R_0'\subset R'$
such that
![]() $R'\otimes _{R_0'}M_0=M$
. Moreover,
$R'\otimes _{R_0'}M_0=M$
. Moreover,
![]() $M'$
is residually a lift of
$M'$
is residually a lift of
![]() $\overline {\rho }$
at every maximal point of
$\overline {\rho }$
at every maximal point of
![]() $\operatorname {\mathrm {Spa}} R'$
, so M is as well. By [Reference Wang-EricksonWE18, Theorem 3.8],
$\operatorname {\mathrm {Spa}} R'$
, so M is as well. By [Reference Wang-EricksonWE18, Theorem 3.8],
![]() $M_0$
corresponds to a
$M_0$
corresponds to a
![]() $\operatorname {\mathrm {Spa}} R_0'$
-point of
$\operatorname {\mathrm {Spa}} R_0'$
-point of
![]() $\operatorname {\mathrm {Spf}} R_{\overline {\rho }}^\square $
, and by construction M corresponds to a
$\operatorname {\mathrm {Spf}} R_{\overline {\rho }}^\square $
, and by construction M corresponds to a
![]() $\operatorname {\mathrm {Spa}} R'$
-point of
$\operatorname {\mathrm {Spa}} R'$
-point of
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
deforming
$X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
deforming
![]() $M'$
. Since
$M'$
. Since
![]() $M'$
corresponds to a
$M'$
corresponds to a
![]() $\operatorname {\mathrm {Spa}} (R'/I)$
-point of the Zariski-open subspace
$\operatorname {\mathrm {Spa}} (R'/I)$
-point of the Zariski-open subspace
![]() $V\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
, the image of the morphism
$V\subset X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
, the image of the morphism
![]() $\operatorname {\mathrm {Spa}} R'\rightarrow X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
also lands in V. Since D is trianguline with regular parameters and trivialized quotients, the morphism
$\operatorname {\mathrm {Spa}} R'\rightarrow X_{\mathrm {{tri}},\overline {\rho }}^{\square }$
also lands in V. Since D is trianguline with regular parameters and trivialized quotients, the morphism
![]() $\operatorname {\mathrm {Spa}} R'\rightarrow V$
lifts to a morphism
$\operatorname {\mathrm {Spa}} R'\rightarrow V$
lifts to a morphism
![]() $\operatorname {\mathrm {Spa}} R'\rightarrow V^\square $
.
$\operatorname {\mathrm {Spa}} R'\rightarrow V^\square $
.
The claim that
![]() $V^\square \rightarrow \mathcal {S}_d^\square $
has relative dimension
$V^\square \rightarrow \mathcal {S}_d^\square $
has relative dimension
![]() $d^2$
follows because ‘changing the framing’ makes
$d^2$
follows because ‘changing the framing’ makes
![]() $V^\square $
a
$V^\square $
a
![]() $\left (\operatorname {\mathrm {GL}}_d\right )^{\mathrm {{an}}}$
-torsor over its image in
$\left (\operatorname {\mathrm {GL}}_d\right )^{\mathrm {{an}}}$
-torsor over its image in
![]() $\mathcal {S}_d^\square $
.
$\mathcal {S}_d^\square $
.
Now, we can compute the dimension. By Proposition 2.2.7, we see that
![]() $V^\square $
is equidimensional of dimension
$V^\square $
is equidimensional of dimension
![]() $d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] + d$
(resp.
$d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] + d$
(resp.
![]() $d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] + d + \dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
). Since
$d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] + d + \dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
). Since
![]() $V^\square \rightarrow V$
is a
$V^\square \rightarrow V$
is a
![]() ${\mathbf {G}}_{m,V}^d$
-torsor, it follows that V is equidimensional of dimension
${\mathbf {G}}_{m,V}^d$
-torsor, it follows that V is equidimensional of dimension
![]() $d^2+\frac {d(d+1)}{2}[K:{\mathbf {Q}}_p]$
(resp.
$d^2+\frac {d(d+1)}{2}[K:{\mathbf {Q}}_p]$
(resp.
![]() $d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] +\dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
. Finally,
$d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p] +\dim \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
. Finally,
![]() $V\subset X$
is Zariski-dense, so we are done.
$V\subset X$
is Zariski-dense, so we are done.
For the last part, we define
![]() $V^{\square ,\psi ,\underline \kappa }$
via the pullback
$V^{\square ,\psi ,\underline \kappa }$
via the pullback

where
![]() $Y:=\widehat {({\mathscr {O}}_K^{\times })^d}$
and the morphism
$Y:=\widehat {({\mathscr {O}}_K^{\times })^d}$
and the morphism
![]() $\operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}\rightarrow {\mathbf {G}}_{m,Y}$
is given by
$\operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}\rightarrow {\mathbf {G}}_{m,Y}$
is given by
![]() $\underline \kappa $
and
$\underline \kappa $
and
![]() $\delta _\psi $
. Since
$\delta _\psi $
. Since
![]() $V^\square \rightarrow {\mathbf {G}}_{m,Y}$
is smooth, its image is open, and the preimage in
$V^\square \rightarrow {\mathbf {G}}_{m,Y}$
is smooth, its image is open, and the preimage in
![]() $\operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is open, as well.
$\operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is open, as well.
Remark 2.3.3. Suppose that
![]() $x\in \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is a maximal point such that the fiber of
$x\in \operatorname {\mathrm {Spa}} R^{\mathrm {{an}}}$
is a maximal point such that the fiber of
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
contains a point
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
contains a point
![]() $(\rho _x,\underline \delta _x)$
such that
$(\rho _x,\underline \delta _x)$
such that
![]() $\underline \delta _x$
is a regular parameter for
$\underline \delta _x$
is a regular parameter for
![]() $D_{\mathrm {rig}}(\rho _x)$
. Then if we apply Proposition 2.3.2 with
$D_{\mathrm {rig}}(\rho _x)$
. Then if we apply Proposition 2.3.2 with
![]() $R=k(x)^+$
, we see that every irreducible component of the fiber containing
$R=k(x)^+$
, we see that every irreducible component of the fiber containing
![]() $(\rho _x,\underline \delta _x)$
has dimension
$(\rho _x,\underline \delta _x)$
has dimension
![]() $d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p]$
.
$d^2 + \frac {d(d-1)}{2}[K:{\mathbf {Q}}_p] + d[K:{\mathbf {Q}}_p]$
.
Example 2.3.4. We return to the setting of Example 2.2.9, where
![]() $K={\mathbf {Q}}_p$
,
$K={\mathbf {Q}}_p$
,
![]() $d=2$
,
$d=2$
,
![]() $R={\mathbf {Z}}_p[\![T_0]\!]$
corresponds to integral weight space for a split maximal torus of
$R={\mathbf {Z}}_p[\![T_0]\!]$
corresponds to integral weight space for a split maximal torus of
![]() $\operatorname {\mathrm {GL}}_2/{\mathbf {Z}}_p$
,
$\operatorname {\mathrm {GL}}_2/{\mathbf {Z}}_p$
,
![]() $\psi _0:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}\rightarrow R^{\times }$
is an unramified character, and there is a universal pair of characters
$\psi _0:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}\rightarrow R^{\times }$
is an unramified character, and there is a universal pair of characters
![]() $\lambda _1,\lambda _2:{\mathbf {Z}}_p^{\times }\rightrightarrows R^{\times }$
. We again set
$\lambda _1,\lambda _2:{\mathbf {Z}}_p^{\times }\rightrightarrows R^{\times }$
. We again set
![]() $\psi :=\psi _0\left ( \lambda _1\lambda _2 \chi _{\mathrm {{cyc}}}\right )^{-1}$
and
$\psi :=\psi _0\left ( \lambda _1\lambda _2 \chi _{\mathrm {{cyc}}}\right )^{-1}$
and
![]() $\underline \kappa :(\lambda _2^{-1},\left (\lambda _1\chi _{\mathrm {{cyc}}}\right )^{-1})$
. Then if
$\underline \kappa :(\lambda _2^{-1},\left (\lambda _1\chi _{\mathrm {{cyc}}}\right )^{-1})$
. Then if
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
is nonempty, each irreducible component is six-dimensional.
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
is nonempty, each irreducible component is six-dimensional.
Moreover, suppose there is a characteristic-p point
![]() $(\rho _x,\underline \delta _x)$
with specified weight and determinant such that
$(\rho _x,\underline \delta _x)$
with specified weight and determinant such that
![]() $\rho _x$
is trianguline with regular parameter
$\rho _x$
is trianguline with regular parameter
![]() $\delta _x$
. Then the fiber over
$\delta _x$
. Then the fiber over
![]() $\underline \delta _x|_{({\mathbf {Z}}_p^{\times })^2}$
is four-dimensional; since this is one of
$\underline \delta _x|_{({\mathbf {Z}}_p^{\times })^2}$
is four-dimensional; since this is one of
![]() $p-1$
disjoint characteristic-p fibers, we see that the irreducible component containing
$p-1$
disjoint characteristic-p fibers, we see that the irreducible component containing
![]() $(\rho _x,\underline \delta _x)$
contains a dense open characteristic-
$(\rho _x,\underline \delta _x)$
contains a dense open characteristic-
![]() $0$
subspace, consisting of points in
$0$
subspace, consisting of points in
![]() $U_{\mathrm {{tri}}}^\square (\overline {\rho })^{\mathrm {reg}}$
(in the notation of [Reference Breuil, Hellmann and SchraenBHS17, Définition 2.4]).
$U_{\mathrm {{tri}}}^\square (\overline {\rho })^{\mathrm {reg}}$
(in the notation of [Reference Breuil, Hellmann and SchraenBHS17, Définition 2.4]).
Now, we consider a global setup. Let F be a number field, and suppose that
![]() $\overline {\rho }:\operatorname {\mathrm {Gal}}_{F}\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
is an absolutely irreducible representation, unramified outside a finite set of primes S.
$\overline {\rho }:\operatorname {\mathrm {Gal}}_{F}\rightarrow \operatorname {\mathrm {GL}}_d({\mathbf {F}})$
is an absolutely irreducible representation, unramified outside a finite set of primes S.
Then the homomorphisms
for each
![]() $v\mid p$
induce a morphism
$v\mid p$
induce a morphism
 $$\begin{align*}\left(\operatorname{\mathrm{Spa}} R_{\overline{\rho},S}^\square\right)^{\mathrm{{an}}}\times \prod_{v\mid p}\mathcal{T}^d\rightarrow \prod_{v\mid p}\left(\left(\operatorname{\mathrm{Spa}} R_{\overline{\rho}_v}^\square\right)^{\mathrm{{an}}}\times\mathcal{T}^d\right) \end{align*}$$
$$\begin{align*}\left(\operatorname{\mathrm{Spa}} R_{\overline{\rho},S}^\square\right)^{\mathrm{{an}}}\times \prod_{v\mid p}\mathcal{T}^d\rightarrow \prod_{v\mid p}\left(\left(\operatorname{\mathrm{Spa}} R_{\overline{\rho}_v}^\square\right)^{\mathrm{{an}}}\times\mathcal{T}^d\right) \end{align*}$$
and we define
![]() $X_{\mathrm {{tri}},\overline {\rho },S}^\square $
to be the preimage of
$X_{\mathrm {{tri}},\overline {\rho },S}^\square $
to be the preimage of
![]() $\prod _{v\mid p}X_{\mathrm {{tri}},\overline {\rho }_v}^\square $
.
$\prod _{v\mid p}X_{\mathrm {{tri}},\overline {\rho }_v}^\square $
.
If R is a complete local Noetherian
![]() ${\mathbf {Z}}_p$
-algebra with maximal ideal
${\mathbf {Z}}_p$
-algebra with maximal ideal
![]() $\mathfrak {m}_R$
and finite residue field, and
$\mathfrak {m}_R$
and finite residue field, and
![]() $\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
is a continuous character such that
$\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
is a continuous character such that
![]() $\det \overline {\rho } = \psi \mod \mathfrak {m}_R$
, the homomorphisms
$\det \overline {\rho } = \psi \mod \mathfrak {m}_R$
, the homomorphisms
and
induce a sequence of morphisms
where
![]() $\psi _v:=\psi |_{\operatorname {\mathrm {Gal}}_{F_v}}$
. We define
$\psi _v:=\psi |_{\operatorname {\mathrm {Gal}}_{F_v}}$
. We define
![]() $X_{\mathrm {{tri}},\overline {\rho },S}^{\square ,\psi }$
and
$X_{\mathrm {{tri}},\overline {\rho },S}^{\square ,\psi }$
and
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
to be the preimages of
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi }$
to be the preimages of
![]() $\prod _{v\mid p}X_{\mathrm {{tri}},\overline {\rho }_v}^{\square ,\psi _v}$
in
$\prod _{v\mid p}X_{\mathrm {{tri}},\overline {\rho }_v}^{\square ,\psi _v}$
in
![]() $\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho },S}^{\square ,\psi }\right )^{\mathrm {{an}}}\times \prod _{v\mid p}\mathcal {T}^d$
and
$\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho },S}^{\square ,\psi }\right )^{\mathrm {{an}}}\times \prod _{v\mid p}\mathcal {T}^d$
and
![]() $\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }\right )^{\mathrm {{an}}}\times \prod _{v\mid p}\mathcal {T}^d$
, respectively.
$\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi }\right )^{\mathrm {{an}}}\times \prod _{v\mid p}\mathcal {T}^d$
, respectively.
If we additionally have d-tuples of characters
![]() $\underline \kappa _v:=(\kappa _{v,1},\ldots ,\kappa _{v,d})$
, where
$\underline \kappa _v:=(\kappa _{v,1},\ldots ,\kappa _{v,d})$
, where
![]() $\kappa _{v,i}:{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is a continuous character, and we set
$\kappa _{v,i}:{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathscr {O}}(X)^{\times }$
is a continuous character, and we set
![]() $X:=\left (\operatorname {\mathrm {Spa}} R\right )^{\mathrm {{an}}}$
, we may form the spaces
$X:=\left (\operatorname {\mathrm {Spa}} R\right )^{\mathrm {{an}}}$
, we may form the spaces

In particular, suppose we have fixed a neat level
![]() $K=K^pI$
, as in Sections 3 and 4, and consider the ring
$K=K^pI$
, as in Sections 3 and 4, and consider the ring
![]() $R={\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]$
corresponding to integral weight space. Since
$R={\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]$
corresponding to integral weight space. Since
![]() $T_0=\prod _{v\mid p}(\operatorname {\mathrm {Res}}_{{\mathscr {O}}_{F_v}/{\mathbf {Z}}_p}T_v)({\mathbf {Z}}_p)$
, we have homomorphisms
$T_0=\prod _{v\mid p}(\operatorname {\mathrm {Res}}_{{\mathscr {O}}_{F_v}/{\mathbf {Z}}_p}T_v)({\mathbf {Z}}_p)$
, we have homomorphisms
![]() ${\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\rightarrow R$
, and hence morphisms
${\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\rightarrow R$
, and hence morphisms
![]() $\operatorname {\mathrm {Spa}} R\rightarrow \operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]$
. Suppose we have a determinant character
$\operatorname {\mathrm {Spa}} R\rightarrow \operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]$
. Suppose we have a determinant character
![]() $\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
, and a set of weights
$\psi :\operatorname {\mathrm {Gal}}_F\rightarrow R^{\times }$
, and a set of weights
![]() $\underline \kappa _v:=(\kappa _{v,1},\ldots ,\kappa _{v,d}):{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
for each
$\underline \kappa _v:=(\kappa _{v,1},\ldots ,\kappa _{v,d}):{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
for each
![]() $v\mid p$
such that
$v\mid p$
such that
![]() $\psi |_{\operatorname {\mathrm {Gal}}_{F_v}}$
and
$\psi |_{\operatorname {\mathrm {Gal}}_{F_v}}$
and
![]() $\underline \kappa _v$
are compatible for all v and such that
$\underline \kappa _v$
are compatible for all v and such that
![]() $\psi _v$
and
$\psi _v$
and
![]() $\underline \kappa _v$
factor through
$\underline \kappa _v$
factor through
![]() ${\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\rightarrow R$
for all v, that is, they depend only on the projection to
${\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\rightarrow R$
for all v, that is, they depend only on the projection to
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]$
.
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]$
.
Proposition 2.3.5. Under the above assumptions, there is an open subspace
![]() $Z\subset \mathscr {W}_F$
such that
$Z\subset \mathscr {W}_F$
such that
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }|_Z\rightarrow Z$
is equidimensional of dimension
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }|_Z\rightarrow Z$
is equidimensional of dimension
![]() $\lvert \Sigma _p\rvert (d^2-1)+[F:{\mathbf {Q}}]\frac {d(d-1)}{2}$
.
$\lvert \Sigma _p\rvert (d^2-1)+[F:{\mathbf {Q}}]\frac {d(d-1)}{2}$
.
Proof. Viewing
![]() $\psi _v$
as a character
$\psi _v$
as a character
![]() $\operatorname {\mathrm {Gal}}_{F_v}\rightarrow {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\times }$
and viewing
$\operatorname {\mathrm {Gal}}_{F_v}\rightarrow {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\times }$
and viewing
![]() $\underline \kappa _v=(\kappa _{v,1},\ldots ,\kappa _{v,d})$
as a d-tuple of characters
$\underline \kappa _v=(\kappa _{v,1},\ldots ,\kappa _{v,d})$
as a d-tuple of characters
![]() ${\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\times }$
, we have a pullback diagram
${\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\times }$
, we have a pullback diagram

The right vertical morphism has relative dimension
 $$\begin{align*}\sum_{v\mid p}\left(d^2-1 + [F_v:{\mathbf{Q}}_p]\frac{d(d-1)}{2}\right) = \lvert\Sigma_p\rvert(d^2-1)+[F:{\mathbf{Q}}]\frac{d(d-1)}{2} \end{align*}$$
$$\begin{align*}\sum_{v\mid p}\left(d^2-1 + [F_v:{\mathbf{Q}}_p]\frac{d(d-1)}{2}\right) = \lvert\Sigma_p\rvert(d^2-1)+[F:{\mathbf{Q}}]\frac{d(d-1)}{2} \end{align*}$$
over an open subspace of
![]() $\prod _{v\mid p}\left (\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\right )^{\mathrm {{an}}}$
, so the morphism
$\prod _{v\mid p}\left (\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]\right )^{\mathrm {{an}}}$
, so the morphism
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }\rightarrow \mathscr {W}_F$
does, as well.
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }\rightarrow \mathscr {W}_F$
does, as well.
The case we will be most interested in is the case where
![]() $F/{\mathbf {Q}}$
is cyclic and totally split at p, and
$F/{\mathbf {Q}}$
is cyclic and totally split at p, and
![]() $d=2$
. In that case,
$d=2$
. In that case,
![]() $X_{\mathrm {{tri}},\overline {\rho }_v}^{\square ,\psi _v,\underline \kappa _v}\rightarrow \operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\mathrm {{an}}}$
has relative dimension
$X_{\mathrm {{tri}},\overline {\rho }_v}^{\square ,\psi _v,\underline \kappa _v}\rightarrow \operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\mathrm {{an}}}$
has relative dimension
![]() $4$
over an open subspace of
$4$
over an open subspace of
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\mathrm {{an}}}$
for each
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![T_v({\mathscr {O}}_{F_v})]\!]^{\mathrm {{an}}}$
for each
![]() $v\mid p$
, and hence
$v\mid p$
, and hence
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }\rightarrow \mathscr {W}_F$
has relative dimension
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ,\underline \kappa }\rightarrow \mathscr {W}_F$
has relative dimension
![]() $4[F:{\mathbf {Q}}]$
over an open subspace of
$4[F:{\mathbf {Q}}]$
over an open subspace of
![]() $\mathscr {W}_F$
.
$\mathscr {W}_F$
.
2.4 Trianguline deformation rings
We have constructed the trianguline varieties
![]() $X_{\mathrm {{tri}},\overline {\rho }}^\square $
and
$X_{\mathrm {{tri}},\overline {\rho }}^\square $
and
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
as subspaces of the (nonquasicompact) pseudorigid space
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
as subspaces of the (nonquasicompact) pseudorigid space
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}},d}{\times }_{{\mathbf {Z}}}\widehat {({\mathscr {O}}_K^{\times })^d}\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
. However, the advantage of working with general pseudorigid spaces is that we can construct integral models, so long as we bound the slope.
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}},d}{\times }_{{\mathbf {Z}}}\widehat {({\mathscr {O}}_K^{\times })^d}\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
. However, the advantage of working with general pseudorigid spaces is that we can construct integral models, so long as we bound the slope.
We will apply this to find formal models for pieces of our trianguline varieties. Recall that, when K is a finite extension of
![]() ${\mathbf {Q}}_p$
and
${\mathbf {Q}}_p$
and
![]() $\overline {\rho }$
is a representation of
$\overline {\rho }$
is a representation of
![]() $\operatorname {\mathrm {Gal}}_K$
, we defined
$\operatorname {\mathrm {Gal}}_K$
, we defined
![]() $X_{\mathrm {{tri}},\overline {\rho }}^\square $
and
$X_{\mathrm {{tri}},\overline {\rho }}^\square $
and
![]() $X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
as analytic subspaces of
$X_{\mathrm {{tri}},\overline {\rho }}^{\square ,\psi ,\underline \kappa }$
as analytic subspaces of
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
and
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
and
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
, respectively. By construction,
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
, respectively. By construction,
![]() $\operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
has a quasicompact integral model, but
$\operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
has a quasicompact integral model, but
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
does not; in particular, it is not equal to the analytic locus of
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}\times \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
does not; in particular, it is not equal to the analytic locus of
![]() $\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\left \langle T,T^{-1}\right \rangle $
(and similarly for
$\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^{\square }\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\left \langle T,T^{-1}\right \rangle $
(and similarly for
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
).
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]\times \left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^{\square }\right )^{\mathrm {{an}}}$
).
In order to construct integral models of annuli, we begin with an illustrative example.
Example 2.4.1. Suppose
![]() $R={\mathbf {Z}}_p[\![u]\!]$
and h is an integer. We may cover
$R={\mathbf {Z}}_p[\![u]\!]$
and h is an integer. We may cover
![]() $Y:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![u]\!]\right )^{\mathrm {{an}}}$
with the open affinoid subspaces
$Y:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![u]\!]\right )^{\mathrm {{an}}}$
with the open affinoid subspaces
![]() $U_1:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Q}}_p\left \langle \frac u p\right \rangle \right )$
and
$U_1:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Q}}_p\left \langle \frac u p\right \rangle \right )$
and
![]() $U_2:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![u]\!]\left \langle \frac p u\right \rangle \left [\frac 1 u\right ]\right )$
; their intersection is the circle
$U_2:=\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![u]\!]\left \langle \frac p u\right \rangle \left [\frac 1 u\right ]\right )$
; their intersection is the circle
![]() $U_1\cap U_2=\operatorname {\mathrm {Spa}}\left ({\mathbf {Q}}_p\left \langle \frac u p, \frac p u\right \rangle \right )$
.
$U_1\cap U_2=\operatorname {\mathrm {Spa}}\left ({\mathbf {Q}}_p\left \langle \frac u p, \frac p u\right \rangle \right )$
.
The annulus
![]() $C_{U_1,h}$
is affinoid, with coordinate ring
$C_{U_1,h}$
is affinoid, with coordinate ring
 $$\begin{align*}{\mathbf{Q}}_p\left\langle \frac u p,p^hT,T_2\right\rangle/(TT_2-p^h) = {\mathbf{Q}}_p\left\langle \frac u p,T,T_1,T_2\right\rangle/(T_1-p^hT,TT_2-p^h). \end{align*}$$
$$\begin{align*}{\mathbf{Q}}_p\left\langle \frac u p,p^hT,T_2\right\rangle/(TT_2-p^h) = {\mathbf{Q}}_p\left\langle \frac u p,T,T_1,T_2\right\rangle/(T_1-p^hT,TT_2-p^h). \end{align*}$$
Restricting to
![]() $U_1\cap U_2$
, we obtain an affinoid with coordinate ring
$U_1\cap U_2$
, we obtain an affinoid with coordinate ring
 $$\begin{align*}{\mathbf{Z}}_p[\![u]\!]\left\langle \frac u p,\frac p u,T,T_1,T_2\right\rangle\left[\frac 1 u\right]/(T_1-u^h\left(\frac p u\right)^hT,TT_2-u^h\left(\frac p u\right)^h). \end{align*}$$
$$\begin{align*}{\mathbf{Z}}_p[\![u]\!]\left\langle \frac u p,\frac p u,T,T_1,T_2\right\rangle\left[\frac 1 u\right]/(T_1-u^h\left(\frac p u\right)^hT,TT_2-u^h\left(\frac p u\right)^h). \end{align*}$$
Writing
![]() $T_1':=\left (\frac u p\right )^hT_1$
and
$T_1':=\left (\frac u p\right )^hT_1$
and
![]() $T_2':=\left (\frac u p\right )^hT_2$
, we get
$T_2':=\left (\frac u p\right )^hT_2$
, we get
 $$\begin{align*}{\mathbf{Z}}_p[\![u]\!]\left\langle \frac u p,\frac p u,T,T_1',T_2'\right\rangle\left[\frac 1 u\right]/(T_1'-u^hT,TT_2'-u^h) \end{align*}$$
$$\begin{align*}{\mathbf{Z}}_p[\![u]\!]\left\langle \frac u p,\frac p u,T,T_1',T_2'\right\rangle\left[\frac 1 u\right]/(T_1'-u^hT,TT_2'-u^h) \end{align*}$$
which is also the restriction of
![]() $C_{U_2,h}$
to
$C_{U_2,h}$
to
![]() $U_1\cap U_2$
.
$U_1\cap U_2$
.
The affinoid spaces
![]() $C_{U_i,h}$
and
$C_{U_i,h}$
and
![]() $C_{U_1\cap U_2,h}$
have integral models, compatible with gluing. Thus, we see that
$C_{U_1\cap U_2,h}$
have integral models, compatible with gluing. Thus, we see that
![]() $C_{Y,h}$
in this case admits a formal model which lives over the blow-up
$C_{Y,h}$
in this case admits a formal model which lives over the blow-up
![]() $\mathrm {Bl}_{(p,u)}R$
.
$\mathrm {Bl}_{(p,u)}R$
.
Returning to the general case, we may choose a
![]() ${\mathbf {Z}}_p$
-basis for the torsion-free part of
${\mathbf {Z}}_p$
-basis for the torsion-free part of
![]() ${\mathscr {O}}_K^{\times }$
and corresponding coordinates on
${\mathscr {O}}_K^{\times }$
and corresponding coordinates on
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
. Then we may consider relative annuli over
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
. Then we may consider relative annuli over
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![\widehat {{\mathscr {O}}_K^{\times }}]\!]$
; as above, these annuli glue to a space
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![\widehat {{\mathscr {O}}_K^{\times }}]\!]$
; as above, these annuli glue to a space
![]() $\mathcal {T}_h$
which has an integral model
$\mathcal {T}_h$
which has an integral model
![]() $\mathfrak {T}_h$
over the blow-up
$\mathfrak {T}_h$
over the blow-up
![]() $\mathrm {Bl}_I{\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]$
(where
$\mathrm {Bl}_I{\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]$
(where
![]() $I=\cap \mathfrak {m}$
is the intersection of the maximal ideals of
$I=\cap \mathfrak {m}$
is the intersection of the maximal ideals of
![]() ${\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]$
). Similarly, given some integer
${\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]$
). Similarly, given some integer
![]() $d\geq 1$
, we may define relative annuli
$d\geq 1$
, we may define relative annuli
![]() $\mathcal {T}_h^d\subset \mathcal {T}^d$
over
$\mathcal {T}_h^d\subset \mathcal {T}^d$
over
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]^{\mathrm {{an}}}$
, which have integral models
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathscr {O}}_K^{\times })^d]\!]^{\mathrm {{an}}}$
, which have integral models
![]() $\mathfrak {T}_h^d$
.
$\mathfrak {T}_h^d$
.
Now, we may set
and
When F is a totally real field and
![]() $\overline {\rho }$
is a representation of
$\overline {\rho }$
is a representation of
![]() $\operatorname {\mathrm {Gal}}_F$
unramified outside a finite set of places S, we may similarly define bounded global trianguline varieties
$\operatorname {\mathrm {Gal}}_F$
unramified outside a finite set of places S, we may similarly define bounded global trianguline varieties
![]() $X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^\square $
and
$X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^\square $
and
![]() $X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
as subspaces of
$X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
as subspaces of
![]() $\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \times \prod _{v\mid p}\mathcal {T}_h^d\right )^{\mathrm {{an}}}$
and
$\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \times \prod _{v\mid p}\mathcal {T}_h^d\right )^{\mathrm {{an}}}$
and
![]() $\left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^\square \times \prod _{v\mid p}\mathcal {T}_h^d\right )^{\mathrm {{an}}}$
, respectively.
$\left (\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{\overline {\rho }}^\square \times \prod _{v\mid p}\mathcal {T}_h^d\right )^{\mathrm {{an}}}$
, respectively.
Remark 2.4.2. We emphasize that these bounded trianguline varieties are not canonical; they depend on a choice of coordinates on
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
. This may seem strange, but we will use our bounded trianguline varieties to study bounded-slope pieces of eigenvarieties, and the construction of these pieces of eigenvarieties also depends on a choice of pseudouniformizer in the coefficients.
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![{\mathscr {O}}_K^{\times }]\!]^{\mathrm {{an}}}$
. This may seem strange, but we will use our bounded trianguline varieties to study bounded-slope pieces of eigenvarieties, and the construction of these pieces of eigenvarieties also depends on a choice of pseudouniformizer in the coefficients.
Remark 2.4.3. For our purposes, we in fact only need to consider relative annuli and bounded trianguline varieties over some affinoid subspace U of weight space. Nevertheless, for the sake of completeness we treat them here over all of weight space.
Now, we restrict to the case
![]() $K={\mathbf {Q}}_p$
, and we choose coordinates
$K={\mathbf {Q}}_p$
, and we choose coordinates
![]() $z_1,\ldots ,z_d$
on each component of
$z_1,\ldots ,z_d$
on each component of
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]^{\mathrm {{an}}}$
. Write
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]^{\mathrm {{an}}}$
. Write
![]() $h=a/b$
, where
$h=a/b$
, where
![]() $a,b$
are nonnegative relatively prime integers. We will construct an integral model of
$a,b$
are nonnegative relatively prime integers. We will construct an integral model of
![]() $X_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }$
using Corollary A.0.2.
$X_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }$
using Corollary A.0.2.
For
![]() $z\in \{p,z_1,\ldots ,z_d\}$
, we get an affinoid
$z\in \{p,z_1,\ldots ,z_d\}$
, we get an affinoid
![]() $U_z:=\operatorname {\mathrm {Spa}} R_z$
, where
$U_z:=\operatorname {\mathrm {Spa}} R_z$
, where
![]() $R_z:={\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]\left \langle \frac {p}{z},\frac {z_1}{z},\ldots ,\frac {z_d}{z}\right \rangle \left [\frac 1 z\right ]$
with ring of integers
$R_z:={\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]\left \langle \frac {p}{z},\frac {z_1}{z},\ldots ,\frac {z_d}{z}\right \rangle \left [\frac 1 z\right ]$
with ring of integers
![]() $R_{z,0}$
, inside
$R_{z,0}$
, inside
![]() $\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]^{\mathrm {{an}}}$
. Then the restriction of
$\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![({\mathbf {Z}}_p^{\times })^{d}]\!]^{\mathrm {{an}}}$
. Then the restriction of
![]() $\mathcal {T}_h^d$
to
$\mathcal {T}_h^d$
to
![]() $U_z$
has the presentation
$U_z$
has the presentation
 $$\begin{align*}\operatorname{\mathrm{Spa}} {\mathbf{Z}}_p[\![({\mathbf{Z}}_p^{\times})^{d}]\!]\left\langle \frac{p}{z},\frac{z_1}{z},\ldots,\frac{z_d}{z}, z^aT_1^{\pm b},\ldots, z^aT_d^{\pm b}\right\rangle\left[\frac 1 z\right]. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spa}} {\mathbf{Z}}_p[\![({\mathbf{Z}}_p^{\times})^{d}]\!]\left\langle \frac{p}{z},\frac{z_1}{z},\ldots,\frac{z_d}{z}, z^aT_1^{\pm b},\ldots, z^aT_d^{\pm b}\right\rangle\left[\frac 1 z\right]. \end{align*}$$
Over this space, there is a d-tuple
![]() $\delta _1,\ldots ,\delta _d:{\mathbf {Q}}_p^{\times }\rightrightarrows R_z^{\times }$
, where
$\delta _1,\ldots ,\delta _d:{\mathbf {Q}}_p^{\times }\rightrightarrows R_z^{\times }$
, where
![]() $\delta _i(p)=T_i$
and
$\delta _i(p)=T_i$
and
![]() $(\delta _i|_{{\mathbf {Z}}_p^{\times }})$
is the restriction of the universal character on
$(\delta _i|_{{\mathbf {Z}}_p^{\times }})$
is the restriction of the universal character on
![]() $({\mathbf {Z}}_p^{\times })^d$
.
$({\mathbf {Z}}_p^{\times })^d$
.
Given an affinoid
![]() $\operatorname {\mathrm {Spa}} R\subset \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
with pseudouniformizer
$\operatorname {\mathrm {Spa}} R\subset \left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
with pseudouniformizer
![]() $u\in R$
, there is a
$u\in R$
, there is a
![]() $(\varphi ,\Gamma )$
-module
$(\varphi ,\Gamma )$
-module
![]() $D_R$
of rank d over
$D_R$
of rank d over
![]() $\operatorname {\mathrm {Spa}} R$
. To study the bounded trianguline variety, we first study morphisms
$\operatorname {\mathrm {Spa}} R$
. To study the bounded trianguline variety, we first study morphisms
![]() $D_R\rightarrow \Lambda _{R,\mathrm {rig},{\mathbf {Q}}_p}(\delta _d)$
. Equivalently, we consider the twist
$D_R\rightarrow \Lambda _{R,\mathrm {rig},{\mathbf {Q}}_p}(\delta _d)$
. Equivalently, we consider the twist
![]() $D_R(\delta _d^{-1})$
over the (nonquasicompact) space
$D_R(\delta _d^{-1})$
over the (nonquasicompact) space
![]() $\operatorname {\mathrm {Spa}} R\times \operatorname {\mathrm {Spa}} R_z\left \langle z^hT_d^{\pm 1}\right \rangle $
and consider morphisms
$\operatorname {\mathrm {Spa}} R\times \operatorname {\mathrm {Spa}} R_z\left \langle z^hT_d^{\pm 1}\right \rangle $
and consider morphisms
![]() $D_R(\delta _d^{-1})\rightarrow \Lambda _{R,\mathrm {rig},{\mathbf {Q}}_p}$
to the trivial rank-
$D_R(\delta _d^{-1})\rightarrow \Lambda _{R,\mathrm {rig},{\mathbf {Q}}_p}$
to the trivial rank-
![]() $1\ (\varphi ,\Gamma )$
-module.
$1\ (\varphi ,\Gamma )$
-module.
We wish to first consider the closure
![]() $\overline Z_R$
of
$\overline Z_R$
of
in
![]() $\operatorname {\mathrm {Spa}} R_0\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
$\operatorname {\mathrm {Spa}} R_0\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
There is a nonzero morphism at precisely the points
![]() $x\in \operatorname {\mathrm {Spa}} R\times \operatorname {\mathrm {Spa}} R_z$
, where
$x\in \operatorname {\mathrm {Spa}} R\times \operatorname {\mathrm {Spa}} R_z$
, where
![]() $H^0(D_R^\vee (\delta _d)_x)$
is nonvanishing; equivalently (by Tate duality), at precisely the points where
$H^0(D_R^\vee (\delta _d)_x)$
is nonvanishing; equivalently (by Tate duality), at precisely the points where
![]() $H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}})_x)$
is nonvanishing. We write
$H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}})_x)$
is nonvanishing. We write
![]() $Z_R'$
for the support of
$Z_R'$
for the support of
![]() $H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}})_x)$
.
$H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}})_x)$
.
The closure of
![]() $Z_R$
is a priori defined as a subspace of the locus
$Z_R$
is a priori defined as a subspace of the locus
We first claim that there is a closed subspace of
whose restriction to this subspace is our original closure.
By [Reference BellovinBel23a, Proposition 5.2] (more precisely, by the proof of the corresponding result [Reference Kedlaya, Pottharst and XiaoKPX14, Proposition 3.3] in characteristic
![]() $0$
),
$0$
),
![]() $H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}}))$
vanishes if
$H^2(D_R(\delta _d^{-1}\chi _{\mathrm {{cyc}}}))$
vanishes if
![]() $T_d$
is sufficiently u-adically small. Here, ‘sufficiently small’ depends only on
$T_d$
is sufficiently u-adically small. Here, ‘sufficiently small’ depends only on
![]() $D_R$
, not on the twist by
$D_R$
, not on the twist by
![]() $\delta _d|_{{\mathbf {Z}}_p^{\times }}$
. Thus,
$\delta _d|_{{\mathbf {Z}}_p^{\times }}$
. Thus,
![]() $Z_R'$
is contained in the locus
$Z_R'$
is contained in the locus
![]() $\{T_d\geq u^N\}$
for some
$\{T_d\geq u^N\}$
for some
![]() $N\gg 0$
. Since
$N\gg 0$
. Since
![]() $\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
is covered by the loci
$\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
is covered by the loci
![]() $\{\lvert T_d\rvert \geq \lvert u^{2N}\rvert \}$
and
$\{\lvert T_d\rvert \geq \lvert u^{2N}\rvert \}$
and
![]() $\{\lvert T_d\rvert \leq \lvert u^{2N}\rvert \}$
, the closure of
$\{\lvert T_d\rvert \leq \lvert u^{2N}\rvert \}$
, the closure of
![]() $Z_R$
is well-behaved in
$Z_R$
is well-behaved in
![]() $\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
$\operatorname {\mathrm {Spa}} R\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
We next consider the intersection of
![]() $Z_R$
with
$Z_R$
with
that is, to the locus where
![]() $T_d$
is not very u-adically large. We may apply [Reference BellovinBel23a, Corollary 5.3] to the universal twist of
$T_d$
is not very u-adically large. We may apply [Reference BellovinBel23a, Corollary 5.3] to the universal twist of
![]() $D_R$
over this space, and we conclude that
$D_R$
over this space, and we conclude that
![]() $Z_R'$
is contained in the subspace
$Z_R'$
is contained in the subspace
![]() $\{\lvert z^{N'}\rvert \leq \lvert u\rvert \}$
for some
$\{\lvert z^{N'}\rvert \leq \lvert u\rvert \}$
for some
![]() $N'\gg 0$
. Since
$N'\gg 0$
. Since
![]() $Z_R\subset Z_R'$
, the same is true of
$Z_R\subset Z_R'$
, the same is true of
![]() $Z_R$
and its Zariski closure
$Z_R$
and its Zariski closure
![]() $\overline Z_R$
.
$\overline Z_R$
.
On the other hand, if
![]() $T_d$
is u-adically large, say, if
$T_d$
is u-adically large, say, if
![]() $T_d\geq u^{-1}$
, then we have the pair of inequalities
$T_d\geq u^{-1}$
, then we have the pair of inequalities
This implies we are over the (affinoid) subspace
This lets us study the points consisting of a Galois representation together with a first step in a triangulation and their Zariski-closure; in order to proceed by induction and study the points consisting of Galois representations together with a full triangulation, we will need the following lemma:
Lemma 2.4.4. Let R be a pseudoaffinoid algebra with pseudouniformizer
![]() $u\in R$
, and let D be a family of
$u\in R$
, and let D be a family of
![]() $(\varphi ,\Gamma )$
-modules of rank d over R such that
$(\varphi ,\Gamma )$
-modules of rank d over R such that
![]() $H^0(k(x)\otimes _RD^\vee )$
is nonzero at a Zariski-dense set of maximal points
$H^0(k(x)\otimes _RD^\vee )$
is nonzero at a Zariski-dense set of maximal points
![]() $x\in \operatorname {\mathrm {Spa}} R$
. Then there is a finite affinoid cover
$x\in \operatorname {\mathrm {Spa}} R$
. Then there is a finite affinoid cover
![]() $\{U_i\}$
of
$\{U_i\}$
of
![]() $\operatorname {\mathrm {Spa}} R$
and a collection of proper morphisms
$\operatorname {\mathrm {Spa}} R$
and a collection of proper morphisms
![]() $\pi _i:\widetilde U_i\rightarrow U_i$
such that
$\pi _i:\widetilde U_i\rightarrow U_i$
such that
-
1. There are morphisms
 $\lambda _i:\pi _i^\ast D\rightarrow \Lambda _{\widetilde U_i,\mathrm {rig},{\mathbf {Q}}_p}\otimes \mathscr {L}$
, for some line bundle
$\lambda _i:\pi _i^\ast D\rightarrow \Lambda _{\widetilde U_i,\mathrm {rig},{\mathbf {Q}}_p}\otimes \mathscr {L}$
, for some line bundle
 $\mathscr {L}$
on
$\mathscr {L}$
on
 $\widetilde U_i$
$\widetilde U_i$
-
2. The kernel of
 $\lambda _i$
is a family of
$\lambda _i$
is a family of
 $(\varphi ,\Gamma )$
-modules of rank
$(\varphi ,\Gamma )$
-modules of rank
 $d-1$
$d-1$
Proof. After replacing
![]() $\operatorname {\mathrm {Spa}} R$
with a connected component of its normalization, we may assume that
$\operatorname {\mathrm {Spa}} R$
with a connected component of its normalization, we may assume that
![]() $\operatorname {\mathrm {Spa}} R$
is normal and irreducible. Using [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.6(2)], there is a proper birational morphism
$\operatorname {\mathrm {Spa}} R$
is normal and irreducible. Using [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.6(2)], there is a proper birational morphism
![]() $f:X_{R}\rightarrow \operatorname {\mathrm {Spa}} R$
such that
$f:X_{R}\rightarrow \operatorname {\mathrm {Spa}} R$
such that
![]() $H^i(f^\ast D^\vee )$
is flat for
$H^i(f^\ast D^\vee )$
is flat for
![]() $i=0$
and has Tor-dimension at most
$i=0$
and has Tor-dimension at most
![]() $1$
for
$1$
for
![]() $i=1,2$
. For any
$i=1,2$
. For any
![]() $x\in X$
, we have an exact sequence
$x\in X$
, we have an exact sequence
(where we have used the low-degree exact sequences coming from the base-change spectral sequence cf. [Reference BellovinBel23a, Corollary 3.12] and the assumption that
![]() $H^i(f^\ast D^\vee )$
has Tor-dimension at most
$H^i(f^\ast D^\vee )$
has Tor-dimension at most
![]() $1$
for
$1$
for
![]() $i=1,2$
). Since we assumed that
$i=1,2$
). Since we assumed that
![]() $H^0(k(x)\otimes _RD^\vee )$
is nonzero at a Zariski-dense set of maximal points
$H^0(k(x)\otimes _RD^\vee )$
is nonzero at a Zariski-dense set of maximal points
![]() $x\in \operatorname {\mathrm {Spa}} R$
, we see that
$x\in \operatorname {\mathrm {Spa}} R$
, we see that
![]() $H^0(f^\ast D^\vee )$
is projective of nonzero rank.
$H^0(f^\ast D^\vee )$
is projective of nonzero rank.
Let
![]() $g:Y_{R}\rightarrow X_R$
be the projective space
$g:Y_{R}\rightarrow X_R$
be the projective space
![]() $\underline{\mathrm{Proj}}\left (\operatorname {\mathrm {Sym}} H^0(f^\ast D^\vee \right )^\vee )$
over
$\underline{\mathrm{Proj}}\left (\operatorname {\mathrm {Sym}} H^0(f^\ast D^\vee \right )^\vee )$
over
![]() $X_R$
. Since
$X_R$
. Since
![]() $g:Y_R\rightarrow X_R$
is flat, we have
$g:Y_R\rightarrow X_R$
is flat, we have
![]() $g^\ast H^i(f^\ast D)\xrightarrow \sim H^i(g^\ast f^\ast D)$
for all i, and moreover,
$g^\ast H^i(f^\ast D)\xrightarrow \sim H^i(g^\ast f^\ast D)$
for all i, and moreover,
![]() $g^\ast f^\ast D$
retains the property that
$g^\ast f^\ast D$
retains the property that
![]() $H^0(g^\ast f^\ast D)$
is flat (of nonzero rank) and
$H^0(g^\ast f^\ast D)$
is flat (of nonzero rank) and
![]() $H^i(g^\ast f^\ast D)$
has Tor-dimension at most
$H^i(g^\ast f^\ast D)$
has Tor-dimension at most
![]() $1$
for
$1$
for
![]() $i=1,2$
.
$i=1,2$
.
Over
![]() $Y_R$
, there is a universal quotient
$Y_R$
, there is a universal quotient
![]() $g^\ast H^0(f^\ast D^\vee )^\vee \twoheadrightarrow {\mathscr {O}}_{Y_R}(1)$
, which induces an injection
$g^\ast H^0(f^\ast D^\vee )^\vee \twoheadrightarrow {\mathscr {O}}_{Y_R}(1)$
, which induces an injection
![]() ${\mathscr {O}}_{Y_R}(-1)\rightarrow g^\ast H^0(f^\ast D^\vee )$
with projective cokernel. If we consider the composition
${\mathscr {O}}_{Y_R}(-1)\rightarrow g^\ast H^0(f^\ast D^\vee )$
with projective cokernel. If we consider the composition
we may again dualize to obtain a morphism
![]() $\lambda :g^\ast f^\ast D\rightarrow {\mathscr {O}}_{Y_R}(1)\otimes \Lambda _{Y_R,\mathrm {rig},{\mathbf {Q}}_p}$
.
$\lambda :g^\ast f^\ast D\rightarrow {\mathscr {O}}_{Y_R}(1)\otimes \Lambda _{Y_R,\mathrm {rig},{\mathbf {Q}}_p}$
.
There is a finite affinoid cover
![]() $\{\operatorname {\mathrm {Spa}} R_j'\}$
of
$\{\operatorname {\mathrm {Spa}} R_j'\}$
of
![]() $Y_R$
trivializing
$Y_R$
trivializing
![]() ${\mathscr {O}}_{Y_R}(1)$
; we let
${\mathscr {O}}_{Y_R}(1)$
; we let
![]() $\lambda _j$
denote the restriction of
$\lambda _j$
denote the restriction of
![]() $\lambda $
to
$\lambda $
to
![]() $\operatorname {\mathrm {Spa}} R_j'$
. For any
$\operatorname {\mathrm {Spa}} R_j'$
. For any
![]() $x\in \operatorname {\mathrm {Spa}} R_j'$
, we again have an exact sequence
$x\in \operatorname {\mathrm {Spa}} R_j'$
, we again have an exact sequence
This implies in particular that the specialization of
![]() $\lambda _j$
is nonzero. If x has characteristic-p residue field, this implies that the specialization of
$\lambda _j$
is nonzero. If x has characteristic-p residue field, this implies that the specialization of
![]() $\lambda _j$
is surjective. As in the proof of [Reference BellovinBel23a, Lemma 5.7], this implies that there is an affinoid subdomain
$\lambda _j$
is surjective. As in the proof of [Reference BellovinBel23a, Lemma 5.7], this implies that there is an affinoid subdomain
![]() $V_j=\{\lvert p\rvert \leq \lvert u^{r_j}\rvert \}\subset \operatorname {\mathrm {Spa}} R_j'$
containing the locus
$V_j=\{\lvert p\rvert \leq \lvert u^{r_j}\rvert \}\subset \operatorname {\mathrm {Spa}} R_j'$
containing the locus
![]() $\{p=0\}$
over which
$\{p=0\}$
over which
![]() $\lambda _j$
is surjective.
$\lambda _j$
is surjective.
Let
![]() $N:=\max \{r_j\}$
and set
$N:=\max \{r_j\}$
and set
![]() $U_1:=\{\lvert p\rvert \leq \lvert u^N\rvert \}\subset \operatorname {\mathrm {Spa}} R$
. Then the preimage
$U_1:=\{\lvert p\rvert \leq \lvert u^N\rvert \}\subset \operatorname {\mathrm {Spa}} R$
. Then the preimage
![]() $(f\circ g)^{-1}\left (U_1\right )$
is contained in
$(f\circ g)^{-1}\left (U_1\right )$
is contained in
![]() $\cup _j V_j$
. We will set
$\cup _j V_j$
. We will set
![]() $\widetilde U_1:=(f\circ g)^{-1}\left (U_1\right )$
. Then by construction,
$\widetilde U_1:=(f\circ g)^{-1}\left (U_1\right )$
. Then by construction,
![]() $\pi _1:\widetilde U_1\rightarrow U$
is surjective and
$\pi _1:\widetilde U_1\rightarrow U$
is surjective and
is surjective, so its kernel is a family of
![]() $(\varphi ,\Gamma )$
-modules of rank
$(\varphi ,\Gamma )$
-modules of rank
![]() $d-1$
.
$d-1$
.
On the other hand, set
![]() $U_2:=\{\lvert u^N\rvert \leq \lvert p\rvert \}\subset \operatorname {\mathrm {Spa}} R$
. Then the preimage
$U_2:=\{\lvert u^N\rvert \leq \lvert p\rvert \}\subset \operatorname {\mathrm {Spa}} R$
. Then the preimage
![]() $(f\circ g)^{-1}\left (U_2\right )$
is quasicompact and contained in the characteristic-
$(f\circ g)^{-1}\left (U_2\right )$
is quasicompact and contained in the characteristic-
![]() $0$
locus of
$0$
locus of
![]() $Y_R$
, so we may apply the techniques of the proof of [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.9]. More precisely, we let
$Y_R$
, so we may apply the techniques of the proof of [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.9]. More precisely, we let
![]() $h:U_2'\rightarrow (f\circ g)^{-1}\left (U_2\right )$
be a proper birational morphism so that
$h:U_2'\rightarrow (f\circ g)^{-1}\left (U_2\right )$
be a proper birational morphism so that
![]() $H^i((f\circ g\circ h)^\ast D/t)$
is flat for
$H^i((f\circ g\circ h)^\ast D/t)$
is flat for
![]() $i=0$
and has Tor-dimension at most
$i=0$
and has Tor-dimension at most
![]() $1$
for
$1$
for
![]() $i=1, 2$
(again using [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.6(2)]). This lets us deduce that
$i=1, 2$
(again using [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.6(2)]). This lets us deduce that
![]() $h^\ast \lambda |_{U_2'}$
is surjective away from a proper Zariski-closed subspace, and locally on
$h^\ast \lambda |_{U_2'}$
is surjective away from a proper Zariski-closed subspace, and locally on
![]() $U_2'$
, its cokernel is killed by a power of t. Then we make a further blow-up
$U_2'$
, its cokernel is killed by a power of t. Then we make a further blow-up
![]() $\widetilde U_2\rightarrow U_2'$
such that over
$\widetilde U_2\rightarrow U_2'$
such that over
![]() $U_2$
, the kernel of
$U_2$
, the kernel of
![]() $\lambda $
is a family of
$\lambda $
is a family of
![]() $(\varphi ,\Gamma )$
-modules of rank
$(\varphi ,\Gamma )$
-modules of rank
![]() $d-1$
, as desired.
$d-1$
, as desired.
This permits us to use induction to deduce the following:
Corollary 2.4.5. Let R be a pseudoaffinoid algebra with pseudouniformizer
![]() $u\in R$
, and let D be a family of rank-
$u\in R$
, and let D be a family of rank-
![]() $d\ (\varphi ,\Gamma )$
-modules over R. Consider the Zariski closure Z of the locus in
$d\ (\varphi ,\Gamma )$
-modules over R. Consider the Zariski closure Z of the locus in
![]() $\operatorname {\mathrm {Spa}} R_0\times \operatorname {\mathrm {Spa}} R_{z,0}\times {\mathbf {G}}_{m,R}^d$
corresponding to points
$\operatorname {\mathrm {Spa}} R_0\times \operatorname {\mathrm {Spa}} R_{z,0}\times {\mathbf {G}}_{m,R}^d$
corresponding to points
![]() $x=(D_x,\underline \delta _x)$
, where
$x=(D_x,\underline \delta _x)$
, where
![]() $\lvert \delta _{i,x}(p)^{\pm 1}\rvert \leq \lvert z\rvert ^{-h}$
for all i, and
$\lvert \delta _{i,x}(p)^{\pm 1}\rvert \leq \lvert z\rvert ^{-h}$
for all i, and
![]() $\underline \delta _x$
is a regular parameter of
$\underline \delta _x$
is a regular parameter of
![]() $D_x$
. Then there is some
$D_x$
. Then there is some
![]() $N'\gg 0$
such that
$N'\gg 0$
such that
This is precisely the condition we need to apply Corollary A.0.2, so the closure we are interested in is well-behaved in
![]() $\operatorname {\mathrm {Spf}} R_0\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
$\operatorname {\mathrm {Spf}} R_0\mathop {\widehat \otimes } R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
.
Letting
![]() $\operatorname {\mathrm {Spa}} R$
range over a (finite) cover of
$\operatorname {\mathrm {Spa}} R$
range over a (finite) cover of
![]() $\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
, we obtain a closed subspace of
$\left (\operatorname {\mathrm {Spa}} R_{\overline {\rho }}^\square \right )^{\mathrm {{an}}}$
, we obtain a closed subspace of
![]() $\operatorname {\mathrm {Spf}} R_{\overline \rho }^\square \times \operatorname {\mathrm {Spa}} R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
. Letting z range over
$\operatorname {\mathrm {Spf}} R_{\overline \rho }^\square \times \operatorname {\mathrm {Spa}} R_{z,0}\left \langle z^aT_i^b,T_i'\right \rangle /(T_i^bT_i'-z^a)$
. Letting z range over
![]() $\{p,z_1,\ldots ,z_d\}$
, in turn, we may glue to get a closed subspace of
$\{p,z_1,\ldots ,z_d\}$
, in turn, we may glue to get a closed subspace of
![]() $\operatorname {\mathrm {Spf}} R_0\times \mathfrak {T}_h^d$
, yielding the desired integral models of pieces of trianguline varieties:
$\operatorname {\mathrm {Spf}} R_0\times \mathfrak {T}_h^d$
, yielding the desired integral models of pieces of trianguline varieties:
Corollary 2.4.6. Suppose that
![]() $\overline {\rho }$
is a representation of
$\overline {\rho }$
is a representation of
![]() $\operatorname {\mathrm {Gal}}_K$
, where K is a finite extension of
$\operatorname {\mathrm {Gal}}_K$
, where K is a finite extension of
![]() ${\mathbf {Q}}_p$
, or of
${\mathbf {Q}}_p$
, or of
![]() $\operatorname {\mathrm {Gal}}_F$
, where F is a totally real number field (in which case we assume
$\operatorname {\mathrm {Gal}}_F$
, where F is a totally real number field (in which case we assume
![]() $\rho $
is unramified outside a finite set of places S). Then there are formal schemes
$\rho $
is unramified outside a finite set of places S). Then there are formal schemes
![]() $\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }$
(resp.
$\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }$
(resp.
![]() $\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square }$
) and
$\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square }$
) and
![]() $\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }$
(resp.
$\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }$
(resp.
![]() $\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
), which are affine over
$\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
), which are affine over
![]() $\mathfrak {T}_h$
, such that
$\mathfrak {T}_h$
, such that
![]() $\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },\leq h}^\square $
(resp.
$\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },\leq h}^\square $
(resp.
![]() $\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^\square $
) and
$\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^\square $
) and
![]() $\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }$
(resp.
$\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },\leq h}^{\square ,\psi ,\underline \kappa }$
(resp.
![]() $\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
).
$\left (\mathfrak {X}_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }\right )^{\mathrm {{an}}}=X_{\mathrm {{tri}},\overline {\rho },S,\leq h}^{\square ,\psi ,\underline \kappa }$
).
3 Extended eigenvarieties
3.1 Definitions
We briefly recall the construction of extended eigenvarieties in the two cases of interest to us. Fix a number field F and a reductive group
![]() ${{\mathrm{{H}}}}$
over F which is split at all places above p; then we define
${{\mathrm{{H}}}}$
over F which is split at all places above p; then we define
![]() ${\mathbf {G}}:=\operatorname {\mathrm {Res}}_{F/{\mathbf {Q}}}{{\mathrm{{H}}}}$
. If we choose split models
${\mathbf {G}}:=\operatorname {\mathrm {Res}}_{F/{\mathbf {Q}}}{{\mathrm{{H}}}}$
. If we choose split models
![]() ${{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
over
${{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
over
![]() ${\mathscr {O}}_{F_v}$
for each place
${\mathscr {O}}_{F_v}$
for each place
![]() $v\mid p$
, along with split maximal tori and Borel subgroups
$v\mid p$
, along with split maximal tori and Borel subgroups
![]() $\operatorname {\mathrm {T}}_v\subset {\mathbf {B}}_v\subset {{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
, we obtain an integral model
$\operatorname {\mathrm {T}}_v\subset {\mathbf {B}}_v\subset {{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
, we obtain an integral model
![]() ${\mathbf {G}}_{{\mathbf {Z}}_p}:=\prod _{v\mid p}{{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
of
${\mathbf {G}}_{{\mathbf {Z}}_p}:=\prod _{v\mid p}{{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
of
![]() ${\mathbf {G}}$
, as well as closed subgroup schemes
${\mathbf {G}}$
, as well as closed subgroup schemes
Let
![]() $T_0:=\operatorname {\mathrm {T}}({\mathbf {Z}}_p)$
, and let the Iwahori subgroup
$T_0:=\operatorname {\mathrm {T}}({\mathbf {Z}}_p)$
, and let the Iwahori subgroup
![]() $I\subset {\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {Z}}_p)$
be the preimage of
$I\subset {\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {Z}}_p)$
be the preimage of
![]() ${\mathbf {B}}({\mathbf {F}}_p)$
under the reduction map
${\mathbf {B}}({\mathbf {F}}_p)$
under the reduction map
![]() ${\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {Z}}_p)\rightarrow {\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {F}}_p)$
.
${\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {Z}}_p)\rightarrow {\mathbf {G}}_{{\mathbf {Z}}_p}({\mathbf {F}}_p)$
.
We choose a tame level by choosing compact open subgroups
![]() $K_\ell \subset {\mathbf {G}}({\mathbf {Q}}_\ell )$
for each prime
$K_\ell \subset {\mathbf {G}}({\mathbf {Q}}_\ell )$
for each prime
![]() $\ell \neq p$
, such that
$\ell \neq p$
, such that
![]() $K_\ell =\mathcal {G}({\mathbf {Z}}_\ell )$
for almost all primes
$K_\ell =\mathcal {G}({\mathbf {Z}}_\ell )$
for almost all primes
![]() $\ell $
(where
$\ell $
(where
![]() $\mathcal {G}$
is some reductive model of
$\mathcal {G}$
is some reductive model of
![]() ${\mathbf {G}}$
over
${\mathbf {G}}$
over
![]() ${\mathbf {Z}}[1/M]$
for some integer M). Then we put
${\mathbf {Z}}[1/M]$
for some integer M). Then we put
![]() $K^p:=\prod _{\ell \neq p}K_\ell $
and
$K^p:=\prod _{\ell \neq p}K_\ell $
and
![]() $K:=K^pI$
; we assume throughout that K contains an open normal subgroup
$K:=K^pI$
; we assume throughout that K contains an open normal subgroup
![]() $K'$
such that
$K'$
such that
![]() $[K:K']$
is prime to p and
$[K:K']$
is prime to p and
which is the neatness hypothesis of [Reference Johansson and NewtonJN19b].Footnote
1
If
![]() ${\mathbf {Z}}$
denotes the center of
${\mathbf {Z}}$
denotes the center of
![]() ${\mathbf {G}}$
, we let
${\mathbf {G}}$
, we let
![]() $Z(K):={\mathbf {Z}}({\mathbf {Q}})\cap K$
and let
$Z(K):={\mathbf {Z}}({\mathbf {Q}})\cap K$
and let
![]() $\overline {Z(K)}\subset T_0$
denote its p-adic closure. We also let
$\overline {Z(K)}\subset T_0$
denote its p-adic closure. We also let
![]() $K_\infty \subset {\mathbf {G}}({\mathbf {R}})$
be a maximal compact and connected subgroup at infinity, and let
$K_\infty \subset {\mathbf {G}}({\mathbf {R}})$
be a maximal compact and connected subgroup at infinity, and let
![]() $Z_\infty ^\circ \subset Z_\infty =:{\mathbf {Z}}({\mathbf {R}})$
denote the identity component.
$Z_\infty ^\circ \subset Z_\infty =:{\mathbf {Z}}({\mathbf {R}})$
denote the identity component.
Finally, let
![]() $\Sigma \subset T_0$
be the kernel of some splitting of the inclusion
$\Sigma \subset T_0$
be the kernel of some splitting of the inclusion
![]() $T_0\subset \operatorname {\mathrm {T}}({\mathbf {Q}}_p)$
; there are then certain submonoids
$T_0\subset \operatorname {\mathrm {T}}({\mathbf {Q}}_p)$
; there are then certain submonoids
![]() $\Sigma ^{\mathrm {cpt}}\subset \Sigma ^+\subset \Sigma $
, and we fix some
$\Sigma ^{\mathrm {cpt}}\subset \Sigma ^+\subset \Sigma $
, and we fix some
![]() $t\in \Sigma ^{\mathrm {cpt}}$
.
$t\in \Sigma ^{\mathrm {cpt}}$
.
In the cases of interest to us, F will be a totally real field, completely split at p, and
![]() ${{\mathrm{{H}}}}$
will be either
${{\mathrm{{H}}}}$
will be either
![]() $\operatorname {\mathrm {GL}}_2$
or the reductive group
$\operatorname {\mathrm {GL}}_2$
or the reductive group
![]() $\underline D^{\times }$
corresponding to the units of a totally definite quaternion algebra over F split at every place above p. Fixing isomorphisms
$\underline D^{\times }$
corresponding to the units of a totally definite quaternion algebra over F split at every place above p. Fixing isomorphisms
![]() $D_v\xrightarrow {\sim }\operatorname {\mathrm {Mat}}_2(F_v)$
for each place v where D is split, we may define integral models of
$D_v\xrightarrow {\sim }\operatorname {\mathrm {Mat}}_2(F_v)$
for each place v where D is split, we may define integral models of
![]() ${{\mathrm{{H}}}}_v$
via
${{\mathrm{{H}}}}_v$
via
![]() ${{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}(R_0):=\left (R_0\otimes \operatorname {\mathrm {Mat}}_2({\mathscr {O}}_{F_v})\right )^{\times }$
for all
${{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}(R_0):=\left (R_0\otimes \operatorname {\mathrm {Mat}}_2({\mathscr {O}}_{F_v})\right )^{\times }$
for all
![]() ${\mathscr {O}}_{F_v}$
-algebras
${\mathscr {O}}_{F_v}$
-algebras
![]() $R_0$
(whether
$R_0$
(whether
![]() ${{\mathrm{{H}}}}=\operatorname {\mathrm {GL}}_2$
or
${{\mathrm{{H}}}}=\operatorname {\mathrm {GL}}_2$
or
![]() $\underline D^{\times }$
). In either case, we let
$\underline D^{\times }$
). In either case, we let
![]() ${\mathbf {B}}_v\subset {{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
be the standard upper-triangular Borel and we let
${\mathbf {B}}_v\subset {{\mathrm{{H}}}}_{{\mathscr {O}}_{F_v}}$
be the standard upper-triangular Borel and we let
![]() $\operatorname {\mathrm {T}}_v\subset {\mathbf {B}}_v$
be the standard diagonal maximal torus.
$\operatorname {\mathrm {T}}_v\subset {\mathbf {B}}_v$
be the standard diagonal maximal torus.
For either choice of
![]() ${{\mathrm{{H}}}}$
, the adelic subgroup
${{\mathrm{{H}}}}$
, the adelic subgroup
![]() $K(N)\subset \left ({\mathbf {A}}_{F,f}\otimes {{\mathrm{{H}}}}(F)\right )^{\times }$
of full level N is neat for
$K(N)\subset \left ({\mathbf {A}}_{F,f}\otimes {{\mathrm{{H}}}}(F)\right )^{\times }$
of full level N is neat for
![]() $N\geq 3$
such that N is prime to the finite places v where
$N\geq 3$
such that N is prime to the finite places v where
![]() ${{\mathrm{{H}}}}_v\neq \operatorname {\mathrm {GL}}_2$
. Thus, if we assume
${{\mathrm{{H}}}}_v\neq \operatorname {\mathrm {GL}}_2$
. Thus, if we assume
![]() $p\geq 5$
, we may take
$p\geq 5$
, we may take
![]() $K^p$
arbitrary.
$K^p$
arbitrary.
For either choice of
![]() ${{\mathrm{{H}}}}$
, we define
${{\mathrm{{H}}}}$
, we define
![]() $\Sigma _v^+:=\left \{\left (\begin {smallmatrix}\varpi _v^{a_1} & 0 \\ 0 & \varpi _v^{a_2}\end {smallmatrix}\right ) \mid a_2\geq a_1\right \}$
and
$\Sigma _v^+:=\left \{\left (\begin {smallmatrix}\varpi _v^{a_1} & 0 \\ 0 & \varpi _v^{a_2}\end {smallmatrix}\right ) \mid a_2\geq a_1\right \}$
and
![]() $\Delta _v:=I_v\Sigma _v^+I_v$
. Similarly, we define
$\Delta _v:=I_v\Sigma _v^+I_v$
. Similarly, we define
![]() $\Sigma ^+:=\prod _{v\mid p}\Sigma _v^+$
and
$\Sigma ^+:=\prod _{v\mid p}\Sigma _v^+$
and
![]() $\Delta _p:=I\Sigma ^+I=\prod _{v\mid p}\Delta _v$
. Then we fix
$\Delta _p:=I\Sigma ^+I=\prod _{v\mid p}\Delta _v$
. Then we fix
![]() $U_{\varpi _v}:=\left [I_v\left (\begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix}\right )I_v\right ]\in I_v\backslash {{\mathrm{{H}}}}(F_v)/I_v$
and
$U_{\varpi _v}:=\left [I_v\left (\begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix}\right )I_v\right ]\in I_v\backslash {{\mathrm{{H}}}}(F_v)/I_v$
and
![]() $U_p:=\prod _{v\mid p}U_{\varpi _v}$
.
$U_p:=\prod _{v\mid p}U_{\varpi _v}$
.
For each prime
![]() $\ell \neq p$
, we fix a monoid
$\ell \neq p$
, we fix a monoid
![]() $\Delta _\ell \subset {\mathbf {G}}({\mathbf {Q}}_\ell )$
containing
$\Delta _\ell \subset {\mathbf {G}}({\mathbf {Q}}_\ell )$
containing
![]() $K_\ell $
, which is equal to
$K_\ell $
, which is equal to
![]() ${\mathbf {G}}({\mathbf {Q}}_\ell )$
when
${\mathbf {G}}({\mathbf {Q}}_\ell )$
when
![]() $K_\ell =\mathcal {G}({\mathbf {Z}}_\ell )$
such that
$K_\ell =\mathcal {G}({\mathbf {Z}}_\ell )$
such that
![]() $(\Delta _\ell , K_\ell )$
is a Hecke pair and the Hecke algebra
$(\Delta _\ell , K_\ell )$
is a Hecke pair and the Hecke algebra
![]() $\mathbb {T}(\Delta _\ell , K_\ell )$
over
$\mathbb {T}(\Delta _\ell , K_\ell )$
over
![]() ${\mathbf {Z}}_p$
is commutative. Then we define
${\mathbf {Z}}_p$
is commutative. Then we define
![]() $\Delta ^p:=\prod _{\ell \neq p}^\prime \Delta _\ell $
and
$\Delta ^p:=\prod _{\ell \neq p}^\prime \Delta _\ell $
and
![]() $\Delta :=\Delta ^p\Delta _p$
. We write
$\Delta :=\Delta ^p\Delta _p$
. We write
![]() $\mathbb {T}(\Delta ^p,K^p):=\otimes _{\ell \neq p}\mathbb {T}(\Delta _\ell , K_\ell )$
and
$\mathbb {T}(\Delta ^p,K^p):=\otimes _{\ell \neq p}\mathbb {T}(\Delta _\ell , K_\ell )$
and
![]() $\mathbb {T}(\Delta ,K):=\otimes _\ell \mathbb {T}(\Delta _\ell , K_\ell )$
for the corresponding global Hecke algebras.
$\mathbb {T}(\Delta ,K):=\otimes _\ell \mathbb {T}(\Delta _\ell , K_\ell )$
for the corresponding global Hecke algebras.
A weight is a continuous homomorphism
![]() $\kappa :T_0\rightarrow R^{\times }$
which is trivial on
$\kappa :T_0\rightarrow R^{\times }$
which is trivial on
![]() $Z(K)$
, where R is a pseudoaffinoid algebra over
$Z(K)$
, where R is a pseudoaffinoid algebra over
![]() ${\mathbf {Z}}_p$
. We define weight space
${\mathbf {Z}}_p$
. We define weight space
![]() $\mathscr {W}$
via
$\mathscr {W}$
via
It can be written explicitly as the analytic locus of
![]() $\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!],{\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]\right )$
. Then
$\operatorname {\mathrm {Spa}}\left ({\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!],{\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]\right )$
. Then
![]() $\mathscr {W}$
is equidimensional of dimension
$\mathscr {W}$
is equidimensional of dimension
![]() $1+[F:{\mathbf {Q}}]+\mathfrak {d}$
, where
$1+[F:{\mathbf {Q}}]+\mathfrak {d}$
, where
![]() $\mathfrak {d}$
is the defect in Leopoldt’s conjecture for F and p.
$\mathfrak {d}$
is the defect in Leopoldt’s conjecture for F and p.
The next step is to construct a sheaf of Hecke modules over weight space such that
![]() $U_p$
acts compactly and admits a Fredholm determinant. We will actually use two such sheaves. If
$U_p$
acts compactly and admits a Fredholm determinant. We will actually use two such sheaves. If
![]() $\kappa :T_0\rightarrow R^{\times }$
is a weight, then [Reference Johansson and NewtonJN16] construct certain modules of analytic functions
$\kappa :T_0\rightarrow R^{\times }$
is a weight, then [Reference Johansson and NewtonJN16] construct certain modules of analytic functions
![]() $\mathcal {A}_{\kappa }^r$
and distributions
$\mathcal {A}_{\kappa }^r$
and distributions
![]() $\mathcal {D}_{\kappa }^r$
. Here,
$\mathcal {D}_{\kappa }^r$
. Here,
![]() $r\in (r_{\kappa },1)$
, where
$r\in (r_{\kappa },1)$
, where
![]() $r_{\kappa }\in [1/p,1)$
. When
$r_{\kappa }\in [1/p,1)$
. When
![]() $r_{\kappa }\in (1/p,1)$
, they also construct
$r_{\kappa }\in (1/p,1)$
, they also construct
![]() $\mathcal {A}_{\kappa }^{<r}$
and
$\mathcal {A}_{\kappa }^{<r}$
and
![]() $\mathcal {D}_{\kappa }^{<r}$
so that
$\mathcal {D}_{\kappa }^{<r}$
so that
![]() $\mathcal {D}_{\kappa }^r$
is the dual of
$\mathcal {D}_{\kappa }^r$
is the dual of
![]() $\mathcal {A}_{\kappa }^{<r}$
and
$\mathcal {A}_{\kappa }^{<r}$
and
![]() $\mathcal {A}_{\kappa }^r$
is the dual of
$\mathcal {A}_{\kappa }^r$
is the dual of
![]() $\mathcal {D}_{\kappa }^{<r}$
. As in [Reference Hansen and NewtonHN17], we fix augmented Borel–Serre complexes
$\mathcal {D}_{\kappa }^{<r}$
. As in [Reference Hansen and NewtonHN17], we fix augmented Borel–Serre complexes
![]() $C_{\bullet }^{\mathrm {BM}}(K,-)$
and
$C_{\bullet }^{\mathrm {BM}}(K,-)$
and
![]() $C_{c}^{\bullet }(K,-)$
for Borel–Moore homology and compactly supported cohomology, respectively, and we consider
$C_{c}^{\bullet }(K,-)$
for Borel–Moore homology and compactly supported cohomology, respectively, and we consider
as well as
Now,
![]() $\mathcal {A}_{\kappa }^r$
and
$\mathcal {A}_{\kappa }^r$
and
![]() $\mathcal {D}_{\kappa }^r$
are potentially orthonormalizable, so
$\mathcal {D}_{\kappa }^r$
are potentially orthonormalizable, so
![]() $C_\ast ^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r):=\oplus _i C_i^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r)$
and
$C_\ast ^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r):=\oplus _i C_i^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r)$
and
![]() $C_c^\ast (K,\mathcal {D}_{\kappa }^r):=\oplus _iC_c^i(K,\mathcal {D}_{\kappa }^r)$
are, as well. Since
$C_c^\ast (K,\mathcal {D}_{\kappa }^r):=\oplus _iC_c^i(K,\mathcal {D}_{\kappa }^r)$
are, as well. Since
![]() $U_p$
acts compactly on
$U_p$
acts compactly on
![]() $\mathcal {A}_{\kappa }^r$
and
$\mathcal {A}_{\kappa }^r$
and
![]() $\mathcal {D}_{\kappa }^r$
, this implies that there are Fredholm determinants
$\mathcal {D}_{\kappa }^r$
, this implies that there are Fredholm determinants
![]() $F_{\kappa }^{r,\prime }$
and
$F_{\kappa }^{r,\prime }$
and
![]() $F_{\kappa }^r$
for its action on
$F_{\kappa }^r$
for its action on
![]() $C_\ast ^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r)$
and
$C_\ast ^{\mathrm {BM}}(K,\mathcal {A}_{\kappa }^r)$
and
![]() $C_c^\ast (K,\mathcal {D}_{\kappa }^r)$
, respectively.
$C_c^\ast (K,\mathcal {D}_{\kappa }^r)$
, respectively.
It turns out that
![]() $F_{\kappa }^{r,\prime }$
and
$F_{\kappa }^{r,\prime }$
and
![]() $F_{\kappa }^r$
are independent of r by [Reference Johansson and NewtonJN16, Proposition 4.1.2]; we set
$F_{\kappa }^r$
are independent of r by [Reference Johansson and NewtonJN16, Proposition 4.1.2]; we set
![]() $\mathscr {D}_{\kappa }:=\varprojlim _r\mathcal {D}_{\kappa }^r$
and
$\mathscr {D}_{\kappa }:=\varprojlim _r\mathcal {D}_{\kappa }^r$
and
![]() $\mathscr {A}_{\kappa }:=\varinjlim _r\mathcal {A}_{\kappa }^r$
, and we write
$\mathscr {A}_{\kappa }:=\varinjlim _r\mathcal {A}_{\kappa }^r$
, and we write
![]() $F_{\kappa }$
and
$F_{\kappa }$
and
![]() $F_{\kappa }^\prime $
for the Fredholm determinants of
$F_{\kappa }^\prime $
for the Fredholm determinants of
![]() $U_p$
on
$U_p$
on
![]() $C_c^\ast (K,\mathscr {D}_{\kappa })$
and
$C_c^\ast (K,\mathscr {D}_{\kappa })$
and
![]() $C_\ast ^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })$
, respectively. Then
$C_\ast ^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })$
, respectively. Then
![]() $F_{\kappa }$
and
$F_{\kappa }$
and
![]() $F_{\kappa }^\prime $
define spectral varieties
$F_{\kappa }^\prime $
define spectral varieties
![]() $\mathscr {Z}\subset {\mathbf {A}}_{\mathscr {W}_F}^1$
and
$\mathscr {Z}\subset {\mathbf {A}}_{\mathscr {W}_F}^1$
and
![]() $\mathscr {Z}^\prime \subset {\mathbf {A}}_{\mathscr {W}_F}^1$
. We let
$\mathscr {Z}^\prime \subset {\mathbf {A}}_{\mathscr {W}_F}^1$
. We let
![]() $\pi :\mathscr {Z}\rightarrow \mathscr {W}_F$
and
$\pi :\mathscr {Z}\rightarrow \mathscr {W}_F$
and
![]() $\pi ':\mathscr {Z}'\rightarrow \mathscr {W}_F$
be the projection on the first factor; they are flat morphisms of pseudorigid spaces.
$\pi ':\mathscr {Z}'\rightarrow \mathscr {W}_F$
be the projection on the first factor; they are flat morphisms of pseudorigid spaces.
By [Reference Johansson and NewtonJN16, Theorem 2.3.2],
![]() $\mathscr {Z}$
has a cover by open affinoid subspaces V such that
$\mathscr {Z}$
has a cover by open affinoid subspaces V such that
![]() $U:=\pi (V)$
is an open affinoid subspace of
$U:=\pi (V)$
is an open affinoid subspace of
![]() $\mathscr {W}_F$
and
$\mathscr {W}_F$
and
![]() $\pi |_V:V\rightarrow U$
is finite of constant degree. This implies that over such a V, F factors as
$\pi |_V:V\rightarrow U$
is finite of constant degree. This implies that over such a V, F factors as
![]() $F_V=Q_VS_V$
where
$F_V=Q_VS_V$
where
![]() $Q_V$
is a multiplicative polynomial of degree
$Q_V$
is a multiplicative polynomial of degree
![]() $\deg \pi |_V$
,
$\deg \pi |_V$
,
![]() $S_V$
is a Fredholm series, and
$S_V$
is a Fredholm series, and
![]() $Q_V$
and
$Q_V$
and
![]() $S_V$
are relatively prime.
$S_V$
are relatively prime.
If such a factorization exists, we may make
![]() $C_c^{\bullet }(K,\mathscr {D}_V)$
into a complex of
$C_c^{\bullet }(K,\mathscr {D}_V)$
into a complex of
![]() ${\mathscr {O}}_{\mathscr {Z}}$
-modules by letting T act via
${\mathscr {O}}_{\mathscr {Z}}$
-modules by letting T act via
![]() $U_p^{-1}$
. Then the assignment
$U_p^{-1}$
. Then the assignment
![]() $V\mapsto \ker Q_V^\ast (U_p)\subset C^{\bullet }(K,\mathscr {D}_{V})$
defines a bounded complex
$V\mapsto \ker Q_V^\ast (U_p)\subset C^{\bullet }(K,\mathscr {D}_{V})$
defines a bounded complex
![]() $\mathscr {K}^{\bullet }$
of coherent
$\mathscr {K}^{\bullet }$
of coherent
![]() ${\mathscr {O}}_{\mathscr {Z}}$
-modules, where
${\mathscr {O}}_{\mathscr {Z}}$
-modules, where
![]() $Q_V^\ast (T):=T^{\deg Q_V}Q_V(1/T)$
. If
$Q_V^\ast (T):=T^{\deg Q_V}Q_V(1/T)$
. If
![]() $V=\pi ^{-1}(U)$
, where
$V=\pi ^{-1}(U)$
, where
![]() $(U,h)$
is a slope datum, then
$(U,h)$
is a slope datum, then
![]() $\mathscr {K}^{\bullet }$
is the slope-
$\mathscr {K}^{\bullet }$
is the slope-
![]() $\leq h$
subcomplex of
$\leq h$
subcomplex of
![]() $C_c^{\bullet }(K,\mathscr {D}_V)$
. We set
$C_c^{\bullet }(K,\mathscr {D}_V)$
. We set
which is a coherent sheaf on
![]() $\mathscr {Z}$
.
$\mathscr {Z}$
.
Such factorizations exist locally, by an extension of a result of [Reference Ash and StevensAS]:
Proposition 3.1.1. Let R be a pseudoaffinoid algebra, and let
![]() $x_0\in \operatorname {\mathrm {Spa}} R$
be a maximal point. Let
$x_0\in \operatorname {\mathrm {Spa}} R$
be a maximal point. Let
![]() $F(T)\in R\{\!\{T\}\!\}$
be a Fredholm power series, and fix
$F(T)\in R\{\!\{T\}\!\}$
be a Fredholm power series, and fix
![]() $h\in {\mathbf {Q}}$
. Suppose
$h\in {\mathbf {Q}}$
. Suppose
![]() $F_{x_0}\neq 0$
, and let
$F_{x_0}\neq 0$
, and let
![]() $F_{x_0}=Q_{0}S_{0}$
be the slope
$F_{x_0}=Q_{0}S_{0}$
be the slope
![]() $\leq h$
-factorization of the specialization of F at
$\leq h$
-factorization of the specialization of F at
![]() $x_0$
. Then there is an open affinoid subspace
$x_0$
. Then there is an open affinoid subspace
![]() $U\subset \operatorname {\mathrm {Spa}} R$
containing
$U\subset \operatorname {\mathrm {Spa}} R$
containing
![]() $x_0$
such that
$x_0$
such that
![]() $F_U$
has a slope
$F_U$
has a slope
![]() $\leq h$
-factorization
$\leq h$
-factorization
![]() $F_U=QS$
with Q specializing to
$F_U=QS$
with Q specializing to
![]() $Q_0$
and S specializing to
$Q_0$
and S specializing to
![]() $S_0$
at
$S_0$
at
![]() $x_0$
.
$x_0$
.
Proof. The existence of the factorization of
![]() $F_{x_0}$
follows from the version of the Weierstrass preparation theorem proved in [Reference Ash and StevensAS, Lemma 4.4.3]. Then the proof of the proposition is nearly identical to that of [Reference Ash and StevensAS, Theorem 4.5.1], up to replacing p with u and translating the numerical inequalities into rational localization conditions.
$F_{x_0}$
follows from the version of the Weierstrass preparation theorem proved in [Reference Ash and StevensAS, Lemma 4.4.3]. Then the proof of the proposition is nearly identical to that of [Reference Ash and StevensAS, Theorem 4.5.1], up to replacing p with u and translating the numerical inequalities into rational localization conditions.
Since spectral varieties are flat over weight space, we will be able to use the following result to show that slope factorizations exist:
Theorem 3.1.2 [Reference ConradCon06, Theorem A.1.2].
Let
![]() $f:X\rightarrow Y$
be a flat map of pseudorigid spaces. Then f is finite if and only it is quasicompact and separated with finite fibers, and its fiber rank is locally constant on Y.
$f:X\rightarrow Y$
be a flat map of pseudorigid spaces. Then f is finite if and only it is quasicompact and separated with finite fibers, and its fiber rank is locally constant on Y.
Remark 3.1.3. This result is stated in [Reference ConradCon06] for classical rigid spaces, but the proof goes through unchanged for pseudorigid spaces. The input from non-Archimedean geometry is the theory of formal models (and flattening results) of [Reference Bosch and LütkebohmertBL93a], [Reference Bosch and LütkebohmertBL93b]; Although the authors had in mind applications to classical rigid analytic spaces, they worked in sufficient generality that their results hold in the more general pseudorigid context. One uses this theory to reduce to the corresponding algebraic result of [Reference Deligne and RapoportDR73, Lemma II.1.19].
We further observe that we have inclusions
![]() $\mathcal {D}_{\kappa }^r\subset \mathcal {D}_{\kappa }^{<r}\subset \mathcal {D}_{\kappa }^s$
for any
$\mathcal {D}_{\kappa }^r\subset \mathcal {D}_{\kappa }^{<r}\subset \mathcal {D}_{\kappa }^s$
for any
![]() $r_{\kappa }\leq s<r$
. Thus, the fact that
$r_{\kappa }\leq s<r$
. Thus, the fact that
![]() $F_{\kappa }^r=F_{\kappa }^s$
implies that
$F_{\kappa }^r=F_{\kappa }^s$
implies that
![]() $\mathscr {M}_c^\ast = \oplus _i H_c^i(K,\mathscr {D}_{\kappa }^{<r})_{\leq h}$
for any
$\mathscr {M}_c^\ast = \oplus _i H_c^i(K,\mathscr {D}_{\kappa }^{<r})_{\leq h}$
for any
![]() $r>r_{\kappa }$
.
$r>r_{\kappa }$
.
We may carry out the same procedure for the action of
![]() $U_p$
on
$U_p$
on
![]() $C_\ast ^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })$
and obtain a coherent sheaf
$C_\ast ^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })$
and obtain a coherent sheaf
![]() $\mathscr {M}_\ast ^{\mathrm {BM}}=\oplus _iH_i^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })_{\leq h}$
on
$\mathscr {M}_\ast ^{\mathrm {BM}}=\oplus _iH_i^{\mathrm {BM}}(K,\mathscr {A}_{\kappa })_{\leq h}$
on
![]() $\mathscr {Z}^{\prime }$
. Let
$\mathscr {Z}^{\prime }$
. Let
![]() $\mathbb {T}$
denote either
$\mathbb {T}$
denote either
![]() $\mathbb {T}(\Delta ^p,K^p)$
or
$\mathbb {T}(\Delta ^p,K^p)$
or
![]() $\mathbb {T}(\Delta ,K)$
. Both
$\mathbb {T}(\Delta ,K)$
. Both
![]() $\mathscr {M}_c^\ast $
and
$\mathscr {M}_c^\ast $
and
![]() $\mathscr {M}_\ast ^{\mathrm {BM}}$
are Hecke modules, so we have constructed eigenvariety data
$\mathscr {M}_\ast ^{\mathrm {BM}}$
are Hecke modules, so we have constructed eigenvariety data
![]() $(\mathscr {Z},\mathscr {M}_c^\ast ,\mathbb {T},\psi )$
and
$(\mathscr {Z},\mathscr {M}_c^\ast ,\mathbb {T},\psi )$
and
![]() $(\mathscr {Z}^\prime ,\mathscr {M}_\ast ^{\mathrm {BM}},\mathbb {T},\psi ')$
(where
$(\mathscr {Z}^\prime ,\mathscr {M}_\ast ^{\mathrm {BM}},\mathbb {T},\psi ')$
(where
![]() $\psi :\mathbb {T}\rightarrow \operatorname {\mathrm {End}}_{{\mathscr {O}}_{\mathscr {Z}}}(\mathscr {M}_c^\ast )$
and
$\psi :\mathbb {T}\rightarrow \operatorname {\mathrm {End}}_{{\mathscr {O}}_{\mathscr {Z}}}(\mathscr {M}_c^\ast )$
and
![]() $\psi ':\mathbb {T}\rightarrow \operatorname {\mathrm {End}}_{{\mathscr {O}}_{\mathscr {Z}^\prime }}(\mathscr {M}_\ast ^{\mathrm {BM}})$
give the Hecke-module structures).
$\psi ':\mathbb {T}\rightarrow \operatorname {\mathrm {End}}_{{\mathscr {O}}_{\mathscr {Z}^\prime }}(\mathscr {M}_\ast ^{\mathrm {BM}})$
give the Hecke-module structures).
Finally, we may construct eigenvarieties from the eigenvariety data. Let
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\mathscr {T}^\prime $
denote the sheaves of
$\mathscr {T}^\prime $
denote the sheaves of
![]() ${\mathscr {O}}_{\mathscr {Z}}$
-algebras generated by the images of
${\mathscr {O}}_{\mathscr {Z}}$
-algebras generated by the images of
![]() $\psi $
and
$\psi $
and
![]() $\psi '$
, respectively; in particular, if
$\psi '$
, respectively; in particular, if
![]() $\mathscr {Z}_{U,h}\subset \mathscr {Z}$
is an open affinoid corresponding to the slope datum
$\mathscr {Z}_{U,h}\subset \mathscr {Z}$
is an open affinoid corresponding to the slope datum
![]() $(U,h)$
, then
$(U,h)$
, then
and
Then we set
and
and we have finite morphisms
![]() $q:\mathscr {X}_{{\mathbf {G}}}\rightarrow \mathscr {Z}$
and
$q:\mathscr {X}_{{\mathbf {G}}}\rightarrow \mathscr {Z}$
and
![]() $q':\mathscr {X}_{{\mathbf {G}}}^\prime \rightarrow \mathscr {Z}^\prime $
, and
$q':\mathscr {X}_{{\mathbf {G}}}^\prime \rightarrow \mathscr {Z}^\prime $
, and
![]() ${\mathbf {Z}}_p$
-algebra homomorphisms
${\mathbf {Z}}_p$
-algebra homomorphisms
![]() $\phi _{\mathscr {X}}:\mathbb {T}\rightarrow {\mathscr {O}}(\mathscr {X}_{{\mathbf {G}}}^{\mathbb {T}})$
and
$\phi _{\mathscr {X}}:\mathbb {T}\rightarrow {\mathscr {O}}(\mathscr {X}_{{\mathbf {G}}}^{\mathbb {T}})$
and
![]() $\phi _{\mathscr {X}'}:\mathbb {T}\rightarrow {\mathscr {O}}(\mathscr {X}_{{\mathbf {G}}}^{\mathbb {T},\prime })$
. If the choice of Hecke operators is clear from context, we will drop
$\phi _{\mathscr {X}'}:\mathbb {T}\rightarrow {\mathscr {O}}(\mathscr {X}_{{\mathbf {G}}}^{\mathbb {T},\prime })$
. If the choice of Hecke operators is clear from context, we will drop
![]() $\mathbb {T}$
from the notation.
$\mathbb {T}$
from the notation.
If
![]() $\mathbb {T}=\mathbb {T}(\Delta ,K)$
, then unlike [Reference Johansson and NewtonJN16], we are adding the Hecke operators
$\mathbb {T}=\mathbb {T}(\Delta ,K)$
, then unlike [Reference Johansson and NewtonJN16], we are adding the Hecke operators
![]() $U_{\varpi _v}$
at places
$U_{\varpi _v}$
at places
![]() $v\mid p$
to our Hecke algebras (and hence to the coordinate rings of our eigenvarieties), not just the controlling operator
$v\mid p$
to our Hecke algebras (and hence to the coordinate rings of our eigenvarieties), not just the controlling operator
![]() $U_p$
.
$U_p$
.
3.2 The middle-degree eigenvariety
When
![]() $F={\mathbf {Q}}$
and
$F={\mathbf {Q}}$
and
![]() ${\mathbf {G}}={{\mathrm{{H}}}}=\operatorname {\mathrm {GL}}_2$
, for any fixed slope h such that
${\mathbf {G}}={{\mathrm{{H}}}}=\operatorname {\mathrm {GL}}_2$
, for any fixed slope h such that
![]() $C_c^{\bullet }(K,\mathscr {D}_{\kappa })$
has a slope-
$C_c^{\bullet }(K,\mathscr {D}_{\kappa })$
has a slope-
![]() $\leq h$
decomposition, the complex
$\leq h$
decomposition, the complex
![]() $C_c^{\bullet }(K,\mathscr {D}_{\kappa })_{\leq h}$
has cohomology only in degree
$C_c^{\bullet }(K,\mathscr {D}_{\kappa })_{\leq h}$
has cohomology only in degree
![]() $1$
, and
$1$
, and
![]() $H_c^1(K,\mathscr {D}_{\kappa })_{\leq h}$
is projective. As a result, the eigencurve is reduced and equidimensional, and classical points are very Zariski-dense. For a general totally real field F, the situation is more complicated. The complex
$H_c^1(K,\mathscr {D}_{\kappa })_{\leq h}$
is projective. As a result, the eigencurve is reduced and equidimensional, and classical points are very Zariski-dense. For a general totally real field F, the situation is more complicated. The complex
![]() $C_c^{\bullet }(K,\mathscr {D}_{\kappa })_{\leq h}$
lives in degrees
$C_c^{\bullet }(K,\mathscr {D}_{\kappa })_{\leq h}$
lives in degrees
![]() $[0,2d]$
, and we are still primarily interested in the degree-d cohomology; indeed, the discussion of [Reference HarderHar87, §3.6] shows that cuspidal cohomological automorphic forms contribute only to middle degree cohomology in the classical finite-dimensional classical analogue. However, there is no reason to expect the other cohomology groups to vanish.
$[0,2d]$
, and we are still primarily interested in the degree-d cohomology; indeed, the discussion of [Reference HarderHar87, §3.6] shows that cuspidal cohomological automorphic forms contribute only to middle degree cohomology in the classical finite-dimensional classical analogue. However, there is no reason to expect the other cohomology groups to vanish.
Instead, following [Reference Bergdall and HansenBH17] we will sketch the construction of an open subspace
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, where
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, where
![]() $H_c^i(K,\mathscr {D}_{\kappa })$
vanishes for
$H_c^i(K,\mathscr {D}_{\kappa })$
vanishes for
![]() $i\neq d$
; by [Reference Bergdall and HansenBH17, Theorem B.0.1], all classical points of
$i\neq d$
; by [Reference Bergdall and HansenBH17, Theorem B.0.1], all classical points of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
whose associated Galois representation have sufficiently large residual image lie in
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
whose associated Galois representation have sufficiently large residual image lie in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
. The cohomology and base change result [Reference Johansson and NewtonJN16, Theorem 4.2.1] shows that the locus where
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
. The cohomology and base change result [Reference Johansson and NewtonJN16, Theorem 4.2.1] shows that the locus where
![]() $H_c^i(K,\mathscr {D}_{\kappa })=0$
for
$H_c^i(K,\mathscr {D}_{\kappa })=0$
for
![]() $i\geq d+1$
is open, but we need to use the homology complexes
$i\geq d+1$
is open, but we need to use the homology complexes
![]() $C_{\bullet }^{\mathrm {BM}}(K,\mathcal {A}_{\kappa })$
to control
$C_{\bullet }^{\mathrm {BM}}(K,\mathcal {A}_{\kappa })$
to control
![]() $H_c^i(K,\mathscr {D}_{\kappa })$
for
$H_c^i(K,\mathscr {D}_{\kappa })$
for
![]() $i\leq d-1$
.
$i\leq d-1$
.
As in [Reference Bergdall and HansenBH17], the key points are a base change result for Borel–Moore homology, and a universal coefficients theorem relating it to compactly supported cohomology:
Proposition 3.2.1.
-
• There is a third-quadrant spectral sequence
 $$\begin{align*}E_2^{i,j} = \operatorname{\mathrm{Tor}}_{-i}^R(H_{-j}^{\mathrm{BM}}(K,\mathscr{A}_{\kappa})_{\leq h},S)\Rightarrow H_{-i-j}^{\mathrm{BM}}(K,\mathscr{A}_{\kappa_S})_{\leq h} \end{align*}$$
$$\begin{align*}E_2^{i,j} = \operatorname{\mathrm{Tor}}_{-i}^R(H_{-j}^{\mathrm{BM}}(K,\mathscr{A}_{\kappa})_{\leq h},S)\Rightarrow H_{-i-j}^{\mathrm{BM}}(K,\mathscr{A}_{\kappa_S})_{\leq h} \end{align*}$$
-
• There is a second-quadrant spectral sequence
 $$\begin{align*}E_2^{i,j}=\operatorname{\mathrm{Ext}}_R^i(H_j^{\mathrm{BM}}(K,\mathscr{A}_{\kappa})_{\leq h},R)\Rightarrow H_c^{i+j}(K,\mathscr{D}_{\kappa})_{\leq h} \end{align*}$$
$$\begin{align*}E_2^{i,j}=\operatorname{\mathrm{Ext}}_R^i(H_j^{\mathrm{BM}}(K,\mathscr{A}_{\kappa})_{\leq h},R)\Rightarrow H_c^{i+j}(K,\mathscr{D}_{\kappa})_{\leq h} \end{align*}$$
These are spectral sequences of
![]() $\mathbb {T}(\Delta ,K)$
-modules.
$\mathbb {T}(\Delta ,K)$
-modules.
The proof uses both the fact that
![]() $\mathcal {D}_{\kappa }^{<r}$
is the continuous dual of
$\mathcal {D}_{\kappa }^{<r}$
is the continuous dual of
![]() $\mathcal {A}_{\kappa }^r$
and the fact that
$\mathcal {A}_{\kappa }^r$
and the fact that
![]() $H_c^i(K,\mathcal {D}_{\kappa }^{<r})_{\leq h}=H_c^i(K,\mathcal {D}_{\kappa }^r)_{\leq h}$
for all
$H_c^i(K,\mathcal {D}_{\kappa }^{<r})_{\leq h}=H_c^i(K,\mathcal {D}_{\kappa }^r)_{\leq h}$
for all
![]() $r>r_{\kappa }$
.
$r>r_{\kappa }$
.
Proposition 3.2.2. If
![]() $(U,h)$
is a slope datum, then we have a natural commuting diagram
$(U,h)$
is a slope datum, then we have a natural commuting diagram

Thus, we have a morphism
![]() $\tau :\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{\mathrm {{red}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^\prime $
and a closed immersion
$\tau :\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{\mathrm {{red}}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^\prime $
and a closed immersion
![]() $i:\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{\mathrm {{red}}}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
.
$i:\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{\mathrm {{red}}}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
.
Definition 3.2.3.
By construction, a point
![]() $x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of weight
$x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
of weight
![]() $\lambda _x$
lies in the Zariski-open subspace
$\lambda _x$
lies in the Zariski-open subspace
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
if and only if
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
if and only if
![]() $H_c^j(K,k_x\otimes \mathscr {D}_{\lambda _x})_{\mathfrak {m}_x}=0$
for all
$H_c^j(K,k_x\otimes \mathscr {D}_{\lambda _x})_{\mathfrak {m}_x}=0$
for all
![]() $j\neq d$
(where
$j\neq d$
(where
![]() $\mathfrak {m}_x$
is the maximal ideal of the Hecke algebra corresponding to x).
$\mathfrak {m}_x$
is the maximal ideal of the Hecke algebra corresponding to x).
Proposition 3.2.4.
-
1. The coherent sheaf
 $\mathscr {M}_c^d|_{\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}}$
is flat over
$\mathscr {M}_c^d|_{\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}}$
is flat over
 $\mathscr {W}$
.
$\mathscr {W}$
. -
2.
 $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
is covered by open affinoids W such that W is a connected component of
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
is covered by open affinoids W such that W is a connected component of
 $(\pi \circ q)^{-1}(U)$
, where
$(\pi \circ q)^{-1}(U)$
, where
 $(U,h)$
is some slope datum, and
$(U,h)$
is some slope datum, and
 $\mathscr {T}(W)$
acts faithfully on
$\mathscr {T}(W)$
acts faithfully on
 $\mathscr {M}_c^d(W)\cong e_WH_c^d(K,\mathscr {D}_{\kappa })_{\leq h}$
(where
$\mathscr {M}_c^d(W)\cong e_WH_c^d(K,\mathscr {D}_{\kappa })_{\leq h}$
(where
 $e_W$
is the idempotent projector restricting from
$e_W$
is the idempotent projector restricting from
 $(\pi \circ q)^{-1}(U)$
to W).
$(\pi \circ q)^{-1}(U)$
to W).
Proof. This follows from the base change spectral sequence, and the criterion for flatness.
3.3 Jacquet–Langlands
The classical Jacquet–Langlands correspondence lets us transfer automorphic forms between
![]() $\operatorname {\mathrm {GL}}_2$
and quaternionic algebraic groups. Over
$\operatorname {\mathrm {GL}}_2$
and quaternionic algebraic groups. Over
![]() ${\mathbf {Q}}$
, this correspondence was interpolated in [Reference ChenevierChe05] to give a closed immersion of eigencurves
${\mathbf {Q}}$
, this correspondence was interpolated in [Reference ChenevierChe05] to give a closed immersion of eigencurves
![]() $\mathscr {X}_{D^{\times }/{\mathbf {Q}}}^{\mathrm {rig}}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}^{\mathrm {rig}}$
; this interpolation was given for general totally real fields in [Reference BirkbeckBir19]. We give the corresponding result for extended eigenvarieties. However, as we have elected to work with the eigenvariety for
$\mathscr {X}_{D^{\times }/{\mathbf {Q}}}^{\mathrm {rig}}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}}}^{\mathrm {rig}}$
; this interpolation was given for general totally real fields in [Reference BirkbeckBir19]. We give the corresponding result for extended eigenvarieties. However, as we have elected to work with the eigenvariety for
![]() $\operatorname {\mathrm {GL}}_2/F$
constructed in [Reference Johansson and NewtonJN16] via overconvergent cohomology, instead of the eigenvariety constructed from Hilbert modular forms, we will never get an isomorphism of eigenvarieties, even when
$\operatorname {\mathrm {GL}}_2/F$
constructed in [Reference Johansson and NewtonJN16] via overconvergent cohomology, instead of the eigenvariety constructed from Hilbert modular forms, we will never get an isomorphism of eigenvarieties, even when
![]() $[F:{\mathbf {Q}}]$
is even.
$[F:{\mathbf {Q}}]$
is even.
Let D be a totally definite quaternion algebra over F, split at every place above p, and let
![]() $\mathfrak {d}_D$
be its discriminant. For any ideal
$\mathfrak {d}_D$
be its discriminant. For any ideal
![]() $\mathfrak {n}\subset {\mathscr {O}}_F$
with
$\mathfrak {n}\subset {\mathscr {O}}_F$
with
![]() $(\mathfrak {d}_D,\mathfrak {n})=1$
, we define the subgroup
$(\mathfrak {d}_D,\mathfrak {n})=1$
, we define the subgroup
![]() $K_1^{\underline D^{\times }}(\mathfrak {n})\subset ({\mathscr {O}}_D\otimes \widehat {{\mathbf {Z}}})^{\times }$
$K_1^{\underline D^{\times }}(\mathfrak {n})\subset ({\mathscr {O}}_D\otimes \widehat {{\mathbf {Z}}})^{\times }$
We may define a similar subgroup
![]() $K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})\subset \operatorname {\mathrm {Res}}_{{\mathscr {O}}_F/{\mathbf {Z}}_p}\operatorname {\mathrm {GL}}_2(\widehat {{\mathbf {Z}}})$
.
$K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})\subset \operatorname {\mathrm {Res}}_{{\mathscr {O}}_F/{\mathbf {Z}}_p}\operatorname {\mathrm {GL}}_2(\widehat {{\mathbf {Z}}})$
.
A classical algebraic weight is a tuple
![]() $(k_\sigma )\in {\mathbf {Z}}_{\geq 2}^{\Sigma _\infty }$
together with a tuple
$(k_\sigma )\in {\mathbf {Z}}_{\geq 2}^{\Sigma _\infty }$
together with a tuple
![]() $(v_\sigma )\in {\mathbf {Z}}^{\Sigma _\infty }$
such that
$(v_\sigma )\in {\mathbf {Z}}^{\Sigma _\infty }$
such that
![]() $(k_\sigma )+(v_\sigma ) = (r,\ldots ,r)$
for some
$(k_\sigma )+(v_\sigma ) = (r,\ldots ,r)$
for some
![]() $r\in {\mathbf {Z}}$
, where
$r\in {\mathbf {Z}}$
, where
![]() $\Sigma _\infty $
is the set of embeddings
$\Sigma _\infty $
is the set of embeddings
![]() $F\hookrightarrow {\mathbf {R}}$
. Set
$F\hookrightarrow {\mathbf {R}}$
. Set
![]() $e_1:=(\frac {r+k_\sigma }{2})$
and
$e_1:=(\frac {r+k_\sigma }{2})$
and
![]() $e_2:=(\frac {r-k_\sigma }{2})$
, and define characters
$e_2:=(\frac {r-k_\sigma }{2})$
, and define characters
![]() $\kappa _i:F^{\times }\rightarrow {\mathbf {R}}^{\times }$
for
$\kappa _i:F^{\times }\rightarrow {\mathbf {R}}^{\times }$
for
![]() $i=1,2$
via
$i=1,2$
via
Then
![]() $(\kappa _1,\kappa _2)$
is a character on
$(\kappa _1,\kappa _2)$
is a character on
![]() $\operatorname {\mathrm {T}}({\mathbf {Z}})$
which is trivial on a finite-index subgroup of the center
$\operatorname {\mathrm {T}}({\mathbf {Z}})$
which is trivial on a finite-index subgroup of the center
![]() $Z_G({\mathbf {Z}})={\mathscr {O}}_F^{\times }$
.
$Z_G({\mathbf {Z}})={\mathscr {O}}_F^{\times }$
.
Then we have the classical Jacquet–Langlands correspondence:
Theorem 3.3.1. Let
![]() $\kappa $
be a classical weight, and let
$\kappa $
be a classical weight, and let
![]() $\mathfrak {n}\subset {\mathscr {O}}_F$
be an ideal such that
$\mathfrak {n}\subset {\mathscr {O}}_F$
be an ideal such that
![]() $(\mathfrak {n},\mathfrak {d}_D)=1$
. There is a Hecke-equivariant isomorphism of spaces of cusp forms
$(\mathfrak {n},\mathfrak {d}_D)=1$
. There is a Hecke-equivariant isomorphism of spaces of cusp forms
We will interpolate this correspondence to a closed immersion
![]() $\mathscr {X}_{\underline D^{\times }}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, where the source has tame level
$\mathscr {X}_{\underline D^{\times }}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, where the source has tame level
![]() $K_1^{\underline D^{\times }}(\mathfrak {n})$
and the target has tame level
$K_1^{\underline D^{\times }}(\mathfrak {n})$
and the target has tame level
![]() $K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})$
. We use the interpolation theorem of [Reference Johansson and NewtonJN19a]:
$K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})$
. We use the interpolation theorem of [Reference Johansson and NewtonJN19a]:
Theorem 3.3.2 [Reference Johansson and NewtonJN19a, Theorem 3.2.1].
Let
![]() $\mathfrak {D}_i=(\mathscr {Z}_i,\mathscr {M}_i,\mathbb {T}_i,\psi _i)$
for
$\mathfrak {D}_i=(\mathscr {Z}_i,\mathscr {M}_i,\mathbb {T}_i,\psi _i)$
for
![]() $i=1,2$
be eigenvariety data, with corresponding eigenvarieties
$i=1,2$
be eigenvariety data, with corresponding eigenvarieties
![]() $\mathscr {X}_i$
, and suppose we have the following:
$\mathscr {X}_i$
, and suppose we have the following:
-
• A morphism
 $j:\mathscr {Z}_1\rightarrow \mathscr {Z}_2$
$j:\mathscr {Z}_1\rightarrow \mathscr {Z}_2$
-
• A
 ${\mathbf {Z}}_p$
-algebra homomorphism
${\mathbf {Z}}_p$
-algebra homomorphism
 $\mathbb {T}_2\rightarrow \mathbb {T}_1$
$\mathbb {T}_2\rightarrow \mathbb {T}_1$
-
• A subset
 $\mathscr {X}^{\mathrm {cl}}\subset \mathscr {X}_1$
of maximal points such that the
$\mathscr {X}^{\mathrm {cl}}\subset \mathscr {X}_1$
of maximal points such that the
 $\mathbb {T}_2$
-eigensystem of x appears in
$\mathbb {T}_2$
-eigensystem of x appears in
 $\mathscr {M}_2(j(\pi _1(x)))$
for all
$\mathscr {M}_2(j(\pi _1(x)))$
for all
 $x\in \mathscr {X}^{\mathrm {cl}}$
.
$x\in \mathscr {X}^{\mathrm {cl}}$
.
Let
![]() $\overline {\mathscr {X}}\subset \mathscr {X}_1$
denote the Zariski closure of
$\overline {\mathscr {X}}\subset \mathscr {X}_1$
denote the Zariski closure of
![]() $\mathscr {X}^{\mathrm {cl}}$
(with its underlying reduced structure). Then there is a canonical morphism
$\mathscr {X}^{\mathrm {cl}}$
(with its underlying reduced structure). Then there is a canonical morphism
![]() $i:\overline {\mathscr {X}}\rightarrow \mathscr {X}_2$
lying over j, such that
$i:\overline {\mathscr {X}}\rightarrow \mathscr {X}_2$
lying over j, such that
![]() $\phi _{\overline {\mathscr {X}}}\circ \sigma = i^\ast \circ \phi _{\mathscr {X}_2}$
. If j is a closed immersion and
$\phi _{\overline {\mathscr {X}}}\circ \sigma = i^\ast \circ \phi _{\mathscr {X}_2}$
. If j is a closed immersion and
![]() $\sigma $
is a surjection, then i is a closed immersion.
$\sigma $
is a surjection, then i is a closed immersion.
We remark that in the presence of integral structures, we can make a sharper statement:
Corollary 3.3.3. With notation as above, suppose that the
![]() $\mathscr {Z}_i=\operatorname {\mathrm {Spa}} R_i$
are affinoid, with
$\mathscr {Z}_i=\operatorname {\mathrm {Spa}} R_i$
are affinoid, with
![]() $R_{i,0}\subset R_i$
rings of definition such that j is induced by a morphism
$R_{i,0}\subset R_i$
rings of definition such that j is induced by a morphism
![]() $\operatorname {\mathrm {Spf}} R_{1,0}\rightarrow \operatorname {\mathrm {Spf}} R_{2,0}$
, and suppose that
$\operatorname {\mathrm {Spf}} R_{1,0}\rightarrow \operatorname {\mathrm {Spf}} R_{2,0}$
, and suppose that
![]() $M_i:=\Gamma (\mathscr {Z}_i,\mathscr {M}_i)$
admit
$M_i:=\Gamma (\mathscr {Z}_i,\mathscr {M}_i)$
admit
![]() $R_{i,0}$
-lattices
$R_{i,0}$
-lattices
![]() $M_{i,0}$
stable under the actions of
$M_{i,0}$
stable under the actions of
![]() $\mathbb {T}_i$
. Let
$\mathbb {T}_i$
. Let
![]() $R_{i,0}':=\operatorname {\mathrm {im}}\left (R_{i,0}\otimes \mathbb {T}_i\rightarrow \operatorname {\mathrm {End}}_{R_{i,0}}(M_{i,0})\right )$
, and let
$R_{i,0}':=\operatorname {\mathrm {im}}\left (R_{i,0}\otimes \mathbb {T}_i\rightarrow \operatorname {\mathrm {End}}_{R_{i,0}}(M_{i,0})\right )$
, and let
![]() $\overline {\mathscr {X}}_0$
denote the closure of
$\overline {\mathscr {X}}_0$
denote the closure of
![]() $\mathscr {X}^{\mathrm {cl}}$
in
$\mathscr {X}^{\mathrm {cl}}$
in
![]() $\operatorname {\mathrm {Spf}} R_{1,0}'$
. Then there is a morphism
$\operatorname {\mathrm {Spf}} R_{1,0}'$
. Then there is a morphism
![]() $j_0:\overline {\mathscr {X}}_0\rightarrow \operatorname {\mathrm {Spf}} R_{2,0}'$
.
$j_0:\overline {\mathscr {X}}_0\rightarrow \operatorname {\mathrm {Spf}} R_{2,0}'$
.
Proof. As in the proof of [Reference Johansson and NewtonJN19a, Theorem 3.2.1], one reduces to the case where
![]() $R_0:=R_{1,0}=R_{2,0}$
and
$R_0:=R_{1,0}=R_{2,0}$
and
![]() $\mathbb {T}:=\mathbb {T}_1=\mathbb {T}_2$
, and one considers the actions of
$\mathbb {T}:=\mathbb {T}_1=\mathbb {T}_2$
, and one considers the actions of
![]() $\mathbb {T}_1\oplus \mathbb {T}_2$
on
$\mathbb {T}_1\oplus \mathbb {T}_2$
on
![]() $M_{1,0}\oplus M_{2,0}$
. Then we have quotients
$M_{1,0}\oplus M_{2,0}$
. Then we have quotients
Since
![]() $\overline {\mathscr {X}}\subset \mathscr {X}_2$
and
$\overline {\mathscr {X}}\subset \mathscr {X}_2$
and
![]() $\operatorname {\mathrm {Spf}} R_{3,0}$
is separated, we have
$\operatorname {\mathrm {Spf}} R_{3,0}$
is separated, we have
![]() $\overline {\mathscr {X}}_0\subset \operatorname {\mathrm {Spf}} R_{2,0}'$
, as desired.
$\overline {\mathscr {X}}_0\subset \operatorname {\mathrm {Spf}} R_{2,0}'$
, as desired.
We take
![]() $\mathscr {Z}_1=\mathscr {Z}_2=\mathscr {W}_F\times {\mathbf {G}}_m$
. In order to define
$\mathscr {Z}_1=\mathscr {Z}_2=\mathscr {W}_F\times {\mathbf {G}}_m$
. In order to define
![]() $\mathbb {T}=\mathbb {T}_1=\mathbb {T}_2$
, we set
$\mathbb {T}=\mathbb {T}_1=\mathbb {T}_2$
, we set
 $$\begin{align*}\Delta_{v} = \begin{cases} \operatorname{\mathrm{GL}}_2(F_v) &\mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \\ {K_1^{\underline D^{\times}}(\mathfrak{n})}_v &\mbox{ if } v\mid \mathfrak{d}_D\mathfrak{n}. \end{cases} \end{align*}$$
$$\begin{align*}\Delta_{v} = \begin{cases} \operatorname{\mathrm{GL}}_2(F_v) &\mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \\ {K_1^{\underline D^{\times}}(\mathfrak{n})}_v &\mbox{ if } v\mid \mathfrak{d}_D\mathfrak{n}. \end{cases} \end{align*}$$
For
![]() $v\mid p$
, we take
$v\mid p$
, we take
![]() $\Delta _{v}$
as in §3.1. In other words,
$\Delta _{v}$
as in §3.1. In other words,
![]() $\mathbb {T}$
is the commutative
$\mathbb {T}$
is the commutative
![]() ${\mathbf {Z}}_p$
-algebra generated by
${\mathbf {Z}}_p$
-algebra generated by
![]() $T_v:=[K_v\left ( \begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix} \right )K_v]$
and
$T_v:=[K_v\left ( \begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix} \right )K_v]$
and
![]() $S_v:=[K_v\left ( \begin {smallmatrix}\varpi _v & \\ & \varpi _v\end {smallmatrix} \right )K_v]$
for
$S_v:=[K_v\left ( \begin {smallmatrix}\varpi _v & \\ & \varpi _v\end {smallmatrix} \right )K_v]$
for
![]() $v\nmid p\mathfrak {d}_D\mathfrak {n}$
and
$v\nmid p\mathfrak {d}_D\mathfrak {n}$
and
![]() $U_{\varpi _v}$
for
$U_{\varpi _v}$
for
![]() $v\mid p$
.
$v\mid p$
.
However, we cannot immediately combine this interpolation theorem with the Jacquet–Langlands correspondence because our choice of weight space means that classical weights may not be Zariski dense unless Leopoldt’s conjecture is true. More precisely, given a classical algebraic weight, we constructed a character on
![]() $\operatorname {\mathrm {T}}({\mathbf {Z}})$
trivial on a finite-index subgroup of
$\operatorname {\mathrm {T}}({\mathbf {Z}})$
trivial on a finite-index subgroup of
![]() ${\mathscr {O}}_F^{\times }$
, and conversely, characters on
${\mathscr {O}}_F^{\times }$
, and conversely, characters on
![]() $\operatorname {\mathrm {T}}({\mathbf {Z}})$
trivial on a finite-index subgroup of
$\operatorname {\mathrm {T}}({\mathbf {Z}})$
trivial on a finite-index subgroup of
![]() ${\mathscr {O}}_F^{\times }$
yield classical algebraic weights. This equivalence relies on Dirichlet’s unit theorem.
${\mathscr {O}}_F^{\times }$
yield classical algebraic weights. This equivalence relies on Dirichlet’s unit theorem.
This means that there are two natural definitions of p-adic families of weights,
![]() $\mathscr {W}_F'=\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![(\operatorname {\mathrm {Res}}_{{\mathscr {O}}_F/{\mathbf {Z}}_p}{\mathbf {G}}_m)\times {\mathbf {Z}}_p^{\times }]\!]^{\mathrm {{an}}}$
interpolating classical algebraic weights, and
$\mathscr {W}_F'=\operatorname {\mathrm {Spa}} {\mathbf {Z}}_p[\![(\operatorname {\mathrm {Res}}_{{\mathscr {O}}_F/{\mathbf {Z}}_p}{\mathbf {G}}_m)\times {\mathbf {Z}}_p^{\times }]\!]^{\mathrm {{an}}}$
interpolating classical algebraic weights, and
![]() $\mathscr {W}_F$
interpolating characters on
$\mathscr {W}_F$
interpolating characters on
![]() $T_0$
, and the equivalence of those two definitions depends on Leopoldt’s conjecture.
$T_0$
, and the equivalence of those two definitions depends on Leopoldt’s conjecture.
Fortunately, the gap between these weight spaces can be controlled: There is a closed embedding
![]() $\mathscr {W}_F'\hookrightarrow \mathscr {W}_F$
, and the twisting action by characters on
$\mathscr {W}_F'\hookrightarrow \mathscr {W}_F$
, and the twisting action by characters on
![]() ${\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}$
defines a surjective map
${\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}$
defines a surjective map
We say that a weight
![]() $\lambda \in \mathscr {W}_F^{\mathrm {rig}}(\overline {{\mathbf {Q}}}_p)$
is twist classical if it is in the
$\lambda \in \mathscr {W}_F^{\mathrm {rig}}(\overline {{\mathbf {Q}}}_p)$
is twist classical if it is in the
![]() $\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of a classical weight. Then twist classical weights are very Zariski dense in
$\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of a classical weight. Then twist classical weights are very Zariski dense in
![]() $\mathscr {W}_F$
.
$\mathscr {W}_F$
.
In addition, we may define a twisting action on Hecke modules, as in [Reference Bergdall and HansenBH17]. Let
![]() $\operatorname {\mathrm {Gal}}_{F,p}$
denote the Galois group of the maximal abelian extension of F unramified away from p and
$\operatorname {\mathrm {Gal}}_{F,p}$
denote the Galois group of the maximal abelian extension of F unramified away from p and
![]() $\infty $
, and let
$\infty $
, and let
![]() $\eta :\operatorname {\mathrm {Gal}}_{F,p}\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
be a continuous character. Global class field theory implies that
$\eta :\operatorname {\mathrm {Gal}}_{F,p}\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
be a continuous character. Global class field theory implies that
![]() $\operatorname {\mathrm {Gal}}_{F,p}$
fits into an exact sequence
$\operatorname {\mathrm {Gal}}_{F,p}$
fits into an exact sequence
where
![]() $\mathrm {Cl}_F^+$
is the narrow class group of F (and hence finite). Suppose M is an R-module equipped with an R-linear left
$\mathrm {Cl}_F^+$
is the narrow class group of F (and hence finite). Suppose M is an R-module equipped with an R-linear left
![]() $\Delta _p$
-action. Then we may define a new left
$\Delta _p$
-action. Then we may define a new left
![]() $\Delta _p$
-module
$\Delta _p$
-module
![]() $M(\eta ):=M\otimes \eta ^{-1}|_{{\mathscr {O}}_{F,p}^{\times }}$
, where the action of
$M(\eta ):=M\otimes \eta ^{-1}|_{{\mathscr {O}}_{F,p}^{\times }}$
, where the action of
![]() $g\in \Delta _p$
is given by
$g\in \Delta _p$
is given by
In particular,
![]() $\mathscr {D}_{\kappa }(\eta )\cong \mathscr {D}_{\eta ^{-1}\cdot \kappa }$
by [Reference Bergdall and HansenBH17, Lemma 5.5.2], and there is an isomorphism
$\mathscr {D}_{\kappa }(\eta )\cong \mathscr {D}_{\eta ^{-1}\cdot \kappa }$
by [Reference Bergdall and HansenBH17, Lemma 5.5.2], and there is an isomorphism
Suppose
![]() $x\in \mathscr {X}_{\underline D^{\times }}(\overline {{\mathbf {Q}}}_p)$
is a point with
$x\in \mathscr {X}_{\underline D^{\times }}(\overline {{\mathbf {Q}}}_p)$
is a point with
![]() $\mathrm {wt}(x)=:\lambda $
, corresponding to the system of Hecke eigenvalues
$\mathrm {wt}(x)=:\lambda $
, corresponding to the system of Hecke eigenvalues
![]() $\psi _x:\mathbb {T}\rightarrow \overline {{\mathbf {Q}}}_p$
. Then we define a new system of Hecke eigenvalues via
$\psi _x:\mathbb {T}\rightarrow \overline {{\mathbf {Q}}}_p$
. Then we define a new system of Hecke eigenvalues via
 $$\begin{align*}\mathrm{tw}_\eta(\psi_x)(T) = \begin{cases} \eta(\varpi_v)\psi_x(T) & \mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \mbox{ and } T=T_v \\ \eta(\varpi_v)^2\psi_x(T) & \mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \mbox{ and } T=S_v \\ \eta(\varpi_v)\psi_x(T) & \mbox{ if } v\mid p. \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{tw}_\eta(\psi_x)(T) = \begin{cases} \eta(\varpi_v)\psi_x(T) & \mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \mbox{ and } T=T_v \\ \eta(\varpi_v)^2\psi_x(T) & \mbox{ if } v\nmid p\mathfrak{d}_D\mathfrak{n} \mbox{ and } T=S_v \\ \eta(\varpi_v)\psi_x(T) & \mbox{ if } v\mid p. \end{cases} \end{align*}$$
Then it follows from [Reference Bergdall and HansenBH17, Proposition 5.5.5] that
![]() $\mathrm {tw}_\eta (\psi _x)$
corresponds to a point
$\mathrm {tw}_\eta (\psi _x)$
corresponds to a point
![]() $\mathrm {tw}_\eta (x)\in \mathscr {X}_{\underline D^{\times }}$
of weight
$\mathrm {tw}_\eta (x)\in \mathscr {X}_{\underline D^{\times }}$
of weight
![]() $\eta ^{-1}|_{{\mathscr {O}}_{F,p}^{\times }}\cdot \kappa $
.
$\eta ^{-1}|_{{\mathscr {O}}_{F,p}^{\times }}\cdot \kappa $
.
We say that a point
![]() $x\in \mathscr {X}_{\underline D^{\times }}(\overline {{\mathbf {Q}}}_p)$
is twist classical if it is in the
$x\in \mathscr {X}_{\underline D^{\times }}(\overline {{\mathbf {Q}}}_p)$
is twist classical if it is in the
![]() $\widehat {\operatorname {\mathrm {Gal}}_{F,p}}(\overline {{\mathbf {Q}}}_p)$
-orbit of a point corresponding to a classical system of Hecke eigenvalues.
$\widehat {\operatorname {\mathrm {Gal}}_{F,p}}(\overline {{\mathbf {Q}}}_p)$
-orbit of a point corresponding to a classical system of Hecke eigenvalues.
Proposition 3.3.4. Twist classical points are very Zariski dense in
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
Proof. Recall that
![]() $\mathscr {X}_{\underline D^{\times }}$
admits a cover by affinoid pseudorigid spaces of the form
$\mathscr {X}_{\underline D^{\times }}$
admits a cover by affinoid pseudorigid spaces of the form
![]() $\operatorname {\mathrm {Spa}} \mathscr {T}(\mathscr {Z}_{U,h})$
, where
$\operatorname {\mathrm {Spa}} \mathscr {T}(\mathscr {Z}_{U,h})$
, where
![]() $\pi :\mathscr {Z}_{U,h}\rightarrow U$
is finite of constant degree, and
$\pi :\mathscr {Z}_{U,h}\rightarrow U$
is finite of constant degree, and
We write
![]() $U=\operatorname {\mathrm {Spa}} R$
for some pseudoaffinoid algebra R over
$U=\operatorname {\mathrm {Spa}} R$
for some pseudoaffinoid algebra R over
![]() ${\mathbf {Z}}_p$
. We will show that
${\mathbf {Z}}_p$
. We will show that
![]() $\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})\rightarrow \operatorname {\mathrm {Spec}} R$
carries irreducible components surjectively onto irreducible components, and we will construct a Zariski dense set of maximal points
$\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})\rightarrow \operatorname {\mathrm {Spec}} R$
carries irreducible components surjectively onto irreducible components, and we will construct a Zariski dense set of maximal points
![]() $W_{U,h}^{\mathrm {tw-cl}}\subset U$
such that the points of
$W_{U,h}^{\mathrm {tw-cl}}\subset U$
such that the points of
![]() $\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {tw-cl}})$
are twist classical. By [Reference ChenevierChe04, Lemme 6.2.8], this implies the desired result.
$\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {tw-cl}})$
are twist classical. By [Reference ChenevierChe04, Lemme 6.2.8], this implies the desired result.
To see that irreducible components of
![]() $\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})$
map surjectively onto irreducible components of
$\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})$
map surjectively onto irreducible components of
![]() $\operatorname {\mathrm {Spec}} R$
, we observe that D is totally definite, so the associated Shimura manifold is a finite set of points and
$\operatorname {\mathrm {Spec}} R$
, we observe that D is totally definite, so the associated Shimura manifold is a finite set of points and
![]() $H_c^\ast (K,\mathscr {D}_U)$
vanishes outside degree
$H_c^\ast (K,\mathscr {D}_U)$
vanishes outside degree
![]() $0$
. The base change spectral sequence of [Reference Johansson and NewtonJN16, Theorem 4.2.1] implies that the formation of
$0$
. The base change spectral sequence of [Reference Johansson and NewtonJN16, Theorem 4.2.1] implies that the formation of
![]() $H^0(K,\mathscr {D}_U)_{\leq h}$
commutes with arbitrary base change on U, which implies that
$H^0(K,\mathscr {D}_U)_{\leq h}$
commutes with arbitrary base change on U, which implies that
![]() $H^0(K,\mathscr {D}_U)_{\leq h}$
is flat. Then [Reference ChenevierChe04, Lemme 6.2.10] implies that
$H^0(K,\mathscr {D}_U)_{\leq h}$
is flat. Then [Reference ChenevierChe04, Lemme 6.2.10] implies that
![]() $\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})\rightarrow \operatorname {\mathrm {Spec}} R$
carries irreducible components surjectively onto irreducible components, as desired.
$\operatorname {\mathrm {Spec}}\mathscr {T}(\mathscr {Z}_{U,h})\rightarrow \operatorname {\mathrm {Spec}} R$
carries irreducible components surjectively onto irreducible components, as desired.
Thus, it remains to construct
![]() $W_{U,h}^{\mathrm {tw-cl}}$
. Birkbeck proved a ‘small slope implies classical’ result [Reference BirkbeckBir19, Theorem 4.3.7] and constructed a set
$W_{U,h}^{\mathrm {tw-cl}}$
. Birkbeck proved a ‘small slope implies classical’ result [Reference BirkbeckBir19, Theorem 4.3.7] and constructed a set
![]() $W_{U,h}^{\mathrm {cl}}$
Zariski dense in
$W_{U,h}^{\mathrm {cl}}$
Zariski dense in
![]() $U\cap \mathscr {W}_F'$
such that the points of
$U\cap \mathscr {W}_F'$
such that the points of
![]() $\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {cl}})$
are classical (see the proof of [Reference BirkbeckBir19, Theorem 6.1.9]). Setting
$\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {cl}})$
are classical (see the proof of [Reference BirkbeckBir19, Theorem 6.1.9]). Setting
![]() $W_{U,h}^{\mathrm {tw-cl}}$
to be the
$W_{U,h}^{\mathrm {tw-cl}}$
to be the
![]() $\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of
$\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of
![]() $W_{U,h}^{\mathrm {cl}}$
, [Reference Bergdall and HansenBH17, Lemma 6.3.1] implies that points of
$W_{U,h}^{\mathrm {cl}}$
, [Reference Bergdall and HansenBH17, Lemma 6.3.1] implies that points of
![]() $\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {tw-cl}})$
are twist classical, and we are done.
$\mathrm {wt}^{-1}(W_{U,h}^{\mathrm {tw-cl}})$
are twist classical, and we are done.
As a corollary, we deduce that
![]() $\mathscr {X}_{\underline D^{\times }}$
has no components supported entirely in characteristic p:
$\mathscr {X}_{\underline D^{\times }}$
has no components supported entirely in characteristic p:
Corollary 3.3.5.
![]() $\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is Zariski dense in
$\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is Zariski dense in
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
We may use similar arguments to show that
![]() $\mathscr {X}_{\underline D^{\times }}$
is reduced:
$\mathscr {X}_{\underline D^{\times }}$
is reduced:
Proposition 3.3.6. The eigenvariety
![]() $\mathscr {X}_{\underline D^{\times }}$
is reduced.
$\mathscr {X}_{\underline D^{\times }}$
is reduced.
Proof. We first show that
![]() $\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is reduced. By [Reference Johansson and NewtonJN16, Proposition 6.1.2] (which adapts [Reference ChenevierChe05, Proposition 3.9]), it is enough to find a Zariski dense set of twist classical weights
$\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is reduced. By [Reference Johansson and NewtonJN16, Proposition 6.1.2] (which adapts [Reference ChenevierChe05, Proposition 3.9]), it is enough to find a Zariski dense set of twist classical weights
![]() $W_{U,h}^{{\mathrm{ss}}}\subset U\subset \mathscr {W}_F^{\mathrm {rig}}$
for each slope datum
$W_{U,h}^{{\mathrm{ss}}}\subset U\subset \mathscr {W}_F^{\mathrm {rig}}$
for each slope datum
![]() $(U,h)$
such that
$(U,h)$
such that
![]() $\mathscr {M}(\mathscr {Z}_{U,h})_{\kappa }$
is a semisimple Hecke module for all
$\mathscr {M}(\mathscr {Z}_{U,h})_{\kappa }$
is a semisimple Hecke module for all
![]() $\kappa \in W_{U,h}^{{\mathrm{ss}}}$
. Birkbeck [Reference BirkbeckBir19, Lemma 6.1.12] constructed sets
$\kappa \in W_{U,h}^{{\mathrm{ss}}}$
. Birkbeck [Reference BirkbeckBir19, Lemma 6.1.12] constructed sets
![]() $W_{U,h}^{\prime ,{\mathrm{ss}}}$
Zariski dense in
$W_{U,h}^{\prime ,{\mathrm{ss}}}$
Zariski dense in
![]() $U\cap \mathscr {W}_F^{\prime ,\mathrm {rig}}$
with this property, and we will again use twisting by p-adic characters to construct
$U\cap \mathscr {W}_F^{\prime ,\mathrm {rig}}$
with this property, and we will again use twisting by p-adic characters to construct
![]() $W_{U,h}^{{\mathrm{ss}}}$
.
$W_{U,h}^{{\mathrm{ss}}}$
.
If
![]() $\eta :{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
is a character, we have an isomorphism
$\eta :{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
is a character, we have an isomorphism
By [Reference Bergdall and HansenBH17, Proposition 5.5.5],
![]() $\mathrm {tw}_\eta $
is Hecke-equivariant up to scalars, so
$\mathrm {tw}_\eta $
is Hecke-equivariant up to scalars, so
![]() $\mathscr {M}(\mathscr {Z}_{U,h})_{\kappa }$
is a semisimple Hecke module if and only if
$\mathscr {M}(\mathscr {Z}_{U,h})_{\kappa }$
is a semisimple Hecke module if and only if
![]() $\mathscr {M}(\mathscr {Z}_{\eta ^{-1}\cdot U,h})_{\eta ^{-1}\cdot \kappa }$
is. Thus, we may take
$\mathscr {M}(\mathscr {Z}_{\eta ^{-1}\cdot U,h})_{\eta ^{-1}\cdot \kappa }$
is. Thus, we may take
![]() $W_{U,h}^{{\mathrm{ss}}}$
to be the
$W_{U,h}^{{\mathrm{ss}}}$
to be the
![]() $\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of
$\widehat {{\mathscr {O}}_{F,p}^{\times }/\overline {{\mathscr {O}}_F^{\times ,+}}}(\overline {{\mathbf {Q}}}_p)$
-orbit of
![]() $\cup _{U'}W_{U',h}^{\prime ,{\mathrm{ss}}}$
, as
$\cup _{U'}W_{U',h}^{\prime ,{\mathrm{ss}}}$
, as
![]() $(U',h)$
varies through slope data, and we see that
$(U',h)$
varies through slope data, and we see that
![]() $\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is reduced.
$\mathscr {X}_{\underline D^{\times }}^{\mathrm {rig}}$
is reduced.
Now, let
![]() $X\subset \mathscr {X}_{\underline D^{\times }}$
be an open affinoid subspace, and let
$X\subset \mathscr {X}_{\underline D^{\times }}$
be an open affinoid subspace, and let
![]() $\{X_i\}$
be an open affinoid cover of the rigid analytic locus
$\{X_i\}$
be an open affinoid cover of the rigid analytic locus
![]() $X^{\mathrm {rig}}\subset X$
. Since
$X^{\mathrm {rig}}\subset X$
. Since
![]() $X\smallsetminus X^{\mathrm {rig}}$
contains no open subset of X, the natural map
$X\smallsetminus X^{\mathrm {rig}}$
contains no open subset of X, the natural map
is injective. Each
![]() ${\mathscr {O}}(X_i)$
is reduced, so
${\mathscr {O}}(X_i)$
is reduced, so
![]() ${\mathscr {O}}(X)$
is, as well.
${\mathscr {O}}(X)$
is, as well.
Now, the Jacquet–Langlands correspondence for eigenvarieties follows immediately:
Corollary 3.3.7. There is a closed immersion
![]() $\mathscr {X}_{\underline D^{\times }}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
interpolating the classical Jacquet–Langlands correspondence on (twist) classical points, where the source has tame level
$\mathscr {X}_{\underline D^{\times }}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
interpolating the classical Jacquet–Langlands correspondence on (twist) classical points, where the source has tame level
![]() $K_1^{\underline D^{\times }}(\mathfrak {n})$
and the target has tame level
$K_1^{\underline D^{\times }}(\mathfrak {n})$
and the target has tame level
![]() $K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})$
.
$K_1^{\operatorname {\mathrm {GL}}_2/F}(\mathfrak {n})$
.
In particular, if
![]() $[F:{\mathbf {Q}}]$
is even, we can find D split at all finite places and ramified at all infinite places. Then we may take in particular
$[F:{\mathbf {Q}}]$
is even, we can find D split at all finite places and ramified at all infinite places. Then we may take in particular
![]() $\mathfrak {n}={\mathscr {O}}_F$
to obtain a morphism of eigenvarieties of tame level
$\mathfrak {n}={\mathscr {O}}_F$
to obtain a morphism of eigenvarieties of tame level
![]() $1$
.
$1$
.
3.4 Cyclic base change
Fix an integer
![]() $N\in {\mathbf {N}}$
, and let S be a finite set of primes containing every prime dividing
$N\in {\mathbf {N}}$
, and let S be a finite set of primes containing every prime dividing
![]() $pN$
. For any number field F, we again let
$pN$
. For any number field F, we again let
![]() $K_F^p\subset \operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
be the compact open subgroup given by
$K_F^p\subset \operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
be the compact open subgroup given by
and we let
![]() $K_F:=K_F^pI$
. We also define the Hecke algebra
$K_F:=K_F^pI$
. We also define the Hecke algebra
There is a homomorphism
![]() $\sigma _F^S:\mathbb {T}_F^S\rightarrow \mathbb {T}_{{\mathbf {Q}}}^S$
induced by unramified local Langlands and restriction of Weil representations from
$\sigma _F^S:\mathbb {T}_F^S\rightarrow \mathbb {T}_{{\mathbf {Q}}}^S$
induced by unramified local Langlands and restriction of Weil representations from
![]() $W_F$
to
$W_F$
to
![]() $W_{\mathbf {Q}}$
.
$W_{\mathbf {Q}}$
.
Similarly, there is a morphism of weight spaces
![]() $\mathscr {W}_{{\mathbf {Q}},0}\hookrightarrow \mathscr {W}_{\mathbf {Q}}\rightarrow \mathscr {W}_F$
induced by the norm map
$\mathscr {W}_{{\mathbf {Q}},0}\hookrightarrow \mathscr {W}_{\mathbf {Q}}\rightarrow \mathscr {W}_F$
induced by the norm map
![]() $T_{F,0}\rightarrow T_{{\mathbf {Q}},0}$
.
$T_{F,0}\rightarrow T_{{\mathbf {Q}},0}$
.
In the special case where
![]() $F/{\mathbf {Q}}$
is cyclic, the classical base change map produces cuspidal automorphic representations of
$F/{\mathbf {Q}}$
is cyclic, the classical base change map produces cuspidal automorphic representations of
![]() $\operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
from certain cuspidal automorphic representations of
$\operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
from certain cuspidal automorphic representations of
![]() $\operatorname {\mathrm {GL}}_2({\mathbf {A}}_{{\mathbf {Q}}})$
, and [Reference Johansson and NewtonJN19a] interpolated it to a morphism of eigenvarieties:
$\operatorname {\mathrm {GL}}_2({\mathbf {A}}_{{\mathbf {Q}}})$
, and [Reference Johansson and NewtonJN19a] interpolated it to a morphism of eigenvarieties:
Theorem 3.4.1 [Reference Johansson and NewtonJN19a, Theorem 4.3.1].Footnote 2
There is a finite morphism
lying over
![]() $\mathscr {W}_{{\mathbf {Q}}}\rightarrow \mathscr {W}_F$
and compatible with the homomorphism
$\mathscr {W}_{{\mathbf {Q}}}\rightarrow \mathscr {W}_F$
and compatible with the homomorphism
![]() $\sigma _F^S$
.
$\sigma _F^S$
.
Here, the source includes only cuspidal components with a Zariski-dense set of forms without complex multiplication by an imaginary quadratic subfield of F.
Let
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})=\left \langle \tau \right \rangle $
. Then a cuspidal automorphic representation
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})=\left \langle \tau \right \rangle $
. Then a cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
is in the image of the base change map if and only if
$\operatorname {\mathrm {GL}}_2({\mathbf {A}}_F)$
is in the image of the base change map if and only if
![]() $\pi \circ \tau \cong \pi $
. In particular, the systems of Hecke eigenvalues of base-changed representations must be fixed by
$\pi \circ \tau \cong \pi $
. In particular, the systems of Hecke eigenvalues of base-changed representations must be fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
.
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
.
This characterization of the image of the classical base change map permits us to prove automorphy lifting theorems by passing to a more convenient solvable extension. We therefore wish to characterize the image of the interpolated base change map when F is totally real and completely split at p (so that the ‘F - ncm’ condition is vacuous). We further assume that
![]() $[F:{\mathbf {Q}}]$
is prime to p.
$[F:{\mathbf {Q}}]$
is prime to p.
We will study the ‘
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus’ in the
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus’ in the
![]() $\operatorname {\mathrm {GL}}_{2/F}$
-eigenvariety
$\operatorname {\mathrm {GL}}_{2/F}$
-eigenvariety
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
and show that it is the image of the cyclic base change map; Xiang [Reference XiangXia18] used a similar idea to construct p-adic families of essentially self-dual automorphic representations.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
and show that it is the image of the cyclic base change map; Xiang [Reference XiangXia18] used a similar idea to construct p-adic families of essentially self-dual automorphic representations.
Remark 3.4.2. We expect that it is possible to construct a base change morphism and characterize its image for more general cyclic extensions of number fields
![]() $F'/F$
; however, for simplicity (and compatibility with [Reference Johansson and NewtonJN19a]) we have chosen to restrict to this setting.
$F'/F$
; however, for simplicity (and compatibility with [Reference Johansson and NewtonJN19a]) we have chosen to restrict to this setting.
We first observe that
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
acts on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
acts on
![]() $\operatorname {\mathrm {GL}}_{2/F}$
, stabilizing
$\operatorname {\mathrm {GL}}_{2/F}$
, stabilizing
![]() $\operatorname {\mathrm {T}}\subset {\mathbf {B}}$
and I, and also stabilizing the tame level
$\operatorname {\mathrm {T}}\subset {\mathbf {B}}$
and I, and also stabilizing the tame level
![]() $K_F^p$
. Next, observe that
$K_F^p$
. Next, observe that
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
acts on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
acts on
![]() $\mathbb {T}_F^S$
via
$\mathbb {T}_F^S$
via
![]() $(\tau \cdot T)(g)=T(\tau ^{-1}(g))$
for all
$(\tau \cdot T)(g)=T(\tau ^{-1}(g))$
for all
![]() $T\in \mathbb {T}_F^S$
and
$T\in \mathbb {T}_F^S$
and
![]() $g\in \operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f})$
. Then for any
$g\in \operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f})$
. Then for any
![]() $\delta \in \Delta $
,
$\delta \in \Delta $
,
![]() $(\tau \cdot [K_F\delta K_F])(g) = [K_F\tau ^{-1}(\delta )K_F](g)$
; in particular,
$(\tau \cdot [K_F\delta K_F])(g) = [K_F\tau ^{-1}(\delta )K_F](g)$
; in particular,
![]() $\tau \cdot U_{\varpi _v}=U_{\tau (v)}$
, and hence
$\tau \cdot U_{\varpi _v}=U_{\tau (v)}$
, and hence
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
fixes
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
fixes
![]() $U_p$
. Similarly, we have an action of
$U_p$
. Similarly, we have an action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
![]() $\mathscr {W}_{\mathbf {Q}}$
given via
$\mathscr {W}_{\mathbf {Q}}$
given via
![]() $(\tau \cdot \lambda )(g) = \lambda (\tau ^{-1}(g))$
; the image of
$(\tau \cdot \lambda )(g) = \lambda (\tau ^{-1}(g))$
; the image of
![]() $\mathscr {W}_{{\mathbf {Q}}}$
in
$\mathscr {W}_{{\mathbf {Q}}}$
in
![]() $\mathscr {W}_F$
is the diagonal locus, that is, exactly the
$\mathscr {W}_F$
is the diagonal locus, that is, exactly the
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus.
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
-fixed locus.
Since
![]() $U_p$
is fixed by
$U_p$
is fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, we see that if
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, we see that if
![]() $\kappa $
is a weight fixed by
$\kappa $
is a weight fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, then the Fredholm determinant
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, then the Fredholm determinant
![]() $F_{\kappa }(T)$
of the action of
$F_{\kappa }(T)$
of the action of
![]() $U_p$
on
$U_p$
on
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
is fixed by
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
is fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. Thus, we have a spectral variety
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. Thus, we have a spectral variety
![]() $\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\subset \mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\times {\mathbf {A}}^{1,\mathrm {an}}$
over
$\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\subset \mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\times {\mathbf {A}}^{1,\mathrm {an}}$
over
![]() $\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
.
$\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
.
Lemma 3.4.3. Let
![]() $\kappa :T_0\rightarrow R^{\times }$
be a weight fixed by
$\kappa :T_0\rightarrow R^{\times }$
be a weight fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. There is an action of
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. There is an action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
and if
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
and if
![]() $\mathscr {D}_{\kappa }$
admits a slope-
$\mathscr {D}_{\kappa }$
admits a slope-
![]() $\leq h$
decomposition, the action of
$\leq h$
decomposition, the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
stabilizes
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
stabilizes
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })_{\leq h}$
.
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })_{\leq h}$
.
Proof. Referring to the definition of
![]() $\mathscr {D}_{\kappa }$
for an arbitrary weight
$\mathscr {D}_{\kappa }$
for an arbitrary weight
![]() $\kappa $
, we have
$\kappa $
, we have
![]() $\mathscr {D}_{\kappa }=\varprojlim \mathcal {D}_{\kappa }^r$
, where
$\mathscr {D}_{\kappa }=\varprojlim \mathcal {D}_{\kappa }^r$
, where
![]() $\mathcal {D}_{\kappa }^r$
is the completion of a module
$\mathcal {D}_{\kappa }^r$
is the completion of a module
![]() $\mathcal {D}_{\kappa }$
with respect to a norm
$\mathcal {D}_{\kappa }$
with respect to a norm
![]() $\|\cdot \|_r$
. The module
$\|\cdot \|_r$
. The module
![]() $\mathcal {D}_{\kappa }$
itself is the continuous dual of the space
$\mathcal {D}_{\kappa }$
itself is the continuous dual of the space
![]() $\mathcal {A}_{\kappa }\subset \mathcal {C}(I,R)$
of continuous functions
$\mathcal {A}_{\kappa }\subset \mathcal {C}(I,R)$
of continuous functions
![]() $f:I\rightarrow R$
such that
$f:I\rightarrow R$
such that
![]() $f(gb)=\kappa (b)f(g)$
for all
$f(gb)=\kappa (b)f(g)$
for all
![]() $g\in I$
and
$g\in I$
and
![]() $b\in B_0$
. It follows that we have a map
$b\in B_0$
. It follows that we have a map
![]() $\tau :\mathcal {A}_{\kappa }\rightarrow \mathcal {A}_{\tau (\kappa )}$
(since the action of
$\tau :\mathcal {A}_{\kappa }\rightarrow \mathcal {A}_{\tau (\kappa )}$
(since the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
preserves both I and
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
preserves both I and
![]() $B_0$
). If
$B_0$
). If
![]() $\kappa $
is fixed by
$\kappa $
is fixed by
![]() $\tau $
, we obtain a dual action of
$\tau $
, we obtain a dual action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
![]() $\mathcal {D}_{\kappa }$
, and hence
$\mathcal {D}_{\kappa }$
, and hence
![]() $\mathcal {D}_{\kappa }^r$
and
$\mathcal {D}_{\kappa }^r$
and
![]() $\mathscr {D}_{\kappa }$
.
$\mathscr {D}_{\kappa }$
.
Since
![]() $K_F^p$
is also stable under the action of
$K_F^p$
is also stable under the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
and the actions of
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
and the actions of
![]() $K_F^p$
and
$K_F^p$
and
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
![]() $\mathscr {D}_{\kappa }$
commute, by functoriality we obtain an action of
$\mathscr {D}_{\kappa }$
commute, by functoriality we obtain an action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
on
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
. Moreover, the action of
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
. Moreover, the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
fixes the Hecke operator
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
fixes the Hecke operator
![]() $U_p$
, so [Reference Johansson and NewtonJN16, Proposition 2.2.11] implies that the action of
$U_p$
, so [Reference Johansson and NewtonJN16, Proposition 2.2.11] implies that the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
also preserves
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
also preserves
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })_{\leq h}$
.
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })_{\leq h}$
.
Lemma 3.4.4. Let
![]() $\kappa :T_0\rightarrow R^{\times }$
be a weight fixed by
$\kappa :T_0\rightarrow R^{\times }$
be a weight fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. For any
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. For any
![]() $T\in \mathbb {T}_F^S$
, we have
$T\in \mathbb {T}_F^S$
, we have
![]() $\tau \cdot T = \tau \circ T\circ \tau ^{-1}$
as operators on
$\tau \cdot T = \tau \circ T\circ \tau ^{-1}$
as operators on
![]() $C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
.
$C^{\bullet }(K_F,\mathscr {D}_{\kappa })$
.
Proof. We may assume
![]() $T=[K_F\delta K_F]$
for some
$T=[K_F\delta K_F]$
for some
![]() $\delta \in \Delta $
. Then
$\delta \in \Delta $
. Then
![]() $\tau \cdot [K_F\delta K_F] = [K_F\tau (\delta )K_F]$
, and the corresponding morphism
$\tau \cdot [K_F\delta K_F] = [K_F\tau (\delta )K_F]$
, and the corresponding morphism
is induced by the conjugation map
![]() $\tau (\delta )K_F\tau (\delta )^{-1}\rightarrow K_F$
and the map
$\tau (\delta )K_F\tau (\delta )^{-1}\rightarrow K_F$
and the map
![]() $\mathscr {D}_{\kappa }\rightarrow \mathscr {D}_{\kappa }$
given by
$\mathscr {D}_{\kappa }\rightarrow \mathscr {D}_{\kappa }$
given by
![]() $d\mapsto \tau (\delta )\cdot d$
. But
$d\mapsto \tau (\delta )\cdot d$
. But
![]() $\tau (\delta ) K_F\tau (\delta )^{-1} = \tau \left (\delta \tau ^{-1}(K_F) \delta ^{-1}\right )$
, so we may factor the conjugation map as
$\tau (\delta ) K_F\tau (\delta )^{-1} = \tau \left (\delta \tau ^{-1}(K_F) \delta ^{-1}\right )$
, so we may factor the conjugation map as
Similarly,
![]() $d\mapsto \tau (\delta )\cdot d$
factors as
$d\mapsto \tau (\delta )\cdot d$
factors as
![]() $\tau \circ T\circ \tau ^{-1}$
, so our morphism of complexes also factors as desired.
$\tau \circ T\circ \tau ^{-1}$
, so our morphism of complexes also factors as desired.
We may restrict
![]() $\mathscr {M}_c^\ast $
to
$\mathscr {M}_c^\ast $
to
![]() $\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/Q)}$
; we denote this restriction by
$\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/Q)}$
; we denote this restriction by
![]() $\mathscr {H}^\ast $
and by abuse of notation, we again use
$\mathscr {H}^\ast $
and by abuse of notation, we again use
![]() $\mathscr {T}$
to denote the sheaf generated by the image of
$\mathscr {T}$
to denote the sheaf generated by the image of
![]() $\mathbb {T}_F^S$
in
$\mathbb {T}_F^S$
in
![]() $\mathscr {E}nd_{\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}\left (\mathscr {H}^\ast \right )$
. Then the slice of the eigenvariety
$\mathscr {E}nd_{\mathscr {Z}^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}\left (\mathscr {H}^\ast \right )$
. Then the slice of the eigenvariety
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
over
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
over
![]() $\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is, by definition,
$\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is, by definition,
![]() $\underline{\mathrm{Spa}} \mathscr {T}$
.
$\underline{\mathrm{Spa}} \mathscr {T}$
.
Both
![]() $\mathbb {T}(\Delta ^p,K_F^p)$
and
$\mathbb {T}(\Delta ^p,K_F^p)$
and
![]() $\operatorname {\mathrm {End}}_{{\mathscr {O}}(V)}\left (\mathscr {H}^\ast \right )$
have actions of
$\operatorname {\mathrm {End}}_{{\mathscr {O}}(V)}\left (\mathscr {H}^\ast \right )$
have actions of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, and Lemma 3.4.4 implies that they are compatible. Thus,
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
, and Lemma 3.4.4 implies that they are compatible. Thus,
![]() $\mathscr {T}(V)$
and
$\mathscr {T}(V)$
and
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S|_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}$
have actions of
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S|_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}$
have actions of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
.
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
.
The subspace of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
fixed by
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
corresponds to the sheaf
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
corresponds to the sheaf
![]() $V\mapsto \mathscr {T}(V)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
of coinvariants of
$V\mapsto \mathscr {T}(V)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
of coinvariants of
![]() $\mathscr {T}$
. Since
$\mathscr {T}$
. Since
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
is a finite group with order prime to p,
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
is a finite group with order prime to p,
![]() $\mathscr {T}(V)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is a
$\mathscr {T}(V)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is a
![]() ${\mathscr {O}}_{\mathscr {W}_F}(V)$
-linear direct summand of
${\mathscr {O}}_{\mathscr {W}_F}(V)$
-linear direct summand of
![]() $\mathscr {T}(V)$
.
$\mathscr {T}(V)$
.
The above discussion gives us a closed subspace
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}\hookrightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
.
We let
and we let
![]() $\overline {\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }}$
denote its Zariski closure in
$\overline {\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }}$
denote its Zariski closure in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
.
Lemma 3.4.5. Classical points are very Zariski dense in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
.
Proof. If
![]() $(U,h)$
is a slope datum and
$(U,h)$
is a slope datum and
![]() $W\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
is a connected affinoid subspace of the preimage of U, then
$W\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^S$
is a connected affinoid subspace of the preimage of U, then
![]() $\mathscr {T}(W)=e_W\mathscr {T}(U)$
and
$\mathscr {T}(W)=e_W\mathscr {T}(U)$
and
![]() $\mathscr {M}_c^\ast (W)\cong e_WH_c^\ast (K,\mathscr {D}_U)_{\leq h}$
, where
$\mathscr {M}_c^\ast (W)\cong e_WH_c^\ast (K,\mathscr {D}_U)_{\leq h}$
, where
![]() $e_W$
is the idempotent projector to W. If
$e_W$
is the idempotent projector to W. If
![]() $W\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}^S$
, then
$W\subset \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}^S$
, then
![]() $\mathscr {M}_c^\ast \cong e_WH_c^d(K,\mathscr {D}_U)_{\leq h}$
and
$\mathscr {M}_c^\ast \cong e_WH_c^d(K,\mathscr {D}_U)_{\leq h}$
and
![]() $H_c^d(K,\mathscr {D}_U)_{\leq h}$
is a projective
$H_c^d(K,\mathscr {D}_U)_{\leq h}$
is a projective
![]() ${\mathscr {O}}_{\mathscr {W}_F}(U)$
-module. It follows that the restriction of
${\mathscr {O}}_{\mathscr {W}_F}(U)$
-module. It follows that the restriction of
![]() $\mathscr {M}_c^\ast $
to
$\mathscr {M}_c^\ast $
to
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is a vector bundle over U.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is a vector bundle over U.
By [Reference ChenevierChe04, Lemme 6.2.10],
![]() $\mathscr {T}(U)$
is
$\mathscr {T}(U)$
is
![]() ${\mathscr {O}}_{\mathscr {W}_F}(U)$
-torsion-free, and it remains torsion-free after any flat base change on U. Since
${\mathscr {O}}_{\mathscr {W}_F}(U)$
-torsion-free, and it remains torsion-free after any flat base change on U. Since
![]() $\mathscr {T}(U)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is a direct summand of
$\mathscr {T}(U)_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
is a direct summand of
![]() $\mathscr {T}(U)$
, the same property holds for the coinvariants.
$\mathscr {T}(U)$
, the same property holds for the coinvariants.
Now, we may apply [Reference ChenevierChe04, Lemme 6.2.10] again to conclude that
![]() $W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is equidimensional of dimension
$W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is equidimensional of dimension
![]() $\dim {\mathscr {O}}_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}(U)$
, and every irreducible component of
$\dim {\mathscr {O}}_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}(U)$
, and every irreducible component of
![]() $W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
surjects onto an irreducible component of
$W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
surjects onto an irreducible component of
![]() $\operatorname {\mathrm {Spec}} {\mathscr {O}}_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}(U)$
.
$\operatorname {\mathrm {Spec}} {\mathscr {O}}_{\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}}(U)$
.
If
![]() $x\in W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
has a classical weight that is sufficiently large (where ‘sufficiently large’ depends on h), then x corresponds to a classical Hilbert modular form. But sufficiently large classical weights are very Zariski dense in
$x\in W\cap \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
has a classical weight that is sufficiently large (where ‘sufficiently large’ depends on h), then x corresponds to a classical Hilbert modular form. But sufficiently large classical weights are very Zariski dense in
![]() $\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
, so [Reference ChenevierChe04, Lemme 6.2.8] implies that classical points are very Zariski dense in
$\mathscr {W}_F^{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})}$
, so [Reference ChenevierChe04, Lemme 6.2.8] implies that classical points are very Zariski dense in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S,\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
.
Remark 3.4.6. The proof Lemma 3.4.5 is the only time we use our assumption that
![]() $\lvert \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})\rvert $
is prime to p. If we restricted to the rigid analytic locus (where p is invertible, so that
$\lvert \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})\rvert $
is prime to p. If we restricted to the rigid analytic locus (where p is invertible, so that
![]() $\mathscr {T}_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}}$
is unconditionally a direct summand of
$\mathscr {T}_{\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}}$
is unconditionally a direct summand of
![]() $\mathscr {T}$
, this assumption would be unnecessary.
$\mathscr {T}$
, this assumption would be unnecessary.
Corollary 3.4.7. The image of the cyclic base change morphism in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}^S$
is exactly
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}^S$
is exactly
![]() $\overline {\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }}$
.
$\overline {\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }}$
.
Proof. Since the cyclic base change morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
is finite, it has closed image. Moreover, cyclic base change carries any classical point of
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
is finite, it has closed image. Moreover, cyclic base change carries any classical point of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
to a point of
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
to a point of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
; since
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
; since
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is closed in
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is closed in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, it contains the entire image of the cyclic base change morphism. On the other hand, every classical point of
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, it contains the entire image of the cyclic base change morphism. On the other hand, every classical point of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is in the image of cyclic base change, by the classical theorem, so Lemma 3.4.5 implies the desired result.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}^{S, \operatorname {\mathrm {Gal}}(F/{\mathbf {Q}}),\circ }$
is in the image of cyclic base change, by the classical theorem, so Lemma 3.4.5 implies the desired result.
3.5 Galois representations
In [Reference Johansson and NewtonJN16, §5.4], the authors construct families of Galois determinants (in the sense of [Reference ChenevierChe14]) over the eigenvarieties
![]() $\mathscr {X}_{\mathbf {G}}$
when
$\mathscr {X}_{\mathbf {G}}$
when
![]() $\mathbf {G}=\operatorname {\mathrm {Res}}_{F/{\mathbf {Q}}}\operatorname {\mathrm {GL}}_n$
and F is totally real or CM, and prove that they satisfy local-global compatibility at places away from p and the level. Then the Jacquet–Langlands correspondence lets us deduce the following:
$\mathbf {G}=\operatorname {\mathrm {Res}}_{F/{\mathbf {Q}}}\operatorname {\mathrm {GL}}_n$
and F is totally real or CM, and prove that they satisfy local-global compatibility at places away from p and the level. Then the Jacquet–Langlands correspondence lets us deduce the following:
Theorem 3.5.1. Let D be a quaternion algebra over a totally real field F, such that F is totally split at p and D is split at all places above p. Let
![]() $K=K^pI\subset ({\mathbf {A}}_{F,f}\otimes D)^{\times }$
be the level, and let S be the set of finite places v of F for which D is ramified or
$K=K^pI\subset ({\mathbf {A}}_{F,f}\otimes D)^{\times }$
be the level, and let S be the set of finite places v of F for which D is ramified or
![]() $K_v\neq \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
. Then there is a continuous two-dimensional Galois determinant
$K_v\neq \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
. Then there is a continuous two-dimensional Galois determinant
![]() $D:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow {\mathscr {O}}(\mathscr {X}_{\underline D^{\times }})^+$
such that
$D:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow {\mathscr {O}}(\mathscr {X}_{\underline D^{\times }})^+$
such that
for all
![]() $v\notin S$
, where
$v\notin S$
, where
![]() $P_v(X)$
is the standard Hecke polynomial.
$P_v(X)$
is the standard Hecke polynomial.
Moreover, if
![]() $v\mid p$
, then for every maximal point
$v\mid p$
, then for every maximal point
![]() $x\in \mathscr {X}_{\underline D^{\times }}$
of weight
$x\in \mathscr {X}_{\underline D^{\times }}$
of weight
![]() $\kappa _x=(\kappa _{x,1},\kappa _{x,2})$
, we let
$\kappa _x=(\kappa _{x,1},\kappa _{x,2})$
, we let
![]() $\psi :{\mathscr {O}}(\mathscr {X}_{\underline D^{\times }})^+\rightarrow k(x)^+$
denote the corresponding specialization map. Then there is a proper Zariski-closed subspace
$\psi :{\mathscr {O}}(\mathscr {X}_{\underline D^{\times }})^+\rightarrow k(x)^+$
denote the corresponding specialization map. Then there is a proper Zariski-closed subspace
![]() $Z\subset \mathscr {X}_{\underline D^{\times }}$
such that for
$Z\subset \mathscr {X}_{\underline D^{\times }}$
such that for
![]() $x\notin Z$
, the Galois representation corresponding to
$x\notin Z$
, the Galois representation corresponding to
![]() $D_x|_{\operatorname {\mathrm {Gal}}_{F,v}}$
is trianguline with parameters
$D_x|_{\operatorname {\mathrm {Gal}}_{F,v}}$
is trianguline with parameters
![]() $\delta _1,\delta _2:F_v^{\times }\rightrightarrows k(v)^{\times }$
, where
$\delta _1,\delta _2:F_v^{\times }\rightrightarrows k(v)^{\times }$
, where
and
Proof. It only remains to check local-global compatibility at places above p. But this is true for noncritical classical points by work of Saito, Blasius–Rogawski, and Skinner, and it is true for twists of those classical points by the definition of twisting. Then the result follows from [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.10] and [Reference BellovinBel23a, Theorem 6.8].
Remark 3.5.2. For each point
![]() $x\in \mathscr {X}_{\underline D^{\times }}$
, there is a residual Galois determinant
$x\in \mathscr {X}_{\underline D^{\times }}$
, there is a residual Galois determinant
![]() $\overline D_x$
valued in a finite field. These residual Galois determinants are constant on each connected component of
$\overline D_x$
valued in a finite field. These residual Galois determinants are constant on each connected component of
![]() $\mathscr {X}_{\underline D^{\times }}$
, as a consequence of [Reference ChenevierChe14, Lemma 3.10].
$\mathscr {X}_{\underline D^{\times }}$
, as a consequence of [Reference ChenevierChe14, Lemma 3.10].
As in Corollary 3.3.3, we can make a sharper local statement in the presence of integral structures. Suppose
![]() $\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight, where R is a pseudoaffinoid algebra equipped with a norm adapted to
$\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight, where R is a pseudoaffinoid algebra equipped with a norm adapted to
![]() $\kappa $
, and
$\kappa $
, and
![]() $R_0\subset R$
is the corresponding unit ball (so in particular,
$R_0\subset R$
is the corresponding unit ball (so in particular,
![]() $\kappa $
takes values in
$\kappa $
takes values in
![]() $R_0$
). If
$R_0$
). If
![]() $(\operatorname {\mathrm {Spa}} R,h)$
is a slope datum, for any
$(\operatorname {\mathrm {Spa}} R,h)$
is a slope datum, for any
![]() $r>r_{\kappa }$
we define
$r>r_{\kappa }$
we define
and
Corollary 3.5.3. With hypotheses and notation as above, there is a two-dimensional Galois determinant
![]() $D_0:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow \mathbb {T}_{\kappa ,\leq h}^{<r,\circ ,\mathrm {red}}$
such that
$D_0:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow \mathbb {T}_{\kappa ,\leq h}^{<r,\circ ,\mathrm {red}}$
such that
Proof. This is a corollary of the construction of [Reference Johansson and NewtonJN16, §5.4], rather than of Theorem 3.5.1. For each maximal point
![]() $x\in \operatorname {\mathrm {Spa}} R$
with residue field L and ring of integers
$x\in \operatorname {\mathrm {Spa}} R$
with residue field L and ring of integers
![]() ${\mathscr {O}}_L$
, let
${\mathscr {O}}_L$
, let
![]() $\kappa _x$
be the composition of
$\kappa _x$
be the composition of
![]() $\kappa $
with
$\kappa $
with
![]() $R_0\rightarrow {\mathscr {O}}_L$
. By [Reference Johansson and NewtonJN16, Corollary 5.3.2(2)] combined with Corollary 3.3.3, there is a two-dimensional Galois determinant
$R_0\rightarrow {\mathscr {O}}_L$
. By [Reference Johansson and NewtonJN16, Corollary 5.3.2(2)] combined with Corollary 3.3.3, there is a two-dimensional Galois determinant
![]() $D_x:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow \mathbb {T}_{\kappa _x,\leq h}^{<r,\circ ,\mathrm {red}}$
valued in the reduced quotient of
$D_x:\operatorname {\mathrm {Gal}}_{F,S}\rightarrow \mathbb {T}_{\kappa _x,\leq h}^{<r,\circ ,\mathrm {red}}$
valued in the reduced quotient of
![]() $\mathbb {T}_{\kappa _x,\leq h}^{<r,\circ }$
. We have an injection
$\mathbb {T}_{\kappa _x,\leq h}^{<r,\circ }$
. We have an injection
where the x range over maximal points of
![]() $\operatorname {\mathrm {Spa}} R$
. The ring
$\operatorname {\mathrm {Spa}} R$
. The ring
![]() $\mathbb {T}_{\kappa ,\leq h}^{<r,\circ ,\mathrm {red}}$
is compact since it is a finite
$\mathbb {T}_{\kappa ,\leq h}^{<r,\circ ,\mathrm {red}}$
is compact since it is a finite
![]() $R_0$
-module, so by [Reference ChenevierChe14, Example 2.3.2] the
$R_0$
-module, so by [Reference ChenevierChe14, Example 2.3.2] the
![]() $\mathbb {T}_{\kappa _x,\leq h}^{<r,\circ ,\mathrm {red}}$
-valued determinants glue to
$\mathbb {T}_{\kappa _x,\leq h}^{<r,\circ ,\mathrm {red}}$
-valued determinants glue to
![]() $D_0$
.
$D_0$
.
3.6 Quaternionic sub-eigenvarieties
In order to study suitable spaces of overconvergent quaternionic modular forms, we will need to define and study eigenvarieties parametrizing quaternionic modular forms with certain auxiliary data fixed. We let F be a totally real number field totally split at p, and we let D be a totally definite quaternion algebra over F, split at all places above p. We fix a level
![]() $K\subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
and monoid
$K\subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
and monoid
![]() $K\subset \Delta \subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
, and we set
$K\subset \Delta \subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
, and we set
![]() $\mathbb {T}$
to be either
$\mathbb {T}$
to be either
![]() $\mathbb {T}(\Delta ^p,K^p)$
or
$\mathbb {T}(\Delta ^p,K^p)$
or
![]() $\mathbb {T}(\Delta ,K)$
.
$\mathbb {T}(\Delta ,K)$
.
In order to construct an eigenvariety for
![]() $\underline D$
, we fixed a Borel–Serre complex
$\underline D$
, we fixed a Borel–Serre complex
![]() $C_c^{\bullet }(K,-)$
and we considered the cohomology
$C_c^{\bullet }(K,-)$
and we considered the cohomology
![]() $C_c^{\bullet }(K,\mathscr {D}_{\kappa })$
. However, because we assumed D is totally definite, the associated Shimura manifold is a finite set of points, and so the cohomology of
$C_c^{\bullet }(K,\mathscr {D}_{\kappa })$
. However, because we assumed D is totally definite, the associated Shimura manifold is a finite set of points, and so the cohomology of
![]() $C_c^{\bullet }(K,-)=C^{\bullet }(K,-)$
vanishes outside of degree
$C_c^{\bullet }(K,-)=C^{\bullet }(K,-)$
vanishes outside of degree
![]() $0$
.
$0$
.
Thus, we can give an extremely concrete description of the automorphic forms of interest to us and of the Hecke operators acting on them. Suppose that M is a left
![]() $R[\Delta ]$
-module, for some pseudoaffinoid algebra R. Then if
$R[\Delta ]$
-module, for some pseudoaffinoid algebra R. Then if
![]() $f:D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }\rightarrow M$
is a function and
$f:D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }\rightarrow M$
is a function and
![]() $\gamma \in \Delta $
, we define
$\gamma \in \Delta $
, we define
![]() ${}_\gamma |f$
via
${}_\gamma |f$
via
![]() ${}_\gamma |f(g) = \gamma \cdot f(g\gamma )$
. Then
${}_\gamma |f(g) = \gamma \cdot f(g\gamma )$
. Then
We can describe the Hecke operator
![]() $[KgK]:H^0(K,M)\rightarrow H^0(K,M)$
explicitly for any
$[KgK]:H^0(K,M)\rightarrow H^0(K,M)$
explicitly for any
![]() $g\in \Delta $
; we decompose the double coset
$g\in \Delta $
; we decompose the double coset
![]() $KgK=\coprod _i g_iK$
as a finite disjoint union of cosets, and we have
$KgK=\coprod _i g_iK$
as a finite disjoint union of cosets, and we have
The first piece of auxiliary data we want to fix is the central character. If
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R_0^{\times }$
is a continuous character such that
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R_0^{\times }$
is a continuous character such that
![]() $\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
agrees with the action of
$\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
agrees with the action of
![]() $K_v\cap {\mathscr {O}}_{F_v}^{\times }$
on M for all finite places v of F, we may extend the action of K on M to an action of
$K_v\cap {\mathscr {O}}_{F_v}^{\times }$
on M for all finite places v of F, we may extend the action of K on M to an action of
![]() $K\cdot {\mathbf {A}}_{F,f}^{\times }$
by letting
$K\cdot {\mathbf {A}}_{F,f}^{\times }$
by letting
![]() ${\mathbf {A}}_{F,f}^{\times }$
act by
${\mathbf {A}}_{F,f}^{\times }$
act by
![]() $\xi $
. Then we define
$\xi $
. Then we define
If we write
![]() $D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K=\coprod _{i\in I}D^{\times } g_i K{\mathbf {A}}_{F,f}^{\times }$
for some finite set of elements
$D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K=\coprod _{i\in I}D^{\times } g_i K{\mathbf {A}}_{F,f}^{\times }$
for some finite set of elements
![]() $g_i\in ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }$
, the natural map
$g_i\in ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }$
, the natural map
 $$ \begin{align*} H^0(K,M)[\xi] &\rightarrow \oplus_{i\in I}M^{(K{\mathbf{A}}_{F,f}^{\times}\cap g_i^{-1}D^{\times} g_i)/F^{\times}} \\ f &\mapsto (f(g_i)) \end{align*} $$
$$ \begin{align*} H^0(K,M)[\xi] &\rightarrow \oplus_{i\in I}M^{(K{\mathbf{A}}_{F,f}^{\times}\cap g_i^{-1}D^{\times} g_i)/F^{\times}} \\ f &\mapsto (f(g_i)) \end{align*} $$
is an isomorphism.
The calculations of [Reference TaylorTay06, Lemma 1.1] show that
![]() $(K{\mathbf {A}}_{F,f}^{\times }\cap g_i^{-1}D^{\times } g_i)/F^{\times }$
is a finite group with order prime to p for all i (since we assumed
$(K{\mathbf {A}}_{F,f}^{\times }\cap g_i^{-1}D^{\times } g_i)/F^{\times }$
is a finite group with order prime to p for all i (since we assumed
![]() $p\neq 2$
). Thus, if M is a potentially orthonormalizable Banach R-module, then so is
$p\neq 2$
). Thus, if M is a potentially orthonormalizable Banach R-module, then so is
![]() $H^0(K,M)[\xi ]$
, and we will be able to apply the formalism of slope decompositions to quaternionic modular forms with fixed central character. More precisely, we may consider the action of a compact operator U on
$H^0(K,M)[\xi ]$
, and we will be able to apply the formalism of slope decompositions to quaternionic modular forms with fixed central character. More precisely, we may consider the action of a compact operator U on
![]() $H^0(K,M)[\xi ]$
. If
$H^0(K,M)[\xi ]$
. If
![]() $H^0(K,M)[\xi ]$
admits a slope-
$H^0(K,M)[\xi ]$
admits a slope-
![]() $\leq h$
-decomposition, then
$\leq h$
-decomposition, then
![]() $H^0(K,M)[\xi ]_{\leq h}$
is a finite R-module which is a direct summand of
$H^0(K,M)[\xi ]_{\leq h}$
is a finite R-module which is a direct summand of
![]() $H^0(K,M)[\xi ]$
. Since
$H^0(K,M)[\xi ]$
. Since
![]() $H^0(K,M)[\xi ]$
is potentially orthonormalizable,
$H^0(K,M)[\xi ]$
is potentially orthonormalizable,
![]() $H^0(K,M)[\xi ]_{\leq h}$
satisfies the property (Pr) of [Reference BuzzardBuz07] and by [Reference BuzzardBuz07, Lemma 2.11] it is actually projective as an R-module.
$H^0(K,M)[\xi ]_{\leq h}$
satisfies the property (Pr) of [Reference BuzzardBuz07] and by [Reference BuzzardBuz07, Lemma 2.11] it is actually projective as an R-module.
The coefficient modules of interest to us are the modules of distributions
![]() $\mathscr {D}_{\kappa }$
constructed in [Reference Johansson and NewtonJN16], and we fix a character
$\mathscr {D}_{\kappa }$
constructed in [Reference Johansson and NewtonJN16], and we fix a character
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
as above. The operator
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
as above. The operator
![]() $U_p$
commutes with the action of
$U_p$
commutes with the action of
![]() ${\mathbf {A}}_{F,f}^{\times }/F^{\times }$
on
${\mathbf {A}}_{F,f}^{\times }/F^{\times }$
on
![]() $\mathscr {D}_{\kappa }$
given by
$\mathscr {D}_{\kappa }$
given by
![]() $\xi $
, so
$\xi $
, so
![]() $U_p$
acts compactly on
$U_p$
acts compactly on
![]() $C^\ast (K,\mathscr {D}_{\kappa })[\xi ]$
. We may construct a corresponding spectral variety
$C^\ast (K,\mathscr {D}_{\kappa })[\xi ]$
. We may construct a corresponding spectral variety
![]() $\mathscr {Z}_\xi $
and eigenvariety datum
$\mathscr {Z}_\xi $
and eigenvariety datum
![]() $(\mathscr {Z}_\xi , \mathscr {M}_{\xi },\mathbb {T},\psi )$
, where
$(\mathscr {Z}_\xi , \mathscr {M}_{\xi },\mathbb {T},\psi )$
, where
![]() $\mathscr {M}_{\xi }$
is the coherent sheaf on
$\mathscr {M}_{\xi }$
is the coherent sheaf on
![]() $\mathscr {Z}_\xi $
coming from factorizations of the characteristic power series of
$\mathscr {Z}_\xi $
coming from factorizations of the characteristic power series of
![]() $U_p$
; we write
$U_p$
; we write
![]() $\mathscr {X}_{\underline D^{\times },\xi }$
for the corresponding eigenvariety.
$\mathscr {X}_{\underline D^{\times },\xi }$
for the corresponding eigenvariety.
By construction,
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]_{\leq h}$
is a projective R-module whenever
$H^0(K,\mathscr {D}_{\kappa })[\xi ]_{\leq h}$
is a projective R-module whenever
![]() $(U,h)$
is a slope datum. Then [Reference ChenevierChe04, Lemme 6.2.10] implies that if
$(U,h)$
is a slope datum. Then [Reference ChenevierChe04, Lemme 6.2.10] implies that if
![]() $\mathscr {M}_{\xi }$
is nonzero,
$\mathscr {M}_{\xi }$
is nonzero,
![]() $\mathscr {X}_{\underline D^{\times },\xi }$
is equidimensional of the same dimension as
$\mathscr {X}_{\underline D^{\times },\xi }$
is equidimensional of the same dimension as
![]() $\mathscr {W}_F$
.
$\mathscr {W}_F$
.
Moreover, for each maximal point
![]() $x\in \mathscr {X}_{\underline D^{\times },\xi }$
, the corresponding Hecke eigensystem appears in
$x\in \mathscr {X}_{\underline D^{\times },\xi }$
, the corresponding Hecke eigensystem appears in
![]() $\mathscr {X}_{\underline D^{\times }}$
(with unrestricted central character), by construction. Then the interpolation theorem [Reference Johansson and NewtonJN19a, Theorem 3.2.1] implies that there is a closed immersion
$\mathscr {X}_{\underline D^{\times }}$
(with unrestricted central character), by construction. Then the interpolation theorem [Reference Johansson and NewtonJN19a, Theorem 3.2.1] implies that there is a closed immersion
![]() $\mathscr {X}_{\underline D^{\times },\xi }^{\mathrm {{red}}}\hookrightarrow \mathscr {X}_{\underline D^{\times }}$
, and dimension considerations imply that its image is a union of irreducible components of
$\mathscr {X}_{\underline D^{\times },\xi }^{\mathrm {{red}}}\hookrightarrow \mathscr {X}_{\underline D^{\times }}$
, and dimension considerations imply that its image is a union of irreducible components of
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
This implies in particular that as
![]() $(U,h)$
runs over slope data for
$(U,h)$
runs over slope data for
![]() $C^\ast (K,\mathscr {D}_{\kappa })[\xi ]$
, the sets
$C^\ast (K,\mathscr {D}_{\kappa })[\xi ]$
, the sets
![]() $W_{U,h}^{\prime ,\mathrm {ss}}\subset U$
of semisimple weights constructed in Proposition 3.3.6 are Zariski dense. Then we may repeat the argument of that proposition to conclude that
$W_{U,h}^{\prime ,\mathrm {ss}}\subset U$
of semisimple weights constructed in Proposition 3.3.6 are Zariski dense. Then we may repeat the argument of that proposition to conclude that
![]() $\mathscr {X}_{\underline D^{\times },\xi }$
is itself reduced.
$\mathscr {X}_{\underline D^{\times },\xi }$
is itself reduced.
We have shown the following:
Proposition 3.6.1. Given a character
![]() $\xi : {\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
as above, there is an eigenvariety
$\xi : {\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
as above, there is an eigenvariety
![]() $\mathscr {X}_{\underline D^{\times },\xi }$
of quaternionic modular forms with central character
$\mathscr {X}_{\underline D^{\times },\xi }$
of quaternionic modular forms with central character
![]() $\xi $
. It is reduced and equidimensional, and it is naturally identified as a (possibly empty) union of irreducible components of
$\xi $
. It is reduced and equidimensional, and it is naturally identified as a (possibly empty) union of irreducible components of
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
We also wish to introduce eigenvarieties localized at maximal ideals of Hecke algebras. Let
![]() $\mathfrak {m}\subset \mathbb {T}$
be a maximal ideal. By Theorem 3.5.1 and Remark 3.5.2, the residual Hecke eigenvalues are locally constant on
$\mathfrak {m}\subset \mathbb {T}$
be a maximal ideal. By Theorem 3.5.1 and Remark 3.5.2, the residual Hecke eigenvalues are locally constant on
![]() $\mathscr {X}_{\underline D^{\times }}$
. It follows that the restrictions
$\mathscr {X}_{\underline D^{\times }}$
. It follows that the restrictions
![]() $\mathscr {M}_{\mathfrak {m}}$
and
$\mathscr {M}_{\mathfrak {m}}$
and
![]() $\mathscr {M}_{\xi ,\mathfrak {m}}$
are supported on unions of connected components of
$\mathscr {M}_{\xi ,\mathfrak {m}}$
are supported on unions of connected components of
![]() $\mathscr {Z}$
, which we write
$\mathscr {Z}$
, which we write
![]() $\mathscr {Z}_{\mathfrak {m}}$
and
$\mathscr {Z}_{\mathfrak {m}}$
and
![]() $\mathscr {Z}_{\xi ,\mathfrak {m}}$
, respectively. In particular, if
$\mathscr {Z}_{\xi ,\mathfrak {m}}$
, respectively. In particular, if
![]() $(U,h)$
is a slope datum, then
$(U,h)$
is a slope datum, then
![]() $H^0(K,\mathscr {D}_U)_{\leq h,\mathfrak {m}}$
and
$H^0(K,\mathscr {D}_U)_{\leq h,\mathfrak {m}}$
and
![]() $H^0(K,\mathscr {D}_U)_{\leq h,\xi ,\mathfrak {m}}$
are again finite projective
$H^0(K,\mathscr {D}_U)_{\leq h,\xi ,\mathfrak {m}}$
are again finite projective
![]() ${\mathscr {O}}(U)$
-modules. Then an identical argument shows the following:
${\mathscr {O}}(U)$
-modules. Then an identical argument shows the following:
Proposition 3.6.2. Given a character
![]() $\xi : {\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
as above and a maximal ideal
$\xi : {\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
as above and a maximal ideal
![]() $\mathfrak {m}\subset \mathbb {T}$
as above, for any choice of Hecke algebra
$\mathfrak {m}\subset \mathbb {T}$
as above, for any choice of Hecke algebra
![]() $\mathbb {T}'$
(possibly different from
$\mathbb {T}'$
(possibly different from
![]() $\mathbb {T}$
) there are eigenvarieties
$\mathbb {T}$
) there are eigenvarieties
![]() $\mathscr {X}_{\underline D^{\times },\mathfrak {m}}^{\mathbb {T}'}$
and
$\mathscr {X}_{\underline D^{\times },\mathfrak {m}}^{\mathbb {T}'}$
and
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{\mathbb {T}'}$
of quaternionic modular forms localized at
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{\mathbb {T}'}$
of quaternionic modular forms localized at
![]() $\mathfrak {m}$
. They are reduced and equidimensional, and they are naturally identified as (possibly empty) unions of connected components of
$\mathfrak {m}$
. They are reduced and equidimensional, and they are naturally identified as (possibly empty) unions of connected components of
![]() $\mathscr {X}_{\underline D^{\times }}^{\mathbb {T}'}$
.
$\mathscr {X}_{\underline D^{\times }}^{\mathbb {T}'}$
.
Remark 3.6.3. We write
![]() $h=m/n$
and consider the closed ball
$h=m/n$
and consider the closed ball
![]() $\mathbb {B}_{U,h}:=\{\lvert T^n\rvert \leq \lvert u^{-m}\rvert \}\subset \mathbb {A}_U^1$
for some open affinoid
$\mathbb {B}_{U,h}:=\{\lvert T^n\rvert \leq \lvert u^{-m}\rvert \}\subset \mathbb {A}_U^1$
for some open affinoid
![]() $U\subset \mathscr {W}_F$
. Setting
$U\subset \mathscr {W}_F$
. Setting
![]() $Z_{U,h}:=\mathscr {Z}_{\mathfrak {m}}\cap \mathbb {B}_{U,h}$
(resp.
$Z_{U,h}:=\mathscr {Z}_{\mathfrak {m}}\cap \mathbb {B}_{U,h}$
(resp.
![]() $Z_{U,h}:=\mathscr {Z}_{\xi ,\mathfrak {m}}\cap \mathbb {B}_{U,h}$
), we abuse terminology slightly and say that
$Z_{U,h}:=\mathscr {Z}_{\xi ,\mathfrak {m}}\cap \mathbb {B}_{U,h}$
), we abuse terminology slightly and say that
![]() $(U,h)$
is a slope datum for
$(U,h)$
is a slope datum for
![]() $\mathscr {X}_{\underline D^{\times },\mathfrak {m}}$
(resp.
$\mathscr {X}_{\underline D^{\times },\mathfrak {m}}$
(resp.
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}$
) if
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}$
) if
![]() $Z_{U,h}\rightarrow U$
is finite of constant degree.
$Z_{U,h}\rightarrow U$
is finite of constant degree.
4 Overconvergent quaternionic modular forms
4.1 Definitions
We will use overconvergent cohomology to define and study spaces of overconvergent quaternionic modular forms. Maintaining our notation from § 3.1, and in particular § 3.6, we fix a level
![]() $K\subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
and monoid
$K\subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
and monoid
![]() $K\subset \Delta \subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
, and we set
$K\subset \Delta \subset \left ({\mathbf {A}}_{F,f}\otimes _F D\right )^{\times }$
, and we set
![]() $\mathbb {T}$
to be either
$\mathbb {T}$
to be either
![]() $\mathbb {T}(\Delta ^p,K^p)$
or
$\mathbb {T}(\Delta ^p,K^p)$
or
![]() $\mathbb {T}(\Delta ,K)$
.
$\mathbb {T}(\Delta ,K)$
.
The coefficients for our families of overconvergent modular forms will be a pseudoaffinoid algebra R over
![]() ${\mathbf {Z}}_p$
; we set
${\mathbf {Z}}_p$
; we set
![]() $U:=\operatorname {\mathrm {Spa}} R$
. We also fix a pseudouniformizer
$U:=\operatorname {\mathrm {Spa}} R$
. We also fix a pseudouniformizer
![]() $u\in R$
. If
$u\in R$
. If
![]() $\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight, we choose a norm
$\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight, we choose a norm
![]() $\lvert \cdot \rvert $
on R so that
$\lvert \cdot \rvert $
on R so that
![]() $\lvert \cdot \rvert $
is adapted to
$\lvert \cdot \rvert $
is adapted to
![]() $\kappa $
and multiplicative with respect to u, and
$\kappa $
and multiplicative with respect to u, and
![]() $\log _p\lvert \cdot \rvert $
is discrete (which we may do, by Lemma 4.1.1 below). Then the unit ball
$\log _p\lvert \cdot \rvert $
is discrete (which we may do, by Lemma 4.1.1 below). Then the unit ball
![]() $R_0\subset R$
is a ring of definition containing u.
$R_0\subset R$
is a ring of definition containing u.
Fix some
![]() $r\geq r_{\kappa }$
. We let
$r\geq r_{\kappa }$
. We let
![]() $\mathcal {D}_{\kappa }^{r, \circ }\subset \mathcal {D}_{\kappa }^r$
denote the unit ball, and we also consider larger modules of distributions
$\mathcal {D}_{\kappa }^{r, \circ }\subset \mathcal {D}_{\kappa }^r$
denote the unit ball, and we also consider larger modules of distributions
![]() $\mathcal {D}_{\kappa }^{<r}\supset \mathcal {D}_{\kappa }^r$
, with unit ball
$\mathcal {D}_{\kappa }^{<r}\supset \mathcal {D}_{\kappa }^r$
, with unit ball
![]() $\mathcal {D}_{\kappa }^{<r,\circ }\subset \mathcal {D}_{\kappa }^{<r}$
. Following §3.6, we also fix a character
$\mathcal {D}_{\kappa }^{<r,\circ }\subset \mathcal {D}_{\kappa }^{<r}$
. Following §3.6, we also fix a character
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R^{\times }$
such that
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R^{\times }$
such that
![]() $\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
agrees with the action of
$\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
agrees with the action of
![]() $K_v\cap {\mathscr {O}}_{F_v}^{\times }$
on
$K_v\cap {\mathscr {O}}_{F_v}^{\times }$
on
![]() $\mathcal {D}_{\kappa }^r$
, that is, such that
$\mathcal {D}_{\kappa }^r$
, that is, such that
![]() $\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
is trivial for
$\xi |_{K_v\cap {\mathscr {O}}_{F_v}^{\times }}$
is trivial for
![]() $v\nmid p$
and
$v\nmid p$
and
![]() $\xi |_{I_v\cap {\mathscr {O}}_{F_v}^{\times }}$
is equal to the action of
$\xi |_{I_v\cap {\mathscr {O}}_{F_v}^{\times }}$
is equal to the action of
![]() $I_v\cap {\mathscr {O}}_{F_v}^{\times }$
on
$I_v\cap {\mathscr {O}}_{F_v}^{\times }$
on
![]() $\mathcal {D}_{\kappa }^r$
for
$\mathcal {D}_{\kappa }^r$
for
![]() $v\mid p$
.
$v\mid p$
.
The construction of the required norm on R is a variant of [Reference Johansson and NewtonJN16, Lemma 3.3.1], and we refer to that paper for the terminology:
Lemma 4.1.1. If R is a pseudoaffinoid algebra over
![]() ${\mathbf {Z}}_p$
and
${\mathbf {Z}}_p$
and
![]() $\kappa :T_0/\overline {Z(K)}$
is a weight, there is a norm
$\kappa :T_0/\overline {Z(K)}$
is a weight, there is a norm
![]() $\lvert \cdot \rvert $
on R such that
$\lvert \cdot \rvert $
on R such that
![]() $\lvert \cdot \rvert $
is adapted to
$\lvert \cdot \rvert $
is adapted to
![]() $\kappa $
and multiplicative with respect to u, the unit ball
$\kappa $
and multiplicative with respect to u, the unit ball
![]() $R_0$
is Noetherian, and
$R_0$
is Noetherian, and
![]() $\log _p\lvert \cdot \rvert $
is discrete.
$\log _p\lvert \cdot \rvert $
is discrete.
Proof. Choose a Noetherian ring of definition
![]() $R_0\subset R$
formally of finite type over
$R_0\subset R$
formally of finite type over
![]() ${\mathbf {Z}}_p$
. As in the proof of [Reference Johansson and NewtonJN16, Lemma 3.3.1],
${\mathbf {Z}}_p$
. As in the proof of [Reference Johansson and NewtonJN16, Lemma 3.3.1],
![]() $\kappa (T_0)\subset R^\circ $
and
$\kappa (T_0)\subset R^\circ $
and
![]() $\kappa (T_\epsilon )\subset 1+R^{\circ \circ }$
; since both groups are topologically finitely generated, we may replace
$\kappa (T_\epsilon )\subset 1+R^{\circ \circ }$
; since both groups are topologically finitely generated, we may replace
![]() $R_0$
with a finite integral extension and assume that
$R_0$
with a finite integral extension and assume that
![]() $\kappa (T_0)\subset R_0$
, and we may find some integer
$\kappa (T_0)\subset R_0$
, and we may find some integer
![]() $m\geq 1$
so that
$m\geq 1$
so that
![]() $\kappa (T_\epsilon )^m\subset 1+uR_0$
.
$\kappa (T_\epsilon )^m\subset 1+uR_0$
.
Let
![]() $R':=R[u^{1/m}]$
, let
$R':=R[u^{1/m}]$
, let
![]() $R_0':=R_0[u^{1/m}]$
and let
$R_0':=R_0[u^{1/m}]$
and let
![]() $u':=u^{1/m}$
. Then
$u':=u^{1/m}$
. Then
![]() $R'$
is a finite R-module, so it has a canonical topology, and the subspace topology it induces on R agrees with the original topology on R. Now, for any
$R'$
is a finite R-module, so it has a canonical topology, and the subspace topology it induces on R agrees with the original topology on R. Now, for any
![]() $a\in {\mathbf {R}}_{>1}$
we may define a norm
$a\in {\mathbf {R}}_{>1}$
we may define a norm
![]() $\lvert \cdot \rvert '$
on
$\lvert \cdot \rvert '$
on
![]() $R'$
via
$R'$
via
The restriction of
![]() $\lvert \cdot \rvert '$
to R has the desired properties.
$\lvert \cdot \rvert '$
to R has the desired properties.
When U is a subspace of
![]() $\mathscr {W}_F$
, we can make a more precise statement. In this case, R is reduced, so the ring of power-bounded elements
$\mathscr {W}_F$
, we can make a more precise statement. In this case, R is reduced, so the ring of power-bounded elements
![]() $R_0:=R^\circ $
is a ring of definition. Then we may define a norm
$R_0:=R^\circ $
is a ring of definition. Then we may define a norm
![]() $\lvert \cdot \rvert $
on R via
$\lvert \cdot \rvert $
on R via
Lemma 4.1.2. If U is a rational subspace of
![]() $\mathscr {W}_F$
and
$\mathscr {W}_F$
and
![]() $\kappa $
is the restriction of the universal character on
$\kappa $
is the restriction of the universal character on
![]() $\mathscr {W}_F$
, then
$\mathscr {W}_F$
, then
![]() $\lvert \cdot \rvert $
is adapted to
$\lvert \cdot \rvert $
is adapted to
![]() $\kappa $
.
$\kappa $
.
The proof is essentially identical to that of [Reference Johansson and NewtonJN16, Lemma 6.3.1].
Recall that we have Fredholm power series
and
and they are independent of
![]() $r\geq r_{\kappa }$
, by [Reference Johansson and NewtonJN16, Proposition 4.1.2].
$r\geq r_{\kappa }$
, by [Reference Johansson and NewtonJN16, Proposition 4.1.2].
If
![]() $H^0(K,\mathcal {D}_{\kappa }^r)$
(resp.
$H^0(K,\mathcal {D}_{\kappa }^r)$
(resp.
![]() $H^0(K,\mathcal {D}_{\kappa }^r)[\xi ]$
) admits a slope
$H^0(K,\mathcal {D}_{\kappa }^r)[\xi ]$
) admits a slope
![]() $\leq h$
-factorization, then the formalism of slope decompositions implies that we have a decomposition
$\leq h$
-factorization, then the formalism of slope decompositions implies that we have a decomposition
resp.
for all
![]() $r\geq r_{\kappa }$
, and the decomposition is independent of r.
$r\geq r_{\kappa }$
, and the decomposition is independent of r.
Moreover, if
![]() $r'\in [r_{\kappa },r)$
, the inclusions
$r'\in [r_{\kappa },r)$
, the inclusions
induce an isomorphism
![]() $H^0(K,\mathcal {D}_{\kappa }^r)_{\leq h}\xrightarrow {\sim }H^0(K,\mathcal {D}_{\kappa }^{r'})_{\leq h}$
. We may therefore define
$H^0(K,\mathcal {D}_{\kappa }^r)_{\leq h}\xrightarrow {\sim }H^0(K,\mathcal {D}_{\kappa }^{r'})_{\leq h}$
. We may therefore define
and
We make the additional definitions
and
We are now in a position to define spaces of overconvergent quaternionic modular forms, together with an integral structure and Hecke algebras:
Definition 4.1.3. Suppose that
![]() $H^0(K,\mathcal {D}_{\kappa }^{<r})$
admits a slope-
$H^0(K,\mathcal {D}_{\kappa }^{<r})$
admits a slope-
![]() $\leq h$
-decomposition, where
$\leq h$
-decomposition, where
![]() $h=a/b$
for
$h=a/b$
for
![]() $a,b$
positive and relatively prime integers. We define the modular forms of weight
$a,b$
positive and relatively prime integers. We define the modular forms of weight
![]() $\kappa $
and slope-
$\kappa $
and slope-
![]() $\leq h$
to be the module
$\leq h$
to be the module
it is a module over the Hecke algebra
We define two modules of integral overconvergent modular forms (and corresponding Hecke algebras). As in § 3.5, we set
and
We also define a second lattice
which is stable under the operators
![]() $u^aU_{\varpi _v}^{-b}$
, as well; we set
$u^aU_{\varpi _v}^{-b}$
, as well; we set
If
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R_0^{\times }$
is a continuous character as above and
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow R_0^{\times }$
is a continuous character as above and
![]() $H^0(K,\mathcal {D}_{\kappa }^{<r})[\xi ]$
admits a slope-
$H^0(K,\mathcal {D}_{\kappa }^{<r})[\xi ]$
admits a slope-
![]() $\leq h$
decomposition, we define the modular forms with central character
$\leq h$
decomposition, we define the modular forms with central character
![]() $\xi $
to be
$\xi $
to be
![]() $S_{\kappa ,\xi }(K)_{\leq h}:= H^0(K,\mathscr {D}_{\kappa })[\xi ]_{\leq h}$
and similarly for integral modular forms with central character
$S_{\kappa ,\xi }(K)_{\leq h}:= H^0(K,\mathscr {D}_{\kappa })[\xi ]_{\leq h}$
and similarly for integral modular forms with central character
![]() $\xi $
.
$\xi $
.
Remark 4.1.4. We expect that
![]() $S_{\kappa }^{\circ }(K)_{\leq h}$
and the corresponding Hecke algebra
$S_{\kappa }^{\circ }(K)_{\leq h}$
and the corresponding Hecke algebra
![]() $\mathbb {T}_{\kappa ,\leq h}^{\circ }$
depend on r, but we have suppressed that from the notation for the sake of compactness.
$\mathbb {T}_{\kappa ,\leq h}^{\circ }$
depend on r, but we have suppressed that from the notation for the sake of compactness.
Remark 4.1.5. We will write
![]() $\mathbb {T}_{K,\kappa ,\leq h}^{<r,\circ }$
and
$\mathbb {T}_{K,\kappa ,\leq h}^{<r,\circ }$
and
![]() $\mathbb {T}_{K,\kappa ,\leq h}^{\circ }$
for these Hecke algebras if the level is not clear from context.
$\mathbb {T}_{K,\kappa ,\leq h}^{\circ }$
for these Hecke algebras if the level is not clear from context.
We again write
![]() $h=a/b$
with
$h=a/b$
with
![]() $a,b$
positive and relatively prime integers. If
$a,b$
positive and relatively prime integers. If
![]() $S_{\kappa }(K)_{\leq h}$
(resp.
$S_{\kappa }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }(K)_{\leq h}$
has rank d, then the characteristic polynomial of
$S_{\kappa ,\xi }(K)_{\leq h}$
has rank d, then the characteristic polynomial of
![]() $u^aU_{\varpi _v}^{-b}$
is a monic degree-d polynomial over R. By the definition of a slope decomposition, its roots are integral at every rank-
$u^aU_{\varpi _v}^{-b}$
is a monic degree-d polynomial over R. By the definition of a slope decomposition, its roots are integral at every rank-
![]() $1$
point of
$1$
point of
![]() $\operatorname {\mathrm {Spa}} R$
. Hence, the coefficients actually live in
$\operatorname {\mathrm {Spa}} R$
. Hence, the coefficients actually live in
![]() $R^\circ $
and
$R^\circ $
and
![]() $u^aU_{\varpi _v}^{-b}$
is power-bounded on
$u^aU_{\varpi _v}^{-b}$
is power-bounded on
![]() $S_{\kappa }(K)_{\leq h}$
(resp.
$S_{\kappa }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }(K)_{\leq h}$
. In particular, if R is reduced and
$S_{\kappa ,\xi }(K)_{\leq h}$
. In particular, if R is reduced and
![]() $R_0=R^\circ $
, we see that
$R_0=R^\circ $
, we see that
![]() $S_{\kappa }^{\circ }(K)_{\leq h}$
(resp.
$S_{\kappa }^{\circ }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }^{\circ }(K)_{\leq h}$
) is given concretely by
$S_{\kappa ,\xi }^{\circ }(K)_{\leq h}$
) is given concretely by
 $$\begin{align*}\sum_{(i_v)\in \{0,\ldots,d-1\}^{\Sigma_p}}\prod_{v\mid p}(u^aU_{\varpi_v}^{-b})^{i_v}\left( S_{\kappa}^{<r,\circ}(K)_{\leq h} \right). \end{align*}$$
$$\begin{align*}\sum_{(i_v)\in \{0,\ldots,d-1\}^{\Sigma_p}}\prod_{v\mid p}(u^aU_{\varpi_v}^{-b})^{i_v}\left( S_{\kappa}^{<r,\circ}(K)_{\leq h} \right). \end{align*}$$
In particular,
![]() $U_p^{b(d-1)}\left ( S_{\kappa }^{\circ }(K)_{\leq h} \right )\subset S_{\kappa }^{<r,\circ }(K)_{\leq h}$
(and similarly for
$U_p^{b(d-1)}\left ( S_{\kappa }^{\circ }(K)_{\leq h} \right )\subset S_{\kappa }^{<r,\circ }(K)_{\leq h}$
(and similarly for
![]() $S_{\kappa ,\xi }^{\circ }(K)_{\leq h}$
).
$S_{\kappa ,\xi }^{\circ }(K)_{\leq h}$
).
We now fix a choice of Hecke algebra. Let S denote the set of places of F such that
![]() $v\mid p$
, D is ramified at v, or
$v\mid p$
, D is ramified at v, or
![]() $K_v\neq \mathcal {O}_{D,v}^{\times }$
. For
$K_v\neq \mathcal {O}_{D,v}^{\times }$
. For
![]() $v\notin S$
, we define
$v\notin S$
, we define
for some fixed uniformizer
![]() $\varpi _v$
of
$\varpi _v$
of
![]() ${\mathscr {O}}_{F_v}$
.
${\mathscr {O}}_{F_v}$
.
We define the Hecke algebra
![]() $\mathbb {T}$
to be the free commutative
$\mathbb {T}$
to be the free commutative
![]() ${\mathbf {Z}}_p$
-algebra generated by
${\mathbf {Z}}_p$
-algebra generated by
![]() $\{U_{\varpi _v}\}_{v\mid p}$
and
$\{U_{\varpi _v}\}_{v\mid p}$
and
![]() $\{S_w, T_w\}_{w\notin S}$
. Since
$\{S_w, T_w\}_{w\notin S}$
. Since
![]() $\Delta _p$
acts on the modules of distributions
$\Delta _p$
acts on the modules of distributions
![]() $\mathcal {D}_{\kappa }^{<r,\circ }$
and Hecke operators away from p preserve the slope decomposition, we may view
$\mathcal {D}_{\kappa }^{<r,\circ }$
and Hecke operators away from p preserve the slope decomposition, we may view
![]() $S_{\kappa }^{<r,\circ }(K)_{\leq h}$
as a
$S_{\kappa }^{<r,\circ }(K)_{\leq h}$
as a
![]() $\mathbb {T}$
-module.
$\mathbb {T}$
-module.
We also describe the so-called diamond operators after modifying the tame level
![]() $K^p$
. Suppose we have a finite set Q of places of F such that for each
$K^p$
. Suppose we have a finite set Q of places of F such that for each
![]() $v\in Q$
,
$v\in Q$
,
![]() $v\nmid p$
,
$v\nmid p$
,
![]() $\operatorname {\mathrm {Nm}} v\equiv 1\quad\pmod p$
, D is split at v, and
$\operatorname {\mathrm {Nm}} v\equiv 1\quad\pmod p$
, D is split at v, and
![]() $K_v=\operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
. For each
$K_v=\operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
. For each
![]() $v\in Q$
, we again let
$v\in Q$
, we again let
![]() $K_0(v)\subset {{\mathrm{{H}}}}(F_v)$
denote the subgroup
$K_0(v)\subset {{\mathrm{{H}}}}(F_v)$
denote the subgroup
![]() $\left \{\left (\begin {smallmatrix}\ast & \ast \\ 0 & \ast \end {smallmatrix}\right )\quad\mod v\right \}$
, and we consider the homomorphism
$\left \{\left (\begin {smallmatrix}\ast & \ast \\ 0 & \ast \end {smallmatrix}\right )\quad\mod v\right \}$
, and we consider the homomorphism
given by composing
with the projection to the p-power quotient
![]() $k(v)^{\times }\rightarrow \Delta _v$
. Let
$k(v)^{\times }\rightarrow \Delta _v$
. Let
![]() $K^-(v)$
denote the group
$K^-(v)$
denote the group
for each
![]() $v\in Q$
, and let
$v\in Q$
, and let
and
Then
![]() $K_0(v)/K^-(v)\cong \Delta _v$
, and every
$K_0(v)/K^-(v)\cong \Delta _v$
, and every
![]() $h\in \Delta _Q:=\prod _{v\in Q}\Delta _v$
gives rise to a Hecke operator
$h\in \Delta _Q:=\prod _{v\in Q}\Delta _v$
gives rise to a Hecke operator
on
![]() $S_{\kappa }^{<r,\circ }(K^-(Q))$
, where
$S_{\kappa }^{<r,\circ }(K^-(Q))$
, where
![]() $\widetilde h$
is a lift of h to
$\widetilde h$
is a lift of h to
![]() $K_0(Q)$
;
$K_0(Q)$
;
![]() $\left \langle h\right \rangle $
is independent of the choice of
$\left \langle h\right \rangle $
is independent of the choice of
![]() $\widetilde h$
.
$\widetilde h$
.
We let
![]() $\mathbb {T}_Q^-$
be the free commutative
$\mathbb {T}_Q^-$
be the free commutative
![]() ${\mathbf {Z}}_p$
-algebra generated by
${\mathbf {Z}}_p$
-algebra generated by
![]() $\{U_{\varpi _v}\}_{v\mid p}$
,
$\{U_{\varpi _v}\}_{v\mid p}$
,
![]() $\{S_v, T_v\}_{v\notin S}$
, and
$\{S_v, T_v\}_{v\notin S}$
, and
![]() $\{U_{\varpi _v}\}_{v\in Q}$
, where
$\{U_{\varpi _v}\}_{v\in Q}$
, where
![]() $U_{\varpi _v}:=[K^-(v)\left (\begin {smallmatrix}1 & 0 \\ 0 & \varpi _v\end {smallmatrix}\right )K^-(v)]$
; it acts naturally on
$U_{\varpi _v}:=[K^-(v)\left (\begin {smallmatrix}1 & 0 \\ 0 & \varpi _v\end {smallmatrix}\right )K^-(v)]$
; it acts naturally on
![]() $S_{\kappa }^{<r,\circ }(K^-(Q))_{\leq h}$
, and we let
$S_{\kappa }^{<r,\circ }(K^-(Q))_{\leq h}$
, and we let
![]() $\mathbb {T}_{K^-(Q),\leq h}^{<r,\circ }$
denote the
$\mathbb {T}_{K^-(Q),\leq h}^{<r,\circ }$
denote the
![]() $R_0$
-algebra its image generates in
$R_0$
-algebra its image generates in
![]() $\operatorname {\mathrm {End}}_{R_0}(S_{\kappa }^{<r,\circ }(K^-(Q))_{\leq h})$
. Similarly, we let
$\operatorname {\mathrm {End}}_{R_0}(S_{\kappa }^{<r,\circ }(K^-(Q))_{\leq h})$
. Similarly, we let
![]() $\mathbb {T}_{0,Q}$
be the free commutative
$\mathbb {T}_{0,Q}$
be the free commutative
![]() ${\mathbf {Z}}_p$
-algebra generated by
${\mathbf {Z}}_p$
-algebra generated by
![]() $\{U_{\varpi _v}\}_{v\mid p}$
,
$\{U_{\varpi _v}\}_{v\mid p}$
,
![]() $\{S_v, T_v\}_{v\notin S}$
, and
$\{S_v, T_v\}_{v\notin S}$
, and
![]() $\{U_{\varpi _v}\}_{v\in Q}$
, where
$\{U_{\varpi _v}\}_{v\in Q}$
, where
![]() $U_{\varpi _v}:=[K_0(v)\left (\begin {smallmatrix}1 & 0 \\ 0 & \varpi _v\end {smallmatrix}\right )K_0(v)]$
.
$U_{\varpi _v}:=[K_0(v)\left (\begin {smallmatrix}1 & 0 \\ 0 & \varpi _v\end {smallmatrix}\right )K_0(v)]$
.
4.2 Integral overconvergent quaternionic modular forms
We need to make a closer study of the structure of the integral modules of distributions and their finite-slope subspaces.
Lemma 4.2.1. If
![]() $\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight and
$\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight and
![]() $H^0(K,\mathscr {D}_{\kappa })$
(resp.
$H^0(K,\mathscr {D}_{\kappa })$
(resp.
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]$
) admits a slope-
$H^0(K,\mathscr {D}_{\kappa })[\xi ]$
) admits a slope-
![]() $\leq h$
-decomposition, then
$\leq h$
-decomposition, then
![]() $S_{\kappa }(K)_{\leq h}$
(resp.
$S_{\kappa }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }(K)_{\leq h}$
) is a finite projective R-module. If the Fredholm power series
$S_{\kappa ,\xi }(K)_{\leq h}$
) is a finite projective R-module. If the Fredholm power series
![]() $F_{\kappa }$
has a slope
$F_{\kappa }$
has a slope
![]() $\leq h$
-factorization, then
$\leq h$
-factorization, then
![]() $S_{\kappa }(K)_{\leq h}$
(resp.
$S_{\kappa }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }(K)_{\leq h}$
) is compatible with arbitrary base change on R.
$S_{\kappa ,\xi }(K)_{\leq h}$
) is compatible with arbitrary base change on R.
Proof. We prove the result for
![]() $H^0(K,\mathscr {D}_{\kappa })$
;
$H^0(K,\mathscr {D}_{\kappa })$
;
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]$
is handled similarly. It is enough to handle the case where the tame level is neat. Then
$H^0(K,\mathscr {D}_{\kappa })[\xi ]$
is handled similarly. It is enough to handle the case where the tame level is neat. Then
![]() $S_{\kappa }(K)_{\leq h}$
is a direct summand of the potentially orthonormalizable Banach R-module
$S_{\kappa }(K)_{\leq h}$
is a direct summand of the potentially orthonormalizable Banach R-module
![]() $H^0(K,\mathscr {D}_{\kappa })$
which is finitely generate over R, so by [Reference BuzzardBuz07, Lemma 2.11] is projective.
$H^0(K,\mathscr {D}_{\kappa })$
which is finitely generate over R, so by [Reference BuzzardBuz07, Lemma 2.11] is projective.
If the Fredholm power series
![]() $F_{\kappa }$
has a slope-
$F_{\kappa }$
has a slope-
![]() $\leq h$
-factorization, then the slope decomposition is functorial in R, by [Reference Johansson and NewtonJN16, Theorem 2.2.13].
$\leq h$
-factorization, then the slope decomposition is functorial in R, by [Reference Johansson and NewtonJN16, Theorem 2.2.13].
Corollary 4.2.2. If
![]() $\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight and
$\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
is a weight and
![]() $H^0(K,\mathscr {D}_{\kappa })$
(resp.
$H^0(K,\mathscr {D}_{\kappa })$
(resp.
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]$
) admits a slope-
$H^0(K,\mathscr {D}_{\kappa })[\xi ]$
) admits a slope-
![]() $\leq h$
-decomposition, then
$\leq h$
-decomposition, then
![]() $S_{\kappa }^{<r, \circ }(K)_{\leq h}$
(resp.
$S_{\kappa }^{<r, \circ }(K)_{\leq h}$
(resp.
![]() $S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h}$
) is a finite
$S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h}$
) is a finite
![]() $R_0$
-module.
$R_0$
-module.
Proof. This follows from the equality
![]() $H^0(K,\mathcal {D}_{\kappa }^r)_{\leq h}=H^0(K,\mathcal {D}_{\kappa }^{<r})_{\leq h}$
and the fact that
$H^0(K,\mathcal {D}_{\kappa }^r)_{\leq h}=H^0(K,\mathcal {D}_{\kappa }^{<r})_{\leq h}$
and the fact that
![]() $\mathcal {D}_{\kappa }^{<r,\circ }$
is bounded in
$\mathcal {D}_{\kappa }^{<r,\circ }$
is bounded in
![]() $\mathcal {D}_{\kappa }^{<r}$
.
$\mathcal {D}_{\kappa }^{<r}$
.
Now, we consider the behavior of
![]() $H^0(K,\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}$
under change of coefficients. Let
$H^0(K,\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}$
under change of coefficients. Let
![]() $\kappa _R:T_0/\overline {Z(K)}\rightarrow R^{\times }$
be a weight. If
$\kappa _R:T_0/\overline {Z(K)}\rightarrow R^{\times }$
be a weight. If
![]() $f:R\rightarrow R'$
is a homomorphism of pseudoaffinoid algebras, we let
$f:R\rightarrow R'$
is a homomorphism of pseudoaffinoid algebras, we let
![]() $\kappa _{R^{\prime }}$
denote the composition
$\kappa _{R^{\prime }}$
denote the composition
![]() $T_0/\overline {Z(K)}\xrightarrow {\kappa _R}R^{\times }\xrightarrow {f}{R'}^{\times }$
. By [Reference Johansson and NewtonJN16, Corollary A.14], f is topologically of finite type, so we have a surjection
$T_0/\overline {Z(K)}\xrightarrow {\kappa _R}R^{\times }\xrightarrow {f}{R'}^{\times }$
. By [Reference Johansson and NewtonJN16, Corollary A.14], f is topologically of finite type, so we have a surjection
![]() $R\left \langle X_1,\ldots ,X_n\right \rangle \twoheadrightarrow R'$
. If R is equipped with a norm adapted to
$R\left \langle X_1,\ldots ,X_n\right \rangle \twoheadrightarrow R'$
. If R is equipped with a norm adapted to
![]() $\kappa _R$
and
$\kappa _R$
and
![]() $R_0\subset R$
is the corresponding ring of definition, with
$R_0\subset R$
is the corresponding ring of definition, with
![]() $u\in R_0$
a pseudouniformizer, we define
$u\in R_0$
a pseudouniformizer, we define
![]() $R_0':=R_0\left \langle X_1,\ldots ,X_n\right \rangle $
and
$R_0':=R_0\left \langle X_1,\ldots ,X_n\right \rangle $
and
![]() $u':=f(u)$
.
$u':=f(u)$
.
Let
![]() $a:=\lvert u\rvert _R$
. We define a norm
$a:=\lvert u\rvert _R$
. We define a norm
![]() $\lvert \cdot \rvert _{R^{\prime }}$
on
$\lvert \cdot \rvert _{R^{\prime }}$
on
![]() $R'$
via
$R'$
via
Then
![]() $R_0'$
is the unit ball of
$R_0'$
is the unit ball of
![]() $R'$
with respect to
$R'$
with respect to
![]() $\lvert \cdot \rvert _{R^{\prime }}$
, and
$\lvert \cdot \rvert _{R^{\prime }}$
, and
![]() $\lvert u'\rvert _{R^{\prime }} = \vert u\rvert _R$
. Moreover, if
$\lvert u'\rvert _{R^{\prime }} = \vert u\rvert _R$
. Moreover, if
![]() $\lvert \cdot \rvert _R$
is adapted to
$\lvert \cdot \rvert _R$
is adapted to
![]() $\kappa _R$
, then
$\kappa _R$
, then
![]() $\lvert \cdot \rvert _{R^{\prime }}$
is adapted to
$\lvert \cdot \rvert _{R^{\prime }}$
is adapted to
![]() $\kappa _{R^{\prime }}$
.
$\kappa _{R^{\prime }}$
.
Lemma 4.2.3. With notation as above, suppose that
![]() $f:R_0\rightarrow R_0'$
is a finite map. Then the natural map
$f:R_0\rightarrow R_0'$
is a finite map. Then the natural map
![]() $R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is a topological isomorphism (with respect to the
$R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is a topological isomorphism (with respect to the
![]() $u'$
-adic topology), where the completed tensor product is taken with respect to the u-adic topology on
$u'$
-adic topology), where the completed tensor product is taken with respect to the u-adic topology on
![]() $\mathcal {D}_{\kappa _R}^{<r,\circ }$
and the
$\mathcal {D}_{\kappa _R}^{<r,\circ }$
and the
![]() $u'$
-adic topology on
$u'$
-adic topology on
![]() $R_0'$
.
$R_0'$
.
Proof. We first check that the morphism
![]() $R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is an isomorphism of
$R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is an isomorphism of
![]() $R_0'$
-modules. The discussion after [Reference Johansson and NewtonJN16, Proposition 3.2.7] shows that
$R_0'$
-modules. The discussion after [Reference Johansson and NewtonJN16, Proposition 3.2.7] shows that
where
![]() $n_R(r,u,\alpha ):= \left \lfloor \frac {\lvert \alpha \rvert \log _pr}{\log _p\lvert u\rvert _R}\right \rfloor $
,
$n_R(r,u,\alpha ):= \left \lfloor \frac {\lvert \alpha \rvert \log _pr}{\log _p\lvert u\rvert _R}\right \rfloor $
,
![]() $\mathbf {n}$
is a certain (noncanonical but explicit) finite set (depending only on the group-theoretic data we fixed at the beginning of §3), and
$\mathbf {n}$
is a certain (noncanonical but explicit) finite set (depending only on the group-theoretic data we fixed at the beginning of §3), and
![]() $\alpha $
is a multi-index (and similarly for
$\alpha $
is a multi-index (and similarly for
![]() $\mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
). Now,
$\mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
). Now,
![]() $R_0'$
is a finitely presented
$R_0'$
is a finitely presented
![]() $R_0$
-module, and for any finitely presented
$R_0$
-module, and for any finitely presented
![]() $R_0$
-module M, the natural morphism
$R_0$
-module M, the natural morphism
![]() $M\otimes _{R_0}\prod _\alpha R_0\cdot u^{-n_R(r,u,\alpha )}\mathbf {b}^\alpha \rightarrow \prod _\alpha M\cdot u^{-n_R(r,u,\alpha )}\mathbf {b}^\alpha $
is an isomorphism. By construction,
$M\otimes _{R_0}\prod _\alpha R_0\cdot u^{-n_R(r,u,\alpha )}\mathbf {b}^\alpha \rightarrow \prod _\alpha M\cdot u^{-n_R(r,u,\alpha )}\mathbf {b}^\alpha $
is an isomorphism. By construction,
![]() $n_R(r,u,\alpha ) = n_{R^{\prime }}(r,u',\alpha )$
for all
$n_R(r,u,\alpha ) = n_{R^{\prime }}(r,u',\alpha )$
for all
![]() $\alpha $
, so the claim follows.
$\alpha $
, so the claim follows.
Finally, the morphism
![]() $R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is clearly continuous, so the open mapping theorem implies that it is a topological isomorphism.
$R_0'\mathop {\widehat \otimes }_{R_0}\mathcal {D}_{\kappa _R}^{<r,\circ }\rightarrow \mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ }$
is clearly continuous, so the open mapping theorem implies that it is a topological isomorphism.
Corollary 4.2.4. With notation as above, suppose that
![]() $f:R_0\rightarrow R_0'$
is a finite map. If
$f:R_0\rightarrow R_0'$
is a finite map. If
![]() $F_{\kappa }$
has a slope
$F_{\kappa }$
has a slope
![]() $\leq h$
-factorization, then the natural map
$\leq h$
-factorization, then the natural map
is surjective.
Proof. Writing
![]() $D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K=\coprod _{i\in I}D^{\times } g_i K$
for some finite set of elements
$D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K=\coprod _{i\in I}D^{\times } g_i K$
for some finite set of elements
![]() $g_i\in ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }$
, we have an isomorphism
$g_i\in ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }$
, we have an isomorphism
For every map
![]() $R\rightarrow R'$
as above, Lemma 4.2.3 implies that the base change map
$R\rightarrow R'$
as above, Lemma 4.2.3 implies that the base change map
is an isomorphism. Moreover, the calculations of [Reference TaylorTay06, Lemma 1.1] show that the order of
![]() $(K{\mathbf {A}}_{F,f}^{\times }\cap g_i^{-1}D^{\times } g_i)/F^{\times }$
is prime to p for all i, so the base change map
$(K{\mathbf {A}}_{F,f}^{\times }\cap g_i^{-1}D^{\times } g_i)/F^{\times }$
is prime to p for all i, so the base change map
![]() $R_0'\mathop {\widehat \otimes }_{R_0}H^0(K,\mathcal {D}_{\kappa _R}^{<r,\circ })[\xi ]\rightarrow H^0(K,\mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ })[\xi ]$
is an isomorphism.
$R_0'\mathop {\widehat \otimes }_{R_0}H^0(K,\mathcal {D}_{\kappa _R}^{<r,\circ })[\xi ]\rightarrow H^0(K,\mathcal {D}_{\kappa _{R^{\prime }}}^{<r,\circ })[\xi ]$
is an isomorphism.
Now, we have a commutative diagram

(where the fact that the right vertical arrow is an isomorphism follows from Lemma 4.2.1). This implies first of all that the map
![]() $R'\otimes _{R}H^0\left (K,\mathcal {D}_{\kappa _R}^{<r}\right )[\xi ]\rightarrow H^0\left (K,\mathcal {D}_{\kappa _{R^{\prime }}}^{<r}\right )[\xi ]$
carries
$R'\otimes _{R}H^0\left (K,\mathcal {D}_{\kappa _R}^{<r}\right )[\xi ]\rightarrow H^0\left (K,\mathcal {D}_{\kappa _{R^{\prime }}}^{<r}\right )[\xi ]$
carries
![]() $R_0'\otimes _{R_0}S_{\kappa _R,\xi }^{<r,\circ }(K)_{\leq h}$
to
$R_0'\otimes _{R_0}S_{\kappa _R,\xi }^{<r,\circ }(K)_{\leq h}$
to
![]() $S_{\kappa _{R^{\prime }},\xi }^{<r,\circ }(K)_{\leq h}$
.
$S_{\kappa _{R^{\prime }},\xi }^{<r,\circ }(K)_{\leq h}$
.
To prove surjectivity, we may lift
![]() $f\in S_{\kappa _{R^{\prime }},\xi }^{<r,\circ }(K)_{\leq h}$
to an element of
$f\in S_{\kappa _{R^{\prime }},\xi }^{<r,\circ }(K)_{\leq h}$
to an element of
![]() $R_0'\mathop {\widehat \otimes }_{R_0} H^0\left (K,\mathcal {D}_{\kappa _R}^{<r,\circ }\right )[\xi ]$
since the left vertical arrow is an isomorphism. Its image in
$R_0'\mathop {\widehat \otimes }_{R_0} H^0\left (K,\mathcal {D}_{\kappa _R}^{<r,\circ }\right )[\xi ]$
since the left vertical arrow is an isomorphism. Its image in
![]() $R'\otimes _RH^0\left (K,\mathcal {D}_{\kappa _R}^{<r}\right )[\xi ]_{\leq h}$
is therefore an element of
$R'\otimes _RH^0\left (K,\mathcal {D}_{\kappa _R}^{<r}\right )[\xi ]_{\leq h}$
is therefore an element of
![]() $R_0'\otimes _{R_0}S_{\kappa _R,\xi }^{<r,\circ }(K)_{\leq h}$
in the preimage of f.
$R_0'\otimes _{R_0}S_{\kappa _R,\xi }^{<r,\circ }(K)_{\leq h}$
in the preimage of f.
We may also extend [Reference KisinKis09a, Lemma 2.1.4] and [Reference KisinKis09a, Lemma 2.1.7] to statements about families of integral overconvergent modular forms.
Proposition 4.2.5. Let
![]() $\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
be a weight, and let
$\kappa :T_0/\overline {Z(K)}\rightarrow R^{\times }$
be a weight, and let
![]() $\chi :\Delta _Q\rightarrow R^{\times }$
be a character. For any finite set of primes Q as in § 4.1, suppose that
$\chi :\Delta _Q\rightarrow R^{\times }$
be a character. For any finite set of primes Q as in § 4.1, suppose that
![]() $H^0(K_0(Q),\mathscr {D}_{\kappa })$
and
$H^0(K_0(Q),\mathscr {D}_{\kappa })$
and
![]() $H^0(K^-(Q),\mathscr {D}_{\kappa })$
admit slope-
$H^0(K^-(Q),\mathscr {D}_{\kappa })$
admit slope-
![]() $\leq h$
-decompositions. Then the natural map
$\leq h$
-decompositions. Then the natural map
 $$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q=\chi}\rightarrow S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}^{\Delta_Q=\chi} \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q=\chi}\rightarrow S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}^{\Delta_Q=\chi} \end{align*}$$
is an isomorphism.
Here,
![]() $\left (S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}\right )_{\Delta _Q=\chi }$
is the maximal quotient of
$\left (S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}\right )_{\Delta _Q=\chi }$
is the maximal quotient of
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
on which
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
on which
![]() $\Delta _Q$
acts by
$\Delta _Q$
acts by
![]() $\chi $
; if
$\chi $
; if
![]() $\chi $
is the trivial character, this is simply the coinvariants.
$\chi $
is the trivial character, this is simply the coinvariants.
Proof. We first assume that K is neat. Writing
![]() $D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _FD)^{\times }/K_0(Q) = \sqcup _{i\in I}D^{\times } g_iK_0(Q)$
, we have a finite disjoint union
$D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _FD)^{\times }/K_0(Q) = \sqcup _{i\in I}D^{\times } g_iK_0(Q)$
, we have a finite disjoint union
We claim that
![]() $\Delta _Q$
acts freely on
$\Delta _Q$
acts freely on
![]() $D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K^-(Q)$
. But if
$D^{\times }\backslash ({\mathbf {A}}_{F,f}\otimes _F D)^{\times }/K^-(Q)$
. But if
![]() $D^{\times } g_ih_j K^-(Q) = D^{\times } g_{i'}h_{j'}K^-(Q)$
, then the neatness hypothesis 3.1.1 implies that
$D^{\times } g_ih_j K^-(Q) = D^{\times } g_{i'}h_{j'}K^-(Q)$
, then the neatness hypothesis 3.1.1 implies that
![]() $i=i'$
and
$i=i'$
and
![]() $j=j'$
. Hence, we have
$j=j'$
. Hence, we have
and we can write
 $$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r,\circ})[\xi]\right)_{\Delta_Q=\chi}\xrightarrow\sim H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r,\circ})[\xi]^{\Delta_Q=\chi} \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r,\circ})[\xi]\right)_{\Delta_Q=\chi}\xrightarrow\sim H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r,\circ})[\xi]^{\Delta_Q=\chi} \end{align*}$$
and
 $$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r})[\xi]\right)_{\Delta_Q=\chi}\xrightarrow\sim H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r})[\xi]^{\Delta_Q=\chi}. \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle:\left(H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r})[\xi]\right)_{\Delta_Q=\chi}\xrightarrow\sim H^0(K^-(Q),\mathcal{D}_{\kappa}^{<r})[\xi]^{\Delta_Q=\chi}. \end{align*}$$
If
![]() $K'\vartriangleleft K$
with
$K'\vartriangleleft K$
with
![]() $K'$
neat and
$K'$
neat and
![]() $[K:K']$
prime to p, then
$[K:K']$
prime to p, then
![]() $\sum _{h\in \Delta _Q}\chi (d)\left \langle h\right \rangle $
induces diagrams
$\sum _{h\in \Delta _Q}\chi (d)\left \langle h\right \rangle $
induces diagrams

and

Using [Reference Johansson and NewtonJN16, Proposition 2.2.11], for any level K we obtain an isomorphism
 $$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle: S_{\kappa,\xi}(K^-(Q)_{\leq h})_{\Delta_Q}\xrightarrow\sim S_{\kappa,\xi}(K_0(Q))_{\leq h}. \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle: S_{\kappa,\xi}(K^-(Q)_{\leq h})_{\Delta_Q}\xrightarrow\sim S_{\kappa,\xi}(K_0(Q))_{\leq h}. \end{align*}$$
Then we have a diagram

where
![]() $I_{\Delta _Q,\chi }\subset R_0[\Delta _Q]$
denotes the ideal generated by the elements
$I_{\Delta _Q,\chi }\subset R_0[\Delta _Q]$
denotes the ideal generated by the elements
![]() $\left \langle h\right \rangle -\chi (h)$
for
$\left \langle h\right \rangle -\chi (h)$
for
![]() $h\in \Delta _Q$
. A diagram chase shows that we have the desired isomorphism
$h\in \Delta _Q$
. A diagram chase shows that we have the desired isomorphism
 $$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle: \left(S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q=\chi}\xrightarrow\sim S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}^{\Delta_Q=\chi}.\\[-40pt] \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\chi(h)^{-1}\left\langle h\right\rangle: \left(S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q=\chi}\xrightarrow\sim S_{\kappa,\xi}^{<r,\circ}(K^-(Q))_{\leq h}^{\Delta_Q=\chi}.\\[-40pt] \end{align*}$$
Now, assume that R is a local field with uniformizer u, that is, a finite extension of
![]() ${\mathbf {Q}}_p$
or
${\mathbf {Q}}_p$
or
![]() ${\mathbf {F}}_p(\!(u)\!)$
. Then by [Reference Ash and StevensAS, Theorem 4.4.2], it is automatic that
${\mathbf {F}}_p(\!(u)\!)$
. Then by [Reference Ash and StevensAS, Theorem 4.4.2], it is automatic that
![]() $H^0(K,\mathscr {D}_{\kappa })$
and
$H^0(K,\mathscr {D}_{\kappa })$
and
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]$
admit slope-
$H^0(K,\mathscr {D}_{\kappa })[\xi ]$
admit slope-
![]() $\leq h$
-decompositions (and that
$\leq h$
-decompositions (and that
![]() $F_{\kappa }$
and
$F_{\kappa }$
and
![]() $F_{\kappa ,\xi }$
admit slope-
$F_{\kappa ,\xi }$
admit slope-
![]() $\leq h$
-factorizations).
$\leq h$
-factorizations).
Proposition 4.2.6. If R is a local field, with ring of integers
![]() $R_0$
and uniformizer
$R_0$
and uniformizer
![]() $u\in R_0$
, the module
$u\in R_0$
, the module
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
is finite projective over
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
is finite projective over
![]() $R_0[\Delta _Q]$
.
$R_0[\Delta _Q]$
.
Proof. To check that
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is projective over
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is projective over
![]() $R_0[\Delta _Q]$
, we may replace
$R_0[\Delta _Q]$
, we may replace
![]() $R_0$
with a finite extension, so we may assume that
$R_0$
with a finite extension, so we may assume that
![]() $R_0$
contains the values of all characters
$R_0$
contains the values of all characters
![]() $\chi :\Delta _Q\rightarrow \overline {R}^{\times }$
. If
$\chi :\Delta _Q\rightarrow \overline {R}^{\times }$
. If
![]() $\Delta _v$
has order
$\Delta _v$
has order
![]() $p^{n_v}$
, we can write
$p^{n_v}$
, we can write
![]() $R_0[\Delta _Q]$
explicitly (but noncanonically) as
$R_0[\Delta _Q]$
explicitly (but noncanonically) as
![]() $R_0[\{x_v\}_{v\mid p}]/(\{x_v^{p^{n_v}}-1)$
; this assumption implies that the polynomials
$R_0[\{x_v\}_{v\mid p}]/(\{x_v^{p^{n_v}}-1)$
; this assumption implies that the polynomials
![]() $x_v^{p^{n_v}}-1$
split completely, and the ideals
$x_v^{p^{n_v}}-1$
split completely, and the ideals
![]() $I_{\Delta _Q,\chi }$
introduced above are the nonmaximal prime ideals of
$I_{\Delta _Q,\chi }$
introduced above are the nonmaximal prime ideals of
![]() $R_0[\Delta _Q]$
.
$R_0[\Delta _Q]$
.
On the other hand, we have a family of surjections
The target is a lattice in
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]_{\leq h}^{\Delta _Q=\chi }$
; since
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]_{\leq h}^{\Delta _Q=\chi }$
; since
![]() $R_0$
is a discrete valuation ring,
$R_0$
is a discrete valuation ring,
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}^{\Delta _Q=\chi }$
is free of some rank
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}^{\Delta _Q=\chi }$
is free of some rank
![]() $d_\chi $
. Since
$d_\chi $
. Since
![]() $R_0[\Delta _Q]$
is a local ring,
$R_0[\Delta _Q]$
is a local ring,
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}$
can be generated by
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}$
can be generated by
![]() $d_{\chi }$
elements as a
$d_{\chi }$
elements as a
![]() $R_0[\Delta _Q]$
-module.
$R_0[\Delta _Q]$
-module.
Furthermore,
![]() $R_0[\Delta _Q]_{\Delta _Q=\chi }\cong R_0$
. Since
$R_0[\Delta _Q]_{\Delta _Q=\chi }\cong R_0$
. Since
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}^{\Delta _Q=\chi }$
cannot be generated as an
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r,\circ })[\xi ]_{\leq h}^{\Delta _Q=\chi }$
cannot be generated as an
![]() $R_0$
-module by fewer than
$R_0$
-module by fewer than
![]() $d_\chi $
elements, this implies that the ranks
$d_\chi $
elements, this implies that the ranks
![]() $d_\chi $
agree for all characters
$d_\chi $
agree for all characters
![]() $\chi $
; call this number d.
$\chi $
; call this number d.
We therefore have a presentation of
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
:
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
:
Since the surjection
![]() $R_0[\Delta _Q]^{\oplus d}\rightarrow S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is an isomorphism modulo each
$R_0[\Delta _Q]^{\oplus d}\rightarrow S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is an isomorphism modulo each
![]() $I_{\Delta _Q,\chi }$
, the image of
$I_{\Delta _Q,\chi }$
, the image of
![]() $R_0[\Delta _Q]^{\oplus d'}$
in
$R_0[\Delta _Q]^{\oplus d'}$
in
![]() $R_0[\Delta _Q]^{\oplus d}$
is contained in
$R_0[\Delta _Q]^{\oplus d}$
is contained in
![]() $I_{\Delta _Q,\chi }R_0[\Delta _Q]^{\oplus d}$
. In particular, if
$I_{\Delta _Q,\chi }R_0[\Delta _Q]^{\oplus d}$
. In particular, if
![]() $d'\neq 0$
, then the Fitting ideals of
$d'\neq 0$
, then the Fitting ideals of
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
are contained in
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
are contained in
![]() $\cap _\chi I_{\Delta _Q,\chi }$
.
$\cap _\chi I_{\Delta _Q,\chi }$
.
On the other hand, the module
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]$
is potentially orthonormalizable as an
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]$
is potentially orthonormalizable as an
![]() $R[\Delta _Q]$
-module, so by [Reference Johansson and NewtonJN16, Theorem 2.2.2]
$R[\Delta _Q]$
-module, so by [Reference Johansson and NewtonJN16, Theorem 2.2.2]
![]() $H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]_{\leq h}$
is a finite projective
$H^0(K^-(Q),\mathcal {D}_{\kappa }^{<r})[\xi ]_{\leq h}$
is a finite projective
![]() $R[\Delta _Q]$
-module. In particular, for each prime
$R[\Delta _Q]$
-module. In particular, for each prime
![]() $\mathfrak {p}\subset R[\Delta _Q]$
, there is some integer
$\mathfrak {p}\subset R[\Delta _Q]$
, there is some integer
![]() $d_{\mathfrak {p}}\leq d$
such that
$d_{\mathfrak {p}}\leq d$
such that
![]() $\operatorname {\mathrm {Fitt}}_{k}(S_{\kappa ,\xi }(K^-(Q))_{\leq h,\mathfrak {p}})=0$
for
$\operatorname {\mathrm {Fitt}}_{k}(S_{\kappa ,\xi }(K^-(Q))_{\leq h,\mathfrak {p}})=0$
for
![]() $k<d_{\mathfrak {p}}$
and
$k<d_{\mathfrak {p}}$
and
![]() $\operatorname {\mathrm {Fitt}}_{k}(S_{\kappa ,\xi }(K^-(Q))_{\leq h,\mathfrak {p}})=R[\Delta _Q]_{\mathfrak {p}}$
for
$\operatorname {\mathrm {Fitt}}_{k}(S_{\kappa ,\xi }(K^-(Q))_{\leq h,\mathfrak {p}})=R[\Delta _Q]_{\mathfrak {p}}$
for
![]() $k\geq d_{\mathfrak {p}}$
. But the formation of Fitting ideals is functorial in the coefficients, and
$k\geq d_{\mathfrak {p}}$
. But the formation of Fitting ideals is functorial in the coefficients, and
![]() $\cap _\chi I_{\Delta _Q,\chi }$
does not generate the unit ideal in
$\cap _\chi I_{\Delta _Q,\chi }$
does not generate the unit ideal in
![]() $R[\Delta _Q]$
, so
$R[\Delta _Q]$
, so
![]() $d'=0$
and
$d'=0$
and
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is free of rank d over
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q)_{\leq h})$
is free of rank d over
![]() $R_0[\Delta _Q]$
.
$R_0[\Delta _Q]$
.
We may consider characteristic polynomials of operators on
![]() $S_{\kappa ,\xi }(K^-(Q))_{\leq h}$
, viewed as either a rank-d projective
$S_{\kappa ,\xi }(K^-(Q))_{\leq h}$
, viewed as either a rank-d projective
![]() $R[\Delta _Q]$
-module, or as a rank-
$R[\Delta _Q]$
-module, or as a rank-
![]() $d\lvert \Delta _Q]$
projective R-module. In particular, we have seen that if
$d\lvert \Delta _Q]$
projective R-module. In particular, we have seen that if
![]() $h=a/b$
, the R-linear characteristic polynomial of
$h=a/b$
, the R-linear characteristic polynomial of
![]() $u^aU_{\varpi _v}^{-b}$
has coefficients in
$u^aU_{\varpi _v}^{-b}$
has coefficients in
![]() $R^\circ $
. Using properties of circulant matrices, we see that the
$R^\circ $
. Using properties of circulant matrices, we see that the
![]() $R[\Delta _Q]$
-linear characteristic polynomial of
$R[\Delta _Q]$
-linear characteristic polynomial of
![]() $u^aU_{\varpi _v}^{-b}$
has coefficients in
$u^aU_{\varpi _v}^{-b}$
has coefficients in
![]() $R^\circ [\Delta _Q]$
.
$R^\circ [\Delta _Q]$
.
Corollary 4.2.7. Let notation be as above, and let d denote the rank of
![]() $S_{\kappa ,\xi }(K_0(Q))_{\leq h}$
. Suppose that R is reduced and
$S_{\kappa ,\xi }(K_0(Q))_{\leq h}$
. Suppose that R is reduced and
![]() $R_0=R^\circ $
. Then the natural map
$R_0=R^\circ $
. Then the natural map
 $$\begin{align*}\sum_{h\in\Delta_Q}\left\langle h\right\rangle:\left(S_{\kappa,\xi}^{\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q}\rightarrow S_{\kappa,\xi}^{\circ}(K_0(Q))_{\leq h} \end{align*}$$
$$\begin{align*}\sum_{h\in\Delta_Q}\left\langle h\right\rangle:\left(S_{\kappa,\xi}^{\circ}(K^-(Q))_{\leq h}\right)_{\Delta_Q}\rightarrow S_{\kappa,\xi}^{\circ}(K_0(Q))_{\leq h} \end{align*}$$
is surjective, and its kernel is annihilated by
![]() $u^{(d-1)a}$
.
$u^{(d-1)a}$
.
Proof. Since
![]() $u^aU_{\varpi _v}^{-b}$
is power-bounded for all
$u^aU_{\varpi _v}^{-b}$
is power-bounded for all
![]() $v\mid p$
on both
$v\mid p$
on both
![]() $S_{\kappa ,\xi }(K_0(Q))_{\leq h}$
and
$S_{\kappa ,\xi }(K_0(Q))_{\leq h}$
and
![]() $S_{\kappa ,\xi }(K^-(Q))_{\leq h}$
, by assumption, and
$S_{\kappa ,\xi }(K^-(Q))_{\leq h}$
, by assumption, and
![]() $U_{\varpi _v}$
commutes with the diamond operators, surjectivity follows.
$U_{\varpi _v}$
commutes with the diamond operators, surjectivity follows.
To study the kernel of
![]() $\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
, we first observe that for
$\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
, we first observe that for
![]() $f\in S_{\kappa ,\xi }^{\circ }(K^-(Q))_{\leq h}$
,
$f\in S_{\kappa ,\xi }^{\circ }(K^-(Q))_{\leq h}$
,
![]() $U_p^{b(d-1)}(f)\in S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
. Suppose
$U_p^{b(d-1)}(f)\in S_{\kappa ,\xi }^{<r,\circ }(K^-(Q))_{\leq h}$
. Suppose
![]() $f\in S_{\kappa ,\xi }^\circ (K^-(Q))_{\leq h}$
is in the kernel of
$f\in S_{\kappa ,\xi }^\circ (K^-(Q))_{\leq h}$
is in the kernel of
![]() $\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
. Since
$\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
. Since
![]() $U_p$
commutes with the diamond operators,
$U_p$
commutes with the diamond operators,
![]() $(u^aU_{p}^{-b})^{d-1}(f)$
is also in the kernel of
$(u^aU_{p}^{-b})^{d-1}(f)$
is also in the kernel of
![]() $\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
, and by Proposition 4.2.6 it actually lives in
$\sum _{h\in \Delta _Q}\left \langle h\right \rangle $
, and by Proposition 4.2.6 it actually lives in
![]() $I_{\Delta _Q}S_{\kappa ,\xi }^{<r}(K^-(Q))_{\leq h}$
. But then
$I_{\Delta _Q}S_{\kappa ,\xi }^{<r}(K^-(Q))_{\leq h}$
. But then
as desired.
Proposition 4.2.8. Suppose that
![]() $\kappa $
is an open weight such that
$\kappa $
is an open weight such that
![]() $\operatorname {\mathrm {Spa}} R$
contains a Zariski-dense set of classical weights, and suppose that
$\operatorname {\mathrm {Spa}} R$
contains a Zariski-dense set of classical weights, and suppose that
![]() $F_{\kappa }$
admits a slope
$F_{\kappa }$
admits a slope
![]() $\leq h$
-factorization. Let
$\leq h$
-factorization. Let
![]() $A_v, B_v\in \mathbb {T}_K^{<r,\circ }$
be lifts of
$A_v, B_v\in \mathbb {T}_K^{<r,\circ }$
be lifts of
![]() $\alpha _v, \beta _v$
, respectively. Then the map
$\alpha _v, \beta _v$
, respectively. Then the map
is an isomorphism (where we view
![]() $S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
as a submodule of
$S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
as a submodule of
![]() $S_{\kappa ,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}}$
).
$S_{\kappa ,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}}$
).
Proof. We may assume
![]() $Q=\{v\}$
, by induction on the size of Q. Then the source and the target are finite
$Q=\{v\}$
, by induction on the size of Q. Then the source and the target are finite
![]() $R_0$
-modules. After inverting u, [Reference KisinKis09a, Lemma 2.1.7] implies that the map is an isomorphism when specialized to any sufficiently large classical weight. It follows that
$R_0$
-modules. After inverting u, [Reference KisinKis09a, Lemma 2.1.7] implies that the map is an isomorphism when specialized to any sufficiently large classical weight. It follows that
![]() $S_{\kappa ,\xi }(K)_{\leq h,\mathfrak {m}}$
and
$S_{\kappa ,\xi }(K)_{\leq h,\mathfrak {m}}$
and
![]() $S_{\kappa ,\xi }(K_0(Q))_{\leq h,\mathfrak {m}_{Q,0}}$
have the same rank over R. We claim that it suffices to check that
$S_{\kappa ,\xi }(K_0(Q))_{\leq h,\mathfrak {m}_{Q,0}}$
have the same rank over R. We claim that it suffices to check that
![]() $U_{\varpi _v}-B_v$
is surjective after specializing at every maximal ideal of
$U_{\varpi _v}-B_v$
is surjective after specializing at every maximal ideal of
![]() $R_0$
. Indeed, this implies that
$R_0$
. Indeed, this implies that
is a surjection of projective R-modules of the same rank, so it is injective. Then the kernel of
![]() $U_{\varpi _v}-B_v$
on
$U_{\varpi _v}-B_v$
on
![]() $S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
is u-torsion. But
$S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
is u-torsion. But
![]() $S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
has no u-torsion, by definition, so the kernel is trivial.
$S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
has no u-torsion, by definition, so the kernel is trivial.
Thus, we need to check that
is surjective for any specialization
![]() $R_0\rightarrow {\mathbf {F}}'$
at a maximal ideal. There is some maximal point
$R_0\rightarrow {\mathbf {F}}'$
at a maximal ideal. There is some maximal point
![]() $x\in \operatorname {\mathrm {Spa}} R$
with residue field
$x\in \operatorname {\mathrm {Spa}} R$
with residue field
![]() $R_x$
and ring of integers
$R_x$
and ring of integers
![]() $R_{x,0}$
such that
$R_{x,0}$
such that
![]() $R_0\rightarrow {\mathbf {F}}'$
factors through
$R_0\rightarrow {\mathbf {F}}'$
factors through
![]() $R_0\rightarrow R_{x,0}$
, and by Corollary 4.2.4 the maps
$R_0\rightarrow R_{x,0}$
, and by Corollary 4.2.4 the maps
![]() $R_{x,0}\otimes _{R_0}S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}\rightarrow S_{\kappa _x,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
and
$R_{x,0}\otimes _{R_0}S_{\kappa ,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}\rightarrow S_{\kappa _x,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
and
![]() $R_{x,0}\otimes _{R_0}S_{\kappa ,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}_{0,Q}}\rightarrow S_{\kappa _x,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}_{Q,0}}$
are surjective. It therefore suffices to prove that
$R_{x,0}\otimes _{R_0}S_{\kappa ,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}_{0,Q}}\rightarrow S_{\kappa _x,\xi }^{<r,\circ }(K_0(Q))_{\leq h,\mathfrak {m}_{Q,0}}$
are surjective. It therefore suffices to prove that
is surjective. But this is a map of vector spaces of the same dimension, so it is enough to prove injectivity.
The module
![]() ${\mathbf {F}}'\otimes _{R_0}S_{\kappa _x,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
is a finite module over the Artin local ring
${\mathbf {F}}'\otimes _{R_0}S_{\kappa _x,\xi }^{<r,\circ }(K)_{\leq h,\mathfrak {m}}$
is a finite module over the Artin local ring
![]() $\mathbb {T}_{\mathfrak {m}}/\pi $
, so if the kernel of
$\mathbb {T}_{\mathfrak {m}}/\pi $
, so if the kernel of
![]() $U_{\varpi _v}-B_v$
is nontrivial, it contains
$U_{\varpi _v}-B_v$
is nontrivial, it contains
![]() $f\neq 0$
which is
$f\neq 0$
which is
![]() $\mathfrak {m}$
-torsion. In particular,
$\mathfrak {m}$
-torsion. In particular,
![]() $T_v(f)=(\alpha _v+\beta _v)x$
and
$T_v(f)=(\alpha _v+\beta _v)x$
and
![]() $U_{\varpi _v}(f)=\beta _v$
.
$U_{\varpi _v}(f)=\beta _v$
.
Since
 $$\begin{align*}[K_0(v)\left(\begin{smallmatrix}1 & \\ & \varpi_v\end{smallmatrix}\right)K_0(v)] = \coprod_{\alpha\in k_v}\left( \begin{smallmatrix}1 & \\ \widetilde\alpha\varpi_v & \varpi_v\end{smallmatrix} \right)K_0(v), \end{align*}$$
$$\begin{align*}[K_0(v)\left(\begin{smallmatrix}1 & \\ & \varpi_v\end{smallmatrix}\right)K_0(v)] = \coprod_{\alpha\in k_v}\left( \begin{smallmatrix}1 & \\ \widetilde\alpha\varpi_v & \varpi_v\end{smallmatrix} \right)K_0(v), \end{align*}$$
where
![]() $\widetilde \alpha $
denotes a lift of
$\widetilde \alpha $
denotes a lift of
![]() $\alpha $
, we have
$\alpha $
, we have
But
![]() $\left (\begin {smallmatrix}1 & \\ \widetilde \alpha \varpi _v & \varpi _v\end {smallmatrix}\right ) = \left (\begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix}\right )\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )$
and
$\left (\begin {smallmatrix}1 & \\ \widetilde \alpha \varpi _v & \varpi _v\end {smallmatrix}\right ) = \left (\begin {smallmatrix}1 & \\ & \varpi _v\end {smallmatrix}\right )\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )$
and
![]() ${}_{\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )}|f = f$
, since f is fixed by
${}_{\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )}|f = f$
, since f is fixed by
![]() $\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
by assumption, so
$\left (\begin {smallmatrix}1 & \\ \widetilde \alpha & 1 \end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
by assumption, so
Similarly, we have
 $$\begin{align*}[\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})\left(\begin{smallmatrix}1 & \\ & \varpi_v\end{smallmatrix}\right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})] = \left( \begin{smallmatrix}\varpi_v & \\ & 1\end{smallmatrix} \right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})\bigsqcup \coprod_{\alpha\in k_v}\left( \begin{smallmatrix}1 & \\ \widetilde\alpha & \varpi_v \end{smallmatrix}\right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v}) \end{align*}$$
$$\begin{align*}[\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})\left(\begin{smallmatrix}1 & \\ & \varpi_v\end{smallmatrix}\right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})] = \left( \begin{smallmatrix}\varpi_v & \\ & 1\end{smallmatrix} \right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v})\bigsqcup \coprod_{\alpha\in k_v}\left( \begin{smallmatrix}1 & \\ \widetilde\alpha & \varpi_v \end{smallmatrix}\right)\operatorname{\mathrm{GL}}_2({\mathscr{O}}_{F_v}) \end{align*}$$
so
Now, for any
![]() $\alpha \in k(v)$
,
$\alpha \in k(v)$
,
so
But
since f is fixed by
![]() $\left (\begin {smallmatrix}1 & \\ & \varpi _v \end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
, so
$\left (\begin {smallmatrix}1 & \\ & \varpi _v \end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_2({\mathscr {O}}_{F_v})$
, so
![]() $\alpha _v=\beta _v$
, which contradicts our assumption.
$\alpha _v=\beta _v$
, which contradicts our assumption.
Corollary 4.2.9. With notation as above, the map
is an isomorphism.
4.3 Varying the level
We record some results on the existence of slope decompositions as we vary the tame level. Fix a set of places Q as above, and fix a maximal ideal
![]() $\mathfrak {m}\subset \mathbb {T}$
which corresponds to the residual Hecke eigenvalues at some maximal point of
$\mathfrak {m}\subset \mathbb {T}$
which corresponds to the residual Hecke eigenvalues at some maximal point of
![]() $\mathscr {X}_{\underline D^{\times }}$
. There is a corresponding Galois representation
$\mathscr {X}_{\underline D^{\times }}$
. There is a corresponding Galois representation
![]() $\overline {\rho }_{\mathfrak {m}}:\operatorname {\mathrm {Gal}}_F\rightarrow \operatorname {\mathrm {GL}}_2({\mathbf {F}})$
for some finite field
$\overline {\rho }_{\mathfrak {m}}:\operatorname {\mathrm {Gal}}_F\rightarrow \operatorname {\mathrm {GL}}_2({\mathbf {F}})$
for some finite field
![]() ${\mathbf {F}}$
; it is unramified at all places of Q and the characteristic polynomial of
${\mathbf {F}}$
; it is unramified at all places of Q and the characteristic polynomial of
![]() $\overline {\rho }_{\mathfrak {m}}(\mathrm {{Frob}}_v)$
is
$\overline {\rho }_{\mathfrak {m}}(\mathrm {{Frob}}_v)$
is
![]() $X^2-T_vX+\operatorname {\mathrm {Nm}}(v)S_v$
for all
$X^2-T_vX+\operatorname {\mathrm {Nm}}(v)S_v$
for all
![]() $v\in Q$
. After replacing
$v\in Q$
. After replacing
![]() ${\mathbf {F}}$
with a quadratic extension if necessary, we may assume that each such characteristic polynomial has roots
${\mathbf {F}}$
with a quadratic extension if necessary, we may assume that each such characteristic polynomial has roots
![]() $\{\alpha _v,\beta _v\}$
in
$\{\alpha _v,\beta _v\}$
in
![]() ${\mathbf {F}}$
; we assume that
${\mathbf {F}}$
; we assume that
![]() $\alpha _v\beta _v^{-1}\notin \{1,\operatorname {\mathrm {Nm}}(v)^{\pm }\}$
.
$\alpha _v\beta _v^{-1}\notin \{1,\operatorname {\mathrm {Nm}}(v)^{\pm }\}$
.
Let
![]() $E/{\mathbf {Q}}_p$
be a finite extension with ring of integers
$E/{\mathbf {Q}}_p$
be a finite extension with ring of integers
![]() ${\mathscr {O}}_E$
, uniformizer
${\mathscr {O}}_E$
, uniformizer
![]() $\pi $
and residue field containing
$\pi $
and residue field containing
![]() ${\mathbf {F}}$
, and replace the Hecke algebras
${\mathbf {F}}$
, and replace the Hecke algebras
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\mathbb {T}_{Q,0}$
with
$\mathbb {T}_{Q,0}$
with
![]() ${\mathscr {O}}_E\otimes _{{\mathbf {Z}}_p}\mathbb {T}$
and
${\mathscr {O}}_E\otimes _{{\mathbf {Z}}_p}\mathbb {T}$
and
![]() ${\mathscr {O}}_E\otimes _{{\mathscr {O}}_E}\mathbb {T}_{Q,0}$
, respectively. Similarly, replace the coefficient module
${\mathscr {O}}_E\otimes _{{\mathscr {O}}_E}\mathbb {T}_{Q,0}$
, respectively. Similarly, replace the coefficient module
![]() $\mathscr {D}_{\kappa }$
with its base-change to
$\mathscr {D}_{\kappa }$
with its base-change to
![]() ${\mathscr {O}}_E$
so that the Hecke algebras continue to act (the upshot is that we also base-change the resulting eigenvarieties from
${\mathscr {O}}_E$
so that the Hecke algebras continue to act (the upshot is that we also base-change the resulting eigenvarieties from
![]() ${\mathbf {Z}}_p$
to
${\mathbf {Z}}_p$
to
![]() ${\mathscr {O}}_E$
, but we suppress this from the notation). Fix a root
${\mathscr {O}}_E$
, but we suppress this from the notation). Fix a root
![]() $\alpha _v\in \mathbb {F}$
of each characteristic polynomial, and fix a lift
$\alpha _v\in \mathbb {F}$
of each characteristic polynomial, and fix a lift
![]() $A_v\in {\mathscr {O}}_E$
of each
$A_v\in {\mathscr {O}}_E$
of each
![]() $\alpha _v$
. Then we define
$\alpha _v$
. Then we define
![]() $\mathfrak {m}_{Q,0}\subset \mathbb {T}_{Q,0}$
to be the maximal ideal generated by
$\mathfrak {m}_{Q,0}\subset \mathbb {T}_{Q,0}$
to be the maximal ideal generated by
![]() $\mathfrak {m}\cap \mathbb {T}_{Q,0}$
and
$\mathfrak {m}\cap \mathbb {T}_{Q,0}$
and
![]() $U_{\varpi _v}-A_v$
for all
$U_{\varpi _v}-A_v$
for all
![]() $v\in Q$
.
$v\in Q$
.
Lemma 4.3.1. Fix a central character
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
. Then there is an isomorphism
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
. Then there is an isomorphism
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}_{Q,0}}\xrightarrow {\sim }\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_Q(0),\mathbb {T}_{Q,0}}$
, compatible with the respective morphisms to
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}_{Q,0}}\xrightarrow {\sim }\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_Q(0),\mathbb {T}_{Q,0}}$
, compatible with the respective morphisms to
![]() $\mathscr {W}_F$
.
$\mathscr {W}_F$
.
Proof. Let
![]() $S_{\kappa }(K)_{\leq h,\mathfrak {m}}:=\mathbb {T}_{\mathfrak {m}}\otimes _{\mathbb {T}}S_{\kappa }(K)_{\leq h}$
, and similarly for
$S_{\kappa }(K)_{\leq h,\mathfrak {m}}:=\mathbb {T}_{\mathfrak {m}}\otimes _{\mathbb {T}}S_{\kappa }(K)_{\leq h}$
, and similarly for
![]() $S_{\kappa }(K_Q(0))_{\leq h,\mathfrak {m}_{Q,0}}$
. By [Reference KisinKis09a, Lemma 2.1.7], for any slope h and any sufficiently large classical weight
$S_{\kappa }(K_Q(0))_{\leq h,\mathfrak {m}_{Q,0}}$
. By [Reference KisinKis09a, Lemma 2.1.7], for any slope h and any sufficiently large classical weight
![]() $\kappa $
, we have an isomorphism of
$\kappa $
, we have an isomorphism of
![]() $\mathbb {T}_{Q,0}$
-modules
$\mathbb {T}_{Q,0}$
-modules
By construction, classical points are dense in
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}_{Q,0}}$
and
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}_{Q,0}}$
and
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_Q(0),\mathbb {T}_{Q,0}}$
, so we may use [Reference Johansson and NewtonJN19a, Theorem 3.2.1] to construct morphisms of eigenvarieties
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_Q(0),\mathbb {T}_{Q,0}}$
, so we may use [Reference Johansson and NewtonJN19a, Theorem 3.2.1] to construct morphisms of eigenvarieties
and
These morphisms are mutually inverse, so they are isomorphisms.
Corollary 4.3.2. Fix a central character
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
. Let
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
. Let
![]() $U=\operatorname {\mathrm {Spa}} R\subset \mathscr {W}_F$
be a connected affinoid open, corresponding to a weight
$U=\operatorname {\mathrm {Spa}} R\subset \mathscr {W}_F$
be a connected affinoid open, corresponding to a weight
![]() $\kappa $
, and fix
$\kappa $
, and fix
![]() $h\in \mathbb {Q}_{>0}$
. Then
$h\in \mathbb {Q}_{>0}$
. Then
![]() $(U,h)$
is a slope datum for
$(U,h)$
is a slope datum for
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K}$
if and only if it is a slope datum for
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K}$
if and only if it is a slope datum for
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_0(Q)}$
.
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_0(Q)}$
.
Proof. We write
![]() $h=m/n$
and consider the closed ball
$h=m/n$
and consider the closed ball
![]() $\mathbb {B}_{U,h}:=\{\lvert T^n\rvert \leq \lvert u^{-m}\rvert \}\subset \mathbb {A}_U^1$
. If
$\mathbb {B}_{U,h}:=\{\lvert T^n\rvert \leq \lvert u^{-m}\rvert \}\subset \mathbb {A}_U^1$
. If
![]() $\mathscr {Z}$
and
$\mathscr {Z}$
and
![]() $\mathscr {Z}'$
denote the spectral varieties for
$\mathscr {Z}'$
denote the spectral varieties for
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K}$
and
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K}$
and
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_0(Q)}$
, respectively, we set
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q,0}}^{K_0(Q)}$
, respectively, we set
![]() $Z_{U,h}:=\mathscr {Z}\cap \mathbb {B}_{U,h}$
and
$Z_{U,h}:=\mathscr {Z}\cap \mathbb {B}_{U,h}$
and
![]() $Z_{U,h}':=\mathscr {Z}'\cap \mathbb {B}_{U,h}$
. We need to show that
$Z_{U,h}':=\mathscr {Z}'\cap \mathbb {B}_{U,h}$
. We need to show that
![]() $Z_{U,h}\rightarrow U$
is finite with constant degree if and only if
$Z_{U,h}\rightarrow U$
is finite with constant degree if and only if
![]() $Z_{U,h}'\rightarrow U$
is.
$Z_{U,h}'\rightarrow U$
is.
Since the morphisms
![]() $\mathscr {Z}\rightarrow \mathscr {W}_F$
and
$\mathscr {Z}\rightarrow \mathscr {W}_F$
and
![]() $\mathscr {Z}'\rightarrow \mathscr {W}_F$
are flat and we have assumed U is connected, it is enough to prove that
$\mathscr {Z}'\rightarrow \mathscr {W}_F$
are flat and we have assumed U is connected, it is enough to prove that
![]() $Z_{U,h}\rightarrow U$
is finite if and only if
$Z_{U,h}\rightarrow U$
is finite if and only if
![]() $Z_{U,h}'\rightarrow U$
is. To see this, it is enough to show the same statement about the morphisms
$Z_{U,h}'\rightarrow U$
is. To see this, it is enough to show the same statement about the morphisms
![]() $Z_{U,h}^{\mathrm {{red}}}, Z_{U,h}^{',\mathrm {red}}\rightarrow U$
on the underlying reduced subspaces.
$Z_{U,h}^{\mathrm {{red}}}, Z_{U,h}^{',\mathrm {red}}\rightarrow U$
on the underlying reduced subspaces.
Setting
![]() $\mathbb {T}:={\mathscr {O}}_E$
, we have
$\mathbb {T}:={\mathscr {O}}_E$
, we have
and
Then as in Lemma 4.3.1, we have an isomorphism
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}}\rightarrow \mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K_0(Q),\mathbb {T}}$
compatible with the respective morphisms to
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K,\mathbb {T}}\rightarrow \mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}}^{K_0(Q),\mathbb {T}}$
compatible with the respective morphisms to
![]() $\mathscr {W}_F$
, and the result follows.
$\mathscr {W}_F$
, and the result follows.
We may also compare slope data for
![]() $\mathscr {X}_{\underline D^{\times }}^{K_0(Q)}$
and
$\mathscr {X}_{\underline D^{\times }}^{K_0(Q)}$
and
![]() $\mathscr {X}_{\underline D^{\times }}^{K^-(Q)}$
:
$\mathscr {X}_{\underline D^{\times }}^{K^-(Q)}$
:
Lemma 4.3.3. Fix a central character
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W})^{\times }$
. Let
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W})^{\times }$
. Let
![]() $U=\operatorname {\mathrm {Spa}} R\subset \mathscr {W}_F$
be an affinoid open, corresponding to a weight
$U=\operatorname {\mathrm {Spa}} R\subset \mathscr {W}_F$
be an affinoid open, corresponding to a weight
![]() $\kappa $
, and fix
$\kappa $
, and fix
![]() $h\in \mathbb {Q}_{>0}$
. Then
$h\in \mathbb {Q}_{>0}$
. Then
![]() $(U,h)$
is a slope datum for
$(U,h)$
is a slope datum for
![]() $\mathscr {X}_{\underline D,\xi }^{K_0(Q)}$
if and only if it is a slope datum for
$\mathscr {X}_{\underline D,\xi }^{K_0(Q)}$
if and only if it is a slope datum for
![]() $\mathscr {X}_{\underline D,\xi }^{K^-(Q)}$
.
$\mathscr {X}_{\underline D,\xi }^{K^-(Q)}$
.
Proof. Let
![]() $\mathscr {Z}$
and
$\mathscr {Z}$
and
![]() $\mathscr {Z}'$
be the spectral varieties for
$\mathscr {Z}'$
be the spectral varieties for
![]() $\mathscr {X}_{\underline D,\xi }^{K_0(Q)}$
and
$\mathscr {X}_{\underline D,\xi }^{K_0(Q)}$
and
![]() $\mathscr {X}_{\underline D,\xi }^{K^-(Q)}$
, respectively, and let
$\mathscr {X}_{\underline D,\xi }^{K^-(Q)}$
, respectively, and let
![]() $x\in U$
be a maximal point. Then by Proposition 4.2.6 the module
$x\in U$
be a maximal point. Then by Proposition 4.2.6 the module
![]() $H^0(K^-(Q),\mathscr {D}_{\kappa _x})[\xi ]_{\leq h}$
is finite projective over
$H^0(K^-(Q),\mathscr {D}_{\kappa _x})[\xi ]_{\leq h}$
is finite projective over
![]() $k_x[\Delta _Q]$
of constant rank, and the natural map
$k_x[\Delta _Q]$
of constant rank, and the natural map
![]() $H^0(K^-(Q),\mathscr {D}_{\kappa _x})[\xi ]_{\leq h,\Delta _Q}\rightarrow H^0(K_0(Q),\mathscr {D}_{\kappa _x})_{\leq h}$
is an isomorphism. It follows that the fiber of
$H^0(K^-(Q),\mathscr {D}_{\kappa _x})[\xi ]_{\leq h,\Delta _Q}\rightarrow H^0(K_0(Q),\mathscr {D}_{\kappa _x})_{\leq h}$
is an isomorphism. It follows that the fiber of
![]() $Z_{U,h}$
over x is finite of order d if and only if the fiber of
$Z_{U,h}$
over x is finite of order d if and only if the fiber of
![]() $\mathscr {Z}'$
over x is finite of order
$\mathscr {Z}'$
over x is finite of order
![]() $d\lvert \Delta _Q\rvert $
. Since spectral varieties are flat over weight space, the result follows from Theorem 3.1.2.
$d\lvert \Delta _Q\rvert $
. Since spectral varieties are flat over weight space, the result follows from Theorem 3.1.2.
5 Patching and modularity
5.1 Setup
Let us recall our goal. Assume
![]() $p\geq 5$
. Fix a non-Archimedean characteristic p local field L with ring of integers
$p\geq 5$
. Fix a non-Archimedean characteristic p local field L with ring of integers
![]() ${\mathscr {O}}_L$
, residue field
${\mathscr {O}}_L$
, residue field
![]() ${\mathbf {F}}_q$
and uniformizer u. Fix a continuous odd representation
${\mathbf {F}}_q$
and uniformizer u. Fix a continuous odd representation
![]() $\overline {\rho }:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathbf {F}}_q)$
such that:
$\overline {\rho }:\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathbf {F}}_q)$
such that:
-
•
 $\overline {\rho }$
is modular
$\overline {\rho }$
is modular -
•
 $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}(\zeta _p)}}$
is absolutely irreducible
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}(\zeta _p)}}$
is absolutely irreducible -
• The image of
 $\overline {\rho }$
contains
$\overline {\rho }$
contains
 $\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
$\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
-
•
 $\overline {\rho }$
is unramified at all places away from p
$\overline {\rho }$
is unramified at all places away from p -
•
 $\overline {\rho } \not \sim \chi \otimes \left (\begin {smallmatrix} \overline \chi _{\mathrm {{cyc}}} & \ast \\ & 1\end {smallmatrix}\right )$
for any character
$\overline {\rho } \not \sim \chi \otimes \left (\begin {smallmatrix} \overline \chi _{\mathrm {{cyc}}} & \ast \\ & 1\end {smallmatrix}\right )$
for any character
 $\chi :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow {\mathbf {F}}_q^{\times }$
.
$\chi :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow {\mathbf {F}}_q^{\times }$
.
The assumption that
![]() $\overline {\rho }$
has large image is stronger than the typical hypothesis. This is because we need to use [Reference Bergdall and HansenBH17, Theorem B.0.1] to ensure that we can work with middle-degree eigenvarieties for Hilbert modular forms.
$\overline {\rho }$
has large image is stronger than the typical hypothesis. This is because we need to use [Reference Bergdall and HansenBH17, Theorem B.0.1] to ensure that we can work with middle-degree eigenvarieties for Hilbert modular forms.
We wish to prove the following modularity theorem:
Theorem 5.1.1. Suppose
![]() $\rho :\operatorname {\mathrm {Gal}}_{\mathbf {Q}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathscr {O}}_L)$
is a continuous odd representation unramified away from p and trianguline at p with regular parameters, whose reduction modulo u is as above. Then
$\rho :\operatorname {\mathrm {Gal}}_{\mathbf {Q}}\rightarrow \operatorname {\mathrm {GL}}_2({\mathscr {O}}_L)$
is a continuous odd representation unramified away from p and trianguline at p with regular parameters, whose reduction modulo u is as above. Then
![]() $\rho $
is the twist of a Galois representation arising from an overconvergent modular form.
$\rho $
is the twist of a Galois representation arising from an overconvergent modular form.
The predicted weight
![]() $\kappa $
can be read off from the parameters of the triangulation, as can the predicted slope h.
$\kappa $
can be read off from the parameters of the triangulation, as can the predicted slope h.
More precisely, we will show that
![]() $\rho $
corresponds to a class in
$\rho $
corresponds to a class in
![]() $S_{\kappa }(K)_{\leq h}$
, where
$S_{\kappa }(K)_{\leq h}$
, where
![]() $K=I\cdot K_1(N)^p = I\cdot \prod _{\ell \neq p,\ell \nmid N}\operatorname {\mathrm {GL}}_2({\mathbf {Q}}_\ell )\cdot \prod _{\ell \mid N}K_1(\ell )$
for some
$K=I\cdot K_1(N)^p = I\cdot \prod _{\ell \neq p,\ell \nmid N}\operatorname {\mathrm {GL}}_2({\mathbf {Q}}_\ell )\cdot \prod _{\ell \mid N}K_1(\ell )$
for some
![]() $N\geq 5$
prime to p. To do this, we will consider an open weight
$N\geq 5$
prime to p. To do this, we will consider an open weight
![]() $\kappa :T_0\rightarrow {\mathscr {O}}(U)^{\times }$
, where
$\kappa :T_0\rightarrow {\mathscr {O}}(U)^{\times }$
, where
![]() $U\subset \mathscr {W}$
contains a point corresponding to
$U\subset \mathscr {W}$
contains a point corresponding to
![]() $\kappa $
and
$\kappa $
and
![]() $(U,h)$
is a slope datum, and we will study the spaces
$(U,h)$
is a slope datum, and we will study the spaces
![]() $S_{\kappa }(K^-(Q))_{\leq h}$
for varying sets of primes Q.
$S_{\kappa }(K^-(Q))_{\leq h}$
for varying sets of primes Q.
5.2 Patched eigenvarieties
In this section, we construct local pieces of patched quaternionic eigenvarieties, using the language of ultrafilters of [Reference ScholzeSch18, §9]. We fix a totally real field F split at all places above p and a totally definite quaternion algebra D over F, which is ramified at all infinite places and split at all finite places. We also fix the tame level
![]() $K^p:=\operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f}^p)$
. We further assume that
$K^p:=\operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f}^p)$
. We further assume that
![]() $F/{\mathbf {Q}}$
is abelian, so that Leopoldt’s conjecture is known to hold. Unlike [Reference ScholzeSch18], we do not assume that F has a unique prime above p; we let
$F/{\mathbf {Q}}$
is abelian, so that Leopoldt’s conjecture is known to hold. Unlike [Reference ScholzeSch18], we do not assume that F has a unique prime above p; we let
![]() $\Sigma _p:=\{v\mid p\}$
. We expect these hypotheses can be relaxed considerably, but this is not necessary for our applications. Fix some finite extension
$\Sigma _p:=\{v\mid p\}$
. We expect these hypotheses can be relaxed considerably, but this is not necessary for our applications. Fix some finite extension
![]() $E/{\mathbf {Q}}_p$
with residue field containing
$E/{\mathbf {Q}}_p$
with residue field containing
![]() $\mathbf {F}_q$
.
$\mathbf {F}_q$
.
Recall that there are Galois deformation rings
![]() $R_{\overline {\rho },\Sigma _p}^{\square }$
and
$R_{\overline {\rho },\Sigma _p}^{\square }$
and
![]() $R_{\overline {\rho },\Sigma _p}$
, parametrizing deformations of
$R_{\overline {\rho },\Sigma _p}$
, parametrizing deformations of
![]() $\overline {\rho }$
unramified outside of
$\overline {\rho }$
unramified outside of
![]() $\Sigma _p$
, where
$\Sigma _p$
, where
![]() $R_{\overline {\rho }}^{\square }$
additionally parametrizes framings of the deformations at places of
$R_{\overline {\rho }}^{\square }$
additionally parametrizes framings of the deformations at places of
![]() $\Sigma _p$
. There is also a local framed deformation ring
$\Sigma _p$
. There is also a local framed deformation ring
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square }:=\mathop {\widehat \otimes }_{v\in \Sigma _p}R_{\overline {\rho }_v}^{\square }$
, where
$R_{\overline {\rho },\mathrm {loc}}^{\square }:=\mathop {\widehat \otimes }_{v\in \Sigma _p}R_{\overline {\rho }_v}^{\square }$
, where
![]() $R_{\overline {\rho }_v}^{\square }$
parametrizes framed deformations of
$R_{\overline {\rho }_v}^{\square }$
parametrizes framed deformations of
![]() $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_{F_v}}$
, and there is a natural map
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_{F_v}}$
, and there is a natural map
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square }\rightarrow R_{\overline {\rho }}^{\square }$
.
$R_{\overline {\rho },\mathrm {loc}}^{\square }\rightarrow R_{\overline {\rho }}^{\square }$
.
We define a distinguished family of characters
![]() $\eta _{\mathrm {univ}}:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
over integral weight space. We have a universal weight
$\eta _{\mathrm {univ}}:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
over integral weight space. We have a universal weight
![]() $\underline \lambda =(\lambda _1,\lambda _2)$
, where each
$\underline \lambda =(\lambda _1,\lambda _2)$
, where each
![]() $\lambda _i$
is a character
$\lambda _i$
is a character
![]() $\prod _{v\in \Sigma _p}{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
, and we define
$\prod _{v\in \Sigma _p}{\mathscr {O}}_{F_v}^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
, and we define
![]() $\eta _v:{\mathscr {O}}_{F_v}^{\times }\cong {\mathbf {Z}}_p^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
via
$\eta _v:{\mathscr {O}}_{F_v}^{\times }\cong {\mathbf {Z}}_p^{\times }\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
via
![]() $\eta (x):=\left (\lambda _1|_{{\mathscr {O}}_{F_v}^{\times }}(x)\lambda _2|_{{\mathscr {O}}_{F_v}^{\times }}(x)\right )^{-1}$
. Then because we have assumed that Leopoldt’s conjecture holds for F, we see that
$\eta (x):=\left (\lambda _1|_{{\mathscr {O}}_{F_v}^{\times }}(x)\lambda _2|_{{\mathscr {O}}_{F_v}^{\times }}(x)\right )^{-1}$
. Then because we have assumed that Leopoldt’s conjecture holds for F, we see that
![]() $\eta _v$
is independent of
$\eta _v$
is independent of
![]() $v\in \Sigma $
; global class field theory gives us a corresponding character
$v\in \Sigma $
; global class field theory gives us a corresponding character
![]() $\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
, which we restrict to
$\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow {\mathbf {Z}}_p[\![T_0/\overline {Z(K)}]\!]^{\times }$
, which we restrict to
![]() $\operatorname {\mathrm {Gal}}_F$
to obtain
$\operatorname {\mathrm {Gal}}_F$
to obtain
![]() $\eta _{\mathrm {univ}}$
.
$\eta _{\mathrm {univ}}$
.
We fix an unramified continuous character
![]() $\psi _0:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]^{\times }$
such that the reduction
$\psi _0:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]^{\times }$
such that the reduction
![]() $\overline \psi _0$
modulo the maximal ideal satisfies
$\overline \psi _0$
modulo the maximal ideal satisfies
![]() $\det \overline {\rho }=\overline \psi _0\overline \eta _{\mathrm {univ}}\overline \chi _{\mathrm {{cyc}}}^{-1}$
, and we set
$\det \overline {\rho }=\overline \psi _0\overline \eta _{\mathrm {univ}}\overline \chi _{\mathrm {{cyc}}}^{-1}$
, and we set
![]() $\psi :=\psi _0\eta _{\mathrm {univ}}$
and
$\psi :=\psi _0\eta _{\mathrm {univ}}$
and
![]() $\psi ':=\psi _0\eta _{\mathrm {univ}}\chi _{\mathrm {{cyc}}}^{-1}$
. Then we constructed quotients
$\psi ':=\psi _0\eta _{\mathrm {univ}}\chi _{\mathrm {{cyc}}}^{-1}$
. Then we constructed quotients
 $$ \begin{align*} {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\Sigma_p}^{\square}&\twoheadrightarrow R_{\overline{\rho},\Sigma_p}^{\square,\psi'} \\ {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\mathrm{loc}}^{\square}&\twoheadrightarrow R_{\overline{\rho},\mathrm{loc}}^{\square,\psi'} \\ {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\Sigma_p}&\twoheadrightarrow R_{\overline{\rho},\Sigma_p}^{\psi'} \end{align*} $$
$$ \begin{align*} {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\Sigma_p}^{\square}&\twoheadrightarrow R_{\overline{\rho},\Sigma_p}^{\square,\psi'} \\ {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\mathrm{loc}}^{\square}&\twoheadrightarrow R_{\overline{\rho},\mathrm{loc}}^{\square,\psi'} \\ {\mathscr{O}}_E[\![T_0/\overline{Z(K)}]\!]\mathop{\widehat\otimes} R_{\overline{\rho},\Sigma_p}&\twoheadrightarrow R_{\overline{\rho},\Sigma_p}^{\psi'} \end{align*} $$
parametrizing families of deformations with fixed determinants.
We also define families of weights
![]() $\underline \kappa _v$
over
$\underline \kappa _v$
over
![]() $\mathscr {W}_F$
via
$\mathscr {W}_F$
via
In order to find sets of Taylor–Wiles primes, we impose the following standard hypotheses:
-
1.
 $p\geq 5$
$p\geq 5$
-
2.
 $\overline {\rho }|_{F(\zeta _p)}$
is absolutely irreducible
$\overline {\rho }|_{F(\zeta _p)}$
is absolutely irreducible -
3. If
 $p=5$
and
$p=5$
and
 $\overline {\rho }$
has projective image
$\overline {\rho }$
has projective image
 $\operatorname {\mathrm {PGL}}_2({\mathbf {F}}_5)$
, the kernel of
$\operatorname {\mathrm {PGL}}_2({\mathbf {F}}_5)$
, the kernel of
 $\overline {\rho }$
does not fix
$\overline {\rho }$
does not fix
 $F(\zeta _5)$
$F(\zeta _5)$
Then we have the following relative version of [Reference KisinKis09a, Proposition 2.2.4] (since we assumed p splits completely in F,
![]() $[F:{\mathbf {Q}}]=\lvert \Sigma _p\rvert $
):
$[F:{\mathbf {Q}}]=\lvert \Sigma _p\rvert $
):
Proposition 5.2.1. Let
![]() $g:=\dim _{{\mathbf {F}}_q}H^1(\operatorname {\mathrm {Gal}}_{F,\Sigma _p},\operatorname {\mathrm {ad}}^0\overline {\rho }(1))-1$
. Then for each positive integer n, there exists a finite set
$g:=\dim _{{\mathbf {F}}_q}H^1(\operatorname {\mathrm {Gal}}_{F,\Sigma _p},\operatorname {\mathrm {ad}}^0\overline {\rho }(1))-1$
. Then for each positive integer n, there exists a finite set
![]() $Q_n$
of places of F, disjoint from
$Q_n$
of places of F, disjoint from
![]() $\Sigma _p$
, of cardinality
$\Sigma _p$
, of cardinality
![]() $g+1$
such that
$g+1$
such that
-
1. for all
 $v\in Q_n$
,
$v\in Q_n$
,
 $\operatorname {\mathrm {Nm}}(v)\equiv 1\quad\pmod {p^n}$
, and
$\operatorname {\mathrm {Nm}}(v)\equiv 1\quad\pmod {p^n}$
, and
 $\overline {\rho }(\mathrm {Frob}_v)$
has distinct eigenvalues
$\overline {\rho }(\mathrm {Frob}_v)$
has distinct eigenvalues -
2. the global relative Galois deformation ring
 $R_{\overline {\rho },\Sigma _p\cup Q_n}^{\square ,\psi '}$
parametrizing families of deformations with determinant
$R_{\overline {\rho },\Sigma _p\cup Q_n}^{\square ,\psi '}$
parametrizing families of deformations with determinant
 $\psi $
unramified outside
$\psi $
unramified outside
 $\Sigma _p\cup Q_n$
can be topologically generated as an
$\Sigma _p\cup Q_n$
can be topologically generated as an
 $R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}$
-algebra by g elements.
$R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}$
-algebra by g elements.
Proof. This follows from Lemma 2.1.1, as in [Reference KisinKis09b, Proposition 3.2.5].
We fix such a set
![]() $Q_n$
for each
$Q_n$
for each
![]() $n\geq 1$
, as well as a nonprincipal ultrafilter
$n\geq 1$
, as well as a nonprincipal ultrafilter
![]() $\mathfrak {F}$
on
$\mathfrak {F}$
on
![]() $\{n\geq 1\}$
(more precisely, on its power set, ordered by inclusion). For notational convenience, we set
$\{n\geq 1\}$
(more precisely, on its power set, ordered by inclusion). For notational convenience, we set
![]() $Q_0:=\emptyset $
, and we let
$Q_0:=\emptyset $
, and we let
![]() $Q_n':=Q_n\cup \Sigma _p$
. For each n, we again let
$Q_n':=Q_n\cup \Sigma _p$
. For each n, we again let
![]() $K^-(Q_n)\subset K_0(Q_n)\subset G({\mathbf {A}}_{F,f}^p)\cong \operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f}^p)$
be the compact open subgroups
$K^-(Q_n)\subset K_0(Q_n)\subset G({\mathbf {A}}_{F,f}^p)\cong \operatorname {\mathrm {GL}}_2({\mathbf {A}}_{F,f}^p)$
be the compact open subgroups
Let
![]() $\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
be the central character corresponding to
$\xi :{\mathbf {A}}_{F,f}^{\times }/F^{\times }\rightarrow {\mathscr {O}}(\mathscr {W}_F)^{\times }$
be the central character corresponding to
![]() $\psi $
via class field theory.
$\psi $
via class field theory.
Now, we analyze the eigenvarieties
![]() $\mathscr {X}_{\underline D^{\times }}^{K^-(Q_n)}$
. Let
$\mathscr {X}_{\underline D^{\times }}^{K^-(Q_n)}$
. Let
![]() $\kappa $
be a weight valued in a reduced pseudoaffinoid
$\kappa $
be a weight valued in a reduced pseudoaffinoid
![]() ${\mathbf {Z}}_p$
-algebra R, and write
${\mathbf {Z}}_p$
-algebra R, and write
![]() $U:=\operatorname {\mathrm {Spa}} R$
. Assume that the Fredholm determinant corresponding to
$U:=\operatorname {\mathrm {Spa}} R$
. Assume that the Fredholm determinant corresponding to
![]() $H^0(K,\mathscr {D}_{\kappa })[\xi ]$
admits a slope-
$H^0(K,\mathscr {D}_{\kappa })[\xi ]$
admits a slope-
![]() $\leq h$
-factorization for some slope
$\leq h$
-factorization for some slope
![]() $h=a/b$
(where
$h=a/b$
(where
![]() $a,b$
are relatively prime nonnegative integers); by Corollary 4.3.2 and Lemma 4.3.3, the Fredholm determinants corresponding to
$a,b$
are relatively prime nonnegative integers); by Corollary 4.3.2 and Lemma 4.3.3, the Fredholm determinants corresponding to
![]() $H^0(K_0(Q_n),\mathscr {D}_{\kappa })[\xi ]$
and
$H^0(K_0(Q_n),\mathscr {D}_{\kappa })[\xi ]$
and
![]() $H^0(K^-(Q_n),\mathscr {D}_{\kappa })[\xi ]$
also admit slope-
$H^0(K^-(Q_n),\mathscr {D}_{\kappa })[\xi ]$
also admit slope-
![]() $\leq h$
-factorizations. We also assume that R can be equipped with a norm adapted to
$\leq h$
-factorizations. We also assume that R can be equipped with a norm adapted to
![]() $\kappa $
such that the corresponding unit ball is the ring of definition
$\kappa $
such that the corresponding unit ball is the ring of definition
![]() $R_0=R^\circ $
; this is possible, for example, if U is an affinoid open or a maximal point in
$R_0=R^\circ $
; this is possible, for example, if U is an affinoid open or a maximal point in
![]() $\mathscr {W}_F$
by Lemma 4.1.2. Then we fix some
$\mathscr {W}_F$
by Lemma 4.1.2. Then we fix some
![]() $r>r_{\kappa }$
.
$r>r_{\kappa }$
.
The modularity of the residual representation
![]() $\overline {\rho }$
means that
$\overline {\rho }$
means that
![]() $\overline {\rho }$
corresponds to a maximal ideal
$\overline {\rho }$
corresponds to a maximal ideal
![]() $\mathfrak {m}\subset \mathbb {T}$
. For each
$\mathfrak {m}\subset \mathbb {T}$
. For each
![]() $v\in Q_n$
, we fix a root
$v\in Q_n$
, we fix a root
![]() $\alpha _v$
of the characteristic polynomial
$\alpha _v$
of the characteristic polynomial
![]() $X^2-T_vX+\operatorname {\mathrm {Nm}}(v)S_v$
of
$X^2-T_vX+\operatorname {\mathrm {Nm}}(v)S_v$
of
![]() $\overline {\rho }(\mathrm {Frob}_v)$
(increasing
$\overline {\rho }(\mathrm {Frob}_v)$
(increasing
![]() ${\mathbf {F}}_q$
, and hence E, if necessary), and we consider the corresponding maximal ideal
${\mathbf {F}}_q$
, and hence E, if necessary), and we consider the corresponding maximal ideal
![]() $\mathfrak {m}_{Q_n}\subset \mathbb {T}_{Q_n}^-$
(as in § 3.6).
$\mathfrak {m}_{Q_n}\subset \mathbb {T}_{Q_n}^-$
(as in § 3.6).
Then we have a collection of diagrams

The preimage
![]() $\mathrm {wt}^{-1}(U)$
in the slope-
$\mathrm {wt}^{-1}(U)$
in the slope-
![]() $\leq h$
part of the eigenvariety has the form
$\leq h$
part of the eigenvariety has the form
![]() $\operatorname {\mathrm {Spa}}\left (\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h},\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^\circ \right )$
, and since
$\operatorname {\mathrm {Spa}}\left (\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h},\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^\circ \right )$
, and since
![]() $\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q_n}}^{K^-(Q_n)}$
is reduced,
$\mathscr {X}_{\underline D^{\times },\xi ,\mathfrak {m}_{Q_n}}^{K^-(Q_n)}$
is reduced,
![]() $\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^\circ \subset \mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}$
is a ring of definition.
$\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^\circ \subset \mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}$
is a ring of definition.
For each n, the module of overconvergent modular forms
![]() $S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
is a
$S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
is a
![]() $\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}$
-module, and it is projective as an R-module; let d be its rank over R. The
$\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}$
-module, and it is projective as an R-module; let d be its rank over R. The
![]() $\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^{<r,\circ }$
-submodule
$\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^{<r,\circ }$
-submodule
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h}$
is a lattice in
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h}$
is a lattice in
![]() $S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
. Recall from Definition 4.1.3 that there is a second lattice
$S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
. Recall from Definition 4.1.3 that there is a second lattice
 $$\begin{align*}S_{\kappa,\xi}^{\circ}(K^-(Q_n))_{\leq h}:=\sum_{v\mid p}\sum_{i\geq 0} (u^aU_{\varpi_v}^{-b})^i\left( S_{\kappa,\xi}^{<r,\circ}(K^-(Q_n))_{\leq h} \right) \end{align*}$$
$$\begin{align*}S_{\kappa,\xi}^{\circ}(K^-(Q_n))_{\leq h}:=\sum_{v\mid p}\sum_{i\geq 0} (u^aU_{\varpi_v}^{-b})^i\left( S_{\kappa,\xi}^{<r,\circ}(K^-(Q_n))_{\leq h} \right) \end{align*}$$
which is stable under the operators
![]() $u^aU_{\varpi _v}^{-b}$
, as well.
$u^aU_{\varpi _v}^{-b}$
, as well.
Let
![]() $R_{\overline {\rho },Q_n'}^{\psi '}|_U$
denote the localization
$R_{\overline {\rho },Q_n'}^{\psi '}|_U$
denote the localization
![]() $R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]} R_{\overline {\rho },Q_n'}^{\psi '}$
; the formal scheme
$R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]} R_{\overline {\rho },Q_n'}^{\psi '}$
; the formal scheme
![]() $\operatorname {\mathrm {Spf}} R_{\overline {\rho },Q_n'}^{\psi '}|_U$
is an integral model for the pseudorigid space
$\operatorname {\mathrm {Spf}} R_{\overline {\rho },Q_n'}^{\psi '}|_U$
is an integral model for the pseudorigid space
![]() $U\times \operatorname {\mathrm {Spa}} R_{\overline {\rho },Q_n'}^{\psi '}$
. Similarly, we will write
$U\times \operatorname {\mathrm {Spa}} R_{\overline {\rho },Q_n'}^{\psi '}$
. Similarly, we will write
![]() $R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }|_U$
for the localization
$R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }|_U$
for the localization
![]() $R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]}R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }$
and
$R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]}R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }$
and
![]() $R_{\mathrm {{tri}},\overline {\rho },\mathrm {loc},\leq h}^{\square ,\psi ',\underline \kappa }|_{U}$
for the localization
$R_{\mathrm {{tri}},\overline {\rho },\mathrm {loc},\leq h}^{\square ,\psi ',\underline \kappa }|_{U}$
for the localization
![]() $R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]}R_{\mathrm {{tri}},\overline {\rho },\mathrm {loc},\leq h}^{\square ,\psi ',\underline \kappa }$
. Using the existence of Galois representations, we see that
$R_0\mathop {\widehat \otimes }_{{\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]}R_{\mathrm {{tri}},\overline {\rho },\mathrm {loc},\leq h}^{\square ,\psi ',\underline \kappa }$
. Using the existence of Galois representations, we see that
![]() $\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^{\circ }$
is a
$\mathbb {T}_{K^-(Q_n),\kappa ,\xi ,\leq h}^{\circ }$
is a
![]() $R_{\overline {\rho },Q_n'}^{\psi '}|_U$
-algebra.
$R_{\overline {\rho },Q_n'}^{\psi '}|_U$
-algebra.
By Lemma 4.2.6,
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is a finite
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is a finite
![]() $R_0[\Delta _{Q_n}]$
-module, with
$R_0[\Delta _{Q_n}]$
-module, with
Since the augmentation ideal
![]() $I_{\Delta _{Q_n}}$
is contained in the Jacobson radical of
$I_{\Delta _{Q_n}}$
is contained in the Jacobson radical of
![]() $R_0[\Delta _{Q_n}]$
, this implies that
$R_0[\Delta _{Q_n}]$
, this implies that
![]() $S_{\kappa ,\xi }^{<r,\circ }(K_0(Q_n))_{\leq h,\mathfrak {m}_{0,Q_n}}$
and
$S_{\kappa ,\xi }^{<r,\circ }(K_0(Q_n))_{\leq h,\mathfrak {m}_{0,Q_n}}$
and
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
can be generated by the same number of elements (over
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
can be generated by the same number of elements (over
![]() $R_0$
and
$R_0$
and
![]() $R_0[\Delta _{Q_n}]$
, respectively).
$R_0[\Delta _{Q_n}]$
, respectively).
Similarly,
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is a finite
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is a finite
![]() $R_0[\Delta _{Q_n}]$
-module. Since
$R_0[\Delta _{Q_n}]$
-module. Since
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is generated by
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is generated by
![]() $d^{\lvert \Sigma _p\rvert }$
translates of
$d^{\lvert \Sigma _p\rvert }$
translates of
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
, we see that the number of generators of
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
, we see that the number of generators of
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
over
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
over
![]() $R_0[\Delta _{Q_n}]$
is bounded independently of n.
$R_0[\Delta _{Q_n}]$
is bounded independently of n.
Set
![]() $j=4\lvert \Sigma _p\rvert -1$
and
$j=4\lvert \Sigma _p\rvert -1$
and
![]() $k=\lvert Q_n\rvert = g+1$
. Using local-global compatibility at places in
$k=\lvert Q_n\rvert = g+1$
. Using local-global compatibility at places in
![]() $Q_n$
, there is a homomorphism
$Q_n$
, there is a homomorphism
![]() $R_0\mathop {\widehat \otimes } {\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]\rightarrow R_{\overline {\rho },Q_n'}^{\psi '}|_U$
such that the action of
$R_0\mathop {\widehat \otimes } {\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]\rightarrow R_{\overline {\rho },Q_n'}^{\psi '}|_U$
such that the action of
![]() $R_0\mathop {\widehat \otimes } {\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]$
on
$R_0\mathop {\widehat \otimes } {\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]$
on
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))^\circ _{\leq h,\mathfrak {m}_{Q_n}^-}$
is compatible with the action of
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))^\circ _{\leq h,\mathfrak {m}_{Q_n}^-}$
is compatible with the action of
![]() $R_0[\Delta _{Q_n}]$
via a fixed surjection
$R_0[\Delta _{Q_n}]$
via a fixed surjection
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]\rightarrow R_0[\Delta _{Q_n}]$
.
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_1,\ldots ,y_{k}]\!]\rightarrow R_0[\Delta _{Q_n}]$
.
We observe that we may view
![]() $S_{\kappa ,\xi }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
as a module over
$S_{\kappa ,\xi }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
as a module over
![]() $\operatorname {\mathrm {Spa}} R[\Delta _Q]{\times }_U C_{U,h}$
, where
$\operatorname {\mathrm {Spa}} R[\Delta _Q]{\times }_U C_{U,h}$
, where
![]() $C_{U,h}$
is the annulus of radius h, by letting the coordinate on
$C_{U,h}$
is the annulus of radius h, by letting the coordinate on
![]() $C_{U,h}$
act as
$C_{U,h}$
act as
![]() $U_p^{-1}$
.
$U_p^{-1}$
.
Now, we consider local-global compatibility at places in
![]() $\Sigma _p$
. Recall that the actions of
$\Sigma _p$
. Recall that the actions of
![]() $u^{a}U_{\varpi _v}^b$
and
$u^{a}U_{\varpi _v}^b$
and
![]() $u^{a}U_{\varpi _v}^{-b}$
on
$u^{a}U_{\varpi _v}^{-b}$
on
![]() $S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
are power-bounded for all
$S_{\kappa ,\xi }(K^-(Q_n))_{\leq h}$
are power-bounded for all
![]() $v\mid p$
. Thus, we can make
$v\mid p$
. Thus, we can make
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
into a module over
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
into a module over
![]() $R_{\overline {\rho },Q_n'}^{\psi '}|_U\left \langle p^{h}T_1^{\pm 1},\ldots ,p^{h}T_{\lvert \Sigma _p\rvert }^{\pm 1}\right \rangle $
by letting
$R_{\overline {\rho },Q_n'}^{\psi '}|_U\left \langle p^{h}T_1^{\pm 1},\ldots ,p^{h}T_{\lvert \Sigma _p\rvert }^{\pm 1}\right \rangle $
by letting
![]() $T_i$
act as
$T_i$
act as
![]() $U_{\varpi _{v_i}}^{-1}$
. But local-global compatibility tells us that, over the analytic locus,
$U_{\varpi _{v_i}}^{-1}$
. But local-global compatibility tells us that, over the analytic locus,
![]() $S_{\kappa ,\xi }(K^-(Q_n))$
is supported on the trianguline locus, so
$S_{\kappa ,\xi }(K^-(Q_n))$
is supported on the trianguline locus, so
![]() $S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is actually a
$S_{\kappa ,\xi }^{\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
is actually a
![]() $R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\psi ',\underline \kappa }|_U$
-module, where the coordinates of
$R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\psi ',\underline \kappa }|_U$
-module, where the coordinates of
![]() ${\mathbf {G}}_m^{\Sigma _p}$
act as
${\mathbf {G}}_m^{\Sigma _p}$
act as
![]() $U_{\varpi _v}^{-1}$
.
$U_{\varpi _v}^{-1}$
.
Since
![]() $R_{\overline {\rho },Q_n'}^{\psi '}\rightarrow R_{\overline {\rho },Q_n'}^{\square ,\psi '}$
is formally smooth of dimension j, we may construct a homomorphism
$R_{\overline {\rho },Q_n'}^{\psi '}\rightarrow R_{\overline {\rho },Q_n'}^{\square ,\psi '}$
is formally smooth of dimension j, we may construct a homomorphism
compatible with
such that
![]() $y_{k+1},\ldots ,y_{k+j}$
are the framing variables. Finally, we fix a surjection
$y_{k+1},\ldots ,y_{k+j}$
are the framing variables. Finally, we fix a surjection
![]() $R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}[\![x_1,\ldots ,x_g]\!]\twoheadrightarrow R_{\overline {\rho },Q_n'}^{\square ,\psi '}$
and a map
$R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}[\![x_1,\ldots ,x_g]\!]\twoheadrightarrow R_{\overline {\rho },Q_n'}^{\square ,\psi '}$
and a map
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_1,\ldots ,y_{k+j}]\!]\rightarrow R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}[\![x_1,\ldots ,x_g]\!]$
such that the corresponding diagram
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_1,\ldots ,y_{k+j}]\!]\rightarrow R_{\overline {\rho },\mathrm {loc}}^{\square ,\psi '}[\![x_1,\ldots ,x_g]\!]$
such that the corresponding diagram

commutes.
Now, we can patch. We add framing variables by setting
and
so that
for all
![]() $n\geq 1$
, and
$n\geq 1$
, and
for all
![]() $n\geq 1$
.
$n\geq 1$
.
For any open ideal
![]() $I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, we define
$I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, we define
and
Here, the homomorphism
![]() $\prod _{n\geq 1}R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I\rightarrow R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I$
is the localization map coming from our choice of nonprincipal ultrafilter.
$\prod _{n\geq 1}R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I\rightarrow R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I$
is the localization map coming from our choice of nonprincipal ultrafilter.
Passing to the inverse limit, we obtain the patched modules
and
Similarly, we may define patched global deformation rings
![]() $R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h,I}^{\square ,\psi ',\underline \kappa }|_U$
and Hecke algebras
$R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h,I}^{\square ,\psi ',\underline \kappa }|_U$
and Hecke algebras
![]() $\mathbb {T}_{\infty ,\kappa ,\leq h,I}^{<r,\circ }$
and
$\mathbb {T}_{\infty ,\kappa ,\leq h,I}^{<r,\circ }$
and
![]() $\mathbb {T}_{\infty ,\kappa ,\leq h,I}^\circ $
via
$\mathbb {T}_{\infty ,\kappa ,\leq h,I}^\circ $
via
Setting
![]() $R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U:=\varprojlim _I R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h,I}^{\square ,\psi ',\underline \kappa }|_ U$
,
$R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U:=\varprojlim _I R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h,I}^{\square ,\psi ',\underline \kappa }|_ U$
,
![]() $\mathbb {T}_{\infty ,\kappa ,\leq h}^{<r,\circ }:=\varprojlim _I \mathbb {T}_{\infty ,\kappa ,\leq h,I}^{<r,\circ }$
, and
$\mathbb {T}_{\infty ,\kappa ,\leq h}^{<r,\circ }:=\varprojlim _I \mathbb {T}_{\infty ,\kappa ,\leq h,I}^{<r,\circ }$
, and
![]() $\mathbb {T}_{\infty ,\kappa ,\leq h}^\circ :=\varprojlim _I \mathbb {T}_{\infty ,\kappa ,\leq h,I}^\circ $
, we have a sequence of homomorphisms
$\mathbb {T}_{\infty ,\kappa ,\leq h}^\circ :=\varprojlim _I \mathbb {T}_{\infty ,\kappa ,\leq h,I}^\circ $
, we have a sequence of homomorphisms
compatible with their actions on
![]() $M_\infty $
.
$M_\infty $
.
Note that for each open ideal I, we have a surjection
Hence, we have a surjection
and a closed immersion
Furthermore, since
![]() $R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_i)\cong R_{\mathrm {{tri}},\overline {\rho },\Sigma _p,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
for all n, we see that
$R_{\mathrm {{tri}},\overline {\rho },Q_n',\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_i)\cong R_{\mathrm {{tri}},\overline {\rho },\Sigma _p,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
for all n, we see that
![]() $R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_i)\cong R_{\mathrm {{tri}},\overline {\rho },\Sigma _p,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
.
$R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_i)\cong R_{\mathrm {{tri}},\overline {\rho },\Sigma _p,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
.
Lemma 5.2.2. The patched modules
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
are finite over
$M_\infty $
are finite over
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
. In particular, they are complete.
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
. In particular, they are complete.
Proof. The powers of the ideal
![]() $(u,y_1,\ldots ,y_{k+j})$
are cofinal in the set of open ideals of
$(u,y_1,\ldots ,y_{k+j})$
are cofinal in the set of open ideals of
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, and for any open ideals
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, and for any open ideals
![]() $I\subset I'\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, the natural maps
$I\subset I'\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
, the natural maps
![]() $M_I^{<r}/I'\rightarrow M_{I'}^{<r}$
and
$M_I^{<r}/I'\rightarrow M_{I'}^{<r}$
and
![]() $M_I/I'\rightarrow M_{I'}$
are isomorphisms. Then [Sta18, Tag 09B8] implies that
$M_I/I'\rightarrow M_{I'}$
are isomorphisms. Then [Sta18, Tag 09B8] implies that
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
are complete and
$M_\infty $
are complete and
![]() $M_\infty ^{<r}/I\cong M_I^{<r}$
and
$M_\infty ^{<r}/I\cong M_I^{<r}$
and
![]() $M_\infty /I\cong M_I$
for all open ideals
$M_\infty /I\cong M_I$
for all open ideals
![]() $I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
.
$I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
.
We have
which is
![]() $R_0$
-finite. Since the number of generators of
$R_0$
-finite. Since the number of generators of
![]() $M_n/(u,y_1,\ldots ,y_{k+j})$
over
$M_n/(u,y_1,\ldots ,y_{k+j})$
over
![]() $R_0$
is bounded independently of n,
$R_0$
is bounded independently of n,
![]() $M_\infty /(u,y_1,\ldots ,y_{k+j})$
is
$M_\infty /(u,y_1,\ldots ,y_{k+j})$
is
![]() $R_0$
-finite. Hence, by [Reference MatsumuraMat89, Theorem 8.4],
$R_0$
-finite. Hence, by [Reference MatsumuraMat89, Theorem 8.4],
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
are
$M_\infty $
are
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
-finite.
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
-finite.
Proposition 5.2.3. If
![]() $R=L$
is a field with ring of integers
$R=L$
is a field with ring of integers
![]() ${\mathscr {O}}_L$
, then
${\mathscr {O}}_L$
, then
![]() $M_\infty ^{<r}$
is a finite projective
$M_\infty ^{<r}$
is a finite projective
![]() ${\mathscr {O}}_L[\![y_1,\ldots ,y_{k+j}]\!]$
-module.
${\mathscr {O}}_L[\![y_1,\ldots ,y_{k+j}]\!]$
-module.
Proof. We claim it is enough to show that, for any open ideal I,
![]() $M_n^{<r}/I$
is a free
$M_n^{<r}/I$
is a free
![]() ${\mathscr {O}}_L[\![y_i]\!]/I$
-module of rank d for all
${\mathscr {O}}_L[\![y_i]\!]/I$
-module of rank d for all
![]() $n\gg 0$
. Indeed, because our ultrafilter is nonprincipal, this implies that
$n\gg 0$
. Indeed, because our ultrafilter is nonprincipal, this implies that
![]() $M_I^{<r}$
is also a free
$M_I^{<r}$
is also a free
![]() ${\mathscr {O}}_L[\![y_i]\!]/I$
-module of rank d (since the localization
${\mathscr {O}}_L[\![y_i]\!]/I$
-module of rank d (since the localization
![]() $\prod _{n\geq 1}{\mathscr {O}}_L[\![y_i]\!]/I\rightarrow {\mathscr {O}}_L[\![y_i]\!]/I$
factors through the localization
$\prod _{n\geq 1}{\mathscr {O}}_L[\![y_i]\!]/I\rightarrow {\mathscr {O}}_L[\![y_i]\!]/I$
factors through the localization
![]() $\prod _{n\geq 1}{\mathscr {O}}_L[\![y_i]\!]/I\rightarrow \prod _{n\geq n_0}{\mathscr {O}}_L[\![y_i]\!]/I$
for any
$\prod _{n\geq 1}{\mathscr {O}}_L[\![y_i]\!]/I\rightarrow \prod _{n\geq n_0}{\mathscr {O}}_L[\![y_i]\!]/I$
for any
![]() $n_0\geq 1$
). Since
$n_0\geq 1$
). Since
![]() $M_\infty ^{<r}$
is
$M_\infty ^{<r}$
is
![]() $(u,y_1,\ldots ,y_{k+j})$
-adically separated, [Reference MatsumuraMat89, Theorem 22.3] implies that
$(u,y_1,\ldots ,y_{k+j})$
-adically separated, [Reference MatsumuraMat89, Theorem 22.3] implies that
![]() $M_\infty ^{<r}$
is flat over
$M_\infty ^{<r}$
is flat over
![]() ${\mathscr {O}}_L[\![y_i]\!]$
and hence projective.
${\mathscr {O}}_L[\![y_i]\!]$
and hence projective.
By Proposition 4.2.6,
![]() $S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h}$
is a projective
$S_{\kappa ,\xi }^{<r,\circ }(K^-(Q_n))_{\leq h}$
is a projective
![]() $R_0[\Delta _{Q_n}]$
-module of rank d for all n. Then for
$R_0[\Delta _{Q_n}]$
-module of rank d for all n. Then for
![]() $n\gg 0$
(depending on I),
$n\gg 0$
(depending on I),
![]() $M_n^{<r}/I$
is free over
$M_n^{<r}/I$
is free over
![]() ${\mathscr {O}}_L[\![y_i]\!]$
of rank d, so we are done.
${\mathscr {O}}_L[\![y_i]\!]$
of rank d, so we are done.
The modules
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
behave well under finite base change, in particular, under passage to closed subspaces of U:
$M_\infty $
behave well under finite base change, in particular, under passage to closed subspaces of U:
Lemma 5.2.4. Let
![]() $f:R_0\rightarrow R_0'$
be a finite morphism, where
$f:R_0\rightarrow R_0'$
be a finite morphism, where
![]() $R_0'$
is a Noetherian ring of definition in a pseudoaffinoid algebra. Let
$R_0'$
is a Noetherian ring of definition in a pseudoaffinoid algebra. Let
![]() $\kappa '$
be the weight
$\kappa '$
be the weight
![]() $f\circ \kappa $
, and let
$f\circ \kappa $
, and let
![]() ${M_\infty '}^{<r}$
denote the patched module constructed from the modules of modular forms
${M_\infty '}^{<r}$
denote the patched module constructed from the modules of modular forms
![]() $S_{\kappa ',\xi }^{<r,\circ }(K_{Q_n}^-)_{\leq h,\mathfrak {m}_{Q_n}^-}$
. Then the natural maps
$S_{\kappa ',\xi }^{<r,\circ }(K_{Q_n}^-)_{\leq h,\mathfrak {m}_{Q_n}^-}$
. Then the natural maps
and
are surjections.
Proof. We treat the first map; the second is similar. Let
![]() $M_n':={\mathbf {Z}}_p[\![y_{k+1},\ldots ,y_{k+j}]\!]\otimes _{{\mathbf {Z}}_p}S_{\kappa ',\xi }^{<r,\circ }(K_{Q_n}^-)_{\leq h,\mathfrak {m}_{Q_n}^-}$
. The open ideals
$M_n':={\mathbf {Z}}_p[\![y_{k+1},\ldots ,y_{k+j}]\!]\otimes _{{\mathbf {Z}}_p}S_{\kappa ',\xi }^{<r,\circ }(K_{Q_n}^-)_{\leq h,\mathfrak {m}_{Q_n}^-}$
. The open ideals
![]() $I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
generate open ideals of
$I\subset R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
generate open ideals of
![]() $R_0'\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
and are cofinal, so it suffices to show that we have a surjection
$R_0'\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
and are cofinal, so it suffices to show that we have a surjection
The left side is isomorphic to
![]() $R_0'\otimes _{R_0}M_I$
(because
$R_0'\otimes _{R_0}M_I$
(because
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I$
is discrete, by construction). Since each map
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]/I$
is discrete, by construction). Since each map
![]() $R_0'\otimes _{R_0}M_n\rightarrow M_n'$
is surjective (by Lemma 4.2.3, and since the transition maps
$R_0'\otimes _{R_0}M_n\rightarrow M_n'$
is surjective (by Lemma 4.2.3, and since the transition maps
![]() $\prod _{n=1}^{k+1}M_n\rightarrow \prod _{n=1}^kM_n$
are surjective, the Mittag–Leffler condition implies that the natural map
$\prod _{n=1}^{k+1}M_n\rightarrow \prod _{n=1}^kM_n$
are surjective, the Mittag–Leffler condition implies that the natural map
is surjective.
We have constructed two coherent
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
-modules,
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
-modules,
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
;
$M_\infty $
;
![]() $M_\infty $
is naturally a
$M_\infty $
is naturally a
![]() $R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
-module, but
$R_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
-module, but
![]() $M_\infty ^{<r}$
is projective when U is a point, making its support over
$M_\infty ^{<r}$
is projective when U is a point, making its support over
![]() $R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
easier to analyze.
$R_0\mathop {\widehat \otimes }{\mathbf {Z}}_p[\![y_i]\!]$
easier to analyze.
We now pass to the loci of the corresponding map
where
![]() $u\neq 0$
, and we consider the analytification
$u\neq 0$
, and we consider the analytification
![]() $M_\infty ^{\mathrm {{an}}}$
of
$M_\infty ^{\mathrm {{an}}}$
of
![]() $M_\infty $
as a coherent sheaf over
$M_\infty $
as a coherent sheaf over
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
.
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
.
Lemma 5.2.5. The support of
![]() $M_\infty ^{\mathrm {{an}}}$
is a Zariski-closed subspace of dimension
$M_\infty ^{\mathrm {{an}}}$
is a Zariski-closed subspace of dimension
 $$\begin{align*}\dim \operatorname{\mathrm{Spa}} R_0\mathop{\widehat\otimes}{\mathbf{Z}}_p[\![y_i]\!]\left[\frac 1 u\right] = \dim U + (g+1)+(4\lvert\Sigma_p\rvert-1) = \dim U + g + 4\lvert\Sigma_p\rvert. \end{align*}$$
$$\begin{align*}\dim \operatorname{\mathrm{Spa}} R_0\mathop{\widehat\otimes}{\mathbf{Z}}_p[\![y_i]\!]\left[\frac 1 u\right] = \dim U + (g+1)+(4\lvert\Sigma_p\rvert-1) = \dim U + g + 4\lvert\Sigma_p\rvert. \end{align*}$$
Proof. If
![]() $x:R\rightarrow L$
is a maximal point and
$x:R\rightarrow L$
is a maximal point and
![]() ${\mathscr {O}}_L$
is the ring of integers of L, it suffices to show that
${\mathscr {O}}_L$
is the ring of integers of L, it suffices to show that
![]() ${\mathscr {O}}_L\otimes _{R_0}M_\infty $
is supported on all of
${\mathscr {O}}_L\otimes _{R_0}M_\infty $
is supported on all of
![]() $\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. We set
$\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. We set
![]() $\kappa ':=x\circ \kappa $
and we let
$\kappa ':=x\circ \kappa $
and we let
![]() ${M_\infty '}^{<r}$
and
${M_\infty '}^{<r}$
and
![]() $M_\infty '$
be the patched modules constructed from the modules
$M_\infty '$
be the patched modules constructed from the modules
![]() $S_{\kappa ',\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
and
$S_{\kappa ',\xi }^{<r,\circ }(K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
and
![]() $S_{\kappa ',\xi }^\circ (K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
, respectively. Since the natural map
$S_{\kappa ',\xi }^\circ (K^-(Q_n))_{\leq h,\mathfrak {m}_{Q_n}^-}$
, respectively. Since the natural map
is surjective, it suffices to show that
![]() $M_\infty '$
is supported on all of
$M_\infty '$
is supported on all of
![]() $\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. To see this, we consider the natural morphism
$\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. To see this, we consider the natural morphism
![]() ${M_\infty '}^{<r}\rightarrow M_\infty '$
.
${M_\infty '}^{<r}\rightarrow M_\infty '$
.
We will show that
![]() ${M_\infty '}^{<r}\rightarrow M_\infty '$
is an isomorphism over a dense open subspace of
${M_\infty '}^{<r}\rightarrow M_\infty '$
is an isomorphism over a dense open subspace of
![]() $\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. Let
$\operatorname {\mathrm {Spec}} {\mathscr {O}}_L[\![y_i]\!]$
. Let
![]() $P_n$
be the cokernel of
$P_n$
be the cokernel of
![]() ${M_n'}^{<r}\rightarrow M_n'$
, and let P be the cokernel of
${M_n'}^{<r}\rightarrow M_n'$
, and let P be the cokernel of
![]() ${M_\infty '}^{<r}\rightarrow M_\infty '$
. Since the cokernel of
${M_\infty '}^{<r}\rightarrow M_\infty '$
. Since the cokernel of
is finite and u-power-torsion,
![]() $P_n$
is also u-power-torsion.
$P_n$
is also u-power-torsion.
There is some integer
![]() $k_0\geq 0$
such that
$k_0\geq 0$
such that
and by Corollary 4.2.7 the kernel of
is annihilated by
![]() $u^{(d-1)a}$
. Hence, there is some
$u^{(d-1)a}$
. Hence, there is some
![]() $N\gg 0$
such that
$N\gg 0$
such that
![]() $u^NP_n\subset (y_i)P_n$
for all n, and by devissage, the modules
$u^NP_n\subset (y_i)P_n$
for all n, and by devissage, the modules
![]() $P_n/(y_i)^kP_n$
are annihilated by
$P_n/(y_i)^kP_n$
are annihilated by
![]() $u^{kN}$
for all
$u^{kN}$
for all
![]() $k, n\geq 0$
.
$k, n\geq 0$
.
Next, we observe that we have exact sequences
for all n. Indeed, there are surjections
But
![]() $M_n^{<r}$
is projective over
$M_n^{<r}$
is projective over
![]() ${\mathscr {O}}_L[\![y_1]\!]$
, so
${\mathscr {O}}_L[\![y_1]\!]$
, so
![]() $M_n^{<r}/(y_i)^k$
has no u-torsion, whereas
$M_n^{<r}/(y_i)^k$
has no u-torsion, whereas
![]() $\operatorname {\mathrm {Tor}}_1^{{\mathscr {O}}_L[\![y_i]\!]}({\mathscr {O}}_L[\![y_i]\!]/(y_i)^k, P_n)$
is entirely u-power-torsion because
$\operatorname {\mathrm {Tor}}_1^{{\mathscr {O}}_L[\![y_i]\!]}({\mathscr {O}}_L[\![y_i]\!]/(y_i)^k, P_n)$
is entirely u-power-torsion because
![]() $P_n$
is.
$P_n$
is.
Let
![]() $J_k\subset {\mathscr {O}}_L[\![y_i]\!]$
be the ideal generated by
$J_k\subset {\mathscr {O}}_L[\![y_i]\!]$
be the ideal generated by
![]() $u^{Nk}$
and
$u^{Nk}$
and
![]() $(y_i)^k$
. Then the Tor long exact sequence gives us exact sequences
$(y_i)^k$
. Then the Tor long exact sequence gives us exact sequences
Moreover,
Let
![]() $P_{J_k}$
denote the localization of
$P_{J_k}$
denote the localization of
![]() $\prod _{n\geq 1}P_n/J_k$
at the ideal corresponding to our chosen ultrafilter. We have an exact sequence
$\prod _{n\geq 1}P_n/J_k$
at the ideal corresponding to our chosen ultrafilter. We have an exact sequence
and since the set
![]() $\{J_k\}$
is cofinal in the set of open ideals of
$\{J_k\}$
is cofinal in the set of open ideals of
![]() ${\mathscr {O}}_L[\![y_i]\!]$
, an exact sequence
${\mathscr {O}}_L[\![y_i]\!]$
, an exact sequence
But since
![]() $u^NP\subset (y_i)P$
, P is supported on a proper closed subscheme of
$u^NP\subset (y_i)P$
, P is supported on a proper closed subscheme of
![]() $\operatorname {\mathrm {Spf}} {\mathscr {O}}_L[\![y_i]\!]$
; away from the support of P, the map
$\operatorname {\mathrm {Spf}} {\mathscr {O}}_L[\![y_i]\!]$
; away from the support of P, the map
![]() ${M_\infty '}^{<r}\rightarrow M_\infty '$
is an isomorphism, as desired.
${M_\infty '}^{<r}\rightarrow M_\infty '$
is an isomorphism, as desired.
The support of
![]() $M_\infty ^{\mathrm {{an}}}$
over
$M_\infty ^{\mathrm {{an}}}$
over
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
is a Zariski-closed subspace, whose dimension must therefore be
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
is a Zariski-closed subspace, whose dimension must therefore be
 $$\begin{align*}\dim \operatorname{\mathrm{Spa}} R_0\mathop{\widehat\otimes}{\mathbf{Z}}_p[\![y_i]\!]\left[\frac 1 u\right] = \dim U + g + 4\lvert\Sigma_p\rvert. \end{align*}$$
$$\begin{align*}\dim \operatorname{\mathrm{Spa}} R_0\mathop{\widehat\otimes}{\mathbf{Z}}_p[\![y_i]\!]\left[\frac 1 u\right] = \dim U + g + 4\lvert\Sigma_p\rvert. \end{align*}$$
But the morphism
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ',\underline \kappa }|_U\rightarrow U$
has relative dimension
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {loc}}^{\square ,\psi ',\underline \kappa }|_U\rightarrow U$
has relative dimension
![]() $4\lvert \Sigma _p\rvert $
over an open subspace of U by Proposition 2.3.5, so any nonempty irreducible components have total dimension
$4\lvert \Sigma _p\rvert $
over an open subspace of U by Proposition 2.3.5, so any nonempty irreducible components have total dimension
![]() $\dim U+4\lvert \Sigma _p\rvert $
. It follows that the support of
$\dim U+4\lvert \Sigma _p\rvert $
. It follows that the support of
![]() $M_\infty ^{\mathrm {{an}}}$
on
$M_\infty ^{\mathrm {{an}}}$
on
![]() $X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
is the union of irreducible components.
$X_{\mathrm {{tri}},\overline {\rho },\mathrm {{loc}},\leq h}^{\square ,\psi ',\underline \kappa }|_U\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![x_i]\!]$
is the union of irreducible components.
Finally, since we have a closed embedding
we conclude that the support of
![]() $M_\infty $
on
$M_\infty $
on
![]() $X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ,\underline \kappa }|_U$
is also a union of irreducible components, which we denote
$X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ,\underline \kappa }|_U$
is also a union of irreducible components, which we denote
![]() $\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
.
$\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
.
We have a sequence of morphisms
(where we send the product of the factors of
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
in the definition of the trianguline varieties to the factor of
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
in the definition of the trianguline varieties to the factor of
![]() ${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
on the right, corresponding to the action of
${\mathbf {G}}_m^{\operatorname {\mathrm {ad}}}$
on the right, corresponding to the action of
![]() $U_p^{-1}$
);
$U_p^{-1}$
);
![]() $M_\infty $
is a finite module on
$M_\infty $
is a finite module on
![]() $X_{\mathrm {{tri}},\overline {\rho },\infty }^{\square ,\psi ',\underline \kappa }|_U$
whose pushforward to
$X_{\mathrm {{tri}},\overline {\rho },\infty }^{\square ,\psi ',\underline \kappa }|_U$
whose pushforward to
![]() ${\mathbf {G}}_{m,U}^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![y_i]\!]$
is also finite.
${\mathbf {G}}_{m,U}^{\operatorname {\mathrm {ad}}}\times \operatorname {\mathrm {Spa}}{\mathbf {Z}}_p[\![y_i]\!]$
is also finite.
We summarize this discussion:
Theorem 5.2.6. There is a space
![]() $\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
(which we call the patched eigenvariety over U), a finite module
$\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
(which we call the patched eigenvariety over U), a finite module
![]() $M_\infty $
supported on
$M_\infty $
supported on
![]() $\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
, (which we call the patched module) and a morphism
$\mathscr {X}_{\underline D^{\times },U,\leq h}^{\infty ,\psi ,\underline \kappa }$
, (which we call the patched module) and a morphism
whose image is the union of irreducible components.
Since this morphism factors through the global trianguline variety, we also deduce the following corollary:
Corollary 5.2.7. The support of
![]() $M_\infty /(y_1,\ldots ,y_{k})$
in the trianguline variety over
$M_\infty /(y_1,\ldots ,y_{k})$
in the trianguline variety over
![]() $X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_1,\ldots ,y_{k})\cong X_{\mathrm {{tri}},\Sigma _p,\overline {\rho },\leq h}^{\square ,\psi ',\underline \kappa }|_U$
is a union of irreducible components.
$X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U/(y_1,\ldots ,y_{k})\cong X_{\mathrm {{tri}},\Sigma _p,\overline {\rho },\leq h}^{\square ,\psi ',\underline \kappa }|_U$
is a union of irreducible components.
Remark 5.2.8. We carried out this construction locally because it is difficult to study the behavior of
![]() $M_\infty ^{<r}$
and
$M_\infty ^{<r}$
and
![]() $M_\infty $
under rational localization; we have not checked that the analytic patched modules
$M_\infty $
under rational localization; we have not checked that the analytic patched modules
![]() $M_\infty ^{\mathrm {{an}}}$
form a coherent sheaf. However, because specialization maps induce surjections on patched modules, as
$M_\infty ^{\mathrm {{an}}}$
form a coherent sheaf. However, because specialization maps induce surjections on patched modules, as
![]() $(U,h)$
varies over slope data, the supports of patched modules glue to a global patched eigenvariety
$(U,h)$
varies over slope data, the supports of patched modules glue to a global patched eigenvariety
![]() $\mathscr {X}_{\underline D^{\times }}^{\infty ,\psi ,\underline \kappa }$
.
$\mathscr {X}_{\underline D^{\times }}^{\infty ,\psi ,\underline \kappa }$
.
5.3 Modularity
We are now in a position to prove Theorem 5.1.1. We will say that a Galois representation
![]() $\rho $
is modular if it comes from a point on the extended eigenvariety.
$\rho $
is modular if it comes from a point on the extended eigenvariety.
Proposition 5.3.1. Let
![]() $F/{\mathbf {Q}}$
be a real quadratic extension split at p such that the image of
$F/{\mathbf {Q}}$
be a real quadratic extension split at p such that the image of
![]() $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
![]() $\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
. Then
$\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
. Then
![]() $\rho :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2(L)$
is modular if and only if
$\rho :\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}}\rightarrow \operatorname {\mathrm {GL}}_2(L)$
is modular if and only if
![]() $\rho |_{\operatorname {\mathrm {Gal}}_F}$
is modular.
$\rho |_{\operatorname {\mathrm {Gal}}_F}$
is modular.
Proof. We have the cyclic base-change morphism
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
from §3.4, so if
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
from §3.4, so if
![]() $\rho $
corresponds to
$\rho $
corresponds to
![]() $x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
, then
$x\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
, then
![]() $\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to the image of x in
$\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to the image of x in
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
. To show the other direction, we note that if
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/F,\mathrm {mid}}$
. To show the other direction, we note that if
![]() $\rho |_{\operatorname {\mathrm {Gal}}_F}$
is associated to
$\rho |_{\operatorname {\mathrm {Gal}}_F}$
is associated to
![]() $x'\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, then the corresponding eigenvalues are fixed by
$x'\in \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, then the corresponding eigenvalues are fixed by
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. Since we assumed that the image of
$\operatorname {\mathrm {Gal}}(F/{\mathbf {Q}})$
. Since we assumed that the image of
![]() $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
![]() $\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
, by [Reference Bergdall and HansenBH17, Theorem B.0.1] we may apply Corollary 3.4.7 to conclude that
$\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
, by [Reference Bergdall and HansenBH17, Theorem B.0.1] we may apply Corollary 3.4.7 to conclude that
![]() $x'$
is in the image of
$x'$
is in the image of
![]() $\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
.
$\mathscr {X}_{\operatorname {\mathrm {GL}}_2/{\mathbf {Q}},\mathrm {cusp}}$
.
Choose
![]() $F/{\mathbf {Q}}$
a real quadratic extension split at p. We may additionally choose F such that the image of
$F/{\mathbf {Q}}$
a real quadratic extension split at p. We may additionally choose F such that the image of
![]() $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
contains
![]() $\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
, by requiring that
$\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
, by requiring that
![]() $\ell $
splits in F for
$\ell $
splits in F for
![]() $\ell $
in some finite set of primes S of
$\ell $
in some finite set of primes S of
![]() ${\mathbf {Q}}$
such that
${\mathbf {Q}}$
such that
![]() $\{\overline {\rho }(\mathrm {Frob}_\ell )\}_{\ell \in S}$
generate
$\{\overline {\rho }(\mathrm {Frob}_\ell )\}_{\ell \in S}$
generate
![]() $\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
. Maintaining the notation of the previous section, we let
$\operatorname {\mathrm {SL}}_2({\mathbf {F}}_p)$
. Maintaining the notation of the previous section, we let
![]() $D/F$
be a totally definite quaternion algebra, split at all finite places, and we let
$D/F$
be a totally definite quaternion algebra, split at all finite places, and we let
![]() $R:={\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]$
. The Jacquet–Langlands correspondence gives us a morphism of eigenvarieties
$R:={\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]$
. The Jacquet–Langlands correspondence gives us a morphism of eigenvarieties
![]() $\mathscr {X}_{\underline D^{\times }}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, so it suffices to show that
$\mathscr {X}_{\underline D^{\times }}\rightarrow \mathscr {X}_{\operatorname {\mathrm {GL}}_2/F}$
, so it suffices to show that
![]() $\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to a point on
$\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to a point on
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
Theorem 5.3.2.
![]() $\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to a point on
$\rho |_{\operatorname {\mathrm {Gal}}_F}$
corresponds to a point on
![]() $\mathscr {X}_{\underline D^{\times }}$
.
$\mathscr {X}_{\underline D^{\times }}$
.
Remark 5.3.3. There is some
![]() $h\in {\mathbf {Q}}_{\geq 0}$
such that
$h\in {\mathbf {Q}}_{\geq 0}$
such that
![]() $\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
is trianguline with parameter of slope-
$\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
is trianguline with parameter of slope-
![]() $\leq h$
for each
$\leq h$
for each
![]() $v\mid p$
, and there is some open affinoid
$v\mid p$
, and there is some open affinoid
![]() $U\subset \mathscr {W}_F$
containing the weight of
$U\subset \mathscr {W}_F$
containing the weight of
![]() $\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
such that
$\rho |_{\operatorname {\mathrm {Gal}}_{F_v}}$
such that
![]() $(U,h)$
is a slope datum for
$(U,h)$
is a slope datum for
![]() $\mathscr {X}_{\underline D^{\times }}$
. In the following proof, we will work with a patched eigenvariety
$\mathscr {X}_{\underline D^{\times }}$
. In the following proof, we will work with a patched eigenvariety
![]() $X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
. However, since our arguments only require working sufficiently close to the boundary, we are always free to shrink U (or increase h). For compactness of exposition and notation, we therefore suppress
$X_{\mathrm {{tri}},\overline {\rho },\infty ,\leq h}^{\square ,\psi ',\underline \kappa }|_U$
. However, since our arguments only require working sufficiently close to the boundary, we are always free to shrink U (or increase h). For compactness of exposition and notation, we therefore suppress
![]() $(U,h)$
from the proof.
$(U,h)$
from the proof.
Note that we may also arrange
![]() $(U,h)$
so that the slope-
$(U,h)$
so that the slope-
![]() $\leq h$
part of
$\leq h$
part of
![]() $\mathscr {X}_{\underline D^{\times }}|_U$
is nonempty. Indeed, we have assumed that
$\mathscr {X}_{\underline D^{\times }}|_U$
is nonempty. Indeed, we have assumed that
![]() $\overline {\rho }$
is modular, so there are components of
$\overline {\rho }$
is modular, so there are components of
![]() $\mathscr {X}_{\underline D^{\times }}$
with residual Galois representation
$\mathscr {X}_{\underline D^{\times }}$
with residual Galois representation
![]() $\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
. Then [Reference Johansson and NewtonJN19b, Corollary 4.2.4] shows that such components contain classical points with parallel weight
$\overline {\rho }|_{\operatorname {\mathrm {Gal}}_F}$
. Then [Reference Johansson and NewtonJN19b, Corollary 4.2.4] shows that such components contain classical points with parallel weight
![]() $2$
, and the proof shows that we may find such points arbitrarily close to the boundary by varying the p-nebentypus. Such classical points have slope-
$2$
, and the proof shows that we may find such points arbitrarily close to the boundary by varying the p-nebentypus. Such classical points have slope-
![]() $\leq 1$
, so we may ensure nonemptiness by increasing h (and shrinking U, if necessary).
$\leq 1$
, so we may ensure nonemptiness by increasing h (and shrinking U, if necessary).
Proof. Let
![]() $\rho _0:=\rho |_{\operatorname {\mathrm {Gal}}_F}$
. We have assumed that
$\rho _0:=\rho |_{\operatorname {\mathrm {Gal}}_F}$
. We have assumed that
![]() $\rho |_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}}$
is trianguline, so we may write
$\rho |_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}}$
is trianguline, so we may write
![]() $D_{\mathrm {rig}}(\rho |_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}})$
as an extension of rank-
$D_{\mathrm {rig}}(\rho |_{\operatorname {\mathrm {Gal}}_{{\mathbf {Q}}_p}})$
as an extension of rank-
![]() $1\ (\varphi ,\Gamma )$
-modules:
$1\ (\varphi ,\Gamma )$
-modules:
for characters
![]() $\delta _1,\delta _2:{\mathbf {Q}}_p^{\times }\rightrightarrows L^{\times }$
. After twisting, we may assume that
$\delta _1,\delta _2:{\mathbf {Q}}_p^{\times }\rightrightarrows L^{\times }$
. After twisting, we may assume that
![]() $\delta _1|_{{\mathbf {Z}}_p^{\times }}$
is trivial. We fix a weight
$\delta _1|_{{\mathbf {Z}}_p^{\times }}$
is trivial. We fix a weight
![]() $\kappa _0$
according to
$\kappa _0$
according to
![]() $\delta _1|_{{\mathbf {Z}}_p^{\times }}$
and
$\delta _1|_{{\mathbf {Z}}_p^{\times }}$
and
![]() $\delta _2|_{{\mathbf {Z}}_p^{\times }}$
, and we fix an unramified character
$\delta _2|_{{\mathbf {Z}}_p^{\times }}$
, and we fix an unramified character
![]() $\psi _0:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]^{\times }$
deforming
$\psi _0:\operatorname {\mathrm {Gal}}_F\rightarrow {\mathscr {O}}_E[\![T_0/\overline {Z(K)}]\!]^{\times }$
deforming
![]() $\chi _{\mathrm {{cyc}}}\kappa _{0,1}\kappa _{0,2}\det \rho |_{\operatorname {\mathrm {Gal}}_F}$
.
$\chi _{\mathrm {{cyc}}}\kappa _{0,1}\kappa _{0,2}\det \rho |_{\operatorname {\mathrm {Gal}}_F}$
.
It is enough to show that the point
![]() $x_0\in X_{\mathrm {{tri}},\overline {\rho }_0}^{\square ,\psi ',\underline \kappa }$
corresponding to
$x_0\in X_{\mathrm {{tri}},\overline {\rho }_0}^{\square ,\psi ',\underline \kappa }$
corresponding to
![]() $\rho _0$
is in the support of the patched module
$\rho _0$
is in the support of the patched module
![]() ${M}_\infty $
. To see this, we treat separately the cases when
${M}_\infty $
. To see this, we treat separately the cases when
![]() $\rho $
is ordinary or nonordinary at p.
$\rho $
is ordinary or nonordinary at p.
We first assume that
![]() $\rho $
is ordinary at p. Then
$\rho $
is ordinary at p. Then
![]() $\rho _0|_{\operatorname {\mathrm {Gal}}_{F_v}}$
has the form
$\rho _0|_{\operatorname {\mathrm {Gal}}_{F_v}}$
has the form
for each
![]() $v\mid p$
, where
$v\mid p$
, where
![]() $\chi _{i,v}:\operatorname {\mathrm {Gal}}_{F_v}\rightrightarrows {\mathscr {O}}_E^{\times }$
are characters.
$\chi _{i,v}:\operatorname {\mathrm {Gal}}_{F_v}\rightrightarrows {\mathscr {O}}_E^{\times }$
are characters.
We wish to consider the slope-
![]() $0$
trianguline variety, which is the same as considering ordinary deformations of these extensions (with determinant fixed). The characters
$0$
trianguline variety, which is the same as considering ordinary deformations of these extensions (with determinant fixed). The characters
![]() $\chi _{i,v}|_{{\mathscr {O}}_{F_v}}$
deform over weight space, and the unramified characters specified by
$\chi _{i,v}|_{{\mathscr {O}}_{F_v}}$
deform over weight space, and the unramified characters specified by
![]() $\chi _{1,v}(p)$
correspond to a point on
$\chi _{1,v}(p)$
correspond to a point on
![]() $\operatorname {\mathrm {Spf}} {\mathscr {O}}_E[\![\{t_v\}_{v\mid p}]\!]$
. Note that since we specify a determinant at every point of weight space, deforming
$\operatorname {\mathrm {Spf}} {\mathscr {O}}_E[\![\{t_v\}_{v\mid p}]\!]$
. Note that since we specify a determinant at every point of weight space, deforming
![]() $\chi _{1,v}(p)$
also uniquely deforms
$\chi _{1,v}(p)$
also uniquely deforms
![]() $\chi _{2,v}(p)$
.
$\chi _{2,v}(p)$
.
Thus, we see that the space
is the moduli space of pairs of characters. Moreover, away from a Zariski-closed subspace of this space, the space of extensions of the universal characters is a rank-
![]() $1$
vector bundle. In particular, since
$1$
vector bundle. In particular, since
![]() $\kappa _0$
is regular, over an open neighborhood of
$\kappa _0$
is regular, over an open neighborhood of
![]() $\kappa _0$
in
$\kappa _0$
in
![]() $\mathscr {W}_F$
, this moduli space is irreducible (and contains the point corresponding to
$\mathscr {W}_F$
, this moduli space is irreducible (and contains the point corresponding to
![]() $\rho _0$
). Adding framing variables and passing from extensions to Galois representations preserve irreducibility of the moduli space.
$\rho _0$
). Adding framing variables and passing from extensions to Galois representations preserve irreducibility of the moduli space.
Thus, it suffices to show that the ordinary patched module for some characteristic
![]() $0$
weight
$0$
weight
![]() $\kappa _1$
sufficiently near the boundary is supported on the fiber of this moduli space. We choose
$\kappa _1$
sufficiently near the boundary is supported on the fiber of this moduli space. We choose
![]() $\kappa _1$
so that it is parallel. But the ordinary part of the Coleman–Mazur eigencurve is finite flat and surjective over weight space, so we may choose ordinary overconvergent eigenforms of appropriate weight and transfer them to
$\kappa _1$
so that it is parallel. But the ordinary part of the Coleman–Mazur eigencurve is finite flat and surjective over weight space, so we may choose ordinary overconvergent eigenforms of appropriate weight and transfer them to
![]() $\underline D^{\times }$
, where they contribute to the support of the patched module, as desired.
$\underline D^{\times }$
, where they contribute to the support of the patched module, as desired.
We now assume that
![]() $\rho $
is not ordinary at p so that
$\rho $
is not ordinary at p so that
![]() $\rho _0$
is not ordinary at either place above p. Since the parameters of
$\rho _0$
is not ordinary at either place above p. Since the parameters of
![]() $D_{\mathrm {rig}}(\rho )$
were assumed regular,
$D_{\mathrm {rig}}(\rho )$
were assumed regular,
![]() $x_0$
is a smooth point of
$x_0$
is a smooth point of
![]() $X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }$
. Therefore,
$X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }$
. Therefore,
![]() $x_0$
is contained in a unique irreducible component V of
$x_0$
is contained in a unique irreducible component V of
![]() $X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }$
, and we can find an open affinoid neighborhood
$X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }$
, and we can find an open affinoid neighborhood
![]() $V'\subset V$
of
$V'\subset V$
of
![]() $x_0$
so that
$x_0$
so that
![]() $V'$
contains no ordinary parameters.
$V'$
contains no ordinary parameters.
It follows that
![]() $\rho _0$
can be analytically deformed to characteristic
$\rho _0$
can be analytically deformed to characteristic
![]() $0$
(as in Example 2.3.4). In fact, the morphism
$0$
(as in Example 2.3.4). In fact, the morphism
![]() $X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }\rightarrow \mathscr {W}_F$
is smooth in a neighborhood of
$X_{\mathrm {{tri}},\overline {\rho }_0,\mathrm {{loc}}}^{\square ,\psi ',\underline \kappa }\rightarrow \mathscr {W}_F$
is smooth in a neighborhood of
![]() $x_0$
; in particular, it is open, and we may assume that the weights corresponding to the first term in the triangulation remain trivial as we deform, at both places above p.
$x_0$
; in particular, it is open, and we may assume that the weights corresponding to the first term in the triangulation remain trivial as we deform, at both places above p.
Recall that for any p-adic field
![]() $K/{\mathbf {Q}}_p$
, given a character
$K/{\mathbf {Q}}_p$
, given a character
![]() $\delta :K^{\times }\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
, its weight
$\delta :K^{\times }\rightarrow \overline {{\mathbf {Q}}}_p^{\times }$
, its weight
![]() $(\mathrm {wt}_\sigma (\delta ))_{\sigma :K\hookrightarrow \overline {{\mathbf {Q}}}_p}$
is the tuple such that
$(\mathrm {wt}_\sigma (\delta ))_{\sigma :K\hookrightarrow \overline {{\mathbf {Q}}}_p}$
is the tuple such that
We say that
![]() $\delta $
is locally algebraic of weight
$\delta $
is locally algebraic of weight
![]() $(k_\sigma )_\sigma $
if
$(k_\sigma )_\sigma $
if
![]() $\mathrm {wt}_\sigma (\delta )=k_\sigma \in {\mathbf {Z}}$
for all
$\mathrm {wt}_\sigma (\delta )=k_\sigma \in {\mathbf {Z}}$
for all
![]() $\sigma $
; equivalently, the restriction of
$\sigma $
; equivalently, the restriction of
![]() $\delta $
to some open subgroup of
$\delta $
to some open subgroup of
![]() ${\mathscr {O}}_K^{\times }$
is
${\mathscr {O}}_K^{\times }$
is
![]() $\chi _{\underline k}:=x\mapsto \prod _\sigma \sigma (x)^{-k_\sigma }$
. If
$\chi _{\underline k}:=x\mapsto \prod _\sigma \sigma (x)^{-k_\sigma }$
. If
![]() $\underline \delta $
is the parameter of a trianguline
$\underline \delta $
is the parameter of a trianguline
![]() $(\varphi ,\Gamma )$
-module, we say that it is locally algebraic of strongly dominant weight if
$(\varphi ,\Gamma )$
-module, we say that it is locally algebraic of strongly dominant weight if
![]() $\delta _{i,\sigma }$
is locally algebraic of weight
$\delta _{i,\sigma }$
is locally algebraic of weight
![]() $(k_{i,\sigma })$
and
$(k_{i,\sigma })$
and
![]() $k_{i,\sigma }<k_{i+1,\sigma }$
, for all i and
$k_{i,\sigma }<k_{i+1,\sigma }$
, for all i and
![]() $\sigma $
.
$\sigma $
.
We claim that there is some locally algebraic strongly dominant
![]() $\kappa _1\in \mathscr {W}_F^{\mathrm {rig}}$
such that the fiber
$\kappa _1\in \mathscr {W}_F^{\mathrm {rig}}$
such that the fiber
![]() $V^{\mathrm {rig}}|_{\kappa _1}$
is equidimensional of dimension
$V^{\mathrm {rig}}|_{\kappa _1}$
is equidimensional of dimension
![]() $8$
. Indeed, since we chose a deformation of
$8$
. Indeed, since we chose a deformation of
![]() $(\rho _0,\underline \delta )$
keeping
$(\rho _0,\underline \delta )$
keeping
![]() $\delta _1|_{{\mathscr {O}}_{F,p}^{\times }}$
trivial, it is enough to see that there are points of
$\delta _1|_{{\mathscr {O}}_{F,p}^{\times }}$
trivial, it is enough to see that there are points of
![]() $\operatorname {\mathrm {Spf}} {\mathbf {Z}}_p[\![{\mathbf {Z}}_p^{\times }]\!]^{\mathrm {rig}}$
which are locally algebraic of positive weight arbitrarily close to the boundary, which follows from the calculations of, for example, [Reference Johansson and NewtonJN19b, §2.7]. In fact, we can choose
$\operatorname {\mathrm {Spf}} {\mathbf {Z}}_p[\![{\mathbf {Z}}_p^{\times }]\!]^{\mathrm {rig}}$
which are locally algebraic of positive weight arbitrarily close to the boundary, which follows from the calculations of, for example, [Reference Johansson and NewtonJN19b, §2.7]. In fact, we can choose
![]() $\kappa _1$
to be locally algebraic of weights
$\kappa _1$
to be locally algebraic of weights
![]() $\{0,1\}$
at both places above p.
$\{0,1\}$
at both places above p.
We further claim that we may assume that
![]() $V^{',\mathrm {rig}}|_{\kappa _1}$
consists of points corresponding to Galois representations which are potentially Barsotti–Tate at both places above p. Indeed, two-dimensional (characteristic
$V^{',\mathrm {rig}}|_{\kappa _1}$
consists of points corresponding to Galois representations which are potentially Barsotti–Tate at both places above p. Indeed, two-dimensional (characteristic
![]() $0$
)
$0$
)
![]() $(\varphi ,\Gamma _{{\mathbf {Q}}_p})$
-modules are classified in [Reference ColmezCol08, §3.3], and after possibly replacing
$(\varphi ,\Gamma _{{\mathbf {Q}}_p})$
-modules are classified in [Reference ColmezCol08, §3.3], and after possibly replacing
![]() $\kappa _1$
with a weight closer to the boundary which is locally algbraic of weights
$\kappa _1$
with a weight closer to the boundary which is locally algbraic of weights
![]() $\{0,1\}$
, the corresponding
$\{0,1\}$
, the corresponding
![]() $(\varphi ,\Gamma _{{\mathbf {Q}}_p})$
-modules are crystabelline.
$(\varphi ,\Gamma _{{\mathbf {Q}}_p})$
-modules are crystabelline.
Now, it suffices to show that the patched module for weight
![]() $\kappa _1$
is supported on all of
$\kappa _1$
is supported on all of
![]() $V^{',\mathrm {rig}}|_{\kappa _1}$
. But a dense open subspace of
$V^{',\mathrm {rig}}|_{\kappa _1}$
. But a dense open subspace of
![]() $V^{',\mathrm {rig}}|_{\kappa _1}$
is a subspace of the generic fiber of one of the potentially Barsotti–Tate deformation rings constructed in [Reference KisinKis09c]. Then we may apply [Reference KisinKis09b, Theorem 3.4.11] (with some hypotheses relaxed in [Reference GeeGee06]).
$V^{',\mathrm {rig}}|_{\kappa _1}$
is a subspace of the generic fiber of one of the potentially Barsotti–Tate deformation rings constructed in [Reference KisinKis09c]. Then we may apply [Reference KisinKis09b, Theorem 3.4.11] (with some hypotheses relaxed in [Reference GeeGee06]).
A Extensions of Zariski-closed subsets
The paper [Reference LourençoLou17] proves Riemann extension theorems for functions on normal pseudorigid spaces and normal excellent formal schemes; in this appendix, we use those results to extend certain Zariski-closed adic subsets (in the sense of [Reference Johansson and NewtonJN19a, §2.1]) of pseudorigid spaces over missing subsets of codimension at least
![]() $2$
.
$2$
.
Proposition A.0.1. Let
![]() $\mathfrak {X}$
be a normal excellent formal scheme, which is nowhere discrete. If
$\mathfrak {X}$
be a normal excellent formal scheme, which is nowhere discrete. If
![]() $Z\subset X:=\mathfrak {X}^{\mathrm {{an}}}$
is a Zariski-closed adic subset, then there is a closed formal subscheme
$Z\subset X:=\mathfrak {X}^{\mathrm {{an}}}$
is a Zariski-closed adic subset, then there is a closed formal subscheme
![]() $\mathfrak {Z}\subset \mathfrak {X}$
such that
$\mathfrak {Z}\subset \mathfrak {X}$
such that
![]() $Z=\mathfrak {Z}^{\mathrm {{an}}}$
.
$Z=\mathfrak {Z}^{\mathrm {{an}}}$
.
Proof of Proposition A.0.1.
We may assume that
![]() $\mathfrak {X}=\operatorname {\mathrm {Spf}} R$
, where R is a normal excellent domain with ideal of definition
$\mathfrak {X}=\operatorname {\mathrm {Spf}} R$
, where R is a normal excellent domain with ideal of definition
![]() $J=(f_1,\ldots ,f_n)$
. Then by the definitions of [Reference Johansson and NewtonJN19a, §2.1], there is a coherent sheaf
$J=(f_1,\ldots ,f_n)$
. Then by the definitions of [Reference Johansson and NewtonJN19a, §2.1], there is a coherent sheaf
![]() $\mathcal {I}\subset {\mathscr {O}}_X$
of ideals such that
$\mathcal {I}\subset {\mathscr {O}}_X$
of ideals such that
![]() $Z=\{x\in X\mid \mathcal {I}_x\neq {\mathscr {O}}_{X,x}\}$
. We need to show that there is an ideal
$Z=\{x\in X\mid \mathcal {I}_x\neq {\mathscr {O}}_{X,x}\}$
. We need to show that there is an ideal
![]() $I\subset R$
whose associated sheaf agrees with
$I\subset R$
whose associated sheaf agrees with
![]() $\mathcal {I}$
on X.
$\mathcal {I}$
on X.
We define
![]() $\mathcal {I}^+:=\mathcal {I}\cap {\mathscr {O}}_X^+$
, and we set
$\mathcal {I}^+:=\mathcal {I}\cap {\mathscr {O}}_X^+$
, and we set
![]() $I:=\Gamma (X,\mathcal {I}^+)$
; by [Reference LourençoLou17, Proposition 6.2],
$I:=\Gamma (X,\mathcal {I}^+)$
; by [Reference LourençoLou17, Proposition 6.2],
![]() $R=\Gamma (X,{\mathscr {O}}_X^+)$
, so we may view I as an ideal of R. It remains to show that for each affinoid open subspace
$R=\Gamma (X,{\mathscr {O}}_X^+)$
, so we may view I as an ideal of R. It remains to show that for each affinoid open subspace
![]() $\operatorname {\mathrm {Spa}} R'\subset X$
,
$\operatorname {\mathrm {Spa}} R'\subset X$
,
![]() $R'\otimes _RI=\mathcal {I}(\operatorname {\mathrm {Spa}} R')$
. To see this, we observe that we have a finite cover
$R'\otimes _RI=\mathcal {I}(\operatorname {\mathrm {Spa}} R')$
. To see this, we observe that we have a finite cover
![]() $X=\cup _i\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
, so it suffices to check this with
$X=\cup _i\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
, so it suffices to check this with
![]() $R'=\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
.
$R'=\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
.
Setting
![]() $R_i:=R\left \langle \frac {J}{f_i}\right \rangle $
and
$R_i:=R\left \langle \frac {J}{f_i}\right \rangle $
and
![]() $U_i=\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
, we have an exact sequence of R-modules
$U_i=\operatorname {\mathrm {Spa}} R\left \langle \frac {J}{f_i}\right \rangle $
, we have an exact sequence of R-modules
For any fixed index
![]() $i_0$
, we may tensor with
$i_0$
, we may tensor with
![]() $R_{i_0}^\circ $
and complete
$R_{i_0}^\circ $
and complete
![]() $f_{i_0}$
-adically; as R is Noetherian, our sequence
$f_{i_0}$
-adically; as R is Noetherian, our sequence
 $$\begin{align*}0\rightarrow R_{i_0}^\circ\mathop{\widehat\otimes}_RI\rightarrow \prod_i\left(R_{i_0}^\circ\mathop{\widehat\otimes}_R\mathcal{I}^+(U_i)\right)\rightrightarrows \prod_{i,j}\left(R_{i_0}^\circ\mathop{\widehat\otimes}_R\mathcal{I}^+(U_i\cap U_j)\right) \end{align*}$$
$$\begin{align*}0\rightarrow R_{i_0}^\circ\mathop{\widehat\otimes}_RI\rightarrow \prod_i\left(R_{i_0}^\circ\mathop{\widehat\otimes}_R\mathcal{I}^+(U_i)\right)\rightrightarrows \prod_{i,j}\left(R_{i_0}^\circ\mathop{\widehat\otimes}_R\mathcal{I}^+(U_i\cap U_j)\right) \end{align*}$$
remains exact. But
![]() $R_{i_0}^\circ \mathop {\widehat \otimes }_R\mathcal {I}^+(U_i)$
generates
$R_{i_0}^\circ \mathop {\widehat \otimes }_R\mathcal {I}^+(U_i)$
generates
![]() $\mathcal {I}(U_{i_0}\cap U_i)$
and
$\mathcal {I}(U_{i_0}\cap U_i)$
and
![]() $R_{i_0}^\circ \mathop {\widehat \otimes }_R\mathcal {I}^+(U_i\cap U_j)$
generates
$R_{i_0}^\circ \mathop {\widehat \otimes }_R\mathcal {I}^+(U_i\cap U_j)$
generates
![]() $\mathcal {I}(U_{i_0}\cap U_i\cap U_j)$
after inverting a pseudouniformizer
$\mathcal {I}(U_{i_0}\cap U_i\cap U_j)$
after inverting a pseudouniformizer
![]() $u_{i_0}$
of
$u_{i_0}$
of
![]() $R_{i_0}$
for all
$R_{i_0}$
for all
![]() $i,j$
, and
$i,j$
, and
![]() $\{U_{i_0}\cap U_i\}_i$
is a cover of
$\{U_{i_0}\cap U_i\}_i$
is a cover of
![]() $U_{i_0}$
, so in fact
$U_{i_0}$
, so in fact
![]() $R_{i_0}\mathop {\widehat \otimes }_RI=\mathcal {I}(U_{i_0})$
, as desired.
$R_{i_0}\mathop {\widehat \otimes }_RI=\mathcal {I}(U_{i_0})$
, as desired.
Corollary A.0.2. Let E be a p-adic field, let
![]() $\mathfrak {X}=\operatorname {\mathrm {Spa}} R_1$
, where
$\mathfrak {X}=\operatorname {\mathrm {Spa}} R_1$
, where
![]() $R_1:={\mathscr {O}}_E[\![x_1,\ldots ,x_{n_1}]\!]\left \langle y_1,\ldots ,y_{n_2}\right \rangle /I$
, and let
$R_1:={\mathscr {O}}_E[\![x_1,\ldots ,x_{n_1}]\!]\left \langle y_1,\ldots ,y_{n_2}\right \rangle /I$
, and let
![]() $\mathfrak {Y}:=\operatorname {\mathrm {Spa}} R_2$
, where
$\mathfrak {Y}:=\operatorname {\mathrm {Spa}} R_2$
, where
![]() $R_2={\mathscr {O}}_E[\![z_1,\ldots ,z_{m_1}]\!]\left \langle w_1,\ldots ,w_{m_2}\right \rangle /J$
. Suppose that
$R_2={\mathscr {O}}_E[\![z_1,\ldots ,z_{m_1}]\!]\left \langle w_1,\ldots ,w_{m_2}\right \rangle /J$
. Suppose that
![]() $R_1$
has dimension at least
$R_1$
has dimension at least
![]() $2$
. Suppose that
$2$
. Suppose that
![]() $Z\subset \mathfrak {X}^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}\mathfrak {Y}$
is a Zariski-closed subset and that there is some integer
$Z\subset \mathfrak {X}^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}\mathfrak {Y}$
is a Zariski-closed subset and that there is some integer
![]() $N\geq 1$
such that
$N\geq 1$
such that
![]() $Z\cap \operatorname {\mathrm {Spa}} R_1\left \langle \frac p u, \left \{\frac {x_i}{u}\right \}\right \rangle \left [\frac 1 u\right ]\times \mathfrak {Y}$
is contained in the rational domain
$Z\cap \operatorname {\mathrm {Spa}} R_1\left \langle \frac p u, \left \{\frac {x_i}{u}\right \}\right \rangle \left [\frac 1 u\right ]\times \mathfrak {Y}$
is contained in the rational domain
![]() $\{z_j^N\leq u\neq 0 \text { for all } j=1,\ldots ,m\}$
for each
$\{z_j^N\leq u\neq 0 \text { for all } j=1,\ldots ,m\}$
for each
![]() $u\in \{\varpi _E,x_1,\ldots ,x_{n_1}\}$
. Then there is a closed formal subscheme
$u\in \{\varpi _E,x_1,\ldots ,x_{n_1}\}$
. Then there is a closed formal subscheme
![]() $\mathfrak {Z}\subset \mathfrak {X}\mathop {\widehat \otimes }_{{\mathscr {O}}_E}\mathfrak {Y}$
such that
$\mathfrak {Z}\subset \mathfrak {X}\mathop {\widehat \otimes }_{{\mathscr {O}}_E}\mathfrak {Y}$
such that
![]() $\mathfrak {Z}^{\mathrm {{an}}}\cap (\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}\mathfrak {Y}=Z$
(where the intersection is taken inside
$\mathfrak {Z}^{\mathrm {{an}}}\cap (\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}\mathfrak {Y}=Z$
(where the intersection is taken inside
![]() $\left (\operatorname {\mathrm {Spa}} R_1\mathop {\widehat \otimes }_{{\mathscr {O}}_E}R_2\right )^{\mathrm {{an}}}$
).
$\left (\operatorname {\mathrm {Spa}} R_1\mathop {\widehat \otimes }_{{\mathscr {O}}_E}R_2\right )^{\mathrm {{an}}}$
).
Proof. Replacing Z with
![]() $Z\cap V(I)^{\mathrm {{an}}}\cap V(J)^{\mathrm {{an}}}$
, we may assume that
$Z\cap V(I)^{\mathrm {{an}}}\cap V(J)^{\mathrm {{an}}}$
, we may assume that
![]() $I=J=(0)$
so that
$I=J=(0)$
so that
![]() $R_1={\mathscr {O}}_E[\![\{x_i\}]\!]\left \langle \{y_k\}\right \rangle $
and
$R_1={\mathscr {O}}_E[\![\{x_i\}]\!]\left \langle \{y_k\}\right \rangle $
and
![]() $R_2={\mathscr {O}}_E[\![\{z_j\}]\!]\left \langle \{w_\ell \}\right \rangle $
. Then by Proposition A.0.1 it suffices to extend Z to a Zariski-closed subset of
$R_2={\mathscr {O}}_E[\![\{z_j\}]\!]\left \langle \{w_\ell \}\right \rangle $
. Then by Proposition A.0.1 it suffices to extend Z to a Zariski-closed subset of
![]() $\left (\operatorname {\mathrm {Spa}} R_1\mathop {\widehat \otimes }_{{\mathscr {O}}_E}R_2\right )^{\mathrm {{an}}}$
. This analytic locus, in turn, is covered by the affinoid pseudorigid spaces
$\left (\operatorname {\mathrm {Spa}} R_1\mathop {\widehat \otimes }_{{\mathscr {O}}_E}R_2\right )^{\mathrm {{an}}}$
. This analytic locus, in turn, is covered by the affinoid pseudorigid spaces
 $$\begin{align*}\mathcal{V}_u:=\operatorname{\mathrm{Spa}} {\mathscr{O}}_E[\![\{x_i\}_i,\{z_j\}_j]\!]\left\langle \frac{\varpi_E}{u},\left\{\frac{x_i}{u}\right\}_i,\{y_k\}_k, \left\{\frac{z_j}{u}\right\}_j,\{w_\ell\}_\ell\right\rangle\left[\frac 1 u\right] \end{align*}$$
$$\begin{align*}\mathcal{V}_u:=\operatorname{\mathrm{Spa}} {\mathscr{O}}_E[\![\{x_i\}_i,\{z_j\}_j]\!]\left\langle \frac{\varpi_E}{u},\left\{\frac{x_i}{u}\right\}_i,\{y_k\}_k, \left\{\frac{z_j}{u}\right\}_j,\{w_\ell\}_\ell\right\rangle\left[\frac 1 u\right] \end{align*}$$
for
![]() $u\in \{\varpi _E,x_1,\ldots ,x_{n_1}\}$
and
$u\in \{\varpi _E,x_1,\ldots ,x_{n_1}\}$
and
 $$\begin{align*}\mathcal{V}_{z_{j_0}}:=\operatorname{\mathrm{Spa}} {\mathscr{O}}_E[\![\{x_i\}_i,\{z_j\}_j]\!]\left\langle\frac{\varpi_E}{z_{j_0}}, \left\{\frac{x_i}{z_{j_0}}\right\}_i,\{y_k\}_k,\left\{\frac{z_j}{z_{j_0}}\right\}_j,\{w_\ell\}_\ell\right\rangle\left[\frac{1}{z_{j_0}}\right] \end{align*}$$
$$\begin{align*}\mathcal{V}_{z_{j_0}}:=\operatorname{\mathrm{Spa}} {\mathscr{O}}_E[\![\{x_i\}_i,\{z_j\}_j]\!]\left\langle\frac{\varpi_E}{z_{j_0}}, \left\{\frac{x_i}{z_{j_0}}\right\}_i,\{y_k\}_k,\left\{\frac{z_j}{z_{j_0}}\right\}_j,\{w_\ell\}_\ell\right\rangle\left[\frac{1}{z_{j_0}}\right] \end{align*}$$
for
![]() $j_0=1,\ldots ,m$
. Since the
$j_0=1,\ldots ,m$
. Since the
![]() $\mathcal {V}_u$
are contained in
$\mathcal {V}_u$
are contained in
![]() $(\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}R_2$
, we only need to extend the intersections
$(\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}R_2$
, we only need to extend the intersections
![]() $Z\cap \mathcal {V}_{z_{j_0}}$
to Zariski-closed subsets of
$Z\cap \mathcal {V}_{z_{j_0}}$
to Zariski-closed subsets of
![]() $\mathcal {V}_{z_{j_0}}$
.
$\mathcal {V}_{z_{j_0}}$
.
We can cover each
![]() $\mathcal {V}_{z_{j_0}}$
by its open subspaces defined by inequalities
$\mathcal {V}_{z_{j_0}}$
by its open subspaces defined by inequalities
for
![]() $i=1,\ldots , n_1$
and
$i=1,\ldots , n_1$
and
so it suffices to find suitable Zariski-closed subsets of each of these spaces.
By assumption,
![]() $Z\cap \mathcal {V}_{z_{j_0},2}$
is empty. Moreover,
$Z\cap \mathcal {V}_{z_{j_0},2}$
is empty. Moreover,
and
since the conditions
![]() $\lvert z_{j_0}^{N+1}\rvert \leq \lvert \varpi _E\rvert $
and
$\lvert z_{j_0}^{N+1}\rvert \leq \lvert \varpi _E\rvert $
and
![]() $z_{j_0}\neq 0$
imply
$z_{j_0}\neq 0$
imply
![]() $\varpi _E\neq 0$
(and similarly for
$\varpi _E\neq 0$
(and similarly for
![]() $\{\lvert z_{j_0}^{N+1}\rvert \leq \lvert x_{i}\rvert \}$
and
$\{\lvert z_{j_0}^{N+1}\rvert \leq \lvert x_{i}\rvert \}$
and
![]() $z_{j_0}\neq 0$
). Thus,
$z_{j_0}\neq 0$
). Thus,
![]() $Z\cap \mathcal {V}_{z_{j_0},p,2}$
,
$Z\cap \mathcal {V}_{z_{j_0},p,2}$
,
![]() $Z\cap \mathcal {V}_{z_{j_0},i,2}$
are defined by sheaves of ideals which agree on intersections
$Z\cap \mathcal {V}_{z_{j_0},i,2}$
are defined by sheaves of ideals which agree on intersections
![]() $\mathcal {V}_{z_{j_0},i,1}\cap \mathcal {V}_{z_{j_0},i',1}$
.
$\mathcal {V}_{z_{j_0},i,1}\cap \mathcal {V}_{z_{j_0},i',1}$
.
By construction, these sheaves agree on the overlaps
![]() $\mathcal {V}_{z_{j_0},p,1}\cap \mathcal {V}_{z_{j_0},p,2}=\{\lvert z_{j_0}^{N+1}\rvert =\lvert \varpi _E\rvert \}$
and
$\mathcal {V}_{z_{j_0},p,1}\cap \mathcal {V}_{z_{j_0},p,2}=\{\lvert z_{j_0}^{N+1}\rvert =\lvert \varpi _E\rvert \}$
and
![]() $\mathcal {V}_{z_{j_0},i,1}\cap \mathcal {V}_{z_{j_0},i,2}=\{\lvert z_{j_0}^{N+1}\rvert =\lvert x_i\rvert \}$
. We have therefore extended the sheaf of ideals defining
$\mathcal {V}_{z_{j_0},i,1}\cap \mathcal {V}_{z_{j_0},i,2}=\{\lvert z_{j_0}^{N+1}\rvert =\lvert x_i\rvert \}$
. We have therefore extended the sheaf of ideals defining
![]() $Z\cap \mathcal {V}_{z_{j_0}}\cap (\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}R_2$
to a sheaf of ideals on all of
$Z\cap \mathcal {V}_{z_{j_0}}\cap (\operatorname {\mathrm {Spa}} R_1)^{\mathrm {{an}}}{\times }_{{\mathscr {O}}_E}R_2$
to a sheaf of ideals on all of
![]() $\mathcal {V}_{z_{j_0}}$
, as desired.
$\mathcal {V}_{z_{j_0}}$
, as desired.
Acknowledgements
I would like to thank A. Caraiani, T. Gee, J. Newton and V. Pilloni for many helpful conversations, as well as useful comments on earlier versions of this paper. I would also like to thank the anonymous referee for reading this paper extremely carefully and making many helpful comments.
Competing interest
The authors have no competing interest to declare.